Pavel Hejbal. Tecplot
|
|
|
- Vladislav Kříž
- před 6 lety
- Počet zobrazení:
Transkript
1 Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Pavel Hejbal Vizualizace numerických řešení parciálních diferenciálních rovnic pomocí balíku Tecplot Katedra numerické matematiky Vedoucí bakalářské práce: Doc. RNDr. Vít Dolejší, Ph.D. Studijní program: Matematika, Obecná matematika 2006
2 Děkuji panu docentu Dolejšímu za ochotu a vstřícnost, kterou mi věnoval během všech konzultací, a za velmi cenné rady a připomínky při tvorbě této práce. Prohlašuji, že jsem svou bakalářskou práci napsal samostatně a výhradně s použitím citovaných pramenů. Souhlasím se zapůjčováním práce a jejím zveřejňováním. V Praze dne Pavel Hejbal 2
3 Obsah 1 Mechanika tekutin 5 2 Popis vstupních dat 7 3 Řešení úlohy Triangulace Hodnoty aproximace Animace 15 5 Ukázky výsledků 16 Literatura 19 3
4 Název práce: Vizualizace numerických řešení parciálních diferenciálních rovnic pomocí balíku Tecplot Autor: Pavel Hejbal Katedra: Katedra numerické matematiky Vedoucí bakalářské práce: Doc. RNDr. Vít Dolejší, Ph.D. vedoucího: Abstrakt: V předložené práci se zabýváme vizualizací numerických řešení parciálních diferenciálních rovnic získaných nespojitou Galerkinovou metodou, která dává po částech polynomiální, ale nespojitou aproximaci. Pro vizualizaci chceme použít komerční software Tecplot, který však umožňuje vizualizovat pouze spojitou, po částech lineární funkci. Cílem této práce je vytvořit vhodný interface mezi výstupem nespojité Galerkinovy metody a vstupem programu Tecplot, což znamená navrhnout a posléze implementovat algoritmy, které aproximují nespojitou, po částech polynomiální funkci novou spojitou a po částech lineární funkcí. Na závěr se věnujeme tvorbě softwarových prostředků, které použitím zmíněných algoritmů umožní automaticky generovat animace numerického řešení. Klíčová slova: Tecplot, nespojitá Galerkinova metoda, triangulace Title: Vizualization of numerical solutions of partial differential equations with the aid of software Tecplot Author: Pavel Hejbal Department: Department of Numerical Mathematics Supervisor: Doc. RNDr. Vít Dolejší, Ph.D. Supervisor s address: Vit.Dolejsi@mff.cuni.cz Abstract: In the present work we deal with the vizualization of numerical solutions of partial differential equations obtained by discontinuous Galerkin finite element method, which gives a discontinuous piecewise polynomial approximation. For the vizualization we would like to use commercial software Tecplot, which enables to display only continuous piecewise linear function. The aim of this work is to create interface between the output of the discontinuous Galerkin finite element method and the input of the Tecplot. Therefore we propose and implement algorithms, which approximate discontinuous piecewise polynomial function by the function, which is continuous and piecewise linear. In the end of this work we turn to create software products, which could automatically generate animations of numerical solutions, with the aid of mentioned algorithms. Keywords: Tecplot, discontinuous Galerkin method, triangulation 4
5 Kapitola 1 Mechanika tekutin Studium proudění kapalin a plynů nachází uplatnění v mnoha rozmanitých oblastech vědy i techniky jako je např. letectví a aeronautika, automobilový průmysl, strojírenství (konstrukce turbín a kompresorů), chemický a potravinářský průmysl (mísicí zařízení, proudění chemicky reagujících tekutin), medicína (proudění krve v cévách), biologie, meteorologie, hydrologie, oceánografie či ochrana životního prostředí. Ke zkoumání proudění je možné využít dva přístupy. Jednak pomocí experimentů, které sice přinášejí realistický obraz skutečného proudění, ovšem jejich uskutečnění je často nákladné a zároveň časově náročné. Druhou možností je použití matematických modelů. Většina z nich umožňuje převést úlohu na řešení soustavy parciálních diferenciálních rovnic vyjadřujících základní fyzikální zákony zachování hmoty, hybnosti, momentu hybnosti a energie. Počítačová dynamika tekutin (známá pod zkratkou CFD = Computational Fluid Dynamics) se zabývá numerickým řešením takových soustav. Cílem tohoto oboru je vytvoření počítačové simulace proudění, získané na základě aplikace vhodných numerických metod a výpočtových algoritmů, která bude srovnatelná s výsledky experimentů. Tato práce se zabývá závěrečnou fází tohoto procesu, kterou je vizualizace řešení. V poslední době se při řešení soustav diferenciálních rovnic popisujících proudění používají metody vyššího řádu, uved me například ADGFEM (Adaptive Discontinuous Galerkin Finite Element Method), v současnosti vyvíjený na Katedře numerické matematiky, viz [1], [2], [3]. Touto metodou se získá po částech polynomiální aproximace. Většina dnes dostupného softwaru ovšem umožňuje vizualizovat pouze funkce po částech konstantní nebo spojité a po částech lineární, jako v případě komerčního softwaru TECPLOT, jehož licenci zakoupila matematická sekce na MFF. Cílem této práce je tedy vytvořit interface mezi výsledky nespojité Galerkinovy metody a vstupem programu Tecplot. To znamená navrhnout, a následně implementovat vhodný algoritmus, který aproximuje nespojitou po částech polynomiální funkci takovou funkcí, která je spojitá a po částech lineární. Výstupem vytvořeného programu je soubor 5
6 přímo zpracovatelný programem Tecplot. 6
7 Kapitola 2 Popis vstupních dat V této části se podrobněji seznámíme s podobou výsledků nespojité Galerkinovy metody a uvedeme formát vstupních dat. Necht Ω R 2 je oblast, která je rozdělena na uzavřené trojúhelníky {K i }, přičemž platí: K o i K o j =, i j Množinu všech {K i }, pokrývajících Ω, nazýváme triangulací. V našem případě pracujeme pouze s konformními triangulacemi, které splňují následující podmínku: K i K j = 1 bod celá hrana, i j Triangulace, která není konformní, se nazývá nekonformní. Jeden ze dvou souborů, který náš program obdrží na vstup, bude specifikovat triangulaci {K i }. To znamená, že v něm budou zapsány souřadnice uzlových bodů triangulace a dále jejich trojice, definující jednotlivé trojúhelníky. Numerické řešení, získané pomocí nespojité Galerkinovy metody, patří do prostoru S h nespojitých po částech polynomiálních funkcí: S h = {v h, v h Ki P k (K i ), K i } kde P k (K i ) označuje prostor polynomů nejvýše k-tého stupně na elementu K i. Každý polynom definovaný na daném elementu je v naší úloze určen svými funkčními hodnotami na následující množině uzlů: 3 {x = λ i a i, λ j {0, 1 i=1 k,..., k 1 3 k, 1}, j {1, 2, 3}, λ i = 1} i=1 kde a 1, a 2, a 3 jsou vrcholy daného trojúhelníku. 7
8 p p p3 5 Obrázek 2.1: Uzly definující polynomiální funkci 2 Počet uzlů pro dané k je: d(k) = (k + 1)(k + 2) 2 Funkce z prostoru S h je tedy jednoznačně určena svými hodnotami v d(k) bodech pro každý trojúhelník. Na obrázku 2.1 jsou znázorněny tři případy k = 1, 2, 3, na které se v naší práci omezíme. Element, na kterém je definován polynom stupně i, budeme nadále označovat p i. Polynom prvního stupně je určen třemi body ve vrcholech elementu. V případě p 2 známe navíc hodnoty ve středech hran. Podobně u p 3, kde je známa též hodnota v těžišti trojúhelníku. Funkční hodnoty definující numerické řešení jsou dány samostatným vstupním souborem. V rámci této práce se věnujeme aplikacím z numerické simulace stlačitelného proudění, které je popsáno čtyřmi veličinami: hustota, hybnost ( R 2 ) a energie. Uved me příklad části tohoto souboru:
9 Čtveřice řádků odpovídá jednomu z elementů. Každý ze čtyř řádků přísluší jedné z veličin. Na začátku každého řádku je uvedeno celé číslo nabývající hodnot 1, 2, nebo 3, které určuje stupeň polynomu na daném elementu. Dále již následují funkční hodnoty v takovém pořadí, jak je uvedeno na obrázku 2.1. V úloze předpokládáme, že na daném elementu je stupeň polynomu stejný pro všechny veličiny. 9
10 Kapitola 3 Řešení úlohy V předchozí kapitole jsme popsali všechna vstupní data, můžeme tedy přikročit k samotnému řešení úlohy. Naším cílem bude vytvořit soubor, ve kterém bude popsána nová triangulace, a dále právě jedna hodnota aproximace v každém uzlu této triangulace. Tecplot tyto data vizualizuje jako spojitou a na každém trojúhelníku lineární funkci. 3.1 Triangulace Aby byla maximálně využita všechna vstupní data, je potřeba vhodným způsobem zjemnit zadanou sít. V případě p 2 a p 3 máme totiž k dispozici řešení nejen v uzlových bodech, ale i v ostatních bodech na hranách sítě, eventuálně uvnitř elementu. Právě v těchto bodech budeme chtít rozšiřovat původní triangulaci. Pokud neznáme hodnoty nikde mimo uzlové body, což je případ polynomiální aproximace řádu jedna, nemá velký smysl původní triangulaci nějak měnit. Tato aproximace je totiž po částech lineární a naším cílem je taktéž po částech lineární aproximace, ale navíc spojitá. Je proto nutné určit právě jednu hodnotu v každém uzlu. Počítáním hodnot v uzlech výsledné triangulace se budeme zabývat v příští podkapitole. Uvažujme nyní polynomiální aproximaci vyššího řádu než jedna. Tentokrát budeme zjemňovat zadanou triangulaci. První fáze dělení elementů je zachycena na obrázku 3.1. Trojúhelník typu p 2 a p 3 se rozdělí na více elementů podle schématu na obrázku. Pokud provedeme toto dělění pro všechny patřičné trojúhelníky a jestliže se stupně polynomů zadaných na elementech této triangulace budou lišit, získáme nekonformní triangulaci. Naším cílem je ovšem vytvořit konformní triangulaci, což znamená, že je nutné provést dodatečná dělení. Nyní probereme základní případy, které mohou nastat. Pokud vedle sebe budou ležet elementy stejného typu, není třeba provádět další dělení, nebot výsledná triangulace bude konformní. Uvažujme tentokrát element typu p 2 a jeho sousední element typu p 1. Abychom získali konformní triangulaci, element p 1 se rozdělí na dva 10
11 p2 p3 Obrázek 3.1: Vnitřní dělění trojúhelníku trojúhelníky. Podobně se řeší soused p 3, jak je patrné z obrázku 3.2. Je na něm vidět, že element p 1 se může dělit popsaným způsobem vícekrát. Pokud by element p 1 měl tři sousedy typu p 3, rozdělí se na sedm elementů, jak je vidět na obrázku 3.3. Zbývá situace, kdy spolu sousedí elementy typu p 2 a p 3. Dělení trojúhelníků potom probíhá opět podobným způsobem. Hanging node, což je bod, který leží uvnitř hrany jednoho trojúhelníku a současně je vrcholem jiného trojúhelníku, je propojen hranou s protějším bodem. Pro názornost je uveden obrázek 3.4 zachycující případ, kde leží p 2 mezi dvěma p Hodnoty aproximace Nyní už známe podobu první části výstupního souboru, zbývá ted ještě určit hodnoty naší aproximace v uzlech nové triangulace. Z polynomiální aproximace známe hodnoty v d(k) bodech na daném trojúhelníku, který je typu p k. Z předchozí podkapitoly plyne, že sjednocení těchto bodů jednoznačně odpovídá právě všem uzlům nové triangulace. Abychom získali pro každý uzel jednu hodnotu, spočítáme vhodný průměr hodnot zadaných v tomto bodě, popřípadě i hodnot v bodech ležících v blízkosti daného uzlu. Je-li uzel uvnitř hrany ležící na hranici Ω, nebo leží-li v těžišti trojúhelníku p 3, známe v něm ze vstupu jedinou hodnotu, která se přímo přenese i do naší nové aproximace. Pokud bod leží na společné hraně dvou původních elementů stejného 11
12 Obrázek 3.2: Dělení trojúhelníků typu p 1 (značeno červeně) Obrázek 3.3: Dělení trojúhelníku typu p 1, který má tři sousedy p 3 12
13 Obrázek 3.4: element p 2 leží mezi dvěma p 3. Červeně jsou vyznačena dodatečná dělení. typu, nebo pokud je uzlem v původní triangulaci, máme v tomto bodě ze vstupu k dispozici různý počet hodnot polynomiální aproximace. Jednotlivé hodnoty v tomto bodě dávají polynomy zadané na trojúhelnících, jejichž hrany obsahují tento bod. Za hodnotu aproximace zde vezmeme jednoduše aritmetický průměr těchto hodnot. Stejně se řeší případ uzlů, ležících na hranici p 1 a elementu jiného b z f x y g a Obrázek 3.5: f je polynom stupně 3, g je polynom stupně 2 typu. Výsledkem bude opět aritmetický průměr hodnot dvou polynomů v tomto bodě. Rozdíl spočívá v tom, že hodnotu polynomu na p 1 nemáme zadanou přímo na vstupu. Funkční hodnota lineární funkce se však jedno- 13
14 duše dopočítá. Zbývají už jen uzly ležící na společné hraně trojúhelníků p 2 a p 3. Označme x, y, z body na společné hraně stejně jako na obrázku 3.5. Polynom na p 3 označme f a polynom na p 2 značme g. Naše aproximace u bude nabývat v uzlech na hraně následujících hodnot: u(x) = u(y) = 3f(x) + 2g(y) + u(a) 6 2g(y) + f(x) + f(z) 4 Uzel z je symetrický případ uzlu x. Hodnota aproximace v bodě x závisí na hodnotě stejné aproximace v bodě a. To však není ve sporu, nebot algoritmus nejprve vypočte hodnoty ve vrcholech trojúhelníků původní triangulace, které ovšem nezávisí na hodnotách v uzlech uvnitř hran. Na závěr kapitoly dodejme, že program nedává aproximace původních veličin. Ve výstupním souboru budou hodnoty následujících veličin: hustota, rychlost ( R 2 ), tlak, Machovo číslo. 14
15 Kapitola 4 Animace V předchozích kapitolách jsme popsali výstup programu, kterým je datový soubor, jenž lze načíst přímo do programu Tecplot. V něm si uživatel může vytvořit grafický výstup svého numerického řešení. Tecplot umožňuje navíc vytvářet animace a exportovat je ve formátu AVI. Aby uživatel při vytváření animaci použitím více datových souborů popsaných ve druhé kapitole nemusel zdlouhavě zpracovávat každý soubor jednotlivě, a poté každý zvlášt importovat do Tecplotu, vytvořil jsem softwarové prostředky pro Unixový operační systém, které celý tento proces automatizují. Jednotlivé úkony jsou prováděny pomocí shell skriptu. První z nich slouží k načtení více datových souborů, které pak uživatel může dále zpracovávat v interaktivním prostředí Tecplotu. Jediné, co uživatel musí udělat po spuštění skriptu, je určit, která data vytvořená ADGFEM chce vizualizovat. Skript už dále zajistí vytvoření všech datových souborů a dále vygeneruje speciální makrosoubor, který se následně předá Tecplotu. To má za následek spuštění interaktivního režimu, ve kterém jsou načtena všechna data určená uživatelem. Druhý shell script svým použitím navazuje na první skript, pomocí kterého se uživatel seznámil s grafickou podobou výsledků a mohl se rozhodnout, z kterých dat bude chtít vytvořit animaci. Prostřednictvím druhého skriptu může uživatel rychle a jednoduše generovat animaci ve formátu AVI. V tomto případě se pro urychlení nespouští grafické prostředí Tecplotu. Uživatel po spuštění skriptu vybere datové soubory a veličinu, zvolí si rychlost a velikost animace. Poté se podobně jako v předchozím případě automaticky vytvoří makrosoubor, jenž se předá Tecplotu a zajistí tak vytvoření příslušného video souboru. Popsané programy jsou k dispozici na přiloženém CD. 15
16 Kapitola 5 Ukázky výsledků V této kapitole jsou ukázky výsledných vizualizací numerického řešení vytvořené Tecplotem. Obrázky 5.1, 5.2 a 5.3 zachycují typický testovací příklad pro transonické proudění, kterým je proudění nevazké stlačitelné tekutiny GAMM kanálem, viz [1],[2],[3]. Na obrázku 5.4 je příklad nestacionárního proudění nevazké stlačitelné tekutiny přes dopředný schod, viz [4] y x y x Obrázek 5.1: Nahoře je původní triangulace s elementy typu p 3 a níže výsledná triangulace. 16
17 Obrázek 5.2: Tlak nevazké stlačitelné tekutiny při proudění GAMM kanálem Obrázek 5.3: Machovo číslo stlačitelné tekutiny při proudění GAMM kanálem 17
18 Obrázek 5.4: Ukázky z animace hustoty stlačitelné tekutiny při proudění přes dopředný schod 18
19 Literatura [1] V. Dolejší: Discontinuous Galerkin method for the numerical simulation of unsteady compressible flow, WSEAS Transactions on Systems, 5 (5): , [2] V. Dolejší, M. Feistauer: A Semi-implicit Discontinuous Galerkin Finite Element Method for the Numerical Solution of Inviscid Compressible Flow, J. Comput. Phys., 198 (2): , [3] V. Dolejší: On the Discontinuous Galerkin Method for the Numerical Solution of the Navier Stokes Equations, Int. J. Numer. Methods Fluids, 45: , [4] Woodward, Paul; Colella, Phillip: The numerical simulation of twodimensional fluid flow with strong shocks. J. Comput. Phys. 54, (1984) 19
MATEMATIKA V MEDICÍNĚ
 MATEMATIKA V MEDICÍNĚ Tomáš Oberhuber Fakulta jaderná a fyzikálně inženýrská České vysoké učení technické v Praze Matematika pro život TOMÁŠ OBERHUBER (FAKULTA JADERNÁ A FYZIKÁLNĚ INŽENÝRSKÁ MATEMATIKA
MATEMATIKA V MEDICÍNĚ Tomáš Oberhuber Fakulta jaderná a fyzikálně inženýrská České vysoké učení technické v Praze Matematika pro život TOMÁŠ OBERHUBER (FAKULTA JADERNÁ A FYZIKÁLNĚ INŽENÝRSKÁ MATEMATIKA
INOVACE ODBORNÉHO VZDĚLÁVÁNÍ NA STŘEDNÍCH ŠKOLÁCH ZAMĚŘENÉ NA VYUŽÍVÁNÍ ENERGETICKÝCH ZDROJŮ PRO 21. STOLETÍ A NA JEJICH DOPAD NA ŽIVOTNÍ PROSTŘEDÍ
 INOVACE ODBORNÉHO VZDĚLÁVÁNÍ NA STŘEDNÍCH ŠKOLÁCH ZAMĚŘENÉ NA VYUŽÍVÁNÍ ENERGETICKÝCH ZDROJŮ PRO 21. STOLETÍ A NA JEJICH DOPAD NA ŽIVOTNÍ PROSTŘEDÍ CZ.1.07/1.1.00/08.0010 NUMERICKÉ SIMULACE ING. KATEŘINA
INOVACE ODBORNÉHO VZDĚLÁVÁNÍ NA STŘEDNÍCH ŠKOLÁCH ZAMĚŘENÉ NA VYUŽÍVÁNÍ ENERGETICKÝCH ZDROJŮ PRO 21. STOLETÍ A NA JEJICH DOPAD NA ŽIVOTNÍ PROSTŘEDÍ CZ.1.07/1.1.00/08.0010 NUMERICKÉ SIMULACE ING. KATEŘINA
Colloquium FLUID DYNAMICS 2007 Institute of Thermomechanics AS CR, v. v. i., Prague, October 24-26, 2007 p.1
 Colloquium FLUID DYNAMICS 27 Institute of Thermomechanics AS CR, v. v. i., Prague, October 24-26, 27 p.1 NUMERICKÉ ŘEŠENÍ STACIONÁRNÍHO A NESTACIONÁRNÍHO TRANSSONICKÉHO PROUDĚNÍ VE VNĚJŠÍ AERODYNAMICE
Colloquium FLUID DYNAMICS 27 Institute of Thermomechanics AS CR, v. v. i., Prague, October 24-26, 27 p.1 NUMERICKÉ ŘEŠENÍ STACIONÁRNÍHO A NESTACIONÁRNÍHO TRANSSONICKÉHO PROUDĚNÍ VE VNĚJŠÍ AERODYNAMICE
Propojení matematiky, fyziky a počítačů
 Propojení matematiky, fyziky a počítačů Název projektu: Věda pro život, život pro vědu Registrační číslo: CZ..7/.3./45.9 V Ústí n. L., únor 5 Ing. Radek Honzátko, Ph.D. Propojení matematiky, fyziky a počítačů
Propojení matematiky, fyziky a počítačů Název projektu: Věda pro život, život pro vědu Registrační číslo: CZ..7/.3./45.9 V Ústí n. L., únor 5 Ing. Radek Honzátko, Ph.D. Propojení matematiky, fyziky a počítačů
Počítačová dynamika tekutin (CFD) Řešení rovnic. - metoda konečných objemů -
 Počítačová dynamika tekutin (CFD) Řešení rovnic - metoda konečných objemů - Rozdělení parciálních diferenciálních rovnic 2 Obecná parciální diferenciální rovnice se dvěma nezávislými proměnnými x a y:
Počítačová dynamika tekutin (CFD) Řešení rovnic - metoda konečných objemů - Rozdělení parciálních diferenciálních rovnic 2 Obecná parciální diferenciální rovnice se dvěma nezávislými proměnnými x a y:
Katedra geotechniky a podzemního stavitelství
 Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Metoda okrajových prvků (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Metoda okrajových prvků (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
Studentská tvůrčí činnost 2009
 Studentská tvůrčí činnost 2009 Numerické řešení proudového pole v kompresorové lopatkové mříži Balcarová Lucie Vedoucí práce: Prof. Ing. P. Šafařík, CSc. a Ing. T. Hyhlík, PhD. Numerické řešení proudového
Studentská tvůrčí činnost 2009 Numerické řešení proudového pole v kompresorové lopatkové mříži Balcarová Lucie Vedoucí práce: Prof. Ing. P. Šafařík, CSc. a Ing. T. Hyhlík, PhD. Numerické řešení proudového
Stabilizace Galerkin Least Squares pro
 Fakulta strojní ČVUT Ústav technické matematiky Stabilizace Galerkin Least Squares pro MKP na řešení proudění o vyšších Reynoldsových číslech Ing. Jakub Šístek Doc. RNDr. Pavel Burda, CSc. RNDr. Jaroslav
Fakulta strojní ČVUT Ústav technické matematiky Stabilizace Galerkin Least Squares pro MKP na řešení proudění o vyšších Reynoldsových číslech Ing. Jakub Šístek Doc. RNDr. Pavel Burda, CSc. RNDr. Jaroslav
U Úvod do modelování a simulace systémů
 U Úvod do modelování a simulace systémů Vyšetřování rozsáhlých soustav mnohdy nelze provádět analytickým výpočtem.často je nutné zkoumat chování zařízení v mezních situacích, do kterých se skutečné zařízení
U Úvod do modelování a simulace systémů Vyšetřování rozsáhlých soustav mnohdy nelze provádět analytickým výpočtem.často je nutné zkoumat chování zařízení v mezních situacích, do kterých se skutečné zařízení
Simulace (nejen) fyzikálních jevů na počítači
 Simulace (nejen) fyzikálních jevů na počítači V. Kučera Katedra numerické matematiky, MFFUK Praha 7.2.2013 Aerodynamický flutter Tacoma bridge, 1940 Fyzikální model Realita je komplikovaná Navier-Stokesovy
Simulace (nejen) fyzikálních jevů na počítači V. Kučera Katedra numerické matematiky, MFFUK Praha 7.2.2013 Aerodynamický flutter Tacoma bridge, 1940 Fyzikální model Realita je komplikovaná Navier-Stokesovy
Tento dokument obsahuje zadání pro semestrální programy z PAA. Vypracování. vypracovanou úlohu podle níže uvedených zadání. To mimo jiné znamená, že
 Kapitola Zadání Tento dokument obsahuje zadání pro semestrální programy z PAA. Vypracování alespoň jedné úlohy je nutnou podmínkou pro úspěšné složení zkoušky resp. získaní (klasifikovaného) zápočtu (viz.
Kapitola Zadání Tento dokument obsahuje zadání pro semestrální programy z PAA. Vypracování alespoň jedné úlohy je nutnou podmínkou pro úspěšné složení zkoušky resp. získaní (klasifikovaného) zápočtu (viz.
Voronoiův diagram. RNDr. Petra Surynková, Ph.D. Univerzita Karlova v Praze Matematicko-fyzikální fakulta
 12 RNDr., Ph.D. Katedra didaktiky matematiky Univerzita Karlova v Praze Matematicko-fyzikální fakulta petra.surynkova@mff.cuni.cz http://surynkova.info Definice V( P) nad množinou bodů P { p v rovině 1,
12 RNDr., Ph.D. Katedra didaktiky matematiky Univerzita Karlova v Praze Matematicko-fyzikální fakulta petra.surynkova@mff.cuni.cz http://surynkova.info Definice V( P) nad množinou bodů P { p v rovině 1,
Počítačová dynamika tekutin (CFD) Základní rovnice. - laminární tok -
 Počítačová dynamika tekutin (CFD) Základní rovnice - laminární tok - Základní pojmy 2 Tekutina nemá vlastní tvar působením nepatrných tečných sil se částice tekutiny snadno uvedou do pohybu (výjimka některé
Počítačová dynamika tekutin (CFD) Základní rovnice - laminární tok - Základní pojmy 2 Tekutina nemá vlastní tvar působením nepatrných tečných sil se částice tekutiny snadno uvedou do pohybu (výjimka některé
VYBRANÉ PARTIE Z NUMERICKÉ MATEMATIKY
 VYBRANÉ PARTIE Z NUMERICKÉ MATEMATIKY Jan Krejčí 31. srpna 2006 jkrejci@physics.ujep.cz http://physics.ujep.cz/~jkrejci Obsah 1 Přímé metody řešení soustav lineárních rovnic 3 1.1 Gaussova eliminace...............................
VYBRANÉ PARTIE Z NUMERICKÉ MATEMATIKY Jan Krejčí 31. srpna 2006 jkrejci@physics.ujep.cz http://physics.ujep.cz/~jkrejci Obsah 1 Přímé metody řešení soustav lineárních rovnic 3 1.1 Gaussova eliminace...............................
FLUENT přednášky. Metoda konečných objemů (MKO)
 FLUENT přednášky Metoda konečných objemů (MKO) Pavel Zácha zdroj: [Bakker, 2008], [Vodička, 2011], [Runchal, 2008], [Kozubková, 2008] Historie - zřejmě nestarší způsob řešení parciálních diferenciálních
FLUENT přednášky Metoda konečných objemů (MKO) Pavel Zácha zdroj: [Bakker, 2008], [Vodička, 2011], [Runchal, 2008], [Kozubková, 2008] Historie - zřejmě nestarší způsob řešení parciálních diferenciálních
Podobnostní transformace
 Schurova věta 1 Podobnostní transformace a výpočet vlastních čísel Obecný princip: Úloha: Řešíme-li matematickou úlohu, je často velmi vhodné hledat její ekvivalentní formulaci tak, aby se řešení úlohy
Schurova věta 1 Podobnostní transformace a výpočet vlastních čísel Obecný princip: Úloha: Řešíme-li matematickou úlohu, je často velmi vhodné hledat její ekvivalentní formulaci tak, aby se řešení úlohy
1 Polynomiální interpolace
 Polynomiální interpolace. Metoda neurčitých koeficientů Příklad.. Nalezněte polynom p co nejmenšího stupně, pro který platí p() = 0, p(2) =, p( ) = 6. Řešení. Polynom hledáme metodou neurčitých koeficientů,
Polynomiální interpolace. Metoda neurčitých koeficientů Příklad.. Nalezněte polynom p co nejmenšího stupně, pro který platí p() = 0, p(2) =, p( ) = 6. Řešení. Polynom hledáme metodou neurčitých koeficientů,
Martin Lísal. Úvod do MPI
 Martin Lísal září 2003 PARALELNÍ POČÍTÁNÍ Úvod do MPI 1 1 Co je to paralelní počítání? Paralelní počítání je počítání na paralelních počítačích či jinak řečeno využití více než jednoho procesoru při výpočtu
Martin Lísal září 2003 PARALELNÍ POČÍTÁNÍ Úvod do MPI 1 1 Co je to paralelní počítání? Paralelní počítání je počítání na paralelních počítačích či jinak řečeno využití více než jednoho procesoru při výpočtu
Jana Dannhoferová Ústav informatiky, PEF MZLU
 Počítačová grafika Křivky Jana Dannhoferová (jana.dannhoferova@mendelu.cz) Ústav informatiky, PEF MZLU Základní vlastnosti křivek křivka soustava parametrů nějaké rovnice, která je posléze generativně
Počítačová grafika Křivky Jana Dannhoferová (jana.dannhoferova@mendelu.cz) Ústav informatiky, PEF MZLU Základní vlastnosti křivek křivka soustava parametrů nějaké rovnice, která je posléze generativně
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY STUDIE TURBÍNY S VÍŘIVÝM OBĚŽNÝM KOLEM STUDY OF TURBINE WITH SIDE CHANNEL RUNNER
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ENERGETICKÝ ÚSTAV FACULTY OF MECHANICAL ENGINEERING ENERGY INSTITUTE STUDIE TURBÍNY S VÍŘIVÝM OBĚŽNÝM KOLEM STUDY
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ENERGETICKÝ ÚSTAV FACULTY OF MECHANICAL ENGINEERING ENERGY INSTITUTE STUDIE TURBÍNY S VÍŘIVÝM OBĚŽNÝM KOLEM STUDY
VYUŽITÍ MATLABU PRO VÝUKU NUMERICKÉ MATEMATIKY Josef Daněk Centrum aplikované matematiky, Západočeská univerzita v Plzni. Abstrakt
 VYUŽITÍ MATLABU PRO VÝUKU NUMERICKÉ MATEMATIKY Josef Daněk Centrum aplikované matematiky, Západočeská univerzita v Plzni Abstrakt Současný trend snižování počtu kontaktních hodin ve výuce nutí vyučující
VYUŽITÍ MATLABU PRO VÝUKU NUMERICKÉ MATEMATIKY Josef Daněk Centrum aplikované matematiky, Západočeská univerzita v Plzni Abstrakt Současný trend snižování počtu kontaktních hodin ve výuce nutí vyučující
Afinita je stručný název pro afinní transformaci prostoru, tj.vzájemně jednoznačné afinní zobrazení bodového prostoru A n na sebe.
 4 Afinita Afinita je stručný název pro afinní transformaci prostoru, tj.vzájemně jednoznačné afinní zobrazení bodového prostoru A n na sebe. Poznámka. Vzájemně jednoznačným zobrazením rozumíme zobrazení,
4 Afinita Afinita je stručný název pro afinní transformaci prostoru, tj.vzájemně jednoznačné afinní zobrazení bodového prostoru A n na sebe. Poznámka. Vzájemně jednoznačným zobrazením rozumíme zobrazení,
Vzor textu na deskách bakalářské práce. Univerzita Karlova v Praze Pedagogická fakulta BAKALÁŘSKÁ PRÁCE. Jméno Příjmení
 Vzor textu na deskách bakalářské práce Univerzita Karlova v Praze Pedagogická fakulta BAKALÁŘSKÁ PRÁCE Rok Jméno Příjmení Vzor titulní strany bakalářské práce Univerzita Karlova v Praze Pedagogická fakulta
Vzor textu na deskách bakalářské práce Univerzita Karlova v Praze Pedagogická fakulta BAKALÁŘSKÁ PRÁCE Rok Jméno Příjmení Vzor titulní strany bakalářské práce Univerzita Karlova v Praze Pedagogická fakulta
APROXIMACE KŘIVEK V MATLABU NEWTONŮV INTERPOLAČNÍ POLYNOM CURVE FITTING IN MATLAB NEWTON INTERPOLATION POLYNOMIAL
 APROXIMACE KŘIVEK V MATLABU NEWTONŮV INTERPOLAČNÍ POLYNOM CURVE FITTING IN MATLAB NEWTON INTERPOLATION POLYNOMIAL Jiří Kulička 1 Anotace: Článek se zabývá odvozením, algoritmizací a popisem konstrukce
APROXIMACE KŘIVEK V MATLABU NEWTONŮV INTERPOLAČNÍ POLYNOM CURVE FITTING IN MATLAB NEWTON INTERPOLATION POLYNOMIAL Jiří Kulička 1 Anotace: Článek se zabývá odvozením, algoritmizací a popisem konstrukce
V předchozí kapitole jsme podstatným způsobem rozšířili naši představu o tom, co je to číslo. Nadále jsou pro nás důležité především vlastnosti
 Kapitola 5 Vektorové prostory V předchozí kapitole jsme podstatným způsobem rozšířili naši představu o tom, co je to číslo. Nadále jsou pro nás důležité především vlastnosti operací sčítání a násobení
Kapitola 5 Vektorové prostory V předchozí kapitole jsme podstatným způsobem rozšířili naši představu o tom, co je to číslo. Nadále jsou pro nás důležité především vlastnosti operací sčítání a násobení
Globální matice konstrukce
 Globální matice konstrukce Z matic tuhosti a hmotnosti jednotlivých prvků lze sestavit globální matici tuhosti a globální matici hmotnosti konstrukce, které se využijí v řešení základní rovnice MKP: [m]{
Globální matice konstrukce Z matic tuhosti a hmotnosti jednotlivých prvků lze sestavit globální matici tuhosti a globální matici hmotnosti konstrukce, které se využijí v řešení základní rovnice MKP: [m]{
Modelování proudění ve vysokém rozlišení
 Modelování proudění ve vysokém rozlišení Vladimír Fuka vedoucí práce: doc. RNDr. Josef Brechler, CSc. Cíle práce Vytvořit základ počítačového modelu proudění. Vyzkoušet některé nové postupy. Ověřit funkčnost
Modelování proudění ve vysokém rozlišení Vladimír Fuka vedoucí práce: doc. RNDr. Josef Brechler, CSc. Cíle práce Vytvořit základ počítačového modelu proudění. Vyzkoušet některé nové postupy. Ověřit funkčnost
Aplikovaná numerická matematika
 Aplikovaná numerická matematika 6. Metoda nejmenších čtverců doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních
Aplikovaná numerická matematika 6. Metoda nejmenších čtverců doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních
Hydromechanické procesy Počítačová dynamika tekutin (CFD) - úvod -
 Hydromechanické procesy Počítačová dynamika tekutin (CFD) - úvod - M. Jahoda Co je CFD? 2 Computational Fluid Dynamics (CFD) je moderní metoda jak získat představu o proudění tekutin, přenosu tepla a hmoty,
Hydromechanické procesy Počítačová dynamika tekutin (CFD) - úvod - M. Jahoda Co je CFD? 2 Computational Fluid Dynamics (CFD) je moderní metoda jak získat představu o proudění tekutin, přenosu tepla a hmoty,
Výpočet stlačitelného proudění metodou konečných objemů
 Výpočet stlačitelného proudění metodou konečných objemů Petra Punčochářová Ústav technické matematiky, Fakulta strojní, Vysoké učení technické v Praze Vedoucí práce: Prof. RNDr. K. Kozel DrSc. Úvod V 80.
Výpočet stlačitelného proudění metodou konečných objemů Petra Punčochářová Ústav technické matematiky, Fakulta strojní, Vysoké učení technické v Praze Vedoucí práce: Prof. RNDr. K. Kozel DrSc. Úvod V 80.
MATEMATIKA III. Olga Majlingová. Učební text pro prezenční studium. Předběžná verze
 Fakulta strojního inženýrství Univerzity J. E. Purkyně v Ústí nad Labem Pasteurova 7 Tel.: 475 285 511 400 96 Ústí nad Labem Fax: 475 285 566 Internet: www.ujep.cz E-mail: kontakt@ujep.cz MATEMATIKA III
Fakulta strojního inženýrství Univerzity J. E. Purkyně v Ústí nad Labem Pasteurova 7 Tel.: 475 285 511 400 96 Ústí nad Labem Fax: 475 285 566 Internet: www.ujep.cz E-mail: kontakt@ujep.cz MATEMATIKA III
Transformujte diferenciální výraz x f x + y f do polárních souřadnic r a ϕ, které jsou definovány vztahy x = r cos ϕ a y = r sin ϕ.
 Ukázka 1 Necht má funkce z = f(x, y) spojité parciální derivace. Napište rovnici tečné roviny ke grafu této funkce v bodě A = [ x 0, y 0, z 0 ]. Transformujte diferenciální výraz x f x + y f y do polárních
Ukázka 1 Necht má funkce z = f(x, y) spojité parciální derivace. Napište rovnici tečné roviny ke grafu této funkce v bodě A = [ x 0, y 0, z 0 ]. Transformujte diferenciální výraz x f x + y f y do polárních
1 Přesnost metody konečných prvků
 1 PŘESNOST METODY KONEČNÝCH PRVKŮ 1 1 Přesnost metody konečných prvků Metoda konečných prvků je založena na diskretizaci původní spojité konstrukce soustavou prvků (nebo obecněji na diskretizaci slabé
1 PŘESNOST METODY KONEČNÝCH PRVKŮ 1 1 Přesnost metody konečných prvků Metoda konečných prvků je založena na diskretizaci původní spojité konstrukce soustavou prvků (nebo obecněji na diskretizaci slabé
APLIKACE SIMULAČNÍHO PROGRAMU ANSYS PRO VÝUKU MIKROELEKTROTECHNICKÝCH TECHNOLOGIÍ
 APLIKACE SIMULAČNÍHO PROGRAMU ANSYS PRO VÝUKU MIKROELEKTROTECHNICKÝCH TECHNOLOGIÍ 1. ÚVOD Ing. Psota Boleslav, Doc. Ing. Ivan Szendiuch, CSc. Ústav mikroelektroniky, FEKT VUT v Brně, Technická 10, 602
APLIKACE SIMULAČNÍHO PROGRAMU ANSYS PRO VÝUKU MIKROELEKTROTECHNICKÝCH TECHNOLOGIÍ 1. ÚVOD Ing. Psota Boleslav, Doc. Ing. Ivan Szendiuch, CSc. Ústav mikroelektroniky, FEKT VUT v Brně, Technická 10, 602
9. přednáška z předmětu GIS1 Digitální model reliéfu a odvozené povrchy. Vyučující: Ing. Jan Pacina, Ph.D.
 9. přednáška z předmětu GIS1 Digitální model reliéfu a odvozené povrchy Vyučující: Ing. Jan Pacina, Ph.D. e-mail: jan.pacina@ujep.cz Lehký úvod Digitální modely terénu jsou dnes v geoinformačních systémech
9. přednáška z předmětu GIS1 Digitální model reliéfu a odvozené povrchy Vyučující: Ing. Jan Pacina, Ph.D. e-mail: jan.pacina@ujep.cz Lehký úvod Digitální modely terénu jsou dnes v geoinformačních systémech
Aproximace funkcí. Numerické metody 6. května FJFI ČVUT v Praze
 Aproximace funkcí Numerické metody 6. května 2018 FJFI ČVUT v Praze 1 Úvod Dělení Interpolace 1D Více dimenzí Minimalizace Důvody 1 Dělení Dělení - Získané data zadané data 2 Dělení - Získané data Obecně
Aproximace funkcí Numerické metody 6. května 2018 FJFI ČVUT v Praze 1 Úvod Dělení Interpolace 1D Více dimenzí Minimalizace Důvody 1 Dělení Dělení - Získané data zadané data 2 Dělení - Získané data Obecně
Přijímací zkouška na MFF UK v Praze
 Přijímací zkouška na MFF UK v Praze pro bakalářské studijní programy fyzika, informatika a matematika 017, varianta A U každé z deseti úloh je nabízeno pět odpovědí: a, b, c, d, e. Vaším úkolem je u každé
Přijímací zkouška na MFF UK v Praze pro bakalářské studijní programy fyzika, informatika a matematika 017, varianta A U každé z deseti úloh je nabízeno pět odpovědí: a, b, c, d, e. Vaším úkolem je u každé
Rovinná úloha v MKP. (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v. prostorové úlohy: u, v, w
 Rovinná úloha v MKP Hledané deformační veličiny viz klasická teorie pružnosti (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v desky: w, ϕ x, ϕ y prostorové úlohy: u,
Rovinná úloha v MKP Hledané deformační veličiny viz klasická teorie pružnosti (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v desky: w, ϕ x, ϕ y prostorové úlohy: u,
Počítačová dynamika tekutin užitečný nástroj pro inženýry
 Počítačová dynamika tekutin užitečný nástroj pro inženýry M. Jahoda Úvod Počítačová dynamika tekutin (Computational Fluid Dynamics, CFD) je moderní metoda, která se zabývá prouděním tekutin, přenosem tepla
Počítačová dynamika tekutin užitečný nástroj pro inženýry M. Jahoda Úvod Počítačová dynamika tekutin (Computational Fluid Dynamics, CFD) je moderní metoda, která se zabývá prouděním tekutin, přenosem tepla
APLIKACE. Poznámky Otázky
 APLIKACE Následující úlohy lze zhruba rozdělit na geometrické, algebraické a úlohy popisující různé stavy v některých oblastech jiných věd, např. fyziky nebo ekonomie. GEOMETRICKÉ ÚLOHY Mezi typické úlohy
APLIKACE Následující úlohy lze zhruba rozdělit na geometrické, algebraické a úlohy popisující různé stavy v některých oblastech jiných věd, např. fyziky nebo ekonomie. GEOMETRICKÉ ÚLOHY Mezi typické úlohy
přenosu tepla seznámí s teoretickou stránkou této problematiky, kterou si dále osvojují v následných
 Koncepce virtuální laboratoře přenosu tepla Volavý, Jaroslav 1 & Knotek, Stanislav 2 & Jícha, Miroslav 3 1 Ing., VUT v Brně, Fakulta strojního inženýrství, Enegetický ústav, Odbor termomechaniky a techniky
Koncepce virtuální laboratoře přenosu tepla Volavý, Jaroslav 1 & Knotek, Stanislav 2 & Jícha, Miroslav 3 1 Ing., VUT v Brně, Fakulta strojního inženýrství, Enegetický ústav, Odbor termomechaniky a techniky
Modelování zdravotně významných částic v ovzduší v podmínkách městské zástavby
 Modelování zdravotně významných částic v ovzduší v podmínkách městské zástavby Jiří Pospíšil, Miroslav Jícha pospisil.j@fme.vutbr.cz Vysoké učení technické v Brně Fakulta strojního inženýrství Energetický
Modelování zdravotně významných částic v ovzduší v podmínkách městské zástavby Jiří Pospíšil, Miroslav Jícha pospisil.j@fme.vutbr.cz Vysoké učení technické v Brně Fakulta strojního inženýrství Energetický
Matematické modely a způsoby jejich řešení. Kateřina Růžičková
 Matematické modely a způsoby jejich řešení Kateřina Růžičková Rovnice matematické fyziky Přednáška převzata od Doc. Rapanta Parciální diferencíální rovnice Diferencialní rovnice obsahujcí parcialní derivace
Matematické modely a způsoby jejich řešení Kateřina Růžičková Rovnice matematické fyziky Přednáška převzata od Doc. Rapanta Parciální diferencíální rovnice Diferencialní rovnice obsahujcí parcialní derivace
GRAFICKÉ ŘEŠENÍ ROVNIC A JEJICH SOUSTAV
 GRAFICKÉ ŘEŠENÍ ROVNIC A JEJICH SOUSTAV Mgr. Jitka Nováková SPŠ strojní a stavební Tábor Abstrakt: Grafické řešení rovnic a jejich soustav je účinná metoda, jak vysvětlit, kolik různých řešení může daný
GRAFICKÉ ŘEŠENÍ ROVNIC A JEJICH SOUSTAV Mgr. Jitka Nováková SPŠ strojní a stavební Tábor Abstrakt: Grafické řešení rovnic a jejich soustav je účinná metoda, jak vysvětlit, kolik různých řešení může daný
Metoda konečných prvků Charakteristika metody (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika)
 Inovace studijního oboru Geotechnika Reg. č. CZ.1.07/2.2.00/28.0009 Metoda konečných prvků Charakteristika metody (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika) Doc. RNDr.
Inovace studijního oboru Geotechnika Reg. č. CZ.1.07/2.2.00/28.0009 Metoda konečných prvků Charakteristika metody (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika) Doc. RNDr.
Potenciální proudění
 Hydromechanické procesy Potenciální proudění + plíživé obtékání koule M. Jahoda Proudění tekutiny Pohyby elementu tekutiny 2 čas t čas t + dt obecný pohyb posunutí lineární deformace rotace úhlová deformace
Hydromechanické procesy Potenciální proudění + plíživé obtékání koule M. Jahoda Proudění tekutiny Pohyby elementu tekutiny 2 čas t čas t + dt obecný pohyb posunutí lineární deformace rotace úhlová deformace
Diskrétní řešení vzpěru prutu
 1 z 5 Diskrétní řešení vzpěru prutu Discrete solution of beam buckling Petr Frantík Abstract Here is described discrete method for solution of beam buckling. The beam is divided into a number of tough
1 z 5 Diskrétní řešení vzpěru prutu Discrete solution of beam buckling Petr Frantík Abstract Here is described discrete method for solution of beam buckling. The beam is divided into a number of tough
Univerzita Karlova v Praze
 [Vzor: Pevná deska bakalářské práce není součástí elektronické verze] Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Rok Jméno a příjmení autora [Vzor :Titulní strana bakalářské
[Vzor: Pevná deska bakalářské práce není součástí elektronické verze] Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Rok Jméno a příjmení autora [Vzor :Titulní strana bakalářské
FP - SEMINÁŘ Z NUMERICKÉ MATEMATIKY. Katedra matematiky a didaktiky matematiky Technická univerzita v Liberci
 FP - SEMINÁŘ Z NUMERICKÉ MATEMATIKY Dana Černá http://www.fp.tul.cz/kmd/ Katedra matematiky a didaktiky matematiky Technická univerzita v Liberci OBSAH A CÍLE SEMINÁŘE: Opakování a procvičení vybraných
FP - SEMINÁŘ Z NUMERICKÉ MATEMATIKY Dana Černá http://www.fp.tul.cz/kmd/ Katedra matematiky a didaktiky matematiky Technická univerzita v Liberci OBSAH A CÍLE SEMINÁŘE: Opakování a procvičení vybraných
Řešení 1D vedení tepla metodou sítí a metodou
 ENumerická analýza transportních procesů - NTP2 Přednáška č. 9 Řešení 1D vedení tepla metodou sítí a metodou konečných objemů Metoda sítí (metoda konečných diferencí - MKD) Metoda sítí Základní myšlenka
ENumerická analýza transportních procesů - NTP2 Přednáška č. 9 Řešení 1D vedení tepla metodou sítí a metodou konečných objemů Metoda sítí (metoda konečných diferencí - MKD) Metoda sítí Základní myšlenka
Software pro modelování chování systému tlakové kanalizační sítě Popis metodiky a ukázka aplikace
 Optimalizace systémů tlakových kanalizací pomocí matematického modelování jejich provozních stavů Software pro modelování chování systému tlakové kanalizační sítě Popis metodiky a ukázka aplikace Ing.
Optimalizace systémů tlakových kanalizací pomocí matematického modelování jejich provozních stavů Software pro modelování chování systému tlakové kanalizační sítě Popis metodiky a ukázka aplikace Ing.
2. Schurova věta. Petr Tichý. 3. října 2012
 2. Schurova věta Petr Tichý 3. října 2012 1 Podobnostní transformace a výpočet vlastních čísel Obecný princip: Úloha: Řešíme-li matematickou úlohu, je často velmi vhodné hledat její ekvivalentní formulaci
2. Schurova věta Petr Tichý 3. října 2012 1 Podobnostní transformace a výpočet vlastních čísel Obecný princip: Úloha: Řešíme-li matematickou úlohu, je často velmi vhodné hledat její ekvivalentní formulaci
5. Lokální, vázané a globální extrémy
 5 Lokální, vázané a globální extrémy Studijní text Lokální extrémy 5 Lokální, vázané a globální extrémy Definice 51 Řekneme, že f : R n R má v bodě a Df: 1 lokální maximum, když Ka, δ Df tak, že x Ka,
5 Lokální, vázané a globální extrémy Studijní text Lokální extrémy 5 Lokální, vázané a globální extrémy Definice 51 Řekneme, že f : R n R má v bodě a Df: 1 lokální maximum, když Ka, δ Df tak, že x Ka,
Příspěvek do konference STČ 2008: Numerické modelování obtékání profilu NACA 0012 dvěma nemísitelnými tekutinami
 Příspěvek do konference STČ 2008: Numerické modelování obtékání profilu NACA 0012 dvěma nemísitelnými tekutinami (Numerical Modelling of Flow of Two Immiscible Fluids Past a NACA 0012 profile) Ing. Tomáš
Příspěvek do konference STČ 2008: Numerické modelování obtékání profilu NACA 0012 dvěma nemísitelnými tekutinami (Numerical Modelling of Flow of Two Immiscible Fluids Past a NACA 0012 profile) Ing. Tomáš
K velkým datům přes matice a grafy
 K velkým datům přes matice a grafy Miroslav Tůma Katedra numerické matematiky, MFF UK mirektuma@karlin.mff.cuni.cz MFF UK, 10.4.2019 1 / 70 Outline 1 Motivace 2 Šíření infekční choroby 3 Jiné motivace
K velkým datům přes matice a grafy Miroslav Tůma Katedra numerické matematiky, MFF UK mirektuma@karlin.mff.cuni.cz MFF UK, 10.4.2019 1 / 70 Outline 1 Motivace 2 Šíření infekční choroby 3 Jiné motivace
Vzor textu na deskách diplomové práce. Univerzita Karlova v Praze Pedagogická fakulta DIPLOMOVÁ PRÁCE. Jméno Příjmení
 Vzor textu na deskách diplomové práce Univerzita Karlova v Praze Pedagogická fakulta DIPLOMOVÁ PRÁCE Rok Jméno Příjmení Vzor titulní strany diplomové práce Univerzita Karlova v Praze Pedagogická fakulta
Vzor textu na deskách diplomové práce Univerzita Karlova v Praze Pedagogická fakulta DIPLOMOVÁ PRÁCE Rok Jméno Příjmení Vzor titulní strany diplomové práce Univerzita Karlova v Praze Pedagogická fakulta
Aplikovaná numerická matematika - ANM
 Aplikovaná numerická matematika - ANM 3 Řešení soustav lineárních rovnic iterační metody doc Ing Róbert Lórencz, CSc České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových
Aplikovaná numerická matematika - ANM 3 Řešení soustav lineárních rovnic iterační metody doc Ing Róbert Lórencz, CSc České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových
Vzpěr jednoduchého rámu, diferenciální operátory. Lenka Dohnalová
 1 / 40 Vzpěr jednoduchého rámu, diferenciální operátory Lenka Dohnalová ČVUT, fakulta stavební, ZS 2015/2016 katedra stavební mechaniky a katedra matematiky, Odborné vedení: doc. Ing. Jan Zeman, Ph.D.,
1 / 40 Vzpěr jednoduchého rámu, diferenciální operátory Lenka Dohnalová ČVUT, fakulta stavební, ZS 2015/2016 katedra stavební mechaniky a katedra matematiky, Odborné vedení: doc. Ing. Jan Zeman, Ph.D.,
Pokyny pro vypracování bakalářských, diplomových a rigorózních prací na Přírodovědecké fakultě MU
 Opatření děkana Přírodovědecké fakulty Masarykovy univerzity č. 12 / 2018 Pokyny pro vypracování bakalářských, diplomových a rigorózních prací na Přírodovědecké fakultě MU (ve znění účinném od 15.12.2018)
Opatření děkana Přírodovědecké fakulty Masarykovy univerzity č. 12 / 2018 Pokyny pro vypracování bakalářských, diplomových a rigorózních prací na Přírodovědecké fakultě MU (ve znění účinném od 15.12.2018)
Úvod do přesnosti MKP, generace sítí a metod řešení soustav lineárních rovnic
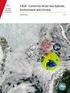 ENumerická analýza transportních procesů - NTP2 Přednáška č. 8 Úvod do přesnosti MKP, generace sítí a metod řešení soustav lineárních rovnic Úvod do přesnosti metody konečných prvků Úvod do přesnosti metody
ENumerická analýza transportních procesů - NTP2 Přednáška č. 8 Úvod do přesnosti MKP, generace sítí a metod řešení soustav lineárních rovnic Úvod do přesnosti metody konečných prvků Úvod do přesnosti metody
Přijímací zkouška na MFF UK v Praze
 Přijímací zkouška na MFF UK v Praze pro bakalářské studijní programy fyzika, informatika a matematika 2016, varianta A U každé z deseti úloh je nabízeno pět odpovědí: a, b, c, d, e. Vaším úkolem je u každé
Přijímací zkouška na MFF UK v Praze pro bakalářské studijní programy fyzika, informatika a matematika 2016, varianta A U každé z deseti úloh je nabízeno pět odpovědí: a, b, c, d, e. Vaším úkolem je u každé
SEMESTRÁLNÍ PRÁCE X. Aproximace křivek Numerické vyhlazování
 KATEDRA ANALYTICKÉ CHEMIE FAKULTY CHEMICKO TECHNOLOGICKÉ UNIVERSITA PARDUBICE - Licenční studium chemometrie LS96/1 SEMESTRÁLNÍ PRÁCE X. Aproximace křivek Numerické vyhlazování Praha, leden 1999 0 Úloha
KATEDRA ANALYTICKÉ CHEMIE FAKULTY CHEMICKO TECHNOLOGICKÉ UNIVERSITA PARDUBICE - Licenční studium chemometrie LS96/1 SEMESTRÁLNÍ PRÁCE X. Aproximace křivek Numerické vyhlazování Praha, leden 1999 0 Úloha
 Interpolace Uvažujme třídu funkcí jedné proměnné ψ(x; a 0,..., a n ), kde a 0,..., a n jsou parametry, které popisují jednotlivé funkce této třídy. Mějme dány body x 0, x 1,..., x n, x i x k, i, k = 0,
Interpolace Uvažujme třídu funkcí jedné proměnné ψ(x; a 0,..., a n ), kde a 0,..., a n jsou parametry, které popisují jednotlivé funkce této třídy. Mějme dány body x 0, x 1,..., x n, x i x k, i, k = 0,
MATICE. a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij]
![MATICE. a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij] MATICE. a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij]](/thumbs/58/41721403.jpg) MATICE Matice typu m/n nad tělesem T je soubor m n prvků z tělesa T uspořádaných do m řádků a n sloupců: a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij] a m1 a m2 a mn Prvek a i,j je prvek matice A na místě
MATICE Matice typu m/n nad tělesem T je soubor m n prvků z tělesa T uspořádaných do m řádků a n sloupců: a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij] a m1 a m2 a mn Prvek a i,j je prvek matice A na místě
South Bohemia Mathematical Letters Volume 23, (2015), No. 1, DĚLENÍ KRUHU NA OBLASTI ÚVOD
 South Bohemia Mathematical Letters Volume 23, (2015), No. 1, 113-122. DĚLENÍ KRUHU NA OBLASTI MAREK VEJSADA ABSTRAKT. V textu se zabývám řešením následujícího problému: Zvolíme na kružnici určitý počet
South Bohemia Mathematical Letters Volume 23, (2015), No. 1, 113-122. DĚLENÍ KRUHU NA OBLASTI MAREK VEJSADA ABSTRAKT. V textu se zabývám řešením následujícího problému: Zvolíme na kružnici určitý počet
Dnešní látka: Literatura: Kapitoly 3 a 4 ze skript Karel Rektorys: Matematika 43, ČVUT, Praha, Text přednášky na webové stránce přednášejícího.
 Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
MODELOVÁNÍ SHALLOW WATER
 Západočeská univerzita Fakulta aplikovaných věd Matematické metody v aplikovaných vědách a ve vzdělávání MODELOÁNÍ SHLLOW WTER KRISTÝN HDŠOÁ ziraf@students.zcu.cz 1 ÚOD Dostala jsem za úkol namodelovat
Západočeská univerzita Fakulta aplikovaných věd Matematické metody v aplikovaných vědách a ve vzdělávání MODELOÁNÍ SHLLOW WTER KRISTÝN HDŠOÁ ziraf@students.zcu.cz 1 ÚOD Dostala jsem za úkol namodelovat
Numerické řešení 2D stlačitelného proudění s kondenzací. Michal Seifert
 Numerické řešení 2D stlačitelného proudění s kondenzací Michal Seifert Úkoly diplomové práce Popsat matematické modely proudící tekutiny Popis numerických metod založených na metodě konečných objemů Porovnání
Numerické řešení 2D stlačitelného proudění s kondenzací Michal Seifert Úkoly diplomové práce Popsat matematické modely proudící tekutiny Popis numerických metod založených na metodě konečných objemů Porovnání
Základy tvorby výpočtového modelu
 Základy tvorby výpočtového modelu Zpracoval: Jaroslav Beran Pracoviště: Technická univerzita v Liberci katedra textilních a jednoúčelových strojů Tento materiál vznikl jako součást projektu In-TECH 2,
Základy tvorby výpočtového modelu Zpracoval: Jaroslav Beran Pracoviště: Technická univerzita v Liberci katedra textilních a jednoúčelových strojů Tento materiál vznikl jako součást projektu In-TECH 2,
PARAMETRICKÁ STUDIE VÝPOČTU KOMBINACE JEDNOKOMPONENTNÍCH ÚČINKŮ ZATÍŽENÍ
 PARAMETRICKÁ STUDIE VÝPOČTU KOMBINACE JEDNOKOMPONENTNÍCH ÚČINKŮ ZATÍŽENÍ Ing. David KUDLÁČEK, Katedra stavební mechaniky, Fakulta stavební, VŠB TUO, Ludvíka Podéště 1875, 708 33 Ostrava Poruba, tel.: 59
PARAMETRICKÁ STUDIE VÝPOČTU KOMBINACE JEDNOKOMPONENTNÍCH ÚČINKŮ ZATÍŽENÍ Ing. David KUDLÁČEK, Katedra stavební mechaniky, Fakulta stavební, VŠB TUO, Ludvíka Podéště 1875, 708 33 Ostrava Poruba, tel.: 59
Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice
 Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice Vektorové podprostory K množina reálných nebo komplexních čísel, U vektorový prostor nad K. Lineární kombinace vektorů u 1, u 2,...,u
Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice Vektorové podprostory K množina reálných nebo komplexních čísel, U vektorový prostor nad K. Lineární kombinace vektorů u 1, u 2,...,u
Opatření děkana č. 1/2012 Pokyny pro vypracování bakalářských, diplomových a rigorózních prací na Přírodovědecké fakultě MU
 Opatření děkana č. 1/2012 Pokyny pro vypracování bakalářských, diplomových a rigorózních prací na Přírodovědecké fakultě MU Bakalářské, diplomové a rigorózní práce odevzdávané k obhajobě na Přírodovědecké
Opatření děkana č. 1/2012 Pokyny pro vypracování bakalářských, diplomových a rigorózních prací na Přírodovědecké fakultě MU Bakalářské, diplomové a rigorózní práce odevzdávané k obhajobě na Přírodovědecké
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ
 ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
Interpolace, ortogonální polynomy, Gaussova kvadratura
 Interpolace, ortogonální polynomy, Gaussova kvadratura Petr Tichý 20. listopadu 2013 1 Úloha Lagrangeovy interpolace Dán omezený uzavřený interval [a, b] a v něm n + 1 různých bodů x 0, x 1,..., x n. Nechť
Interpolace, ortogonální polynomy, Gaussova kvadratura Petr Tichý 20. listopadu 2013 1 Úloha Lagrangeovy interpolace Dán omezený uzavřený interval [a, b] a v něm n + 1 různých bodů x 0, x 1,..., x n. Nechť
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
Buněčné automaty a mřížkové buněčné automaty pro plyny. Larysa Ocheretna
 Buněčné automaty a mřížkové buněčné automaty pro plyny Larysa Ocheretna Obsah Buněčný automat: princip modelu, vymezení pojmů Mřížkový buněčný automat pro plyny Příklady aplikace principů mřížkových buněčných
Buněčné automaty a mřížkové buněčné automaty pro plyny Larysa Ocheretna Obsah Buněčný automat: princip modelu, vymezení pojmů Mřížkový buněčný automat pro plyny Příklady aplikace principů mřížkových buněčných
Numerické řešení modelu proudění v porézní hornině s puklinou
 Numerické řešení modelu proudění v porézní hornině s puklinou Martin Hanek Úvod Vedoucí práce prof. RNDr. Pavel Burda, CSc. Zajímá nás jednofázová tekutina v puklině porézní horniny. Studie je provedena
Numerické řešení modelu proudění v porézní hornině s puklinou Martin Hanek Úvod Vedoucí práce prof. RNDr. Pavel Burda, CSc. Zajímá nás jednofázová tekutina v puklině porézní horniny. Studie je provedena
Nelineární obvody. V nelineárních obvodech však platí Kirchhoffovy zákony.
 Nelineární obvody Dosud jsme se zabývali analýzou lineárních elektrických obvodů, pasivní lineární prvky měly zpravidla konstantní parametr, v těchto obvodech platil princip superpozice a pro analýzu harmonického
Nelineární obvody Dosud jsme se zabývali analýzou lineárních elektrických obvodů, pasivní lineární prvky měly zpravidla konstantní parametr, v těchto obvodech platil princip superpozice a pro analýzu harmonického
Elektronické obvody analýza a simulace
 Elektronické obvody analýza a simulace Jiří Hospodka katedra Teorie obvodů, 804/B3 ČVUT FEL 4. října 2006 Jiří Hospodka (ČVUT FEL) Elektronické obvody analýza a simulace 4. října 2006 1 / 7 Charakteristika
Elektronické obvody analýza a simulace Jiří Hospodka katedra Teorie obvodů, 804/B3 ČVUT FEL 4. října 2006 Jiří Hospodka (ČVUT FEL) Elektronické obvody analýza a simulace 4. října 2006 1 / 7 Charakteristika
Nelineární analýza materiálů a konstrukcí (V-132YNAK) Přednáška 2 Princip metody konečných prvků
 Nelineární analýza materiálů a konstrukcí (V-132YNAK) Přednáška 2 Princip metody konečných prvků Petr Kabele petr.kabele@fsv.cvut.cz people.fsv.cvut.cz/~pkabele Petr Kabele, 2007-2014 Obsah Variační principy
Nelineární analýza materiálů a konstrukcí (V-132YNAK) Přednáška 2 Princip metody konečných prvků Petr Kabele petr.kabele@fsv.cvut.cz people.fsv.cvut.cz/~pkabele Petr Kabele, 2007-2014 Obsah Variační principy
INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ. Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ.1.07/2.2.00/28.
 INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ107/2200/280141 Soustavy lineárních rovnic Michal Botur Přednáška 4 KAG/DLA1M: Lineární
INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ Modernizace studijního programu Matematika na PřF Univerzity Palackého v Olomouci CZ107/2200/280141 Soustavy lineárních rovnic Michal Botur Přednáška 4 KAG/DLA1M: Lineární
NUMERICKÁ SIMULACE PROUDĚNÍ DVOUFÁZOVÉ VLHKÉ PÁRY OHYBEM POTRUBÍ Numerical simulation of two phase wet steam flow in pipeline elbow
 NUMERICKÁ SIMULACE PROUDĚNÍ DVOUFÁZOVÉ VLHKÉ PÁRY OHYBEM POTRUBÍ Numerical simulation of two phase wet steam flow in pipeline elbow Šťastný Miroslav 1, Střasák Pavel 2 1 Západočeská univerzita v Plzni,
NUMERICKÁ SIMULACE PROUDĚNÍ DVOUFÁZOVÉ VLHKÉ PÁRY OHYBEM POTRUBÍ Numerical simulation of two phase wet steam flow in pipeline elbow Šťastný Miroslav 1, Střasák Pavel 2 1 Západočeská univerzita v Plzni,
Diferenciální rovnice
 Diferenciální rovnice Průvodce studiem Touto kapitolou se náplň základního kurzu bakalářské matematiky uzavírá. Je tomu tak mimo jiné proto, že jsou zde souhrnně využívány poznatky získané studiem předchozích
Diferenciální rovnice Průvodce studiem Touto kapitolou se náplň základního kurzu bakalářské matematiky uzavírá. Je tomu tak mimo jiné proto, že jsou zde souhrnně využívány poznatky získané studiem předchozích
8.3). S ohledem na jednoduchost a názornost je výhodné seznámit se s touto Základní pojmy a vztahy. Definice
 9. Lineární diferenciální rovnice 2. řádu Cíle Diferenciální rovnice, v nichž hledaná funkce vystupuje ve druhé či vyšší derivaci, nazýváme diferenciálními rovnicemi druhého a vyššího řádu. Analogicky
9. Lineární diferenciální rovnice 2. řádu Cíle Diferenciální rovnice, v nichž hledaná funkce vystupuje ve druhé či vyšší derivaci, nazýváme diferenciálními rovnicemi druhého a vyššího řádu. Analogicky
SVOČ FST Bc. Václav Sláma, Zahradní 861, Strakonice Česká republika
 VÝPOČET PROUDĚNÍ V NADBANDÁŽOVÉ UCPÁVCE PRVNÍHO STUPNĚ OBĚŽNÉHO KOLA BUBNOVÉHO ROTORU TURBÍNY SVOČ FST 2011 Bc. Václav Sláma, Zahradní 861, 386 01 Strakonice Česká republika Bc Jan Čulík, Politických vězňů
VÝPOČET PROUDĚNÍ V NADBANDÁŽOVÉ UCPÁVCE PRVNÍHO STUPNĚ OBĚŽNÉHO KOLA BUBNOVÉHO ROTORU TURBÍNY SVOČ FST 2011 Bc. Václav Sláma, Zahradní 861, 386 01 Strakonice Česká republika Bc Jan Čulík, Politických vězňů
Křivky a plochy technické praxe
 Kapitola 7 Křivky a plochy technické praxe V technické praxi se setkáváme s tím, že potřebujeme křivky a plochy, které se dají libovolně upravovat a zároveň je jejich matematické vyjádření jednoduché.
Kapitola 7 Křivky a plochy technické praxe V technické praxi se setkáváme s tím, že potřebujeme křivky a plochy, které se dají libovolně upravovat a zároveň je jejich matematické vyjádření jednoduché.
Matematika (CŽV Kadaň) aneb Úvod do lineární algebry Matice a soustavy rovnic
 Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
Vlastnosti pravděpodobnosti, geometrická pravděpodobnost
 Vlastnosti pravděpodobnosti, geometrická pravděpodobnost 1. Přátelé Igor a Dano si domluví schůzku mezi 9.00 a 10.00. Jejich příchody na dané místo jsou náhodné v rámci smluveného časového intervalu. Každý
Vlastnosti pravděpodobnosti, geometrická pravděpodobnost 1. Přátelé Igor a Dano si domluví schůzku mezi 9.00 a 10.00. Jejich příchody na dané místo jsou náhodné v rámci smluveného časového intervalu. Každý
VE 2D A 3D. Radek Výrut. Abstrakt Tento článek obsahuje postupy pro výpočet Minkowského sumy dvou množin v rovině a pro výpočet Minkowského sumy
 25. KONFERENCE O GEOMETRII A POČÍTAČOVÉ GRAFICE Radek Výrut VÝPOČET MINKOWSKÉHO SUMY VE 2D A 3D Abstrakt Tento článek obsahuje postupy pro výpočet Minkowského sumy dvou množin v rovině a pro výpočet Minkowského
25. KONFERENCE O GEOMETRII A POČÍTAČOVÉ GRAFICE Radek Výrut VÝPOČET MINKOWSKÉHO SUMY VE 2D A 3D Abstrakt Tento článek obsahuje postupy pro výpočet Minkowského sumy dvou množin v rovině a pro výpočet Minkowského
Arnoldiho a Lanczosova metoda
 Arnoldiho a Lanczosova metoda 1 Částečný problém vlastních čísel Ne vždy je potřeba (a někdy to není ani technicky možné) nalézt celé spektrum dané matice (velké řídké matice). Úloze, ve které chceme aproximovat
Arnoldiho a Lanczosova metoda 1 Částečný problém vlastních čísel Ne vždy je potřeba (a někdy to není ani technicky možné) nalézt celé spektrum dané matice (velké řídké matice). Úloze, ve které chceme aproximovat
Numerická matematika 1
 Numerická matematika 1 Obsah 1 Řešení nelineárních rovnic 3 1.1 Metoda půlení intervalu....................... 3 1.2 Metoda jednoduché iterace..................... 4 1.3 Newtonova metoda..........................
Numerická matematika 1 Obsah 1 Řešení nelineárních rovnic 3 1.1 Metoda půlení intervalu....................... 3 1.2 Metoda jednoduché iterace..................... 4 1.3 Newtonova metoda..........................
PRAKTIKUM I. Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. Pracoval: Pavel Ševeček stud. skup.: F/F1X/11 dne:
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM I. Úloha č. VII Název: Studium kmitů vázaných oscilátorů Pracoval: Pavel Ševeček stud. skup.: F/F1X/11 dne: 27. 2. 2012 Odevzdal
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM I. Úloha č. VII Název: Studium kmitů vázaných oscilátorů Pracoval: Pavel Ševeček stud. skup.: F/F1X/11 dne: 27. 2. 2012 Odevzdal
Stefan Ratschan. Fakulta informačních technologíı. Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti 1 / 16
 Modelování fyzikálního okoĺı Stefan Ratschan Katedra číslicového návrhu Fakulta informačních technologíı České vysoké učení technické v Praze 25. října 2011 Evropský sociální fond Praha & EU: Investujeme
Modelování fyzikálního okoĺı Stefan Ratschan Katedra číslicového návrhu Fakulta informačních technologíı České vysoké učení technické v Praze 25. října 2011 Evropský sociální fond Praha & EU: Investujeme
Hledání extrémů funkcí
 Hledání extrémů funkcí Budeme se zabývat téměř výhradně hledáním minima. Přes nost nalezeného extrému Obecně není hledání extrému tak přesné jako řešení rovnic. Demonstrovat to můžeme na příkladu hledání
Hledání extrémů funkcí Budeme se zabývat téměř výhradně hledáním minima. Přes nost nalezeného extrému Obecně není hledání extrému tak přesné jako řešení rovnic. Demonstrovat to můžeme na příkladu hledání
Převedení okrajové úlohy na sled
 Převedení okrajové úlohy na sled úloh počátečních 1 Jiří Taufer Abstrakt Tento příspěvek je věnován řešení okrajových problémů pro soustavu okrajových obyčejných diferenciálních lineárních rovnic metodami,
Převedení okrajové úlohy na sled úloh počátečních 1 Jiří Taufer Abstrakt Tento příspěvek je věnován řešení okrajových problémů pro soustavu okrajových obyčejných diferenciálních lineárních rovnic metodami,
CFD simulace teplotně-hydraulické charakteristiky na modelu palivové tyči v oblasti distanční mřížky
 Konference ANSYS 011 CFD simulace teplotně-hydraulické charakteristiky na modelu palivové tyči v oblasti distanční mřížky D. Lávička Západočeská univerzita v Plzni, Katedra energetických strojů a zařízení,
Konference ANSYS 011 CFD simulace teplotně-hydraulické charakteristiky na modelu palivové tyči v oblasti distanční mřížky D. Lávička Západočeská univerzita v Plzni, Katedra energetických strojů a zařízení,
Katedra geotechniky a podzemního stavitelství
 Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Metoda oddělených elementů (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Metoda oddělených elementů (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
Fakt. Každou soustavu n lineárních ODR řádů n i lze eliminací převést ekvivalentně na jednu lineární ODR
 DEN: ODR teoreticky: soustavy rovnic Soustava lineárních ODR 1 řádu s konstantními koeficienty je soustava ve tvaru y 1 = a 11 y 1 + a 12 y 2 + + a 1n y n + b 1 (x) y 2 = a 21 y 1 + a 22 y 2 + + a 2n y
DEN: ODR teoreticky: soustavy rovnic Soustava lineárních ODR 1 řádu s konstantními koeficienty je soustava ve tvaru y 1 = a 11 y 1 + a 12 y 2 + + a 1n y n + b 1 (x) y 2 = a 21 y 1 + a 22 y 2 + + a 2n y
CFD simulace vícefázového proudění na nakloněné desce: porovnání smáčivosti různých kapalin. Martin Šourek
 CFD simulace vícefázového proudění na nakloněné desce: porovnání smáčivosti různých kapalin Martin Šourek VŠCHT Praha Ústav matematiky Praha 13. Prosince 2016 Úvod Model Výsledky Závěr Úvod 13.12.2016
CFD simulace vícefázového proudění na nakloněné desce: porovnání smáčivosti různých kapalin Martin Šourek VŠCHT Praha Ústav matematiky Praha 13. Prosince 2016 Úvod Model Výsledky Závěr Úvod 13.12.2016
