Středoškolská technika Algoritmus pro bezztrátovou kompresi dat
|
|
|
- Milada Procházková
- před 8 lety
- Počet zobrazení:
Transkript
1 Středoškolská technika 2016 Setkání a prezentace prací středoškolských studentů na ČVUT Algoritmus pro bezztrátovou kompresi dat Štěpán Pešout Gymnázium, Vlašim, Tylova 271 Tylova 271, Vlašim Agloritmus pro bezztrátovou kompresi dat 1/7
2 Úvod Co je to komprese a jak ji dělíme Když mluvíme v informatice o kompresi, jde o nějaké zmenšování dat. Rozlišujeme dva základní typy ztrátovou a bezztrátovou. První druh se používá typicky u mediálních souborů, tedy u hudby, obrázků nebo videa. Nevýhodou je to, že tento typ komprese nenávratně poškodí takový soubor; zůstane sice běžně čitelný, ale sníží se jeho kvalita. Naopak je velmi výhodné to, že se data rapidně zmenší (tedy lepší kompresní poměr). Snižovat velikost (a zároveň kvalitu) je možné v podstatě do nekonečna (obr. 1). Obr. 1: Ztráta kvality v závislosti na kompresním poměru Zdroj: Dalším druhem komprese je bezztrátová. Ta se používá, pokud je nutné zachování kvality nebo pokud by ztrátou byť jen jediné informace došlo k nečitenlosti dat toto se objevuje typicky u textových souborů. Nevýhodou je obecně horší kompresní poměr, což znamená, že se data příliš nezmenší. Bezztrátové algoritmy zpravidla využívají redundantní data; to jsou taková, která se opakují (jsou v podstatě navíc) a je proto možné je uvést jen jednou a podruhé jen odkaz na ně. Zde je příklad: Vstup: aaabbbbccc Výstup: 3a4b3c Důležitost komprimování Zmenšování dat je důležité, protože se objem dat na celém světě zdvojnásobí za přibližně každé dva roky. Komprese souborů proto velmi šetří prostor od kapesních zařízení po datová centra. Skoro každý máme smartphone představme si to tedy na tomto příkladu. Máme v paměti telefonu 64 GB místa a chceme prostor zcela zaplnit filmy ve FullHD rozlišení, které mají v průměru každý 2 GB. Pokud nepoužijeme kompresi, můžeme si stáhnout maximálně 32 filmů. Pokud s tím nejsme spokojeni, máme 2 možnosti: 1. Použít bezztrátovou kompresi a filmy zmenšit v průměru třeba na 70 % jejich původní velikosti tedy na 1,4 GB pro každý z nich. Takových filmů potom do paměti vměstnáme asi 45. Agloritmus pro bezztrátovou kompresi dat 2/7
3 2. Použít ztrátovou kompresi a spokojit se tak s horší kvalitou. Řekněme, že za kompromis mezi kvalitou a velikostí budeme považovat zmenšení na 40 % původní velikosti. Každý film bude potom zabírat 800 MB. Do paměti potom uložíme asi 80 takovýchto filmů. Popis samotného kompresního algoritmu Hlavní myšlenka Algoritmus převede vstupní data na číslo, se kterým se dále pracuje (vizte podrobný popis níže). Poté je výsledek vyjádřen v původním kódování. V podstatě neexistuje způsob, jak vyjádřit k+1 informací k informacemi, aby to fungovalo při jakémkoli k. Dokázal jsem, že to není možné v rámci jedné číselné soustavy. Z toho tedy vyplývá, že kompresní poměr bezztrátové komprese je vždy závislý na míře redundance vstupních dat. Vstupní data Vstupní a výstupní kódování je Base64. Toto kódování používá (jak už z názvu vyplývá) 64 různých znaků jedná se o malá a velká písmena anglické abecedy (52 znaků), o čísla (10 znaků), o lomítko (/) a znak plus (+). Funguje to tak, že z každých 3 libovolných znaků (1 znak = 256 možností) v kódování Base64 vzniknou 4 znaky. Pokud tedy počet znaků není dělitelný třemi, po převodu se na konec řetězce Base64 přidá odpovídající počet znaků =, tak, aby byl počet znaků dělitelný čtyřmi. Znak rovnítka nepoužívám v tabulce z toho důvodu, že v delším řetězci jsou 1 až 3 nezkomprimované znaky zanedbatelné a po dokončení komprese se přidají na konec řetězce. Důvodem, proč používám Base64 je mimo jiné i to, že 64 znaků se přesně vejde do tabulky 8 na 8 znaků. Poté se každý znak převede na dvouciferné číslo (viz tabulka). Pokud však použijeme hodnoty popisků v horní řadě a levém sloupci, dostaneme číslo které je de facto v osmičkové soustavě. To je důležitá informace (důvod popisuji dále v textu) a A b B c C d D 1 e E f F g G h H 2 i I j J k K l L 3 m M n N o O p P 4 q Q r R s S t T 5 u U v V w W x X 6 y Y z Z / + Agloritmus pro bezztrátovou kompresi dat 3/7
4 Je tedy zřejmé, že mohu reprezentovat libovolný znak z tabulky podle hodnoty v horním řádku a levém sloupci. Není přitom zapotřebí žádného oddělování mezi znaky vyjádřenými čísly, neboť zápis každého ze znaků je roven právě jednomu číslu, které je vždy dvouciferné. Výsledný číselný řetězec nazývejme x. Například: Informační znaky Vstup: Ahoj Výstup: Dále v textu IZ. Jedná se o n znaků v kódování Base64 (tedy 64 n kombinací), které se přidají na začátek řetězce a neprovádí se u nich komprese. Slouží k zapsání, zda a jakým způsobem proběhly obě metody komprese, které popisuji níže. Číslo n se mění pode toho, kolik místa pro zápis informací v IZ je potřeba. Velikost n se uvede před IZ jako dvouciferné číslo. Pokud je například n=5, před řetězec se zapíše jako 05. Obecně je ale snaha o to, aby mělo n co nejnižší možnou hodnotu. První metoda Číslo je převedeno do dvojkové soustavy. Ve výsledku jsou nahrazeny nuly a jedničky počty těchto znaků. Využívá se také toho, že číslo ve dvojkové soustavě začíná vždy jedničkou. Pokud bude tento počet roven 8, zapíše se jako nula. Od 10 výše se používají znaky malé anglické abecedy, tedy a až z. Ačkoli je následující situace velmi málo pravděpodobná, může se stát, že bude pohromadě více znaků jednoho druhu, než 35. V takovém případě se první metoda neprovede, což se zapíše do IZ. Vždy určíme číselnou soustavu o nejnižším možném základu a výsledek poté převedeme zpět do osmičkové soustavy. Uvedu příklad: Vstup (tj. x): (37017) 8 Převod do dvojkové soustavy: x 8 = ( ) 2 Nahrazení počty znaků: 554 Převod zpět do osmičkové soustavy: (554) 6 = (326) 8 Tato úprava řetězce se neprovede, pokud platí, že délka výstupu délka x. V opačném případě se do x přiřadí výstup této metody. Informace o tom, zda došlo k nahrazení a jestli se převádělo z jiné číselné soustavy se zapíše do IZ. Pokud se to vyplatí, následuje další provedení první metody a takto do té doby, dokud nepřestane platit zmíněná nerovnice délka výstupu délka x. Kolikrát se povedlo metodu provést, je zaneseno v IZ. Druhá metoda Zde se pracuje s číselnými soustavami o základu v intervalu <8; 36>, přiřemž základy leží v Z. Agloritmus pro bezztrátovou kompresi dat 4/7
5 Začněme se základem 8. Nejprve se určí, která dvojice čísel se nejčastěji v řetězci vyskytuje. Takováto dvojice je poté všude nahrazena číslem 8. Výsledek je převeden zpět do osmičkové soustavy a délka odečtena od délky původního řetězce. Výsledek tohoto rozdílu se zapíše společně s informací, že šlo o dvojice a osmičkovou číselnou soustavu. Obdobně se pokračuje i u trojic, čtveřic, apod. Záleží na délce vstupu, jak dlouhé budou skupiny číslic. Nejdelší skupina je vždy třísetina délky vstupu (výjimkou jsou dvojice, které se hledají vždy). Najde se nejčastěji se opakující skupina číslic a ta se nahradí číslem 8. Poté dojde opět k převodu do osmičkové soustavy a k výpočtu rozdílu délky původního řetězce a výstupu. Zapíše se rozdíl zároveň s informací, o jak velkou skupinu čísel šlo. Nyní máme v podstatě tabulku skupin čísel a rozdílů. Vybere se výstupní řetězec odpovídající nejvyššímu rozdílu. Informace o tom se zapíše. Nyní vysvětím, jak funguje nahrazování v rámci soustav o vyšším základu. Funguje to v podstatě stejně jako v rámci devítkové soustavy, jen se hledají větší počty opakujících se skupin čísel, které se nahrazují znaky z příslušné soustavy. V číselné soustavě o základu r bude tedy algoritmus hledat a nahrazovat r 8 nejčastěji se opakujících skupin pomocí znaků, které osmišková soustava neobsahuje. Poté je výstupní řetězec převeden zpět do osmičkové soustavy a obdobně vypočítán rozdíl. Toto se provede (jak jsem již zmínil) v rámci všech číselných soustav o celočíselných základech v intervalu <8; 36>. Informace o tom, u jak velké skupiny čísel v rámci jaké číselné soustavy se povedlo dosáhnout nejvyššího rozdílu, se zapíše. Opět se nám tedy vytvořila tabulka, ve které díky rozdílům vidíme, kde došlo k největšímu zkrácení. Informace o tom se zapíše do IZ. Podle informací, které máme, se může znovu vytvořit nejkratší výstupní řetězec (abychom nemuseli všechny výsledné řetězce ukládat). Tento pak nahradí původní vstupní řetězec, který jsme měli před druhou metodou za předpokladu, že je nejkratší řetězec kratší, než vstupní. Výsledek této operace se opět objeví v IZ. Uvedu příklad (pro jedenáctkovou soustavu při hledání dvojic). Volím záměrně takový vstup, aby bylo vidět zkrácení: Vstup: Vyhledání, které 3 se opakují nejčastěji: Jedná se o dvojice 52, 23 a 31 Nahrazení: a6824a49 Převod do osmičkové soustavy: ( ) 8 Rozdíl délek: 5 (došlo tedy ke zkrácení) Druhá metoda je zacyklená; provádí se do té doby, než neexistuje žádný výstupní řetězec, který by byl kratší, než vstupní. Kolikrát se metoda provedla a o jaké nejkratší řetězce šlo, se zapíše do IZ. Zkomprimování díky výpočtům z druhé metody Shrňme si, co máme v IZ: Agloritmus pro bezztrátovou kompresi dat 5/7
6 1. kolikrát se provedla první metoda spolu s informací, jak se v jednotlivých opakováních převádělo na úrovni číselných soustav; 2. jaká kombinace délek nahrazovaných skupin v rámci jakých číselných soustav vede vždy po převodech na osmičkovou soustavu k nejkratšímu výstupnímu řetězci a zda tento řetězec není delší, než ten vstupní. Pokud je délka výstupu z druhé metody větší nebo stejná než délka vstupu a zároveň se nepovedlo provést první metodu, můžeme prohlásit, že komprese se nevyplatí a algoritmus tedy spolu s touto informací vrátí původní řetězec. Jestliže předchozí podmínka neplatí, vezme se řetězec ve stavu před druhou metodou (přičemž nezáleží na tom, zda se provedla metoda první) a podle kombinace uvedené v IZ jej algoritmus zkrátí. Když se povede zkrátit řetězec pomocí první nebo druhé metody, celý algoritmus se zopakuje. Informace o tom, kolikrát se komprese opakovala, je zanesena v IZ. Převod zpět do Base64 Pokud se komprese vyplatila, máme její výstup jako číslo v osmičkové soustavě. Aby se uživateli vypsala hodnota v původním kódování, převedeme jej podle tabulky uvedené u vstupních dat. Například: Vstup: Výstup: Ahoj Může se stát, že číslo bude mít lichý počet míst. Poslední číslice se takovém případě odstraní, aby se mohla použít tabulka. Do IZ poté zapíšeme, zda došlo k odstranění a pokud ano, tak o jakou číslici šlo. Dekomprese V IZ máme napsány informace o průběhu komprese oběma metodami. Algoritmus tedy převede data z Base64 do číselného formátu pomocí tabulky uvedené na straně č. 3. Pomocí dat z IZ se provede dekomprese. Představme si, že jsme například komprimovali takto: 1. Převedení z Base64 na číslo podle tabulky 2. Provedla se první metoda, nepřevádělo se. 3. Provedla se druhá metoda, k největšímu zkrácení došlo v soustavě o základu 24 při nahrazování trojic. 4. Provedla se první metoda, převádělo se z trojkové soustavy. 5. Převedení na kódování Base64 podle tabulky Dekomprese je tedy v podstatě obráceně provdená komprese v závislosti na datech v IZ: 1. Převedení z Base64 na číslo podle tabulky 2. Číslo se převede z trojkové do osmičkové soustavy a zapíše se pomocí střídavého nahrazování počtů znaků nulami a jedničkami. Následuje převod z dvojkové zpět do osmičkové soustavy. Agloritmus pro bezztrátovou kompresi dat 6/7
7 3. Číslo se převede do soustavy o základu 24, kde nahradíme znaky nepatřící do osmičkové soustavy trojicemi znaků tak, jak je uvedeno v IZ. 4. Číslo se zapíše se pomocí střídavého nahrazování počtů znaků nulami a jedničkami. Následuje převod z dvojkové zpět do osmičkové soustavy. 5. Převedení na kódování Base64 podle tabulky Závěr Kompresní poměr Vzhledem k tomu, že lze jen těžko říci, jaká bude míra redundance vstupních dat, nemůžeme spočítat kompresní poměr, který bude platit vždycky. Co mohu tedy říci je to, že při kompresi textu dojde nejspíše k většímu zkrácení, než například u mediálních souborů. Pokud zvážíme, že text v anglickém jazyce používá pouze kolem 60 různých znaků, což je asi jedna čtvrtina z celkových 256, je jasné, že se znaky budou opakovat častěji i po převodu na Base64. Využití V tuto chvíli jde pouze o sepsanou koncepci, ale pokud bych toto později nakódoval a distribuoval, domnívám se, že by algoritmus mohl najít využití zejména v pamětech mobilních zažízení nebo na cloudu. Tam se uživatelé potýkají s malou kapacitou a za rozšíření prostoru si musí připlácet. Agloritmus pro bezztrátovou kompresi dat 7/7
Základní jednotky používané ve výpočetní technice
 Základní jednotky používané ve výpočetní technice Nejmenší jednotkou informace je bit [b], který může nabývat pouze dvou hodnot 1/0 (ano/ne, true/false). Tato jednotka není dostatečná pro praktické použití,
Základní jednotky používané ve výpočetní technice Nejmenší jednotkou informace je bit [b], který může nabývat pouze dvou hodnot 1/0 (ano/ne, true/false). Tato jednotka není dostatečná pro praktické použití,
Identifikátor materiálu: ICT-1-19
 Identifikátor materiálu: ICT-1-19 Předmět Informační a komunikační technologie Téma materiálu Komprimace, archivace dat Autor Ing. Bohuslav Nepovím Anotace Student si procvičí / osvojí komprimaci, archivaci
Identifikátor materiálu: ICT-1-19 Předmět Informační a komunikační technologie Téma materiálu Komprimace, archivace dat Autor Ing. Bohuslav Nepovím Anotace Student si procvičí / osvojí komprimaci, archivaci
Číselné soustavy a převody mezi nimi
 Číselné soustavy a převody mezi nimi Základní požadavek na počítač je schopnost zobrazovat a pamatovat si čísla a provádět operace s těmito čísly. Čísla mohou být zobrazena v různých číselných soustavách.
Číselné soustavy a převody mezi nimi Základní požadavek na počítač je schopnost zobrazovat a pamatovat si čísla a provádět operace s těmito čísly. Čísla mohou být zobrazena v různých číselných soustavách.
Textové, datumové a časové funkce
 Textové, datumové a časové funkce EU peníze středním školám Didaktický učební materiál Anotace Označení DUMU: VY_32_INOVACE_IT4.15 Předmět: IVT Tematická oblast: Microsoft Office 2007 Autor: Ing. Vladimír
Textové, datumové a časové funkce EU peníze středním školám Didaktický učební materiál Anotace Označení DUMU: VY_32_INOVACE_IT4.15 Předmět: IVT Tematická oblast: Microsoft Office 2007 Autor: Ing. Vladimír
Kódováni dat. Kódy používané pro strojové operace
 Kódováni dat Před zpracováním dat například v počítači je třeba znaky převést do tvaru, kterému počítač rozumí, tj. přiřadit jim určité kombinace bitů. Tomuto převodu se říká kódování. Kód je předpis pro
Kódováni dat Před zpracováním dat například v počítači je třeba znaky převést do tvaru, kterému počítač rozumí, tj. přiřadit jim určité kombinace bitů. Tomuto převodu se říká kódování. Kód je předpis pro
Jednoduché cykly 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. 45.
 Jednoduché cykly Tento oddíl obsahuje úlohy na první procvičení práce s cykly. Při řešení každé ze zde uvedených úloh stačí použít vedle podmíněných příkazů jen jediný cyklus. Nepotřebujeme používat ani
Jednoduché cykly Tento oddíl obsahuje úlohy na první procvičení práce s cykly. Při řešení každé ze zde uvedených úloh stačí použít vedle podmíněných příkazů jen jediný cyklus. Nepotřebujeme používat ani
Výroková logika II. Negace. Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0).
 Výroková logika II Negace Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0). Na konkrétních příkladech si ukážeme, jak se dají výroky negovat. Obecně se výrok dá negovat tak, že před
Výroková logika II Negace Již víme, že negace je změna pravdivostní hodnoty výroku (0 1; 1 0). Na konkrétních příkladech si ukážeme, jak se dají výroky negovat. Obecně se výrok dá negovat tak, že před
Digitalizace signálu (obraz, zvuk)
 Digitalizace signálu (obraz, zvuk) Základem pro digitalizaci obrazu je převod světla na elektrické veličiny. K převodu světla na elektrické veličiny slouží např. čip CCD. Zkratka CCD znamená Charged Coupled
Digitalizace signálu (obraz, zvuk) Základem pro digitalizaci obrazu je převod světla na elektrické veličiny. K převodu světla na elektrické veličiny slouží např. čip CCD. Zkratka CCD znamená Charged Coupled
Úvod do řešení lineárních rovnic a jejich soustav
 Úvod do řešení lineárních rovnic a jejich soustav Rovnice je zápis rovnosti dvou výrazů, ve kterém máme najít neznámé číslo (neznámou). Po jeho dosazení do rovnice musí platit rovnost. Existuje-li takové
Úvod do řešení lineárních rovnic a jejich soustav Rovnice je zápis rovnosti dvou výrazů, ve kterém máme najít neznámé číslo (neznámou). Po jeho dosazení do rovnice musí platit rovnost. Existuje-li takové
4a) Racionální čísla a početní operace s nimi
 Racionální čísla a početní operace s nimi Množinu racionálních čísel získáme z množiny čísel celých, jejím rozšířením o čísla desetinná s ukončeným des. rozvojem nebo periodická a zlomky, které lze na
Racionální čísla a početní operace s nimi Množinu racionálních čísel získáme z množiny čísel celých, jejím rozšířením o čísla desetinná s ukončeným des. rozvojem nebo periodická a zlomky, které lze na
Číselné soustavy. Ve světě počítačů se využívají tři základní soustavy:
 Číselné soustavy Ve světě počítačů se využívají tři základní soustavy: dekadická binární hexadecimální patří mezi soustavy poziční, tj. desítková hodnota každé číslice (znaku) závisí na její pozici vzhledem
Číselné soustavy Ve světě počítačů se využívají tři základní soustavy: dekadická binární hexadecimální patří mezi soustavy poziční, tj. desítková hodnota každé číslice (znaku) závisí na její pozici vzhledem
Cykly a pole 103. 104. 105. 106. 107. 108. 109. 110. 111. 112. 113. 114. 115. 116.
 Cykly a pole Tato část sbírky je tvořena dalšími úlohami na práci s cykly. Na rozdíl od předchozího oddílu se zde již v řešeních úloh objevuje více cyklů, ať už prováděných po sobě nebo vnořených do sebe.
Cykly a pole Tato část sbírky je tvořena dalšími úlohami na práci s cykly. Na rozdíl od předchozího oddílu se zde již v řešeních úloh objevuje více cyklů, ať už prováděných po sobě nebo vnořených do sebe.
1. Základní pojmy a číselné soustavy
 1. Základní pojmy a číselné soustavy 1.1. Základní pojmy Hardware (technické vybavení počítače) Souhrnný název pro veškerá fyzická zařízení, kterými je počítač vybaven. Software (programové vybavení počítače)
1. Základní pojmy a číselné soustavy 1.1. Základní pojmy Hardware (technické vybavení počítače) Souhrnný název pro veškerá fyzická zařízení, kterými je počítač vybaven. Software (programové vybavení počítače)
Převody mezi číselnými soustavami
 Převody mezi číselnými soustavami 1. Převod čísla do dekadické soustavy,kde Z je celé číslo, pro které platí a Řešením je převod pomocí Hornerova schématu Příklad: Převeďte číslo F 3 = 2101 do soustavy
Převody mezi číselnými soustavami 1. Převod čísla do dekadické soustavy,kde Z je celé číslo, pro které platí a Řešením je převod pomocí Hornerova schématu Příklad: Převeďte číslo F 3 = 2101 do soustavy
Výhody a nevýhody jednotlivých reprezentací jsou shrnuty na konci kapitoly.
 Kapitola Reprezentace grafu V kapitole?? jsme se dozvěděli, co to jsou grafy a k čemu jsou dobré. rzo budeme chtít napsat nějaký program, který s grafy pracuje. le jak si takový graf uložit do počítače?
Kapitola Reprezentace grafu V kapitole?? jsme se dozvěděli, co to jsou grafy a k čemu jsou dobré. rzo budeme chtít napsat nějaký program, který s grafy pracuje. le jak si takový graf uložit do počítače?
IB112 Základy matematiky
 IB112 Základy matematiky Řešení soustavy lineárních rovnic, matice, vektory Jan Strejček IB112 Základy matematiky: Řešení soustavy lineárních rovnic, matice, vektory 2/53 Obsah Soustava lineárních rovnic
IB112 Základy matematiky Řešení soustavy lineárních rovnic, matice, vektory Jan Strejček IB112 Základy matematiky: Řešení soustavy lineárních rovnic, matice, vektory 2/53 Obsah Soustava lineárních rovnic
Největší společný dělitel
 1..1 Největší společný dělitel Předpoklady: 01016 Číslo Číslo nsn Platí pravidlo "nsn získáme jako součin obou čísel"? = 1 = Násobící pravidlo platí. 1 = Násobící pravidlo platí. 1 = Násobící pravidlo
1..1 Největší společný dělitel Předpoklady: 01016 Číslo Číslo nsn Platí pravidlo "nsn získáme jako součin obou čísel"? = 1 = Násobící pravidlo platí. 1 = Násobící pravidlo platí. 1 = Násobící pravidlo
1.5.2 Číselné soustavy II
 .. Číselné soustavy II Předpoklady: Př. : Převeď do desítkové soustavy čísla. a) ( ) b) ( ) 4 c) ( ) 6 = + + + = 7 + 9 + = a) = 4 + 4 + 4 = 6 + 4 + = 9 b) 4 = 6 + 6 + 6 = 6 + 6 + = 6 + + = 69. c) 6 Pedagogická
.. Číselné soustavy II Předpoklady: Př. : Převeď do desítkové soustavy čísla. a) ( ) b) ( ) 4 c) ( ) 6 = + + + = 7 + 9 + = a) = 4 + 4 + 4 = 6 + 4 + = 9 b) 4 = 6 + 6 + 6 = 6 + 6 + = 6 + + = 69. c) 6 Pedagogická
( ) Jako základ mocnin nemusíme používat jen 10. Pokud není jasné, že číslo je uvedeno v desítkové soustavě, píšeme jej takto: ( 12054 ) 10
 .. Číselné soustavy I Předpoklady: základní početní operace Pedagogická poznámka: Tato a následující hodina není součástí klasické gymnaziální sady. Upřímně řečeno nevím proč. Jednak se všichni studenti
.. Číselné soustavy I Předpoklady: základní početní operace Pedagogická poznámka: Tato a následující hodina není součástí klasické gymnaziální sady. Upřímně řečeno nevím proč. Jednak se všichni studenti
ZLOMKY A RACIONÁLNÍ ČÍSLA. Pojem zlomku. Zlomek zápis části celku. a b. a je část, b je celek, zlomková čára
 9... ZLOMKY A RACIONÁLNÍ ČÍSLA Pojem zlomku Zlomek zápis části celku a b a je část, b je celek, zlomková čára Každé číslo zapsané zlomkem lze vyjádřit jako číslo desetinné 7 Zlomková čára je dělící čára
9... ZLOMKY A RACIONÁLNÍ ČÍSLA Pojem zlomku Zlomek zápis části celku a b a je část, b je celek, zlomková čára Každé číslo zapsané zlomkem lze vyjádřit jako číslo desetinné 7 Zlomková čára je dělící čára
Identifikátor materiálu: ICT-1-02
 Identifikátor materiálu: ICT-1-02 Předmět Informační a komunikační technologie Téma materiálu Data a informace Autor Ing. Bohuslav Nepovím Anotace Student si procvičí / osvojí základní pojmy jako data,
Identifikátor materiálu: ICT-1-02 Předmět Informační a komunikační technologie Téma materiálu Data a informace Autor Ing. Bohuslav Nepovím Anotace Student si procvičí / osvojí základní pojmy jako data,
ČÍSELNÉ SOUSTAVY PŘEVODY
 ČÍSELNÉ SOUSTAVY V každodenním životě je soustava desítková (decimální, dekadická) o základu Z=10. Tato soustava používá číslice 0, 1, 2, 3, 4, 5, 6, 7, 8 a 9, není však vhodná pro počítače nebo číslicové
ČÍSELNÉ SOUSTAVY V každodenním životě je soustava desítková (decimální, dekadická) o základu Z=10. Tato soustava používá číslice 0, 1, 2, 3, 4, 5, 6, 7, 8 a 9, není však vhodná pro počítače nebo číslicové
Fz =a z + a z +...+a z +a z =
 Polyadické číselné soustavy - převody M-místná skupina prvků se z-stavovou abecedou umožňuje zobrazit z m čísel. Zjistíme, že stačí vhodně zvolit číslo m, abychom mohli zobrazit libovolné číslo menší než
Polyadické číselné soustavy - převody M-místná skupina prvků se z-stavovou abecedou umožňuje zobrazit z m čísel. Zjistíme, že stačí vhodně zvolit číslo m, abychom mohli zobrazit libovolné číslo menší než
Nerovnice a nerovnice v součinovém nebo v podílovém tvaru
 Variace 1 Nerovnice a nerovnice v součinovém nebo v podílovém tvaru Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz
Variace 1 Nerovnice a nerovnice v součinovém nebo v podílovém tvaru Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz
Nejvyšší řád čísla bit č. 7 bit č. 6 bit č.5 bit č. 4 bit č. 3 bit č. 2 bit č. 1 bit č. 0
 Číselné soustavy Cílem této kapitoly je sezn{mit se se z{kladními jednotkami používanými ve výpočetní technice. Poznat číselné soustavy, kódy a naučit se převody mezi číselnými soustavami. Klíčové pojmy:
Číselné soustavy Cílem této kapitoly je sezn{mit se se z{kladními jednotkami používanými ve výpočetní technice. Poznat číselné soustavy, kódy a naučit se převody mezi číselnými soustavami. Klíčové pojmy:
ŘEŠENÍ KVADRATICKÝCH A ZLOMKOVÝCH NEROVNIC V ŠESTI BODECH
 (Tento text je součástí výkladu k definičním oborům, tam najdete další příklady a pokud chcete část tohoto textu někde použít, můžete čerpat ze stažené kompletní verze definičních oborů ve formátu.doc.)
(Tento text je součástí výkladu k definičním oborům, tam najdete další příklady a pokud chcete část tohoto textu někde použít, můžete čerpat ze stažené kompletní verze definičních oborů ve formátu.doc.)
Výběr báze. u n. a 1 u 1
 Výběr báze Mějme vektorový prostor zadán množinou generátorů. To jest V = M, kde M = {u,..., u n }. Pokud je naším úkolem najít nějakou bázi V, nejpřímočařejším postupem je napsat si vektory jako řádky
Výběr báze Mějme vektorový prostor zadán množinou generátorů. To jest V = M, kde M = {u,..., u n }. Pokud je naším úkolem najít nějakou bázi V, nejpřímočařejším postupem je napsat si vektory jako řádky
3. Reálná čísla. většinou racionálních čísel. V analytických úvahách, které praktickým výpočtům
 RACIONÁLNÍ A IRACIONÁLNÍ ČÍSLA Význačnými množinami jsou číselné množiny K nejvýznamnějším patří množina reálných čísel, obsahující jako podmnožiny množiny přirozených, celých, racionálních a iracionálních
RACIONÁLNÍ A IRACIONÁLNÍ ČÍSLA Význačnými množinami jsou číselné množiny K nejvýznamnějším patří množina reálných čísel, obsahující jako podmnožiny množiny přirozených, celých, racionálních a iracionálních
Matematika (CŽV Kadaň) aneb Úvod do lineární algebry Matice a soustavy rovnic
 Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
x 0; x = x (s kladným číslem nic nedělá)
 .. Funkce absolutní hodnota Předpoklady: 08, 07 x - zničí znaménko čísla, všechna čísla změní na nezáporná Jak vyjádřit matematicky? Pomocí číselné osy: x je vzdálenost obrazu čísla na číselné ose od počátku.
.. Funkce absolutní hodnota Předpoklady: 08, 07 x - zničí znaménko čísla, všechna čísla změní na nezáporná Jak vyjádřit matematicky? Pomocí číselné osy: x je vzdálenost obrazu čísla na číselné ose od počátku.
Čtvrtek 8. prosince. Pascal - opakování základů. Struktura programu:
 Čtvrtek 8 prosince Pascal - opakování základů Struktura programu: 1 hlavička obsahuje název programu, použité programové jednotky (knihovny), definice konstant, deklarace proměnných, všechny použité procedury
Čtvrtek 8 prosince Pascal - opakování základů Struktura programu: 1 hlavička obsahuje název programu, použité programové jednotky (knihovny), definice konstant, deklarace proměnných, všechny použité procedury
Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto
 Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto Registrační číslo projektu Šablona Autor Název materiálu CZ.1.07/1.5.00/34.0951 III/2 INOVACE A ZKVALITNĚNÍ VÝUKY PROSTŘEDNICTVÍM ICT Mgr. Jana
Gymnázium Vysoké Mýto nám. Vaňorného 163, 566 01 Vysoké Mýto Registrační číslo projektu Šablona Autor Název materiálu CZ.1.07/1.5.00/34.0951 III/2 INOVACE A ZKVALITNĚNÍ VÝUKY PROSTŘEDNICTVÍM ICT Mgr. Jana
Soustavy více rovnic o více neznámých III
 2..15 Soustavy více rovnic o více neznámých III Předpoklady: 214 Největší problém při řešení soustav - výroba trojúhelníkového tvaru (tedy vyrábění nul). Postup v dosavadních příkladech byl rychlý - využíval
2..15 Soustavy více rovnic o více neznámých III Předpoklady: 214 Největší problém při řešení soustav - výroba trojúhelníkového tvaru (tedy vyrábění nul). Postup v dosavadních příkladech byl rychlý - využíval
M - Příprava na 1. zápočtový test - třída 3SA
 M - Příprava na 1. zápočtový test - třída 3SA Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento
M - Příprava na 1. zápočtový test - třída 3SA Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento
STRUKTURA RASTROVÝCH DAT
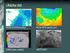 STRUKTURA RASTROVÝCH DAT dva typy rastrové vrstvy v GIS 1) Digitální obraz TV, počítač, mobil - obrazovka obraz z bodů mapa - mřížka s barevnými plochami 2) Rastrová data data pro analýzu a) binární -
STRUKTURA RASTROVÝCH DAT dva typy rastrové vrstvy v GIS 1) Digitální obraz TV, počítač, mobil - obrazovka obraz z bodů mapa - mřížka s barevnými plochami 2) Rastrová data data pro analýzu a) binární -
II. Úlohy na vložené cykly a podprogramy
 II. Úlohy na vložené cykly a podprogramy Společné zadání pro příklady 1. - 10. začíná jednou ze dvou možností popisu vstupních dat. Je dána posloupnost (neboli řada) N reálných (resp. celočíselných) hodnot.
II. Úlohy na vložené cykly a podprogramy Společné zadání pro příklady 1. - 10. začíná jednou ze dvou možností popisu vstupních dat. Je dána posloupnost (neboli řada) N reálných (resp. celočíselných) hodnot.
Kompresní algoritmy grafiky. Jan Janoušek F11125
 Kompresní algoritmy grafiky Jan Janoušek F11125 K čemu je komprese dobrá? Pokud je třeba skladovat datově náročné soubory. Např. pro záznam obrazu, hudby a hlavně videa je třeba skladovat překvapivě mnoho
Kompresní algoritmy grafiky Jan Janoušek F11125 K čemu je komprese dobrá? Pokud je třeba skladovat datově náročné soubory. Např. pro záznam obrazu, hudby a hlavně videa je třeba skladovat překvapivě mnoho
Číslo materiálu. Datum tvorby Srpen 2012
 Číslo projektu Číslo materiálu Název školy Autor Tematická oblast Ročník CZ.1.07/1.5.00/34.0581 VY_32_INOVACE_CTE_2.MA_03_Převod čísel mezi jednotlivými číselnými soustavami Střední odborná škola a Střední
Číslo projektu Číslo materiálu Název školy Autor Tematická oblast Ročník CZ.1.07/1.5.00/34.0581 VY_32_INOVACE_CTE_2.MA_03_Převod čísel mezi jednotlivými číselnými soustavami Střední odborná škola a Střední
Soustavy dvou lineárních rovnic o dvou neznámých I
 .3.10 Soustavy dvou lineárních rovnic o dvou neznámých I Předpoklady: 308 Pedagogická poznámka: Hodina má trochu netradiční charakter. U každé metody si studenti opíší postup a pak ho zkusí uplatnit na
.3.10 Soustavy dvou lineárních rovnic o dvou neznámých I Předpoklady: 308 Pedagogická poznámka: Hodina má trochu netradiční charakter. U každé metody si studenti opíší postup a pak ho zkusí uplatnit na
1 Linearní prostory nad komplexními čísly
 1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
Funkce a lineární funkce pro studijní obory
 Variace 1 Funkce a lineární funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce
Variace 1 Funkce a lineární funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce
Data v počítači. Informační data. Logické hodnoty. Znakové hodnoty
 Data v počítači Informační data (elementární datové typy) Logické hodnoty Znaky Čísla v pevné řádové čárce (celá čísla) v pohyblivé (plovoucí) řád. čárce (reálná čísla) Povelová data (instrukce programu)
Data v počítači Informační data (elementární datové typy) Logické hodnoty Znaky Čísla v pevné řádové čárce (celá čísla) v pohyblivé (plovoucí) řád. čárce (reálná čísla) Povelová data (instrukce programu)
M - Příprava na pololetní písemku č. 1
 M - Příprava na pololetní písemku č. 1 Určeno pro třídy 3SA, 3SB. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací o programu naleznete
M - Příprava na pololetní písemku č. 1 Určeno pro třídy 3SA, 3SB. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase. Více informací o programu naleznete
aneb jak se to tam všechno vejde?
 768 576 KOMPRIMACE aneb jak se to tam všechno vejde? Položme si hned na začátku zdánlivě nepodstatnou otázku: Kolik místa zabere dvouhodinový film na CD nebo DVD? Uvažujme následující příklad: rozlišení
768 576 KOMPRIMACE aneb jak se to tam všechno vejde? Položme si hned na začátku zdánlivě nepodstatnou otázku: Kolik místa zabere dvouhodinový film na CD nebo DVD? Uvažujme následující příklad: rozlišení
Algoritmizace a programování
 Algoritmizace a programování Výrazy Operátory Výrazy Verze pro akademický rok 2012/2013 1 Operace, operátory Unární jeden operand, operátor se zapisuje ve většině případů před operand, v některých případech
Algoritmizace a programování Výrazy Operátory Výrazy Verze pro akademický rok 2012/2013 1 Operace, operátory Unární jeden operand, operátor se zapisuje ve většině případů před operand, v některých případech
1.5.1 Číselné soustavy
 .. Číselné soustavy Předpoklady: základní početní operace Pedagogická poznámka: Tato hodina není součástí klasické gymnaziální sady. Upřímně řečeno nevím proč. Jednak se všichni studenti určitě setkávají
.. Číselné soustavy Předpoklady: základní početní operace Pedagogická poznámka: Tato hodina není součástí klasické gymnaziální sady. Upřímně řečeno nevím proč. Jednak se všichni studenti určitě setkávají
Soustavy více rovnic o více neznámých II
 2..14 Soustavy více rovnic o více neznámých II Předpoklady: 21 Největší problém při řešení soustav = výroba trojúhelníkového tvaru (tedy vyrábění nul). Postup v dosavadních příkladech byl rychlý - využíval
2..14 Soustavy více rovnic o více neznámých II Předpoklady: 21 Největší problém při řešení soustav = výroba trojúhelníkového tvaru (tedy vyrábění nul). Postup v dosavadních příkladech byl rychlý - využíval
Algoritmus pro hledání nejkratší cesty orientovaným grafem
 1.1 Úvod Algoritmus pro hledání nejkratší cesty orientovaným grafem Naprogramoval jsem v Matlabu funkci, která dokáže určit nejkratší cestu v orientovaném grafu mezi libovolnými dvěma vrcholy. Nastudoval
1.1 Úvod Algoritmus pro hledání nejkratší cesty orientovaným grafem Naprogramoval jsem v Matlabu funkci, která dokáže určit nejkratší cestu v orientovaném grafu mezi libovolnými dvěma vrcholy. Nastudoval
9.1.1 Základní kombinatorická pravidla I
 9.. Základní kombinatorická pravidla I Předpoklady: Př. : Ve třídě je 7 děvčat a 3 kluků. Kolik máme možností jak vybrat dvojici klukholka, která bude mít projev na maturitním plese? Vybíráme ze 7 holek
9.. Základní kombinatorická pravidla I Předpoklady: Př. : Ve třídě je 7 děvčat a 3 kluků. Kolik máme možností jak vybrat dvojici klukholka, která bude mít projev na maturitním plese? Vybíráme ze 7 holek
1. lekce. do souboru main.c uložíme následující kód a pomocí F9 ho zkompilujeme a spustíme:
 1. lekce 1. Minimální program do souboru main.c uložíme následující kód a pomocí F9 ho zkompilujeme a spustíme: #include #include int main() { printf("hello world!\n"); return 0; 2.
1. lekce 1. Minimální program do souboru main.c uložíme následující kód a pomocí F9 ho zkompilujeme a spustíme: #include #include int main() { printf("hello world!\n"); return 0; 2.
Čísla v plovoucířádovéčárce. INP 2008 FIT VUT v Brně
 Čísla v plovoucířádovéčárce INP 2008 FIT VUT v Brně Čísla v pevné vs plovoucí řádové čárce Pevnářádováčárka FX bez desetinné části (8 bitů) Přímý kód: 0 až 255 Doplňkový kód: -128 až 127 aj. s desetinnou
Čísla v plovoucířádovéčárce INP 2008 FIT VUT v Brně Čísla v pevné vs plovoucí řádové čárce Pevnářádováčárka FX bez desetinné části (8 bitů) Přímý kód: 0 až 255 Doplňkový kód: -128 až 127 aj. s desetinnou
1.2.3 Racionální čísla I
 .2. Racionální čísla I Předpoklady: 002 Racionální jsou všechna čísla, která můžeme zapsat ve tvaru zlomku p q, kde p Z, q N. Například 2 ; ; 2 ; 6 ; umožňují počítat s částmi celků (třeba polovina dortu),
.2. Racionální čísla I Předpoklady: 002 Racionální jsou všechna čísla, která můžeme zapsat ve tvaru zlomku p q, kde p Z, q N. Například 2 ; ; 2 ; 6 ; umožňují počítat s částmi celků (třeba polovina dortu),
( ) ( ) 2.8.2 Lineární rovnice s parametrem II. Předpoklady: 2801
 .8. Lineární rovnice s parametrem II Předpoklady: 80 Pedagogická poznámka: Zvládnutí zápisu a obecného postupu (dělení podle hodnot parametru) při řešení parametrických rovnic v této hodině je zásadní
.8. Lineární rovnice s parametrem II Předpoklady: 80 Pedagogická poznámka: Zvládnutí zápisu a obecného postupu (dělení podle hodnot parametru) při řešení parametrických rovnic v této hodině je zásadní
Hledání kořenů rovnic jedné reálné proměnné metoda půlení intervalů Michal Čihák 23. října 2012
 Hledání kořenů rovnic jedné reálné proměnné metoda půlení intervalů Michal Čihák 23. října 2012 Problém hledání kořenů rovnice f(x) = 0 jeden ze základních problémů numerické matematiky zároveň i jeden
Hledání kořenů rovnic jedné reálné proměnné metoda půlení intervalů Michal Čihák 23. října 2012 Problém hledání kořenů rovnice f(x) = 0 jeden ze základních problémů numerické matematiky zároveň i jeden
Inovace výuky prostřednictvím ICT v SPŠ Zlín, CZ.1.07/1.5.00/34.0333 Vzdělávání v informačních a komunikačních technologií
 VY_32_INOVACE_31_18 Škola Název projektu, reg. č. Vzdělávací oblast Vzdělávací obor Tematický okruh Téma Tematická oblast Název Autor Vytvořeno, pro obor, ročník Anotace Přínos/cílové kompetence Střední
VY_32_INOVACE_31_18 Škola Název projektu, reg. č. Vzdělávací oblast Vzdělávací obor Tematický okruh Téma Tematická oblast Název Autor Vytvořeno, pro obor, ročník Anotace Přínos/cílové kompetence Střední
1.2.3 Racionální čísla I
 .2. Racionální čísla I Předpoklady: 002 Pedagogická poznámka: Hodina je trochu netypická, na jejím začátku provedu výklad (spíše opakování), který nechám na tabuli a potom až do konce řeší žáci zbytek
.2. Racionální čísla I Předpoklady: 002 Pedagogická poznámka: Hodina je trochu netypická, na jejím začátku provedu výklad (spíše opakování), který nechám na tabuli a potom až do konce řeší žáci zbytek
63. ročník Matematické olympiády 2013/2014
 63. ročník Matematické olympiády 2013/2014 Úlohy ústředního kola kategorie P 2. soutěžní den Na řešení úloh máte 4,5 hodiny čistého času. Při soutěži je zakázáno používat jakékoliv pomůcky kromě psacích
63. ročník Matematické olympiády 2013/2014 Úlohy ústředního kola kategorie P 2. soutěžní den Na řešení úloh máte 4,5 hodiny čistého času. Při soutěži je zakázáno používat jakékoliv pomůcky kromě psacích
7. přednáška Systémová analýza a modelování. Přiřazovací problém
 Přiřazovací problém Přiřazovací problémy jsou podtřídou logistických úloh, kde lze obecně říci, že m dodavatelů zásobuje m spotřebitelů. Dalším specifikem je, že kapacity dodavatelů (ai) i požadavky spotřebitelů
Přiřazovací problém Přiřazovací problémy jsou podtřídou logistických úloh, kde lze obecně říci, že m dodavatelů zásobuje m spotřebitelů. Dalším specifikem je, že kapacity dodavatelů (ai) i požadavky spotřebitelů
Závěrečná zkouška z informatiky 2011
 Závěrečná zkouška z informatiky 2011 1) Číslo A je v dvojkové soustavě a má hodnotu 1101011. Číslo B je v šestnáctkové soustavě a má hodnotu FF3. Vypočítejte : A * B a výsledek napište v desítkové soustavě.
Závěrečná zkouška z informatiky 2011 1) Číslo A je v dvojkové soustavě a má hodnotu 1101011. Číslo B je v šestnáctkové soustavě a má hodnotu FF3. Vypočítejte : A * B a výsledek napište v desítkové soustavě.
Vektory a matice. Obsah. Aplikovaná matematika I. Carl Friedrich Gauss. Základní pojmy a operace
 Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
Funkce. Definiční obor a obor hodnot
 Funkce Definiční obor a obor hodnot Opakování definice funkce Funkce je předpis, který každému číslu z definičního oboru, který je podmnožinou množiny všech reálných čísel R, přiřazuje právě jedno reálné
Funkce Definiční obor a obor hodnot Opakování definice funkce Funkce je předpis, který každému číslu z definičního oboru, který je podmnožinou množiny všech reálných čísel R, přiřazuje právě jedno reálné
1. lekce. do souboru main.c uložíme následující kód a pomocí F9 ho zkompilujeme a spustíme:
 1. lekce 1. Minimální program do souboru main.c uložíme následující kód a pomocí F9 ho zkompilujeme a spustíme: #include #include int main() { printf("hello world!\n"); return 0; 2.
1. lekce 1. Minimální program do souboru main.c uložíme následující kód a pomocí F9 ho zkompilujeme a spustíme: #include #include int main() { printf("hello world!\n"); return 0; 2.
Videosekvence. vznik, úpravy, konverze formátů, zachytávání videa...
 Videosekvence vznik, úpravy, konverze formátů, zachytávání videa... VIDEOSEKVENCE (VIDEO) Sekvence obrázků rychle po sobě jdoucích (např. 60 snímků za sekundu) tak, že vznikne pro diváka iluze pohybu.
Videosekvence vznik, úpravy, konverze formátů, zachytávání videa... VIDEOSEKVENCE (VIDEO) Sekvence obrázků rychle po sobě jdoucích (např. 60 snímků za sekundu) tak, že vznikne pro diváka iluze pohybu.
3 Jednoduché datové typy 2 3.1 Interpretace čísel v paměti počítače... 3. 4 Problémy s matematickými operacemi 5
 Obsah Obsah 1 Číselné soustavy 1 2 Paměť počítače 1 2.1 Měření objemu paměti počítače................... 1 3 Jednoduché datové typy 2 3.1 Interpretace čísel v paměti počítače................. 3 4 Problémy
Obsah Obsah 1 Číselné soustavy 1 2 Paměť počítače 1 2.1 Měření objemu paměti počítače................... 1 3 Jednoduché datové typy 2 3.1 Interpretace čísel v paměti počítače................. 3 4 Problémy
Dělitelnost čísel, nejmenší společný násobek, největší společný dělitel
 Variace 1 Dělitelnost čísel, nejmenší společný násobek, největší společný dělitel Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu
Variace 1 Dělitelnost čísel, nejmenší společný násobek, největší společný dělitel Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu
Kolekce ArrayList. Deklarace proměnných. Import. Vytvoření prázdné kolekce. napsal Pajclín
 Kolekce ArrayList napsal Pajclín Tento článek jsem se rozhodl věnovat kolekci ArrayList, protože je to jedna z nejpoužívanějších. Tento článek není kompletním popisem třídy ArrayList, ale budu se snažit
Kolekce ArrayList napsal Pajclín Tento článek jsem se rozhodl věnovat kolekci ArrayList, protože je to jedna z nejpoužívanějších. Tento článek není kompletním popisem třídy ArrayList, ale budu se snažit
DATABÁZE MS ACCESS 2010
 DATABÁZE MS ACCESS 2010 KAPITOLA 5 PRAKTICKÁ ČÁST TABULKY POPIS PROSTŘEDÍ Spuštění MS Access nadefinovat název databáze a cestu k uložení databáze POPIS PROSTŘEDÍ Nahoře záložky: Soubor (k uložení souboru,
DATABÁZE MS ACCESS 2010 KAPITOLA 5 PRAKTICKÁ ČÁST TABULKY POPIS PROSTŘEDÍ Spuštění MS Access nadefinovat název databáze a cestu k uložení databáze POPIS PROSTŘEDÍ Nahoře záložky: Soubor (k uložení souboru,
Číselné soustavy v mikroprocesorové technice Mikroprocesorová technika a embedded systémy
 Ústav radioelektroniky Vysoké učení technické v Brně Číselné soustavy v mikroprocesorové technice Mikroprocesorová technika a embedded systémy Přednáška 8 doc. Ing. Tomáš Frýza, Ph.D. listopad 2012 Obsah
Ústav radioelektroniky Vysoké učení technické v Brně Číselné soustavy v mikroprocesorové technice Mikroprocesorová technika a embedded systémy Přednáška 8 doc. Ing. Tomáš Frýza, Ph.D. listopad 2012 Obsah
Komprese dat (Komprimace dat)
 Komprese dat (Komprimace dat) Př.: zakódovat slovo ARARAUNA K K 2 četnost absolutní relativní A 4,5 N,25 R 2,25 U,25 kód K : kód K 2 :... 6 bitů... 4 bitů prefixový kód: žádné kódové slovo není prefixem
Komprese dat (Komprimace dat) Př.: zakódovat slovo ARARAUNA K K 2 četnost absolutní relativní A 4,5 N,25 R 2,25 U,25 kód K : kód K 2 :... 6 bitů... 4 bitů prefixový kód: žádné kódové slovo není prefixem
Slovní úlohy I
 ..1 Slovní úlohy I Předpoklady: 0008 Pedagogická poznámka: Slovní úlohy jsou problém, hlavně pro to, že neexistuje jednoznačný algoritmus na jejich řešení. Této první hodiny se však problémy netýkají,
..1 Slovní úlohy I Předpoklady: 0008 Pedagogická poznámka: Slovní úlohy jsou problém, hlavně pro to, že neexistuje jednoznačný algoritmus na jejich řešení. Této první hodiny se však problémy netýkají,
Vyhledávání. doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava. Prezentace ke dni 12.
 Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 12. září 2016 Jiří Dvorský (VŠB TUO) Vyhledávání 201 / 344 Osnova přednášky
Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 12. září 2016 Jiří Dvorský (VŠB TUO) Vyhledávání 201 / 344 Osnova přednášky
Racionální čísla. teorie řešené úlohy cvičení tipy k maturitě výsledky. Víš, že. Naučíš se
 teorie řešené úlohy cvičení tipy k maturitě výsledky Víš, že racionální v matematice znamená poměrový nebo podílový, zatímco v běžné řeči ho užíváme spíše ve významu rozumový? zlomky používali již staří
teorie řešené úlohy cvičení tipy k maturitě výsledky Víš, že racionální v matematice znamená poměrový nebo podílový, zatímco v běžné řeči ho užíváme spíše ve významu rozumový? zlomky používali již staří
Lineární funkce, rovnice a nerovnice 4 lineární nerovnice
 Lineární funkce, rovnice a nerovnice 4 lineární nerovnice 4.1 ekvivalentní úpravy Při řešení lineárních nerovnic používáme ekvivalentní úpravy (tyto úpravy nijak neovlivní výsledek řešení). Jsou to především
Lineární funkce, rovnice a nerovnice 4 lineární nerovnice 4.1 ekvivalentní úpravy Při řešení lineárních nerovnic používáme ekvivalentní úpravy (tyto úpravy nijak neovlivní výsledek řešení). Jsou to především
Maticí typu (m, n), kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru:
 3 Maticový počet 3.1 Zavedení pojmu matice Maticí typu (m, n, kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru: a 11 a 12... a 1k... a 1n a 21 a 22...
3 Maticový počet 3.1 Zavedení pojmu matice Maticí typu (m, n, kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru: a 11 a 12... a 1k... a 1n a 21 a 22...
8. lekce Úvod do jazyka C 3. část Základní příkazy jazyka C Miroslav Jílek
 8. lekce Úvod do jazyka C 3. část Základní příkazy jazyka C Miroslav Jílek 1/41 Základní příkazy Všechny příkazy se píšou malými písmeny! Za většinou příkazů musí být středník (;)! 2/41 Základní příkazy
8. lekce Úvod do jazyka C 3. část Základní příkazy jazyka C Miroslav Jílek 1/41 Základní příkazy Všechny příkazy se píšou malými písmeny! Za většinou příkazů musí být středník (;)! 2/41 Základní příkazy
Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ.1.07/1.5.00/34.0205
 Střední průmyslová škola strojnická Olomouc, tř.7. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ..07/.5.00/34.0205 Šablona: III/2 Informační technologie
Střední průmyslová škola strojnická Olomouc, tř.7. listopadu 49 Výukový materiál zpracovaný v rámci projektu Výuka moderně Registrační číslo projektu: CZ..07/.5.00/34.0205 Šablona: III/2 Informační technologie
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
Způsoby realizace této funkce:
 KOMBINAČNÍ LOGICKÉ OBVODY U těchto obvodů je výstup určen jen výhradně kombinací vstupních veličin. Hodnoty výstupních veličin nezávisejí na předcházejícím stavu logického obvodu, což znamená, že kombinační
KOMBINAČNÍ LOGICKÉ OBVODY U těchto obvodů je výstup určen jen výhradně kombinací vstupních veličin. Hodnoty výstupních veličin nezávisejí na předcházejícím stavu logického obvodu, což znamená, že kombinační
Vyhledávání. doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava. Prezentace ke dni 21.
 Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 21. září 2018 Jiří Dvorský (VŠB TUO) Vyhledávání 242 / 433 Osnova přednášky
Vyhledávání doc. Mgr. Jiří Dvorský, Ph.D. Katedra informatiky Fakulta elektrotechniky a informatiky VŠB TU Ostrava Prezentace ke dni 21. září 2018 Jiří Dvorský (VŠB TUO) Vyhledávání 242 / 433 Osnova přednášky
Tabulkový procesor. Základní rysy
 Tabulkový procesor Tabulkový procesor je počítačový program zpracovávající data uložená v buňkách tabulky. Program umožňuje použití vzorců pro práci s daty a zobrazuje výsledné hodnoty podle vstupních
Tabulkový procesor Tabulkový procesor je počítačový program zpracovávající data uložená v buňkách tabulky. Program umožňuje použití vzorců pro práci s daty a zobrazuje výsledné hodnoty podle vstupních
Kapitola 1. Signály a systémy. 1.1 Klasifikace signálů
 Kapitola 1 Signály a systémy 1.1 Klasifikace signálů Signál představuje fyzikální vyjádření informace, obvykle ve formě okamžitých hodnot určité fyzikální veličiny, která je funkcí jedné nebo více nezávisle
Kapitola 1 Signály a systémy 1.1 Klasifikace signálů Signál představuje fyzikální vyjádření informace, obvykle ve formě okamžitých hodnot určité fyzikální veličiny, která je funkcí jedné nebo více nezávisle
2.8.6 Čísla iracionální, čísla reálná
 .8.6 Čísla iracionální, čísla reálná Předpoklady: 0080 Př. : Doplň tabulku (všechny sloupce je možné vypočítat bez kalkulačky). 00 x 0 0,0004 00 900,69 6 8 x 0,09 0, x 0 0,0004 00 x 0 0,0 0 6 6 900 0 00
.8.6 Čísla iracionální, čísla reálná Předpoklady: 0080 Př. : Doplň tabulku (všechny sloupce je možné vypočítat bez kalkulačky). 00 x 0 0,0004 00 900,69 6 8 x 0,09 0, x 0 0,0004 00 x 0 0,0 0 6 6 900 0 00
Úlohy krajského kola kategorie C
 67. ročník matematické olympiády Úlohy krajského kola kategorie C 1. Najděte nejmenší přirozené číslo končící čtyřčíslím 2018, které je násobkem čísla 2017. 2. Pro celá čísla x, y, z platí x 2 + y z =
67. ročník matematické olympiády Úlohy krajského kola kategorie C 1. Najděte nejmenší přirozené číslo končící čtyřčíslím 2018, které je násobkem čísla 2017. 2. Pro celá čísla x, y, z platí x 2 + y z =
Popis programu EnicomD
 Popis programu EnicomD Pomocí programu ENICOM D lze konfigurovat výstup RS 232 přijímačů Rx1 DIN/DATA a Rx1 DATA (přidělovat textové řetězce k jednotlivým vysílačům resp. tlačítkům a nastavovat parametry
Popis programu EnicomD Pomocí programu ENICOM D lze konfigurovat výstup RS 232 přijímačů Rx1 DIN/DATA a Rx1 DATA (přidělovat textové řetězce k jednotlivým vysílačům resp. tlačítkům a nastavovat parametry
MATA Př 3. Číselné soustavy. Desítková soustava (dekadická) základ 10, číslice 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
 MATA Př 3 Číselné soustavy Poziční číselná soustava je dnes převládající způsob písemné reprezentace čísel dokonce pokud se dnes mluví o číselných soustavách, jsou tím obvykle myšleny soustavy poziční.
MATA Př 3 Číselné soustavy Poziční číselná soustava je dnes převládající způsob písemné reprezentace čísel dokonce pokud se dnes mluví o číselných soustavách, jsou tím obvykle myšleny soustavy poziční.
Cvičení 5 - Inverzní matice
 Cvičení 5 - Inverzní matice Pojem Inverzní matice Buď A R n n. A je inverzní maticí k A, pokud platí, AA = A A = I n. Matice A, pokud existuje, je jednoznačná. A stačí nám jen jedna rovnost, aby platilo,
Cvičení 5 - Inverzní matice Pojem Inverzní matice Buď A R n n. A je inverzní maticí k A, pokud platí, AA = A A = I n. Matice A, pokud existuje, je jednoznačná. A stačí nám jen jedna rovnost, aby platilo,
Nejvyšší řád čísla bit č. 7 bit č. 6 bit č.5 bit č. 4 bit č. 3 bit č. 2 bit č. 1 bit č. 0
 Číselné soustavy Cílem této kapitoly je sezn{mit se se z{kladními jednotkami používanými ve výpočetní technice. Poznat číselné soustavy, umět v nich prov{dět z{kladní aritmetické operace a naučit se převody
Číselné soustavy Cílem této kapitoly je sezn{mit se se z{kladními jednotkami používanými ve výpočetní technice. Poznat číselné soustavy, umět v nich prov{dět z{kladní aritmetické operace a naučit se převody
Řešení slovních úloh pomocí lineárních rovnic
 Řešení slovních úloh pomocí lineárních rovnic Řešení slovních úloh představuje spojení tří, dnes bohužel nelehkých, úloh porozumění čtenému textu (pochopení zadání), jeho matematizaci (převedení na rovnici)
Řešení slovních úloh pomocí lineárních rovnic Řešení slovních úloh představuje spojení tří, dnes bohužel nelehkých, úloh porozumění čtenému textu (pochopení zadání), jeho matematizaci (převedení na rovnici)
PŘÍMKA A JEJÍ VYJÁDŘENÍ V ANALYTICKÉ GEOMETRII
 PŘÍMKA A JEJÍ VYJÁDŘENÍ V ANALYTICKÉ GEOMETRII V úvodu analytické geometrie jsme vysvětlili, že její hlavní snahou je popsat geometrické útvary (body, vektory, přímky, kružnice,...) pomocí čísel nebo proměnných.
PŘÍMKA A JEJÍ VYJÁDŘENÍ V ANALYTICKÉ GEOMETRII V úvodu analytické geometrie jsme vysvětlili, že její hlavní snahou je popsat geometrické útvary (body, vektory, přímky, kružnice,...) pomocí čísel nebo proměnných.
P4 Ukecaný program InterLoS 2014
 P4 Ukecaný program Stáhněte si zdrojový kód P4-ukecany.c, zkopilujte jej pomocí kompilátoru jazyka C a spusťte. Program je psaný podle standartu C89, takže by měl jít zkompilovat libovolným C kompilátorem,
P4 Ukecaný program Stáhněte si zdrojový kód P4-ukecany.c, zkopilujte jej pomocí kompilátoru jazyka C a spusťte. Program je psaný podle standartu C89, takže by měl jít zkompilovat libovolným C kompilátorem,
KOMPRIMACE. aneb Aby to zabralo méně místa
 KOMPRIMACE aneb Aby to zabralo méně místa Komprimace nebo také komprese je jednoduše řečeno sbalení či spakování dat na mnohem menší velikost. Ve skutečnosti se jedná o vypuštění nadbytečné informace takovým
KOMPRIMACE aneb Aby to zabralo méně místa Komprimace nebo také komprese je jednoduše řečeno sbalení či spakování dat na mnohem menší velikost. Ve skutečnosti se jedná o vypuštění nadbytečné informace takovým
Algoritmy I. Číselné soustavy přečíst!!! ALGI 2018/19
 Algoritmy I Číselné soustavy přečíst!!! Číselné soustavy Každé číslo lze zapsat v poziční číselné soustavě ve tvaru: a n *z n +a n-1 *z n-1 +. +a 1 *z 1 +a 0 *z 0 +a -1 *z n-1 +a -2 *z -2 +.. V dekadické
Algoritmy I Číselné soustavy přečíst!!! Číselné soustavy Každé číslo lze zapsat v poziční číselné soustavě ve tvaru: a n *z n +a n-1 *z n-1 +. +a 1 *z 1 +a 0 *z 0 +a -1 *z n-1 +a -2 *z -2 +.. V dekadické
HROMADNÉ ÚPRAVY NAJÍT A NAHRADIT
 HROMADNÉ ÚPRAVY NAJÍT A NAHRADIT Funkce Najít a nahradit slouží k rychlému vyhledávání určitých slov a jejich nahrazování jinými slovy. Lze hledat i určité varianty slov a nahrazovat je buď hromadně (všechny
HROMADNÉ ÚPRAVY NAJÍT A NAHRADIT Funkce Najít a nahradit slouží k rychlému vyhledávání určitých slov a jejich nahrazování jinými slovy. Lze hledat i určité varianty slov a nahrazovat je buď hromadně (všechny
KFC/SEM, KFC/SEMA Rovnice, nerovnice
 KFC/SEM, KFC/SEMA Rovnice, nerovnice Požadované dovednosti: Řešení lineárních rovnic a nerovnic Řešení kvadratických rovnic Řešení rovnic s odmocninou Řešení rovnic s parametrem Řešení rovnic s absolutní
KFC/SEM, KFC/SEMA Rovnice, nerovnice Požadované dovednosti: Řešení lineárních rovnic a nerovnic Řešení kvadratických rovnic Řešení rovnic s odmocninou Řešení rovnic s parametrem Řešení rovnic s absolutní
Pythagorova věta
 .8.19 Pythagorova věta Předpoklady: 00801 Pedagogická poznámka: Z následujícího příkladu rýsuje každý žák pouze jeden bod podle toho, v jakém sedí oddělení. Př. 1: Narýsuj pravoúhlý trojúhelník: a) ABC:
.8.19 Pythagorova věta Předpoklady: 00801 Pedagogická poznámka: Z následujícího příkladu rýsuje každý žák pouze jeden bod podle toho, v jakém sedí oddělení. Př. 1: Narýsuj pravoúhlý trojúhelník: a) ABC:
FUNKCE 3. Autor: Mgr. Dana Kaprálová. Datum (období) tvorby: září, říjen 2013. Ročník: sedmý. Vzdělávací oblast: Informatika a výpočetní technika
 FUNKCE 3 Autor: Mgr. Dana Kaprálová Datum (období) tvorby: září, říjen 2013 Ročník: sedmý Vzdělávací oblast: Informatika a výpočetní technika 1 Anotace: Žáci se seznámí se základní obsluhou tabulkového
FUNKCE 3 Autor: Mgr. Dana Kaprálová Datum (období) tvorby: září, říjen 2013 Ročník: sedmý Vzdělávací oblast: Informatika a výpočetní technika 1 Anotace: Žáci se seznámí se základní obsluhou tabulkového
9 Kolmost vektorových podprostorů
 9 Kolmost vektorových podprostorů Od kolmosti dvou vektorů nyní přejdeme ke kolmosti dvou vektorových podprostorů. Budeme se zabývat otázkou, kdy jsou dva vektorové podprostory na sebe kolmé a jak to poznáme.
9 Kolmost vektorových podprostorů Od kolmosti dvou vektorů nyní přejdeme ke kolmosti dvou vektorových podprostorů. Budeme se zabývat otázkou, kdy jsou dva vektorové podprostory na sebe kolmé a jak to poznáme.
Kódy a kódování dat. Binární (dvojkové) kódy. Kód Aikenův
 Kódy a kódování dat Kódování je proces, při kterém se každému znaku nebo postupnosti znaků daného souboru znaků jednoznačně přiřadí znak nebo postupnost znaků z jiného souboru znaků. Kódování je tedy transformace
Kódy a kódování dat Kódování je proces, při kterém se každému znaku nebo postupnosti znaků daného souboru znaků jednoznačně přiřadí znak nebo postupnost znaků z jiného souboru znaků. Kódování je tedy transformace
EU-OPVK: VY_32_INOVACE_FIL12 Vojtěch Filip, 2014
 Číslo projektu CZ.1.07/1.5.00/34.0036 Tématický celek Inovace výuky ICT na BPA Název projektu Inovace a individualizace výuky Název materiálu Komprese a archivace dat Číslo materiálu VY_32_INOVACE_FIL12
Číslo projektu CZ.1.07/1.5.00/34.0036 Tématický celek Inovace výuky ICT na BPA Název projektu Inovace a individualizace výuky Název materiálu Komprese a archivace dat Číslo materiálu VY_32_INOVACE_FIL12
