Vlastnosti Fourierovy transformace
|
|
|
- Pavla Horáčková
- před 10 lety
- Počet zobrazení:
Transkript
1 Vlastnosti Fourierovy transformace Linearita Fourierova transformace je lineární (všechny druhy :-) ), je tedy homogenní a aditivní Homogenita: změna amplitudy v časové oblasti způsobí stejnou změnu amplitudy ve frekvenční oblasti
2 Aditivita: něco přidám v časové oblasti a přidá se to i ve frekvenční (nezávisle)
3 Komprese / expanze Když signál natáhnu v časové oblasti, smrskne se mi ve frekvenční a obráceně Příklad: gaussovka (jejím obrazem je opět gaussovka)
4 Posunutí v časové oblasti Při posunutí v časové oblasti zůstává magnituda stejná a mění se pouze fáze
5 Jaká informace je ukryta ve fázi? Vezmu jednoduchý signál, provedu DFT, převedu do polárních souřadnic, postupně nahradím magnitudu a fázi náhodnými čísly a následně zrekonstruuji zpět do časové oblasti (IDFT) Ve fázi je dobře vidět poloha hran. Proč? Hrana v časové oblasti vznikne, když na stejném místě roste současně hodně sinusovek musí mít stejnou fázi zobecnění: hodně informace o tvaru signálu v časové oblasti je schováno ve fázi. Naopak na fázi moc nezáleží u signálů, kde na tvaru moc nezáleží a informace je schovaná ve frekvencích, např. audio signál. % vygeneruji jednoduchy signal clear all x(1:50) = 0; x(51:100) = linspace(0.9,1.2,50); x(101:299) = 0; % provedu DFT a prevod do polarnich souradnic [ReX ImX] = DFT(x); [XMag, XPha] = RectToPolar(ReX,ImX); % nahodna faze z intervalu pi / pi XPha0 = (rand(1,length(xmag))-0.5)*2*pi; % rekonstrukce jen z magnitudy [X2r X2i] = PolarToRect(XMag,XPha0); x2 = IDFT(X2r, X2i); % rekonstrukce jen z faze XMag0 = rand(1,length(xmag)); [X3r X3i] = PolarToRect(XMag0,XPha); x3 = IDFT(X3r, X3i); % a ted spolecne namalujeme subplot(3,1,1); plot(x); title('originalni signal'); subplot(3,1,2); plot(x2) title('rekonstrukce z magnitudy'); subplot(3,1,3); plot(x3) title('rekonstrukce z faze');
6 Periodicita signálu v časové oblasti DFT považuje časový signál za periodický. Když něco uděláme se spektrem, před převedením zpět do časové oblasti, může být výsledný časový signál delší, nevejde se do daného počtu vzorků. Příklad cirkulární konvoluce (přednáška o aplikacích konvoluce pomocí DFT)
7 Periodicita signálu ve frekvenční oblasti Záporné frekvence od -0,5 do 0 vzorkovací frekvence Zrcadlový obraz: magnituda sudá, fáze lichá Záporná frekvence, co je to za podivnost?
8 Amplitudová modulace Modulace spojení (merging) dvou signálů Amplitudová modulace násobení Obálka nosné = původní signál Násobení v časové oblasti = konvoluce ve frekvenční Nosná je puls výsledek konvoluce je posun Výsledek ve frekvenční oblasti Nosná zůstane Spektrum originálu se tam objeví Objeví se ještě něco dalšího! Co to je? Negativní frekvence! Více o modulacích v PDF GenerováníSignálu
9 % amplitudova modulace - ukazka zapornych frekvenci clear all; [Y,FS,NBITS]=wavread('mechanika2.wav'); y2 = Y'; Y2 = fft(y2); delka = length(y2); delkas = length(y2) / FS; % delka signalu v sekundach % vytvoreni nosne (na frekvenci napr. ctvrtiny vzorkovacky originalu) t = linspace(0,delkas,delka); nosna = sin(fs/4*2*pi*t); NOS = fft(nosna); % amplitudova modulace - nasobeni signalu v casove oblasti hloubkamodulace = 1; am = nosna.* (1 + hloubkamodulace * y2); % tomu by mela odpovidat konvoluce ve frekvencni % a protoze jadro je puls, tak se to jen posune a zjevi % se zaporne frekvence AM = fft(am); % a ted uz to jen namalujeme subplot(3,1,1); plot(abs(y2(1:delka/2))); axis([0 delka/2 0 max(abs(y2))]); title('frekvence audio'); subplot(3,1,2); plot(abs(nos(1:delka/2))); axis([0 delka/2 0 max(abs(nos))]); title('frekvence nosna'); subplot(3,1,3); plot(abs(am(1:delka/2))); axis([0 delka/ ]); title('frekvence amplitudove modulace'); Totéž v Matlabu
10 Užitečné dvojice Každému signálu v časové oblasti odpovídá nějaký signál ve frekvenční oblasti a obráceně. Existují dvojice (časová/frekvenční) které jsou užitečnější než jiné. Například obdélníkovému pulsu odpovídá funkce sinc, gaussovce gaussovka, atd. Impuls / konstanta (viz slide komprese/expanze komprese na puls, expanze na konstantu)
11 Funkce sinc / Obdélníkový puls clear all t = linspace(-10,10); y = sinc(t); subplot(2,2,1) plot(t,y); axis tight xlabel('cas (sec)');ylabel('amplituda'); title('funkce sinc') Y = fft(y); subplot(2,2,2) Ym = abs(y(1:length(y)/2)); f = linspace(0,0.5,length(ym)); plot(f,ym); axis tight xlabel('frekvence (Hz)');ylabel('Amplituda'); title('spektrum funkce sinc') from = -100; to = 100; points = 1500; t = linspace(from,to,points); y = sinc(t); subplot(2,2,3) plot(t,y); axis tight xlabel('cas (sec)');ylabel('amplituda'); title('funkce sinc') Y = fft(y); subplot(2,2,4) Tvz = (to-from)/points; fvz = 1/Tvz; Ym = abs(y(1:length(y)/2)); f = linspace(0,0.5*fvz,length(ym)); plot(f,ym); axis tight xlabel('frekvence (Hz)');ylabel('Amplituda'); title('spektrum funkce sinc') sinc( a) = sin ( π a) π a
12 Obdélníkový puls / funkce sinc Cvičení: pořádně prozkoumejte funkci sinc, bude se nám hodit do budoucna (proč asi?) vyzkoušejte další dvojice (trojúhelník, gaussovka,, využijte matlabovské funkce tripuls apod. viz help)
13 Chirp signál Chrip signál je užitečná věcička v aplikacích jako je radar. Jeho frekvenční odezva vypadá následovně: 2 Magnituda je konstantní, fáze klesá podle vztahu Faze() i = αi + βi. Z toho jsme schopni vygenerovat příslušné ReX a ImX složky (potřebujeme PolarToRect funkci) a následně pomocí IDFT i impulsní odezvu: IDFT Když tedy do systému s takovou odezvou pustíme jednu delta funkci, dostaneme divoký signál který začíná na nízkých frekvencích, které se postupně zvyšují. K čemu je to dobré?
14 Chirp signál je reverzibilní, když pustíme chirp signál do antichirp systému, dostaneme zpátky jediný puls. Antichirp signál bude mít opět magnitudu konstantní a fázi obrácenou. Docílíme toho tak, že převrátíme zleva doprava impulsní odezvu. DFT Převrácená impulsní odezva ReX a ImX vypadají podobně, co ta fáze??? A k čemu to teda je????
15 Aplikace chirp signálu Radar: vezmu směrovou anténu a vypustím z ní krátký impuls rádiových vln. Ta letí a letí, až narazí na nepřátelské letadlo a vrátí se. Vlna letí rychle, čím je impuls delší, tím je horší rozlišení (1 mikrosekunda je cca 300 m), takže potřebuji co nejkratší impuls. Aby vlna doletěla (a detekovatelná část se odrazila), potřebuji do ní nacpat určité množství energie. Čím víc, tím líp. Co nejvíc energie co nejkratší puls shoří mi to Řešení: využiji chirp signál! Napřed mám impuls, než odletí z antény tak ho přehodím na chirp, dostanu zpátky chirp, ten převedu zpátky na impuls a můžu nepřítele sejmout raz dva. Cvičení: prozkoumejte chirp signál Vygenerujte podobné obrázky jako v přednáškových slidech
[ n. Konvoluce. = 0 jinak. 0 jinak. Užitečné signály (diskrétní verze) Jednotkový skok 1 pro n = 0
 Užitečné signály (diskrétní verze) Konvoluce σ Jednotkový skok [ n] Jednotkový impuls (delta funkce) Posunutý jednotkový impuls 1 pro n 0 1 pro n = 0 δ = δ [ n] [ n k] = 0 jinak 0 jinak Proč jsou užitečné?
Užitečné signály (diskrétní verze) Konvoluce σ Jednotkový skok [ n] Jednotkový impuls (delta funkce) Posunutý jednotkový impuls 1 pro n 0 1 pro n = 0 δ = δ [ n] [ n k] = 0 jinak 0 jinak Proč jsou užitečné?
Fourierova transformace
 Fourierova transformace Jean Baptiste Joseph Fourier (768-83) Jeho obdivovatel (nedatováno) Opáčko harmonických signálů Spojitý harmonický signál ( ) = cos( ω + ϕ ) x t C t C amplituda ω úhlová frekvence
Fourierova transformace Jean Baptiste Joseph Fourier (768-83) Jeho obdivovatel (nedatováno) Opáčko harmonických signálů Spojitý harmonický signál ( ) = cos( ω + ϕ ) x t C t C amplituda ω úhlová frekvence
Úvod do zpracování signálů
 1 / 25 Úvod do zpracování signálů Karel Horák Rozvrh přednášky: 1. Spojitý a diskrétní signál. 2. Spektrum signálu. 3. Vzorkovací věta. 4. Konvoluce signálů. 5. Korelace signálů. 2 / 25 Úvod do zpracování
1 / 25 Úvod do zpracování signálů Karel Horák Rozvrh přednášky: 1. Spojitý a diskrétní signál. 2. Spektrum signálu. 3. Vzorkovací věta. 4. Konvoluce signálů. 5. Korelace signálů. 2 / 25 Úvod do zpracování
31ZZS 9. PŘEDNÁŠKA 24. listopadu 2014
 3ZZS 9. PŘEDNÁŠKA 24. listopadu 24 SPEKTRÁLNÍ ANALÝZA Fourierovy řady Diskrétní Fourierovy řady Fourierova transformace Diskrétní Fourierova transformace Spektrální analýza Zobrazení signálu ve frekvenční
3ZZS 9. PŘEDNÁŠKA 24. listopadu 24 SPEKTRÁLNÍ ANALÝZA Fourierovy řady Diskrétní Fourierovy řady Fourierova transformace Diskrétní Fourierova transformace Spektrální analýza Zobrazení signálu ve frekvenční
Lineární a adaptivní zpracování dat. 2. SYSTÉMY a jejich popis v časové doméně a frekvenční doméně
 Lineární a adaptivní zpracování dat 2. SYSTÉMY a jejich popis v časové doméně a frekvenční doméně Daniel Schwarz Investice do rozvoje vzdělávání Osnova Opakování: signály a systémy Vlastnosti systémů Systémy
Lineární a adaptivní zpracování dat 2. SYSTÉMY a jejich popis v časové doméně a frekvenční doméně Daniel Schwarz Investice do rozvoje vzdělávání Osnova Opakování: signály a systémy Vlastnosti systémů Systémy
Lineární a adaptivní zpracování dat. 2. SYSTÉMY a jejich popis v časové doméně a frekvenční doméně
 Lineární a adaptivní zpracování dat 2. SYSTÉMY a jejich popis v časové doméně a frekvenční doméně Daniel Schwarz Investice do rozvoje vzdělávání Osnova Opakování: signály a systémy Vlastnosti systémů Systémy
Lineární a adaptivní zpracování dat 2. SYSTÉMY a jejich popis v časové doméně a frekvenční doméně Daniel Schwarz Investice do rozvoje vzdělávání Osnova Opakování: signály a systémy Vlastnosti systémů Systémy
Lineární a adaptivní zpracování dat. 3. SYSTÉMY a jejich popis ve frekvenční oblasti
 Lineární a adaptivní zpracování dat 3. SYSTÉMY a jejich popis ve frekvenční oblasti Daniel Schwarz Osnova Opakování: systémy a jejich popis v časové oblasti Fourierovy řady Frekvenční charakteristika systémů
Lineární a adaptivní zpracování dat 3. SYSTÉMY a jejich popis ve frekvenční oblasti Daniel Schwarz Osnova Opakování: systémy a jejich popis v časové oblasti Fourierovy řady Frekvenční charakteristika systémů
SIGNÁLY A SOUSTAVY, SIGNÁLY A SYSTÉMY
 SIGNÁLY A SOUSTAVY, SIGNÁLY A SYSTÉMY TEMATICKÉ OKRUHY Signály se spojitým časem Základní signály se spojitým časem (základní spojité signály) Jednotkový skok σ (t), jednotkový impuls (Diracův impuls)
SIGNÁLY A SOUSTAVY, SIGNÁLY A SYSTÉMY TEMATICKÉ OKRUHY Signály se spojitým časem Základní signály se spojitým časem (základní spojité signály) Jednotkový skok σ (t), jednotkový impuls (Diracův impuls)
A7B31ZZS 10. PŘEDNÁŠKA Návrh filtrů 1. prosince 2014
 A7B3ZZS. PŘEDNÁŠKA Návrh filtrů. prosince 24 Návrhy jednoduchých filtrů Návrhy složitějších filtrů Porovnání FIR a IIR Nástroje pro návrh FIR filtrů v MATLABu Nástroje pro návrh IIR filtrů v MATLABu Kvantování
A7B3ZZS. PŘEDNÁŠKA Návrh filtrů. prosince 24 Návrhy jednoduchých filtrů Návrhy složitějších filtrů Porovnání FIR a IIR Nástroje pro návrh FIR filtrů v MATLABu Nástroje pro návrh IIR filtrů v MATLABu Kvantování
Fourierova transformace
 Fourierova transformace EO Přednáška Pavel Máša ÚVODEM Známe Fourierovy řady v komplexním tvaru f(t) = 1X k= 1 A k e jk! t Spektrum této řady je diskrétní A k = 1 T Obvody tedy musíme řešit v HUS člen
Fourierova transformace EO Přednáška Pavel Máša ÚVODEM Známe Fourierovy řady v komplexním tvaru f(t) = 1X k= 1 A k e jk! t Spektrum této řady je diskrétní A k = 1 T Obvody tedy musíme řešit v HUS člen
Rekurentní filtry. Matlab
 Rekurentní filtry IIR filtry filtry se zpětnou vazbou a nekonečnou impulsní odezvou Výstupní signál je závislý na vstupu a minulém výstupu. Existují různé konvence zápisu, pozor na to! Někde je záporná
Rekurentní filtry IIR filtry filtry se zpětnou vazbou a nekonečnou impulsní odezvou Výstupní signál je závislý na vstupu a minulém výstupu. Existují různé konvence zápisu, pozor na to! Někde je záporná
Úloha D - Signál a šum v RFID
 1. Zadání: Úloha D - Signál a šum v RFID Změřte úrovně užitečného signálu a šumu v přenosovém řetězci systému RFID v závislosti na čtecí vzdálenosti. Zjistěte maximální čtecí vzdálenost daného RFID transpondéru.
1. Zadání: Úloha D - Signál a šum v RFID Změřte úrovně užitečného signálu a šumu v přenosovém řetězci systému RFID v závislosti na čtecí vzdálenosti. Zjistěte maximální čtecí vzdálenost daného RFID transpondéru.
X31ZZS 3. PŘEDNÁŠKA 6. října Periodické průběhy Fourierovy řady Spektrum Barva zvuku Aplikace
 X31ZZS 3. PŘEDNÁŠKA 6. října 214 Periodické průběhy Fourierovy řady Spektrum Barva zvuku Aplikace Fourierovy řady Jean Baptiste Fourier (francouzský matematik 1768-183) Harmonická analýza Libovolný periodický
X31ZZS 3. PŘEDNÁŠKA 6. října 214 Periodické průběhy Fourierovy řady Spektrum Barva zvuku Aplikace Fourierovy řady Jean Baptiste Fourier (francouzský matematik 1768-183) Harmonická analýza Libovolný periodický
A2B31SMS 3. PŘEDNÁŠKA 15. října 2015
 A2B31SMS 3. PŘEDNÁŠKA 15. října 215 ADITIVNÍ SYNTÉZA Harmonická analýza Harmonická syntéza Fourierovy řady Spektrum Barva zvuku Aditivní syntéza a spektrální modelování Parciály Fourierovy řady Jean Baptiste
A2B31SMS 3. PŘEDNÁŠKA 15. října 215 ADITIVNÍ SYNTÉZA Harmonická analýza Harmonická syntéza Fourierovy řady Spektrum Barva zvuku Aditivní syntéza a spektrální modelování Parciály Fourierovy řady Jean Baptiste
Systémy. Systém: souhrn souvisejících prvků, sdružený do nějakého smysluplného celku
 Systémy Systém: souhrn souvisejících prvků, sdružený do nějakého smysluplného celku Pro nás: krabička něco dělající se signály: xt, xn něco do ní leze vstup ( ) [ ] něco z ní leze ven výstup yt ( ), yn
Systémy Systém: souhrn souvisejících prvků, sdružený do nějakého smysluplného celku Pro nás: krabička něco dělající se signály: xt, xn něco do ní leze vstup ( ) [ ] něco z ní leze ven výstup yt ( ), yn
Filtrace obrazu ve frekvenční oblasti
 Filtrace obrazu ve frekvenční oblasti Václav Hlaváč České vysoké učení technické v Praze Český institut informatiky, robotiky a kybernetiky 166 36 Praha 6, Jugoslávských partyzánů 1580/3 http://people.ciirc.cvut.cz/hlavac,
Filtrace obrazu ve frekvenční oblasti Václav Hlaváč České vysoké učení technické v Praze Český institut informatiky, robotiky a kybernetiky 166 36 Praha 6, Jugoslávských partyzánů 1580/3 http://people.ciirc.cvut.cz/hlavac,
FILTRACE VE FOURIEROVSKÉM SPEKTRU
 1/18 FILTRACE VE FOURIEROVSKÉM SPEKTRU (patří do lineárních integrálních transformací) Václav Hlaváč Fakulta elektrotechnická ČVUT v Praze katedra kybernetiky, Centrum strojového vnímání hlavac@fel.cvut.cz
1/18 FILTRACE VE FOURIEROVSKÉM SPEKTRU (patří do lineárních integrálních transformací) Václav Hlaváč Fakulta elektrotechnická ČVUT v Praze katedra kybernetiky, Centrum strojového vnímání hlavac@fel.cvut.cz
Digitalizace převod AS DS (analogový diskrétní signál )
 Digitalizace signálu v čase Digitalizace převod AS DS (analogový diskrétní signál ) v amplitudě Obvykle převod spojité předlohy (reality) f 1 (t/x,...), f 2 ()... připomenutí Digitalizace: 1. vzorkování
Digitalizace signálu v čase Digitalizace převod AS DS (analogový diskrétní signál ) v amplitudě Obvykle převod spojité předlohy (reality) f 1 (t/x,...), f 2 ()... připomenutí Digitalizace: 1. vzorkování
doc. Dr. Ing. Elias TOMEH Elias Tomeh / Snímek 1
 doc. Dr. Ing. Elias TOMEH e-mail: elias.tomeh@tul.cz Elias Tomeh / Snímek 1 Frekvenční spektrum Dělení frekvenčního pásma (počet čar) Průměrování Časovou váhovou funkci Elias Tomeh / Snímek 2 Vzorkovací
doc. Dr. Ing. Elias TOMEH e-mail: elias.tomeh@tul.cz Elias Tomeh / Snímek 1 Frekvenční spektrum Dělení frekvenčního pásma (počet čar) Průměrování Časovou váhovou funkci Elias Tomeh / Snímek 2 Vzorkovací
Dodatky k FT: 1. (2D digitalizace) 2. Více o FT 3. Více k užití filtrů. 7. přednáška předmětu Zpracování obrazů
 Dodatky k FT:. (D digitalizace. Více o FT 3. Více k užití filtrů 7. přednáška předmětu Zpracování obrazů Martina Mudrová 4 Pořízení digitálního obrazu Obvykle: Proces transformace spojité předlohy (reality
Dodatky k FT:. (D digitalizace. Více o FT 3. Více k užití filtrů 7. přednáška předmětu Zpracování obrazů Martina Mudrová 4 Pořízení digitálního obrazu Obvykle: Proces transformace spojité předlohy (reality
Akustika. 3.1 Teorie - spektrum
 Akustika 3.1 Teorie - spektrum Rozklad kmitů do nejjednodušších harmonických Spektrum Spektrum Jedna harmonická vlna = 1 frekvence Dvě vlny = 2 frekvence Spektrum 3 vlny = 3 frekvence Spektrum Další vlny
Akustika 3.1 Teorie - spektrum Rozklad kmitů do nejjednodušších harmonických Spektrum Spektrum Jedna harmonická vlna = 1 frekvence Dvě vlny = 2 frekvence Spektrum 3 vlny = 3 frekvence Spektrum Další vlny
Při návrhu FIR filtru řešíme obvykle následující problémy:
 Návrh FIR filtrů Při návrhu FIR filtru řešíme obvykle následující problémy: volba frekvenční odezvy požadovaného filtru; nejčastěji volíme ideální charakteristiku normovanou k Nyquistově frekvenci, popř.
Návrh FIR filtrů Při návrhu FIR filtru řešíme obvykle následující problémy: volba frekvenční odezvy požadovaného filtru; nejčastěji volíme ideální charakteristiku normovanou k Nyquistově frekvenci, popř.
Lineární a adpativní zpracování dat. 3. Lineární filtrace I: Z-transformace, stabilita
 Lineární a adpativní zpracování dat 3. Lineární filtrace I: Z-transformace, stabilita Daniel Schwarz Investice do rozvoje vzdělávání Osnova Opakování: signály, systémy, jejich vlastnosti a popis v časové
Lineární a adpativní zpracování dat 3. Lineární filtrace I: Z-transformace, stabilita Daniel Schwarz Investice do rozvoje vzdělávání Osnova Opakování: signály, systémy, jejich vlastnosti a popis v časové
KTE/TEVS - Rychlá Fourierova transformace. Pavel Karban. Katedra teoretické elektrotechniky Fakulta elektrotechnická Západočeská univerzita v Plzni
 KTE/TEVS - Rychlá Fourierova transformace Pavel Karban Katedra teoretické elektrotechniky Fakulta elektrotechnická Západočeská univerzita v Plzni 10.11.011 Outline 1 Motivace FT Fourierova transformace
KTE/TEVS - Rychlá Fourierova transformace Pavel Karban Katedra teoretické elektrotechniky Fakulta elektrotechnická Západočeská univerzita v Plzni 10.11.011 Outline 1 Motivace FT Fourierova transformace
Základní metody číslicového zpracování signálu a obrazu část II.
 A4M38AVS Aplikace vestavěných systémů Přednáška č. 8 Základní metody číslicového zpracování signálu a obrazu část II. Radek Sedláček, katedra měření, ČVUT FEL, 2015 Obsah přednášky Převzorkování decimace,
A4M38AVS Aplikace vestavěných systémů Přednáška č. 8 Základní metody číslicového zpracování signálu a obrazu část II. Radek Sedláček, katedra měření, ČVUT FEL, 2015 Obsah přednášky Převzorkování decimace,
A2B31SMS 11. PŘEDNÁŠKA 4. prosince 2014
 A2B31SMS 11. PŘEDNÁŠKA 4. prosince 214 Číslicové audio efekty Hřebenové filtry Fázovací filtry Dozvuky Konvoluční reverb Schroederův algoritmus modelování dozvuku Číslicové audio efekty Filtrace - DP,
A2B31SMS 11. PŘEDNÁŠKA 4. prosince 214 Číslicové audio efekty Hřebenové filtry Fázovací filtry Dozvuky Konvoluční reverb Schroederův algoritmus modelování dozvuku Číslicové audio efekty Filtrace - DP,
Spektrální analýza a diskrétní Fourierova transformace. Honza Černocký, ÚPGM
 Spektrální analýza a diskrétní Fourierova transformace Honza Černocký, ÚPGM Povídání o cosinusovce 2 Argument cosinusovky 0 2p a pak každé 2p perioda 3 Cosinusovka s diskrétním časem Úkol č. 1: vyrobit
Spektrální analýza a diskrétní Fourierova transformace Honza Černocký, ÚPGM Povídání o cosinusovce 2 Argument cosinusovky 0 2p a pak každé 2p perioda 3 Cosinusovka s diskrétním časem Úkol č. 1: vyrobit
Zvuk. 1. základní kmitání. 2. šíření zvuku
 Zvuk 1. základní kmitání - vzduchem se šíří tlakové vzruchy (vzruchová vlna), zvuk je systémem zhuštěnin a zředěnin - podstatou zvuku je kmitání zdroje zvuku a tím způsobené podélné vlnění elastického
Zvuk 1. základní kmitání - vzduchem se šíří tlakové vzruchy (vzruchová vlna), zvuk je systémem zhuštěnin a zředěnin - podstatou zvuku je kmitání zdroje zvuku a tím způsobené podélné vlnění elastického
Komplexní obálka pásmového signálu
 České vysoké učení technické v Praze, Fakulta elektrotechnická X37SGS Signály a systémy Komplexní obálka pásmového signálu Daniel Tureček 8.11.8 1 Úkol měření Nalezněte vzorky komplexní obálky pásmového
České vysoké učení technické v Praze, Fakulta elektrotechnická X37SGS Signály a systémy Komplexní obálka pásmového signálu Daniel Tureček 8.11.8 1 Úkol měření Nalezněte vzorky komplexní obálky pásmového
1 Zpracování a analýza tlakové vlny
 1 Zpracování a analýza tlakové vlny 1.1 Cíl úlohy Prostřednictvím této úlohy se naučíte a zopakujete: analýzu biologických signálů v časové oblasti, analýzu biologických signálů ve frekvenční oblasti,
1 Zpracování a analýza tlakové vlny 1.1 Cíl úlohy Prostřednictvím této úlohy se naučíte a zopakujete: analýzu biologických signálů v časové oblasti, analýzu biologických signálů ve frekvenční oblasti,
Číslicové zpracování signálů a Fourierova analýza.
 Číslicové zpracování signálů a Fourierova analýza www.kme.zcu.cz/kmet/exm 1 Obsah prezentace 1. Úvod a motivace 2. Data v časové a frekvenční oblasti 3. Fourierova analýza teoreticky 4. Fourierova analýza
Číslicové zpracování signálů a Fourierova analýza www.kme.zcu.cz/kmet/exm 1 Obsah prezentace 1. Úvod a motivace 2. Data v časové a frekvenční oblasti 3. Fourierova analýza teoreticky 4. Fourierova analýza
VYUŽITÍ MATLABU PRO PODPORU VÝUKY A PŘI ŘEŠENÍ VÝZKUMNÝCH ÚKOLŮ NA KATEDŘE KOMUNIKAČNÍCH A INFORMAČNÍCH SYSTÉMŮ
 VYUŽITÍ MATLABU PRO PODPORU VÝUKY A PŘI ŘEŠENÍ VÝZKUMNÝCH ÚKOLŮ NA KATEDŘE KOMUNIKAČNÍCH A INFORMAČNÍCH SYSTÉMŮ Markéta Mazálková Katedra komunikačních a informačních systémů Fakulta vojenských technologií,
VYUŽITÍ MATLABU PRO PODPORU VÝUKY A PŘI ŘEŠENÍ VÝZKUMNÝCH ÚKOLŮ NA KATEDŘE KOMUNIKAČNÍCH A INFORMAČNÍCH SYSTÉMŮ Markéta Mazálková Katedra komunikačních a informačních systémů Fakulta vojenských technologií,
Osnova. Idea ASK/FSK/PSK ASK Amplitudové... Strana 1 z 16. Celá obrazovka. Konec Základy radiotechniky
 Pulsní kódová modulace, amplitudové, frekvenční a fázové kĺıčování Josef Dobeš 24. října 2006 Strana 1 z 16 Základy radiotechniky 1. Pulsní modulace Strana 2 z 16 Pulsní šířková modulace (PWM) PAM, PPM,
Pulsní kódová modulace, amplitudové, frekvenční a fázové kĺıčování Josef Dobeš 24. října 2006 Strana 1 z 16 Základy radiotechniky 1. Pulsní modulace Strana 2 z 16 Pulsní šířková modulace (PWM) PAM, PPM,
Lineární a adaptivní zpracování dat. 1. ÚVOD: SIGNÁLY a SYSTÉMY
 Lineární a adaptivní zpracování dat 1. ÚVOD: SIGNÁLY a SYSTÉMY Daniel Schwarz Investice do rozvoje vzdělávání Osnova Úvodní informace o předmětu Signály, časové řady klasifikace, příklady, vlastnosti Vzorkovací
Lineární a adaptivní zpracování dat 1. ÚVOD: SIGNÁLY a SYSTÉMY Daniel Schwarz Investice do rozvoje vzdělávání Osnova Úvodní informace o předmětu Signály, časové řady klasifikace, příklady, vlastnosti Vzorkovací
Primární zpracování radarového signálu dopplerovská filtrace
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE K13137 - Katedra radioelektroniky A2M37RSY Jméno Stud. rok Stud. skupina Ročník Lab. skupina Václav Dajčar 2011/2012 2. 101 - Datum zadání Datum odevzdání Klasifikace
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE K13137 - Katedra radioelektroniky A2M37RSY Jméno Stud. rok Stud. skupina Ročník Lab. skupina Václav Dajčar 2011/2012 2. 101 - Datum zadání Datum odevzdání Klasifikace
Číslicové filtry. Honza Černocký, ÚPGM
 Číslicové filtry Honza Černocký, ÚPGM Aliasy Digitální filtry Diskrétní systémy Systémy s diskrétním časem atd. 2 Na co? Úprava signálů Zdůraznění Potlačení Detekce 3 Zdůraznění basy 4 Zdůraznění výšky
Číslicové filtry Honza Černocký, ÚPGM Aliasy Digitální filtry Diskrétní systémy Systémy s diskrétním časem atd. 2 Na co? Úprava signálů Zdůraznění Potlačení Detekce 3 Zdůraznění basy 4 Zdůraznění výšky
polyfázové filtry (multirate filters) cascaded integrator comb filter (CIC) A0M38SPP - Signálové procesory v praxi - přednáška 8 2
 A0M38SPP - Signálové procesory v praxi - přednáška 8 2 Decimace snížení vzorkovací frekvence Interpolace zvýšení vzorkovací frekvence Obecné převzorkování signálu faktorem I/D Efektivní způsoby implementace
A0M38SPP - Signálové procesory v praxi - přednáška 8 2 Decimace snížení vzorkovací frekvence Interpolace zvýšení vzorkovací frekvence Obecné převzorkování signálu faktorem I/D Efektivní způsoby implementace
ZPRACOVÁNÍ SIGNÁLŮ Z MECHANICKÝCH. Jiří Tůma
 ZPRACOVÁNÍ SIGNÁLŮ Z MECHANICKÝCH SYSTÉMŮ UŽITÍM FFT Jiří Tůma Štramberk 1997 ii Anotace Cílem této knihy je systematicky popsat metody analýzy signálů z mechanických systémů a strojních zařízení. Obsahem
ZPRACOVÁNÍ SIGNÁLŮ Z MECHANICKÝCH SYSTÉMŮ UŽITÍM FFT Jiří Tůma Štramberk 1997 ii Anotace Cílem této knihy je systematicky popsat metody analýzy signálů z mechanických systémů a strojních zařízení. Obsahem
Fouriérova transformace, konvoluce, dekonvoluce, Fouriérovské integrály
 co byste měli umět po dnešní lekci: používat funkce pro výpočet FFT (Fast Fourier Transformation) spočítat konvoluci/dekonvoluci pomocí FFT použít FFT při výpočtu určitých integrálů vědět co je nízko\vysoko
co byste měli umět po dnešní lekci: používat funkce pro výpočet FFT (Fast Fourier Transformation) spočítat konvoluci/dekonvoluci pomocí FFT použít FFT při výpočtu určitých integrálů vědět co je nízko\vysoko
Cvi ení 2. Cvi ení 2. Modelování systém a proces. Mgr. Lucie Kárná, PhD. March 5, 2018
 Modelování systém a proces Mgr. Lucie Kárná, PhD karna@fd.cvut.cz March 5, 2018 1 Gracké moºnosti Matlabu 2 Zobrazení signálu 3 4 Analýza signálu Gracké moºnosti Matlabu Základní gracké p íkazy I Graf
Modelování systém a proces Mgr. Lucie Kárná, PhD karna@fd.cvut.cz March 5, 2018 1 Gracké moºnosti Matlabu 2 Zobrazení signálu 3 4 Analýza signálu Gracké moºnosti Matlabu Základní gracké p íkazy I Graf
B2M31SYN SYNTÉZA AUDIO SIGNÁLŮ
 B2M31SYN SYNTÉZA AUDIO SIGNÁLŮ zima 2016-2017 Roman Čmejla cmejla@fel.cvut.cz B2, místn.525 tel. 224 3522 36 http://sami.fel.cvut.cz/sms/ A2B31SMS - SYNTÉZA MULTIMEDIÁLNÍCH SIGNÁLŮ zima 2015-2016 http://sami.fel.cvut.cz/sms/
B2M31SYN SYNTÉZA AUDIO SIGNÁLŮ zima 2016-2017 Roman Čmejla cmejla@fel.cvut.cz B2, místn.525 tel. 224 3522 36 http://sami.fel.cvut.cz/sms/ A2B31SMS - SYNTÉZA MULTIMEDIÁLNÍCH SIGNÁLŮ zima 2015-2016 http://sami.fel.cvut.cz/sms/
SIGNÁLY A LINEÁRNÍ SYSTÉMY
 SIGNÁLY A LINEÁRNÍ SYSTÉMY prof. Ing. Jiří Holčík, CSc. holcik@iba.muni.cziba.muni.cz II. SIGNÁLY ZÁKLADNÍ POJMY SIGNÁL - DEFINICE SIGNÁL - DEFINICE Signál je jev fyzikální, chemické, biologické, ekonomické
SIGNÁLY A LINEÁRNÍ SYSTÉMY prof. Ing. Jiří Holčík, CSc. holcik@iba.muni.cziba.muni.cz II. SIGNÁLY ZÁKLADNÍ POJMY SIGNÁL - DEFINICE SIGNÁL - DEFINICE Signál je jev fyzikální, chemické, biologické, ekonomické
SIGNÁLY A LINEÁRNÍ SYSTÉMY
 SIGNÁLY A LINEÁRNÍ SYSTÉMY prof. Ing. Jiří Holčík, CSc. holcik@iba.muni.cz II. SIGNÁLY ZÁKLADNÍ POJMY SIGNÁL - DEFINICE SIGNÁL - DEFINICE Signál je jev fyzikální, chemické, biologické, ekonomické či jiné
SIGNÁLY A LINEÁRNÍ SYSTÉMY prof. Ing. Jiří Holčík, CSc. holcik@iba.muni.cz II. SIGNÁLY ZÁKLADNÍ POJMY SIGNÁL - DEFINICE SIGNÁL - DEFINICE Signál je jev fyzikální, chemické, biologické, ekonomické či jiné
Signál v čase a jeho spektrum
 Signál v čase a jeho spektrum Signály v časovém průběhu (tak jak je vidíme na osciloskopu) můžeme dělit na periodické a neperiodické. V obou případech je lze popsat spektrálně určit jaké kmitočty v sobě
Signál v čase a jeho spektrum Signály v časovém průběhu (tak jak je vidíme na osciloskopu) můžeme dělit na periodické a neperiodické. V obou případech je lze popsat spektrálně určit jaké kmitočty v sobě
Zpráva k semestrální práci z B2M31SYN Syntéza audio signálů
 Zpráva k semestrální práci z B2M31SYN Syntéza audio signálů Část 1 - Syntéza orchestrálních nástrojů pro symfonickou báseň B.Smetany "Vltava" Cílem této části práce je syntetizovat symfonickou báseň B.Smetany
Zpráva k semestrální práci z B2M31SYN Syntéza audio signálů Část 1 - Syntéza orchestrálních nástrojů pro symfonickou báseň B.Smetany "Vltava" Cílem této části práce je syntetizovat symfonickou báseň B.Smetany
Magnetická rezonance (2)
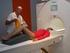 NMR spektroskopie Principy zobrazování Fourierovské MRI Magnetická rezonance (2) J. Kybic, J. Hornak 1, M. Bock, J. Hozman 2008 2013 1 http://www.cis.rit.edu/htbooks/mri/ NMR spektroskopie Principy zobrazování
NMR spektroskopie Principy zobrazování Fourierovské MRI Magnetická rezonance (2) J. Kybic, J. Hornak 1, M. Bock, J. Hozman 2008 2013 1 http://www.cis.rit.edu/htbooks/mri/ NMR spektroskopie Principy zobrazování
Opakování z předmětu TES
 Opakování z předmětu TES A3B35ARI 6..6 Vážení studenti, v následujících měsících budete každý týden z předmětu Automatické řízení dostávat domácí úkol z látky probrané v daném týdnu na přednáškách. Jsme
Opakování z předmětu TES A3B35ARI 6..6 Vážení studenti, v následujících měsících budete každý týden z předmětu Automatické řízení dostávat domácí úkol z látky probrané v daném týdnu na přednáškách. Jsme
A2B31SMS 2. PŘEDNÁŠKA 9. října 2017 Číslicové signály
 A2B3SMS 2. PŘEDNÁŠKA 9. října 27 Číslicové signály Aperiodické Periodické Aplikace Zvuky telefonu Hudební stupnice Tónová volba Tabulková (wavetable) syntéza Tabulkový oscilátor Interpolace Pitch posunutí
A2B3SMS 2. PŘEDNÁŠKA 9. října 27 Číslicové signály Aperiodické Periodické Aplikace Zvuky telefonu Hudební stupnice Tónová volba Tabulková (wavetable) syntéza Tabulkový oscilátor Interpolace Pitch posunutí
Interpolace a aproximace dat.
 Numerické metody Interpolace a aproximace dat. Interpolace dat křivkou (funkcí) - křivka (graf funkce) prochází daty (body) přesně. Aproximace dat křivkou (funkcí) - křivka (graf funkce) prochází daty
Numerické metody Interpolace a aproximace dat. Interpolace dat křivkou (funkcí) - křivka (graf funkce) prochází daty (body) přesně. Aproximace dat křivkou (funkcí) - křivka (graf funkce) prochází daty
ÚPGM FIT VUT Brno,
 Systémy s diskrétním časem Jan Černocký ÚPGM FIT VUT Brno, cernocky@fit.vutbr.cz 1 LTI systémy v tomto kursu budeme pracovat pouze se systémy lineárními a časově invariantními. Úvod k nim jsme viděli již
Systémy s diskrétním časem Jan Černocký ÚPGM FIT VUT Brno, cernocky@fit.vutbr.cz 1 LTI systémy v tomto kursu budeme pracovat pouze se systémy lineárními a časově invariantními. Úvod k nim jsme viděli již
Multimediální systémy
 Multimediální systémy Jan Outrata KATEDRA INFORMATIKY UNIVERZITA PALACKÉHO V OLOMOUCI přednášky Získání obsahu Jan Outrata (Univerzita Palackého v Olomouci) Multimediální systémy Olomouc, září prosinec
Multimediální systémy Jan Outrata KATEDRA INFORMATIKY UNIVERZITA PALACKÉHO V OLOMOUCI přednášky Získání obsahu Jan Outrata (Univerzita Palackého v Olomouci) Multimediální systémy Olomouc, září prosinec
BPC2E_C09 Model komunikačního systému v Matlabu
 BPCE_C9 Model komunikačního systému v Matlabu Cílem cvičení je vyzkoušet si sestavit skripty v Matlabu pro model jednoduchého komunikačního systému pro přenos obrázků. Úloha A. Sestavte model komunikačního
BPCE_C9 Model komunikačního systému v Matlabu Cílem cvičení je vyzkoušet si sestavit skripty v Matlabu pro model jednoduchého komunikačního systému pro přenos obrázků. Úloha A. Sestavte model komunikačního
Quantization of acoustic low level signals. David Bursík, Miroslav Lukeš
 KVANTOVÁNÍ ZVUKOVÝCH SIGNÁLŮ NÍZKÉ ÚROVNĚ Abstrakt Quantization of acoustic low level signals David Bursík, Miroslav Lukeš Při testování kvality A/D převodníků se používají nejrůznější testovací signály.
KVANTOVÁNÍ ZVUKOVÝCH SIGNÁLŮ NÍZKÉ ÚROVNĚ Abstrakt Quantization of acoustic low level signals David Bursík, Miroslav Lukeš Při testování kvality A/D převodníků se používají nejrůznější testovací signály.
Při návrhu FIR filtru řešíme obvykle následující problémy:
 Návrh FIR filtrů Při návrhu FIR filtru řešíme obvykle následující problémy: volba frekvenční odezvy požadovaného filtru; nejčastěji volíme ideální charakteristiku normovanou k Nyquistově frekvenci, popř.
Návrh FIR filtrů Při návrhu FIR filtru řešíme obvykle následující problémy: volba frekvenční odezvy požadovaného filtru; nejčastěji volíme ideální charakteristiku normovanou k Nyquistově frekvenci, popř.
Vlastnosti a modelování aditivního
 Vlastnosti a modelování aditivního bílého šumu s normálním rozdělením kacmarp@fel.cvut.cz verze: 0090913 1 Bílý šum s normálním rozdělením V této kapitole se budeme zabývat reálným gaussovským šumem n(t),
Vlastnosti a modelování aditivního bílého šumu s normálním rozdělením kacmarp@fel.cvut.cz verze: 0090913 1 Bílý šum s normálním rozdělením V této kapitole se budeme zabývat reálným gaussovským šumem n(t),
VY_32_INOVACE_E 15 03
 Název a adresa školy: Střední škola průmyslová a umělecká, Opava, příspěvková organizace, Praskova 399/8, Opava, 746 01 Název operačního programu: OP Vzdělávání pro konkurenceschopnost, oblast podpory
Název a adresa školy: Střední škola průmyslová a umělecká, Opava, příspěvková organizace, Praskova 399/8, Opava, 746 01 Název operačního programu: OP Vzdělávání pro konkurenceschopnost, oblast podpory
Frekvenční analýza optických zobrazovacích systémů
 OPT/OZI L05 Frekvenční analýza optických zobrazovacích systémů obecný model vstupní pupila výstupní pupila v z u y z o x z i difrakčně limitovaný zobrazovací systém: rozbíhavá sférická vlna od bodového
OPT/OZI L05 Frekvenční analýza optických zobrazovacích systémů obecný model vstupní pupila výstupní pupila v z u y z o x z i difrakčně limitovaný zobrazovací systém: rozbíhavá sférická vlna od bodového
9. PRINCIPY VÍCENÁSOBNÉHO VYUŽITÍ PŘENOSOVÝCH CEST
 9. PRINCIPY VÍCENÁSOBNÉHO VYUŽITÍ PŘENOSOVÝCH CEST Modulace tvoří základ bezdrátového přenosu informací na velkou vzdálenost. V minulosti se ji využívalo v telekomunikacích při vícenásobném využití přenosových
9. PRINCIPY VÍCENÁSOBNÉHO VYUŽITÍ PŘENOSOVÝCH CEST Modulace tvoří základ bezdrátového přenosu informací na velkou vzdálenost. V minulosti se ji využívalo v telekomunikacích při vícenásobném využití přenosových
Lineární a adaptivní zpracování dat. 2. SYSTÉMY a jejich popis v časové doméně
 Lineární a adaptivní zpracování dat 2. SYSTÉMY a jejich popis v časové doméně Daniel Schwarz Investice do rozvoje vzdělávání Osnova Opakování: signály Systémy: definice, několik příkladů Vlastnosti systémů
Lineární a adaptivní zpracování dat 2. SYSTÉMY a jejich popis v časové doméně Daniel Schwarz Investice do rozvoje vzdělávání Osnova Opakování: signály Systémy: definice, několik příkladů Vlastnosti systémů
Geometrické transformace
 1/15 Předzpracování v prostoru obrazů Geometrické transformace Václav Hlaváč, Jan Kybic Fakulta elektrotechnická ČVUT v Praze katedra kybernetiky, Centrum strojového vnímání hlavac@fel.cvut.cz http://cmp.felk.cvut.cz/
1/15 Předzpracování v prostoru obrazů Geometrické transformace Václav Hlaváč, Jan Kybic Fakulta elektrotechnická ČVUT v Praze katedra kybernetiky, Centrum strojového vnímání hlavac@fel.cvut.cz http://cmp.felk.cvut.cz/
B2M31SYN 3. PŘEDNÁŠKA 17. října 2018
 B2M31SYN 3. PŘEDNÁŠKA 17. října 218 ADITIVNÍ SYNTÉZA Harmonická analýza Harmonická syntéza Fourierovy řady Hudební nástroje Barva zvuku Spektrum Aditivní syntéza a spektrální modelování Parciály Fourierovy
B2M31SYN 3. PŘEDNÁŠKA 17. října 218 ADITIVNÍ SYNTÉZA Harmonická analýza Harmonická syntéza Fourierovy řady Hudební nástroje Barva zvuku Spektrum Aditivní syntéza a spektrální modelování Parciály Fourierovy
25.z-6.tr ZS 2015/2016
 Ústav technologie, mechanizace a řízení staveb Teorie měření a regulace Typové členy 2 25.z-6.tr ZS 2015/2016 2015 - Ing. Václav Rada, CSc. TEORIE ŘÍZENÍ třetí část tématu předmětu pokračuje. A oblastí
Ústav technologie, mechanizace a řízení staveb Teorie měření a regulace Typové členy 2 25.z-6.tr ZS 2015/2016 2015 - Ing. Václav Rada, CSc. TEORIE ŘÍZENÍ třetí část tématu předmětu pokračuje. A oblastí
Náhodné signály. Honza Černocký, ÚPGM
 Náhodné signály Honza Černocký, ÚPGM Signály ve škole a v reálném světě Deterministické Rovnice Obrázek Algoritmus Kus kódu } Můžeme vypočítat Málo informace! Náhodné Nevíme přesně Pokaždé jiné Především
Náhodné signály Honza Černocký, ÚPGM Signály ve škole a v reálném světě Deterministické Rovnice Obrázek Algoritmus Kus kódu } Můžeme vypočítat Málo informace! Náhodné Nevíme přesně Pokaždé jiné Především
SIGNÁLY A LINEÁRNÍ SYSTÉMY
 SIGNÁLY A LINEÁRNÍ SYSTÉMY prof. Ing. Jiří Holčík, CSc. holcik@iba.muni.cz, Kamenice 3, 4. patro, dv.č.424 INVESTICE Institut DO biostatistiky ROZVOJE VZDĚLÁVÁNÍ a analýz IV. FREKVENČNÍ TRASFORMACE SPOJITÉ
SIGNÁLY A LINEÁRNÍ SYSTÉMY prof. Ing. Jiří Holčík, CSc. holcik@iba.muni.cz, Kamenice 3, 4. patro, dv.č.424 INVESTICE Institut DO biostatistiky ROZVOJE VZDĚLÁVÁNÍ a analýz IV. FREKVENČNÍ TRASFORMACE SPOJITÉ
Transformace obrazu Josef Pelikán KSVI MFF UK Praha
 Transformace obrazu 99725 Josef Pelikán KSVI MFF UK Praha email: Josef.Pelikan@mff.cuni.cz WWW: http://cgg.ms.mff.cuni.cz/~pepca/ Transformace 2D obrazu dekorelace dat potlačení závislosti jednotlivých
Transformace obrazu 99725 Josef Pelikán KSVI MFF UK Praha email: Josef.Pelikan@mff.cuni.cz WWW: http://cgg.ms.mff.cuni.cz/~pepca/ Transformace 2D obrazu dekorelace dat potlačení závislosti jednotlivých
Zpráva k semestrální práci
 ČVUT FEL Zpráva k semestrální práci A2B31SMS Jan Vimr 2017/2018 1. Postup Zadáním semestrální práce byla syntéza libovolného hudebního nástroje pro skladbu: Let čmeláka Nikolaj Rimskij Korsakov, dále odevzdat
ČVUT FEL Zpráva k semestrální práci A2B31SMS Jan Vimr 2017/2018 1. Postup Zadáním semestrální práce byla syntéza libovolného hudebního nástroje pro skladbu: Let čmeláka Nikolaj Rimskij Korsakov, dále odevzdat
BPC2E_C08 Parametrické 3D grafy v Matlabu
 BPC2E_C08 Parametrické 3D grafy v Matlabu Cílem cvičení je procvičit si práci se soubory a parametrickými 3D grafy v Matlabu. Úloha A. Protože budete řešit transformaci z kartézských do sférických souřadnic,
BPC2E_C08 Parametrické 3D grafy v Matlabu Cílem cvičení je procvičit si práci se soubory a parametrickými 3D grafy v Matlabu. Úloha A. Protože budete řešit transformaci z kartézských do sférických souřadnic,
magnetizace M(t) potom, co těsně po rychlé změně získal vzorek magnetizaci M 0. T 1, (2)
 1 Pracovní úkoly Pulsní metoda MR (část základní) 1. astavení optimálních excitačních podmínek signálu FID 1 H ve vzorku pryže 2. Měření závislosti amplitudy signálu FID 1 H ve vzorku pryže na délce excitačního
1 Pracovní úkoly Pulsní metoda MR (část základní) 1. astavení optimálních excitačních podmínek signálu FID 1 H ve vzorku pryže 2. Měření závislosti amplitudy signálu FID 1 H ve vzorku pryže na délce excitačního
ednáška a telefonní modemy Ing. Bc. Ivan Pravda
 11.předn ednáška Telefonní přístroje, modulační metody a telefonní modemy Ing. Bc. Ivan Pravda Telefonní přístroj princip funkce - klasická analogová telefonní přípojka (POTS Plain Old Telephone Service)
11.předn ednáška Telefonní přístroje, modulační metody a telefonní modemy Ing. Bc. Ivan Pravda Telefonní přístroj princip funkce - klasická analogová telefonní přípojka (POTS Plain Old Telephone Service)
Zpráva k semestrální práci z předmětu Syntéza audio signálů. Vypracoval: Jakub Krista Zimní semestr 2016/2017 Datum odevzdání:
 Zpráva k semestrální práci z předmětu Syntéza audio signálů Vypracoval: Jakub Krista Zimní semestr 2016/2017 Datum odevzdání: 31.12.2016 Obsah 1. Úvod... 2 2. Použité druhy syntéz... 3 2.1 Aditivní syntéza...
Zpráva k semestrální práci z předmětu Syntéza audio signálů Vypracoval: Jakub Krista Zimní semestr 2016/2017 Datum odevzdání: 31.12.2016 Obsah 1. Úvod... 2 2. Použité druhy syntéz... 3 2.1 Aditivní syntéza...
3. AMPLITUDOVĚ MODULOVANÉ SIGNÁLY
 3. AMPLITUDOVĚ MODULOVANÉ SIGNÁLY Modulací nazýváme proces při kterém je jedním signálem přetvář en jiný signál za účelem př enosu informace. Př i amplitudové modulaci dochází k ovlivňování amplitudy nosného
3. AMPLITUDOVĚ MODULOVANÉ SIGNÁLY Modulací nazýváme proces při kterém je jedním signálem přetvář en jiný signál za účelem př enosu informace. Př i amplitudové modulaci dochází k ovlivňování amplitudy nosného
7. ODE a SIMULINK. Nejprve velmi jednoduchý příklad s numerických řešením. Řešme rovnici
 7. ODE a SIMULINK Jednou z často používaných aplikací v Matlabu je modelování a simulace dynamických systémů. V zásadě můžeme postupovat buď klasicky inženýrsky (popíšeme systém diferenciálními rovnicemi
7. ODE a SIMULINK Jednou z často používaných aplikací v Matlabu je modelování a simulace dynamických systémů. V zásadě můžeme postupovat buď klasicky inženýrsky (popíšeme systém diferenciálními rovnicemi
Předmět A3B31TES/Př. 13
 Předmět A3B31TES/Př. 13 PS 1 1 Katedra teorie obvodů, místnost č. 523, blok B2 Přednáška 13: Kvantování, modulace, stavový popis PS Předmět A3B31TES/Př. 13 květen 2015 1 / 28 Obsah 1 Kvantování 2 Modulace
Předmět A3B31TES/Př. 13 PS 1 1 Katedra teorie obvodů, místnost č. 523, blok B2 Přednáška 13: Kvantování, modulace, stavový popis PS Předmět A3B31TES/Př. 13 květen 2015 1 / 28 Obsah 1 Kvantování 2 Modulace
Teorie měření a regulace
 Ústav technologie, mechanizace a řízení staveb Teorie měření a regulace 22.z-3.tr ZS 2015/2016 2015 - Ing. Václav Rada, CSc. TEORIE ŘÍZENÍ druhá část tématu předmětu pokračuje. oblastí matematických pomůcek
Ústav technologie, mechanizace a řízení staveb Teorie měření a regulace 22.z-3.tr ZS 2015/2016 2015 - Ing. Václav Rada, CSc. TEORIE ŘÍZENÍ druhá část tématu předmětu pokračuje. oblastí matematických pomůcek
Řešení diferenciálních rovnic v MATLABu
 Řešení diferenciálních rovnic v MATLABu Základy algoritmizace a programování Přednáška 23. listopadu 2011 Co řešíme Obyčejné diferenciální rovnice prvního řádu: separovatelné lineární exaktní druhého řádu,
Řešení diferenciálních rovnic v MATLABu Základy algoritmizace a programování Přednáška 23. listopadu 2011 Co řešíme Obyčejné diferenciální rovnice prvního řádu: separovatelné lineární exaktní druhého řádu,
Diskretizace. 29. dubna 2015
 MSP: Domácí příprava č. 3 Vnitřní a vnější popis diskrétních systémů Dopředná Z-transformace Zpětná Z-transformace Řešení diferenčních rovnic Stabilita diskrétních systémů Spojování systémů Diskretizace
MSP: Domácí příprava č. 3 Vnitřní a vnější popis diskrétních systémů Dopředná Z-transformace Zpětná Z-transformace Řešení diferenčních rovnic Stabilita diskrétních systémů Spojování systémů Diskretizace
Analýza lineárních regulačních systémů v časové doméně. V Modelice (ale i v Simulinku) máme blok TransfeFunction
 Analýza lineárních regulačních systémů v časové doméně V Modelice (ale i v Simulinku) máme blok TransfeFunction Studijní materiály http://physiome.cz/atlas/sim/regulacesys/ Khoo: Physiological Control
Analýza lineárních regulačních systémů v časové doméně V Modelice (ale i v Simulinku) máme blok TransfeFunction Studijní materiály http://physiome.cz/atlas/sim/regulacesys/ Khoo: Physiological Control
Modulace a šum signálu
 Modulace a šum signálu PATRIK KANIA a ŠTĚPÁN URBAN Nejlepší laboratoř molekulové spektroskopie vysokého rozlišení Ústav analytické chemie, VŠCHT Praha kaniap@vscht.cz a urbans@vscht.cz http://www.vscht.cz/anl/lmsvr
Modulace a šum signálu PATRIK KANIA a ŠTĚPÁN URBAN Nejlepší laboratoř molekulové spektroskopie vysokého rozlišení Ústav analytické chemie, VŠCHT Praha kaniap@vscht.cz a urbans@vscht.cz http://www.vscht.cz/anl/lmsvr
MĚŘENÍ ÚHLOVÝCH KMITŮ ZA ROTACE
 26. mezinárodní konference DIAGO 27 TECHNICKÁ DIAGNOSTIKA STROJŮ A VÝROBNÍCH ZAŘÍZENÍ MĚŘENÍ ÚHLOVÝCH KMITŮ ZA ROTACE Jiří TŮMA VŠB Technická Univerzita Ostrava Osnova Motivace Kalibrace měření Princip
26. mezinárodní konference DIAGO 27 TECHNICKÁ DIAGNOSTIKA STROJŮ A VÝROBNÍCH ZAŘÍZENÍ MĚŘENÍ ÚHLOVÝCH KMITŮ ZA ROTACE Jiří TŮMA VŠB Technická Univerzita Ostrava Osnova Motivace Kalibrace měření Princip
Flexibilita jednoduché naprogramování a přeprogramování řídícího systému
 Téma 40 Jiří Cigler Zadání Číslicové řízení. Digitalizace a tvarování. Diskrétní systémy a jejich vlastnosti. Řízení diskrétních systémů. Diskrétní popis spojité soustavy. Návrh emulací. Nelineární řízení.
Téma 40 Jiří Cigler Zadání Číslicové řízení. Digitalizace a tvarování. Diskrétní systémy a jejich vlastnosti. Řízení diskrétních systémů. Diskrétní popis spojité soustavy. Návrh emulací. Nelineární řízení.
UNIVERZITA PARDUBICE. Fakulta elektrotechniky a informatiky. Fourierovy Řady Jakub Jeřábek
 UNIVERZITA PARDUBICE Fakulta elektrotechniky a informatiky Fourierovy Řady Jakub Jeřábek Bakalářská práce 2012 Prohlášení autora Prohlašuji, že jsem tuto práci vypracoval samostatně. Veškeré literární
UNIVERZITA PARDUBICE Fakulta elektrotechniky a informatiky Fourierovy Řady Jakub Jeřábek Bakalářská práce 2012 Prohlášení autora Prohlašuji, že jsem tuto práci vypracoval samostatně. Veškeré literární
Modulační syntéza 8. prosince 2014
 ZZS-12 Modulační syntéza 8. prosince 2014 Amplitudová modulace Syntetické zvony Jednoduché syntetické FM nástroje Syntetické zvuky vítr Kruhová modulace t f f t f f t f t f m c m c c m ) ( 2 cos 2 1 )
ZZS-12 Modulační syntéza 8. prosince 2014 Amplitudová modulace Syntetické zvony Jednoduché syntetické FM nástroje Syntetické zvuky vítr Kruhová modulace t f f t f f t f t f m c m c c m ) ( 2 cos 2 1 )
pi Ludolfovo číslo π = 3,14159 e Eulerovo číslo e = 2,71828 (lze spočítat jako exp(1)), např. je v Octave, v MATLABu tato konstanta e není
 realmax maximální použitelné reálné kladné číslo realmin minimální použitelné reálné kladné číslo (v absolutní hodnotě, tj. číslo nejblíž k nule které lze použít) 0 pi Ludolfovo číslo π = 3,14159 e Eulerovo
realmax maximální použitelné reálné kladné číslo realmin minimální použitelné reálné kladné číslo (v absolutní hodnotě, tj. číslo nejblíž k nule které lze použít) 0 pi Ludolfovo číslo π = 3,14159 e Eulerovo
PSK1-5. Frekvenční modulace. Úvod. Vyšší odborná škola a Střední průmyslová škola, Božetěchova 3 Ing. Marek Nožka. Název školy: Vzdělávací oblast:
 PSK1-5 Název školy: Autor: Anotace: Vzdělávací oblast: Předmět: Tematická oblast: Výsledky vzdělávání: Klíčová slova: Druh učebního materiálu: Vyšší odborná škola a Střední průmyslová škola, Božetěchova
PSK1-5 Název školy: Autor: Anotace: Vzdělávací oblast: Předmět: Tematická oblast: Výsledky vzdělávání: Klíčová slova: Druh učebního materiálu: Vyšší odborná škola a Střední průmyslová škola, Božetěchova
Rozprostřené spektrum. Multiplex a mnohonásobný přístup
 Rozprostřené spektrum Multiplex a mnohonásobný přístup Multiplex Přenos více nezávislých informačních signálů jedním přenosovým prostředím (mezi dvěma body) Multiplexování MPX Vratný proces sdružování
Rozprostřené spektrum Multiplex a mnohonásobný přístup Multiplex Přenos více nezávislých informačních signálů jedním přenosovým prostředím (mezi dvěma body) Multiplexování MPX Vratný proces sdružování
DIGITÁLNÍ KOMUNIKACE S OPTICKÝMI VLÁKNY. Digitální signál bude rekonstruován přijímačem a přiváděn do audio zesilovače.
 DIGITÁLNÍ KOMUNIKACE S OPTICKÝMI VLÁKNY 104-4R Pomocí stavebnice Optel sestavte optický systém, který umožní přenos zvuku. Systém bude vysílat audio informaci prostřednictvím optického kabelu jako sekvenci
DIGITÁLNÍ KOMUNIKACE S OPTICKÝMI VLÁKNY 104-4R Pomocí stavebnice Optel sestavte optický systém, který umožní přenos zvuku. Systém bude vysílat audio informaci prostřednictvím optického kabelu jako sekvenci
Zpracování obrazů. Honza Černocký, ÚPGM
 Zpracování obrazů Honza Černocký, ÚPGM 1D signál 2 Obrázky 2D šedotónový obrázek (grayscale) Několikrát 2D barevné foto 3D lékařské zobrazování, vektorová grafika, point-clouds (hloubková mapa, Kinect)
Zpracování obrazů Honza Černocký, ÚPGM 1D signál 2 Obrázky 2D šedotónový obrázek (grayscale) Několikrát 2D barevné foto 3D lékařské zobrazování, vektorová grafika, point-clouds (hloubková mapa, Kinect)
SYNTÉZA AUDIO SIGNÁLŮ
 SYNTÉZA AUDIO SIGNÁLŮ R. Čmejla Fakulta elektrotechnická, ČVUT v Praze Abstrakt Příspěvek pojednává o technikách číslicové audio syntézy vyučovaných v předmětu Syntéza multimediálních signálů na Elektrotechnické
SYNTÉZA AUDIO SIGNÁLŮ R. Čmejla Fakulta elektrotechnická, ČVUT v Praze Abstrakt Příspěvek pojednává o technikách číslicové audio syntézy vyučovaných v předmětu Syntéza multimediálních signálů na Elektrotechnické
Funkce komplexní proměnné a integrální transformace
 Funkce komplexní proměnné a integrální transformace Fourierovy řady I. Marek Lampart Text byl vytvořen v rámci realizace projektu Matematika pro inženýry 21. století (reg. č. CZ.1.07/2.2.00/07.0332), na
Funkce komplexní proměnné a integrální transformace Fourierovy řady I. Marek Lampart Text byl vytvořen v rámci realizace projektu Matematika pro inženýry 21. století (reg. č. CZ.1.07/2.2.00/07.0332), na
VOLBA ČASOVÝCH OKEN A PŘEKRYTÍ PRO VÝPOČET SPEKTER ŠIROKOPÁSMOVÝCH SIGNÁLŮ
 VOLBA ČASOVÝCH OKEN A PŘEKRYTÍ PRO VÝPOČET SPEKTER ŠIROKOPÁSOVÝCH SIGNÁLŮ Jiří TŮA, VŠB Technická univerzita Ostrava Petr Czyž, Halla Visteon Autopal Services, sro Nový Jičín 2 Anotace: Referát se zabývá
VOLBA ČASOVÝCH OKEN A PŘEKRYTÍ PRO VÝPOČET SPEKTER ŠIROKOPÁSOVÝCH SIGNÁLŮ Jiří TŮA, VŠB Technická univerzita Ostrava Petr Czyž, Halla Visteon Autopal Services, sro Nový Jičín 2 Anotace: Referát se zabývá
 Úkol 1 Zpráva k semestrální práci k předmětu B2M31SYN Syntéza audio signálů Lukáš Krauz krauzluk@fel.cvut.cz Hlavním cílem této úlohy bylo vytvořit za pomoci MIDI souboru, obsahující noty a stopy k jednotlivým
Úkol 1 Zpráva k semestrální práci k předmětu B2M31SYN Syntéza audio signálů Lukáš Krauz krauzluk@fel.cvut.cz Hlavním cílem této úlohy bylo vytvořit za pomoci MIDI souboru, obsahující noty a stopy k jednotlivým
Vstupní signál protne zvolenou úroveň. Na základě získaných údajů se dá spočítat perioda signálu a kmitočet. Obrázek č.2
 2. Vzorkovací metoda Určení kmitočtu z vzorkovaného průběhu. Tato metoda založena na pozorování vstupního signálu pomocí osciloskopu a nastavení určité úrovně, pro zjednodušování považujeme úroveň nastavenou
2. Vzorkovací metoda Určení kmitočtu z vzorkovaného průběhu. Tato metoda založena na pozorování vstupního signálu pomocí osciloskopu a nastavení určité úrovně, pro zjednodušování považujeme úroveň nastavenou
Klasifikace hudebních stylů
 Klasifikace hudebních stylů Martin Šimonovský (mys7@seznam.cz) Rozpoznávání hudby úloha z oblasti DSP klasifikace dle hudebních stylů
Klasifikace hudebních stylů Martin Šimonovský (mys7@seznam.cz) Rozpoznávání hudby úloha z oblasti DSP klasifikace dle hudebních stylů
CW01 - Teorie měření a regulace
 Ústav technologie, mechanizace a řízení staveb CW01 - Teorie měření a regulace ZS 2014/2015 tm-ch-spec. 1.p 2014 - Ing. Václav Rada, CSc. Ústav technologie, mechanizace a řízení staveb Teorie měření a
Ústav technologie, mechanizace a řízení staveb CW01 - Teorie měření a regulace ZS 2014/2015 tm-ch-spec. 1.p 2014 - Ing. Václav Rada, CSc. Ústav technologie, mechanizace a řízení staveb Teorie měření a
" Furierova transformace"
 UNIVERZITA JANA EVANGELISTY PURKYNĚ V ÚSTÍ NAD LABEM FAKULTA ŽIVOTNÍHO PROSTŘEDÍ " Furierova transformace" Seminární práce z předmětu Dálkový průzkum Země Marcela Bartošová, Veronika Bláhová OŽP, 3.ročník
UNIVERZITA JANA EVANGELISTY PURKYNĚ V ÚSTÍ NAD LABEM FAKULTA ŽIVOTNÍHO PROSTŘEDÍ " Furierova transformace" Seminární práce z předmětu Dálkový průzkum Země Marcela Bartošová, Veronika Bláhová OŽP, 3.ročník
Biofyzikální ústav LF MU Brno. jarní semestr 2011
 pro obor Ošetřovatelská péče v gerontologii Biofyzikální ústav LF MU Brno jarní semestr 2011 Obsah letmý dotyk teorie systémů klasifikace a analýza biosignálů Co je signál? Co je biosignál? Co si počít
pro obor Ošetřovatelská péče v gerontologii Biofyzikální ústav LF MU Brno jarní semestr 2011 Obsah letmý dotyk teorie systémů klasifikace a analýza biosignálů Co je signál? Co je biosignál? Co si počít
v Praze mezi kanály EEG Ondřej Drbal 5. ročník, stud. sk. 9
 České vysoké učení technické v Praze Algoritmy pro měření zpoždění mezi kanály EEG Ondřej Drbal 5. ročník, stud. sk. 9 31. března 23 Obsah 1 Zadání 1 2 Uvedení do problematiky měření zpoždění signálů 1
České vysoké učení technické v Praze Algoritmy pro měření zpoždění mezi kanály EEG Ondřej Drbal 5. ročník, stud. sk. 9 31. března 23 Obsah 1 Zadání 1 2 Uvedení do problematiky měření zpoždění signálů 1
MĚŘENÍ A ANALÝZA ELEKTROAKUSTICKÝCH SOUSTAV NA MODELECH. Petr Kopecký ČVUT, Fakulta elektrotechnická, Katedra Radioelektroniky
 MĚŘENÍ A ANALÝZA ELEKTROAKUSTICKÝCH SOUSTAV NA MODELECH Petr Kopecký ČVUT, Fakulta elektrotechnická, Katedra Radioelektroniky Při návrhu elektroakustických soustav, ale i jiných systémů, je vhodné nejprve
MĚŘENÍ A ANALÝZA ELEKTROAKUSTICKÝCH SOUSTAV NA MODELECH Petr Kopecký ČVUT, Fakulta elektrotechnická, Katedra Radioelektroniky Při návrhu elektroakustických soustav, ale i jiných systémů, je vhodné nejprve
Analýza a zpracování digitálního obrazu
 Analýza a zpracování digitálního obrazu Úlohy strojového vidění lze přibližně rozdělit do sekvence čtyř funkčních bloků: Předzpracování veškerých obrazových dat pomocí filtrací (tj. transformací obrazové
Analýza a zpracování digitálního obrazu Úlohy strojového vidění lze přibližně rozdělit do sekvence čtyř funkčních bloků: Předzpracování veškerých obrazových dat pomocí filtrací (tj. transformací obrazové
Laplaceova transformace
 Laplaceova transformace Modelování systémů a procesů (11MSP) Bohumil Kovář, Jan Přikryl, Miroslav Vlček Ústav aplikované matematiky ČVUT v Praze, Fakulta dopravní 5. přednáška 11MSP pondělí 23. března
Laplaceova transformace Modelování systémů a procesů (11MSP) Bohumil Kovář, Jan Přikryl, Miroslav Vlček Ústav aplikované matematiky ČVUT v Praze, Fakulta dopravní 5. přednáška 11MSP pondělí 23. března
