MASARYKOVA UNIVERZITA
|
|
|
- Veronika Veselá
- před 8 lety
- Počet zobrazení:
Transkript
1 MASARYKOVA UNIVERZITA PŘÍRODOVĚDECKÁ FAKULTA DIPLOMOVÁ PRÁCE Bc. PAVLA HOLUBÁŘOVÁ MATEMATICKÉ METODY JIŠTĚNÍ OPČNÍCH PORTFOLIÍ (MATHEMATICAL METHODS OF HEDGING OPTION PORTFOLIOS) doc. RNDr. MARTIN KOLÁŘ, Ph.D. Studijní program: Aplikovaná matematika Studijní obor: Finanční matematika BRNO 2011
2 Název: Matematické metody jištění opčních portfolií Autor: Bc. Pavla Holubářová Ústav matematiky a statistiky Přírodovědecké fakulty, MU Vedoucí diplomové práce: doc. RNDr. Martin Kolář, Ph.D. Abstrakt Předmětem diplomové práce je jištění opčních portfolií. Začátek práce je věnován úvodu do teorie opcí. Následuje část věnovaná Black-Scholesovu modelu, kde jdou uvedeny předpoklady modelu, odvození Black-Scholesovy rovnice a její následné analytické řešení za pomocí transformace na rovnici vedení tepla. Závěr práce se věnuje hedgingu a popisu jednotlivých jistících strategíí s následnou aplikací na příkladu s reálnými daty. Klíčová slova opce, oceňování opcí, Brownůw pohyb, Black-Scholesův model, delta hedging, stop loss, jištění Title: Mathematical methods of hedging option portfolios Author: Bc. Pavla Holubářová Department of Mathematics and Statistics, Faculty of Science, MU Supervisor: doc. RNDr. Martin Kolář, Ph.D. Abstract The goal of this thesis is hedging of options. In the first part are described the basics of option theory. Following part deals with Black-Scholes model, derivation of the Black-Scholes equation and its analytical solving with transformation to the heat equation. The last part of the thesis is about hedging and involves descriptions of the hedging strategies and aplications of these strategies in the example with real data. Keywords option, option valuation, Brownian motion, Black-Scholes model, delta hedging, hedging, stop loss
3 Poděkování Na tomto místě bych v prvé řadě ráda poděkovala doc. RNDr. Martinu Kolářovi, Ph.D. za vedení mé práce, poskytnuté rady a dodávání motivace v průběhu vypracovávání. Dále bych chtěla poděkovat svým rodičům a svému příteli za psychickou podporu, kterou mi během práce poskytovali. Prohlášení Prohlašuji, že jsem diplomovou práci Matematické metody jištění opčních portfolií vypracovala samostatně pod vedením pana doc. RNDr. Martina Koláře, Ph.D. a uvedla v ní všechny použité literární a jiné odborné zdroje. V Brně dne 18. září 2011
4 Obsah Úvod 3 1 Úvod k opcím Obchodování s opcemi Typy opcí Black-Scholesova rovnice Předpoklady Black-Scholesova modelu Brownův pohyb Odvození Black-Scholesovy rovnice Okrajové podmínky Analytické řešení Black-Scholesovy rovnice Rovnice vedení tepla Odvození Black-Scholesova vzorce Hedging opcí Opční charakteristiky Delta Gama Vega Theta Rho Zajišťovací strategie Statický hedging Dynamický hedging Aplikace zajišťovacích strategií na zvolené opční portfolio Opce na akcie společnosti AXA Krytá pozice Stop loss Delta hedging Shrnutí Opce na ACCOR S.A Krytá pozice Stop loss Delta hedging Shrnutí
5 5.3 Srovnání jednotlivých zajišťovacích strategií Závěr 60 Literatura 63 Seznam obrázků 65 Seznam tabulek 69 A Delta hedging - AXA 70 B Delta hedging - ACCOR 86 C Značení 102 2
6 Úvod Tato práce se zabývá metodami jištění opčních portfolií, přičemž pro oceňování opcí bude využito známého Black-Scholesova modelu. Text je celkem členěn do pěti kapitol, kdy se bude postupovat od teoretických východisek až ke konečné aplikaci těchto poznatků v praktické části práce. První kapitola bude, jak již bylo naznačeno, věnována teoretickému úvodu do opcí, kde si pojem opce zadefinujeme a dále si tento finanční derivát blíže představíme z hlediska jeho vlastností, obchodování s ním a uvedeme si základní typy opcí. Protože k ocenění budeme využívat Black-Scholesův model, bude druhá kapitola věnována právě odvození Black- Scholesovy rovnice. Přestože tento model představili pánové Black a Scholes již v 70. letech. 20. století, i dnes je investory často využíván prostřednictvím svých modifikací. Na začátek kapitoly budou uvedeny předpoklady modelu - bude představen tzv. ideální trh. Jelikož se v celé práci budou využívat opce na akcie, rozebereme si poté blíže jeden z předpokladů ohledně modelování vývoje ceny akcie, kterým je Brownůw pohyb. Na konci kapitoly pak bude odvozena Black-Scholesova rovnice. Obsahem následující kapitoly bude analytické řešení této rovnice, jejímž řešením je Black-Scholesův vzorec pro oceňování opcí. Ten budeme potřebovat nejen k zjištění hodnoty opce, ale využijeme ho i nadále při zajišťování opcí. K řešení rovnice budeme muset nejprve stanovit okrajové a koncové podmínky rovnice za účelem jednoznačnosti řešení. Ke konečnému vyřešení pak využijeme rovnice vedení tepla. Další kapitola se již bude zabývat zajišťěním, neboli hedgingem. Nejprve si úděláme obecný úvod k hedgingu a popíšeme si tzv. opční charakteristiky, které jsou základem některých jistících strategií. Poté již přejdeme k představení jednotlivých 3
7 zajišťovacích strategií, které budou rozčleněny do dvou skupin na statické a dynamické. Dále bude popsána podstata každé z těchto strategií s následným názorným předvedením na příkladu. Poslední kapitola pak bude věnována aplikaci uvedených jistících strategií na portfolio opcí, jehož podkladem budou reálná tržní data. Následně pak budou výsledky jednotlivých strategií v našem příkladě zhodnoceny, především se zaměříme na strategie stop loss a delta hedging. 4
8 1 Úvod k opcím Současné finanční trhy nabízejí investorům velké množství různých finančních produktů. Velmi rozšířenými a též oblíbenými investičními nástroji jsou finanční deriváty, jejichž hodnota je odvozena od hodnoty jiného finančního instrumentu. Tento instrument se označuje jako podkladové aktivum a nejčastěji se jedná o úrokové míry, měny, akcie, komodity či akciové indexy. Podstatou derivátů je nesoulad mezi časem uzavření obchodu a jeho vypořádáním. Základními typy finančních derivátů jsou forwardy, futures, swapy a opce. Právě posledním jmenovaným typem se bude tato práce zabývat, přičemž jako podklad opce je zvolena akcie, neboť jsou akciové opce na trhu obchodovány v největších objemech. Opce je kontrakt uzavřený mezi dvěma stranami - vlastníkem opce (kupující) a upisovatelem opce (prodávající). Definice 1 Opce jsou instrumenty, jejichž vlastník má právo koupit, resp. prodat sjednané množství daného podkladového aktiva za předem dohodnutou cenu a v předem stanoveném čase. Upisovatel opce má naopak povinnost vlastníkovi opce toto aktivum prodat, resp. koupit. Cena podkladu, na níž se obě strany dopředu dohodly, se nazývá realizační cena a dobu, kdy má být kontrakt vypořádán, pak nazýváme časem expirace. Dalšími důležitými parametry kontraktu je obchodovaný počet podkladového aktiva (nejčastěji 100 ks a násobky 100), datum uzavření a o jaký druh opce se jedná. 1.1 Obchodování s opcemi Opce jsou obchodovány jednak na burzách, jednak tzv. přes přepážku (over-thecounter, zkráceně OTC). Opce obchodované na burzách jsou standardizované - jsou pevně stanoveny parametry sjednávaného obchodu (například množství dodaných akcií, čas plnění obchodu)- a tím je zvýšena jejich likvidita. Mezi významné opční 5
9 burzy patří Chicago Board Options Exchange (CBOE) či London International Financial Futures and Options Exchange (LIFFE). Opce obchodované na OTC trzích jsou oproti burzám vytvořené dle potřeb konkrétního zákazníka, neboť podmínky obchodu si sjednávají smluvní strany samy. Důsledkem je snížená likvidita opce (je težší nalézt protistranu, které by vyhovovaly stejné podmínky). Opce jsou investory využívány pro zajištění rizika, spekulaci či arbitráž. Původním motivem pro nákup opcí bylo zajištění (hedging) proti fluktuacím v ceně podkladu. Opce investorovi umožňují zafixovat si cenu aktiva pro budoucí obchod. Častějším důvodem obchodování s opcemi je však v současnosti spekulace na vývoj kurzu podkladového aktiva a s ní využívání pákového efektu opcí, pomocí něhož mohou investoři znásobit své potencionální zisky (ale též ztráty). Posledním důvodem je využití opce k arbitráži, kdy se investor snaží využít rozdílů v cenách derivátu na různých trzích či mezi promptním a termínovým trhem, čímž může dosáhnout bezrizikového zisku. 1.2 Typy opcí Základní členění opcí rozlišuje opce na kupní opce (call) a prodejní opce (put). V případě kupní opce má její vlastník právo nakoupit podkladové aktivum a upisovatel opce má povinnost mu ho prodat. Naopak prodejní opce představuje pro vlastníka právo prodat podkladové aktivum, kdežto pro upisovatele povinnost toto aktivum v případě uplatnění opce nakoupit. Dle možnosti vypořádání opce členíme opce na evropské a americké. Zatímco evropské opce může jejich vlastník uplatnit pouze v čase expirace, tj. na konci životnosti opce, americké opce lze uplatnit kdykoliv během jejich životnosti. V dalším textu budou uvažovány pouze opce evropské. Vlastník kupní opce ji při expiraci (v čase T ) uplatní pouze v případě, že cena akcie bude větší než realizační cena, S T > K, a opce je tzv. v penězích (in the money, zkráceně ITM). V případě, že se obě ceny rovnají, S t = K, tj. opce je na penězích (at the money, ATM) je jedno, zda vlastník opci uplatní či ne. Bude-li S t < K, pak je opce mimo peníze (out of the money, OTM) a nebude uplatněna, neboť je levnější pořídit akcii přímo na trhu. 6
10 Obrázek 1.1: Výplatní funkce evropské kupní a prodejní opce. Majitel prodejní opce taktéž opci uplatní v případě, že skončí ITM (u put opce S t < K) či ATM, zatímco při S t > K je opce OTM a tudíž bezcenná. Hodnotu opce při expiraci lze popsat pomocí výplatní funkce V (S T, T ) opce, call : V C = max(s T K, 0), put : V P = max(k S T, 0), (1.1) které jsou vykresleny na obrázku (1.1). Protože vlastník opce si může vybrat, zda opci uplatní či ne, má oproti upisovateli jistou výhodu, za níž upisovateli opce platí při uzavření kontraktu tzv. opční prémii. Tato prémie se skládá ze dvou složek. První složku tvoří vnitřní hodnota opce - hodnota získaná okamžitým uplatněním opce, kterou vypočítáme dosazením aktuální hodnoty akcie do vzorce (1.1) místo S T, tedy např. pro call opci činí vnitřní hodnota max(s t K, 0). Tato hodnota je vždy nezáporná. Druhou složku prémie tvoří časová hodnota opce - rozdíl mezi prémií a vnitřní hodnotou opce. Už víme, jaká je hodnota opce při expiraci. Otázkou ovšem zůstává hodnota opce během životnosti a tím i velikost opční prémie. Jaká je správná hodnota opce? Existuje několik modelů pro oceňování opcí, které se snaží tuto hodnotu nalézt. Tím nejznámnějším a také nejrozšířenějším, z něhož bude i tato práce vycházet, je Black-Scholesův model. 7
11 2 Black-Scholesova rovnice První významný a přelomový oceňovací model představil ve své práci již v roce 1900 francouzský matematik Louis Bachelier 1. Další důležitý převrat v oceňování pak způsobili svou prací The Pricing of Options and Corporate Liabilities z roku 1973 pánové Black a Scholes, když vyřešili otázku oceňování opcí ve spojitém čase. Problém totiž transformovali na řešení parabolické parciální diferenciální rovnice, přičemž podstatou odvození této rovnice byla konstrukce bezrizikového portfolia ob sahujícího akcie a opce. Pozoruhodným aspektem modelu je jeho nezávislost na pos tojích investora k riziku i jeho očekáváních. Za způsob odvození vzorce pro oceňování evropského typu opcí nakonec obdržel pan Scholes Nobelovu cenu za ekonomii. Tato kapitola je věnována odvození Black-Scholesovy rovnice a následně také jejím analytickým řešením, čímž se dospěje k známemu oceňovacímu vzorci. Nejprve si však uveďme předpoklady Black-Scholesova modelu. 2.1 Předpoklady Black-Scholesova modelu Zjednodušující předpoklady, tzv. ideální podmínky na trhu, s nimiž byl Black- Scholesův vzorec odvozen, jsou následující 2 : - bezriziková úroková míra je známá a konstantní po celou dobu, - cena akcie se vyvíjí dle geometrického Brownova pohybu, - volatilita akcie je konstantní, - akcie nevyplácí dividendy, - opce je evropského typu, - neuvažujeme žádné transakční náklady (spread, komise, daně a jiné poplatky), - lze nakoupit a prodat jakékoliv množství akcií, - je povolen prodej nakrátko (short selling) a to po celou potřebnou dobu. 1 Přehled jednotlivých modelů oceňování opcí viz Haug, [7] 2 viz Black, Scholes, [2], str
12 Jako další zjednodušující podmínky uveďme, že uvažujeme pouze jednu cenu akcie (tedy nákupní i prodejní cena je stejná), stejně tak je pouze jedna bezriziková úroková míra pro půjčování a výpůjčky. Trh je vždy likvidní bez příležitosti k arbitráži, přičemž se obchoduje kontinuálně. Přestože se jedná o zjednodušující podmínky, některé jsou až nereálné (např. konstantní volatilita, neexistence nákladů aj.), je Black-Scholesův model využíván i v dnešním reálném obchodním prostředí. Zkušení investoři, kteří ho používají, jsou si totiž dobře vědomi jeho nedostatků a omezení, někdy si pro své potřeby model modifikují např. přidáním dalších parametrů. Původní model tak položil základy pro vznik nových a lepších způsobů oceňování opcí. V této práci bude též využit lehce modifikovaný model, neboť oproti původnímu Black-Scholesovu modelu budou uvažovány výplaty dividend z akcií, čímž bude model o něco reálnější. Za výše uvedených předpokladů hodnota opce V závisí pouze na ceně podkladového aktiva S t a času t, tedy V = V (S t, t). Black-Scholesův vzorec pro výpočet hodnoty opce vypadá následovně kde call : V C (S t, t) = S t e q(t t) N(d 1 ) Ke r(t t) N(d 2 ), put : V P (S t, t) = Ke r(t t) N( d 2 ) S t e q(t t) N( d 1 ), d 1 = ln S + (r q + 1 K 2 σ2 )(T t) σ, T t d 2 = d 1 σ T t a N(.) je distribuční funkce standardního normálního rozdělení, tj. N(x) = 1 2π x e y 2 dy. 9
13 Vztah mezi hodnotou kupní a prodejní opce se stejným podkladem, expirační dobou a realizační cenou lze vyjádřit jako V C + Ke r(t t) + S t e q(t t) = V P + S t. Tento vztah se nazývá put-call parita. Známe-li hodnotu kupní opce, můžeme z ní odvodit hodnotu odpovídající prodejní opce a naopak. Ještě než přejdeme k odvození samotné rovnice, podívejme se blíže na klíčový předpoklad modelu, kterým je vývoj ceny podkladu dle geometrického Brownova pohybu. 2.2 Brownův pohyb Přestože je ve skutečnosti vývoj ceny akcie po částech spojitý a navíc s diskrétními skoky, bude pro nás v našem modelu vhodnou aproximací tohoto vývoje spojitý proces. Konkrétně pro modelování vývoje ceny akcie, jak je uvedeno v předpokladech modelu, využijeme Brownův pohyb. Definice 2 Stochastický proces ve spojitém časem {W t, t 0} se nazývá standardní Brownův pohyb (též Wienerův proces) jestliže platí: W 0 = 0, trajektorie jsou spojité, pro každé t 0 = 0 < t 1 < t 2... < t n jsou přírůstky (W t1 W t0 ), (W t2 W t1 ),...(W tn W tn 1 ) náhodnými proměnnými a navzájem nezávislé, pro každé 0 s t je přírůstek (W t W s ) N(0, t s). Obecný Brownův pohyb lze vyjádřit pomocí stochastické diferenciální rovnice jako dx t = µdt + σdw t, 10
14 Obrázek 2.1: Wienerův proces (vlevo) a geometrický Brownův pohyb. kde µ značí drift a σ volatilitu. Zatímco µdt představuje deterministickou složku Brownova pohybu, σdw t je složkou fluktuační (náhodnou). Spíše něž Brownův pohyb však pro modelování náhodného vývoje ceny aktiva využijeme geometrický Brownův pohyb, neboť standardní Brownův pohyb může nabývat i záporných hodnot, což je v případě kotace ceny akcie nežádoucí. Definice 3 Nechť {X t, t 0} je Brownův pohyb s parametry µ a σ a y 0 R +, pak se systém náhodných proměnných {Y t, t 0}, kde Y (t) = y 0 e X(t), t 0, nazývá geometrický Brownův pohyb 3. Ve tvaru stochastické diferenciální rovnice lze geometrický Brownův pohyb vyjádřit takto: dy t = µy t dt + σy t dw t. Protože Brownův pohyp, resp. Wienerův proces není diferencovatelný, je při práci s ním třeba použít jiných pravidel než nabízí diferenciální počet a sice stochastický kalkulus. Základním nástrojem tohoto počtu je Itôovo lemma. 3 viz Ševčovič, [6], str.24 11
15 Lemma 1 (Itôovo lemma) Nechť f(x, t) je dvakrát spojitě diferencovatelná funkce, tj. třídy C 2, a X t je řešením stochastické diferenciální rovnice ve tvaru dx t = µ(x t, t)dt + σ(x t, t)dw t. Pak df je také stochastický proces daný vztahem df = f ( f x dx + t + 1 ) 2 σ2 (X t, t) 2 f dt. x 2 Důkaz např. viz Melicherčík, [11], str Právě na základě aplikace tohoto lemmatu jsme schopni odvodit Black-Scholesovu rovnici, která má pro náš případ akcie vyplácející spojitě dividendu s roční dividendovou mírou q, pro q > 0 tvar V t + (r q)sv S σ2 S 2 V SS rv = 0, kde dolní indexy značí parciální derivaci podle odpovídající proměnné. 2.3 Odvození Black-Scholesovy rovnice Black-Scholesova rovnice popisuje časový vývoj ceny opce na akcii jakožto funkci ceny akcie S a času t. Základním předpokladem modelu je zmíněný geometrický Brownův pohyb pro modelování náhodného vývoje ceny akcie jako funkce času, S = S(t). Protože uvažujeme vyplácení dividend, držbou akcie za krátký časový okamžik dt činí dividenda qsdt. Vyplácení dividend má však za následek pokles v ceně akcie. To se projeví v rovnici popisující geometrický Brownův pohyb sníženým trendem, tj. ds = (µ q)sdt + σsdw, (2.1) kde ds je změna ceny akcie za časový okamžik dt, µ je očekávaný výnos akcie, σ 12
16 je volatilita časového vývoje ceny akcie, dw je přírůstek Wienerova procesu. Tuto rovnici lze napsat také ve tvaru ds S = (µ q)dt + σdw, neboť spíše než absolutní změna ceny akcie bude podstatnější relativní změna ceny a model bude nezávislý na volbě jednotek. Nechť hodnota opce V (S, t) je dostatečně hladká funkce a S = S(t) vyhovuje rovnici (2.1). Z Itôova lemmatu plyne, že dv = (V t + (µ q)sv S + 12 σ2 S 2 V SS ) dt + σsv S dw, kde dolní indexy opět značí parciální derivaci. Uvažujme portfolio Π složené z jedné upsané opce o ceně V a akcií o ceně S, tedy hodnota portfolia v čase t činí Π = V + S. (2.2) Za nekonečně malý časový okamžik dt se hodnota portfolia změní o dπ = dv + (ds + qs). Dosazením za ds a dv dostáváme, že dπ = σs( V S + )dw ( (µ q)s( V S + ) + 1 ) 2 σ2 S 2 V SS + V t qs dt. Volbou = V S lze z rovnice odstranit náhodný člen dw a zároveň s ním zmizí také člen s driftem µ q, což znamená, že hodnota opce nebude záviset na očekávané míře růstu akcie. Celkově je tedy nekonečně malá změna portfolia rovna 13
17 dπ = ( 1 2 σ2 S 2 V SS qsv S + V t ) dt (2.3) a je zcela deterministická. Touto volbou jsme tak vytvořili portfolio neutrální vůči stochastickým fluktuacím v ceně podkladové akcie. Z předpokladu konstantní bezrizikové úrokové míry r, neexistence arbitráže a neexistence jakýchkoliv poplatků na trhu musí být výnos portfolia roven výnosu jakéhokoliv jiného bezrizikového instrumentu na trhu. Proto platí, že dπ = rπdt. Dosazením za dπ z (2.3) a Π z (2.2) tedy rv + rsv S = V t 1 2 σ2 S 2 V SS + qsv S. Snadnou úpravou nakonec obdržíme kýženou Black-Scholesovu parciální diferenciální rovnici V t + (r q)sv S σ2 S 2 V SS rv = 0. (2.4) Obecně mají parciální diferenciální rovnice samy o sobě mnoho řešení, my však potřebujeme, aby byla hodnota opce jedinečná a nemohly tak vzniknout arbitrážní příležitosti. Upřesnění řešení rovnice dosáhneme stanovením okrajových podmínek. 2.4 Okrajové podmínky Nejčastějším typem rovnic, které se objevují v případě finančních problémů, jsou parabolické parciální diferenciální rovnice Také v případě rovnice (2.4) se jedná o rovnici parabolickou, avšak zpětnou parabolickou rovnici. Standardní i zpětná parabolická rovnice jsou matematicky ekvivalentní, pouze u zpětných pro specifikaci řešení uvádíme koncovou podmínku namísto počáteční. Zaměřme se nejprve na evropskou kupní opci s hodnotou V C (S, t). Koncovou podmínku pro kupní opci již známe, je to hodnota opce v čase t = T, tedy je stejná 14
18 jako výplatní funkce opce V C (S T, T ) = max(s T K, 0). Cenu akcie S uvažujeme na intervalu [0, ). Hodnota opce na akcii s kurzem S = 0 bude zřejmě nulová, jak je patrné z rovnice (2.1), neboť pro S = 0 je též ds = 0, a proto se hodnota akcie nemůže změnit. Za tohoto stavu bude kupní opce bezcenná, tj. V C (0, t) = 0. V případě S bude hodnota akcie růst velmi rychle. Hodnota opce se bude postupně přibližovat ceně S, avšak diskontované o dividendovou míru q, a realizační hodnota opce K s rostoucím S bude ztrácet na významu. Opce bude s vysokou pravděpodobností v době expirace uplatněna. Proto pro S platí, že lim V C(S, t) Se q(t t) = Ke r(t t). S Čím více se bude cena akcie blížit nekonečnu, tím více bude zanedbatelná hodnota realizační ceny, proto V C (S, t) Se q(t t), S. U okrajových podmínek pro evropskou prodejní opci budeme postupovat obdobně. Stejně jako u kupní opce, koncovou podmínku prodejní opce již známe, je jí výplatní funkce opce, V P (S T, T ) = max(k S T, 0). V případě S = 0 se hodnota akcie nemění a opce tak bude nakonci uplatněna se ziskem K. Hodnota opce při S = 0 je tak rovna současné hodnotě realizační ceny K (hodnotu musíme diskontovat o míru r) 15
19 V P (0, t) = Ke r(t t). Naopak při vysokých hodnotách ceny akcie, S, se opce bude stávat postupně bezcennou, proto lim V P (S, t) = 0. S Koncové a okrajové podmínky evropských opcí jsou shrnuty v tabulce (2.1). Call opce Put opce V C (S T, T ) = max(s T K, 0) V P (S T, T ) = max(k S T, 0) V C (0, t) = 0 r(t t) V P (0, t) = Ke V C (S, t) Se q(t t), S V P (S, t) 0, S Tabulka 2.1: Přehled okrajových a koncových podmínek pro evropský typ opcí. Stanovením těchto podmínek jsme schopni nalézt explicitní řešení Black-Scholesovy rovnice (2.4). 16
20 3 Analytické řešení Black-Scholesovy rovnice V předešlé kapitole jsme na základě vytvoření bezrizikového portfolia odvodili Black- Scholesovu rovnici pro evropské opce na akcii vyplácející spojitě dividendu. Tato kapitola bude věnována řešení uvedené rovnice a tím odvození známého vzorce pro oceňování opcí. Na začátek však připomeňme tvar řešené rovnice: V t σ2 S 2 2 V V + (r q) S S2 S rv = 0, (3.1) kde S(t) > 0, 0 t T. Jedná se o parciální diferenciální rovnici, která je - lineární, - parabolická, - s nekonstantními koeficienty. Obecně jsou parciální diferenciální rovnice těžko řešitelné, mezi ty snáze řešitelné patří rovnice lineární s konstantními koeficienty. Příkladem takové rovnice je rovnice vedení tepla, jejíž řešení lze zkonstruovat pomocí standardních metod. 3.1 Rovnice vedení tepla Rovnice vedení tepla popisuje šíření tepla různými materiály v průběhu času. Pro jednodimenzionální prostor má homogenní rovnice vedení tepla tvar u τ (x, τ) = a 2 u (x, τ), x2 kde u(x, t) je teplota v bodě x v čase τ pro < x < a τ 0, a je konstanta. 17
21 Jedná se o snad nejznámnější příklad parabolické parciální diferenciální rovnice. Výhodou je její řešitelnost pomocí standardních metod, jakými jsou separ ace proměnných a Fourierova transformace. Fundamentálním řešení rovnice vedení tepla je G(x, τ) = 1 2 x 2 aπτ e 4aτ. (3.2) Řešení rovnice vedení tepla s počáteční podmínkou pak lze vyjádřit jako u(x, τ) = G(x s, τ) u(s, 0)ds. (3.3) Právě pro svou řešitelnost bývá rovnice vedení tepla využívána při řešení finančních problémů. Jak již bylo zmíněno, většina těchto problémů je popsána parabolickými parciálnimi rovnicemi. Ty se vhodnými transformacemi převedou na rovnici vedení tepla a vyřeší. Také v případě řešení Black-Scholesovy rovnice se postupuje stejně. Prvním krokem bude převedení rovnice (3.1) na standardní parabolickou rovnici s konstantními koeficienty. Za tímto účelem zavedeme nové proměnné x a τ, kde x = ln S K, τ = (T t)σ2, a funkci u(x, τ), pro níž platí, že u(x, τ) = 1 K V (S, t) = V (Kex, T τ/σ 2 ). (3.4) K Obecně je definována pro x kladné i záporné a pro τ 0. Touto změnou proměných dostáváme V t = ( σ 2 )Ku τ, V S = K S u x, V SS = K S 2 (u xx u x ), 18
22 dolní indexy značí parciální derivaci dle příslušné proměnné. Dosadíme-li výrazy do rovnice (3.1), obdržíme po úpravě rovnici s konstantními koeficienty tvaru u τ = 1 2 u xx + ( r q 1 ) u σ 2 x r u. (3.5) 2 σ2 Pro zjednodušení označme γ = r σ 2, α = q σ 2, β = r q σ 2 1 2, pak po dosazení do rovnice (3.5) u τ = 1 2 u xx + βu x γu = 0 (3.6) Podívejme se nyní blíže na jednotlivé členy pravé strany této rovnice a jejich vliv na řešení 1. Uvažujme počáteční podmínku tvaru u 0 (x) = 1 2πτo e x2 2τo. (3.7) Funkce u 0 (x) popisuje Gaussův pulz, přičemž plocha (M): 1 střed: M 1 šířka: M Rovnice difúze: u 0(x) dx = 1, xu 0(x) dx = 0, x2 u 0 (x) dx = τ 0. u τ = 1 2 u xx Řešením této rovnice při dané počáteční podmínce je funkce u 1 (x, τ) = 1 2π(τo + τ) e x2 2(τo+τ), tedy Gaussův pulz s plochou 1, středem v nule a šířkou τ 0 + τ, znázorněn na obr. (3.1). Z finančního hlediska je difúze důsledkem volatility podkladového aktiva, 1 zpracováno dle Almgren, [1], str
23 neboť hodnota opce v daném čase a při dané ceně podkladu závisí na budoucích hodnotách opce, tj. i na rozmezí pohybu budoucích cen podkladového aktiva. Obrázek 3.1: Řešení rovnice difúze. Transportní rovnice (konvekce): u τ = βu x Řešením rovnice konvekce je funkce u 2 (x, τ) = 1 2πτo e (x+βτ)2 2τo, Gaussův pulz s plochou 1, se středem v x = βτ a šířkou τ 0, viz obr. (3.3). Platí tedy, že u 2 (x, τ) = u 0 (x + βτ). V souvislosti s financemi konvekce vzniká v důsledku bezrizikového očekávaného růstu v ceně podkladu. Při aktuální ceně podkladu S je současná hodnota podkladu v čase T, S T, kterou potřebujeme pro ocenění opce, rovna e (r q)t S. Rovnice rozptylu (disipace): u τ = γu Řešením rovnice při dané počáteční podmínce je funkce u 3 (x, τ) = e γτ 2πτo e x2 2τo. Tento Gaussův pulz, viz obr. (??), má plochu rovnu e γτ, střed v nule a šířku τ 0. Platí, že u 3 (x, τ) = e γτ u 0 (x). Vrátíme-li se opět k našemu finančnímu problému, 20
24 Obrázek 3.2: Řešení rovnice konvekce. pak disipace odpovídá časové hodnotě opce. Např. současná hodnota hodnoty opce při expiraci je e rt V (S, T ). Obrázek 3.3: Řešení rovnice disipace. Budeme-li uvažovat všechny tři členy najednou, pak z výše uvedených poznatků vyplývá, že při počáteční podmínce (3.7) má rovnice (3.6) řešení ve tvaru u(x, τ) = e γτ 2 2π(τ0 + τ) e (x+βτ) 2(τ0+τ), (3.8) což je Gaussův pulz s plochou e γτ, středem v x = βτ a šířkou τ 0 + τ znázorněný na obr.(3.4). 21
25 Obrázek 3.4: Řešení rovnice u τ = 1 2 u xx + βu x γu = 0. V tabulce (3.1) jsou pro přehlednost uvedena řešení rovnic pro jednotlivé případy. Plocha Střed Šířka u(x, 0) = u 0 (x) 1 0 τ0 u τ = 1u 2 xx 1 0 τ0 + τ u τ = βu x 1 βτ τ0 u τ = γu e γτ 0 τ0 u τ = 1 u 2 xx + β u x γ u e γτ βτ τ0 + τ Tabulka 3.1: Vliv členů rovnice u τ = 1u 2 xx + βu x γu = 0 na její řešení. Dalším krokem při transformaci rovnice (3.6) na rovnici vedení tepla bude eliminace členů βu x a γu, k čemuž využijeme uvedené poznatky o jejich vlivu na řešení rovnice. Člen γu lze velmi jednoduše odstranit zavedením nové proměnné ũ(x, τ), přičemž u(x, τ) = e γτ ũ(x, τ). Funkce ũ(x, τ) představuje diskontovanou hodnotu opce. Dosazením za jednotlivé parciální derivace a následnou úpravou dostáváme, že ũ = 1 2ũxx + ũ x. (3.9) Zbývá již jen odstranit člen konvekce. Eliminaci lze provést dvěma způsoby. První možností je posunutí souřadnic pomocí zavedení proměnné x = x + βτ, načež 22
26 budeme hledat novou funkci v(x, τ) takovou, že ũ(x, τ) = v(x + βτ, τ) = v(x, τ). Druhou možností je opět využít vhodný diskontní faktor, tentokrát však závislý na x i τ. Pro novou funkci v(x, τ) tak bude platit ũ(x, τ) = e ax bτ v(x, τ), kde a, b jsou konstantní. Aby tato funkce ũ splňovala rovnici (3.9), musí pro v platit v τ = 1 2 v xx + ( a + β)v x + ( 1 2 a2 βa + b)v. Volbou a = β a b = 1 2 β2 získáme hledanou rovnici vedení tepla ve tvaru v τ = 1 2 v xx. (3.10) Obecně je tato rovnice uvažována pro x R a τ 0. Protože však má opce životnost pouze do času T, budeme rovnici uvažovat pro 0 τ σ 2 T. Celou transformaci rovnice Black-Scholesovy rovnice na rovnici vedení tepla shrnuje následující tabulka (3.2). S = Ke x, t = T τ σ 2, β = r q σ 2 1, 2 r γ = σ 2 V (S, t) = Ke γτ βx 1 2 β2τ v(x, τ) Tabulka 3.2: Transformace Black-Scholesovy rovnice na rovnici vedení tepla. Společně s původní rovnicí (2.4) se transformují také koncové a okrajové podmínky. Využijeme-li tabulky (3.2), pak z koncových podmínek pro Black-Scholesovu rovnici obdržíme podmínky počáteční ve tvaru 23
27 v C (x, 0) = max(e (β+1)x e βx, 0), v P (x, 0) = max(e βx e (β+1)x, 0). (3.11) a okrajové podmínky call : v C (x, τ) e (β+1)x+ 1 2 (β+1)2τ e βx+ 1 2 β2τ, x, v C (x, τ) o(1), x, put : v P (x, τ) o(1), x, v P (x, τ) e βx+ 1 2 β2τ e (β+1)x+ 1 2 (β+1)2τ, x. 3.2 Odvození Black-Scholesova vzorce Další postup pro odvození Black-Scholesova vzorce byl naznačen již v podkapitole 3.1. Máme-li rovnici převedenu na rovnici vedení tepla, nalezneme její řešení, které zpětně transformujeme do původních proměnných. Fundamentální řešení pro rovnici (3.10) je rovno G = 1 2πτ e x2 2τ. Řešením naší rovnice vedení tepla s počáteční podmínkou je v(x, τ) = G(x s, τ)v(s, 0) ds. Jako první si odvodíme oceňovací vzorec pro kupní opci. Dosadíme-li do integrálu za G a počáteční podmínku pro danou opci, viz (3.11), lze řešení zapsat jako v C (x, τ) = 1 2πτ e (x s)2 2τ max(e (β+1)s e βs, 0) ds = 1 2πτ 0 e (x s)2 2τ (e (β+1)s e βs )ds = I 1 I 2, 24
28 kde I 1 = 1 e (x s)2 2τ e (β+1)s ds, I 2 = 1 2πτ 2πτ e (x s)2 2τ e βs ds. 0 Úpravou na čtverec v exponentu a vhodnou substitucí obdržíme 0 x+τ(β+1) I 1 = e 1 2 τ(β+1)2 +(β+1)x 1 τ 2π x+τβ I 2 = e 1 2 τβ2 +βx 1 τ 2π ( e y2 1 x + τ(β + 1) ) 2 dy = e 2 τ(β+1)2 +(β+1)x N τ e y2 2 dy = e 1 2 τβ2 +βx N ( x + τβ ) τ Nyní převedeme I 1, I 2 zpět do původních proměnných S, t, viz tabulka (3.2). ( ) ln S/K + (r q + σ 2 Ke γτ βx 1 2 τβ2 I 1 = Se q(t t) )(T t) 2 N σ = Se q(t t) N(d 1 ) T t ( ) ln S/K (r q σ 2 Ke γτ βx 1 2 τβ2 I 2 = Ke r(t t) )(T t) 2 N σ = Ke r(t t) N(d 2 ) T t Celkově tedy dostáváme, že V C (S, t) = Se q(t t) N(d 1 ) Ke r(t t) N(d 2 ), (3.12) což je hledaný Black-Scholesův vzorec pro kupní opci na akcii vyplácející spojitě dividendu. Analogicky se odvodí i vzorec pro prodejní opci, V P (S, t) = Ke r(t t) N( d 2 ) Se q(t t) N( d 1 ), (3.13) když použijeme příslušnou počáteční podmínku. Druhou možností je odvodit vzorec pro prodejní opci z put-call parity, V P (S, t) = V C (S, t) Se q(t t) + Ke r(t t), 25
29 přičemž platí, že 1 N(d 1 ) = N( d 1 ). 26
30 4 Hedging opcí Stejně jako u jiných finančních instrumentů obnáší také obchodování s opcemi investiční rizika. Tato rizika a jejich negativní dopady se investoři snaží pokud možno co nejvíce minimalizovat pomocí řízení rizik, neboli risk managementu. V rámci tohoto řízení jsou rizika spojená s drženým portfoliem vyhledávána, důkladně analyzována, zajištěna a nadále průběžně monitorována 1. Zajištění se proti riziku pomocí investice do vhodného instrumentu se nazývá hedging - investor spolu s investicí do vybraného aktiva zároveň zaujímá pozici ve zvoleném zajišťovacím aktivu, které minimalizuje pohyby ceny investice. Nevhodně zvolený jistící instrument může naopak riziko pozice zvyšovat. Protože mezi ziskem a rizikem panuje určitá rovnováha, snížíme-li riziko dané investice, činíme tak většinou na úkor jejího zisku, navíc vytvoření zajištění představuje pro investora další náklady. Na zajištění lze též nahlížet jako na určitý druh investice, jejímž ziskem je snížené riziko. Účinnost zajištění velmi závisí na korelaci mezi drženým a zajišťovacím aktivem. Investoři se snaží nalézt takový instrument, který co nejpřesněji replikuje výnosy jejich portfolia, čímž umožňuje riziko co nejvíce snížit 2. Pokud investor zcela eliminuje riziko opční pozice tak, že zajištovací instrument vždy vyplatí jen tolik, aby byla pokryta ztráta opce a nic víc (neboť větší krytí znamená také další náklady), pak se jedná o perfektní hedging. V praxi je však téměř nemožné takovýto jistící instrument nalézt. Existují však instrumenty s velmi dobrou korelací a velmi obdobným vývojem ceny k vývoji ceny drženého aktiva. Přestože nejde o perfektní hedging, i jejich účinnost může být velmi vysoká. Protože je však pozice kryta jen částečně, existují tu reziduální rizika, na která by se nemělo zapomenout. Na vývoj hodnoty opce mají vliv různé faktory, především pak parametry vstupující do Black-Scholesova vzorce, na něž se v této práci zaměříme. Jsou jimi: 1 viz Ward, [14], str viz Ward, [14], str
31 - aktuální hodnota podkladového aktiva S t, - bezriziková úroková míra r, - realizační cena K, - volatilita podkladu σ, - čas zbývající do expirace T t, - dividendová míra q. Jejich vliv na hodnotu opce vyjadřují tzv. opční charakteristiky, jimiž se zabývá následující podkapitola. 4.1 Opční charakteristiky V reálném tržním prostředí působí všechny faktory na hodnotu opce současně. Při řízení rizika však bývají jednotlivé faktory analyzovány nejprve jednotlivě, tj. uvažuje se změna pouze v jednom z parametrů, přičemž ostatní zůstávají konstantní. Citlivost hodnoty opce na tyto jednotlivé faktory se pak měří pomocí opčních charakteristik. Mezi ty hlavní patří delta ( ), gama (Γ), theta (Θ), vega (Υ) a rho (ρ) Delta Významnou opční charakteristikou je delta opce, která měří citlivost hodnoty opce, vypočtené na základě Black-Scholesova vzorce, na ceně podkladového aktiva. Udává, o kolik se změní cena opce, změní-li se cena podkladového aktiva o jednu jednotku. Na deltu lze proto nahlížet jako na přibližnou velikost zisku/ztráty při změně ceny podkladu. Delta opce je definována jako = V S. Ze vzorce (3.12) můžeme snadno odvodit explicitní vzorec pro výpočet delty evropské kupní opce C = V C S = e q(t t) N(d 1 ), (4.1) 28
32 a z (3.13) vzorec pro deltu evropské put opce P = V P S = e q(t t) N( d 1 ) (4.2) Delta kupní opce je vždy kladná, hodnoty jsou z intervalu 0 až 1. Delta prodejní opce má naopak vždy zápornou hodnotu z intervalu -1 až 0. Protože se investiční portfolio většinou skládá z více jak jedné opce, využívají investoři tzv. poziční deltu, která je sumou jednotlivých delt vynásobených příslušným počtem opcí v portfoliu. Delty nakoupených opcí se přičítají, naopak delty upsaných opcí se odečítají. Poziční delta umožňuje investorovi změřit, o kolik se změní hodnota celého opčního portfolia, změní-li se cena podkladové akcie. Během životnosti opce se však delta mění. Také na ní působí rozličné faktory, ovlivňující její hodnotu, nejvíce pak cena podkladu a čas zbývající do expirace. Například s tím, jak se mění hodnota akcie, mění se hodnota delty následovně: pro opce hluboko OTM je delta blízko nuly, pro opce ATM se pohybuje kolem hodnoty 0,5 pro kupní opci, resp. -0,5 pro opci prodejní. Čím více je opce ITM, tím více roste delta kupní opce a blíží se k jedné, resp. klesá k -1 pro opce prodejní. Delta je investory nejvíce využívanou charakteristikou opčních portfolií, přestože hodnoty vypočítané dle uvedených vzorců jsou pouze teoretické, neboť se neuvažují změny ostatních parametrů. Avšak vypočtené hodnoty jsou užitečným nástrojem, jak vyjádřit přibližné riziko spojené s pohybem ceny podkladové akcie za malý časový interval. Mají tak své uplatnění při zajišťování opčních portfolií Gama Vedle delty je další nejčastěji analyzovanou charakteristikou gama, která měří citlivost změny delty opce na změnách ceny podkladové akcie. Tedy nám udává, jak moc se mění delta opce v souvislosti s pohybem ceny podkladu o 1 peněžní jednotku. Je-li gama vysoká, pak se delta mění velmi rychle a naopak. 29
33 Z matematického hlediska je gama definována jako Γ = S = 2 V S 2. Zderivováním již námi odvozených vztahů (4.1) a (4.2) pro deltu dostaneme Γ = 2 V C S 2 = 2 V P S 2 = e q(t t) σs T t N (d 1 ). Hodnota gamy je proto stejná jak pro kupní, tak pro prodejní opce při stejné realizační ceně a stejné expiraci. Poziční gamu opět získáme sečtením gam jednotlivých opcí. Největší hodnotu má gama pro opci na penězích. S tím, jak se opce pohybuje směrem mimo peníze či naopak ITM, její hodnota klesá. Obdobně jako delta opce, je i gama důležitá pro zajišťování opčních portfolií, především proto, že udává citlivost delty opce na podkladové akcii Vega Dalším z faktorů, který vedle ceny podkladového aktiva ovlivňuje hodnotu opce, je volatilita podkladové akcie. Přestože Black-Scholesův model předpokládá volatilitu konstantní, ve skutečnosti tomu tak není a volatilita se v průběhu času mění. Citlivost opce na změny volatility je kvantifikována charakteristikou vega 3. Obvykle je vega vyjadřována jako velikost změny hodnoty opce při změně volatility o 1 %. Vega opce je určena předpisem: Z Black-Scholesova vzorce dostaneme Υ = V σ. Υ = V C σ = V P σ = Se q(t t) T tn (d 1 ). 3 Vega jako jediná z opčních charakteristik není řeckým písmenem, bývá proto někdy označena také jako kappa či lambda 30
34 Vega je shodná pro kupní i prodejní opce a je vždy kladná. Jednotlivé opce však na volatilitu reagují s odlišnou intenzitou. Největší hodnotu má faktor pro opci ATM a rychle klesá pro opce ITM i OTM Theta Protože opční prémie obsahuje určitou časovou hodnotu, je faktorem ovlivňujícím opční cenu také čas. Oproti ostatním faktorům má tu vlastnost, že ovlivňuje cenu opce, i když jsou trhy zavřené. Parametr, který měří závislost hodnoty opce na plynutí času se nazývá theta. Nejčastěji bývá vyjadřována jako velikost změny opční hodnoty za jeden den. Obvykle je theta definována jako první derivace ceny opce dle času, avšak protože opční cena závisí především na čase zbývajícím do expirace, lze thetu definovat jako Θ = V t = V τ, kde τ = T t je čas zbývající do expirace. Odvozený analytický vzorec pro evropskou kupní a prodejní opci je následující Θ C = V C τ = qse qτ N(d 1 ) Se qτ σ 2 τ N (d 1 ) rke rτ N(d 2 ), Θ P = V P τ = rke rτ N( d 2 ) qse qτ N( d 1 ) Se qτ σ 2 τ N (d 1 ). Hodnota thety pro call opce je vždy záporná, pro put opce může být i kladná. Nejvyšší hodnoty má theta pro opci ATM a postupně klesá s přechodem mimo peníze či do peněz. Dále pro thetu opce ATM a ITM platí, že s blížící se dobou expirace theta roste, pro opce OTM naopak klesá. Narozdíl od předešlých charakteristik, nebývá theta obchodníky příliš využívána a pokud, tak spíše pro odhad změny ceny portfolia vlivem plynutí času. Při výpočtu poziční thety pro držené opce je theta negativní, neboť jejich hodnota s časem klesá. Naopak upsání opce bude mít thetu kladnou. 31
35 4.1.5 Rho Poslední charakteristikou, která je řazena mezi základní a kterou si představíme, je rho. Parametr rho vypovídá o vlivu úrokové míry na cenu opce. Většinou se vyjadřuje jako velikost změny opční hodnoty při změně v úrokové míře o 1 %. Vypočítat rho můžeme derivací opční hodnoty podle úrokové míry, tj. ρ = V r. Z Black-Scholesova vzorce pak dostaneme, že ρ C = V C r = (T t)ke r(t t) N(d 2 ), ρ P = V P r = (T t)ke r(t t) N( d 2 ). Pro kupní opce je ρ vždy kladné, naproti tomu u put opce záporné. Hodnoty parametru ρ jsou zpravidla nízké a v čase se příliš nemění, proto patří k méně využívaným charakteristikám. Vyšší je rho pro opce s delší životností, pro krátké životnosti bývají zanedbatelné. Velikost rho je také vyšší, čím více je opce v penězích. S tím, jak se opce přesouvá mimo peníze, hodnota ρ klesá. 4.2 Zajišťovací strategie Investor má při jištění své pozice na výběr z různých instrumentů a několika různých zajišťovacích strategií. Přičemž špatná volba jištění může mít negativní dopad na investorovo portfolio a tak namísto aby snižoval daná rizka naopak je zvyšuje. Tato podkapitola byla zpracována na základě Hull, [8], kap. 17. Než si představíme některé zajišťovací strategie, podívejme se nejprve na situaci, kdy se investor nijak proti riziku nezajištuje a jeho pozice je tzv. nekrytá. Investor prodá či nakoupí opční kontrakty ale současně s nákupem nevytváří žádné zajištění pro případ, že by se cena podkladu pro investora vyvíjela špatným směrem. Investor 32
36 zůstává vystaven velkému riziku, neboť za určitých okolností může takováto strategie vést k neomezeným ztrátám a sice v situaci, kdy opce bude na konci životnosti uplatněna. Upisovatel v případě kupní opce musí nakoupit na trhu akcie dráže, než je následně prodá vlastníkovi opce. U prodejní opce naopak prodává akcie na trhu mnohem levněji, než-li je předtím od vlastníka nakoupil. To však neznamená, že tato strategie nemůže také přinést zisk. Pokud opce na konci nebude uplatněna, upisovatel nemusí žádné opce od vlastníka opce ani nakoupit ani prodat a nemá tak žádné dodatečné náklady, přičemž jeho ziskem je opční prémie. Příklad Uvažujme investora, který se rozhodl nijak nekrýt své opční portfolio, které je tvořeno 10 prodanými kupními opcemi na akcie společnosti ABC, jejichž aktuální cena na trhu činí 8 EUR/ks. Realizační cena opce je K = 10 EUR a cena za kontrakt 30 EUR (na 100ks), tedy obdržená prémie je 300 EUR. Jestliže cena akcie vystoupá v době expirace k 20 EUR/ks, pak vlastník opci uplatní a bude od upisovatele chtít nakoupit 1000 ks akcie za dohodnutou cenu 10 EUR/ks. Investor musí nejprve požadované akcie koupit na trhu za EUR, aby je však následně prodal za pouhých EUR. Ztráta tak celkem činí = 9700EUR. Pakliže cena akcie klesne v době expirace na 5 EUR/ks, opce uplatněna nebude a zisk upisovatele činí 300 EUR Statický hedging O tomto druhu zajištění napovídá mnohé už jeho název. Investor svou pozici sice na začátku zajistí ale dále již do zajištění nijak nezasahuje a nepřizpůsobuje ho vývoji situace na trhu. Strategie tak obnáší náklady pouze při jejím vytváření. Příkladem statického hedgingu je strategie kryté pozice. 33
37 Krytá pozice Pro zajištění své pozice může investor zvolit velmi jednoduchou jistící strategii kryté pozice. Investor s prodejem opčního kontraktu zároveň vytvoří vhodnou pozici v podkladovém aktivu, aby se tak zajistil v případě pohybu ceny opačným směrem, než by si investor přál. Upíše-li kupní opci, nakoupí potřebný počet akcií, upíše-li prodejní opci, pak musí akcie naopak shortovat. Pozici kryje tolika akciemi, kolik bude třeba v případě uplatnění opce. V průběhu životnosti opce zajištění nijak dále nemění. Tato strategie funguje poměrně dobře v případě, že opce skončí při expiraci ITM a bude nakonci uplatněna. Avšak v ostatních případech může také tato strategie znamenat pro investora velké ztráty, neboť v případě opce OTM nijak upisovatele nechrání. Buď drží akcie, jejichž hodnota od nákupu klesla až pod realizační cenu, takže případným prodejem akcií se náklady investorovi nevrátí, nebo na krátko prodal akcie, jejichž cena postupně vzrostla, takže jejich zpětný odkup bude nákladnější. Příklad Uvažujme investora z předchozího příkladu, avšak tentokrát se rozhodl svou pozici zajistit a držet ji krytou, tzn. co nejdříve s prodejem call opcí investor nakoupí 1000 ks akcií společnosti ABC celkem za EUR. Pokud cena akcie vystoupá na 20 EUR, pak vlastník opce uplatní a koupí od investora akcie za EUR. Zisk investora činí = 2300EUR. Jestliže však cena akcie klesne na 5 EUR, opce nebude uplatněna a investorem držené akcie mají nyní cenu pouze 5000 EUR. Celkem upisovatel tratí = 2700EUR Dynamický hedging Některá portfolia se pomocí statického hedgingu zajistit nedají. Namísto toho využívají strategie dynamické, při kterých se zajištění průběžně přizpůsobuje. Kromě 34
38 pořizovacích nákladů tak investor oproti statickému hedgingu vydává i náklady na přizpůsobování zajištění. Stop-loss Poměrně jednoduchou dynamicky zajišťovací strategií je stop-loss strategie, jejíž podstatou je střídavé držení kryté a nekryté pozice s tím, jak se vyvíjí cena podkladové akcie a tím i možnost uplatnění opce při expiraci. Hranici pro držení kryté či nekryté pozice představuje realizační cena opce. Jak tato strategie funguje si ukažme na příkladu upsání kupní opce. Příklad Uvažujme investora, který prodal jednu kupní opci a chce se zajistit proti riziku. Pokud se bude cena podkladu držet nad realizační cenou, pak by opce na konci byla uplatněna a investor bude muset dodat vlastníkovi opce akcie. Aby se zajistil, vytvoří si krytou pozici - nakoupí akcie. Tyto akcie drží po dobu, po kterou se cena podkladové akcie pohybuje nad realizační cenou. Naopak klesne-li cena podkladu pod realizační cenu, opce uplatněna nebude a investor může držet pozici nekrytou - jakmile cena protne hranici směrem dolů, prodá případně držené akcie. Tím si zajistí, že v čase expirace T bude v případě uplatnění opce držet potřebná akcie, naopak bude-li opce bezcenná, žádné držet nebude. Na první pohled se může tato strategie zdát jako perfektní. Investor zkrátka sleduje vývoj ceny podkladu a jakmila tato protne stanovenou hranici směrem vzhůru, nakoupí akcie, jakmile ji protne směrem dolů, prodá akcie. Problém však je, že ve chvíli kdy akcie protne hranici, investor ještě neví, kterým směrem se cena bude dále pohybovat. Tedy musí počkat na další vývoj, a proto případně obchoduje akcie za cenu vždy lehce nad či lehce pod hranicí, tj. za K + ɛ či K ɛ, kde ɛ je nějaké malé kladné číslo. Neuvažují-li se transakční náklady, musí investor i tak při každém páru operací nákup-prodej vynaložit náklady ve výši 2ɛ. Výši těchto nákladů lze eliminovat vyšší frekvencí monitorování vývoje ceny. Na druhou stranu má ale vyšší frekvence sledování ceny za následek růst počtu provedených transakcí (pro ɛ blížící se nule poroste frekvence k nekonečnu), což v reálném obchodním prostředí povede k nárůstu transakčních nákladů. 35
39 Proto ani strategie stop loss není příliš vhodným způsobem zajištění. Může se stát, že investor vynaloží vysoké náklady na zajištění a opce nakonec nebude vůbec uplatněna. Delta Hedging K jištění portfolií využívají mnozí investoři již námi zmíněné opční charakteristiky, především pak delty, gamy a vegy. Zaměřme se nyní na deltu, která měří citlivost hodnoty opce na ceně podkladového aktiva. Snahou investora bude samozřejmě co nejmenší citlivost a tedy i co nejnižší delta, nejlépe nulová. Neboť to znamená, že se změnou v ceně podkladu se cena opce nezmění. Portfolio s nulovou deltou se nazývá delta-neutrální a tento způsob zajištění jako delta-hedging. Vhodným nástrojem pro vynulování delty bude samo podkladové aktivum, neboť jeho delta je rovna jedné. Protože se však delta v čase mění a investorova pozice je tak jištěna jen po krátký časový úsek, bude třeba jištění v čase přizpůsobovat, tzv. rebalancovat, a proto ho také neustále monitorovat. Ukažme si nyní, jak deltahedging pracuje na následujícím příkladu. Příklad Uvažujme investora, který prodal 10 call opcí na akcii firmy ABC, jejíž aktuální cena činí 53 EUR. Je-li delta opce 0,771, pak poziční delta je 0,771 x 1000 = Poziční deltu tak neutralizujeme nákupem 771 ks akcí firmy ABC. Pokud však následující den cena akcie vzroste na 53,12 EUR, změní se také delta opce a sice na 0,693. Delta portfolia (včetně držených akcií) je nyní 78, tedy je nyní potřeba 78 ks akcií prodat, aby byla delta opět nulová. Gama Hedging Gama měří, jak rychle se mění delta v závislosti na změně v ceně podkladu, a slouží tak k předpovídání vývoje delty dané opce. Záměrem investora bude co nejvíce gamu eliminovat, protože pak se bude také snižovat citlivost delty na změnu v ceně podkladové akcie a investice bude chráněna i proti větším výkyvům v ceně podkladu. Princip neutralizace gamy je stejný jako u delta hedgingu. K vynulování gamy však nelze nyní použít podkladového aktiva, neboť gama akcie je rovna 0. Investor tedy 36
40 potřebuje instrument, který nebude na podkladu lineárně závislý. Využít tak lze např. další opci. Nesmí se však zapomenout, že přidání opce do portfolia změní jeho deltu a je proto třeba následně portfolio i delta-neutralizovat. Ukažme si opět vše na příkladu. Příklad Uvažujme opět investora z předešlého příkladu. Delta-neutrální portfolio má gamu rovnu 1200, kterou chce investor neutralizovat. K dispozici má opci s deltou 0,52 a gamou 1,5. Aby gamu portfolia vynuloval, bude třeba 1200/1,5 ks opce, tj. 800 ks. Nákupem těchto opcí se však změní také delta portfolia, která nyní činí 800 x 0,52 = 416. Proto je třeba nyní 416 ks podkladových akcií prodat, aby byla delta opět nulová a portfolio bylo zajištěno proti výkyvům v ceně podkladové akcie. Vega Hedging Přestože Black-Scholesův model předpokládá konstantní volatilitu podkladové akcie, bylo později prokázáno, že volatilita se v čase mění a ovlivňuje tak hodnotu opcí. Chce-li se investor zajistit proti vlivu volatility na hodnotu opce ve svém portfoliu, může k tomu opět využít příslušné opční charakteristiky, v případě volatility je jí Υ, a snažit se ji neutralizovat. Vega podkladové akcie je rovna 0 a nelze ji proto využít. Investor bude nyní k zajištění potřebovat minimálně 2 odlišné deriváty podkladové akcie, např. 2 různé opce, viz následující příklad. Nesmíme se ale opět zapomenout, že přidáním dalších aktiv do portfolia se změní gama i delta. Příklad Opět uvažujme investora z předešlých 2 příkladů, který drží delta-neutrální portfolio. Gama tohoto portfolia činí 1200, vega pak Pro zajištění má investor k dispozici dvě různé opce, kde 1 = 0, 52, 2 = 0, 63, Γ 1 = 1, 5, Γ 2 = 2, Υ 1 = 1, 3 a Υ 2 = 1, 6. Pro gama- i vega-neutrální portfolio musí platit , 3ω 1 + 1, 6ω 2 = 0, , 5ω 1 + 2ω 2 = 0. 37
41 Dostaneme, že ω 1 = a ω 2 = 22800, tj. nakoupíme ks první opce a prodáme ks druhé opce. Delta portfolia tak bude činit x 0, x 0,63 = Prodejem 1028 ks podkladové akcie nakonec portfolio i deltaneutralizujeme. Bohužel hedging pomocí zmíněných opčních charakteristik je v praxi, kde nejsou ideální podmínky na trhu, velmi obtížný. Problémem jsou hlavně vysoké transakční náklady v důsledku častého rebalancování. Proto se tyto strategie pro malá portfolia nevyplatí. U větších portfolií se využívá delta hedgingu většinou se rebalancuje z důvodu transakčních nákladů maximálně jednou denně. Udržování nulové gamy a vegy už je ale velmi komplikované. Je velmi obtížné nalézt na trhu takové nelineární instrumenty, které je možné obchodovat v požadovaném množství. 38
Matematicko-fyzikální fakulta Univerzity Karlovy
 Oceňování finančních derivátů ve spojitém čase Václav Kozmík Matematicko-fyzikální fakulta Univerzity Karlovy 4. 10. 2010 Úvod Stochastický kalkulus Wienerův proces stochastické procesy Itoovo lemma změna
Oceňování finančních derivátů ve spojitém čase Václav Kozmík Matematicko-fyzikální fakulta Univerzity Karlovy 4. 10. 2010 Úvod Stochastický kalkulus Wienerův proces stochastické procesy Itoovo lemma změna
Finanční management. Nejefektivnější portfolio (leží na hranici) dle Markowitze: Polemika o významu dividendové politiky
 Finanční management Dividendová politika, opce, hranice pro cenu opce, opční techniky Nejefektivnější portfolio (leží na hranici dle Markowitze: existuje jiné s vyšším výnosem a nižší směrodatnou odchylkou
Finanční management Dividendová politika, opce, hranice pro cenu opce, opční techniky Nejefektivnější portfolio (leží na hranici dle Markowitze: existuje jiné s vyšším výnosem a nižší směrodatnou odchylkou
Příprava na zkoušky odborné způsobilosti na finančních trzích
 Příprava na zkoušky odborné způsobilosti na finančních trzích Deriváty II opce a opční strategie Opce Poskytuje vlastníkovi opce nikoli povinnost, ale právo k nákupu nebo prodeji určitého podkladového
Příprava na zkoušky odborné způsobilosti na finančních trzích Deriváty II opce a opční strategie Opce Poskytuje vlastníkovi opce nikoli povinnost, ale právo k nákupu nebo prodeji určitého podkladového
Finanční trhy Úvod do finančních derivátů
 Finanční trhy Úvod do finančních derivátů Ing. Gabriela Oškrdalová e-mail: oskrdalova@mail.muni.cz Tento studijní materiál byl vytvořen jako výstup z projektu č. CZ.1.07/2.2.00/15.0189. 2.2.2013 Finanční
Finanční trhy Úvod do finančních derivátů Ing. Gabriela Oškrdalová e-mail: oskrdalova@mail.muni.cz Tento studijní materiál byl vytvořen jako výstup z projektu č. CZ.1.07/2.2.00/15.0189. 2.2.2013 Finanční
Tomáš Cipra: Matematika cenných papírů. Professional Publishing, Praha 2013 (288 stran, ISBN: ) ÚVOD.. 7
 Tomáš Cipra: Matematika cenných papírů. Professional Publishing, Praha 2013 (288 stran, ISBN: 978-80-7431-079-9) OBSAH ÚVOD.. 7 1. DLUHOPISY.. 9 1.1. Dluhopisy v praxi... 9 1.1.1. Princip dluhopisů 9 1.1.2.
Tomáš Cipra: Matematika cenných papírů. Professional Publishing, Praha 2013 (288 stran, ISBN: 978-80-7431-079-9) OBSAH ÚVOD.. 7 1. DLUHOPISY.. 9 1.1. Dluhopisy v praxi... 9 1.1.1. Princip dluhopisů 9 1.1.2.
Změna hodnoty pozice v důsledku změn tržních cen.
 Tržní riziko Změna hodnoty pozice v důsledku změn tržních cen. Akciové riziko Měnové riziko Komoditní riziko Úrokové riziko Odvozená rizika... riz. volatility, riz. korelace Pozice (saldo hodnoty očekávaných
Tržní riziko Změna hodnoty pozice v důsledku změn tržních cen. Akciové riziko Měnové riziko Komoditní riziko Úrokové riziko Odvozená rizika... riz. volatility, riz. korelace Pozice (saldo hodnoty očekávaných
Stochastické diferenciální rovnice
 KDM MFF UK, Praha Aplikace matematiky pro učitele 15.11.2011 Kermack-McKendrickův model Kermack-McKendrickův model s vakcinací Model pro nemoc s rychlým šířením a krátkou dobou léčby. Příkladem takovéto
KDM MFF UK, Praha Aplikace matematiky pro učitele 15.11.2011 Kermack-McKendrickův model Kermack-McKendrickův model s vakcinací Model pro nemoc s rychlým šířením a krátkou dobou léčby. Příkladem takovéto
Změna hodnoty pozice v důsledku změn tržních cen.
 Tržní riziko Změna hodnoty pozice v důsledku změn tržních cen. Akciové riziko Měnové riziko Komoditní riziko Úrokové riziko Odvozená rizika... riz. volatility, riz. korelace Pozice (saldo hodnoty očekávaných
Tržní riziko Změna hodnoty pozice v důsledku změn tržních cen. Akciové riziko Měnové riziko Komoditní riziko Úrokové riziko Odvozená rizika... riz. volatility, riz. korelace Pozice (saldo hodnoty očekávaných
Strategie Covered Call
 Strategie Covered Call Tato strategie vzniká kombinací pozice na podkladovém aktivu a výpisem call opce na toto aktivum. Řada obchodníků bohužel neví, že s pomocí této strategie mohou zvýšit výnosnost
Strategie Covered Call Tato strategie vzniká kombinací pozice na podkladovém aktivu a výpisem call opce na toto aktivum. Řada obchodníků bohužel neví, že s pomocí této strategie mohou zvýšit výnosnost
DERIVÁTOVÝ TRH. Druhy derivátů
 DERIVÁTOVÝ TRH Definice derivátu - nejobecněji jsou deriváty nástrojem řízení rizik (zejména tržních a úvěrových), deriváty tedy nejsou investičními nástroji - definice dle US GAAP: derivát je finančním
DERIVÁTOVÝ TRH Definice derivátu - nejobecněji jsou deriváty nástrojem řízení rizik (zejména tržních a úvěrových), deriváty tedy nejsou investičními nástroji - definice dle US GAAP: derivát je finančním
Metodický list - Finanční deriváty
 Metodický list - Finanční deriváty Základní odborná literatura vydaná VŠFS: [0] Záškodný,P., Pavlát,V., Budík,J.: Finanční deriváty a jejich oceňování.všfs,praha 2007 Tato literatura platí v plném rozsahu,
Metodický list - Finanční deriváty Základní odborná literatura vydaná VŠFS: [0] Záškodný,P., Pavlát,V., Budík,J.: Finanční deriváty a jejich oceňování.všfs,praha 2007 Tato literatura platí v plném rozsahu,
Přemysl Bejda.
 premyslbejda@gmail.com 2010 Obsah 1 2 3 Obchodovatelnost Cena rizika Obsah 1 2 3 Obchodovatelnost Cena rizika Obsah 1 2 3 Obchodovatelnost Cena rizika Itôovo lemma Lemma (Itôovo) Necht X t je stochastický
premyslbejda@gmail.com 2010 Obsah 1 2 3 Obchodovatelnost Cena rizika Obsah 1 2 3 Obchodovatelnost Cena rizika Obsah 1 2 3 Obchodovatelnost Cena rizika Itôovo lemma Lemma (Itôovo) Necht X t je stochastický
Martin Chudoba. Seminář - Stochastické modelování v ekonomii a financích KPMS MFF UK. dluhopisů pomocí. Black-Scholesova modelu. M.Chudoba.
 Martin Chudoba s Seminář - Stochastické modelování v ekonomii a financích KPMS MFF UK 18.10.2010 Uvažujeme bezkupónový dluhopis vyplácející jednotku v čase T Za předpokladu konstantní úrokové míry r pro
Martin Chudoba s Seminář - Stochastické modelování v ekonomii a financích KPMS MFF UK 18.10.2010 Uvažujeme bezkupónový dluhopis vyplácející jednotku v čase T Za předpokladu konstantní úrokové míry r pro
1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004.
 Prostá regresní a korelační analýza 1 1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004. Problematika závislosti V podstatě lze rozlišovat mezi závislostí nepodstatnou, čili náhodnou
Prostá regresní a korelační analýza 1 1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004. Problematika závislosti V podstatě lze rozlišovat mezi závislostí nepodstatnou, čili náhodnou
Měnové opce v TraderGO
 Měnové opce v TraderGO Upozornění Informace sdělené v rámci této prezentace NEJSOU investičním doporučením, projevem osobního investičního poradenství ani nabídkou k nákupu či prodeji investičních nástrojů.
Měnové opce v TraderGO Upozornění Informace sdělené v rámci této prezentace NEJSOU investičním doporučením, projevem osobního investičního poradenství ani nabídkou k nákupu či prodeji investičních nástrojů.
FINANČNÍ A INVESTIČNÍ MATEMATIKA 2
 FINANČNÍ A INVESTIČNÍ MATEMATIKA 2 Metodický list č. 1 Název tématického celku: Dluhopisy a dluhopisové portfolio I. Cíl: Základním cílem tohoto tematického celku je popsat dluhopisy jako investiční instrumenty,
FINANČNÍ A INVESTIČNÍ MATEMATIKA 2 Metodický list č. 1 Název tématického celku: Dluhopisy a dluhopisové portfolio I. Cíl: Základním cílem tohoto tematického celku je popsat dluhopisy jako investiční instrumenty,
8.3). S ohledem na jednoduchost a názornost je výhodné seznámit se s touto Základní pojmy a vztahy. Definice
 9. Lineární diferenciální rovnice 2. řádu Cíle Diferenciální rovnice, v nichž hledaná funkce vystupuje ve druhé či vyšší derivaci, nazýváme diferenciálními rovnicemi druhého a vyššího řádu. Analogicky
9. Lineární diferenciální rovnice 2. řádu Cíle Diferenciální rovnice, v nichž hledaná funkce vystupuje ve druhé či vyšší derivaci, nazýváme diferenciálními rovnicemi druhého a vyššího řádu. Analogicky
3.1.1. Výpočet vnitřní hodnoty obligace (dluhopisu)
 Využití poměrových ukazatelů pro fundamentální analýzu cenných papírů Principem této analýzy je stanovení, zda je cenný papír na kapitálovém trhu podhodnocen, správně oceněn, nebo nadhodnocen. Analýza
Využití poměrových ukazatelů pro fundamentální analýzu cenných papírů Principem této analýzy je stanovení, zda je cenný papír na kapitálovém trhu podhodnocen, správně oceněn, nebo nadhodnocen. Analýza
1 Odvození poptávkové křivky
 Odvození poptávkové křivky Optimalizační chování domácností (maximalizace užitku) vzhledem k rozpočtovému omezení. Nejprve odvodíme deterministický model, který potom rozšíříme o stochastické prvky. Odvozené
Odvození poptávkové křivky Optimalizační chování domácností (maximalizace užitku) vzhledem k rozpočtovému omezení. Nejprve odvodíme deterministický model, který potom rozšíříme o stochastické prvky. Odvozené
Rovnovážné modely v teorii portfolia
 3. září 2013, Podlesí Obsah Portfolio a jeho charakteristiky Definice portfolia Výnosnost a riziko aktiv Výnosnost a riziko portfolia Klasická teorie portfolia Markowitzův model Tobinův model CAPM - model
3. září 2013, Podlesí Obsah Portfolio a jeho charakteristiky Definice portfolia Výnosnost a riziko aktiv Výnosnost a riziko portfolia Klasická teorie portfolia Markowitzův model Tobinův model CAPM - model
Informace. o finančních nástrojích a rizicích spojených s investováním
 Informace o finančních nástrojích a rizicích spojených s investováním Společnost QuantOn Solutions, o. c. p., a. s. (Dále jen QuantOn Solutions nebo i obchodník) poskytuje klientovi v souladu s 73d odst.
Informace o finančních nástrojích a rizicích spojených s investováním Společnost QuantOn Solutions, o. c. p., a. s. (Dále jen QuantOn Solutions nebo i obchodník) poskytuje klientovi v souladu s 73d odst.
Finanční deriváty ŘÍZENÍ RIZIK I
 Finanční deriváty Smlouvy, jimiž se neobchoduje s podkladovými aktivy, ale právy na ně (=> obchody s rizikem ). Hodnota vzniká zprostředkovaně přes hodnotu podkladového aktiva nebo ukazatele. Existence
Finanční deriváty Smlouvy, jimiž se neobchoduje s podkladovými aktivy, ale právy na ně (=> obchody s rizikem ). Hodnota vzniká zprostředkovaně přes hodnotu podkladového aktiva nebo ukazatele. Existence
1. Náhodný vektor (X, Y ) má diskrétní rozdělení s pravděpodobnostní funkcí p, kde. p(x, y) = a(x + y + 1), x, y {0, 1, 2}.
 VIII. Náhodný vektor. Náhodný vektor (X, Y má diskrétní rozdělení s pravděpodobnostní funkcí p, kde p(x, y a(x + y +, x, y {,, }. a Určete číslo a a napište tabulku pravděpodobnostní funkce p. Řešení:
VIII. Náhodný vektor. Náhodný vektor (X, Y má diskrétní rozdělení s pravděpodobnostní funkcí p, kde p(x, y a(x + y +, x, y {,, }. a Určete číslo a a napište tabulku pravděpodobnostní funkce p. Řešení:
FINANČNÍ A INVESTIČNÍ MATEMATIKA Metodický list č. 1
 FINANČNÍ A INVESTIČNÍ MATEMATIKA Metodický list č. 1 Název tématického celku: Úroková sazba a výpočet budoucí hodnoty Cíl: Základním cílem tohoto tematického celku je vysvětlit pojem úroku a roční úrokové
FINANČNÍ A INVESTIČNÍ MATEMATIKA Metodický list č. 1 Název tématického celku: Úroková sazba a výpočet budoucí hodnoty Cíl: Základním cílem tohoto tematického celku je vysvětlit pojem úroku a roční úrokové
Příručka k měsíčním zprávám ING fondů
 Příručka k měsíčním zprávám ING fondů ING Investment Management vydává každý měsíc aktuální zprávu ke každému fondu, která obsahuje základní informace o fondu, jeho aktuální výkonnosti, složení portfolia
Příručka k měsíčním zprávám ING fondů ING Investment Management vydává každý měsíc aktuální zprávu ke každému fondu, která obsahuje základní informace o fondu, jeho aktuální výkonnosti, složení portfolia
Oceňování akcií a. Brno 2012
 Oceňování akcií a dluhopisů Brno 2012 Osnova 1 Oceňování akcií 2 Akcie Představují podíl na majetku akciové společnosti. Držení je spojeno s řadou práv- právo účasti na hlasování na valné hromadě, právo
Oceňování akcií a dluhopisů Brno 2012 Osnova 1 Oceňování akcií 2 Akcie Představují podíl na majetku akciové společnosti. Držení je spojeno s řadou práv- právo účasti na hlasování na valné hromadě, právo
11. přednáška 10. prosince Kapitola 3. Úvod do teorie diferenciálních rovnic. Obyčejná diferenciální rovnice řádu n (ODR řádu n) je vztah
 11. přednáška 10. prosince 2007 Kapitola 3. Úvod do teorie diferenciálních rovnic. Obyčejná diferenciální rovnice řádu n (ODR řádu n) je vztah F (x, y, y, y,..., y (n) ) = 0 mezi argumentem x funkce jedné
11. přednáška 10. prosince 2007 Kapitola 3. Úvod do teorie diferenciálních rovnic. Obyčejná diferenciální rovnice řádu n (ODR řádu n) je vztah F (x, y, y, y,..., y (n) ) = 0 mezi argumentem x funkce jedné
CENNÉ PA CENNÉ PÍRY PÍR
 CENNÉ PAPÍRY ve finančních institucích dr. Malíková 1 Operace s cennými papíry Banky v operacích s cennými papíry (CP) vystupují jako: 1. Investor do CP 2. Emitent CP 3. Obchodník s CP Klasifikace a operace
CENNÉ PAPÍRY ve finančních institucích dr. Malíková 1 Operace s cennými papíry Banky v operacích s cennými papíry (CP) vystupují jako: 1. Investor do CP 2. Emitent CP 3. Obchodník s CP Klasifikace a operace
Příručka k měsíčním zprávám ING fondů
 Příručka k měsíčním zprávám ING fondů ING Investment Management vydává každý měsíc aktuální zprávu ke každému fondu, která obsahuje základní informace o fondu, jeho aktuální výkonnosti, složení portfolia
Příručka k měsíčním zprávám ING fondů ING Investment Management vydává každý měsíc aktuální zprávu ke každému fondu, která obsahuje základní informace o fondu, jeho aktuální výkonnosti, složení portfolia
Deriváty termínové operace
 Deriváty termínové operace Deriváty jsou termínové obchody, které jsou odvozeny od obchodů s jinými, tzv. podkladovými aktivy. Termínové obchody - obchody, které jsou sjednány v okamžiku podpisu kontraktu
Deriváty termínové operace Deriváty jsou termínové obchody, které jsou odvozeny od obchodů s jinými, tzv. podkladovými aktivy. Termínové obchody - obchody, které jsou sjednány v okamžiku podpisu kontraktu
Členění termínových obchodů z hlediska jejich základních
 Členění termínových obchodů z hlediska jejich základních vlastností a způsobů obchodovatelnosti TERMÍNOVÉ OBCHODY Neodvolatelné /tzv. pevné/ termínové obchody Termínové kontrakty typu forward a futures
Členění termínových obchodů z hlediska jejich základních vlastností a způsobů obchodovatelnosti TERMÍNOVÉ OBCHODY Neodvolatelné /tzv. pevné/ termínové obchody Termínové kontrakty typu forward a futures
KOUPENÉ A PRODANÉ OPCE VERTIKÁLNÍ SPREADY
 KAPITOLA 3 KOUPENÉ A PRODANÉ OPCE VERTIKÁLNÍ SPREADY Vertikální spread je kombinace koupené a prodané put nebo call opce se stejným expiračním měsícem. Výraz spread se používá proto, že riziko je rozložené
KAPITOLA 3 KOUPENÉ A PRODANÉ OPCE VERTIKÁLNÍ SPREADY Vertikální spread je kombinace koupené a prodané put nebo call opce se stejným expiračním měsícem. Výraz spread se používá proto, že riziko je rozložené
X = x, y = h(x) Y = y. hodnotám x a jedné hodnotě y. Dostaneme tabulku hodnot pravděpodobnostní
 ..08 8cv7.tex 7. cvičení - transformace náhodné veličiny Definice pojmů a základní vzorce Je-li X náhodná veličina a h : R R je měřitelná funkce, pak náhodnou veličinu Y, která je definovaná vztahem X
..08 8cv7.tex 7. cvičení - transformace náhodné veličiny Definice pojmů a základní vzorce Je-li X náhodná veličina a h : R R je měřitelná funkce, pak náhodnou veličinu Y, která je definovaná vztahem X
12. Křivkové integrály
 12 Křivkové integrály Definice 121 Jednoduchou po částech hladkou křivkou v prostoru R n rozumíme množinu bodů [x 1,, x n ], které jsou dány parametrickými rovnicemi x 1 = ϕ 1 t), x 2 = ϕ 2 t), x n = ϕ
12 Křivkové integrály Definice 121 Jednoduchou po částech hladkou křivkou v prostoru R n rozumíme množinu bodů [x 1,, x n ], které jsou dány parametrickými rovnicemi x 1 = ϕ 1 t), x 2 = ϕ 2 t), x n = ϕ
Téma 22. Ondřej Nývlt
 Téma 22 Ondřej Nývlt nyvlto1@fel.cvut.cz Náhodná veličina a náhodný vektor. Distribuční funkce, hustota a pravděpodobnostní funkce náhodné veličiny. Střední hodnota a rozptyl náhodné veličiny. Sdružené
Téma 22 Ondřej Nývlt nyvlto1@fel.cvut.cz Náhodná veličina a náhodný vektor. Distribuční funkce, hustota a pravděpodobnostní funkce náhodné veličiny. Střední hodnota a rozptyl náhodné veličiny. Sdružené
Tématické okruhy. 4. Investiční nástroje investiční nástroje, cenné papíry, druhy a vlastnosti
 Seznam tématických okruhů a skupin tématických okruhů ( 4 odst. 2 vyhlášky o druzích odborných obchodních činností obchodníka s cennými papíry vykonávaných prostřednictvím makléře, o druzích odborné specializace
Seznam tématických okruhů a skupin tématických okruhů ( 4 odst. 2 vyhlášky o druzích odborných obchodních činností obchodníka s cennými papíry vykonávaných prostřednictvím makléře, o druzích odborné specializace
Finanční deriváty II.
 Ing. Martin Širůček, Ph.D. Katedra financí a účetnictví sirucek.martin@svse.cz sirucek@gmail.com Finanční deriváty II. strana 2 Obsah přednášky Princip opcí Druhy opcí Cena a spekulační efekt Kurzovní
Ing. Martin Širůček, Ph.D. Katedra financí a účetnictví sirucek.martin@svse.cz sirucek@gmail.com Finanční deriváty II. strana 2 Obsah přednášky Princip opcí Druhy opcí Cena a spekulační efekt Kurzovní
Příloha k prezentaci BRODIS hodnotový OPFKI QIIS
 Příloha k prezentaci BRODIS hodnotový OPFKI QIIS V následující prezentaci se seznámíme s investičními principy, kterým věříme a na základě kterých jsme si nechali vytvořit BRODIS hodnotový OPFKI. Tyto
Příloha k prezentaci BRODIS hodnotový OPFKI QIIS V následující prezentaci se seznámíme s investičními principy, kterým věříme a na základě kterých jsme si nechali vytvořit BRODIS hodnotový OPFKI. Tyto
rovnic), Definice y + p(x)y = q(x), Je-li q(x) = 0 na M, nazývá se y + p(x)y =
 Cíle Přehled základních typů diferenciálních rovnic prvního řádu zakončíme pojednáním o lineárních rovnicích, které patří v praktických úlohách k nejfrekventovanějším. Ukážeme například, že jejich řešení
Cíle Přehled základních typů diferenciálních rovnic prvního řádu zakončíme pojednáním o lineárních rovnicích, které patří v praktických úlohách k nejfrekventovanějším. Ukážeme například, že jejich řešení
Opční strategie Vertikální spread
 Opční strategie Vertikální spread Bull Call Spread Tato strategie kombinuje nákup kupní opce (long call) a prodej kupní opce (short call) s odlišnými realizačními cenami, přičemž platí, že strike u nakoupené
Opční strategie Vertikální spread Bull Call Spread Tato strategie kombinuje nákup kupní opce (long call) a prodej kupní opce (short call) s odlišnými realizačními cenami, přičemž platí, že strike u nakoupené
MERTON C. ROBERT, SCHOLES S. MYRON
 MERTON C. ROBERT, SCHOLES S. MYRON Abstrakt: Ekonomičtí profesoři Black, Merton a Scholes, jejichž výzkum se zaměřil na modely oceňování opcí, se svojí prací zasloužili o dynamický rozvoj trhu finančních
MERTON C. ROBERT, SCHOLES S. MYRON Abstrakt: Ekonomičtí profesoři Black, Merton a Scholes, jejichž výzkum se zaměřil na modely oceňování opcí, se svojí prací zasloužili o dynamický rozvoj trhu finančních
1. Přednáška. Ing. Miroslav Šulai, MBA
 N_OFI_2 1. Přednáška Počet pravděpodobnosti Statistický aparát používaný ve financích Ing. Miroslav Šulai, MBA 1 Počet pravděpodobnosti -náhodné veličiny 2 Počet pravděpodobnosti -náhodné veličiny 3 Jevy
N_OFI_2 1. Přednáška Počet pravděpodobnosti Statistický aparát používaný ve financích Ing. Miroslav Šulai, MBA 1 Počet pravděpodobnosti -náhodné veličiny 2 Počet pravděpodobnosti -náhodné veličiny 3 Jevy
9. T r a n s f o r m a c e n á h o d n é v e l i č i n y
 9. T r a n s f o r m a c e n á h o d n é v e l i č i n y Při popisu procesů zpracováváme vstupní údaj, hodnotu x tak, že výstupní hodnota y závisí nějakým způsobem na vstupní, je její funkcí y = f(x).
9. T r a n s f o r m a c e n á h o d n é v e l i č i n y Při popisu procesů zpracováváme vstupní údaj, hodnotu x tak, že výstupní hodnota y závisí nějakým způsobem na vstupní, je její funkcí y = f(x).
Necht tedy máme přirozená čísla n, k pod pojmem systém lineárních rovnic rozumíme rovnice ve tvaru
 2. Systémy lineárních rovnic V této kapitole se budeme zabývat soustavami lineárních rovnic s koeficienty z pole reálných případně komplexních čísel. Uvádíme podmínku pro existenci řešení systému lineárních
2. Systémy lineárních rovnic V této kapitole se budeme zabývat soustavami lineárních rovnic s koeficienty z pole reálných případně komplexních čísel. Uvádíme podmínku pro existenci řešení systému lineárních
INFORMACE O RIZICÍCH
 INFORMACE O RIZICÍCH PPF banka a.s. se sídlem Praha 6, Evropská 2690/17, PSČ: 160 41, IČ: 47116129, zapsaná v obchodním rejstříku vedeném Městským soudem v Praze, oddíl B, vložka 1834 (dále jen Obchodník)
INFORMACE O RIZICÍCH PPF banka a.s. se sídlem Praha 6, Evropská 2690/17, PSČ: 160 41, IČ: 47116129, zapsaná v obchodním rejstříku vedeném Městským soudem v Praze, oddíl B, vložka 1834 (dále jen Obchodník)
Účetnictví finančních institucí. Cenné papíry a deriváty
 Účetnictví finančních institucí Cenné papíry a deriváty 1 BANKOVNÍ ÚČETNICTVÍ ÚČTOVÁ TŘÍDA 3 Od klasických služeb, které představují přijímání vkladů a poskytování úvěrů, banky postupně přecházejí k službám
Účetnictví finančních institucí Cenné papíry a deriváty 1 BANKOVNÍ ÚČETNICTVÍ ÚČTOVÁ TŘÍDA 3 Od klasických služeb, které představují přijímání vkladů a poskytování úvěrů, banky postupně přecházejí k službám
Bankovní účetnictví - účtová třída 3 1
 Bankovní účetnictví Cenné papíry a deriváty Bankovní účetnictví - účtová třída 3 1 BANKOVNÍ ÚČETNICTVÍ ÚČTOVÁ TŘÍDA 3 Od klasických služeb, které představují přijímání vkladů a poskytování úvěrů, banky
Bankovní účetnictví Cenné papíry a deriváty Bankovní účetnictví - účtová třída 3 1 BANKOVNÍ ÚČETNICTVÍ ÚČTOVÁ TŘÍDA 3 Od klasických služeb, které představují přijímání vkladů a poskytování úvěrů, banky
Jiří Neubauer. Katedra ekonometrie, FVL, UO Brno kancelář 69a, tel
 Katedra ekonometrie, FVL, UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Výsledky některých náhodných pokusů jsou přímo vyjádřeny číselně (např. při hodu kostkou padne 6). Náhodnou veličinou
Katedra ekonometrie, FVL, UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Výsledky některých náhodných pokusů jsou přímo vyjádřeny číselně (např. při hodu kostkou padne 6). Náhodnou veličinou
I. D i s k r é t n í r o z d ě l e n í
 6. T y p y r o z d ě l e n í Poznámka: V odst. 5.5-5.10 jsme uvedli příklady náhodných veličin a jejich distribučních funkcí. Poznali jsme, že se od sebe liší svým typem. V příkladech 5.5, 5.6 a 5.8 jsme
6. T y p y r o z d ě l e n í Poznámka: V odst. 5.5-5.10 jsme uvedli příklady náhodných veličin a jejich distribučních funkcí. Poznali jsme, že se od sebe liší svým typem. V příkladech 5.5, 5.6 a 5.8 jsme
10. cvičení z PST. 5. prosince T = (n 1) S2 X. (n 1) s2 x σ 2 q χ 2 (n 1) (1 α 2 ). q χ 2 (n 1) 2. 2 x. (n 1) s. x = 1 6. x i = 457.
 0 cvičení z PST 5 prosince 208 0 (intervalový odhad pro rozptyl) Soubor (70, 84, 89, 70, 74, 70) je náhodným výběrem z normálního rozdělení N(µ, σ 2 ) Určete oboustranný symetrický 95% interval spolehlivosti
0 cvičení z PST 5 prosince 208 0 (intervalový odhad pro rozptyl) Soubor (70, 84, 89, 70, 74, 70) je náhodným výběrem z normálního rozdělení N(µ, σ 2 ) Určete oboustranný symetrický 95% interval spolehlivosti
Matematická analýza ve Vesmíru. Jiří Bouchala
 Matematická analýza ve Vesmíru Jiří Bouchala Katedra aplikované matematiky jiri.bouchala@vsb.cz www.am.vsb.cz/bouchala - p. 1/19 typu: m x (sin x, cos x) R(x, ax +...)dx. Matematická analýza ve Vesmíru.
Matematická analýza ve Vesmíru Jiří Bouchala Katedra aplikované matematiky jiri.bouchala@vsb.cz www.am.vsb.cz/bouchala - p. 1/19 typu: m x (sin x, cos x) R(x, ax +...)dx. Matematická analýza ve Vesmíru.
Úvod do analýzy cenných papírů. Dagmar Linnertová 5. Října 2009
 Úvod do analýzy cenných papírů Dagmar Linnertová 5. Října 2009 Investice a investiční rozhodování Každý je potenciální investor Nevynaložením prostředků na svou současnou potřebu se jí tímto vzdává Mít
Úvod do analýzy cenných papírů Dagmar Linnertová 5. Října 2009 Investice a investiční rozhodování Každý je potenciální investor Nevynaložením prostředků na svou současnou potřebu se jí tímto vzdává Mít
p(x) = P (X = x), x R,
 6. T y p y r o z d ě l e n í Poznámka: V odst. 5.5-5.10 jsme uvedli příklady náhodných veličin a jejich distribučních funkcí. Poznali jsme, že se od sebe liší svým typem. V příkladech 5.5, 5.6 a 5.8 jsme
6. T y p y r o z d ě l e n í Poznámka: V odst. 5.5-5.10 jsme uvedli příklady náhodných veličin a jejich distribučních funkcí. Poznali jsme, že se od sebe liší svým typem. V příkladech 5.5, 5.6 a 5.8 jsme
Náklady kapitálu. Finanční struktura by měla korespondovat s majetkovou strukturou z hlediska časovosti. Stálá aktiva. Dlouhodobý.
 Náklady na kapitál Náklady kapitálu Finanční struktura by měla korespondovat s majetkovou strukturou z hlediska časovosti Aktiva (majetek) Stálá aktiva Oběžná aktiva Dlouhodobý majetek Trvalý OM Dlouhodobý
Náklady na kapitál Náklady kapitálu Finanční struktura by měla korespondovat s majetkovou strukturou z hlediska časovosti Aktiva (majetek) Stálá aktiva Oběžná aktiva Dlouhodobý majetek Trvalý OM Dlouhodobý
Matematika (CŽV Kadaň) aneb Úvod do lineární algebry Matice a soustavy rovnic
 Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
INTEGRÁLY S PARAMETREM
 INTEGRÁLY S PARAMETREM b a V kapitole o integraci funkcí více proměnných byla potřeba funkce g(x) = f(x, y) dy proměnné x. Spojitost funkce g(x) = b a f(x, y) dy proměnné x znamená vlastně prohození limity
INTEGRÁLY S PARAMETREM b a V kapitole o integraci funkcí více proměnných byla potřeba funkce g(x) = f(x, y) dy proměnné x. Spojitost funkce g(x) = b a f(x, y) dy proměnné x znamená vlastně prohození limity
Produkty finančních trhů a jejich rizika. Ostatní produkty
 Produkty finančních trhů a jejich rizika Ostatní produkty datum platnosti a účinnosti od 01. 09. 2014 Obsah Úvod 3 Vysvětlivky 4 Popis rizik 4 Obecné 4 Charakteristiky opcí 5 Seznam zkratek 6 Riziko ztráty
Produkty finančních trhů a jejich rizika Ostatní produkty datum platnosti a účinnosti od 01. 09. 2014 Obsah Úvod 3 Vysvětlivky 4 Popis rizik 4 Obecné 4 Charakteristiky opcí 5 Seznam zkratek 6 Riziko ztráty
Finanční deriváty. Základní druhy finančních investičních instrumentů. Vymezení termínových obchodů. spotový versus termínový obchod (resp.
 Ing. Martin Širůček, Ph.D. Katedra financí a účetnictví sirucek.martin@svse.cz sirucek@gmail.com Finanční deriváty strana 2 Základní druhy finančních investičních instrumentů strana 3 Vymezení termínových
Ing. Martin Širůček, Ph.D. Katedra financí a účetnictví sirucek.martin@svse.cz sirucek@gmail.com Finanční deriváty strana 2 Základní druhy finančních investičních instrumentů strana 3 Vymezení termínových
Optimální řízení pro geometrický Brownův pohyb
 1/39 Optimální řízení pro geometrický Brownův pohyb Lenka Slámová Katedra pravděpodobnosti a matematické statistiky Matematicko fyzikální fakulta Univerzity Karlovy Stochastické modelování v ekonomii a
1/39 Optimální řízení pro geometrický Brownův pohyb Lenka Slámová Katedra pravděpodobnosti a matematické statistiky Matematicko fyzikální fakulta Univerzity Karlovy Stochastické modelování v ekonomii a
Finanční rizika. podniku, způsoben rizikového faktoru. že e protistrana. hodnoty podniku, způsoben. ností ŘÍZENÍ RIZIK I
 Finanční rizika Tržní riziko je pravděpodobnost podobnost změny hodnoty podniku, způsoben sobené změnou tržní hodnoty rizikového faktoru. Kreditní riziko je pravděpodobnost podobnost změny hodnoty podniku,
Finanční rizika Tržní riziko je pravděpodobnost podobnost změny hodnoty podniku, způsoben sobené změnou tržní hodnoty rizikového faktoru. Kreditní riziko je pravděpodobnost podobnost změny hodnoty podniku,
SR (CZK/EUR) 26,512 27,122 3 měs. IR CZK p.a. 6,24 7,44 3 měs. IR EUR p.a. 3,86 4,62 a) přímá kotace Nákupní forwardový kurs vypočítáme takto: SR 100
 Příklad č. 1 Na základě následujících kotací spotového kursu eura v korunách a tříměsíčních úrokových měr na korunová a eurová aktiva vypočítejte nákupní a prodejní tříměsíční forwardový kurs eura v korunách
Příklad č. 1 Na základě následujících kotací spotového kursu eura v korunách a tříměsíčních úrokových měr na korunová a eurová aktiva vypočítejte nákupní a prodejní tříměsíční forwardový kurs eura v korunách
KMA/MAB. Kamila Matoušková (A07142) Plzeň, 2009 EFEKTIVNÍ PORFÓLIO V MARKOWITZOVĚ SMYSLU
 EFEKTIVNÍ PORFÓLIO V MARKOWITZOVĚ SMYSLU KMA/MAB Kamila Matoušková (A07142) Plzeň, 2009 Obsahem práce je vytvoření efektivního portfolia v Markowitzově smyslu.z akcií obchodovaných na SPADu. Dále je uvažována
EFEKTIVNÍ PORFÓLIO V MARKOWITZOVĚ SMYSLU KMA/MAB Kamila Matoušková (A07142) Plzeň, 2009 Obsahem práce je vytvoření efektivního portfolia v Markowitzově smyslu.z akcií obchodovaných na SPADu. Dále je uvažována
Náhodný vektor. Náhodný vektor. Hustota náhodného vektoru. Hustota náhodného vektoru. Náhodný vektor je dvojice náhodných veličin (X, Y ) T = ( X
 Náhodný vektor Náhodný vektor zatím jsme sledovali jednu náhodnou veličinu, její rozdělení a charakteristiky často potřebujeme vyšetřovat vzájemný vztah několika náhodných veličin musíme sledovat jejich
Náhodný vektor Náhodný vektor zatím jsme sledovali jednu náhodnou veličinu, její rozdělení a charakteristiky často potřebujeme vyšetřovat vzájemný vztah několika náhodných veličin musíme sledovat jejich
Aplikovaná numerická matematika
 Aplikovaná numerická matematika 6. Metoda nejmenších čtverců doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních
Aplikovaná numerická matematika 6. Metoda nejmenších čtverců doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních
Pojmy z kombinatoriky, pravděpodobnosti, znalosti z kapitoly náhodná veličina, znalost parciálních derivací, dvojného integrálu.
 6. NÁHODNÝ VEKTOR Průvodce studiem V počtu pravděpodobnosti i v matematické statistice se setkáváme nejen s náhodnými veličinami, jejichž hodnotami jsou reálná čísla, ale i s takovými, jejichž hodnotami
6. NÁHODNÝ VEKTOR Průvodce studiem V počtu pravděpodobnosti i v matematické statistice se setkáváme nejen s náhodnými veličinami, jejichž hodnotami jsou reálná čísla, ale i s takovými, jejichž hodnotami
ROVNICE NA ČASOVÝCH ŠKÁLÁCH A NÁHODNÉ PROCESY. Michal Friesl
 Robust 14, Jetřichovice ROVNICE NA ČASOVÝCH ŠKÁLÁCH A NÁHODNÉ PROCESY Michal Friesl Katedra matematiky Fakulta aplikovaných věd Západočeská univerzita v Plzni Robust 14, Jetřichovice ÚVOD Úvod Analýzníkům
Robust 14, Jetřichovice ROVNICE NA ČASOVÝCH ŠKÁLÁCH A NÁHODNÉ PROCESY Michal Friesl Katedra matematiky Fakulta aplikovaných věd Západočeská univerzita v Plzni Robust 14, Jetřichovice ÚVOD Úvod Analýzníkům
9. T r a n s f o r m a c e n á h o d n é v e l i č i n y
 9. T r a n s f o r m a c e n á h o d n é v e l i č i n Při popisu procesů zpracováváme vstupní údaj, hodnotu x tak, že výstupní hodnota závisí nějakým způsobem na vstupní, je její funkcí = f(x). Pokud
9. T r a n s f o r m a c e n á h o d n é v e l i č i n Při popisu procesů zpracováváme vstupní údaj, hodnotu x tak, že výstupní hodnota závisí nějakým způsobem na vstupní, je její funkcí = f(x). Pokud
8 Střední hodnota a rozptyl
 Břetislav Fajmon, UMAT FEKT, VUT Brno Této přednášce odpovídá kapitola 10 ze skript [1]. Také je k dispozici sbírka úloh [2], kde si můžete procvičit příklady z kapitol 2, 3 a 4. K samostatnému procvičení
Břetislav Fajmon, UMAT FEKT, VUT Brno Této přednášce odpovídá kapitola 10 ze skript [1]. Také je k dispozici sbírka úloh [2], kde si můžete procvičit příklady z kapitol 2, 3 a 4. K samostatnému procvičení
Základy teorie finančních investic
 Ing. Martin Širůček, Ph.D. Katedra financí a účetnictví sirucek.martin@svse.cz sirucek@gmail.com Základy teorie finančních investic strana 2 Úvod do teorie investic Pojem investice Rozdělení investic a)
Ing. Martin Širůček, Ph.D. Katedra financí a účetnictví sirucek.martin@svse.cz sirucek@gmail.com Základy teorie finančních investic strana 2 Úvod do teorie investic Pojem investice Rozdělení investic a)
Investiční služby, Investiční nástroje a rizika s nimi související
 Investiční služby, Investiční nástroje a rizika s nimi související Předmětem tohoto materiálu je popis investičních služeb poskytovaných ATLANTIK finanční trhy, a.s. (dále jen Obchodník ), investičních
Investiční služby, Investiční nástroje a rizika s nimi související Předmětem tohoto materiálu je popis investičních služeb poskytovaných ATLANTIK finanční trhy, a.s. (dále jen Obchodník ), investičních
Všeobecná rovnováha 1 Statistický pohled
 Makroekonomická analýza přednáška 4 1 Všeobecná rovnováha 1 Statistický pohled Předpoklady Úspory (resp.spotřeba) a investice (resp.kapitál), kterými jsme se zabývali v minulých lekcích, jsou spolu s technologickým
Makroekonomická analýza přednáška 4 1 Všeobecná rovnováha 1 Statistický pohled Předpoklady Úspory (resp.spotřeba) a investice (resp.kapitál), kterými jsme se zabývali v minulých lekcích, jsou spolu s technologickým
MODELY ŘÍZENÍ ZÁSOB nákladově orientované modely poptávka pořizovací lhůta dodávky předstih objednávky deterministické stochastické
 MODELY ŘÍZENÍ ZÁSOB Význam zásob spočívá především v tom, že - vyrovnávají časový nebo prostorový nesoulad mezi výrobou a spotřebou - zajišťují plynulou výrobu nebo plynulé dodávky zboží i při nepředvídaných
MODELY ŘÍZENÍ ZÁSOB Význam zásob spočívá především v tom, že - vyrovnávají časový nebo prostorový nesoulad mezi výrobou a spotřebou - zajišťují plynulou výrobu nebo plynulé dodávky zboží i při nepředvídaných
Charakterizace rozdělení
 Charakterizace rozdělení Momenty f(x) f(x) f(x) μ >μ 1 σ 1 σ >σ 1 g 1 g σ μ 1 μ x μ x x N K MK = x f( x) dx 1 M K = x N CK = ( x M ) f( x) dx ( xi M 1 C = 1 K 1) N i= 1 K i K N i= 1 K μ = E ( X ) = xf
Charakterizace rozdělení Momenty f(x) f(x) f(x) μ >μ 1 σ 1 σ >σ 1 g 1 g σ μ 1 μ x μ x x N K MK = x f( x) dx 1 M K = x N CK = ( x M ) f( x) dx ( xi M 1 C = 1 K 1) N i= 1 K i K N i= 1 K μ = E ( X ) = xf
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
3.1. Newtonovy zákony jsou základní zákony klasické (Newtonovy) mechaniky
 3. ZÁKLADY DYNAMIKY Dynamika zkoumá příčinné souvislosti pohybu a je tedy zdůvodněním zákonů kinematiky. K pojmům používaným v kinematice zavádí pojem hmoty a síly. Statický výpočet Dynamický výpočet -
3. ZÁKLADY DYNAMIKY Dynamika zkoumá příčinné souvislosti pohybu a je tedy zdůvodněním zákonů kinematiky. K pojmům používaným v kinematice zavádí pojem hmoty a síly. Statický výpočet Dynamický výpočet -
Statistika a spolehlivost v lékařství Charakteristiky spolehlivosti prvků I
 Statistika a spolehlivost v lékařství Charakteristiky spolehlivosti prvků I Příklad Tahová síla papíru používaného pro výrobu potravinových sáčků je důležitá charakteristika kvality. Je známo, že síla
Statistika a spolehlivost v lékařství Charakteristiky spolehlivosti prvků I Příklad Tahová síla papíru používaného pro výrobu potravinových sáčků je důležitá charakteristika kvality. Je známo, že síla
Obchodní instrumenty. 1. Bez páky: A) Akcie B) ETF. 2. S pákou: A) Futures B) Opce C) CFD D) Forex
 CO TO JE BURZA? Burza Místo, kde se obchodují všechny finanční instrumenty Striktní dohled kontrolních orgánů Místo, kde se střetává nabídka s poptávkou Právnická osoba, a.s. Obchodník s cennými papíry
CO TO JE BURZA? Burza Místo, kde se obchodují všechny finanční instrumenty Striktní dohled kontrolních orgánů Místo, kde se střetává nabídka s poptávkou Právnická osoba, a.s. Obchodník s cennými papíry
Diferenciální rovnice
 Obyčejné diferenciální rovnice - studijní text pro cvičení v předmětu Matematika - 2. Studijní materiál byl připraven pracovníky katedry E. Novákovou, M. Hyánkovou a L. Průchou za podpory grantu IG ČVUT
Obyčejné diferenciální rovnice - studijní text pro cvičení v předmětu Matematika - 2. Studijní materiál byl připraven pracovníky katedry E. Novákovou, M. Hyánkovou a L. Průchou za podpory grantu IG ČVUT
Pojistná matematika. Úmrtnostní tabulky, komutační čísla a jejich použití. Silvie Kafková
 Úmrtnostní tabulky, komutační čísla a jejich použití 2015 Osnova 1 Délka života 2 Intenzita úmrtnosti 3 Úmrtnostní Tabulky 4 Komutační čísla Obsah 1 Délka života 2 Intenzita úmrtnosti 3 Úmrtnostní Tabulky
Úmrtnostní tabulky, komutační čísla a jejich použití 2015 Osnova 1 Délka života 2 Intenzita úmrtnosti 3 Úmrtnostní Tabulky 4 Komutační čísla Obsah 1 Délka života 2 Intenzita úmrtnosti 3 Úmrtnostní Tabulky
Základy matematiky pro FEK
 Základy matematiky pro FEK 8. přednáška Blanka Šedivá KMA zimní semestr 2016/2017 Blanka Šedivá (KMA) Základy matematiky pro FEK zimní semestr 2016/2017 1 / 14 Derivace funkce U lineárních funkcí ve tvaru
Základy matematiky pro FEK 8. přednáška Blanka Šedivá KMA zimní semestr 2016/2017 Blanka Šedivá (KMA) Základy matematiky pro FEK zimní semestr 2016/2017 1 / 14 Derivace funkce U lineárních funkcí ve tvaru
Finanční deriváty. Základní druhy finančních investičních instrumentů. Vymezení termínových obchodů. spotový versus termínový obchod (resp.
 Ing. Martin Širůček, Ph.D. Katedra financí a účetnictví sirucek.martin@svse.cz sirucek@gmail.com Finanční deriváty strana 2 Základní druhy finančních investičních instrumentů strana 3 Vymezení termínových
Ing. Martin Širůček, Ph.D. Katedra financí a účetnictví sirucek.martin@svse.cz sirucek@gmail.com Finanční deriváty strana 2 Základní druhy finančních investičních instrumentů strana 3 Vymezení termínových
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Vektory Definice 011 Vektorem aritmetického prostorur n budeme rozumět uspořádanou n-tici reálných čísel x 1, x 2,, x n Definice 012 Definice sčítání
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Vektory Definice 011 Vektorem aritmetického prostorur n budeme rozumět uspořádanou n-tici reálných čísel x 1, x 2,, x n Definice 012 Definice sčítání
Investiční nástroje a rizika s nimi související
 Investiční nástroje a rizika s nimi související CENNÉ PAPÍRY Dokumentace: Banka uzavírá s klientem standardní smlouvy dle typu kontraktu (Komisionářská smlouva, repo smlouva, mandátní smlouva). AKCIE je
Investiční nástroje a rizika s nimi související CENNÉ PAPÍRY Dokumentace: Banka uzavírá s klientem standardní smlouvy dle typu kontraktu (Komisionářská smlouva, repo smlouva, mandátní smlouva). AKCIE je
Strukturované investiční instrumenty
 Ing. Martin Širůček, Ph.D. Strukturované investiční instrumenty Katedra financí a účetnictví sirucek.martin@svse.cz sirucek@gmail.com strana 2 Základní charakteristika finanční investiční instrumenty slučující
Ing. Martin Širůček, Ph.D. Strukturované investiční instrumenty Katedra financí a účetnictví sirucek.martin@svse.cz sirucek@gmail.com strana 2 Základní charakteristika finanční investiční instrumenty slučující
Parciální derivace a diferenciál
 Parciální derivace a diferenciál Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem
Parciální derivace a diferenciál Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem
OBECNÉ POKYNY K OPRAVÁM MODIFIKOVANÉ DURACE EBA/GL/2016/09 04/01/2017. Obecné pokyny
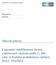 EBA/GL/2016/09 04/01/2017 Obecné pokyny k opravám modifikované durace u dluhových nástrojů podle čl. 340 odst. 3 druhého pododstavce nařízení (EU) č. 575/2013 1. Dodržování předpisů a oznamovací povinnost
EBA/GL/2016/09 04/01/2017 Obecné pokyny k opravám modifikované durace u dluhových nástrojů podle čl. 340 odst. 3 druhého pododstavce nařízení (EU) č. 575/2013 1. Dodržování předpisů a oznamovací povinnost
Vybrané poznámky k řízení rizik v bankách
 Vybrané poznámky k řízení rizik v bankách Seminář z aktuárských věd Petr Myška 7.11.2008 Obsah přednášky Oceňování nestandartních instrumentů finančních trhů Aplikace analytických vzorců Simulační techniky
Vybrané poznámky k řízení rizik v bankách Seminář z aktuárských věd Petr Myška 7.11.2008 Obsah přednášky Oceňování nestandartních instrumentů finančních trhů Aplikace analytických vzorců Simulační techniky
Definice 7.1 Nechť je dán pravděpodobnostní prostor (Ω, A, P). Zobrazení. nebo ekvivalentně
 7 Náhodný vektor Nezávislost náhodných veličin Definice 7 Nechť je dán pravděpodobnostní prostor (Ω, A, P) Zobrazení X : Ω R n, které je A-měřitelné, se nazývá (n-rozměrný) náhodný vektor Měřitelností
7 Náhodný vektor Nezávislost náhodných veličin Definice 7 Nechť je dán pravděpodobnostní prostor (Ω, A, P) Zobrazení X : Ω R n, které je A-měřitelné, se nazývá (n-rozměrný) náhodný vektor Měřitelností
TEORETICKÉ PŘEDPOKLADY Garantovaných produktů
 TEORETICKÉ PŘEDPOKLADY Garantovaných produktů 1 Výnosově -rizikový profil Knockoutprodukty Warrants Výnosová-šance Garantované produkty Dluhopisy Diskontové produkty Airbag Bonus Indexové produkty Akciové
TEORETICKÉ PŘEDPOKLADY Garantovaných produktů 1 Výnosově -rizikový profil Knockoutprodukty Warrants Výnosová-šance Garantované produkty Dluhopisy Diskontové produkty Airbag Bonus Indexové produkty Akciové
Úvod do teorie portfolia. CAPM model. APT model Výhody vs. nevýhody modelů CML SML. Beta faktor
 Radka Domanská 1 Úvod do teorie portfolia CML CAPM model SML Beta faktor APT model Výhody vs. nevýhody modelů 2 Množina dostupných portfolií Všechna možná portfolia, která mohou být vytvořena ze skupiny
Radka Domanská 1 Úvod do teorie portfolia CML CAPM model SML Beta faktor APT model Výhody vs. nevýhody modelů 2 Množina dostupných portfolií Všechna možná portfolia, která mohou být vytvořena ze skupiny
Mikroekonomie Nabídka, poptávka
 Téma cvičení č. 2: Mikroekonomie Nabídka, poptávka Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Podstatné z minulého cvičení Matematický pojmový aparát v Mikroekonomii Důležité minulé cvičení kontrolní
Téma cvičení č. 2: Mikroekonomie Nabídka, poptávka Ing. Jaroslav ŠETEK, Ph.D. Katedra ekonomiky, JČU Podstatné z minulého cvičení Matematický pojmový aparát v Mikroekonomii Důležité minulé cvičení kontrolní
pouze u některých typů rovnic a v tomto textu se jím nebudeme až na
 Matematika II 7.1. Zavedení diferenciálních rovnic Definice 7.1.1. Rovnice tvaru F(y (n), y (n 1),, y, y, x) = 0 se nazývá diferenciální rovnice n-tého řádu pro funkci y = y(x). Speciálně je F(y, y, x)
Matematika II 7.1. Zavedení diferenciálních rovnic Definice 7.1.1. Rovnice tvaru F(y (n), y (n 1),, y, y, x) = 0 se nazývá diferenciální rovnice n-tého řádu pro funkci y = y(x). Speciálně je F(y, y, x)
Úvod. www.csob.cz. Nástroje sloužící k zajištění rizika pohybu úrokových měr. Finanční trhy. Identifikace rizika. Definice a rozsah rizika
 Nástroje sloužící k zajištění rizika pohybu úrokových měr Úvod Každý podnikatelský subjekt čelí nejistotě. Budoucnost je doposud nenapsaná kapitola a můžeme jen s menšími či většími úspěchy odhadovat,
Nástroje sloužící k zajištění rizika pohybu úrokových měr Úvod Každý podnikatelský subjekt čelí nejistotě. Budoucnost je doposud nenapsaná kapitola a můžeme jen s menšími či většími úspěchy odhadovat,
2D transformací. červen Odvození transformačního klíče vybraných 2D transformací Metody vyrovnání... 2
 Výpočet transformačních koeficinetů vybraných 2D transformací Jan Ježek červen 2008 Obsah Odvození transformačního klíče vybraných 2D transformací 2 Meto vyrovnání 2 2 Obecné vyjádření lineárních 2D transformací
Výpočet transformačních koeficinetů vybraných 2D transformací Jan Ježek červen 2008 Obsah Odvození transformačního klíče vybraných 2D transformací 2 Meto vyrovnání 2 2 Obecné vyjádření lineárních 2D transformací
Doc. RNDr. Martin Kolář, Ph.D. Mgr. Lenka Křivánková
 Oceňování finančních derivátů Doc. RNDr. Martin Kolář, Ph.D. Mgr. Lenka Křivánková 1 Tento učební text vznikl za přispění Evropského sociálního fondu a státního rozpočtu ČR prostřednictvím Operačního programu
Oceňování finančních derivátů Doc. RNDr. Martin Kolář, Ph.D. Mgr. Lenka Křivánková 1 Tento učební text vznikl za přispění Evropského sociálního fondu a státního rozpočtu ČR prostřednictvím Operačního programu
E S E J MĚNOVÉ FUTURES A MĚNOVÉ OPCE
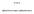 E S E J MĚNOVÉ FUTURES A MĚNOVÉ OPCE Úvod Měnovými operacemi se nazývají prodeje a nákupy cizích měn, zejména pro zprostředkování obchodů se službami a kapitálovými transakcemi 1. Jednotlivé subjekty provádějící
E S E J MĚNOVÉ FUTURES A MĚNOVÉ OPCE Úvod Měnovými operacemi se nazývají prodeje a nákupy cizích měn, zejména pro zprostředkování obchodů se službami a kapitálovými transakcemi 1. Jednotlivé subjekty provádějící
MASARYKOVA UNIVERZITA PŘÍRODOVĚDECKÁ FAKULTA
 MASARYKOVA UNIVERZITA PŘÍRODOVĚDECKÁ FAKULTA ÚSTAV MATEMATIKY A STATISTIKY MODELY STOCHASTICKÉ VOLATILITY Diplomová práce Martin Diviš Vedoucí práce: Mgr. Ondřej Pokora, Ph.D. Brno 2015 Bibliografický
MASARYKOVA UNIVERZITA PŘÍRODOVĚDECKÁ FAKULTA ÚSTAV MATEMATIKY A STATISTIKY MODELY STOCHASTICKÉ VOLATILITY Diplomová práce Martin Diviš Vedoucí práce: Mgr. Ondřej Pokora, Ph.D. Brno 2015 Bibliografický
Normální rozložení a odvozená rozložení
 I Normální rozložení a odvozená rozložení I.I Normální rozložení Data, se kterými pracujeme, pocházejí z různých rozložení. Mohou být vychýlena (doleva popř. doprava, nebo v nich není na první pohled vidět
I Normální rozložení a odvozená rozložení I.I Normální rozložení Data, se kterými pracujeme, pocházejí z různých rozložení. Mohou být vychýlena (doleva popř. doprava, nebo v nich není na první pohled vidět
PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU
 PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU 6.1 Křivkový integrál 1. druhu Definice 1. Množina R n se nazývá prostá regulární křivka v R n právě tehdy, když existuje vzájemně jednoznačné zobrazení
PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU 6.1 Křivkový integrál 1. druhu Definice 1. Množina R n se nazývá prostá regulární křivka v R n právě tehdy, když existuje vzájemně jednoznačné zobrazení
Funkce jedné proměnné
 Funkce jedné proměnné Příklad - V následujících příkladech v případě a) pro funkce dané rovnicí zjistěte zda jsou rostoucí klesající nebo konstantní vypočítejte průsečíky grafu s osami souřadnic a graf
Funkce jedné proměnné Příklad - V následujících příkladech v případě a) pro funkce dané rovnicí zjistěte zda jsou rostoucí klesající nebo konstantní vypočítejte průsečíky grafu s osami souřadnic a graf
