Program EduBeam. Uživatelský manuál. 13. března Vít Šmilauer, Bořek Patzák, Jan Stránský
|
|
|
- Magdalena Urbanová
- před 6 lety
- Počet zobrazení:
Transkript
1 Program EduBeam Uživatelský manuál 13. března 2018 Vít Šmilauer, Bořek Patzák, Jan Stránský České vysoké učení technické v Praze Fakulta stavební Katedra mechaniky Thákurova Praha 6
2 Obsah 1 Úvod 3 2 Posloupnost zadávání dat 3 3 Příklad 2D prutové konstrukce 4 4 Vliv smyku a přechod na zjednodušenou deformační metodu 9 5 Závěr 9 2
3 1 Úvod Program EduBeam je open-source konečněprvkový program, který slouží převážně pro řešení vnitřních sil na staticky určitých i neurčitých 2D rovinných přímých prutových konstrukcí v lineárně elastické oblasti. EduBeam je primárně určen pro výuku studentů a pro výpočty jednodušších konstrukcí, například příhradových konstrukcí, prostých a spojitých nosníků, rámů, krovů, které se běžně probírají ve výuce. Výstupem programu jsou Grafické průběhy vnitřních sil (N, V, M). Deformované tvary konstrukce. Reakce. Matice tuhosti prutových prvků a matice tuhosti konstrukce. Vektor zatížení prutových prvků a vektor zatížení konstrukce. EduBeam umožňuje ukládat řešenou úlohu, exportovat výsledky ve formě tabulek či ukládat screenshoty ve formě bitmap. Je také vybaven funkcí Undo/Redo. EduBeam neobsahuje mnoho uživatelsky příjemných funkcí, které jsou dostupné v komerčních programech (databáze materiálů, databáze průřezů, DXF/DWG import, dimenzování, posudky průřezů, výkaz materiálu, BIM...). Role univerzity je seznámit studenty s různými metodami řešení a proto není ani naším cílem vytvářet konkurenci komerčním programům, která by stála mnoho času a úsilí. Naším cílem je poskytnout zdarma studentům program, který obsahuje základní filosofii metody konečných prvků s aplikací na prutové konstrukce. V současné době tvoří metoda konečných prvků naprosto dominantní přístup pro řešení lineárních i nelineárních úloh stavební mechaniky. EduBeam je napsán v jazyce Python 2.7 a poskytuje možnost dalšího rozšíření s přístupen ke zdrojovým kódům. V tomto směru jsme otevření k jakékoli další spolupráci. EduBeam s příklady lze získat na edubeam:edubeam. K dispozici je exe soubor pro Windows, který je zkompilován pomocí programu PyInstaller. Pro další zájemce jsou ke stažení zdrojové py soubory, které běží na všech operačních systémech, vyžadují však instalaci Pythonu 2.7 a dalších knihoven. EduBeam lze spouštět s různými parametry, které získáte spuštěním z terminálu s parametrem -h, například $ edubeam.exe -h Jazyk EduBeamu se automaticky zjistí z nastavení locales. Český jazyk se násilně zapne pomocí parametru -l cz, anglický -l en. 2 Posloupnost zadávání dat Všechny komerční i nekomerční softwary pro analýzu metodou konečných prvků mají prakticky stejnou posloupnost úkonů. Posloupnost vyplývá z formulace metody konečných prvků, kdy je potřeba nakonec řešit podmínky rovnováhy na konstrukci pomocí rovnice Kr = f (1) 3
4 kde K je redukovaná matice tuhosti konstrukce, r je vektor neznámých posunutí či natočení a f je vektor zatížení. Pro sestavení matice K je potřeba provést lokalizaci příspěvků tuhosti jednotlivých prvků, která závisí na geometrii a materiálových vlastnostech. Sekvence zadávání vstupních dat, výpočtu a vyhodnocení obvykle probíhá stejným způsobem pro všechny programy. Pro případ 2D lineární analýzy prutové konstrukce v programu EduBeam vypadá konkrétně takto Zadání materiálů - specifikuje se modul pružnosti, smykový modul pružnosti, součinitel délkové teplotní roztažnosti. Zadání průřezů - zadávají se průřezové charakteristiky plocha A, moment setrvačnosti I y, výška průřezu h, součinitel vlivu smyku κ. Zadání geometrie - zadání uzlů, podpor, prutů, kloubů. Je možné také zadat více oddělených konstrukcí, redukovaná matice tuhosti konstrukce K se pak skládá z více vzájemně nezávislých submatic jednotlivých konstrukcí. Zadání zatížení - zadání uzlových sil a momentů, spojitých prutových zatížení, poklesů podpor, teploty na dolním a horním povrchu prutu. Vytvoření sítě - v programu EduBeam odpovídá síť přímo zadaným 2D prutům, není tedy potřeba síť dále vytvářet. Řešení soustavy rovnic dle (1). Postprocessing Vykreslení výsledků, tj. vnitřních sil N,V,M, průhybů konstrukce. Přístup do matic tuhostí a vektorů zatížení na jednotlivých prvcích i celé konstrukci. 3 Příklad 2D prutové konstrukce Na uvedeném příkladu vysvětlíme zadání dat a analýzu konstrukce. Cílem je určit průběhy vnitřních sil a deformovaného tvaru dle obr. 1. Nejprve zadáme materiál Upravit Přidat Přidat materiál. Jednotky si lze zvolit libovolně, typicky zvolíme systém jednotek kn, kpa, m. Zadá se tedy E= kpa, G= kpa (ovlivňuje pouze vliv na smykovou tuhost průřezu, která zde nehraje roli), α = C 1. Po zadání materiálu se napíše informativní hláška v konzoli, že materiál byl přidán, viz obr. 2. Název materiálu může být libovolný, zde je název Mat. Dále se přidá průřez. Na zadaném obdélníkovém průřezu b = 0.3 m, h = 0.54 m ručně vypočítáme A = = m 2, I y = = m 4, h = 0.54 m, κ = Opět zadáme pomocí Upravit Přidat Přidat průřez. Název je Obdélník, viz obr. 3. Úlohu uložíme Soubor Uložit. EduBeam implicitně obsahuje materiál DefaultMat, který má parametry betonu a implicitní průřez DefaultCS, který představuje obdélník m. Všechny zadané materiály a průřezy lze upravovat a mazat pod volbou Upravit Upravit či Upravit Smazat. Také lze využít zpětných a dopředných kroků Upravit Zpět či Upravit Vpřed. Většině příkazů jsou navíc přiřazeny standardní zkratky, například Ctrl+S uloží soubor. V dolním okně je konzole, která vypisuje standardní a chybové hlášky EduBeamu. 4
5 K +20 K K +20 K φ =0.006e-3 rad [m, kn] E=30 GPa 0.54 α=12. e-6 1/K Obrázek 1: Příklad prutové konstrukce pro analýzu. Obrázek 2: Zadání materiálu. Obrázek 3: Zadání průřezu. Úloha má celkem šest uzlů (styčníků). Styčník 4 bychom nemuseli vkládat, Edu- Beam umožňuje vložit obecnou polohu síly na prut. Vložíme standardně šest uzlů pomocí Upravit Přidat Přidat uzel, viz obr. 4. Zde je nejlepší metoda zadávat přímo souřadnice, také by šlo zadávat uzly pomocí myši. Rolovací kolečko myši je Zoom, klik kolečka s Ctrl je posun, klik kolečka se Shift je spojitý Zoom. Souřadné osy x,z jsou standardně doprava a dolů. V průběhu zadání lze zadávat okrajové podmínky na prutech - podpory. My je zadáme nyní pomocí Upravit Upravit Upravit uzel, nebo kliknutím pravým tlačítkem přímo na uzel. Po zadání máme následující obr. 5. 5
6 Obrázek 4: Zadání uzlů. Obrázek 5: Zadání okrajových podmínek (podpor). Zadání prvků (=prutů) se provede pomocí Upravit Přidat Přidat prvek. Koncové uzly prvků lze vybrat myší nebo z levého panelu, viz obr. 6. Zároveň se přiřadí materiál a průřez každému prvku pro správné sestavení matice tuhosti prvku K. Každý prut může mít kloubové uložení, v takovém případě proběhne automatická statická kondenzace neznámého natočení v místě kloubového uložení. Obrázek 6: Zadání prutů. 6
7 Zatížení na konstrukci jsou zde čtyř typů; osamělá síla, předepsané natočení, spojité konstantní zatížení a zatížení teplotou. Nejdříve se definuje zatěžovací stav, kterému se přiřadí dané zatížení. EduBeam implicitně definuje jeden zatěžovací stav Default_loadcase, který se zobrazuje vlevo nahoře. Pro naše účely necháme tento implicitní zatěžovací stav. Pro skutečnou analýzu by se definovaly zatěžovací stavy pro mezní stav použitelnosti, mezní stav únosnosti a dále by šly vytvářet kombinace zatížení. Takováto analýza není předmětem tohoto příkladu. Uzlové zatížení se přidá Upravit Přidat Přidat uzlové zatížení. Zatížení přiřadíme uzlu 4, složky zatížení přepočteme do požadovaného globálního systému; F x = / = 18 kn, F z = 30 2/ = 24 kn. Předepsané přemístění se vloží pomocí Upravit Přidat Přidat předepsané přemístění. Do uzlu 6 se zadá ϕ = rad, viz obr. 7. Směr kladné rotace je dle pravidla pravé ruky, tzn. proti směru hodinových ručiček. Spojité zatížení se vloží pomocí Upravit Přidat Přidat prvkové zatížení. Typ: Spojité. Směr: Z. Teplota se vloží pomocí Upravit Přidat Přidat prvkové zatížení. Typ: Teplota. Teplota v těžišti průřezu je T c = = 30 C, teplotní rozdíl T d T h = = 20 C. Veškeré silové i nesilové zatížení konstrukce je na obr. 8. Tím máme připraveno zadání úlohy pro výpočet dle (1). Obrázek 7: Zatížení osamělou silou a natočením podpory. Obrázek 8: Veškeré silové i nesilové zatížení konstrukce. Výpočet se provede pomocí Výpočet Výpočet úlohy. V konzoli se zobrazí počet rovnic a předepsaných stupňů volnosti. Pro šest uzlů vychází 6 3 = 18 neznámých. Z toho již 5 stupňů volnosti odpovídá zadaným podporám. Celkem se tedy řeší 18 5 = 13 neznámých. Pro zobrazení výsledků je nutné přepnout EduBeam do postprocesoru pomocí Výpočet PostProcesor. Nyní lze zobrazit deformovaný tvar na obr. 9. Obr. 10 ukazuje průběh ohybového momentu, dále lze zobrazit vnitřní síly N, V, či vykreslit vnější 7
8 reakce. Obrázek 9: Výsledná deformace konstrukce. Obrázek 10: Výsledný průběh momentů. Řešení lze zobrazit v přehledné tabulce Tabulka Výsledky Výsledky do tabulky. V tabulce lze přepínat mezi výsledky v Uzlech (posuny, natočení, reakce) a na Prvcích (koncové deformace, koncové síly, normálová síla). Ve výběru Tabulka lze zvolit další možnosti výsledků. Patří sem matice tuhosti jednotlivých prvků v lokální a globální souřadné soustavě, koncové posuny, koncové síly. Dále pak neredukovaná matice tuhosti celé konstrukce, posuny všech uzlů a příslušných sil. Hodnoty z tabulky lze kopírovat např. do Excelu či LibreOffice pro další zpracování. Obrázek 11: Tabulka výsledků v uzlech. EduBeam umožňuje export kreslící plochy do png bitmapy pomocí Soubor Exportovat grafiku. Tím supluje funkci printscreen, která je dostupná na většině operačních systémů. 8
9 4 Vliv smyku a přechod na zjednodušenou deformační metodu Program EduBeam řeší prutové konstrukce obecnou deformační metodou (ODM) včetně smykové deformace. V případě potřeby lze provést redukci na zjednodušenou deformační metodu (ZDM), která se často používá při ručních výpočtech a zrušit vliv smykové deformace. Zjednodušení lze snadno ukázat pomocí principu virtuálních sil. Uvažujme virtuální deformaci od jednotkového impulzu na konstrukci δ, jejíž převrácená hodnota je tuhost k = 1/δ a prozkoumejme jednotlivé příspěvky silových členů δ = MM dx + EI y L }{{} Vliv křivosti NN EA dx L }{{} Vliv protažení střednice + V V κga dx L }{{} Vliv smykové deformace kde M, N, V jsou virtuální průběhy sil pro odpovídající jednotkový impulz pro výpočet δ. Vliv smykové deformace značí Timošenkův (Mindlinův, Reissnerův) prut, kdy průřez po deformaci již nezůstává kolmý ke střednici prutu. Celková deformace δ vlivem smykového zkosení naroste a tuhost k naopak poklesne. Pokud nechceme se smykovou deformací počítat, lze nastavit smykový součinitel κ >> 1. Nastavení G na velkou hodnotu může být riskantní, neboť ho lze určit z Poissonova čísla a z Youngova modulu pružnosti pro izotropní materiál. Některé programy modul pružnosti ve smyku G tímto způsobem počítají. Pro redukci ODM na ZDM potřebujeme zajistit EA. To lze zařídit zadáním A, neboť E se vyskytuje i v ohybové tuhosti průřezu. Při nastavení velké plochy A dojde automaticky ke zrušení vlivu smyku a počítá se pouze Euler-Bernoulliův prut s nestlačitelnou střednicí. 5 Závěr Program EduBeam slouží zejména pro studijní účely. Správnost řešení se rutině testuje na 31 základních konstrukcích, kde je známé řešení analytické. Přesto se mohou objevit mnohé chyby. Budeme rádi, pokud se zapojíte do vylepšování EduBeamu, ať už aktivním programováním či hlášením chyb. Chyby prosím hlašte autorům Edubeamu (vit.smilauer (at) fsv.cvut.cz). Uveďte verzi EduBeamu, operační systém, detailní popis chyby a jak k ní došlo. Nejlépe ještě přiložte vstupní soubor xml s vaší úlohou. (2) 9
Stavební mechanika přednáška, 10. dubna 2017
 Stavební mechanika 3 7. přednáška, 10. dubna 2017 Stavební mechanika 3 7. přednáška, 10. dubna 2017 Obecná deformační metoda 8) poznámky k využití symetrie 9) využití výpočetních programů 10) kontrola
Stavební mechanika 3 7. přednáška, 10. dubna 2017 Stavební mechanika 3 7. přednáška, 10. dubna 2017 Obecná deformační metoda 8) poznámky k využití symetrie 9) využití výpočetních programů 10) kontrola
Princip virtuálních posunutí (obecný princip rovnováhy)
 SMA2 Přednáška 05 Princip virtuálních posunutí Deformační metoda Matice tuhosti prutu pro tah/tlak Matice tuhosti prutu pro ohyb Program EduBeam Příklady Copyright (c) 2012 Vít Šmilauer Czech Technical
SMA2 Přednáška 05 Princip virtuálních posunutí Deformační metoda Matice tuhosti prutu pro tah/tlak Matice tuhosti prutu pro ohyb Program EduBeam Příklady Copyright (c) 2012 Vít Šmilauer Czech Technical
Přednáška 1 Obecná deformační metoda, podstata DM
 Statika stavebních konstrukcí II., 3.ročník bakalářského studia Přednáška 1 Obecná deformační metoda, podstata DM Základní informace o výuce předmětu SSK II Metody řešení staticky neurčitých konstrukcí
Statika stavebních konstrukcí II., 3.ročník bakalářského studia Přednáška 1 Obecná deformační metoda, podstata DM Základní informace o výuce předmětu SSK II Metody řešení staticky neurčitých konstrukcí
Zjednodušená deformační metoda (2):
 Stavební mechanika 1SM Přednášky Zjednodušená deformační metoda () Prut s kloubově připojeným koncem (statická kondenzace). Řešení rovinných rámů s posuvnými patry/sloupy. Prut s kloubově připojeným koncem
Stavební mechanika 1SM Přednášky Zjednodušená deformační metoda () Prut s kloubově připojeným koncem (statická kondenzace). Řešení rovinných rámů s posuvnými patry/sloupy. Prut s kloubově připojeným koncem
Stavební mechanika 3 132SM3 Přednášky. Deformační metoda: ZDM pro rámy s posuvnými styčníky, využití symetrie, výpočetní programy a kontrola výsledků.
 Stavební mechanika 12SM Přednášky Deformační metoda: ZDM pro rámy s posuvnými styčníky, využití symetrie, výpočetní programy a kontrola výsledků. Porovnání ODM a ZDM Příklad 1: (viz předchozí přednáška)
Stavební mechanika 12SM Přednášky Deformační metoda: ZDM pro rámy s posuvnými styčníky, využití symetrie, výpočetní programy a kontrola výsledků. Porovnání ODM a ZDM Příklad 1: (viz předchozí přednáška)
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6
 OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
Princip virtuálních posunutí (obecný princip rovnováhy)
 SMA Přednáška 5 Princip virtuálních posunutí Deformační metoda Matice tuhosti prutu pro tahtlak Matice tuhosti prutu pro ohyb Program EduBeam Příklady Copyright (c) Vít Šmilauer Czech Technical University
SMA Přednáška 5 Princip virtuálních posunutí Deformační metoda Matice tuhosti prutu pro tahtlak Matice tuhosti prutu pro ohyb Program EduBeam Příklady Copyright (c) Vít Šmilauer Czech Technical University
Posouzení mikropilotového základu
 Inženýrský manuál č. 36 Aktualizace 06/2017 Posouzení mikropilotového základu Program: Soubor: Skupina pilot Demo_manual_36.gsp Cílem tohoto inženýrského manuálu je vysvětlit použití programu GEO5 SKUPINA
Inženýrský manuál č. 36 Aktualizace 06/2017 Posouzení mikropilotového základu Program: Soubor: Skupina pilot Demo_manual_36.gsp Cílem tohoto inženýrského manuálu je vysvětlit použití programu GEO5 SKUPINA
Vybrané okruhy znalostí z předmětů stavební mechanika, pružnost a pevnost důležité i pro studium předmětů KP3C a KP5A - navrhování nosných konstrukcí
 Vybrané okruhy znalostí z předmětů stavební mechanika, pružnost a pevnost důležité i pro studium předmětů KP3C a KP5A - navrhování nosných konstrukcí Skládání a rozklad sil Skládání a rozklad sil v rovině
Vybrané okruhy znalostí z předmětů stavební mechanika, pružnost a pevnost důležité i pro studium předmětů KP3C a KP5A - navrhování nosných konstrukcí Skládání a rozklad sil Skládání a rozklad sil v rovině
Spojitý nosník. Příklady
 Spojitý nosník Příklady Příklad, zadání A = konst. =, m I = konst. =,6 m 4 E = konst. = GPa q =kn / m F kn 3 = M = 5kNm F = 5kN 8 F3 = 8kN 4,5 . způsob řešení n p = (nepočítáme pootočení ve styčníku č.3)
Spojitý nosník Příklady Příklad, zadání A = konst. =, m I = konst. =,6 m 4 E = konst. = GPa q =kn / m F kn 3 = M = 5kNm F = 5kN 8 F3 = 8kN 4,5 . způsob řešení n p = (nepočítáme pootočení ve styčníku č.3)
Téma 12, modely podloží
 Téma 1, modely podloží Statika stavebních konstrukcí II., 3.ročník bakalářského studia Úvod Winklerův model podloží Pasternakův model podloží Pružný poloprostor Nosník na pružném Winklerově podloží, řešení
Téma 1, modely podloží Statika stavebních konstrukcí II., 3.ročník bakalářského studia Úvod Winklerův model podloží Pasternakův model podloží Pružný poloprostor Nosník na pružném Winklerově podloží, řešení
Pružnost a plasticita II CD03
 Pružnost a plasticita II CD3 uděk Brdečko VUT v Brně, Fakulta stavební, Ústav stavební mechanik tel: 5447368 email: brdecko.l @ fce.vutbr.cz http://www.fce.vutbr.cz/stm/brdecko.l/html/distcz.htm Obsah
Pružnost a plasticita II CD3 uděk Brdečko VUT v Brně, Fakulta stavební, Ústav stavební mechanik tel: 5447368 email: brdecko.l @ fce.vutbr.cz http://www.fce.vutbr.cz/stm/brdecko.l/html/distcz.htm Obsah
Postup zadávání základové desky a její interakce s podložím v programu SCIA
 Postup zadávání základové desky a její interakce s podložím v programu SCIA Tloušťka desky h s = 0,4 m. Sloupy 0,6 x 0,6m. Zatížení: rohové sloupy N 1 = 800 kn krajní sloupy N 2 = 1200 kn střední sloupy
Postup zadávání základové desky a její interakce s podložím v programu SCIA Tloušťka desky h s = 0,4 m. Sloupy 0,6 x 0,6m. Zatížení: rohové sloupy N 1 = 800 kn krajní sloupy N 2 = 1200 kn střední sloupy
ZDM PŘÍMÉ NOSNÍKY. Příklad č. 1. Miloš Hüttner SMR2 ZDM přímé nosníky cvičení 09. Zadání
 iloš Hüttner SR D přímé nosníky cvičení 09 adání D PŘÍÉ NOSNÍKY Příklad č. 1 Vykreslete průběhy vnitřních sil na konstrukci zobrazené na Obr. 1. Příklad převzat z katedrové wikipedie (originál ke stažení
iloš Hüttner SR D přímé nosníky cvičení 09 adání D PŘÍÉ NOSNÍKY Příklad č. 1 Vykreslete průběhy vnitřních sil na konstrukci zobrazené na Obr. 1. Příklad převzat z katedrové wikipedie (originál ke stažení
Výpočet přetvoření a dimenzování pilotové skupiny
 Inženýrský manuál č. 18 Aktualizace: 08/2018 Výpočet přetvoření a dimenzování pilotové skupiny Program: Soubor: Skupina pilot Demo_manual_18.gsp Cílem tohoto inženýrského manuálu je vysvětlit použití programu
Inženýrský manuál č. 18 Aktualizace: 08/2018 Výpočet přetvoření a dimenzování pilotové skupiny Program: Soubor: Skupina pilot Demo_manual_18.gsp Cílem tohoto inženýrského manuálu je vysvětlit použití programu
BO009 KOVOVÉ MOSTY 1 NÁVOD NA VÝPOČET VNITŘNÍCH SIL NA PODÉLNÝCH VÝZTUHÁCH ORTOTROPNÍ MOSTOVKY. AUTOR: Ing. MARTIN HORÁČEK, Ph.D.
 BO009 KOVOVÉ MOSTY 1 NÁVOD NA VÝPOČET VNITŘNÍCH SIL NA PODÉLNÝCH VÝZTUHÁCH ORTOTROPNÍ MOSTOVKY AUTOR: Ing. MARTIN HORÁČEK, Ph.D. Obsah Stanovení pérové konstanty poddajné podpory... - 3-1.1 Princip stanovení
BO009 KOVOVÉ MOSTY 1 NÁVOD NA VÝPOČET VNITŘNÍCH SIL NA PODÉLNÝCH VÝZTUHÁCH ORTOTROPNÍ MOSTOVKY AUTOR: Ing. MARTIN HORÁČEK, Ph.D. Obsah Stanovení pérové konstanty poddajné podpory... - 3-1.1 Princip stanovení
Zadejte ručně název první kapitoly. Manuál. Rozhraní pro program ETABS
 Zadejte ručně název první kapitoly Manuál Rozhraní pro program ETABS Všechny informace uvedené v tomto dokumentu mohou být změněny bez předchozího upozornění. Žádnou část tohoto dokumentu není dovoleno
Zadejte ručně název první kapitoly Manuál Rozhraní pro program ETABS Všechny informace uvedené v tomto dokumentu mohou být změněny bez předchozího upozornění. Žádnou část tohoto dokumentu není dovoleno
1/7. Úkol č. 9 - Pružnost a pevnost A, zimní semestr 2011/2012
 Úkol č. 9 - Pružnost a pevnost A, zimní semestr 2011/2012 Úkol řešte ve skupince 2-3 studentů. Den narození zvolte dle jednoho člena skupiny. Řešení odevzdejte svému cvičícímu. Na symetrické prosté krokevní
Úkol č. 9 - Pružnost a pevnost A, zimní semestr 2011/2012 Úkol řešte ve skupince 2-3 studentů. Den narození zvolte dle jednoho člena skupiny. Řešení odevzdejte svému cvičícímu. Na symetrické prosté krokevní
STRUČNÝ NÁVOD PRO POUŽÍVÁNÍ PROGRAMU SCIA ENGINEER (RÁMOVÉ KONSTRUKCE)
 STRUČNÝ NÁVOD PRO POUŽÍVÁNÍ PROGRAMU SCIA ENGINEER 2012.0 (RÁMOVÉ KONSTRUKCE) http://www.scia-online.com/ STUDENTSKÁ VERZE PROGRAMU SCIA ENGINEER 2012.0 http://www.scia-campus.com/ STAŽENÍ STUDENTSKÉ VERZE
STRUČNÝ NÁVOD PRO POUŽÍVÁNÍ PROGRAMU SCIA ENGINEER 2012.0 (RÁMOVÉ KONSTRUKCE) http://www.scia-online.com/ STUDENTSKÁ VERZE PROGRAMU SCIA ENGINEER 2012.0 http://www.scia-campus.com/ STAŽENÍ STUDENTSKÉ VERZE
Betonové konstrukce (S) Přednáška 3
 Betonové konstrukce (S) Přednáška 3 Obsah Účinky předpětí na betonové prvky a konstrukce Silové působení kabelu na beton Ekvivalentní zatížení Staticky neurčité účinky předpětí Konkordantní kabel, Lineární
Betonové konstrukce (S) Přednáška 3 Obsah Účinky předpětí na betonové prvky a konstrukce Silové působení kabelu na beton Ekvivalentní zatížení Staticky neurčité účinky předpětí Konkordantní kabel, Lineární
Beton 3D Výuková příručka Fine s. r. o. 2010
 Zadání Cílem tohoto příkladu je navrhnout a posoudit výztuž šestiúhelníkového železobetonového sloupu (výška průřezu 20 cm) o výšce 2 m namáhaného normálovou silou 400 kn, momentem My=2,33 knm a momentem
Zadání Cílem tohoto příkladu je navrhnout a posoudit výztuž šestiúhelníkového železobetonového sloupu (výška průřezu 20 cm) o výšce 2 m namáhaného normálovou silou 400 kn, momentem My=2,33 knm a momentem
Dvě varianty rovinného problému: rovinná napjatost. rovinná deformace
 Rovinný problém Řešíme plošné konstrukce zatížené a uložené v jejich střednicové rovině. Dvě varianty rovinného problému: rovinná napjatost rovinná deformace 17 Rovinná deformace 1 Obsahuje složky deformace
Rovinný problém Řešíme plošné konstrukce zatížené a uložené v jejich střednicové rovině. Dvě varianty rovinného problému: rovinná napjatost rovinná deformace 17 Rovinná deformace 1 Obsahuje složky deformace
NEXIS 32 rel. 3.50. Železobetonový nosník
 SCIA CZ, s. r. o. Slavíčkova 1a 638 00 Brno tel. 545 193 526 545 193 535 fax 545 193 533 E-mail info.brno@scia.cz www.scia.cz Systém programů pro projektování prutových a stěnodeskových konstrukcí NEXIS
SCIA CZ, s. r. o. Slavíčkova 1a 638 00 Brno tel. 545 193 526 545 193 535 fax 545 193 533 E-mail info.brno@scia.cz www.scia.cz Systém programů pro projektování prutových a stěnodeskových konstrukcí NEXIS
Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady. Část 1 - Test
 Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových charakteristik, oficiální přehled
Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových charakteristik, oficiální přehled
IDEA Frame 4. Uživatelská příručka
 Uživatelská příručka IDEA Frame IDEA Frame 4 Uživatelská příručka Uživatelská příručka IDEA Frame Obsah 1.1 Požadavky programu... 6 1.2 Pokyny k instalaci programu... 6 2 Základní pojmy... 7 3 Ovládání...
Uživatelská příručka IDEA Frame IDEA Frame 4 Uživatelská příručka Uživatelská příručka IDEA Frame Obsah 1.1 Požadavky programu... 6 1.2 Pokyny k instalaci programu... 6 2 Základní pojmy... 7 3 Ovládání...
Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil
 Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil Souřadný systém, v rovině i prostoru Síla bodová: vektorová veličina (kluzný, vázaný vektor - využití),
Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil Souřadný systém, v rovině i prostoru Síla bodová: vektorová veličina (kluzný, vázaný vektor - využití),
PRUŽNOST A PLASTICITA I
 Otázky k procvičování PRUŽNOST A PLASTICITA I 1. Kdy je materiál homogenní? 2. Kdy je materiál izotropní? 3. Za jakých podmínek můžeme použít princip superpozice účinků? 4. Vysvětlete princip superpozice
Otázky k procvičování PRUŽNOST A PLASTICITA I 1. Kdy je materiál homogenní? 2. Kdy je materiál izotropní? 3. Za jakých podmínek můžeme použít princip superpozice účinků? 4. Vysvětlete princip superpozice
Téma 3 Úvod ke staticky neurčitým prutovým konstrukcím
 Stavební mechanika, 2.ročník bakalářského studia AST Téma 3 Úvod ke staticky neurčitým prutovým konstrukcím Katedra stavební mechaniky Fakulta stavební, VŠB - Technická univerzita Ostrava Osnova přednášky
Stavební mechanika, 2.ročník bakalářského studia AST Téma 3 Úvod ke staticky neurčitým prutovým konstrukcím Katedra stavební mechaniky Fakulta stavební, VŠB - Technická univerzita Ostrava Osnova přednášky
písemky (3 příklady) Výsledná známka je stanovena zkoušejícím na základě celkového počtu bodů ze semestru, ze vstupního testu a z písemky.
 POŽADAVKY KE ZKOUŠCE Z PP I Zkouška úrovně Alfa (pro zájemce o magisterské studium) Zkouška sestává ze vstupního testu (10 otázek, výběr správné odpovědi ze čtyř možností, rozsah dle sloupečku Požadavky)
POŽADAVKY KE ZKOUŠCE Z PP I Zkouška úrovně Alfa (pro zájemce o magisterské studium) Zkouška sestává ze vstupního testu (10 otázek, výběr správné odpovědi ze čtyř možností, rozsah dle sloupečku Požadavky)
Pružnost a pevnost. 2. přednáška, 10. října 2016
 Pružnost a pevnost 2. přednáška, 10. října 2016 Prut namáhaný jednoduchým ohybem: rovnoměrně ohýbaný prut nerovnoměrně ohýbaný prut příklad výpočet napětí a ohybu vliv teplotních měn příklad nerovnoměrné
Pružnost a pevnost 2. přednáška, 10. října 2016 Prut namáhaný jednoduchým ohybem: rovnoměrně ohýbaný prut nerovnoměrně ohýbaný prut příklad výpočet napětí a ohybu vliv teplotních měn příklad nerovnoměrné
Obsah. 1. Obecná vylepšení Úpravy Prvky Zatížení Výpočet Posudky a výsledky Dokument...
 Novinky 2/2016 Obsah 1. Obecná vylepšení...3 2. Úpravy...7 3. Prvky...9 4. Zatížení... 11 5. Výpočet...4 6. Posudky a výsledky...5 7. Dokument...8 2 1. Obecná vylepšení Nové možnosti otáčení modelu, zobrazení
Novinky 2/2016 Obsah 1. Obecná vylepšení...3 2. Úpravy...7 3. Prvky...9 4. Zatížení... 11 5. Výpočet...4 6. Posudky a výsledky...5 7. Dokument...8 2 1. Obecná vylepšení Nové možnosti otáčení modelu, zobrazení
Namáhání ostění kolektoru
 Inženýrský manuál č. 23 Aktualizace 06/2016 Namáhání ostění kolektoru Program: MKP Soubor: Demo_manual_23.gmk Cílem tohoto manuálu je vypočítat namáhání ostění raženého kolektoru pomocí metody konečných
Inženýrský manuál č. 23 Aktualizace 06/2016 Namáhání ostění kolektoru Program: MKP Soubor: Demo_manual_23.gmk Cílem tohoto manuálu je vypočítat namáhání ostění raženého kolektoru pomocí metody konečných
Katedra geotechniky a podzemního stavitelství
 Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Metoda okrajových prvků (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Metoda okrajových prvků (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
Posouzení stability svahu
 Inženýrský manuál č. 25 Aktualizace 07/2016 Posouzení stability svahu Program: MKP Soubor: Demo_manual_25.gmk Cílem tohoto manuálu je vypočítat stupeň stability svahu pomocí metody konečných prvků. Zadání
Inženýrský manuál č. 25 Aktualizace 07/2016 Posouzení stability svahu Program: MKP Soubor: Demo_manual_25.gmk Cílem tohoto manuálu je vypočítat stupeň stability svahu pomocí metody konečných prvků. Zadání
Ing. Jakub Kršík Ing. Tomáš Pail. Navrhování betonových konstrukcí 1D
 Ing. Jakub Kršík Ing. Tomáš Pail Navrhování betonových konstrukcí 1D Úvod Nové moduly dostupné v Hlavním stromě Beton 15 Původní moduly dostupné po aktivaci ve Funkcionalitě projektu Staré posudky betonu
Ing. Jakub Kršík Ing. Tomáš Pail Navrhování betonových konstrukcí 1D Úvod Nové moduly dostupné v Hlavním stromě Beton 15 Původní moduly dostupné po aktivaci ve Funkcionalitě projektu Staré posudky betonu
Cvičení software Groma základní seznámení
 Cvičení software Groma základní seznámení 4 2 3 1 Obr. 1: Hlavní okno programu Groma v.11. Hlavní okno 1. Ikony základních geodetických úloh, lze je vyvolat i z menu Výpočty. 2. Ikona základního nastavení
Cvičení software Groma základní seznámení 4 2 3 1 Obr. 1: Hlavní okno programu Groma v.11. Hlavní okno 1. Ikony základních geodetických úloh, lze je vyvolat i z menu Výpočty. 2. Ikona základního nastavení
Libor Kasl 1, Alois Materna 2
 SROVNÁNÍ VÝPOČETNÍCH MODELŮ DESKY VYZTUŽENÉ TRÁMEM Libor Kasl 1, Alois Materna 2 Abstrakt Příspěvek se zabývá modelováním desky vyztužené trámem. Jsou zde srovnány různé výpočetní modely model s prostorovými
SROVNÁNÍ VÝPOČETNÍCH MODELŮ DESKY VYZTUŽENÉ TRÁMEM Libor Kasl 1, Alois Materna 2 Abstrakt Příspěvek se zabývá modelováním desky vyztužené trámem. Jsou zde srovnány různé výpočetní modely model s prostorovými
Nový způsob práce s průběžnou klasifikací lze nastavit pouze tehdy, je-li průběžná klasifikace v evidenčním pololetí a školním roce prázdná.
 Průběžná klasifikace Nová verze modulu Klasifikace žáků přináší novinky především v práci s průběžnou klasifikací. Pro zadání průběžné klasifikace ve třídě doposud existovaly 3 funkce Průběžná klasifikace,
Průběžná klasifikace Nová verze modulu Klasifikace žáků přináší novinky především v práci s průběžnou klasifikací. Pro zadání průběžné klasifikace ve třídě doposud existovaly 3 funkce Průběžná klasifikace,
Postup při výpočtu prutové konstrukce obecnou deformační metodou
 Vysoké učení technické v Brně Fakulta stavební Ústav stavební mechaniky Postup při výpočtu prutové konstrukce obecnou deformační metodou Petr Frantík Obsah 1 Vytvoření modelu 2 2 Styčníkové vektory modelu
Vysoké učení technické v Brně Fakulta stavební Ústav stavební mechaniky Postup při výpočtu prutové konstrukce obecnou deformační metodou Petr Frantík Obsah 1 Vytvoření modelu 2 2 Styčníkové vektory modelu
IDEA Slab 5. Uživatelská příručka
 Uživatelská příručka IDEA Slab IDEA Slab 5 Uživatelská příručka Uživatelská příručka IDEA Slab Obsah 1.1 Požadavky programu... 4 1.2 Pokyny k instalaci programu... 4 2 Základní pojmy... 5 3 Ovládání...
Uživatelská příručka IDEA Slab IDEA Slab 5 Uživatelská příručka Uživatelská příručka IDEA Slab Obsah 1.1 Požadavky programu... 4 1.2 Pokyny k instalaci programu... 4 2 Základní pojmy... 5 3 Ovládání...
FAKULTA STAVEBNÍ. Telefon: WWW:
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ ZÁKLADY METODY KONEČNÝCH PRVKŮ Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast10.vsb.cz/brozovsky/
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ ZÁKLADY METODY KONEČNÝCH PRVKŮ Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast10.vsb.cz/brozovsky/
Zde je uveden abecední seznam důležitých pojmů interaktivního učebního textu
 index 1 Rejstřík Zde je uveden abecední seznam důležitých pojmů interaktivního učebního textu Pružnost a pevnost. U každého termínu je uvedeno označení kapitoly a čísla obrazovek, na nichž lze pojem nalézt.
index 1 Rejstřík Zde je uveden abecední seznam důležitých pojmů interaktivního učebního textu Pružnost a pevnost. U každého termínu je uvedeno označení kapitoly a čísla obrazovek, na nichž lze pojem nalézt.
Prizmatické prutové prvky zatížené objemovou změnou po výšce průřezu (teplota, vlhkost, smrštění )
 1 Prizmatické prutové prvky zatížené objemovou změnou po výšce průřezu (teplota, vlhkost, smrštění ) 1. Rozšířený Hookeův zákon pro jednoosou napjatost Základním materiálovým vztahem lineární teorie pružnosti
1 Prizmatické prutové prvky zatížené objemovou změnou po výšce průřezu (teplota, vlhkost, smrštění ) 1. Rozšířený Hookeův zákon pro jednoosou napjatost Základním materiálovým vztahem lineární teorie pružnosti
Platnost Bernoulli Navierovy hypotézy
 Přednáška 03 Diferenciální rovnice ohybu prutu Platnost Bernoulli Navierovy hypotézy Schwedlerovy věty Rovnováha na segmentech prutu Clebschova metoda integrace Příklady Copyright (c) 011 Vít Šmilauer
Přednáška 03 Diferenciální rovnice ohybu prutu Platnost Bernoulli Navierovy hypotézy Schwedlerovy věty Rovnováha na segmentech prutu Clebschova metoda integrace Příklady Copyright (c) 011 Vít Šmilauer
Pružnost a pevnost (132PRPE), paralelka J2/1 (ZS 2015/2016) Písemná část závěrečné zkoušky vzorové otázky a příklady.
 Pružnost a pevnost (132PRPE), paralelka J2/1 (ZS 2015/2016) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových
Pružnost a pevnost (132PRPE), paralelka J2/1 (ZS 2015/2016) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových
Pružnost a pevnost. zimní semestr 2013/14
 Pružnost a pevnost zimní semestr 2013/14 Organizace předmětu Přednášející: Prof. Milan Jirásek, B322 Konzultace: pondělí 10:00-10:45 nebo dle dohody E-mail: Milan.Jirasek@fsv.cvut.cz Webové stránky předmětu:
Pružnost a pevnost zimní semestr 2013/14 Organizace předmětu Přednášející: Prof. Milan Jirásek, B322 Konzultace: pondělí 10:00-10:45 nebo dle dohody E-mail: Milan.Jirasek@fsv.cvut.cz Webové stránky předmětu:
Tvorba výpočtového modelu MKP
 Tvorba výpočtového modelu MKP Jaroslav Beran (KTS) Modelování a simulace Tvorba výpočtového modelu s využitím MKP zahrnuje: Tvorbu (import) geometrického modelu Generování sítě konečných prvků Definování
Tvorba výpočtového modelu MKP Jaroslav Beran (KTS) Modelování a simulace Tvorba výpočtového modelu s využitím MKP zahrnuje: Tvorbu (import) geometrického modelu Generování sítě konečných prvků Definování
Tutoriál programu ADINA
 Nelineární analýza materiálů a konstrukcí (V-132YNAK) Tutoriál programu ADINA Petr Kabele petr.kabele@fsv.cvut.cz people.fsv.cvut.cz/~pkabele Petr Kabele, 2007-2010 1 Výstupy programu ADINA: Preprocesor
Nelineární analýza materiálů a konstrukcí (V-132YNAK) Tutoriál programu ADINA Petr Kabele petr.kabele@fsv.cvut.cz people.fsv.cvut.cz/~pkabele Petr Kabele, 2007-2010 1 Výstupy programu ADINA: Preprocesor
Co je nového 2017 R2
 Co je nového 2017 R2 Co je nového v GRAITEC Advance BIM Designers - 2017 R2 Obsah STRUCTURAL BIM DESIGNERS... 4 STEEL STRUCTURE DESIGNER 2017 R2... 4 Možnost "Připojit osu do uzlu"... 4 Zarovnání" otvorů...
Co je nového 2017 R2 Co je nového v GRAITEC Advance BIM Designers - 2017 R2 Obsah STRUCTURAL BIM DESIGNERS... 4 STEEL STRUCTURE DESIGNER 2017 R2... 4 Možnost "Připojit osu do uzlu"... 4 Zarovnání" otvorů...
FIN3D Výukovápříručka
 www.fine.cz FIN3D Výukovápříručka Zadání Tento příklad ukáže výpočet a posouzení konstrukce zobrazené na obrázku. Sloupy jsou z trubek, trámy profil I. Materiál ocel Fe 360. Zatížení na trámy je svislé
www.fine.cz FIN3D Výukovápříručka Zadání Tento příklad ukáže výpočet a posouzení konstrukce zobrazené na obrázku. Sloupy jsou z trubek, trámy profil I. Materiál ocel Fe 360. Zatížení na trámy je svislé
SolidWorks. SW je parametrický 3D modelář a umožňuje. Postup práce v SW: Prostředí a ovládání
 SolidWorks Prostředí a ovládání SW je parametrický 3D modelář a umožňuje objemové a plošné modelování práci s rozsáhlými sestavami automatické generování výrobních výkresu spojení mezi modelováním dílu,
SolidWorks Prostředí a ovládání SW je parametrický 3D modelář a umožňuje objemové a plošné modelování práci s rozsáhlými sestavami automatické generování výrobních výkresu spojení mezi modelováním dílu,
POŽADAVKY KE ZKOUŠCE Z PP I
 POŽADAVKY KE ZKOUŠCE Z PP I Zkouška úrovně Alfa (pro zájemce o magisterské studium) Zkouška sestává ze o vstupního testu (10 otázek, výběr správné odpovědi ze čtyř možností, rozsah dle sloupečku Požadavky)
POŽADAVKY KE ZKOUŠCE Z PP I Zkouška úrovně Alfa (pro zájemce o magisterské studium) Zkouška sestává ze o vstupního testu (10 otázek, výběr správné odpovědi ze čtyř možností, rozsah dle sloupečku Požadavky)
Kapitola 24. Numerické řešení pažící konstrukce
 Kapitola 24. Numerické řešení pažící konstrukce Cílem tohoto manuálu je vypočítat deformace kotvené stěny z ocelových štětovnic a dále zjistit průběhy vnitřních sil pomocí metody konečných prvků. Zadání
Kapitola 24. Numerické řešení pažící konstrukce Cílem tohoto manuálu je vypočítat deformace kotvené stěny z ocelových štětovnic a dále zjistit průběhy vnitřních sil pomocí metody konečných prvků. Zadání
Výpočet konsolidace pod silničním náspem
 Inženýrský manuál č. 11 Aktualizace: 06/2018 Výpočet konsolidace pod silničním náspem Program: Soubor: Sedání Demo_manual_11.gpo V tomto inženýrském manuálu je vysvětlen výpočet časového průběhu sedání
Inženýrský manuál č. 11 Aktualizace: 06/2018 Výpočet konsolidace pod silničním náspem Program: Soubor: Sedání Demo_manual_11.gpo V tomto inženýrském manuálu je vysvětlen výpočet časového průběhu sedání
Analýza stavebních konstrukcí
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Analýza stavebních konstrukcí Příklady Petr Konvalinka prof. Ing. Petr Konvalinka, CSc. a kolektiv 009 prof. Ing. Petr Konvalinka, CSc. Ing. Dagmar Jandeková, Ph.D.
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Analýza stavebních konstrukcí Příklady Petr Konvalinka prof. Ing. Petr Konvalinka, CSc. a kolektiv 009 prof. Ing. Petr Konvalinka, CSc. Ing. Dagmar Jandeková, Ph.D.
A x A y. α = 30. B y. A x =... kn A y =... kn B y =... kn. Vykreslení N, V, M. q = 2kN/m M = 5kNm. F = 10 kn A c a b d ,5 2,5 L = 10
 Vzorový příklad k 1. kontrolnímu testu Prostý nosník Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A y y q = kn/m M = 5kNm F = 10 kn A c a b d 1 1 3,5,5 L = 10 α B B y x α = 30
Vzorový příklad k 1. kontrolnímu testu Prostý nosník Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A y y q = kn/m M = 5kNm F = 10 kn A c a b d 1 1 3,5,5 L = 10 α B B y x α = 30
Rovinná úloha v MKP. (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v. prostorové úlohy: u, v, w
 Rovinná úloha v MKP Hledané deformační veličiny viz klasická teorie pružnosti (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v desky: w, ϕ x, ϕ y prostorové úlohy: u,
Rovinná úloha v MKP Hledané deformační veličiny viz klasická teorie pružnosti (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v desky: w, ϕ x, ϕ y prostorové úlohy: u,
Co je nového 2019 R2
 Co je nového 2019 R2 Obsah AKTUALIZACE... 4 NOVÁ VERZE ITALSKÉ NORMY NTC 2018... 4 Změna koeficientů zatížení pro ostatní stálé zatížení... 4 Doplnění nových tříd betonu... 5 Nové a aktualizované odkazy
Co je nového 2019 R2 Obsah AKTUALIZACE... 4 NOVÁ VERZE ITALSKÉ NORMY NTC 2018... 4 Změna koeficientů zatížení pro ostatní stálé zatížení... 4 Doplnění nových tříd betonu... 5 Nové a aktualizované odkazy
Materiálové vlastnosti: Poissonův součinitel ν = 0,3. Nominální mez kluzu (ocel S350GD + Z275): Rozměry průřezu:
 Řešený příklad: Výpočet momentové únosnosti ohýbaného tenkostěnného C-profilu dle ČSN EN 1993-1-3. Ohybová únosnost je stanovena na základě efektivního průřezového modulu. Materiálové vlastnosti: Modul
Řešený příklad: Výpočet momentové únosnosti ohýbaného tenkostěnného C-profilu dle ČSN EN 1993-1-3. Ohybová únosnost je stanovena na základě efektivního průřezového modulu. Materiálové vlastnosti: Modul
IDEA Corbel 5. Uživatelská příručka
 Uživatelská příručka IDEA Corbel IDEA Corbel 5 Uživatelská příručka Uživatelská příručka IDEA Corbel Obsah 1.1 Požadavky programu... 3 1.2 Pokyny k instalaci programu... 3 2 Základní pojmy... 4 3 Ovládání...
Uživatelská příručka IDEA Corbel IDEA Corbel 5 Uživatelská příručka Uživatelská příručka IDEA Corbel Obsah 1.1 Požadavky programu... 3 1.2 Pokyny k instalaci programu... 3 2 Základní pojmy... 4 3 Ovládání...
Analýza stavebních konstrukcí
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Analýza stavebních konstrukcí Příklady Petr Konvalinka prof. Ing. Petr Konvalinka, CSc. a kolektiv 2009 prof. Ing. Petr Konvalinka, CSc. Ing. Dagmar Jandeková Ing.
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Analýza stavebních konstrukcí Příklady Petr Konvalinka prof. Ing. Petr Konvalinka, CSc. a kolektiv 2009 prof. Ing. Petr Konvalinka, CSc. Ing. Dagmar Jandeková Ing.
Výpočet sedání kruhového základu sila
 Inženýrský manuál č. 22 Aktualizace 06/2016 Výpočet sedání kruhového základu sila Program: MKP Soubor: Demo_manual_22.gmk Cílem tohoto manuálu je popsat řešení sedání kruhového základu sila pomocí metody
Inženýrský manuál č. 22 Aktualizace 06/2016 Výpočet sedání kruhového základu sila Program: MKP Soubor: Demo_manual_22.gmk Cílem tohoto manuálu je popsat řešení sedání kruhového základu sila pomocí metody
3. kapitola. Průběhy vnitřních sil na lomeném nosníku. Janek Faltýnek SI J (43) Teoretická část: Příkladová část: Stavební mechanika 2
 3. kapitola Stavební mechanika Janek Faltýnek SI J (43) Průběhy vnitřních sil na lomeném nosníku Teoretická část: Naším úkolem je v tomto příkladu vyšetřit průběh vnitřních sil na lomeném rovinném nosníku
3. kapitola Stavební mechanika Janek Faltýnek SI J (43) Průběhy vnitřních sil na lomeném nosníku Teoretická část: Naším úkolem je v tomto příkladu vyšetřit průběh vnitřních sil na lomeném rovinném nosníku
Martin NESLÁDEK. 14. listopadu 2017
 Martin NESLÁDEK Faculty of mechanical engineering, CTU in Prague 14. listopadu 2017 1 / 22 Poznámky k úlohám řešeným MKP Na přesnost simulace pomocí MKP a prostorové rozlišení výsledků má vliv především:
Martin NESLÁDEK Faculty of mechanical engineering, CTU in Prague 14. listopadu 2017 1 / 22 Poznámky k úlohám řešeným MKP Na přesnost simulace pomocí MKP a prostorové rozlišení výsledků má vliv především:
Pružnost a plasticita CD03
 Pružnost a plasticita CD03 Luděk Brdečko VUT v Brně, Fakulta stavební, Ústav stavební mechaniky tel: 541147368 email: brdecko.l @ fce.vutbr.cz http://www.fce.vutbr.cz/stm/brdecko.l/html/distcz.htm Obsah
Pružnost a plasticita CD03 Luděk Brdečko VUT v Brně, Fakulta stavební, Ústav stavební mechaniky tel: 541147368 email: brdecko.l @ fce.vutbr.cz http://www.fce.vutbr.cz/stm/brdecko.l/html/distcz.htm Obsah
Generace zatěžovacích případů
 Zatížení na nosník se v programu Betonový výsek zadává stejným způsobem jako v ostatních programech FIN EC zadávají se průběhy vnitřních sil pro jednotlivé zatěžovací případy. Pro usnadnění zadávání je
Zatížení na nosník se v programu Betonový výsek zadává stejným způsobem jako v ostatních programech FIN EC zadávají se průběhy vnitřních sil pro jednotlivé zatěžovací případy. Pro usnadnění zadávání je
Numerické řešení pažící konstrukce
 Inženýrský manuál č. 24 Aktualizace 06/2016 Numerické řešení pažící konstrukce Program: MKP Soubor: Demo_manual_24.gmk Cílem tohoto manuálu je vypočítat deformace kotvené stěny z ocelových štětovnic a
Inženýrský manuál č. 24 Aktualizace 06/2016 Numerické řešení pažící konstrukce Program: MKP Soubor: Demo_manual_24.gmk Cílem tohoto manuálu je vypočítat deformace kotvené stěny z ocelových štětovnic a
IDEA Column 5. Uživatelská příručka
 Uživatelská příručka IDEA Column IDEA Column 5 Uživatelská příručka Uživatelská příručka IDEA Column Obsah 1.1 Požadavky programu... 5 1.2 Pokyny k instalaci programu... 5 2 Základní pojmy... 6 3 Ovládání...
Uživatelská příručka IDEA Column IDEA Column 5 Uživatelská příručka Uživatelská příručka IDEA Column Obsah 1.1 Požadavky programu... 5 1.2 Pokyny k instalaci programu... 5 2 Základní pojmy... 6 3 Ovládání...
Klasifikace rámů a složitějších patrových konstrukcí
 Klasifikace rámů a složitějších patrových konstrukcí Klasifikace závisí na geometrii i zatížení řešit pro každou kombinaci zatížení!! 1. Konstrukce řešené podle teorie 1. řádu (α > 10): F α 10 Pro dané
Klasifikace rámů a složitějších patrových konstrukcí Klasifikace závisí na geometrii i zatížení řešit pro každou kombinaci zatížení!! 1. Konstrukce řešené podle teorie 1. řádu (α > 10): F α 10 Pro dané
Definujte poměrné protažení (schematicky nakreslete a uved te jednotky) Napište hlavní kroky postupu při posouzení prutu na vzpěrný tlak.
 00001 Definujte mechanické napětí a uved te jednotky. 00002 Definujte normálové napětí a uved te jednotky. 00003 Definujte tečné (tangenciální, smykové) napětí a uved te jednotky. 00004 Definujte absolutní
00001 Definujte mechanické napětí a uved te jednotky. 00002 Definujte normálové napětí a uved te jednotky. 00003 Definujte tečné (tangenciální, smykové) napětí a uved te jednotky. 00004 Definujte absolutní
Výpočet sedání osamělé piloty
 Inženýrský manuál č. 14 Aktualizace: 06/2018 Výpočet sedání osamělé piloty Program: Pilota Soubor: Demo_manual_14.gpi Cílem tohoto inženýrského manuálu je vysvětlit použití programu GEO 5 PILOTA pro výpočet
Inženýrský manuál č. 14 Aktualizace: 06/2018 Výpočet sedání osamělé piloty Program: Pilota Soubor: Demo_manual_14.gpi Cílem tohoto inženýrského manuálu je vysvětlit použití programu GEO 5 PILOTA pro výpočet
NEXIS 32 rel. 3.60 Samostatný betonový průřez
 SCIA CZ, s. r. o. Slavíčkova 1a 638 00 Brno tel. 545 193 526 545 193 535 fax 545 193 533 E-mail info.brno@scia.cz www.scia.cz Systém programů pro projektování prutových a stěnodeskových konstrukcí NEXIS
SCIA CZ, s. r. o. Slavíčkova 1a 638 00 Brno tel. 545 193 526 545 193 535 fax 545 193 533 E-mail info.brno@scia.cz www.scia.cz Systém programů pro projektování prutových a stěnodeskových konstrukcí NEXIS
IDEA Column 6. Uživatelská příručka
 Uživatelská příručka IDEA Column IDEA Column 6 Uživatelská příručka Uživatelská příručka IDEA Column Obsah 1.1 Požadavky programu... 5 1.2 Pokyny k instalaci programu... 5 2 Základní pojmy... 6 3 Ovládání...
Uživatelská příručka IDEA Column IDEA Column 6 Uživatelská příručka Uživatelská příručka IDEA Column Obsah 1.1 Požadavky programu... 5 1.2 Pokyny k instalaci programu... 5 2 Základní pojmy... 6 3 Ovládání...
STATIKA STAVEBNÍCH KONSTRUKCÍ I
 VŠB Technická univerzita Ostrava Fakulta stavební, Ludvíka Podéště 1875, 708 33 Ostrava Ivan Kološ, Martin Krejsa, Stanislav Pospíšil, Oldřich Sucharda STATIKA STAVEBNÍCH KONSTRUKCÍ I Vzdělávací pomůcka
VŠB Technická univerzita Ostrava Fakulta stavební, Ludvíka Podéště 1875, 708 33 Ostrava Ivan Kološ, Martin Krejsa, Stanislav Pospíšil, Oldřich Sucharda STATIKA STAVEBNÍCH KONSTRUKCÍ I Vzdělávací pomůcka
Návrh kotvené pažící stěny
 Inženýrský manuál č. 6 Aktualizace: 03/2018 Návrh kotvené pažící stěny Program: Pažení posudek Soubor: Demo_manual_06.gp2 V tomto inženýrském manuálu je provedeno ověření návrhu kotvené pažící konstrukce
Inženýrský manuál č. 6 Aktualizace: 03/2018 Návrh kotvené pažící stěny Program: Pažení posudek Soubor: Demo_manual_06.gp2 V tomto inženýrském manuálu je provedeno ověření návrhu kotvené pažící konstrukce
Analýza stavebních konstrukcí
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Analýza stavebních konstrukcí Příklady Petr Konvalinka prof. Ing. Petr Konvalinka, CSc. a kolektiv 009 prof. Ing. Petr Konvalinka, CSc. Ing. Dagmar Jandeková Ing. Radoslav
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Analýza stavebních konstrukcí Příklady Petr Konvalinka prof. Ing. Petr Konvalinka, CSc. a kolektiv 009 prof. Ing. Petr Konvalinka, CSc. Ing. Dagmar Jandeková Ing. Radoslav
Novinky v programu RFEM Modelování
 Novinky v programu RFEM 4 1. Modelování Linie a plochy NURBS Modelování v RFEMu 4 bylo rozšířeno o nový typ linií a ploch NURBS (Non-Uniform Rational B-Splines). Tyto matematicky definované linie a plochy
Novinky v programu RFEM 4 1. Modelování Linie a plochy NURBS Modelování v RFEMu 4 bylo rozšířeno o nový typ linií a ploch NURBS (Non-Uniform Rational B-Splines). Tyto matematicky definované linie a plochy
Nosné desky. 1. Kirchhoffova teorie ohybu tenkých desek (h/l < 1/10) 3. Mindlinova teorie pro tlusté desky (h/l < 1/5)
 Nosné desky Deska je těleso, které má jeden rozměr mnohem menší než rozměry zbývající. Zatížení desky je orientováno výhradně kolmo k její střednicové rovině. 1. Kirchhoffova teorie ohybu tenkých desek
Nosné desky Deska je těleso, které má jeden rozměr mnohem menší než rozměry zbývající. Zatížení desky je orientováno výhradně kolmo k její střednicové rovině. 1. Kirchhoffova teorie ohybu tenkých desek
Konstrukční systémy vícepodlažních budov Přednáška 5 Stěnové systémy Doc. Ing. Hana Gattermayerová,CSc Obsah
 Konstrukční systémy vícepodlažních budov Přednáška 5 Doc. Ing. Hana Gattermayerová,CSc gatter@fsv.cvut.cz Literatura Obsah Rojík: Konstrukční systémy vícepodlažních budov, CVUT 1979, předběžné a podrobné
Konstrukční systémy vícepodlažních budov Přednáška 5 Doc. Ing. Hana Gattermayerová,CSc gatter@fsv.cvut.cz Literatura Obsah Rojík: Konstrukční systémy vícepodlažních budov, CVUT 1979, předběžné a podrobné
α = 210 A x =... kn A y =... kn A M =... knm
 Vzorový příklad k 1. kontrolnímu testu Konzola Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A M A y y q = kn/m M = - 5kNm A α B c a b d F = 10 kn 1 1 3,5,5 L = 10 x α = 10 A
Vzorový příklad k 1. kontrolnímu testu Konzola Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A M A y y q = kn/m M = - 5kNm A α B c a b d F = 10 kn 1 1 3,5,5 L = 10 x α = 10 A
PLASTOVÁ AKUMULAČNÍ, SEDIMENTAČNÍ A RETENČNÍ NÁDRŽ HN A VN POSOUZENÍ PLASTOVÉ NÁDRŽE VN-2 STATICKÝ POSUDEK
 PLASTOVÁ AKUMULAČNÍ, SEDIMENTAČNÍ A RETENČNÍ NÁDRŽ HN A VN POSOUZENÍ PLASTOVÉ NÁDRŽE VN-2 STATICKÝ POSUDEK - - 20,00 1 [0,00; 0,00] 2 [0,00; 0,38] +z 2,00 3 [0,00; 0,72] 4 [0,00; 2,00] Geometrie konstrukce
PLASTOVÁ AKUMULAČNÍ, SEDIMENTAČNÍ A RETENČNÍ NÁDRŽ HN A VN POSOUZENÍ PLASTOVÉ NÁDRŽE VN-2 STATICKÝ POSUDEK - - 20,00 1 [0,00; 0,00] 2 [0,00; 0,38] +z 2,00 3 [0,00; 0,72] 4 [0,00; 2,00] Geometrie konstrukce
Výpočet svislé únosnosti a sedání skupiny pilot
 Inženýrský manuál č. 17 Aktualizace: 04/2016 Výpočet svislé únosnosti a sedání skupiny pilot Proram: Soubor: Skupina pilot Demo_manual_17.sp Úvod Cílem tohoto inženýrského manuálu je vysvětlit použití
Inženýrský manuál č. 17 Aktualizace: 04/2016 Výpočet svislé únosnosti a sedání skupiny pilot Proram: Soubor: Skupina pilot Demo_manual_17.sp Úvod Cílem tohoto inženýrského manuálu je vysvětlit použití
Výpočet svislé únosnosti a sedání pilot vyšetřovaných na základě zkoušek CPT
 Inženýrský manuál č. 15 Aktualizace: 07/2018 Výpočet svislé únosnosti a sedání pilot vyšetřovaných na základě zkoušek CPT Program: Soubor: Pilota CPT Demo_manual_15.gpn Cílem tohoto inženýrského manuálu
Inženýrský manuál č. 15 Aktualizace: 07/2018 Výpočet svislé únosnosti a sedání pilot vyšetřovaných na základě zkoušek CPT Program: Soubor: Pilota CPT Demo_manual_15.gpn Cílem tohoto inženýrského manuálu
Stavební mechanika 2 (K132SM02)
 Stavební mechanika 2 (K132SM02) Přednáší: doc. Ing. Matěj Lepš, Ph.D. Katedra mechaniky K132 místnost D2034 e-mail: matej.leps@fsv.cvut.cz konzultační hodiny budou upřesněny později https://mech.fsv.cvut.cz/student/
Stavební mechanika 2 (K132SM02) Přednáší: doc. Ing. Matěj Lepš, Ph.D. Katedra mechaniky K132 místnost D2034 e-mail: matej.leps@fsv.cvut.cz konzultační hodiny budou upřesněny později https://mech.fsv.cvut.cz/student/
IDEA Frame 6. Uživatelská příručka
 Uživatelská příručka IDEA Frame IDEA Frame 6 Uživatelská příručka Uživatelská příručka IDEA Frame Obsah 1.1. Požadavky programu... 6 1.2. Pokyny k instalaci programu... 6 2 Základní pojmy... 7 3 Ovládání...
Uživatelská příručka IDEA Frame IDEA Frame 6 Uživatelská příručka Uživatelská příručka IDEA Frame Obsah 1.1. Požadavky programu... 6 1.2. Pokyny k instalaci programu... 6 2 Základní pojmy... 7 3 Ovládání...
IDEA RCS 8 Reinforced Concrete Section
 Uživatelská příručka IDEA IDEA RCS 8 Reinforced Concrete Section Uživatelská příručka Uživatelská příručka IDEA Obsah 1.1 Požadavky programu... 9 1.2 Pokyny k instalaci programu... 9 2 Základní pojmy...
Uživatelská příručka IDEA IDEA RCS 8 Reinforced Concrete Section Uživatelská příručka Uživatelská příručka IDEA Obsah 1.1 Požadavky programu... 9 1.2 Pokyny k instalaci programu... 9 2 Základní pojmy...
Program předmětu YMVB. 1. Modelování konstrukcí ( ) 2. Lokální modelování ( )
 Program předmětu YMVB 1. Modelování konstrukcí (17.2.2012) 1.1 Globální a lokální modelování stavebních konstrukcí Globální modely pro konstrukce jako celek, lokální modely pro návrh výztuže detailů a
Program předmětu YMVB 1. Modelování konstrukcí (17.2.2012) 1.1 Globální a lokální modelování stavebních konstrukcí Globální modely pro konstrukce jako celek, lokální modely pro návrh výztuže detailů a
Projevy dotvarování na konstrukcích (na úrovni průřezových modelů)
 PŘEDNÁŠKY Projevy dotvarování na konstrukcích (na úrovni průřezových modelů) Volné dotvarování Vázané dotvarování Dotvarování a geometrická nelinearita Volné dotvarování Vývoj deformací není omezován staticky
PŘEDNÁŠKY Projevy dotvarování na konstrukcích (na úrovni průřezových modelů) Volné dotvarování Vázané dotvarování Dotvarování a geometrická nelinearita Volné dotvarování Vývoj deformací není omezován staticky
Téma 8 Příčně zatížený rám a rošt
 Statika stavebních konstrukcí I.,.ročník bakalářského studia Téma 8 Příčně zatížený rám a rošt Základní vlastnosti příčně zatíženého rámu Jednoduchý příčně zatížený otevřený rám Základní vlastnosti roštu
Statika stavebních konstrukcí I.,.ročník bakalářského studia Téma 8 Příčně zatížený rám a rošt Základní vlastnosti příčně zatíženého rámu Jednoduchý příčně zatížený otevřený rám Základní vlastnosti roštu
Únosnost kompozitních konstrukcí
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta strojní Ústav letadlové techniky Únosnost kompozitních konstrukcí Optimalizační výpočet kompozitních táhel konstantního průřezu Technická zpráva Pořadové číslo:
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta strojní Ústav letadlové techniky Únosnost kompozitních konstrukcí Optimalizační výpočet kompozitních táhel konstantního průřezu Technická zpráva Pořadové číslo:
RFEM 5 RSTAB 8. Novinky. Dlubal Software. Strana. Obsah. Version: 5.05.0029 / 8.05.0029. Nové přídavné moduly. Hlavní programy.
 Dlubal Software Obsah Strana 1 Nové přídavné moduly Hlavní programy 3 Přídavné moduly 3 Novinky RFEM 5 & RSTAB 8 Version: 5.05.009 / 8.05.009 (C) www.gbi-statik.de Dlubal Software s.r.o. Statické a dynamické
Dlubal Software Obsah Strana 1 Nové přídavné moduly Hlavní programy 3 Přídavné moduly 3 Novinky RFEM 5 & RSTAB 8 Version: 5.05.009 / 8.05.009 (C) www.gbi-statik.de Dlubal Software s.r.o. Statické a dynamické
STATIKA. Vyšetřování reakcí soustav. Úloha jednoduchá. Ústav mechaniky a materiálů K618
 STATIKA Vyšetřování reakcí soustav Úloha jednoduchá Ústav mechaniky a materiálů K618 1 Zadání Posuďte statickou určitost a vyšetřete reakce rovinné soustavy zadané dle obrázku: q 0 M Dáno: L = 2 m M =
STATIKA Vyšetřování reakcí soustav Úloha jednoduchá Ústav mechaniky a materiálů K618 1 Zadání Posuďte statickou určitost a vyšetřete reakce rovinné soustavy zadané dle obrázku: q 0 M Dáno: L = 2 m M =
Rekapitulace princip virtuálních sil pro tah/tlak
 SMA Přednáška Doplňková virtuální práce momentů Metody integrace dvou spojitých funkcí Doplňková virtuální práce posouvajících sil Vliv rovnoměrné a nerovnoměrné teploty Formulace principu virtuálních
SMA Přednáška Doplňková virtuální práce momentů Metody integrace dvou spojitých funkcí Doplňková virtuální práce posouvajících sil Vliv rovnoměrné a nerovnoměrné teploty Formulace principu virtuálních
Kapitola 4. Tato kapitole se zabývá analýzou vnitřních sil na rovinných nosnících. Nejprve je provedena. Každý prut v rovině má 3 volnosti (kap.1).
 Kapitola 4 Vnitřní síly přímého vodorovného nosníku 4.1 Analýza vnitřních sil na rovinných nosnících Tato kapitole se zabývá analýzou vnitřních sil na rovinných nosnících. Nejprve je provedena rekapitulace
Kapitola 4 Vnitřní síly přímého vodorovného nosníku 4.1 Analýza vnitřních sil na rovinných nosnících Tato kapitole se zabývá analýzou vnitřních sil na rovinných nosnících. Nejprve je provedena rekapitulace
IDEA Connection Release Listopad 2014 Nová a vylepšená funkcionalita
 strana 1/12 Hello colleagues, IDEA Connection Release Listopad 2014 Nová a vylepšená funkcionalita strana 2/12 Hello colleagues, Uprostřed listopadu jsem dokončili další verzi IDEA Connection s řadu zajímavých
strana 1/12 Hello colleagues, IDEA Connection Release Listopad 2014 Nová a vylepšená funkcionalita strana 2/12 Hello colleagues, Uprostřed listopadu jsem dokončili další verzi IDEA Connection s řadu zajímavých
Příklad 7 Průhyb nosníku - složitější případ
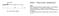 Příklad 7 Průhyb nosníku - složitější případ Zadání Nosník s proměnným průřezem je na obrázku. Průřezy a jsou obdélníkové, výška prvního průřezu je, násobkem výšky druhého průřezu. a) Pomocí metody integrace
Příklad 7 Průhyb nosníku - složitější případ Zadání Nosník s proměnným průřezem je na obrázku. Průřezy a jsou obdélníkové, výška prvního průřezu je, násobkem výšky druhého průřezu. a) Pomocí metody integrace
Výukovápříručka. Ocelové spoje
 Výukovápříručka Ocelové spoje Obsah Oboustranný přípoj nosníku na sloup...3 Šroubovaný přípoj úhelníků na styčníkový plech...19 Šroubovaný přípoj úhelníků na styčníkový plech...28 2 Oboustranný přípoj
Výukovápříručka Ocelové spoje Obsah Oboustranný přípoj nosníku na sloup...3 Šroubovaný přípoj úhelníků na styčníkový plech...19 Šroubovaný přípoj úhelníků na styčníkový plech...28 2 Oboustranný přípoj
TENSOR NAPĚTÍ A DEFORMACE. Obrázek 1: Volba souřadnicového systému
 TENSOR NAPĚTÍ A DEFORMACE Obrázek 1: Volba souřadnicového systému Pole posunutí, deformace, napětí v materiálovém bodě {u} = { u v w } T (1) Obecně 9 složek pole napětí lze uspořádat do matice [3x3] -
TENSOR NAPĚTÍ A DEFORMACE Obrázek 1: Volba souřadnicového systému Pole posunutí, deformace, napětí v materiálovém bodě {u} = { u v w } T (1) Obecně 9 složek pole napětí lze uspořádat do matice [3x3] -
ROBOTIKA M3A 2018/2019 ING. VLADIMÍR VYHŇÁK
 ROBOTIKA M3A 2018/2019 ING. VLADIMÍR VYHŇÁK Návrh robotizovaných pracovišť Program ABB Robot Studio (dále jen ABB-RS) slouží k přípravě programů průmyslových robotů a jejich nejbližší periférie, k jejich
ROBOTIKA M3A 2018/2019 ING. VLADIMÍR VYHŇÁK Návrh robotizovaných pracovišť Program ABB Robot Studio (dále jen ABB-RS) slouží k přípravě programů průmyslových robotů a jejich nejbližší periférie, k jejich
Statika 1. Reakce na rovinných staticky určitých konstrukcích. Miroslav Vokáč ČVUT v Praze, Fakulta architektury.
 reálných 3. přednáška Reakce na rovinných staticky určitých konstrukcích Miroslav Vokáč miroslav.vokac@cvut.cz ČVUT v Praze, Fakulta architektury 21. března 2016 Dřevěný trámový strop - Anežský klášter
reálných 3. přednáška Reakce na rovinných staticky určitých konstrukcích Miroslav Vokáč miroslav.vokac@cvut.cz ČVUT v Praze, Fakulta architektury 21. března 2016 Dřevěný trámový strop - Anežský klášter
