MATEMATICKÝ MODEL CÉVNÍ STĚNY DVOUŠKÁLOVÁ METODA HOMOGENIZACE S UVAŽOVÁNÍM VELKÝCH DEFORMACÍ
|
|
|
- Tereza Musilová
- před 8 lety
- Počet zobrazení:
Transkript
1 MATEMATICKÝ MODEL CÉVNÍ STĚNY DVOUŠKÁLOVÁ METODA HOMOGENIZACE S UVAŽOVÁNÍM VELKÝCH DEFORMACÍ Vladimír LUKEŠ, Eduard ROHAN 2 Abstract: Cévní stěna je modelována pomocí dvouškálové metody homogenizace, která umožňuje respektovat složitou mikrostrukturu stěny. Použit je nelineární matematický model s uvažováním velkých deformací a hyperelastickým materiálovým vztahem. Homogenizovaný model je rozšířen o elastická vlákna, která reprezentují vnější a vnitřní elastickou vrstvu na povrchu cévní stěny. Problém je linearizován pomocí aktualizované Lagrangeovy formulace a řešen iteračně metodou konečných prvků. Key words: arterial wall, homogenization, large deformation, updated Lagrangian formulation. ÚVOD Stávající modely cévní stěny, viz např. [, 2], bývají založeny na superpozici deformačních energií, které přísluší jejím jednotlivým složkám, jimiž jsou mezibuněčná hmota (matrice), svalová vlákna (uskupení svalových buněk) a další vláknité struktury obsahující elastin a kolagen. Takový přístup umožňuje zohlednění anizotropie tkáně i jejích základních charakteristik při zachování velmi přístupné implementovatelnosti modelu. e zřejmé, že mnohé materiálové nelinearity měkké tkáně, jak jsou pozorovány na makroškále, mají svůj původ v interakcích a geometrických nelinearitách deformující se mikrostruktury. Tento fenomen lze vystihnout s použitím víceškálového modelování, které odráží hierarchické uspořádání materiálu, od nanostruktury vláknitých komponent, přes buněčnou úroveň, až po makroskopické měřítko, kde pozorujeme chování celých orgánů. Dvouškálová metoda homogenizace je jednou z alternativ popisu tohoto hierarchického modelování. V tomto příspěvku je představen zjednodušený model buněčné úrovně cévní stěny, který je založen na existenci periodicky se opakující základní buňky obsahující matrici a nestlačitelnou inkluzi. Navazujeme tak na výsledky předchozího studia metody homogenizace v kontextu popisu měkkých tkání [5, 3]. Uvažovaný přístup je možné dále rozšířit o viskoelastické chování některých složek mikrostruktury i o popis svalové kontrakce [5, 6]... Stěna cévy Stěna artérií je složena ze tří vrstev, jejichž mohutnost a složení závisí na typu cévy. U středních arterií je dominantní střední svalová vrstva (media) obsahující převážně hladké svalové buňky, viz obr.. Tato vrstva je ohraničena na svém vnitřním a vnějším povrchu elastinem ve formě vláknitých lamel a je z mechanického hlediska podstatná, zatímco vnitřní intima a vnější adveticia plní jiné fyziologické funkce. Uspořádání svalových buněk medie je spirální až kruhovité a umožňuje změnu průsvitu cév. Ing. Vladimír Lukeš, Katedra mechaniky, ZČU, Univerzitní 22, 306 4, Plzeň, lukes@kme.zcu.cz 2 doc. Dr. Ing. Eduard Rohan, Katedra mechaniky, ZČU, Univerzitní 22, 306 4, Plzeň, rohan@kme.zcu.cz
2 V. Lukeš, E. Rohan Endothel Elastica interna Tunica intima Tunica media Tunica adventitia Smooth muscle cell Elastica externa Tunica media Obr.. Fotografie a schéma cévní stěny..2. Matematický model cévní stěny V této práci je cévní stěna modelována pomocí dvouškálové metody homogenizace s uvažováním velkých deformací. Použit je hyperelastický materiálový model. Na mikroskopické úrovni je za základní periodicky se opakující jednotku zvolen zjednodušený model hladké svalové buňky, jež se skládá z elastického cytoskeletu a vlastního endoplazmatu. Ve zde uvažované matematické abstrakci sestává základní referenční buňka z hyperelastické matrice a nestlačitelné inkluze, aproximující jen pasivní chování buňky. Cévu považujeme za osově symetrickou a na makroskopické úrovni modelujeme pouze malý výřez stěny s okrajovými podmínkami odpovídajícími osové symetrii. Tento výřez reprezentuje střední svalovou vrstvu artérie. Na výřezu jsou též definována elastická vlákna, která odpovídají elastickým vrstvám na vnějším a vnitřním povrchu stěny cévy. 2. DVOUŠKÁLOVÁ METODA HOMOGENIZACE 2.. Rovnice rovnováhy V aktualizované Lagrangeově formulaci má rovnice rovnováhy následující tvar (viz [3, 4]) Z Ω Lτkl ( u) e (v) Z dx + τ δη ( u; v) dx = Ω = L(v) Z Ω τ e (v) dx, v V0 (Ω), () kde e (u) = 2 ( j ui + i uj ) je lineární část deformačního tenzoru, δη (u; v) = 2 ( i uk j vk + i vk j uk ) je nelineární část deformačního tenzoru, Lτ (u) je Lieova derivace Kirchhoffova napětí, τ je Kirchhoffovo napětí a L(v) je virtuální práce vnějších sil. V0 (Ω) {v [W,2 (Y )]n v = 0 na ΩD } je prostor přípustných posuvů na oblasti Ω. V této práci je použit neo-hookovský hyperelastický materiálový model, napětí je pak dáno vztahem τ = I p + µ 2/3 dev b, (2) kde = det F, b = F F T (F je deformační gradient), µ je materiálový parametr a p je hydrostatický tlak. e-li materiál stlačitelný, lze tlak vyjádřit vztahem závisejícím na parametru γ: p = γ( ). (3)
3 Matematický model cévní stěny 2.2. Homogenizovaný model V tomto odstavci jsou shrnuty rovnice dvouškálového modelování hyperelastického materiálu s nestlačitelnými inkluzemi, viz [3, 4]. Uvažujeme dvě měřítka, makroskopické v souřadnicích x a mikroskopické v souřadnicích y. Tato měřítka jsou svázána bezrozměrným parametrem ε, y = x/ε. V procesu homogenizace uvažujeme, že heterogenity na mikroškále jsou velmi malé a proto můžeme vzít ε 0 +. Tím získáme limitní model, který je použitelný pro dostatečně malé ε > 0 vystihující konkrétní reálnou situaci. Na makroskopické oblasti definujeme oscilující koeficienty µ, x γ, x µ ε (x) =, γ ε (x) = 0, x T ε γ, x T ε. (4) t Y Γ t T ε m Γ u Obr. 2. Mikroskopická a makroskopická oblast. Rovnici rovnováhy () a konstitutivní vztah pro tlak (3) lze přepsat do tvaru tt Kε D e kl ( u ε )e (v ε ) dx ε p ε div v ε dx + τ ε δη ( u ε ; v ε ) dx + ε kl + T ε ε m p ε uε i vj ε = L(v ε ) x j x i T ε ε m ε m τ ε e (v ε ) ε dx + ε γ ε pε q dx = T ε p ε div v ε, v ε V 0 () (5) q div u ε dx, q L 2 (). (6) Formálně je možné odvodit homogenizovaný model pomocí metody asymptotických rozvojů. Řešení, pole posuvů a tlaků, hledáme ve tvaru asymptotického Y-periodického rozvoje (podle parametru ε) u ε (x) = u 0 (x) + ε u (x, y) +..., p ε (x) = p 0 (x, y) + ε p (x, y) +... (7) ejich dosazením to (5)-(6) a vhodnou volbou testovacích funkcí odvodíme rovnice mikroskopické a makroskopické úlohy deformovatelného tělesa, které se řeší v iteracích. Řešení mikroúlohy (přírůstek tlaku a posuvů) hledáme ve formě charakteristických funkcí χ, π a π u i (x, y) = χ rs i (x, y) s x u 0 r(x), (8) p 0 (x, y) = π rs (x, y) s x u 0 r(x), (9) p 0 (x) = π rs (x) s x u 0 r(x). (0) Toto nám umožňuje definovat a řešit makroskopický a mikroskopický problém odděleně. Mikroskopický problém: Pro pevné x (každý bod ) najít χ H # (Y ), π L 2 (Y ) a π IR takové, že (r, s =, 2, (3)): a Ym (χ rs Π rs, w) + b Ym (χ rs Π rs, w) (π rs, div y w) Ym + ( π rs, div y w) Ym = 0, w H # (Y ), () ( γ πrs, q) + (q, div y χ rs ) Ym (q, div y Π rs ) Ym = 0, q L 2 (Y ), (2) (, div y χ rs ) Ym = T δ rs (3)
4 V. Lukeš, E. Rohan kde Π rs i y s δ ri, H # (Y ) {v [W,2 (Y )] n v je Y poriodická, Y v(y) dy = 0} je prostor přípustných posuvů a bilineární formy a Ym (u, v) a b Ym (u, v) jsou definovány následovně a Ym (u, v) = b Ym (u, v) = ( D tt K kl ) + p 0 δ δ kl e y kl (u) ey (v) dy, (4) ( ) τ δ kl p 0 δ kj δ li y i u k y j v l dy. (5) Makroskopický problém: Definujeme symetrický (platí kl = kl, ale kl ji kl) tenzor homogenizovaných koeficientů ˆQ kl ˆQ kl [ ( c Y Π kl χ kl, Π χ ) + ( ) ] γ π, π kl + p 0 (δ kl δ il δ δ kl ), (6) Y kde bilineární forma c Y (u, v) = a Y (u, v)+b Y (u, v). Pro známé homogenizované koeficienty ˆQ kl a průměrná napětí Ŝ = τ dy chceme vypočítat makroskopická posunutí u 0 V () taková, že Y ˆQ kl l x u 0 k j x v i dx = L(v) Ŝ e x (v) dx, v = V 0 (). (7) Homogenizované koeficienty ˆQ kl a průměrná napětí Ŝ je nutné znát ve všech bodech makroskopické oblasti. Problém je nutno vzhledem k nelinearitám řešit iteračním algoritmem. 3. ELASTICKÁ VLÁKNA Elastické vrstvy v cévní stěně je možno modelovat zavedením elastických vláken do homogenizovaného modelu. V každém bodě vnitřní a vnější válcových ploch, které vymezují vrstvu medie, definujeme směrový jednotkový vektor vlákna ν, viz obr.3 ve dvou tzv. preferenčních směrech určujících dvě protiběžné spirály. Cauchyho napětí ve vlákně r-tého směru je dáno vztahem [r] σ fib = σ [r] ν [r] j, (8) kde σ je skalár Cauchyho napětí ve směru vlákna. Směrový vektor vlákna, v počáteční konfiguraci značen ν, je průběžně aktualizován pomocí deformačního gradientu F λ [r] ν [r] i Prodloužení ve směru vlákna λ je dáno vztahem = F ν [r] j. (9) λ 2 [r] = δ ki F ν [r] j F kl ν [r] l = ( ν [r]) T C ν [r], (20) kde C = F T F je pravý Cauchy Greenův deformační tenzor. Nyní použeme výše uvedené vztahy a přepíšeme napětí (8) do nového tvaru, ve kterém použeme velikost druhého Piola Kirchhoffovo napětí S (napětí ve směru vlákna) [r] σ fib = σ [r] ν [r] j = λ2 [r] ν [r] j S(λ 2 [r] ). (2) Napětí S je definováno pomocí funkce deformační energie jako (zavedeme θ = λ 2 ) S(θ) = 2 W (θ). (22) θ
5 Matematický model cévní stěny V tomto modelu byla funkce deformační energie zvolena ve tvaru kubické funkce { W (θ) = E 6 θ3, pro θ 0 0, pro θ < 0. (23) Protože vlákna nekladou při kompresi odpor, je v případě zkrácení vlákna funkce deformační energie rovna nule. Celkový příspěvek napětí od všech vláken v daném bodě je dán součtem jednotlivých napětích ve vláknech, můžeme tedy psát σ fib = r [r] σ fib = r 2 W (λ 2 λ2 [r] ) [r] (λ 2 [r] ) ν [r] j. (24) Podobně jako v případě napětí, vlákna přispějí i svou tuhostí do celkového tenzoru tuhosti soustavy D fib kl = 2 W (λ 2 4 λ 4 [r] ) [r] ν [r] r (λ 2 [r] )2 j ν [r] k ν[r] l, (25) kde se opět sčítá přes všechna vlákna definovaná v daném bodě. Pro numerické řešení jsou vlákna definována ve vybraných uzlech MKP sítě prostřednictvím směrových vektorů. α α Obr. 3. Vlákna definovaná v MKP modelu. 4. NUMERICKÝ PŘÍKLAD Na makroskopické úrovni máme výřez cévní stěny (okrajové podmínky odpovídají osové symetrii) a tento výřez je zatížen uvnitř přetlakem. Na následujícím obrázku vlevo je vidět deformace stěny v případě, kdy nejsou definována žádná vlákna. Vpravo vidíme situaci při stejném silovém působení ale za přítomnosti elastických vláken na vnitřním a vnějším povrchu (viz obr.3, α = 25 ). Na druhém obrázku vidíme makroskopickou oblast a hodnoty napětí, tlaku a deformace na mikrostruktuře ve vyznačeném bodě makrooblasti. Obr. 4. Deformace stěny vlevo model bez vláken, vpravo s vlákny.
6 V. Lukeš, E. Rohan a) b) Obr. 5. Deformovaná mikroskopická buňka a) celková deformace, b) napětí, c) tlak. c) 5. ZÁVĚRY V příspěvku je prezentován matematický model cévní stěny založený na dvouškálové metodě homogenizace pro velké deformace. Uvedený přístup umožňuje zohlednit charakteristické vlastnosti mikrostruktury a vysledovat jak jejich případná změna ovlivní chování cévu jako celek. Zavedení elastických vláken do homogenizovaného modelu cévní stěny je dalším krokem k realističtějšímu matematickému popisu chování cév, zde rozšířenému o popis elastických lamel ve vrstvě medie. Pro další zdokonalení modelu je nezbytné uvažovat jev kontrakce svalových buněk a jevy spojené s redistribucí kapalných složek hmoty tvořící cévní tkáň v tomto ohledu bude možné navázat na dílčí výsledky z oblasti homogenizace porézních materiálů, viz [5, 6]. Numerické simulace jsou prováděny vlastními programovými prostředky a algoritmy v jazyce C. Poděkování: Příspěvek byl podpořen projektem Fondu rozvoje vysokých škol č. 352/2004/G3 a projektem LN00B084. LITERATURA [] Holzapfel G. A.: Nonlinear Solid Mechanics.. Wiley, Chichester, [2] Rohan E., Cimrman R.: Sensitivity analysis and material identification for activated smooth muscle, Computer Assisted Mechanics and Engrg. Science 9, 59 54, [3] Rohan E.: Mathematical Modellinf of Soft Tissues. Habilitation Thesis. ZČU, Plzeň, [4] Rohan, E. (2003) Sensitivity strategies in modelling heterogeneous media undergoing finite deformation. Math. and Computers in Simul., 6, [5] Rohan, E. (2004) Modelling large deformation induced microflow in soft biological tissues. (submitted for publication, 2004). [6] Rohan E., Cimrman R.: Numerical Modelling and Homogenized Constitutive Law of Large Deforming Porous Media. In Proc. of the Seventh International Conference on Computational Structures Technology, B.H.V. Topping and C.A. Mota Soares (Eds.) Civil-Comp Press 2004.
Mikrostruktura tkáně a matematické modely cév. Katedra mechaniky. Ing. Vladimír LUKEŠ. školitel: doc. Dr. Ing. Eduard ROHAN. Fakulta aplikovaných
 ZÁPADOČESKÁ UNIVERZITA V PLZNI Katedra mechaniky Fakulta aplikovaných věd Mikrostruktura tkáně a matematické modely cév Ing. Vladimír LUKEŠ školitel: doc. Dr. Ing. Eduard ROHAN Plzeň, leden 2005 Obsah
ZÁPADOČESKÁ UNIVERZITA V PLZNI Katedra mechaniky Fakulta aplikovaných věd Mikrostruktura tkáně a matematické modely cév Ing. Vladimír LUKEŠ školitel: doc. Dr. Ing. Eduard ROHAN Plzeň, leden 2005 Obsah
TENSOR NAPĚTÍ A DEFORMACE. Obrázek 1: Volba souřadnicového systému
 TENSOR NAPĚTÍ A DEFORMACE Obrázek 1: Volba souřadnicového systému Pole posunutí, deformace, napětí v materiálovém bodě {u} = { u v w } T (1) Obecně 9 složek pole napětí lze uspořádat do matice [3x3] -
TENSOR NAPĚTÍ A DEFORMACE Obrázek 1: Volba souřadnicového systému Pole posunutí, deformace, napětí v materiálovém bodě {u} = { u v w } T (1) Obecně 9 složek pole napětí lze uspořádat do matice [3x3] -
c B. Patzák 2012, verze 01
 Úvod do nelineárních problémů c B. Patzák (borek.patzak@fsv.cvut.cz), 2012, verze 01 Příklady nelineárního chování Problém vedení tepla, kde vlastnosti materiálu (koeficient vedení tepla) závisí na aktuální
Úvod do nelineárních problémů c B. Patzák (borek.patzak@fsv.cvut.cz), 2012, verze 01 Příklady nelineárního chování Problém vedení tepla, kde vlastnosti materiálu (koeficient vedení tepla) závisí na aktuální
Rozdíly mezi MKP a MHP, oblasti jejich využití.
 Rozdíly mezi, oblasti jejich využití. Obě metody jsou vhodné pro určitou oblast problémů. základě MKP vyžaduje rozdělení těles na vhodný počet prvků, jejichž analýza je poměrně snadná a pro většinu částí
Rozdíly mezi, oblasti jejich využití. Obě metody jsou vhodné pro určitou oblast problémů. základě MKP vyžaduje rozdělení těles na vhodný počet prvků, jejichž analýza je poměrně snadná a pro většinu částí
Biomechanika srdečněcévnísoustavy a konstitutivnímodelování
 Biomechanika srdečněcévnísoustavy a konstitutivnímodelování Biomechanika a lékařsképřístroje Biomechanika I LukášHorný Laboratoř biomechaniky člověka Ústavu mechaniky Fakulty strojní ČVUT v Praze M Konstitutivní
Biomechanika srdečněcévnísoustavy a konstitutivnímodelování Biomechanika a lékařsképřístroje Biomechanika I LukášHorný Laboratoř biomechaniky člověka Ústavu mechaniky Fakulty strojní ČVUT v Praze M Konstitutivní
FAKULTA STAVEBNÍ. Telefon: WWW:
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ ZÁKLADY METODY KONEČNÝCH PRVKŮ Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast10.vsb.cz/brozovsky/
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ ZÁKLADY METODY KONEČNÝCH PRVKŮ Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast10.vsb.cz/brozovsky/
Nelineární úlohy při výpočtu konstrukcí s využitím MKP
 Nelineární úlohy při výpočtu konstrukcí s využitím MKP Obsah přednášky Lineární a nelineární úlohy Typy nelinearit (geometrická, materiálová, kontakt,..) Příklady nelineárních problémů Teorie kontaktu,
Nelineární úlohy při výpočtu konstrukcí s využitím MKP Obsah přednášky Lineární a nelineární úlohy Typy nelinearit (geometrická, materiálová, kontakt,..) Příklady nelineárních problémů Teorie kontaktu,
Vlastnosti a zkoušení materiálů. Přednáška č.4 Úvod do pružnosti a pevnosti
 Vlastnosti a zkoušení materiálů Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze
Vlastnosti a zkoušení materiálů Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze
Nelineární problémy a MKP
 Nelineární problémy a MKP Základní druhy nelinearit v mechanice tuhých těles: 1. materiálová (plasticita, viskoelasticita, viskoplasticita,...) 2. geometrická (velké posuvy a natočení, stabilita konstrukcí)
Nelineární problémy a MKP Základní druhy nelinearit v mechanice tuhých těles: 1. materiálová (plasticita, viskoelasticita, viskoplasticita,...) 2. geometrická (velké posuvy a natočení, stabilita konstrukcí)
Autor: Vladimír Švehla
 Bulletin of Applied Mechanics 1, 55 64 (2005) 55 Využití Castiglianovy věty při výpočtu deformací staticky určité případy zatížení tahem a tlakem Autor: Vladimír Švehla České vysoké učení technické, akulta
Bulletin of Applied Mechanics 1, 55 64 (2005) 55 Využití Castiglianovy věty při výpočtu deformací staticky určité případy zatížení tahem a tlakem Autor: Vladimír Švehla České vysoké učení technické, akulta
Obecný Hookeův zákon a rovinná napjatost
 Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
KONSTITUČNÍ VZTAHY. 1. Tahová zkouška
 1. Tahová zkouška Tahová zkouška se provádí dle ČSN EN ISO 6892-1 (aktualizována v roce 2010) Je nejčastější mechanickou zkouškou kovových materiálů. Zkoušky se realizují na trhacích strojích, kde se zkušební
1. Tahová zkouška Tahová zkouška se provádí dle ČSN EN ISO 6892-1 (aktualizována v roce 2010) Je nejčastější mechanickou zkouškou kovových materiálů. Zkoušky se realizují na trhacích strojích, kde se zkušební
8. Základy lomové mechaniky. Únava a lomová mechanika Pavel Hutař, Luboš Náhlík
 Únava a lomová mechanika Koncentrace napětí nesingulární koncentrátor napětí singulární koncentrátor napětí 1 σ = σ + a r 2 σ max = σ 1 + 2( / ) r 0 ; σ max Nekonečný pás s eliptickým otvorem [Pook 2000]
Únava a lomová mechanika Koncentrace napětí nesingulární koncentrátor napětí singulární koncentrátor napětí 1 σ = σ + a r 2 σ max = σ 1 + 2( / ) r 0 ; σ max Nekonečný pás s eliptickým otvorem [Pook 2000]
Dvě varianty rovinného problému: rovinná napjatost. rovinná deformace
 Rovinný problém Řešíme plošné konstrukce zatížené a uložené v jejich střednicové rovině. Dvě varianty rovinného problému: rovinná napjatost rovinná deformace 17 Rovinná deformace 1 Obsahuje složky deformace
Rovinný problém Řešíme plošné konstrukce zatížené a uložené v jejich střednicové rovině. Dvě varianty rovinného problému: rovinná napjatost rovinná deformace 17 Rovinná deformace 1 Obsahuje složky deformace
Nosné desky. 1. Kirchhoffova teorie ohybu tenkých desek (h/l < 1/10) 3. Mindlinova teorie pro tlusté desky (h/l < 1/5)
 Nosné desky Deska je těleso, které má jeden rozměr mnohem menší než rozměry zbývající. Zatížení desky je orientováno výhradně kolmo k její střednicové rovině. 1. Kirchhoffova teorie ohybu tenkých desek
Nosné desky Deska je těleso, které má jeden rozměr mnohem menší než rozměry zbývající. Zatížení desky je orientováno výhradně kolmo k její střednicové rovině. 1. Kirchhoffova teorie ohybu tenkých desek
Rovinná úloha v MKP. (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v. prostorové úlohy: u, v, w
 Rovinná úloha v MKP Hledané deformační veličiny viz klasická teorie pružnosti (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v desky: w, ϕ x, ϕ y prostorové úlohy: u,
Rovinná úloha v MKP Hledané deformační veličiny viz klasická teorie pružnosti (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v desky: w, ϕ x, ϕ y prostorové úlohy: u,
Analýza napjatosti PLASTICITA
 Analýza napjatosti PLASTICITA TENZOR NAPĚTÍ Teplota v daném bodě je skalár, je to tenzor nultého řádu, který nezávisí na změně souřadného systému Síla je vektor, je to tenzor prvního řádu, v trojrozměrném
Analýza napjatosti PLASTICITA TENZOR NAPĚTÍ Teplota v daném bodě je skalár, je to tenzor nultého řádu, který nezávisí na změně souřadného systému Síla je vektor, je to tenzor prvního řádu, v trojrozměrném
vztažný systém obecné napětí předchozí OBSAH další
 p05 1 5. Deformace těles S deformací jako složkou mechanického pohybu jste se setkali už ve statice. Běžně je chápána jako změna rozměrů a tvaru tělesa. Lze ji popsat změnami vzdáleností různých dvou bodů
p05 1 5. Deformace těles S deformací jako složkou mechanického pohybu jste se setkali už ve statice. Běžně je chápána jako změna rozměrů a tvaru tělesa. Lze ji popsat změnami vzdáleností různých dvou bodů
Stabilizace Galerkin Least Squares pro
 Fakulta strojní ČVUT Ústav technické matematiky Stabilizace Galerkin Least Squares pro MKP na řešení proudění o vyšších Reynoldsových číslech Ing. Jakub Šístek Doc. RNDr. Pavel Burda, CSc. RNDr. Jaroslav
Fakulta strojní ČVUT Ústav technické matematiky Stabilizace Galerkin Least Squares pro MKP na řešení proudění o vyšších Reynoldsových číslech Ing. Jakub Šístek Doc. RNDr. Pavel Burda, CSc. RNDr. Jaroslav
Mechanika s Inventorem
 Mechanika s Inventorem 2. Základní pojmy CAD data FEM výpočty Petr SCHILLING, autor přednášky Ing. Kateřina VLČKOVÁ, obsahová korekce Optimalizace Tomáš MATOVIČ, publikace 1 Obsah přednášky: Lagrangeův
Mechanika s Inventorem 2. Základní pojmy CAD data FEM výpočty Petr SCHILLING, autor přednášky Ing. Kateřina VLČKOVÁ, obsahová korekce Optimalizace Tomáš MATOVIČ, publikace 1 Obsah přednášky: Lagrangeův
Nelineární analýza materiálů a konstrukcí (V-132YNAK) Přednáška 2 Princip metody konečných prvků
 Nelineární analýza materiálů a konstrukcí (V-132YNAK) Přednáška 2 Princip metody konečných prvků Petr Kabele petr.kabele@fsv.cvut.cz people.fsv.cvut.cz/~pkabele Petr Kabele, 2007-2014 Obsah Variační principy
Nelineární analýza materiálů a konstrukcí (V-132YNAK) Přednáška 2 Princip metody konečných prvků Petr Kabele petr.kabele@fsv.cvut.cz people.fsv.cvut.cz/~pkabele Petr Kabele, 2007-2014 Obsah Variační principy
Martin NESLÁDEK. 14. listopadu 2017
 Martin NESLÁDEK Faculty of mechanical engineering, CTU in Prague 14. listopadu 2017 1 / 22 Poznámky k úlohám řešeným MKP Na přesnost simulace pomocí MKP a prostorové rozlišení výsledků má vliv především:
Martin NESLÁDEK Faculty of mechanical engineering, CTU in Prague 14. listopadu 2017 1 / 22 Poznámky k úlohám řešeným MKP Na přesnost simulace pomocí MKP a prostorové rozlišení výsledků má vliv především:
7. Základní formulace lineární PP
 p07 1 7. Základní formulace lineární PP Podle tvaru závislosti mezi vnějšími silami a deformačně napěťovými parametry tělesa dělíme pružnost a pevnost na lineární a nelineární. Lineární pružnost vyšetřuje
p07 1 7. Základní formulace lineární PP Podle tvaru závislosti mezi vnějšími silami a deformačně napěťovými parametry tělesa dělíme pružnost a pevnost na lineární a nelineární. Lineární pružnost vyšetřuje
Lineární stabilita a teorie II. řádu
 Lineární stabilita a teorie II. řádu Sestavení podmínek rovnováhy na deformované konstrukci Konstrukce s a bez počáteční imperfekce Výpočet s malými vs. s velkými deformacemi ANKC-C 1 Zatěžovacídráhy [Šejnoha,
Lineární stabilita a teorie II. řádu Sestavení podmínek rovnováhy na deformované konstrukci Konstrukce s a bez počáteční imperfekce Výpočet s malými vs. s velkými deformacemi ANKC-C 1 Zatěžovacídráhy [Šejnoha,
Metoda konečných prvků Charakteristika metody (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika)
 Inovace studijního oboru Geotechnika Reg. č. CZ.1.07/2.2.00/28.0009 Metoda konečných prvků Charakteristika metody (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika) Doc. RNDr.
Inovace studijního oboru Geotechnika Reg. č. CZ.1.07/2.2.00/28.0009 Metoda konečných prvků Charakteristika metody (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika) Doc. RNDr.
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV MECHANIKY TĚLES, MECHATRONIKY A BIOMECHANIKY Komentovaný metodický list č. 1/4 Vytvořil: Ing. Oldřich Ševeček & Ing. Tomáš Profant, Ph.D.
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV MECHANIKY TĚLES, MECHATRONIKY A BIOMECHANIKY Komentovaný metodický list č. 1/4 Vytvořil: Ing. Oldřich Ševeček & Ing. Tomáš Profant, Ph.D.
Základy matematické teorie pružnosti Tenzor napětí a tenzor deformace Statické (Cauchyho) rovnice. Geometrické rovnice
 Přednáška 1 Základy matematické teorie pružnosti Tenzor napětí a tenzor deformace Statické (Cauchyho) rovnice Rozšířený Hookův zákon Geometrické rovnice Ondřej Jiroušek Ústav mechaniky a materiálů Fakulta
Přednáška 1 Základy matematické teorie pružnosti Tenzor napětí a tenzor deformace Statické (Cauchyho) rovnice Rozšířený Hookův zákon Geometrické rovnice Ondřej Jiroušek Ústav mechaniky a materiálů Fakulta
Numerické metody. Numerické modelování v aplikované geologii. David Mašín. Ústav hydrogeologie, inženýrské geologie a užité geofyziky
 Numerické modelování v aplikované geologii David Mašín Ústav hydrogeologie, inženýrské geologie a užité geofyziky Přírodovědecká fakulta Karlova Univerzita v Praze Přednášky pro obor Geotechnologie David
Numerické modelování v aplikované geologii David Mašín Ústav hydrogeologie, inženýrské geologie a užité geofyziky Přírodovědecká fakulta Karlova Univerzita v Praze Přednášky pro obor Geotechnologie David
7 Lineární elasticita
 7 Lineární elasticita Elasticita je schopnost materiálu pružně se deformovat. Deformace ideálně elastických látek je okamžitá (časově nezávislá) a dokonale vratná. Působí-li na infinitezimální objemový
7 Lineární elasticita Elasticita je schopnost materiálu pružně se deformovat. Deformace ideálně elastických látek je okamžitá (časově nezávislá) a dokonale vratná. Působí-li na infinitezimální objemový
Zjednodušená deformační metoda (2):
 Stavební mechanika 1SM Přednášky Zjednodušená deformační metoda () Prut s kloubově připojeným koncem (statická kondenzace). Řešení rovinných rámů s posuvnými patry/sloupy. Prut s kloubově připojeným koncem
Stavební mechanika 1SM Přednášky Zjednodušená deformační metoda () Prut s kloubově připojeným koncem (statická kondenzace). Řešení rovinných rámů s posuvnými patry/sloupy. Prut s kloubově připojeným koncem
Obr. 0.1: Nosník se spojitým zatížením.
 Každý test obsahuje jeden příklad podobný níže uvedeným tpovým příkladům a několik otázek vbraných z níže uvedených testových otázek. Za příklad je možno získat maimálně bodů, celkový počet bodů z testu
Každý test obsahuje jeden příklad podobný níže uvedeným tpovým příkladům a několik otázek vbraných z níže uvedených testových otázek. Za příklad je možno získat maimálně bodů, celkový počet bodů z testu
FAKULTA STAVEBNÍ NELINEÁRNÍ MECHANIKA. Telefon: WWW:
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ NELINEÁRNÍ MECHANIKA Bakalářské studium, 4. ročník Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ NELINEÁRNÍ MECHANIKA Bakalářské studium, 4. ročník Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz
1 Ohyb desek - mindlinovské řešení
 1 OHYB DESEK - MINDLINOVSKÉ ŘEŠENÍ 1 1 Ohyb desek - mindlinovské řešení Kinematika přemístění Posun w se po tloušťce desky mění málo (vzhledem k hodnotě průhybu) w(x, y, z) = w(x, y) Normály ke střednicové
1 OHYB DESEK - MINDLINOVSKÉ ŘEŠENÍ 1 1 Ohyb desek - mindlinovské řešení Kinematika přemístění Posun w se po tloušťce desky mění málo (vzhledem k hodnotě průhybu) w(x, y, z) = w(x, y) Normály ke střednicové
ÚVOD DO MODELOVÁNÍ V MECHANICE
 ÚVO O MOELOVÁNÍ V MECHNICE MECHNIK KOMPOZITNÍCH MTERIÁLŮ 2 Přednáška č. 7 Robert Zemčík 1 Zebry normální Zebry zdeformované 2 Zebry normální Zebry zdeformované 3 Zebry normální 4 Zebry zdeformované protažené?
ÚVO O MOELOVÁNÍ V MECHNICE MECHNIK KOMPOZITNÍCH MTERIÁLŮ 2 Přednáška č. 7 Robert Zemčík 1 Zebry normální Zebry zdeformované 2 Zebry normální Zebry zdeformované 3 Zebry normální 4 Zebry zdeformované protažené?
Aproximace posuvů [ N ],[G] Pro každý prvek se musí nalézt vztahy
![Aproximace posuvů [ N ],[G] Pro každý prvek se musí nalézt vztahy Aproximace posuvů [ N ],[G] Pro každý prvek se musí nalézt vztahy](/thumbs/97/130835283.jpg) Aproimace posuvů Pro každý prvek se musí nalézt vztahy kde jsou prozatím neznámé transformační matice. Neznámé funkce posuvů se obvykle aproimují ve formě mnohočlenů kartézských souřadnic. Například 1.
Aproimace posuvů Pro každý prvek se musí nalézt vztahy kde jsou prozatím neznámé transformační matice. Neznámé funkce posuvů se obvykle aproimují ve formě mnohočlenů kartézských souřadnic. Například 1.
Geometricky válcová momentová skořepina
 Geometricky válcová momentová skořepina Dalším typem tenkostěnnéo rotačně souměrnéo tělesa je geometricky válcová momentová skořepina. Typický souřadnicový systém je opět systém s osami z, r, a t. Geometricky
Geometricky válcová momentová skořepina Dalším typem tenkostěnnéo rotačně souměrnéo tělesa je geometricky válcová momentová skořepina. Typický souřadnicový systém je opět systém s osami z, r, a t. Geometricky
PRUŽNOST A PEVNOST II
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ PRUŽNOST A PEVNOST II Navazující magisterské studium, 1. ročník Alois Materna (přednášky) Jiří Brožovský (cvičení) Kancelář: LP C 303/1
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ PRUŽNOST A PEVNOST II Navazující magisterské studium, 1. ročník Alois Materna (přednášky) Jiří Brožovský (cvičení) Kancelář: LP C 303/1
Termomechanika 10. přednáška Doc. Dr. RNDr. Miroslav Holeček
 Termomechanika 10. přednáška Doc. Dr. RNDr. Miroslav Holeček Upozornění: Tato prezentace slouží výhradně pro výukové účely Fakulty strojní Západočeské univerzity v Plzni. Byla sestavena autorem s využitím
Termomechanika 10. přednáška Doc. Dr. RNDr. Miroslav Holeček Upozornění: Tato prezentace slouží výhradně pro výukové účely Fakulty strojní Západočeské univerzity v Plzni. Byla sestavena autorem s využitím
Náhradní ohybová tuhost nosníku
 Náhradní ohybová tuhost nosníku Autoři: Doc. Ing. Jiří PODEŠVA, Ph.D., Katedra mechaniky, Fakulta strojní, VŠB - Technická univerzita Ostrava, e-mail: jiri.podesva@vsb.cz Anotace: Výpočty ocelových výztuží
Náhradní ohybová tuhost nosníku Autoři: Doc. Ing. Jiří PODEŠVA, Ph.D., Katedra mechaniky, Fakulta strojní, VŠB - Technická univerzita Ostrava, e-mail: jiri.podesva@vsb.cz Anotace: Výpočty ocelových výztuží
AUTORIZOVANÝ SOFTWARE. MatFEM
 AUTORIZOVANÝ SOFTWARE MatFEM OBECNÝ ŘEŠIČ NA BÁZI METODY KONEČNÝCH PRVKŮ V SYSTÉMU MATLAB Autor: Ing. Vladimír Lukeš, Ph.D. doc. Dr. Ing. Eduard Rohan Číslo projektu: Číslo výsledku: Odpovědný pracovník:
AUTORIZOVANÝ SOFTWARE MatFEM OBECNÝ ŘEŠIČ NA BÁZI METODY KONEČNÝCH PRVKŮ V SYSTÉMU MATLAB Autor: Ing. Vladimír Lukeš, Ph.D. doc. Dr. Ing. Eduard Rohan Číslo projektu: Číslo výsledku: Odpovědný pracovník:
Katedra geotechniky a podzemního stavitelství
 Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Metoda oddělených elementů (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Metoda oddělených elementů (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
12 DYNAMIKA SOUSTAVY HMOTNÝCH BODŮ
 56 12 DYNAMIKA SOUSTAVY HMOTNÝCH BODŮ Těžiště I. impulsová věta - věta o pohybu těžiště II. impulsová věta Zákony zachování v izolované soustavě hmotných bodů Náhrada pohybu skutečných objektů pohybem
56 12 DYNAMIKA SOUSTAVY HMOTNÝCH BODŮ Těžiště I. impulsová věta - věta o pohybu těžiště II. impulsová věta Zákony zachování v izolované soustavě hmotných bodů Náhrada pohybu skutečných objektů pohybem
NELINEÁRNÍ MECHANIKA
 VYSOKÉ UČENÍ ECHNICKÉ V BRNĚ FAKULA SAVEBNÍ Doc.Ing.Ivan Němec, CSc. NELINEÁRNÍ MECHANIKA MODUL D7 M1 ZÁKLADY NELINEÁRNÍ MECHANIKY SUDIJNÍ OPORY PRO SUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU SUDIA Doc.Ing.Ivan
VYSOKÉ UČENÍ ECHNICKÉ V BRNĚ FAKULA SAVEBNÍ Doc.Ing.Ivan Němec, CSc. NELINEÁRNÍ MECHANIKA MODUL D7 M1 ZÁKLADY NELINEÁRNÍ MECHANIKY SUDIJNÍ OPORY PRO SUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU SUDIA Doc.Ing.Ivan
Vícerozměrné úlohy pružnosti
 Přednáška 07 Rovinná napjatost nosné stěny Rovinná deformace Hlavní napětí Mohrova kružnice Metoda konečných prvků pro rovinnou napjatost Laméovy rovnice Příklady Copyright (c) 011 Vít Šmilauer Czech Technical
Přednáška 07 Rovinná napjatost nosné stěny Rovinná deformace Hlavní napětí Mohrova kružnice Metoda konečných prvků pro rovinnou napjatost Laméovy rovnice Příklady Copyright (c) 011 Vít Šmilauer Czech Technical
Úlohy nejmenších čtverců
 Úlohy nejmenších čtverců Petr Tichý 7. listopadu 2012 1 Problémy nejmenších čtverců Ax b Řešení Ax = b nemusí existovat, a pokud existuje, nemusí být jednoznačné. Často má smysl hledat x tak, že Ax b.
Úlohy nejmenších čtverců Petr Tichý 7. listopadu 2012 1 Problémy nejmenších čtverců Ax b Řešení Ax = b nemusí existovat, a pokud existuje, nemusí být jednoznačné. Často má smysl hledat x tak, že Ax b.
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6
 OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
Summer Workshop of Applied Mechanics. Závislost míry tuhosti laminátové desky na orientaci vrstev a její maximalizace
 Summer Workshop of Applied Mechanics June 22 Department of Mechanics Facult of Mechanical Engineering Czech Technical Universit in Prague Závislost mír tuhosti laminátové desk na orientaci vrstev a její
Summer Workshop of Applied Mechanics June 22 Department of Mechanics Facult of Mechanical Engineering Czech Technical Universit in Prague Závislost mír tuhosti laminátové desk na orientaci vrstev a její
12. Prostý krut Definice
 p12 1 12. Prostý krut 12.1. Definice Prostý krut je označení pro namáhání přímého prizmatického prutu, jestliže jsou splněny prutové předpoklady, příčné průřezy se nedeformují, pouze se vzájemně natáčejí
p12 1 12. Prostý krut 12.1. Definice Prostý krut je označení pro namáhání přímého prizmatického prutu, jestliže jsou splněny prutové předpoklady, příčné průřezy se nedeformují, pouze se vzájemně natáčejí
Technologie a procesy sušení dřeva
 strana 1 Technologie a procesy sušení dřeva 5. Deformačně-napěťové pole ve dřevě během sušení Vytvořeno s podporou projektu Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v
strana 1 Technologie a procesy sušení dřeva 5. Deformačně-napěťové pole ve dřevě během sušení Vytvořeno s podporou projektu Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v
Polární rozklad deformačního gradientu a tenzory přetvoření
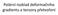 Polární rozklad deformačního gradientu a tenzory přetvoření https://en.wikipedia.org/wiki/finite_strain_theory Deformační gradient Musí tedy existovat jednoznačné zobrazení konfigurace : 1 t t x X, a inversní
Polární rozklad deformačního gradientu a tenzory přetvoření https://en.wikipedia.org/wiki/finite_strain_theory Deformační gradient Musí tedy existovat jednoznačné zobrazení konfigurace : 1 t t x X, a inversní
1.1 Shrnutí základních poznatků
 1.1 Shrnutí základních poznatků Pojmem nádoba obvykle označujeme součásti strojů a zařízení, které jsou svým tvarem a charakterem namáhání shodné s dutými tělesy zatíženými vnitřním, popř. i vnějším tlakem.sohledemnatopovažujemezanádobyrůznápotrubíakotlovátělesa,alenapř.i
1.1 Shrnutí základních poznatků Pojmem nádoba obvykle označujeme součásti strojů a zařízení, které jsou svým tvarem a charakterem namáhání shodné s dutými tělesy zatíženými vnitřním, popř. i vnějším tlakem.sohledemnatopovažujemezanádobyrůznápotrubíakotlovátělesa,alenapř.i
ÚVOD DO MODELOVÁNÍ V MECHANICE
 ÚVOD DO MODELOVÁNÍ V MECHANICE PRUŽNOST A PEVNOST Přednáška č. 5 Prof. Ing. Vladislav Laš. CSc. MECHANIKA PODDAJNÝCH TĚLES Úkolem PP z inženýrského hlediska je navrhnout součásti nebo konstrukce, které
ÚVOD DO MODELOVÁNÍ V MECHANICE PRUŽNOST A PEVNOST Přednáška č. 5 Prof. Ing. Vladislav Laš. CSc. MECHANIKA PODDAJNÝCH TĚLES Úkolem PP z inženýrského hlediska je navrhnout součásti nebo konstrukce, které
Modelování a aproximace v biomechanice
 Modelování a aproximace v biomechanice Během většiny lidské aktivity působí v jednom okamžiku víc než jedna skupina svalů. Je-li úkolem analyzovat síly působící v kloubech a svalech během určité lidské
Modelování a aproximace v biomechanice Během většiny lidské aktivity působí v jednom okamžiku víc než jedna skupina svalů. Je-li úkolem analyzovat síly působící v kloubech a svalech během určité lidské
Úvod do analytické mechaniky
 Úvod do analytické mechaniky Vektorová mechanika, která je někdy nazývána jako Newtonova, vychází bezprostředně z principů, které jsou vyjádřeny vztahy mezi vektorovými veličinami. V tomto případě např.
Úvod do analytické mechaniky Vektorová mechanika, která je někdy nazývána jako Newtonova, vychází bezprostředně z principů, které jsou vyjádřeny vztahy mezi vektorovými veličinami. V tomto případě např.
Pružnost a pevnost I
 Stránka 1 teoretické otázk 2007 Ing. Tomáš PROFANT, Ph.D. verze 1.1 OBSAH: 1. Tenzor napětí 2. Věta o sdruženosti smkových napětí 3. Saint Venantův princip 4. Tenzor deformace (přetvoření) 5. Geometrická
Stránka 1 teoretické otázk 2007 Ing. Tomáš PROFANT, Ph.D. verze 1.1 OBSAH: 1. Tenzor napětí 2. Věta o sdruženosti smkových napětí 3. Saint Venantův princip 4. Tenzor deformace (přetvoření) 5. Geometrická
Dynamika vázaných soustav těles
 Dynamika vázaných soustav těles Většina strojů a strojních zařízení, s nimiž se setkáváme v praxi, lze považovat za soustavy těles. Složitost dané soustavy závisí na druhu řešeného případu. Základem pro
Dynamika vázaných soustav těles Většina strojů a strojních zařízení, s nimiž se setkáváme v praxi, lze považovat za soustavy těles. Složitost dané soustavy závisí na druhu řešeného případu. Základem pro
4. Napjatost v bodě tělesa
 p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
POČÍTAČOVÉ SIMULACE DVOUOSÝCH TAHOVÝCH ZKOUŠEK MĚKKÝCH BIOLOGICKÝCH TKÁNÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV MECHANIKY TĚLES, MECHATRONIKY A BIOMECHANIKY FACULTY OF MECHANICAL ENGINEERING INSTITUTE OF SOLID MECHANICS,
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV MECHANIKY TĚLES, MECHATRONIKY A BIOMECHANIKY FACULTY OF MECHANICAL ENGINEERING INSTITUTE OF SOLID MECHANICS,
Nauka o materiálu. Přednáška č.4 Úvod do pružnosti a pevnosti
 Nauka o materiálu Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze kluzu R e, odpovídající
Nauka o materiálu Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze kluzu R e, odpovídající
Stavební mechanika 3 132SM3 Přednášky. Deformační metoda: ZDM pro rámy s posuvnými styčníky, využití symetrie, výpočetní programy a kontrola výsledků.
 Stavební mechanika 12SM Přednášky Deformační metoda: ZDM pro rámy s posuvnými styčníky, využití symetrie, výpočetní programy a kontrola výsledků. Porovnání ODM a ZDM Příklad 1: (viz předchozí přednáška)
Stavební mechanika 12SM Přednášky Deformační metoda: ZDM pro rámy s posuvnými styčníky, využití symetrie, výpočetní programy a kontrola výsledků. Porovnání ODM a ZDM Příklad 1: (viz předchozí přednáška)
Vibrace atomů v mřížce, tepelná kapacita pevných látek
 Vibrace atomů v mřížce, tepelná kapacita pevných látek Atomy vázané v mřížce nejsou v klidu. Míru jejich pohybu vyjadřuje podobně jako u plynů a kapalin teplota. - Elastické vlny v kontinuu neatomární
Vibrace atomů v mřížce, tepelná kapacita pevných látek Atomy vázané v mřížce nejsou v klidu. Míru jejich pohybu vyjadřuje podobně jako u plynů a kapalin teplota. - Elastické vlny v kontinuu neatomární
2D transformací. červen Odvození transformačního klíče vybraných 2D transformací Metody vyrovnání... 2
 Výpočet transformačních koeficinetů vybraných 2D transformací Jan Ježek červen 2008 Obsah Odvození transformačního klíče vybraných 2D transformací 2 Meto vyrovnání 2 2 Obecné vyjádření lineárních 2D transformací
Výpočet transformačních koeficinetů vybraných 2D transformací Jan Ježek červen 2008 Obsah Odvození transformačního klíče vybraných 2D transformací 2 Meto vyrovnání 2 2 Obecné vyjádření lineárních 2D transformací
Cvičení 7 (Matematická teorie pružnosti)
 VŠB Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti (339) Pružnost a pevnost v energetice (Návo do cvičení) Cvičení 7 (Matematická teorie pružnosti) Autor: Jaroslav Rojíček Verze:
VŠB Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti (339) Pružnost a pevnost v energetice (Návo do cvičení) Cvičení 7 (Matematická teorie pružnosti) Autor: Jaroslav Rojíček Verze:
 2.1. OBĚHOVÁ SOUSTAVA Aorta Hornı duta z ı la Leve plicnı tepny Prave plicnı tepny Plicnı kmen Leva sı n Leve plicnı z ı ly Aorta lnı chlopen Prave plicnı z ı ly Plicnı chlopen Mitra lnı chlopen Prava
2.1. OBĚHOVÁ SOUSTAVA Aorta Hornı duta z ı la Leve plicnı tepny Prave plicnı tepny Plicnı kmen Leva sı n Leve plicnı z ı ly Aorta lnı chlopen Prave plicnı z ı ly Plicnı chlopen Mitra lnı chlopen Prava
TENKOSTĚNNÉ A SPŘAŽENÉ KONSTRUKCE
 1 TENKOSTĚNNÉ A SPŘAŽENÉ KONSTRUKCE Michal Jandera Obsah přednášek 1. Stabilita stěn, nosníky třídy 4.. Tenkostěnné za studena tvarované profily: Výroba, chování průřezů, chování prutů. 3. Tenkostěnné
1 TENKOSTĚNNÉ A SPŘAŽENÉ KONSTRUKCE Michal Jandera Obsah přednášek 1. Stabilita stěn, nosníky třídy 4.. Tenkostěnné za studena tvarované profily: Výroba, chování průřezů, chování prutů. 3. Tenkostěnné
Tvorba výpočtového modelu MKP
 Tvorba výpočtového modelu MKP Jaroslav Beran (KTS) Modelování a simulace Tvorba výpočtového modelu s využitím MKP zahrnuje: Tvorbu (import) geometrického modelu Generování sítě konečných prvků Definování
Tvorba výpočtového modelu MKP Jaroslav Beran (KTS) Modelování a simulace Tvorba výpočtového modelu s využitím MKP zahrnuje: Tvorbu (import) geometrického modelu Generování sítě konečných prvků Definování
OPTIMALIZACE A MULTIKRITERIÁLNÍ HODNOCENÍ FUNKČNÍ ZPŮSOBILOSTI POZEMNÍCH STAVEB D24FZS
 OPTIMALIZACE A MULTIKRITERIÁLNÍ HODNOCENÍ FUNKČNÍ ZPŮSOBILOSTI POZEMNÍCH STAVEB Optimalizace a multikriteriální hodnocení funkční způsobilosti pozemních staveb Anotace: Optimalizace objektů pozemních staveb
OPTIMALIZACE A MULTIKRITERIÁLNÍ HODNOCENÍ FUNKČNÍ ZPŮSOBILOSTI POZEMNÍCH STAVEB Optimalizace a multikriteriální hodnocení funkční způsobilosti pozemních staveb Anotace: Optimalizace objektů pozemních staveb
Studentská tvůrčí činnost 2009
 Studentská tvůrčí činnost 2009 Numerické řešení proudového pole v kompresorové lopatkové mříži Balcarová Lucie Vedoucí práce: Prof. Ing. P. Šafařík, CSc. a Ing. T. Hyhlík, PhD. Numerické řešení proudového
Studentská tvůrčí činnost 2009 Numerické řešení proudového pole v kompresorové lopatkové mříži Balcarová Lucie Vedoucí práce: Prof. Ing. P. Šafařík, CSc. a Ing. T. Hyhlík, PhD. Numerické řešení proudového
ANALÝZA KONSTRUKCÍ. 5. přednáška
 ANALÝZA KONSTRUKCÍ 5. přednáška Nosné stěny rovinná napjatost Způsoby výpočtu napjatosti: Deformační metodou Primární neznámé: posuny u(,y), v(,y) Výchozí rovnice: statické Silovou metodou Primární neznámá:
ANALÝZA KONSTRUKCÍ 5. přednáška Nosné stěny rovinná napjatost Způsoby výpočtu napjatosti: Deformační metodou Primární neznámé: posuny u(,y), v(,y) Výchozí rovnice: statické Silovou metodou Primární neznámá:
Prostorové konstrukce. neznámé parametry: u, v w. (prvky se středostranovými uzly)
 Konečné prvk pro řešení 3D úloh Prostorové konstrukce neznámé parametr: u, v w volba různého počtu uzlů a neznámých v uzlech možnost zakřivených hran prvků (prvk se středostranovými uzl) Opakování: Geometrické
Konečné prvk pro řešení 3D úloh Prostorové konstrukce neznámé parametr: u, v w volba různého počtu uzlů a neznámých v uzlech možnost zakřivených hran prvků (prvk se středostranovými uzl) Opakování: Geometrické
Co jsme udělali: Au = f, u D(A)
 Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Nespojitá vlákna. Nanokompozity
 Nespojitá vlákna Nanokompozity Pro 5. ročník nanomateriály Fakulta mechatroniky Katedra materiálu Strojní fakulty Technická univerzita v Liberci Doc. Ing. Karel Daďourek, 2010 Vliv nespojitých vláken Uspořádaná
Nespojitá vlákna Nanokompozity Pro 5. ročník nanomateriály Fakulta mechatroniky Katedra materiálu Strojní fakulty Technická univerzita v Liberci Doc. Ing. Karel Daďourek, 2010 Vliv nespojitých vláken Uspořádaná
Numerické modelování interakce proudění a pružného tělesa v lidském vokálním traktu
 Numerické modelování interakce proudění a pružného tělesa v lidském vokálním traktu Vedoucí práce: doc. Ing. Petr Šidlof, Ph.D. Bc. Petra Tisovská 22. května 2018 Studentská 2 461 17 Liberec 2 petra.tisovska@tul.cz
Numerické modelování interakce proudění a pružného tělesa v lidském vokálním traktu Vedoucí práce: doc. Ing. Petr Šidlof, Ph.D. Bc. Petra Tisovská 22. května 2018 Studentská 2 461 17 Liberec 2 petra.tisovska@tul.cz
Markovské metody pro modelování pravděpodobnosti
 Markovské metody pro modelování pravděpodobnosti rizikových stavů 1 Markovský řetězec Budeme uvažovat náhodný proces s diskrétním časem (náhodnou posloupnost) X(t), t T {0, 1, 2,... } s konečnou množinou
Markovské metody pro modelování pravděpodobnosti rizikových stavů 1 Markovský řetězec Budeme uvažovat náhodný proces s diskrétním časem (náhodnou posloupnost) X(t), t T {0, 1, 2,... } s konečnou množinou
Dnešní látka: Literatura: Kapitoly 3 a 4 ze skript Karel Rektorys: Matematika 43, ČVUT, Praha, Text přednášky na webové stránce přednášejícího.
 Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Fakt. Každou soustavu n lineárních ODR řádů n i lze eliminací převést ekvivalentně na jednu lineární ODR
 DEN: ODR teoreticky: soustavy rovnic Soustava lineárních ODR 1 řádu s konstantními koeficienty je soustava ve tvaru y 1 = a 11 y 1 + a 12 y 2 + + a 1n y n + b 1 (x) y 2 = a 21 y 1 + a 22 y 2 + + a 2n y
DEN: ODR teoreticky: soustavy rovnic Soustava lineárních ODR 1 řádu s konstantními koeficienty je soustava ve tvaru y 1 = a 11 y 1 + a 12 y 2 + + a 1n y n + b 1 (x) y 2 = a 21 y 1 + a 22 y 2 + + a 2n y
Václav Uruba home.zcu.cz/~uruba ZČU FSt, KKE Ústav termomechaniky AV ČR, v.v.i., ČVUT v Praze, FS, UK MFF
 Václav Uruba uruba@fst.zcu.cz home.zcu.cz/~uruba ZČU FSt, KKE Ústav termomechaniky AV ČR, v.v.i., ČVUT v Praze, FS, UK MFF 13.10.2014 Mechanika tekutin 1/13 1 Mechanika tekutin - přednášky 1. Úvod, pojmy,
Václav Uruba uruba@fst.zcu.cz home.zcu.cz/~uruba ZČU FSt, KKE Ústav termomechaniky AV ČR, v.v.i., ČVUT v Praze, FS, UK MFF 13.10.2014 Mechanika tekutin 1/13 1 Mechanika tekutin - přednášky 1. Úvod, pojmy,
Řešení kontaktní úlohy v MKP s ohledem na efektivitu výpočtu
 Řešení kontaktní úlohy v MKP s ohledem na efektivitu výpočtu Jan Hynouš Abstrakt Tato práce se zabývá řešením kontaktní úlohy v MKP s ohledem na efektivitu výpočtu. Na její realizaci se spolupracovalo
Řešení kontaktní úlohy v MKP s ohledem na efektivitu výpočtu Jan Hynouš Abstrakt Tato práce se zabývá řešením kontaktní úlohy v MKP s ohledem na efektivitu výpočtu. Na její realizaci se spolupracovalo
které charakterizují danou fyzikální situaci. souvislostí). Může být formulován jako soustava rovnic a nerovnic.
 1. Přednáška Obsah: Úvod do tvorby matematických modelů jako okrajové úlohy pro diferenciální rovnici. Příklad 1D vedení tepla a lineární pružnost. Diferenciální, variační, energetická formulace úloh.
1. Přednáška Obsah: Úvod do tvorby matematických modelů jako okrajové úlohy pro diferenciální rovnici. Příklad 1D vedení tepla a lineární pružnost. Diferenciální, variační, energetická formulace úloh.
Globální matice konstrukce
 Globální matice konstrukce Z matic tuhosti a hmotnosti jednotlivých prvků lze sestavit globální matici tuhosti a globální matici hmotnosti konstrukce, které se využijí v řešení základní rovnice MKP: [m]{
Globální matice konstrukce Z matic tuhosti a hmotnosti jednotlivých prvků lze sestavit globální matici tuhosti a globální matici hmotnosti konstrukce, které se využijí v řešení základní rovnice MKP: [m]{
Modelovánía experimentální zjišťovánímechanických vlastností nelineárních materiálů
 Modelovánía experimentální zjišťovánímechanických vlastností nelineárních materiálů Biomechanika a lékařsképřístroje Projekt II LukášHorný Laboratoř biomechaniky člověka Ústavu mechaniky Fakulty strojní
Modelovánía experimentální zjišťovánímechanických vlastností nelineárních materiálů Biomechanika a lékařsképřístroje Projekt II LukášHorný Laboratoř biomechaniky člověka Ústavu mechaniky Fakulty strojní
OHYB (Napjatost) M A M + qc a + b + c ) M A = 2M qc a + b + c )
 3.3 Řešené příklady Příklad 1: Pro nosník na obrázku vyšetřete a zakreslete reakce, T (x) a M(x). Dále určete M max a proveďte dimenzování pro zadaný průřez. Dáno: a = 0.5 m, b = 0.3 m, c = 0.4 m, d =
3.3 Řešené příklady Příklad 1: Pro nosník na obrázku vyšetřete a zakreslete reakce, T (x) a M(x). Dále určete M max a proveďte dimenzování pro zadaný průřez. Dáno: a = 0.5 m, b = 0.3 m, c = 0.4 m, d =
Termomechanika 9. přednáška Doc. Dr. RNDr. Miroslav Holeček
 Termomechanika 9. přednáška Doc. Dr. RNDr. Miroslav Holeček Upozornění: Tato prezentace slouží výhradně pro výukové účely Fakulty strojní Západočeské univerzity v Plzni. Byla sestavena autorem s využitím
Termomechanika 9. přednáška Doc. Dr. RNDr. Miroslav Holeček Upozornění: Tato prezentace slouží výhradně pro výukové účely Fakulty strojní Západočeské univerzity v Plzni. Byla sestavena autorem s využitím
Literatura: Kapitoly 3, 4 a 2 d) ze skript Karel Rektorys: Matematika 43, ČVUT, Praha, Text přednášky na webové stránce přednášejícího.
 Předmět: MA4 Dnešní látka: Nehomogenní okrajové podmínky. Pokračování OÚ pro PDR (jen pro fajnšmekry). Jednoznačnost zobecněného řešení. Metoda sítí v 1D. Přibližné řešení okrajových úloh. Aproximace vlastních
Předmět: MA4 Dnešní látka: Nehomogenní okrajové podmínky. Pokračování OÚ pro PDR (jen pro fajnšmekry). Jednoznačnost zobecněného řešení. Metoda sítí v 1D. Přibližné řešení okrajových úloh. Aproximace vlastních
10. Elasto-plastická lomová mechanika
 (J-integrál) Únava a lomová mechanika J-integrál je zobecněním hnací síly trhliny a umožňuje použití i v případech plastické deformace většího rozsahu: d J = A U da ( ) A práce vnějších sil působících
(J-integrál) Únava a lomová mechanika J-integrál je zobecněním hnací síly trhliny a umožňuje použití i v případech plastické deformace většího rozsahu: d J = A U da ( ) A práce vnějších sil působících
Reologické modely technických materiálů při prostém tahu a tlaku
 . lekce Reologické modely technických materiálů při prostém tahu a tlaku Obsah. Základní pojmy Vnitřní síly napětí. Základní reologické modely technických materiálů 3.3 Elementární reologické modely creepu
. lekce Reologické modely technických materiálů při prostém tahu a tlaku Obsah. Základní pojmy Vnitřní síly napětí. Základní reologické modely technických materiálů 3.3 Elementární reologické modely creepu
Definice 1.1. Nechť je M množina. Funkci ρ : M M R nazveme metrikou, jestliže má následující vlastnosti:
 Přednáška 1. Definice 1.1. Nechť je množina. Funkci ρ : R nazveme metrikou, jestliže má následující vlastnosti: (1 pro každé x je ρ(x, x = 0; (2 pro každé x, y, x y, je ρ(x, y = ρ(y, x > 0; (3 pro každé
Přednáška 1. Definice 1.1. Nechť je množina. Funkci ρ : R nazveme metrikou, jestliže má následující vlastnosti: (1 pro každé x je ρ(x, x = 0; (2 pro každé x, y, x y, je ρ(x, y = ρ(y, x > 0; (3 pro každé
Příloha č. 1. amplitudová charakteristika filtru fázová charakteristika filtru / frekvence / Hz. 1. Určení proudové hustoty
 Příloha č. 1 Při hodnocení expozice nízkofrekvenčnímu elektromagnetickému poli (0 Hz 10 MHz) je určující veličinou modifikovaná proudová hustota J mod indukovaná v tělesné tkáni. Jak je uvedeno v nařízení
Příloha č. 1 Při hodnocení expozice nízkofrekvenčnímu elektromagnetickému poli (0 Hz 10 MHz) je určující veličinou modifikovaná proudová hustota J mod indukovaná v tělesné tkáni. Jak je uvedeno v nařízení
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY
 VYSOKÉ UČENÍ TEHNIKÉ V BRNĚ BRNO UNIVERSITY OF TEHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ FAULTY OF MEHANIAL ENGINEERING ÚSTAV MEHANIKY TĚLES, MEHATRONIKY A BIOMEHANIKY INSTITUTE OF SOLID MEHANIS, MEHATRONIS
VYSOKÉ UČENÍ TEHNIKÉ V BRNĚ BRNO UNIVERSITY OF TEHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ FAULTY OF MEHANIAL ENGINEERING ÚSTAV MEHANIKY TĚLES, MEHATRONIKY A BIOMEHANIKY INSTITUTE OF SOLID MEHANIS, MEHATRONIS
Kritéria porušení laminy
 Kap. 4 Kritéria porušení laminy Inormační a vzdělávací centrum kompozitních technologií & Ústav mechaniky, biomechaniky a mechatroniky S ČVU v Praze.. 007-6.. 007 Úvod omové procesy vyvolané v jednosměrovém
Kap. 4 Kritéria porušení laminy Inormační a vzdělávací centrum kompozitních technologií & Ústav mechaniky, biomechaniky a mechatroniky S ČVU v Praze.. 007-6.. 007 Úvod omové procesy vyvolané v jednosměrovém
geologie a užité geofyziky Karlova Univerzita, Praha v geomechanice I
 1 Ústav hydrogeologie, inženýrské geologie a užité geofyziky Karlova Univerzita, Praha Přednášky pro předmět Matematické modelování v geomechanice I 3. část numerické metody David Mašín 2 Obsah Výstavba
1 Ústav hydrogeologie, inženýrské geologie a užité geofyziky Karlova Univerzita, Praha Přednášky pro předmět Matematické modelování v geomechanice I 3. část numerické metody David Mašín 2 Obsah Výstavba
Vzpěr jednoduchého rámu, diferenciální operátory. Lenka Dohnalová
 1 / 40 Vzpěr jednoduchého rámu, diferenciální operátory Lenka Dohnalová ČVUT, fakulta stavební, ZS 2015/2016 katedra stavební mechaniky a katedra matematiky, Odborné vedení: doc. Ing. Jan Zeman, Ph.D.,
1 / 40 Vzpěr jednoduchého rámu, diferenciální operátory Lenka Dohnalová ČVUT, fakulta stavební, ZS 2015/2016 katedra stavební mechaniky a katedra matematiky, Odborné vedení: doc. Ing. Jan Zeman, Ph.D.,
Interpolace, ortogonální polynomy, Gaussova kvadratura
 Interpolace, ortogonální polynomy, Gaussova kvadratura Petr Tichý 20. listopadu 2013 1 Úloha Lagrangeovy interpolace Dán omezený uzavřený interval [a, b] a v něm n + 1 různých bodů x 0, x 1,..., x n. Nechť
Interpolace, ortogonální polynomy, Gaussova kvadratura Petr Tichý 20. listopadu 2013 1 Úloha Lagrangeovy interpolace Dán omezený uzavřený interval [a, b] a v něm n + 1 různých bodů x 0, x 1,..., x n. Nechť
b) Maximální velikost zrychlení automobilu, nemají-li kola prokluzovat, je a = f g. Automobil se bude rozjíždět po dobu t = v 0 fg = mfgv 0
 Řešení úloh. kola 58. ročníku fyzikální olympiády. Kategorie A Autoři úloh: J. Thomas, 5, 6, 7), J. Jírů 2,, 4).a) Napíšeme si pohybové rovnice, ze kterých vyjádříme dobu jízdy a zrychlení automobilu A:
Řešení úloh. kola 58. ročníku fyzikální olympiády. Kategorie A Autoři úloh: J. Thomas, 5, 6, 7), J. Jírů 2,, 4).a) Napíšeme si pohybové rovnice, ze kterých vyjádříme dobu jízdy a zrychlení automobilu A:
ROVINNÁ ÚLOHA. Všechny veličiny (geometrie, materiálové vlastnosti, zatížení) jsou nezávislé na jedné prostorové proměnné
 ROVINNÁ ÚLOHA Rovinná úloha Všechny veličiny (geometrie, materiálové vlastnosti, zatížení) jsou nezávislé na jedné prostorové proměnné Rovinná napjatost Rovinná deformace Rotačně symetrická úloha Rovinná
ROVINNÁ ÚLOHA Rovinná úloha Všechny veličiny (geometrie, materiálové vlastnosti, zatížení) jsou nezávislé na jedné prostorové proměnné Rovinná napjatost Rovinná deformace Rotačně symetrická úloha Rovinná
ÚVOD DO TERMODYNAMIKY
 ÚVOD DO TERMODYNAMIKY Termodynamika: Nauka o obecných zákonitostech, kterými se se řídí transformace CELKOVÉ energie makroskopických systémů v její různé formy. Je založena na výsledcích experimentílních
ÚVOD DO TERMODYNAMIKY Termodynamika: Nauka o obecných zákonitostech, kterými se se řídí transformace CELKOVÉ energie makroskopických systémů v její různé formy. Je založena na výsledcích experimentílních
Termomechanika 11. přednáška Doc. Dr. RNDr. Miroslav Holeček
 Termomechanika 11. přednáška Doc. Dr. RNDr. Miroslav Holeček Upozornění: Tato prezentace slouží výhradně pro výukové účely Fakulty strojní Západočeské univerzity v Plzni. Byla sestavena autorem s využitím
Termomechanika 11. přednáška Doc. Dr. RNDr. Miroslav Holeček Upozornění: Tato prezentace slouží výhradně pro výukové účely Fakulty strojní Západočeské univerzity v Plzni. Byla sestavena autorem s využitím
1 Přesnost metody konečných prvků
 1 PŘESNOST METODY KONEČNÝCH PRVKŮ 1 1 Přesnost metody konečných prvků Metoda konečných prvků je založena na diskretizaci původní spojité konstrukce soustavou prvků (nebo obecněji na diskretizaci slabé
1 PŘESNOST METODY KONEČNÝCH PRVKŮ 1 1 Přesnost metody konečných prvků Metoda konečných prvků je založena na diskretizaci původní spojité konstrukce soustavou prvků (nebo obecněji na diskretizaci slabé
Katedra geotechniky a podzemního stavitelství
 Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Modelování zatížení tunelů (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Modelování zatížení tunelů (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
Biomechanika II. Modely napjatosti a deformace cév, vliv zbytkových napětí a aktivní vlastnosti. Lukáš Horný
 Biomechanika II Modely napjatosti a deformace cév, vliv zbytkových napětí a aktivní vlastnosti ČVUT v Praze, fakulta strojní, ústav mechaniky, biomechaniky a mechatroniky Obor: Biomechanika a lékařské
Biomechanika II Modely napjatosti a deformace cév, vliv zbytkových napětí a aktivní vlastnosti ČVUT v Praze, fakulta strojní, ústav mechaniky, biomechaniky a mechatroniky Obor: Biomechanika a lékařské
