POZEMNÍ KOMUNIKACE I.

Transkript

1 VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ PETR HOLCNER POZEMNÍ KOMUNIKACE I. MODUL BM0-M0 SMROVÉ EŠENÍ POZEMNÍCH KOMUNIKACÍ STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA

2 Pozemní komunikace I. Modul BM0-M0 Petr Holcner, Brno (40) -

3 Obsah OBSAH Úvod...5. Cíle...5. Požadované znalosti Doba potebná ke studiu Klíová slova...5 Polomry smrových oblouk...7. Minimální polomr otáení geometrie vozidla...7. Minimální polomr smrového oblouku úvod Minimální polomr smrového oblouku bezpenost proti peklopení vozidla Minimální polomr smrového oblouku bezpenost proti usmyknutí vozidla....5 Minimální polomr smrového oblouku bezpenost podle SN Bezpenost smrových polomr navržených podle normy Pechodnice a její výpoet Kivost a její prbh ve smrovém oblouku Klotoidická pechodnice Vytyovací hodnoty klotoidy Výpoet hlavních vytyovacích hodnot klotoidy Výpoet podrobných bod klotoidy Délka pechodnice Pechodnice ve smrových obloucích Výpoet symetrických oblouk Volba parametru a úhlová podmínka pro symetrický oblouk Postup výpotu Tabulky I. geometrická podobnost klotoid Výpoet a vytyení nesymetrických oblouk Volba parametru a úhlová podmínka pro nesymetrický oblouk Postup výpotu Složené oblouky Postup vytyení pechodnicového oblouku Závr Shrnutí Studijní prameny Seznam použité literatury Seznam doplkové studijní literatury Odkazy na další studijní zdroje a prameny (40) -

4

5 Úvod Úvod Návrh trasy pozemních komunikací v sob zahrnuje smrovou složku a výškovou složku. Smrové ešení vidíme názorn v situaních výkresech, do podélných profil se dostává pouze v podob schématického popisu. Naopak výškové ešení je názorn zobrazené v podélných profilech, do situace se dostane nanejvýš v podob popisu u sklonovník, pokud jsou vbec vykresleny. Pro smrové ešení a pro výškové ešení se navrhuje samostatn podle požadavk normy, ale je nutné si uvdomovat, že trasa pozemní komunikace je v sob zahrnuje smrovou i výškovou složku ešení. Tento text se ale soustedí pouze na smrové ešení oddlen od výškového ešení. Výškové ešení, vzájemné vztahy výškového a smrového ešení, zásady trasování jsou vysvtlené v modulu BM0-M0.. Cíle Cílem je zvládnout smrové ešení pozemních komunikací. Draz je kladen na pochopení, z eho jsou odvozeny návrhové parametry. Na to navazuje struný výet nejdležitjších parametr požadovaných normou SN Projektování silnic a dálnic. Absolvent bude schopný poítat rznými metodami jednotlivé prvky smrového ešení a z nich složené motivy. Bude vdt, jaké jsou možnosti a omezení návrhu smrového ešení. Spoítané oblouky bude umt vytyit.. Požadované znalosti Následující text pedpokládá základní znalosti matematiky a fyziky. Pedpokládá se absolvovaný úvod do pozemních komunikací na úrovni BO0 Konstrukce a dopravní stavby, základní znalost geodézie, znalost ortogonálního a polárního vytyování bod, znalost hlavních vytyovacích prvk smrového oblouku..3 Doba potebná ke studiu Asi 8 hodin..4 Klíová slova Osa komunikace, smrový oblouk, kružnicový oblouk, pechodnice, klotoida, kivost, polomr, parametr klotoidy, návrhové prvky, bezpenost, píný sklon. - 5 (40) -

6

7 Polomry smrových oblouk Polomry smrových oblouk Je žádoucí navrhovat takové smrové ešení, které bude respektovat reálné možnosti prjezdu vozidla smrovým obloukem. Opan eeno, není vhodné, aby se po vozovce pohybovala vozidla, která nerespektují nebo nemohou respektovat osu (smrové ešení) komunikace. V píném ezu má dopravní proud (a tedy každé vozidlo) vymezený prostor, který se nazývá jízdní pruh, a za normálních okolností by se vozidlo mlo pohybovat výhradn v tomto prostoru. To je mimo jiné pedepsáno v Zákon o provozu na pozemních komunikacích. 364/000 Sb. v Smr a zpsob jízdy: () Na pozemní komunikaci se jezdí vpravo, a pokud tomu nebrání zvláštní okolnosti, pi pravém okraji vozovky, pokud není stanoveno jinak. Návrh smrového ešení je tedy za rzných okolností podízen rzným dále uvedeným požadavkm.. Minimální polomr otáení geometrie vozidla Za velmi nízkých rychlostí, nap. pi parkování nebo pi pojíždní mimo veejné komunikace je rozhodující minimální polomr otáení vozidla. Absolutní minimum použitelného polomru (za pedpokladu prjezdu obloukem najednou bez vracení) je dáno vlastnostmi vozidla. V technické dokumentaci lze vtšinou najít vnjší obrysový prmr otáení. Pro vozidla stejné kategorie jsou si tyto hodnoty blízké (nap. Škoda Fabia 0,48, Škoda Octavia 0,8, Ford Focus 0,9). Tomu odpovídá polomr otáení na vnitní hran asi 3,4 m, v ose asi 4,4 m. Velikost tohoto minimálního polomru závisí pedevším na rozvoru náprav a na rejdovém úhlu (maximální úhel natoení kol iditelné nápravy od polohy pro pímou jízdu). Pokud budeme uvažovat nejen o stop vozidla, ale o potebném prostoru pro pohyb vozidla, budou dležité i rozmry karosérie, pedevším pevisy karosérie. Minimální polomry otáení jsou samozejm velmi rozdílné pro rzné typy vozidel nejvtší budou pro nákladní soupravy a menší pro autobusy, tžká a lehká nákladní vozidla, dodávky a osobní automobily. Samozejm jsou geometrické vlastnosti vozidel odlišné pro rzné znaky a typy vozidel v každé kategorii. Minimální polomr otáení je tedy nutn vztažen k uvažovanému typu vozidla, které se bude po komunikaci pohybovat. Tento minimální polomr najde uplatnní pi návrhu neveejných obslužných komunikací jako nap.píjezd do garáže na vlastním pozemku a pi urování rozmr manipulaních ploch na parkovištích. Nejmenší hodnoty smrových polomr, které se vyskytují v normových pedpisech jsou v SN Projektování kižovatek na silniních komunikacích v l. 6.9.: Nejmenší polomr vnitní hrany jízdních pruh u kižovatek silnic a místních komunikací je m. Nejmenší doporuený polomr u komunikací obslužných je 9 m, pípustný je 6 m U existujících komunikací lze najít na kižovatkách i polomry obrubník v hodnotách podstatn nižších, které pak už mají charakter zaoblení a nikoliv vymezení jízdní dráhy (nap. u budovy fakulty kižovatka Veveí Resslova i - 7 (40) -

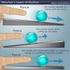
8 Pozemní komunikace I. Modul BM0-M0 Veveí Rybkova). Je nutné ale k takovému místu pistupovat s vdomím, že plocha, kterou potebuje vozidlo k pohybu bude výrazn odlišná od plochy takto vymezené obrubníkem. Jde tedy už o pípad, kdy návrh smrového ešení nerespektuje reálné možnosti vozidla. Pohyb po takto malých polomrech je možný jen pi extrémn malých rychlostech. Nap. metrová hodnota polomru podle SN odpovídá návrhové rychlosti 0 km/h pi píném sklonu %. Pokuste se odhadnout nebo zmit polomry na mstských kižovatkách a porovnejte je s polomry otáení osobních vozidel, nákladních vozidel a autobus. Umožují všechny kižovatky pohyb vozidel podle navržených polomr? Na kižovatkách je rozhodující obrubníková hrana a její polomr.. Minimální polomr smrového oblouku úvod Mimo výše uvedené pípady se samozejm pedpokládá, že dopravní proud a jednotlivá vozidla se budou pohybovat pibližn stálou rychlostí. Rozhodn je nežádoucí, aby vozidla musela náhle mnit rychlost kvli smrovým obloukm. Prakticky je tento pirozený požadavek zajištný tím, že na pozemních komunikacích (mimo kižovatek) je pro poteby projektování pedepsaná (v dlouhých souvislých tazích) návrhová rychlost. Ta platí pro smrov pímé ešení, ale i pro všechny smrové oblouky na trase. Polomr smrového oblouku pak odpovídá této návrhové rychlosti. Jak je vysvtleno dále, polomr závisí i na velikosti dostedného píného sklonu (klopení) komunikace. Názorným píkladem klopení z jiné oblasti je úprava cyklistické dráhy na velodromu s extrémním klopením, která umožuje prjezd velmi malých polomr vysokou rychlostí (závodní cyklisté jezdí vlastn rychlostí srovnatelnou s automobily kolem 60 km/h). Jednostopé vozidlo (závodní kolo) pkn demonstruje, co se pi prjezdu smrovým obloukem dje. Pi prjezdu obloukem psobí na cyklistu i jeho stroj odstedivá síla pímo úmrná druhé mocnin rychlosti a nepímo úmrná polomru oblouku. Jednostopé vozidlo se musí vklánt do oblouku tak, aby výslednice odstedivých sil a tíhové síly smovala do místa opory, tj. pedního a zadního kola bicyklu. Jinými slovy do stopy (reprezentované vpodstat dvma body), ve které se bicykl pohybuje. Jízdní kolo nemá žádnou jinou oporu, cyklista udržuje kolo pi jízd v souladu s výslednicí odstedivé a tíhové síly. Rovina proložená jízdní stopou a tžištm cyklisty (vetn jeho stroje) je rovinou, ve které musí ležet výslednice sil. Tedy naklonní kola nám (kteí se na cyklistu díváme zvenku) dává výstižnou informaci o výsledných silách. Cyklista by mohl samozejm zatáet i na vodorovném velodromu, ale bylo by nebezpeí (od jisté hraniní rychlosti by to byla jistota), že tecí a adhezní síly neudrží kola v požadované stop a po smyku cyklista havaruje. Smrové oblouky na velodromu jsou tedy klopené. Ideální pípad je ten, kdy povrch bude kolmý k výslednici sil. Pak nebude existovat v míst styku kola s dráhou žádná boní síla a cyklista nedostane smyk. Cyklistická dráha se tedy navrhuje zhruba ve sklonu, který je kolmý k bicyklu pi prjezdu pedpokládanou rychlostí. Je pravdou, že ne všichni cyklisté dosahují stejné rychlosti a pro- - 8 (40) -

9 Polomry smrových oblouk to není každý prjezd za ideálních podmínek (kolo kolmé k povrchu). Zvlášt patrné to je v pípadech, kdy se z rzných dvod (teba kvli taktice nebo už po závodu) pokouší cyklista projíždt obloukem velmi pomalu. Dost asto se stává, že uklouzne na velikém sklonu dol a havaruje. Zkušenosti z cyklistického velodromu nám pomohou lépe pochopit požadavky na klopení pozemních komunikací. Pro danou návrhovou rychlost budeme stanovovat polomr smrového oblouku spolu s dostedným píným sklonem ve smrovém oblouku. Návrhová rychlost v n, minimální polomr smrového oblouku R min a píný sklon p% jsou spolu vzájemn provázány. Na silnicích mají obdobné vlastnosti jako kola motocykly. Automobily se odlišují pedevším tím, že se opírají o plochu (urenou tymi koly), nikoliv o pímku, jako jednostopá vozidla. Znamená to, že automobily se nemohou vklánt do zatáky. Na druhé stran jsou stabilnjší s ohledem na peklopení, ale tato stabilita je rovnž limitována. K usmyknutí ale mže dojít zrovna tak, jako u cyklisty, který jede pomalu po naklopené dráze nebo rychle po nenaklopené dráze. Na rozdíl od cyklistického velodromu na silnicích musíme zaruit i bezpenost vozidlm, která se pohybují pomalu nebo stojí, dostedný sklon tedy je na silnicích podstatn menší než na závodní dráze pro cyklisty, i když se auta pohybují rychleji. Je nutné na pozemních silnicích zajistit bezpenost proti peklopení a bezpenost proti usmyknutí. Píný sklon ale musí být bezpený i pro vozidla pohybující se malou rychlostí za nevhodných adhezních podmínek (pi náledí) z tohoto plyne omezení maximálního dostedného sklonu a pokud nemžeme navrhovat píný libovoln velký, existuje pro návrhovou rychlost i absolutní limit smrového polomru. Pedstavte si, že jste vezeni nejdív po pímém úseku a následn smrovým obloukem, který má nulové klopení. Jednou pokus absolvujete s automobilem a jednou na motocyklu (jde o jeden z mála vyrobených kapotovaných motocykl)a nevidíte pitom ven. Uvnit v kabin auta máte zavšené závaží na niti kyvadlo, stejné kyvadlo máte zavšené v motocyklu. Poznáte uvnit v aut a uvnit v motocyklu podle náklonu kyvadlo, že projíždíte smrovým obloukem? Je možné vymyslet takové ešení, že v žádném pípad nepoznáte podle kyvadla prjezd smrovým obloukem? Mají tyto úvahy njaký význam pro návrh polomr smrových oblouk?.3 Minimální polomr smrového oblouku bezpenost proti peklopení vozidla Pedpokládáme vozidlo projíždjící smrovým obloukem o neznámém polomru R. Smrový oblouk je klopený smrem ke stedu oblouku (dostedný sklon). Na vozidlo, které se pohybuje ve smrovém oblouk psobí tyto síly: tíha vozidla Q m g v Q v C m odstedivá síla R g R Na obrázku je sklon vyjádený jako úhel mený od vodorovné roviny. Tíhová síla G je orientována svisle (ve shod s gravitací), odstedivá síla je oriento- - 9 (40) -

10 Pozemní komunikace I. Modul BM0-M0-0 (40) - vaná vodorovn. Pro další úvahy rozložíme síly psobící na vozidlo (v tžišti vozidla) do smru rovnobžného s povrchem vozovky a do smru kolmého k povrchu vozovky. Vozidlo je popsáno svou šíkou (rozchod b) a výškou tžišt h. Minimální polomr bude pi pevn daných rozmrech vozidla závislý na návrhové rychlosti a píném sklonu vozovky. Bezpenost vozidla proti pevržení vozidla se posuzuje s použitím moment síly. Kritický stav nastává ve chvíli, kdy souet všech moment sil vzhledem k bodu otáení (na obrázku je oznaen O) je nulový. Momentová rovnice má v následujících tech ádcích tento tvar: ( ) ( ) ( ) ( ) + + h b b h R g v h b Q b h R g v Q h Q b Q b C h C sin cos sin cos sin cos sin cos 0 sin cos sin cos V prvním ádku je momentová rovnice vyjádena s pomocí odstedivé a tíhové síly. Do druhého ádku je odstedivá síla vyjádena pomocí tíhové síly a gravitaního zrychlení: R v g Q R v m C Po úprav ve tetím ádku ve vztahu nefiguruje ani hmotnost ani tíha. Polomr není závislý na hmotnosti vozidla, ale pouze na rychlosti a na geometrii vozidla, jak je vidt dále: + h b b h g v R sin cos sin cos

11 Polomry smrových oblouk Další úpravy smují ke zjednodušení vztahu. Vynásobíme itatele i jmenovatele cos. Zatím jsme uvažovali o rovnovážném vztahu a pro nj zjišovali nutný polomr. Vtší polomry nám budou vyhovovat, proto nahradíme rovnost nerovností. v R g ( h b tg ) ( b + h tg ) v g p% h b 00 p% b + h 00 Tangentu úhlu jsme nahradili píným sklonem, který se bžn používá pro popis píného sklonu. Dosazením do šíky a výšky tžišt zkoumaného vozidla za b a h najdeme minimální polomr, zaruující bezpenost vozidla proti pevržení pi dané rychlosti a píném sklonu vozovky. Dosate rozmry a odhadnutou výšku tžišt pro osobní automobil a pro špatn naložený nákladní automobil (tžký náklad ve velké výšce - vysoká poloha tžišt) a zjistte pro tato vozidla polomr bezpený proti peklopení pi píných sklonech 0 %,,5% (základní píný sklon) a 6%. Porovnejte dále s polomry bezpenými proti usmyknutí..4 Minimální polomr smrového oblouku bezpenost proti usmyknutí vozidla Opt jako v pedchozím pípadu pedpokládáme prjezd smrovým obloukem pi daném dostedném píném sklonu. Hledáme polomr, pi kterém nastane rovnováha sil psobících smrem ven a smrem do oblouku. Uvažujeme opt s odstedivou silou C a tíhovou silou Q, jak jsou definovány výše. Bezpenost vozidla proti usmyknutí se posuzuje soutem sil rovnobžných s povrchem vozovky. Kritický stav nastává ve chvíli, kdy je souet sil psobících ve smru ven z oblouku a ve smru opaném nulový. Smrem z oblouku psobí složka odstedivé síly rovnobžná s povrchem. Proti usmyknutí psobí pedevším tecí síla (ta je úmrná silám psobícím kolmo k povrchu a koeficientu tení f). V pípad nenulového dostedného píného sklonu pispívá ke tení i složka odstedivé síly kolmá k povrchu a složka tíhové síly rovnobžná s povrchem. Rovnice silové rovnováhy vypadá takto: ( Q cos + C sin ) f C cos Q sin Rovnici upravíme vydlením cos a zmníme ji na nerovnici: ( Q + C tg ) f + Q tg C Q ( f + C tg ) C ( f tg ) Q v C po dosazení g R - (40) -

12 Pozemní komunikace I. Modul BM0-M0 Q ( f + tg ) ( f tg ) v R g Q g v R ( f tg ) ( f + tg ) zjistíme, že minimální polomr závisí na rychlosti, na úhlu (resp. na píném sklonu) a na koeficientu tení. Bezpenost proti usmyknutí není nijak závislá na geometrických charakteristikách vozidla nezávisí ani na šíce vozidla ani na výšce tžišt. Protože hodnota f*tg je relativn malá (asi do 0,05), v dalších úvahách ji zanedbáme a v itateli bude místo ( f tg ). Pak vypadá použitelný vzorec následovn (po dosazení pevodu jednotek u návrhové rychlosti protože návrhová rychlost se bžn udává v km/h a do vzorce potebujeme m/s): vn R g R 7 ( f + tg ) v n ( f ± 0,0 p% ) Minimální polomr je závislý na návrhové rychlosti v n a na píném sklonu p%. Záporné znaménko se použije v pípad, že sklon není dostedný, ale sm- uje ven z oblouku. Po dosazení reálných hodnot rozmr a reálných koeficient tení (uvažuje se pomrn nízký koeficient tení f pro špatné adhezní podmínky o hodnot pibližn 0,) se prokáže, že podmínka pro usmyknutí je písnjší. Potvrzuje to i bžná zkušenost, dostat vozidlo do smyku je snazší a bžnjší než pevrátit vozidlo. Spoítejte polomry bezpené proti usmyknutí pro koeficient tení f0,% pi píných sklonech 0 %,,5% (základní píný sklon) a 6%. Porovnejte s polomry bezpenými proti peklopení, které jste spoítali výše..5 Minimální polomr smrového oblouku bezpenost podle SN SN vychází ze vztahu pro bezpenost proti usmyknutí, kde je polomr oblouku pímo úmrný druhé mocnin rychlosti, ale nezávisí nijak na geometrických charakteristikách vozidla. Vztah je zjednodušen do následující po podoby: R min const. v p% n Pípadné zmny názoru na míru bezpenosti lze pak snadno zavést do normy zmnou velikosti koeficientu. V souasnosti se používají dva rzné koeficienty - const.0,3 pro rychlosti v n 80 km/h a const.0,36 pro rychlosti v n >80 km/h, viz SN 73 60, píloha C, str (40) -

13 Polomry smrových oblouk Pro projekní poteby jsou píslušné minimální polomry v norm tabelovány v podob, jak je dále uvedeno. Porovnejte díve spoítané polomry bezpené proti peklopení a proti usmyknutí s normovými hodnotami..6 Bezpenost smrových polomr navržených podle normy Nutno dodat, že koeficient tení nabývá hodnot ve velikém rozsahu a pro extrémní hodnoty není zajištno, že k usmyknutí nedojde. V takových pípadech platí ustanovení silniních pedpis o pizpsobení jízdy podmínkám. Naopak za dobrých podmínek dokážou auta projíždt smrovým obloukem vtší rychlostí, než je uvažovaná rychlost návrhová nebo smrodatná. Pojem bezpenosti tak, jak ho používá norma, nelze brát jako absolutní bezpenost, ale statisticky jako pijatelnou míru bezpenosti, ne které se shodli normotvrci a spolenost a která je podložena empiricky. Další nutným upozornním je, že takto navržené polomry nezaruují automaticky dostatené bezpené rozhledové vzdálenosti ve smrovém oblouku v šíce silniní koruny. V tabulce je upozornní, že polomry vpravo od perušované áry je teba rozhledové vzdálenosti ovit, pípadn zaruit úpravami v blízkosti komunikace. - 3 (40) -

14 Pozemní komunikace I. Modul BM0-M0 Další v norm uvedené upozornní se týká nutnosti provit výsledný sklon (pro polomry vpravo od plné áry). Norma totiž na jiném míst omezuje velikost výsledného sklonu a jeho pekroení hrozí pi soubhu velkého píného s velkým podélným sklonem. Naopak norma umožuje pro velké polomry smrových oblouk nepoužít dostedný sklon. To mže být v nkterých pípadech výhodné a používá se dost asto na dálnicích, kde se takto velké polomry vyskytují. Lze se takto vyhnout nutnosti oklápní (zmny píného sklonu) mezi protismrnými oblouky (je to výhodné pro odvodnní komunikace, protože na ní pak nejsou místa s nulovým píným sklonem). Na dálnicích lze s nedostedným píným sklonem odvodovat povrch vozovky k píkopm, nemusí se budovat odvodnní u stedového pásu. Tyto úpravy jsou ale možné pouze pro velké polomry viz pravý sloupec tabulky. Spoítejte pro normové polomry a píné sklony rychlost bezpenou proti usmyknutí pro koeficient tení f0,05 (náledí, namrzající déš) a porovnejte s návrhovou rychlostí. Pi jízd na náledí pak vhodn aplikujte bezpenou rychlost. - 4 (40) -

15 Pechodnice a její výpoet 3 Pechodnice a její výpoet Doposud jsme se zabývali polomrem smrového oblouku s jakýmsi automatickým pedpokladem, že oblouk znamená kružnici. Je to pravda, ale ne úplná. Podstatnou ástí (tém) každého oblouku je pechodnice. SN ist kružnicový oblouk pipouští, ale jen v pípad, že odsun oskulaní kružnice použité pechodnice (bude vysvtleno dále) je menší, než 0,5 m. Rozhodn ale takové smrové ešení norma nedoporuuje. Pechodnice je pro poteby smrových oblouk kivka, která plynule mní svou kivost a v míst napojení na jiné smrové prvky (kružnice nebo pímky) má kivost stejnou jako napojované prvky. Nejastji se používá pechodnice zvaná klotoida, která je popsána níže. Krom klotoidy se jako pechodnice mohou používat následující kivky: lemniskáta kubická parabola (používá se asto v železniním stavitelství kvadratická parabola (je použitelná pro vytyení oblouku pouhým pásmem nebo primitivním mítkem v podob provazu, není to však oblouk normový a pechodnice nemá v míst dotyku nulovou kivost parabola tvrtého stupn sinusoida (nulová kivost je v inflexním bod sinusoidy Schrammova kivka Odhadnte, jaký je prbh kivosti tzv. volantové kivky, což je trajektorie vykreslená pi reálném prjezdu vozidla obloukem. Navrhnte vhodný model volantové kivky a porovnejte ho s klotoidickým obloukem, který je popsán v dalším textu. 3. Kivost a její prbh ve smrovém oblouku Kivost je definovaná jako inverzní hodnota k polomru. ρ R Pro kružnici má tedy kivost konstantní hodnotu (polomr je konstantní) po celé délce kružnice. Na pímce má kivost nulovou hodnotu ρ 0 platí tedy, že: R protože R ρ Graf kivosti smrového motivu tena kružnice tena, který je uvedený v následujícím obrázku, dokazuje, že tento motiv je nevýhodný pro jízdu vozidla. - 5 (40) -

16 Pozemní komunikace I. Modul BM0-M0 V bod dotyku vzniká tzv. píný ráz, za pedpokladu, že vozidlo je pevn vedeno (proto vzniká píný ráz u kolejových vozidel, pokud je oblouk bez pechodnice nebo je špatn provedený). Jako píný ráz je vnímána neplynulá, skoková zmna zrychlení. Graf kivosti je totožný s grafem dostedivého zrychlení. Silniní vozidla nejsou pevn vedená, píný ráz u nich nevzniká, ale je to za tu cenu, že se mohou odchylovat od dráhy urené vytyenou naprojektovanou kivkou. Pokud by vozidlo mlo dodržet trajektorii tena kružnice tena, musel by idi pi konstantní nenulové rychlosti nastavit polomr dráhy na požadovanou kružnici (otoit volantem do konené polohy) za nulový as v míst skokové zmny kivosti. To není možné. Jinou možností je zmnit v bod dotyku rychlost na nulovou, nastavit polomr a pokraovat v jízd. To zase není moc praktické, rozumné a užitené. Bžný zpsob ešení tohoto rozporu je odchýlit se trajektorií od vytyené dráhy. Pi malých odchylkách to neznamená nic nebezpeného, pi velikých (v závislosti na polomru, rychlosti, rychlosti zmny kivosti, šíce jízdního pruhu) to mže vést ke kolizi s vozidly v jiném pruhu nebo k vyjetí mimo vozovku). Zásadní zpsob, jak se vypoádat s tímto problémem je použít oblouk s pechodnicí. Pokuste se s libovolným vozidlem nakreslit volantovou kivku ve tvaru pímka, kružnice, pímka a vysvtlete, pro není toto ešení vhodné pro bžný provoz. - 6 (40) -

17 Pechodnice a její výpoet 3. Klotoidická pechodnice Použití pechodnice umožní prjezd kolejového vozidla obloukem bez píného rázu a pro silniní vozidla umožní návrh smrového ešení blízkého realistické trajektorii. V silniním stavitelství se bžn používá jako pechodnice klotoida. Platí pro ni to, co je uvedeno v obecné definici pechodnice, ale navíc je jednoznan upesnná závislost kivosti na délce klotoidy (pesnji na vzdálenosti od za- átku klotoidy, tj. od bodu s nulovou kivostí. Má lineární závislost kivosti na délce (na vzdálenosti od zaátku klotoidy). Zde je uvedený graf kivosti oblouku kružnicového s klotoidickými pechodnicemi (ervená tenká ára) v porovnání s prbhem kivosti ist kružnicového oblouku (tlustá fialová ára). Svtle zelená tenká ára imituje volantovou kivku, což je název pro skutenou pirozenou trajektorii, která není matematicky definovaná a každý idi ji pi každém prjezdu vykreslí po svém. Proti ist kružnicovému oblouku má oblouk s klotoidickými pechodnicemi píznivjší prbh a trajektorie se s ním mže shodovat s dostatenou pesností. Slovní definice klotoidy je následující: Klotoida je kivka, která mní svou kivost v lineární závislosti na délce. Za délku se považuje vzdálenost od zaátku klotoidy ke zkoumanému bodu a kivostí je mínna píslušná kivost klotoidy ve zkoumaném bod. Zaátek klotoidy má nulovou kivost. Defininí popis (lineární závislost kivosti na délce) lze zapsat vztahem: ρ l konst, resp. l konst, resp. l R const. R konst - 7 (40) -

18 Pozemní komunikace I. Modul BM0-M0 Ten poslední výraz je používaný jako základní rovnice klotoidy. Klotoida je tedy definovaná základní rovnicí klotoidy: l R const. ρ Tato rovnice vyjaduje skutenost, že kivost klotoidy v bod vzdáleném od zaátku klotoidy o l je pímo úmrná práv délce l (tedy kivost je lineárn závislá na délce). Jako konstanta se volí druhá mocnina parametru klotoidy A. Základní rovnice klotoidy se nejastji píše ve tvaru: A l R Tímto zpsobem je pro každou hodnotu parametru A definována jednoznan kivka, která je nekonen dlouhá a má tvar spirály, která se zavíjí sama do sebe s rostoucí kivostí (klesajícím polomrem oskulaní kružnice) pro vzdálenjší body). Klotoidy s rzným parametrem A jsou si geometricky podobné a liší se svými rozmry v pomru parametr. Parametr klotoidy A udává velikost klotoidy. V nekonené délce l se klotoida blíží bodu o souadnicích: x y A π V tomto vztahu je názorn vidt, že pro rostoucí parametr se zvtšuje velikost klotoidy v pímé úme k velikosti parametru A. R Zde uvedený obrázek je pevzatý z kde si mžete vyzkoušet libovolné výpoty klotoid (ve skutenosti ale neumíme poítat prbh klotoidy nekonen dlouhé, pestože je definovaná, v tomto pípad je omezení spoitatelné délky úhlem zhruba 34 rad, což je asi 60 grad). Zpsobem, který je zde použitý, mžeme tedy vypoítat klotoidu, která se do sebe zavine 5,4 krát. Je jasné, že tak dlouhou klotoidu pro praktické poteby nepotebujeme, bžn vystaíme s klotoidami v úhlovém rozsahu až 50 grad. V následujícím ob- - 8 (40) -

19 Pechodnice a její výpoet rázku je ve stejném prostedí spoítaná tatáž klotoida o stejném parametru ale s desetkrát menší délkou s prakticky použitelným koncovým úhlem 0,37 grad. Ješt jednou zdrazuji, jde o stejnou klotoidu, pouze z ní použijeme kratší ást. Nutno dodat, že nejastjší koncové úhly klotoid jsou ješt menší - do 0 grad. Na tomto píkladu vidíme, že klotoida je jednoznan definovaná svým parametrem A jako nekonen dlouhá kivka s lineárním nárstem kivosti. Parametr A uruje rychlost nárstu kivosti a tím velikost klotoidy. Z takto definované klotoidy o nekonené délce si vybíráme vhodnou použitelnou ást. Nejastji potebujeme tu ást, která má na zaátku nulovou kivost a na konci definovaný polomr kivosti. V základní rovnici klotoidy, která platí pro libovolný bod na délce klotoidy a tedy i pro koncový bod klotoidy, A l R vidíme, že pro jednoznaný popis klotoidy (ve smyslu klotoida o požadovaném parametru A a požadované délce nebo koncovém polomru) potebujeme dva parametry. Napíklad parametr A a délku l. Jak uvidíme dále, je možné zadat klotoidu i jinými zpsoby. V dalším obrázku grafu kivosti uvažujeme o nulové kivosti na zaátku oblouku a o kivosti /R uprosted oblouku. Vidíme, že mžeme mnit rychlost zmny kivosti, tedy navrhovat pro daný koncový polomr klotoidy s rzným parametrem A. Velmi rychlá zmna znamená malou délku klotoidy (malý parametr A) a limitem je ist kružnicový oblouk, kde délka klotoidy l 0. Nejdelší možná klotoida je omezená délkou kružnicové ásti oblouku, která zbývá, o 0. Jak uvidíme dále, z geometrických vlastností klotoidy plyne, že tuto podmínku mžeme pehledn zformulovat jako úhlovou podmínku. Všimnte si rovnž dležité skutenosti, že klotoidy zvtšují celkovou délku oblouku. Pibližn platí, že polovina délky klotoidy je na úkor pvodního ist kružnicového oblouku a polovina prodlužuje celkovou délku oblouku. Strmjší klotoidy (menší parametr A) prodlužují oblouk mén, pozvolnjší klotoidy (vtší parametr A) znamenají delší oblouk. - 9 (40) -

20 Pozemní komunikace I. Modul BM0-M0 Na adrese si vyzkoušejte vliv parametru klotoidy a délky klotoidy na koncový polomr a na koncový úhel. Na Ústavu pozemních komunikací nebo v knihovn FAST si vypjete klotoidické tabulky (Veselý, Kašpárek: Klotoida) a rovnž si ovte praktický vztah koncového úhlu, délky klotoidy, koncového polomru a parametru. 3.3 Vytyovací hodnoty klotoidy Zatím známe ke klotoid ti charakteristiky parametr A, délku klotoidy l a R polomr oskulaní kružnice v koncovém bod klotoidy. Tyto hodnoty jsou provázány vztahem, který jsme nazvali základní rovnice klotoidy. Z ní vidíme, že k jednoznanému urení potebn ásti klotoidy staí dva ze tí výše uvedených údaj, tetí dopoítáme. A l R Význam parametru byl vysvtlený již výše. Význam délky je snad zejmý, pro upesnní lze uvést, že se jedná o délku menou po klotoidické kivce! od za- átku klotoidy až do koncového bodu, pro který provádíme výpoet. Polomr R je polomr oskulaní kružnice této klotoidy v tomto bod. Základní rovnice platí pro libovolný zkoumaný bod klotoidy. Další základní charakteristikou klotoidy je koncový úhel klotoidy. Ten je definovaný jako úhel, který spolu svírají teny klotoidy v poátením a v koncovém bod, jak je vidt z obrázku. Dležitý je vztah koncového úhlu (jedná se úhel v obloukových jednotkách radiánech) k délce klotoidy a koncovému polomru: l τ R - 0 (40) -

21 Pechodnice a její výpoet Dozvídáme se, že úhel oblouku klotoidického je pi stejné délce oblouku poloviní, než u kružnicového oblouku. Užitenjší je pro nás pevrácená informace, že pro stejný úhel je klotoida dvakrát delší, než kružnice o stejném polomru jako je koncový polomr klotoidy. Hlavn tento vztah umožuje pevést zadané hodnoty na koncový úhel, se kterým pak pracuje výpoetní algoritmus. Doposud uvedené charakteristiky klotoidy umožují pímý výpoet (postup bude dále vysvtlen) celého souboru hlavních vytyovacích hodnot. Následující charakteristiky taky mohou jednoznan klotoidu definovat, ale neumožují pímý výpoet. Dalšími hlavními vytyovacími hodnotami tedy jsou (viz obrázek): x,y pravoúhlé souadnice koncového bodu x S poloha paty kolmice spuštné ze stedu oskulaní kružnice na hlavní tenu x M s t poloha prseíku koncové teny s hlavní tenou délka koncové teny R odsun oskulaní kružnice od hlavní teny z vzeptí, vrcholová vzdálenost, vzdálenost prseíku teen od vrcholu oblouku (tato hodnota má rozumný význam jen pro ist pechodnicový symetrický oblouk bez kružnicové ásti) - (40) -

22 Pozemní komunikace I. Modul BM0-M0 3.4 Výpoet hlavních vytyovacích hodnot klotoidy Podstatou výpotu a hlavním problémem je výpoet souadnic koncového bodu x, y. Vstupními hodnotami jsou libovolné dv ze ty základních charakteristik umožujících pímý výpoet (A, l, R, ). Pro výpoet podle níže uvedeného algoritmu potebujeme délku l a koncový úhel. V pípad poteby dopoítáme pomocí výše uvedených základních vztah. Souadnice koncového bodu mžeme s pedem zvolenou pesností (neexistuje pesný analytický vztah) jako souet rozumného potu len nekonen dlouhé matematické ady: x y n n l l ( ) ( ) n+ n+ τ n ( 4 n 3) ( n ) τ n! ( 4 n ) ( n )! Úhel τ se dosazuje v radiánech. ada velmi rychle konverguje, staí porovnávat absolutní velikost každého lenu ady se stanovenou pesností bžn 0,00m). Pro bžné výpoty staí asto první ti leny. Ze souadnic koncového bodu se další vytyovací hodnoty snadno dopoítají pomocí goniometrických vztah, které lze snadno odvodit z pravoúhlých trojúhelník ve výpoetním schématu. Dále jsou uvedené píslušné vztahy pro jejich výpoet z x a y. Vytyení je vztažené k zaátku klotoidy. x R sin τ x S x M ( ) x y cot g ( τ ) - (40) -

23 Pechodnice a její výpoet s t y sin( τ ) R y R ( cos( τ )) z y cos( τ ) Výše uvedené výpoty vtšinou nebudete sami opakovan provádt, ale jsou základem specializovaných výpoetních a grafických softwar, které se bžn používají pi projektování. Znalost tohoto postupu a jeho pochopení je však velmi dležité, protože dává pedstavu, jaký výpoet je možný a jaký ne. Nebudete pak od SW žádat nemožné, což mže skonit obtížn odhalitelnou chybou. Pomocí výše uvedeného postupu byly spoítány Klotoidické tabulky, které lze rovnž použít pi projektování. Jejich nevýhodou ve srovnání se SW je samozejm vtší pracnost a chybjící interaktivita vzhledem k výkresu, ale výhodou je jejich názornost a pehlednost. Odvote výše uvedené vztahy pro výpoet vytyovacích hodnot x S, x M, s t, R, z. Pepokládejte, že pravoúhlé souadnice x, y koncového bodu znáte. 3.5 Výpoet podrobných bod klotoidy Osa se krom hlavních bod vytyuje rovnž v podrobných bodech, ty jsou standardn popsány svým staniením (nejastji v celých násobcích 0 m). Vytyit podrobný bod na klotoid tedy znamená vytyit bod na klotoid, který je daný svou vzdáleností od zaátku klotoidy (po výpotu staniení). Pro vytyování se používá polární nebo ortogonální metoda. Za poátek sou- adnicové soustavy (polární nebo ortogonální) pro vytyení podrobných bod na klotoid se volí nejastji zaátek klotoidy a orientace je dána tenou klotoidy v zaátku. Výpoet vytyení podrobného bodu je pak výpoet totožný s výpotem souadnic x, y, jak je výše uvedeno pro hlavní vytyovací hodnoty. Jen je zapotebí stanovit vzdálenost vytyovaného bodu od zaátku klotoidy. Vtšinou se požaduje vytyení podrobných bod v celých násobcích dvaceti metr staniení, odtud tedy vyplyne požadavek na polohu vytyovaného bodu. Z ortogonálního vytyení (souadnice x,y) snadno pepoítáme vytyení polární, pokud je teba. Lze použít i starobylé vytyovací tabulky. Pro snadné vytyení podrobných bod je urena ást II. Klotoidických tabulek (autoi Veselý, Kašpárek). Ta obsahuje spoítané x-ové a y-ové souadnice pro ortogonální vytyení v konkrétních vzdálenostech l od zaátku klotoidy. Tyto výpoty jsou tam nachystány pro širokou škálu klotoid s okrouhlými parametry. Mezi délkami lze interpretovat. Mezi parametry rovnž, ale dvojí interpolace by už znamenala naprostou ztrátu výhody rychlého a snadného vytyení. Proto se parametry klotoid bžn volí (pokud je to možné) takové, které se vyskytují v tabulkách II. Pro polární vytyení lze potebné hodnoty pepoítat z ortogonálních nebo použít tabulku III. Ta je opt spoítaná pro jednotkovou klotoidu s parametrem 00, takže je zapotebí pepoítávat skutenou vytyovanou délku a poté inter- - 3 (40) -

24 Pozemní komunikace I. Modul BM0-M0 polovat mezi tabulkovými hodnotami, což je pracné a zdlouhavé. Tabulky III. jsou seazeny (na rozdíl od tab. I.) podle délky. Spoítejte nebo najdte v tabulkách pro klotoidu vhodn zvoleného rozmru aspo 6 podrobných bod a vyneste od hlavní (poátení) teny pravoúhlými souadnicemi na milimetrový papír nebo v prostedí grafického editoru. - 4 (40) -

25 Délka pechodnice 4 Délka pechodnice Požadavky na délku pechodnice jsou tyto: ) pechodnice má být tak dlouhá, aby pírstek odstedivého zrychlení za jednotku asu byl v mezích zaruujících pimený komfort jízdy Pírstek odstedivého zrychlení k by se ml držet v doporuených mezích, což je k0,3 až 0,6 m/s 3 (Chochol, Lehovec, Pošvá, Rondoš: Cesty a dianice, str. 87) a v k t R t Z toho: t v R k a protože pro konstantní rychlost na délce pechodnice platí: L v t, pro délku L lze psát: 3 v v L v t v R k k R Pokud chceme do vztahu rychlost vkládat v km/h místo v m/s (a silniái to tak vtšinou chtjí), ve vztahu se objeví pepotový koeficient: L 3 v 3 3,6 k R 3 v 47 k R Když za R dosadíme podle SN (pro v n 80 km/h) 0,3 vn Rmin p%, dostaneme závislost délky pechodnice L na návrhové rychlosti v n : 3 vn v p% L 0,3 vn 47 k 0,3 47 k p% Pak pro k0,3 a pro píný sklon v hodnot (napíklad) 3% vychází délka L asi 0,7 * v n, pro k0,3 a pro píný sklon v hodnot (napíklad) 6% vychází délka L asi,4 * v n. Pro parametr A klotoidy definované základní rovnicí závislost parametru na rychlosti: A R L lze pak psát v v v A R A 47 k R 47 k a potom 47 k Práv parametr klotoidy udává rychlost zmny kivosti, které odpovídá rychlost zmny dostedivého zrychlení. - 5 (40) -

26 Pozemní komunikace I. Modul BM0-M0 ) pechodnice má být tak dlouhá, aby as potebný na zmnu polomru trajektorie z pímky na hodnotu na konci pechodnice odpovídal možnostem vozidla a idie Doba potebná ke zmn kivosti trajektorie (natoení volantu do polohy odpovídající polomru oblouku) závisí na hodnot polomru, rychlosti vozidla, typu vozidla a jeho konstrukci (nákladní osobní, s nebo bez posilovae ízení, stabilita vozidla), na reakních asech idie aj. Tato doba se uvádí v hodnotách pibližn 3 až 5 sekund (Chochol, Lehovec, Pošvá, Rondoš: Cesty a dianice, str. 88). Potom délka pechodnice je: L 3 v až 5 v pro rychlost v m/s L 0,8 vn až, 4 v n pro návrhovou rychlost v km/h 3) pechodnice má být tak dlouhá, aby zmna píného sklonu provádná na délce pechodnice odpovídala požadavkm a délku a sklon vzestupnice (požadavky na vzestupnice a sestupnice specifikuje SN v l. 8. a l. 8.3) Pedpokládá se, že vzestupnice (zmna píného sklonu) se provede na délku pechodnice. Pak je limitem délky pechodnice minimální a maximální sklon vzestupnice. 4) délka pechodnice má vyhovt estetickým a jízdn-psychologickým požadavkm Tyto požadavky nelze definovat jednoznan. Jejich uplatnní závisí na zkušenostech projektanta. Obecn lze íci, že pro velké polomry oblouk je vhodné používat dlouhé pechodnice, což znamená, že parametr pechodnic pro velké polomry bude mnohem vtší. 5) minimální délka pechodnice podle SN ) doporuená délka pechodnice podle SN Požadavky SN jsou na následujícím obrázku. Mezi uvedenými pravidly je samozejm nejdležitjší závazné minimum normy (bod 5) v norm l , jist stojí zato je ješt jednou opsat. Minimální délka klotoidy závisí na zpsobu klopení a je lmin, 0v n pro klopení kolem osy jízdního pásu lmin, 5v n pro klopení kolem vnjší hrany vodicího proužku. Délka pechodnice z tohoto vztahu je v metrech, návrhová rychlost po silniásku v km/h. Projektanti se asto piklánjí k pechodnicím o délce blízké minimální. Rozumným dvodem pro výbr spíše kratších pechodnic je spolehlivé odvodnní vozovky. Zmna píného sklonu se totiž vtšinou provádí na celou délku pechodnice a krátká pechodnice pak znamená minimalizaci úseku s píným sklonem blízkým nule. - 6 (40) -

27 Délka pechodnice Porovnejte délky pechodnic podle bod ) až 6). - 7 (40) -

28 Pozemní komunikace I. Modul BM0-M0 5 Pechodnice ve smrových obloucích Pro správný návrh smrového ešení je nutné používat pechodnice. Jejich délka musí být delší než minimální (podle pedcházejícího textu), shora délka omezena není. Polomr oblouku R musí být vtší než minimální (podle textu v pedcházející pednášce). Oblouk je limitován úhlem S, který spolu svírají teny, respektive strany smrového (tenového) polygonu. Nejbžnjší ešení smrového oblouku je takové, že kružnicová ást oblouku je napojena na teny krajovými pechodnicemi. Ty mohou být symetrické parametry i délka klotoid v oblouku jsou shodné - (graf kivosti takového motivu jsme již vidli výše) nebo mohou být nesymetrické zvolíme pro klotoidy rzné parametry a klotoidy jsou pak rzn dlouhé (graf kivosti takového motivu následuje). V grafu kivostí je ješt pedstaven jeden reprezentant tzv. složených oblouk je to svtle modrý graf. O složeném oblouku se hovoí, pokud se v nm vyskytuje více než jeden kružnicový oblouk. I takové ešení je možné, jeho výpoet ale nebude popsán v tomto textu. Oblouky se složené z jednotlivých prvk (kružnicových oblouk a klotoid) se navrhují jako plynulé a hladké oblouky. Tím je mínno pedevším, že v každém bod oblouku existuje práv jedna tena. Jinými slovy, jednotlivé prvky na sebe navazujeme tak, aby mly spolenou tenu. To musí být splnno vždy Další podmínka je mén silná, jde o to, aby na sebe jednotlivé na sebe navazující prvky mly v bod napojení stejnou kivost. Prakticky nejsou malé odchylky na závadu a norma dokonce pipouští výjimen napojení dvou stejnosmrných oblouk, jejichž polomry jsou v pomru až :. Uvažte, jaký je vliv parametru klotoidy na délku klotoidy a na délku celého oblouku. - 8 (40) -

29 Výpoet symetrických oblouk 6 Výpoet symetrických oblouk Za symetrické oblouky se oznaují všechny ty, které jsou symetrické kolem osy, která plí úhel doplkový ke stedovému úhlu S. Takové oblouky mají dv dležité vlastnosti: ) staí poítat pouze polovinu oblouku (aspo pro hlavní body, pro podrobné nebývají umístny symetricky), ) délka hlavní teny je totožná pro ob sousedící strany tenového polygonu. To znamená, že symetrické oblouky úspšn užijeme tam, kde se nám podaí navrhnout tenový polygon s pibližn stejn dlouhými stranami, nebo tam, kde rezignujeme na inflexní ešení a jsme ochotní vkládat mezi nkteré oblouky mezipímé. 6. Volba parametru a úhlová podmínka pro symetrický oblouk ) Parametr blížící se nule znamená délku klotoidy blížící se nule a ešení blízké prostému kružnicovému oblouku. Koncový úhel klotoidy τ je velmi malý, blíží se nule. ) Pro minimální délku pechodnice L min dostáváme ze základní rovnice klotoidy A R L parametr rozumn použitelné klotoidy. Koncový min úhel klotoidy τ nabývá hodnot v rozmezí 0 < τ < S Smrový motiv se nazývá kružnicový oblouk se symetrickými pechodnicemi. 3) Délku klotoidy, parametr klotoidy a koncový úhel klotoidy τ nemžeme zvtšovat libovoln. Jsme limitováni stedovým úhlem S tak, že τ S. Smrový motiv, kde τ S nazýváme symetrický ist pechodnicový oblouk (symetrická biklotoida). Kivost /R je dosažena práv jen v koncovém bod klotoidy v tzv. vrcholu oblouku. Celková délka oblouku L+L je dvojnásobná proti délce o ist kružnicového oblouku o stejném polomru. Odpovídajícím zpsobem se prodlouží délka hlavní teny t takového motivu. ist pechodnicový oblouk budeme používat tam, kde potebujeme dosáhnout maximální délky teny pi daném polomru a v pípadech, kdy požadujeme co nejpomalejší nárst kivosti. Jaká je souvislost mezi vrcholovým úhlem tenového polygonu a délkou pechodnic?. 6. Postup výpotu Oblouk je zadán jednou z vytyovacích hodnot klotoidy (v tomto píkladu koncovým polomrem R) a stedovým (vrcholovým) úhlem S, který spolu svírají teny smrového polygonu. Je to úhel, který máme k dispozici pro navrhovaný oblouk. Musíme pi volb parametru klotoid dodržet podmínku 3) z pedcházejícího odstavce. Nemžeme tedy libovoln zvtšovat délku klotoidy (tzn. nemžeme libovoln zvtšovat parametr), protože koncový úhel klotoidy se zvtšuje. Parametr klotoidy tedy musíme zvolit rozumn, aby vyhovl norm a jiným požadavkm a abychom nepekroili zmiovanou podmínku 3). - 9 (40) -

30 Pozemní komunikace I. Modul BM0-M0 Pro zadaný polomr zvolíme vhodnou pechodnici. S využitím základních vztah: A l R l τ R dopoítáme potebné hodnoty úhlu, délky, parametru a ovíme návrh podle úhlové podmínky. Uríme hlavní vytyovací hodnoty klotoidy, jak bylo ukázáno výše v kapitole Výpoet hlavních vytyovacích hodnot klotoidy. Cílem dalšího výpotu je umožnit vytyení celého motivu do tenového (smrového) polygonu. Výpoet tedy musí dospt až k urení délky hlavní teny T, která udává vzdálenost zaátku klotoidy od vrcholu tenového polygonu. Až se nám podaí vytyit zaátek klotoidy (oblouku), budeme umt vytyit všechny další potebné hodnoty vytyovací hodnoty jsou totiž vztaženy k zaátku klotoidy. Po bližším prozkoumání schématu vidíme, že pro výpoet délky hlavní teny T mžeme použít hlavní vytyovací hodnoty klotoidy. V obrázku vidíme, že délka hlavní teny T x S + t S x S je jednou ze spoítaných vytyovacích hodnot. t S se snadno dopoítáme. Když si pedstavíme kružnici soustednou s kružnicovou ástí oblouku. Tato pomocná kružnice má polomr r+r a dotká se hlavních teen. t S je pak délka teny této pomocné kružnice. Tu umíme velmi snadno spoítat t S S ( r + r). tg - 30 (40) -

31 Výpoet symetrických oblouk Dále musíme spoítat vytyovací hodnoty pro kružnicovou ást. Úhel 0 jsme vlastn už poítali pi ovování úhlové podmínky. τ 0 S Je to úhel, který spolu svírají teny kružnicové ásti oblouku. Hlavní vytyovací hodnoty kružnice a její vytyení zvládáme z dívjšího studia: S t R tg x R sin S S y R cos z R S cos π R o S 400 Pak už T dopoítáme a úloha je vyešená a motiv lze vytyit. Dkladn prozkoumejte výpoetní a vytyovací schéma. Uvdomte si vzájemnou polohu oskulaní kružnice, jejího stedu, teen oblouku. Rozmyslete a vyzkoušejte, jaký vliv bude mít zmna parametru klotoid na délku klotoidy, na délku oblouku, na velikost odsunu oskulaní kružnice a na délku kružnice. 6.3 Tabulky I. geometrická podobnost klotoid Pro praktické použití (v dob, kdy výpoetní technika nebyla bžn dostupná) byly spoítány Klotoidické tabulky (autoi Veselý, Kašpárek), které lze s úspchem a úinn používat. Jejich pochopení je dležité pro pochopení vlastností klotoidy. Jejich ást I. má univerzální platnost. ást I. obsahuje vypoítané vytyovací hodnoty pro jednu konkrétní klotoidu o parametru A 00 (tzv. jednotkový parametr) v rozsahu koncového úhlu klotoidy τ od 0 g do 35 g. Spoítané hodnoty jsou seazeny podle τ, úhly se liší o malou hodnotu. Pro konkrétní hodnoty τ tedy máme výpoet hotový (pro jednotkovou klotoidu) a hodnoty mžeme rovnou opsat. Pro mezilehlé hodnoty použijeme lineární interpolaci mezi dvma nejbližšími hodnotami. Mezi tabulkovými hodnotami se vyskytuje i koncový polomr R, ten ale bude odlišný od našeho požadovaného polomru. V dalším postupu využijeme geometrické podobnosti klotoid. Každá jednotlivá klotoida (nekonen dlouhá kivka) je definovaná rychlostí zmny kivosti a je jednoznan popsaná svým parametrem A. Všechny takové klotoidy jsou si geometricky podobné. To platí i pro ásti rzných klotoid (s rzným parametrem A). Pokud se zabýváme dvma rznými klotoidami se stejným koncovým úhlem klotoidy τ, platí pro n geometrická podobnost. Pro všechny rozmry, - 3 (40) -

32 Pozemní komunikace I. Modul BM0-M0 které lze na klotoidách o stejném koncovém úhlu τ urit, platí, že pomr všech rozmr je shodný s pomrem parametr tchto klotoid: A A l R R x x S S x x M M s s t t Pitom, nutno zdraznit a opakovat: τ τ z z Jednoduchým pepotem lze tedy urit pro požadovaný polomr správný parametr a dopoítat všechny vytyovací hodnoty. Takto lze i urit vytyovací hodnoty pro klotoidu danou jiným požadavkem, teba, parametrem klotoidy, délkou klotoidy, délkou teny, odsunem oskulaní kružnice, Koncový úhel klotoidy τ je pevn daný jako polovina úhlu seveného tenami oblouku. t t Ovte geometrickou podobnost klotoid na adrese x x y y - 3 (40) -

33 Výpoet a vytyení nesymetrických oblouk 7 Výpoet a vytyení nesymetrických oblouk Protože vtšinou usilujeme o inflexní ešení a teny, které jsou k dispozici pro smrový oblouk nebývají stejné délky na obou stranách, nevystaíme vždy se symetrickými oblouky. Rozdíly v délce stran polygonu mžeme ásten kompenzovat nesymetrickým ešením oblouku. Nesymetrie se dociluje použitím pechodnic s rozdílným parametrem, tedy s rznou délkou a rozdílným koncovým úhlem. Typickým takovým motivem je kružnicový oblouk s nesymetrickými pechodnicemi. 7. Volba parametru a úhlová podmínka pro nesymetrický oblouk Délku (a parametr) oblouku, jak jsem se již díve dovdli, nemžeme volit libovoln. Úhlová podmínka má pro nesymetrické oblouky tuto podobu: τ τ < + Pípustné je ješt ešení za podmínky τ τ + S S kdy se jedná o ist pechodnicový oblouk nesymetrickou biklotoidu. 7. Postup výpotu Zadání mže být rzné, ale musí umožnit zjištní délek klotoid a koncových úhl ze známých základních vztah. Musí tedy být zadány nebo zvoleny v souladu s požadavky normovými a jinými dva defininí parametry (40) -

34 Pozemní komunikace I. Modul BM0-M0 Dále tedy pedpokládáme zadaný stedový úhel S, polomr kružnicové ásti oblouku R a koncové úhly τ.a τ Obdobn tedy platí tento postup: ) Dopoítáme stedový úhel 0 pipadající na kružnicovou ást oblouku a ovíme, jestli je vtší než nula (nebo aspo roven pro ist pechodnicový oblouk). τ 0 S τ ) Uríme hlavní vytyovací hodnoty klotoidy, jak bylo ukázáno výše v kapitole Výpoet hlavních vytyovacích hodnot klotoidy. Výpoet lze samozejm provést pomocí známých tabulek I. (Veselý, Kašpárek), pi pesném dodržení úhl τ.a τ je nutné interpolovat. Ve vtšin praktických pípad je možné si práci zjednodušit a nedodržet úhly τ.a τ (a tím pádem A, A a l, l ) pesn podle zadání. Praktické rozdíly jsou malé a mohou být asto akceptovány. Ve vtšin pípad je mnit i polomr. Všechny zmny se ale musí udržet v rámci pedepsaných normových hodnot. Pak mžeme použít i tabulek IV. (Veselý, Kašpárek). Tam jsou pímo spoítány vytyovací hodnoty pro konkrétní klotoidické pechodnice s vybranými okrouhlými parametry a vybranými okrouhlými koncovými polomry. Další výhodou krom tohoto pohodlného výpotu (opsání spoítaných hodnot) je snadné vytyení podrobných bod, kde mžeme opisovat spoítané hodnoty pro ortogonální vytyení klotoid s okrouhlými parametry pi konkrétních délkách l v tabulkách II. (Veselý, Kašpárek). 3) Abychom mohli motiv vytyit, musíme urit délky hlavních teen t a t. Uváží se odsuny oskulaní kružnice R a R. Z výše ukázaného schématu se budeme zabývat ástí blízko prseíku hlavních teen V a prseíku pomocných teen V (ty se dotýkají oskulaní kružnice a jsou rovnobžné s hlavními). Oblast je oznaena v obrázku obdélníkem a zde ji vidíme v detailu. Nejdíve spoítáme délku teen oskulaní kružnice, to je vzdálenost - 34 (40) -

35 Výpoet a vytyení nesymetrických oblouk bod dotyku od prseíku pomocných teen V. Protože kružnice sama o sob je symetrická, jsou ob teny stejn dlouhé: S t t R tg a b a b 4) Ve vyšrafovaných trojúhelnících provedeme následující výpoty: R tg ( ) R sin S R tg ( ) S ( ) S R sin ( ) S 5) Potom délky hlavních teen spoítáme jako souet pomocné teny oskulaní kružnice t t, píslušných stran trojúhelník a, b, a, b a píslušných vytyovacích hodnot x S a x S obou klotoid: t t a + b + x S t t a + b + x S 6) Vytyení motivu je standardní. Podrobný postup je uvedený níže. Nejdíve se na teny vynese od vrcholu délka hlavních teen a tím se získá zaátek a konec oblouku. Odtud se vynášejí další hlavní vytyovací hodnoty a podrobné body. Kružnicová ást oblouku, se vytyuje od teen kružnice. Ty získáme jako prodloužení koncových teen klotoidy. Tento výpoet je univerzálním výpotem pro libovolné oblouky s dvma krajními pechodnicemi. Mžete si ho ovit i pro oblouky s velkým stedovým úhlem (nad 00 g ). Používá se teba pro vratné rampy na mimoúrov- ových kižovatkách. Za nkterých okolností ( S >00 g )vychází délka teny záporná, což znamená, že se prseík teen dostane na opanou stranu vzhledem ke smrové ose (40) -

36 Pozemní komunikace I. Modul BM0-M0 8 Složené oblouky Složené oblouky jsou ty oblouky, které se skládají z více prvk. Víme z dívjška, že za geometrické prvky smrového ešení se používají pímka (ta se v oblouku samozejm neužívá), kružnice a pechodnice (víme, že se bžn používá klotoida). Díve probrané smrové motivy (kružnicový oblouk, kružnicový oblouk se symetrickými nebo nesymetrickými pechodnicemi, ist pechodnicový oblouk symetrický nebo nesymetrický) se v bžné mluv za složené neoznaují. Za složené se oznaují ty, které jsou složitjší než výše uvedené. Je to nap. už i kružnicový oblouk s více než jedním polomrem. Dále to jsou pechodnicové oblouky s kružnicemi, ve kterých je použit více než jeden kružnicový oblouk. A dále ist pechodnicový oblouk s více než dvma pechodnicemi. Poslední dva pípady se vyznaují tím, že se v nich vyskytuje mezilehlá pechodnice. Úvodní tvrzení tedy opravíme. Složené oblouky jsou: složené kružnicové oblouky (pi moderním trasování se prakticky neužívají) pechodnicové oblouky, ve kterých se vyskytuje mezilehlá pechodnice (navíc ke krajovým pechodnicím) složené oblouky mají více než jeden kružnicový oblouk (mže být i o nulové délce Názorn lze ukázat složené oblouky v diagramech kivosti oblouk. Vytyovací schéma složených oblouk bývá ponkud složitjší. Výpoet je pomrn pracný a záleží na vstupních podmínkách pro výpoet. Pokud je výpoet provádný njakým SW, nemusí nás jeho složitost píliš trápit. Je však na nás, abychom zadali takové okrajové podmínky, které rozumný výpoet umožní. Použití složených oblouk mže být motivováno tmito okolnostmi: - 36 (40) -