MATEMATICKÁ KARTOGRAFIE
|
|
|
- Vítězslav Sedláček
- před 8 lety
- Počet zobrazení:
Transkript
1 VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KARTOGRAFIE MODUL 5 NEPRAVÁ ZOBRAZENÍ STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA
2 Matematická kartografie Modul Miloslav Švec, Brno (17) -
3 Obsah OBSAH 1 Úvod Cíle Požadované znalosti Doba potebná ke studiu Klíová slova...5 Nepravá zobrazení (pseudozobrazení) Nepravá kuželová zobrazení...6. Nepravá azimutální zobrazení Zobrazení odvozená z jednoduchých azimutálních zobrazení v píné poloze Nepravá válcová zobrazení Mnohokuželová (polykónická) zobrazení Závr Shrnutí Studijní prameny Seznam použité literatury Seznam doplkové studijní literatury Odkazy na další studijní zdroje a prameny (17) -
4
5 Úvod 1 Úvod 1.1 Cíle Matematická kartografie patí k základním teroretickým pedmtm studijních program geodézie a kartografie. Vytváí pedpoklady pro zvládnutí obecných a praktických úloh jak obecné geodézie, tak pedevším obecné kartografie. Moduly pedmtu jsou koncipovány jako ucelené celky. Pesto na sebe teoreticky navazují. Opora Matematická kartografie je tvoena tmito moduly: Referenní plochy a souadnicové systémy Kartografická zkreslení Kartografické zobrazení Jednoduchá zobrazení Nepravá azimutální zobrazení 1. Požadované znalosti Pedmt vyžaduje dobré matematické základy. Jedná se o zvládnutí základ matematické analýzy, pedevším diferenciálního potu jedné a více promnných, integrálního potu, základ diferenciálních rovnic a nkterých partií deskriptivní a diferenciální geometrie. 1.3 Doba potebná ke studiu Pedmt je vyuován jako povinný v prvním roníku navazujícího magisterského studijního programu Geodézie a kartografie v rozsahu hodiny pednášky a 1 hodiny cviení za týden, tedy celkem 39 hodin za semestr. Jako u každého teoretického pedmtu se pedpokládá alespo stelná asová zátž pi samostudiu. 1.4 Klíová slova Matematická kartografie, referenní plocha, zobrazení, mapa, elipsoid, souadnicové soustavy - 5 (17) -
6 Matematická kartografie Modul Nepravá zobrazení (pseudozobrazení) Zobrazení jednoduché nepravé kuželové ρ = f ( U ), ε = g( V ) = nv ρ = f ( U ), ε = g( U,V ) azimutální ρ = f ( U ), ε = V ρ = f ( U ), ε = g( U,V ) válcové X = f ( V ) = nv, Y = g( U ) X = f ( U,V ), Y = g( U ) Zemské rovnobžky v nepravých zobrazeních zstávají zobrazeny stejn jako v jednoduchých, tj. kuželových a azimutálních jako soustedné kružnice, ve válcových jako pímky rovnobžné s rovníkem. Poledníky se obecn zobrazují jako kivky. Dvod zavádní nepravých zobrazení zlepšit vlastnosti sítí, zmírnit narstání délkových zkreslení v rovnobžkách. Nepravá zobrazení se užívají pouze u map velmi malých mítek referenní plocha je koule..1 Nepravá kuželová zobrazení Bonneovo zobrazení O Q V P P o U o U V S r r o V S Q ε ρ r P P o r o O J Zobrazovací rovnice ρ = ρ + ε = o R RcosU V ρ ( U U ) o - 6 (17) -
7 Nepravá zobrazení Zkreslení m p = tgθ = 1 + V o RcosU ( ϑ) = VsinU, P = 1 tg 180 sinu RcosU ρ, m ρ r = 1 Bonneovo (18. stol.) zobrazení je ekvidistantní v rovnobžkách a ekvivalentní.. Nepravá azimutální zobrazení Wernerovo Stabovo zobrazení (16. stol.) Je mezním pípadem Bonneova zobrazení pro Zobrazovací rovnice ρ = R o o =. U 90 o RcosU ( 90 U ), ε = V Sted rovnobžkových kružnic leží v obraze pólu a poledníky vyplují celý horizont. ρ - 7 (17) -
8 Matematická kartografie Modul.3 Zobrazení odvozená z jednoduchých azimutálních zobrazení v píné poloze Aitovovo zobrazení (19. stol.) Afinní prmt píného ekvidistantního azimutálního zobrazení Postelova na rovinu, procházející rovníkem této sít a odklonnou od její roviny o 60 o Hammerovo zobrazení - 8 (17) -
9 Nepravá zobrazení Wagnerovo zobrazení Upravené Aitovovo zobrazení Winkelova kombinovaná zobrazení Globulární zobrazení Zobrazení zemské polokoule do kružnice, rovník a stední poledník jsou pímé a na sebe kolmé..4 Nepravá válcová zobrazení Nejširší škála používaných a možných zobrazení Mercatorovo Sansonovo zobrazení (17. a 18. stol.) Zobrazovací rovnice pro poátek v prseíku obrazu rovníku a stedního poledníku X Odtud eliminací U dostaneme ( U,V ), Y = RU g( U ) = RV cos U = f = X Y RV cos R =. - 9 (17) -
10 Matematická kartografie Modul Pro = konst. ( poledník) V, dostaneme rovnici sinusoidy poledník se zobrazí jako sinusoida sinusoidální zobrazení. Zkreslení m 1 = 1 + V sin U, mr = 1, tg =, P VsinU p ϑ = 1 Mollweidovo zobrazení (19. stol.) Základní poledník je pímý a zkresluje se, ostatní poledníky jsou eliptické, rovnobžky jsou pímé, zobrazení není ekvidistantní, je ekvivalentní (17) -
11 Nepravá zobrazení Collignovo zobrazení (19. stol.) Zobrazení zempisné sít samými pímkami Eckertovo zobrazení (0. stol.) Eckertovo zobrazení s pímkovými obrazy poledník - 11 (17) -
12 Matematická kartografie Modul Eckertovo zobrazení s eliptickými obrazy poledník Eckertovo zobrazení se sinusoidálními obrazy poledník - 1 (17) -
13 Nepravá zobrazení.5 Mnohokuželová (polykónická) zobrazení Pi jednoduchém kuželovém zobrazení v normální poloze se zobrazuje na jediný pláš kužele rovnobžky se V zobrazují jako soustedné kružnice. A Pi mnohokuželovém zobrazení se zobrazuje na nekonený poet kužel, každý zobrazuje práv jen tu rovnobžku, ve které se daný kužel dotýká referenní plochy. Rovnobžky se zobrazují opt jako kružnice, ale nesoustedné. Obecné zobrazovací rovnice ( U ), i = g( U ), h( U,V ) ρ = f ε = A O B C A 1 O 1 C 1 B 1 V B V C S V A X i V B ε ρ V C S C C 1 B B 1 A A 1 O O 1 Y - 13 (17) -
14 Matematická kartografie Modul Hasslerovo ekvidistantní zobrazení (19. stol.) Základní polykónické zobrazení ekvidistantní v rovnobžkách s nezkresleným stedním poledníkem. Zobrazovací rovnice ρ = Rcotg U, i = ρ + RU, ε = V sinu Pro konstrukní práce platí X = i ρ cos ε, Y = ρ sinε Zkreslení tgθ = m r = 1, ε sinε cosε sec U P = 1 + cotg, m p U sin = 1 + ε Grintenovo kruhové zobrazení (19. stol.) cotg U sin ε secθ Lambertovo Lagrangeovo konformní kruhové zobrazení - 14 (17) -
15 Nepravá zobrazení Polyedrická zobrazení Zobrazení referenní plochy po vymezených ástech Díve již Cassini-Soldner a Gaussovo konformní zobrazení (17) -
16
17 Závr 3 Závr 3.1 Shrnutí S rozvojem výpoetní techniky se používá stále více tzv. nepravých zobrazení. Modul uvádí nkteré z nich. Obsáhlé pehledy lze najít na internetových stránkách nap. [5] až [8]. 3. Studijní prameny 3..1 Seznam použité literatury [1] Hojovec, V. a kol. Kartografie, GPK Praha Seznam doplkové studijní literatury [] Daniš, M., Valko, J. Matematická kartografia, SVŠT Bratislava 1987 [3] Srnka, E. Matematická kartografie, VAAZ, Brno 1977 [4] Böhm, J. Matematická kartografie, VŠT, Brno Odkazy na další studijní zdroje a prameny [5] [6] [7] [8] (17) -
MATEMATICKÁ KARTOGRAFIE
 VYSOKÉ UENÍ TECHNICKÉ V BN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KATOGAFIE MODUL 3 KATOGAFICKÉ ZOBAZENÍ STUDIJNÍ OPOY PO STUDIJNÍ POGAMY S KOMBINOVANOU FOMOU STUDIA Matematická kartografie Modul 3
VYSOKÉ UENÍ TECHNICKÉ V BN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KATOGAFIE MODUL 3 KATOGAFICKÉ ZOBAZENÍ STUDIJNÍ OPOY PO STUDIJNÍ POGAMY S KOMBINOVANOU FOMOU STUDIA Matematická kartografie Modul 3
MATEMATICKÁ KARTOGRAFIE
 VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KARTOGRAFIE MODUL KARTOGRAFICKÁ ZKRESLENÍ STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Matematická kartografie
VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KARTOGRAFIE MODUL KARTOGRAFICKÁ ZKRESLENÍ STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Matematická kartografie
Jiří Cajthaml. ČVUT v Praze, katedra geomatiky. zimní semestr 2014/2015
 Kartografie 1 - přednáška 8 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Nepravá zobrazení zachovávají některé charakteristiky jednoduchých zobrazení (tvar rovnoběžek) některé
Kartografie 1 - přednáška 8 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Nepravá zobrazení zachovávají některé charakteristiky jednoduchých zobrazení (tvar rovnoběžek) některé
1 Nepravá zobrazení. 4 Zobrazení odvozené z jednoduchých azimutálních (modifikované. Obsah. 3 Nepravá azimutální zobrazení.
 Obsah 1 Nepravá zobrazení 2 3 4 Zobrazení odvozené z jednoduchých azimutálních (modifikované zobrazení) 5 Zobrazení Evropy Nepravá zobrazení: jednoduché nepravé kuželové ρ = f (U), ɛ = g(v ) = nv ρ = f
Obsah 1 Nepravá zobrazení 2 3 4 Zobrazení odvozené z jednoduchých azimutálních (modifikované zobrazení) 5 Zobrazení Evropy Nepravá zobrazení: jednoduché nepravé kuželové ρ = f (U), ɛ = g(v ) = nv ρ = f
MATEMATICKÁ KARTOGRAFIE
 VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KARTOGRAFIE MODUL 1 REFERENNÍ PLOCHY A SOUADNICOVÉ SYSTÉMY STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Mtemtická
VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KARTOGRAFIE MODUL 1 REFERENNÍ PLOCHY A SOUADNICOVÉ SYSTÉMY STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Mtemtická
Matematické metody v kartografii. Nepravá zobrazení. Polykónická zobrazení. (11.)
 Matematické metody v kartografii Nepravá zobrazení. Polykónická zobrazení. (11.) 1. Společné vlastnosti nepravých zobrazení Jedna ze souřadnicových funkcí je funkcí zeměpisné šířky i délky Obrazy rovnoběţek:
Matematické metody v kartografii Nepravá zobrazení. Polykónická zobrazení. (11.) 1. Společné vlastnosti nepravých zobrazení Jedna ze souřadnicových funkcí je funkcí zeměpisné šířky i délky Obrazy rovnoběţek:
Jiří Cajthaml. ČVUT v Praze, katedra geomatiky. zimní semestr 2014/2015
 Kartografie 1 - přednáška 9 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Polykónická zobrazení někdy také mnohokuželová zobecnění kuželových zobrazení použito je nekonečně mnoho
Kartografie 1 - přednáška 9 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Polykónická zobrazení někdy také mnohokuželová zobecnění kuželových zobrazení použito je nekonečně mnoho
Jiří Cajthaml. ČVUT v Praze, katedra geomatiky. zimní semestr 2014/2015
 Kartografie 1 - přednáška 5 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Válcová zobrazení obrazem poledníků jsou úsečky, které mají konstantní rozestupy obrazem rovnoběžek jsou
Kartografie 1 - přednáška 5 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Válcová zobrazení obrazem poledníků jsou úsečky, které mají konstantní rozestupy obrazem rovnoběžek jsou
Matematické metody v kartografii. Členění kartografických zobrazení. Zobrazení z elipsoidu na kouli (5.)
 Matematické metody v kartografii Členění kartografických zobrazení. Zobrazení z elipsoidu na kouli (5.) 1. Členění kartografických zobrazení: Existuje velkémnožstvíkarografických zobrazení. Lze je členit
Matematické metody v kartografii Členění kartografických zobrazení. Zobrazení z elipsoidu na kouli (5.) 1. Členění kartografických zobrazení: Existuje velkémnožstvíkarografických zobrazení. Lze je členit
Matematické metody v kartografii. Volba a identifikace zobrazení. Zobrazení použitá v ČR. Kritéria pro hodnocení kartografických zobrazení(13)
 Matematické metody v kartografii Volba a identifikace zobrazení. Zobrazení použitá v ČR. Kritéria pro hodnocení kartografických zobrazení(3) Volba kartografického zobrazení Parametry ovlivňující volbu
Matematické metody v kartografii Volba a identifikace zobrazení. Zobrazení použitá v ČR. Kritéria pro hodnocení kartografických zobrazení(3) Volba kartografického zobrazení Parametry ovlivňující volbu
PŘEHLED JEVNOSTI ZOBRAZENÍ
 Úhlojevná (konformní Plochojevná (ekvivalentní Délkojevná (ekvidistatntí Vyrovnávací (kompenzační PŘEHLED JEVNOSTI ZOBRAZENÍ (azimutální Stereografická (cylindické Mercatorovo zobrazení (loodroma jako
Úhlojevná (konformní Plochojevná (ekvivalentní Délkojevná (ekvidistatntí Vyrovnávací (kompenzační PŘEHLED JEVNOSTI ZOBRAZENÍ (azimutální Stereografická (cylindické Mercatorovo zobrazení (loodroma jako
Jiří Cajthaml. ČVUT v Praze, katedra geomatiky. zimní semestr 2014/2015
 Kartografie 1 - přednáška 1 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Úvod přednášky, cvičení, zápočty, zkoušky Jiří Cajthaml (přednášky, cvičení) potřebné znalosti: vzorce
Kartografie 1 - přednáška 1 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Úvod přednášky, cvičení, zápočty, zkoušky Jiří Cajthaml (přednášky, cvičení) potřebné znalosti: vzorce
Zobrazení. Geografická kartografie Přednáška 4
 Zobrazení Geografická kartografie Přednáška 4 kartografické zobrazení způsob, který každému bodu na referenční ploše přiřazuje právě jeden bod na zobrazovací ploše (výjimkou jsou ovšem singulární body)
Zobrazení Geografická kartografie Přednáška 4 kartografické zobrazení způsob, který každému bodu na referenční ploše přiřazuje právě jeden bod na zobrazovací ploše (výjimkou jsou ovšem singulární body)
Jiří Cajthaml. ČVUT v Praze, katedra geomatiky. zimní semestr 2014/2015
 Kartografie 1 - přednáška 6 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Kartografická zobrazení použitá na našem území důležitá jsou zejména zobrazení pro státní mapová díla v
Kartografie 1 - přednáška 6 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Kartografická zobrazení použitá na našem území důležitá jsou zejména zobrazení pro státní mapová díla v
Matematické metody v kartografii. Kruhová zobrazení. Polyedrická a neklasifikovaná zobrazení (12)
 Matematické metody v kartografii Kruhová zobrazení. Polyedrická a neklasifikovaná zobrazení (12) Kruhová zobrazení Společné vlastnosti: Síť poledníků/rovnoběžek tvořena pouze kruhovými oblouky Středy rovnoběžkových
Matematické metody v kartografii Kruhová zobrazení. Polyedrická a neklasifikovaná zobrazení (12) Kruhová zobrazení Společné vlastnosti: Síť poledníků/rovnoběžek tvořena pouze kruhovými oblouky Středy rovnoběžkových
Základy kartografie. RNDr. Petra Surynková, Ph.D.
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta RNDr., Ph.D. petra.surynkova@mff.cuni.cz www.surynkova.info Kartografie Vědní obor zabývající se znázorněním zemského povrchu a nebeských těles
Univerzita Karlova v Praze Matematicko-fyzikální fakulta RNDr., Ph.D. petra.surynkova@mff.cuni.cz www.surynkova.info Kartografie Vědní obor zabývající se znázorněním zemského povrchu a nebeských těles
Základy kartografie, topografické plochy
 Základy kartografie, topografické plochy morava@karlin.mff.cuni.cz Katedra didaktiky matematiky MFF UK, Praha Aplikace matematiky pro učitele, 3. ledna 2012 Základní pojmy Kartografie věda zabývající se
Základy kartografie, topografické plochy morava@karlin.mff.cuni.cz Katedra didaktiky matematiky MFF UK, Praha Aplikace matematiky pro učitele, 3. ledna 2012 Základní pojmy Kartografie věda zabývající se
Matematické metody v kartografii. Jednoduchá azimutální zobrazení. Azimutální projekce. UPS. (10.)
 Matematické metody v kartografii Jednoduchá azimutální zobrazení. Azimutální projekce. UPS. (10.) 1. Jednoduchá azimutální zobrazení Společné vlastnosti: Jednoduché zobrazení, zobrazuje na tečnou rovinu
Matematické metody v kartografii Jednoduchá azimutální zobrazení. Azimutální projekce. UPS. (10.) 1. Jednoduchá azimutální zobrazení Společné vlastnosti: Jednoduché zobrazení, zobrazuje na tečnou rovinu
Jiří Cajthaml. ČVUT v Praze, katedra geomatiky. zimní semestr 2014/2015
 Kartografie 1 - přednáška 2 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Kartografické zobrazení kartografické zobrazení vzájemné přiřazení polohy bodů na dvou různých referenčních
Kartografie 1 - přednáška 2 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Kartografické zobrazení kartografické zobrazení vzájemné přiřazení polohy bodů na dvou různých referenčních
Geodézie a pozemková evidence
 2012, Brno Ing.Tomáš Mikita, Ph.D. Geodézie a pozemková evidence Přednáška č.2 - Kartografická zobrazení, souřadnicové soustavy Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské
2012, Brno Ing.Tomáš Mikita, Ph.D. Geodézie a pozemková evidence Přednáška č.2 - Kartografická zobrazení, souřadnicové soustavy Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské
Celkem existuje asi 300 zobrazení, používá se jen několik desítek.
 ÁKLADY KARTOGRAFIE RO SŠ KARTOGRAFICKÉ OBRAENÍ Kartografické zobrazení je způsob, který každému bodu na referenčním elipsoidu resp. referenční kouli přiřazuje body v rovině. Určení věrných obrazů bodů
ÁKLADY KARTOGRAFIE RO SŠ KARTOGRAFICKÉ OBRAENÍ Kartografické zobrazení je způsob, který každému bodu na referenčním elipsoidu resp. referenční kouli přiřazuje body v rovině. Určení věrných obrazů bodů
Jednoduchá zobrazení. Podpořeno z projektu FRVŠ 584/2011.
 Podpořeno z projektu FRVŠ 584/2011. Obsah Jednoduchá zobrazení 1 Jednoduchá zobrazení 2 Obsah Jednoduchá zobrazení 1 Jednoduchá zobrazení 2 Společné vlastnosti jednoduchých zobrazení: Zobrazovací ref.
Podpořeno z projektu FRVŠ 584/2011. Obsah Jednoduchá zobrazení 1 Jednoduchá zobrazení 2 Obsah Jednoduchá zobrazení 1 Jednoduchá zobrazení 2 Společné vlastnosti jednoduchých zobrazení: Zobrazovací ref.
Matematická kartografie. Černý J., Kočandrlová M.: Konstruktivní geometrie, ČVUT. Referenční plochy
 Matematická kartografie Buchar.: Matematická kartografie 10, ČVUT; Černý J., Kočandrlová M.: Konstruktivní geometrie, ČVUT Referenční plochy referenční elipsoid (sféroid) zploštělý rotační elipsoid Besselův
Matematická kartografie Buchar.: Matematická kartografie 10, ČVUT; Černý J., Kočandrlová M.: Konstruktivní geometrie, ČVUT Referenční plochy referenční elipsoid (sféroid) zploštělý rotační elipsoid Besselův
Geodézie pro architekty. Úvod do geodézie
 Geodézie pro architekty Úvod do geodézie Geodézie pro architekty Ing. Tomáš Křemen, Ph.D. B905 http://k154.fsv.cvut.cz/~kremen/ tomas.kremen@fsv.cvut.cz Doporučená literatura: Hánek, P. a kol.: Stavební
Geodézie pro architekty Úvod do geodézie Geodézie pro architekty Ing. Tomáš Křemen, Ph.D. B905 http://k154.fsv.cvut.cz/~kremen/ tomas.kremen@fsv.cvut.cz Doporučená literatura: Hánek, P. a kol.: Stavební
Stavební geodézie. Úvod do geodézie. Ing. Tomáš Křemen, Ph.D.
 Stavební geodézie Úvod do geodézie Ing. Tomáš Křemen, Ph.D. Stavební geodézie SG01 Ing. Tomáš Křemen, Ph.D. B905 http://k154.fsv.cvut.cz/~kremen/ tomas.kremen@fsv.cvut.cz Doporučená literatura: Hánek,
Stavební geodézie Úvod do geodézie Ing. Tomáš Křemen, Ph.D. Stavební geodézie SG01 Ing. Tomáš Křemen, Ph.D. B905 http://k154.fsv.cvut.cz/~kremen/ tomas.kremen@fsv.cvut.cz Doporučená literatura: Hánek,
Matematické metody v kartografii. Jednoduchá válcová zobrazení. Válcové projekce. Gaussovo zobrazení. (6.+7.)
 Matematické metody v kartografii Jednoduchá válcová zobrazení. Válcové projekce. Gaussovo zobrazení. (6.+7.) 1. Jednoduchá zobrazení Společné vlastnosti: Zobrazovací plocha představována pláštěm kužele,
Matematické metody v kartografii Jednoduchá válcová zobrazení. Válcové projekce. Gaussovo zobrazení. (6.+7.) 1. Jednoduchá zobrazení Společné vlastnosti: Zobrazovací plocha představována pláštěm kužele,
Pr niky ploch a t les
 Gymnázium Christiana Dopplera, Zborovská 45, Praha 5 RONÍKOVÁ PRÁCE Prniky ploch a tles Vypracoval: Tomáš Martínek ída: 4.C Školní rok: 2013/2014 Seminá: Deskriptivní geometrie Prohlašuji, že jsem svou
Gymnázium Christiana Dopplera, Zborovská 45, Praha 5 RONÍKOVÁ PRÁCE Prniky ploch a tles Vypracoval: Tomáš Martínek ída: 4.C Školní rok: 2013/2014 Seminá: Deskriptivní geometrie Prohlašuji, že jsem svou
Kartografie I. RNDr. Ladislav Plánka, CSc. Institut geodézie a důlního měřictví, Hornicko-geologická fakulta, VŠB TU Ostrava
 Kartografie I Matematické a geometrické základy kartografických děl RNDr. Ladislav Plánka, CSc. Institut geodézie a důlního měřictví, Hornicko-geologická fakulta, VŠB TU Ostrava Podkladové materiály pro
Kartografie I Matematické a geometrické základy kartografických děl RNDr. Ladislav Plánka, CSc. Institut geodézie a důlního měřictví, Hornicko-geologická fakulta, VŠB TU Ostrava Podkladové materiály pro
Srovnání konformních kartografických zobrazení pro zvolené
 Srovnání konformních kartografických zobrazení pro zvolené území (návod na cvičení) 1 Úvod Cílem úlohy je srovnání vlastnosti jednoduchých konformních zobrazení a jejich posouzení z hlediska vhodnosti
Srovnání konformních kartografických zobrazení pro zvolené území (návod na cvičení) 1 Úvod Cílem úlohy je srovnání vlastnosti jednoduchých konformních zobrazení a jejich posouzení z hlediska vhodnosti
Podpořeno z projektu FRVŠ 584/2011.
 Podpořeno z projektu FRVŠ 584/2011. Obsah Křovákovo zobrazení 1 Křovákovo zobrazení Obsah Křovákovo zobrazení 1 Křovákovo zobrazení Podpořeno z projektu FRVŠ 584/2011. Křovákovo zobrazení Křovákovo zobrazení
Podpořeno z projektu FRVŠ 584/2011. Obsah Křovákovo zobrazení 1 Křovákovo zobrazení Obsah Křovákovo zobrazení 1 Křovákovo zobrazení Podpořeno z projektu FRVŠ 584/2011. Křovákovo zobrazení Křovákovo zobrazení
APROXIMACE KŘOVÁKOVA ZOBRAZENÍ PRO GEOGRAFICKÉ ÚČELY
 APROXIMACE KŘOVÁKOVA ZOBRAZENÍ PRO GEOGRAFICKÉ ÚČELY Radek Dušek, Jan Mach Katedra fyzické geografie a geoekologie, Přírodovědecká fakulta, Ostravská univerzita, Ostrava Gymnázium Omská, Praha Abstrakt
APROXIMACE KŘOVÁKOVA ZOBRAZENÍ PRO GEOGRAFICKÉ ÚČELY Radek Dušek, Jan Mach Katedra fyzické geografie a geoekologie, Přírodovědecká fakulta, Ostravská univerzita, Ostrava Gymnázium Omská, Praha Abstrakt
Detekce kartografického zobrazení z množiny bodů, praktické zkušenosti
 Detekce kartografického zobrazení z množiny bodů, praktické zkušenosti Tomáš Bayer Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta, Univerzita Karlova v Praze, Albertov 6, 10 78,
Detekce kartografického zobrazení z množiny bodů, praktické zkušenosti Tomáš Bayer Katedra aplikované geoinformatiky a kartografie, Přírodovědecká fakulta, Univerzita Karlova v Praze, Albertov 6, 10 78,
Úvodní ustanovení. Geodetické referenční systémy
 430/2006 Sb. NAŘÍZENÍ VLÁDY ze dne 16. srpna 2006 o stanovení geodetických referenčních systémů a státních mapových děl závazných na území státu a zásadách jejich používání ve znění nařízení vlády č. 81/2011
430/2006 Sb. NAŘÍZENÍ VLÁDY ze dne 16. srpna 2006 o stanovení geodetických referenčních systémů a státních mapových děl závazných na území státu a zásadách jejich používání ve znění nařízení vlády č. 81/2011
Gymnázium Christiana Dopplera, Zborovská 45, Praha 5. Kartografické projekce
 Gymnázium Christiana Dopplera, Zborovská 45, Praha 5 ROČNÍKOVÁ PRÁCE Kartografické projekce Vypracoval: Jiří Novotný Třída: 4.C Školní rok: 2013/2014 Seminář: Deskriptivní geometrie Prohlašuji, že jsem
Gymnázium Christiana Dopplera, Zborovská 45, Praha 5 ROČNÍKOVÁ PRÁCE Kartografické projekce Vypracoval: Jiří Novotný Třída: 4.C Školní rok: 2013/2014 Seminář: Deskriptivní geometrie Prohlašuji, že jsem
SPŠ STAVEBNÍ České Budějovice MAPOVÁNÍ. JS pro 3. ročník S3G
 SPŠ STAVEBNÍ České Budějovice MAPOVÁNÍ JS pro 3. ročník S3G ROZPIS TÉMAT PRO ŠK. ROK 2018/2019 1) Kartografické zobrazení na území ČR Cassiny-Soldnerovo zobrazení Obecné konformní kuželové zobrazení Gauss-Krügerovo
SPŠ STAVEBNÍ České Budějovice MAPOVÁNÍ JS pro 3. ročník S3G ROZPIS TÉMAT PRO ŠK. ROK 2018/2019 1) Kartografické zobrazení na území ČR Cassiny-Soldnerovo zobrazení Obecné konformní kuželové zobrazení Gauss-Krügerovo
4. EZY NA KUŽELÍCH 4.1. KUŽELOVÁ PLOCHA, KUŽEL
 4. EZY NA KUŽELÍCH 4.1. KUŽELOVÁ PLOCHA, KUŽEL Definice : Je dána kružnice k ležící v rovin a mimo ni bod V. Všechny pímky jdoucí bodem V a protínající kružnici k tvoí kruhovou kuželovou plochu. Tyto pímky
4. EZY NA KUŽELÍCH 4.1. KUŽELOVÁ PLOCHA, KUŽEL Definice : Je dána kružnice k ležící v rovin a mimo ni bod V. Všechny pímky jdoucí bodem V a protínající kružnici k tvoí kruhovou kuželovou plochu. Tyto pímky
Jiří Cajthaml. ČVUT v Praze, katedra geomatiky. zimní semestr 2014/2015
 Kartografie 1 - přednáška 7 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 válcové konformní zobrazení v transverzální poloze někdy také nazýváno transverzální Mercatorovo nebo Gauss-Krügerovo
Kartografie 1 - přednáška 7 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 válcové konformní zobrazení v transverzální poloze někdy také nazýváno transverzální Mercatorovo nebo Gauss-Krügerovo
Matematické metody v kartografii. Přednáška 3. Důležité křivky na kouli a elipsoidu. Loxodroma a ortodroma.
 Matematické metody v kartografii Přednáška 3. Důležité křivky na kouli a elipsoidu. Loxodroma a ortodroma. . Přehled důležitých křivek V matematické kartografii existují důležité křivky, které jdou po
Matematické metody v kartografii Přednáška 3. Důležité křivky na kouli a elipsoidu. Loxodroma a ortodroma. . Přehled důležitých křivek V matematické kartografii existují důležité křivky, které jdou po
Kartografie - úvod, historie a rozdělení Matematická kartografie Kartografická zobrazení
 Kartografie - úvod, historie a rozdělení Matematická kartografie Kartografická zobrazení Kartografie přednáška 1 Kartografie obor zabývající se zobrazováním zakřivené části Zemského povrchu do rovinné
Kartografie - úvod, historie a rozdělení Matematická kartografie Kartografická zobrazení Kartografie přednáška 1 Kartografie obor zabývající se zobrazováním zakřivené části Zemského povrchu do rovinné
GIS Geografické informační systémy
 GIS Geografické informační systémy Kartografie Glóbus představuje zmenšený a zjednodušený, 3rozměrný model zemského povrchu; všechny délky na glóbu jsou zmenšeny v určitém poměru; úhly a tvary a velikosti
GIS Geografické informační systémy Kartografie Glóbus představuje zmenšený a zjednodušený, 3rozměrný model zemského povrchu; všechny délky na glóbu jsou zmenšeny v určitém poměru; úhly a tvary a velikosti
8. Deskriptivní geometrie
 8. Deskriptivní geometrie 337 Volitelný pedmt - dvouletý Vzdlávací oblast: Matematika a její aplikace Vzdlávací obor: Matematika a její aplikace Vyuovací pedmt: Deskriptivní geometrie 1. Charakteristika
8. Deskriptivní geometrie 337 Volitelný pedmt - dvouletý Vzdlávací oblast: Matematika a její aplikace Vzdlávací obor: Matematika a její aplikace Vyuovací pedmt: Deskriptivní geometrie 1. Charakteristika
Zobrazování zemského povrchu
 Zobrazování zemského povrchu Země je kulatá Mapy jsou placaté Zemský povrch je zvlněný a země není kulatá Fyzický povrch potřebuji promítnout na nějaký matematicky popsatelný povrch http://photojournal.jpl.nasa.gov/jpeg/pia03399.jpg
Zobrazování zemského povrchu Země je kulatá Mapy jsou placaté Zemský povrch je zvlněný a země není kulatá Fyzický povrch potřebuji promítnout na nějaký matematicky popsatelný povrch http://photojournal.jpl.nasa.gov/jpeg/pia03399.jpg
Referenční plochy a souřadnice na těchto plochách Zeměpisné, pravoúhlé, polární a kartografické souřadnice
 Referenční plochy a souřadnice na těchto plochách Zeměpisné, pravoúhlé, polární a kartografické souřadnice Kartografie přednáška 5 Referenční plochy souřadnicových soustav slouží k lokalizaci bodů, objektů
Referenční plochy a souřadnice na těchto plochách Zeměpisné, pravoúhlé, polární a kartografické souřadnice Kartografie přednáška 5 Referenční plochy souřadnicových soustav slouží k lokalizaci bodů, objektů
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ BAKALÁŘSKÁ PRÁCE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ BAKALÁŘSKÁ PRÁCE PRAHA 2014 Sandra PÁNKOVÁ ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ STUDIJNÍ PROGRAM GEODÉZIE A KARTOGRAFIE STUDIJNÍ OBOR
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ BAKALÁŘSKÁ PRÁCE PRAHA 2014 Sandra PÁNKOVÁ ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ STUDIJNÍ PROGRAM GEODÉZIE A KARTOGRAFIE STUDIJNÍ OBOR
154GUI1 Geodézie pro UIS 1
 154GUI1 Geodézie pro UIS 1 Přednášející: Ing. Tomáš Křemen, Ph.D; Místnost: B905 Email: tomas.kremen@fsv.cvut.cz WWW: k154.fsv.cvut.cz/~kremen Literatura: [1] Ratiborský, J.: Geodézie 10. 2. vyd. Praha:
154GUI1 Geodézie pro UIS 1 Přednášející: Ing. Tomáš Křemen, Ph.D; Místnost: B905 Email: tomas.kremen@fsv.cvut.cz WWW: k154.fsv.cvut.cz/~kremen Literatura: [1] Ratiborský, J.: Geodézie 10. 2. vyd. Praha:
SPŠSTAVEBNÍČeskéBudějovice MAPOVÁNÍ. Gauss-Krügerovo zobrazení UTM
 SPŠSTAVEBNÍČeskéBudějovice MAPOVÁNÍ Gauss-Krügerovo zobrazení UTM 1 Předmluva Mapování v novém Křovákově kuželovém konformním zobrazení mělo dobrou přesnost a značné výhody, ale ty měly využití jen lokální
SPŠSTAVEBNÍČeskéBudějovice MAPOVÁNÍ Gauss-Krügerovo zobrazení UTM 1 Předmluva Mapování v novém Křovákově kuželovém konformním zobrazení mělo dobrou přesnost a značné výhody, ale ty měly využití jen lokální
ení Francie Zuzana Ženíšková
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakultaa stavební Obor geodézie a kartografie Katedra mapování a kartografie BAKALÁŘSKÁ PRÁCE Ekvivalentní zobraze ení Francie Vedoucí bakalářské práce: Ing. Petr Buchar,
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakultaa stavební Obor geodézie a kartografie Katedra mapování a kartografie BAKALÁŘSKÁ PRÁCE Ekvivalentní zobraze ení Francie Vedoucí bakalářské práce: Ing. Petr Buchar,
Geoinformatika. IV Poloha v prostoru
 Geoinformatika IV Poloha v prostoru jaro 2017 Petr Kubíček kubicek@geogr.muni.cz Laboratory on Geoinformatics and Cartography (LGC) Institute of Geography Masaryk University Czech Republic Složky geografických
Geoinformatika IV Poloha v prostoru jaro 2017 Petr Kubíček kubicek@geogr.muni.cz Laboratory on Geoinformatics and Cartography (LGC) Institute of Geography Masaryk University Czech Republic Složky geografických
Definice : Jsou li povrchové pímky kolmé k rovin, vzniká kolmá kruhová válcová plocha a pomocí roviny také kolmý kruhový válec.
 3. EZY NA VÁLCÍCH 3.1. VÁLCOVÁ PLOCHA, VÁLEC Definice : Je dána kružnice k ležící v rovin a pímka a rznobžná s rovinou. Všechny pímky rovnobžné s pímkou a protínající kružnici k tvoí kruhovou válcovou
3. EZY NA VÁLCÍCH 3.1. VÁLCOVÁ PLOCHA, VÁLEC Definice : Je dána kružnice k ležící v rovin a pímka a rznobžná s rovinou. Všechny pímky rovnobžné s pímkou a protínající kružnici k tvoí kruhovou válcovou
ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE. Matematika AA01. Cvičení, zimní semestr DOMÁCÍ ÚLOHY. Jan Šafařík
 Vysoké učení technické v Brně Stavební fakulta ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE Matematika AA0 Cvičení, zimní semestr DOMÁCÍ ÚLOHY Jan Šafařík Brno c 2005 () Jsou dány matice A = AB BA. [ AB BA
Vysoké učení technické v Brně Stavební fakulta ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE Matematika AA0 Cvičení, zimní semestr DOMÁCÍ ÚLOHY Jan Šafařík Brno c 2005 () Jsou dány matice A = AB BA. [ AB BA
Transformace dat mezi různými datovými zdroji
 Transformace dat mezi různými datovými zdroji Zpracovali: Datum prezentace: BUČKOVÁ Dagmar, BUC061 MINÁŘ Lukáš, MIN075 09. 04. 2008 Obsah Základní pojmy Souřadnicové systémy Co to jsou transformace Transformace
Transformace dat mezi různými datovými zdroji Zpracovali: Datum prezentace: BUČKOVÁ Dagmar, BUC061 MINÁŘ Lukáš, MIN075 09. 04. 2008 Obsah Základní pojmy Souřadnicové systémy Co to jsou transformace Transformace
MAPOVÁNÍ. Všeobecné základy map JS pro 2. ročník S2G 1. ročník G1Z
 MAPOVÁNÍ Všeobecné základy map JS pro 2. ročník S2G 1. ročník G1Z Všeobecné základy MAP Mapování řeší problém znázornění nepravidelného zemského povrchu do roviny Vychází se z: 1) geometrických základů
MAPOVÁNÍ Všeobecné základy map JS pro 2. ročník S2G 1. ročník G1Z Všeobecné základy MAP Mapování řeší problém znázornění nepravidelného zemského povrchu do roviny Vychází se z: 1) geometrických základů
GIS Geografické informační systémy. Daniela Ďuráková, Jan Gaura Katedra informatiky, FEI
 GIS Geografické informační systémy Daniela Ďuráková, Jan Gaura Katedra informatiky, FEI jan.gaura@vsb.cz http://mrl.cs.vsb.cz/people/gaura Kartografie Stojí na pomezí geografie a geodezie. Poskytuje vizualizaci
GIS Geografické informační systémy Daniela Ďuráková, Jan Gaura Katedra informatiky, FEI jan.gaura@vsb.cz http://mrl.cs.vsb.cz/people/gaura Kartografie Stojí na pomezí geografie a geodezie. Poskytuje vizualizaci
Geodézie Přednáška. Souřadnicové systémy Souřadnice na referenčních plochách
 Geodézie Přednáška Souřadnicové systémy Souřadnice na referenčních plochách strana 2 každý stát nebo skupina států si volí pro souvislé zobrazení celého území vhodný souřadnicový systém slouží k lokalizaci
Geodézie Přednáška Souřadnicové systémy Souřadnice na referenčních plochách strana 2 každý stát nebo skupina států si volí pro souvislé zobrazení celého území vhodný souřadnicový systém slouží k lokalizaci
KINEMATICKÁ GEOMETRIE V ROVIN
 KINEMATICKÁ GEOMETRIE V ROVIN Kivka je jednoparametrická množina bod X(t), jejíž souadnice jsou dány funkcemi: x = x(t), y = y(t), t I R. Tena kivky je urena bodem dotyku X a teným vektorem o souadnicích
KINEMATICKÁ GEOMETRIE V ROVIN Kivka je jednoparametrická množina bod X(t), jejíž souadnice jsou dány funkcemi: x = x(t), y = y(t), t I R. Tena kivky je urena bodem dotyku X a teným vektorem o souadnicích
Pro mapování na našem území bylo použito následujících souřadnicových systémů:
 SOUŘADNICOVÉ SYSTÉMY Pro mapování na našem území bylo použito následujících souřadnicových systémů: 1. SOUŘADNICOVÉ SYSTÉMY STABILNÍHO KATASTRU V první polovině 19. století bylo na našem území mapováno
SOUŘADNICOVÉ SYSTÉMY Pro mapování na našem území bylo použito následujících souřadnicových systémů: 1. SOUŘADNICOVÉ SYSTÉMY STABILNÍHO KATASTRU V první polovině 19. století bylo na našem území mapováno
Tisk Základních map R
 Tisk Základních map R ESKÉ VYSOKÉ UENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA MAPOVÁNÍ A KARTOGRAFIE Semestrální práce z pedmtu Kartografická polygrafie a reprografie Ve
Tisk Základních map R ESKÉ VYSOKÉ UENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA MAPOVÁNÍ A KARTOGRAFIE Semestrální práce z pedmtu Kartografická polygrafie a reprografie Ve
Souřadnicov. Cassini Soldnerovo zobrazení. Cassini-Soldnerovo. b) Evropský terestrický referenční systém m (ETRS), adnicové systémy
 Závazné referenční systémy dle 430/2006 Sb. Souřadnicov adnicové systémy na území Nařízen zení vlády o stanovení geodetických referenčních systémů a státn tních mapových děl d l závazných z na území státu
Závazné referenční systémy dle 430/2006 Sb. Souřadnicov adnicové systémy na území Nařízen zení vlády o stanovení geodetických referenčních systémů a státn tních mapových děl d l závazných z na území státu
Kartografické projekce
 GYMNÁZIUM CHRISTIANA DOPPLERA Zborovská 45, Praha 5 Ročníková práce z deskriptivní geometrie Kartografické projekce Vypracoval: Nguyen, Viet Bach, 4.C Školní rok: 2011/2012 Zadavatel: Mgr. Ondřej Machů
GYMNÁZIUM CHRISTIANA DOPPLERA Zborovská 45, Praha 5 Ročníková práce z deskriptivní geometrie Kartografické projekce Vypracoval: Nguyen, Viet Bach, 4.C Školní rok: 2011/2012 Zadavatel: Mgr. Ondřej Machů
Seminář z geoinformatiky
 Seminář z geoinformatiky Úvod Přednášející: Ing. M. Čábelka cabelka@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie PřF UK v Praze Úvod - Přednášející: Ing. Miroslav Čábelka, - rozsah hodin:
Seminář z geoinformatiky Úvod Přednášející: Ing. M. Čábelka cabelka@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie PřF UK v Praze Úvod - Přednášející: Ing. Miroslav Čábelka, - rozsah hodin:
K154SG01 Stavební geodézie
 K154SG01 Stavební geodézie Přednášející: Doc. Ing. Martin Štroner, Ph.D; Místnost: B912 Email: martin.stroner@fsv.cvut.cz Literatura: [1] Hánek, P. a kol.: Stavební geodézie. Česká technika -nakladatelství
K154SG01 Stavební geodézie Přednášející: Doc. Ing. Martin Štroner, Ph.D; Místnost: B912 Email: martin.stroner@fsv.cvut.cz Literatura: [1] Hánek, P. a kol.: Stavební geodézie. Česká technika -nakladatelství
Topografické mapování KMA/TOMA
 Topografické mapování KMA/TOMA ZÁPADOČESKÁ UNIVERZITA V PLZNI Fakulta aplikovaných věd - KMA oddělení geomatiky Ing. Martina Vichrová, Ph.D. vichrova@kma.zcu.cz Vytvoření materiálů bylo podpořeno prostředky
Topografické mapování KMA/TOMA ZÁPADOČESKÁ UNIVERZITA V PLZNI Fakulta aplikovaných věd - KMA oddělení geomatiky Ing. Martina Vichrová, Ph.D. vichrova@kma.zcu.cz Vytvoření materiálů bylo podpořeno prostředky
ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE. Matematika I/2 BA07. Cvičení, zimní semestr
 Vysoké učení technické v Brně Stavební fakulta ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE Matematika I/ BA07 Cvičení, zimní semestr DOMÁCÍ ÚLOHY Jan Šafařík Brno c 0 () Integrace užitím základních vzorců.
Vysoké učení technické v Brně Stavební fakulta ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE Matematika I/ BA07 Cvičení, zimní semestr DOMÁCÍ ÚLOHY Jan Šafařík Brno c 0 () Integrace užitím základních vzorců.
Zeměpisné souřadnice Zeměpisná šířka rovnoběžce poledníky Zeměpisná délka
 Zeměpisné souřadnice Pro určení polohy na zemském povrchu používáme souřadnicovou soustavu. Počátek souřadnic leží ve středu Země S. Rovina proložená středem Země kolmo na osu otáčení je rovina rovníku
Zeměpisné souřadnice Pro určení polohy na zemském povrchu používáme souřadnicovou soustavu. Počátek souřadnic leží ve středu Země S. Rovina proložená středem Země kolmo na osu otáčení je rovina rovníku
( ) ( ) 2 2 B A B A ( ) ( ) ( ) B A B A B A
 Vzdálenost dvou bod, sted úseky Ž Vzdálenost dvou bod Pi vyšetování vzájemné polohy bod, pímek a rovin lze použít libovolnou vhodn zvolenou soustavu souadnic (afinní). však pi vyšetování metrických vlastností
Vzdálenost dvou bod, sted úseky Ž Vzdálenost dvou bod Pi vyšetování vzájemné polohy bod, pímek a rovin lze použít libovolnou vhodn zvolenou soustavu souadnic (afinní). však pi vyšetování metrických vlastností
Maturitní témata z matematiky
 Maturitní témata z matematiky G y m n á z i u m J i h l a v a Výroky, množiny jednoduché výroky, pravdivostní hodnoty výroků, negace operace s výroky, složené výroky, tabulky pravdivostních hodnot důkazy
Maturitní témata z matematiky G y m n á z i u m J i h l a v a Výroky, množiny jednoduché výroky, pravdivostní hodnoty výroků, negace operace s výroky, složené výroky, tabulky pravdivostních hodnot důkazy
GEODETICKÉ VÝPOČTY I.
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 2.ročník GEODETICKÉ VÝPOČTY I. PRAVOÚHLÉ SOUŘADNICE V ČR ZOBRAZOVÁNÍ POLOHY BODŮ (SOUSTAVY) Soustavu souřadnic lze označit jako vzájemně jednoznačné
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 2.ročník GEODETICKÉ VÝPOČTY I. PRAVOÚHLÉ SOUŘADNICE V ČR ZOBRAZOVÁNÍ POLOHY BODŮ (SOUSTAVY) Soustavu souřadnic lze označit jako vzájemně jednoznačné
Výsledky úloh. 1. Úpravy výrazů + x 0, 2x 1 2 2, x Funkce. = f) a 2.8. ( ) ( ) 1.6. , klesající pro a ( 0, ) ), rostoucí pro s (, 1)
 Výsledky úloh. Úpravy výrazů.. +, + R.., a 0, a b.., a ± b, a b a b a +.. + a +, 0, a.., a 0; ± ; n + a.. a + b 9, > 0.7., a ± b a b m n.8., m 0, n 0, m n.9. a, a > 0 m + n.0., ;0; ;;.., k.. tg, k sin.
Výsledky úloh. Úpravy výrazů.. +, + R.., a 0, a b.., a ± b, a b a b a +.. + a +, 0, a.., a 0; ± ; n + a.. a + b 9, > 0.7., a ± b a b m n.8., m 0, n 0, m n.9. a, a > 0 m + n.0., ;0; ;;.., k.. tg, k sin.
4. Matematická kartografie
 4. Země má nepravidelný tvar, který je dán půsoením mnoha sil, zejména gravitační a odstředivé (vzhledem k rotaci Země). Odstředivá síla způsouje, že tvar Země je zploštělý, tj. zemský rovník je dále od
4. Země má nepravidelný tvar, který je dán půsoením mnoha sil, zejména gravitační a odstředivé (vzhledem k rotaci Země). Odstředivá síla způsouje, že tvar Země je zploštělý, tj. zemský rovník je dále od
REKONSTRUKCE ASTROLÁBU POMOCÍ STEREOGRAFICKÉ PROJEKCE
 REKONTRUKCE ATROLÁBU POMOCÍ TEREOGRAFICKÉ PROJEKCE Václav Jára 1 1 tereografická projekce a její vlastnosti tereografická projekce kulové plochy je středové promítání z bodu této kulové plochy do tečné
REKONTRUKCE ATROLÁBU POMOCÍ TEREOGRAFICKÉ PROJEKCE Václav Jára 1 1 tereografická projekce a její vlastnosti tereografická projekce kulové plochy je středové promítání z bodu této kulové plochy do tečné
! " # $ % # & ' ( ) * + ), -
 ! " # $ % # & ' ( ) * + ), - INDIVIDUÁLNÍ VÝUKA MATEMATIKA METODIKA Kuželosek Mgr. Petra Dunovská bezen 9 Obtížnost této kapitol matematik je dána tím, že se pi výkladu i ešení úloh komplexn vužívají vdomosti
! " # $ % # & ' ( ) * + ), - INDIVIDUÁLNÍ VÝUKA MATEMATIKA METODIKA Kuželosek Mgr. Petra Dunovská bezen 9 Obtížnost této kapitol matematik je dána tím, že se pi výkladu i ešení úloh komplexn vužívají vdomosti
ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE. Matematika I/1 BA06. Cvičení, zimní semestr
 Vysoké učení technické v Brně Stavební fakulta ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE Matematika I/1 BA06 Cvičení, zimní semestr DOMÁCÍ ÚLOHY Jan Šafařík Brno c 2014 1 (1) Určete rovnici kručnice o
Vysoké učení technické v Brně Stavební fakulta ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE Matematika I/1 BA06 Cvičení, zimní semestr DOMÁCÍ ÚLOHY Jan Šafařík Brno c 2014 1 (1) Určete rovnici kručnice o
Souřadnicové systémy Souřadnice na referenčních plochách
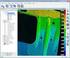 Geodézie přednáška 2 Souřadnicové systémy Souřadnice na referenčních plochách Ústav geoinformačních technologií Lesnická a dřevařská fakulta ugt.mendelu.cz tel.: 545134015 Souřadnicové systémy na území
Geodézie přednáška 2 Souřadnicové systémy Souřadnice na referenčních plochách Ústav geoinformačních technologií Lesnická a dřevařská fakulta ugt.mendelu.cz tel.: 545134015 Souřadnicové systémy na území
GYMNÁZIUM CHEB SEMINÁRNÍ PRÁCE
 GYMNÁZIUM CHEB SEMINÁRNÍ PRÁCE Relace Cheb, 006 Radek HÁJEK Prohlášení Prohlašuji, že jsem seminární práci na téma: Relace vypracoval zcela sám za použití pramen uvedených v piložené bibliograii na poítai
GYMNÁZIUM CHEB SEMINÁRNÍ PRÁCE Relace Cheb, 006 Radek HÁJEK Prohlášení Prohlašuji, že jsem seminární práci na téma: Relace vypracoval zcela sám za použití pramen uvedených v piložené bibliograii na poítai
GA06 Deskriptivní geometrie pro obor Geodézie a kartografie Úvod do kartografie.
 GA06 Deskriptivní geometrie pro obor Geodézie a kartografie Úvod do kartografie. Květoslava Prudilová Jan Šafařík přednášková skupina P-G1G1, učebna C311 zimní semestr 2018-2019 21. listopad 2018 Základní
GA06 Deskriptivní geometrie pro obor Geodézie a kartografie Úvod do kartografie. Květoslava Prudilová Jan Šafařík přednášková skupina P-G1G1, učebna C311 zimní semestr 2018-2019 21. listopad 2018 Základní
GEODETICKÉ VÝPOČTY I.
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 2.ročník GEODETICKÉ VÝPOČTY I. PRAVOÚHLÉ SOUŘADNICE V ČR ZOBRAZOVÁNÍ POLOHY BODŮ (SOUSTAVY) Soustavu souřadnic lze označit jako vzájemně jednoznačné
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 2.ročník GEODETICKÉ VÝPOČTY I. PRAVOÚHLÉ SOUŘADNICE V ČR ZOBRAZOVÁNÍ POLOHY BODŮ (SOUSTAVY) Soustavu souřadnic lze označit jako vzájemně jednoznačné
LEMOVÁNÍ I ZADÁNÍ: VUT - FSI, ÚST Odbor technologie tváení kov a plast
 Cviení. Jméno/skupina Speciální technologie tváení ZADÁNÍ: Vypoítejte energosilové parametry vyskytující se pi tváení souástí z plechu metodou lemování. Pro tváení souástí byl v pípad lemování otvor použit
Cviení. Jméno/skupina Speciální technologie tváení ZADÁNÍ: Vypoítejte energosilové parametry vyskytující se pi tváení souástí z plechu metodou lemování. Pro tváení souástí byl v pípad lemování otvor použit
Šroubový pohyb rovnoměrný pohyb složený z posunutí a rotace. Šroubovice dráha hmotného bodu při šroubovém pohybu
 ŠROUBOVICE Šroubový pohyb rovnoměrný pohyb složený z posunutí a rotace Šroubovice dráha hmotného bodu při šroubovém pohybu ZÁKLADNÍ POJMY osa šroubovice o nosná válcová plocha (r poloměr řídicí kružnice
ŠROUBOVICE Šroubový pohyb rovnoměrný pohyb složený z posunutí a rotace Šroubovice dráha hmotného bodu při šroubovém pohybu ZÁKLADNÍ POJMY osa šroubovice o nosná válcová plocha (r poloměr řídicí kružnice
JIHOČESKÁ UNIVERZITA V ČESKÝCH BUDĚJOVICÍCH ZEMĚDĚLSKÁ FAKULTA
 JIHOČESKÁ UNIVERZITA V ČESKÝCH BUDĚJOVICÍCH ZEMĚDĚLSKÁ FAKULTA Studijní program: Studijní obor: Zadávající katedra: Vedoucí katedry: B4106 Zemědělská specializace Pozemkové úpravy a převody nemovitostí
JIHOČESKÁ UNIVERZITA V ČESKÝCH BUDĚJOVICÍCH ZEMĚDĚLSKÁ FAKULTA Studijní program: Studijní obor: Zadávající katedra: Vedoucí katedry: B4106 Zemědělská specializace Pozemkové úpravy a převody nemovitostí
2. EZY NA JEHLANECH. Píklad 47 : Sestrojte ez pravidelného tybokého jehlanu ABCDV rovinou.
 2. EZY NA JEHLANECH Píklad 47 : Sestrojte ez pravidelného tybokého jehlanu ABCDV rovinou. Popis konstrukce : Podobn jako u píkladu 41 je výhodné proložit nkterými dvma hranami jehlanu rovinu kolmou k pdorysn.
2. EZY NA JEHLANECH Píklad 47 : Sestrojte ez pravidelného tybokého jehlanu ABCDV rovinou. Popis konstrukce : Podobn jako u píkladu 41 je výhodné proložit nkterými dvma hranami jehlanu rovinu kolmou k pdorysn.
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Vyšší geodézie 2 2/6 Transformace souřadnic z ETRF2000 do
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Vyšší geodézie 2 2/6 Transformace souřadnic z ETRF2000 do
Souřadnicové systémy v geodatech resortu ČÚZK a jejich transformace
 Souřadnicové systémy v geodatech resortu ČÚZK a jejich transformace Zeměměřický úřad, Jan Řezníček Praha, 2018 Definice matematická pravidla (rovnice) jednoznačné přidružení souřadnic k prostorovým informacím
Souřadnicové systémy v geodatech resortu ČÚZK a jejich transformace Zeměměřický úřad, Jan Řezníček Praha, 2018 Definice matematická pravidla (rovnice) jednoznačné přidružení souřadnic k prostorovým informacím
ANOTACE nově vytvořených/inovovaných materiálů
 ANOTACE nově vytvořených/inovovaných materiálů Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast CZ.1.07/1.5.00/34.1017 III/2 - Inovace a zkvalitnění výuky prostřednictvím ICT Analytická
ANOTACE nově vytvořených/inovovaných materiálů Číslo projektu Číslo a název šablony klíčové aktivity Tematická oblast CZ.1.07/1.5.00/34.1017 III/2 - Inovace a zkvalitnění výuky prostřednictvím ICT Analytická
Jihoeská univerzita v eských Budjovicích Pedagogická fakulta
 Jihoeská univerzita v eských Budjovicích Pedagogická fakulta Konstrukní úlohy ešené pomocí Cabri geometrie Miroslava Lutzová Finanní matematika 2001-2004 Vedoucí diplomové práce: Mgr. Pavel Leischner Most,
Jihoeská univerzita v eských Budjovicích Pedagogická fakulta Konstrukní úlohy ešené pomocí Cabri geometrie Miroslava Lutzová Finanní matematika 2001-2004 Vedoucí diplomové práce: Mgr. Pavel Leischner Most,
SOUŘADNICOVÉ SYSTÉMY. SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 3.ročník
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 3.ročník SOUŘADNICOVÉ SYSTÉMY GEOID, REFERENČNÍ ELIPSOID, REFERENČNÍ KOULE S JTSK S - 42 WGS 84 TRANSFORMACE SUŘADNICOVÝCH SYSTÉMŮ REFERENČNÍ SYSTÉMY
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 3.ročník SOUŘADNICOVÉ SYSTÉMY GEOID, REFERENČNÍ ELIPSOID, REFERENČNÍ KOULE S JTSK S - 42 WGS 84 TRANSFORMACE SUŘADNICOVÝCH SYSTÉMŮ REFERENČNÍ SYSTÉMY
Trojúhelníky. a jejich různé středy. Součet vnitřních úhlů trojúhelníku = 180 neboli π radiánů.
 Úvod V této knize předkládáme čtenáři základní matematické a fyzikální vzorce v přívětivé a snadno použitelné podobě. Využití čísel a symbolů k modelování, předpovídání a ovládání reality je mocnou zbraní
Úvod V této knize předkládáme čtenáři základní matematické a fyzikální vzorce v přívětivé a snadno použitelné podobě. Využití čísel a symbolů k modelování, předpovídání a ovládání reality je mocnou zbraní
L I C H O B Ž N Í K (2 HODINY) ? Co to vlastn lichobžník je? Podívej se napíklad na následující obrázky:
 L I C H O B Ž N Í K (2 HODINY)? Co to vlastn lichobžník je? Podívej se napíklad na následující obrázky: Na obrázcích je vyobrazena hospodáská budova a židlika, kterou urit mají tvoji rodie na chodb nebo
L I C H O B Ž N Í K (2 HODINY)? Co to vlastn lichobžník je? Podívej se napíklad na následující obrázky: Na obrázcích je vyobrazena hospodáská budova a židlika, kterou urit mají tvoji rodie na chodb nebo
TÍHOVÉ ZRYCHLENÍ TEORETICKÝ ÚVOD. 9, m s.
 TÍHOVÉ ZRYCHLENÍ TEORETICKÝ ÚVOD Soustavu souřadnic spojenou se Zemí můžeme považovat prakticky za inerciální. Jen při několika jevech vznikají odchylky, které lze vysvětlit vlastním pohybem Země vzhledem
TÍHOVÉ ZRYCHLENÍ TEORETICKÝ ÚVOD Soustavu souřadnic spojenou se Zemí můžeme považovat prakticky za inerciální. Jen při několika jevech vznikají odchylky, které lze vysvětlit vlastním pohybem Země vzhledem
Přednášející: Ing. M. Čábelka Katedra aplikované geoinformatiky a kartografie PřF UK v Praze
 Seminář z geoinformatiky Úvod do geodézie Seminář z geo oinform matiky Přednášející: Ing. M. Čábelka cabelka@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie PřF UK v Praze Úvod do geodézie
Seminář z geoinformatiky Úvod do geodézie Seminář z geo oinform matiky Přednášející: Ing. M. Čábelka cabelka@natur.cuni.cz Katedra aplikované geoinformatiky a kartografie PřF UK v Praze Úvod do geodézie
Základní topologické pojmy:
 Křivky Marie Ennemond Camille Jordan (88 9): Křivka je množina bodů, která je surjektivním obrazem nějakého intervalu Giuseppe Peano (858 9): Zobrazení intervalu na čtverec Wacław Franciszek Sierpiński
Křivky Marie Ennemond Camille Jordan (88 9): Křivka je množina bodů, která je surjektivním obrazem nějakého intervalu Giuseppe Peano (858 9): Zobrazení intervalu na čtverec Wacław Franciszek Sierpiński
Úvodní informace. 17. února 2018
 Úvodní informace Funkce více proměnných Přednáška první 17. února 2018 Obsah 1 Úvodní informace. 2 Funkce více proměnných Definiční obor Limita a spojitost Derivace, diferencovatelnost, diferenciál Úvodní
Úvodní informace Funkce více proměnných Přednáška první 17. února 2018 Obsah 1 Úvodní informace. 2 Funkce více proměnných Definiční obor Limita a spojitost Derivace, diferencovatelnost, diferenciál Úvodní
8 Plochy - vytvoření, rozdělení, tečná rovina a normála. Šroubové plochy - přímkové, cyklické. Literatura:
 8 Plochy - vytvoření, rozdělení, tečná rovina a normála. Šroubové plochy - přímkové, cyklické. Literatura: (1)Poláček, J., Doležal, M.: Základy deskriptivní a konstruktivní geometrie, díl 5, Křivky a plochy
8 Plochy - vytvoření, rozdělení, tečná rovina a normála. Šroubové plochy - přímkové, cyklické. Literatura: (1)Poláček, J., Doležal, M.: Základy deskriptivní a konstruktivní geometrie, díl 5, Křivky a plochy
OSTRAVSKÁ UNIVERZITA P Ř ÍRODOVĚ DECKÁ FAKULTA ÚVOD DO KARTOGRAFIE LUDĚ K KRTIČ KA
 OSTRAVSKÁ UNIVERZITA P Ř ÍRODOVĚ DECKÁ FAKULTA ÚVOD DO KARTOGRAFIE LUDĚ K KRTIČ KA OSTRAVA 2007 2 Název: Úvod do kartografie Autor: Mgr. Luděk Krtička Vydání: první, 2007 Počet stran: 87 Recenzovali: Ing.
OSTRAVSKÁ UNIVERZITA P Ř ÍRODOVĚ DECKÁ FAKULTA ÚVOD DO KARTOGRAFIE LUDĚ K KRTIČ KA OSTRAVA 2007 2 Název: Úvod do kartografie Autor: Mgr. Luděk Krtička Vydání: první, 2007 Počet stran: 87 Recenzovali: Ing.
Matematické metody v kartografii
 Mtemtické metody v krtogrfii. Přednášk Referenční elipsoid zákldní vzthy. Poloměry křivosti. Délky poledníkového rovnoběžkového oblouku. 1. Zákldní vzthy n rotčním elipoidu Rotční elipsoid dán následujícími
Mtemtické metody v krtogrfii. Přednášk Referenční elipsoid zákldní vzthy. Poloměry křivosti. Délky poledníkového rovnoběžkového oblouku. 1. Zákldní vzthy n rotčním elipoidu Rotční elipsoid dán následujícími
System Projection Aplikace pro souřadnicové přepočty a základní geodetické úlohy (Uživatelský manuál) Jan Ježek, Radek Sklenička červen 2004
 System Projection Aplikace pro souřadnicové přepočty a základní geodetické úlohy (Uživatelský manuál) Jan Ježek, Radek Sklenička červen 2004 1 Obsah Úvod 3 1 Základní ovládání 4 1.1 Výběr zobrazení a jeho
System Projection Aplikace pro souřadnicové přepočty a základní geodetické úlohy (Uživatelský manuál) Jan Ježek, Radek Sklenička červen 2004 1 Obsah Úvod 3 1 Základní ovládání 4 1.1 Výběr zobrazení a jeho
Prbh funkce Jaroslav Reichl, 2006
 rbh funkce Jaroslav Reichl, 6 Vyšetování prbhu funkce V tomto tetu je vzorov vyešeno nkolik úloh na vyšetení prbhu funkce. i ešení úlohy jsou využity základní vlastnosti diferenciálního potu.. ešený píklad
rbh funkce Jaroslav Reichl, 6 Vyšetování prbhu funkce V tomto tetu je vzorov vyešeno nkolik úloh na vyšetení prbhu funkce. i ešení úlohy jsou využity základní vlastnosti diferenciálního potu.. ešený píklad
Matematika vzorce. Ing. Petr Šídlo. verze
 Matematika vzorce Ing. Petr Šídlo verze 0050409 Obsah Jazyk matematiky 3. Výrokový počet.......................... 3.. Logické spojky...................... 3.. Tautologie výrokového počtu...............
Matematika vzorce Ing. Petr Šídlo verze 0050409 Obsah Jazyk matematiky 3. Výrokový počet.......................... 3.. Logické spojky...................... 3.. Tautologie výrokového počtu...............
Ing. Jiří Fejfar, Ph.D. Souřadné systémy
 Ing. Jiří Fejfar, Ph.D. Souřadné systémy SRS (Spatial reference system) CRS (Coordinate Reference system) Kapitola 1: Základní pojmy Základní prostorové pojmy Geografický prostor Prostorové vztahy (geometrie,
Ing. Jiří Fejfar, Ph.D. Souřadné systémy SRS (Spatial reference system) CRS (Coordinate Reference system) Kapitola 1: Základní pojmy Základní prostorové pojmy Geografický prostor Prostorové vztahy (geometrie,
Obsah a průběh zkoušky 1PG
 Obsah a průběh zkoušky PG Zkouška se skládá z písemné a ústní části. Písemná část (cca 6 minut) dvě konstrukční úlohy dle části po. bodech a jedna úloha výpočetní úloha dle části za bodů. Ústní část jedna
Obsah a průběh zkoušky PG Zkouška se skládá z písemné a ústní části. Písemná část (cca 6 minut) dvě konstrukční úlohy dle části po. bodech a jedna úloha výpočetní úloha dle části za bodů. Ústní část jedna
KMA/G2 Geometrie 2 9. až 11. cvičení
 KMA/G2 Geometrie 2 9. až 11. cvičení 1. Rozhodněte, zda kuželosečka k je regulární nebo singulární: a) k : x 2 0 + 2x 0x 1 x 0 x 2 + x 2 1 2x 1x 2 + x 2 2 = 0; b) k : x 2 0 + x2 1 + x2 2 + 2x 0x 1 = 0;
KMA/G2 Geometrie 2 9. až 11. cvičení 1. Rozhodněte, zda kuželosečka k je regulární nebo singulární: a) k : x 2 0 + 2x 0x 1 x 0 x 2 + x 2 1 2x 1x 2 + x 2 2 = 0; b) k : x 2 0 + x2 1 + x2 2 + 2x 0x 1 = 0;
