Hartreeho-Fockova metoda (HF)
|
|
|
- Ludvík Bartoš
- před 6 lety
- Počet zobrazení:
Transkript
1 Staonární Shrödngerova rovne H Ψ = EΨ Metoda konfgurační nterake Metoda vázanýh klastrů Poruhová teore Zahrnutí el. korelae Bornova-Oppenhemerova aproxmae Model nezávslýh elektronů Vlnová funke ve tvaru Slaterova determnantu MO LCAO + varační prnp Hartreeho-Fokova metoda (HF) Separae σ-π Neemprké π-elektronové metody Zanedbání některýh ntegrálů Emprké parametry Sememprké π-elektronové metody Zanedbání elektronové repulse Hükelova metoda MO Zanedbání některýh ntegrálů Emprké parametry Sememprké metody (NDO, AM1, PM3) Metoda EHT Zanedbání elektronové repulse Separae σ-π
2 Aproxmae vedouí k HMO Bornova-Oppenhemerova aproxmae Model nenteragujííh elektronů úplné zanedbání elektronové repulse H = h E = ε Ψ( 1, 2,..., N ) = ϕ( ) MO LCAO aproxmae ϕ = µ µ χ µ Separae σ-π: báze AO je tvořena pouze p z atomovým orbtaly na uhlíku Využtí varačního prnpu energ vyjádříme jako funk rozvojovýh koef. μ - Vzhledem k úplnému zanedbání elektronové repulse vede varační prnp jednoduše na systém sekulárníh rovn: Překryvový ntegrál S = χ χ dτ = δ µν µ ν µν... 1 pro μ=ν... 0 pro μ ν H = χ h χ dτ µν µ ν... α pro μ=ν... Coulombký nt.... β pro μ ν... Rezonanční nt. (pouze pro atomy spojené vazbou) ( H ε S ) + ( H ε S ) ( H ε S ) = n 1n 1n ( H ε S ) + ( H ε S ) ( H ε S ) = n 2n 2n... ( H ε S ) + ( H ε S ) ( H ε S ) = 0 1 n1 n n2 n2 n nn nn Žádné ntegály se nemusí v rám HMO počítat! Dosadíme do sekulárníh rovn.
3 Symetre a její využtí v HMO Operae symetre převede systém do stavu nerozlštelného od původního stavu Operae symetre Prvek symetre Žádná změna Identta Zradlení v rovně Rovna symetre σ Rotae podél n-četné osy n-četná rotační osa C n Inverze Inverzní entrum Příklad: obdélník Například Rovna σ xy σ xy σˆ xy 4 3 =
4 Jestlže systém má určtý prvek symetre, pak vlnová funke popsujíí tento systém musí být vlastní funkí příslušného operátoru symetre => MO musí být vlastní funkí opeátou symetre => Působením operátoru musíme získat tutéž funk vynásobenou konstantou => Tato konstanta konstanta může být pouze ±1 Vlnová funke symetrká S (vzhledem k příslušné opera symetre) Vlnová funke antsymetrká A 4 3 σ xy ϕ = 1χ1+ 2χ2 + 3χ3 + 4χ4 ˆ xy = ± σ ϕ ϕ Oˆ ϕ = ϕ Oˆ ϕ = ϕ ˆ σ xy ϕ = χ + χ + χ + χ = = ˆ σ xy ϕ = χ χ χ χ = =
5 HMO pro systémy s heteroatomy HMO lze použít pro systémy, které obsahují heterotaomy v konjuga s π-elektrony uhlíkového skeletu. V případě čstě uhlíkovýh konjugovanýh systémů jsme pro ntegrály v sekulárníh rovníh použly: ˆ ef χ H χ = H = α = α µ µ µµ ˆ ef χ H χ = H = β = β µ ν µν α má význam onzačního potenálu v 2p z AO uhlíku Podobně zavedeme pro ostatní elementy α X v závslost na jejh elektronegatvtě: αx = αc + hxβ h < h < h ( pyrdn) < h ( keton) < h B C N O Cl C CC Podobně zavedeme parametry β xy odpovídajíí síle vazby. Například C=N vazba v pyrdnu je zhurba stejná jako C=C vazba v benzenu. C-N vazba v anlnu je ale určtě slabší, tudíž β CN <1. β XY = kxy β
6 HMO metoda rozšířená na systémy s heteroatomy Coulombké ntegrály: α X = α C + h X β Resonanční ntegrály: β XY = k XY β CC Atom Příklad h X (β) Vazba k XY B borazol -1 B=N, B=C 0.7 C naftalen, 0 C=C 1 C hexatren 0 C=C 1.1 N pyrdn 0,5 C=N 1 N pyrdnoný katon 2,0 C=N+ 1 N pyrol, anln 1,5 C-N 0,8 N ntrl 0,5 C N 1,4 N ntrobenzen 2,0 C=N 0,8 N=O 0,7 O keton 1,0 C=O, C O - 1,0 O furan 2,0 C O 0,8 S thoketon 0,5 C=S 0,9 S thofen, thofenol 1,0 C S 0,7 F fluorbenzen 3 C F 0,7 Cl hlorbenzen 2 C Cl 0,4 Br brombenzen 1,5 C Br 0,3 I jodbenzen 1,3 C I 0,25
7 Využtí HMO Celková π-elektronová energe: q p µ = W = Delokalzační energe: DE = W m.w Et π-elektronové hustoty: Řády vazeb: Volná valene: µν = nµ n ε n µ ν F N p = µ max µν (Pro uhlík ) 3 π-elektronové náboje na atomeh elektroflní substtue (př. Pyrdn má tyto 0.950, a v poloháh para, meta a orto. Fotohemké reake jde pouze o změnu obsazovaíh čísel. Radkálová substtue určená volnou valení
8 Konstruke HMO s využtím symetre Vlastní funke Hamltonánu musí respektovat symetr systému. Vlastní funke Hamltonánu lze vzít jako báz reprezentae grupy. Je třeba konstruovat symetrky adaptované orbtaly. ϕ ˆ dr = P p = χ ( RO ) ˆ p g r r r z R z R Dmenze r Řád grupy p z atomový orbtal Operátor symetre Charakter operae symetre R pro r χ
9 Charater table for D 6h pont group E 2C 6 2C 3 C 2 3C' 2 3C'' 2 2S 3 2S 6 σ h 3σ d 3σ v Lnear, rotatons Quadrat A 1g x 2 +y 2, z 2 A 2g R z B 1g B 2g E 1g (R x, R y ) (xz, yz) E 2g (x 2 -y 2, xy) A 1u A 2u z B 1u B 2u E 1u (x, y) E 2u Charater table for C 6v pont group E 2C 6 (z) 2C 3 (z) C 2 (z) 3σ v 3σ d lnear, rotatons quadrat A z x 2 +y 2, z 2 A R z B B E (x, y) (R x, R y ) (xz, yz) E (x 2 -y 2, xy)
Lambertův-Beerův zákon
 Lambertův-Beerův zákon Intenzta záření po průchodu kavtou se vzorkem: Integrovaný absorpční koecent: I nal = I ntal e ε c L A = ε ( ~ ν ) d~ ν Bezjednotková včna síla osclátoru: v cm -1 = 4.3 10 9 A Síla
Lambertův-Beerův zákon Intenzta záření po průchodu kavtou se vzorkem: Integrovaný absorpční koecent: I nal = I ntal e ε c L A = ε ( ~ ν ) d~ ν Bezjednotková včna síla osclátoru: v cm -1 = 4.3 10 9 A Síla
Molekuly. w konstrukce zkusmé funkce ve tvaru LCAO. atomový orbital - známe. rozvojový koeficient neznáme - počítáme
 Zdroje w Zdroje nejsou důsledně továny, za ož se hluboe omlouvám w Některé zdroje w L. Pela: Ideas of Quantum Chemstry w Gaussan: WhtePages w do. P. Nahtgall přednášky z podzmní školy w do. P. Jurečka
Zdroje w Zdroje nejsou důsledně továny, za ož se hluboe omlouvám w Některé zdroje w L. Pela: Ideas of Quantum Chemstry w Gaussan: WhtePages w do. P. Nahtgall přednášky z podzmní školy w do. P. Jurečka
Ab initio výpočty v chemii a biochemii
 Ab initio výpočty v chemii a biochemii Doc. RNDr. Ing. Jaroslav Burda, CSc., jaroslav.burda@mff.cuni.cz Dr. Vladimír Sychrovský vladimir.sychrovsky@uochb.cas.cz Studijní literatura Szabo A., Ostlund N.S.
Ab initio výpočty v chemii a biochemii Doc. RNDr. Ing. Jaroslav Burda, CSc., jaroslav.burda@mff.cuni.cz Dr. Vladimír Sychrovský vladimir.sychrovsky@uochb.cas.cz Studijní literatura Szabo A., Ostlund N.S.
Překryv orbitalů. Vznik vazby překryvem orbitalů na dvou různých atomech A, B Obsazeno dvojicí elektronů Ψ = Ψ A Ψ Β
 Překryv orbitalů Vznik vazby překryvem orbitalů na dvou různých atomech A, B Obsazeno dvojicí elektronů Ψ = Ψ A Ψ Β Podmínky překryvu: Vhodná symetrie, znaménko vlnové funkce Vhodná energie, srovnatelná,
Překryv orbitalů Vznik vazby překryvem orbitalů na dvou různých atomech A, B Obsazeno dvojicí elektronů Ψ = Ψ A Ψ Β Podmínky překryvu: Vhodná symetrie, znaménko vlnové funkce Vhodná energie, srovnatelná,
Hartre-Fock method (HF)
 Cofgurato Iteracto (CI) Coupled Clusters (CC) Perturbato Theory (PT, MP) Electro correlato H Ψ = EΨ Bor-Oppehemer approxmato Model of depedet electros Product wave fucto (Slater determat) MO LCAO Hartre-Fock
Cofgurato Iteracto (CI) Coupled Clusters (CC) Perturbato Theory (PT, MP) Electro correlato H Ψ = EΨ Bor-Oppehemer approxmato Model of depedet electros Product wave fucto (Slater determat) MO LCAO Hartre-Fock
ÚVOD DO KVANTOVÉ CHEMIE
 ÚVOD DO KVANTOVÉ CHEME. Navození kvantové mechanky Postuláty kvantové mechanky, základy operátorové algebry, navození kvantové mechanky, jednoduché modely.. Vodíkový atom 3. Základní aproxmace používané
ÚVOD DO KVANTOVÉ CHEME. Navození kvantové mechanky Postuláty kvantové mechanky, základy operátorové algebry, navození kvantové mechanky, jednoduché modely.. Vodíkový atom 3. Základní aproxmace používané
Symetrie Platonovská tělesa
 Symetrie Platonovská tělesa 1 Symetrie Virus rýmy Virus obrny Virus slintavky a kulhavky 2 Symetrie molekul Jak jsou atomy v molekule uspořádány = ekvivalentní atomy 3 Prvky a operace symetrie Značka Prvek
Symetrie Platonovská tělesa 1 Symetrie Virus rýmy Virus obrny Virus slintavky a kulhavky 2 Symetrie molekul Jak jsou atomy v molekule uspořádány = ekvivalentní atomy 3 Prvky a operace symetrie Značka Prvek
Symetrie Platonovská tělesa
 Symetrie Platonovská tělesa 1 Symetrie Virus rýmy Virus obrny Virus slintavky a kulhavky 2 Symetrie molekul Jak jsou atomy v molekule uspořádány = ekvivalentní atomy 3 Prvky a operace symetrie Značk a
Symetrie Platonovská tělesa 1 Symetrie Virus rýmy Virus obrny Virus slintavky a kulhavky 2 Symetrie molekul Jak jsou atomy v molekule uspořádány = ekvivalentní atomy 3 Prvky a operace symetrie Značk a
 !!! #!! # % & ()!+ %& #( ) +,,!,!!./0./01 2 34 % 00 (1!#! #! #23 + )!!,,5,!+ 4)!005!! 6 )! %,76!,8, )! 44 %!! #! #236!!1 1 5 6 5+!!1 ( 9 9!5 6 + /+ # % 7 8 % : 4; 2,/! = %
!!! #!! # % & ()!+ %& #( ) +,,!,!!./0./01 2 34 % 00 (1!#! #! #23 + )!!,,5,!+ 4)!005!! 6 )! %,76!,8, )! 44 %!! #! #236!!1 1 5 6 5+!!1 ( 9 9!5 6 + /+ # % 7 8 % : 4; 2,/! = %
Atom vodíku. Nejjednodušší soustava: p + e Řešitelná exaktně. Kulová symetrie. Potenciální energie mezi p + e. e =
 Atom vodíku Nejjednodušší soustava: p + e Řešitelná exaktně Kulová symetrie Potenciální energie mezi p + e V 2 e = 4πε r 0 1 Polární souřadnice využití kulové symetrie atomu Ψ(x,y,z) Ψ(r,θ, φ) x =? y=?
Atom vodíku Nejjednodušší soustava: p + e Řešitelná exaktně Kulová symetrie Potenciální energie mezi p + e V 2 e = 4πε r 0 1 Polární souřadnice využití kulové symetrie atomu Ψ(x,y,z) Ψ(r,θ, φ) x =? y=?
Molekulová vibrace dvojatomové molekuly. Disociační křivka dvojatomové molekuly
 Molekulová vbrace dvojatomové molekuly Dsocační křvka dvojatomové molekuly x Potencální energe, E Repulsvní síly x Přtažlvé síly síly x Pro malé odchylky [(x-x ) ] možno aproxmovat parabolou, jak plyne
Molekulová vbrace dvojatomové molekuly Dsocační křvka dvojatomové molekuly x Potencální energe, E Repulsvní síly x Přtažlvé síly síly x Pro malé odchylky [(x-x ) ] možno aproxmovat parabolou, jak plyne
Operátory a maticové elementy
 Operátory a matice Operátory a maticové elementy operátory je výhodné reprezentovat maticemi maticové elementy operátorů jsou dány vztahy mezi Slaterovými determinanty obsahujícími ortonormální orbitaly
Operátory a matice Operátory a maticové elementy operátory je výhodné reprezentovat maticemi maticové elementy operátorů jsou dány vztahy mezi Slaterovými determinanty obsahujícími ortonormální orbitaly
17 Vlastnosti molekul
 17 Vlastnosti molekul Experimentálně molekuly charakterizujeme pomocí nejrůznějších vlastností: můžeme změřit třeba NMR posuny, elektrické či magnetické parametry či třeba jejich optickou otáčivost. Tyto
17 Vlastnosti molekul Experimentálně molekuly charakterizujeme pomocí nejrůznějších vlastností: můžeme změřit třeba NMR posuny, elektrické či magnetické parametry či třeba jejich optickou otáčivost. Tyto
Mul$determinantální metody: CASSCF
 Mul$determinantální metody: CASSCF Mul%konfiguračni (mnohadeterninantálni MC SCF) metody použivají narozdíl od metody Hartreeho- Focka pro popis N- elektronového systému větší počet Slaterových determinantů.
Mul$determinantální metody: CASSCF Mul%konfiguračni (mnohadeterninantálni MC SCF) metody použivají narozdíl od metody Hartreeho- Focka pro popis N- elektronového systému větší počet Slaterových determinantů.
11 Kvantová teorie molekul
 11 Kvantová teore molekul Pops molekul v rámc kvantové teore je ústředním tématem kvantové cheme. Na rozdíl od atomů nejsou molekuly centrálně symetrcké, což výpočty jejch vlastností komplkuje. V důsledku
11 Kvantová teore molekul Pops molekul v rámc kvantové teore je ústředním tématem kvantové cheme. Na rozdíl od atomů nejsou molekuly centrálně symetrcké, což výpočty jejch vlastností komplkuje. V důsledku
16 Semiempirické přístupy
 16 Semiempirické přístupy V této kapitole se podíváme na skupinu semiempirických metod. Ačkoli semiempirické metody také vycházejí z řešení elektronové Schrödingerovy rovnice, jejich rovnice obsahují dodatečné
16 Semiempirické přístupy V této kapitole se podíváme na skupinu semiempirických metod. Ačkoli semiempirické metody také vycházejí z řešení elektronové Schrödingerovy rovnice, jejich rovnice obsahují dodatečné
METODY VÝPOČETNÍ CHEMIE
 METODY VÝPOČETNÍ CHEMIE Metody výpočetní chemie Ab initio metody Semiempirické metody Molekulová mechanika Molekulová simulace Ab initio metody Ab initio - od počátku Metody kvantově-mechanické vycházejí
METODY VÝPOČETNÍ CHEMIE Metody výpočetní chemie Ab initio metody Semiempirické metody Molekulová mechanika Molekulová simulace Ab initio metody Ab initio - od počátku Metody kvantově-mechanické vycházejí
Teorie Molekulových Orbitalů (MO)
 Teorie Molekulových Orbitalů (MO) Kombinace atomových orbitalů na všech atomech v molekule Vhodná symetrie Vhodná (podobná) energie Z n AO vytvoříme n MO Pro začátek dvouatomové molekuly: H 2, F 2, CO,...
Teorie Molekulových Orbitalů (MO) Kombinace atomových orbitalů na všech atomech v molekule Vhodná symetrie Vhodná (podobná) energie Z n AO vytvoříme n MO Pro začátek dvouatomové molekuly: H 2, F 2, CO,...
VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE FAKULTA INFORMATIKY A STATISTIKY Katedra statistiky a pravděpodobnosti STATISTIKA VZORCE PRO 4ST201
 VYOKÁ ŠKOLA EKONOMICKÁ V RAZE FAKULTA INFORMATIKY A TATITIKY Kaedra a a ravděodobo TATITIKA VZORCE RO 4T verze.3 oledí aualzace: 4.9.9 KT 9 oá aa,,..., ɶ < z < + < z < + +,5 z +, 5 z H H H G... G... R
VYOKÁ ŠKOLA EKONOMICKÁ V RAZE FAKULTA INFORMATIKY A TATITIKY Kaedra a a ravděodobo TATITIKA VZORCE RO 4T verze.3 oledí aualzace: 4.9.9 KT 9 oá aa,,..., ɶ < z < + < z < + +,5 z +, 5 z H H H G... G... R
Born-Oppenheimerova aproximace
 Born-Oppenheimerova aproximace Oddělení elektronického a jaderného pohybu Jádra 2000 x těžší než elektrony elektrony kvantová chemie, popis systému (do 100 atomů) na základě vlastností elektronů (jádra
Born-Oppenheimerova aproximace Oddělení elektronického a jaderného pohybu Jádra 2000 x těžší než elektrony elektrony kvantová chemie, popis systému (do 100 atomů) na základě vlastností elektronů (jádra
Atomové a molekulové orbitaly Ion molekuly vodíku. Molekula vodíku Heitler-Londonovou metodou. Metoda LCAO. Báze atomových orbitalů.
 Atomové a molekulové orbitaly Ion molekuly vodíku. Molekula vodíku Heitler-Londonovou metodou. Metoda LCAO. Báze atomových orbitalů. Ion molekuly vodíku H + 2 První použití metody je demonstrováno při
Atomové a molekulové orbitaly Ion molekuly vodíku. Molekula vodíku Heitler-Londonovou metodou. Metoda LCAO. Báze atomových orbitalů. Ion molekuly vodíku H + 2 První použití metody je demonstrováno při
elektrony v pevné látce verze 1. prosince 2016
 F6122 Základy fyziky pevných látek seminář elektrony v pevné látce verze 1. prosince 2016 1 Drudeho model volných elektronů 1 1.1 Mathiessenovo pravidlo............................................... 1
F6122 Základy fyziky pevných látek seminář elektrony v pevné látce verze 1. prosince 2016 1 Drudeho model volných elektronů 1 1.1 Mathiessenovo pravidlo............................................... 1
Modelové výpočty na H 2 a HeH +
 Modelové výpočty na H 2 a HeH + Minimální báze Všechny teoretické poznatky je užitečné ilustrovat modelovým výpočtem. Budeme aplikovat Hartree-Fockovy výpočty na uzavřených slupkách systémů H 2 a HeH +.
Modelové výpočty na H 2 a HeH + Minimální báze Všechny teoretické poznatky je užitečné ilustrovat modelovým výpočtem. Budeme aplikovat Hartree-Fockovy výpočty na uzavřených slupkách systémů H 2 a HeH +.
Dvě varianty rovinného problému: rovinná napjatost. rovinná deformace
 Rovinný problém Řešíme plošné konstrukce zatížené a uložené v jejich střednicové rovině. Dvě varianty rovinného problému: rovinná napjatost rovinná deformace 17 Rovinná deformace 1 Obsahuje složky deformace
Rovinný problém Řešíme plošné konstrukce zatížené a uložené v jejich střednicové rovině. Dvě varianty rovinného problému: rovinná napjatost rovinná deformace 17 Rovinná deformace 1 Obsahuje složky deformace
Korelační energie. Celkovou elektronovou energii molekuly lze experimentálně určit ze vztahu. E vib. = E at. = 39,856, E d
 Korelační energe Referenční stavy Energ molekul a atomů lze vyjádřt vzhledem k různým referenčním stavům. V kvantové mechance za referenční stav s nulovou energí bereme stav odpovídající nenteragujícím
Korelační energe Referenční stavy Energ molekul a atomů lze vyjádřt vzhledem k různým referenčním stavům. V kvantové mechance za referenční stav s nulovou energí bereme stav odpovídající nenteragujícím
John Dalton Amadeo Avogadro
 Spojením atomů vznikají molekuly... John Dalton 1766 1844 Amadeo Avogadro 1776 1856 Výpočet molekuly 2, metoda valenční vazby Walter eitler 1904 1981 Fritz W. London 1900 1954 Teorie molekulových orbitalů
Spojením atomů vznikají molekuly... John Dalton 1766 1844 Amadeo Avogadro 1776 1856 Výpočet molekuly 2, metoda valenční vazby Walter eitler 1904 1981 Fritz W. London 1900 1954 Teorie molekulových orbitalů
13 Elektronová struktura molekul
 13 Elektronová struktura molekul Ústředním úkolem kvantové chemie po zavedení Bornovy-Oppenheimerovy aproximace je výpočet elektronové energie molekul Ĥ e ψ e ( r, R) = E e ( R)ψ e ( r, R), (13.1) kde
13 Elektronová struktura molekul Ústředním úkolem kvantové chemie po zavedení Bornovy-Oppenheimerovy aproximace je výpočet elektronové energie molekul Ĥ e ψ e ( r, R) = E e ( R)ψ e ( r, R), (13.1) kde
VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE FAKULTA INFORMATIKY A STATISTIKY Katedra statistiky a pravděpodobnosti STATISTIKA VZORCE PRO 4ST201
 VYOKÁ ŠKOLA EKONOMICKÁ V RAZE FAKULTA INFORMATIKY A TATITIKY Kaedra a a ravděodobo TATITIKA VZORCE RO 4T verze. oledí aalzace:.9.8 KT 8 oá aa,,..., % z z,5 z, 5 z H H H G... G... R ma - m ( ( ( ( ( ( V
VYOKÁ ŠKOLA EKONOMICKÁ V RAZE FAKULTA INFORMATIKY A TATITIKY Kaedra a a ravděodobo TATITIKA VZORCE RO 4T verze. oledí aalzace:.9.8 KT 8 oá aa,,..., % z z,5 z, 5 z H H H G... G... R ma - m ( ( ( ( ( ( V
Laserová technika prosince Katedra fyzikální elektroniky.
 Laserová technika 1 Aktivní prostředí Šíření rezonančního záření dvouhladinovým prostředím Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 22. prosince 2016 Program
Laserová technika 1 Aktivní prostředí Šíření rezonančního záření dvouhladinovým prostředím Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 22. prosince 2016 Program
Kvantová teorie elementární základy
 Kvtová teore elemetárí zákldy Toy Hey, Ptrk Wlters Nový kvtový vesmír Překld Mrt Žofk, váz. s přeblem, 43 str, ISBN 8-7363--, řd zp Co byste měl zát l Zářeí čerého těles by Jeff Juste https://www.youtube.om/plylst?
Kvtová teore elemetárí zákldy Toy Hey, Ptrk Wlters Nový kvtový vesmír Překld Mrt Žofk, váz. s přeblem, 43 str, ISBN 8-7363--, řd zp Co byste měl zát l Zářeí čerého těles by Jeff Juste https://www.youtube.om/plylst?
ρ = 0 (nepřítomnost volných nábojů)
 Učební text k přednášce UFY Světlo v izotropním látkovém prostředí Maxwellovy rovnice v izotropním látkovém prostředí: B rot + D rot H ( r, t) div D ρ rt, ( ) div B a materiálové vztahy D ε pro dielektrika
Učební text k přednášce UFY Světlo v izotropním látkovém prostředí Maxwellovy rovnice v izotropním látkovém prostředí: B rot + D rot H ( r, t) div D ρ rt, ( ) div B a materiálové vztahy D ε pro dielektrika
Orbitaly, VSEPR 1 / 18
 rbitaly, VSEPR Rezonanční struktury, atomové a molekulové orbitaly, hybridizace, určování tvaru molekuly pomocí teorie VSEPR, úvod do symetrie molekul, dipólový moment 1 / 18 Formální náboj Rozdíl mezi
rbitaly, VSEPR Rezonanční struktury, atomové a molekulové orbitaly, hybridizace, určování tvaru molekuly pomocí teorie VSEPR, úvod do symetrie molekul, dipólový moment 1 / 18 Formální náboj Rozdíl mezi
Přednáška IX: Elektronová spektroskopie II.
 Přednáška IX: Elektronová spektroskopie II. 1 Försterův resonanční přenos energie Pravděpodobnost (rychlost) přenosu je určená jako: k ret 1 = τ 0 D R r 0 6 0 τ D R 0 r Doba života donoru v excitovaném
Přednáška IX: Elektronová spektroskopie II. 1 Försterův resonanční přenos energie Pravděpodobnost (rychlost) přenosu je určená jako: k ret 1 = τ 0 D R r 0 6 0 τ D R 0 r Doba života donoru v excitovaném
Hartreeho-Fockova metoda (HF)
 Stacionární Schrödingerova rovnice H Ψ = EΨ Metoda konfigurační interakce Metoda vázaných klastrů Poruchová teorie Zahrnutí el. korelace Bornova-Oppenheimerova aproximace Model nezávislých elektronů Vlnová
Stacionární Schrödingerova rovnice H Ψ = EΨ Metoda konfigurační interakce Metoda vázaných klastrů Poruchová teorie Zahrnutí el. korelace Bornova-Oppenheimerova aproximace Model nezávislých elektronů Vlnová
Orbitaly, VSEPR. Zdeněk Moravec, 16. listopadu / 21
 rbitaly, VSEPR Rezonanční struktury, atomové a molekulové orbitaly, hybridizace, určování tvaru molekuly pomocí teorie VSEPR, úvod do symetrie molekul, dipólový moment Zdeněk Moravec, http://z-moravec.net
rbitaly, VSEPR Rezonanční struktury, atomové a molekulové orbitaly, hybridizace, určování tvaru molekuly pomocí teorie VSEPR, úvod do symetrie molekul, dipólový moment Zdeněk Moravec, http://z-moravec.net
Úvod do parciálních diferenciálních rovnic. 2 Kanonický tvar lineárních PDR 2. řádu pro funkce
 Příklady na cvičení k přednášce NMMA334 Úvod do parciálních diferenciálních rovnic 1 Kanonický tvar lineárních PDR 2. řádu pro funkce dvou proměnných 1. Určete typ parciální diferenciální rovnice u xx
Příklady na cvičení k přednášce NMMA334 Úvod do parciálních diferenciálních rovnic 1 Kanonický tvar lineárních PDR 2. řádu pro funkce dvou proměnných 1. Určete typ parciální diferenciální rovnice u xx
Přehled Ab Initio a semiempirických metod
 Přehled Ab Initio a semiempirických metod Pokud se vám bude zdát, že je v tom nějaký blud, tak tam asi je. Budu rád, když mě na něj upozorníte. Ab initio metody - od počátku, z prvotních principů, tzn.
Přehled Ab Initio a semiempirických metod Pokud se vám bude zdát, že je v tom nějaký blud, tak tam asi je. Budu rád, když mě na něj upozorníte. Ab initio metody - od počátku, z prvotních principů, tzn.
Diferenˇcní rovnice Diferenciální rovnice Matematika IV Matematika IV Program
 Program Diferenční rovnice Program Diferenční rovnice Diferenciální rovnice Program Frisch a Samuelson: Systém je dynamický, jestliže jeho chování v čase je určeno funkcionální rovnicí, jejíž neznámé závisí
Program Diferenční rovnice Program Diferenční rovnice Diferenciální rovnice Program Frisch a Samuelson: Systém je dynamický, jestliže jeho chování v čase je určeno funkcionální rovnicí, jejíž neznámé závisí
Prověřování Standardního modelu
 Prověřování Standardního modelu 1) QCD hluboce nepružný rozptyl, elektron (mion) proton, strukturní funkce fotoprodukce γ proton produkce gluonů v e + e produkce jetů, hadronů 2) Elektroslabá torie interference
Prověřování Standardního modelu 1) QCD hluboce nepružný rozptyl, elektron (mion) proton, strukturní funkce fotoprodukce γ proton produkce gluonů v e + e produkce jetů, hadronů 2) Elektroslabá torie interference
X = x, y = h(x) Y = y. hodnotám x a jedné hodnotě y. Dostaneme tabulku hodnot pravděpodobnostní
 ..08 8cv7.tex 7. cvičení - transformace náhodné veličiny Definice pojmů a základní vzorce Je-li X náhodná veličina a h : R R je měřitelná funkce, pak náhodnou veličinu Y, která je definovaná vztahem X
..08 8cv7.tex 7. cvičení - transformace náhodné veličiny Definice pojmů a základní vzorce Je-li X náhodná veličina a h : R R je měřitelná funkce, pak náhodnou veličinu Y, která je definovaná vztahem X
Dr. Petr Jizba. I. Relativistická QM a dráhové integrály. Ia. Bezspinová částice a bosonová struna
 Příklady k předmětu Metody Funkconálního Integrálu Dr Petr Jzba I Relatvstcká QM a dráhové ntegrály Ia Bezspnová částce a bosonová struna Příklad 1: Dokažte, že na úrovn pohybových rovnc jsou následující
Příklady k předmětu Metody Funkconálního Integrálu Dr Petr Jzba I Relatvstcká QM a dráhové ntegrály Ia Bezspnová částce a bosonová struna Příklad 1: Dokažte, že na úrovn pohybových rovnc jsou následující
Víceatomové molekuly s jedním centrálním atomem
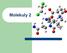 Molekuly 2 Víceatomové molekuly s jedním centrálním atomem l u tříatomových molekul se uplatňuje směr vazby l dvě atomové spojnice (vazby) svírají vazebný úhel O H H Hybridizace l MO-LCAO se v empirických
Molekuly 2 Víceatomové molekuly s jedním centrálním atomem l u tříatomových molekul se uplatňuje směr vazby l dvě atomové spojnice (vazby) svírají vazebný úhel O H H Hybridizace l MO-LCAO se v empirických
PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU
 PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU 6.1 Křivkový integrál 1. druhu Definice 1. Množina R n se nazývá prostá regulární křivka v R n právě tehdy, když existuje vzájemně jednoznačné zobrazení
PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU 6.1 Křivkový integrál 1. druhu Definice 1. Množina R n se nazývá prostá regulární křivka v R n právě tehdy, když existuje vzájemně jednoznačné zobrazení
y ds, z T = 1 z ds, kde S = S
 Plošné integrály příklad 5 Určete souřadnice těžiště části roviny xy z =, která leží v prvním oktantu x >, y >, z >. Řešení: ouřadnice těžiště x T, y T a z T homogenní plochy lze určit pomocí plošných
Plošné integrály příklad 5 Určete souřadnice těžiště části roviny xy z =, která leží v prvním oktantu x >, y >, z >. Řešení: ouřadnice těžiště x T, y T a z T homogenní plochy lze určit pomocí plošných
Dvojné a trojné integrály příklad 3. x 2 y dx dy,
 Spočtěte = { x, y) ; 4x + y 4 }. Dvojné a trojné integrály příklad 3 x y dx dy, Řešení: Protože obor integrace je symetrický vzhledem k ose x, tj. vzhledem k substituci [x; y] [x; y], a funkce fx, y) je
Spočtěte = { x, y) ; 4x + y 4 }. Dvojné a trojné integrály příklad 3 x y dx dy, Řešení: Protože obor integrace je symetrický vzhledem k ose x, tj. vzhledem k substituci [x; y] [x; y], a funkce fx, y) je
Hamiltonián popisující atom vodíku ve vnějším magnetickém poli:
 Orbitální a spinový magnetický moment a jejich interakce s vnějším polem Vše na příkladu atomu H: Elektron (e - ) a jádro (u atomu H pouze p + ) mají vlastní magnetický moment (= spin). Tyto dva dipóly
Orbitální a spinový magnetický moment a jejich interakce s vnějším polem Vše na příkladu atomu H: Elektron (e - ) a jádro (u atomu H pouze p + ) mají vlastní magnetický moment (= spin). Tyto dva dipóly
Elektronový obal atomu
 Elektronový obal atomu Chemické vlastnosti atomů (a molekul) jsou určeny vlastnostmi elektronového obalu. Chceme znát energii a prostorové rozložení elektronů Znalosti o elektronovém obalu byly získány
Elektronový obal atomu Chemické vlastnosti atomů (a molekul) jsou určeny vlastnostmi elektronového obalu. Chceme znát energii a prostorové rozložení elektronů Znalosti o elektronovém obalu byly získány
OPVK CZ.1.07/2.2.00/
 18.2.2013 OPVK CZ.1.07/2.2.00/28.0184 Cvičení z NMR OCH/NMR Mgr. Tomáš Pospíšil, Ph.D. LS 2012/2013 18.2.2013 NMR základní principy NMR Nukleární Magnetická Resonance N - nukleární (studujeme vlastnosti
18.2.2013 OPVK CZ.1.07/2.2.00/28.0184 Cvičení z NMR OCH/NMR Mgr. Tomáš Pospíšil, Ph.D. LS 2012/2013 18.2.2013 NMR základní principy NMR Nukleární Magnetická Resonance N - nukleární (studujeme vlastnosti
3. Absorpční spektroskopie
 3. Absorpční spetrosope Lambert-Beerův záon Nechť olmovaný svaze ntenzty (λ) dopadá na homogenní planparalelní vrstvu tloušťy l. (λ) (x) Př průchodu vrstvou (x, x+dx) se ntenzta dx sníží o d = -α(λ) (λ,x)
3. Absorpční spetrosope Lambert-Beerův záon Nechť olmovaný svaze ntenzty (λ) dopadá na homogenní planparalelní vrstvu tloušťy l. (λ) (x) Př průchodu vrstvou (x, x+dx) se ntenzta dx sníží o d = -α(λ) (λ,x)
Substituce ve vícenásobném integrálu verze 1.1
 Úvod Substituce ve vícenásobném integrálu verze. Následující text popisuje výpočet vícenásobných integrálů pomocí věty o substituci. ěl by sloužit především studentům předmětu ATEAT k přípravě na zkoušku.
Úvod Substituce ve vícenásobném integrálu verze. Následující text popisuje výpočet vícenásobných integrálů pomocí věty o substituci. ěl by sloužit především studentům předmětu ATEAT k přípravě na zkoušku.
Druhé kvantování. Slaterův determinant = χ χ
 Druhé kvntování Druhé kvntování žádná nová fyzk! jný formlsmus upltnění prncpu ntsymetre bez použtí Slterových determnntů. Antsymetrcké vlstnost vlnových funkcí jsou přeneseny n lgebrcké vlstnost dných
Druhé kvntování Druhé kvntování žádná nová fyzk! jný formlsmus upltnění prncpu ntsymetre bez použtí Slterových determnntů. Antsymetrcké vlstnost vlnových funkcí jsou přeneseny n lgebrcké vlstnost dných
Část 5.2 Lokalizovaný požár
 Část 5.2 Lokalizovaný požár P. Schaumann, T. Trautmann University of Hannover J. Žižka České vysoké učení technické v Praze 1 ZADÁNÍ Cílem příkladu je určit teplotu ocelového nosníku, který je součástí
Část 5.2 Lokalizovaný požár P. Schaumann, T. Trautmann University of Hannover J. Žižka České vysoké učení technické v Praze 1 ZADÁNÍ Cílem příkladu je určit teplotu ocelového nosníku, který je součástí
Poznámky k přednášce o grupách
 Mchal Lenc Poznámky ke grupám 465 Poznámky k přednášce o grupách Defnce a příklady grup Příklad : Cyklcká grupa o čtyřech prvcích Příklad : Grupy matc Příklad : Grupa O(n) 4 Příklad 4: Grupa U(n) 4 5 Příklad
Mchal Lenc Poznámky ke grupám 465 Poznámky k přednášce o grupách Defnce a příklady grup Příklad : Cyklcká grupa o čtyřech prvcích Příklad : Grupy matc Příklad : Grupa O(n) 4 Příklad 4: Grupa U(n) 4 5 Příklad
Úvod do teorie odhadu. Ing. Michael Rost, Ph.D.
 Úvod do teorie odhadu Ing. Michael Rost, Ph.D. Náhodný výběr Náhodným výběrem ze základního souboru populace, která je popsána prostřednictvím hustoty pravděpodobnosti f(x, θ), budeme nazývat posloupnost
Úvod do teorie odhadu Ing. Michael Rost, Ph.D. Náhodný výběr Náhodným výběrem ze základního souboru populace, která je popsána prostřednictvím hustoty pravděpodobnosti f(x, θ), budeme nazývat posloupnost
3 Základní modely reaktorů
 3 Základní modely reaktorů Rovnce popsující chování reakční směs v reaktoru (v čase a prostoru) vycházejí z blančních rovnc pro hmotu, energ a hybnost. Blanc lze formulovat pro extenzvní velčnu B v obecném
3 Základní modely reaktorů Rovnce popsující chování reakční směs v reaktoru (v čase a prostoru) vycházejí z blančních rovnc pro hmotu, energ a hybnost. Blanc lze formulovat pro extenzvní velčnu B v obecném
Teorie krystalového pole (ligandového)
 Teorie krystalového pole (ligandového) Literatura Title page Svatopluk Krupička: Fyzika feritů a příbuzných magnetických kysličníků Antonín A. Vlček: Struktura vlastnosti koordinačních sloučenin C.E. Housecroft,
Teorie krystalového pole (ligandového) Literatura Title page Svatopluk Krupička: Fyzika feritů a příbuzných magnetických kysličníků Antonín A. Vlček: Struktura vlastnosti koordinačních sloučenin C.E. Housecroft,
Kinetika spalovacích reakcí
 Knetka spalovacích reakcí Základy knetky spalování - nauka o průběhu spalovacích reakcí a závslost rychlost reakcí na různých faktorech Hlavní faktory: - koncentrace reagujících látek - teplota - tlak
Knetka spalovacích reakcí Základy knetky spalování - nauka o průběhu spalovacích reakcí a závslost rychlost reakcí na různých faktorech Hlavní faktory: - koncentrace reagujících látek - teplota - tlak
Relativistická kvantová mechanika
 Relatvstcká kvantová mechanka Mchal Lenc Poznámky k přednášce v jarním semestru Obrazy Postulát o kvantové kausaltě Evoluční operátor 3 Schrödngerův a Hesenbergův obraz 3 4 Interakční obraz4 Relatvta a
Relatvstcká kvantová mechanka Mchal Lenc Poznámky k přednášce v jarním semestru Obrazy Postulát o kvantové kausaltě Evoluční operátor 3 Schrödngerův a Hesenbergův obraz 3 4 Interakční obraz4 Relatvta a
VÝPOČETNÍ CHEMIE V ANALÝZE STRUKTURY
 VÝPOČETNÍ CHEMIE V ANALÝZE STRUKTURY A VLASTNOSTÍ MOLEKUL Michal Čajan Katedra anorganické chemie PřF UP v Olomouci MOLEKULOVÉ MODELOVÁNÍ V CHEMII MOLEKULOVÉ MODELOVÁNÍ aplikace zobrazení a analýza strukturních
VÝPOČETNÍ CHEMIE V ANALÝZE STRUKTURY A VLASTNOSTÍ MOLEKUL Michal Čajan Katedra anorganické chemie PřF UP v Olomouci MOLEKULOVÉ MODELOVÁNÍ V CHEMII MOLEKULOVÉ MODELOVÁNÍ aplikace zobrazení a analýza strukturních
Elektromagnetické pole je generováno elektrickými náboji a jejich pohybem. Je-li zdroj charakterizován nábojovou hustotou ( r r
 Záření Hertzova dipólu, kulové vlny, Rovnice elektromagnetického pole jsou vektorové diferenciální rovnice a podle symetrie bývá vhodné je řešit v křivočarých souřadnicích. Základní diferenciální operátory
Záření Hertzova dipólu, kulové vlny, Rovnice elektromagnetického pole jsou vektorové diferenciální rovnice a podle symetrie bývá vhodné je řešit v křivočarých souřadnicích. Základní diferenciální operátory
Stavba hmoty. Atomová teorie Korpuskulární model látky - chemické
 Stavba hmoty Atomová teorie Korpuskulární model látky - chemické látky jsou složeny z mikroskopických, chemicky dále neděčástic atomů. Později byl model rozšířen na molekuly a ionty (chemický druh - specie).
Stavba hmoty Atomová teorie Korpuskulární model látky - chemické látky jsou složeny z mikroskopických, chemicky dále neděčástic atomů. Později byl model rozšířen na molekuly a ionty (chemický druh - specie).
Mezimolekulové interakce
 Mezimolekulové interakce Interakce molekul reaktivně vzniká či zaniká kovalentní vazba překryv elektronových oblaků, mění se vlastnosti nereaktivně vznikají molekulové komplexy slabá, nekovalentní, nechemická,
Mezimolekulové interakce Interakce molekul reaktivně vzniká či zaniká kovalentní vazba překryv elektronových oblaků, mění se vlastnosti nereaktivně vznikají molekulové komplexy slabá, nekovalentní, nechemická,
Elektromagnetické záření. lineárně polarizované záření. Cirkulárně polarizované záření
 Elektromagnetické záření lineárně polarizované záření Cirkulárně polarizované záření Levotočivé Pravotočivé 1 Foton Jakékoli elektromagnetické vlnění je kvantováno na fotony, charakterizované: Vlnovou
Elektromagnetické záření lineárně polarizované záření Cirkulárně polarizované záření Levotočivé Pravotočivé 1 Foton Jakékoli elektromagnetické vlnění je kvantováno na fotony, charakterizované: Vlnovou
Elektronový obal atomu
 Elektronový obal atomu Ondřej Havlíček.ročník F-Vt/SŠ Jsoucno je vždy něco, co jsme si sami zkonstruovali ve své mysli. Podstata takovýchto konstrukcí nespočívá v tom, že by byly odvozeny ze smyslových
Elektronový obal atomu Ondřej Havlíček.ročník F-Vt/SŠ Jsoucno je vždy něco, co jsme si sami zkonstruovali ve své mysli. Podstata takovýchto konstrukcí nespočívá v tom, že by byly odvozeny ze smyslových
Syntetická geometrie I
 Shodnost Pedagogická fakulta 2016 www.karlin.mff.cuni.cz/~zamboj/ Vzdálenost dvou bodů Necht A, B, C ρ. Vzdálenost dvou bodů A, B v rovině je číslo AB a platí AB 0 AB = 0 A = B AB = BA pozitivně definitní
Shodnost Pedagogická fakulta 2016 www.karlin.mff.cuni.cz/~zamboj/ Vzdálenost dvou bodů Necht A, B, C ρ. Vzdálenost dvou bodů A, B v rovině je číslo AB a platí AB 0 AB = 0 A = B AB = BA pozitivně definitní
Fyzika atomového jádra
 Fyzika atomového jádra (NJSF064) František Knapp http://www-ucjf.troja.mff.cuni.cz/~knapp/jf/ frantisek.knapp@mff.cuni.cz Slupkový model jádra evidence magických čísel: hmoty, separační energie, vazbové
Fyzika atomového jádra (NJSF064) František Knapp http://www-ucjf.troja.mff.cuni.cz/~knapp/jf/ frantisek.knapp@mff.cuni.cz Slupkový model jádra evidence magických čísel: hmoty, separační energie, vazbové
Teorie chemické vazby a molekulární geometrie Molekulární geometrie VSEPR
 Geometrie molekul Lewisovy vzorce poskytují informaci o tom které atomy jsou spojeny vazbou a o jakou vazbu se jedná (topologie molekuly). Geometrické uspořádání molekuly je charakterizováno: Délkou vazeb
Geometrie molekul Lewisovy vzorce poskytují informaci o tom které atomy jsou spojeny vazbou a o jakou vazbu se jedná (topologie molekuly). Geometrické uspořádání molekuly je charakterizováno: Délkou vazeb
Oddělení pohybu elektronů a jader
 Oddělení pohybu elektronů a ader Adiabatická aproximace Born-Oppenheimerova aproximace Důležité vztahy sou 4, 5, 7, 0,,, udělal sem to zbytečně podrobně, e to samostatný okruh Separace translačního pohybu:
Oddělení pohybu elektronů a ader Adiabatická aproximace Born-Oppenheimerova aproximace Důležité vztahy sou 4, 5, 7, 0,,, udělal sem to zbytečně podrobně, e to samostatný okruh Separace translačního pohybu:
Řešit atom vodíku znamená nalézt řešení Schrödingerovy rovnice s příslušným hamiltoniánem. 1 4πǫ 0. 2m e
 8 Atom vodíku Správné řešení atomu vodíku je jedním z velkých vítězství kvantové mechaniky. Podle klasické fyziky náboj, který se pohybuje se zrychlením (elektron obíhající vodíkové jádro proton), by měl
8 Atom vodíku Správné řešení atomu vodíku je jedním z velkých vítězství kvantové mechaniky. Podle klasické fyziky náboj, který se pohybuje se zrychlením (elektron obíhající vodíkové jádro proton), by měl
ck f Podmínka pro nalezení nejvhodnější variační funkce (minimální energie): = 0
 Varačí teorém W Φ H Φ = ΦΦ E 0 Aproxmatví vlová fukce dává eerg, která je vždy větší (ebo rova) E 0 Leárí varačí fukce: Φ = k k W Podmíka pro alezeí ejvhodější varačí fukce (mmálí eerge): = 0 ck f c =>
Varačí teorém W Φ H Φ = ΦΦ E 0 Aproxmatví vlová fukce dává eerg, která je vždy větší (ebo rova) E 0 Leárí varačí fukce: Φ = k k W Podmíka pro alezeí ejvhodější varačí fukce (mmálí eerge): = 0 ck f c =>
Variační počet 2. Prof. RNDr. Olga Krupková, DrSc. Autorizovaný zápis přednášek (letní semestr 2004/2005) Zapsal Jan Šustek
 Prof. RNDr. Olga Krupková, DrSc. Autorizovaný zápis přednášek (letní semestr 2004/2005) Zapsal Jan Šustek Obsah Seznam použitých symbolů a konvencí.............................................. 2 0. Opakování.........................................................................
Prof. RNDr. Olga Krupková, DrSc. Autorizovaný zápis přednášek (letní semestr 2004/2005) Zapsal Jan Šustek Obsah Seznam použitých symbolů a konvencí.............................................. 2 0. Opakování.........................................................................
Nosné desky. 1. Kirchhoffova teorie ohybu tenkých desek (h/l < 1/10) 3. Mindlinova teorie pro tlusté desky (h/l < 1/5)
 Nosné desky Deska je těleso, které má jeden rozměr mnohem menší než rozměry zbývající. Zatížení desky je orientováno výhradně kolmo k její střednicové rovině. 1. Kirchhoffova teorie ohybu tenkých desek
Nosné desky Deska je těleso, které má jeden rozměr mnohem menší než rozměry zbývající. Zatížení desky je orientováno výhradně kolmo k její střednicové rovině. 1. Kirchhoffova teorie ohybu tenkých desek
Variační počet 2. Prof. RNDr. Olga Krupková, DrSc. Obsahuje 1413 hypertextových odkazů. Autorizovaný zápis přednášek (letní semestr 2004/2005)
 Prof. RNDr. Olga Krupková, DrSc. Autorizovaný zápis přednášek (letní semestr 2004/2005) Obsahuje 1413 hypertextových odkazů Zapsal Jan Šustek Aktualizováno 29. května 2005 Obsah Seznam použitých symbolů
Prof. RNDr. Olga Krupková, DrSc. Autorizovaný zápis přednášek (letní semestr 2004/2005) Obsahuje 1413 hypertextových odkazů Zapsal Jan Šustek Aktualizováno 29. května 2005 Obsah Seznam použitých symbolů
VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE FAKULTA INFORMATIKY A STATISTIKY Katedra statistiky a pravděpodobnosti STATISTIKA VZORCE. k bakalářské zkoušce
 VYOKÁ ŠKOLA EKONOMCKÁ V RAZE FAKULTA NFORMATKY A TATTKY Kaeda a a avděodobo TATTKA VZORCE baalářé zošce veze 3. oledí aalzace: 3.9.7 KT 7 oá aa Rozděleí čeoí,,..., Kval % z ůmě H H H G... Rozěí R ma -
VYOKÁ ŠKOLA EKONOMCKÁ V RAZE FAKULTA NFORMATKY A TATTKY Kaeda a a avděodobo TATTKA VZORCE baalářé zošce veze 3. oledí aalzace: 3.9.7 KT 7 oá aa Rozděleí čeoí,,..., Kval % z ůmě H H H G... Rozěí R ma -
Syntetická geometrie I
 Shodnost Pedagogická fakulta 2018 www.karlin.mff.cuni.cz/~zamboj/ Vzdálenost dvou bodů Definice (Vzdálenost) Necht A, B, C ρ. Vzdálenost dvou bodů A, B v rovině je číslo AB a platí AB 0 AB = 0 A = B AB
Shodnost Pedagogická fakulta 2018 www.karlin.mff.cuni.cz/~zamboj/ Vzdálenost dvou bodů Definice (Vzdálenost) Necht A, B, C ρ. Vzdálenost dvou bodů A, B v rovině je číslo AB a platí AB 0 AB = 0 A = B AB
Matematika 4 FSV UK, LS Miroslav Zelený
 Matematika 4 FSV UK, LS 2017-18 Miroslav Zelený 13. Diferenční rovnice 14. Diferenciální rovnice se separovanými prom. 15. Lineární diferenciální rovnice prvního řádu 16. Lineární diferenciální rovnice
Matematika 4 FSV UK, LS 2017-18 Miroslav Zelený 13. Diferenční rovnice 14. Diferenciální rovnice se separovanými prom. 15. Lineární diferenciální rovnice prvního řádu 16. Lineární diferenciální rovnice
ATOM VODÍKU MODEL : STOJÍCÍ BODOVÉ JÁDRO A ELEKTRON VZÁJEMNĚ ELEKTROSTATICKY INTERAGUJÍCÍ SCHRÖDINGEROVA ROVNICE PRO PŘÍPAD POTENCIÁLNÍ ENERGIE.
 ATOMY + MOLEKULY ATOM VODÍKU MODEL : STOJÍCÍ BODOVÉ JÁDRO A ELEKTRON VZÁJEMNĚ ELEKTROSTATICKY INTERAGUJÍCÍ SCHRÖDINGEROVA ROVNICE H ˆψ = Eψ PRO PŘÍPAD POTENCIÁLNÍ ENERGIE Vˆ = Ze 2 4πε o r ŘEŠENÍ HLEDÁME
ATOMY + MOLEKULY ATOM VODÍKU MODEL : STOJÍCÍ BODOVÉ JÁDRO A ELEKTRON VZÁJEMNĚ ELEKTROSTATICKY INTERAGUJÍCÍ SCHRÖDINGEROVA ROVNICE H ˆψ = Eψ PRO PŘÍPAD POTENCIÁLNÍ ENERGIE Vˆ = Ze 2 4πε o r ŘEŠENÍ HLEDÁME
Detekce nabitých částic Jak se ztrácí energie průchodem částice hmotou?
 Detekce nabitých částic Jak se ztrácí energie průchodem částice hmotou? 10/20/2004 1 Bethe Blochova formule (1) je maximální možná předaná energie elektronu N r e - vogadrovo čislo - klasický poloměr elektronu
Detekce nabitých částic Jak se ztrácí energie průchodem částice hmotou? 10/20/2004 1 Bethe Blochova formule (1) je maximální možná předaná energie elektronu N r e - vogadrovo čislo - klasický poloměr elektronu
k + q. Jestliže takový dipól kmitá s frekvencí ν (odpovídající
 Vlastnosti kmitajíího dipólu Podle klasiké teoie je nejefektivnějším zdojem elektomagnetikého záření kmitajíí elektiký dipól. Intenzita jeho záření o několik řádů převyšuje intenzity ostatníh zdojů záření
Vlastnosti kmitajíího dipólu Podle klasiké teoie je nejefektivnějším zdojem elektomagnetikého záření kmitajíí elektiký dipól. Intenzita jeho záření o několik řádů převyšuje intenzity ostatníh zdojů záření
Příloha-výpočet motoru
 Příloha-výpočet motoru 1.Zadané parametry motoru: vrtání d : 77mm zdvih z: 87mm kompresní poměr ε : 10.6 atmosférický tlak p 1 : 98000Pa teplota nasávaného vzduchu T 1 : 353.15K adiabatický exponent κ
Příloha-výpočet motoru 1.Zadané parametry motoru: vrtání d : 77mm zdvih z: 87mm kompresní poměr ε : 10.6 atmosférický tlak p 1 : 98000Pa teplota nasávaného vzduchu T 1 : 353.15K adiabatický exponent κ
Balmerova série vodíku
 Balmerova série vodíku Eva Bartáková, SGAGY Kladno, evebartak@centrum.cz Adam Fadrhonc, SSOU a U, Černá za Bory, Pardubice, adam@kve.cz Lukáš Malina, gymn. Christiana Dopplera, Praha, lukas-malina@seznam.cz
Balmerova série vodíku Eva Bartáková, SGAGY Kladno, evebartak@centrum.cz Adam Fadrhonc, SSOU a U, Černá za Bory, Pardubice, adam@kve.cz Lukáš Malina, gymn. Christiana Dopplera, Praha, lukas-malina@seznam.cz
VYBRANÉ DOSIMETRICKÉ VELIČINY A VZTAHY MEZI NIMI
 VYBRANÉ DOSIMETRICKÉ VELIČINY A VZTAHY MEZI NIMI Přehled dosimrických veličin: Daniel KULA (verze 1.0), 1. Aktivita: Definice veličiny: Poč radioaktivních přeměn v radioaktivním materiálu, vztažený na
VYBRANÉ DOSIMETRICKÉ VELIČINY A VZTAHY MEZI NIMI Přehled dosimrických veličin: Daniel KULA (verze 1.0), 1. Aktivita: Definice veličiny: Poč radioaktivních přeměn v radioaktivním materiálu, vztažený na
Geometricky válcová momentová skořepina
 Geometricky válcová momentová skořepina Dalším typem tenkostěnnéo rotačně souměrnéo tělesa je geometricky válcová momentová skořepina. Typický souřadnicový systém je opět systém s osami z, r, a t. Geometricky
Geometricky válcová momentová skořepina Dalším typem tenkostěnnéo rotačně souměrnéo tělesa je geometricky válcová momentová skořepina. Typický souřadnicový systém je opět systém s osami z, r, a t. Geometricky
Rovinná monochromatická vlna v homogenním, neabsorbujícím, jednoosém anizotropním prostředí
 Rovinná monochromatická vlna v homogenním, neabsorbujícím, jednoosém anizotropním prostředí r r Další předpoklad: nemagnetické prostředí B = µ 0 H izotropně. Veškerá anizotropie pochází od interakce elektrických
Rovinná monochromatická vlna v homogenním, neabsorbujícím, jednoosém anizotropním prostředí r r Další předpoklad: nemagnetické prostředí B = µ 0 H izotropně. Veškerá anizotropie pochází od interakce elektrických
VÍTEJTE V MIKROSVĚTĚ
 VÍTEJTE V MIKROSVĚTĚ Klasická vs. Moderní fyzika Klasická fyzika fyzika obyčejných věcí viditelných pouhým okem Moderní fyzika Relativita zabývá se tím co se pohybuje rychle nebo v silovém gravitačním
VÍTEJTE V MIKROSVĚTĚ Klasická vs. Moderní fyzika Klasická fyzika fyzika obyčejných věcí viditelných pouhým okem Moderní fyzika Relativita zabývá se tím co se pohybuje rychle nebo v silovém gravitačním
Řešení: Nejprve musíme napsat parametrické rovnice křivky C. Asi nejjednodušší parametrizace je. t t dt = t 1. x = A + ( B A ) t, 0 t 1,
 Určete Křivkový integrál příklad 4 x ds, kde {x, y ; y ln x, x 3}. Řešení: Nejprve musíme napsat parametrické rovnice křivky. Asi nejjednodušší parametrizace je Tedy daný integrál je x ds x t, y ln t,
Určete Křivkový integrál příklad 4 x ds, kde {x, y ; y ln x, x 3}. Řešení: Nejprve musíme napsat parametrické rovnice křivky. Asi nejjednodušší parametrizace je Tedy daný integrál je x ds x t, y ln t,
Matematika I A ukázkový test 1 pro 2018/2019
 Matematka I A ukázkový test 1 pro 2018/2019 1. Je dána soustava rovnc s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napšte Frobenovu větu (předpoklady + tvrzení). b) Vyšetřete
Matematka I A ukázkový test 1 pro 2018/2019 1. Je dána soustava rovnc s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napšte Frobenovu větu (předpoklady + tvrzení). b) Vyšetřete
MATEMATIKA II - vybrané úlohy ze zkoušek v letech
 MATEMATIKA II - vybrané úlohy ze zkoušek v letech 2009 2012 doplněné o další úlohy 3. část KŘIVKOVÉ INTEGRÁLY, GREENOVA VĚTA, POTENIÁLNÍ POLE, PLOŠNÉ INTEGRÁLY, GAUSSOVA OSTROGRADSKÉHO VĚTA 7. 4. 2013
MATEMATIKA II - vybrané úlohy ze zkoušek v letech 2009 2012 doplněné o další úlohy 3. část KŘIVKOVÉ INTEGRÁLY, GREENOVA VĚTA, POTENIÁLNÍ POLE, PLOŠNÉ INTEGRÁLY, GAUSSOVA OSTROGRADSKÉHO VĚTA 7. 4. 2013
KLASICKÁ MECHANIKA. Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny.
 MECHANIKA 1 KLASICKÁ MECHANIKA Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny. Klasická mechanika rychlosti těles jsou mnohem menší než rychlost světla ve
MECHANIKA 1 KLASICKÁ MECHANIKA Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny. Klasická mechanika rychlosti těles jsou mnohem menší než rychlost světla ve
Odhady - Sdružené rozdělení pravděpodobnosti
 Odhady - Sdružené rozdělení pravděpodobnosti 4. listopadu 203 Kdybych chtěl znát maximum informací o náhodné veličině, musel bych znát všechny hodnoty, které mohou padnout, a jejich pravděpodobnosti. Tedy
Odhady - Sdružené rozdělení pravděpodobnosti 4. listopadu 203 Kdybych chtěl znát maximum informací o náhodné veličině, musel bych znát všechny hodnoty, které mohou padnout, a jejich pravděpodobnosti. Tedy
Jednokapalinové přiblížení (MHD-magnetohydrodynamika)
 Jenokapalinové přiblížení (HD-magnetohyroynamika) Zákon zachování hmoty zákony zachování počtu elektronů a iontů násobeny hmotnostmi a sečteny n e + iv = ( nu ) ni + iv( nu i i) = e e iv ( u ) (1) t ρ
Jenokapalinové přiblížení (HD-magnetohyroynamika) Zákon zachování hmoty zákony zachování počtu elektronů a iontů násobeny hmotnostmi a sečteny n e + iv = ( nu ) ni + iv( nu i i) = e e iv ( u ) (1) t ρ
7. Analýza rozptylu.
 7. Analýza rozptylu. Uvedeme obecnou ideu, která je založena na minimalizaci chyby metodou nejmenších čtverců. Nejdříve uvedeme několik základních tvrzení. Uvažujeme náhodný vektor Y = (Y, Y,..., Y n a
7. Analýza rozptylu. Uvedeme obecnou ideu, která je založena na minimalizaci chyby metodou nejmenších čtverců. Nejdříve uvedeme několik základních tvrzení. Uvažujeme náhodný vektor Y = (Y, Y,..., Y n a
1 Topologie roviny a prostoru
 1 Topologie roviny a prostoru 1.1 Základní pojmy množin Intervaly a okolí Intervaly v rovině nebo prostoru jsou obdélníky nebo hranoly se stranami rovnoběžnými s osami souřadnic. Podmnožiny intervalů se
1 Topologie roviny a prostoru 1.1 Základní pojmy množin Intervaly a okolí Intervaly v rovině nebo prostoru jsou obdélníky nebo hranoly se stranami rovnoběžnými s osami souřadnic. Podmnožiny intervalů se
PŘÍKLADY K MATEMATICE 3 - VÍCENÁSOBNÉ INTEGRÁLY. x 2. 3+y 2
 PŘÍKLADY K ATEATICE 3 - VÍCENÁSOBNÉ INTEGRÁLY ZDENĚK ŠIBRAVA.. Dvojné integrály.. Vícenásobné intergrály Příklad.. Vypočítejme dvojný integrál x 3 + y da, kde =, 3,. Řešení: Funkce f(x, y) = x je na obdélníku
PŘÍKLADY K ATEATICE 3 - VÍCENÁSOBNÉ INTEGRÁLY ZDENĚK ŠIBRAVA.. Dvojné integrály.. Vícenásobné intergrály Příklad.. Vypočítejme dvojný integrál x 3 + y da, kde =, 3,. Řešení: Funkce f(x, y) = x je na obdélníku
Relativistická kinematika
 Relativistická kinematika 1 Formalismus čtyřhybnosti Pro řešení relativistických kinematických úloh lze často s výhodou použít formalismus čtyřhybnosti. Čtyřhybnost je čtyřvektor, který v sobě zahrnuje
Relativistická kinematika 1 Formalismus čtyřhybnosti Pro řešení relativistických kinematických úloh lze často s výhodou použít formalismus čtyřhybnosti. Čtyřhybnost je čtyřvektor, který v sobě zahrnuje
Kvantová teorie atomů
 Kvantová teorie atomů Kdo otevřel Pandořinu skříňku? l při studiu záření abs. černého tělesa (hvězda) použil Max von Planck (1900, NP 1918) předpoklad, že oscilátor má diskrétní spektrum, s velikostí kvanta
Kvantová teorie atomů Kdo otevřel Pandořinu skříňku? l při studiu záření abs. černého tělesa (hvězda) použil Max von Planck (1900, NP 1918) předpoklad, že oscilátor má diskrétní spektrum, s velikostí kvanta
1. Kvantové jámy. Tabulka 1: Efektivní hmotnosti nosičů v krystalech GaAs, AlAs, v jednotkách hmotnosti volného elektronu m o.
 . Kvantové jámy Pokročilé metody růstu krystalů po jednotlivých vrstvách (jako MBE) dovolují vytvořit si v krystalu libovolný potenciál. Jeden z hojně používaných materiálů je: GaAs, AlAs a jejich ternární
. Kvantové jámy Pokročilé metody růstu krystalů po jednotlivých vrstvách (jako MBE) dovolují vytvořit si v krystalu libovolný potenciál. Jeden z hojně používaných materiálů je: GaAs, AlAs a jejich ternární

