Univerzita Karlova v Praze Matematicko-fyzikální fakulta. Markowitzův model. Optimalizace II s aplikací ve financích.
|
|
|
- Denis Vacek
- před 8 lety
- Počet zobrazení:
Transkript
1 Univerzita Karlova v Praze Matematicko-fyzikální fakulta Markowitzův model Optimalizace II s aplikací ve financích Lucia Jarešová léto 2006
2 Obsah 1 Zadání úlohy 3 2 Markowitzův model 4 3 Výběr titulů 5 4 Odhady vstupních parametrů modelu 9 5 Vyřešení úloh 12 6 Míry rizika 21 7 Výsledky 22 2
3 1 ZADÁNÍÚLOHY 1 Zadání úlohy Jste správcem akciových portfólií. Potřebujete, mimo jiné, připravit pro své klienty vhodná akciová portfolia pro investování 2 miliónů Kč na období jednoho roku. Očekáváte, že se klient bude chtít poradit v otázce složení vhodného akciového portfólia a rozhodli jste se využít Markowitzův model pro selekci. Zvolte vhodné tituly(8-10). Víte, že výběru titulů předchází globální a odvětvová analýza a proto vyberete tituly, které jsou v souladu s vaší predikcí vývoje na finančních trzích. Úkoly: a) Sestavte efektivní hranici portfólií(graficky prezentujte), vyberte některá portfólia na efektivní hranici a uveďte jejich složení(váhy) a očekávané výnosnosti titulů zastoupených v portfóliu. b) Jak se změní efektivní hranice pokud budete mít možnost investovat do bezrizikového aktiva (depozitavbance)ssazbou...(naleznětesami)? c) Jak se změní efektivní hranice pokud budete mít možnost výpůjček od správce porfolia až do 30% hodnoty portfólia, pro jednoduchost předpokládejte že výpůjční sazba je stejná jako depozitní, dokázali by jste zohlednit rozdílnou výpůjční a depozitní sazbu(nalezněte její sazbu sami a určete efektivní portfólia)? d) Co když budete mít povoleny krátké prodeje, až do 30% počátečního vkladu? Nakreslete efektivní hranici v tomto případě. e) V souladu s vnitřní politikou investiční společnosti, kterou zastupujete, nesmíte navrhnout portfólia, kde některý z titulů přesáhne 15% váhu v celkovém portfóliu. Nakreslete hranici efektivních portfólií v tomto případě. Zdůvodněte jak jste získali odhady vstupních parametrů modelu, jaké jste volili tituly a proč (zejména s ohledem na rizika která model zohledňuje a velikost investované částky). Efektivní hranice počítejte numericky, stačí aproximace pro dostatečně hustý nosič. Pozor na frekvenci dat z kterých parametry odhadujete, pozor na štěpení akcií a dividendy, pozor na měnu, směnné kurzy. V případech a)-e) vyberte některé z efektivních porfólií a spočtěte VAR(95%). 3
4 2 MARKOWITZŮVMODEL 2 Markowitzův model Markowitzův model se týká především investic do portfolia akcií a využívá celé řady zjednodušujících předpokladů: ideální trh bez transakčních nákladů a bez arbitráže obchodování s neomezeně dělitenými dokumenty na trhu obchodují pouze malí racionální investoři, kteří využívají shodných informací, a to hodnot očekávaných výnosností akcií a rozptylů a kovariancí těchto výnosností, investují ve stejném čase na jedno stejně dlouhé období investoři se chovají racionálně, tj. upřednostňují větší výnosy před menšími výnosy a menší riziko před větším rizikem Základní model: Uvažujeme investici do J akcií, jednotková investice do j-té z nich dává ve zvoleném období náhodnou výnosnost ρ j. Rozdělenívektoru ρ=(ρ 1,...,ρ J ) jecharakterizovánoznámýmvektoremstředníchhodnotr=eρ aznámouvariančnímaticív=var ρ=[cov(ρ i,ρ j );i,j=1,...,j]. Složeníportfoliajeurčenováhami x 1,x 2,...,x J,kterémusísplňovatpodmínku J x j =1. j=1 Tato podmínka může být případně nahrazena nebo doplněna jinými, pokud to vyžaduje situace (např. existuje-li možnost půjčky, nejsou-li povoleny krátké prodeje apod.). Očekávanývýnos portfoliasváhamix=(x 1,...,x J ) budemechápatjakostředníhodnotu jeho celkové výnosnosti J r(x)=ex ρ=x r= x j r j. j=1 Riziko portfolia budeme chápat jako hodnotou rozptylu nebo standartní odchylky jeho očekávané výnosnosti J J σ 2 (x)=var(x ρ)=x Vx= cov(ρ i,ρ j )x i x j. i=1 j=1 4
5 3 VÝBĚRTITULŮ 3 Výběr titulů Velmi limitujícím faktorem pro výběr titulů do našeho modelu byla dostupnost dat. Na stránkách věnujícím se akciím(např. se zobrazuje historie kurzů najednou maximálněpro50dníanašímcílembylosehnatconejdelšíhistoriidatprolepšíodhadyvstupních parametrů modelu. Kopírování dat z těchto stránek navíc vyžaduje další úpravy, protože data se nám uloží jako řetězec znaků s mezerami. Finanční portály nabízí placené služby, kde jsou dostupné aktuální informace a analýzy a prognózy trhu, včetně možnosti stažení historických dat vývoje kurzu akcií v excelovkém souboru. Pro akcie obchodované v zahraničí bychom potřebovali i data k vývoji kurzu měny, abychom mohli hodnoty přepočítat vzhledem k jedné měně. Měnový vývoj totiž může velmi výrazně negativně oblivnit vývoj celkové investice i v případě pozitivního vývoje kurzu akcie. Protože sehnat data k vývoji kurzuměnyjeještěobtížnějšínežsehnatdatakvývojikurzuakcie,rozhodlajsemsezaměřitnaakcie obchodované na českém trhu. Velkou nevýhodou českého trhu je malý počet obchodovatelných likvidních akcií. Ve SPADu(Systém pro Podporu trhu Akcií a Dluhopisů) se v současnosti obchoduje pouze 9 titulů(cetv, ČEZ, Erste Bank, Komerční banka, ORCO, Philip Morris, Telefónica, UnipetrolaZentiva),navícjezdemožnékupovataprodávatpouzevelkémnožstvíakcií,tzv.loty,cožje pro náš model nevyhovující vzhledem k částce, kterou chceme investovat(1 lot slojí řádově milion). Obchodovat s akciemi je dále možné v RM systému a v KOBOSu(KOntinuální Burzovní Obchodní Systém), kde je možné prodávat a kupovat menší množství akcií. Pro obchodování v KOBOSu je výhodné použít některý z investičních portálů(např. které nabízí obchodování s malými objemy za poměrně nízké poplatky(ve srovnání například s RM-systémem). Některé navíc nabízí i možnost úvěru na maržové obchody, které díky pákovému efektu mohou znásobit výnos vlastního kapitálu, ale bohužel mohou i znásobit případnou ztrátu. Větší zisk je tedy doprovázen větším rizikem. Portál nabízí maržový úvěr v korunách se sazbou 7,5% p.a. s čtvtletním úročením(tj. efektivní úroková míra je 7,71% p.a.). Mým hlavním hlediskem pro výběr titulů byla dostatečně dlouhá historie vývoje kurzu, likvidita akcie a vzestupný trend vývoje kurzů za posledních pár let. Za dostatečně dlouhou historií jsem zvolila dobu od , tedy datum, kdy na trh vstoupily akcie Erste Bank. Tímto omezením nám bohužel vypadly SPADové tituly Zentiva, CETV a ORCO, které se obchodují teprve krátkou dobu. Vývoj kurzu těchto titulů od začátku jejich obchodování je převážně rostoucí a očekává se i další pozitivní vývoj v budoucnosti, navíc SPADové tituly jsou velmi likvidní. Z těchto důvodů je určitě škoda, že jsme tyto tituly vynechali z další analýzy, ale délka jejich historie by neumožňovala dobré odhady vstupních parametrů pro Markowitzův model, protože pro odhad variančí matice výnosností jednotlivých titulů bychom museli použít stejně dlouhou historii pro všechny tituly. Program R sice umožňuje počítat varianční matici i z dat různých délek, výsledná matice ale nemusí být pozitivně semidefinitní, což by mohlo vést k následným problémům při optimalizaci(minimalizovaná kvadratická forma by pak nemusela být konvexní). Kromě velmi likvidních SPADových titulů bylo nutné vybrat i další tituly. Tady jsem se řídila hlavně grafickým znázorněním vývoje kurzů akcí(viz Obrázek 1) a velikostí vyplacených dividend (viz Tabulka 2), protože dividenda je důležitým zdrojem výnosu akcie a její vyplacení způsobí pokles hodnoty kurzu přibližně o hodnotu akcie. Zároveň jsem se snažila vybírat tituly, jejichž hodnota kurzusečastomění.kurztotižreagujenaobchodovánísdanýmstitulem,tedyakciesvíceproměnlivým grafem bývají likvidnější než akcie, jejichž graf zůstává delší dobu na stejných hodnotách. Pro další analýzu jsem nakonec vybrala tituly uvedené v Tabulce 1. 5
6 3 VÝBĚRTITULŮ Tabulka 1: Tituly vybrané pro další analýzu číslo název titulu označení proměnné 1 ČEZ cez 2 Erste Bank erste 3 Komerční banka kb 4 Philip Morris ČR philip 5 Telefónica telef 6 Unipetrol unipet 7 Pražská energetika prener 8 Setuza setuza 9 Stavby silnic a železnic ssz 10 Východočeská plynárenská vcplyn Grafyakciípoužitýchvmodeluaindexupx V grafech jsou zachyceny hodnoty od do Datum posledního pozorování je , svislá čára v grafu vyznačuje datum před jedním rokem, tj Pro zajímavost uvádím ještě graf vývoje akciového indexu PX(Obrázek 2). Vývoj akciového indexu bývá spojen s výnosností trhu. Báze indexu PX ale obsahuje pouze SPADové tituly, kde váha titulu je určena poměrem zastoupení titulu na trhu. Obrázek 1: akcie (a) ČEZ (b) Erste bank 6
7 3 VÝBĚRTITULŮ (c) Komerční banka (d) Philip Morris (e) Telefónica (f) Unipetrol (g) Pražská Energetika 7 (h) Setuza
8 3 VÝBĚRTITULŮ (g) SSŽ (h) Východočeská plynárenská Obrázek 2: index px 8
9 4 ODHADY VSTUPNÍCH PARAMETRŮ MODELU 4 Odhady vstupních parametrů modelu Data vývoje kurzu akcií obsahují hodnoty kurzu v obchodních dnech od do pro 10 titulů, k dispozici máme celkem 972 pozorování hodnot kurzů všech akcií. Frekvence těchto dat je denní, ale ne všechny dny jsou obchodní. Z tohoto důvodu jsem vytvořila novou proměnnou čas označenou t, která udává pořadové číslo obchodního dne. Plánovaný investiční horizont je jeden rok. V době od do je 252 obchodních dní, tento počet pozorování zvolíme za období jednoho roku. Kromě hodnot kurzu je nutné při odhadu výnosností dané akcie počítat i s vyplacenými dividendami na jednu akcií. Hodnoty vyplacených dividend jsou uvedeny v Tabulce 2. V posledním sloupci této tabulky jsou uvedeny rozhodné dny pro výplatu dividend v roce Tabulka 2: Vyplacené dividendy v letech j název rozhodnýden kurz cez 2,5 4, (1.86%) 2 erste (2.36%) 3 kb 11, (7.55%) 4 philip (9.59%) 5 telef 0 57, (9.86%) 6 unipet (0%) 7 prener (5.15%) 8 setuza (0%) 9 ssz 37,4 46,75 110, (12.63%) 10 vcplyn , (3.87%) V posledním sloupci je v závorce uvedeno, jakou část hodnoty kurzu dne tvoří dividenda vyplacená v roce Nárok na vyplacení dividendy má pouze ten, kdo je vlastníkem dané akcie během rozhodného dne. Den následující po rozhodném dnu se zvyšuje prodej dané akcie. Převys nabídky této akcie se projeví snížením kurzu. Toto snížení kurzu se považuje za vliv vyplacené dividendy a proto právě den po rozhodném dnu v roce 2006 budeme v modelu považovat za den vyplacení dividendy. Dny vyplacení dividend v minulých letech stanovíme tak, aby u daného titulu během 252 dní došlo vždy právě kjednomuvyplacenídividendy.tedyje-li t 0 denvyplacenídividendyvroce2006,budeden t dnem vyplacení dividendy v roce 2005, podobně v ostatních letech. Data: Dne proběhlo u akcií Erste Bank štěpení v poměru 1:4. Hodnotu kurzu před tímto datem a hodnotu dividendy v letech 2002, 2003 a 2004 jsem proto upravila vydělením čtyřmi. U ostatních akcií v uvažovaném období ke štěpení nedošlo. Následující označení už uvažuje upravené hodnoty. y j,t hodnotakurzuakcie jvčase t t=1,...,t=972 9
10 4 ODHADY VSTUPNÍCH PARAMETRŮ MODELU j=1,...,j=10 d j,t vyplacenádividendaakcie jvčase t, pokudčas tneníčasemvyplácenídividendy,je d j,t =0 výnosnostakcie jvčase t r j,t Očekávaná výnosnost akcie j v čase t spočítáme podle vzorce: r j,t = y j,t y j,t t k=t d j,k y j,t j=1,...,10; t=253,...,972 Očekávané výnosnosti nám vyjdou v procentech, u každého titulu dostaneme 720 pozorování hodnot výnosností. Z Tabulky 2 vidíme, že u akcií Telefónicy je datum vyplacení dividendy až v září. Tato dividendajevesrovnánísminulýmidvěmaletypoměrněvelkáaispojenífiremčeskýtelecoma Eurotel v Telefónicu naznačuje další pozitivní vývoj. S touto dividendou ale v našem modelu nepočítáme, protože její vyplacení proběhne teprve v budoucnosti a parametry modelu odhadujeme na základě historických dat. V modelu tedy tato informace vůbec není zachycena. Odhadyparametrůr,Vavýnosnostítržníhoportfolia r M : Odhadyparametrůr=(r 1,...,r 10 ) av=[v i,j ;i,j=1,...,10]spočítámejakoprůměraempirickouvariančnímaticizvýnosností r j,t přesproměnnoučas t. výnos r= cez erste kb philip telef unipet prener setuza ssz vcplyn = diag(v) riziko Odhad varianční matice V: cez erste kb philip telef unipet prener setuza ssz vcplyn 0 1 cez erste kb philip telef unipet prener setuza B C A vcplyn
11 4 ODHADY VSTUPNÍCH PARAMETRŮ MODELU Odmocněním prvků na diagonále varianční matice dostaneme standartní odchylky výnosností akcí, kteréjsoumíramirizikjednotlivýchakcií(vizvektor diag(v)). Dále uvádím empirickou korelační matici výnosností. Pro lepší diverzifikaci portfolia je důležité, aby některé složky portfolia byly záporně korelované. cez erste kb philip telef unipet prener setuza ssz vcplyn 0 1 cez 1 erste kb philip telef R= unipet prener setuza B C A vcplyn
12 5 VYŘEŠENÍÚLOH 5 Vyřešení úloh Eficientní portfolia Podle předpokladu dávají investoři přednost portfoliím s vyšším výnosem a menším rizikem. výnos r(x)=r x riziko σ 2 (x)=x Vx Portfoliosváhamix splňujícímipodmínky(p)nazvemeeficientnívzhledemkestředníhodnotě a rozptylu(mean-variance efficient), jestliže neexistují jiné váhy x splňujícími podmínky(p), pro kteréje r(x) r(x ) σ 2 (x) σ 2 (x )aaspoňjednaznerovnostíjeostrá.podmínky(p)jsou všechny dodatečné podmínky omezení na váhy. Eficientní portfolia můžeme hledat jako řešení optimalizačních úloh, kde množina X všech přípustnýchřešení(vah)xjeurčenapodmínkami(p). Například můžeme řešit optimalizační úlohu závislou na parametru kde λ 0jeparametrmodelujícíinvestorůvvztahkriziku. Nebo můžeme použít přístup ε-constrained max x X r x λx Vx, (1) min x X x Vx (2) za r x r p, kdeparametremjenastavenáminimálníhodnota r p přijatelné(očekávané)výnosnostiportfolia. Přístup, kde bychom maximalizovali očekávaný výnos při dané horní mezi pro rozptyl není výhodný, protože by množina přípustných řešení byla určena nelineárními podmínkami. Já jsem pro vyřešení příkladů zvolila postup(2). Kvadratické programování v MATLABu Pro vyřešení optimalizačních úloh jsem použila program MATLAB, který obsahuje Optimization Toolbox pro řešení úloh lineárního i nelineárního programování. Při řešení zadaných úloh jsem z tohoto toolboxu vystačila s funkcí quadprog(), která slouží pro hledání optimálního řešení úlohy kvadratického programování. Úloha kvadratického programování: 1 min x 2 x Hx+f x 12
13 5 VYŘEŠENÍÚLOH za Ax b Aeqx = beq H,A,Aeq...matice f,b,beq...vektory Tuto úlohu vyřešíme v MATLABu pomocí příkazu: x = quadprog(h,f,a,b,aeq,beq) Ve všech úlohách je množina přípustných řešení konvexní polyedr(je omezená a určená lineárními omezeními), navíc jsem omezení vždy volila tak, aby množina přípustných řešení byla neprázdná. Pokud je navíc matice H pozitivně definitní, je účelová funkce ryze konvexní a je zaručena existence a jednoznačnost minima. Navíc vzhledem k tomu, že H je regulární, algoritmus funkce quadprog() vždy zkonverguje a to právě k optimálnímu řešení. V případě, že H je singulární a pozitivně semidefinitní je pořád zaručena existence minima, ale toto minimum už nemusí být určeno jednoznačně a algoritmus funkce quadprog() nemusí konvergovat. Pokud zkonverguje, je díky konvexnosti funkce zaručeno, že řešení je optimální, ale nemusí být eficientní podle naší definice. Například by se mohlo stát, že existuje více optimálních řešení, které majírozdílnouočekávanouvýnosnost 1,aalgoritmusfunkcenašelřešení,kterémáminimálnírozptyl, ale které nedává mezi optimálními maximální očekávaný výnos. Protože mým cílem je spočítat efektivní hranici, rozhodla jsem se v příkladech se singulární maticí H nerovnostr x r p nahraditrovnostír x=r p.nejdřívejsemsispočítalaintervalmožných hodnotparametru r p apotomjsemúlohuřešilaprorovnoměrnýnosičztohotointervalu.tímto způsobem jsem pro různé nastavené možné očekávané výnosnosti minimalizovala riziko. Dále jsem využila další možnosti funkce quadprog(), a to informace jestli úloha zkonvergovala. Použijeme-li tuto funkci ve tvaru [x, fval, exitflag] = quadprog(h,f,a,b,aeq,beq), dostaneme jako výstup kromě optimálního řešení ještě proměnné f val a exitf lag. Proměnná f val obsahuje optimální hodnotu účelové funkce. Proměnná exitf lag vypovídá o ukončujících podmínkách funkce quadprog(): exitflag >0 zkonvergovalokřešeníx exitf lag = 0 maximální počet iterací byl překročen exitf lag < 0 problém je neomezený, nepřípustný nebo nekonverguje. Protože MATLAB do proměnné x uloží nějaké hodnoty i v případě, že optimální řešení nalezeno nebylo, doplnila jsem program v případě, kdy jsou možné i singulární matice, testem, jestli funkce zkonvergovala k nějakému řešení(tj. je-li exitf lag > 0) a zakreslovala jsem pouze tyto řešení. Víme-li, že bylo nalezeno nějaké řešení, víme díky konvexnosti, že je optimální a zároveň víme hodnotu jeho očekávané výnosnosti(podmínka). Pokud existuje jiné optimální řešení, je hodnota 1 Vomezenídávámepouzedolníhraniciproočekávanývýnos 13
14 5 VYŘEŠENÍÚLOH jeho očekávané výnosnosti stejná a výsledkem je stejný bod na efektivní hranici. Nejednoznačnost optimálního řešení v tomto případě tedy nevadí. Problémem by mohlo být, kdyby většina úloh nezkonvergovala a výsledkem by bylo málo bodů na nakreslení efektivní hranice, k tomu ale v našem případě nedošlo. Řešení úloh a)-e) Při řešení úloh jsem vždy nejdříve úvahou nebo vyřešením optimalizační úlohy určila meze pro očekávanouvýnosnost r min a r max.zvolilajsemparametr krokamezníhodnotu r p jsemvolilapostupně jako r min +i krok;i=0,...,k.vhodnouvolbouparametru krokjsemzaručila,že r min +k krok= r max.prozískanéhodnotyxjsemspočítaladvojice[σ(x),r(x)]kterétvoříefektivníhranici. Dále používám značení: I n jednotkovámaticedimenzen 1,1 n sloupcovývektorjedniček 0,0 n sloupcovývektornul 0 n,m maticenulorozměrechnam J=10 počettitulůakcií a) Sestavte efektivní hranici portfólií(graficky prezentujte), vyberte některá portfólia na efektivní hranici a uveďte jejich složení(váhy) a očekávané výnosnosti titulů zastoupených v portfóliu. Obrázek 3: Pouze možnost investovat do akcií r(x) efektivní hranice σ(x) Hodnotu r min spočítámepomocívyřešeníúlohy(minimalizujemerizikobezohledunavýnos): min x x Vx za x 0, x 1=1 optimálnířešení x G r min = r(x G )=r x G =
15 5 VYŘEŠENÍÚLOH Hodnota r max = jemaximálníhodnotavektorur. Váhy x dostaneme řešením úlohy min x x Vx za r x r p 1 x = 1 x 0 Vstupy funkce quadprog(): ( r A= I J ) H=2 V f=0 J ( ) rp b= Aeq=1 0 J beq=1 b) Jak se změní efektivní hranice pokud budete mít možnost investovat do bezrizikového aktiva (depozitavbance)ssazbou...(naleznětesami)? Obrázek 4: Navíc možnost ukládání peněz r(x) efektivní hranice σ(x) Jako možnost investovat do bezrizikového aktiva jsem zvolila uložení peněz na termínovaný vklad s dobou uložení 1 rok. Úroková míra těchto vkladů závisí na výšce vkladu. Využila jsem srovnání termínovaných vkladů na Nejlepší nabídku tohoto produktu z bank má v současnosti Waldviertler Sparkasse, kde se úroková míra pohybuje v rozmezí 1, 3 2, 05% p.a. podle velikosti vkládané částky(do 2 milionů Kč). Zajímavá je také nabídka družstevní záložny Fio, kde se úrokové míryvkladunarokpohybujívrozmezí3 3,6%p.a..DružstevnízáložnaFiojevsočasnostinejvětší družstevní záložna, která vznikla v roce 1996 a jako jedna z prvních splnila jednotné podmínky EU prospořitelníaúvěrnídružstva.pokolapsuzáložennakonci90letunásalepořádpřetrváváurčitá nedůvěra v ukládání peněz do družstevních záložen. Propotřebymodelujsemzvolilajakobezrizikovouúrokovoumíru r 0 hodnotu2%p.a.. 15
16 5 VYŘEŠENÍÚLOH Při investování očekáváme aspoň takový výnos, který bychom dostali uložením všech peněz do bezrizikovéhoaktiva,tedy r min =2. Hodnota r max = jeopětmaximálníhodnotavektorur. Kroměproměnných x j ;j=1,...,jurčujícíchváhuinvesticedotitulu j,uvažujemeještěproměnnou x 0 určujícíváhuinvesticedobezrizikovéhoaktiva.očekávanývýnosje r 0 x 0 +r xapodmínka naváhysezměnína x 0 +1 x=1.vyjádřením x 0 =1 1 xadosazenímdostanemevzorecpro očekávanývýnos r 0 +(r 1) x. Váhyxdostanemeřešenímnásledujícíúlohy,váhu x 0 dopočítámezpodmínkyprováhy min x x Vx za r 0 +(r 1) x r p 1 x 1 x 0 Vstupy funkce quadprog(): A= (r 1) 1 J I J H=2 V f=0 J (r p r 0 ) b= 1 0 J Aeq=0 beq=0 c) Jak se změní efektivní hranice pokud budete mít možnost výpůjček od správce porfolia až do 30% hodnoty portfólia, pro jednoduchost předpokládejte, že výpůjční sazba je stejná jako depozitní, dokázali by jste zohlednit rozdílnou výpůjční a depozitní sazbu(nalezněte její sazbu sami a určete efektivní portfólia)? Obrázek 5: Navíc možnost ukládání a půjčování peněz r(x) efektivní hranice σ(x) 16
17 5 VYŘEŠENÍÚLOH Možnost půjčky do 30% hodnoty portfolia nám umožní hradit ze svého pouze 70% hodnoty portfolia, tedy nám dovolí sestavit portfolio o hodnotě až 10/7 našeho současného kapitálu. Při kapitálu 2 miliony může být hodnota našeho portfolia až Kč. Jako výpujční sazbu jsem použila úrokovou sazbu maržového úvěru nabízenou portálem 7,5%p.a. s čtvrtletním úročením, tj. efektivní úroková míra je cca 7,7135%. Tyto maržové obchody jsou u investorů velmi oblíbené, protože způsobují tzv. pákový efekt, kterým se znásobí výnos z našeho vloženého kapitálu. Větší výnos je ale provázen větším rizikem, protože stejným způsobem se znásobí případná ztráta. Vzhledem k tomu, že ve skutečnosti je výpujční vždy sazba větší než depozitní, rozhodla jsem se úlohuřešitprorozdílnésazby.dále r puj =(( /4) 4 1) 100jevýpujčnísazbaar 0 =2 je opět depozitní sazba. Vzhledem k možnosti půjčky je nutné upravit podmínku na váhy. Velikost půjčkyoznačíme P.Platí0 P 3 7.Proměnná x 0určujeváhuinvesticedobezrizikovéhoaktiva. Podmínkanaváhymápotomtvar: x 0 +1 x=1+p. Vzorecproočekávanývýnosje: r 0 x 0 +r x r puj P. Opětplatí r min = r 0 =2.Očekávanývýnosnejvýnosnějšíhotitulujevětšínežvýpujčnísazba,takže maximální očekávaný výnos dostaneme, když si půjčíme maximum a vše investujeme do titulu s největšímočekávanýmvýnosem,tedy r max = 10 7 max(r) 3 7 r puj= Hledanéproměnnéjsoutedy P, x 0 ax,kteréjsouřešenímnásledujícíúlohy.protožemámevíc proměnných než je dimenze matice V, bude matice H singulární, proto použijeme pro výnos omezení srovností. min P,x x Vx za r 0 x 0 +r x r puj P 0,x = r p P+ x 0 +1 x = 1 x 0 x 0 0 P 0 P 3 7 Vstupyfunkcequadprog():vektorproměnnýchje (P, x 0,x ) A= ( 02,2 0 H=2 2,J 0 J,2 V J J 0 J 0 J I J J ) ( ) rpuj r Aeq= 0 r J b= f=0 J+2 beq= J 3/7 ( rp 1 ) d) Co když budete mít povoleny krátké prodeje, až do 30% počátečního vkladu? Nakreslete efektivní hranici v tomto případě. Povolení krátkých prodejů nahrává spekulantům na pokles kurzu akcie. Investor prodá akcie, které vlastníněkdojinýanakonciobdobíjezasekoupízpět.pokudkurzklesl,nakoupiljezpátkylevněji 17
18 5 VYŘEŠENÍÚLOH Obrázek 6: Navíc povoleny krátké prodeje r(x) efektivní hranice σ(x) a vydělal na rozdílu cen. V Markowitzově modelu se povolení krátkých prodejů modeluje pomocí povolení záporných koeficientů vah. Váhyxdostanemeřešenímnásledujícíúlohy,kdex jevektorzápornýchčástívektorux,tj. x j = max(0, x j ).Musíplatit,žesoučetzápornýchčástívahnesmíbýtvětšínež30%. min x x Vx za r x r p 1 x = 1 1 x 0.3 Platí,že x j = x + j x j.definujmevektoryamaticim ( ) x + y= =(x + 1,...,x+ J,x 1,...,x J ) M= ( I J ) I J x Pomocínichdostanemevztahy x=my a 1 x = ( 0 J 1 J ) y. Původní úlohu tak můžeme přepsat na následující úlohu. Vzhledem k tomu, že matice v kvadratické formě je tady singulární, používám opět v omezení na výnos rovnost. Přibyla nám podmínka na nezápornost proměnných. min y y M VMy za r My = r p 1 My = 1 ( 0 1 ) y 0.3 y 0 Vstupy funkce quadprog(): H=2 M VM f=0 2J 18
19 5 VYŘEŠENÍÚLOH Aeq= A= ( r M 1 M ( I2J ) 0 J 1 b= J ) ( ) r = r 1 1 Optimální řešení původní úlohy získáme ze vztahu x = My. ( 02J 0.3 ) beq= ( rp 1 ) Ještějenutnéurčithodnoty r min a r max.prospočítání r min vyřešímestejnouoptimalizačníúlohu, vekterévynechámeomezeníproočekávanývýnos.maticeh,aavektoryfabbudoustejné.v matici Aeq a vektoru beq zůstane pouze spodní řádek, tj. Aeq= ( 1 M ) = ( 1 1 ) beq=1 Výsledkemje r min =r x=r My= Maximální očekávaný výnos dostaneme, když maximální možnou částku(tj. 130%počátečního vkladu) investujeme do aktiva s největším očekávaným výnosem a 30% počátečního vkladu si půjčíme prodejemcizího aktivasnejmenšímočekávanýmvýnosem,proto r max =1.3 max(r) 0.3 min(r)= e) V souladu s vnitřní politikou investiční společnosti, kterou zastupujete, nesmíte navrhnout portfólia, kde některý z titulů přesáhne 15% váhu v celkovém portfóliu. Nakreslete hranici efektivních portfólií v tomto případě. Obrázek7:Maximálníváha1tituluvportfoliuje15% r(x) efektivní hranice σ(x) Řešenítétoúlohyjejednoduché,stačíkpřípaduzaa)přidatpodmínku,žekaždé x j musíbýtmenší než Váhy x tedy dostaneme řešením úlohy min x x Vx za r x r p 1 x = 1 x 0 x J 19
20 5 VYŘEŠENÍÚLOH Vstupy funkce quadprog(): A= r I J I J H=2 V f=0 J r p b= 0 J Aeq=1 beq= J Hodnotu r min opětspočítámevyřešenímoptimalizačníúlohy,kdevynechámepodmínkunaočekávanývýnos.profunkciquadprog()sezměnípouzematiceaavektorb. ( ) ( ) IJ 0 A= b= J I J J Výsledkemje r min = Maximální očekávaný výnos dostaneme, když postupně rozložíme investice maximálně do aktiv s největším očekávaným výnosem. Tedy 15% do aktiva s největším očekávaným výnosem, dalších 15% doaktivasdruhýmnejvětšímočekávanýmvýnosematd.,vyjdenám r max = VMATLABu jsem použila opět funkci quadprog(), kde jsem v podmínkách použila stejné matice jako při počítání r min,pouzematicihjsemnahradilaprázdnoumaticíapoložilajsemf= r,cožodpovídá maximalizaci výnosu nez ohledu na riziko. 20
21 6 MÍRYRIZIKA 6 Míry rizika VaR(Value at Risk) VaRjetakováhodnota,ževýnosmenšínežVaRnastanesmaloupravděpodobností1 α(většinou α=0.95,varsepakoznačujejako95%var).proportfoliosváhamixanáhodnýmivýnosnostmi ρplatí: P(ρ x <VaR α (x))=1 α data matice dat historických výnosnosti, případě možnosti půjčky nebo ukládání penězpřidámesloupeckonstant r 0 nebo r puj x vektor vah složení portfolia ret = data x vektor pozorování historických výnosností portfolia ˆµ průměr pozorování ve vektoru ret ˆσ standartní odchylka pozorování ve vektoru ret Neparametrický VaR Neparametrický VaR budeme v našem případě počítat na základě historických dat jako empirický pětiprocentní kvantil. V MATLABu použijeme následující příkaz. VaR 0.95 (x) = prctile(ret,0.05) Parametrický VaR Parametrický VaR se počítá za předpokladu, že výnosnosti jsou normálně rozdělené se střední hodnotou µarozptylem σ 2. pvar 0.95 (x)=ˆµ+ˆσ u 0.05, kde u 0.05 =Φ 1 (0.05)jepětiprocentníkvantilnormálníhorozdělení. CVaR( Conditional Value at Risk) CVaR α (x)jepodmíněnástředníhodnotavýnosnostímenšíchnežvar α (x). CVaR α (x)=e(ρ x ρ x <VaR α (x)) ZdatodhadnemeCVaR 0.95 (x)jakoprůměrvšechpozorovánímenšíchnežvar 0.95 (x). 21
22 7 VÝSLEDKY 7 Výsledky Obrázek 8: Efektivní hranice a)-e) r(x) a) Pouze moznost investovat do akcii 20 b) Navic moznost ukladani penez c) Navic moznost ukladani a pujcovani penez d) Navic povoleny kratke prodeje e) Max. vaha 1 titulu je 15% σ(x) Obrázek 9: Efektivní hranice a)-e)- detail r(x) σ(x) 22
23 7 VÝSLEDKY a) Máme pouze možnost investovat do akcií. Parametry r(x) σ(x) VaR 0.95(x) pvar 0.95 (x) CVaR 0.95(x) Váhy cez 0.00% 6.11% 19.20% 31.94% 45.61% 61.61% 81.78% % erste 3.72% 12.09% 16.50% 25.77% 29.72% 28.36% 16.10% 0.00% kb 10.30% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% philip 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% telef 14.37% 2.03% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% unipet 0.00% 0.00% 0.00% 5.50% 8.49% 7.69% 2.12% 0.00% prener 32.75% 38.65% 31.34% 11.58% 0.00% 0.00% 0.00% 0.00% setuza 12.82% 14.59% 8.86% 1.13% 0.00% 0.00% 0.00% 0.00% ssz 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% vcplyn 26.03% 26.53% 24.10% 24.08% 16.18% 2.34% 0.00% 0.00% Investované částky cez erste kb philip telef unipet prener setuza ssz vcplyn
24 7 VÝSLEDKY b) Kromě možnosti investovat do akcií máme možnost peníze uložit do bezrizikového aktiva s úrokovou sazbou 2%. Parametry r(x) σ(x) VaR 0.95(x) pvar 0.95 (x) CVaR 0.95(x) Váhy uložit % 78.74% 52.76% 12.60% 0.00% 0.00% 0.00% 0.00% cez 0.00% 1.47% 3.26% 6.03% 23.46% 43.65% 69.98% % erste 0.00% 2.64% 5.86% 10.84% 19.20% 29.88% 24.23% 0.00% kb 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% philip 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% telef 0.00% 0.07% 0.15% 0.29% 0.00% 0.00% 0.00% 0.00% unipet 0.00% 0.00% 0.00% 0.00% 1.40% 8.59% 5.79% 0.00% prener 0.00% 8.37% 18.60% 34.41% 25.63% 0.00% 0.00% 0.00% setuza 0.00% 3.10% 6.90% 12.76% 6.41% 0.00% 0.00% 0.00% ssz 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% vcplyn 0.00% 5.61% 12.47% 23.07% 23.90% 17.88% 0.00% 0.00% Investované částky uložit cez erste kb philip telef unipet prener setuza ssz vcplyn
Cvičení z optimalizace Markowitzův model
 Cvičení z optimalizace Markowitzův model Vojtěch Franc, 29 1 Úvod V tomto cvičení se budeme zabývat aplikací kvadratického programování v ekonomii a sice v úloze, jejímž cílem bude optimalizovat portfolio
Cvičení z optimalizace Markowitzův model Vojtěch Franc, 29 1 Úvod V tomto cvičení se budeme zabývat aplikací kvadratického programování v ekonomii a sice v úloze, jejímž cílem bude optimalizovat portfolio
Změna hodnoty pozice v důsledku změn tržních cen.
 Tržní riziko Změna hodnoty pozice v důsledku změn tržních cen. Akciové riziko Měnové riziko Komoditní riziko Úrokové riziko Odvozená rizika... riz. volatility, riz. korelace Pozice (saldo hodnoty očekávaných
Tržní riziko Změna hodnoty pozice v důsledku změn tržních cen. Akciové riziko Měnové riziko Komoditní riziko Úrokové riziko Odvozená rizika... riz. volatility, riz. korelace Pozice (saldo hodnoty očekávaných
Změna hodnoty pozice v důsledku změn tržních cen.
 Tržní riziko Změna hodnoty pozice v důsledku změn tržních cen. Akciové riziko Měnové riziko Komoditní riziko Úrokové riziko Odvozená rizika... riz. volatility, riz. korelace Pozice (saldo hodnoty očekávaných
Tržní riziko Změna hodnoty pozice v důsledku změn tržních cen. Akciové riziko Měnové riziko Komoditní riziko Úrokové riziko Odvozená rizika... riz. volatility, riz. korelace Pozice (saldo hodnoty očekávaných
Optimalizace portfolia a míry rizika. Pavel Sůva
 Základní seminář 6. října 2009 Obsah Úloha optimalizace portfolia Markowitzův model Míry rizika Value-at-Risk Conditional Value-at-Risk Drawdown míry rizika Minimalizační formule Optimalizační modely Empirická
Základní seminář 6. října 2009 Obsah Úloha optimalizace portfolia Markowitzův model Míry rizika Value-at-Risk Conditional Value-at-Risk Drawdown míry rizika Minimalizační formule Optimalizační modely Empirická
Markowitzův model. Josef Orel, Pavel Sůva. 22. června Markowitzův model Stáhnutí a úprava dat Vstupní data a odhad parametrů 10
 Markowitzův model Optimalizace II s aplikací ve financích zápočtová úloha Josef Orel, Pavel Sůva 22. června 2010 Obsah 1 Zadání 2 2 Markowitzův model 3 2.1 Formulace základní úlohy a značení......................
Markowitzův model Optimalizace II s aplikací ve financích zápočtová úloha Josef Orel, Pavel Sůva 22. června 2010 Obsah 1 Zadání 2 2 Markowitzův model 3 2.1 Formulace základní úlohy a značení......................
Obecná úloha lineárního programování. Úloha LP a konvexní množiny Grafická metoda. Jiří Neubauer. Katedra ekonometrie FEM UO Brno
 Přednáška č. 3 Katedra ekonometrie FEM UO Brno Optimalizace portfolia Investor se s pomocí makléře rozhoduje mezi následujícími investicemi: akcie A, akcie B, státní pokladniční poukázky, dluhopis A, dluhopis
Přednáška č. 3 Katedra ekonometrie FEM UO Brno Optimalizace portfolia Investor se s pomocí makléře rozhoduje mezi následujícími investicemi: akcie A, akcie B, státní pokladniční poukázky, dluhopis A, dluhopis
Časová hodnota peněz (2015-01-18)
 Časová hodnota peněz (2015-01-18) Základní pojem moderní teorie financí. Říká nám, že peníze svoji hodnotu v čase mění. Díky časové hodnotě peněz jsme schopni porovnat různé investiční nebo úvěrové nabídky
Časová hodnota peněz (2015-01-18) Základní pojem moderní teorie financí. Říká nám, že peníze svoji hodnotu v čase mění. Díky časové hodnotě peněz jsme schopni porovnat různé investiční nebo úvěrové nabídky
KMA/MAB. Kamila Matoušková (A07142) Plzeň, 2009 EFEKTIVNÍ PORFÓLIO V MARKOWITZOVĚ SMYSLU
 EFEKTIVNÍ PORFÓLIO V MARKOWITZOVĚ SMYSLU KMA/MAB Kamila Matoušková (A07142) Plzeň, 2009 Obsahem práce je vytvoření efektivního portfolia v Markowitzově smyslu.z akcií obchodovaných na SPADu. Dále je uvažována
EFEKTIVNÍ PORFÓLIO V MARKOWITZOVĚ SMYSLU KMA/MAB Kamila Matoušková (A07142) Plzeň, 2009 Obsahem práce je vytvoření efektivního portfolia v Markowitzově smyslu.z akcií obchodovaných na SPADu. Dále je uvažována
Fakta a mýty o investování i riziku. Monika Laušmanová Radek Urban
 Fakta a mýty o investování i riziku Monika Laušmanová Radek Urban 1 Mýtus: Mezi investováním a utrácením není skoro žádný rozdíl Utrácení - koupě kabelky 35 000 30 000 Cena kabelky 25 000 20 000 15 000
Fakta a mýty o investování i riziku Monika Laušmanová Radek Urban 1 Mýtus: Mezi investováním a utrácením není skoro žádný rozdíl Utrácení - koupě kabelky 35 000 30 000 Cena kabelky 25 000 20 000 15 000
3. Zajištěný fond. Odvaz s minimálním rizikem.
 3. Zajištěný fond Odvaz s minimálním rizikem. 1 4 DŮVODY PROČ INVESTOVAT do 3. Zajištěného fondu 1 Jistota návratnost 106 % vložené investice Podstupujete minimální riziko - fond způsobem svého investování
3. Zajištěný fond Odvaz s minimálním rizikem. 1 4 DŮVODY PROČ INVESTOVAT do 3. Zajištěného fondu 1 Jistota návratnost 106 % vložené investice Podstupujete minimální riziko - fond způsobem svého investování
Parametrické programování
 Parametrické programování Příklad 1 Parametrické pravé strany Firma vyrábí tři výrobky. K jejich výrobě potřebuje jednak surovinu a jednak stroje, na kterých dochází ke zpracování. Na první výrobek jsou
Parametrické programování Příklad 1 Parametrické pravé strany Firma vyrábí tři výrobky. K jejich výrobě potřebuje jednak surovinu a jednak stroje, na kterých dochází ke zpracování. Na první výrobek jsou
FINANČNÍ A INVESTIČNÍ MATEMATIKA Metodický list č. 1
 FINANČNÍ A INVESTIČNÍ MATEMATIKA Metodický list č. 1 Název tématického celku: Úroková sazba a výpočet budoucí hodnoty Cíl: Základním cílem tohoto tematického celku je vysvětlit pojem úroku a roční úrokové
FINANČNÍ A INVESTIČNÍ MATEMATIKA Metodický list č. 1 Název tématického celku: Úroková sazba a výpočet budoucí hodnoty Cíl: Základním cílem tohoto tematického celku je vysvětlit pojem úroku a roční úrokové
Příloha k prezentaci BRODIS hodnotový OPFKI QIIS
 Příloha k prezentaci BRODIS hodnotový OPFKI QIIS V následující prezentaci se seznámíme s investičními principy, kterým věříme a na základě kterých jsme si nechali vytvořit BRODIS hodnotový OPFKI. Tyto
Příloha k prezentaci BRODIS hodnotový OPFKI QIIS V následující prezentaci se seznámíme s investičními principy, kterým věříme a na základě kterých jsme si nechali vytvořit BRODIS hodnotový OPFKI. Tyto
Cíl: seznámení s pojetím peněz v ekonomické teorii a s fungováním trhu peněz. Peníze jako prostředek směny, zúčtovací jednotka a uchovatel hodnoty.
 Vysoká škola finanční a správní, o. p. s. Akademický rok 2006/07, letní semestr Kombinované studium Předmět: Makroekonomie (Bc.) Metodický list č. 3 7) Peníze a trh peněz. 8) Otevřená ekonomika 7) Peníze
Vysoká škola finanční a správní, o. p. s. Akademický rok 2006/07, letní semestr Kombinované studium Předmět: Makroekonomie (Bc.) Metodický list č. 3 7) Peníze a trh peněz. 8) Otevřená ekonomika 7) Peníze
Úročení a časová hodnota peněz
 Úročení a časová hodnota peněz V přednášce budou představeny základní pojmy z finanční matematiky. 1 Jednoduché úročení a diskontování V případě jednoduchého úročení nedochází k připisování úroku k původnímu
Úročení a časová hodnota peněz V přednášce budou představeny základní pojmy z finanční matematiky. 1 Jednoduché úročení a diskontování V případě jednoduchého úročení nedochází k připisování úroku k původnímu
Finančnítrhy. Kolektivníinvestování
 Finančnítrhy Kolektivníinvestování Princip kolektivního investování Podstatou podnikání formou kolektivního investování je shromažďování peněžních prostředků od předem neurčeného a neomezeného počtu osob
Finančnítrhy Kolektivníinvestování Princip kolektivního investování Podstatou podnikání formou kolektivního investování je shromažďování peněžních prostředků od předem neurčeného a neomezeného počtu osob
Investiční životní pojištění
 Přehled fondů ČSOB - konzervativní fond Opatrný investor, který nerad riskuje a požaduje mírně převýšit výnosy z termínovaných vkladů u bank. ČSOB růstový fond Opatrný investor, který je ovšem ochoten
Přehled fondů ČSOB - konzervativní fond Opatrný investor, který nerad riskuje a požaduje mírně převýšit výnosy z termínovaných vkladů u bank. ČSOB růstový fond Opatrný investor, který je ovšem ochoten
Statistická analýza dat
 Statistická analýza dat Jméno: Podpis: Cvičení Zkouška (písemná + ústní) 25 Celkem 50 Známka Pokyny k vypracování: doba řešení je 120min, jasně zodpovězte pokud možno všechny otázky ze zadání, pracujte
Statistická analýza dat Jméno: Podpis: Cvičení Zkouška (písemná + ústní) 25 Celkem 50 Známka Pokyny k vypracování: doba řešení je 120min, jasně zodpovězte pokud možno všechny otázky ze zadání, pracujte
Investiční principy, kterým věříme a které využíváme při individuálním hodnotovém investičním poradenství
 Investiční principy, kterým věříme a které využíváme při individuálním hodnotovém investičním poradenství J a ro s l av H l av i c a, č e r ve n e c 2 0 1 4 V následující prezentaci se seznámíte s našimi
Investiční principy, kterým věříme a které využíváme při individuálním hodnotovém investičním poradenství J a ro s l av H l av i c a, č e r ve n e c 2 0 1 4 V následující prezentaci se seznámíte s našimi
ST 14.1. 8:00, E 127 PO 19.1. 16:00, E 127 ČT 22.1. 8:00, E 127 ST 28.1. 16:00, E 127. Komerční bankovnictví 1 / VŠFS ZS 2008/09
 Zkouškové termíny ST 14.1. 8:00, E 127 PO 19.1. 16:00, E 127 ČT 22.1. 8:00, E 127 ST 28.1. 16:00, E 127 1 Vymezení cenných papírů (CP) CP jsou v zákoně vymezeny výčtem: Akcie, zatímní listy, poukázky na
Zkouškové termíny ST 14.1. 8:00, E 127 PO 19.1. 16:00, E 127 ČT 22.1. 8:00, E 127 ST 28.1. 16:00, E 127 1 Vymezení cenných papírů (CP) CP jsou v zákoně vymezeny výčtem: Akcie, zatímní listy, poukázky na
Finanční gramotnost pro SŠ -10. modul Investování a pasivní příjem
 Modul č. 10 Ing. Miroslav Škvára O investicích O investování likvidita výnosnost rizikovost Kam mám investovat? Mnoho začínajících investorů se ptá, kam je nejlepší investovat? Všichni investiční poradci
Modul č. 10 Ing. Miroslav Škvára O investicích O investování likvidita výnosnost rizikovost Kam mám investovat? Mnoho začínajících investorů se ptá, kam je nejlepší investovat? Všichni investiční poradci
Příručka k měsíčním zprávám ING fondů
 Příručka k měsíčním zprávám ING fondů ING Investment Management vydává každý měsíc aktuální zprávu ke každému fondu, která obsahuje základní informace o fondu, jeho aktuální výkonnosti, složení portfolia
Příručka k měsíčním zprávám ING fondů ING Investment Management vydává každý měsíc aktuální zprávu ke každému fondu, která obsahuje základní informace o fondu, jeho aktuální výkonnosti, složení portfolia
III) Podle závislosti na celkovém ekonomickém vývoji či na vývoji v jednotlivé firmě a) systematické tržní, b) nesystematické jedinečné.
 Měření rizika Podnikatelské riziko představuje možnost, že dosažené výsledky podnikání se budou kladně či záporně odchylovat od předpokládaných výsledků. Toto riziko vzniká např. při zavádění nových výrobků
Měření rizika Podnikatelské riziko představuje možnost, že dosažené výsledky podnikání se budou kladně či záporně odchylovat od předpokládaných výsledků. Toto riziko vzniká např. při zavádění nových výrobků
PENÍZE, BANKY, FINANČNÍ TRHY
 PENÍZE, BANKY, FINANČNÍ TRHY Úročení 2 1. Jednoduché úročení Kapitál, Jistina označení pro peněžní částku Úrok odměna věřitele, u dlužníka je to cena za úvěr = CENA PENĚZ Doba splatnosti doba, po kterou
PENÍZE, BANKY, FINANČNÍ TRHY Úročení 2 1. Jednoduché úročení Kapitál, Jistina označení pro peněžní částku Úrok odměna věřitele, u dlužníka je to cena za úvěr = CENA PENĚZ Doba splatnosti doba, po kterou
Příručka k měsíčním zprávám ING fondů
 Příručka k měsíčním zprávám ING fondů ING Investment Management vydává každý měsíc aktuální zprávu ke každému fondu, která obsahuje základní informace o fondu, jeho aktuální výkonnosti, složení portfolia
Příručka k měsíčním zprávám ING fondů ING Investment Management vydává každý měsíc aktuální zprávu ke každému fondu, která obsahuje základní informace o fondu, jeho aktuální výkonnosti, složení portfolia
Varianta Pravděpodobnost Výnos A 1 Výnos A 2 1 0,1 1% 0,1 3% 0,3 2 0,2 12% 2,4 28% 5,6 3 0,3 6% 1,8 14% 4,2
 Dobrý den. Kladno, 22. 3. 2007 21:35 Chtěl bych se všem omluvit za ten závěr přednášky. Bohužel mě chyba v jednom z příkladů vykolejila natolik, že jsem se již velice těžko soustředil na svůj výkon. Chtěl
Dobrý den. Kladno, 22. 3. 2007 21:35 Chtěl bych se všem omluvit za ten závěr přednášky. Bohužel mě chyba v jednom z příkladů vykolejila natolik, že jsem se již velice těžko soustředil na svůj výkon. Chtěl
k riziku a ve svém důsledku vedlo použití modelu k diverzifikaci portfolia.
 MARKOWITZŮV MODEL OPTIMÁLNÍ VOLBY PORTFOLIA PŘEDPOKLADY, DATA, ALTERNATIVY Jitka Dupačová - příprava k přednášce pro ČSOB a Analýze investic Za zakladatele moderní teorie portfolia je pokládán H. Markowitz
MARKOWITZŮV MODEL OPTIMÁLNÍ VOLBY PORTFOLIA PŘEDPOKLADY, DATA, ALTERNATIVY Jitka Dupačová - příprava k přednášce pro ČSOB a Analýze investic Za zakladatele moderní teorie portfolia je pokládán H. Markowitz
K n = lim K 0.(1 + i/m) m.n. K n = K 0.e i.n. Stav kapitálu při spojitém úročení:
 Finanční matematika Spojité úročení Doposud při výpočtu stavu kapitálu na konci doby uložení byl proveden za (tacitního) předpokladu, že četnost připisování úroku za 1 rok m je konečné číslo délka jednoho
Finanční matematika Spojité úročení Doposud při výpočtu stavu kapitálu na konci doby uložení byl proveden za (tacitního) předpokladu, že četnost připisování úroku za 1 rok m je konečné číslo délka jednoho
Komerční banka. Akumulovat Sázka na dividendu a oživení
 Günter Hohberger (Analytik) +43 (0)50100-17354 Shrnutí a překlad anglického originálu Martin Krajhanzl (Analytik), mkrajhanzl@csas.cz 19.9.2013 Komerční banka Akumulovat Sázka na dividendu a oživení Vyšší
Günter Hohberger (Analytik) +43 (0)50100-17354 Shrnutí a překlad anglického originálu Martin Krajhanzl (Analytik), mkrajhanzl@csas.cz 19.9.2013 Komerční banka Akumulovat Sázka na dividendu a oživení Vyšší
Value at Risk. Karolína Maňáková
 Value at Risk Karolína Maňáková Value at risk Historická metoda Model-Building přístup Lineární model variance a kovariance Metoda Monte Carlo Stress testing a Back testing Potenciální ztráta s danou pravděpodobností
Value at Risk Karolína Maňáková Value at risk Historická metoda Model-Building přístup Lineární model variance a kovariance Metoda Monte Carlo Stress testing a Back testing Potenciální ztráta s danou pravděpodobností
Investiční dotazník a poučení o aspektech obchodování s cennými papíry
 Investiční dotazník a poučení o aspektech obchodování s cennými papíry vyžadovaný v souladu s 15h a 15i zákona o podnikání na kapitálovém trhu Upozornění pro zákazníky: Vyplnění tohoto dotazníku je dobrovolné.
Investiční dotazník a poučení o aspektech obchodování s cennými papíry vyžadovaný v souladu s 15h a 15i zákona o podnikání na kapitálovém trhu Upozornění pro zákazníky: Vyplnění tohoto dotazníku je dobrovolné.
Cvičení 5 - Inverzní matice
 Cvičení 5 - Inverzní matice Pojem Inverzní matice Buď A R n n. A je inverzní maticí k A, pokud platí, AA = A A = I n. Matice A, pokud existuje, je jednoznačná. A stačí nám jen jedna rovnost, aby platilo,
Cvičení 5 - Inverzní matice Pojem Inverzní matice Buď A R n n. A je inverzní maticí k A, pokud platí, AA = A A = I n. Matice A, pokud existuje, je jednoznačná. A stačí nám jen jedna rovnost, aby platilo,
Komoditní zajištěný fond. Odvažte se s minimálním rizikem.
 Komoditní zajištěný fond Odvažte se s minimálním rizikem. 4 DŮVODY PROČ INVESTOVAT do Komoditního zajištěného fondu 1 Jistota návratnost 105 % vložené investice Podstupujete minimální riziko - fond způsobem
Komoditní zajištěný fond Odvažte se s minimálním rizikem. 4 DŮVODY PROČ INVESTOVAT do Komoditního zajištěného fondu 1 Jistota návratnost 105 % vložené investice Podstupujete minimální riziko - fond způsobem
FRP 6. cvičení Měření rizika
 FRP 6. cvičení Měření rizika Podnikatelské riziko představuje možnost, že dosažené výsledky podnikání se budou kladně či záporně odchylovat od předpokládaných výsledků. Toto riziko vzniká např. při zavádění
FRP 6. cvičení Měření rizika Podnikatelské riziko představuje možnost, že dosažené výsledky podnikání se budou kladně či záporně odchylovat od předpokládaných výsledků. Toto riziko vzniká např. při zavádění
naopak více variant odpovědí, bude otázka hodnocena jako nesprávně zodpovězená.
 Datum:... Jméno:... Přijímací řízení pro akademický rok 28/9 na magisterské studijní obor Finanční informatiky a statistika Písemná část přijímací zkoušky z matematiky Za každou správnou odpověd se získávají
Datum:... Jméno:... Přijímací řízení pro akademický rok 28/9 na magisterské studijní obor Finanční informatiky a statistika Písemná část přijímací zkoušky z matematiky Za každou správnou odpověd se získávají
Lineární programování
 Lineární programování Petr Tichý 19. prosince 2012 1 Outline 1 Lineární programování 2 Optimalita a dualita 3 Geometrie úlohy 4 Simplexová metoda 2 Lineární programování Lineární program (1) min f(x) za
Lineární programování Petr Tichý 19. prosince 2012 1 Outline 1 Lineární programování 2 Optimalita a dualita 3 Geometrie úlohy 4 Simplexová metoda 2 Lineární programování Lineární program (1) min f(x) za
FINANČNÍ A INVESTIČNÍ MATEMATIKA 2
 FINANČNÍ A INVESTIČNÍ MATEMATIKA 2 Metodický list č. 1 Název tématického celku: Dluhopisy a dluhopisové portfolio I. Cíl: Základním cílem tohoto tematického celku je popsat dluhopisy jako investiční instrumenty,
FINANČNÍ A INVESTIČNÍ MATEMATIKA 2 Metodický list č. 1 Název tématického celku: Dluhopisy a dluhopisové portfolio I. Cíl: Základním cílem tohoto tematického celku je popsat dluhopisy jako investiční instrumenty,
Úvod do teorie portfolia. CAPM model. APT model Výhody vs. nevýhody modelů CML SML. Beta faktor
 Radka Domanská 1 Úvod do teorie portfolia CML CAPM model SML Beta faktor APT model Výhody vs. nevýhody modelů 2 Množina dostupných portfolií Všechna možná portfolia, která mohou být vytvořena ze skupiny
Radka Domanská 1 Úvod do teorie portfolia CML CAPM model SML Beta faktor APT model Výhody vs. nevýhody modelů 2 Množina dostupných portfolií Všechna možná portfolia, která mohou být vytvořena ze skupiny
Vyjadřují se v procentech z hodnoty vloženého kapitálu. Někdy se pro jejich označení používá termín cena kapitálu.
 1. Cena kapitálu Náklady kapitálu představují pro podnik výdaj, který musí zaplatit za získání různých forem kapitálu (tj. za získání např. různých forem dluhů, akciového kapitálu, nerozděleného zisku
1. Cena kapitálu Náklady kapitálu představují pro podnik výdaj, který musí zaplatit za získání různých forem kapitálu (tj. za získání např. různých forem dluhů, akciového kapitálu, nerozděleného zisku
Investičníčinnost. Existují různá pojetí investiční činnosti: Z pohledu ekonomické teorie. Podnikové pojetí investic
 Investičníčinnost Existují různá pojetí investiční činnosti: Z pohledu ekonomické teorie Podnikové pojetí investic Klasifikace investic v podniku 1) Hmotné (věcné, fyzické, kapitálové) investice 2) Nehmotné
Investičníčinnost Existují různá pojetí investiční činnosti: Z pohledu ekonomické teorie Podnikové pojetí investic Klasifikace investic v podniku 1) Hmotné (věcné, fyzické, kapitálové) investice 2) Nehmotné
Krátkodobé cenné papíry a Skonto obsah přednášky
 Krátkodobé cenné papíry a Skonto obsah přednášky 1) Vybrané krátkodobé cenné papíry 2) Skonto není cenný papír, ale použito obdobných principů jako u krátkodobých cenných papírů Vybrané krátkodobé cenné
Krátkodobé cenné papíry a Skonto obsah přednášky 1) Vybrané krátkodobé cenné papíry 2) Skonto není cenný papír, ale použito obdobných principů jako u krátkodobých cenných papírů Vybrané krátkodobé cenné
Obecná úloha lineárního programování
 Obecná úloha lineárního programování Úloha Maximalizovat hodnotu c T x (tzv. účelová funkce) za podmínek Ax b (tzv. omezující podmínky) kde A je daná reálná matice typu m n a c R n, b R m jsou dané reálné
Obecná úloha lineárního programování Úloha Maximalizovat hodnotu c T x (tzv. účelová funkce) za podmínek Ax b (tzv. omezující podmínky) kde A je daná reálná matice typu m n a c R n, b R m jsou dané reálné
Vysvětlivky k měsíčním reportům fondů RCM
 Vysvětlivky k měsíčním reportům fondů RCM Rozhodný den Pokud není u jednotlivých údajů uvedeno žádné konkrétní datum, platí údaje k tomuto rozhodnému dni. Kategorie investic Třída aktiv a její stručný
Vysvětlivky k měsíčním reportům fondů RCM Rozhodný den Pokud není u jednotlivých údajů uvedeno žádné konkrétní datum, platí údaje k tomuto rozhodnému dni. Kategorie investic Třída aktiv a její stručný
Stav Půjčky Splátky Kurzové Změna Stav
 II. Státní dluh 1. Vývoj státního dluhu V 2013 došlo ke zvýšení celkového státního dluhu o 47,9 mld. Kč z 1 667,6 mld. Kč na 1 715,6 mld. Kč. Znamená to, že v průběhu 2013 se tento dluh zvýšil o 2,9 %.
II. Státní dluh 1. Vývoj státního dluhu V 2013 došlo ke zvýšení celkového státního dluhu o 47,9 mld. Kč z 1 667,6 mld. Kč na 1 715,6 mld. Kč. Znamená to, že v průběhu 2013 se tento dluh zvýšil o 2,9 %.
Jak mohu splnit svá očekávání
 Jak mohu splnit svá očekávání Investiční strategie SPOLEHLIVÝ PARTNER PRO ÚSPĚŠNÉ INVESTOVÁNÍ Každý z nás má své specifické cíle, kterých může prostřednictvím investování dosáhnout. Pro někoho je důležité
Jak mohu splnit svá očekávání Investiční strategie SPOLEHLIVÝ PARTNER PRO ÚSPĚŠNÉ INVESTOVÁNÍ Každý z nás má své specifické cíle, kterých může prostřednictvím investování dosáhnout. Pro někoho je důležité
II. Vývoj státního dluhu
 II. Vývoj státního dluhu V 1. čtvrtletí 2014 došlo ke zvýšení celkového státního dluhu z 1 683,3 mld. Kč na 1 683,4 mld. Kč, což znamená, že v průběhu 1. čtvrtletí 2014 se tento dluh prakticky nezměnil.
II. Vývoj státního dluhu V 1. čtvrtletí 2014 došlo ke zvýšení celkového státního dluhu z 1 683,3 mld. Kč na 1 683,4 mld. Kč, což znamená, že v průběhu 1. čtvrtletí 2014 se tento dluh prakticky nezměnil.
Obligace II obsah přednášky
 Obligace II obsah přednášky 1) Durace obligace 2) Durace portfolia 3) Obchodování obligací kurzovní lístky Durace definice Durace udává střední dobu splatnosti obligace (tento pojem zavedl v roce 1938
Obligace II obsah přednášky 1) Durace obligace 2) Durace portfolia 3) Obchodování obligací kurzovní lístky Durace definice Durace udává střední dobu splatnosti obligace (tento pojem zavedl v roce 1938
Manažerská ekonomika KM IT
 KVANTITATIVNÍ METODY INFORMAČNÍ TECHNOLOGIE (zkouška č. 3) Cíl předmětu Získat základní znalosti v oblasti práce s ekonomickými ukazateli a daty, osvojit si znalosti finanční a pojistné matematiky, zvládnout
KVANTITATIVNÍ METODY INFORMAČNÍ TECHNOLOGIE (zkouška č. 3) Cíl předmětu Získat základní znalosti v oblasti práce s ekonomickými ukazateli a daty, osvojit si znalosti finanční a pojistné matematiky, zvládnout
Finanční trhy. Finanční aktiva
 Finanční trhy Finanční aktiva Magický trojúhelník investování (I) Riziko Výnos Likvidita Magický trojúhelník investování (II) Tři prvky magického trojúhelníku (výnos, riziko a likvidita) vytváří určitý
Finanční trhy Finanční aktiva Magický trojúhelník investování (I) Riziko Výnos Likvidita Magický trojúhelník investování (II) Tři prvky magického trojúhelníku (výnos, riziko a likvidita) vytváří určitý
Úlohy nejmenších čtverců
 Úlohy nejmenších čtverců Petr Tichý 7. listopadu 2012 1 Problémy nejmenších čtverců Ax b Řešení Ax = b nemusí existovat, a pokud existuje, nemusí být jednoznačné. Často má smysl hledat x tak, že Ax b.
Úlohy nejmenších čtverců Petr Tichý 7. listopadu 2012 1 Problémy nejmenších čtverců Ax b Řešení Ax = b nemusí existovat, a pokud existuje, nemusí být jednoznačné. Často má smysl hledat x tak, že Ax b.
KB POVINNÝ KONZERVATIVNÍ FOND
 KB POVINNÝ KONZERVATIVNÍ FOND Fond v kontextu nepříznivého dění na dluhopisových trzích poklesl Zápornou výkonnost zaznamenaly všechny nejkonzervativnější fondy v odvětví Na výkonnosti se negativně odrazil
KB POVINNÝ KONZERVATIVNÍ FOND Fond v kontextu nepříznivého dění na dluhopisových trzích poklesl Zápornou výkonnost zaznamenaly všechny nejkonzervativnější fondy v odvětví Na výkonnosti se negativně odrazil
Trh kapitálu. Doc. Ing. Jana Korytárová, Ph.D. Úspory a investice. Procesy, které v ekonomice probíhají lze shrnout následující tabulkou :
 Trh kapitálu Doc. Ing. Jana Korytárová, Ph.D. Úspory a investice Nabídku na trhu kapitálu tvoří úspory (Saving, S). Procesy, které v ekonomice probíhají lze shrnout následující tabulkou : produkt P věcná
Trh kapitálu Doc. Ing. Jana Korytárová, Ph.D. Úspory a investice Nabídku na trhu kapitálu tvoří úspory (Saving, S). Procesy, které v ekonomice probíhají lze shrnout následující tabulkou : produkt P věcná
Finanční trhy Kolektivní investování
 Finanční trhy Kolektivní investování Ing. Gabriela Oškrdalová e-mail: oskrdalova@mail.muni.cz Tento studijní materiál byl vytvořen jako výstup z projektu č. CZ.1.07/2.2.00/15.0189. 2.2.2013 Kolektivní
Finanční trhy Kolektivní investování Ing. Gabriela Oškrdalová e-mail: oskrdalova@mail.muni.cz Tento studijní materiál byl vytvořen jako výstup z projektu č. CZ.1.07/2.2.00/15.0189. 2.2.2013 Kolektivní
3 Jednoduchý a složený úrok, budoucí a současná hodnota, střadatel, fondovatel, nestejné peněžní proudy
 3 Jednoduchý a složený úrok, budoucí a současná hodnota, střadatel, fondovatel, nestejné peněžní proudy Stejné nominální částky mají v různých obdobích různou hodnotu tj. koruna dnes má jinou hodnotu,
3 Jednoduchý a složený úrok, budoucí a současná hodnota, střadatel, fondovatel, nestejné peněžní proudy Stejné nominální částky mají v různých obdobích různou hodnotu tj. koruna dnes má jinou hodnotu,
Úvod. Kapitálové statky výrobek není určen ke spotřebě, ale k další výrobě (postupná spotřeba) amortizace Finanční kapitál cenné papíry
 TRH KAPITÁLU Úvod Kapitálové statky výrobek není určen ke spotřebě, ale k další výrobě (postupná spotřeba) amortizace Finanční kapitál cenné papíry Vznik díky odložené spotřebě Nutná kompenzace možnost
TRH KAPITÁLU Úvod Kapitálové statky výrobek není určen ke spotřebě, ale k další výrobě (postupná spotřeba) amortizace Finanční kapitál cenné papíry Vznik díky odložené spotřebě Nutná kompenzace možnost
Úvod do analýzy cenných papírů. Dagmar Linnertová 5. Října 2009
 Úvod do analýzy cenných papírů Dagmar Linnertová 5. Října 2009 Investice a investiční rozhodování Každý je potenciální investor Nevynaložením prostředků na svou současnou potřebu se jí tímto vzdává Mít
Úvod do analýzy cenných papírů Dagmar Linnertová 5. Října 2009 Investice a investiční rozhodování Každý je potenciální investor Nevynaložením prostředků na svou současnou potřebu se jí tímto vzdává Mít
Hodnocení ekonomické efektivnosti projektů Průměrný výnos z investice, doba návratnosti, ČSH, VVP
 Hodnocení ekonomické efektivnosti projektů Průměrný výnos z investice, doba návratnosti, ČSH, VVP Investice je charakterizována jako odložená spotřeba. Podnikové investice jsou ty statky, které nejsou
Hodnocení ekonomické efektivnosti projektů Průměrný výnos z investice, doba návratnosti, ČSH, VVP Investice je charakterizována jako odložená spotřeba. Podnikové investice jsou ty statky, které nejsou
Investiční instrumenty a portfolio výnos, riziko, likvidita Úvod do finančních aktiv. Ing. Gabriela Oškrdalová e-mail: oskrdalova@mail.muni.
 Finanční trhy Investiční instrumenty a portfolio výnos, riziko, likvidita Úvod do finančních aktiv Ing. Gabriela Oškrdalová e-mail: oskrdalova@mail.muni.cz Tento studijní materiál byl vytvořen jako výstup
Finanční trhy Investiční instrumenty a portfolio výnos, riziko, likvidita Úvod do finančních aktiv Ing. Gabriela Oškrdalová e-mail: oskrdalova@mail.muni.cz Tento studijní materiál byl vytvořen jako výstup
Rovnovážné modely v teorii portfolia
 3. září 2013, Podlesí Obsah Portfolio a jeho charakteristiky Definice portfolia Výnosnost a riziko aktiv Výnosnost a riziko portfolia Klasická teorie portfolia Markowitzův model Tobinův model CAPM - model
3. září 2013, Podlesí Obsah Portfolio a jeho charakteristiky Definice portfolia Výnosnost a riziko aktiv Výnosnost a riziko portfolia Klasická teorie portfolia Markowitzův model Tobinův model CAPM - model
maticeteorie 1. Matice A je typu 2 4, matice B je typu 4 3. Jakých rozměrů musí být matice X, aby se dala provést
 Úlohy k zamyšlení 1. Zdůvodněte, proč třetí řádek Hornerova schématu pro vyhodnocení polynomu p v bodě c obsahuje koeficienty polynomu r, pro který platí p(x) = (x c) r(x) + p(c). 2. Dokažte, že pokud
Úlohy k zamyšlení 1. Zdůvodněte, proč třetí řádek Hornerova schématu pro vyhodnocení polynomu p v bodě c obsahuje koeficienty polynomu r, pro který platí p(x) = (x c) r(x) + p(c). 2. Dokažte, že pokud
Švýcarský frank za 35 let posílil o 63% oproti dolaru. Přesto se Švýcarům vyplatilo investovat do světových akcií!
 Švýcarský frank za 35 let posílil o 63% oproti dolaru. Přesto se Švýcarům vyplatilo investovat do světových akcií! Autor: Ing. Tomáš Tyl 7.6. 2011 Schválil: Ing. Vladimír Fichtner Výnosy akcií překonají
Švýcarský frank za 35 let posílil o 63% oproti dolaru. Přesto se Švýcarům vyplatilo investovat do světových akcií! Autor: Ing. Tomáš Tyl 7.6. 2011 Schválil: Ing. Vladimír Fichtner Výnosy akcií překonají
Lineární programování
 24.9.205 Lineární programování Radim Farana Podklady pro výuku pro akademický rok 203/204 Obsah Úloha lineárního programování. Formulace úlohy lineárního programování. Typické úlohy lineárního programování.
24.9.205 Lineární programování Radim Farana Podklady pro výuku pro akademický rok 203/204 Obsah Úloha lineárního programování. Formulace úlohy lineárního programování. Typické úlohy lineárního programování.
19.10.2015. Finanční matematika. Čas ve finanční matematice. Finanční matematika v osobních a rodinných financích
 Finanční matematika v osobních a rodinných financích Garant: Ing. Martin Širůček, Ph.D. Lektor: Ing. Martin Širůček, Ph.D. - doktorské studium oboru Finance na Provozně ekonomické fakultě Mendelovy univerzity
Finanční matematika v osobních a rodinných financích Garant: Ing. Martin Širůček, Ph.D. Lektor: Ing. Martin Širůček, Ph.D. - doktorské studium oboru Finance na Provozně ekonomické fakultě Mendelovy univerzity
KAPITOLA 4: PENĚŽNÍ TRH
 KAPITOLA 4: PENĚŽNÍ TRH Vysoká škola technická a ekonomická v Českých Budějovicích Institute of Technology And Business In České Budějovice Tento učební materiál vznikl v rámci projektu "Integrace a podpora
KAPITOLA 4: PENĚŽNÍ TRH Vysoká škola technická a ekonomická v Českých Budějovicích Institute of Technology And Business In České Budějovice Tento učební materiál vznikl v rámci projektu "Integrace a podpora
Jak splním svoje očekávání
 Jak splním svoje očekávání Zlatá investice SPOLEHLIVÝ PARTNER PRO ÚSPĚŠNÉ INVESTOVÁNÍ Proč investovat do zlata? Cena (USD) Vývoj ceny zlata v letech 2000 až 2012 Zdroj: Bloomberg Investice do zlata je
Jak splním svoje očekávání Zlatá investice SPOLEHLIVÝ PARTNER PRO ÚSPĚŠNÉ INVESTOVÁNÍ Proč investovat do zlata? Cena (USD) Vývoj ceny zlata v letech 2000 až 2012 Zdroj: Bloomberg Investice do zlata je
Cíl: seznámení s pojetím peněz v ekonomické teorii a s fungováním trhu peněz. Peníze jako prostředek směny, zúčtovací jednotka a uchovatel hodnoty.
 Vysoká škola finanční a správní, o. p. s. Akademický rok 2007/08, letní semestr Kombinované studium Předmět: Makroekonomie (Bc.) Metodický list č. 3 7) Peníze a trh peněz 8) Otevřená ekonomika 9) Hospodářské
Vysoká škola finanční a správní, o. p. s. Akademický rok 2007/08, letní semestr Kombinované studium Předmět: Makroekonomie (Bc.) Metodický list č. 3 7) Peníze a trh peněz 8) Otevřená ekonomika 9) Hospodářské
INDEXY KAPITÁLOVÝCH TRHŮ V ČR A VE SVĚTĚ. Michaela Ambrožová
 INDEXY KAPITÁLOVÝCH TRHŮ V ČR A VE SVĚTĚ Michaela Ambrožová Co je index? akciový index je statistickou veličinou, měří změny v portfoliu akcií reprezentujících část celkového akciového trhu, hlavní úkol:
INDEXY KAPITÁLOVÝCH TRHŮ V ČR A VE SVĚTĚ Michaela Ambrožová Co je index? akciový index je statistickou veličinou, měří změny v portfoliu akcií reprezentujících část celkového akciového trhu, hlavní úkol:
Nové trendy v investování
 AC Innovation s.r.o. Projekt: Praktický průvodce ekonomikou aneb My se trhu nebojíme! Registrační číslo: CZ.1.07/1.1.34/02.0039 Vzdělávací oblast: Nové trendy v investování Ing. Yveta Tomášková, Ph. D.
AC Innovation s.r.o. Projekt: Praktický průvodce ekonomikou aneb My se trhu nebojíme! Registrační číslo: CZ.1.07/1.1.34/02.0039 Vzdělávací oblast: Nové trendy v investování Ing. Yveta Tomášková, Ph. D.
Čistá současná hodnota a vnitřní výnosové procento
 Čistá současná hodnota a vnitřní výnosové procento Co je to čistá současná hodnota? Čistá současná hodnota představuje rozdíl mezi diskontovanými peněžními příjmy z určité činnosti a výdaji na tuto činnost.
Čistá současná hodnota a vnitřní výnosové procento Co je to čistá současná hodnota? Čistá současná hodnota představuje rozdíl mezi diskontovanými peněžními příjmy z určité činnosti a výdaji na tuto činnost.
CVIČENÍ ZE ZÁKLADŮ FINANCÍ
 CVIČENÍ ZE ZÁKLADŮ FINANCÍ 9.. 0 Veronika Kajurová Katedra financí kancelář č. 0 vkajurova@mail.muni.cz PROGRAM DNEŠNÍHO TUTORIÁLU Část I. - Časová hodnota peněz Příklady - opakování Část II. - Podnikové
CVIČENÍ ZE ZÁKLADŮ FINANCÍ 9.. 0 Veronika Kajurová Katedra financí kancelář č. 0 vkajurova@mail.muni.cz PROGRAM DNEŠNÍHO TUTORIÁLU Část I. - Časová hodnota peněz Příklady - opakování Část II. - Podnikové
Charakteristika rizika
 Charakteristika rizika Riziko je možnost, že se dosažené výsledky podnikání budou příznivě či nepříznivě odchylovat od předpokládaných výsledků. Odchylky od předpokladu jsou: a) příznivé b) nepříznivé
Charakteristika rizika Riziko je možnost, že se dosažené výsledky podnikání budou příznivě či nepříznivě odchylovat od předpokládaných výsledků. Odchylky od předpokladu jsou: a) příznivé b) nepříznivé
N i investiční náklady, U roční úspora ročních provozních nákladů
 Technicko-ekonomická optimalizace cílem je určení nejvýhodnějšího řešení pro zamýšlenou akci Vždy existují nejméně dvě varianty nerealizace projektu nulová varianta realizace projektu Konstrukce variant
Technicko-ekonomická optimalizace cílem je určení nejvýhodnějšího řešení pro zamýšlenou akci Vždy existují nejméně dvě varianty nerealizace projektu nulová varianta realizace projektu Konstrukce variant
MATERIÁL NA JEDNÁNÍ Zastupitelstva města Doksy
 MATERIÁL NA JEDNÁNÍ Zastupitelstva města Doksy Jednání zastupitelstva města dne: 2. 0. 206 Věc: Portfolio města Předkládá: Ing. Eva Burešová, starostka města Zpracoval (a): Ing. Pavinská, VFO MěÚ Doksy
MATERIÁL NA JEDNÁNÍ Zastupitelstva města Doksy Jednání zastupitelstva města dne: 2. 0. 206 Věc: Portfolio města Předkládá: Ing. Eva Burešová, starostka města Zpracoval (a): Ing. Pavinská, VFO MěÚ Doksy
INVESTOVÁNÍ A PASIVNÍ PŘÍJEM
 pracovní list k tématu INVESTOVÁNÍ A PASIVNÍ PŘÍJEM Individuální práce A) Práce v hodině Úkol č. 1: Rozhodněte, zda se jedná o úvěrový či investiční (spořicí) produkt: Kontokorent Hypotéka Dluhopis Spotřebitelský
pracovní list k tématu INVESTOVÁNÍ A PASIVNÍ PŘÍJEM Individuální práce A) Práce v hodině Úkol č. 1: Rozhodněte, zda se jedná o úvěrový či investiční (spořicí) produkt: Kontokorent Hypotéka Dluhopis Spotřebitelský
Hledání extrémů funkcí
 Hledání extrémů funkcí Budeme se zabývat téměř výhradně hledáním minima. Přes nost nalezeného extrému Obecně není hledání extrému tak přesné jako řešení rovnic. Demonstrovat to můžeme na příkladu hledání
Hledání extrémů funkcí Budeme se zabývat téměř výhradně hledáním minima. Přes nost nalezeného extrému Obecně není hledání extrému tak přesné jako řešení rovnic. Demonstrovat to můžeme na příkladu hledání
Funkce jedné proměnné
 Funkce jedné proměnné Příklad - V následujících příkladech v případě a) pro funkce dané rovnicí zjistěte zda jsou rostoucí klesající nebo konstantní vypočítejte průsečíky grafu s osami souřadnic a graf
Funkce jedné proměnné Příklad - V následujících příkladech v případě a) pro funkce dané rovnicí zjistěte zda jsou rostoucí klesající nebo konstantní vypočítejte průsečíky grafu s osami souřadnic a graf
INVESTIČNÍ DOTAZNÍK. 1. Identifikace zákazníka. 2. Investiční cíle zákazníka. Jméno a příjmení / obchodní firma / název: RČ/IČ: bytem/sídlo:
 INVESTIČNÍ DOTAZNÍK Investiční dotazník je předkládán v souladu s ust. 15h a 15i zákona č. 256/2004 Sb., o podnikání na kapitálovém trhu, ve znění pozdějších předpisů zákazníkovi společnosti B22 Finance
INVESTIČNÍ DOTAZNÍK Investiční dotazník je předkládán v souladu s ust. 15h a 15i zákona č. 256/2004 Sb., o podnikání na kapitálovém trhu, ve znění pozdějších předpisů zákazníkovi společnosti B22 Finance
Náklady kapitálu. Finanční struktura by měla korespondovat s majetkovou strukturou z hlediska časovosti. Stálá aktiva. Dlouhodobý.
 Náklady na kapitál Náklady kapitálu Finanční struktura by měla korespondovat s majetkovou strukturou z hlediska časovosti Aktiva (majetek) Stálá aktiva Oběžná aktiva Dlouhodobý majetek Trvalý OM Dlouhodobý
Náklady na kapitál Náklady kapitálu Finanční struktura by měla korespondovat s majetkovou strukturou z hlediska časovosti Aktiva (majetek) Stálá aktiva Oběžná aktiva Dlouhodobý majetek Trvalý OM Dlouhodobý
Investiční produkty v rámci finanční skupiny České spořitelny
 Fakulta ekonomických studií Katedra financí a finančních služeb Navazující magisterské studium kombinované Bankovnictví ZS 2011 Investiční produkty v rámci finanční skupiny České spořitelny Struktura nabídky
Fakulta ekonomických studií Katedra financí a finančních služeb Navazující magisterské studium kombinované Bankovnictví ZS 2011 Investiční produkty v rámci finanční skupiny České spořitelny Struktura nabídky
Numerické metody a programování. Lekce 8
 Numerické metody a programování Lekce 8 Optimalizace hledáme bod x, ve kterém funkce jedné nebo více proměnných f x má minimum (maximum) maximalizace f x je totéž jako minimalizace f x Minimum funkce lokální:
Numerické metody a programování Lekce 8 Optimalizace hledáme bod x, ve kterém funkce jedné nebo více proměnných f x má minimum (maximum) maximalizace f x je totéž jako minimalizace f x Minimum funkce lokální:
Numerické metody optimalizace - úvod
 Numerické metody optimalizace - úvod Petr Tichý 16. února 2015 1 Organizace přednášek a cvičení 13 přednášek a cvičení. Zápočet: úloha programování a testování úloh v Matlabu. Další informace na blogu
Numerické metody optimalizace - úvod Petr Tichý 16. února 2015 1 Organizace přednášek a cvičení 13 přednášek a cvičení. Zápočet: úloha programování a testování úloh v Matlabu. Další informace na blogu
Pojem investování a druhy investic
 Investiční činnost Pojem investování a druhy investic Rozhodování o investicích Zdroje financování investic Hodnocení efektivnosti investic Metody hodnocení investic Ukazatele hodnocení efektivnosti investic
Investiční činnost Pojem investování a druhy investic Rozhodování o investicích Zdroje financování investic Hodnocení efektivnosti investic Metody hodnocení investic Ukazatele hodnocení efektivnosti investic
Technická Analýza. Fio, banka, a.s. Fio, banka, a.s. 15/06/10
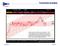 Technická Analýza Fio, banka, a.s. Pražský index PX se vrátil do hranic úzkého sideway (1080 1200). Hranice 1300 bodů růst zastavila a došlo ke korekci. Hlavní významnou rezistencí zůstává horní hranice
Technická Analýza Fio, banka, a.s. Pražský index PX se vrátil do hranic úzkého sideway (1080 1200). Hranice 1300 bodů růst zastavila a došlo ke korekci. Hlavní významnou rezistencí zůstává horní hranice
Finanční management. Nejefektivnější portfolio (leží na hranici) dle Markowitze: Přímka kapitálového trhu
 Finanční anageent Příka kapitálového trhu, odel CAPM, systeatické a nesysteatické riziko Příka kapitálového trhu Čí vyšší e sklon křivky, tí vyšší e nechuť investora riskovat. očekávaný výnos Množina všech
Finanční anageent Příka kapitálového trhu, odel CAPM, systeatické a nesysteatické riziko Příka kapitálového trhu Čí vyšší e sklon křivky, tí vyšší e nechuť investora riskovat. očekávaný výnos Množina všech
zisk : srovnávaná veličina (hodnocená,vstupní)
 4. přednáška Finanční analýza podniku - FucAn Návaznost na minulou přednášku Elementární metody a) analýza absolutních ukazatelů b) analýza rozdílových a tokových ukazatelů c) analýza poměrových ukazatelů
4. přednáška Finanční analýza podniku - FucAn Návaznost na minulou přednášku Elementární metody a) analýza absolutních ukazatelů b) analýza rozdílových a tokových ukazatelů c) analýza poměrových ukazatelů
Finanční gramotnost pro školy. Senior lektoři: Karel KOŘENÝ Petr PAVLÁSEK
 Finanční gramotnost pro školy Senior lektoři: Karel KOŘENÝ Petr PAVLÁSEK r. 2012 1. Zlatá pravidla Pokud chcete dosáhnout finanční nezávislosti, musíte plánovat, být disciplinovaní a rozhodnuti ovládat
Finanční gramotnost pro školy Senior lektoři: Karel KOŘENÝ Petr PAVLÁSEK r. 2012 1. Zlatá pravidla Pokud chcete dosáhnout finanční nezávislosti, musíte plánovat, být disciplinovaní a rozhodnuti ovládat
SR (CZK/EUR) 26,512 27,122 3 měs. IR CZK p.a. 6,24 7,44 3 měs. IR EUR p.a. 3,86 4,62 a) přímá kotace Nákupní forwardový kurs vypočítáme takto: SR 100
 Příklad č. 1 Na základě následujících kotací spotového kursu eura v korunách a tříměsíčních úrokových měr na korunová a eurová aktiva vypočítejte nákupní a prodejní tříměsíční forwardový kurs eura v korunách
Příklad č. 1 Na základě následujících kotací spotového kursu eura v korunách a tříměsíčních úrokových měr na korunová a eurová aktiva vypočítejte nákupní a prodejní tříměsíční forwardový kurs eura v korunách
D D P. e e e. ...požadovaná výnosová míra D...očekávané dividendy P. očekávaná prodejní cena. D n. n nekonečno. e e e e
 Téma 8: Chování cen akcií a investiční management Struktura přednášky: 1. Chování cen akcií fundamentální a technická analýza a teorie efektivních trhů. Riziko a výnos Markowitzův model 3. Kapitálový trh
Téma 8: Chování cen akcií a investiční management Struktura přednášky: 1. Chování cen akcií fundamentální a technická analýza a teorie efektivních trhů. Riziko a výnos Markowitzův model 3. Kapitálový trh
RELAX BONUS CERTIFIKÁT
 RELAX BONUS CERTIFIKÁT NA AKCIE ŽCEZ A.S., ERSTE BANK AG, TELEFONICA O2 CZECH REPUBLIC, KOMERCNÍ Ž BANKA A.S. WKN HV5AGG VYUZIJTE ŠANCE NA 40 % BONUS! Š CTYRI Ž Ž JEDNÍM TAHEM Přejete si atraktivní výnosový
RELAX BONUS CERTIFIKÁT NA AKCIE ŽCEZ A.S., ERSTE BANK AG, TELEFONICA O2 CZECH REPUBLIC, KOMERCNÍ Ž BANKA A.S. WKN HV5AGG VYUZIJTE ŠANCE NA 40 % BONUS! Š CTYRI Ž Ž JEDNÍM TAHEM Přejete si atraktivní výnosový
I) Vlastní kapitál 1) Základní jmění /upsaný kapitál/ 2) Kapitálové fondy: - ážio/disážio - dary - vklady společníků 3)Fondy ze zisku: - rezervní
 Náklady na kapitál I) Vlastní kapitál 1) Základní jmění /upsaný kapitál/ 2) Kapitálové fondy: - ážio/disážio - dary - vklady společníků 3)Fondy ze zisku: - rezervní fond - statutární a ostatní fondy 4)
Náklady na kapitál I) Vlastní kapitál 1) Základní jmění /upsaný kapitál/ 2) Kapitálové fondy: - ážio/disážio - dary - vklady společníků 3)Fondy ze zisku: - rezervní fond - statutární a ostatní fondy 4)
IAS 39: Účtování a oceňování
 IAS 39: Účtování a oceňování Josef Jílek člen Standards Advice Review Group březen 2007 Program Definice Zajišťovací účetnictví Vložené deriváty Deriváty na vlastní kapitálové nástroje Odúčtování aktiv
IAS 39: Účtování a oceňování Josef Jílek člen Standards Advice Review Group březen 2007 Program Definice Zajišťovací účetnictví Vložené deriváty Deriváty na vlastní kapitálové nástroje Odúčtování aktiv
Téma: Investice do akcií společnosti ČEZ
 Matematika a byznys Téma: Investice do akcií společnosti ČEZ Alena Švédová A07146 Investice do akcií společnosti ČEZ ÚVOD Tímto tématem, které jsem si pro tuto práci zvolila, bych chtěla poukázat na to,
Matematika a byznys Téma: Investice do akcií společnosti ČEZ Alena Švédová A07146 Investice do akcií společnosti ČEZ ÚVOD Tímto tématem, které jsem si pro tuto práci zvolila, bych chtěla poukázat na to,
Poptávka po penězích
 Poptávka po penězích 1. Neoklasické teorie poptávky po penězích - tradiční: Fisherova, Marshallova, cambridgeská - moderní: Friedmanova 2. Keynesiánská teorie poptávky po penězích tradiční: Keynesova moderní:
Poptávka po penězích 1. Neoklasické teorie poptávky po penězích - tradiční: Fisherova, Marshallova, cambridgeská - moderní: Friedmanova 2. Keynesiánská teorie poptávky po penězích tradiční: Keynesova moderní:
Cenné papíry základní charakteristika
 Cenné papíry základní charakteristika Cenný papír nebo zápis v příslušné evidenci spojený s nárokem,. Jejich podobu, údaje a možné operace upravují zákony.. Emitent (výstavce) Osoba, která. státní CP (státní
Cenné papíry základní charakteristika Cenný papír nebo zápis v příslušné evidenci spojený s nárokem,. Jejich podobu, údaje a možné operace upravují zákony.. Emitent (výstavce) Osoba, která. státní CP (státní
Analýzy a doporučení. Doporučení: Držet Cílová cena: 923 Kč. 28.4.2011 Změna doporučení na DRŽET z KOUPIT
 Fio banka, a.s. Fio Analýzy a doporučení Změna cílové ceny společnosti ČEZ Doporučení: Držet Cílová cena: 923 Kč 28.4.2011 Změna doporučení na DRŽET z KOUPIT K dnešnímu dni měníme naše doporučení u energetické
Fio banka, a.s. Fio Analýzy a doporučení Změna cílové ceny společnosti ČEZ Doporučení: Držet Cílová cena: 923 Kč 28.4.2011 Změna doporučení na DRŽET z KOUPIT K dnešnímu dni měníme naše doporučení u energetické
II. Vývoj státního dluhu
 II. Vývoj státního dluhu V 2015 došlo ke snížení celkového státního dluhu z 1 663,7 mld. Kč na 1 663,1 mld. Kč, tj. o 0,6 mld. Kč, přičemž vnitřní státní dluh se zvýšil o 1,6 mld. Kč, zatímco korunová
II. Vývoj státního dluhu V 2015 došlo ke snížení celkového státního dluhu z 1 663,7 mld. Kč na 1 663,1 mld. Kč, tj. o 0,6 mld. Kč, přičemž vnitřní státní dluh se zvýšil o 1,6 mld. Kč, zatímco korunová
Regresní analýza 1. Regresní analýza
 Regresní analýza 1 1 Regresní funkce Regresní analýza Důležitou statistickou úlohou je hledání a zkoumání závislostí proměnných, jejichž hodnoty získáme při realizaci experimentů Vzhledem k jejich náhodnému
Regresní analýza 1 1 Regresní funkce Regresní analýza Důležitou statistickou úlohou je hledání a zkoumání závislostí proměnných, jejichž hodnoty získáme při realizaci experimentů Vzhledem k jejich náhodnému
Důvodová zpráva. Správu aktiv města Jablonce nad Nisou vykonává na základě uzavřené smlouvy společnost J&T Banka, a.s.
 Důvodová zpráva Správu aktiv města Jablonce nad Nisou vykonává na základě uzavřené smlouvy společnost J&T Banka, a.s. V únoru byla správcem inkasována odměna za správu roku 2018 ve výši 462 914,97 Kč a
Důvodová zpráva Správu aktiv města Jablonce nad Nisou vykonává na základě uzavřené smlouvy společnost J&T Banka, a.s. V únoru byla správcem inkasována odměna za správu roku 2018 ve výši 462 914,97 Kč a
ČESKÝ AKCIOVÝ TRH - MĚSÍČNÍ KOMENTÁŘ ČEZ
 ČESKÝ AKCIOVÝ TRH - MĚSÍČNÍ KOMENTÁŘ ČEZ AKCIOVÉ TRHY ČERVENEC 2003 ČEZ ZVÝŠIT VÁHU (vůči indexu PX 50) 2. 7. 2003 ANALYTIK Karel Tregler BLOOMBERG CEZ CP (+420) 261 319 081 CENA (30. 6. 2003) 105,64 Kč
ČESKÝ AKCIOVÝ TRH - MĚSÍČNÍ KOMENTÁŘ ČEZ AKCIOVÉ TRHY ČERVENEC 2003 ČEZ ZVÝŠIT VÁHU (vůči indexu PX 50) 2. 7. 2003 ANALYTIK Karel Tregler BLOOMBERG CEZ CP (+420) 261 319 081 CENA (30. 6. 2003) 105,64 Kč
RELAX BONUS CERTIFIKÁT
 RELAX BONUS CERTIFIKÁT NA AKCIE SPOLECNOSTÍ Ž ŽCEZ A.S., ERSTE BANK AG ZENTIVA A.S., KOMERCNÍ Ž BANKA A.S. WKN HV5ACZ VYUZIJTE ŠANCE NA 15 18 %* BONUS! Š CTYRI Ž Ž JEDNÍM TAHEM Přejete si atraktivní výnosový
RELAX BONUS CERTIFIKÁT NA AKCIE SPOLECNOSTÍ Ž ŽCEZ A.S., ERSTE BANK AG ZENTIVA A.S., KOMERCNÍ Ž BANKA A.S. WKN HV5ACZ VYUZIJTE ŠANCE NA 15 18 %* BONUS! Š CTYRI Ž Ž JEDNÍM TAHEM Přejete si atraktivní výnosový
