! " # $ % # & ' ( ) * + ), -
|
|
|
- František Müller
- před 7 lety
- Počet zobrazení:
Transkript
1 ! " # $ % # & ' ( ) * + ), - INDIVIDUÁLNÍ VÝUKA MATEMATIKA METODIKA Kuželosek Mgr. Petra Dunovská bezen 9 Obtížnost této kapitol matematik je dána tím, že se pi výkladu i ešení úloh komplexn vužívají vdomosti a dovednosti z matematik získané v nižších ronících. Pro zvládnutí uiva b mli studenti umt upravovat výraz, ešit rovnice a jejich soustav vetn iracionálních rovnic a rovnic s absolutní hodnotou, lineární a kvadratické rovnice s parametrem, funkce hlavn lineární, kvadratické a lineárn lomené. Dále je potebná znalost analtické geometrie v rovin, zejména operace s vektor a rovnice pímk v rovin. Vhodnými pomckami pro výuku jsou matematické tabulk pro SŠ, kalkulaka, model kuželu a válce pro pedstavu pojmu kuželoseka, poíta, promítaka, internet, polstrenová deska pokrtá papírem s provázkem, špendlík a tužka pro konstrukci kuželosek. 1
2 I.kapitola Pojem KUŽELOSEKA a její rovnice Kuželosek jsou množin bod v rovin, které lze získat jako prnik rotaní kuželové ploch a rovin. Protínáme-li kužel rovinou kolmou na osu smetrie rotaního kuželu, výslednou kuželosekou je kružnice.protínáme-li kužel rovinou rovnobžnou práv s jednou z povrchových pímek plášt kuželu, výslednou kuželosekou je parabola.protínáme-li kužel rovinou, která svírá s osou smetrie rotaního kuželu úhel menší než 9 a vtší než polovina vrcholového úhlu kuželu, výslednou kuželosekou je elipsa. Rovina pitom protíná všechn povrchové pímk plášt kužele a není ted s žádnou z nich rovnobžná. Protínáme-li kužel rovinou, která svírá s osou smetrie rotaního kuželu úhel menší než polovina vrcholového úhlu kuželu, výslednou kuželosekou je hperbola; pitom rovina je rovnobžná práv se dvma povrchovými pímkami kuželu. K vsvtlení pojm je vhodné použít model kuželu a následující obrázk: Definice kuželoseek: Kružnice je množina všech bod rovin, které mají od daného bodu, stedu kružnice, danou vzdálenost, polomr kružnice. Elipsa je množina všech bod X rovin, pro které se souet XE + XF, vzdáleností bodu X od daných bod E, F této rovin, rovná danému íslu vtšímu než EF. Bod E a F se nazývají ohniska elips. Hperbola je množina všech bod X rovin, pro které se XE - XF rovná danému kladnému íslu, které je menší než EF. Bod E, F jsou dva rzné bod rovin a nazývají se ohniska hperbol. Parabola je množina všech bod rovin, které mají stejnou vzdálenost od bodu rovin F a od pímk q, která bodem F neprochází. Bod F se nazývá ohnisko, pímka q ídicí pímka parabol. Ke konstrukci kuželoseek podle jejich definic je možné použít polstrenovou desku s papírem, špendlík, tužkou a provázkem. Tto konstrukce je možné také vidt na internetu a je možné je promítat: Kuželosek zadáváme pomocí obecné rovnice, stedové rovnice (kružnice, elipsa, hperbola) i vrcholové rovnice (parabola).
3 Všechn tp rovnic kuželoseek, souadnice sted, vrchol, ohnisek a potebné nákres kuželoseek také nalezneme v Matematických tabulkách pro SŠ, které lze použít i pi výkladu, nebo je možné obrázk a rovnice promítat viz uvádné odkaz: ešené píklad na jednotlivé kuželosek: 1) Urete sted a polomr kružnice dané rovnicí x - x =. Doplníme výraz x - x a + 4 na druhé mocnin dvojlen (x 1) a ( + ): x - x = (x - 1) + ( + ) - 16 = (x - 1) + ( + ) = 16 Sted zadané kružnice je bod S[1; -] a její polomr r = 4. ) Urete sted, ohniska a hlavní poloosu elips dané rovnicí 5x x =. Nejprve obecnou rovnici upravíme na rovnici stedovou: 5x x = 5x + 15x = 5(x + 6x) + 9( - 4) + 6 = 5(x + 6x + 9-9) + 9( ) + 6 = 5(x + ) ( - ) = 5(x + ) + 9( - ) = 5 ted x ( ) Ze stedové rovnice snadno uríme jak sted elips, tak její hlavní osu a vedlejší poloosu. Navíc rozpoznáme i orientaci její hlavní os viz obrázek: ) Najdte sted, ohniska a hlavní vrchol hperbol, dané rovnicí: 9x - 9x =.
4 Podobn jako u pedchozích píklad upravíme obecnou rovnici na stedovou, ze které dokážeme celou adu údaj pímo víst. 9(x - 5) - 16( + ) x 5 = -144 pevedeme na tvar Z této rovnice uríme souadnice stedu hperbol, její hlavní a vedlejší poloosu. Sted S má souadnice S[5; -], hlavní poloosa a = 4, vedlejší poloosa b =. Z a a b dopoítáme výstednost e = 5. Tvar stedové rovnice odpovídá hperbole, jejíž hlavní osa je rovnobžná s osou. To nám staí k urení souadnic ohnisek E, F a hlavních vrchol A, B; E[5; ], F[5; -8], A[5; ] a B[5; -6]. 4) Najdte vrcholovou rovnici parabol urené ohniskem E[; 4] a ídicí pímkou q: = -. Vrchol V hledané parabol leží mezi bodem E a pímkou q. Platí, že V o, EV = Vq = p. Ze vzdálenosti E a q a jejich poloh mžeme urit jeho souadnice. Protože Eq = 6, mžeme íci, že souadnice vrcholu V jsou [; 1]. Z toho už jednoduše vjádíme vrcholovou rovnici: (x - ) = 1( - 1) Metodické poznámk k ešeným píkladm i k píkladm na další procviování: a)vsvtlit, jaký je rozdíl v obecných rovnicích jednotlivých kuželoseek, jak se z obecné rovnice odhadne, o jakou kuželoseku se mže jednat, pokud rovnice kuželoseku pedstavuje. b)vsvtlit postup pevádní obecné rovnice na stedovou nebo vrcholovou a obrácen. Ze stedové rovnice (u parabol z vrcholové rovnice) kuželoseku bezpen poznáme. c)všechn kuželosek je vhodné znázornit a popisovat pomocí obrázku. d)je teba umt pracovat s obrázk a vztah v tabulkách, rozumt pojmm hlavní a vedlejší vrchol, ohniska, sted, výstednost ( excentricita), hlavní a vedlejší poloos, asmptot hperbol, vrchol a ídící pímka parabol. Další píklad k procviení: 1) Najdte stedovou a obecnou rovnici kružnice se stedem S[; 5] a polomrem r =. (x - ) + ( - 5) =, x - 6x =. ) Zjistte, zda bod A[; 1], B[; 5], C[4; 5] a D[-1; ] leží na stejné kružnici. 4
5 stedová rovnice kružnice, urená bod A, B a C, je: (x - ) + ( - ) = 5. Zkusíme-li dosadit souadnice bodu D, zjistíme, že získaná rovnost neplatí, to znamená, že bod D neleží na stejné kružnici jako bod A, B a C. ) Urete výstednost elips s hlavním vrcholem A[-1; 1], vedlejším vrcholem B[4; -] a stedem S[4; 1]. ze vztahu a = b + e dopoítáme výstednost e = 4. 4) Najdte stedovou rovnici elips se stedem S[; ], výstedností e = 4 a hlavním vrcholem A[-; ]. vedlejší poloosu b vpoítáme ze vztahu b = a e, b =. 5) Najdte obecnou rovnici elips, která má sted S[; 1], hlavní vrchol A[; 6] a ohnisko E[; -]. 5x + 9-1x =. 6) Urete obecnou rovnici parabol s vrcholem V[; -1], jejíž ídicí pímkou je osa. - 8x =. 7) Najdte ohnisko, vrchol a ídicí pímku parabol, která je dána rovnicí x - 4x =. z vrcholové rovnice (x - ) = 4( - ) uríme souadnice vrcholu V[; ], ohnisko E má souadnice E[; ] a ídicí pímka q dané parabol má rovnici = 1. 8) Urete stedovou rovnici a asmptot hperbol se stedem S[; -1], ohniskem E[7; -1] a vrcholem A[5; -1]. a = SA =, e = SE = 5, b = 4, asmptot: 4x =, 4x =. 9) Napište obecnou rovnici hperbol s asmptotami a 1 : x =, a : x = a vrcholem A[; ]. 9x x =. 5
6 II.kapitola Kuželoseka a pímka Pímka mže mít s kuželosekou, 1, nebo spolené bod. Jednotlivé možnosti jsou uveden v tabulce. V rovnici pímk se asto vsktuje uritý parametr, jehož hodnotu urujeme nejastji pomocí diskriminantu kvadratické rovnice. kuželoseka spol. bod 1 spol. bod spol. bod kružnice Pímka vn Pímka je tenou Pímka je senou kružnice (D<). kružnice kružnice (D>). elipsa hperbola parabola Pímka vn elips (D<). Pímka vn vtví hperbol(d<), nebo pímo asmptota hperbol. Pímka vn parabol(d<). (D = ). Pímka je tenou elips (D = ). Pímka je tenou hperbol (D = ), nebo je rovnobžná s asmptotou hperbol. Pímka je tenou parabol (D = ), nebo rovnobžná s osou parabol. Pímka je senou elips (D>). Pímka je senou hperbol (D>). Pímka je senou parabol (D>). D diskriminant kvadratické rovnice (ešíme kvadratickou rovnici s parametrem) Z rovnice pímk vjádíme jednu neznámou, dosadíme do rovnice kuželosek a poítáme diskriminant kvadratické rovnice. Vzájemné poloh hperbol a parabol s pímkou, které nejdou ešit pomocí diskriminantu, ešíme jako vzájemnou polohu pímek pomocí vektor( rovnobžnost vektor). Pokud máme napsat rovnici ten k dané kuželosece v bod, který na kuželosece leží, použijeme obecné rovnice teen, které najdeme v tabulkách. Zde nemusíme ešit rovnici s parametrem. Pokud píšeme rovnici ten z bodu, který na kuželosece neleží, postupujeme takto: a)u kružnice mžeme vužít rovnici polár, tj. pímk spojující bod dotku. (Pímka daná rovnicí (x - m)(x 1 - m) + ( - n)( 1 - n) = r se nazývá polára bodu X 1 [x 1 ; 1 ] vzhledem ke kružnici k se stedem S[m; n] a polomrem r.) Prseík polár s kružnicí jsou bod, které na kružnici leží a t již lze použít k zápisu rovnic teen podle tabulek. Rovnice polár je rovnž v tabulkách. b)u všech kuželoseek uríme pomocí soustav rovnic nejprve bod dotku kuželosek a pímk a pak mžeme napsat rovnice teen. 6
7 Vzájemnou polohu kuželoseek a pímk ilustrují obrázk: (kružnice a pímka) (elipsa a pímka) (hperbola a pímka) 7
8 (parabola a pímka) Píklad ešené nebo s náznakem 1) Najdte prseík pímk p(a, u) a kružnice (x - ) + ( - ) = 4, je-li A[-1; 4] a u = (1; -1). parametrick vjádíme pímku p: x = -1 + t, = 4 - t; t. Do stedové rovnice kružnice dosadíme souadnice x a z parametrické rovnice pímk p. Získáme kvadratickou rovnici t - 6t + 8 =. Podle diskriminantu D této rovnice, lze rozhodnout, jaká je vzájemná poloha dané pímk a kružnice. Je-li D <, rovnice nemá v ešení a pímka p je vnjší pímkou kružnice. Je-li D =, rovnice má jedno (dvojnásobné ešení) a pímka p je tenou kružnice. Nakonec, je-li D >, rovnice má dv ešení a pímka p je senou kružnice. V našem pípad je D = 4 a rovnice má dv t 1 = 4 a t =. Tto dv hodnot parametru dosadíme do parametrické rovnice pímk p a získáme souadnice bod P1[; ] a P[1; ], které jsou hledanými prseík. ) Najdte rovnici ten kružnice x - x = v jejím bod T[4; -]. Stedová rovnice kružnice je (x - 1) + ( - ) = 5. Rovnice ten t v bod T[x ; ] má tvar: (x - 1)(x - 1) + ( - )( - ) = 5. Po dosazení bodu T do této rovnice ten a po úprav na obecnou rovnici pímk dostaneme t: x =. ) Najdte spolené bod pímk x = a parabol ( - ) = (x - 1). ešíme soustavu rovnic. Z rovnice pímk nejprve vjádíme nap. = x + 5 a dosadíme do rovnice parabol. Hledáme ešení kvadratické rovnice. Poet ešení urí vzájemnou polohu pímk a parabol. Navíc získáme jednu ze souadnic hledaných prseík. Kvadratická rovnice x + x + = nemá žádné ešení, a proto mžeme íci, že zadaná pímka a parabola nemají žádný spolený bod, pímka je vnjší pímkou parabol. 4) Najdte ten ke kružnici k: x - x =, které procházejí bodem B[5; 1]. Nejprve uríme stedovou rovnici kružnice k: (x - 1) + ( + ) = 16, bod B na kružnici neleží. Uríme rovnici polár: (x - 1)(5-1) + ( + )(1 + ) = 16, ted x + - =. Prseík polár a kružnice bod T 1 [1; 1] a T [5; -] jsou bod dotku. Obecná rovnice ten kružnice k v bod T 1 je: (x - 1)(1-1) + ( + )(1+ ) = 16, ted = 1. 8
9 Obecná rovnice ten kružnice k v bod T je (x - 1)(5-1) + ( + )(- + ) = 16, ted x = 5. 5) Urete délku ttiv, kterou vtíná pímka p na kuželosece k. p : x ; k : x x 1 Prseík jsou P ; ; 1 P ; prseík, pro vzdálenosti dvou bod (resp. délku úsek) platí: P x x 1P 1 1, ted, délka ttiv je vzdálenost P P ) Urete tenu kuželosek x 9 5, která je rovnobžná s pímkou p : x. rovnice hledané ten t : ax b c, tena je rovnobžná s pímkou p, její rovnice je ted t : x c. ešíme soustavu x 9 5 x c Z lineární rovnice vjádíme jednu neznámou (nap. x), dosadíme ji do kvadratické rovnice, a pak ešíme kvadratickou rovnici s parametrem c. Jelikož se jedná o tenu, musí být D =.. 9 D b 6c c c c 6c c 6c 618 4ac c D 144c 6 c t : x 5 5 c5, ted existují dv hledané ten: Metodické poznámk k uvedeným úlohám: 9
10 a)pi hledání spolených bod kuželosek a pímk ešíme vžd soustavu rovnic, z rovnice pímk dosazujeme do rovnice kuželosek. Z potu ešení soustav uríme poet spolených bod, vpoteme ob souadnice prseík. b) Pipomeneme ešení kvadratické rovnice s parametrem a vliv diskriminantu na poet ešení rovnice. Zapisujeme všechna ešení (nap. všechn ten). c) Pokud píšeme rovnici ten, která prochází daným bodem, vžd ovíme, zda bod na dané kuželosece leží nebo neleží. d) Pro lepší pedstavu situace kreslíme obrázk a používáme tabulk s konkrétními obrázk. Další píklad k procviení: 1) Urete vzájemnou polohu pímk p a kuželosek k. p : x 1 ; k : x 4 ( sena kuželosek) ) Urete tenu kuželosek x x, která se jí dotýká v teném T ;. ( rovnice ten: t : 5x 1 ) T bod ) Urete tenu kuželosek, pro kterou platí a) tena je vedena bodem ; M (nejedná se o tený bod!) a kuželoseka má rovnici x ( t : x 4 9 ) b) tena je kolmá na pímku p : x a kuželoseka má rovnici x 4 1 ( : x t ) 4) Napište rovnici ten ke kružnici x - 6x =, která je rovnobžná s pímkou p: x =. ( t 1 : x =, t : x = ) Test na závr Je možné použít tento test: zeloseck 1
11 Použitá literatura a ostatní materiál: Matematické tabulk pro SŠ - rzné Nadžda Kubešová, Eva Cibulková : Matematika pehled stedoškolského uiva,. vd.,tebí: Petra Velanová, 7, edice Maturita V píloze na dalších stránkách jsou uveden píklad z pedchozích stránek tak, ab mohl být v pípad poteb kopírován pro práci student pi hodinách individuální výuk. 11
12 I.kapitola Pojem KUŽELOSEKA a její rovnice ešené píklad na jednotlivé kuželosek: 1) Urete sted a polomr kružnice dané rovnicí x - x =. ) Urete sted, ohniska a hlavní poloosu elips dané rovnicí 5x x =. ) Najdte sted, ohniska a hlavní vrchol hperbol, dané rovnicí: 9x - 9x =. 4) Najdte vrcholovou rovnici parabol urené ohniskem E[; 4] a ídicí pímkou q: = -. Další píklad k procviení: 1) Najdte stedovou a obecnou rovnici kružnice se stedem S[; 5] a polomrem r =. ) Zjistte, zda bod A[; 1], B[; 5], C[4; 5] a D[-1; ] leží na stejné kružnici. ) Urete výstednost elips s hlavním vrcholem A[-1; 1], vedlejším vrcholem B[4; -] a stedem S[4; 1]. 4) Najdte stedovou rovnici elips se stedem S[; ], výstedností e = 4 a hlavním vrcholem A[-; ]. 5) Najdte obecnou rovnici elips, která má sted S[; 1], hlavní vrchol A[; 6] a ohnisko E[; -]. 6) Urete obecnou rovnici parabol s vrcholem V[; -1], jejíž ídicí pímkou je osa. 7) Najdte ohnisko, vrchol a ídicí pímku parabol, která je dána rovnicí x - 4x =. 8) Urete stedovou rovnici a asmptot hperbol se stedem S[; -1], ohniskem E[7; -1] a vrcholem A[5; -1]. 9) Napište obecnou rovnici hperbol s asmptotami a 1 : x =, a : x = a vrcholem A[; ]. II.kapitola Kuželoseka a pímka Píklad ešené nebo s náznakem 1) Najdte prseík pímk p(a, u) a kružnice (x - ) + ( - ) = 4, je-li A[-1; 4] a u = (1; -1). ) Najdte rovnici ten kružnice x - x = v jejím bod T[4; -]. ) Najdte spolené bod pímk x = a parabol ( - ) = (x - 1). 4) Najdte ten ke kružnici k: x - x =, které procházejí bodem B[5; 1]. 5) Urete délku ttiv, kterou vtíná pímka p na kuželosece k. p : x ; k : x x 1 6) Urete tenu kuželosek x 9 5, která je rovnobžná s pímkou p : x. 1
13 Další píklad k procviení: 1) Urete vzájemnou polohu pímk p a kuželosek k. p : x 1 ; k : x 4 ) Urete tenu kuželosek x x, která se jí dotýká v teném T ;. T bod ) Urete tenu kuželosek, pro kterou platí: M ; (nejedná se o tený bod!) a kuželoseka a) tena je vedena bodem má rovnici x b) tena je kolmá na pímku p : x a kuželoseka má rovnici x 4 1 4) Napište rovnici ten ke kružnici x - 6x =, která je rovnobžná s pímkou p: x =. ( t 1 : x =, t : x = ) 1
X = A + tu. Obr x = a 1 + tu 1 y = a 2 + tu 2, t R, y = kx + q, k, q R (6.1)
 .6. Analtická geometrie lineárních a kvadratických útvarů v rovině. 6.1. V této kapitole budeme studovat geometrické úloh v rovině analtick, tj. lineární a kvadratické geometrické útvar vjádříme pomocí
.6. Analtická geometrie lineárních a kvadratických útvarů v rovině. 6.1. V této kapitole budeme studovat geometrické úloh v rovině analtick, tj. lineární a kvadratické geometrické útvar vjádříme pomocí
4. EZY NA KUŽELÍCH 4.1. KUŽELOVÁ PLOCHA, KUŽEL
 4. EZY NA KUŽELÍCH 4.1. KUŽELOVÁ PLOCHA, KUŽEL Definice : Je dána kružnice k ležící v rovin a mimo ni bod V. Všechny pímky jdoucí bodem V a protínající kružnici k tvoí kruhovou kuželovou plochu. Tyto pímky
4. EZY NA KUŽELÍCH 4.1. KUŽELOVÁ PLOCHA, KUŽEL Definice : Je dána kružnice k ležící v rovin a mimo ni bod V. Všechny pímky jdoucí bodem V a protínající kružnici k tvoí kruhovou kuželovou plochu. Tyto pímky
Definice : Jsou li povrchové pímky kolmé k rovin, vzniká kolmá kruhová válcová plocha a pomocí roviny také kolmý kruhový válec.
 3. EZY NA VÁLCÍCH 3.1. VÁLCOVÁ PLOCHA, VÁLEC Definice : Je dána kružnice k ležící v rovin a pímka a rznobžná s rovinou. Všechny pímky rovnobžné s pímkou a protínající kružnici k tvoí kruhovou válcovou
3. EZY NA VÁLCÍCH 3.1. VÁLCOVÁ PLOCHA, VÁLEC Definice : Je dána kružnice k ležící v rovin a pímka a rznobžná s rovinou. Všechny pímky rovnobžné s pímkou a protínající kružnici k tvoí kruhovou válcovou
Gymnázium, Brno, Elgartova 3
 Gymnázium, Brno, Elgartova 3 GE - Vyšší kvalita výuky CZ.1.07/1.5.00/34.0925 IV/2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma: Analytická geometrie
Gymnázium, Brno, Elgartova 3 GE - Vyšší kvalita výuky CZ.1.07/1.5.00/34.0925 IV/2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma: Analytická geometrie
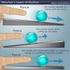
Odvození středové rovnice kružnice se středem S [m; n] a o poloměru r. Bod X ležící na kružnici má souřadnice [x; y].
![Odvození středové rovnice kružnice se středem S [m; n] a o poloměru r. Bod X ležící na kružnici má souřadnice [x; y]. Odvození středové rovnice kružnice se středem S [m; n] a o poloměru r. Bod X ležící na kružnici má souřadnice [x; y].](/thumbs/91/104981778.jpg) Konzultace č. 6: Rovnice kružnice, poloha přímky a kružnice Literatura: Matematika pro gymnázia: Analytická geometrie, kap. 5.1 a 5. Sbírka úloh z matematiky pro SOŠ a studijní obory SOU. část, kap. 6.1
Konzultace č. 6: Rovnice kružnice, poloha přímky a kružnice Literatura: Matematika pro gymnázia: Analytická geometrie, kap. 5.1 a 5. Sbírka úloh z matematiky pro SOŠ a studijní obory SOU. část, kap. 6.1
obecná rovnice kružnice a x 2 b y 2 c x d y e=0 1. Napište rovnici kružnice, která má střed v počátku soustavy souřadnic a prochází bodem A[-3;2].
![obecná rovnice kružnice a x 2 b y 2 c x d y e=0 1. Napište rovnici kružnice, která má střed v počátku soustavy souřadnic a prochází bodem A[-3;2]. obecná rovnice kružnice a x 2 b y 2 c x d y e=0 1. Napište rovnici kružnice, která má střed v počátku soustavy souřadnic a prochází bodem A[-3;2].](/thumbs/59/44051949.jpg) Kružnice množina bodů, které mají od středu stejnou vzdálenost pojmy: bod na kružnici X [x, y]; poloměr kružnice r pro střed S[0; 0]: SX =r x 0 2 y 0 2 =r x 2 y 2 =r 2 pro střed S[m; n]: SX =r x m 2 y
Kružnice množina bodů, které mají od středu stejnou vzdálenost pojmy: bod na kružnici X [x, y]; poloměr kružnice r pro střed S[0; 0]: SX =r x 0 2 y 0 2 =r x 2 y 2 =r 2 pro střed S[m; n]: SX =r x m 2 y
UNIVERZITA PALACKÉHO V OLOMOUCI. Bakaláská práce. Analytická geometrie kuželoseek
 UNIVERZITA PALACKÉHO V OLOMOUCI PEDAGOGICKÁ FAKULTA Katedra matematiky Bakaláská práce Martin Krbec, DiS. Analytická geometrie kuželoseek Olomouc 2013 vedoucí práce: Mgr. David Nocar, Ph.D. Prohlášení
UNIVERZITA PALACKÉHO V OLOMOUCI PEDAGOGICKÁ FAKULTA Katedra matematiky Bakaláská práce Martin Krbec, DiS. Analytická geometrie kuželoseek Olomouc 2013 vedoucí práce: Mgr. David Nocar, Ph.D. Prohlášení
2. EZY NA JEHLANECH. Píklad 47 : Sestrojte ez pravidelného tybokého jehlanu ABCDV rovinou.
 2. EZY NA JEHLANECH Píklad 47 : Sestrojte ez pravidelného tybokého jehlanu ABCDV rovinou. Popis konstrukce : Podobn jako u píkladu 41 je výhodné proložit nkterými dvma hranami jehlanu rovinu kolmou k pdorysn.
2. EZY NA JEHLANECH Píklad 47 : Sestrojte ez pravidelného tybokého jehlanu ABCDV rovinou. Popis konstrukce : Podobn jako u píkladu 41 je výhodné proložit nkterými dvma hranami jehlanu rovinu kolmou k pdorysn.
Inovace a zkvalitnění výuky prostřednictvím ICT (III/2)
 Projekt: Příjemce: Digitální učební materiál ve škole, registrační číslo projektu CZ..07/.5.00/3.057 Střední zdravotnická škola a Všší odborná škola zdravotnická, Husova 3, 37 60 České Budějovice Název
Projekt: Příjemce: Digitální učební materiál ve škole, registrační číslo projektu CZ..07/.5.00/3.057 Střední zdravotnická škola a Všší odborná škola zdravotnická, Husova 3, 37 60 České Budějovice Název
Pr niky ploch a t les
 Gymnázium Christiana Dopplera, Zborovská 45, Praha 5 RONÍKOVÁ PRÁCE Prniky ploch a tles Vypracoval: Tomáš Martínek ída: 4.C Školní rok: 2013/2014 Seminá: Deskriptivní geometrie Prohlašuji, že jsem svou
Gymnázium Christiana Dopplera, Zborovská 45, Praha 5 RONÍKOVÁ PRÁCE Prniky ploch a tles Vypracoval: Tomáš Martínek ída: 4.C Školní rok: 2013/2014 Seminá: Deskriptivní geometrie Prohlašuji, že jsem svou
17 Kuželosečky a přímky
 17 Kuželosečky a přímky 17.1 Poznámka: Polára bodu M ke kuželosečce Nechť X = [x 0,y 0 ] je bod. Zavedeme následující úpravy: x x 0 x y y 0 y xy (x 0 y + xy 0 )/ x (x 0 + x)/ y (y 0 + y)/ (x m) (x 0 m)(x
17 Kuželosečky a přímky 17.1 Poznámka: Polára bodu M ke kuželosečce Nechť X = [x 0,y 0 ] je bod. Zavedeme následující úpravy: x x 0 x y y 0 y xy (x 0 y + xy 0 )/ x (x 0 + x)/ y (y 0 + y)/ (x m) (x 0 m)(x
R O V N O B Ž N Í K (2 HODINY)
 R O V N O B Ž N Í K (2 HODINY)? Co to vlastn rovnobžník je? Na obrázku je dopravní znaka, která íká, že vzdálenost k železninímu pejezdu je 1 m (dva pruhy, jeden pruh pedstavuje vzdálenost 80 m): Pozorn
R O V N O B Ž N Í K (2 HODINY)? Co to vlastn rovnobžník je? Na obrázku je dopravní znaka, která íká, že vzdálenost k železninímu pejezdu je 1 m (dva pruhy, jeden pruh pedstavuje vzdálenost 80 m): Pozorn
M N O Ž I N Y B O D D A N É V L A S T N O S T I V R O V I N 3 HODINY
 M N O Ž I N Y B O D D A N É V L A S T N O S T I V R O V I N 3 HODINY V této kapitole se budeme zabývat množinami (skupinami) bod, které spojuje njaká spolená vlastnost. Tato vlastnost je pro všechny body
M N O Ž I N Y B O D D A N É V L A S T N O S T I V R O V I N 3 HODINY V této kapitole se budeme zabývat množinami (skupinami) bod, které spojuje njaká spolená vlastnost. Tato vlastnost je pro všechny body
Prbh funkce Jaroslav Reichl, 2006
 rbh funkce Jaroslav Reichl, 6 Vyšetování prbhu funkce V tomto tetu je vzorov vyešeno nkolik úloh na vyšetení prbhu funkce. i ešení úlohy jsou využity základní vlastnosti diferenciálního potu.. ešený píklad
rbh funkce Jaroslav Reichl, 6 Vyšetování prbhu funkce V tomto tetu je vzorov vyešeno nkolik úloh na vyšetení prbhu funkce. i ešení úlohy jsou využity základní vlastnosti diferenciálního potu.. ešený píklad
8. Deskriptivní geometrie
 8. Deskriptivní geometrie 337 Volitelný pedmt - dvouletý Vzdlávací oblast: Matematika a její aplikace Vzdlávací obor: Matematika a její aplikace Vyuovací pedmt: Deskriptivní geometrie 1. Charakteristika
8. Deskriptivní geometrie 337 Volitelný pedmt - dvouletý Vzdlávací oblast: Matematika a její aplikace Vzdlávací obor: Matematika a její aplikace Vyuovací pedmt: Deskriptivní geometrie 1. Charakteristika
Kuželosečky. Copyright c 2006 Helena Říhová
 Kuželosečk Copright c 2006 Helena Říhová Obsah 1 Kuželosečk 3 1.1 Kružnice... 3 1.1.1 Tečnakekružnici..... 3 1.2 lipsa.... 4 1.2.1 Rovniceelips...... 5 1.2.2 Tečnakelipse... 7 1.2.3 Konstrukceelips.....
Kuželosečk Copright c 2006 Helena Říhová Obsah 1 Kuželosečk 3 1.1 Kružnice... 3 1.1.1 Tečnakekružnici..... 3 1.2 lipsa.... 4 1.2.1 Rovniceelips...... 5 1.2.2 Tečnakelipse... 7 1.2.3 Konstrukceelips.....
10. Analytická geometrie kuželoseček 1 bod
 10. Analytická geometrie kuželoseček 1 bod 10.1. Kružnice opsaná obdélníku ABCD, kde A[2, 3], C[8, 3], má rovnici a) x 2 10x + y 2 + 7 = 0, b) (x 3) 2 + (y 3) 2 = 36, c) x 2 + 10x + y 2 18 = 0, d) (x 10)
10. Analytická geometrie kuželoseček 1 bod 10.1. Kružnice opsaná obdélníku ABCD, kde A[2, 3], C[8, 3], má rovnici a) x 2 10x + y 2 + 7 = 0, b) (x 3) 2 + (y 3) 2 = 36, c) x 2 + 10x + y 2 18 = 0, d) (x 10)
Kapitola 5. Seznámíme se ze základními vlastnostmi elipsy, hyperboly a paraboly, které
 Kapitola 5 Kuželosečky Seznámíme se ze základními vlastnostmi elipsy, hyperboly a paraboly, které společně s kružnicí jsou známy pod společným názvem kuželosečky. Říká se jim tak proto, že každou z nich
Kapitola 5 Kuželosečky Seznámíme se ze základními vlastnostmi elipsy, hyperboly a paraboly, které společně s kružnicí jsou známy pod společným názvem kuželosečky. Říká se jim tak proto, že každou z nich
ANALYTICKÁ GEOMETRIE HYPERBOLY
 Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol ANALYTICKÁ
Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol ANALYTICKÁ
Michal Zamboj. January 4, 2018
 Meziřádky mezi kuželosečkami - doplňkový materiál k přednášce Geometrie Michal Zamboj January 4, 018 Pozn. Najdete-li chybu, neváhejte mi napsat, může to ušetřit tápání Vašich kolegů. Pozn. v dokumentu
Meziřádky mezi kuželosečkami - doplňkový materiál k přednášce Geometrie Michal Zamboj January 4, 018 Pozn. Najdete-li chybu, neváhejte mi napsat, může to ušetřit tápání Vašich kolegů. Pozn. v dokumentu
GYMNÁZIUM CHEB SEMINÁRNÍ PRÁCE
 GYMNÁZIUM CHEB SEMINÁRNÍ PRÁCE Relace Cheb, 006 Radek HÁJEK Prohlášení Prohlašuji, že jsem seminární práci na téma: Relace vypracoval zcela sám za použití pramen uvedených v piložené bibliograii na poítai
GYMNÁZIUM CHEB SEMINÁRNÍ PRÁCE Relace Cheb, 006 Radek HÁJEK Prohlášení Prohlašuji, že jsem seminární práci na téma: Relace vypracoval zcela sám za použití pramen uvedených v piložené bibliograii na poítai
37. PARABOLA V ANALYTICKÉ GEOMETRII
 37.. Napiš rovnici paraboly, která má osu rovnoběžnou s osou y a prochází body A 0; 60, B 4; 8, C 8;36. 0m p60n 4m p8n 8m p36n m p pn 0 6 8 6 mm p pn 64 6 7 3 mm p pn 6 8m64 p 3 64 6m9 p Je-li osa rovnoběžná
37.. Napiš rovnici paraboly, která má osu rovnoběžnou s osou y a prochází body A 0; 60, B 4; 8, C 8;36. 0m p60n 4m p8n 8m p36n m p pn 0 6 8 6 mm p pn 64 6 7 3 mm p pn 6 8m64 p 3 64 6m9 p Je-li osa rovnoběžná
Vlastní čísla a vlastní vektory
 5 Vlastní čísla a vlastní vektor Poznámka: Je-li A : V V lineární zobrazení z prostoru V do prostoru V někd se takové zobrazení nazývá lineárním operátorem, pak je přirozeným požadavkem najít takovou bázi
5 Vlastní čísla a vlastní vektor Poznámka: Je-li A : V V lineární zobrazení z prostoru V do prostoru V někd se takové zobrazení nazývá lineárním operátorem, pak je přirozeným požadavkem najít takovou bázi
2.1 Pokyny k otev eným úlohám. 2.2 Pokyny k uzav eným úlohám. Testový sešit neotvírejte, po kejte na pokyn!
 MATEMATIKA základní úrove obtížnosti DIDAKTICKÝ TEST Maximální bodové hodnocení: 50 bod Hranice úspšnosti: 33 % Základní informace k zadání zkoušky Didaktický test obsahuje 26 úloh. asový limit pro ešení
MATEMATIKA základní úrove obtížnosti DIDAKTICKÝ TEST Maximální bodové hodnocení: 50 bod Hranice úspšnosti: 33 % Základní informace k zadání zkoušky Didaktický test obsahuje 26 úloh. asový limit pro ešení
VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C)
 VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C) max. 3 body 1 Zjistěte, zda vektor u je lineární kombinací vektorů a, b, je-li u = ( 8; 4; 3), a = ( 1; 2; 3), b = (2; 0; 1). Pokud ano, zapište tuto lineární kombinaci.
VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C) max. 3 body 1 Zjistěte, zda vektor u je lineární kombinací vektorů a, b, je-li u = ( 8; 4; 3), a = ( 1; 2; 3), b = (2; 0; 1). Pokud ano, zapište tuto lineární kombinaci.
ANALYTICKÁ GEOMETRIE INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ
 ANALYTICKÁ GEOMETRIE Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu
ANALYTICKÁ GEOMETRIE Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu
Základy matematiky kombinované studium 714 0365/06
 Základy matematiky kombinované studium 714 0365/06 1. Některé základní pojmy: číselné množiny, intervaly, operace s intervaly (sjednocení, průnik), kvantifikátory, absolutní hodnota čísla, vzorce: 2. Algebraické
Základy matematiky kombinované studium 714 0365/06 1. Některé základní pojmy: číselné množiny, intervaly, operace s intervaly (sjednocení, průnik), kvantifikátory, absolutní hodnota čísla, vzorce: 2. Algebraické
L I C H O B Ž N Í K (2 HODINY) ? Co to vlastn lichobžník je? Podívej se napíklad na následující obrázky:
 L I C H O B Ž N Í K (2 HODINY)? Co to vlastn lichobžník je? Podívej se napíklad na následující obrázky: Na obrázcích je vyobrazena hospodáská budova a židlika, kterou urit mají tvoji rodie na chodb nebo
L I C H O B Ž N Í K (2 HODINY)? Co to vlastn lichobžník je? Podívej se napíklad na následující obrázky: Na obrázcích je vyobrazena hospodáská budova a židlika, kterou urit mají tvoji rodie na chodb nebo
KINEMATICKÁ GEOMETRIE V ROVIN
 KINEMATICKÁ GEOMETRIE V ROVIN Kivka je jednoparametrická množina bod X(t), jejíž souadnice jsou dány funkcemi: x = x(t), y = y(t), t I R. Tena kivky je urena bodem dotyku X a teným vektorem o souadnicích
KINEMATICKÁ GEOMETRIE V ROVIN Kivka je jednoparametrická množina bod X(t), jejíž souadnice jsou dány funkcemi: x = x(t), y = y(t), t I R. Tena kivky je urena bodem dotyku X a teným vektorem o souadnicích
1.1 Napište středovou rovnici kružnice, která má střed v počátku soustavy souřadnic a prochází bodem
 Analytická geometrie - kružnice Napište středovou rovnici kružnice, která má střed v počátku soustavy souřadnic a prochází bodem A = ; 5 [ ] Napište středový i obecný tvar rovnice kružnice, která má střed
Analytická geometrie - kružnice Napište středovou rovnici kružnice, která má střed v počátku soustavy souřadnic a prochází bodem A = ; 5 [ ] Napište středový i obecný tvar rovnice kružnice, která má střed
ANALYTICKÁ GEOMETRIE ELIPSY
 Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol ANALYTICKÁ
Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol ANALYTICKÁ
Příklady k analytické geometrii kružnice a vzájemná poloha kružnice a přímky
 Příklady k analytické geometrii kružnice a vzájemná poloha kružnice a přímky Př. 1: Určete rovnice všech kružnic, které procházejí bodem A = * 6; 9+, mají střed na přímce p: x + 3y 18 = 0 a jejich poloměr
Příklady k analytické geometrii kružnice a vzájemná poloha kružnice a přímky Př. 1: Určete rovnice všech kružnic, které procházejí bodem A = * 6; 9+, mají střed na přímce p: x + 3y 18 = 0 a jejich poloměr
Analytická geometrie kvadratických útvarů v rovině
 Analytická geometrie kvadratických útvarů v rovině V následujícím textu se budeme postupně zabývat kružnicí, elipsou, hyperbolou a parabolou, které souhrnně označujeme jako kuželosečky. Současně budeme
Analytická geometrie kvadratických útvarů v rovině V následujícím textu se budeme postupně zabývat kružnicí, elipsou, hyperbolou a parabolou, které souhrnně označujeme jako kuželosečky. Současně budeme
JAK NA HYPERBOLU S GEOGEBROU
 Trendy ve vzdělávání 015 JAK NA HYPERBOLU S GEOGEBROU KRIEG Jaroslav, CZ Resumé Článek ukazuje, jak pomocí GeoGebry snadno řešit úlohy, které vedou na konstrukci hyperboly, případně jak lehce zkonstruovat
Trendy ve vzdělávání 015 JAK NA HYPERBOLU S GEOGEBROU KRIEG Jaroslav, CZ Resumé Článek ukazuje, jak pomocí GeoGebry snadno řešit úlohy, které vedou na konstrukci hyperboly, případně jak lehce zkonstruovat
KRUŽNICE, KRUH, KULOVÁ PLOCHA, KOULE
 Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol KRUŽNICE,
Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol KRUŽNICE,
( ) ( ) 2 2 B A B A ( ) ( ) ( ) B A B A B A
 Vzdálenost dvou bod, sted úseky Ž Vzdálenost dvou bod Pi vyšetování vzájemné polohy bod, pímek a rovin lze použít libovolnou vhodn zvolenou soustavu souadnic (afinní). však pi vyšetování metrických vlastností
Vzdálenost dvou bod, sted úseky Ž Vzdálenost dvou bod Pi vyšetování vzájemné polohy bod, pímek a rovin lze použít libovolnou vhodn zvolenou soustavu souadnic (afinní). však pi vyšetování metrických vlastností
Michal Zamboj. December 23, 2016
 Meziřádky mezi kuželosečkami - doplňkový materiál k přednášce Geometrie Michal Zamboj December 3, 06 Pozn. Najdete-li chybu, neváhejte mi napsat, může to ušetřit tápání Vašich kolegů. Pozn. v dokumentu
Meziřádky mezi kuželosečkami - doplňkový materiál k přednášce Geometrie Michal Zamboj December 3, 06 Pozn. Najdete-li chybu, neváhejte mi napsat, může to ušetřit tápání Vašich kolegů. Pozn. v dokumentu
O P A K O V Á N Í A P R O H L O U B E N Í U I V A O J E D N O D U C H Ý C H K O N S T R U K C Í C H 1,5 HODINY
 O P A K O V Á N Í A P R O H L O U B E N Í U I V A O J E D N O D U C H Ý C H K O N S T R U K C Í C H 1,5 HODINY Díve, než spolen pikroíme k uivu o množinách bod, pokusíme se zopakovat nkteré jednoduché
O P A K O V Á N Í A P R O H L O U B E N Í U I V A O J E D N O D U C H Ý C H K O N S T R U K C Í C H 1,5 HODINY Díve, než spolen pikroíme k uivu o množinách bod, pokusíme se zopakovat nkteré jednoduché
Definice Tečna paraboly je přímka, která má s parabolou jediný společný bod,
 5.4 Parabola Parabola je křivka, která vznikne řezem rotační kuželové plochy rovinou, jestliže odchylka roviny řezu od osy kuželové plochy je stejná jako odchylka povrchových přímek plochy a rovina řezu
5.4 Parabola Parabola je křivka, která vznikne řezem rotační kuželové plochy rovinou, jestliže odchylka roviny řezu od osy kuželové plochy je stejná jako odchylka povrchových přímek plochy a rovina řezu
prostorová definice (viz obrázek vlevo nahoře): elipsa je průsečnou křivkou rovinného
 Elipsa Výklad efinice a ohniskové vlastnosti prostorová definice (viz obrázek vlevo nahoře): elipsa je průsečnou křivkou rovinného řezu na rotační kuželové ploše, jestliže řezná rovina není kolmá k ose
Elipsa Výklad efinice a ohniskové vlastnosti prostorová definice (viz obrázek vlevo nahoře): elipsa je průsečnou křivkou rovinného řezu na rotační kuželové ploše, jestliže řezná rovina není kolmá k ose
Parametrická rovnice přímky v rovině
 Parametrická rovnice přímky v rovině Nechť je v kartézské soustavě souřadnic dána přímka AB. Nechť vektor u = B - A. Pak libovolný bod X[x; y] leží na přímce AB právě tehdy, když vektory u a X - A jsou
Parametrická rovnice přímky v rovině Nechť je v kartézské soustavě souřadnic dána přímka AB. Nechť vektor u = B - A. Pak libovolný bod X[x; y] leží na přímce AB právě tehdy, když vektory u a X - A jsou
ANALYTICKÁ GEOMETRIE PARABOLY
 Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol ANALYTICKÁ
Projekt ŠABLONY NA GVM Gymnázium Velké Meziříčí registrační číslo projektu: CZ.1.07/1.5.00/34.0948 IV-2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol ANALYTICKÁ
Matematika I, část I. Rovnici (1) nazýváme vektorovou rovnicí roviny ABC. Rovina ABC prochází bodem A a říkáme, že má zaměření u, v. X=A+r.u+s.
 3.4. Výklad Předpokládejme, že v prostoru E 3 jsou dány body A, B, C neležící na jedné přímce. Těmito body prochází jediná rovina, kterou označíme ABC. Určíme vektory u = B - A, v = C - A, které jsou zřejmě
3.4. Výklad Předpokládejme, že v prostoru E 3 jsou dány body A, B, C neležící na jedné přímce. Těmito body prochází jediná rovina, kterou označíme ABC. Určíme vektory u = B - A, v = C - A, které jsou zřejmě
ICT podporuje moderní způsoby výuky CZ.1.07/1.5.00/ Matematika analytická geometrie. Mgr. Pavel Liška
 Název projektu ICT podporuje moderní způsoby výuky Číslo projektu CZ.1.07/1.5.00/34.0717 Název školy Gymnázium, Turnov, Jana Palacha 804, přísp. organizace Číslo a název šablony klíčové aktivity IV/2 Inovace
Název projektu ICT podporuje moderní způsoby výuky Číslo projektu CZ.1.07/1.5.00/34.0717 Název školy Gymnázium, Turnov, Jana Palacha 804, přísp. organizace Číslo a název šablony klíčové aktivity IV/2 Inovace
May 31, Rovnice elipsy.notebook. Elipsa 2. rovnice elipsy. SOŠ InterDact Most, Mgr.Petra Mikolášková
 Elipsa 2 rovnice elipsy SOŠ InterDact Most, Mgr.Petra Mikolášková 1 Název školy Autor Název šablony Číslo projektu Předmět SOŠ InterDACT s.r.o. Most Mgr. Petra Mikolášková III/2_Inovace a zkvalitnění výuky
Elipsa 2 rovnice elipsy SOŠ InterDact Most, Mgr.Petra Mikolášková 1 Název školy Autor Název šablony Číslo projektu Předmět SOŠ InterDACT s.r.o. Most Mgr. Petra Mikolášková III/2_Inovace a zkvalitnění výuky
ANALYTICKÁ GEOMETRIE INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ. Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky
 ANALYTICKÁ GEOMETRIE Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu
ANALYTICKÁ GEOMETRIE Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu
Cyklografie. Cyklický průmět bodu
 Cyklografie Cyklografie je nelineární zobrazovací metoda - bodům v prostoru odpovídají kružnice v rovině a naopak. Úlohy v rovině pak převádíme na řešení prostorových úloh, např. pomocí cyklografie řešíme
Cyklografie Cyklografie je nelineární zobrazovací metoda - bodům v prostoru odpovídají kružnice v rovině a naopak. Úlohy v rovině pak převádíme na řešení prostorových úloh, např. pomocí cyklografie řešíme
Vzdělávací materiál. vytvořený v projektu OP VK CZ.1.07/1.5.00/34.0211. Anotace. Analytická geometrie. Hyperbola VY_32_INOVACE_M0119.
 Vzdělávací materiál vytvořený v projektu OP VK Název školy: Gymnázium, Zábřeh, náměstí Osvobození 20 Číslo projektu: Název projektu: Číslo a název klíčové aktivity: CZ.1.07/1.5.00/34.0211 Zlepšení podmínek
Vzdělávací materiál vytvořený v projektu OP VK Název školy: Gymnázium, Zábřeh, náměstí Osvobození 20 Číslo projektu: Název projektu: Číslo a název klíčové aktivity: CZ.1.07/1.5.00/34.0211 Zlepšení podmínek
Projekt OPVK - CZ.1.07/1.1.00/ Matematika pro všechny. Univerzita Palackého v Olomouci
 Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Geometrie Různé metody řešení Téma: Analytická geometrie v prostoru, vektory, přímky Autor:
Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Geometrie Různé metody řešení Téma: Analytická geometrie v prostoru, vektory, přímky Autor:
7.5.1 Středová a obecná rovnice kružnice
 7.5.1 Středová a obecná rovnice kružnice Předpoklady: kružnice, 505, 7103, 730 Pedagogická poznámka: Pro tuto hodinu (a mnoho dalších hodin v kapitole o kuželosečkách) je rozhodující, aby studenti uměli
7.5.1 Středová a obecná rovnice kružnice Předpoklady: kružnice, 505, 7103, 730 Pedagogická poznámka: Pro tuto hodinu (a mnoho dalších hodin v kapitole o kuželosečkách) je rozhodující, aby studenti uměli
Píkazy pro kreslení.
 Píkazy pro kreslení. Tento text je psán pro AUTOCAD 2006, eskou modifikaci. V jiných verzích se proto vyskytnou odchylky. Jsou to píkazy, které umožují nakreslit jednotlivé entity v AUTOCADu. Z menu je
Píkazy pro kreslení. Tento text je psán pro AUTOCAD 2006, eskou modifikaci. V jiných verzích se proto vyskytnou odchylky. Jsou to píkazy, které umožují nakreslit jednotlivé entity v AUTOCADu. Z menu je
Analytická geometrie lineárních útvarů
 ) Na přímce: a) Souřadnice bodu na přímce: Analtická geometrie lineárních útvarů Bod P nazýváme počátek - jeho souřadnice je P [0] Nalevo od počátku leží čísla záporná, napravo čísla kladná. Každý bod
) Na přímce: a) Souřadnice bodu na přímce: Analtická geometrie lineárních útvarů Bod P nazýváme počátek - jeho souřadnice je P [0] Nalevo od počátku leží čísla záporná, napravo čísla kladná. Každý bod
KOMPLEXNÍ ČÍSLA INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ
 KOMPLEXNÍ ČÍSLA Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu INVESTICE
KOMPLEXNÍ ČÍSLA Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu INVESTICE
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ
 ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
Pravdpodobnost výskytu náhodné veliiny na njakém intervalu urujeme na základ tchto vztah: f(x)
 NÁHODNÁ VELIINA Náhodná veliina je veliina, jejíž hodnota je jednoznan urena výsledkem náhodného pokusu (je-li tento výsledek dán reálným íslem). Jde o reálnou funkci definovanou na základním prostoru
NÁHODNÁ VELIINA Náhodná veliina je veliina, jejíž hodnota je jednoznan urena výsledkem náhodného pokusu (je-li tento výsledek dán reálným íslem). Jde o reálnou funkci definovanou na základním prostoru
Důkazy vybraných geometrických konstrukcí
 Gymnázium Christiana Dopplera, Zborovská 45, Praha 5 Ročníková práce Důkazy vybraných geometrických konstrukcí Vypracovala: Ester Sgallová Třída: 8.M Školní rok: 015/016 Seminář : Deskriptivní geometrie
Gymnázium Christiana Dopplera, Zborovská 45, Praha 5 Ročníková práce Důkazy vybraných geometrických konstrukcí Vypracovala: Ester Sgallová Třída: 8.M Školní rok: 015/016 Seminář : Deskriptivní geometrie
Definice: Kružnice je množina bodů v rovině, které mají od daného bodu (střed S) stejnou vzdálenost
 Kuželosečky Kružnice Definice: Kružnice je množina bodů v rovině, které mají od daného bodu (střed S) stejnou vzdálenost (poloměr r).?! Co získáme, když v definici výraz stejnou nahradíme stejnou nebo
Kuželosečky Kružnice Definice: Kružnice je množina bodů v rovině, které mají od daného bodu (střed S) stejnou vzdálenost (poloměr r).?! Co získáme, když v definici výraz stejnou nahradíme stejnou nebo
M - Kvadratická funkce
 M - Kvadratická funkce Autor: Mgr. Jaromír Juřek Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento dokument byl kompletně
M - Kvadratická funkce Autor: Mgr. Jaromír Juřek Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento dokument byl kompletně
Kuželoseč ky. 1.1 Elipsa
 Kuželoseč ky 1.1 Elipsa Definice: Elipsa je množina všech bodů v 2, které mají od dvou pevných (různých) bodů v 2, zvaných ohniska (značíme F 1, F 2 ), stálý součet vzdáleností rovný 2a, který je větší
Kuželoseč ky 1.1 Elipsa Definice: Elipsa je množina všech bodů v 2, které mají od dvou pevných (různých) bodů v 2, zvaných ohniska (značíme F 1, F 2 ), stálý součet vzdáleností rovný 2a, který je větší
DRUHY ROVNOBŽNÍK A JEJICH VLASTNOSTI 1 HODINA
 DRUHY ROVNOBŽNÍK A JEJICH VLASTNOSTI HODINA Podívej se na následující obrázek: Na obrázku je rovnobžník s vyznaeným pravým úhlem. Odpovídej na otázky:? Jaká je velikost vnitního úhlu pi vrcholu C? Je rovna
DRUHY ROVNOBŽNÍK A JEJICH VLASTNOSTI HODINA Podívej se na následující obrázek: Na obrázku je rovnobžník s vyznaeným pravým úhlem. Odpovídej na otázky:? Jaká je velikost vnitního úhlu pi vrcholu C? Je rovna
Hyperbola. Předpoklady: 7507, 7512
 7.5.6 Hperbola Předpoklad: 7507, 75 Pedagogická poznámka: Na první pohled se nezdá, že b hodina bla příliš zaplněná, ale kreslení obrázků studentům (spíše studentkám) docela trvá. Je dobré vsvětlit, že
7.5.6 Hperbola Předpoklad: 7507, 75 Pedagogická poznámka: Na první pohled se nezdá, že b hodina bla příliš zaplněná, ale kreslení obrázků studentům (spíše studentkám) docela trvá. Je dobré vsvětlit, že
Analytická geometrie v E 3 - kvadriky
 Analtická geometrie v E 3 - kvadrik ROVNICE KVADRIKY ( v ákladní a posunuté poloe) Kvadrik v ákladní poloe - střed nebo vrchol leží v počátku ( vi příloha na konci) Posunutí v rovnici nahradíme všechn
Analtická geometrie v E 3 - kvadrik ROVNICE KVADRIKY ( v ákladní a posunuté poloe) Kvadrik v ákladní poloe - střed nebo vrchol leží v počátku ( vi příloha na konci) Posunutí v rovnici nahradíme všechn
M - Analytická geometrie pro třídu 4ODK
 M - Analytická geometrie pro třídu 4ODK Autor: Mgr. Jaromír Juřek Kopírování a jakékoliv další využití výukového materiálu je dovoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE Tento dokument
M - Analytická geometrie pro třídu 4ODK Autor: Mgr. Jaromír Juřek Kopírování a jakékoliv další využití výukového materiálu je dovoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE Tento dokument
1.13 Klasifikace kvadrik
 5 KAPITOLA 1. KVADRIKY JAKO PLOCHY. STUPNĚ 1.13 Klasifikace kvadrik V této části provedeme klasifikaci kvadrik. Vyšetříme všechny případy, které mohou různou volbou koeficientů v rovnici kvadriky a 11
5 KAPITOLA 1. KVADRIKY JAKO PLOCHY. STUPNĚ 1.13 Klasifikace kvadrik V této části provedeme klasifikaci kvadrik. Vyšetříme všechny případy, které mohou různou volbou koeficientů v rovnici kvadriky a 11
Projekt OPVK - CZ.1.07/1.1.00/ Matematika pro všechny. Univerzita Palackého v Olomouci
 Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Závislosti a funkční vztahy Gradovaný řetězec úloh Téma: Kvadratická funkce Autor: Kubešová
Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Závislosti a funkční vztahy Gradovaný řetězec úloh Téma: Kvadratická funkce Autor: Kubešová
GYMNÁZIUM CHEB. SEMINÁRNÍ PRÁCE Grafy funkcí sbírka ešených úloh. Radek HÁJEK, 8.A Radka JIROUŠKOVÁ, 8.A Cheb, 2006 Petr NEJTEK, 8.
 GYMNÁZIUM CHEB SEMINÁRNÍ PRÁCE Grafy funkcí sbírka ešených úloh Radek HÁJEK, 8.A Radka JIROUŠKOVÁ, 8.A Cheb, 006 Petr NEJTEK, 8.A Prohlášení Prohlašujeme, že jsme seminární práci na téma: Grafy funkcí
GYMNÁZIUM CHEB SEMINÁRNÍ PRÁCE Grafy funkcí sbírka ešených úloh Radek HÁJEK, 8.A Radka JIROUŠKOVÁ, 8.A Cheb, 006 Petr NEJTEK, 8.A Prohlášení Prohlašujeme, že jsme seminární práci na téma: Grafy funkcí
Matematika I, část I Vzájemná poloha lineárních útvarů v E 3
 3.6. Vzájemná poloha lineárních útvarů v E 3 Výklad A. Vzájemná poloha dvou přímek Uvažujme v E 3 přímky p, q: p: X = A + ru q: X = B + sv a hledejme jejich společné body, tj. hledejme takové hodnoty parametrů
3.6. Vzájemná poloha lineárních útvarů v E 3 Výklad A. Vzájemná poloha dvou přímek Uvažujme v E 3 přímky p, q: p: X = A + ru q: X = B + sv a hledejme jejich společné body, tj. hledejme takové hodnoty parametrů
KVADRATICKÉ FUNKCE. + bx + c, největší hodnotu pro x = a platí,
 KVADRATICKÉ FUNKCE Definice Kvadratická funkce je každá funkce na množině R (tj. o definičním ooru R), daná ve tvaru y = ax + x + c, kde a je reálné číslo různé od nuly,, c, jsou liovolná reálná čísla.
KVADRATICKÉ FUNKCE Definice Kvadratická funkce je každá funkce na množině R (tj. o definičním ooru R), daná ve tvaru y = ax + x + c, kde a je reálné číslo různé od nuly,, c, jsou liovolná reálná čísla.
14. přednáška. Přímka
 14 přednáška Přímka Začneme vyjádřením přímky v prostoru Přímku v prostoru můžeme vyjádřit jen parametricky protože obecná rovnice přímky v prostoru neexistuje Přímka v prostoru je určena bodem A= [ a1
14 přednáška Přímka Začneme vyjádřením přímky v prostoru Přímku v prostoru můžeme vyjádřit jen parametricky protože obecná rovnice přímky v prostoru neexistuje Přímka v prostoru je určena bodem A= [ a1
Variace. Kvadratická funkce
 Variace 1 Kvadratická funkce Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratická funkce Kvadratická
Variace 1 Kvadratická funkce Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Kvadratická funkce Kvadratická
Analytická geometrie. c ÚM FSI VUT v Brně
 19. září 2007 Příklad 1. Příklad 2. Příklad 3. Příklad 1. Určete obecnou rovnici roviny, která prochází body A = [0, 1, 2], B = [ 1, 0, 3], C = [3, 1, 0]. Příklad 1. A = [0, 1, 2], B = [ 1, 0, 3], C =
19. září 2007 Příklad 1. Příklad 2. Příklad 3. Příklad 1. Určete obecnou rovnici roviny, která prochází body A = [0, 1, 2], B = [ 1, 0, 3], C = [3, 1, 0]. Příklad 1. A = [0, 1, 2], B = [ 1, 0, 3], C =
Digitální učební materiál
 Digitální učební materiál Číslo projektu CZ07/500/34080 Název projektu Zkvalitnění výuky prostřednictvím ICT Číslo a název šablony klíčové aktivity III/ Inovace a zkvalitnění výuky prostřednictvím ICT
Digitální učební materiál Číslo projektu CZ07/500/34080 Název projektu Zkvalitnění výuky prostřednictvím ICT Číslo a název šablony klíčové aktivity III/ Inovace a zkvalitnění výuky prostřednictvím ICT
Matematika 1 MA1. 1 Analytická geometrie v prostoru - základní pojmy. 4 Vzdálenosti. 12. přednáška ( ) Matematika 1 1 / 32
 Matematika 1 12. přednáška MA1 1 Analytická geometrie v prostoru - základní pojmy 2 Skalární, vektorový a smíšený součin, projekce vektoru 3 Přímky a roviny 4 Vzdálenosti 5 Příčky mimoběžek 6 Zkouška;
Matematika 1 12. přednáška MA1 1 Analytická geometrie v prostoru - základní pojmy 2 Skalární, vektorový a smíšený součin, projekce vektoru 3 Přímky a roviny 4 Vzdálenosti 5 Příčky mimoběžek 6 Zkouška;
Modernizace výuky na Fakultě stavební VUT v Brně v rámci bakalářských a magisterských studijních programů CZ.04.1.03/3.2.15.2/0292
 Modernizace výuky na Fakultě stavební VUT v Brně v rámci bakalářských a magisterských studijních programů CZ.04.1.03/3.2.15.2/0292 Název předmětu: Vyrovnávací kurz z matematiky Zabezpečující ústav: Ústav
Modernizace výuky na Fakultě stavební VUT v Brně v rámci bakalářských a magisterských studijních programů CZ.04.1.03/3.2.15.2/0292 Název předmětu: Vyrovnávací kurz z matematiky Zabezpečující ústav: Ústav
M - Příprava na 1. čtvrtletku pro třídy 2P a 2VK
 M - Příprava na 1. čtvrtletku pro třídy P a VK Autor: Mgr. Jaromír Juřek Kopírování a jakékoliv další využití výukového materiálu dovoleno pouze s odkazem na www.jarjurek.cz. VARIACE 1 Tento dokument byl
M - Příprava na 1. čtvrtletku pro třídy P a VK Autor: Mgr. Jaromír Juřek Kopírování a jakékoliv další využití výukového materiálu dovoleno pouze s odkazem na www.jarjurek.cz. VARIACE 1 Tento dokument byl
NEWTONOVY POHYBOVÉ ZÁKONY
 NEWTONOVY POHYBOVÉ ZÁKONY Metodika Mgr. Michal Schovánek kvten 2010 Newtonovy pohybové zákony patí mezi nejobtížnjší kapitoly stedoškolské mechaniky. Popisované situace jsou sice jednoduše demonstrovatelné,
NEWTONOVY POHYBOVÉ ZÁKONY Metodika Mgr. Michal Schovánek kvten 2010 Newtonovy pohybové zákony patí mezi nejobtížnjší kapitoly stedoškolské mechaniky. Popisované situace jsou sice jednoduše demonstrovatelné,
Analytická geometrie. přímka vzájemná poloha přímek rovina vzájemná poloha rovin. Název: XI 3 21:42 (1 z 37)
 Analytická geometrie přímka vzájemná poloha přímek rovina vzájemná poloha rovin Název: XI 3 21:42 (1 z 37) Název: XI 3 21:42 (2 z 37) Rovnice přímky a) parametrická A B A B C A X Název: XI 3 21:42 (3 z
Analytická geometrie přímka vzájemná poloha přímek rovina vzájemná poloha rovin Název: XI 3 21:42 (1 z 37) Název: XI 3 21:42 (2 z 37) Rovnice přímky a) parametrická A B A B C A X Název: XI 3 21:42 (3 z
7.5.8 Středová rovnice elipsy
 758 Středová rovnice elips Předpokld: 750, 7507 Př : Vrchol elips leží v odech A[ ;], B [ 3;], [ ;5], [ ; 3] elips souřdnice jejích ohnisek Urči prmetr Zdné souřdnice už n první pohled vpdjí podezřele,
758 Středová rovnice elips Předpokld: 750, 7507 Př : Vrchol elips leží v odech A[ ;], B [ 3;], [ ;5], [ ; 3] elips souřdnice jejích ohnisek Urči prmetr Zdné souřdnice už n první pohled vpdjí podezřele,
11. VEKTOROVÁ ALGEBRA A ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ
 11. VEKTOROVÁ ALGEBRA A ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ Dovednosti: 1. Chápat pojmy orientovaná úsečka a vektor a geometrický význam součtu, rozdílu a reálného násobku orientovaných úseček a vektorů..
11. VEKTOROVÁ ALGEBRA A ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ Dovednosti: 1. Chápat pojmy orientovaná úsečka a vektor a geometrický význam součtu, rozdílu a reálného násobku orientovaných úseček a vektorů..
+ 2y. a y = 1 x 2. du x = nxn 1 f(u) 2x n 3 yf (u)
 Diferenciální počet příklad 1 Dokažte, že funkce F, = n f 2, kde f je spojitě diferencovatelná funkce, vhovuje vztahu + 2 = nf ; 0 Řešení: Označme u = 2. Pak je F, = n fu a platí Podle vět o derivaci složené
Diferenciální počet příklad 1 Dokažte, že funkce F, = n f 2, kde f je spojitě diferencovatelná funkce, vhovuje vztahu + 2 = nf ; 0 Řešení: Označme u = 2. Pak je F, = n fu a platí Podle vět o derivaci složené
Deskriptivní geometrie 2
 Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra matematiky Deskriptivní geometrie 2 Pomocný učební text - díl II Světlana Tomiczková Plzeň 4. května 2011 verze 1.0 Obsah 1 Středové promítání
Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra matematiky Deskriptivní geometrie 2 Pomocný učební text - díl II Světlana Tomiczková Plzeň 4. května 2011 verze 1.0 Obsah 1 Středové promítání
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ
 ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Mgr. Zora Hauptová ANALYTICKÁ GEOMETRIE PŘÍMKY TEST VY_32_INOVACE_MA_3_20 OPVK 1.5 EU peníze středním školám CZ.1.07/1.500/34.0116 Modernizace výuky na učilišti
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Mgr. Zora Hauptová ANALYTICKÁ GEOMETRIE PŘÍMKY TEST VY_32_INOVACE_MA_3_20 OPVK 1.5 EU peníze středním školám CZ.1.07/1.500/34.0116 Modernizace výuky na učilišti
7.5.3 Hledání kružnic II
 753 Hledání kružnic II Předpoklady: 750 Pedagogická poznámka: Tato hodina patří mezi vůbec nejtěžší Není reálné předpokládat, že by většina studentů dokázala samostatně přijít na řešení, po čase na rozmyšlenou
753 Hledání kružnic II Předpoklady: 750 Pedagogická poznámka: Tato hodina patří mezi vůbec nejtěžší Není reálné předpokládat, že by většina studentů dokázala samostatně přijít na řešení, po čase na rozmyšlenou
1. Několik základních pojmů ze středoškolské matematiky. Na začátku si připomeneme následující pojmy:
 Opakování středoškolské matematiky Slovo úvodem: Tato pomůcka je určena zejména těm studentům presenčního i kombinovaného studia na VŠFS, kteří na středních školách neprošli dostatečnou průpravou z matematiky
Opakování středoškolské matematiky Slovo úvodem: Tato pomůcka je určena zejména těm studentům presenčního i kombinovaného studia na VŠFS, kteří na středních školách neprošli dostatečnou průpravou z matematiky
MATEMATICKÁ KARTOGRAFIE
 VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KARTOGRAFIE MODUL 5 NEPRAVÁ ZOBRAZENÍ STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Matematická kartografie Modul
VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KARTOGRAFIE MODUL 5 NEPRAVÁ ZOBRAZENÍ STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Matematická kartografie Modul
CVIČNÝ TEST 9 OBSAH. Mgr. Václav Zemek. I. Cvičný test 2 II. Autorské řešení 5 III. Klíč 17 IV. Záznamový list 19
 CVIČNÝ TEST 9 Mgr. Václav Zemek OBSAH I. Cvičný test 2 II. Autorské řešení 5 III. Klíč 17 IV. Záznamový list 19 I. CVIČNÝ TEST 1 Vypočítejte (7,5 10 3 2 10 2 ) 2. Výsledek zapište ve tvaru a 10 n, kde
CVIČNÝ TEST 9 Mgr. Václav Zemek OBSAH I. Cvičný test 2 II. Autorské řešení 5 III. Klíč 17 IV. Záznamový list 19 I. CVIČNÝ TEST 1 Vypočítejte (7,5 10 3 2 10 2 ) 2. Výsledek zapište ve tvaru a 10 n, kde
3.6. ANALYTICKÁ GEOMETRIE PARABOLY
 3.6. ANALYTICKÁ GEOMETRIE PARABOLY V této kapitole se dozvíte: jak je geometricky definována kuželosečka zvaná parabola; co je to ohnisko, řídící přímka, vrchol, osa, parametr paraboly; tvar vrcholové
3.6. ANALYTICKÁ GEOMETRIE PARABOLY V této kapitole se dozvíte: jak je geometricky definována kuželosečka zvaná parabola; co je to ohnisko, řídící přímka, vrchol, osa, parametr paraboly; tvar vrcholové
Tematický plán uiva z matematiky pro 6. roník na školní rok 2009-2010
 Tematický plán uiva z matematiky pro 6. roník na školní rok 2009-2010 Msíc: Záí Uivo: Shrnutí a opakování uiva z 5.roníku Pirozená ísla íselná osa, porovnávání, zaokrouhlování, operace s nimi, pevody,
Tematický plán uiva z matematiky pro 6. roník na školní rok 2009-2010 Msíc: Záí Uivo: Shrnutí a opakování uiva z 5.roníku Pirozená ísla íselná osa, porovnávání, zaokrouhlování, operace s nimi, pevody,
Obecná rovnice kvadratické funkce : y = ax 2 + bx + c Pokud není uvedeno jinak, tak definičním oborem řešených funkcí je množina reálných čísel.
 5. Funkce 9. ročník 5. Funkce ZOPAKUJTE SI : 8. ROČNÍK KAPITOLA. Funkce. 5.. Kvadratická funkce Obecná rovnice kvadratické funkce : y = ax + bx + c Pokud není uvedeno jinak, tak definičním oborem řešených
5. Funkce 9. ročník 5. Funkce ZOPAKUJTE SI : 8. ROČNÍK KAPITOLA. Funkce. 5.. Kvadratická funkce Obecná rovnice kvadratické funkce : y = ax + bx + c Pokud není uvedeno jinak, tak definičním oborem řešených
Analytická geometrie přímky, roviny (opakování středoškolské látky) = 0. Napište obecnou rovnici. 8. Jsou dány body A [ 2,3,
 Analytická geometrie přímky roviny opakování středoškolské látk Jsou dány body A [ ] B [ 5] a C [ 6] a) přímky AB b) osy úsečky AB c) přímky na které leží výška vc trojúhelníka ABC d) přímky na které leží
Analytická geometrie přímky roviny opakování středoškolské látk Jsou dány body A [ ] B [ 5] a C [ 6] a) přímky AB b) osy úsečky AB c) přímky na které leží výška vc trojúhelníka ABC d) přímky na které leží
Projekt OPVK - CZ.1.07/1.1.00/ Matematika pro všechny. Univerzita Palackého v Olomouci
 Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Závislosti a funkční vztahy Gradovaný řetězec úloh Téma: graf funkce, derivace funkce a její
Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Závislosti a funkční vztahy Gradovaný řetězec úloh Téma: graf funkce, derivace funkce a její
Funkce jedné reálné proměnné. lineární kvadratická racionální exponenciální logaritmická s absolutní hodnotou
 Funkce jedné reálné proměnné lineární kvadratická racionální exponenciální logaritmická s absolutní hodnotou lineární y = ax + b Průsečíky s osami: Px [-b/a; 0] Py [0; b] grafem je přímka (získá se pomocí
Funkce jedné reálné proměnné lineární kvadratická racionální exponenciální logaritmická s absolutní hodnotou lineární y = ax + b Průsečíky s osami: Px [-b/a; 0] Py [0; b] grafem je přímka (získá se pomocí
Gymnázium Jiřího Ortena, Kutná Hora. Průřezová témata Poznámky. Téma Školní výstupy Učivo (pojmy) volné rovnoběžné promítání průmětna
 Předmět: Matematika Náplň: Stereometrie, Analytická geometrie Třída: 3. ročník a septima Počet hodin: 4 hodiny týdně Pomůcky: PC a dataprojektor, učebnice Stereometrie Volné rovnoběžné promítání Zobrazí
Předmět: Matematika Náplň: Stereometrie, Analytická geometrie Třída: 3. ročník a septima Počet hodin: 4 hodiny týdně Pomůcky: PC a dataprojektor, učebnice Stereometrie Volné rovnoběžné promítání Zobrazí
Jihoeská univerzita v eských Budjovicích Pedagogická fakulta
 Jihoeská univerzita v eských Budjovicích Pedagogická fakulta Konstrukní úlohy ešené pomocí Cabri geometrie Miroslava Lutzová Finanní matematika 2001-2004 Vedoucí diplomové práce: Mgr. Pavel Leischner Most,
Jihoeská univerzita v eských Budjovicích Pedagogická fakulta Konstrukní úlohy ešené pomocí Cabri geometrie Miroslava Lutzová Finanní matematika 2001-2004 Vedoucí diplomové práce: Mgr. Pavel Leischner Most,
Rovnice přímky vypsané příklady. Parametrické vyjádření přímky
 Rovnice přímky vypsané příklady Zdroj: Vše kromě příkladu 3.4: http://kdm.karlin.mff.cuni.cz/diplomky/jan_koncel/rovina.php?kapitola=parametrickevyjadre ni Příklady 3.5 a 3.7-1 a 3: http://kdm.karlin.mff.cuni.cz/diplomky/jan_koncel/rovina.php?kapitola=obecnarovnice
Rovnice přímky vypsané příklady Zdroj: Vše kromě příkladu 3.4: http://kdm.karlin.mff.cuni.cz/diplomky/jan_koncel/rovina.php?kapitola=parametrickevyjadre ni Příklady 3.5 a 3.7-1 a 3: http://kdm.karlin.mff.cuni.cz/diplomky/jan_koncel/rovina.php?kapitola=obecnarovnice
11. VEKTOROVÁ ALGEBRA A ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ. u. v = u v + u v. Umět ho aplikovat při
 . VEKTOROVÁ ALGEBRA A ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ Dovednosti:. Chápat pojmy orientovaná úsečka a vektor a geometrický význam součtu, rozdílu a reálného násobku orientovaných úseček a vektorů..
. VEKTOROVÁ ALGEBRA A ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ Dovednosti:. Chápat pojmy orientovaná úsečka a vektor a geometrický význam součtu, rozdílu a reálného násobku orientovaných úseček a vektorů..
SEZNAM ANOTACÍ. CZ.1.07/1.5.00/ III/2 Inovace a zkvalitnění výuky prostřednictvím ICT VY_32_INOVACE_MA4 Analytická geometrie
 SEZNAM ANOTACÍ Číslo projektu Číslo a název šablony klíčové aktivity Označení sady DUM Tematická oblast CZ.1.07/1.5.00/34.0527 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT VY_32_INOVACE_MA4 Analytická
SEZNAM ANOTACÍ Číslo projektu Číslo a název šablony klíčové aktivity Označení sady DUM Tematická oblast CZ.1.07/1.5.00/34.0527 III/2 Inovace a zkvalitnění výuky prostřednictvím ICT VY_32_INOVACE_MA4 Analytická
Tematický plán uiva z matematiky pro 6. roník na školní rok 2011-2012
 Tematický plán uiva z matematiky pro 6. roník na školní rok 2011-2012 Msíc: Záí Uivo: Shrnutí a opakování uiva z 5.roníku Pirozená ísla íselná osa, porovnávání, zaokrouhlování, operace s nimi, pevody,
Tematický plán uiva z matematiky pro 6. roník na školní rok 2011-2012 Msíc: Záí Uivo: Shrnutí a opakování uiva z 5.roníku Pirozená ísla íselná osa, porovnávání, zaokrouhlování, operace s nimi, pevody,
Opakování k maturitě matematika 4. roč. TAD 2 <
 8.. Otázka číslo Mocniny a odmocniny. b.) Zjednodušte: 6 b. b Opakování k maturitě matematika. roč. TAD : 6.) Zjednodušte: 6 6.) Vypočtěte: a. y : ( a. y ) =.) Usměrněte zlomek =.. Otázka číslo Lineární
8.. Otázka číslo Mocniny a odmocniny. b.) Zjednodušte: 6 b. b Opakování k maturitě matematika. roč. TAD : 6.) Zjednodušte: 6 6.) Vypočtěte: a. y : ( a. y ) =.) Usměrněte zlomek =.. Otázka číslo Lineární
Hledání parabol
 7.5.1 Hledání arabol Předoklad: 751, 7513 Pedagogická oznámka: Studenti jsou o řekonání očátečních roblémů s aměti vcelku úsěšní, všichni většinou zvládnou alesoň rvních ět říkladů. Hodinu organizuji tak,
7.5.1 Hledání arabol Předoklad: 751, 7513 Pedagogická oznámka: Studenti jsou o řekonání očátečních roblémů s aměti vcelku úsěšní, všichni většinou zvládnou alesoň rvních ět říkladů. Hodinu organizuji tak,
