Záznam o ústní zkou²ce z p edm tu 01RMF (akademický ²kolní rok 2015/2016) P íjmení a jméno Datum Hodnocení Písemka Celkové hodnocení Podpis studenta
|
|
|
- Barbora Staňková
- před 8 lety
- Počet zobrazení:
Transkript
1 báze v Hilbertov prostoru obory excentricity parciální diferenciální rovnice (a metoda jejich detekce pro PDR druhého ádu pro funkci dvou prom nných) fundamentální e²ení operátoru 1. ➋ Dokaºte: f( x), g( x) L 2 (G) f( x)g ( x) L 1 (G). ➌ Z jakého d vodu nem ºe být rovnost ( L[f(t)](p), φ(p) ) = ( f(t), L[φ(p)](t) ) prohlá²ena za denici zobecn né Laplaceovy transformace? ➍ O em pojednává Hellinger v-toeplitz v teorém? K emu ho lze vyuºít? ➎ Vyslovte a dokaºte v tu o omezenosti Volterrova integrálního operátoru a v²ech jeho mocnin. ➏ Vyslovte a dokaºte v tu o vyhlazení charakteristické funkce omezené oblasti G E r.
2 2. L p a L p násobení funkcí v D (E r ) a anní transformace (z stává výsledek t chto operací skute n v D (E r )?) komutující operátory obor nulovosti zobecn né funkce ➋ Pro klasické funkce dokaºte rovnost ( ) f f( x) g( x) = x k x k Jaké p edpoklady pro f( x) a g( x) je nutno uvaºovat? g( x). ➌ Vyslovte a dokaºte v tu o klasickém Laplaceov obrazu derivace. ➍ Vyslovte a dokaºte v tu o Fourierov obrazu fundamentálního e²ení. ➎ Dokaºte: f( x) L 2 (G) H G µ(h) < + f( x) L 1 (H). ➏ Dokaºte, ºe transforma ní vztahy odvozené z e²ení rovnice y = λ 1,2 (x, y) skute n p evád jí parabolickou diferenciální rovnici do normálního tvaru.
3 hustota derivace v D geometrická násobnost vlastního ísla operátoru (jaké vlastnosti má geometrická násobnost u operátoru s ist bodovým spektrem a jak to souvisí s po tem vlastních ísel?) 3. ➋ Dokaºte: Nech S = {f 1 (x), f 2 (x),...} je maximální ortonormální mnoºina na Hilbertov prostoru H a g(x) H. Nech pro kaºdé k N : g f k = 0. Pak g( x) = 0. ➌ Vyslovte a dokaºte v tu o derivaci klasického Laplaceova obrazu. ➍ Vyslovte a dokaºte základní v tu o e²ení diferenciální rovnice v D. ➎ Dokaºte: f n (x) = s(x) g( x) H fn g = s g. n=1 n=1 ➏ Dokaºte, ºe Fourierova transformace je zobrazení z S (E r ) do S (E r ). D kaz demonstrujte na p ípad r = 1.
4 4. skalární sou in na prostoru funkcí (a n které p íklady) D(G) a D (G) Volterrova integrální rovnice a Volterrovo jádro separabilní Hilbert v prostor ➋ Dokaºte: L[Θ(t) t 0 f(τ) dτ] = F (p) p ➌ Dokaºte, ºe pro libovolnou testovací funkci φ(x) D(R) existuje K R + 0 x, y R (x y) platí φ(x) φ(y) x y K. tak, ºe pro kaºdé ➍ Vyslovte a dokaºte v tu o hermiticit sloºeného operátoru K L. ➎ Z jakého d vodu nelze p ijmout rovnost ( f g, φ( x) ) = ( f( x) g( y), φ( x + y) ) za denici konvoluce v D? Podrobn vysv tlete na p íklad. ➏ Prezentujte detailn konstrukci Legendreových polynom.
5 5. D a D reg Cauchyova úloha pro vlnovou rovnici a její p evod do D rezolventa integrální rovnice ➋ Odvo te obrazy F[δ µ ] a F[sin(αx)]. ➌ Vyslovte a dokaºte v tu o posunutí tenzorového sou inu. ➍ Diskutujte pojem unfoldované spektrum operátoru. Jakým zp sobem se konstruuje p íslu²ná operátorová báze v H? ➎ Vyslovte a dokaºte v tu o omezenosti Fredholmova integrálního operátoru na Banachov prostoru C σ (Ḡ) i na prostoru kvadraticky integrabilních funkcí L 2(G). ➏ Prezentujte detailn konstrukci Hermiteových polynom.
6 konvergence na prostoru zobecn ných funkcí Cauchyova úloha pro Schrödingerovu rovnici a její p evod do D nosi zobecn né funkce a zobecn ná funkce s pozitivním nosi em 6. ➋ Vyslovte a dokaºte v tu o násobení tenzorového sou inu funkcí a( y) (f( x) g( y) ). ➌ Jak souvisí hodnota funkcionálního diskriminantu d(x, y) s typem excentricity parciální diferenciální rovnice? Dokaºte. ➍ Dokaºte následující tvrzení (tzv. lemma o kruhovém spektru): Nech L : H H je operátor s ist bodovým spektrem, pro který platí, ºe σ( L) leºí na jednotkové kruºnici v Gaussov rovin. Dokaºte, ºe vzdálenost obraz dvou funkcí z H se aplikací operátoru L nem ní. ➎ Vyslovte a dokaºte v tu o e²ení Fredholmovy integrální rovnice se separabilním jádrem. ➏ Dokaºte komutativitu tenzorového sou inu.
7 operace rovnosti, s ítání a násobení na prostoru D (E r ) (z jakého d vodu z stávají výsledky t chto operací v D (E r )?) Diracova prostá vrstva Co je faktorová funkce a faktorový prostor funkcí? 7. ➋ Dokaºte rovnost D (1,1,...,1) Θ µ ( x) = δ µ ( x). ➌ Dokaºte, ºe jsou-li f, g regulární distribuce s generátory f( x), g( x) L 1 (E r ), pak f g existuje a je také regulární. Co je jejím generátorem? ➍ Dokaºte, ºe je-li Fredholm v operátor zadán spojitým jádrem, pak lze volit Dom( K) = C σ (Ḡ) i Dom( K) = L 2 (G). ➎ Dokaºte, ºe konverguje-li (η k ) k=1 také. k jedni ce, pak ( η k + η ) k x j k=1 ➏ Vyslovte a dokaºte v tu o vlastních íslech integrálního operátoru se separabilním jádrem.
8 8. Hilbert v prostor funkcí a konvergence podle normy tenzorový sou in v D spojitost operátoru t ída funcí D sep (E r+s ) a její zásadní vztah k D(E r+s ) ➋ Nech φ( x) D(E r ). Za jakých p edpoklad platí a( x)φ( x) D(E r )? Své tvrzení dokaºte. Jaká je alternativa tohoto tvrzení pro φ( x) S (E r )? ➌ Vyslovte a dokaºte v tu o limit obrazu pro klasickou Laplaceovu transformaci. ➍ Vyslovte a dokaºte v tu o reálnosti kvadratické formy hermiteovského operátoru. Ob implikace dokaºte. Co lze z tohoto tvrzení odvodit pro vlastní ísla hermiteovského operátoru? ➎ Dokaºte, ºe je-li Volterr v operátor zadán spojitým jádrem, pak lze volit Dom( K) = C σ ( 0, a ). ➏ Vyslovte a dokaºte v tu o derivaci konvoluce zobecn ných funkcí.
9 hlavní hodnota integrálu konvoluce v D omezenost operátoru 9. ➋ Vyslovte a dokaºte v ty o vztahu klasického a zobecn ného e²ení parciální diferenciální rovnice L(u) = f( x). ➌ Vyslovte a dokaºte v tu o obrazu konvoluce pro klasickou Laplaceovu transformaci. ➍ Vyslovte a dokaºte v tu o ortogonalit vlastních funkcí. ➎ Vyslovte a dokaºte v tu o e²ení Volterrovy integrální rovnice metodou postupných aproximací. ➏ Dokaºte v tu: Nech f, g D a g je nitní. Pak existuje konvoluce f g a pro kaºdou testovací funkci φ( x) D platí ( f g, φ( x) ) = ( f( x) g( y), η( y)φ( x + y) ), kde η( y) je libovolná testovací funkce, která je na okolí nosi e supp(g) rovna jedné.
10 10. lokáln integrabilní funkce (kde se tento pojem uplat uje v teorii zobecn ných funkcí?) Diracova δ funkce a centrovaná δ funkce operátor s ist bodovým spektrem ➋ Uvaºujme integrální rovnici µ K(φ) + f( x) = φ( x) a mnoºiny W 0 := {φ( x) Dom( K) : µ K(φ) = φ( x)} a W f := {φ( x) Dom( K) : µ K(φ)+f( x) = φ( x)}. Diskutujte, jaké vlastnosti ob mnoºiny spl ují a jaká je mezi nimi vazba. Jak tyto vlastnosti souvisejí s po tem e²ení rovnice s pravou stranou a bez pravé strany? ➌ Dokaºte spojitost tenzorového sou inu. ➍ Podle denice ukaºte, ºe δ f = f δ = f. ➎ Dokaºte, ºe Volterr v operátor se spojitým jádrem je lineární, spojitý a omezený na deni ním oboru Dom( K) = C σ ( 0, a ). ➏ Zodpov zte a va²e tvrzení podpo te korektním výpo tem: Nech u(x, t) C 1 (R 2 ) \ C 2 (R 2 ). Nech w(x, t) je zobecn ná funkce generovaná klasickou funkcí Θ(t)u(x, t). ƒemu je v D (R 2 ) roven výraz w (x, t)? t
11 11. kone ná ást (partie nie) superstejnom rná konvergence ve Schwartzov prostoru kvadratická a bilineární forma indukovaná operátorem ➋ Diskutujte vztah mezi L, L 1, L 2 a L loc. Jednotlivá tvrzení zd vodn te. ➌ Vyslovte a dokaºte v tu o vztahu stejnom rné konvergence a konvergence podle normy na L (w) 2 (G), kde µ(g) <. ➍ Vyslovte a dokaºte v tu o asociativit konvoluce v D +(R). ➎ Formulujte Cauchyovu úlohu pro dopravní rovnici a p eve te ji do e i zobecn ných funkcí. ➏ Odvo te metodu pro hledání transforma ních vztah pro hyperbolickou PDR druhého ádu pro funkci dvou prom nných.
12 12. superstejnom rná konvergence v prostoru testovacích funkcí Cauchyova úloha pro rovnici vedení tepla a její p evod do D Neumannova ada integrální rovnice (dokaºte její regulární konvergenci pro Fredholm v i Volterr v integrální operátor) ➋ Leºí Heavisideova, resp. Diracova funkce (v etn centrovaných variant) v D +(E r )? Podrobn komentujte. ➌ Dokaºte, ºe zobrazení F : S S je spojité. ➍ Vyslovte a dokaºte v tu o derivaci tenzorového sou inu. ➎ Dokaºte, ºe je-li f( x) L 1 (E r ), pak F[f( x)] existuje. ➏ Dokaºte v tu: Nech S = {f 1 ( x), f 2 ( x),..., f k ( x),...} je báze v separabilním Hilbertov prostoru H tvo ená vlastními funkcemi operátoru L s ist bodovým spektrem. Ozna me µ k vlastní íslo p íslu²né vlastní funkci f k ( x). Nech U = {µ 1, µ 2,..., µ k,...}. Pak σ( L) = U.
13 13. funkcionál (jeho spojitost a linearita) Heavisideova a centrovaná Heavisideova funkce (klasická a zobecn ná) hermiticita operátoru okolí mnoºiny ➋ Z denice hermiticity operátoru odvo te podmínku pro jádro K ( x, y) integrálního operátoru K denovaného na L 2 (G) posta ující pro to, aby K byl hermiteovský. ➌ Dokaºte, ºe je-li f( x) S, pak F[f( x)] existuje. ➍ Vyslovte a dokaºte v tu o existenci konvoluce pro klasické funkce. ➎ Vyslovte a dokaºte v tu o e²ení Fredholmovy integrální rovnice metodou iterovaných jader. ➏ Jak vypadá obecný vztah pro laplaceovskou inverzi? Vztah d kladn rozeberte a jeho aplikací odvo te Laplace v vzor k obrazu F (s) = Θ(s)/s.
14 14. spojitost skalárního sou inu Sochockého distribuce typy denitnosti operátoru nitní distribuce ➋ Vyslovte v tu o zjednodu²ení denice zobecn né konvoluce za p edpokladu, ºe ob funkce f, g budou ze t ídy D +(R). K emu lze takové zjednodu²ení dále vyuºít? ➌ Dokaºte, ºe je-li f(t) P(R), pak L[f(t)] existuje. ➍ Vyslovte a dokaºte v tu o e²ení Fredholmovy integrální rovnice metodou postupných aproximací. ➎ Co zajímavého lze demonstrovat na konvoluci Θ δ 1? ➏ Odvo te metodu detekce normaliza ních transforma ních vztah pro diferenciální rovnici s konstantními koecienty.
15 15. Fourierova ada funkce f H, Fourierovy koecienty prostory S (E r ) a S (E r ) posloupnost konvergující k jedni ce (+ p íklad konstrukce) ➋ Vyslovte a dokaºte v tu o vektorovém prostoru vlastních funkcí. Jak souvisí tato v ta s pojmem geometrická násobnost? ➌ Rozhodn te o platnosti následující implikace: f(x) S (R) Dom(f) (0, + ) L[f] existuje. ➍ Vyslovte a dokaºte v tu o zám n klasického laplaceovského obrazu a vzoru v ur itém integrálu. ➎ Dokaºte Sochockého vzorce a v²echny kroky d kazu korektn zd vodn te. ➏ Dokaºte v tu: Konvoluce zobecn ných funkcí je na D +(R) spojitá v obou argumentech, tj. pro libovolnou zobecn nou funkci g D +(R) a libovolnou posloupnost zobecn ných funkcí f k D +(R), která v D (R) konverguje k funkci f D +(R), platí rovnosti lim (f k g) D = f g, lim (g f k) D = g f. k k
16 16. Parseval v vzorec, Parsevalova rovnost a Besselova nerovnost (diskuse jejich vztah) klasická Laplaceova transformace funkcionální σ norma (diskutujte, pro jde o normu a na co je t eba dát p i denici funkcionální σ normy pozor) ➋ Dokaºte, ºe centrovaná Diracova δ funkce je singulární. ➌ Dokaºte: Nech φ( x), ψ( x) S (E r ) a φ, ψ jsou regulární distribuce generované funkcemi φ( x), ψ( x) S (E r ). Pak v S (E r ) platí rovnost ( F[φ], ψ( x) ) = ( φ, F[ψ( x)]). Pro se tato v ta dokazuje je²t p ed zavedením Fourierovy transformace na prostoru temperovaných distribucí? ➍ Dokaºte, ºe kaºdý skalární sou in na Hilbertov prostoru H je spojitý. Jaký je d sledek této vlastnosti? ➎ Odvo te tvar jádra integrálního operátoru K 2 pro Volterr v integrální operátor. Je operátor K 2 také Volterrova typu? ➏ Vyslovte a dokaºte v tu o harmonickém e²ení vlnové rovnice a rovnice vedení tepla.
17 17. parciální diferenciální operátor druhého ádu a jeho vlastnosti (zapi²te tvar operátoru v multiindexové notaci) klasická Fourieova transformace t ídy W 0 a W f pro parciální diferenciální operátor L a jejich vztah konvergence ve t íd temperovaných distribucí ➋ Za jakých podmínek platí implikace Dokaºte a srovnejte. limnorm f n( x) = f( x) H limnorm L ( f n ( x) ) = L ( f( x) )? n n limnorm n f n( x) = f( x) H lim n L(f n ) g = L(f) g. ➌ Dokaºte komutativitu konvoluce (v L 1 i v D ). ➍ Vyslovte a dokaºte v tu o derivaci obrazu ve Fourierov transformaci (v S i S ). ➎ Vyslovte a dokaºte v tu o e²ení Volterrovy integrální rovnice metodou iterovaných jader. ➏ e²te rovnici x m f(x) = 0 v S (R) a znalosti jejího e²ení uºijte p i odvození Fourierova obrazu jednotkové funkce.
18 18. klasikace parciálních diferenciálních rovnic druhého ádu Fourierova transformace v S (E r ) integrální rovnice (typologie integrálních rovnic) ➋ Dokaºte rovnost δ µ = δ( x µ). ƒemu se rovná supp(δ µ )? Své tvrzení dokaºte. ➌ Vyslovte a dokaºte v tu o substituci ve vzoru ve Fourierov transformaci (v S i S ). ➍ Vyslovte a dokaºte v tu o omezenosti spojitého operátoru. ➎ Vyslovte a dokaºte v tu o Parsevalov vzorci a Parsevalov rovnosti. ➏ Dokaºte v tu: Operátor s ist bodovým spektrem, pro který σ( L) R, je hermiteovský.
19 19. zobecn ná alternativa pro klasickou funkci 1 x µ diferenciální operátor v D a e²ení diferenciální rovnice v D jádro integrálního operátoru a jeho spojitost, resp. separabilita ➋ Vyslovte a dokaºte v tu o parciální derivaci sou inu zobecn ných funkcí. ➌ Vyslovte a dokaºte v tu o Fourierov obrazu konvoluce v S. ➍ Vyslovte a dokaºte v tu o harmonickém e²ení dopravní rovnice. ➎ Jak lze rozepsat δ( x) D (E r ) za pomoci tenzorového sou inu? Dokaºte. K s ist bodovým spektrem, ➏ Dokaºte v tu: Nech je dán Fredholm v integrální operátor jehoº deni ním oborem je L 2 (G). Nech soubor σ unf ( K) = (λ 1, λ 2, λ 3...) je unfoldovaným spektrem tohoto operátoru a B = { φ 1 ( x), φ 2 ( x), φ 3 ( x)... } p íslu²ná operátorová báze. Nech ada k=1 λ k konverguje. Pak integrální jádro takového operátoru m ºe být p epsáno do tvaru K ( x, y) = l=1 λ lφ l ( x)φ l ( y).
20 20. prostor testovacích funkcí a p íklady Cauchyova úloha pro oby ejnou diferenciální rovnici a její p evod do D mez integrálního jádra a d kaz její kone nosti ➋ Vyslovte a dokaºte v tu o zobecn né derivaci skokové funkce. ➌ ƒemu se rovná L[ f(t) t ] a za jakých p edpoklad? Dokaºte. ➍ Dokaºte Besselovu nerovnost. ➎ Pro v D neexistuje 1 x? Jak se absence této distribuce e²í? ➏ Vyslovte a dokaºte tvrzení o tvaru Fourierovy inverzní transformace v S i S. Uºijte faktu, ºe F[1] = (2π) r δ( ξ).
21 21. Cimrmanovy bu inky linearita a spojitost funkcionálu nad D(E r ) - denici demonstrujte na p íklad ( f, φ( x) ) = Banach v prostor C σ (J) ➋ Dokaºte, ºe δ µ D (E r ) a Θ µ D (E r ). φ( µ 2 x) d x ( µ E r ). ➌ Vyslovte a dokaºte v tu o obrazu derivace ve Fourierov transformaci (v S i S ). ➍ Vyslovte v tu o Fourierov rozvoji a diskutujte, jakým zp sobem lze dokázat. ➎ Za jakých podmínek platí vlastnost R f(x)g(x) dx = F (x)g(x) dx z Fourierova desa- R tera? Dokaºte. ➏ Dokaºte: Nech S = {f 1 (x), f 2 (x),...} je ortonormální mnoºina na Hilbertov prostoru H a g(x) H. Ozna me a k := g f k. Pak existuje limita limnorm n n a k f k (x) = a k f k (x) H. k=1 Ozna íme-li tuto limitu h(x), pak navíc pro kaºdé k N platí: g h fk = 0. k=1
Zkou²ková písemná práce. 1/A z p edm tu 01RMF
 Příjmení a jméno 1 2 3 4 5 CELKEM Zkou²ková písemná práce. 1/A z p edm tu 01RMF 15/01/2016, 9:00 10:00 ➊ Je funkcionál denovaný p edpisem ze t ídy D (G), kde G = (1, + ). Vysv tlete! ( g; φ(x)) := R φ(x)
Příjmení a jméno 1 2 3 4 5 CELKEM Zkou²ková písemná práce. 1/A z p edm tu 01RMF 15/01/2016, 9:00 10:00 ➊ Je funkcionál denovaný p edpisem ze t ídy D (G), kde G = (1, + ). Vysv tlete! ( g; φ(x)) := R φ(x)
Zápo tová písemná práce. 1 z p edm tu 01RMF varianta A
 Zápo tová písemná práce. 1 z p edm tu 1MF varianta A tvrtek 19. listopadu 215, 13:215:2 ➊ (5 bod ) Nech f (x), g(x) L 1 () a f (x) dx = A, x f (x) dx = µ, Vypo ítejte, emu se rovná z( f g)(z) dz. g(x)
Zápo tová písemná práce. 1 z p edm tu 1MF varianta A tvrtek 19. listopadu 215, 13:215:2 ➊ (5 bod ) Nech f (x), g(x) L 1 () a f (x) dx = A, x f (x) dx = µ, Vypo ítejte, emu se rovná z( f g)(z) dz. g(x)
Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A
 Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A st eda 19. listopadu 2015, 11:2013:20 ➊ (3 body) Pro diferenciální operátor ˆL je mnoºina W q denována p edpisem W q = { y(x) Dom( ˆL) : ˆL(y(x))
Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A st eda 19. listopadu 2015, 11:2013:20 ➊ (3 body) Pro diferenciální operátor ˆL je mnoºina W q denována p edpisem W q = { y(x) Dom( ˆL) : ˆL(y(x))
Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A
 Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A úterý 6. prosince 2016, 13:2015:20 ➊ (8 bod ) Vy²et ete stejnom rnou konvergenci ady na mnoºin R +. n=2 x n 1 1 4n 2 + x 2 ln 2 (n) ➋ (5 bod ) Detailn
Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A úterý 6. prosince 2016, 13:2015:20 ➊ (8 bod ) Vy²et ete stejnom rnou konvergenci ady na mnoºin R +. n=2 x n 1 1 4n 2 + x 2 ln 2 (n) ➋ (5 bod ) Detailn
Katedra matematiky Fakulty jaderné a fyzikálně inženýrské ČVUT v Praze Příjmení a jméno ➊ ➋ ➌ ➍ ➎ ➏ Bonus
 Zkoušková písemná práce č 1 z předmětu 1RMF čtvrtek 16 ledna 214, 9: 11: ➊ 11 bodů) Ve třídě zobecněných funkcí vypočítejte itu x ) n n2 sin 2 P 1 n x) ➋ 6 bodů) Aplikací Laplaceovy transformace vypočtěte
Zkoušková písemná práce č 1 z předmětu 1RMF čtvrtek 16 ledna 214, 9: 11: ➊ 11 bodů) Ve třídě zobecněných funkcí vypočítejte itu x ) n n2 sin 2 P 1 n x) ➋ 6 bodů) Aplikací Laplaceovy transformace vypočtěte
nazvu obecnou PDR pro neznámou funkci
 Denice. Bu n N a Ω R d otev ená, d 2. Vztah tvaru F (x, u(x), Du(x),..., D (n 1) u(x), D (n) u(x)) = 0 x Ω (1) nazvu obecnou PDR pro neznámou funkci u : Ω R d R Zde je daná funkce. F : Ω R R d R dn 1 R
Denice. Bu n N a Ω R d otev ená, d 2. Vztah tvaru F (x, u(x), Du(x),..., D (n 1) u(x), D (n) u(x)) = 0 x Ω (1) nazvu obecnou PDR pro neznámou funkci u : Ω R d R Zde je daná funkce. F : Ω R R d R dn 1 R
Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A
 Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A úterý 28. listopadu 2017, 9:2011:20 ➊ (8 bod ) Lze nebo nelze k rozhodnutí o stejnom rné konvergence ady ( 1) n+1 x ln(n) n 6 + n 2 x 4 na intervalu
Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A úterý 28. listopadu 2017, 9:2011:20 ➊ (8 bod ) Lze nebo nelze k rozhodnutí o stejnom rné konvergence ady ( 1) n+1 x ln(n) n 6 + n 2 x 4 na intervalu
Rovnice matematické fyziky cvičení pro akademický školní rok 2013-2014
 Harmonogram výuky předmětu Rovnice matematické fyziky cvičení pro akademický školní rok 2013-2014 Vedoucí cvičení: ing. Václav Klika, Ph.D. & MSc. Karolína Korvasová & & ing. Matěj Tušek, Ph.D. Katedra
Harmonogram výuky předmětu Rovnice matematické fyziky cvičení pro akademický školní rok 2013-2014 Vedoucí cvičení: ing. Václav Klika, Ph.D. & MSc. Karolína Korvasová & & ing. Matěj Tušek, Ph.D. Katedra
Zápo tová písemná práce. 1 z p edm tu 01MAB4 varianta A
 Zápo tová písemná práce. 1 z p edm tu 01MAB4 varianta A 18. dubna 2016, 11:2013:20 ➊ (1 bod) Nalezn te kritický bod soustavy generujících rovnic e x 6y 6z 2 + 12z = 13, 2e 2x 6y z 3 = 6. Uºijte faktu,
Zápo tová písemná práce. 1 z p edm tu 01MAB4 varianta A 18. dubna 2016, 11:2013:20 ➊ (1 bod) Nalezn te kritický bod soustavy generujících rovnic e x 6y 6z 2 + 12z = 13, 2e 2x 6y z 3 = 6. Uºijte faktu,
Zkou²ková písemná práce. 1 z p edm tu 01MAB4
 Zkou²ková písemná práce. 1 z p edm tu 01MAB4 25/05/2017, 9:00 11:00 ➊ (9 bod ) Nech je dvojrozm rná Lebesgueova míra generována vytvo ujícími funkcemi φ(x) = Θ(x)x 2 a ψ(y) = 7y. Vypo t te míru mnoºiny
Zkou²ková písemná práce. 1 z p edm tu 01MAB4 25/05/2017, 9:00 11:00 ➊ (9 bod ) Nech je dvojrozm rná Lebesgueova míra generována vytvo ujícími funkcemi φ(x) = Θ(x)x 2 a ψ(y) = 7y. Vypo t te míru mnoºiny
Zkou²ková písemná práce. 1 z p edm tu 01MAB4
 Zkou²ková písemná práce. 1 z p edm tu 1MAB4 29/5/218, 9: 11: ➊ (8 bod ) Pro parametry a > a b R vypo t te ur itý integrál e ax2 cos(bx2 ) 1 x Uºijte v tu o derivaci integrálu s parametrem. Spln ní p edpokladu
Zkou²ková písemná práce. 1 z p edm tu 1MAB4 29/5/218, 9: 11: ➊ (8 bod ) Pro parametry a > a b R vypo t te ur itý integrál e ax2 cos(bx2 ) 1 x Uºijte v tu o derivaci integrálu s parametrem. Spln ní p edpokladu
Zkou²ková písemná práce. 1 z p edm tu 01MAB4
 Katedra matematiky Fakulty jaderné a fyzikálně inženýrské ČVU v Praze Zkou²ková písemná práce. 1 z p edm tu 1MAB4 25/5/216, 9: 11: ➊ (11 bod ) Vypo ítejte abstraktní plo²nou míru mnoºiny M = (x, y) R 2
Katedra matematiky Fakulty jaderné a fyzikálně inženýrské ČVU v Praze Zkou²ková písemná práce. 1 z p edm tu 1MAB4 25/5/216, 9: 11: ➊ (11 bod ) Vypo ítejte abstraktní plo²nou míru mnoºiny M = (x, y) R 2
1. Spo t te limity (m ºete pouºívat l'hospitalovo pravidlo) x cotg x 1. c) lim. g) lim e x 1. cos(x) =
 I. L'HOSPITALOVO PRAVIDLO A TAYLOR V POLYNOM. Spo t te limity (m ºete pouºívat l'hospitalovo pravidlo) a) lim tg sin ( + ) / e e) lim a a i) lim a a, a > P ipome me si: 3 tg 4 2 tg b) lim 3 sin 4 2 sin
I. L'HOSPITALOVO PRAVIDLO A TAYLOR V POLYNOM. Spo t te limity (m ºete pouºívat l'hospitalovo pravidlo) a) lim tg sin ( + ) / e e) lim a a i) lim a a, a > P ipome me si: 3 tg 4 2 tg b) lim 3 sin 4 2 sin
Požadavky k písemné přijímací zkoušce z matematiky do navazujícího magisterského studia pro neučitelské obory
 Požadavky k písemné přijímací zkoušce z matematiky do navazujícího magisterského studia pro neučitelské obory Zkouška ověřuje znalost základních pojmů, porozumění teorii a schopnost aplikovat teorii při
Požadavky k písemné přijímací zkoušce z matematiky do navazujícího magisterského studia pro neučitelské obory Zkouška ověřuje znalost základních pojmů, porozumění teorii a schopnost aplikovat teorii při
22 Základní vlastnosti distribucí
 M. Rokyta, MFF UK: Aplikovaná matematika IV kap. 22: Základní vlastnosti distribucí 5 22 Základní vlastnosti distribucí 22.1 Temperované distribuce Definice. O funkci ϕ C (R m ) řekneme, že je rychle klesající
M. Rokyta, MFF UK: Aplikovaná matematika IV kap. 22: Základní vlastnosti distribucí 5 22 Základní vlastnosti distribucí 22.1 Temperované distribuce Definice. O funkci ϕ C (R m ) řekneme, že je rychle klesající
I. VRSTEVNICE FUNKCE, OTEV ENÉ A UZAV ENÉ MNOšINY
 I. VRSTEVNICE FUNKCE, OTEV ENÉ A UZAV ENÉ MNOšINY 1. Ur ete a nakreslete deni ní obor a vrstevnice funkcí: a) f(, y) = + y b) f(, y) = y c) f(, y) = 2 + y 2 d) f(, y) = 2 y 2 e) f(, y) = y f) f(, y) =
I. VRSTEVNICE FUNKCE, OTEV ENÉ A UZAV ENÉ MNOšINY 1. Ur ete a nakreslete deni ní obor a vrstevnice funkcí: a) f(, y) = + y b) f(, y) = y c) f(, y) = 2 + y 2 d) f(, y) = 2 y 2 e) f(, y) = y f) f(, y) =
Text m ºe být postupn upravován a dopl ován. Datum poslední úpravy najdete u odkazu na staºení souboru. Veronika Sobotíková
 Tento text není samostatným studijním materiálem. Jde jen o prezentaci promítanou na p edná²kách, kde k ní p idávám slovní komentá. N které d leºité ásti látky pí²u pouze na tabuli a nejsou zde obsaºeny.
Tento text není samostatným studijním materiálem. Jde jen o prezentaci promítanou na p edná²kách, kde k ní p idávám slovní komentá. N které d leºité ásti látky pí²u pouze na tabuli a nejsou zde obsaºeny.
Skalární sou in. Úvod. Denice skalárního sou inu
 Skalární sou in Jedním ze zp sob, jak m ºeme dva vektory kombinovat, je skalární sou in. Výsledkem skalárního sou inu dvou vektor, jak jiº název napovídá, je skalár. V tomto letáku se nau íte, jak vypo
Skalární sou in Jedním ze zp sob, jak m ºeme dva vektory kombinovat, je skalární sou in. Výsledkem skalárního sou inu dvou vektor, jak jiº název napovídá, je skalár. V tomto letáku se nau íte, jak vypo
Záznam o ústní zkoušce z předmětu 01MAB4 (akademický školní rok 2017/2018) Příjmení a jméno studenta Finální hodnocení Datum ústní zkoušky
 hladká funkce na oblasti G E r 1. matematickým zápisem vystihněte geometrickou interpretaci abstraktního Lebesgueova integrálu Kam míří gradf( a)? Své tvrzení podpořte výpočtem. Jaký je rozdíl mezi symboly
hladká funkce na oblasti G E r 1. matematickým zápisem vystihněte geometrickou interpretaci abstraktního Lebesgueova integrálu Kam míří gradf( a)? Své tvrzení podpořte výpočtem. Jaký je rozdíl mezi symboly
5. Aplikace diferenciálního a integrálního po tu v jedné dimenzi ZS 2017/18 1 / 32
 5. Aplikace diferenciálního a integrálního po tu v jedné dimenzi Tomá² Sala MÚ UK, MFF UK ZS 2017/18 5. Aplikace diferenciálního a integrálního po tu v jedné dimenzi ZS 2017/18 1 / 32 5.1 Funkce spojité
5. Aplikace diferenciálního a integrálního po tu v jedné dimenzi Tomá² Sala MÚ UK, MFF UK ZS 2017/18 5. Aplikace diferenciálního a integrálního po tu v jedné dimenzi ZS 2017/18 1 / 32 5.1 Funkce spojité
Úvod do parciálních diferenciálních rovnic. 2 Kanonický tvar lineárních PDR 2. řádu pro funkce
 Příklady na cvičení k přednášce NMMA334 Úvod do parciálních diferenciálních rovnic 1 Kanonický tvar lineárních PDR 2. řádu pro funkce dvou proměnných 1. Určete typ parciální diferenciální rovnice u xx
Příklady na cvičení k přednášce NMMA334 Úvod do parciálních diferenciálních rovnic 1 Kanonický tvar lineárních PDR 2. řádu pro funkce dvou proměnných 1. Určete typ parciální diferenciální rovnice u xx
ZS: 2018/2019 NMAF063 F/3 Josef MÁLEK. Matematika pro fyziky III
 ZS: 2018/2019 NMAF063 F/3 Josef MÁLEK Matematika pro fyziky III OBECNÉ INFORMACE A SYLABUS Přednášející: Cvičící: Josef Málek Tomáš Los, Michal Pavelka, Michal Pavelka, Vít Průša Termíny přednášek: čtvrtek
ZS: 2018/2019 NMAF063 F/3 Josef MÁLEK Matematika pro fyziky III OBECNÉ INFORMACE A SYLABUS Přednášející: Cvičící: Josef Málek Tomáš Los, Michal Pavelka, Michal Pavelka, Vít Průša Termíny přednášek: čtvrtek
19 Hilbertovy prostory
 M. Rokyta, MFF UK: Aplikovaná matematika III kap. 19: Hilbertovy prostory 34 19 Hilbertovy prostory 19.1 Úvod, základní pojmy Poznámka (připomenutí). Necht (X,(, )) je vektorový prostor se skalárním součinem
M. Rokyta, MFF UK: Aplikovaná matematika III kap. 19: Hilbertovy prostory 34 19 Hilbertovy prostory 19.1 Úvod, základní pojmy Poznámka (připomenutí). Necht (X,(, )) je vektorový prostor se skalárním součinem
NMAF063 Matematika pro fyziky III Zápočtová písemná práce B Termín pro odevzdání 4. ledna 2019
 Jméno: Příklad 2 3 4 5 Celkem bodů Bodů 20 20 20 20 20 00 Získáno Zápočtová písemná práce určená k domácímu vypracování. Nutnou podmínkou pro získání zápočtu je zisk více jak 50 bodů. Pravidla jsou následující:.
Jméno: Příklad 2 3 4 5 Celkem bodů Bodů 20 20 20 20 20 00 Získáno Zápočtová písemná práce určená k domácímu vypracování. Nutnou podmínkou pro získání zápočtu je zisk více jak 50 bodů. Pravidla jsou následující:.
1 Existence e²ení systému diferenciálních rovnic. 2 Jednozna nost e²ení pro systém diferenciálních rovnic
 1 Existence e²ení systému diferenciálních rovnic Denice. Funkci x : I R n, I otev ený interval, nazveme e²ením (DR), jestliºe 1. t I : (x(t), t) Ω 2. t I : x (t) vlastní 3. t I : x (t) = f(x(t), t) Lemma
1 Existence e²ení systému diferenciálních rovnic Denice. Funkci x : I R n, I otev ený interval, nazveme e²ením (DR), jestliºe 1. t I : (x(t), t) Ω 2. t I : x (t) vlastní 3. t I : x (t) = f(x(t), t) Lemma
Parciální diferenciální rovnice
 Parciální diferenciální rovnice Obsah kurzu Co bude obsahovat... úvod do PDR odvození některých PDR klasická teorie lineárních PDR 1. a 2. řádu řešení poč. a okraj. úloh vlastnosti řešení souvislost s
Parciální diferenciální rovnice Obsah kurzu Co bude obsahovat... úvod do PDR odvození některých PDR klasická teorie lineárních PDR 1. a 2. řádu řešení poč. a okraj. úloh vlastnosti řešení souvislost s
M4140 Vybrané partie z matematické analýzy Přírodovědecká fakulta MU
 M4140 Vybrané partie z matematické analýzy Přírodovědecká fakulta MU jaro 2010 Rozsah 4/2/0. 6 kr. Ukončení: zk. 1) Obyčejné diferenciální rovnice: 1.1. Úvod základní pojmy, přímé metody řešení některých
M4140 Vybrané partie z matematické analýzy Přírodovědecká fakulta MU jaro 2010 Rozsah 4/2/0. 6 kr. Ukončení: zk. 1) Obyčejné diferenciální rovnice: 1.1. Úvod základní pojmy, přímé metody řešení některých
VYBRANÉ APLIKACE RIEMANNOVA INTEGRÁLU I. OBSAH A DÉLKA. (f(x) g(x)) dx.
 VYBRANÉ APLIKACE RIEMANNOVA INTEGRÁLU I. OBSAH A DÉLKA. Výpo et obsahu rovinných ploch a) Plocha ohrani ená k ivkami zadanými v kartézských sou adnicích. Obsah S rovinné plochy ohrani ené dv ma spojitými
VYBRANÉ APLIKACE RIEMANNOVA INTEGRÁLU I. OBSAH A DÉLKA. Výpo et obsahu rovinných ploch a) Plocha ohrani ená k ivkami zadanými v kartézských sou adnicích. Obsah S rovinné plochy ohrani ené dv ma spojitými
Věta o sedlovém bodu a Fredholmova alternativa
 Věta o sedlovém bodu a Fredholmova alternativa Petr Tomiczek Fakulta Aplikovaných věd Západočeská univerzita Plzeň 2006 obsah 1 Rozklad Hilbertova prostoru Uzavřený lineární a samoadjungovaný operátor
Věta o sedlovém bodu a Fredholmova alternativa Petr Tomiczek Fakulta Aplikovaných věd Západočeská univerzita Plzeň 2006 obsah 1 Rozklad Hilbertova prostoru Uzavřený lineární a samoadjungovaný operátor
2. Určte hromadné body, limitu superior a limitu inferior posloupností: 2, b n = n. n n n.
 Písemka matematika 3 s řešením 1. Vypočtěte lim n( 1 + n 2 n), n lim n (( 1 + 1 n e ) n ) n. 1/2, 1/ e 2. Určte hromadné body, limitu superior a limitu inferior posloupností: a n = sin nπ ( 2, b n = n
Písemka matematika 3 s řešením 1. Vypočtěte lim n( 1 + n 2 n), n lim n (( 1 + 1 n e ) n ) n. 1/2, 1/ e 2. Určte hromadné body, limitu superior a limitu inferior posloupností: a n = sin nπ ( 2, b n = n
24. Parciální diferenciální rovnice
 24. Parciální diferenciální rovnice Aplikovaná matematika IV, NMAF074 M. Rokyta, KMA MFF UK LS 2011/12 24.1 Rovnice vedení tepla Definice (Rovnice vedení tepla) Parciální diferenciální rovnici c(x)ρ(x)
24. Parciální diferenciální rovnice Aplikovaná matematika IV, NMAF074 M. Rokyta, KMA MFF UK LS 2011/12 24.1 Rovnice vedení tepla Definice (Rovnice vedení tepla) Parciální diferenciální rovnici c(x)ρ(x)
I. Diferenciální rovnice. 3. Rovnici y = x+y+1. převeďte vhodnou transformací na rovnici homogenní (vzniklou
 Typy příkladů pro I. část písemky ke zkoušce z MA II I. Diferenciální rovnice. 1. Určete obecné řešení rovnice y = y sin x.. Určete řešení rovnice y = y x splňující počáteční podmínku y(1) = 0. 3. Rovnici
Typy příkladů pro I. část písemky ke zkoušce z MA II I. Diferenciální rovnice. 1. Určete obecné řešení rovnice y = y sin x.. Určete řešení rovnice y = y x splňující počáteční podmínku y(1) = 0. 3. Rovnici
POŽADAVKY K SOUBORNÉ ZKOUŠCE Z MATEMATIKY
 POŽADAVKY K SOUBORNÉ ZKOUŠCE Z MATEMATIKY Bakalářský studijní program B1101 (studijní obory - Aplikovaná matematika, Matematické metody v ekonomice, Aplikovaná matematika pro řešení krizových situací)
POŽADAVKY K SOUBORNÉ ZKOUŠCE Z MATEMATIKY Bakalářský studijní program B1101 (studijní obory - Aplikovaná matematika, Matematické metody v ekonomice, Aplikovaná matematika pro řešení krizových situací)
DERIVACE FUNKCE KOMPLEXNÍ PROMĚNNÉ
 DERIVACE FUNKCE KOMPLEXNÍ PROMĚNNÉ vlastnosti holomorfní DERIVACE U reálných funkcí více reálných proměnných nebylo možné definovat derivaci analogicky definici reálné jedné reálné proměnné (nešlo dělit...)
DERIVACE FUNKCE KOMPLEXNÍ PROMĚNNÉ vlastnosti holomorfní DERIVACE U reálných funkcí více reálných proměnných nebylo možné definovat derivaci analogicky definici reálné jedné reálné proměnné (nešlo dělit...)
Numerické řešení nelineárních rovnic
 Numerické řešení nelineárních rovnic Mirko Navara http://cmp.felk.cvut.cz/ navara/ Centrum strojového vnímání, katedra kybernetiky FEL ČVUT Karlovo náměstí, budova G, místnost 104a http://math.feld.cvut.cz/nemecek/nummet.html
Numerické řešení nelineárních rovnic Mirko Navara http://cmp.felk.cvut.cz/ navara/ Centrum strojového vnímání, katedra kybernetiky FEL ČVUT Karlovo náměstí, budova G, místnost 104a http://math.feld.cvut.cz/nemecek/nummet.html
Katedra matematiky Fakulty jaderné a fyzikálně inženýrské ČVUT v Praze Příjmení a jméno ➊ ➋ ➌ ➍ ➎ ➏ Bonus
 Zkoušková písemná práce č. 1 z předmětu 01MAB4 pondělí 25. května 2015, 9:00 11:00 Vypočítejte integrál y d(, y), kde Ω Objekt Ω načrtněte do obrázku! Ω = { (, y) R 2 :, y 0 4 + y 4 1 ( 4 + y 4 ) 3 16
Zkoušková písemná práce č. 1 z předmětu 01MAB4 pondělí 25. května 2015, 9:00 11:00 Vypočítejte integrál y d(, y), kde Ω Objekt Ω načrtněte do obrázku! Ω = { (, y) R 2 :, y 0 4 + y 4 1 ( 4 + y 4 ) 3 16
Obraz matematický objekt. Spojitý obraz f c : (Ω c R 2 ) R
 Obraz matematický objekt Spojitý obraz f c : (Ω c R 2 ) R Obraz matematický objekt Spojitý obraz f c : (Ω c R 2 ) R Diskrétní obraz f d : (Ω {0... n 1 } {0... n 2 }) {0... f max } Obraz matematický objekt
Obraz matematický objekt Spojitý obraz f c : (Ω c R 2 ) R Obraz matematický objekt Spojitý obraz f c : (Ω c R 2 ) R Diskrétní obraz f d : (Ω {0... n 1 } {0... n 2 }) {0... f max } Obraz matematický objekt
Vektor náhodných veli in - práce s více prom nnými
 Vektor náhodných veli in - práce s více prom nnými 12. kv tna 2015 N kdy k popisu n jaké situace pot ebujeme více neº jednu náhodnou veli inu. Nap. v k, hmotnost, vý²ku. Mezi t mito veli inami mohou být
Vektor náhodných veli in - práce s více prom nnými 12. kv tna 2015 N kdy k popisu n jaké situace pot ebujeme více neº jednu náhodnou veli inu. Nap. v k, hmotnost, vý²ku. Mezi t mito veli inami mohou být
Otázky k ústní zkoušce, přehled témat A. Číselné řady
 Otázky k ústní zkoušce, přehled témat 2003-2004 A Číselné řady Vysvětlete pojmy částečný součet řady, součet řady, řadonverguje, řada je konvergentní Formulujte nutnou podmínku konvergence řady a odvoďte
Otázky k ústní zkoušce, přehled témat 2003-2004 A Číselné řady Vysvětlete pojmy částečný součet řady, součet řady, řadonverguje, řada je konvergentní Formulujte nutnou podmínku konvergence řady a odvoďte
Binární operace. Úvod. Pomocný text
 Pomocný text Binární operace Úvod Milí e²itelé, binární operace je pom rn abstraktní téma, a tak bude ob as pot eba odprostit se od konkrétních p íklad a podívat se na v c s ur itým nadhledem. Nicmén e²ení
Pomocný text Binární operace Úvod Milí e²itelé, binární operace je pom rn abstraktní téma, a tak bude ob as pot eba odprostit se od konkrétních p íklad a podívat se na v c s ur itým nadhledem. Nicmén e²ení
Diferenˇcní rovnice Diferenciální rovnice Matematika IV Matematika IV Program
 Program Diferenční rovnice Program Diferenční rovnice Diferenciální rovnice Program Frisch a Samuelson: Systém je dynamický, jestliže jeho chování v čase je určeno funkcionální rovnicí, jejíž neznámé závisí
Program Diferenční rovnice Program Diferenční rovnice Diferenciální rovnice Program Frisch a Samuelson: Systém je dynamický, jestliže jeho chování v čase je určeno funkcionální rovnicí, jejíž neznámé závisí
Reálná ísla a posloupnosti Jan Malý
 Reálná ísla a posloupnosti Jan Malý Obsah 1. Reálná ísla 1 2. Posloupnosti 2 3. Hlub²í v ty o itách 4 1. Reálná ísla 1.1. Úmluva (T leso). Pod pojmem t leso budeme v tomto textu rozum t pouze komutativní
Reálná ísla a posloupnosti Jan Malý Obsah 1. Reálná ísla 1 2. Posloupnosti 2 3. Hlub²í v ty o itách 4 1. Reálná ísla 1.1. Úmluva (T leso). Pod pojmem t leso budeme v tomto textu rozum t pouze komutativní
Státní závěrečná zkouška z oboru Matematika a její použití v přírodních vědách
 Státní závěrečná zkouška z oboru Matematika a její použití v přírodních vědách Ústní zkouška z oboru Náročnost zkoušky je podtržena její ústní formou a komisionálním charakterem. Předmětem bakalářské zkoušky
Státní závěrečná zkouška z oboru Matematika a její použití v přírodních vědách Ústní zkouška z oboru Náročnost zkoušky je podtržena její ústní formou a komisionálním charakterem. Předmětem bakalářské zkoušky
SIGNÁLY A SOUSTAVY, SIGNÁLY A SYSTÉMY
 SIGNÁLY A SOUSTAVY, SIGNÁLY A SYSTÉMY TEMATICKÉ OKRUHY Signály se spojitým časem Základní signály se spojitým časem (základní spojité signály) Jednotkový skok σ (t), jednotkový impuls (Diracův impuls)
SIGNÁLY A SOUSTAVY, SIGNÁLY A SYSTÉMY TEMATICKÉ OKRUHY Signály se spojitým časem Základní signály se spojitým časem (základní spojité signály) Jednotkový skok σ (t), jednotkový impuls (Diracův impuls)
e²ení systém lineárních rovnic pomocí s ítací, dosazovací a srovnávací metody
 e²ení systém lineárních rovnic pomocí s ítací, dosazovací a srovnávací metody V praxi se asto setkávame s p ípady, kdy je pot eba e²it více rovnic, takzvaný systém rovnic, obvykle s více jak jednou neznámou.
e²ení systém lineárních rovnic pomocí s ítací, dosazovací a srovnávací metody V praxi se asto setkávame s p ípady, kdy je pot eba e²it více rovnic, takzvaný systém rovnic, obvykle s více jak jednou neznámou.
K oddílu VI.1 obecné slabé topologie Příklad 1. Necht X = C([0, 1]) s topologií bodové konvergence na [0, 1]. Popište všechny
![K oddílu VI.1 obecné slabé topologie Příklad 1. Necht X = C([0, 1]) s topologií bodové konvergence na [0, 1]. Popište všechny K oddílu VI.1 obecné slabé topologie Příklad 1. Necht X = C([0, 1]) s topologií bodové konvergence na [0, 1]. Popište všechny](/thumbs/102/155153373.jpg) FUNKCIONÁLNÍ ANALÝZA 1 PŘÍKLADY PRO POROZUMĚNÍ LÁTCE ZS 2016/2017 PŘÍKLADY KE KAPITOLE VI K oddílu VI.1 obecné slabé topologie Příklad 1. Necht X = C([0, 1]) s topologií bodové konvergence na [0, 1]. Popište
FUNKCIONÁLNÍ ANALÝZA 1 PŘÍKLADY PRO POROZUMĚNÍ LÁTCE ZS 2016/2017 PŘÍKLADY KE KAPITOLE VI K oddílu VI.1 obecné slabé topologie Příklad 1. Necht X = C([0, 1]) s topologií bodové konvergence na [0, 1]. Popište
Poznámky k Fourierově transformaci
 Poznámky k Fourierově transformaci V těchto poznámkách jsou uvedeny základní vlastnosti jednorozměrné Fourierovy transformace a její aplikace na jednoduché modelové případy. Pro určitost jsou sdružené
Poznámky k Fourierově transformaci V těchto poznámkách jsou uvedeny základní vlastnosti jednorozměrné Fourierovy transformace a její aplikace na jednoduché modelové případy. Pro určitost jsou sdružené
Semestrální práce z p edm tu URM (zadání), 2014/2015:
 Semestrální práce z p edm tu URM (zadání), 2014/2015: 1. Vyzna te na globusu cestu z jihu Grónska na jih Afriky, viz Obrázek 1. V po áte ní a cílové destinaci bude zapíchnutý ²pendlík sm ující do st edu
Semestrální práce z p edm tu URM (zadání), 2014/2015: 1. Vyzna te na globusu cestu z jihu Grónska na jih Afriky, viz Obrázek 1. V po áte ní a cílové destinaci bude zapíchnutý ²pendlík sm ující do st edu
Dolní odhad síly pro ztrátu stability obecného prutu
 ƒeské vysoké u ení technické v Praze 9. února 216 Vedoucí seminární práce: doc. RNDr. Ivana Pultarová, Ph.D. prof. Ing. Milan Jirásek, DrSc. Osnova 1 2 Cíl práce Cíl práce Nalézt velikost síly, která zp
ƒeské vysoké u ení technické v Praze 9. února 216 Vedoucí seminární práce: doc. RNDr. Ivana Pultarová, Ph.D. prof. Ing. Milan Jirásek, DrSc. Osnova 1 2 Cíl práce Cíl práce Nalézt velikost síly, která zp
Státnice - Rekurzivní a rekurzivn spo etné mnoºiny
 Kapitola 1 Státnice - Rekurzivní a rekurzivn spo etné mnoºiny 1.1 Rekurzivn spo etné mnoºiny Denice (Rekurzivní a rekurzivn spo etná mnoºina) Charakteristická funkce mnoºiny M ozna uje charakteristickou
Kapitola 1 Státnice - Rekurzivní a rekurzivn spo etné mnoºiny 1.1 Rekurzivn spo etné mnoºiny Denice (Rekurzivní a rekurzivn spo etná mnoºina) Charakteristická funkce mnoºiny M ozna uje charakteristickou
Okruhy k bakalářské státní závěrečné zkoušce (2015) Matematická analýza
 Okruhy k bakalářské státní závěrečné zkoušce (2015) Matematická analýza 1. Funkce, graf funkce, inverzní funkce, operace s funkcemi, trigonometrické funkce, mocninná funkce, exponenciální funkce, logaritmická
Okruhy k bakalářské státní závěrečné zkoušce (2015) Matematická analýza 1. Funkce, graf funkce, inverzní funkce, operace s funkcemi, trigonometrické funkce, mocninná funkce, exponenciální funkce, logaritmická
Integrování jako opak derivování
 Integrování jako opak derivování V tomto dokumentu budete seznámeni s derivováním b ºných funkcí a budete mít moºnost vyzkou²et mnoho zp sob derivace. Jedním z nich je proces derivování v opa ném po adí.
Integrování jako opak derivování V tomto dokumentu budete seznámeni s derivováním b ºných funkcí a budete mít moºnost vyzkou²et mnoho zp sob derivace. Jedním z nich je proces derivování v opa ném po adí.
FOURIEROVA TRANSFORMACE FOURIEROVA VĚTA
 FOURIEROVA TRANSFORMACE FOURIEROVA VĚTA V kapitole o Fourierových řadách byla dokázána Fourierova věta (připomeňte si, že f(x = (f(x + + f(x /2: VĚTA Necht f je po částech hladká na R a R f konverguje
FOURIEROVA TRANSFORMACE FOURIEROVA VĚTA V kapitole o Fourierových řadách byla dokázána Fourierova věta (připomeňte si, že f(x = (f(x + + f(x /2: VĚTA Necht f je po částech hladká na R a R f konverguje
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %% KLÍČOVÉPOJMY %%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %% KLÍČOVÉPOJMY %%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% norma normovaný lineární prostor metrika indukovaná normou
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %% KLÍČOVÉPOJMY %%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% norma normovaný lineární prostor metrika indukovaná normou
FOURIEROVA ANALÝZA- ZÁPISKY Z PŘEDNÁŠEK
 FOUIEOVA ANALÝZA- ZÁPISKY Z PŘEDNÁŠEK JAN MALÝ Obsah 1. Fourierovy řady klasika 1 2. Fourierovy řady v Hilbertově prostoru 3 3. Sčítání Fourierových řad 4 4. Distribuce 6 5. Distribuce jako funkcionály*
FOUIEOVA ANALÝZA- ZÁPISKY Z PŘEDNÁŠEK JAN MALÝ Obsah 1. Fourierovy řady klasika 1 2. Fourierovy řady v Hilbertově prostoru 3 3. Sčítání Fourierových řad 4 4. Distribuce 6 5. Distribuce jako funkcionály*
Komplexní analýza. Laplaceova transformace. Martin Bohata. Katedra matematiky FEL ČVUT v Praze
 Komplexní analýza Laplaceova transformace Martin Bohata Katedra matematiky FEL ČVUT v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Laplaceova transformace 1 / 18 Definice Definice Laplaceovou
Komplexní analýza Laplaceova transformace Martin Bohata Katedra matematiky FEL ČVUT v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Laplaceova transformace 1 / 18 Definice Definice Laplaceovou
15 Maticový a vektorový počet II
 M. Rokyta, MFF UK: Aplikovaná matematika III kap. 15: Maticový a vektorový počet II 1 15 Maticový a vektorový počet II 15.1 Úvod Opakování z 1. ročníku (z kapitoly 8) Označení. Množinu všech reálných resp.
M. Rokyta, MFF UK: Aplikovaná matematika III kap. 15: Maticový a vektorový počet II 1 15 Maticový a vektorový počet II 15.1 Úvod Opakování z 1. ročníku (z kapitoly 8) Označení. Množinu všech reálných resp.
Interpolace, ortogonální polynomy, Gaussova kvadratura
 Interpolace, ortogonální polynomy, Gaussova kvadratura Petr Tichý 20. listopadu 2013 1 Úloha Lagrangeovy interpolace Dán omezený uzavřený interval [a, b] a v něm n + 1 různých bodů x 0, x 1,..., x n. Nechť
Interpolace, ortogonální polynomy, Gaussova kvadratura Petr Tichý 20. listopadu 2013 1 Úloha Lagrangeovy interpolace Dán omezený uzavřený interval [a, b] a v něm n + 1 různých bodů x 0, x 1,..., x n. Nechť
MKI Funkce f(z) má singularitu v bodě 0. a) Stanovte oblast, ve které konverguje hlavní část Laurentova rozvoje funkce f(z) v bodě 0.
 MKI -00 Funkce f(z) má singularitu v bodě 0. a) Stanovte oblast, ve které konverguje hlavní část Laurentova rozvoje funkce f(z) v bodě 0. V jakém rozmezí se může pohybovat poloměr konvergence regulární
MKI -00 Funkce f(z) má singularitu v bodě 0. a) Stanovte oblast, ve které konverguje hlavní část Laurentova rozvoje funkce f(z) v bodě 0. V jakém rozmezí se může pohybovat poloměr konvergence regulární
Limity funkcí v nevlastních bodech. Obsah
 Limity funkcí v nevlastních bodech V tomto letáku si vysv tlíme, co znamená, kdyº funkce mí í do nekone na, mínus nekone na nebo se blíºí ke konkrétnímu reálnému íslu, zatímco x jde do nekone na nebo mínus
Limity funkcí v nevlastních bodech V tomto letáku si vysv tlíme, co znamená, kdyº funkce mí í do nekone na, mínus nekone na nebo se blíºí ke konkrétnímu reálnému íslu, zatímco x jde do nekone na nebo mínus
Projekty - Úvod do funkcionální analýzy
 Projekty - Úvod do funkcionální analýzy Projekt č. 1. Nechť a, b R, a < b. Dokažte, že prostor C( a, b ) = f : R R: f je spojitá na D(f) = a, b s metrikou je úplný. ρ(f, g) = max f(x) g(x) x a,b Projekt
Projekty - Úvod do funkcionální analýzy Projekt č. 1. Nechť a, b R, a < b. Dokažte, že prostor C( a, b ) = f : R R: f je spojitá na D(f) = a, b s metrikou je úplný. ρ(f, g) = max f(x) g(x) x a,b Projekt
Záludnosti velkých dimenzí
 Jan Vybíral KM/FJFI/ƒVUT 6. listopadu 2017 1/28 Warm-up Dva problémy na zah átí Geometrie R d Kolik bod je t eba rozmístit v jednotkové krychli [0, 1] d v dimenzi d, aby v kaºdém kvádru o objemu 1/10 leºel
Jan Vybíral KM/FJFI/ƒVUT 6. listopadu 2017 1/28 Warm-up Dva problémy na zah átí Geometrie R d Kolik bod je t eba rozmístit v jednotkové krychli [0, 1] d v dimenzi d, aby v kaºdém kvádru o objemu 1/10 leºel
Primitivní funkce a Riemann uv integrál Lineární algebra Taylor uv polynom Extrémy funkcí více prom ˇenných Matematika III Matematika III Program
 Program Primitivní funkce a Riemannův integrál Program Primitivní funkce a Riemannův integrál Lineární algebra Program Primitivní funkce a Riemannův integrál Lineární algebra Taylorův polynom Program Primitivní
Program Primitivní funkce a Riemannův integrál Program Primitivní funkce a Riemannův integrál Lineární algebra Program Primitivní funkce a Riemannův integrál Lineární algebra Taylorův polynom Program Primitivní
FOURIEROVA TRANSFORMACE
 FOURIEROVA TRANSFORMACE FOURIEROVA VĚTA V kapitole o Fourierových řadách byla dokázána (připomeňte si, že f(x) = (f(x + ) + f(x ))/2): VĚTA. Necht f je po částech hladká na R a R f konverguje. Potom f(x)
FOURIEROVA TRANSFORMACE FOURIEROVA VĚTA V kapitole o Fourierových řadách byla dokázána (připomeňte si, že f(x) = (f(x + ) + f(x ))/2): VĚTA. Necht f je po částech hladká na R a R f konverguje. Potom f(x)
ŘADY KOMPLEXNÍCH FUNKCÍ
 ŘADY KOMPLEXNÍCH FUNKCÍ OBECNÉ VLASTNOSTI Řady komplexních čísel z n byly částečně probírány v kapitole o číselných řadách. Definice říká, že n=0 z n = z, jestliže z je limita částečných součtů řady z
ŘADY KOMPLEXNÍCH FUNKCÍ OBECNÉ VLASTNOSTI Řady komplexních čísel z n byly částečně probírány v kapitole o číselných řadách. Definice říká, že n=0 z n = z, jestliže z je limita částečných součtů řady z
Katedra matematiky Fakulty jaderné a fyzikálně inženýrské ČVUT v Praze. Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A
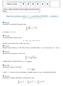 Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A středa 19. listopadu 2014, 11:20 13:20 ➊ (8 bodů) Rozhodněte o stejnoměrné konvergenci řady n 3 n ( ) 1 e xn2 x 2 +n 2 na množině A = 0, + ). ➋
Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A středa 19. listopadu 2014, 11:20 13:20 ➊ (8 bodů) Rozhodněte o stejnoměrné konvergenci řady n 3 n ( ) 1 e xn2 x 2 +n 2 na množině A = 0, + ). ➋
MATEMATIKA IV - PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE - ZÁPISKY Z. Obsah. 1. Parciální diferenciální rovnice obecně. 2. Kvaazilineární rovnice prvního řádu
 MATEMATIKA IV - PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE - ZÁPISKY Z PŘEDNÁŠEK JAN MALÝ Obsah 1. Parciální diferenciální rovnice obecně 1. Kvaazilineární rovnice prvního řádu 1 3. Lineární rovnice druhého řádu
MATEMATIKA IV - PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE - ZÁPISKY Z PŘEDNÁŠEK JAN MALÝ Obsah 1. Parciální diferenciální rovnice obecně 1. Kvaazilineární rovnice prvního řádu 1 3. Lineární rovnice druhého řádu
Co je to tensor... Vektorový prostor
 Vektorový prostor Co je to tensor... Tato ást je tu jen pro p ipomenutí, pokud nevíte co je to vektorový prostor, tak tení tohoto textu ukon ete na konci této v ty, neb zbytek textu by pro Vás nebyl ni
Vektorový prostor Co je to tensor... Tato ást je tu jen pro p ipomenutí, pokud nevíte co je to vektorový prostor, tak tení tohoto textu ukon ete na konci této v ty, neb zbytek textu by pro Vás nebyl ni
2. Ur íme sudost/lichost funkce a pr se íky s osami. 6. Na záv r na rtneme graf vy²et ované funkce. 8x. x 2 +4
 Pr b h funkce V této jednotce si ukáºeme jak postupovat p i vy²et ování pr b hu funkce. P edpokládáme znalost po ítání derivací a limit, které jsou dob e popsány v p edchozích letácích tohoto bloku. P
Pr b h funkce V této jednotce si ukáºeme jak postupovat p i vy²et ování pr b hu funkce. P edpokládáme znalost po ítání derivací a limit, které jsou dob e popsány v p edchozích letácích tohoto bloku. P
které charakterizují danou fyzikální situaci. souvislostí). Může být formulován jako soustava rovnic a nerovnic.
 1. Přednáška Obsah: Úvod do tvorby matematických modelů jako okrajové úlohy pro diferenciální rovnici. Příklad 1D vedení tepla a lineární pružnost. Diferenciální, variační, energetická formulace úloh.
1. Přednáška Obsah: Úvod do tvorby matematických modelů jako okrajové úlohy pro diferenciální rovnici. Příklad 1D vedení tepla a lineární pružnost. Diferenciální, variační, energetická formulace úloh.
PRIMITIVNÍ FUNKCE. Primitivní funkce primitivní funkce. geometrický popis integrály 1 integrály 2 spojité funkce konstrukce prim.
 PRIMITIVNÍ FUNKCE V předchozích částech byly zkoumány derivace funkcí a hlavním tématem byly funkce, které derivace mají. V této kapitole se budou zkoumat funkce, které naopak jsou derivacemi jiných funkcí
PRIMITIVNÍ FUNKCE V předchozích částech byly zkoumány derivace funkcí a hlavním tématem byly funkce, které derivace mají. V této kapitole se budou zkoumat funkce, které naopak jsou derivacemi jiných funkcí
Obsah. 1 Lineární prostory 2
 Obsah 1 Lineární prostory 2 2 Úplné prostory 2 2.1 Metrické prostory.................................... 2 2.2 Banachovy prostory................................... 3 2.3 Lineární funkcionály..................................
Obsah 1 Lineární prostory 2 2 Úplné prostory 2 2.1 Metrické prostory.................................... 2 2.2 Banachovy prostory................................... 3 2.3 Lineární funkcionály..................................
Matematika I A ukázkový test 1 pro 2014/2015
 Matematika I A ukázkový test 1 pro 2014/2015 1. Je dána soustava rovnic s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napište Frobeniovu větu (existence i počet řešení). b)
Matematika I A ukázkový test 1 pro 2014/2015 1. Je dána soustava rovnic s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napište Frobeniovu větu (existence i počet řešení). b)
P íklad 1 (Náhodná veli ina)
 P íklad 1 (Náhodná veli ina) Uvaºujeme experiment: házení mincí. Výsledkem pokusu je rub nebo líc, ºe padne hrana neuvaºujeme. Pokud hovo íme o náhodné veli in, musíme p epsat výsledky pokusu do mnoºiny
P íklad 1 (Náhodná veli ina) Uvaºujeme experiment: házení mincí. Výsledkem pokusu je rub nebo líc, ºe padne hrana neuvaºujeme. Pokud hovo íme o náhodné veli in, musíme p epsat výsledky pokusu do mnoºiny
se nazývá charakter grupy G. Dále budeme uvaºovat pouze kone né grupy G. Charaktery tvo í také grupu, s násobením denovaným
 Charaktery a Diskrétní Fourierova transforace Nejd leºit j²í kvantový algorite je Diskrétní Fourierova transforace (DFT) D vody jsou dva: DFT je pro kvantové po íta e exponenciáln rychlej²í neº pro po
Charaktery a Diskrétní Fourierova transforace Nejd leºit j²í kvantový algorite je Diskrétní Fourierova transforace (DFT) D vody jsou dva: DFT je pro kvantové po íta e exponenciáln rychlej²í neº pro po
Rovnice a nerovnice. Posloupnosti.
 .. Veronika Sobotíková katedra matematiky, FEL ƒvut v Praze, http://math.feld.cvut.cz/ 30. srpna 2018.. 1/75 (v reálném oboru) Rovnicí resp. nerovnicí v reálném oboru rozumíme zápis L(x) P(x), kde zna
.. Veronika Sobotíková katedra matematiky, FEL ƒvut v Praze, http://math.feld.cvut.cz/ 30. srpna 2018.. 1/75 (v reálném oboru) Rovnicí resp. nerovnicí v reálném oboru rozumíme zápis L(x) P(x), kde zna
PRIMITIVNÍ FUNKCE DEFINICE A MOTIVACE
 PIMITIVNÍ FUNKCE V předchozích částech byly zkoumány derivace funkcí a hlavním tématem byly funkce, které derivace mají. V této kapitole se budou zkoumat funkce, které naopak jsou derivacemi jiných funkcí
PIMITIVNÍ FUNKCE V předchozích částech byly zkoumány derivace funkcí a hlavním tématem byly funkce, které derivace mají. V této kapitole se budou zkoumat funkce, které naopak jsou derivacemi jiných funkcí
VYSOKÁ ŠKOLA POLYTECHNICKÁ JIHLAVA. Katedra matematiky. Matematika 2. pro technické obory. Petr Gurka, Stanislava Dvořáková
 VYSOKÁ ŠKOLA POLYTECHNICKÁ JIHLAVA Katedra matematiky Matematika 2 pro technické obory Petr Gurka, Stanislava Dvořáková 2019 Petr Gurka, Stanislava Dvořáková Matematika 2 pro technické obory 1. vydání
VYSOKÁ ŠKOLA POLYTECHNICKÁ JIHLAVA Katedra matematiky Matematika 2 pro technické obory Petr Gurka, Stanislava Dvořáková 2019 Petr Gurka, Stanislava Dvořáková Matematika 2 pro technické obory 1. vydání
Definice 1.1. Nechť je M množina. Funkci ρ : M M R nazveme metrikou, jestliže má následující vlastnosti:
 Přednáška 1. Definice 1.1. Nechť je množina. Funkci ρ : R nazveme metrikou, jestliže má následující vlastnosti: (1 pro každé x je ρ(x, x = 0; (2 pro každé x, y, x y, je ρ(x, y = ρ(y, x > 0; (3 pro každé
Přednáška 1. Definice 1.1. Nechť je množina. Funkci ρ : R nazveme metrikou, jestliže má následující vlastnosti: (1 pro každé x je ρ(x, x = 0; (2 pro každé x, y, x y, je ρ(x, y = ρ(y, x > 0; (3 pro každé
Vektory. Vektorové veli iny
 Vektor je veli ina, která má jak velikost tak i sm r. Ob tyto vlastnosti musí být uvedeny, aby byl vektor stanoven úpln. V této ásti je návod, jak vektory zapsat, jak je s ítat a od ítat a jak je pouºívat
Vektor je veli ina, která má jak velikost tak i sm r. Ob tyto vlastnosti musí být uvedeny, aby byl vektor stanoven úpln. V této ásti je návod, jak vektory zapsat, jak je s ítat a od ítat a jak je pouºívat
1. (18 bod ) Náhodná veli ina X je po et rub p i 400 nezávislých hodech mincí. a) Pomocí ƒeby²evovy nerovnosti odhadn te pravd podobnost
 (8 bod ) Náhodná veli ina X je po et rub p i nezávislých hodech mincí a) Pomocí ƒeby²evovy nerovnosti odhadn te pravd podobnost P ( X EX < ) (9 bod ) b) Formulujte centrální limitní v tu a pomocí ní vypo
(8 bod ) Náhodná veli ina X je po et rub p i nezávislých hodech mincí a) Pomocí ƒeby²evovy nerovnosti odhadn te pravd podobnost P ( X EX < ) (9 bod ) b) Formulujte centrální limitní v tu a pomocí ní vypo
MATEMATIKA IV - ZÁPISKY Z PŘEDNÁŠEK FOURIEROVA ANALÝZA A PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE
 MATEMATIKA IV - ZÁPISKY Z PŘEDNÁŠEK FOUIEOVA ANALÝZA A PACIÁLNÍ DIFEENCIÁLNÍ OVNICE JAN MALÝ Obsah 1. Fourierovy řady klasika. Fourierovy řady v Hilbertově prostoru 3 3. Sčítání Fourierových řad 5 4. Fourierova
MATEMATIKA IV - ZÁPISKY Z PŘEDNÁŠEK FOUIEOVA ANALÝZA A PACIÁLNÍ DIFEENCIÁLNÍ OVNICE JAN MALÝ Obsah 1. Fourierovy řady klasika. Fourierovy řady v Hilbertově prostoru 3 3. Sčítání Fourierových řad 5 4. Fourierova
Úlohy k přednášce NMAG 101 a 120: Lineární algebra a geometrie 1 a 2,
 Úlohy k přednášce NMAG a : Lineární algebra a geometrie a Verze ze dne. května Toto je seznam přímočarých příkladů k přednášce. Úlohy z tohoto seznamu je nezbytně nutné umět řešit. Podobné typy úloh se
Úlohy k přednášce NMAG a : Lineární algebra a geometrie a Verze ze dne. května Toto je seznam přímočarých příkladů k přednášce. Úlohy z tohoto seznamu je nezbytně nutné umět řešit. Podobné typy úloh se
P ÍPRAVY NA HODINU MATEMATIKA
 Modernizace výuky v rámci odborných a všeobecných p edm t st ední školy. íslo projektu: CZ.1.07/1.1.10/01.0021 P ÍPRAVY NA HODINU MATEMATIKA Tyto p ípravy na hodinu jsou spolufinancovány Evropským sociálním
Modernizace výuky v rámci odborných a všeobecných p edm t st ední školy. íslo projektu: CZ.1.07/1.1.10/01.0021 P ÍPRAVY NA HODINU MATEMATIKA Tyto p ípravy na hodinu jsou spolufinancovány Evropským sociálním
Lineární algebra : Skalární součin a ortogonalita
 Lineární algebra : Skalární součin a ortogonalita (15. přednáška) František Štampach, Karel Klouda frantisek.stampach@fit.cvut.cz, karel.klouda@fit.cvut.cz Katedra aplikované matematiky Fakulta informačních
Lineární algebra : Skalární součin a ortogonalita (15. přednáška) František Štampach, Karel Klouda frantisek.stampach@fit.cvut.cz, karel.klouda@fit.cvut.cz Katedra aplikované matematiky Fakulta informačních
Teorie měření a regulace
 Ústav technologie, mechanizace a řízení staveb Teorie měření a regulace 22.z-3.tr ZS 2015/2016 2015 - Ing. Václav Rada, CSc. TEORIE ŘÍZENÍ druhá část tématu předmětu pokračuje. oblastí matematických pomůcek
Ústav technologie, mechanizace a řízení staveb Teorie měření a regulace 22.z-3.tr ZS 2015/2016 2015 - Ing. Václav Rada, CSc. TEORIE ŘÍZENÍ druhá část tématu předmětu pokračuje. oblastí matematických pomůcek
Obsah. Pouºité zna ení 1
 Obsah Pouºité zna ení 1 1 Úvod 3 1.1 Opera ní výzkum a jeho disciplíny.......................... 3 1.2 Úlohy matematického programování......................... 3 1.3 Standardní maximaliza ní úloha lineárního
Obsah Pouºité zna ení 1 1 Úvod 3 1.1 Opera ní výzkum a jeho disciplíny.......................... 3 1.2 Úlohy matematického programování......................... 3 1.3 Standardní maximaliza ní úloha lineárního
QR, b = QS, c = QP. Dokaºte ºe vzdálenost bodu P od roviny spl uje. a (b c) d =
 . cvi ení -Opakování geometrie IR n, p íklady () Najd te velikost úhlu mezi hlavní diagonálou krychle a diagonálou jedné ze stran, která s ní má spole ný vrchol. (2) Dokaºte ºe x y = y x. (3) Dokaºte ºe
. cvi ení -Opakování geometrie IR n, p íklady () Najd te velikost úhlu mezi hlavní diagonálou krychle a diagonálou jedné ze stran, která s ní má spole ný vrchol. (2) Dokaºte ºe x y = y x. (3) Dokaºte ºe
Občas se používá značení f x (x 0, y 0 ), resp. f y (x 0, y 0 ). Parciální derivace f. rovnoběžného s osou y a z:
 PARCIÁLNÍ DERIVACE Jak derivovat reálné funkce více proměnných aby bylo možné tyto derivace použít podobně jako derivace funkcí jedné proměnné? Jestliže se okopíruje definice z jedné proměnné dostane se
PARCIÁLNÍ DERIVACE Jak derivovat reálné funkce více proměnných aby bylo možné tyto derivace použít podobně jako derivace funkcí jedné proměnné? Jestliže se okopíruje definice z jedné proměnné dostane se
Požadavky ke zkoušce. Ukázková písemka
 Požadavky ke zkoušce Zkouška z předmětu MATEMATIKA 1 má dvě části Písemná část: Písemná část se ještě dále rozděluje na praktickou část písemku a teoretickou část test. Písemka trvá 90 minut a je v ní
Požadavky ke zkoušce Zkouška z předmětu MATEMATIKA 1 má dvě části Písemná část: Písemná část se ještě dále rozděluje na praktickou část písemku a teoretickou část test. Písemka trvá 90 minut a je v ní
K oddílu I.1 základní pojmy, normy, normované prostory
 ÚVOD DO FUNKCIONÁLNÍ ANALÝZY PŘÍKLADY PRO POROZUMĚNÍ LÁTCE ZS 2015/2016 PŘÍKLADY KE KAPITOLE I K oddílu I1 základní pojmy, normy, normované prostory Příklad 1 Necht X je reálný vektorový prostor a : X
ÚVOD DO FUNKCIONÁLNÍ ANALÝZY PŘÍKLADY PRO POROZUMĚNÍ LÁTCE ZS 2015/2016 PŘÍKLADY KE KAPITOLE I K oddílu I1 základní pojmy, normy, normované prostory Příklad 1 Necht X je reálný vektorový prostor a : X
18 Fourierovy řady Úvod, základní pojmy
 M. Rokyta, MFF UK: Aplikovaná matematika III kap. 18: Fourierovy řady 7 18 Fourierovy řady 18.1 Úvod, základní pojmy Otázka J. Fouriera: Lze každou periodickou funkci napsat jako součet nějakých "elementárních"
M. Rokyta, MFF UK: Aplikovaná matematika III kap. 18: Fourierovy řady 7 18 Fourierovy řady 18.1 Úvod, základní pojmy Otázka J. Fouriera: Lze každou periodickou funkci napsat jako součet nějakých "elementárních"
Ztráta stability prost podep eného Timo²enkova prutu
 Ztráta stability prost podep eného Timo²enkova prutu ƒeské vysoké u ení technické v Praze 12. zá í 2016 Vedoucí seminární práce: prof. Ing. Milan Jirásek, DrSc. Osnova 1 2 3 4 Cíl práce Cíl práce Nalézt
Ztráta stability prost podep eného Timo²enkova prutu ƒeské vysoké u ení technické v Praze 12. zá í 2016 Vedoucí seminární práce: prof. Ing. Milan Jirásek, DrSc. Osnova 1 2 3 4 Cíl práce Cíl práce Nalézt
Netradiční výklad tradičních témat
 Netradiční výklad tradičních témat J. Musilová, P. Musilová: Matematika pro porozumění i praxi I. VUTIUM, Brno 2006 (291 s.), 2009 (349 s.). J. Musilová, P. Musilová: Matematika pro porozumění i praxi
Netradiční výklad tradičních témat J. Musilová, P. Musilová: Matematika pro porozumění i praxi I. VUTIUM, Brno 2006 (291 s.), 2009 (349 s.). J. Musilová, P. Musilová: Matematika pro porozumění i praxi
OBECNOSTI KONVERGENCE V R N
 FUNKCE VÍCE PROMĚNNÝCH V reálných situacích závisejí děje obvykle na více proměnných než jen na jedné (např. na teplotě i na tlaku), závislost na jedné proměnné je spíše výjimkou. OBECNOSTI Reálná funkce
FUNKCE VÍCE PROMĚNNÝCH V reálných situacích závisejí děje obvykle na více proměnných než jen na jedné (např. na teplotě i na tlaku), závislost na jedné proměnné je spíše výjimkou. OBECNOSTI Reálná funkce
DRN: Kořeny funkce numericky
 DRN: Kořeny funkce numericky Kořenem funkce f rozumíme libovolné číslo r splňující f(r) = 0. Fakt. Nechť f je funkce na intervalu a, b. Jestliže f(a) f(b) < 0 (tj. f(a) a f(b) mají opačná znaménka) a f
DRN: Kořeny funkce numericky Kořenem funkce f rozumíme libovolné číslo r splňující f(r) = 0. Fakt. Nechť f je funkce na intervalu a, b. Jestliže f(a) f(b) < 0 (tj. f(a) a f(b) mají opačná znaménka) a f
ÚVOD DO FUNKCIONÁLNÍ ANALÝZY. Jiří Bouchala
 ÚVOD DO FUNKCIONÁLNÍ ANALÝZY Jiří Bouchala Text byl vytvořen v rámci realizace projektu Matematika pro inženýry 21. století (reg. č. CZ.1.7/2.2./7.332), na kterém se společně podílela Vysoká škola báňská
ÚVOD DO FUNKCIONÁLNÍ ANALÝZY Jiří Bouchala Text byl vytvořen v rámci realizace projektu Matematika pro inženýry 21. století (reg. č. CZ.1.7/2.2./7.332), na kterém se společně podílela Vysoká škola báňská
Program SMP pro kombinované studium
 Zadání příkladů k procvičení na seminář Program SMP pro kombinované studium Nejdůležitější typy příkladů - minimum znalostí před zkouškovou písemkou 1) Matice 1. Pro matice 1 0 2 1 0 3 B = 7 3 4 4 2 0
Zadání příkladů k procvičení na seminář Program SMP pro kombinované studium Nejdůležitější typy příkladů - minimum znalostí před zkouškovou písemkou 1) Matice 1. Pro matice 1 0 2 1 0 3 B = 7 3 4 4 2 0
Exponenciála matice a její užití. fundamentálních matic. Užití mocninných řad pro rovnice druhého řádu
 1 Tutoriál č. 3 Exponenciála matice a její užití řešení Cauchyovy úlohy pro lineární systémy užitím fundamentálních matic. Užití mocninných řad pro rovnice druhého řádu 0.1 Exponenciála matice a její užití
1 Tutoriál č. 3 Exponenciála matice a její užití řešení Cauchyovy úlohy pro lineární systémy užitím fundamentálních matic. Užití mocninných řad pro rovnice druhého řádu 0.1 Exponenciála matice a její užití
Požadavky ke zkoušce
 Požadavky ke zkoušce Zkouška z předmětu MATEMATIKA 2 má dvě části Písemná část: Písemná část se ještě dále rozděluje na praktickou část písemku a teoretickou část test. Písemka trvá 90 minut a je v ní
Požadavky ke zkoušce Zkouška z předmětu MATEMATIKA 2 má dvě části Písemná část: Písemná část se ještě dále rozděluje na praktickou část písemku a teoretickou část test. Písemka trvá 90 minut a je v ní
