MĚSTSKÁ KOLEJOVÁ DOPRAVA
|
|
|
- Břetislav Hruška
- před 9 lety
- Počet zobrazení:
Transkript
1 MĚSTSKÁ KOLEJOVÁ DOPRAVA cvičení z předmětu 12MKDP ZS 2015/2016 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Ing. Vojtěch Novotný budova Horská, kancelář A433 VojtechNovotny@gmail.com
2 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Oblouky tramvajových tratí
3
4 oblouky tramvajových tratí minimální poloměr oblouku R lim = 50 m, ve stísněných poměrech R min = 20 m v uliční síti bez převýšení, jinak podobně jako na železnici Při malých poloměrech oblouků R < 1000 m musíme řešit problematiku vzájemného míjení tramvajových vlaků v oblouku
5 průjezdní průřez x obrys vozidla průjezdní průřez vymezuje minimální vzdálenosti pro vně ležící stavby, zařízení, předměty, kolejová i nekolejová vozidla na sousedních kolejích a nekolejová vozidla v sousedních jízdních pruzích (od osy obrysu vozidla a spojnice TK) obrys vozidla vymezuje dovolené vzdálenosti všech bodů na povrchu vozidel (od osy obrysu vozidla a spojnice TK)
6 průjezdní průřez x obrys vozidla přímá přímá
7 průjezdní průřez x obrys vozidla oblouk směrový oblouk
8 průjezdní průřez x obrys vozidla oblouk
9 oblouky tramvajových tratí
10 oblouky tramvajových tratí foto: Ing. Ondřej Havlena
11 návrh dvoukolejné trati v oblouku Vstupní parametry: střední poloměr R s vrcholový úhel α osová vzdálenost kolejí v přilehlém úseku Ve směrovém oblouku je v drtivé většině případů potřeba rozšířit osovou vzdálenost
12 oblouky tramvajových tratí ZÁKLADNÍ TYPY TRAMVAJOVÝCH OBLOUKŮ: dle způsobu rozšíření osové vzdálenosti oblouk s přechodnicemi oblouk s přechodovým kružnicovým obloukem oblouk s přechodovým kružnicovým obloukem s mezipřímou
13
14
15 Úloha 2 Návrh tramvajové tratě v oblouku ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612)
16 Úloha 2 Návrh tramvajové tratě v oblouku Navrhněte a narýsujte dvoukolejnou tramvajovou trať v oblouku Vstupní údaje: r s m střední poloměr dvoukolejného oblouku α vrcholový úhel směrového oblouku e p m osová vzdálenost kolejí (v přilehlých traťových úsecích) r S : [m] úhel [ ] e p [m] 3,00 3,05 3,10 3,15 3,20 3,25 3,30
17 Úloha 2 Návrh parametry oblouku 1. VÝPOČET POLOMĚRU VNĚJŠÍHO OBLOUKU R e : R e = r s + e p 2 R e [m] poloměr vnějšího oblouku r s [m] střední poloměr dvoukolejného oblouku e p [m] osová vzdálenost kolejí v přilehlých traťových úsecích
18 Úloha 2 Návrh parametry oblouku 2. URČENÍ HODNOTY δ i(re) : δ i(re) rozšíření vnitřní části průjezdného průřezu pro vnější kolej Tabulka 1
19 Úloha 2 Návrh parametry oblouku 3. VÝPOČET POLOMĚRU VNITŘNÍHO OBLOUKU R i : R i = R e 1, 35 δ i Re 0, 3 δ i Ri 1, 35 R i [m] poloměr vnitřního oblouku R e [m] poloměr vnějšího oblouku δ i(re) [m] rozšíření vnitřní části průjezdného průřezu vnějšího oblouku δ a(ri) [m] rozšíření vnější části průjezdného průřezu vnitřního oblouku
20 Úloha 2 Návrh parametry oblouku 3. VÝPOČET POLOMĚRU VNITŘNÍHO OBLOUKU R i : přes pomocný poloměr R pom R pom = R e 3 δ i Re R pom [m] pomocný poloměr R e [m] poloměr vnějšího oblouku δ i(re) [m] rozšíření vnitřní části průjezdného průřezu vnějšího oblouku
21 Úloha 2 Návrh parametry oblouku 4. URČENÍ HODNOTY δ a(rpom) : δ a(rpom) hodnota teoretického rozšíření vnější části průjezdného průřezu pro pomocný poloměr Tabulka 2
22 Úloha 2 Návrh parametry oblouku 5. VÝPOČET POLOMĚRU VNITŘNÍHO OBLOUKU R i (krokově): 1. krok R i1 = R pom δ a Rpom a v Tabulce 2 nalezneme δ a Ri1 - pokud δ a Ri1 = δ a Rpom, potom R i1 = R i - pokud δ a Ri1 δ a Rpom, pokračuji krokem 2
23 Úloha 2 Návrh parametry oblouku 5. VÝPOČET POLOMĚRU VNITŘNÍHO OBLOUKU R i (krokově): 2. krok R i2 = R pom δ a Ri1 a v Tabulce 2 nalezneme δ a Ri2 - pokud δ a Ri2 = δ a Ri1, potom R i2 = R i - pokud δ a Ri2 δ a Ri1, pokračuji krokem 3 a tak dále až do n-tého kroku
24 Úloha 2 Návrh parametry oblouku 6. VÝPOČET OSOVÉ VZDÁLENOSTI KOLEJÍ V OBLOUKU e O = R e R i 7. VÝPOČET ROZŠÍŘENÍ OSOVÉ VZDÁLENOSTI KOLEJÍ V OBLOUKU = e o e p
25 Úloha 2 Návrh vytyčovací prvky oblouku VYTYČOVACÍ PRVKY PŘECHODOVÉHO OBLOUKU S MEZIPŘÍMOU
26 Úloha 2 Návrh vytyčovací prvky oblouku VYTYČOVACÍ PRVKY PŘECHODOVÉHO OBLOUKU S MEZIPŘÍMOU Vstupní údaje: poloměr přechodového oblouku: R p = 120 m délka mezipřímé: m = 6 m úhel φ přechodového oblouku: φ = 2. arctg m + m R p R i 2. R p R i
27 Úloha 2 Návrh vytyčovací prvky oblouku VNĚJŠÍ OBLOUK: délka tečny vnějšího oblouku t e : t e = R e. tg α 2 délka vnějšího oblouku v ose koleje d e : d e = R e. arc α = R e. π 180. α VNITŘNÍ OBLOUK: délka tečny vnitřního oblouku t i : t i = R i. tg α 2 φ délka vnitřního oblouku v ose koleje d i : d i = R i. arc α 2φ π = R i α 2φ
28 Úloha 2 Návrh vytyčovací prvky oblouku PŘECHODOVÝ OBLOUK: délka tečny přechodového oblouku oblouku t p : t p = R p. tg φ 2 délka vnějšího oblouku v ose koleje d e : d p = R p. arc φ = R p. π 180. φ vzdálenost počátku přechodového oblouku a počátku vnějšího oblouku t x : t x = R p R i. sin φ + m. cos φ
29 Úloha 2 Návrh vytyčovací prvky oblouku
30 Úloha 2 maximální rychlost v oblouku VÝPOČET MAXIMÁLNÍ RYCHLOSTI PRŮJEZDU OBLOUKEM Maximální rychlost průjezdu obloukem bez převýšení v = 150. a n. R i 11, 5 [km. h 1 ] Výpočet proveďte postupně pro hodnoty nevyrovnaného bočního zrychlení: a n1 = 0, 5 m. s 2 a n2 = 0, 8 m. s 2
31 Úloha 2 Návrh tramvajové tratě v oblouku Výstupem z Úlohy 2 bude: Vytyčovací výkres směrového oblouku tramvajové trati v měřítku 1:200 Výpočty parametrů a vytyčovacích prvků směrového oblouku tramvajové trati (obecný vzorec dosazení výsledek)
32 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Děkuji za pozornost Otázky?
PROJEKTOVÁNÍ KOLEJOVÉ DOPRAVY
 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) PROJEKTOVÁNÍ KOLEJOVÉ DOPRAVY cvičení z předmětu 12PKD úvodní informace Projektování kolejové dopravy (12PKD) cvičení Ing. Vojtěch Novotný
ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) PROJEKTOVÁNÍ KOLEJOVÉ DOPRAVY cvičení z předmětu 12PKD úvodní informace Projektování kolejové dopravy (12PKD) cvičení Ing. Vojtěch Novotný
ŽELEZNIČNÍ TRATĚ A STANICE
 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) ŽELEZNIČNÍ TRATĚ A STANICE cvičení z předmětu 12ZTS letní semestr 2015/2016 úvodní informace Železniční tratě a stanice (12ZTS) cvičení Ing.
ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) ŽELEZNIČNÍ TRATĚ A STANICE cvičení z předmětu 12ZTS letní semestr 2015/2016 úvodní informace Železniční tratě a stanice (12ZTS) cvičení Ing.
MĚSTSKÁ KOLEJOVÁ DOPRAVA
 MĚSTSKÁ KOLEJOVÁ DOPRAVA cvičení z předmětu 12MKDP ZS 2015/2016 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Ing. Vojtěch Novotný budova Horská, kancelář A433 VojtechNovotny@gmail.com
MĚSTSKÁ KOLEJOVÁ DOPRAVA cvičení z předmětu 12MKDP ZS 2015/2016 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Ing. Vojtěch Novotný budova Horská, kancelář A433 VojtechNovotny@gmail.com
PROJEKTOVÁNÍ KOLEJOVÉ DOPRAVY
 PROJEKTOVÁNÍ KOLEJOVÉ DOPRAVY cvičení z předmětu 12PKD ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Úloha 2 Železniční stanice vytyčovací výkres zhlaví ČVUT v Praze Fakulta dopravní Ústav
PROJEKTOVÁNÍ KOLEJOVÉ DOPRAVY cvičení z předmětu 12PKD ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Úloha 2 Železniční stanice vytyčovací výkres zhlaví ČVUT v Praze Fakulta dopravní Ústav
ZADÁNÍ ročníkového projektu pro III.a IV.ročník studijního oboru: Konstrukce a dopravní stavby
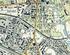
 ZADÁNÍ ročníkového projektu pro III.a IV.ročník studijního oboru: Konstrukce a dopravní stavby I. V daném mapovém podkladu v měřítku 1:10 000 vypracujte návrh spojení mezi body A a B na úrovni vyhledávací
ZADÁNÍ ročníkového projektu pro III.a IV.ročník studijního oboru: Konstrukce a dopravní stavby I. V daném mapovém podkladu v měřítku 1:10 000 vypracujte návrh spojení mezi body A a B na úrovni vyhledávací
MĚSTSKÁ KOLEJOVÁ DOPRAVA
 MĚSTSKÁ KOLEJOVÁ DOPRAVA cvičení z předmětu 12MKDP ZS 2015/2016 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Ing. Vojtěch Novotný budova Horská, kancelář A433 VojtechNovotny@gmail.com
MĚSTSKÁ KOLEJOVÁ DOPRAVA cvičení z předmětu 12MKDP ZS 2015/2016 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Ing. Vojtěch Novotný budova Horská, kancelář A433 VojtechNovotny@gmail.com
MĚSTSKÁ KOLEJOVÁ DOPRAVA
 MĚSTSKÁ KOLEJOVÁ DOPRAVA cvičení z předmětu 12MKDP ZS 2014/2015 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Ing. Vojtěch Novotný budova Horská, kancelář A433 VojtechNovotny@gmail.com
MĚSTSKÁ KOLEJOVÁ DOPRAVA cvičení z předmětu 12MKDP ZS 2014/2015 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Ing. Vojtěch Novotný budova Horská, kancelář A433 VojtechNovotny@gmail.com
100 1500 1200 1000 875 750 675 600 550 500 - - 775 650 550 500 450 400 350 325 - -
 Prostý kružnicový oblouk Prostý kružnicový oblouk se používá buď jako samostatné řešení změny směru osy nebo nám slouží jako součást směrové změny v kombinaci s přechodnicemi nebo složenými oblouky. Nejmenší
Prostý kružnicový oblouk Prostý kružnicový oblouk se používá buď jako samostatné řešení změny směru osy nebo nám slouží jako součást směrové změny v kombinaci s přechodnicemi nebo složenými oblouky. Nejmenší
ZÁKLADY DOPRAVNÍHO INŽENÝRSTVÍ
 ZÁKLADY DOPRAVNÍHO INŽENÝRSTVÍ cvičení z předmětu 12ZYDI ZS 2015/2016 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Ing. Vojtěch Novotný budova Horská, kancelář A433 novotvo4@fd.cvut.cz
ZÁKLADY DOPRAVNÍHO INŽENÝRSTVÍ cvičení z předmětu 12ZYDI ZS 2015/2016 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Ing. Vojtěch Novotný budova Horská, kancelář A433 novotvo4@fd.cvut.cz
MĚSTSKÁ KOLEJOVÁ DOPRAVA
 MĚSTSKÁ KOLEJOVÁ DOPRAVA cvičení z předmětu 12MKDP ZS 2015/2016 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Ing. Vojtěch Novotný budova Horská, kancelář A433 VojtechNovotny@gmail.com
MĚSTSKÁ KOLEJOVÁ DOPRAVA cvičení z předmětu 12MKDP ZS 2015/2016 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Ing. Vojtěch Novotný budova Horská, kancelář A433 VojtechNovotny@gmail.com
VÝHYBKY A ZHLAVÍ ŽELEZNIČNÍ STANICE
 VÝHYBKY A ZHLAVÍ ŽELEZNIČNÍ STANICE POMŮCKA PRO CVIČENÍ Z PŘEDMĚTU ŽELEZNIČNÍ STAVBY 2 (ZST2) Kolejiště železniční stanice sestává ze staničních kolejí a ze zhlaví, kde se jednotlivé koleje propojují.
VÝHYBKY A ZHLAVÍ ŽELEZNIČNÍ STANICE POMŮCKA PRO CVIČENÍ Z PŘEDMĚTU ŽELEZNIČNÍ STAVBY 2 (ZST2) Kolejiště železniční stanice sestává ze staničních kolejí a ze zhlaví, kde se jednotlivé koleje propojují.
VYTYČENÍ OSY KOMUNIKACE. PRAXE 4. ročník Ing. D. Mlčková
 VYTYČENÍ OSY KOMUNIKACE PRAXE 4. ročník Ing. D. Mlčková Zadání: Vypracujte projekt pro výstavbu komunikace S 9,5/60 v prostoru Louky v katastrálním území Nové Městečko Přílohy: 1) Technická zpráva 2)
VYTYČENÍ OSY KOMUNIKACE PRAXE 4. ročník Ing. D. Mlčková Zadání: Vypracujte projekt pro výstavbu komunikace S 9,5/60 v prostoru Louky v katastrálním území Nové Městečko Přílohy: 1) Technická zpráva 2)
Mezipřímé (nejen) v kolejových spojeních a rozvětveních
 Mezipřímé (nejen) v kolejových spojeních a rozvětveních 1. Přechodová kolejnice Délka: - v hlavní koleji dl. 12,5 m - v ostatních kolejích 10,0 m - ve staničním zhlaví nejméně 4,0 m Vzdálenost přechodového
Mezipřímé (nejen) v kolejových spojeních a rozvětveních 1. Přechodová kolejnice Délka: - v hlavní koleji dl. 12,5 m - v ostatních kolejích 10,0 m - ve staničním zhlaví nejméně 4,0 m Vzdálenost přechodového
ZÁKLADNÍ POJMY Z TRASOVÁNÍ
 ZÁKLADNÍ POJMY Z TRASOVÁNÍ Vrstevnice = čára spojující body terénu se nadmořskou výškou stejnou Interval vrstevnic (ekvidistance) = výškový rozdíl mezi vrstevnicemi Spádnice = čára udávající průběh spádu
ZÁKLADNÍ POJMY Z TRASOVÁNÍ Vrstevnice = čára spojující body terénu se nadmořskou výškou stejnou Interval vrstevnic (ekvidistance) = výškový rozdíl mezi vrstevnicemi Spádnice = čára udávající průběh spádu
Analýza současného stavu tratě Praha Beroun přes Rudnou u Prahy
 ČVUT V PRAZE Fakulta dopravní, Ústav dopravních systémů K612 Analýza současného stavu tratě Praha Beroun přes Rudnou u Prahy Projekt Železniční síť České republiky a Evropy Vypracovali: Filip Štajner 3
ČVUT V PRAZE Fakulta dopravní, Ústav dopravních systémů K612 Analýza současného stavu tratě Praha Beroun přes Rudnou u Prahy Projekt Železniční síť České republiky a Evropy Vypracovali: Filip Štajner 3
kv,o... koeficient růstu osobní dopravy kv,n... koeficient růstu nákladní dopravy IV, kv,o, kv,n... uvažovat pro rok ukončení provozu (2045)
 STANOVENÍ KATEGORIE SILNICE kv,o... koeficient růstu osobní dopravy kv,n... koeficient růstu nákladní dopravy IV, kv,o, kv,n... uvažovat pro rok ukončení provozu (2045) I 50 V X Y Y X X Y Y X I O IO k
STANOVENÍ KATEGORIE SILNICE kv,o... koeficient růstu osobní dopravy kv,n... koeficient růstu nákladní dopravy IV, kv,o, kv,n... uvažovat pro rok ukončení provozu (2045) I 50 V X Y Y X X Y Y X I O IO k
Seminář ACRI ve spolupráci s ÚNMZ a Sdružením dopravních podniků Praha, 15.1.2015. DIPRO, spol s.r.o.
 Seminář ACRI ve spolupráci s ÚNMZ a Sdružením dopravních podniků Praha, 15.1.2015 DIPRO, spol s.r.o. SEZNAM NOREM URČENÝCH K REVIZI PRVNÍ ETAPA: ČSN 28 0318 PRŮJEZDNÉ PRŮŘEZY TRAMVAJOVÝCH TRATÍ ČSN 28
Seminář ACRI ve spolupráci s ÚNMZ a Sdružením dopravních podniků Praha, 15.1.2015 DIPRO, spol s.r.o. SEZNAM NOREM URČENÝCH K REVIZI PRVNÍ ETAPA: ČSN 28 0318 PRŮJEZDNÉ PRŮŘEZY TRAMVAJOVÝCH TRATÍ ČSN 28
č.. 8 Dokumenty o GPK na VRT
 Vysokorychlostní železniční tratě L u k á š Přednáška č.. 8 T ý f a Ústav dopravních systémů (K612) Geometrické a další parametry koleje na vysokorychlostních tratích Anotace: Dokumenty určující parametry
Vysokorychlostní železniční tratě L u k á š Přednáška č.. 8 T ý f a Ústav dopravních systémů (K612) Geometrické a další parametry koleje na vysokorychlostních tratích Anotace: Dokumenty určující parametry
NÁVRH TRASY POZEMNÍ KOMUNIKACE. Michal RADIMSKÝ
 NÁVRH TRASY POZEMNÍ KOMUNIKACE Michal RADIMSKÝ TRASA PK trasou pozemní komunikace (PK) rozumíme prostorovou čáru, určující směrový i výškový průběh dané komunikace trasa PK je spojnicí středů povrchu silniční
NÁVRH TRASY POZEMNÍ KOMUNIKACE Michal RADIMSKÝ TRASA PK trasou pozemní komunikace (PK) rozumíme prostorovou čáru, určující směrový i výškový průběh dané komunikace trasa PK je spojnicí středů povrchu silniční
Infrastruktura kolejové dopravy
 07 Infrastruktura kolejové dopravy u k á š T ý f a ČUT v Praze Fakulta dopravní Anotace: Téma č. Geometrické parametry železniční koleje geometrické a konstrukční uspořádání železniční koleje převýšení
07 Infrastruktura kolejové dopravy u k á š T ý f a ČUT v Praze Fakulta dopravní Anotace: Téma č. Geometrické parametry železniční koleje geometrické a konstrukční uspořádání železniční koleje převýšení
ORGANIZACE A ŘÍZENÍ MHD cvičení z předmětu 12OMHD LS 2014/2015
 ORGANIZACE A ŘÍZENÍ MHD cvičení z předmětu 12OMHD LS 2014/2015 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Ing. Vojtěch Novotný budova Horská, kancelář A433 VojtechNovotny@gmail.com ČVUT
ORGANIZACE A ŘÍZENÍ MHD cvičení z předmětu 12OMHD LS 2014/2015 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Ing. Vojtěch Novotný budova Horská, kancelář A433 VojtechNovotny@gmail.com ČVUT
od zadaného bodu, vzdálenost. Bod je střed, je poloměr kružnice. Délka spojnice dvou bodů kružnice, která prochází středem
 Kružnice Kružnice je množina všech bodů roviny, které mají od zadaného bodu, vzdálenost. Bod je střed, je poloměr kružnice. Délka spojnice dvou bodů kružnice, která prochází středem je průměr kružnice.
Kružnice Kružnice je množina všech bodů roviny, které mají od zadaného bodu, vzdálenost. Bod je střed, je poloměr kružnice. Délka spojnice dvou bodů kružnice, která prochází středem je průměr kružnice.
L J Kompendium informací o LCS Úvod Součásti LCS Lesní cesty Dělení lesních cest... 13
 OBSAH L J Kompendium informací o LCS...12 1.1 Úvod... 1.2 Součásti LCS... 12 1.3 Lesní cesty... 1.4 Dělení lesních cest... 13 1.4.1 Dělení podle probíhající části dopravního procesu...13 1.4.2 Dělení dle
OBSAH L J Kompendium informací o LCS...12 1.1 Úvod... 1.2 Součásti LCS... 12 1.3 Lesní cesty... 1.4 Dělení lesních cest... 13 1.4.1 Dělení podle probíhající části dopravního procesu...13 1.4.2 Dělení dle
Výpočet křivosti křivek ve stavební praxi
 Přechodnice podle Nördlinga (kubická parabola) Vypočtěte křivost Nördlingovy přechodnice v bodě x=0 a x=l x y( x) 6LR x- vzdálenost bodu přechodnice od začátku přechodnice v tečně y- kolmá vzdálenost bodu
Přechodnice podle Nördlinga (kubická parabola) Vypočtěte křivost Nördlingovy přechodnice v bodě x=0 a x=l x y( x) 6LR x- vzdálenost bodu přechodnice od začátku přechodnice v tečně y- kolmá vzdálenost bodu
ČESKÁ TECHNICKÁ NORMA
 ČESKÁ TECHNICKÁ NORMA ICS 93.100 Březen 2015 ČSN 28 0318 Průjezdné průřezy tramvajových tratí a obrysy pro vozidla provozovaná na tramvajových dráhách Track gauge and contour lines for tramways Nahrazení
ČESKÁ TECHNICKÁ NORMA ICS 93.100 Březen 2015 ČSN 28 0318 Průjezdné průřezy tramvajových tratí a obrysy pro vozidla provozovaná na tramvajových dráhách Track gauge and contour lines for tramways Nahrazení
Seminář ACRI ve spolupráci s ÚNMZ a Sdružením dopravních podniků Praha, DIPRO, spol s.r.o.
 Seminář ACRI ve spolupráci s ÚNMZ a Sdružením dopravních podniků Praha, 17.12.2013 DIPRO, spol s.r.o. SEZNAM NOREM URČENÝCH K REVIZI PRVNÍ ETAPA: Projednání konceptu revize ČSN: ČSN 28 0318 PRŮJEZDNÉ PRŮŘEZY
Seminář ACRI ve spolupráci s ÚNMZ a Sdružením dopravních podniků Praha, 17.12.2013 DIPRO, spol s.r.o. SEZNAM NOREM URČENÝCH K REVIZI PRVNÍ ETAPA: Projednání konceptu revize ČSN: ČSN 28 0318 PRŮJEZDNÉ PRŮŘEZY
Výukový materiál zpracován v rámci projektu EU peníze školám
 Výukový materiál zpracován v rámci projektu EU peníze školám Registrační číslo projektu: CZ.1.07/1.5.00/34.0230 šablona III / 2 č. materiálu VY_32_INOVACE_399 Jméno autora : Ing. Stanislav Skalický Třída
Výukový materiál zpracován v rámci projektu EU peníze školám Registrační číslo projektu: CZ.1.07/1.5.00/34.0230 šablona III / 2 č. materiálu VY_32_INOVACE_399 Jméno autora : Ing. Stanislav Skalický Třída
KOMENTÁŘ KE VZOROVÉMU LISTU SVĚTLÝ TUNELOVÝ PRŮŘEZ DVOUKOLEJNÉHO TUNELU
 KOMENTÁŘ KE VZOROVÉMU LISTU SVĚTLÝ TUNELOVÝ PRŮŘEZ DVOUKOLEJNÉHO TUNELU OBSAH 1. ÚVOD... 3 1.1. Předmět a účel... 3 1.2. Platnost a závaznost použití... 3 2. SOUVISEJÍCÍ NORMY A PŘEDPISY... 3 3. ZÁKLADNÍ
KOMENTÁŘ KE VZOROVÉMU LISTU SVĚTLÝ TUNELOVÝ PRŮŘEZ DVOUKOLEJNÉHO TUNELU OBSAH 1. ÚVOD... 3 1.1. Předmět a účel... 3 1.2. Platnost a závaznost použití... 3 2. SOUVISEJÍCÍ NORMY A PŘEDPISY... 3 3. ZÁKLADNÍ
METRO. Doc. Ing. Pavel Hánek, CSc. Uvedené materiály jsou pouze podkladem přednášek předmětu 154GP10.
 METRO Doc. Ing. Pavel Hánek, CSc. Uvedené materiály jsou pouze podkladem přednášek předmětu 154GP10. 2014 OCHRANNÉ PÁSMO METRA Ochranné pásmo 30 m na obě strany nebo vně od osy tunelu Obvod dráhy 1,5 m
METRO Doc. Ing. Pavel Hánek, CSc. Uvedené materiály jsou pouze podkladem přednášek předmětu 154GP10. 2014 OCHRANNÉ PÁSMO METRA Ochranné pásmo 30 m na obě strany nebo vně od osy tunelu Obvod dráhy 1,5 m
Provozování autobusů a trolejbusů VHD na tramvajovém tělese
 Provozování autobusů a trolejbusů VHD na tramvajovém tělese // sdružený tramvajový a autobusový/trolejbusový pás // dodatečné zavedení provozu autobusů a trolejbusů VHD na tramvajovém tělese // Vojtěch
Provozování autobusů a trolejbusů VHD na tramvajovém tělese // sdružený tramvajový a autobusový/trolejbusový pás // dodatečné zavedení provozu autobusů a trolejbusů VHD na tramvajovém tělese // Vojtěch
SYLABUS 9. PŘEDNÁŠKY Z INŢENÝRSKÉ GEODÉZIE
 SYLABUS 9. PŘEDNÁŠKY Z INŢENÝRSKÉ GEODÉZIE (Řešení kruţnicových oblouků v souřadnicích) 3. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. prosinec 2015
SYLABUS 9. PŘEDNÁŠKY Z INŢENÝRSKÉ GEODÉZIE (Řešení kruţnicových oblouků v souřadnicích) 3. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. prosinec 2015
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ, OBOR GEODÉZIE A KARTOGRAFIE KATEDRA GEODÉZIE A POZEMKOVÝCH ÚPRAV název předmětu
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ, OBOR GEODÉZIE A KARTOGRAFIE KATEDRA GEODÉZIE A POZEMKOVÝCH ÚPRAV název předmětu VÝUKA V TERÉNU Z GEODÉZIE 1, 2 - VY1 kód úlohy název úlohy K PŘÍMÉ
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ, OBOR GEODÉZIE A KARTOGRAFIE KATEDRA GEODÉZIE A POZEMKOVÝCH ÚPRAV název předmětu VÝUKA V TERÉNU Z GEODÉZIE 1, 2 - VY1 kód úlohy název úlohy K PŘÍMÉ
dx se nazývá diferenciál funkce f ( x )
 6 Výklad Definice 6 Nechť je 0 vnitřním bodem definičního oboru D f funkce f ( ) Funkce proměnné d = 0 definovaná vztahem df ( 0) = f ( 0) d se nazývá diferenciál funkce f ( ) v bodě 0, jestliže platí
6 Výklad Definice 6 Nechť je 0 vnitřním bodem definičního oboru D f funkce f ( ) Funkce proměnné d = 0 definovaná vztahem df ( 0) = f ( 0) d se nazývá diferenciál funkce f ( ) v bodě 0, jestliže platí
METRO Doc. Ing. Pavel Hánek, CSc. Uvedené materiály jsou pouze podkladem přednášek předmětu 154IG4. OCHRANNÉ PÁSMO METRA
 METRO Doc. Ing. Pavel Hánek, CSc. Uvedené materiály jsou pouze podkladem přednášek předmětu 154IG4. 2015 OCHRANNÉ PÁSMO METRA Ochranné pásmo 30 m na obě strany nebo vně od osy tunelu Obvod dráhy 1,5 m
METRO Doc. Ing. Pavel Hánek, CSc. Uvedené materiály jsou pouze podkladem přednášek předmětu 154IG4. 2015 OCHRANNÉ PÁSMO METRA Ochranné pásmo 30 m na obě strany nebo vně od osy tunelu Obvod dráhy 1,5 m
Modernizace výuky na Fakultě stavební VUT v Brně v rámci bakalářských a magisterských studijních programů CZ / /0292
 Modernizace výuky na Fakultě stavební VUT v Brně v rámci bakalářských a magisterských studijních programů CZ.04.1.03/3.2.15.2/0292 Název kurzu: Městské komunikace PŘEDNÁŠKA ČÍSLO 4 Návrhové prvky místních
Modernizace výuky na Fakultě stavební VUT v Brně v rámci bakalářských a magisterských studijních programů CZ.04.1.03/3.2.15.2/0292 Název kurzu: Městské komunikace PŘEDNÁŠKA ČÍSLO 4 Návrhové prvky místních
PROJEKTOVÁNÍ KOLEJOVÉ DOPRAVY
 PROJEKTOVÁNÍ KOLEJOVÉ DOPRAVY cvičení z předmětu 12PKD ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Úloha 2 Železniční stanice dopravní schéma stanice ČVUT v Praze Fakulta dopravní Ústav
PROJEKTOVÁNÍ KOLEJOVÉ DOPRAVY cvičení z předmětu 12PKD ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Úloha 2 Železniční stanice dopravní schéma stanice ČVUT v Praze Fakulta dopravní Ústav
Obecná rovnice kvadratické funkce : y = ax 2 + bx + c Pokud není uvedeno jinak, tak definičním oborem řešených funkcí je množina reálných čísel.
 5. Funkce 9. ročník 5. Funkce ZOPAKUJTE SI : 8. ROČNÍK KAPITOLA. Funkce. 5.. Kvadratická funkce Obecná rovnice kvadratické funkce : y = ax + bx + c Pokud není uvedeno jinak, tak definičním oborem řešených
5. Funkce 9. ročník 5. Funkce ZOPAKUJTE SI : 8. ROČNÍK KAPITOLA. Funkce. 5.. Kvadratická funkce Obecná rovnice kvadratické funkce : y = ax + bx + c Pokud není uvedeno jinak, tak definičním oborem řešených
5. P L A N I M E T R I E
 5. P L A N I M E T R I E 5.1 Z Á K L A D N Í P L A N I M E T R I C K É P O J M Y Bod (definice, značení, znázornění) Přímka (definice, značení, znázornění) Polopřímka (definice, značení, znázornění, počáteční
5. P L A N I M E T R I E 5.1 Z Á K L A D N Í P L A N I M E T R I C K É P O J M Y Bod (definice, značení, znázornění) Přímka (definice, značení, znázornění) Polopřímka (definice, značení, znázornění, počáteční
DIPRO, spol s.r.o. VĚCNÝ ZÁMĚR
 DIPRO, spol s.r.o. VĚCNÝ ZÁMĚR SEZNAM NOREM URČENÝCH K REVIZI ČSN 28 0318 PRŮJEZDNÉ PRŮŘEZY TRAMVAJOVÝCH TRATÍ ČSN 28 0337 OBRYSSY PROP TRAMVAJOVÉ VOZIDLA ČSN 73 6405 PROJKETOVÁNÍ TRAMVAJOVÝCH TRATÍ ČSN
DIPRO, spol s.r.o. VĚCNÝ ZÁMĚR SEZNAM NOREM URČENÝCH K REVIZI ČSN 28 0318 PRŮJEZDNÉ PRŮŘEZY TRAMVAJOVÝCH TRATÍ ČSN 28 0337 OBRYSSY PROP TRAMVAJOVÉ VOZIDLA ČSN 73 6405 PROJKETOVÁNÍ TRAMVAJOVÝCH TRATÍ ČSN
PŘECHODNICE. Matematicky lze klotoidu odvodit z hlediska bezpečnosti jízdy vozidla pro křivku, které vozidlo vytváří po přechodnici a její tvar je:
 PŘECHODNICE V silničním stavitelství používáme jako přechodnicové křivky klotoidu. Klotoida (radioida) tvarově představuje spirálu o nekonečné délce, blížící se k ohnisku, kde poloměr oblouku je nulový
PŘECHODNICE V silničním stavitelství používáme jako přechodnicové křivky klotoidu. Klotoida (radioida) tvarově představuje spirálu o nekonečné délce, blížící se k ohnisku, kde poloměr oblouku je nulový
SEZNAM NOREM URČENÝCH K REVIZI
 DIPRO, spols.r.o. s.r.o. SEZNAM NOREM URČENÝCH K REVIZI PRVNÍ ETAPA: ČSN 28 0318 PRŮJEZDNÉ PRŮŘEZY TRAMVAJOVÝCH TRATÍ ČSN 28 0337 OBRYSY PRO TRAMVAJOVÁ VOZIDLA 10/2013 schváleno zařazení do plánu přípravy
DIPRO, spols.r.o. s.r.o. SEZNAM NOREM URČENÝCH K REVIZI PRVNÍ ETAPA: ČSN 28 0318 PRŮJEZDNÉ PRŮŘEZY TRAMVAJOVÝCH TRATÍ ČSN 28 0337 OBRYSY PRO TRAMVAJOVÁ VOZIDLA 10/2013 schváleno zařazení do plánu přípravy
Pokyny pro řešení příkladů z předmětu Mechanika v dopravě pro obor. Pozemní doprava AR 2006/2007
 Pokyny pro řešení příkladů z předmětu Mechanika v dopravě pro obor Pozemní doprava AR 2006/2007 Tyto příklady slouží k procvičení základních problematik probíraných na přednáškách tohoto předmětu. Jednotlivé
Pokyny pro řešení příkladů z předmětu Mechanika v dopravě pro obor Pozemní doprava AR 2006/2007 Tyto příklady slouží k procvičení základních problematik probíraných na přednáškách tohoto předmětu. Jednotlivé
Ing. Aleš Polzer Ing. Petra Cihlářová Doc. Ing. Miroslav Píška, CSc. Technologie výroby II Obsah kapitoly
 Vysoké učení technické v rně Fakulta strojního inženýrství Ústav strojírenské technologie Odbor obrábění éma: 4. cvičení - Soustružení II Okruhy: Geometrie lamače třísky soustružnického nože Vypracoval:
Vysoké učení technické v rně Fakulta strojního inženýrství Ústav strojírenské technologie Odbor obrábění éma: 4. cvičení - Soustružení II Okruhy: Geometrie lamače třísky soustružnického nože Vypracoval:
BM03 MĚSTSKÉ KOMUNIKACE
 BM03 MĚSTSKÉ KOMUNIKACE 3. týden Rozhledy, přechody pro chodce a místa pro přecházení, zastávky autobusu Miroslav Patočka kancelář C330 email: patocka.m@fce.vutbr.cz Martin Novák kancelář C331 email: novak.m@fce.vutbr.cz
BM03 MĚSTSKÉ KOMUNIKACE 3. týden Rozhledy, přechody pro chodce a místa pro přecházení, zastávky autobusu Miroslav Patočka kancelář C330 email: patocka.m@fce.vutbr.cz Martin Novák kancelář C331 email: novak.m@fce.vutbr.cz
VÝŠKOVÉ NÁVRHOVÉ PRVKY
 VÝŠKOVÉ NÁVRHOVÉ PRVKY 1 VÝŠKOVÉ NÁVRHOVÉ PRVKY Výškový průběh trasy silniční komunikace, který se znázorňuje v podélném profilu, je určen niveletou. Niveleta se skládá z přímých částí, které mají různý
VÝŠKOVÉ NÁVRHOVÉ PRVKY 1 VÝŠKOVÉ NÁVRHOVÉ PRVKY Výškový průběh trasy silniční komunikace, který se znázorňuje v podélném profilu, je určen niveletou. Niveleta se skládá z přímých částí, které mají různý
Cyklometrické funkce
 4 Cyklometrické funkce V minulé kapitole jsme zkoumali první funkci inverzní ke funkci goniometrické (tyto funkce se nazývají cyklometrické) funkci y = arcsin x (inverzní k funkci y = sin x ) Př: Nakresli
4 Cyklometrické funkce V minulé kapitole jsme zkoumali první funkci inverzní ke funkci goniometrické (tyto funkce se nazývají cyklometrické) funkci y = arcsin x (inverzní k funkci y = sin x ) Př: Nakresli
Návody na výpočty směrových a sklonových poměrů dle zadání do cvičení
 Návody na výpočty měrových a klonových poměrů dle zadání do cvičení Kombinované tudium BO01, čát Dopravní tavby Ad 1) Návrh obou měrových oblouků bez přechodnic a) Změřte tředové úhly pomocí tangenty úhlu
Návody na výpočty měrových a klonových poměrů dle zadání do cvičení Kombinované tudium BO01, čát Dopravní tavby Ad 1) Návrh obou měrových oblouků bez přechodnic a) Změřte tředové úhly pomocí tangenty úhlu
Cyklometrické funkce
 4..7 Cyklometrické funkce Předpoklady: 46 Cyklometrické funkce: funkce inverzní k funkcím goniometrickým z minulé hodiny známe první cyklometrickou funkci y = arcsin x (inverzní k funkci y = sin x ). Př.
4..7 Cyklometrické funkce Předpoklady: 46 Cyklometrické funkce: funkce inverzní k funkcím goniometrickým z minulé hodiny známe první cyklometrickou funkci y = arcsin x (inverzní k funkci y = sin x ). Př.
ORGANIZACE A ŘÍZENÍ MHD cvičení z předmětu 12OMHD LS 2014/2015
 ORGANIZACE A ŘÍZENÍ MHD cvičení z předmětu 12OMHD LS 2014/2015 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Ing. Vojtěch Novotný budova Horská, kancelář A433 VojtechNovotny@gmail.com ČVUT
ORGANIZACE A ŘÍZENÍ MHD cvičení z předmětu 12OMHD LS 2014/2015 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Ing. Vojtěch Novotný budova Horská, kancelář A433 VojtechNovotny@gmail.com ČVUT
REKONSTRUKCE ŽELEZNIČNÍ STANICE STUDENEC TECHNICKÁ ZPRÁVA. BRNO, listopad 2005 upravil Richard Svoboda
 REKONSTRUKCE ŽELEZNIČNÍ STANICE STUDENEC TECHNICKÁ ZPRÁVA BRNO, listopad 2005 upravil Richard Svoboda 1 Obsah Tady bude obsah 2 1. Úvod 1.1 Zásady pro vypracování Železniční stanice Studenec leží na trati
REKONSTRUKCE ŽELEZNIČNÍ STANICE STUDENEC TECHNICKÁ ZPRÁVA BRNO, listopad 2005 upravil Richard Svoboda 1 Obsah Tady bude obsah 2 1. Úvod 1.1 Zásady pro vypracování Železniční stanice Studenec leží na trati
Sada 3 Inženýrské stavby
 S třední škola stavební Jihlava Sada 3 Inženýrské stavby 12. Trasování žel. tratí, speciální dráhy Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284
S třední škola stavební Jihlava Sada 3 Inženýrské stavby 12. Trasování žel. tratí, speciální dráhy Digitální učební materiál projektu: SŠS Jihlava šablony registrační číslo projektu:cz.1.09/1.5.00/34.0284
ORGANIZACE A ŘÍZENÍ MHD cvičení z předmětu 12OMHD LS 2014/2015
 ORGANIZACE A ŘÍZENÍ MHD cvičení z předmětu 12OMHD LS 2014/2015 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Ing. Vojtěch Novotný budova Horská, kancelář A433 VojtechNovotny@gmail.com Úloha
ORGANIZACE A ŘÍZENÍ MHD cvičení z předmětu 12OMHD LS 2014/2015 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Ing. Vojtěch Novotný budova Horská, kancelář A433 VojtechNovotny@gmail.com Úloha
ICT podporuje moderní způsoby výuky CZ.1.07/1.5.00/ Matematika planimetrie. Mgr. Tomáš Novotný
 Název projektu ICT podporuje moderní způsoby výuky Číslo projektu CZ.1.07/1.5.00/34.0717 Název školy Gymnázium, Turnov, Jana Palacha 804, přísp. organizace Číslo a název šablony klíčové aktivity IV/2 Inovace
Název projektu ICT podporuje moderní způsoby výuky Číslo projektu CZ.1.07/1.5.00/34.0717 Název školy Gymnázium, Turnov, Jana Palacha 804, přísp. organizace Číslo a název šablony klíčové aktivity IV/2 Inovace
Přednáška č. 9 ŽELEZNICE. 1. Dráhy
 Přednáška č. 9 ŽELEZNICE 1. Dráhy Dráhy definuje zákon o drahách (č. 266/1994). Dráhou je cesta určená k pohybu drážních vozidel včetně pevných zařízení potřebných k zajištění bezpečnosti a plynulosti
Přednáška č. 9 ŽELEZNICE 1. Dráhy Dráhy definuje zákon o drahách (č. 266/1994). Dráhou je cesta určená k pohybu drážních vozidel včetně pevných zařízení potřebných k zajištění bezpečnosti a plynulosti
Pokyny pro řešení příkladů z předmětu Mechanika v dopravě pro obor. Dopravní prostředky. ak. rok. 2006/07
 Pokyny pro řešení příkladů z předmětu Mechanika v dopravě pro obor Dopravní prostředky ak. rok. 26/7 Tyto příklady slouží k procvičení základních problematik probíraných na přednáškách tohoto předmětu.
Pokyny pro řešení příkladů z předmětu Mechanika v dopravě pro obor Dopravní prostředky ak. rok. 26/7 Tyto příklady slouží k procvičení základních problematik probíraných na přednáškách tohoto předmětu.
11.12.2011. Pravý odbočovací pruh PŘÍKLAD. Místní sběrná komunikace dvoupruhová s oboustranným chodníkem. L d s 10
 11.1.011 SMK Příklad PravýOdbočovací.ppt SILNIČNÍ A MĚSTSKÉ KOMUNIKACE programu č.3 B Návrhstykovékřižovatky s pravým odbočovacím pruhem Návrh křižovatky: Nakreslete ve vhodném měřítku situační výkres
11.1.011 SMK Příklad PravýOdbočovací.ppt SILNIČNÍ A MĚSTSKÉ KOMUNIKACE programu č.3 B Návrhstykovékřižovatky s pravým odbočovacím pruhem Návrh křižovatky: Nakreslete ve vhodném měřítku situační výkres
POZEMNÍ KOMUNIKACE VE MĚSTECH A OBCÍCH
 Obsah: POZEMNÍ KOMUNIKACE VE MĚSTECH A OBCÍCH 1. Předpisy 2. Rozdělení pozemních komunikací 3. Připojování pozemních komunikací 4. Rozhledové poměry 5. Výhybny a obratiště 6. Odstavné a parkovací plochy
Obsah: POZEMNÍ KOMUNIKACE VE MĚSTECH A OBCÍCH 1. Předpisy 2. Rozdělení pozemních komunikací 3. Připojování pozemních komunikací 4. Rozhledové poměry 5. Výhybny a obratiště 6. Odstavné a parkovací plochy
Správa železniční dopravní cesty, státní organizace. Železniční svršek DOPLŇUJÍCÍ TECHNICKÉ PODMÍNKY PRO GEOMETRICKÉ A PROSTOROVÉ USPOŘÁDÁNÍ KOLEJÍ
 Správa železniční dopravní cesty, státní organizace SŽDC S3 díl XVI Železniční svršek DOPLŇUJÍCÍ TECHNICKÉ PODMÍNKY PRO GEOMETRICKÉ A PROSTOROVÉ USPOŘÁDÁNÍ KOLEJÍ Účinnost od 1. října 2008 ve znění změny
Správa železniční dopravní cesty, státní organizace SŽDC S3 díl XVI Železniční svršek DOPLŇUJÍCÍ TECHNICKÉ PODMÍNKY PRO GEOMETRICKÉ A PROSTOROVÉ USPOŘÁDÁNÍ KOLEJÍ Účinnost od 1. října 2008 ve znění změny
Hodnocení vodicích vlastností lokomotivy v obloucích velmi malých poloměrů podle nové vyhlášky UIC 518:2009
 Vědeckotechnický sborník ČD č. 29/1 Jaromír Zelenka 1 Hodnocení vodicích vlastností lokomotivy v obloucích velmi malých poloměrů podle nové vyhlášky UIC 518:9 Klíčová slova: vodicí vlastnosti lokomotivy,
Vědeckotechnický sborník ČD č. 29/1 Jaromír Zelenka 1 Hodnocení vodicích vlastností lokomotivy v obloucích velmi malých poloměrů podle nové vyhlášky UIC 518:9 Klíčová slova: vodicí vlastnosti lokomotivy,
Konstrukční uspořádání koleje
 Konstrukční uspořádání koleje Otto Plášek, doc. Ing. Ph.. Ústv železničních konstrukcí stveb Tto prezentce byl vytvořen pro studijní účely studentů. ročníku mgisterského studi oboru Geodézie krtogrfie
Konstrukční uspořádání koleje Otto Plášek, doc. Ing. Ph.. Ústv železničních konstrukcí stveb Tto prezentce byl vytvořen pro studijní účely studentů. ročníku mgisterského studi oboru Geodézie krtogrfie
Přednáška č. 4 PŘÍČNÉ USPOŘÁDÁNÍ POZEMNÍ KOMUNIKACE. 1. Základní názvosloví silniční komunikace
 Přednáška č. 4 PŘÍČNÉ USPOŘÁDÁNÍ POZEMNÍ KOMUNIKACE 1. Základní názvosloví silniční komunikace DVOUPRUHOVÁ SILNICE 1 - směrový sloupek, 2 - svah výkopu, 3 - hranice silničního pozemku, 4 - mezník, 5 -
Přednáška č. 4 PŘÍČNÉ USPOŘÁDÁNÍ POZEMNÍ KOMUNIKACE 1. Základní názvosloví silniční komunikace DVOUPRUHOVÁ SILNICE 1 - směrový sloupek, 2 - svah výkopu, 3 - hranice silničního pozemku, 4 - mezník, 5 -
Projekt OPVK - CZ.1.07/1.1.00/ Matematika pro všechny. Univerzita Palackého v Olomouci
 Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Závislosti a funkční vztahy Gradovaný řetězec úloh Téma: graf funkce, derivace funkce a její
Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Závislosti a funkční vztahy Gradovaný řetězec úloh Téma: graf funkce, derivace funkce a její
Kapitola 5. Seznámíme se ze základními vlastnostmi elipsy, hyperboly a paraboly, které
 Kapitola 5 Kuželosečky Seznámíme se ze základními vlastnostmi elipsy, hyperboly a paraboly, které společně s kružnicí jsou známy pod společným názvem kuželosečky. Říká se jim tak proto, že každou z nich
Kapitola 5 Kuželosečky Seznámíme se ze základními vlastnostmi elipsy, hyperboly a paraboly, které společně s kružnicí jsou známy pod společným názvem kuželosečky. Říká se jim tak proto, že každou z nich
Dopravní a liniové stavby 12 Železniční infrastruktura
 Dopravní a liniové stavby 12 Železniční infrastruktura 2.1. Konstrukce železničních vozidel Dvojkolí. U železničních vozidel jsou běžně kola pevně nalisována na nápravách a vytvářejí tak dvojkolí, která
Dopravní a liniové stavby 12 Železniční infrastruktura 2.1. Konstrukce železničních vozidel Dvojkolí. U železničních vozidel jsou běžně kola pevně nalisována na nápravách a vytvářejí tak dvojkolí, která
Konstruktivní geometrie - LI. Konstruktivní geometrie - LI () Kótované promítání 1 / 44
 Kótované promítání Konstruktivní geometrie - LI Konstruktivní geometrie - LI () Kótované promítání 1 / 44 Obsah 1 Polohové úlohy 2 Spád přímky a roviny Konstruktivní geometrie - LI () Kótované promítání
Kótované promítání Konstruktivní geometrie - LI Konstruktivní geometrie - LI () Kótované promítání 1 / 44 Obsah 1 Polohové úlohy 2 Spád přímky a roviny Konstruktivní geometrie - LI () Kótované promítání
ÚROVŇOVÁ KŘIŽOVATKA (POKRAČOVÁNÍ)
 ÚROVŇOVÁ KŘIŽOVATKA (POKRAČOVÁNÍ) KONSTRUKCE STYKOVÉ KŘIŽOVATKY (POKRAČOVÁNÍ) krok V. konstrukce nároží použití kroku V. v závislosti na typu křižovatky (postup uveden pro směr CB neplatí pouze pro SÚK
ÚROVŇOVÁ KŘIŽOVATKA (POKRAČOVÁNÍ) KONSTRUKCE STYKOVÉ KŘIŽOVATKY (POKRAČOVÁNÍ) krok V. konstrukce nároží použití kroku V. v závislosti na typu křižovatky (postup uveden pro směr CB neplatí pouze pro SÚK
Vzdálenosti od hranice obvodu dráhy 1. dráhy celostátní, regionální 60 30
 Ústav územního rozvoje, Jakubské nám. 3, 602 00 Brno Tel.: +420542423111, www.uur.cz, e-mail: sekretariat@uur.cz LIMITY VYUŽITÍ ÚZEMÍ Dostupnost: http://www.uur.cz/default.asp?id=2591 2.5.101 OCHRANNÁ
Ústav územního rozvoje, Jakubské nám. 3, 602 00 Brno Tel.: +420542423111, www.uur.cz, e-mail: sekretariat@uur.cz LIMITY VYUŽITÍ ÚZEMÍ Dostupnost: http://www.uur.cz/default.asp?id=2591 2.5.101 OCHRANNÁ
TUNELY 2. Doc. Ing. Pavel Hánek, CSc. Následující stránky jsou doplňkem přednášek předmětu 154GP10 PROFILY TUNELŮ
 TUNELY Doc. Ing. Pavel Hánek, CSc. Následující stránky jsou doplňkem přednášek předmětu 154GP10 017 ÚČEL A. Dopravní železniční (jednokolejné, dvoukolejné) silniční podzemní městské dráhy B. Rozvody průplavní,
TUNELY Doc. Ing. Pavel Hánek, CSc. Následující stránky jsou doplňkem přednášek předmětu 154GP10 017 ÚČEL A. Dopravní železniční (jednokolejné, dvoukolejné) silniční podzemní městské dráhy B. Rozvody průplavní,
T E R M I N O L O G I E
 825-4 Objekty podzemní tunely T E R M I N O L O G I E B Beton prostý je beton bez výztuže nebo s výztuží hmotnosti do 15 kg/m 3. Beton stříkaný je konstrukce vytvořená pneumatickým nanášením betonové směsi.
825-4 Objekty podzemní tunely T E R M I N O L O G I E B Beton prostý je beton bez výztuže nebo s výztuží hmotnosti do 15 kg/m 3. Beton stříkaný je konstrukce vytvořená pneumatickým nanášením betonové směsi.
Délka oblouku křivky
 Přechodnice podle Blosse Vypočtěte délku oblouku Blossovy přechodnice na intervalu 0, L Např pro vysokorychlostní tratě mezi ČR a Německem je R 6500m, L 198m 4 1 y ) ( R 4L 5 10L ( 2 3 - vzdálenost bodu
Přechodnice podle Blosse Vypočtěte délku oblouku Blossovy přechodnice na intervalu 0, L Např pro vysokorychlostní tratě mezi ČR a Německem je R 6500m, L 198m 4 1 y ) ( R 4L 5 10L ( 2 3 - vzdálenost bodu
Dopravní technika technologie
 Pokyny pro řešení příkladů z předmětu Mechanika pohybu vozidel pro obor Dopravní technika technologie AR 2012/2013 Tyto příklady slouží k procvičení základních problematik probíraných na přednáškách tohoto
Pokyny pro řešení příkladů z předmětu Mechanika pohybu vozidel pro obor Dopravní technika technologie AR 2012/2013 Tyto příklady slouží k procvičení základních problematik probíraných na přednáškách tohoto
SYLABUS 10. PŘEDNÁŠKY Z INŢENÝRSKÉ GEODÉZIE
 SYLABUS 10 PŘEDNÁŠKY Z INŢENÝRSKÉ GEODÉZIE (Přechodnice, přechodnicové a výškové oblouky) 3 ročník bakalářského studia studijní program G studijní obor G doc Ing Jaromír Procházka, CSc prosinec 2015 1
SYLABUS 10 PŘEDNÁŠKY Z INŢENÝRSKÉ GEODÉZIE (Přechodnice, přechodnicové a výškové oblouky) 3 ročník bakalářského studia studijní program G studijní obor G doc Ing Jaromír Procházka, CSc prosinec 2015 1
SYLABUS 8. PŘEDNÁŠKY Z INŽENÝRSKÉ GEODÉZIE
 SYLABUS 8 PŘEDNÁŠKY Z INŽENÝRSKÉ GEODÉZIE (Vytyčování kružnicových oblouků) 3 ročník bakalářského studia studijní program G studijní obor G doc Ing Jaromír Procházka CSc listopad 2015 1 11 VYTYČOVÁNÍ OBLOUKŮ
SYLABUS 8 PŘEDNÁŠKY Z INŽENÝRSKÉ GEODÉZIE (Vytyčování kružnicových oblouků) 3 ročník bakalářského studia studijní program G studijní obor G doc Ing Jaromír Procházka CSc listopad 2015 1 11 VYTYČOVÁNÍ OBLOUKŮ
zlepšení image veřejné dopravy
 Úspěšný, atraktivní a konkurenceschopný systém veřejné dopravy musí disponovat takovou infrastrukturou, která poskytuje pro její provoz podmínky umožňující dosažení příslušných ukazatelů kvality veřejné
Úspěšný, atraktivní a konkurenceschopný systém veřejné dopravy musí disponovat takovou infrastrukturou, která poskytuje pro její provoz podmínky umožňující dosažení příslušných ukazatelů kvality veřejné
ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE. Matematika 0A1. Cvičení, zimní semestr. Samostatné výstupy. Jan Šafařík
 Vysoké učení technické v Brně Stavební fakulta ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE Matematika 0A1 Cvičení, zimní semestr Samostatné výstupy Jan Šafařík Brno c 2003 Obsah 1. Výstup č.1 2 2. Výstup
Vysoké učení technické v Brně Stavební fakulta ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE Matematika 0A1 Cvičení, zimní semestr Samostatné výstupy Jan Šafařík Brno c 2003 Obsah 1. Výstup č.1 2 2. Výstup
Analýza trati Česká Lípa - Lovosice Studentský projekt Železniční síť ČR a Evropy
 ČVUT V PRAZE FAKULTA DOPRAVNÍ Analýza trati Česká Lípa - Lovosice Studentský projekt Železniční síť ČR a Evropy Studenti: Jan Baloun, Matěj Mareš, Robert Plocek, Jiří Tylich Vedoucí projektu: Lukáš Týfa,
ČVUT V PRAZE FAKULTA DOPRAVNÍ Analýza trati Česká Lípa - Lovosice Studentský projekt Železniční síť ČR a Evropy Studenti: Jan Baloun, Matěj Mareš, Robert Plocek, Jiří Tylich Vedoucí projektu: Lukáš Týfa,
Vzorové příklady k přijímacím zkouškám. 1) Doplňte číselné řady o další dvě čísla. a) 3, 6, 12, 24, 48, 96,... b) 875, 764, 653, 542, 431,...
 Vzorové příklady k přijímacím zkouškám ) Doplňte číselné řady o další dvě čísla. a), 6,, 4, 48, 96,... b) 87, 764, 6, 4, 4,... c), 6, 8,,, 0, 6,... d),,, 7,,, 7, 9,,... e) ; ; ; ; ; 8 ) Doplňte číslo místo.
Vzorové příklady k přijímacím zkouškám ) Doplňte číselné řady o další dvě čísla. a), 6,, 4, 48, 96,... b) 87, 764, 6, 4, 4,... c), 6, 8,,, 0, 6,... d),,, 7,,, 7, 9,,... e) ; ; ; ; ; 8 ) Doplňte číslo místo.
UNIVERZITA. PARDUBICE Dopravní fakulta Jana Pernera. Katedra dopravních prostředků a diagnostiky. Oddělení kolejových vozidel
 UNIVERZITA PARDUBICE Dopravní fakulta Jana Pernera Katedra dopravních prostředků a diagnostiky Oddělení kolejových vozidel Dislokované pracoviště Česká Třebová Slovanská 452 56 2 Česká Třebová www.upce.cz/dfjp
UNIVERZITA PARDUBICE Dopravní fakulta Jana Pernera Katedra dopravních prostředků a diagnostiky Oddělení kolejových vozidel Dislokované pracoviště Česká Třebová Slovanská 452 56 2 Česká Třebová www.upce.cz/dfjp
Konstrukční uspořádání koleje
 Konstrukční uspořádání koleje Rozchod a rozšíření rozchodu koleje Otto Plášek, doc. Ing. Ph.D. Ústav železničních konstrukcí a staveb Tato prezentace byla vytvořen pro studijní účely studentů 3. ročníku
Konstrukční uspořádání koleje Rozchod a rozšíření rozchodu koleje Otto Plášek, doc. Ing. Ph.D. Ústav železničních konstrukcí a staveb Tato prezentace byla vytvořen pro studijní účely studentů 3. ročníku
KŘIŽOVATKY Úrovňové křižovatky (neokružní). Návrhové prvky
 KŘIŽOVATKY Úrovňové křižovatky (neokružní). Návrhové prvky KŘIŽ 04 Úrovňové Rozhledy.ppt 2 Související předpis ČSN 73 6102 Projektování křižovatek na pozemních komunikacích, listopad 2007 kapitola 5.2.9
KŘIŽOVATKY Úrovňové křižovatky (neokružní). Návrhové prvky KŘIŽ 04 Úrovňové Rozhledy.ppt 2 Související předpis ČSN 73 6102 Projektování křižovatek na pozemních komunikacích, listopad 2007 kapitola 5.2.9
Oblouky Malého železničního zkušebního okruhu jako zkušební trať exponovaných zkušebních úseků podle vyhlášky UIC 518
 VĚDECKOTECHNICKÝ SBORNÍK ČD ROK 1999 ČÍSLO 7 Antonín Vaněček Oblouky Malého železničního zkušebního okruhu jako zkušební trať exponovaných zkušebních úseků podle vyhlášky UIC 518 Klíčová slova: Vyhláška
VĚDECKOTECHNICKÝ SBORNÍK ČD ROK 1999 ČÍSLO 7 Antonín Vaněček Oblouky Malého železničního zkušebního okruhu jako zkušební trať exponovaných zkušebních úseků podle vyhlášky UIC 518 Klíčová slova: Vyhláška
Infrastruktura kolejové dopravy
 Infrastruktura kolejové dopravy L u k á š T ý f a ČVUT FD, Ústav dopravních systémů (K612) Téma č.. 11 Kombinované kolejové systémy Anotace: definice, princip způsoby využití pro obsluhu území provozní
Infrastruktura kolejové dopravy L u k á š T ý f a ČVUT FD, Ústav dopravních systémů (K612) Téma č.. 11 Kombinované kolejové systémy Anotace: definice, princip způsoby využití pro obsluhu území provozní
Analýza vodicích vlastností dieselelektrické lokomotivy s novým podvozkem CZ LOKO pomocí simulačních výpočtů
 Jaromír Zelenka 1 Analýza vodicích vlastností dieselelektrické lokomotivy s novým podvozkem CZ LOKO pomocí simulačních výpočtů Klíčová slova: dvounápravový podvozek dieselelektrické lokomotivy, simulační
Jaromír Zelenka 1 Analýza vodicích vlastností dieselelektrické lokomotivy s novým podvozkem CZ LOKO pomocí simulačních výpočtů Klíčová slova: dvounápravový podvozek dieselelektrické lokomotivy, simulační
ŠROUBOVICE. 1) Šroubový pohyb. 2) Základní pojmy a konstrukce
 1) Šroubový pohyb ŠROUBOVICE Šroubový pohyb vznikne složením dvou pohybů : otočení kolem dané osy o a posunutí ve směru této osy. Velikost posunutí je přitom přímo úměrná otočení. Konstantou této přímé
1) Šroubový pohyb ŠROUBOVICE Šroubový pohyb vznikne složením dvou pohybů : otočení kolem dané osy o a posunutí ve směru této osy. Velikost posunutí je přitom přímo úměrná otočení. Konstantou této přímé
NÁVRH VÝŠKOVÉHO ŘEŠENÍ 2 VARIANTY:
 NÁVRH VÝŠKOVÉHO ŘEŠENÍ 2 VARIANTY: 1. velkorysá (červená barva) - co nejnižší provozní náklady není nutné respektovat terén, možno použít větších zemních prací - málo (cca do 4) výškových oblouků - velké
NÁVRH VÝŠKOVÉHO ŘEŠENÍ 2 VARIANTY: 1. velkorysá (červená barva) - co nejnižší provozní náklady není nutné respektovat terén, možno použít větších zemních prací - málo (cca do 4) výškových oblouků - velké
ZÁKLADY DOPRAVNÍHO INŽENÝRSTVÍ
 ZÁKLADY DOPRAVNÍHO INŽENÝRSTVÍ cvičení z předmětu 12ZYDI ZS 2015/2016 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Ing. Vojtěch Novotný budova Horská, kancelář A433 novotvo4@fd.cvut.cz
ZÁKLADY DOPRAVNÍHO INŽENÝRSTVÍ cvičení z předmětu 12ZYDI ZS 2015/2016 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Ing. Vojtěch Novotný budova Horská, kancelář A433 novotvo4@fd.cvut.cz
MATEMATIKA III. π π π. Program - Dvojný integrál. 1. Vypočtěte dvojrozměrné integrály v obdélníku D: ( ), (, ): 0,1, 0,3, (2 4 ), (, ) : 1,3, 1,1,
 MATEMATIKA III Program - vojný integrál. Vpočtěte dvojrozměrné integrál v obdélníku : + dd = { < > < > } ( 3), (, ) : 0,, 0,, dd = { < > < > } ( 4 ), (, ) :,3,,, + dd = { < > < > } ( ), (, ):,0,,, + dd=
MATEMATIKA III Program - vojný integrál. Vpočtěte dvojrozměrné integrál v obdélníku : + dd = { < > < > } ( 3), (, ) : 0,, 0,, dd = { < > < > } ( 4 ), (, ) :,3,,, + dd = { < > < > } ( ), (, ):,0,,, + dd=
AXONOMETRIE. Rozměry ve směru os (souřadnice bodů) jsou násobkem příslušné jednotky.
 AXONOMETRIE 1) Princip, základní pojmy Axonometrie je rovnoběžné promítání do průmětny různoběžné se souřadnicovými rovinami. Kvádr v axonometrii : {O,x,y,z} souřadnicový systém XYZ - axonometrická průmětna
AXONOMETRIE 1) Princip, základní pojmy Axonometrie je rovnoběžné promítání do průmětny různoběžné se souřadnicovými rovinami. Kvádr v axonometrii : {O,x,y,z} souřadnicový systém XYZ - axonometrická průmětna
Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny. Univerzita Palackého v Olomouci
 Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Geometrie Různé metody řešení Téma: Kružnice, kruh, tečny, obsahy, goniometrické funkce, integrace
Projekt OPVK - CZ.1.07/1.1.00/26.0047 Matematika pro všechny Univerzita Palackého v Olomouci Tematický okruh: Geometrie Různé metody řešení Téma: Kružnice, kruh, tečny, obsahy, goniometrické funkce, integrace
Napojení komunikace Bílina Kostomlaty na dopravní síť v Bílině
 Napojení komunikace Bílina Kostomlaty na dopravní síť v Bílině Technická pomoc TECHNICKÁ ZPRÁVA Zak. č. 4527/TP Arch. č. DO-6-12701 Březen 2016 Zpracovatel: Báňské projekty Teplice a. s. Kollárova 11,
Napojení komunikace Bílina Kostomlaty na dopravní síť v Bílině Technická pomoc TECHNICKÁ ZPRÁVA Zak. č. 4527/TP Arch. č. DO-6-12701 Březen 2016 Zpracovatel: Báňské projekty Teplice a. s. Kollárova 11,
Vzdálenosti od hranice obvodu dráhy 1. dráhy celostátní, regionální 60 30
 Ústav územního rozvoje, Jakubské nám. 3, 658 34 Brno Tel.: +420542423111, www.uur.cz, e-mail: sekretariat@uur.cz LIMITY VYUŽITÍ ÚZEMÍ Dostupnost: http://www.uur.cz/default.asp?id=2591 2.5.101 OCHRANNÁ
Ústav územního rozvoje, Jakubské nám. 3, 658 34 Brno Tel.: +420542423111, www.uur.cz, e-mail: sekretariat@uur.cz LIMITY VYUŽITÍ ÚZEMÍ Dostupnost: http://www.uur.cz/default.asp?id=2591 2.5.101 OCHRANNÁ
3 ZÁSADY ŘEŠENÍ PRO OSOBY SE SLUCHOVÝM POSTIŽENÍM
 B.4. BEZBARIÉROVÉ UŽÍVÁNÍ Obsah 1 ZÁSADY ŘEŠENÍ PRO OSOBY S OMEZENOU SCHOPNOSTÍ POHYBU 1.1 Komunikace pro chodce - chodníky 1.2 Přechody pro chodce, místa pro přecházení 1.3 Nástupiště veřejné dopravy
B.4. BEZBARIÉROVÉ UŽÍVÁNÍ Obsah 1 ZÁSADY ŘEŠENÍ PRO OSOBY S OMEZENOU SCHOPNOSTÍ POHYBU 1.1 Komunikace pro chodce - chodníky 1.2 Přechody pro chodce, místa pro přecházení 1.3 Nástupiště veřejné dopravy
Geometrie. 1 Metrické vlastnosti. Odchylku boční hrany a podstavy. Odchylku boční stěny a podstavy
 1 Metrické vlastnosti 9000153601 (level 1): Úhel vyznačený na obrázku znázorňuje: eometrie Odchylku boční hrany a podstavy Odchylku boční stěny a podstavy Odchylku dvou protilehlých hran Odchylku podstavné
1 Metrické vlastnosti 9000153601 (level 1): Úhel vyznačený na obrázku znázorňuje: eometrie Odchylku boční hrany a podstavy Odchylku boční stěny a podstavy Odchylku dvou protilehlých hran Odchylku podstavné
STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJÍRENSKÁ a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191. Obor M/01 STROJÍRENSTVÍ
 STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJÍRENSKÁ a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Obor 23-41-M/01 STROJÍRENSTVÍ 1. ročník TECHNICKÉ KRESLENÍ PRAVIDLA PRO KÓTOVÁNÍ SOUČÁSTÍ
STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJÍRENSKÁ a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Obor 23-41-M/01 STROJÍRENSTVÍ 1. ročník TECHNICKÉ KRESLENÍ PRAVIDLA PRO KÓTOVÁNÍ SOUČÁSTÍ
BM03 MĚSTSKÉ KOMUNIKACE
 BM03 MĚSTSKÉ KOMUNIKACE 2. týden Návrh směrového řešení, parkoviště Miroslav Patočka kancelář C330 email: patocka.m@fce.vutbr.cz Martin Novák kancelář C331 email: novak.m@fce.vutbr.cz NÁPLŇ CVIČENÍ Odevzdání
BM03 MĚSTSKÉ KOMUNIKACE 2. týden Návrh směrového řešení, parkoviště Miroslav Patočka kancelář C330 email: patocka.m@fce.vutbr.cz Martin Novák kancelář C331 email: novak.m@fce.vutbr.cz NÁPLŇ CVIČENÍ Odevzdání
ŽELEZNIČNÍ ZASTÁVKA OSTRAVA ZÁBŘEH S NÁVRHEM PŘESTUPU NA MHD
 VŠB-Technická univerzita Ostrava Fakulta stavební Studentská vědecká odborná činnost Akademický rok 2009/2010 ŽELEZNIČNÍ ZASTÁVKA OSTRAVA ZÁBŘEH S NÁVRHEM PŘESTUPU NA MHD RAILWAY STOP OSTRAVA ZÁBŘEH WITH
VŠB-Technická univerzita Ostrava Fakulta stavební Studentská vědecká odborná činnost Akademický rok 2009/2010 ŽELEZNIČNÍ ZASTÁVKA OSTRAVA ZÁBŘEH S NÁVRHEM PŘESTUPU NA MHD RAILWAY STOP OSTRAVA ZÁBŘEH WITH
MDT 624. 02 OBOROVÁ NORMA Schválena: 20. 9. 1980 Federální ministerstvo dopravy
 MDT 624. 02 OBOROVÁ NORMA Schválena: 20. 9. 1980 Federální ministerstvo dopravy PROSTOROVÉ USPOŘÁDÁNÍ VRAT NAD KOLEJEMI ROZCHODU 1435 mm a 1520 (1524) mm TNŽ 73 6388 Tato norma platí pro prostorové uspořádání
MDT 624. 02 OBOROVÁ NORMA Schválena: 20. 9. 1980 Federální ministerstvo dopravy PROSTOROVÉ USPOŘÁDÁNÍ VRAT NAD KOLEJEMI ROZCHODU 1435 mm a 1520 (1524) mm TNŽ 73 6388 Tato norma platí pro prostorové uspořádání
Diferenciální počet funkcí více proměnných
 Vysoké učení technické v Brně Fakulta strojního inženýrství Diferenciální počet funkcí více proměnných Doc RNDr Miroslav Doupovec, CSc Neřešené příklady Matematika II OBSAH Obsah I Diferenciální počet
Vysoké učení technické v Brně Fakulta strojního inženýrství Diferenciální počet funkcí více proměnných Doc RNDr Miroslav Doupovec, CSc Neřešené příklady Matematika II OBSAH Obsah I Diferenciální počet
, = , = , = , = Pokud primitivní funkci pro proměnnou nevidíme, pomůžeme si v tuto chvíli jednoduchou substitucí = +2 +1, =2 1 = 1 2 1
 ŘEŠENÉ PŘÍKLADY Z MB ČÁST 7 Příklad 1 a) Vypočtěte hmotnost oblasti ohraničené přímkami =1,=3,=1,= jestliže její hustota je dána funkcí 1,= ++1 b) Vypočtěte statický moment čtverce ohraničeného přímkami
ŘEŠENÉ PŘÍKLADY Z MB ČÁST 7 Příklad 1 a) Vypočtěte hmotnost oblasti ohraničené přímkami =1,=3,=1,= jestliže její hustota je dána funkcí 1,= ++1 b) Vypočtěte statický moment čtverce ohraničeného přímkami
Revitalizace vodního toku
 Revitalizace vodního toku ČSN 01 3105 společně pro výkresy, velikosti, popisování, materiály, formáty a skládání výkresů, měřítka, čáry, kótování, ČSN 01 3402 popisové pole ČSN 01 3160 zásady oprav a změn
Revitalizace vodního toku ČSN 01 3105 společně pro výkresy, velikosti, popisování, materiály, formáty a skládání výkresů, měřítka, čáry, kótování, ČSN 01 3402 popisové pole ČSN 01 3160 zásady oprav a změn
