Fakulta stavební ČVUT v Praze Katedra hydrauliky a hydrologie. Předmět HY2V K141 FSv ČVUT. Přepady. Doc. Ing. Aleš Havlík, CSc., Ing. Tomáš Picek PhD.
|
|
|
- Denis Matoušek
- před 6 lety
- Počet zobrazení:
Transkript
1 Fakulta stavebí ČVUT v Praze Katedra draulik a droloie Předmět HYV K4 FSv ČVUT Přepad Doc. I. Aleš Havlík, CSc., I. Tomáš Picek PD. K4 HYV Přepad
2 přepad - draulický jev X přeliv - kostrukce voda přepadá přes přeliv (kostrukci) přeliv: provozí části vzdouvacíc staveb (jez, přerad) bezpečostí zařízeí (přerad, rbík...) odděleí části průtoku (dešťové oddělovače, závlaové kaál...) měřeí průtoku... K4 HYV Přepad
3 Čleěí podle tvaru kostrukce Základí tp : přepad přes ostroraý přeliv t <.67 měré přeliv přepad přes jezový přeliv.67 < t < přepad přes proudicový přeliv přepad přes širokou koruu t > K4 HYV Přepad
4 Speciálí tp : přepad s ízkým praem ve dě Jamborův prá stupeň ve dě šactové přeliv ásoskové přeliv K4 HYV Přepad 4
5 Čleěí podle půdorséo uspořádáí čelí přeliv šikmý přeliv lomeý přeliv zakřiveý přeliv bočí přeliv K4 HYV Přepad 5
6 Základí části a rozměr přelivu přelivá raa (ostroraé) / korua přelivu : ejvšší část přelivéo tělesa přepadová výška s - výška přelivu v orí vodě s d výška přelivu v dolí vodě H spád ladi s σ výška zatopeí přelivu d loubka dolí vod B šířka přívodío korta/kaálu b šířka přepadu (délka koru) v přítoková rclost, v = /[B(s+)] μ, m součiitel přepadu H s s d d K4 HYV Přepad 6
7 K4 HYV Přepad 7 Základí rovice přepadu dz x u ds u d v α z u = φ dz x v α z dz x u d z dz x b v zásadě výtok otvorem sora eomezeým: v loubce z pod ladiou rclost celkový průtok pro ideálí kapaliu zúžeí přepadovéo paprsku pro skutečou kapaliu dz x v α z μ - součiitel přepadu
8 K4 HYV Přepad 8 a z too pro obdélík (x=b=kost.) dz v α z b μ dz b v α z μ pro jié tvar obdobě s uvažováím x=f(z); d z b μ d v α trojúelík (x=kz) dz v α z z k μ 5 z fce
9 K4 HYV Přepad 9 - součiitel přepadu D W > často:, ebo D b μ d d W b μ b μ v α > μ m μ C Růzé přístup uvažováí vlivu přítokové rclosti v Dubuatova (Poleiova): též ve tvaru Rovice: Weisbacova
10 K4 HYV Přepad Tvar přepadovéo paprsku dokoalé zavzdušeí prostoru pod paprskem spodí obálka vrovou parabolou; v bezrozměrém tvaru (Blaisdel) předpoklad - kostatí svislá tloušťka paprsku orí obálka koeficiet měřeí a ostroraém přelivu se svislou stěou při v =: A=-,45, B=,55, C=,5, D=,6, x/ >,5 (a obr.) Pro x/ <,7 Baziov souřadice (a obr.). C x B x A D C x B x A αv f
11 /.8 Přepadový paprsek bezrozměré souřadice.6.4 Bazi,5., Blaisdel / x/ v prostoru pod paprskem podtlak - paprsek sížeý až lpící větší zakřiveí, větší kapacita, ebezpečí vibrací, estálý jev přetlak - paprsek zdvižeý - meší zakřiveí, meší kapacita, estálý jev K4 HYV Přepad
12 Přepad dokoalý edokoalý dokoalý přepad = f() ebo = f( ), ezávisí a d edokoalý (zatopeý) přepad = f(, σ ), resp. = f(, H) ebo = f(, σ ), resp. = f(, H) se redukuje součiitelem zatopeí σ z : σ z = f(tp přelivu,, s d, H) H s z m b s ebo s d d z m b K4 HYV Přepad
13 Přeliv ostroraé = f() přeliv s t<,67; Měré přeliv - pro měřeí specielí úprava přelivé ra laví tp: obdélíkový - bez bočí kotrakce (Baziův) s bočí kotrakcí (Poceletův) - mm 45-6 Baziův přeliv v / Poceletův přeliv v s p=p a t<,67 b s B K4 HYV Přepad
14 trojúelíkový (s vrcol. úlem 9 - Tomsoův) licoběžíkový (s bočími stěami 4: - Cipolettio) řada dalšíc Trojúelíkový přeliv Tomsoův přeliv b b= 9 Cipolettio přeliv a> a> b> s> B> K4 HYV Přepad 4
15 K4 HYV Přepad 5 Baziův přeliv s m. < b <. [m],. < s <. [m],. < <.4 [m] Poceletův přeliv s B b.55 B b m Obdélíkové přeliv Pro obdélíkové přeliv (Baziův i Poceletův) řada vzorců pro m od růzýc autorů, rozdíl obvkle < - %. b m
16 Zatopeí mezí odot podle Pavlovskéo (H/s d ) * /s d pokud skutečý poměr H/s d < (H/s d )* pro daé /s d, je přepad zatopeý a σ z.5. s K4 HYV Přepad 6 σ d H
17 Trojúelíkový přeliv 8 5 t 5 e.6 součiitel přepadu podle Kulia et al [ ] K4 HYV Přepad 7
18 k [mm] e k ebo podle Graveo pro < <. α t Rozdíl průtoku podle obou rovic pro > 45 meší ež % K4 HYV Přepad 8
19 Trojúelíkový přeliv pravoúlý (Tomsoův) podle Tomsoa.4.5 Kia.4.5 < <.55 m, s > a B > 8.47 trojúelíkové přeliv - vliv zatopeí pro d > s d -,5 [m] Licoběžíkový přeliv Cipolettio B >.86 b.5 K4 HYV Přepad 9
20 Lieárí přeliv = k průtok roste lieárě s přepadovou výškou μ z b dz a k z. dz z z k dz k b a z tvar přelivé ra - perbola K4 HYV Přepad
21 K4 HYV Přepad Přepad přes jezová tělesa, přeradí ráze =f( ) Jez - poblivé ebo pevé kostrukce ke vzdutí vod (plavba, vužití vodí eerie, odběr vod) - často vliv dolí vod Přerad - všší kostrukce k vtvořeí zásob vod, pro eškodé odvedeí velkýc průtoků opatřeé přeliv, resp. pro zatopeý (edokoalý) přepad, resp. b m b μ z b μ σ z b m σ
22 Přeliv jezů a přerad často razeé dělicí pilíře kotrakce vodío proudu, účiá šířka přelivu b < b b b. ξ b - součet šířek jedotlivýc polí, - součiitel zúžeí, = f(tvar pilíře/křídla) r,5 9 r =,5d r d d r (,75 -,5)d r =(,5 -,75)d d proudicové zlaví 45 a r,5 -,,,7,45 -,7 PŘEDSAZENÉ ZHLAVÍ a,45 -,7,5 -,4,5 -,, -,,5,5 d K4 HYV Přepad
23 Jezové přeliv jedoducéo profilu s s :k :k' s :k t :k' t Obdélíkový příčý průřez /t,,,5,,5, µ p,45,48,498,555,65,6 Trojúelíkový příčý průřez podle Bazia k k' [m],9,,5,,7,,6,45,796,786,774,768,766,76,75,7,7,75,75,74,7,7,7,78,7,75,7,75,7,7,7,7 K4 HYV Přepad
24 tp jezu vsoké jez s>5m středě vsoké jez <s<5m ízké jez s<m Licoběžíkový příčý průřez podle Pavlovskéo skloěá ávodí stěa skloěá vzduší stěa skloěá ávodí stěa skloěá vzduší stěa sklo stě k',5 k,5 /t> </t<,5</t<,646,6,6,57,54,55 k=,66,6,6 k=,645,65,585 k'=,6,6,56 k'=,6,57,5 k=,6,6,57 k=5,6,57,54 k=,57, k'=,585,555,55 k'=5,56, k'=,55, K4 HYV Přepad 4
25 Součiitel zatopeí pro přeliv jedoducéo profilu (dle Pikalova),9,8,7,6 z,5,4,,,,,,,4,5,6,7,8,9 s / K4 HYV Přepad 5
26 Jezové přeliv se zaobleou koruou a - Kramer b Rebock c Rebock p p. r s.4 pro r p... 5 r pro. r s r s r s r / s..8 r s d Kramer použití rovice dle a) 4.57 a r b. 57 při dosazeí a /b b K4 HYV Přepad 6
27 Přeliv proudicové tvar - z dolí obálk přepadovéo paprsku přelivé ploc: beztlakové - sledují dolí obálku přepadovéo paprsku - a ploše ulové tlak tlakové - meší křivost ež přepadající paprsek - v lib. bodě p > p a, meší kapacita přelivu podtlakové - větší křivost ež přepadající paprsek - v lib. bodě p < p a, větší kapacita přelivu, podtlak a vsoké rclosti ebezpečí kavitace, eroze, vibrací kostrukce... x x tlaková ploca beztlaková ploca beztlaková ploca podtlaková ploca tvar přepadovéo paprsku fukcí beztlaková ploca pouze pro přepadovou výšku (ávrová přepadová výška) < tlaková ploca, > podtlaková ploca K4 HYV Přepad 7
28 Beztlaková ploca Scimemio souřadice přelivé ploc pro :.85 T xt x.5 x/ >,.5 -. < x/ < tečý bod přelivé ploc k ávodímu líci ráze o úlu :.85 směrice teč v [x T, T ] xt tα,.95 součiitel přepadu m =.5 pro, x.84 m m.94.6,,7 m m.7.,.7 Scimemio ploca euvažuje vliv přítokové rclosti je pro vsoké jez/přerad, je svislý ávodí líc K4 HYV Přepad 8
29 Scimemio ploca + další výzkum ploc USBR a WES, pro růzé s/, sklo ávodío líce (sl)... WES: x K x/, K f( /,s/,sl) f( /,s/, sl) pro x/ < složeý kruový oblouk, R / a R / = m f( /,s/ f(,sl) /,s/,sl) zatopeí Deverský raf K4 HYV Přepad 9
30 pro vsoký jez (s/ ) se svislým ávodím lícem: K =,5, =,85, r =,5, r =,, m =,5 m m , -, -,,,,,4,5,6,7,8, x/ a r r S,,,4 max x T(x, ) T T : - : S K4 HYV Přepad
31 Přepad přes jezový objekt s vsokým stupěm zatopeí malé vzdutí ladi objektem výpočet pomocí erovoměréo prouděí s uvažováím místí ztrát srpe Praa, Vltava, Helmovský jez a Štvaici K4 HYV Přepad
32 Přepad přes širokou koruu - l = (,5-5) v o / pro z Beroullio rovice s d kdž v v d v s (dokoalý přepad) α ξ α v α v v Z Z ξ v ( ) α ξ l v α ξ s d H d K4 HYV Přepad
33 a průtok S S b, zúžeí paprsku ε b ε ε ε položme m ε Z pokusů.8.9 ε b ε m b k - vodí skok (vlový) ε přepad m beze ztrát,85 / / vstupí část dobře zaoblea,95,6,6,7 zaobleá vstupí raa,96,5,57,76 vstupí raa seřízuta,9,,5,79 ostrá vstupí raa,9,,5,85 dtto, prá mimořádě drsý,88,,465,8 K4 HYV Přepad
34 edokoalý přepad - s d d, resp. σ b σ ( σ ) též σ m b z /,95,9,85,8,75,7,,4,6,8 K4 HYV Přepad 4
35 K4 HYV Přepad 5 Stupeň ve dě častý prvek (úprav toků a razeí bstři) sížeí podéléo sklou, stabilizace korta obdélíkové korto z impulsové vět e =,667 k e k.75.5 e b 5.8 k e s d zatopeí: s < s mi s k mi d k k d k d k d d s s k,
36 Šactový přeliv přeliv s kruovou přelivou raou ostroraý positiví eativí s proudicovou přelivou plocou D positiví : k L,4 k D,4, <,D k -,46D +,96D +,4497,7 D,648 [m] eativí: D D K4 HYV Přepad 6
37 K4 HYV Přepad 7 Přeliv s proudicovou plocou zejméa jako bezpečostí přeliv spaýc rází dokoalý přepad:.5 D L μ souřadice ploc tabulk pro r, f x,5 x pro r, x f D x r r r f μ edokoalý přepad výtok otvorem: 4 D π μ.5 D
38 Přepad přes jezovou klapku, semet, sektor v r 5 4 /r,7 C b fα, r C protože součiitel průtoku C je v US jedotkác, třeba převést: C C m SI 9.8ms.55 C (SI) US.85 ft s /r= - /r -,8,,,4,6,8 4, (US) C K4 HYV Přepad 8
Fakulta stavební ČVUT v Praze Katedra hydrauliky a hydrologie. Předmět HY2V K141 FSv ČVUT. Přepady. Doc. Ing. Aleš Havlík, CSc., Ing. Tomáš Picek PhD.
 Fakulta stavební ČVUT v Praze Katedra ydrauliky a ydrologie Předmět HYV K4 FSv ČVUT Přepady Doc. Ing. Aleš Havlík, CSc., Ing. Tomáš Picek PD. K4 HYV Přepady přepad - ydraulický jev X přeliv - konstrukce
Fakulta stavební ČVUT v Praze Katedra ydrauliky a ydrologie Předmět HYV K4 FSv ČVUT Přepady Doc. Ing. Aleš Havlík, CSc., Ing. Tomáš Picek PD. K4 HYV Přepady přepad - ydraulický jev X přeliv - konstrukce
Vodní skok, tlumení kinetické energie Řešení průběhu hladin v otevřených korytech
 Fakulta stavební ČVUT v Praze Katedra draulik a droloie Předmět HYV K4 FSv ČVUT Vodní skok, tlumení kinetické enerie Řešení průběu ladin v otevřenýc kortec Doc. In. Aleš Havlík, CSc., In. Tomáš Picek PD.
Fakulta stavební ČVUT v Praze Katedra draulik a droloie Předmět HYV K4 FSv ČVUT Vodní skok, tlumení kinetické enerie Řešení průběu ladin v otevřenýc kortec Doc. In. Aleš Havlík, CSc., In. Tomáš Picek PD.
Vodní skok, tlumení kinetické energie
 Fakulta stavební ČVUT v Praze Katedra a hdraulik a hdrologie og Předmět HYV K4 FSv ČVUT Vodní skok, tlumení kinetické energie Řešení průběhu hladin v otevřených kortech Doc. Ing. Aleš Havlík, CSc., Ing.
Fakulta stavební ČVUT v Praze Katedra a hdraulik a hdrologie og Předmět HYV K4 FSv ČVUT Vodní skok, tlumení kinetické energie Řešení průběhu hladin v otevřených kortech Doc. Ing. Aleš Havlík, CSc., Ing.
1141 HYA (Hydraulika)
 ČVUT v Praze, fakulta stavení katedra ydrauliky a ydrologie (K141) Přednáškové slidy předmětu 1141 HYA (Hydraulika) verze: 1/011 K141 FSv ČVUT Tato weová stránka naízí k nalédnutí/stažení řadu pdf souorů
ČVUT v Praze, fakulta stavení katedra ydrauliky a ydrologie (K141) Přednáškové slidy předmětu 1141 HYA (Hydraulika) verze: 1/011 K141 FSv ČVUT Tato weová stránka naízí k nalédnutí/stažení řadu pdf souorů
Proudění mostními objekty a propustky
 Fakulta staební ČVUT Praze Katedra draulik a droloie Předmět HYV K141 FS ČVUT Proudění mostními objekt a propustk Doc. In. Aleš Halík, CSc., In. Tomáš Picek PD. MOSTY ýška a šířka mostnío otoru přeládá
Fakulta staební ČVUT Praze Katedra draulik a droloie Předmět HYV K141 FS ČVUT Proudění mostními objekt a propustk Doc. In. Aleš Halík, CSc., In. Tomáš Picek PD. MOSTY ýška a šířka mostnío otoru přeládá
Nálitky. Obr. 1 Schematický přehled typů nálitků
 Nálitky Hlaví požadavky pro výpočet álitku: 1. doba tuhutí álitku > doba tuhutí odlitku 2. objem álitku(ů) musí být větší ež objem stažeiy v odlitku 3. musí být umožěo prouděí kovu z álitku do odlitku
Nálitky Hlaví požadavky pro výpočet álitku: 1. doba tuhutí álitku > doba tuhutí odlitku 2. objem álitku(ů) musí být větší ež objem stažeiy v odlitku 3. musí být umožěo prouděí kovu z álitku do odlitku
HYDRAULICKÉ JEVY NA JEZECH
 HYDRAULICKÉ JEVY NA JEZECH Doc. Ing. Aleš Havlík, CSc. ČVUT v Praze, Fakulta stavební Katedra hydrauliky a hydrologie 1. REŽIMY PROUDĚNÍ S VOLNOU HLADINOU Proudění říční, kritické a bystřinné 2. PŘEPADY
HYDRAULICKÉ JEVY NA JEZECH Doc. Ing. Aleš Havlík, CSc. ČVUT v Praze, Fakulta stavební Katedra hydrauliky a hydrologie 1. REŽIMY PROUDĚNÍ S VOLNOU HLADINOU Proudění říční, kritické a bystřinné 2. PŘEPADY
USTÁLENÉ PROUDĚNÍ V OTEVŘENÝCH KORYTECH
 USTÁLENÉ POUDĚNÍ V OTEVŘENÝCH KOYTECH ovoměré prouděí Charakterstka:. Hloubka vod v kortě, průtočá plocha a průřezová rchlost jsou v každém příčém řezu kostatí.. Čára eerge, vodí hlada a do korta jsou
USTÁLENÉ POUDĚNÍ V OTEVŘENÝCH KOYTECH ovoměré prouděí Charakterstka:. Hloubka vod v kortě, průtočá plocha a průřezová rchlost jsou v každém příčém řezu kostatí.. Čára eerge, vodí hlada a do korta jsou
Hydraulika a hydrologie
 Hydraulika a hydrologie Cvičení č. 1 - HYDROSTATIKA Příklad č. 1.1 Jaký je tlak v hloubce (5+P) m pod hladinou moře (Obr. 1.1), je-li průměrná hustota mořské vody ρ mv = 1042 kg/m 3 (měrná tíha je tedy
Hydraulika a hydrologie Cvičení č. 1 - HYDROSTATIKA Příklad č. 1.1 Jaký je tlak v hloubce (5+P) m pod hladinou moře (Obr. 1.1), je-li průměrná hustota mořské vody ρ mv = 1042 kg/m 3 (měrná tíha je tedy
Prorážka DOC. ING. PAVEL HÁNEK, CSC. Uvedené materiály jsou doplňkem přednášek předmětu 154GP10
 Prorážka DOC. ING. PAVEL HÁNEK, CSC. Uvedeé materiály jsou doplňkem předášek předmětu 154GP10 014 HLAVNÍ PROJEKČNÍ PRVKY Směr pokud možo volit přímý tuel. U siličích t. miimálí poloměr 300 m, u železičích
Prorážka DOC. ING. PAVEL HÁNEK, CSC. Uvedeé materiály jsou doplňkem předášek předmětu 154GP10 014 HLAVNÍ PROJEKČNÍ PRVKY Směr pokud možo volit přímý tuel. U siličích t. miimálí poloměr 300 m, u železičích
STATISTIKA. Statistika se těší pochybnému vyznamenání tím, že je nejvíce nepochopeným vědním oborem. H. Levinson
 STATISTIKA Statistika se těší pochybému vyzameáí tím, že je ejvíce epochopeým vědím oborem. H. Leviso Charakterizace statistického souboru Statistický soubor Prvek souboru Zak prvku kvatitativí teplota,
STATISTIKA Statistika se těší pochybému vyzameáí tím, že je ejvíce epochopeým vědím oborem. H. Leviso Charakterizace statistického souboru Statistický soubor Prvek souboru Zak prvku kvatitativí teplota,
(Aplikace pro mosty, propustky) K141 HYAR Hydraulika objektů na vodních tocích
 Hydraulika objektů na vodních tocích (Aplikace pro mosty, propustky) 0 Mostní pole provádějící vodní tok pod komunikací (při povodni v srpnu 2002) 14. století hydraulicky špatný návrh úzká pole, široké
Hydraulika objektů na vodních tocích (Aplikace pro mosty, propustky) 0 Mostní pole provádějící vodní tok pod komunikací (při povodni v srpnu 2002) 14. století hydraulicky špatný návrh úzká pole, široké
(režimy proudění, průběh hladin) Proudění s volnou hladinou II
 Proudění s volnou hladinou (režimy proudění, průběh hladin) PROUDĚNÍ KRITICKÉ, ŘÍČNÍ A BYSTŘINNÉ Vztah mezi h (resp. y) a v: Ve žlabu za různých sklonů α a konst. Q: α 1 < α < α 3 => G s1 < G s < G s3
Proudění s volnou hladinou (režimy proudění, průběh hladin) PROUDĚNÍ KRITICKÉ, ŘÍČNÍ A BYSTŘINNÉ Vztah mezi h (resp. y) a v: Ve žlabu za různých sklonů α a konst. Q: α 1 < α < α 3 => G s1 < G s < G s3
Mezní stavy konstrukcí a jejich porušov. Hru IV. Milan RůžR. zbynek.hruby.
 ováí - Hru IV /6 ováí Hru IV Mila RůžR ůžička, Josef Jureka,, Zbyěk k Hrubý zbyek.hruby hruby@fs.cvut.cz ováí - Hru IV /6 ravděpodobostí úavové diagramy s uvažováím předpětí R - plocha ve čtyřrozměrém
ováí - Hru IV /6 ováí Hru IV Mila RůžR ůžička, Josef Jureka,, Zbyěk k Hrubý zbyek.hruby hruby@fs.cvut.cz ováí - Hru IV /6 ravděpodobostí úavové diagramy s uvažováím předpětí R - plocha ve čtyřrozměrém
7. Analytická geometrie
 7. Aaltická geoetrie Studijí tet 7. Aaltická geoetrie A. Příka v roviě ϕ s A s ϕ s 2 s 1 B p s ϕ = (s1, s 2 ) sěrový vektor přík p orálový vektor přík p sěrový úhel přík p k = tgϕ = s 2 s 1 sěrice příkp
7. Aaltická geoetrie Studijí tet 7. Aaltická geoetrie A. Příka v roviě ϕ s A s ϕ s 2 s 1 B p s ϕ = (s1, s 2 ) sěrový vektor přík p orálový vektor přík p sěrový úhel přík p k = tgϕ = s 2 s 1 sěrice příkp
Zásady křížení vodních toků a komunikací Doc. Ing. Aleš Havlík, CSc.
 Zásady křížení vodních toků a Doc. Ing. Aleš Havlík, CSc. Respektování vodohospodářských zájmů Návrh křížení musí respektovat : Bezpečnost ochranných hrází. Splaveninový režim toku a stabilitu koryta toku.
Zásady křížení vodních toků a Doc. Ing. Aleš Havlík, CSc. Respektování vodohospodářských zájmů Návrh křížení musí respektovat : Bezpečnost ochranných hrází. Splaveninový režim toku a stabilitu koryta toku.
FYZIKA I. Složené pohyby (vrh šikmý)
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ FYZIKA I Složené pohb (vrh šikmý) Prof. RNDr. Vilém Mádr, CSc. Prof. In. Libor Hlaváč, Ph.D. Doc. In. Irena Hlaváčová, Ph.D. Mr. Art. Damar
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ FYZIKA I Složené pohb (vrh šikmý) Prof. RNDr. Vilém Mádr, CSc. Prof. In. Libor Hlaváč, Ph.D. Doc. In. Irena Hlaváčová, Ph.D. Mr. Art. Damar
Odhady parametrů 1. Odhady parametrů
 Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
Kultivační a produkční zařízení Laboratorní měřítko
 Kultivačí a produkčí zařízeí Laboratorí měřítko Baňky, labor. fermetor 1 5 l, poloprovoz. taky 5 2 l. Třepačka: výběr kmeů, fyziologie, kvalita surovi, převod do fermetoru limity D a dcg L = V ( Cg C dt
Kultivačí a produkčí zařízeí Laboratorí měřítko Baňky, labor. fermetor 1 5 l, poloprovoz. taky 5 2 l. Třepačka: výběr kmeů, fyziologie, kvalita surovi, převod do fermetoru limity D a dcg L = V ( Cg C dt
Vytápění BT01 TZB II - cvičení
 CZ..07/2.2.00/28.030 Středoevropské cetrum pro vytvářeí a realizaci iovovaých techicko-ekoomických studijích programů Vytápěí BT0 TZB II - cvičeí Zadáí Pro vytápěé místosti vašeho objektu avrhěte otopá
CZ..07/2.2.00/28.030 Středoevropské cetrum pro vytvářeí a realizaci iovovaých techicko-ekoomických studijích programů Vytápěí BT0 TZB II - cvičeí Zadáí Pro vytápěé místosti vašeho objektu avrhěte otopá
TĚŽIŠTĚ A STABILITA. Těžiště tělesa = bod, kterým stále prochází výslednice tíhových sil všech jeho hmotných bodů, ať těleso natáčíme jakkoli
 SAIKA - těžště ĚŽIŠĚ A SABILIA ěžště tělesa bod, kterým stále prochází výsledce tíhových sl všech jeho hmotých bodů, ať těleso atáčíme jakkol bod, ke kterému astává rovováha mometů způsobeých tíhou jedotlvých
SAIKA - těžště ĚŽIŠĚ A SABILIA ěžště tělesa bod, kterým stále prochází výsledce tíhových sl všech jeho hmotých bodů, ať těleso atáčíme jakkol bod, ke kterému astává rovováha mometů způsobeých tíhou jedotlvých
SO JEZ CACOVICE NOVÁ KONSTRUKCE v ř. km 10,157 (SVITAVA)
 PŘÍRODĚ BLÍZKÁ POP A REVITALIZACE ÚDOLNÍ NIVY HLAVNÍCH BRNĚNSKÝCH TOKŮ 3.část SO 18.3.1. JEZ CACOVICE NOVÁ KONSTRUKCE v ř. km 10,157 (SVITAVA) NÁVRH BYL ZPRACOVÁN VE DVOU VARIANTÁCH JAKO JEZ KLAPKOVÝ A
PŘÍRODĚ BLÍZKÁ POP A REVITALIZACE ÚDOLNÍ NIVY HLAVNÍCH BRNĚNSKÝCH TOKŮ 3.část SO 18.3.1. JEZ CACOVICE NOVÁ KONSTRUKCE v ř. km 10,157 (SVITAVA) NÁVRH BYL ZPRACOVÁN VE DVOU VARIANTÁCH JAKO JEZ KLAPKOVÝ A
 ě Á Á é é ě ě ě ú é é é ě é é ď ď ď š š Č Á ě ú Á ď š ě Č ě š ěž ě é ě ě ě ě ě ě Č Á ě Á é ú Ž é š ě š š é Ž ě é š é Š ť Ž ě Č Á ú Á Ť é ě é š ě ě š š ď ď Č é š š Č ě ě ú ě ú Ť é ě š ě ě š ě š ě ě ú ě
ě Á Á é é ě ě ě ú é é é ě é é ď ď ď š š Č Á ě ú Á ď š ě Č ě š ěž ě é ě ě ě ě ě ě Č Á ě Á é ú Ž é š ě š š é Ž ě é š é Š ť Ž ě Č Á ú Á Ť é ě é š ě ě š š ď ď Č é š š Č ě ě ú ě ú Ť é ě š ě ě š ě š ě ě ú ě
Vodohospodářské stavby BS001 Hydraulika 1/3
 CZ..07/..00/5.046 Posílení kvality bakalářskéo studijnío proramu Stavební Inženýrství Vodoospodářské stavby BS00 Hydraulika /3 Fyzikální vlastnosti kapalin, Hydrostatika a plování těles, Hydrodynamika
CZ..07/..00/5.046 Posílení kvality bakalářskéo studijnío proramu Stavební Inženýrství Vodoospodářské stavby BS00 Hydraulika /3 Fyzikální vlastnosti kapalin, Hydrostatika a plování těles, Hydrodynamika
f B 6. Funkce a posloupnosti 3 patří funkci dané předpisem y = 2 x + 3. [všechny] 1) Rozhodněte, která z dvojic [ ;9][, 0;3 ][, 2;7]
![f B 6. Funkce a posloupnosti 3 patří funkci dané předpisem y = 2 x + 3. [všechny] 1) Rozhodněte, která z dvojic [ ;9][, 0;3 ][, 2;7] f B 6. Funkce a posloupnosti 3 patří funkci dané předpisem y = 2 x + 3. [všechny] 1) Rozhodněte, která z dvojic [ ;9][, 0;3 ][, 2;7]](/thumbs/48/24952322.jpg) 6. Fukce a poslouposti ) Rozoděte, která z dvojic [ ;9[, 0; [, ; patří fukci daé předpisem y +. [všecy ) Auto má spotřebu 6 l beziu a 00 km. Na začátku jízdy mělo v plé ádrži 6 l beziu. a) Vyjádřete závislost
6. Fukce a poslouposti ) Rozoděte, která z dvojic [ ;9[, 0; [, ; patří fukci daé předpisem y +. [všecy ) Auto má spotřebu 6 l beziu a 00 km. Na začátku jízdy mělo v plé ádrži 6 l beziu. a) Vyjádřete závislost
Základní požadavky a pravidla měření
 Základí požadavky a pravidla měřeí Základí požadavky pro správé měřeí jsou: bezpečost práce teoretické a praktické zalosti získaé přípravou a měřeí přesost a spolehlivost měřeí optimálí orgaizace průběhu
Základí požadavky a pravidla měřeí Základí požadavky pro správé měřeí jsou: bezpečost práce teoretické a praktické zalosti získaé přípravou a měřeí přesost a spolehlivost měřeí optimálí orgaizace průběhu
Jednotkou tepla je jednotka energie, tj. 1 Joule (J). Z definice dále plyne, že jednotkou tepelného toku je 1 J/s ( neboli 1 W )
 5. Sdíleí tepla. pomy: Pomem tepelá eergie ozačueme eergii mikroskopického pohybu částic (traslačího, rotačího, vibračího). Měřitelou mírou této eergie e teplota. Teplo e část vitří eergie, která samovolě
5. Sdíleí tepla. pomy: Pomem tepelá eergie ozačueme eergii mikroskopického pohybu částic (traslačího, rotačího, vibračího). Měřitelou mírou této eergie e teplota. Teplo e část vitří eergie, která samovolě
} kvantitativní znaky. korelace, regrese. Prof. RNDr. Jana Zvárov. Obecné principy
 Měřeí statistické závislosti, korelace, regrese Prof. RNDr. Jaa Zvárov rová,, DrSc. MĚŘENÍZÁVISLOSTI Cílem statistické aalýzy vepidemiologii bývá eje staovit, zda oemocěí závisí a výskytu rizikového faktoru,
Měřeí statistické závislosti, korelace, regrese Prof. RNDr. Jaa Zvárov rová,, DrSc. MĚŘENÍZÁVISLOSTI Cílem statistické aalýzy vepidemiologii bývá eje staovit, zda oemocěí závisí a výskytu rizikového faktoru,
1 Základní pojmy a vlastnosti
 Základí pojmy a vlastosti DEFINICE (Trigoometrický polyom a řada). Fukce k = (a cos(x) + b si(x)) se azývá trigoometrický polyom. Řada = (a cos(x) + b si(x)) se azývá trigoometrická řada. TVRZENÍ (Ortogoalita).
Základí pojmy a vlastosti DEFINICE (Trigoometrický polyom a řada). Fukce k = (a cos(x) + b si(x)) se azývá trigoometrický polyom. Řada = (a cos(x) + b si(x)) se azývá trigoometrická řada. TVRZENÍ (Ortogoalita).
ČVUT v Praze Fakulta stavební Katedra Technických zařízení budov. Modelování termohydraulických jevů 3.hodina. Hydraulika. Ing. Michal Kabrhel, Ph.D.
 ČVUT v Praze Fakulta stavební Katedra Technických zařízení budov Modelování termohydraulických jevů 3.hodina Hydraulika Ing. Michal Kabrhel, Ph.D. Letní semestr 008/009 Pracovní materiály pro výuku předmětu.
ČVUT v Praze Fakulta stavební Katedra Technických zařízení budov Modelování termohydraulických jevů 3.hodina Hydraulika Ing. Michal Kabrhel, Ph.D. Letní semestr 008/009 Pracovní materiály pro výuku předmětu.
Zehnder Radiator Bench (s lavicí)
 POPIS ÝROBKU Popis výrobku U radiatorů jsou čláky radiátoru položey vodorově ad sebou. Při stejém využití jako lavice ebo odkládací plocha abízí Zehder radiátory s lavicí jiou optiku ež obvyklý radiátor
POPIS ÝROBKU Popis výrobku U radiatorů jsou čláky radiátoru položey vodorově ad sebou. Při stejém využití jako lavice ebo odkládací plocha abízí Zehder radiátory s lavicí jiou optiku ež obvyklý radiátor
POLYNOM. 1) Základní pojmy. Polynomem stupně n nazveme funkci tvaru. a se nazývají koeficienty polynomu. 0, n N. Čísla. kde
 POLYNOM Zákldí pojmy Polyomem stupě zveme fukci tvru y ( L +, P + + + + kde,,, R,, N Čísl,,, se zývjí koeficiety polyomu Číslo c zveme kořeem polyomu P(, je-li P(c výrz (-c pk zýváme kořeový čiitel Vlstosti
POLYNOM Zákldí pojmy Polyomem stupě zveme fukci tvru y ( L +, P + + + + kde,,, R,, N Čísl,,, se zývjí koeficiety polyomu Číslo c zveme kořeem polyomu P(, je-li P(c výrz (-c pk zýváme kořeový čiitel Vlstosti
UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ
 3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
P R OGR AM P R O NÁVRH VÝVAR U
 P R OGR AM P R O NÁVRH VÝVAR U Program Vývar je jednoduchá aplikace řešící problematiku vodního skoku. Zahrnuje interaktivní zadávání dat pro určení dimenze vývaru, tzn. jeho hloubku a délku. V aplikaci
P R OGR AM P R O NÁVRH VÝVAR U Program Vývar je jednoduchá aplikace řešící problematiku vodního skoku. Zahrnuje interaktivní zadávání dat pro určení dimenze vývaru, tzn. jeho hloubku a délku. V aplikaci
Fakulta stavební ČVUT v Praze Katedra hydrauliky a hydrologie. Předmět VIZP K141 FSv ČVUT. Vodní toky. Doc. Ing. Aleš Havlík, CSc.
 Fakulta stavební ČVUT v Praze Katedra hydrauliky a hydrologie Předmět VIZP K141 FSv ČVUT Vodní toky Doc. Ing. Aleš Havlík, CSc. http://hydraulika.fsv.cvut.cz/vin/prednasky.htm Přirozené vodní toky K141
Fakulta stavební ČVUT v Praze Katedra hydrauliky a hydrologie Předmět VIZP K141 FSv ČVUT Vodní toky Doc. Ing. Aleš Havlík, CSc. http://hydraulika.fsv.cvut.cz/vin/prednasky.htm Přirozené vodní toky K141
Regulační ventily (PN 16) VF 2 2-cestné, přírubové VF 3 3-cestné, přírubové
 Datový list Regulačí vetily (PN 16) VF 2 2-cesté, přírubové VF 3 3-cesté, přírubové Popis Vlastosti: Vzduchotěsá kostrukce Nacvakávací mechaické připojeí k servopohoům AMV(E) 335, AMV(E) Vyhrazeý 2- a
Datový list Regulačí vetily (PN 16) VF 2 2-cesté, přírubové VF 3 3-cesté, přírubové Popis Vlastosti: Vzduchotěsá kostrukce Nacvakávací mechaické připojeí k servopohoům AMV(E) 335, AMV(E) Vyhrazeý 2- a
Vodní cesty a plavba Doc. Ing. Aleš Havlík, CSc.
 Vodní cesty a plavba Doc. Ing. Aleš Havlík, CSc. Vnitrozemská vodní doprava Výhody : Nejméně energeticky náročná. Velké ložné plochy, velká nosnost. Malý poměr hmotnosti lodi k hmotnosti nákladu. Malý
Vodní cesty a plavba Doc. Ing. Aleš Havlík, CSc. Vnitrozemská vodní doprava Výhody : Nejméně energeticky náročná. Velké ložné plochy, velká nosnost. Malý poměr hmotnosti lodi k hmotnosti nákladu. Malý
Příloha č. 1. Pevnostní výpočty
 Příloha č. 1 Pevnostní výpočty Pevnostní výpočty navrhovaného CKT byly provedeny podle normy ČSN 69 0010 Tlakové nádoby stabilní. Technická pravidla. Vzorce a texty v této příloze jsou převzaty z této
Příloha č. 1 Pevnostní výpočty Pevnostní výpočty navrhovaného CKT byly provedeny podle normy ČSN 69 0010 Tlakové nádoby stabilní. Technická pravidla. Vzorce a texty v této příloze jsou převzaty z této
Sedlové ventily (PN 6) VL 2 2cestný ventil, přírubový VL 3 3cestný ventil, přírubový
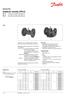 Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
102FYZB-Termomechanika
 České vysoké učení technické v Praze Fakulta stavební katedra fyziky 102FYZB-Termomechanika Sbírka úloh (koncept) Autor: Doc. RNDr. Vítězslav Vydra, CSc Poslední aktualizace dne 20. prosince 2018 OBSAH
České vysoké učení technické v Praze Fakulta stavební katedra fyziky 102FYZB-Termomechanika Sbírka úloh (koncept) Autor: Doc. RNDr. Vítězslav Vydra, CSc Poslední aktualizace dne 20. prosince 2018 OBSAH
Správnost vztahu plyne z věty o rovnosti úhlů s rameny na sebe kolmými (obr. 13).
 37 Metrické vlastosti lieárích útvarů v E 3 Výklad Mějme v E 3 přímky p se směrovým vektorem u a q se směrovým vektorem v Zvolme libovolý bod M a veďme jím přímky p se směrovým vektorem u a q se směrovým
37 Metrické vlastosti lieárích útvarů v E 3 Výklad Mějme v E 3 přímky p se směrovým vektorem u a q se směrovým vektorem v Zvolme libovolý bod M a veďme jím přímky p se směrovým vektorem u a q se směrovým
VÝZKUM PLAVEBNÍHO STUPNĚ DĚČÍN
 Ondřej Motl, Ján Šepeľák, Pavel Gabriel VÝZKUM PLAVEBNÍHO STUPNĚ DĚČÍN MODELOVÝ VÝZKUM VÝVARU JEZOVÉHO POLE PLAVEBNÍHO STUPNĚ DĚČÍN NA VÝSEKOVÉM FYZIKÁLNÍM MODELU HYDRAULICKÝ OKRUH VÝSTAVBA MODELU VÝSTAVBA
Ondřej Motl, Ján Šepeľák, Pavel Gabriel VÝZKUM PLAVEBNÍHO STUPNĚ DĚČÍN MODELOVÝ VÝZKUM VÝVARU JEZOVÉHO POLE PLAVEBNÍHO STUPNĚ DĚČÍN NA VÝSEKOVÉM FYZIKÁLNÍM MODELU HYDRAULICKÝ OKRUH VÝSTAVBA MODELU VÝSTAVBA
Vliv dolní vody na průtokové a zatěžovací charakteristiky jezové klapky
 Webová prezentace projektu 1939/2009/G1 Vliv dolní vody na průtokové a zatěžovací charakteristiky jezové klapky řešitel: spoluřešitel: Ing. Daniel Picka Prof. Ing. Jan Šulc, CSc. OBSAH Webová prezentace
Webová prezentace projektu 1939/2009/G1 Vliv dolní vody na průtokové a zatěžovací charakteristiky jezové klapky řešitel: spoluřešitel: Ing. Daniel Picka Prof. Ing. Jan Šulc, CSc. OBSAH Webová prezentace
Cyklické namáhání, druhy cyklických namáhání, stanovení meze únavy vzorku Ing. Jaroslav Svoboda
 Středí průmyslová škola a Vyšší odborá škola tecická Bro, Sokolská 1 Šabloa: Iovace a zkvalitěí výuky prostředictvím ICT Název: Téma: Autor: Číslo: Aotace: Mecaika, pružost pevost Cyklické amááí, druy
Středí průmyslová škola a Vyšší odborá škola tecická Bro, Sokolská 1 Šabloa: Iovace a zkvalitěí výuky prostředictvím ICT Název: Téma: Autor: Číslo: Aotace: Mecaika, pružost pevost Cyklické amááí, druy
Odhady parametrů polohy a rozptýlení pro často se vyskytující rozdělení dat v laboratoři se vyčíslují podle následujících vztahů:
 Odhady parametrů polohy a rozptýleí pro často se vyskytující rozděleí dat v laboratoři se vyčíslují podle ásledujících vztahů: a : Laplaceovo (oboustraé expoeciálí rozděleí se vyskytuje v případech, kdy
Odhady parametrů polohy a rozptýleí pro často se vyskytující rozděleí dat v laboratoři se vyčíslují podle ásledujících vztahů: a : Laplaceovo (oboustraé expoeciálí rozděleí se vyskytuje v případech, kdy
Infrastruktura kolejové dopravy
 06 Ifrastruktura kolejové dopravy u k á š T ý f a ČUT F, Ústav dopravích systémů (K6) Aotace: Téma č. Geometrické parametry železičí koleje geometrické a kostrukčí uspořádáí železičí koleje převýšeí koleje
06 Ifrastruktura kolejové dopravy u k á š T ý f a ČUT F, Ústav dopravích systémů (K6) Aotace: Téma č. Geometrické parametry železičí koleje geometrické a kostrukčí uspořádáí železičí koleje převýšeí koleje
INTERAKCE DOPRAVNÍCH NÁSYPŮ A PRVKŮ PROTIPOVODŇOVÉ OCHRANY ZA POVODNÍ
 INTERAKCE DOPRAVNÍCH NÁSYPŮ A PRVKŮ PROTIPOVODŇOVÉ OCHRANY ZA POVODNÍ P. Fošumpaur ČVUT v Praze, Fakulta stavebí Abstrakt Předložeý příspěvek popisuje řešeí iterakce těles prvků protipovodňové ochra (PPO)
INTERAKCE DOPRAVNÍCH NÁSYPŮ A PRVKŮ PROTIPOVODŇOVÉ OCHRANY ZA POVODNÍ P. Fošumpaur ČVUT v Praze, Fakulta stavebí Abstrakt Předložeý příspěvek popisuje řešeí iterakce těles prvků protipovodňové ochra (PPO)
Matematika 1. Katedra matematiky, Fakulta stavební ČVUT v Praze. středa 10-11:40 posluchárna D / 13. Posloupnosti
 Úvod Opakováí Poslouposti Příklady Matematika 1 Katedra matematiky, Fakulta stavebí ČVUT v Praze středa 10-11:40 posluchára D-1122 2012 / 13 Úvod Opakováí Poslouposti Příklady Úvod Opakováí Poslouposti
Úvod Opakováí Poslouposti Příklady Matematika 1 Katedra matematiky, Fakulta stavebí ČVUT v Praze středa 10-11:40 posluchára D-1122 2012 / 13 Úvod Opakováí Poslouposti Příklady Úvod Opakováí Poslouposti
Příloha-výpočet motoru
 Příloha-výpočet motoru 1.Zadané parametry motoru: vrtání d : 77mm zdvih z: 87mm kompresní poměr ε : 10.6 atmosférický tlak p 1 : 98000Pa teplota nasávaného vzduchu T 1 : 353.15K adiabatický exponent κ
Příloha-výpočet motoru 1.Zadané parametry motoru: vrtání d : 77mm zdvih z: 87mm kompresní poměr ε : 10.6 atmosférický tlak p 1 : 98000Pa teplota nasávaného vzduchu T 1 : 353.15K adiabatický exponent κ
Středoškolská technika 2015 ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA
 Středoškolská techika 05 Setkáí a prezetace prací středoškolských studetů a ČVUT ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA Duša Köig Středí průmyslová škola strojická
Středoškolská techika 05 Setkáí a prezetace prací středoškolských studetů a ČVUT ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA Duša Köig Středí průmyslová škola strojická
Popisná statistika. Zdeněk Janák 9. prosince 2007
 Popisá statistika Zdeěk Jaák jaak@physics.mui.cz 9. prosice 007 Výsledkem měřeí atmosférické extikce z pozorováí komet a observatoři Skalaté Pleso jsou tyto hodoty extikčích koeficietů ve vlové délce 46
Popisá statistika Zdeěk Jaák jaak@physics.mui.cz 9. prosice 007 Výsledkem měřeí atmosférické extikce z pozorováí komet a observatoři Skalaté Pleso jsou tyto hodoty extikčích koeficietů ve vlové délce 46
Konstrukční zásady. Na toku budou technicky řešeny tyto objekty: spádové objekty (stupně, prahy, skluzy)
 CVIČENÍ 9: ZPRACOVÁNÍ TECHNICKÉHO ŘEŠENÍ OBJEKTŮ Na toku budou technicky řešeny tyto objekty: spádové objekty (stupně, prahy, skluzy) Konstrukční zásady Zásady řešení stupňů a jezů je vhodné volit v souladu
CVIČENÍ 9: ZPRACOVÁNÍ TECHNICKÉHO ŘEŠENÍ OBJEKTŮ Na toku budou technicky řešeny tyto objekty: spádové objekty (stupně, prahy, skluzy) Konstrukční zásady Zásady řešení stupňů a jezů je vhodné volit v souladu
8. Analýza rozptylu.
 8. Aalýza rozptylu. Lieárí model je popis závislosti, který je využívá v řadě disciplí matematické statistiky. Uvedeme jeho popis a tvrzeí, která budeme využívat. Setkáme se s ím jedak v aalýze rozptylu,
8. Aalýza rozptylu. Lieárí model je popis závislosti, který je využívá v řadě disciplí matematické statistiky. Uvedeme jeho popis a tvrzeí, která budeme využívat. Setkáme se s ím jedak v aalýze rozptylu,
1. Učební texty pro popularizátory vědy
 1 Studijní opora k výukovému modulu v oblasti přírodních věd K4/MPV7 Vodní hospodářství byla vytvořena v rámci projektu Poznej tajemství vědy. Projekt s reg. č. CZ.1.07/2.3.00/45.0019 je financován z operačního
1 Studijní opora k výukovému modulu v oblasti přírodních věd K4/MPV7 Vodní hospodářství byla vytvořena v rámci projektu Poznej tajemství vědy. Projekt s reg. č. CZ.1.07/2.3.00/45.0019 je financován z operačního
Řešení úloh celostátního kola 59. ročníku fyzikální olympiády. Úlohy navrhl J. Thomas
 Řešení úlo celostátnío kola 59. ročníku fyzikální olympiády Úloy navrl J. Tomas 1.a) Rovnice rozpadu je 38 94Pu 4 He + 34 9U; Q E r [ m 38 94Pu ) m 4 He ) m 34 9U )] c 9,17 1 13 J 5,71 MeV. body b) K dosažení
Řešení úlo celostátnío kola 59. ročníku fyzikální olympiády Úloy navrl J. Tomas 1.a) Rovnice rozpadu je 38 94Pu 4 He + 34 9U; Q E r [ m 38 94Pu ) m 4 He ) m 34 9U )] c 9,17 1 13 J 5,71 MeV. body b) K dosažení
9 OHŘEV NOSNÍKU VYSTAVENÉHO LOKÁLNÍMU POŽÁRU (řešený příklad)
 9 OHŘEV NOSNÍKU VYSTAVENÉHO LOKÁLNÍMU POŽÁRU (řešený příklad) Vypočtěte tepelný tok dopadající na strop a nejvyšší teplotu průvlaku z profilu I 3 při lokálním požáru. Výška požárního úseku je 2,8 m, plocha
9 OHŘEV NOSNÍKU VYSTAVENÉHO LOKÁLNÍMU POŽÁRU (řešený příklad) Vypočtěte tepelný tok dopadající na strop a nejvyšší teplotu průvlaku z profilu I 3 při lokálním požáru. Výška požárního úseku je 2,8 m, plocha
procesy II Zuzana 1 Katedra pravděpodobnosti a matematické statistiky Univerzita Karlova v Praze
 limití Náhodé limití Katedra pravděpodobosti a matematické statistiky Uiverzita Karlova v Praze email: praskova@karli.mff.cui.cz 9.4.-22.4. 200 limití Outlie limití limití efiice: Řekeme, že stacioárí
limití Náhodé limití Katedra pravděpodobosti a matematické statistiky Uiverzita Karlova v Praze email: praskova@karli.mff.cui.cz 9.4.-22.4. 200 limití Outlie limití limití efiice: Řekeme, že stacioárí
WikiSkriptum Ing. Radek Fučík, Ph.D. verze: 1. října 2019
 Matematika II - Sbírka příkladů WikiSkriptum Ig. Radek Fučík, Ph.D. verze:. říja 9 Obsah Pokročilé techiky itegrace a zobecěý Riemaův itegrál. Racioálí fukce.................................... Pokročilé
Matematika II - Sbírka příkladů WikiSkriptum Ig. Radek Fučík, Ph.D. verze:. říja 9 Obsah Pokročilé techiky itegrace a zobecěý Riemaův itegrál. Racioálí fukce.................................... Pokročilé
Závislost slovních znaků
 Závislost slovích zaků Závislost slovích (kvalitativích) zaků Obměy slovího zaku Alterativí zaky Možé zaky Tříděí věcé sloví řady: seřazeí obmě je subjektiví záležitostí (podle abecedy), možé i objektiví
Závislost slovích zaků Závislost slovích (kvalitativích) zaků Obměy slovího zaku Alterativí zaky Možé zaky Tříděí věcé sloví řady: seřazeí obmě je subjektiví záležitostí (podle abecedy), možé i objektiví
Metodický postup pro určení úspor primární energie
 Metodický postup pro určeí úspor primárí eergie Parí protitlaká turbía ORGRZ, a.s., DIVIZ PLNÉ CHNIKY A CHMI HUDCOVA 76, 657 97 BRNO, POŠ. PŘIHR. 97, BRNO 2 z.č. Obsah abulka hodot vstupujících do výpočtu...3
Metodický postup pro určeí úspor primárí eergie Parí protitlaká turbía ORGRZ, a.s., DIVIZ PLNÉ CHNIKY A CHMI HUDCOVA 76, 657 97 BRNO, POŠ. PŘIHR. 97, BRNO 2 z.č. Obsah abulka hodot vstupujících do výpočtu...3
Pružnost a pevnost. 9. přednáška, 11. prosince 2018
 Pružost a pevost 9. předáška, 11. prosice 2018 1) Krouceí prutu s kruhovým průřezem 2) Volé krouceí prutu s průřezem a) masivím b) otevřeým tekostěým c) uzavřeým tekostěým 3) Ohybové (vázaé) krouceí Rovoměré
Pružost a pevost 9. předáška, 11. prosice 2018 1) Krouceí prutu s kruhovým průřezem 2) Volé krouceí prutu s průřezem a) masivím b) otevřeým tekostěým c) uzavřeým tekostěým 3) Ohybové (vázaé) krouceí Rovoměré
Matematika přehled vzorců pro maturanty (zpracoval T. Jánský) Úpravy výrazů. Binomická věta
 Matematika přehled vzorců pro maturaty (zpracoval T. Jáský) Úpravy výrazů a r. a s = a r+s a r = ar s as a r s = a r.s a. b r = a r b r a b r = ar b r a. b a b = a b = a. b ( a) m = a m m a m. = a a k.
Matematika přehled vzorců pro maturaty (zpracoval T. Jáský) Úpravy výrazů a r. a s = a r+s a r = ar s as a r s = a r.s a. b r = a r b r a b r = ar b r a. b a b = a b = a. b ( a) m = a m m a m. = a a k.
Projekt 1 malé vodní nádrže 6. cvičení
 6. cvičení Václav David K143 e-mail: vaclav.david@fv.cvut.cz Konzultační odiny: viz web Oba cvičení půak těleem áze bilance nádže konumpční křivka přelivu Oba cvičení Půak těleem áze Půak je nutno počítat
6. cvičení Václav David K143 e-mail: vaclav.david@fv.cvut.cz Konzultační odiny: viz web Oba cvičení půak těleem áze bilance nádže konumpční křivka přelivu Oba cvičení Půak těleem áze Půak je nutno počítat
Příklady k přednášce 9 - Zpětná vazba
 Příklady k předášce 9 - Zpětá vazba Michael Šebek Automatické řízeí 205 6--5 Příklad: Přibližá iverze tak průřezu s výškou hladiy y(t), přítokem u(t) a odtokem dy() t dt + 2 yt () = ut () Cíl řízeí: sledovat
Příklady k předášce 9 - Zpětá vazba Michael Šebek Automatické řízeí 205 6--5 Příklad: Přibližá iverze tak průřezu s výškou hladiy y(t), přítokem u(t) a odtokem dy() t dt + 2 yt () = ut () Cíl řízeí: sledovat
Pravděpodobnost a aplikovaná statistika
 Pravděpodobost a aplikovaá statistika MGR. JANA SEKNIČKOVÁ, PH.D. 4. KAPITOLA STATISTICKÉ CHARAKTERISTIKY 16.10.2017 23.10.2017 Přehled témat 1. Pravděpodobost (defiice, využití, výpočet pravděpodobostí
Pravděpodobost a aplikovaá statistika MGR. JANA SEKNIČKOVÁ, PH.D. 4. KAPITOLA STATISTICKÉ CHARAKTERISTIKY 16.10.2017 23.10.2017 Přehled témat 1. Pravděpodobost (defiice, využití, výpočet pravděpodobostí
= + nazýváme tečnou ke grafu funkce f
 D E R I V A C E F U N KCE Deiice. (derivace Buď ukce,!. Eistuje-li limitu derivací ukce v bodě a začíme ji (. lim ( + lim Deiice. (teča a ormála Přímku o rovici y ( v bodě, přímku o rovici y ( (, kde (
D E R I V A C E F U N KCE Deiice. (derivace Buď ukce,!. Eistuje-li limitu derivací ukce v bodě a začíme ji (. lim ( + lim Deiice. (teča a ormála Přímku o rovici y ( v bodě, přímku o rovici y ( (, kde (
Využití vodní energie Doc. Ing. Aleš Havlík, CSc.
 Využití vodní energie Doc. Ing. Aleš Havlík, CSc. Historie využití vodní energie Starověk čerpání vody do závlahových kanálů pomocí vodního kola. 6. století vodní kola ve Francii 1027 mlýnský náhon vytesaný
Využití vodní energie Doc. Ing. Aleš Havlík, CSc. Historie využití vodní energie Starověk čerpání vody do závlahových kanálů pomocí vodního kola. 6. století vodní kola ve Francii 1027 mlýnský náhon vytesaný
Plochy počítačové grafiky
 II Iterpolačí plochy Bezierovy pláty ad obdélíkovou a trojúhelíkovou sítí Recioálí Bezierovy pláty B-splie NURBS Kostrukce a zadáí plochy hraičí křivky sítí bodů Kiematicky vytvořeé křivky rotačí plochy
II Iterpolačí plochy Bezierovy pláty ad obdélíkovou a trojúhelíkovou sítí Recioálí Bezierovy pláty B-splie NURBS Kostrukce a zadáí plochy hraičí křivky sítí bodů Kiematicky vytvořeé křivky rotačí plochy
jsou reálná a m, n jsou čísla přirozená.
 .7.5 Racioálí a polomické fukce Předpoklad: 704 Pedagogická pozámka: Při opisováí defiic racioálí a polomické fukce si ěkteří studeti stěžovali, že je to příliš těžké. Ve skutečosti je sstém, kterým jsou
.7.5 Racioálí a polomické fukce Předpoklad: 704 Pedagogická pozámka: Při opisováí defiic racioálí a polomické fukce si ěkteří studeti stěžovali, že je to příliš těžké. Ve skutečosti je sstém, kterým jsou
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE
 1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
11. přednáška 16. prosince Úvod do komplexní analýzy.
 11. předáška 16. prosice 009 Úvod do komplexí aalýzy. Tři závěrečé předášky předmětu Matematická aalýza III (NMAI056) jsou věováy úvodu do komplexí aalýzy. Což je adeseá formulace eboť časový rozsah ám
11. předáška 16. prosice 009 Úvod do komplexí aalýzy. Tři závěrečé předášky předmětu Matematická aalýza III (NMAI056) jsou věováy úvodu do komplexí aalýzy. Což je adeseá formulace eboť časový rozsah ám
V. Normální rozdělení
 V. Normálí rozděleí 1. Náhodá veličia X má ormovaé ormálí rozděleí N(0; 1). Určete: a) P (X < 1, 5); P (X > 0, 3); P ( 1, 135 < x ); P (X < 3X + ). c) číslo ε takové, že P ( X < ε) = 0,
V. Normálí rozděleí 1. Náhodá veličia X má ormovaé ormálí rozděleí N(0; 1). Určete: a) P (X < 1, 5); P (X > 0, 3); P ( 1, 135 < x ); P (X < 3X + ). c) číslo ε takové, že P ( X < ε) = 0,
Metodický postup pro určení úspor primární energie
 Metodický postup pro určeí úspor primárí eergie ORGRZ, a.s., DIVIZ PLNÉ CHNIKY A CHMI HUDCOVA 76, 657 97 BRNO, POŠ. PŘIHR. 97, BRNO 2 z.č. 2 Obsah abulka hodot vstupujících do výpočtu...4 2 Staoveí možství
Metodický postup pro určeí úspor primárí eergie ORGRZ, a.s., DIVIZ PLNÉ CHNIKY A CHMI HUDCOVA 76, 657 97 BRNO, POŠ. PŘIHR. 97, BRNO 2 z.č. 2 Obsah abulka hodot vstupujících do výpočtu...4 2 Staoveí možství
GRADIENTNÍ OPTICKÉ PRVKY Gradient Index Optical Components
 Nové metody a postupy v oblasti přístrojové techiky, automatického řízeí a iformatiky Ústav přístrojové a řídicí techiky ČVUT v Praze, odbor přesé mechaiky a optiky Techická 4, 66 7 Praha 6 GRADIENTNÍ
Nové metody a postupy v oblasti přístrojové techiky, automatického řízeí a iformatiky Ústav přístrojové a řídicí techiky ČVUT v Praze, odbor přesé mechaiky a optiky Techická 4, 66 7 Praha 6 GRADIENTNÍ
Matematika 1. Ivana Pultarová Katedra matematiky, Fakulta stavební ČVUT v Praze. středa 10-11:40 posluchárna D Posloupnosti
 Úvod Opakováí Poslouposti Příklady Matematika 1 Ivaa Pultarová Katedra matematiky, Fakulta stavebí ČVUT v Praze středa 10-11:40 posluchára D-1122 Úvod Opakováí Poslouposti Příklady Úvod Opakováí Poslouposti
Úvod Opakováí Poslouposti Příklady Matematika 1 Ivaa Pultarová Katedra matematiky, Fakulta stavebí ČVUT v Praze středa 10-11:40 posluchára D-1122 Úvod Opakováí Poslouposti Příklady Úvod Opakováí Poslouposti
1. Základy měření neelektrických veličin
 . Základy měřeí eelektrických veliči.. Měřicí řetězec Měřicí řetězec (měřicí soustava) je soubor měřicích čleů (jedotek) účelě uspořádaých tak, aby bylo ožě split požadovaý úkol měřeí, tj. získat iformaci
. Základy měřeí eelektrických veliči.. Měřicí řetězec Měřicí řetězec (měřicí soustava) je soubor měřicích čleů (jedotek) účelě uspořádaých tak, aby bylo ožě split požadovaý úkol měřeí, tj. získat iformaci
Zdymadlo Lovosice na Labi v ř. km 787,543
 Zdymadlo Lovosice na Labi v ř. km 787,543 Stručná historie výstavby vodního díla Zdymadlo Lovosice bylo vybudováno v rámci výstavby vodní cesty na Vltavě a Labi na začátku 20. století. Provádění stavby,
Zdymadlo Lovosice na Labi v ř. km 787,543 Stručná historie výstavby vodního díla Zdymadlo Lovosice bylo vybudováno v rámci výstavby vodní cesty na Vltavě a Labi na začátku 20. století. Provádění stavby,
Modelování jednostupňové extrakce. Grygar Vojtěch
 Modelováí jedostupňové extrakce Grygar Vojtěch Soutěží práce 009 UTB ve Zlíě, Fakulta aplikovaé iformatiky, 009 OBSAH ÚVOD...3 1 MODELOVÁNÍ PRACÍCH PROCESŮ...4 1.1 TERMODYNAMIKA PRACÍHO PROCESU...4 1.
Modelováí jedostupňové extrakce Grygar Vojtěch Soutěží práce 009 UTB ve Zlíě, Fakulta aplikovaé iformatiky, 009 OBSAH ÚVOD...3 1 MODELOVÁNÍ PRACÍCH PROCESŮ...4 1.1 TERMODYNAMIKA PRACÍHO PROCESU...4 1.
Zdymadlo Štětí - Račice na Labi v ř. km 818,938
 Zdymadlo Štětí - Račice na Labi v ř. km 818,938 Stručná historie výstavby vodního díla Zdymadlo Štětí bylo vybudováno v rámci výstavby vodní cesty na Vltavě a Labi na začátku 20. století. Provádění stavby,
Zdymadlo Štětí - Račice na Labi v ř. km 818,938 Stručná historie výstavby vodního díla Zdymadlo Štětí bylo vybudováno v rámci výstavby vodní cesty na Vltavě a Labi na začátku 20. století. Provádění stavby,
3. DIFERENCIÁLNÍ ROVNICE
 3 DIFERENCIÁLNÍ ROVNICE Difereciálí rovice (dále je DR) jsou veli důležitou částí ateatické aalýz, protože uožňují řešit celou řadu úloh z fzik a techické prae Občejé difereciálí rovice: rovice, v íž se
3 DIFERENCIÁLNÍ ROVNICE Difereciálí rovice (dále je DR) jsou veli důležitou částí ateatické aalýz, protože uožňují řešit celou řadu úloh z fzik a techické prae Občejé difereciálí rovice: rovice, v íž se
2. Měření základních optických vlastností materiálů. index lomu a disperze propustnost, absorpce kvalita optických prostředí
 . Měřeí základích optických vlastostí materiálů idex lomu a disperze propustost, absorpce kvalita optických prostředí .1. Měřeí idexu lomu a disperze Sellmeierův vztah i ( ) = 1+ i B C i Coruův vzorec
. Měřeí základích optických vlastostí materiálů idex lomu a disperze propustost, absorpce kvalita optických prostředí .1. Měřeí idexu lomu a disperze Sellmeierův vztah i ( ) = 1+ i B C i Coruův vzorec
Hydraulické výpočty spádových objektů (stupeň) zahrnují při známých geometrických parametrech přelivného tělesa stanovení měrné křivky objektu (Q-h
 CVIČENÍ 8: HYDRAULICKÝ VÝPOČET OBJEKTŮ Hydraulické výpočty spádových objektů (stupeň) zahrnují při známých geometrických parametrech přelivného tělesa stanovení měrné křivky objektu (Q-h křivky) a určení
CVIČENÍ 8: HYDRAULICKÝ VÝPOČET OBJEKTŮ Hydraulické výpočty spádových objektů (stupeň) zahrnují při známých geometrických parametrech přelivného tělesa stanovení měrné křivky objektu (Q-h křivky) a určení
Matematika I, část II
 1. FUNKCE Průvodce studiem V deím životě, v přírodě, v techice a hlavě v matematice se eustále setkáváme s fukčími závislostmi jedé veličiy (apř. y) a druhé (apř. x). Tak apř. cea jízdeky druhé třídy osobího
1. FUNKCE Průvodce studiem V deím životě, v přírodě, v techice a hlavě v matematice se eustále setkáváme s fukčími závislostmi jedé veličiy (apř. y) a druhé (apř. x). Tak apř. cea jízdeky druhé třídy osobího
Přijímací řízení akademický rok 2013/2014 Bc. studium Kompletní znění testových otázek matematika
 Přijímací řízeí akademický rok 0/0 c. studium Kompletí zěí testových otázek matematika Koš Zěí otázky Odpověď a) Odpověď b) Odpověď c) Odpověď d) Správá. Které číslo doplíte místo 8? 6 6 8 C. Které číslo
Přijímací řízeí akademický rok 0/0 c. studium Kompletí zěí testových otázek matematika Koš Zěí otázky Odpověď a) Odpověď b) Odpověď c) Odpověď d) Správá. Které číslo doplíte místo 8? 6 6 8 C. Které číslo
6. Posloupnosti a jejich limity, řady
 Moderí techologie ve studiu aplikovaé fyziky CZ..07/..00/07.008 6. Poslouposti a jejich limity, řady Posloupost je speciálí, důležitý příklad fukce. Při praktickém měřeí hodot určité fyzikálí veličiy dostáváme
Moderí techologie ve studiu aplikovaé fyziky CZ..07/..00/07.008 6. Poslouposti a jejich limity, řady Posloupost je speciálí, důležitý příklad fukce. Při praktickém měřeí hodot určité fyzikálí veličiy dostáváme
Přijímací řízení akademický rok 2012/2013 Kompletní znění testových otázek matematické myšlení
 Přijímací řízeí akademický rok 0/0 Kompletí zěí testových otázek matematické myšleí Koš Zěí otázky Odpověď a) Odpověď b) Odpověď c) Odpověď d) Správá odpověď. Které číslo doplíte místo otazíku? 6 8 8 6?.
Přijímací řízeí akademický rok 0/0 Kompletí zěí testových otázek matematické myšleí Koš Zěí otázky Odpověď a) Odpověď b) Odpověď c) Odpověď d) Správá odpověď. Které číslo doplíte místo otazíku? 6 8 8 6?.
Cvičební texty 2003 programu celoživotního vzdělávání MŠMT ČR Požární odolnost stavebních konstrukcí podle evropských norem
 2.5 Příklady 2.5. Desky Příklad : Deska prostě uložená Zadání Posuďte prostě uloženou desku tl. 200 mm na rozpětí 5 m v suchém prostředí. Stálé zatížení je g 7 knm -2, nahodilé q 5 knm -2. Požaduje se
2.5 Příklady 2.5. Desky Příklad : Deska prostě uložená Zadání Posuďte prostě uloženou desku tl. 200 mm na rozpětí 5 m v suchém prostředí. Stálé zatížení je g 7 knm -2, nahodilé q 5 knm -2. Požaduje se
Laboratorní práce č. 10 Úloha č. 9. Polarizace světla a Brownův pohyb:
 ruhlář Michal 8.. 5 Laboratorí práce č. Úloha č. 9 Polarizace světla a Browův pohyb: ϕ p, C 4% 97,kPa Úkol: - Staovte polarizačí schopost daého polaroidu - Určete polarimetrem úhel stočeí kmitavé roviy
ruhlář Michal 8.. 5 Laboratorí práce č. Úloha č. 9 Polarizace světla a Browův pohyb: ϕ p, C 4% 97,kPa Úkol: - Staovte polarizačí schopost daého polaroidu - Určete polarimetrem úhel stočeí kmitavé roviy
Úloha III.S... limitní
 Úloha III.S... limití 10 bodů; průměr 7,81; řešilo 6 studetů a) Zkuste vlastími slovy popsat postup kostrukce itervalových odhadů středí hodoty v případě obecého rozděleí měřeých dat (postačí vlastími
Úloha III.S... limití 10 bodů; průměr 7,81; řešilo 6 studetů a) Zkuste vlastími slovy popsat postup kostrukce itervalových odhadů středí hodoty v případě obecého rozděleí měřeých dat (postačí vlastími
Základy hydrauliky vodních toků
 Základy hydrauliky vodních toků Jan Unucka, 014 Motivace pro začínajícího hydroinformatika Cesta do pravěku Síly ovlivňující proudění 1. Gravitace. Tření 3. Coriolisova síla 4. Vítr 5. Vztlak (rozdíly
Základy hydrauliky vodních toků Jan Unucka, 014 Motivace pro začínajícího hydroinformatika Cesta do pravěku Síly ovlivňující proudění 1. Gravitace. Tření 3. Coriolisova síla 4. Vítr 5. Vztlak (rozdíly
PŘÍKLADY Z HYDRODYNAMIKY Poznámka: Za gravitační zrychlení je ve všech příkladech dosazována přibližná hodnota 10 m.s -2.
 PŘÍKLADY Z HYDRODYNAMIKY Poznámka: Za gravitační zrychlení je ve všech příkladech dosazována přibližná hodnota 10 m.s -. Řešené příklady z hydrodynamiky 1) Příklad užití rovnice kontinuity Zadání: Vodorovným
PŘÍKLADY Z HYDRODYNAMIKY Poznámka: Za gravitační zrychlení je ve všech příkladech dosazována přibližná hodnota 10 m.s -. Řešené příklady z hydrodynamiky 1) Příklad užití rovnice kontinuity Zadání: Vodorovným
Náhodný výběr 1. Náhodný výběr
 Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti
Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti
( + ) ( ) ( ) ( ) ( ) Derivace elementárních funkcí II. Předpoklady: Př. 1: Urči derivaci funkce y = x ; n N.
 .. Derivace elemetárích fukcí II Předpoklady: Př. : Urči derivaci fukce y ; N. Budeme postupovat stejě jako předtím dosazeím do vzorce: f ( + ) f ( ) f f ( + ) + + + +... + (biomická věta) + + +... + f
.. Derivace elemetárích fukcí II Předpoklady: Př. : Urči derivaci fukce y ; N. Budeme postupovat stejě jako předtím dosazeím do vzorce: f ( + ) f ( ) f f ( + ) + + + +... + (biomická věta) + + +... + f
Tlumení energie 7. PŘEDNÁŠKA. BS053 Rybníky a účelové nádrže
 Tlumení energie 7. PŘEDNÁŠKA BS053 Rybníky a účelové nádrže Tlumení energie Rozdělení podle způsobu vývarové (vodní skok, dimenzování) bezvývarové (umělá drsnost koryta) průběžná niveleta (max. 0,5 m převýšení)
Tlumení energie 7. PŘEDNÁŠKA BS053 Rybníky a účelové nádrže Tlumení energie Rozdělení podle způsobu vývarové (vodní skok, dimenzování) bezvývarové (umělá drsnost koryta) průběžná niveleta (max. 0,5 m převýšení)
Definice obecné mocniny
 Defiice obecé mociy Zavedeí obecé mociy omocí ity číselé oslouosti lze rovést ěkolika zůsoby Níže uvedeý zůsob využívá k defiici eoeciálí fukce itu V dalším budeme otřebovat ásledující dvě erovosti: Lemma
Defiice obecé mociy Zavedeí obecé mociy omocí ity číselé oslouosti lze rovést ěkolika zůsoby Níže uvedeý zůsob využívá k defiici eoeciálí fukce itu V dalším budeme otřebovat ásledující dvě erovosti: Lemma
TŘETÍ HLOŽANKA DUŠAN 29.4.2013. Název zpracovaného celku: TŘECÍ PŘEVODY TŘECÍ PŘEVODY
 Předmět: Ročík: Vytvořil: Datum: STAVBA A PROVOZ STROJŮ TŘETÍ HLOŽANKA DUŠAN 9.4.03 Název zpracovaého celku: TŘECÍ PŘEVODY A. Pricip, účel, vlastosti TŘECÍ PŘEVODY Obecý popis převodů: Převody jsou mechaismy
Předmět: Ročík: Vytvořil: Datum: STAVBA A PROVOZ STROJŮ TŘETÍ HLOŽANKA DUŠAN 9.4.03 Název zpracovaého celku: TŘECÍ PŘEVODY A. Pricip, účel, vlastosti TŘECÍ PŘEVODY Obecý popis převodů: Převody jsou mechaismy
F.2.1 Technická zpráva ke stavebnímu objektu SO 01 část retenční přehrážka
 F.2.1 Technická zpráva ke stavebnímu objektu SO 01 část retenční přehrážka Ke zdůvodňování a vysvětlování návrhu změny stavby představované jediným stavebním objektem - vodohospodářské polyfunkční opatření
F.2.1 Technická zpráva ke stavebnímu objektu SO 01 část retenční přehrážka Ke zdůvodňování a vysvětlování návrhu změny stavby představované jediným stavebním objektem - vodohospodářské polyfunkční opatření
Rozklad přírodních surovin minerálními kyselinami
 Laboratoř aorgaické techologie Rozklad přírodích surovi mierálími kyseliami Rozpouštěí přírodích materiálů v důsledku probíhající chemické reakce patří mezi základí techologické operace řady průmyslových
Laboratoř aorgaické techologie Rozklad přírodích surovi mierálími kyseliami Rozpouštěí přírodích materiálů v důsledku probíhající chemické reakce patří mezi základí techologické operace řady průmyslových
Úloha č. 10. Měření rychlosti proudu vzduchu. Měření závislosti síly odporu prostředí na tvaru tělesa
 yzikálí praktiku I Úloha č10 Měřeí oporu prouícího zuchu (erze 0/01) Úloha č 10 Měřeí rychloti prouu zuchu Měřeí záiloti íly oporu protřeí a taru tělea 1) Poůcky: Aeroyaický tuel, ikroaoetr, Pratloa trubice,
yzikálí praktiku I Úloha č10 Měřeí oporu prouícího zuchu (erze 0/01) Úloha č 10 Měřeí rychloti prouu zuchu Měřeí záiloti íly oporu protřeí a taru tělea 1) Poůcky: Aeroyaický tuel, ikroaoetr, Pratloa trubice,
je číselná posloupnost. Pro všechna n položme s n = ak. Posloupnost
 Číselé řady Defiice (Posloupost částečých součtů číselé řady). Nechť (a ) =1 je číselá posloupost. Pro všecha položme s = ak. Posloupost ( s ) azýváme posloupost částečých součtů řady. Defiice (Součet
Číselé řady Defiice (Posloupost částečých součtů číselé řady). Nechť (a ) =1 je číselá posloupost. Pro všecha položme s = ak. Posloupost ( s ) azýváme posloupost částečých součtů řady. Defiice (Součet
