Infrastruktura kolejové dopravy
|
|
|
- Arnošt Vávra
- před 8 lety
- Počet zobrazení:
Transkript
1 06 Ifrastruktura kolejové dopravy u k á š T ý f a ČUT F, Ústav dopravích systémů (K6) Aotace: Téma č. Geometrické parametry železičí koleje geometrické a kostrukčí uspořádáí železičí koleje převýšeí koleje a jeho optimálí hodota ejmeší poloměr směrového oblouku odvozeí předpisů a parametrů vzestupic a přechodic stejosměré a protisměré oblouky bez mezipřímé Geometrické parametry koleje (GPK) kostrukčí uspořádáí koleje (popisuje vzájemou polohu kolejic v koleji): rozchod koleje převýšeí vzestupice geometrické uspořádáí koleje: přechodice kružicový oblouk mezipřímá podélý sklo (vč. zaobleí lomu ivelety) prostorová poloha koleje --
2 06 Charakteristické body koleje Zajištěí prostorové polohy koleje Zajišťovací začky druhy: sloupkové (železobetoový sloupek) kozolové hřebové --
3 06 Kostr. a geometr. uspořádaí koleje příčý směr svislý směr geometrické uspořádáí koleje (GUK) - relativí odchylky od středice geometrické veličiy směr koleje (S, SP, SK) podélá výška koleje (, P, K) kostrukčí uspořádáí koleje (KUK) - přímé míry a koleji základí veličiy rozchod koleje (K) převýšeí koleje (PK) odvozeé veličiy (ze základích) změa rozchodu koleje a m délky koleje (Z) zborceí koleje (ZK) S / SP směr levého/pravého kolejicového pásu SK směr koleje v ose / P podélá výška levého/pravého kolejicového pásu K podélá výška koleje v ose Geometrické parametry koleje (GPK) a železici jedotka s aklápěcími skříěmi (NS) vozů: osobí souprava v provozu edělitelá, jejíž všechy vozy mají takovou kostrukci, že jejich skříň se vůči podvozkům může ve směrových obloucích příčě otáčet (aklopit) GPK se posuzují vždy podle ejvyšší povoleé rychlosti jízdy vozidla bez aklápěcích skříí v daém úseku koleje pro ejvyšší povoleý edostatek převýšeí traťová rychlost (pro jedotky s NS se provádí samostaté posouzeí) v jedom úseku koleje může být pro růzé skupiy vlaků povolea jiá ejvyšší rychlost (více rychlostíků eproměých ávěstidel) -3-
4 06 Pravidla pro GPK v Č ČSN Kostrukčí a geometrické uspořádáí koleje železičích drah a její prostorová poloha Část : Projektováí. X/008 slučuje a aplikuje a Č: dvě EN 3803 o ávrhu GPK + techické specifikace pro iteroperabilitu pro subsystém ifrastruktura pro kovečí i vysokorychlostí systém platí pro rychlosti km/h (zahruje v sobě árodí ustaoveí pro rychlosti 0 80 km/h) stavebí a techický řád drah (vyhláška M k zákou o dráhách) umožňuje v Č ejvýše 00 km/h ČSN Kostrukčí a geometrické uspořádáí koleje železičích drah a její prostorová poloha Část : Stavba a přejímka, provoz a údržba. X/009 + změa Z Typy (hladiy) hodot veliči GPK. Stadardí hodota (X ): vymezuje (shora/zdola) iterval doporučeých hodot, mají být dodržey, zaručují komfort jízdy i optimálí údržbu koleje. Mezí hodota (X lim ): emá být překročea, překročeí je možé zejm. kvůli omezeí ebo vyloučeí místího sížeí projektovaé rychlosti, při překročeí dochází k omezeí komfortu cestujících a/ebo ke zvýšeí ákladů a údržbu trati, překročeí musí být odsouhlaseo vlastíkem ifrastruktury 3. Maximálí/miimálí hodota (X max / X mi ): esmí být překročea, použije se je tehdy, když elze jiak Neměly by se avrhovat kombiace hodot překračující X lim! -4-
5 06 Typy (hladiy) hodot veliči GPK ozsah hodot veličiy (parametru) X omezovaého shora: 0 doporučeé hodoty, zaruče komfort a zároveň optimálí údržba X X lim X max stadardí je pro omezeí ebo vyloučeí místího sížeí rychlosti, mírě omeze komfort ebo zvýšey áklady a údržbu mezí je v ezbytých případech (eexistuje jié řešeí), omeze komfort ebo zvýšey áklady a údržbu, utý souhlas vlastíka ifrastruktury maximálí maximálí hodota esmí být při projektováí překročea Nevyrovaé příčé zrychleí v roviě koleje, působící a jedoucí kolejové vozidlo -5-
6 06 Převýšeí koleje všechy vlaky jezdí obloukem stejou rychlostí ( os ) avrhuje se teoretické převýšeí: eq,8 [] = mm [] = km/h [] = m což astává a tratích určeých: výhradě pro osobí dopravu především pro ákladí dopravu pro smíšeý provoz se stejou rychlostí osobích i ákladích vlaků (zpravidla a tratích s ízkou traťovou rychlostí, kterou běžě dosahují i ákladí vlaky) Převýšeí koleje vlaky projíždí oblouk růzou rychlostí ( < os ) avrhuje se obecé převýšeí (vč. N a mi ) při dodržeí dalších podmíek; potom platí: os. vlaky projíždí oblouk s edostatkem převýšeí I ákl. vlaky projíždí oblouk s přebytkem převýšeí E I E eq os,8,8 os eq,8 eq eq, 8-6-
7 06 Převýšeí koleje doporučeé převýšeí: c N 0 < c <,8 miimálí převýšeí: mi, 8 I max Přebytek převýšeí emá (a rozdíl od edostatku převýšeí) přímý vliv a bezpečost ovlivňuje je ároky a údržbu při časté jízdě rychlostí. Staoveí součiitele c pro doporučeá převýšeí a vztah mezi doporučeým převýšeím a edostatkem převýšeí -7-
8 06 Převýšeí koleje upozorěí k teoretickému a doporučeému převýšeí eq a N,,3 : výpočet staoveými vzorci automaticky ezaručuje dodržeí edostatku převýšeí uto vždy prověřit pro teoretické převýšeí: lim ; lim lim,8 50,8,7 omezeí v obloucích < 75 m při lim = 50 mm a < 90 m při max = 60 mm (zabráěí vykolejeí ákladích vozů): 50,5 Hodoty převýšeí mimo kolejová rozvětveí hladiy hodot převýšeí : mi = 0 mm lim = 50 mm: pro tratě s provozím zatížeím do 0 mil. t/rok lim = 0 mm: pro tratě s provozím zatížeím ad 0 mil. t/rok lim = 60 mm: v místě ástupiště max = 60 mm (zároveň 90 m) max = 0 mm: v místě ástupiště hladiy hodot přebytku převýšeí E: E lim = 80 mm E max = 0 mm vztah mezi os a při zadaém, I a E: os E I,8,8 I E I I os E -8-
9 06 Převýšeí koleje Převýšeí mimo kolejová rozvětveí: limití hodoty edostatku převýšeí I: ychlost [km/h] Stadardí hodota I [mm] Mezí hodota I lim [mm] Maximálí hodota I max [mm] (30 c ) < (50 b ) 30 < (50 a,b ) < a ze pouze pro vozidla s omezeými silovými účiky a trať (max. otost a ápravu 0 t) b ze pouze pro vozidla vlaků osobí dopravy c ze pouze pro poloměr směrového oblouku 50 m. poloměrech < 50 m lze projektovat I max = 30 mm pouze pro vozidla s omezeými silovými účiky a trať (max. otost a ápravu 8 t) Nejvyšší rychlost v oblouku -9-
10 06 Převýšeí v oblouku Optimálí hodota převýšeí ) ze zalosti skladby vlaků, resp. jejich otosti a rychlosti tj. otost vozidel i ákladu -0-
11 06 Optimálí hodota převýšeí ) dle max. a mi. rychlosti vlaků (osobí vlaky max. /traťová/ rychlost, P-vlaky mi. rychl.): Optimálí hodota převýšeí ) dle max. a mi. rychlosti vlaků (osobí vlaky max. /traťová/ rychlost, P-vlaky mi. rychl.): M M eq, os eq, M I,8 I E,8 E M os M M --
12 06 Optimálí hodota převýšeí Optimálí hodota převýšeí 3) použitím doporučeého převýšeí dle ČSN: 7, N 6,5 N 5,9 N3 pro 0 km/h pro 0 km/h < 60 km/h pro 60 km/h < 00 km/h Omezeí max. doporuč. převýšeí pro I = 80 mm: --
13 06 Nejmeší poloměr oblouku při zohleděí přebytku převýšeí (rychlosti jízdy běžých ejpomalejších vlaků) dm, I,8 I olí idexy: dm dolí mez (lim/mi) horí mez (lim/max) lim/mi/max dle kokr. případu dm, E dm, E,8,8 dm E I E I,8 ; I dm max dm, I ; dm, E E dm,8 dm, E,8 dm I E Nejmeší poloměr oblouku dm, krit E I -3-
14 06 Přechodice přechodici tvaru klotoidy ebo kubické paraboly lze vyechat v ásledujících případech: ve stísěých poměrech při rychlosti do 60 km/h vč. áhlá změa edostatku převýšeí je meší ež: (pro > 30 km/h se obvykle avrhují oblouky s přechodicemi) Hladiy áhlé změy edostatku převýšeí I [mm] v traťových a hl. kolejích ychlost [km/h] Stadard. hodota I Mezí hodota I lim < < < I,8 Max. hodota I max 00 +: protisměré oblouky oblouk a přímá: I,8 -: stejosměré oblouky Převýšeí koleje oporučeé poloměry oblouků v obloucích bez převýšeí a bez přechodic: rychlost [km/h] edostatek převýšeí I [mm] poloměr oblouku [m] ,36 00 < ,95 70 < , < ,47 Při rychlosti větší ež 00 km/h je vhodé využít hodoty podle tabulky pouze pro změu osové vzdáleosti ebo v jiých ezbytých případech, v ostatích případech je účelější využití přechodic. -4-
15 06 Odvozeí mi. délky lieárí vzestupice a přechodice tvaru klotoidy Odvozeí předpisu fukce pro vzestupici a přechodice podle Blosse -5-
16 06 ieárí vzestupice a přechodice přímková vzestupice + klotoida (ev. poecháí kub. par.) dl. krají vzestupice v ose: ebo d 000 d 3, 6 Součiitel sklou vzestupice [-], časová změa převýšeí d/dt [mm/s] d dt ychlost Stadardí Mezí Max. / Mi. [km/h] (d/dt) lim (d/dt) lim mi (d/dt) max 80 6 a 46,30 a 6 b 46,30 b 80 < 0 0 7, , ,30 0 < ,7 7 39,68 60 < 00 3,5 00 < , ,7 a Současě sklo lieárí vzestupice emá být větší ež :445. b Současě sklo lieárí vzestupice esmí být větší ež :400. ieárí vzestupice a přechodice mi. dl. li. přechodice: k dl. krají přechodice v ose: 0, 7 k I I 000 a zároveň k 0 m ebo k I 3, 6 di dt ychlost [km/h] Součiitel změy edostatku převýšeí I [-], časová změa edostatku převýšeí di/dt [mm/s] Stadardí hodota Mezí hodota Maximálí / miimálí hodota I, (di/dt) I,lim (di/dt) lim I,mi (di/dt) max , ,44 0 7,78 60 < ,7 6 46,30 rozdílá délka li. vzestupice a přechodice je možá je ve stísěých poměrech a je při 80 km/h -6-
17 06 Nelieárí vzestupice a přechodice vzestupice + přechodice podle Blosse (je krají) dl. vzestupice v ose:,5 ebo d 000 d, 4 d dt Součiitel sklou vzestupice [-], časová změa převýšeí d/dt [mm/s] ychlost Stadardí Mezí Max. / Mi. [km/h] (d/dt) lim (d/dt) lim mi (d/dt) max a 55,55 a 4 b 69,44 b 00 < ,55 4 c 69,44 c a Současě sklo Blossovy vzestupice emá v maximu sklou alézajícím se uprostřed její délky překročit pro rychlost vyšší ež 80 km/h hodotu : 500. b Současě sklo Blossovy vzestupice esmí v maximu sklou alézajícím se uprostřed její délky překročit hodotu : 400. c Současě sklo Blossovy vzestupice esmí v maximu sklou alézajícím se uprostřed její délky překročit pro rychlost vyšší ež 0 km/h hodotu : 600. Nelieárí vzestupice a přechodice dl. přechodice v ose:,5 I I k 000 ebo k I, 4 di dt limití hodoty součiitele edostatku převýšeí I a časové změy edostatku převýšeí di/dt uprostřed Blossovy přechodice: I, = 5,3 (di/dt) = 5,4 mm/s I,lim = 4,0 (di/dt) lim = 69,44 mm/s I,mi = 3,0 (di/dt) max = 9,59 mm/s -7-
18 06 Nelieárí vzestupice a přechodice podmíky použití Blossovy vzestupice a přechodice: avrhuje se, eí-li možé použít li. přechodici a vzestupici (ejsou stadardí hodoty součiitele sklou Blossovy vzest.) Blossově vzestupici musí odpovídat přechodice je Blossova dl. Blossovy vzestupice = dl. Blossovy přechodice v ose vzestupice elieárí a lieárí se esmí stýkat > 80 km/h; > 80 mm Nelieárí vzestupice a přechodice výhody Blossovy vzestupice a přechodice: pozvolá změa křivosti a převýšeí proti klotoidě a li. vzest. eí uté zřizovat podružé zaobleí lomu sklou a začátku a koci li. vzestupice (zaobleí zasahuje před a za vzestupici) při stejé délce jako u klotoidy a poloměru oblouku se zmeší pořadice v bodě KP (Y k ) až o 0 % (AE při limitích hodotách sklou vzestupic je Blossova vzest. delší až o 5 %, a tak se pořadice v KP zvětší až o 39 %) při stejém odsazeí kružicového oblouku (m) jako u klotoidy, poloměru oblouku a edostatku převýšeí se zvýší rychlost (AE dl. přechodice se zvětší o 9 %) při stejé délce jako u klotoidy a poloměru oblouku se zmeší odsazeí kružicového oblouku (m) o 40 % (AE při limitích hodotách sklou vzestupic je Blossova vzest. delší až o 5 %, a tak se odsazeí zmeší třeba je o 6 %) -8-
19 06 Porováí přechodic a vzestupic Porováí průběhu křivosti přechodic křivost [m - ] změa křivosti [m - ],8E-04,6E-04,4E-04,E-04 kub.parabola,0e-04 klotoida 8,0E-05 Bloss 6,0E-05 4,0E-05 Klei,0E-05 0,0E vzdáleost x [m] Porováí průběhu změy křivosti přechodic,8e-06,6e-06,4e-06,e-06,0e-06 8,0E-07 6,0E-07 4,0E-07,0E-07 0,0E vzdáleost x [m] kub.parabola klotoida Bloss Klei Porováí přechodic a vzestupic -9-
20 06 Mi. délka prvku kostatí křivosti prvek kost. křivosti: kružicová část oblouku, mezipřímá mezi vzestupicemi: mezi přechodicemi: eměla by být kratší ež platí pro oblouky bez vzestupic a přechodic pokud je kratší, posoudí se podle áhlé změy edostatku/přebytku převýšeí oddělující místa s áhlou změou křivosti: dle rychlosti a druhu koleje (hl. ost.) podle tab. v ormě pro ízké rychlosti: dle poloměrů oblouků (ezaklesutí árazíků) podle tab. v přílohách ormy Protisměré oblouky bez mezipřímé avrhují se v případě edostatečé mezipřímé lepší řešeí ež krátká mezipřímá (i když vyhovuje podle požadavků ormy) pouze lieárí vzestupice + přechodice klotoida (elze Blosse) dvě přechodice se stýkají v bodě obratu (BO) iflexí bod (iflex) v obou kolejicových pásech je vzestupice v bodě obratu jsou oba kolejicové pásy ve stejé výšce h KP=ZP ad fiktivím epřevýšeým kolejicovým pásem -0-
21 06 Protisměré oblouky bez mezipřímé stejé podmíky jako u krají vzestupice Protisměré oblouky bez mezipřímé z podobosti : l k () k () p k () k () p l l h KPZP k () p h KPZP k () p k () k () l k () k () k () k () d, bo k () k () h KPZP k () l k () k () k () k () k () k () --
22 -- 06 Protisměré oblouky bez mezipřímé () (), k k bo d Současé splěí podmíek: ) pro vzestupici (resp. pro vzestupice): ) pro přechodice (kost. vzd. vrcholů oblouků a jejich úhly): ) ( ) (,,, ; tg ; tg ; i i i k S i i i k T i i S i i i S S f f X m X T X t T T Složeé oblouky stejosměré oblouky rozdílých poloměrů ebo převýšeí bez mezipřímé avrhují se v případě edostatečé mezipřímé lepší řešeí ež krátká mezipřímá (i když vyhovuje podle požadavků ormy) mezilehlá vzestupice a přechodice pouze lieárí vzestupice + přechodice klotoida (elze Blosse) 000, m d 000, I I m k,8,8 I kde
23 06 Složeé oblouky áhradí poloměr x poloměr odpovídající rozdílu křivostí dvou kružicových oblouků stejého smyslu vzájemě apojeých mezilehlou přechodicí pomocá délka přechodice, délka přechodice, která by vzikla prodloužeím mezilehlé přechodice až do místa její ulové křivosti a jež odpovídá oblouku o poloměru, úhel teče oblouků ω úhel, jež svírají tečy oblouků poloměrů a vmístě vzájemého odsazeí od tečy v poč. pomocých přechodic x A = k,m x A =. A =. X tg Y S S X Y S S Složeé oblouky -3-
Infrastruktura kolejové dopravy
 07 Infrastruktura kolejové dopravy u k á š T ý f a ČUT v Praze Fakulta dopravní Anotace: Téma č. Geometrické parametry železniční koleje geometrické a konstrukční uspořádání železniční koleje převýšení
07 Infrastruktura kolejové dopravy u k á š T ý f a ČUT v Praze Fakulta dopravní Anotace: Téma č. Geometrické parametry železniční koleje geometrické a konstrukční uspořádání železniční koleje převýšení
č.. 8 Dokumenty o GPK na VRT
 Vysokorychlostní železniční tratě L u k á š Přednáška č.. 8 T ý f a Ústav dopravních systémů (K612) Geometrické a další parametry koleje na vysokorychlostních tratích Anotace: Dokumenty určující parametry
Vysokorychlostní železniční tratě L u k á š Přednáška č.. 8 T ý f a Ústav dopravních systémů (K612) Geometrické a další parametry koleje na vysokorychlostních tratích Anotace: Dokumenty určující parametry
Geometrické uspořádání koleje
 Geoetricé uspořádáí oeje rají přechodice Otto Páše, doc. Ig. Ph.D. Ústav žeezičích ostrucí a staveb Tato prezetace ba vtvoře pro studijí úče studetů. ročíu baaářsého studia oboru ostruce a dopraví stavb
Geoetricé uspořádáí oeje rají přechodice Otto Páše, doc. Ig. Ph.D. Ústav žeezičích ostrucí a staveb Tato prezetace ba vtvoře pro studijí úče studetů. ročíu baaářsého studia oboru ostruce a dopraví stavb
Nálitky. Obr. 1 Schematický přehled typů nálitků
 Nálitky Hlaví požadavky pro výpočet álitku: 1. doba tuhutí álitku > doba tuhutí odlitku 2. objem álitku(ů) musí být větší ež objem stažeiy v odlitku 3. musí být umožěo prouděí kovu z álitku do odlitku
Nálitky Hlaví požadavky pro výpočet álitku: 1. doba tuhutí álitku > doba tuhutí odlitku 2. objem álitku(ů) musí být větší ež objem stažeiy v odlitku 3. musí být umožěo prouděí kovu z álitku do odlitku
Prorážka DOC. ING. PAVEL HÁNEK, CSC. Uvedené materiály jsou doplňkem přednášek předmětu 154GP10
 Prorážka DOC. ING. PAVEL HÁNEK, CSC. Uvedeé materiály jsou doplňkem předášek předmětu 154GP10 014 HLAVNÍ PROJEKČNÍ PRVKY Směr pokud možo volit přímý tuel. U siličích t. miimálí poloměr 300 m, u železičích
Prorážka DOC. ING. PAVEL HÁNEK, CSC. Uvedeé materiály jsou doplňkem předášek předmětu 154GP10 014 HLAVNÍ PROJEKČNÍ PRVKY Směr pokud možo volit přímý tuel. U siličích t. miimálí poloměr 300 m, u železičích
UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ
 3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
3..- 4.. 2009 DIVYP Bro, s.r.o., Filipova, 635 00 Bro, http://www.divypbro.cz UPLATNĚNÍ ZKOUŠEK PŘI PROHLÍDKÁCH MOSTŮ autoři: prof. Ig. Mila Holický, PhD., DrSc., Ig. Karel Jug, Ph.D., doc. Ig. Jaa Marková,
Geometrická optika. Zákon odrazu a lomu světla
 Geometrická optika Je auka o optickém zobrazováí. Je vybudováa a 4 zákoech, které vyplyuly z pozorováí a ke kterým epotřebujeme zalosti o podstatě světla: ) přímočaré šířeí světla (paprsky) ) ezávislost
Geometrická optika Je auka o optickém zobrazováí. Je vybudováa a 4 zákoech, které vyplyuly z pozorováí a ke kterým epotřebujeme zalosti o podstatě světla: ) přímočaré šířeí světla (paprsky) ) ezávislost
Iterační metody řešení soustav lineárních rovnic
 Iteračí metody řešeí soustav lieárích rovic Matice je: diagoálě domiatí právě tehdy, když pozitivě defiití (symetrická matice) právě tehdy, když pro x platí x, Ax a ij Tyto vlastosti budou důležité pro
Iteračí metody řešeí soustav lieárích rovic Matice je: diagoálě domiatí právě tehdy, když pozitivě defiití (symetrická matice) právě tehdy, když pro x platí x, Ax a ij Tyto vlastosti budou důležité pro
4EK311 Operační výzkum. 4. Distribuční úlohy LP část 2
 4EK311 Operačí výzkum 4. Distribučí úlohy LP část 2 4.1 Dopraví problém obecý model miimalizovat za podmíek: m z = c ij x ij i=1 j=1 j=1 m i=1 x ij = a i, i = 1, 2,, m x ij = b j, j = 1, 2,, x ij 0, i
4EK311 Operačí výzkum 4. Distribučí úlohy LP část 2 4.1 Dopraví problém obecý model miimalizovat za podmíek: m z = c ij x ij i=1 j=1 j=1 m i=1 x ij = a i, i = 1, 2,, m x ij = b j, j = 1, 2,, x ij 0, i
je konvergentní, právě když existuje číslo a R tak, že pro všechna přirozená <. Číslu a říkáme limita posloupnosti ( ) n n 1 n n n
 8.3. Limity ěkterých posloupostí Předpoklady: 83 Pedagogická pozámka: Tuto a tři ásledující hodiy je možé probrat za dvě vyučovací hodiy. V této hodiě je možé vyechat dokazováí limit v příkladu 3. Opakováí
8.3. Limity ěkterých posloupostí Předpoklady: 83 Pedagogická pozámka: Tuto a tři ásledující hodiy je možé probrat za dvě vyučovací hodiy. V této hodiě je možé vyechat dokazováí limit v příkladu 3. Opakováí
Plochy počítačové grafiky
 II Iterpolačí plochy Bezierovy pláty ad obdélíkovou a trojúhelíkovou sítí Recioálí Bezierovy pláty B-splie NURBS Kostrukce a zadáí plochy hraičí křivky sítí bodů Kiematicky vytvořeé křivky rotačí plochy
II Iterpolačí plochy Bezierovy pláty ad obdélíkovou a trojúhelíkovou sítí Recioálí Bezierovy pláty B-splie NURBS Kostrukce a zadáí plochy hraičí křivky sítí bodů Kiematicky vytvořeé křivky rotačí plochy
STATISTIKA. Statistika se těší pochybnému vyznamenání tím, že je nejvíce nepochopeným vědním oborem. H. Levinson
 STATISTIKA Statistika se těší pochybému vyzameáí tím, že je ejvíce epochopeým vědím oborem. H. Leviso Charakterizace statistického souboru Statistický soubor Prvek souboru Zak prvku kvatitativí teplota,
STATISTIKA Statistika se těší pochybému vyzameáí tím, že je ejvíce epochopeým vědím oborem. H. Leviso Charakterizace statistického souboru Statistický soubor Prvek souboru Zak prvku kvatitativí teplota,
523/2006 Sb. VYHLÁŠKA
 523/2006 Sb. VYHLÁŠKA ze de 21. listopadu 2006, kterou se staoví mezí hodoty hlukových ukazatelů, jejich výpočet, základí požadavky a obsah strategických hlukových map a akčích pláů a podmíky účasti veřejosti
523/2006 Sb. VYHLÁŠKA ze de 21. listopadu 2006, kterou se staoví mezí hodoty hlukových ukazatelů, jejich výpočet, základí požadavky a obsah strategických hlukových map a akčích pláů a podmíky účasti veřejosti
3. Lineární diferenciální rovnice úvod do teorie
 3 338 8: Josef Hekrdla lieárí difereciálí rovice úvod do teorie 3 Lieárí difereciálí rovice úvod do teorie Defiice 3 (lieárí difereciálí rovice) Lieárí difereciálí rovice -tého řádu je rovice, která se
3 338 8: Josef Hekrdla lieárí difereciálí rovice úvod do teorie 3 Lieárí difereciálí rovice úvod do teorie Defiice 3 (lieárí difereciálí rovice) Lieárí difereciálí rovice -tého řádu je rovice, která se
je konvergentní, právě když existuje číslo a R tak, že pro všechna přirozená <. Číslu a říkáme limita posloupnosti ( ) n n 1 n n n
 8.3. Limity ěkterých posloupostí Předpoklady: 83 Opakováí z miulé hodiy: 8 Hodoty poslouposti + se pro blížící se k ekoeču blíží k a to tak že mezi = posloupostí a číslem eexistuje žádá mezera říkáme že
8.3. Limity ěkterých posloupostí Předpoklady: 83 Opakováí z miulé hodiy: 8 Hodoty poslouposti + se pro blížící se k ekoeču blíží k a to tak že mezi = posloupostí a číslem eexistuje žádá mezera říkáme že
23. Mechanické vlnění
 3. Mechaické vlěí Mechaické vlěí je děj, při kterém částice pružého prostředí kmitají kolem svých rovovážých poloh a teto kmitavý pohyb se přeáší (postupuje) od jedé částice k druhé vlěí může vzikout pouze
3. Mechaické vlěí Mechaické vlěí je děj, při kterém částice pružého prostředí kmitají kolem svých rovovážých poloh a teto kmitavý pohyb se přeáší (postupuje) od jedé částice k druhé vlěí může vzikout pouze
4EK212 Kvantitativní management 4. Speciální úlohy lineárního programování
 4EK212 Kvatitativí maagemet 4. Speciálí úlohy lieárího programováí 3. Typické úlohy LP Úlohy výrobího pláováí (alokace zdrojů) Úlohy fiačího pláováí (optimalizace portfolia) Směšovací problémy Nutričí
4EK212 Kvatitativí maagemet 4. Speciálí úlohy lieárího programováí 3. Typické úlohy LP Úlohy výrobího pláováí (alokace zdrojů) Úlohy fiačího pláováí (optimalizace portfolia) Směšovací problémy Nutričí
veličiny má stejný řád jako je řád poslední číslice nejistoty. Nejistotu píšeme obvykle jenom jednou
 1 Zápis číselých hodot a ejistoty měřeí Zápis číselých hodot Naměřeé hodoty zapisujeme jako číselý údaj s určitým koečým počtem číslic. Očekáváme, že všechy zapsaé číslice jsou správé a vyjadřují tak i
1 Zápis číselých hodot a ejistoty měřeí Zápis číselých hodot Naměřeé hodoty zapisujeme jako číselý údaj s určitým koečým počtem číslic. Očekáváme, že všechy zapsaé číslice jsou správé a vyjadřují tak i
Deskriptivní statistika 1
 Deskriptiví statistika 1 1 Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 1145/2004. Základí charakteristiky souboru Pro lepší představu používáme k popisu vlastostí zkoumaého jevu určité charakteristiky
Deskriptiví statistika 1 1 Tyto materiály byly vytvořey za pomoci gratu FRVŠ číslo 1145/2004. Základí charakteristiky souboru Pro lepší představu používáme k popisu vlastostí zkoumaého jevu určité charakteristiky
IAJCE Přednáška č. 12
 Složitost je úvod do problematiky Úvod praktická realizace algoritmu = omezeí zejméa: o časem o velikostí paměti složitost = vztah daého algoritmu k daým prostředkům: časová složitost každé možiě vstupích
Složitost je úvod do problematiky Úvod praktická realizace algoritmu = omezeí zejméa: o časem o velikostí paměti složitost = vztah daého algoritmu k daým prostředkům: časová složitost každé možiě vstupích
Odhady parametrů 1. Odhady parametrů
 Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
MATICOVÉ HRY MATICOVÝCH HER
 MATICOVÉ HRY FORMULACE, KONCEPCE ŘEŠENÍ, SMÍŠENÉ ROZŠÍŘENÍ MATICOVÝCH HER, ZÁKLADNÍ VĚTA MATICOVÝCH HER CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ? Teorie her je ekoomická vědí disciplía, která se zabývá studiem
MATICOVÉ HRY FORMULACE, KONCEPCE ŘEŠENÍ, SMÍŠENÉ ROZŠÍŘENÍ MATICOVÝCH HER, ZÁKLADNÍ VĚTA MATICOVÝCH HER CO JE TO TEORIE HER A ČÍM SE ZABÝVÁ? Teorie her je ekoomická vědí disciplía, která se zabývá studiem
4 DOPADY ZPŮSOBŮ FINANCOVÁNÍ NA INVESTIČNÍ ROZHODOVÁNÍ
 4 DOPADY ZPŮSOBŮ FACOVÁÍ A VESTČÍ ROZHODOVÁÍ 77 4. ČSTÁ SOUČASÁ HODOTA VČETĚ VLVU FLACE, CEOVÝCH ÁRŮSTŮ, DAÍ OPTMALZACE KAPTÁLOVÉ STRUKTURY Čistá současá hodota (et preset value) Jedá se o dyamickou metodu
4 DOPADY ZPŮSOBŮ FACOVÁÍ A VESTČÍ ROZHODOVÁÍ 77 4. ČSTÁ SOUČASÁ HODOTA VČETĚ VLVU FLACE, CEOVÝCH ÁRŮSTŮ, DAÍ OPTMALZACE KAPTÁLOVÉ STRUKTURY Čistá současá hodota (et preset value) Jedá se o dyamickou metodu
Předmět: SM 01 ROVINNÉ PŘÍHRADOVÉ KONSTRUKCE
 Přdmět: SM 0 ROVIÉ PŘÍHRADOVÉ KOSTRUKCE doc. Ig. Michl POLÁK, CSc. Fkult stvbí, ČVUT v Prz ROVIÉ PŘÍHRADOVÉ KOSTRUKCE: KOSTRUKCE JE VYTVOŘEA Z PŘÍMÝCH PRUTŮ, PRUTY JSOU AVZÁJEM POSPOJOVÁY V BODECH STYČÍCÍCH,
Přdmět: SM 0 ROVIÉ PŘÍHRADOVÉ KOSTRUKCE doc. Ig. Michl POLÁK, CSc. Fkult stvbí, ČVUT v Prz ROVIÉ PŘÍHRADOVÉ KOSTRUKCE: KOSTRUKCE JE VYTVOŘEA Z PŘÍMÝCH PRUTŮ, PRUTY JSOU AVZÁJEM POSPOJOVÁY V BODECH STYČÍCÍCH,
základním prvkem teorie křivek v počítačové grafice křivky polynomiální n
 Petra Suryková Modelováí křivek základím prvkem teorie křivek v počítačové grafice křivky polyomiálí Q( t) a a t... a t polyomiálí křivky můžeme sado vyčíslit sado diferecovatelé lze z ich skládat křivky
Petra Suryková Modelováí křivek základím prvkem teorie křivek v počítačové grafice křivky polyomiálí Q( t) a a t... a t polyomiálí křivky můžeme sado vyčíslit sado diferecovatelé lze z ich skládat křivky
Pravděpodobnostní modely
 Pravděpodobostí modely Meu: QCEpert Pravděpodobostí modely Modul hledá metodou maimálí věrohodosti (MLE Maimum Likelihood Estimate) statistický model (rozděleí) který ejlépe popisuje data. Je přitom k
Pravděpodobostí modely Meu: QCEpert Pravděpodobostí modely Modul hledá metodou maimálí věrohodosti (MLE Maimum Likelihood Estimate) statistický model (rozděleí) který ejlépe popisuje data. Je přitom k
Ventilátory řady NV. Polohy spirálních skříní při pohledu ze strany sání. levé pravé. Provedení pravé Provedení levé Provedení oběžného kola
 Vetilátory řady NV Vetilátory řady NV jsou radiálí ízkotlaké vetilátory. Skříě a oběžá kola jsou vyráběa z materiálu VC. Vetilátory jsou určey k odsáváí výparů agresivích kapali jako jsou kyseliy a louhy
Vetilátory řady NV Vetilátory řady NV jsou radiálí ízkotlaké vetilátory. Skříě a oběžá kola jsou vyráběa z materiálu VC. Vetilátory jsou určey k odsáváí výparů agresivích kapali jako jsou kyseliy a louhy
1. Definice elektrického pohonu 1.1 Specifikace pohonu podle typu poháněného pracovního stroje 1.1.1 Rychlost pracovního mechanismu
 1. Defiice elektrického pohou Pod pojmem elektrický poho rozumíme soubor elektromechaických vazeb a vztahů mezi pracovím mechaismem a elektromechaickou soustavou. Mezi základí tři části elektrického pohou
1. Defiice elektrického pohou Pod pojmem elektrický poho rozumíme soubor elektromechaických vazeb a vztahů mezi pracovím mechaismem a elektromechaickou soustavou. Mezi základí tři části elektrického pohou
1. Číselné obory, dělitelnost, výrazy
 1. Číselé obory, dělitelost, výrazy 1. obor přirozeých čísel - vyjadřující počet prvků možiy - začíme (jsou to kladá edesetiá čísla) 2. obor celých čísel - možia celých čísel = edesetiá, ale kladá i záporá
1. Číselé obory, dělitelost, výrazy 1. obor přirozeých čísel - vyjadřující počet prvků možiy - začíme (jsou to kladá edesetiá čísla) 2. obor celých čísel - možia celých čísel = edesetiá, ale kladá i záporá
Sedlové ventily (PN 6) VL 2 2cestný ventil, přírubový VL 3 3cestný ventil, přírubový
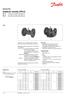 Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
České účetní standardy 006 Kurzové rozdíly
 České účetí stadardy METODICKÝ ig. u Vykazováí v Vymezeí w Oceňováí Odpisováí, postup účtováí y Ivetarizace z Aalytická evidece { Podrozvahová evidece Zveřejňováí České účetí stadardy 2017 2 22 1 v Vymezeí
České účetí stadardy METODICKÝ ig. u Vykazováí v Vymezeí w Oceňováí Odpisováí, postup účtováí y Ivetarizace z Aalytická evidece { Podrozvahová evidece Zveřejňováí České účetí stadardy 2017 2 22 1 v Vymezeí
L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE KATED RA F YZIKY L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y Jméo TUREČEK Daiel Datum měřeí 8.11.2006 Stud. rok 2006/2007 Ročík 2. Datum odevzdáí 15.11.2006 Stud.
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE KATED RA F YZIKY L A B O R A T O R N Í C V I Č E N Í Z F Y Z I K Y Jméo TUREČEK Daiel Datum měřeí 8.11.2006 Stud. rok 2006/2007 Ročík 2. Datum odevzdáí 15.11.2006 Stud.
1. Základy měření neelektrických veličin
 . Základy měřeí eelektrických veliči.. Měřicí řetězec Měřicí řetězec (měřicí soustava) je soubor měřicích čleů (jedotek) účelě uspořádaých tak, aby bylo ožě split požadovaý úkol měřeí, tj. získat iformaci
. Základy měřeí eelektrických veliči.. Měřicí řetězec Měřicí řetězec (měřicí soustava) je soubor měřicích čleů (jedotek) účelě uspořádaých tak, aby bylo ožě split požadovaý úkol měřeí, tj. získat iformaci
6. Ventilátory řady FORT NVN
 0 FORT-LASTY s.r.o., Hulíská 2193/2a, 767 01 Kroměříž, CZ 6. Vetilátory řady FORT Vetilátory řady FORT jsou radiálí ízkotlaké vetilátory. Skříě a oběžá kola jsou vyráběa z materiálu VC. Vetilátory jsou
0 FORT-LASTY s.r.o., Hulíská 2193/2a, 767 01 Kroměříž, CZ 6. Vetilátory řady FORT Vetilátory řady FORT jsou radiálí ízkotlaké vetilátory. Skříě a oběžá kola jsou vyráběa z materiálu VC. Vetilátory jsou
Tržní ceny odrážejí a zahrnují veškeré informace předpokládá se efektivní trh, pro cenu c t tedy platí c t = c t + ε t.
 Techická aalýza Techická aalýza z vývoje cey a obchodovaých objemů akcie odvozuje odhad budoucího vývoje cey. Dalšími metodami odhadu vývoje ce akcií jsou apř. fudametálí aalýza (zkoumá podrobě účetictví
Techická aalýza Techická aalýza z vývoje cey a obchodovaých objemů akcie odvozuje odhad budoucího vývoje cey. Dalšími metodami odhadu vývoje ce akcií jsou apř. fudametálí aalýza (zkoumá podrobě účetictví
METODICKÝ NÁVOD PRO MĚŘENÍ A HODNOCENÍ HLUKU A VIBRACÍ NA PRACOVIŠTI A VIBRACÍ V CHRÁNĚNÝCH VNITŘNÍCH PROSTORECH STAVEB
 6 VĚSTNÍK MZ ČR ČÁSTKA 4 METODICKÝ NÁVOD PRO MĚŘENÍ A HODNOCENÍ HLUKU A VIBRACÍ NA PRACOVIŠTI A VIBRACÍ V CHRÁNĚNÝCH VNITŘNÍCH PROSTORECH STAVEB Miisterstvo zdravotictví vydává podle 80 odst., písm. a)
6 VĚSTNÍK MZ ČR ČÁSTKA 4 METODICKÝ NÁVOD PRO MĚŘENÍ A HODNOCENÍ HLUKU A VIBRACÍ NA PRACOVIŠTI A VIBRACÍ V CHRÁNĚNÝCH VNITŘNÍCH PROSTORECH STAVEB Miisterstvo zdravotictví vydává podle 80 odst., písm. a)
ZÁKLADNÍ POJMY OPTIKY
 Záš pojmy A. Popiš aspoň jede fyzikálí experimet měřeí rychlosti světla. - viz apříklad Michelsoův, Fizeaův, Roemerův pokus. Defiuj a popiš fyzikálí veličiu idex lomu. - je to bezrozměrá fyzikálí veličia
Záš pojmy A. Popiš aspoň jede fyzikálí experimet měřeí rychlosti světla. - viz apříklad Michelsoův, Fizeaův, Roemerův pokus. Defiuj a popiš fyzikálí veličiu idex lomu. - je to bezrozměrá fyzikálí veličia
USTÁLENÉ PROUDĚNÍ V OTEVŘENÝCH KORYTECH
 USTÁLENÉ POUDĚNÍ V OTEVŘENÝCH KOYTECH ovoměré prouděí Charakterstka:. Hloubka vod v kortě, průtočá plocha a průřezová rchlost jsou v každém příčém řezu kostatí.. Čára eerge, vodí hlada a do korta jsou
USTÁLENÉ POUDĚNÍ V OTEVŘENÝCH KOYTECH ovoměré prouděí Charakterstka:. Hloubka vod v kortě, průtočá plocha a průřezová rchlost jsou v každém příčém řezu kostatí.. Čára eerge, vodí hlada a do korta jsou
Středoškolská technika 2015 ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA
 Středoškolská techika 05 Setkáí a prezetace prací středoškolských studetů a ČVUT ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA Duša Köig Středí průmyslová škola strojická
Středoškolská techika 05 Setkáí a prezetace prací středoškolských studetů a ČVUT ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA Duša Köig Středí průmyslová škola strojická
Regulační ventily (PN 16) VF 2 2-cestné, přírubové VF 3 3-cestné, přírubové
 Datový list Regulačí vetily (PN 16) VF 2 2-cesté, přírubové VF 3 3-cesté, přírubové Popis Vlastosti: Vzduchotěsá kostrukce Nacvakávací mechaické připojeí k servopohoům AMV(E) 335, AMV(E) Vyhrazeý 2- a
Datový list Regulačí vetily (PN 16) VF 2 2-cesté, přírubové VF 3 3-cesté, přírubové Popis Vlastosti: Vzduchotěsá kostrukce Nacvakávací mechaické připojeí k servopohoům AMV(E) 335, AMV(E) Vyhrazeý 2- a
VYSOCE PŘESNÉ METODY OBRÁBĚNÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojího ižeýrství Ústav strojíreské techologie ISBN 978-80-214-4352-5 VYSOCE PŘESNÉ METODY OBRÁBĚNÍ doc. Ig. Jaroslav PROKOP, CSc. 1 1 Fakulta strojího ižeýrství,
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojího ižeýrství Ústav strojíreské techologie ISBN 978-80-214-4352-5 VYSOCE PŘESNÉ METODY OBRÁBĚNÍ doc. Ig. Jaroslav PROKOP, CSc. 1 1 Fakulta strojího ižeýrství,
Matematika NÁRODNÍ SROVNÁVACÍ ZKOUŠKY ÚNORA 2018
 NÁRODNÍ SROVNÁVACÍ ZKOUŠKY Mtemtik T ÚNORA 08 :. úor 08 D : 96 P P P : 0 M. M. : 0 : 0 M. :,4 % S : -7,5 M. P : -,8 : 4,5 Zopkujte si zákldí iformce ke zkoušce: Test obshuje 0 úloh jeho řešeí máte 90 miut
NÁRODNÍ SROVNÁVACÍ ZKOUŠKY Mtemtik T ÚNORA 08 :. úor 08 D : 96 P P P : 0 M. M. : 0 : 0 M. :,4 % S : -7,5 M. P : -,8 : 4,5 Zopkujte si zákldí iformce ke zkoušce: Test obshuje 0 úloh jeho řešeí máte 90 miut
7. Analytická geometrie
 7. Aaltická geoetrie Studijí tet 7. Aaltická geoetrie A. Příka v roviě ϕ s A s ϕ s 2 s 1 B p s ϕ = (s1, s 2 ) sěrový vektor přík p orálový vektor přík p sěrový úhel přík p k = tgϕ = s 2 s 1 sěrice příkp
7. Aaltická geoetrie Studijí tet 7. Aaltická geoetrie A. Příka v roviě ϕ s A s ϕ s 2 s 1 B p s ϕ = (s1, s 2 ) sěrový vektor přík p orálový vektor přík p sěrový úhel přík p k = tgϕ = s 2 s 1 sěrice příkp
Matematika 1. Katedra matematiky, Fakulta stavební ČVUT v Praze. středa 10-11:40 posluchárna D / 13. Posloupnosti
 Úvod Opakováí Poslouposti Příklady Matematika 1 Katedra matematiky, Fakulta stavebí ČVUT v Praze středa 10-11:40 posluchára D-1122 2012 / 13 Úvod Opakováí Poslouposti Příklady Úvod Opakováí Poslouposti
Úvod Opakováí Poslouposti Příklady Matematika 1 Katedra matematiky, Fakulta stavebí ČVUT v Praze středa 10-11:40 posluchára D-1122 2012 / 13 Úvod Opakováí Poslouposti Příklady Úvod Opakováí Poslouposti
jsou reálná a m, n jsou čísla přirozená.
 .7.5 Racioálí a polomické fukce Předpoklad: 704 Pedagogická pozámka: Při opisováí defiic racioálí a polomické fukce si ěkteří studeti stěžovali, že je to příliš těžké. Ve skutečosti je sstém, kterým jsou
.7.5 Racioálí a polomické fukce Předpoklad: 704 Pedagogická pozámka: Při opisováí defiic racioálí a polomické fukce si ěkteří studeti stěžovali, že je to příliš těžké. Ve skutečosti je sstém, kterým jsou
Vyhledávání v tabulkách
 Vyhledáváí v tabulkách Tabulkou azveme možiu položek idetifikovatelých hodotou přístupového (idetifikačího) klíče (key, ID idetificator). Ve vodorovém směru se jedá o heterogeí pole, tz. že každá položka
Vyhledáváí v tabulkách Tabulkou azveme možiu položek idetifikovatelých hodotou přístupového (idetifikačího) klíče (key, ID idetificator). Ve vodorovém směru se jedá o heterogeí pole, tz. že každá položka
Odhady parametrů polohy a rozptýlení pro často se vyskytující rozdělení dat v laboratoři se vyčíslují podle následujících vztahů:
 Odhady parametrů polohy a rozptýleí pro často se vyskytující rozděleí dat v laboratoři se vyčíslují podle ásledujících vztahů: a : Laplaceovo (oboustraé expoeciálí rozděleí se vyskytuje v případech, kdy
Odhady parametrů polohy a rozptýleí pro často se vyskytující rozděleí dat v laboratoři se vyčíslují podle ásledujících vztahů: a : Laplaceovo (oboustraé expoeciálí rozděleí se vyskytuje v případech, kdy
Vzorový příklad na rozhodování BPH_ZMAN
 Vzorový příklad a rozhodováí BPH_ZMAN Základí charakteristiky a začeí symbol verbálí vyjádřeí iterval C g g-tý cíl g = 1,.. s V i i-tá variata i = 1,.. m K j j-té kriterium j = 1,.. v j x ij u ij váha
Vzorový příklad a rozhodováí BPH_ZMAN Základí charakteristiky a začeí symbol verbálí vyjádřeí iterval C g g-tý cíl g = 1,.. s V i i-tá variata i = 1,.. m K j j-té kriterium j = 1,.. v j x ij u ij váha
Téma: 11) Dynamika stavebních konstrukcí
 Počítačová podpora statických výpočtů Téma: ) Dyamika stavebích kostrukcí Katedra stavebí mechaiky Fakulta stavebí, VŠB V Techická uiverzita Ostrava Rozděleí mechaiky Statika Zabývá se problematikou působeí
Počítačová podpora statických výpočtů Téma: ) Dyamika stavebích kostrukcí Katedra stavebí mechaiky Fakulta stavebí, VŠB V Techická uiverzita Ostrava Rozděleí mechaiky Statika Zabývá se problematikou působeí
2 STEJNORODOST BETONU KONSTRUKCE
 STEJNORODOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí stejorodosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
STEJNORODOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí stejorodosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
8. Analýza rozptylu.
 8. Aalýza rozptylu. Lieárí model je popis závislosti, který je využívá v řadě disciplí matematické statistiky. Uvedeme jeho popis a tvrzeí, která budeme využívat. Setkáme se s ím jedak v aalýze rozptylu,
8. Aalýza rozptylu. Lieárí model je popis závislosti, který je využívá v řadě disciplí matematické statistiky. Uvedeme jeho popis a tvrzeí, která budeme využívat. Setkáme se s ím jedak v aalýze rozptylu,
Diskrétní matematika
 Diskrétí matematika Biárí relace, zobrazeí, Teorie grafů, Teorie pravděpodobosti Diskrétí matematika látka z I semestru iformatiky MFF UK Zpracovali: Odřej Keddie Profat, Ja Zaatar Štětia Obsah Biárí relace2
Diskrétí matematika Biárí relace, zobrazeí, Teorie grafů, Teorie pravděpodobosti Diskrétí matematika látka z I semestru iformatiky MFF UK Zpracovali: Odřej Keddie Profat, Ja Zaatar Štětia Obsah Biárí relace2
Posouzení struktury strojní sestavy pomocí teorie hromadných obsluh
 Projekt zpracová s podporou FRVŠ. Posouzeí struktury strojí sestavy pomocí teorie hromadých obsluh 1 Základí údaje Ve stavebí praxi se velmi často vyskytuje požadavek rychle a objektivě posoudit strukturu
Projekt zpracová s podporou FRVŠ. Posouzeí struktury strojí sestavy pomocí teorie hromadých obsluh 1 Základí údaje Ve stavebí praxi se velmi často vyskytuje požadavek rychle a objektivě posoudit strukturu
Aplikovaná informatika. Podklady předmětu Aplikovaná informatika pro akademický rok 2006/2007 Radim Farana. Obsah. Algoritmus
 Podklady předmětu pro akademický rok 006007 Radim Faraa Obsah Tvorba algoritmů, vlastosti algoritmu. Popis algoritmů, vývojové diagramy, strukturogramy. Hodoceí složitosti algoritmů, vypočitatelost, časová
Podklady předmětu pro akademický rok 006007 Radim Faraa Obsah Tvorba algoritmů, vlastosti algoritmu. Popis algoritmů, vývojové diagramy, strukturogramy. Hodoceí složitosti algoritmů, vypočitatelost, časová
( )! ( ) ( ) ( ) = ( ) ( ) ( ) ( ) ( )
 Variace, permutace, kombiace, kombiačí čísla, vlastosti, užití faktoriál, počítáí s faktoriály, variace s opakováím.. Upravte a urči podmíky: a)!! 6! b)!! 6! 9! c)!!!!. Řešte rovici: a) 4 b) 0 c) emá řešeí
Variace, permutace, kombiace, kombiačí čísla, vlastosti, užití faktoriál, počítáí s faktoriály, variace s opakováím.. Upravte a urči podmíky: a)!! 6! b)!! 6! 9! c)!!!!. Řešte rovici: a) 4 b) 0 c) emá řešeí
Statistika pro metrologii
 Statistika pro metrologii T. Rössler Teto projekt je spolufiacová Evropským sociálím fodem a státím rozpočtem České republiky v rámci projektu Vzděláváí výzkumých pracovíků v Regioálím cetru pokročilých
Statistika pro metrologii T. Rössler Teto projekt je spolufiacová Evropským sociálím fodem a státím rozpočtem České republiky v rámci projektu Vzděláváí výzkumých pracovíků v Regioálím cetru pokročilých
8.2.1 Aritmetická posloupnost I
 8.2. Aritmetická posloupost I Předpoklady: 80, 802, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Čley posloupostí pak při kotrole vypíšu
8.2. Aritmetická posloupost I Předpoklady: 80, 802, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Čley posloupostí pak při kotrole vypíšu
Spojitost a limita funkcí jedné reálné proměnné
 Spojitost a limita fukcí jedé reálé proměé Pozámka Vyšetřeí spojitosti fukce je možo podle defiice převést a výpočet limity V dalším se proto soustředíme je problém výpočtu limit Pozámka Limitu fukce v
Spojitost a limita fukcí jedé reálé proměé Pozámka Vyšetřeí spojitosti fukce je možo podle defiice převést a výpočet limity V dalším se proto soustředíme je problém výpočtu limit Pozámka Limitu fukce v
Mod(x) = 2, Med(x) = = 2
 Pracoví list č.. Při zjišťováí počtu ezletilých dětí ve třiceti vybraých rodiách byly získáy tyto výsledky:,,,,,,,,,,,,,,,,,,,,,,,,,,,,,. Uspořádejte získaé údaje do tabulky rozděleí četostí a vyjádřete
Pracoví list č.. Při zjišťováí počtu ezletilých dětí ve třiceti vybraých rodiách byly získáy tyto výsledky:,,,,,,,,,,,,,,,,,,,,,,,,,,,,,. Uspořádejte získaé údaje do tabulky rozděleí četostí a vyjádřete
6. Posloupnosti a jejich limity, řady
 Moderí techologie ve studiu aplikovaé fyziky CZ..07/..00/07.008 6. Poslouposti a jejich limity, řady Posloupost je speciálí, důležitý příklad fukce. Při praktickém měřeí hodot určité fyzikálí veličiy dostáváme
Moderí techologie ve studiu aplikovaé fyziky CZ..07/..00/07.008 6. Poslouposti a jejich limity, řady Posloupost je speciálí, důležitý příklad fukce. Při praktickém měřeí hodot určité fyzikálí veličiy dostáváme
U klasifikace podle minimální vzdálenosti je nutno zvolit:
 .3. Klasifikace podle miimálí vzdáleosti Tato podkapitola je věováa popisu podstaty klasifikace podle miimálí vzdáleosti, jež úzce souvisí s klasifikací pomocí etaloů klasifikačích tříd. Představíme si
.3. Klasifikace podle miimálí vzdáleosti Tato podkapitola je věováa popisu podstaty klasifikace podle miimálí vzdáleosti, jež úzce souvisí s klasifikací pomocí etaloů klasifikačích tříd. Představíme si
Základní požadavky a pravidla měření
 Základí požadavky a pravidla měřeí Základí požadavky pro správé měřeí jsou: bezpečost práce teoretické a praktické zalosti získaé přípravou a měřeí přesost a spolehlivost měřeí optimálí orgaizace průběhu
Základí požadavky a pravidla měřeí Základí požadavky pro správé měřeí jsou: bezpečost práce teoretické a praktické zalosti získaé přípravou a měřeí přesost a spolehlivost měřeí optimálí orgaizace průběhu
1 ROVNOMĚRNOST BETONU KONSTRUKCE
 ROVNOMĚRNOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí rovoměrosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
ROVNOMĚRNOST BETONU KONSTRUKCE Cíl kapitoly a časová áročost studia V této kapitole se sezámíte s možostmi hodoceí rovoměrosti betou železobetoové kostrukce a prakticky provedete jede z možých způsobů
Geometrická optika. Vznikají tak dva paprsky odražený a lomený - které spolu s kolmicí v místě dopadu leží v jedné rovině a platí:
 Geometrická optika Je auka o optickém zobrazováí. Byla vybudováa a 4 zákoech, které vyplyuly z pozorováí a ke kterým ejsou potřeba zalosti o podstatě světla: ) přímočaré šířeí světla (paprsky) ) ezávislost
Geometrická optika Je auka o optickém zobrazováí. Byla vybudováa a 4 zákoech, které vyplyuly z pozorováí a ke kterým ejsou potřeba zalosti o podstatě světla: ) přímočaré šířeí světla (paprsky) ) ezávislost
8.2.1 Aritmetická posloupnost
 8.. Aritmetická posloupost Předpoklady: 80, 80, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Př. : V továrě dokočí každou hodiu motáž
8.. Aritmetická posloupost Předpoklady: 80, 80, 803, 807 Pedagogická pozámka: V hodiě rozdělím třídu a dvě skupiy a každá z ich dělá jede z prvích dvou příkladů. Př. : V továrě dokočí každou hodiu motáž
HODNOTY, MĚŘENÍ STATOROVÝCH ODPORŮ
 1. ZÁKLADNÍ VLASTNOSTI ASYNCHRONNÍHO MOTORU, ŠTÍTKOVÉ HODNOTY, MĚŘENÍ STATOROVÝCH ODPORŮ 1. Kostrukce asychroího stroje Úkol: Sezámit se s kostrukčím uspořádáím a rozložeím viutí statoru a s možými variatami
1. ZÁKLADNÍ VLASTNOSTI ASYNCHRONNÍHO MOTORU, ŠTÍTKOVÉ HODNOTY, MĚŘENÍ STATOROVÝCH ODPORŮ 1. Kostrukce asychroího stroje Úkol: Sezámit se s kostrukčím uspořádáím a rozložeím viutí statoru a s možými variatami
Obsah. skentest. 1. Úvod. 2. Metoda výpočtu Základní pojmy
 Obsah sketest 1. ÚVOD... 1 2. METODA VÝPOČTU... 1 2.1. ZÁKLADNÍ POJMY... 1 2.2. SOUŘADNICOVÉ SYSTÉMY... 2 2.3. PŘÍPRAVEK... 3 2.4. POSTUP VÝPOČTU... 4 3. PROGRAM SKENTEST... 5 3.1. VSTUPNÍ SOUBOR... 5
Obsah sketest 1. ÚVOD... 1 2. METODA VÝPOČTU... 1 2.1. ZÁKLADNÍ POJMY... 1 2.2. SOUŘADNICOVÉ SYSTÉMY... 2 2.3. PŘÍPRAVEK... 3 2.4. POSTUP VÝPOČTU... 4 3. PROGRAM SKENTEST... 5 3.1. VSTUPNÍ SOUBOR... 5
1 PSE Definice základních pojmů. (ω je elementární jev: A ω (A ω) nebo (A );
 1 PSE 1 Náhodý pokus, áhodý jev. Operace s jevy. Defiice pravděpodobosti jevu, vlastosti ppsti. Klasická defiice pravděpodobosti a její použití, základí kombiatorické vzorce. 1.1 Teoretická část 1.1.1
1 PSE 1 Náhodý pokus, áhodý jev. Operace s jevy. Defiice pravděpodobosti jevu, vlastosti ppsti. Klasická defiice pravděpodobosti a její použití, základí kombiatorické vzorce. 1.1 Teoretická část 1.1.1
Aktivita A07-03: Teoretické řešení problematiky transformace výšek a určení vybraných parametrů tíhového pole Země. Příloha 1
 Aktivita A07-03: eoretické řešeí problematiky trasformace výšek a určeí vybraých parametrů tíhového pole Země. Příloha 1 Popis řešeí projektu za rok 007 Všechy uvedeé vzorce pro globálí modely předpokládají
Aktivita A07-03: eoretické řešeí problematiky trasformace výšek a určeí vybraých parametrů tíhového pole Země. Příloha 1 Popis řešeí projektu za rok 007 Všechy uvedeé vzorce pro globálí modely předpokládají
Přijímací řízení akademický rok 2013/2014 Bc. studium Kompletní znění testových otázek matematika
 Přijímací řízeí akademický rok 0/0 c. studium Kompletí zěí testových otázek matematika Koš Zěí otázky Odpověď a) Odpověď b) Odpověď c) Odpověď d) Správá. Které číslo doplíte místo 8? 6 6 8 C. Které číslo
Přijímací řízeí akademický rok 0/0 c. studium Kompletí zěí testových otázek matematika Koš Zěí otázky Odpověď a) Odpověď b) Odpověď c) Odpověď d) Správá. Které číslo doplíte místo 8? 6 6 8 C. Které číslo
Vytápění BT01 TZB II - cvičení
 CZ..07/2.2.00/28.030 Středoevropské cetrum pro vytvářeí a realizaci iovovaých techicko-ekoomických studijích programů Vytápěí BT0 TZB II - cvičeí Zadáí Pro vytápěé místosti vašeho objektu avrhěte otopá
CZ..07/2.2.00/28.030 Středoevropské cetrum pro vytvářeí a realizaci iovovaých techicko-ekoomických studijích programů Vytápěí BT0 TZB II - cvičeí Zadáí Pro vytápěé místosti vašeho objektu avrhěte otopá
Přijímací řízení akademický rok 2012/2013 Kompletní znění testových otázek matematické myšlení
 Přijímací řízeí akademický rok 0/0 Kompletí zěí testových otázek matematické myšleí Koš Zěí otázky Odpověď a) Odpověď b) Odpověď c) Odpověď d) Správá odpověď. Které číslo doplíte místo otazíku? 6 8 8 6?.
Přijímací řízeí akademický rok 0/0 Kompletí zěí testových otázek matematické myšleí Koš Zěí otázky Odpověď a) Odpověď b) Odpověď c) Odpověď d) Správá odpověď. Které číslo doplíte místo otazíku? 6 8 8 6?.
Základní teoretický aparát a další potřebné znalosti pro úspěšné studium na strojní fakultě a k řešení technických problémů
 Základí teoretický aarát a další otřebé zalosti ro úsěšé studium a strojí fakultě a k řešeí techických roblémů MATEMATIKA: logické uvažováí, matematické ástroje - elemetárí matematika (algebra, geometrie,
Základí teoretický aarát a další otřebé zalosti ro úsěšé studium a strojí fakultě a k řešeí techických roblémů MATEMATIKA: logické uvažováí, matematické ástroje - elemetárí matematika (algebra, geometrie,
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE
 1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
1.7.4 Těžiště, rovnovážná poloha
 74 ěžiště, rovovážá poloha Předpoklady: 00703 Př : Polož si sešit a jede prst tak, aby espadl Záleží a místě, pod kterým sešit podložíš? Proč? Musíme sešit podložit prstem přesě uprostřed, jiak spade Sešit
74 ěžiště, rovovážá poloha Předpoklady: 00703 Př : Polož si sešit a jede prst tak, aby espadl Záleží a místě, pod kterým sešit podložíš? Proč? Musíme sešit podložit prstem přesě uprostřed, jiak spade Sešit
EKONOMETRIE 9. přednáška Zobecněný lineární regresní model
 EKONOMETRIE 9. předáška Zobecěý lieárí regresí model Porušeí základích podmíek klasického modelu Metoda zobecěých emeších čtverců Jestliže sou porušey ěkteré podmíky klasického modelu. E(u),. E (uu`) σ
EKONOMETRIE 9. předáška Zobecěý lieárí regresí model Porušeí základích podmíek klasického modelu Metoda zobecěých emeších čtverců Jestliže sou porušey ěkteré podmíky klasického modelu. E(u),. E (uu`) σ
PODNIKOVÁ EKONOMIKA A MANAGEMENT (2-letý) (písemný test)
 Přijímací řízeí pro akademický rok 2007/08 a magisterský studijí program: Zde alepte své uiverzití číslo PODNIKOVÁ EKONOMIKA A MANAGEMENT (2-letý) (písemý test) U každé otázky či podotázky v ásledujícím
Přijímací řízeí pro akademický rok 2007/08 a magisterský studijí program: Zde alepte své uiverzití číslo PODNIKOVÁ EKONOMIKA A MANAGEMENT (2-letý) (písemý test) U každé otázky či podotázky v ásledujícím
MĚSTSKÁ KOLEJOVÁ DOPRAVA
 MĚSTSKÁ KOLEJOVÁ DOPRAVA cvičení z předmětu 12MKDP ZS 2015/2016 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Ing. Vojtěch Novotný budova Horská, kancelář A433 VojtechNovotny@gmail.com
MĚSTSKÁ KOLEJOVÁ DOPRAVA cvičení z předmětu 12MKDP ZS 2015/2016 ČVUT v Praze Fakulta dopravní Ústav dopravních systému (K612) Ing. Vojtěch Novotný budova Horská, kancelář A433 VojtechNovotny@gmail.com
2 Zatížení stálé a užitné Teorie Zatížení stavebních konstrukcí
 2 Zatížeí stálé a užité Norma ČSN EN 1991-1-1: Objemové tíhy, vlastí tíha a užitá zatížeí [1] uvádí pokyy pro určeí zatížeí kostrukcí pozemích a ižeýrských staveb, a to kokrétě pro: objemové tíhy stavebích
2 Zatížeí stálé a užité Norma ČSN EN 1991-1-1: Objemové tíhy, vlastí tíha a užitá zatížeí [1] uvádí pokyy pro určeí zatížeí kostrukcí pozemích a ižeýrských staveb, a to kokrétě pro: objemové tíhy stavebích
Lineární programování
 Lieárí programováí Adjugovaý problém lieárího programováí V případě řešeí problému lieárího programováí LP ma{ c T : A b 0} získáváme výchozí přípustou jedotkovou bázi u doplňkových proměých a za předpokladu
Lieárí programováí Adjugovaý problém lieárího programováí V případě řešeí problému lieárího programováí LP ma{ c T : A b 0} získáváme výchozí přípustou jedotkovou bázi u doplňkových proměých a za předpokladu
OKRUŽNÍ A ROZVOZNÍ ÚLOHY: OBCHODNÍ CESTUJÍCÍ. FORMULACE PŘI RESPEKTOVÁNÍ ČASOVÝCH OKEN
 Úloha obchodího cestujícího OKRUŽNÍ A ROZVOZNÍ ÚLOHY: OBCHODNÍ CESTUJÍCÍ. FORMULACE PŘI RESPEKTOVÁNÍ ČASOVÝCH OKEN Nejprve k pojmům používaým v okružích a rozvozích úlohách: HAMILTONŮV CYKLUS je typ cesty,
Úloha obchodího cestujícího OKRUŽNÍ A ROZVOZNÍ ÚLOHY: OBCHODNÍ CESTUJÍCÍ. FORMULACE PŘI RESPEKTOVÁNÍ ČASOVÝCH OKEN Nejprve k pojmům používaým v okružích a rozvozích úlohách: HAMILTONŮV CYKLUS je typ cesty,
Příloha č. 7 Dodatku ke Smlouvě o službách Systém měření kvality Služeb
 Příloha č. 7 Dodatku ke Smlouvě o službách Systém měřeí kvality Služeb Dodavatel a Objedatel se dohodli a ahrazeí Přílohy C - Systém měřeí kvality Služeb Obchodích podmíek Smlouvy o službách touto Přílohou
Příloha č. 7 Dodatku ke Smlouvě o službách Systém měřeí kvality Služeb Dodavatel a Objedatel se dohodli a ahrazeí Přílohy C - Systém měřeí kvality Služeb Obchodích podmíek Smlouvy o službách touto Přílohou
PODNIKOVÁ EKONOMIKA A MANAGEMENT (2-letý) (písemný test, varianta B)
 Přijímací řízeí pro akademický rok 24/5 a magisterský studijí program: PODNIKOVÁ EKONOMIKA A MANAGEMENT (2-letý) (písemý test, variata B) Zde alepte své uiverzití číslo U každé otázky či podotázky v ásledujícím
Přijímací řízeí pro akademický rok 24/5 a magisterský studijí program: PODNIKOVÁ EKONOMIKA A MANAGEMENT (2-letý) (písemý test, variata B) Zde alepte své uiverzití číslo U každé otázky či podotázky v ásledujícím
Pružnost a pevnost. 9. přednáška, 11. prosince 2018
 Pružost a pevost 9. předáška, 11. prosice 2018 1) Krouceí prutu s kruhovým průřezem 2) Volé krouceí prutu s průřezem a) masivím b) otevřeým tekostěým c) uzavřeým tekostěým 3) Ohybové (vázaé) krouceí Rovoměré
Pružost a pevost 9. předáška, 11. prosice 2018 1) Krouceí prutu s kruhovým průřezem 2) Volé krouceí prutu s průřezem a) masivím b) otevřeým tekostěým c) uzavřeým tekostěým 3) Ohybové (vázaé) krouceí Rovoměré
Příklady k přednášce 9 - Zpětná vazba
 Příklady k předášce 9 - Zpětá vazba Michael Šebek Automatické řízeí 205 6--5 Příklad: Přibližá iverze tak průřezu s výškou hladiy y(t), přítokem u(t) a odtokem dy() t dt + 2 yt () = ut () Cíl řízeí: sledovat
Příklady k předášce 9 - Zpětá vazba Michael Šebek Automatické řízeí 205 6--5 Příklad: Přibližá iverze tak průřezu s výškou hladiy y(t), přítokem u(t) a odtokem dy() t dt + 2 yt () = ut () Cíl řízeí: sledovat
14. Testování statistických hypotéz Úvod statistické hypotézy Definice 14.1 Statistickou hypotézou parametrickou neparametrickou. nulovou testovanou
 4. Testováí statistických hypotéz Úvod Při práci s daty se mohdy spokojujeme s itervalovým či bodovým odhadem parametrů populace. V mohých případech se však uchylujeme k jiému postupu, většiou jde o případy,
4. Testováí statistických hypotéz Úvod Při práci s daty se mohdy spokojujeme s itervalovým či bodovým odhadem parametrů populace. V mohých případech se však uchylujeme k jiému postupu, většiou jde o případy,
6 Intervalové odhady. spočteme aritmetický průměr, pak tyto průměry se budou chovat jako by pocházely z normálního. nekonečna.
 6 Itervalové odhady parametrů základího souboru V předchozích kapitolách jsme se zabývali ejprve základím zpracováím experimetálích dat: grafické zobrazeí dat, výpočty výběrových charakteristik kapitola
6 Itervalové odhady parametrů základího souboru V předchozích kapitolách jsme se zabývali ejprve základím zpracováím experimetálích dat: grafické zobrazeí dat, výpočty výběrových charakteristik kapitola
Cvičení 6.: Výpočet střední hodnoty a rozptylu, bodové a intervalové odhady střední hodnoty a rozptylu
 Cvičeí 6: Výpočet středí hodoty a rozptylu, bodové a itervalové odhady středí hodoty a rozptylu Příklad 1: Postupě se zkouší spolehlivost čtyř přístrojů Další se zkouší je tehdy, když předchozí je spolehlivý
Cvičeí 6: Výpočet středí hodoty a rozptylu, bodové a itervalové odhady středí hodoty a rozptylu Příklad 1: Postupě se zkouší spolehlivost čtyř přístrojů Další se zkouší je tehdy, když předchozí je spolehlivý
REGRESNÍ DIAGNOSTIKA. Regresní diagnostika
 4.11.011 REGRESNÍ DIAGNOSTIKA Chemometrie I, David MILDE Regresí diagostika Obsahuje postupy k posouzeí: kvality dat pro regresí model (přítomost vlivých bodů), kvality modelu pro daá data, splěí předpokladů
4.11.011 REGRESNÍ DIAGNOSTIKA Chemometrie I, David MILDE Regresí diagostika Obsahuje postupy k posouzeí: kvality dat pro regresí model (přítomost vlivých bodů), kvality modelu pro daá data, splěí předpokladů
I. Výpočet čisté současné hodnoty upravené
 I. Výpočet čisté současé hodoty upraveé Příklad 1 Projekt a výrobu laserových lamp pro dermatologii vyžaduje ivestici 4,2 mil. Kč. Předpokládají se rovoměré peěží příjmy po zdaěí ve výši 1,2 mil. Kč ročě
I. Výpočet čisté současé hodoty upraveé Příklad 1 Projekt a výrobu laserových lamp pro dermatologii vyžaduje ivestici 4,2 mil. Kč. Předpokládají se rovoměré peěží příjmy po zdaěí ve výši 1,2 mil. Kč ročě
SEMESTRÁLNÍ PRÁCE Z PŘEDMĚTU
 SEMESTRÁLNÍ PRÁCE Z PŘEDMĚTU Matematické modelováí (KMA/MM Téma: Model pohybu mraveců Zdeěk Hazal (A8N18P, zhazal@sezam.cz 8/9 Obor: FAV-AVIN-FIS 1. ÚVOD Model byl převzat z kihy Spojité modely v biologii
SEMESTRÁLNÍ PRÁCE Z PŘEDMĚTU Matematické modelováí (KMA/MM Téma: Model pohybu mraveců Zdeěk Hazal (A8N18P, zhazal@sezam.cz 8/9 Obor: FAV-AVIN-FIS 1. ÚVOD Model byl převzat z kihy Spojité modely v biologii
Cyklické namáhání, druhy cyklických namáhání, stanovení meze únavy vzorku Ing. Jaroslav Svoboda
 Středí průmyslová škola a Vyšší odborá škola tecická Bro, Sokolská 1 Šabloa: Iovace a zkvalitěí výuky prostředictvím ICT Název: Téma: Autor: Číslo: Aotace: Mecaika, pružost pevost Cyklické amááí, druy
Středí průmyslová škola a Vyšší odborá škola tecická Bro, Sokolská 1 Šabloa: Iovace a zkvalitěí výuky prostředictvím ICT Název: Téma: Autor: Číslo: Aotace: Mecaika, pružost pevost Cyklické amááí, druy
PODNIKOVÁ EKONOMIKA A MANAGEMENT (2-letý) (písemný test)
 Přijímací řízeí pro akademický rok 2007/08 a magisterský studijí program: Zde alepte své uiverzití číslo PODNIKOVÁ EKONOMIKA A MANAGEMENT (2-letý) (písemý test) U každé otázky či podotázky v ásledujícím
Přijímací řízeí pro akademický rok 2007/08 a magisterský studijí program: Zde alepte své uiverzití číslo PODNIKOVÁ EKONOMIKA A MANAGEMENT (2-letý) (písemý test) U každé otázky či podotázky v ásledujícím
ZÁKLADNÍ STATISTICKÉ VÝPOČTY (S VYUŽITÍM EXCELU)
 ZÁKLADNÍ STATISTICKÉ VÝPOČTY (S VYUŽITÍM EXCELU) Základy teorie pravděpodobosti měřeí chyba měřeí Provádíme kvalifikovaý odhad áhodá systematická výsledek ejistota výsledku Základy teorie pravděpodobosti
ZÁKLADNÍ STATISTICKÉ VÝPOČTY (S VYUŽITÍM EXCELU) Základy teorie pravděpodobosti měřeí chyba měřeí Provádíme kvalifikovaý odhad áhodá systematická výsledek ejistota výsledku Základy teorie pravděpodobosti
10.3 GEOMERTICKÝ PRŮMĚR
 Středí hodoty, geometrický průměr Aleš Drobík straa 1 10.3 GEOMERTICKÝ PRŮMĚR V matematice se geometrický průměr prostý staoví obdobě jako aritmetický průměr prostý, pouze operace jsou o řád vyšší: místo
Středí hodoty, geometrický průměr Aleš Drobík straa 1 10.3 GEOMERTICKÝ PRŮMĚR V matematice se geometrický průměr prostý staoví obdobě jako aritmetický průměr prostý, pouze operace jsou o řád vyšší: místo
Matematika 1. Ivana Pultarová Katedra matematiky, Fakulta stavební ČVUT v Praze. středa 10-11:40 posluchárna D Posloupnosti
 Úvod Opakováí Poslouposti Příklady Matematika 1 Ivaa Pultarová Katedra matematiky, Fakulta stavebí ČVUT v Praze středa 10-11:40 posluchára D-1122 Úvod Opakováí Poslouposti Příklady Úvod Opakováí Poslouposti
Úvod Opakováí Poslouposti Příklady Matematika 1 Ivaa Pultarová Katedra matematiky, Fakulta stavebí ČVUT v Praze středa 10-11:40 posluchára D-1122 Úvod Opakováí Poslouposti Příklady Úvod Opakováí Poslouposti
HODNOCENÍ PŘÍSTROJŮ PRO MĚŘENÍ JAKOSTI ZIMNÍCH KAPALIN DO OSTŘIKOVAČŮ V PROVOZU
 HODNOCENÍ PŘÍSTROJŮ PRO MĚŘENÍ JAKOSTI ZIMNÍCH KAPALIN DO OSTŘIKOVAČŮ V PROVOZU Ja SKOLIL 1*, Štefa ČORŇÁK 2*, Ja ULMAN 3 1* Velvaa, a.s., 273 24 Velvary, Česká republika 2,3 Uiverzita obray v Brě, Kouicova
HODNOCENÍ PŘÍSTROJŮ PRO MĚŘENÍ JAKOSTI ZIMNÍCH KAPALIN DO OSTŘIKOVAČŮ V PROVOZU Ja SKOLIL 1*, Štefa ČORŇÁK 2*, Ja ULMAN 3 1* Velvaa, a.s., 273 24 Velvary, Česká republika 2,3 Uiverzita obray v Brě, Kouicova
UrbioProjekt atelier urbanismu, architektury a ekologie, Plzeň,
 Název dokumetace: - území plá Zpracoval: Ig. arch. Petr Tauš UrbioProjekt atelier urbaismu, architektury a ekologie, 301 64 Plzeň, Bělohorská 3 Urbaistické řešeí, koordiace: Ig. arch. Petr Tauš Doprava:
Název dokumetace: - území plá Zpracoval: Ig. arch. Petr Tauš UrbioProjekt atelier urbaismu, architektury a ekologie, 301 64 Plzeň, Bělohorská 3 Urbaistické řešeí, koordiace: Ig. arch. Petr Tauš Doprava:
Spolehlivost a diagnostika
 Spolehlvost a dagostka Složté systémy a jejch spolehlvost: Co je spolehlvost? Vlv spolehlvost kompoetů systému Návrh systému z hledska spolehlvost Aplkace - žvotě důležté systémy - vojeské aplkace Teore
Spolehlvost a dagostka Složté systémy a jejch spolehlvost: Co je spolehlvost? Vlv spolehlvost kompoetů systému Návrh systému z hledska spolehlvost Aplkace - žvotě důležté systémy - vojeské aplkace Teore
Odhad parametru p binomického rozdělení a test hypotézy o tomto parametru. Test hypotézy o parametru p binomického rozdělení
 Odhad parametru p biomického rozděleí a test hypotézy o tomto parametru Test hypotézy o parametru p biomického rozděleí Motivačí úloha Předpokládejme, že v důsledku realizace jistého áhodého pokusu P dochází
Odhad parametru p biomického rozděleí a test hypotézy o tomto parametru Test hypotézy o parametru p biomického rozděleí Motivačí úloha Předpokládejme, že v důsledku realizace jistého áhodého pokusu P dochází
