říkali spíš latinsky: divide et impera). Tato zásada se pak osvědčila nejen ve starořímské
|
|
|
- Stanislava Černá
- před 9 lety
- Počet zobrazení:
Transkript
1 1. Rozdìl a panuj Potkáme-li spletitý problém, často pomáhá rozdělit ho na jednodušší části a s těmi se pak vypořádat postupně. Jak říkali staří Římané: rozděl a panuj (oni to říkali spíš latinsky: divide et impera). Tato zásada se pak osvědčila nejen ve starořímské politice, ale také o dvě tisíciletí později při návrhu algoritmů. Nás v této kapitole bude přirozeně zajímat zejména algoritmická stránka věci. Naším cílem bude rozkládat zadaný problém na menší podproblémy a z jejich výsledků pak skládat řešení celého problému. S jednotlivými podproblémy potom naložíme stejně opět je rozložíme na ještě menší a tak budeme pokračovat, než se dostaneme k tak jednoduchým vstupům, že je už umíme vyřešit přímo. Myšlenka je to trochu bláznivá, ale často vede k překvapivě jednoduchému, rychlému a obvykle rekurzivnímu algoritmu. Postupně ji použijeme na třídění posloupností, násobení čísel i matic a hledání k-tého nejmenšího ze zadaných prvků. Nejprve si tuto techniku ovšem vyzkoušejme na jednoduchém hlavolamu známém pod názvem Hanojské věže Hanojské vì¾e Legenda vypráví, že v daleké Hanoji stojí starobylý klášter. V jeho sklepení se skrývá rozlehlá jeskyně, v níž stojí tři sloupy. Na nich je navlečeno celkem 64 zlatých disků různých velikostí. Za úsvitu věků byly všechny disky srovnané podle velikosti na prvním sloupu: největší disk dole, nejmenší nahoře. Od té doby mniši každý den za hlaholu zvonů obřadně přenesou nejvyšší disk z některého sloupu na jiný sloup. Tradice jim přitom zakazuje položit větší disk na menší a také zopakovat již jednou použité rozmístění disků. Říká se, že až se všechny disky opět sejdou na jednom sloupu, nastane konec světa. Nabízí se samozřejmě otázka, za jak dlouho se mnichům může podařit splnit svůj úkol a celou věž z disků přenést. Zamysleme se nad tím rovnou pro obecný počet disků a očíslujme si je podle velikosti od 1 (nejmenší disk) do N (největší). Také si označme sloupy: na sloupu A budou disky na počátku, na sloup B je chceme přemístit a sloup C můžeme používat jako pomocný. Stav hry při přenášení největšího disku
2 Ať už zvolíme jakýkoliv postup, někdy během něj musíme přemístit největší disk na sloup B. V tomto okamžiku musí být na jiném sloupu samotný největší disk a všechny ostatní disky na zbývajícím sloupu (viz obrázek). Nabízí se tedy nejprve přemístit disky 1,..., N 1 z A na C, pak přesunout disk N z A na B a konečně přestěhovat disky 1,..., N 1 z C na B. Tím jsme tedy problém přesunu věže výšky N převedli na dva problémy s věží výšky N 1. Ty ovšem můžeme vyřešit stejně, tedy rekurzivním zavoláním téhož algoritmu. Zastavíme se až u věže výšky 1, kterou zvládneme přemístit jedním tahem. Algoritmus bude vypadat takto: Algoritmus Hanoj Vstup: Výška věže N; sloupy A (zdrojový), B (cílový), C (pomocný). 1. Pokud je N = 1, přesuneme disk 1 z A na B. 2. Jinak: 3. Zavoláme Hanoj(N 1; A, C, B). 4. Přesuneme disk N z A na B. 5. Zavoláme Hanoj(N 1; C, B, A). Průběh algoritmu Hanoj pro N = 3 Ujistěme se, že náš algoritmus při přenášení věží neporuší pravidla. Když v kroku 3 přesouváme disk z A na B, o všech menších discích víme, že jsou na věži C, takže na ně určitě nic nepoložíme. Taktéž nikdy nepoužijeme žádnou konfiguraci dvakrát. K tomu si stačí uvědomit, že se konfigurace navštívené během obou rekurzivních volání liší polohou N-tého disku. Spočítejme, kolik tahů náš algoritmus spotřebuje. Pokud si označíme T (N) počet tahů použitý pro věž výšky N, bude platit: T (1) = 1, T (N) = 2 T (N 1) + 1. Z tohoto vztahu okamžitě zjistíme, že T (2) = 3, T (3) = 7 a T (4) = 15. Nabízí se, že by mohlo platit T (N) = 2 N 1. To snadno ověříme indukcí: Pro N = 1 je tvrzení pravdivé. Pokud platí pro N 1, dostaneme: T (N) = 2 (2 N 1 1) + 1 = 2 2 N = 2 N 1. Časová složitost algoritmu je tedy exponenciální. Ve cvičení ale snadno ukážeme, že exponenciální počet tahů je nejlepší možný. Pro N = 64 tedy mniši budou pracovat minimálně , dní, takže konce světa se alespoň po nejblizších pár biliard let nemusíme obávat
3 Cvičení: 1. Dokažte, že algoritmus Hanoj je nejlepší možný, tedy že 2 N 1 tahů je opravdu potřeba. 2. Přidejme k regulím hanojských mnichů ještě jedno pravidlo: je zakázáno přenášet disky přímo ze sloupu A na B nebo opačně (každý přesun se tedy musí uskutečnit přes sloup C). I nyní je problém řešitelný. Jak a s jakou časovou složitostí? 3. Dokažte, že algoritmus z předchozího cvičení navštíví každé korektní rozmístění disků mezi sloupy (tj. takové, v němž nikde neleží větší disk na menším) právě jednou. 4. Vymyslete algoritmus, který pro zadané rozmístění disků na sloupy co nejrychleji přemístí všechny disky na libovolný jeden sloup. 5*. Navrhněte takové řešení Hanojských věží, které místo rekurze bude umět z pořadového čísla tahu rovnou určit, který disk přesunout a kam Tøídìní sléváním { Mergesort Zopakujme si, jakým způsobem jsme vyřešili úlohu z minulé kapitoly. Nejprve jsme ji rozložili na dvě úlohy menší (věže výšky N 1), ty jsme vyřešili rekurzivně, a pak jsme z jejich výsledků přidáním jednoho tahu utvořili výsledek úlohy původní. Podívejme se nyní, jak se podobný přístup osvědčí na problému třídění posloupnosti, který jsme již zkoumali v jedné z předchozích kapitol. Dostaneme-li posloupnost N prvků, jistě ji můžeme rozdělit na dvě části poloviční délky (řekněme prvních N/2 a zbývajících N/2 prvků). Ty setřídíme rekurzivním zavoláním téhož algoritmu. Setříděné poloviny posléze slijeme dohromady do jedné setříděné posloupnosti a máme výsledek. Když ještě ošetříme triviální případ N = 1, aby se nám rekurze zastavila (na to není radno zapomínat), dostaneme následující algoritmus. Říká se mu třídění sléváním neboli MergeSort. Algoritmus MergeSort (třídění sléváním) Vstup: Posloupnost a 1,..., a N k setřídění. Výstup: Setříděná posloupnost b 1,..., b N. 1. Pokud N = 1, vrátíme jako výsledek b 1 = a 1 a skončíme. 2. x 1,..., x N/2 MergeSort(a 1,..., a N/2 ) 3. y 1,..., y N/2 MergeSort(a N/2 +1,..., a N ) 4. b 1,..., b N Merge(x 1,..., x N/2 ; y 1,..., y N/2 ) Procedura Merge se stará o samotné slévání. To zařídíme snadno: Pokud chceme slít posloupnosti x 1 x 2... x m a y 1 y 2... y n, bude výsledná posloupnost začínat menším z prvků x 1 a y 1. Tento prvek z příslušné vstupní posloupnosti přesuneme na výstup a pokračujeme stejným způsobem. Pokud to byl (řekněme) prvek x 1, zbývá nám slít x 2,..., x m s y 1,..., y n. Dalším prvkem výstupu tedy bude minimum z x 2 a y 1. To opět přesuneme, a tak dále, než se buď x nebo y vyprázdní
4 Algoritmus Merge (slévání) Vstup: Setříděné posloupnosti x 1,..., x m a y 1,..., y n. Výstup: Setříděná posloupnost z 1,..., z m+n. 1. i 1, j 1 (zbývá slít x i,..., x m a y j,..., y n ) 2. k 1 (výsledek se objeví v z k,..., z m+n ) 3. Dokud i m a j n, opakujeme: 4. Je-li x i y j, přesuneme prvek z x: z k x i, i i Jinak přesouváme z y: z k y j, j j k k Je-li i m, zkopírujeme zbylá x: z k,..., z m+n x i,..., x m. 8. Je-li j n, zkopírujeme zbylá y: z k,..., z m+n y j,..., y n. Rozbor složitosti Nyní si rozmysleme, kolik času tříděním strávíme. Slévání má lineární časovou složitost (Merge pouze přesouvá prvky a každý přesune právě jednou). Složitost samotného třídění můžeme popsat takto: T (1) = 1, T (N) = 2 T (N/2) + cn. První rovnost nám popisuje, co se stane, když už v posloupnosti zbývá jediný prvek. Dobu trvání této operace jsme si přitom zvolili za jednotku času. Druhá rovnost pak odpovídá zajímavé části algoritmu. Čas cn potřebujeme na rozdělení posloupnosti a slití setříděných kusů. Mimo to voláme dvakrát sebe sama na vstup velikosti N/2, což pokaždé trvá T (N/2). (Zde se dopouštíme malého podvůdku a předpokládáme, že N je mocnina dvojky, a proto se nemusíme starat o zaokrouhlování. V kapitole 1.4 uvidíme, že to opravdu neuškodí.) Jak tuto rekurentní rovnici vyřešíme? Zkusme si v druhém vztahu za T (N/2) dosadit podle téže rovnice: To můžeme dále rozepsat na: T (N) = 2 (2 T (N/4) + cn/2) + cn = = 4 T (N/4) + 2cN. T (N) = 4 (2 T (N/8) + cn/4) + 2cN = 8 T (N/8) + 3cN. Obecně po k rozepsáních: T (N) = 2 k T (N/2 k ) + kcn. Nyní si zvolme k tak, aby N/2 k bylo rovno jedné, čili k = log 2 N. Dostaneme: T (N) = 2 log 2 N T (1) + log 2 N cn. = N + cn log 2 N
5 Časová složitost Mergesortu je tedy Θ(N log N), což zní velice nadějně vyrovná se nejrychlejšímu algoritmu z kapitoly o třídění, totiž Heapsortu, a je přitom daleko jednodušší. Jeho slabinou ale je spotřeba paměti. Zatímco Heapsort si vystačil se vstupním polem a pár pomocnými proměnnými, naše procedura Merge sama o sobě pracuje se dvěma N-prvkovými poli. Pojďme dokázat, že lineární množství pomocné paměti (to je paměť, do které nepočítáme velikost vstupu a výstupu) Mergesortu také úplně stačí. Zavoláme-li funkci MergeSort na vstup velikosti N, potřebujeme si pamatovat lokální proměnné této funkce (poloviny vstupu a jejich setříděné verze dohromady Θ(N) paměti) a pak také, kam se z funkce máme vrátit (na to stačí konstantní množství paměti). Mimo to nějakou paměť spotřebují obě rekurzivní volání, ale jelikož vždy běží nejvýše jedno z nich, stačí ji započítat jen jednou. Opět dostaneme jednoduchou rekurentní rovnici: M(1) = 1, M(N) = cn + M(N/2) pro nějakou kladnou konstantu c. To nám pro M(N) dává geometrickou řadu cn + cn/2 + cn/4 +..., která má součet Θ(N). Prostorová složitost je tedy opravdu lineární. Výhody třídění sléváním se naplno projeví tehdy, když chceme třídit data v seznamech, ke kterým neumíme přistupovat napřeskáčku. Mergesort totiž prvky vždy prochází postupně jeden po druhém. Navíc ani nemusíme do pomocných posloupností data kopírovat, stačí vytvářet nové seznamy z původních prvků. Paměťové nároky jednoho volání funkce Merge se proto smrsknou na konstantní a celého Mergesortu na Θ(log N). math Stromy rekurze Někdy je jednodušší místo počítání s rekurencemi odhadnout složitost úvahou o stromu rekurzivních volání. Nakresleme si strom, jehož vrcholy budou odpovídat jednotlivým podúlohám, které řešíme. Kořen je původní úloha velikosti N, jeho dva synové podúlohy velikosti N/2. Pak následují 4 podúlohy velikosti N/4, a tak dále až k listům, což jsou podúlohy o jednom prvku. Obecně i-tá hladina bude mít 2 i vrcholů pro podúlohy velikosti N/2 i, takže hladin bude celkem log 2 N. Strom rekurze algoritmu MergeSort
6 Rozmysleme si nyní, kolik času kde trávíme. Rozdělování i slévání jsou lineární, takže jeden vrchol na i-té hladině spotřebuje čas Θ(N/2 i ). Celá i-tá hladina přispěje časem 2 i Θ(N/2 i ) = Θ(N). Když tento čas sečteme přes všechny hladiny, dostaneme celkovou časovou složitost Θ(N log N). Všimněte si, že tento stromový důkaz docela věrně odpovídá tomu, jak jsme předtím rozepisovali rekurenci. Situace po k-tém rozepsání totiž popisuje řez stromem rekurze na k-té hladině. Vyšší hladiny jsme již sečetli, nižší nás teprve čekají. I prostorové nároky algoritmu můžeme vyčíst ze stromu. V každém vrcholu potřebujeme paměť lineární s velikostí podúlohy, ve vrcholu na i-té hladině tedy Θ(N/2 i ). V paměti je vždy vrchol, který právě zpracováváme, a všichni jeho předci. Maximálně tedy nějaká cesta z kořene do listu. Sečteme-li prostor zabraný vrcholy na takové cestě, dostaneme Θ(N) + Θ(N/2) + Θ(N/4) Θ(1) = Θ(N). Cvičení: 1. Naprogramujte Mergesort bez rekurze. V k-tém průchodu si představujte, že pole je rozdělené na bloky o 2 k prvcích, a vždy slévejte dvojice sousedních bloků. 2. Naprogramujte třídění seznamu pomocí Mergesortu. Jde to snáze rekurzivně nebo cyklem? 3. Popište třídící algoritmus, který bude vstup rozkládat na více než dvě části a ty pak rekurzivně třídit. Může být rychlejší než Mergesort? 4*. Naše procedura Merge potřebuje lineární pomocnou paměť, což je nešikovné. Poměrně složitým trikem lze paměťové nároky srazit až na konstantu při zachování lineární časové složitosti. Zkuste objevit, jak je snížit alespoň na O( n) Násobení èísel Při třídění metodou Rozděl a panuj jsme získali algoritmus, který byl sice elegantnější než předchozí třídící algoritmy, ale měl stejnou časovou složitost. Pojďme se nyní podívat na příklad, kdy nám tato metoda pomůže k efektivnějšímu algoritmu. Půjde o násobení dlouhých čísel. Mějme N-ciferná čísla X a Y, která chceme vynásobit. Rozdělme si je na horních N/2 a dolních N/2 cifer (pro jednoduchost opět předpokládejme, že N je mocnina dvojky). Platí tedy: X = A 10 N/2 + B, Y = C 10 N/2 + D pro nějaká (N/2)-ciferná čísla A, B, C, D. Hledaný součin XY pak můžeme zapsat jako: XY = AC 10 N + (AD + BC) 10 N/2 + BD. Spočítáme tedy rekurzivně součiny AC, AD, BC a BD a pak z nich složíme výsledek. Skládání obnáší několik 2N-ciferných sčítání a několik násobení mocninou desítky, to druhé ovšem není nic jiného, než doplňování nul na konec čísla. Řešíme
7 tedy čtyři podproblémy poloviční velikosti a k tomu spotřebujeme lineární čas. Pro časovou složitost proto platí: T (1) = 1, T (N) = 4 T (N/2) + Θ(N). Podobně jako minule, i zde k vyřešení rovnice stačí rozmyslet si, jak vypadá strom rekurzivních volání. Na jeho i-té hladině se nachází 4 i vrcholů s podproblémy o N/2 i cifrách. V každém vrcholu tedy trávíme čas Θ(N/2 i ) a na celé hladině 4 i Θ(N/2 i ) = Θ(2 i N). Jelikož hladin je opět log 2 N, strávíme jenom na poslední hladině čas Θ(2 log 2 N N) = Θ(N 2 ). Oproti běžnému školnímu násobení jsme si tedy vůbec nepomohli. První pokus o násobení rekurzí Po tomto neúspěchu se svého plánu ovšem nevzdáme, nýbrž nahlédneme, že ze zmíněných čtyř násobení poloviční velikosti můžeme jedno ušetřit. Když vynásobíme (A+B) (C+D), dostaneme AC+AD+BC+BD. To se od závorky (AD+BC), kterou potřebujeme, liší jen o AC + BD. Tyto dva členy nicméně známe, takže je můžeme odečíst. Získáme následující formulku pro XY : XY = AC 10 N + ((A + B)(C + D) AC BD) 10 N/2 + BD. Časová složitost se touto úpravou změní následovně: T (N) = 3 T (N/2) + Θ(N). Sledujme, jak se změnil strom: na i-té hladině nalezneme 3 i vrcholů s (N/2 i )- cifernými problémy a jeho hloubka bude nadále činit log 2 N. Na i-té hladině nyní dohromady trávíme čas Θ(N (3/2) i ), v součtu přes všechny hladiny dostaneme: T (N) = Θ(N [(3/2) 0 + (3/2) (3/2) log 2 N ]). Výraz v hranatých závorkách je geometrická řada s kvocientem 3/2. Tu můžeme sečíst obvyklým způsobem na (3/2) 1+log 2 N 1. 3/
8 Strom rekurze algoritmu Násob Když zanedbáme konstanty, obdržíme (3/2) log 2 N. To dále upravíme na (2 log 2 (3/2) ) log 2 N = 2 log 2 (3/2) log 2 N = (2 log 2 N ) log 2 (3/2) = N log 2 (3/2) = N log Časová složitost našeho algoritmu tedy činí Θ(N N log ) = Θ(N log 2 3 ) Θ(N 1,59 ). To je již podstatně lepší než obvyklý kvadratický algoritmus. Paměti nám přitom bude stačit lineárně mnoho (viz cvičení 1.3.3). Algoritmus Násob Vstup: N-ciferná čísla X a Y Výstup: Součin Z = XY 1. Pokud N 1, vrátíme Z = XY a skončíme. 2. k = N/2 3. A X/10 k, B X mod 10 k 4. C Y/10 k, D Y mod 10 k 5. P Násob(A, C) 6. Q Násob(B, D) 7. R Násob(A + B, C + D) 8. Z P 10 N + (R P Q) 10 k + Q Zbývá dodat, že naším algoritmem vývoj neskončil a existují i asymptoticky rychlejší metody. Ty jednodušší z nich využívají podobný princip rozkladu na podproblémy, ovšem s více částmi (viz cvičení ). Pokročilejší algoritmy jsou ale obvykle založeny na Fourierově transformaci. Arnold Schönhage v roce 1979 ukázal, že tímto způsobem lze dokonce dosáhnout lineární časové složitosti. Násobení je tedy, alespoň teoreticky, stejně těžké jako sčítání a odčítání. Ve cvičeních navíc odvodíme, že dělit lze stejně rychle jako násobit. Cvičení: 1. Pozornému čtenáři jistě neuniklo, že se v našem rozboru časové složitosti skrývá drobná chybička: čísla A + B a C + D mohou mít více než N/2 cifer, konkrétně N/ Ukažte, že to časovou složitost algoritmu neovlivní. 2. Problému z předchozího cvičení se lze také vyhnout jednoduchou úpravou algoritmu. Změnte 7. krok algoritmu tak, aby volal Násob na N/2-ciferná čísla
9 3. Dokažte, že funkce Násob má lineární prostorovou složitost. (Podobnou úvahou jako u Mergesortu.) 4. Algoritmus Násob je sice pro velká N rychlejší než školní násobení, ale pro malé vstupy se ho nevyplatí použít, protože režie na rekurzi a spojování mezivýsledků bude daleko větší než čas spotřebovaný kvadratickým algoritmem. Často proto pomůže zkřížit chytrý rekurzivní algoritmus s nějakým primitivním. Pokud velikosti vstupu klesne pod vhodně zvolenou konstantu N 0, rekurzi zastavíme a použijeme hrubou sílu. Zkuste si takový hybridní algoritmus pro násobení naprogramovat a experimentálně zjistit nejvýhodnější hodnotu pro N 0. 5*. Zrychlete algoritmus Násob tím, že budete číslo dělit na tři části a rekurzivně počítat pět součinů. Nazveme-li části čísla X po řadě X 2, X 1, X 0 a analogicky pro Y, budeme počítat tyto součiny: W 0 = X 0 Y 0, W 1 = (X 2 + X 1 + X 0 )(Y 2 + Y 1 + Y 0 ), W 2 = (X 2 X 1 + X 0 )(Y 2 Y 1 + Y 0 ), W 3 = (4X 2 + 2X 1 + X 0 )(4Y 2 + 2Y 1 + Y 0 ), W 4 = (4X 2 2X 1 + X 0 )(4Y 2 2Y 1 + Y 0 ). Ukažte, že součin XY lze zapsat jako lineární kombinaci těchto mezivýsledků. Jakou bude mít tento algoritmus časovou složitost? 6**. Pomocí nápovědy k předchozímu cvičení ukažte, jak pro libovolné r 1 čísla dělit na r + 1 částí a rekurzivně počítat 2r + 1 součinů. Co z toho plyne pro časovou složitost násobení? Může se hodit Kuchařková věta z následující podkapitoly. 7*. Z rychlého násobení můžeme odvodit i efektivní algoritmus pro dělení. Hodí se k tomu Newtonova iterační metoda řešení rovnic, zvaná též metoda tečen. Vyzkoušíme si ji na výpočtu N cifer podílu 1/a pro 2 N 1 a < 2 N. Uvážíme funkci f(x) = 1/x a. Tato funkce nabývá nulové hodnoty pro x = 1/a a její obr derivace je f (x) = 1/x 2. Budeme vytvářet posloupnost aproximací kořene této funkce. Za počáteční aproximaci x 0 zvolíme 2 N, hodnotu x i+1 získáme z x i tak, že sestrojíme tečnu ke grafu funkce f v bodě (x i, f(x i )) a vezmeme si x-ovou souřadnici průsečíku této tečny s osou x. Pro tuto souřadnici platí x i+1 = x i f(x i )/f (x i ) = 2x i ax 2 i. Posloupnost x 0, x 1, x 2,... velmi rychle konverguje ke kořeni x = 1/a a k jejímu výpočtu stačí pouze sčítání, odčítání a násobení čísel. Rozmyslete si, jak tímto způsobem dělit libovolné číslo libovolným. 8**. Dokažte, že newtonovské dělení z minulého cvičení nalezne podíl po O(log N) iteracích. Pracuje tedy v čase O(M(N) log N), kde M(N) je čas potřebný na vynásobení dvou N-ciferných čísel. 9**. Logaritmu v předchozím odhadu se lze zbavit, pokud funkce M(N) roste alespoň lineárně, čili platí M(cN) = O(cM(N)) pro každé c 1. Stačí pak v k-té iteraci algoritmu počítat pouze s 2 Θ(k) -cifernými čísly, čímž složitost klesne na O(M(N) + M(N/2) + M(N/4) +...) = O(M(N) (1 + 1/2 + 1/4 +...)) = O(M(N)). Dělení je tedy stejně těžké jako násobení
10 10. Jak pomocí metody Rozděl a panuj vypsat N-ciferné číslo v soustavě o daném základu? Může se hodit výsledek předchozího cvičení. 1.4.* Slo¾itost rekurzivních algoritmù U předchozích algoritmů založených na principu Rozděl a panuj jsme pozorovali několik různých časových složitostí: Θ(2 N ) u Hanojských věží, Θ(N log N) u Mergesortu a Θ(N 1,59 ) u násobení čísel. Hned se nabízí otázka, jestli v těchto složitostech lze nalézt nějaký řád. Pojďme to zkusit: Uvažme rekurzivní algoritmus, který vstup rozloží na a podproblémů velikosti N/b a z jejich výsledků složí celkovou odpověď v čase Θ(N c ). 1 Dovolíme-li si opět zamést pod rohožku případné zaokrouhlování předpokladem, že N je mocninou čísla b, bude příslušná rekurence vypadat takto: T (1) = 1, T (N) = a T (N/b) + Θ(N c ). Použijeme osvědčenou metodu založenou na stromu rekurze. Jak tento strom vypadá? Každý vnitřní vrchol stromu má přesně a synů, takže na i-té hladině se nachází a i vrcholů. Velikost problému se zmenšuje b-krát, proto na i-té hladině leží podproblémy velikosti N/b i. Po log b N hladinách se tudíž rekurze zastaví. Nyní počítejme, kolik času kde strávíme. V jednom vrcholu i-té hladiny je to Θ((N/b i ) c ), na celé hladině pak Θ(a i (N/b i ) c ). Tento výraz snadno upravíme na Θ(N c (a/b c ) i ), což v součtu přes všechny hladiny dá: Θ(N c [(a/b c ) 0 + (a/b c ) (a/b c ) log b N ]). Výraz v hranatých závorkách je opět nějaká geometrická řada, tentokrát s kvocientem q = a/b c. Její chování bude proto záviset na tom, jak velký je kvocient: q = 1: Všechny členy řady jsou rovny jedné, takže se řada sečte na log b N + 1. Tomu odpovídá časová složitost T (N) = Θ(N c log N). Tak se chová například Mergesort na všech hladinách stromu se vykonává stejné množství práce. q < 1: I kdyby řada byla nekonečná, bude mít součet nejvýše 1/(1 q), a to je konstanta. Dostaneme tedy T (N) = Θ(N c ). To znamená, že podstatnou část času trávíme v kořeni stromu a zbytek je zanedbatelný. Algoritmus tohoto typu jsme ještě nepotkali. q > 1: Řadu sečteme na (q 1+log b N 1)/(q 1) = Θ(q log b N ), dominantní je tentokrát čas trávený v listech. To jsme už viděli u algo- 1 Do tohoto schématu nám nezapadají Hanojské věže, ale ty jsou neobvyklé i tím, že jejich podproblémy jsou jen o jedničku menší než původní problém. Mimo to algoritmy s exponenciální složitostí jsou poněkud nepraktické
11 ritmu na násobení čísel, zkusme tedy výraz upravit obdobně: q log b N = ( a b c ) logb N = a log b N (b c ) log b N = blogb a logb N b c log b N = = (blog b N ) log b a (b log b N ) c = N logb a N c. Vyjde nám T (N) = Θ(N c q log b N ) = Θ(N log b a ). Zbývá maličkost: vymést zpod rohožky případ, kdy N není mocninou čísla b. Tehdy dělení na podproblémy nebude úplně rovnoměrné některé budou mít velikost N/b, jiné N/b. My se ale komplikovanému počítání vyhneme následující úvahou: označme si N nejbližší nižší mocninu b a N + nejbližší vyšší. Jelikož časová složitost s rostoucím N jistě neklesá, leží T (N) mezi T (N ) a T (N + ). Jenže N a N + se liší jen b-krát, což se do T (...) ve všech třech typech chování promítne pouze konstantou. Proto jsou T (N ) i T (N + ) asymptoticky stejné a taková musí být i T (N). 2 Zjistili jsme tedy, že hledaná funkce T (N) se vždy chová jedním ze tří popsaných způsobů. To můžeme shrnout do následující kuchařkové věty, známé také pod anglickým názvem Master theorem: Věta: (Kuchařka na řešení rekurencí) Rekurentní rovnice T (N) = a T (N/b) + Θ(N c ), T (1) = 1 má pro konstanty a 1, b > 1, c 0 řešení: T (N) = Θ(N c log N), pokud a/b c = 1; T (N) = Θ(N c ), pokud a/b c < 1; T (N) = Θ(N log b a ), pokud a/b c > 1. obr Cvičení: 1. Nalezněte nějaký algoritmus, který odpovídá druhému typu chování (q < 1). 2*. Vylepšete kuchařkovou větu, aby pokrývala i případy, v nichž se velikosti podproblémů liší až o nějakou konstantu. To by se hodilo například u násobení čísel. 3**. Kuchařka pro různě hladové jedlíky: Jak by věta vypadala, kdybychom problém dělili na nestejně velké části? Tedy kdyby rekurence měla tvar T (N) = T (β 1 N)+ T (β 2 N) T (β a N) + Θ(N c ) Násobení matic { Strassenùv algoritmus Nejen násobením čísel živ jest matematik. Často je potřeba násobit i složitější matematické objekty, zejména pak čtvercové matice. Pokud počítáme součin dvou math matic tvaru N N přesně podle definice, potřebujeme Θ(N 3 ) kroků. Jak v roce 2 To trochu připomíná Větu o policajtech z matematické analýzy. Vlastně říkáme, že pokud f(n) g(n) h(n) a existuje nějaká funkce z(n) taková, že f(n) = Θ(z(n)) a h(n) = Θ(z(n)), pak také platí g(n) = Θ(z(n))
12 1969 ukázal pan Volker Strassen, i zde dělení na menší podproblémy přináší ovoce v podobě rychlejšího algoritmu. Nejprve si rozmyslíme, že stačí umět násobit matice, jejichž velikost je mocnina dvojky. Jinak stačí matice doplnit vpravo a dole nulami a nahlédnout, že vynásobením takto orámovaných matic získáme stejným způsobem orámovaný součin původních matic. Navíc orámované matice obsahují nejvýše čtyřikrát tolik prvků, takže se nemusíme obávat, že bychom tím algoritmus podstatně zpomalili. Mějme tedy matice X a Y, obě tvaru N N pro N = 2 k. Rozdělíme si je na čtvrtiny (budeme jim říkat bloky): matici X na A až D, matici Y na P až S, všechny formátu N/2 N/2. Pomocí těchto bloků můžeme snadno zapsat jednotlivé bloky součinu X Y : ( A B X Y = C D ) ( ) ( P Q AP + BR AQ + BS = R S CP + DR CQ + DS Tento vztah vlastně vypadá úplně stejně jako klasická definice násobení matic, jen zde jednotlivá písmena nezastupují čísla, nýbrž bloky. Jedno násobení matic N N jsme tedy převedli na 8 násobení matic poloviční velikosti. Letmým nahlédnutím do kuchařkové věty z minulé kapitoly zjistíme, že tak získáme opět kubický algoritmus. 3 Stejně jako u násobení čísel nás zachrání, že dovedeme jedno násobení ušetřit. Jen příslušné formule jsou daleko komplikovanější a připomínají králíka vytaženého z klobouku. Neprozradíme vám, jak kouzelník pan Strassen svůj trik vymyslel (sami neznáme žádný systematický postup, jak na to přijít), ale když už vzorce známe, není těžké ověřit, že opravdu fungují (viz cvičení). Formulky vypadají takto: ( ) T1 + T X Y = 4 T 5 + T 7 T 3 + T 5, T 2 + T 4 T 1 T 2 + T 3 + T 6 kde: T 1 = (A + D) (P + S), T 5 = (A + B) S, T 2 = (C + D) P, T 6 = (C A) (P + Q), T 3 = A (Q S), T 7 = (B D) (R + S). T 4 = D (R P ), Stačí nám tedy provést 7 násobení menších matic a 18 maticových součtů a rozdílů. Součty a rozdíly umíme počítat v čase Θ(N 2 ), takže časovou složitost celého algoritmu bude popisovat rekurence T (N) = 7T (N/2) + Θ(N 2 ). Podle kuchařkové věty je jejím řešením T (N) = Θ(N log 2 7 ) Θ(N 2,807 ). Pro úplnost dodejme, že jsou známy i efektivnější algoritmy, které jsou ovšem mnohem složitější a které se vyplatí používat až pro opravdu obří matice. Nejrychlejší z nich (Coppersmithův-Winogradův) dosahuje složitosti Θ(N 2,376 ) a mnozí se domnívají, že k Θ(N 2 ) se lze libovolně přiblížit. 3 Obvyklá terminologie je tu poněkud zavádějící N zde neznačí velikost vstupu, nýbrž počet řádků matice; vstup je tedy velký N 2. )
13 Cvičení: 1. Dokažte Strassenovy vzorce. Návod: T 1 = T 4 = + T 5 = + + T 7 = + + T 1 + T 4 T 5 + T 7 = + + = AP + BR. 2. Rychlé násobení matic je základem rychlých algoritmů pro další operace z lineární algebry. Vymyslete algoritmus pro výpočet inverze trojúhelníkové matice Hledání k-tého nejmen¹ího prvku { Quickselect Při použití metody Rozděl a panuj se někdy ukáže, že některé z částí, na které jsme vstup rozdělili, nemusíme vůbec zpracovávat. Typickým příkladem je následující algoritmus na hledání k-tého nejmenšího prvku posloupnosti. Dostaneme-li na vstupu nějakou posloupnost prvků, jeden z nich si vybereme a budeme mu říkat pivot. Zadané prvky poté rozhrneme na tři části: doleva půjdou prvky menší než pivot, doprava prvky větší než pivot a uprostřed zůstanou ty, které se pivotovi rovnají. Tyto části budeme značit po řadě L, P a S. Kdybychom posloupnost setřídili, musí v ní vystupovat nejdříve všechny prvky z levé části, pak prvky z části střední a konečně ty z pravé. Pokud je tedy k L, musí se hledaný prvek nalézat nalevo a musí tam být k-tý nejmenší (žádný prvek z jiné části ho nemohl předběhnout). Podobně je-li L < k L + S, padne hledaný prvek v setříděné posloupnosti tam, kde leží S, a tedy je roven pivotovi. A konečně pro k > L + S se musí nacházet v pravé části a musí tam být (k L S )-tý nejmenší. Ze tří částí vstupu jsme si tedy vybrali jednu a v ní opět hledáme několikátý nejmenší prvek, na což samozřejmě použijeme rekurzi. Vznikne následující algoritmus, obvykle známý pod názvem Quickselect: Algoritmus QuickSelect Vstup: Posloupnost prvků X = x 1,..., x N a číslo k (1 k N). Výstup: y = k-tý nejmenší prvek v X. 1. Pokud N = 1, vrátíme y = x 1 a skončíme. 2. p některý z prvků x 1,..., x N (pivot) 3. L prvky v X, které jsou menší než p 4. P prvky v X, které jsou větší než p 5. S prvky v X, které jsou rovny p 6. Pokud k L, pak y QuickSelect(L, k). 7. Jinak je-li k L + S, nastavíme y p. 8. Jinak y QuickSelect(P, k L S )
14 Správnost algoritmů je evidentní, ale jak to bude s časovou složitostí? Pokaždé strávíme lineární čas rozdělováním posloupnosti a pak se zavoláme rekurzivně na menší vstup. O kolik menší bude, to závisí zejména na volbě pivota. Jestliže si ho budeme vybírat nešikovně, například jako největší prvek vstupu, skončí N 1 prvků nalevo. Pokud navíc bude k = 1, budeme se rekurzivně volat vždy na tuto obří levou část. Ta se pak opět zmenší pouhou o jedničku a tak dále, takže celková časová složitost vyjde Θ(N) + Θ(N 1) Θ(1) = Θ(N 2 ). Obecněji pokud rozdělujeme vstup nerovnoměrně, hrozí nám, že nepřítel zvolí k tak, aby nás vždy vehnal do té větší části. Ideální obranou by tedy pochopitelně bylo volit za pivota medián posloupnosti. 4 Tehdy bude nalevo i napravo nejvýše N/2 prvků (alespoň jeden je uprostřed) a ať už si během rekurze vybereme levou nebo pravou část, N bude exponenciálně klesat. Algoritmus pak doběhne v čase Θ(N) + Θ(N/2) + Θ(N/4) Θ(1) = Θ(N). Medián ovšem není jediným pivotem, pro kterého algoritmus poběží lineárně. Zkusme za pivota zvolit lžimedián tak budeme říkat prvku, který leží v prostředních dvou čtvrtinách setříděné posloupnosti. Tehdy bude nalevo i napravo nejvýše 3/4 N a velikost vstupu bude opět exponenciálně klesat, byť o chlup pomaleji: Θ(N) + Θ(3/4 N) + Θ((3/4) 2 N) Θ(1). To je opět geometrická řada se součtem Θ(N). Ani medián, ani lžimedián bohužel neumíme rychle najít. Jakého pivota tedy v algoritmu používat? Ukazuje se, že na tom příliš nezáleží můžeme zvolit třeba prvek x N/2 nebo si hodit kostkou (totiž pseudonáhodným generátorem) a vybrat ze všech x i náhodně. Algoritmus pak bude mít lineární časovou složitost v průměrném případě. Co to přesně znamená a jak to dokázat, odložíme do kapitoly 1.9. V praxi tento přístup každopádně funguje výtečně. Prozatím se spokojíme s intuitivním vysvětlením: Alespoň polovina všech prvků jsou lžimediány, takže pokud se budeme trefovat náhodně (nebo pevně, ale vstup bude dobře zamíchaný ), často se strefíme do lžimediánu a algoritmus bude postupovat kupředu dostatečně rychle. Cvičení: 1. Proč navrhujeme volit za pivota prvek x N/2 a ne třeba x 1 nebo x N? 2. Student Šťoura si místo lžimediánů za pivoty volí ještě lživější mediány, které leží v prostředních šesti osminách vstupu. Jaké dosahuje časové složitosti? 3. Jak by dopadlo, kdybychom na vstupu dostali posloupnost reálných čísel a jako pivota používali aritmetický průměr? 4. Uvědomte si, že binární vyhledávání je také algoritmus typu Rozděl a panuj, v němž velikost vstupu exponenciálně klesá. Spočítejte jeho časovou složitost metodami z této kapitoly. Čím se liší od Quickselectu? 4 Medián je prvek, pro který platí, že nejvýše polovina prvků je menší než on a nejvýše polovina větší; tuto vlastnost má N/2 -tý a N/2 -tý nejmenší prvek
15 1.7. Je¹tì jednou tøídìní { Quicksort Rozdělování vstupu podle pivota, které se osvědčilo v minulé kapitole, můžeme použít i ke třídění dat. Připomeňme si, že rozdělíme-li vstup na levou, pravou a střední část, budou v setříděné posloupnosti vystupovat nejdříve prvky z levé části, pak ty z prostřední a nakonec prvky z části pravé. Můžeme tedy rekurzivně setřídit levou a pravou část (prostřední je sama od sebe setříděná), pak části poskládat ve správném pořadí a získat setříděnou posloupnost. Tomuto třídícímu algoritmu se říká Quicksort. 5 Algoritmus QuickSort Vstup: Posloupnost prvků X = x 1,..., x N k setřídění. Výstup: Setříděná posloupnost Y. 1. Pokud N 1, vrátíme Y = X a skončíme. 2. p některý z prvků x 1,..., x N (pivot) 3. L prvky v X, které jsou menší než p 4. P prvky v X, které jsou větší než p 5. S prvky v X, které jsou rovny p 6. Rekurzivně setřídíme části: 7. L QuickSort(L) 8. P QuickSort(P ) 9. Slepíme části za sebe: Y L, S, P. Dobrou představu o rychlosti algoritmu nám jako obvykle dá strom rekurzivních volání. V kořeni máme celý vstup, na první hladině jeho levou a pravou část, na druhé hladině levé a pravé části těchto částí, a tak dále, až v listech triviální posloupnosti délky 1. Rekurzivní volání na vstup nulové délky do stromu kreslit nebudeme a rovnou je zabudujeme do jejich otců. Jelikož rozkládání vstupu i skládání výsledku jistě pokaždé stihneme v lineárním čase, trávíme v každém vrcholu čas přímo úměrný velikosti příslušného podproblému. Pro libovolnou hladinu navíc platí, že podproblémy, které na ní leží, mají dohromady nejvýše N prvků vznikly totiž rozdělením vstupu na disjunktní části a ještě se nám při tom některé prvky (pivoti) poztrácely. Na jedné hladině proto trávíme čas O(N). Tvar stromu a s ním i časová složitost samozřejmě opět stojí a padají s volbou pivota. Pokud za pivoty volíme mediány nebo alespoň lžimediány, klesají velikosti podproblémů exponenciálně (na i-té hladině O((3/4) i N)), takže strom je vyvážený a má hloubku O(log N). V součtu přes všechny hladiny proto časová složitost činí O(N log N). 5 Za jménem se často skrývá příběh. Quicksort (což znamená Rychlotřidič ) přišel ke svému jménu tak, že v roce 1961, kdy vznikl, byl prvním třídícím algoritmem se složitostí O(N log N) aspoň v průměrném případě
16 Jestliže naopak volíme pivoty nešťastně jako (řekněme) největší prvky vstupu, oddělí se na každé hladině od vstupu jen úsek o jednom prvku a hladin bude Θ(N). To povede na kvadratickou časovou složitost. Horší případ již nenastane, neboť na každé hladině přijdeme alespoň o prvek, který se stal pivotem. Quicksort při dobré a špatné volbě pivota Podobně jako u Quickselectu, i zde je mnoho dobrých pivotů, se kterými se algoritmus chová efektivně (alespoň polovina prvků jsou lžimediány). V praxi proto opět funguje spoléhat na náhodný generátor nebo dobře zamíchaný vstup. V kapitole 1.9 pak vypočteme, že Quicksort s náhodnou volbou pivota má časovou složitost O(N log N) v průměrném případě. Quicksort v praxi Závěrem si dovolme krátkou poznámku o praktických implementacích Quicksortu. Ačkoliv tento algoritmus mezi ostatními třídícími algoritmy na první pohled ničím nevyniká, u většiny překladačů se v roli standardní funkce pro třídění setkáte právě s ním. Důvodem této nezvyklé popularity není móda, nýbrž praktické zkušenosti. Dobře vyladěná implementace Quicksortu totiž na reálném počítači běží výrazně rychleji než jiné třídící algoritmy. Cesta od našeho poměrně obecně formulovaného algoritmu k takto propracovanému programu je samozřejmě složitá a vyžaduje mimo mistrného zvládnutí programátorského řemesla i detailní znalost konkrétního počítače. My si ukážeme alespoň první kroky této cesty. Především Quicksort upravíme tak, aby prvky zbytečně nekopíroval. Vstup dostane jako ostatní třídící algoritmy v poli a pak bude pouze prvky uvnitř tohoto pole prohazovat. Rekurzivně tedy budeme třídit různé úseky společného pole. Kterým úsekem se máme právě zabývat, vymezíme snadno indexy krajních prvků. Levý okraj úseku (ten blíže k začátku pole) budeme značit l, pravý pak r. Rozdělování nám zjednoduší, budeme-li vstup dělit jen na dvě části namísto tří prvky rovné pivotovi mohou bez újmy na korektnosti přijít jak nalevo, tak napravo. Budeme postupovat následovně: Použijeme dva indexy i a j. První z nich bude procházet tříděným úsekem zleva doprava a přeskakovat prvky, které mají zůstat nalevo; druhý index půjde zprava doleva a bude přeskakovat prvky patřící do pravé části. Levý index se tudíž zastaví na prvním prvku, který je vlevo, ale patří doprava; podobně pravý index se zastaví na nejbližším prvku vpravo, který patří
17 doleva. Stačí tedy tyto dva prvky prohodit a pokračovat stejným způsobem dál, až se indexy setkají. Nyní máme obě části uložené v souvislých úsecích pole, takže je můžeme rekurzivně setřídit. Navíc se tyto úseky vyskytují přesně tam, kde mají ležet v setříděné posloupnosti, takže slepovací krok 9 původního Quicksortu můžeme zcela vynechat. Algoritmus QuickSort2 Vstup: Pole P [1... N], indexy l a r úseku, který třídíme. Výstup: Úsek P [l... r] je setříděn. 1. Pokud l r, ihned skončíme. 2. p některý z prvků P [l],..., P [r] (pivot) 3. i = l, j = r 4. Dokud i j, opakujeme: 5. Dokud P [i] < p, zvyšujeme i o Dokud P [j] > p, snižujeme j o Je-li i < j, prohodíme P [i] a P [j]. 8. Je-li i j, pak i i + 1, j j Rekurzivně setřídíme části: 10. QuickSort2(P, l, j) 11. QuickSort2(P, i, r) Popsanými úpravami jsme jistě nezhoršili časovou složitost: V krocích 2 8 zpracujeme každý prvek úseku nejvýše jednou, celkově tedy rozdělováním trávíme čas lineární s délkou úseku, s čímž naše analýza časové složitosti počítala. Naopak jsme se zbavili zbytečného kopírování prvků do pomocné paměti. Další možná vylepšení ponecháváme čtenáři jako cvičení s nápovědou. Cvičení: 1. Rozmyslete si, že procedura QuickSort2 je korektní. Zejména si uvědomte, co se stane, když si jako pivota vybereme nejmenší nebo největší prvek úseku nebo když dokonce budou všechny prvky v úseku stejné. Ani tehdy během kroků 4 8 nemohou indexy i, j opustit tříděný úsek a každá z částí, na které se rekurzivně zavoláme, bude ostře menší než původní vstup. 2. Vlastní zásobník: Abychom netrávili tolik času rekurzivním voláním a předáváním parametrů, nahradíme rekurzi naším vlastním zásobníkem, na kterém si budeme pamatovat začátky a konce úseků, které nám ještě zbývá setřídit. 3. Šetříme pamětí: Vylepšíme postup z minulého cvičení tak, že dvojici rekurzivních volání v krocích 7 a 8 nahradíme uložením většího úseku na zásobník a pokračováním tříděním menšího úseku. Dokažte, že po této úpravě může být v libovolný okamžik na zásobníku jen O(log N) úseků, což je také celkové množství pomocné paměti, které algoritmus spotřebuje. Fix! Fix: Obrázek situace
18 4. Včas se zastavíme: Podobně jako při násobení čísel (cvičení 1.3.4) se i u Quicksortu hodí zastavit rekurzi předčasně (pro N menší než vhodná konstanta N 0 ) a přepnout na některý z kvadratických třídících algoritmů. Vyzkoušejte si najít hodnotu N 0, pro kterou algoritmus běží nejrychleji. 5. Medián ze tří: Oblíbený trik na výběr pivota je spočítat medián z prvního, prostředního a posledního prvku úseku. Předpokládáme-li, že na vstupu dostaneme náhodnou permutaci čísel 1,..., N, jaká je pravděpodobnost, že takový pivot bude lžimediánem? 1.8. k-tý nejmen¹í prvek v lineárním èase Algoritmus Quickselect pro hledání k-tého nejmenšího prvku, který jsme potkali v kapitole 1.6, pracuje v lineárním čase pouze v průměrném případě. Nyní si ukážeme, jak ho upravit, aby tuto časovou složitost měl vždy. Jediné, co změníme, bude volba pivota. Prvky si nejprve seskupíme do pětic (není-li poslední pětice úplná, doplníme ji nekonečně velkými hodnotami). Poté nalezneme medián každé pětice a z těchto mediánů rekurzivním zavoláním našeho algoritmu spočítáme opět medián. Ten pak použijeme jako pivota k rozdělení vstupu na levou, střední a pravou část a pokračujeme jako v původním Quickselectu. Celý algoritmus bude vypadat takto: Algoritmus LinearSelect Vstup: Posloupnost prvků X = x 1,..., x N a číslo k (1 k N). Výstup: y = k-tý nejmenší prvek v X. 1. Pokud N 5, úlohu vyřešíme triviálním algoritmem. 2. Prvky rozdělíme na pětice P 1,..., P N/5. 3. Spočítáme mediány pětic: m i medián P i. 4. Najdeme pivota: p LinearSelect(m 1,..., m N/5 ; N/10 ). 5. L, P, S prvky z X, které jsou menší než p, větší než p, rovny p. 6. Pokud k L, pak y LinearSelect(L, k). 7. Jinak je-li k L + S, nastavíme y p. 8. Jinak y LinearSelect(P, k L S ). Abychom chování algoritmu pochopili, uvědomíme si nejdříve, že vybraný pivot není příliš daleko od mediánu celé posloupnosti X. K tomu nám pomůže obrázek. Pětice a jejich mediány
19 Překreslíme si do něj vstup a každou pětici uspořádáme zdola nahoru. Mediány pětic tedy budou ležet v prostředním řádku. Pětice si ještě přeházíme tak, aby jejich mediány rostly zleva doprava. (Pozor, algoritmus nic takového nedělá, pouze my při jeho analýze!) Navíc budeme pro jednoduchost předpokládat, že pětic je lichý počet a že všechny prvky jsou navzájem různé. Náš pivot (medián mediánů pětic) se tedy na obrázku nachází přesně uprostřed. Mediány všech pětic, které leží napravo od něj, jsou proto větší než pivot. Všechny prvky umístěné nad nimi jsou ještě větší, takže celý obdélník, jehož levým dolním rohem je pivot, padne v našem algoritmu do části P nebo S. Počítejme, kolik obsahuje prvků: Všech pětic je N/5, polovina z nich ( N/10 pětic) zasahuje do našeho obdélníku, a to třemi prvky. To celkem dává alespoň 3/10 N prvků, o kterých s jistotou víme, že se neobjeví v L. Levá část proto měří nejvýše 7/10 N. Podobně nahlédneme, že napravo je také nejvýše 7/10 N prvků stačí uvážit obdélník, který se rozprostírá od pivota doleva dolů. Všechny jeho prvky leží v L nebo S a opět jich je minimálně 3/10 N. Tato úvaha nám pomůže v odhadu časové složitosti: Rozdělovaní na pětice a počítání jejich mediánů je lineární pětice jsou konstantně velké, takže medián jedné spočítáme sebehloupějším algoritmem za konstantní čas. Dělení posloupnosti na části L, P a S a rozhodování, do které z částí se vydat, trvá také Θ(N). Poprvé voláme LinearSelect rekurzivně ve 4. kroku na N/5 prvků. Podruhé ho voláme v kroku 6 nebo 8, a to na levou nebo pravou část vstupu. Jak už víme, každá z nich měří nejvýše 7/10 N. Pro časovou složitost v nejhorším případě proto dostaneme následující rekurentní rovnici (konstant jsme se zbavili vhodnou volbou jednotky času): T (1) = O(1), T (N) = T (N/5) + T (7/10 N) + N. Metody z předchozích kapitol jsou na vyřešení této rekurence krátké (s výjimkou obecného postupu z cvičení 1.4.3). Pomůže nám válečná lest: uhodneme, že T (N) = cn, a ověříme si dosazením, že existuje taková konstanta c, pro kterou tato funkce naši rekurenci splňuje: cn = 1/5 cn + 7/10 cn + N = = 9/10 cn + N. Tato rovnost platí pro c = 10. Náš algoritmus tedy opravdu hledá k-tý nejmenší prvek v lineárním čase
20 Nyní bychom mohli upravit Quicksort, aby jako pivota použil vždy medián spočítaný tímto algoritmem. Pak by třídil v čase Θ(N log N) i v nejhorším případě. Příliš praktický takový algoritmus ale není. Jak asi tušíte, naše dvojitě rekurzivní hledání mediánu je sice asymptoticky lineární, ale konstanty, které v jeho složitosti vystupují, nejsou zrovna malé. Bývá proto užitečnější volit pivota náhodně a smířit se s tím, že občas promarníme jeden průchod kvůli nešikovnému pivotovi, než si třídění stále brzdit důmyslným vybíráním kvalitních pivotů. Cvičení: 1. Rozmyslete si, že našemu algoritmu nevadí, když prvky na vstupu nebudou navzájem různé. 2. Upravte funkci LinearSelect tak, aby si vystačila s konstantně velkou pomocnou pamětí. 3. Jak bude vypadat strom rekurzivních volání funkce LinearSelect? Kolik bude mít listů? Jak dlouhá bude nejkratší a nejdelší větev? 4. Proč při vybírání k-tého nejmenšího prvku používáme zrovna pětice? Fungoval by algoritmus s trojicemi? Nebo se sedmicemi? Byl by pak stále lineární? 5*. Na medián se můžeme dívat také tak, že je to patník na půli cesty od minima k maximu. Jinými slovy, mezi minimem a mediánem leží přibližně stejně prvků jako mezi mediánem a maximem. Co kdybychom chtěli mezi minimum a maximum co nejrovnoměrněji rozmístit více patníků? Přesněji: pro n-prvkovou množinu prvků X a číslo ε (0 < ε < 1) definujeme ε-síť jako posloupnost min X = x 0 < x 1 <... < x 1/ε = max X prvků vybraných z X tak, aby se mezi x i a x i+1 vždy nacházelo nejvýše εn prvků z X. Pro ε = 1/2 tedy počítáme minimum, medián a maximum, pro ε = 1/4 přidáme prvky ve čtvrtinách,..., a při ε = 1/n už třídíme. Složitost hledaní ε-sítě se tedy v zavislosti na hodnotě ε bude pohybovat mezi O(n) a O(n log n). Najděte algoritmus s časovou složitostí O(n log(1/ε)). 1.9.* Pravdìpodobnostní algoritmy U algoritmů založených na výběru pivota (Quickselect a Quicksort) jsme spoléhali na to, že pokud budeme pivota volit náhodně, bude se algoritmus chovat dobře. V této kapitole využijeme základní aparát teorie pravděpodobnosti k tomu, abychom těmto tvrzením dali smysl. TODO: Někde v knize bychom se měli zmínit o náhodných číslech a pravděpodobnostních algoritmech. Také by mělo padnout, že je zásadní rozdíl mezi průměrnou worst-case složitostí pp. algoritmu a složitostí deterministického algoritmu průměrovanou přes všechny vstupy. Že je mezi tím nějaký vztah (Yaův princip), to už je bezpečně mimo náš dosah. Jak se náhodná čísla generují? Tak dlouho se chodí se džbánem... Začněme jednoduchým příkladem: budeme chodit se džbánem pro vodu tak math
21 dlouho, než se utrhne ucho, což při každém pokusu nastane náhodně s pravděpodobností p (0 < p < 1), nezávisle na výsledcích předchozích pokusů. Kolik pokusů v průměru podnikneme? Označme si T počet kroků, po kterém k utržení ucha dojde. To je nějaká náhodná veličina a nás bude zajímat její střední hodnota E[T ]. Spočítáme ji jednoduchým trikem (jak jinak než rekurzivním): V každém případě provedeme první pokus. Pokud se ucho utrhne (což nastane s pravděpodobností p), hra končí. Pokud se neutrhne (pravděpodobnost 1 p), dostaneme se do přesně stejné situace, jako předtím náš ideální džbán totiž nemá žádnou paměť. Z toho vyjde následující rovnice pro E[T ]: E[T ] = 1 + p 0 + (1 p) E[T ]. Vyřešíme-li, dostaneme E[T ] = 1/p. Tento výsledek se nám bude často hodit, formulujme si ho proto jako lemma: Lemma: (O džbánu) Čekáme-li na náhodný jev, který nastane s pravděpodobností p, dočkáme se ve střední hodnotě po 1/p pokusech. Mediány, lžimediány a Quickselect Úvaha o džbánu nám dává jednoduchý algoritmus, pomocí kterého umíme najít lžimedián posloupnosti N prvků: Vybereme si rovnoměrně náhodně jeden z prvků posloupnosti; tím rovnoměrně myslíme tak, aby všechny prvky měly stejnou pravděpodobnost. Pak ověříme, jestli jsme si vybrali lžimedián. Pokud ne, na vše zapomeneme a postup opakujeme. Kolik pokusů budeme potřebovat, než algoritmus skončí? Lžimediány tvoří alespoň polovinu prvků, tedy pravděpodobnost, že se do nějakého strefíme, je minimálně 1/2. Podle lemmatu o džbánu tedy střední hodnota počtu pokusů bude nejvýše 2. (Počet pokusů v nejhorším případě ovšem neumíme omezit nijak při dostatečné smůle můžeme stále vybírat nejmenší prvek. Že se to stane, má ale nulovou pravděpodobnost.) Nyní už snadno spočítáme časovou složitost našeho algoritmu. Jeden pokus trvá Θ(N), střední hodnota počtu pokusů je O(1), takže střední hodnota časové složitosti je Θ(N). Obvykle budeme zkráceně mluvit o průměrné časové složitosti. Pokud tento výpočet lžimediánu použijeme v Quickselectu, získáme algoritmus pro hledání k-tého nejmenšího prvku s průměrnou složitostí Θ(N). Dobrá, tím jsme se ale šalamounsky vyhnuli otázce, jakou průměrnou složitost má původní Quickselect s rovnoměrně náhodnou volbou pivota. Tu odhadneme snadno: Rozdělíme si běh algoritmu na fáze. Fáze bude končit v okamžiku, kdy si za pivota zvolíme lžimedián. Fáze se skládá z kroků spočívajících v náhodné volbě pivota, lineárně dlouhém výpočtu a zahození části vstupu. Už víme, že lžimedián se průměrně podaří najít za dva kroky, tudíž jedna fáze trvá v průměru lineárně dlouho. Navíc si všimneme, že během každé fáze se vstup zmenší alespoň o čtvrtinu. K tomu totiž stačil samotný poslední krok, ostatní kroky mohou situaci jedině zlepšit. Průměrnou složitost celého algoritmu pak vyjádříme jako součet průměrných složitostí jednotlivých fází: Θ(N)+Θ((3/4) N)+Θ((3/4) 2 N)+... = Θ(N). term
22 Indikátory a Quicksort Podíváme-li se na výpočet v minulém odstavci s odstupem, všimneme si, že se opírá zejména o linearitu střední hodnoty ta říká, že E[X + Y ] = E[X] + E[Y ]. Časovou složitost celého algoritmu jsme vyjádřili jako součet složitostí fází. Přitom fázi jsme si nadefinovali tak, aby se již chovala dostatečně průhledně. Podobně můžeme analyzovat i Quicksort, jen se nám bude hodit složitost rozložit na daleko více veličin. Mimo to si všimneme, že Quicksort na každé porovnání provede jen O(1) dalších operací, takže postačí odhadnout počet provedených porovnání. Očíslujeme si prvky podle pořadí v setříděné posloupnosti y 1,..., y N. Zavedeme náhodné veličiny C ij pro 1 i < j N tak, aby platilo C ij = 1 právě tehdy, když během výpočtu došlo k porovnání y i s y j. V opačném případě je C ij = 0. Proměnným, které nabývají hodnoty 0 nebo 1 podle toho, zda nějaká událost nastala, se obvykle říká indikátory. Počet všech porovnání je tudíž roven součtu všech indikátorů C ij. Zamysleme se nyní nad tím, kdy může být C ij = 1. Algoritmus porovnává pouze s pivotem, takže jedna z hodnot y i, y j se těsně předtím musí stát pivotem. Navíc všechny hodnoty y i+1,..., y j 1 se ještě pivoty stát nesměly, jelikož jinak by y i a y j už byly rozděleny v různých částech posloupnosti. Jinými slovy, C ij je rovno jedné právě tehdy, když se z hodnot y i, y i+1,..., y j stane jako první pivotem buď y i nebo y j. A poněvadž pivota vybíráme rovnoměrně náhodně, má každý z prvků y i,..., y j stejnou pravděpodobnost, že se stane pivotem jako první, totiž 1/(j i+1). Proto C ij = 1 nastane s pravděpodobností 2/(j i + 1). Nyní si stačí uvědomit, že když indikátory nabývají pouze hodnot 0 a 1, je jejich střední hodnota rovna právě pravděpodobnosti jedničky, tedy také 2/(j i+1). Sečtením přes všechny dvojice (i, j) pak dostaneme pro počet všech porovnání: E[C] = 1 i<j N 2 j i + 1 N 2 d N 1 d. Nerovnost na pravé straně platí díky tomu, že rozdíly j i+1 se nacházejí v intervalu 2, N a každým rozdílem přispěje nejvýše N různých dvojic (i, j). Poslední suma je tzv. harmonická suma, jejíž hodnota je lnn + O(1). Spočítali jsme tedy, že střední hodnota časové složitosti Quicksortu s rovnoměrně náhodnou volbou pivota je O(N log N). Chování na náhodném vstupu Když jsme poprvé přemýšleli o tom, jak volit pivota, všimli jsme si, že pokud volíme pivota pevně, náš algoritmus není odolný proti zlomyslnému uživateli. Takový uživatel může na vstupu zadat šikovně sestrojenou posloupnost, která algoritmus donutí vybrat si v každém kroku pivota nešikovně, takže poběží kvadraticky dlouho. Tomu jsme se přirozeně vyhnuli náhodnou volbou pivota pro sebezlotřilejší vstup math
23 doběhneme v průměru rychle. Hodí se ale také vědět, že i pro pevnou volbu pivota je špatných vstupů málo. Zavedeme si proto ještě jeden druh složitosti algoritmů, tentokrát opět deterministických (bez náhodného generátoru). Bude to složitost v průměru přes vstupy. Jinými slovy algoritmus bude mít pevný průběh, ale budeme mu dávat náhodný vstup a počítat, jak dlouho v průměru poběží. Co to ale takový náhodný vstup je? U našich dvou problémů to docela dobře vystihuje náhodná permutace vybereme si rovnoměrně náhodně jednu z N! permutací množiny {1, 2,..., N}. Jak Quicksort, tak Quickselect se pak budou chovat velmi podobně, jako když měly pevný vstup, ale volily náhodně pivota. Pokud je na vstupu rovnoměrně náhodná permutace, je její prostřední prvek rovnoměrně náhodně vybrané číslo z množiny {1, 2,..., N}. Vybereme-li si ho za pivota a rozdělíme vstup na levou a pravou část, obě části budou opět náhodné permutace, takže se na nich algoritmus bude opět chovat tímto způsobem. Můzeme tedy analýzu z této kapitoly použít i na tento druh průměru se stejným výsledkem. Cvičení: 1. Ideální mince: Mějme počítač, jehož náhodným generátorem je ideální mince. Jinými slovy, máme funkci random, ze které na každé zavolání vypadne jeden rovnoměrně náhodný bit vygenerovaný nezávisle na předchozích bitech. Jak pomocí takové funkce generovat rovnoměrně náhodná přirozená čísla od 1 do N? Minimalizujte průměrný počet hodů mincí. 2. Ukažte, že v předchozím cvičení nelze počet hodů mincí v nejhorším případě nijak omezit, leda že by N bylo mocninou dvojky. 3. Míchání karet: Popište algoritmus, který v lineárním čase vygeneruje náhodnou permutaci množiny {1, 2,..., N}. 4. V mnoha programovacích jazycích je k dispozici funkci random, která nám vrátí rovnoměrně (pseudo)náhodné číslo z pevně daného intervalu. Lidé ji často používají pro generování čísel v rozsahu od 0 do N 1 tak, že spočtou random mod N. Jaký se v tom skrývá háček? 5. Náhodná k-tice: Na vstupu je číslo k > 1 a posloupnost navzájem různých přirozených čísel ukončená nulou. Vymyslete algoritmus, který z této posloupnosti vybere rovnoměrně náhodně k-tici čísel. Vstup může být tak dlouhý, že se celý nevejde do paměti; k-tice se tam spolehlivě vejde. 6*. Míchání podruhé: Vasil Vasiljevič míchá karty takto: připraví si N prázdných přihrádek. Pak postupně umisťuje čísla 1,..., N do přihrádek tak, že vždy vybere rovnoměrně náhodně přihrádku a pokud v ní již něco je, vybírá znovu. Kolik pokusů bude v průměru potřebovat? 7. Lemma o džbánu můžeme dokázat i přímo podle definice střední hodnoty: Pravděpodobnost, že ucho se poprvé utrhne při i-tém pokusu, je rovna p(1 p) i 1. Proto E[T ] = i=1 ip(1 p)i 1 = p/(1 p) i=1 i(1 p)i. Podobnou sumu jsme ovšem již potkali při analýze stavění haldy zespodu. Sečtěte ji. odkaz
říkali spíš latinsky: divide et impera). Tato zásada se pak osvědčila nejen ve starořímské
 1. Rozdìl a panuj Potkáme-li spletitý problém, často pomáhá rozdělit ho na jednodušší části a s těmi se pak vypořádat postupně. Jak říkali staří Římané: rozděl a panuj (oni to říkali spíš latinsky: divide
1. Rozdìl a panuj Potkáme-li spletitý problém, často pomáhá rozdělit ho na jednodušší části a s těmi se pak vypořádat postupně. Jak říkali staří Římané: rozděl a panuj (oni to říkali spíš latinsky: divide
1. Rozdìl a panuj Hanojské vì¾e
 1. Rozdìl a panuj Potkáme-li spletitý problém, často pomáhá rozdělit ho na jednodušší části a s těmi se pak vypořádat postupně. Jak říkali staří Římané: rozděl a panuj. 1 Tato zásada se pak osvědčila nejen
1. Rozdìl a panuj Potkáme-li spletitý problém, často pomáhá rozdělit ho na jednodušší části a s těmi se pak vypořádat postupně. Jak říkali staří Římané: rozděl a panuj. 1 Tato zásada se pak osvědčila nejen
13. Třídící algoritmy a násobení matic
 13. Třídící algoritmy a násobení matic Minulou přednášku jsme probírali QuickSort, jeden z historicky prvních třídících algoritmů, které překonaly kvadratickou složitost aspoň v průměrném případě. Proč
13. Třídící algoritmy a násobení matic Minulou přednášku jsme probírali QuickSort, jeden z historicky prvních třídících algoritmů, které překonaly kvadratickou složitost aspoň v průměrném případě. Proč
Na začátku rozdělíme práci a určíme, které podproblémy je potřeba vyřešit. Tyto
 Kapitola 1 Rozděl a panuj Rozděl a panuj je programovací metoda. Často se označuje latinsky Divide et Empera nebo anglicky Divide and Conquer. Vychází z toho, že umíme zadaný problém rozložit na menší
Kapitola 1 Rozděl a panuj Rozděl a panuj je programovací metoda. Často se označuje latinsky Divide et Empera nebo anglicky Divide and Conquer. Vychází z toho, že umíme zadaný problém rozložit na menší
Prohledávání do šířky = algoritmus vlny
 Prohledávání do šířky = algoritmus vlny - souběžně zkoušet všechny možné varianty pokračování výpočtu, dokud nenajdeme řešení úlohy průchod stromem všech možných cest výpočtu do šířky, po vrstvách (v každé
Prohledávání do šířky = algoritmus vlny - souběžně zkoušet všechny možné varianty pokračování výpočtu, dokud nenajdeme řešení úlohy průchod stromem všech možných cest výpočtu do šířky, po vrstvách (v každé
DobSort. Úvod do programování. DobSort Implementace 1/3. DobSort Implementace 2/3. DobSort - Příklad. DobSort Implementace 3/3
 DobSort Úvod do programování Michal Krátký 1,Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programování, 2004/2005 V roce 1980 navrhl Dobosiewicz variantu (tzv. DobSort),
DobSort Úvod do programování Michal Krátký 1,Jiří Dvorský 1 1 Katedra informatiky VŠB Technická univerzita Ostrava Úvod do programování, 2004/2005 V roce 1980 navrhl Dobosiewicz variantu (tzv. DobSort),
Intervalové stromy. Představme si, že máme posloupnost celých čísel p 0, p 1,... p N 1, se kterou budeme. 1. Změna jednoho čísla v posloupnosti.
 Intervalové stromy Představme si, že máme posloupnost celých čísel p 0, p 1,... p N 1, se kterou budeme průběžně provádět tyto dvě operace: 1. Změna jednoho čísla v posloupnosti. 2. Zjištění součtu čísel
Intervalové stromy Představme si, že máme posloupnost celých čísel p 0, p 1,... p N 1, se kterou budeme průběžně provádět tyto dvě operace: 1. Změna jednoho čísla v posloupnosti. 2. Zjištění součtu čísel
z nich byla poprvé dokázána v 19. století velikány analytické teorie čísel (Pafnutij Lvovič Čebyšev, Charles-Jean de la Vallée Poussin a další).
 0. Tři věty o prvočíslech Martin Mareš Úvodem Při analýze algoritmů se často využívají různá tvrzení o prvočíslech. Většina z nich byla poprvé dokázána v 9. století velikány analytické teorie čísel (Pafnutij
0. Tři věty o prvočíslech Martin Mareš Úvodem Při analýze algoritmů se často využívají různá tvrzení o prvočíslech. Většina z nich byla poprvé dokázána v 9. století velikány analytické teorie čísel (Pafnutij
Numerická matematika 1
 Numerická matematika 1 Obsah 1 Řešení nelineárních rovnic 3 1.1 Metoda půlení intervalu....................... 3 1.2 Metoda jednoduché iterace..................... 4 1.3 Newtonova metoda..........................
Numerická matematika 1 Obsah 1 Řešení nelineárních rovnic 3 1.1 Metoda půlení intervalu....................... 3 1.2 Metoda jednoduché iterace..................... 4 1.3 Newtonova metoda..........................
V každém kroku se a + b zmenší o min(a, b), tedy vždy alespoň o 1. Jestliže jsme na začátku dostali 2
 Euklidův algoritmus Doprovodný materiál pro cvičení Programování I. NPRM044 Autor: Markéta Popelová Datum: 31.10.2010 Euklidův algoritmus verze 1.0 Zadání: Určete největšího společného dělitele dvou zadaných
Euklidův algoritmus Doprovodný materiál pro cvičení Programování I. NPRM044 Autor: Markéta Popelová Datum: 31.10.2010 Euklidův algoritmus verze 1.0 Zadání: Určete největšího společného dělitele dvou zadaných
Lingebraické kapitolky - Analytická geometrie
 Lingebraické kapitolky - Analytická geometrie Jaroslav Horáček KAM MFF UK 2013 Co je to vektor? Šipička na tabuli? Ehm? Množina orientovaných úseček majících stejný směr. Prvek vektorového prostoru. V
Lingebraické kapitolky - Analytická geometrie Jaroslav Horáček KAM MFF UK 2013 Co je to vektor? Šipička na tabuli? Ehm? Množina orientovaných úseček majících stejný směr. Prvek vektorového prostoru. V
1 Linearní prostory nad komplexními čísly
 1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
Mimo samotné správnosti výsledku vypočteného zapsaným algoritmem je ještě jedno
 12 Délka výpočtu algoritmu Mimo samotné správnosti výsledku vypočteného zapsaným algoritmem je ještě jedno neméně důležité hledisko k posouzení vhodnosti algoritmu k řešení zadané úlohy. Jedná se o čas,
12 Délka výpočtu algoritmu Mimo samotné správnosti výsledku vypočteného zapsaným algoritmem je ještě jedno neméně důležité hledisko k posouzení vhodnosti algoritmu k řešení zadané úlohy. Jedná se o čas,
Jednoduchá exponenciální rovnice
 Jednoduchá exponenciální rovnice Z běžné rovnice se exponenciální stává, pokud obsahuje proměnnou v exponentu. Obecně bychom mohli exponenciální rovnici zapsat takto: a f(x) = b g(x), kde a, b > 0. Typickým
Jednoduchá exponenciální rovnice Z běžné rovnice se exponenciální stává, pokud obsahuje proměnnou v exponentu. Obecně bychom mohli exponenciální rovnici zapsat takto: a f(x) = b g(x), kde a, b > 0. Typickým
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
(4x) 5 + 7y = 14, (2y) 5 (3x) 7 = 74,
 1. V oboru celých čísel řešte soustavu rovnic (4x) 5 + 7y = 14, (2y) 5 (3x) 7 = 74, kde (n) k značí násobek čísla k nejbližší číslu n. (P. Černek) Řešení. Z první rovnice dané soustavy plyne, že číslo
1. V oboru celých čísel řešte soustavu rovnic (4x) 5 + 7y = 14, (2y) 5 (3x) 7 = 74, kde (n) k značí násobek čísla k nejbližší číslu n. (P. Černek) Řešení. Z první rovnice dané soustavy plyne, že číslo
Úlohy krajského kola kategorie C
 67. ročník matematické olympiády Úlohy krajského kola kategorie C 1. Najděte nejmenší přirozené číslo končící čtyřčíslím 2018, které je násobkem čísla 2017. 2. Pro celá čísla x, y, z platí x 2 + y z =
67. ročník matematické olympiády Úlohy krajského kola kategorie C 1. Najděte nejmenší přirozené číslo končící čtyřčíslím 2018, které je násobkem čísla 2017. 2. Pro celá čísla x, y, z platí x 2 + y z =
0. Lineární rekurence Martin Mareš, 2010-07-04
 0 Lineární rekurence Martin Mareš, 2010-07-04 V tomto krátkém textu se budeme zabývat lineárními rekurencemi, tj posloupnostmi definovanými rekurentní rovnicí typu A n+k = c 0 A n + c 1 A n+1 + + c k 1
0 Lineární rekurence Martin Mareš, 2010-07-04 V tomto krátkém textu se budeme zabývat lineárními rekurencemi, tj posloupnostmi definovanými rekurentní rovnicí typu A n+k = c 0 A n + c 1 A n+1 + + c k 1
(Cramerovo pravidlo, determinanty, inverzní matice)
 KMA/MAT1 Přednáška a cvičení, Lineární algebra 2 Řešení soustav lineárních rovnic se čtvercovou maticí soustavy (Cramerovo pravidlo, determinanty, inverzní matice) 16 a 21 října 2014 V dnešní přednášce
KMA/MAT1 Přednáška a cvičení, Lineární algebra 2 Řešení soustav lineárních rovnic se čtvercovou maticí soustavy (Cramerovo pravidlo, determinanty, inverzní matice) 16 a 21 října 2014 V dnešní přednášce
Rozděl a panuj. Často se setkáme s úlohami, které lze snadno rozdělit na nějaké menší úlohy a z jejich
 Rozděl a panuj Často se setkáme s úlohami, které lze snadno rozdělit na nějaké menší úlohy a z jejich výsledků zase snadno složit výsledek původní velké úlohy. Přitom menší úlohy můžeme řešit opět týmž
Rozděl a panuj Často se setkáme s úlohami, které lze snadno rozdělit na nějaké menší úlohy a z jejich výsledků zase snadno složit výsledek původní velké úlohy. Přitom menší úlohy můžeme řešit opět týmž
V předchozí kapitole jsme podstatným způsobem rozšířili naši představu o tom, co je to číslo. Nadále jsou pro nás důležité především vlastnosti
 Kapitola 5 Vektorové prostory V předchozí kapitole jsme podstatným způsobem rozšířili naši představu o tom, co je to číslo. Nadále jsou pro nás důležité především vlastnosti operací sčítání a násobení
Kapitola 5 Vektorové prostory V předchozí kapitole jsme podstatným způsobem rozšířili naši představu o tom, co je to číslo. Nadále jsou pro nás důležité především vlastnosti operací sčítání a násobení
CVIČNÝ TEST 15. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17
 CVIČNÝ TEST 15 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT K ÚLOZE 1 Je dána čtvercová mřížka, v níž každý čtverec má délku
CVIČNÝ TEST 15 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT K ÚLOZE 1 Je dána čtvercová mřížka, v níž každý čtverec má délku
Matematika (CŽV Kadaň) aneb Úvod do lineární algebry Matice a soustavy rovnic
 Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
NPRG030 Programování I, 2018/19 1 / :03:07
 NPRG030 Programování I, 2018/19 1 / 20 3. 12. 2018 09:03:07 Vnitřní třídění Zadání: Uspořádejte pole délky N podle hodnot prvků Měřítko efektivity: * počet porovnání * počet přesunů NPRG030 Programování
NPRG030 Programování I, 2018/19 1 / 20 3. 12. 2018 09:03:07 Vnitřní třídění Zadání: Uspořádejte pole délky N podle hodnot prvků Měřítko efektivity: * počet porovnání * počet přesunů NPRG030 Programování
Základy algoritmizace a programování
 Základy algoritmizace a programování Složitost algoritmů. Třídění Přednáška 8 16. listopadu 2009 Který algoritmus je "lepší"? Různé algoritmy, které řeší stejnou úlohu zbytek = p % i; zbytek = p - p/i*i;
Základy algoritmizace a programování Složitost algoritmů. Třídění Přednáška 8 16. listopadu 2009 Který algoritmus je "lepší"? Různé algoritmy, které řeší stejnou úlohu zbytek = p % i; zbytek = p - p/i*i;
5. Náhodná veličina. 2. Házíme hrací kostkou dokud nepadne šestka. Náhodná veličina nabývá hodnot z posloupnosti {1, 2, 3,...}.
 5. Náhodná veličina Poznámka: Pro popis náhodného pokusu jsme zavedli pojem jevového pole S jako množiny všech možných výsledků a pravděpodobnost náhodných jevů P jako míru výskytů jednotlivých výsledků.
5. Náhodná veličina Poznámka: Pro popis náhodného pokusu jsme zavedli pojem jevového pole S jako množiny všech možných výsledků a pravděpodobnost náhodných jevů P jako míru výskytů jednotlivých výsledků.
1 Mnohočleny a algebraické rovnice
 1 Mnohočleny a algebraické rovnice 1.1 Pojem mnohočlenu (polynomu) Připomeňme, že výrazům typu a 2 x 2 + a 1 x + a 0 říkáme kvadratický trojčlen, když a 2 0. Číslům a 0, a 1, a 2 říkáme koeficienty a písmenem
1 Mnohočleny a algebraické rovnice 1.1 Pojem mnohočlenu (polynomu) Připomeňme, že výrazům typu a 2 x 2 + a 1 x + a 0 říkáme kvadratický trojčlen, když a 2 0. Číslům a 0, a 1, a 2 říkáme koeficienty a písmenem
přirozený algoritmus seřadí prvky 1,3,2,8,9,7 a prvky 4,5,6 nechává Metody řazení se dělí:
 Metody řazení ve vnitřní a vnější paměti. Algoritmy řazení výběrem, vkládáním a zaměňováním. Heapsort, Shell-sort, Radix-sort, Quicksort. Řazení sekvenčních souborů. Řazení souborů s přímým přístupem.
Metody řazení ve vnitřní a vnější paměti. Algoritmy řazení výběrem, vkládáním a zaměňováním. Heapsort, Shell-sort, Radix-sort, Quicksort. Řazení sekvenčních souborů. Řazení souborů s přímým přístupem.
1 Mnohočleny a algebraické rovnice
 1 Mnohočleny a algebraické rovnice 1.1 Pojem mnohočlenu (polynomu) Připomeňme, že výrazům typu a 2 x 2 + a 1 x + a 0 říkáme kvadratický trojčlen, když a 2 0. Číslům a 0, a 1, a 2 říkáme koeficienty a písmenem
1 Mnohočleny a algebraické rovnice 1.1 Pojem mnohočlenu (polynomu) Připomeňme, že výrazům typu a 2 x 2 + a 1 x + a 0 říkáme kvadratický trojčlen, když a 2 0. Číslům a 0, a 1, a 2 říkáme koeficienty a písmenem
Algoritmizace Dynamické programování. Jiří Vyskočil, Marko Genyg-Berezovskyj 2010
 Dynamické programování Jiří Vyskočil, Marko Genyg-Berezovskyj 2010 Rozděl a panuj (divide-and-conquer) Rozděl (Divide): Rozděl problém na několik podproblémů tak, aby tyto podproblémy odpovídaly původnímu
Dynamické programování Jiří Vyskočil, Marko Genyg-Berezovskyj 2010 Rozděl a panuj (divide-and-conquer) Rozděl (Divide): Rozděl problém na několik podproblémů tak, aby tyto podproblémy odpovídaly původnímu
64. ročník matematické olympiády Řešení úloh krajského kola kategorie A
 64. ročník matematické olympiády Řešení úloh krajského kola kategorie A 1. Středy stran AC, BC označme postupně, N. Střed kružnice vepsané trojúhelníku KLC označme I. Úvodem poznamenejme, že body K, L
64. ročník matematické olympiády Řešení úloh krajského kola kategorie A 1. Středy stran AC, BC označme postupně, N. Střed kružnice vepsané trojúhelníku KLC označme I. Úvodem poznamenejme, že body K, L
PŘEDNÁŠKA 2 POSLOUPNOSTI
 PŘEDNÁŠKA 2 POSLOUPNOSTI 2.1 Zobrazení 2 Definice 1. Uvažujme libovolné neprázdné množiny A, B. Zobrazení množiny A do množiny B je definováno jako množina F uspořádaných dvojic (x, y A B, kde ke každému
PŘEDNÁŠKA 2 POSLOUPNOSTI 2.1 Zobrazení 2 Definice 1. Uvažujme libovolné neprázdné množiny A, B. Zobrazení množiny A do množiny B je definováno jako množina F uspořádaných dvojic (x, y A B, kde ke každému
ALGORITMY A DATOVÉ STRUKTURY
 Název tématického celku: Cíl: ALGORITMY A DATOVÉ STRUKTURY Metodický list č. 1 Časová složitost algoritmů Základním cílem tohoto tematického celku je vysvětlení potřebných pojmů a definic nutných k popisu
Název tématického celku: Cíl: ALGORITMY A DATOVÉ STRUKTURY Metodický list č. 1 Časová složitost algoritmů Základním cílem tohoto tematického celku je vysvětlení potřebných pojmů a definic nutných k popisu
12. Lineární programování
 . Lineární programování. Lineární programování Úloha lineárního programování (lineární optimalizace) je jedním ze základních problémů teorie optimalizace. Našim cílem je nalézt maximum (resp. minimum)
. Lineární programování. Lineární programování Úloha lineárního programování (lineární optimalizace) je jedním ze základních problémů teorie optimalizace. Našim cílem je nalézt maximum (resp. minimum)
1 Řešení soustav lineárních rovnic
 1 Řešení soustav lineárních rovnic 1.1 Lineární rovnice Lineární rovnicí o n neznámých x 1,x 2,..., x n s reálnými koeficienty rozumíme rovnici ve tvaru a 1 x 1 + a 2 x 2 +... + a n x n = b, (1) kde koeficienty
1 Řešení soustav lineárních rovnic 1.1 Lineární rovnice Lineární rovnicí o n neznámých x 1,x 2,..., x n s reálnými koeficienty rozumíme rovnici ve tvaru a 1 x 1 + a 2 x 2 +... + a n x n = b, (1) kde koeficienty
Obecná informatika. Matematicko-fyzikální fakulta Univerzity Karlovy v Praze. Podzim 2012
 Obecná informatika Přednášející Putovních přednášek Matematicko-fyzikální fakulta Univerzity Karlovy v Praze Podzim 2012 Přednášející Putovních přednášek (MFF UK) Obecná informatika Podzim 2012 1 / 18
Obecná informatika Přednášející Putovních přednášek Matematicko-fyzikální fakulta Univerzity Karlovy v Praze Podzim 2012 Přednášející Putovních přednášek (MFF UK) Obecná informatika Podzim 2012 1 / 18
2.7.6 Rovnice vyšších řádů
 6 Rovnice vyšších řádů Předpoklady: 50, 05 Pedagogická poznámka: Pokud mám jenom trochu čas probírám látku této hodiny ve dvou vyučovacích hodinách V první probíráme separaci kořenů, v druhé pak snížení
6 Rovnice vyšších řádů Předpoklady: 50, 05 Pedagogická poznámka: Pokud mám jenom trochu čas probírám látku této hodiny ve dvou vyučovacích hodinách V první probíráme separaci kořenů, v druhé pak snížení
a počtem sloupců druhé matice. Spočítejme součin A.B. Označme matici A.B = M, pro její prvky platí:
 Řešené příklady z lineární algebry - část 1 Typové příklady s řešením Příklady jsou určeny především k zopakování látky před zkouškou, jsou proto řešeny se znalostmi učiva celého semestru. Tento fakt se
Řešené příklady z lineární algebry - část 1 Typové příklady s řešením Příklady jsou určeny především k zopakování látky před zkouškou, jsou proto řešeny se znalostmi učiva celého semestru. Tento fakt se
Praha & EU: investujeme do vaší budoucnosti. Daniel Turzík, Miroslava Dubcová,
 E-sbírka příkladů Seminář z matematiky Evropský sociální fond Praha & EU: investujeme do vaší budoucnosti Daniel Turzík, Miroslava Dubcová, Pavla Pavlíková Obsah 1 Úpravy výrazů................................................................
E-sbírka příkladů Seminář z matematiky Evropský sociální fond Praha & EU: investujeme do vaší budoucnosti Daniel Turzík, Miroslava Dubcová, Pavla Pavlíková Obsah 1 Úpravy výrazů................................................................
Maticí typu (m, n), kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru:
 3 Maticový počet 3.1 Zavedení pojmu matice Maticí typu (m, n, kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru: a 11 a 12... a 1k... a 1n a 21 a 22...
3 Maticový počet 3.1 Zavedení pojmu matice Maticí typu (m, n, kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru: a 11 a 12... a 1k... a 1n a 21 a 22...
Jak pracovat s absolutními hodnotami
 Jak pracovat s absolutními hodnotami Petr Matyáš 1 Co to je absolutní hodnota Absolutní hodnota čísla a, dále ji budeme označovat výrazem a, je jeho vzdálenost od nuly na ose x, tedy je to vždy číslo kladné.
Jak pracovat s absolutními hodnotami Petr Matyáš 1 Co to je absolutní hodnota Absolutní hodnota čísla a, dále ji budeme označovat výrazem a, je jeho vzdálenost od nuly na ose x, tedy je to vždy číslo kladné.
Funkce a lineární funkce pro studijní obory
 Variace 1 Funkce a lineární funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce
Variace 1 Funkce a lineární funkce pro studijní obory Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. 1. Funkce
Anotace. Informace o praktiku z programování!!! Direktivy překladače Soubory (textové) Quicksort Metoda rozděl a panuj
 Anotace Informace o praktiku z programování!!! Direktivy překladače Soubory (textové) Quicksort Metoda rozděl a panuj Direktivy překladače Překladač kontroluje plno věcí, například: zda nekoukáme za konec
Anotace Informace o praktiku z programování!!! Direktivy překladače Soubory (textové) Quicksort Metoda rozděl a panuj Direktivy překladače Překladač kontroluje plno věcí, například: zda nekoukáme za konec
CVIČNÝ TEST 12. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 6 III. Klíč 19 IV. Záznamový list 21
 CVIČNÝ TEST 12 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 19 IV. Záznamový list 21 I. CVIČNÝ TEST VÝCHOZÍ TEXT K ÚLOZE 1 Písmena A, B, C a D vyjadřují každé jednu z číslic
CVIČNÝ TEST 12 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 19 IV. Záznamový list 21 I. CVIČNÝ TEST VÝCHOZÍ TEXT K ÚLOZE 1 Písmena A, B, C a D vyjadřují každé jednu z číslic
Řešení úloh z TSP MU SADY S 1
 Řešení úloh z TSP MU SADY S 1 projekt RESENI-TSP.CZ úlohy jsou vybírány z dříve použitých TSP MU autoři řešení jsou zkušení lektoři vzdělávací agentury Kurzy-Fido.cz Masarykova univerzita nabízí uchazečům
Řešení úloh z TSP MU SADY S 1 projekt RESENI-TSP.CZ úlohy jsou vybírány z dříve použitých TSP MU autoři řešení jsou zkušení lektoři vzdělávací agentury Kurzy-Fido.cz Masarykova univerzita nabízí uchazečům
Polynomy. Mgr. Veronika Švandová a Mgr. Zdeněk Kříž, Ph. D. 1.1 Teorie Zavedení polynomů Operace s polynomy...
 Polynomy Obsah Mgr. Veronika Švandová a Mgr. Zdeněk Kříž, Ph. D. 1 Základní vlastnosti polynomů 2 1.1 Teorie........................................... 2 1.1.1 Zavedení polynomů................................
Polynomy Obsah Mgr. Veronika Švandová a Mgr. Zdeněk Kříž, Ph. D. 1 Základní vlastnosti polynomů 2 1.1 Teorie........................................... 2 1.1.1 Zavedení polynomů................................
Posloupnosti a jejich limity
 KMA/MAT Přednáška č. 7, Posloupnosti a jejich ity 5. listopadu 203 Motivační příklady Prozkoumejme, zatím laicky, následující posloupnosti: Posloupnost, 4, 9,..., n 2,... : Hodnoty rostou nade všechny
KMA/MAT Přednáška č. 7, Posloupnosti a jejich ity 5. listopadu 203 Motivační příklady Prozkoumejme, zatím laicky, následující posloupnosti: Posloupnost, 4, 9,..., n 2,... : Hodnoty rostou nade všechny
Nerovnice, grafy, monotonie a spojitost
 Nerovnice, grafy, monotonie a spojitost text pro studenty Fakulty přírodovědně-humanitní a pedagogické TU v Liberci vzniklý za podpory fondu F Martina Šimůnková 29. prosince 2016 1 Úvod Na druhém stupni
Nerovnice, grafy, monotonie a spojitost text pro studenty Fakulty přírodovědně-humanitní a pedagogické TU v Liberci vzniklý za podpory fondu F Martina Šimůnková 29. prosince 2016 1 Úvod Na druhém stupni
Tento text je stručným shrnutím těch tvrzení Ramseyovy teorie, která zazněla
 Ramseyovy věty Martin Mareš Tento text je stručným shrnutím těch tvrzení Ramseyovy teorie, která zazněla na mé letošní přednášce z Kombinatoriky a grafů I Předpokládá, že čtenář se již seznámil se základní
Ramseyovy věty Martin Mareš Tento text je stručným shrnutím těch tvrzení Ramseyovy teorie, která zazněla na mé letošní přednášce z Kombinatoriky a grafů I Předpokládá, že čtenář se již seznámil se základní
Kolik existuje různých stromů na pevně dané n-prvkové množině vrcholů?
 Kapitola 9 Matice a počet koster Graf (orientovaný i neorientovaný) lze popsat maticí, a to hned několika různými způsoby. Tématem této kapitoly jsou incidenční matice orientovaných grafů a souvislosti
Kapitola 9 Matice a počet koster Graf (orientovaný i neorientovaný) lze popsat maticí, a to hned několika různými způsoby. Tématem této kapitoly jsou incidenční matice orientovaných grafů a souvislosti
Informatika 8. třída/6
 Rekurze Jedním z důležitých principů pro návrh procedur je tzv. rekurze. Nejlépe uvidíme tento princip na příkladech dvou velmi jednoduchých procedur (hvězdička označuje násobení). Rekurze vlastně označuje
Rekurze Jedním z důležitých principů pro návrh procedur je tzv. rekurze. Nejlépe uvidíme tento princip na příkladech dvou velmi jednoduchých procedur (hvězdička označuje násobení). Rekurze vlastně označuje
Úlohy krajského kola kategorie A
 64. ročník matematické olympiády Úlohy krajského kola kategorie A 1. Je dán trojúhelník ABC s tupým úhlem při vrcholu C. Osa o 1 úsečky AC protíná stranu AB v bodě K, osa o 2 úsečky BC protíná stranu AB
64. ročník matematické olympiády Úlohy krajského kola kategorie A 1. Je dán trojúhelník ABC s tupým úhlem při vrcholu C. Osa o 1 úsečky AC protíná stranu AB v bodě K, osa o 2 úsečky BC protíná stranu AB
Nechť je číselná posloupnost. Pro všechna položme. Posloupnost nazýváme posloupnost částečných součtů řady.
 Číselné řady Definice (Posloupnost částečných součtů číselné řady). Nechť je číselná posloupnost. Pro všechna položme. Posloupnost nazýváme posloupnost částečných součtů řady. Definice (Součet číselné
Číselné řady Definice (Posloupnost částečných součtů číselné řady). Nechť je číselná posloupnost. Pro všechna položme. Posloupnost nazýváme posloupnost částečných součtů řady. Definice (Součet číselné
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Vektory Definice 011 Vektorem aritmetického prostorur n budeme rozumět uspořádanou n-tici reálných čísel x 1, x 2,, x n Definice 012 Definice sčítání
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Vektory Definice 011 Vektorem aritmetického prostorur n budeme rozumět uspořádanou n-tici reálných čísel x 1, x 2,, x n Definice 012 Definice sčítání
Obsah. Metodický list Metodický list Metodický list Metodický list
 METODICKÉ LISTY Z MATEMATIKY pro gymnázia a základní vzdělávání Jaroslav Švrček a kolektiv Rámcový vzdělávací program pro gymnázia Vzdělávací oblast: Matematika a její aplikace Tematický okruh: Závislosti
METODICKÉ LISTY Z MATEMATIKY pro gymnázia a základní vzdělávání Jaroslav Švrček a kolektiv Rámcový vzdělávací program pro gymnázia Vzdělávací oblast: Matematika a její aplikace Tematický okruh: Závislosti
- funkce, které integrujete aproximujte jejich Taylorovými řadami a ty následně zintegrujte. V obou případech vyzkoušejte Taylorovy řady
 Vzorové řešení domácího úkolu na 6. 1. 1. Integrály 1 1 x2 dx, ex2 dx spočítejte přibližně následují metodou - funkce, které integrujete aproximujte jejich Taylorovými řadami a ty následně zintegrujte.
Vzorové řešení domácího úkolu na 6. 1. 1. Integrály 1 1 x2 dx, ex2 dx spočítejte přibližně následují metodou - funkce, které integrujete aproximujte jejich Taylorovými řadami a ty následně zintegrujte.
 Interpolace Uvažujme třídu funkcí jedné proměnné ψ(x; a 0,..., a n ), kde a 0,..., a n jsou parametry, které popisují jednotlivé funkce této třídy. Mějme dány body x 0, x 1,..., x n, x i x k, i, k = 0,
Interpolace Uvažujme třídu funkcí jedné proměnné ψ(x; a 0,..., a n ), kde a 0,..., a n jsou parametry, které popisují jednotlivé funkce této třídy. Mějme dány body x 0, x 1,..., x n, x i x k, i, k = 0,
Operace s maticemi. 19. února 2018
 Operace s maticemi Přednáška druhá 19. února 2018 Obsah 1 Operace s maticemi 2 Hodnost matice (opakování) 3 Regulární matice 4 Inverzní matice 5 Determinant matice Matice Definice (Matice). Reálná matice
Operace s maticemi Přednáška druhá 19. února 2018 Obsah 1 Operace s maticemi 2 Hodnost matice (opakování) 3 Regulární matice 4 Inverzní matice 5 Determinant matice Matice Definice (Matice). Reálná matice
Řešení čtvrté série (14. dubna 2009)
 13. Tento seminář pro Vás připravuje vzdělávací agentura Kurzy-Fido.cz...s námi TSP zvládnete! Řešení čtvrté série (14. dubna 2009) Řešení společně připravili lektoři Aleph.cz a Kurzy-Fido.cz Úlohy z varianty
13. Tento seminář pro Vás připravuje vzdělávací agentura Kurzy-Fido.cz...s námi TSP zvládnete! Řešení čtvrté série (14. dubna 2009) Řešení společně připravili lektoři Aleph.cz a Kurzy-Fido.cz Úlohy z varianty
Matematická analýza pro informatiky I. Limita posloupnosti (I)
 Matematická analýza pro informatiky I. 3. přednáška Limita posloupnosti (I) Jan Tomeček tomecek@inf.upol.cz http://aix-slx.upol.cz/ tomecek/index Univerzita Palackého v Olomouci 25. února 2011 tomecek@inf.upol.cz
Matematická analýza pro informatiky I. 3. přednáška Limita posloupnosti (I) Jan Tomeček tomecek@inf.upol.cz http://aix-slx.upol.cz/ tomecek/index Univerzita Palackého v Olomouci 25. února 2011 tomecek@inf.upol.cz
Cvičení 5 - Inverzní matice
 Cvičení 5 - Inverzní matice Pojem Inverzní matice Buď A R n n. A je inverzní maticí k A, pokud platí, AA = A A = I n. Matice A, pokud existuje, je jednoznačná. A stačí nám jen jedna rovnost, aby platilo,
Cvičení 5 - Inverzní matice Pojem Inverzní matice Buď A R n n. A je inverzní maticí k A, pokud platí, AA = A A = I n. Matice A, pokud existuje, je jednoznačná. A stačí nám jen jedna rovnost, aby platilo,
Algoritmická matematika 3 Mgr. Petr Osička, Ph.D. ZS 2014. Rozděl a panuj
 Algoritmická matematika 3 KMI/ALM3 Mgr. Petr Osička, Ph.D. ZS 2014 1 Základní princip Rozděl a panuj Technika rozděl a panuj je založená na následující myšlence. Z dané vstupní instance I vygenerujeme
Algoritmická matematika 3 KMI/ALM3 Mgr. Petr Osička, Ph.D. ZS 2014 1 Základní princip Rozděl a panuj Technika rozděl a panuj je založená na následující myšlence. Z dané vstupní instance I vygenerujeme
5. Lokální, vázané a globální extrémy
 5 Lokální, vázané a globální extrémy Studijní text Lokální extrémy 5 Lokální, vázané a globální extrémy Definice 51 Řekneme, že f : R n R má v bodě a Df: 1 lokální maximum, když Ka, δ Df tak, že x Ka,
5 Lokální, vázané a globální extrémy Studijní text Lokální extrémy 5 Lokální, vázané a globální extrémy Definice 51 Řekneme, že f : R n R má v bodě a Df: 1 lokální maximum, když Ka, δ Df tak, že x Ka,
Derivace funkcí více proměnných
 Derivace funkcí více proměnných Pro studenty FP TUL Martina Šimůnková 16. května 019 1. Derivace podle vektoru jako funkce vektoru. Pro pevně zvolenou funkci f : R d R n a bod a R d budeme zkoumat zobrazení,
Derivace funkcí více proměnných Pro studenty FP TUL Martina Šimůnková 16. května 019 1. Derivace podle vektoru jako funkce vektoru. Pro pevně zvolenou funkci f : R d R n a bod a R d budeme zkoumat zobrazení,
1 Lineární prostory a podprostory
 Lineární prostory a podprostory Přečtěte si: Učebnice AKLA, kapitola první, podkapitoly. až.4 včetně. Cvičení. Které z následujících množin jsou lineárními prostory s přirozenými definicemi operací?. C
Lineární prostory a podprostory Přečtěte si: Učebnice AKLA, kapitola první, podkapitoly. až.4 včetně. Cvičení. Které z následujících množin jsou lineárními prostory s přirozenými definicemi operací?. C
= - rovnost dvou výrazů, za x můžeme dosazovat různá čísla, tím měníme
 - FUNKCE A ROVNICE Následující základní znalosti je nezbytně nutné umět od okamžiku probrání až do konce kapitoly (většinou do napsání čtvrtletní písemné práce, na výjimky z tohoto pravidla bude upozorněno).
- FUNKCE A ROVNICE Následující základní znalosti je nezbytně nutné umět od okamžiku probrání až do konce kapitoly (většinou do napsání čtvrtletní písemné práce, na výjimky z tohoto pravidla bude upozorněno).
Riemannův určitý integrál
 Riemannův určitý integrál 1. Motivační příklad Příklad (Motivační příklad pro zavedení Riemannova integrálu). Nechť,. Vypočtěme obsah vybarvené oblasti ohraničené grafem funkce, osou a svislými přímkami
Riemannův určitý integrál 1. Motivační příklad Příklad (Motivační příklad pro zavedení Riemannova integrálu). Nechť,. Vypočtěme obsah vybarvené oblasti ohraničené grafem funkce, osou a svislými přímkami
Semestrální z předmětu MM
 Semestrální z předmětu MM práce Diferenční rovnice Jméno a příjmení: Osobní číslo: Studijní skupina: Obor: E-mail: Jan Forejt A07026 1. ročník, komb. studium Matematika forejt@cs.mfcr.cz Datum odevzdání:
Semestrální z předmětu MM práce Diferenční rovnice Jméno a příjmení: Osobní číslo: Studijní skupina: Obor: E-mail: Jan Forejt A07026 1. ročník, komb. studium Matematika forejt@cs.mfcr.cz Datum odevzdání:
Univerzita Karlova v Praze Pedagogická fakulta
 Univerzita Karlova v Praze Pedagogická fakulta SEMINÁRNÍ PRÁCE Z METOD ŘEŠENÍ 1 TEORIE ČÍSEL 000/001 Cifrik, M-ZT Příklad ze zadávacích listů 10 101 Dokažte, že číslo 101 +10 je dělitelné číslem 51 Důkaz:
Univerzita Karlova v Praze Pedagogická fakulta SEMINÁRNÍ PRÁCE Z METOD ŘEŠENÍ 1 TEORIE ČÍSEL 000/001 Cifrik, M-ZT Příklad ze zadávacích listů 10 101 Dokažte, že číslo 101 +10 je dělitelné číslem 51 Důkaz:
Extrémy funkce dvou proměnných
 Extrémy funkce dvou proměnných 1. Stanovte rozměry pravoúhlé vodní nádrže o objemu 32 m 3 tak, aby dno a stěny měly nejmenší povrch. Označme rozměry pravoúhlé nádrže x, y, z (viz obr.). ak objem této nádrže
Extrémy funkce dvou proměnných 1. Stanovte rozměry pravoúhlé vodní nádrže o objemu 32 m 3 tak, aby dno a stěny měly nejmenší povrch. Označme rozměry pravoúhlé nádrže x, y, z (viz obr.). ak objem této nádrže
bin arn ı vyhled av an ı a bst Karel Hor ak, Petr Ryˇsav y 23. bˇrezna 2016 Katedra poˇ c ıtaˇ c u, FEL, ˇ CVUT
 binární vyhledávání a bst Karel Horák, Petr Ryšavý 23. března 2016 Katedra počítačů, FEL, ČVUT Příklad 1 Naimplementujte binární vyhledávání. Upravte metodu BinarySearch::binarySearch. 1 Příklad 2 Mysĺım
binární vyhledávání a bst Karel Horák, Petr Ryšavý 23. března 2016 Katedra počítačů, FEL, ČVUT Příklad 1 Naimplementujte binární vyhledávání. Upravte metodu BinarySearch::binarySearch. 1 Příklad 2 Mysĺım
řešeny numericky 6 Obyčejné diferenciální rovnice řešeny numericky
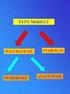 řešeny numericky řešeny numericky Břetislav Fajmon, UMAT FEKT, VUT Brno Na minulé přednášce jsme viděli některé klasické metody a přístupy pro řešení diferenciálních rovnic: stručně řečeno, rovnice obsahující
řešeny numericky řešeny numericky Břetislav Fajmon, UMAT FEKT, VUT Brno Na minulé přednášce jsme viděli některé klasické metody a přístupy pro řešení diferenciálních rovnic: stručně řečeno, rovnice obsahující
Zpracoval: hypspave@fel.cvut.cz 7. Matematická indukce a rekurse. Řešení rekurentních (diferenčních) rovnic s konstantními koeficienty.
 Zpracoval: hypspave@fel.cvut.cz 7. Matematická indukce a rekurse. Řešení rekurentních (diferenčních) rovnic s konstantními koeficienty. (A7B01MCS) I. Matematická indukce a rekurse. Indukční principy patří
Zpracoval: hypspave@fel.cvut.cz 7. Matematická indukce a rekurse. Řešení rekurentních (diferenčních) rovnic s konstantními koeficienty. (A7B01MCS) I. Matematická indukce a rekurse. Indukční principy patří
Vyvažování a rotace v BVS, všude se předpokládá AVL strom
 Vyvažování a rotace v BVS, všude se předpokládá AVL strom 1. Jednoduchá levá rotace v uzlu u má operační složitost a) závislou na výšce levého podstromu uzlu u b) mezi O(1) a Θ(n) c) závislou na hloubce
Vyvažování a rotace v BVS, všude se předpokládá AVL strom 1. Jednoduchá levá rotace v uzlu u má operační složitost a) závislou na výšce levého podstromu uzlu u b) mezi O(1) a Θ(n) c) závislou na hloubce
Úlohy klauzurní části školního kola kategorie B
 65. ročník matematické olympiády Úlohy klauzurní části školního kola kategorie B 1. Kolika způsoby je možno vyplnit čtvercovou tabulku 3 3 čísly,, 3, 3, 3, 4, 4, 4, 4 tak, aby součet čísel v každém čtverci
65. ročník matematické olympiády Úlohy klauzurní části školního kola kategorie B 1. Kolika způsoby je možno vyplnit čtvercovou tabulku 3 3 čísly,, 3, 3, 3, 4, 4, 4, 4 tak, aby součet čísel v každém čtverci
CVIČNÝ TEST 48. OBSAH I. Cvičný test 2. Mgr. Tomáš Kotler. II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17
 CVIČNÝ TEST 48 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 Je dán konvexní čtyřúhelník, jehož vnitřní
CVIČNÝ TEST 48 Mgr. Tomáš Kotler OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 15 IV. Záznamový list 17 I. CVIČNÝ TEST VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 Je dán konvexní čtyřúhelník, jehož vnitřní
Náplň. v.0.03 16.02.2014. - Jednoduché příklady na práci s poli v C - Vlastnosti třídění - Způsoby (algoritmy) třídění
 Náplň v.0.03 16.02.2014 - Jednoduché příklady na práci s poli v C - Vlastnosti třídění - Způsoby (algoritmy) třídění Spojení dvou samostatně setříděných polí void Spoj(double apole1[], int adelka1, double
Náplň v.0.03 16.02.2014 - Jednoduché příklady na práci s poli v C - Vlastnosti třídění - Způsoby (algoritmy) třídění Spojení dvou samostatně setříděných polí void Spoj(double apole1[], int adelka1, double
7B. Výpočet limit L Hospitalovo pravidlo
 7B. Výpočet it L Hospitalovo pravidlo V prai často potřebujeme určit itu výrazů, které vzniknou operacemi nebo složením několika spojitých funkcí. Většinou pomohou pravidla typu ita součtu násobku, součinu,
7B. Výpočet it L Hospitalovo pravidlo V prai často potřebujeme určit itu výrazů, které vzniknou operacemi nebo složením několika spojitých funkcí. Většinou pomohou pravidla typu ita součtu násobku, součinu,
Příklad 1. Řešení 1a Máme vyšetřit lichost či sudost funkce ŘEŠENÉ PŘÍKLADY Z M1A ČÁST 3
 Příklad 1 Zjistěte, zda jsou dané funkce sudé nebo liché, případně ani sudé ani liché: a) =ln b) = c) = d) =4 +1 e) =sin cos f) =sin3+ cos+ Poznámka Všechny tyto úlohy řešíme tak, že argument funkce nahradíme
Příklad 1 Zjistěte, zda jsou dané funkce sudé nebo liché, případně ani sudé ani liché: a) =ln b) = c) = d) =4 +1 e) =sin cos f) =sin3+ cos+ Poznámka Všechny tyto úlohy řešíme tak, že argument funkce nahradíme
Kongruence na množině celých čísel
 121 Kapitola 4 Kongruence na množině celých čísel 4.1 Relace kongruence na množině celých čísel Vraťme se k úvahám o dělení se zbytkem. Na základní škole jsme se naučili, že když podělíme číslo 11 číslem
121 Kapitola 4 Kongruence na množině celých čísel 4.1 Relace kongruence na množině celých čísel Vraťme se k úvahám o dělení se zbytkem. Na základní škole jsme se naučili, že když podělíme číslo 11 číslem
Úlohy domácí části I. kola kategorie C
 6. ročník Matematické olympiády Úlohy domácí části I. kola kategorie C 1. Určete všechny dvojice (x, y) reálných čísel, která vyhovují soustavě rovnic (x + )2 = y, (y )2 = x + 8. Řešení. Vzhledem k tomu,
6. ročník Matematické olympiády Úlohy domácí části I. kola kategorie C 1. Určete všechny dvojice (x, y) reálných čísel, která vyhovují soustavě rovnic (x + )2 = y, (y )2 = x + 8. Řešení. Vzhledem k tomu,
CVIČNÝ TEST 5. OBSAH I. Cvičný test 2. Mgr. Václav Zemek. II. Autorské řešení 6 III. Klíč 17 IV. Záznamový list 19
 CVIČNÝ TEST 5 Mgr. Václav Zemek OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 17 IV. Záznamový list 19 I. CVIČNÝ TEST 1 Zjednodušte výraz (2x 5) 2 (2x 5) (2x + 5) + 20x. 2 Určete nejmenší trojciferné
CVIČNÝ TEST 5 Mgr. Václav Zemek OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 17 IV. Záznamový list 19 I. CVIČNÝ TEST 1 Zjednodušte výraz (2x 5) 2 (2x 5) (2x + 5) + 20x. 2 Určete nejmenší trojciferné
Binární vyhledávací stromy pokročilé partie
 Binární vyhledávací stromy pokročilé partie KMI/ALS lekce Jan Konečný 30.9.204 Literatura Cormen Thomas H., Introduction to Algorithms, 2nd edition MIT Press, 200. ISBN 0-262-5396-8 6, 3, A Knuth Donald
Binární vyhledávací stromy pokročilé partie KMI/ALS lekce Jan Konečný 30.9.204 Literatura Cormen Thomas H., Introduction to Algorithms, 2nd edition MIT Press, 200. ISBN 0-262-5396-8 6, 3, A Knuth Donald
Matematika IV 9. týden Vytvořující funkce
 Matematika IV 9. týden Vytvořující funkce Jan Slovák Masarykova univerzita Fakulta informatiky jaro 2015 Obsah přednášky 1 Vytvořující funkce a Fibonacciho čísla 2 Vytvořující funkce - připomenutí 3 Řešení
Matematika IV 9. týden Vytvořující funkce Jan Slovák Masarykova univerzita Fakulta informatiky jaro 2015 Obsah přednášky 1 Vytvořující funkce a Fibonacciho čísla 2 Vytvořující funkce - připomenutí 3 Řešení
Necht tedy máme přirozená čísla n, k pod pojmem systém lineárních rovnic rozumíme rovnice ve tvaru
 2. Systémy lineárních rovnic V této kapitole se budeme zabývat soustavami lineárních rovnic s koeficienty z pole reálných případně komplexních čísel. Uvádíme podmínku pro existenci řešení systému lineárních
2. Systémy lineárních rovnic V této kapitole se budeme zabývat soustavami lineárních rovnic s koeficienty z pole reálných případně komplexních čísel. Uvádíme podmínku pro existenci řešení systému lineárních
Doba běhu daného algoritmu/programu. 1. Který fragment programu z následujících dvou proběhne rychleji?
 1 Doba běhu daného algoritmu/programu 1. Který fragment programu z následujících dvou proběhne rychleji? int n = 100; int sum = 0; for (i = 0; i < n; i++) for (j = 0; j < i; j++) sum += i+j; int n = 75;
1 Doba běhu daného algoritmu/programu 1. Který fragment programu z následujících dvou proběhne rychleji? int n = 100; int sum = 0; for (i = 0; i < n; i++) for (j = 0; j < i; j++) sum += i+j; int n = 75;
Ukážeme si lineární algoritmus, který pro pevné k rozhodne, zda vstupní. stromový rozklad. Poznamenejme, že je-li k součástí vstupu, pak rozhodnout
 Ukážeme si lineární algoritmus, který pro pevné k rozhodne, zda vstupní graf má stromovou šířku nejvýše k, a je-li tomu tak, také vrátí příslušný stromový rozklad. Poznamenejme, že je-li k součástí vstupu,
Ukážeme si lineární algoritmus, který pro pevné k rozhodne, zda vstupní graf má stromovou šířku nejvýše k, a je-li tomu tak, také vrátí příslušný stromový rozklad. Poznamenejme, že je-li k součástí vstupu,
V exponenciální rovnici se proměnná vyskytuje v exponentu. Obecně bychom mohli exponenciální rovnici zapsat takto:
 Eponenciální rovnice V eponenciální rovnici se proměnná vyskytuje v eponentu. Obecně bychom mohli eponenciální rovnici zapsat takto: a ( ) f ( ) f kde a > 0, b > 0 b Příkladem velmi jednoduché eponenciální
Eponenciální rovnice V eponenciální rovnici se proměnná vyskytuje v eponentu. Obecně bychom mohli eponenciální rovnici zapsat takto: a ( ) f ( ) f kde a > 0, b > 0 b Příkladem velmi jednoduché eponenciální
Algoritmus pro generování normálních magických čtverců
 1.1 Úvod Algoritmus pro generování normálních magických čtverců Naprogramoval jsem v Matlabu funkci, která dokáže vypočítat magický čtverec libovolného přípustného rozměru. Za pomocí tří algoritmů, které
1.1 Úvod Algoritmus pro generování normálních magických čtverců Naprogramoval jsem v Matlabu funkci, která dokáže vypočítat magický čtverec libovolného přípustného rozměru. Za pomocí tří algoritmů, které
2. Určete jádro KerL zobrazení L, tj. nalezněte alespoň jednu jeho bázi a určete jeho dimenzi.
 Řešené příklady z lineární algebry - část 3 Typové příklady s řešením Příklad 3.1: Zobrazení L: P 3 R 23 je zobrazení z prostoru P 3 všech polynomů do stupně 3 (včetně nulového polynomu) do prostoru R
Řešené příklady z lineární algebry - část 3 Typové příklady s řešením Příklad 3.1: Zobrazení L: P 3 R 23 je zobrazení z prostoru P 3 všech polynomů do stupně 3 (včetně nulového polynomu) do prostoru R
POSLOUPNOSTI A ŘADY INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ. Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky
 POSLOUPNOSTI A ŘADY Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu
POSLOUPNOSTI A ŘADY Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu
61. ročník matematické olympiády III. kolo kategorie A. Hradec Králové, března 2012
 61. ročník matematické olympiády III. kolo kategorie Hradec Králové, 5. 8. března 01 MO 1. Najděte všechna celá čísla n, pro něž je n 4 3n + 9 prvočíslo. (leš Kobza) Řešení. Zadaný výraz lze jednoduchou
61. ročník matematické olympiády III. kolo kategorie Hradec Králové, 5. 8. března 01 MO 1. Najděte všechna celá čísla n, pro něž je n 4 3n + 9 prvočíslo. (leš Kobza) Řešení. Zadaný výraz lze jednoduchou
Diskrétní matematika. DiM /01, zimní semestr 2016/2017
 Diskrétní matematika Petr Kovář petr.kovar@vsb.cz Vysoká škola báňská Technická univerzita Ostrava DiM 470-2301/01, zimní semestr 2016/2017 O tomto souboru Tento soubor je zamýšlen především jako pomůcka
Diskrétní matematika Petr Kovář petr.kovar@vsb.cz Vysoká škola báňská Technická univerzita Ostrava DiM 470-2301/01, zimní semestr 2016/2017 O tomto souboru Tento soubor je zamýšlen především jako pomůcka
JčU - Cvičení z matematiky pro zemědělské obory (doc. RNDr. Nýdl, CSc & spol.) Minitest MT4
 ŘEŠENÍ MINITESTŮ JčU - Cvičení z matematiky pro zemědělské obory (doc. RNDr. Nýdl, CSc & spol.) Minitest MT4. Z daných tří soustav rovnic o neznámých x, x vyberte právě všechny ty, které jsou regulární.
ŘEŠENÍ MINITESTŮ JčU - Cvičení z matematiky pro zemědělské obory (doc. RNDr. Nýdl, CSc & spol.) Minitest MT4. Z daných tří soustav rovnic o neznámých x, x vyberte právě všechny ty, které jsou regulární.
Dynamické programování
 Dynamické programování prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (BI-EFA)
Dynamické programování prof. Ing. Pavel Tvrdík CSc. Katedra počítačových systémů Fakulta informačních technologií České vysoké učení technické v Praze c Pavel Tvrdík, 2010 Efektivní algoritmy (BI-EFA)
Operace s maticemi
 Operace s maticemi Seminář druhý 17.10. 2018 Obsah 1 Operace s maticemi 2 Hodnost matice 3 Regulární matice 4 Inverzní matice Matice Definice (Matice). Reálná matice typu m n je obdélníkové schema A =
Operace s maticemi Seminář druhý 17.10. 2018 Obsah 1 Operace s maticemi 2 Hodnost matice 3 Regulární matice 4 Inverzní matice Matice Definice (Matice). Reálná matice typu m n je obdélníkové schema A =
POSLOUPNOSTI A ŘADY INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ
 POSLOUPNOSTI A ŘADY Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu
POSLOUPNOSTI A ŘADY Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu
ANTAGONISTICKE HRY 172
 5 ANTAGONISTICKÉ HRY 172 Antagonistický konflikt je rozhodovací situace, v níž vystupují dva inteligentní rozhodovatelé, kteří se po volbě svých rozhodnutí rozdělí o pevnou částku, jejíž výše nezávisí
5 ANTAGONISTICKÉ HRY 172 Antagonistický konflikt je rozhodovací situace, v níž vystupují dva inteligentní rozhodovatelé, kteří se po volbě svých rozhodnutí rozdělí o pevnou částku, jejíž výše nezávisí
Algoritmus pro hledání nejkratší cesty orientovaným grafem
 1.1 Úvod Algoritmus pro hledání nejkratší cesty orientovaným grafem Naprogramoval jsem v Matlabu funkci, která dokáže určit nejkratší cestu v orientovaném grafu mezi libovolnými dvěma vrcholy. Nastudoval
1.1 Úvod Algoritmus pro hledání nejkratší cesty orientovaným grafem Naprogramoval jsem v Matlabu funkci, která dokáže určit nejkratší cestu v orientovaném grafu mezi libovolnými dvěma vrcholy. Nastudoval
Věta 12.3 : Věta 12.4 (princip superpozice) : [MA1-18:P12.7] rovnice typu y (n) + p n 1 (x)y (n 1) p 1 (x)y + p 0 (x)y = q(x) (6)
![Věta 12.3 : Věta 12.4 (princip superpozice) : [MA1-18:P12.7] rovnice typu y (n) + p n 1 (x)y (n 1) p 1 (x)y + p 0 (x)y = q(x) (6) Věta 12.3 : Věta 12.4 (princip superpozice) : [MA1-18:P12.7] rovnice typu y (n) + p n 1 (x)y (n 1) p 1 (x)y + p 0 (x)y = q(x) (6)](/thumbs/96/128965676.jpg) 1. Lineární diferenciální rovnice řádu n [MA1-18:P1.7] rovnice typu y n) + p n 1 )y n 1) +... + p 1 )y + p 0 )y = q) 6) počáteční podmínky: y 0 ) = y 0 y 0 ) = y 1 y n 1) 0 ) = y n 1. 7) Věta 1.3 : Necht
1. Lineární diferenciální rovnice řádu n [MA1-18:P1.7] rovnice typu y n) + p n 1 )y n 1) +... + p 1 )y + p 0 )y = q) 6) počáteční podmínky: y 0 ) = y 0 y 0 ) = y 1 y n 1) 0 ) = y n 1. 7) Věta 1.3 : Necht
