Kapitola 12. Spočítejte průřezové charakteristiky průřezu dle obrázku 12.1 vlevo. Rozměry jsou v [mm].
|
|
|
- Matyáš Havel
- před 5 lety
- Počet zobrazení:
Transkript
1 Kapitola 12 Průřezové charakteristiky V této kapitole bude na příkladech vysvětlen výpočet průřezových charakteristik složených průřezů [1], které jsou potřebné jak pro dimenzování prutů (stanovení únosnosti, napětí i přetvoření (předmět Pružnost a plasticita)), tak i při výpočtu staticky neurčitých konstrukcí (předměty Pružnost a plasticita i další navazující). V prvním příkladu 12.1 je uveden popis výpočtu i s podrobným komentářem, čímž je částečně vysvětlena také teorie dané problematiky Příklad - složený průřez 1 Spočítejte průřezové charakteristiky průřezu dle obrázku 12.1 vlevo. Rozměry jsou v [mm]. Obrázek 12.1: Schéma průřezu příkladu Plocha složeného průřezu [m 2 ] Každý složený průřez je potřeba rozdělit na dílčí základní plochy. Možností se nabízí více, např. obr. Výsledná plocha průřezu je pak dána součtem dílčích základních. Pro řešení 134
2 průřezových charakteristik námi zadaného průřezu je použito rozdělení dle obr uprostřed nebo obr A 1 = = 400 [mm 2 ], A 2 = = 800 [mm 2 ], A 3 = = 1000 [mm 2 ], (12.1) A = A i = 2, [mm 2 ] = 2, [m 2 ]. V případě otvoru v průřezu se při výpočtu celkové plochy jeho dílčí plocha odečítá. 2 Statický moment plochy [m 3 ] Stejně jako statický moment síly (kap. 2) je možné definovat statický moment plochy vztažený k libovolné ose (S x, S z ). Pokud není určeno jinak, je u výpočtu těžiště (viz dále) výhodné pomocnou(výchozí) souřadnou soustavu xz, ke které bude počítán statický moment plochy vést s počátkem v levém horním rohu složeného průřezu (obr. 12.2). Tím je zajištěno, že všechny dílčí plochy i vzdálenosti jejich těžišt jsou v kladném směru os. Velikost momentu je dán součinem velikosti plochy a její vzdálenosti od osy, přičemž působiště příslušné plochy je uvažováno její těžiště. Znaménková konvence statického momentu plochy je shodná jako u statického momentu síly (kladný směr otáčení je proti směru hodinových ručiček). Velikosti dílčích ploch jsou známy z (12.1), polohy dílčích těžišt lze jednoduše definovat dle obr Statický moment plochy se používá při výpočtu těžiště složené plochy, viz následující kapitola. S x,i = A i z Ti [m 3 ], S z,i = A i x Ti [m 3 ]. (12.2) Stejně jako u soustav sil (kap. 2) platí: Součet statických momentů všech dílčích ploch průřezu k libovolné ose je je shodný se statickým momentem celkové plochy ke stejné ose. 135
3 Obrázek 12.2: Schéma pro výpočet těžiště průřezu příkladu
4 3 Poloha těžiště složeného průřezu [m] Těžiště složeného obrazce se počítá ze známých vztahů, které byly získány s využitím pravidla uvedeného v poznámce výše: x T = Ai x T,i Ai [m], (12.3) z T = Ai z T,i Ai [m]. (12.4) Pro odvození těchto vztahů je potřeba zavést do těžišt dílčích ploch T i fiktivní síly o velikosti daných ploch A i ve směru os x nebo z dle obr Tím se získají 2 soustavy fiktivních rovnoběžných sil, které mají shodné vlastnosti se skutečnou soustavou rovnoběžných sil(kap. 2). Definováním statického středu těchto rovnoběžných sil jsou dány souřadnice těžiště složeného obrazce. x T = Ai x T,i Ai = A 1 x T,1 +A 2 x T,2 +A 3 x T,3 A = ,2 10 3, = 35,0 [mm]. (12.5) z T = Ai z T,i Ai = A 1 z T,1 +A 2 z T,2 +A 3 z T,3 A = ,2 10 3, = 39,09 [mm]. (12.6) Pomocí vztahů (12.5) a (12.6) jsou definovány souřadnice těžiště celého složeného obrazce vzhledem k pomocným osám x; z : T [35,0 ; 39,09] [mm]. Tímto bodem jsou vedeny těžištní osy x t ;z t (obr dole), které se tímto stávají základními osami dalšího výpočtu a pomocné (x; z) již nebudou jeho součástí. V případě otvoru v průřezu, budou členy příslušné tomuto otvoru [ A i x T,i ] v rovnici (12.5) a [ A i z T,i ] v rovnici (12.6) odečítány. Pro následující výpočty bude třeba stanovit vzdálenosti těžišt dílčích ploch T i od obou os těžištních x t ; z t. Vzdálenosti tzv.ramena se vyjadřují ve skutečných hodnotách (nikoli absolutních).je-litěžištědílčíplochyt i vkladnémsměruodosyx t (případněz t ),mávzdálenost tohoto těžiště od příslušné osy kladnou hodnotu, je-li v záporném směru od těžištních os, má hodnotu zápornou. Ramena těžišt T i od osy x t se značí c i, od osy z t pak d i a jsou dány vztahy: 137
5 c i = z T,i z T [m], d i = x T,i x T [m]. (12.7) c 1 = z T,1 z T = 5 39,09 = 34,09 [mm], c 2 = z T,2 z T = 30 39,09 = 9,09 [mm], c 3 = z T,3 z T = 60 39,09 = 20,91 [mm]. (12.8) d 1 = x T,1 x T = = 15,0 [mm], d 2 = x T,2 x T = = 5,0 [mm], d 3 = x T,3 x T = = 10,0 [mm]. (12.9) 4 Momenty setrvačnosti (MS) základních průřezů [m 4 ] Moment setrvačnosti je kvadratický moment plochy vztažený k jedné (libovolné) ose a je definován základním obecným vztahem: I x = z 2 da [m 4 ], A (12.10) I z = x 2 da [m 4 ], kde x,z je vzdálenost plochy A od definované osy z, respektive x. A MS nabývá nejnižší hodnoty, je-li vztažen k osám procházejících těžištěm, jedná se o centrální moment setrvačnosti, těžištní osy pak centrální osy setrvačnosti. MS nabývá pouze kladných hodnot, nebot vzdálenost x, respektive z jsou 2krát mocněny a je tudíž jedno, zda se jedná o vzdálenost v kladném či záporném směru od sledované osy. Ve stavební mechanice bývá nejčastějším požadavkem stanovení právě tohoto centrálního MS. V běžné praxi se však často hovoří o momentu setrvačnosti s tím, že se automaticky uvažuje centrální moment setrvačnosti. Rovnice pro výpočet momentů setrvačnosti (centrálních MS) základních průřezů Řešením integrálů (12.10) se získají známé vzorce pro MS základních průřezů (kruh, mezikruží, obdélník, čtverec, trojúhelník...). Zadaný složený průřez příkladu 12.1 je tvořen třemi obdélníky. Rovnice pro výpočet momentu setrvačnosti obdélníku k jeho vlastním těžištním osám v obecném tvaru jsou: I x = 1 12 b h3 [m 4 ], I z = 1 12 h b3 [m 4 ]. (12.11) 138
6 Platí obecné pravidlo, že veličina, která je v základních rovnicích (12.11) mocněna představuje rozměr, jež je kolmý k dané ose. Konkrétně viz. (12.12) a (12.13). Momenty setrvačnosti dílčích ploch zadaného průřezu JednáseomomentysetrvačnostiI x,i ; I z,i dílčíchplocha i vztaženýchkjejichvlastnímtěžištním osám x t,i ; z t,i : I x,1 = = 3, [mm 4 ] = 3, [m 4 ], I x,2 = = 0, [mm 4 ] = 0, [m 4 ], I x,3 = = 33, [mm 4 ] = 33, [m 4 ]. I z,1 = = 53, [mm 4 ] = 53, [m 4 ], I z,2 = = 26, [mm 4 ] = 26, [m 4 ], I z,3 = = 208, [mm 4 ] = 208, [m 4 ]. (12.12) (12.13) 5 Momenty setrvačnosti průřezů k posunutým osám [m 4 ] MS průřezu k libovolné posunuté ose (x), resp. (z) je definován tzv. Steinerovou větou: I x = I x +A c 2 [m 4 ], I z = I z +A d 2 [m 4 ], kde: A [m 2 ]... plocha průřezu, I x, I z [m 4 ]... centrální momenty setrvačnosti průřezu, c, d [m]... vzdálenost těžiště průřezu od posunuté osy x, resp. z. (12.14) 6 Centrální momenty setrvačnosti složeného průřezu [m 4 ] Moment setrvačnosti složeného průřezu k určité ose je dán součtem momentů setrvačnosti dílčích ploch k této ose. Pokud se jedná o osu procházející těžištěm, jedná se o centrální MS. Matematicky toto popisuje opět Steinerova věta (??): I x = (I x,i +A i c 2 i) [m 4 ], I z = (I z,i +A i d 2 i) [m 4 ], kde: A i [m 2 ]... plocha dílčích průřezů (12.1), I x,i, I z,i [m 4 ]... momenty setrvačnosti (centrální) dílčích průřezů (12.12) a (12.13), c i, d i [m]... ramena těžišt (12.8) a (12.9), (12.15) 139
7 a tím: I x = [ I x,1 +A 1 c 2 1 ]+[ I x,2 +A 2 c 2 2 ]+[ I x,3 +A 3 c 2 3 ] = [ 3, ( 34,9) 2 ] +[ 106, ( 9,09) 2 ] +[ 33, (20,91) 2 ] = 1, [mm 4 ] = 1, [m 4 ], (12.16) I z = [ I z,1 +A 1 d 2 1 ]+[ I z,2 +A 2 d 2 2 ]+[ I z,3 +A 3 d 2 3 ] = [ 53, ( 15,0) 2 ] +[ 26, ( 5,,0) 2 ] +[ 208, (10,0) 2 ] = 0, [mm 4 ] = 0, [m 4 ]. (12.17) Člen [ I x,1 + A 1 c 2 1 ] v rovnici (12.16) vyjadřuje moment setrvačnosti průřezu 1 vztažený k těžištníoseceléhoprůřezux t.analogickytoplatíprodalšíčlenyiprůřezyvrovnicích(12.16)a(12.17). Součtem momentů setrvačnosti všech dílčích průřezů vzhledem těžištní ose se získá centrální moment setrvačnosti celého průřezu, což je slovní vyjádření Steinerovy věty (12.14) i rovnic (12.16) a (12.17). Vpřípaděotvoruvprůřezu,budoučlenypříslušnétomutootvoru[ I x,i +A i c 2 i ] vrovnici(12.16) a [ I z,i +A i d 2 i ] v rovnici (12.17) odečítány. 7 Deviační moment [m 4 ] Deviační moment je důležitou veličinou pro definování hlavních centrálních MS (kap. 6). Jedná se o kvadratický moment plochy vztažený k dvěma vzájemně kolmým osám a je definován základním obecným vztahem: kde: A [m 2 ]... plocha průřezu, D xz = x [m]... vzdálenost plochy A od definované osy z, z [m]... vzdálenost plochy A od definované osy x, A x z da [m 4 ], (12.18) Deviační moment nabývá kladných i záporných hodnot, znaménko závisí na součinu vzdáleností os x z. Pro jednoose či dvouose symetrické průřezy má vždy nulovou hodnotu. 140
8 Stejně jako momenty setrvačnosti i deviační momenty je možné vztahovat k libovolným(vzájemně kolmým) osám nebo k osám (vzájemně kolmým) procházejících těžištěm. V druhém případě se jedná o centrální deviační moment. Ve stavební mechanice bývá nejčastějším požadavkem stanovení právě tohoto centrálního deviačního momentu. V běžné praxi se však často hovoří o deviačním momentu s tím, že se automaticky uvažuje centrální deviační moment. Deviační momenty dílčích ploch zadaného průřezu Zadaný složený průřez příkladu 12.1 je tvořen třemi obdélníky. Jedná se o symerické průřezy, tudíž deviační momenty k jejich vlastním těžištním osám jsou nulové. D xz,1 = D xz,2 = D xz,3 = 0 [m 4 ]. (12.19) Deviační moment průřezu k posunutým osám [m 4 ] Deviační moment průřezu k libovolné posunutým osám x, z nabývá kladných i záporných hodnot a stejně jako momenty setrvačnosti je definován Steinerovou větou: D xz = D xz +A c d [m 4 ], (12.20) kde: A [m 2 ]... plocha průřezu, D xz [m 4 ]... deviační moment průřezu vztažený k jeho vlastním těžištním osám, c, d [m]... vzdálenost těžiště průřezu od posunuté osy (x), resp. (z). Deviační moment složeného průřezu [m 4 ] Deviační moment složeného průřezu k určité ose je dán součtem momentů setrvačnosti dílčích ploch k této ose. Matematicky toto popisuje opět Steinerova věta (12.20): D xz = (D xz,i +A i c i d i ) [m 4 ], (12.21) kde: A i [m 2 ]... plocha dílčích průřezů (12.1), D xz,i [m 4 ]... deviační momenty dílčích průřezů, tady v důsledku symetrie D xz,i = 0, c i, d i [m]... ramena těžišt (12.8) a (12.9), a tím: D xz = [ D xz,1 +A 1 c 1 d 1 ]+[ D xz,2 +A 2 c 2 d 2 ]+[ D xz,3 +A 3 c 3 d 3 ] = [ 0+0, ( 34,09) ( 15,0) ] +[ 0+0, ( 9,09) ( 5,0) ] +[ ,91 10,0 ] = 0, [mm 4 ] = 0, [m 4 ]. (12.22) 141
9 V případě otvoru v průřezu, budou členy příslušné tomuto otvoru [ D xz,i +A i c i d i ] v rovnici (12.22) odečítány. 8 Hlavní centrální momenty setrvačnosti průřezu [m 4 ] Hlavní centrální momenty setrvačnosti I 1 I max ; I 2 I min jsou kvadratické momenty plochy vztažené k jedné z pootočených, vzájemně kolmých těžištních os x 1 ;z 2, přičemž k jedné z os, např. x 1 nabývá maximálních hodnot a k druhé ose, tedy z 2 minimálních hodnot. Hlavní centrální MS jsou dány vztahem: I 1,2 = 1 2 (I x +I z )± 1 2 (I x I z ) 2 +4 D 2 xz [m 4 ], (12.23) kde: I x, I z [m 4 ]... centrální momenty setrvačnosti průřezu, D xz [m 4 ]... deviační moment průřezu (centrální), a tím: I 1 = 1 2 (I x +I z )+ 1 2 (I x I z ) 2 +4 D 2 xz = 1 2 (1, , ) (1, ,49833) 2 +4 (0, ) 2 = 1, [mm 4 ] = 1, [m 4 ], (12.24) I 2 = 1 2 (I x +I z ) 1 2 (I x I z ) 2 +4 D 2 xz = 1 2 (1, , ) 1 2 (1, ,49833) 2 +4 (0, ) 2 = 0, [mm 4 ] = 0, [m 4 ], (12.25) U symetrického průřezu není třeba I 1 ; I 2 počítat, nebot hlavní centrální moment setrvačnosti je shodný s centrálním momentem setrvačnosti s tím, že I 1 je větší z I x ; I z a I 2 menší z I x ; I z. 9 Natočení hlavních centrálních os Natočení hlavních centrálních os x 1 ;z 2, tedy os, ke kterým jsou vztaženy hlavní centrální MS I 1 ; I 2 se spočítají ze vztahů: tgα 1 = I 1 I x = 1, , = 0,5288 [ ] D xz 0, α 1 = 27,87 [ ], (12.26) 142
10 Obrázek 12.3: Schéma k hlavním centrálním MS příkladu 12.1 tgα 2 = I 2 I x = 0, , = 1,8915 [ ] D xz 0, α 2 = 62,13 [ ], (12.27) Úhel α 1 definuje pootočení těžištní osy x t od hlavní centrální osy x 1, úhel α 2 pak pootočení rovněž těžištní osy x t od hlavní centrální osy z 2. Kladný směr vede od kladného směru osy x ke kladnému směru osy z, tedy ve směru chodu hodinových ručiček, viz obrázek 12.3 vlevo. Úhlel α 2 má zápornou hodnotu, čemuž odpovídá pootočení osy x t od osy z 2 v záporném směru (proti chodu hodinových ručiček). V inženýrské praxi se výsledky této úlohy využívají k případnému pootočení průřezu o úhel α 1. Tím je dosaženo, že osa x t se stává hlavní centrální osou x 1 (x t x 1 ) a daný průřez má v této poloze největší hodnotu momentu setrvačnosti a tím i největší tuhost ohybu vzhledem k ose x, viz obrázek 12.3 vpravo. MS daného průřezu vzhledem k ose z je v tomto případě nejmenší. Dojde-li k pootočení průřezu o úhel α 2 (je záporný-bude se jednat o pootočení proti směru chodu hodinových ručiček), bude dosaženo největší hodnoty MS i ohybové tuhosti vzhledem k ose z. Shodné hodnoty I 1 ; I 2 budou dosaženy i při pootočení průřezu o dalších 180 [ ], tedy celkově o 207,87 [ ]. Schématicky tuto situaci vystihuje řešení v příkladu Invariant součtu momentů setrvačnosti Součet momentů setrvačnosti ke dvěma vzájemně kolmým osám setrvačnosti se při otáčení obou os kolem počátku nemění, zůstává invariantní. Musí být tedy splněna podmínka: I x +I z = I 1 +I 2. (12.28) 143
11 Po dosazení: (1, , ) = (1, , ) (1, ) [m 4 ] = (1, ) [m 4 ]. (12.29) Podmínka je splněna. 11 Polární moment setrvačnosti [m 4 ] Polární moment setrvačnosti je kvadratický moment plochy vztažený k jednomu bodu a je definován základním obecným vztahem: I p = Po dosazení s odkazem na (odkazbenebda,,,,,,) se získá: kde: A i [m 2 ]... plocha průřezu, p [m]... vzdálenost plochy A od definovaného bodu P, A p 2 da [m 4 ]. (12.30) I p = I x +I z [m 4 ], (12.31) I x [m 4 ]... moment setrvačnosti plochy vztažený k ose x s počátkem v bodu P, I z [m 4 ]... moment setrvačnosti plochy vztažený k ose z s počátkem v bodu P. Polární moment setrvačnosti nabývá pouze kladných hodnot. Stejně jako momenty setrvačnosti i polární moment setrvačnosti je možné vztahovat k libovolnému bodu nebo k přímo k těžišti. V druhém případě se jedná o centrální polární moment setrvačnosti. Ve stavební mechanice bývá nejčastějším požadavkem stanovení právě tohoto centrálního polárního momentu setrvačnosti. V běžné praxi se však často hovoří o polárním momentu setrvačnosti s tím, že se automaticky uvažuje centrální polární moment setrvačnosti. Polární moment setrvačnosti složeného průřezu [m 4 ] Polární moment setrvačnosti složeného průřezu se počítá ve vztahu (12.31). Pro průřez z příkladu 12.1 má (centrální) polární moment setrvačnosti hodnotu: I p = I x +I z = 1, , = 1, [mm 4 ] = 1, [m 4 ]. (12.32) 144
12 12 Rekapitulace základních pojmů Moment setrvačnosti (MS) I x ; I z [m 4 ] - kvadratický moment plochy vztažený k libovolné ose x resp. z. Centrální moment setrvačnosti I x I xt ; I z I zt [m 4 ] - kvadratický moment plochy vztažený k jedné z těžištních os x t ; z t. MomentsetrvačnostiI x ; I z [m 4 ] -kvadratickýmomentplochyvztaženýklibovolnépootočené ose x resp. z. Hlavní moment setrvačnosti I 1 I max ; I 2 I min [m 4 ] - kvadratický moment plochy vztažený k jedné z pootočených, vzájemně kolmých os x 1 ; z 2, přičemž k jedné (x 1) nabývá maximálních a k druhé (z 2) minimálních hodnot. Hlavní centrální moment setrvačnosti I 1 I max ; I 2 I min [m 4 ] - kvadratický moment plochy vztažený k jedné z pootočených, vzájemně kolmých těžištních os x t,1 ; z t,2, přičemž k jedné (x t,1 ) nabývá maximálních a k druhé (z t,2 ) minimálních hodnot. U symetrického průřezu je hlavní centrální moment setrvačnosti shodný s centrálním momentem setrvačnosti. Deviační moment D xz [m 4 ] - kvadratický moment plochy vztažený ke dvěma vzájemně kolmým osám x ; z. CentrálnídeviačnímomentD xz [m 4 ] -kvadratickýmomentplochyvztaženýkedvěmavzájemně kolmým těžištním osám x t ; z t. Polární moment setrvačnosti I p - kvadratický moment plochy vztažený k jednomu bodu (pólu). Centrální polární moment setrvačnosti I p - kvadratický moment plochy vztažený k těžišti. Osy setrvačnosti - libovolně umístěné osy (např.(x; z)), obr. 12.2), ke kterým jsou MS vztaženy. Centrální osy setrvačnosti - vzájemně kolmé osy procházející těžištěm x t ; z t. Hlavníosysetrvačnosti-vzájemněkolméosyx 1 ; z 2 pootočenétak,žei 1 I x,max ; I 2 I z,min. Hlavní centrální osy setrvačnosti - vzájemně kolmé osy procházející těžištěm x t,1 ; z t,2 pootočené tak, že I 1 I xt,max ; I 2 I zt,min. 145
13 12.2. PŘÍKLAD - SLOŽENÝ PRŮŘEZ Příklad - složený průřez 2 Spočítejte průřezové charakteristiky průřezu, který má shodné rozměry jako v příkladu 12.1, ale jeho výchozí poloha je oproti předešlému zadání změněna dle obrázku 12.4 vlevo. Rozměry jsou v [mm]. Obrázek 12.4: Schéma k příkladu 12.2 Výsledky řešení Schéma k řešení hlavních centrálních momentů viz obr uprostřed a vpravo. x T = 30,91 [mm], z T = 35,00 [mm], c 1 = 15,0 [mm], c 2 = 5,0 [mm], c 3 = 10,0 [mm], d 1 = 25,91 [mm], d 2 = 0,91 [mm], d 3 = 29,09 [mm], I x = 0, [mm 4 ], I z = 1, [mm 4 ], D xz = 0, [mm 4 ], I p = 1, [mm 4 ], I 1 = 1, [mm 4 ], I 2 = 0, [mm 4 ], α 1 = 62,13 [ ], α 2 = 27,87 [ ]. (12.33) 146
14 12.3. PŘÍKLAD - SLOŽENÝ PRŮŘEZ Příklad - složený průřez 3 Spočítejte průřezové charakteristiky průřezu dle obrázku 12.5 vlevo. Rozměry jsou v [mm]. Obrázek 12.5: Schéma příkladu 12.3 Výsledky řešení Jedná se o složený svařovaný průřez, jehož jednu z dílčích ploch tvoří normalizovaný válcovaný průřez (A 2 U180). Plocha i hodnota momentů setrvačnosti válcovaného průřezu (12.34) jsou získané z ocelářských tabulek. Schéma k řešení těžiště průřezu i MS viz obr uprostřed a vpravo. A 2 = 2, [mm 2 ], I x = 13, [mm 4 ], I z = 1, [mm 4 ]. (12.34) 147
15 12.4. PŘÍKLAD - SLOŽENÝ PRŮŘEZ 4 x T = 20,82 [mm], z T = 90,00 [mm], c 1 = c 2 = 0 [mm], d 1 = 15,82 [mm], d 2 = 8,48 [mm], (12.35) I x = 16, [mm 4 ], I z = 1, [mm 4 ], I p = 18, [mm 4 ], D xz = 0 [mm 4 ]... symetrie, I 1 = I x... symetrie, I 2 = I z... symetrie. (12.36) 12.4 Příklad - složený průřez 4 Spočítejte průřezové charakteristiky průřezu, který má shodné rozměry jako v příkladu 12.3, ale jeho výchozí poloha je oproti předešlému zadání pootočena o 90 dle obrázku 12.6 nahoře. Rozměry jsou v [mm]. Výsledky řešení Schéma k řešení těžiště průřezu i MS viz obr uprostřed a dole. A 2 = 2, [mm 2 ], I x = 1, [mm 4 ], I z = 13, [mm 4 ]. (12.37) x T = 90,00 [mm], z T = 20,82 [mm], d 1 = d 2 = 0 [mm], c 1 = 15,82 [mm], c 2 = 8,48 [mm], (12.38) 148
16 12.4. PŘÍKLAD - SLOŽENÝ PRŮŘEZ 4 Obrázek 12.6: Schéma příkladu 12.4 I x = 1, [mm 4 ], I z = 16, [mm 4 ], I p = 18, [mm 4 ], D xz = 0 [mm 4 ]... symetrie, I 1 = I x... symetrie, I 2 = I z... symetrie. (12.39) 149
17 12.5. PŘÍKLAD - SLOŽENÝ PRŮŘEZ Příklad - složený průřez 5 Obrázek 12.7: Schéma příkladu 12.5 Spočítejte průřezové charakteristiky průřezu dle obrázku Rozměry jsou v [mm]. Výsledky řešení A 1 = 4, [mm 2 ], A 2 = 0, [mm 2 ], x T = 42,86 [mm], z T = 32,14 [mm], d 1 = 2,86 [mm], d 2 = 22,86 [mm], c 1 = 2,14 [mm], c 2 = 17,14 [mm], (12.40) I x = 1, [mm 4 ], I z = 2, [mm 4 ], I p = 3, [mm 4 ], D xz = 0, [mm 4 ], I 1 = 2, [mm 4 ], I 2 = 1, [mm 4 ], α 1 = 78,56 [ ], α 2 = 11,44 [ ]. (12.41) 150
18 12.5. PŘÍKLAD - SLOŽENÝ PRŮŘEZ 5 Kontrola invariantu součtu MS: (I x +I z ) = (I 1 +I 2 ) (1, , ) = (2, , ) (3, ) [mm 4 ] = (3, ) [mm 4 ]. (12.42) Podmínka je splněna. Schéma natočení hlavních centrálních os setrvačnosti viz obr Obrázek 12.8: Schéma natočení hlavních centrálních os setrvačnosti příkladu 12.5 Jelikož průřez 2 je otvor, je nutné ve všech rovnicích členy týkající se tohoto průřezu odečítat. 151
19 12.6. PŘÍKLAD - SLOŽENÝ PRŮŘEZ Příklad - složený průřez 6 Obrázek 12.9: Schéma příkladu 12.6 Spočítejte průřezové charakteristiky průřezu dle obrázku Rozměry jsou v [m]. Výsledky řešení A 1 = 0,2826 [m 2 ], A 2 = 0,0314 [m 2 ], x T = 0,2875 [m], z T = 0,3 [m], d 1 = 0,0125 [m], d 2 = 0,1125 [m], c 1 = c 2 = 0 [m], (12.43) I x = 62, [m 4 ], I z = 59, [m 4 ], I p = 122, [m 4 ], D xz = 0 [m 4 ]... symetrie, (12.44) I 1 = I x... symetrie, I 2 = I z... symetrie. (12.45) 152
20 12.7. PŘÍKLAD - SLOŽENÝ PRŮŘEZ Příklad - složený průřez 7 Obrázek 12.10: Schéma příkladu 12.7 Spočítejte průřezové charakteristiky průřezu dle obrázku Rozměry jsou v [cm]. Výsledky řešení A 1 = 20, [mm 2 ], A 2 = 0, [mm 2 ], x T = 81,24 [mm], z T = 79,17 [mm], d 1 = 1,24 [mm], d 2 = 31,24 [mm], c 1 = 0,83 [mm], c 2 = 20,83 [mm], I x = 31, [mm 4 ], I z = 31, [mm 4 ], I p = 63, [mm 4 ], D xz = 49, [mm 4 ] I 1 = 32, [mm 4 ], I 2 = 31, [mm 4 ], α 1 = 31,5 [ ], α 2 = 58,5 [ ]. (12.46) (12.47) 153
PRUŽNOST A PEVNOST 2 V PŘÍKLADECH
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ PRUŽNOST A PEVNOST V PŘÍKLADECH Kvadratický moment II doc. Ing. Karel Frydrýšek, Ph.D., ING-PAED IGIP Ing. Milan Sivera Ing. Richard Klučka
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ PRUŽNOST A PEVNOST V PŘÍKLADECH Kvadratický moment II doc. Ing. Karel Frydrýšek, Ph.D., ING-PAED IGIP Ing. Milan Sivera Ing. Richard Klučka
1. Úvod do pružnosti a pevnosti
 1. Úvod do pružnosti a pevnosti Mechanika je nejstarší vědní obor a její nedílnou součástí je nauka o pružnosti a pevnosti. Pružností nazýváme schopnost pevných těles získat po odstranění vnějších účinků
1. Úvod do pružnosti a pevnosti Mechanika je nejstarší vědní obor a její nedílnou součástí je nauka o pružnosti a pevnosti. Pružností nazýváme schopnost pevných těles získat po odstranění vnějších účinků
Steinerova věta a průřezové moduly. Znění a použití Steinerovy věty. Určeno pro druhý ročník strojírenství M/01. Vytvořeno červen 2013
 Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Inovace a zkvalitnění výuky prostřednictvím ICT Název: Téma: Autor: Číslo: Anotace: Mechanika, pružnost pevnost Steinerova
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Inovace a zkvalitnění výuky prostřednictvím ICT Název: Téma: Autor: Číslo: Anotace: Mechanika, pružnost pevnost Steinerova
III/2-1 Inovace a zkvalitnění výuky prostřednictvím ICT
 Název školy Název projektu Registrační číslo projektu Autor Střední průmyslová škola strojírenská a azyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Modernizace výuky CZ.1.07/1.5.00/34.1003
Název školy Název projektu Registrační číslo projektu Autor Střední průmyslová škola strojírenská a azyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Modernizace výuky CZ.1.07/1.5.00/34.1003
Veličiny charakterizující geometrii ploch
 Veličiny charakterizující geometrii ploch Jedná se o veličiny charakterizující geometrii průřezu tělesa. Obrázek 1: Těleso v rovině. Těžiště plochy Souřadnice těžiště plochy, na které je hmota rovnoměrně
Veličiny charakterizující geometrii ploch Jedná se o veličiny charakterizující geometrii průřezu tělesa. Obrázek 1: Těleso v rovině. Těžiště plochy Souřadnice těžiště plochy, na které je hmota rovnoměrně
Osové a deviační momenty setrvačnosti ploch (opakování ze 4. cvičení) Momenty setrvačnosti k otočeným osám Kroucení kruhových a mezikruhových průřezů
 Jedenácté cvičení bude vysvětlovat tuto problematiku: Osové a deviační momenty setrvačnosti ploch (opakování ze 4. cvičení) Momenty setrvačnosti k otočeným osám Kroucení kruhových a mezikruhových průřezů
Jedenácté cvičení bude vysvětlovat tuto problematiku: Osové a deviační momenty setrvačnosti ploch (opakování ze 4. cvičení) Momenty setrvačnosti k otočeným osám Kroucení kruhových a mezikruhových průřezů
Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil
 Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil Souřadný systém, v rovině i prostoru Síla bodová: vektorová veličina (kluzný, vázaný vektor - využití),
Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil Souřadný systém, v rovině i prostoru Síla bodová: vektorová veličina (kluzný, vázaný vektor - využití),
K výsečovým souřadnicím
 3. cvičení K výsečovým souřadnicím Jak již bylo řečeno, výsečové souřadnice přiřazujeme bodům na střednici otevřeného průřezu, jejich soustava je dána pólem B a výsečovým počátkem M 0. Velikost výsečové
3. cvičení K výsečovým souřadnicím Jak již bylo řečeno, výsečové souřadnice přiřazujeme bodům na střednici otevřeného průřezu, jejich soustava je dána pólem B a výsečovým počátkem M 0. Velikost výsečové
PRŮŘEZOVÉ CHARAKTERISTIKY
 . cvičení PRŮŘEZOVÉ CHRKTERISTIKY Poznámka Pojem průřezu zavádíme u prutových konstrukčních prvků. Průřez je rovinný obrazec, který vznikne myšleným řezem vedeným kolmo k podélné ose nedeformovaného prutu,
. cvičení PRŮŘEZOVÉ CHRKTERISTIKY Poznámka Pojem průřezu zavádíme u prutových konstrukčních prvků. Průřez je rovinný obrazec, který vznikne myšleným řezem vedeným kolmo k podélné ose nedeformovaného prutu,
Momenty setrvačnosti a deviační momenty
 Momenty setrvačnosti a deviační momenty Momenty setrvačnosti a deviační momenty charakterizují spolu shmotností a statickými momenty hmoty rozložení hmotnosti tělesa vprostoru. Jako takové se proto vyskytují
Momenty setrvačnosti a deviační momenty Momenty setrvačnosti a deviační momenty charakterizují spolu shmotností a statickými momenty hmoty rozložení hmotnosti tělesa vprostoru. Jako takové se proto vyskytují
1 Veličiny charakterizující geometrii ploch
 1 Veličiny charakterizující geometrii ploch Jedná se o veličiny charakterizující geometrii průřezu tělesa. Obrázek 1: Těleso v rovině. Těžiště plochy Souřadnice těžiště plochy, na které je hmota rovnoměrně
1 Veličiny charakterizující geometrii ploch Jedná se o veličiny charakterizující geometrii průřezu tělesa. Obrázek 1: Těleso v rovině. Těžiště plochy Souřadnice těžiště plochy, na které je hmota rovnoměrně
Kapitola 8. prutu: rovnice paraboly z = k x 2 [m], k = z a x 2 a. [m 1 ], (8.1) = z b x 2 b. rovnice sklonu střednice prutu (tečna ke střednici)
![Kapitola 8. prutu: rovnice paraboly z = k x 2 [m], k = z a x 2 a. [m 1 ], (8.1) = z b x 2 b. rovnice sklonu střednice prutu (tečna ke střednici) Kapitola 8. prutu: rovnice paraboly z = k x 2 [m], k = z a x 2 a. [m 1 ], (8.1) = z b x 2 b. rovnice sklonu střednice prutu (tečna ke střednici)](/thumbs/61/45546970.jpg) Kapitola 8 Vnitřní síly rovinně zakřiveného prutu V této kapitole bude na příkladech vysvětleno řešení vnitřních sil rovinně zakřivených nosníků, jejichž střednici tvoří oblouk ve tvaru kvadratické paraboly[1].
Kapitola 8 Vnitřní síly rovinně zakřiveného prutu V této kapitole bude na příkladech vysvětleno řešení vnitřních sil rovinně zakřivených nosníků, jejichž střednici tvoří oblouk ve tvaru kvadratické paraboly[1].
5. Statika poloha střediska sil
 5. Statika poloha střediska sil 5.1 Rovnoběžné sily a jejich střed Uvažujeme soustavu vzájemně rovnoběžných sil v prostoru s pevnými působišti. Každá síla má působiště dané polohovým vektorem. Všechny
5. Statika poloha střediska sil 5.1 Rovnoběžné sily a jejich střed Uvažujeme soustavu vzájemně rovnoběžných sil v prostoru s pevnými působišti. Každá síla má působiště dané polohovým vektorem. Všechny
PRUŽNOST A PEVNOST 2 V PŘÍKLADECH
 VYSOKÁ ŠKOLA BÁŇSKÁ TECNICKÁ UNIVEZITA OSTAVA FAKULTA STOJNÍ PUŽNOST A PEVNOST V PŘÍKLADEC Kvadratický moment I doc. Ing. Karel Frydrýšek, Ph.D., ING-PAED IGIP Ing. Milan Sivera Ing. ichard Klučka Ing.
VYSOKÁ ŠKOLA BÁŇSKÁ TECNICKÁ UNIVEZITA OSTAVA FAKULTA STOJNÍ PUŽNOST A PEVNOST V PŘÍKLADEC Kvadratický moment I doc. Ing. Karel Frydrýšek, Ph.D., ING-PAED IGIP Ing. Milan Sivera Ing. ichard Klučka Ing.
R β α. Obrázek 1: Zadání - profil složený ze třech elementárních obrazců: 1 - rovnoramenný pravoúhlý trojúhelník, 2 - čtverec, 3 - kruhová díra
 Zadání: Vypočtěte polohu těžiště, momenty setrvačnosti a deviační moment k centrálním osám a dále určete hlavní centrální momenty setrvačnosti, poloměry setrvačnosti a natočení hlavních centrálních os
Zadání: Vypočtěte polohu těžiště, momenty setrvačnosti a deviační moment k centrálním osám a dále určete hlavní centrální momenty setrvačnosti, poloměry setrvačnosti a natočení hlavních centrálních os
Klopením rozumíme ztrátu stability při ohybu, při které dojde k vybočení prutu z roviny jeho prvotního ohybu (viz obr.). Obr.
 . cvičení Klopení nosníků Klopením rozumíme ztrátu stability při ohybu, při které dojde k vybočení prutu z roviny jeho prvotního ohybu (viz obr.). Obr. Ilustrace klopení Obr. Ohýbaný prut a tvar jeho ztráty
. cvičení Klopení nosníků Klopením rozumíme ztrátu stability při ohybu, při které dojde k vybočení prutu z roviny jeho prvotního ohybu (viz obr.). Obr. Ilustrace klopení Obr. Ohýbaný prut a tvar jeho ztráty
Podmínky k získání zápočtu
 Podmínky k získání zápočtu 18 až 35 bodů 7 % aktivní účast, omluvená neúčast Odevzdání programů Testy: 8 nepovinných testů (-2 body nebo -3 body) 3 povinné testy s ohodnocením 5 bodů (povoleny 2 opravné
Podmínky k získání zápočtu 18 až 35 bodů 7 % aktivní účast, omluvená neúčast Odevzdání programů Testy: 8 nepovinných testů (-2 body nebo -3 body) 3 povinné testy s ohodnocením 5 bodů (povoleny 2 opravné
Kapitola 2. o a paprsek sil lze ztotožnit s osou x (obr.2.1). sil a velikost rovnou algebraickému součtu sil podle vztahu R = F i, (2.
 Kapitola 2 Přímková a rovinná soustava sil 2.1 Přímková soustava sil Soustava sil ležící ve společném paprsku se nazývá přímková soustava sil [2]. Působiště všech sil m i lze posunout do společného bodu
Kapitola 2 Přímková a rovinná soustava sil 2.1 Přímková soustava sil Soustava sil ležící ve společném paprsku se nazývá přímková soustava sil [2]. Působiště všech sil m i lze posunout do společného bodu
1. Změřte momenty setrvačnosti kvádru vzhledem k hlavním osám setrvačnosti.
 1 Pracovní úkoly 1. Změřte momenty setrvačnosti kvádru vzhledem k hlavním osám setrvačnosti.. Určete složky jednotkového vektoru ve směru zadané obecné osy rotace kvádru v souřadné soustavě dané hlavními
1 Pracovní úkoly 1. Změřte momenty setrvačnosti kvádru vzhledem k hlavním osám setrvačnosti.. Určete složky jednotkového vektoru ve směru zadané obecné osy rotace kvádru v souřadné soustavě dané hlavními
Průmyslová střední škola Letohrad. Ing. Soňa Chládková. Sbírka příkladů. ze stavební mechaniky
 Průmyslová střední škola Letohrad Ing. Soňa Chládková Sbírka příkladů ze stavební mechaniky 2014 Tento projekt je realizovaný v rámci OP VK a je financovaný ze Strukturálních fondů EU (ESF) a ze státního
Průmyslová střední škola Letohrad Ing. Soňa Chládková Sbírka příkladů ze stavební mechaniky 2014 Tento projekt je realizovaný v rámci OP VK a je financovaný ze Strukturálních fondů EU (ESF) a ze státního
Průřezové charakteristiky základních profilů.
 Stření průmyslová škola a Vyšší oborná škola technická Brno, Sokolská 1 Šablona: Inovace a zkvalitnění výuky prostřenictvím ICT Název: Téma: Autor: Číslo: Anotace: Mechanika, pružnost pevnost Průřezové
Stření průmyslová škola a Vyšší oborná škola technická Brno, Sokolská 1 Šablona: Inovace a zkvalitnění výuky prostřenictvím ICT Název: Téma: Autor: Číslo: Anotace: Mechanika, pružnost pevnost Průřezové
NAMÁHÁNÍ NA OHYB NAMÁHÁNÍ NA OHYB
 Předmět: Ročník: Vytvořil: Datum: MECHANIKA DRUHÝ ŠČERBOVÁ M. PAVELKA V. 12. KVĚTNA 2013 Název zpracovaného celku: NAMÁHÁNÍ NA OHYB NAMÁHÁNÍ NA OHYB Nejdůleţitější konstrukční prvek pro ohyb je nosník.
Předmět: Ročník: Vytvořil: Datum: MECHANIKA DRUHÝ ŠČERBOVÁ M. PAVELKA V. 12. KVĚTNA 2013 Název zpracovaného celku: NAMÁHÁNÍ NA OHYB NAMÁHÁNÍ NA OHYB Nejdůleţitější konstrukční prvek pro ohyb je nosník.
6.3 Momenty setrvačnosti a deviační momenty rovinných obrazců. yda. 1) I y, I z > 0. 2) I y, I z závisí na vzdálenosti plochy od osy II I I I I
 6.3 Moment setrvačnosti a deviační moment rovinných obraců Statické moment rovinného obrace -k ose xiální moment setrvačnosti rovinného obrace -k ose -k ose Pon.: 1), > 0 S d d d. S d -k ose [m 3 ] [m
6.3 Moment setrvačnosti a deviační moment rovinných obraců Statické moment rovinného obrace -k ose xiální moment setrvačnosti rovinného obrace -k ose -k ose Pon.: 1), > 0 S d d d. S d -k ose [m 3 ] [m
Hydromechanické procesy Hydrostatika
 Hydromechanické procesy Hydrostatika M. Jahoda Hydrostatika 2 Hydrostatika se zabývá chováním tekutin, které se vzhledem k ohraničujícímu prostoru nepohybují - objem tekutiny bude v klidu, pokud výslednice
Hydromechanické procesy Hydrostatika M. Jahoda Hydrostatika 2 Hydrostatika se zabývá chováním tekutin, které se vzhledem k ohraničujícímu prostoru nepohybují - objem tekutiny bude v klidu, pokud výslednice
Veronika Drobná VB1STI02 Ing. Michalcová Vladimíra, Ph.D.
 Příklad 1: 3;4 3;4 = =4 9 2;1,78 = = 4 9 4=16 9 =1,78 =2 =2 2 4 9 =16 9 1 = 1+ =0,49 = 1+ =0,872 =0 =10 6+ 2,22=0 =3,7 6+ 2,22=0 =3,7 + =0 3,7+3,7=0 0=0 =60,64 =0 =0 + =0 =3,7 á čá 5+ 2,22=0 =3,7 5+ 2,22+
Příklad 1: 3;4 3;4 = =4 9 2;1,78 = = 4 9 4=16 9 =1,78 =2 =2 2 4 9 =16 9 1 = 1+ =0,49 = 1+ =0,872 =0 =10 6+ 2,22=0 =3,7 6+ 2,22=0 =3,7 + =0 3,7+3,7=0 0=0 =60,64 =0 =0 + =0 =3,7 á čá 5+ 2,22=0 =3,7 5+ 2,22+
ZÁKLADNÍ PŘÍPADY NAMÁHÁNÍ
 7. cvičení ZÁKLADNÍ PŘÍPADY NAMÁHÁNÍ V této kapitole se probírají výpočty únosnosti průřezů (neboli posouzení prvků na prostou pevnost). K porušení materiálu v tlačených částech průřezu dochází: mezní
7. cvičení ZÁKLADNÍ PŘÍPADY NAMÁHÁNÍ V této kapitole se probírají výpočty únosnosti průřezů (neboli posouzení prvků na prostou pevnost). K porušení materiálu v tlačených částech průřezu dochází: mezní
OTÁZKY VSTUPNÍHO TESTU PP I LS 2010/2011
 OTÁZKY VSTUPNÍHO TESTU PP I LS 010/011 Pomocí Thumovy definice, s využitím vrubové citlivosti q je definován vztah mezi součiniteli vrubu a tvaru jako: Součinitel tvaru α je podle obrázku definován jako:
OTÁZKY VSTUPNÍHO TESTU PP I LS 010/011 Pomocí Thumovy definice, s využitím vrubové citlivosti q je definován vztah mezi součiniteli vrubu a tvaru jako: Součinitel tvaru α je podle obrázku definován jako:
Mechanika tuhého tělesa
 Mechanika tuhého tělesa Tuhé těleso je ideální těleso, jehož tvar ani objem se působením libovolně velkých sil nemění Síla působící na tuhé těleso má pouze pohybové účinky Pohyby tuhého tělesa Posuvný
Mechanika tuhého tělesa Tuhé těleso je ideální těleso, jehož tvar ani objem se působením libovolně velkých sil nemění Síla působící na tuhé těleso má pouze pohybové účinky Pohyby tuhého tělesa Posuvný
Kapitola 4. Tato kapitole se zabývá analýzou vnitřních sil na rovinných nosnících. Nejprve je provedena. Každý prut v rovině má 3 volnosti (kap.1).
 Kapitola 4 Vnitřní síly přímého vodorovného nosníku 4.1 Analýza vnitřních sil na rovinných nosnících Tato kapitole se zabývá analýzou vnitřních sil na rovinných nosnících. Nejprve je provedena rekapitulace
Kapitola 4 Vnitřní síly přímého vodorovného nosníku 4.1 Analýza vnitřních sil na rovinných nosnících Tato kapitole se zabývá analýzou vnitřních sil na rovinných nosnících. Nejprve je provedena rekapitulace
Příklad 7 Průhyb nosníku - složitější případ
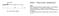 Příklad 7 Průhyb nosníku - složitější případ Zadání Nosník s proměnným průřezem je na obrázku. Průřezy a jsou obdélníkové, výška prvního průřezu je, násobkem výšky druhého průřezu. a) Pomocí metody integrace
Příklad 7 Průhyb nosníku - složitější případ Zadání Nosník s proměnným průřezem je na obrázku. Průřezy a jsou obdélníkové, výška prvního průřezu je, násobkem výšky druhého průřezu. a) Pomocí metody integrace
4. Statika základní pojmy a základy rovnováhy sil
 4. Statika základní pojmy a základy rovnováhy sil Síla je veličina vektorová. Je určena působištěm, směrem, smyslem a velikostí. Působiště síly je bod, ve kterém se přenáší účinek síly na těleso. Směr
4. Statika základní pojmy a základy rovnováhy sil Síla je veličina vektorová. Je určena působištěm, směrem, smyslem a velikostí. Působiště síly je bod, ve kterém se přenáší účinek síly na těleso. Směr
OHYB (Napjatost) M A M + qc a + b + c ) M A = 2M qc a + b + c )
 3.3 Řešené příklady Příklad 1: Pro nosník na obrázku vyšetřete a zakreslete reakce, T (x) a M(x). Dále určete M max a proveďte dimenzování pro zadaný průřez. Dáno: a = 0.5 m, b = 0.3 m, c = 0.4 m, d =
3.3 Řešené příklady Příklad 1: Pro nosník na obrázku vyšetřete a zakreslete reakce, T (x) a M(x). Dále určete M max a proveďte dimenzování pro zadaný průřez. Dáno: a = 0.5 m, b = 0.3 m, c = 0.4 m, d =
1. výpočet reakcí R x, R az a R bz - dle kapitoly 3, q = q cosα (5.1) kolmých (P ). iz = P iz sinα (5.2) iz = P iz cosα (5.3) ix = P ix cosα (5.
 Kapitola 5 Vnitřní síly přímého šikmého nosníku Pojem šikmý nosník je používán dle publikace [1] pro nosník ležící v souřadnicové rovině xz, který je vůči vodorovné ose x pootočen o úhel α. Pro šikmou
Kapitola 5 Vnitřní síly přímého šikmého nosníku Pojem šikmý nosník je používán dle publikace [1] pro nosník ležící v souřadnicové rovině xz, který je vůči vodorovné ose x pootočen o úhel α. Pro šikmou
1 Tuhé těleso a jeho pohyb
 1 Tuhé těleso a jeho pohyb Tuhé těleso (TT) působením vnějších sil se nemění jeho tvar ani objem nedochází k jeho deformaci neuvažuje se jeho částicová struktura, těleso považujeme za tzv. kontinuum spojité
1 Tuhé těleso a jeho pohyb Tuhé těleso (TT) působením vnějších sil se nemění jeho tvar ani objem nedochází k jeho deformaci neuvažuje se jeho částicová struktura, těleso považujeme za tzv. kontinuum spojité
Měření momentu setrvačnosti
 Měření momentu setrvačnosti Úkol : 1. Zjistěte pro dané těleso moment setrvačnosti, prochází-li osa těžištěm. 2. Zjistěte moment setrvačnosti daného tělesa k dané ose metodou torzních kmitů. Pomůcky :
Měření momentu setrvačnosti Úkol : 1. Zjistěte pro dané těleso moment setrvačnosti, prochází-li osa těžištěm. 2. Zjistěte moment setrvačnosti daného tělesa k dané ose metodou torzních kmitů. Pomůcky :
Statika 1. Vnitřní síly na prutech. Miroslav Vokáč 11. dubna ČVUT v Praze, Fakulta architektury. Statika 1. M.
 Definování 4. přednáška prutech iroslav okáč miroslav.vokac@cvut.cz ČUT v Praze, Fakulta architektury 11. dubna 2016 prutech nitřní síly síly působící uvnitř tělesa (desky, prutu), které vznikají působením
Definování 4. přednáška prutech iroslav okáč miroslav.vokac@cvut.cz ČUT v Praze, Fakulta architektury 11. dubna 2016 prutech nitřní síly síly působící uvnitř tělesa (desky, prutu), které vznikají působením
Prizmatické prutové prvky zatížené objemovou změnou po výšce průřezu (teplota, vlhkost, smrštění )
 1 Prizmatické prutové prvky zatížené objemovou změnou po výšce průřezu (teplota, vlhkost, smrštění ) 1. Rozšířený Hookeův zákon pro jednoosou napjatost Základním materiálovým vztahem lineární teorie pružnosti
1 Prizmatické prutové prvky zatížené objemovou změnou po výšce průřezu (teplota, vlhkost, smrštění ) 1. Rozšířený Hookeův zákon pro jednoosou napjatost Základním materiálovým vztahem lineární teorie pružnosti
Namáhání na tah, tlak
 Namáhání na tah, tlak Pro namáhání na tah i tlak platí stejné vztahy a rovnice. Velikost normálového napětí v tahu, resp. tlaku vypočítáme ze vztahu: resp. kde je napětí v tahu, je napětí v tlaku (dále
Namáhání na tah, tlak Pro namáhání na tah i tlak platí stejné vztahy a rovnice. Velikost normálového napětí v tahu, resp. tlaku vypočítáme ze vztahu: resp. kde je napětí v tahu, je napětí v tlaku (dále
Měření tíhového zrychlení matematickým a reverzním kyvadlem
 Úloha č. 3 Měření tíhového zrychlení matematickým a reverzním kyvadlem Úkoly měření: 1. Určete tíhové zrychlení pomocí reverzního a matematického kyvadla. Pro stanovení tíhového zrychlení, viz bod 1, měřte
Úloha č. 3 Měření tíhového zrychlení matematickým a reverzním kyvadlem Úkoly měření: 1. Určete tíhové zrychlení pomocí reverzního a matematického kyvadla. Pro stanovení tíhového zrychlení, viz bod 1, měřte
písemky (3 příklady) Výsledná známka je stanovena zkoušejícím na základě celkového počtu bodů ze semestru, ze vstupního testu a z písemky.
 POŽADAVKY KE ZKOUŠCE Z PP I Zkouška úrovně Alfa (pro zájemce o magisterské studium) Zkouška sestává ze vstupního testu (10 otázek, výběr správné odpovědi ze čtyř možností, rozsah dle sloupečku Požadavky)
POŽADAVKY KE ZKOUŠCE Z PP I Zkouška úrovně Alfa (pro zájemce o magisterské studium) Zkouška sestává ze vstupního testu (10 otázek, výběr správné odpovědi ze čtyř možností, rozsah dle sloupečku Požadavky)
Těžiště. Fyzikální význam těžiště:
 ěžště Fykální výnam těžště: a) hmotný bod se soustředěnou hmotností útvaru b) bod, ve kterém le hmotný útvar vystavený tíe podepřít prot posunutí anž by docháelo k rotac ěžště je chápáno jako statcký střed
ěžště Fykální výnam těžště: a) hmotný bod se soustředěnou hmotností útvaru b) bod, ve kterém le hmotný útvar vystavený tíe podepřít prot posunutí anž by docháelo k rotac ěžště je chápáno jako statcký střed
POŽADAVKY KE ZKOUŠCE Z PP I
 POŽADAVKY KE ZKOUŠCE Z PP I Zkouška úrovně Alfa (pro zájemce o magisterské studium) Zkouška sestává ze o vstupního testu (10 otázek, výběr správné odpovědi ze čtyř možností, rozsah dle sloupečku Požadavky)
POŽADAVKY KE ZKOUŠCE Z PP I Zkouška úrovně Alfa (pro zájemce o magisterské studium) Zkouška sestává ze o vstupního testu (10 otázek, výběr správné odpovědi ze čtyř možností, rozsah dle sloupečku Požadavky)
Přijímací zkouška na navazující magisterské studium Studijní program Fyzika obor Učitelství fyziky matematiky pro střední školy
 Přijímací zkouška na navazující magisterské studium 013 Studijní program Fyzika obor Učitelství fyziky matematiky pro střední školy Studijní program Učitelství pro základní školy - obor Učitelství fyziky
Přijímací zkouška na navazující magisterské studium 013 Studijní program Fyzika obor Učitelství fyziky matematiky pro střední školy Studijní program Učitelství pro základní školy - obor Učitelství fyziky
Přetvořené ose nosníku říkáme ohybová čára. Je to rovinná křivka.
 OHYBOVÁ ČÁRA ZA PROSTÉHO OHYBU - rovinné průřez zůstávají po deformaci rovinnými, avšak natáčejí se. - při prostém ohbu hlavní centrální osa setrvačnosti všech průřezů leží v rovině vnějších sil, která
OHYBOVÁ ČÁRA ZA PROSTÉHO OHYBU - rovinné průřez zůstávají po deformaci rovinnými, avšak natáčejí se. - při prostém ohbu hlavní centrální osa setrvačnosti všech průřezů leží v rovině vnějších sil, která
3.4.2 Rovnováha Rovnováha u centrální rovinné silové soustavy nastává v případě, že výsledná síla nahrazující soustavu je rovna nule. Tedy. Obr.17.
 Obr.17. F F 1x = F.cos α1,..., Fnx = F. cos 1y = F.sin α1,..., Fny = F. sin α α n n. Původní soustava je nyní nahrazena děma soustavami sil ve směru osy x a ve směru osy y. Tutu soustavu nahradíme dvěma
Obr.17. F F 1x = F.cos α1,..., Fnx = F. cos 1y = F.sin α1,..., Fny = F. sin α α n n. Původní soustava je nyní nahrazena děma soustavami sil ve směru osy x a ve směru osy y. Tutu soustavu nahradíme dvěma
Střední škola automobilní Ústí nad Orlicí
 Síla Základní pojmy Střední škola automobilní Ústí nad Orlicí vzájemné působení těles, které mění jejich pohybový stav nebo tvar zobrazuje se graficky jako úsečka se šipkou ve zvoleném měřítku m f je vektor,
Síla Základní pojmy Střední škola automobilní Ústí nad Orlicí vzájemné působení těles, které mění jejich pohybový stav nebo tvar zobrazuje se graficky jako úsečka se šipkou ve zvoleném měřítku m f je vektor,
SYLABUS 9. PŘEDNÁŠKY Z INŢENÝRSKÉ GEODÉZIE
 SYLABUS 9. PŘEDNÁŠKY Z INŢENÝRSKÉ GEODÉZIE (Řešení kruţnicových oblouků v souřadnicích) 3. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. prosinec 2015
SYLABUS 9. PŘEDNÁŠKY Z INŢENÝRSKÉ GEODÉZIE (Řešení kruţnicových oblouků v souřadnicích) 3. ročník bakalářského studia studijní program G studijní obor G doc. Ing. Jaromír Procházka, CSc. prosinec 2015
Obsah. 2 Moment síly Dvojice sil Rozklad sil 4. 6 Rovnováha 5. 7 Kinetická energie tuhého tělesa 6. 8 Jednoduché stroje 8
 Obsah 1 Tuhé těleso 1 2 Moment síly 2 3 Skládání sil 3 3.1 Skládání dvou různoběžných sil................. 3 3.2 Skládání dvou rovnoběžných, různě velkých sil......... 3 3.3 Dvojice sil.............................
Obsah 1 Tuhé těleso 1 2 Moment síly 2 3 Skládání sil 3 3.1 Skládání dvou různoběžných sil................. 3 3.2 Skládání dvou rovnoběžných, různě velkých sil......... 3 3.3 Dvojice sil.............................
Materiálové vlastnosti: Poissonův součinitel ν = 0,3. Nominální mez kluzu (ocel S350GD + Z275): Rozměry průřezu:
 Řešený příklad: Výpočet momentové únosnosti ohýbaného tenkostěnného C-profilu dle ČSN EN 1993-1-3. Ohybová únosnost je stanovena na základě efektivního průřezového modulu. Materiálové vlastnosti: Modul
Řešený příklad: Výpočet momentové únosnosti ohýbaného tenkostěnného C-profilu dle ČSN EN 1993-1-3. Ohybová únosnost je stanovena na základě efektivního průřezového modulu. Materiálové vlastnosti: Modul
PROBLÉMY STABILITY. 9. cvičení
 PROBLÉMY STABILITY 9. cvičení S pojmem ztráty stability tvaru prvku se posluchač zřejmě již setkal v teorii pružnosti při studiu prutů namáhaných osovým tlakem (viz obr.). Problematika je však obecnější
PROBLÉMY STABILITY 9. cvičení S pojmem ztráty stability tvaru prvku se posluchač zřejmě již setkal v teorii pružnosti při studiu prutů namáhaných osovým tlakem (viz obr.). Problematika je však obecnější
MECHANIKA TUHÉHO TĚLESA
 MECHANIKA TUHÉHO TĚLESA. Základní teze tuhé těleso ideální těleso, které nemůže být deformováno působením žádné (libovolně velké) vnější síly druhy pohybu tuhého tělesa a) translace (posuvný pohyb) všechny
MECHANIKA TUHÉHO TĚLESA. Základní teze tuhé těleso ideální těleso, které nemůže být deformováno působením žádné (libovolně velké) vnější síly druhy pohybu tuhého tělesa a) translace (posuvný pohyb) všechny
Deformace nosníků při ohybu.
 Číslo projektu CZ.1.07/ 1.1.36/ 02.0066 Autor Pavel Florík Předmět Mechanika Téma Deformace nosníků při ohybu Metodický pokyn výkladový text s ukázkami Deformace nosníků při ohybu. Příklad č.2 Zalomený
Číslo projektu CZ.1.07/ 1.1.36/ 02.0066 Autor Pavel Florík Předmět Mechanika Téma Deformace nosníků při ohybu Metodický pokyn výkladový text s ukázkami Deformace nosníků při ohybu. Příklad č.2 Zalomený
Teorie prostého smyku se v technické praxi používá k výpočtu styků, jako jsou nýty, šrouby, svorníky, hřeby, svary apod.
 Výpočet spojovacích prostředků a spojů (Prostý smyk) Průřez je namáhán na prostý smyk: působí-li na něj vnější síly, jejichž účinek lze ekvivalentně nahradit jedinou posouvající silou T v rovině průřezu
Výpočet spojovacích prostředků a spojů (Prostý smyk) Průřez je namáhán na prostý smyk: působí-li na něj vnější síly, jejichž účinek lze ekvivalentně nahradit jedinou posouvající silou T v rovině průřezu
MĚŘENÍ MOMENTU SETRVAČNOSTI Z DOBY KYVU
 Úloha č 5 MĚŘENÍ MOMENTU SETRVAČNOSTI Z DOBY KYVU ÚKOL MĚŘENÍ: Určete moment setrvačnosti ruhové a obdélníové desy vzhledem jednotlivým osám z doby yvu Vypočtěte moment setrvačnosti ruhové a obdélníové
Úloha č 5 MĚŘENÍ MOMENTU SETRVAČNOSTI Z DOBY KYVU ÚKOL MĚŘENÍ: Určete moment setrvačnosti ruhové a obdélníové desy vzhledem jednotlivým osám z doby yvu Vypočtěte moment setrvačnosti ruhové a obdélníové
Ohyb nastává, jestliže v řezu jakožto vnitřní účinek působí ohybový moment, tj. dvojice sil ležící v rovině kolmé k rovině řezu.
 Ohyb přímých prutů nosníků Ohyb nastává, jestliže v řeu jakožto vnitřní účinek působí ohybový moment, tj dvojice sil ležící v rovině kolmé k rovině řeu Ohybový moment určíme jako součet momentů od všech
Ohyb přímých prutů nosníků Ohyb nastává, jestliže v řeu jakožto vnitřní účinek působí ohybový moment, tj dvojice sil ležící v rovině kolmé k rovině řeu Ohybový moment určíme jako součet momentů od všech
Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady. Část 1 - Test
 Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových charakteristik, oficiální přehled
Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových charakteristik, oficiální přehled
Přímková a rovinná soustava sil
 Přímková a rovinná soustava sil 1) Souřadný systém - v prostoru - v rovině + y + 2) Síla P ( nebo F) - vektorová veličina - působiště velikost orientace Soustavy sil - přehled Soustavy sil můžeme rodělit
Přímková a rovinná soustava sil 1) Souřadný systém - v prostoru - v rovině + y + 2) Síla P ( nebo F) - vektorová veličina - působiště velikost orientace Soustavy sil - přehled Soustavy sil můžeme rodělit
Pružnost a pevnost (132PRPE), paralelka J2/1 (ZS 2015/2016) Písemná část závěrečné zkoušky vzorové otázky a příklady.
 Pružnost a pevnost (132PRPE), paralelka J2/1 (ZS 2015/2016) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových
Pružnost a pevnost (132PRPE), paralelka J2/1 (ZS 2015/2016) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových
Betonové konstrukce (S) Přednáška 3
 Betonové konstrukce (S) Přednáška 3 Obsah Účinky předpětí na betonové prvky a konstrukce Silové působení kabelu na beton Ekvivalentní zatížení Staticky neurčité účinky předpětí Konkordantní kabel, Lineární
Betonové konstrukce (S) Přednáška 3 Obsah Účinky předpětí na betonové prvky a konstrukce Silové působení kabelu na beton Ekvivalentní zatížení Staticky neurčité účinky předpětí Konkordantní kabel, Lineární
Zjednodušená deformační metoda (2):
 Stavební mechanika 1SM Přednášky Zjednodušená deformační metoda () Prut s kloubově připojeným koncem (statická kondenzace). Řešení rovinných rámů s posuvnými patry/sloupy. Prut s kloubově připojeným koncem
Stavební mechanika 1SM Přednášky Zjednodušená deformační metoda () Prut s kloubově připojeným koncem (statická kondenzace). Řešení rovinných rámů s posuvnými patry/sloupy. Prut s kloubově připojeným koncem
BIOMECHANIKA. 3,Geometrie lidského těla, těžiště, stabilita, moment síly
 BIOMECHANIKA 3,Geometrie lidského těla, těžiště, stabilita, moment síly Studijní program, obor: Tělesná výchovy a sport Vyučující: PhDr. Martin Škopek, Ph.D. TĚŽIŠTĚ TĚLESA Tuhé těleso je složeno z velkého
BIOMECHANIKA 3,Geometrie lidského těla, těžiště, stabilita, moment síly Studijní program, obor: Tělesná výchovy a sport Vyučující: PhDr. Martin Škopek, Ph.D. TĚŽIŠTĚ TĚLESA Tuhé těleso je složeno z velkého
Statika 2. Vybrané partie z plasticity. Miroslav Vokáč 2. prosince ČVUT v Praze, Fakulta architektury.
 ocelových 5. přednáška Vybrané partie z plasticity Miroslav Vokáč miroslav.vokac@klok.cvut.cz ČVUT v Praze, Fakulta architektury 2. prosince 2015 Pracovní diagram ideálně pružného materiálu ocelových σ
ocelových 5. přednáška Vybrané partie z plasticity Miroslav Vokáč miroslav.vokac@klok.cvut.cz ČVUT v Praze, Fakulta architektury 2. prosince 2015 Pracovní diagram ideálně pružného materiálu ocelových σ
Střední průmyslová škola strojírenská a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191
 Název školy Název projektu Registrační číslo projektu Autor Název šablony Střední průmyslová škola strojírenská a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Modernizace výuky
Název školy Název projektu Registrační číslo projektu Autor Název šablony Střední průmyslová škola strojírenská a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Modernizace výuky
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6
 OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
Cvičení 1. Napjatost v bodě tělesa Hlavní napětí Mezní podmínky ve víceosé napjatosti
 Cvičení 1 Napjatost v bodě tělesa Hlavní napětí Mezní podmínky ve víceosé napjatosti Napjatost v bodě tělesa Napjatost (napěťový stav) v bodě tělesa je množinou obecných napětí ve všech řezech, které lze
Cvičení 1 Napjatost v bodě tělesa Hlavní napětí Mezní podmínky ve víceosé napjatosti Napjatost v bodě tělesa Napjatost (napěťový stav) v bodě tělesa je množinou obecných napětí ve všech řezech, které lze
Předmět: Ročník: Vytvořil: Datum: ŠČERBOVÁ M. PAVELKA V. NOSNÍKY
 Předmět: Ročník: Vytvořil: Datum: MECHNIK PRVNÍ ŠČERBOVÁ M. PVELK V. 15. ZÁŘÍ 2012 Název zpracovaného celku: NOSNÍKY ) NOSNÍKY ZTÍŽENÉ OBECNOU SOUSTVOU SIL Obecný postup při matematickém řešení reakcí
Předmět: Ročník: Vytvořil: Datum: MECHNIK PRVNÍ ŠČERBOVÁ M. PVELK V. 15. ZÁŘÍ 2012 Název zpracovaného celku: NOSNÍKY ) NOSNÍKY ZTÍŽENÉ OBECNOU SOUSTVOU SIL Obecný postup při matematickém řešení reakcí
PRUŽNOST A PLASTICITA I
 Otázky k procvičování PRUŽNOST A PLASTICITA I 1. Kdy je materiál homogenní? 2. Kdy je materiál izotropní? 3. Za jakých podmínek můžeme použít princip superpozice účinků? 4. Vysvětlete princip superpozice
Otázky k procvičování PRUŽNOST A PLASTICITA I 1. Kdy je materiál homogenní? 2. Kdy je materiál izotropní? 3. Za jakých podmínek můžeme použít princip superpozice účinků? 4. Vysvětlete princip superpozice
Zakřivený nosník. Rovinně zakřivený nosník v rovinné úloze geometrie, reakce, vnitřní síly. Stavební statika, 1.ročník bakalářského studia
 Stavební statika, 1.ročník bakalářského studia Zakřivený nosník Rovinně zakřivený nosník v rovinné úloze geometrie, reakce, vnitřní síly Katedra stavební mechaniky Fakulta stavební, VŠB - Technická univerzita
Stavební statika, 1.ročník bakalářského studia Zakřivený nosník Rovinně zakřivený nosník v rovinné úloze geometrie, reakce, vnitřní síly Katedra stavební mechaniky Fakulta stavební, VŠB - Technická univerzita
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ PRŮVODCE GB01-P03 MECHANIKA TUHÝCH TĚLES
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ Prof. RNDr. Zdeněk Chobola,CSc., Vlasta Juránková,CSc. FYZIKA PRŮVODCE GB01-P03 MECHANIKA TUHÝCH TĚLES STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ Prof. RNDr. Zdeněk Chobola,CSc., Vlasta Juránková,CSc. FYZIKA PRŮVODCE GB01-P03 MECHANIKA TUHÝCH TĚLES STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU
α = 210 A x =... kn A y =... kn A M =... knm
 Vzorový příklad k 1. kontrolnímu testu Konzola Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A M A y y q = kn/m M = - 5kNm A α B c a b d F = 10 kn 1 1 3,5,5 L = 10 x α = 10 A
Vzorový příklad k 1. kontrolnímu testu Konzola Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A M A y y q = kn/m M = - 5kNm A α B c a b d F = 10 kn 1 1 3,5,5 L = 10 x α = 10 A
A x A y. α = 30. B y. A x =... kn A y =... kn B y =... kn. Vykreslení N, V, M. q = 2kN/m M = 5kNm. F = 10 kn A c a b d ,5 2,5 L = 10
 Vzorový příklad k 1. kontrolnímu testu Prostý nosník Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A y y q = kn/m M = 5kNm F = 10 kn A c a b d 1 1 3,5,5 L = 10 α B B y x α = 30
Vzorový příklad k 1. kontrolnímu testu Prostý nosník Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A y y q = kn/m M = 5kNm F = 10 kn A c a b d 1 1 3,5,5 L = 10 α B B y x α = 30
5. Stanovení tíhového zrychlení reverzním kyvadlem a studium gravitačního pole
 5. Stanovení tíhového zrychlení reverzním kyvadlem a studium gravitačního pole 5.1. Zadání úlohy 1. Určete velikost tíhového zrychlení pro Prahu reverzním kyvadlem.. Stanovte chybu měření tíhového zrychlení.
5. Stanovení tíhového zrychlení reverzním kyvadlem a studium gravitačního pole 5.1. Zadání úlohy 1. Určete velikost tíhového zrychlení pro Prahu reverzním kyvadlem.. Stanovte chybu měření tíhového zrychlení.
4. Napjatost v bodě tělesa
 p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
TÍHOVÉ ZRYCHLENÍ TEORETICKÝ ÚVOD. 9, m s.
 TÍHOVÉ ZRYCHLENÍ TEORETICKÝ ÚVOD Soustavu souřadnic spojenou se Zemí můžeme považovat prakticky za inerciální. Jen při několika jevech vznikají odchylky, které lze vysvětlit vlastním pohybem Země vzhledem
TÍHOVÉ ZRYCHLENÍ TEORETICKÝ ÚVOD Soustavu souřadnic spojenou se Zemí můžeme považovat prakticky za inerciální. Jen při několika jevech vznikají odchylky, které lze vysvětlit vlastním pohybem Země vzhledem
12. Prostý krut Definice
 p12 1 12. Prostý krut 12.1. Definice Prostý krut je označení pro namáhání přímého prizmatického prutu, jestliže jsou splněny prutové předpoklady, příčné průřezy se nedeformují, pouze se vzájemně natáčejí
p12 1 12. Prostý krut 12.1. Definice Prostý krut je označení pro namáhání přímého prizmatického prutu, jestliže jsou splněny prutové předpoklady, příčné průřezy se nedeformují, pouze se vzájemně natáčejí
Pružnost a pevnost R. Halama/L. Adámková/F. Fojtík/K. Frydrýšek/M. Šofer/J. Rojíček/M. Fusek
 Pružnost a pevnost R. Halama/. Adámková/F. Fojtík/K. Frydrýšek/M. Šofer/J. Rojíček/M. Fusek Text byl vytvořen v rámci realizace projektu Matematika pro inženýry. století (reg. č. CZ..07/..00/07.0), na
Pružnost a pevnost R. Halama/. Adámková/F. Fojtík/K. Frydrýšek/M. Šofer/J. Rojíček/M. Fusek Text byl vytvořen v rámci realizace projektu Matematika pro inženýry. století (reg. č. CZ..07/..00/07.0), na
(3) Vypočítejte moment setrvačnosti kvádru vzhledem k zadané obecné ose rotace.
 STUDUM OTÁčENÍ TUHÉHO TěLESA TEREZA ZÁBOJNÍKOVÁ 1. Pracovní úkol (1) Změřte momenty setrvačnosti kvádru vzhledem k hlavním osám setrvačnosti. (2) Určete složky jednotkového vektoru ve směru zadané obecné
STUDUM OTÁčENÍ TUHÉHO TěLESA TEREZA ZÁBOJNÍKOVÁ 1. Pracovní úkol (1) Změřte momenty setrvačnosti kvádru vzhledem k hlavním osám setrvačnosti. (2) Určete složky jednotkového vektoru ve směru zadané obecné
Mgr. Tomáš Kotler. I. Cvičný test 2 II. Autorské řešení 7 III. Klíč 15 IV. Záznamový list 17
 Mgr. Tomáš Kotler I. Cvičný test 2 II. Autorské řešení 7 III. Klíč 15 IV. Záznamový list 17 VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 Je dán rovinný obrazec, v obrázku vyznačený barevnou výplní, který představuje
Mgr. Tomáš Kotler I. Cvičný test 2 II. Autorské řešení 7 III. Klíč 15 IV. Záznamový list 17 VÝCHOZÍ TEXT A OBRÁZEK K ÚLOZE 1 Je dán rovinný obrazec, v obrázku vyznačený barevnou výplní, který představuje
3. Vypočítejte chybu, které se dopouštíte idealizací reálného kyvadla v rámci modelu kyvadla matematického.
 Pracovní úkoly. Změřte místní tíhové zrychlení g metodou reverzního kyvadla. 2. Změřte místní tíhové zrychlení g metodou matematického kyvadla. 3. Vypočítejte chybu, které se dopouštíte idealizací reálného
Pracovní úkoly. Změřte místní tíhové zrychlení g metodou reverzního kyvadla. 2. Změřte místní tíhové zrychlení g metodou matematického kyvadla. 3. Vypočítejte chybu, které se dopouštíte idealizací reálného
2.5 Rovnováha rovinné soustavy sil
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 2.5 Rovnováha rovinné soustavy sil Rovnováha sil je stav, kdy na těleso působí více sil, ale jejich výslednice
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 2.5 Rovnováha rovinné soustavy sil Rovnováha sil je stav, kdy na těleso působí více sil, ale jejich výslednice
Obecný Hookeův zákon a rovinná napjatost
 Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
F - Mechanika tuhého tělesa
 F - Mechanika tuhého tělesa Učební text pro studenty dálkového studia a shrnující text pro studenty denního studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem
F - Mechanika tuhého tělesa Učební text pro studenty dálkového studia a shrnující text pro studenty denního studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem
Euklidovský prostor. Funkce dvou proměnných: základní pojmy, limita a spojitost.
 Euklidovský prostor. Funkce dvou proměnných: základní pojmy, limita a spojitost. Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a
Euklidovský prostor. Funkce dvou proměnných: základní pojmy, limita a spojitost. Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a
Předmět: MATEMATIKA Ročník: PRVNÍ Měsíc: učivo:. ZÁŘÍ ŘÍJEN LISTOPAD PROSINEC
 Předmět: MATEMATIKA Ročník: PRVNÍ Měsíc: učivo:. ZÁŘÍ Úvod k učivu o přirozeném čísle. Numerace do 5, čtení čísel 0-5. Vytváření souborů o daném počtu předmětů. Znaménka méně, více, rovná se, porovnávání
Předmět: MATEMATIKA Ročník: PRVNÍ Měsíc: učivo:. ZÁŘÍ Úvod k učivu o přirozeném čísle. Numerace do 5, čtení čísel 0-5. Vytváření souborů o daném počtu předmětů. Znaménka méně, více, rovná se, porovnávání
16. Matematický popis napjatosti
 p16 1 16. Matematický popis napjatosti Napjatost v bodě tělesa jsme definovali jako množinu obecných napětí ve všech řezech, které lze daným bodem tělesa vést. Pro jednoznačný matematický popis napjatosti
p16 1 16. Matematický popis napjatosti Napjatost v bodě tělesa jsme definovali jako množinu obecných napětí ve všech řezech, které lze daným bodem tělesa vést. Pro jednoznačný matematický popis napjatosti
Pružnost a pevnost R. Halama, L. Adámková, F. Fojtík, K. Frydrýšek, M. Šofer, J. Rojíček, M. Fusek
 Pružnost a pevnost R. Halama, L. Adámková, F. Fojtík, K. Frydrýšek, M. Šofer, J. Rojíček, M. Fusek Text byl vytvořen v rámci realizace projektu Matematika pro inženýry 21. století (reg. č. CZ.1.07/2.2.00/07.0332),
Pružnost a pevnost R. Halama, L. Adámková, F. Fojtík, K. Frydrýšek, M. Šofer, J. Rojíček, M. Fusek Text byl vytvořen v rámci realizace projektu Matematika pro inženýry 21. století (reg. č. CZ.1.07/2.2.00/07.0332),
Kˇriv e pruty Martin Fiˇser Martin Fiˇ ser Kˇ riv e pruty
 Obsah Dimenzování křivého tenkého prutu zde Deformace v daném místě prutu zde Castiglianova věta zde Dimenzování křivého tenkého prutu Mějme obecný křivý prut z homogeního izotropního materiálu. Obrázek:
Obsah Dimenzování křivého tenkého prutu zde Deformace v daném místě prutu zde Castiglianova věta zde Dimenzování křivého tenkého prutu Mějme obecný křivý prut z homogeního izotropního materiálu. Obrázek:
Libor Kasl 1, Alois Materna 2
 SROVNÁNÍ VÝPOČETNÍCH MODELŮ DESKY VYZTUŽENÉ TRÁMEM Libor Kasl 1, Alois Materna 2 Abstrakt Příspěvek se zabývá modelováním desky vyztužené trámem. Jsou zde srovnány různé výpočetní modely model s prostorovými
SROVNÁNÍ VÝPOČETNÍCH MODELŮ DESKY VYZTUŽENÉ TRÁMEM Libor Kasl 1, Alois Materna 2 Abstrakt Příspěvek se zabývá modelováním desky vyztužené trámem. Jsou zde srovnány různé výpočetní modely model s prostorovými
Skládání různoběžných kmitů. Skládání kolmých kmitů. 1) harmonické kmity stejné frekvence :
 Skládání různoběžných kmitů Uvědomme si principiální bod tohoto problému : na jediný hmotný bod působí dvě nezávislé pružné síl ve dvou různých směrech. Jednotlivé mechanické pohb, které se budou skládat,
Skládání různoběžných kmitů Uvědomme si principiální bod tohoto problému : na jediný hmotný bod působí dvě nezávislé pružné síl ve dvou různých směrech. Jednotlivé mechanické pohb, které se budou skládat,
BIOMECHANIKA DYNAMIKA NEWTONOVY POHYBOVÉ ZÁKONY, VNITŘNÍ A VNĚJŠÍ SÍLY ČASOVÝ A DRÁHOVÝ ÚČINEK SÍLY
 BIOMECHANIKA DYNAMIKA NEWTONOVY POHYBOVÉ ZÁKONY, VNITŘNÍ A VNĚJŠÍ SÍLY ČASOVÝ A DRÁHOVÝ ÚČINEK SÍLY ROTAČNÍ POHYB TĚLESA, MOMENT SÍLY, MOMENT SETRVAČNOSTI DYNAMIKA Na rozdíl od kinematiky, která se zabývala
BIOMECHANIKA DYNAMIKA NEWTONOVY POHYBOVÉ ZÁKONY, VNITŘNÍ A VNĚJŠÍ SÍLY ČASOVÝ A DRÁHOVÝ ÚČINEK SÍLY ROTAČNÍ POHYB TĚLESA, MOMENT SÍLY, MOMENT SETRVAČNOSTI DYNAMIKA Na rozdíl od kinematiky, která se zabývala
Z hlediska pružnosti a pevnosti si lze stav napjatosti
 S T R O J N IC K Á P Ř ÍR U Č K A část 7, díl 4, kapitola 1, str. 1 7/4.1 T Y P Y N A P J A T O S T I A T R A N S F O R M A C E N A P J A T O S T I Pojmem napjatost roumíme stav určitého bodu tělesa, který
S T R O J N IC K Á P Ř ÍR U Č K A část 7, díl 4, kapitola 1, str. 1 7/4.1 T Y P Y N A P J A T O S T I A T R A N S F O R M A C E N A P J A T O S T I Pojmem napjatost roumíme stav určitého bodu tělesa, který
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV MECHANIKY TĚLES, MECHATRONIKY A BIOMECHANIKY Komentovaný metodický list č. 1/4 Vytvořil: Ing. Oldřich Ševeček & Ing. Tomáš Profant, Ph.D.
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV MECHANIKY TĚLES, MECHATRONIKY A BIOMECHANIKY Komentovaný metodický list č. 1/4 Vytvořil: Ing. Oldřich Ševeček & Ing. Tomáš Profant, Ph.D.
Fyzika 2 - rámcové příklady Magnetické pole - síla na vodič, moment na smyčku
 Fyzika 2 - rámcové příklady Magnetické pole - síla na vodič, moment na smyčku 1. Určete skalární a vektorový součin dvou obecných vektorů a a popište, jak závisí výsledky těchto součinů na úhlu mezi vektory.
Fyzika 2 - rámcové příklady Magnetické pole - síla na vodič, moment na smyčku 1. Určete skalární a vektorový součin dvou obecných vektorů a a popište, jak závisí výsledky těchto součinů na úhlu mezi vektory.
NAMÁHÁNÍ NA KRUT NAMÁHÁNÍ NA KRUT
 Φd Předmět: Ročník: Vytvořil: Datum: MECHANIKA DRUHÝ ŠČERBOVÁ M. PAVELKA V. 8. KVĚTNA 2013 Název zpracovaného celku: NAMÁHÁNÍ NA KRUT NAMÁHÁNÍ NA KRUT KRUT KRUHOVÝCH PRŮŘEZŮ Součást je namáhána na krut
Φd Předmět: Ročník: Vytvořil: Datum: MECHANIKA DRUHÝ ŠČERBOVÁ M. PAVELKA V. 8. KVĚTNA 2013 Název zpracovaného celku: NAMÁHÁNÍ NA KRUT NAMÁHÁNÍ NA KRUT KRUT KRUHOVÝCH PRŮŘEZŮ Součást je namáhána na krut
2) Nulový bod stroje používáme k: a) Kalibraci stroje b) Výchozímu bodu vztažného systému c) Určení korekcí nástroje
 1) K čemu používáme u CNC obráběcího stroje referenční bod stroje: a) Kalibraci stroje a souřadného systému b) Zavedení souřadného systému stroje c) K výměně nástrojů 2) Nulový bod stroje používáme k:
1) K čemu používáme u CNC obráběcího stroje referenční bod stroje: a) Kalibraci stroje a souřadného systému b) Zavedení souřadného systému stroje c) K výměně nástrojů 2) Nulový bod stroje používáme k:
1/7. Úkol č. 9 - Pružnost a pevnost A, zimní semestr 2011/2012
 Úkol č. 9 - Pružnost a pevnost A, zimní semestr 2011/2012 Úkol řešte ve skupince 2-3 studentů. Den narození zvolte dle jednoho člena skupiny. Řešení odevzdejte svému cvičícímu. Na symetrické prosté krokevní
Úkol č. 9 - Pružnost a pevnost A, zimní semestr 2011/2012 Úkol řešte ve skupince 2-3 studentů. Den narození zvolte dle jednoho člena skupiny. Řešení odevzdejte svému cvičícímu. Na symetrické prosté krokevní
TUHÉ TĚLESO. Mgr. Jan Ptáčník - GJVJ - Fyzika - Mechanika - 1. ročník
 TUHÉ TĚLESO Mgr. Jan Ptáčník - GJVJ - Fyzika - Mechanika - 1. ročník Tuhé těleso Tuhé těleso je ideální těleso, jehož objem ani tvar se účinkem libovolně velkých sil nemění. Pohyb tuhého tělesa: posuvný
TUHÉ TĚLESO Mgr. Jan Ptáčník - GJVJ - Fyzika - Mechanika - 1. ročník Tuhé těleso Tuhé těleso je ideální těleso, jehož objem ani tvar se účinkem libovolně velkých sil nemění. Pohyb tuhého tělesa: posuvný
trubku o délce l. Prut (nebo trubka) bude namáhán kroutícím momentem M K [Nm]. Obrázek 1: Prut namáhaný kroutícím momentem.
![trubku o délce l. Prut (nebo trubka) bude namáhán kroutícím momentem M K [Nm]. Obrázek 1: Prut namáhaný kroutícím momentem. trubku o délce l. Prut (nebo trubka) bude namáhán kroutícím momentem M K [Nm]. Obrázek 1: Prut namáhaný kroutícím momentem.](/thumbs/99/141481369.jpg) Namáhání krutem Uvažujme přímý prut neměnného kruhového průřezu (Obr.2), popřípadě trubku o délce l. Prut (nebo trubka) bude namáhán kroutícím momentem M K [Nm]. Obrázek : Prut namáhaný kroutícím momentem.
Namáhání krutem Uvažujme přímý prut neměnného kruhového průřezu (Obr.2), popřípadě trubku o délce l. Prut (nebo trubka) bude namáhán kroutícím momentem M K [Nm]. Obrázek : Prut namáhaný kroutícím momentem.
ZÁKLADNÍ ÚLOHY TEORIE PLASTICITY Teoretické příklady
 Teorie plasticity VŠB TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ KATEDRA PRUŽNOSTI A PEVNOSTI ZÁKLADNÍ ÚLOHY TEORIE PLASTICITY Teoretické příklady 1. ŘEŠENÝ PŘÍKLAD NA TAH ŘEŠENÍ DLE DOVOLENÝCH NAMÁHÁNÍ
Teorie plasticity VŠB TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ KATEDRA PRUŽNOSTI A PEVNOSTI ZÁKLADNÍ ÚLOHY TEORIE PLASTICITY Teoretické příklady 1. ŘEŠENÝ PŘÍKLAD NA TAH ŘEŠENÍ DLE DOVOLENÝCH NAMÁHÁNÍ
12 DYNAMIKA SOUSTAVY HMOTNÝCH BODŮ
 56 12 DYNAMIKA SOUSTAVY HMOTNÝCH BODŮ Těžiště I. impulsová věta - věta o pohybu těžiště II. impulsová věta Zákony zachování v izolované soustavě hmotných bodů Náhrada pohybu skutečných objektů pohybem
56 12 DYNAMIKA SOUSTAVY HMOTNÝCH BODŮ Těžiště I. impulsová věta - věta o pohybu těžiště II. impulsová věta Zákony zachování v izolované soustavě hmotných bodů Náhrada pohybu skutečných objektů pohybem
