NMR spektroskopie vysokého rozlišení v kapalné a pevné fázi spinový hamiltonián, typy interakcí, projevy ve spektrech
|
|
|
- Ludvík Pešan
- před 8 lety
- Počet zobrazení:
Transkript
1 NMR spektroskopie vysokého rozlišení v kapalné a pevné fázi spinový hamiltonián, typy interakcí, projevy ve spektrech Spinový hamiltonián Hamiltonián soustavy jader a elektronů v magnetickém poli lze zapsat ve tvaru = H L ( q)+ H L, σ (q, σ ), H () kde H L (q) je člen nezávislý na spinových proměnných (především coulombická interakce) a HL, σ ( q, σ ) obsahuje členy popisující vzájemné interakce magnetických momentů (spinů) s externím magnetickým polem a eventuálně jadernou kvadrupólovou interakci. Předpokládejme: HL, σ H L HL, σ = A j ( σ ) Y j (q) j n vlastní vektor H L (q) s vlastní hodnotou E (n ) (q) degenerace vůči spinovým proměnným: n m = n m, m vlastní stavy H L, σ Pak v. řádu poruchového počtu máme: () E n,m = n m H L, σ n m = n Y j n m A j m = Λ j, n m A j m, j () j kde Λ j,n n Y j n. Pro efektivní spinový hamiltonián v. řádu poruchového počtu pak dostáváme: () H S, n= Λ j, n A j, () j přičemž n obvykle značí základní stav. Podobně v. řádu poruchového počtu máme: ( ) H () S, n= H S,n + Λ i j,n Ai A j, (4) i,j kde Λ i j,n = n' n Y i n ' n ' Y j n E (n ) E (n ' ). Magnetická interakce jader a elektronů Interakce spinu jádra s elektronovým spinem a orbitálním momentem elektronů popisuje hamiltonián:
2 = ( p +e A) +V + H S O + μ B s rot A, H me (5) je kde V popisuje elektrostatickou interakci, H S O spin-orbitální interakci, s je spin elektronu a A vektorový potenciál magnetického pole vytvářeného jaderným magnetickým momentem. Pro jádro v počátku souřadnic máme: μ μ r, div A= A=, 4π r (6) kde r je polohový vektor elektronu a μ = γ I I je magnetický dipólový moment jádra. Hamiltonián (5) lze rozepsat: = p +V + e ( p A+ A p )+ e A + H S O+ μ B s rot A. H me me me Podívejme se nyní na člen (7) e A p) : ( p A+ me a p obecně nekomutují, ale platí: p A+ A p = A p +div A A ψ p ( A ψ) div ( A ψ )= A grad. neboť: p A ψ+ ψ div A Dále: e e μ ( μ r ) p e μ μ (r p ) e μ μ l μ μ B μ l μ γ e μ l A p = = = = = me me 4 π me 4 π me 4 π r π r π r r r μb e e, γe me me Tedy dostáváme že výše uvažovaný člen popisuje interakci jaderného momentu a orbitálního momentu elektronu. Odhadněme nyní působení elektronového orbitálního momentu: například pro fluor máme 8,9 =, kde a je Bohrův poloměr. Magnetické pole vytvořené elektronem na jádře r p a μ μb l má velikost cca 6 T. Ale v typických experimentech v pevných látkách a π r molekulách se obvykle nepozorují tak velká pole daná elektronovými orbitálními momenty. Příčinou jsou uzavřené slupky a elektrony zúčastňující se vazeb příspěvky se vzájemně kompenzují. Dále u paramagnetických iontů je příčinou tzv. zamrzání orbitálního momentu, tj. základní stav iontu v krystalovém poli (poli okolních nábojů) v prvním přiblížení již není vlastním stavem lz, ale jejich lineární kombinací, která má lz = (toto však neplatí pro ionty vzácných zemin částečně obsazená slupka 4f je odstíněná vnějšími elektrony okolí ji ovlivní méně). ( ) Dále se podívejme na člen μ B s rot A : Zdlouhavou úpravou při níž se použijí jednak identity pro pro diferenciální úpravy a jednak = 4 π δ (), dostaneme spolu s elektronové vlnové funkce atom ψ r l kolem : Δ r ()
3 orbitálním členem hamiltonián hyperjemné interakce: [ ( ] μ l r (s r ) 8 Hh f = γe γ I I + s + π s δ (r ). π r r r ) (8) Význam jednotlivých členů je: Orbitální člen + Dipól-dipólová interakce magnetických mo mentů (spin elektronu - jaderný spin) + Fermiho kontaktní interakce (pro elektrony s nenulovou pravděpodobností výskytu v místě jádra). Efektivní magnetické pole na jádře: [ ( ] μ l r ( s r ) 8 Bh f = γ e + s + π s δ (r ). π r r r ) (9) Možná zobecnění: ) více elektronů superpozice jednoelektronových příspěvků, vzájemná elektrostatická interakce ) jiné než atomové vlnové funkce - ψ( r ) pomocí rozvoje (kulové funkce centrované na daném jádře, oddělit nultý člen) Je-li výsledný (elektronový) orbitální moment atomu L z =, resp. L z =, pak Hh f = I A S, () kde S je spin atomu (elektronový) a A je tenzor hyperjemné interakce. Soustava elektronů a jader ve vnějším poli Uvažujme soustavu jader a elektronů. Jádra označme indexem k a elektrony indexem i. Oproti předchozímu případu dostáváme následující změny: Zeemanovská interakce jaderných magnetických momentů v externím poli: Z I = γ k I k B μk B k () k Vektorový potenciál pro i-tý elektron: Ai = Ai + Aik, () r( i) kde Ai =B je dán vnějším polem a představuje působení vnějšího pole na i-tý elektron. A μ μ k r (ik) (ik ) představuje působení mezi k-tým jaderným momentem a i.tým elektronem a r Aik = (ik ) 4 π (r ) je poloha elektronu vůči jádru. Hamiltonián je potom tedy roven:
4 = ( p i +e A i )+V + H S O + μ B si rot A i μk B. H me i i k () Sledujme nyní členy popisující magnetické interakce a obsahující operátory jaderných magnetických momentů (jaderných spinů): Elektronové a jaderné magnetické momenty v externím poli zeemanovské členy: Z I = μk B jaderný magnetický moment v externím poli (4) Z S = μ B si B elektronový spin (5) e Z l = p i A i=μ B B li elektronový orbitální moment me i i (6) k i V případě diamagnetických látek se členy Z S a Z l v. řádu poruchového počtu neuplatní v základním stavu je výsledný elektronový spin i orbitální moment nulový. (Podobně i v případě zamrzlého orbitálního momentu u paramagnetik se Z l v. řádu neuplatní.) Příspěvek e A : me i Tento příspěvek je kvadratický v B a pro NMR je nevýznamný nezávisí na spinových operátorech. Magnetická interakce jader a elektronů hyperjemná μ μ μ l O = μ B p i Aik= B k(ik ) ik, 4 π k i (r ) k i (7) (ik ) kde lik = r p i. μ B μ ( si r( ik) )( μk r( ik) ) S = si μ k (ik ) 4 π k i (r (ik )) (r ) ( ) μ 6 π μ B S = si μ k δ (r (ik) ) 4π k i (8) (9) ( μ B= γ e, μ k= γ k Ik ). Pro diamagnetické látky se tyto členy v. řádu poruchového počtu opět neuplatní. Nové členy (které se v. řádu uplatní): interakce jaderného magnetického momentu a elektronových magnetických momentů vyvolaná působením externího magnetického pole a pole jiných magnetických momentů (např. ostatních jader) na elektronový systém (polarizace elektronového systému) 4
5 dva bilineární členy: člen bilineární ve složkách μ k, B, tj. Ik, B : (i ) (ik) B r μ μk r e e O = Ai Aik =. me k i me k i 4 π ( r (ik )) () Tento člen představuje interakci mezi jadernými magnetickými momenty a magnetickým polem proudů (el.) vyvolaných Larmorovou precesí elektronů ve vnějším magnetickém poli. Dochází k posunu rezonanční frekvence z hodnoty γ k B (stínění, chemický posuv). člen bilineární ve složkách μ k, μk ', tj. Ik, Ik ' μk rik μk ' r ik ' e e μ. O = A A = ik ik ' me i k k ' me 4 π i k k ' r ik r ik ' () Tento člen představuje vazbu mezi dvěma jadernými magnetickými momenty μ k, μk ' zprostředkovanou elektrony (nepřímá interakce mezi jadernými spiny), (nepřímá dipól-dipólová interakce, J-vazba). Chemický posun O pro jedno jádro (tedy) bez interakce přes k): μ e μ e γ (i ) ( i) O = ( B r ) ( μ r ) (i) = ( B r( i) ) ( I r ( i) ) (i) = 4 π me i (r ) 4 π me i (r ). μ e γ (i ) (i ) (i ) (i ) = ( B r )( r I )+( B I )( r r )) (i) ( 4 π me i (r ) () Definujme tenzor σ d, tak aby ψ O ψ =B σ dμ, () kde ψ je elektronová vlnová funkce v základním stavu. Tedy σ d je symetrický a má složky: ( σ d ) jl = ψ μ e x(i) x (il ) ( r (i) ) δ jl ) ψ. (i) ( j 4 π me i (r ) (4) Tenzor σ d nazýváme tenzorem diamagnetického stínění. Sdružení s Z I dostaneme v hamiltoniánu Z I γ I ( σ d ) B. (5) 5
6 V kapalinách se projeví rychlé izotropní rotace molekul. Nediagonální členy σ d jsou antisymetrické v souřadnicích a jejich časové středování dá. Dále při rotaci souřadného systému se obecně σd. zachovává stopa, neboť stopa je invariant tenzoru a diagonální členy se tedy středují k / Tr Dosazením dostaneme: Tr σd= μ e. 4 π me i r (i ) (6) Definujme skalární veličinu σ d : μ e. σ d = Tr σd= π me i r (i) (7) Sdružením s Z I pak máme Z I γ I ( σ d ) B. (8) Vidíme, že skutečně jde o efekt stínění vnějšího magnetického pole, neboť σ >, tedy ( σ d ) B <B. Vedle tohoto diamagnetického stínění (daného O ) dostaneme bilineární formu v μ, B také v. řádu poruchové teorie. Odtud dostaneme tzv. paramagnetické stínění popsané tenzorem σ p, resp v kapalinách,po časovém středování vlivem rychlých rotací molekul, skalární veličinou σ p σ p= Tr σ p. (9) Součtem diamagnetického a paramagnetického příspěvku dostaneme tenzor chemického posuvu (stínění) σ = σ d +σ p. () A ve spinovém hamiltoniánu se objeví člen γ I ( σ ) B. Pro kapaliny dostaneme chemický posuv (konstantu stínění): σ =σ d +σ p. () A ve spinovém hamiltoniánu se objeví člen γ I ( σ ) B. Rezonanční frekvence jsou posunuty. Speciálně v kapalinách na hodnotu γ ( σ ) B. Frekvenční posuv je úměrný externímu poli B. Hodnoty chemických posuvů jsou citlivé na chemické vazby v okolí atomu s rezonujícím jádrem, závisí na teplotě, ph, rozpouštědle. Chemický posuv v monokrystalech Tenzor σ je symetrický a tedy ho lze diagonalizovat. Hlavní osy tenzoru i σ, j σ, k σ jsou definované vzhledem ke krystalu. Hlavní hodnoty tenzoru označme σ x x, σ y y, σ z z. Je třeba si uvědomit, že 6
7 pole B nemusí ležet v hlavní ose tenzoru σ. Proto vektorem k označíme směr pole B : B= B k, dále zavedeme φ, θ jako souřadnice k v systému hlavních os σ a označíme: α x =k i σ =sin θ cos φ α y =k j σ =sin θ sin φ. α z =k k σ =cos θ () Spinový hamiltonián: H S = γ B I z+ γ B k σ I. () Platí, že Zeemanovská interakce chemický posuv. Proto budeme postupovat poruchovým počtem s použitím aproximace energetických hladin v. řádu uvážíme pouze část poruchy komutující s hamiltoniánem Zeemanovské interakce (pro. řád je důležitá jen komutující část): H S = γ B I z+ γ B Iz ( αx σ x x +α y σ y y +α z σ z z ) (4) ω= ω+ ωa sin θ cos θ+ ωb sin θ sin φ+ω c cos θ, (5) kde ωa = γ B σ x x, podobně ωb, ωc. Předpokládejme, že σ z z je výrazně odlišný od σ x x σ y y. cos φ = (+cos φ ), sin φ= ( cos φ) dostaneme: Úpravou pomocí vztahů [ H S = γ B Iz ( σ x x +σ y y +σ z z ) ( σ z z σ x x σ y y ) ( cos θ ) (σ x x σ y y )sin θ cos φ (6) Označme: σ LOngitudal ( σ z z σ x x σ y y ), σtransversal ( σ x x σ y y ) (7) pak: [ ] H S = γ B I z Tr σ +σ LO ( cos θ ) σtr sin θ cos φ. (8) Chemický posuv v polykrystalech Je potřeba provést superpozici všech možných orientací hlavních os σ vzhledem k B a uvážit relativní četnosti 7 ]
8 θ... π, P ( θ )= sin θ φ... π, P ( φ )=. π Chemický posuv v kapalinách Rychlé rotace molekul. Izotropní geometrické členy u σ LO i σtr se středují k, zbývá člen s Tr σ σ, a tedy H S = γ I z B ( σ ). (9) Nepřímá interakce mezi jadernými magnetickými momenty Podobně jako u chemického posuvu z O pro dvojici jader k, k ' dostaneme bilineární formu ve složkách Ik, Ik '. A spolu s opravami vyšších řádů lze dospět k tenzoru nepřímé dipól-dipólové h (spin-spinové) interakce J a ve spinovém hamiltoniánu dostat člen h Ik J Ik ', který je nezávislý na vnějším poli. Z tenzoru je možno oddělit část s nulovou stopou: J =J ' +J ' ' J ' ' = Tr J E, J ' =J Tr J E (4) kde J ' je tzv. pseudodipólová interakce a J ' ' je tzv. pseudovýměnná interakce (skalární). Speciálně v kapalinách díky rychlým molekulárním pohybům zbyde jen skalární interakce (J-vazba) a ve spinovém hamiltoniánu příspěvek h Ik J Ik '. Spektroskopie NMR vysokého rozlišení v kapalinách Pro NMR v kapalinách je důležitý rychlý, izotropní pohyb molekul, který vede k časovému středování interakcí. Po tomto středování zbyde jen stopa tenzoru popisujícího danou interakci. Ta σ a pro neje pro přímou dipól-dipólovou interakci nulová, pro chemický posuv označíme σ Tr přímou dipól-dipólovou interakci (J-vazbu) zavedeme označení J Tr J. s. Lze dosáhnout relativního rozlišení ve T (nutná homogenita a stabilita pole téhož řádu). Vlastní šířka jednoduché rezonanční křivky spektru až Spinový hamiltonián HHR = γ k B ( σk ) Ikz + h J k,k ' Ik I k ', k k<k ' 8 (4)
9 zahrnuje Zeemanovskou interakci, chemický posuv a J-vazbu. indexy k, k ' značí jádra. Chemický posuv Závisí na rozložení elektronové hustoty kolem jádra. Pro jádra izotopů s větším počtem elektronů jr větší interval možných chemických posunů. Udává se vzhledem ke zvolenému standardu pro daný izotop jako hodnota δ (toto se dělá proto, že σ je malé oproti jedničce a neznáme dostatečně přesně hodnotu B ): ω ω σ σ δ= ω standardu 6= standardu 6. standardu σ (4) standardu Protože σ standardu,je δ=( σ standardu σ ) 6. (4) δ se udává v bezrozměrných jednotkách ppm. Standard: rozpustný v běžně používaných rozpouštědlech stálý nesmí interagovat malá závislost jeho chemického posuvu na teplotě, koncentraci, jeho čára ve spektru je singlet nepřekrývá rezonanční křivky měřených látek Obvyklý standard je tetrametylsilan (TMS) Si(CH)4, je použitelný pro spektra jader H, C, 9Si. Používají se i jiné standardy. Orientačně lze využít například známé polohy čar rozpouštědla (pro H je rozpouštědlo často deuterované, ale bývá přítomný zbytkový signál H), nebo lze škálu odvodit z rezonance D (lock) v závislosti na chemikálii obsahující tento izotop a rozpouštědle. Poznámka: Ve spektroskopii NMR vysokého rozlišení je zvykem frekvenční osu spekter škálovat buď v δ (ppm), nebo ve frekvenčních rozdílech (Hz) mezi rezonancí studované čáry a standardu. V obojím případě bývá orientace této osy taková, že vynášené hodnoty rostou směrem doleva. To vzniklo zřejmě historicky, aby spektra nebyla na pohled pravolevě převrácena oproti spektrům v minulosti měřeným kontinuální metodou při pevné frekvenci a proměnném vnějším poli, kdy na vodorovné ose bylo vynášeno magnetické pole zleva doprava od menších hodnot k větším. Tedy více vpravo jsou rezonanční čáry více stíněných jader (dříve při pevné frekvenci bylo na jejich rezonanci potřeba větší pole, dnes při konstantním vnějším poli rezonují na menší frekvenci). V jiných oborech spektroskopie NMR, méně spjatých s chemií a biologií taková konvence není. Chemické posuvy experimentální data 9
10
11
12 J-vazba Konstanty J jsou nezávislé na vnějším poli. Uvádějí se v jednotkách frekvence (Hz). Dosah interakce i přes několik chemických vazeb. Označení: indexy vlevo nahoře počet vazeb indexy vlevo dole jádra mezi kterými daná interakce nastává J-vazba experimentální data
13
14 4
15 Poznámky: Standardně měřené H spektrum = FID. Standardní C spektrum je tzv. dekaplované spektrum viz otázka o dekaplingu.díky tomuto postupu spektrum obsahuje jednoduché (nerozštěpené) čáry pro každou hodnotu chemického posuvu. Obecně ovšem jsou zkresleny intenzity čar, takže neodpovídají relativní četnosti jader. Spektra C měřená bez dekaplingu obsahují kromě jednoduchých čar (např. pro kvartérní uhlíky) i čáry rozštěpené do multipletů a mohou být proto napohled nepřehledná. Navíc mají vzhledem ke slabé intenzitě rezonance C, relativně dlouhým relaxačním dobám T a rozdělení intenzity čáry do multipletů horší poměr signál / šum. Projevy chemického posuvu a J-vazby ve spektrech NMR kapalin Spinový hamiltonián: k k k ' HHR = γ k B ( σk ) I z + h J k,k ' I I. k (4) k<k ' Speciálně: jádra, jaderné spiny I, S = : HHR = ω I Iz ω S S z +h J I S = ω I I z ω S S z +h J ( I S + I S + Iz S z ), kde ω I = γ I B ( σ I ), ω S = γs B ( σ S ) posuv). (44) (tj. zahrnují Zeemanovskou interakci + chemický a) Stejná jádra, stejný chemický posuv (ekvivalentní jádra) ω I =ωs = ωσ Vlastní vektory H z ( + H σ ) Vlastní hodnoty H z + H σ + +, + -, - + 4, - -, ωσ ωσ Řešení diagonalizací maticové reprezentace HHR v bázi vlastních vektorů H z : 5
16 Vlastní vektory HHR Vlastní hodnoty HHR ωσ + π J π J ' ( ) π J ω σ+ π J ' ( ) Pravděpodobnosti přechodů: i Ix + S x j = ( i I+ + S+ j + i I- + S - j ). (45) Závěry: J-vazba způsobí stejný posuv energetických hladin u, ',4. Posuv hladiny ' je sice jiný, ale pravděpodobnost přechodu z ' nebo na ' je nulová. => J-vazba mezi dvěma ekvivalentními jádry nevyvolá štěpení ve spektru (rezonanční frekvence zůstane ωσ ). To platí obecně i pro vyšší počet jader než dvě. b) případ ω I ωs Tento případ splňují například jádra dvou různých izotopů s nenulovým spinem, ale i stejný izotop, avšak různé chemické posuvy. Předpokládejme ω I <ωs. Vlastní vektory H z ( + H σ ) Vlastní hodnoty H z + H σ + + ( ω I + ωs ) + - ( ω I ωs ) - + ( ω ω S ) I ( ω +ω S ) I HHR zapíšeme v maticové reprezentaci vlastních stavů H z : 6
17 ( ω I +ω S )+ π J ( ω I ω S ) π J π J. HHR = π J ( ω I ω S ) π J ( ω I +ω S )+ π J ( ) (46) Řešení: nalezení vlastních hodnot a vektorů: Vektory + + a zůstávají vlastními vektory i pro HHR, s vlastními hodnotami uvedenými na diagonále. Nutno diagonalizovat submatici. Tím dostaneme vlastní hodnoty a nové lineární kombinace z vektorů + - a - +. Poznámka (trik): Normalizace a kolmost vlastních vektorů pro výpočet je výhodné hledat nové vlastní vektory ve tvaru ' =cos φ + - +sin φ - +, ' = sin φ + - +cos φ - + (47) kde φ je neznámá z intervalu ( 9, 9 ). Výsledek: Vlastní vektory HHR Vlastní hodnoty HHR + + ( ω I + ωs )+ π J ' =cos φ + - +sin φ - + ' = sin φ + - +cos φ - + (ω I ωs )+4 π J π J ( ω I +ω S )+ π J ( ω I ω S )+4 π J π J kde ω I ω S ( ω I ω S ) +4 π J π J. tg φ = = π J ω I ω S + ( ω I ω S )+4 π J (48) Pravděpodobnosti přechodů indukovaných rf polem: P =P 4 (cos φ+sin φ), (49) P =P 4 (cos φ sin φ). (5) V dalším budeme diskutovat dva případy: 7
18 A. ω S ω I π J B. ω S ω I π J (dominantní chemický posuv) (chemický posuv a J-vazba jsou srovnatelné) Ad. A: Schéma energetických hladin pro ω S ω I π J : (Předp. ω I >ωs, J > ) φ= vypnutá J-vazba zapnutá J-vazba Frekvence přechodů: ω ω() S = ωs π J () ω4 ωs =ω S +π J. ω ω() I =ω I π J ω4 ω(i )=ω I +π J (5) Pravděpodobnosti přechodů jsou stejné. Spektrum: Původní čáry jsou rozštěpeny na dublety. 8
19 Ad. B: Dostaneme štěpení čar ve spektru a intenzity v závislosti na J ωs ω I. Zvolme pevně ω S ω I = Hz, pak spektrum vypadá následovně: π Štěpení (v Hz) je stále rovno J, jsou zde dvě různé pravděpodobnosti přechodů => intenzity čar. Případ více spinů. Bázi tvořili součiny jednočásticových vlastních vek torů. Dimenze báze byla 4. Diagonalizace maticové reprezentace vedla na subdeterminanty: Dosud jsme řešili případ dvou spinů I, S = Zobecnění pro N spinů I : (k ) ( N I +) možností pro m =M ( N I +) subdeterminantů. Řád subdeterminantu je dám počtem kombinací, jak složit dané M obecně může být vysoké číslo. Možno využít případnou symetrii molekuly některé z hodnot σ k, J k,k ' mohou být stejné ekvivalentní jádra. Rozlišujeme dva druhy ekvivalence dvou jader. Jednak ekvivalenci chemickou, kdy dvě jádra jsou chemicky ekvivalentní pokud je možné je zaměnit operací symetrie (tj. mají 9
20 stejné chemické okolí, stejnou rezonanční frekvenci). A jednak ekvivalenci magnetickou, přičemž magnetická ekvivalence představuje silnější požadavek než ekvivalence chemická: dvě jádra jsou magneticky ekvivalentní, jestliže jsou chemicky ekvivalentní a mají identické interakční konstanty se všemi dalšími jádry v molekule (nebo v molekule nejsou žádná další magneticky aktivní jádra). Mezi magneticky ekvivalentními jádry pak nedochází k štěpení vlivem J-vazby. Hamiltonián: ) ) (G (G HHR = ωg I (G I ' ). z + h J G, G' I G (5) G <G' Kde indexy G,G ' označují skupiny ekvivalentních jader (uvnitř skupiny jsou posuvy stejné, tudíž se můžeme zabývat jen interakcemi mezi jednotlivými skupinami). A I (G) = I ( k) (5) k je součet ve skupině ekvivalentních jader (vazba mezi ekvivalentními jádry nevyvolá štěpení čar). Omezíme se na na slabou J-vazbu (ve srovnání s chemickým posuvem, spektra. řádu ). Zavedeme následující značení: skupinu ekvivalentních jader označíme velkým písmenem a počet jader ve skupině označíme indexem: A, B,....Rozdíl v chemických posuvech jednotlivých skupin vyjádříme vzdáleností písmen v abecedě A X.... Př.: pro dvě skupiny ekvivalentních jader: A, B stejný izotop, různé chemické posuvy A, X buď různé izotopy, nebo stejný izotop, ale velmi různé chemické posuvy. ) (X ) (A) (X ) HHR = ω A I (A I. z ω X I z +h J A X I (54) Bez J-vazby degenerované hladiny ( ) EM A M X = ω A M A ω X M X. (55) J-vazba oprava v. přiblížení ( A) (X ) M A M X h J A X I I M A M X =M A M X h J A X nesnímá degeneraci. (56)
21 Pro dané M A, M X : EM A MX = ω A M A ω X M X +M A M X h J A B. (57) Přechody pro Δ (M A+M X )=±. Spektrum X (přechody se změnou M X ) Pro dané M A a změna Δ M X =±. Frekvence přechodu: ω X +M A π J A X. Multiplet ve spektru X, celkem I (k ) N A + ekvidistantních čar vzdálených o π J A X. Spektrum A (přechody se změnou M A ) Pro dané M X a změna Δ M A =±. Frekvence přechodu: ω A+M X π J A X. Multiplet ve spektru X, celkem I (k ) N X + ekvidistantních čar vzdálených o π J A X. Těžiště multipletu zůstává na místě daném chemickým posuvem, tj. ω A pro spektrum A, ω X pro spektrum X. Vzdálenost těžišť je tedy ω A ω X. Př.: Systém AX, oba spiny / : multiplet A += čáry multiplet X += čáry tj. dublety. Př.: Systém AX, oba spiny / : multiplet A +=4 čáry kvartet multiplet X += čáry triplet Intenzity čar v multipletu A, resp. X jsou úměrné počtu různých kombinací pro složení M X,resp. MA: Spektrum A: MX počet kombinací / / / /
22 Spektrum X: MX počet kombinací - (Pascalův trojúhelník) máme větší počet různých M A a tedy více čar ve spektru X, obecně větší po čet kombinací pro stejné M A. Pozn.: Pro spiny A> Z obrázku výše je vidět výhoda velkých polí - J A B nezávisí na Bext, ale ω I ω S π Bext.
23
24 Složitější molekuly Více skupin vzájemně interagujících J-vazbou => složitá multipletní struktura, překryvy čar ve spektru. Jak zjednodušit spektra (zbavit se multipletní struktury)? Izotopová záměna selektivně. Dekapling (viz. otázka věnovaná dekaplingu). 4
Hamiltonián popisující atom vodíku ve vnějším magnetickém poli:
 Orbitální a spinový magnetický moment a jejich interakce s vnějším polem Vše na příkladu atomu H: Elektron (e - ) a jádro (u atomu H pouze p + ) mají vlastní magnetický moment (= spin). Tyto dva dipóly
Orbitální a spinový magnetický moment a jejich interakce s vnějším polem Vše na příkladu atomu H: Elektron (e - ) a jádro (u atomu H pouze p + ) mají vlastní magnetický moment (= spin). Tyto dva dipóly
OPVK CZ.1.07/2.2.00/
 18.2.2013 OPVK CZ.1.07/2.2.00/28.0184 Cvičení z NMR OCH/NMR Mgr. Tomáš Pospíšil, Ph.D. LS 2012/2013 18.2.2013 NMR základní principy NMR Nukleární Magnetická Resonance N - nukleární (studujeme vlastnosti
18.2.2013 OPVK CZ.1.07/2.2.00/28.0184 Cvičení z NMR OCH/NMR Mgr. Tomáš Pospíšil, Ph.D. LS 2012/2013 18.2.2013 NMR základní principy NMR Nukleární Magnetická Resonance N - nukleární (studujeme vlastnosti
Úvod do strukturní analýzy farmaceutických látek
 Úvod do strukturní analýzy farmaceutických látek Garant předmětu: doc. Ing. Bohumil Dolenský, Ph.D. A28, linka 40, dolenskb@vscht.cz Nukleární Magnetická Rezonance II. Příprava předmětu byla podpořena
Úvod do strukturní analýzy farmaceutických látek Garant předmětu: doc. Ing. Bohumil Dolenský, Ph.D. A28, linka 40, dolenskb@vscht.cz Nukleární Magnetická Rezonance II. Příprava předmětu byla podpořena
Skoro každý prvek má nějaký stabilní isotop s nenulovým spinem. (Výjimky: Ar, Tc, Ce, Pm)
 Gyromagnetická částice, jev magnetické rezonance Pojmy s kterýma se můžete setkat: u elektronů lze Bohrův magneton Zkoumat NMR lze jen ty jádra, které mají nenulový jaderný spin: Několik systematických
Gyromagnetická částice, jev magnetické rezonance Pojmy s kterýma se můžete setkat: u elektronů lze Bohrův magneton Zkoumat NMR lze jen ty jádra, které mají nenulový jaderný spin: Několik systematických
Elektromagnetické pole je generováno elektrickými náboji a jejich pohybem. Je-li zdroj charakterizován nábojovou hustotou ( r r
 Záření Hertzova dipólu, kulové vlny, Rovnice elektromagnetického pole jsou vektorové diferenciální rovnice a podle symetrie bývá vhodné je řešit v křivočarých souřadnicích. Základní diferenciální operátory
Záření Hertzova dipólu, kulové vlny, Rovnice elektromagnetického pole jsou vektorové diferenciální rovnice a podle symetrie bývá vhodné je řešit v křivočarých souřadnicích. Základní diferenciální operátory
Od kvantové mechaniky k chemii
 Od kvantové mechaniky k chemii Jan Řezáč UOCHB AV ČR 19. září 2017 Jan Řezáč (UOCHB AV ČR) Od kvantové mechaniky k chemii 19. září 2017 1 / 33 Úvod Vztah mezi molekulovou strukturou a makroskopickými vlastnostmi
Od kvantové mechaniky k chemii Jan Řezáč UOCHB AV ČR 19. září 2017 Jan Řezáč (UOCHB AV ČR) Od kvantové mechaniky k chemii 19. září 2017 1 / 33 Úvod Vztah mezi molekulovou strukturou a makroskopickými vlastnostmi
SPEKTROSKOPIE NUKLEÁRNÍ MAGNETICKÉ REZONANCE
 SPEKTROSKOPIE NUKLEÁRNÍ MAGNETICKÉ REZONANCE Obecné základy nedestruktivní metoda strukturní analýzy zabývá se rezonancí atomových jader nutná podmínka pro měření spekter: nenulový spin atomového jádra
SPEKTROSKOPIE NUKLEÁRNÍ MAGNETICKÉ REZONANCE Obecné základy nedestruktivní metoda strukturní analýzy zabývá se rezonancí atomových jader nutná podmínka pro měření spekter: nenulový spin atomového jádra
Základy Mössbauerovy spektroskopie. Libor Machala
 Základy Mössbauerovy spektroskopie Libor Machala Rudolf L. Mössbauer 1958: jev bezodrazové rezonanční absorpce záření gama atomovým jádrem 1961: Nobelova cena Analogie s rezonanční absorpcí akustických
Základy Mössbauerovy spektroskopie Libor Machala Rudolf L. Mössbauer 1958: jev bezodrazové rezonanční absorpce záření gama atomovým jádrem 1961: Nobelova cena Analogie s rezonanční absorpcí akustických
NMR spektroskopie. Úvod
 NMR spektroskopie Úvod Zkratka NMR znamená Nukleární Magnetická Rezonance. Jde o analytickou metodu, která na základě absorpce radiofrekvenčního záření vzorkem umístěným v silném magnetickém poli poskytuje
NMR spektroskopie Úvod Zkratka NMR znamená Nukleární Magnetická Rezonance. Jde o analytickou metodu, která na základě absorpce radiofrekvenčního záření vzorkem umístěným v silném magnetickém poli poskytuje
Spektra 1 H NMR. Velmi zjednodušeně! Bohumil Dolenský
 Spektra 1 MR Velmi zjednodušeně! Bohumil Dolenský Spektra 1 MR... Počet signálů C 17 18 2 O 2 MeO Počet signálů = počet neekvivalentních skupin OMe = informace o symetrii molekuly Spektrum 1 MR... Počet
Spektra 1 MR Velmi zjednodušeně! Bohumil Dolenský Spektra 1 MR... Počet signálů C 17 18 2 O 2 MeO Počet signálů = počet neekvivalentních skupin OMe = informace o symetrii molekuly Spektrum 1 MR... Počet
NMR spektroskopie rádiové frekvence jádra spinovou rezonancí jader spinový moment lichý počet
 NMR spektroskopie NMR spektroskopie Nukleární Magnetická Resonance - spektroskopická metoda založená na měření absorpce elektromagnetického záření (rádiové frekvence asi od 4 do 900 MHz). Na rozdíl od
NMR spektroskopie NMR spektroskopie Nukleární Magnetická Resonance - spektroskopická metoda založená na měření absorpce elektromagnetického záření (rádiové frekvence asi od 4 do 900 MHz). Na rozdíl od
Základní parametry 1 H NMR spekter
 LEKCE 1a Základní parametry 1 NMR spekter Počet signálů ve spektru (zjištění počtu skupin chemicky ekvivalentních jader) Integrální intenzita (intenzita pásů závisí na počtu jader) Chemický posun (polohy
LEKCE 1a Základní parametry 1 NMR spekter Počet signálů ve spektru (zjištění počtu skupin chemicky ekvivalentních jader) Integrální intenzita (intenzita pásů závisí na počtu jader) Chemický posun (polohy
Atom vodíku. Nejjednodušší soustava: p + e Řešitelná exaktně. Kulová symetrie. Potenciální energie mezi p + e. e =
 Atom vodíku Nejjednodušší soustava: p + e Řešitelná exaktně Kulová symetrie Potenciální energie mezi p + e V 2 e = 4πε r 0 1 Polární souřadnice využití kulové symetrie atomu Ψ(x,y,z) Ψ(r,θ, φ) x =? y=?
Atom vodíku Nejjednodušší soustava: p + e Řešitelná exaktně Kulová symetrie Potenciální energie mezi p + e V 2 e = 4πε r 0 1 Polární souřadnice využití kulové symetrie atomu Ψ(x,y,z) Ψ(r,θ, φ) x =? y=?
spinový rotační moment (moment hybnosti) kvantové číslo jaderného spinu I pro NMR - jádra s I 0
 Spektroskopie NMR - teoretické základy spin nukleonů, spin jádra, kvantová čísla energetické stavy jádra v magnetickém poli rezonanční podmínka - instrumentace pulsní metody, pulsní sekvence relaxační
Spektroskopie NMR - teoretické základy spin nukleonů, spin jádra, kvantová čísla energetické stavy jádra v magnetickém poli rezonanční podmínka - instrumentace pulsní metody, pulsní sekvence relaxační
LEKCE 1b. Základní parametry 1 H NMR spekter. Symetrie v NMR spektrech: homotopické, enantiotopické, diastereotopické protony (skupiny)*
 Základní parametry 1 NMR spekter LEKCE 1b Symetrie v NMR spektrech: homotopické, enantiotopické, diastereotopické protony (skupiny)* 3.5 3.0 2.5 2.0 1.5 Základní parametry 1 NMR spekter Počet signálů ve
Základní parametry 1 NMR spekter LEKCE 1b Symetrie v NMR spektrech: homotopické, enantiotopické, diastereotopické protony (skupiny)* 3.5 3.0 2.5 2.0 1.5 Základní parametry 1 NMR spekter Počet signálů ve
Úvod do strukturní analýzy farmaceutických látek
 Úvod do strukturní analýzy farmaceutických látek Garant předmětu: doc. Ing. Bohumil Dolenský, Ph.D. A28, linka 40, dolenskb@vscht.cz Nukleární Magnetická Rezonance I. Příprava předmětu byla podpořena projektem
Úvod do strukturní analýzy farmaceutických látek Garant předmětu: doc. Ing. Bohumil Dolenský, Ph.D. A28, linka 40, dolenskb@vscht.cz Nukleární Magnetická Rezonance I. Příprava předmětu byla podpořena projektem
Nukleární magnetická rezonance (NMR)
 Nukleární magnetická rezonance (NMR) Nukleární magnetické rezonance (NMR) princip ZDROJ E = h. elektro-magnetické záření E energie záření h Plankova konstanta frekvence záření VZOREK E E 1 E 0 DETEKTOR
Nukleární magnetická rezonance (NMR) Nukleární magnetické rezonance (NMR) princip ZDROJ E = h. elektro-magnetické záření E energie záření h Plankova konstanta frekvence záření VZOREK E E 1 E 0 DETEKTOR
Laserová technika prosince Katedra fyzikální elektroniky.
 Laserová technika 1 Aktivní prostředí Šíření rezonančního záření dvouhladinovým prostředím Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 22. prosince 2016 Program
Laserová technika 1 Aktivní prostředí Šíření rezonančního záření dvouhladinovým prostředím Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 22. prosince 2016 Program
přičemž předpokládáme A malé, U zahrnuje coulombické členy. Když roznásobíme závorku, p 2 reprezentuje kinetickou energii nabitých částic, člen
 Výběrová pravidla Absorpce/stim. emise Kde se výběrová pravidla vezmou? Použijeme semiklasické přiblížení, tzn. s nabitými částicemi (s indexy 1...N) zacházíme kvantově, s vnějším elektromagnetickým polem
Výběrová pravidla Absorpce/stim. emise Kde se výběrová pravidla vezmou? Použijeme semiklasické přiblížení, tzn. s nabitými částicemi (s indexy 1...N) zacházíme kvantově, s vnějším elektromagnetickým polem
Orbitaly, VSEPR 1 / 18
 rbitaly, VSEPR Rezonanční struktury, atomové a molekulové orbitaly, hybridizace, určování tvaru molekuly pomocí teorie VSEPR, úvod do symetrie molekul, dipólový moment 1 / 18 Formální náboj Rozdíl mezi
rbitaly, VSEPR Rezonanční struktury, atomové a molekulové orbitaly, hybridizace, určování tvaru molekuly pomocí teorie VSEPR, úvod do symetrie molekul, dipólový moment 1 / 18 Formální náboj Rozdíl mezi
Fyzika IV. 1) orbitální magnetický moment (... moment proudové smyčky) gyromagnetický poměr: kvantování: Bohrův magneton: 2) spinový magnetický moment
 λ=21 cm 1) orbitální magnetický moment (... moment proudové smyčky) μ I S gyromagnetický poměr: kvantování: Bohrův magneton: 2) spinový magnetický moment 2 Zeemanův jev - rozštěpení spektrálních čar v
λ=21 cm 1) orbitální magnetický moment (... moment proudové smyčky) μ I S gyromagnetický poměr: kvantování: Bohrův magneton: 2) spinový magnetický moment 2 Zeemanův jev - rozštěpení spektrálních čar v
Nukleární Overhauserův efekt (NOE)
 Nukleární Overhauserův efekt (NOE) NOE je důsledek dipolární interakce mezi dvěma jádry. Vzniká přímou interakcí volně přes prostor, tudíž není ovlivněn chemickými vazbami jako nepřímá spin-spinová interakce.
Nukleární Overhauserův efekt (NOE) NOE je důsledek dipolární interakce mezi dvěma jádry. Vzniká přímou interakcí volně přes prostor, tudíž není ovlivněn chemickými vazbami jako nepřímá spin-spinová interakce.
Orbitaly, VSEPR. Zdeněk Moravec, 16. listopadu / 21
 rbitaly, VSEPR Rezonanční struktury, atomové a molekulové orbitaly, hybridizace, určování tvaru molekuly pomocí teorie VSEPR, úvod do symetrie molekul, dipólový moment Zdeněk Moravec, http://z-moravec.net
rbitaly, VSEPR Rezonanční struktury, atomové a molekulové orbitaly, hybridizace, určování tvaru molekuly pomocí teorie VSEPR, úvod do symetrie molekul, dipólový moment Zdeněk Moravec, http://z-moravec.net
ATOMOVÁ SPEKTROMETRIE
 ATOMOVÁ SPEKTROMETRIE Atomová spektrometrie valenčních e - 1. OES (AES). AAS 3. AFS 1 Atomová spektra čárová spektra Tok záření P - množství zářivé energie (Q E ) přenesené od zdroje za jednotku času.
ATOMOVÁ SPEKTROMETRIE Atomová spektrometrie valenčních e - 1. OES (AES). AAS 3. AFS 1 Atomová spektra čárová spektra Tok záření P - množství zářivé energie (Q E ) přenesené od zdroje za jednotku času.
Elementární částice. 1. Leptony 2. Baryony 3. Bosony. 4. Kvarkový model 5. Slabé interakce 6. Partonový model
 Elementární částice 1. Leptony 2. Baryony 3. Bosony 4. Kvarkový model 5. Slabé interakce 6. Partonový model I.S. Hughes: Elementary Particles M. Leon: Particle Physics W.S.C. Williams Nuclear and Particle
Elementární částice 1. Leptony 2. Baryony 3. Bosony 4. Kvarkový model 5. Slabé interakce 6. Partonový model I.S. Hughes: Elementary Particles M. Leon: Particle Physics W.S.C. Williams Nuclear and Particle
Nukleární magnetická rezonance (NMR)
 Nukleární magnetická rezonance (NMR) Mgr. Zdeněk Moravec, Ph.D. Úvod Zkratka NMR znamená Nukleární Magnetická Rezonance. Jde o analytickou metodu, která na základě absorpce radiofrekvenčního záření vzorkem
Nukleární magnetická rezonance (NMR) Mgr. Zdeněk Moravec, Ph.D. Úvod Zkratka NMR znamená Nukleární Magnetická Rezonance. Jde o analytickou metodu, která na základě absorpce radiofrekvenčního záření vzorkem
ZÁKLADY SPEKTROMETRIE NUKLEÁRNÍ MAGNETICKÉ REZONANCE
 ZÁKLADY SPEKTROMETRIE NUKLEÁRNÍ MAGNETICKÉ REZONANCE Co to je NMR? nedestruktivní spektroskopická metoda využívající magnetických vlastností atomových jader ke studiu struktury molekul metoda č.1 pro určování
ZÁKLADY SPEKTROMETRIE NUKLEÁRNÍ MAGNETICKÉ REZONANCE Co to je NMR? nedestruktivní spektroskopická metoda využívající magnetických vlastností atomových jader ke studiu struktury molekul metoda č.1 pro určování
Vektory a matice. Obsah. Aplikovaná matematika I. Carl Friedrich Gauss. Základní pojmy a operace
 Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
Metody spektrální. Metody molekulové spektroskopie NMR. Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
 Metody spektrální Metody molekulové spektroskopie NMR Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Spektroskopie NMR - teoretické základy spin nukleonů, spin jádra, kvantová čísla
Metody spektrální Metody molekulové spektroskopie NMR Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Spektroskopie NMR - teoretické základy spin nukleonů, spin jádra, kvantová čísla
Zajímavé vlastnosti sluneční atmosféry: magnetická a rychlostní pole
 Zajímavé vlastnosti sluneční atmosféry: magnetická a rychlostní pole Spektroskopie (nejen) ve sluneční fyzice LS 2011/2012 Michal Švanda Astronomický ústav MFF UK Astronomický ústav AV ČR Vliv na tvar
Zajímavé vlastnosti sluneční atmosféry: magnetická a rychlostní pole Spektroskopie (nejen) ve sluneční fyzice LS 2011/2012 Michal Švanda Astronomický ústav MFF UK Astronomický ústav AV ČR Vliv na tvar
17 Vlastnosti molekul
 17 Vlastnosti molekul Experimentálně molekuly charakterizujeme pomocí nejrůznějších vlastností: můžeme změřit třeba NMR posuny, elektrické či magnetické parametry či třeba jejich optickou otáčivost. Tyto
17 Vlastnosti molekul Experimentálně molekuly charakterizujeme pomocí nejrůznějších vlastností: můžeme změřit třeba NMR posuny, elektrické či magnetické parametry či třeba jejich optickou otáčivost. Tyto
COSY + - podmínky měření a zpracování dat ztráta rozlišení ve spektru. inphase dublet, disperzní. antiphase dublet, absorpční
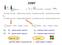 y x COSY 90 y chem. posuv J vazba 90 x : : inphase dublet, disperzní inphase dublet, disperzní antiphase dublet, absorpční antiphase dublet, absorpční diagonální pík krospík + - - + podmínky měření a zpracování
y x COSY 90 y chem. posuv J vazba 90 x : : inphase dublet, disperzní inphase dublet, disperzní antiphase dublet, absorpční antiphase dublet, absorpční diagonální pík krospík + - - + podmínky měření a zpracování
NMR spektroskopie Instrumentální a strukturní analýza
 NMR spektroskopie Instrumentální a strukturní analýza prof. RNDr. Zdeněk Friedl, CSc. Použitá a doporučená literatura Solomons T.W.G., Fryhle C.B.: Organic Chemistry, 8th Ed., Wiley 2004. Günther H.: NMR
NMR spektroskopie Instrumentální a strukturní analýza prof. RNDr. Zdeněk Friedl, CSc. Použitá a doporučená literatura Solomons T.W.G., Fryhle C.B.: Organic Chemistry, 8th Ed., Wiley 2004. Günther H.: NMR
Optické spektroskopie 1 LS 2014/15
 Optické spektroskopie 1 LS 2014/15 Martin Kubala 585634179 mkubala@prfnw.upol.cz 1.Úvod Velikosti objektů v přírodě Dítě ~ 1 m (10 0 m) Prst ~ 2 cm (10-2 m) Vlas ~ 0.1 mm (10-4 m) Buňka ~ 20 m (10-5 m)
Optické spektroskopie 1 LS 2014/15 Martin Kubala 585634179 mkubala@prfnw.upol.cz 1.Úvod Velikosti objektů v přírodě Dítě ~ 1 m (10 0 m) Prst ~ 2 cm (10-2 m) Vlas ~ 0.1 mm (10-4 m) Buňka ~ 20 m (10-5 m)
Necht L je lineární prostor nad R. Operaci : L L R nazýváme
 Skalární součin axiomatická definice odvození velikosti vektorů a úhlu mezi vektory geometrická interpretace ortogonalita vlastnosti ortonormálních bázi [1] Definice skalárního součinu Necht L je lineární
Skalární součin axiomatická definice odvození velikosti vektorů a úhlu mezi vektory geometrická interpretace ortogonalita vlastnosti ortonormálních bázi [1] Definice skalárního součinu Necht L je lineární
Dolenský, VŠCHT Praha, pracovní verze 1
 1. Multiplicita_INDA Interpretujte multiplety všech signálů spektra. Všechny multiplety jsou důsledkem interakce výhradně s jádry s magnetickým jaderným spinem 1/2, a nejsou významně komplikovány přítomností
1. Multiplicita_INDA Interpretujte multiplety všech signálů spektra. Všechny multiplety jsou důsledkem interakce výhradně s jádry s magnetickým jaderným spinem 1/2, a nejsou významně komplikovány přítomností
Učební texty k státní bakalářské zkoušce Matematika Skalární součin. študenti MFF 15. augusta 2008
 Učební texty k státní bakalářské zkoušce Matematika Skalární součin študenti MFF 15. augusta 2008 1 10 Skalární součin Požadavky Vlastnosti v reálném i komplexním případě Norma Cauchy-Schwarzova nerovnost
Učební texty k státní bakalářské zkoušce Matematika Skalární součin študenti MFF 15. augusta 2008 1 10 Skalární součin Požadavky Vlastnosti v reálném i komplexním případě Norma Cauchy-Schwarzova nerovnost
Maticí typu (m, n), kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru:
 3 Maticový počet 3.1 Zavedení pojmu matice Maticí typu (m, n, kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru: a 11 a 12... a 1k... a 1n a 21 a 22...
3 Maticový počet 3.1 Zavedení pojmu matice Maticí typu (m, n, kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru: a 11 a 12... a 1k... a 1n a 21 a 22...
Oddělení pohybu elektronů a jader
 Oddělení pohybu elektronů a ader Adiabatická aproximace Born-Oppenheimerova aproximace Důležité vztahy sou 4, 5, 7, 0,,, udělal sem to zbytečně podrobně, e to samostatný okruh Separace translačního pohybu:
Oddělení pohybu elektronů a ader Adiabatická aproximace Born-Oppenheimerova aproximace Důležité vztahy sou 4, 5, 7, 0,,, udělal sem to zbytečně podrobně, e to samostatný okruh Separace translačního pohybu:
Elektronový obal atomu
 Elektronový obal atomu Vlnění o frekvenci v se může chovat jako proud částic (kvant - fotonů) o energii E = h.v Částice pohybující se s hybností p se může chovat jako vlna o vlnové délce λ = h/p Kde h
Elektronový obal atomu Vlnění o frekvenci v se může chovat jako proud částic (kvant - fotonů) o energii E = h.v Částice pohybující se s hybností p se může chovat jako vlna o vlnové délce λ = h/p Kde h
Jiří Brus. (Verze 1.0.1-2005) (neupravená a neúplná)
 Jiří Brus (Verze 1.0.1-2005) (neupravená a neúplná) Ústav makromolekulární chemie AV ČR, Heyrovského nám. 2, Praha 6 - Petřiny 162 06 e-mail: brus@imc.cas.cz Transverzální magnetizace, která vykonává precesi
Jiří Brus (Verze 1.0.1-2005) (neupravená a neúplná) Ústav makromolekulární chemie AV ČR, Heyrovského nám. 2, Praha 6 - Petřiny 162 06 e-mail: brus@imc.cas.cz Transverzální magnetizace, která vykonává precesi
4. Napjatost v bodě tělesa
 p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
Dekapling, koherentní transfer polarizace, nukleární Overhauserův jev
 Dekapling Dekapling, koherentní transfer polarizace, nukleární Overhauserův jev Dekaplingem rozumíme odstranění vlivu J-vazby XA na na spektra jader A působením dalšího radiofrekvenčního pole ( ω X )na
Dekapling Dekapling, koherentní transfer polarizace, nukleární Overhauserův jev Dekaplingem rozumíme odstranění vlivu J-vazby XA na na spektra jader A působením dalšího radiofrekvenčního pole ( ω X )na
Analýza napjatosti PLASTICITA
 Analýza napjatosti PLASTICITA TENZOR NAPĚTÍ Teplota v daném bodě je skalár, je to tenzor nultého řádu, který nezávisí na změně souřadného systému Síla je vektor, je to tenzor prvního řádu, v trojrozměrném
Analýza napjatosti PLASTICITA TENZOR NAPĚTÍ Teplota v daném bodě je skalár, je to tenzor nultého řádu, který nezávisí na změně souřadného systému Síla je vektor, je to tenzor prvního řádu, v trojrozměrném
Nukleární Overhauserův efekt (NOE)
 LEKCE 8 Nukleární verhauserův efekt (NE) určení prostorové struktury molekul využití REY spektroskopie projevy NE a chemické výměny v jednom systému Nukleární verhauserův efekt (NE) důsledek dipolární
LEKCE 8 Nukleární verhauserův efekt (NE) určení prostorové struktury molekul využití REY spektroskopie projevy NE a chemické výměny v jednom systému Nukleární verhauserův efekt (NE) důsledek dipolární
Fyzika atomového jádra
 Fyzika atomového jádra (NJSF064) František Knapp http://www.ipnp.cz/knapp/jf/ frantisek.knapp@mff.cuni.cz Literatura [1] S.G. Nilsson, I. Rangarsson: Shapes and shells in nuclear structure [2] R. Casten:
Fyzika atomového jádra (NJSF064) František Knapp http://www.ipnp.cz/knapp/jf/ frantisek.knapp@mff.cuni.cz Literatura [1] S.G. Nilsson, I. Rangarsson: Shapes and shells in nuclear structure [2] R. Casten:
terminologie předchozí kapitoly: (ϕ, Ω) - plocha, S - geometrický obraz plochy
 2. Plošný integrál. Poznámka. Obecně: integrování přes k-rozměrné útvary (k-plochy) v R n. Omezíme se na případ k = 2, n = 3. Definice. Množina S R 3 se nazve plocha, pokud S = ϕ(), kde R 2 je otevřená
2. Plošný integrál. Poznámka. Obecně: integrování přes k-rozměrné útvary (k-plochy) v R n. Omezíme se na případ k = 2, n = 3. Definice. Množina S R 3 se nazve plocha, pokud S = ϕ(), kde R 2 je otevřená
Strukturní analýza. NMR spektroskopie
 Strukturní analýza NMR spektroskopie RNDr. Zdeněk Tošner, Ph.D. lavova 8, místnost 020 tel. 22195 1323 tosner@natur.cuni.cz www.natur.cuni.cz/nmr/vyuka.html Literatura Böhm, Smrčková-Voltrová: Strukturní
Strukturní analýza NMR spektroskopie RNDr. Zdeněk Tošner, Ph.D. lavova 8, místnost 020 tel. 22195 1323 tosner@natur.cuni.cz www.natur.cuni.cz/nmr/vyuka.html Literatura Böhm, Smrčková-Voltrová: Strukturní
doc. Ing. Richard Hrabal, CSc. Ing. Hana Dvořáková, CSc. RNDr. Jan Lang, PhD. Číslo dveří A 42, telefon 3805,
 Vyučující: doc. Ing. Richard rabal, CSc. Ing. ana Dvořáková, CSc. RNDr. Jan Lang, PhD. Číslo dveří A 42, telefon 3805, e-mail hrabalr@vscht.cz Termín: každé pondělí od 8.30 do 11.30 Místo: posluchárna
Vyučující: doc. Ing. Richard rabal, CSc. Ing. ana Dvořáková, CSc. RNDr. Jan Lang, PhD. Číslo dveří A 42, telefon 3805, e-mail hrabalr@vscht.cz Termín: každé pondělí od 8.30 do 11.30 Místo: posluchárna
Všechno, co jste kdy chtěli vědět o maticích, ale báli jste se zeptat
 Všechno, co jste kdy chtěli vědět o maticích, ale báli jste se zeptat Čtvercová matice n n, např. může reprezentovat: A = A A 2 A 3 A 2 A 22 A 23 A 3 A 32 A 33 matici koeficientů soustavy n lineárních
Všechno, co jste kdy chtěli vědět o maticích, ale báli jste se zeptat Čtvercová matice n n, např. může reprezentovat: A = A A 2 A 3 A 2 A 22 A 23 A 3 A 32 A 33 matici koeficientů soustavy n lineárních
Diskutujte, jak široký bude pás spojený s fosforescencí versus fluorescencí. Udělejte odhad v cm -1.
 S použitím modelu volného elektronu (=částice v krabici) spočtěte vlnovou délku a vlnočet nejdlouhovlnějšího elektronového přechodu u molekuly dekapentaenu a oktatetraenu. Diskutujte polohu absorpčního
S použitím modelu volného elektronu (=částice v krabici) spočtěte vlnovou délku a vlnočet nejdlouhovlnějšího elektronového přechodu u molekuly dekapentaenu a oktatetraenu. Diskutujte polohu absorpčního
Fyzika atomového jádra
 Fyzika atomového jádra (NJSF064) František Knapp http://www-ucjf.troja.mff.cuni.cz/~knapp/jf/ frantisek.knapp@mff.cuni.cz Slupkový model jádra evidence magických čísel: hmoty, separační energie, vazbové
Fyzika atomového jádra (NJSF064) František Knapp http://www-ucjf.troja.mff.cuni.cz/~knapp/jf/ frantisek.knapp@mff.cuni.cz Slupkový model jádra evidence magických čísel: hmoty, separační energie, vazbové
Matematika B101MA1, B101MA2
 Matematika B101MA1, B101MA2 Zařazení předmětu: povinný předmět 1.ročníku bc studia 2 semestry Rozsah předmětu: prezenční studium 2 + 2 kombinované studium 16 + 0 / semestr Zakončení předmětu: ZS zápočet
Matematika B101MA1, B101MA2 Zařazení předmětu: povinný předmět 1.ročníku bc studia 2 semestry Rozsah předmětu: prezenční studium 2 + 2 kombinované studium 16 + 0 / semestr Zakončení předmětu: ZS zápočet
Lineární algebra : Skalární součin a ortogonalita
 Lineární algebra : Skalární součin a ortogonalita (15. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 30. dubna 2014, 09:00 1 2 15.1 Prehilhertovy prostory Definice 1. Buď V LP nad
Lineární algebra : Skalární součin a ortogonalita (15. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 30. dubna 2014, 09:00 1 2 15.1 Prehilhertovy prostory Definice 1. Buď V LP nad
Ab initio výpočty v chemii a biochemii
 Ab initio výpočty v chemii a biochemii Doc. RNDr. Ing. Jaroslav Burda, CSc., jaroslav.burda@mff.cuni.cz Dr. Vladimír Sychrovský vladimir.sychrovsky@uochb.cas.cz Studijní literatura Szabo A., Ostlund N.S.
Ab initio výpočty v chemii a biochemii Doc. RNDr. Ing. Jaroslav Burda, CSc., jaroslav.burda@mff.cuni.cz Dr. Vladimír Sychrovský vladimir.sychrovsky@uochb.cas.cz Studijní literatura Szabo A., Ostlund N.S.
8 Matice a determinanty
 M Rokyta, MFF UK: Aplikovaná matematika II kap 8: Matice a determinanty 1 8 Matice a determinanty 81 Matice - definice a základní vlastnosti Definice Reálnou resp komplexní maticí A typu m n nazveme obdélníkovou
M Rokyta, MFF UK: Aplikovaná matematika II kap 8: Matice a determinanty 1 8 Matice a determinanty 81 Matice - definice a základní vlastnosti Definice Reálnou resp komplexní maticí A typu m n nazveme obdélníkovou
LEKCE 7. Interpretace 13 C NMR spekter. Využití 2D experimentů. Zpracování, výpočet a databáze NMR spekter (ACD/Labs, Topspin, Mnova) ppm
 LEKCE 7 Interpretace 13 C MR spekter Využití 2D experimentů ppm 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0 6.5 6.5 6.0 5.5 5.0 4.5 4.0 3.5 3.0 2.5 2.0 1.5 1.0 ppm Zpracování, výpočet a databáze MR spekter
LEKCE 7 Interpretace 13 C MR spekter Využití 2D experimentů ppm 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0 6.5 6.5 6.0 5.5 5.0 4.5 4.0 3.5 3.0 2.5 2.0 1.5 1.0 ppm Zpracování, výpočet a databáze MR spekter
Definice 13.1 Kvadratická forma v n proměnných s koeficienty z tělesa T je výraz tvaru. Kvadratická forma v n proměnných je tak polynom n proměnných s
 Kapitola 13 Kvadratické formy Definice 13.1 Kvadratická forma v n proměnných s koeficienty z tělesa T je výraz tvaru f(x 1,..., x n ) = a ij x i x j, kde koeficienty a ij T. j=i Kvadratická forma v n proměnných
Kapitola 13 Kvadratické formy Definice 13.1 Kvadratická forma v n proměnných s koeficienty z tělesa T je výraz tvaru f(x 1,..., x n ) = a ij x i x j, kde koeficienty a ij T. j=i Kvadratická forma v n proměnných
Operátory a maticové elementy
 Operátory a matice Operátory a maticové elementy operátory je výhodné reprezentovat maticemi maticové elementy operátorů jsou dány vztahy mezi Slaterovými determinanty obsahujícími ortonormální orbitaly
Operátory a matice Operátory a maticové elementy operátory je výhodné reprezentovat maticemi maticové elementy operátorů jsou dány vztahy mezi Slaterovými determinanty obsahujícími ortonormální orbitaly
1. Náhodný vektor (X, Y ) má diskrétní rozdělení s pravděpodobnostní funkcí p, kde. p(x, y) = a(x + y + 1), x, y {0, 1, 2}.
 VIII. Náhodný vektor. Náhodný vektor (X, Y má diskrétní rozdělení s pravděpodobnostní funkcí p, kde p(x, y a(x + y +, x, y {,, }. a Určete číslo a a napište tabulku pravděpodobnostní funkce p. Řešení:
VIII. Náhodný vektor. Náhodný vektor (X, Y má diskrétní rozdělení s pravděpodobnostní funkcí p, kde p(x, y a(x + y +, x, y {,, }. a Určete číslo a a napište tabulku pravděpodobnostní funkce p. Řešení:
Fyzika IV Dynamika jader v molekulách
 Dynamika jader v molekulách vibrace rotace Dynamika jader v molekulách rotační energetické hladiny (dvouatomová molekula) moment setrvačnosti kolem osy procházející těžištěm osa těžiště m2 m1 r2 r1 R moment
Dynamika jader v molekulách vibrace rotace Dynamika jader v molekulách rotační energetické hladiny (dvouatomová molekula) moment setrvačnosti kolem osy procházející těžištěm osa těžiště m2 m1 r2 r1 R moment
Lineární algebra : Metrická geometrie
 Lineární algebra : Metrická geometrie (16. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 6. května 2014, 10:42 1 2 Úvod Zatím jsme se lineární geometrii věnovali v kapitole o lineárních
Lineární algebra : Metrická geometrie (16. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 6. května 2014, 10:42 1 2 Úvod Zatím jsme se lineární geometrii věnovali v kapitole o lineárních
12.NMR spektrometrie při analýze roztoků
 Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti 12.NMR spektrometrie při analýze roztoků Pavel Matějka pavel.matejka@vscht.cz pavel.matejka@gmail.com 12.NMR spektrometrie při analýze
Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti 12.NMR spektrometrie při analýze roztoků Pavel Matějka pavel.matejka@vscht.cz pavel.matejka@gmail.com 12.NMR spektrometrie při analýze
Dnešní látka: Literatura: Kapitoly 3 a 4 ze skript Karel Rektorys: Matematika 43, ČVUT, Praha, Text přednášky na webové stránce přednášejícího.
 Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Řešit atom vodíku znamená nalézt řešení Schrödingerovy rovnice s příslušným hamiltoniánem. 1 4πǫ 0. 2m e
 8 Atom vodíku Správné řešení atomu vodíku je jedním z velkých vítězství kvantové mechaniky. Podle klasické fyziky náboj, který se pohybuje se zrychlením (elektron obíhající vodíkové jádro proton), by měl
8 Atom vodíku Správné řešení atomu vodíku je jedním z velkých vítězství kvantové mechaniky. Podle klasické fyziky náboj, který se pohybuje se zrychlením (elektron obíhající vodíkové jádro proton), by měl
Kapitola 3. Magnetické vlastnosti látky. 3.1 Diamagnetismus
 Kapitola 3 Magnetické vlastnosti látky Velká část magnetických projevů je zejména u paramagnetických a feromagnetických látek způsobena především spinovým magnetickým momentem. Pokud se po sečtení všech
Kapitola 3 Magnetické vlastnosti látky Velká část magnetických projevů je zejména u paramagnetických a feromagnetických látek způsobena především spinovým magnetickým momentem. Pokud se po sečtení všech
Atomové a molekulové orbitaly Ion molekuly vodíku. Molekula vodíku Heitler-Londonovou metodou. Metoda LCAO. Báze atomových orbitalů.
 Atomové a molekulové orbitaly Ion molekuly vodíku. Molekula vodíku Heitler-Londonovou metodou. Metoda LCAO. Báze atomových orbitalů. Ion molekuly vodíku H + 2 První použití metody je demonstrováno při
Atomové a molekulové orbitaly Ion molekuly vodíku. Molekula vodíku Heitler-Londonovou metodou. Metoda LCAO. Báze atomových orbitalů. Ion molekuly vodíku H + 2 První použití metody je demonstrováno při
Autor: martina urbanová, jiří brus. Základní experimentální postupy NMR spektroskopie pevného stavu
 Autor: martina urbanová, jiří brus Základní experimentální postupy NMR spektroskopie pevného stavu Obsah přednášky anizotropní interakce v pevných látkách techniky rušení anizotropie jaderných interakcí
Autor: martina urbanová, jiří brus Základní experimentální postupy NMR spektroskopie pevného stavu Obsah přednášky anizotropní interakce v pevných látkách techniky rušení anizotropie jaderných interakcí
ESR, spinový hamiltonián a spektra
 ER, spnový hamltonán a spektra NMR k k získávání důležtých nformací o struktuře látky využívá gyromagnetckých vlastností atomových jader. Podobně ER (EPR) využívá k obdobným účelům gyromagnetckých vlastností
ER, spnový hamltonán a spektra NMR k k získávání důležtých nformací o struktuře látky využívá gyromagnetckých vlastností atomových jader. Podobně ER (EPR) využívá k obdobným účelům gyromagnetckých vlastností
LEKCE 2b. NMR a chiralita, posunová činidla. Interpretace 13 C NMR spekter
 LEKCE 2b NMR a chiralita, posunová činidla Interpretace 13 C NMR spekter Stanovení optické čistoty Enantiomery jsou nerozlišitelné v NMR spektroskopii není možné rozlišit enantiomer od racemátu!!! Enantiotopické
LEKCE 2b NMR a chiralita, posunová činidla Interpretace 13 C NMR spekter Stanovení optické čistoty Enantiomery jsou nerozlišitelné v NMR spektroskopii není možné rozlišit enantiomer od racemátu!!! Enantiotopické
příkladů do cvičení. V textu se objeví i pár detailů, které jsem nestihl (na které jsem zapomněl) a(b u) = (ab) u, u + ( u) = 0 = ( u) + u.
 Několik řešených příkladů do Matematiky Vektory V tomto textu je spočteno několik ukázkových příkladů které vám snad pomohou při řešení příkladů do cvičení. V textu se objeví i pár detailů které jsem nestihl
Několik řešených příkladů do Matematiky Vektory V tomto textu je spočteno několik ukázkových příkladů které vám snad pomohou při řešení příkladů do cvičení. V textu se objeví i pár detailů které jsem nestihl
7 Analytické vyjádření shodnosti
 7 Analytické vyjádření shodnosti 7.1 Analytická vyjádření shodných zobrazení v E 2 Osová souměrnost Osová souměrnost O(o) podle osy o s obecnou rovnicí o : ax + by + c =0: x = x 2a (ax + by + c) a 2 +
7 Analytické vyjádření shodnosti 7.1 Analytická vyjádření shodných zobrazení v E 2 Osová souměrnost Osová souměrnost O(o) podle osy o s obecnou rovnicí o : ax + by + c =0: x = x 2a (ax + by + c) a 2 +
Základy NMR 2D spektroskopie
 Základy NMR 2D spektroskopie Jaroslav Kříž Ústav makromolekulární chemie AV ČR v.v.i. puls 1D : d 1 Fourierova transformace časového rozvoje odezvy dá 1D spektrum 2D: d 1 d 1 d 1 d 0 d 0 + in 0 d 0 + 2in
Základy NMR 2D spektroskopie Jaroslav Kříž Ústav makromolekulární chemie AV ČR v.v.i. puls 1D : d 1 Fourierova transformace časového rozvoje odezvy dá 1D spektrum 2D: d 1 d 1 d 1 d 0 d 0 + in 0 d 0 + 2in
Postup při interpretaci NMR spekter neznámého vzorku
 Postup při interpretaci NMR spekter neznámého vzorku VŠCT 2017, Bohumil Dolenský, dolenskb@vscht.cz Tento text byl vypracován pro projekt Inovace předmětu Semestrální práce oboru analytická chemie I. Slouží
Postup při interpretaci NMR spekter neznámého vzorku VŠCT 2017, Bohumil Dolenský, dolenskb@vscht.cz Tento text byl vypracován pro projekt Inovace předmětu Semestrální práce oboru analytická chemie I. Slouží
plochy oddělí. Dále určete vzdálenost d mezi místem jeho dopadu na
 Přijímací zkouška z fyziky 01 - Nav. Mgr. - varianta A Příklad 1 (5 bodů) Koule o poloměru R=10 cm leží na vodorovné rovině. Z jejího nejvyššího bodu vypustíme s nulovou počáteční rychlostí bod o hmotností
Přijímací zkouška z fyziky 01 - Nav. Mgr. - varianta A Příklad 1 (5 bodů) Koule o poloměru R=10 cm leží na vodorovné rovině. Z jejího nejvyššího bodu vypustíme s nulovou počáteční rychlostí bod o hmotností
Vlastní čísla a vlastní vektory
 5 Vlastní čísla a vlastní vektor Poznámka: Je-li A : V V lineární zobrazení z prostoru V do prostoru V někd se takové zobrazení nazývá lineárním operátorem, pak je přirozeným požadavkem najít takovou bázi
5 Vlastní čísla a vlastní vektor Poznámka: Je-li A : V V lineární zobrazení z prostoru V do prostoru V někd se takové zobrazení nazývá lineárním operátorem, pak je přirozeným požadavkem najít takovou bázi
O Minimální počet valencí potřebných ke spojení vícevazných atomů = (24 C + 3 O + 7 N 1) * 2 = 66 valencí
 Jméno a příjmení:_bohumil_dolenský_ Datum:_10.12.2010_ Fakulta:_FCHI_ Kruh:_ÚACh_ 1. Sepište seznam signálů 1 H dle klesajícího chemického posunu (včetně nečistot), uveďte chemický posun, multiplicitu
Jméno a příjmení:_bohumil_dolenský_ Datum:_10.12.2010_ Fakulta:_FCHI_ Kruh:_ÚACh_ 1. Sepište seznam signálů 1 H dle klesajícího chemického posunu (včetně nečistot), uveďte chemický posun, multiplicitu
Spektrální metody NMR I. opakování
 Spektrální metody NMR I opakování Využití NMR určování chemické struktury přírodní látky, organická syntéza konstituce, konformace, konfigurace ověření čistoty studium dynamických procesů reakční kinetika
Spektrální metody NMR I opakování Využití NMR určování chemické struktury přírodní látky, organická syntéza konstituce, konformace, konfigurace ověření čistoty studium dynamických procesů reakční kinetika
Příklad 1: Komutační relace [d/dx, x] Příklad 2: Operátor B = i d/dx
![Příklad 1: Komutační relace [d/dx, x] Příklad 2: Operátor B = i d/dx Příklad 1: Komutační relace [d/dx, x] Příklad 2: Operátor B = i d/dx](/thumbs/91/106542832.jpg) 1 Příklad 1: Komutační relace [d/, x] Mějme na dva operátory: ˆ d/ a ˆ 5 D X x, například na prvek x působí takto Určeme jejich komutátor ˆ 5 d 5 4 ˆ 5 5 6 D x x 5 x, X x xx x ˆ ˆ ˆ ˆ ˆ ˆ d d [ DX, ] f
1 Příklad 1: Komutační relace [d/, x] Mějme na dva operátory: ˆ d/ a ˆ 5 D X x, například na prvek x působí takto Určeme jejich komutátor ˆ 5 d 5 4 ˆ 5 5 6 D x x 5 x, X x xx x ˆ ˆ ˆ ˆ ˆ ˆ d d [ DX, ] f
Greenova funkce pro dvoubodové okrajové úlohy pro obyčejné diferenciální rovnice
 Greenova funkce pro dvoubodové okrajové úlohy pro obyčejné diferenciální rovnice Jan Tomeček Tento stručný text si klade za cíl co nejrychlejší uvedení do teorie Greenových funkcí pro obyčejné diferenciální
Greenova funkce pro dvoubodové okrajové úlohy pro obyčejné diferenciální rovnice Jan Tomeček Tento stručný text si klade za cíl co nejrychlejší uvedení do teorie Greenových funkcí pro obyčejné diferenciální
Afinita je stručný název pro afinní transformaci prostoru, tj.vzájemně jednoznačné afinní zobrazení bodového prostoru A n na sebe.
 4 Afinita Afinita je stručný název pro afinní transformaci prostoru, tj.vzájemně jednoznačné afinní zobrazení bodového prostoru A n na sebe. Poznámka. Vzájemně jednoznačným zobrazením rozumíme zobrazení,
4 Afinita Afinita je stručný název pro afinní transformaci prostoru, tj.vzájemně jednoznačné afinní zobrazení bodového prostoru A n na sebe. Poznámka. Vzájemně jednoznačným zobrazením rozumíme zobrazení,
Příklad 3 (25 bodů) Jakou rychlost musí mít difrakčním úhlu 120? -částice, abychom pozorovali difrakční maximum od rovin d hkl = 0,82 Å na
 Přijímací zkouška z fyziky 01 - Nav. Mgr. - varianta A Příklad 1 (5 bodů) Koule o poloměru R=10 cm leží na vodorovné rovině. Z jejího nejvyššího bodu vypustíme s nulovou počáteční rychlostí bod o hmotností
Přijímací zkouška z fyziky 01 - Nav. Mgr. - varianta A Příklad 1 (5 bodů) Koule o poloměru R=10 cm leží na vodorovné rovině. Z jejího nejvyššího bodu vypustíme s nulovou počáteční rychlostí bod o hmotností
Úvod do moderní fyziky. lekce 3 stavba a struktura atomu
 Úvod do moderní fyziky lekce 3 stavba a struktura atomu Vývoj představ o stavbě atomu 1904 J. J. Thomson pudinkový model atomu 1909 H. Geiger, E. Marsden experiment s ozařováním zlaté fólie alfa částicemi
Úvod do moderní fyziky lekce 3 stavba a struktura atomu Vývoj představ o stavbě atomu 1904 J. J. Thomson pudinkový model atomu 1909 H. Geiger, E. Marsden experiment s ozařováním zlaté fólie alfa částicemi
Definice : Definice :
 KAPITOLA 7: Spektrální analýza operátorů a matic [PAN16-K7-1] Definice : Necht H je komplexní Hilbertův prostor. Řekneme, že operátor T B(H) je normální, jestliže T T = T T. Operátor T B(H) je normální
KAPITOLA 7: Spektrální analýza operátorů a matic [PAN16-K7-1] Definice : Necht H je komplexní Hilbertův prostor. Řekneme, že operátor T B(H) je normální, jestliže T T = T T. Operátor T B(H) je normální
Teorie chemické vazby a molekulární geometrie Molekulární geometrie VSEPR
 Geometrie molekul Lewisovy vzorce poskytují informaci o tom které atomy jsou spojeny vazbou a o jakou vazbu se jedná (topologie molekuly). Geometrické uspořádání molekuly je charakterizováno: Délkou vazeb
Geometrie molekul Lewisovy vzorce poskytují informaci o tom které atomy jsou spojeny vazbou a o jakou vazbu se jedná (topologie molekuly). Geometrické uspořádání molekuly je charakterizováno: Délkou vazeb
Základy maticového počtu Matice, determinant, definitnost
 Základy maticového počtu Matice, determinant, definitnost Petr Liška Masarykova univerzita 18.9.2014 Matice a vektory Matice Matice typu m n je pravoúhlé (nebo obdélníkové) schéma, které má m řádků a n
Základy maticového počtu Matice, determinant, definitnost Petr Liška Masarykova univerzita 18.9.2014 Matice a vektory Matice Matice typu m n je pravoúhlé (nebo obdélníkové) schéma, které má m řádků a n
Zdrojem většiny příkladů je sbírka úloh 1. cvičení ( ) 2. cvičení ( )
 Příklady řešené na cvičení LA II - LS 1/13 Zdrojem většiny příkladů je sbírka úloh http://kam.mff.cuni.cz/~sbirka/ 1. cvičení (..13) 1. Rozhodněte, které z následujících operací jsou skalárním součinem
Příklady řešené na cvičení LA II - LS 1/13 Zdrojem většiny příkladů je sbírka úloh http://kam.mff.cuni.cz/~sbirka/ 1. cvičení (..13) 1. Rozhodněte, které z následujících operací jsou skalárním součinem
Lineární algebra : Vlastní čísla, vektory a diagonalizace
 Lineární algebra : Vlastní čísla, vektory a diagonalizace (14. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 21. dubna 2014, 19:37 1 2 14.1 Vlastní čísla a vlastní vektory Nechť je
Lineární algebra : Vlastní čísla, vektory a diagonalizace (14. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 21. dubna 2014, 19:37 1 2 14.1 Vlastní čísla a vlastní vektory Nechť je
ATOMOVÁ SPEKTROMETRIE
 ATOMOVÁ SPEKTROMETRIE doc. Ing. David MILDE, Ph.D. tel.: 585634443 E-mail: david.milde@upol.cz (c) -017 Doporučená literatura Černohorský T., Jandera P.: Atomová spektrometrie. Univerzita Pardubice 1997.
ATOMOVÁ SPEKTROMETRIE doc. Ing. David MILDE, Ph.D. tel.: 585634443 E-mail: david.milde@upol.cz (c) -017 Doporučená literatura Černohorský T., Jandera P.: Atomová spektrometrie. Univerzita Pardubice 1997.
Zeemanův jev. 1 Úvod (1)
 Zeemanův jev Tereza Gerguri (Gymnázium Slovanské náměstí, Brno) Stanislav Marek (Gymnázium Slovanské náměstí, Brno) Michal Schulz (Gymnázium Komenského, Havířov) Abstrakt Cílem našeho experimentu je dokázat
Zeemanův jev Tereza Gerguri (Gymnázium Slovanské náměstí, Brno) Stanislav Marek (Gymnázium Slovanské náměstí, Brno) Michal Schulz (Gymnázium Komenského, Havířov) Abstrakt Cílem našeho experimentu je dokázat
Překryv orbitalů. Vznik vazby překryvem orbitalů na dvou různých atomech A, B Obsazeno dvojicí elektronů Ψ = Ψ A Ψ Β
 Překryv orbitalů Vznik vazby překryvem orbitalů na dvou různých atomech A, B Obsazeno dvojicí elektronů Ψ = Ψ A Ψ Β Podmínky překryvu: Vhodná symetrie, znaménko vlnové funkce Vhodná energie, srovnatelná,
Překryv orbitalů Vznik vazby překryvem orbitalů na dvou různých atomech A, B Obsazeno dvojicí elektronů Ψ = Ψ A Ψ Β Podmínky překryvu: Vhodná symetrie, znaménko vlnové funkce Vhodná energie, srovnatelná,
Využití magneticko-rezonanční tomografie v měřicí technice. Ing. Jan Mikulka, Ph.D. Ing. Petr Marcoň
 Využití magneticko-rezonanční tomografie v měřicí technice Ing. Jan Mikulka, Ph.D. Ing. Petr Marcoň Osnova Podstata nukleární magnetické rezonance (MR) Historie vývoje MR Spektroskopie MRS Tomografie MRI
Využití magneticko-rezonanční tomografie v měřicí technice Ing. Jan Mikulka, Ph.D. Ing. Petr Marcoň Osnova Podstata nukleární magnetické rezonance (MR) Historie vývoje MR Spektroskopie MRS Tomografie MRI
(Cramerovo pravidlo, determinanty, inverzní matice)
 KMA/MAT1 Přednáška a cvičení, Lineární algebra 2 Řešení soustav lineárních rovnic se čtvercovou maticí soustavy (Cramerovo pravidlo, determinanty, inverzní matice) 16 a 21 října 2014 V dnešní přednášce
KMA/MAT1 Přednáška a cvičení, Lineární algebra 2 Řešení soustav lineárních rovnic se čtvercovou maticí soustavy (Cramerovo pravidlo, determinanty, inverzní matice) 16 a 21 října 2014 V dnešní přednášce
ČÁST V F Y Z I K Á L N Í P O L E. 18. Gravitační pole 19. Elektrostatické pole 20. Elektrický proud 21. Magnetické pole 22. Elektromagnetické pole
 Kde se nacházíme? ČÁST V F Y Z I K Á L N Í P O L E 18. Gravitační pole 19. Elektrostatické pole 20. Elektrický proud 21. Magnetické pole 22. Elektromagnetické pole Mapování elektrického pole -jak? Detektorem.Intenzita
Kde se nacházíme? ČÁST V F Y Z I K Á L N Í P O L E 18. Gravitační pole 19. Elektrostatické pole 20. Elektrický proud 21. Magnetické pole 22. Elektromagnetické pole Mapování elektrického pole -jak? Detektorem.Intenzita
Kapitola 11: Vektory a matice:
 Kapitola 11: Vektory a matice: Prostor R n R n = {(x 1,, x n ) x i R, i = 1,, n}, n N x = (x 1,, x n ) R n se nazývá vektor x i je i-tá souřadnice vektoru x rovnost vektorů: x = y i = 1,, n : x i = y i
Kapitola 11: Vektory a matice: Prostor R n R n = {(x 1,, x n ) x i R, i = 1,, n}, n N x = (x 1,, x n ) R n se nazývá vektor x i je i-tá souřadnice vektoru x rovnost vektorů: x = y i = 1,, n : x i = y i
Nekovalentní interakce
 Nekovalentní interakce Jan Řezáč UOCHB AV ČR 3. listopadu 2016 Jan Řezáč (UOCHB AV ČR) Nekovalentní interakce 3. listopadu 2016 1 / 28 Osnova 1 Teorie 2 Typy nekovalentních interakcí 3 Projevy v chemii
Nekovalentní interakce Jan Řezáč UOCHB AV ČR 3. listopadu 2016 Jan Řezáč (UOCHB AV ČR) Nekovalentní interakce 3. listopadu 2016 1 / 28 Osnova 1 Teorie 2 Typy nekovalentních interakcí 3 Projevy v chemii
ZÁKLADNÍ EXPERIMENTÁLNÍ
 Kurz praktické NMR spektroskopie 10. - 12. říjen 2011, Praha ZÁKLADNÍ EXPERIMENTÁLNÍ POSTUPY NMR ROZTOKŮ A KAPALIN Jana Svobodová Ústav Makromolekulární chemie AV ČR, v.v.i. Bruker 600 Avance III PŘÍSTROJOVÉ
Kurz praktické NMR spektroskopie 10. - 12. říjen 2011, Praha ZÁKLADNÍ EXPERIMENTÁLNÍ POSTUPY NMR ROZTOKŮ A KAPALIN Jana Svobodová Ústav Makromolekulární chemie AV ČR, v.v.i. Bruker 600 Avance III PŘÍSTROJOVÉ
Fyzika atomového jádra (FAJ) Petr Veselý Ústav Jaderné fyziky, Česká Akademie Věd www-ucjf.troja.mff.cuni.cz/~vesely/faj/faj.pdf
 Fyzika atomového jádra (FAJ) Petr Veselý Ústav Jaderné fyziky, Česká Akademie Věd www-ucjf.troja.mff.cuni.cz/~vesely/faj/faj.pdf Letní semestr 2017 Motivace Studium jaderné struktury: - široká škála systémů
Fyzika atomového jádra (FAJ) Petr Veselý Ústav Jaderné fyziky, Česká Akademie Věd www-ucjf.troja.mff.cuni.cz/~vesely/faj/faj.pdf Letní semestr 2017 Motivace Studium jaderné struktury: - široká škála systémů
Aplikovaná numerická matematika
 Aplikovaná numerická matematika 6. Metoda nejmenších čtverců doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních
Aplikovaná numerická matematika 6. Metoda nejmenších čtverců doc. Ing. Róbert Lórencz, CSc. České vysoké učení technické v Praze Fakulta informačních technologií Katedra počítačových systémů Příprava studijních
