Užití systému Mathematica při hodnocení. Doc. RNDr. Jan Hurt, CSc.
|
|
|
- Hana Štěpánková
- před 9 lety
- Počet zobrazení:
Transkript
1 Bakalářská práce Užití systému Mathematica při hodnocení finančních derivátů Jan Hanák Vedoucí bakalářské práce Doc. RNDr. Jan Hurt, CSc. Praha 2004
2 Obsah 1 Úvod 3 2 Finanční deriváty Definice Použití derivátů Klasifikace derivátů Forwardy Futures Swapy Opční deriváty Hodnocení opčních derivátů Cena opce při splatnosti Evropské opce Put call parita Black Scholesova formule Americké opce Binomické stromy Cox Ross Rubinsteinův model Jarrow Ruddův model Greeks míry citlivosti Užití systému Mathematica Výpočet ceny evropské opce Výpočet ceny americké opce Cox Ross Rubinsteinův model Jarrow Ruddův model Greeks Konvergence numerických procedur Závěr 23
3 1 Úvod Systém Mathematica je komerční technický výpočetní systém vyvinutý společností Wolfram Research. První verze tohoto softwaru byla uvedena v roce 1988 a hlavním iniciátorem byl Stephen Wolfram. Jak se dá systém Mathematica využít pro hodnocení finančních derivátů? Nejjednodušší by samozřejmě bylo natáhnout si rozšiřující balík funkcí Derivatives Expert, jež nabízí širokou paletu nástrojů pro práci s finančními deriváty. Tento balík však není standartní součástí systému, a tak nám zbývá možnost využít programové prostředí systému Mathematica, s jehož pomocí můžeme naprogramovat vlastní procedury pro hodnocení finančních derivátů. V úvodní kapitole nejprve vyložím definici, použití a klasifikaci finančních derivátů z obecného hlediska. V teoretické části se omezím pouze na opční deriváty s podkladovým aktivem akcií nevyplácející dividendy. Pro jejich ocenění použiji Black Schlolesovu formuli pro evropské opce a metodu binomických stromů pro opce americké. V další kapitole oceňovací modely popsané v teoretické části budu algoritmizovat pomocí systému Mathematica a jednotlivé modely porovnám mezi sebou. Hlavním cílem mé práce je tedy využití systému Mathematica a s jeho pomocí naprogramovat numerické procedury pro výpočet opční prémie evropských a amerických opcí. Dalším cílem je také analýza problému konvergence jednotlivých numerických procedur a jejich vzájemné porovnání.
4 2 Finanční deriváty 2.1 Definice Finanční deriváty (derivative securities) jsou definovány 1 jako finanční nástroje splňující následující kritéria: jejich hodnota závisí na změně ceny jiných instrumentů (tzv. bazických nebo podkladových instrumentů) při jejich pořízení není třeba vydat žádné finanční prostředky nebo je množství potřebných prostředků značně nižší než cena podkladového aktiva splatnost derivátového kontraktu je delší než splatnost odpovídajících spotových obchodů Použití derivátů Deriváty slouží různým segmentům společnosti a uspokojují potřeby v závislosti na skupině uživatelů: generování zisku tvůrců trhu zatímco pro skupinu tvůrců trhu jsou deriváty jako celek ziskové, skupina konečných uživatelů je v souhrnu ztrátová zajišt ování (hedging) jedná se o ochranu hodnoty určitého nástroje či portfolia nástrojů proti nepříznivému vývoji úrokových měr, akciového trhu, měnového kurzu, cen komodit či rizikovosti určitého subjektu. Příkladem zajištění je pokrytí, kdy se sjedná operace přesně opačná vůči zajišt ované operaci. Opakem zajišt ování je spekulace spekulace (trading) jedná se převzetí rizik vývoje úrokových měr, akciového trhu, měnového kurzu, cen komodit či rizikovosti určitého subjektu. Spekulant vstupuje na derivátový trh ve snaze profitovat na cenovém vývoji, který předpokládá tím, že akceptuje riziko arbitráž, tj. využití cenových rozdílů vznikajících z teritoriálního nebo časového hlediska 1 Nejpodrobnější definici finančních derivátů najdeme ve standardu FAS 133 (výtah je uveden v [11]) obecně přijímaných účetních zásad USA (US generally accepted accounting principles, US GAAP). 2 Kromě výše uvedené definice, která vychází z mezinárodních účetních standardů (international accounting standards, IAS) a platí pro banky a některé finanční instituce, existují v české legislativě dvě další definice, a to v zákonu o cenných papírech a v devizovém zákonu. V praxi to znamená, že tyto tři (bohužel velmi rozdílné) definice derivátů v české legislativě vymezují rozdílnou množinu nástrojů.
5 deriváty jako forma odměny (remuneration derivative) zaměstnance či člena statutárního orgánu. Od výše uvedených derivátů se liší zejména tím, že nejsou sjednány za tržních podmínek podvody mnoho derivátů nesleduje kterýkoli z výše uvedených cílů, ale slouží k finančním podvodům spočívajícím v převodu peněz mezi různými subjekty. Motivem takových převodů je krácení daní (zejména daně z příjmu) a tunelování některého subjektu jiným subjektem poskytují informace o cenách podkladových nástrojů v budoucnosti (price discovery). 2.3 Klasifikace derivátů Klasifikace derivátů je možná z několika hledisek: podle typu bazického instrumentu (podléhajícího aktiva) se rozlišují komoditní deriváty, úrokové deriváty (kontrakty na budoucí nákup či prodej úrokových instrumentů jako je depozitum, úvěr, krátkodobý či dlouhodobý dluhopis), měnové deriváty, akciové deriváty a deriváty na akciový index podle způsobu jejich obchodování se hovoří o burzovních a OTC (over the counter) derivátech podle práv, která z derivátového kontraktu vyplývají pro jednotlivé strany, se rozlišují pevné a opční kontrakty. Pevné (či nepodmíněné) deriváty představují termínový obchod, který jsou oba (nevyvázaní) účastníci povinni k datu splatnosti uskutečnit bez ohledu na to, jaká je k tomuto datu skutečná cena bazického instrumentu. Pevné deriváty se vyznačují tím, že vstup do takového termínového kontraktu je obvykle pro obě strany bezplatný. Mezi pevné deriváty řadíme forwardy, futures a swapy Forwardy Forwardy jsou individuálně sjednané termínové obchody (většinou se tedy jedná o OTC deriváty) na budoucí závazný nákup či prodej určitého množství podkladového instrumentu za předem dohodnutou forwardovou cenu.
6 2.3.2 Futures Futures jsou standardizované (standardizovaný typ podkladového aktiva, množství, datum splatnosti aj.) forwardové kontrakty obchodované na derivátové burze. Ceny futures jsou kótovány denně a řídí se nabídkou a poptávkou. Narozdíl od forwardů existuje u futures každodenní tržní přeceňování (marking to market), každodenní vypořádání a možnost odstoupení od sjednaného kontratku v libovolném čase jeho odprodejem na likvidním sekundárním trhu Swapy Swapy jsou OTC deriváty s vypořádáním (výměnou, dodáním) podkladových nástrojů ve více okamžicích v budoucnosti, tj. představuje několik forwardů s postupnou výměnou podkladových aktiv. Může se jednat o dohodu o budoucí směně úrokových plateb odvozené od stejné nominální hodnoty, ale definovaných odlišným způsobem (tzv. úrokový swap), případně dohodu o směně úrokových plateb vztahujících se ke kapitálovým částkám denominovaným v různých měnách, kdy navíc dochází také ke směně příslušných kapitálových částek (tzv. měnový swap) Opční deriváty Opční (či podmíněné) deriváty představují termínový obchod, při němž jeden z účastníků (kupující, držitel opce, holder) získává právo (nikoli povinnost) uskutečnit tento obchod k datu splatnosti (evropská opce, European option) nebo kdykoli do splatnosti (americká opce, American option). Postavení druhého účastníka (prodávající, upisovatel, writer) je pasivní, nebot je závislý na rozhodnutí účastníka v aktivním postavení. Kupující musí při vstupu do opčního kontraktu za svou výhodu (právo) zaplatit prodávajícímu určitou opční prémii (cenu opce, option premium). Opce jsou obchodovány jak jako standardizované burzovní, tak jako OTC deriváty. Existují kupní opce (call options, calls), jejichž držitel má právo koupit a upisovatel povinnost prodat podkladové aktivum za předem sjednaných podmínek (datum splatnosti opce, množství a realizační cena bazického instrumentu), a prodejní opce (put options, puts), jejichž držitel má právo prodat a upisovatel povinnost koupit podkladové aktivum za předem sjednaných podmínek.
7 Opční listy (warranty) jsou v podstatě kupní opce, které emitent vydává k nákupu určitého počtu svých akcií nebo dluhopisů. Opční list bývá často původně součástí dluhopisu, po oddělení je s ním však možné obchodovat jako se samostatným cenným papírem. Stropy (caps) zaručují kupujícímu právo na průběžné plnění od jejich prodejce ve formě úrokového rozdílu, pokud příslušná úroková sazba stoupne nad sjednanou mez. Podobně dna (floors) zaručují držiteli právo na průběžné plnění od jejich prodejce ve formě úrokového rozdílu, pokud příslušná úroková sazba klesne pod sjednanou mez. Konečně kupující obojků (colars) dostává průběžně plnění od jejich prodejce, pokud příslušná úroková sazba stoupne nad sjednanou mez a poskytuje průběžně plnění jejich prodejci, pokud příslušná úroková sazba klesne pod sjednanou mez. Exotické opce (exotic options) jsou velice různorodé opce, většinou nestandardního mimoburzovního typu se složitějším systémem plnění, které jsou často navrhovány finančními institucemi dle okamžitých potřeb trhu (jsou často šité na míru klientům). Příkladem jsou složené opce (compound options, tj. opce na opce), as-you-like-it options (u těchto obcí se může kupující po určité době rozhodnout, zda to budou kupní nebo prodejní opce), binární opce (binary options, tj. opce z nichž plyne v případě ziskovosti konstantní částka, at je výše zisku, která by plynula z klasické opce jakákoliv). Další typy opčních derivátů jsou např. opce na futures, swapce (swaptions, tj. opce na swapy), kapce (captions, tj. opce na stropy) aj.
8 3 Hodnocení opčních derivátů 3.1 Cena opce při splatnosti V případě obyčejných (plain vanilla) opcí je cena call opce, resp. put opce, při splatnosti dána jako C T = max(s T X; 0), resp. P T = max(x S T ; 0), (1) kde S T je cena podkladového aktiva v čase T (při splatnosti opce) a X je sjednaná realizační cena (strike price). Ceny opcí (opční prémie) v časech t < T jsou v případě opcí obchodovatelných na burze určeny nabídkou a poptávkou. Ceny OTC opcí se pak odhadují na základě vhodného matematického modelu nebo na základě numerické simulace. 3.2 Evropské opce Put call parita Termínem put call parita se označuje vztah mezi opčními prémiemi navzájem si odpovídajících opcí call a put (tj. se stejným podkladovým aktivem, stejnou realizační cenou a stejnou dobou do splatnosti). Používá se například pro výpočet opční prémie nebo odvození vlastností opce put na základě vypočtené opční prémie nebo odvozených vlastností opce call. Put call parita má tvar kde P t... opční prémie opce put v čase t C t... opční prémie opce call v čase t S t... cena podkladového aktiva v čase t X... realizační cena opce (strike price) T t... doba do splatnosti opce r... bezriziková úroková míra. P t = C t + Xe r(t t) S t, (2)
9 3.2.2 Black Scholesova formule Pro určení opční prémie evropské opce se používá známý Black Scholesův vzorec (Black Scholesova formule), který se pro call opce obvykle zapisuje ve tvaru (při zachování stejného značení) C t = S t N(d 1 ) Xe r(t t) N(d 2 ), (3) kde N(.) je distribuční funkce standardizovaného normálního rozdělení N(0,1) a d 1 = ln(s t/x) + (r + σ 2 /2)(T t) σ (4) T t d 2 = ln(s t/x) + (r σ 2 /2)(T t) σ = d 1 σ T t, (5) T t kde σ je tzv. volatilita ceny podkladové akcie (volatilita se zpravidla stanovuje na základě historických údajů ceny akcie). Black Scholesův vzorec pro opční prémii evropské put opce dostaneme ze vzorce (3) snadno pomocí put call parity (2) ve tvaru P t = Xe r(t t) N( d 2 ) S t N( d 1 ). (6) Pro odvození 3 Black Schlolesovy formule se musíme omezit těmito předpoklady: neexistence arbitráže (předpoklad úplnosti trhu), hodnotící úroková míra r je bezriziková (předpoklad rizikově neutrálního světa) a konstantní během sledovaného období, volatilita σ je konstantní pro různé realizační ceny a model akciových cen vychází z Wienerova procesu (více v [2]). 3.3 Americké opce Binomické stromy Pro určení opční prémie amerických opcí již Black Scholesova formule (3) nestačí 4 a je nutné přistoupit k některému numerickému modelu. Ve své práci jsem zvolil binomický model oceňování opcí. 3 Odvození Black Schlolesovy formule najdeme například v [1], [2] a [7]. 4 Zde je nutné poznamenat, že cena opční prémie pro americkou opci call je shodná s opční prémií odpovídající evropské opce, nebot předčasné uplatnění americké opce nepředstavuje pro jejího držitele žádnou výhodu. Tvrzení vyplývá z následující nerovnosti: C A t C E t S t Xe r(t t) > S t X, kde C A t je cena americké opce, C E t je cena evropské opce a S t X je zisk z předčasného uplatnění opce. Z tohoto důvodu by bylo možné pro výpočet opční prémie americké opce call použít Black Scholesovu formuli (3).
10 Model binomického stromu se používá jako diskrétní aproximace modelů ve spojitém čase, která při infinitezimálním zkracování příslušných diskrétních časových intervalů konverguje k příslušnému spojitému modelu. Aproximace binomickým modelem je založena na představě, že pro změnu hodnoty S 0 (cena podkladové akcie v čase 0) během krátkého časového intervalu t jsou jen dvě možnosti: hodnota podkladové akcie S 0 bud vzroste na hodnotu S 0 u (u > 1) s pravděpodobností p (0 < p < 1), nebo klesne na hodnotu S 0 d (d < 1) s pravděpodobností (1 p). Parametry p, u a d musí dávat korektní hodnotu průměru a rozptylu ceny akcie během časového intervalu délky t. Očekávaná hodnota akcie na konci tohoto intervalu je Se r t, kde S je hodnota na začátku časového intervalu r je bezriziková úroková míra (opět předpokládáme rizikově neutrální svět). Očekávaná hodnota akcie se rovná její střední hodnotě, tj. psu + (1 p)sd = Se r t, neboli Pro rozptyl obdobně platí pu + (1 p)d = e r t. (7) pu 2 + (1 p)d 2 [pu + (1 p)d] 2 = e 2r t (e σ2 t 1), (8) kde na levé straně rovnice je rozptyl stanovený pomocí binomického modelu po uplynutí času t a výraz na pravé straně je tentýž rozptyl stanovený pomocí spojitého modelu, tzv. difuzního procesu, který vychází ze zobecněného Wienerova procesu, což je nejčastěji využívaný markovský proces (více v [2]). Rovnice (8) se obvykle zapisuje ve tvaru p(1 p)(u d) 2 = e 2r t (e σ2 t 1), nebo pu 2 + (1 p)d 2 = e (2r+σ2 ) t (9) Pro malá t je možné výraz e σ2 t rozvést v Taylorovu řadu 1+σ 2 t+o[ t] 2 a tím rovnici (8), resp. (9) aproximovat 5 na tvar: Dosazením p z (7) a úpravě dostaneme pu 2 + (1 p)d 2 e 2r t = σ 2 t. (10) e r t (u + d) ud e 2r t = σ 2 t. (11) 5 Porovnáním rozdílu přesných a přibližných hodnot se zabývá odstavec (4.4) Konvergence numerických procedur.
11 Rovnice (7) a (9), resp. (7) a aproximující (11) nám dávají dvě podmínky na parametry p, u a d. Podle určení třetí doplňující podmínky získáme rozdílné modely binomických stromů. Cox, Ross a Rubinstein použili v [4] podmínku u = 1/d a p = 1/2 poprvé použili Jarrow a Rudd v [10]. Pomocí binomického modelu určíme cenu americké opce v čase t = 0. Vývoj budeme modelovat v n krocích, tj. t = T/n. (i, j) znamená j tý uzel binomického stromu v čase i t, i = 0, 1,..., n, j = 0, 1,..., i. Cenu opce v uzlu (i, j) označíme jako f ij. Cena podkladové akcie v uzlu (i, j) je rovna S 0 u j d i j (12) a pomocí ní budeme simulovat budoucí ceny podkladové akcie. Předpokládejme, že americkou put opci budeme realizovat v okamžiku T, tj. po n krocích. Podle (1) a (12) je její cena v čase T : f nj = max(x S 0 u j d n j, 0), j = 0, 1,..., n. (13) Pro zjištění opční prémie budeme postupovat zpětným algoritmem skrz vytvořený binomický strom: cenu opce v uzlu (i, j) určíme pomocí střední diskontované ceny opce v uzlech (i + 1, j + 1) a (i + 1, j), přičemž víme, že přechod mezi danými uzly je uskutečněn s danou pravděpodobností p, resp. (1 p). Bez uvažování předčasné realizace je cena opce v uzlu (i, j) rovna f ij = e r t (pf i+1,j+1 + (1 p)f i+1,j ), i = 0,..., n 1, j = 0,..., i. (14) Pro případ možné předčasné realizace musíme též uvažovat vnitřní cenu americké put opce v uzlu (i, j) max(x S 0 u j d i j, 0). (15) Opci uplatním pokud (15) > (14), ale musím se podívat do minulosti, jestli jsem ji neuplatnil někdy dříve. Neboli pro cenu opce v uzlu (i, j) platí f ij = max ( X S 0 u j d i j, e r t (pf i+1,j+1 + (1 p)f i+1,j ) ), (16) i = 0, 1,..., n 1, j = 0, 1,..., i. Postupujeme tedy rekurentně skrz vytvořený binomický strom až do f 00, čímž obdržíme odhad hodnoty opční prémie americké put opce v čase t = 0. Obdobně pro cenu americké call opce v uzlu (i, j) dostaneme f ij = max ( S 0 u j d i j X, e r t (pf i+1,j+1 + (1 p)f i+1,j ) ), (17) i = 0, 1,..., n 1, j = 0, 1,..., i.
12 3.3.2 Cox Ross Rubinsteinův model Řešením systému rovnic (7) a (9) s dodatečnou podmínkou u = 1/d (např. pomocí systému Mathematica) obdržíme hodnoty pro parametry p, u a d: u CRR = 1 ) (1 2 e r t + e (2r+σ2) t + 4e 2r t + (1 + e (2r+σ2 ) t ) 2 d CRR = 1 ) (1 2 e r t + e (2r+σ2) t 4e 2r t + (1 + e (2r+σ2 ) t ) 2 (18) [ p CRR = 1 4e 2r t + 2e (2r+σ2) t + e 2(2r+σ2 ) t (1 + e 2r t ( 2 + e σ2 t ))... 4e 2r t + (1 + e (2r+σ2 ) t ) 2 ] / [ 2(1 + e 2r t ( 4 + 2e σ2 t + e 2(r+σ2 ) t )) ]. Označme f = e r t a g = e (r+σ2 ) t. Rovnice (18) pak po úpravě můžeme napsat v přehlednějším tvaru jako: u CRR = 1 2 ( ) f + g + (f + g) 2 4 d CRR = 1 ( ) f + g (f + g) p CRR = 1 1 f + g 2/f. 2 (f + g) 2 4 (19) Řešením rovnice (7) a aproximující rovnice (11) s dodatečnou podmínkou u = 1/d dostaneme dvě řešení (jedno s + a druhé s ) pro přibližné hodnoty parametrů p, u a d: u CRRAp1 = 1 + e 2r t + σ 2 t ± 2e r t 4e 2r t + (1 + e 2r t + σ 2 t) 2 d CRRAp1 = 1 ) (1 2 e r t + e 2r t + σ 2 t ± 4e 2r t + (1 + e 2r t + σ 2 t) 2 p CRRAp1 = e 1 2r t σ 2 t + = er t d 2 4e 2r t + (1 + e 2r t + σ 2 t) 2 u d. (20)
13 Rovnice (20) je opět možno pro malé t zjednodušit 6 rozvinutím exponenciálních funkcí v Taylorovy řady. Po úpravě dostaneme: u CRRAp2 = e σ t, d CRRAp2 = e σ t, p CRRAp2 = er t d u d. (21) Jarrow Ruddův model Řešením systému rovnic (7) a (9) s dodatečnou podmínkou p = 1/2 obdržíme přesné hodnoty parametrů u a d: u JR = e r t (1 + ) ) e σ2 t 1, d JR = e (1 r t e σ2 t 1. (22) Pokud opět využijeme Taylorův rozvoj pro exponenciální funkci dostaneme v praxi často používanou aproximaci 7 : u JRAp1 = 1 + r t + σ t, d JRAp1 = 1 + r t σ t. (23) Řešením soustavy rovnic (7) a aproximující (11) s dodatečnou podmínkou p = 1/2 získáme odhady u a d: u JRAp2 = e r t + σ t, d JRAp2 = e r t σ t (24) a aplikací Taylorova rozvoje dospějeme ke stejnému výsledku (23) jako při aproximaci přesných hodnot u a d. 6 Tyto zjednodušující aproximace najdeme např. v [2] a [6]. 7 Jarrow a Rudd v [10] pro svůj výpočet použili odlišné odhady od výše uvedených: u JR = e (r σ2 /2) t e σ t, d JR = e (r σ2 /2) t e σ t.
14 3.4 Greeks míry citlivosti Greeks rozumíme míry gamma, delta, rho, theta a vega. Tyto míry měří citlivost plynoucí ze změny faktorů, které ovlivňují výši opční prémie. Podle Black Scholesovy formule (3) je cena evropské opce funkcí pěti proměnných, což lze symbolicky zapsat jako V = V (S t, X, r, T t, σ). Greeks měří citlivost změny funkce V na její jednotlivé parametry, neboli se jedná o parciální derivace funkce V podle příslušné proměnné (více v [2]). Dalším způsobem jak změřit některé řecké míry je odhad pomocí binomického stromu. Pro jejich výpočet nebudeme používat funkci V pro výpočet teoretické opční prémie, ale funkci f ij (16) pro výpočet ceny opce v uzlu (i, j). Míra delta popisuje citlivost opční prémie na změnu ceny bazické akcie a může být odhadnuta jako f/ S, kde S je malá změna ceny podkladové akcie a f je odpovídající změna opční prémie. V čase t máme dva odhady pro cenu opce: f 11 pro cenu akcie S 0 u a f 10 pro cenu akcie S 0 d. Delta pak tedy spočteme jako = f 11 f 10 S 0 u S 0 d. (25) Pro určení míry gamma, která popisuje citlivost míry delta na změnu ceny bazické akcie, vezmeme dva odhady v čase 2 t. První je (f 22 f 21 )/(S 0 u 2 S 0 ) a druhý (f 21 f 20 )/(S 0 S 0 d 2 ). Gamma je pak změna v delta odhadech vydělená polovinou rozdílu krajních hodnot ceny akcie v čase 2 t: Γ = (f 22 f 21 )/(S 0 u 2 S 0 ) (f 21 f 20 )/(S 0 S 0 d 2 ). (26) 1/2(S 0 u 2 S 0 d 2 ) Další mírou, kterou můžeme získat přímo z binomického stromu, je theta. Theta popisuje citlivost opční prémie na změnu doby do splatnosti. Odhadem je Θ = f 21 f 00. (27) 2 t
15 4 Užití systému Mathematica V následující kapitole jsou algoritmizovány procedury pro výpočet opční prémie evropských a amerických opcí teoreticky popsaných v předchozí kapitole a jsou naprogramované a odladěné v systému Mathematica. 4.1 Výpočet ceny evropské opce Procedura pro výpočet opční prémie evropské opce call pomocí Black Scholesovy formule (3) vypadá takto (není to však jediný způsob): Needs[ Statistics NormalDistribution ] No[x ] := CDF[NormalDistribution[0, 1], x] call[s, X, σ, r, T, t ] := Module[{d1, d2}, d1 = (Log [S/X] + (r + σ 2 /2) (T t))/(σ T t ); d2 = (Log [S/X] + (r σ 2 /2) (T t))/(σ T t ); S No[d1] X Exp[ r (T t)] No[d2] ] Obdobně pro evropskou put: put[s, X, σ, r, T, t ] := Module[{d1, d2}, d1 = (Log [S/X] + (r + σ 2 /2) (T t))/(σ T t ); d2 = (Log [S/X] + (r σ 2 /2) (T t))/(σ T t ); X Exp[ r (T t)] No[ d2] S No[ d1] ] Poznámka: Vzhledem k tomu, že jsem si definoval vlastní funkci pro výpočet hodnoty distribuční funkce standardizovaného normálního rozdělení N(0,1) No[x], která používá funkci NormalDistribution, která je obsažena ve standartním statistickém balíku Statistics NormalDistribution, je nutné tento balík nejprve natáhnout pomocí příkazu Needs. 4.2 Výpočet ceny americké opce Procedury pro výpočet opčních prémií amerických opcí vychází z algoritmu popsaném v odstavci (3.3.1). Jedná se zejména o vzorec (16) pro opce put, resp. (17) pro call. Tento vzorec využívá rekurzivní funkce BinStrom, která vytvoří binomický strom na základě určených parametrů p, u a d.
16 4.2.1 Cox Ross Rubinsteinův model Pro určení opční prémie na základě Cox Ross Rubinsteinova modelu použijeme pro parametry p, u, d rovnice (19). Procedura pro výpočet ceny americké call opce pak vypadá takto: CRRcall[S, X, σ, r, T, n ] := Module[{f, g, u, d, p, OpcniPremie, BinStrom}, f = Exp[ r T/n]; g = Exp[(r + σ 2 ) T/n]; u = 1/2(f + g + (f + g) 2 4 ); d = 1/2(f + g (f + g) 2 4 ); p = (1/f d)/(u d); BinStrom[i, j ] := BinStrom[i, j] = If[i == n, Max[S u j d n j X, 0], Max[S u j d i j X, Exp[ r T/n] (p BinStrom[i + 1, j + 1] + (1 p) BinStrom[i + 1, j])]]; OpcniPremie = BinStrom[0, 0]; Clear[BinStrom]; OpcniPremie] Obdobně pro americkou put 8 : CRRput[S, X, σ, r, T, n ] := Module[{f, g, u, d, p, OpcniPremie, BinStrom}, f = Exp[ r T/n]; g = Exp[(r + σ 2 ) T/n]; u = 1/2(f + g + (f + g) 2 4 ); d = 1/2(f + g (f + g) 2 4 ); p = (1/f d)/(u d); BinStrom[i, j ] := BinStrom[i, j] = If[i == n, Max[X S u j d n j, 0], Max[X S u j d i j, Exp[ r T/n] (p BinStrom[i + 1, j + 1] + (1 p) BinStrom[i + 1, j])]]; OpcniPremie = BinStrom[0, 0]; Clear[BinStrom]; OpcniPremie] Při použití aproximujících rovnic (20) dostaneme: CRRcallAp1[S, X, σ, r, T, n ] := Module[{u, d, p, OpcniPremie, BinStrom}, u = 2 Exp[r T/n] / (1 + Exp[2 r T/n] + σ 2 T/n ± Sqrt( 4 Exp[2 r T/n] + (1 + Exp[2 r T/n] + σ 2 T/n) 2 )); d = 1/2 Exp[(r T/n] (1 + Exp[2 r T/n] + σ 2 T/n ± Sqrt( 4 Exp[2 r T/n] + (1 + Exp[2 r T/n] + σ 2 T/n) 2 )); p = (Exp[r T/n] d)/(u d); BinStrom[i, j ] := BinStrom[i, j] = If[i == n, Max[S u j d n j X, 0], Max[S u j d i j X, Exp[ r T/n] (p BinStrom[i + 1, j + 1] + (1 p) BinStrom[i + 1, j])]]; OpcniPremie = BinStrom[0, 0]; Clear[BinStrom]; OpcniPremie] 8 V dalším textu se omezím pouze na americké opce call, nebot procedury pro výpočet opční prémie americké put jsou téměř totožné: put využívá vzorec (16) a call (17).
17 A nakonec při použití rovnic (21): CRRcallAp2[S, X, σ, r, T, n ] := Module[{u, d, p, OpcniPremie, BinStrom}, u = Exp[σ T/n]; d = Exp[ σ T/n]; p = (Exp[r T/n] d)/(u d); BinStrom[i, j ] := BinStrom[i, j] = If[i == n, Max[S u j d n j X, 0], Max[S u j d i j X, Exp[ r T/n] (p BinStrom[i + 1, j + 1] + (1 p) BinStrom[i + 1, j])]]; OpcniPremie = BinStrom[0, 0]; Clear[BinStrom]; OpcniPremie] Jarrow Ruddův model Pro určení opční prémie na základě Jarrow Ruddova modelu použijeme pro parametry p, u, d rovnice (22): JRcall[S, X, σ, r, T, n ] := Module[{u, d, p, OpcniPremie, BinStrom}, p = 1/2; u = Exp[r T/n] (1 + Exp[σ 2 T/n] 1); d = Exp[r T/n] (1 Exp[σ 2 T/n] 1); BinStrom[i, j ] := BinStrom[i, j] = If[i == n, Max[S u j d n j X, 0], Max[S u j d i j X, Exp[ r T/n] (p BinStrom[i + 1, j + 1] + (1 p) BinStrom[i + 1, j])]]; OpcniPremie = BinStrom[0, 0]; Clear[BinStrom]; OpcniPremie] Při použití aproximujících rovnic (23) a (24) dostaneme: JRcallAp1[S, X, σ, r, T, n ] := Module[{u, d, p, OpcniPremie, BinStrom}, p = 1/2; u = Exp[r T/n] + σ T/n; d = Exp[r T/n] σ T/n; BinStrom[i, j ] := BinStrom[i, j] = If[i == n, Max[S u j d n j X, 0], Max[S u j d i j X, Exp[ r T/n] (p BinStrom[i + 1, j + 1] + (1 p) BinStrom[i + 1, j])]]; OpcniPremie = BinStrom[0, 0]; Clear[BinStrom]; OpcniPremie] JRcallAp2[S, X, σ, r, T, n ] := Module[{u, d, p, OpcniPremie, BinStrom}, p = 1/2; u = 1 + r T/n + σ T/n; d = 1 + r T/n σ T/n; BinStrom[i, j ] := BinStrom[i, j] = If[i == n, Max[S u j d n j X, 0], Max[S u j d i j X, Exp[ r T/n] (p BinStrom[i + 1, j + 1] + (1 p) BinStrom[i + 1, j])]]; OpcniPremie = BinStrom[0, 0]; Clear[BinStrom]; OpcniPremie]
18 4.3 Greeks Pro výpočet Greeks popsaných v odstavci (3.4) můžeme použít kterýkoli výše zmíněný model binomického stromu. Zde uvedu pouze proceduru vycházející z Cox Ross Rubinsteinova modelu americké opce call: Greeks[S, X, σ, r, T, n ]:=Module[{f,g,u,d,p,Delta,Gamma,Theta,BinStrom}, f = Exp[ r T/n]; g = Exp[(r + σ 2 ) T/n]; u = 1/2(f + g + (f + g) 2 4 ); d = 1/2(f + g (f + g) 2 4 ); p = (1/f d)/(u d); BinStrom[i, j ] := BinStrom[i, j] = If[i == n, Max[S u j d n j X, 0], Max[S u j d i j X, Exp[ r T/n] (p BinStrom[i + 1, j + 1] + (1 p) BinStrom[i + 1, j])]]; Delta = (BinStrom[1, 0] BinStrom[1, 1])/(u d) S; Gamma = 2 ((BinStrom[2, 2] BinStrom[2, 1])/(u 2 1) S (BinStrom[2, 1] BinStrom[2, 0])/(1 d 2 ) S)/(u 2 d 2 ) S; Theta = (BinStrom[2, 1] BinStrom[0, 0])/(2 T/n); Clear[BinStrom]; {Delta, Gamma, Theta}] 4.4 Konvergence numerických procedur Nejprve provedu srovnání 9 opční prémie americké call opce vypočtené pomocí Black Scholesovy formule (3) a ceny opce vypočtené pomocí binomického modelu (uvádím srovnání pouze pro Cox Ross Rubinsteinův model). Podle poznámky 4 by opční prémie měly být shodné Při srovnávání se v celém odstavci omezím na tyto opce: call na podkladovou akcii v hodnotě 9, realizační cenou 10, volatilitou 20%, bezrizikovou úrokovou mírou 10%, splatností za 1 rok a put na podkladovou akcii v hodnotě 45, realizační cenou 50, volatilitou 40%, bezrizikovou úrokovou mírou 10%, splatností za 5 měsíců.
19 Z grafu je vidět, že rozdíl mezi cenou opce vypočtené pomocí Black Scholesovy formule (3) a cenou opce vypočtené pomocí Cox Ross Rubinsteinova modelu pro vzrůstající n (tj. počet kroků v binomickém stromu) konverguje k nule, neboli opční prémie americké call opce vycházející z binomického modelu konverguje pro n blížící se nekonečnu k opční prémii získané pomocí Black Scholesova vzorce. Z odstavce (3.3.1) vyplývá, že při t blížící se nule, resp. při n blížící se nekonečnu ( t = T/n, lim n T/n = 0), aproximace binomickým modelem konverguje k příslušnému modelu spojitému. Položme si otázku, pro jak velké n lze získat rozumné výsledky? Podívejme se nejprve na grafy znázorňující cenu opční prémie získanou pomocí binomického modelu v závislosti na n. Cox Ross Rubinsteinův model (první graf je pro opci call, druhý pro put):
20 Jarrow Ruddův model (první graf je pro opci call, druhý pro put): Jaké n nám tedy zaručí, že dostaneme rozumné výsledky? Hull ve své knize [6] uvádí, že již pro n=30. Vzhledem k tomu, že konvergence uvedených procedur není monotónní a opční prémie v závislosti na n silně osciluje (viz. grafy), není to tak jednoznačné tvrzení. Pokud vyberu nešt astné n, může se mi daný výsledek od přesného výrazně odlišovat. Závěr je tedy takový, že konvergence není přesvědčivá a n=30 není dostačující. Jak se liší konvergence jednotlivých binomických modelů algoritmizovaných v odstavci (4.2)? Zejména se zaměřím na porovnání Cox Ross Rubinsteinova a Jarrow Ruddova modelu a na porovnání těchto modelů oproti jejich aproximacím v závislosti na počtu uskutečněných kroků v binomickém stromu.
21 Porovnání Cox Ross Rubinsteinova (19) a Jarrow Ruddova (22) modelu je znázorněno na následujích grafech 10 : Rozdíl mezi přesným Cox Ross Rubinsteinovým modelem (19) a jeho aproximací (20) (řešení s ) ukazují tyto grafy: Rozdíl mezi přesným Cox Ross Rubinsteinovým modelem (19) a jeho aproximací (21) je znázorněn následujícími grafy: Snadno nahlédneme, že rozdíl mezi použitými aproximacemi je značný: přiblížení vycházející z (20) je o mnoho nepřesnější (zejména pro malé n) a její 10 V celém odstavci platí, že grafy zobrazené vlevo znázorňují opce call a grafy zobrazené vpravo znázorňují opce put.
22 použití pro praktický výpočet je nasnadě. Zde se můžeme podívat na rozdíly mezi jednotlivými aproximacemi (20) a (21) vynesené do grafu: Rozdíl mezi použitými aproximacemi (23) a (24) Jarrow Ruddova modelu již není zdaleka tak dramatický jako v případě Cox Ross Rubinsteinova modelu: Z grafického znázornění vyplývá, že rozdíl mezi použitými aproximacemi je v řádu tisícin již pro malé n. Rozdíly mezi přesným Jarrow Ruddovým modelem (22) a jeho aproximací (23) nebo (24) ilustrují následující grafy:
Finanční trhy Úvod do finančních derivátů
 Finanční trhy Úvod do finančních derivátů Ing. Gabriela Oškrdalová e-mail: oskrdalova@mail.muni.cz Tento studijní materiál byl vytvořen jako výstup z projektu č. CZ.1.07/2.2.00/15.0189. 2.2.2013 Finanční
Finanční trhy Úvod do finančních derivátů Ing. Gabriela Oškrdalová e-mail: oskrdalova@mail.muni.cz Tento studijní materiál byl vytvořen jako výstup z projektu č. CZ.1.07/2.2.00/15.0189. 2.2.2013 Finanční
DERIVÁTOVÝ TRH. Druhy derivátů
 DERIVÁTOVÝ TRH Definice derivátu - nejobecněji jsou deriváty nástrojem řízení rizik (zejména tržních a úvěrových), deriváty tedy nejsou investičními nástroji - definice dle US GAAP: derivát je finančním
DERIVÁTOVÝ TRH Definice derivátu - nejobecněji jsou deriváty nástrojem řízení rizik (zejména tržních a úvěrových), deriváty tedy nejsou investičními nástroji - definice dle US GAAP: derivát je finančním
Tomáš Cipra: Matematika cenných papírů. Professional Publishing, Praha 2013 (288 stran, ISBN: ) ÚVOD.. 7
 Tomáš Cipra: Matematika cenných papírů. Professional Publishing, Praha 2013 (288 stran, ISBN: 978-80-7431-079-9) OBSAH ÚVOD.. 7 1. DLUHOPISY.. 9 1.1. Dluhopisy v praxi... 9 1.1.1. Princip dluhopisů 9 1.1.2.
Tomáš Cipra: Matematika cenných papírů. Professional Publishing, Praha 2013 (288 stran, ISBN: 978-80-7431-079-9) OBSAH ÚVOD.. 7 1. DLUHOPISY.. 9 1.1. Dluhopisy v praxi... 9 1.1.1. Princip dluhopisů 9 1.1.2.
Příprava na zkoušky odborné způsobilosti na finančních trzích
 Příprava na zkoušky odborné způsobilosti na finančních trzích Deriváty II opce a opční strategie Opce Poskytuje vlastníkovi opce nikoli povinnost, ale právo k nákupu nebo prodeji určitého podkladového
Příprava na zkoušky odborné způsobilosti na finančních trzích Deriváty II opce a opční strategie Opce Poskytuje vlastníkovi opce nikoli povinnost, ale právo k nákupu nebo prodeji určitého podkladového
Metodický list - Finanční deriváty
 Metodický list - Finanční deriváty Základní odborná literatura vydaná VŠFS: [0] Záškodný,P., Pavlát,V., Budík,J.: Finanční deriváty a jejich oceňování.všfs,praha 2007 Tato literatura platí v plném rozsahu,
Metodický list - Finanční deriváty Základní odborná literatura vydaná VŠFS: [0] Záškodný,P., Pavlát,V., Budík,J.: Finanční deriváty a jejich oceňování.všfs,praha 2007 Tato literatura platí v plném rozsahu,
Členění termínových obchodů z hlediska jejich základních
 Členění termínových obchodů z hlediska jejich základních vlastností a způsobů obchodovatelnosti TERMÍNOVÉ OBCHODY Neodvolatelné /tzv. pevné/ termínové obchody Termínové kontrakty typu forward a futures
Členění termínových obchodů z hlediska jejich základních vlastností a způsobů obchodovatelnosti TERMÍNOVÉ OBCHODY Neodvolatelné /tzv. pevné/ termínové obchody Termínové kontrakty typu forward a futures
Finanční deriváty II.
 Ing. Martin Širůček, Ph.D. Katedra financí a účetnictví sirucek.martin@svse.cz sirucek@gmail.com Finanční deriváty II. strana 2 Obsah přednášky Princip opcí Druhy opcí Cena a spekulační efekt Kurzovní
Ing. Martin Širůček, Ph.D. Katedra financí a účetnictví sirucek.martin@svse.cz sirucek@gmail.com Finanční deriváty II. strana 2 Obsah přednášky Princip opcí Druhy opcí Cena a spekulační efekt Kurzovní
CENNÉ PA CENNÉ PÍRY PÍR
 CENNÉ PAPÍRY ve finančních institucích dr. Malíková 1 Operace s cennými papíry Banky v operacích s cennými papíry (CP) vystupují jako: 1. Investor do CP 2. Emitent CP 3. Obchodník s CP Klasifikace a operace
CENNÉ PAPÍRY ve finančních institucích dr. Malíková 1 Operace s cennými papíry Banky v operacích s cennými papíry (CP) vystupují jako: 1. Investor do CP 2. Emitent CP 3. Obchodník s CP Klasifikace a operace
ST 14.1. 8:00, E 127 PO 19.1. 16:00, E 127 ČT 22.1. 8:00, E 127 ST 28.1. 16:00, E 127. Komerční bankovnictví 1 / VŠFS ZS 2008/09
 Zkouškové termíny ST 14.1. 8:00, E 127 PO 19.1. 16:00, E 127 ČT 22.1. 8:00, E 127 ST 28.1. 16:00, E 127 1 Vymezení cenných papírů (CP) CP jsou v zákoně vymezeny výčtem: Akcie, zatímní listy, poukázky na
Zkouškové termíny ST 14.1. 8:00, E 127 PO 19.1. 16:00, E 127 ČT 22.1. 8:00, E 127 ST 28.1. 16:00, E 127 1 Vymezení cenných papírů (CP) CP jsou v zákoně vymezeny výčtem: Akcie, zatímní listy, poukázky na
Vybrané poznámky k řízení rizik v bankách
 Vybrané poznámky k řízení rizik v bankách Seminář z aktuárských věd Petr Myška 7.11.2008 Obsah přednášky Oceňování nestandartních instrumentů finančních trhů Aplikace analytických vzorců Simulační techniky
Vybrané poznámky k řízení rizik v bankách Seminář z aktuárských věd Petr Myška 7.11.2008 Obsah přednášky Oceňování nestandartních instrumentů finančních trhů Aplikace analytických vzorců Simulační techniky
Univerzita Karlova v Praze Matematicko-fyzikální fakulta
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Andrea Voráčková Investiční strategie finančních derivátů Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské
Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Andrea Voráčková Investiční strategie finančních derivátů Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské
Informace. o finančních nástrojích a rizicích spojených s investováním
 Informace o finančních nástrojích a rizicích spojených s investováním Společnost QuantOn Solutions, o. c. p., a. s. (Dále jen QuantOn Solutions nebo i obchodník) poskytuje klientovi v souladu s 73d odst.
Informace o finančních nástrojích a rizicích spojených s investováním Společnost QuantOn Solutions, o. c. p., a. s. (Dále jen QuantOn Solutions nebo i obchodník) poskytuje klientovi v souladu s 73d odst.
Bezkuponové dluhopisy centrálních bank Poukázky České národní banky a bezkupónové dluhopisy vydané zahraničními centrálními bankami.
 POPIS ČÍSELNÍKU : : BA0088 Druhy cenných papírů a odvozených kontraktů (derivátů) Hierarchická klasifikace druhů cenných papírů podle jejich ekonomické formy a obsahu (věcného charakteru) s návazností
POPIS ČÍSELNÍKU : : BA0088 Druhy cenných papírů a odvozených kontraktů (derivátů) Hierarchická klasifikace druhů cenných papírů podle jejich ekonomické formy a obsahu (věcného charakteru) s návazností
Bankovní účetnictví - účtová třída 3 1
 Bankovní účetnictví Cenné papíry a deriváty Bankovní účetnictví - účtová třída 3 1 BANKOVNÍ ÚČETNICTVÍ ÚČTOVÁ TŘÍDA 3 Od klasických služeb, které představují přijímání vkladů a poskytování úvěrů, banky
Bankovní účetnictví Cenné papíry a deriváty Bankovní účetnictví - účtová třída 3 1 BANKOVNÍ ÚČETNICTVÍ ÚČTOVÁ TŘÍDA 3 Od klasických služeb, které představují přijímání vkladů a poskytování úvěrů, banky
Účetnictví finančních institucí. Cenné papíry a deriváty
 Účetnictví finančních institucí Cenné papíry a deriváty 1 BANKOVNÍ ÚČETNICTVÍ ÚČTOVÁ TŘÍDA 3 Od klasických služeb, které představují přijímání vkladů a poskytování úvěrů, banky postupně přecházejí k službám
Účetnictví finančních institucí Cenné papíry a deriváty 1 BANKOVNÍ ÚČETNICTVÍ ÚČTOVÁ TŘÍDA 3 Od klasických služeb, které představují přijímání vkladů a poskytování úvěrů, banky postupně přecházejí k službám
Měnové opce v TraderGO
 Měnové opce v TraderGO Upozornění Informace sdělené v rámci této prezentace NEJSOU investičním doporučením, projevem osobního investičního poradenství ani nabídkou k nákupu či prodeji investičních nástrojů.
Měnové opce v TraderGO Upozornění Informace sdělené v rámci této prezentace NEJSOU investičním doporučením, projevem osobního investičního poradenství ani nabídkou k nákupu či prodeji investičních nástrojů.
Deriváty termínové operace
 Deriváty termínové operace Deriváty jsou termínové obchody, které jsou odvozeny od obchodů s jinými, tzv. podkladovými aktivy. Termínové obchody - obchody, které jsou sjednány v okamžiku podpisu kontraktu
Deriváty termínové operace Deriváty jsou termínové obchody, které jsou odvozeny od obchodů s jinými, tzv. podkladovými aktivy. Termínové obchody - obchody, které jsou sjednány v okamžiku podpisu kontraktu
Tématické okruhy. 4. Investiční nástroje investiční nástroje, cenné papíry, druhy a vlastnosti
 Seznam tématických okruhů a skupin tématických okruhů ( 4 odst. 2 vyhlášky o druzích odborných obchodních činností obchodníka s cennými papíry vykonávaných prostřednictvím makléře, o druzích odborné specializace
Seznam tématických okruhů a skupin tématických okruhů ( 4 odst. 2 vyhlášky o druzích odborných obchodních činností obchodníka s cennými papíry vykonávaných prostřednictvím makléře, o druzích odborné specializace
Produkty finančních trhů a jejich rizika. Devizové produkty a produkty peněžního trhu
 Produkty finančních trhů a jejich rizika Devizové produkty a produkty peněžního trhu datum platnosti a účinnosti od 01. 09. 2014 Obsah Úvod 3 Vysvětlivky 4 rizik 4 Obecné 4 Charakteristiky opcí 5 Seznam
Produkty finančních trhů a jejich rizika Devizové produkty a produkty peněžního trhu datum platnosti a účinnosti od 01. 09. 2014 Obsah Úvod 3 Vysvětlivky 4 rizik 4 Obecné 4 Charakteristiky opcí 5 Seznam
FAKULTA EKONOMICKÁ. Diplomová práce. Matematické modely oceňování finančních derivátů základy teorie a vybrané aplikace
 ZÁPADOČESKÁ UNIVERZITA V PLZNI FAKULTA EKONOMICKÁ Diplomová práce Matematické modely oceňování finančních derivátů základy teorie a vybrané aplikace Mathematical models of financial derivatives pricing
ZÁPADOČESKÁ UNIVERZITA V PLZNI FAKULTA EKONOMICKÁ Diplomová práce Matematické modely oceňování finančních derivátů základy teorie a vybrané aplikace Mathematical models of financial derivatives pricing
[1m] [DOCO30_11.03.00] Objem obchodů s CP - jiný než obhosp. vztah. Nákup Prodej. Objem obchodů s inv. nástroji za sledované období
![[1m] [DOCO30_11.03.00] Objem obchodů s CP - jiný než obhosp. vztah. Nákup Prodej. Objem obchodů s inv. nástroji za sledované období [1m] [DOCO30_11.03.00] Objem obchodů s CP - jiný než obhosp. vztah. Nákup Prodej. Objem obchodů s inv. nástroji za sledované období](/thumbs/24/2391093.jpg) [1m] [DOCO30_11.03.00] Objem obchodů s CP - jiný než obhosp. vztah Nákup Prodej Objem obchodů s inv. nástroji za sledované období 1 2 Zákazníci celkem 1 49158717 46596447 Banka 2 34323419 35567005 Pojišťovna
[1m] [DOCO30_11.03.00] Objem obchodů s CP - jiný než obhosp. vztah Nákup Prodej Objem obchodů s inv. nástroji za sledované období 1 2 Zákazníci celkem 1 49158717 46596447 Banka 2 34323419 35567005 Pojišťovna
FINANČNÍ A INVESTIČNÍ MATEMATIKA 2
 FINANČNÍ A INVESTIČNÍ MATEMATIKA 2 Metodický list č. 1 Název tématického celku: Dluhopisy a dluhopisové portfolio I. Cíl: Základním cílem tohoto tematického celku je popsat dluhopisy jako investiční instrumenty,
FINANČNÍ A INVESTIČNÍ MATEMATIKA 2 Metodický list č. 1 Název tématického celku: Dluhopisy a dluhopisové portfolio I. Cíl: Základním cílem tohoto tematického celku je popsat dluhopisy jako investiční instrumenty,
FINANČNÍ A INVESTIČNÍ MATEMATIKA Metodický list č. 1
 FINANČNÍ A INVESTIČNÍ MATEMATIKA Metodický list č. 1 Název tématického celku: Úroková sazba a výpočet budoucí hodnoty Cíl: Základním cílem tohoto tematického celku je vysvětlit pojem úroku a roční úrokové
FINANČNÍ A INVESTIČNÍ MATEMATIKA Metodický list č. 1 Název tématického celku: Úroková sazba a výpočet budoucí hodnoty Cíl: Základním cílem tohoto tematického celku je vysvětlit pojem úroku a roční úrokové
Finanční deriváty. Základní druhy finančních investičních instrumentů. Vymezení termínových obchodů. spotový versus termínový obchod (resp.
 Ing. Martin Širůček, Ph.D. Katedra financí a účetnictví sirucek.martin@svse.cz sirucek@gmail.com Finanční deriváty strana 2 Základní druhy finančních investičních instrumentů strana 3 Vymezení termínových
Ing. Martin Širůček, Ph.D. Katedra financí a účetnictví sirucek.martin@svse.cz sirucek@gmail.com Finanční deriváty strana 2 Základní druhy finančních investičních instrumentů strana 3 Vymezení termínových
FINANČNÍ DERIVÁTY A JEJICH MOŽNÉ VYUŽITÍ V PODNIKOVÉ PRAXI
 Masarykova univerzita Ekonomicko-správní fakulta Studijní obor: Finanční podnikání FINANČNÍ DERIVÁTY A JEJICH MOŽNÉ VYUŽITÍ V PODNIKOVÉ PRAXI Financial derivatives and their possible utilization in business
Masarykova univerzita Ekonomicko-správní fakulta Studijní obor: Finanční podnikání FINANČNÍ DERIVÁTY A JEJICH MOŽNÉ VYUŽITÍ V PODNIKOVÉ PRAXI Financial derivatives and their possible utilization in business
Přehled obchodů pro zákazníky podle investičních nástrojů - DOCO30_21 - Objem obchodů s CP - jiný než obhosp. vztah
 Přehled obchodů pro zákazníky podle investičních nástrojů - DOCO30_21 - Objem obchodů s CP - jiný než obhosp. vztah Objem obchodů s inv. nástroji za sledované období Nákup Prodej Investiční CP Akcie nebo
Přehled obchodů pro zákazníky podle investičních nástrojů - DOCO30_21 - Objem obchodů s CP - jiný než obhosp. vztah Objem obchodů s inv. nástroji za sledované období Nákup Prodej Investiční CP Akcie nebo
ZÁPADOČESKÁ UNIVERZITA V PLZNI FAKULTA EKONOMICKÁ
 ZÁPADOČESKÁ UNIVERZITA V PLZNI FAKULTA EKONOMICKÁ Diplomová práce Finanční deriváty - jejich oceňování a využití v podnikových financích Financial derivatives - their pricing and application in the corporate
ZÁPADOČESKÁ UNIVERZITA V PLZNI FAKULTA EKONOMICKÁ Diplomová práce Finanční deriváty - jejich oceňování a využití v podnikových financích Financial derivatives - their pricing and application in the corporate
Finanční deriváty ŘÍZENÍ RIZIK I
 Finanční deriváty Smlouvy, jimiž se neobchoduje s podkladovými aktivy, ale právy na ně (=> obchody s rizikem ). Hodnota vzniká zprostředkovaně přes hodnotu podkladového aktiva nebo ukazatele. Existence
Finanční deriváty Smlouvy, jimiž se neobchoduje s podkladovými aktivy, ale právy na ně (=> obchody s rizikem ). Hodnota vzniká zprostředkovaně přes hodnotu podkladového aktiva nebo ukazatele. Existence
AKTIVA A JEJICH STRUKTURA, OCEŇOVÁNÍ
 AKTIVA A JEJICH STRUKTURA, OCEŇOVÁNÍ 5.5 POHLEDÁVKY - podstata, charakteristika, oceňování, postupy účtování, vykazování v rozvaze, odlišnosti vůči mezinárodní regulaci dle IAS/IFRS Pohledávku lze charakterizovat
AKTIVA A JEJICH STRUKTURA, OCEŇOVÁNÍ 5.5 POHLEDÁVKY - podstata, charakteristika, oceňování, postupy účtování, vykazování v rozvaze, odlišnosti vůči mezinárodní regulaci dle IAS/IFRS Pohledávku lze charakterizovat
Produkty finančních trhů a jejich rizika. Ostatní produkty
 Produkty finančních trhů a jejich rizika Ostatní produkty datum platnosti a účinnosti od 01. 09. 2014 Obsah Úvod 3 Vysvětlivky 4 Popis rizik 4 Obecné 4 Charakteristiky opcí 5 Seznam zkratek 6 Riziko ztráty
Produkty finančních trhů a jejich rizika Ostatní produkty datum platnosti a účinnosti od 01. 09. 2014 Obsah Úvod 3 Vysvětlivky 4 Popis rizik 4 Obecné 4 Charakteristiky opcí 5 Seznam zkratek 6 Riziko ztráty
ZÁPADOČESKÁ UNIVERZITA V PLZNI
 ZÁPADOČESKÁ UNIVERZITA V PLZNI FAKULTA EKONOMICKÁ Diplomová práce Vypracování souboru procedur s finančním zaměřením především na oceňování opcí Development of a set of financially oriented procedures
ZÁPADOČESKÁ UNIVERZITA V PLZNI FAKULTA EKONOMICKÁ Diplomová práce Vypracování souboru procedur s finančním zaměřením především na oceňování opcí Development of a set of financially oriented procedures
Finanční deriváty. Základní druhy finančních investičních instrumentů. Vymezení termínových obchodů. spotový versus termínový obchod (resp.
 Ing. Martin Širůček, Ph.D. Katedra financí a účetnictví sirucek.martin@svse.cz sirucek@gmail.com Finanční deriváty strana 2 Základní druhy finančních investičních instrumentů strana 3 Vymezení termínových
Ing. Martin Širůček, Ph.D. Katedra financí a účetnictví sirucek.martin@svse.cz sirucek@gmail.com Finanční deriváty strana 2 Základní druhy finančních investičních instrumentů strana 3 Vymezení termínových
Produkty finančních trhů. Ostatní produkty
 Produkty finančních trhů Verze 3.2, říjen 2008 Obsah Úvod... 1 Vysvětlivky... 2 Popis rizik... 2 Obecné.... 2 Charakteristiky opcí... 3 Seznam zkratek... 4 Riziko ztráty investované částky...4 Daňové dopady...
Produkty finančních trhů Verze 3.2, říjen 2008 Obsah Úvod... 1 Vysvětlivky... 2 Popis rizik... 2 Obecné.... 2 Charakteristiky opcí... 3 Seznam zkratek... 4 Riziko ztráty investované částky...4 Daňové dopady...
Produkty finančních trhů a jejich rizika. Produkty devizových a peněžních transakcí
 Produkty finančních trhů a jejich rizika Verze 0.5, září 2009 Obsah Úvod... 1 Vysvětlivky... 2 rizik... 2 Obecné... 2 Charakteristiky opcí... 3 Seznam zkratek... 4 Riziko ztráty investované částky... 4
Produkty finančních trhů a jejich rizika Verze 0.5, září 2009 Obsah Úvod... 1 Vysvětlivky... 2 rizik... 2 Obecné... 2 Charakteristiky opcí... 3 Seznam zkratek... 4 Riziko ztráty investované částky... 4
Finanční deriváty II.
 Ing. Martin Širůček, Ph.D. Katedra financí a účetnictví sirucek.martin@svse.cz sirucek@gmail.com Finanční deriváty II. strana 2 Obsah přednášky Princip opcí Druhy opcí Cena opce a spekulační efekt Kurzovní
Ing. Martin Širůček, Ph.D. Katedra financí a účetnictví sirucek.martin@svse.cz sirucek@gmail.com Finanční deriváty II. strana 2 Obsah přednášky Princip opcí Druhy opcí Cena opce a spekulační efekt Kurzovní
Hlášení o druzích a rozsahu poskytnutých investičních služeb
 ČESKÁ NÁRODNÍ BANKA Výkaz: OCP (ČNB) 31-4 Datový soubor: DOCOS31 Hlášení o druzích a rozsahu poskytnutých investičních služeb Část 1: Přehled obchodů pro zákazníky dle sektorů Datová oblast: DOCO3_11 CP
ČESKÁ NÁRODNÍ BANKA Výkaz: OCP (ČNB) 31-4 Datový soubor: DOCOS31 Hlášení o druzích a rozsahu poskytnutých investičních služeb Část 1: Přehled obchodů pro zákazníky dle sektorů Datová oblast: DOCO3_11 CP
Matematicko-fyzikální fakulta Univerzity Karlovy
 Oceňování finančních derivátů ve spojitém čase Václav Kozmík Matematicko-fyzikální fakulta Univerzity Karlovy 4. 10. 2010 Úvod Stochastický kalkulus Wienerův proces stochastické procesy Itoovo lemma změna
Oceňování finančních derivátů ve spojitém čase Václav Kozmík Matematicko-fyzikální fakulta Univerzity Karlovy 4. 10. 2010 Úvod Stochastický kalkulus Wienerův proces stochastické procesy Itoovo lemma změna
 N_MF_B Mezinárodní finance B 4. Devizové operace forwardové operace uzavřená a otevřená devizová pozice, hedging swapové devizové operace. Parita úrokové míry Nekrytá úroková parita - Covered Covered Interest
N_MF_B Mezinárodní finance B 4. Devizové operace forwardové operace uzavřená a otevřená devizová pozice, hedging swapové devizové operace. Parita úrokové míry Nekrytá úroková parita - Covered Covered Interest
Zajištění kurzového rizika pomocí derivátů devizového trhu
 Bankovní institut vysoká škola Praha Finančnictví a ekonomických disciplín Zajištění kurzového rizika pomocí derivátů devizového trhu Bakalářská práce Autor: Ondřej Švec Bankovnictví, Bankovní management
Bankovní institut vysoká škola Praha Finančnictví a ekonomických disciplín Zajištění kurzového rizika pomocí derivátů devizového trhu Bakalářská práce Autor: Ondřej Švec Bankovnictví, Bankovní management
Strukturované investiční instrumenty
 Ing. Martin Širůček, Ph.D. Strukturované investiční instrumenty Katedra financí a účetnictví sirucek.martin@svse.cz sirucek@gmail.com strana 2 Základní charakteristika finanční investiční instrumenty slučující
Ing. Martin Širůček, Ph.D. Strukturované investiční instrumenty Katedra financí a účetnictví sirucek.martin@svse.cz sirucek@gmail.com strana 2 Základní charakteristika finanční investiční instrumenty slučující
Hlášení o druzích a rozsahu poskytnutých investičních služeb
 ČESKÁ NÁRODNÍ BANKA Výkaz: OCP (ČNB) 31-4 Datový soubor: DOCOS31 Hlášení o druzích a rozsahu poskytnutých investičních služeb Část 1: Přehled obchodů pro zákazníky dle sektorů Datová oblast: DOCO3_11 CP
ČESKÁ NÁRODNÍ BANKA Výkaz: OCP (ČNB) 31-4 Datový soubor: DOCOS31 Hlášení o druzích a rozsahu poskytnutých investičních služeb Část 1: Přehled obchodů pro zákazníky dle sektorů Datová oblast: DOCO3_11 CP
Investiční nástroje a rizika s nimi související
 Investiční nástroje a rizika s nimi související CENNÉ PAPÍRY Dokumentace: Banka uzavírá s klientem standardní smlouvy dle typu kontraktu (Komisionářská smlouva, repo smlouva, mandátní smlouva). AKCIE je
Investiční nástroje a rizika s nimi související CENNÉ PAPÍRY Dokumentace: Banka uzavírá s klientem standardní smlouvy dle typu kontraktu (Komisionářská smlouva, repo smlouva, mandátní smlouva). AKCIE je
Hlášení o druzích a rozsahu poskytnutých investičních služeb
 Česká národní banka OCP (ČNB) 31-04 Hlášení o druzích a rozsahu poskytnutých investičních služeb Datový soubor: DOCOS31.02.00 Sestavil: jmeno osoby Telefon: telefon Podpis oprávněné osoby: Komentář: Banka:
Česká národní banka OCP (ČNB) 31-04 Hlášení o druzích a rozsahu poskytnutých investičních služeb Datový soubor: DOCOS31.02.00 Sestavil: jmeno osoby Telefon: telefon Podpis oprávněné osoby: Komentář: Banka:
Finanční management. Nejefektivnější portfolio (leží na hranici) dle Markowitze: Polemika o významu dividendové politiky
 Finanční management Dividendová politika, opce, hranice pro cenu opce, opční techniky Nejefektivnější portfolio (leží na hranici dle Markowitze: existuje jiné s vyšším výnosem a nižší směrodatnou odchylkou
Finanční management Dividendová politika, opce, hranice pro cenu opce, opční techniky Nejefektivnější portfolio (leží na hranici dle Markowitze: existuje jiné s vyšším výnosem a nižší směrodatnou odchylkou
Zahraniční investiční nástroje Obchody s CP (Σ)
 Přehled obchodů pro zákazníky podle investičních nástrojů - DOCO30_21 - Objem obchodů s CP - jiný než obhosp. vztah Objem obchodů s inv. nástroji za sledované období Nákup Prodej 1 2 Investiční CP (Σ)
Přehled obchodů pro zákazníky podle investičních nástrojů - DOCO30_21 - Objem obchodů s CP - jiný než obhosp. vztah Objem obchodů s inv. nástroji za sledované období Nákup Prodej 1 2 Investiční CP (Σ)
'Hlášení o druzích a rozsahu poskytnutých investičních služeb
 Česká národní banka OCP (ČNB) 31-04 'Hlášení o druzích a rozsahu poskytnutých investičních služeb Datový soubor: DOCOS31.04.00 Sestavil: P. Gross Telefon: 221 191 286 Podpis oprávněné osoby: Komentář:
Česká národní banka OCP (ČNB) 31-04 'Hlášení o druzích a rozsahu poskytnutých investičních služeb Datový soubor: DOCOS31.04.00 Sestavil: P. Gross Telefon: 221 191 286 Podpis oprávněné osoby: Komentář:
Spotové operace 4 Custody převody 5
 Přehled obchodů pro zákazníky podle investičních nástrojů - DOCO3_21 - Objem obchodů s CP - jiný než obhosp. vztah Objem obchodů s inv. nástroji za sledované období Nákup Prodej 1 2 Investiční CP (Σ) 1
Přehled obchodů pro zákazníky podle investičních nástrojů - DOCO3_21 - Objem obchodů s CP - jiný než obhosp. vztah Objem obchodů s inv. nástroji za sledované období Nákup Prodej 1 2 Investiční CP (Σ) 1
Zajištění měnových rizik
 Ing.František Janatka,CSc. Zajištění měnových rizik Měnová rizika souvisejí s vývojem světové ekonomiky, měnovými kurzy a dalšími faktory -představují značná rizika, v současné době zejména pro české vývozce
Ing.František Janatka,CSc. Zajištění měnových rizik Měnová rizika souvisejí s vývojem světové ekonomiky, měnovými kurzy a dalšími faktory -představují značná rizika, v současné době zejména pro české vývozce
Obchodní instrumenty. 1. Bez páky: A) Akcie B) ETF. 2. S pákou: A) Futures B) Opce C) CFD D) Forex
 CO TO JE BURZA? Burza Místo, kde se obchodují všechny finanční instrumenty Striktní dohled kontrolních orgánů Místo, kde se střetává nabídka s poptávkou Právnická osoba, a.s. Obchodník s cennými papíry
CO TO JE BURZA? Burza Místo, kde se obchodují všechny finanční instrumenty Striktní dohled kontrolních orgánů Místo, kde se střetává nabídka s poptávkou Právnická osoba, a.s. Obchodník s cennými papíry
MASARYKOVA UNIVERZITA V BRNĚ
 MASARYKOVA UNIVERZITA V BRNĚ Ekonomicko-správní fakulta Jana Hnátková (UČO 174727) Finanční podnikání Magisterské (prezenční) studium Imatrikulační ročník 2005 Téma: Finanční deriváty Finanční trhy (PFFITR)
MASARYKOVA UNIVERZITA V BRNĚ Ekonomicko-správní fakulta Jana Hnátková (UČO 174727) Finanční podnikání Magisterské (prezenční) studium Imatrikulační ročník 2005 Téma: Finanční deriváty Finanční trhy (PFFITR)
Seznam studijní literatury
 Seznam studijní literatury Zákon o účetnictví, Vyhlášky 500 a 501/2002 České účetní standardy (o CP) Kovanicová, D.: Finanční účetnictví, Světový koncept, Polygon, Praha 2002 nebo později Standard č. 28,
Seznam studijní literatury Zákon o účetnictví, Vyhlášky 500 a 501/2002 České účetní standardy (o CP) Kovanicová, D.: Finanční účetnictví, Světový koncept, Polygon, Praha 2002 nebo později Standard č. 28,
Hlášení o druzích a rozsahu poskytnutých investičních služeb za 2. čtvrtletí 2010 Publikováno na internetu dne 30. července 2010
 Hlášení o druzích a rozsahu poskytnutých investičních služeb za 2. čtvrtletí 2010 Publikováno na internetu dne 30. července 2010 OCP (ČNB) 31-04 Hlášení o druzích a rozsahu poskytnutých investičních služeb
Hlášení o druzích a rozsahu poskytnutých investičních služeb za 2. čtvrtletí 2010 Publikováno na internetu dne 30. července 2010 OCP (ČNB) 31-04 Hlášení o druzích a rozsahu poskytnutých investičních služeb
Úvod. www.csob.cz. Nástroje sloužící k zajištění rizika pohybu úrokových měr. Finanční trhy. Identifikace rizika. Definice a rozsah rizika
 Nástroje sloužící k zajištění rizika pohybu úrokových měr Úvod Každý podnikatelský subjekt čelí nejistotě. Budoucnost je doposud nenapsaná kapitola a můžeme jen s menšími či většími úspěchy odhadovat,
Nástroje sloužící k zajištění rizika pohybu úrokových měr Úvod Každý podnikatelský subjekt čelí nejistotě. Budoucnost je doposud nenapsaná kapitola a můžeme jen s menšími či většími úspěchy odhadovat,
Ocenění finančních derivátů a jejich účetní zachycení v podniku Moravský Peněžní Ústav spořitelní družstvo. Bc. Petr Gibala
 Ocenění finančních derivátů a jejich účetní zachycení v podniku Moravský Peněžní Ústav spořitelní družstvo Bc. Petr Gibala Diplomová práce 2017 ABSTRAKT Cílem této diplomové práce je vypracovat projekt
Ocenění finančních derivátů a jejich účetní zachycení v podniku Moravský Peněžní Ústav spořitelní družstvo Bc. Petr Gibala Diplomová práce 2017 ABSTRAKT Cílem této diplomové práce je vypracovat projekt
Hlášení o druzích a rozsahu poskytnutých investičních služeb
 Česká národní banka OCP (ČNB) 3-04 Hlášení o druzích a rozsahu poskytnutých investičních služeb Datový soubor: DOCOS3.02.00 Sestavil: odd. Externích výkazů Telefon: Podpis oprávněné osoby: Komentář: Banka:
Česká národní banka OCP (ČNB) 3-04 Hlášení o druzích a rozsahu poskytnutých investičních služeb Datový soubor: DOCOS3.02.00 Sestavil: odd. Externích výkazů Telefon: Podpis oprávněné osoby: Komentář: Banka:
INFORMACE O RIZICÍCH
 INFORMACE O RIZICÍCH PPF banka a.s. se sídlem Praha 6, Evropská 2690/17, PSČ: 160 41, IČ: 47116129, zapsaná v obchodním rejstříku vedeném Městským soudem v Praze, oddíl B, vložka 1834 (dále jen Obchodník)
INFORMACE O RIZICÍCH PPF banka a.s. se sídlem Praha 6, Evropská 2690/17, PSČ: 160 41, IČ: 47116129, zapsaná v obchodním rejstříku vedeném Městským soudem v Praze, oddíl B, vložka 1834 (dále jen Obchodník)
Investiční služby investiční nástroje
 Investiční služby investiční nástroje Podnikání na kapitálovém trhu Mgr. Bc. Kristýna Chalupecká Hlavní body přednášky Investiční nástroje Subjekty investování Investiční služby Dle Zákona č. 256/2004
Investiční služby investiční nástroje Podnikání na kapitálovém trhu Mgr. Bc. Kristýna Chalupecká Hlavní body přednášky Investiční nástroje Subjekty investování Investiční služby Dle Zákona č. 256/2004
Hlášení o druzích a rozsahu poskytnutých investičních služeb
 ČESKÁ NÁRODNÍ BANKA Výkaz: OCP (ČNB) 31-04 Datový soubor: DOCOS31 Hlášení o druzích a rozsahu poskytnutých investičních služeb Část 1: Přehled obchodů pro zákazníky dle sektorů Datová oblast: DOCO30_11
ČESKÁ NÁRODNÍ BANKA Výkaz: OCP (ČNB) 31-04 Datový soubor: DOCOS31 Hlášení o druzích a rozsahu poskytnutých investičních služeb Část 1: Přehled obchodů pro zákazníky dle sektorů Datová oblast: DOCO30_11
Strategie Covered Call
 Strategie Covered Call Tato strategie vzniká kombinací pozice na podkladovém aktivu a výpisem call opce na toto aktivum. Řada obchodníků bohužel neví, že s pomocí této strategie mohou zvýšit výnosnost
Strategie Covered Call Tato strategie vzniká kombinací pozice na podkladovém aktivu a výpisem call opce na toto aktivum. Řada obchodníků bohužel neví, že s pomocí této strategie mohou zvýšit výnosnost
Systematizace derivátních finančních nástrojů
 Systematizace derivátních finančních nástrojů Peter Mokrička 1 Abstrakt Příspěvek se zabývá vymezením a systematizací derivátních finančních nástrojů, rozlišuje pojmy deriváty a derivátní finanční nástroje,
Systematizace derivátních finančních nástrojů Peter Mokrička 1 Abstrakt Příspěvek se zabývá vymezením a systematizací derivátních finančních nástrojů, rozlišuje pojmy deriváty a derivátní finanční nástroje,
Hlášení o druzích a rozsahu poskytnutých investičních služeb za 4. čtvrtletí 2007. Publikováno na internetu dne 1.února 2008
 Hlášení o druzích a rozsahu poskytnutých investičních služeb za 4. čtvrtletí 2007 Publikováno na internetu dne 1.února 2008 Hlášení o druzích a rozsahu poskytnutých investičních služeb za 4.Q.2007 Česká
Hlášení o druzích a rozsahu poskytnutých investičních služeb za 4. čtvrtletí 2007 Publikováno na internetu dne 1.února 2008 Hlášení o druzích a rozsahu poskytnutých investičních služeb za 4.Q.2007 Česká
Finanční rizika. podniku, způsoben rizikového faktoru. že e protistrana. hodnoty podniku, způsoben. ností ŘÍZENÍ RIZIK I
 Finanční rizika Tržní riziko je pravděpodobnost podobnost změny hodnoty podniku, způsoben sobené změnou tržní hodnoty rizikového faktoru. Kreditní riziko je pravděpodobnost podobnost změny hodnoty podniku,
Finanční rizika Tržní riziko je pravděpodobnost podobnost změny hodnoty podniku, způsoben sobené změnou tržní hodnoty rizikového faktoru. Kreditní riziko je pravděpodobnost podobnost změny hodnoty podniku,
Investiční bankovnictví 4
 Metodický list pro soustředění kombinovaného studia předmětu Investiční bankovnictví 4 Metodický list číslo 1 Název tématického celku: Investiční bankovnictví - analýzy Cíl: Cílem tématického celku je
Metodický list pro soustředění kombinovaného studia předmětu Investiční bankovnictví 4 Metodický list číslo 1 Název tématického celku: Investiční bankovnictví - analýzy Cíl: Cílem tématického celku je
INVESTIČNÍ DOTAZNÍK. 1. Obecné informace
 INVESTIČNÍ DOTAZNÍK 1. Obecné informace (a) (b) (c) (d) Banka předkládá tento Investiční dotazník Klientovi za účelem kvalifikovaného poskytování Investičních služeb Bankou. Poskytnuté informace bude Banka
INVESTIČNÍ DOTAZNÍK 1. Obecné informace (a) (b) (c) (d) Banka předkládá tento Investiční dotazník Klientovi za účelem kvalifikovaného poskytování Investičních služeb Bankou. Poskytnuté informace bude Banka
Ing. Ondřej Audolenský
 České vysoké učení technické v Praze Fakulta elektrotechnická Katedra ekonomiky, manažerství a humanitních věd Ing. Ondřej Audolenský Vedoucí: Prof. Ing. Oldřich Starý, CSc. Rizika podnikání malých a středních
České vysoké učení technické v Praze Fakulta elektrotechnická Katedra ekonomiky, manažerství a humanitních věd Ing. Ondřej Audolenský Vedoucí: Prof. Ing. Oldřich Starý, CSc. Rizika podnikání malých a středních
Konverzní faktory, koeficienty a metody používané při výpočtu kapitálových požadavků k úvěrovému riziku obchodního portfolia a k tržnímu riziku
 Příloha č. 20 Konverzní faktory, koeficienty a metody používané při výpočtu kapitálových požadavků k úvěrovému riziku obchodního portfolia a k tržnímu riziku A. Vypořádací riziko Konverzní faktory pro
Příloha č. 20 Konverzní faktory, koeficienty a metody používané při výpočtu kapitálových požadavků k úvěrovému riziku obchodního portfolia a k tržnímu riziku A. Vypořádací riziko Konverzní faktory pro
Obchodování s deriváty v praxi
 Obchodování s deriváty v praxi Praha 17.4.2012 Patria Direct, člen skupiny KBC group. Patria Direct, a.s., Jungmannova 24, 110 00 Praha 1, tel.: +420 221 424 240, fax: +420 221 424 179, e-mail: info@patria-direct.cz,
Obchodování s deriváty v praxi Praha 17.4.2012 Patria Direct, člen skupiny KBC group. Patria Direct, a.s., Jungmannova 24, 110 00 Praha 1, tel.: +420 221 424 240, fax: +420 221 424 179, e-mail: info@patria-direct.cz,
Základy teorie finančních investic
 Ing. Martin Širůček, Ph.D. Katedra financí a účetnictví sirucek.martin@svse.cz sirucek@gmail.com Základy teorie finančních investic strana 2 Úvod do teorie investic Pojem investice Rozdělení investic a)
Ing. Martin Širůček, Ph.D. Katedra financí a účetnictví sirucek.martin@svse.cz sirucek@gmail.com Základy teorie finančních investic strana 2 Úvod do teorie investic Pojem investice Rozdělení investic a)
Změna hodnoty pozice v důsledku změn tržních cen.
 Tržní riziko Změna hodnoty pozice v důsledku změn tržních cen. Akciové riziko Měnové riziko Komoditní riziko Úrokové riziko Odvozená rizika... riz. volatility, riz. korelace Pozice (saldo hodnoty očekávaných
Tržní riziko Změna hodnoty pozice v důsledku změn tržních cen. Akciové riziko Měnové riziko Komoditní riziko Úrokové riziko Odvozená rizika... riz. volatility, riz. korelace Pozice (saldo hodnoty očekávaných
Finanční deriváty a nutnost jejich studia
 Finanční deriváty a nutnost jejich studia Bohuslav Sekerka, katedra účetnictví a financí SVŠES v Praze Tento příspěvek chce upozornit na využití finančních derivátů v podnikání a na nutnost zařadit do
Finanční deriváty a nutnost jejich studia Bohuslav Sekerka, katedra účetnictví a financí SVŠES v Praze Tento příspěvek chce upozornit na využití finančních derivátů v podnikání a na nutnost zařadit do
OBECNÉ POKYNY K OPRAVÁM MODIFIKOVANÉ DURACE EBA/GL/2016/09 04/01/2017. Obecné pokyny
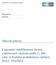 EBA/GL/2016/09 04/01/2017 Obecné pokyny k opravám modifikované durace u dluhových nástrojů podle čl. 340 odst. 3 druhého pododstavce nařízení (EU) č. 575/2013 1. Dodržování předpisů a oznamovací povinnost
EBA/GL/2016/09 04/01/2017 Obecné pokyny k opravám modifikované durace u dluhových nástrojů podle čl. 340 odst. 3 druhého pododstavce nařízení (EU) č. 575/2013 1. Dodržování předpisů a oznamovací povinnost
3.1.1. Výpočet vnitřní hodnoty obligace (dluhopisu)
 Využití poměrových ukazatelů pro fundamentální analýzu cenných papírů Principem této analýzy je stanovení, zda je cenný papír na kapitálovém trhu podhodnocen, správně oceněn, nebo nadhodnocen. Analýza
Využití poměrových ukazatelů pro fundamentální analýzu cenných papírů Principem této analýzy je stanovení, zda je cenný papír na kapitálovém trhu podhodnocen, správně oceněn, nebo nadhodnocen. Analýza
Zajištění kurzového rizika
 Zajištění kurzového rizika Riziko směnného kurzu Riziko, že v budoucnu nastane neočekávaná situace Riziko, že v budoucnu dojde k nepříznivému vývoji kurzu Cíl zajištění kurzového rizika Ošetřit budoucí
Zajištění kurzového rizika Riziko směnného kurzu Riziko, že v budoucnu nastane neočekávaná situace Riziko, že v budoucnu dojde k nepříznivému vývoji kurzu Cíl zajištění kurzového rizika Ošetřit budoucí
Změna hodnoty pozice v důsledku změn tržních cen.
 Tržní riziko Změna hodnoty pozice v důsledku změn tržních cen. Akciové riziko Měnové riziko Komoditní riziko Úrokové riziko Odvozená rizika... riz. volatility, riz. korelace Pozice (saldo hodnoty očekávaných
Tržní riziko Změna hodnoty pozice v důsledku změn tržních cen. Akciové riziko Měnové riziko Komoditní riziko Úrokové riziko Odvozená rizika... riz. volatility, riz. korelace Pozice (saldo hodnoty očekávaných
SR (CZK/EUR) 26,512 27,122 3 měs. IR CZK p.a. 6,24 7,44 3 měs. IR EUR p.a. 3,86 4,62 a) přímá kotace Nákupní forwardový kurs vypočítáme takto: SR 100
 Příklad č. 1 Na základě následujících kotací spotového kursu eura v korunách a tříměsíčních úrokových měr na korunová a eurová aktiva vypočítejte nákupní a prodejní tříměsíční forwardový kurs eura v korunách
Příklad č. 1 Na základě následujících kotací spotového kursu eura v korunách a tříměsíčních úrokových měr na korunová a eurová aktiva vypočítejte nákupní a prodejní tříměsíční forwardový kurs eura v korunách
6. Banka a finanční trh, vlastní operace banky s cennými papíry, operace pro klienta, investiční činnosti bank
 6. Banka a finanční trh, vlastní operace banky s cennými papíry, operace pro klienta, investiční činnosti bank Finanční trh je trhem peněz a kapitálu. Banky vstupují na tento trh jako zprostředkovatelé
6. Banka a finanční trh, vlastní operace banky s cennými papíry, operace pro klienta, investiční činnosti bank Finanční trh je trhem peněz a kapitálu. Banky vstupují na tento trh jako zprostředkovatelé
Finanční deriváty v podmínkách České republiky
 Bankovní institut vysoká škola Praha Katedra Finančních obchodů Finanční deriváty v podmínkách České republiky Bakalářská práce Autor: Vedoucí práce: Jana Pražáková, DiS, Bankovnictví, Bankovní management
Bankovní institut vysoká škola Praha Katedra Finančních obchodů Finanční deriváty v podmínkách České republiky Bakalářská práce Autor: Vedoucí práce: Jana Pražáková, DiS, Bankovnictví, Bankovní management
Mezinárodní finanční trhy
 Úvod Ing. Jan Vejmělek, Ph.D., CFA jan_vejmelek@kb.cz Investiční bankovnictví Náplň kurzu Úvod do mezinárodních finančních trhů Devizový trh a jeho instrumenty Mezinárodní finanční instituce Teorie mezinárodního
Úvod Ing. Jan Vejmělek, Ph.D., CFA jan_vejmelek@kb.cz Investiční bankovnictví Náplň kurzu Úvod do mezinárodních finančních trhů Devizový trh a jeho instrumenty Mezinárodní finanční instituce Teorie mezinárodního
Oceňování akcií a. Brno 2012
 Oceňování akcií a dluhopisů Brno 2012 Osnova 1 Oceňování akcií 2 Akcie Představují podíl na majetku akciové společnosti. Držení je spojeno s řadou práv- právo účasti na hlasování na valné hromadě, právo
Oceňování akcií a dluhopisů Brno 2012 Osnova 1 Oceňování akcií 2 Akcie Představují podíl na majetku akciové společnosti. Držení je spojeno s řadou práv- právo účasti na hlasování na valné hromadě, právo
IAS 39: Účtování a oceňování
 IAS 39: Účtování a oceňování Josef Jílek člen Standards Advice Review Group březen 2007 Program Definice Zajišťovací účetnictví Vložené deriváty Deriváty na vlastní kapitálové nástroje Odúčtování aktiv
IAS 39: Účtování a oceňování Josef Jílek člen Standards Advice Review Group březen 2007 Program Definice Zajišťovací účetnictví Vložené deriváty Deriváty na vlastní kapitálové nástroje Odúčtování aktiv
KMA/MAB. Kamila Matoušková (A07142) Plzeň, 2009 EFEKTIVNÍ PORFÓLIO V MARKOWITZOVĚ SMYSLU
 EFEKTIVNÍ PORFÓLIO V MARKOWITZOVĚ SMYSLU KMA/MAB Kamila Matoušková (A07142) Plzeň, 2009 Obsahem práce je vytvoření efektivního portfolia v Markowitzově smyslu.z akcií obchodovaných na SPADu. Dále je uvažována
EFEKTIVNÍ PORFÓLIO V MARKOWITZOVĚ SMYSLU KMA/MAB Kamila Matoušková (A07142) Plzeň, 2009 Obsahem práce je vytvoření efektivního portfolia v Markowitzově smyslu.z akcií obchodovaných na SPADu. Dále je uvažována
VYSOKÁ ŠKOLA POLYTECHNICKÁ JIHLAVA Obor Finance a řízení. Opční obchody a jejich porovnání s jiný m zvolený m derivátový m kontraktem
 VYSOKÁ ŠKOLA POLYTECHNICKÁ JIHLAVA Obor Finance a řízení Opční obchody a jejich porovnání s jiný m zvolený m derivátový m kontraktem Bakalářská práce Autor: Lukáš Křen Vedoucí práce: Ing. Petr Jiříček
VYSOKÁ ŠKOLA POLYTECHNICKÁ JIHLAVA Obor Finance a řízení Opční obchody a jejich porovnání s jiný m zvolený m derivátový m kontraktem Bakalářská práce Autor: Lukáš Křen Vedoucí práce: Ing. Petr Jiříček
Přemysl Bejda.
 premyslbejda@gmail.com 2010 Obsah 1 2 3 Obchodovatelnost Cena rizika Obsah 1 2 3 Obchodovatelnost Cena rizika Obsah 1 2 3 Obchodovatelnost Cena rizika Itôovo lemma Lemma (Itôovo) Necht X t je stochastický
premyslbejda@gmail.com 2010 Obsah 1 2 3 Obchodovatelnost Cena rizika Obsah 1 2 3 Obchodovatelnost Cena rizika Obsah 1 2 3 Obchodovatelnost Cena rizika Itôovo lemma Lemma (Itôovo) Necht X t je stochastický
Telefonní číslo:
 Sdělení klíčových informací Účel Tento dokument Vám poskytne klíčové informace o tomto investičním produktu. Nejde o propagační materiál. Poskytnutí těchto informací vyžaduje zákon, aby Vám pomohly porozumět
Sdělení klíčových informací Účel Tento dokument Vám poskytne klíčové informace o tomto investičním produktu. Nejde o propagační materiál. Poskytnutí těchto informací vyžaduje zákon, aby Vám pomohly porozumět
Pehled obhospodaovaného majetku Datová oblast: DOCO30_31 Objem obhospodaovaných cenných papír
 Pehled obhospodaovaného majetku Datová oblast: DOCO30_31 Objem obhospodaovaných cenných papír inv. nástroje k A B C 1 Investiní CP Tuzemské a zahraniní investiní nástroje 1 0 Akcie nebo obdobné CP (obchodovatelné
Pehled obhospodaovaného majetku Datová oblast: DOCO30_31 Objem obhospodaovaných cenných papír inv. nástroje k A B C 1 Investiní CP Tuzemské a zahraniní investiní nástroje 1 0 Akcie nebo obdobné CP (obchodovatelné
Hlášení o druzích a rozsahu poskytnutých investičních služeb za 1. čtvrtletí 2007
 Hlášení o druzích a rozsahu poskytnutých investičních služeb za 1. čtvrtletí 27 HVB Bank Czech Republic a.s. Vydáno dne 3. dubna 27 HVB Bank Czech Republic a.s. nám. Republiky 3a/29 11 Praha 1 Hlášení
Hlášení o druzích a rozsahu poskytnutých investičních služeb za 1. čtvrtletí 27 HVB Bank Czech Republic a.s. Vydáno dne 3. dubna 27 HVB Bank Czech Republic a.s. nám. Republiky 3a/29 11 Praha 1 Hlášení
Úvod do analýzy cenných papírů. Dagmar Linnertová 5. Října 2009
 Úvod do analýzy cenných papírů Dagmar Linnertová 5. Října 2009 Investice a investiční rozhodování Každý je potenciální investor Nevynaložením prostředků na svou současnou potřebu se jí tímto vzdává Mít
Úvod do analýzy cenných papírů Dagmar Linnertová 5. Října 2009 Investice a investiční rozhodování Každý je potenciální investor Nevynaložením prostředků na svou současnou potřebu se jí tímto vzdává Mít
INVESTIČNÍ DOTAZNÍK - PRÁVNICKÁ OSOBA
 INVESTIČNÍ DOTAZNÍK - PRÁVNICKÁ OSOBA Zákazník Obchodní název IČO: CIF: Sídlo: Ulice: Obec: PSČ: Země: (dále též jen "Zákazník") UniCredit Bank Czech Republic and Slovakia, a.s., se sídlem Praha 4, Želetavská
INVESTIČNÍ DOTAZNÍK - PRÁVNICKÁ OSOBA Zákazník Obchodní název IČO: CIF: Sídlo: Ulice: Obec: PSČ: Země: (dále též jen "Zákazník") UniCredit Bank Czech Republic and Slovakia, a.s., se sídlem Praha 4, Želetavská
SYLABUS PŘEDMĚTU PREZENČNÍ STUDIUM Slezská univerzita v Opavě Obchodně podnikatelská fakulta v Karviné Platnost akreditace do Kód studijního
 SYLABUS PŘEDMĚTU PREZENČNÍ STUDIUM Slezská univerzita v Opavě Obchodně podnikatelská fakulta v Karviné Platnost akreditace do Kód studijního PPMA Kód katedry FIN Název studijního Portfolio management Portfolio
SYLABUS PŘEDMĚTU PREZENČNÍ STUDIUM Slezská univerzita v Opavě Obchodně podnikatelská fakulta v Karviné Platnost akreditace do Kód studijního PPMA Kód katedry FIN Název studijního Portfolio management Portfolio
00001350_IS_0644 K_M vztah (05_01) Stránka 1
 00001350_IS_0644 K_M vztah (05_01) Stránka 1 05_01 Objem obchodu s cennymi papiry uzavrenych pro zakazniky v ramci komisionarskeho nebo mandatniho vztahu Nakup (celkovy obrat) za sledovane Prodej (celkovy
00001350_IS_0644 K_M vztah (05_01) Stránka 1 05_01 Objem obchodu s cennymi papiry uzavrenych pro zakazniky v ramci komisionarskeho nebo mandatniho vztahu Nakup (celkovy obrat) za sledovane Prodej (celkovy
Zajištění kurzového rizika pomocí derivátů devizového trhu
 Bankovní institut vysoká škola Praha Finančnictví a ekonomických disciplín Zajištění kurzového rizika pomocí derivátů devizového trhu Bakalářská práce Autor: Ondřej Švec Bankovnictví, Bankovní management
Bankovní institut vysoká škola Praha Finančnictví a ekonomických disciplín Zajištění kurzového rizika pomocí derivátů devizového trhu Bakalářská práce Autor: Ondřej Švec Bankovnictví, Bankovní management
ZAJIŠTĚNÍ KURZOVÉHO RIZIKA
 ČESKÁ ZEMĚDĚLSKÁ UNIVERZITA Provozně ekonomická fakulta Katedra obchodu a financí TEZE K DP ZAJIŠTĚNÍ KURZOVÉHO RIZIKA U VYBRANÉ OBCHODNÍ TRANSAKCE Vedoucí diplomové práce: Vypracoval: Ing. Jana Žehrová
ČESKÁ ZEMĚDĚLSKÁ UNIVERZITA Provozně ekonomická fakulta Katedra obchodu a financí TEZE K DP ZAJIŠTĚNÍ KURZOVÉHO RIZIKA U VYBRANÉ OBCHODNÍ TRANSAKCE Vedoucí diplomové práce: Vypracoval: Ing. Jana Žehrová
Pokroky matematiky, fyziky a astronomie
 Pokroky matematiky, fyziky a astronomie Carmen Simerská Úvod do finančních derivátú, zvláště forwardů a opcí Pokroky matematiky, fyziky a astronomie, Vol. 56 (2011), No. 4, 313 322 Persistent URL: http://dml.cz/dmlcz/142021
Pokroky matematiky, fyziky a astronomie Carmen Simerská Úvod do finančních derivátú, zvláště forwardů a opcí Pokroky matematiky, fyziky a astronomie, Vol. 56 (2011), No. 4, 313 322 Persistent URL: http://dml.cz/dmlcz/142021
FIMO 6 Finanční a komoditní deriváty v MO
 FIMO 6 Finanční a komoditní deriváty v MO Obecná charakteristika Finanční instrumenty s širokým uplatněním v MO. 3 základní ekonomické charakteristiky: Deriváty jsou termínové kontrakty. Sjednány dnes,
FIMO 6 Finanční a komoditní deriváty v MO Obecná charakteristika Finanční instrumenty s širokým uplatněním v MO. 3 základní ekonomické charakteristiky: Deriváty jsou termínové kontrakty. Sjednány dnes,
nákup 3,20( 5,18) 1,62
 a) ( FRF/DEM nákup 3,20( 5,18) 1,62 prodej 3,42( 5,26 1,54) b) 1. Prodej DEM v bance A: 617 284 USD (1 000 000 : 1,62) 2. Prodej USD v bance B: 3197531 FRF (617 284 x 5,18) 3. Prodej FRF v bance C: 1 005513
a) ( FRF/DEM nákup 3,20( 5,18) 1,62 prodej 3,42( 5,26 1,54) b) 1. Prodej DEM v bance A: 617 284 USD (1 000 000 : 1,62) 2. Prodej USD v bance B: 3197531 FRF (617 284 x 5,18) 3. Prodej FRF v bance C: 1 005513
TEORETICKÉ PŘEDPOKLADY Garantovaných produktů
 TEORETICKÉ PŘEDPOKLADY Garantovaných produktů 1 Výnosově -rizikový profil Knockoutprodukty Warrants Výnosová-šance Garantované produkty Dluhopisy Diskontové produkty Airbag Bonus Indexové produkty Akciové
TEORETICKÉ PŘEDPOKLADY Garantovaných produktů 1 Výnosově -rizikový profil Knockoutprodukty Warrants Výnosová-šance Garantované produkty Dluhopisy Diskontové produkty Airbag Bonus Indexové produkty Akciové
Univerzita Pardubice Fakulta ekonomicko-správní Ústav matematiky a kvantitativních metod. Oceňování finančních derivátů.
 Univerzita Pardubice Fakulta ekonomicko-správní Ústav matematiky a kvantitativních metod Oceňování finančních derivátů Marcela Škodová Bakalářská práce 2012 PROHLÁŠENÍ Prohlašuji, že jsem tuto práci
Univerzita Pardubice Fakulta ekonomicko-správní Ústav matematiky a kvantitativních metod Oceňování finančních derivátů Marcela Škodová Bakalářská práce 2012 PROHLÁŠENÍ Prohlašuji, že jsem tuto práci
Telefonní číslo:
 Sdělení klíčových informací Účel Tento dokument Vám poskytne klíčové informace o tomto investičním produktu. Nejde o propagační materiál. Poskytnutí těchto informací vyžaduje zákon, aby Vám pomohly porozumět
Sdělení klíčových informací Účel Tento dokument Vám poskytne klíčové informace o tomto investičním produktu. Nejde o propagační materiál. Poskytnutí těchto informací vyžaduje zákon, aby Vám pomohly porozumět
Nakup (celkovy obrat) za sledovane ctvrtleti
 05_01 Objem obchodu s cennymi papiry uzavrenych pro zakazniky v ramci komisionarskeho nebo mandatniho vztahu Nakup (celkovy obrat) za sledovane Prodej (celkovy obrat) za sledovane A B 001 002 1. Investicni
05_01 Objem obchodu s cennymi papiry uzavrenych pro zakazniky v ramci komisionarskeho nebo mandatniho vztahu Nakup (celkovy obrat) za sledovane Prodej (celkovy obrat) za sledovane A B 001 002 1. Investicni
KOUPENÉ A PRODANÉ OPCE VERTIKÁLNÍ SPREADY
 KAPITOLA 3 KOUPENÉ A PRODANÉ OPCE VERTIKÁLNÍ SPREADY Vertikální spread je kombinace koupené a prodané put nebo call opce se stejným expiračním měsícem. Výraz spread se používá proto, že riziko je rozložené
KAPITOLA 3 KOUPENÉ A PRODANÉ OPCE VERTIKÁLNÍ SPREADY Vertikální spread je kombinace koupené a prodané put nebo call opce se stejným expiračním měsícem. Výraz spread se používá proto, že riziko je rozložené
