Šířka a tvar spektrální čáry Martin Šubr, 2013
|
|
|
- Simona Pavlíková
- před 8 lety
- Počet zobrazení:
Transkript
1 Šířka a tvar spektrální čáry Martin Šubr, 2013 Úvod Ukazuje se, že žádná spektrální čára není dokonale úzká (dokonalá delta funkce). Pomocí spektrálních přístrojů s dostatečně vysokým rozlišením bychom zjistili, že každá čára má ve skutečnosti nějakou nenulovou šířku dω ukazuje se, že každá spektrální čára má jistou přirozenou šířku, která může být dále dalšími mechanismy rozšířena, buďto homogenně nebo nehomogenně. Nechť střed spektrální čáry leží na frekvenci ω 0. Pak obvykle dω/ω 0 1 (mluvíme o kvasimonochromatickém světle). Pokud je spektrální čára širší, mluvíme obvykle o pásu (např. elektronové přechody mají často strukturu spíše pásů, zatímco u vibračních a rotačních přechodů mluvíme spíše o čarách). Jako míru šířky takovéto čáry zavádíme obvykle veličinu FWHM (full width at half of maximum). Platí: dω = de = df = dν = dλ. ω 0 E 0 f 0 ν 0 λ 0 První čtyři rovnosti jsou jasné, protože úhlová frekvence, energie, frekvence a vlnočet jsou si veličiny vzájemně úměrné. Poslední rovnost je taky jasná, pokud diferencujeme vztah mezi frekvencí a vlnovou délkou a dosadíme do příslušných vztahů. Příklad: Pokud čára zabírá oblast řekněme od 499 do 501 nm, má pološířku 2 nm a její FWHM je 2/500 = 0,004. Totéž číslo ale dostaneme, pokud převedeme vlnové délky 499nm a 501 nm na frekvence a dělíme rozdíl těchto frekvencí frekvencí příslušející vlnové délce 500 nm. Přirozená šířka spektrální čáry Přirozenou šířku spektrální čáry můžeme objasnit na základě klasického modelu, poloklasického i zcela kvantového. Klasický model, který vysvětluje přirozený tvar spektrální čáry, je Lorentzův model. Je to sice možná až příliš hrubá aproximace, ale i tak to vyjde. V Lorentzově modelu předpokládáme, že elektron je vázaný k jádru na pružince, tj. vratná síla je přímo úměrná vzdálenosti elektronu od jádra. Napíšemeli si Newtonovu rovnici pro tlumený harmonický oscilátor mx + mγx + kx = qe a dosadíme-li do něj závislost elektrického pole E ve tvaru komplexní exponenciály (E = E 0 e iωt ), můžeme hledat tvar výchylky x rovněž ve tvaru komplexní exponenciály x = x 0 e iωt. Z matematického hlediska je totiž řešení výše uvedené obyčejné diferenciální rovnice součtem řešení homogenní rovnice a partikulárního řešení rovnice s pravou stranou. V dostatečně dlouhém čase však bude řešení homogenní části rovnice utlumeno (díky nenulové konstantě tlumení γ), proto stačí uvažovat jen partikulární řešení. Řešení pro x má tedy tvar komplexní exponenciály, které má reálnou a imaginární část (x 0 vyjde obecně komplexní, ale komu by se to nelíbilo, může si celý výpočet provést jen se siny a kosiny, je to užitečný, i když o něco delší postup ). Reálná i imaginární část x vyjdou ve tvaru Lorentzových křivek. Imaginární část přitom udává energii záření absorbovanou
2 v látce. Jelikož imaginární část x je absorpční Lorentzova křivka, má i profil spektrální čáry tvar Lorentzovy křivky (tedy nedochází pouze k absorpci přesně frekvence ω 0, ale s menší mírou dochází i k absorpci okolních frekvencí). Konstanta γ pak přímo souvisí s pološířkou Lorentzovy křivky (pološířka křivky je buďto γ nebo 2γ, to se mi teď přesně nechce počítat ). Jiný (semikvantový nebo kvantový) pohled na věc je tento: Když se odvozuje Fermiho zlaté pravidlo (viz jiná otázka), tak se tam dojde k tomu, že pravděpodobnost přechodu mezi dvěma stacionárními stavy atomu nebo molekuly za jednotku času je součinem nějaké prostorové části (integrál, jehož nulovost nebo nenulovost souvisí s výběrovými pravidly, objeví se tam v prvním přiblížení elektrický dipólový moment přechodu atd ) a delta funkce s argumentem (ω ω 0 ), což říká, že absorpce (nebo emise) má rezonanční charakter. Ve skutečnosti však musíme uvážit konečnou dobu života vyšších excitovaných stavů, tedy relaxační mechanismy, které omezují dobu setrvání molekuly ve vyšších excitovaných stavech. Každá molekula totiž za čas ztratí část své energie a ať už zářivým, nebo nezářivým přechodem, a dostane se zpátky do základního stavu (obsazovací čísla jednotlivých hladin v rovnováze určuje Boltzmannovo rozdělení). Skutečně, když se v jednom kroku odvozování Fermiho zlatého pravidla doba života vyšších excitovaných stavů zahrne fenomenologicky tak, že klesá exponenciálně s nějakou časovou konstantou, tak výsledný tvar Fermiho pravidla již nebude obsahovat delta funkci, ale bude to absorpční Lorentzova křivka s pološířkou (navíc ale musíme ještě provést tu aproximaci, že se díváme na tu molekulu v časech delších, než je ta samotná doba života (což většinou děláme) jinak by se ten vzorec totiž ještě trochu zkomplikoval...) Připomenutí: Výpočet se provádí tak, že v době působení poruchy se vlnová funkce rozvine do řady vlastních funkcí neporušeného hamiltoniánu (semiklasický přístup), popř. do direktního součtu vlastních funkcí neporušeného hamiltoniánu a stavů pole (úplně kvantový přístup zde by vyšla navíc i spontánní emise). Pak se řeší rovnice pro ty vývojové koeficienty semikonzervativním postupem s takovou počáteční podmínkou, že na počátku byl celkový stav molekuly nějaký čistý stav. Aby vyšel Lorentzovský profil spektrální čáry, tak musíme právě tuto počáteční podmínku vynásobit klesající exponenciálou exp( t) zkrátka tam tu konečnou dobu vyšších kvantových stavů musíme dodat fenomenologicky. K odhadu pološířky spektrální čáry můžou dobře posloužit i relace neurčitosti mezi energií a časem: E t h. Říká to zhruba to, že čím kratší je doba setrvání molekuly v excitovaném stavu, tím delší musí být neurčitost ve vyzářené energii, a tím je vlastně spektrální čára rozmazanější. Např. u vysokotlakých výbojek dochází ke srážkám elektronů s molekulami častěji, než u nízkotlakých výbojek, tudíž excitované stavy molekul u výbojek s vyšším tlakem žijí kratší dobu a jejich spektrální čára je oproti čarám nízkotlakých výbojek značně rozšířená (může být rozšířená dokonce až to spojitého spektra). V jaderné fyzice lze zase měřit velice krátké poločasy rozpadu některých jader tak, že se namísto přímo této doby, která může být i velmi krátká, měří pološířky rozpadových křivek, a z relací neurčitosti se dopočítá právě poločas rozpadu. Analogie: Velice krátký laserový puls může mít dobu trvání pouze několik period světelných vln. Z relací neurčitosti dostáváme, že spektrum takovéhoto pulsu je velice široké ( bílé světlo obsahuje všechny možné vlnové délky, a to i tehdy, pokud je laser naladěn na jednu konkrétní vlnovou délku!) Je to vlastně i obecná vlastnost Fourierovy transformace (FT), že FT převádí koncentrovanější funkci na zředěnější a naopak (FT funkce sin x na celém intervalu je rovna delta
3 funkci, FT oseknuté sinové funkce je funkce typu sin y /y, FT Gaussiánu s velkou pološířkou je Gaussián s malou pološířkou a naopak, totéž pro Lorentzovu křivku ). Jinak ty relace neurčitosti můžeme chápat čistě formální analogii k relacím neurčitosti mezi hybností a souřadnicí (pro operátor energie máme v kvantové mechanice výraz ih t, ačkoliv pro čas jako takový přesně vzato v kvantové mechanice žádný operátor nemáme). Mechanismy rozšíření spektrální čáry Přirozená šířka čáry může být dále rozšířená buďto homogenně nebo nehomogenně. Příkladem homogenního rozšíření je rozšíření sycením. Jedná se o to, když budeme zvyšovat intenzitu dopadajícího světla (prostorovou hustotu spektrální hustoty energie s frekvencí odpovídající energetickému rozdílu dvou uvažovaných hladin), bude se v rovnovážném stavu zvyšovat populace vyšší hladiny a snižovat populace základního stavu. Pozor: Toto neříká nic o tom, když se na ty dva uvažované stavy koukneme třeba po 100 ps od excitace, že ten vyšší stav ještě nestačil během takto krátké doby deexcitovat! Ve skutečnosti se jedná o to, jak se změní rozdíl populací základní a vyšší excitované hladiny v rovnovážném stavu v důsledku intenzívního záření musí se napsat rovnice vyjadřující, že počet přechodů zdola nahoru je v rovnovážném stavu stejný, jako počet přechodů shora dolů (zahrnout musíme všechny zářivé i nezářivé přechody), popř. složitější soustavu rovnic, která může zahrnovat i další vyšší excitované stavy, a pak to vyjde. Ukáže se, že čára si v tomto případě zanechává Lorentzův tvar, ale její pološířka se rozšiřuje a výška snižuje (protože je méně molekul v základním stavu), integrální intenzita přitom zůstává zachována. Toto rozšíření se projevuje u všech molekul stejně, proto mluvíme o homogenním rozšíření. Příkladem nehomogenního rozšíření spektrální čáry je teplotní rozšíření neboli rozšíření Dopplerovým jevem. Jak známo, Dopplerův jev je jev, kdy pozorovatel pohybující se vůči zdroji záření vnímá posunutou frekvenci oproti frekvenci, kterou emituje zdroj záření ve své klidové soustavě. Pokud bychom tedy uvažovali jednu molekulu plynu, která se pohybuje vůči laboratorní soustavě, a zkoumali např. její emisní spektrum (analogicky bychom mohli zkoumat její absorpční spektrum, ale to je velmi podobné, a na emisním spektru se to líp vysvětluje ), tak tato molekula emituje trochu jinou frekvenci, než jakou vnímá detektor spojený s laboratorní soustavou. Rozdíl těchto frekvencí je dán skalárním součinem rychlosti molekuly a vlnového vektoru emitované vlny. Vzhledem k tomu, že celková emise (nebo absorpce) je daná souborem velkého počtu molekul, z nichž každá má jinou rychlost (velikost i směr) a každá z těchto molekul emituje (absorbuje) na trochu jiné frekvenci, je výsledný profil spektrální čáry daný superpozicí profilů jednotlivých čar také bychom mohli říct, že výsledná rozšířená čára je obálkovou křivkou jednotlivých Lorentzových křivek příslušejících jednotlivým molekulám, které jsou ovšem díky Dopplerovu jevu centrované na trochu jiných frekvencích, a také vždy jiný počet molekul emituje nebo absorbuje na té a té frekvenci... Rozložení velikostí rychlostí molekul v plynu se řídí Maxwell-Boltzmannovým rozdělením: dn v N = Kv2 e mv2 2kT dv
4 Nám ale nejde až tolik o rozdělení velikosti rychlostí molekul v plynu, ale zajímá nás i jejich směr! Pokud zvolíme směr osy z ve směru vlnového vektoru, pak podíl molekul se složkou velikosti rychlosti v z je dn v z N = Ce mv 2 z 2kT dv z Dosadíme-li za diferenciál z-ové složky rychlosti diferenciál frekvence (ze vztahu mezi rychlostí molekuly a změny frekvence dané Dopplerovým jevem), dostaneme vztah, ze kterého vyčteme relativní podíl molekul, které emitují na intervalu frekvencí (ω, ω + dω). Tedy: Protože rozložení rychlostí molekul plynu je Gaussovské, bude i výsledný tvar spektrální čáry Gaussovský. Pološířka čáry bude dω = ω c 8kTln2 m Šířka čáry tedy roste s teplotou a klesá s hmotností pohybujících se částic. Pro většinu spekter ve viditelné i IR oblasti je teplotní mechanismus rozšíření obvykle dominantní, takováto pološířka je zhruba 10 až 100 větší, než pološířka daná přirozeným profilem spektrální čáry. Dopplerovské rozšíření je dominantním mechanismem rozšíření zejména u plynů. Pokud se projevuje zároveň víc mechanismů rozšíření, tj. zanedbáním jednoho z mechanismů by spektrální čára měla čistě Lorentzovský/čistě Gaussovský tvar, bude výsledný profil spektrální čáry dán konvolucí těchto dvou profilů. Tvar spektrální čáry daný konvolucí Lorentzova a Gaussova profilu se nazývá Voigtův profil. Nicméně, často je jeden z mechanismů rozšíření dominantní, tj. pokud je např. pološířka křivky daná Dopplerovským rozšířením mnohem větší, než pološířka Lorentzovy křivky u přirozené šířky čáry, tak je výsledná pološířka čáry daná převážně tou pološířkou Gaussovy křivky (také bychom mohli říct součtem pološířky Gaussovy křivky a Lorentzovy křivky, ale to obecně pro srovnatelné pološířky neplatí)! Toto lze trochu víc zobecnit: Výsledný profil spektrální čáry je daný konvolucí tvaru přirozené šířky spektrální čáry a funkce, která popisuje distribuci rezonančních frekvencí (mluvíme o nehomogenním rozšíření). Distribuci rezonančních frekvencí je u tepelného rozšířená daná právě tím Dopplerovým jevem, ale obecně se může jednat např. o distribuci danou různým chemickým okolím molekul, pokud jsou tyto molekuly zabudovány např. do nějaké matrice. Pak je otázkou, jestli tuto distribuční funkci umíme vůbec nějak popsat... I v NMR něco podobného platí... Rozšíření srážkami (tlakové) může být pružné nebo nepružné. U nepružných srážek vedou srážky molekul B s molekulami A k deexcitaci molekul A, tudíž snižování doby, po kterou je molekula A ve vyšším excitovaném stavu, tudíž ke zvýšení pološířky spektrální čáry. Rychlostní konstantu deexcitace lze napsat jako součet rychlostní konstanty (Einsteinova koeficientu) spontánní emise a rychlostní konstanty dané srážkami. Právě rychlostní konstanta daná srážkami je za dané teploty úměrná tlaku plynu, tj. při vyšším tlaku se molekuly častěji potkávají, a průměrná doba jejich života je kratší. V plynu ovšem souvisí tlak s teplotou a objemem, takže se vše dá dopočítat pomocí stavové rovnice. Např. zvýšení tlaku za stálé teploty způsobí rozšíření čáry, avšak zvýšení teploty za stálého tlaku
5 naopak zúžení čáry, protože se zvýší objem a tím klesne objemová hustota částic. Např. izochorické zvýšení teploty pak způsobí i zvýšení tlaku, tudíž se pak bude projevovat jak mechanismus tlakového rozšíření, tak mechanismus teplotního rozšíření. Pak záleží na tom, který z těchto dvou mechanismů je dominantní, obecně se ale projevují oba dva. Tlakové rozšíření je ovšem rozšíření homogenní, neboť za jednotku času (srovnatelnou s dobou, po kterou obvykle měříme) prodělá každá molekula velké množství srážek, přičemž pro opravdu velký počet molekul jsou počty srážek, které prodělá každá molekula, víceméně stejné. U pružných srážek způsobí kolize molekuly B s molekulou A pouze změnu struktury elektronových hladin molekuly A, což vede obvykle ke snížení frekvence přechodu mezi 2 stavy molekuly A, než jaká byla tato frekvence při nekonečné vzdálenosti molekul A a B. Jelikož distribuce vzdáleností, na kterou se dostane molekula B k molekule A, můžeme opět vyjádřit statisticky, má i výsledná rozšířená spektrální čára příslušný tvar (který však nemusí být nutně symetrický závisí právě na tvaru oné distribuční funkce). Pro odpudivé síly mezi A a B se střed čáry posune k nižším vlnočtům a při přitažlivých silách k vyšším vlnočtům, neboť při přitažlivých silách jsou elektronové oblaky obou molekul víc rozptýleny mezi obě tyto molekuly, čímž dochází k výraznému snížení energie u základní hladiny a výslednému zvýšení energetického rozdílu mezi oběma hladinami molekuly A (obě hladiny se posouvají energeticky dolů, ale ta spodní o něco víc ). Další faktory ovlivňující tvar spektrální čáry Nějaké další poznámky, které mě napadly, které mohou způsobovat, že spektrální čáry mohou mít další, těžko definovatelné patvary: V praktiku jsme mohli pozorovat IR a Ramanova spektra sloučeniny CCl 4. Chlor ovšem patří mezi prvky, u něhož se mohou vyskytovat dva různé izotopy, a to na rozdíl od většiny lehčích prvků prakticky ve stejném přirozeném izotopovém zastoupení. Jelikož frekvence vibrací závisí na hmotnostech kmitajících jader, jsou trochu odlišné i frekvence vibrací skupiny jader, jichž se zúčastní izotopy 35 Cl a 36 Cl. Ve spektru se to pak projeví jakýmsi hrbem na té spektrální čáře, protože se jedná v podstatě o překryv dvou jednoduchých čar. Pokud je např. u vibračních spekter nezanedbatelná absorpce vyšších excitovaných stavů (typicky druhého excitovaného stavu), můžeme ve spektru pozorovat i čáru odpovídající absorpci např. z druhého do třetího excitovaného stavu (samozřejmě s mnohem menší intenzitou). Odpovídající frekvence je ale obvykle o něco menší než frekvence odpovídající absorpci ze základního do prvního excitovaného stavu, a to kvůli anharmonicitě. Ve spektru se toto projeví jako jakýsi malý kopeček směrem k oblasti nižších frekvencí vůči původní čáře, případně může tento kopeček s původní čarou splynout. U elektronových spekter mluvíme spíše o elektronových pásech, než o čarách. Mimo toho, že u elektronových spekter můžeme pozorovat 1 čistě elektronovou čáru (absorpci ze základního do základního vibračního stavu prvního excitovaného elektronového stavu u pevných látek mluvíme o tzv. zero phonon line), tak můžeme pozorovat i elektronověvibrační přechody, kde se obecně mění jak elektronový, tak vibrační stav. Dokonce se ukazuje, že za jistých podmínek (změna rovnovážné polohy jader při změně elektronového stavu) může být pravděpodobnější přechod do prvního vibračního excitovaného stavu
6 prvního elektronového stavu, než do jeho základního vibračního stavu. Stejně tak při nenulové teplotě bychom mohli pozorovat satelitní čáry na nižších frekvencích příslušející přechodům z vyšších vibračních stavů základního elektronového stavu. Molekula s N atomy má však 3N-6 vibračních stupňů volnosti, proto je množství takovýchto přechodů, které můžeme pozorovat, velmi velké. Místo toho, že bychom pozorovali nějakou satelitní struktura vibračních čar 3N-6 krát přeloženou přes sebe, tak se díky teplotě a interakci s rozpouštědlem všechny tyto vibrační satelity slijí dohromady a vytvoří jeden velký elektronový pás. Takovou specialitou je rozšíření čáry průletem. Pokud měříme např. s úzkým laserovým svazkem plynný vzorek, jehož některé molekuly se pohybují velmi vysokou rychlostí, tak ve skutečnosti určitý počet molekul interaguje s laserovým svazkem jen velice krátkou dobu. To opět podle relací neurčitosti přináší určité rozšíření příslušné spektrální čáry. Hole burning: Pokud máme nehomogenně rozšířenou spektrální čáru (např. Dopplerovsky, tj. každá molekula absorbuje/emituje na trochu jiné frekvenci) a vzorek ozáříme silným (kvazi)monochromatickým světlem (s pološířkou menší, než pološířka Dopplerovsky rozšířené čáry), jehož frekvence ovšem spadá to intervalu frekvencí té Dopplerovsky rozšířené čáry, dojde k jevu, který se označuje jako Hole burning. Na této konkrétní frekvenci totiž dojde ke zvýšení obsazenosti vyšších hladin (viz odstavec o rozšíření sycením), tj. absorpce na této konkrétní frekvenci bude snížená; ve spektrální čáře se objeví tzv. Bennetův zářez. Pokud tato vypálíme zářez přímo do střední frekvence uvažované Dopplerovsky rozšířené čáry, nazývá se tento zářez Lambův zářez. Zdroje: V. Kapsa: Teoretické základy molekulární spektroskopie (přednáška) W. Demtroder Atoms, Molecules and Photons Tam najdete víc, než se podařilo vecpat sem do toho dokumentu, hlavně některé vzorce, které jsem tady okomentoval často jen slovně...
Elektromagnetické záření. lineárně polarizované záření. Cirkulárně polarizované záření
 Elektromagnetické záření lineárně polarizované záření Cirkulárně polarizované záření Levotočivé Pravotočivé 1 Foton Jakékoli elektromagnetické vlnění je kvantováno na fotony, charakterizované: Vlnovou
Elektromagnetické záření lineárně polarizované záření Cirkulárně polarizované záření Levotočivé Pravotočivé 1 Foton Jakékoli elektromagnetické vlnění je kvantováno na fotony, charakterizované: Vlnovou
Laserová technika prosince Katedra fyzikální elektroniky.
 Laserová technika 1 Aktivní prostředí Šíření rezonančního záření dvouhladinovým prostředím Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 22. prosince 2016 Program
Laserová technika 1 Aktivní prostředí Šíření rezonančního záření dvouhladinovým prostředím Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 22. prosince 2016 Program
SPEKTRÁLNÍ METODY. Ing. David MILDE, Ph.D. Katedra analytické chemie Tel.: ; (c) David MILDE,
 SEKTRÁLNÍ METODY Ing. David MILDE, h.d. Katedra analytické chemie Tel.: 585634443; E-mail: david.milde@upol.cz (c) -2008 oužitá a doporučená literatura Němcová I., Čermáková L., Rychlovský.: Spektrometrické
SEKTRÁLNÍ METODY Ing. David MILDE, h.d. Katedra analytické chemie Tel.: 585634443; E-mail: david.milde@upol.cz (c) -2008 oužitá a doporučená literatura Němcová I., Čermáková L., Rychlovský.: Spektrometrické
ATOMOVÁ SPEKTROMETRIE
 ATOMOVÁ SPEKTROMETRIE Atomová spektrometrie valenčních e - 1. OES (AES). AAS 3. AFS 1 Atomová spektra čárová spektra Tok záření P - množství zářivé energie (Q E ) přenesené od zdroje za jednotku času.
ATOMOVÁ SPEKTROMETRIE Atomová spektrometrie valenčních e - 1. OES (AES). AAS 3. AFS 1 Atomová spektra čárová spektra Tok záření P - množství zářivé energie (Q E ) přenesené od zdroje za jednotku času.
Optické spektroskopie 1 LS 2014/15
 Optické spektroskopie 1 LS 2014/15 Martin Kubala 585634179 mkubala@prfnw.upol.cz 1.Úvod Velikosti objektů v přírodě Dítě ~ 1 m (10 0 m) Prst ~ 2 cm (10-2 m) Vlas ~ 0.1 mm (10-4 m) Buňka ~ 20 m (10-5 m)
Optické spektroskopie 1 LS 2014/15 Martin Kubala 585634179 mkubala@prfnw.upol.cz 1.Úvod Velikosti objektů v přírodě Dítě ~ 1 m (10 0 m) Prst ~ 2 cm (10-2 m) Vlas ~ 0.1 mm (10-4 m) Buňka ~ 20 m (10-5 m)
13. Spektroskopie základní pojmy
 základní pojmy Spektroskopicky významné OPTICKÉ JEVY absorpce absorpční spektrometrie emise emisní spektrometrie rozptyl rozptylové metody Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
základní pojmy Spektroskopicky významné OPTICKÉ JEVY absorpce absorpční spektrometrie emise emisní spektrometrie rozptyl rozptylové metody Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti
Úvod do laserové techniky KFE FJFI ČVUT Praha Michal Němec, 2014. Plynové lasery. Plynové lasery většinou pracují v kontinuálním režimu.
 Aktivní prostředí v plynné fázi. Plynové lasery Inverze populace hladin je vytvářena mezi energetickými hladinami některé ze složek plynu - atomy, ionty nebo molekuly atomární, iontové, molekulární lasery.
Aktivní prostředí v plynné fázi. Plynové lasery Inverze populace hladin je vytvářena mezi energetickými hladinami některé ze složek plynu - atomy, ionty nebo molekuly atomární, iontové, molekulární lasery.
Úvod do spektrálních metod pro analýzu léčiv
 Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Úvod do spektrálních metod pro analýzu léčiv Pavel Matějka, Vadym Prokopec pavel.matejka@vscht.cz pavel.matejka@gmail.com Vadym.Prokopec@vscht.cz
Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti Úvod do spektrálních metod pro analýzu léčiv Pavel Matějka, Vadym Prokopec pavel.matejka@vscht.cz pavel.matejka@gmail.com Vadym.Prokopec@vscht.cz
ATOMOVÁ SPEKTROMETRIE
 ATOMOVÁ SPEKTROMETRIE doc. Ing. David MILDE, Ph.D. tel.: 585634443 E-mail: david.milde@upol.cz (c) -017 Doporučená literatura Černohorský T., Jandera P.: Atomová spektrometrie. Univerzita Pardubice 1997.
ATOMOVÁ SPEKTROMETRIE doc. Ing. David MILDE, Ph.D. tel.: 585634443 E-mail: david.milde@upol.cz (c) -017 Doporučená literatura Černohorský T., Jandera P.: Atomová spektrometrie. Univerzita Pardubice 1997.
Fyzika IV Dynamika jader v molekulách
 Dynamika jader v molekulách vibrace rotace Dynamika jader v molekulách rotační energetické hladiny (dvouatomová molekula) moment setrvačnosti kolem osy procházející těžištěm osa těžiště m2 m1 r2 r1 R moment
Dynamika jader v molekulách vibrace rotace Dynamika jader v molekulách rotační energetické hladiny (dvouatomová molekula) moment setrvačnosti kolem osy procházející těžištěm osa těžiště m2 m1 r2 r1 R moment
Od kvantové mechaniky k chemii
 Od kvantové mechaniky k chemii Jan Řezáč UOCHB AV ČR 19. září 2017 Jan Řezáč (UOCHB AV ČR) Od kvantové mechaniky k chemii 19. září 2017 1 / 33 Úvod Vztah mezi molekulovou strukturou a makroskopickými vlastnostmi
Od kvantové mechaniky k chemii Jan Řezáč UOCHB AV ČR 19. září 2017 Jan Řezáč (UOCHB AV ČR) Od kvantové mechaniky k chemii 19. září 2017 1 / 33 Úvod Vztah mezi molekulovou strukturou a makroskopickými vlastnostmi
INSTRUMENTÁLNÍ METODY
 INSTRUMENTÁLNÍ METODY ACH/IM David MILDE, 2014 Dělení instrumentálních metod Spektrální metody (MILDE) Separační metody (JIROVSKÝ) Elektroanalytické metody (JIROVSKÝ) Ostatní: imunochemické, radioanalytické,
INSTRUMENTÁLNÍ METODY ACH/IM David MILDE, 2014 Dělení instrumentálních metod Spektrální metody (MILDE) Separační metody (JIROVSKÝ) Elektroanalytické metody (JIROVSKÝ) Ostatní: imunochemické, radioanalytické,
Diskutujte, jak široký bude pás spojený s fosforescencí versus fluorescencí. Udělejte odhad v cm -1.
 S použitím modelu volného elektronu (=částice v krabici) spočtěte vlnovou délku a vlnočet nejdlouhovlnějšího elektronového přechodu u molekuly dekapentaenu a oktatetraenu. Diskutujte polohu absorpčního
S použitím modelu volného elektronu (=částice v krabici) spočtěte vlnovou délku a vlnočet nejdlouhovlnějšího elektronového přechodu u molekuly dekapentaenu a oktatetraenu. Diskutujte polohu absorpčního
Molekulová spektroskopie 1. Chemická vazba, UV/VIS
 Molekulová spektroskopie 1 Chemická vazba, UV/VIS 1 Chemická vazba Silová interakce mezi dvěma atomy. Chemické vazby jsou soudržné síly působící mezi jednotlivými atomy nebo ionty v molekulách. Chemická
Molekulová spektroskopie 1 Chemická vazba, UV/VIS 1 Chemická vazba Silová interakce mezi dvěma atomy. Chemické vazby jsou soudržné síly působící mezi jednotlivými atomy nebo ionty v molekulách. Chemická
Úvod do moderní fyziky. lekce 3 stavba a struktura atomu
 Úvod do moderní fyziky lekce 3 stavba a struktura atomu Vývoj představ o stavbě atomu 1904 J. J. Thomson pudinkový model atomu 1909 H. Geiger, E. Marsden experiment s ozařováním zlaté fólie alfa částicemi
Úvod do moderní fyziky lekce 3 stavba a struktura atomu Vývoj představ o stavbě atomu 1904 J. J. Thomson pudinkový model atomu 1909 H. Geiger, E. Marsden experiment s ozařováním zlaté fólie alfa částicemi
Úvod do laserové techniky
 Úvod do laserové techniky Látka jako soubor kvantových soustav Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické v Praze petr.koranda@gmail.com 18. září 2018 Světlo jako elektromagnetické
Úvod do laserové techniky Látka jako soubor kvantových soustav Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické v Praze petr.koranda@gmail.com 18. září 2018 Světlo jako elektromagnetické
Metody nelineární optiky v Ramanově spektroskopii
 Metody nelineární optiky v Ramanově spektroskopii Využití optických nelinearit umožňuje přejít od tradičního studia rozptylu světla na fluktuacích, teplotních elementárních excitacích, ke studiu rozptylu
Metody nelineární optiky v Ramanově spektroskopii Využití optických nelinearit umožňuje přejít od tradičního studia rozptylu světla na fluktuacích, teplotních elementárních excitacích, ke studiu rozptylu
Spektrometrické metody. Luminiscenční spektroskopie
 Spektrometrické metody Luminiscenční spektroskopie luminiscence molekul a pevných látek šířka spektrální čar a doba života luminiscence polarizace luminiscence korekce luminiscenčních spekter vliv aparatury
Spektrometrické metody Luminiscenční spektroskopie luminiscence molekul a pevných látek šířka spektrální čar a doba života luminiscence polarizace luminiscence korekce luminiscenčních spekter vliv aparatury
Látka jako soubor kvantových soustav
 Opakování pojmů Látka jako soubor kvantovýh soustav - foton - kvantování energie - kvantová soustava systém vázanýh části (atom, molekula, iont), jehož energie je kvantována - základní stav kvantové soustavy
Opakování pojmů Látka jako soubor kvantovýh soustav - foton - kvantování energie - kvantová soustava systém vázanýh části (atom, molekula, iont), jehož energie je kvantována - základní stav kvantové soustavy
Základy Mössbauerovy spektroskopie. Libor Machala
 Základy Mössbauerovy spektroskopie Libor Machala Rudolf L. Mössbauer 1958: jev bezodrazové rezonanční absorpce záření gama atomovým jádrem 1961: Nobelova cena Analogie s rezonanční absorpcí akustických
Základy Mössbauerovy spektroskopie Libor Machala Rudolf L. Mössbauer 1958: jev bezodrazové rezonanční absorpce záření gama atomovým jádrem 1961: Nobelova cena Analogie s rezonanční absorpcí akustických
Kinetická teorie ideálního plynu
 Přednáška 10 Kinetická teorie ideálního plynu 10.1 Postuláty kinetické teorie Narozdíl od termodynamiky kinetická teorie odvozuje makroskopické vlastnosti látek (např. tlak, teplotu, vnitřní energii) na
Přednáška 10 Kinetická teorie ideálního plynu 10.1 Postuláty kinetické teorie Narozdíl od termodynamiky kinetická teorie odvozuje makroskopické vlastnosti látek (např. tlak, teplotu, vnitřní energii) na
ABSORPČNÍ A EMISNÍ SPEKTRÁLNÍ METODY
 ABSORPČNÍ A EMISNÍ SPEKTRÁLNÍ METODY 1 Fyzikální základy spektrálních metod Monochromatický zářivý tok 0 (W, rozměr m 2.kg.s -3 ): Absorbován ABS Propuštěn Odražen zpět r Rozptýlen s Bilance toků 0 = +
ABSORPČNÍ A EMISNÍ SPEKTRÁLNÍ METODY 1 Fyzikální základy spektrálních metod Monochromatický zářivý tok 0 (W, rozměr m 2.kg.s -3 ): Absorbován ABS Propuštěn Odražen zpět r Rozptýlen s Bilance toků 0 = +
ZÁŘENÍ V ASTROFYZICE
 ZÁŘENÍ V ASTROFYZICE Plazmový vesmír Uvádí se, že 99 % veškeré hmoty ve vesmíru je v plazmovém skupenství (hvězdy, mlhoviny, ) I na Zemi se vyskytuje plazma, např. v podobě blesků, polárních září Ve sluneční
ZÁŘENÍ V ASTROFYZICE Plazmový vesmír Uvádí se, že 99 % veškeré hmoty ve vesmíru je v plazmovém skupenství (hvězdy, mlhoviny, ) I na Zemi se vyskytuje plazma, např. v podobě blesků, polárních září Ve sluneční
Vybrané spektroskopické metody
 Vybrané spektroskopické metody a jejich porovnání s Ramanovou spektroskopií Předmět: Kapitoly o nanostrukturách (2012/2013) Autor: Bc. Michal Martinek Školitel: Ing. Ivan Gregora, CSc. Obsah přednášky
Vybrané spektroskopické metody a jejich porovnání s Ramanovou spektroskopií Předmět: Kapitoly o nanostrukturách (2012/2013) Autor: Bc. Michal Martinek Školitel: Ing. Ivan Gregora, CSc. Obsah přednášky
přičemž předpokládáme A malé, U zahrnuje coulombické členy. Když roznásobíme závorku, p 2 reprezentuje kinetickou energii nabitých částic, člen
 Výběrová pravidla Absorpce/stim. emise Kde se výběrová pravidla vezmou? Použijeme semiklasické přiblížení, tzn. s nabitými částicemi (s indexy 1...N) zacházíme kvantově, s vnějším elektromagnetickým polem
Výběrová pravidla Absorpce/stim. emise Kde se výběrová pravidla vezmou? Použijeme semiklasické přiblížení, tzn. s nabitými částicemi (s indexy 1...N) zacházíme kvantově, s vnějším elektromagnetickým polem
OPVK CZ.1.07/2.2.00/
 18.2.2013 OPVK CZ.1.07/2.2.00/28.0184 Cvičení z NMR OCH/NMR Mgr. Tomáš Pospíšil, Ph.D. LS 2012/2013 18.2.2013 NMR základní principy NMR Nukleární Magnetická Resonance N - nukleární (studujeme vlastnosti
18.2.2013 OPVK CZ.1.07/2.2.00/28.0184 Cvičení z NMR OCH/NMR Mgr. Tomáš Pospíšil, Ph.D. LS 2012/2013 18.2.2013 NMR základní principy NMR Nukleární Magnetická Resonance N - nukleární (studujeme vlastnosti
10. Energie a její transformace
 10. Energie a její transformace Energie je nejdůležitější vlastností hmoty a záření. Je obsažena v každém kousku hmoty i ve světelném paprsku. Je ve vesmíru a všude kolem nás. S energií se setkáváme na
10. Energie a její transformace Energie je nejdůležitější vlastností hmoty a záření. Je obsažena v každém kousku hmoty i ve světelném paprsku. Je ve vesmíru a všude kolem nás. S energií se setkáváme na
Hamiltonián popisující atom vodíku ve vnějším magnetickém poli:
 Orbitální a spinový magnetický moment a jejich interakce s vnějším polem Vše na příkladu atomu H: Elektron (e - ) a jádro (u atomu H pouze p + ) mají vlastní magnetický moment (= spin). Tyto dva dipóly
Orbitální a spinový magnetický moment a jejich interakce s vnějším polem Vše na příkladu atomu H: Elektron (e - ) a jádro (u atomu H pouze p + ) mají vlastní magnetický moment (= spin). Tyto dva dipóly
Plazmové metody. Základní vlastnosti a parametry plazmatu
 Plazmové metody Základní vlastnosti a parametry plazmatu Atom je základní částice běžné hmoty. Částice, kterou již chemickými prostředky dále nelze dělit a která definuje vlastnosti daného chemického prvku.
Plazmové metody Základní vlastnosti a parametry plazmatu Atom je základní částice běžné hmoty. Částice, kterou již chemickými prostředky dále nelze dělit a která definuje vlastnosti daného chemického prvku.
Elektronová a absorpční spektroskopie, Vibrační spektroskopie (absorpční a Ramanova rozptylu)
 Elektronová a absorpční spektroskopie, Vibrační spektroskopie (absorpční a Ramanova rozptylu) Průchod optického záření absorbujícím prostředím V dipólové aproximaci platí Einsteinův vztah pro pravděpodobnost
Elektronová a absorpční spektroskopie, Vibrační spektroskopie (absorpční a Ramanova rozptylu) Průchod optického záření absorbujícím prostředím V dipólové aproximaci platí Einsteinův vztah pro pravděpodobnost
Světlo jako elektromagnetické záření
 Světlo jako elektromagnetické záření Základní pojmy: Homogenní prostředí prostředí, jehož dané vlastnosti jsou ve všech místech v prostředí stejné. Izotropní prostředí prostředí, jehož dané vlastnosti
Světlo jako elektromagnetické záření Základní pojmy: Homogenní prostředí prostředí, jehož dané vlastnosti jsou ve všech místech v prostředí stejné. Izotropní prostředí prostředí, jehož dané vlastnosti
Elektromagnetické pole je generováno elektrickými náboji a jejich pohybem. Je-li zdroj charakterizován nábojovou hustotou ( r r
 Záření Hertzova dipólu, kulové vlny, Rovnice elektromagnetického pole jsou vektorové diferenciální rovnice a podle symetrie bývá vhodné je řešit v křivočarých souřadnicích. Základní diferenciální operátory
Záření Hertzova dipólu, kulové vlny, Rovnice elektromagnetického pole jsou vektorové diferenciální rovnice a podle symetrie bývá vhodné je řešit v křivočarých souřadnicích. Základní diferenciální operátory
Stručný úvod do spektroskopie
 Vzdělávací soustředění studentů projekt KOSOAP Slunce, projevy sluneční aktivity a využití spektroskopie v astrofyzikálním výzkumu Stručný úvod do spektroskopie Ing. Libor Lenža, Hvězdárna Valašské Meziříčí,
Vzdělávací soustředění studentů projekt KOSOAP Slunce, projevy sluneční aktivity a využití spektroskopie v astrofyzikálním výzkumu Stručný úvod do spektroskopie Ing. Libor Lenža, Hvězdárna Valašské Meziříčí,
Úloha 5: Spektrometrie záření α
 Petra Suková, 3.ročník 1 Úloha 5: Spektrometrie záření α 1 Zadání 1. Proveďte energetickou kalibraci α-spektrometru a určete jeho rozlišení. 2. Určeteabsolutníaktivitukalibračníhoradioizotopu 241 Am. 3.
Petra Suková, 3.ročník 1 Úloha 5: Spektrometrie záření α 1 Zadání 1. Proveďte energetickou kalibraci α-spektrometru a určete jeho rozlišení. 2. Určeteabsolutníaktivitukalibračníhoradioizotopu 241 Am. 3.
ρ = 0 (nepřítomnost volných nábojů)
 Učební text k přednášce UFY Světlo v izotropním látkovém prostředí Maxwellovy rovnice v izotropním látkovém prostředí: B rot + D rot H ( r, t) div D ρ rt, ( ) div B a materiálové vztahy D ε pro dielektrika
Učební text k přednášce UFY Světlo v izotropním látkovém prostředí Maxwellovy rovnice v izotropním látkovém prostředí: B rot + D rot H ( r, t) div D ρ rt, ( ) div B a materiálové vztahy D ε pro dielektrika
CHARAKTERIZACE MATERIÁLU II
 CHARAKTERIZACE MATERIÁLU II Vyučující a zkoušející Ing. Martin Kormunda, Ph.D. - CN320 Konzultační hodiny: Po 10-12, St 13 14 nebo dle dohody Doc. RNDr. Jaroslav Pavlík, CS.c. - CN Konzultační hodiny:
CHARAKTERIZACE MATERIÁLU II Vyučující a zkoušející Ing. Martin Kormunda, Ph.D. - CN320 Konzultační hodiny: Po 10-12, St 13 14 nebo dle dohody Doc. RNDr. Jaroslav Pavlík, CS.c. - CN Konzultační hodiny:
Poznámky k Fourierově transformaci
 Poznámky k Fourierově transformaci V těchto poznámkách jsou uvedeny základní vlastnosti jednorozměrné Fourierovy transformace a její aplikace na jednoduché modelové případy. Pro určitost jsou sdružené
Poznámky k Fourierově transformaci V těchto poznámkách jsou uvedeny základní vlastnosti jednorozměrné Fourierovy transformace a její aplikace na jednoduché modelové případy. Pro určitost jsou sdružené
Kvantová fyzika atomárních soustav letní semestr VIII. KOTLÁŘSKÁ 23. DUBNA 2014
 F40 Kvantová fyzika atomárních soustav letní semestr 03-04 VIII. Vibrace víceatomových molekul cvičení KOTLÁŘSKÁ 3. DUBNA 04 Úvodem capsule o maticích a jejich diagonalisaci definice "vibračních módů"
F40 Kvantová fyzika atomárních soustav letní semestr 03-04 VIII. Vibrace víceatomových molekul cvičení KOTLÁŘSKÁ 3. DUBNA 04 Úvodem capsule o maticích a jejich diagonalisaci definice "vibračních módů"
Příklad 1: Komutační relace [d/dx, x] Příklad 2: Operátor B = i d/dx
![Příklad 1: Komutační relace [d/dx, x] Příklad 2: Operátor B = i d/dx Příklad 1: Komutační relace [d/dx, x] Příklad 2: Operátor B = i d/dx](/thumbs/91/106542832.jpg) 1 Příklad 1: Komutační relace [d/, x] Mějme na dva operátory: ˆ d/ a ˆ 5 D X x, například na prvek x působí takto Určeme jejich komutátor ˆ 5 d 5 4 ˆ 5 5 6 D x x 5 x, X x xx x ˆ ˆ ˆ ˆ ˆ ˆ d d [ DX, ] f
1 Příklad 1: Komutační relace [d/, x] Mějme na dva operátory: ˆ d/ a ˆ 5 D X x, například na prvek x působí takto Určeme jejich komutátor ˆ 5 d 5 4 ˆ 5 5 6 D x x 5 x, X x xx x ˆ ˆ ˆ ˆ ˆ ˆ d d [ DX, ] f
Přednášky z lékařské biofyziky Biofyzikální ústav Lékařské fakulty Masarykovy univerzity, Brno
 Přednášky z lékařské biofyziky Biofyzikální ústav Lékařské fakulty Masarykovy univerzity, Brno 1 Přednášky z lékařské biofyziky Biofyzikální ústav Lékařské fakulty Masarykovy univerzity, Brno Struktura
Přednášky z lékařské biofyziky Biofyzikální ústav Lékařské fakulty Masarykovy univerzity, Brno 1 Přednášky z lékařské biofyziky Biofyzikální ústav Lékařské fakulty Masarykovy univerzity, Brno Struktura
V mnoha běžných případech v optickém oboru je zanedbáváno silové působení magnetické složky elektromagnetického pole na náboje v látce str. 3 6.
 Nekvantový popis interakce světla s pasivní látkou Zcela nekvantová fyzika nemůže interakci elektromagnetického záření s látkou popsat, např. atom jako soustava kladných a záporných nábojů by vůbec nebyl
Nekvantový popis interakce světla s pasivní látkou Zcela nekvantová fyzika nemůže interakci elektromagnetického záření s látkou popsat, např. atom jako soustava kladných a záporných nábojů by vůbec nebyl
Emise vyvolaná působením fotonů nebo částic
 Emise vyvolaná působením fotonů nebo částic PES (fotoelektronová spektroskopie) XPS (rentgenová fotoelektronová spektroskopie), ESCA (elektronová spektroskopie pro chemickou analýzu) UPS (ultrafialová
Emise vyvolaná působením fotonů nebo částic PES (fotoelektronová spektroskopie) XPS (rentgenová fotoelektronová spektroskopie), ESCA (elektronová spektroskopie pro chemickou analýzu) UPS (ultrafialová
Balmerova série. F. Grepl 1, M. Benc 2, J. Stuchlý 3 Gymnázium Havlíčkův Brod 1, Gymnázium Mnichovo Hradiště 2, Gymnázium Šumperk 3
 Balmerova série F. Grepl 1, M. Benc 2, J. Stuchlý 3 Gymnázium Havlíčkův Brod 1, Gymnázium Mnichovo Hradiště 2, Gymnázium Šumperk 3 Grepl.F@seznam.cz Abstrakt: Metodou dělených svazků jsme určili lámavý
Balmerova série F. Grepl 1, M. Benc 2, J. Stuchlý 3 Gymnázium Havlíčkův Brod 1, Gymnázium Mnichovo Hradiště 2, Gymnázium Šumperk 3 Grepl.F@seznam.cz Abstrakt: Metodou dělených svazků jsme určili lámavý
KMS cvičení 6. Ondřej Marek
 KMS cvičení 6 Ondřej Marek NETLUMENÝ ODDAJNÝ SYSTÉM S DOF analytické řešení k k Systém se stupni volnosti popisují pohybové rovnice: x m m x m x + k + k x k x = m x k x + k x = k x m x k x x m k x x m
KMS cvičení 6 Ondřej Marek NETLUMENÝ ODDAJNÝ SYSTÉM S DOF analytické řešení k k Systém se stupni volnosti popisují pohybové rovnice: x m m x m x + k + k x k x = m x k x + k x = k x m x k x x m k x x m
Vibrace atomů v mřížce, tepelná kapacita pevných látek
 Vibrace atomů v mřížce, tepelná kapacita pevných látek Atomy vázané v mřížce nejsou v klidu. Míru jejich pohybu vyjadřuje podobně jako u plynů a kapalin teplota. - Elastické vlny v kontinuu neatomární
Vibrace atomů v mřížce, tepelná kapacita pevných látek Atomy vázané v mřížce nejsou v klidu. Míru jejich pohybu vyjadřuje podobně jako u plynů a kapalin teplota. - Elastické vlny v kontinuu neatomární
E g IZOLANT POLOVODIČ KOV. Zakázaný pás energií
 Polovodiče To jestli nazýváme danou látku polovodičem, závisí především na jejích vlastnostech ve zvoleném teplotním oboru. Obecně jsou to látky s 0 ev < Eg < ev. KOV POLOVODIČ E g IZOLANT Zakázaný pás
Polovodiče To jestli nazýváme danou látku polovodičem, závisí především na jejích vlastnostech ve zvoleném teplotním oboru. Obecně jsou to látky s 0 ev < Eg < ev. KOV POLOVODIČ E g IZOLANT Zakázaný pás
Skalární a vektorový popis silového pole
 Skalární a vektorový popis silového pole Elektrické pole Elektrický náboj Q [Q] = C Vlastnost materiálových objektů Interakce (vzájemné silové působení) Interakci (vzájemné silové působení) mezi dvěma
Skalární a vektorový popis silového pole Elektrické pole Elektrický náboj Q [Q] = C Vlastnost materiálových objektů Interakce (vzájemné silové působení) Interakci (vzájemné silové působení) mezi dvěma
Základy spektroskopie a její využití v astronomii
 Ing. Libor Lenža, Hvězdárna Valašské Meziříčí, p. o. Základy spektroskopie a její využití v astronomii Hvězdárna Valašské Meziříčí, p. o. Krajská hvezdáreň v Žiline Světlo x záření Jak vypadá spektrum?
Ing. Libor Lenža, Hvězdárna Valašské Meziříčí, p. o. Základy spektroskopie a její využití v astronomii Hvězdárna Valašské Meziříčí, p. o. Krajská hvezdáreň v Žiline Světlo x záření Jak vypadá spektrum?
Laserová technika prosince Katedra fyzikální elektroniky.
 Laserová technika 1 Aktivní prostředí Šíření optických impulsů v aktivním prostředí Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz. prosince 016 Program přednášek
Laserová technika 1 Aktivní prostředí Šíření optických impulsů v aktivním prostředí Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz. prosince 016 Program přednášek
SPEKTROSKOPICKÉ VLASTNOSTI LÁTEK (ZÁKLADY SPEKTROSKOPIE)
 SPEKTROSKOPICKÉ VLASTNOSTI LÁTEK (ZÁKLADY SPEKTROSKOPIE) Elektromagnetické vlnění SVĚTLO Charakterizace záření Vlnová délka - (λ) : jednotky: m (obvykle nm) λ Souvisí s povahou fotonu Charakterizace záření
SPEKTROSKOPICKÉ VLASTNOSTI LÁTEK (ZÁKLADY SPEKTROSKOPIE) Elektromagnetické vlnění SVĚTLO Charakterizace záření Vlnová délka - (λ) : jednotky: m (obvykle nm) λ Souvisí s povahou fotonu Charakterizace záření
6.2.8 Vlnová funkce. ψ nemá (zatím?) žádný fyzikální smysl, fyzikální smysl má funkce. Předpoklady: 060207
 6..8 Vlnová funkce ředpoklady: 06007 edagogická poznámka: Tato hodina není příliš středoškolská. Zařadil jsem ji kvůli tomu, aby žáci měli alespoň přibližnou představu o tom, jak se v kvantové fyzice pracuje.
6..8 Vlnová funkce ředpoklady: 06007 edagogická poznámka: Tato hodina není příliš středoškolská. Zařadil jsem ji kvůli tomu, aby žáci měli alespoň přibližnou představu o tom, jak se v kvantové fyzice pracuje.
- Rayleighův rozptyl turbidimetrie, nefelometrie - Ramanův rozptyl. - fluorescence - fosforescence
 ROZPTYLOVÉ a EMISNÍ metody - Rayleighův rozptyl turbidimetrie, nefelometrie - Ramanův rozptyl - fluorescence - fosforescence Ramanova spektroskopie Každá čára Ramanova spektra je svými vlastnostmi závislá
ROZPTYLOVÉ a EMISNÍ metody - Rayleighův rozptyl turbidimetrie, nefelometrie - Ramanův rozptyl - fluorescence - fosforescence Ramanova spektroskopie Každá čára Ramanova spektra je svými vlastnostmi závislá
16. Franck Hertzův experiment
 16. Franck Hertzův experiment Zatímco zahřáté těleso vysílá spojité spektrum elektromagnetického záření, mají např. zahřáté páry kovů nebo plyny, v nichž probíhá elektrický výboj, spektrum čárové. V uvedených
16. Franck Hertzův experiment Zatímco zahřáté těleso vysílá spojité spektrum elektromagnetického záření, mají např. zahřáté páry kovů nebo plyny, v nichž probíhá elektrický výboj, spektrum čárové. V uvedených
12 DYNAMIKA SOUSTAVY HMOTNÝCH BODŮ
 56 12 DYNAMIKA SOUSTAVY HMOTNÝCH BODŮ Těžiště I. impulsová věta - věta o pohybu těžiště II. impulsová věta Zákony zachování v izolované soustavě hmotných bodů Náhrada pohybu skutečných objektů pohybem
56 12 DYNAMIKA SOUSTAVY HMOTNÝCH BODŮ Těžiště I. impulsová věta - věta o pohybu těžiště II. impulsová věta Zákony zachování v izolované soustavě hmotných bodů Náhrada pohybu skutečných objektů pohybem
Balmerova série vodíku
 Balmerova série vodíku Josef Navrátil 1, Barbora Pavlíková 2, Pavel Mičulka 3 1 Gymnázium Ivana Olbrachta, pepa.navratil.ez@volny.cz 2 Gymnázium Jeseník, barca@progeo-sys.cz 3 Gymnázium a SOŠ Frýdek Místek,
Balmerova série vodíku Josef Navrátil 1, Barbora Pavlíková 2, Pavel Mičulka 3 1 Gymnázium Ivana Olbrachta, pepa.navratil.ez@volny.cz 2 Gymnázium Jeseník, barca@progeo-sys.cz 3 Gymnázium a SOŠ Frýdek Místek,
Fluorescence (luminiscence)
 Fluorescence (luminiscence) Patří mezi luminiscenční metody fotoluminiscence. Luminiscence efekt, kdy excitované molekuly či atomy vyzařují světlo při přechodu z excitovaného do základního stavu. Podle
Fluorescence (luminiscence) Patří mezi luminiscenční metody fotoluminiscence. Luminiscence efekt, kdy excitované molekuly či atomy vyzařují světlo při přechodu z excitovaného do základního stavu. Podle
Teplota jedna ze základních jednotek soustavy SI, vyjadřována je v Kelvinech (značka K) další používané stupnice: Celsiova, Fahrenheitova
 1 Rozložení, distribuce tepla Teplota je charakteristika tepelného stavu hmoty je to stavová veličina, charakterizující termodynamickou rovnováhu systému. Teplo vyjadřuje kinetickou energii částic. Teplota
1 Rozložení, distribuce tepla Teplota je charakteristika tepelného stavu hmoty je to stavová veličina, charakterizující termodynamickou rovnováhu systému. Teplo vyjadřuje kinetickou energii částic. Teplota
Laserová technika 1. Rychlostní rovnice pro Q-spínaný laser. 22. prosince Katedra fyzikální elektroniky.
 Laserová technika 1 Aktivní prostředí Rychlostní rovnice pro Q-spínaný laser Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 22. prosince 2016 Program přednášek
Laserová technika 1 Aktivní prostředí Rychlostní rovnice pro Q-spínaný laser Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 22. prosince 2016 Program přednášek
R10 F Y Z I K A M I K R O S V Ě T A. R10.1 Fotovoltaika
 Fyzika pro střední školy II 84 R10 F Y Z I K A M I K R O S V Ě T A R10.1 Fotovoltaika Sluneční záření je spojeno s přenosem značné energie na povrch Země. Její velikost je dána sluneční neboli solární
Fyzika pro střední školy II 84 R10 F Y Z I K A M I K R O S V Ě T A R10.1 Fotovoltaika Sluneční záření je spojeno s přenosem značné energie na povrch Země. Její velikost je dána sluneční neboli solární
37 MOLEKULY. Molekuly s iontovou vazbou Molekuly s kovalentní vazbou Molekulová spektra
 445 37 MOLEKULY Molekuly s iontovou vazbou Molekuly s kovalentní vazbou Molekulová spektra Soustava stabilně vázaných atomů tvoří molekulu. Podle počtu atomů hovoříme o dvoj-, troj- a více atomových molekulách.
445 37 MOLEKULY Molekuly s iontovou vazbou Molekuly s kovalentní vazbou Molekulová spektra Soustava stabilně vázaných atomů tvoří molekulu. Podle počtu atomů hovoříme o dvoj-, troj- a více atomových molekulách.
3.1. Newtonovy zákony jsou základní zákony klasické (Newtonovy) mechaniky
 3. ZÁKLADY DYNAMIKY Dynamika zkoumá příčinné souvislosti pohybu a je tedy zdůvodněním zákonů kinematiky. K pojmům používaným v kinematice zavádí pojem hmoty a síly. Statický výpočet Dynamický výpočet -
3. ZÁKLADY DYNAMIKY Dynamika zkoumá příčinné souvislosti pohybu a je tedy zdůvodněním zákonů kinematiky. K pojmům používaným v kinematice zavádí pojem hmoty a síly. Statický výpočet Dynamický výpočet -
Fyzika IV. g( ) Vibrace jader atomů v krystalové mříži
 Vibrace jader atomů v krystalové mříži v krystalu máme N základních buněk, v každé buňce s atomů, které kmitají kolem rovnovážných poloh výchylky kmitů jsou malé (Taylorův rozvoj): harmonická aproximace
Vibrace jader atomů v krystalové mříži v krystalu máme N základních buněk, v každé buňce s atomů, které kmitají kolem rovnovážných poloh výchylky kmitů jsou malé (Taylorův rozvoj): harmonická aproximace
Luminiscence. emise světla látkou, která je způsobená: světlem (fotoluminiscence) fluorescence, fosforescence. chemicky (chemiluminiscence)
 Luminiscence Luminiscence emise světla látkou, která je způsobená: světlem (fotoluminiscence) fluorescence, fosforescence chemicky (chemiluminiscence) teplem (termoluminiscence) zvukem (sonoluminiscence)
Luminiscence Luminiscence emise světla látkou, která je způsobená: světlem (fotoluminiscence) fluorescence, fosforescence chemicky (chemiluminiscence) teplem (termoluminiscence) zvukem (sonoluminiscence)
(Následující odstavce jsou zde uvedeny jen pro zájemce.) , sin2π, (2)
 Studium difrakčních jevů TEORIE doplněk: Odvození výrazů pro difrakční maxima (popř. minima) na štěrbině, dvojštěrbině a mřížce jsou zpravidla uvedena na středoškolské úrovni, což je založeno na vhodném
Studium difrakčních jevů TEORIE doplněk: Odvození výrazů pro difrakční maxima (popř. minima) na štěrbině, dvojštěrbině a mřížce jsou zpravidla uvedena na středoškolské úrovni, což je založeno na vhodném
Fyzika laserů. 4. dubna Katedra fyzikální elektroniky.
 Fyzika laserů Přitahováni frekvencí. Spektrum laserového záření. Modelocking Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 4. dubna 2013 Program přednášek 1.
Fyzika laserů Přitahováni frekvencí. Spektrum laserového záření. Modelocking Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 4. dubna 2013 Program přednášek 1.
Kovy - model volných elektronů
 Kovy - model volných elektronů Kovová vazba 1. Preferuje ji většina prvků vyskytujících se v přírodě. Kov je tvořen kladně nabitými ionty (s konfigurací vzácného plynu) a relativně velmi volnými elektrony.
Kovy - model volných elektronů Kovová vazba 1. Preferuje ji většina prvků vyskytujících se v přírodě. Kov je tvořen kladně nabitými ionty (s konfigurací vzácného plynu) a relativně velmi volnými elektrony.
Fyzika IV. -ezv -e(z-zv) kov: valenční elektrony vodivostní elektrony. Elektronová struktura pevných látek model volných elektronů
 Elektronová struktura pevných látek model volných elektronů 1897: J.J. Thomson - elektron jako částice 1900: P. Drude: kinetická teorie plynů - kov jako plyn elektronů Drudeho model elektrony se mezi srážkami
Elektronová struktura pevných látek model volných elektronů 1897: J.J. Thomson - elektron jako částice 1900: P. Drude: kinetická teorie plynů - kov jako plyn elektronů Drudeho model elektrony se mezi srážkami
4 Přenos energie ve FS
 4 Přenos energie ve FS Petr Ilík KF a CH, PřF UP Přenos energie (excitace) do C - 1-1 molekula chl je i při vysoké ozářenosti excitována max. 10x za sekundu neefektivní pro C - nténní systém s mnoha pigmenty
4 Přenos energie ve FS Petr Ilík KF a CH, PřF UP Přenos energie (excitace) do C - 1-1 molekula chl je i při vysoké ozářenosti excitována max. 10x za sekundu neefektivní pro C - nténní systém s mnoha pigmenty
VIBRAČNÍ SPEKTROMETRIE
 VIBRAČNÍ SPEKTROMETRIE (c) -2012 RAMANOVA SPEKTROMETRIE 1 PRINCIP METODY Měří se rozptýlené záření, které vzniká interakcí monochromatického záření z viditelné oblasti s molekulami vzorku za současné změny
VIBRAČNÍ SPEKTROMETRIE (c) -2012 RAMANOVA SPEKTROMETRIE 1 PRINCIP METODY Měří se rozptýlené záření, které vzniká interakcí monochromatického záření z viditelné oblasti s molekulami vzorku za současné změny
6 PŘEDNÁŠKA 6: Stav kvantového systému, úplná množina pozorovatelných. Operátor momentu hybnosti a kvadrátu momentu hybnosti.
 6 PŘEDNÁŠKA 6: Stav kvantového systému, úplná množina pozorovatelných Operátor momentu hybnosti a kvadrátu momentu hybnosti Víme už tedy téměř vše o operátorech Jsou to vlastně měřící přístroje v kvantové
6 PŘEDNÁŠKA 6: Stav kvantového systému, úplná množina pozorovatelných Operátor momentu hybnosti a kvadrátu momentu hybnosti Víme už tedy téměř vše o operátorech Jsou to vlastně měřící přístroje v kvantové
Základy vakuové techniky
 Základy vakuové techniky Střední rychlost plynů Rychlost molekuly v p = (2 k N A ) * (T/M 0 ), N A = 6. 10 23 molekul na mol (Avogadrova konstanta), k = 1,38. 10-23 J/K.. Boltzmannova konstanta, T.. absolutní
Základy vakuové techniky Střední rychlost plynů Rychlost molekuly v p = (2 k N A ) * (T/M 0 ), N A = 6. 10 23 molekul na mol (Avogadrova konstanta), k = 1,38. 10-23 J/K.. Boltzmannova konstanta, T.. absolutní
Anizotropie fluorescence
 Anizotropie fluorescence Pokročilé biofyzikální metody v experimentální biologii Ctirad Hofr 6 1 Jev anizotropie Jestliže dochází k excitaci světlem kmitajícím v jedné rovině, emise fluorescence se často
Anizotropie fluorescence Pokročilé biofyzikální metody v experimentální biologii Ctirad Hofr 6 1 Jev anizotropie Jestliže dochází k excitaci světlem kmitajícím v jedné rovině, emise fluorescence se často
10A1_IR spektroskopie
 C6200-Biochemické metody 10A1_IR spektroskopie Petr Zbořil IR spektroskopie Excitace vibračních a rotačních přechodů Valenční vibrace n Deformační vibrace d IR spektroskopie N atomů = 3N stupňů volnosti
C6200-Biochemické metody 10A1_IR spektroskopie Petr Zbořil IR spektroskopie Excitace vibračních a rotačních přechodů Valenční vibrace n Deformační vibrace d IR spektroskopie N atomů = 3N stupňů volnosti
7. Měření fluorescence při excitaci kontinuálním světlem ( steady-state )
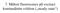 7. Měření fluorescence při excitaci kontinuálním světlem ( steady-state ) Steady-state měření Excitujeme kontinuálním světlem, měříme intenzitu emise (počet emitovaných fotonů) Obvykle nedetekujeme všechny
7. Měření fluorescence při excitaci kontinuálním světlem ( steady-state ) Steady-state měření Excitujeme kontinuálním světlem, měříme intenzitu emise (počet emitovaných fotonů) Obvykle nedetekujeme všechny
1. Kvantové jámy. Tabulka 1: Efektivní hmotnosti nosičů v krystalech GaAs, AlAs, v jednotkách hmotnosti volného elektronu m o.
 . Kvantové jámy Pokročilé metody růstu krystalů po jednotlivých vrstvách (jako MBE) dovolují vytvořit si v krystalu libovolný potenciál. Jeden z hojně používaných materiálů je: GaAs, AlAs a jejich ternární
. Kvantové jámy Pokročilé metody růstu krystalů po jednotlivých vrstvách (jako MBE) dovolují vytvořit si v krystalu libovolný potenciál. Jeden z hojně používaných materiálů je: GaAs, AlAs a jejich ternární
Luminiscence. Luminiscence. Fluorescence. emise světla látkou, která je způsobená: světlem (fotoluminiscence) chemicky (chemiluminiscence)
 Luminiscence Luminiscence emise světla látkou, která je způsobená: světlem (fotoluminiscence) fluorescence, fosforescence chemicky (chemiluminiscence) teplem (termoluminiscence) zvukem (sonoluminiscence)
Luminiscence Luminiscence emise světla látkou, která je způsobená: světlem (fotoluminiscence) fluorescence, fosforescence chemicky (chemiluminiscence) teplem (termoluminiscence) zvukem (sonoluminiscence)
Praktikum III - Optika
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK Praktikum III - Optika Úloha č. 13 Název: Vlastnosti rentgenového záření Pracoval: Matyáš Řehák stud.sk.: 13 dne: 3. 4. 2008 Odevzdal
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK Praktikum III - Optika Úloha č. 13 Název: Vlastnosti rentgenového záření Pracoval: Matyáš Řehák stud.sk.: 13 dne: 3. 4. 2008 Odevzdal
plochy oddělí. Dále určete vzdálenost d mezi místem jeho dopadu na
 Přijímací zkouška z fyziky 01 - Nav. Mgr. - varianta A Příklad 1 (5 bodů) Koule o poloměru R=10 cm leží na vodorovné rovině. Z jejího nejvyššího bodu vypustíme s nulovou počáteční rychlostí bod o hmotností
Přijímací zkouška z fyziky 01 - Nav. Mgr. - varianta A Příklad 1 (5 bodů) Koule o poloměru R=10 cm leží na vodorovné rovině. Z jejího nejvyššího bodu vypustíme s nulovou počáteční rychlostí bod o hmotností
Měření absorbce záření gama
 Měření absorbce záření gama Úkol : 1. Změřte záření gama přirozeného pozadí. 2. Změřte záření gama vyzářené gamazářičem. 3. Změřte záření gama vyzářené gamazářičem přes absorbátor. 4. Naměřené závislosti
Měření absorbce záření gama Úkol : 1. Změřte záření gama přirozeného pozadí. 2. Změřte záření gama vyzářené gamazářičem. 3. Změřte záření gama vyzářené gamazářičem přes absorbátor. 4. Naměřené závislosti
Příklad 3 (25 bodů) Jakou rychlost musí mít difrakčním úhlu 120? -částice, abychom pozorovali difrakční maximum od rovin d hkl = 0,82 Å na
 Přijímací zkouška z fyziky 01 - Nav. Mgr. - varianta A Příklad 1 (5 bodů) Koule o poloměru R=10 cm leží na vodorovné rovině. Z jejího nejvyššího bodu vypustíme s nulovou počáteční rychlostí bod o hmotností
Přijímací zkouška z fyziky 01 - Nav. Mgr. - varianta A Příklad 1 (5 bodů) Koule o poloměru R=10 cm leží na vodorovné rovině. Z jejího nejvyššího bodu vypustíme s nulovou počáteční rychlostí bod o hmotností
Metody charakterizace nanomaterálů I
 Vybrané metody spektráln lní analýzy Metody charakterizace nanomaterálů I RNDr. Věra Vodičková, PhD. Molekulová spektroskopie atomy a molekuly mohou měnit svůj energetický stav přijetím nebo vyzářením
Vybrané metody spektráln lní analýzy Metody charakterizace nanomaterálů I RNDr. Věra Vodičková, PhD. Molekulová spektroskopie atomy a molekuly mohou měnit svůj energetický stav přijetím nebo vyzářením
Fyzika laserů. 7. března Katedra fyzikální elektroniky.
 Fyzika laserů Poloklasický popis šíření elmg. záření v rezonančním prostředí. Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 7. března 2013 Program přednášek
Fyzika laserů Poloklasický popis šíření elmg. záření v rezonančním prostředí. Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 7. března 2013 Program přednášek
Laserová technika 1. Rychlostní rovnice pro Q-spínaný laser. 16. prosince 2013. Katedra fyzikální elektroniky. jan.sulc@fjfi.cvut.
 Laserová technika 1 Aktivní prostředí Rychlostní rovnice pro Q-spínaný laser Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 16. prosince 2013 Program přednášek
Laserová technika 1 Aktivní prostředí Rychlostní rovnice pro Q-spínaný laser Jan Šulc Katedra fyzikální elektroniky České vysoké učení technické jan.sulc@fjfi.cvut.cz 16. prosince 2013 Program přednášek
NMR spektroskopie. Úvod
 NMR spektroskopie Úvod Zkratka NMR znamená Nukleární Magnetická Rezonance. Jde o analytickou metodu, která na základě absorpce radiofrekvenčního záření vzorkem umístěným v silném magnetickém poli poskytuje
NMR spektroskopie Úvod Zkratka NMR znamená Nukleární Magnetická Rezonance. Jde o analytickou metodu, která na základě absorpce radiofrekvenčního záření vzorkem umístěným v silném magnetickém poli poskytuje
Spektroskopické metody. převážně ve viditelné, ultrafialové a blízké infračervené oblasti
 Spektroskopické metody převážně ve viditelné, ultrafialové a blízké infračervené oblasti Elektromagnetické záření Elektromagnetické záření je postupné vlnění elektromagnetického pole složeného z kombinace
Spektroskopické metody převážně ve viditelné, ultrafialové a blízké infračervené oblasti Elektromagnetické záření Elektromagnetické záření je postupné vlnění elektromagnetického pole složeného z kombinace
Balmerova série, určení mřížkové a Rydbergovy konstanty
 Balmerova série, určení mřížkové a Rydbergovy konstanty V tomto laboratorním cvičení zkoumáme spektrální čáry 1. řádu vodíku a rtuti pomocí difrakční mřížky (mřížkového spektroskopu). Známé spektrální
Balmerova série, určení mřížkové a Rydbergovy konstanty V tomto laboratorním cvičení zkoumáme spektrální čáry 1. řádu vodíku a rtuti pomocí difrakční mřížky (mřížkového spektroskopu). Známé spektrální
Elementární částice. 1. Leptony 2. Baryony 3. Bosony. 4. Kvarkový model 5. Slabé interakce 6. Partonový model
 Elementární částice 1. Leptony 2. Baryony 3. Bosony 4. Kvarkový model 5. Slabé interakce 6. Partonový model I.S. Hughes: Elementary Particles M. Leon: Particle Physics W.S.C. Williams Nuclear and Particle
Elementární částice 1. Leptony 2. Baryony 3. Bosony 4. Kvarkový model 5. Slabé interakce 6. Partonový model I.S. Hughes: Elementary Particles M. Leon: Particle Physics W.S.C. Williams Nuclear and Particle
Daniel Franta Ústav fyzikální elektroniky, Přírodovědecká fakulta, Masarykova univerzita
 Pokročilé disperzní modely v optice tenkých vrstev Lekce 3: Kvantově mechanický popis Thomas-Reiche-Kuhnovo (TRK) sumační pravidlo; Fermiho zlaté pravidlo; dipólová aproximace; dielektrická odezva Daniel
Pokročilé disperzní modely v optice tenkých vrstev Lekce 3: Kvantově mechanický popis Thomas-Reiche-Kuhnovo (TRK) sumační pravidlo; Fermiho zlaté pravidlo; dipólová aproximace; dielektrická odezva Daniel
Nerovnovážné systémy Onsagerova hypotéza, fluktuačně disipační teorém
 Nerovnovážné systémy Onsagerova hypotéza, fluktuačně disipační teorém Omezení se na nerovnážné systémy v blízkosti rovnováhy Chování systému lze popsat v rámci linear response theory (teorie lineární odezvy)
Nerovnovážné systémy Onsagerova hypotéza, fluktuačně disipační teorém Omezení se na nerovnážné systémy v blízkosti rovnováhy Chování systému lze popsat v rámci linear response theory (teorie lineární odezvy)
11. přednáška 10. prosince Kapitola 3. Úvod do teorie diferenciálních rovnic. Obyčejná diferenciální rovnice řádu n (ODR řádu n) je vztah
 11. přednáška 10. prosince 2007 Kapitola 3. Úvod do teorie diferenciálních rovnic. Obyčejná diferenciální rovnice řádu n (ODR řádu n) je vztah F (x, y, y, y,..., y (n) ) = 0 mezi argumentem x funkce jedné
11. přednáška 10. prosince 2007 Kapitola 3. Úvod do teorie diferenciálních rovnic. Obyčejná diferenciální rovnice řádu n (ODR řádu n) je vztah F (x, y, y, y,..., y (n) ) = 0 mezi argumentem x funkce jedné
Látkové množství n poznámky 6.A GVN
 Látkové množství n poznámky 6.A GVN 10. září 2007 charakterizuje látky z hlediska počtu částic (molekul, atomů, iontů), které tato látka obsahuje je-li v tělese z homogenní látky N částic, pak látkové
Látkové množství n poznámky 6.A GVN 10. září 2007 charakterizuje látky z hlediska počtu částic (molekul, atomů, iontů), které tato látka obsahuje je-li v tělese z homogenní látky N částic, pak látkové
Pokročilé cvičení z fyzikální chemie KFC/POK2 Vibrační spektroskopie
 Pokročilé cvičení z fyzikální chemie KFC/POK2 Vibrační spektroskopie Vibrace molekul mohou být měřeny buď pomocí absorpce infračerveného záření, nebo pomocí neelastického rozptylu záření, tzn. Ramanova
Pokročilé cvičení z fyzikální chemie KFC/POK2 Vibrační spektroskopie Vibrace molekul mohou být měřeny buď pomocí absorpce infračerveného záření, nebo pomocí neelastického rozptylu záření, tzn. Ramanova
Přednáška IX: Elektronová spektroskopie II.
 Přednáška IX: Elektronová spektroskopie II. 1 Försterův resonanční přenos energie Pravděpodobnost (rychlost) přenosu je určená jako: k ret 1 = τ 0 D R r 0 6 0 τ D R 0 r Doba života donoru v excitovaném
Přednáška IX: Elektronová spektroskopie II. 1 Försterův resonanční přenos energie Pravděpodobnost (rychlost) přenosu je určená jako: k ret 1 = τ 0 D R r 0 6 0 τ D R 0 r Doba života donoru v excitovaném
Funkce komplexní proměnné a integrální transformace
 Funkce komplexní proměnné a integrální transformace Fourierovy řady I. Marek Lampart Text byl vytvořen v rámci realizace projektu Matematika pro inženýry 21. století (reg. č. CZ.1.07/2.2.00/07.0332), na
Funkce komplexní proměnné a integrální transformace Fourierovy řady I. Marek Lampart Text byl vytvořen v rámci realizace projektu Matematika pro inženýry 21. století (reg. č. CZ.1.07/2.2.00/07.0332), na
Charakteristiky optoelektronických součástek
 FYZIKÁLNÍ PRAKTIKUM Ústav fyziky FEKT VUT BRNO Spolupracoval Jan Floryček Jméno a příjmení Jakub Dvořák Ročník 1 Měřeno dne Předn.sk.-Obor BIA 27.2.2007 Stud.skup. 13 Odevzdáno dne Příprava Opravy Učitel
FYZIKÁLNÍ PRAKTIKUM Ústav fyziky FEKT VUT BRNO Spolupracoval Jan Floryček Jméno a příjmení Jakub Dvořák Ročník 1 Měřeno dne Předn.sk.-Obor BIA 27.2.2007 Stud.skup. 13 Odevzdáno dne Příprava Opravy Učitel
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/ Vlnění
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Vlnění Vhodíme-li na klidnou vodní hladinu kámen, hladina se jeho dopadem rozkmitá a z místa rozruchu se začnou
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Vlnění Vhodíme-li na klidnou vodní hladinu kámen, hladina se jeho dopadem rozkmitá a z místa rozruchu se začnou
Elektronový obal atomu
 Elektronový obal atomu Vlnění o frekvenci v se může chovat jako proud částic (kvant - fotonů) o energii E = h.v Částice pohybující se s hybností p se může chovat jako vlna o vlnové délce λ = h/p Kde h
Elektronový obal atomu Vlnění o frekvenci v se může chovat jako proud částic (kvant - fotonů) o energii E = h.v Částice pohybující se s hybností p se může chovat jako vlna o vlnové délce λ = h/p Kde h
III. STRUKTURA A VLASTNOSTI PLYNŮ
 III. STRUKTURA A VLASTNOSTI PLYNŮ 3.1 Ideální plyn a) ideální plyn model, předpoklady: 1. rozměry molekul malé (ve srovnání se střední vzdáleností molekul). molekuly na sebe navzálem silově nepůsobí (mimo
III. STRUKTURA A VLASTNOSTI PLYNŮ 3.1 Ideální plyn a) ideální plyn model, předpoklady: 1. rozměry molekul malé (ve srovnání se střední vzdáleností molekul). molekuly na sebe navzálem silově nepůsobí (mimo
Molekulová fyzika a termika:
 Molekulová fyzika a termika: 1. Měření teploty: 2. Délková roztažnost a Objemová roztažnost látek 3. Bimetal 4. Anomálie vody 5. Částicová stavba látek, vlastnosti látek 6. Atomová hmotnostní konstanta
Molekulová fyzika a termika: 1. Měření teploty: 2. Délková roztažnost a Objemová roztažnost látek 3. Bimetal 4. Anomálie vody 5. Částicová stavba látek, vlastnosti látek 6. Atomová hmotnostní konstanta
