Obsah. Obsah OBSAH... 1
|
|
|
- Hynek Fišer
- před 7 lety
- Počet zobrazení:
Transkript
1 Obsah Obsah OBSAH SOUADNICOVÉ SOUSTAVY PRAVOÚHLÉ A SFÉRICKÉ SOUADNICOVÉ SOUSTAVY TRANSFORMACE POMOCÍ ROTANÍCH ÚHL EULEROVSKÉHO TYPU ASTRONOMICKÉ SOUADNICOVÉ SOUSTAVY Obzorníková souadnicová soustava Rovníkové souadnicové soustavy Ekliptikální souadnicová soustava Transformace mezi astronomickými souadnicovými soustavami ZDÁNLIVÝ DENNÍ POHYB HVZD VÝCHOD A ZÁPAD HVZD CIRKUMPOLÁRNÍ HVZDY SOUMRAKY PRCHOD ELONGACÍ (MAXIMÁLNÍ DIGRESÍ) PRCHOD HVZD PRVNÍM VERTIKÁLEM....4 PRCHOD HVZD MÍSTNÍM POLEDNÍKEM HORNÍ A DOLNÍ KULMINACE... 3 NERUŠENÝ KEPLEROVSKÝ POHYB ODVOZENÍ KEPLEROVÝCH ZÁKON A DALŠÍCH ZÁKLADNÍCH VZTAH Sestavení pohybových rovnic Gravitaní konstanta URENÍ POLOHY A SLOŽEK POSTUPNÉ RYCHLOSTI Dráhové elementy Urení polohy v rovin dráhy Urení polohy v prostoru Rozklad postupné rychlosti do prostorových složek NAUKA O ASE - ASOMÍRA JULIÁNSKÉ DATUM STANDARDNÍ EPOCHY A PEVODY VELIIN ROTANÍ ASY Rotaní asy hvzdné Rotaní asy slunení a asová rovnice Soustava svtových as Vztah mezi hvzdnými a sluneními asy Pásmový as datová ára a letní asy ASY DEFINOVANÉ FYZIKÁLN Atomový as ízený (koordinovaný) as DYNAMICKÉ ASY Terestrický dynamický as Barycentrický dynamický as PEVODY AS DEFINICE ROK KALENDÁE Juliánský kalendá Gregoriánský kalendá ZMNY SOUADNIC VLASTNÍ POHYB HVZDY PRECESE A NUTACE Rozdlení precese a nutace Výpoet precese a nutace ABERACE
2 Obsah Denní aberace Roní aberace Planetární (družicová) aberace PARALAXA Denní paralaxa Roní paralaxa ASTRONOMICKÁ REFRAKCE Elementární odvození refrakního vzorce Vliv refrakce na obzorníkové souadnice z a a STEDNÍ PRAVÁ A ZDÁNLIVÁ MÍSTA HVZD (KOSMICKÝCH TLES) POHYB PÓLU KATALOGY HVZD ASTRONOMICKÉ ROENKY GEODETICKÁ ASTRONOMIE UŽITÍ ASTRONOMICKÝCH VELIIN V ASTRONOMICKO-GEODETICKÉ SÍTI (AGS) Užití astronomických zempisných souadnic v AGS Užití astronomických azimut v AGS ASTRONOMICKO-GEODETICKÁ SÍ NA ÚZEMÍ ESKOSLOVENSKA Mení astronomických zempisných souadnic Mení astronomických azimut METODY NIŽŠÍ PESNOSTI SOUBŽNÉ UROVÁNÍ ZEMPISNÝCH SOUADNIC NIŽŠÍ PESNOSTI Poetn-grafická metoda Metoda zenitových vzdáleností a as UROVÁNÍ ZEMPISNÉ ŠÍKY NIŽŠÍ PESNOSTI - METODA ZENITOVÝCH VZDÁLENOSTÍ A AS UROVÁNÍ ZEMPISNÉ DÉLKY NIŽŠÍ PESNOSTI - METODA ZENITOVÝCH VZDÁLENOSTÍ A AS UROVÁNÍ AZIMUTU NIŽŠÍ PESNOSTI Opticko-mechanické pomcky k vytýení poledníku Vytýení poledníku pomocí tabulky azimut Polárky Urování azimutu pozemního cíle pomocí hodinového úhlu METODY VYŠŠÍ PESNOSTI UROVÁNÍ ZEMPISNÉ ŠÍKY VYŠŠÍ PESNOSTI Metoda rozdílu zenitových vzdáleností - Horrebowova-Talcottova metoda UROVÁNÍ ZEMPISNÉ DÉLKY VYŠŠÍ PESNOSTI Metoda prchod hvzd místním poledníkem Metoda stejných výšek (MSV) - Cingerova metoda UROVÁNÍ AZIMUTU VYŠŠÍ PESNOSTI SOUASNÉ UROVÁNÍ ZEMPISNÝCH SOUADNIC VYŠŠÍ PESNOSTI - METODY STEJNÝCH VÝŠEK (MSV) SOUASNÉ UROVÁNÍ ZEMPISNÝCH SOUADNIC A AZIMUTU... 99
3 Kapitola 1 Souadnicové soustavy 1 Souadnicové soustavy 1.1 Pravoúhlé a sférické souadnicové soustavy Polohu libovolného bodu v euklidovském prostoru dimenze 3 (E 3 ) ve kterém budeme pracovat mžeme popsat rznými typy souadnic. Ve sférické astronomii se nejast ji používá 1) pravoúhlá souadnicová soustava ) sférická souadnicová soustava. 1) Pravoúhlá souadnicová soustava Ti navzájem kolmé jednotkové vektory i j k umíst né ve zvoleném poátku O v E 3 (viz obrázek 1.1) tvoí pravoúhlou (ortogonální) souadnicovou soustavu. Pímky které jsou nositelkami vektor i j k nazýváme souadnicovými osami. Obrázek 1.1: Pravoúhlá souadnicová soustava Polohu libovolného bodu R který mžeme považovat za koncový bod vektoru r umíst ného v poátku O vyjádíme jednoznan jako lineární kombinaci vektor i j k (1.1.1) r = x. i + y. j + z. k Veliiny x y z pak nazýváme souadnicemi bodu R. Vynásobíme-li postupn výraz (1.1.1) skalárn vektory i j k dostáváme v dsledku ortogonality vektor i j k (1.1.) x = r. i y = r. j z = r. k. Vzpomeneme-li si na geometrický význam skalárního souinu dvou vektor vidíme že souadnice x y z vznikají jako prm t vektoru r na souadnicové osy. V pípad že i r bude jednotkový vektor platí (1.1.3) x = cos α y = cos β z = cos γ 3
4 Kapitola 1 Souadnicové soustavy kde α β γ jsou úhly které svírá vektor r se souadnicovými osami. Souadnice jednotkového vektoru pak nazýváme smrové kosiny. Z definice plyne že splují podmínku x + y + z = 1. Souadnicová soustava mže být pravotoivá jak je tomu na obrázku 1.1 kdy pi pohledu od konce osy z pejdeme od osy x k ose y otoením o 9 o proti sm ru hodinových ruiek - tedy v matematicky kladném (a geodeticky záporném) smyslu podobn od osy y k ose z. Levotoivá soustava by m la orientaci os obrácen. ) Sférická souadnicová soustava Sférickou souadnicovou soustavu tvoí základní rovina a základní sm r jehož poátek leží v základní rovin. Za základní rovinu si zvolme rovinu xy tvoenou poátkem O a souadnicovými osami x a y za základní smr pak sm r osy x. Polohu bodu R v prostoru pak urují ti souadnice r... délka prvodie r λ... úhel mezi osou x a prm tem r do roviny xy ϕ...úhel mezi prvodiem r a rovinou xy. Veliiny r ϕ λ se nazývají sférické souadnice bodu R. Z obrázku 1. platí a dále tedy x = r cos ϕ cos λ (1.1.4) y = r cos ϕ sin λ z = r sin ϕ respektive inverzní vztahy Obrázek 1.: Sférická souadnicová soustava OR = r cosϕ x = OR cos λ y = OR sin λ z = r sin ϕ 4
5 Kapitola 1 Souadnicové soustavy (1.1.5) r + = x + y z y λ = arctan x z z ϕ = arc cot = arcsin. x + y r Souadnicové soustavy mžeme v prostoru umístit a orientovat rzným zpsobem. Pokud bude orientace v prostoru resp. v t lese i na jeho povrchu uritým zpsobem realizována mžeme mluvit o souadnicovém systému. 1. Transformace pomocí rotaních úhl eulerovského typu Pedpokládejme že chceme provést pechod ze soustavy S do soustavy S. Zvolme proto dv pomocné kartézské souadnicové soustavy S 1 (x 1 y 1 z 1 ) S (x y z ) a definujme postupnou transformaci následujícím zpsobem: a) Pechod z S do S 1 : Soustavu S 1 natoíme vi S tak že ztotožníme poátky O a osy z a z 1 osa x 1 je vi x pootoena v matematicky kladném smyslu o úhel ω v rovin xy viz obr. 1.3a stejn tak osa y 1 vi y. Pak mžeme psát (1..1) Ozname x y z (1..) Z ( ω) cosω = sinω cosω = sinω sinω cosω sinω cosω x. y. 1 z transformaní matici kterou mžeme chápat jako pootoení kolem osy z o úhel ω vedoucí ke ztotožn ní obou soustav. 1 a) b) c) Obrázek 1.3 a b c: Transformace pomocí postupných rotací b) Pechod z S 1 do S : Soustavu S umístíme vi S 1 tak že ztotožníme poátky O a osy x 1 a x osa y je vi y 1 pootoena v matematicky kladném smyslu o úhel ε v rovin y 1 z 1 viz obrázek 1.3b stejn tak osa z vi z 1. Na základ výsledk pedchozího odstavce pak mžeme op t psát 5
6 Kapitola 1 Souadnicové soustavy (1..3) Ozname x y z (1..4) X ( ε ) 1 = 1 = x1 cosε sinε. y1. sinε cosε z1 cosε sinε 6 sinε cosε transformaní matici kterou op t mžeme chápat jako pootoení kolem osy x o úhel ε vedoucí ke ztotožn ní obou soustav. c) Pechod z S do S : Soustavu S umístíme vi S tak že ztotožníme poátky O a osy y a y osa z je vi z pootoena v matematicky kladném smyslu o úhel ψ v rovin x z viz obr. 1.3c stejn tak osa x vi x. Analogicky k pedchozímu pak mžeme op t psát: (1..5) Ozname (1..6) ( ) Y ψ x cosψ sinψ x = y 1. y. z sinψ cosψ z cosψ sinψ = 1 sinψ cosψ transformaní matici která reprezentuje pootoení kolem osy y o úhel ψ. Spojíme-li nyní výsledky (1..1) až (1..6) lze pro pechod (transformaci) ze soustavy S do S psát: (1..7) S = Y(ψ) X(ε) Z(ω) S = R ψεω S když jsme ješt položili (1..8) R ψεω = Y(ψ) X(ε) Z(ω). Transformaní matice Y(ψ) X(ε) Z(ω) budeme dále velmi asto používat. Povšimn me si že v podstat nezáleží jakým symbolem jsme oznaili rotaní úhly dležité je pouze zachovat vždy (matematicky) kladný smr otáení. Nejdležit jším výsledkem tohoto odstavce je skutenost že transformaci z jedné euklidovské soustavy do druhé chápeme jako posloupnost otáení o známé elementární úhly takovým zpsobem abychom ztotožnili osy pvodní a nové soustavy. V prostoru E 3 pro takové ztotožn ní vystaíme se temi rotacemi ale obecn jich mže být více ve speciálních pípadech poloh os naopak mén. Další dležitou vlastností matic Y(ψ) X(ε) Z(ω) je že jsou ortonormální tedy platí: (1..9) Y(ψ). Y T (ψ) = E Y -1 (ψ) = Y T (ψ) = Y(-ψ) a podobn pro X(ε) a Z(ω). V dsledku (1..9) píšeme pro zp tnou transformaci z S do S
7 Kapitola 1 Souadnicové soustavy (1..1) S = ( Y(ψ). X(ε). Z(ω) ) -1. S = Z T (ω). X T (ε). Y T (ψ). S. Jak uvidíme v dalších odstavcích budeme v pevážné míe pracovat s transformacemi jednotkových vektor pjde nám pedevším o transformaci smr; vzdálenosti se neuvažují. V n kterých pípadech - zvlášt pi transfomaci geodetických referenních systém - se stává že úhly ψεω nabývají velmi malých hodnot v tšinou mén než 5. V tomto pípad si pak mžeme dovolit zjednodušení a položit cosψ = 1 sinψ = ψ obdobn pro ε ω. Dále položit ε.ω = atd. Pro R ψεω z (1..8) pak platí (1..11) R ψεω 1 ψ 1 1 ω 1 ω ψ = ε ω ω ε { } = ψ 1 ε 1 1 ψ ε 1 kde {} jsou leny druhého ádu. 1.3 Astronomické souadnicové soustavy Pomocí astronomických souadnicových soustav vyjadujeme polohu kosmických t les (hv zdy kvasary Slunce družice) v prostoru a to nejast ji pomocí sférických nebo pravoúhlých prostorových souadnic. Abychom mohli zavést sférickou souadnicovou soustavu musíme zvolit sféru (kouli) s uritým polom rem a základní sm ry a roviny které je možné fyzikáln realizovat. Z matematického hlediska je vhodné zvolit polom r koule roven 1 (Gaussova sféra). Za základní sm ry zvolíme: svislici v daném bod pozorování nebo smr rotaní osy Zem nebo smr k pólu ekliptiky. Za základní roviny volíme: rovinu horizontu (obzorníku) v daném bod pozorování nebo rovinu rovníku nebo rovinu ekliptiky (ekliptika je rovina ve které vykonává Zem pohyb kolem Slunce anebo z hlediska pozorovatele na Zemi ve které je zdánliv umíst no Slunce na obloze). Podle základních smr a rovin rozd lujeme sférické souadnicové soustavy na: obzorníkovou souadnicovou soustavu rovníkovou souadnicovou soustavu (závislou na ase) rovníkovou souadnicovou soustavu (nezávislou na ase) ekliptikální souadnicovou soustavu galaktickou souadnicovou soustavu N které z uvedených souadnicových soustav d líme ješt podle polohy stedu koule na topocentrickou geocentrickou heliocentrickou obecn objektocentrickou nebo poátek mže být ve stedu jiných t les nap. M síce planet barycentrickou (poátek je v t žišti nap. slunení soustavy) 7
8 Kapitola 1 Souadnicové soustavy Souadnicové soustavy které jsou vázány na hmotný útvar a které se pohybují vzhledem k základnímu (nehybnému) prostoru rovnomrn a pímoae nazýváme inerciální souadnicové soustavy. Tak napíklad souadnicová soustava vázaná na systém velmi vzdálených zdroj kosmického záení (kvasary) tvoí inerciální soustavu naopak jakákoliv souadnicová soustava pevn spojená s rotující Zemí není inerciální Obzorníková souadnicová soustava Základním sm rem obzorníkové souadnicové soustavy je sm r svislice v bod T ze kterého pozorujeme kosmické objekty. Do tohoto bodu umístíme sted jednotkové koule O - viz obrázek 1.4. Svislice protne jednotkovou kouli v bod Z který nazýváme zenit (nadhlavník) a v bod N a který nazýváme nadir. Rovina kolmá ke svislici procházející bodem O se nazývá rovina obzorníku. Protíná jednotkovou kouli v hlavní kružnici která se nazývá obzorník nebo též horizont. Horizont rozd luje kouli na dv poloviny z nichž pouze horní je viditelná. Vedeme-li rovnob žku s rotaní osou bodem O protíná jednotkovou kouli v severním pólu P n a jižním pólu P s. Obrázek 1.4: Obzorníková soustava Hlavní kružnice procházející zenitem a nadirem se nazývají výškové kružnice (vertikály). Z nich jsou dv význané a to místní poledník (meridián) a první vertikál. Místní poledník definujeme jako kružnici procházející zenitem nadirem severním a jižním pólem. Rovina proložená touto kružnicí se nazývá rovina místního poledníku. Slunce pi svém zdánlivém pohybu po obloze prochází touto rovinou v pravé místní poledne (termíny budou upesn ny v dalších odstavcích) proto název poledník. Rovina prvního vertikálu prochází zenitem a nadirem a je kolmá na rovinu místního poledníku. Prsenice této roviny s jednotkovou koulí se nazývá první vertikál. Prseíky místního poledníku resp. prvního vertikálu s obzorníkem se nazývají severní bod N jižní bod S západní bod W a východní bod E. Pravoúhlou souadnicovou soustavu x o y o z o zavedeme podle obrázku
9 Kapitola 1 Souadnicové soustavy Obzorník a poledník definují obzorníkovou soustavu. Sférické souadnice se nazývají azimut a a zenitová vzdálenost z resp. výška hvzdy h. Zvolme na jednotkové kružnici polohu hv zdy H a proložme hv zdou svislou rovinu (rovinu vertikálu). Azimut a je pak úhel který svírá rovina vertikálu s rovinou místního poledníku. M í se od jižní vtve místního poledníku v matematicky záporném smyslu (k západu) a nabývá hodnot v intervalu o až 36 o. Zenitová vzdálenost z je úhel m ený po výškové kružnici od zenitu ke hv zd. Nabývá hodnot o až 18 o. Výška hv zdy h je úhel který svírá sm r ke hv zd s rovinou obzorníku. Mezi výškou a zenitovou vzdáleností platí jednoduchý vztah (1.3.1) z + h = 9 o. Vodorovná rovina proložená hv zdou H protne jednotkovou kouli ve vedlejší kružnici která se nazývá almukantarat. Hv zdy které se nacházejí na almukantaratu mají stejnou zenitovou vzdálenost. Poznámka: Slovo almukantarat je arabského pvodu. V obzorníkové soustav se souadnice hv zdy m ní jednak v závislosti na ase v dsledku rotace Zem za druhé se zm nou pozorovacího místa protože každému bodu na Zemi náleží v závislosti na zem pisné šíce ϕ a zem pisné délce λ jiný obzorník a zenit. Astronomická zem pisná šíka v obzorníkové soustav se rovná výšce severního pólu P n nad obzorem (horizontem) tedy (1.3.) h Pn = ϕ. Orientujme pravotoivou pravoúhlou souadnicovou soustavu tak že osa +x o bude procházet jižním bodem S osa +z o zenitem Z a osa +y o východním bodem E. Aplikujme vztahy (1.1.4) na jednotkovou kouli. Obdržíme vztahy mezi systémem sm rových kosin (x y z) v obzorníkové soustav a obzorníkovými souadnicemi ve tvaru x (1.3.3) S o = y z o cos h cosa sin z cos a = h a z a = cos sin sin sin sin h cos z (kde index o znaí obzorníkovou soustavu) respektive y (1.3.4) a = arctan h = arcsin z z = arccos z. o o x 1.3. Rovníkové souadnicové soustavy o Základním sm rem rovníkové soustavy je sm r osy rotace Zem která protne jednotkovou kouli v severním sv tovém pólu P n a jižním sv tovém pólu P s viz obrázek 1.5. Základní rovinou je rovina rovníku kolmá k ose rotace vedená bodem O. Rovina rovníku protne kouli v hlavní kružnici kterou nazýváme svtovým rovníkem. Roviny procházející sv tovými póly nazveme deklinaními rovinami jejich prsenice s jednotkovou koulí nazýváme deklinaní kružnice - viz obr Polohu hv zdy vi rovníku uruje souadnice zvaná deklinace δ. Je to úhlová vzdálenost hv zdy od rovníku m ená podél deklinaní kružnice. Deklinace nabývá hodnot v intervalu -9 o až 9 o m eno od jižního pólu k severnímu pólu. Vedlejší roviny rovnob žné s rovinou rovníku protínají jednotkovou kouli v 9
10 Kapitola 1 Souadnicové soustavy kružnicích které se nazývají deklinaní rovnobžky. Po deklinaních rovnob žkách hv zdy vykonávají svj zdánlivý denní pohyb jako odraz skutené rotace Zem. Polohu hv zdy vi pólu mžeme také vyjádit pomocí pólové vzdálenosti p. Je to úhlová vzdálenost hv zdy m ená po deklinaní kružnici od severního pólu. Pro deklinaci a pólovou vzdálenost platí jednoduchý vztah δ + p = 9 o. Druhou rovníkovou souadnici mžeme volit dv ma zpsoby podle zvolené pomocné základní roviny. Rozlišujeme tak první a druhou rovníkovou souadnicovou soustavu S r1 a S r. Obrázek 1.5: Rovníková soustava S r1 Obrázek 1.6: Rovníková soustava S r 1) První rovníková souadnicová soustava S r1 závislá na ase V první rovníkové souadnicové soustav - viz obr zvolíme za základní rovinu rovinu místního poledníku. Polohu hv zdy pak uruje hodinový úhel t a deklinace δ která již byla definována. Hodinový úhel je úhel který svírá rovina místního poledníku s deklinaní rovinou procházející hv zdou. M íme ho od jižní v tve místního poledníku v matematicky záporném smyslu. Mže nabývat hodnot o až 36 o v tšinou ho však vyjadujeme v hodinové míe v intervalu h až 4 h. Jak vyplývá z definice hodinový úhel je závislý na poloze místního poledníku. Ten však v dsledku rotace Zem m ní neustále svou polohu vi hv zdám a z toho vyplývá i zm na hodinového úhlu. První rovníková soustava je tedy vázána na Zemi a spolu s ní rotuje. Má proto zásadní význam pro m ení asu odvozeného z rotace Zem to je také dvod pro je hodinový úhel vyjadován v hodinové míe. Podle obrázku 1.5 též platí že úhel který svírá rovina rovníku s rovinou obzorníku je roven 9 o - ϕ. 1
11 Kapitola 1 Souadnicové soustavy Orientujme pravotoivou pravoúhlou souadnicovou soustavu tak že osa +x r1 bude procházet prseíkem místního poledníku s rovníkem osa +z r1 severním pólem P n a osa +y r1 východním bodem E. Aplikujme vztahy (1.1.4) na jednotkovou kouli. Obdržíme vztahy mezi systémem sm rových kosin (x y z) r1 v první rovníkové soustav a rovníkovými souadnicemi t δ v téže soustav ve tvaru (1.3.5) S r respektive 1 x = y z r1 cosδ cost = cosδ sint sinδ y (1.3.6) t = arctan δ = arcsin zr1. x ) Druhá rovníková souadnicová soustava S r nezávislá na ase r1 Zem obíhá kolem Slunce v rovin která svírá s rovinou sv tového rovníku úhel pibližn rovný 3.5 o a nazývá se rovina ekliptiky. Název pochází z eckého slova ekleipsis a znamená zatm ní. Pozorovateli na Zemi se skutený pohyb Zem kolem Slunce jeví jako zdánlivý pohyb Slunce po obloze po hlavní kružnici zvané ekliptika. Ekliptika protíná sv tový rovník ve dvou bodech - obr Prseík kterým prochází Slunce v den jarní rovnodennosti nazýváme jarní bod a oznauje se astronomickým symbolem souhv zdí Berana - Aries (beran). Druhý prseík kterým prochází Slunce v den podzimní rovnodennosti se nazývá podzimní bod a oznauje se symbolem - Libra (váhy). Za pomocnou základní rovinu druhé rovníkové soustavy zvolíme deklinaní rovinu procházející jarním bodem. Takto vytvoenou deklinaní kružnici zvolíme za nulovou. Polohu hv zd v této soustav urujeme pomocí rektascenze α a již definované deklinace δ. Rektascenze je úhel mezi deklinaní rovinou procházející jarním bodem a deklinaní rovinou hv zdy nebo na jednotkové kouli úhel mezi jarním bodem a deklinaní kružnicí. Pi definici pravoúhlé soustavy podle obr. 1.6 se α m í v matematicky kladném smyslu od jarního bodu v intervalu h až 4 h. (N kdy se také oznauje AR z latinského ascensio recta - pravá vzdálenost). Porovnáme-li ob rovníkové souadnicové soustavy vidíme že deklinace je v obou soustavách stejná nezávislá na rotaci Zem a na poloze místa pozorovatele ale hodinový úhel a rektascenze se liší. Uv domme si že rektascenze nezávisí na poloze místa pozorovatele ani na rotaci Zem protože se m í od jarního bodu. Z t chto dvod druhá rovníková soustava nerotuje - je tak do jisté míry nezávislá na ase - a proto se využívá na sestavení katalog souadnic hv zd efemerid (souadnic) Slunce M síce a planet. Poznámka: Nezávislost na ase není úplná protože jak uvidíme v kapitole 5 zabývající se precesí a nutací mní jarní bod rovina rovníku a ekliptiky polohu vi stálicím. Tato zmna je však ádov menší než zmna hodinového úhlu o 36 o za den. Orientujme pravotoivou pravoúhlou souadnicovou soustavu tak že osa +x r bude procházet jarním bodem osa +z r severním pólem P n a osa +y r tvoí pravotoivou sou- adnicovou soustavu. Aplikujme vztahy (1.1.4) na jednotkovou kouli. Obdržíme vztahy mezi 11
12 Kapitola 1 Souadnicové soustavy systémem sm rových kosin (x y z) ve druhé rovníkové soustav a rovníkovými souadnicemi α δ v téže soustav ve tvaru (1.3.7) S r respektive x = y z r cosδ cosα = cosδ sinα sinδ y (1.3.8) α = arctan δ = arcsin zr. x Ekliptikální souadnicová soustava r Základní rovinou ekliptikální souadnicové soustavy S e je rovina ekliptiky která protíná jednotkovou kouli v hlavní kružnici zvané ekliptika - viz obrázek 1.6. Ekliptika svírá s rovníkem úhel ε který se nazývá sklon ekliptiky. Prsenice roviny ekliptiky a roviny rovníku sm uje do jarního respektive podzimního bodu jak již bylo uvedeno výše. Hlavním sm rem je sm r kolmý k rovin ekliptiky protíná kouli v pólech ekliptiky P e a P e. Hlavní roviny proložené osou ekliptiky protínají kouli v šíkových kružnicích. Šíkovou kružnici procházející jarním bodem zvolíme za výchozí (nulovou). Obrázek 1.6: Ekliptikální soustava S e Polohu hv zdy H v ekliptikální souadnicové soustav vyjadujeme ekliptikální délkou λ a ekliptikální šíkou β. Ekliptikální délka je úhel který svírá nulová šíková rovina s šíkovou rovinou vedenou hv zdou. M í se od jarního bodu v matematicky kladném smyslu v intervalu o až 36 o. Ekliptikální šíka je úhel který svírá sm r ke hv zd OH s rovinou ekliptiky m í se podél šíkové kružnice. Nabývá hodnot -9 o až 9 o pi m ení od P e sm rem k P e. Orientujme pravotoivou pravoúhlou souadnicovou soustavu tak že osa +x e bude procházet jarním bodem osa +z e pólem P e a osa +y e tvoí pravotoivý systém. Aplikujme vztahy 1
13 Kapitola 1 Souadnicové soustavy (1.1.4) na jednotkovou kouli. Obdržíme vztahy mezi systémem sm rových kosin (x y z) e v ekliptikální soustav a ekliptikálními souadnicemi λ β v téže soustav ve tvaru (1.3.9) S e respektive x = y z e cosβ cosλ = cosβ sinλ sin β y (1.3.1) λ = arctan β = arcsin ze. x e Galaktická souadnicová soustava je vázána na galaktický rovník a galaktický pól. V geodetické astronomii se nepoužívá proto se jí nebudeme více zabývat. Pehled typ souadnicových soustav a souadnic je uveden v Tabulce 1.1. Tabulka Pehled typ souadnicových soustav používaných ve sférické a geodetické astronomii Soustava sférické souadnice zpsob mení mat. smr mení od obzorníková astronomický azimut a jižní v tve poledníku S o zenitová vzdálenost z zenitu 1. rovníková hodinový úhel t jižní v tve poledníku S r1 deklinace δ rovníku. rovníková rektascenze α + jarního bodu S r deklinace δ rovníku ekliptikální ekliptikální délka λ + jarního bodu S e ekliptikální šíka β ekliptiky Transformace mezi astronomickými souadnicovými soustavami Nech S o = (x y z) T o jsou obzorníkové pravoúhlé souadnice (sm rové kosiny) S r1 = (x y z) T r1 jsou pravoúhlé souadnice 1. rovníkové soustavy a S r = (x y z) T r jsou pravoúhlé souadnice. rovníkové soustavy téže hv zdy H na jednotkové sfée. Transformace S o S r1 Podle obrázku 1.7a vidíme že ze soustavy S r1 pejdeme do S o pootoením soustavy o úhel 9 o - ϕ kolem osy y o = y r1 v matematicky kladném smyslu. Naopak ze soustavy S o pejdeme do S r1 otáením kolem téže osy v opaném smyslu tedy (1.3.11) S S o r1 = Y ( 9 ϕ) S r1 = Y ( ϕ 9 ) S o kde transformaní matice Y je definována výrazem (1..6). Dosadíme-li nyní za S o z (1.3.3) a za S r1 z (1.3.5) do první rovnice (1.3.11) dostáváme (1.3.1) sin z cosa = sinδ cosϕ + cosδ sinϕ cost sin z sin a = cosδ sin t. cos z = sinδ sinϕ + cosδ cosϕ cost 13
14 Kapitola 1 Souadnicové soustavy Vyd líme-li druhou rovnici první a druhou rovnici tetí máme pro a a z (1.3.13) sin t tan a = sinϕ cost tanδ cosϕ tan z = sin t cos cos tan sin sin a ( ϕ t + δ ϕ) Podobn ze druhé rovnice (1.3.11) vyjde (1.3.14) cosδ cost = cos z cosϕ + sin z sinϕ cosa cosδ sin t = sin z sin a sinδ = cos z sinϕ sin z cosϕ cosa a stejným postupem jako výše pro t a δ (1.3.15) sin a tan t = cot z cosϕ + sinϕ cosa tanδ = ( ϕ ϕ ) cot z sin cos cosa sin t sin a.. a) b) Obrázek 1.7 ab: Transformace mezi astronomickými souadnicovými soustavami S o S r1 S r Ve výrazech (1.3.13) a (1.3.15) urujeme kvadranty podle znaménka funkcí sinus a kosinus piemž itatel písluší sinu a jmenovatel kosinu. V pípad že se jmenovatel blíží nule použijeme inverzní funkce. Poznámka: Pi výpotech na kalkulakách je výhodné pro urení úhlu používat funkci arctan se dvma argumenty nebo jí ekvivalentní funkci. K výrazm (1.3.1) až (1.3.15) mžeme také dosp t aplikujeme-li na nautický trojúhelník - viz obrázek vty sférické trigonometrie. V pípad (1.3.1) jde pak o sinuskosinovou sinovou a kosinovou vtu aplikovanou na zenitovou vzdálenost z a azimut a v pípad (1.3.14) o sinuskosinovou sinovou a kosinovou vtu aplikovanou na deklinaci δ a hodinový úhel t. Pro úplnost uvedeme ješt výraz pro paralaktický úhel q urený na základ sinové a sinuskosinové vty aplikované na z a q 14
15 Kapitola 1 Souadnicové soustavy (1.3.16) Jejich d lením dostaneme (1.3.17) tan q = sin z sinq = cosϕ sin t. sin z cosq = sinϕ cosδ cosϕ sinδ cost sin t tanϕ cosδ sinδ cost. Obrázek 1.7 c: Transformace mezi S r a S e Obrázek 1.8: Nautický trojúhelník Transformace S r1 S r Podle obrázku 1.7b a s použitím výsledk odstavce 1. vidíme že ze soustavy S r1 pejdeme do S r pootoením o úhel s který svírá rovina místního poledníku s deklinaní rovinou procházející jarním bodem kolem osy z r1 z r v matematicky záporném smyslu. Naopak ze soustavy S r pejdeme do S r1 otáením kolem téže osy v opaném smyslu tedy (1.3.18) ( s) ( s) S = Z S r r1 S = Z S r1 r. Úhel s se nazývá místní hvzdný as. Z hlediska soustavy S r1 je s hodinovým úhlem jarního bodu tedy docházíme k dležité definici: místní hvzdný as s je roven hodinovému úhlu jarního bodu. Dosazením do výrazu (1.3.18) z (1..) (1.3.5) a (1.3.7) dostáváme vztah mezi rektascenzí α a hodinovým úhlem t který je též okamžit zejmý z obrázku 1.7b (1.3.19) t = s - α. Z posledního výrazu plyne zajímavý výsledek. V pípad prchodu hvzdy místním poledníkem (t = pesn ji v pípad horní kulminace viz kap. ) je místní hvzdný as 15
16 Kapitola 1 Souadnicové soustavy roven rektascenzi hvzdy. Tato skutenost je dležitá pro urování místního hv zdného asu v pípad že známe rektascenzi hv zdy. Poznámka: Ze zavedení soustavy S r1 je patrné že hodinový úhel má co init s asem. Pedstavíme-li si místo hvzdy Slunce je zejmé že v horní kulminaci kdy t = bude (místní) slunení as + 1 hod (slunení as je z praktických dvod zvtšen o 1 h) pro t = 1 h bude místní slunení as = 13 h atd. Podobn je tomu s hvzdným asem. Na základ analogie se zavedením sluneního asu je zejmé že funkci Slunce zde pebírá fiktivní hvzda - jarní bod v pípad hvzdného asu není však nutno pidávat 1 h. Transformace S o S r Pro transformaci mezi obzorníkovou soustavou a druhou rovníkovou soustavou mžeme využít kombinace již odvozených výraz (1.3.11) a (1.3.18). Pak platí (1.3.) S S o r = Y = Z o ( 9 ϕ) Z( s) S r o ( s) Y ( ϕ 9 ) S o kde význam matic Y Z je vysv tlen v odstavci 1.. Dosazením za S o S r1 S r a Y Z bychom op t získali transformaní vztahy mezi azimutem a zenitovou vzdáleností z a rektascenzí α deklinací δ. Prakticky se této pímé transformace používá zídka. Transformace S e S r Podle obrázku 1.7c a s použitím výsledk odstavce 1. vidíme že ze soustavy S r pejdeme do S e pootoením o úhel ε který svírá rovina rovníku s rovinou ekliptiky kolem osy x e x r v matematicky kladném smyslu. Naopak ze soustavy S e pejdeme do S r otáením kolem téže osy v opaném smyslu tedy (1.3.1) ( ε) r ( ε) S = X S e S = X S r e kde transformaní matice X je definována výrazem (1..4). Dosadíme-li op t za S e z (1.3.9) a za S r z (1.3.7) lze pro vztahy mezi β λ a α δ psát (1.3.) a pro zp tnou transformaci máme (1.3.3) cosβ sin λ = sinδ sin ε + cosδ cosε sinα cosβ cosλ = cosδ cosα sin β = sinδ cosε cosδ sin ε sinα cosδ sinα = sin β sin ε + cosβ cosε sin λ cosδ cosα = cosβ cosλ. sinδ = sin β cosε + cosβ sin ε sin λ Podobn jako v pedchozích pípadech lze k výrazm (1.3.) a (1.3.3) dojít aplikací sinuskosinové sinové a kosinové vty sférické trigonometrie na sférický trojúhelník na obr
17 Kapitola 1 Souadnicové soustavy Obrázek 1.9: Sférický trojúhelník v pípad transformace mezi S r a S e 17
18 Kapitola Zdánlivý denní pohyb hvzd Zdánlivý denní pohyb hvzd Zdánlivý denní pohyb hv zd zpsobuje skutená rotace Zem. Zem se otoí kolem osy rotace jednou za 4 hodin hv zdného asu (pesn jší definice bude uvedena v kapitole 4) sm r pohybu se d je od západu k východu. Pozorovateli stojícímu na povrchu Zem se však zdá že se otáí obloha a to sm rem od východu k západu. Zdánlivého pohybu oblohy se úastní všechna t lesa která se nacházejí v kosmickém prostoru. Podle rzné polohy hv zdy vi základním sm rm a rovinám budeme uvažovat adu pípad. Ne všechny hv zdy totiž vycházejí a zapadají procházejí prvním vertikálem ap. Trochu jiná situace též nastává je-li místo pozorovatele umíst no na severní nebo na jižní polokouli. Z tohoto dvodu se ve svých následujících úvahách omezíme na místo pozorovatele na severní polokouli zhruba v zem pisných šíkách odpovídajících stední Evrop tedy kolem 5 severní zem pisné šíky. Pro jižní polokouli a pro δ < píslušné nerovnosti vynásobené -1 a upravené..1 Východ a západ hvzd cirkumpolární hvzdy soumraky Podle obrázku.1a jsou zejmé následující skutenosti: a) Hv zda o deklinaci δ o o (.1.1) ϕ 9 < δ < 9 ϕ vychází i zapadá. Pro hv zdu pro kterou platí o < δ < 9 o - ϕ je denní oblouk (= hv zda je nad obzorem) v tší než noní (= hv zda je pod obzorem). Pi δ = je denní oblouk roven nonímu a pi o > δ > ϕ - 9 o je noní oblouk delší než denní oblouk. Poznámka: Oznaení denní oblouk a noní oblouk je logické v pípad že hvzdou je Slunce. a) b) Obrázek.1 ab: Východ a západ hvzd V souvislosti s východem a západem Slunce mluvíme také o soumraku. Soumraky rozd lujeme na n kolik typ a platí pro n (z je zenitová vzdálenost Slunce): 18
19 Kapitola Zdánlivý denní pohyb hvzd 1) soumrak obanský nastává nejsou-li vid t žádné hv zdy a platí-li: 9 o < z < 96 o ) soumrak nautický (námoní naviganí) nastává jsou-li vid t nejjasn jší hv zdy a horizont a platí-li: 96 o < z < 1 o 3) soumrak astronomický nastává jsou-li vid t i slabé hv zdy a horizont a platí-li: 1 o < z < 18 o 4) astronomická noc nastává platí-li: z > 18 o. b) Hv zda pro jejíž deklinaci δ platí (.1.) o δ 9 ϕ 9 nezapadá je stále nad obzorem. Taková hv zda se nazývá cirkumpolární (obtonová).. Prchod elongací (maximální digresí) Hv zdy s deklinací v intervalu o (..1) δ ϕ 9 nebo též o ϕ δ 9 mají svou zdánlivou dráhu v severní polovin místního poledníku. Tyto hv zdy neprocházejí I. vertikálem ale procházejí naopak tak zvanou elongací (maximální digresí) - viz obrázek.. V pípad západní elongace je paralaktický úhel q roven 9 o v pípad východní elongace q = 7 o. Tyto pípady mají svj význam pi urování zem pisných souadnic n kterými metodami geodetické astronomie. Vyšetujme jak se v pípad prchodu hv zdy elongací m ní s asem azimut a zenitová vzdálenost. Obrázek.: Prchod hvzdy elongací (maximální digresí) V pípad elongace lze ukázat že zm na azimutu je nulová. V elongaci je tedy diferenciální pohyb v azimutu nulový a azimut zde dosahuje svých extrémních hodnot. Dalším rozborem zjistíme že pro pípad zenitové vzdálenosti jde rovn ž o extrémy. Tedy velikost asové zmny zenitové vzdálenosti je v pípad západní elongace nejvtší a v pípad východní elongace nejmenší. 19
20 Kapitola Zdánlivý denní pohyb hvzd.3 Prchod hvzd prvním vertikálem Hv zdy s deklinací v intervalu (.3.1) δ ϕ ϕ neboli ϕ ϕ procházejí prvním vertikálem - viz obr..1a. Východní i západní prchod je soum rný vi místnímu poledníku. Napíšeme-li sinovou a sinuskosinovou v tu pro nautický trojúhelník pro zenitovou vzdálenost z a azimut a mžeme vypoítat hodinový úhel t a zenitovou vzdálenost z..4 Prchod hvzd místním poledníkem horní a dolní kulminace Prochází-li hv zda místním poledníkem íkáme že kulminuje. Pokud hv zda prochází poledníkem mezi body P n a S (viz obr..1a) jde o horní kulminaci v pípad prchodu mezi body P n a N jde o dolní kulminaci. Podle obrázku.3 mžeme tak rozlišit ti pípady prchodu místním poledníkem. 1) Hv zda H 1 leží na jih od zenitu a na jih od severního pólu P n. Pro zenitovou vzdálenost z hodinový úhel t a azimut a pak platí (.4.1) z = δ h S h o ϕ 1 t1 = a1 = kde S znamená že jde o jižní hv zdu h horní kulminaci a jednika znaí H 1 z obrázku. Obrázek.3: Prchod hvzd místním poledníkem ) Hv zda H leží na sever od zenitu a na jih od severního pólu P n. Pro zenitovou vzdálenost z hodinový úhel t a azimut a pak platí (.4.) z = ϕ 18 h N h o δ t = a = kde N znamená že jde o severní hv zdu h horní kulminaci a dvojka znaí H z obrázku.
21 Kapitola Zdánlivý denní pohyb hvzd 3) Hv zda H 3 leží na sever od zenitu a na sever od severního pólu P n. Pro zenitovou vzdálenost z hodinový úhel t a azimut a pak platí (.4.3) d o h o z N = 18 δ 3 ϕ t3 = 1 a = kde N znamená že jde o severní hv zdu d horní kulminaci a trojka znaí H 3 z obrázku. Ve všech pípadech platí pro vztah místního hv zdného asu s rektascenze α hv zdy a hodinový úhel t h h (.4.4) s = t + α = + α h 1 Na základ všech tí pípad prchodu poledníkem a rovnice (.4.4) mžeme nyní upesnit vztah mezi rektascenzí a místním hv zdným asem: místní hvzdný as je roven rektascenzi hvzdy v okamžiku prchodu horní kulminací. A jaké jsou zm ny obzorníkových souadnic pi prchodu místním poledníkem? Zm na zenitové vzdálenosti je ve všech 3 pípadech nulová. Zm na azimutu je maximální v 1. a 3. pípad a minimální v. pípad. 1
22 Kapitola 3 Nerušený keplerovský pohyb 3 Nerušený keplerovský pohyb V této kapitole budou nejprve odvozeny ti Keplerovy zákony popisující relativní pohyb v prostoru vedlejšího t lesa m vi základnímu t lesu M viz obrázek 3.. T lesa budeme považovat za hmotné body o hmotnostech m a M na n ž nepsobí žádné negravitaní vlivy a z gravitaních jen ty kterými psobí vzájemn na sebe. Dále budou uvedeny vzorce urující další základní vztahy které souvisí s relativním pohybem t lesa m. Žádaným a základním výsledkem bude urení polohy a složek rychlosti v obecném ase. Strun bude pojednáno i o vztazích mezi soustavou rovníkovou a dráhovou a to mezi souadnicemi a složkami postupné rychlosti. 3.1 Odvození Keplerových zákon a dalších základních vztah V roce 169 byly Keplerem v jeho díle Astronomia nova formulovány prvé dva jeho zákony o pohybu planet kolem Slunce. V roce 1618 formuloval zákon tetí. V pvodním Keplerov vyjádení bylo zn ní t chto zákon následující: Zákon 1. (Nyní je uvád n jako druhý.) Jak se má plocha CDE k polovin doby ob hu danou nám 18 o tak se má plocha CAG anebo CAH k délce dob v CG nebo CH. Proto se stává plocha CGA mírou doby nebo stední anomálie která odpovídá oblouku excentru CG nebo stední anomálie m í pece dobu obrázek 3.1. Zákon. (Nyní je uvád n jako prvý.) Planet Marsu náleží jako tvar pouze a jedin dokonalá elipsa. Zákon 3. Je však zcela jisté a dokonale souhlasí že logaritmus pom ru mezi dobami ob h dvou libovolných planet je pesn pldruhým násobkem logaritmu pom ru stedních vzdáleností t.j. drah samotných. Obrázek 3.1: K formulaci Keplerových zákon
23 Kapitola 3 Nerušený keplerovský pohyb Tyto zákony byly Keplerem odvozeny na základ bohatých pozorování vykonaných jím a jeho pedchdci pedevším Tycho Brahem. I když jejich objevení vyžadovalo dlouhou adu let vyerpávající práce byl pesto kladný výsledek podpoen i n kolika náhodn vhodnými okolnostmi. Tak pedevším pro studium byla zvolena planeta Mars jejíž dráha je znan výstedná a pohyb relativn rychlý. Mimo to pesnost observaního materiálu který byl Keplerovi k dispozici byla 1 takže neukázal poruchy v pohybu Marsu ádov 1 velké zpsobené pedevším Jupiterem které by odvození základního tvaru dráhy zkomplikovaly. V souasné dob jsou Keplerovy zákony formulovány takto: 1. Planety se pohybují v elipsách blízkých kružnicím o spoleném ohnisku ve Slunci (pesnji v tžišti (barycentru) slunení soustavy). Plošná rychlost t.j. plocha opsaná prvodiem za jednotku asu je konstantní 3. Pomr druhé mocniny obžné doby vzhledem ke tetí mocnin hlavní poloosy je konstantní Jak již bylo eeno byly zákony odvozeny na základ observaního materiálu m ly tudíž experimentální charakter a to až do doby Newtonovy. Isaak Newton ve svém díle z roku 1687 Philosophiae naturalis principia mathematica definuje svj gravitaní zákon na jehož základ teoreticky dokazuje platnost Keplerových zákon. Tím tyto zákony nabyly obecné platnosti pro pohyb libovolných dvou tles kolem sebe nepsobí-li žádné další vn jší a vnitní síly Sestavení pohybových rovnic Obrázek 3.: Vztah mezi tlesy M a m Nejprve vysv tlíme pojem síly tak jak ho definoval Newton jednak v gravitaním zákon a jednak ve druhém pohybovém zákon. Zvolme pravoúhlou prostorovou souadnicovou soustavu x y z s poátkem O v obecném bod kterou budeme považovat za inerciální. Vi ní se bude pohybovat jak t leso m tak i základní t leso M. Jejich vzájemnou polohu uruje vektor (3.1.1) r = ρ m ρ M. Gravitaní zákon definuje sílu F vztahem 3
24 Kapitola 3 Nerušený keplerovský pohyb (3.1.) F = G Mm r r 3 kde G je gravitaní Newtonova-Cavendishova konstanta (bližší vysv tlení je v odstavci 3.1.). Tatáž síla psobí jak na hmotnost m tak i na hmotnost M jenže v opaném sm ru. V rovnici (3.1.) se pak zm ní znaménko. Podle druhého pohybového zákona se projevuje gravitaní úinek hmotnosti M tím že hmotnosti m udílí zrychlení γ m a naopak. Takže (3.1.3) F = γ m m F = γ M. Spojením rovnic (3.1.) a (3.1.3) získáme M m (3.1.4) γ m = G r γ G r 3 M = 3 r r Derivujeme-li výraz (3.1.1) podle asu platí d r d ρm d ρm = r = dt dt dt a jelikož platí ρ m = γ m a ρ M = γ M je (3.1.5) + r r µ r = kde 3 (3.1.6) µ = G( M + m ) M m. = ρ ρ je n kdy nazýváno gravitaním parametrem. Nejast ji platí m << M takže (3.1.7) µ GM a pedstavuje tzv. centrickou gravitaní konstantu t lesa M. Tak nap. pro Zemi kde M = M se jedná o geocentrickou gravitaní konstantu GM bližší viz odst Rozepíšeme-li rovnici (3.1.5) do složek získáme ti pohybové rovnice x (3.1.8) y z x + µ = y + = z + µ = 3 3 r r r 3 které popisují relativní pohyb t lesa m vi t lesu M v soustav s osami x y z a s poátkem C = M viz obrázek 3.. ešení pohybových rovnic (3.1.5) resp. (3.1.8) pedstavuje teorii nerušeného keplerovského pohybu. Integrace závisí na šesti integraních konstantách nebo se jedná o ti diferenciální rovnice druhého ádu. V odstavci 3..1 budou prezentovány šesti dráhovými elementy. Ze získaných vztah pedevším z rovnice (3.1.5) resp. (3.1.8) je možno získat další vztahy podstatné dležitosti pro pohyb dvou t les (keplerovský pohyb). Pesn platí že pohyb tlesa m kolem tlesa M (ale i naopak) se d je v rovin dané rovnicí (3.1.9) c x + c y + c z 1 3 = a procházející poátkem C = M. Koeficienty c 1 c a c 3 jsou konstantní co do velikosti i sm ru a nazývají se plošné integrály. Jsou složkami plošného vektoru c a pedstavují sm rové parametry normály N k rovin dráhy viz obr M 4
25 Kapitola 3 Nerušený keplerovský pohyb Platí že (3.1.1) a pro sm rové kosiny N platí c = c1 + c + Obrázek 3.3: Keplerovská elipsa c1 c c3 (3.1.11) = sin i sin Ω = sin i cos Ω = cosi c c c c 3 kde i je sklon roviny dráhy a je rektascenze výstupního uzlu roviny dráhy viz kapitola Symboly c 1 c a c 3 pedstavují integraní konstanty. Derivováním rovnice podle asu mžeme ješt získat vztah (3.1.1) c x + c y + c z kdy 1 3 = x y z jsou složky postupné rychlosti V viz obr Ve sledu postupu 1 následuje druhý Keplerv zákon který praví že dvojnásobek plochy opsané prvodiem za dobu t t je (3.1.13) S = c t t ) ( kde c je dvojnásobná plošná rychlost centrického prvodie r. Pro složky vektoru c pak platí (3.1.14) c yz zy c = zx xz c = xy yx 1 = 3 a pedstavují prm t c do prm ten yz zx xy. První Keplerv zákon zní že t lesa (planety) se pohybují kolem centrálního t lesa (Slunce) po elipsách v jejichž spoleném ohnisku je t žišt Slunce 3. Nejast ji je vyjadován rovnicí 1 Viz. nap. Kabelá J. Kostelecký J.: Geodetická astronomie 1. VUT. 1 str. 44 To vše z pohybových rovnic (3.1.5) resp. (3.1.8) odvozených Newtonem 5
26 Kapitola 3 Nerušený keplerovský pohyb (3.1.15) a(1 e ) r = 1+ ecos v v které e je íselná výstednost a hlavní poloosa a p = a(1 e ) je parametr. Úhel v je pravá anomálie a poítá se od hlavní poloosy 36 viz. obr 3.3. Tetí Keplerv zákon v exaktní form má tvar 3 a G( M + m) (3.1.16) = = konst. T 4π C A neboli od sm ru k pericentru A od do kde T je doba ob hu t lesa m kolem centrálního t lesa M. Jiný jeho tvar je 3 (3.1.17) n a = k ( M + m) = µ = GM kde n je stední / prm rná úhlová rychlost. Jestliže rovnici (3.1.16) sestavíme pro dv t lesa m 1 a m pak získáme pibližný tvar tetího Keplerova zákona (3.1.18) a a 1 3 T = T pi zanedbání hmotnosti m 1 << M a m << M. Dležitým vztahem je integrál živé síly (vis viva) 1 (3.1.19) V = GM r a 1 který dává možnost zjišt ní postupné rychlosti V pi znalosti pouze prvodie. Je zejmé že pravá strana rovnice musí být kladná tudíž (3.1.) r < a a pohyb je možný pouze uvnit kružnice o polom ru a. Není-li tomu tak nejedná se již o pohyb keplerovský. Druh kuželoseky dráhy - viz rovnice (3.1.15) - v závislosti na velikosti V je možno získat podle velikosti poloosy a z tabulky 3.1. Tabulka Druh kuželoseky dráhy v závislosti na hlavní poloose a a velikosti postupné rychlosti V Hlavní poloosa a Postupná rychlost V Kuželoseka z rovnice (3.1.19) a = r V = µ / r kružnice a > V < µ / r elipsa a V = µ / r parabola a < V > µ / r hyperbola 3 Lépe barycentrum Slunení soustavy 6
27 Kapitola 3 Nerušený keplerovský pohyb Z rovnice (3.1.19) též vyplývá že se rychlost V zmenšuje pi vzdalování t lesa m od základního t lesa M. Pi r a platí V. Integrál živé síly je projevem kinetické energie. Zákon zachování energie zní: (3.1.1) 1 mv + µ m 1 µ m = r a což je výraz konstantní. Prvý a druhý len na levé stran vyjaduje kinetickou a potenciální energii t les m. Na pravé stran vystupuje celková mechanická energie která je konstantní po celou dobu pohybu t lesa m nap. družice v prostoru. Rovnice (3.1.1) definuje zákon zachování energie Gravitaní konstanta V rovnici (3.1.6) a (3.1.16) vystupuje konstanta G která ve spojení s hmotností M základního t lesa vytváí tzv. centrickou gravitaní konstantu GM t lesa M. Její hodnoty pro rzná t lesa slunení soustavy uvádí tabulka 3.. Tabulka 3. - Centrické gravitaní konstanty Gravitaní konstanta Základní (centrální) t leso Oznaení Hodnota [m 3.s - ] Heliocentrická Slunce GM x 1 13 Geocentrická Zem GM x 1 9 Selenocentrická M síc GM x 1 9 Areocentrická Mars GM x 1 9 Afroditocentrická Venuše GM x 1 9 Oznaení GM se užívá ve spojitosti s družicemi a je tedy nov jšího data. Díve a nyní ješt ve fyzice a nebeské mechanice se na místo G užívá k což je již zmín ná gravitaní Newtonova-Cavendishova konstanta - viz výraz (3.1.). Její souasná nejpravd podobn jší hodnota je G = k = (6673 ± 1) m 3. s -. kg -1. V nebeské mechanice pirozených kosmických t les se tradin užívá Gaussovy gravitaní konstanty k která je podle rovnice (3.1.16) vyjádena vztahem (3.1.) k ( M m) + = π T a 3 Rovnice sdružuje ti fyzikální veliiny: hmotnost as a délku. Gaussem byla zvolena za jednotku délky hlavní poloosa zemské dráhy a položena rovna 1. Je oznaována jako astronomická jednotka a ve zkratce je zapisována jako AU. Za jednotku hmotnosti zvolil hmotnost Slunce takže hmotnosti ostatních t les jsou vyjádeny pom rem (3.1.3) hmotnost t lesa hmotnost Slunce 7
28 Kapitola 3 Nerušený keplerovský pohyb pro Zemi vychází tento pom r 1/ Za dobu T ob hu Zem kolem Slunce pijal stedních dní která pedstavuje dobu siderického roku (viz kap. 4). Získal hodnotu (3.1.4) 3 / ( astron.jednotkadélky) ( stední den)( hmotnostslunce) k = /. V souasné dob je známo že Gaussem zavedené íselné hodnoty t.j. hmotnost Zem a ob žná doba nejsou zcela správné. Jelikož však uvedená hodnota sloužila k etným výpotm a je vlastn hodnotou konvenní byla tato hodnota pijata Mezinárodní astronomickou unií jako nem nná. Délku hlavní poloosy dráhy Zem v rozm ru astronomické jednotky je pak nutné z tohoto vzorce vypoítat. Pro nov jší hodnoty T a m Zem vychází a = 1.. Gaussovu gravitaní konstantu je ovšem možné urit i pro jiné jednotky. 3. Urení polohy a složek postupné rychlosti V tomto odstavci budou nejprve uvedeny rzné druhy dráhových element poté bude urena poloha vedlejšího t lesa a složky postupné rychlosti v rovin dráhy a nakonec i v prostoru. Rovn ž bude v nována pozornost transformacím Dráhové elementy Existuje šest dráhových element které odpovídají šesti integraním konstantám. Prozatím jsme jich získali p t. Vnjší dráhové elementy viz obr. 3.3 urují orientaci dráhy v prostoru a jsou jimi rektascenze výstupního uzlu Ω. Poítáme ji od sm ru k jarnímu bodu ve smyslu matematicky kladném v rovin rovníku v intervalu o až 36 o sklon roviny dráhy i (n kdy se též znaí I). Poítáme jej od roviny rovníku matematicky kladn v intervalu o až 18 o. Pi i 9 ) jde o pohyb pímý (prográdní) pi i = 9 o jde o o o polární dráhu a pi i ( 9 18 jde o pohyb zp tný (retrográdní) argument pericentra ω. Poítáme jej od výstupního uzlu Ω v rovin dráhy v matematicky kladném smyslu v intervalu o až 36 o. Takto definované vn jší dráhové elementy se používají nap. pi popisu pohybu družic obíhajících kolem Zem. Pro planety obíhající kolem Slunce (pesn ji kolem barycentra slunení soustavy) je vztažnou rovinou rovina ekliptiky takže napíklad nepjde o rektascenzi ale délku výstupního uzlu ap. Pevod souadnic bodu mezi ekliptikální soustavou a rovníkovou soustavou je popsán v kapitole 1. Vnitní dáhové elementy popisují pohyb v rovin dráhy a jsou jimi (viz obrázek 3.4): hlavní poloosa dráhy a íselná výstednost (excentricita) e as τ prchodu pericentrem A Vn jší i vnitní dráhové elementy mohou být nahrazeny jinými. Jsou jimi nap. 8
29 Kapitola 3 Nerušený keplerovský pohyb π = Ω + ω ε = π + M kde M je stední anomálie v ase t epochy. Stední anomálie M v obecném ase t je pak dána výrazem (3..1) M = M + n( t t ) kde n je stední úhlová rychlost. Obrázek 3.4: Keplerovský pohyb - rovina dráhy Pro dráhu blízkou rovin rovníku (resp. ekliptiky) se volí vn jší dráhové elementy f = tan i sin Ω g = tan i cosω ímž se odstrauje singularita pi i resp. i 18. Pro dráhu blízkou dráze kruhové (e ) se volí za vnitní dráhové elementy h = e sin π k = e cosπ resp. λ = M + ω h = esinω k = ecosω ímž se odstrauje singularita pi e =. 3.. Urení polohy v rovin dráhy Jsou dány vnitní dráhové elementy a e τ pípadn M v ase epochy t. Pro obecný as t uríme souadnice r v resp. ξ η. Díve než uvedeme výsledné vzorce je teba definovat další veliiny a nalézt potebné vzájemné vztahy. V pedchozím textu jsme dokázali viz rovnici (3.1.9) že pohyb vedlejšího t lesa m vi základnímu t lesu M se d je v rovin procházející poátkem C = M. Jelikož nejast jším tvarem dráhy um lých družic Zem je elipsa budeme studovat pouze eliptický pohyb v rovin dráhy. Zvolme souadnicovou soustavu viz obrázek 3.4 s poátkem op t v bod C který je totožný s ohniskem elipsy. Není-li t leso M hmotným bodem pak C = M leží v barycentru. Kladná osa ξ sm uje k pericentru A a kladná osa η je k ní kolmá. Orientace dráhy vi výstupnímu uzlu Ω je dána úhlem ω tj. argumentem pericentra. Sted elipsy je S hlavní poloosa a vedlejší poloosa b = a 1 e a geometrická výstednost SC = ae kde e je íselná výstednost (excentricita). Nejbližším bodem dráhy vzhledem k poátku je pericentrum A a jeho prvodi je a(1 - e). Nejvzdálen jším je apocentrum B a jeho prvodi je a(1 + e). Je-li základním t lesem Slunce (Zem ap.) hovoíme o periheliu (perigeu ap.) a o afeliu (apogeu ap.). eské výrazy jsou písluní (pízemí) a odsluní (odzemí). Obecná poloha P je 9
30 Kapitola 3 Nerušený keplerovský pohyb dána bu pravoúhlými souadnicemi ξ η nebo polárními souadnicemi r a v. Nejast ji bude rovnice elipsy vyjádena v polárním tvaru viz též rovnici (3.1.15). (3..) ( 1 e ) a r = 1+ e cos v kde a (1 - e ) = p a p je parametr elipsy který odpovídá pravé anomálii v = 9 o. Zaveme dále pojmy excentrická anomálie E a stední anomálie M. Excentrická anomálie E odpovídá na obr. 3.4 bodm P P které jsou afinní vi bodu P a leží tedy na soustedných kružnicích o polom rech a a b. Body P P se fiktivn pohybují po t chto kružnicích nerovnom rn. Stední anomálie M odpovídá fiktivnímu bodu P který se pohybuje rovnom rn nap. po kružnici o polom ru a. Jestliže se t leso nachází v pericentru i v apocentru platí že P = P = P. Pro 1. a. kvadrant platí že v > E > M a pro 3. a 4. kvadrant platí že v < E < M. Pistupme nyní k odvození potebných vztah. Stední anomálie M Pomocí rovnice (3.1.17) uríme stední úhlovou rychlost GM (3..3) n =. 3 a Podle obrázku 3.4 pak platí (3..4) M n( t ) = τ resp. (3..5) M = M + n( t t ) viz též rovnici (3..1). Pi praktickém ešení je nutné v novat pozornost rozm rovým jednotkám. Vyjádení prvodie r jako funkce excentrické anomálie E (3..6) Pak takže Podle obrázku 3.4 platí že ( ) ξ = r cos v = a cos E ae = a cos E e η = r sin v = b sin E = a 1 e sin E. [( ) ( 1 ) ] ( 1 cos cos ) r = a cose e + e sin E r = a e E + e E (3..7) r = a( e E) 1 cos. Vztah mezi excentrickou E a pravou anomálií v Z rovnic (3..6) vyplývá že 3
31 Kapitola 3 Nerušený keplerovský pohyb tan a vzhledem k (3..7) dále platí takže tan ( cos ) ( cos ) v 1 cos v r a E e = = 1+ cos v r + a E e ( 1+ )( 1 cos ) ( 1 e)( 1+ cos E) v e E = v 1+ e E (3..8) tan = tan 1 e Plošné integrály. Plošné integrály c 1 c c 3 byly v rovnici (3.1.14) vyjádeny v tírozm rném prostoru. Pro pohyb t lesa sledovaný v jeho dráze bude platit (3..9) = c = c = c = ξ η η ξ c1 3 kde c je dvojnásobek plošné rychlosti opsané prvodiem. Z rovnic (3..6) vyplývá že (3..1) ξ = r cos v r sin v v η = r sin v + r cos v v. Výrazy (3..1) a (3..6) dosadíme do druhé rovnice (3..9) a po úprav dostaneme (3..11) c = r v což vyplývá i z geometrické pedstavy nebo c je plocha infinitezimálního obdélníku o stranách r a r v. Vztah mezi stední M a excentrickou anomálií E - Keplerova rovnice Vyjdeme z výrazu pro integrál živé síly (3.1.19) postupnou rychlost V vyjádíme pomocí složek r = Vr a r v = Vn viz obrázek 3.5. Získáme 1 (3..1) V = r + r v = Vr + Vn = µ. r a Z rovnice (3..11) a z odvozování 1. Keplerova zákona vyplývá že c µ p (3..13) v = = r r takže r µ p 1 + = µ. Po vynásobení výrazem r dostaneme r r a rr = µ a e ( r a ) a z toho okamžit a (3..14) r ( ) a e r a dr = µ a dt. 31
Obr. 4 Změna deklinace a vzdálenosti Země od Slunce v průběhu roku
 4 ZÁKLADY SFÉRICKÉ ASTRONOMIE K posouzení proslunění budovy nebo oslunění pozemku je vždy nutné stanovit polohu slunce na obloze. K tomu slouží vztahy sférické astronomie slunce. Pro sledování změn slunečního
4 ZÁKLADY SFÉRICKÉ ASTRONOMIE K posouzení proslunění budovy nebo oslunění pozemku je vždy nutné stanovit polohu slunce na obloze. K tomu slouží vztahy sférické astronomie slunce. Pro sledování změn slunečního
Sférická trigonometrie v matematické geografii a astronomii
 Sférická trigonometrie v matematické geografii a astronomii Mgr. Hana Lakomá, Ph.D., Mgr. Veronika Douchová 00 Tento učební materiál vznikl v rámci grantu FRVŠ F1 066. 1 Základní pojmy sférické trigonometrie
Sférická trigonometrie v matematické geografii a astronomii Mgr. Hana Lakomá, Ph.D., Mgr. Veronika Douchová 00 Tento učební materiál vznikl v rámci grantu FRVŠ F1 066. 1 Základní pojmy sférické trigonometrie
Filip Hroch. Astronomické pozorování. Filip Hroch. Výpočet polohy planety. Drahové elementy. Soustava souřadnic. Pohyb po elipse
 ÚTFA,Přírodovědecká fakulta MU, Brno, CZ březen 2005 březnového tématu Březnové téma je věnováno klasické sférické astronomii. Úkol se skládá z měření, výpočtu a porovnání výsledků získaných v obou částech.
ÚTFA,Přírodovědecká fakulta MU, Brno, CZ březen 2005 březnového tématu Březnové téma je věnováno klasické sférické astronomii. Úkol se skládá z měření, výpočtu a porovnání výsledků získaných v obou částech.
MASARYKOVA UNIVERZITA PEDAGOGICKÁ FAKULTA KATEDRA GEOGRAFIE. Planetární geografie seminář
 MASARYKOA UNIERZITA PEDAGOGICKÁ FAKULTA KATEDRA GEOGRAFIE květen 2008 I Měření vzdáleností ve vesmíru 1) ýpočet hodnoty pc a ly ze známé AU a převod těchto hodnot. 1 AU = 150 10 6 km Z definice paralaxy
MASARYKOA UNIERZITA PEDAGOGICKÁ FAKULTA KATEDRA GEOGRAFIE květen 2008 I Měření vzdáleností ve vesmíru 1) ýpočet hodnoty pc a ly ze známé AU a převod těchto hodnot. 1 AU = 150 10 6 km Z definice paralaxy
GEODETICKÁ ASTRONOMIE A KOSMICKÁ GEODEZIE I
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ JAN FIXEL, RADOVAN MACHOTKA GEODETICKÁ ASTRONOMIE A KOSMICKÁ GEODEZIE I MODUL 01 SFÉRICKÁ ASTRONOMIE STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ JAN FIXEL, RADOVAN MACHOTKA GEODETICKÁ ASTRONOMIE A KOSMICKÁ GEODEZIE I MODUL 01 SFÉRICKÁ ASTRONOMIE STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU
pohyb hvězdy ve vesmírném prostoru vlastní pohyb hvězdy pohyb, změna, souřadné soustavy vzhledem ke stálicím precese,
 Změny souřadnic nebeských těles pohyb hvězdy ve vesmírném prostoru vlastní pohyb hvězdy vlastní pohyb max. 10 /rok, v průměru 0.013 /rok pohyb, změna, souřadné soustavy vzhledem ke stálicím precese, nutace,
Změny souřadnic nebeských těles pohyb hvězdy ve vesmírném prostoru vlastní pohyb hvězdy vlastní pohyb max. 10 /rok, v průměru 0.013 /rok pohyb, změna, souřadné soustavy vzhledem ke stálicím precese, nutace,
MATEMATICKÁ KARTOGRAFIE
 VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KARTOGRAFIE MODUL KARTOGRAFICKÁ ZKRESLENÍ STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Matematická kartografie
VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KARTOGRAFIE MODUL KARTOGRAFICKÁ ZKRESLENÍ STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Matematická kartografie
Korekce souřadnic. 2s [ rad] R. malé změny souřadnic, které je nutno uvažovat při stanovení polohy astronomických objektů. výška pozorovatele
![Korekce souřadnic. 2s [ rad] R. malé změny souřadnic, které je nutno uvažovat při stanovení polohy astronomických objektů. výška pozorovatele Korekce souřadnic. 2s [ rad] R. malé změny souřadnic, které je nutno uvažovat při stanovení polohy astronomických objektů. výška pozorovatele](/thumbs/51/28250241.jpg) OPT/AST L07 Korekce souřadnic malé změny souřadnic, které je nutno uvažovat při stanovení polohy astronomických objektů výška pozorovatele konečný poloměr země R výška h objektu závisí na výšce s stanoviště
OPT/AST L07 Korekce souřadnic malé změny souřadnic, které je nutno uvažovat při stanovení polohy astronomických objektů výška pozorovatele konečný poloměr země R výška h objektu závisí na výšce s stanoviště
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Geodetická astronomie 3/6 Aplikace keplerovského pohybu
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Geodetická astronomie 3/6 Aplikace keplerovského pohybu
Interpretace pozorování planet na obloze a hvězdné obloze
 Interpretace pozorování planet na obloze a hvězdné obloze - role vztažné soustavy - modely Sluneční soustavy stejná pozorování je možné vysvětlit různými modely! heliocentrický x geocentrický model Tanec
Interpretace pozorování planet na obloze a hvězdné obloze - role vztažné soustavy - modely Sluneční soustavy stejná pozorování je možné vysvětlit různými modely! heliocentrický x geocentrický model Tanec
Interpretace pozorování planet na obloze a hvězdné obloze
 Interpretace pozorování planet na obloze a hvězdné obloze - role vztažné soustavy - modely Sluneční soustavy stejná pozorování je možné vysvětlit různými modely! heliocentrický x geocentrický model Tanec
Interpretace pozorování planet na obloze a hvězdné obloze - role vztažné soustavy - modely Sluneční soustavy stejná pozorování je možné vysvětlit různými modely! heliocentrický x geocentrický model Tanec
Interpretace pozorování planet na obloze a hvězdné obloze
 Interpretace pozorování planet na obloze a hvězdné obloze - role vztažné soustavy - modely Sluneční soustavy stejná pozorování je možné vysvětlit různými modely! heliocentrický x geocentrický model Tanec
Interpretace pozorování planet na obloze a hvězdné obloze - role vztažné soustavy - modely Sluneční soustavy stejná pozorování je možné vysvětlit různými modely! heliocentrický x geocentrický model Tanec
Obsah. 1 Sférická astronomie Základní problémy sférické astronomie... 8
 Obsah 1 Sférická astronomie 3 1.1 Základní pojmy sférické astronomie................. 3 1.2 Souřadnicové soustavy........................ 5 1.2.1 Azimutální souřadnicový systém............... 6 1.2.2 Ekvatoreální
Obsah 1 Sférická astronomie 3 1.1 Základní pojmy sférické astronomie................. 3 1.2 Souřadnicové soustavy........................ 5 1.2.1 Azimutální souřadnicový systém............... 6 1.2.2 Ekvatoreální
KLASICKÁ MECHANIKA. Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny.
 MECHANIKA 1 KLASICKÁ MECHANIKA Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny. Klasická mechanika rychlosti těles jsou mnohem menší než rychlost světla ve
MECHANIKA 1 KLASICKÁ MECHANIKA Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny. Klasická mechanika rychlosti těles jsou mnohem menší než rychlost světla ve
4. EZY NA KUŽELÍCH 4.1. KUŽELOVÁ PLOCHA, KUŽEL
 4. EZY NA KUŽELÍCH 4.1. KUŽELOVÁ PLOCHA, KUŽEL Definice : Je dána kružnice k ležící v rovin a mimo ni bod V. Všechny pímky jdoucí bodem V a protínající kružnici k tvoí kruhovou kuželovou plochu. Tyto pímky
4. EZY NA KUŽELÍCH 4.1. KUŽELOVÁ PLOCHA, KUŽEL Definice : Je dána kružnice k ležící v rovin a mimo ni bod V. Všechny pímky jdoucí bodem V a protínající kružnici k tvoí kruhovou kuželovou plochu. Tyto pímky
Základní jednotky v astronomii
 v01.00 Základní jednotky v astronomii Ing. Neliba Vlastimil AK Kladno 2005 Délka - l Slouží pro určení vzdáleností ve vesmíru Základní jednotkou je metr metr je definován jako délka, jež urazí světlo ve
v01.00 Základní jednotky v astronomii Ing. Neliba Vlastimil AK Kladno 2005 Délka - l Slouží pro určení vzdáleností ve vesmíru Základní jednotkou je metr metr je definován jako délka, jež urazí světlo ve
Jiří Cajthaml. ČVUT v Praze, katedra geomatiky. zimní semestr 2014/2015
 Kartografie 1 - přednáška 1 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Úvod přednášky, cvičení, zápočty, zkoušky Jiří Cajthaml (přednášky, cvičení) potřebné znalosti: vzorce
Kartografie 1 - přednáška 1 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Úvod přednášky, cvičení, zápočty, zkoušky Jiří Cajthaml (přednášky, cvičení) potřebné znalosti: vzorce
MATEMATICKÁ KARTOGRAFIE
 VYSOKÉ UENÍ TECHNICKÉ V BN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KATOGAFIE MODUL 3 KATOGAFICKÉ ZOBAZENÍ STUDIJNÍ OPOY PO STUDIJNÍ POGAMY S KOMBINOVANOU FOMOU STUDIA Matematická kartografie Modul 3
VYSOKÉ UENÍ TECHNICKÉ V BN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KATOGAFIE MODUL 3 KATOGAFICKÉ ZOBAZENÍ STUDIJNÍ OPOY PO STUDIJNÍ POGAMY S KOMBINOVANOU FOMOU STUDIA Matematická kartografie Modul 3
Astronomická pozorování
 KLASICKÁ ASTRONOMIE Astronomická pozorování Základní úloha při pozorování nějakého děje, zejména pohybu těles je stanovení jeho polohy (rychlosti) v daném okamžiku Astronomie a poziční astronomie Souřadnicové
KLASICKÁ ASTRONOMIE Astronomická pozorování Základní úloha při pozorování nějakého děje, zejména pohybu těles je stanovení jeho polohy (rychlosti) v daném okamžiku Astronomie a poziční astronomie Souřadnicové
b) Maximální velikost zrychlení automobilu, nemají-li kola prokluzovat, je a = f g. Automobil se bude rozjíždět po dobu t = v 0 fg = mfgv 0
 Řešení úloh. kola 58. ročníku fyzikální olympiády. Kategorie A Autoři úloh: J. Thomas, 5, 6, 7), J. Jírů 2,, 4).a) Napíšeme si pohybové rovnice, ze kterých vyjádříme dobu jízdy a zrychlení automobilu A:
Řešení úloh. kola 58. ročníku fyzikální olympiády. Kategorie A Autoři úloh: J. Thomas, 5, 6, 7), J. Jírů 2,, 4).a) Napíšeme si pohybové rovnice, ze kterých vyjádříme dobu jízdy a zrychlení automobilu A:
Úvod do nebeské mechaniky
 OPT/AST L09 Úvod do nebeské mechaniky pohyby astronomických těles ve společném gravitačním poli obecně: chaotický systém nestabilní numerické řešení speciální případ: problém dvou těles analytické řešení
OPT/AST L09 Úvod do nebeské mechaniky pohyby astronomických těles ve společném gravitačním poli obecně: chaotický systém nestabilní numerické řešení speciální případ: problém dvou těles analytické řešení
Zpracoval Zdeněk Hlaváč. 1. Definujte hlavní kružnici kulové plochy. Uveďte příklady hlavních kružnic na zeměkouli.
 Teoretické otázky ke zkoušce z NEBESKÉ MECHANIKY Zpracoval Zdeněk Hlaváč A) Základní formulace 1. Definujte hlavní kružnici kulové plochy. Uveďte příklady hlavních kružnic na zeměkouli. 2. Popište pojmy
Teoretické otázky ke zkoušce z NEBESKÉ MECHANIKY Zpracoval Zdeněk Hlaváč A) Základní formulace 1. Definujte hlavní kružnici kulové plochy. Uveďte příklady hlavních kružnic na zeměkouli. 2. Popište pojmy
Definice : Jsou li povrchové pímky kolmé k rovin, vzniká kolmá kruhová válcová plocha a pomocí roviny také kolmý kruhový válec.
 3. EZY NA VÁLCÍCH 3.1. VÁLCOVÁ PLOCHA, VÁLEC Definice : Je dána kružnice k ležící v rovin a pímka a rznobžná s rovinou. Všechny pímky rovnobžné s pímkou a protínající kružnici k tvoí kruhovou válcovou
3. EZY NA VÁLCÍCH 3.1. VÁLCOVÁ PLOCHA, VÁLEC Definice : Je dána kružnice k ležící v rovin a pímka a rznobžná s rovinou. Všechny pímky rovnobžné s pímkou a protínající kružnici k tvoí kruhovou válcovou
2. Kinematika bodu a tělesa
 2. Kinematika bodu a tělesa Kinematika bodu popisuje těleso nebo také bod, který se pohybuje po nějaké trajektorii, křivce nebo jinak definované dráze v závislosti na poloze bodu na dráze, rychlosti a
2. Kinematika bodu a tělesa Kinematika bodu popisuje těleso nebo také bod, který se pohybuje po nějaké trajektorii, křivce nebo jinak definované dráze v závislosti na poloze bodu na dráze, rychlosti a
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV MATEMATIKY FACULTY OF MECHANICAL ENGINEERING INSTITUTE OF MATHEMATICS UŽITÍ SFÉRICKÉ GEOMETRIE V ZEMĚPISE
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV MATEMATIKY FACULTY OF MECHANICAL ENGINEERING INSTITUTE OF MATHEMATICS UŽITÍ SFÉRICKÉ GEOMETRIE V ZEMĚPISE
6. Vektorový počet Studijní text. 6. Vektorový počet
 6. Vektorový počet Budeme se pohybovat v prostoru R n, což je kartézská mocnina množiny reálných čísel R; R n = R R. Obvykle nám bude stačit omezení na případy n = 1, 2, 3; nicméně teorie je platná obecně.
6. Vektorový počet Budeme se pohybovat v prostoru R n, což je kartézská mocnina množiny reálných čísel R; R n = R R. Obvykle nám bude stačit omezení na případy n = 1, 2, 3; nicméně teorie je platná obecně.
REKONSTRUKCE ASTROLÁBU POMOCÍ STEREOGRAFICKÉ PROJEKCE
 REKONTRUKCE ATROLÁBU POMOCÍ TEREOGRAFICKÉ PROJEKCE Václav Jára 1 1 tereografická projekce a její vlastnosti tereografická projekce kulové plochy je středové promítání z bodu této kulové plochy do tečné
REKONTRUKCE ATROLÁBU POMOCÍ TEREOGRAFICKÉ PROJEKCE Václav Jára 1 1 tereografická projekce a její vlastnosti tereografická projekce kulové plochy je středové promítání z bodu této kulové plochy do tečné
! " # $ % # & ' ( ) * + ), -
 ! " # $ % # & ' ( ) * + ), - INDIVIDUÁLNÍ VÝUKA MATEMATIKA METODIKA Kuželosek Mgr. Petra Dunovská bezen 9 Obtížnost této kapitol matematik je dána tím, že se pi výkladu i ešení úloh komplexn vužívají vdomosti
! " # $ % # & ' ( ) * + ), - INDIVIDUÁLNÍ VÝUKA MATEMATIKA METODIKA Kuželosek Mgr. Petra Dunovská bezen 9 Obtížnost této kapitol matematik je dána tím, že se pi výkladu i ešení úloh komplexn vužívají vdomosti
Jiří Cajthaml. ČVUT v Praze, katedra geomatiky. zimní semestr 2014/2015
 Kartografie 1 - přednáška 2 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Kartografické zobrazení kartografické zobrazení vzájemné přiřazení polohy bodů na dvou různých referenčních
Kartografie 1 - přednáška 2 Jiří Cajthaml ČVUT v Praze, katedra geomatiky zimní semestr 2014/2015 Kartografické zobrazení kartografické zobrazení vzájemné přiřazení polohy bodů na dvou různých referenčních
Lineární algebra : Metrická geometrie
 Lineární algebra : Metrická geometrie (16. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 6. května 2014, 10:42 1 2 Úvod Zatím jsme se lineární geometrii věnovali v kapitole o lineárních
Lineární algebra : Metrická geometrie (16. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 6. května 2014, 10:42 1 2 Úvod Zatím jsme se lineární geometrii věnovali v kapitole o lineárních
FYZIKA I. Gravitační pole. Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D. Doc. Ing. Irena Hlaváčová, Ph.D. Mgr. Art.
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERITA OSTRAVA FAKULTA STROJNÍ FYIKA I Gravitační pole Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D. Doc. Ing. Irena Hlaváčová, Ph.D. Mgr. Art. Dagmar Mádrová
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERITA OSTRAVA FAKULTA STROJNÍ FYIKA I Gravitační pole Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D. Doc. Ing. Irena Hlaváčová, Ph.D. Mgr. Art. Dagmar Mádrová
Seriál VII.IV Astronomické souřadnice
 Výfučtení: Astronomické souřadnice Představme si naši oblíbenou hvězdu, kterou chceme ukázat našemu kamarádovi. Kamarád je ale zrovna na dovolené, a tak mu ji nemůžeme ukázat přímo. Rádi bychom mu tedy
Výfučtení: Astronomické souřadnice Představme si naši oblíbenou hvězdu, kterou chceme ukázat našemu kamarádovi. Kamarád je ale zrovna na dovolené, a tak mu ji nemůžeme ukázat přímo. Rádi bychom mu tedy
KINEMATICKÁ GEOMETRIE V ROVIN
 KINEMATICKÁ GEOMETRIE V ROVIN Kivka je jednoparametrická množina bod X(t), jejíž souadnice jsou dány funkcemi: x = x(t), y = y(t), t I R. Tena kivky je urena bodem dotyku X a teným vektorem o souadnicích
KINEMATICKÁ GEOMETRIE V ROVIN Kivka je jednoparametrická množina bod X(t), jejíž souadnice jsou dány funkcemi: x = x(t), y = y(t), t I R. Tena kivky je urena bodem dotyku X a teným vektorem o souadnicích
Projekty - Vybrané kapitoly z matematické fyziky
 Projekty - Vybrané kapitoly z matematické fyziky Klára Švarcová klara.svarcova@tiscali.cz 1 Obsah 1 Průlet tělesa skrz Zemi 3 1.1 Zadání................................. 3 1. Řešení.................................
Projekty - Vybrané kapitoly z matematické fyziky Klára Švarcová klara.svarcova@tiscali.cz 1 Obsah 1 Průlet tělesa skrz Zemi 3 1.1 Zadání................................. 3 1. Řešení.................................
X = A + tu. Obr x = a 1 + tu 1 y = a 2 + tu 2, t R, y = kx + q, k, q R (6.1)
 .6. Analtická geometrie lineárních a kvadratických útvarů v rovině. 6.1. V této kapitole budeme studovat geometrické úloh v rovině analtick, tj. lineární a kvadratické geometrické útvar vjádříme pomocí
.6. Analtická geometrie lineárních a kvadratických útvarů v rovině. 6.1. V této kapitole budeme studovat geometrické úloh v rovině analtick, tj. lineární a kvadratické geometrické útvar vjádříme pomocí
MATEMATICKÁ KARTOGRAFIE
 VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KARTOGRAFIE MODUL 5 NEPRAVÁ ZOBRAZENÍ STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Matematická kartografie Modul
VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KARTOGRAFIE MODUL 5 NEPRAVÁ ZOBRAZENÍ STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Matematická kartografie Modul
7. Gravitační pole a pohyb těles v něm
 7. Gravitační pole a pohyb těles v něm Gravitační pole - existuje v okolí každého hmotného tělesa - představuje formu hmoty - zprostředkovává vzájemné silové působení mezi tělesy Newtonův gravitační zákon:
7. Gravitační pole a pohyb těles v něm Gravitační pole - existuje v okolí každého hmotného tělesa - představuje formu hmoty - zprostředkovává vzájemné silové působení mezi tělesy Newtonův gravitační zákon:
1.6.9 Keplerovy zákony
 1.6.9 Keplerovy zákony Předpoklady: 1608 Pedagogická poznámka: K výkladu této hodiny používám freewareový program Celestia (3D simulátor vesmíru), který umožňuje putovat vesmírem a sledovat ho z různých
1.6.9 Keplerovy zákony Předpoklady: 1608 Pedagogická poznámka: K výkladu této hodiny používám freewareový program Celestia (3D simulátor vesmíru), který umožňuje putovat vesmírem a sledovat ho z různých
5a. Globální referenční systémy Parametry orientace Země (EOP) Aleš Bezděk
 5a. Globální referenční systémy Parametry orientace Země (EOP) Aleš Bezděk Teoretická geodézie 4 FSV ČVUT 2017/2018 LS 1 Celková orientace zemského tělesa, tj. precese-nutace+pohyb pólu+vlastní rotace,
5a. Globální referenční systémy Parametry orientace Země (EOP) Aleš Bezděk Teoretická geodézie 4 FSV ČVUT 2017/2018 LS 1 Celková orientace zemského tělesa, tj. precese-nutace+pohyb pólu+vlastní rotace,
Odchylka ekliptiky od roviny Galaxie
 Jiří Kapr 1, Jakub Fuis 2, Tomáš Bárta 3 1 Gymnázium Plasy, Plasy 2 Gymnázium Botičská, Praha 3 Gymnázium Nad Štolou, Praha Týden Vědy, 2010 Jiří Kapr 1, Jakub Fuis 2, Tomáš Bárta 3 1 Gymnázium Plasy,
Jiří Kapr 1, Jakub Fuis 2, Tomáš Bárta 3 1 Gymnázium Plasy, Plasy 2 Gymnázium Botičská, Praha 3 Gymnázium Nad Štolou, Praha Týden Vědy, 2010 Jiří Kapr 1, Jakub Fuis 2, Tomáš Bárta 3 1 Gymnázium Plasy,
Cyklografie. Cyklický průmět bodu
 Cyklografie Cyklografie je nelineární zobrazovací metoda - bodům v prostoru odpovídají kružnice v rovině a naopak. Úlohy v rovině pak převádíme na řešení prostorových úloh, např. pomocí cyklografie řešíme
Cyklografie Cyklografie je nelineární zobrazovací metoda - bodům v prostoru odpovídají kružnice v rovině a naopak. Úlohy v rovině pak převádíme na řešení prostorových úloh, např. pomocí cyklografie řešíme
ČASOMÍRA ROTAČNÍ ČASY FYZIKÁLNĚ DEFINOVANÉ ČASY JULIÁNSKÉ DATUM
 ČASOMÍRA ROTAČNÍ ČASY FYZIKÁLNĚ DEFINOVANÉ ČASY JULIÁNSKÉ DATUM Hynčicová Tereza, H2IGE1 2014 ČAS Jedna ze základních fyzikálních veličin Využívá se k určení časových údajů sledovaných jevů Časovou škálu
ČASOMÍRA ROTAČNÍ ČASY FYZIKÁLNĚ DEFINOVANÉ ČASY JULIÁNSKÉ DATUM Hynčicová Tereza, H2IGE1 2014 ČAS Jedna ze základních fyzikálních veličin Využívá se k určení časových údajů sledovaných jevů Časovou škálu
Pravdpodobnost výskytu náhodné veliiny na njakém intervalu urujeme na základ tchto vztah: f(x)
 NÁHODNÁ VELIINA Náhodná veliina je veliina, jejíž hodnota je jednoznan urena výsledkem náhodného pokusu (je-li tento výsledek dán reálným íslem). Jde o reálnou funkci definovanou na základním prostoru
NÁHODNÁ VELIINA Náhodná veliina je veliina, jejíž hodnota je jednoznan urena výsledkem náhodného pokusu (je-li tento výsledek dán reálným íslem). Jde o reálnou funkci definovanou na základním prostoru
Skalární a vektorový popis silového pole
 Skalární a vektorový popis silového pole Elektrické pole Elektrický náboj Q [Q] = C Vlastnost materiálových objektů Interakce (vzájemné silové působení) Interakci (vzájemné silové působení) mezi dvěma
Skalární a vektorový popis silového pole Elektrické pole Elektrický náboj Q [Q] = C Vlastnost materiálových objektů Interakce (vzájemné silové působení) Interakci (vzájemné silové působení) mezi dvěma
Analytická geometrie lineárních útvarů
 ) Na přímce: a) Souřadnice bodu na přímce: Analtická geometrie lineárních útvarů Bod P nazýváme počátek - jeho souřadnice je P [0] Nalevo od počátku leží čísla záporná, napravo čísla kladná. Každý bod
) Na přímce: a) Souřadnice bodu na přímce: Analtická geometrie lineárních útvarů Bod P nazýváme počátek - jeho souřadnice je P [0] Nalevo od počátku leží čísla záporná, napravo čísla kladná. Každý bod
Vzdálenosti a východ Slunce
 Vzdálenosti a východ Slunce Zdeněk Halas KDM MFF UK, 2011 Aplikace matem. pro učitele Zdeněk Halas (KDM MFF UK, 2011) Vzdálenosti a východ Slunce Aplikace matem. pro učitele 1 / 8 Osnova Zdeněk Halas (KDM
Vzdálenosti a východ Slunce Zdeněk Halas KDM MFF UK, 2011 Aplikace matem. pro učitele Zdeněk Halas (KDM MFF UK, 2011) Vzdálenosti a východ Slunce Aplikace matem. pro učitele 1 / 8 Osnova Zdeněk Halas (KDM
Derivace goniometrických funkcí
 Derivace goniometrických funkcí Shrnutí Jakub Michálek, Tomáš Kučera Odvodí se základní vztahy pro derivace funkcí sinus a cosinus za pomoci věty o třech itách, odvodí se také několik typických it pomocí
Derivace goniometrických funkcí Shrnutí Jakub Michálek, Tomáš Kučera Odvodí se základní vztahy pro derivace funkcí sinus a cosinus za pomoci věty o třech itách, odvodí se také několik typických it pomocí
Mnohé problémy analýzy dynamických systémů vedou k řešení diferenciální rovnice (4.1)
 4 Řešení odezev dynamických systémů ve fázové rovině 4.1 Základní pojmy teorie fázové roviny Mnohé problémy analýzy dynamických systémů vedou k řešení diferenciální rovnice ( ) x+ F x, x = (4.1) kde F(
4 Řešení odezev dynamických systémů ve fázové rovině 4.1 Základní pojmy teorie fázové roviny Mnohé problémy analýzy dynamických systémů vedou k řešení diferenciální rovnice ( ) x+ F x, x = (4.1) kde F(
( ) ( ) 2 2 B A B A ( ) ( ) ( ) B A B A B A
 Vzdálenost dvou bod, sted úseky Ž Vzdálenost dvou bod Pi vyšetování vzájemné polohy bod, pímek a rovin lze použít libovolnou vhodn zvolenou soustavu souadnic (afinní). však pi vyšetování metrických vlastností
Vzdálenost dvou bod, sted úseky Ž Vzdálenost dvou bod Pi vyšetování vzájemné polohy bod, pímek a rovin lze použít libovolnou vhodn zvolenou soustavu souadnic (afinní). však pi vyšetování metrických vlastností
VYBRANÉ APLIKACE RIEMANNOVA INTEGRÁLU I. OBSAH A DÉLKA. (f(x) g(x)) dx.
 VYBRANÉ APLIKACE RIEMANNOVA INTEGRÁLU I. OBSAH A DÉLKA. Výpo et obsahu rovinných ploch a) Plocha ohrani ená k ivkami zadanými v kartézských sou adnicích. Obsah S rovinné plochy ohrani ené dv ma spojitými
VYBRANÉ APLIKACE RIEMANNOVA INTEGRÁLU I. OBSAH A DÉLKA. Výpo et obsahu rovinných ploch a) Plocha ohrani ená k ivkami zadanými v kartézských sou adnicích. Obsah S rovinné plochy ohrani ené dv ma spojitými
Obsah. Obsah. 2.3 Pohyby v radiálním poli Doplňky 16. F g = κ m 1m 2 r 2 Konstantu κ nazýváme gravitační konstantou.
 Obsah Obsah 1 Newtonův gravitační zákon 1 2 Gravitační pole 3 2.1 Tíhové pole............................ 5 2.2 Radiální gravitační pole..................... 8 2.3..................... 11 3 Doplňky 16
Obsah Obsah 1 Newtonův gravitační zákon 1 2 Gravitační pole 3 2.1 Tíhové pole............................ 5 2.2 Radiální gravitační pole..................... 8 2.3..................... 11 3 Doplňky 16
Urení rychlosti svtla Römerovou metodou
 Urení rychlosti svtla Römerovou metodou Informace pro uitele Obtížnost: 4. roník SŠ Cíle: Cílem tohoto cviení je uit rychlost svtla tak, jak ji zmil Olaf Ch. Römer. Studenti si jednak procvií základy planimetrie,
Urení rychlosti svtla Römerovou metodou Informace pro uitele Obtížnost: 4. roník SŠ Cíle: Cílem tohoto cviení je uit rychlost svtla tak, jak ji zmil Olaf Ch. Römer. Studenti si jednak procvií základy planimetrie,
Téma: Úvod(Souřadnice a základy sférické trigonometrie)
 Téma: Úvod(Souřadnice a základy sférické trigonometrie) Zpracoval Doc. RNDr. Zdeněk Hlaváč, CSc Kartézské souřadnicové soustavy Pravoúhlá pravotočivá kartézská souřadnicová soustava v třírozměrném Euklidovském
Téma: Úvod(Souřadnice a základy sférické trigonometrie) Zpracoval Doc. RNDr. Zdeněk Hlaváč, CSc Kartézské souřadnicové soustavy Pravoúhlá pravotočivá kartézská souřadnicová soustava v třírozměrném Euklidovském
terminologie předchozí kapitoly: (ϕ, Ω) - plocha, S - geometrický obraz plochy
 2. Plošný integrál. Poznámka. Obecně: integrování přes k-rozměrné útvary (k-plochy) v R n. Omezíme se na případ k = 2, n = 3. Definice. Množina S R 3 se nazve plocha, pokud S = ϕ(), kde R 2 je otevřená
2. Plošný integrál. Poznámka. Obecně: integrování přes k-rozměrné útvary (k-plochy) v R n. Omezíme se na případ k = 2, n = 3. Definice. Množina S R 3 se nazve plocha, pokud S = ϕ(), kde R 2 je otevřená
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Kosmická geodézie 5/ Určování astronomických zeměpisných
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ OBOR GEODÉZIE A KARTOGRAFIE KATEDRA VYŠŠÍ GEODÉZIE název předmětu úloha/zadání název úlohy Kosmická geodézie 5/ Určování astronomických zeměpisných
R β α. Obrázek 1: Zadání - profil složený ze třech elementárních obrazců: 1 - rovnoramenný pravoúhlý trojúhelník, 2 - čtverec, 3 - kruhová díra
 Zadání: Vypočtěte polohu těžiště, momenty setrvačnosti a deviační moment k centrálním osám a dále určete hlavní centrální momenty setrvačnosti, poloměry setrvačnosti a natočení hlavních centrálních os
Zadání: Vypočtěte polohu těžiště, momenty setrvačnosti a deviační moment k centrálním osám a dále určete hlavní centrální momenty setrvačnosti, poloměry setrvačnosti a natočení hlavních centrálních os
Úvodní informace. 17. února 2018
 Úvodní informace Funkce více proměnných Přednáška první 17. února 2018 Obsah 1 Úvodní informace. 2 Funkce více proměnných Definiční obor Limita a spojitost Derivace, diferencovatelnost, diferenciál Úvodní
Úvodní informace Funkce více proměnných Přednáška první 17. února 2018 Obsah 1 Úvodní informace. 2 Funkce více proměnných Definiční obor Limita a spojitost Derivace, diferencovatelnost, diferenciál Úvodní
Hvězdářský zeměpis Obloha a hvězdná obloha
 Hvězdářský zeměpis Obloha a hvězdná obloha směr = polopřímka, spojující oči, kterými sledujeme svět kolem sebe, s daným objektem obzor = krajina, kterou obzíráme, v našem dohledu (budovy, stromy, kopce)
Hvězdářský zeměpis Obloha a hvězdná obloha směr = polopřímka, spojující oči, kterými sledujeme svět kolem sebe, s daným objektem obzor = krajina, kterou obzíráme, v našem dohledu (budovy, stromy, kopce)
Matematická analýza III.
 2. Parciální derivace Miroslav Hušek, Lucie Loukotová UJEP 2010 Parciální derivace jsou zobecněním derivace funkce jedné proměnné. V této kapitole poznáme jejich základní vlastnosti a využití. Co bychom
2. Parciální derivace Miroslav Hušek, Lucie Loukotová UJEP 2010 Parciální derivace jsou zobecněním derivace funkce jedné proměnné. V této kapitole poznáme jejich základní vlastnosti a využití. Co bychom
4. Napjatost v bodě tělesa
 p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
Matematická kartografie. Černý J., Kočandrlová M.: Konstruktivní geometrie, ČVUT. Referenční plochy
 Matematická kartografie Buchar.: Matematická kartografie 10, ČVUT; Černý J., Kočandrlová M.: Konstruktivní geometrie, ČVUT Referenční plochy referenční elipsoid (sféroid) zploštělý rotační elipsoid Besselův
Matematická kartografie Buchar.: Matematická kartografie 10, ČVUT; Černý J., Kočandrlová M.: Konstruktivní geometrie, ČVUT Referenční plochy referenční elipsoid (sféroid) zploštělý rotační elipsoid Besselův
Obecný Hookeův zákon a rovinná napjatost
 Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
Kinematika tuhého tělesa. Pohyb tělesa v rovině a v prostoru, posuvný a rotační pohyb
 Kinematika tuhého tělesa Pohyb tělesa v rovině a v prostoru, posuvný a rotační pohyb Úvod Tuhé těleso - definice všechny body tělesa mají stálé vzájemné vzdálenosti těleso se nedeformuje, nemění tvar počet
Kinematika tuhého tělesa Pohyb tělesa v rovině a v prostoru, posuvný a rotační pohyb Úvod Tuhé těleso - definice všechny body tělesa mají stálé vzájemné vzdálenosti těleso se nedeformuje, nemění tvar počet
Referenční plochy a souřadnice na těchto plochách Zeměpisné, pravoúhlé, polární a kartografické souřadnice
 Referenční plochy a souřadnice na těchto plochách Zeměpisné, pravoúhlé, polární a kartografické souřadnice Kartografie přednáška 5 Referenční plochy souřadnicových soustav slouží k lokalizaci bodů, objektů
Referenční plochy a souřadnice na těchto plochách Zeměpisné, pravoúhlé, polární a kartografické souřadnice Kartografie přednáška 5 Referenční plochy souřadnicových soustav slouží k lokalizaci bodů, objektů
BIOMECHANIKA KINEMATIKA
 BIOMECHANIKA KINEMATIKA MECHANIKA Mechanika je nejstarším oborem fyziky (z řeckého méchané stroj). Byla původně vědou, která se zabývala konstrukcí strojů a jejich činností. Mechanika studuje zákonitosti
BIOMECHANIKA KINEMATIKA MECHANIKA Mechanika je nejstarším oborem fyziky (z řeckého méchané stroj). Byla původně vědou, která se zabývala konstrukcí strojů a jejich činností. Mechanika studuje zákonitosti
Necht L je lineární prostor nad R. Operaci : L L R nazýváme
 Skalární součin axiomatická definice odvození velikosti vektorů a úhlu mezi vektory geometrická interpretace ortogonalita vlastnosti ortonormálních bázi [1] Definice skalárního součinu Necht L je lineární
Skalární součin axiomatická definice odvození velikosti vektorů a úhlu mezi vektory geometrická interpretace ortogonalita vlastnosti ortonormálních bázi [1] Definice skalárního součinu Necht L je lineární
Rychlost, zrychlení, tíhové zrychlení
 Úloha č. 3 Rychlost, zrychlení, tíhové zrychlení Úkoly měření: 1. Sestavte nakloněnou rovinu a změřte její sklon.. Změřte závislost polohy tělesa na čase a stanovte jeho rychlost a zrychlení. 3. Určete
Úloha č. 3 Rychlost, zrychlení, tíhové zrychlení Úkoly měření: 1. Sestavte nakloněnou rovinu a změřte její sklon.. Změřte závislost polohy tělesa na čase a stanovte jeho rychlost a zrychlení. 3. Určete
Vzdálenosti ve sluneční soustavě: paralaxy a Keplerovy zákony
 Vzdálenosti ve sluneční soustavě: paralaxy a Keplerovy zákony Astronomové při sledování oblohy zaznamenávají především úhly a pozorují něco, co se nazývá nebeská sféra. Nicméně, hvězdy nejsou od Země vždy
Vzdálenosti ve sluneční soustavě: paralaxy a Keplerovy zákony Astronomové při sledování oblohy zaznamenávají především úhly a pozorují něco, co se nazývá nebeská sféra. Nicméně, hvězdy nejsou od Země vždy
Pohyby HB v některých význačných silových polích
 Pohyby HB v některých význačných silových polích Pohyby HB Gravitační pole Gravitační pole v blízkém okolí Země tíhové pole Pohyb v gravitačním silovém poli Keplerova úloha (podrobné řešení na semináři)
Pohyby HB v některých význačných silových polích Pohyby HB Gravitační pole Gravitační pole v blízkém okolí Země tíhové pole Pohyb v gravitačním silovém poli Keplerova úloha (podrobné řešení na semináři)
Úvod do nebeské mechaniky
 OPT/AST L09 Úvod do nebeské mechaniky pohyby astronomických těles ve společném gravitačním poli obecně: chaotický systém nestabilní numerické řešení speciální případ: problém dvou těles analytické řešení
OPT/AST L09 Úvod do nebeské mechaniky pohyby astronomických těles ve společném gravitačním poli obecně: chaotický systém nestabilní numerické řešení speciální případ: problém dvou těles analytické řešení
PLANETA ZEMĚ A JEJÍ POHYBY. Maturitní otázka č. 1
 PLANETA ZEMĚ A JEJÍ POHYBY Maturitní otázka č. 1 TVAR ZEMĚ Geoid = skutečný tvar Země Nelze vyjádřit matematicky Rotační elipsoid rovníkový poloměr = 6 378 km vzdálenost od středu Země k pólu = 6 358 km
PLANETA ZEMĚ A JEJÍ POHYBY Maturitní otázka č. 1 TVAR ZEMĚ Geoid = skutečný tvar Země Nelze vyjádřit matematicky Rotační elipsoid rovníkový poloměr = 6 378 km vzdálenost od středu Země k pólu = 6 358 km
Matematika 1 MA1. 1 Analytická geometrie v prostoru - základní pojmy. 4 Vzdálenosti. 12. přednáška ( ) Matematika 1 1 / 32
 Matematika 1 12. přednáška MA1 1 Analytická geometrie v prostoru - základní pojmy 2 Skalární, vektorový a smíšený součin, projekce vektoru 3 Přímky a roviny 4 Vzdálenosti 5 Příčky mimoběžek 6 Zkouška;
Matematika 1 12. přednáška MA1 1 Analytická geometrie v prostoru - základní pojmy 2 Skalární, vektorový a smíšený součin, projekce vektoru 3 Přímky a roviny 4 Vzdálenosti 5 Příčky mimoběžek 6 Zkouška;
4. Lineární diferenciální rovnice rovnice 1. ádu
 4. Lineární diferenciální rovnice rovnice. ádu y + p( ) y = (4.) L[ y] = y + p( ) y p q jsou spojité na I = (ab) a < b. Z obecné teorie vyplývá že množina všech ešení rovnice (4.) na intervalu I (tzv.
4. Lineární diferenciální rovnice rovnice. ádu y + p( ) y = (4.) L[ y] = y + p( ) y p q jsou spojité na I = (ab) a < b. Z obecné teorie vyplývá že množina všech ešení rovnice (4.) na intervalu I (tzv.
Nejprve si připomeňme z geometrie pojem orientovaného úhlu a jeho velikosti.
 U. 4. Goniometrie Nejprve si připomeňme z geometrie pojem orientovaného úhlu a jeho velikosti. 4.. Orientovaný úhel a jeho velikost. Orientovaným úhlem v rovině rozumíme uspořádanou dvojici polopřímek
U. 4. Goniometrie Nejprve si připomeňme z geometrie pojem orientovaného úhlu a jeho velikosti. 4.. Orientovaný úhel a jeho velikost. Orientovaným úhlem v rovině rozumíme uspořádanou dvojici polopřímek
Dvojné a trojné integrály příklad 3. x 2 y dx dy,
 Spočtěte = { x, y) ; 4x + y 4 }. Dvojné a trojné integrály příklad 3 x y dx dy, Řešení: Protože obor integrace je symetrický vzhledem k ose x, tj. vzhledem k substituci [x; y] [x; y], a funkce fx, y) je
Spočtěte = { x, y) ; 4x + y 4 }. Dvojné a trojné integrály příklad 3 x y dx dy, Řešení: Protože obor integrace je symetrický vzhledem k ose x, tj. vzhledem k substituci [x; y] [x; y], a funkce fx, y) je
MATEMATIKA II - vybrané úlohy ze zkoušek v letech
 MATEMATIKA II - vybrané úlohy ze zkoušek v letech 2009 2012 doplněné o další úlohy 3. část KŘIVKOVÉ INTEGRÁLY, GREENOVA VĚTA, POTENIÁLNÍ POLE, PLOŠNÉ INTEGRÁLY, GAUSSOVA OSTROGRADSKÉHO VĚTA 7. 4. 2013
MATEMATIKA II - vybrané úlohy ze zkoušek v letech 2009 2012 doplněné o další úlohy 3. část KŘIVKOVÉ INTEGRÁLY, GREENOVA VĚTA, POTENIÁLNÍ POLE, PLOŠNÉ INTEGRÁLY, GAUSSOVA OSTROGRADSKÉHO VĚTA 7. 4. 2013
Eudoxovy modely. Apollónios (225 př. Kr.) ukázal, že oba přístupy jsou při aplikaci na Slunce ekvivalentní. Deferent, epicykl a excentr
 Počátek goniometrie Eudoxovy modely Deferent, epicykl a excentr Apollónios (225 př Kr) ukázal, že oba přístupy jsou při aplikaci na Slunce ekvivalentní Zdeněk Halas (KDM MFF UK) Goniometrie v antice 25
Počátek goniometrie Eudoxovy modely Deferent, epicykl a excentr Apollónios (225 př Kr) ukázal, že oba přístupy jsou při aplikaci na Slunce ekvivalentní Zdeněk Halas (KDM MFF UK) Goniometrie v antice 25
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ
 ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
Otázku, kterými body prochází větev implicitní funkce řeší následující věta.
 1 Implicitní funkce Implicitní funkce nejsou funkce ve smyslu definice, že funkce bodu z definičního oboru D přiřadí právě jednu hodnotu z oboru hodnot H. Přesnější termín je funkce zadaná implicitně.
1 Implicitní funkce Implicitní funkce nejsou funkce ve smyslu definice, že funkce bodu z definičního oboru D přiřadí právě jednu hodnotu z oboru hodnot H. Přesnější termín je funkce zadaná implicitně.
základy astronomie 1 praktikum 3. Astronomické souřadnice
 základy astronomie 1 praktikum 3. Astronomické souřadnice 1 Úvod Znalost a správné používání astronomických souřadnic patří k základní výbavě astronoma. Bez nich se prostě neobejdete. Nejde ale jen o znalost
základy astronomie 1 praktikum 3. Astronomické souřadnice 1 Úvod Znalost a správné používání astronomických souřadnic patří k základní výbavě astronoma. Bez nich se prostě neobejdete. Nejde ale jen o znalost
i=1 Přímka a úsečka. Body, které leží na přímce procházející body a a b můžeme zapsat pomocí parametrické rovnice
 I. Funkce dvou a více reálných proměnných 1. Úvod Značení: V textu budeme používat označení: N pro množinu všech přirozených čísel; R pro množinu všech reálných čísel; R n pro množinu všech uspořádaných
I. Funkce dvou a více reálných proměnných 1. Úvod Značení: V textu budeme používat označení: N pro množinu všech přirozených čísel; R pro množinu všech reálných čísel; R n pro množinu všech uspořádaných
MATEMATIKA II - vybrané úlohy ze zkoušek ( 2015)
 MATEMATIKA II - vybrané úlohy ze zkoušek ( 2015 doplněné o další úlohy 13. 4. 2015 Nalezené nesrovnalosti ve výsledcích nebo připomínky k tomuto souboru sdělte laskavě F. Mrázovi ( e-mail: Frantisek.Mraz@fs.cvut.cz.
MATEMATIKA II - vybrané úlohy ze zkoušek ( 2015 doplněné o další úlohy 13. 4. 2015 Nalezené nesrovnalosti ve výsledcích nebo připomínky k tomuto souboru sdělte laskavě F. Mrázovi ( e-mail: Frantisek.Mraz@fs.cvut.cz.
Fyzika 1 - rámcové příklady Kinematika a dynamika hmotného bodu, gravitační pole
 Fyzika 1 - rámcové příklady Kinematika a dynamika hmotného bodu, gravitační pole 1. Určete skalární a vektorový součin dvou obecných vektorů AA a BB a popište, jak závisí výsledky těchto součinů na úhlu
Fyzika 1 - rámcové příklady Kinematika a dynamika hmotného bodu, gravitační pole 1. Určete skalární a vektorový součin dvou obecných vektorů AA a BB a popište, jak závisí výsledky těchto součinů na úhlu
České vysoké učení technické v Praze. Vývoj systému pro automatické určování azimutu z měření na Slunce
 České vysoké učení technické v Praze fakulta stavební Vývoj systému pro automatické určování azimutu z měření na Slunce Developement of system for automatic azimuth determination based on Sun observations
České vysoké učení technické v Praze fakulta stavební Vývoj systému pro automatické určování azimutu z měření na Slunce Developement of system for automatic azimuth determination based on Sun observations
Vzorce a recepty nebeské mechaniky
 Vzorce a recepty nebeské mechaniky Verze 3.0 Petr Scheirich, 2004 http://nebmech.astronomy.cz Obsah 1 Úvod 1 2 Souřadnice na obloze 1 3 Pohyb po kuželosečce 4 4 Elipsa 6 5 Pohybpoelipse 7 6 Parabola 10
Vzorce a recepty nebeské mechaniky Verze 3.0 Petr Scheirich, 2004 http://nebmech.astronomy.cz Obsah 1 Úvod 1 2 Souřadnice na obloze 1 3 Pohyb po kuželosečce 4 4 Elipsa 6 5 Pohybpoelipse 7 6 Parabola 10
Skládání různoběžných kmitů. Skládání kolmých kmitů. 1) harmonické kmity stejné frekvence :
 Skládání různoběžných kmitů Uvědomme si principiální bod tohoto problému : na jediný hmotný bod působí dvě nezávislé pružné síl ve dvou různých směrech. Jednotlivé mechanické pohb, které se budou skládat,
Skládání různoběžných kmitů Uvědomme si principiální bod tohoto problému : na jediný hmotný bod působí dvě nezávislé pružné síl ve dvou různých směrech. Jednotlivé mechanické pohb, které se budou skládat,
19 Eukleidovský bodový prostor
 19 Eukleidovský bodový prostor Eukleidovským bodovým prostorem rozumíme afinní bodový prostor, na jehož zaměření je definován skalární součin. Víme, že pomocí skalárního součinu jsou definovány pojmy norma
19 Eukleidovský bodový prostor Eukleidovským bodovým prostorem rozumíme afinní bodový prostor, na jehož zaměření je definován skalární součin. Víme, že pomocí skalárního součinu jsou definovány pojmy norma
Další plochy technické praxe
 Další plochy technické praxe Dosud studované plochy mají široké využití jak ve stavební tak ve strojnické praxi. Studovali jsme možnosti jejich konstrukcí, vlastností i využití v praxi. Kromě těchto ploch
Další plochy technické praxe Dosud studované plochy mají široké využití jak ve stavební tak ve strojnické praxi. Studovali jsme možnosti jejich konstrukcí, vlastností i využití v praxi. Kromě těchto ploch
9.1 Definice a rovnice kuželoseček
 9. Kuželosečky a kvadriky 9.1 Definice a rovnice kuželoseček Kuželosečka - řez na kruhovém kuželi, množina bodů splňujících kvadratickou rovnici ve dvou proměnných. Elipsa parametricky: X(t) = (a cos t,
9. Kuželosečky a kvadriky 9.1 Definice a rovnice kuželoseček Kuželosečka - řez na kruhovém kuželi, množina bodů splňujících kvadratickou rovnici ve dvou proměnných. Elipsa parametricky: X(t) = (a cos t,
Analytická geometrie přímky, roviny (opakování středoškolské látky) = 0. Napište obecnou rovnici. 8. Jsou dány body A [ 2,3,
 Analytická geometrie přímky roviny opakování středoškolské látk Jsou dány body A [ ] B [ 5] a C [ 6] a) přímky AB b) osy úsečky AB c) přímky na které leží výška vc trojúhelníka ABC d) přímky na které leží
Analytická geometrie přímky roviny opakování středoškolské látk Jsou dány body A [ ] B [ 5] a C [ 6] a) přímky AB b) osy úsečky AB c) přímky na které leží výška vc trojúhelníka ABC d) přímky na které leží
Substituce ve vícenásobném integrálu verze 1.1
 Úvod Substituce ve vícenásobném integrálu verze. Následující text popisuje výpočet vícenásobných integrálů pomocí věty o substituci. ěl by sloužit především studentům předmětu ATEAT k přípravě na zkoušku.
Úvod Substituce ve vícenásobném integrálu verze. Následující text popisuje výpočet vícenásobných integrálů pomocí věty o substituci. ěl by sloužit především studentům předmětu ATEAT k přípravě na zkoušku.
Práce, energie a další mechanické veličiny
 Práce, energie a další mechanické veličiny Úvod V předchozích přednáškách jsme zavedli základní mechanické veličiny (rychlost, zrychlení, síla, ) Popis fyzikálních dějů usnadňuje zavedení dalších fyzikálních
Práce, energie a další mechanické veličiny Úvod V předchozích přednáškách jsme zavedli základní mechanické veličiny (rychlost, zrychlení, síla, ) Popis fyzikálních dějů usnadňuje zavedení dalších fyzikálních
TÍHOVÉ ZRYCHLENÍ TEORETICKÝ ÚVOD. 9, m s.
 TÍHOVÉ ZRYCHLENÍ TEORETICKÝ ÚVOD Soustavu souřadnic spojenou se Zemí můžeme považovat prakticky za inerciální. Jen při několika jevech vznikají odchylky, které lze vysvětlit vlastním pohybem Země vzhledem
TÍHOVÉ ZRYCHLENÍ TEORETICKÝ ÚVOD Soustavu souřadnic spojenou se Zemí můžeme považovat prakticky za inerciální. Jen při několika jevech vznikají odchylky, které lze vysvětlit vlastním pohybem Země vzhledem
MANUÁL K ŘEŠENÍ TESTOVÝCH ÚLOH
 Krok za krokem k nové maturitě Maturita nanečisto 005 MA4 MANUÁL K ŘEŠENÍ TESTOVÝCH ÚLOH Matematika rozšířená úroveň Vážení vyučující! ředmětoví koordinátoři Centra pro zjišťování výsledků vzdělávání pro
Krok za krokem k nové maturitě Maturita nanečisto 005 MA4 MANUÁL K ŘEŠENÍ TESTOVÝCH ÚLOH Matematika rozšířená úroveň Vážení vyučující! ředmětoví koordinátoři Centra pro zjišťování výsledků vzdělávání pro
Michal Zamboj. January 4, 2018
 Meziřádky mezi kuželosečkami - doplňkový materiál k přednášce Geometrie Michal Zamboj January 4, 018 Pozn. Najdete-li chybu, neváhejte mi napsat, může to ušetřit tápání Vašich kolegů. Pozn. v dokumentu
Meziřádky mezi kuželosečkami - doplňkový materiál k přednášce Geometrie Michal Zamboj January 4, 018 Pozn. Najdete-li chybu, neváhejte mi napsat, může to ušetřit tápání Vašich kolegů. Pozn. v dokumentu
Zavedeme-li souřadnicový systém {0, x, y, z}, pak můžeme křivku definovat pomocí vektorové funkce.
 KŘIVKY Křivka = dráha pohybujícího se bodu = = množina nekonečného počtu bodů, které závisí na parametru (čase). Proto můžeme křivku také nazvat jednoparametrickou množinou bodů. Zavedeme-li souřadnicový
KŘIVKY Křivka = dráha pohybujícího se bodu = = množina nekonečného počtu bodů, které závisí na parametru (čase). Proto můžeme křivku také nazvat jednoparametrickou množinou bodů. Zavedeme-li souřadnicový
Píkazy pro kreslení.
 Píkazy pro kreslení. Tento text je psán pro AUTOCAD 2006, eskou modifikaci. V jiných verzích se proto vyskytnou odchylky. Jsou to píkazy, které umožují nakreslit jednotlivé entity v AUTOCADu. Z menu je
Píkazy pro kreslení. Tento text je psán pro AUTOCAD 2006, eskou modifikaci. V jiných verzích se proto vyskytnou odchylky. Jsou to píkazy, které umožují nakreslit jednotlivé entity v AUTOCADu. Z menu je
Téma: Fáze Měsíce a planet, zdánlivý pohyb oblohy na planetách
 Téma: Fáze Měsíce a planet, zdánlivý pohyb oblohy na planetách Zpracoval Doc. RNDr. Zdeněk Hlaváč, Cc Vlivem vzájemné polohy lunce, Země a dalšího tělesa(např. jiné planety nebo Měsíce) dochází k jevu,
Téma: Fáze Měsíce a planet, zdánlivý pohyb oblohy na planetách Zpracoval Doc. RNDr. Zdeněk Hlaváč, Cc Vlivem vzájemné polohy lunce, Země a dalšího tělesa(např. jiné planety nebo Měsíce) dochází k jevu,
14. přednáška. Přímka
 14 přednáška Přímka Začneme vyjádřením přímky v prostoru Přímku v prostoru můžeme vyjádřit jen parametricky protože obecná rovnice přímky v prostoru neexistuje Přímka v prostoru je určena bodem A= [ a1
14 přednáška Přímka Začneme vyjádřením přímky v prostoru Přímku v prostoru můžeme vyjádřit jen parametricky protože obecná rovnice přímky v prostoru neexistuje Přímka v prostoru je určena bodem A= [ a1
NEWTONOVY POHYBOVÉ ZÁKONY
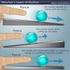 NEWTONOVY POHYBOVÉ ZÁKONY Metodika Mgr. Michal Schovánek kvten 2010 Newtonovy pohybové zákony patí mezi nejobtížnjší kapitoly stedoškolské mechaniky. Popisované situace jsou sice jednoduše demonstrovatelné,
NEWTONOVY POHYBOVÉ ZÁKONY Metodika Mgr. Michal Schovánek kvten 2010 Newtonovy pohybové zákony patí mezi nejobtížnjší kapitoly stedoškolské mechaniky. Popisované situace jsou sice jednoduše demonstrovatelné,
