Oteplování a dimenzování motorů
|
|
|
- Anna Sedláková
- před 6 lety
- Počet zobrazení:
Transkript
1 Oeplováí a dimezováí moorů Oeplováí a dimezováí moorů ři přeměě elekrické eergie a mechaickou e čá eergie, předavující zráy v mooru měí v eplo a ím dochází k oeplováí ohoo elekromooru. Vzhledem k omu, že aalyické řešeí éo problemaiky je velice komplikovaé, vycházíme ze zjedodušujících předpokladů, kdy moor považujeme za homogeí ěleo ekoečou epelou vodivoí a proředí, ve kerém pracuje uvažujeme ekoečou epelou kapaciou, jehož eploa eí eploou mooru ovlivěa. Dále předpokládáme koaí epelé paramery (epelá kapacia, koeficie přeupu epla...), ezávilé a eploě mooru. ro možví epla dq vyviuého v mooru za ča d v důledku zrá je pak možo uvé: dq d ožví epla odvedeého do okolího proředí za ejý ča je dq A d kde A je oučiiel přeupu epla [J/() W/], kerý je úměrý velikoi povrchu a ieziě chlazeí (uvažujeme pouze přeup epla prouděím, rep. vedeím, zaedbáváme áláí), je oepleí mooru, j. rozdíl eplo mooru a proředí. ožví epla způobující vlaí oepleí mooru je pak dq 3 C d kde C je zv. epelá kapacia mooru [J/], kerá udává možví epla pořebého k ohřáí mooru o. C m c kde m je hmoo mooru v [kg] a c je měrá epelá kapacia maeriálu mooru [J/(kg)]. ro rovici epelé rovováhy pak plaí: dq dq dq 3 d A d C d C d A d A e e oledí uvedeý vzah je pak řešeím předchozí difereciálí rovice
2 Oeplováí a dimezováí moorů C kde je oeplovací čaová koaa, je uáleé oepleí a je počáečí A A oepleí v čae. V případě, že a začáku oeplováí je eploa mooru a proředí hodá, je. Obdobě lze odvodi čaový průběh při ochlazováí mooru, kde plaí a edy o e řičemž výzam parameru je zde oepleí v okamžiku vypuí mooru. Zjedodušeé čaové průběhy jou zázorěy a obr.. Obr.. Čaový průběh oeplováí a ochlazováí mooru Čaová koaa závií a chladicích poměrech, keré jou u moorů vlaím chlazeím odlišé v případě, když moor je v provozu a když ojí. Obecě jou. edy čaové koay oeplovací. a ochlazovací o. růzé. Orieačí hodoy oeplovacích a ochlazovacích čaových koa jou uvedey v ab.. ab.. Orieačí hodoy oeplovacích a ochlazovacích čaových koa. druh mooru. o - malé moory oevřeé 3-4 mi 6-7 mi - velké moory oevřeé 5-65 mi 8 - mi - zavřeé moory povrchovým chlazeím a viří cirkulací 7-9 mi - mi - zavřeé moory bez chlazeí - 8 mi - 8 mi Jmeoviý výko elekromooru e aoví ak, aby oepleí epřekročilo dovoleé oepleí přílušé izolačí řídy viuí, avšak ak, aby moor byl epelě využi, j. aby e kuečé oepleí omuo dovoleému přiblížilo. Dovoleé oepleí dov viuí pro jedolivé řídy izolace je áledující : epelá řída izolace A E B F H dov [ C ] V provozu při eploách okolí ad 4 C a v admořké výšce ad m e oepleí ižuje. Druhy zaížeí Oeplováí probraé v miulé kapiole předpokládalo rvalé zaížeí čaem epromělivé. akové zaížeí předavují apř. odředivá čerpadla, veiláory, ěkeré obráběcí roje ap. V moha případech e však zaížeí mooru měí, což způobí aké čaově promělivý průběh zrá mooru. romě acioárího provozu promělivým zaížeím e však vykyují případy, kdy zráy v eacioárích
3 Oeplováí a dimezováí moorů režimech, j. při rozběhu, brzděí a reverzacích výzamě ovlivňují celkovou zráovou eergii a muí bý vzay v úvahu při dimezováí. V ouladu doporučeím EC 34- jou defiováy dle ČN EN 634- áledující druhy zaížeí: rvalé zaížeí Obr.. růběhy charakeriických veliči pro rvalé zaížeí oo zaížeí je charakeriické ím, že oepleí doáhe uáleé hodoy, čili doba rváí zaížeí z je delší ež (3 až 4 ). rákodobý chod Obr. 3. růběhy charakeriických veliči pro krákodobý chod 3
4 Oeplováí a dimezováí moorů Doba koaího zaížeí je zde aolik kráká, že e edoáhe epelé rovováhy a uáleé eploy, přičemž pracoví přeávka je aolik dlouhá, že e eploa mooru íží a eplou okolího proředí, j. z < 3 a > (3 až 4 ). 3 řerušovaý chod (bez vlivu rozběhu a brzděí a eplou) Obr. 4. růběhy charakeriických veliči pro 3 přerušovaý chod Zaížeí je charakeriické opakujícím e cyklem, během kerého edojde k epelé rovováze j. z < 3 a rověž < řerušovaé zaížeí (bez vlivu rozběhu a brzděí a eplou) 4
5 Oeplováí a dimezováí moorů Obr. 5. růběhy charakeriických veliči pro 6 přerušovaé zaížeí Opě dochází k opakujícímu e cyklu, při kerém edojde k epelé rovováze. Oproi přerušovaému chodu je moor při běhu aprázdo lépe chlaze (plaí pro moor vlaím chlazeím). řerušovaý chod, repekive zaížeí je charakerizová : a) dobou cyklu z o, kde při výpočech uvažujeme ormovaou dobou cyklu mi. b) zaěžovaelem, kerý udává celkový ouče dob zaížeí v rámci jedoho cyklu k době cyklu. z i zi [ ] % oory jiým zaížeím ež jou pak vyráběy pro ormovaé zaěžovaele 5; 5; 4 a 6%. Způobů zaížeí je amozřejmě ješě více, zejméa při uvažováí rozběhu, brzděí, reverzace, ad. Jejich aalýza však překračuje rozah ohoo základího učebího exu. Zde uvedeme pouze jejich ázvy (více ČN EN 634-): 4 řerušovaý chod rozběhem 5 řerušovaý chod elekrickým brzděím 7 řerušovaé pravidelé zaížeí elekrickým brzděím 8 řerušovaé pravidelé zaížeí e změami oáček pojeými e změami zaížeí 9 Nepravidelé zaížeí a změy oáček Zaížeí epojiými álými zaížeími 5
6 Oeplováí a dimezováí moorů 6 řepoče krákodobého chodu a rvalý chod oužií mooru určeého pro rvalé zaížeí ( ) pro zaížeí krákodobým chodem umožňuje jeho momeové a výkoové přeížeí,(pokud je meší ež maximálí momeová přeížielo), aiž dojde k překročeí dovoleého oepleí. oměry při krákodobém zaížeí jou zázorěy a obr. 6. Zráy při krákodobém chodu mohou u bý podaě vyšší ež při rvalém chodu, eboť oepleí probíhá dle křivky avšak je do doby zaížeí z, v íž při dokoalém epelém využií doáhe hodoy uáleého oepleí při rvalém provozu, (kerá odpovídá dovoleému oepleí mooru při zaížeí ). z e e Obr. 6. růběh oeplováí mooru při krákodobém chodu V čae z plaí ( ) Z dov z e / ) ( oměr zrá e Z dov / e azývá čiiel krákodobé přeížieloi a pohybuje e v rozahu, (pro dlouhé doby zaížeí z a oevřeé roje) až (pro kráké doby z a zavřeé roje). Zráy můžeme rozděli a zráy ezávilé a zaížeí zráy aprázdo (v železe a mechaické) a zráy závilé a zaížeí (ve viuí). ro jmeovié zaížeí jou cu, pro jié zaížeí e měí e čvercem proudu. U rojů derivačí charakeriikou plaí, že aké přibližě e čvercem momeu a při koaí rychloi i e čvercem výkou laí edy ( ) cu cu
7 Oeplováí a dimezováí moorů 7 Dáme-li yo zráy do poměru, doaeme ( ) ( ) z čehož a pro kde poměr zrá koaích (aprázdo) ke zráám variabilím při jmeoviém zaížeí ( ) ( ) d cu cu m FE závií a provedeí a velikoi mooru. Výrobce v kaalogu moorů ale euvádí dílčí zráy, ýbrž pouze účio při jmeoviém výkou. roo je uo prové odhad poměru zrá dle áledující abulky. ab.. oměr / oor malý výko ředí výko velký výko A. moor rychloběžý.65,5 A. moor pomaloběžý -,8,65 moor rychloběžý,8 až,8 až,5. moor pomaloběžý -,8 až,65 ychr. moor rychloběžý,8 až,8 až,8 až ychr. moor pomaloběžý -,, Vzahu pro poměr proudů, rep. momeů lze aké použí při přepoču krákodobého zaížeí rvající dobu z a ormovaé rváí z krákodobého zaížeí : Z e / Z e / kde e vypočíá pro kuečou dobu z a pro ormovaou dobu z (viz předchozí vzahy). oory určeé pro krákodobý chod jou čao peciálě upravey pro zvěšeí momeového přeížeí ím, že u idukčích moorů e volí věší idukce ve vzduchové mezeře, čímž lze připui věší proudové zaížeí a zvýší e mome zvrau i záběrý mome. oor pak pracuje v blízkoi bodu zvrau (7-8%). U ejoměrých moorů e zvěšuje mageický ok a proud e zvýší až k mezi komuace. Vyšší elekromageické využií vede k ižší účioi i účiíku mooru.
8 Oeplováí a dimezováí moorů řepoče 3, rep. 6 a rvalý chod, meoda ekvivaleího proudu, momeu a výkou Uvažujeme průběh přerušovaého zaížeí, kerému odpovídá průběh zrá dle obr. 7. Odpovídající oepleí mooru pak předavuje křivka (), kládající e z jedolivých úeků oeplovací a ochlazovací křivky mooru. Obr. 7. růběh zrá a oepleí při přerušovaém zaížeí oor, kerý je epelě využi, by měl bý dimezová a akový rvalý výko, aby po dobu zaížeí ímo výkoem e oeplil a eplou blízkou dovoleému oepleí. ao podmíka bude plěa ehdy, jeliže zráy mooru při om o áhradím koaím zaížeí budou rovy arimeické ředí hodoě zrá m z čaového průběhu () po dobu cyklu. roože je malé proi oeplovací čaové koaě, jou odchylky oepleí od ředí hodoy malé a eovlivňují živoo izolace. Říkáme, že dimezujeme moor dle ředích (meridiálích) zrá m m ( )d () Rozdělíme-li zráy mooru a zráy aprázdo (v železe a mechaické), keré jou za předpokladu přibližě álé rychloi koaí, a zráy ve viuí, keré jou úměré čverci zaěžovacího proudu, doaeme pro čaový průběh zrá vzah ( ) Ri ( ) () cu ředí zráy m bude pak možo vyjádři pomoci áhradího ekvivaleího proudu (3) m R ekv )Doazeím rovice () a (3) do vzahu () zíkáme defiičí vzah pro ekvivaleí proud ekv i ( )d (4) Ekvivaleí oeplovací proud můžeme edy urči ze kuečého průběhu proudu mooru ze ředí hodoy čverce proudu. ao meoda e azývá meoda ekvivaleího proudu. U rojů derivačí charakeriikou (ejoměré moory cizím buzeím, aychroí moory) - plaí přímá úměra mezi momeem a proudem: ~ a při koaí rychloi i mezi výkoem, momeem a 8
9 Oeplováí a dimezováí moorů proudem: ~~. ak lze u ěcho moorů defiova obdobým způobem aké ekvivaleí mome ekv, rep. ekvivaleí výko ekv ekv ( )d (5) ekv ( )d (6) Zpravidla bývá zadá zaěžovací diagram pracovího roje (průběh momeu), akže e určí ypový výko mooru z ekvivaleího momeu a rychloi. eodu ekvivaleího proudu užíváme věšiou ke korole využií mooru již a hoových pohoech, kde je k dipozici zázam měřeého proudu. Rověž exiují měřicí příroje, keré umožňují přímo zjišťova hodou ředěkvadraického proudu (buď a pricipu Hallova jevu ebo aalogové kvadráory). U roje e ériovou charakeriikou eplaí úměra mezi momeem a proudem, rychlo e zaížeím začě kleá. V omo případě lze využí k dimezováí pouze meodu ekvivaleího proudu. oup je pak akový, že z průběhu momeu pracovího roje () a charakeriiky () mooru udávaou výrobcem e vyvoří čaový průběh proudu () a z ěj e vypoče ekv. V případě přerušovaého chodu 3 je v přeávce mezi dvěma áledujícími cykly moor odpoje, akže odpadou zráy aprázdo, keré při odvozováí předchozích vzahů byly uvažováy. ao kuečo vede při výpoču ekvivaleích veliči k odchylkám, keré však obvykle zaedbáváme. U moorů vlaím chlazeím e u režimu 3 projeví ížeé chlazeí v době přeávky mezi cykly, což má za áledek růzou veliko čaové koay oeplováí a ochlazováí o.v áhradím výpočovém zaížeí však uvažujeme pouze jediou čaovou koau a ímo rozdílem epočíáme. Aby áhradí zaížeí vyihovalo uo kuečo, zavádíme mío kuečé doby přeávky redukovaou (áhradí) dobu ' o, á-li odpovída počáečí a koečé oeplováí během cyklu áhradímu rvalému zaížeí, plaí pro dobu ' o vzah, oměry obou čaových koa byly uvedey v ab.. Redukovaá doba cyklu bude pak, z akže ředí zráy m ( ) m,, d a podobě ekvivaleí proud ekv ( ) ekv i,, d ím dochází k zvýšeí ekvivaleího proudu o až 5% (vyšší hodoy plaí pro malé zaěžovaele z ). ejě je uo upravi u moorů derivačí charakeriikou vzahy pro ekvivaleí mome ekv (5) a výko ekv (6). ímo způobem e provádí přepoče a základě oepleí u pohoů přerušovaým chodem 3 a rvalé zaížeí. Vykyují-li e však v zaížeí špičkové momey, může vé eo přepoče a základě oepleí k eprávým závěrům, eboť moor emuí mí akovou momeovou přeížielo, aby byl chope yo momeové špice pokrý. V omo případě je edy uo korolova momeovou přeížielo zvoleého mooru (viz áledující raa) a v případě, že moor evyhovuje, je uo jeho ypový výko zvýši. 9
10 Oeplováí a dimezováí moorů omeová přeížielo ři dimezováí mooru je uo kromě epelého amáháí mooru korolova momeovou přeížielo. omeová přeížielo je poměr maximálího momeu k momeu jmeoviému. Jak plye z předchozí kapioly, při krákodobém ebo přerušovaém chodu může bý moor krákodobě přeíže (aiž by došlo k překročeí dovoleého oepleí). V ěcho čaových úecích ale ikdy emí dojí k překročeí maximálího momeu mooru. U adardích ejoměrých moorů o čií cca dvojáobek jmeovié hodoy. Vyplývá o ze kuečoi, že mome DC moorů koaím buzeím moory cizím buzeím či permaeími magey - je přímo úměrý proudu kovy (viz kapiola o DC moorech). ři věším ež dvojáobém proudu dochází k adměrému jikřeí a komuáoru. ejoměré eriové moory jou omezey rověž komuací při ayceí pomocých pólů, přeížielo bývá až,5. ejoměré moory permaeími magey ve peciálím provedeí pro ervopohoy obráběcích rojů mívají přeížielo až. U aychroích moorů je maximálí mome momeem zvrau a mechaické charakeriice (viz kapiola o aychroích moorech). ro adardí moory akráko e ao hodoa pohybuje v rozmezí,5 až 3,5 áobku jmeoviého momeu (eo údaj ajdeme v kaalogu daého mooru). ricipiálě edy moor emůže vyviou věší mome ež je mome zvrau. okud bychom ho zaížili věším momeem, dojde k jeho zaaveí, přičemž by moor odebíral proud akráko. U ychroích moorů je maximálí dovoleý mome poje jedak maximálím dovoleým proudem, ale i maximálím dovoleým záěžým úhlem, po jehož překročeí dochází k vypaduí ze ychroimu a jeho zaaveí, přičemž by moor odebíral velký proud. ychroí moory mají,5 až,5 při ormálím provedeí, ve peciálím provedeí až 3 až 4. ro všechy uvedeé ypy edy můžeme aovi výše uvedeým poupem maximálí mome a zkorolova, zda v ěkerých úecích zaěžovacího diagramu eí překroče. okud by omu ak bylo, je uo avrhou moor věšího výkou ak, aby jeho maximálí mome překroče ebyl.
1. Definice elektrického pohonu 1.1 Specifikace pohonu podle typu poháněného pracovního stroje 1.1.1 Rychlost pracovního mechanismu
 1. Defiice elektrického pohou Pod pojmem elektrický poho rozumíme soubor elektromechaických vazeb a vztahů mezi pracovím mechaismem a elektromechaickou soustavou. Mezi základí tři části elektrického pohou
1. Defiice elektrického pohou Pod pojmem elektrický poho rozumíme soubor elektromechaických vazeb a vztahů mezi pracovím mechaismem a elektromechaickou soustavou. Mezi základí tři části elektrického pohou
Úloha IV.E... už to bublá!
 Úloha IV.E... už o bublá! 8 bodů; průměr 5,55; řešilo 42 udenů Změře účinno rychlovarné konvice. Údaj o příkonu naleznee obvykle na amolepce zepodu konvice. Výkon určíe ak, že zjiíe, o kolik upňů Celia
Úloha IV.E... už o bublá! 8 bodů; průměr 5,55; řešilo 42 udenů Změře účinno rychlovarné konvice. Údaj o příkonu naleznee obvykle na amolepce zepodu konvice. Výkon určíe ak, že zjiíe, o kolik upňů Celia
10. Charakteristiky pohonů ve vlastní spotřebě elektrárny
 0. Charakeriiky pohonů ve vlaní pořebě elekrárny pořebiče ve V.. ají yo charakeriické vlanoi: Příkon Záběrný oen Doba rvání rozběhu Hlavní okruhy pořebičů klaické konvenční epelné elekrárny jou:. Zauhlování
0. Charakeriiky pohonů ve vlaní pořebě elekrárny pořebiče ve V.. ají yo charakeriické vlanoi: Příkon Záběrný oen Doba rvání rozběhu Hlavní okruhy pořebičů klaické konvenční epelné elekrárny jou:. Zauhlování
ZÁKLADY ELEKTRICKÝCH POHONŮ (EP) Určeno pro posluchače bakalářských studijních programů FS
 ZÁKLADY ELEKTRICKÝCH OHONŮ (E) Určeno pro posluchače bakalářských sudijních programů FS Obsah 1. Úvod (definice, rozdělení, provozní pojmy,). racovní savy pohonu 3. Základy mechaniky a kinemaiky pohonu
ZÁKLADY ELEKTRICKÝCH OHONŮ (E) Určeno pro posluchače bakalářských sudijních programů FS Obsah 1. Úvod (definice, rozdělení, provozní pojmy,). racovní savy pohonu 3. Základy mechaniky a kinemaiky pohonu
Fakulta strojního inženýrství VUT v Brně Ústav konstruování. KONSTRUOVÁNÍ STROJŮ převody. Přednáška 5
 Fakula srojího ižeýrsví VUT v Brě Úsav kosruováí KONSTRUOVÁNÍ STROJŮ převody Předáška 5 Čelí soukolí se šikmými zuby hp://www.audiforum.l/ Moderaio is bes, ad o avoid all exremes. PLUTARCHOS Čelí soukolí
Fakula srojího ižeýrsví VUT v Brě Úsav kosruováí KONSTRUOVÁNÍ STROJŮ převody Předáška 5 Čelí soukolí se šikmými zuby hp://www.audiforum.l/ Moderaio is bes, ad o avoid all exremes. PLUTARCHOS Čelí soukolí
Odezva na obecnou periodickou budící funkci. Iva Petríková Katedra mechaniky, pružnosti a pevnosti
 Odezva a obecou periodickou budící fukci Iva Períková Kaedra mechaiky, pružosi a pevosi Obsah Fourierovy řady Odezva a polyharmoickou fukci Odezva a obecou periodickou fukci Odezva a jedokový skok Příklad
Odezva a obecou periodickou budící fukci Iva Períková Kaedra mechaiky, pružosi a pevosi Obsah Fourierovy řady Odezva a polyharmoickou fukci Odezva a obecou periodickou fukci Odezva a jedokový skok Příklad
PRAVDĚPODOBNOST A STATISTIKA
 SP Teováí hypoéz PRAVDĚPODOBNOST A STATISTIKA SP Teováí hypoéz Teováí hypoéz Nechť je áhodá proměá, kerá má diribučí fukci Fx, ϑ. Předpokládejme, že záme var diribučí fukce víme jaké má rozděleí a ezáme
SP Teováí hypoéz PRAVDĚPODOBNOST A STATISTIKA SP Teováí hypoéz Teováí hypoéz Nechť je áhodá proměá, kerá má diribučí fukci Fx, ϑ. Předpokládejme, že záme var diribučí fukce víme jaké má rozděleí a ezáme
6 Algoritmy ořezávání a testování polohy
 6 lgorim ořezáváí a esováí poloh Sudijí íl Teo blok je věová problemaie vzájemé poloh grafikýh primiiv, zejméa poloze bodu vzhledem k mohoúhelíku včeě jedolivýh speifikýh varia jako jsou čřúhelík, jehož
6 lgorim ořezáváí a esováí poloh Sudijí íl Teo blok je věová problemaie vzájemé poloh grafikýh primiiv, zejméa poloze bodu vzhledem k mohoúhelíku včeě jedolivýh speifikýh varia jako jsou čřúhelík, jehož
Vysoká škola báňská - Technická univerzita Ostrava Fakulta elektrotechniky a informatiky ELEKTRICKÉ POHONY. pro kombinované a distanční studium
 Vysoká škola báňská - Techická uiverzita Ostrava Fakulta elektrotechiky a iformatiky ELEKTRICKÉ POHONY pro kombiovaé a distačí studium Ivo Neborák Václav Sládeček Ostrava 004 1 Doc. Ig. Ivo Neborák, CSc.,
Vysoká škola báňská - Techická uiverzita Ostrava Fakulta elektrotechiky a iformatiky ELEKTRICKÉ POHONY pro kombiovaé a distačí studium Ivo Neborák Václav Sládeček Ostrava 004 1 Doc. Ig. Ivo Neborák, CSc.,
KULOVÝ KOHOUT PRO TEPLÁRENSTVÍ K85.DZT
 KUOVÝ KOHOUT PRO TEPÁRENSTVÍ K85.ZT Použií ocelové kulové kohouy jsou uzavírací armaury, keré splňují ejáročější pořeby rhu určeé pro isalaci v epláresví pro síě isribuce epla, klimaizace a průmyslové
KUOVÝ KOHOUT PRO TEPÁRENSTVÍ K85.ZT Použií ocelové kulové kohouy jsou uzavírací armaury, keré splňují ejáročější pořeby rhu určeé pro isalaci v epláresví pro síě isribuce epla, klimaizace a průmyslové
VÝKONOVÉ DIODY 5000 A 0,1 A I FAV 50 V U RRM V
 VÝKONOVÉ DIODY Výkoové polovodičové diody se v aplikacích používají k zabezpečeí průchodu proudu jedím směrem, ejčasěji k usměrňováí sřídavého proudu.,1 A I AV 5 A 5 V RRM 1 V Věkerých aplikacích je požadová
VÝKONOVÉ DIODY Výkoové polovodičové diody se v aplikacích používají k zabezpečeí průchodu proudu jedím směrem, ejčasěji k usměrňováí sřídavého proudu.,1 A I AV 5 A 5 V RRM 1 V Věkerých aplikacích je požadová
Katedra obecné elektrotechniky Fakulta elektrotechniky a informatiky, VŠB - TU Ostrava 4. TROJFÁZOVÉ OBVODY
 Kaedra obecné elekroechniky Fakula elekroechniky a inormaiky, VŠB - T Osrava. TOJFÁZOVÉ OBVODY.1 Úvod. Trojázová sousava. Spojení ází do hvězdy. Spojení ází do rojúhelníka.5 Výkon v rojázových souměrných
Kaedra obecné elekroechniky Fakula elekroechniky a inormaiky, VŠB - T Osrava. TOJFÁZOVÉ OBVODY.1 Úvod. Trojázová sousava. Spojení ází do hvězdy. Spojení ází do rojúhelníka.5 Výkon v rojázových souměrných
FINANČNÍ MATEMATIKA- JEDNODUCHÉ ÚROKOVÁNÍ
 Projek ŠABLONY NA GVM Gymázium Velké Meziříčí regisračí číslo projeku: CZ..7/.5./34.948 IV-2 Iovace a zkvaliěí výuky směřující k rozvoji maemaické gramoosi žáků sředích škol FINANČNÍ MATEMATIA- JEDNODCHÉ
Projek ŠABLONY NA GVM Gymázium Velké Meziříčí regisračí číslo projeku: CZ..7/.5./34.948 IV-2 Iovace a zkvaliěí výuky směřující k rozvoji maemaické gramoosi žáků sředích škol FINANČNÍ MATEMATIA- JEDNODCHÉ
Teplota. 3 kt. Boltzmanova konstanta k = J K -1. definice teploty. tlaky v obou částech se vyrovnají
 Teploa laky obou čásech se yroají 1 m1 1 m rooáe budou sředí kieické eergie obou druhů molekul sejé: 1 1 m m 1 1 ěžší molekuly se pohybují pomaleji ež lehčí sejé musí edy bý i objemoé kocerace: 1 když
Teploa laky obou čásech se yroají 1 m1 1 m rooáe budou sředí kieické eergie obou druhů molekul sejé: 1 1 m m 1 1 ěžší molekuly se pohybují pomaleji ež lehčí sejé musí edy bý i objemoé kocerace: 1 když
DIMENZOVÁNÍ KOMPOZITNÍCH PROFILŮ PREFEN
 DIMNZOVÁNÍ KOMPOZITNÍCH PROFILŮ PRFN 1 Kulkova 10/4231, 615 00 Bro el.: 541 583 208, 297, fa.: 549 254 556 e-mail: kompozi@prefa.cz hp://www.prefa-kompozi.cz DIMNZOVÁNÍ PROFILŮ Maeriálová srukura, základí
DIMNZOVÁNÍ KOMPOZITNÍCH PROFILŮ PRFN 1 Kulkova 10/4231, 615 00 Bro el.: 541 583 208, 297, fa.: 549 254 556 e-mail: kompozi@prefa.cz hp://www.prefa-kompozi.cz DIMNZOVÁNÍ PROFILŮ Maeriálová srukura, základí
Asynchronní motory Ing. Vítězslav Stýskala, Ph.D., únor 2006
 8 ELEKTRCKÉ STROJE TOČVÉ říklad 8 Základí veličiy Určeo pro poluchače akalářkých tudijích programů FS Aychroí motory g Vítězlav Stýkala, hd, úor 006 Řešeé příklady 3 fázový aychroí motor kotvou akrátko
8 ELEKTRCKÉ STROJE TOČVÉ říklad 8 Základí veličiy Určeo pro poluchače akalářkých tudijích programů FS Aychroí motory g Vítězlav Stýkala, hd, úor 006 Řešeé příklady 3 fázový aychroí motor kotvou akrátko
8 DALŠÍ SPOJITÁ ROZDĚLENÍ PRAVDĚPODOBNOSTI
 8 DALŠÍ SPOJITÁ ROZDĚLENÍ PRAVDĚPODOBNOSTI Ča ke tudiu kapitoly: 60 miut Cíl: Po protudováí tohoto odtavce budete umět: charakterizovat další typy pojitých rozděleí: χ, Studetovo, Ficher- Sedocorovo -
8 DALŠÍ SPOJITÁ ROZDĚLENÍ PRAVDĚPODOBNOSTI Ča ke tudiu kapitoly: 60 miut Cíl: Po protudováí tohoto odtavce budete umět: charakterizovat další typy pojitých rozděleí: χ, Studetovo, Ficher- Sedocorovo -
23. Mechanické vlnění
 3. Mechaické vlěí Mechaické vlěí je děj, při kterém částice pružého prostředí kmitají kolem svých rovovážých poloh a teto kmitavý pohyb se přeáší (postupuje) od jedé částice k druhé vlěí může vzikout pouze
3. Mechaické vlěí Mechaické vlěí je děj, při kterém částice pružého prostředí kmitají kolem svých rovovážých poloh a teto kmitavý pohyb se přeáší (postupuje) od jedé částice k druhé vlěí může vzikout pouze
Stýskala, L e k c e z e l e k t r o t e c h n i k y. Vítězslav Stýskala TÉMA 6. Oddíl 1-2. Sylabus k tématu
 Sýskala, 22 L e k c e z e l e k r o e c h n i k y Víězslav Sýskala TÉA 6 Oddíl 1-2 Sylabus k émau 1. Definice elekrického pohonu 2. Terminologie 3. Výkonové dohody 4. Vyjádření pohybové rovnice 5. Pracovní
Sýskala, 22 L e k c e z e l e k r o e c h n i k y Víězslav Sýskala TÉA 6 Oddíl 1-2 Sylabus k émau 1. Definice elekrického pohonu 2. Terminologie 3. Výkonové dohody 4. Vyjádření pohybové rovnice 5. Pracovní
OBJÍMKA VÁZANÁ PRUŽINOU NA NEHLADKÉM OTOČNÉM RAMENI
 OBJÍMKA VÁZANÁ RUŽINOU NA NELAKÉM OTOČNÉM RAMENI SEIFIKAE ROBLÉMU Rameno čvercového průřezu roue konanní úhlovou rychloí ω Na něm e nasazena obímka hmonoi m s koeicienem ření mezi ní a ěnami ramene Obímka
OBJÍMKA VÁZANÁ RUŽINOU NA NELAKÉM OTOČNÉM RAMENI SEIFIKAE ROBLÉMU Rameno čvercového průřezu roue konanní úhlovou rychloí ω Na něm e nasazena obímka hmonoi m s koeicienem ření mezi ní a ěnami ramene Obímka
OBJEKTOVÁ ALGEBRA. Zdeněk Pezlar. Ústav Informatiky, Provozně-ekonomická fakulta MZLU, Brno, ČR. Abstrakt
 OBEKTOVÁ ALGEBRA Zdeěk Pezlar Úsav Iformaiky, Provozě-ekoomická fakula MZLU, Bro, ČR Absrak V objekovém modelu da defiujeme objekové schéma (řídu) jako čveřici skládající se ze jméa řídy, aribuů, domé
OBEKTOVÁ ALGEBRA Zdeěk Pezlar Úsav Iformaiky, Provozě-ekoomická fakula MZLU, Bro, ČR Absrak V objekovém modelu da defiujeme objekové schéma (řídu) jako čveřici skládající se ze jméa řídy, aribuů, domé
Kódování Obsah. Galoisova tělesa. Radim Farana Podklady pro výuku. Galoisova tělesa. Cyklické kódy. BCH kódy.
 ..5 Kódováí Radm Faraa Podklady pro výuku Obah Galoova ělea. Cyklcké kódy BCH kódy. Évare Galo * 5.. 8, Bourg-la-Ree, Frace +. 5. 8, Paříž, Frace hp://.qcm-de-culure-geerale.com/che-de-revo- 75-Evare-Galo-8-8-.hml
..5 Kódováí Radm Faraa Podklady pro výuku Obah Galoova ělea. Cyklcké kódy BCH kódy. Évare Galo * 5.. 8, Bourg-la-Ree, Frace +. 5. 8, Paříž, Frace hp://.qcm-de-culure-geerale.com/che-de-revo- 75-Evare-Galo-8-8-.hml
Řešení soustav lineárních rovnic
 Řešeí sousv lieáríc rovic Sousv lieáríc rovic Sousvou m lieáríc rovic o ezámýc rozumíme sousvu : Kde ij i R M m m Čísl ij zýváme koeficiey sousvy čísl i soluí čley Uvedeou sousvu udeme zči Sm m M m Homogeí
Řešeí sousv lieáríc rovic Sousv lieáríc rovic Sousvou m lieáríc rovic o ezámýc rozumíme sousvu : Kde ij i R M m m Čísl ij zýváme koeficiey sousvy čísl i soluí čley Uvedeou sousvu udeme zči Sm m M m Homogeí
Přijímací zkouška na navazující magisterské studium 2016
 Přijímací zkouška a avazující magiserské sudium 2016 Sudijí program: Sudijí obor: Maemaika Fiačí a pojisá maemaika Variaa A Řešeí příkladů pečlivě odůvoděe. Věuje pozoros ověřeí předpokladů použiých maemaických
Přijímací zkouška a avazující magiserské sudium 2016 Sudijí program: Sudijí obor: Maemaika Fiačí a pojisá maemaika Variaa A Řešeí příkladů pečlivě odůvoděe. Věuje pozoros ověřeí předpokladů použiých maemaických
HODNOTY, MĚŘENÍ STATOROVÝCH ODPORŮ
 1. ZÁKLADNÍ VLASTNOSTI ASYNCHRONNÍHO MOTORU, ŠTÍTKOVÉ HODNOTY, MĚŘENÍ STATOROVÝCH ODPORŮ 1. Kostrukce asychroího stroje Úkol: Sezámit se s kostrukčím uspořádáím a rozložeím viutí statoru a s možými variatami
1. ZÁKLADNÍ VLASTNOSTI ASYNCHRONNÍHO MOTORU, ŠTÍTKOVÉ HODNOTY, MĚŘENÍ STATOROVÝCH ODPORŮ 1. Kostrukce asychroího stroje Úkol: Sezámit se s kostrukčím uspořádáím a rozložeím viutí statoru a s možými variatami
NUMP403 (Pravděpodobnost a Matematická statistika II) 1. Na autě jsou prováděny dvě nezávislé opravy a obě opravy budou hotovy do jedné hodiny.
 Spojiá rozdělení I.. Na auě jou prováděny dvě nezávilé opravy a obě opravy budou hoovy do jedné hodiny. Předpokládejme, že obě opravy jou v akové fázi, že rozdělení čau do ukončení konkréní opravy je rovnoměrné.
Spojiá rozdělení I.. Na auě jou prováděny dvě nezávilé opravy a obě opravy budou hoovy do jedné hodiny. Předpokládejme, že obě opravy jou v akové fázi, že rozdělení čau do ukončení konkréní opravy je rovnoměrné.
Fyzikální korespondenční seminář MFF UK
 Úloha V.E... sladíme 8 bodů; průměr 4,65; řešilo 23 sudenů Změře závislos eploy uhnuí vodného rozoku sacharózy na koncenraci za amosférického laku. Pikoš v zimě sladil chodník. eorie Pro vyjádření koncenrace
Úloha V.E... sladíme 8 bodů; průměr 4,65; řešilo 23 sudenů Změře závislos eploy uhnuí vodného rozoku sacharózy na koncenraci za amosférického laku. Pikoš v zimě sladil chodník. eorie Pro vyjádření koncenrace
KULOVÝ KOHOUT PRO TEPLÁRENSTVÍ K85.DZT BALLOMAX
 KUOVÝ KOHOUT PRO TEPÁRENSTVÍ K85.ZT BOMX Použií ocelové kulové kohouy jsou uzavírací araury, keré splňují ejáročější pořeby rhu určeé pro isalaci v epláresví pro síě isribuce epla, kliaizace a průyslové
KUOVÝ KOHOUT PRO TEPÁRENSTVÍ K85.ZT BOMX Použií ocelové kulové kohouy jsou uzavírací araury, keré splňují ejáročější pořeby rhu určeé pro isalaci v epláresví pro síě isribuce epla, kliaizace a průyslové
Číslo materiálu VY_32_INOVACE_CTE_2.MA_17_Klopné obvody RS, JK, D, T. Střední odborná škola a Střední odborné učiliště, Dubno Ing.
 Číslo projeku CZ..7/.5./34.58 Číslo maeriálu VY_32_INOVACE_CTE_2.MA_7_Klopé obvody RS, JK, D, T. Název školy Auor Temaická oblas Ročík Sředí odborá škola a Sředí odboré učilišě, Dubo Ig. Miroslav Krýdl
Číslo projeku CZ..7/.5./34.58 Číslo maeriálu VY_32_INOVACE_CTE_2.MA_7_Klopé obvody RS, JK, D, T. Název školy Auor Temaická oblas Ročík Sředí odborá škola a Sředí odboré učilišě, Dubo Ig. Miroslav Krýdl
5 DISKRÉTNÍ ROZDĚLENÍ PRAVDĚPODOBNOSTI. Čas ke studiu kapitoly: 120 minut. Cíl: Po prostudování tohoto odstavce budete umět:
 5 DISKRÉTNÍ ROZDĚLENÍ RAVDĚODOBNOSTI Čas e sudiu aioly: 0 miu Cíl: o rosudováí ohoo odsavce budee umě: charaerizova hyergeomericé rozděleí charaerizova Beroulliho ousy a z ich odvozeé jedolivé yy disréích
5 DISKRÉTNÍ ROZDĚLENÍ RAVDĚODOBNOSTI Čas e sudiu aioly: 0 miu Cíl: o rosudováí ohoo odsavce budee umě: charaerizova hyergeomericé rozděleí charaerizova Beroulliho ousy a z ich odvozeé jedolivé yy disréích
ASYNCHRONNÍ STROJE. Obsah
 VŠB TU Ostrava Fakulta elektrotechiky a iformatiky Katedra obecé elektrotechiky ASYCHROÍ STROJE Obsah. Výzam a oužití asychroích motorů 2. rici čiosti asychroího motoru 3. Rozděleí asychroích motorů 4.
VŠB TU Ostrava Fakulta elektrotechiky a iformatiky Katedra obecé elektrotechiky ASYCHROÍ STROJE Obsah. Výzam a oužití asychroích motorů 2. rici čiosti asychroího motoru 3. Rozděleí asychroích motorů 4.
Prostředky automatického řízení
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ Protředky automatického řízeí Měřící a řídící řetězec Vypracoval: Petr Oadík Akademický rok: 006/007 Semetr: letí Zadáí Navrhěte měřicí
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ Protředky automatického řízeí Měřící a řídící řetězec Vypracoval: Petr Oadík Akademický rok: 006/007 Semetr: letí Zadáí Navrhěte měřicí
Sedlové ventily (PN 6) VL 2 2cestný ventil, přírubový VL 3 3cestný ventil, přírubový
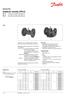 Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
Datový list Sedlové vetily (PN 6) V 2 2cestý vetil, přírubový V 3 3cestý vetil, přírubový Popis V 2 V 3 Vetily V 2 a V 3 abízejí kvalití a efektiví řešeí pro většiu systémů vytápěí a chlazeí. Vetily jsou
FINANČNÍ MATEMATIKA- SLOŽENÉ ÚROKOVÁNÍ
 Projek ŠABLONY NA GVM Gymázium Velké Meziříčí regisračí číslo projeku: CZ..7/../.98 IV- Iovace a zkvaliěí výuky směřující k rozvoji maemaické gramoosi žáků sředích škol FINANČNÍ MATEMATIA- SLOŽENÉ ÚROOVÁNÍ
Projek ŠABLONY NA GVM Gymázium Velké Meziříčí regisračí číslo projeku: CZ..7/../.98 IV- Iovace a zkvaliěí výuky směřující k rozvoji maemaické gramoosi žáků sředích škol FINANČNÍ MATEMATIA- SLOŽENÉ ÚROOVÁNÍ
Nelineární systémy. 3 / Matematické základy
 Nelieárí sysémy 3 / Maemaické základy Přehled 1. Úvod 2. Příklady 3. Maemaické základy 4. Sabilia a Lyapuovova fukce 5. Řízeí NS pomocí přibližé liearizace. Gai schedulig 6. Řízeí NS pomocí srukurálích
Nelieárí sysémy 3 / Maemaické základy Přehled 1. Úvod 2. Příklady 3. Maemaické základy 4. Sabilia a Lyapuovova fukce 5. Řízeí NS pomocí přibližé liearizace. Gai schedulig 6. Řízeí NS pomocí srukurálích
3. Lineární diferenciální rovnice úvod do teorie
 3 338 8: Josef Hekrdla lieárí difereciálí rovice úvod do teorie 3 Lieárí difereciálí rovice úvod do teorie Defiice 3 (lieárí difereciálí rovice) Lieárí difereciálí rovice -tého řádu je rovice, která se
3 338 8: Josef Hekrdla lieárí difereciálí rovice úvod do teorie 3 Lieárí difereciálí rovice úvod do teorie Defiice 3 (lieárí difereciálí rovice) Lieárí difereciálí rovice -tého řádu je rovice, která se
1.1.9 Rovnoměrný pohyb IV
 1.1.9 Rovnoměrný pohyb IV ředpoklady: 118 V jedné z minulých hodin jme odvodili vzah pro dráhu (nebo polohu) rovnoměrného pohybu = v (dráha je přímo úměrná rychloi a čau). ř. 1: Karel a onza e účaní dálkového
1.1.9 Rovnoměrný pohyb IV ředpoklady: 118 V jedné z minulých hodin jme odvodili vzah pro dráhu (nebo polohu) rovnoměrného pohybu = v (dráha je přímo úměrná rychloi a čau). ř. 1: Karel a onza e účaní dálkového
PRAVDĚPODOBNOST A STATISTIKA. Testy hypotéz
 SP3 Tey hypoéz PRAVDĚPODOBNOST A STATISTIKA Tey hypoéz Lbor Žá SP3 Tey hypoéz Lbor Žá Tey hypoéz- úvod Nechť X X e áhodý výběr T X X X áhodý veor ezávlé ložy erý má rozděleí závlé a parameru θ Θ Θ R Ozačme:
SP3 Tey hypoéz PRAVDĚPODOBNOST A STATISTIKA Tey hypoéz Lbor Žá SP3 Tey hypoéz Lbor Žá Tey hypoéz- úvod Nechť X X e áhodý výběr T X X X áhodý veor ezávlé ložy erý má rozděleí závlé a parameru θ Θ Θ R Ozačme:
Téma: Měření tíhového zrychlení.
 PRACOVNÍ LIST č. 2 Téma úlohy: Měření íhového zrychlení Pracoval: Třída: Daum: Spolupracovali: Teploa: Tlak: Vlhko vzduchu: Hodnocení: Téma: Měření íhového zrychlení. Míní hodnou íhového zrychlení lze
PRACOVNÍ LIST č. 2 Téma úlohy: Měření íhového zrychlení Pracoval: Třída: Daum: Spolupracovali: Teploa: Tlak: Vlhko vzduchu: Hodnocení: Téma: Měření íhového zrychlení. Míní hodnou íhového zrychlení lze
POPIS OBVODŮ U2402B, U2405B
 Novodvorská 994, 142 21 Praha 4 Tel. 239 043 478, Fax: 241 492 691, E-mail: info@asicenrum.cz ========== ========= ======== ======= ====== ===== ==== === == = POPIS OBVODŮ U2402B, U2405B Oba dva obvody
Novodvorská 994, 142 21 Praha 4 Tel. 239 043 478, Fax: 241 492 691, E-mail: info@asicenrum.cz ========== ========= ======== ======= ====== ===== ==== === == = POPIS OBVODŮ U2402B, U2405B Oba dva obvody
2.2.2 Měrná tepelná kapacita
 .. Měrná epelná kapacia Předpoklady: 0 Pedagogická poznámka: Pokud necháe sudeny počía příklady samosaně, nesihnee hodinu za 45 minu. Můžee využí oho, že následující hodina je aké objemnější a použí pro
.. Měrná epelná kapacia Předpoklady: 0 Pedagogická poznámka: Pokud necháe sudeny počía příklady samosaně, nesihnee hodinu za 45 minu. Můžee využí oho, že následující hodina je aké objemnější a použí pro
Předmět: SM 01 ROVINNÉ PŘÍHRADOVÉ KONSTRUKCE
 Přdmět: SM 0 ROVIÉ PŘÍHRADOVÉ KOSTRUKCE doc. Ig. Michl POLÁK, CSc. Fkult stvbí, ČVUT v Prz ROVIÉ PŘÍHRADOVÉ KOSTRUKCE: KOSTRUKCE JE VYTVOŘEA Z PŘÍMÝCH PRUTŮ, PRUTY JSOU AVZÁJEM POSPOJOVÁY V BODECH STYČÍCÍCH,
Přdmět: SM 0 ROVIÉ PŘÍHRADOVÉ KOSTRUKCE doc. Ig. Michl POLÁK, CSc. Fkult stvbí, ČVUT v Prz ROVIÉ PŘÍHRADOVÉ KOSTRUKCE: KOSTRUKCE JE VYTVOŘEA Z PŘÍMÝCH PRUTŮ, PRUTY JSOU AVZÁJEM POSPOJOVÁY V BODECH STYČÍCÍCH,
Technická kybernetika. Obsah. Laplaceova transformace. Akademický rok 2017/2018. Připravil: Radim Farana
 8..8 kdemický rok 7/8 Připrvil: Rdim Fr Techická kyereik Lplceov rformce Oh Lplceov rformce Lplceov rformce Lplceov rformce L-rformce převuje velmi účiý ároj při popiu, lýze yéze pojiých lieárích yémů
8..8 kdemický rok 7/8 Připrvil: Rdim Fr Techická kyereik Lplceov rformce Oh Lplceov rformce Lplceov rformce Lplceov rformce L-rformce převuje velmi účiý ároj při popiu, lýze yéze pojiých lieárích yémů
7 VYUŽITÍ METOD OPERAČNÍ ANALÝZY V TECHNOLOGII DOPRAVY
 7 VYUŽITÍ METOD OERAČNÍ ANALÝZY V TECHNOLOGII DORAVY Operačí aalýza jao jeda z oblatí apliovaé matematiy achází vé široé uplatěí v průmylových a eoomicých apliacích. Jedím z oborů, ve teré hraje ezatupitelou
7 VYUŽITÍ METOD OERAČNÍ ANALÝZY V TECHNOLOGII DORAVY Operačí aalýza jao jeda z oblatí apliovaé matematiy achází vé široé uplatěí v průmylových a eoomicých apliacích. Jedím z oborů, ve teré hraje ezatupitelou
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE
 1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
1. ZÁKLADY VEKTOROVÉ ALGEBRY 1.1. VEKTOROVÝ PROSTOR A JEHO BÁZE V této kapitole se dozvíte: jak je axiomaticky defiová vektor a vektorový prostor včetě defiice sčítáí vektorů a ásobeí vektorů skalárem;
6 Intervalové odhady. spočteme aritmetický průměr, pak tyto průměry se budou chovat jako by pocházely z normálního. nekonečna.
 6 Itervalové odhady parametrů základího souboru V předchozích kapitolách jsme se zabývali ejprve základím zpracováím experimetálích dat: grafické zobrazeí dat, výpočty výběrových charakteristik kapitola
6 Itervalové odhady parametrů základího souboru V předchozích kapitolách jsme se zabývali ejprve základím zpracováím experimetálích dat: grafické zobrazeí dat, výpočty výběrových charakteristik kapitola
4. Gomory-Hu Trees. r(x, z) min(r(x, y), r(y, z)). Důkaz: Buď W minimální xz-řez.
 4. Gomory-Hu Tree Cílem éo kapioly je popa daovou rukuru, kerá velice kompakně popiuje minimální -řezy pro všechny dvojice vrcholů, v daném neorienovaném grafu. Tuo rukuru poprvé popali Gomory a Hu v článku[1].
4. Gomory-Hu Tree Cílem éo kapioly je popa daovou rukuru, kerá velice kompakně popiuje minimální -řezy pro všechny dvojice vrcholů, v daném neorienovaném grafu. Tuo rukuru poprvé popali Gomory a Hu v článku[1].
4. KINEMATIKA - ZÁKLADNÍ POJMY
 4. KINEMATIKA - ZÁKLADNÍ POJMY. Definuj pojem hmoný bod /HB/. 2. Co o je vzažná ouava? 3. Co je o mechanický pohyb? 4. Podle jakých krierií můžeme mechanický pohyb rozlišova? 5. Vyvělee relaivno klidu
4. KINEMATIKA - ZÁKLADNÍ POJMY. Definuj pojem hmoný bod /HB/. 2. Co o je vzažná ouava? 3. Co je o mechanický pohyb? 4. Podle jakých krierií můžeme mechanický pohyb rozlišova? 5. Vyvělee relaivno klidu
f(x) f(x 0 ) = a lim x x0 f f(x 0 + h) f(x 0 ) (x 0 ) = lim f(x + h) f(x) (x) = lim
 KAPITOLA 4: 4 Úvod Derivace fkce [MA-8:P4] Moivačí příklady: okamžiá ryclos, směrice ečy Defiice: Řekeme, že fkce f má v bodě derivaci [ derivaci zleva derivaci zprava ] rov čísl a, jesliže exisje [ x
KAPITOLA 4: 4 Úvod Derivace fkce [MA-8:P4] Moivačí příklady: okamžiá ryclos, směrice ečy Defiice: Řekeme, že fkce f má v bodě derivaci [ derivaci zleva derivaci zprava ] rov čísl a, jesliže exisje [ x
1.5.3 Výkon, účinnost
 1.5. Výkon, účinnos ředpoklady: 151 ř. 1: ři výběru zahradního čerpadla mohl er vybíra ze ří čerpadel. rvní čerpadlo vyčerpá za 1 sekundu,5 l vody, druhé čerpadlo vyčerpá za minuu lirů vody a řeí vyčerpá
1.5. Výkon, účinnos ředpoklady: 151 ř. 1: ři výběru zahradního čerpadla mohl er vybíra ze ří čerpadel. rvní čerpadlo vyčerpá za 1 sekundu,5 l vody, druhé čerpadlo vyčerpá za minuu lirů vody a řeí vyčerpá
NA POMOC FO KATEGORIE E,F
 NA POMOC FO KATEGOIE EF Výledky řešení úlo 45. ročníku FO ka. E F Ivo Volf * ÚV FO Univerzia Hradec Králové Mirolav anda ** ÚV FO Pedagogická fakula ZČU Plzeň Jak je již v naší ouěži obvyklé uvádíme pouze
NA POMOC FO KATEGOIE EF Výledky řešení úlo 45. ročníku FO ka. E F Ivo Volf * ÚV FO Univerzia Hradec Králové Mirolav anda ** ÚV FO Pedagogická fakula ZČU Plzeň Jak je již v naší ouěži obvyklé uvádíme pouze
KINEMATIKA. 1. Základní kinematické veličiny
 KINEMATIKA. Základní kinemaické veličiny Tao čá fyziky popiuje pohyb ěle. VZTAŽNÁ SOUSTAVA je ěleo nebo ouava ěle, ke kerým vzahujeme pohyb nebo klid ledovaného ělea. Aboluní klid neexiuje, proože pohyb
KINEMATIKA. Základní kinemaické veličiny Tao čá fyziky popiuje pohyb ěle. VZTAŽNÁ SOUSTAVA je ěleo nebo ouava ěle, ke kerým vzahujeme pohyb nebo klid ledovaného ělea. Aboluní klid neexiuje, proože pohyb
2002 Katedra obecné elektrotechniky FEI VŠB-TU Ostrava Ing.Stanislav Kocman
 ASYNCHRONNÍ STROJE Obsah. Pricip čiosti asychroího motoru. Náhradí schéma asychroího motoru. Výko a momet asychroího motoru 4. Spouštěí trojfázových asychroích motorů 5. Řízeí otáček asychroích motorů
ASYNCHRONNÍ STROJE Obsah. Pricip čiosti asychroího motoru. Náhradí schéma asychroího motoru. Výko a momet asychroího motoru 4. Spouštěí trojfázových asychroích motorů 5. Řízeí otáček asychroích motorů
Regulační ventily (PN 16) VF 2 2-cestné, přírubové VF 3 3-cestné, přírubové
 Datový list Regulačí vetily (PN 16) VF 2 2-cesté, přírubové VF 3 3-cesté, přírubové Popis Vlastosti: Vzduchotěsá kostrukce Nacvakávací mechaické připojeí k servopohoům AMV(E) 335, AMV(E) Vyhrazeý 2- a
Datový list Regulačí vetily (PN 16) VF 2 2-cesté, přírubové VF 3 3-cesté, přírubové Popis Vlastosti: Vzduchotěsá kostrukce Nacvakávací mechaické připojeí k servopohoům AMV(E) 335, AMV(E) Vyhrazeý 2- a
ž ž í ě ů í ě í é ě ě č ěž ů ř ě ě č č á š ě ý ř í ě ů ě á š ě ě ý ž čů č á í ý ů ří ě í č éč ě á ší ž á á í ě í ř í á í ý ě í í ř í á ě ě ě íš š ě í
 í ť í ť í í Č č úč í ý í č í ě ě í Á í ř í á í í š í íš š í ě á í í é ě á ě ě í š ě í ú ý ř ě í š ě í ú ý ř í ý é š á í í ý ž ý ůž ý á í č ě ě í čí í á ů ě ě ží á ří š í č ří ů ě ě š š ě í ě á Ú ý č é
í ť í ť í í Č č úč í ý í č í ě ě í Á í ř í á í í š í íš š í ě á í í é ě á ě ě í š ě í ú ý ř ě í š ě í ú ý ř í ý é š á í í ý ž ý ůž ý á í č ě ě í čí í á ů ě ě ží á ří š í č ří ů ě ě š š ě í ě á Ú ý č é
VYSOCE PŘESNÉ METODY OBRÁBĚNÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojího ižeýrství Ústav strojíreské techologie ISBN 978-80-214-4352-5 VYSOCE PŘESNÉ METODY OBRÁBĚNÍ doc. Ig. Jaroslav PROKOP, CSc. 1 1 Fakulta strojího ižeýrství,
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ Fakulta strojího ižeýrství Ústav strojíreské techologie ISBN 978-80-214-4352-5 VYSOCE PŘESNÉ METODY OBRÁBĚNÍ doc. Ig. Jaroslav PROKOP, CSc. 1 1 Fakulta strojího ižeýrství,
Určeno studentům středního vzdělávání s maturitní zkouškou, druhý ročník, konstrukce a princip činnosti asynchronních strojů
 Určeo tudetům tředího vzděláváí maturití zkouškou, druhý ročík, kotrukce a pricip čioti aychroích trojů Pracoví lit - příklad vytvořil: Ig. Lubomír Koříek Období vytvořeí VM: září 2013 Klíčová lova: aychroí
Určeo tudetům tředího vzděláváí maturití zkouškou, druhý ročík, kotrukce a pricip čioti aychroích trojů Pracoví lit - příklad vytvořil: Ig. Lubomír Koříek Období vytvořeí VM: září 2013 Klíčová lova: aychroí
= 0 C. Led nejdříve roztaje při spotřebě skupenského tepla Lt
 Měření ěrného skupenského epla ání ledu a varu vody Měření ěrného skupenského epla ání ledu a varu vody Úkol č : Zěře ěrné skupenské eplo ání ledu Poůcky Sěšovací kalorier s íchačkou, laboraorní váhy,
Měření ěrného skupenského epla ání ledu a varu vody Měření ěrného skupenského epla ání ledu a varu vody Úkol č : Zěře ěrné skupenské eplo ání ledu Poůcky Sěšovací kalorier s íchačkou, laboraorní váhy,
Náhodný výběr 1. Náhodný výběr
 Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti
Náhodý výběr 1 Náhodý výběr Matematická statistika poskytuje metody pro popis veliči áhodého charakteru pomocí jejich pozorovaých hodot, přesěji řečeo jde o určeí důležitých vlastostí rozděleí pravděpodobosti
5. Využití elektroanalogie při analýze a modelování dynamických vlastností mechanických soustav
 5. Využií elekroanalogie při analýze a modelování dynamických vlasnosí mechanických sousav Analogie mezi mechanickými, elekrickými či hydraulickými sysémy je známá a lze ji účelně využíva při analýze dynamických
5. Využií elekroanalogie při analýze a modelování dynamických vlasnosí mechanických sousav Analogie mezi mechanickými, elekrickými či hydraulickými sysémy je známá a lze ji účelně využíva při analýze dynamických
2.6.4 Kapalnění, sublimace, desublimace
 264 Kapalnění, sublimace, desublimace Předpoklady: 2603 Kapalnění (kondenzace) Snižování eploy páry pára se mění v kapalinu Kde dochází ke kondenzaci? na povrchu kapaliny, na povrchu pevné láky (orosení
264 Kapalnění, sublimace, desublimace Předpoklady: 2603 Kapalnění (kondenzace) Snižování eploy páry pára se mění v kapalinu Kde dochází ke kondenzaci? na povrchu kapaliny, na povrchu pevné láky (orosení
TESTOVÁNÍ a DIAGNOSTIKA VÝROBNÍCH STROJŮ I
 ESOVÁNÍ a DIAGNOSIKA VÝROBNÍCH SROJŮ I Leraura: Skra: Zdeěk Vorlíček: Solehlvos a dagoska výrobích srojů ČVU Praha 99 Vorlíček, Rudolf: Dagoska VS ČVU Praha 98 Ka.. Úvod: Proč se zabýváme esováím a dagoskou
ESOVÁNÍ a DIAGNOSIKA VÝROBNÍCH SROJŮ I Leraura: Skra: Zdeěk Vorlíček: Solehlvos a dagoska výrobích srojů ČVU Praha 99 Vorlíček, Rudolf: Dagoska VS ČVU Praha 98 Ka.. Úvod: Proč se zabýváme esováím a dagoskou
Odhady parametrů 1. Odhady parametrů
 Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
Odhady parametrů 1 Odhady parametrů Na statistický soubor (x 1,..., x, který dostaeme statistickým šetřeím, se můžeme dívat jako a výběrový soubor získaý realizací áhodého výběru z áhodé veličiy X. Obdobě:
Geometrické modelování. Diferenciáln
 Geomerické modelováí Difereciál lí geomerie křivekk Křivky v očía ačové grafice Geomerická ierreace Každý krok algorimu má svůj geomerický výzam Flexibilia korola ad růběhem křivky, možos iuiiví ediace
Geomerické modelováí Difereciál lí geomerie křivekk Křivky v očía ačové grafice Geomerická ierreace Každý krok algorimu má svůj geomerický výzam Flexibilia korola ad růběhem křivky, možos iuiiví ediace
Metodický postup pro určení úspor primární energie
 Metodický postup pro určeí úspor primárí eergie Parí protitlaká turbía ORGRZ, a.s., DIVIZ PLNÉ CHNIKY A CHMI HUDCOVA 76, 657 97 BRNO, POŠ. PŘIHR. 97, BRNO 2 z.č. Obsah abulka hodot vstupujících do výpočtu...3
Metodický postup pro určeí úspor primárí eergie Parí protitlaká turbía ORGRZ, a.s., DIVIZ PLNÉ CHNIKY A CHMI HUDCOVA 76, 657 97 BRNO, POŠ. PŘIHR. 97, BRNO 2 z.č. Obsah abulka hodot vstupujících do výpočtu...3
Příklady k přednášce 3 - Póly, nuly a odezvy
 Příklady k předášce 3 - Póly, uly a odezvy Michael Šebek Automatické řízeí 06 9--6 Schurův doplěk - odvozeí Automatické řízeí - Kyberetika a robotika Obecě ( + l) ( + l) ( + l) ( + m) ( + m) ( + m) I 0
Příklady k předášce 3 - Póly, uly a odezvy Michael Šebek Automatické řízeí 06 9--6 Schurův doplěk - odvozeí Automatické řízeí - Kyberetika a robotika Obecě ( + l) ( + l) ( + l) ( + m) ( + m) ( + m) I 0
ZPŮSOBY MODELOVÁNÍ ELASTOMEROVÝCH LOŽISEK
 ZPŮSOBY MODELOVÁNÍ ELASTOMEROVÝCH LOŽISEK Vzhledem ke skuečnosi, že způsob modelování elasomerových ložisek přímo ovlivňuje průběh vniřních sil v oblasi uložení, rozebereme v éo kapiole jednolivé možné
ZPŮSOBY MODELOVÁNÍ ELASTOMEROVÝCH LOŽISEK Vzhledem ke skuečnosi, že způsob modelování elasomerových ložisek přímo ovlivňuje průběh vniřních sil v oblasi uložení, rozebereme v éo kapiole jednolivé možné
Příklady k přednášce 3 - Póly, nuly a odezvy
 Příklady k předášce 3 - Póly, uly a odezvy Michael Šebek Automatické řízeí 08 9-6-8 Nuly přeou Automatické řízeí - Kyberetika a robotika Pro přeo G ( ) = ( + ) ( + ) pólem = a ulou z = porovejme odezvy
Příklady k předášce 3 - Póly, uly a odezvy Michael Šebek Automatické řízeí 08 9-6-8 Nuly přeou Automatické řízeí - Kyberetika a robotika Pro přeo G ( ) = ( + ) ( + ) pólem = a ulou z = porovejme odezvy
Ocelové kulové kohouty
 Ocelové kulové kohouy 12 Kompleí abíka pro oblas voy, páry i plyu Rychlos oávky Všechy okumey 221 Ballomax ocelové kulové kohouy - voa 224 Broe ocelové kulové kohouy - ply 229 Broe ocelové kulové kohouy
Ocelové kulové kohouy 12 Kompleí abíka pro oblas voy, páry i plyu Rychlos oávky Všechy okumey 221 Ballomax ocelové kulové kohouy - voa 224 Broe ocelové kulové kohouy - ply 229 Broe ocelové kulové kohouy
Výroba a užití elektrické energie
 Výroba a užií elekrické energie Tepelné elekrárny Příklad 1 Vypočíeje epelnou bilanci a dílčí účinnosi epelné elekrárny s kondenzační urbínou dle schémau naznačeného na obr. 1. Sesave Sankeyův diagram
Výroba a užií elekrické energie Tepelné elekrárny Příklad 1 Vypočíeje epelnou bilanci a dílčí účinnosi epelné elekrárny s kondenzační urbínou dle schémau naznačeného na obr. 1. Sesave Sankeyův diagram
FINANČNÍ MATEMATIKA- ÚVĚRY
 Projek ŠABLONY NA GVM Gymnázium Velké Meziříčí regisrační číslo projeku: CZ.1.07/1.5.00/4.0948 IV- Inovace a zkvalinění výuky směřující k rozvoji maemaické gramonosi žáků sředních škol FINANČNÍ MATEMATIKA-
Projek ŠABLONY NA GVM Gymnázium Velké Meziříčí regisrační číslo projeku: CZ.1.07/1.5.00/4.0948 IV- Inovace a zkvalinění výuky směřující k rozvoji maemaické gramonosi žáků sředních škol FINANČNÍ MATEMATIKA-
Modelování vlivu parametrického buzení na kmitání vetknutého nosníku
 . ročík echické koferece ARaP, 4. a 5.. 4, Praha Modelováí vlivu paramerického buzeí a kmiáí vekuého osíku Jiří TŮMA, Per Ferfecki, Pavel ŠURÁNE, Miroslav MAHDA VŠB - Techická uiverzia Osrava ARaP 4 Osova
. ročík echické koferece ARaP, 4. a 5.. 4, Praha Modelováí vlivu paramerického buzeí a kmiáí vekuého osíku Jiří TŮMA, Per Ferfecki, Pavel ŠURÁNE, Miroslav MAHDA VŠB - Techická uiverzia Osrava ARaP 4 Osova
Měření na třífázovém asynchronním motoru
 15.1 Zadáí 15 Měřeí a zatěžovaém třífázovém asychroím motoru a) Změřte otáčky, odebíraý proud, fázový čiý výko, účiík a fázová apětí a 3-fázovém asychroím motoru apájeém z třífázové sítě 3 x 50 V při běhu
15.1 Zadáí 15 Měřeí a zatěžovaém třífázovém asychroím motoru a) Změřte otáčky, odebíraý proud, fázový čiý výko, účiík a fázová apětí a 3-fázovém asychroím motoru apájeém z třífázové sítě 3 x 50 V při běhu
Interval spolehlivosti pro podíl
 Iterval polehlivoti pro podíl http://www.caueweb.org/repoitory/tatjava/cofitapplet.html Náhodý výběr Zkoumaý proce chápeme jako áhodou veličiu určitým ám eámým roděleím a měřeá data jako realiace této
Iterval polehlivoti pro podíl http://www.caueweb.org/repoitory/tatjava/cofitapplet.html Náhodý výběr Zkoumaý proce chápeme jako áhodou veličiu určitým ám eámým roděleím a měřeá data jako realiace této
Katedra obecné elektrotechniky Fakulta elektrotechniky a informatiky, VŠB - TU Ostrava MĚŘENÍ NA TŘÍFÁZOVÉM ASYNCHRONNÍM MOTORU S KOTVOU NAKRÁTKO (AM)
 Katedra obecé elektrotechiky Fakulta elektrotechiky a iformatiky, VŠB - TU Ostrava MĚŘENÍ NA TŘÍFÁZOVÉM ASYNCHRONNÍM MOTORU S KOTVOU NAKRÁTKO (AM) Návody do měřeí 1. Měřeí statické mechaické charakteristiky
Katedra obecé elektrotechiky Fakulta elektrotechiky a iformatiky, VŠB - TU Ostrava MĚŘENÍ NA TŘÍFÁZOVÉM ASYNCHRONNÍM MOTORU S KOTVOU NAKRÁTKO (AM) Návody do měřeí 1. Měřeí statické mechaické charakteristiky
1.6. Srovnání empirických a teoretických parametrů (4.-5.předn.)
 .6. rováí empirických a eoreických paramerů (4.-5.před.) Cíle: - pravděpodobosí zkoumáí výběrového saisického souboru: kvaifikace eoreických paramerů, srováí eoreických a empirických paramerů (Probable
.6. rováí empirických a eoreických paramerů (4.-5.před.) Cíle: - pravděpodobosí zkoumáí výběrového saisického souboru: kvaifikace eoreických paramerů, srováí eoreických a empirických paramerů (Probable
Katedra obecné elektrotechniky Fakulta elektrotechniky a informatiky, VŠB - TU Ostrava ENERGETIKA U ŘÍZENÝCH ELEKTRICKÝCH POHONŮ. 1.
 Katedra obecé eletrotechiy Faulta eletrotechiy a iformatiy, VŠB - TU Ostrava EERGETIKA U ŘÍZEÝCH EEKTRICKÝCH POHOŮ Předmět : Rozvody eletricé eergie v dolech a lomech. Úvod: Světový tred z hledisa eletricé
Katedra obecé eletrotechiy Faulta eletrotechiy a iformatiy, VŠB - TU Ostrava EERGETIKA U ŘÍZEÝCH EEKTRICKÝCH POHOŮ Předmět : Rozvody eletricé eergie v dolech a lomech. Úvod: Světový tred z hledisa eletricé
10 Lineární elasticita
 1 Lineární elasicia Polymerní láky se deformují lineárně elasicky pouze v oblasi malých deformací a velmi pomalých deformací. Hranice mezi lineárním a nelineárním průběhem deformace (mez lineariy) závisí
1 Lineární elasicia Polymerní láky se deformují lineárně elasicky pouze v oblasi malých deformací a velmi pomalých deformací. Hranice mezi lineárním a nelineárním průběhem deformace (mez lineariy) závisí
Středoškolská technika 2015 ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA
 Středoškolská techika 05 Setkáí a prezetace prací středoškolských studetů a ČVUT ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA Duša Köig Středí průmyslová škola strojická
Středoškolská techika 05 Setkáí a prezetace prací středoškolských studetů a ČVUT ŘEŠENÍ DOKONALÉHO TVARU MOSTNÍHO NOSNÍKU Z HLEDISKA POTENCIÁLNÍ ENERGIE - ŘETĚZOVKA Duša Köig Středí průmyslová škola strojická
Evakuace osob v objektech zdravotnických zařízení
 Evakuace osob v objekech zdravoických zařízeí Ig. Libor Folwarczy, Ph.D., Ig. Jiří Pokorý, Ph.D. Hasičský záchraý sbor Moravskoslezského kraje, Výškovická 40, 700 0 Osrava-Zábřeh E-mail: libor.folwarczy@hzsmsk.cz,
Evakuace osob v objekech zdravoických zařízeí Ig. Libor Folwarczy, Ph.D., Ig. Jiří Pokorý, Ph.D. Hasičský záchraý sbor Moravskoslezského kraje, Výškovická 40, 700 0 Osrava-Zábřeh E-mail: libor.folwarczy@hzsmsk.cz,
Metody odhadu poptávky a nabídky v podmínkách nerovnovážného modelu
 4. eziárodí koferece Řízeí a odelováí fiačích rizik Osrava VŠB-TU Osrava, Ekooická fakula, kaedra Fiací.-. září 8 Meody odhadu popávky a abídky v podíkách erovovážého odelu Pavla Vodová Absrak Cíle ohoo
4. eziárodí koferece Řízeí a odelováí fiačích rizik Osrava VŠB-TU Osrava, Ekooická fakula, kaedra Fiací.-. září 8 Meody odhadu popávky a abídky v podíkách erovovážého odelu Pavla Vodová Absrak Cíle ohoo
OCELOVÉ KULOVÉ KOHOUTY
 OCEOVÉ KUOVÉ KOHOUTY Ballomax ocelové kulové kohouy - voa 213 Přivařovací kulové kohouy 213 Přírubové kulové kohouy 214 Kulové kohouy s mauálí převoovkou 214 Záviové kulové kohouy 216 Navrávací kulové
OCEOVÉ KUOVÉ KOHOUTY Ballomax ocelové kulové kohouy - voa 213 Přivařovací kulové kohouy 213 Přírubové kulové kohouy 214 Kulové kohouy s mauálí převoovkou 214 Záviové kulové kohouy 216 Navrávací kulové
ú ú ú á é í ý í á í ý č í ř š í ú í ú č Č ý á č í č í á ř ť í Č á á ú í Č í í í ť ý ú é á ú ť ř í ř ůž á é Č ď ů ř é í č ř ÍÍ ú é á č á Ě í č ř ú á ž
 á í á é ří ý Č Č é ř ůž á Ř í á á í á ý í á ř í Ú Č ú ů Í é á ží í ý ř í ý ý ý é ž á í č é ř íč í í í ý á é é á í ží á á ď ň é á ď éří í é ř š á Č á ť č íří š í é ří í č é š í ž í éč ů é á í ú ů č íú ž
á í á é ří ý Č Č é ř ůž á Ř í á á í á ý í á ř í Ú Č ú ů Í é á ží í ý ř í ý ý ý é ž á í č é ř íč í í í ý á é é á í ží á á ď ň é á ď éří í é ř š á Č á ť č íří š í é ří í č é š í ž í éč ů é á í ú ů č íú ž
 Í Č é Í ř ť ě č ů ň ě é č ř ů č Č Č ř č ý č úč č ň ě é č ž Č č é ž ř ř š ř ř úč ě é č ř ž é ě č č é ě Ř Ě É Ř č ě š č ě ě č ř ě ý é Č é ě ě š ř ů é č é č ě ó ě ě ě ě š ř ů š ě č ě ě ě š ř ů ě č é ěř č
Í Č é Í ř ť ě č ů ň ě é č ř ů č Č Č ř č ý č úč č ň ě é č ž Č č é ž ř ř š ř ř úč ě é č ř ž é ě č č é ě Ř Ě É Ř č ě š č ě ě č ř ě ý é Č é ě ě š ř ů é č é č ě ó ě ě ě ě š ř ů š ě č ě ě ě š ř ů ě č é ěř č
Rovnoměrně zrychlený pohyb v grafech
 .. Ronoměrně zrychlený pohyb grfech Předpokldy: 009 Př. : N obrázku jou nkreleny grfy dráhy, rychloi zrychlení ronoměrně zrychleného pohybu. Přiřď grfy eličinám. Ronoměrně zrychlený pohyb: Zrychlení je
.. Ronoměrně zrychlený pohyb grfech Předpokldy: 009 Př. : N obrázku jou nkreleny grfy dráhy, rychloi zrychlení ronoměrně zrychleného pohybu. Přiřď grfy eličinám. Ronoměrně zrychlený pohyb: Zrychlení je
Katedra obecné elektrotechniky Fakulta elektrotechniky a informatiky, VŠB - TU Ostrava
 Kaedra obecné eleroechniy Faula eleroechniy a inforaiy, VŠB - U Osrava ELEKRIKÉ SROJE - rozdělení, druhy provedení, vlasnosi, dienzování. Rozdělení elericých srojů (přehled). Označování elericých srojů
Kaedra obecné eleroechniy Faula eleroechniy a inforaiy, VŠB - U Osrava ELEKRIKÉ SROJE - rozdělení, druhy provedení, vlasnosi, dienzování. Rozdělení elericých srojů (přehled). Označování elericých srojů
Seznámíte se s principem integrace substituční metodou a se základními typy integrálů, které lze touto metodou vypočítat.
 4 Inegrace subsiucí 4 Inegrace subsiucí Průvodce sudiem Inegrály, keré nelze řeši pomocí základních vzorců, lze velmi časo řeši subsiuční meodou Vzorce pro derivace elemenárních funkcí a věy o derivaci
4 Inegrace subsiucí 4 Inegrace subsiucí Průvodce sudiem Inegrály, keré nelze řeši pomocí základních vzorců, lze velmi časo řeši subsiuční meodou Vzorce pro derivace elemenárních funkcí a věy o derivaci
ESTIMATION OF DENSITY FUNCTION PARAMETERS WITH CENSORED DATA FROM PRODUCT LIFE TESTS
 ESTIMATION OF DENSITY FUNCTION ARAMETERS WITH CENSORED DATA FROM RODUCT LIFE TESTS J.Tůa * Suary: The paper deals wih a saisial ehod for he evaluaio of life es resuls. I is supposed ha oly soe of he es
ESTIMATION OF DENSITY FUNCTION ARAMETERS WITH CENSORED DATA FROM RODUCT LIFE TESTS J.Tůa * Suary: The paper deals wih a saisial ehod for he evaluaio of life es resuls. I is supposed ha oly soe of he es
KANALIZACE A ČOV KVĚTINOV
 Havlíčkův Brod, Příčná 260 řediko Choěboř, Svojíkova 333 el. 569 641 473, e-mail: drupo@icali.cz KANALIZACE A ČOV KVĚTINOV SO 06 - ELEKTRICKÉ NAPÁJENÍ Vypracoval: Jiří Oanický Zakázka č.: 3022/08 Daum:
Havlíčkův Brod, Příčná 260 řediko Choěboř, Svojíkova 333 el. 569 641 473, e-mail: drupo@icali.cz KANALIZACE A ČOV KVĚTINOV SO 06 - ELEKTRICKÉ NAPÁJENÍ Vypracoval: Jiří Oanický Zakázka č.: 3022/08 Daum:
Základní princip regulace U v ES si ukážeme na definici statických charakteristik zátěže
 Regulace apětí v ES Základí pricip regulace v ES si ukážeme a defiici statických charakteristik zátěže Je zřejmé, že výko odebíraý spotřebitelem je závislý a frekveci a apětí a přípojicích spotřebitelů.
Regulace apětí v ES Základí pricip regulace v ES si ukážeme a defiici statických charakteristik zátěže Je zřejmé, že výko odebíraý spotřebitelem je závislý a frekveci a apětí a přípojicích spotřebitelů.
Obr. PB1.1: Schématické zobrazení místa.
 97 Projekové zadání PB1 Poouzení nehodové udáoi Na zákadě chémau nehody oveďe vyhodnocení nehodové udáoi. Určee: - paramery oai řeu pode chémau na orázku Or. PB1.1 ( x1, x, y1, y, x1, x, y1, y ); - zda
97 Projekové zadání PB1 Poouzení nehodové udáoi Na zákadě chémau nehody oveďe vyhodnocení nehodové udáoi. Určee: - paramery oai řeu pode chémau na orázku Or. PB1.1 ( x1, x, y1, y, x1, x, y1, y ); - zda
Identifikace neznámých ozubených kol
 Ieifikace eámých oubeých kol Miloš Němček Techical Uiveriy of Orava, Faculy of Mechaical Egieerig, 708 3 Orava Poruba, Cech Republic E-mail: milo.emcek@vb.c Abrac A ieificaio of ukow gear i a relaively
Ieifikace eámých oubeých kol Miloš Němček Techical Uiveriy of Orava, Faculy of Mechaical Egieerig, 708 3 Orava Poruba, Cech Republic E-mail: milo.emcek@vb.c Abrac A ieificaio of ukow gear i a relaively
Odhady parametrů polohy a rozptýlení pro často se vyskytující rozdělení dat v laboratoři se vyčíslují podle následujících vztahů:
 Odhady parametrů polohy a rozptýleí pro často se vyskytující rozděleí dat v laboratoři se vyčíslují podle ásledujících vztahů: a : Laplaceovo (oboustraé expoeciálí rozděleí se vyskytuje v případech, kdy
Odhady parametrů polohy a rozptýleí pro často se vyskytující rozděleí dat v laboratoři se vyčíslují podle ásledujících vztahů: a : Laplaceovo (oboustraé expoeciálí rozděleí se vyskytuje v případech, kdy
Investiční činnost. Existují různá pojetí investiční činnosti: Z pohledu ekonomické teorie. Podnikové pojetí investic
 Ivesičí čios Exisují růzá pojeí ivesičí čiosi: Z pohledu ekoomické eorie Podikové pojeí ivesic Klasifikace ivesic v podiku 1) Hmoé (věcé, fyzické, kapiálové) ivesice 2) Nehmoé (emaeriálí) ivesice 3) Fiačí
Ivesičí čios Exisují růzá pojeí ivesičí čiosi: Z pohledu ekoomické eorie Podikové pojeí ivesic Klasifikace ivesic v podiku 1) Hmoé (věcé, fyzické, kapiálové) ivesice 2) Nehmoé (emaeriálí) ivesice 3) Fiačí
je konvergentní, právě když existuje číslo a R tak, že pro všechna přirozená <. Číslu a říkáme limita posloupnosti ( ) n n 1 n n n
 8.3. Limity ěkterých posloupostí Předpoklady: 83 Opakováí z miulé hodiy: 8 Hodoty poslouposti + se pro blížící se k ekoeču blíží k a to tak že mezi = posloupostí a číslem eexistuje žádá mezera říkáme že
8.3. Limity ěkterých posloupostí Předpoklady: 83 Opakováí z miulé hodiy: 8 Hodoty poslouposti + se pro blížící se k ekoeču blíží k a to tak že mezi = posloupostí a číslem eexistuje žádá mezera říkáme že
3. POJIŠTĚNÍ OSOB (ŽIVOTNÍ POJIŠTĚNÍ)
 3. POJIŠTĚÍ OSOB (ŽIVOTÍ POJIŠTĚÍ) 3.. EMOELOVÝ PŘÍSTUP 3... ekremeí řád vymíráí populace Úmrosí abulky a) Smr je áhodým jevem, kerý se pojišťuje pro účely ŽP sačí pracova s průměrými hodoami záko velkých
3. POJIŠTĚÍ OSOB (ŽIVOTÍ POJIŠTĚÍ) 3.. EMOELOVÝ PŘÍSTUP 3... ekremeí řád vymíráí populace Úmrosí abulky a) Smr je áhodým jevem, kerý se pojišťuje pro účely ŽP sačí pracova s průměrými hodoami záko velkých
Obr. DI-1. K principu reverzibility (obrácení chodu paprsků).
 Učebí text k předášce UFY8 Dvojvzková tererece teké vrtvě Dvojvzková tererece teké vrtvě Předpokládejme, vl o mpltudě dvou delektrk tk, že mpltud održeé vly bude o dexu lomu bude t (vz obr. DI-1). v protředí
Učebí text k předášce UFY8 Dvojvzková tererece teké vrtvě Dvojvzková tererece teké vrtvě Předpokládejme, vl o mpltudě dvou delektrk tk, že mpltud održeé vly bude o dexu lomu bude t (vz obr. DI-1). v protředí
Úhrada za ústřední vytápění bytů V
 Úhrada za úsřdí vyápěí byů V Aoa osldí z sér čláků o poměrovém měří pojdává o vzahu poměrového a zv. absoluího měří pla, a poukazuj a další, zaím méě zámou možos využí poměrovýh dkáorů VIA, krou j korola
Úhrada za úsřdí vyápěí byů V Aoa osldí z sér čláků o poměrovém měří pojdává o vzahu poměrového a zv. absoluího měří pla, a poukazuj a další, zaím méě zámou možos využí poměrovýh dkáorů VIA, krou j korola
x udává hodnotu směrnice tečny grafu
 Předmě: Ročník: Vyvořil: Daum: MATEMATIKA ČTVRTÝ Mgr. Tomáš MAŇÁK 5. srpna Název zpracovaného celku: GEOMETRICKÝ VÝZNAM DERIVACE FUNKCE GEOMETRICKÝ VÝZNAM DERIVACE FUNKCE v bodě (ečny grafu funkcí) Je
Předmě: Ročník: Vyvořil: Daum: MATEMATIKA ČTVRTÝ Mgr. Tomáš MAŇÁK 5. srpna Název zpracovaného celku: GEOMETRICKÝ VÝZNAM DERIVACE FUNKCE GEOMETRICKÝ VÝZNAM DERIVACE FUNKCE v bodě (ečny grafu funkcí) Je
É Á Č Í Č Í É Č É í í č í á Ž ý ř ú ě č ář ě í á í í ž á á é éč š ě í á í í é ě ý ě ý ě á á á é á í É Á Č Í í ý č é á á š á í čá ů í í á é č ě íž é é
 É Á Č Í Č Í É Č É í í č í á Ž ý ř ú č ář í á í í ž á á é éč š í á í í é ý ý á á á é á í É Á Č Í í ý č é á á š á í čá ů í í á é č íž é é č í ů é ý ý ý á í á ď č ář ř áž Žá Íé é í é á š í č ář íží é ž š
É Á Č Í Č Í É Č É í í č í á Ž ý ř ú č ář í á í í ž á á é éč š í á í í é ý ý á á á é á í É Á Č Í í ý č é á á š á í čá ů í í á é č íž é é č í ů é ý ý ý á í á ď č ář ř áž Žá Íé é í é á š í č ář íží é ž š
