Tento text doplňuje návod k úloze Měření momentu setrvačnosti uvedený ve skriptech Úvod do fyzikálních měření. V žádném případě si neklade za cíl být

5.4.6 Objemy a povrchy rotačních těles I

5.4.6 Objey a povchy otačních těle I Předpoklady: 050405 Pedagogická poznáka: Stejně jako u nohotěnů i u otačních těle e vzoce po objey a obahy e neodvozují, žáci ohou využívat tabulky a cíle hodin je,

Seznámíte se s další aplikací určitého integrálu výpočtem obsahu pláště rotačního tělesa.

.4. Obsh pláště otčního těles.4. Obsh pláště otčního těles Cíle Seznámíte se s dlší plikcí učitého integálu výpočtem obshu pláště otčního těles. Předpokládné znlosti Předpokládáme, že jste si postudovli

DOPLŇKOVÉ TEXTY BB01 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ TUHÉ TĚLESO

DOPLŇKOÉ TXTY BB0 PAL SCHAUR INTRNÍ MATRIÁL FAST UT BRNĚ TUHÉ TĚLSO Tuhé těleso je těleso, o teé latí, že libovolná síla ůsobící na těleso nezůsobí jeho defoaci, ale ůže ít ouze ohybový účine. Libovolná

Pohyb tělesa, základní typy pohybů, pohyb posuvný a rotační. Obsah přednášky : typy pohybů tělesa posuvný pohyb rotační pohyb geometrie hmot

Pohyb tělesa, základní typy pohybů, pohyb posuvný a otační Obsah přednášky : typy pohybů tělesa posuvný pohyb otační pohyb geoetie hot Pohyb tělesa, základní typy pohybů, pohyb posuvný a otační posuvný

URČITÝ INTEGRÁL. Motivace:

Motivce: URČITÝ INTEGRÁL Pomocí učitého integálu můžeme vpočítt: Osh ovinného ozce. Ojem otčního těles. Délku ovinné křivk. Dlší vužití učitého integálu: ve zice, chemii, ekonomii Histoická poznámk: Deinici

2.9.14 Věty o logaritmech I

.9.1 Věty o itmech I Předpokldy: 910 Pedgogická poznámk: Tto náledující hodin e djí tihnout njednou, pokud oželíte počítání v tbulce někteé příkldy n konci příští hodiny. Přijde mi to tochu škod, nžím

Laboratorní práce č. 3: Kmitání mechanického oscilátoru

Přírodní vědy oderně a interaktivně FYZIKA 4. ročník šetiletého a. ročník čtyřletého tudia Laboratorní práce č. : Kitání echanického ocilátoru G Gynáziu Hranice Přírodní vědy oderně a interaktivně FYZIKA

Dynamika tuhého tělesa. Petr Šidlof

Dnaika tuhého tělesa Pet Šidlof Dnaika tuhého tělesa Pvní věta ipulsová F dp dt a t Zchlení těžiště Výslednice vnějších sil F A F B F C Celková hbnost soustav p p i Hotnost soustav i těžiště soustav se

Gravitační pole. a nepřímo úměrná čtverci vzdáleností r. r r

Newtonův avitační zákon: Gavitační pole ezi dvěa tělesy o hotnostech 1 a, kteé jsou od sebe vzdáleny o, působí stejně velké síly vzájené přitažlivosti, jejichž velikost je přío úěná součinu hotností 1

Zvyšování kvality výuky technických oborů

Zvšování kvlit výuk technických ooů Klíčová ktivit IV Inovce zkvlitnění výuk měřující k ozvoji mtemtické gmotnoti žáků tředních škol Tém IV1 Algeické výz, výz mocninmi odmocninmi Kitol 1 Duhá odmocnin

Orientační odhad zatížitelnosti mostů pozemních komunikací v návaznosti na ČSN a TP200

Orientční odhd ztížitelnoti motů pozemních komunikcí v návznoti n ČSN 73 6222 TP200 Úvod Ztížitelnot motů PK e muí tnovit jedním z náledujících potupů podle ČSN 73 6222, kpitol 6 : - podrobný ttický výpočet

F9 SOUSTAVA HMOTNÝCH BODŮ

F9 SOUSTAVA HMOTNÝCH BODŮ Evopský sociální fon Ph & EU: Investujee o vší buoucnosti F9 SOUSTAVA HMOTNÝCH BODŮ Nyní se nučíe popisovt soustvu hotných boů Přepokláeje, že áe N hotných boů 1,,, N N násleující

GEOMETRICKÉ APLIKACE INTEGRÁLNÍHO POČTU

Integální počet funkcí jedné eálné poměnné - 4. - GEOMETRICKÉ APLIKACE INTEGRÁLNÍHO POČTU PŘÍKLAD Učete plochu pod gfem funkce f ( x) = sinx n intevlu,. Ploch pod gfem nezáponé funkce f(x) se n intevlu,

Obsah přednášky : Dynamika mechanismů. dynamika mechanismů - metoda uvolňování, dynamika mechanismů - metoda redukce

Obsh přednášky : Dynik echnisů dynik echnisů - etod uvolňování, dynik echnisů - etod edukce Dynik echnisů Dynik echnisů pojednává o vzthu ezi sili, působícíi n soustvu těles - echnisus, pohybe echnisu,

s N, r > s platí: Základní požadavek na krásu matematického pravidla: Musí být co nejobecnější s minimem a a = a = a. Nemohli bychom ho upravit tak,

.6. Mocniny celý ocnitele I Předpokldy: 6, 6 Př. : Kteé ze dvou pvidel je teticky hezčí? ) Po kždé R, N pltí: +. ) Po kždé R,, N, > pltí:. Zákldní poždvek n káu tetického pvidl: Muí ýt co nejoecnější inie

Algebraický výraz je číselný výraz s proměnou. V těchto výrazech se vyskytují vedle reálných čísel také proměnné. Například. 4a 4,5x + 6,78 7t.

9 očník - lomený lgeický vý, lineání ovnice nenámo ve jmenovteli Lomený lgeický vý Lineání ovnice nenámo ve jmenovteli Doočjeme žákům okovt voce t ( ) od úv vý n očin Lomený vý Číelné vý jo vý v nichž

Základní principy fyziky semestrální projekt. Studium dynamiky kladky, závaží a vozíku

Zákldní principy fyziky seestrální projekt Studiu dyniky kldky, závží vozíku Petr Luzr I/4 008/009 Zákldní principy fyziky Seestrální projekt Projekt zdl: Projekt vyprcovl: prof. In. rntišek Schuer, DrSc.

metoda uvolňování metoda redukce G 1 G 2

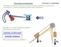Dynik echnisů Dynik echnisů pojednává o vzthu ezi sili, působícíi n soustvu těles - echnisus, pohybe echnisu, těito sili způsobené. Seznáíe se se dvě zákldníi etodi řešení dyniky echnisů. etod uvolňování

VÝPOČET HLAVNÍCH ROZMĚRŮ ČTYŘTAKTNÍHO SPALOVACÍHO MOTORU

Pítový alovací troj je teelný otor, kde e čát energie vzniklá álení aliva řeění v tlakovou energii. Tato energie oocí vhodného echaniu e ění v echanickou energii. Jako nejoužívanější echaniu k řeěně tlakové

Exponenciální výrazy a rovnice

Epoeciálí výzy ovice Epoeciálí výzy ovice - jou ovice výzy ezáou v epoetu = 7 + + + + = 7 = 6 + + 6 Pvidl po počítáí ocii Při úpvě výzů ocii řešeí epoeciálích ovic je tře dodžovt áledující pvidl (jou uvede

Název školy. Moravské gymnázium Brno s.r.o. Mgr. Marie Chadimová Mgr. Věra Jeřábková. Autor. Matematika 02a Racionální čísla. Text a příklady.

Čílo ojektu CZ..07/..00/4.074 Název školy Movké gymnázium Bno..o. Auto Temtiká olt Mg. Mie Chdimová Mg. Vě Jeřáková Mtemtik 0 Rionální číl. Text říkldy. Ročník. Dtum tvoy.. 0 Anote ) o žáky jko text látky,

Dynamika tuhého tělesa

Dnaika tuhého tělesa Pet Šidlof ECHNCKÁ UNVERZA V LBERC Fakulta echatonik, infoatik a eioboových studií ento ateiál vnikl v áci pojektu ESF CZ..7/../7.47 Reflexe požadavků půslu na výuku v oblasti autoatického

a q provedeme toto nahrazení a dostane soustavu dvou rovnic o dvou neznámých: jsou nenulová čísla (jinak by na pravé straně rovnice byla 0)

..9 Úlohy geometickou poloupotí Předpokldy: 0, 0 Pedgogická pozámk: Při řešeí příkldů potupujeme tk, by Ti ejpomlejší počítli lepoň příkldy,,,. Souh vzoců pvidel po geometickou poloupot: + - pozávcí zmeí

Molekulová fyzika. Reálný plyn. Prof. RNDr. Emanuel Svoboda, CSc.

Molekulová fyzik Reálný lyn Prof. RNDr. Enuel Svood, CSc. Reálný lyn Existence vzájeného silového ůsoení ezi částicei (tzv. vn der Wlsovské síly) Odudivá síl ezi částicei (interkce řekryvová) ři dosttečně

Odraz na kulové ploše Duté zrcadlo

Odz n kulové ploše Duté zcdlo o.. os zcdl V.. vchol zcdl S.. střed zcdl (kul. ploch).. polomě zcdl (kul. ploch) Ppsek vchází z odu A n ose zcdl po odzu n zcdle dopdá do nějkého odu B n ose. Podle oázku

Geometrické a fyzikální aplikace určitého integrálu. = b a. je v intervalu a, b záporná, je integrál rovněž záporný.

4. přednášk Geometické zikální plikce učitého integálu Geometické plikce. Osh ovinného útvu A. Pokud se jedná o ovinný útv omezený osou přímkmi gem spojité nezáponé unkce pk je jeho osh dán učitým integálem

Obsah dnešní přednášky : Obecný rovinný pohyb tělesa. Teorie současných pohybů, Coriolisovo zrychlení, dynamika obecného rovinného pohybu.

Obsh dnešní řednášky : Obecný oinný ohyb těles. eoie součsných ohybů, Coiolisoo zychlení, dynik obecného oinného ohybu. Obecný oinný ohyb zákldní ozkld. osu osu = A otce = A otce A A A A efeenční bod sueosice

7.5.12 Parabola. Předpoklady: 7501, 7507. Pedagogická poznámka: Na všechny příklady je potřeba asi jeden a půl vyučovací hodiny.

75 Paabola Předoklad: 750, 7507 Pedagogická oznámka: Na všechn říklad je otřeba asi jeden a ůl vučovací hodin Paabolu už známe: matematika: Gafem každé kvadatické funkce = a + b + c je aabola fzika: Předmět,

11. cvičení z Matematiky 2

11. cvičení z Mateatiky. - 6. května 16 11.1 Vypočtěte 1 x + y + z dv, kde : x + y + z 1. Věta o substituci á analogický tva a podínky pouze zanedbatelné nožiny nyní zahnují i plochy, oviny atd.: f dv

Teorie současných pohybů, Coriolisovo zrychlení, dynamika obecného rovinného pohybu.

Obsh dnešní řednášky : Alikoná echnik, 4. řednášk Obecný oinný ohyb těles. eoie součsných ohybů, Coiolisoo zychlení, dynik obecného oinného ohybu. Obecný oinný ohyb zákldní ozkld. Alikoná echnik, 4. řednášk

Dráhy planet. 28. července 2015

Dáhy plnet Pet Šlecht 28. čevence 205 Výpočet N střední škole se zpvidl učí, že dáhy plnet jsou elipsy se Sluncem v ohnisku. Tké se učí, že tento fkt je možné dokázt z Newtonov gvitčního zákon. Příslušný

KONSTRUKTIVNÍ GEOMETRIE. Mgr. Petra Pirklová, Ph.D. kmd.fp.tul.cz Budova G, 4. patro

KONSTRUKTIVNÍ GEOMETRIE Mg. Pet Piklová, Ph.D. kmd.fp.tul.cz Budov G, 4. pto SYLBUS. Mongeovo pomítání.. nltická geometie v E 3. 3. Vektoová funkce jedné eálné poměnné. Křivk. 4. Šoubovice - konstuktivní

Výpočty za použití zákonů pro ideální plyn

ýočty za oužití zákonů ro ideální lyn Látka v lynné stavu je tvořena volnýi atoy(onoatoickýi olekulai), ionty nebo olekulai. Ideální lyn- olekuly na sebe neůsobí žádnýi silai, jejich obje je ve srovnání

vzhledem k ose kolmé na osu geometrickou a procházející hmotným středem válce. c) kužel o poloměru R, výšce h, hmotnosti m

8. Mechanika tuhého tělesa 8.. Základní poznatky Souřadnice x 0, y 0, z 0 hmotného středu tuhého tělesa x = x dm m ( m) 0, y = y dm m ( m) 0, z = z dm m ( m) 0. Poznámka těžiště tuhého tělesa má v homogenním

3.1.7 Kyvadlo. Předpoklady: 3106

37 Kyvado ředpokady: 306 edaoická poznámka: Ceý obsah hodiny není možné stihnout za 45 minut Je třeba se ozhodnout, co je podstatné: testování vzoce paktickým sestojováním kyvade, povídání o kyvadových

Univerzita Karlova v Praze Pedagogická fakulta

Uivezit lov v Pze Pedgogiká fkult SEMINÁRNÍ PRÁCE Z POLYNOMICÉ ALGEBRY ZVOLENÝ POLYNOM / CIFRI Zdáí: Zvol olyom f ( x) stuě 6 tkový y 6 f ( ) { 87868}. Uči všehy kořey s ásoostí. Vyováí: Zdáí vyhovuje

25 Měrný náboj elektronu

5 Měrný náboj elektronu ÚKOL Stnovte ěrný náboj elektronu e výsledek porovnejte s tbulkovou hodnotou. TEORIE Poěr náboje elektronu e hotnosti elektronu nzýváe ěrný náboj elektronu. Jednou z ožných etod

= b a. V případě, že funkce f(x) je v intervalu <a,b> záporná, je integrál rovněž záporný.

5. přednášk APLIKAE URČITÉHO INTERÁLU Pomocí integálního počtu je možné vpočítt osh ovinných útvů ojem otčních těles délk ovinných křivek. Velké upltnění má učitý integál tké ve zice chemii. eometické

( a ) s. Exponenciální rovnice teorie. Exponenciální rovnice ukázkové úlohy. Příklad 1.

eg. č. pojektu CZ..07/..0/0.0007 Eponenciální ovnice teoie - ovnice, ve kteých e neznámá vykytuje v eponentu Řešíme je v záviloti n typu ovnice několik zákldními metodmi. A. metod převedení n tejný zákld

8. Elementární funkce

Historie přírodních věd potvrzuje, že většinu reálně eistujících dějů lze reprezentovt mtemtickými model, které jsou popsán tzv. elementárními funkcemi. Elementární funkce je kždá funkce, která vznikne

Obsah. 2 Moment síly Dvojice sil Rozklad sil 4. 6 Rovnováha 5. 7 Kinetická energie tuhého tělesa 6. 8 Jednoduché stroje 8

Obsah 1 Tuhé těleso 1 2 Moment síly 2 3 Skládání sil 3 3.1 Skládání dvou různoběžných sil................. 3 3.2 Skládání dvou rovnoběžných, různě velkých sil......... 3 3.3 Dvojice sil.............................

C Charakteristiky silničních motorových vozidel

C Chaaktetky lnčních otoových vozel Toto téa e zabývá záklaní etoa tanovení někteých povozních chaaktetk lnčních otoových vozel, kteé pak náleně louží k pouzování užtných vlatnotí těchto vozel. Stanovení

Téma: Analýza kmitavého pohybu harmonického oscilátoru

PRACOVNÍ LIST č. Téa úlohy: Analýza kitavého pohybu haronického ocilátoru Pracoval: Třída: Datu: Spolupracovali: Teplota: Tlak: Vlhkot vzduchu: Hodnocení: Téa: Analýza kitavého pohybu haronického ocilátoru

a polohovými vektory r k

Mechania hmotných soustav Hmotná soustava (HS) je supina objetů, o teých je vhodné uvažovat jao o celu Pvy HS se pohybují účinem sil N a) vnitřních: Σ ( F + F + L+ F ) 0 i 1 i1 b) vnějších: síly od objetů,

1.2.4 Racionální čísla II

.2.4 Racionální číla II Předoklady: 20 Pedagogická oznámka: S říkladem 0 je třeba začít nejozději 0 minut řed koncem hodiny. Př. : Sečti. Znázorni vůj otu graficky. 2 2 = = 2 Sčítáme netejné čáti muíme

Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Inovace a zkvalitnění výuky prostřednictvím ICT

Střední půmyslová škola a Vyšší odboná škola technická Bno, Sokolská 1 Šablona: Inovace a zkvalitnění výuky postřednictvím ICT Název: Téma: Auto: Číslo: Anotace: Mechanika, dynamika Pohybová ovnice po

DOPLŇKOVÉ TEXTY BB01 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ ENERGIE

DOPLŇKOVÉ TEXTY BB1 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ ENERGIE Obsa Energie... 1 Kinetická energie... 1 Potenciální energie... Konzervativní síla... Konzervativníu silovéu oli odovídá dru otenciální

Funkce. Mgr. Jarmila Zelená. Gymnázium, SOŠ a VOŠ Ledeč nad Sázavou

Funkce Mg. Jmil Zelená Gymnázium, SOŠ VOŠ Ledeč nd Sázvou Eponenciální ovnice VY INOVACE_05 M Gymnázium, SOŠ VOŠ Ledeč nd Sázvou Eponenciální ovnice = ovnice, ve kteých se neznámá vyskytuje v eponentu

LINEÁRNÍ TRANSFORMACE V ROVINĚ

LINEÁRNÍ TRANSFORMACE V ROVINĚ Kil Mleček Dgr Szrková FSv ČVUT Prh Thákurov 7 66 9 Prh 6 ČR e-il: kil@tfsvvutz SjF STU Brtislv Ná Slood 7 8 3 Brtislv SR e-il: szrkov@sjfstusk Astrkt V řísěvku je osý geoetriký

( ) 1.2.19 Zákon zachování hybnosti II. Předpoklady: 010218

..9 Záon zchoání hybnoti II Předoldy: 8 Pedgogicá ozná: Cíl hodiny je jednoduchý. Studenti by e ěli nučit ottně rozhodot, j bude ydt dození onrétní ituce do záon zchoání hybnoti. Jde o jednu z nejleších

3. Kvadratické rovnice

CZ..07/..08/0.0009. Kvdrtické rovnice se v tetice oznčuje lgebrická rovnice druhého stupně, tzn. rovnice o jedné neznáé, ve které neznáá vystupuje ve druhé ocnině (²). V zákldní tvru vypdá následovně:

Automaty a gramatiky. Trochu motivace. Roman Barták, KTIML. rní jazyky. Regulárn. Kleeneova věta. L = { w w=babau w=uabbv w=ubaa, u,v {a,b}* }

ochu motivce L = { w w=u w=uv w=u, u,v {,}* } Automty gmtiky Romn Bták, KIML tk@ktiml.mff.cuni.cz htt://ktiml.mff.cuni.cz/~tk L = L L L, kde L = { w w=u, u {,}* }, L = { w w=uv, u,v {,}* } L = { w w=u,

Hlavní body. Úvod do dynamiky. Dynamika translačních pohybů Dynamika rotačních pohybů

Mechanka dynaka Hlavní body Úvod do dynaky. Dynaka tanslačních pohybů Dynaka otačních pohybů Úvod do dynaky Mechanka by byla neúplná, kdyby se nezabývala, důvody poč se tělesa dávají do pohybu, zychlují,

K přednášce NUFY080 Fyzika I prozatímní učební materiál, verze 01 Keplerova úloha Leoš Dvořák, MFF UK Praha, Keplerova úloha

K řednášce NUFY080 Fyzika I ozatímní učební mateiál, veze 01 Keleova úloha eoš Dvořák, MFF UK Paha, 014 Keleova úloha Chceme sočítat, jak se ohybuje hmotný bod gavitačně řitahovaný nehybným silovým centem.

Hmotnostní tok výfukových plynů turbinou, charakteristika turbiny

Hotnostní tok výfukových lynů tubinou, chaakteistika tubiny c 0 c v v Hotnostní tok tubinou lze osat ovnicí / ED cs /ED je edukovaný ůtokový ůřez celé tubiny Úloha je řešena jako ůtok stlačitelné tekutiny

1 Tuhé těleso a jeho pohyb

1 Tuhé těleso a jeho pohyb Tuhé těleso (TT) působením vnějších sil se nemění jeho tvar ani objem nedochází k jeho deformaci neuvažuje se jeho částicová struktura, těleso považujeme za tzv. kontinuum spojité

3.4.3 Množiny bodů dané vlastnosti I

3.4.3 Množiny odů dné vlstnosti I Předpoldy: 3401 Něteé z těchto množin už známe. J je definován užnice ( ; )? Množin všech odů oviny, teé mjí od středu vzdálenost. Předchozí vět znmená dvě věci: Vzdálenost

ř é Ů é ř ž ř é é ř ž ř Ů ř ř ř Ú é Í ř ř ř é Ž é Í ř é Ý ř ř é é é é ř ř ř é é ř é é ř é Ž ř Ý é ří ř Ř é ř ř Ž Ů ř ř ř Š Í ří ř ř řň é ř Ú řň é ř řň é ř Š ř ž é ř Ž ř Ž ř ř ř Ž Á Ž Ž Š ř ř ř ř ř é é

Příklad 22 : Kapacita a rozložení intenzity elektrického pole v deskovém kondenzátoru s jednoduchým dielektrikem

Příkld 22 : Kpcit rozložení intenzity elektrického pole v deskovém kondenzátoru s jednoduchým dielektrikem Předpokládné znlosti: Elektrické pole mezi dvěm nbitými rovinmi Příkld 2 Kpcit kondenzátoru je

( a) Okolí bodu

0..5 Okolí bodu Předpokldy: 40 Pedgogická poznámk: Hodin zjevně překrčuje možnosti většiny studentů v 45 minutách. Myslím, že nemá cenu přethovt do dlší hodiny, příkldy s redukovnými okolími nejsou nutné,

TECHNICKÁ UNIVERZITA V LIBERCI Katedra fyziky, Hálkova 6, Liberec

TECHNICKÁ UNIVERITA V LIBERCI Ktedr fyziky, Hálkov 6, 46 7 Liberec htt://www.f.tul.cz/kfy/bs_uf_r.html POŽADAVKY PRO PŘIJÍMACÍ KOUŠKY FYIKY Akdemický rok: 008/009 fkult edgogická Témtické okruhy. Kinemtik

Vlnová teorie. Ing. Bc. Michal Malík, Ing. Bc. Jiří Primas. TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií

Ing. Bc. Michl Mlík, Ing. Bc. Jiří Prims ECHNICKÁ UNIVERZIA V LIBERCI Fkult mechtroniky, informtiky mezioborových studií ento mteriál vznikl v rámci projektu ESF CZ.1.7/../7.47, který je spolufinncován

LABORATORNÍ CVIČENÍ Z FYZIKY

ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE KATEDRA FYZIKY ABORATORNÍ CVIČENÍ Z FYZIKY Jéno: Petr Česák Datu ěření: 7.. Studijní rok: 999-, Ročník: Datu odevzdání:.5. Studijní skupina: 5 aboratorní skupina: Klasifikace:

Sbírka úloh z matematiky pro 9.ročník Lomené výrazy ZŠ Třešť

Sík úloh z tetik po 9.očík I. Loeé výz ZŠ Třešť . Loeý výz je zloek. Jeovtel zloku e eí ovt ule. U loeých výzů učujee vžd podík, po kteé á loeý výz l. Řešeý příkld Uči podík, po kteé jí výz l, řeš dlší

4. TROJFÁZOVÉ OBVODY

Katedra obecné elektrotechniky Fakulta elektrotechniky a inforatiky, VŠB - T Otrava 4. TROJFÁZOVÉ OBVODY rčeno pro poluchače všech bakalářkých tudijních prograů FS 4. Úvod 4. Trojfázová outava 4. Spojení

3.1.8 Přeměny energie v mechanickém oscilátoru

3..8 Přeěny energie v echanické oscilátoru Předoklady: 0050, 03007 Pedagogická oznáka: Odvození zákona zachování energie rovádí na vodorovné ružině, rotože je říočařejší. Pro zájece je uvedeno na konci

PLANIMETRIE ZÁKLADNÍ POJMY PŘÍMKA A JEJÍ ČÁSTI

Předmět: Ročník: ytvořil: Dtum: MTEMTIK DRUHÝ Mg. Tomáš MŇÁK 17. květn 2012 Název zcovného celku: PLNIMETRIE ZÁKLDNÍ POJMY Plnimetie = geometie v ovině. Zákldními útvy eukleidovské geometie jsou: bod římk

FYZIKA I. Mechanická energie. Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D. Doc. Ing. Irena Hlaváčová, Ph.D. Mgr. Art.

VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ FYZIKA I Mechanická enegie Pof. RND. Vilém Mád, CSc. Pof. Ing. Libo Hlaváč, Ph.D. Doc. Ing. Iena Hlaváčová, Ph.D. Mg. At. Dagma Mádová Ostava

Pístový efekt výtahů ve stavebních objektech

Pístový efekt výthů ve stvebních objektech Ing. Jiří Pokorný, Ph.D. Hsičský záchrnný sbor Morvskoslezského krje úzení odbor Opv Těšínská 39, 746 01 Opv e-il: jiripokorny@ujil.cz Klíčová slov Pístový efekt,

VYVAŽOVÁNÍ VNĚJŠÍCH ÚČINKŮ ZPŮSOBENÝCH SETRVAČNÝMI SILAMI OD ROTAČNÍCH A POSUVNÝCH HMOT

VYVAŽOVÁNÍ VNĚJŠÍCH ÚČINKŮ ZPŮSOBENÝCH SETRVAČNÝMI SILAMI OD ROTAČNÍCH A POSUVNÝCH HMOT Předěte vyvažování jsou sekundání síly vyvolané účinky ohybujících se hot otačních a osuvných. o Setvačná síla otačních

Automaty a gramatiky. Pro připomenutí. Roman Barták, KTIML. Důkaz věty o dvousměrných automatech (1)

4 Automty gmtiky omn Bták, KTIML tk@ktiml.mff.cuni.cz htt://ktiml.mff.cuni.cz/~tk Po řiomenutí Automt může tké ovládt čtecí hlvu dvousměný (dvoucestný) utomt řechodová funkce: Q X Q {-,,+} Slovo w je řijto

VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY MĚŘENÍ HMOTNOSTNÍCH PARAMETRŮ VOZIDEL

VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY ÚSTAV SOUDNÍHO INŽENÝRSTVÍ INSTITUTE OF FORENSIC ENGINEERING MĚŘENÍ HMOTNOSTNÍCH PARAMETRŮ VOZIDEL MEASUREMENT OF THE WEIGHT PARAMETERS OF VEHICLES

Odraz na kulové ploše

Odz n kulové ploše Duté zcdlo o.. os zcdl V.. vchol zcdl S.. střed zcdl (kul. ploch).. polomě zcdl (kul. ploch) Ppsek vchází z odu A n ose zcdl po odzu n zcdle dopdá do nějkého odu B n ose. tojúhelníků

Cílem kapitoly je zvládnutí řešení determinantů čtvercových matic.

temtk I část I Determty mtc řádu Determty mtc řádu Cíle Cílem ktoly je zvládutí řešeí ermtů čtvercových mtc Defce Determtem (řádu ) čtvercové mtce řádu jejímž rvky j jsou reálá (oř komlexí) čísl zýváme

II. kolo kategorie Z5

II. kolo ktegorie Z5 Z5 II 1 Z prvé kpsy klhot jsem přendl 4 pětikoruny do levé kpsy z levé kpsy jsem přendl 16 dvoukorun do prvé kpsy. Teď mám v levé kpse o 13 korun méně než v prvé. Ve které kpse jsem

Obecný rovinný pohyb. teorie současných pohybů, Coriolisovo zrychlení dynamika obecného rovinného pohybu,

Obecný oinný pohyb ynik, 7. přednášk Obsh přednášky : teoie součsných pohybů, Coiolisoo zychlení dynik obecného oinného pohybu, ob studi : si 1,5 hodiny Cíl přednášky : seznáit studenty se zákldy teoie

3.2.8 Oblouková míra. Předpoklady:

3..8 Oblouková mía Předpoklady: Pedagogická poznámka: Tato hodina zabee přibližně jednu a půl vyučovací hodiny. Na 45 minut je možné hodinu zkátit buď vynecháním někteých převodů na konci (vzhledem k tomu,

Dynamika mechanismů. dynamika mechanismů - metoda uvolňování, dynamika mechanismů - metoda redukce. asi 1,5 hodiny

Dynaika echanisů Dynaika I, 0. přednáška Obsah přednášky : dynaika echanisů - etoda uvolňování, dynaika echanisů - etoda edukce Doba studia : asi,5 hodiny Cíl přednášky : seznáit studenty se dvěa základníi

13. Exponenciální a logaritmická funkce

@11 1. Eponenciální logritmická funkce Mocninná funkce je pro r libovolné nenulové reálné číslo dán předpisem f: y = r, r R, >0 Eponent r je konstnt je nezávisle proměnná. Definičním oborem jsou pouze

ZÁKLADY ROBOTIKY Denavit-Hartenbergova transformace

ZÁKLADY ROBOIKY Denvt-Hrtenbergov trnforme Ing. Joef Černohorký, Ph.D. ECHNICKÁ UNIVERZIA V LIBERCI Fkult mehtronky, nformtky mezoborovýh tuí ento mterál vznkl v rám projektu ESF CZ..7/../7.47 Reflexe

Seminární práce z fyziky

Seminání páce z fyziky školní ok 005/006 Jakub Dundálek 3.A Jiáskovo gymnázium v Náchodě Přeměny mechanické enegie Přeměna mechanické enegie na ovnoamenné houpačce Název: Přeměna mechanické enegie na ovnoamenné

Posouzení stability svahu

Verifikční nuál č. 3 Aktulizce 04/016 Posouzení stbility svhu Progr: Soubor: Stbilit svhu Deo_v_03.gst V toto verifikční nuálu je uveden ruční výpočet posouzení stbility svhu posouzení stbility svhu zbezpečeného

ROVNOBĚŽNÉ PROMÍTÁNÍ, VOLNÉ ROVNOBĚŽNÉ PROMÍTÁNÍ

Technická univerzit v Liberci Fkult přírodovědně-humnitní pedgogická Ktedr mtemtiky didktiky mtemtiky ROVNOĚŽNÉ PROMÍTÁNÍ, VOLNÉ ROVNOĚŽNÉ PROMÍTÁNÍ Pomocný učební text Petr Pirklová Liberec, září 2013

Předmět: Ročník: Vytvořil: Datum: MATEMATIKA TŘETÍ MGR. JÜTTNEROVÁ Název zpracovaného celku: GEOMETRICKÁ POSLOUPNOST A JEJÍ UŽITÍ

Předmět: Ročík: Vytvořil: Dtum: MATEMATIKA TŘETÍ MGR JÜTTNEROVÁ Název zprcového celku: GEOMETRICKÁ POSLOUPNOST A JEJÍ UŽITÍ GEOMETRICKÁ POSLOUPNOST Defiice: Poloupot e zývá geometrická právě tehdy, když

1.2.2 Síly II. Předpoklady: 1201

1.. Síly II Předoklady: 101 Oakování z minulé hodiny: Pohyb a jeho změny zůobují íly. Pro každou ravou ílu můžeme najít: ůvodce (těleo, které ji zůobuje), cíl (těleo, na které íla ůobí), artnerkou ílu

Klíčové pojmy Vypište hlavní pojmy: b) Tíhová síla. c) Tíha. d) Gravitační zrychlení. e) Intenzita gravitačního pole

Pojekt Efektivní Učení Refomou oblastí gymnaziálního vzdělávání je spolufinancován Evopským sociálním fondem a státním ozpočtem České epubliky. GRAVITAČNÍ POLE Teoie Slovně i matematicky chaakteizujte

VYVAŽOVÁNÍ VNĚJŠÍCH ÚČINKŮ ZPŮSOBENÝCH SETRVAČNÝMI SILAMI OD ROTAČNÍCH A POSUVNÝCH HMOT

VYVAŽOVÁNÍ VNĚJŠÍCH ÚČINKŮ ZPŮSOBENÝCH SETRVAČNÝMI SILAMI OD ROTAČNÍCH A POSUVNÝCH HMOT Předěte vyvažování jsou sekundání síly vyvolané účinky ohybujících se hot otačních a osuvných. Fo Setvačná síla otačních

Lineární nerovnice a jejich soustavy

teorie řešené úlohy cvičení tipy k mturitě výsledky Lineární nerovnice jejich soustvy Víš, že pojem nerovnice není opkem pojmu rovnice? lineární rovnice má většinou jediné řešení, kdežto lineární nerovnice

S t e j n o s měrné stroje Ing. Vítězslav Stýskala, Ph.D., únor 2006

8. ELEKTRICKÉ STROJE TOČIVÉ rčeno pro posluchče bklářských studijních progrmů FS S t e j n o s měrné stroje Ing. Vítězslv Stýskl, Ph.D., únor 6 Řešené příkldy Příkld 8. Mechnické chrkteristiky Stejnosměrný

( ) ( ) ( ) Exponenciální rovnice. 17.3. Řeš v R rovnici: 3 + 9 + 27 = ŘEŠENÍ: Postup z předešlého výpočtu doplníme využitím dalšího vztahu: ( ) t s t

7. EXPONENCIÁLNÍ ROVNICE 7.. Řeš v R rovnice: ) 5 b) + c) 7 0 d) ( ) 0,5 ) 5 7 5 7 K { } c) 7 0 K d) ( ) b) + 0 + 0 K ( ) 5 0 5, 7 K { 5;7} Strtegie: potřebujeme zíkt tkový tvr rovnice, kd je n obou trnách

LABORATORNÍ CVIČENÍ Z FYZIKY

ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE KATEDRA FYZIKY LABORATORNÍ CVIČENÍ Z FYZIKY méno Stanilav Matoušek Datum měření 16. 5. 5 Stud. rok 4/5 Ročník 1. Datum odevzdání 3. 5. 5 Stud. kupina 158/45 Lab. kupina

Cavendishův pokus: Určení gravitační konstanty,,vážení Země

Cavendishův pokus: Učení gavitační konstanty,,vážení Země Jiří Kist - Mendlovo gymnázium, Opava, SO@seznam.cz Teeza Steinhatová - gymnázium J. K. Tyla Hadec Kálové, SteinT@seznam.cz 1. Úvod Abstakt: Cílem

ňď Ó Ó Š ť ř ř ř Č ř ť ř Ř Š Ě Č Č ř Č Ý Ě ť Ě ť ř ý ř Ř ť ň Ě Ý ř Ě ř ř ň ť Š Š Š ň ť Ó ť Á ť ř Ů Ú Ě Č ť ň Š ř Ď Č Š ň Ř Ě ň ý řň ř ř ř Č Š ť Š Š Š Ú Š Á Ý Ú Š Š Š Š Š ť Á ť ť Ě ť ť ť ř Ú Ú Ú Š Ů Š ý

Řešení úloh 1. kola 51. ročníku fyzikální olympiády. Kategorie D = s v 2

Řešení úloh 1. kola 51. ročníku fyzikální olympiády. Kategorie D Autor úloh: J. Jírů 1.a) Dobaprvníjízdynaprvníčtvrtinětratije 1 4 1 4 48 t 1 = = h= 1 v 1 60 60 h=1min anazbývajícíčátitrati t = 4 v = 4

Mechanika hmotného bodu

Mechanika hmotného bodu Pohybové zákony klaické fyziky Volný hmotný bod = hmotný bod (HB), na kteý nepůobí žádné íly (je to abtaktní objekt). Ineciální vztažná (ouřadná) outava = vztažná (ouřadná) outava,

N. Určete velikosti sil, kterými trám působí na vzpěry.

0. Tué těeo 0 N 0. béníoá tená e ozěy 0 c 90 c je otáčiá oe oy joucí její třee oé oině ey. N eu ůobí íy oe obázu. Učete eiot ě ýenéo oentu íy ě otáčení ey, teý tento oent íy zůobí. 0 N 0 c 0 N 90 c 0 N

Nakloněná rovina II

1215 Nkloněná rovin II Předokldy: 1214 Pomůcky: siloměr 2,5 N, sd n měření řecí síly Pedoická oznámk: V éo následující hodině se nerobírá žádná nová lák Přeso jde o oměrně důležié hodiny, roože žáci se

( t) ( t) ( ( )) ( ) ( ) ( ) Vzdálenost bodu od přímky I. Předpoklady: 7308

731 Vzdálenost odu od římky I Předokldy: 7308 Pedgogiká oznámk: Pokud máte málo čsu, můžete odvodit vzore ez smosttné ráe studentů oužít některý z říkldů z dlší hodiny Tím jednu ze dvou hodin ro vzdálenost

Hustota plynů - jak ji změřit?

eletrh náadů učitelů fyziky 9 Hustota lynů - jak ji zěřit? ER SÁDEK, UKÁŠ AWERA edagogická fakulta U, Brno Abstrakt ěření hustoty evných látek a kaalin je běžná laboratorní úloha na řadě škol, nicéně ěření

5.1.5 Základní vztahy mezi body, přímkami a rovinami

5.1.5 Zákldní vzthy mezi body, přímkmi rovinmi Předpokldy: 510 Prostor má tři rozměry, skládá se z bodů přímk - jednorozměrná podmnožin prostoru (množin bodů), rovin - dvojrozměrná podmnožin prostoru (množin