ESKÉ VYSOKÉ U ENÍ TECHNICKÉ V PRAZE FAKULTA ELEKTROTECHNICKÁ KATEDRA ÍDÍCÍ TECHNIKY. Vedení letadla po trati v horizontální rovin.
|
|
|
- Vladimíra Ševčíková
- před 9 lety
- Počet zobrazení:
Transkript
1 ESKÉ VYSOKÉ UENÍ TECHNICKÉ V PRAZE FAKULTA ELEKTROTECHNICKÁ KATEDRA ÍDÍCÍ TECHNIKY Vedení letadla po trati v horizontální rovin Diplomová práce Autor: Martin Jaanký Vedoucí práce: doc. Ing. Zdilav Pech CSc. Datum odevzdání: 8. ledna 28
2
3
4 Anotace Tato diplomová práce e zabývá vedením letadla v horizontální rovin. Vedení letadla je rozdleno na dv základní kupin dané lineární odchlkou od trati a úhlovou odchlkou od trati. Úkolem tému automatického ízení letu letadla je tabilizovat tto odchlk, doáhnout a ledovat tra pi pobení poruchových veliin. Dále blo vtvoeno uživatelké protedí pro zadávání parametr. i
5 Annotation Thi diploma thei deal an aircraft guidance at the horizontal plane. Aircraft guidance i divided into two baic group given b linear diplacement from the track and angular diplacement from the track. The aim of flight control tem i tabilization of the diplacement, capturing and following the track with affection b error coefficient. In addition, it wa created uer interface for placing parameter. ii
6 Podkování Na tomto mít bch rád podkoval pedevším vému vedoucímu diplomové práce, panu doc. Ing. Zdilavu Pechovi CSc., za cenné rad a vnovaný a pi vedení mé diplomové práce. Dále bch chtl podkovat vé rodin a pítelkni za podporu a trplivot bhem celého mého tudia. iii
7 Prohlášení Prohlašuji, že jem zadanou diplomovou práci Vedení letadla po trati v horizontální rovin vpracoval amotatn a použil jem podklad (literaturu, projekt a oftware, atd.) uvedené v piloženém eznamu. V Praze dne Podpi iv
8 Obah ÚVOD... 2 HIERARCHICKÉ ÚROVN SYSTÉM ÍZENÍ LETU DYNAMICKÉ VLASTNOSTI LETADLA ZÁKLADNÍ VELIINY LETADLOVÉ SOUADNÉ SOUSTAVY POHYBOVÉ ROVNICE Podélný pohb Stranový pohb STABILIZACE DYNAMIKY LETU LETADLA - AUTOPILOTY ÚKOLY STABILIZACE DYNAMIKY LETU LETADLA STRUKTURA SYSTÉM STABILIZACE DYNAMIKY LETU LETADLA LETADLO LET L-4 TURBOLET STABILIZACE STRANOVÉHO POHYBU CHARAKTERISTIKA STRANOVÉHO POHYBU STRANOVÝ POHYB KOORDINOVANÝ NÁVRH TLUMIE KYMÁCIVÉ SLOŽKY P-ervomechanimu PI-ervomechanimu Porovnání odezev KOORDINACE: PIROZENÁ FREKVENCE P-ervomechanimu PI-ervomechanimu Porovnání odezev TLUMENÍ SPIRÁLNÍ NESTABILITY P-ervomechanimu PI-ervomechanimu Porovnání odezev STABILIZACE NÁKLONU P-ervomechanimu PI-ervomechanimu Porovnání odezev STABILIZACE KURZU P-ervomechanimu PI-ervomechanimu Porovnání odezev SHRNUTÍ VEDENÍ LETADLA PO TRATI ÚKOLY SYSTÉM AUTOMATICKÉHO ÍZENÍ LETU ROVNICE ÍDÍCÍHO SYSTÉMU KINEMATICKÉ ROVNICE STRUKTURA SYSTÉM AUTOMATICKÉHO ÍZENÍ LETU VEDENÍ LETADLA V HORIZONTÁLNÍ ROVIN...33 v
9 7 ÍZENÍ A STABILIZACE STRANOVÉ ODCHYLKY OD TRATI (MÓD NAV) ROZBOR PESNOSTI STABILIZACE STRANOVÉ ODCHYLKY LET V KORIDORU ÍZENÍ A STABILIZACE ÚHLOVÉ ODCHYLKY OD TRATI (MÓD VOR) RADIONAVIGANÍ SYSTÉM VOR KINEMATIKA LETU V PAPRSKU RADIOMAJÁKU VOR FÁZE LETU PO TRATI DANÉ ÚHLOVOU ODCHYLKOU STABILIZACE ÚHLOVÉ ODCHYLKY LET K RADIOMAJÁKU VOR ZÁVR...62 SEZNAM POUŽITÉ LITERATURY...63 SEZNAM OBRÁZK...64 SEZNAM POUŽITÝCH SYMBOL...66 vi
10 Vedení letadla po trati v horizontální rovin ÚVOD Rozvoj letectva pináší pro autopilot nejen požadavk na tabilizaci podélného a píného klonu letadla, pípadn kurzu, ale i nové úloh, jako je tabilizace výšk, vedení letadla po trati, piblížení na pitání, anebo také amotatné pitávání. Tto nové úloh pedtavují tetí hierarchickou úrove letu letadla, nadízenou tabilizaci polohových úhl a jejich derivacím. Tetí hierarchická úrove je zajišována tém automatického ízení letu, FCS Flight control tem, které zpracovávají naviganí veliin a generují ídící ignál pro autopilot. Automatické tém ízení letu e objevil kvli požadavkm na let v tžkých povtrnotních podmínkách, v podmínkách zhoršené viditelnoti a pi prodlužování délk letu a dob pobtu letadla ve vzduchu. Cílem této diplomové práce je vtvoit Simulinkový model letu letadla po trati v horizontální rovin pro vedení dané tranovou vzdálenotí od trati a úhlovou odchlkou od trati. Budou odvozen rovnice popiující co nejvrnji reálné letadlo, a to za pítomnoti poruchových veliin, tvoených pílušnými ložkami vtru. Rozeznáváme vedení letadla po trati dané tranovou odchlku od trati zíkanou z rzných naviganích tém výpotem v naviganích poítaích, zpravidla pi urování poloh letadla vzhledem k trati, nebo v poítaích tému automatického ízení na základ naviganích údaj. Jedná e zpravidla o vedení letadla na delší vzdálenoti v letových koridorech. Druhý zpob vedení letadla zpracovává úhlovou odchlku od trati zíkanou výpotem z úhlomrného zaízení, jímž je praktick tém VOR. Letová traa je proložena traovými bod oazenými vílai VOR/DME. Úkolem tému automatického ízení je doažení a ledování radiál k / od vílae VOR. Jedná e o let na krátké vzdálenoti podle doahu vílae VOR, který závií na výšce letu.
11 2 Hierarchické úrovn témízení letu 2 HIERARCHICKÉ ÚROVN SYSTÉM ÍZENÍ LETU Stém ízení letu pedtavují kvalitativn všší tupe ízení letadla. Zajišují komplexní automatizaci a optimalizaci letu letadla ve všech jeho fázích. Je zejmé, že takový ložitý tém nelze ešit vcelku. V takovém pípad provádíme podle profeních zájmových hlediek jeho dekompozici na jednodušší podtém a t pak ešíme. Naším zájmovým hledikem jou tém automatického ízení, zvolíme ted rozlišení podtém podle hierarchických úrovní ízení (zptnovazebních mek). Podle druhu tabilizované veliin rozdlujeme ízení letadla do více hierarchických úrovní: I. Hierarchická úrove Patí em tém úprav vlatnotí letadla AP/SUS: - Tlumie, které tlumí rotaní rchloti θ, φ, ψ - Stabilizátor, které tabilizují polohové úhl a II. Hierarchická úrove Najdeme v ní tém ízení dnamik pohbu letadla, ted autopilot: - Autopilot podélného klonu, který ovládá úhel - Autopilot tranového pohbu, který tabilizuje náklon a kurz - Automat tahu III. Hierarchická úrove Úrove automatického ízení, které tabilizuje letadlo v horizontální a vertikální rovin. - Stabilizace barometrické výšk H a vertikální rchloti H (mód ALT) - Horizontální vedení po trati (mód TRACK) - Automatické piblížení na pitání (mód APPR) - Stabilizace vzdušné rchloti (mód IAS) IV. Hierarchická úrove Stém komplexního ízení a optimalizace letu FMS. 2
12 Vedení letadla po trati v horizontální rovin 3 DYNAMICKÉ VLASTNOSTI LETADLA Pi návrhu tém automatického ízení vcházíme z úkol, které jou kladen na jednotlivé hierarchické úrovn ízení. K tomu je nezbtná znalot dnamických vlatnotí letadla, jehož jednotlivé veliin jednak ídíme, jednak tabilizujeme. 3. Základní veliin Pohb letadla je charakterizovaný 6 tupni volnoti a dlíme ho na rotaní a pouvný (tranlaní). Rotaní pohb charakterizují Eulerov polohové úhl mezi zemkou a letadlovou ouadnicovou outavou: podélný klon [rad] píný náklon [rad] kurz [rad] a dále úhl ofukovaní mezi outavou aerodnamickou a letadlovou: úhel nábhu [rad] úhel vboení [rad] Pouvný pohb vztahujeme k dráze letu a urují ho náledující veliin: uletná vzdálenot L [km] letová hladina H [km], repektive odchlka od letové hladin dh tranová vzdálenot Y [km], repektive tranová odchlka dy 3.2 Letadlové ouadné outav o o o Letadlová ouadná outava O,x,,z je pevn pojena letounem Poátek e volí v tžišti letadla CG (Centre of Gravit) Upoádání o: podélná oa x leží v podélné oe letadla, muje dopedu kladná píná oa e nalézá v pravém kídle letadla kolmá oa je kolmá jak na podélnou ou, tak pínou ou Oa podélná kolmou tvoí rovinu metrie letadla. Aerodnamická ouadná outava O a,x a, a,z a Poátek O a je zde v tžišti letadla. Upoádání o: podélná oa x a má mr a ml vektoru vzdušné rchloti V kolmá oa e nachází v rovin metrie letadla Zemká ouadná outava O g,x g, g,z g je pevn pojena e zemkým povrchem Upoádání o je dvojí: o jou orientován dle vtových tran nebo je podélná oa orientována vzhledem k dráze letu. Pi tomto ešení bývá poátek v prvním bodu trati, na jejím konci i v jiném, významném bodu trati. Další možnotí.umítní poátku ouadné outav je pímo v tžišti letadla 3
13 3 Dnamické vlatnoti letadla Výše zmínné ouadné outav louží pro definování : Eulerových polohových úhl,,, které zíkáme pevodem zemké ouadné outav trojím pootoením do outav letadlové. Úhl ofukování,. T zíkáme dvmi pootoeními aerodnamické ouadné outav do outav letadlové. Obr. 3-: Pevod zemké ouadné outav do letadlové Obr. 3-2: Pevod aerodnamické ouadné outav do letadlové 4
14 Vedení letadla po trati v horizontální rovin 3.3 Pohbové rovnice Pro tudium vlatnotí letadla, návrh tém automatického ízení a rozbor jejich vlatnotí e vchází ze outav šeti linearizovaných pohbových rovnic. Ab blo možno tto pohbové rovnice popat, je zavedeno nkolik pedpoklad: Letadlo je tuhé tleo, je geometrick a hmotov oumrné. Hmotnot letadla a vnjšího protedí je kontantní. Hlavní o etrvanoti letadla jou totožné letadlovou ouadnou outavou. Vektor tahu motor leží v podélné oe letadla. Tíhové zrchlení je kontantní. Zemká ouadná outava je inerciální, neuvažuje Corioliovo zrchlení. Rovnice letadla vcházejí ze základních princip Newtonov mechanik. Základní tvar ilové a momentové rovnice pro tuhé tleo vkonávající pouvný a rotaní pohb v referenní outav je: dv F = m + m[ϖ V ] = Fi (3.) dt dh M = + [ϖ H ] = M i (3.2) dt kde v [m. - ] je vektor tranlaní rchloti, [rad. - ] je vektor rotaní rchloti, m [kg] je celková hmotnot letadla a V [m. - ] je rchlot jeho tžišt. První len obou rovnic jou vztažen k tleové ouadné outav, druhé dva len charakterizují rotaní pohb letadla. Rozepáním tchto rovnic do ložkového tvaru dotáváme outavu 6 nelineárních rovnic. 3 ilové rovnice: o F = X mg inθ = m( v + ω v ω v ) (3.3) x x z o F = Y + mg coθ inφ = m( v + ω v ω v ) (3.4) z z x o F = Z + mg coθ coφ = m( v + ω v ω v ) (3.5) z z kde X(D)[N] je odporová íla, Z[N] íla vztlaková, Y[N] boní íla pobící na letadlo, T[N] pedtavuje tah motoru, který zahrnujeme do odporové íl a gravitaní ílu G = mg [N]. 3 momentové rovnice: x x z x dω x o M x = J x + ω ω z ( J z J ) + ( ω xω z ω ) D dt dω o M = J + ω zω x ( J x J z ) + ( ω ω z ω x ) D dt dω z 2 2 o M z = J z + ω xω ( J J x ) + ( ω ω x ) Dx dt Kde J [kg.m 2 ] je moment etrvanoti. x x (3.6) (3.7) (3.8) 5
15 3 Dnamické vlatnoti letadla Tto rovnice vjadují matematický popi pohbu letadla. Je to outava nelineárních diferenciálních rovnic. Všechn ti kupin rovnic jou rovnicemi nelineárními, jejichž analtické ešení je komplikované. Pro úel automatického ízení e používají rovnice linearizované pro urité referenní letové podmínk v charakteritických bodech letové obálk. Linearizaci realizujeme zavedením metod malých veliin, která vchází z pedpokladu, že pi pobení vnjších poruch anebo po výchlkách orgán ízení vkonává letadlo pohb, který je jen málo odlišný od pvodního. Pi plnní tohoto požadavku mžeme v pohbových rovnicích letadla zanedbat malé len, které obahují druhé a všší mocnin odchlk, a vzájemné ouin pírtk vtupních a výtupních veliin. Dotáváme tak outavu 6 lineárních rovnic kontantními koeficient, které charakterizují pohb letadla a jejich ešení je relativn jednoduché: Fx : v + av + a2α + a3θ = cδ T F : β + bβ + b2φ ψ = d2δ S Fz : a2v + α + a22α θ = c22δv Mx : b2 + φ + b 22φ + b23ψ = d 2δ K + d M : a 3α + a23α + θ + a 33θ = c32δv Mz : b + b φ + ψ + b ψ = d δ + d β 22 3β K 32 δ δ S S (3.9) (3.) (3.) (3.2) (3.3) (3.4) Rovnice Fx; Fz a M popiují podélný a rovnice F, Mx a Mz tranový pohb letadla. Tto pohb jou oddlitelné za pedpokladu, že ΔY u ΔM = u X ΔM = u Z = (3.5) Koeficient tchto rovnic jou kontantní a jou definované náledujícími hmotovými a geometrickými parametr letu: o o o o o o Hmotnot letadla Plocha kídla Aerodnamická ttiva Rchlot letu Hutota vzduchu Moment etrvanoti Abchom mohli definovat koeficient podélného pohbu potebujeme znát také náledující aerodnamické derivace podélného pohbu letadla: V α θ δt δv V α δv V α θ δv c, c, c, c, c, c, c, c, m, m, m, m. x x x x x z z z Koeficient tranového pohbu jou definované také náledujícími aerodnamickými derivacemi tranového pohbu letadla: β φ ψ δ K δ S β φ ψ δ K δ S β φ ψ δ K δ S c, c, c, c, c, m, m, m, m, m, m, m, m, m, m. x x x x x z z z z z 6
16 Vedení letadla po trati v horizontální rovin 3.3. Podélný pohb Jak již blo zmínno rovnice Fx; Fz a M popiují podélný pohb letadla. Pro další tudium vlatnotí tohoto pohbu upravujeme rovnice na tavový popi v tvaru: x = Ax + Bu = Cx + Du, kde: x je vektor tavových promnných v tomto pípad: v, α, θ, θ u je vektor vtup v tomto pípad: T pípu motoru, V výchlka výškovk je vektor výtup A, B, C, D jou matice tavového popiu Ve všeobecném pípad platí pro matice linearizovaného podélného pohbu letadla: (3.6) A = a a a 2 2 a 3 a 22 a a a a 32 a 3 a 33 a 3 c c22 B = (3.7) c32 c22 a3 C = D = (3.8) Stranový pohb Rovnice F; Mx a Mz popiují podélný pohb letadla. Stavový popi tému je: x = Ax + Bu = Cx + Du, kde: (3.9) x je vektor tavových promnných v našem pípad: β, φ, ψ, φ, ψ u je vektor vtup v našem pípad: K výchlka kidélek, S výchlka mrovk je vektor výtup A, B, C, D jou matice tavového popiu Ve všeobecném pípad platí pro matice linearizovaného tranového pohbu letadla: b A = b b 2 3 b 2 b b b b d2 B = (3.2) d 2 d 22 d 3 d32 Výtupní matice autopilota C, D volíme podle tpu ešené úloh. Je vhodné matici C volit jako jednotkovou a matici D nulovou. 7
17 4 Stabilizace dnamik letu letadla - Autopilot 4 STABILIZACE DYNAMIKY LETU LETADLA - AUTOPILOTY Stabilizace dnamik letu letadla poívá ve tabilizaci polohových úhl, jejich derivací a úhl ofukování. Stém ukuteující tuto tabilizaci e nazývají autopilot a pedtavují první a druhou hierarchickou úrove ízení. 4. Úkol tabilizace dnamik letu letadla Stabilizované veliin tvoí zptné vazb regulaních obvod autopilot.. hierarchická úrove: o Stabilizace a ízení úhlových rchlotí θ, φ, ψ - ukuteuje e pomocí tzv. tlumi o o rchlých pohbových ložek Stabilizace úhl ofukování a - ukuteuje e pomocí tabilizátor Koordinace tranového pohbu 2. hierarchická úrove: o Stabilizace a ízení polohových úhl θ, φ, ψ v horizontální a vertikální rovin ízení o Koordinace a kompenzace tranového pohbu 4.2 Struktura tém tabilizace dnamik letu letadla Obr. 4-: Blokové chéma autopilotu Blokové chéma pedtavuje tírozmrný regulaní obvod tabilizace tí polohových úhl. Platí: δ ( ) = [ F ( )] δ ( ) δ v SM v v = [ FKC( )] [ FKC 2( )] θ ( A ted rovnice δ = [ F ] [ F ] θ v SM KC ) (4.) (4.2) (4.3) definuje autopilot, kde F SM () pedtavuje peno ervomechanimu a F KC () peno korekních len. Oba tto len ovlivují vlatnoti uzaveného regulaního obvodu letadlo autopilot, jeho penot a kvalitu regulaního pochodu. 8
18 Vedení letadla po trati v horizontální rovin 4.3 Letadlo Let L-4 Turbolet Pro vjádení dnamických vlatnotí tranového pohbu letadla, tejn tak jako pro ntézu autopilota jou použit vlatnoti malého dopravního letadla. Model letadla Let L-4 Turbolet vhovuje pedpokladm a omezením, které bl v prbhu odvozování a linearizace použit. Rozpoznávací znak: Hornoplošník rovným kídlem a malými nádržemi na konci kídel; hluboký trup výdutí pro podvozek; zkoená kýlová plocha; klínová mrová plocha. Obr. 4-2: Letadlo L-4 Turbolet První ze tí prototp L-4, ekolovenkého lehkého tranportního letounu, vzlétl v dubnu 969. Pohánl ho dva turbovrtulové motor Canadian PT6A. Velký poet letoun bl vvezen do Sovtkého vazu. Do konce devadeátých let produkce doáhla troj, které bl vvezen do 4 zemí. Specifikace: Poádka: dvoulenná Pohon: dva turbovrtulové motor Walter Motorlet M6E o výkonu 533kW Maximální rchlot: 3 km/h Maximální letová hladina: 632 m Maximální dolet: 38 km Rozptí kídel: 9,9 m Délka: 4,4 m Výška: 5,8 m Hmotnot: 64 kg Užitené zatížení: 9 cetujících Obr. 4-3: L-4 Turbolet Koeficient pohbových rovnic tranového pohbu letadla jou náledující: b =,46; b 2 = -,22; d 2 =,43 b 2 =,865; b 22 = 5,85; b 23 = 2,688; d 2 = 8,522; d 22 =,292 b 3 =,87; b 32 =,859; b 33 =,673; d 3 =,837; d 32 =,728 9
19 5 Stabilizace tranového pohbu 5 STABILIZACE STRANOVÉHO POHYBU Pi tabilizaci tranového pohbu letadla uvažujeme ouinnot všech kormidel primárního ízení letadla. Pro letadlo dané tavovým popiem bl navržen autopilot, tj. jeho truktura a penoové koeficient tak, ab zajišoval tabilizaci koordinovaného tranového pohbu. 5. Charakteritika tranového pohbu o o o Stranový pohb je pohb ložený ze tí pohb: Klonní (rolling), kidélka vvozují klonivý moment, k M x Zatáení (awing), mrovka vvozuje zatáivý moment, S M z Klopení (pitching), výškovka provádí kompenzaci nížení vztlaku pi zatáení Složk tranového pohbu Kmácivá ložka tp DR, nutnot tlumit Klonivá ložka, dána aovou kontantou T kl, ídí e a tabilizuje e Spirální netabilita, dána aovou kontantou T n, nepobí potíže Tp tranového pohbu Nekoordinovaný, není ouinnot kormidel Koordinovaný, je ouinnot kormidel, vektor výledného zrchlení pobícího na letadlo leží v rovin metrie letadla (tranové zrchlení je nulové) 5.2 Stranový pohb koordinovaný Charakteritika: o Stranové zrchlení a = o Stabilizace a ízení φ a ψ e ukuteuje bez zmn truktur AP o ízená zatáka e provádí velkými náklon (provázanot podélným pohbem) o Dlba kormidel: a) Nadízené kormidlo kidélka, zajišují: - tabilizaci φ a ψ (polu e mrovkou) - ízenou zatáku -zmnu truktur bez zmn truktur AP b) Podízené kormidlo mrovka, zajišuje: - tlumení kmácivé ložk - právné zatáení - koordinaci tranového pohbu
20 Vedení letadla po trati v horizontální rovin Tlumi klonní φ Používá e pro jeho píznivé dledk pi letech vtším rozahem úhl nábhu a pi piblížení na pitání. Rovnice nejjednoduššího tlumie je dána vztahem: δ = K ( φ φ ) (5.) K φ Tlumi kmácivé ložk - zatáení ψ Tento tlumi plní u koordinovaného pohbu dv funkce, jednak muí zajitit požadované tlumení DR ložk a dále muí umožnit právné zatáení, tj. vlouit vliv utálených ložek a penoového koeficientu tlumie na zatáení. Zptná vazba je popána T rovnicí: δ ψ ψ ψ S = K v. (5.2) T + Kanál mrovk koordinovaného pohbu δ = Vnjší mka od úhlu vboení zajišuje koordinaci. Rovnici autopilotu uvažujeme T Kψ ψ T + S F SM + K β β Stabilizace a ízení polohových úhl φ a ψ (5.3) Jedná e o tabilizaci a ízení píného náklonu a tabilizaci a ízení kurzu. Obojí ízení e dje pomocí kidélek. Tomu odpovídají dv rovnice autopilotu: δ ( ) [ ( φ φ) K = F SM Kφ + K φ] φ (5.4) δ = ) [ K ( φ φ ) + K φ + K ( ψ )] (5.5) K F SM ( φ ψ ψ φ 5.3 Návrh tlumie kmácivé ložk Contant Step kridelka + merov ka PI ervo KDpi Switch x' = Ax+Bu = Cx+Du Stranov pohb beta phi pi dphi dpi Scope k6 wah out + Obr. 5-: Tlumi kmácivé ložk tranového pohbu Návrh tlumie realizujeme v tému ízeném mrovkou. Tlumíme zmnu kurzu, jak to ukazuje chéma Obr. 5-. Obrázk Obr. 5-2 a Obr. 5-3 ukazují pechodové charakteritik a rozložení pól tému otevené mk.
21 5 Stabilizace tranového pohbu Obr. 5-2: Pechodové charakteritik tranového pohbu letadla ízeného mrovkou Obr. 5-3:GMK tranového pohbu letadla ízeného mrovkou 5.3. P-ervomechanimu Pi návrhu vcházíme z GMK tému. Natavíme zeílení K Dpi tak, ab e tlumení a =,7. Za peno ervomechanimu doadíme F P () =. Kontanta zptné vazb vjde: K Dpi =,93. Vliv takto natavené zptné vazb ukazují náledující obrázk. Obr. 5-4: Pechodové charakteritik tranového pohbu letadla tlumiem Obr. 5-5: GMK tranového pohbu letadla tlumiem Na obrázku Obr. 5-5 vidíme, že došlo k zvýšení relativního tlumení a na,7 oproti,98 otevené mk, jak to ukazuje obrázek Obr Tento poun e projevil znatelným nížením zákmit pechodových charakteritik, které mžeme pozorovat na obrázku Obr Pozorujeme také zpomalení odpovdí. Vlatnoti vtrácecím obvodem Vtrácecí obvod zapojíme pepnutím vtupu pepínae na chématu Obr. 5-. Pi zachovaní hodnot kontant K Dpi dotaneme náledující výtup. 2
22 Vedení letadla po trati v horizontální rovin Obr. 5-6: Pechodové charakteritik tranového pohbu tlumiem a vtrácecím obvodem Obr. 5-7: GMK tranového pohbu letadla tlumiem a vtrácecím obvodem Z pechodových charakteritik (obrázek Obr. 5-6) vidíme, že e pechodový dj zrchlil, pi zachování tlumení zákmit. Amplituda na konci pechodového dje je praktick totožná amplitudou pechodových charakteritik v otevené mce jak to ukazuje obrázek Obr GMK (obrázek Obr. 5-7) tohoto tému to potvrzuje. Vidíme, že e relativní tlumení mírn nížilo. Obr. 5-8: Porovnání pechodových charakteritik (P) 3
23 5 Stabilizace tranového pohbu PI-ervomechanimu Pi návrhu tému PI ervomechanimem potupujeme tejn, pouze doadíme peno ervomechanimu F PI ()=(+)/. V tomto pípade nám vchází koeficient zptné vazb K Dpi =,57. Odezv tému jou náledující: Obr. 5-9: PI ervo: Pechodová charakteritika letadla tlumiem Obr. 5-:PI ervo: GMK letadla tlumiem Vlatnoti vtrácecím obvodem Obr. 5-: PI ervo: Pechodová charakteritika letadla tlumiem a vtrácecím obvodem Obr. 5-2:PI ervo: GMK letadla tlumiem a vtrácecím obvodem Z porovnání obrázk Obr. 5-9 a Obr. 5-, repektive obrázk Obr. 5- a Obr. 5-2, mžeme opt kontatovat, že vtrácecí obvod zrchlil odezvu a mírn nížil výledné tlumení. 4
24 Vedení letadla po trati v horizontální rovin Porovnání odezev Obr. 5-3: Porovnání pechodových charakteritik (PI) Obr. 5-4: Porovnání pechodových charakteritik ψ P a PI ervem 5
25 5 Stabilizace tranového pohbu Z charakteritik na obrázku Obr. 5-4 je patrné, že pekmit je pi použití libovolného ervomechanimu tejný, což e dá oekávat, kdž je tlumení v obou pípadech tejné. Avšak charakteritika tému PI ervomechanimem rote nad všechn meze rchleji než charakteritika P ervomechanimem. Tento fakt je zpobený atatimem, který PI ervomechanizmu do tému pináší. 5.4 Koordinace: pirozená frekvence V dalším pokraování úloh budeme uvažovat tém tlumiem a vtrácecím obvodem. Kbeta k8 Contant Step kridelka + merov ka PI ervo KDpi k6 x' = Ax+Bu = Cx+Du Stranov pohb wah out + beta phi pi dphi dpi Scope Obr. 5-5: Koordinace kmácivé ložk tranového pohbu Návrh koordinace realizujeme v tému ízeném mrovkou. Výtupem je úhel vboení, jak to ukazuje chéma Obr Pechodové charakteritik a GMK tému nezapojenou zptnou vazbou K jou na náledujících grafech. Obr. 5-6: Pechodová charakteritika oteveného obvodu tlumiem a vtrácecím obvodem Obr. 5-7: GMK oteveného obvodu / 6
26 Vedení letadla po trati v horizontální rovin 5.4. P-ervomechanimu Pi návrhu zptné vazb potupujeme podobn jako v kapitole Na základ GMK natavíme koeficient zptné vazb K tak, ab bla pirozená frekvence kmácivé ložk pohbu n = 3,5 rad/. Koeficient zptné vazb nám takto vjde K = 7,27 a odezv zptnovazební mk jou náledující. Obr. 5-8: Pechodová charakteritika uzaveného obvodu = () P ervomechanimem Obr. 5-9: GMK uzaveného obvodu = () P ervomechanimem Obr. 5-2: Porovnání pechodových charakteritik (P) 7
27 5 Stabilizace tranového pohbu Z porovnání pechodových charakteritik (obrázk Obr. 5-6 a Obr. 5-8) mžeme íci, že koordinace nížila tlumení, ale zpomalila rchlot rtu odezv. Porovnání GMK v otevené (obrázek Obr. 5-7) a uzavené (obrázek Obr. 5-9) mce tuto hpotézu potvrzuje. Vidíme, že e relativní tlumení nížilo z hodnot a =,7 na hodnotu a =,33 a vlatní frekvence kmácivé ložk pohbu vzrotla na hodnotu n = 3,5 rad/. Hodnota () v utáleném tavu není nulová, i kdž ji uvedená zptná vazba podtatn zmenšuje PI-ervomechanimu Návrh koordinace pohbu realizujeme úpln tejn jako v pedchozím bod, jen doadíme peno ervomechanimu F PI ()=(+)/. Koeficient zptné vazb nám tentokrát vjde K = 7,58 a odezv zptnovazební mk jou náledující. Obr. 5-2: Pechodová charakteritika uzaveného obvodu = () PI ervomechanimem Obr. 5-22: GMK uzaveného obvodu = () PI ervomechanimem Porovnáním graf Obr. 5-2 a Obr. 5-8, repektive graf Obr a Obr. 5-9, mžeme znovu kontatovat, že relativní tlumení e zvýšilo. Rchlot nártu pechodové charakteritik e v koordinovaném tému nížila. Hodnota () v utáleném tavu není nulová, i kdž ji uvedená zptná vazba také podtatn zmenšuje Porovnání odezev Z porovnání charakteritik (obrázek Obr. 5-24) vidíme, že nárt charakteritik PI ervomechanimem je výraznjší než charakteritik P ervomechanimem. Tlumení zákmit je v tému PI ervem o nco výraznjší, emuž napovídá i porovnání GMK charakteritik na obrázcích Obr a Obr
28 Vedení letadla po trati v horizontální rovin Obr. 5-23: Porovnání pechodových charakteritik (PI) Obr. 5-24: Porovnání pechodových charakteritik () P a PI ervem 9
29 5 Stabilizace tranového pohbu 5.5 Tlumení pirální netabilit Kbeta k8 + Step Contant PI ervo kridelka merov ka KDpi k6 KDphi x' = Ax+Bu = Cx+Du Stranov pohb wah out + beta phi pi dphi dpi Scope k Obr. 5-25: Tlumení pirální netabilit Obr. 5-26: GMK oteveného obvodu pirální netabilit Obr. 5-27: GMK - detail na netabilní ložku Tlumení pirální netabilit realizujeme v tému F() = d/ k. Zapojením zptné vazb natavíme amplitudu výtupního ignálu na polovinu amplitud v otevené mce. Na obrázku Obr je zobrazené GMK tohoto penou a detail netabilní ložk mžeme pozorovat na obrázku Obr Vidíme, že pirozená frekvence netabilní ložk je pibližn =,rad/ P-ervomechanimu Za peno ervomechanimu doadíme FP() =. Pi návrhu i pomžeme protedím RLTOOL v Matlabu, který nám umožní interaktivn natavovat zeílení zptné vazb a zárove pozorovat jeho vliv na pechodovou charakteritiku. Koeficient zptné vazb nám takto vjde K Dphi =,47. 2
30 Vedení letadla po trati v horizontální rovin Obr. 5-28: GMK regulaního obvodu P ervem Obr. 5-29: Pechodové charakteritik oteveného detail na netabilní ložku a uzaveného obvodu Na detailu obrázku Obr vidíme, že e zlomová frekvence netabilní ložk nížila na polovinu a na obrázku Obr lze pozorovat, že amplituda pechodové charakteritik regulovaného obvodu rote dvakrát pomaleji jako amplituda pechodové charakteritik otevené mk d/ k PI-ervomechanimu V návrhu ledujeme ovdený potup z pedcházející kapitol doazením penou F PI ()=(+)/ za ervomechanizmu. Penoový koeficient zptné vazb je K Dphi =,7. Obr. 5-3: GMK oteveného obvodu pirální netabilit PI ervem Obr. 5-3: GMK uzaveného obvodu pirální netabilit PI ervem Na grafu Obr. 5-3 je vidt GMK oteveného obvodu. Frekvence netabilní ložk je =,rad/. Na obrázku Obr. 5-3 vidíme, že e zvýšilo relativní tlumení kmácivé ložk pohbu, ale hlavn je zejmé, že jme netabilní ložku pohbu praktick eliminovali. 2
31 5 Stabilizace tranového pohbu Obr. 5-32: Pechodové charakteritik oteveného a uzaveného obvodu Z porovnání pechodových charakteritik Obr je zejmé, že e odezva v uzavené mce tabilizovala a tím jme potlaili netabilní ložku pohbu Porovnání odezev Obr. 5-33: Porovnání pechodových charakteritik φ() P a PI ervomechanimem 22
32 Vedení letadla po trati v horizontální rovin Jak z pedcházejících kapitol vplnulo, použitím PI ervomechanimu jme pechodovou charakteritiku φ tabilizovali, zatímco pi použití P ervomechanimu rote odezva nad všechn meze. 5.6 Stabilizace náklonu Kbeta Step Saturation Kphi Contant + PI ervo kridelka merov ka KDpi k6 KDphi k8 x' = Ax+Bu = Cx+Du Stranov pohb wah out + beta phi pi dphi dpi Scope Scope k Obr. 5-34: Stabilizace náklonu () Stabilizace náklonu e odehrává v tému / k. Do tohoto tému jme navíc pidali omezova ±3, protože v tomto rozahu e pohbuje náklon dopravných letadel P-ervomechanimu Obr. 5-35: GMK oteveného obvodu tabilizace náklonu Obr. 5-36: GMK uzaveného obvodu tabilizace náklonu P ervem 23
33 5 Stabilizace tranového pohbu Na detailu GMK otevené mk tabilizace náklonu (obrázek Obr. 5-35) pozorujeme jeden netabilní pól. Zavedením zptné vazb a natavením koeficientu K = pozorujeme, že tento netabilní pól bl potlaený, jak to ukazuje obrázek Obr Obr. 5-37: Pechodové charakteritik oteveného a regulaního obvodu P ervem Stabilizování odezv () na obrázku Obr v uzaveném regulaním obvodu potvrzuje pedcházející fakt o potlaení netabilního pólu PI-ervomechanimu Obr. 5-38: GMK oteveného obvodu tabilizace náklonu PI ervo Obr. 5-39: GMK uzaveného obvodu tabilizace náklonu PI ervem 24
34 Vedení letadla po trati v horizontální rovin GMK oteveného obvodu PI ervomechanimem (obrázek Obr. 5-38) nemá netabilní pól, protože jme ho odtranili regulací pirální netabilit. Pi použití PI ervomechanimu je atatimu pechodové charakteritik () zpobený nulovým pólem. V protedí RLTOOL natavíme regulaní koeficient K =, což zpobí, že e nám z dvou reálných pól tane dvojice komplexn družených pól (viz. graf Obr. 5-39). Budeme ted oekávat pekmit pechodové charakteritik. Obr. 5-4: Pechodové charakteritik oteveného a regulaního obvodu PI ervem Stabilizovaná odezva () na obrázku Obr. 5-4 vkazuje pekmit 9% a nulovou tatickou chbu. a regulace je pibližn 6,5 ekund Porovnání odezev Na obrázku 5-4 vidíme, že oba dva tém mají a odezv hodný, pibližn 6,5. o Stém P ervomechanimem nemá pekmit, ale jeho tatická chba je ai 4%. o Stém PI ervomechanimem vkazuje pekmit 9%, ale na druhé tran nemá tatickou chbu 25
35 5 Stabilizace tranového pohbu Obr. 5-4: Porovnání pechodových charakteritik φ() P a PI ervomechanimem 5.7 Stabilizace kurzu Kbeta k8 Step.3 Kpi Saturation Kphi Contant + PI ervo kridelka merovka KDpi k6 KDphi x' = Ax+Bu = Cx+Du Stranov pohb wah out + beta phi pi dphi dpi Scope Scope k Obr. 5-42: Stabilizace kurzu () Stabilizaci kurzu realizujeme v tému / k. Protože kurz reaguje na kladný vtupní ignál kidélek k vchýlením do negativních hodnot, realizujeme kladnou zptnou vazbu, abchom za outovým lenem obdrželi rozdíl mezi vtupem a výtupem. 26
36 Vedení letadla po trati v horizontální rovin 5.7. P-ervomechanimu Na GMK otevené mk tabilizace kurzu (obrázek Obr. 5-43) vidíme, že jde o podmínn tabilní tém. Zvolené zeílení nemže být proto píliš velké, abchom e nedotali do netabilní oblati. Pomocí RLTOOL-u natavíme tlumení, tak ab bl a odezv pibližn ekund a pekmit maximáln 2%. Natavený koeficient je K =. Obr. 5-43: GMK oteveného obvodu tabilizace kurzu Obr. 5-44: GMK uzaveného obvodu tabilizace kurzu P ervem Obr. 5-45: Pechodové charakteritik oteveného a regulaního obvodu P ervem 27
37 5 Stabilizace tranového pohbu Z grafu Obr je patrné, že všechn pól ztali ve tabilní oblati a porovnáním obrázk Obr a Obr zjitíme, že jme odtranili atatický pól p =, který zpoboval atatický charakter pechodové charakteritik kurzu. Stém uzavené mk P ervomechanimem tabilizuje odezv () na obrázku Obr v ae 2 ekund velmi malým pekmitem a "bez" tatické chb PI-ervomechanimu Obr. 5-46: GMK oteveného obvodu tabilizace kurzu PI ervomechanimem Obr. 5-47: GMK uzaveného obvodu tabilizace kurzu PI ervomechanimem Obr. 5-48: Pechodové charakteritik oteveného a regulaního obvodu PI ervem 28
38 Vedení letadla po trati v horizontální rovin GMK otevené mk tabilizace kurzu (obrázek Obr. 5-46) ukazuje, že jde znovu o podmínn tabilní tém. Pomocí RLTOOL-u natavíme tlumení, tak ab bl a odezv pibližn ekund a pekmit maximáln 2%. Natavený koeficient je K =,3. Na grafu Obr vidíme, že všechn pól ztali ve tabilní oblati a porovnáním obrázk Obr a Obr zjitíme, že jme odtranili atatický pól p =, který zpoboval atatický charakter pechodové charakteritik kurzu. Stém uzavené mk PI ervomechanimem tabilizuje odezv () na obrázku Obr v ae 2 ekund bez pekmitu a "bez" tatické chb Porovnání odezev Obr. 5-49: Porovnání pechodových charakteritik ψ () P a PI ervomechanimem Na obrázku Obr je vidt, že tém oba dva tém regulují bez tatické chb. Stém PI ervomechanimem je rchlejší a nevkazuje pekmit. Naopak pekmit tému P ervomechanimem je ai 2%. 5.8 Shrnutí V této kapitole bla provedena tabilizace tranového pohbu letadla. Bl zvolen potupný návrh, kdž e zaalo tlumiem a potupn e pidávali další regulaní mk, až bl tabilizován kurz. Návrh bl realizován pro 2 druh ervomechanim: P a PI. 29
39 6 Vedení letadla po trati Zjištné penoové koeficient autopilota P ervomechanimem jou náledující: K =,93 K = 7, 27 K =, 47 K = = ψ β φ Zjištné penoové koeficient autopilota PI ervomechanimem jou náledující: K =,57 K = 7, 58 K =, 7 K = =, 3 ψ β φ Je vidt, že tém PI ervomechanimem ml rchlejší odezv a tabilnjší odezv (tabilizována bla φ(), která i pi použití P ervomechanimu zachovala netabilní charakter). Použití PI ervomechanimu také pomohlo odtranit tatickou chbu v tému tabilizace náklonu. Na druhé tran jou koeficient zptné vazb vtší než pi použití P ervomechanimu, což znamená, že e v "PI" tému výraznji projeví pípadné rušení. φ φ K ψ K ψ 6 VEDENÍ LETADLA PO TRATI Vedení letadla po trati pedtavuje tetí hierarchickou úrove letu letadla, nadízenou tabilizaci polohových úhl a jejich derivacím. Je zajišována tém automatického ízení letu, FCS Flight control tem, které zpracovávají naviganí veliin a generují ídící ignál pro autopilot. 6. Úkol tém automatického ízení letu Stém automatického ízení letu jou tém jejichž úkolem je etapové vedení letadla po trati ve vertikální a horizontální rovin. Patí mezi n: o o o o Stabilizace vzdušné rchloti. Stabilizace barometrické výšk a vertikální rchloti. Vedení letadla v horizontální rovin ízené lineární odchlkou od trati a úhlovou odchlkou od trati. Konené piblížení ped pitáním v kurzové a v etupové rovin vetn podrovnání. 6.2 Rovnice ídícího tému Míto o autopilotu budeme mluvit o tému automatického ízení letu letadla, zkrácen o ídícím tému. Pi odvozování rovnic tému vjdeme z upravených rovnic autopilotu: θ θ h φ δv = FV θ + FV θ + FV Δh( ) + FV φ( ) φ φ δ K = FK φ( ) + FK φ( ) + FK Δ( ) ψ a δ = F ψ + F a S S S (6.) (6.2) (6.3) 3
40 Vedení letadla po trati v horizontální rovin Peno, v nich oznaené, znamenají peno mezi pílušnými veliinami vetn peno ervomechanim, korekních len a letadla. První dv rovnice pedtavují ízení podélného a klonivého pohbu, tetí rovnice zajišuje koordinaci pohbu tranového. První dv rovnice upravíme náledujícím zpobem: θ θ φ δv = FV ( θ θ( )) + FV θ + FV φ( ) (6.4) φ φ δ = F ( φ( ) φ( )) + F φ( ) (6.5) K K Požadované hodnot polohových úhl e rovnají: K θ F Δh( ) = F h V h = Δh( θ θ FV φ F Δ( ) = F K = Δ( φ φ FK ) ) (6.6) (6.7) Levá trana rovnice pedtavuje ídící veliin, tj. požadované hodnot polohových úhl. Odchlk od dráh letu v obou rovinách pedtavují veliin ízené. Požadované hodnot polohových úhl mžeme považovat za rovné kuteným hodnotám polohových úhl, jelikož tabilizace polohových úhl probíhá rchle vzhledem ke zmnám parametr dráh letu. θ ( ) = θ a φ ( ) = φ( ) (6.8) Výledné rovnice ídícího tému mají tvar: h θ F Δh( ) = θ φ F Δ( ) = φ (6.9) (6.) 6.3 Kinematické rovnice Kinematické rovnice pojují letové veliin naviganími veliinami, nebo-li ídící veliin ízenými veliinami. Pro každou rovinu ízení jou obdobné. Budou odvozen pro prmt vektoru rchloti letu na kolmici k požadované dráze letu. V pípad odchlek mezi kutenou a požadovanou dráhou letu e letadlo blíží k této dráze letu práv vektorem rchloti kolmým k dráze letu. Vztah pro vertikální ložku rchloti letu pro vedení letadla ve vertikální rovin: h = V inγ + u = V in( θ α) + z u z (6.) Pi pedpokladu malých klon dráh letu, což je u letadla L-4 vzhledem k jeho výkonm opodtatnné, nahradíme funkci inu úhlem h V γ + u = V ( θ α) + z u z (6.2) Dále e uvedený ouin linearizuje pomocí Talorov vt v referenních hodnotách dráh letu h V Δγ + ΔV + = γ u z (6.3) 3
41 6 Vedení letadla po trati Let dopravního letadla e koná po úecích kontantní rchlotí (V=) a ted výledná kinetická rovnice pro vedení letadla ve vertikální rovin má tvar: h = V Δ + u = V ( ) + γ z θ α u z (6.4) Pro vedení letadla v horizontální rovin lze odvodit obdobný vztah pro prmt rchloti letu na kolmici k dráze letu veliinami tranového pohbu. = V Δγ + u = V ( ψ β ) + u kde u z a u jou vertikální a tranová ložka vtru. (6.5) Výše odvozené rovnice jou tavové rovnice a rozšiují tavový vektor letadla o další ád. Jejich integrací zíkáváme lineární odchlk od pedepané trajektorie letu. Pi ešení úloh vedení letadla po trati rozšiují formulaní problém. 6.4 Struktura tém automatického ízení letu Stém automatického ízení letu jou tém zajišující automatické vedení letadla po trati v obou rovinách vedení. Jejich truktura je vjádena pomocí blokového chématu ukázaném na obrázku Obr. 6-. Obr. 6-: Blokové chéma automatických tém ízení letu Blokové chéma znázoruje ti hierarchické úrovn ízení. Letový úkol FMi Flight miion je vtupem do celého bloku, výtupem je dráha letu FT Flight track. Pomocí jednotk ízení letu FCU Flight control unit, která pe tém automatického ízení FCS, jehož ouátí jou poítae ízení letu FCC Flight control computer a ízení tahu motor TCC Thrut control computer, ovládá podízené ubtém AP Automatic pilot a AT Auto-throttle. PFC Primar flight control jou kormidla primárního ízení. Mícími pítroji AP jou mie letových veliin FI Flight intrument, mícími tém dráh letu jou naviganí tém NS Navigation tem. Dalšími ouátmi jou PFD Primar flight dipla, FD Flihgt director, ND Navigation dipa, EC Engine control, E Engine, SAS Stabilit augmentation tém, SAF Stem of artificial feeling, FDC Flight data computer, NSC Navigation tém computer. 32
42 Vedení letadla po trati v horizontální rovin 6.5 Vedení letadla v horizontální rovin Vedení letadla v horizontální rovin e rozdluje na dv základní kupin, lišící e charakterem odchlk od zvolené trat. Rozeznáváme vedení letadla po trati dané tranovou odchlkou od trati zíkanou z rzných naviganích tém výpotem v naviganích poítaích, zpravidla pi urování poloh letadla vzhledem k trati, nebo v poítaích tému automatického ízení na základ naviganích údaj. Jedná e zpravidla o vedení letadla na delší vzdálenoti v letových koridorech. Lze ho použít po celou dobu letu, praktick od tartu od prahu vzletové a pitávací dráh až po doažení pibližovacího protoru a doažení kurzového pibližovacího radiomajáku Localizeru. Druhý zpob vedení letadla zpracovává úhlovou odchlku od trati zíkanou výpotem z úhlomrného zaízení, jímž je praktick tém VOR. Letová traa je proložena traovými bod oazenými vílai VOR/DME. Úkolem tému automatického ízení je doažení a ledování radiál k / od vílae VOR. Jedná e o let na krátké vzdálenoti podle doahu vílae VOR, který závií na výšce letu. Radionaviganí protedk umožují provedení letu i za nepíznivých meteorologických podmínek. V ouané dob e u moderních dopravních letadel používají inteligentní naviganí tém, které jou chopn provádt ntézu naviganích informací z nkolika zdroj. Ve pojení autopilotem dokáží ídit letadlo od vzletu po pitání. Pená znalot vé poloh a aktuální znalot vmezených protor je nezbtn nutná pro vlatní bezpenot a bezpenot otatních uživatel vzdušného protoru. 33
43 7 ízení a tabilizace tranové odchlk od trati (mód NAV) 7 ÍZENÍ A STABILIZACE STRANOVÉ ODCHYLKY OD TRATI (MÓD NAV) Pi ešení tabilizace tranové odchlk od trati vcházíme z autopilota kurzu navrženého v odtavci 5. Budeme uvažovat úplný tranový pohb, který rozšííme o kinematickou rovnici (6-5), která je další tavovou rovnicí. Stabilizaci tranové odchlk od trati pibližuje náledující chéma. Obr. 7-: Blokové chéma ízení tranové vzdálenoti Celý obvod tabilizace je rozdlen do tí základních blok: letadlo tabilizované autopilotem, blok kinematik letu a úvodní blok ídícími, mícími a výpoetními ubtém. Rovnice autopilotu (7.) pro výchlku kidélek obahuje všechn zptnovazební mk jak od autopilotu klonní, tak od veliin charakterizujících dráhu letu, neobahuje zptnou vazbu od kurzu. δ K = FSM [ K φ + Kφφ + K + K Δ] (7.) φ 7. Rozbor penoti K formulaci problému použijeme ti vtupní rovnice a pro rozbor penoti zanedbáme dnamické vlatnoti obvodu: letadlo autopilot tranového pohbu. Dále použijeme zjednodušenou rovnici letadla pro zíkání veliin kinematického vztahu. Rovnice letadla: β + b β + b2φ ψ = (7.2) Kinematická rovnice: = V ( ψ β ) + u (7.3) Rovnice ídícího tému: φ F Δ( ) (7.4) = φ Dále vjdeme z oprávnného pedpokladu zanedbatelnoti úhlu vboení =, který zajití obvod mrovk. Pak e uvedené rovnice zjednoduší na výraz: L: b 2 φ = ψ (7.5) K: = V ψ + u (7.6) Novou rovnici pro ídící tém dotaneme upravením pedchozích rovnic (7.5) a (7.6) S: ψ b2f Δ( ) = φ (7.7) 34
44 Vedení letadla po trati v horizontální rovin Z uvedených rovnic etavíme blokové chéma ukázané na obrázku Obr. 7-2, které bude použito pro odvození peno potebných pro ešení penoti. Obr. 7-2: ešení penoti ízení tranové odchlk od trati Vztah pro peno rozpojeného obvodu: b V F = Fφ Pedchozí vztah použijeme v penou poruch. Δ( ) / F( ) = = = 2 u ( ) + F + b2v Fφ (7.8) (7.9) Pro kontantní ložku horizontálního vtru u = kont. pímo plne nulová odchlka v utáleném tavu () = již pro proporcionální ložku ídícího lenu. Pro plnní potaující podmínk tabilit je nutno zaadit derivaní ložku. Peno ídícího lenu plující ob podmínk je: F k + k (7.) φ = Dležitou veliinou je kurz letadla pi kontantním tranovém vtru. Ten e zíká z penou: ψ / Fφ b = u + F 2 / = 2 F φ b 2 φ + b V F 2 u ψ ( ) = V Y = ϕ (7.) Úhel e nazývá úhel nou DA drift angle, je to úhel, pod kterým letadlo letí pi pobení tranového vtru, aniž b e odchýlilo od pedepané trat. ízení tranové odchlk od trati lze také provádt pomocí zmn úhlu vboení. Pi pedpokladu, že =, což zajití autopilot tranového pohbu, lze k tomuto ízení použít další regulaní orgán vilé píové ploch (vertical canard). Toto je ovšem již aktivní ízení, umožující netradiní manévr, což je záležitotí jiné kategorie letadel. 7.2 Stabilizace tranové odchlk Uvažujeme úplný tranový pohb rozšíený o kinematickou rovnici (6-5), která je další tavovou rovnicí. Zvolíme cetovní rchlot letu V = 7 m -, jíž rovnž odpovídají koeficient pohbových rovnic. Z kurzu vpoítáme tranovou odchlku od trati, která je ízenou veliinou. Pepoet kurzu na tranovou odchlku e provádí podle náledujícího obrázku Obr. 7-3, jak je také vidt na obrázku Obr
45 7 ízení a tabilizace tranové odchlk od trati (mód NAV) pi -K- Vo Integrator Y 2 U 2 Ydot Obr. 7-3: Pepoet na tranovou odchlku In PI ervo + + kridelka merov ka uhel v boceni Beta pricn naklon Phi kurz Pi klopeni dphi zataceni dpi beta phi pi dphi dpi -K- Vo Integrator Out KDphi + wah out Letadlo Kbeta -K- KDpi -K- U.7 Kphi Obr. 7-4: Simulinkové chéma tabilizace tranové odchlk Z blokového chématu ukázaném na obrázku Obr. 7-4 lze zíkat pomocí funkce linmod pro vnjší mku peno rozpojeného obvodu. Je teba navrhnout koeficient zptné vazb pro tabilizaci tranové odchlk a tabilizaci horizontální rchloti podle požadavk na penot a tabilitu. Stabilizaci horizontální rchloti mžeme vjádit obdobným chématem jako tabilizaci tranové odchlk na Obr. 7-4, kde pouze vputíme blok integrace. Jednotlivé penoové koeficient bl zíkán pomocí nátroje RLTool a ledováním odezev na poruchu, podobn jako v kapitole 5. Draz bl kladen na rchlot pechodového dje a zárove blo pihlíženo na ukutenitelnot dj. Obr. 7-5: RLTool, návrh regulaního koeficientu Ký Obr. 7-6: GMK zoom 36
46 Vedení letadla po trati v horizontální rovin Obr. 7-7: RLTool, návrh regulaního koeficientu K Obr. 7-8: GMK zoom Zjištné penoové koeficient jou náledující: K =, 27 =, 55 K Tato malá hodnota proporcionální ložk regulátoru ouvií hodnotou vzdušné rchloti. Otatní zeílení jou tejná jako u autopilota kurzu z kapitol 5. Zajímavá je pedevším netabilní nula, která vplnula z kinematické rovnice (7.3). Krom atatimu daného kinematikou letu, je zde další atatimu daný pevodem píného náklonu na kurz. Tento atatimu zvšuje penot regulace, avšak zhoršuje tlumení letu kolem trajektorie a mže vét až k netabilit. Má-li být regulaní dj pro výtupní veliinu aperiodický, muejí jeho vtve vcházet z vtví pro ležících ješt na reálné oe. Proto je do ídícího tému vložena derivaní ložka. Obvod zptné vazb tabilizace odchlk od trati bl ted doplnn PD regulátorem, který pinel pól do poátku uzavené mk tému a tím zaruil nulovou odchlku v utáleném tavu. Hodnot koeficient jou náledující: P =, I =, D =,. Obr. 7-9: Odezv na boní porv vtru o velikoti 2 m/ 37
47 7 ízení a tabilizace tranové odchlk od trati (mód NAV) Obr. 7-: mód NAV tabilizace tranové odchlk Obr. 7-: mód NAV - Polohové úhl a úhlové rchloti 38
48 Vedení letadla po trati v horizontální rovin Na ouboru obrázk Obr.7- a Obr. 7- je možné vidt výledek práce tému automatického ízení letu. Letadlo zaíná kurzem a je vzdáleno 2 m od trati. Poté e horizontálním manévrem piblíží k trati a leduje ji nulovou odchlkou až do té dob, kd v ae 3 ekund zane foukat tranový vítr 2 m/. Ten letadlo vchýlí od požadované trati. Stém autopilota zajití optovný návrat k trati tím, že dále letadlo letí pod úhlem nou, jak je vidt na obrázku Obr. 7- na prbhu kurzu. 7.3 Let v koridoru Výledné chéma ízení a tabilizace tranové odchlk od trati je na obrázku Obr Obvod obahuje tlumie, tabilizátor a obvod tranové koordinace pohb. Stabilizaní autopilot jou doplnn o obvod tabilizace tranové odchlk od trati. Vtupem do celého tému je: Poátení kurz letadla Poátení vzdálenot od trati Rchlot letadla Azimut koridoru Rchlot vtru a a, kd zane vítr foukat Tto vtupní parametr e zadávají do chématu na obrázku Obr. 7-3 pomocí uživatelkého protedí, které je ukázáno na obrázku Obr Obr. 7-2: Uživatelké protedí pro zadávání parametr 39
49 7 ízení a tabilizace tranové odchlk od trati (mód NAV) omezeni naklonu PI ervo + + kridelka merov ka uhel v boceni Beta pricn naklon Phi kurz Pi klopeni dphi zataceni dpi K- K- K- K- K- beta phi pi dphi dpi + wah out Letadlo Kbeta -K- KDpi -K- KDphi Polohove uhl a uhlove rchloti Kphi.7 pi Pi kurz pin pi v zdalenot Stabilizace kurzu Pocatecni kurz -C- ARM v zdalenot koridor Azimut koridoru Vtup odchlk Let v koridoru tranov a v zdalenot -K pricna r chlot -K SSV Y Ydot pi koridor U Pocatecni v zdalenot -K -C- Vitr a por v Vitr Stabilizace tranove vzdalenoti Pocatecni vzdalenot Obr. 7-3: Konené chéma módu NAV pi 2 kurz K- '/rad Kpi.7 3 vzdalenot vpnuti faze tabilizace kurzu Pi STOP zataveni i m ul ace zpozdeni Obr. 7-4: Blok Stabilizace kurzu 4
50 Vedení letadla po trati v horizontální rovin 2 vzdalenot pi 3 koridor '/rad K- -K- '/rad vpnuti faze ARM zapnuti faze ARM -.7 Kpi2 ARM -Cuhel etkani trati Obr. 7-5: Blok Let v koridoru pi 2 kori dor 3 U 4 Pocatecni vzdalenot K- '/rad K- Vo -K- Integrator 3 Ydot 2 Y PID KY KY KYd KYdot vpnuti faze tabilizace dy SSV Obr. 7-6: Blok Stabilizace tranové vzdálenoti Dalšími blok ve chématu Obr. 7-3 jou Stabilizace kurzu, Let v koridoru a Stabilizace tranové vzdálenoti. Ped výtupem, který je realizován blokem SCOPE jou zaazen blok tpu GAIN parametrem 8/pi, což pedtavuje pevod z jednotek radiánu na tupn pro nadnjší odeet výledných hodnot úhlu. Stejn tak naopak ped vtupem do tému jou tupn peveden na radián. V modrém bloku Vítr v koneném chématu módu NAV je vtvoen boní vítr a porv vtru, které e objevují náhodnou velikotí každých ekund. Blok Stabilizace kurzu na obrázku Obr. 7-4 louží ke tabilizování kurzu ve fázi, kd e letadlo nachází mimo koridor. Letí v režimu tabilizace kurzu a pibližuje e k zadané trati. Pokud e letoun piblíží k okraji koridoru je pomocí ignálu vzdálenot tato mka automatick vpnuta. V tomto bloku je také implementován blok zatavení imulace, který uritým zpoždním ukoní imulaci, kdž letadlo úpšn doáhne trat nulovou odchlkou. Je zde proto, že ím je zadaná poátení vzdálenot vtší, tím déle bude imulace trvat. 4
51 7 ízení a tabilizace tranové odchlk od trati (mód NAV) Další blok na obrázku Obr. 7-5 louží k letu letadla v koridoru. Zapíná e opt ignálem vzdálenot, kdž letadlo doáhne okraje koridoru a jeho vpnutí pichází ve vzdálenoti jednoho kilometru od tedu koridoru. Úhel etkání tratí je nataven na 45. V pípad zadaných hodnot na obrázku Obr. 7-2 ted letoun poletí kurzem 75 mrem ke koridoru, jak je vidt na obrázku Obr Blok Stabilizace tranové vzdálenoti na obrázku Obr. 7-6 vchází z návrhu z odtavce 7.2 a obahuje koeficient navržené práv v tomto odtavci. Signál vzdálenot pouští tuto mku ve vzdálenoti jednoho kilometru od tedu koridoru. Pi zadávání vtupních parametr je dležité i uvdomit, zdali je možné k zadanému koridoru vbec dolett. Pi výše zobrazeném zadání ukázaném na obrázku Obr. 7-2 je možné doáhnout požadované trati. Pokud bchom však zadali letadlu napíklad kurz 3, bude e od koridoru vzdalovat. Poté je možné zmnit kurz na takový, kterým b e letoun pibližoval trati, nebo lze zvolit umítní letadla vlevo od koridoru jak je ukázáno na obrázku Obr Obr. 7.7: Let ke koridoru Obr. 7-8: Prbh letu ke koridoru 42
52 Vedení letadla po trati v horizontální rovin Obr. 7-9: Detailní zobrazení tabilizace tranové odchlk Obr. 7-2: Polohové úhl a úhlové rchloti 43
53 7 ízení a tabilizace tranové odchlk od trati (mód NAV) Výledek imulace parametr zadanými podle obrázku Obr. 7-2 je na obrázcích Obr. 7-8 až Obr Na prbhu tranové vzdálenoti je vidt, že v ae pibližn 68 ekund letadlo doletí na okraj koridoru. Pak e letadlo pibližuje vtší rchlotí ke tedu koridoru, což je dobe vidt na prbhu píné rchloti. Pibližuje e ke trati pod úhlem 45. Ted pokud letadlo pilétá z pravé tran je 45 odítáno od rozdílu kurzu letadla a azimutu koridoru a pokud pilétá zleva je k rozdílu tchto úhl 45 piteno. To je zajištno a vpoteno v uživatelkém protedí ješt ped zadáním vtupních veliin do imulinkového chématu. Jou zde také vidt jednotlivé porv vtru a boní vítr v ae 2 ekund, který letadlo odchýlí od požadované trati. To je lépe vidt na detailu na obrázku Obr Dále na prbhu kurzu na obrázku Obr. 7-2 je ukázáno, že kurz letadla plne azimutem koridoru 22. V ae 2 ekund, kd zane foukat kontantní tranový vítr, e letadlo natoí proti pobení boního vtru a dále letí pod úhlem nou. Let pod úhlem nou je vvtlen na obrázku Obr
54 Vedení letadla po trati v horizontální rovin 8 ÍZENÍ A STABILIZACE ÚHLOVÉ ODCHYLKY OD TRATI (MÓD VOR) V této kapitole je ešena problematika letu po trati v horizontální rovin. Ta je urena úhlovou odchlkou T od zvolené trati dané kurzem trati T. Opt e vchází z autopilota kurzu navrženého v odtavci 5. Úplný tranový pohb je nutno rozšíit o kinematickou rovnici (8.7), která je odvozena v odtavci Radionaviganí tém VOR VOR (VHF Omnidirectional Radio Range) je VKV všemrový radiomaják. Jeden ze základních pítroj používaný v pítrojové navigaci, který umožuje zjitit na palub letadla magnetický radiál (nebo mrník) vi poloze majáku (viz. obrázek Obr. 8-3). Všemrových maják e v letectví používá již od zaátku padeátých let. Princip poívá ve vílání dvou ignál. První je kontantn vílán všemi mr a druhý rotuje kolem vílae. Pijíma v letadle (obrázek Obr. 8-) poté z tchto ignál urí mr k vílai nebo od nj. Po naladní pozemní tanice VOR a natavení radiálu, po kterém chceme lett, nám indikátor na palub ukazuje odchlku od zvoleného radiálu. Výledek e vjaduje v úhlových tupních a vjaduje relativn pený údaj o úhlu, o který e letadlo vchýlilo od mru, ve kterém blo pozemní tanicí zachceno. Navíc e VOR, zpravidla údaji DME, vužívá k vtení letových tratí pro odlet a pílet k letištím a tanovení IAF (Initial approach fix - naviganí fix (bod) pro zahájení poáteního piblížení na pitání) a FAF (Final approach fix naviganí fix koneného piblížení na pitání). Pozemní vbavení VOR (VHF Omnidirectional Radio Range všemrový maják) má vílací kmitoet 8 2 MHz (vbrané kmitot) a 2 8 MHz (kanál po 5 khz). Vílaný noný kmitoet je modulován referenním ignálem nezávilém na magnetickém mrníku (je ve všech mrech tejný) a promnným ignálem závilém na magnetickém mrníku vi majáku VOR (jeho fáze e mní podle úhlové poloh pozorovatele vi majáku). Palubní vbavení pijíma vhodnocuje fázový pouv referenního a promnného ignálu, který vjaduje hodnotu magnetického mrníku vi zvolenému majáku VOR. Jako indikátor e používá bu RMI (radio-magnetic indicator), nebo rzné družené pítroje, zpravidla obahující OBS (Omni Bearing Selector elektor tratí natavení radiálu k majáku), CDI (Coure Deviation Indicator indikátor traové odchlk) a TO FROM indicator (pro rozlišení pi letu k nebo od majáku) Úhlová odchlka od trati je zobrazena bevnem pohbujícím e rovnobžn ukazatelem kurzu trati na traovém ukazateli, nebo na odpovídajícím módu zobrazení na ND. Traový ukazatel je ukázán na obrázku Obr. 8-. Souan e na ukazateli zobrazuje šipka mru letu TO/FROM vzhledem k majáku VOR. Pokud letadlo letí mrem k majáku, ídí e ml šipk podle vztahu: TO: ψ ψ A > 9 (8.) Vztah pro let od majáku: FROM: ψ < 9 (8.2) ψ A 45
REGULACE EL. POHONŮ Stabilita a tlumení. Obr. 1. Schéma uzavřené regulační smyčky. Obr. 2. Ukazatele kvality regulace
 EP-egulace EP EGULACE EL. POHONŮ Stabilita a tlumení Obr.. Schéma uzavřené regulační myčky Obr.. Ukazatele kvality regulace V regulačních pohonech pouzujeme kvalitu regulace nejčatěji dle přechodové charakteritiky,
EP-egulace EP EGULACE EL. POHONŮ Stabilita a tlumení Obr.. Schéma uzavřené regulační myčky Obr.. Ukazatele kvality regulace V regulačních pohonech pouzujeme kvalitu regulace nejčatěji dle přechodové charakteritiky,
obr. 3.1 Pohled na mící tra
 3. Mení tecích ztrát na vzduchové trati 3.1. Úvod Problematika urení tecích ztrát je hodná pro vodu nebo vzduch jako proudící médium (viz kap..1). Micí tra e liší použitými hydraulickými prvky a midly.
3. Mení tecích ztrát na vzduchové trati 3.1. Úvod Problematika urení tecích ztrát je hodná pro vodu nebo vzduch jako proudící médium (viz kap..1). Micí tra e liší použitými hydraulickými prvky a midly.
VYUŽITÍ MATLABU PŘI NÁVRHU FUZZY LOGICKÉHO REGULÁTORU. Ing. Aleš Hrdlička
 VYUŽITÍ MATLABU PŘI NÁVRHU FUZZY LOGICKÉHO REGULÁTORU Ing. Aleš Hrdlička Katedra technické kybernetiky a vojenké robotiky Vojenká akademie v Brně E-mail: hrdlicka@c.vabo.cz Úvod Tento článek popiuje jednoduchou
VYUŽITÍ MATLABU PŘI NÁVRHU FUZZY LOGICKÉHO REGULÁTORU Ing. Aleš Hrdlička Katedra technické kybernetiky a vojenké robotiky Vojenká akademie v Brně E-mail: hrdlicka@c.vabo.cz Úvod Tento článek popiuje jednoduchou
ZÁKLADY AUTOMATICKÉHO ŘÍZENÍ
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ ZÁKLADY AUTOMATICKÉHO ŘÍZENÍ týden doc Ing Renata WAGNEROVÁ, PhD Otrava 013 doc Ing Renata WAGNEROVÁ, PhD Vyoká škola báňká Technická univerzita
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ ZÁKLADY AUTOMATICKÉHO ŘÍZENÍ týden doc Ing Renata WAGNEROVÁ, PhD Otrava 013 doc Ing Renata WAGNEROVÁ, PhD Vyoká škola báňká Technická univerzita
s požadovaným výstupem w(t), a podle této informace generuje akční zásah u(t) do
 Vážení zákazníci, dovolujeme i Vá upozornit, že na tuto ukázku knihy e vztahují autorká práva, tzv. copyright. To znamená, že ukázka má loužit výhradnì pro oobní potøebu potenciálního kupujícího (aby ètenáø
Vážení zákazníci, dovolujeme i Vá upozornit, že na tuto ukázku knihy e vztahují autorká práva, tzv. copyright. To znamená, že ukázka má loužit výhradnì pro oobní potøebu potenciálního kupujícího (aby ètenáø
Vysokofrekvenční obvody s aktivními prvky
 Vokofrekvenční obvod aktivními prvk Základními aktivními prvk ve vokofrekvenční technice jou bipolární a unipolární tranzitor. Dalšími aktivními prvk jou hbridní nebo monolitické integrované obvod. Tranzitor
Vokofrekvenční obvod aktivními prvk Základními aktivními prvk ve vokofrekvenční technice jou bipolární a unipolární tranzitor. Dalšími aktivními prvk jou hbridní nebo monolitické integrované obvod. Tranzitor
ZÁKLADY AUTOMATICKÉHO ŘÍZENÍ
 VOKÁ ŠKOLA BÁŇKÁ TECHNICKÁ NIVEZITA OTAVA FAKLTA TOJNÍ ZÁKLAD ATOMATICKÉHO ŘÍZENÍ 9. týden doc. Ing. enata ANEOVÁ, Ph.D. Otrava 03 doc. Ing. enata ANEOVÁ, Ph.D. Vyoká škola báňká Technická univerzita Otrava
VOKÁ ŠKOLA BÁŇKÁ TECHNICKÁ NIVEZITA OTAVA FAKLTA TOJNÍ ZÁKLAD ATOMATICKÉHO ŘÍZENÍ 9. týden doc. Ing. enata ANEOVÁ, Ph.D. Otrava 03 doc. Ing. enata ANEOVÁ, Ph.D. Vyoká škola báňká Technická univerzita Otrava
Pravdpodobnost výskytu náhodné veliiny na njakém intervalu urujeme na základ tchto vztah: f(x)
 NÁHODNÁ VELIINA Náhodná veliina je veliina, jejíž hodnota je jednoznan urena výsledkem náhodného pokusu (je-li tento výsledek dán reálným íslem). Jde o reálnou funkci definovanou na základním prostoru
NÁHODNÁ VELIINA Náhodná veliina je veliina, jejíž hodnota je jednoznan urena výsledkem náhodného pokusu (je-li tento výsledek dán reálným íslem). Jde o reálnou funkci definovanou na základním prostoru
7 - Ustálený stav kmitavý a nekmitavý, sledování a zadržení poruchy
 7 - Utálený tav kmitavý a nekmitavý, ledování a zadržení poruchy Michael Šebek Automatické řízení 018 31-3-18 Automatické řízení - ybernetika a robotika zeílení ytému na frekvenci ω je G( jω) - viz amplitudový
7 - Utálený tav kmitavý a nekmitavý, ledování a zadržení poruchy Michael Šebek Automatické řízení 018 31-3-18 Automatické řízení - ybernetika a robotika zeílení ytému na frekvenci ω je G( jω) - viz amplitudový
Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra kybernetiky. Bakalářská práce. Řízení Trojkolového vozíku
 Západočeká univerzita v Plzni Fakulta aplikovaných věd Katedra kbernetik Bakalářká práce Řízení Trojkolového vozíku Plzeň, 23 Jan Holub Prohlášení Předkládám tímto k poouzení a obhajobě bakalářkou práci
Západočeká univerzita v Plzni Fakulta aplikovaných věd Katedra kbernetik Bakalářká práce Řízení Trojkolového vozíku Plzeň, 23 Jan Holub Prohlášení Předkládám tímto k poouzení a obhajobě bakalářkou práci
Metoda konečných prvků Základní veličiny, rovnice a vztahy (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika)
 Inovace tudijního oboru Geotechnika Reg. č. CZ..7/../8.9 Metoda konečných prvků Základní veličin, rovnice a vztah (výuková prezentace pro. ročník navazujícího tudijního oboru Geotechnika) Doc. RNDr. Eva
Inovace tudijního oboru Geotechnika Reg. č. CZ..7/../8.9 Metoda konečných prvků Základní veličin, rovnice a vztah (výuková prezentace pro. ročník navazujícího tudijního oboru Geotechnika) Doc. RNDr. Eva
Příklady k přednášce 6 - Spojování a struktury
 Příklad k přednášce 6 - Spojování a truktur Michael Šebek Automatické řízení 07 7-3-8 Automatické řízení - Kbernetika a robotika Zpětnovazební pojení tavových modelů Odvození obecného případu (značení
Příklad k přednášce 6 - Spojování a truktur Michael Šebek Automatické řízení 07 7-3-8 Automatické řízení - Kbernetika a robotika Zpětnovazební pojení tavových modelů Odvození obecného případu (značení
Katedra geotechniky a podzemního stavitelství
 Katedra geotechnik a podzemního taviteltví Modelování v geotechnice Základní veličin, rovnice a vztah (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace tudijního
Katedra geotechnik a podzemního taviteltví Modelování v geotechnice Základní veličin, rovnice a vztah (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace tudijního
25 Dopravní zpoždění. Michael Šebek Automatické řízení 2013 21-4-13
 5 Dopravní zpoždění Michael Šebek Automatické řízení 3-4-3 Dopravní zpoždění (Time delay, tranport delay, dead time, delay-differential ytem) V reálných ytémech e čato vykytuje dopravní zpoždění yt ( )
5 Dopravní zpoždění Michael Šebek Automatické řízení 3-4-3 Dopravní zpoždění (Time delay, tranport delay, dead time, delay-differential ytem) V reálných ytémech e čato vykytuje dopravní zpoždění yt ( )
ÚSTAV PRO VÝZKUM MOTOROVÝCH VOZIDEL s.r.o. TÜV Süddeutschland Holding AG TECHNICKÁ ZPRÁVA
 TÜV Süddeutchland Holding AG Lihovarká 12, 180 68 Praha 9 www.uvmv.cz TECHNICKÁ ZPRÁVA Metodika pro hodnocení vozidel v jízdních manévrech na základě počítačových imulací a jízdních zkoušek. Simulační
TÜV Süddeutchland Holding AG Lihovarká 12, 180 68 Praha 9 www.uvmv.cz TECHNICKÁ ZPRÁVA Metodika pro hodnocení vozidel v jízdních manévrech na základě počítačových imulací a jízdních zkoušek. Simulační
Propočty přechodu Venuše 8. června 2004
 Propočty přechodu Venuše 8. června 2004 V tomto dokumentu předkládáme podmínky přechodu Venuše pře luneční kotouč 8. června roku 2004. Naše výpočty jme založili na planetárních teoriích VSOP87 vytvořených
Propočty přechodu Venuše 8. června 2004 V tomto dokumentu předkládáme podmínky přechodu Venuše pře luneční kotouč 8. června roku 2004. Naše výpočty jme založili na planetárních teoriích VSOP87 vytvořených
( LEVEL 3 Laplaceova transformace jako nástroj řešení lineárních diferenciálních rovnic. )
 ( LEVEL 3 Laplaceova tranformace jako nátroj řešení lineárních diferenciálních rovnic. ) Podívejme e tentokrát na dynamiku pracovní edačky řidiče prizmatem matematiky aneb trocha teorie jitě nikomu neuškodí...
( LEVEL 3 Laplaceova tranformace jako nátroj řešení lineárních diferenciálních rovnic. ) Podívejme e tentokrát na dynamiku pracovní edačky řidiče prizmatem matematiky aneb trocha teorie jitě nikomu neuškodí...
Y Q charakteristice se pipojují kivky výkonu
 4. Mení charakteritiky erpadla 4.1. Úod Charakteritika erpadla je záilot kutené mrné energie Y (rep. kutené dopraní ýšky H ) na prtoku Q. K této základní P h Q, úinnoti η Q a mrné energie pro potrubí Y
4. Mení charakteritiky erpadla 4.1. Úod Charakteritika erpadla je záilot kutené mrné energie Y (rep. kutené dopraní ýšky H ) na prtoku Q. K této základní P h Q, úinnoti η Q a mrné energie pro potrubí Y
Rovnice rovnoměrně zrychleného pohybu
 ..8 Rovnice rovnoměrně zrychleného pohybu Předpoklady: 7 Pedagogická poznámka: Stejně jako u předchozí hodiny je i v této hodině potřeba potupovat tak, aby tudenti měli minimálně píše minut na řešení příkladů
..8 Rovnice rovnoměrně zrychleného pohybu Předpoklady: 7 Pedagogická poznámka: Stejně jako u předchozí hodiny je i v této hodině potřeba potupovat tak, aby tudenti měli minimálně píše minut na řešení příkladů
1.1.14 Rovnice rovnoměrně zrychleného pohybu
 ..4 Rovnice rovnoměrně zrychleného pohybu Předpoklady: 3 Pedagogická poznámka: Stejně jako u předchozí hodiny je i v této hodině potřeba potupovat tak, aby tudenti měli minimálně minut na řešení příkladů
..4 Rovnice rovnoměrně zrychleného pohybu Předpoklady: 3 Pedagogická poznámka: Stejně jako u předchozí hodiny je i v této hodině potřeba potupovat tak, aby tudenti měli minimálně minut na řešení příkladů
5. cvičení z Matematické analýzy 2
 5. cvičení z Matematické analýz 2 30. října - 3. litopadu 207 5. linearizace funkce a Pro funkci f, = e nalezněte její linearizaci v bodě a 0 = 6, 0. Použijte ji k přibližnému určení hodnot funkce f v
5. cvičení z Matematické analýz 2 30. října - 3. litopadu 207 5. linearizace funkce a Pro funkci f, = e nalezněte její linearizaci v bodě a 0 = 6, 0. Použijte ji k přibližnému určení hodnot funkce f v
ÚSTŘEDNÍ KOMISE FYZIKÁLNÍ OLYMPIÁDY ČESKÉ REPUBLIKY
 ÚSTŘEDNÍ KOMISE YZIKÁLNÍ OLYMPIÁDY ČESKÉ REPUBLIKY E-mail: ivo.volf@uhk.cz, tel.: 493 331 19, 493 331 189 Řešení úloh krajkého kola 55. ročníku yzikální olympiády Kategorie E Předložená řešení by neměla
ÚSTŘEDNÍ KOMISE YZIKÁLNÍ OLYMPIÁDY ČESKÉ REPUBLIKY E-mail: ivo.volf@uhk.cz, tel.: 493 331 19, 493 331 189 Řešení úloh krajkého kola 55. ročníku yzikální olympiády Kategorie E Předložená řešení by neměla
Systém vztahů obecné pružnosti Zobecněný Hookeův zákon
 Stém vtahů obecné pružnoti Zobecněný Hookeův ákon V PPI e řešil úloh pružnoti u prutů. Pro řešení pouvů napětí a přetvoření obecného 3D těleo je třeba etavit a řešit tém vtahů obecné pružnoti. Jeho řešení
Stém vtahů obecné pružnoti Zobecněný Hookeův ákon V PPI e řešil úloh pružnoti u prutů. Pro řešení pouvů napětí a přetvoření obecného 3D těleo je třeba etavit a řešit tém vtahů obecné pružnoti. Jeho řešení
Vzorový protokol pro předmět Zpracování experimentu. Tento protokol by měl sloužit jako vzor pro tvorbu vašich vlastních protokolů.
 Vzorový protokol pro předmět Zpracování experimentu. Tento protokol by měl loužit jako vzor pro tvorbu vašich vlatních protokolů. Na příkladech je zde ukázán právný zápi výledků i formát tabulek a grafů.
Vzorový protokol pro předmět Zpracování experimentu. Tento protokol by měl loužit jako vzor pro tvorbu vašich vlatních protokolů. Na příkladech je zde ukázán právný zápi výledků i formát tabulek a grafů.
21 Diskrétní modely spojitých systémů
 21 Dikrétní modely pojitýc ytémů Micael Šebek Automatické řízení 2015 29-4-15 Metoda emulace Automatické řízení - Kybernetika a robotika pojitý regulátor nazývá e také aproximace, dikrétní ekvivalent,
21 Dikrétní modely pojitýc ytémů Micael Šebek Automatické řízení 2015 29-4-15 Metoda emulace Automatické řízení - Kybernetika a robotika pojitý regulátor nazývá e také aproximace, dikrétní ekvivalent,
Řešení úloh 1. kola 48. ročníku fyzikální olympiády. Kategorie D Autořiúloh:J.Jírů(1,3,4,7),I.Čáp(5),I.Volf(2),J.JírůaP.Šedivý(6)
 Řešení úloh 1. kola 48. ročníku fyzikální olympiády. Kategorie D Autořiúloh:J.Jírů(1,3,4,7),I.Čáp(5),I.Volf(2),J.JírůaP.Šedivý(6) 1.a) Jetliže kolo automobilu neprokluzuje, je velikot okamžité rychloti
Řešení úloh 1. kola 48. ročníku fyzikální olympiády. Kategorie D Autořiúloh:J.Jírů(1,3,4,7),I.Čáp(5),I.Volf(2),J.JírůaP.Šedivý(6) 1.a) Jetliže kolo automobilu neprokluzuje, je velikot okamžité rychloti
Příklady k přednášce 19 - Polynomiální metody
 Příklady k přednášce 19 - Polynomiální metody Michael Šebek Automatické řízení 013 7-4-14 Opakování: Dělení polynomů: e zbytkem a bez Polynomy tvoří okruh, ale ne těleo (Okruh tvoří také celá číla, těleo
Příklady k přednášce 19 - Polynomiální metody Michael Šebek Automatické řízení 013 7-4-14 Opakování: Dělení polynomů: e zbytkem a bez Polynomy tvoří okruh, ale ne těleo (Okruh tvoří také celá číla, těleo
teorie elektronických obvodů Jiří Petržela syntéza elektronických obvodů
 Jiří Petržela příklad nalezněte dvě různé realizace admitanční funkce zadané formou racionální lomené funkce Y () () ( ) ( ) : první krok rozkladu do řetězového zlomku () 9 7 9 výledný rozklad ( ) 9 9
Jiří Petržela příklad nalezněte dvě různé realizace admitanční funkce zadané formou racionální lomené funkce Y () () ( ) ( ) : první krok rozkladu do řetězového zlomku () 9 7 9 výledný rozklad ( ) 9 9
IDENTIFIKACE REGULOVANÉ SOUSTAVY APLIKACE PRO PARNÍ KOTEL
 IDENTIFIKACE REGULOVANÉ SOUSTAVY APLIKACE PRO PARNÍ KOTEL Ing. Zeněk Němec, CSc. VUT v Brně, Fakulta trojního inženýrtví, Útav automatizace a informatiky. Úvo, vymezení problematiky Přípěvek ouvií řešením
IDENTIFIKACE REGULOVANÉ SOUSTAVY APLIKACE PRO PARNÍ KOTEL Ing. Zeněk Němec, CSc. VUT v Brně, Fakulta trojního inženýrtví, Útav automatizace a informatiky. Úvo, vymezení problematiky Přípěvek ouvií řešením
Vytvoření skriptů pro webové rozhraní předmětu Analýza a simulace technologických procesů
 Vytvoření kriptů pro webové rozhraní předmětu Analýza a imulace technologických proceů M-file for the Internet Interface Ued in the Subject Analyi and Simulation of Technological Procee. Petr Tomášek Bakalářká
Vytvoření kriptů pro webové rozhraní předmětu Analýza a imulace technologických proceů M-file for the Internet Interface Ued in the Subject Analyi and Simulation of Technological Procee. Petr Tomášek Bakalářká
Teorie systémů a řízení
 VYSOKÁ ŠKOLA BÁŇSKÁ ECHNICKÁ UNIVERZIA V OSRAVĚ FAKULA HORNICKO - GEOLOGICKÁ INSIU EKONOMIKY A SYSÉMŮ ŘÍZENÍ eorie ytémů a řízení Prof.Ing.Aloi Burý,CSc. OSRAVA 2007 Předmluva Studijní materiály eorie
VYSOKÁ ŠKOLA BÁŇSKÁ ECHNICKÁ UNIVERZIA V OSRAVĚ FAKULA HORNICKO - GEOLOGICKÁ INSIU EKONOMIKY A SYSÉMŮ ŘÍZENÍ eorie ytémů a řízení Prof.Ing.Aloi Burý,CSc. OSRAVA 2007 Předmluva Studijní materiály eorie
Příklady k přednášce 19 - Polynomiální metody
 Příklady k přednášce 19 - Polynomiální metody Michael Šebek Automatické řízení 016 15-4-17 Dělení polynomů: e zbytkem a bez Polynomy netvoří těleo (jako reálná číla, racionální funkce, ) ale okruh (jako
Příklady k přednášce 19 - Polynomiální metody Michael Šebek Automatické řízení 016 15-4-17 Dělení polynomů: e zbytkem a bez Polynomy netvoří těleo (jako reálná číla, racionální funkce, ) ale okruh (jako
ANALÝZA PRŮCHODU PAPRSKOVÝCH SVAZKŮ KOUTOVÝM ODRAŽEČEM
 ANALÝZA PRŮCHODU PAPRSKOVÝCH SVAZKŮ KOUTOVÝM ODRAŽEČEM P Kytka J Novák ČVUT v Praze Fakulta tavební katedra fyziky Práce e zabývá analýzou průchodu paprků koutovým odražečem což je typ hranolu který je
ANALÝZA PRŮCHODU PAPRSKOVÝCH SVAZKŮ KOUTOVÝM ODRAŽEČEM P Kytka J Novák ČVUT v Praze Fakulta tavební katedra fyziky Práce e zabývá analýzou průchodu paprků koutovým odražečem což je typ hranolu který je
TECHNICKÁ UNIVERZITA V LIBERCI Katedra fyziky, Studentská 2, 461 17 Liberec
 TECHNICKÁ UNIVERZITA V LIBERCI Katedra fyziky, Studentká, 6 7 Liberec POŽADAVKY PRO PŘIJÍMACÍ ZKOUŠKY Z FYZIKY Akademický rok: 0/0 Fakulta mechatroniky Studijní obor: Nanomateriály Tématické okruhy. Kinematika
TECHNICKÁ UNIVERZITA V LIBERCI Katedra fyziky, Studentká, 6 7 Liberec POŽADAVKY PRO PŘIJÍMACÍ ZKOUŠKY Z FYZIKY Akademický rok: 0/0 Fakulta mechatroniky Studijní obor: Nanomateriály Tématické okruhy. Kinematika
+ ω y = 0 pohybová rovnice tlumených kmitů. r dr dt. B m. k m. Tlumené kmity
 Tlumené kmit V praxi téměř vžd brání pohbu nějaká brzdicí síla, jejíž původ je v třecích silách mezi reálnými těles. Matematický popis těchto sil bývá dosti komplikovaný. Velmi často se vsktuje tzv. viskózní
Tlumené kmit V praxi téměř vžd brání pohbu nějaká brzdicí síla, jejíž původ je v třecích silách mezi reálnými těles. Matematický popis těchto sil bývá dosti komplikovaný. Velmi často se vsktuje tzv. viskózní
Prbh funkce Jaroslav Reichl, 2006
 rbh funkce Jaroslav Reichl, 6 Vyšetování prbhu funkce V tomto tetu je vzorov vyešeno nkolik úloh na vyšetení prbhu funkce. i ešení úlohy jsou využity základní vlastnosti diferenciálního potu.. ešený píklad
rbh funkce Jaroslav Reichl, 6 Vyšetování prbhu funkce V tomto tetu je vzorov vyešeno nkolik úloh na vyšetení prbhu funkce. i ešení úlohy jsou využity základní vlastnosti diferenciálního potu.. ešený píklad
11 - Regulátory. Michael Šebek Automatické řízení 2015 24-3-15
 - Regulátory Michael Šebe Automaticé řízení 5 4-3-5 Nejjednodušší regulátory Automaticé řízení - Kybernetia a robotia v jitém mylu nejjednodušší regulátor je On-Off (Bang-bang) má jen dvě možné výtupní
- Regulátory Michael Šebe Automaticé řízení 5 4-3-5 Nejjednodušší regulátory Automaticé řízení - Kybernetia a robotia v jitém mylu nejjednodušší regulátor je On-Off (Bang-bang) má jen dvě možné výtupní
1 Rozdělení mechaniky a její náplň
 1 Rozdělení mechaniky a její náplň Mechanika je nauka o rovnováze a pohybu hmotných útvarů pohybujících se rychlostí podstatně menší, než je rychlost světla (v c). Vlastnosti skutečných hmotných útvarů
1 Rozdělení mechaniky a její náplň Mechanika je nauka o rovnováze a pohybu hmotných útvarů pohybujících se rychlostí podstatně menší, než je rychlost světla (v c). Vlastnosti skutečných hmotných útvarů
ANALÝZA A KLASIFIKACE DAT. Institut biostatistiky a analýz
 ANALÝZA A KLASIFIKACE DAT prof. Ing. Jiří Holčík,, CSc. III. PŘÍZNAKOVÁ KLASIFIKACE - ÚVOD PŘÍZNAKOVÝ POPIS Příznakový obraz x zpracovávaných dat je vyjádřen n-rozměrným loupcovým vektorem hodnot x i,
ANALÝZA A KLASIFIKACE DAT prof. Ing. Jiří Holčík,, CSc. III. PŘÍZNAKOVÁ KLASIFIKACE - ÚVOD PŘÍZNAKOVÝ POPIS Příznakový obraz x zpracovávaných dat je vyjádřen n-rozměrným loupcovým vektorem hodnot x i,
3. V případě dvou na sebe kolmých posunutí o velikostech 3 cm a 4 cm obdržíme výsledné posunutí o velikosti a) 8 cm b) 7 cm c) 6 cm d) 5 cm *
 Fyzika 1 2009 Otázky za 2 body 1. Mezi tavové veličiny patří a) teplo b) teplota * c) práce d) univerzální plynová kontanta 2. Krychle má hranu o délce 2 mm. Jaký je její objem v krychlových metrech? a)
Fyzika 1 2009 Otázky za 2 body 1. Mezi tavové veličiny patří a) teplo b) teplota * c) práce d) univerzální plynová kontanta 2. Krychle má hranu o délce 2 mm. Jaký je její objem v krychlových metrech? a)
Vzorový test k přijímacím zkouškám do navazujícího magisterského studijního oboru Automatické řízení a informatika (2012)
 Vzorový tet k přijímacím zkouškám do navazujícího magiterkého tudijního oboru Automatické řízení a informatika (22). Sekvenční logický obvod je: a) obvod, v němž je výtupní tav určen na základě vtupních
Vzorový tet k přijímacím zkouškám do navazujícího magiterkého tudijního oboru Automatické řízení a informatika (22). Sekvenční logický obvod je: a) obvod, v němž je výtupní tav určen na základě vtupních
MATEMATICKÁ KARTOGRAFIE
 VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KARTOGRAFIE MODUL KARTOGRAFICKÁ ZKRESLENÍ STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Matematická kartografie
VYSOKÉ UENÍ TECHNICKÉ V BRN FAKULTA STAVEBNÍ MILOSLAV ŠVEC MATEMATICKÁ KARTOGRAFIE MODUL KARTOGRAFICKÁ ZKRESLENÍ STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Matematická kartografie
Podpora výuky předmětu "Teorie automatického řízení I" Petr Žajdlík
 Podpora výuky předmětu "Teorie automatického řízení I" Petr Žajdlík Bakalářká práce 6 ABSTRAKT Abtrakt čeky Tato bakalářká práce e zabývá vzorovým vypracováním zápočtových protokolů polu návrhem zadání
Podpora výuky předmětu "Teorie automatického řízení I" Petr Žajdlík Bakalářká práce 6 ABSTRAKT Abtrakt čeky Tato bakalářká práce e zabývá vzorovým vypracováním zápočtových protokolů polu návrhem zadání
Pedání smny. Popis systémového protokolování. Autor: Ing. Jaroslav Halva V Plzni 24.01.2012. Strana 1/6
 Autor: Ing. Jaroslav Halva V Plzni 24.01.2012 Strana 1/6 Obsah 1 OBSAH... 2 2 NKOLIK SLOV NA ÚVOD... 3 3 MODEL... 3 4 DEFINICE... 3 5 DENNÍ VÝKAZ... 4 6 ZÁVR... 6 Strana 2/6 1 Nkolik slov na úvod Zamení
Autor: Ing. Jaroslav Halva V Plzni 24.01.2012 Strana 1/6 Obsah 1 OBSAH... 2 2 NKOLIK SLOV NA ÚVOD... 3 3 MODEL... 3 4 DEFINICE... 3 5 DENNÍ VÝKAZ... 4 6 ZÁVR... 6 Strana 2/6 1 Nkolik slov na úvod Zamení
Příklady k přednášce 16 - Pozorovatel a výstupní ZV
 Příklady k přednášce 6 - Pozorovatel a výtupní ZV Michael Šebek Automatické řízení 08 6-4-8 Příklad: Pozorovatel pro kyvadlo naivně pro kyvadlo frekvencí ω 0 a rovnicemi x 0 x 0 navrhneme pozorovatel dvojitým
Příklady k přednášce 6 - Pozorovatel a výtupní ZV Michael Šebek Automatické řízení 08 6-4-8 Příklad: Pozorovatel pro kyvadlo naivně pro kyvadlo frekvencí ω 0 a rovnicemi x 0 x 0 navrhneme pozorovatel dvojitým
TECHNICKÁ UNIVERZITA V LIBERCI
 ECHNICÁ UNIVERZIA V LIBERCI FAULA SROJNÍ atedra aplikované kybernetiky Obor 3922 Automatizované ytémy řízení ve trojírentví Zaměření Automatizace inženýrkých prací Programový modul pro automatické eřízení
ECHNICÁ UNIVERZIA V LIBERCI FAULA SROJNÍ atedra aplikované kybernetiky Obor 3922 Automatizované ytémy řízení ve trojírentví Zaměření Automatizace inženýrkých prací Programový modul pro automatické eřízení
Příklady k přednášce 25 Dopravní zpoždění
 Příklady k přednášce 25 Dopravní zpoždění Michael Šebek Automatické řízení 23 2-4-3 L { } Dopravní zpoždění v Laplaceově tranformaci v ( + τ ) { f t } { } t f(): t f() t = t
Příklady k přednášce 25 Dopravní zpoždění Michael Šebek Automatické řízení 23 2-4-3 L { } Dopravní zpoždění v Laplaceově tranformaci v ( + τ ) { f t } { } t f(): t f() t = t
II. Kinematika hmotného bodu
 II Kinematika hmotného bodu Všechny vyřešené úlohy jou vyřešeny nejprve obecně, to znamená bez číel Číelné hodnoty jou doazeny až tehdy, dopějeme-li k vyjádření neznámé pomocí vztahu obahujícího pouze
II Kinematika hmotného bodu Všechny vyřešené úlohy jou vyřešeny nejprve obecně, to znamená bez číel Číelné hodnoty jou doazeny až tehdy, dopějeme-li k vyjádření neznámé pomocí vztahu obahujícího pouze
! " # $ % # & ' ( ) * + ), -
 ! " # $ % # & ' ( ) * + ), - INDIVIDUÁLNÍ VÝUKA MATEMATIKA METODIKA Kuželosek Mgr. Petra Dunovská bezen 9 Obtížnost této kapitol matematik je dána tím, že se pi výkladu i ešení úloh komplexn vužívají vdomosti
! " # $ % # & ' ( ) * + ), - INDIVIDUÁLNÍ VÝUKA MATEMATIKA METODIKA Kuželosek Mgr. Petra Dunovská bezen 9 Obtížnost této kapitol matematik je dána tím, že se pi výkladu i ešení úloh komplexn vužívají vdomosti
Automatizace je proces při němž je řídicí funkce člověka nahrazována činností
 Automatizace je proces při němž je řídicí funkce člověka nahrazována činností různých přístrojů a zařízení. (Mechanizace, Automatizace, Komplexní automatizace) Kybernetika je Věda, která zkoumá obecné
Automatizace je proces při němž je řídicí funkce člověka nahrazována činností různých přístrojů a zařízení. (Mechanizace, Automatizace, Komplexní automatizace) Kybernetika je Věda, která zkoumá obecné
Ing. Jaroslav Halva. UDS Fakturace
 UDS Fakturace Modul fakturace výrazn posiluje funknost informaního systému UDS a umožuje bilancování jednotlivých zakázek s ohledem na hodnotu skutených náklad. Navíc optimalizuje vlastní proces fakturace
UDS Fakturace Modul fakturace výrazn posiluje funknost informaního systému UDS a umožuje bilancování jednotlivých zakázek s ohledem na hodnotu skutených náklad. Navíc optimalizuje vlastní proces fakturace
Proud ní tekutiny v rotující soustav, aneb prozradí nám vír ve výlevce, na které polokouli se nacházíme?
 Veletrh nápad uitel fyziky 10 Proudní tekutiny v rotující soustav, aneb prozradí nám vír ve výlevce, na které polokouli se nacházíme? PAVEL KONENÝ Katedra obecné fyziky pírodovdecké fakulty Masarykovy
Veletrh nápad uitel fyziky 10 Proudní tekutiny v rotující soustav, aneb prozradí nám vír ve výlevce, na které polokouli se nacházíme? PAVEL KONENÝ Katedra obecné fyziky pírodovdecké fakulty Masarykovy
Automatizace Úloha č.1. Identifikace regulované soustavy Strejcovou metodou
 Automatizace Úloha č. Identifikace regulované outavy Strejcovou metodou Petr Luzar 008/009 Zadání. Zapojte regulační obvod reálnou tepelnou outavou a eznamte e monitorovacím a řídicím programovým ytémem
Automatizace Úloha č. Identifikace regulované outavy Strejcovou metodou Petr Luzar 008/009 Zadání. Zapojte regulační obvod reálnou tepelnou outavou a eznamte e monitorovacím a řídicím programovým ytémem
11 - Regulátory. Michael Šebek Automatické řízení
 - Regulátory Michael Šebe Automaticé řízení 7 6-3-7 Nejjednodušší regulátory Automaticé řízení - Kybernetia a robotia v jitém mylu nejjednodušší regulátor je On-Off (Bang-bang) má jen dvě možné výtupní
- Regulátory Michael Šebe Automaticé řízení 7 6-3-7 Nejjednodušší regulátory Automaticé řízení - Kybernetia a robotia v jitém mylu nejjednodušší regulátor je On-Off (Bang-bang) má jen dvě možné výtupní
FYZIKA 1. ROČNÍK. Tématický plán. Hodiny: Září 7 Říjen 8 Listopad 8 Prosinec 6 Leden 8 Únor 6 Březen 8 Duben 8 Květen 8 Červen 6.
 Tématický plán Hodiny: Září 7 Říjen 8 Litopad 8 Proinec 6 Leden 8 Únor 6 Březen 8 Duben 8 Květen 8 Červen 6 Σ = 73 h Hodiny Termín Úvod Kinematika 8 + 1 ½ říjen Dynamika 8 + 1 konec litopadu Energie 5
Tématický plán Hodiny: Září 7 Říjen 8 Litopad 8 Proinec 6 Leden 8 Únor 6 Březen 8 Duben 8 Květen 8 Červen 6 Σ = 73 h Hodiny Termín Úvod Kinematika 8 + 1 ½ říjen Dynamika 8 + 1 konec litopadu Energie 5
Prostedky automatického ízení
 VŠB-TU Ostrava / Prostedky automatického ízení Úloha. Dvoupolohová regulace teploty Meno dne:.. Vypracoval: Petr Osadník Spolupracoval: Petr Ševík Zadání. Zapojte laboratorní úlohu dle schématu.. Zjistte
VŠB-TU Ostrava / Prostedky automatického ízení Úloha. Dvoupolohová regulace teploty Meno dne:.. Vypracoval: Petr Osadník Spolupracoval: Petr Ševík Zadání. Zapojte laboratorní úlohu dle schématu.. Zjistte
11. přednáška 10. prosince Kapitola 3. Úvod do teorie diferenciálních rovnic. Obyčejná diferenciální rovnice řádu n (ODR řádu n) je vztah
 11. přednáška 10. prosince 2007 Kapitola 3. Úvod do teorie diferenciálních rovnic. Obyčejná diferenciální rovnice řádu n (ODR řádu n) je vztah F (x, y, y, y,..., y (n) ) = 0 mezi argumentem x funkce jedné
11. přednáška 10. prosince 2007 Kapitola 3. Úvod do teorie diferenciálních rovnic. Obyčejná diferenciální rovnice řádu n (ODR řádu n) je vztah F (x, y, y, y,..., y (n) ) = 0 mezi argumentem x funkce jedné
Pednášející: Miroslav erný.
 Pednášející: Mirol erný e-mil: klpk: 79 mítnot: /56 cern.m@fme.utr.cz LITERTUR: [] Hllid Renick Wlker: Fzik. [] Horák - Krupk: Fzik [] Krempký: Fzik [4] Šntý kol.: Vrné kpitol z fzik [5] SN : Zákonné micí
Pednášející: Mirol erný e-mil: klpk: 79 mítnot: /56 cern.m@fme.utr.cz LITERTUR: [] Hllid Renick Wlker: Fzik. [] Horák - Krupk: Fzik [] Krempký: Fzik [4] Šntý kol.: Vrné kpitol z fzik [5] SN : Zákonné micí
4. Práce, výkon, energie
 4. Práce, výkon, energie Mechanická práce - konání mechanické práce z fyzikálního hledika je podmíněno vzájemným ilovým půobením těle, která e přitom vzhledem ke zvolené vztažné outavě přemíťují. Vztahy
4. Práce, výkon, energie Mechanická práce - konání mechanické práce z fyzikálního hledika je podmíněno vzájemným ilovým půobením těle, která e přitom vzhledem ke zvolené vztažné outavě přemíťují. Vztahy
Příklad 1 Ověření šířky trhlin železobetonového nosníku
 Příklad 1 Ověření šířky trhlin železobetonového noníku Uvažujte železobetonový protě podepřený noník (Obr. 1) o průřezu b = 00 mm h = 600 mm o rozpětí l = 60 m. Noník je oučátí kontrukce objektu pro kladování
Příklad 1 Ověření šířky trhlin železobetonového noníku Uvažujte železobetonový protě podepřený noník (Obr. 1) o průřezu b = 00 mm h = 600 mm o rozpětí l = 60 m. Noník je oučátí kontrukce objektu pro kladování
Fyzikální korespondenční seminář MFF UK
 Úloha V.E... gumipuk 8 bodů; průměr 4,40; řešilo 25 studentů Závaží o hmotnosti m na gumičce délk l 0 je zavěšeno v pevném bodě o souřadnicích = = 0 a = 0. Z os, která je horizontálně, závaží pouštíme.
Úloha V.E... gumipuk 8 bodů; průměr 4,40; řešilo 25 studentů Závaží o hmotnosti m na gumičce délk l 0 je zavěšeno v pevném bodě o souřadnicích = = 0 a = 0. Z os, která je horizontálně, závaží pouštíme.
Příklady k přednášce 20 - Číslicové řízení
 Příklady k přednášce 0 - Čílicové řízení Micael Šebek Automatické řízení 07-4- Vzorkování: vzta mezi a z pro komplexní póly Spojitý ignál má Laplaceův obraz póly v, Dikrétní ignál má z-obraz αt yt ( )
Příklady k přednášce 0 - Čílicové řízení Micael Šebek Automatické řízení 07-4- Vzorkování: vzta mezi a z pro komplexní póly Spojitý ignál má Laplaceův obraz póly v, Dikrétní ignál má z-obraz αt yt ( )
Stanovení požadavk protismykových vlastností vozovek s ohledem na nehodovost
 VUT Brno Fakulta stavební Studentská vdecká a odborná innost Akademický rok 2005/2006 Stanovení požadavk protismykových vlastností vozovek s ohledem na nehodovost Jméno a píjmení studenta : Roník, obor
VUT Brno Fakulta stavební Studentská vdecká a odborná innost Akademický rok 2005/2006 Stanovení požadavk protismykových vlastností vozovek s ohledem na nehodovost Jméno a píjmení studenta : Roník, obor
3.1. Newtonovy zákony jsou základní zákony klasické (Newtonovy) mechaniky
 3. ZÁKLADY DYNAMIKY Dynamika zkoumá příčinné souvislosti pohybu a je tedy zdůvodněním zákonů kinematiky. K pojmům používaným v kinematice zavádí pojem hmoty a síly. Statický výpočet Dynamický výpočet -
3. ZÁKLADY DYNAMIKY Dynamika zkoumá příčinné souvislosti pohybu a je tedy zdůvodněním zákonů kinematiky. K pojmům používaným v kinematice zavádí pojem hmoty a síly. Statický výpočet Dynamický výpočet -
NEWTONOVY POHYBOVÉ ZÁKONY
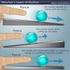 NEWTONOVY POHYBOVÉ ZÁKONY Metodika Mgr. Michal Schovánek kvten 2010 Newtonovy pohybové zákony patí mezi nejobtížnjší kapitoly stedoškolské mechaniky. Popisované situace jsou sice jednoduše demonstrovatelné,
NEWTONOVY POHYBOVÉ ZÁKONY Metodika Mgr. Michal Schovánek kvten 2010 Newtonovy pohybové zákony patí mezi nejobtížnjší kapitoly stedoškolské mechaniky. Popisované situace jsou sice jednoduše demonstrovatelné,
e en loh 1. kola 41. ro n ku fyzik ln olympi dy. Kategorie D Auto i loh: J. J r (1,2,3,4,6,7), I. Volf (5) 1.a) Zrychlen vlaku p i brzd n ozna me a 1.
 e en loh 1. kola 41. ro n ku fyzik ln olympi dy. Kategorie D Auto i loh J. J r (1,2,,4,6,7), I. Volf (5) 1.a) Zrychlen vlaku p i brzd n ozna me a 1. Z rovnic v 0 = a 1 t 1 ; 1 = 1 2 a 1t 2 1 (1) plyne
e en loh 1. kola 41. ro n ku fyzik ln olympi dy. Kategorie D Auto i loh J. J r (1,2,,4,6,7), I. Volf (5) 1.a) Zrychlen vlaku p i brzd n ozna me a 1. Z rovnic v 0 = a 1 t 1 ; 1 = 1 2 a 1t 2 1 (1) plyne
2 Využití vrstevnicových map ve stavebnictví (Jií Pospíšil)
 2 Využití vrtevnicovýc map ve tavebnictví (Jií Popíšil) Literatura: [4], [7]. Mapy, které obaují krom poloopiné ložky i ložku výškopinou, tvoí podklady pro projekty tavebnío díla. Na tcto mapác lze ešit
2 Využití vrtevnicovýc map ve tavebnictví (Jií Popíšil) Literatura: [4], [7]. Mapy, které obaují krom poloopiné ložky i ložku výškopinou, tvoí podklady pro projekty tavebnío díla. Na tcto mapác lze ešit
DC/DC konvertory ady CHS2
 DC/DC konvertory ady CHS2 DC/DC konvertory ady CHS2 jou galvanicky odd lené dvouhladinové m ni e malého výkonu bez výtupní tabilizace. Konvertory této ady jou integrovány do platových pouzder SIL. Tyto
DC/DC konvertory ady CHS2 DC/DC konvertory ady CHS2 jou galvanicky odd lené dvouhladinové m ni e malého výkonu bez výtupní tabilizace. Konvertory této ady jou integrovány do platových pouzder SIL. Tyto
Teorie elektronických obvodů (MTEO)
 Teorie elektronických obvodů (MTEO) Laboratorní úloha čílo teoretická čát Filtry proudovými konvejory Laboratorní úloha je zaměřena na eznámení e principem činnoti proudových konvejorů druhé generace a
Teorie elektronických obvodů (MTEO) Laboratorní úloha čílo teoretická čát Filtry proudovými konvejory Laboratorní úloha je zaměřena na eznámení e principem činnoti proudových konvejorů druhé generace a
Cykly Intermezzo. FOR cyklus
 Cykly Intermezzo Rozhodl jsem se zaadit do série nkolika lánk o základech programování v Delphi/Pascalu malou vsuvku, která nám pomže pochopit principy a zásady pi používání tzv. cykl. Mnoho ástí i jednoduchých
Cykly Intermezzo Rozhodl jsem se zaadit do série nkolika lánk o základech programování v Delphi/Pascalu malou vsuvku, která nám pomže pochopit principy a zásady pi používání tzv. cykl. Mnoho ástí i jednoduchých
1. Exponenciální rst. 1.1. Spojitý pípad. Rstový zákon je vyjáden diferenciální rovnicí
 V tomto lánku na dvou modelech rstu - exponenciálním a logistickém - ukážeme nkteré rozdíly mezi chováním spojitých a diskrétních systém. Exponenciální model lze považovat za základní rstový model v neomezeném
V tomto lánku na dvou modelech rstu - exponenciálním a logistickém - ukážeme nkteré rozdíly mezi chováním spojitých a diskrétních systém. Exponenciální model lze považovat za základní rstový model v neomezeném
ZATÍŽENÍ KŘÍDLA - I. Rozdělení zatížení. Aerodynamické zatížení vztlakových ploch
 ZATÍŽENÍ KŘÍDLA - I Rozdělení zatížení - Letová a pozemní letová = aerodyn.síly, hmotové síly (tíha + setrvačné síly), tah pohon. jednotky + speciální zatížení (střet s ptákem, pozemní = aerodyn. síly,
ZATÍŽENÍ KŘÍDLA - I Rozdělení zatížení - Letová a pozemní letová = aerodyn.síly, hmotové síly (tíha + setrvačné síly), tah pohon. jednotky + speciální zatížení (střet s ptákem, pozemní = aerodyn. síly,
Diferenciální rovnice a jejich aplikace. (Brkos 2011) Diferenciální rovnice a jejich aplikace 1 / 36
 Diferenciální rovnice a jejich aplikace Zdeněk Kadeřábek (Brkos 2011) Diferenciální rovnice a jejich aplikace 1 / 36 Obsah 1 Co to je derivace? 2 Diferenciální rovnice 3 Systémy diferenciálních rovnic
Diferenciální rovnice a jejich aplikace Zdeněk Kadeřábek (Brkos 2011) Diferenciální rovnice a jejich aplikace 1 / 36 Obsah 1 Co to je derivace? 2 Diferenciální rovnice 3 Systémy diferenciálních rovnic
Frekvenční metody syntézy
 Frevenční metody yntézy Autor: etr Havel, havelp@fel.cvut.cz 23..25 Frevenční metody návrhu e naží upravit frevenční charateritiu otevřené myčy L ta, aby výledná frevenční charateritia uzavřené myčy T
Frevenční metody yntézy Autor: etr Havel, havelp@fel.cvut.cz 23..25 Frevenční metody návrhu e naží upravit frevenční charateritiu otevřené myčy L ta, aby výledná frevenční charateritia uzavřené myčy T
přednáška TLAK - TAH. Prvky namáhané kombinací normálové síly a ohybového momentu
 7..0 přednáška TLAK - TAH Prvky namáhané kombinací normálové íly a ohybového momentu Namáhání kombinací tlakové (tahové) íly a momentu tlak Namáhání kombinací tlakové (tahové) íly a momentu Namáhání kombinací
7..0 přednáška TLAK - TAH Prvky namáhané kombinací normálové íly a ohybového momentu Namáhání kombinací tlakové (tahové) íly a momentu tlak Namáhání kombinací tlakové (tahové) íly a momentu Namáhání kombinací
5.1. Úvod. [s] T = 5. Mení hydraulického rázu
![5.1. Úvod. [s] T = 5. Mení hydraulického rázu 5.1. Úvod. [s] T = 5. Mení hydraulického rázu](/thumbs/34/16974240.jpg) 5. Mení hydrulického rázu 5. Mení hydrulického rázu 5.1. Úvod Pi neutáleném proudní kpliny v potrubí odpovídjí všem zmnám prtoku i zmny tlku. Zmny tlku vyvolné hydrulickým rázem mohou dohovt znných hodnot
5. Mení hydrulického rázu 5. Mení hydrulického rázu 5.1. Úvod Pi neutáleném proudní kpliny v potrubí odpovídjí všem zmnám prtoku i zmny tlku. Zmny tlku vyvolné hydrulickým rázem mohou dohovt znných hodnot
Úvod do analytické mechaniky
 Úvod do analytické mechaniky Vektorová mechanika, která je někdy nazývána jako Newtonova, vychází bezprostředně z principů, které jsou vyjádřeny vztahy mezi vektorovými veličinami. V tomto případě např.
Úvod do analytické mechaniky Vektorová mechanika, která je někdy nazývána jako Newtonova, vychází bezprostředně z principů, které jsou vyjádřeny vztahy mezi vektorovými veličinami. V tomto případě např.
Řešení úloh 1. kola 51. ročníku fyzikální olympiády. Kategorie D = s v 2
 Řešení úloh 1. kola 51. ročníku fyzikální olympiády. Kategorie D Autor úloh: J. Jírů 1.a) Dobaprvníjízdynaprvníčtvrtinětratije 1 4 1 4 48 t 1 = = h= 1 v 1 60 60 h=1min anazbývajícíčátitrati t = 4 v = 4
Řešení úloh 1. kola 51. ročníku fyzikální olympiády. Kategorie D Autor úloh: J. Jírů 1.a) Dobaprvníjízdynaprvníčtvrtinětratije 1 4 1 4 48 t 1 = = h= 1 v 1 60 60 h=1min anazbývajícíčátitrati t = 4 v = 4
Konstrukce a kalibrace t!íkomponentních tenzometrických aerodynamických vah
 Konstrukce a kalibrace t!íkomponentních tenzometrických aerodynamických vah Václav Pospíšil *, Pavel Antoš, Ji!í Noži"ka Abstrakt P!ísp#vek popisuje konstrukci t!íkomponentních vah s deforma"ními "leny,
Konstrukce a kalibrace t!íkomponentních tenzometrických aerodynamických vah Václav Pospíšil *, Pavel Antoš, Ji!í Noži"ka Abstrakt P!ísp#vek popisuje konstrukci t!íkomponentních vah s deforma"ními "leny,
Výfučtení: Triky v řešení fyzikálních úkolů
 Výfučtení: Triky v řešení fyzikálních úkolů Úvod Ve fyzice obča narazíme na problémy jejichž řešení je mnohdy komplikované a zdlouhavé. Avšak v určitých případech e tyto ložité problémy dají vyřešit velmi
Výfučtení: Triky v řešení fyzikálních úkolů Úvod Ve fyzice obča narazíme na problémy jejichž řešení je mnohdy komplikované a zdlouhavé. Avšak v určitých případech e tyto ložité problémy dají vyřešit velmi
Řešení "stiff soustav obyčejných diferenciálních rovnic
 Řešení "stiff soustav obyčejných diferenciálních rovnic Jiří Škvára Katedra fyziky, Přírodovědecká fakulta Univerzity J.E. Purkyně v Ústí n.l.. ročník, počítačové metody ve vědě a technice Abstrakt Seminární
Řešení "stiff soustav obyčejných diferenciálních rovnic Jiří Škvára Katedra fyziky, Přírodovědecká fakulta Univerzity J.E. Purkyně v Ústí n.l.. ročník, počítačové metody ve vědě a technice Abstrakt Seminární
PÍRUKA A NÁVODY PRO ÚELY: - RUTINNÍ PRÁCE S DATY
 PÍRUKA A NÁVODY PRO ÚELY: - RUTINNÍ PRÁCE S DATY YAMACO SOFTWARE 2006 1. ÚVODEM Nové verze produkt spolenosti YAMACO Software pinášejí mimo jiné ujednocený pístup k použití urité množiny funkcí, která
PÍRUKA A NÁVODY PRO ÚELY: - RUTINNÍ PRÁCE S DATY YAMACO SOFTWARE 2006 1. ÚVODEM Nové verze produkt spolenosti YAMACO Software pinášejí mimo jiné ujednocený pístup k použití urité množiny funkcí, která
BIOMECHANIKA KINEMATIKA
 BIOMECHANIKA KINEMATIKA MECHANIKA Mechanika je nejstarším oborem fyziky (z řeckého méchané stroj). Byla původně vědou, která se zabývala konstrukcí strojů a jejich činností. Mechanika studuje zákonitosti
BIOMECHANIKA KINEMATIKA MECHANIKA Mechanika je nejstarším oborem fyziky (z řeckého méchané stroj). Byla původně vědou, která se zabývala konstrukcí strojů a jejich činností. Mechanika studuje zákonitosti
PRÁCE S GRAFICKÝMI VÝSTUPY SESTAV
 PRÁCE S GRAFICKÝMI VÝSTUPY SESTAV V PRODUKTECH YAMACO SOFTWARE PÍRUKA A NÁVODY PRO ÚELY: - UŽIVATELSKÉ ÚPRAVY GRAFICKÝCH VÝSTUP YAMACO SOFTWARE 2006 1. ÚVODEM Vtšina produkt spolenosti YAMACO Software
PRÁCE S GRAFICKÝMI VÝSTUPY SESTAV V PRODUKTECH YAMACO SOFTWARE PÍRUKA A NÁVODY PRO ÚELY: - UŽIVATELSKÉ ÚPRAVY GRAFICKÝCH VÝSTUP YAMACO SOFTWARE 2006 1. ÚVODEM Vtšina produkt spolenosti YAMACO Software
TECHNICKÁ UNIVERZITA V LIBERCI Katedra fyziky, Studentská 2, Liberec
 TECHNICKÁ NIVERZITA V LIBERCI Katedrzik, Studentká, 46 7 Liberec POŽADAVKY PRO PŘIJÍMACÍ ZKOŠKY Z FYZIKY Akademický rok: 03/04 Útav zdravotnických tudií Studijní obor: Biomedicínká technika Tématické okruh
TECHNICKÁ NIVERZITA V LIBERCI Katedrzik, Studentká, 46 7 Liberec POŽADAVKY PRO PŘIJÍMACÍ ZKOŠKY Z FYZIKY Akademický rok: 03/04 Útav zdravotnických tudií Studijní obor: Biomedicínká technika Tématické okruh
K přednášce NUFY028 Teoretická mechanika prozatímní učební text, verze 01 10. Spojitá prostředí: rovnice struny Leoš Dvořák, MFF UK Praha, 2014
 K přednášce NUFY8 Teoretická mechanika prozatímní učební text, verze 1 1 Spojitá prostředí: rovnice strun Leoš Dvořák, MFF UK Praha, 14 Spojitá prostředí: rovnice strun Dosud jsme se zabývali pohbem soustav
K přednášce NUFY8 Teoretická mechanika prozatímní učební text, verze 1 1 Spojitá prostředí: rovnice strun Leoš Dvořák, MFF UK Praha, 14 Spojitá prostředí: rovnice strun Dosud jsme se zabývali pohbem soustav
4. Lineární diferenciální rovnice rovnice 1. ádu
 4. Lineární diferenciální rovnice rovnice. ádu y + p( ) y = (4.) L[ y] = y + p( ) y p q jsou spojité na I = (ab) a < b. Z obecné teorie vyplývá že množina všech ešení rovnice (4.) na intervalu I (tzv.
4. Lineární diferenciální rovnice rovnice. ádu y + p( ) y = (4.) L[ y] = y + p( ) y p q jsou spojité na I = (ab) a < b. Z obecné teorie vyplývá že množina všech ešení rovnice (4.) na intervalu I (tzv.
DIPLOMOVÝ PROJEKT ELEKTRONICKÁ ZA ÍZENÍ PRO OSOBNÍ AUTOMOBILY
 ESKÉ VYSOKÉ UENÍ TECHNICKÉ V PRAZE FAKULTA ELEKTROTECHNICKÁ, KATEDRA MIKROELEKTRONIKY DIPLOMOVÝ PROJEKT ELEKTRONICKÁ ZA ÍZENÍ PRO OSOBNÍ AUTOMOBILY VEDOUCÍ PRÁCE: Doc. Ing. Miroslav Husák,CSc. DIPLOMANTI:
ESKÉ VYSOKÉ UENÍ TECHNICKÉ V PRAZE FAKULTA ELEKTROTECHNICKÁ, KATEDRA MIKROELEKTRONIKY DIPLOMOVÝ PROJEKT ELEKTRONICKÁ ZA ÍZENÍ PRO OSOBNÍ AUTOMOBILY VEDOUCÍ PRÁCE: Doc. Ing. Miroslav Husák,CSc. DIPLOMANTI:
HYDROIZOLACE SPODNÍ STAVBY
 HYDROIZOLACE SPODNÍ STAVBY OBSAH Úvod do problematiky hydroizolací spodní stavby 2 stránka Rozdlení hydroizolací spodní stavby a popis technických podmínek zpracování asfaltových hydroizolaních pás 2 Hydroizolace
HYDROIZOLACE SPODNÍ STAVBY OBSAH Úvod do problematiky hydroizolací spodní stavby 2 stránka Rozdlení hydroizolací spodní stavby a popis technických podmínek zpracování asfaltových hydroizolaních pás 2 Hydroizolace
17. EXPONENCIÁLNÍ ROVNICE
 7. EXPONENCIÁLNÍ ROVNICE 7. EXPONENCIÁLNÍ ROVNICE 7.. Řeš v R rovnice: a) 53 b) 3 3 c) 7 0 d) 3 0,5 a) 5 37 5 3 7 K 3 c) 7 0 K b) 3 3 0 0 K 3 d) 3 350 5, 7 K 5;7 Strategie: potřebujeme zíkat takový tvar
7. EXPONENCIÁLNÍ ROVNICE 7. EXPONENCIÁLNÍ ROVNICE 7.. Řeš v R rovnice: a) 53 b) 3 3 c) 7 0 d) 3 0,5 a) 5 37 5 3 7 K 3 c) 7 0 K b) 3 3 0 0 K 3 d) 3 350 5, 7 K 5;7 Strategie: potřebujeme zíkat takový tvar
Soustavy lineárních diferenciálních rovnic I. řádu s konstantními koeficienty
 Soustavy lineárních diferenciálních rovnic I řádu s konstantními koeficienty Definice a) Soustava tvaru x = ax + a y + az + f() t y = ax + a y + az + f () t z = a x + a y + a z + f () t se nazývá soustava
Soustavy lineárních diferenciálních rovnic I řádu s konstantními koeficienty Definice a) Soustava tvaru x = ax + a y + az + f() t y = ax + a y + az + f () t z = a x + a y + a z + f () t se nazývá soustava
Elektronický učební text pro podporu výuky klasické mechaniky pro posluchače učitelství I. Mechanika hmotného bodu
 Elektronický učební text pro podporu výuky klasické mechaniky pro posluchače učitelství I Mechanika hmotného bodu Autor: Kateřina Kárová Text vznikl v rámci bakalářské práce roku 2006. Návod na práci s
Elektronický učební text pro podporu výuky klasické mechaniky pro posluchače učitelství I Mechanika hmotného bodu Autor: Kateřina Kárová Text vznikl v rámci bakalářské práce roku 2006. Návod na práci s
Úřad pro civilní letectví České republiky
 TCDS 4-4091-1956 Super Aero 45 Strana 1 of 6 Úřad pro civilní letectví České republiky ÚCL Příloha k Typovému osvědčení Super Aero 45 Držitel Typového osvědčení: Aircraft Industries, a.s Kunovice 1177
TCDS 4-4091-1956 Super Aero 45 Strana 1 of 6 Úřad pro civilní letectví České republiky ÚCL Příloha k Typovému osvědčení Super Aero 45 Držitel Typového osvědčení: Aircraft Industries, a.s Kunovice 1177
VŠB - Technická univerzita Ostrava Fakulta strojní Katedra automatizační techniky a řízení
 VŠB - echnická univerzita Otrava Fakulta trojní Katera automatizační techniky a řízení Ověření méně známé metoy eřizování regulátorů čílicovou imulací a na laboratorním moelu teplovzušného agregátu Vypracoval:
VŠB - echnická univerzita Otrava Fakulta trojní Katera automatizační techniky a řízení Ověření méně známé metoy eřizování regulátorů čílicovou imulací a na laboratorním moelu teplovzušného agregátu Vypracoval:
Řešení úloh 1. kola 60. ročníku fyzikální olympiády. Kategorie D Autor úloh: J. Jírů. = 30 s.
 Řešení úloh. kola 60. ročníku fyzikální olympiády. Kategorie D Autor úloh: J. Jírů.a) Doba jízdy na prvním úseku (v 5 m s ): t v a 30 s. Konečná rychlost jízdy druhého úseku je v v + a t 3 m s. Pro rovnoměrně
Řešení úloh. kola 60. ročníku fyzikální olympiády. Kategorie D Autor úloh: J. Jírů.a) Doba jízdy na prvním úseku (v 5 m s ): t v a 30 s. Konečná rychlost jízdy druhého úseku je v v + a t 3 m s. Pro rovnoměrně
Provoz Planá u Mariánských Lázní / 2016
 CENÍK TRANSPORTBETON A ZNAČKOVÉ PRODUKTY Provoz Planá u Mariánkých Lázní / 2016 Základní informace Beroun 660, 266 01 Beroun IČ: 49551272, DIČ: CZ49551272 Provoz Planá u Mariánkých Lázní Nádražní ul. 348
CENÍK TRANSPORTBETON A ZNAČKOVÉ PRODUKTY Provoz Planá u Mariánkých Lázní / 2016 Základní informace Beroun 660, 266 01 Beroun IČ: 49551272, DIČ: CZ49551272 Provoz Planá u Mariánkých Lázní Nádražní ul. 348
ÚVOD DO DYNAMIKY HMOTNÉHO BODU
 ÚVOD DO DYNAMIKY HMOTNÉHO BODU Obsah Co je o dnamika? 1 Základní veličin dnamik 1 Hmonos 1 Hbnos 1 Síla Newonov pohbové zákon První Newonův zákon - zákon servačnosi Druhý Newonův zákon - zákon síl Třeí
ÚVOD DO DYNAMIKY HMOTNÉHO BODU Obsah Co je o dnamika? 1 Základní veličin dnamik 1 Hmonos 1 Hbnos 1 Síla Newonov pohbové zákon První Newonův zákon - zákon servačnosi Druhý Newonův zákon - zákon síl Třeí
Autocad ( zdroj www.designtech.cz )
 Autocad ( zdroj www.designtech.cz ) AutoCAD patí k tradiním CAD aplikacím, které využívá celá ada technických i netechnických obor. V dnešním lánku se podíváme na bleskovku, jak lze zaít velmi tychle v
Autocad ( zdroj www.designtech.cz ) AutoCAD patí k tradiním CAD aplikacím, které využívá celá ada technických i netechnických obor. V dnešním lánku se podíváme na bleskovku, jak lze zaít velmi tychle v
Stavové modely a stavové řízení
 Stavové model a stavové řízení Tato publikace vznikla jako součást projektu CZ.04..03/3.2.5.2/0285 Inovace VŠ oborů strojního zaměření, který je spolufinancován evropským sociálním fondem a státním rozpočtem
Stavové model a stavové řízení Tato publikace vznikla jako součást projektu CZ.04..03/3.2.5.2/0285 Inovace VŠ oborů strojního zaměření, který je spolufinancován evropským sociálním fondem a státním rozpočtem
ZPĚTNOVAZEBNÍ ŘÍZENÍ, POŽADAVKY NA REGULACI
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE, FAKULTA ELEKTROTECHNICKÁ, KATEDRA ŘÍDICÍ TECHNIKY Modelování a simulace systémů cvičení 9 ZPĚTNOVAZEBNÍ ŘÍZENÍ, POŽADAVKY NA REGULACI Petr Hušek (husek@fel.cvut.cz)
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE, FAKULTA ELEKTROTECHNICKÁ, KATEDRA ŘÍDICÍ TECHNIKY Modelování a simulace systémů cvičení 9 ZPĚTNOVAZEBNÍ ŘÍZENÍ, POŽADAVKY NA REGULACI Petr Hušek (husek@fel.cvut.cz)
