1.7 Magnetické pole stacionárního proudu
|
|
|
- Kryštof Macháček
- před 8 lety
- Počet zobrazení:
Transkript
1 1.7 Magnetické poe stacionárního proudu Pohybující se e. náboje (e. proud) vytvářejí magnetické poe. Naopak poe působí siou na pohybující se e. náboje E. proud, Ohmův zákon v diferenciáním tvaru ρ... hustota pohybujícího se náboje, v... rychost pohybujícího se náboje Definice proudové hustoty i ρ v, i = i ( r, t). Náboj, který proteče poškou d za časový interva dt: dq = ρd = ρ v d dt = i d dt = id cos αdt = id }{{} dt i Proud di pochou d: di = dq dt = i d Cekový proud I tekoucí pochou : I = di = i d
2 peciání případ: i = konst,... rovinná pocha komá k I I = i d = id cos 0 = i i = I (proudová hustota = proud jednotkovou pochou komou k i )
3 1.7.2 E. proud ve vodičích Z vodiče protékaného proudem vyděíme maý váeček s osou ve směru poe. Pro něj napíšeme Ohmův zákon. U = RI, U = E, I = i, R = 1 γ (γ... měrná e. vodivost) E = 1 γ i, E = 1 γ i, i = γ E Ohmův zákon v dif. tvaru Poznámka: Uvnitř baterií působí vede e. si E i síy eektrochemické povahy ε. Pak i = γ( ε + E ), i = γ(ε E). nehomogenních a anizotropních prostředích je závisost i = i ( E ) sožitější, Ohmův zákon nepatí Rovnice kontinuity Experiment ukazuje, že patí zákon zachování e. náboje. Tento zákon zachování e. náboje chceme formuovat okáně. prostředí protékaném proudem zvoíme ibovonou uzavřenou pochu. Za čas dt vyteče z objemu náboj dq výtok = i d dt (viz úvahy v bodu 1.7.2). Náboj, který za čas dt z objemu vyteče je roven úbytku náboje v tomto objemu, dq výtok = dq úbytek. Q(t) = ρ( r, t)d, Q(t + dt) = ρ( r, t + dt)d
4 dq úbytek = Q(t) Q(t + dt) = [ρ( r, t) ρ( r, t + dt)]d i d dt = [ρ( r, t) ρ( r, t + dt)]d ρ( r, t) ρ( r, t + dt) d + } dt {{ } ρ t (v imitě dt 0) [ ρ t + div i ] i d = 0 div i d (Gaussova věta) d = 0 ρ t + div i = 0 Posední rovnice patí díky tomu, že objem je ibovoný. Poznámka: Rovnice kontinuity je obecnou okání formuací zákona zachování spojitě rozožených veičin. Např.: ρ... hustota náboje, i... tok náboje zákon zachování náboje ρ... hustota hmotnosti, i... tok hmotnosti zákon zachování hmotnosti ρ... hustota energie, i... tok energie zákon zachování energie, atd. Tok i nemusí mít ani tvar i = ρ v (např. v kvantové fyzice tok pravděpodobnosti) iové účinky magnetického poe iové účinky popisujeme pomocí vektoru magnetické indukce B. 1. Bodový náboj F mg = Q v B ( F emg = Q( E + v B )) Př.: Pohyb bodového náboje v homogenním magnetickém poi Osu z zvoíme ve směru poe, B = (0, 0, B). Řešíme pohybovou rovnici: e sožkách: m d v dt = Q( v B ) m dv x dt = Q(v yb z v z B y ) = QBv y
5 m dv y dt = Q(v zb x v x B z ) = QBv x m dv z dt = Q(v xb y v y B x ) = 0 Zavedeme cykotronovou frekvenci ω QB m : dv x dt dv y dt = ωv y = ωv x dv z dt = 0 Daší integrací určíme souřadnice: v x = v 0 cos(ωt + ϕ) v y = v 0 sin(ωt + ϕ) v z = v z0 (ověřit dosazením) dx dt = v x x = x 0 + v 0 sin(ωt + ϕ) ω dy dt = v y y = y 0 + v 0 cos(ωt + ϕ) ω dz dt = v z z = z 0 + v z0 t (Konstanty v 0, ϕ, v z0, x 0, y 0, z 0 jsou určeny počáteční rychostí a poohou.) Závěr: Náboj Q se v rovině komé k magnetickému poi pohybuje po kružnici: v 2 x + v 2 y = v 2 0 = konst. (x x 0 ) 2 + (y y 0 ) 2 = v2 0 ω 2 e směru poe se náboj pohybuje s konstantní rychostí v z0. 2. Objemový proudový eement d protékaný proudovou hustotou i = ρ v dq = ρd, d E mg = dq v B = ρd v B, d F mg = i B d Ceková mg. sía působící na objem : F mg = d F mg = i B d 3. ía působící na eement d úzkého vodiče (drát), protékaný proudem I
6 d = d, id = id = Id, i d i d = Id... přechod od objemových vodičů k vodičům ineárním d F mg = d i B = Id B B = konst.,... přímí vodič F mg = Id B = I B (třední škoa: F mg = BI sin α + pravido evé ruky) Zdroje magnetického poe Zdroji mg. poe jsou pohybující se náboje - proudy. Biotův-avartův zákon (anaogie Couombova zákona v eektrostatice): 1. Objemové proudy d B = µ 0 i d R 4π R 3 B = d B = µ 0 4π i ( r ) R d R 3
7 2. Lineární proudy i d Id d B = µ 0 4π I d R R 3 B = d B = µ 0 4π I d R R 3 Biotův-avartův zákon patí pouze pro stacionární proudy (nezávisost i, I, B na čase). Př.: Magnetické poe přímého vodiče d = dx, d B = µ 0 4π I d R, B = R 3 šechny příspěvky d B jsou rovnoběžné B = db d B db = µ 0 dxr sin α I 4π R 3
8 yjádření všech veičin pomocí úhu α: R = (směr B komo z papíru) a, x = acotg α, dx = a sin α db = µ a 0 4π I dα sin α sin 2 α a 2 sin 2 α B = µ π 0 I sin αdα 4π a 0 2 sin 2 α dα = µ 0 I sin αdα 4π a = µ 0 I 2π a Z Biotova-avartova zákona ze odvodit soustavu dif. rovnic pro B : div B = 0, rot B = µ 0 i Integrání formuace: div B = 0 div B d = 0 B d = 0 rot B = µ 0 i Interpretace první rovnice: div B = 0 B d = 0 div E = ρ ε 0 E d = Q ε 0 rot B d = µ 0 i d B d = µ0 I neexistují mg. náboje (ρ mg = 0, Q mg = 0). Mohy by však existovat mg. dipóy, sožené z opačných mg. nábojů (anaogie e. dipóů). Mg. dipóy skutečně existují, jsou ae vytvářeny uzavřenými proudovými smyčkami. Interpretace pomocí siočar: eektrostatice siočáry začínají na kadných a končí na záporných nábojích. teorii mg. poe neexistují mg. náboje, siočáry tedy nemají počátek a konec, jsou uzavřené nebo jdou z nekonečna do nekonečna Řešení mg. poe pomocí vektorového potenciáu A... vektorový potenciá div B = 0 B ( r ) = rot A ( r ) rot B = µ 0 i rot (rot A ) grad (div A ) A = µ 0 i A grad (div A ) = µ0 i
9 Rovnice pro A je zatím dost sožitá. Při jejím zjednodušení využijeme nejednoznačnosti vektorového potenciáu A k danému poio B. kutečně nechť f( r ) je ibovoná derivovatená skaární funkce. Derivujeme pomocí ní nový potenciá A = A + grad f. Pak rot A = rot } {{ A} + rot grad f = B B 0 Potenciá A vyhovuje proto stejné rovnici jako A : A grad (div A ) = µ 0 i Dosud ibovonou funkci f zvoíme tak, aby div A = 0: 0 = div A = div ( A + grad f) = div A + div (grad f), f = div A f hrnutí: B = rot A, A = µ 0 i (Poissonova rovnice - umíme ji řešit), div A = 0 (Lorentzova nebo kaibrační podmínka). daším vynecháme čárku: A A. Nejdříve vyřešíme Poissonovu rovnici: A ( µ 0 i ( r ) r ) = 4π R d R ( r r ) d = dx dy dz Řešení pro jednoduchost přepíšeme do formy, patné pro tenký uzavřený vodič: i d Id, d d r, A ( r ) = µ 0 4π I (Je-i poe stacionární, nesmí nikde přibývat ani ubývat e. náboj proudové smyčky musí být uzavřené.) Je třeba ještě ověřit, zda je u řešení Poissonovy rovnice spněna Lorentzova podmínka div A = 0: d r R
10 A x x = µ 0 4π I x div A = A x x + A y y + A z z dx ( r r ) = µ 0 4π I 1 x ( r r ) = 1 x ( r r ), A x x = µ 0 4π dx 1 x ( r r ) ( ) 1 dx x R div A = µ 0 4π [ ( ) 1 dx + ( ) 1 dy + ( ) ] 1 dz = µ 0 x R y R z R 4π ( ) 1 d = 0 R (obecně df = 0 pro ibovonou funkci f) ektorový potenciá vyhovuje dif. rovnici a Lorentzově podmínce. B ( r ) = rot A ( µ 0 r ) = 4π rot ( d r ( r r ) Magnetické poe v átkovém prostředí ede makroskopických (voných) proudů přispívají k mg. poi proudy atomární a moekuární (magnetizační, vázané). Můžeme si je modeově představit jako uzavřené proudové smyčky, vytvořené eektrony obíhající okoo jader nebo vytvořené rotací (spinem) eektronů a atomových jader. Magnetický dipó (uzavřená proudová smyčka) ) A ( µ 0 r ) = 4π d R, B = rot A =... (Biot-avart)
11 Pro veké vzdáenosti r r od proudové smyčky je: ěta: 1 R = 1 ( r r ) 1 r r r + r 3 A ( µ 0 r ) 4π I 1 r Důkaz: tokesova věta: d 0 + µ 0 4π I 1 r 3 (viz odvození pro e. dipó) ( r r )d, d = 0 r ( r r )d = r F d = rot F d Za funkci F ( r ) dosadíme c f( r ), kde c = (c x, c y, c z ) je ibovoný konstantní vektor. Úprava evé strany: F d = c fd Úprava pravé strany: rot F d = ( f = c x d y z d z [ y (c zf) ] [ z (c yf) d x + z (c xf) ] [ x (c zf) d y + x (c yf) ] y (c xf) d z = ) f } {{ y } (d grad f) x ) x d f x z +c y ( d z f (d grad f) y ) y d f y = c (d grad f) x +c z ( d x f tokesova věta pro F = c f dává tedy: c fd = c d grad f (d grad f) z Rovnost patí pro ibovoný vektor c, musí se proto rovnat integráy: f( r )d = d grad f( r ) Integrační proměnnou r nejdříve přeznačíme na r, r r, a poté za f( r ) dosadíme r r ( r bereme jako parametr či konstantu). Pak
12 grad f( r ) = x (xx +yy +zz ) i + y (xx +yy +zz ) j + z (xx +yy +zz ) k = Tedy: = x i + y j + z k = r. ( r r )d = d r = r A ( µ 0 r r ) 4π I r 3 Zavedeme mg. dipóový moment m I : e sožkách: A ( µ 0 m r r ) 4π r 3, B = rot A B x = (rot A ) x = y A z z A y = µ { 0 4π y (m xy m y x)(x 2 + y 2 + z 2 ) 3 } z (m zx m x z)(x 2 + y 2 + z 2 ) 3 2 =... = µ { 0 3 m xx + m y y + m z z x 1 } 4π r 5 r m 3 x ektorový zápis mg. poe eementárního dipóu: Anaogie s poem e. dipóu: { } µ 0 m r B = 3 1 r m 4π r 5 r 3 { } 1 p r E = 3 1 r p 4πε 0 r 5 r 3 Ovšem p = Q, m = I. Couomb původně vycháze z představy m = Q m (Q m... magnetický náboj). ektor magnetizace Eementární dipóy (atomové, moekuární,...) m i, M = mi, suma přes jednotkový objem; épe m M = i, suma přes maý objem ; M = n m (n... hustota dip. momentů, m... střední mg. dip. moment). ektor magnetizace = hustota mg. dip. momentů. 2
13 Poe zmagnetovaných těes (magnetů) d m = M( r )d, d B = µ 0 4π B ( r ) = d B = µ 0 4π 3d m R R 5 M( 3 r ) R R 5 R d m R 3 M( r ) R 3 d Pro veké vzdáenosti od magnetu, r r, je přibižně R = r r r a kde m [ ] B ( µ 0 m r m r ) 3, 4π r 5 r 3 M( r )d je cekový dipóový moment magnetu. yjádření magnetizačních proudů pomocí magnetizace Probém: rovnici mg. poe rot B = µ 0 i ( B d = µ0 I) je proud tvořen tokem voných nábojů a tokem magnetizačním: i = i vo + i mg, I = I vo + I mg. Neznámý magnetizační proud chceme z rovnice eiminovat.
14 daném prostředí zvome ibovonou křivku, ohraničující pochu. K magnetizačnímu proudu Img přispívají pouze dipóy, ežící dostatečně bízko hranice. m 1 = I dipóový moment jednoho dipóu (např. atomu; uzavřenou proudovou smyčku vytváří např. obíhající eektron). Na úseku d křivky přispívají k magnetizačnímu toku pouze ty dipóy, jejich středy eží v objemu d = 1 d. Jim odpovídá magnetizační proud : Pak d I mg = nd I 1 = n 1 I } {{ 1 d = Md } počet dipóů v objemu d m 1 I mg = di mg = Md B d = µ0 I vo + Md B M d = I vo µ0
15 Definujme vektor e. intenzity H B µ 0 M, ( B = µ 0H + M). Pak H d = Ivo Díky přechodu od B k H pracujeme pouze s měřitenými vonými proudy. Ae H =? Diferenciání tvar zákona cekového proudu: H d = rot H d, I vo = rot H d = i vo d i vo d rot H = i vo Jiné odvození diferenciání formy zákona cekového proudu: Magnetizační proud pomocí vektoru magnetizace: I mg = Md = rot Md Magnetizační proud pomocí proudové hustoty: I mg = i mg d i mg = rot M, rot B = µ 0 i = µ0 ( i vo + i mg ) = µ 0 ( i vo + rot M) rot B M µ0 H = i vo, rot H = i vo Materiáový vztah
16 M = M( B ), resp. M = M( H ), feromagnetika, sožitá závisost M = M(H). Magneticky měkká prostředí M ψ m H, ψm... magnetická susceptibiita. Na rozdí od e. susceptibiita ψ e může být kadná (átky paramagnetické) i záporná (átky diamagnetické). B = µ0 ( H + M) µ 0 (1 + ψ } {{ m ) } H = µ H } µ r {{ } µ µ r... reativní permeabiita, µ... permeabiita prostředí, µ = µ( r ), rot B = rot H = i µ vo. Pokud µ = konst. rot B = µ i vo, rot B = µ 0 ( i vo + i mg ). daším textu přeznačení i vo i, I vo I, tedy např. rot H = i.
MAGNETICKÉ POLE. 1. Stacionární magnetické pole I I I I I N S N N
 MAGETCKÉ POLE 1. Stacionární magnetické poe V E S T C E D O R O Z V O J E V Z D Ě L Á V Á Í je část prostoru, kde se veičiny popisující magnetické poe nemění s časem. Vzniká v bízkosti stacionárních vodičů
MAGETCKÉ POLE 1. Stacionární magnetické poe V E S T C E D O R O Z V O J E V Z D Ě L Á V Á Í je část prostoru, kde se veičiny popisující magnetické poe nemění s časem. Vzniká v bízkosti stacionárních vodičů
Jev elektromagnetické indukce
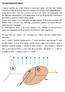 Jev eektromagnetické indukce V minuých kapitoách jsme si jistě uvědomii, že pojmy kid a pohyb, které byy vemi významné u mechanických dějů, při zkoumání eektrických a magnetických jevů nabyy přímo zásadní
Jev eektromagnetické indukce V minuých kapitoách jsme si jistě uvědomii, že pojmy kid a pohyb, které byy vemi významné u mechanických dějů, při zkoumání eektrických a magnetických jevů nabyy přímo zásadní
3.9. Energie magnetického pole
 3.9. nergie agnetického poe 1. Uět odvodit energii agnetického poe cívky tak, aby bya vyjádřena poocí paraetrů obvodu (I a L).. Znát vztah pro energii agnetického poe cívky jako funkci veičin charakterizujících
3.9. nergie agnetického poe 1. Uět odvodit energii agnetického poe cívky tak, aby bya vyjádřena poocí paraetrů obvodu (I a L).. Znát vztah pro energii agnetického poe cívky jako funkci veičin charakterizujících
Práce vykonaná v elektrickém poli, napětí, potenciál Vzájemná souvislost mezi intenzitou elektrického pole, napětím a potenciálem Práce vykonaná v
 Páce vykonaná v eektickém poi, napětí, potenciá Vzájemná souvisost mezi intenzitou eektického poe, napětím a potenciáem Páce vykonaná v eektostatickém poi po uzavřené dáze Gadient skaání funkce Skaání
Páce vykonaná v eektickém poi, napětí, potenciá Vzájemná souvisost mezi intenzitou eektického poe, napětím a potenciáem Páce vykonaná v eektostatickém poi po uzavřené dáze Gadient skaání funkce Skaání
Couloumbuv zákon stejne jako vetsina zakonu elektrostatiky jsou velmi podobna zakonum gravitacniho pole.
 1) Eektrostaticke poe, Cooumbuv zákon, Permitivita kazde dve teesa nabite eektrickym nabojem Q na sebe pusobi vzajemnou siou. Ta je vysise pomoci Couombovyho zákona: F = 1 4 Q Q 1 2 r r 2 0 kde první cast
1) Eektrostaticke poe, Cooumbuv zákon, Permitivita kazde dve teesa nabite eektrickym nabojem Q na sebe pusobi vzajemnou siou. Ta je vysise pomoci Couombovyho zákona: F = 1 4 Q Q 1 2 r r 2 0 kde první cast
OTÁZKY Z TEORIE ELEKTROMAGNETICKÉHO POLE Letní semestr 2003/2004 poslední úprava 25. června 2004
 OTÁZKY Z TEORIE ELEKTROMAGNETICKÉHO POLE Letní semestr 2003/2004 posední úprava 25. června 2004 1. ía současně působící na eektrický náboj v eektrickém a magnetickém poi (Lorentzova sía) [ ] F m = Q E
OTÁZKY Z TEORIE ELEKTROMAGNETICKÉHO POLE Letní semestr 2003/2004 posední úprava 25. června 2004 1. ía současně působící na eektrický náboj v eektrickém a magnetickém poi (Lorentzova sía) [ ] F m = Q E
ČÁST V F Y Z I K Á L N Í P O L E. 18. Gravitační pole 19. Elektrostatické pole 20. Elektrický proud 21. Magnetické pole 22. Elektromagnetické pole
 Kde se nacházíme? ČÁST V F Y Z I K Á L N Í P O L E 18. Gravitační pole 19. Elektrostatické pole 20. Elektrický proud 21. Magnetické pole 22. Elektromagnetické pole Mapování elektrického pole -jak? Detektorem.Intenzita
Kde se nacházíme? ČÁST V F Y Z I K Á L N Í P O L E 18. Gravitační pole 19. Elektrostatické pole 20. Elektrický proud 21. Magnetické pole 22. Elektromagnetické pole Mapování elektrického pole -jak? Detektorem.Intenzita
Z toho se η využije na zajištění funkcí automobilu a na překonání odporu vzduchu. l 100 km. 2 body b) Hledáme minimum funkce θ = 1.
 Řešení úoh. koa 59. ročníku fyzikání oympiády. Kategorie A Autor úoh: J. Thomas.a) Na dráze vt bude zapotřebí objem paiva V θ θv t. Při jeho spáení se získá tepo Q mh ρv H ρθvh t. Z toho se η využije na
Řešení úoh. koa 59. ročníku fyzikání oympiády. Kategorie A Autor úoh: J. Thomas.a) Na dráze vt bude zapotřebí objem paiva V θ θv t. Při jeho spáení se získá tepo Q mh ρv H ρθvh t. Z toho se η využije na
STACIONÁRNÍ MAGNETICKÉ POLE. Mgr. Jan Ptáčník - GJVJ - Fyzika - Elektřina a magnetismus - 3. ročník
 STACIONÁRNÍ MAGNETICKÉ POLE Mgr. Jan Ptáčník - GJVJ - Fyzika - Elektřina a magnetismus - 3. ročník Magnetické pole Vytváří se okolo trvalého magnetu. Magnetické pole vodiče Na základě experimentů bylo
STACIONÁRNÍ MAGNETICKÉ POLE Mgr. Jan Ptáčník - GJVJ - Fyzika - Elektřina a magnetismus - 3. ročník Magnetické pole Vytváří se okolo trvalého magnetu. Magnetické pole vodiče Na základě experimentů bylo
Skalární a vektorový popis silového pole
 Skalární a vektorový popis silového pole Elektrické pole Elektrický náboj Q [Q] = C Vlastnost materiálových objektů Interakce (vzájemné silové působení) Interakci (vzájemné silové působení) mezi dvěma
Skalární a vektorový popis silového pole Elektrické pole Elektrický náboj Q [Q] = C Vlastnost materiálových objektů Interakce (vzájemné silové působení) Interakci (vzájemné silové působení) mezi dvěma
Řešení úloh 1. kola 60. ročníku fyzikální olympiády. Kategorie B Autoři úloh: J. Thomas (1, 2, 3, 4, 5, 7), M. Jarešová (6)
 Řešení úoh 1. koa 60. ročníku fyzikání oympiády. Kategorie B Autoři úoh: J. Thomas (1, 2, 3, 4, 5, 7), M. Jarešová (6) h 1.a) Protože vzdáenost bodů K a O je cos α, je doba etu kuičky z bodu K do bodu
Řešení úoh 1. koa 60. ročníku fyzikání oympiády. Kategorie B Autoři úoh: J. Thomas (1, 2, 3, 4, 5, 7), M. Jarešová (6) h 1.a) Protože vzdáenost bodů K a O je cos α, je doba etu kuičky z bodu K do bodu
UNIVERZITA PARDUBICE FAKULTA CHEMICKO-TECHNOLOGICKÁ. katedra fyziky ZÁKLADY FYZIKY II. Pro obory DMML, TŘD a AID prezenčního studia DFJP
 UNIVERZITA PARDUBICE FAKULTA CHEMICKO-TECHNOLOGICKÁ katedra fyziky ZÁKLADY FYZIKY II Pro obory DMML, TŘD a AID prezenčního studia DFJP RNDr Jan Z a j í c, CSc, 005 4 MAGNETICKÉ JEVY 4 NESTACIONÁRNÍ ELEKTROMAGNETICKÉ
UNIVERZITA PARDUBICE FAKULTA CHEMICKO-TECHNOLOGICKÁ katedra fyziky ZÁKLADY FYZIKY II Pro obory DMML, TŘD a AID prezenčního studia DFJP RNDr Jan Z a j í c, CSc, 005 4 MAGNETICKÉ JEVY 4 NESTACIONÁRNÍ ELEKTROMAGNETICKÉ
MAGNETICKÉ POLE V REÁLNÉM PROSTŘEDÍ ( MAGNETIKA)
 MAGNETICKÉ POLE V REÁLNÉM PROSTŘEDÍ ( MAGNETIKA) Aplikace : Magnetický HD Snímání binárního signálu u HD HD vývoj hustota záznamu PC hard disk drive capacity (in GB). The vertical axis is logarithmic,
MAGNETICKÉ POLE V REÁLNÉM PROSTŘEDÍ ( MAGNETIKA) Aplikace : Magnetický HD Snímání binárního signálu u HD HD vývoj hustota záznamu PC hard disk drive capacity (in GB). The vertical axis is logarithmic,
Magnetické vlastnosti látek (magnetik) jsou důsledkem orbitálního a rotačního pohybu elektronů. Obíhající elektrony představují elementární proudové
 MAGNETICKÉ POLE V LÁTCE, MAXWELLOVY ROVNICE MAGNETICKÉ VLASTNOSTI LÁTEK Magnetické vlastnosti látek (magnetik) jsou důsledkem orbitálního a rotačního pohybu elektronů. Obíhající elektrony představují elementární
MAGNETICKÉ POLE V LÁTCE, MAXWELLOVY ROVNICE MAGNETICKÉ VLASTNOSTI LÁTEK Magnetické vlastnosti látek (magnetik) jsou důsledkem orbitálního a rotačního pohybu elektronů. Obíhající elektrony představují elementární
1. Dva dlouhé přímé rovnoběžné vodiče vzdálené od sebe 0,75 cm leží kolmo k rovine obrázku 1. Vodičem 1 protéká proud o velikosti 6,5A směrem od nás.
 Příklady: 30. Magnetické pole elektrického proudu 1. Dva dlouhé přímé rovnoběžné vodiče vzdálené od sebe 0,75 cm leží kolmo k rovine obrázku 1. Vodičem 1 protéká proud o velikosti 6,5A směrem od nás. a)
Příklady: 30. Magnetické pole elektrického proudu 1. Dva dlouhé přímé rovnoběžné vodiče vzdálené od sebe 0,75 cm leží kolmo k rovine obrázku 1. Vodičem 1 protéká proud o velikosti 6,5A směrem od nás. a)
Obvody s rozprostřenými parametry
 Obvody s rozprostřenými parametry EO2 Přednáška 12 Pave Máša - Vedení s rozprostřenými parametry ÚVODEM Každá kroucená dvojinka UTP patch kabeu je samostaným vedením s rozprostřenými parametry Impedance
Obvody s rozprostřenými parametry EO2 Přednáška 12 Pave Máša - Vedení s rozprostřenými parametry ÚVODEM Každá kroucená dvojinka UTP patch kabeu je samostaným vedením s rozprostřenými parametry Impedance
Transformujte diferenciální výraz x f x + y f do polárních souřadnic r a ϕ, které jsou definovány vztahy x = r cos ϕ a y = r sin ϕ.
 Ukázka 1 Necht má funkce z = f(x, y) spojité parciální derivace. Napište rovnici tečné roviny ke grafu této funkce v bodě A = [ x 0, y 0, z 0 ]. Transformujte diferenciální výraz x f x + y f y do polárních
Ukázka 1 Necht má funkce z = f(x, y) spojité parciální derivace. Napište rovnici tečné roviny ke grafu této funkce v bodě A = [ x 0, y 0, z 0 ]. Transformujte diferenciální výraz x f x + y f y do polárních
Gyrační poloměr jako invariant relativistického pohybu. 2 Nerovnoměrný pohyb po kružnici v R 2
 Gyrační poloměr jako invariant relativistického pohybu nabité částice v konfiguraci rovnoběžného konstantního vnějšího elektromagnetického pole 1 Popis problému Uvažujme pohyb nabité částice v E 3 v takové
Gyrační poloměr jako invariant relativistického pohybu nabité částice v konfiguraci rovnoběžného konstantního vnějšího elektromagnetického pole 1 Popis problému Uvažujme pohyb nabité částice v E 3 v takové
2.1 Stáčivost v závislosti na koncentraci opticky aktivní látky
 1 Pracovní úkoy 1. Změřte závisost stočení poarizační roviny na koncentraci vodního roztoku gukozy v rozmezí 0 500 g/. Pro jednu zvoenou koncentraci proveďte 5 měření úhu stočení poarizační roviny. Jednu
1 Pracovní úkoy 1. Změřte závisost stočení poarizační roviny na koncentraci vodního roztoku gukozy v rozmezí 0 500 g/. Pro jednu zvoenou koncentraci proveďte 5 měření úhu stočení poarizační roviny. Jednu
Obsah PŘEDMLUVA 11 ÚVOD 13 1 Základní pojmy a zákony teorie elektromagnetického pole 23
 Obsah PŘEDMLUVA... 11 ÚVOD... 13 0.1. Jak teoreticky řešíme elektrotechnické projekty...13 0.2. Dvojí význam pojmu pole...16 0.3. Elektromagnetické pole a technické projekty...20 1. Základní pojmy a zákony
Obsah PŘEDMLUVA... 11 ÚVOD... 13 0.1. Jak teoreticky řešíme elektrotechnické projekty...13 0.2. Dvojí význam pojmu pole...16 0.3. Elektromagnetické pole a technické projekty...20 1. Základní pojmy a zákony
Inovace předmětů studijních programů strojního inženýrství v oblasti teplotního namáhání
 Grantový projekt FRVŠ MŠMT č.97/7/f/a Inovace předmětů studijních programů strojního inženýrství v obasti tepotního namáhání Některé apikace a ukázky konkrétních řešení tepeného namáhání těes. Autorky:
Grantový projekt FRVŠ MŠMT č.97/7/f/a Inovace předmětů studijních programů strojního inženýrství v obasti tepotního namáhání Některé apikace a ukázky konkrétních řešení tepeného namáhání těes. Autorky:
VEKTOROVÁ POLE Otázky
 VEKTOROVÁ POLE VEKTOROVÁ POLE Je-li A podmnožina roviny a f je zobrazení A do R 2, které je dáno souřadnicemi f 1, f 2, tj., f(x, y) = (f 1 (x, y), f 2 (x, y)) pro (x, y) A, lze chápat dvojici (f 1 (x,
VEKTOROVÁ POLE VEKTOROVÁ POLE Je-li A podmnožina roviny a f je zobrazení A do R 2, které je dáno souřadnicemi f 1, f 2, tj., f(x, y) = (f 1 (x, y), f 2 (x, y)) pro (x, y) A, lze chápat dvojici (f 1 (x,
Modelování kmitavých soustav s jedním stupněm volnosti
 Modeování kmitavých soustav s jedním stupněm vonosti Zpracova Doc. RNDr. Zdeněk Haváč, CSc 1. Zákadní mode Zákadním modeem kmitavé soustavy s jedním stupněm vonosti je tzv. diskrétní podéně kmitající mode,
Modeování kmitavých soustav s jedním stupněm vonosti Zpracova Doc. RNDr. Zdeněk Haváč, CSc 1. Zákadní mode Zákadním modeem kmitavé soustavy s jedním stupněm vonosti je tzv. diskrétní podéně kmitající mode,
Přehled veličin elektrických obvodů
 Přehled veličin elektrických obvodů Ing. Martin Černík, Ph.D Projekt ESF CZ.1.7/2.2./28.5 Modernizace didaktických metod a inovace. Elektrický náboj - základní vlastnost některých elementárních částic
Přehled veličin elektrických obvodů Ing. Martin Černík, Ph.D Projekt ESF CZ.1.7/2.2./28.5 Modernizace didaktických metod a inovace. Elektrický náboj - základní vlastnost některých elementárních částic
1 Funkce dvou a tří proměnných
 1 Funkce dvou a tří proměnných 1.1 Pojem funkce více proměnných Definice Funkce dvou proměnných je předpis, který každému bodu z R 2 (tj. z roviny) přiřazuje jediné reálné číslo. z = f(x, y), D(f) R 2
1 Funkce dvou a tří proměnných 1.1 Pojem funkce více proměnných Definice Funkce dvou proměnných je předpis, který každému bodu z R 2 (tj. z roviny) přiřazuje jediné reálné číslo. z = f(x, y), D(f) R 2
Magnetické pole se projevuje silovými účinky - magnety přitahují železné kovy.
 Magnetické pole Vznik a zobrazení magnetického pole Magnetické pole vzniká kolem pohybujících se elektrických nábojů. V případě elektromagnetů jde o pohyb volných elektronů (nosičů elektrického náboje)
Magnetické pole Vznik a zobrazení magnetického pole Magnetické pole vzniká kolem pohybujících se elektrických nábojů. V případě elektromagnetů jde o pohyb volných elektronů (nosičů elektrického náboje)
Kapitola 11: Lineární diferenciální rovnice 1/15
 Kapitola 11: Lineární diferenciální rovnice 1/15 Lineární diferenciální rovnice 2. řádu Definice: Lineární diferenciální rovnice 2-tého řádu je rovnice tvaru kde: y C 2 (I) je hledaná funkce a 0 (x)y +
Kapitola 11: Lineární diferenciální rovnice 1/15 Lineární diferenciální rovnice 2. řádu Definice: Lineární diferenciální rovnice 2-tého řádu je rovnice tvaru kde: y C 2 (I) je hledaná funkce a 0 (x)y +
VEKTOROVÁ POLE VEKTOROVÁ POLE
 Je-li A podmnožina roviny a f je zobrazení A do R 2, které je dáno souřadnicemi f 1, f 2, tj., f(x, y) = (f 1 (x, y), f 2 (x, y)) pro (x, y) A, lze chápat dvojici (f 1 (x, y), f 2 (x, y)) jako vektor s
Je-li A podmnožina roviny a f je zobrazení A do R 2, které je dáno souřadnicemi f 1, f 2, tj., f(x, y) = (f 1 (x, y), f 2 (x, y)) pro (x, y) A, lze chápat dvojici (f 1 (x, y), f 2 (x, y)) jako vektor s
1 Rozdělení mechaniky a její náplň
 1 Rozdělení mechaniky a její náplň Mechanika je nauka o rovnováze a pohybu hmotných útvarů pohybujících se rychlostí podstatně menší, než je rychlost světla (v c). Vlastnosti skutečných hmotných útvarů
1 Rozdělení mechaniky a její náplň Mechanika je nauka o rovnováze a pohybu hmotných útvarů pohybujících se rychlostí podstatně menší, než je rychlost světla (v c). Vlastnosti skutečných hmotných útvarů
Zapnutí a vypnutí proudu spínačem S.
 ELEKTROMAGNETICKÁ INDUKCE Dva Faradayovy pokusy odpovídají na otázku zda může vzniknout elektrický proud vlivem magnetického pole Pohyb tyčového magnetu k (od) vodivé smyčce s měřidlem, nebo smyčkou k
ELEKTROMAGNETICKÁ INDUKCE Dva Faradayovy pokusy odpovídají na otázku zda může vzniknout elektrický proud vlivem magnetického pole Pohyb tyčového magnetu k (od) vodivé smyčce s měřidlem, nebo smyčkou k
Přijímací zkouška na navazující magisterské studium 2015
 Přijímací zkouška na navazující magisterské studium 205 Studijní program: Studijní obory: Fyzika FFUM Varianta A Řešení příkladů pečlivě odůvodněte. Příklad (25 bodů) Pro funkci f(x) := e x 2. Určete definiční
Přijímací zkouška na navazující magisterské studium 205 Studijní program: Studijní obory: Fyzika FFUM Varianta A Řešení příkladů pečlivě odůvodněte. Příklad (25 bodů) Pro funkci f(x) := e x 2. Určete definiční
7 Základní elektromagnetické veličiny a jejich měření
 7 Základní elektromagnetické veličiny a jejich měření Intenzity elektrického a magnetického pole, elektrická a magnetická indukce. Materiálové vztahy. Měrné metody elektrických a magnetických veličin.
7 Základní elektromagnetické veličiny a jejich měření Intenzity elektrického a magnetického pole, elektrická a magnetická indukce. Materiálové vztahy. Měrné metody elektrických a magnetických veličin.
Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 2. 3. 2018 Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
2. 3. 2018 Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
Magnetické pole - stacionární
 Magnetické pole - stacionární magnetické pole, jehož charakteristické veličiny se s časem nemění kolem vodiče s elektrickým polem je magnetické pole Magnetické indukční čáry Uzavřené orientované křivky,
Magnetické pole - stacionární magnetické pole, jehož charakteristické veličiny se s časem nemění kolem vodiče s elektrickým polem je magnetické pole Magnetické indukční čáry Uzavřené orientované křivky,
MFT - Matamatika a fyzika pro techniky
 MFT - Matamatika a fyzika pro techniky Pro každou přednášku by zde měl být seznam klíčových témat, odkaz na literaturu, zápočtový příklad k řešení a další příklady k procvičování převážně ze sbírky příkladů
MFT - Matamatika a fyzika pro techniky Pro každou přednášku by zde měl být seznam klíčových témat, odkaz na literaturu, zápočtový příklad k řešení a další příklady k procvičování převážně ze sbírky příkladů
Hlavní body - elektromagnetismus
 Elektromagnetismus Hlavní body - elektromagnetismus Lorenzova síla, hmotový spektrograf, Hallův jev Magnetická síla na proudovodič Mechanický moment na proudovou smyčku Faradayův zákon elektromagnetické
Elektromagnetismus Hlavní body - elektromagnetismus Lorenzova síla, hmotový spektrograf, Hallův jev Magnetická síla na proudovodič Mechanický moment na proudovou smyčku Faradayův zákon elektromagnetické
Otázku, kterými body prochází větev implicitní funkce řeší následující věta.
 1 Implicitní funkce Implicitní funkce nejsou funkce ve smyslu definice, že funkce bodu z definičního oboru D přiřadí právě jednu hodnotu z oboru hodnot H. Přesnější termín je funkce zadaná implicitně.
1 Implicitní funkce Implicitní funkce nejsou funkce ve smyslu definice, že funkce bodu z definičního oboru D přiřadí právě jednu hodnotu z oboru hodnot H. Přesnější termín je funkce zadaná implicitně.
Měřicí a řídicí technika Bakalářské studium 2007/2008. odezva. odhad chování procesu. formální matematický vztah s neznámými parametry
 MODELOVÁNÍ základní pojmy a postupy principy vytváření deterministických matematických modelů vybrané základní vztahy používané při vytváření matematických modelů ukázkové příklady Základní pojmy matematický
MODELOVÁNÍ základní pojmy a postupy principy vytváření deterministických matematických modelů vybrané základní vztahy používané při vytváření matematických modelů ukázkové příklady Základní pojmy matematický
F7 MOMENT SETRVAČNOSTI
 F7 MOMENT ETRVAČNOTI Evropský sociání fond Praha & EU: Investujeme do vaší budoucnosti F7 MOMENT ETRVAČNOTI V této části si spočteme některé jednoduché příkady na rotační pohyby a seznámíme se s někoika
F7 MOMENT ETRVAČNOTI Evropský sociání fond Praha & EU: Investujeme do vaší budoucnosti F7 MOMENT ETRVAČNOTI V této části si spočteme některé jednoduché příkady na rotační pohyby a seznámíme se s někoika
7 Gaussova věta 7 GAUSSOVA VĚTA. Použitím Gaussovy věty odvod te velikost vektorů elektrické indukce a elektrické intenzity pro
 7 Gaussova věta Zadání Použitím Gaussovy věty odvod te velikost vektorů elektrické indukce a elektrické intenzity pro následující nabitá tělesa:. rovnoměrně nabitou kouli s objemovou hustotou nábojeρ,
7 Gaussova věta Zadání Použitím Gaussovy věty odvod te velikost vektorů elektrické indukce a elektrické intenzity pro následující nabitá tělesa:. rovnoměrně nabitou kouli s objemovou hustotou nábojeρ,
Matematika pro chemické inženýry
 Matematika pro chemické inženýry Drahoslava Janovská Plošný integrál Přednášky Z 216-217 ponzorováno grantem VŠCHT Praha, PIGA 413-17-6642, 216 Povinná látka. Bude v písemkách a bude se zkoušet při ústní
Matematika pro chemické inženýry Drahoslava Janovská Plošný integrál Přednášky Z 216-217 ponzorováno grantem VŠCHT Praha, PIGA 413-17-6642, 216 Povinná látka. Bude v písemkách a bude se zkoušet při ústní
Elektromagnetismus 163
 Elektromagnetismus 163 I I H= 2πr Magnetické pole v blízkosti vodi e s proudem x r H Relativní permeabilita Materiály paramagnetické feromagnetické (nap. elezo, nikl, kobalt) diamagnetické Ve vzduchu je
Elektromagnetismus 163 I I H= 2πr Magnetické pole v blízkosti vodi e s proudem x r H Relativní permeabilita Materiály paramagnetické feromagnetické (nap. elezo, nikl, kobalt) diamagnetické Ve vzduchu je
ELEKTRICKÝ PROUD ELEKTRICKÝ ODPOR (REZISTANCE) REZISTIVITA
 ELEKTRICKÝ PROD ELEKTRICKÝ ODPOR (REZISTANCE) REZISTIVITA 1 ELEKTRICKÝ PROD Jevem Elektrický proud nazveme usměrněný pohyb elektrických nábojů. Např.:- proud vodivostních elektronů v kovech - pohyb nabitých
ELEKTRICKÝ PROD ELEKTRICKÝ ODPOR (REZISTANCE) REZISTIVITA 1 ELEKTRICKÝ PROD Jevem Elektrický proud nazveme usměrněný pohyb elektrických nábojů. Např.:- proud vodivostních elektronů v kovech - pohyb nabitých
Téma 4 Výpočet přímého nosníku
 Stavební statika, 1.ročník bakaářského studia Téma 4 Výpočet přímého nosníku Výpočet nosníku v osové úoze Výpočet nosníku v příčné úoze ve svisé a vodorovné havní rovině Výpočet nosníku v krutové úoze
Stavební statika, 1.ročník bakaářského studia Téma 4 Výpočet přímého nosníku Výpočet nosníku v osové úoze Výpočet nosníku v příčné úoze ve svisé a vodorovné havní rovině Výpočet nosníku v krutové úoze
14. cvičení z Matematické analýzy 2
 4. cvičení z atematické analýzy 2 8. - 2. ledna 28 4. (Greenova věta) Použijte Greenovu větu k nalezení práce síly F (x, y) (2xy 3, 4x 2 y 2 ) vykonané na částici podél křivky Γ, která je hranicí oblasti
4. cvičení z atematické analýzy 2 8. - 2. ledna 28 4. (Greenova věta) Použijte Greenovu větu k nalezení práce síly F (x, y) (2xy 3, 4x 2 y 2 ) vykonané na částici podél křivky Γ, která je hranicí oblasti
7 Kvantová částice v centrálně symetrickém potenciálu.
 7 Kvantová částice v centráně symetrickém potenciáu. Představte si, že hodíte kámen do vody a chcete popsat vny, které vzniknou. Protože hadina je D, můžete vny popsat funkcí f x, y. Ae pokud jste chytří,
7 Kvantová částice v centráně symetrickém potenciáu. Představte si, že hodíte kámen do vody a chcete popsat vny, které vzniknou. Protože hadina je D, můžete vny popsat funkcí f x, y. Ae pokud jste chytří,
FYZIKA II. Petr Praus 6. Přednáška elektrický proud
 FYZIKA II Petr Praus 6. Přednáška elektrický proud Osnova přednášky Elektrický proud proudová hustota Elektrický odpor a Ohmův zákon měrná vodivost driftová rychlost Pohyblivost nosičů náboje teplotní
FYZIKA II Petr Praus 6. Přednáška elektrický proud Osnova přednášky Elektrický proud proudová hustota Elektrický odpor a Ohmův zákon měrná vodivost driftová rychlost Pohyblivost nosičů náboje teplotní
8.3). S ohledem na jednoduchost a názornost je výhodné seznámit se s touto Základní pojmy a vztahy. Definice
 9. Lineární diferenciální rovnice 2. řádu Cíle Diferenciální rovnice, v nichž hledaná funkce vystupuje ve druhé či vyšší derivaci, nazýváme diferenciálními rovnicemi druhého a vyššího řádu. Analogicky
9. Lineární diferenciální rovnice 2. řádu Cíle Diferenciální rovnice, v nichž hledaná funkce vystupuje ve druhé či vyšší derivaci, nazýváme diferenciálními rovnicemi druhého a vyššího řádu. Analogicky
Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
Extrémy funkce dvou proměnných
 Extrémy funkce dvou proměnných 1. Stanovte rozměry pravoúhlé vodní nádrže o objemu 32 m 3 tak, aby dno a stěny měly nejmenší povrch. Označme rozměry pravoúhlé nádrže x, y, z (viz obr.). ak objem této nádrže
Extrémy funkce dvou proměnných 1. Stanovte rozměry pravoúhlé vodní nádrže o objemu 32 m 3 tak, aby dno a stěny měly nejmenší povrch. Označme rozměry pravoúhlé nádrže x, y, z (viz obr.). ak objem této nádrže
Stacionární magnetické pole. Kolem trvalého magnetu existuje magnetické pole.
 Magnetické pole Stacionární magnetické pole Kolem trvalého magnetu existuje magnetické pole. Stacionární magnetické pole Pilinový obrazec magnetického pole tyčového magnetu Stacionární magnetické pole
Magnetické pole Stacionární magnetické pole Kolem trvalého magnetu existuje magnetické pole. Stacionární magnetické pole Pilinový obrazec magnetického pole tyčového magnetu Stacionární magnetické pole
GE - Vyšší kvalita výuky CZ.1.07/1.5.00/
 Gymnázium, Brno, Elgartova 3 GE - Vyšší kvalita výuky CZ.1.07/1.5.00/34.0925 IV/2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma : Diferenciální a integrální
Gymnázium, Brno, Elgartova 3 GE - Vyšší kvalita výuky CZ.1.07/1.5.00/34.0925 IV/2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma : Diferenciální a integrální
rovnic), Definice y + p(x)y = q(x), Je-li q(x) = 0 na M, nazývá se y + p(x)y =
 Cíle Přehled základních typů diferenciálních rovnic prvního řádu zakončíme pojednáním o lineárních rovnicích, které patří v praktických úlohách k nejfrekventovanějším. Ukážeme například, že jejich řešení
Cíle Přehled základních typů diferenciálních rovnic prvního řádu zakončíme pojednáním o lineárních rovnicích, které patří v praktických úlohách k nejfrekventovanějším. Ukážeme například, že jejich řešení
Elektrické a magnetické pole zdroje polí
 Elektrické a magnetické pole zdroje polí Podstata elektromagnetických jevů Elementární částice s ohledem na elektromagnetické působení Elektrické a magnetické síly a jejich povaha Elektrický náboj a jeho
Elektrické a magnetické pole zdroje polí Podstata elektromagnetických jevů Elementární částice s ohledem na elektromagnetické působení Elektrické a magnetické síly a jejich povaha Elektrický náboj a jeho
1.5. DYNAMIKA OTÁČIVÉHO A SLOŽENÉHO POHYBU TĚLESA
 .5. OTÁČIVÉHO A SLOŽENÉHO POHYBU TĚLESA.5. ZÁKLADNÍ ROVNICE DYNAMIKY PRO ROTAČNÍ POHYB Fz F Z výsednce zrychujících s F m.a n m a t a n r z F Zrychující moment M F. r F. r z z z m.a t r6,5cm ρ r ω,ε r
.5. OTÁČIVÉHO A SLOŽENÉHO POHYBU TĚLESA.5. ZÁKLADNÍ ROVNICE DYNAMIKY PRO ROTAČNÍ POHYB Fz F Z výsednce zrychujících s F m.a n m a t a n r z F Zrychující moment M F. r F. r z z z m.a t r6,5cm ρ r ω,ε r
diferenciální rovnice verze 1.1
 Diferenciální rovnice vyšších řádů, snižování řádu diferenciální rovnice verze 1.1 1 Úvod Následující text popisuje řešení diferenciálních rovnic, konkrétně diferenciálních rovnic vyšších řádů a snižování
Diferenciální rovnice vyšších řádů, snižování řádu diferenciální rovnice verze 1.1 1 Úvod Následující text popisuje řešení diferenciálních rovnic, konkrétně diferenciálních rovnic vyšších řádů a snižování
(1 + v ) (5 bodů) Pozor! Je nutné si uvědomit, že v a f mají opačný směr! Síla působí proti pohybu.
 Přijímací zkouška na navazující magisterské studium - 017 Studijní program Fyzika - všechny obory kromě Učitelství fyziky-matematiky pro střední školy, Varianta A Příklad 1 (5 bodů) Těleso s hmotností
Přijímací zkouška na navazující magisterské studium - 017 Studijní program Fyzika - všechny obory kromě Učitelství fyziky-matematiky pro střední školy, Varianta A Příklad 1 (5 bodů) Těleso s hmotností
Základní otázky pro teoretickou část zkoušky.
 Základní otázky pro teoretickou část zkoušky. Platí shodně pro prezenční i kombinovanou formu studia. 1. Síla současně působící na elektrický náboj v elektrickém a magnetickém poli (Lorentzova síla) 2.
Základní otázky pro teoretickou část zkoušky. Platí shodně pro prezenční i kombinovanou formu studia. 1. Síla současně působící na elektrický náboj v elektrickém a magnetickém poli (Lorentzova síla) 2.
Vzájemné silové působení
 magnet, magnetka magnet zmagnetované těleso. Původně vyrobeno z horniny magnetit, která má sama magnetické vlastnosti dnes ocelové zmagnetované magnety, ferity, neodymové magnety. dva magnetické póly (S-J,
magnet, magnetka magnet zmagnetované těleso. Původně vyrobeno z horniny magnetit, která má sama magnetické vlastnosti dnes ocelové zmagnetované magnety, ferity, neodymové magnety. dva magnetické póly (S-J,
Téma 1: Elektrostatika I - Elektrický náboj Kapitola 22, str. 577 592
 Téma 1: Elektrostatika I - Elektrický náboj Kapitola 22, str. 577 592 Shrnutí: Náboj a síla = Coulombova síla: - Síla jíž na sebe náboje Q působí je stejná - Pozn.: hledám-li velikost, tak jen dosadím,
Téma 1: Elektrostatika I - Elektrický náboj Kapitola 22, str. 577 592 Shrnutí: Náboj a síla = Coulombova síla: - Síla jíž na sebe náboje Q působí je stejná - Pozn.: hledám-li velikost, tak jen dosadím,
ELEKTROMAGNETICKÉ POLE
 ELEKTROMAGNETICKÉ POLE 1. Magnetická síla působící na náboj v magnetickém poli Fyzikové Lorentz a Ampér zjistili, že silové působení magnetického pole na náboj Q, závisí na: 1. velikosti náboje Q, 2. relativní
ELEKTROMAGNETICKÉ POLE 1. Magnetická síla působící na náboj v magnetickém poli Fyzikové Lorentz a Ampér zjistili, že silové působení magnetického pole na náboj Q, závisí na: 1. velikosti náboje Q, 2. relativní
Elektřina a magnetismus UF/01100. Základy elektřiny a magnetismu UF/PA112
 Elektřina a magnetismus UF/01100 Rozsah: 4/2 Forma výuky: přednáška Zakončení: zkouška Kreditů: 9 Dop. ročník: 1 Dop. semestr: letní Základy elektřiny a magnetismu UF/PA112 Rozsah: 3/2 Forma výuky: přednáška
Elektřina a magnetismus UF/01100 Rozsah: 4/2 Forma výuky: přednáška Zakončení: zkouška Kreditů: 9 Dop. ročník: 1 Dop. semestr: letní Základy elektřiny a magnetismu UF/PA112 Rozsah: 3/2 Forma výuky: přednáška
Průvodce studiem. do bodu B se snažíme najít nejkratší cestu. Ve firmách je snaha minimalizovat
 6. Extrémy funkcí více proměnných Průvodce studiem Hledání extrémů je v praxi často řešená úloha. Např. při cestě z bodu A do bodu B se snažíme najít nejkratší cestu. Ve firmách je snaha minimalizovat
6. Extrémy funkcí více proměnných Průvodce studiem Hledání extrémů je v praxi často řešená úloha. Např. při cestě z bodu A do bodu B se snažíme najít nejkratší cestu. Ve firmách je snaha minimalizovat
Substituce ve vícenásobném integrálu verze 1.1
 Úvod Substituce ve vícenásobném integrálu verze. Následující text popisuje výpočet vícenásobných integrálů pomocí věty o substituci. ěl by sloužit především studentům předmětu ATEAT k přípravě na zkoušku.
Úvod Substituce ve vícenásobném integrálu verze. Následující text popisuje výpočet vícenásobných integrálů pomocí věty o substituci. ěl by sloužit především studentům předmětu ATEAT k přípravě na zkoušku.
Sedmé cvičení bude vysvětlovat tuto problematiku:
 Sedmé cvičení bude vysvětlovat tuto problematiku: Velmi stručně o parciálních derivacích Castiglianova věta k čemu slouží Castiglianova věta jak ji použít Castiglianova věta staticky určité přímé nosníky
Sedmé cvičení bude vysvětlovat tuto problematiku: Velmi stručně o parciálních derivacích Castiglianova věta k čemu slouží Castiglianova věta jak ji použít Castiglianova věta staticky určité přímé nosníky
1. Náhodný vektor (X, Y ) má diskrétní rozdělení s pravděpodobnostní funkcí p, kde. p(x, y) = a(x + y + 1), x, y {0, 1, 2}.
 VIII. Náhodný vektor. Náhodný vektor (X, Y má diskrétní rozdělení s pravděpodobnostní funkcí p, kde p(x, y a(x + y +, x, y {,, }. a Určete číslo a a napište tabulku pravděpodobnostní funkce p. Řešení:
VIII. Náhodný vektor. Náhodný vektor (X, Y má diskrétní rozdělení s pravděpodobnostní funkcí p, kde p(x, y a(x + y +, x, y {,, }. a Určete číslo a a napište tabulku pravděpodobnostní funkce p. Řešení:
Přijímací zkouška na navazující magisterské studium 2017 Studijní program: Fyzika Studijní obory: FFUM
 Přijímací zkouška na navazující magisterské studium 207 Studijní program: Fyzika Studijní obory: FFUM Varianta A Řešení příkladů pečlivě odůvodněte. Příklad (25 bodů) Nechť (a) Spočtěte lim n x n. (b)
Přijímací zkouška na navazující magisterské studium 207 Studijní program: Fyzika Studijní obory: FFUM Varianta A Řešení příkladů pečlivě odůvodněte. Příklad (25 bodů) Nechť (a) Spočtěte lim n x n. (b)
+ 2y. a y = 1 x 2. du x = nxn 1 f(u) 2x n 3 yf (u)
 Diferenciální počet příklad 1 Dokažte, že funkce F, = n f 2, kde f je spojitě diferencovatelná funkce, vhovuje vztahu + 2 = nf ; 0 Řešení: Označme u = 2. Pak je F, = n fu a platí Podle vět o derivaci složené
Diferenciální počet příklad 1 Dokažte, že funkce F, = n f 2, kde f je spojitě diferencovatelná funkce, vhovuje vztahu + 2 = nf ; 0 Řešení: Označme u = 2. Pak je F, = n fu a platí Podle vět o derivaci složené
V elektrostatickém poli jsme se zabývali vznikem a vlastnostmi pole v blízkosti nábojů. Elektrické pole jsme popisovali vektorem E.
 MAGNETICKÉ POLE V elektrostatickém poli jsme se zabývali vznikem a vlastnostmi pole v blízkosti nábojů. Elektrické pole jsme popisovali vektorem E. Podobně i magnety vytvářejí pole v každém bodě prostoru.
MAGNETICKÉ POLE V elektrostatickém poli jsme se zabývali vznikem a vlastnostmi pole v blízkosti nábojů. Elektrické pole jsme popisovali vektorem E. Podobně i magnety vytvářejí pole v každém bodě prostoru.
PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU
 PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU 6.1 Křivkový integrál 1. druhu Definice 1. Množina R n se nazývá prostá regulární křivka v R n právě tehdy, když existuje vzájemně jednoznačné zobrazení
PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU 6.1 Křivkový integrál 1. druhu Definice 1. Množina R n se nazývá prostá regulární křivka v R n právě tehdy, když existuje vzájemně jednoznačné zobrazení
4. Statika základní pojmy a základy rovnováhy sil
 4. Statika základní pojmy a základy rovnováhy sil Síla je veličina vektorová. Je určena působištěm, směrem, smyslem a velikostí. Působiště síly je bod, ve kterém se přenáší účinek síly na těleso. Směr
4. Statika základní pojmy a základy rovnováhy sil Síla je veličina vektorová. Je určena působištěm, směrem, smyslem a velikostí. Působiště síly je bod, ve kterém se přenáší účinek síly na těleso. Směr
Matematika II, úroveň A ukázkový test č. 1 (2016) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 22. 2. 2016 Matematika II, úroveň A ukázkový test č. 1 (2016) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
22. 2. 2016 Matematika II, úroveň A ukázkový test č. 1 (2016) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
Dvojné a trojné integrály příklad 3. x 2 y dx dy,
 Spočtěte = { x, y) ; 4x + y 4 }. Dvojné a trojné integrály příklad 3 x y dx dy, Řešení: Protože obor integrace je symetrický vzhledem k ose x, tj. vzhledem k substituci [x; y] [x; y], a funkce fx, y) je
Spočtěte = { x, y) ; 4x + y 4 }. Dvojné a trojné integrály příklad 3 x y dx dy, Řešení: Protože obor integrace je symetrický vzhledem k ose x, tj. vzhledem k substituci [x; y] [x; y], a funkce fx, y) je
11. přednáška 10. prosince Kapitola 3. Úvod do teorie diferenciálních rovnic. Obyčejná diferenciální rovnice řádu n (ODR řádu n) je vztah
 11. přednáška 10. prosince 2007 Kapitola 3. Úvod do teorie diferenciálních rovnic. Obyčejná diferenciální rovnice řádu n (ODR řádu n) je vztah F (x, y, y, y,..., y (n) ) = 0 mezi argumentem x funkce jedné
11. přednáška 10. prosince 2007 Kapitola 3. Úvod do teorie diferenciálních rovnic. Obyčejná diferenciální rovnice řádu n (ODR řádu n) je vztah F (x, y, y, y,..., y (n) ) = 0 mezi argumentem x funkce jedné
Matematická analýza III.
 2. Parciální derivace Miroslav Hušek, Lucie Loukotová UJEP 2010 Parciální derivace jsou zobecněním derivace funkce jedné proměnné. V této kapitole poznáme jejich základní vlastnosti a využití. Co bychom
2. Parciální derivace Miroslav Hušek, Lucie Loukotová UJEP 2010 Parciální derivace jsou zobecněním derivace funkce jedné proměnné. V této kapitole poznáme jejich základní vlastnosti a využití. Co bychom
Atom vodíku. Nejjednodušší soustava: p + e Řešitelná exaktně. Kulová symetrie. Potenciální energie mezi p + e. e =
 Atom vodíku Nejjednodušší soustava: p + e Řešitelná exaktně Kulová symetrie Potenciální energie mezi p + e V 2 e = 4πε r 0 1 Polární souřadnice využití kulové symetrie atomu Ψ(x,y,z) Ψ(r,θ, φ) x =? y=?
Atom vodíku Nejjednodušší soustava: p + e Řešitelná exaktně Kulová symetrie Potenciální energie mezi p + e V 2 e = 4πε r 0 1 Polární souřadnice využití kulové symetrie atomu Ψ(x,y,z) Ψ(r,θ, φ) x =? y=?
MATEMATIKA II - vybrané úlohy ze zkoušek ( 2015)
 MATEMATIKA II - vybrané úlohy ze zkoušek ( 2015 doplněné o další úlohy 13. 4. 2015 Nalezené nesrovnalosti ve výsledcích nebo připomínky k tomuto souboru sdělte laskavě F. Mrázovi ( e-mail: Frantisek.Mraz@fs.cvut.cz.
MATEMATIKA II - vybrané úlohy ze zkoušek ( 2015 doplněné o další úlohy 13. 4. 2015 Nalezené nesrovnalosti ve výsledcích nebo připomínky k tomuto souboru sdělte laskavě F. Mrázovi ( e-mail: Frantisek.Mraz@fs.cvut.cz.
Pohyby částic ve vnějším poli A) Homogenní pole. qb m. cyklotronová frekvence. dt = = 0. 2 ω PČ 1
 Způsob popisu Pohb částic v poli vnějším Pohb částic v selfkonsistentním poli Kinetické rovnice Hdrodnamické rovnice * tekutin * 1 tekutina * magnetohdrodnamika Pohb částic ve vnějším poli A) Homogenní
Způsob popisu Pohb částic v poli vnějším Pohb částic v selfkonsistentním poli Kinetické rovnice Hdrodnamické rovnice * tekutin * 1 tekutina * magnetohdrodnamika Pohb částic ve vnějším poli A) Homogenní
PRAKTIKUM II. Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. úlohač.19 Název: Měření s torzním magnetometrem
 Odděení fyzikáních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM II. úohač.19 Název: Měření s torzním magnetometrem Pracova: Lukáš Ledvina stud.skup.14 dne:16.10.2009 Odevzdadne: Možný počet
Odděení fyzikáních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM II. úohač.19 Název: Měření s torzním magnetometrem Pracova: Lukáš Ledvina stud.skup.14 dne:16.10.2009 Odevzdadne: Možný počet
A x A y. α = 30. B y. A x =... kn A y =... kn B y =... kn. Vykreslení N, V, M. q = 2kN/m M = 5kNm. F = 10 kn A c a b d ,5 2,5 L = 10
 Vzorový příklad k 1. kontrolnímu testu Prostý nosník Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A y y q = kn/m M = 5kNm F = 10 kn A c a b d 1 1 3,5,5 L = 10 α B B y x α = 30
Vzorový příklad k 1. kontrolnímu testu Prostý nosník Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A y y q = kn/m M = 5kNm F = 10 kn A c a b d 1 1 3,5,5 L = 10 α B B y x α = 30
4. Magnetické pole. 4.1. Fyzikální podstata magnetismu. je silové pole, které vzniká v důsledku pohybu elektrických nábojů
 4. Magnetické pole je silové pole, které vzniká v důsledku pohybu elektrických nábojů 4.1. Fyzikální podstata magnetismu Magnetické pole vytváří permanentní (stálý) magnet, nebo elektromagnet. Stálý magnet,
4. Magnetické pole je silové pole, které vzniká v důsledku pohybu elektrických nábojů 4.1. Fyzikální podstata magnetismu Magnetické pole vytváří permanentní (stálý) magnet, nebo elektromagnet. Stálý magnet,
5 Stacionární magnetické pole HRW 28, 29(29, 30)
 5 STACIONÁRNÍ MAGNETICKÉ POLE HRW 28, 29(29, 30) 31 5 Stacionární magnetické pole HRW 28, 29(29, 30) 5.1 Magneticképole,jehozdrojeaúčinkyHRW28(29) 5.1.1 Permanentní magnet Vedle výhradně přitažlivé interakce
5 STACIONÁRNÍ MAGNETICKÉ POLE HRW 28, 29(29, 30) 31 5 Stacionární magnetické pole HRW 28, 29(29, 30) 5.1 Magneticképole,jehozdrojeaúčinkyHRW28(29) 5.1.1 Permanentní magnet Vedle výhradně přitažlivé interakce
ELEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Magnetická síla a moment sil
 ELEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Magnetická síla a moment sil Peter Dourmashkin MIT 006, překlad: Jan Pacák (007) Obsah 6. MAGNETICKÁ SÍLA A MOMENT SIL 3 6.1 ÚKOLY 3 ÚLOHA 1: HMOTNOSTNÍ
ELEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Magnetická síla a moment sil Peter Dourmashkin MIT 006, překlad: Jan Pacák (007) Obsah 6. MAGNETICKÁ SÍLA A MOMENT SIL 3 6.1 ÚKOLY 3 ÚLOHA 1: HMOTNOSTNÍ
LDF MENDELU. Simona Fišnarová (MENDELU) LDR druhého řádu VMAT, IMT 1 / 22
 Lineární diferenciální rovnice druhého řádu Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF)
Lineární diferenciální rovnice druhého řádu Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF)
Kapitola 8: Dvojný integrál 1/26
 Kapitola 8: vojný integrál 1/26 vojný integrál - osnova kapitoly 2/26 dvojný integrál přes obdélník definice výpočet (Fubiniova věta pro obdélník) dvojný integrál přes standardní množinu definice výpočet
Kapitola 8: vojný integrál 1/26 vojný integrál - osnova kapitoly 2/26 dvojný integrál přes obdélník definice výpočet (Fubiniova věta pro obdélník) dvojný integrál přes standardní množinu definice výpočet
FYZIKA II. Petr Praus 7. Přednáška stacionární magnetické pole náboj v magnetickém poli
 FYZIKA II Petr Praus 7. Přednáška stacionární magnetické pole náboj v magnetickém poli Osnova přednášky Stacionární magnetické pole Lorentzova síla Hallův jev Pohyb a urychlování nabitých částic (cyklotron,
FYZIKA II Petr Praus 7. Přednáška stacionární magnetické pole náboj v magnetickém poli Osnova přednášky Stacionární magnetické pole Lorentzova síla Hallův jev Pohyb a urychlování nabitých částic (cyklotron,
TELMG Modul 03: Maxwellovy rovnice. I. a II. MR: aplikací plošného integrálu a Stokesovy věty integrálního počtu
 Difereniální a integrální tvar Maxwellovýh rovni kot James Clerk Maxwell (1831-1879) Integrální tvar Difereniální tvar d I Hdl = I + d dt D D rot H = j+ d II Edl = d dt B B rot E = III D d = Q div D =
Difereniální a integrální tvar Maxwellovýh rovni kot James Clerk Maxwell (1831-1879) Integrální tvar Difereniální tvar d I Hdl = I + d dt D D rot H = j+ d II Edl = d dt B B rot E = III D d = Q div D =
1. Obyčejné diferenciální rovnice
 & 8..8 8: Josef Hekrdla obyčejné diferenciální rovnice-separace proměnných. Obyčejné diferenciální rovnice Rovnice, ve které je neznámá funkcí a v rovnici se vyskytuje spolu se svými derivacemi, se nazývá
& 8..8 8: Josef Hekrdla obyčejné diferenciální rovnice-separace proměnných. Obyčejné diferenciální rovnice Rovnice, ve které je neznámá funkcí a v rovnici se vyskytuje spolu se svými derivacemi, se nazývá
FYZIKA II. Petr Praus 10. Přednáška Magnetické pole v látce
 FYZIKA II Petr Praus 10. Přednáška Magnetické pole v látce Osnova přednášky Magnetické pole v látkovém prostředí, Ampérovy proudové smyčky, veličiny B, M, H materiálové vztahy, susceptibilita a permeabilita
FYZIKA II Petr Praus 10. Přednáška Magnetické pole v látce Osnova přednášky Magnetické pole v látkovém prostředí, Ampérovy proudové smyčky, veličiny B, M, H materiálové vztahy, susceptibilita a permeabilita
NOSNÍK NA PRUŽNÉM PODLOŽÍ (WINKLEROVSKÉM)
 NOSNÍK NA PRUŽNÉ PODLOŽÍ (WINKLEROVSKÉ) Uvažujeme spojitý nosník na pružných podporách. Pružná podpora - odpor je úměrný zatlačení. Pružné podpory velmi blízko sebe - jejich účinek lze nahradit spojitou
NOSNÍK NA PRUŽNÉ PODLOŽÍ (WINKLEROVSKÉ) Uvažujeme spojitý nosník na pružných podporách. Pružná podpora - odpor je úměrný zatlačení. Pružné podpory velmi blízko sebe - jejich účinek lze nahradit spojitou
III. Diferenciál funkce a tečná rovina 8. Diferenciál funkce. Přírůstek funkce. a = (x 0, y 0 ), h = (h 1, h 2 ).
 III. Diferenciál funkce a tečná rovina 8. Diferenciál funkce. Přírůstek funkce = f(x 0 + h 1, y 0 + h 2 ) f(x 0, y 0 ) f u (x 0, y 0 ), kde u = (h 1, h 2 ). ( ) = f(x 0 + h 1, y 0 ) f(x 0, y 0 ) x (x 0,
III. Diferenciál funkce a tečná rovina 8. Diferenciál funkce. Přírůstek funkce = f(x 0 + h 1, y 0 + h 2 ) f(x 0, y 0 ) f u (x 0, y 0 ), kde u = (h 1, h 2 ). ( ) = f(x 0 + h 1, y 0 ) f(x 0, y 0 ) x (x 0,
13. cvičení z Matematické analýzy 2
 . cvičení z atematické analýz 2 5. - 9. května 27. konzervativní pole, potenciál Dokažte, že následující pole jsou konzervativní a najděte jejich potenciál. i F x,, z x 2 +, 2 + x, ze z, ii F x,, z x 2
. cvičení z atematické analýz 2 5. - 9. května 27. konzervativní pole, potenciál Dokažte, že následující pole jsou konzervativní a najděte jejich potenciál. i F x,, z x 2 +, 2 + x, ze z, ii F x,, z x 2
Příklad 33 : Energie elektrického pole deskového kondenzátoru. Ověření vztahu mezi energií, kapacitou a veličinami pole.
 Přík 33 : Energie eektrického poe eskového konenzátoru. Ověření vzthu mezi energií, kpcitou veičinmi poe. Přepokáné znosti: Eektrické poe kpcit eskového konenzátoru Přík V eskovém konenzátoru je eektrické
Přík 33 : Energie eektrického poe eskového konenzátoru. Ověření vzthu mezi energií, kpcitou veičinmi poe. Přepokáné znosti: Eektrické poe kpcit eskového konenzátoru Přík V eskovém konenzátoru je eektrické
Hamiltonián popisující atom vodíku ve vnějším magnetickém poli:
 Orbitální a spinový magnetický moment a jejich interakce s vnějším polem Vše na příkladu atomu H: Elektron (e - ) a jádro (u atomu H pouze p + ) mají vlastní magnetický moment (= spin). Tyto dva dipóly
Orbitální a spinový magnetický moment a jejich interakce s vnějším polem Vše na příkladu atomu H: Elektron (e - ) a jádro (u atomu H pouze p + ) mají vlastní magnetický moment (= spin). Tyto dva dipóly
Stacionární magnetické pole
 Stacionání magnetické poe Vzájemné siové působení vodičů s poudem a pemanentních magnetů Magnetické jevy - známy od středověku, přesnější poznatky 19. stoetí. Stacionání magnetické poe: zdojem je nepohybující
Stacionání magnetické poe Vzájemné siové působení vodičů s poudem a pemanentních magnetů Magnetické jevy - známy od středověku, přesnější poznatky 19. stoetí. Stacionání magnetické poe: zdojem je nepohybující
Přednáška 12 Obecná deformační metoda, nelineární úlohy u prutových soustav
 Statika stavebních konstrukcí II., 3.ročník bakaářského studia Přednáška Obecná deformační metoda, neineární úohy u prutových soustav Fyzikáně neineární úoha Geometricky neineární úoha Konstrukčně neineární
Statika stavebních konstrukcí II., 3.ročník bakaářského studia Přednáška Obecná deformační metoda, neineární úohy u prutových soustav Fyzikáně neineární úoha Geometricky neineární úoha Konstrukčně neineární
Funkce zadané implicitně
 Kapitola 8 Funkce zadané implicitně Začneme několika příklady. Prvním je známá rovnice pro jednotkovou kružnici x 2 + y 2 1 = 0. Tato rovnice popisuje křivku, kterou si však nelze představit jako graf
Kapitola 8 Funkce zadané implicitně Začneme několika příklady. Prvním je známá rovnice pro jednotkovou kružnici x 2 + y 2 1 = 0. Tato rovnice popisuje křivku, kterou si však nelze představit jako graf
Mechanika - kinematika
 Mechanika - kinematika Hlavní body Úvod do mechaniky, kinematika hmotného bodu Pohyb přímočarý rovnoměrný rovnoměrně zrychlený. Pohyb křivočarý. Pohyb po kružnici rovnoměrný rovnoměrně zrychlený Pohyb
Mechanika - kinematika Hlavní body Úvod do mechaniky, kinematika hmotného bodu Pohyb přímočarý rovnoměrný rovnoměrně zrychlený. Pohyb křivočarý. Pohyb po kružnici rovnoměrný rovnoměrně zrychlený Pohyb
Parciální diferenciální rovnice
 Parciální diferenciální rovnice Obsah kurzu Co bude obsahovat... úvod do PDR odvození některých PDR klasická teorie lineárních PDR 1. a 2. řádu řešení poč. a okraj. úloh vlastnosti řešení souvislost s
Parciální diferenciální rovnice Obsah kurzu Co bude obsahovat... úvod do PDR odvození některých PDR klasická teorie lineárních PDR 1. a 2. řádu řešení poč. a okraj. úloh vlastnosti řešení souvislost s
ELEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Gaussův zákon
 ELEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Gaussův zákon Peter Dourmashkin MIT 006, překlad: Jan Pacák (007) Obsah 3. GAUSSŮV ZÁKON 3.1 ALGORITMUS PRO ŘEŠENÍ PROBLÉMŮ POMOCÍ GAUSSOVA ZÁKONA ÚLOHA
ELEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Gaussův zákon Peter Dourmashkin MIT 006, překlad: Jan Pacák (007) Obsah 3. GAUSSŮV ZÁKON 3.1 ALGORITMUS PRO ŘEŠENÍ PROBLÉMŮ POMOCÍ GAUSSOVA ZÁKONA ÚLOHA
