Rozmístěte na šachovnici 6 6 čtyři tchýně 1 tak, aby se navzájem neohrožovaly a právě jedno volné pole zůstalo neohrožené.
|
|
|
- Adam Růžička
- před 8 lety
- Počet zobrazení:
Transkript
1 Úlohy na šachovnici 3. podzimní série Vzorové řešení Úloha 1. Rozmístěte na šachovnici 6 6 čtyři tchýně 1 tak, aby se navzájem neohrožovaly a právě jedno volné pole zůstalo neohrožené. (Martin Töpfer) V této úloze bylo úkolem najít vyhovující rozestavení tchyní. Možností, jak nějaké takové najít, existuje mnoho. My si ukážeme, jaké úvahy nám v hledání mohou pomoci. Začneme pozorováním, že žádné dvě tchyně se nemohou vyskytovat ve stejném řádku ani sloupci, protože by se jinak ohrožovaly tahem věže. Právě čtyři řádky a čtyři sloupce tedy budou obsazeny tchyní. Dva neobsazené řádky a sloupce nám pak určují čtyři políčka, která tchyně nebudou ohrožovat tahem věže. Víme, že jedno z těchto polí musí zůstat neohrožené a zbylá tři musí být tchyněmi ohrožena tahem koně. Nyní se můžeme zaměřit na ta rozestavení, kde jsou neobsazené právě dva prostřední sloupce a dva prostřední řádky. Po chvíli zkoušení pak dojdeme k jednomu z rozestavení na prvních dvou obrázcích (či k rozestavení, které z těchto dvou vznikne tak, že šachovnici otočíme, či překlopíme podle jedné z jejích os symetrie). 6 0Z0ZNZ 5 Z0Z0ZN 4 0Z0Z0Z 3 Z0Z0Z0 2 0M0Z0Z 1 M0Z0Z0 a b c d e f 1 Tchýně je figura pohybující se po šachovnici pomocí tahů koně i věže. 1
2 6 NZ0Z0Z 5 Z0Z0ZN 4 0Z0Z0Z 3 Z0Z0Z0 2 0M0Z0Z 1 Z0Z0M0 a b c d e f 6 NZ0Z0Z 5 ZNZ0Z0 4 0ZNZ0Z 3 Z0Z0Z0 2 0Z0Z0M 1 Z0Z0Z0 a b c d e f Jinou možností je začít s rozestavením čtyř tchyní na hlavní diagonálu šachovnice. Toto ještě není správné řešení, neboť zbývají dvě neohrožená políčka. Přesunutím poslední tchyně však již získáme validní pozici na třetím obrázku. Sešlo se mnoho různých rozestavení a drtivá většina z nich byla správně. Jejich tvůrci si tak zasloužili plný počet bodů. Jak si také někteří řešitelé povšimli, správných řešení je hodně 2. To je mimo jiné způsobeno tím, že otočením či překlopením šachovnice ze správného řešení vyrobíme zase správné řešení. Na závěr opravme jednu gramatickou chybu, ke které nedopatřením v zadání došlo a kterou někteří z Vás postřehli. Slovo tchyně je odvozeno od podstatného jména tchán pomocí přípony -yně, a není tedy důvod psát jej s dlouhým ý, čehož jsme se v zadání dopustili. Omlouváme se a doufáme, že Vás tato nepřesnost při řešení natolik závažného problému, jakým bezpečné rozmístění tchyní jistě je, příliš nerušila. (Václav Rozhoň) Úloha 2. V rozích šachovnice 3 3 stojí dokola postupně Šemík, Rosinanta, Stínovlas a Trojský kůň. Všichni se mohou pohybovat jako šachoví koně a nesmí stát dva na stejném poli. Je možné, aby se za těchto podmínek Šemík s Rosinantou prohodili a ostatní se vrátili na svá původní místa? (Anh Dung Tonda Le) 2 přesněji 340 :) 2
3 Šem Ros Ros Šem Troj Stín Troj Stín Uvažme tahy, kterými se koně mohou pohybovat mezi poli. Sestrojíme graf, jehož vrcholy odpovídají polím šachovnice a hrana spojuje dvě políčka taková, že se z jednoho dá jedním tahem skočit na druhé. Výsledný graf je cyklus a jeden izolovaný vrchol (viz obrázek), ve kterém tahy koní odpovídají pohybu na sousední políčko. Šemík Rosinanta Trojský k Rosinanta Trojský k Šemík Stínovlas Stínovlas Ani v tomto grafu nemohou dva koně stát ve stejném vrcholu. Podíváme-li se, kde stojí Šemík, a půjdeme-li po cyklu po směru hodinových ručiček, nalezneme Rosinantu, Stínovlase a nakonec Trojského koně. Uvedené tahy toto pořadí zachovávají. Rozestavení, do kterého chceme koně rozmístit, má ovšem jiné pořadí, a proto není možné prohodit Šemíka s Rosinantou tak, aby se ostatní vrátili na původní místa. Všimněte si, že můžeme vypustit předpoklad o vracení na původní místa a stále to nepůjde. Mezi Šemíkem a Rosinantou je v cyklu pouze jedno políčko, kde nemohou stát oba Stínovlas a Trojský kůň. Nebo můžeme ze šachovnice odstranit Trojského koně, a přesto hledaná posloupnost tahů nebude existovat. Rozmyslete si, že to dokazuje stejný argument s pořadím koňů v cyklu. Kdybychom uvažovali pouze tři koně a nevyžadovali návrat na původní políčko, existovala by posloupnost tahů, při níž by si Šemík s Rosinantou vyměnili místa. Zhruba třetina řešení se podobala tomu autorskému. Většina těch ostatních se pokoušela o rozbor případů. To není úplně marná cesta, protože na takto malé šachovnici existuje poměrně málo různých situací a většina z nich je navíc v jistém smyslu symetrická. Postup je to ale velmi zdlouhavý a velmi náchylný na chyby. Mnoho řešitelů si snažilo ušetřit práci tím, že vybrali vždy ten nejlepší nebo nejrozumnější tah, ale bez argumentu s cyklem vůbec není jasné, který tah to je. Navíc není vůbec jasné, proč nemá smysl, aby kůň skočil zpět, odkud přišel (dokud se nezmíní rozestavení na kružnici). A jak vlastně může být nějaký tah lepší než jiný, když ani jeden z nich nevede ke zdárnému cíli? Při rozboru případů je nezbytné pozorně prozkoumat všechny možnosti a nezavrhnout nějakou jenom proto, že nevypadá slibně. (Filip Hlásek) 3
4 Úloha 3. Obarvěte sedm polí šachovnice 4 4 tak, aby na ní po odebrání libovolných dvou sloupců a dvou řádků zůstalo alespoň jedno obarvené pole. (Rado Švarc) Nejprve si uvědomíme, že po vyškrtnutí libovolných dvou řádků a sloupců nám z šachovnice zbude čtveřice polí, která původně tvořila rohy obdélníku 3 se stranami rovnoběžnými s okrajem šachovnice. Pro začátek obarvěme horní levý roh šachovnice a přeškrtněme všechna pole ležící na úhlopříčce, v řádku a v sloupci, které obsahují tento roh (viz obrázek). Všimneme si, že žádná čtveřice přeškrtnutých polí netvoří rohy obdélníku. Tudíž všechny obdélníky, které nemají v rohu již obarvené pole, musejí mít v alespoň jednom z rohů některé nepřeškrtnuté pole. Těch už je ale jen 6, tudíž je můžeme obarvit všechna a získáme tak jedno z možných řešení: Nejprve bych rád zmínil, že až na proházení řádků a sloupců měla úloha jediné řešení, celkem jich tedy bylo 96. Vzhledem k malým rozměrům zadané šachovnice bylo častým řešením této úlohy zkoušení několika různých obarvení, dokud nebyla splněna zadaná podmínka. Tento postup se ovšem poměrně velkému počtu řešitelů vymstil, jelikož naprostá většina chybných řešení opomněla jeden či dva nepokryté obdélníky. Špatné řešení bylo obvykle podobné jednomu z následujících dvou obarvení: (Tomáš Novotný) 3 Čtverec je speciálním případem obdélníku. 4
5 Úloha 4. Najděte všechna přirozená n, pro která lze rozdělit šachovnici n n na lichý počet čtverců 2 2 a několik 4 tetromin tvaru T. (Rado Švarc) Nejprve si dokážeme, že n musí být sudé: Čtverec 2 2 i T-tetromino jsou složené ze čtyř čtverečků. Proto 4 n 2, a tedy 2 n. Dále oddělíme dva případy, n = 4k + 2 a n = 4k, kde k je nějaké celé nezáporné číslo. Pro n = 4k+2 je možné pokrýt šachovnici lichým počtem čtverců 2 2 bez použití T-tetromina. Zjevně jich můžeme n/2 = 2k + 1 položit vedle sebe na spodní okraj mřížky. Pak totéž uděláme ve zbylých 2k dvojřádcích a dohromady budeme mít (2k + 1) 2 = 4k 2 + 4k + 1 čtverců 2 2, což je lichý počet. Pro n = 4k obarvíme šachovnici černobíle klasickým způsobem. Protože je n sudé a barvy se pravidelně střídají, je na šachovnici stejně černých i bílých čtverečků. Každý čtverec 2 2 zřejmě zabírá dvě bílá a dvě černá políčka. Naopak T-tetromino pokryje vždy buď jeden bílý a tři černé (nazveme ho černé), nebo jeden černý a tři bílé čtverečky (nazveme ho bílé). Abychom našimi útvary mohli pokrýt celý čtverec n n, určitě potřebujeme zakrýt stejný počet bílých i černých políček. Proto ke každému černému T-tetrominu musí být na šachovnici jedno bílé. Neboli je potřeba použít sudý počet T-tetromin, označme tedy jejich počet jako 2l pro l nezáporné celé číslo. Platí n = 4k, neboli n 2 = 16k 2. A odečteme-li od celkového počtu polí počet polí zabraných T-tetrominy, dostaneme 16k 2 4 (2l) = 8(2k 2 l). Každý čtverec 2 2 zabírá čtyři políčka, do zbytku šachovnice se jich tedy vejde 8(2k 2 l)/4 = 2(2k 2 l), což je sudé číslo. Pro n dělitelné čtyřmi proto nelze šachovnici pokrýt podle zadání. Úloha nedopadla moc dobře, ačkoli ke správné odpovědi dospěli snad všichni, kteří si správně přečetli zadání. Více než polovina řešitelů ale potom nedokázala, že pro n dělitelné čtyřmi se šachovnice pokrýt nedá. Většinou vágně tvrdili, že z T-tetromin se nedá sestavit jiný rozumný tvar než čtverce 4 4, což zaprvé není pravda (lze jimi vyplnit například dvoučtverečkový okraj šachovnice pro n = 4k + 2) a zadruhé (což je mnohem důležitější) to opravdu nemůžeme tvrdit jen proto, že jsme nenašli žádné jiné jejich uspořádání. Pro čtyři nebo pět T-tetromin snad ještě můžeme vyzkoušet všechny možnosti, ale pro tisícové počty by to šlo už opravdu těžko. Stejně tak je potřeba ukázat, že pro n = 4k + 2 řešení opravdu existuje. Snadno si lze totiž představit útvar, který na šachovnici zabere n 2 /4 bílých a n 2 /4 černých čtverečků, a přesto se vedle něj už nevejde druhý, který by pokryl zbytek šachovnice. Na závěr bych ještě poznamenala, jaké problémy působilo slovo tetromino. Řešitelé ho tak půl napůl používali ve středním a mužském rodě, někteří z něj udělali třeba tetramín nebo dokonce triomino a vůbec jim nevadilo, že tak se běžně nazývá útvar o čtvereček menší. (Bára Kociánová) Úloha 5. Kuba a Bára spolu hrají hru. Na začátku mají šachovnici , kde jsou všechna políčka bílá. Kuba v každém svém tahu přebarví nějaký bílý čtverec 2 2 na černo, Bára vždy přebarví nějaká tři bílá políčka tvořící jakkoliv orientované L. Pravidelně se střídají v tazích, přičemž Kuba začíná. Prohrává ten, kdo jako první nemůže táhnout. Který z nich má vyhrávající strategii? (Kuba Krásenský) 4 Nemusí být použito žádné. 5
6 Vyhrávající strategii má Bára. Ve svém prvním tahu si vybere některý z prázdných rohů šachovnice (takový určitě existuje, protože Kuba zatím stihl vybarvit jen jeden čtverec 2 2) a zahraje do něj následovně: Vzniknou tak tři rezervní políčka (v obrázku vyznačena šedě) ve tvaru L taková, že ani jedno z nich nemůže Kuba svým tahem vybarvit. Potom bude hra pokračovat. Bára bude nadále hrát tak, že nebude vybarvovat žádné z rezervních políček. Jelikož v každém tahu ubude bílých políček, tak časem nastane situace, že na šachovnici už nebude žádný bílý čtverec 2 2. Pokud je v této situaci na tahu Kuba, prohrál, protože nemá co zabarvit. Pokud je na tahu Bára, může zabarvit tři rezervní políčka. Po tomto jejím tahu Kuba nemá co zabarvit, takže také prohrál. Úloha byla na pětku celkem jednoduchá a pětibodovými řešeními se to jen hemžilo. Drtivá většina z nich využívala stejnou myšlenku jako to vzorové. Několik řešitelů navrhlo pro Báru strategii takovou, že bude hrát vždy na pozici středově symterickou s předchozím Kubovým tahem tato strategie funguje také, jen je potřeba dát si pozor na pár technických detailů. (Tonda Češík) Úloha 6. Dva kamarádi, Plusík a Mínusík, našli šachovnici 3 3 vyplněnou v nějakém pořadí čísly 1 až 9. Plusík umí ke všem číslům v libovolném čtverci 2 2 přičíst jedničku, Mínusík umí analogicky odčítat. Poté, co si s šachovnicí chvíli takto hráli, objevilo se ve všech jejích políčkách stejné číslo. Kolik to mohlo být? (Rado Švarc) Na začátku je součet čísel na šachovnici rovný 45. Označme p počet tahů Plusíka a m počet tahů Mínusíka. Položme k = p m. Plusík i Mínusík ovlivňují každým svým tahem 4 políčka. Na konci jejich hry tedy bude součet čísel na šachovnici rovný k. Dále označme e hodnotu, která se původně nacházela ve středu šachovnice. Každý tah Plusíka i Mínusíka toto číslo mění, a tak na konci bude hodnota na prostředním políčku rovna e + k. Na konci však má být na všech polích šachovnice stejná hodnota, tudíž jejich součet bude roven devítinásobku čísla na prostředním políčku. Můžeme tedy psát, že k = 9(e + k), 45 = 9e + 5k. To však znamená, že e je dělitelné 5. Jediné číslo, které bylo na počátku napsáno na šachovnici a bylo dělitelné pěti, je 5. Tedy e = 5. Z toho již snadno dopočteme, že 5k = 45 9e = 0, tedy k = 0. Hodnota, která nakonec na šachovnici zůstane, je e + k = 5. Příkladem šachovnice, kde je možné všechny hodnoty změnit na 5, může být 6
7 Plusík jednou zvýší hodnoty v levém horním čtverci a třikrát v pravém horním. Mínusík jednou sníží čísla v pravém dolním a třikrát v levém dolním. Jediné číslo, které mohlo být na všech políčkách šachovnice zároveň je tedy 5. Úlohu bylo možno dokázat mnoha různými postupy. Ti, kteří předvedli rychlé a elegantní řešení, byli odměněni imaginárním bodem. Část řešitelů mylně předpokládala, že se Plusík a Mínusík ve svých tazích musí pravidelně střídat. (Martin Hora) Úloha 7. Na šachovnici stálo 2015 věží, z nichž se žádné dvě neohrožovaly. Náhle se všechny proměnily v tchýně, udělaly jeden tah jako koně a proměnily se zpět ve věže. Dokažte, že nyní se nutně nějaké dvě z nich ohrožují. (Anh Dung Tonda Le) Zavedeme si souřadnice políček tak, že souřadnice levého horního políčka je (1, 1) a souřadnice pravého spodního políčka je (2015, 2015). Pokud se žádné dvě věže neohrožují, musí být každá v řádku i sloupci sama, a protože je věží stejně jako řádků a sloupců, je v každém řádku i sloupci právě jedna věž. Uvažujme nyní součet x-ových a y-ových souřadnic všech věží. Na začátku se žádné dvě věže neohrožovaly, proto se každý řádek i každý sloupec vyskytl v součtu právě jednou. Součet byl tudíž roven = 2 = Předpokládejme, že se ani po tahu žádné dvě věže neohrožují. Potom je součet jejich souřadnic zase , takže se nezměnil. Ale každá věž se pohnula dohromady o tři políčka, změnila tedy součet souřadnic o liché číslo. A protože věží je 2015, dohromady také změnily součet souřadnic o liché číslo, což je spor. Šachovnicové řešení (podle Jana Šorma): Lemma. Mějme šachovnici (2k 1) (2k 1), kde k je přirozené, a na ní 2k 1 věží rozmístěných tak, aby se neohrožovaly. Pokud šachovnici obarvíme šachovnicově tak, aby levé horní políčko bylo černé, pak je na černých políčkách lichý počet věží. Důkaz. Indukcí podle k. Pro šachovnici 1 1 tvrzení platí. (Je tam jedno černé políčko a na něm jedna věž.) Předpokládejme, že tvrzení platí pro 2k 1, a mějme šachovnici (2k +1) (2k +1) a na ní 2k +1 věží rozmístěných tak, aby se neohrožovaly. Každá věž je sama v řádku i ve sloupci. Rozebereme dvě možnosti: (i) Pokud je na černých políčkách pouze jedna věž, tvrzení platí. (ii) Jinak jsou na černých políčkách alespoň dvě věže. Nějaké takové dvě vybereme a odebereme je i s jejich řádky a sloupci. Tím jsme dostali vyhovující šachovnici (2k 1) (2k 1), na kterou použijeme indukční předpoklad, tedy že tam je lichý počet věží na černých políčkách. A pak zpátky přidáme ty dvě, čímž se parita nezmění. 7
8 Nyní je úloha triviální, protože skokem koně změní figura barvu svého políčka. Protože je věží 2015, můžeme použít lemma. Na začátku se neohrožují, je jich lichý počet na černých, a tedy sudý počet na bílých políčkách. Skokem koně změní svou barvu, takže bude na černých políčkách sudý počet věží. Proto se nějaké dvě budou ohrožovat. Řešení pomocí cyklů v permutacích (podle Adama Španěla): Opět si uvědomíme, že když se věže neohrožují, je v každém řádku i v každém sloupci právě jedna. Nyní si celou šachovnici promítneme na osu x (tzn. máme jeden řádek dlouhý 2015 políček). Na každém políčku je právě jedna věž. Předpokládejme pro spor, že se věže po skoku neohrožují. To znamená, že je opět každé políčko zabrané. Nechť první věž skočila na políčko i. Věž, která stála před skokem na i, musela skočit na nějaké jiné políčko. Takto pokračujeme, ale protože je políček jen 2015, musela někdy nějaká věž skočit na políčko 1, čímž nám vznikl cyklus. A my si přesouvání věží rozdělíme na takové cykly. 5 Každá věž mohla skočit o ±2 nebo o ±1 políčko. Aby se cyklus uzavřel, musí být součet skoků 0, což je sudé číslo. Takže počet skoků o 1 musel být sudý. A to platí pro každý cyklus, tedy celkový počet skoků o 1 ve všech řádcích musel být sudý. Proto skoků o 2 byl lichý počet (protože dohromady jich bylo 2015). Ale tutéž úvahu můžeme udělat, pokud si šachovnici promítneme na osu y. Každý kůň skočí o 2 ve směru jedné osy a o 1 ve směru druhé, neboli pokud ve směru x skočil o 2, skočí ve směru y o 1 a opačně. Podle předchozí úvahy ve směru y skočil lichý počet koňů o 1. Ale to je spor, protože aby se neohrožovali, musel by jich o 1 skočit sudý počet. Úloha byla na sedmičku poměrně jednoduchá a tomu také odpovídá počet došlých řešení. Několik řešitelů tvrdilo, že jediné možné vyhovující rozmístění je diagonální, což není pravda (dokonce existuje 2015! vyhovujících rozmístění). 6 Mnoho řešení se snažilo ukázat, že pro nějaké konkrétní rozložení věží se je přesunout nepovede, ale úloha chtěla dokázat, že pro každé vyhovující rozložení věží a každou variantu jejich skoků se nakonec budou nějaké dvě ohrožovat. To je častá chyba v chápání úlohy, dávejte si na to pozor, zbytečně pak ztrácíte body. (Matěj Konečný) Úloha 8. Kouzelníci Štěpán a David si pro Rada připravili trik s šachovnicí n n. Nejprve David odešel pryč, aby nic neviděl ani neslyšel. Poté Štěpán Radovi nakázal, ať na každé políčko položí dle své vůle buď bílý, nebo černý knoflík. Následně ho nechal, aby zvolil libovolné políčko A a sdělil mu, které to je. Nato si Štěpán vybral políčko B (ne nutně různé od A) a změnil barvu knoflíku, který na B ležel. Když potom přišel David, byl schopný pouze z pohledu na šachovnici uhodnout, které políčko A si Rado vybral. Pro která n je tento trik proveditelný? (Rado Švarc) Nejprve předpokládejme, že je možné trik uskutečnit pro šachovnici n n. Jakýkoliv způsob, jakým je možné rozmístit knoflíky na šachovnici, budeme nazývat konfigurací. David je schopen z pouhého pohledu na šachovnici zjistit, které políčko si Rado vybral. Nechť S P je množina všech konfigurací, podle kterých David pozná, že si Rado vybral políčko P. Protože David je schopný se jednoznačně rozhodnout, jsou všechny tyto množiny disjunktní. Nechť M je to políčko šachovnice, které má nejmenší množinu S M. Protože políček je n 2, existuje 2 n2 možných konfigurací. Protože žádná konfigurace neleží ve dvou množinách, každá množina má velikost alespoň S M a celkem je jich n 2, platí n 2 S M 2 n2. 5 Skoky věží odpovídají nějaké permutaci a my pracujeme s jejím rozkladem na cykly. 6 n! se čte n faktoriál a značí to součin n. 8
9 Pro každou konfiguraci z S M existuje n 2 konfigurací, které se od ní liší jen v barvě jednoho knoflíku. Takže celkově je maximálně n 2 S M konfigurací, které se liší jen o jedna od nějaké konfigurace z S M. Ovšem aby byl trik uskutečnitelný i v případě, že si Rado vybere M, musí pro každou konfiguraci existovat konfigurace z S M, která se od ní liší jen v barvě jednoho knoflíku. Protože konfigurací je 2 n2, dostáváme vztah n 2 S M 2 n2. Porovnáním těchto dvou nerovností dostáváme n 2 S M = 2 n2, takže n 2 n2. To znamená, že n musí být mocnina dvou. Nyní ukážeme, že pokud n = 2 k pro nějaké nezáporné celé k, je trik už proveditelný. Pro n = 1 je to lehké David ví, že si Rado zvolil to jediné políčko, které na šachovnici je. Předpokládejme dále, že n > 1. Ukážeme si dva různé způsoby, jak řešení dokončit. Řešení XORem: Budeme používat takzvaný XOR. Nechť a a b jsou nezáporná celá čísla, která se v binární soustavě zapíšou jako a 1 a 2... a k a b 1 b 2... b k (pokud nemají stejný počet cifer, tak to menší doplníme zleva nulami). Pro každé i od jedné do k nechť c i = 0, pokud a i = b i, a c i = 1 v opačném případě. Potom XOR a a b zadefinujeme jako takové číslo a b, které se v binární soustavě zapíše jako c 1 c 2... c k. Například 12 5 = = = 9. Povšimněme si, že a a = 0, a pokud a b = c, pak a c = b. Políčka na šachovnici si označíme čísly od 0 do 2 2k 1. Potom Štěpán s Davidem postupují následovně: Nechť x je XOR čísel všech políček, na které Rado položil černý knoflík a nechť a je číslo políčka A. Potom Štěpán změní barvu knoflíku na políčku s číslem x a (takové existuje, protože na šachovnici jsou právě všechna políčka, jejichž čísla mají 2k nebo méně cifer). Po této změně bude XOR čísel všech políček s černým knoflíkem roven x (x a) = a. Proto si David pouze spočítá XOR všech políček s černým knoflíkem a dostane A. Řešení půlením intervalů (podle Františka Coufa): Všechna políčka šachovnice si pomyslně poskládáme za sebe a vytvoříme pole délky n 2. To rozdělíme na dvě souvislé části, přičemž levou nazveme M 1. Následně si každou z částí rozdělíme na dvě a levé půlky obou vložíme do množiny M 2. Poté opět každý interval rozdělíme na dvě poloviny a ty levé vložíme do M 3. Postupujeme dál a dál, dokud intervaly nejsou velikosti 1. K těm se dostaneme po 2k 1 krocích. Níže uvedený obrázek prezentuje dělení pro šachovnici o šestnácti políčkách, přičemž M i je tvořena všemi šedými částmi v příslušném řádku. M 1 M 2 M 3 M 4 David po příchodu k šachovnici bude postupovat následujícím algoritmem: pokud je v M i sudý počet černých knoflíků, přesune se v i-tém kroku do levé poloviny intervalu, ve kterém právě je, jinak se přesune do pravé. Na příkladu na obrázku vidíme, že v M 1, M 2, M 3 a M 4 jsou postupně 4, 5, 4 a 4 černé knoflíky, a proto se David přesouvá doleva, doprava, doleva a doleva. Za odpověď zvolí to políčko, na kterém skončil. Stačí nám tedy ukázat, že Štěpán umí změnit jeden knoflík tak, aby David skončil přesně na tom políčku, které Rado zvolil. Štěpán ví, jakou posloupnost příkazů doleva a doprava musí David 9
10 vykonat. Proto se podívá, zda by ho v i-tém kroku současná konfigurace posílala na správnou, nebo špatnou stranu. Pokud na špatnou, zapamatuje si množinu M i, jinak si zapamatuje její doplněk. Chce, aby knoflík, který změní, byl ve všech zapamatovaných množinách. Ovšem pomocí jednoduché indukce se lehce ukáže, že průnik prvních i zapamatovaných množin má průnik právě v jednom intervalu délky 2 2k i. Skutečně, pro i = 1 toto platí, a pokud tvrzení platí pro i, pak průnik prvních i+1 zapamatovaných množin je buď levá, nebo pravá půlka průniku prvních i množin. To znamená, že průnik všech množin je interval délky 1, a tudíž Štěpán skutečně najde knoflík, jehož přebarvením se změní parita počtu černých knoflíků právě těch intervalů, které posílaly Davida na špatnou stranu. Díky tomu David najde správné políčko. Úloha byla na osmičku spíše lehká, a protože sestávala ze dvou částí, mnoho řešitelů skutečně tu lehčí vyřešila. Často se ale neshodli na tom, která to je. Krom dvou nastíněných řešení (rozmyslete si, že jde vlastně o to samé řešení, jen jinak zapsané), se objevilo ještě třetí, které úlohu převedlo na obarvování grafu hyperkrychle Q 2 k, což dořešilo indukcí. (Rado Švarc) 10
3. podzimní série Termín odeslání: 7. prosince Upozorňujeme, že první seriálová série má datum odeslání společný s touto sérií.
 Úlohy na šachovnici 3. podzimní série Termín odeslání: 7. prosince 2015 Upozorňujeme, že první seriálová série má datum odeslání společný s touto sérií. Úloha 1. (3 body) Rozmístětenašachovnici6 6čtyřitchýně
Úlohy na šachovnici 3. podzimní série Termín odeslání: 7. prosince 2015 Upozorňujeme, že první seriálová série má datum odeslání společný s touto sérií. Úloha 1. (3 body) Rozmístětenašachovnici6 6čtyřitchýně
Tento text je stručným shrnutím těch tvrzení Ramseyovy teorie, která zazněla
 Ramseyovy věty Martin Mareš Tento text je stručným shrnutím těch tvrzení Ramseyovy teorie, která zazněla na mé letošní přednášce z Kombinatoriky a grafů I Předpokládá, že čtenář se již seznámil se základní
Ramseyovy věty Martin Mareš Tento text je stručným shrnutím těch tvrzení Ramseyovy teorie, která zazněla na mé letošní přednášce z Kombinatoriky a grafů I Předpokládá, že čtenář se již seznámil se základní
zejména Dijkstrův algoritmus pro hledání minimální cesty a hladový algoritmus pro hledání minimální kostry.
 Kapitola Ohodnocené grafy V praktických aplikacích teorie grafů zpravidla graf slouží jako nástroj k popisu nějaké struktury. Jednotlivé prvky této struktury mají často přiřazeny nějaké hodnoty (může jít
Kapitola Ohodnocené grafy V praktických aplikacích teorie grafů zpravidla graf slouží jako nástroj k popisu nějaké struktury. Jednotlivé prvky této struktury mají často přiřazeny nějaké hodnoty (může jít
Jak pracovat s absolutními hodnotami
 Jak pracovat s absolutními hodnotami Petr Matyáš 1 Co to je absolutní hodnota Absolutní hodnota čísla a, dále ji budeme označovat výrazem a, je jeho vzdálenost od nuly na ose x, tedy je to vždy číslo kladné.
Jak pracovat s absolutními hodnotami Petr Matyáš 1 Co to je absolutní hodnota Absolutní hodnota čísla a, dále ji budeme označovat výrazem a, je jeho vzdálenost od nuly na ose x, tedy je to vždy číslo kladné.
Karnaughovy mapy. Pravdivostní tabulka pro tři vstupní proměnné by mohla vypadat například takto:
 Karnaughovy mapy Metoda je použitelná již pro dvě vstupní proměnné, své opodstatnění ale nachází až s větším počtem vstupů, kdy návrh takového výrazu přestává být triviální. Prvním krokem k sestavení logického
Karnaughovy mapy Metoda je použitelná již pro dvě vstupní proměnné, své opodstatnění ale nachází až s větším počtem vstupů, kdy návrh takového výrazu přestává být triviální. Prvním krokem k sestavení logického
Úloha 1A (5 bodů): vyhovuje Úloha 2A (6 bodů): Obrázek 1 Přelévání mléka
 Kategorie mladší Úloha 1A (5 bodů): Jako první využijeme Žofinčin postřeh. Díky němu se nám totiž celá úloha podstatně zjednoduší. Žofinka říká, ať nehledáme 6 nezávislých cifer, ale pouze 3. Poznávací
Kategorie mladší Úloha 1A (5 bodů): Jako první využijeme Žofinčin postřeh. Díky němu se nám totiž celá úloha podstatně zjednoduší. Žofinka říká, ať nehledáme 6 nezávislých cifer, ale pouze 3. Poznávací
Výsledek. Nejméně 14 kostek, nejvíce 38. Návod. Když se podíváme na stavbu shora, vidíme následující tabulku:
 Vzorová řešení Náboj Úloha. Kvádr s délkami hran, a, a má povrch 5. Najděte hodnotu čísla a. Výsledek.. Návod. Povrch kvádru s hranami délek x, y, z je P = xy + xz + zy. Po dosazení 5 = a + a + a můžeme
Vzorová řešení Náboj Úloha. Kvádr s délkami hran, a, a má povrch 5. Najděte hodnotu čísla a. Výsledek.. Návod. Povrch kvádru s hranami délek x, y, z je P = xy + xz + zy. Po dosazení 5 = a + a + a můžeme
1 Zadání Zadání- Náboj 2010 Úloha1.Kvádrsdélkamihran1, a,2amápovrch54.najdětehodnotučísla a.
 Úloha1.Kvádrsdélkamihran1, a,2amápovrch54.najdětehodnotučísla a. Úloha2.Pomocíprávětříosmičekalibovolnýchzesymbolů+,,,/, vytvořtečíslo3.jedensymbol můžete použít i víckrát. Úloha3.Vejtekmělknihuzteoriemnožin,jejížlistybylyčíslovanépostupně0,1,2,3,...
Úloha1.Kvádrsdélkamihran1, a,2amápovrch54.najdětehodnotučísla a. Úloha2.Pomocíprávětříosmičekalibovolnýchzesymbolů+,,,/, vytvořtečíslo3.jedensymbol můžete použít i víckrát. Úloha3.Vejtekmělknihuzteoriemnožin,jejížlistybylyčíslovanépostupně0,1,2,3,...
Intervalové stromy. Představme si, že máme posloupnost celých čísel p 0, p 1,... p N 1, se kterou budeme. 1. Změna jednoho čísla v posloupnosti.
 Intervalové stromy Představme si, že máme posloupnost celých čísel p 0, p 1,... p N 1, se kterou budeme průběžně provádět tyto dvě operace: 1. Změna jednoho čísla v posloupnosti. 2. Zjištění součtu čísel
Intervalové stromy Představme si, že máme posloupnost celých čísel p 0, p 1,... p N 1, se kterou budeme průběžně provádět tyto dvě operace: 1. Změna jednoho čísla v posloupnosti. 2. Zjištění součtu čísel
Kapitola 11. Vzdálenost v grafech. 11.1 Matice sousednosti a počty sledů
 Kapitola 11 Vzdálenost v grafech V každém grafu lze přirozeným způsobem definovat vzdálenost libovolné dvojice vrcholů. Hlavním výsledkem této kapitoly je překvapivé tvrzení, podle kterého lze vzdálenosti
Kapitola 11 Vzdálenost v grafech V každém grafu lze přirozeným způsobem definovat vzdálenost libovolné dvojice vrcholů. Hlavním výsledkem této kapitoly je překvapivé tvrzení, podle kterého lze vzdálenosti
Součin matice A a čísla α definujeme jako matici αa = (d ij ) typu m n, kde d ij = αa ij pro libovolné indexy i, j.
 Kapitola 3 Počítání s maticemi Matice stejného typu můžeme sčítat a násobit reálným číslem podobně jako vektory téže dimenze. Definice 3.1 Jsou-li A (a ij ) a B (b ij ) dvě matice stejného typu m n, pak
Kapitola 3 Počítání s maticemi Matice stejného typu můžeme sčítat a násobit reálným číslem podobně jako vektory téže dimenze. Definice 3.1 Jsou-li A (a ij ) a B (b ij ) dvě matice stejného typu m n, pak
GRAFY A GRAFOVÉ ALGORITMY
 KATEDRA INFORMATIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITA PALACKÉHO GRAFY A GRAFOVÉ ALGORITMY ARNOŠT VEČERKA VÝVOJ TOHOTO UČEBNÍHO TEXTU JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ
KATEDRA INFORMATIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITA PALACKÉHO GRAFY A GRAFOVÉ ALGORITMY ARNOŠT VEČERKA VÝVOJ TOHOTO UČEBNÍHO TEXTU JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ
Lenka Zalabová. Ústav matematiky a biomatematiky, Přírodovědecká fakulta, Jihočeská univerzita. zima 2012
 Algebra - třetí díl Lenka Zalabová Ústav matematiky a biomatematiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích zima 2012 Obsah 1 Dělitelnost 2 Grupy zbytkových tříd 3 Jedna z
Algebra - třetí díl Lenka Zalabová Ústav matematiky a biomatematiky, Přírodovědecká fakulta, Jihočeská univerzita v Českých Budějovicích zima 2012 Obsah 1 Dělitelnost 2 Grupy zbytkových tříd 3 Jedna z
KOMPLEXNÍ ČÍSLA INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ. Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky
 KOMPLEXNÍ ČÍSLA Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu INVESTICE
KOMPLEXNÍ ČÍSLA Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu INVESTICE
Determinant. Definice determinantu. Permutace. Permutace, vlastnosti. Definice: Necht A = (a i,j ) R n,n je čtvercová matice.
 [] Definice determinantu BI-LIN, determinant, 9, P Olšák [2] Determinant je číslo jistým způsobem charakterizující čtvercovou matici det A 0 pro singulární matici, det A 0 pro regulární matici používá
[] Definice determinantu BI-LIN, determinant, 9, P Olšák [2] Determinant je číslo jistým způsobem charakterizující čtvercovou matici det A 0 pro singulární matici, det A 0 pro regulární matici používá
Úloha 2. Obdélník ABCDprotínákružnicivbodech E, F, G, H jakonaobrázku.jestližeplatí AE =3, DH =4a GH =5,určete EF. G C
 Úloha 1. Čitatel i jmenovatel Kennyho zlomku jsou přirozená čísla se součtem 2011. Hodnota zlomku jepřitommenšínež 1 3.Jakánejvětšímůžetatohodnotabýt? Úloha 2. Obdélník Dprotínákružnicivbodech E, F, G,
Úloha 1. Čitatel i jmenovatel Kennyho zlomku jsou přirozená čísla se součtem 2011. Hodnota zlomku jepřitommenšínež 1 3.Jakánejvětšímůžetatohodnotabýt? Úloha 2. Obdélník Dprotínákružnicivbodech E, F, G,
1. jarní série. Barevné úlohy
 Téma: Datumodeslání: 1. jarní série Barevné úlohy ½ º ÒÓÖ ¾¼½¼ ½º ÐÓ Ó Ýµ Háňa má krychli, jejíž stěny jsou tvořeny barevnými skly. Když se Háňa na svou kostku podívá jako na obrázku, vidí v každé ze sedmi
Téma: Datumodeslání: 1. jarní série Barevné úlohy ½ º ÒÓÖ ¾¼½¼ ½º ÐÓ Ó Ýµ Háňa má krychli, jejíž stěny jsou tvořeny barevnými skly. Když se Háňa na svou kostku podívá jako na obrázku, vidí v každé ze sedmi
Sbírka příkladů. verze 1.0 2.1.2005
 Sbírka příkladů verze 1.0 2.1.2005 Rudolf Kryl Sbírka má pomoci studentům k přípravě na praktický test. Student, který umí programovat, umí ladit a zvládne algoritmicky úlohy této sbírky by neměl mít s
Sbírka příkladů verze 1.0 2.1.2005 Rudolf Kryl Sbírka má pomoci studentům k přípravě na praktický test. Student, který umí programovat, umí ladit a zvládne algoritmicky úlohy této sbírky by neměl mít s
3. ročník, 2013/ 2014 Mezinárodní korespondenční seminář iks
 Řešení 3. série Úloha C3. Rovnostranný trojúhelník o straně délky n je vyplněný jednotkovou trojúhelníčkovou mřížkou. Uzavřená lomená čára vede podél této mřížky a každý vrchol mřížky potká právě jednou.
Řešení 3. série Úloha C3. Rovnostranný trojúhelník o straně délky n je vyplněný jednotkovou trojúhelníčkovou mřížkou. Uzavřená lomená čára vede podél této mřížky a každý vrchol mřížky potká právě jednou.
A0M15EZS Elektrické zdroje a soustavy ZS 2011/2012 cvičení 1. Jednotková matice na hlavní diagonále jsou jedničky, všude jinde nuly
 Matice Matice typu (m, n) je uspořádaná m-tice prvků z řádky matice.. Jednotlivé složky této m-tice nazýváme Matice se zapisují Speciální typy matic Nulová matice všechny prvky matice jsou nulové Jednotková
Matice Matice typu (m, n) je uspořádaná m-tice prvků z řádky matice.. Jednotlivé složky této m-tice nazýváme Matice se zapisují Speciální typy matic Nulová matice všechny prvky matice jsou nulové Jednotková
VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE. Optimalizace trasy při revizích elektrospotřebičů
 VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE FAKULTA INFORMATIKY A STATISTIKY Hlavní specializace: Ekonometrie a operační výzkum Název diplomové práce Optimalizace trasy při revizích elektrospotřebičů Diplomant: Vedoucí
VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE FAKULTA INFORMATIKY A STATISTIKY Hlavní specializace: Ekonometrie a operační výzkum Název diplomové práce Optimalizace trasy při revizích elektrospotřebičů Diplomant: Vedoucí
Eufrat a Tigris HRACÍ MATERIÁL PŘÍPRAVA NA HRU. Sestavení monumentů. Příprava hrací desky. Výběr dynastie
 HRACÍ MATERIÁL Eufrat a Tigris 1 hrací deska 153 civilizačních kartiček - 30 černých osady - 57 červených chrámy - 36 modrých farmy - 30 zelených tržiště 8 kartiček katastrof 4 spojovací kartičky 4 kartičky
HRACÍ MATERIÁL Eufrat a Tigris 1 hrací deska 153 civilizačních kartiček - 30 černých osady - 57 červených chrámy - 36 modrých farmy - 30 zelených tržiště 8 kartiček katastrof 4 spojovací kartičky 4 kartičky
Počítačové zpracování obrazu Projekt Učíme se navzájem
 Počítačové zpracování obrazu Projekt Učíme se navzájem Tomáš Pokorný, Vojtěch Přikryl Jaroška 15. ledna 2010 Tomáš Pokorný email: xtompok@gmail.com Jaroška 1 Obsah Abstrakt! 4 Začátky! 5 M&M 5 Původní
Počítačové zpracování obrazu Projekt Učíme se navzájem Tomáš Pokorný, Vojtěch Přikryl Jaroška 15. ledna 2010 Tomáš Pokorný email: xtompok@gmail.com Jaroška 1 Obsah Abstrakt! 4 Začátky! 5 M&M 5 Původní
13. Třídící algoritmy a násobení matic
 13. Třídící algoritmy a násobení matic Minulou přednášku jsme probírali QuickSort, jeden z historicky prvních třídících algoritmů, které překonaly kvadratickou složitost aspoň v průměrném případě. Proč
13. Třídící algoritmy a násobení matic Minulou přednášku jsme probírali QuickSort, jeden z historicky prvních třídících algoritmů, které překonaly kvadratickou složitost aspoň v průměrném případě. Proč
0. Lineární rekurence Martin Mareš, 2010-07-04
 0 Lineární rekurence Martin Mareš, 2010-07-04 V tomto krátkém textu se budeme zabývat lineárními rekurencemi, tj posloupnostmi definovanými rekurentní rovnicí typu A n+k = c 0 A n + c 1 A n+1 + + c k 1
0 Lineární rekurence Martin Mareš, 2010-07-04 V tomto krátkém textu se budeme zabývat lineárními rekurencemi, tj posloupnostmi definovanými rekurentní rovnicí typu A n+k = c 0 A n + c 1 A n+1 + + c k 1
P1 Formule ve sněhu. P2 Double Cola
 P1 Formule ve sněhu Jak je obecně známo, losi mají spoustu různých zálib. Není tedy velkým překvapením, že existují losi, kteří se vyžívají v matematických prapodivnostech. Jeden takový los přišel s následující
P1 Formule ve sněhu Jak je obecně známo, losi mají spoustu různých zálib. Není tedy velkým překvapením, že existují losi, kteří se vyžívají v matematických prapodivnostech. Jeden takový los přišel s následující
Obrázek 1 Rozdělení pozemků
 Kategorie mladší Úloha A (5 bodů): Jak bylo řečeno v zadání, životní nároky různých zvířátek se liší. Některá potřebují obrovské teritorium, zatímco jiným stačí pozemek o velikosti jediného políčka. Jedno
Kategorie mladší Úloha A (5 bodů): Jak bylo řečeno v zadání, životní nároky různých zvířátek se liší. Některá potřebují obrovské teritorium, zatímco jiným stačí pozemek o velikosti jediného políčka. Jedno
Regulární matice. Věnujeme dále pozornost zejména čtvercovým maticím.
 Regulární matice Věnujeme dále pozornost zejména čtvercovým maticím. Věta. Pro každou čtvercovou matici A = (a ij ) řádu n nad tělesem (T, +, ) jsou následující podmínky ekvivalentní: (i) Řádky matice
Regulární matice Věnujeme dále pozornost zejména čtvercovým maticím. Věta. Pro každou čtvercovou matici A = (a ij ) řádu n nad tělesem (T, +, ) jsou následující podmínky ekvivalentní: (i) Řádky matice
Skalární součin je nástroj, jak měřit velikost vektorů a úhly mezi vektory v reálných a komplexních vektorových prostorech.
 Kapitola 9 Skalární součin Skalární součin je nástroj, jak měřit velikost vektorů a úhly mezi vektory v reálných a komplexních vektorových prostorech. Definice 9.1 Je-li x = (x 1,..., x n ) T R n 1 reálný
Kapitola 9 Skalární součin Skalární součin je nástroj, jak měřit velikost vektorů a úhly mezi vektory v reálných a komplexních vektorových prostorech. Definice 9.1 Je-li x = (x 1,..., x n ) T R n 1 reálný
Predispozice pro výuku IKT (2015/2016)
 Konzervatoř P. J. Vejvanovského Kroměříž Predispozice pro výuku IKT (15/16) Základní algoritmy pro počítání s celými a racionálními čísly Adam Šiška 1 Sčítání dvou kladných celých čísel Problém: Jsou dána
Konzervatoř P. J. Vejvanovského Kroměříž Predispozice pro výuku IKT (15/16) Základní algoritmy pro počítání s celými a racionálními čísly Adam Šiška 1 Sčítání dvou kladných celých čísel Problém: Jsou dána
UNIVERSITA PALACKÉHO V OLOMOUCI PŘÍRODOVĚDECKÁ FAKULTA. KATEDRA MATEMATICKÉ ANALÝZY A APLIKACÍ MATEMATIKY školní rok 2009/2010 BAKALÁŘSKÁ PRÁCE
 UNIVERSITA PALACKÉHO V OLOMOUCI PŘÍRODOVĚDECKÁ FAKULTA KATEDRA MATEMATICKÉ ANALÝZY A APLIKACÍ MATEMATIKY školní rok 2009/2010 BAKALÁŘSKÁ PRÁCE Testy dobré shody Vedoucí diplomové práce: RNDr. PhDr. Ivo
UNIVERSITA PALACKÉHO V OLOMOUCI PŘÍRODOVĚDECKÁ FAKULTA KATEDRA MATEMATICKÉ ANALÝZY A APLIKACÍ MATEMATIKY školní rok 2009/2010 BAKALÁŘSKÁ PRÁCE Testy dobré shody Vedoucí diplomové práce: RNDr. PhDr. Ivo
Teorie informace a kódování (KMI/TIK)
 Teorie informace a kódování (KMI/TIK) Bezpečnostní kódy Lukáš Havrlant Univerzita Palackého 13. listopadu 2012 Konzultace V pracovně 5.076. Každý čtvrtek 9.00 11.00. Emaily: lukas@havrlant.cz lukas.havrlant@upol.cz
Teorie informace a kódování (KMI/TIK) Bezpečnostní kódy Lukáš Havrlant Univerzita Palackého 13. listopadu 2012 Konzultace V pracovně 5.076. Každý čtvrtek 9.00 11.00. Emaily: lukas@havrlant.cz lukas.havrlant@upol.cz
1. série. Pohádky. Téma: Datumodeslání:
 Téma: Datumodeslání: º Ò ¾¼¼ 1. série Pohádky ½º ÐÓ Ó Ýµ ¾º ÐÓ Ó Ýµ Princezna si dělá pořádek ve svých truhličkách. Vysype na stůl do dvou hromádek drahokamy º ÐÓ Ó Ýµ naprvníjichje17,nadruhé10.pokaždé,kdyžnaberezjednéhromádkydorukykameny(vždy
Téma: Datumodeslání: º Ò ¾¼¼ 1. série Pohádky ½º ÐÓ Ó Ýµ ¾º ÐÓ Ó Ýµ Princezna si dělá pořádek ve svých truhličkách. Vysype na stůl do dvou hromádek drahokamy º ÐÓ Ó Ýµ naprvníjichje17,nadruhé10.pokaždé,kdyžnaberezjednéhromádkydorukykameny(vždy
Vektory a matice. Obsah. Aplikovaná matematika I. Carl Friedrich Gauss. Základní pojmy a operace
 Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
8. Geometrie vrací úder (sepsal Pavel Klavík)
 8. Geometrie vrací úder (sepsal Pavel Klavík) Když s geometrickými problémy pořádně nezametete, ony vám to vrátí! Ale když užzametat,takurčitěnepodkoberecamístosmetákupoužijtepřímku.vtéto přednášce nás
8. Geometrie vrací úder (sepsal Pavel Klavík) Když s geometrickými problémy pořádně nezametete, ony vám to vrátí! Ale když užzametat,takurčitěnepodkoberecamístosmetákupoužijtepřímku.vtéto přednášce nás
Poté hráči spočtou své Body prestiže a vítězem se stává ten, kdo jich nashromáždil nejvíce.
 Pravidla hry Rokoko Cíl hry V Rokoku se stáváte majitelem oděvnické dílny na dvoře francouzského krále Ludvíka XV., kde se snažíte získat co nejvíce prestiže. Během každého tahu zahrajete kartu jednoho
Pravidla hry Rokoko Cíl hry V Rokoku se stáváte majitelem oděvnické dílny na dvoře francouzského krále Ludvíka XV., kde se snažíte získat co nejvíce prestiže. Během každého tahu zahrajete kartu jednoho
Edita Kolářová ÚSTAV MATEMATIKY
 Přípravný kurs z matematik Edita Kolářová ÚSTAV MATEMATIKY Přípravný kurs z matematik 1 Obsah 1 Přehled použité smbolik 3 Základní pojm matematické logik a teorie množin 4.1 Element matematické logik.........................
Přípravný kurs z matematik Edita Kolářová ÚSTAV MATEMATIKY Přípravný kurs z matematik 1 Obsah 1 Přehled použité smbolik 3 Základní pojm matematické logik a teorie množin 4.1 Element matematické logik.........................
METODICKÉ LISTY Z MATEMATIKY pro gymnázia a základní vzdělávání
 METODICKÉ LISTY Z MATEMATIKY pro gymnázia a základní vzdělávání Jaroslav Švrček a kolektiv Rámcový vzdělávací program pro gymnázia Vzdělávací oblast: Matematika a její aplikace Tematický okruh: Práce s
METODICKÉ LISTY Z MATEMATIKY pro gymnázia a základní vzdělávání Jaroslav Švrček a kolektiv Rámcový vzdělávací program pro gymnázia Vzdělávací oblast: Matematika a její aplikace Tematický okruh: Práce s
1. K o m b i n a t o r i k a
 . K o m b i a t o r i k a V teorii pravděpodobosti a statistice budeme studovat míru výskytu -pravděpodobostvýsledků procesů, které mají áhodý charakter, t.j. při opakováí za stejých podmíek se objevují
. K o m b i a t o r i k a V teorii pravděpodobosti a statistice budeme studovat míru výskytu -pravděpodobostvýsledků procesů, které mají áhodý charakter, t.j. při opakováí za stejých podmíek se objevují
Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice
 Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice Vektorové podprostory K množina reálných nebo komplexních čísel, U vektorový prostor nad K. Lineární kombinace vektorů u 1, u 2,...,u
Vektorové podprostory, lineární nezávislost, báze, dimenze a souřadnice Vektorové podprostory K množina reálných nebo komplexních čísel, U vektorový prostor nad K. Lineární kombinace vektorů u 1, u 2,...,u
Náhodný pokus každá opakovatelná činnost, prováděná za stejných nebo přibližně stejných podmínek, jejíž výsledek je nejistý a závisí na náhodě.
 Základy teorie pravděpodobnosti Náhodný pokus každá opakovatelná činnost, prováděná za stejných nebo přibližně stejných podmínek, jejíž výsledek je nejistý a závisí na náhodě. Náhodný jev jakékoli tvrzení
Základy teorie pravděpodobnosti Náhodný pokus každá opakovatelná činnost, prováděná za stejných nebo přibližně stejných podmínek, jejíž výsledek je nejistý a závisí na náhodě. Náhodný jev jakékoli tvrzení
2 Spojité modely rozhodování
 2 Spojité modely rozhodování Jak již víme z přednášky, diskrétní model rozhodování lze zapsat ve tvaru úlohy hodnocení variant: f(a i ) max, a i A = {a 1, a 2,... a p }, kde f je kriteriální funkce a A
2 Spojité modely rozhodování Jak již víme z přednášky, diskrétní model rozhodování lze zapsat ve tvaru úlohy hodnocení variant: f(a i ) max, a i A = {a 1, a 2,... a p }, kde f je kriteriální funkce a A
Vrcholová barevnost grafu
 Vrcholová barevnost grafu Definice: Necht G = (V, E) je obyčejný graf a k N. Zobrazení φ : V {1, 2,..., k} nazýváme k-vrcholovým obarvením grafu G. Pokud φ(u) φ(v) pro každou hranu {u, v} E, nazveme k-vrcholové
Vrcholová barevnost grafu Definice: Necht G = (V, E) je obyčejný graf a k N. Zobrazení φ : V {1, 2,..., k} nazýváme k-vrcholovým obarvením grafu G. Pokud φ(u) φ(v) pro každou hranu {u, v} E, nazveme k-vrcholové
přirozený algoritmus seřadí prvky 1,3,2,8,9,7 a prvky 4,5,6 nechává Metody řazení se dělí:
 Metody řazení ve vnitřní a vnější paměti. Algoritmy řazení výběrem, vkládáním a zaměňováním. Heapsort, Shell-sort, Radix-sort, Quicksort. Řazení sekvenčních souborů. Řazení souborů s přímým přístupem.
Metody řazení ve vnitřní a vnější paměti. Algoritmy řazení výběrem, vkládáním a zaměňováním. Heapsort, Shell-sort, Radix-sort, Quicksort. Řazení sekvenčních souborů. Řazení souborů s přímým přístupem.
STROMOVE ALGORITMY Prohledavani do sirky (level-order) Po vodorovnejch carach fronta
 STROMOVE ALGORITMY Prohledavani do sirky (level-order) Po vodorovnejch carach vlož do fronty kořen opakuj, dokud není fronta prázdná 1. vyber uzel z fronty a zpracuj jej 2. vlož do fronty levého následníka
STROMOVE ALGORITMY Prohledavani do sirky (level-order) Po vodorovnejch carach vlož do fronty kořen opakuj, dokud není fronta prázdná 1. vyber uzel z fronty a zpracuj jej 2. vlož do fronty levého následníka
Mgr. Karel Pazourek. online prostředí, Operační program Praha Adaptabilita, registrační číslo CZ.2.17/3.1.00/31165.
 Mnohočleny z různých stran Mgr. Karel Pazourek Kurz vznikl v rámci projektu Rozvoj systému vzdělávacích příležitostí pro nadané žáky a studenty v přírodních vědách a matematice s využitím online prostředí,
Mnohočleny z různých stran Mgr. Karel Pazourek Kurz vznikl v rámci projektu Rozvoj systému vzdělávacích příležitostí pro nadané žáky a studenty v přírodních vědách a matematice s využitím online prostředí,
Skalár- veličina určená jedním číselným údajem čas, hmotnost (porovnej životní úroveň, hospodaření firmy, naše poloha podle GPS )
 LINEÁRNÍ ALGEBRA Úvod vektor Skalár- veličina určená jedním číselným údajem čas, hmotnost (porovnej životní úroveň, hospodaření firmy, naše poloha podle GPS ) Kartézský souřadnicový systém -je taková soustava
LINEÁRNÍ ALGEBRA Úvod vektor Skalár- veličina určená jedním číselným údajem čas, hmotnost (porovnej životní úroveň, hospodaření firmy, naše poloha podle GPS ) Kartézský souřadnicový systém -je taková soustava
. Určete hodnotu neznámé x tak, aby
 Fakulta informačních technologií ČVUT v Praze Přijímací zkouška z matematiky 015 Kód uchazeče ID:.................. Varianta: 1 1. Původní cena knihy byla 50 Kč. Pak byla zdražena o 15 %. Jelikož nešla
Fakulta informačních technologií ČVUT v Praze Přijímací zkouška z matematiky 015 Kód uchazeče ID:.................. Varianta: 1 1. Původní cena knihy byla 50 Kč. Pak byla zdražena o 15 %. Jelikož nešla
Funkce zadané implicitně
 Kapitola 8 Funkce zadané implicitně Začneme několika příklady. Prvním je známá rovnice pro jednotkovou kružnici x 2 + y 2 1 = 0. Tato rovnice popisuje křivku, kterou si však nelze představit jako graf
Kapitola 8 Funkce zadané implicitně Začneme několika příklady. Prvním je známá rovnice pro jednotkovou kružnici x 2 + y 2 1 = 0. Tato rovnice popisuje křivku, kterou si však nelze představit jako graf
Často potřebujeme hledat mezi dvěma vrcholy grafu cestu, která je v nějakém
 1. Nejkrat¹í cesty Často potřebujeme hledat mezi dvěma vrcholy grafu cestu, která je v nějakém smyslu optimální typicky nejkratší možná. Už víme, že prohledávání do šířky najde cestu s nejmenším počtem
1. Nejkrat¹í cesty Často potřebujeme hledat mezi dvěma vrcholy grafu cestu, která je v nějakém smyslu optimální typicky nejkratší možná. Už víme, že prohledávání do šířky najde cestu s nejmenším počtem
I. kolo kategorie Z5
 61. ročník Matematické olympiády I. kolo kategorie Z5 Z5 I 1 Tři kamarádi Pankrác, Servác a Bonifác šli o prázdninách na noční procházku přírodním labyrintem. U vstupu dostal každý svíčku a vydali se různými
61. ročník Matematické olympiády I. kolo kategorie Z5 Z5 I 1 Tři kamarádi Pankrác, Servác a Bonifác šli o prázdninách na noční procházku přírodním labyrintem. U vstupu dostal každý svíčku a vydali se různými
2 HRA V EXPLICITNÍM TVARU
 2 HRA V EXPLICITNÍM TVARU 59 Příklad 1 Hra Nim. Uvažujme jednoduchou hru, kdy dva hráči označme je čísly 1, 2 mají před sebou dvě hromádky, z nichž každá je tvořena dvěma fazolemi. Hráč 1 musí vzít z jedné
2 HRA V EXPLICITNÍM TVARU 59 Příklad 1 Hra Nim. Uvažujme jednoduchou hru, kdy dva hráči označme je čísly 1, 2 mají před sebou dvě hromádky, z nichž každá je tvořena dvěma fazolemi. Hráč 1 musí vzít z jedné
Přehled učiva matematiky 7. ročník ZŠ
 Přehled učiva matematiky 7. ročník ZŠ I. ARITMETIKA 1. Zlomky a racionální čísla Jestliže rozdělíme něco (= celek) na několik stejných dílů, nazývá se každá část celku zlomkem. Zlomek tři čtvrtiny = tři
Přehled učiva matematiky 7. ročník ZŠ I. ARITMETIKA 1. Zlomky a racionální čísla Jestliže rozdělíme něco (= celek) na několik stejných dílů, nazývá se každá část celku zlomkem. Zlomek tři čtvrtiny = tři
4. Lineární nerovnice a jejich soustavy
 4. Lineární nerovnice a jejich soustavy 9. ročník 4. Lineární nerovnice a jejich soustavy 5 > 0 ostrá nerovnost 5.0 50 neostrá nerovnost ( používáme pouze čísla) ZNAKY NEROVNOSTI: > je větší než < je menší
4. Lineární nerovnice a jejich soustavy 9. ročník 4. Lineární nerovnice a jejich soustavy 5 > 0 ostrá nerovnost 5.0 50 neostrá nerovnost ( používáme pouze čísla) ZNAKY NEROVNOSTI: > je větší než < je menší
Střední škola informačních technologií a sociální péče, Brno, Purkyňova 97. Vybrané části Excelu. Ing. Petr Adamec
 INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ Střední škola informačních technologií a sociální péče, Brno, Purkyňova 97 Vybrané části Excelu Ing. Petr Adamec Brno 2010 Cílem předmětu je seznámení se s programem Excel
INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ Střední škola informačních technologií a sociální péče, Brno, Purkyňova 97 Vybrané části Excelu Ing. Petr Adamec Brno 2010 Cílem předmětu je seznámení se s programem Excel
FAKULTA STAVEBNÍ VUT V BRNĚ PŘIJÍMACÍ ŘÍZENÍ PRO AKADEMICKÝ ROK 2003 2004
 PŘIJÍMACÍ ŘÍZENÍ PRO AKADEMICKÝ ROK 003 004 TEST Z MATEMATIKY PRO PŘIJÍMACÍ ZKOUŠKY ČÍSLO M 0030 Vyjádřete jedním desetinným číslem (4 ½ 4 ¼ ) (4 ½ + 4 ¼ ) Správné řešení: 0,5 Zjednodušte výraz : ( 4)
PŘIJÍMACÍ ŘÍZENÍ PRO AKADEMICKÝ ROK 003 004 TEST Z MATEMATIKY PRO PŘIJÍMACÍ ZKOUŠKY ČÍSLO M 0030 Vyjádřete jedním desetinným číslem (4 ½ 4 ¼ ) (4 ½ + 4 ¼ ) Správné řešení: 0,5 Zjednodušte výraz : ( 4)
Standardně máme zapnutý panel nástrojů Formátování a Standardní.
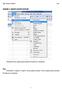 Zapnutí a vypnutí panelů nástrojů Standardně máme zapnutý panel nástrojů Formátování a Standardní. Úkol: Vyzkoušejte si zapnout a vypnout všechny panely nástrojů. Nechte zapnutý panely nástrojů Formátování
Zapnutí a vypnutí panelů nástrojů Standardně máme zapnutý panel nástrojů Formátování a Standardní. Úkol: Vyzkoušejte si zapnout a vypnout všechny panely nástrojů. Nechte zapnutý panely nástrojů Formátování
Přijímačky nanečisto - 2011
 Přijímačky nanečisto - 2011 1. Vypočtěte: 0,5 2 + (-0,5) 2 (- 0,1) 3 = a) 0,001 b) 0,51 c) 0,499 d) 0,501 2. Vypočtěte: a) 0,4 b) - 0,08 c) 2 3 d) 2 3. Určete číslo s tímto rozvinutým zápisem v desítkové
Přijímačky nanečisto - 2011 1. Vypočtěte: 0,5 2 + (-0,5) 2 (- 0,1) 3 = a) 0,001 b) 0,51 c) 0,499 d) 0,501 2. Vypočtěte: a) 0,4 b) - 0,08 c) 2 3 d) 2 3. Určete číslo s tímto rozvinutým zápisem v desítkové
Před první hrou setřiďte karty podle přiloženého pořadníku do drážek v krabici. 500 karet 130 karet peněz Název
 Něco visí ve vzduchu. Správce vypadá, jako by skrýval tajemství. Tvůj věrný sluha tě však varuje. Chystá se spiknutí. Tohle si přece nenecháš líbit. Vymysli vlastní plán, využij svého vlivu a známostí.
Něco visí ve vzduchu. Správce vypadá, jako by skrýval tajemství. Tvůj věrný sluha tě však varuje. Chystá se spiknutí. Tohle si přece nenecháš líbit. Vymysli vlastní plán, využij svého vlivu a známostí.
Gymnázium, Brno. Matice. Závěrečná maturitní práce. Jakub Juránek 4.A Školní rok 2010/11
 Gymnázium, Brno Matice Závěrečná maturitní práce Jakub Juránek 4.A Školní rok 2010/11 Konzultant: Mgr. Aleš Kobza Ph.D. Brno, 2011 Prohlášení Prohlašuji, že jsem předloženou práci zpracoval samostatně
Gymnázium, Brno Matice Závěrečná maturitní práce Jakub Juránek 4.A Školní rok 2010/11 Konzultant: Mgr. Aleš Kobza Ph.D. Brno, 2011 Prohlášení Prohlašuji, že jsem předloženou práci zpracoval samostatně
Brlohovská úloha za 2 body
 Brlohovská úloha za 2 body Určete, kolika nejméně barvami můžeme obarvit naše logo tak, aby žádné dvě sousední oblasti neměly stejnou barvu. Za sousední se považují oblasti, které mají společný více než
Brlohovská úloha za 2 body Určete, kolika nejméně barvami můžeme obarvit naše logo tak, aby žádné dvě sousední oblasti neměly stejnou barvu. Za sousední se považují oblasti, které mají společný více než
POČÍTAČOVÁ GRAFIKA VEKTOROVÁ GRAFIKA POKROČILÉ ČINNOSTI
 POČÍTAČOVÁ GRAFIKA VEKTOROVÁ GRAFIKA POKROČILÉ ČINNOSTI PASTELKA Naším dalším úkolem bude namalovat pastelku. Při tom si vyzkoušíme malování podle vodících linek, různé výplně, transformace i logické operace.
POČÍTAČOVÁ GRAFIKA VEKTOROVÁ GRAFIKA POKROČILÉ ČINNOSTI PASTELKA Naším dalším úkolem bude namalovat pastelku. Při tom si vyzkoušíme malování podle vodících linek, různé výplně, transformace i logické operace.
Marielle Seitz Napiš to do písku Hravé kreslení pro rozvoj koncentrace, jemné motoriky a koordinace pohybů
 Marielle Seitz Napiš to do písku Hravé kreslení pro rozvoj koncentrace, jemné motoriky a koordinace pohybů Téměř všichni lidé se cítí přitahování teplým, jemným pískem. Ve vlhkém stavu je písek hutný a
Marielle Seitz Napiš to do písku Hravé kreslení pro rozvoj koncentrace, jemné motoriky a koordinace pohybů Téměř všichni lidé se cítí přitahování teplým, jemným pískem. Ve vlhkém stavu je písek hutný a
Lineární algebra II. Adam Liška. 9. února 2015. Zápisky z přednášek Jiřího Fialy na MFF UK, letní semestr, ak. rok 2007/2008
 Lineární algebra II Zápisky z přednášek Jiřího Fialy na MFF UK, letní semestr, ak rok 2007/2008 Adam Liška 9 února 2015 http://kammffcunicz/~fiala http://wwwadliskacom 1 Obsah 10 Permutace 3 11 Determinant
Lineární algebra II Zápisky z přednášek Jiřího Fialy na MFF UK, letní semestr, ak rok 2007/2008 Adam Liška 9 února 2015 http://kammffcunicz/~fiala http://wwwadliskacom 1 Obsah 10 Permutace 3 11 Determinant
Tabulkové processory MS Excel (OpenOffice Calc)
 Maturitní téma: Tabulkové processory MS Excel (OpenOffice Calc) Charakteristika tabulkového editoru Tabulkový editor (sprematuritníadsheet) se používá všude tam, kde je třeba zpracovávat data uspořádaná
Maturitní téma: Tabulkové processory MS Excel (OpenOffice Calc) Charakteristika tabulkového editoru Tabulkový editor (sprematuritníadsheet) se používá všude tam, kde je třeba zpracovávat data uspořádaná
Maticové operace projekt č. 3
 Dokumentace k projektu pro předměty IZP a IUS Maticové operace projekt č. 3 9.12.2007 Autor: Václav Uhlíř, xuhlir04@stud.fit.vutbr.cz Fakulta Informačních Technologii Vysoké Učení Technické v Brně Obsah
Dokumentace k projektu pro předměty IZP a IUS Maticové operace projekt č. 3 9.12.2007 Autor: Václav Uhlíř, xuhlir04@stud.fit.vutbr.cz Fakulta Informačních Technologii Vysoké Učení Technické v Brně Obsah
(Auto)korelační funkce. 2. 11. 2015 Statistické vyhodnocování exp. dat M. Čada www.fzu.cz/ ~ cada
 (Auto)korelační funkce 1 Náhodné procesy Korelace mezi náhodnými proměnnými má široké uplatnění v elektrotechnické praxi, kde se snažíme o porovnávání dvou signálů, které by měly být stejné. Příkladem
(Auto)korelační funkce 1 Náhodné procesy Korelace mezi náhodnými proměnnými má široké uplatnění v elektrotechnické praxi, kde se snažíme o porovnávání dvou signálů, které by měly být stejné. Příkladem
Pokud není řečeno jinak, pro zápis čísel používáme desítkovou soustavu. V celé sérii jsou proměnné
 Cifry 3. jarní série Termín odeslání: 10. dubna 2017 Pokud není řečeno jinak, pro zápis čísel používáme desítkovou soustavu. V celé sérii jsou proměnné k a n přirozená čísla. Úloha 1. Nechť S(k) značí
Cifry 3. jarní série Termín odeslání: 10. dubna 2017 Pokud není řečeno jinak, pro zápis čísel používáme desítkovou soustavu. V celé sérii jsou proměnné k a n přirozená čísla. Úloha 1. Nechť S(k) značí
28.ročník. Milý řešiteli!
 28.ročník 3.leták Milý řešiteli! Máme tady nový rok a s ním i další sérii KOperníkova Korespondenčního Semináře. Chtěli bychom Ti v tomto roce popřát jen to nejlepší, hodně vyřešených matematických úloh
28.ročník 3.leták Milý řešiteli! Máme tady nový rok a s ním i další sérii KOperníkova Korespondenčního Semináře. Chtěli bychom Ti v tomto roce popřát jen to nejlepší, hodně vyřešených matematických úloh
MATEMATIKA vyšší úroveň obtížnosti
 MATEMATIKA vyšší úroveň obtížnosti DIDAKTICKÝ TEST MAIVD11C0T01 ILUSTRAČNÍ TEST Maximální bodové hodnocení: 50 bodů Hranice úspěšnosti: 33 % 1 Základní informace k zadání zkoušky Didaktický test obsahuje
MATEMATIKA vyšší úroveň obtížnosti DIDAKTICKÝ TEST MAIVD11C0T01 ILUSTRAČNÍ TEST Maximální bodové hodnocení: 50 bodů Hranice úspěšnosti: 33 % 1 Základní informace k zadání zkoušky Didaktický test obsahuje
TEORIE GRAFŮ. Petr Kovář
 TEORIE GRAFŮ Petr Kovář Text byl vytvořen v rámci realizace projektu Matematika pro inženýry 21. století (reg. č. CZ.1.07/2.2.00/07.0332), na kterém se společně podílela Vysoká škola báňská Technická univerzita
TEORIE GRAFŮ Petr Kovář Text byl vytvořen v rámci realizace projektu Matematika pro inženýry 21. století (reg. č. CZ.1.07/2.2.00/07.0332), na kterém se společně podílela Vysoká škola báňská Technická univerzita
Na začátku rozdělíme práci a určíme, které podproblémy je potřeba vyřešit. Tyto
 Kapitola 1 Rozděl a panuj Rozděl a panuj je programovací metoda. Často se označuje latinsky Divide et Empera nebo anglicky Divide and Conquer. Vychází z toho, že umíme zadaný problém rozložit na menší
Kapitola 1 Rozděl a panuj Rozděl a panuj je programovací metoda. Často se označuje latinsky Divide et Empera nebo anglicky Divide and Conquer. Vychází z toho, že umíme zadaný problém rozložit na menší
VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE. Model tahové hry s finančními odměnami
 VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE FAKULTA INFORMATIKY A STATISTIKY Obor: Statistika a ekonometrie Název bakalářské práce Model tahové hry s finančními odměnami Autor: Vedoucí bakalářské práce: Rok: 009 Markéta
VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE FAKULTA INFORMATIKY A STATISTIKY Obor: Statistika a ekonometrie Název bakalářské práce Model tahové hry s finančními odměnami Autor: Vedoucí bakalářské práce: Rok: 009 Markéta
Mária Sadloňová. Fajn MATIKA. 150 řešených příkladů (vzorek)
 Mária adloňová Fajn MATIKA (nejen) na přijímačky 50 řešených příkladů (vorek) 0 Mgr. Mária adloňová FajnMATIKA (nejen) na přijímačky 50 řešených příkladů (reklamní vorek) Mgr. Mária adloňová, 0 Vydavatel
Mária adloňová Fajn MATIKA (nejen) na přijímačky 50 řešených příkladů (vorek) 0 Mgr. Mária adloňová FajnMATIKA (nejen) na přijímačky 50 řešených příkladů (reklamní vorek) Mgr. Mária adloňová, 0 Vydavatel
1 z 7 18.6.2012 8:14. 1. otázka. Které číslo musíme odečíst od čísla 250, aby výsledné číslo bylo osminásobkem čísla 25? 2. otázka
 Stonožka 9 - M 2011 - náhled testu http://ib.scio.cz/test?t=ceow8rrhgtr79v2xq7/zcppky1fbxbzulq... 1 z 7 18.6.2012 8:14 1. otázka Které číslo musíme odečíst od čísla 250, aby výsledné číslo bylo osminásobkem
Stonožka 9 - M 2011 - náhled testu http://ib.scio.cz/test?t=ceow8rrhgtr79v2xq7/zcppky1fbxbzulq... 1 z 7 18.6.2012 8:14 1. otázka Které číslo musíme odečíst od čísla 250, aby výsledné číslo bylo osminásobkem
6. T e s t o v á n í h y p o t é z
 6. T e s t o v á n í h y p o t é z Na základě hodnot z realizace náhodného výběru činíme rozhodnutí o platnosti hypotézy o hodnotách parametrů rozdělení nebo o jeho vlastnostech. Používáme k tomu vhodně
6. T e s t o v á n í h y p o t é z Na základě hodnot z realizace náhodného výběru činíme rozhodnutí o platnosti hypotézy o hodnotách parametrů rozdělení nebo o jeho vlastnostech. Používáme k tomu vhodně
KATEDRA INFORMATIKY UNIVERZITA PALACKÉHO LINEÁRNÍ ALGEBRA 1 OLGA KRUPKOVÁ VÝVOJ TOHOTO UČEBNÍHO TEXTU JE SPOLUFINANCOVÁN
 KATEDRA INFORMATIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITA PALACKÉHO LINEÁRNÍ ALGEBRA 1 OLGA KRUPKOVÁ VÝVOJ TOHOTO UČEBNÍHO TEXTU JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY
KATEDRA INFORMATIKY PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITA PALACKÉHO LINEÁRNÍ ALGEBRA 1 OLGA KRUPKOVÁ VÝVOJ TOHOTO UČEBNÍHO TEXTU JE SPOLUFINANCOVÁN EVROPSKÝM SOCIÁLNÍM FONDEM A STÁTNÍM ROZPOČTEM ČESKÉ REPUBLIKY
Lineární programování
 Lineární programování Petr Tichý 19. prosince 2012 1 Outline 1 Lineární programování 2 Optimalita a dualita 3 Geometrie úlohy 4 Simplexová metoda 2 Lineární programování Lineární program (1) min f(x) za
Lineární programování Petr Tichý 19. prosince 2012 1 Outline 1 Lineární programování 2 Optimalita a dualita 3 Geometrie úlohy 4 Simplexová metoda 2 Lineární programování Lineární program (1) min f(x) za
Zadání projektů z BPC2 pro letní semestr 2007/2008
 Zadání projektů z BPC2 pro letní semestr 2007/2008 Několik poznámek na úvod Projekt může být i konzolová aplikace. Záleží však na typu zadání, ne každé v konzolové aplikace vyřešit lze. Mezi studenty jsou
Zadání projektů z BPC2 pro letní semestr 2007/2008 Několik poznámek na úvod Projekt může být i konzolová aplikace. Záleží však na typu zadání, ne každé v konzolové aplikace vyřešit lze. Mezi studenty jsou
Lineární algebra a analytická geometrie sbírka úloh a ř ešených př íkladů
 Lineární algebra a analytická geometrie sbírka úloh a ř ešených př íkladů Linear algebra and analytic geometry problems and solved examples Klára Javornická Bakalářská práce 2010 UTB ve Zlíně, Fakulta
Lineární algebra a analytická geometrie sbírka úloh a ř ešených př íkladů Linear algebra and analytic geometry problems and solved examples Klára Javornická Bakalářská práce 2010 UTB ve Zlíně, Fakulta
pro bakalářské studijní programy fyzika, informatika a matematika 2018, varianta A
 Přijímací zkouška na MFF UK pro bakalářské studijní programy fyzika, informatika a matematika 2018, varianta A U každé z deseti úloh je nabízeno pět odpovědí: a, b, c, d, e. Vaším úkolem je u každé úlohy
Přijímací zkouška na MFF UK pro bakalářské studijní programy fyzika, informatika a matematika 2018, varianta A U každé z deseti úloh je nabízeno pět odpovědí: a, b, c, d, e. Vaším úkolem je u každé úlohy
5 Rekurze a zásobník. Rekurzivní volání metody
 5 Rekurze a zásobník Při volání metody z metody main() se do zásobníku uloží aktivační záznam obsahující - parametry - návratovou adresu, tedy adresu, kde bude program pokračovat v metodě main () po skončení
5 Rekurze a zásobník Při volání metody z metody main() se do zásobníku uloží aktivační záznam obsahující - parametry - návratovou adresu, tedy adresu, kde bude program pokračovat v metodě main () po skončení
Úlohy domácí části I. kola kategorie C
 6. ročník Matematické olympiády Úlohy domácí části I. kola kategorie C 1. Určete všechny dvojice (x, y) reálných čísel, která vyhovují soustavě rovnic (x + )2 = y, (y )2 = x + 8. Řešení. Vzhledem k tomu,
6. ročník Matematické olympiády Úlohy domácí části I. kola kategorie C 1. Určete všechny dvojice (x, y) reálných čísel, která vyhovují soustavě rovnic (x + )2 = y, (y )2 = x + 8. Řešení. Vzhledem k tomu,
2. Elementární kombinatorika
 2.1. Kombinace, variace, permutace bez opakování 2. Elementární kombinatorika Definice 2.1. Kombinace je neuspořádaná k-tice prvků z dané n-prvkové množiny. Variace je uspořádaná k-tice prvků z dané n-prvkové
2.1. Kombinace, variace, permutace bez opakování 2. Elementární kombinatorika Definice 2.1. Kombinace je neuspořádaná k-tice prvků z dané n-prvkové množiny. Variace je uspořádaná k-tice prvků z dané n-prvkové
Biostatistika a matematické metody epidemiologie- stručné studijní texty
 Biostatistika a matematické metody epidemiologie- stručné studijní texty Bohumír Procházka, SZÚ Praha 1 Co můžeme sledovat Pro charakteristiku nebo vlastnost, kterou chceme sledovat zvolíme termín jev.
Biostatistika a matematické metody epidemiologie- stručné studijní texty Bohumír Procházka, SZÚ Praha 1 Co můžeme sledovat Pro charakteristiku nebo vlastnost, kterou chceme sledovat zvolíme termín jev.
Popis postupu při zpracování atletických závodů dle programu ATLETICKÁ KANCELÁŘ ( Manuál II.část )
 Popis postupu při zpracování atletických závodů dle programu ATLETICKÁ KANCELÁŘ ( Manuál II.část ) Různé samostatné části : 1 -Připojení k AK - 2x kliknout na Internet Explorer - kliknout na pracovat offline
Popis postupu při zpracování atletických závodů dle programu ATLETICKÁ KANCELÁŘ ( Manuál II.část ) Různé samostatné části : 1 -Připojení k AK - 2x kliknout na Internet Explorer - kliknout na pracovat offline
Kapitola 1: Úvodní strana PARTICLER
 Kapitola 1: Úvodní strana PARTICLER OBSAH Úvod 1.O Particleru 2.Popis programu 2.1 Hlavní okno programu 2.1.1 - Horní lišta 2.1.1.1 Soubor 2.1.1.2 Vzhled 2.1.1.3 - Nastavení 2.1.1.4 - Pomoc 2.1.2 - Pracovní
Kapitola 1: Úvodní strana PARTICLER OBSAH Úvod 1.O Particleru 2.Popis programu 2.1 Hlavní okno programu 2.1.1 - Horní lišta 2.1.1.1 Soubor 2.1.1.2 Vzhled 2.1.1.3 - Nastavení 2.1.1.4 - Pomoc 2.1.2 - Pracovní
Kód uchazeče ID:... Varianta: 14
 Fakulta informačních technologií ČVUT v Praze Přijímací zkouška z matematiky 2013 Kód uchazeče ID:.................. Varianta: 14 1. V lednu byla zaměstnancům zvýšena mzda o 16 % prosincové mzdy. Následně
Fakulta informačních technologií ČVUT v Praze Přijímací zkouška z matematiky 2013 Kód uchazeče ID:.................. Varianta: 14 1. V lednu byla zaměstnancům zvýšena mzda o 16 % prosincové mzdy. Následně
Implementace A* algoritmu na konkrétní problém orientace v prostoru budov
 Implementace A* algoritmu na konkrétní problém orientace v prostoru budov Popis problému Orientaci ve známém prostředí lze převést na problém nalezení cesty z místa A do místa B. Obecně platí, že robot
Implementace A* algoritmu na konkrétní problém orientace v prostoru budov Popis problému Orientaci ve známém prostředí lze převést na problém nalezení cesty z místa A do místa B. Obecně platí, že robot
Skořepina v SolidWorks
 Tvorba tenkostěnné součásti v SolidWorks Skořepina v SolidWorks Ing. Richard Němec, 2012 1. Zadání Vymodelujte v SolidWorks tenkostěnnou součást (skořepinu) víčko anténního zesilovače a uložte do souboru
Tvorba tenkostěnné součásti v SolidWorks Skořepina v SolidWorks Ing. Richard Němec, 2012 1. Zadání Vymodelujte v SolidWorks tenkostěnnou součást (skořepinu) víčko anténního zesilovače a uložte do souboru
8 Přednáška z
 8 Přednáška z 3 12 2003 Problém minimální kostry: Dostaneme souvislý graf G = (V, E), w : E R + Našim úkolem je nalézt strom (V, E ) tak, aby výraz e E w(e) nabýval minimální hodnoty Řešení - Hladový (greedy)
8 Přednáška z 3 12 2003 Problém minimální kostry: Dostaneme souvislý graf G = (V, E), w : E R + Našim úkolem je nalézt strom (V, E ) tak, aby výraz e E w(e) nabýval minimální hodnoty Řešení - Hladový (greedy)
Y36BEZ Bezpečnost přenosu a zpracování dat. Úvod. Róbert Lórencz. http://service.felk.cvut.cz/courses/y36bez lorencz@fel.cvut.cz
 Y36BEZ Bezpečnost přenosu a zpracování dat Róbert Lórencz 1. přednáška Úvod http://service.felk.cvut.cz/courses/y36bez lorencz@fel.cvut.cz Róbert Lórencz (ČVUT FEL, 2007) Y36BEZ Bezpečnost přenosu a zpracování
Y36BEZ Bezpečnost přenosu a zpracování dat Róbert Lórencz 1. přednáška Úvod http://service.felk.cvut.cz/courses/y36bez lorencz@fel.cvut.cz Róbert Lórencz (ČVUT FEL, 2007) Y36BEZ Bezpečnost přenosu a zpracování
{Q={1,2};S,T;u(s,t)} (3.3) Prorovnovážnéstrategie s,t vehřesnulovýmsoučtemmusíplatit:
 3 ANTAGONISTICKÉ HRY 3. ANTAGONISTICKÝ KONFLIKT Antagonistický konflikt je rozhodovací situace, v níž vystupují dva inteligentní rozhodovatelé, kteří se po volbě svých rozhodnutí rozdělí o pevnou částku,
3 ANTAGONISTICKÉ HRY 3. ANTAGONISTICKÝ KONFLIKT Antagonistický konflikt je rozhodovací situace, v níž vystupují dva inteligentní rozhodovatelé, kteří se po volbě svých rozhodnutí rozdělí o pevnou částku,
ponožku, nedovede rozeznat její barvu. Kolik nejméně ponožek musí vytáhnout, aby mezi nimi bylo určitě aspoň osm
 Úloha 1J. Malý Pét a je velký drsňák a nosí vždy jen ponožky různých barev. Ve skříni má 30 červených, 40 zelených a 40 modrých ponožek. Tato skříň se však nachází ve sklepě v místech, kde se nesvítí,
Úloha 1J. Malý Pét a je velký drsňák a nosí vždy jen ponožky různých barev. Ve skříni má 30 červených, 40 zelených a 40 modrých ponožek. Tato skříň se však nachází ve sklepě v místech, kde se nesvítí,
Obsah herní sady: 40x dřevěný kámen hrací deska návod
 Obsah herní sady: 40x dřevěný kámen hrací deska návod www.shogi.cz info@shogi.cz /Shogicz Online návod: http://www.shogi.cz/zviratkanavod.pdf CZ Rychlá pravidla 1 Rozestavění kamenů 3 Hrací kameny a pohyb
Obsah herní sady: 40x dřevěný kámen hrací deska návod www.shogi.cz info@shogi.cz /Shogicz Online návod: http://www.shogi.cz/zviratkanavod.pdf CZ Rychlá pravidla 1 Rozestavění kamenů 3 Hrací kameny a pohyb
Kolekce ArrayList. Deklarace proměnných. Import. Vytvoření prázdné kolekce. napsal Pajclín
 Kolekce ArrayList napsal Pajclín Tento článek jsem se rozhodl věnovat kolekci ArrayList, protože je to jedna z nejpoužívanějších. Tento článek není kompletním popisem třídy ArrayList, ale budu se snažit
Kolekce ArrayList napsal Pajclín Tento článek jsem se rozhodl věnovat kolekci ArrayList, protože je to jedna z nejpoužívanějších. Tento článek není kompletním popisem třídy ArrayList, ale budu se snažit
2. Matice, soustavy lineárních rovnic
 Matice, soustavy lineárních rovnic Tento učební text byl podpořen z Operačního programu Praha- Adaptabilita Irena Sýkorová Některé vlastnosti matic Uvažujmečtvercovoumatici A=(a ij ) n n Matice Asenazývásymetrická,jestližeplatí
Matice, soustavy lineárních rovnic Tento učební text byl podpořen z Operačního programu Praha- Adaptabilita Irena Sýkorová Některé vlastnosti matic Uvažujmečtvercovoumatici A=(a ij ) n n Matice Asenazývásymetrická,jestližeplatí
1 Linearní prostory nad komplexními čísly
 1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
Ukážeme si lineární algoritmus, který pro pevné k rozhodne, zda vstupní. stromový rozklad. Poznamenejme, že je-li k součástí vstupu, pak rozhodnout
 Ukážeme si lineární algoritmus, který pro pevné k rozhodne, zda vstupní graf má stromovou šířku nejvýše k, a je-li tomu tak, také vrátí příslušný stromový rozklad. Poznamenejme, že je-li k součástí vstupu,
Ukážeme si lineární algoritmus, který pro pevné k rozhodne, zda vstupní graf má stromovou šířku nejvýše k, a je-li tomu tak, také vrátí příslušný stromový rozklad. Poznamenejme, že je-li k součástí vstupu,
Kapacita. Gaussův zákon elektrostatiky
 Kapacita Dosud jsme se zabývali vztahy mezi náboji ve vakuu. Prostředí mezi náboji jsme charakterizovali permitivitou ε a uvedli jsme, že ve vakuu je ε = 8,854.1-1 C.V -1.m -1. V této kapitole se budeme
Kapacita Dosud jsme se zabývali vztahy mezi náboji ve vakuu. Prostředí mezi náboji jsme charakterizovali permitivitou ε a uvedli jsme, že ve vakuu je ε = 8,854.1-1 C.V -1.m -1. V této kapitole se budeme
