Několik námětů k zamyšlení pro praktické měření na souřadnicových měřicích strojích. Daniel Zachoval & Luboš Zachoval
|
|
|
- Ludvík Pravec
- před 6 lety
- Počet zobrazení:
Transkript
1 Úvodem. Praxe měření na souřadnicových měřicích strojích ukazuje na řadu problémů, které při měření vznikají, a které se nutně projevují v nesprávných výsledcích měření. Protože měření využívá matematický aparát, nelze při něm obcházet zásadní poučky a pravidla, které(á) matematický výpočet obsahuje. Náš příspěvek si klade za cíl pro širokou veřejnost v oboru souřadnicového měření zpřístupnit shrnutí některých takových pouček a pravidel. Jedná se o volný modifikovaný výběr z neautorizované cizojazyčné publikace, který byl použit v diplomové práci Daniela Zachovala. Nepředkládáme tedy nic originálního. Předkládáme příspěvek, který máme k dispozici s přáním, aby pomohl všem, kteří to potřebují a uznají za vhodné. Autoři. 1
2 Příklady strategie měření a postupy měření základních geometrických elementů Příklady správné a špatné polohy snímače: Všechny příklady jsou se sílou materiálu 1 mm, a průměrem doteku snímače 2 mm, kromě zvlášť uvedených odchylek. Obr. č. 1 Příklad měření 2
3 Obr. č. 2 Příklad měření 3
4 Obr. č. 3 Příklad měření 4
5 Obr. č. 4 Příklad měření 5
6 Obr. č. 5 Příklad měření 6
7 Obr. č. 6 Příklad měření 7
8 Měření bodu Body se obecně snímají ve směru normály plochy (vektor kolmý na danou plochu). Je třeba dbát na to, že čím větší je kulička snímače, tím větší chyba vznikne při směru snímání odchylném od směru normály plochy. Obr. č. 7 Měření bodu 8
9 Obr. č. 8 Měření bodu 9
10 Vyrovnání Vyrovnáním se rozumí ustavení měřeného objektu do určitého souřadného systému. Při vyrovnávání dílů s volně tvarovanými plochami je vyrovnání vždy iteraktivní, tzn. opakováním vyrovnání se dosáhne lepšího vyrovnání. Přitom se měří znovu pouze ty elementy, které se mohou během vyrovnávání zlepšit. To jsou v každém případě body, které leží na volně tvarovaných plochách. Elementy, které se nemohou změnit, se musí měřit pouze jednou a během iterakce se mohou pouze zavolat (vyvolat z paměti). K těmto elementům patří, kružnice, válce (jejich průsečíky, obvykle s rovinou), kužely (průsečíky) a koule. Pro ruční vyrovnání platí: Vždy měřit co možná nejméně měřicích elementů s nejkratšími ručními pohyby stroje. Snímané elementy se popisují jako výstup na obrazovce stroje jednoduchou grafikou v pořadí snímání a s jejich polohou na měřeném dílu. V grafice musí být obsažena také poloha dílu na měřicím stroji. U natáčecích/otáčecích snímačů je třeba dbát na to, aby žádná výměna snímače nebyla obsažena v ručním vyrovnání (nebezpečí kolize). Jestliže z důvodů techniky měření nelze natočení snímače vyloučit, musí se do programu napsat stop stroje s příslušnou hláškou na obrazovku. Obsluha měřicího stroje má potom možnost snímač volně objet. Všechny měřicí elementy pro ruční vyrovnání se měří v souřadném systému měřicího stroje. V tomto souřadném systému se provede také spojování. Až jsou všechny elementy pro vyrovnání změřeny, posadí se počátek souřadnic do prvního měřeného bodu prostorového elementu, a to ve všech třech souřadnicích, aby se zabránilo chybě úhlu, která se u větších vzdáleností negativně projevuje. Vyrovnání je uzavřeno tehdy, když všech šest stupňů volnosti souřadného systému je definováno. Šest stupňů volnosti jsou tři souřadnice a tři směry. Točení v prostoru se provede na směrově určeném elementu. Je-li tento element prostřednictvím měření přeurčen, musí se na něm souřadný systém ještě jednou posadit na nulu. K tomu se ale použije ta souřadnice, která je určena směrově definovaným elementem. Přeurčený je ten element, kde se udělalo více sejmutí, než je potřebné. Tzn.: u čáry víc jak 2 snímané body, u roviny víc jak 3 snímané body (nebo spojované body). Tento vyrovnávací postup určí dva stupně volnosti, a to souřadnice a směr. 10
11 Točení v rovině se provede podobně na jednom směrově definovaném elementu. Tím se opět určí dva stupně volnosti. Nyní zbývají dva směry, tím jsou určeny právě čtyři stupně volnosti souřadného systému. Chybí ještě dvě určení souřadnic. Jedno uřčení je stanovení počátku na směrový element v otáčení roviny. Poslední počátek se určí na příslušném elementu. Vyjímky ručního kompletního vyrovnání existují tehdy, když může být měřený díl postaven rovnoběžně s osami. Potom stačí, když se určí počátek všech tří os souřadného systému. Pro vyrovnání CNC platí: Když se změří (nebo spojí) nějaký element, hned se podle něho vyrovnává. Tzn.: hned po určení prostorového elementu (rovina nebo čára) se provede otočení v prostoru s určením počátku v ose (prostorové ose pouze u roviny). V tomto otočeném souřadném systému se provede určení elementu pro otočení roviny a provede se otočení roviny s určením počátku. Jako poslední se určí element pro ještě chybějící souřadnici a stanoví se počátek na příslušném elementu. Tento souřadný systém se musí uložit (ve vývojovém diagramu označeno jako CNC_END). Tímto je díl určený v souřadném systému měřicího stroje. Nyní se musí otočit o příslušný úhel a posunout do souřadného systému auta. V tomto souřadném systému se musí provést kontrola vyrovnání. Měřené výsledky se uloží jako proměnné, aby se mohla zavést smyčka pro opakování. Po kontrole vyrovnání se musí uložený souřadný systém vyrovnání CNC znovu zavolat (RECALL CNC_END), čímž se při zpětném skoku ze smyčky dostaneme do správného souřadného systému a může se měřit dále. Ve smyčce se musí zohlednit všechny proměnné, které byly přiřazeny výsledkům měření. Ve smyčce se zvýší číselná proměnná, aby se mohlo přerušit vyrovnání. Po smyčce se znovu aktivuje souřadný systém auta (RECALL PCS). Tím je vyrovnání dílu ukončeno. Pro lepší porozumění je cely průběh vyrovnání zobrazen v následujícím vývojovém diagramu. 11
12 Obr. č. 9 Průběh vyrovnání 12
13 Měření U větších úloh měření se vytvářejí čtyři různé měřicí programy. Jsou to: Program vyrovnání Program ořezu Program tvaru Program otvorů Průběh programu vyrovnání je popsán v kapitole vyrovnání. U menších rozsahů měřicího programu zde může být na konci přímo startován měřicí program. Jsou-li měřicí programy rozděleny do těchto čtyř variant, kromě vyrovnávacího programu, se vždy začíná v souřadném systému auta. To se dosáhne tím, že se provede kopie souřadného systému, který je aktivní na měřicím stroji. Předpokladem pro to je, že aktivní souřadný systém na měřicím stroji odpovídá také souřadnému sytému vyrovnání. Před vlastním průběhem programu se provede z bezpečnostních důvodů ještě jednou kontrola vyrovnání. Tzn., že se všechny elementy, které byly použity pro vyrovnání, změří ještě jednou. Nesmějí mít žádnou odchylku od jmenovitých hodnot. Zavoláním smyčky výsledků, nebo zastavením měřicího stroje (ruční kontrola obsluhou stroje) se může zkontrolovat výsledek měření. Teprve nyní se může začít s měřicím programem. Aby se kontrola vyrovnání nemusela vždycky programovat znovu, kopíruje se vždy z vyrovnávacího programu (v AUDIMESS pomocí funkce INCLUDE). 13
14 Měření zahnuté hrany Obr. č. 10 Měření zahnuté hrany Určení nejvyššího bodu: Nejvyšší křivka zahnuté hrany se vytvoří, když není k dispozici žádná střední plocha, paralelním posunutím určující plochy až po střed ZSB a vytvořením řezu z posunuté plochy (nebo plochy, která je k dispozici) s plochou poloměru nebo čelní plochou. Tato křivka se nyní může řezat na libovolných místech s teoretickými rovinami. Vzniklé body jsou nejvyšší body (max. bod) na zahnuté hraně. Určí se jméno nejvyššího bodu, když je tento průchozím měřicím bodem. 14
15 Určení bodu prvního sejmutí a měřicího bodu: Bod prvního sejmutí se posune na křivce řezu 8 milimetrů od začátku zakřivení poloměru. Jméno tohoto bodu nemá význam. Měřicí bod se posune na křivce řezu 4 mm od začátku zakřivení poloměru. Jméno bodu se určí, když je tento průběžným měřicím bodem. Určení korekčního bodu: Korekční body se vytvoří rovnoběžně k síti na nejvyšším bodu poloměru. Při vyhodnocení těchto bodů je třeba dbát na to, že se smí posuzovat pouze souřadnice, určující bod. Jména těchto bodů se stanoví podle platného konceptu pro vytváření jména. Měření viditelných hran (vnější hrany) V závislosti na provedení hrany se musí rozlišovat mezi třemi variantami. Pro všechny varianty se měřicí body určují stejně. Měření se rozlišují právě s ohledem na jejich průběh. Začínají ale všechna s nominálním přesazením souřadného systému do bodu prvního sejmutí, aby se případně měření přímo na měřicím stroji mohlo korigovat na jednoduchý druh a způsob. Určení bodů prvního sejmutí a měřicích bodů, příp. rovin: Bod prvního sejmutí se posune 8 mm od začátku zakřivení poloměru na křivce řezu té nejstabilnější plochy. Jméno tohoto bodu nemá význam. Měřicí body se posunou 4 mm od začátku zakřivení poloměru na křivce řezu. Jména těchto bodů se určí, když se jedná o průběžné měřicí body. Když se určí roviny k vytvoření bodů na hraně, leží tyto ve vzdálenosti měřicích bodů. Jejich snímané body leží na poloměru 1 mm kolem vzdálenosti měřicích bodů, popř. ty měřené body, které se použijí pro spojení roviny, leží v této vzdálenosti poloměru. Viz. také příklady pro tyto tři varianty. 15
16 Varianta 1: Hrany, které jsou určeny pravým úhlem a když základní plochy jsou (přibližně) planární. Měření bez určení bodů hrany: Obr. č. 11 Měření hrany Průběh měření: Po posunutí souřadného systému nominálně do bodu prvního sejmutí se změří bod prvního sejmutí ve směru normály. Souřadný systém se posadí na nulu příslušné souřadnice v tomto měřeném bodě. Nyní se změří měřicí bod dvě jako pomocný bod ve směru normály, do kterého se aktivní souřadný systém znovu v příslušné souřadnici posadí na nulu. Nyní se změří měřicí bod jedna ve směru normály. Aktivní souřadný systém se ještě jednou v příslušné souřadnici posadí na nulu. Nyní se může podobně ve směru normály změřit měřicí bod dvě. Zavolá se zpátky souřadný systém auta, aby se výstup výsledků měření provedl ve správném souřadném systému. Z měřicích bodů jedna a dvě se vytvoří transformační body (TR body) a ve směru normály a hlavního souřadného systému se vyhodnotí příslušné tolerance a jména bodů. 16
17 Měření s určením bodů hrany: Obr. č. 12 Měření hrany Průběh měření: Po posunutí souřadného systému nominálně do bodu prvního sejmutí se změří bod prvního sejmutí ve směru normály. Souřadný systém se posadí na nulu v příslušné ose v tomto bodě. Nyní se změří měřicí bod dvě, pomocný bod tři a pomocný bod čtyři. Z těchto tří bodů se spojí roviny dvě. (Pozor: Vektor této roviny musí ukazovat proti směru snímání). V této rovině se otočí souřadný systém v prostoru a v prostorové ose se posadí na nulu. Tím se může měřit měřicí bod jedna, pomocný bod jedna a pomocný bod dvě. Z těchto tří pomocných bodů se podobně spojí rovina jedna. Z roviny jedna a roviny dvě se nyní vytvoří čára řezu. Tyto se s nominální rovinou řezu protnou v bodě hrany. Zavolá se zpátky souřadný systém auta, aby se mohl provést výstup výsledků měření ve správném souřadném systému. Nyní se musí vytvořit z měřicího bodu jedna, měřicího bodu dvě a bodu hrany transformační body (TR body). Měricí body jedna a dvě se vyhodnotí ve směru normály s odpovídajícími tolerancemi a jmény elementů. Bod hrany bude nyní vyhodnocen s odpovídajícími tolerancemi pro souřadnice potřebné pro korekturu přípravků. 17
18 Varianta 2: Hrany, které neurčuje pravý úhel, ale základní plochy jsou (přibližně) planární. Měření vždy s určením bodu hrany. Obr. č. 13 Měření hrany Průběh měření Po posunutí souřadného systému nominálně do bodu prvního sejmutí se změří bod prvního sejmutí ve směru normály. Souřadný systém se posadí na nulu v tomto měřeném bodě v příslušné souřadnici. Nyní se změří pomocný bod jedna a dvě. Z těchto tří bodů se spojí roviny jedna (pozor: vektor roviny musí ukazovat proti směru snímání). V této rovině se otočí souřadný systém v prostoru a posadí na nulu v prostorové ose. Tím se mohou změřit pomocné body 3, 4 a 5, vždy plus nebo mínus 90 stupňů vektoru roviny (v závislosti na směru snímání). Pozor: snímací kulička nesmí být příliš velká, protože korekce poloměru na měřicím stroji zkresluje výsledek měření. Z těchto tří měřených bodů se podobně spojí rovina dvě. Z roviny jedna a dvě se nyní vytvoří čára průřezu. Tato se nyní prořízne nominální rovinou řezu na bod hrany. Souřadný systém se posune podle příslušné souřadnice do tohoto bodu. Aby se vyloučila chyba korekce poloměru (snímací kuličky), změří se ještě jednou pomocné body 3, 4 a 5, ale ve směru normály. Vytvoří se ještě jednou podobně rovina dvě a bod hrany, aby se získala pravá hrana. Také souřadný systém se posadí na nulu v tomto novém bodě hrany. Měřené body jedna a dvě se nyní mohou změřit ve směru normály. Zavolá se zpět souřadný systém auta, aby se mohl provést výstup výsledků měření ve správném souřadném systému. 18
19 Z měřených bodů jedna a dvě a z bodu hrany se nyní musí vytvořit transformační body (TR body). Měřené body jedna a dvě se vyhodnotí ve směru normály s odpovídajícími tolerancemi a jmény bodů. Bod hrany bude nyní vyhodnocen s odpovídajícími tolerancemi pro souřadnice potřebné pro korekturu přípravků. 19
20 Variana 3: Hrany, které nejsou určeny pravým úhlem základní plochy jsou volně tvarované plochy. Měření vždy s určením bodu hrany. Obr. č. 14 Měření hrany Průběh měření: Po nominálním posunutí souřadného systému do prvně sejmutého bodu se tento bod změří ve směru normály. Souřadný systém se v tomto bodě v příslušné tomuto bodu odpovídající souřadnici posadí na nulu. Nyní se v měřeném bodu dvě změří pomocný bod ve směru normály, v kterém se aktivní souřadný systém posadí na nulu v tomuto bodu odpovídající souřadnici. Nyní se změří měřený bod jedna ve směru normály. Aktivní souřadný systém se ještě jednou posadí na nulu v souřadnici odpovídající tomuto bodu. Nyní se může podobně změřit měřený bod dvě ve směru normály. Měřený bod jedna a dvě se nyní posune podél jejich směru normály o libovolnou hodnotu, a vzniknou tím body obratu (move body) jedna a dvě. Pomocí těchto bodů obratu se vytvoří pomocná čára (jedna a dvě) od měřeného bodu jedna k bodu obratu jedna a od měřeného bodu dvě k bodu obratu dvě. Pomocná rovina jedna a dvě se nyní může spojit přes měřený bod jedna a dvě. Těmito dvěma pomocnými rovinami se vytvoří jejich průsečík. Ten se prořízne rovinou řezu a vznikne bod hrany. Zavolá se zpátky souřadný systém auta, abychom dostali výsledek ve správném souřadném systému. 20
21 Nyní se musí vytvořit transformační body (TR body) z měřených bodů jedna a dvě a z bodu hrany. Měřené body jedna a dvě se vyhodnotí ve směru normály s odpovídajícími tolerancemi a jmény elementů. Bod hrany bude nyní vyhodnocen s odpovídajícími tolerancemi pro souřadnice potřebné pro korekturu přípravků. Měření vnitřních hran Vnitřní hrany (Wurzelkanten) se určí stejně jako hrany vnější. Z hlediska techniky měření zde není rozdílu. Měření límce -přesazení (Flanschmesung) Na spojích se musí měřit jejich poloha a délka. K tomu se musí určit bod ořezu a dva body na spoji. Může se volit mezi dvěma variantami, které jsou závislé na dosažitelnosti spoje. Pro obě varianty se měřené body rozdělují stejně. K umístění měřených bodů platí následující pravidlo: Bod ořezu přímo na hraně ořezu u jednoduchých dílů nebo uprostřed mezi ořezy u spojených dílů. Měřený bod jedna na límci by měl být vzdálen od bodu ořezu asi deset procent délky límce. Měřený bod dvě límce by měl být zhruba dvacet procent od ohybu. Varianta jedna: Snímání podle směru jmenovité normály: Obr. č. 15 Měření spoje 21
22 Průběh měření: Po posunutí souřadného systému nominálně do měřicího bodu dvě na límci, se změří bod prvního sejmutí nebo přímo měřený bod dvě na límci ve směru normály. Souřadný systém se posune na nulu v souřadnici odpovídající tomuto měřenému bodu. Pokud se začínalo s bodem prvního sejmutí k určení dílu, měří se nyní měřený bod dvě na límci. Souřadný systém se v příslušné ose posune na nulu. Potom se změří měřený bod jedna na límci a opět se souřadný systém posune na nulu. Nyní se může změřit bod ořezu. Zavolá se zpátky souřadný systém auta, abychom dostali výsledek ve správném souřadném systému. Z měřených bodů jedna a dvě na límci a z bodu ořezu se nyní musí vytvořit transformační body (TR body). Transformované měřené body se vyhodnotí s odpovídajícími tolerancemi a jmény elementů ve směru normály. Podle odchylky se může posoudit poloha popř. délka límce a případně se může změnit. Varianta 2: Snímání podle směru skutečné normály: Obr. č. 16 Měření spoje Průběh měření: Po posunutí souřadného systému nominálně do měřeného bodu dvě límce se změří případně bod prvního sejmutí nebo přímo vyrovnávací rovina. Pokud se začalo měřit s bodem prvního sejmutí k určení polohy dílu, posune se souřadný systém v souřadnici příslušné tomuto měřenému bodu na nulu. Nyní se může změřit vyrovnávací rovina. Souřadný systém se otočí v prostoru a posune se do nuly v prostorové ose. Potom se změří měřené body na límci a bod ořezu. 22
23 Zavolá se zpátky souřadný systém auta, abychom dostali výsledek ve správném souřadném systému. Z měřených bodů jedna a dvě na límci a z bodu ořezu se nyní musí vytvořit transformační body (TR body). Transformované měřené body se vyhodnotí s odpovídajícími tolerancemi a jmény elementů ve směru normály. Podle odchylky se může posoudit poloha popř. délka límce a případně se může změnit. Příklad kombinace jednotlivých metod měření na neznámém obrysu. Vyobrazení jmenovitého a skutečného dílu: Obr. č. 17 Měření neznámého obrysu Průběh měření V tomto příkladě se mají určit ořez, vnitřní hrana a vnější hrana. Měření se začíná na nejstabilnější ploše. Souřadný systém se posune nominálně ve všech třech osách do pomocného bodu H2. Body M1 (rovná se H1), H2 a M2 (rovná se H3) se určí první rovina (E1). Souřadný systém se vyrovná v prostoru a posune se v prostorové ose na nulu. Nyní se určí druhá rovina (E2) prostřednictvím pomocných bodů H4, H5 a H6, které se měří rovnoběžně v ose. Z rovin E1 a E2 se vytvoří čára průsečíku a tato se prořízne nominální rovinou řezu a vznikne bod hrany K1. Souřadný systém se posune v souřadnici odpovídající tomuto bodu na nulu. 23
24 Nyní se změří měřené body jedna a dvě. Souřadný systém se nyní vyrovná v prostoru na druhé rovině a posune se podle prostorové osy na nulu. Měřené body 3 a 4, a pomocné body H7, H8 a H9, které se měří rovnoběžně v ose, se mohou určit. Pomocí bodů H7, H8 a H9 se nyní spojí třetí rovina (E3). Z rovin E2 a E3 se vytvoří čára řezu a tato se prořízne nominální rovinou řezu a vznikne tak bod hrany K2. Souřadný systém se otočí v prostoru v rovině E3 a v prostorové ose na této rovině se posune na nulu. Nyní se mohou určit měřené body 5, 6 a 7. Zavolá se zpátky souřadný systém auta, abychom dostali výsledek ve správném souřadném systému. Z bodů hrany a z měřených bodů se nyní musí vytvořit transformační body (TR body). Transformované měřené body se vyhodnotí s odpovídajícími tolerancemi a jmény elementů ve směru normály. Transformované body hrany se opatří podobně jménem elementu, ale vyhodnotí se pouze v příslušné ose. Kvůli špatné korekci poloměru kuličky snímače se musí v pomocných bodech H4 H9 pracovat s malou kuličkou. Není-li to možné z důvodů techniky měření, musí se roviny E2 a E3 určit s mezivyrovnáním pomocí dvojího měření (prvně rovnoběžně v ose a potom ve směru normály). 24
25 Měření kružnice Zásadně se kružnice musí měřit v lokálním vyrovnání. Postup: Souřadný systém posunout teoreticky do středu kružnice. Změřit rovinu, která určuje polohu kružnice. Souřadný systém vyrovnat v rovině s otočit v prostoru. Posunout počátek v prostorové ose v rovině. Změřit kružnici, obvykle pěti body sejmutí s hloubkou ponoření nula, a vyhodnotit průměr. Zavolat zpátky souřadný systém vyhodnocení. Vytvořit transformační matici uprostřed kružnice a vyhodnotit odpovídající souřadnice. Poznámka: Směr snímacího nástroje musí být ve směru normály k rovině určující kružnici. Měří-li se kružnice s hloubkou ponoření větší než nula, musí se před zavoláním souřadného systému vyhodnocení promítnout střed kružnice do roviny tuto kružnici určující. Počet měřených bodů a hloubka ponoření jsou závislé na požadavcích na měření a na dostupnosti dílu. Příklad špatného měření na kružnici bez vyrovnání: Obr. č. 18 Špatné měření kružnice Poznámka: Skutečný díl je otočen o dvacet stupňů ve vektoru z P2 oproti jmenovitému dílu. Měří se třemi body s hloubkou ponoření 0,5 mm. Jmenovitý průměr kružnice je 10 mm. Průměr kuličky snímače je 3 mm. Bez vyrovnání se sejme P1 příliš hluboko a P3 příliš vysoko. Měření snímaného bodu P2 je OK. Odchylka, způsobená chybou měření, činí u průměru 0,55 mm a v souřadnicích 0,20 mm. 25
26 Snímané body P1, P2 a P3 jsou vyobrazeny shora i ze spod. Obr. č. 19 Měření kružnice 26
27 Obr. č. 20 Měření kružnice 27
28 Obr. č. 21 Měření kružnice 28
29 Měření kružnice z elipsy, která je kótovaná jako kružnice Otvory, které nejsou postaveny ve směru normály k rovině, určující kružnici. Postup varianta jedna: Souřadný systém posunout teoreticky do středu elipsy. Změřit rovinu, která určuje polohu elipsy. Souřadný systém vyrovnat do této roviny pomocí otočit v prostoru. Prostorovou osu posunout v rovině do nuly. Body, které určují kružnici, změřit s odpovídající hloubkou ponoření na eliptickém výřezu. Definovat dvě teoretické roviny, které určují směr průniku. Měřené body promítnout do definované roviny. Promítnuté body spojit do kružnice a z kružnice vyhodnotit průměr. Ze spojených kružnic vytvořit jednu čáru. Vytvořit průsečík z roviny určující elipsu a z vytvořené čáry. Zavolat zpět souřadný systém vyhodnocení. Vytvořit transformační matici pro střed kružnice rovná se průsečík a vyhodnotit příslušné souřadnice. Postup varianta dvě: Souřadný systém posunout teoreticky do středu elipsy. Změřit rovinu, která určuje polohu elipsy. Souřadný systém vyrovnat do této roviny pomocí otočit v prostoru. Prostorovou osu posunout v rovině do nuly. Body, které určují kružnici, změřit s odpovídající hloubkou ponoření na eliptickém výřezu. Definovat jednu teoretickou rovinu, která určuje směr průniku. Měřené body promítnout do definované roviny. Promítnuté body spojit do kružnice a z kružnice vyhodnotit průměr. Vytvořit jednu čáru normálově středem kružnice. Vytvořit průsečík z roviny určující elipsu a z vytvořené čáry. Zavolat zpět souřadný systém vyhodnocení. Vytvořit transformační matici pro střed kružnice rovná se průsečík a vyhodnotit příslušné souřadnice. 29
30 Obr. č. 22 Měření kružnice z elipsy 30
31 Měření podélného otvoru Při měření podélného otvoru se zkontrolují obě protilehlé kružnice, střed, a světlá vzdálenost. Postup poloha v rovině: Souřadný systém posunout teoreticky do středu podélného otvoru. Změřit rovinu, která určuje polohu podélného otvoru. Vyrovnat souřadný systém v rovině pomocí otočit v prostoru. Prostorovou osu posunout na nulu v rovině. Případně změřit dva body na jedné straně podélného otvoru a spojit je do čáry. V této čáře otočit rovinu a příslušnou souřadnici posunout do nuly. Obě kružnice změřit s odpovídající hloubkou ponoření a vyhodnotit průměry. Při hloubce ponoření větší než 0 promítnout oba středy kružnic do roviny určující podélný otvor. Změřit čáru na jedné straně podélného otvoru s odpovídající hloubkou ponoření, nebo použít čáru, která byla použita pro otočení roviny. Změřit bod na druhé straně podélného otvoru s odpovídající hloubkou ponoření. Při hloubce ponoření větší než 0 promítnout bod a čáru do roviny, určující podélný otvor. Vyhodnotit Euklidovskou vzdálenost čára (průmět) a bod (průmět). Vyhodnotit Euklidovskou vzdálenost středů kružnic (průmět). Zavolat zpět souřadný systém vyhodnocení. Vytvořit středový bod z obou měřených kružnic, popř. promítnutých bodů, a vyhodnotit příslušné souřadnice. 31
32 Obr. č. 23 Měření podélného otvoru 32
33 Postup poloha ve dvou rovinách: Souřadný systém posunout teoreticky do středu podélného otvoru. Změřit pomocnou rovinu. Souřadný systém vyrovnat na pomocnou rovinu pomocí otočit v prostoru. Prostorovou osu posunout v pomocné rovině do nuly. Popř. pomocí určení čáry provést otočení roviny posunutím do nuly. Změřit body, které určují kružnici s odpovídající hloubkou ponoření na eliptickém výřezu. Změřit hlavní rovinu, rovná se kótovanou rovinu, která určuje polohu podélného otvoru. Vyrovnat souřadný systém v rovině pomocí otočit v prostoru. Prostorovou osu posunout v rovině do nuly. Změřit hlavní kružnici s odpovídající hloubkou ponoření a vyhodnotit průměr. Při hloubce ponoření větší než 0 promítnout střed kružnice do hlavní roviny. Body měřené v první kružnici promítnout do hlavní roviny. Promítnuté body spojit do kružnice a vyhodnotit průměr. Změřit čáru na jedné straně podélného otvoru s odpovídající hloubkou ponoření. Změřit bod na druhé straně podélného otvoru s odpovídající hloubkou ponoření. Při hloubce ponoření větší než 0 bod a čáru promítnout na rovinu určující podélný otvor. Vyhodnotit Euklidovskou vzdálenost čára (průmět) a bod (průmět). Vyhodnotit Euklidovskou vzdálenost středu hlavní kružnice (průmět) a spojené kružnice. Zavolat zpátky souřadný systém vyhodnocení. Vytvořit střed mezi středem hlavní kružnice (průmět) a spojené kružnice a vyhodnotit příslušné souřadnice. 33
34 Obr. č. 24 Měření podélného otvoru 34
35 Postup poloha v zahnuté ploše: Vytvořit teoretickou kótovanou rovinu, určující polohu podélného otvoru. Posunout souřadný systém teoreticky do středu podélného otvoru. Případně změřit pomocnou rovinu. Souřadný systém vyrovnat do pomocné roviny pomocí otočit v prostoru. Prostorovou osu posunout do nuly v pomocné rovině. Změřit body, které určují výřez s odpovídajícími prvními sejmutími a odpovídající hloubkou ponoření. Měřené body promítnout do kótované roviny. Promítnuté body spojit do jedné čáry a dvou kružnic a vyhodnotit průměr. Vyhodnotit Euklidovskou vzdálenost mezi čarou a protilehlým promítnutím bodem. Vytvořit střed mezi kružnicemi. Tento promítnout do pomocné roviny. Vytvořit bod obratu z promítnutého středu k teoretickému středu. Zavolat zpátky souřadný systém vyhodnocení. Vytvořit TR bod z bodu obratu a vyhodnotit příslušné souřadnice. Poznámka: Neměří-li se pomocná rovina, spojí se pomocná rovina ze tří měřených bodů, nebo rovnoběžným posunutím kótované roviny do měřeného bodu se vytvoří pomocná rovina. Střed podélného otvoru se může exaktně určit pouze pomocí pomocné roviny. 35
36 Obr. č. 19 Měření podélného otvoru 36
37 Měření čtyřhranného otvoru Při měření čtyřhranného otvoru se kontroluje střed a světlá vzdálenost. Postup: Souřadný systém posunout teoreticky do středu čtyřhranného otvoru. Změřit rovinu, která určuje polohu čtyřhranného otvoru. Souřadný systém vyrovnat v rovině pomocí otočit v prostoru. Prostorovou osu posunout do nuly v rovině. Změřit dva body na každé straně čtyřhranného otvoru s odpovídající hloubkou ponoření. Dbát průměru snímací kuličky a sejmout měřené body v příslušné vzdálenosti od rohů. Měří-li se s hloubkou ponoření větší než nula, promítnou se tyto body do roviny určující čtyřhranný otvor. Z měřených příp. promítnutých bodů vytvořit čtyři čáry, dbát při tom na směr těchto čar. Vyhodnotit Euklidovskou vzdálenost čáry (průmět) a bodu (průmět) na dvou protilehlých stranách. Zavolat zpět souřadný systém vyhodnocení. Vytvořit dva proti sobě ležící průsečíky vždy ze dvou čar. Vytvořit střed z obou spojených bodů a vyhodnotit odpovídající souřadnice. Poznámka: Leží-li čtyřhranný otvor ve dvou rovinách nebo v zahnuté ploše, pracuje se s pomocnou rovinou podobně jako při měření podélného otvoru, aby se snímané body mohly exaktně měřit. Měřené body se dále zpracují odpovídajícím způsobem pomocí kótované roviny. 37
38 Úvodem. Praxe měření na souřadnicových měřicích strojích ukazuje na řadu problémů, které při měření vznikají, a které se nutně projevují v nesprávných výsledcích měření. Protože měření využívá matematický aparát, nelze při něm obcházet zásadní poučky a pravidla, které(á) matematický výpočet obsahuje. Náš příspěvek si klade za cíl pro širokou veřejnost v oboru souřadnicového měření zpřístupnit shrnutí některých takových pouček a pravidel. Jedná se o volný modifikovaný výběr z neautorizované cizojazyčné publikace, který byl použit v diplomové práci Daniela Zachovala. Nepředkládáme tedy nic originálního. Předkládáme příspěvek, který máme k dispozici s přáním, aby pomohl všem, kteří to potřebují a uznají za vhodné. Autoři. 1
39 Příklady strategie měření a postupy měření základních geometrických elementů Příklady správné a špatné polohy snímače: Všechny příklady jsou se sílou materiálu 1 mm, a průměrem doteku snímače 2 mm, kromě zvlášť uvedených odchylek. Obr. č. 1 Příklad měření 2
40 Obr. č. 2 Příklad měření 3
41 Obr. č. 3 Příklad měření 4
42 Obr. č. 4 Příklad měření 5
43 Obr. č. 5 Příklad měření 6
44 Obr. č. 6 Příklad měření 7
45 Měření bodu Body se obecně snímají ve směru normály plochy (vektor kolmý na danou plochu). Je třeba dbát na to, že čím větší je kulička snímače, tím větší chyba vznikne při směru snímání odchylném od směru normály plochy. Obr. č. 7 Měření bodu 8
46 Obr. č. 8 Měření bodu 9
47 Vyrovnání Vyrovnáním se rozumí ustavení měřeného objektu do určitého souřadného systému. Při vyrovnávání dílů s volně tvarovanými plochami je vyrovnání vždy iteraktivní, tzn. opakováním vyrovnání se dosáhne lepšího vyrovnání. Přitom se měří znovu pouze ty elementy, které se mohou během vyrovnávání zlepšit. To jsou v každém případě body, které leží na volně tvarovaných plochách. Elementy, které se nemohou změnit, se musí měřit pouze jednou a během iterakce se mohou pouze zavolat (vyvolat z paměti). K těmto elementům patří, kružnice, válce (jejich průsečíky, obvykle s rovinou), kužely (průsečíky) a koule. Pro ruční vyrovnání platí: Vždy měřit co možná nejméně měřicích elementů s nejkratšími ručními pohyby stroje. Snímané elementy se popisují jako výstup na obrazovce stroje jednoduchou grafikou v pořadí snímání a s jejich polohou na měřeném dílu. V grafice musí být obsažena také poloha dílu na měřicím stroji. U natáčecích/otáčecích snímačů je třeba dbát na to, aby žádná výměna snímače nebyla obsažena v ručním vyrovnání (nebezpečí kolize). Jestliže z důvodů techniky měření nelze natočení snímače vyloučit, musí se do programu napsat stop stroje s příslušnou hláškou na obrazovku. Obsluha měřicího stroje má potom možnost snímač volně objet. Všechny měřicí elementy pro ruční vyrovnání se měří v souřadném systému měřicího stroje. V tomto souřadném systému se provede také spojování. Až jsou všechny elementy pro vyrovnání změřeny, posadí se počátek souřadnic do prvního měřeného bodu prostorového elementu, a to ve všech třech souřadnicích, aby se zabránilo chybě úhlu, která se u větších vzdáleností negativně projevuje. Vyrovnání je uzavřeno tehdy, když všech šest stupňů volnosti souřadného systému je definováno. Šest stupňů volnosti jsou tři souřadnice a tři směry. Točení v prostoru se provede na směrově určeném elementu. Je-li tento element prostřednictvím měření přeurčen, musí se na něm souřadný systém ještě jednou posadit na nulu. K tomu se ale použije ta souřadnice, která je určena směrově definovaným elementem. Přeurčený je ten element, kde se udělalo více sejmutí, než je potřebné. Tzn.: u čáry víc jak 2 snímané body, u roviny víc jak 3 snímané body (nebo spojované body). Tento vyrovnávací postup určí dva stupně volnosti, a to souřadnice a směr. 10
48 Točení v rovině se provede podobně na jednom směrově definovaném elementu. Tím se opět určí dva stupně volnosti. Nyní zbývají dva směry, tím jsou určeny právě čtyři stupně volnosti souřadného systému. Chybí ještě dvě určení souřadnic. Jedno uřčení je stanovení počátku na směrový element v otáčení roviny. Poslední počátek se určí na příslušném elementu. Vyjímky ručního kompletního vyrovnání existují tehdy, když může být měřený díl postaven rovnoběžně s osami. Potom stačí, když se určí počátek všech tří os souřadného systému. Pro vyrovnání CNC platí: Když se změří (nebo spojí) nějaký element, hned se podle něho vyrovnává. Tzn.: hned po určení prostorového elementu (rovina nebo čára) se provede otočení v prostoru s určením počátku v ose (prostorové ose pouze u roviny). V tomto otočeném souřadném systému se provede určení elementu pro otočení roviny a provede se otočení roviny s určením počátku. Jako poslední se určí element pro ještě chybějící souřadnici a stanoví se počátek na příslušném elementu. Tento souřadný systém se musí uložit (ve vývojovém diagramu označeno jako CNC_END). Tímto je díl určený v souřadném systému měřicího stroje. Nyní se musí otočit o příslušný úhel a posunout do souřadného systému auta. V tomto souřadném systému se musí provést kontrola vyrovnání. Měřené výsledky se uloží jako proměnné, aby se mohla zavést smyčka pro opakování. Po kontrole vyrovnání se musí uložený souřadný systém vyrovnání CNC znovu zavolat (RECALL CNC_END), čímž se při zpětném skoku ze smyčky dostaneme do správného souřadného systému a může se měřit dále. Ve smyčce se musí zohlednit všechny proměnné, které byly přiřazeny výsledkům měření. Ve smyčce se zvýší číselná proměnná, aby se mohlo přerušit vyrovnání. Po smyčce se znovu aktivuje souřadný systém auta (RECALL PCS). Tím je vyrovnání dílu ukončeno. Pro lepší porozumění je cely průběh vyrovnání zobrazen v následujícím vývojovém diagramu. 11
49 Obr. č. 9 Průběh vyrovnání 12
50 Měření U větších úloh měření se vytvářejí čtyři různé měřicí programy. Jsou to: Program vyrovnání Program ořezu Program tvaru Program otvorů Průběh programu vyrovnání je popsán v kapitole vyrovnání. U menších rozsahů měřicího programu zde může být na konci přímo startován měřicí program. Jsou-li měřicí programy rozděleny do těchto čtyř variant, kromě vyrovnávacího programu, se vždy začíná v souřadném systému auta. To se dosáhne tím, že se provede kopie souřadného systému, který je aktivní na měřicím stroji. Předpokladem pro to je, že aktivní souřadný systém na měřicím stroji odpovídá také souřadnému sytému vyrovnání. Před vlastním průběhem programu se provede z bezpečnostních důvodů ještě jednou kontrola vyrovnání. Tzn., že se všechny elementy, které byly použity pro vyrovnání, změří ještě jednou. Nesmějí mít žádnou odchylku od jmenovitých hodnot. Zavoláním smyčky výsledků, nebo zastavením měřicího stroje (ruční kontrola obsluhou stroje) se může zkontrolovat výsledek měření. Teprve nyní se může začít s měřicím programem. Aby se kontrola vyrovnání nemusela vždycky programovat znovu, kopíruje se vždy z vyrovnávacího programu (v AUDIMESS pomocí funkce INCLUDE). 13
51 Měření zahnuté hrany Obr. č. 10 Měření zahnuté hrany Určení nejvyššího bodu: Nejvyšší křivka zahnuté hrany se vytvoří, když není k dispozici žádná střední plocha, paralelním posunutím určující plochy až po střed ZSB a vytvořením řezu z posunuté plochy (nebo plochy, která je k dispozici) s plochou poloměru nebo čelní plochou. Tato křivka se nyní může řezat na libovolných místech s teoretickými rovinami. Vzniklé body jsou nejvyšší body (max. bod) na zahnuté hraně. Určí se jméno nejvyššího bodu, když je tento průchozím měřicím bodem. 14
52 Určení bodu prvního sejmutí a měřicího bodu: Bod prvního sejmutí se posune na křivce řezu 8 milimetrů od začátku zakřivení poloměru. Jméno tohoto bodu nemá význam. Měřicí bod se posune na křivce řezu 4 mm od začátku zakřivení poloměru. Jméno bodu se určí, když je tento průběžným měřicím bodem. Určení korekčního bodu: Korekční body se vytvoří rovnoběžně k síti na nejvyšším bodu poloměru. Při vyhodnocení těchto bodů je třeba dbát na to, že se smí posuzovat pouze souřadnice, určující bod. Jména těchto bodů se stanoví podle platného konceptu pro vytváření jména. Měření viditelných hran (vnější hrany) V závislosti na provedení hrany se musí rozlišovat mezi třemi variantami. Pro všechny varianty se měřicí body určují stejně. Měření se rozlišují právě s ohledem na jejich průběh. Začínají ale všechna s nominálním přesazením souřadného systému do bodu prvního sejmutí, aby se případně měření přímo na měřicím stroji mohlo korigovat na jednoduchý druh a způsob. Určení bodů prvního sejmutí a měřicích bodů, příp. rovin: Bod prvního sejmutí se posune 8 mm od začátku zakřivení poloměru na křivce řezu té nejstabilnější plochy. Jméno tohoto bodu nemá význam. Měřicí body se posunou 4 mm od začátku zakřivení poloměru na křivce řezu. Jména těchto bodů se určí, když se jedná o průběžné měřicí body. Když se určí roviny k vytvoření bodů na hraně, leží tyto ve vzdálenosti měřicích bodů. Jejich snímané body leží na poloměru 1 mm kolem vzdálenosti měřicích bodů, popř. ty měřené body, které se použijí pro spojení roviny, leží v této vzdálenosti poloměru. Viz. také příklady pro tyto tři varianty. 15
53 Varianta 1: Hrany, které jsou určeny pravým úhlem a když základní plochy jsou (přibližně) planární. Měření bez určení bodů hrany: Obr. č. 11 Měření hrany Průběh měření: Po posunutí souřadného systému nominálně do bodu prvního sejmutí se změří bod prvního sejmutí ve směru normály. Souřadný systém se posadí na nulu příslušné souřadnice v tomto měřeném bodě. Nyní se změří měřicí bod dvě jako pomocný bod ve směru normály, do kterého se aktivní souřadný systém znovu v příslušné souřadnici posadí na nulu. Nyní se změří měřicí bod jedna ve směru normály. Aktivní souřadný systém se ještě jednou v příslušné souřadnici posadí na nulu. Nyní se může podobně ve směru normály změřit měřicí bod dvě. Zavolá se zpátky souřadný systém auta, aby se výstup výsledků měření provedl ve správném souřadném systému. Z měřicích bodů jedna a dvě se vytvoří transformační body (TR body) a ve směru normály a hlavního souřadného systému se vyhodnotí příslušné tolerance a jména bodů. 16
54 Měření s určením bodů hrany: Obr. č. 12 Měření hrany Průběh měření: Po posunutí souřadného systému nominálně do bodu prvního sejmutí se změří bod prvního sejmutí ve směru normály. Souřadný systém se posadí na nulu v příslušné ose v tomto bodě. Nyní se změří měřicí bod dvě, pomocný bod tři a pomocný bod čtyři. Z těchto tří bodů se spojí roviny dvě. (Pozor: Vektor této roviny musí ukazovat proti směru snímání). V této rovině se otočí souřadný systém v prostoru a v prostorové ose se posadí na nulu. Tím se může měřit měřicí bod jedna, pomocný bod jedna a pomocný bod dvě. Z těchto tří pomocných bodů se podobně spojí rovina jedna. Z roviny jedna a roviny dvě se nyní vytvoří čára řezu. Tyto se s nominální rovinou řezu protnou v bodě hrany. Zavolá se zpátky souřadný systém auta, aby se mohl provést výstup výsledků měření ve správném souřadném systému. Nyní se musí vytvořit z měřicího bodu jedna, měřicího bodu dvě a bodu hrany transformační body (TR body). Měricí body jedna a dvě se vyhodnotí ve směru normály s odpovídajícími tolerancemi a jmény elementů. Bod hrany bude nyní vyhodnocen s odpovídajícími tolerancemi pro souřadnice potřebné pro korekturu přípravků. 17
55 Varianta 2: Hrany, které neurčuje pravý úhel, ale základní plochy jsou (přibližně) planární. Měření vždy s určením bodu hrany. Obr. č. 13 Měření hrany Průběh měření Po posunutí souřadného systému nominálně do bodu prvního sejmutí se změří bod prvního sejmutí ve směru normály. Souřadný systém se posadí na nulu v tomto měřeném bodě v příslušné souřadnici. Nyní se změří pomocný bod jedna a dvě. Z těchto tří bodů se spojí roviny jedna (pozor: vektor roviny musí ukazovat proti směru snímání). V této rovině se otočí souřadný systém v prostoru a posadí na nulu v prostorové ose. Tím se mohou změřit pomocné body 3, 4 a 5, vždy plus nebo mínus 90 stupňů vektoru roviny (v závislosti na směru snímání). Pozor: snímací kulička nesmí být příliš velká, protože korekce poloměru na měřicím stroji zkresluje výsledek měření. Z těchto tří měřených bodů se podobně spojí rovina dvě. Z roviny jedna a dvě se nyní vytvoří čára průřezu. Tato se nyní prořízne nominální rovinou řezu na bod hrany. Souřadný systém se posune podle příslušné souřadnice do tohoto bodu. Aby se vyloučila chyba korekce poloměru (snímací kuličky), změří se ještě jednou pomocné body 3, 4 a 5, ale ve směru normály. Vytvoří se ještě jednou podobně rovina dvě a bod hrany, aby se získala pravá hrana. Také souřadný systém se posadí na nulu v tomto novém bodě hrany. Měřené body jedna a dvě se nyní mohou změřit ve směru normály. Zavolá se zpět souřadný systém auta, aby se mohl provést výstup výsledků měření ve správném souřadném systému. 18
56 Z měřených bodů jedna a dvě a z bodu hrany se nyní musí vytvořit transformační body (TR body). Měřené body jedna a dvě se vyhodnotí ve směru normály s odpovídajícími tolerancemi a jmény bodů. Bod hrany bude nyní vyhodnocen s odpovídajícími tolerancemi pro souřadnice potřebné pro korekturu přípravků. 19
57 Variana 3: Hrany, které nejsou určeny pravým úhlem základní plochy jsou volně tvarované plochy. Měření vždy s určením bodu hrany. Obr. č. 14 Měření hrany Průběh měření: Po nominálním posunutí souřadného systému do prvně sejmutého bodu se tento bod změří ve směru normály. Souřadný systém se v tomto bodě v příslušné tomuto bodu odpovídající souřadnici posadí na nulu. Nyní se v měřeném bodu dvě změří pomocný bod ve směru normály, v kterém se aktivní souřadný systém posadí na nulu v tomuto bodu odpovídající souřadnici. Nyní se změří měřený bod jedna ve směru normály. Aktivní souřadný systém se ještě jednou posadí na nulu v souřadnici odpovídající tomuto bodu. Nyní se může podobně změřit měřený bod dvě ve směru normály. Měřený bod jedna a dvě se nyní posune podél jejich směru normály o libovolnou hodnotu, a vzniknou tím body obratu (move body) jedna a dvě. Pomocí těchto bodů obratu se vytvoří pomocná čára (jedna a dvě) od měřeného bodu jedna k bodu obratu jedna a od měřeného bodu dvě k bodu obratu dvě. Pomocná rovina jedna a dvě se nyní může spojit přes měřený bod jedna a dvě. Těmito dvěma pomocnými rovinami se vytvoří jejich průsečík. Ten se prořízne rovinou řezu a vznikne bod hrany. Zavolá se zpátky souřadný systém auta, abychom dostali výsledek ve správném souřadném systému. 20
58 Nyní se musí vytvořit transformační body (TR body) z měřených bodů jedna a dvě a z bodu hrany. Měřené body jedna a dvě se vyhodnotí ve směru normály s odpovídajícími tolerancemi a jmény elementů. Bod hrany bude nyní vyhodnocen s odpovídajícími tolerancemi pro souřadnice potřebné pro korekturu přípravků. Měření vnitřních hran Vnitřní hrany (Wurzelkanten) se určí stejně jako hrany vnější. Z hlediska techniky měření zde není rozdílu. Měření límce -přesazení (Flanschmesung) Na spojích se musí měřit jejich poloha a délka. K tomu se musí určit bod ořezu a dva body na spoji. Může se volit mezi dvěma variantami, které jsou závislé na dosažitelnosti spoje. Pro obě varianty se měřené body rozdělují stejně. K umístění měřených bodů platí následující pravidlo: Bod ořezu přímo na hraně ořezu u jednoduchých dílů nebo uprostřed mezi ořezy u spojených dílů. Měřený bod jedna na límci by měl být vzdálen od bodu ořezu asi deset procent délky límce. Měřený bod dvě límce by měl být zhruba dvacet procent od ohybu. Varianta jedna: Snímání podle směru jmenovité normály: Obr. č. 15 Měření spoje 21
59 Průběh měření: Po posunutí souřadného systému nominálně do měřicího bodu dvě na límci, se změří bod prvního sejmutí nebo přímo měřený bod dvě na límci ve směru normály. Souřadný systém se posune na nulu v souřadnici odpovídající tomuto měřenému bodu. Pokud se začínalo s bodem prvního sejmutí k určení dílu, měří se nyní měřený bod dvě na límci. Souřadný systém se v příslušné ose posune na nulu. Potom se změří měřený bod jedna na límci a opět se souřadný systém posune na nulu. Nyní se může změřit bod ořezu. Zavolá se zpátky souřadný systém auta, abychom dostali výsledek ve správném souřadném systému. Z měřených bodů jedna a dvě na límci a z bodu ořezu se nyní musí vytvořit transformační body (TR body). Transformované měřené body se vyhodnotí s odpovídajícími tolerancemi a jmény elementů ve směru normály. Podle odchylky se může posoudit poloha popř. délka límce a případně se může změnit. Varianta 2: Snímání podle směru skutečné normály: Obr. č. 16 Měření spoje Průběh měření: Po posunutí souřadného systému nominálně do měřeného bodu dvě límce se změří případně bod prvního sejmutí nebo přímo vyrovnávací rovina. Pokud se začalo měřit s bodem prvního sejmutí k určení polohy dílu, posune se souřadný systém v souřadnici příslušné tomuto měřenému bodu na nulu. Nyní se může změřit vyrovnávací rovina. Souřadný systém se otočí v prostoru a posune se do nuly v prostorové ose. Potom se změří měřené body na límci a bod ořezu. 22
60 Zavolá se zpátky souřadný systém auta, abychom dostali výsledek ve správném souřadném systému. Z měřených bodů jedna a dvě na límci a z bodu ořezu se nyní musí vytvořit transformační body (TR body). Transformované měřené body se vyhodnotí s odpovídajícími tolerancemi a jmény elementů ve směru normály. Podle odchylky se může posoudit poloha popř. délka límce a případně se může změnit. Příklad kombinace jednotlivých metod měření na neznámém obrysu. Vyobrazení jmenovitého a skutečného dílu: Obr. č. 17 Měření neznámého obrysu Průběh měření V tomto příkladě se mají určit ořez, vnitřní hrana a vnější hrana. Měření se začíná na nejstabilnější ploše. Souřadný systém se posune nominálně ve všech třech osách do pomocného bodu H2. Body M1 (rovná se H1), H2 a M2 (rovná se H3) se určí první rovina (E1). Souřadný systém se vyrovná v prostoru a posune se v prostorové ose na nulu. Nyní se určí druhá rovina (E2) prostřednictvím pomocných bodů H4, H5 a H6, které se měří rovnoběžně v ose. Z rovin E1 a E2 se vytvoří čára průsečíku a tato se prořízne nominální rovinou řezu a vznikne bod hrany K1. Souřadný systém se posune v souřadnici odpovídající tomuto bodu na nulu. 23
61 Nyní se změří měřené body jedna a dvě. Souřadný systém se nyní vyrovná v prostoru na druhé rovině a posune se podle prostorové osy na nulu. Měřené body 3 a 4, a pomocné body H7, H8 a H9, které se měří rovnoběžně v ose, se mohou určit. Pomocí bodů H7, H8 a H9 se nyní spojí třetí rovina (E3). Z rovin E2 a E3 se vytvoří čára řezu a tato se prořízne nominální rovinou řezu a vznikne tak bod hrany K2. Souřadný systém se otočí v prostoru v rovině E3 a v prostorové ose na této rovině se posune na nulu. Nyní se mohou určit měřené body 5, 6 a 7. Zavolá se zpátky souřadný systém auta, abychom dostali výsledek ve správném souřadném systému. Z bodů hrany a z měřených bodů se nyní musí vytvořit transformační body (TR body). Transformované měřené body se vyhodnotí s odpovídajícími tolerancemi a jmény elementů ve směru normály. Transformované body hrany se opatří podobně jménem elementu, ale vyhodnotí se pouze v příslušné ose. Kvůli špatné korekci poloměru kuličky snímače se musí v pomocných bodech H4 H9 pracovat s malou kuličkou. Není-li to možné z důvodů techniky měření, musí se roviny E2 a E3 určit s mezivyrovnáním pomocí dvojího měření (prvně rovnoběžně v ose a potom ve směru normály). 24
62 Měření kružnice Zásadně se kružnice musí měřit v lokálním vyrovnání. Postup: Souřadný systém posunout teoreticky do středu kružnice. Změřit rovinu, která určuje polohu kružnice. Souřadný systém vyrovnat v rovině s otočit v prostoru. Posunout počátek v prostorové ose v rovině. Změřit kružnici, obvykle pěti body sejmutí s hloubkou ponoření nula, a vyhodnotit průměr. Zavolat zpátky souřadný systém vyhodnocení. Vytvořit transformační matici uprostřed kružnice a vyhodnotit odpovídající souřadnice. Poznámka: Směr snímacího nástroje musí být ve směru normály k rovině určující kružnici. Měří-li se kružnice s hloubkou ponoření větší než nula, musí se před zavoláním souřadného systému vyhodnocení promítnout střed kružnice do roviny tuto kružnici určující. Počet měřených bodů a hloubka ponoření jsou závislé na požadavcích na měření a na dostupnosti dílu. Příklad špatného měření na kružnici bez vyrovnání: Obr. č. 18 Špatné měření kružnice Poznámka: Skutečný díl je otočen o dvacet stupňů ve vektoru z P2 oproti jmenovitému dílu. Měří se třemi body s hloubkou ponoření 0,5 mm. Jmenovitý průměr kružnice je 10 mm. Průměr kuličky snímače je 3 mm. Bez vyrovnání se sejme P1 příliš hluboko a P3 příliš vysoko. Měření snímaného bodu P2 je OK. Odchylka, způsobená chybou měření, činí u průměru 0,55 mm a v souřadnicích 0,20 mm. 25
63 Snímané body P1, P2 a P3 jsou vyobrazeny shora i ze spod. Obr. č. 19 Měření kružnice 26
64 Obr. č. 20 Měření kružnice 27
65 Obr. č. 21 Měření kružnice 28
66 Měření kružnice z elipsy, která je kótovaná jako kružnice Otvory, které nejsou postaveny ve směru normály k rovině, určující kružnici. Postup varianta jedna: Souřadný systém posunout teoreticky do středu elipsy. Změřit rovinu, která určuje polohu elipsy. Souřadný systém vyrovnat do této roviny pomocí otočit v prostoru. Prostorovou osu posunout v rovině do nuly. Body, které určují kružnici, změřit s odpovídající hloubkou ponoření na eliptickém výřezu. Definovat dvě teoretické roviny, které určují směr průniku. Měřené body promítnout do definované roviny. Promítnuté body spojit do kružnice a z kružnice vyhodnotit průměr. Ze spojených kružnic vytvořit jednu čáru. Vytvořit průsečík z roviny určující elipsu a z vytvořené čáry. Zavolat zpět souřadný systém vyhodnocení. Vytvořit transformační matici pro střed kružnice rovná se průsečík a vyhodnotit příslušné souřadnice. Postup varianta dvě: Souřadný systém posunout teoreticky do středu elipsy. Změřit rovinu, která určuje polohu elipsy. Souřadný systém vyrovnat do této roviny pomocí otočit v prostoru. Prostorovou osu posunout v rovině do nuly. Body, které určují kružnici, změřit s odpovídající hloubkou ponoření na eliptickém výřezu. Definovat jednu teoretickou rovinu, která určuje směr průniku. Měřené body promítnout do definované roviny. Promítnuté body spojit do kružnice a z kružnice vyhodnotit průměr. Vytvořit jednu čáru normálově středem kružnice. Vytvořit průsečík z roviny určující elipsu a z vytvořené čáry. Zavolat zpět souřadný systém vyhodnocení. Vytvořit transformační matici pro střed kružnice rovná se průsečík a vyhodnotit příslušné souřadnice. 29
67 Obr. č. 22 Měření kružnice z elipsy 30
68 Měření podélného otvoru Při měření podélného otvoru se zkontrolují obě protilehlé kružnice, střed, a světlá vzdálenost. Postup poloha v rovině: Souřadný systém posunout teoreticky do středu podélného otvoru. Změřit rovinu, která určuje polohu podélného otvoru. Vyrovnat souřadný systém v rovině pomocí otočit v prostoru. Prostorovou osu posunout na nulu v rovině. Případně změřit dva body na jedné straně podélného otvoru a spojit je do čáry. V této čáře otočit rovinu a příslušnou souřadnici posunout do nuly. Obě kružnice změřit s odpovídající hloubkou ponoření a vyhodnotit průměry. Při hloubce ponoření větší než 0 promítnout oba středy kružnic do roviny určující podélný otvor. Změřit čáru na jedné straně podélného otvoru s odpovídající hloubkou ponoření, nebo použít čáru, která byla použita pro otočení roviny. Změřit bod na druhé straně podélného otvoru s odpovídající hloubkou ponoření. Při hloubce ponoření větší než 0 promítnout bod a čáru do roviny, určující podélný otvor. Vyhodnotit Euklidovskou vzdálenost čára (průmět) a bod (průmět). Vyhodnotit Euklidovskou vzdálenost středů kružnic (průmět). Zavolat zpět souřadný systém vyhodnocení. Vytvořit středový bod z obou měřených kružnic, popř. promítnutých bodů, a vyhodnotit příslušné souřadnice. 31
Úlohy na měřicím přístroji TESA 3D MICRO HITE
 Úlohy na měřicím přístroji TESA 3D MICRO HITE Ing. Zdeněk Ondříšek 1 Obsah: 1. 0. 0 Cíle... 3 1. 1. 0 Než začneme... 3 1. 2. 0 Příprava součásti pro měření... 8 2. 0. 0 Úloha č. 1 Měření délky... 14 2.
Úlohy na měřicím přístroji TESA 3D MICRO HITE Ing. Zdeněk Ondříšek 1 Obsah: 1. 0. 0 Cíle... 3 1. 1. 0 Než začneme... 3 1. 2. 0 Příprava součásti pro měření... 8 2. 0. 0 Úloha č. 1 Měření délky... 14 2.
5) Průnik rotačních ploch. A) Osy totožné (a kolmé k půdorysně) Bod R průniku ploch. 1) Pomocná plocha κ
 5) Průnik rotačních ploch Bod R průniku ploch κ, κ : 1) Pomocná plocha κ ) Průniky : l κ κ, l κ κ 3) R l l Volba pomocné plochy pro průnik rotačních ploch závisí na poloze os ploch. Omezíme se pouze na
5) Průnik rotačních ploch Bod R průniku ploch κ, κ : 1) Pomocná plocha κ ) Průniky : l κ κ, l κ κ 3) R l l Volba pomocné plochy pro průnik rotačních ploch závisí na poloze os ploch. Omezíme se pouze na
Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Aleš Najman [ÚLOHA 28 NÁSTROJE EDITACE ]
![Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Aleš Najman [ÚLOHA 28 NÁSTROJE EDITACE ] Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Aleš Najman [ÚLOHA 28 NÁSTROJE EDITACE ]](/thumbs/26/8858069.jpg) Aplikované úlohy Solid Edge SPŠSE a VOŠ Liberec Ing. Aleš Najman [ÚLOHA 28 NÁSTROJE EDITACE ] 1 ÚVOD Úloha 28 je zaměřena na úpravu objektů v modulu Výkres. Úpravou výkresů jsou myšleny operace zaoblení,
Aplikované úlohy Solid Edge SPŠSE a VOŠ Liberec Ing. Aleš Najman [ÚLOHA 28 NÁSTROJE EDITACE ] 1 ÚVOD Úloha 28 je zaměřena na úpravu objektů v modulu Výkres. Úpravou výkresů jsou myšleny operace zaoblení,
Software Form Control
 Měření na kliknutí myši. Tak jednoduchá je kontrola obrobku v obráběcím centru pomocí měřícího softwaru FormControl. Nezáleží na tom, zda má obrobek obecné 3D kontury nebo běžný 2.5D charakter. Uživatel
Měření na kliknutí myši. Tak jednoduchá je kontrola obrobku v obráběcím centru pomocí měřícího softwaru FormControl. Nezáleží na tom, zda má obrobek obecné 3D kontury nebo běžný 2.5D charakter. Uživatel
Cvičení 2 z předmětu CAD I PARAMETRICKÉ 3D MODELOVÁNÍ
 Cvičení 2 z předmětu CAD I PARAMETRICKÉ 3D MODELOVÁNÍ Cílem druhého cvičení je si na jednoduchém modelu hřídele osvojit základní postupy při tvorbě rotační součástky. Především používání pracovních, nebo
Cvičení 2 z předmětu CAD I PARAMETRICKÉ 3D MODELOVÁNÍ Cílem druhého cvičení je si na jednoduchém modelu hřídele osvojit základní postupy při tvorbě rotační součástky. Především používání pracovních, nebo
Obsluha měřicích zařízení kontaktní metody
 T E C H N I C K Á U N I V E R Z I T A V L I B E R C I FAKULTA STROJNÍ KATEDRA VÝROBNÍCH SYSTÉMŮ A AUTOMATIZACE Obsluha měřicích zařízení kontaktní metody Ing. Petr Keller, Ph.D. Ing. Petr Zelený, Ph.D.
T E C H N I C K Á U N I V E R Z I T A V L I B E R C I FAKULTA STROJNÍ KATEDRA VÝROBNÍCH SYSTÉMŮ A AUTOMATIZACE Obsluha měřicích zařízení kontaktní metody Ing. Petr Keller, Ph.D. Ing. Petr Zelený, Ph.D.
Pravoúhlá axonometrie
 Pravoúhlá axonometrie bod, přímka, rovina, bod v rovině, trojúhelník v rovině, průsečnice rovin, průsečík přímky s rovinou, čtverec v půdorysně, kružnice v půdorysně V Rhinu vypneme osy mřížky (tj. červenou
Pravoúhlá axonometrie bod, přímka, rovina, bod v rovině, trojúhelník v rovině, průsečnice rovin, průsečík přímky s rovinou, čtverec v půdorysně, kružnice v půdorysně V Rhinu vypneme osy mřížky (tj. červenou
P R O M Í T Á N Í. rovina π - průmětna vektor s r - směr promítání. a // s r, b// s r,
 P R O M Í T Á N Í Promítání je zobrazení prostorového útvaru do roviny. Je určeno průmětnou a směrem (rovnoběžné) nebo středem (středové) promítání. Princip rovnoběžného promítání rovina π - průmětna vektor
P R O M Í T Á N Í Promítání je zobrazení prostorového útvaru do roviny. Je určeno průmětnou a směrem (rovnoběžné) nebo středem (středové) promítání. Princip rovnoběžného promítání rovina π - průmětna vektor
Cyklografie. Cyklický průmět bodu
 Cyklografie Cyklografie je nelineární zobrazovací metoda - bodům v prostoru odpovídají kružnice v rovině a naopak. Úlohy v rovině pak převádíme na řešení prostorových úloh, např. pomocí cyklografie řešíme
Cyklografie Cyklografie je nelineární zobrazovací metoda - bodům v prostoru odpovídají kružnice v rovině a naopak. Úlohy v rovině pak převádíme na řešení prostorových úloh, např. pomocí cyklografie řešíme
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/ Protokol měření. Kontrola a měření závitů
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Protokol měření Tolerování závitů Kontrola a měření závitů Řetězec norem, které se zabývají závity, zahrnuje
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Protokol měření Tolerování závitů Kontrola a měření závitů Řetězec norem, které se zabývají závity, zahrnuje
Interaktivní modely pro Konstruktivní geometrii
 Interaktivní modely pro Konstruktivní geometrii Jakub Makarovský Abstrakt V příspěvku jsou prezentovány interaktivní modely základních úloh z Konstruktivní geometrie (1. ročník, zimní semestr) zaměřující
Interaktivní modely pro Konstruktivní geometrii Jakub Makarovský Abstrakt V příspěvku jsou prezentovány interaktivní modely základních úloh z Konstruktivní geometrie (1. ročník, zimní semestr) zaměřující
X = A + tu. Obr x = a 1 + tu 1 y = a 2 + tu 2, t R, y = kx + q, k, q R (6.1)
 .6. Analtická geometrie lineárních a kvadratických útvarů v rovině. 6.1. V této kapitole budeme studovat geometrické úloh v rovině analtick, tj. lineární a kvadratické geometrické útvar vjádříme pomocí
.6. Analtická geometrie lineárních a kvadratických útvarů v rovině. 6.1. V této kapitole budeme studovat geometrické úloh v rovině analtick, tj. lineární a kvadratické geometrické útvar vjádříme pomocí
Programovací stanice itnc 530
 Programovací stanice itnc 530 Základy programování výroby jednoduchých součástí na CNC frézce s řídícím systémem HEIDENHAIN VOŠ a SPŠE Plzeň 2011 / 2012 Ing. Lubomír Nový Stanice itnc 530 a možnosti jejího
Programovací stanice itnc 530 Základy programování výroby jednoduchých součástí na CNC frézce s řídícím systémem HEIDENHAIN VOŠ a SPŠE Plzeň 2011 / 2012 Ing. Lubomír Nový Stanice itnc 530 a možnosti jejího
Příklady k analytické geometrii kružnice a vzájemná poloha kružnice a přímky
 Příklady k analytické geometrii kružnice a vzájemná poloha kružnice a přímky Př. 1: Určete rovnice všech kružnic, které procházejí bodem A = * 6; 9+, mají střed na přímce p: x + 3y 18 = 0 a jejich poloměr
Příklady k analytické geometrii kružnice a vzájemná poloha kružnice a přímky Př. 1: Určete rovnice všech kružnic, které procházejí bodem A = * 6; 9+, mají střed na přímce p: x + 3y 18 = 0 a jejich poloměr
MONGEOVO PROMÍTÁNÍ. bylo objeveno a rozvinuto francouzem Gaspardem Mongem (1746 1818) po dlouhou dobu bylo vojenským tajemstvím
 část 1. MONGEOVO PROMÍTÁNÍ kolmé promítání na dvě průmětny (půdorysna, nárysna), někdy se používá i třetí pomocná průmětna bokorysna bylo objeveno a rozvinuto francouzem Gaspardem Mongem (1746 1818) po
část 1. MONGEOVO PROMÍTÁNÍ kolmé promítání na dvě průmětny (půdorysna, nárysna), někdy se používá i třetí pomocná průmětna bokorysna bylo objeveno a rozvinuto francouzem Gaspardem Mongem (1746 1818) po
Práce s texty, Transformace rastru, Připojení GPS
 Školení programu TopoL xt Práce s texty, Transformace rastru, Připojení GPS Obsah: 1. Uživatelské rozhraní (heslovitě, bylo součástí minulých školení) 2. Nastavení programu (heslovitě, bylo součástí minulých
Školení programu TopoL xt Práce s texty, Transformace rastru, Připojení GPS Obsah: 1. Uživatelské rozhraní (heslovitě, bylo součástí minulých školení) 2. Nastavení programu (heslovitě, bylo součástí minulých
TECHNICKÁ DOKUMENTACE
 TECHNICKÁ DOKUMENTACE Jan Petřík 2013 Projekt ESF CZ.1.07/2.2.00/28.0050 Modernizace didaktických metod a inovace výuky technických předmětů. Obsah přednášek 1. Úvod do problematiky tvorby technické dokumentace
TECHNICKÁ DOKUMENTACE Jan Petřík 2013 Projekt ESF CZ.1.07/2.2.00/28.0050 Modernizace didaktických metod a inovace výuky technických předmětů. Obsah přednášek 1. Úvod do problematiky tvorby technické dokumentace
Rozvinutelné plochy. tvoří jednoparametrickou soustavu rovin a tedy obaluje rozvinutelnou plochu Φ. Necht jsou
 Rozvinutelné plochy Rozvinutelná plocha je každá přímková plocha, pro kterou existuje izometrické zobrazení do rov iny, tj. lze ji rozvinout do roviny. Dá se ukázat, že každá rozvinutelná plocha patří
Rozvinutelné plochy Rozvinutelná plocha je každá přímková plocha, pro kterou existuje izometrické zobrazení do rov iny, tj. lze ji rozvinout do roviny. Dá se ukázat, že každá rozvinutelná plocha patří
AXONOMETRIE - 2. část
 AXONOMETRIE - 2. část Průmět přímky K určení přímky stačí její dva libovolné průměty, zpravidla používáme axonometrický průmět a půdorys. Bod ležící na přímce se zobrazí do bodu na přímce v každém průmětu.
AXONOMETRIE - 2. část Průmět přímky K určení přímky stačí její dva libovolné průměty, zpravidla používáme axonometrický průmět a půdorys. Bod ležící na přímce se zobrazí do bodu na přímce v každém průmětu.
Cvičení 6 z předmětu CAD I PARAMETRICKÉ 3D MODELOVÁNÍ VÝKRES
 Cvičení 6 z předmětu CAD I PARAMETRICKÉ 3D MODELOVÁNÍ VÝKRES Cílem cvičení je osvojit si na jednoduchém modelu odlitého obrobku základní postupy při tvorbě výkresu.obrobek je vytvořen z předem vytvořeného
Cvičení 6 z předmětu CAD I PARAMETRICKÉ 3D MODELOVÁNÍ VÝKRES Cílem cvičení je osvojit si na jednoduchém modelu odlitého obrobku základní postupy při tvorbě výkresu.obrobek je vytvořen z předem vytvořeného
Rasterizace je proces při kterém se vektorově definovaná grafika konvertuje na. x 2 x 1
 Kapitola 4 Rasterizace objektů Rasterizace je proces při kterém se vektorově definovaná grafika konvertuje na rastrově definované obrazy. Při zobrazení reálného modelu ve světových souřadnicích na výstupní
Kapitola 4 Rasterizace objektů Rasterizace je proces při kterém se vektorově definovaná grafika konvertuje na rastrově definované obrazy. Při zobrazení reálného modelu ve světových souřadnicích na výstupní
Obsah a průběh zkoušky 1PG
 Obsah a průběh zkoušky PG Zkouška se skládá z písemné a ústní části. Písemná část (cca 6 minut) dvě konstrukční úlohy dle části po. bodech a jedna úloha výpočetní úloha dle části za bodů. Ústní část jedna
Obsah a průběh zkoušky PG Zkouška se skládá z písemné a ústní části. Písemná část (cca 6 minut) dvě konstrukční úlohy dle části po. bodech a jedna úloha výpočetní úloha dle části za bodů. Ústní část jedna
MONGEOVO PROMÍTÁNÍ - 2. část
 MONGEOVO PROMÍTÁNÍ - 2. část ZOBRAZENÍ KRUŽNICE Příklad: V rovině ρ zobrazte kružnici o středu S a poloměru r. kružnice ležící v obecné rovině se v obou průmětech zobrazuje jako elipsa poloměr kružnice
MONGEOVO PROMÍTÁNÍ - 2. část ZOBRAZENÍ KRUŽNICE Příklad: V rovině ρ zobrazte kružnici o středu S a poloměru r. kružnice ležící v obecné rovině se v obou průmětech zobrazuje jako elipsa poloměr kružnice
1. Dva dlouhé přímé rovnoběžné vodiče vzdálené od sebe 0,75 cm leží kolmo k rovine obrázku 1. Vodičem 1 protéká proud o velikosti 6,5A směrem od nás.
 Příklady: 30. Magnetické pole elektrického proudu 1. Dva dlouhé přímé rovnoběžné vodiče vzdálené od sebe 0,75 cm leží kolmo k rovine obrázku 1. Vodičem 1 protéká proud o velikosti 6,5A směrem od nás. a)
Příklady: 30. Magnetické pole elektrického proudu 1. Dva dlouhé přímé rovnoběžné vodiče vzdálené od sebe 0,75 cm leží kolmo k rovine obrázku 1. Vodičem 1 protéká proud o velikosti 6,5A směrem od nás. a)
HVrchlík DVrchlík. Anuloid Hrana 3D síť
 TVORBA PLOCH Plochy mají oproti 3D drátovým modelům velkou výhodu, pro snadnější vizualizaci modelů můžeme skrýt zadní plochy a vytvořit stínované obrázky. Plochy dále umožňují vytvoření neobvyklých tvarů.
TVORBA PLOCH Plochy mají oproti 3D drátovým modelům velkou výhodu, pro snadnější vizualizaci modelů můžeme skrýt zadní plochy a vytvořit stínované obrázky. Plochy dále umožňují vytvoření neobvyklých tvarů.
2) Nulový bod stroje používáme k: a) Kalibraci stroje b) Výchozímu bodu vztažného systému c) Určení korekcí nástroje
 1) K čemu používáme u CNC obráběcího stroje referenční bod stroje: a) Kalibraci stroje a souřadného systému b) Zavedení souřadného systému stroje c) K výměně nástrojů 2) Nulový bod stroje používáme k:
1) K čemu používáme u CNC obráběcího stroje referenční bod stroje: a) Kalibraci stroje a souřadného systému b) Zavedení souřadného systému stroje c) K výměně nástrojů 2) Nulový bod stroje používáme k:
ROTAČNÍ PLOCHY. 1) Základní pojmy
 ROTAČNÍ PLOCHY 1) Základní pojmy Rotační plocha vznikne rotací tvořicí křivky k kolem osy o. Pro zobrazení a konstrukce bude výhodnější nechat rotovat jednotlivé body tvořicí křivky. Trajektorii rotujícího
ROTAČNÍ PLOCHY 1) Základní pojmy Rotační plocha vznikne rotací tvořicí křivky k kolem osy o. Pro zobrazení a konstrukce bude výhodnější nechat rotovat jednotlivé body tvořicí křivky. Trajektorii rotujícího
Základní pojmy a pravidla kótování
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Základní pojmy a pravidla kótování Pro čtení výkresů, tj. určení rozměrů nebo polohy předmětu, jsou rozhodující
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 Základní pojmy a pravidla kótování Pro čtení výkresů, tj. určení rozměrů nebo polohy předmětu, jsou rozhodující
Analytická geometrie (AG)
 Analytická geometrie (AG) - zkoumá geometrické útvary pomocí algebraických a analytických metod Je založena na vektorech a soustavě souřadnic, rozděluje se na AG v rovině a v prostoru. Analytická geometrie
Analytická geometrie (AG) - zkoumá geometrické útvary pomocí algebraických a analytických metod Je založena na vektorech a soustavě souřadnic, rozděluje se na AG v rovině a v prostoru. Analytická geometrie
Deskriptivní geometrie pro střední školy
 Deskriptivní geometrie pro střední školy Mongeovo promítání 1. díl Ivona Spurná Nakladatelství a vydavatelství R www.computermedia.cz Obsah TEMATICKÉ ROZDĚLENÍ DÍLŮ KNIHY DESKRIPTIVNÍ GEOMETRIE 1. díl
Deskriptivní geometrie pro střední školy Mongeovo promítání 1. díl Ivona Spurná Nakladatelství a vydavatelství R www.computermedia.cz Obsah TEMATICKÉ ROZDĚLENÍ DÍLŮ KNIHY DESKRIPTIVNÍ GEOMETRIE 1. díl
1.1 Napište středovou rovnici kružnice, která má střed v počátku soustavy souřadnic a prochází bodem
 Analytická geometrie - kružnice Napište středovou rovnici kružnice, která má střed v počátku soustavy souřadnic a prochází bodem A = ; 5 [ ] Napište středový i obecný tvar rovnice kružnice, která má střed
Analytická geometrie - kružnice Napište středovou rovnici kružnice, která má střed v počátku soustavy souřadnic a prochází bodem A = ; 5 [ ] Napište středový i obecný tvar rovnice kružnice, která má střed
Výukový manuál 1 /64
 1 Vytvoření křížového spojovacího dílu 2 1. Klepněte na ikonu Geomagic Design a otevřete okno Domů. 2. V tomto okně klepněte na Vytvořit nové díly pro vložení do sestavy. 3 1. 2. 3. 4. V otevřeném okně
1 Vytvoření křížového spojovacího dílu 2 1. Klepněte na ikonu Geomagic Design a otevřete okno Domů. 2. V tomto okně klepněte na Vytvořit nové díly pro vložení do sestavy. 3 1. 2. 3. 4. V otevřeném okně
Cvičení 2 PARAMETRICKÉ 3D MODELOVÁNÍ ROTAČNÍ SOUČÁST HŘÍDEL Inventor Professional 2012
 Cvičení 2 PARAMETRICKÉ 3D MODELOVÁNÍ ROTAČNÍ SOUČÁST HŘÍDEL Inventor Professional 2012 Cílem druhého cvičení je osvojení postupů tvorby rotační součástky na jednoduchém modelu hřídele. Především používání
Cvičení 2 PARAMETRICKÉ 3D MODELOVÁNÍ ROTAČNÍ SOUČÁST HŘÍDEL Inventor Professional 2012 Cílem druhého cvičení je osvojení postupů tvorby rotační součástky na jednoduchém modelu hřídele. Především používání
MONGEOVO PROMÍTÁNÍ. ZOBRAZENÍ BODU - sdružení průměten. ZOBRAZENÍ BODU - kartézské souřadnice A[3; 5; 4], B[-4; -6; 2]
![MONGEOVO PROMÍTÁNÍ. ZOBRAZENÍ BODU - sdružení průměten. ZOBRAZENÍ BODU - kartézské souřadnice A[3; 5; 4], B[-4; -6; 2] MONGEOVO PROMÍTÁNÍ. ZOBRAZENÍ BODU - sdružení průměten. ZOBRAZENÍ BODU - kartézské souřadnice A[3; 5; 4], B[-4; -6; 2]](/thumbs/55/35543113.jpg) ZOBRAZENÍ BODU - sdružení průměten MONGEOVO PROMÍTÁNÍ π 1... půdorysna π 2... nárysna x... osa x (průsečnice průměten) sdružení průměten A 1... první průmět bodu A A 2... druhý průmět bodu A ZOBRAZENÍ
ZOBRAZENÍ BODU - sdružení průměten MONGEOVO PROMÍTÁNÍ π 1... půdorysna π 2... nárysna x... osa x (průsečnice průměten) sdružení průměten A 1... první průmět bodu A A 2... druhý průmět bodu A ZOBRAZENÍ
Momenty setrvačnosti a deviační momenty
 Momenty setrvačnosti a deviační momenty Momenty setrvačnosti a deviační momenty charakterizují spolu shmotností a statickými momenty hmoty rozložení hmotnosti tělesa vprostoru. Jako takové se proto vyskytují
Momenty setrvačnosti a deviační momenty Momenty setrvačnosti a deviační momenty charakterizují spolu shmotností a statickými momenty hmoty rozložení hmotnosti tělesa vprostoru. Jako takové se proto vyskytují
Kapitola 5. Seznámíme se ze základními vlastnostmi elipsy, hyperboly a paraboly, které
 Kapitola 5 Kuželosečky Seznámíme se ze základními vlastnostmi elipsy, hyperboly a paraboly, které společně s kružnicí jsou známy pod společným názvem kuželosečky. Říká se jim tak proto, že každou z nich
Kapitola 5 Kuželosečky Seznámíme se ze základními vlastnostmi elipsy, hyperboly a paraboly, které společně s kružnicí jsou známy pod společným názvem kuželosečky. Říká se jim tak proto, že každou z nich
CAD_Inventor -cvičení k modelování a tvorbě technické obrazové dokumentace Vytváření výrobního výkresu rotační součásti - hřídele
 Předmět: Ročník: Vytvořil: Datum: CAD druhý, třetí Petr Machanec 24.8.2012 Název zpracovaného celku: CAD_Inventor -cvičení k modelování a tvorbě technické obrazové dokumentace Vytváření výrobního výkresu
Předmět: Ročník: Vytvořil: Datum: CAD druhý, třetí Petr Machanec 24.8.2012 Název zpracovaného celku: CAD_Inventor -cvičení k modelování a tvorbě technické obrazové dokumentace Vytváření výrobního výkresu
MODELOVÁNÍ V INVENTORU CV
 Vysoká škola báňská Technická univerzita Ostrava Fakulta strojní MODELOVÁNÍ V INVENTORU CV Návody do cvičení předmětu Grafické systémy II Oldřich Učeň Martin Janečka Ostrava 2011 Tyto studijní materiály
Vysoká škola báňská Technická univerzita Ostrava Fakulta strojní MODELOVÁNÍ V INVENTORU CV Návody do cvičení předmětu Grafické systémy II Oldřich Učeň Martin Janečka Ostrava 2011 Tyto studijní materiály
Gymnázium Jiřího Ortena, Kutná Hora. Průřezová témata Poznámky. Téma Školní výstupy Učivo (pojmy) volné rovnoběžné promítání průmětna
 Předmět: Matematika Náplň: Stereometrie, Analytická geometrie Třída: 3. ročník a septima Počet hodin: 4 hodiny týdně Pomůcky: PC a dataprojektor, učebnice Stereometrie Volné rovnoběžné promítání Zobrazí
Předmět: Matematika Náplň: Stereometrie, Analytická geometrie Třída: 3. ročník a septima Počet hodin: 4 hodiny týdně Pomůcky: PC a dataprojektor, učebnice Stereometrie Volné rovnoběžné promítání Zobrazí
Skládání různoběžných kmitů. Skládání kolmých kmitů. 1) harmonické kmity stejné frekvence :
 Skládání různoběžných kmitů Uvědomme si principiální bod tohoto problému : na jediný hmotný bod působí dvě nezávislé pružné síl ve dvou různých směrech. Jednotlivé mechanické pohb, které se budou skládat,
Skládání různoběžných kmitů Uvědomme si principiální bod tohoto problému : na jediný hmotný bod působí dvě nezávislé pružné síl ve dvou různých směrech. Jednotlivé mechanické pohb, které se budou skládat,
Kapitola 2. o a paprsek sil lze ztotožnit s osou x (obr.2.1). sil a velikost rovnou algebraickému součtu sil podle vztahu R = F i, (2.
 Kapitola 2 Přímková a rovinná soustava sil 2.1 Přímková soustava sil Soustava sil ležící ve společném paprsku se nazývá přímková soustava sil [2]. Působiště všech sil m i lze posunout do společného bodu
Kapitola 2 Přímková a rovinná soustava sil 2.1 Přímková soustava sil Soustava sil ležící ve společném paprsku se nazývá přímková soustava sil [2]. Působiště všech sil m i lze posunout do společného bodu
= cos sin = sin + cos = 1, = 6 = 9. 6 sin 9. = 1 cos 9. = 1 sin 9. + 6 cos 9 = 1 0,939692621 6 ( 0,342020143) = 1 ( 0,342020143) + 6 0,939692621
 ŘEŠENÉ PŘÍKLADY Z MA+ULA ČÁST Příklad Bod má vůči souřadné soustavě souřadnice uvedené níže. Vypočtěte jeho souřadnice vzhledem k soustavě, která je vůči otočená dle zadání uvedeného níže. Výsledky zaokrouhlete
ŘEŠENÉ PŘÍKLADY Z MA+ULA ČÁST Příklad Bod má vůči souřadné soustavě souřadnice uvedené níže. Vypočtěte jeho souřadnice vzhledem k soustavě, která je vůči otočená dle zadání uvedeného níže. Výsledky zaokrouhlete
TVORBA VÝROBNÍ DOKUMENTACE CV
 Vysoká škola báňská Technická univerzita Ostrava Fakulta strojní TVORBA VÝROBNÍ DOKUMENTACE CV Návody do cvičení předmětu Výrobní dokumentace v systému CAD Dr. Ing. Jaroslav Melecký Ostrava 2011 Tyto studijní
Vysoká škola báňská Technická univerzita Ostrava Fakulta strojní TVORBA VÝROBNÍ DOKUMENTACE CV Návody do cvičení předmětu Výrobní dokumentace v systému CAD Dr. Ing. Jaroslav Melecký Ostrava 2011 Tyto studijní
8 Plochy - vytvoření, rozdělení, tečná rovina a normála. Šroubové plochy - přímkové, cyklické. Literatura:
 8 Plochy - vytvoření, rozdělení, tečná rovina a normála. Šroubové plochy - přímkové, cyklické. Literatura: (1)Poláček, J., Doležal, M.: Základy deskriptivní a konstruktivní geometrie, díl 5, Křivky a plochy
8 Plochy - vytvoření, rozdělení, tečná rovina a normála. Šroubové plochy - přímkové, cyklické. Literatura: (1)Poláček, J., Doležal, M.: Základy deskriptivní a konstruktivní geometrie, díl 5, Křivky a plochy
Konstruktivní geometrie PODKLADY PRO PŘEDNÁŠKU
 Konstruktivní geometrie & technické kreslení PODKLADY PRO PŘEDNÁŠKU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného
Konstruktivní geometrie & technické kreslení PODKLADY PRO PŘEDNÁŠKU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného
Obsah. 2 Moment síly Dvojice sil Rozklad sil 4. 6 Rovnováha 5. 7 Kinetická energie tuhého tělesa 6. 8 Jednoduché stroje 8
 Obsah 1 Tuhé těleso 1 2 Moment síly 2 3 Skládání sil 3 3.1 Skládání dvou různoběžných sil................. 3 3.2 Skládání dvou rovnoběžných, různě velkých sil......... 3 3.3 Dvojice sil.............................
Obsah 1 Tuhé těleso 1 2 Moment síly 2 3 Skládání sil 3 3.1 Skládání dvou různoběžných sil................. 3 3.2 Skládání dvou rovnoběžných, různě velkých sil......... 3 3.3 Dvojice sil.............................
VŠB TU OSTRAVA, Fakulta bezpečnostního inženýrství. Kreslení strojírenských výkresů. Ing. Eva Veličková
 VŠB TU OSTRAVA, Fakulta bezpečnostního inženýrství Kreslení strojírenských výkresů Ing. Eva Veličková Obsah: 1. Strojírenské výkresy... 2 2. Pravoúhlé promítání, pohledy... 7 3. Zobrazování na strojírenském
VŠB TU OSTRAVA, Fakulta bezpečnostního inženýrství Kreslení strojírenských výkresů Ing. Eva Veličková Obsah: 1. Strojírenské výkresy... 2 2. Pravoúhlé promítání, pohledy... 7 3. Zobrazování na strojírenském
Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Jan Boháček [ÚLOHA 27 NÁSTROJE KRESLENÍ]
![Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Jan Boháček [ÚLOHA 27 NÁSTROJE KRESLENÍ] Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Jan Boháček [ÚLOHA 27 NÁSTROJE KRESLENÍ]](/thumbs/24/3705963.jpg) Aplikované úlohy Solid Edge SPŠSE a VOŠ Liberec Ing. Jan Boháček [ÚLOHA 27 NÁSTROJE KRESLENÍ] 1 CÍL KAPITOLY V této kapitole si představíme Nástroje kreslení pro tvorbu 2D skic v modulu Objemová součást
Aplikované úlohy Solid Edge SPŠSE a VOŠ Liberec Ing. Jan Boháček [ÚLOHA 27 NÁSTROJE KRESLENÍ] 1 CÍL KAPITOLY V této kapitole si představíme Nástroje kreslení pro tvorbu 2D skic v modulu Objemová součást
TÍHOVÉ ZRYCHLENÍ TEORETICKÝ ÚVOD. 9, m s.
 TÍHOVÉ ZRYCHLENÍ TEORETICKÝ ÚVOD Soustavu souřadnic spojenou se Zemí můžeme považovat prakticky za inerciální. Jen při několika jevech vznikají odchylky, které lze vysvětlit vlastním pohybem Země vzhledem
TÍHOVÉ ZRYCHLENÍ TEORETICKÝ ÚVOD Soustavu souřadnic spojenou se Zemí můžeme považovat prakticky za inerciální. Jen při několika jevech vznikají odchylky, které lze vysvětlit vlastním pohybem Země vzhledem
5. Lokální, vázané a globální extrémy
 5 Lokální, vázané a globální extrémy Studijní text Lokální extrémy 5 Lokální, vázané a globální extrémy Definice 51 Řekneme, že f : R n R má v bodě a Df: 1 lokální maximum, když Ka, δ Df tak, že x Ka,
5 Lokální, vázané a globální extrémy Studijní text Lokální extrémy 5 Lokální, vázané a globální extrémy Definice 51 Řekneme, že f : R n R má v bodě a Df: 1 lokální maximum, když Ka, δ Df tak, že x Ka,
Značení krystalografických rovin a směrů
 Značení krystalografických rovin a směrů (studijní text k předmětu SLO/ZNM1) Připravila: Hana Šebestová 1 Potřeba označování krystalografických rovin a směrů vyplývá z anizotropie (směrové závislosti)
Značení krystalografických rovin a směrů (studijní text k předmětu SLO/ZNM1) Připravila: Hana Šebestová 1 Potřeba označování krystalografických rovin a směrů vyplývá z anizotropie (směrové závislosti)
Euklidovský prostor. Funkce dvou proměnných: základní pojmy, limita a spojitost.
 Euklidovský prostor. Funkce dvou proměnných: základní pojmy, limita a spojitost. Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a
Euklidovský prostor. Funkce dvou proměnných: základní pojmy, limita a spojitost. Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a
1 Tuhé těleso a jeho pohyb
 1 Tuhé těleso a jeho pohyb Tuhé těleso (TT) působením vnějších sil se nemění jeho tvar ani objem nedochází k jeho deformaci neuvažuje se jeho částicová struktura, těleso považujeme za tzv. kontinuum spojité
1 Tuhé těleso a jeho pohyb Tuhé těleso (TT) působením vnějších sil se nemění jeho tvar ani objem nedochází k jeho deformaci neuvažuje se jeho částicová struktura, těleso považujeme za tzv. kontinuum spojité
1.1. Spuštění ArchiCADu 16 1.2. Práce s projektem 16. 1.3. Pracovní plocha 19
 Obsah 1 Seznámení s ArchiCADem 15 1.1. Spuštění ArchiCADu 16 1.2. Práce s projektem 16 Vytvoření nového projektu 16 Vytvoření nového projektu při spuštění ArchiCADu 17 Možné způsoby nastavení nového projektu:
Obsah 1 Seznámení s ArchiCADem 15 1.1. Spuštění ArchiCADu 16 1.2. Práce s projektem 16 Vytvoření nového projektu 16 Vytvoření nového projektu při spuštění ArchiCADu 17 Možné způsoby nastavení nového projektu:
Základní úlohy v Mongeově promítání. n 2 A 1 A 1 A 1. p 1 N 2 A 2. x 1,2 N 1 x 1,2. x 1,2 N 1
 Základní úlohy v Mongeově promítání Předpokladem ke zvládnutí zobrazení v Mongeově promítání je znalost základních úloh. Ale k porozumění následujícího textu je třeba umět zobrazit bod, přímku a rovinu
Základní úlohy v Mongeově promítání Předpokladem ke zvládnutí zobrazení v Mongeově promítání je znalost základních úloh. Ale k porozumění následujícího textu je třeba umět zobrazit bod, přímku a rovinu
Obsah 1 Technologie obrábění na CNC obráběcím stroji... 2
 Obsah 1 Technologie obrábění na CNC obráběcím stroji... 2 Souřadnicový systém... 2 Vztažné body... 6 Absolutní odměřování, přírůstkové odměřování... 8 Geometrie nástroje...10 Korekce nástrojů - soustružení...13
Obsah 1 Technologie obrábění na CNC obráběcím stroji... 2 Souřadnicový systém... 2 Vztažné body... 6 Absolutní odměřování, přírůstkové odměřování... 8 Geometrie nástroje...10 Korekce nástrojů - soustružení...13
ŠROUBOVICE. 1) Šroubový pohyb. 2) Základní pojmy a konstrukce
 1) Šroubový pohyb ŠROUBOVICE Šroubový pohyb vznikne složením dvou pohybů : otočení kolem dané osy o a posunutí ve směru této osy. Velikost posunutí je přitom přímo úměrná otočení. Konstantou této přímé
1) Šroubový pohyb ŠROUBOVICE Šroubový pohyb vznikne složením dvou pohybů : otočení kolem dané osy o a posunutí ve směru této osy. Velikost posunutí je přitom přímo úměrná otočení. Konstantou této přímé
Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Aleš Najman [ÚLOHA 38 KONTROLA A POHONY]
![Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Aleš Najman [ÚLOHA 38 KONTROLA A POHONY] Aplikované úlohy Solid Edge. SPŠSE a VOŠ Liberec. Ing. Aleš Najman [ÚLOHA 38 KONTROLA A POHONY]](/thumbs/27/11375045.jpg) Aplikované úlohy Solid Edge SPŠSE a VOŠ Liberec Ing. Aleš Najman [ÚLOHA 38 KONTROLA A POHONY] 1 ÚVOD Úloha 38 popisuje jednu část oblasti sestava programu Solid Edge V20. Tato úloha je v první části zaměřena
Aplikované úlohy Solid Edge SPŠSE a VOŠ Liberec Ing. Aleš Najman [ÚLOHA 38 KONTROLA A POHONY] 1 ÚVOD Úloha 38 popisuje jednu část oblasti sestava programu Solid Edge V20. Tato úloha je v první části zaměřena
0 x 12. x 12. strana Mongeovo promítání - polohové úlohy.
 strana 9 3.1a Sestrojte sdružené průměty stopníků přímek a = AB, b = CD, c = EF. A [-2, 5, 1], B [3/2, 2, 5], C [3, 7, 4], D [5, 2, 4], E [-5, 3, 3], F [-5, 3, 6]. 3.1b Určete parametrické vyjádření přímek
strana 9 3.1a Sestrojte sdružené průměty stopníků přímek a = AB, b = CD, c = EF. A [-2, 5, 1], B [3/2, 2, 5], C [3, 7, 4], D [5, 2, 4], E [-5, 3, 3], F [-5, 3, 6]. 3.1b Určete parametrické vyjádření přímek
11. Měření závitů. Profil metrického závitu je určen jmenovitými rozměry:
 11. Měření závitů Závit je geometricky určen závitovou plochou. Rozeznáváme závit matice (vnitřní) a závit šroubu (vnější). Závitová plocha vznikne pohybem profilu závitu tak, že každý jeho bod opisuje
11. Měření závitů Závit je geometricky určen závitovou plochou. Rozeznáváme závit matice (vnitřní) a závit šroubu (vnější). Závitová plocha vznikne pohybem profilu závitu tak, že každý jeho bod opisuje
TECHNICKÉ KRESLENÍ A CAD. Přednáška č.5
 TECHNICKÉ KRESLENÍ A CAD Přednáška č.5 Řezy a průřezy těles Mnoho součástek - tvarové podrobnosti uvnitř součástky díry, vyfrézované otvory. Lze zobrazit skrytými čarami v mnoha případech na úkor názornosti,
TECHNICKÉ KRESLENÍ A CAD Přednáška č.5 Řezy a průřezy těles Mnoho součástek - tvarové podrobnosti uvnitř součástky díry, vyfrézované otvory. Lze zobrazit skrytými čarami v mnoha případech na úkor názornosti,
Šroubový pohyb rovnoměrný pohyb složený z posunutí a rotace. Šroubovice dráha hmotného bodu při šroubovém pohybu
 ŠROUBOVICE Šroubový pohyb rovnoměrný pohyb složený z posunutí a rotace Šroubovice dráha hmotného bodu při šroubovém pohybu ZÁKLADNÍ POJMY osa šroubovice o nosná válcová plocha (r poloměr řídicí kružnice
ŠROUBOVICE Šroubový pohyb rovnoměrný pohyb složený z posunutí a rotace Šroubovice dráha hmotného bodu při šroubovém pohybu ZÁKLADNÍ POJMY osa šroubovice o nosná válcová plocha (r poloměr řídicí kružnice
STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJÍRENSKÁ a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191. Obor 23-41-M/01 STROJÍRENSTVÍ
 STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJÍRENSKÁ a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Obor 23-41-M/01 STROJÍRENSTVÍ 1. ročník TECHNICKÉ KRESLENÍ ÚVOD A DESKRIPTIVNÍ GEOMETRIE
STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJÍRENSKÁ a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Obor 23-41-M/01 STROJÍRENSTVÍ 1. ročník TECHNICKÉ KRESLENÍ ÚVOD A DESKRIPTIVNÍ GEOMETRIE
ZOBRAZOVÁNÍ A NORMALIZACE V TECHNICKÉ DOKUMENTACI
 ZOBRAZOVÁNÍ A NORMALIZACE V TECHNICKÉ DOKUMENTACI Pravoúhlé rovnoběžné promítání na několik vzájemně kolmých průměten Použití pomocné průmětny Čistě ploché předměty Souměrné součásti Čistě rotační součásti
ZOBRAZOVÁNÍ A NORMALIZACE V TECHNICKÉ DOKUMENTACI Pravoúhlé rovnoběžné promítání na několik vzájemně kolmých průměten Použití pomocné průmětny Čistě ploché předměty Souměrné součásti Čistě rotační součásti
Výukové texty. pro předmět. Automatické řízení výrobní techniky (KKS/ARVT) na téma
 Výukové texty pro předmět Automatické řízení výrobní techniky (KKS/ARVT) na téma Podklady a grafická vizualizace k určení souřadnicových systémů výrobních strojů Autor: Doc. Ing. Josef Formánek, Ph.D.
Výukové texty pro předmět Automatické řízení výrobní techniky (KKS/ARVT) na téma Podklady a grafická vizualizace k určení souřadnicových systémů výrobních strojů Autor: Doc. Ing. Josef Formánek, Ph.D.
STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJÍRENSKÁ a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191. Obor M/01 STROJÍRENSTVÍ
 STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJÍRENSKÁ a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Obor 23-41-M/01 STROJÍRENSTVÍ 1. ročník TECHNICKÉ KRESLENÍ PRAVIDLA PRO KÓTOVÁNÍ SOUČÁSTÍ
STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJÍRENSKÁ a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Obor 23-41-M/01 STROJÍRENSTVÍ 1. ročník TECHNICKÉ KRESLENÍ PRAVIDLA PRO KÓTOVÁNÍ SOUČÁSTÍ
Technická dokumentace
 Technická dokumentace Obor studia: 23-45-L / 01 Mechanik seřizovač VY_32_inovace_FREI10 : Zásady kreslení průřezů a průniků Datum vypracování: 26.11.2012 Vypracoval: Ing. Bohumil Freisleben Motto: průřez
Technická dokumentace Obor studia: 23-45-L / 01 Mechanik seřizovač VY_32_inovace_FREI10 : Zásady kreslení průřezů a průniků Datum vypracování: 26.11.2012 Vypracoval: Ing. Bohumil Freisleben Motto: průřez
FAKULTA STAVEBNÍ VUT V BRNĚ PŘIJÍMACÍ ŘÍZENÍ PRO AKADEMICKÝ ROK
 FAKULTA STAVEBNÍ VUT V BRNĚ PŘIJÍMACÍ ŘÍZENÍ PRO AKADEMICKÝ ROK 00 007 TEST Z MATEMATIKY PRO PŘIJÍMACÍ ZKOUŠKY ČÍSLO FAST-M-00-0. tg x + cot gx a) sinx cos x b) sin x + cos x c) d) sin x e) +. sin x cos
FAKULTA STAVEBNÍ VUT V BRNĚ PŘIJÍMACÍ ŘÍZENÍ PRO AKADEMICKÝ ROK 00 007 TEST Z MATEMATIKY PRO PŘIJÍMACÍ ZKOUŠKY ČÍSLO FAST-M-00-0. tg x + cot gx a) sinx cos x b) sin x + cos x c) d) sin x e) +. sin x cos
Kótované promítání. Úvod. Zobrazení bodu
 Úvod Kótované promítání Každá promítací metoda má z pohledu praxe určité výhody i nevýhody podle toho, co při jejím užití vyžadujeme. Protože u kótovaného promítání jde o zobrazení prostoru na jednu rovinu,
Úvod Kótované promítání Každá promítací metoda má z pohledu praxe určité výhody i nevýhody podle toho, co při jejím užití vyžadujeme. Protože u kótovaného promítání jde o zobrazení prostoru na jednu rovinu,
PARAMETRICKÉ PROGRAMOVÁNÍ SOUČÁSTI V ŘÍDICÍM SYSTÉMU HEIDENHAIN SVOČ FST 2015
 PARAMETRICKÉ PROGRAMOVÁNÍ SOUČÁSTI V ŘÍDICÍM SYSTÉMU HEIDENHAIN SVOČ FST 2015 Bc. Petr Petrek, Západočeská univerzita v Plzni, Univerzitní 8, 306 14 Plzeň Česká republika ABSTRAKT Tato práce se zabývá
PARAMETRICKÉ PROGRAMOVÁNÍ SOUČÁSTI V ŘÍDICÍM SYSTÉMU HEIDENHAIN SVOČ FST 2015 Bc. Petr Petrek, Západočeská univerzita v Plzni, Univerzitní 8, 306 14 Plzeň Česká republika ABSTRAKT Tato práce se zabývá
Rovinné přetvoření. Posunutí (translace) TEORIE K M2A+ULA
 Rovinné přetvoření Rovinné přetvoření, neboli, jak se také často nazývá, geometrická transformace je vlastně lineární zobrazení v prostoru s nějakou soustavou souřadnic. Jde v něm o přepočet souřadnic
Rovinné přetvoření Rovinné přetvoření, neboli, jak se také často nazývá, geometrická transformace je vlastně lineární zobrazení v prostoru s nějakou soustavou souřadnic. Jde v něm o přepočet souřadnic
CNC stroje. Definice souřadného systému, vztažných bodů, tvorba NC programu.
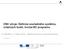 CNC stroje. Definice souřadného systému, vztažných bodů, tvorba NC programu. R. Mendřický, P. Keller (KVS) Elektrické pohony a servomechanismy Definice souřadného systému CNC stroje pro zadání trajektorie
CNC stroje. Definice souřadného systému, vztažných bodů, tvorba NC programu. R. Mendřický, P. Keller (KVS) Elektrické pohony a servomechanismy Definice souřadného systému CNC stroje pro zadání trajektorie
MECHANIKA TUHÉHO TĚLESA
 MECHANIKA TUHÉHO TĚLESA. Základní teze tuhé těleso ideální těleso, které nemůže být deformováno působením žádné (libovolně velké) vnější síly druhy pohybu tuhého tělesa a) translace (posuvný pohyb) všechny
MECHANIKA TUHÉHO TĚLESA. Základní teze tuhé těleso ideální těleso, které nemůže být deformováno působením žádné (libovolně velké) vnější síly druhy pohybu tuhého tělesa a) translace (posuvný pohyb) všechny
tečen a osu o π, V o; plochu omezte hranou vratu a půdorysnou a proved te rozvinutí
 Řešené úlohy Rozvinutelná šroubová plocha v Mongeově promítání Příklad: V Mongeově promítání zobrazte půl závitu rozvinutelné šroubové plochy, jejíž hranou vratu je pravotočivá šroubovice, která prochází
Řešené úlohy Rozvinutelná šroubová plocha v Mongeově promítání Příklad: V Mongeově promítání zobrazte půl závitu rozvinutelné šroubové plochy, jejíž hranou vratu je pravotočivá šroubovice, která prochází
KONSTRUKTIVNÍ GEOMETRIE
 KONSTRUKTIVNÍ GEOMETRIE Přednáška Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipliny společného základu (reg. č. CZ.1.07/2.2.00/28.0021)
KONSTRUKTIVNÍ GEOMETRIE Přednáška Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipliny společného základu (reg. č. CZ.1.07/2.2.00/28.0021)
VÝUKOVÝ MATERIÁL PRO ŽÁKY
 PROJEKT Zlepšení podmínek výuky učebních oborů CZ.1.07./1.1.06/01.0079 Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky VÝUKOVÝ MATERIÁL PRO ŽÁKY Vyučovací
PROJEKT Zlepšení podmínek výuky učebních oborů CZ.1.07./1.1.06/01.0079 Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky VÝUKOVÝ MATERIÁL PRO ŽÁKY Vyučovací
AXONOMETRIE. Rozměry ve směru os (souřadnice bodů) jsou násobkem příslušné jednotky.
 AXONOMETRIE 1) Princip, základní pojmy Axonometrie je rovnoběžné promítání do průmětny různoběžné se souřadnicovými rovinami. Kvádr v axonometrii : {O,x,y,z} souřadnicový systém XYZ - axonometrická průmětna
AXONOMETRIE 1) Princip, základní pojmy Axonometrie je rovnoběžné promítání do průmětny různoběžné se souřadnicovými rovinami. Kvádr v axonometrii : {O,x,y,z} souřadnicový systém XYZ - axonometrická průmětna
manuál CADKON-KROVY CADKON-KROVY kreslení dřevěných konstrukcí pro Autodesk Architectural Desktop
 kreslení dřevěných konstrukcí pro Autodesk Architectural Desktop Stav k 1.2.2007 Vzhledem k tomu, že se náš software průběžně vyvíjí, nemůžeme zaručit, že všechny uvedené údaje v příručce odpovídají aktuálnímu
kreslení dřevěných konstrukcí pro Autodesk Architectural Desktop Stav k 1.2.2007 Vzhledem k tomu, že se náš software průběžně vyvíjí, nemůžeme zaručit, že všechny uvedené údaje v příručce odpovídají aktuálnímu
3. ÚVOD DO ANALYTICKÉ GEOMETRIE 3.1. ANALYTICKÁ GEOMETRIE PŘÍMKY
 3. ÚVOD DO ANALYTICKÉ GEOMETRIE 3.1. ANALYTICKÁ GEOMETRIE PŘÍMKY V této kapitole se dozvíte: jak popsat bod v rovině a v prostoru; vzorec na výpočet vzdálenosti dvou bodů; základní tvary rovnice přímky
3. ÚVOD DO ANALYTICKÉ GEOMETRIE 3.1. ANALYTICKÁ GEOMETRIE PŘÍMKY V této kapitole se dozvíte: jak popsat bod v rovině a v prostoru; vzorec na výpočet vzdálenosti dvou bodů; základní tvary rovnice přímky
Gymnázium, Brno, Elgartova 3
 Gymnázium, Brno, Elgartova 3 GE - Vyšší kvalita výuky CZ.1.07/1.5.00/34.0925 IV/2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma: Analytická geometrie
Gymnázium, Brno, Elgartova 3 GE - Vyšší kvalita výuky CZ.1.07/1.5.00/34.0925 IV/2 Inovace a zkvalitnění výuky směřující k rozvoji matematické gramotnosti žáků středních škol Téma: Analytická geometrie
37. PARABOLA V ANALYTICKÉ GEOMETRII
 37.. Napiš rovnici paraboly, která má osu rovnoběžnou s osou y a prochází body A 0; 60, B 4; 8, C 8;36. 0m p60n 4m p8n 8m p36n m p pn 0 6 8 6 mm p pn 64 6 7 3 mm p pn 6 8m64 p 3 64 6m9 p Je-li osa rovnoběžná
37.. Napiš rovnici paraboly, která má osu rovnoběžnou s osou y a prochází body A 0; 60, B 4; 8, C 8;36. 0m p60n 4m p8n 8m p36n m p pn 0 6 8 6 mm p pn 64 6 7 3 mm p pn 6 8m64 p 3 64 6m9 p Je-li osa rovnoběžná
KRUHOVÁ ŠROUBOVICE A JEJÍ VLASTNOSTI
 KRUHOVÁ ŠROUBOVICE A JEJÍ VLASTNOSTI Šroubový pohyb vzniká složením otáčení kolem osy o a posunutí ve směru osy o, přičemž oba pohyby jsou spojité a rovnoměrné. Jestliže při pohybu po ose "dolů" je otáčení
KRUHOVÁ ŠROUBOVICE A JEJÍ VLASTNOSTI Šroubový pohyb vzniká složením otáčení kolem osy o a posunutí ve směru osy o, přičemž oba pohyby jsou spojité a rovnoměrné. Jestliže při pohybu po ose "dolů" je otáčení
Najíždění na konturu a odjíždění od ní (NORM, KONT, KONTC, KONTT)
 Funkce Předpoklady Syntaxe Prostřednictvím příkazů NORM, KONT, KONTC nebo KONTT je možné při aktivované korekci rádiusu nástroje (G41/G42) přizpůsobit dráhu pro najíždění a odjíždění nástroje na požadovanou
Funkce Předpoklady Syntaxe Prostřednictvím příkazů NORM, KONT, KONTC nebo KONTT je možné při aktivované korekci rádiusu nástroje (G41/G42) přizpůsobit dráhu pro najíždění a odjíždění nástroje na požadovanou
Odvození středové rovnice kružnice se středem S [m; n] a o poloměru r. Bod X ležící na kružnici má souřadnice [x; y].
![Odvození středové rovnice kružnice se středem S [m; n] a o poloměru r. Bod X ležící na kružnici má souřadnice [x; y]. Odvození středové rovnice kružnice se středem S [m; n] a o poloměru r. Bod X ležící na kružnici má souřadnice [x; y].](/thumbs/91/104981778.jpg) Konzultace č. 6: Rovnice kružnice, poloha přímky a kružnice Literatura: Matematika pro gymnázia: Analytická geometrie, kap. 5.1 a 5. Sbírka úloh z matematiky pro SOŠ a studijní obory SOU. část, kap. 6.1
Konzultace č. 6: Rovnice kružnice, poloha přímky a kružnice Literatura: Matematika pro gymnázia: Analytická geometrie, kap. 5.1 a 5. Sbírka úloh z matematiky pro SOŠ a studijní obory SOU. část, kap. 6.1
16. Matematický popis napjatosti
 p16 1 16. Matematický popis napjatosti Napjatost v bodě tělesa jsme definovali jako množinu obecných napětí ve všech řezech, které lze daným bodem tělesa vést. Pro jednoznačný matematický popis napjatosti
p16 1 16. Matematický popis napjatosti Napjatost v bodě tělesa jsme definovali jako množinu obecných napětí ve všech řezech, které lze daným bodem tělesa vést. Pro jednoznačný matematický popis napjatosti
VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C)
 VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C) max. 3 body 1 Zjistěte, zda vektor u je lineární kombinací vektorů a, b, je-li u = ( 8; 4; 3), a = ( 1; 2; 3), b = (2; 0; 1). Pokud ano, zapište tuto lineární kombinaci.
VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C) max. 3 body 1 Zjistěte, zda vektor u je lineární kombinací vektorů a, b, je-li u = ( 8; 4; 3), a = ( 1; 2; 3), b = (2; 0; 1). Pokud ano, zapište tuto lineární kombinaci.
BRICSCAD V15. Objemové modelování
 BRICSCAD V15 Objemové modelování Protea spol. s r.o. Makovského 1339/16 236 00 Praha 6 - Řepy tel.: 235 316 232, 235 316 237 fax: 235 316 038 e-mail: obchod@protea.cz web: www.protea.cz Copyright Protea
BRICSCAD V15 Objemové modelování Protea spol. s r.o. Makovského 1339/16 236 00 Praha 6 - Řepy tel.: 235 316 232, 235 316 237 fax: 235 316 038 e-mail: obchod@protea.cz web: www.protea.cz Copyright Protea
Pedagogická poznámka: Celý obsah se za hodinu stihnout nedá. z ] leží na kulové ploše, právě když platí = r. Dosadíme vzorec pro vzdálenost:
![Pedagogická poznámka: Celý obsah se za hodinu stihnout nedá. z ] leží na kulové ploše, právě když platí = r. Dosadíme vzorec pro vzdálenost: Pedagogická poznámka: Celý obsah se za hodinu stihnout nedá. z ] leží na kulové ploše, právě když platí = r. Dosadíme vzorec pro vzdálenost:](/thumbs/27/10334922.jpg) 753 Kulová plocha Předpoklady: 750 Pedagogická poznámka: Celý obsah se za hodinu stihnout nedá Kulová plocha = kružnice v prostoru Př : Vyslov definici kulové plochy Kulová plocha je množina všech bodů
753 Kulová plocha Předpoklady: 750 Pedagogická poznámka: Celý obsah se za hodinu stihnout nedá Kulová plocha = kružnice v prostoru Př : Vyslov definici kulové plochy Kulová plocha je množina všech bodů
7.5.3 Hledání kružnic II
 753 Hledání kružnic II Předpoklady: 750 Pedagogická poznámka: Tato hodina patří mezi vůbec nejtěžší Není reálné předpokládat, že by většina studentů dokázala samostatně přijít na řešení, po čase na rozmyšlenou
753 Hledání kružnic II Předpoklady: 750 Pedagogická poznámka: Tato hodina patří mezi vůbec nejtěžší Není reálné předpokládat, že by většina studentů dokázala samostatně přijít na řešení, po čase na rozmyšlenou
Zobrazování těles. problematika geometrického modelování. základní typy modelů. datové reprezentace modelů základní metody geometrického modelování
 problematika geometrického modelování manifold, Eulerova rovnost základní typy modelů hranový model stěnový model objemový model datové reprezentace modelů základní metody geometrického modelování těleso
problematika geometrického modelování manifold, Eulerova rovnost základní typy modelů hranový model stěnový model objemový model datové reprezentace modelů základní metody geometrického modelování těleso
Matematika 1 MA1. 1 Analytická geometrie v prostoru - základní pojmy. 4 Vzdálenosti. 12. přednáška ( ) Matematika 1 1 / 32
 Matematika 1 12. přednáška MA1 1 Analytická geometrie v prostoru - základní pojmy 2 Skalární, vektorový a smíšený součin, projekce vektoru 3 Přímky a roviny 4 Vzdálenosti 5 Příčky mimoběžek 6 Zkouška;
Matematika 1 12. přednáška MA1 1 Analytická geometrie v prostoru - základní pojmy 2 Skalární, vektorový a smíšený součin, projekce vektoru 3 Přímky a roviny 4 Vzdálenosti 5 Příčky mimoběžek 6 Zkouška;
STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJÍRENSKÁ a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191. Obor 23-41-M/01 STROJÍRENSTVÍ
 STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJÍRENSKÁ a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Obor 23-41-M/01 STROJÍRENSTVÍ 1. ročník TECHNICKÉ KRESLENÍ PRAVIDLA PRO KÓTOVÁNÍ SOUČÁSTÍ
STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJÍRENSKÁ a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Obor 23-41-M/01 STROJÍRENSTVÍ 1. ročník TECHNICKÉ KRESLENÍ PRAVIDLA PRO KÓTOVÁNÍ SOUČÁSTÍ
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník SOUŘADNICOVÉ SOUSTAVY VE FOTOGRAMMETRII
 SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník SOUŘADNICOVÉ SOUSTAVY VE FOTOGRAMMETRII SOUŘADNICOVÉ SOUSTAVY VE FTM hlavní souřadnicové soustavy systém snímkových souřadnic systém modelových
SPŠS Č.Budějovice Obor Geodézie a Katastr nemovitostí 4.ročník SOUŘADNICOVÉ SOUSTAVY VE FOTOGRAMMETRII SOUŘADNICOVÉ SOUSTAVY VE FTM hlavní souřadnicové soustavy systém snímkových souřadnic systém modelových
Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil
 Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil Souřadný systém, v rovině i prostoru Síla bodová: vektorová veličina (kluzný, vázaný vektor - využití),
Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil Souřadný systém, v rovině i prostoru Síla bodová: vektorová veličina (kluzný, vázaný vektor - využití),
Konstruktivní geometrie - LI. Konstruktivní geometrie - LI () Kótované promítání 1 / 44
 Kótované promítání Konstruktivní geometrie - LI Konstruktivní geometrie - LI () Kótované promítání 1 / 44 Obsah 1 Polohové úlohy 2 Spád přímky a roviny Konstruktivní geometrie - LI () Kótované promítání
Kótované promítání Konstruktivní geometrie - LI Konstruktivní geometrie - LI () Kótované promítání 1 / 44 Obsah 1 Polohové úlohy 2 Spád přímky a roviny Konstruktivní geometrie - LI () Kótované promítání
Fyzika 2 - rámcové příklady Magnetické pole - síla na vodič, moment na smyčku
 Fyzika 2 - rámcové příklady Magnetické pole - síla na vodič, moment na smyčku 1. Určete skalární a vektorový součin dvou obecných vektorů a a popište, jak závisí výsledky těchto součinů na úhlu mezi vektory.
Fyzika 2 - rámcové příklady Magnetické pole - síla na vodič, moment na smyčku 1. Určete skalární a vektorový součin dvou obecných vektorů a a popište, jak závisí výsledky těchto součinů na úhlu mezi vektory.
Deskriptivní geometrie pro střední školy
 Deskriptivní geometrie pro střední školy. díl Ivona Spurná Nakladatelství a vydavatelství R www.computermedia.cz Deskriptivní geometrie Díl Deskriptivní geometrie,. díl Mgr. Ivona Spurná Jazyková úprava:
Deskriptivní geometrie pro střední školy. díl Ivona Spurná Nakladatelství a vydavatelství R www.computermedia.cz Deskriptivní geometrie Díl Deskriptivní geometrie,. díl Mgr. Ivona Spurná Jazyková úprava:
OBSAH. ÚVOD...5 O Advance CADu...5 Kde nalézt informace...5 Použitím Online nápovědy...5. INSTALACE...6 Systémové požadavky...6 Začátek instalace...
 OBSAH ÚVOD...5 O Advance CADu...5 Kde nalézt informace...5 Použitím Online nápovědy...5 INSTALACE...6 Systémové požadavky...6 Začátek instalace...6 SPUŠTĚNÍ ADVANCE CADU...7 UŽIVATELSKÉ PROSTŘEDÍ ADVANCE
OBSAH ÚVOD...5 O Advance CADu...5 Kde nalézt informace...5 Použitím Online nápovědy...5 INSTALACE...6 Systémové požadavky...6 Začátek instalace...6 SPUŠTĚNÍ ADVANCE CADU...7 UŽIVATELSKÉ PROSTŘEDÍ ADVANCE
Je-li dána hranolová nebo jehlanová plocha s podstavou v rovině σ a rovina řezu ρ:
 Kapitola 1 Elementární plochy 1.1 Základní pojmy Elementární plochou budeme rozumět hranolovou, jehlanovou, válcovou, kuželovou a kulovou plochu. Pokud tyto plochy omezíme, popř. přidáme podstavy, můžeme
Kapitola 1 Elementární plochy 1.1 Základní pojmy Elementární plochou budeme rozumět hranolovou, jehlanovou, válcovou, kuželovou a kulovou plochu. Pokud tyto plochy omezíme, popř. přidáme podstavy, můžeme
Pravidla ACES
 Pravidla ACES 2009-2010 Dodatek 3.1 měření modelu na příkladech 3.1 Model Měřítko je 1:12. Rozpětí a délka trupu se mohou lišit nejvíce o +/- 5% od rozměru vycházejícího z měřítka. Veškeré ostatní rozměry
Pravidla ACES 2009-2010 Dodatek 3.1 měření modelu na příkladech 3.1 Model Měřítko je 1:12. Rozpětí a délka trupu se mohou lišit nejvíce o +/- 5% od rozměru vycházejícího z měřítka. Veškeré ostatní rozměry
