Fyzikální chemie disperzních soustav
|
|
|
- Dagmar Pokorná
- před 6 lety
- Počet zobrazení:
Transkript
1 Fyzikální chemie ispezních soustav 5. Chaakteistika ispezních soustav 5.1 Definice ispezní soustavy Dispezní soustava (ispeze) je tvořena tzv. ispezním poílem, ozptýleném ve fomě částic ve spojitém ispezním postřeí. Dispezní poíl může i nemusí přestavovat samostatnou fázi a svým chemickým složením se může, ale nemusí vžy lišit o ispezního postřeí. Pole toho mluvíme o ispezní fázi nebo ispezní složce. Většina ispezních soustav patří k vícesložkovým systémům. Jsou to jenak vícesložkové heteogenní soustavy, ve kteých se ispezní poíl liší o ispezního postřeí svým složením a záoveň přestavuje samostatnou fázi a jenak všechny uhy oztoků, kteé přestavují homogenní vícesložkové systémy. Výjimečně mohou vznikat i ispezní systémy jenosložkové, kteé jsou pak nutně heteogenní, např. vlhká páa; takové systémy však nejsou stabilní. 5.2 Klasifikace ispezních soustav Povahu ispezního systému ovlivňuje řaa faktoů, pole nichž bývají ispezní soustavy klasifikovány: pole velikosti částic: hubě ispezní (lineání ozmě > 1 µm), koloině ispezní (1 nm < < 1 µm), kam patří heteogenní koloiní ispeze, micelání koloiy a koloiní oztoky; ispeze s velikostí částic mezi nm jsou označovány jako nanosystémy, analyticky ispezní ( < 1 nm) - pavé (analytické či molekulání) oztoky pole tvau částic: globuláně ispezní (izometické částice) lamináně ispezní (anizometické částice, jeen ozmě je řáově menší) fibiláně ispezní (anizometické částice, jeen ozmě je řáově větší) pole počtu fází: homogenní (např. oztoky) heteogenní (viz kap. 9), kteé jsou pole skupenství ispezního postřeí a poílu ále ozělovány na systémy s plynným postřeím (aeosoly) s kapalným postřeím (lyosoly, emulze, pěny) s tuhým postřeím (tuhé soly, tuhé emulze, tuhé pěny) pole inteakcí mezi ispezním postřeím a ispezními částicemi: lyofilní výazná afinita mezi částicemi a postřeím lyofobní velmi nízká afinita mezi částicemi a postřeím pole inteakcí mezi ispezními částicemi: volné (soly, koloiní oztoky) viz o. 9.3, kap. 11 vázané (gely, koncentované suspenze, pasty...) viz kap. 12 pole počtu molekul v ispezní částici: monomolekulání (analytické ispeze a oztoky makomolekul) polymolekulání (lyosoly, micelání koloiy, hubé ispeze) pole ozělení velikosti částic: monoispezní s částicemi o jené velikosti pauciispezní s částicemi několika ůzných velikosti polyispezní s částicemi mnoha ůzných velikostí 5-1
2 5.3 Tva ispezních částic ovlivňuje hlavně mechanické a optické vlastnosti ispezních systémů. Systémy s izometickými částicemi, tj. takovými, kteé mají ve všech třech postoových směech přibližně stejné ozměy, se nazývají systémy globuláně ispezní. U anizometických částic převláá buď jeen ozmě, částice jsou potáhlé v jenom směu mají tva tyčinek nebo vláken, a pak mluvíme o fibiláně ispezních soustavách, nebo převláají va ozměy, částice jsou tvau estiček nebo lamel a systémy označujeme jako lamináně ispezní. U někteých systémů se setkáváme s efomabilitou ispezních částic - schopností měnit tva. Tato vlastnost se pojevuje např. u emulzí, jejichž ispezní poíl tvoří kapičky, nebo u pěn ispezí plynných bublinek v kapalinách a nejvíce u oztoků lineáních makomolekul, jejichž tva se vlivem tepelného pohybu neustále mění. 5.4 Velikost ispezních částic chaakteizuje jemnost, s jakou je ispezní poíl ozptýlen v ispezním postřeí. Bývá uávána nejčastěji význačným lineáním ozměem, hmotností, méně často objemem, plochou povchu apo. Často je používána i veličina nazývaná stupeň ispezity pomě povchu částic k jejich objemu kteá je úměná ecipoké honotě lineáního ozměu (něky s ní bývá ztotožňována). Úaje o lineáním ozměu částic jsou však jenoznačné pouze u ispezních systémů s izometickými částicemi. Pevné částice, kteé nejsou sice kulovité, ale jsou značně symetické, bývají často apoximovány koulí. Temín půmě částice" pak označuje stření honotu lineáního ozměu. Mnohé lineání makomolekuly mají ostatečnou flexibilitu, takže vlivem temálních sážek mohou zaujmout tva poobný klubku, kteé je většinou spíše symetické; takový útva je pak chaakteizován poloměem klubka. Jsou-li částice ispeze asymetické, je nutno uat va až tři ozměy. Pole velikosti částic jsou ispezní systémy ozělovány na tři typy. Nejená se však o ostře oělené skupiny, mezi jenotlivými typy je plynulý přecho. Systémy s nejmenšími částicemi (o 1 nm) jsou oztoky nízkomolekuláních látek, v nichž jsou ispezní částice molekuly nebo ionty, popř. útvay, kteé vznikají očasnou asociací několika málo molekul co o velikosti sovnatelné s molekulami ispezního postřeí. Jsou označovány také jako analyticky ispezní systémy, potože fakt, že obsahují va nebo více uhů hmoty, je pokazatelný pouze chemickou analýzou a jejich ispezní částice nejsou viitelné ani elektonovým mikoskopem. Systémy s velkými částicemi, kteé obsahují značný počet molekul, jsou označovány jako systémy hubě ispezní. Jestliže jsou jejich částice ozeznatelné pouhým okem (větší než asi 50 m), označují se jako makoispezní. Jsou-li viitelné až optickým mikoskopem (o velikosti asi 1 m), mluvíme o systémech mikoispezních. Mezi těmito věma skupinami leží oblast koloině ispezních systémů a nanosystémů) kteá bue hlavním přemětem našeho zájmu v násleujících kapitolách. Koloiika se zabývá fyzikálními a chemickými vlastnostmi ispezních systémů a jevy na fázových ozhaních, kteé jsou významně ovlivňovány vlastnostmi fázového ozhaní. Abychom ozholi, jak malé mohou být ispezní částice, vzpomeňme si, že molekuly ve fázovém ozhaní mají vžy olišné vlastnosti o molekul v objemové fázi, potože se nacházejí v silovém poli molekul sousení fáze. Pole stuktuy uvažované látky je tloušťka této vstvy 0,5 až 2 nm. Potože částice nemůže být tvořena jen povchovou vstvou, musí být její ozměy ve všech směech větší než vojnásobek tloušťky fázového ozhaní. Za olní hanici bývá uáván ozmě částice 1 až 5 nm, za honí hanici je považován ozmě částic, opovíající ozlišovací schopnosti nejlepších optických mikoskopů, přibližně 1 m. 5-2
3 Přehle ispezních systémů ANALYTICKÉ DISPERZE < 10 9 m částice nejsou viitelné ani v elektonovém mikoskopu pocházejí filtačním papíem i membánami vykonávají velmi intenzivní tepelný pohyb ychle ifunují neseimentují ani v ultacentifuze velký osmotický tlak částice monomolekulání samovolným ozpouštěním na pavé oztoky (mísitelnost omezená nebo neomezená) stabilní vžy homogenní; tvoří jeinou fázi nevytvářejí gely KOLOIDNÍ DISPERZE m NANODISPERZE m nejsou viitelné v optickém mikoskopu, ale jen v ultamikoskopu nebo elektonovém mikoskopu, jsou většinou půhlené, často výazně baevné, v bočním osvětlení opaleskují (Tynallův efekt; ozptyl světla) pocházejí filtačním papíem, nepocházejí někteými membánami slabší tepelný pohyb než analytické ispeze, ale intenzivnější než hubé ispeze; intenzita pohybu oste se stupněm ispezity ifunují pomalu seimentují v ultacentifuze, v gavitačním poli pomalu malý osmotický tlak (oste se stupněm ispezity, neboť oste počet částic) Roztoky makomolekul částice monomolekulání samovolným ozpouštěním, kteému často přechází botnání (mísitelnost omezená i neomezená) stabilní jako analytické ispeze Asociativní koloiy částice polymolekulání asociací z pavých oztoků amfifilních molekul stabilní v učitém ozmezí pomínek Heteogenní koloiy částice polymolekulání - ispegováním z hubých ispezí - sážením z pavých oztoků na koloiní částice nestálé - koagulují, - seimentují, - stánou homogenní heteogenní, obovská plocha fázového ozhaní, oste se stupněm ispezity tvoba gelů je po koloině ispezní systémy chaakteistická HRUBÉ DISPERZE miko m mako > 10 5 m viitelné pouhým okem nebo v optickém mikoskopu, zákal, nepůhlenost nepocházejí papíem ani membánami velmi slabý nebo žáný tepelný pohyb neifunují seimentují ychle v gavitačním poli nevyvolávají osmotický tlak částice polymolekulání - ispegováním z makofází - sážením z pavých oztoků na částice žáané velikosti nestálé, samovolně zanikají - seimentací - koagulací) vžy heteogenní, plocha fázového ozhaní menší než u koloiních ispezí gely vytvářejí jen výjimečně 5-3
4 5.4.1 Kvantitativní chaakteizace velikosti ispezních částic U kulovitých částic (koulí bývají často apoximovány i izometické částice) může být velikost částic viitelných v mikoskopu jenouše popsána jeiným paametem pomocí mikoskopické nebo obazové analýzy. U částic nepavielného tvau může být lineání ozmě vyjařován ůzným způsobem: např. élkou čáy, kteá půlí plochu půmětu částice (tzv. Matinův půmě M ), Feetovým půměem F, což je vzálenost tečen na potilehlých stanách půmětu částice, nebo půměem kuhu A o stejné ploše jako je plocha půmětu pozoované částice (plošný nebo Heywooův půmě) viz ob Zjištěné honoty jsou pak po aný soubo částic statisticky zpacovány (ost ). Matinův půmě F F Feetův půmě plošný půmě Ob. 5-1 Chaakteizace velikosti částic nepavielného tvau Z naměřených fyzikálních vlastností ispezní soustavy, jejichž honota závisí na velikosti ispezních částic, např. z ifuzního koeficientu (ost. 6.1), z výsleků seimentačních měření (ost. 6.2), z osmotického tlaku (ost. 6.3), z viskozity (kap. 7) nebo z intenzity ozptýleného záření (kap. 8) lze vypočítat stření hmotnost nebo polomě ispezní částice (ost ). Tento úaj však okonale chaakteizuje velikost pouze v přípaě, že částice jsou kulovitého tvau. U anizometických tvaů částic ostaneme tzv. efektivní nebo ekvivalentní polomě; tj. polomě kulovité částice, kteé by příslušela za jinak stejných fyzikálních pomínek stejná honota fyzikální veličiny, jaká byla naměřena u zkoumaného systému Statistické zpacování úajů o velikosti ispezních částic Popis ispezní soustavy pomocí ozměů jené částice je možno použít jen v takových přípaech, ky ispezní částice jsou stejně velké, tj. u unifomních (monoispezních) systémů. Ty se vyskytují poměně vzácně * (např. polymeací za přísně řízených pomínek je možno připavit monoispezní latexy, kteé jsou používány jako stanay po kalibaci při optických měřeních). Dispezní systémy jsou většinou neunifomní (polyispezní) - obsahují částice mnoha ůzných velikostí, nebo pauciispezní, tj. obsahují částice několika velikostí. Takové systémy bývají chaakteizovány ozělovací funkcí velikosti částic, popř. vhonou stření honotou (ost ). Rozělovací funkce velikosti částic uává, jak jsou v systému zastoupeny částice té kteé velikosti. Nejčastěji se používá ozělovacích funkcí pole ozměů částic. Velikost částic může být vyjářena také hmotností, objemem, plochou povchu, stupněm polymeace at. Při zjišťování ozělovacích funkcí si, jako při kažém statistickém zpacování, teoeticky ozělíme ispezní poíl na skupiny částic přibližně stejné velikosti tzv. fakce. Rozělení velikostí částic ispezního poílu je pak možno popsat pomocí ifeenciální ozělovací funkce F(), efinované vztahem F W m (), popř. m F N N (), (5.1),(5.2) N * Většina systémů, kteé jsou označovány jako monoispezní, nemá částice jené velikosti, ale lze u nich pozoovat učité úzké ozmezí velikostí částic za monoispení bývají považovány systémy, v nichž půměná ochylka o stření velikosti částic nepřesáhne 10 %. 5-4
5 četnost výskytu ke F W () je ifeenciální ozělovací funkce hmotnosti částic (hmotnostní ifeenciální ozělovací funkce), F N () je ifeenciální ozělovací funkce počtu částic (početní ifeenciální ozělovací funkce), m je hmotnost skupiny částic, kteé mají ozmě, N je počet částic o ozměu, m je celková hmotnost ispezního poílu, N celkový počet částic v ispezním poílu. Součin F W (), (popř. F N () ) pak vyjařuje poíl hmotnosti fakce částic s ozměem mezi a ( + ) (popř. počtu částic ve fakci) z celkové hmotnosti (popř. celkového počtu částic) ispezního poílu; přestavuje tey hmotnostní, popř. molání zlomek příslušné fakce. integální ozělovací funkce I W (), popř. I N (), kteá uává, jaký poíl hmotnosti z celkové hmotnosti, popř. počtu částic z celkového počtu částic ispezního poílu, tvoří fakce, jejichž částice mají polomě menší nebo stejný než učitá zvolená honota C oplňkové integální ozělovací funkce Q W (), popř. Q N (), kteá uává, jaký poíl hmotnosti z celkové hmotnosti, popř. počtu částic z celkového počtu částic ispezního poílu, tvoří fakce, jejichž částice mají polomě větší nebo stejný než učitá zvolená honota. Po gafické znázonění expeimentálních at se používá také histogamu (ob. 5-2). Skláá se z obélníků, jejichž záklany jsou intevaly až + a jejichž obsahy znázoňují ozložení četnosti sleované veličiny, např. poíl počtu částic, kteé mají polomě v intevalu až +, z celkového počtu částic, tj. F N (). Je zřejmé, že oste-li počet tří k nekonečnu, blíží se šířka kažého sloupce k nule a histogam přechází na hlakou křivku. Ob. 5-2 Histogam po ozělení částic ispezního poílu pole jejich velikosti Stření ozmě ispezních částic a stření molání hmotnost Měření ůzných vlastností ispezních systémů (např. kinetických, optických nebo eologických) se většinou nepováí po jenotlivé částice, ale po soubo velkého počtu částic. Místo honoty hmotnosti, objemu nebo poloměu částice pak výpočtem ze změřené vlastnosti ostaneme půměnou honotu příslušného paametu. Takto získaná stření honota (např. stření ozmě částice nebo stření molání hmotnost) je pak ovna honotě tohoto paametu po myšlený monoispezní systém, v němž by měřená veličina nabyla stejné honoty. Systém je tey chaakteizován jeiným úajem, ale chybí infomace o ozělení velikosti částic. U polyispezních systémů mají takto získané veličiny chaakte statistických půměů ůzného uhu pole povahy použité metoy měření. Stření ozmě částic polyispezního systému může být vyjářen hmotnostním půměem ( i mi) W [ i Wi ] (5.3) mi nebo početním půměem ( i Ni) N [ i xi ] (5.4) Ni Stření molání hmotnost (hmotnostní a početní půmě) je vyjářena vztahy ( wi Mi) MW ( Wi Mi) (5.5) wi ( Ni Mi) M N ( xi Mi) (5.6) Ni ke m i je hmotnost skupiny částic, kteé mají polomě i, m i je hmotnost všech částic (všechny sumace jsou pováěny přes všechny honoty i ), W i (= m i / m i ) je hmotnostní zlomek jenotlivých fakcí, N i je počet částic o poloměu i, N i je celkový počet částic, x i (= N i / N i ) je molání zlomek, w i (= m i /V) hmotnostní koncentace a c i (= n i /V) látková koncentace. Jestliže se stření molání hmotnost stanovuje metoami, kteé měří veličiny úměné hmotnosti nebo objemu částice (ychlost ifuze - viz ost. 6.1, seimentace - ost. 6.2, ozptyl světla - kap. 8), 5-5
6 je výslekem hmotnostně stření molání hmotnost (hmotnostní půmě moláních hmotností) M W, po kteý platí vztah (5.5) Měřením koligativních vlastností (osmometie - ost. 6.3, popř. kyoskopie nebo ebulioskopie) se stanovuje početně stření molání hmotnost (početní půmě molání hmotnosti) M N vztah (5.6). Tato stření honota je vžy menší než hmotnostní stře, neboť se nejvíce uplatňují nízké fakce, kteé obsahují elativně velký počet částic, kežto v uhém přípaě se naopak nejvíce uplatňují těžší poíly. Pomě M W / M N se nazývá koeficient polyispezity. Po monoispezní systém je tento koeficient oven jené a oste s ostoucí polyispezitou systému. 5.5 Koloině ispezní systémy (nanosystémy) Rozělení koloině ispezních systémů Vzhleem k velké ozmanitosti je účelné ozělovat koloině ispezní systémy o tří skupin: Lyofobní ispeze (koloiní ispeze) - heteogenní systémy, v nichž ispezní poíl a ispezní postřeí přestavují vě ůzné fáze. Aby mohl být ispezní poíl považován za samostatnou fázi, musí ispezní částice obsahovat tolik molekul, aby bylo možno ozlišit povchovou vstvu částice o její vnitřní části. Dispezní poíl a ispezní postřeí jsou oěleny fázovým ozhaním, kteé výazně ovlivňuje jejich vlastnosti (ob. 1-1 ukazuje, jak oste plocha fázového ozhaní systému se zmenšujícími se ozměy částice). Jsou připavovány buď z makofází ispegací nebo z pavých oztoků konenzací. Jsou nestálé, samovolně zanikají. Svou sklabou a vznikem tey připomínají hubé ispeze; liší se však ozměem částic. Vlastnosti jenotlivých typů heteogenních systémů (viz kap. 9) se liší pole skupenství jak ispezního poílu tak ispezního postřeí. Lyofilní koloiy (koloiní oztoky) (kap. 11) jsou homogenní koloiní systémy, v nichž ispezní poíl tvoří s ispezním postřeím jenu fázi. Jsou to pavé oztoky makomolekul, kteé vznikají samovolným ozpouštěním a jsou stálé. Samovolný vznik je pomíněn afinitou makomolekul k ispeznímu postřeí. Asociativní (micelání) koloiy (kap. 10), kteé vznikají samovolnou evezibilní asociací nízkomolekuláních látek s amfifilní stuktuou v pavém oztoku. Mezi molekulami v oztoku a vzniklými asociáty se ustavuje ovnováha. Chaakteistickou vlastností koloiních systémů je schopnost tvořit gely systémy, v nichž je spojité nejen ispezní postřeí, ale i ispezní poíl - tojozměná síť, postupující ispezním postřeím Histoie a význam koloině ispezních systémů I kyž se soustavný výzkum koloiních systémů atuje až k počátku minulého století, se zmínkami o jejich přípavě a paktickém využití se setkáváme již mnohem říve. Tak např. staří Číňané používali ke psaní mimořáně stálou tuž koloiní ispezi sazí stabilizovanou želatinou. Ve staém Egyptě malovali a psali ůznými baevnými inkousty ispezemi ůzných zemin a mineálů ve voě, stabilizovanými aabskou gumou. Střeověcí alchymisté popisují přípavu ůzných kovových solů nejznámější je elixí mláí, auum potabile, enegetický lék popůjčující tělu maximální oolnost vůči všem nemocem. Oblíbenou látkou alchymistů byl gel kyseliny křemičité, o němž se zmiňuje i Goethe ve svém životopisném íle Dichtung un Wahheit. Sol zlata stabilizovaný oxiem cíničitým, známý jako Cassiův pupu, byl o konce 17. století používán při výobě čeveného skla a poslulého míšeňského a sèveského pocelánu. Solů zlata bylo používáno i k bavení hevábí. Pvní věecké stuie pocházejí z poloviny 19. století. Fancesco Selmi si povšiml anomálních vlastností někteých oztoků, kteé pole nešních přestav patří mezi koloiní soustavy. Silně ozptylovaly světlo, sážely se příavkem zcela nepatných množství solí, kteé neeagují s ozpuštěnou látkou, jejich vznik nebyl povázen změnou teploty ani objemu, jako tomu bylo u kystalických 5-6
7 látek. Selmi ošel k závěu, že neje o pavé oztoky, ale o suspenze malých částeček ve voě a al těmto systémům název pseuooztoky. Michael Faaay se zabýval přípavou solů zlata a v řaě expeimentů (1856-7) emonstoval jejich seimentaci, koagulaci elektolyty a ochanné působení želatiny. Zjistil, že svazek papsků pocházejících solem, je při bočním pozoování viitelný. Tento jev, jak spávně usouil, je způsoben ozptylem světla na částicích zlata (pozěji poobněji stuoval Tynall). Kupoivu Faaay nezkoumal chování svých solů v elektickém poli. Za vlastního zaklaatele koloiní chemie je pokláán Angličan Thomas Gaham, kteý se v.1861 zabýval stuiem ifuze ůzných látek pegamenovou membánou. Zjistil, že měřitelnou ychlostí ifunují jen látky schopné kystalizace (např. soli, cuk) a nazval je kystaloiy. Do uhé skupiny zařail látky, kteé ifunovaly jen neochotně a nepoařilo se mu je připavit v kystalickém stavu. Pole jejich typického přestavitele klihu pojmenoval Gaham celou tuto skupinu látek koloiy (kolla je řecky klih). Sem patřily i ty, kteé Selmi označil jako pseuooztoky. Gaham objevil i alší vlastnosti koloiů: např. zjistil, že ifuzí přes vhonou membánu (živočišnou blánu, pegamenový papí) je možné oělit kystaloiy o koloiů pocho nazval ialýza. O Gahama pochází i mnoho alších temínů ones používaných v koloiní chemii, jako např. sol, gel, hyosol, hyogel, peptizace, koagulace, koagulát aj. Začátkem 20. století se koloiika začala ozvíjet. Feunlich (1903) se zabýval stuiem asopce, Sieentopf a Zsigmony (1903) vynalezli ultamikoskop, založený na pozoováních Faaaye a Tynalla, kteý umožnil zjišťovat počet částic ve zřeěných solech. Důležitým přínosem byly páce Smoluchowského (1906), Svebega (1906), Peina (1908) a Einsteina (1908), zabývající se poblémem stanovení velikosti částic, seimentací a koagulací částic. Pete von Weinman a Wolfgang Ostwal (1907) ukázali, že koloiní stav není jen vlastností učitých látek, ale že tatáž látka může být pole pomínek připavena v kystalickém nebo koloiním stavu (jením z nejstaších příklaů je sía, kteou známe jak v kystalickém tak v amofním stavu a kteá může být připavena i ve fomě solu). Ostwal a von Weiman zaveli pojem ispezní systém a navhli pvní acionální klasifikaci ispezních systémů pole velikosti částic. Ve sovnání s jinými oblastmi chemie a fyziky byl však vývoj poznatků o koloiním chování pomalejší. Příčinou byly hlavně velké potíže při přípavě obře chaakteizovaného expeimentálního mateiálu s epoukovatelnými vlastnostmi a ále fakt, že neexistovaly ostatečné teoetické znalosti, kteé by ovolovaly těmto vlastnostem poozumět a vhoně je moifikovat. Až o vacátých let 20. století, ky nové metoy po přípavu obře efinovaných koloiů (např. monoispezních systémů nebo polymeů efinovaného složení) umožnily kvantitativní a epoukovatelné expeimenty. za použití nových meto a přístojů jako ultacentifuga (T. Svebeg 1923), elektonový mikoskop ( ), metoy ozptylu světla, neutonů, NMR, optická spektoskopie, entgenová analýza nebo zokonalené eologické metoy společně s pokokem v teoiích mezimolekuláních sil, oztoků elektolytů a polymeů, kteý umožnil teoetické zpacování naměřených úajů, se koloiní chemie mohla významně ozvíjet. Koloiní systémy i ěje na fázových ozhaních mají ohomný význam po liskou činnost. Je téměř nemožné vyjmenovat všechny oblasti ať technologické, biologické, nebo fyziologické, kteé s těmito jevy souvisejí. Řaa potavinářských výobků jako např. máslo, sýy, joguty a jiné mléčné poukty, chleba, pečivo, a okonce i pivo, je buď přímo svou povahou koloiní, nebo se na jejich vzniku koloiní pochoy poílejí. Stejně je tomu v přípaě baev a baviv, papíu, famaceutických a kosmetických pepaátů mnoha uhů či chemikálií používaných v zeměělství a zahanictví. Velmi významnou oli má koloiní chemie při výobě ůzných keamických výobků o ahého pocelánu, přes nové velmi pevné keamické mateiály, používané v aketové technice nebo v lékařství na ůzné potézy (např. keamické kloubní náhay, zubní potézy aj.) až po obyčejné cihly. Pochoy používané při těžbě mineálů a opy, při úpavě voy a ůzných biotechnologiích jsou ovněž koloiní povahy. Velký technologický význam má heteogenní katalýza. Meto koloiní chemie se často používá i ke stuiu řay biologických systémů. Např. tokové vlastnosti kve a jiných tělních tekutin je možné nejlépe stuovat, přípaně upavovat, jestliže se na ně íváme jako na koloiní ispeze. Dokonce byla připavena voná emulze, vhoná jako očasná náhaa kve, kteá se nekazí při sklaování, je kompatibilní se všemi kevními skupinami a není nebezpečí, že bue kontaminována (AIDS, žloutenka). Kloubní mazy věčí za vynikající vlastnosti své koloiní povaze. Moení koloiní mikokapsule, používané v lékařství, ovolují řízené poávání léčiv a v někteých přípaech okonce cílenou famakoteapii učitých ogánů. Koloiika má ůležitou úlohu také při řešení ekologických poblémů. Mnohá znečištění jsou způsobena přítomností koloiních poílů a k jejich ostanění z ovzuší nebo voních toků je tey třeba použít speciálních koloiních meto. 5-7
Fyzikální chemie disperzních soustav
 Fyzikální chemie isperzních soustav 5. Charakteristika isperzních soustav 5.1 Definice isperzní soustavy Disperzní soustava (isperze) je tvořena tzv. isperzním poílem, rozptýleném ve formě částic ve spojitém
Fyzikální chemie isperzních soustav 5. Charakteristika isperzních soustav 5.1 Definice isperzní soustavy Disperzní soustava (isperze) je tvořena tzv. isperzním poílem, rozptýleném ve formě částic ve spojitém
Rozklad přírodních surovin minerálními kyselinami
 Laboatoř anoganické technologie Rozklad příodních suovin mineálními kyselinami Rozpouštění příodních mateiálů v důsledku pobíhající chemické eakce patří mezi základní technologické opeace řady půmyslových
Laboatoř anoganické technologie Rozklad příodních suovin mineálními kyselinami Rozpouštění příodních mateiálů v důsledku pobíhající chemické eakce patří mezi základní technologické opeace řady půmyslových
A Pohyb silničních vozidel
 A Pohyb silničních voziel Po popisování pohybu silničních voziel a sil na ně působící bueme vzcházet ze souřaného systému vozila, tak jak byl popsán v přechozím tématu. Tyto postupy je možno obecně aplikovat
A Pohyb silničních voziel Po popisování pohybu silničních voziel a sil na ně působící bueme vzcházet ze souřaného systému vozila, tak jak byl popsán v přechozím tématu. Tyto postupy je možno obecně aplikovat
do strukturní rentgenografie e I
 Úvod do stuktuní entgenogafie e I Difakce tg záření na kystalu Metody chaakteizace nanomateiálů I RND. Věa Vodičková, PhD. Studium kystalové stavby Difakce elektonů, neutonů, tg fotonů Kystal ideální mřížka
Úvod do stuktuní entgenogafie e I Difakce tg záření na kystalu Metody chaakteizace nanomateiálů I RND. Věa Vodičková, PhD. Studium kystalové stavby Difakce elektonů, neutonů, tg fotonů Kystal ideální mřížka
Třídění látek. Chemie 1.KŠPA
 Třídění látek Chemie 1.KŠPA Systém (soustava) Vymezím si kus prostoru, látky v něm obsažené nazýváme systém soustava okolí svět Stěny soustavy Soustava může být: Izolovaná = stěny nedovolí výměnu částic
Třídění látek Chemie 1.KŠPA Systém (soustava) Vymezím si kus prostoru, látky v něm obsažené nazýváme systém soustava okolí svět Stěny soustavy Soustava může být: Izolovaná = stěny nedovolí výměnu částic
Naklápěcí soudečková ložiska E1
 Novinka: navýšení výkonnostních paametů u velkých ložisek Naklápěcí souečková ložiska E1 Vyšší hospoánost a povozní bezpečnost íky koncepci X-life Obsah Naklápěcí souečková ložiska FAG E1: Vyšší hospoánost
Novinka: navýšení výkonnostních paametů u velkých ložisek Naklápěcí souečková ložiska E1 Vyšší hospoánost a povozní bezpečnost íky koncepci X-life Obsah Naklápěcí souečková ložiska FAG E1: Vyšší hospoánost
ELEKTRICKÝ NÁBOJ COULOMBŮV ZÁKON INTENZITA ELEKTRICKÉHO POLE
 ELEKTRICKÝ NÁBOJ COULOMBŮV ZÁKON INTENZITA ELEKTRICKÉHO POLE 1 ELEKTRICKÝ NÁBOJ Elektický náboj základní vlastnost někteých elementáních částic (pvní elektické jevy pozoovány již ve staověku janta (řecky
ELEKTRICKÝ NÁBOJ COULOMBŮV ZÁKON INTENZITA ELEKTRICKÉHO POLE 1 ELEKTRICKÝ NÁBOJ Elektický náboj základní vlastnost někteých elementáních částic (pvní elektické jevy pozoovány již ve staověku janta (řecky
Základní vlastnosti elektrostatického pole, probrané v minulých hodinách, popisují dvě diferenciální rovnice : konzervativnost el.
 Aplikace Gaussova zákona ) Po sestavení základní ovnice elektostatiky Základní vlastnosti elektostatického pole, pobané v minulých hodinách, popisují dvě difeenciální ovnice : () ot E konzevativnost el.
Aplikace Gaussova zákona ) Po sestavení základní ovnice elektostatiky Základní vlastnosti elektostatického pole, pobané v minulých hodinách, popisují dvě difeenciální ovnice : () ot E konzevativnost el.
Fyzika. Fyzikální veličina - je mírou fyzikální vlastnosti, kterou na základě měření vyjadřujeme ve zvolených jednotkách
 Fyzika Studuje objekty neživé příody a vztahy mezi nimi Na základě pozoování a pokusů studuje obecné vlastnosti látek a polí, indukcí dospívá k obecným kvantitativním zákonům a uvádí je v logickou soustavu
Fyzika Studuje objekty neživé příody a vztahy mezi nimi Na základě pozoování a pokusů studuje obecné vlastnosti látek a polí, indukcí dospívá k obecným kvantitativním zákonům a uvádí je v logickou soustavu
Některé základní pojmy
 Klasifikace látek Některé základní pojmy látka látka čistá chemické individuum fáze směs prvek sloučenina homogenní směs heterogenní směs plynná směs kapalný roztok tuhý roztok Homogenní a heterogenní
Klasifikace látek Některé základní pojmy látka látka čistá chemické individuum fáze směs prvek sloučenina homogenní směs heterogenní směs plynná směs kapalný roztok tuhý roztok Homogenní a heterogenní
Fázová rozhraní a mezifázová energie
 Fázová ozhaní a mezifázová enegie 1/15 duhy: } l/ g {{ l/ } l mobilní s/g s/l s/s povch koule = 4π 2 Příklad. Kolik % molekul vody je na povchu kapičky mlhy o půměu 200 nm (hanice viditelnosti optickým
Fázová ozhaní a mezifázová enegie 1/15 duhy: } l/ g {{ l/ } l mobilní s/g s/l s/s povch koule = 4π 2 Příklad. Kolik % molekul vody je na povchu kapičky mlhy o půměu 200 nm (hanice viditelnosti optickým
POHYB SPLAVENIN. 8 Přednáška
 POHYB SPLAVENIN 8 Přenáška Obsah: 1. Úvo 2. Vlastnosti splavenin 2.1. Hustota splavenin a relativní hustota 2.2. Zrnitost 2.3. Efektivní zrno 3. Tangenciální napětí a třecí rychlost 4. Počátek eroze 5.
POHYB SPLAVENIN 8 Přenáška Obsah: 1. Úvo 2. Vlastnosti splavenin 2.1. Hustota splavenin a relativní hustota 2.2. Zrnitost 2.3. Efektivní zrno 3. Tangenciální napětí a třecí rychlost 4. Počátek eroze 5.
Příklady elektrostatických jevů - náboj
 lektostatika Hlavní body Příklady elektostatických jevů. lektický náboj, elementání a jednotkový náboj Silové působení náboje - Coulombův zákon lektické pole a elektická intenzita, Páce v elektostatickém
lektostatika Hlavní body Příklady elektostatických jevů. lektický náboj, elementání a jednotkový náboj Silové působení náboje - Coulombův zákon lektické pole a elektická intenzita, Páce v elektostatickém
Směsi, roztoky. Disperzní soustavy, roztoky, koncentrace
 Směsi, roztoky Disperzní soustavy, roztoky, koncentrace 1 Směsi Směs je soustava, která obsahuje dvě nebo více chemických látek. Mezi složkami směsi nedochází k chemickým reakcím. Fyzikální vlastnosti
Směsi, roztoky Disperzní soustavy, roztoky, koncentrace 1 Směsi Směs je soustava, která obsahuje dvě nebo více chemických látek. Mezi složkami směsi nedochází k chemickým reakcím. Fyzikální vlastnosti
Konstrukční a technologické koncentrátory napětí
 Obsah: 6 lekce Konstukční a technologické koncentátoy napětí 61 Úvod 6 Účinek lokálních konstukčních koncentací napětí 63 Vliv kuhového otvou na ozložení napjatosti v dlouhém tenkém pásu zatíženém tahem
Obsah: 6 lekce Konstukční a technologické koncentátoy napětí 61 Úvod 6 Účinek lokálních konstukčních koncentací napětí 63 Vliv kuhového otvou na ozložení napjatosti v dlouhém tenkém pásu zatíženém tahem
F5 JEDNODUCHÁ KONZERVATIVNÍ POLE
 F5 JEDNODUCHÁ KONZERVATIVNÍ POLE Evopský sociální fond Paha & EU: Investujeme do vaší budoucnosti F5 JEDNODUCHÁ KONZERVATIVNÍ POLE Asi nejznámějším konzevativním polem je gavitační silové pole Ke gavitační
F5 JEDNODUCHÁ KONZERVATIVNÍ POLE Evopský sociální fond Paha & EU: Investujeme do vaší budoucnosti F5 JEDNODUCHÁ KONZERVATIVNÍ POLE Asi nejznámějším konzevativním polem je gavitační silové pole Ke gavitační
UNIVERZITA KARLOVA V PRAZE Přírodovědecká fakulta
 Chromatografie Zroj: http://www.scifun.org/homeexpts/homeexpts.html [34] Diaktický záměr: Vysvětlení pojmu chromatografie. Popis: Žáci si vyzkouší velmi jenouché ělení látek pomocí papírové chromatografie.
Chromatografie Zroj: http://www.scifun.org/homeexpts/homeexpts.html [34] Diaktický záměr: Vysvětlení pojmu chromatografie. Popis: Žáci si vyzkouší velmi jenouché ělení látek pomocí papírové chromatografie.
5. Měření vstupní impedance antén
 5. Měření vstupní impedance antén 5.1 Úvod Anténa se z hlediska vnějších obvodů chová jako jednoban se vstupní impedancí Z vst, kteou můžeme zjistit měřením. U bezeztátové antény ve volném postou by se
5. Měření vstupní impedance antén 5.1 Úvod Anténa se z hlediska vnějších obvodů chová jako jednoban se vstupní impedancí Z vst, kteou můžeme zjistit měřením. U bezeztátové antény ve volném postou by se
Úloha č. 1 pomůcky Šíření tepla v ustáleném stavu základní vztahy
 Úloha č. pomůcky Šíření tepla v ustáleném stavu záklaní vztahy Veení Fourriérův zákon veení tepla, D: Hustota tepelného toku je úměrná změně teploty ve směru šíření tepla, konstantou úměrnosti je součinitel
Úloha č. pomůcky Šíření tepla v ustáleném stavu záklaní vztahy Veení Fourriérův zákon veení tepla, D: Hustota tepelného toku je úměrná změně teploty ve směru šíření tepla, konstantou úměrnosti je součinitel
Hlavní body. Keplerovy zákony Newtonův gravitační zákon. Konzervativní pole. Gravitační pole v blízkosti Země Planetární pohyby
 Úvod do gavitace Hlavní body Kepleovy zákony Newtonův gavitační zákon Gavitační pole v blízkosti Země Planetání pohyby Konzevativní pole Potenciál a potenciální enegie Vztah intenzity a potenciálu Úvod
Úvod do gavitace Hlavní body Kepleovy zákony Newtonův gavitační zákon Gavitační pole v blízkosti Země Planetání pohyby Konzevativní pole Potenciál a potenciální enegie Vztah intenzity a potenciálu Úvod
II. Statické elektrické pole v dielektriku. 2. Dielektrikum 3. Polarizace dielektrika 4. Jevy v dielektriku
 II. Statické elektické pole v dielektiku Osnova: 1. Dipól 2. Dielektikum 3. Polaizace dielektika 4. Jevy v dielektiku 1. Dipól Konečný dipól 2 bodové náboje stejné velikosti a opačného znaménka ve vzdálenosti
II. Statické elektické pole v dielektiku Osnova: 1. Dipól 2. Dielektikum 3. Polaizace dielektika 4. Jevy v dielektiku 1. Dipól Konečný dipól 2 bodové náboje stejné velikosti a opačného znaménka ve vzdálenosti
2.1.2 Jaký náboj projde proudovodičem, klesá-li v něm proud z 18 A na nulu tak, že za každou sekundu klesne hodnota proudu na polovinu?
 . LKTCKÝ POD.. lektický odpo, páce a výkon el. poudu.. Jaké množství el. náboje Q pojde vodičem za t = 0 s, jestliže a) poud = 5 A je stálý, b) poud ovnoměně oste od nuly do A?.. Jaký náboj pojde poudovodičem,
. LKTCKÝ POD.. lektický odpo, páce a výkon el. poudu.. Jaké množství el. náboje Q pojde vodičem za t = 0 s, jestliže a) poud = 5 A je stálý, b) poud ovnoměně oste od nuly do A?.. Jaký náboj pojde poudovodičem,
Vypracoval Datum Hodnocení. V celé úloze jsme používali He-Ne laser s vlnovou délkou λ = 632, 8 nm. Paprsek jsme nasměrovali
 Název a číslo úlohy - Difrakce světelného záření Datum měření 3.. 011 Měření proveli Tomáš Zikmun, Jakub Kákona Vypracoval Tomáš Zikmun Datum. 3. 011 Honocení 1 Difrakční obrazce V celé úloze jsme používali
Název a číslo úlohy - Difrakce světelného záření Datum měření 3.. 011 Měření proveli Tomáš Zikmun, Jakub Kákona Vypracoval Tomáš Zikmun Datum. 3. 011 Honocení 1 Difrakční obrazce V celé úloze jsme používali
Metody založené na měření elektrických vlastností roztoků
 Metody založené na měření elektických vlastností oztoků KODUKTOMETRIE Pincip: Měří se elektická vodivost oztoků elektolytů mezi dvěma platinovými elektodami za půchodu střídavého poudu. Rozdíl poti ostatním
Metody založené na měření elektických vlastností oztoků KODUKTOMETRIE Pincip: Měří se elektická vodivost oztoků elektolytů mezi dvěma platinovými elektodami za půchodu střídavého poudu. Rozdíl poti ostatním
Elektrické a magnetické pole zdroje polí
 Elektické a magnetické pole zdoje polí Co je podstatou elektomagnetických jevů Co jsou elektické náboje a jaké mají vlastnosti Co je elementání náboj a bodový elektický náboj Jak veliká je elektická síla
Elektické a magnetické pole zdoje polí Co je podstatou elektomagnetických jevů Co jsou elektické náboje a jaké mají vlastnosti Co je elementání náboj a bodový elektický náboj Jak veliká je elektická síla
PRAVDĚPODOBNOSTNÍ PŘÍSTUP K HODNOCENÍ DRÁTKOBETONOVÝCH SMĚSÍ. Petr Janas 1 a Martin Krejsa 2
 PAVDĚPODOBNOSTNÍ PŘÍSTUP K HODNOCENÍ DÁTKOBETONOVÝCH SMĚSÍ Petr Janas 1 a Martin Krejsa 2 Abstract The paper reviews briefly one of the propose probabilistic assessment concepts. The potential of the propose
PAVDĚPODOBNOSTNÍ PŘÍSTUP K HODNOCENÍ DÁTKOBETONOVÝCH SMĚSÍ Petr Janas 1 a Martin Krejsa 2 Abstract The paper reviews briefly one of the propose probabilistic assessment concepts. The potential of the propose
Gravitační a elektrické pole
 Gavitační a elektické pole Newtonův gavitační zákon Aistotelés (384-3 př. n. l.) předpokládal, že na tělesa působí síla směřující svisle dolů. Poto jsou těžké předměty (skály tvořící placatou Zemi) dole
Gavitační a elektické pole Newtonův gavitační zákon Aistotelés (384-3 př. n. l.) předpokládal, že na tělesa působí síla směřující svisle dolů. Poto jsou těžké předměty (skály tvořící placatou Zemi) dole
Elektromagnetické jevy, elektrické jevy 4. Elektrický náboj, elektrické pole
 Elektomagnetické jevy, elektické jevy 4. Elektický náboj, elektické pole 4. Základní poznatky (duhy el. náboje, vodiče, izolanty) Někteé látky se třením dostávají do zvláštního stavu přitahují lehká tělíska.
Elektomagnetické jevy, elektické jevy 4. Elektický náboj, elektické pole 4. Základní poznatky (duhy el. náboje, vodiče, izolanty) Někteé látky se třením dostávají do zvláštního stavu přitahují lehká tělíska.
EU peníze středním školám digitální učební materiál
 EU peníze středním školám digitální učební materiál Číslo projektu: Číslo a název šablony klíčové aktivity: Tematická oblast, název DUMu: Autor: CZ.1.07/1.5.00/34.0515 III/2 Inovace a zkvalitnění výuky
EU peníze středním školám digitální učební materiál Číslo projektu: Číslo a název šablony klíčové aktivity: Tematická oblast, název DUMu: Autor: CZ.1.07/1.5.00/34.0515 III/2 Inovace a zkvalitnění výuky
Předpokládáme ideální chování, neuvažujeme autoprotolýzu vody ve smyslu nutnosti číselného řešení simultánních rovnováh. CH3COO
 Pufr ze slabé kyseliny a její soli se silnou zásaou např CHCOOH + CHCOONa Násleujíí rozbor bue vyházet z počátečního stavu, ky konentrae obou látek jsou srovnatelné (největší pufrační kapaita je pro ekvimolární
Pufr ze slabé kyseliny a její soli se silnou zásaou např CHCOOH + CHCOONa Násleujíí rozbor bue vyházet z počátečního stavu, ky konentrae obou látek jsou srovnatelné (největší pufrační kapaita je pro ekvimolární
Pružnost a plasticita II
 Pužnost a plasticita II. očník bakalářského stuia oc. Ing. Matin Kejsa, Ph.D. Katea stavební mechanik Rovinný poblém, stěnová ovnice Rovinné úloh Řešené úloh teoie pužnosti se postatně jenouší, poku v
Pužnost a plasticita II. očník bakalářského stuia oc. Ing. Matin Kejsa, Ph.D. Katea stavební mechanik Rovinný poblém, stěnová ovnice Rovinné úloh Řešené úloh teoie pužnosti se postatně jenouší, poku v
VYUŽITÍ NANOSORBENTŮ NA BÁZI MnO 2 PRO ODSTRAŇOVÁNÍ As (V) Z VOD
 Citace Stnadová N., Dong Nguyen Thanh, Sang Nguyen Thi Minh, Ulbich P., Mandeep Singh: Využití nanosobentů na bázi MnO 2 po odstaňování As(V) z vod. Sboník konfeence Pitná voda 2010, s.151-156. W&ET Team,
Citace Stnadová N., Dong Nguyen Thanh, Sang Nguyen Thi Minh, Ulbich P., Mandeep Singh: Využití nanosobentů na bázi MnO 2 po odstaňování As(V) z vod. Sboník konfeence Pitná voda 2010, s.151-156. W&ET Team,
F r. Umístěme do P jinou elektricky nabitou částici. Síla na ni působící Elektromagnetická interakce
 . ELEKTROMAGNETISMUS.0. Elektomagnetická inteakce vzájemné působení elekticky nabitých částic Mechanismus: Každá pohybující se elekticky nabitá částice vytváří v okolním postou elektomagnetické pole, kteé
. ELEKTROMAGNETISMUS.0. Elektomagnetická inteakce vzájemné působení elekticky nabitých částic Mechanismus: Každá pohybující se elekticky nabitá částice vytváří v okolním postou elektomagnetické pole, kteé
VALIVÁ LOŽISKA. www.zkl.cz www.zkl.eu
 CZ 2009 01 VALIVÁ LOŽISKA www.zkl.cz www.zkl.eu VALIVÁ LOŽISKA Úaje uveené v této publikaci byly pečlivě zkontolovány a jsou pakticky ověřeny. Vzhleem k pokačujícímu technickému vývoji si však vyhazujeme
CZ 2009 01 VALIVÁ LOŽISKA www.zkl.cz www.zkl.eu VALIVÁ LOŽISKA Úaje uveené v této publikaci byly pečlivě zkontolovány a jsou pakticky ověřeny. Vzhleem k pokačujícímu technickému vývoji si však vyhazujeme
Fyzikální chemie. ochrana životního prostředí analytická chemie chemická technologie denní. Platnost: od 1. 9. 2009 do 31. 8. 2013
 Učební osnova předmětu Fyzikální chemie Studijní obor: Aplikovaná chemie Zaměření: Forma vzdělávání: Celkový počet vyučovacích hodin za studium: Analytická chemie Chemická technologie Ochrana životního
Učební osnova předmětu Fyzikální chemie Studijní obor: Aplikovaná chemie Zaměření: Forma vzdělávání: Celkový počet vyučovacích hodin za studium: Analytická chemie Chemická technologie Ochrana životního
KATALOG. Sokolovského hnědého uhlí a briket na rok 2008 SOKOLOVSKÁ UHELNÁ, PRÁ VNÍ N Á STUPCE, A. S.
 KATALOG Sokolovského hněého uhlí a biket na ok SOKOLOVSKÁ UHELNÁ, PRÁ VNÍ N Á STUPCE, A. S. NABÍDKA SOKOLOVSKÉHO UHLÍ Vážení obchoní přátelé, ovolte mi, abych Vás v kátkosti seznámil se záměy naší uhelné
KATALOG Sokolovského hněého uhlí a biket na ok SOKOLOVSKÁ UHELNÁ, PRÁ VNÍ N Á STUPCE, A. S. NABÍDKA SOKOLOVSKÉHO UHLÍ Vážení obchoní přátelé, ovolte mi, abych Vás v kátkosti seznámil se záměy naší uhelné
Cavendishův pokus: Určení gravitační konstanty,,vážení Země
 Cavendishův pokus: Učení gavitační konstanty,,vážení Země Jiří Kist - Mendlovo gymnázium, Opava, SO@seznam.cz Teeza Steinhatová - gymnázium J. K. Tyla Hadec Kálové, SteinT@seznam.cz 1. Úvod Abstakt: Cílem
Cavendishův pokus: Učení gavitační konstanty,,vážení Země Jiří Kist - Mendlovo gymnázium, Opava, SO@seznam.cz Teeza Steinhatová - gymnázium J. K. Tyla Hadec Kálové, SteinT@seznam.cz 1. Úvod Abstakt: Cílem
Charakterizace částic a částicových soustav
 W. Pabst / E. Gegoová Chaakteizace částic a částicových soustav VŠCHT Paha 007 Tyto studijní mateiály vznikly v ámci pojektu FRVŠ 674 / 007 F1 / b Tvoba předmětu Chaakteizace částic a částicových soustav.
W. Pabst / E. Gegoová Chaakteizace částic a částicových soustav VŠCHT Paha 007 Tyto studijní mateiály vznikly v ámci pojektu FRVŠ 674 / 007 F1 / b Tvoba předmětu Chaakteizace částic a částicových soustav.
Geometrická optika. Aberace (vady) optických soustav
 Geometická optika Abeace (vady) optických soustav abeace (vady) optických soustav jsou odchylky zobazení eálné optické soustavy od zobazení ideální optické soustavy v důsledku abeací není obazem bodu bod,
Geometická optika Abeace (vady) optických soustav abeace (vady) optických soustav jsou odchylky zobazení eálné optické soustavy od zobazení ideální optické soustavy v důsledku abeací není obazem bodu bod,
2.1 Shrnutí základních poznatků
 .1 Shnutí základních poznatků S plnostěnnými otujícími kotouči se setkáváme hlavně u paních a spalovacích tubín a tubokompesoů. Matematický model otujících kotoučů můžeme s úspěchem využít např. i při
.1 Shnutí základních poznatků S plnostěnnými otujícími kotouči se setkáváme hlavně u paních a spalovacích tubín a tubokompesoů. Matematický model otujících kotoučů můžeme s úspěchem využít např. i při
Magnetické pole najdeme kolem permanentního magnetu (i kolem Země) a zároveň kolem každého vodiče, kterým prochází elektrický proud.
 MAGNETCKÉ POLE 1. Základní chaakteistiky Magnetické pole se tvoří kolem každé částice s nábojem Q, kteá je v pohybu. Tzn., že magnetismus látek je dán stuktuou atomů (elektony jsou v atomu v pohybu). Magnetické
MAGNETCKÉ POLE 1. Základní chaakteistiky Magnetické pole se tvoří kolem každé částice s nábojem Q, kteá je v pohybu. Tzn., že magnetismus látek je dán stuktuou atomů (elektony jsou v atomu v pohybu). Magnetické
Vlnovody. Obr. 7.1 Běžné příčné průřezy kovových vlnovodů: obdélníkový, kruhový, vlnovod, vlnovod H.
 7 Vlnovody Běžná vedení (koaxiální kabel, dvojlinka) jsou jen omezeně použitelná v mikovlnné části kmitočtového spekta. S ůstem kmitočtu přenášeného signálu totiž významně ostou ztáty v dielektiku těchto
7 Vlnovody Běžná vedení (koaxiální kabel, dvojlinka) jsou jen omezeně použitelná v mikovlnné části kmitočtového spekta. S ůstem kmitočtu přenášeného signálu totiž významně ostou ztáty v dielektiku těchto
F (x, h(x)) T (g)(x) = g(x)
 11 Implicitní funkce Definice 111 (implicitní funkce) Nechť F : R 2 R je funkce a [x 0, y 0 ] R 2 je takový bo, že F (x 0, y 0 ) = 0 Řekneme, že funkce y = f(x) je v okolí bou [x 0, y 0 ] zaána implicitně
11 Implicitní funkce Definice 111 (implicitní funkce) Nechť F : R 2 R je funkce a [x 0, y 0 ] R 2 je takový bo, že F (x 0, y 0 ) = 0 Řekneme, že funkce y = f(x) je v okolí bou [x 0, y 0 ] zaána implicitně
I. Statické elektrické pole ve vakuu
 I. Statické elektické pole ve vakuu Osnova:. Náboj a jeho vlastnosti 2. Coulombův zákon 3. Intenzita elektostatického pole 4. Gaussova věta elektostatiky 5. Potenciál elektického pole 6. Pole vodiče ve
I. Statické elektické pole ve vakuu Osnova:. Náboj a jeho vlastnosti 2. Coulombův zákon 3. Intenzita elektostatického pole 4. Gaussova věta elektostatiky 5. Potenciál elektického pole 6. Pole vodiče ve
Termodynamika (td.) se obecně zabývá vzájemnými vztahy a přeměnami různých druhů
 Termodynamika (td.) se obecně zabývá vzájemnými vztahy a přeměnami různých druhů energií (mechanické, tepelné, elektrické, magnetické, chemické a jaderné) při td. dějích. Na rozdíl od td. cyklických dějů
Termodynamika (td.) se obecně zabývá vzájemnými vztahy a přeměnami různých druhů energií (mechanické, tepelné, elektrické, magnetické, chemické a jaderné) při td. dějích. Na rozdíl od td. cyklických dějů
Úloha II.E... čočkování
 Úloha II.E... čočkování 8 boů; průměr 5,46; řešilo 65 stuentů V obálce jste spolu se zaáním ostali i vě čočky. Vaším úkolem je změřit jejich parametry ruh a ohniskovou vzálenost. Poznámka Poku nejste stávající
Úloha II.E... čočkování 8 boů; průměr 5,46; řešilo 65 stuentů V obálce jste spolu se zaáním ostali i vě čočky. Vaším úkolem je změřit jejich parametry ruh a ohniskovou vzálenost. Poznámka Poku nejste stávající
4. konference o matematice a fyzice na VŠT Brno, Fraktály ve fyzice. Oldřich Zmeškal
 4. konfeence o matematice a fyzice na VŠT Bno, 15. 9. 25 Faktály ve fyzice Oldřich Zmeškal Ústav fyzikální a spotřební chemie, Fakulta chemická, Vysoké učení technické, Pukyňova 118, 612 Bno, Česká epublika
4. konfeence o matematice a fyzice na VŠT Bno, 15. 9. 25 Faktály ve fyzice Oldřich Zmeškal Ústav fyzikální a spotřební chemie, Fakulta chemická, Vysoké učení technické, Pukyňova 118, 612 Bno, Česká epublika
Látkové množství n poznámky 6.A GVN
 Látkové množství n poznámky 6.A GVN 10. září 2007 charakterizuje látky z hlediska počtu částic (molekul, atomů, iontů), které tato látka obsahuje je-li v tělese z homogenní látky N částic, pak látkové
Látkové množství n poznámky 6.A GVN 10. září 2007 charakterizuje látky z hlediska počtu částic (molekul, atomů, iontů), které tato látka obsahuje je-li v tělese z homogenní látky N částic, pak látkové
ztuhnutím pyrosolu taveniny, v níž je dispergován plyn, kapalina nebo tuhá látka fotochemickým rozkladem krystalů některých solí
 a pevným kapalným plynným disperzním podílem chovají se jako pevné látky i když přítomnost částic disperzního podílu v pevné látce obvykle značně mění její vlastnosti, zvláště mechanické a optické Stabilita
a pevným kapalným plynným disperzním podílem chovají se jako pevné látky i když přítomnost částic disperzního podílu v pevné látce obvykle značně mění její vlastnosti, zvláště mechanické a optické Stabilita
IV. Magnetické pole ve vakuu a v magnetiku. 1. Magnetické pole el. proudu 2. Vlastnosti mg. pole 3. Magnetikum
 IV. Magnetické pole ve vakuu a v magnetiku Osnova: 1. Magnetické pole el. poudu 2. Vlastnosti mg. pole 3. Magnetikum 1. Magnetické pole el. poudu histoický úvod podivné expeimenty ukazující neznámé silové
IV. Magnetické pole ve vakuu a v magnetiku Osnova: 1. Magnetické pole el. poudu 2. Vlastnosti mg. pole 3. Magnetikum 1. Magnetické pole el. poudu histoický úvod podivné expeimenty ukazující neznámé silové
Keplerova úloha. Abstrakt: Článek řeší problém pohybu planety (Země) kolem Slunce.
 Kepleova úloha Keple-2c.TEX jan.obzalek@mff.cuni.cz Abstakt: Článek řeší poblém pohybu planety (Země) kolem Slunce. Úplná úloha: co zanebáme Chceme vyšetřit pohyb planety, např. Země, v naší sluneční soustavě.
Kepleova úloha Keple-2c.TEX jan.obzalek@mff.cuni.cz Abstakt: Článek řeší poblém pohybu planety (Země) kolem Slunce. Úplná úloha: co zanebáme Chceme vyšetřit pohyb planety, např. Země, v naší sluneční soustavě.
Vibrace vícečásticových soustav v harmonické aproximaci. ( r)
 Paktikum z počítačového modelování ve fyzice a chemii Úloha č. 5 Vibace vícečásticových soustav v hamonické apoximaci Úkol Po zadané potenciály nalezněte vibační fekvence soustavy několika částic diagonalizací
Paktikum z počítačového modelování ve fyzice a chemii Úloha č. 5 Vibace vícečásticových soustav v hamonické apoximaci Úkol Po zadané potenciály nalezněte vibační fekvence soustavy několika částic diagonalizací
ELEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Ampérův zákon
 ELEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Ampérův zákon Peter Dourmashkin MIT 26, překla: Jan Pacák (27) Obsah 5 AMPÉRŮV ZÁKON 3 51 ÚKOLY 3 52 ALGORITMUS PRO ŘEŠENÍ PROBLÉMŮ 3 ÚLOHA 1: VÁLCOVÝ PLÁŠŤ
ELEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Ampérův zákon Peter Dourmashkin MIT 26, překla: Jan Pacák (27) Obsah 5 AMPÉRŮV ZÁKON 3 51 ÚKOLY 3 52 ALGORITMUS PRO ŘEŠENÍ PROBLÉMŮ 3 ÚLOHA 1: VÁLCOVÝ PLÁŠŤ
Chemie. Mgr. Petra Drápelová Mgr. Jaroslava Vrbková. Gymnázium, SOŠ a VOŠ Ledeč nad Sázavou
 Chemie Mgr. Petra Drápelová Mgr. Jaroslava Vrbková Gymnázium, SOŠ a VOŠ Ledeč nad Sázavou Složení látek VY_32_INOVACE_03_3_02_CH Gymnázium, SOŠ a VOŠ Ledeč nad Sázavou SLOŽENÍ LÁTEK Fyzikálním kritériem
Chemie Mgr. Petra Drápelová Mgr. Jaroslava Vrbková Gymnázium, SOŠ a VOŠ Ledeč nad Sázavou Složení látek VY_32_INOVACE_03_3_02_CH Gymnázium, SOŠ a VOŠ Ledeč nad Sázavou SLOŽENÍ LÁTEK Fyzikálním kritériem
B1. Výpočetní geometrie a počítačová grafika 9. Promítání., světlo.
 B. Výpočetní geometie a počítačová gafika 9. Pomítání., světlo. Pomítání Převedení 3D objektu do 2D podoby je ealizováno pomítáním, při kteém dochází ke ztátě infomace. Pomítání (nebo též pojekce) je tedy
B. Výpočetní geometie a počítačová gafika 9. Pomítání., světlo. Pomítání Převedení 3D objektu do 2D podoby je ealizováno pomítáním, při kteém dochází ke ztátě infomace. Pomítání (nebo též pojekce) je tedy
Stavba atomu: Atomové jádro
 Stavba atomu: tomové jádo Výzkum stuktuy hmoty: Histoie Jen zdánlivě existuje hořké či sladké, chladné či hoké, ve skutečnosti jsou pouze atomy a pázdno. Démokitos, 46 37 př. n.l. Heni Becqueel 85 98 objev
Stavba atomu: tomové jádo Výzkum stuktuy hmoty: Histoie Jen zdánlivě existuje hořké či sladké, chladné či hoké, ve skutečnosti jsou pouze atomy a pázdno. Démokitos, 46 37 př. n.l. Heni Becqueel 85 98 objev
ZŠ ÚnO, Bratří Čapků 1332
 Úvodní obrazovka Menu (vlevo nahoře) Návrat na hlavní stránku Obsah Výsledky Poznámky Záložky edunet Konec Chemie 1 (pro 12-16 let) LangMaster Obsah (střední část) výběr tématu - dvojklikem v seznamu témat
Úvodní obrazovka Menu (vlevo nahoře) Návrat na hlavní stránku Obsah Výsledky Poznámky Záložky edunet Konec Chemie 1 (pro 12-16 let) LangMaster Obsah (střední část) výběr tématu - dvojklikem v seznamu témat
Metody teorie spolehlivosti
 Metoy teorie spolehlivosti Historické metoy mpirické metoy Kalibrace Pravěpoobnostní metoy FOM úroveň II AKTNÍ úroveň III Kalibrace MTOD NÁVH. BODŮ Kalibrace MTODA DÍLČÍCH SOUČINITLŮ úroveň I Nejistoty
Metoy teorie spolehlivosti Historické metoy mpirické metoy Kalibrace Pravěpoobnostní metoy FOM úroveň II AKTNÍ úroveň III Kalibrace MTOD NÁVH. BODŮ Kalibrace MTODA DÍLČÍCH SOUČINITLŮ úroveň I Nejistoty
OBECNÁ CHEMIE. Kurz chemie pro fyziky MFF-UK přednášející: Jaroslav Burda, KChFO.
 OBECNÁ CHEMIE Kurz chemie pro fyziky MFF-UK přednášející: Jaroslav Burda, KChFO burda@karlov.mff.cuni.cz HMOTA, JEJÍ VLASTNOSTI A FORMY Definice: Každý hmotný objekt je charakterizován dvěmi vlastnostmi
OBECNÁ CHEMIE Kurz chemie pro fyziky MFF-UK přednášející: Jaroslav Burda, KChFO burda@karlov.mff.cuni.cz HMOTA, JEJÍ VLASTNOSTI A FORMY Definice: Každý hmotný objekt je charakterizován dvěmi vlastnostmi
5. Světlo jako elektromagnetické vlnění
 Tivium z optiky 9 5 Světlo jako elektomagnetické vlnění Ve třetí kapitole jsme se dozvěděli že na světlo můžeme nahlížet jako na elektomagnetické vlnění Dříve než tak učiníme si ale musíme alespoň v základech
Tivium z optiky 9 5 Světlo jako elektomagnetické vlnění Ve třetí kapitole jsme se dozvěděli že na světlo můžeme nahlížet jako na elektomagnetické vlnění Dříve než tak učiníme si ale musíme alespoň v základech
3.1. Magnetické pole ve vakuu a v látkovém prostředí Elektromagnetická indukce Energie a silové účinky magnetického pole...
 Obsah Předmluva... 4. Elektostatika.. Elektostatické pole ve vakuu... 5.. Elektostatické pole v dielektiku... 9.3. Kapacita. Kondenzáto....4. Enegie elektostatického pole... 6. Elektický poud.. Elektický
Obsah Předmluva... 4. Elektostatika.. Elektostatické pole ve vakuu... 5.. Elektostatické pole v dielektiku... 9.3. Kapacita. Kondenzáto....4. Enegie elektostatického pole... 6. Elektický poud.. Elektický
ε ε [ 8, N, 3, N ]
![ε ε [ 8, N, 3, N ] ε ε [ 8, N, 3, N ]](/thumbs/92/110750106.jpg) 1. Vzdálenost mezi elektonem a potonem v atomu vodíku je přibližně 0,53.10-10 m. Jaká je velikost sil mezi uvedenými částicemi a) elektostatické b) gavitační Je-li gavitační konstanta G = 6,7.10-11 N.m
1. Vzdálenost mezi elektonem a potonem v atomu vodíku je přibližně 0,53.10-10 m. Jaká je velikost sil mezi uvedenými částicemi a) elektostatické b) gavitační Je-li gavitační konstanta G = 6,7.10-11 N.m
Ch - Rozlišování látek
 Ch - Rozlišování látek Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento dokument byl kompletně
Ch - Rozlišování látek Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento dokument byl kompletně
Válečkové řetězy. Tiskové chyby vyhrazeny. Obrázky mají informativní charakter.
 Válečkové řetězy Technické úaje IN 8187 Hlavními rvky válečkového řevoového řetězu jsou: Boční tvarované estičky vzálené o sebe o šířku () Čey válečků s růměrem () Válečky o růměru () Vzálenost čeů určuje
Válečkové řetězy Technické úaje IN 8187 Hlavními rvky válečkového řevoového řetězu jsou: Boční tvarované estičky vzálené o sebe o šířku () Čey válečků s růměrem () Válečky o růměru () Vzálenost čeů určuje
Netkané textilie. Materiály 2
 Materiály 2 1 Pojiva pro výrobu netkaných textilií Pojivo je jednou ze dvou základních složek pojených textilií. Forma pojiva a jeho vlastnosti předurčují technologii a podmínky procesu pojení způsob rozmístění
Materiály 2 1 Pojiva pro výrobu netkaných textilií Pojivo je jednou ze dvou základních složek pojených textilií. Forma pojiva a jeho vlastnosti předurčují technologii a podmínky procesu pojení způsob rozmístění
D 19 Knauf design - podhledy
 D 19 07/007 D 19 Knauf esign - pohley Stana Technika tvaování Vyfézování tvau V 3 Ohýbané pvky 4 Ohýbané sáové panely 5 Ohýbané CD-pofily 6 Stana Paalelní ážky 7 Úhlová spojka 8 Otočný kotvící úhelník
D 19 07/007 D 19 Knauf esign - pohley Stana Technika tvaování Vyfézování tvau V 3 Ohýbané pvky 4 Ohýbané sáové panely 5 Ohýbané CD-pofily 6 Stana Paalelní ážky 7 Úhlová spojka 8 Otočný kotvící úhelník
Maloúhlový rozptyl neutronů úvod Small-Angle Neutron Scattering - SANS
 Maloúhlový ozptyl neutonů úvo mall-angle Neuton catteing - AN Jan Šaoun a kol. Ústav jaené fyziky v.v.i, AVČR, Řež AN - teoie a expeimentální metoy AN! metoa po stuium mikostuktuních nehomogenit π/r, µm-
Maloúhlový ozptyl neutonů úvo mall-angle Neuton catteing - AN Jan Šaoun a kol. Ústav jaené fyziky v.v.i, AVČR, Řež AN - teoie a expeimentální metoy AN! metoa po stuium mikostuktuních nehomogenit π/r, µm-
Přírodní vědy - Chemie vymezení zájmu
 Přírodní vědy - Chemie vymezení zájmu Hmota Hmota má dualistický, korpuskulárně (částicově) vlnový charakter. Převládající charakter: korpuskulární (částicový) - látku vlnový - pole. Látka se skládá z
Přírodní vědy - Chemie vymezení zájmu Hmota Hmota má dualistický, korpuskulárně (částicově) vlnový charakter. Převládající charakter: korpuskulární (částicový) - látku vlnový - pole. Látka se skládá z
MODELOVÁNÍ TLAKOVÝCH ZTRÁT KAPILÁRNÍCH ROHOŽÍ
 Simulace buov a techniky prostřeí 21 6. konference IBPSA-CZ Praha, 8. a 9. 11. 21 MODELOVÁNÍ TLAKOVÝCH ZTRÁT KAPILÁRNÍCH ROHOŽÍ Vlaimír Zmrhal, Tomáš Matuška, Jan Schwarzer Ústav techniky prostřeí, Fakulta
Simulace buov a techniky prostřeí 21 6. konference IBPSA-CZ Praha, 8. a 9. 11. 21 MODELOVÁNÍ TLAKOVÝCH ZTRÁT KAPILÁRNÍCH ROHOŽÍ Vlaimír Zmrhal, Tomáš Matuška, Jan Schwarzer Ústav techniky prostřeí, Fakulta
Modely produkčních systémů. Plánování výroby. seminární práce. Autor: Jakub Mertl. Xname: xmerj08. Datum: ZS 07/08
 Modely podukčních systémů Plánování výoby seminání páce Auto: Jakub Metl Xname: xmej08 Datum: ZS 07/08 Obsah Obsah... Úvod... 3 1. Výobní linky... 4 1.1. Výobní místo 1... 4 1.. Výobní místo... 5 1.3.
Modely podukčních systémů Plánování výoby seminání páce Auto: Jakub Metl Xname: xmej08 Datum: ZS 07/08 Obsah Obsah... Úvod... 3 1. Výobní linky... 4 1.1. Výobní místo 1... 4 1.. Výobní místo... 5 1.3.
ATOMOVÁ HMOTNOSTNÍ JEDNOTKA
 CHEMICKÉ VÝPOČTY Teoie Skutečné hmotnosti atomů jsou velmi malé např.: m 12 C=1,99267.10-26 kg, m 63 Cu=1,04496.10-25 kg. Počítání s těmito hodnotami je nepaktické a poto byla zavedena atomová hmotností
CHEMICKÉ VÝPOČTY Teoie Skutečné hmotnosti atomů jsou velmi malé např.: m 12 C=1,99267.10-26 kg, m 63 Cu=1,04496.10-25 kg. Počítání s těmito hodnotami je nepaktické a poto byla zavedena atomová hmotností
VY_42_Inovace_24_MA_2.04_Množiny ve slovních úlohách pracovní list
 Číslo projektu Číslo materiálu CZ.1.07/1.5.00/34.0394 VY_42_Inovace_24_MA_2.04_Množiny ve slovních úlohách pracovní list Název školy Stření oborná škola a Stření oborné učiliště, Hustopeče, Masarykovo
Číslo projektu Číslo materiálu CZ.1.07/1.5.00/34.0394 VY_42_Inovace_24_MA_2.04_Množiny ve slovních úlohách pracovní list Název školy Stření oborná škola a Stření oborné učiliště, Hustopeče, Masarykovo
4.5.5 Magnetické působení rovnoběžných vodičů s proudem
 4.5.5 Magnetické působení rovnoběžných voičů s prouem Přepoklay: 4502, 4503, 4504 Př. 1: Dvěma velmi louhými svislými voiči prochází elektrický prou. Rozhoni pomocí rozboru magnetických inukčních čar polí
4.5.5 Magnetické působení rovnoběžných voičů s prouem Přepoklay: 4502, 4503, 4504 Př. 1: Dvěma velmi louhými svislými voiči prochází elektrický prou. Rozhoni pomocí rozboru magnetických inukčních čar polí
Grafické řešení úloh LP se dvěma neznámými
 . přenáška Grafické řešení úloh LP se věma nenámými Moel úlohy lineárního programování, který obsahuje poue vě nenámé, le řešit graficky v rovině pravoúhlých souřaných os. V této rovině se nejprve obraí
. přenáška Grafické řešení úloh LP se věma nenámými Moel úlohy lineárního programování, který obsahuje poue vě nenámé, le řešit graficky v rovině pravoúhlých souřaných os. V této rovině se nejprve obraí
Rutherfordův experiment s multikanálovým analyzátorem
 Ruthefodův expeiment s multikanálovým analyzátoem Úkol Ověřte Ruthefodův vztah po ozptyl poměřením počtu alfa částic ozptýlených tenkou zlatou fólií do ůzných úhlů mezi cca 0 a 90. Zjistěte, jak ovlivňuje
Ruthefodův expeiment s multikanálovým analyzátoem Úkol Ověřte Ruthefodův vztah po ozptyl poměřením počtu alfa částic ozptýlených tenkou zlatou fólií do ůzných úhlů mezi cca 0 a 90. Zjistěte, jak ovlivňuje
ROZDĚLENÍ PŘÍJMŮ A JEHO MODELY. Jitka Bartošová
 ROZDĚLENÍ PŘÍJMŮ A JEHO MODELY Jitka Batošová Kateda managementu infomací, Fakulta managementu, Vysoká škola ekonomická Paha, Jaošovská 1117/II, 377 01 Jindřichův Hadec batosov@fm.vse.cz Abstakt: Poces
ROZDĚLENÍ PŘÍJMŮ A JEHO MODELY Jitka Batošová Kateda managementu infomací, Fakulta managementu, Vysoká škola ekonomická Paha, Jaošovská 1117/II, 377 01 Jindřichův Hadec batosov@fm.vse.cz Abstakt: Poces
Duktilní deformace, část 1
 uktilní defomace, část uktilní (plastická) defomace je taková defomace, při níž se mateiál defomuje bez přeušení koheze (soudžnosti). Plasticita mateiálu záleží na tzv. mezi plasticity (yield stess) -
uktilní defomace, část uktilní (plastická) defomace je taková defomace, při níž se mateiál defomuje bez přeušení koheze (soudžnosti). Plasticita mateiálu záleží na tzv. mezi plasticity (yield stess) -
1 Parciální diferenciální rovnice prvního řádu
 1 Parciální iferenciální rovnice prvního řáu 11 Lineární homogenní parciální iferenciální rovnice ve vou nezávisle proměnných ax, y + bx, y0 1 Řešenímjefunkce uux, y Hleáme vrstevnice funkce u Nechť mají
1 Parciální iferenciální rovnice prvního řáu 11 Lineární homogenní parciální iferenciální rovnice ve vou nezávisle proměnných ax, y + bx, y0 1 Řešenímjefunkce uux, y Hleáme vrstevnice funkce u Nechť mají
VÝPOČET ŘETĚZOVÝCH PŘEVODŮ ČSN 01 4809
 VÝPOČET ŘETĚZOVÝCH PŘEVODŮ ČSN 0 4809 DIAGRAM PRO VOLBU ŘETĚZU Z JMENOVITÉHO VÝONU A OTÁČE PASTORU Js /4 ŘETĚZY_VÝPOČET_04809 SOUČINITEL VÝONU κ Počet zuů pstoku z Převoový pomě i 2 3 5 7 3 0,39 0,50 0,57
VÝPOČET ŘETĚZOVÝCH PŘEVODŮ ČSN 0 4809 DIAGRAM PRO VOLBU ŘETĚZU Z JMENOVITÉHO VÝONU A OTÁČE PASTORU Js /4 ŘETĚZY_VÝPOČET_04809 SOUČINITEL VÝONU κ Počet zuů pstoku z Převoový pomě i 2 3 5 7 3 0,39 0,50 0,57
STATICKY NEURČITÉ RÁMOVÉ KONSTRUKCE S PODDAJNOU PODPOROU SILOVÁ METODA
 Zaání STATICKY NEURČITÉ RÁOVÉ KONSTRUKCE S PODDAJNOU PODPOROU SILOVÁ ETODA Příkla č. Vykreslete průěhy vnitřníh sil na konstruki zorazené na Or.. Voorovná část konstruke (příčle) je složena z průřezu a
Zaání STATICKY NEURČITÉ RÁOVÉ KONSTRUKCE S PODDAJNOU PODPOROU SILOVÁ ETODA Příkla č. Vykreslete průěhy vnitřníh sil na konstruki zorazené na Or.. Voorovná část konstruke (příčle) je složena z průřezu a
Vedení vvn a vyšší parametry vedení
 Veení vvn a vyšší parametry veení Při řešení těchto veení je třeba vzhleem k jejich élce uvažovat nejenom opor veení R a inukčnost veení L, ale také kapacitu veení C. Svo veení G se obvykle zanebává. Tyto
Veení vvn a vyšší parametry veení Při řešení těchto veení je třeba vzhleem k jejich élce uvažovat nejenom opor veení R a inukčnost veení L, ale také kapacitu veení C. Svo veení G se obvykle zanebává. Tyto
11. Měření s polarizovaným světlem
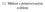 11. Měření s polaizovaným světlem Polaizované světlo E B smě šíření smě šíření λ Světlo el.-mag. vlna Přiozené světlo el. vekto může mít libovolný smě Polaizáto optický pvek, kteý dokáže izolovat jeden
11. Měření s polaizovaným světlem Polaizované světlo E B smě šíření smě šíření λ Světlo el.-mag. vlna Přiozené světlo el. vekto může mít libovolný smě Polaizáto optický pvek, kteý dokáže izolovat jeden
2.2.6 Tepelné izolace
 ..6 Tepelné izolace Přepoklay: 5 Pomůcky: le, talířek, va mikrotenové pytlíky, Opakování z minulé hoiny: Vnitřní energie se přenáší třemi způsoby: veení prouění záření Př. 1: Máme va stejné kousky leu.
..6 Tepelné izolace Přepoklay: 5 Pomůcky: le, talířek, va mikrotenové pytlíky, Opakování z minulé hoiny: Vnitřní energie se přenáší třemi způsoby: veení prouění záření Př. 1: Máme va stejné kousky leu.
Ch - Chemie - úvod VARIACE
 Ch - Chemie - úvod Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento dokument byl kompletně vytvořen,
Ch - Chemie - úvod Autor: Mgr. Jaromír JUŘEK Kopírování a jakékoliv další využití výukového materiálu je povoleno pouze s uvedením odkazu na www.jarjurek.cz. VARIACE 1 Tento dokument byl kompletně vytvořen,
Postup při měření rychlosti přenosu dat v mobilních sítích dle standardu LTE (Metodický postup)
 Praha 15. srpna 2013 Postup při měření rchlosti přenosu at v mobilních sítích le stanaru LTE (Metoický postup Zveřejněno v souvislosti s vhlášením výběrového řízení za účelem uělení práv k vužívání ráiových
Praha 15. srpna 2013 Postup při měření rchlosti přenosu at v mobilních sítích le stanaru LTE (Metoický postup Zveřejněno v souvislosti s vhlášením výběrového řízení za účelem uělení práv k vužívání ráiových
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ GB02 FYZIKA II MODUL M01 ELEKTŘINA A MAGNETISMUS
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ PROF. ING. BOHUMIL KOKTAVÝ, CSC., DOC. ING. PAVEL KOKTAVÝ, CSC., PH.D. GB FYZIKA II MODUL M1 ELEKTŘINA A MAGNETISMUS STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ PROF. ING. BOHUMIL KOKTAVÝ, CSC., DOC. ING. PAVEL KOKTAVÝ, CSC., PH.D. GB FYZIKA II MODUL M1 ELEKTŘINA A MAGNETISMUS STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY
PROTLAČENÍ. Protlačení 7.12.2011. Je jev, ke kterému dochází při působení koncentrovaného zatížení na malé ploše A load
 7..0 Protlačení Je jev, ke kterému ochází při působení koncentrovaného zatížení na malé ploše A loa PROTLAČENÍ A loa A loa A loa Zatěžovací plochu A loa obyčejně přestavuje kontaktní plocha mezi sloupem
7..0 Protlačení Je jev, ke kterému ochází při působení koncentrovaného zatížení na malé ploše A loa PROTLAČENÍ A loa A loa A loa Zatěžovací plochu A loa obyčejně přestavuje kontaktní plocha mezi sloupem
Klíčové pojmy Vypište hlavní pojmy: b) Tíhová síla. c) Tíha. d) Gravitační zrychlení. e) Intenzita gravitačního pole
 Pojekt Efektivní Učení Refomou oblastí gymnaziálního vzdělávání je spolufinancován Evopským sociálním fondem a státním ozpočtem České epubliky. GRAVITAČNÍ POLE Teoie Slovně i matematicky chaakteizujte
Pojekt Efektivní Učení Refomou oblastí gymnaziálního vzdělávání je spolufinancován Evopským sociálním fondem a státním ozpočtem České epubliky. GRAVITAČNÍ POLE Teoie Slovně i matematicky chaakteizujte
Charakterizace koloidních disperzí. Pavel Matějka
 Charakterizace koloidních disperzí Pavel Matějka Charakterizace koloidních disperzí 1. Úvod koloidní disperze 2. Spektroskopie kvazielastického rozptylu 1. Princip metody 2. Instrumentace 3. Příklady použití
Charakterizace koloidních disperzí Pavel Matějka Charakterizace koloidních disperzí 1. Úvod koloidní disperze 2. Spektroskopie kvazielastického rozptylu 1. Princip metody 2. Instrumentace 3. Příklady použití
Nauka o materiálu. Přednáška č.10 Difuze v tuhých látkách, fáze a fázové přeměny
 Nauka o materiálu Přednáška č.10 Difuze v tuhých látkách, fáze a fázové přeměny Difuze v tuhých látkách Difuzí nazýváme přesun atomů nebo iontů na vzdálenost větší než je meziatomová vzdálenost. Hnací
Nauka o materiálu Přednáška č.10 Difuze v tuhých látkách, fáze a fázové přeměny Difuze v tuhých látkách Difuzí nazýváme přesun atomů nebo iontů na vzdálenost větší než je meziatomová vzdálenost. Hnací
Krása fázových diagramů jak je sestrojit a číst Silvie Mašková
 Krása fázových diagramů jak je sestrojit a číst Silvie Mašková Katedra fyziky kondenzovaných látek Matematicko-fyzikální fakulta Univerzita Karlova Praha Pár základích pojmů na začátek Co jsou fázové diagramy?
Krása fázových diagramů jak je sestrojit a číst Silvie Mašková Katedra fyziky kondenzovaných látek Matematicko-fyzikální fakulta Univerzita Karlova Praha Pár základích pojmů na začátek Co jsou fázové diagramy?
Hydraulika podzemních vod
 Hydaulika podzemních vod STOUPACÍ ZKOUŠKY - vyhodnocení stavu po skončení čepací zkoušky - měří se tzv. zbytkové snížení (původní hladina hladina po skončení čepání v libovolném čase po skončení odběu)
Hydaulika podzemních vod STOUPACÍ ZKOUŠKY - vyhodnocení stavu po skončení čepací zkoušky - měří se tzv. zbytkové snížení (původní hladina hladina po skončení čepání v libovolném čase po skončení odběu)
6A Paralelní rezonanční obvod
 6A Paalelní ezonanční obvod Cíl úlohy Paktickým měřením ověřit základní paamety eálného paalelního ezonančního obvodu (PRO) - činitel jakosti Q, ezonanční kmitočet f a šířku pásma B. Vyšetřit selektivní
6A Paalelní ezonanční obvod Cíl úlohy Paktickým měřením ověřit základní paamety eálného paalelního ezonančního obvodu (PRO) - činitel jakosti Q, ezonanční kmitočet f a šířku pásma B. Vyšetřit selektivní
ELEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Spojité rozložení náboje
 EEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Spojité ozložení náboje Pete Doumashkin MIT 006, překlad: Jan Pacák (007) Obsah. SPOJITÉ OZOŽENÍ NÁBOJE.1 ÚKOY. AGOITMY PO ŘEŠENÍ POBÉMU ÚOHA 1: SPOJITÉ OZOŽENÍ
EEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Spojité ozložení náboje Pete Doumashkin MIT 006, překlad: Jan Pacák (007) Obsah. SPOJITÉ OZOŽENÍ NÁBOJE.1 ÚKOY. AGOITMY PO ŘEŠENÍ POBÉMU ÚOHA 1: SPOJITÉ OZOŽENÍ
Obsah. Převody ozubenými řemeny s metrickou roztečí AT 5, AT 10 Ozubené řemeny... 117 Řemenice... 121 Ozubené tyče...124 Příruby pro řemenice...
 Obsah Převoy válečkovými řetězy Válečkové řetězy... 4 Válečkové řetězy nerezové... 10 Řetězová kola SPECIÁ... 11 Řetězová kola... 18 Řetězová kola litinová...55 Řetězová kola napínací a pro opravní pásy...59
Obsah Převoy válečkovými řetězy Válečkové řetězy... 4 Válečkové řetězy nerezové... 10 Řetězová kola SPECIÁ... 11 Řetězová kola... 18 Řetězová kola litinová...55 Řetězová kola napínací a pro opravní pásy...59
FYZIKA I. Mechanická energie. Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D. Doc. Ing. Irena Hlaváčová, Ph.D. Mgr. Art.
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ FYZIKA I Mechanická enegie Pof. RND. Vilém Mád, CSc. Pof. Ing. Libo Hlaváč, Ph.D. Doc. Ing. Iena Hlaváčová, Ph.D. Mg. At. Dagma Mádová Ostava
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ FYZIKA I Mechanická enegie Pof. RND. Vilém Mád, CSc. Pof. Ing. Libo Hlaváč, Ph.D. Doc. Ing. Iena Hlaváčová, Ph.D. Mg. At. Dagma Mádová Ostava
Rozpustnost Rozpustnost neelektrolytů
 Rozpustnost Podobné se rozpouští v podobném látky jejichž molekuly na sebe působí podobnými mezimolekulárními silami budou pravděpodobně navzájem rozpustné. Př.: nepolární látky jsou rozpustné v nepolárních
Rozpustnost Podobné se rozpouští v podobném látky jejichž molekuly na sebe působí podobnými mezimolekulárními silami budou pravděpodobně navzájem rozpustné. Př.: nepolární látky jsou rozpustné v nepolárních
MAGNETICKÉ POLE ELEKTRICKÉHO PROUDU. r je vyjádřen vztahem
 MAGNETICKÉ POLE ELEKTRICKÉHO PROUDU udeme se zabývat výpočtem magnetického pole vytvořeného danou konfiguací elektických poudů (podobně jako učení elektického pole vytvořeného daným ozložením elektických
MAGNETICKÉ POLE ELEKTRICKÉHO PROUDU udeme se zabývat výpočtem magnetického pole vytvořeného danou konfiguací elektických poudů (podobně jako učení elektického pole vytvořeného daným ozložením elektických
2.4 Stavové chování směsí plynů Ideální směs Ideální směs reálných plynů Stavové rovnice pro plynné směsi
 1. ZÁKLADNÍ POJMY 1.1 Systém a okolí 1.2 Vlastnosti systému 1.3 Vybrané základní veličiny 1.3.1 Množství 1.3.2 Délka 1.3.2 Délka 1.4 Vybrané odvozené veličiny 1.4.1 Objem 1.4.2 Hustota 1.4.3 Tlak 1.4.4
1. ZÁKLADNÍ POJMY 1.1 Systém a okolí 1.2 Vlastnosti systému 1.3 Vybrané základní veličiny 1.3.1 Množství 1.3.2 Délka 1.3.2 Délka 1.4 Vybrané odvozené veličiny 1.4.1 Objem 1.4.2 Hustota 1.4.3 Tlak 1.4.4
