Matematické metody v kartografii
|
|
|
- Štěpán Matoušek
- před 6 lety
- Počet zobrazení:
Transkript
1 Mtetické etod krtorii Přednášk 4 5 Krtorická zkreslení. Délkoé zkreslení lošné zkreslení odínk konorit. Tissoto indiktri.
2 . Mtetická krtorie MK Zýá se: Mtetickýi eoetrickýi retr krtorických děl. Přeode údjů z jedné reerenční loch elisoid kole do drhé roin krtorického zorzení tj.. Většino zorzjee ze složitější loch n jednodšší elisoid -> roin. Oě loch jí různo křiost. Důsledke rozdílných křiostí ři zorzoání => znik deorcí oznčoných jko krtorická zkreslení. Mtetická krtorie: Stdje lstnosti zákonitosti krtorických zkreslení. Zýá se teorií krtorických zorzení.
3 . Krtorické zorzení Krtorické zorzení: Předis řiřzje od ležící n jedné reerenční loše oloh n drhé reerenční loše Odozeno teticko cesto. Eistje několik stoek krtorických zorzení. Krtorická rojekce: Vznik eoetricko cesto nř. roítání zridl roítání kole do roin. Zná již e stroěk nř. Ptoleioo zorzení Posán zorzocíi ronicei: Vlstnosti: Sořdnice oecně nkcí některých řídech nkcí jeno neo. Pól je lární od zhlede k zedené sostě kloých sořdnic k k z k : Fnkce ne žd sojité dierencotelné n interlech / / / / / / z LZ z k k k k k k 0 0
4 3. Krtorická ěřítk zkreslení =důsledek zorzení n loch s různýi křiosti. Měřítko s. zkreslení: Měřítko ředstje oěr dierenciálních délkoých neo lošných eleentů. Měřítko je ezrozěrné není řeočítáno n délkoo či lošno hodnot. Zkreslení kzje li ěřítk je řeočteno n délkoo či lošno hodnot. Zkreslení se dáá délkoých lošných či úhloých jednotkách. Měřítko: Měřítko délek: Měřítko loch: P Zkreslení: Délkoé zkreslení: - Úhloé zkreslení: Plošné zkreslení: P- říliš se neožíá
5 4. Délkoé zkreslení Měřítko délek : Poěr dierenciálních zdáleností orze oriinále. Bezrozěrné číslo. ds ds Hodnot : =+{0} se e ětšině řídů líží Zkreslení délek: Udáá li ěřítk n délkoo jednotk. Nejčstěji e tr: c/k d/k >0: Zorzení rodlžje délk <0: Zorzení zkrcje délk s Příkld: = = /k=-.5 c/k. Ekidistntní zorzení: Nezkreslje délk le oze rčité sěr nř. =. Neeistje zorzení které nezkreslolo šechn délk.
6 5. Plošné zkreslení Měřítko loch P Poěr dierenciálních lošných eleentů orze oriinál. Bezrozěrné. P e ětšině řídů >> P dp d Plošné zkreslení: Udáá li ěřítk loch n lošno jednotk Příliš čsto se neožíá. Ekilentní lochojené zorzení Nezkreslje loch. Požito ro olitické sět. Oecný zth ro ěřítko loch: ono sočin ěřítk délek oledník ronoěžce P r úhl ezi orze oledník ronoěžk odození iz dále.
7 6. Úhloé zkreslení Úhloé zkreslení ozdíl úhl ezi dě sosti křiek orze úhle jejich orzů. Nejčstěji se jdřje e stních. Konorní úhlojená zorzení Nezkresljí úhl =0. Požití eodézii elkých ěřítek. Prktick šechn zorzení ro eodézii konorní io Csi- Soldnero. Vzth ezi zkreslení délek úhlů loch: Konorní zorzení: iálně zkresljí loch. Ekilentní zorzení: iálně zkresljí úhl. Koenzční ronácí zorzení: zkresljí še le loch zkresljí éně než konorní zorzení úhl zkresljí éně než ekilentní zorzení.
8 7. Odození délkoého zkreslení /3 Z od P se osne do Q o délkoý eleent ds. To orze odoídá osn o ds.
9 7. Odození délkoého zkreslení /3 d d d d d d ds ds d d ds ds d d d d d d d d d d ds d ds d ds d ds d Pltí: Hodnot d d ředstjí totální dierenciál zorzocích ronic: Délkoé eleent orze oriinále ěřítko: Pltí: d d ]d [ ]d [ ds ds d d d d
10 8. Odození délkoého zkreslení 3/3 Dosdíe z d d Po úrě ýsledný zth ro ěřítko délek: Koeicient s rciálníi dericei nzýáe Gssoýi koeicient. ds ds ]ds [ ds ] [ ds
11 9. Délkoé zkreslení oledník ronoěžce Délkoé zkreslení je nkcí: Poloh od tj. zit Pro oledník ltí: =0 Vzorec se zjednodší dno některé člen. Měřítko délek oledník. Pro oledník ltí: =90 Vzorec se zjednodší oět dno některé člen. Měřítko délek ronoěžce r. r Hodnot eli důležité z nich lze ododit šechn dlší zkreslení lošná i úhloá!!!.
12 0. Podínk konorit / Doszení z r do ronice ro ěřítko délek získáe noý zth. r Z něj lze odit odínk konorit. Podínk konorit: Délkoé zkreslení nkcí oloh nikoli zit r 0 U konorních zorzení délkoé zkreslení nezáisí n zit. Pro ěřítko délek ltí: r
13 . Etréné délkoé zkreslení / Pokd se oloh od neění nekonorního zorzení je ěřítko délek oze nkcí zit. Hledáe ro který zit de ěřítko délek etréní iální neo iniální. Určíe jej rostřednictí derice odle : r 0 Po úrě: t r Ntno drho dericí oěřit zd se jedná o i či ini!!!
14 . Etréné délkoé zkreslení / D zit ro které hodnot délkoého zkreslení etréní: 90 -> jso n see kolé V zit je délkoé zkreslení nejětší je rono zit je délkoé zkreslení nejenší je rono in oř. nok. Hlní rsk Udájí etréní hodnot délkoého zkreslení: = = in zitech. Jediné dojice rků které nekonorních zorzení sírjí rý úhel orze i oriinále Pro konorní zorzení ltí: =
15 3. Výočet hlních rsků Lze je rčit z ronice ro ěřítko délek do které dosdíe hodnot Pltí: es.: in r r
16 4. Zkreslení zit Dán od PQ ležící n ortodroě. V oriinál zit ortodro. V orze zit orz ortodro sěrnice orz ortodro sěrnice orz oledník. Pltí: 80 80
17 5. Odození zthů Pltí: Dosdíe: Pk: Sěrnice orz oledník: Pro =0 Sěrnice orz ronoěžk: Pro =90 d d d d d d t t t t t t t t ds d ds d ds d ds d t t r t
18 6. Zkreslení úhl ezi oledníke ronoěžko Vjdee ze zth ro zkreslení zit ortodro nhrdíe ronoěžko. V oriinál úhel ezi oledníke ronoěžko =90. V orze úhel ezi orze oledník ronoěžk. Sěrník oledník sěrník ronoěžk r r r 80
19 7. Odození zth Princi odození odoný jko ředchozí řídě: Po doszení: t80 t t t r t80 t t d t r d t80 t80 r r t Ortoonální zorzení : Úhel ezi oledníke ronoěžko je roen 90. Všechn jednodchá zorzení + konorní zorzení jso ortoonálni.
20 8. Miální úhloé zkreslení Zkreslení úhl lze jádřit jko zkreslení sěr. Úhloé zkreslení je ted nkcí sěr.. Sořdnicoý ssté 0. Os e sěr hlních rsků. Sořdnicoý ssté orze 0.. tn tn tn d d d d d d d d
21 9. Miální úhloé zkreslení. tn tn 0. tn in tn rctn tn tn tn tn tn tn tn Ze rozdíl rentů: Pltí: Miální úhloé zkreslení:
22 0. Odození lošného zkreslení N séře dán sérický trojúhelník rčený trojicí rcholů: P Q. Zorzí se n trojúhelník P Q Vjdee ze zth ro lošné zkreslení: Pro krtorická zorzení ltí: Ekidistntní: = Konorní: = r =>P= * Ekilentní: * r = jednodché P dol dro doldro tn tn tn r
23 . Odození lošného zkreslení P P tn tn
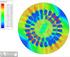
24 . Tissoto indiktri Délkoé zkreslení odě je nkcí zit ohje se interl < in >. Orze nekonečně lé kržnice je důsledk zkreslení elis. Oznčjee ji jko elis zkreslení neo Tissoto indiktri. Vlstnosti: Znázorňje růěh délkoého zkreslení záislosti n zit. U konorních zorzení je kržnicí délkoé zkreslení není nkcí zit Pretr nečárkoné oriinál čárkoné orze: elikost hlní edlejší oloos hlní rsk zit etréních délkoých zkreslení r sěr orz oledník ronoěžk od hlního rsk. t Vzth ezi zit jejich orz: t t t
25 3. Tissoto indiktri oriinále / orze
26 4. Ukázk Tissotoých indiktri zitálního ekidistntního zorzení Georická síť + Tissoto indiktri. Norální oloh. Interl eneroání indiktri <-7090>.
27 5. Měřítko nkcí oloh Měřítko M cí oloh. Poěr di. rleentů délk e sktečnosti ds k n ě ds. Hodnot ds oliněn zkreslení. M Měřítko krtorické: ds k ds Měřítko : ds ds ds dsk M ds M ds Proěnliá eličin ůže se ěnit o desítk/stok rocent. Dík zkreslení se sěre okrjů délk zkresljí zětšjí >. Pozor ři oděřoání zdáleností z!!!
28 6. Měřítko jko nkce oloh M sět M : Merctor-Snson Okrje M : !
29 7. Krtorická zkreslení záěr Krtorická zkreslení záisí n: T krtorického zorzení. Poloze zorzocí loch. Tr zorzoného úzeí. Vzdálenosti od od zákldního oledník či nezkreslené ronoěžk. Krtorická zkreslení níání : Korektní izální je Zkreslení délek loch úhlů do 8%. Vizální oronání do Zkreslení délek loch úhlů do 3%. Krtoetrická nlýz Zkreslení délek loch úhlů do 0.5%.
Analytická geometrie v rovině
 nltická geometrie roině Zč je toho loket (ořnice) ) [ ], [ 7], [ ], [ 5] ; b) = 7 j, = j, = 4 j, = 8 j, = j R M P 9 8 7 6 5 4 ) L[ 7], M[ ] ; b) Q[ ], R[ 5] 9 8 7 6 5 4 4 5 6 7 [ 5], [, 5], [ ] Q 9 5 c),
nltická geometrie roině Zč je toho loket (ořnice) ) [ ], [ 7], [ ], [ 5] ; b) = 7 j, = j, = 4 j, = 8 j, = j R M P 9 8 7 6 5 4 ) L[ 7], M[ ] ; b) Q[ ], R[ 5] 9 8 7 6 5 4 4 5 6 7 [ 5], [, 5], [ ] Q 9 5 c),
Kuželosečky. ( a 0 i b 0 ) a Na obrázku 1 je zakreslena elipsa o poloosách 3 a 7. Pokud střed elipsy se posunul do bodu S x 0
 Generted b Foit PDF Cretor Foit Softwre http://www.foitsoftwre.com For elution onl. Kuželosečk I. Kuželosečk zákldních polohách posunuté to prtie je opkoání látk obkle probírné n střední škole. Kružnice
Generted b Foit PDF Cretor Foit Softwre http://www.foitsoftwre.com For elution onl. Kuželosečk I. Kuželosečk zákldních polohách posunuté to prtie je opkoání látk obkle probírné n střední škole. Kružnice
DUM č. 14 v sadě. Ma-2 Příprava k maturitě a PZ geometrie, analytická geometrie, analýza, komlexní čísla
 rojek GML Brno Docen DUM č. 4 dě M- Přír k mriě PZ geomerie, nlická geomerie, nlý, komlení číl 4. or Mgd Krejčoá Dm.08.0 očník mriní ročník noce DUM nlická geomerie roor - d úloh ýledk. Meriál jo rčen
rojek GML Brno Docen DUM č. 4 dě M- Přír k mriě PZ geomerie, nlická geomerie, nlý, komlení číl 4. or Mgd Krejčoá Dm.08.0 očník mriní ročník noce DUM nlická geomerie roor - d úloh ýledk. Meriál jo rčen
7.2.10 Skalární součin IV
 7.2.10 Sklární sočin IV Předpokld: 7209 Pedgogiká poznámk: Tto hodin je kontet čebnie zláštní. Obshje d důkz jeden příkld z klsiké čebnie. Všehn tři zdání jso znčně obtížná ždjí nápd, proto je řeším normálně
7.2.10 Sklární sočin IV Předpokld: 7209 Pedgogiká poznámk: Tto hodin je kontet čebnie zláštní. Obshje d důkz jeden příkld z klsiké čebnie. Všehn tři zdání jso znčně obtížná ždjí nápd, proto je řeším normálně
FYZIKA I. Rovnoměrný, rovnoměrně zrychlený a nerovnoměrně zrychlený translační pohyb
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ FYZIKA I Ronoměrný, ronoměrně zrychlený neronoměrně zrychlený trnslční pohyb Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hláč, Ph.D. Doc.
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ FYZIKA I Ronoměrný, ronoměrně zrychlený neronoměrně zrychlený trnslční pohyb Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hláč, Ph.D. Doc.
5.4.2 Objemy a povrchy mnohostěnů I
 5.. Objemy orchy mnohostěnů I Předokldy: 51 Význm slo objem i orch je intuitině jsný. Mtemtická definice musí být oněkud řesnější. Okoání z lnimetrie: Obsh obrzce je kldné číslo, řiřzené obrzci tk, že
5.. Objemy orchy mnohostěnů I Předokldy: 51 Význm slo objem i orch je intuitině jsný. Mtemtická definice musí být oněkud řesnější. Okoání z lnimetrie: Obsh obrzce je kldné číslo, řiřzené obrzci tk, že
V = π f 2 (x) dx. f(x) 1 + f 2 (x) dx. x 2 + y 2 = r 2
 Odození zorců pro ýpočet objemů porchů některých těles užitím integrálního počtu Objem rotčního těles, které znikne rotcí funkce y f(x) n interlu, b kolem osy x, lze spočítt podle zorce b V f (x) dx Porch
Odození zorců pro ýpočet objemů porchů některých těles užitím integrálního počtu Objem rotčního těles, které znikne rotcí funkce y f(x) n interlu, b kolem osy x, lze spočítt podle zorce b V f (x) dx Porch
7.2.3 Násobení vektoru číslem I
 7..3 Násobení ektor číslem I Předpoklad: 70 Př. : Zakresli do sosta sořadnic alespoň dě různá místění ektorů: = 3; = 3;0 = ; a) ( ) ( ) c) ( ) - - - x - Pedagogická poznámka: Předchozí příklad není zbtečný.
7..3 Násobení ektor číslem I Předpoklad: 70 Př. : Zakresli do sosta sořadnic alespoň dě různá místění ektorů: = 3; = 3;0 = ; a) ( ) ( ) c) ( ) - - - x - Pedagogická poznámka: Předchozí příklad není zbtečný.
( ) 7.3.3 Vzájemná poloha parametricky vyjádřených přímek I. Předpoklady: 7302
 7.. Vzájemná oloha aramericky yjádřených římek I Předoklady: 70 Pedagogická oznámka: Tao hodina neobsahje říliš mnoho říkladů. Pos elké čási sdenů je oměrně omalý a časo nesihno sočía ani obsah éo hodiny.
7.. Vzájemná oloha aramericky yjádřených římek I Předoklady: 70 Pedagogická oznámka: Tao hodina neobsahje říliš mnoho říkladů. Pos elké čási sdenů je oměrně omalý a časo nesihno sočía ani obsah éo hodiny.
Obsahy - opakování
 .7.0 Obshy - opkoání Předpokldy: 00709 Př. : Vypiš edle sebe zorce pro obsh ronoběžníku, trojúhelníku lichoběžníku. Kždý e šech rintách. Ke kždému zorci nkresli obrázek s yznčenými rozměry, které e zorci
.7.0 Obshy - opkoání Předpokldy: 00709 Př. : Vypiš edle sebe zorce pro obsh ronoběžníku, trojúhelníku lichoběžníku. Kždý e šech rintách. Ke kždému zorci nkresli obrázek s yznčenými rozměry, které e zorci
3.2.7 Příklady řešené pomocí vět pro trojúhelníky
 ..7 Příkldy řešené pomocí ět pro trojúhelníky Předpokldy:, 6 Pedgogická poznámk: U následujících příkldů ( u mnoh dlších příkldů z geometrie) pltí, že nedílnou součástí řešení je nápd (který se tké nemusí
..7 Příkldy řešené pomocí ět pro trojúhelníky Předpokldy:, 6 Pedgogická poznámk: U následujících příkldů ( u mnoh dlších příkldů z geometrie) pltí, že nedílnou součástí řešení je nápd (který se tké nemusí
POVRCH A OBJEM HRANOLU A JEHLANU
 Projekt ŠABLONY NA GM Gymnázim elké Meziříčí registrční číslo rojekt: CZ..07/.5.00/.098 I- Inoce zklitnění ýky směřjící k rozoji mtemtické grmotnosti žáků středních škol PORCH A OBJEM HRANOLU A JEHLANU
Projekt ŠABLONY NA GM Gymnázim elké Meziříčí registrční číslo rojekt: CZ..07/.5.00/.098 I- Inoce zklitnění ýky směřjící k rozoji mtemtické grmotnosti žáků středních škol PORCH A OBJEM HRANOLU A JEHLANU
3. Kvadratické rovnice
 CZ..07/..08/0.0009. Kvdrtické rovnice se v tetice oznčuje lgebrická rovnice druhého stupně, tzn. rovnice o jedné neznáé, ve které neznáá vystupuje ve druhé ocnině (²). V zákldní tvru vypdá následovně:
CZ..07/..08/0.0009. Kvdrtické rovnice se v tetice oznčuje lgebrická rovnice druhého stupně, tzn. rovnice o jedné neznáé, ve které neznáá vystupuje ve druhé ocnině (²). V zákldní tvru vypdá následovně:
Smíšený součin
 7..14 Smíšený součin Předpokldy: 713 Je dán ronoěžnostěn LMNOPR. R O P N M L Jeho ojem umíme spočítt stereometrikým zorem: V = S. p Ronoěžnostěn je tké určen třemi ektory, : R O P N M L jeho ojem musí
7..14 Smíšený součin Předpokldy: 713 Je dán ronoěžnostěn LMNOPR. R O P N M L Jeho ojem umíme spočítt stereometrikým zorem: V = S. p Ronoěžnostěn je tké určen třemi ektory, : R O P N M L jeho ojem musí
DUM č. 10 v sadě. Ma-2 Příprava k maturitě a PZ geometrie, analytická geometrie, analýza, komlexní čísla
 projekt GML Brno Docens DUM č. 10 sadě Ma- Přípraa k matritě a PZ geometrie, analytická geometrie, analýza, komlexní čísla 14. Ator: Magda Krejčoá Datm: 1.08.01 Ročník: matritní ročníky Anotace DUM: Analytická
projekt GML Brno Docens DUM č. 10 sadě Ma- Přípraa k matritě a PZ geometrie, analytická geometrie, analýza, komlexní čísla 14. Ator: Magda Krejčoá Datm: 1.08.01 Ročník: matritní ročníky Anotace DUM: Analytická
cos cos φ ω Převod mechanismu Aplikovaná mechanika, 9. přednáška analytické řešení mechanismu s pravoúhlou kulisou ω, ε φ převod derivace převodu
 Přeod mechnismu nlytické řešení mechnismu s oúhlou kulisou, ε, y y sin y& & cos && y && cos & & && ε cos y& && y ε cos mechnismus s oměnným řeodem ( ) likoná mechnik, 9. řednášk f řeod sin sin deice řeodu
Přeod mechnismu nlytické řešení mechnismu s oúhlou kulisou, ε, y y sin y& & cos && y && cos & & && ε cos y& && y ε cos mechnismus s oměnným řeodem ( ) likoná mechnik, 9. řednášk f řeod sin sin deice řeodu
 Í ž š Ě Í š Ď Ť Í Ó ú ž š Ť š ž ž Ť Ť ž ž Ď Ď š š š š Ť ž ž š ž ň ž Ť š Ť ž š š š Ť ž ž ň š ž ž ž š ž ú ň š Ť Ť Ť Ť ž Í Ť ž ň ž š Ť Ť š š ž ň ž ň Ť ž š ž ž ž ž Ť Ť Í ž Š Í Í Ě Í Ř É É Í Ě ž ž ň š Ž ž ž
Í ž š Ě Í š Ď Ť Í Ó ú ž š Ť š ž ž Ť Ť ž ž Ď Ď š š š š Ť ž ž š ž ň ž Ť š Ť ž š š š Ť ž ž ň š ž ž ž š ž ú ň š Ť Ť Ť Ť ž Í Ť ž ň ž š Ť Ť š š ž ň ž ň Ť ž š ž ž ž ž Ť Ť Í ž Š Í Í Ě Í Ř É É Í Ě ž ž ň š Ž ž ž
Řízení pohybu manipulátoru
 Martin Sábl, Kail Všten, Radek Sekal České soké čení technické Praze, Faklta elektrotechnická ABSTRAKT V sočasné době á inteligentní robotika sé nezastpitelné ísto noha odětích průsl, edicín či ěd. Inteligentní
Martin Sábl, Kail Všten, Radek Sekal České soké čení technické Praze, Faklta elektrotechnická ABSTRAKT V sočasné době á inteligentní robotika sé nezastpitelné ísto noha odětích průsl, edicín či ěd. Inteligentní
Metoda datových obalů DEA
 Metoda datoých obalů DEA Model datoých obalů složí ro hodoceí techické efektiit rodkčích jedotek ssté a základě elosti stů a ýstů. Protože stů a ýstů ůže být íce drhů, řadí se DEA ezi etod icekriteriálího
Metoda datoých obalů DEA Model datoých obalů složí ro hodoceí techické efektiit rodkčích jedotek ssté a základě elosti stů a ýstů. Protože stů a ýstů ůže být íce drhů, řadí se DEA ezi etod icekriteriálího
3.2.5 Pythagorova věta, Euklidovy věty I. α = = Předpoklady: 1107, 3204
 3..5 ythgoro ět, Euklidoy ěty I ředpokldy: 1107, 304 roúhlý trojúhelník = trojúhelník s nitřním úhlem 90 (s prým nitřním úhlem) prý úhel je z nitřníh úhlů nejětší (zýjíí d musí dát dohromdy tké 90 ) strn
3..5 ythgoro ět, Euklidoy ěty I ředpokldy: 1107, 304 roúhlý trojúhelník = trojúhelník s nitřním úhlem 90 (s prým nitřním úhlem) prý úhel je z nitřníh úhlů nejětší (zýjíí d musí dát dohromdy tké 90 ) strn
KINETICKÁ TEORIE PLYNŮ
 KIETICKÁ TEOIE PLYŮ. Cíl a řdoklady - snaží s ysětlit akroskoické choání lynů na základě choání jdnotliých olkul (jjich rychlostí, očtu nárazů na stěnu nádoby, srážk s ostatníi olkulai). Tato tori br úahu
KIETICKÁ TEOIE PLYŮ. Cíl a řdoklady - snaží s ysětlit akroskoické choání lynů na základě choání jdnotliých olkul (jjich rychlostí, očtu nárazů na stěnu nádoby, srážk s ostatníi olkulai). Tato tori br úahu
 ž ž íú ž í í í í ří í í ó ří ů Ž í í í ří ží ž ž ů ů ří í ž ž í í ů ř ž ž ž íú ž í í í ří í í í ó ří ů ž ů í í í ř ž ž ů ů ří ž ží í í ů Ř ř í í Ť ř í í ří Č Ž ř Ť ů í Ž ří í ů ž ří ří ž í ř ů ď í ž ť
ž ž íú ž í í í í ří í í ó ří ů Ž í í í ří ží ž ž ů ů ří í ž ž í í ů ř ž ž ž íú ž í í í ří í í í ó ří ů ž ů í í í ř ž ž ů ů ří ž ží í í ů Ř ř í í Ť ř í í ří Č Ž ř Ť ů í Ž ří í ů ž ří ří ž í ř ů ď í ž ť
 č É Á Á Í š Ě š š Á ú ř í ř í í č ě ě í ě š č é í í ž ě é Í ůž í ě í ší í ě é ě í š Ř š é š ě é í Č ť í Ý ř í č š ď í Č í í š ř ě í é Á í ě ě č ě ě ž ž í Š Í ě ě š ě é ů é ž é é ž ž ů š ě ů é ž č í ž ě
č É Á Á Í š Ě š š Á ú ř í ř í í č ě ě í ě š č é í í ž ě é Í ůž í ě í ší í ě é ě í š Ř š é š ě é í Č ť í Ý ř í č š ď í Č í í š ř ě í é Á í ě ě č ě ě ž ž í Š Í ě ě š ě é ů é ž é é ž ž ů š ě ů é ž č í ž ě
3.3. Operace s vektory. Definice
 Operace s ektory.. Operace s ektory Výklad Definice... Nechť ϕ je úhel do nenloých ektorů, (obr. ). Skalárním sočinem ektorů, rozmíme číslo, které bdeme označoat. (někdy strčně ) a které definjeme roností.
Operace s ektory.. Operace s ektory Výklad Definice... Nechť ϕ je úhel do nenloých ektorů, (obr. ). Skalárním sočinem ektorů, rozmíme číslo, které bdeme označoat. (někdy strčně ) a které definjeme roností.
 Ž ň ů ň ů ů Í Ň Č Á ů ů ů ň Ž Ž Ž ň ň ň Ž ů Í Š Ž ů ó ů ď ů ů ň ď ů ň ň Í ď Í ů Ž Í Í Ž ň ů ů ů ů Í ň Á Íť ň ů ň Ž ů ť ň Ó Ó ň ů ň ň Í ň Í ň ů ů ň ň Ž ň ň ĚŽÍ Í Í Ž Ž Í ó Ž Š ď Š Č Ž Ž Ž Ž ó Ž Ž ÍŽ ď ď
Ž ň ů ň ů ů Í Ň Č Á ů ů ů ň Ž Ž Ž ň ň ň Ž ů Í Š Ž ů ó ů ď ů ů ň ď ů ň ň Í ď Í ů Ž Í Í Ž ň ů ů ů ů Í ň Á Íť ň ů ň Ž ů ť ň Ó Ó ň ů ň ň Í ň Í ň ů ů ň ň Ž ň ň ĚŽÍ Í Í Ž Ž Í ó Ž Š ď Š Č Ž Ž Ž Ž ó Ž Ž ÍŽ ď ď
Základní příklady. 18) Určete velikost úhlu δ, jestliže velikost úhlu α je 27.
 Zákldní příkld 1) Stín věže je dlouhý 55 m stín tče vsoké 1,5 m má v tutéž dou délku 150 cm. Vpočtěte výšku věže. ) Určete měřítko mp, jestliže odélníkové pole o rozměrech 600 m 450 m je n mpě zkresleno
Zákldní příkld 1) Stín věže je dlouhý 55 m stín tče vsoké 1,5 m má v tutéž dou délku 150 cm. Vpočtěte výšku věže. ) Určete měřítko mp, jestliže odélníkové pole o rozměrech 600 m 450 m je n mpě zkresleno
P Y T H A G O R O V A V T A V P R O S T O R U (2 hodiny)
 P Y T H A G O R O V A V T A V P R O T O R U hodiny V této ýkoé hodin si zksíš nkolik málo úloh n žití Pythgoroy ty tlesech. Doosd znáš dobe oze tto tles kádr, krychle jso to lstn tyboké hrnoly, trojboký
P Y T H A G O R O V A V T A V P R O T O R U hodiny V této ýkoé hodin si zksíš nkolik málo úloh n žití Pythgoroy ty tlesech. Doosd znáš dobe oze tto tles kádr, krychle jso to lstn tyboké hrnoly, trojboký
7. SEMINÁŘ Z MECHANIKY
 - 4-7 SEINÁŘ Z ECHANIKY 4 7 Prázdný železniční agón o hotnosti kgse pohbuje rchlostí,9 s po 4 odoroné trati a srazí se s naložený agóne o hotnosti kgstojící klidu s uolněnýi brzdai Jsou-li oba oz při nárazu
- 4-7 SEINÁŘ Z ECHANIKY 4 7 Prázdný železniční agón o hotnosti kgse pohbuje rchlostí,9 s po 4 odoroné trati a srazí se s naložený agóne o hotnosti kgstojící klidu s uolněnýi brzdai Jsou-li oba oz při nárazu
č é č ř č
 Á č ř č Á Á Ň Á č é č ř č Á Ů Ě Í Ý Ř Í Ě É Á Č Ň Í Í Š Á Í Á Ů Ž ČÁ Č ÉÚ Á Í Á Ů É Á Í Ž É Ř ý š ž ř é š ř é ř č é ř é Č é ě ý é ý ú ě š é ý ř é Á ý č ů ú č ř ě ó Á ú č ě ě ů ý ú ů š č é Á ř č ě ř ý č
Á č ř č Á Á Ň Á č é č ř č Á Ů Ě Í Ý Ř Í Ě É Á Č Ň Í Í Š Á Í Á Ů Ž ČÁ Č ÉÚ Á Í Á Ů É Á Í Ž É Ř ý š ž ř é š ř é ř č é ř é Č é ě ý é ý ú ě š é ý ř é Á ý č ů ú č ř ě ó Á ú č ě ě ů ý ú ů š č é Á ř č ě ř ý č
 Ě Ý Í Č í ří í Ř ř ř ří é í í í Ž ř é ř é č ů í é é ž č é č é ž í ů é č í é é ž í í Ž Ž é ú í ř é é Íí ř ů é ž č ů ú í ů ů ú é í í č í í é ř é ů ů í é ř é í ů ž í Í é Í Ř ř ů ř ů ž í é í č í č í í ří í
Ě Ý Í Č í ří í Ř ř ř ří é í í í Ž ř é ř é č ů í é é ž č é č é ž í ů é č í é é ž í í Ž Ž é ú í ř é é Íí ř ů é ž č ů ú í ů ů ú é í í č í í é ř é ů ů í é ř é í ů ž í Í é Í Ř ř ů ř ů ž í é í č í č í í ří í
DOPLŇKOVÉ TEXTY BB01 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ TUHÉ TĚLESO
 DOPLŇKOÉ TXTY BB0 PAL SCHAUR INTRNÍ MATRIÁL FAST UT BRNĚ TUHÉ TĚLSO Tuhé těleso je těleso, o teé latí, že libovolná síla ůsobící na těleso nezůsobí jeho defoaci, ale ůže ít ouze ohybový účine. Libovolná
DOPLŇKOÉ TXTY BB0 PAL SCHAUR INTRNÍ MATRIÁL FAST UT BRNĚ TUHÉ TĚLSO Tuhé těleso je těleso, o teé latí, že libovolná síla ůsobící na těleso nezůsobí jeho defoaci, ale ůže ít ouze ohybový účine. Libovolná
Cvičení č. 2 NÁVRH TEPLOVODNÍHO PODLAHOVÉHO VYTÁPĚNÍ
 SÁLAVÉ A PRŮMYSLOVÉ VYTÁPĚNÍ Cvičení č NÁVRH TEPLOVODNÍHO PODLAHOVÉHO VYTÁPĚNÍ Ing Jindřich Boháč JindrichBohac@fscvtcz +40-435-488 ístnost B1 807 1 Sálavé vytápění = PŘEVÁŽNĚ sálavé vytápění ROZDĚLENÍ
SÁLAVÉ A PRŮMYSLOVÉ VYTÁPĚNÍ Cvičení č NÁVRH TEPLOVODNÍHO PODLAHOVÉHO VYTÁPĚNÍ Ing Jindřich Boháč JindrichBohac@fscvtcz +40-435-488 ístnost B1 807 1 Sálavé vytápění = PŘEVÁŽNĚ sálavé vytápění ROZDĚLENÍ
OBJEMY A POVRCHY TĚLES
 OBJEMY A POVRCHY TĚLES Metodický mteiál do semináře MA SDM Růžen Blžkoá, Ien Budínoá KOMOLÝ JEHLAN Ojem komolého jehlnu Po zjednodušení ododíme zthy po komolý jehln, jehož podstmi jsou čtece. Oznčení:
OBJEMY A POVRCHY TĚLES Metodický mteiál do semináře MA SDM Růžen Blžkoá, Ien Budínoá KOMOLÝ JEHLAN Ojem komolého jehlnu Po zjednodušení ododíme zthy po komolý jehln, jehož podstmi jsou čtece. Oznčení:
 č š š ř ř Í ů č Ě Á Š ŠÁ Ř Ď É Í Ě Í Í čí ž ě č é č ě ý Ž ř ě č ý ě ý ý ř ě š ý ě ť ý é é ě ě é ě é ř é ř Ť ě š ě ž ě é ě é é ů ě é ř ú ý ý é ěř ý ý š ý ý ž é é š ý š ě ý ř ř ř ě š ý ě ý ý ř ě é Ž é é
č š š ř ř Í ů č Ě Á Š ŠÁ Ř Ď É Í Ě Í Í čí ž ě č é č ě ý Ž ř ě č ý ě ý ý ř ě š ý ě ť ý é é ě ě é ě é ř é ř Ť ě š ě ž ě é ě é é ů ě é ř ú ý ý é ěř ý ý š ý ý ž é é š ý š ě ý ř ř ř ě š ý ě ý ý ř ě é Ž é é
É č Ř ů ý ť Ň ť É ť ď ňó ř ř ó ř ř ý ó ř č ó řý ď č ů č ý ř ř ř ň ř č ř ř ř č ť ř ř ď č ř ř ř É Ý ó Ě č Ý ů ý č ó Ř ď š ý ý ý ř ý č Ň č ý ý Ú ť ř ý ů
 č ó Ě č Ý č ý Ú č č ů č š ó ó š ť Ř ň ť Í ř č č ř ů č ý ť č Ť Í č ť č ů č č ů ó Ťř ý ř ť ř ý ý ř ň ř Ž Í ďš č ů ý Ý ř ť É řě ó ň Ě ň ň č Ě č ý ů š č č č ý ň č É č Ř ů ý ť Ň ť É ť ď ňó ř ř ó ř ř ý ó ř č
č ó Ě č Ý č ý Ú č č ů č š ó ó š ť Ř ň ť Í ř č č ř ů č ý ť č Ť Í č ť č ů č č ů ó Ťř ý ř ť ř ý ý ř ň ř Ž Í ďš č ů ý Ý ř ť É řě ó ň Ě ň ň č Ě č ý ů š č č č ý ň č É č Ř ů ý ť Ň ť É ť ď ňó ř ř ó ř ř ý ó ř č
 é á í ů ů ů ů ž š áž š í ě ě ěž Ž ěž é ě č ě Ří í ří ý á ď ě Í Ý ó í řá á í é í é é ň č č á ň í é ý á ř ě č á ě š ř á é ďá ř ř á ý š á í ý ří ý Ž ď ř ě ý ů ží ě ú ě ú ů ř í Íá í í ú é í š ř ě ř ě á ř úř
é á í ů ů ů ů ž š áž š í ě ě ěž Ž ěž é ě č ě Ří í ří ý á ď ě Í Ý ó í řá á í é í é é ň č č á ň í é ý á ř ě č á ě š ř á é ďá ř ř á ý š á í ý ří ý Ž ď ř ě ý ů ží ě ú ě ú ů ř í Íá í í ú é í š ř ě ř ě á ř úř
í é é á š ě í ý ž ď í é žřá čí ř é č í čí á ř á čí é á á á ž ď ř ú ě á í ý ž á ř š í ž ě á š ř ý ř á č í ř á ď ě á á í ě í á ďí é ď ř í č ř ž ř á é č
 ť ď ě ý Ž ý Ž ě ř šá ú é ě é žč ě á ó ž á ě č ď ě ž ří šě í á Ž é á ě č é é ě ě é ě ě ž žě ě řě ě ý á í ě ď ě á ž é á ě ý č ě áú ě á ýž ě ý ú í á ž č ř á ěž ěžš ž ó ě é á ř ě ř ě ž ě á ý í ý š ší á ě ší
ť ď ě ý Ž ý Ž ě ř šá ú é ě é žč ě á ó ž á ě č ď ě ž ří šě í á Ž é á ě č é é ě ě é ě ě ž žě ě řě ě ý á í ě ď ě á ž é á ě ý č ě áú ě á ýž ě ý ú í á ž č ř á ěž ěžš ž ó ě é á ř ě ř ě ž ě á ý í ý š ší á ě ší
Digitální učební materiál
 Digitální učení mteriál Projekt: Digitální učení mteriály e škole registrční číslo projektu CZ.1.07/1..00/4.07 Příjeme: Střední zdrotniká škol Vyšší odorná škol zdrotniká Huso 71 60 České Budějoie Náze
Digitální učení mteriál Projekt: Digitální učení mteriály e škole registrční číslo projektu CZ.1.07/1..00/4.07 Příjeme: Střední zdrotniká škol Vyšší odorná škol zdrotniká Huso 71 60 České Budějoie Náze
KVADRATICKÁ FUNKCE (vlastnosti, grafy)
 KVADRATICKÁ FUNKCE (vlstnosti, gr) Teorie Kvdrtikou unkí se nzývá kždá unke dná předpisem ; R,, R; D( ) je proměnná z příslušného deiničního ooru unke (nejčstěji množin R),, jsou koeiient kvdrtiké unke,
KVADRATICKÁ FUNKCE (vlstnosti, gr) Teorie Kvdrtikou unkí se nzývá kždá unke dná předpisem ; R,, R; D( ) je proměnná z příslušného deiničního ooru unke (nejčstěji množin R),, jsou koeiient kvdrtiké unke,
Teoretický souhrn k 2. až 4. cvičení
 SYSTÉMOVÁ ANALÝZA A MODELOVÁNÍ Teoretcký souhrn k 2. ž 4. cvčení ZS 2009 / 200 . Vyezení zákldních poů.. Systé e Systé e účelově defnovná nožn prvků vze ez n, která spolu se svý vstupy výstupy vykzue ko
SYSTÉMOVÁ ANALÝZA A MODELOVÁNÍ Teoretcký souhrn k 2. ž 4. cvčení ZS 2009 / 200 . Vyezení zákldních poů.. Systé e Systé e účelově defnovná nožn prvků vze ez n, která spolu se svý vstupy výstupy vykzue ko
1.6.7 Složitější typy vrhů
 .6.7 Složitější tp rhů Předpoklad: 66 Pedaoická poznámka: Tato hodina přesahuje běžnou látku, probírám ji pouze případě, že mám přebtek času. Za normálních podmínek není příliš reálné s ětšinou tříd řešit
.6.7 Složitější tp rhů Předpoklad: 66 Pedaoická poznámka: Tato hodina přesahuje běžnou látku, probírám ji pouze případě, že mám přebtek času. Za normálních podmínek není příliš reálné s ětšinou tříd řešit
ň ř š ó ý é í ří í ú ů í ř š í ěř é Š ó ř í ó ó í ó í í ú ů ě ř ň ř š í ěř ó ěř í ú ů ř í ří ř ú í í ó í ó í í í ě ě í ó ě í č ě š í ó ř í á í í ó í ž
 šší á š á ř í š á Ú í ří ě á ě š í ú ůč ů ě š í ě ů ří ě ší ř á ó í í Ú í á ó í ž ó í á ó í ž í šíř í ó ó í í Ú Ů ě ěž ě é š í ě ů ří ě ší ř ó ó í í ú ě ó ó š ě š ě ó ó ší é í š ý á í í ó í é ó é ě á á
šší á š á ř í š á Ú í ří ě á ě š í ú ůč ů ě š í ě ů ří ě ší ř á ó í í Ú í á ó í ž ó í á ó í ž í šíř í ó ó í í Ú Ů ě ěž ě é š í ě ů ří ě ší ř ó ó í í ú ě ó ó š ě š ě ó ó ší é í š ý á í í ó í é ó é ě á á
Automaty a gramatiky. Organizační záležitosti. Přednáška: na webu (http://ktiml.mff.cuni.cz/~bartak/automaty) Proč chodit na přednášku?
 Orgnizční záležitosti Atomty grmtiky Romn Brták, KTIML rtk@ktiml.mff.cni.cz http://ktiml.mff.cni.cz/~rtk Přednášk: n we (http://ktiml.mff.cni.cz/~rtk/tomty) Proč chodit n přednášk? dozvíte se více než
Orgnizční záležitosti Atomty grmtiky Romn Brták, KTIML rtk@ktiml.mff.cni.cz http://ktiml.mff.cni.cz/~rtk Přednášk: n we (http://ktiml.mff.cni.cz/~rtk/tomty) Proč chodit n přednášk? dozvíte se více než
5.2.9 Vzdálenost bodu od roviny
 5..9 zdálenost bodu od roiny ředpokldy: 508 Opkoání z minulé hodiny (definice zdálenosti bodu od přímky): Je dán přímk p bod. zdáleností bodu od přímky p rozumíme zdálenost bodu od bodu, který je ptou
5..9 zdálenost bodu od roiny ředpokldy: 508 Opkoání z minulé hodiny (definice zdálenosti bodu od přímky): Je dán přímk p bod. zdáleností bodu od přímky p rozumíme zdálenost bodu od bodu, který je ptou
Pružnost a plasticita II
 Pružnost plsticit II. ročník klářského studi doc. In. Mrtin Krejs, Ph.D. Ktedr stvení mechnik Řešení nosných stěn pomocí Airho funkce npětí inverzní metod Stěnová rovnice ΔΔ(, ) Stěnová rovnice, nzývná
Pružnost plsticit II. ročník klářského studi doc. In. Mrtin Krejs, Ph.D. Ktedr stvení mechnik Řešení nosných stěn pomocí Airho funkce npětí inverzní metod Stěnová rovnice ΔΔ(, ) Stěnová rovnice, nzývná
2.7.9 Obsah lichoběžníku
 79 Osh lihoěžníku Předpokldy: 00708 Př : Trojúhelník A má osh jednotek Urči oshy trojúhelníků A n ) A ) A ) A Vzore pro osh trojúhelníku: S = osh trojúhelníku se změní, pokud se změní uď strn neo k ní
79 Osh lihoěžníku Předpokldy: 00708 Př : Trojúhelník A má osh jednotek Urči oshy trojúhelníků A n ) A ) A ) A Vzore pro osh trojúhelníku: S = osh trojúhelníku se změní, pokud se změní uď strn neo k ní
Kinematika hmotného bodu
 DOPLŇKOVÉ TEXTY BB1 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ Kinemik hmoného bodu Obsh Klsická mechnik... Vzžný sysém... Polohoý ekor... Trjekorie... Prmerické ronice rjekorie... 3 Příkld 1... 3
DOPLŇKOVÉ TEXTY BB1 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ Kinemik hmoného bodu Obsh Klsická mechnik... Vzžný sysém... Polohoý ekor... Trjekorie... Prmerické ronice rjekorie... 3 Příkld 1... 3
ě č ě ě é é é á á í ří ě ó ě ý Ó ř čá š á Í ó ž í ěš é íď á ž ý š š Š é ř áž í í í ř é á á é Í ď ý ď ž ř óř Í Č ý Ú ě á Ž í í Ž Ó ó ě ě Í ě ž ýď Ž ý č
 č é é é í ří ó ý Ó ř č š Í ó ž í š é íď ž ý š š Š é ř Ž í í í ř é é Í ď ý ď ž ř óř Í Č ý Ú Ž í í Ž Ó ó Í ž ýď Ž ý č í ří Ú č é ř Á Í É ď é ý š Í ý Ž ž Ď Í é ý Í ý ť Ž ř ů č ř Á ž í é Š č š í Ú š š Í ř
č é é é í ří ó ý Ó ř č š Í ó ž í š é íď ž ý š š Š é ř Ž í í í ř é é Í ď ý ď ž ř óř Í Č ý Ú Ž í í Ž Ó ó Í ž ýď Ž ý č í ří Ú č é ř Á Í É ď é ý š Í ý Ž ž Ď Í é ý Í ý ť Ž ř ů č ř Á ž í é Š č š í Ú š š Í ř
LINEÁRNÍ TRANSFORMACE V ROVINĚ
 LINEÁRNÍ TRANSFORMACE V ROVINĚ Kil Mleček Dgr Szrková FSv ČVUT Prh Thákurov 7 66 9 Prh 6 ČR e-il: kil@tfsvvutz SjF STU Brtislv Ná Slood 7 8 3 Brtislv SR e-il: szrkov@sjfstusk Astrkt V řísěvku je osý geoetriký
LINEÁRNÍ TRANSFORMACE V ROVINĚ Kil Mleček Dgr Szrková FSv ČVUT Prh Thákurov 7 66 9 Prh 6 ČR e-il: kil@tfsvvutz SjF STU Brtislv Ná Slood 7 8 3 Brtislv SR e-il: szrkov@sjfstusk Astrkt V řísěvku je osý geoetriký
s N, r > s platí: Základní požadavek na krásu matematického pravidla: Musí být co nejobecnější s minimem a a = a = a. Nemohli bychom ho upravit tak,
 .6. Mocniny celý ocnitele I Předpokldy: 6, 6 Př. : Kteé ze dvou pvidel je teticky hezčí? ) Po kždé R, N pltí: +. ) Po kždé R,, N, > pltí:. Zákldní poždvek n káu tetického pvidl: Muí ýt co nejoecnější inie
.6. Mocniny celý ocnitele I Předpokldy: 6, 6 Př. : Kteé ze dvou pvidel je teticky hezčí? ) Po kždé R, N pltí: +. ) Po kždé R,, N, > pltí:. Zákldní poždvek n káu tetického pvidl: Muí ýt co nejoecnější inie
Přijímací test studijních předpokladů
 Univerzit obrny Přijímcí test stdijních předpokldů Test ze dne 10. 4. 018 (03) Fklt vojenských technologií V kždém příkldě je právě jedn z nbízených vrint řešení správná. Z správně zkrožkovno vrint jso
Univerzit obrny Přijímcí test stdijních předpokldů Test ze dne 10. 4. 018 (03) Fklt vojenských technologií V kždém příkldě je právě jedn z nbízených vrint řešení správná. Z správně zkrožkovno vrint jso
( ) ( ) Pythagorova věta, Euklidovy věty II. γ = 90, je-li dáno: c = 10, c = 6. Předpoklady: 3205
 3..6 Pythgoro ět, Euklidoy ěty II Předpokldy: 305 V kždém proúhlém trojúhelníku s oděsnmi, přeponou pltí: =, =, =, kde je ýšk n přeponu, jsou úseky přepony přilehlé ke strnám,. Kždou z předhozíh ět je
3..6 Pythgoro ět, Euklidoy ěty II Předpokldy: 305 V kždém proúhlém trojúhelníku s oděsnmi, přeponou pltí: =, =, =, kde je ýšk n přeponu, jsou úseky přepony přilehlé ke strnám,. Kždou z předhozíh ět je
Obsah dnešní přednášky : Obecný rovinný pohyb tělesa. Teorie současných pohybů, Coriolisovo zrychlení, dynamika obecného rovinného pohybu.
 Obsh dnešní řednášky : Obecný oinný ohyb těles. eoie součsných ohybů, Coiolisoo zychlení, dynik obecného oinného ohybu. Obecný oinný ohyb zákldní ozkld. osu osu = A otce = A otce A A A A efeenční bod sueosice
Obsh dnešní řednášky : Obecný oinný ohyb těles. eoie součsných ohybů, Coiolisoo zychlení, dynik obecného oinného ohybu. Obecný oinný ohyb zákldní ozkld. osu osu = A otce = A otce A A A A efeenční bod sueosice
 Ž č éří š é š ří í č ó Ž ří š é š ó Ě Ě É Ě Ě ě š čů čů ó ý ů í č ó š ý ó ě ó í Ž ě ó í ř čí Ú á č é ó č éš é č ě ž ó í íš ó ó ý ó ý č ó ě Ť ý ě íř í ě č č ó ý é ů ó é ó á í ě Ť ó ó í ě ý ý ó í íč ó ó
Ž č éří š é š ří í č ó Ž ří š é š ó Ě Ě É Ě Ě ě š čů čů ó ý ů í č ó š ý ó ě ó í Ž ě ó í ř čí Ú á č é ó č éš é č ě ž ó í íš ó ó ý ó ý č ó ě Ť ý ě íř í ě č č ó ý é ů ó é ó á í ě Ť ó ó í ě ý ý ó í íč ó ó
ANALYTICKÁ GEOMETRIE
 Technická niverzit v Liberci Fklt přírodovědně-hmnitní pedgogická Ktedr mtemtiky didktiky mtemtiky NLYTICKÁ GEOMETRIE Pomocný čební text Petr Pirklová Liberec, listopd 2015 NLYTICKÁ GEOMETRIE LINEÁRNÍCH
Technická niverzit v Liberci Fklt přírodovědně-hmnitní pedgogická Ktedr mtemtiky didktiky mtemtiky NLYTICKÁ GEOMETRIE Pomocný čební text Petr Pirklová Liberec, listopd 2015 NLYTICKÁ GEOMETRIE LINEÁRNÍCH
 ď ň Á Ř Č É ř ě ř Ú Č č ě Ž ě ř ě ň ň ř ů ň Ž ě ň š Ň ě ř ř ř č Ž Ž č ř ř ň Ž ň ň ž Í ě š ř ř Č ř š Í ř Ž ó ř ě ů ž ň ř Č ě ř ř Í č ň ů č ř Í ů ů ě ň ů ů ě ň Á Á ů ů ě ň č Ž č ň ů č Ž ň ú Ž ň Ň ň Ž č š
ď ň Á Ř Č É ř ě ř Ú Č č ě Ž ě ř ě ň ň ř ů ň Ž ě ň š Ň ě ř ř ř č Ž Ž č ř ř ň Ž ň ň ž Í ě š ř ř Č ř š Í ř Ž ó ř ě ů ž ň ř Č ě ř ř Í č ň ů č ř Í ů ů ě ň ů ů ě ň Á Á ů ů ě ň č Ž č ň ů č Ž ň ú Ž ň Ň ň Ž č š
 í ý á ř ů ř ě í Ď ě ě ě á ě á ří ý ě í á ř ů ň á ó Š á ř ů ř ě í ě ě ě á ě á íí ý í á á ř ů ř ě í ě ě ě á ě á ří ý ě í Ó ří á ř ů ř ě í ě ě ě á ě á ří ý á ř ů ř ě í ř ý ří í á ř ů ř ě í ě ě ě á ě á ý ě
í ý á ř ů ř ě í Ď ě ě ě á ě á ří ý ě í á ř ů ň á ó Š á ř ů ř ě í ě ě ě á ě á íí ý í á á ř ů ř ě í ě ě ě á ě á ří ý ě í Ó ří á ř ů ř ě í ě ě ě á ě á ří ý á ř ů ř ě í ř ý ří í á ř ů ř ě í ě ě ě á ě á ý ě
Teorie současných pohybů, Coriolisovo zrychlení, dynamika obecného rovinného pohybu.
 Obsh dnešní řednášky : Alikoná echnik, 4. řednášk Obecný oinný ohyb těles. eoie součsných ohybů, Coiolisoo zychlení, dynik obecného oinného ohybu. Obecný oinný ohyb zákldní ozkld. Alikoná echnik, 4. řednášk
Obsh dnešní řednášky : Alikoná echnik, 4. řednášk Obecný oinný ohyb těles. eoie součsných ohybů, Coiolisoo zychlení, dynik obecného oinného ohybu. Obecný oinný ohyb zákldní ozkld. Alikoná echnik, 4. řednášk
5.2.8 Vzdálenost bodu od přímky
 zdálenost bodu od přímky zdálenost bodu od roiny zdálenost roin zdálenost bodu od přímky zdálenost bodu od roiny zdálenost roin 5..8 zdálenost bodu od přímky ředpokldy: 507 edgogická poznámk: Tříd počítá
zdálenost bodu od přímky zdálenost bodu od roiny zdálenost roin zdálenost bodu od přímky zdálenost bodu od roiny zdálenost roin 5..8 zdálenost bodu od přímky ředpokldy: 507 edgogická poznámk: Tříd počítá
Fázové přechody. navzájem nezávislé chemicky čisté látky obsažené v termod.soustavě
 Fázoé řechody Složky soustay s: nazáje nezáislé cheicky čisté látky obsažené terod.soustaě Fáze látky f: hoogenní soubor olekul, který je akroskoické ěřítku ostře ohraničen od jiných souborů olekul, které
Fázoé řechody Složky soustay s: nazáje nezáislé cheicky čisté látky obsažené terod.soustaě Fáze látky f: hoogenní soubor olekul, který je akroskoické ěřítku ostře ohraničen od jiných souborů olekul, které
Matematické metody v kartografii
 Mtemtické metody v krtogrfii. Přednášk Referenční elipsoid zákldní vzthy. Poloměry křivosti. Délky poledníkového rovnoběžkového oblouku. 1. Zákldní vzthy n rotčním elipoidu Rotční elipsoid dán následujícími
Mtemtické metody v krtogrfii. Přednášk Referenční elipsoid zákldní vzthy. Poloměry křivosti. Délky poledníkového rovnoběžkového oblouku. 1. Zákldní vzthy n rotčním elipoidu Rotční elipsoid dán následujícími
 č č č ř ě č ř ě ý ž Č Č úř Č ě Č č č č ě ě ŠÍ ř Ů ú ě ú Ú ý č č Ú ě Ú ě ř ě ž ý Ů ý ř ě ě ž ó ů ý Ú ě ý ý ě ě Ž ě č ž ž Ú ě ý č ž ž ý č ě ě ě Í Ž ě ě ž ě č ý ě ůž ě ý Č ý ř ú ů ě ě ý Č Č ě ý ý Ú ě ý ý
č č č ř ě č ř ě ý ž Č Č úř Č ě Č č č č ě ě ŠÍ ř Ů ú ě ú Ú ý č č Ú ě Ú ě ř ě ž ý Ů ý ř ě ě ž ó ů ý Ú ě ý ý ě ě Ž ě č ž ž Ú ě ý č ž ž ý č ě ě ě Í Ž ě ě ž ě č ý ě ůž ě ý Č ý ř ú ů ě ě ý Č Č ě ý ý Ú ě ý ý
QUADROTORY. Ing. Vlastimil Kříž
 QUADROTORY ng. Vlastiil Kříž Obsah 2 Mateatický odel, říení transforace ei báei (rotace) staoý popis říení Eistující projekt unieritní hobb koerční Quadrotor 3 ožnost isu iniu pohbliých součástek dobrý
QUADROTORY ng. Vlastiil Kříž Obsah 2 Mateatický odel, říení transforace ei báei (rotace) staoý popis říení Eistující projekt unieritní hobb koerční Quadrotor 3 ožnost isu iniu pohbliých součástek dobrý
České vysoké učení technické v Praze Fakulta biomedicínského inženýrství
 Česé vsoé učení technicé v Pre ult iomedicínsého inženýrství Úloh K0/č. 6: Určování oloh těžiště stilometricou lošinou Ing. Ptri Kutíle Ph.D. Ing. dm Žiž (utile@fmi.cvut.c i@fmi.cvut.c) Poděování: Tto
Česé vsoé učení technicé v Pre ult iomedicínsého inženýrství Úloh K0/č. 6: Určování oloh těžiště stilometricou lošinou Ing. Ptri Kutíle Ph.D. Ing. dm Žiž (utile@fmi.cvut.c i@fmi.cvut.c) Poděování: Tto
Ý áš á í é ť š í
 ří ď ě ě é ř ý ří ý é úř á ú ě ě ř ář í ší ž í ř í í Í ř ý áš ě ů é í ď Í ř ý řá óš í áš í ý í ř š í á á ř ří ž ě ž ď š ě í í í á žá ý á Í ÍŽ Š Á Ó ř č í Í é ž é ž á í á á Ž ř ě ž ú á á č ě ě í ěž á í
ří ď ě ě é ř ý ří ý é úř á ú ě ě ř ář í ší ž í ř í í Í ř ý áš ě ů é í ď Í ř ý řá óš í áš í ý í ř š í á á ř ří ž ě ž ď š ě í í í á žá ý á Í ÍŽ Š Á Ó ř č í Í é ž é ž á í á á Ž ř ě ž ú á á č ě ě í ěž á í
Nakloněná rovina III
 6 Nakloněná rovina III Předoklady: 4 Pedagogická oznáka: Následující říklady oět atří do kategorie vozíčků Je saozřejě otázkou, zda tyto říklady v takové nožství cvičit Osobně se i líbí, že se studenti
6 Nakloněná rovina III Předoklady: 4 Pedagogická oznáka: Následující říklady oět atří do kategorie vozíčků Je saozřejě otázkou, zda tyto říklady v takové nožství cvičit Osobně se i líbí, že se studenti
29. OBJEMY A POVRCHY TĚLES
 9. OBJEMY A POVRCHY TĚLES 9.. Vypočítejte poch kádu ABCDEFGH, jestliže ) AB =, BC = b, BH = u b) AB =, BH = u, odchylk AG EH je ϕ H G Poch kádu učíme podle zoce: S = b + c + bc ( ) c E F D b C ) A B u
9. OBJEMY A POVRCHY TĚLES 9.. Vypočítejte poch kádu ABCDEFGH, jestliže ) AB =, BC = b, BH = u b) AB =, BH = u, odchylk AG EH je ϕ H G Poch kádu učíme podle zoce: S = b + c + bc ( ) c E F D b C ) A B u
Univerzita Karlova v Praze Pedagogická fakulta
 Uivezit lov v Pze Pedgogiká fkult SEMINÁRNÍ PRÁCE Z POLYNOMICÉ ALGEBRY ZVOLENÝ POLYNOM / CIFRI Zdáí: Zvol olyom f ( x) stuě 6 tkový y 6 f ( ) { 87868}. Uči všehy kořey s ásoostí. Vyováí: Zdáí vyhovuje
Uivezit lov v Pze Pedgogiká fkult SEMINÁRNÍ PRÁCE Z POLYNOMICÉ ALGEBRY ZVOLENÝ POLYNOM / CIFRI Zdáí: Zvol olyom f ( x) stuě 6 tkový y 6 f ( ) { 87868}. Uči všehy kořey s ásoostí. Vyováí: Zdáí vyhovuje
ž ř í í č í ř í í ř í č ž ý č í í Ú Ý É ú ží ř ň ř ž í í ý č č ží ř í Ř Ž ž ž ž č í Ž ó í Žť žť ú ú ú ú ž ř ž í ú ž ž ž ř čí
 ÍíÍ í ř č ť Í Í ý í ý í í ý ž ř ž ř Í ó ť Í í í í ž ž ř Í ú í ý ý ť í ú ř ží í ř Ž í í í ÓÍ ů í É í č í ží č í Ž ý ú ů č í í ř ž ř č ů č í č ý ří č ý č í í ů ž Ží č í úč ů ý ý ý č č í ů íč Ú ý č č í í
ÍíÍ í ř č ť Í Í ý í ý í í ý ž ř ž ř Í ó ť Í í í í ž ž ř Í ú í ý ý ť í ú ř ží í ř Ž í í í ÓÍ ů í É í č í ží č í Ž ý ú ů č í í ř ž ř č ů č í č ý ří č ý č í í ů ž Ží č í úč ů ý ý ý č č í ů íč Ú ý č č í í
7.3.7 Přímková smršť. Předpoklady: 7306
 737 Přímkoá smršť Předpokldy 7306 Pedgogiká poznámk Hodin znikl jko reke n prní průhod učenií Třeoni se třídou 42011 Ukázlo se, že studenti mjí prolémy s přiřzením spráného ektoru k různým druhům roni
737 Přímkoá smršť Předpokldy 7306 Pedgogiká poznámk Hodin znikl jko reke n prní průhod učenií Třeoni se třídou 42011 Ukázlo se, že studenti mjí prolémy s přiřzením spráného ektoru k různým druhům roni
2. Funkční řady Studijní text. V předcházející kapitole jsme uvažovali řady, jejichž členy byla reálná čísla. Nyní se budeme zabývat studiem
 2. Funkční řd Studijní text 2. Funkční řd V předcházející kpitole jsme uvžovli řd, jejichž člen bl reálná čísl. Nní se budeme zbývt studiem obecnějšího přípdu, kd člen řd tvoří reálné funkce. Definice
2. Funkční řd Studijní text 2. Funkční řd V předcházející kpitole jsme uvžovli řd, jejichž člen bl reálná čísl. Nní se budeme zbývt studiem obecnějšího přípdu, kd člen řd tvoří reálné funkce. Definice
é řě ú čí í řě ú ž ě á á í š ýž ž ž á ě č ž ří é ž í á ý ď á číš š í á ě ě řě í ó í ž é ž í ó ř í ě ší ž é ž é é é řě á ý á ě č ž á á řěč í á á Ž ě ž
 ž í í á ý š á ž ž ý ř ě ů ž Ží ř ě Ž ří í í ž Í ž é ž Řá á č Ú é úř ší úř í ů ý ž ó á ě í é é š ří Ž í ů ě č Ž ří ří í í é á ě á í í ú ú žď č ž Řá á č ŘÁ Á É ý č ý ž íú ě á úř í á ď í ř ř ří č ž ě ž á
ž í í á ý š á ž ž ý ř ě ů ž Ží ř ě Ž ří í í ž Í ž é ž Řá á č Ú é úř ší úř í ů ý ž ó á ě í é é š ří Ž í ů ě č Ž ří ří í í é á ě á í í ú ú žď č ž Řá á č ŘÁ Á É ý č ý ž íú ě á úř í á ď í ř ř ří č ž ě ž á
Lineární algebra. 1) Vektor, lineární závislost a nezávislost. Def.: Číselným vektorem n-rozměrného prostoru nazýváme uspořádanou množinu n čísel
 Lineání lge ) Vekto, lineání záislost nezáislost Def: Číselným ektoem n-ozměného postou nzýáme uspořádnou množinu n čísel,, ) ( n Čísl,, n nzýáme souřdnice ektou, číslo n dimenzí neo ozměem ektou Opece
Lineání lge ) Vekto, lineání záislost nezáislost Def: Číselným ektoem n-ozměného postou nzýáme uspořádnou množinu n čísel,, ) ( n Čísl,, n nzýáme souřdnice ektou, číslo n dimenzí neo ozměem ektou Opece
íž í ě é á ří ž í é á í í éž š ě ž ě ú í í íší ří í á ý ě áší ě í ě čá í ě š é é í áš í á č é čá ří ď ďí ř á š ř á ř ě ě ž ý ě íší ě ě žáďá ž á í ž ě
 š áš ř é ř ě ý ě ě é ý ářů š í ů ý Ú á á ří č á í ě á ě ř ě í ř ý ě í žá á é ř ří á ěř í žá č š ě é ě ě ř ář é á Šú é č á ý í ž ř ě ý ě ší á ý í ží á ě ý ě í ď íč é ě ř á í ě á í ě ří č ý é ý é ě é í á
š áš ř é ř ě ý ě ě é ý ářů š í ů ý Ú á á ří č á í ě á ě ř ě í ř ý ě í žá á é ř ří á ěř í žá č š ě é ě ě ř ář é á Šú é č á ý í ž ř ě ý ě ší á ý í ží á ě ý ě í ď íč é ě ř á í ě á í ě ří č ý é ý é ě é í á
TERMOMECHANIKA 4. První zákon termodynamiky
 FSI VUT Brně, Energetický ústa Odbor termomechaniky a techniky rostředí rof. Ing. Milan Paelek, CSc. TERMOMECHANIKA 4. Prní zákon termodynamiky OSNOVA 4. KAPITOLY. forma I. zákona termodynamiky Objemoá
FSI VUT Brně, Energetický ústa Odbor termomechaniky a techniky rostředí rof. Ing. Milan Paelek, CSc. TERMOMECHANIKA 4. Prní zákon termodynamiky OSNOVA 4. KAPITOLY. forma I. zákona termodynamiky Objemoá
Příklady k přednášce 1. Úvod. Michael Šebek Automatické řízení 2019
 Příklady k řednášce. Úvod Michael Šebek Atomatické řízení 09 08.0.09 Kyvadlo řízené momentem Pohybová rovnice (. Newtonův zákon ro rotaci) J ϕ = M ro moment setrvačnosti J = ml = M Flsinϕ c = M mgl sinϕ
Příklady k řednášce. Úvod Michael Šebek Atomatické řízení 09 08.0.09 Kyvadlo řízené momentem Pohybová rovnice (. Newtonův zákon ro rotaci) J ϕ = M ro moment setrvačnosti J = ml = M Flsinϕ c = M mgl sinϕ
Kinematický model kolového, smykem řízeného robota
 Kineatický odel koloého, syke řízeného roota Šolc rantišek, Toáš Neužil, Jaku Hraec, Jarosla Šeera Astrakt Článek popisuje ateatický odel syke řízeného koloého roota. Root je tořen čtyřkoloý podozke u
Kineatický odel koloého, syke řízeného roota Šolc rantišek, Toáš Neužil, Jaku Hraec, Jarosla Šeera Astrakt Článek popisuje ateatický odel syke řízeného koloého roota. Root je tořen čtyřkoloý podozke u
S t e j n o s měrné stroje Ing. Vítězslav Stýskala, Ph.D., únor 2006
 8. ELEKTRICKÉ STROJE TOČIVÉ rčeno pro posluchče bklářských studijních progrmů FS S t e j n o s měrné stroje Ing. Vítězslv Stýskl, Ph.D., únor 6 Řešené příkldy Příkld 8. Mechnické chrkteristiky Stejnosměrný
8. ELEKTRICKÉ STROJE TOČIVÉ rčeno pro posluchče bklářských studijních progrmů FS S t e j n o s měrné stroje Ing. Vítězslv Stýskl, Ph.D., únor 6 Řešené příkldy Příkld 8. Mechnické chrkteristiky Stejnosměrný
3.2.11 Obvody a obsahy obrazců I
 ..11 Obvody obshy obrzců I Předpokldy: S pomocí vzorců v uvedených v tbulkách řeš následující příkldy Př. 1: Urči výšku lichoběžníku o obshu 54cm zákldnách 7cm 5cm. + c Obsh lichoběžníku: S v Výšk lichoběžníku
..11 Obvody obshy obrzců I Předpokldy: S pomocí vzorců v uvedených v tbulkách řeš následující příkldy Př. 1: Urči výšku lichoběžníku o obshu 54cm zákldnách 7cm 5cm. + c Obsh lichoběžníku: S v Výšk lichoběžníku
ZÁKLADNÍ POZNATKY. p, kde ČÍSELNÉ MNOŽINY (OBORY) N... množina všech přirozených čísel: 1, 2, 3,, n,
 ZÁKLADNÍ POZNATKY ČÍSELNÉ MNOŽINY (OBORY) N... množin všech přirozených čísel: 1, 2, 3,, n, N0... množin všech celých nezáporných čísel (přirozených čísel s nulou: 0,1, 2, 3,, n, Z... množin všech celých
ZÁKLADNÍ POZNATKY ČÍSELNÉ MNOŽINY (OBORY) N... množin všech přirozených čísel: 1, 2, 3,, n, N0... množin všech celých nezáporných čísel (přirozených čísel s nulou: 0,1, 2, 3,, n, Z... množin všech celých
Ž ř ě Ž ů š ř š ě ř š ů ř ř ž ř ě ě ř ě É ř š ř ď Í ě ř ž ř ř ř ě š ž ř ě ě ě ž ž ř ž š ž ů ú ř ď ě É ě š ř ú ř ř ě ž ď š Í ď š ř ú ě ň ě ď ž ě ř ř ó
 ř Ž É Í ř ř ž ěž ú ď ěž ú É ú ú ě Ú š ž ú ď ž ě ď ě ř ž ě ú ř ě š ž ě ř š ž ě ů š ě ř ě ě ě ř ě ř ě ř š ž ň ě š ž Í š ť ž ř š Ž ř ě Ž ů š ř š ě ř š ů ř ř ž ř ě ě ř ě É ř š ř ď Í ě ř ž ř ř ř ě š ž ř ě ě
ř Ž É Í ř ř ž ěž ú ď ěž ú É ú ú ě Ú š ž ú ď ž ě ď ě ř ž ě ú ř ě š ž ě ř š ž ě ů š ě ř ě ě ě ř ě ř ě ř š ž ň ě š ž Í š ť ž ř š Ž ř ě Ž ů š ř š ě ř š ů ř ř ž ř ě ě ř ě É ř š ř ď Í ě ř ž ř ř ř ě š ž ř ě ě
1 Neoklasický model chování spotřebitele
 Neoklasický model choání sotřebitele PŘÍKLAD : PRMÁRNÍ A DUÁLNÍ ÚLOHA Užitek sotřebitele je osán užitkoou funkcí e taru U. Vyjádřete: a. Marshalloy otáky b. Neřímou funkci užitku c. Hicksoy otáky d. Přímou
Neoklasický model choání sotřebitele PŘÍKLAD : PRMÁRNÍ A DUÁLNÍ ÚLOHA Užitek sotřebitele je osán užitkoou funkcí e taru U. Vyjádřete: a. Marshalloy otáky b. Neřímou funkci užitku c. Hicksoy otáky d. Přímou
á ý ě ší čí č í á č ý ář á ž é ó é č ě á š ě ě óš ó á čá čň č ě á á ó í ř é á í íá í á é ř ž ž ě ě ší é í š ů í ě ň ť ó á í Íí í ň í ří ů é ř š í č í
 É Í Á Í á í á í č ý í í č ě í í ý ě í í č š í ří ě ě ý ý ů é ě í á í é é é á ý č ě é č é í í é ě ř é ž í é é ň ř ší á é í ý ý í žň ý á í í í ř ě č ý í é á í í š ý í ě š ář í é á á ď á í ž š é á í ť í ě
É Í Á Í á í á í č ý í í č ě í í ý ě í í č š í ří ě ě ý ý ů é ě í á í é é é á ý č ě é č é í í é ě ř é ž í é é ň ř ší á é í ý ý í žň ý á í í í ř ě č ý í é á í í š ý í ě š ář í é á á ď á í ž š é á í ť í ě
Komplexní čísla. Pojem komplexní číslo zavedeme při řešení rovnice: x 2 + 1 = 0
 Komplexní čísl Pojem komplexní číslo zvedeme př řešení rovnce: x 0 x 0 x - x Odmocnn ze záporného čísl reálně neexstuje. Z toho důvodu se oor reálných čísel rozšíří o dlší číslo : Všechny dlší odmocnny
Komplexní čísl Pojem komplexní číslo zvedeme př řešení rovnce: x 0 x 0 x - x Odmocnn ze záporného čísl reálně neexstuje. Z toho důvodu se oor reálných čísel rozšíří o dlší číslo : Všechny dlší odmocnny
3.1.8 Přeměny energie v mechanickém oscilátoru
 3..8 Přeěny energie v echanické oscilátoru Předoklady: 0050, 03007 Pedagogická oznáka: Odvození zákona zachování energie rovádí na vodorovné ružině, rotože je říočařejší. Pro zájece je uvedeno na konci
3..8 Přeěny energie v echanické oscilátoru Předoklady: 0050, 03007 Pedagogická oznáka: Odvození zákona zachování energie rovádí na vodorovné ružině, rotože je říočařejší. Pro zájece je uvedeno na konci
56. ročník Matematické olympiády. b 1,2 = 27 ± c 2 25
 56. ročník Mtemtické olympiády Úlohy domácí části I. kol ktegorie 1. Njděte všechny dvojice (, ) celých čísel, jež vyhovují rovnici + 7 + 6 + 5 + 4 + = 0. Řešení. Rovnici řešíme jko kvdrtickou s neznámou
56. ročník Mtemtické olympiády Úlohy domácí části I. kol ktegorie 1. Njděte všechny dvojice (, ) celých čísel, jež vyhovují rovnici + 7 + 6 + 5 + 4 + = 0. Řešení. Rovnici řešíme jko kvdrtickou s neznámou
 ůř Í ý Í Ť ý Á Ž Í Á ť Í ť ý ť Ť ě č ě Š ř ú ý š Č ř č ď ř Á Í Í ě ě ř ó ě č ř č ě ř š ě Á Í č ě Í Í Č É ě Š Í Č ě Í ě ů ů ů Č ý ú Ž ří Á Ý Í Á ÍČ ŽÍ Ý Ů ě č ě ě ě ř ě ě ó ž ž ě ýš ě ě ó ě ř ú ě ďý ě Ú
ůř Í ý Í Ť ý Á Ž Í Á ť Í ť ý ť Ť ě č ě Š ř ú ý š Č ř č ď ř Á Í Í ě ě ř ó ě č ř č ě ř š ě Á Í č ě Í Í Č É ě Š Í Č ě Í ě ů ů ů Č ý ú Ž ří Á Ý Í Á ÍČ ŽÍ Ý Ů ě č ě ě ě ř ě ě ó ž ž ě ýš ě ě ó ě ř ú ě ďý ě Ú
Rovnoměrně zrychlený pohyb v grafech
 ..9 Ronoměrně zrychlený pohyb grfech Předpokldy: 4 Př. : N obrázku jsou nkresleny grfy dráhy, rychlosi zrychlení ronoměrně zrychleného pohybu. Přiřď grfy eličinám. s,, ronoměrně zrychlený pohyb: zrychlení
..9 Ronoměrně zrychlený pohyb grfech Předpokldy: 4 Př. : N obrázku jsou nkresleny grfy dráhy, rychlosi zrychlení ronoměrně zrychleného pohybu. Přiřď grfy eličinám. s,, ronoměrně zrychlený pohyb: zrychlení
Základní planimetrické pojmy a poznatky
 teorie řešené úlohy cvičení tiy k mturitě Zákldní lnimetrické ojmy ozntky íš, že očátek geometrie se dtuje do Egyt do třetího tisíciletí ř. n. l.? název geometrie znmenl ůvodně zeměměřičství? (geo = země,
teorie řešené úlohy cvičení tiy k mturitě Zákldní lnimetrické ojmy ozntky íš, že očátek geometrie se dtuje do Egyt do třetího tisíciletí ř. n. l.? název geometrie znmenl ůvodně zeměměřičství? (geo = země,
 ŘÍ ó Ý Ň É Ť Í ň ó Ř Í Í Ň ď ď ď Ě Í Á Ý ó Á ó ď ó Í ó Ř Č ó Ř Ř Á Š Ď ď ď Č Ý Ý Í ň Ý ň Ý Ý ň Í Ý Ó Í Ý ň Ň ď ň ó ó ó ď ň Á Á Á Ě Ě ň ň ň Á Á ó ď Í Ě ď Ď ň Ý ď ó ň Š Í Á ÁŠ Ě Š Í Á ď ď ď ď Ý ň ň Í Ž
ŘÍ ó Ý Ň É Ť Í ň ó Ř Í Í Ň ď ď ď Ě Í Á Ý ó Á ó ď ó Í ó Ř Č ó Ř Ř Á Š Ď ď ď Č Ý Ý Í ň Ý ň Ý Ý ň Í Ý Ó Í Ý ň Ň ď ň ó ó ó ď ň Á Á Á Ě Ě ň ň ň Á Á ó ď Í Ě ď Ď ň Ý ď ó ň Š Í Á ÁŠ Ě Š Í Á ď ď ď ď Ý ň ň Í Ž
Poznámky k cvičením z termomechaniky Cvičení 9.
 Voda a vodní pára Při výpočtech příkladů, které jsou zaěřeny na výpočty vody a vodní páry je důležité si paatovat veličiny, které jsou kritické a z hlediska výpočtu i nezbytné. Jedná se o hodnoty teploty
Voda a vodní pára Při výpočtech příkladů, které jsou zaěřeny na výpočty vody a vodní páry je důležité si paatovat veličiny, které jsou kritické a z hlediska výpočtu i nezbytné. Jedná se o hodnoty teploty
 Ú š šť ž Č Č Č Ž ž š š ž ž š š ď ď Č š š ž š š š Ú š š š š ď š š ď ž š š ď š ů ď ď š Í Ž ů ů ů ů ů š š Ú Í Í ť š š š š ž ů š š š š Ž ž ďš š š Íš Ž š Č š ž Ý ď š Ž š ď ť ž É š š Í š Ž š Č ž ď š Ň ž š óó
Ú š šť ž Č Č Č Ž ž š š ž ž š š ď ď Č š š ž š š š Ú š š š š ď š š ď ž š š ď š ů ď ď š Í Ž ů ů ů ů ů š š Ú Í Í ť š š š š ž ů š š š š Ž ž ďš š š Íš Ž š Č š ž Ý ď š Ž š ď ť ž É š š Í š Ž š Č ž ď š Ň ž š óó
š í ý Í í ý č é á č í ů ý č ě ů á á í é č é á é š á č é ý í á ý ý í ž žá ý ý ř ě ý í ě é ž č é ó é í É é á č ý á ž Ž é ř í ší É ě é ě í á é č ý í ž ří
 š í ý Í í ý č á č í ů ý č ě ů á á í č á š á č ý í á ý ý í ž žá ý ý ř ě ý í ě ž č ó í É á č ý á ž Ž ř í ší É ě ě í á č ý í ž ří í ž ř Ě ř Í ď ář á č ý á í ř š š ě Ž í ý á á ý žá ý ý ž čí Ž í í í í č ř ě
š í ý Í í ý č á č í ů ý č ě ů á á í č á š á č ý í á ý ý í ž žá ý ý ř ě ý í ě ž č ó í É á č ý á ž Ž ř í ší É ě ě í á č ý í ž ří í ž ř Ě ř Í ď ář á č ý á í ř š š ě Ž í ý á á ý žá ý ý ž čí Ž í í í í č ř ě
25 Měrný náboj elektronu
 5 Měrný náboj elektronu ÚKOL Stnovte ěrný náboj elektronu e výsledek porovnejte s tbulkovou hodnotou. TEORIE Poěr náboje elektronu e hotnosti elektronu nzýváe ěrný náboj elektronu. Jednou z ožných etod
5 Měrný náboj elektronu ÚKOL Stnovte ěrný náboj elektronu e výsledek porovnejte s tbulkovou hodnotou. TEORIE Poěr náboje elektronu e hotnosti elektronu nzýváe ěrný náboj elektronu. Jednou z ožných etod
č Ó š í é í é í ž íč é Í é Ť č ž é Ž ě Š š é é čí í í ě í Óč é í Ó íč č í í ě ší íč í š í í í č ě í í č ě í ň ě í ě í ě ší í š í Š Í í é Í ě Ó Ťí ěě ě
 í Š ě čž ť č í í é ž í č í íč í č ě Ž í ě č Ž Ž š é ě ší Ží č íž š ěží é Ží č ě č é Í ňí é č é é Č Í Í Ž Ů Ž í Ť ň í č Ť Ťí Í í ž č í í š Š ň ě í í Ťí č č Ž Ť š š í č ř í íž í Ž í Ó í í í č í í í ě í Ť
í Š ě čž ť č í í é ž í č í íč í č ě Ž í ě č Ž Ž š é ě ší Ží č íž š ěží é Ží č ě č é Í ňí é č é é Č Í Í Ž Ů Ž í Ť ň í č Ť Ťí Í í ž č í í š Š ň ě í í Ťí č č Ž Ť š š í č ř í íž í Ž í Ó í í í č í í í ě í Ť
 ř Ř Š Í í ž í ří ó ří ó Í Í Í Á Í í í č í ř í č í č š íš ěž ú í č Á Ě í čí ě ě Ž Í žď Ď č čí í ú ž Ř Á Á Í ř íš í ž í ž ř č í č í čí ř í č ří š č ří ó č ě č í ó ž ě í ě ě í í ň ď í ž č íč í č í ří š čí
ř Ř Š Í í ž í ří ó ří ó Í Í Í Á Í í í č í ř í č í č š íš ěž ú í č Á Ě í čí ě ě Ž Í žď Ď č čí í ú ž Ř Á Á Í ř íš í ž í ž ř č í č í čí ř í č ří š č ří ó č ě č í ó ž ě í ě ě í í ň ď í ž č íč í č í ří š čí
ý Í č ší í ě í ů ý í ě á íó í í á ě í ě í š í ť é ř š ě Í é é Í á í ří í íř í íž í í í í ů ží í ý í ů í ší ěá Í á é á í í ě ě í ó ý ý í í í ť í á ší í
 ý Í č š ě ů ý ě á ó á ě ě š ť é ř š ě Í é é Í á ř ř ž ů ž ý ů š ěá Í á é á ě ě ó ý ý ť á š ě ž é é č Á ž á Í ř Ě ó é ř á ú Í ě ý é ě š č ý Í ě ř ů ě ú ň Í ť é ě ě š Ě ó á ř č ě ó ů ř ř á Íř ží ř ě č ě
ý Í č š ě ů ý ě á ó á ě ě š ť é ř š ě Í é é Í á ř ř ž ů ž ý ů š ěá Í á é á ě ě ó ý ý ť á š ě ž é é č Á ž á Í ř Ě ó é ř á ú Í ě ý é ě š č ý Í ě ř ů ě ú ň Í ť é ě ě š Ě ó á ř č ě ó ů ř ř á Íř ží ř ě č ě
řá ó á ú ú š š ř č é ě ě á é č ě š č č á ě í Ž š ě ř č é ž ř č é šč š ž é á č ř á ě á ě á é é ž í ř á é ď ě šč í šč ěšť čš ó ž é é ě ž é ď é ší ě ž é
 é é ě í ří í é č á é ě í Ž é í ě ú ť á ď á ý ž ů é ď á ř é č ě ěšť é ě č č ě ú é í í ě í á é ě š ě í ý ý í ú í ó ď ý í ěž í ě á á í ě ý š ě í í é ď Č Á Č ý á ě ě ě ůž ř ě š ě á ě í á é ž í í á ý á á ž
é é ě í ří í é č á é ě í Ž é í ě ú ť á ď á ý ž ů é ď á ř é č ě ěšť é ě č č ě ú é í í ě í á é ě š ě í ý ý í ú í ó ď ý í ěž í ě á á í ě ý š ě í í é ď Č Á Č ý á ě ě ě ůž ř ě š ě á ě í á é ž í í á ý á á ž
Auto během zrychlování z počáteční rychlost 50 km/h se zrychlením dráhu 100 m. Jak dlouho auto zrychlovalo? Jaké rychlosti dosáhlo?
 ..7 Ronoměrně zrychlený pohyb příkldech III Předpokldy: 6 Pedgogická poznámk: Hodinu dělím n dě části: 5 minut n prní d příkldy zbytek n osttní. I když šichni nestihnout spočítt druhý příkld je potřeb,
..7 Ronoměrně zrychlený pohyb příkldech III Předpokldy: 6 Pedgogická poznámk: Hodinu dělím n dě části: 5 minut n prní d příkldy zbytek n osttní. I když šichni nestihnout spočítt druhý příkld je potřeb,

 Riemnnův určitý integrál. Definice 1. Budiž
Riemnnův určitý integrál. Definice 1. Budiž