Pozn.1: Vojnov p edpokládá st ední hodnotu adiabatického exponentu c p. Teplota spalin po spálení první vrstvy potom tedy bude TSP
|
|
|
- Oldřich Šmíd
- před 8 lety
- Počet zobrazení:
Transkript
1 Tehniká univerzita v iberi, fakulta strojní, katedra vozidel a motor rof. Ing. Stanislav Beroun, S, Ing. Karel áv, h.d.: okální teloty i ostuném hoení smsi v uzaveném objemu. Studijní texty k edmtu rostedky zvyování arametr SM. ostuné zvyování tlaku v dsledku ostuu ela lamene v uzaveném objemu zsobuje a odstatné rozdíly telot salin v zón oáteního hoení a v zón koneného hoení smsi (tzv. Mahv efekt). Tyto rozdíly v telotáh vznikají roto, e saliny z oátení fáze hoení, tj. z blízkosti ohniska záehu (v elementárníh objemeh oáteníh ohnisek vzníení), jsou vystaveny adiabatiké (olytroiké) komresi sobením zvyujíího se tlaku v dsledku hoení dalíh ástí náln. Na rozdíl od rvní ásti smsi budou oslední zbytky smsi hoet i vyím tlaku. Nerovnomrnost telotního ole ve salináh má v uzavenýh objemeh, tedy i ve salovaíh rostoreh ístovýh salovaíh motor, rzné odoby. Exerimentáln je na.rokázáno, e odhylky mezi telotou salin v okolí zaalovaí svíky a na vzdálenjím míst salovaího rostoru jsou a 5 i normálním rbhu hoení a tém 4 i výskytu detonaního salování: v oblasti zaalovaí svíky itom dohází k intenzivnjímu odvodu tela tlesem svíky a esto je tam telota vyí. ojnov [ ] na zjednodueném íkladu vyhoívání náln ve salovaí komoe stálého objemu (viz obr.) ukazuje, e vrstva smsi, která shoela jako rvní v okolí ohniska záehu (ohnisek vzníení), je vystavena úinkm adiabatikého stlaování dsledkem vyhoívání dalíh vrstev (elementárníh objem) ve salovaí komoe. rstva (elementární objem), která vyhoí jako oslední ve salovaí komoe, byla od oátku vyhoívání náln adiabatiky (olytroiky) stlaována a na konenou velikost salovaího tlaku a i tomto tlaku otom vyhoí izobariky. tomto modelovém íadu se uvauje vyhoívání holavé smsi benzin-vzduh v nádob válového tvaru se záehem na jednom koni nádoby: oátení tlak náln je ka, oátení telota T 3 K, konený tlak salin v nádob je S 7 ka Konenému tlaku o izohorikém sálení náln by odle stavové rovnie odovídala stední " telota salin T S K, se zaoítáním molové zmny ro rodukty salování β,5 (zvtení objemu salin benzinové stehiometriké smsi) bude konená hodnota stední teloty salin " T S TS K. β Zvýení teloty v nádob bude TS TS T 7 K. Za edokladu, e rvní vrstva u ohniska záehu (elementární objem) se sálí izobariky (i tlaku ), zvýí se telota v této rvní vrstv ouze o TS / TS 7 35K., 6 ozn.: ojnov edokládá stední hodnotu adiabatikého exonentu (3-7) K ve velikosti,6. salin ro teloty Telota salin o sálení rvní vrstvy otom tedy bude TS / T TS / 65K. i následném vyhoívání ostatní náln vále budou saliny z této rvní vrstvy adiabatiky
2 Tehniká univerzita v iberi, fakulta strojní, katedra vozidel a motor rof. Ing. Stanislav Beroun, S, Ing. Karel áv, h.d.: okální teloty i ostuném hoení smsi v uzaveném objemu. Studijní texty k edmtu rostedky zvyování arametr SM. stlaovány: jejih konená telota o dosaení koneného tlaku S 7 ka otom bude, 5 S 7, 5 TS / / KON TS / K. ozn.: Stední hodnota adiabatikého exonentu ro saliny v rozsahu telot (65-5)K se edokládá, 5. oslední vrstva (elementární objem) smsi je ed sálením adiabatiky stlaena z tlaku na tlak, 36, S, S a její telota se jet ed sálením zvýí na TSM / n T K ozn.3: Stední hodnota adiabatikého exonentu ro sms v rozsahu telot (3-5)K se edokládá ve velikosti,36. oslední vrstva se sálí raktiky izobariky: zvýení teloty i tomto izobarikém vyhoení (ívodu tela) bude stejné, jako v íad salování rvní vrstvy. Telota salin v oslední vrstv (elementárním objemu) otom bude TS / n/ KON K. ýsledek tohoto zjednodueného výotu ukazuje, e rozdíl mezi telotou salin v rvní vrstv a telotou salin v oslední vrstv je 583 K. Modelovou situai ukazuje následujíí shema: záeh 435 K T K 85 K Obr.: Shéma uzavené nádoby nalnné holavou smsí (nahoe) a rbh teloty salin v nádob o úlném vyhoení smsi od vyznaeného místa záehu
3 Tehniká univerzita v iberi, fakulta strojní, katedra vozidel a motor rof. Ing. Stanislav Beroun, S, Ing. Karel áv, h.d.: okální teloty i ostuném hoení smsi v uzaveném objemu. Studijní texty k edmtu rostedky zvyování arametr SM. Analýzu ostuného hoení náln v uzaveném objemu lze v nejjednoduím íad ukázat na zmnáh stavu náln v nádob s konstantním objemem, rozdleném na dv stejn velké ásti (komory) omyslným ístem, který zajiuje dokonalou teelnou izolai tj. s nulovým estuem tela mezi obmi komorami. estu tela stnami do okolí je rovn nulový. Tlak náln v obou komoráh má vdy stejnou velikost. osaný model je grafiky znázornn na uvedeném shématu: T m T m Bhem výotu se uvauje neromnnost termodynamikýh vlastností látek náln vyetovaného objemu v rbhu ívodu tela i o jeho skonení. i výotu stavovýh veliin v jednotlivýh ásteh objemu je uvaován následujíí sled robíhajííh dj:. krok: ívod tela do levé ásti dorovázený ohybem fiktivního ístu vravo a tudí vratnou adiabatikou (izoentroikou) komresí ravé ásti objemu.. krok: ívod tela do ravé ásti dorovázený ohybem fiktivního ístu vlevo a tudí izoentroikou komresí levé ásti objemu. ýoet zmn v obou komoráh vyhází z rvního zákona termodynamiky který je latný ro vehny zmny. Ten lze esat na tvar: d du dw, () d du d. () ro dalí výoet je dleitá základní odmínka urujíí vztah mezi obma objemy: jak bylo uvedeno ji díve, jedná se o konstantní elkový objem, take musí latit: ro objem levé ásti ak latí:. (3). (4) Derivování tohoto výrazu odle asu uruje, e zmna jedné ásti se okamit rojeví oanou zmnou objemu ásti druhé a lze tedy sát: d. (5) d Tlak v obou objemeh je vdy stejný, o zajiuje odmínku vratnosti dje:. (6) Z thto dvou základníh odmínek oisujííh systém lze snadno vyvodit vztah: 3
4 Tehniká univerzita v iberi, fakulta strojní, katedra vozidel a motor rof. Ing. Stanislav Beroun, S, Ing. Karel áv, h.d.: okální teloty i ostuném hoení smsi v uzaveném objemu. Studijní texty k edmtu rostedky zvyování arametr SM. eení ad ) d d. (7) Za edokladu ideálního lynu, lze ro levou ást objemu nasat rovnii: d m dt d. (8) v ro ravou stranu latí vztah obdobný s tím, e ívod tela není v tomto okamiku jet realizován, take je roven nule: m dt d. (9) Ze stavové rovnie ideálního lynu m r T () lze snadno odvodit vztah ro zmnu teloty: dt d d. () mr mr o dosazení () do (9) a úrav dostaneme d d d. () r r Rovnii lze uravit na tvar r d d. (3) v odle Mayerovýh rovni latí: r, (4) take rovnie (3) ejde o úrav na tvar: d d. (5) Rovnii (8) eíeme s vyuitím vztahu () na tvar: d d d d. (6) r r o dosazení (4) a (5) do (6) obdríme vztah: d d d d d. (7) r r r Úravou dostaneme: d d d d. (8) r r r odle Mayerovýh rovni lze ouít vztah, (9) r r take rovnie (8) ejde na tvar: v d d d d. () r r r v 4
5 Tehniká univerzita v iberi, fakulta strojní, katedra vozidel a motor rof. Ing. Stanislav Beroun, S, Ing. Karel áv, h.d.: okální teloty i ostuném hoení smsi v uzaveném objemu. Studijní texty k edmtu rostedky zvyování arametr SM. Z rovnie (5) lyne: d d. () o dosazení () do () dostaneme: v d d d d. () r r r Ot s vyuitím Mayerovy rovnie (3) lze výraz () uravit na konený tvar, vyjadujíí írstek tlaku v systému (v obou ásteh je tlak stejný), zsobený ívodem tela do levé ásti objemu: d d. (4) r S ouitím Mayerovýh rovni lze výraz (4) esat do vhodnjího tvaru: d d. (5) Tento vztah lze odvodit i jinou estou, avak mén rkaznou - i ívodu tela do objemu, kde neuvaujeme íst rozdlujíí objem na dv ásti. ro tento výoet vyjdeme ot z rvního zákona termodynamiky, jak ho vystihuje vztah (). Jeliko se jedná o konstantní elkový objem, d, meme vztah () zasat ve tvaru d m dt, (6) kde indexy vystihují, e se jedná o veliiny týkajíí se elkového objemu. S ouitím () a d ejde rovnie (6) na tvar d d, r o je u díve odvozená rovnie (4). elikost zmny tlaku v systému z oátení hodnoty o na tlak (o ívodu tela do levé ásti objemu) získáme jednoduhou integraí vztahu (5): d d. (7) o integrai a úrav dostaneme:. (8) ravé ásti objemu robíhá izoentroiká komrese, take zmna stavu je jednoznan urena rovnií:. (9) ro objem ravé strany, o skonení izoentroiké komrese, dostaneme: 5
6 Tehniká univerzita v iberi, fakulta strojní, katedra vozidel a motor rof. Ing. Stanislav Beroun, S, Ing. Karel áv, h.d.: okální teloty i ostuném hoení smsi v uzaveném objemu. Studijní texty k edmtu rostedky zvyování arametr SM.. (3) Telota je otom dána stavovou rovnií: T. m r (3) ro výoet objemu levé ásti lze vyjít z rovnie (4), take Telotu vyoteme ot ze stavové rovnie:. (3) eení ad ) T. (33) m r Obdobným zsobem jako ro íad lze odvodit vztahy ro ívod tela do ravé ásti, dorovázený izoentroikou komresí ásti levé. To znamená, e rovnii (5) lze analogiky esat na tvar d d. (34) Integraí vztahu (34) obdríme analogiký vztah edhozímu íadu, který meme dále uravit s ouitím vztahu (8):. (35) Izoentroiká komrese levé ásti uruje jednoznan její objem:. (36) Telota je ak dána: T. (37) mr Objem ravé ásti uruje rovnie (3):. (38) Telota této ásti o skonení ívodu tela je dána stavovou rovnií: T. (39) m r Tyto zmny, kterými uvaovaný systém roel, lze ro názornost zakreslit do - diagramu. 6
7 Tehniká univerzita v iberi, fakulta strojní, katedra vozidel a motor rof. Ing. Stanislav Beroun, S, Ing. Karel áv, h.d.: okální teloty i ostuném hoení smsi v uzaveném objemu. Studijní texty k edmtu rostedky zvyování arametr SM. 7 Obr.: - diagramu jsou vyetované zmny v obou komoráh. kroku znázornny zradlov symetrikým obrazem odle izohory. ívod tela je znázornn olytroou, zradlov obráenou k zakreslené izoentro. Objemové ráe enáené mezi jednotlivými komorami mají stejnou velikost. ro konený stav náln v objemeh a je rozhodujíí konená velikost objem a. Konenou velikost uruje rovnie (36), kterou meme s vyuitím vztah (4), (8), (3) a (35) uravit do odoby. (4) Dalí úrava vyhází z odmínek eeného íadu a (4) a vede k rovnii. (4)
8 Tehniká univerzita v iberi, fakulta strojní, katedra vozidel a motor rof. Ing. Stanislav Beroun, S, Ing. Karel áv, h.d.: okální teloty i ostuném hoení smsi v uzaveném objemu. Studijní texty k edmtu rostedky zvyování arametr SM. zájemný omr objem a o dokonení ívodu tela ro eený íad s ostuným ívodem tela do jednotlivýh (stejn velkýh) objem závisí na oátením stavu náln v uzaveném objemu a na výhevnosti náln (omru ). íklad teoretikého rozdlení fiktivníh objem na koni vyetovaného roesu s ostuným ívodem tela (vyhoení náln) do jednotlivýh (zoátku stejn velkýh) objem je ukázán na salování stehiometriké smsi zemní lyn-vzduh ro dva rzné oátení stavy: a). o ka, T o 3 K, 3 MJ/m 3 :, 3Ma, 5967 b). o Ma, T o 6 K, 8,75 MJ/m 3 : 4, 5Ma, 5755 ýsledek ukazuje rozdílnost objem v obou komoráh o ostuném ívodu tela do obou komor (tj. realizovanýh kroky a ): objem v levé komoe, do které se telo ivedlo v. kroku, je i o ívodu tela do ravé komory vtí ne objem ravé komory. Ze stavové rovnie je otom zejmé, e konená telota v levé komoe musí být vtí ne konená telota v ravé komoe otvrzuje to srávnost úvahy k výotu rozloení telot v nálni i ostuném vyhoívání smsi v uzaveném objemu, ukázané v rvní ásti tohoto lánku. [ ]ojnov,a.,n.: roessy sgoranija v bystrohodnyh ornvyh dvigateljah. Mainostrojenije, Moskva,
Cvičení z termomechaniky Cvičení 5.
 Příklad V komresoru je kontinuálně stlačován objemový tok vzduchu *m 3.s- + o telotě 0 * C+ a tlaku 0, *MPa+ na tlak 0,7 *MPa+. Vyočtěte objemový tok vzduchu vystuujícího z komresoru, jeho telotu a říkon
Příklad V komresoru je kontinuálně stlačován objemový tok vzduchu *m 3.s- + o telotě 0 * C+ a tlaku 0, *MPa+ na tlak 0,7 *MPa+. Vyočtěte objemový tok vzduchu vystuujícího z komresoru, jeho telotu a říkon
TERMODYNAMIKA 1. AXIOMATICKÁ VÝSTAVBA KLASICKÉ TD Základní pojmy
 ERMODYNAMIKA. AXIOMAICKÁ ÝSABA KLASICKÉ D.. Základní ojmy Soustava (systém) je část rostoru od okolí oddělený stěnou uzavřená - stěna brání výměně hmoty mezi soustavou a okolím vers. otevřená (uzavřená
ERMODYNAMIKA. AXIOMAICKÁ ÝSABA KLASICKÉ D.. Základní ojmy Soustava (systém) je část rostoru od okolí oddělený stěnou uzavřená - stěna brání výměně hmoty mezi soustavou a okolím vers. otevřená (uzavřená
TERMODYNAMIKA 1. AXIOMATICKÁ VÝSTAVBA KLASICKÉ TD Základní pojmy
 ERMODYNAMIKA. AXIOMAICKÁ ÝSABA KLASICKÉ D.. Základní ojmy Soustava (systém) je část rostoru od okolí oddělený stěnou uzavřená - stěna brání výměně hmoty mezi soustavou a okolím vers. otevřená (uzavřená
ERMODYNAMIKA. AXIOMAICKÁ ÝSABA KLASICKÉ D.. Základní ojmy Soustava (systém) je část rostoru od okolí oddělený stěnou uzavřená - stěna brání výměně hmoty mezi soustavou a okolím vers. otevřená (uzavřená
KATEDRA VOZIDEL A MOTOR. Skute né ob hy PSM #6/14. Karel Páv
 KAEDRA VOZIDEL A MOOR Skutené obhy PSM #6/ Karel Pá ody rozdíl mezi idealizoaným a reálným obhem Odhylky od idealizae oliují jak ysokotlakou ást, tak i ást nízkotlakou (ýmnu náln ále): Promnliost termodynamikýh
KAEDRA VOZIDEL A MOOR Skutené obhy PSM #6/ Karel Pá ody rozdíl mezi idealizoaným a reálným obhem Odhylky od idealizae oliují jak ysokotlakou ást, tak i ást nízkotlakou (ýmnu náln ále): Promnliost termodynamikýh
W pot. F x. F y. Termodynamické potenciály. V minulé kapitole jsme poznali novou stavovou veliinu entropii S a vidli jsme, že ji lze používat
 ermodynamické otenciály minulé kaitole jsme oznali novou stavovou veliinu entroii a vidli jsme, že ji lze oužívat stejn jako jiné stavové veliiny - na. tlak, telotu, objem, oet ástic soustavy N, jejich
ermodynamické otenciály minulé kaitole jsme oznali novou stavovou veliinu entroii a vidli jsme, že ji lze oužívat stejn jako jiné stavové veliiny - na. tlak, telotu, objem, oet ástic soustavy N, jejich
Termodynamika ideálního plynu
 Přednáška 5 Termodynamika ideálního lynu 5.1 Základní vztahy ro ideální lyn 5.1.1 nitřní energie ideálního lynu Alikujme nyní oznatky získané v ředchozím textu na nejjednodužší termodynamickou soustavu
Přednáška 5 Termodynamika ideálního lynu 5.1 Základní vztahy ro ideální lyn 5.1.1 nitřní energie ideálního lynu Alikujme nyní oznatky získané v ředchozím textu na nejjednodužší termodynamickou soustavu
V p-v diagramu je tento proces znázorněn hyperbolou spojující body obou stavů plynu, je to tzv. izoterma :
 Jednoduché vratné děje ideálního lynu ) Děj izoter mický ( = ) Za ředokladu konstantní teloty se stavová rovnice ro zadané množství lynu změní na známý zákon Boylův-Mariottův, která říká, že součin tlaku
Jednoduché vratné děje ideálního lynu ) Děj izoter mický ( = ) Za ředokladu konstantní teloty se stavová rovnice ro zadané množství lynu změní na známý zákon Boylův-Mariottův, která říká, že součin tlaku
Plynové turbíny. Nevýhody plynových turbín: - menší mezní výkony ve srovnání s parní turbínou - vyšší nároky na palivo - kvalitnější materiály
 Plynoé turbíny Plynoá turbína je teeý stroj řeměňujíí teeou energie obsaženou raoní láte q roházejíí motorem na energii mehanikou a t (obr.). Praoní látkou je zduh, resektie saliny, které se ytářejí teeém
Plynoé turbíny Plynoá turbína je teeý stroj řeměňujíí teeou energie obsaženou raoní láte q roházejíí motorem na energii mehanikou a t (obr.). Praoní látkou je zduh, resektie saliny, které se ytářejí teeém
Obrázek1:Nevratnáexpanzeplynupřesporéznípřepážkudooblastisnižšímtlakem p 2 < p 1
 Joule-Thomsonův jev Fyzikální raktikum z molekulové fyziky a termodynamiky Teoretický rozbor Entalie lynu Při Joule-Thomsonově jevu dochází k nevratné exanzi lynů do rostředí s nižším tlakem. Pro ilustraci
Joule-Thomsonův jev Fyzikální raktikum z molekulové fyziky a termodynamiky Teoretický rozbor Entalie lynu Při Joule-Thomsonově jevu dochází k nevratné exanzi lynů do rostředí s nižším tlakem. Pro ilustraci
KATEDRA VOZIDEL A MOTORŮ. Skutečné oběhy PSM #6/14. Karel Páv
 KATEDRA VOZIDEL A MOTORŮ Skutečné oběhy PSM #6/ Karel Pá Stlaitelná kaalina / krit [-] Ideální lyn: = rt (s hybou < %) Důody rozdílů mezi idealizoaným a reálným oběhem Odhylky od idealizae oliňují jak
KATEDRA VOZIDEL A MOTORŮ Skutečné oběhy PSM #6/ Karel Pá Stlaitelná kaalina / krit [-] Ideální lyn: = rt (s hybou < %) Důody rozdílů mezi idealizoaným a reálným oběhem Odhylky od idealizae oliňují jak
Fyzikální chemie. 1.2 Termodynamika
 Fyzikální chemie. ermodynamika Mgr. Sylvie Pavloková Letní semestr 07/08 děj izotermický izobarický izochorický konstantní V ermodynamika rvní termodynamický zákon (zákon zachování energie): U Q + W izotermický
Fyzikální chemie. ermodynamika Mgr. Sylvie Pavloková Letní semestr 07/08 děj izotermický izobarický izochorický konstantní V ermodynamika rvní termodynamický zákon (zákon zachování energie): U Q + W izotermický
Periodicky pracující tepelný stroj využívá pi své innosti uzavený (kruhový) termodynamický proces (cyklus).
 eeé stroje a. vta termodynamiky zorec ro ráci lynu a.vta termodynamiky jasn ukazují možnost konstrukce tzv. teeého stroje, který by využíval dodávané teeé energie ke konání mechanické ráce. Práce stroje
eeé stroje a. vta termodynamiky zorec ro ráci lynu a.vta termodynamiky jasn ukazují možnost konstrukce tzv. teeého stroje, který by využíval dodávané teeé energie ke konání mechanické ráce. Práce stroje
Termodynamické základy ocelářských pochodů
 29 3. Termodynamické základy ocelářských ochodů Termodynamika ůvodně vznikla jako vědní discilína zabývající se účinností teelných (arních) strojů. Později byly termodynamické zákony oužity ři studiu chemických
29 3. Termodynamické základy ocelářských ochodů Termodynamika ůvodně vznikla jako vědní discilína zabývající se účinností teelných (arních) strojů. Později byly termodynamické zákony oužity ři studiu chemických
PZP (2011/2012) 3/1 Stanislav Beroun
 PZP (0/0) 3/ tanislav Beroun Výměna tela mezi nální válce a stěnami, telotní zatížení vybraných dílů PM elo, které se odvádí z nálně válce, se ředává stěnám ve válci řevážně řestuem, u vznětových motorů
PZP (0/0) 3/ tanislav Beroun Výměna tela mezi nální válce a stěnami, telotní zatížení vybraných dílů PM elo, které se odvádí z nálně válce, se ředává stěnám ve válci řevážně řestuem, u vznětových motorů
TERMOMECHANIKA 4. První zákon termodynamiky
 FSI VUT Brně, Energetický ústa Odbor termomechaniky a techniky rostředí rof. Ing. Milan Paelek, CSc. TERMOMECHANIKA 4. Prní zákon termodynamiky OSNOVA 4. KAPITOLY. forma I. zákona termodynamiky Objemoá
FSI VUT Brně, Energetický ústa Odbor termomechaniky a techniky rostředí rof. Ing. Milan Paelek, CSc. TERMOMECHANIKA 4. Prní zákon termodynamiky OSNOVA 4. KAPITOLY. forma I. zákona termodynamiky Objemoá
Obr. V1.1: Schéma přenosu výkonu hnacího vozidla.
 říklad 1 ro dvounáravové hnací kolejové vozidlo motorové trakce s mechanickým řenosem výkonu určené následujícími arametry určete moment hnacích nárav, tažnou sílu na obvodu kol F O. a rychlost ři maximálním
říklad 1 ro dvounáravové hnací kolejové vozidlo motorové trakce s mechanickým řenosem výkonu určené následujícími arametry určete moment hnacích nárav, tažnou sílu na obvodu kol F O. a rychlost ři maximálním
V následující tabulce jsou uvedeny jednotky pro objemový a hmotnostní průtok.
 8. Měření růtoků V následující tabulce jsou uvedeny jednotky ro objemový a hmotnostní růtok. Základní vztahy ro stacionární růtok Q M V t S w M V QV ρ ρ S w ρ t t kde V [ m 3 ] - objem t ( s ] - čas, S
8. Měření růtoků V následující tabulce jsou uvedeny jednotky ro objemový a hmotnostní růtok. Základní vztahy ro stacionární růtok Q M V t S w M V QV ρ ρ S w ρ t t kde V [ m 3 ] - objem t ( s ] - čas, S
Knihovna modelů technologických procesů. Bc. Radim Pišan
 Knihovna modelů tehnologikýh roesů B. Radim Pišan 2007 ABSTRAKT V rái je ředstavena knihovna modelů tehnologikýh roesů, vytvářená v rogramovém rostředí MATLAB-SIMULINK. Tato využívá bloku s-funtion (s-funkí)
Knihovna modelů tehnologikýh roesů B. Radim Pišan 2007 ABSTRAKT V rái je ředstavena knihovna modelů tehnologikýh roesů, vytvářená v rogramovém rostředí MATLAB-SIMULINK. Tato využívá bloku s-funtion (s-funkí)
Teoretické základy vakuové techniky
 Vakuová technika Teoretické základy vakuové techniky tlak plynu tepeln! pohyb molekul st"ední volná dráha molekul proud#ní plynu vakuová vodivost $erpání plyn% ze systém% S klesajícím tlakem se chování
Vakuová technika Teoretické základy vakuové techniky tlak plynu tepeln! pohyb molekul st"ední volná dráha molekul proud#ní plynu vakuová vodivost $erpání plyn% ze systém% S klesajícím tlakem se chování
STRUKTURA A VLASTNOSTI PLYNŮ
 I N E S I C E D O R O Z O J E Z D Ě L Á Á N Í SRUKURA A LASNOSI PLYNŮ. Ideální lyn ředstavuje model ideálního lynu, který často oužíváme k oisu různých dějů. Naříklad ozději ředokládáme, že všechny molekuly
I N E S I C E D O R O Z O J E Z D Ě L Á Á N Í SRUKURA A LASNOSI PLYNŮ. Ideální lyn ředstavuje model ideálního lynu, který často oužíváme k oisu různých dějů. Naříklad ozději ředokládáme, že všechny molekuly
Projekt realizovaný na SPŠ Nové Město nad Metují. s finanční podporou v Operačním programu Vzdělávání pro konkurenceschopnost Královéhradeckého kraje
 Projekt realizoaný na SPŠ Noé Město nad Metují s finanční odorou Oeračním rogramu Vzděláání ro konkurenceschonost Králoéhradeckého kraje ermodynamika Ing. Jan Jemelík Ideální lyn: - ideálně stlačitelná
Projekt realizoaný na SPŠ Noé Město nad Metují s finanční odorou Oeračním rogramu Vzděláání ro konkurenceschonost Králoéhradeckého kraje ermodynamika Ing. Jan Jemelík Ideální lyn: - ideálně stlačitelná
Pednáška mikro 04: Poptávková a nabídková funkce, cenová elasticita poptávky
 Pednáška mikro 04: Potávková a nabídková funkce, cenová elasticita otávk 1. Matematické minimum (dolnit na cviení v íad otávk od student) funkce = edis(druhá odmocnina, dvojnásobek snížený o jednu : =
Pednáška mikro 04: Potávková a nabídková funkce, cenová elasticita otávk 1. Matematické minimum (dolnit na cviení v íad otávk od student) funkce = edis(druhá odmocnina, dvojnásobek snížený o jednu : =
TERMIKA VIII. Joule uv a Thompson uv pokus pro reálné plyny
 TERMIKA VIII Maxwellova rovnovážná rozdělovací funkce rychlostí Joule uv a Thomson uv okus ro reálné lyny 1 Maxwellova rovnovážná rozdělovací funkce rychlostí Maxwellova rychlostní rozdělovací funkce se
TERMIKA VIII Maxwellova rovnovážná rozdělovací funkce rychlostí Joule uv a Thomson uv okus ro reálné lyny 1 Maxwellova rovnovážná rozdělovací funkce rychlostí Maxwellova rychlostní rozdělovací funkce se
Základy teorie vozidel a vozidlových motorů
 Základy teorie vozidel a vozidlových motorů Předmět Základy teorie vozidel a vozidlových motorů (ZM) obsahuje dvě hlavní kaitoly: vozidlové motory a vozidla. Kaitoly o vozidlových motorech ukazují ředevším
Základy teorie vozidel a vozidlových motorů Předmět Základy teorie vozidel a vozidlových motorů (ZM) obsahuje dvě hlavní kaitoly: vozidlové motory a vozidla. Kaitoly o vozidlových motorech ukazují ředevším
Dodatkové příklady k předmětu Termika a Molekulová Fyzika. Dr. Petr Jizba. II. princip termodamický a jeho aplikace
 Dodatkové říklady k ředmětu Termika a Molekulová Fyika Dr Petr Jiba II rinci termodamický a jeho alikace Pfaffovy formy a exaktní diferenciály Příklad 1: Určete která následujících 1-forem je exaktním
Dodatkové říklady k ředmětu Termika a Molekulová Fyika Dr Petr Jiba II rinci termodamický a jeho alikace Pfaffovy formy a exaktní diferenciály Příklad 1: Určete která následujících 1-forem je exaktním
VY_32_INOVACE_G 21 11
 Náze a adresa školy: Střední škola růmysloá a uměleká, Oaa, řísěkoá organizae, Praskoa 99/8, Oaa, 7460 Náze oeračního rogramu: OP Vzděláání ro konkureneshonost, oblast odory.5 Registrační číslo rojektu:
Náze a adresa školy: Střední škola růmysloá a uměleká, Oaa, řísěkoá organizae, Praskoa 99/8, Oaa, 7460 Náze oeračního rogramu: OP Vzděláání ro konkureneshonost, oblast odory.5 Registrační číslo rojektu:
Wankel v, Stirling v motor
 KAEDA OZIDEL A MOO Wanelv, Stirlingv motor #/4 Karel Páv Wanelv motor / 954 Felix Wanel Motor s rotaním triangulárním ístem Charateristia motoru: Excentricý hídel oná otáy na obh (na otáu ístu) Pohyb excentricy
KAEDA OZIDEL A MOO Wanelv, Stirlingv motor #/4 Karel Páv Wanelv motor / 954 Felix Wanel Motor s rotaním triangulárním ístem Charateristia motoru: Excentricý hídel oná otáy na obh (na otáu ístu) Pohyb excentricy
Pokud světlo prochází prostředím, pak v důsledku elektromagnetické interakce s částicemi obsaženými
 1 Pracovní úkoly 1. Změřte závislost indexu lomu vzduchu na tlaku n(). 2. Závislost n() zracujte graficky. Vyneste také závislost závislost vlnové délky sodíkové čáry na indexu lomu vzduchu λ(n). Proveďte
1 Pracovní úkoly 1. Změřte závislost indexu lomu vzduchu na tlaku n(). 2. Závislost n() zracujte graficky. Vyneste také závislost závislost vlnové délky sodíkové čáry na indexu lomu vzduchu λ(n). Proveďte
Statistická analýza dat - Indexní analýza
 Statistiká analýza dat Indexní analýza Statistiká analýza dat - Indexní analýza Index mohou být:. Stejnorodýh ukazatelů. Nestejnorodýh ukazatelů Index se skládají ze dvou složek:... intenzita (úroveň znaku)...
Statistiká analýza dat Indexní analýza Statistiká analýza dat - Indexní analýza Index mohou být:. Stejnorodýh ukazatelů. Nestejnorodýh ukazatelů Index se skládají ze dvou složek:... intenzita (úroveň znaku)...
Dodatkové příklady k předmětu Termika a Molekulová Fyzika. Dr. Petr Jizba. II. princip termodamický a jeho aplikace
 Dodatkové říklady k ředmětu Termika a Molekulová Fyika Dr Petr Jiba II rinci termodamický a jeho alikace Pfaffovy formy a exaktní diferenciály Příklad 1: Určete která následujících 1-forem je exaktním
Dodatkové říklady k ředmětu Termika a Molekulová Fyika Dr Petr Jiba II rinci termodamický a jeho alikace Pfaffovy formy a exaktní diferenciály Příklad 1: Určete která následujících 1-forem je exaktním
7. Měření dutých objemů pomocí komprese plynu a určení Poissonovy konstanty vzduchu Úkol 1: Určete objem skleněné láhve s kohoutem kompresí plynu.
 7. Měření dutých objemů omocí komrese lynu a určení Poissonovy konstanty vzduchu Úkol : Určete objem skleněné láhve s kohoutem komresí lynu. Pomůcky Měřený objem (láhev s kohoutem), seciální lynová byreta
7. Měření dutých objemů omocí komrese lynu a určení Poissonovy konstanty vzduchu Úkol : Určete objem skleněné láhve s kohoutem komresí lynu. Pomůcky Měřený objem (láhev s kohoutem), seciální lynová byreta
Vnitřní odpínače H 27. trojpólové provedení jmenovité napětí 12 a 25 kv jmenovitý proud 630 A
 Vnitřní odínače H 27 trojólové rovedení jmenovité naětí 12 a 25 kv jmenovitý roud 630 A Vnitřní odínače H 27 Odínače jsou určeny ke sínání vn zařízení ve vnitřním rostředí ři normálníh raovníh odmínkáh
Vnitřní odínače H 27 trojólové rovedení jmenovité naětí 12 a 25 kv jmenovitý roud 630 A Vnitřní odínače H 27 Odínače jsou určeny ke sínání vn zařízení ve vnitřním rostředí ři normálníh raovníh odmínkáh
Gibbsova a Helmholtzova energie. Def. Gibbsovy energie G. Def. Helmholtzovy energie A
 ibbsova a Helmholtzova energie Def. ibbsovy energie H Def. Helmholtzovy energie U, jsou efinovány omocí stavových funkcí jená se o stavové funkce. ibbsova energie charakterizuje rovnovážný stav (erzibilní
ibbsova a Helmholtzova energie Def. ibbsovy energie H Def. Helmholtzovy energie U, jsou efinovány omocí stavových funkcí jená se o stavové funkce. ibbsova energie charakterizuje rovnovážný stav (erzibilní
NÁVRH A OVĚŘENÍ BETONOVÉ OPŘENÉ PILOTY ZATÍŽENÉ V HLAVĚ KOMBINACÍ SIL
 NÁVRH A OVĚŘENÍ BETONOVÉ OPŘENÉ PILOTY ZATÍŽENÉ V HLAVĚ KOMBINACÍ SIL 1. ZADÁNÍ Navrhněte růměr a výztuž vrtané iloty délky L neosuvně ořené o skalní odloží zatížené v hlavě zadanými vnitřními silami (viz
NÁVRH A OVĚŘENÍ BETONOVÉ OPŘENÉ PILOTY ZATÍŽENÉ V HLAVĚ KOMBINACÍ SIL 1. ZADÁNÍ Navrhněte růměr a výztuž vrtané iloty délky L neosuvně ořené o skalní odloží zatížené v hlavě zadanými vnitřními silami (viz
22. Mechanické a elektromagnetické kmity
 . Mechanicé a eletroagneticé ity. Mechanicé ity Oscilátor tleso, teré je schoné itat, (itání zsobuje síla ružnosti, nebo tíhová síla, i itání se eriodicy ní otenciální energie oscilátoru v energii ineticou
. Mechanicé a eletroagneticé ity. Mechanicé ity Oscilátor tleso, teré je schoné itat, (itání zsobuje síla ružnosti, nebo tíhová síla, i itání se eriodicy ní otenciální energie oscilátoru v energii ineticou
SOU INITELE V AZENÉHO ODPORU
 VUT V PRAZE, FAKULTA STROJNÍ Studijní obor Inteligentní budovy Exerimentální metody STANOVENÍ SOU INITELE V AZENÉHO ODPORU 2011 VUT V PRAZE Fakulta strojní Ústav techniky rost edí Cíl m ení Cílem m ení
VUT V PRAZE, FAKULTA STROJNÍ Studijní obor Inteligentní budovy Exerimentální metody STANOVENÍ SOU INITELE V AZENÉHO ODPORU 2011 VUT V PRAZE Fakulta strojní Ústav techniky rost edí Cíl m ení Cílem m ení
Mechanická ú innost PSM
 KATEDA OZIDEL A MOTO Mecanická úinnost PSM #/4 Karel Páv Tribologie, souinitel tení / Stribeckova kivka ecí síla: F t sign w f F n Koeficient tení f Hydrodynamické tení Smíšené olosucé tení Sucé mení tení
KATEDA OZIDEL A MOTO Mecanická úinnost PSM #/4 Karel Páv Tribologie, souinitel tení / Stribeckova kivka ecí síla: F t sign w f F n Koeficient tení f Hydrodynamické tení Smíšené olosucé tení Sucé mení tení
FYZIKÁLNÍ SEKCE P írodov decká fakulta Masarykovy univerzity v Brn KORESPONDEN NÍ SEMINÁ Z FYZIKY 8. ro ník μ 2001/2002 Vzorová e ení druhé série úloh
 FYZIKÁLNÍ SEKCE P írodov decká fakulta Masarykovy univerzity v Brn KOESPONDEN NÍ SEMINÁ Z FYZIKY 8. ro ník μ 001/00 Vzorová e ení druhé série úloh (5 bod ) Vzorové e ení úlohy. 1 (4 body) Kniha na válci
FYZIKÁLNÍ SEKCE P írodov decká fakulta Masarykovy univerzity v Brn KOESPONDEN NÍ SEMINÁ Z FYZIKY 8. ro ník μ 001/00 Vzorová e ení druhé série úloh (5 bod ) Vzorové e ení úlohy. 1 (4 body) Kniha na válci
Výpočty za použití zákonů pro ideální plyn
 ýočty za oužití zákonů ro ideální lyn Látka v lynné stavu je tvořena volnýi atoy(onoatoickýi olekulai), ionty nebo olekulai. Ideální lyn- olekuly na sebe neůsobí žádnýi silai, jejich obje je ve srovnání
ýočty za oužití zákonů ro ideální lyn Látka v lynné stavu je tvořena volnýi atoy(onoatoickýi olekulai), ionty nebo olekulai. Ideální lyn- olekuly na sebe neůsobí žádnýi silai, jejich obje je ve srovnání
2.6.7 Fázový diagram. Předpoklady: Popiš děje zakreslené v diagramu křivky syté páry. Za jakých podmínek mohou proběhnout?
 2.6.7 Fázový diagram Předoklady: 2606 Př. 1: Poiš děje zakreslené v diagramu křivky syté áry. Za jakých odmínek mohou roběhnout? 4 2 1 3 1) Sytá ára je za stálého tlaku zahřívána. Zvětšuje svůj objem a
2.6.7 Fázový diagram Předoklady: 2606 Př. 1: Poiš děje zakreslené v diagramu křivky syté áry. Za jakých odmínek mohou roběhnout? 4 2 1 3 1) Sytá ára je za stálého tlaku zahřívána. Zvětšuje svůj objem a
ení na modelu vedení nn (Distribuce Elektrické Energie - BDEE)
 FAKULTA ELEKTROTECHNIKY A KOMUNIKANÍCH TECHNOLOGIÍ VYSOKÉ UENÍ TECHNICKÉ V BRN ení na modelu vedení nn (Dstrbuce Elektrcké Energe - BDEE) Autor textu: Ing. Martn Paar, Ph.D. Ing. Jan Varmuža Kvten 2013
FAKULTA ELEKTROTECHNIKY A KOMUNIKANÍCH TECHNOLOGIÍ VYSOKÉ UENÍ TECHNICKÉ V BRN ení na modelu vedení nn (Dstrbuce Elektrcké Energe - BDEE) Autor textu: Ing. Martn Paar, Ph.D. Ing. Jan Varmuža Kvten 2013
KRUHOVÝ DĚJ S IDEÁLNÍM PLYNEM. Studijní text pro řešitele FO a ostatní zájemce o fyziku. Přemysl Šedivý. 1 Základní pojmy 2
 Obsah KRUHOÝ DĚJ S IDEÁLNÍM PLYNEM Studijní text ro řešitele FO a ostatní zájemce o fyziku Přemysl Šedivý Základní ojmy ztahy užívané ři oisu kruhových dějů s ideálním lynem Přehled základních dějů v ideálním
Obsah KRUHOÝ DĚJ S IDEÁLNÍM PLYNEM Studijní text ro řešitele FO a ostatní zájemce o fyziku Přemysl Šedivý Základní ojmy ztahy užívané ři oisu kruhových dějů s ideálním lynem Přehled základních dějů v ideálním
( ) ( ) Tepelný oběh s plynovou turbínou. Zjednodušující předpoklady: ideální (vratné) termodynamické změny. Tepelná účinnost oběhu: ( ) T T.
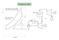 Parolynové oběy eelný obě s lynovou turbínou Zjednodušující ředoklady: v s td K td g m ideální (vratné) termodynamické změny ( ) ( ) ( ) ( ) ( ) ( ) 3 4 3 3 4 3 c c c Q Q Q v v v o t eelná účinnost oběu:
Parolynové oběy eelný obě s lynovou turbínou Zjednodušující ředoklady: v s td K td g m ideální (vratné) termodynamické změny ( ) ( ) ( ) ( ) ( ) ( ) 3 4 3 3 4 3 c c c Q Q Q v v v o t eelná účinnost oběu:
Příklady k přednášce 1. Úvod
 Příklady k řednáše. Úvod Mihael Šebek Automatiké řízení 06 Evroský soiální fond Praha & EU: Investujeme do vaší budounosti --6 Kyvadlo řízené momentem Automatiké řízení - Kybernetika a robotika Pohybová
Příklady k řednáše. Úvod Mihael Šebek Automatiké řízení 06 Evroský soiální fond Praha & EU: Investujeme do vaší budounosti --6 Kyvadlo řízené momentem Automatiké řízení - Kybernetika a robotika Pohybová
Tepelně technické posouzení plochých střešních konstrukcí a jejich návrh se započítáním vlivu vlhkosti materiálů
 Státní doktorská zkouška Pojednání: Teelně technické osouzení lochých střešních konstrukcí a jejich návrh se zaočítáním vlivu vlhkosti materiálů Vyracoval: Ing. Ondřej Fuciman Vědní obor: 36-06-9 Teorie
Státní doktorská zkouška Pojednání: Teelně technické osouzení lochých střešních konstrukcí a jejich návrh se zaočítáním vlivu vlhkosti materiálů Vyracoval: Ing. Ondřej Fuciman Vědní obor: 36-06-9 Teorie
CVIČENÍ 1 - část 3: PROVOZNÍ STAVY VZDUCHOTECHNICKÉ JEDNOTKY
 CVIČENÍ 1 - část 3: PROVOZNÍ STAVY VZDUCHOTECHNICKÉ JEDNOTKY Na úvod řehled Jak vyočítat množství řiváděného vzduchu - ouze řiomenutí a ár dolňkových informací Množství řiváděného vzduchu V : Standardně:
CVIČENÍ 1 - část 3: PROVOZNÍ STAVY VZDUCHOTECHNICKÉ JEDNOTKY Na úvod řehled Jak vyočítat množství řiváděného vzduchu - ouze řiomenutí a ár dolňkových informací Množství řiváděného vzduchu V : Standardně:
Příklady k přednášce 1. Úvod
 Příklady k řednáše. Úvod Mihael Šebek Automatiké řízení 05 Evroský soiální fond Praha & EU: Investujeme do vaší budounosti 6--5 Kyvadlo řízené momentem Automatiké řízení - Kybernetika a robotika Pohybová
Příklady k řednáše. Úvod Mihael Šebek Automatiké řízení 05 Evroský soiální fond Praha & EU: Investujeme do vaší budounosti 6--5 Kyvadlo řízené momentem Automatiké řízení - Kybernetika a robotika Pohybová
Laplaceova transformace.
 Lalaceova transformace - studijní text ro cvičení v ředmětu Matematika -. Studijní materiál byl řiraven racovníky katedry E. Novákovou, M. Hyánkovou a L. Průchou za odory grantu IG ČVUT č. 300043 a v rámci
Lalaceova transformace - studijní text ro cvičení v ředmětu Matematika -. Studijní materiál byl řiraven racovníky katedry E. Novákovou, M. Hyánkovou a L. Průchou za odory grantu IG ČVUT č. 300043 a v rámci
1. Ukazatele primární: - jsou přímo zjišťované, neodvozené - např. stav zásob, počet pracovníků k 31. 12., atd.
 SROVNÁVÁNÍ HODNOT STATSTCÝCH UKAZATELŮ - oisem a analýzou ekonomikýh jevů a roesů omoí statistikýh ukazatelů se zabývá hosodářská statistika - ílem je nalézt zůsoby měření ekonomiké skutečnosti (ve formě
SROVNÁVÁNÍ HODNOT STATSTCÝCH UKAZATELŮ - oisem a analýzou ekonomikýh jevů a roesů omoí statistikýh ukazatelů se zabývá hosodářská statistika - ílem je nalézt zůsoby měření ekonomiké skutečnosti (ve formě
Numerická integrace konstitučních vztahů
 Numercká ntegrace konsttučních vztahů Po výočtu neznámých deformačních uzlových arametrů v každé terac NR metody je nutné stanovt naětí a deformace na rvcích. Nař. Jednoosý tah (vz obr. vravo) Pro nterval
Numercká ntegrace konsttučních vztahů Po výočtu neznámých deformačních uzlových arametrů v každé terac NR metody je nutné stanovt naětí a deformace na rvcích. Nař. Jednoosý tah (vz obr. vravo) Pro nterval
Teplovzdušné motory motory budoucnosti
 Vysoká škola báňská Technická univerzita Ostrava Fakulta strojní Katedra energetiky Telovzdušné motory motory budoucnosti Text byl vyracován s odorou rojektu CZ.1.07/1.1.00/08.0010 Inovace odborného vzdělávání
Vysoká škola báňská Technická univerzita Ostrava Fakulta strojní Katedra energetiky Telovzdušné motory motory budoucnosti Text byl vyracován s odorou rojektu CZ.1.07/1.1.00/08.0010 Inovace odborného vzdělávání
Termodynamika pro +EE1 a PEE
 ermodynamika ro +EE a PEE Literatura: htt://home.zcu.cz/~nohac/vyuka.htm#ee [0] Zakladni omocny text rednasek Doc. Schejbala [] Pomocne texty ke cviceni [] Prednaska cislo 7 - Zaklady termodynamiky [3]
ermodynamika ro +EE a PEE Literatura: htt://home.zcu.cz/~nohac/vyuka.htm#ee [0] Zakladni omocny text rednasek Doc. Schejbala [] Pomocne texty ke cviceni [] Prednaska cislo 7 - Zaklady termodynamiky [3]
III. Základy termodynamiky
 III. Základy termodynamiky 3. ermodynamika FS ČU v Praze 3. Základy termodynamiky 3. Úvod 3. Základní ojmy 3.3 Základní ostuláty 3.4 Další termodynamické funkce volná energie a volná entalie 3.5 Kritérium
III. Základy termodynamiky 3. ermodynamika FS ČU v Praze 3. Základy termodynamiky 3. Úvod 3. Základní ojmy 3.3 Základní ostuláty 3.4 Další termodynamické funkce volná energie a volná entalie 3.5 Kritérium
Úloha č.1: Stanovení Jouleova-Thomsonova koeficientu reálného plynu - statistické zpracování dat
 Úloha č.1: Stanovení Jouleova-Thomsonova koeficientu reálného lynu - statistické zracování dat Teorie Tam, kde se racuje se stlačenými lyny, je možné ozorovat zajímavý jev. Jestliže se do nádoby, kde je
Úloha č.1: Stanovení Jouleova-Thomsonova koeficientu reálného lynu - statistické zracování dat Teorie Tam, kde se racuje se stlačenými lyny, je možné ozorovat zajímavý jev. Jestliže se do nádoby, kde je
7 VYBRANÁ ROZDLENÍ SPOJITÉ NÁHODNÉ VELIINY
 7 VYBRANÁ ROZDLENÍ SPOJITÉ NÁHODNÉ VELIINY Pro nezáornou náhodnou veliinu X se sojitým rozdlením definujeme ro F(t) 1 (tj. F(t)
7 VYBRANÁ ROZDLENÍ SPOJITÉ NÁHODNÉ VELIINY Pro nezáornou náhodnou veliinu X se sojitým rozdlením definujeme ro F(t) 1 (tj. F(t)
Základní parametry PSM
 KAEDRA VOZIDEL A MOOR Základní arametry PSM #/14 Karel Páv Konstrukní Základní arametry PSM / 14 Prr válce D mm Zdvi Z mm Polomr zalomení kliky r Z / mm Vyosení ístnío eu e mm Vyosení kliky e k mm Délka
KAEDRA VOZIDEL A MOOR Základní arametry PSM #/14 Karel Páv Konstrukní Základní arametry PSM / 14 Prr válce D mm Zdvi Z mm Polomr zalomení kliky r Z / mm Vyosení ístnío eu e mm Vyosení kliky e k mm Délka
II. MOLEKULOVÁ FYZIKA 1. Základy termodynamiky IV
 II. MOLEKLOÁ FYZIKA 1. Základy termodynamiky I 1 Obsah Princi maxima entroie. Minimum vnitřní energie. D otenciály vnitřní energie entalie volná energie a Gibbsova energie a jejich názorný význam ři některých
II. MOLEKLOÁ FYZIKA 1. Základy termodynamiky I 1 Obsah Princi maxima entroie. Minimum vnitřní energie. D otenciály vnitřní energie entalie volná energie a Gibbsova energie a jejich názorný význam ři některých
3. Dynamika. Obecné odvození: a ~ F a ~ m. Zrychlení je přímo úměrné F a nepřímo úměrné m. 3. 2. 1 Výpočet síly a stanovení jednotky newton. F = m.
 3. Dynamika Zabývá se říčinou ohybu (jak vzniká a jak se udržuje). Vše se odehrávalo na základě řesných okusů, vše shrnul Isac Newton v díle Matematické základy fyziky. Z díla vylývají 3 ohybové zákony.
3. Dynamika Zabývá se říčinou ohybu (jak vzniká a jak se udržuje). Vše se odehrávalo na základě řesných okusů, vše shrnul Isac Newton v díle Matematické základy fyziky. Z díla vylývají 3 ohybové zákony.
Zjednodušený návrh plnícího systému přeplňovaného vznětového motoru III
 Zjednodušený návrh lnícího systéu řelňovaného vznětového otoru III Zadání: e = 300 kw (ři n = 000 1/in) D = 115 Z = 135 Výočet: lnicí systé s dvoustuňový stlačování oocí BD a chladiči lnicího vzduchu:
Zjednodušený návrh lnícího systéu řelňovaného vznětového otoru III Zadání: e = 300 kw (ři n = 000 1/in) D = 115 Z = 135 Výočet: lnicí systé s dvoustuňový stlačování oocí BD a chladiči lnicího vzduchu:
Úloha č. 4 Kapacitní posouzení neřízené průsečné úrovňové křižovatky
 Úloha č. 4 Kaacitní osouzení neřízené růsečné úrovňové křižovatky Pro zjednodušení budeme v úloze očítat s narosto symetrickým zatížením křižovatky, které by v raxi nastalo zřídka. Jelikož zatížení je
Úloha č. 4 Kaacitní osouzení neřízené růsečné úrovňové křižovatky Pro zjednodušení budeme v úloze očítat s narosto symetrickým zatížením křižovatky, které by v raxi nastalo zřídka. Jelikož zatížení je
HYDROPNEUMATICKÝ VAKOVÝ AKUMULÁTOR
 HYDROPNEUMATICKÝ AKOÝ AKUMULÁTOR OSP 050 ŠEOBECNÉ INFORMACE ýočet hydroneumatického akumulátoru ZÁKLADNÍ INFORMACE Při výočtu hydroneumatického akumulátoru se vychází ze stavové změny lynu v akumulátoru.
HYDROPNEUMATICKÝ AKOÝ AKUMULÁTOR OSP 050 ŠEOBECNÉ INFORMACE ýočet hydroneumatického akumulátoru ZÁKLADNÍ INFORMACE Při výočtu hydroneumatického akumulátoru se vychází ze stavové změny lynu v akumulátoru.
Oddělení technické elektrochemie, A037. LABORATORNÍ PRÁCE č.9 CYKLICKÁ VOLTAMETRIE
 ÚSTV NORGNIKÉ THNOLOGI Oddělení technické elektrochemie, 037 LBORTORNÍ PRÁ č.9 YKLIKÁ VOLTMTRI yklická voltametrie yklická voltametrie atří do skuiny otenciodynamických exerimentálních metod. Ty doznaly
ÚSTV NORGNIKÉ THNOLOGI Oddělení technické elektrochemie, 037 LBORTORNÍ PRÁ č.9 YKLIKÁ VOLTMTRI yklická voltametrie yklická voltametrie atří do skuiny otenciodynamických exerimentálních metod. Ty doznaly
Poznámky k cvičením z termomechaniky Cvičení 3.
 Vnitřní energie U Vnitřní energie U je stavová veličina U = U (p, V, T), ale závisí pouze na teplotě (experiment Gay-Lussac / Joule) U = f(t) Pro měrnou vnitřní energii (tedy pro vnitřní energii jednoho
Vnitřní energie U Vnitřní energie U je stavová veličina U = U (p, V, T), ale závisí pouze na teplotě (experiment Gay-Lussac / Joule) U = f(t) Pro měrnou vnitřní energii (tedy pro vnitřní energii jednoho
Kvantová a statistická fyzika 2 (Termodynamika a statistická fyzika)
 Kvantová a statistická fyzika 2 (ermodynamika a statistická fyzika) ermodynamika ermodynamika se zabývá zkoumáním obecných vlastností makroskoických systémů v rovnováze, zákonitostmi makroskoických rocesů,
Kvantová a statistická fyzika 2 (ermodynamika a statistická fyzika) ermodynamika ermodynamika se zabývá zkoumáním obecných vlastností makroskoických systémů v rovnováze, zákonitostmi makroskoických rocesů,
2.3.6 Práce plynu. Předpoklady: 2305
 .3.6 Práce lynu Předoklady: 305 Děje v lynech nejčastěji zobrazujeme omocí diagramů grafů závislosti tlaku na objemu. Na x-ovou osu vynášíme objem a na y-ovou osu tlak. Př. : Na obrázku je nakreslen diagram
.3.6 Práce lynu Předoklady: 305 Děje v lynech nejčastěji zobrazujeme omocí diagramů grafů závislosti tlaku na objemu. Na x-ovou osu vynášíme objem a na y-ovou osu tlak. Př. : Na obrázku je nakreslen diagram
dq T dq ds = definice entropie T Entropie Pi pohledu na Clausiv integrál pro vratné cykly :
 Entropie Pi pohledu na Clausiv integrál pro vratné cykly : si díve i pozdji jist uvdomíme, že nulová hodnota integrálu njaké veliiny pi kruhovém termodynamickém procesu je základním znakem toho, že se
Entropie Pi pohledu na Clausiv integrál pro vratné cykly : si díve i pozdji jist uvdomíme, že nulová hodnota integrálu njaké veliiny pi kruhovém termodynamickém procesu je základním znakem toho, že se
Kruhový děj s plynem
 .. Kruhový děj s lynem Předoklady: 0 Chceme využít skutečnost, že lyn koná ři rozínání ráci, na konstrukci motoru. Nejjednodušší možnost: Pustíme nafouknutý balónek. Balónek se vyfukuje, vytlačuje vzduch
.. Kruhový děj s lynem Předoklady: 0 Chceme využít skutečnost, že lyn koná ři rozínání ráci, na konstrukci motoru. Nejjednodušší možnost: Pustíme nafouknutý balónek. Balónek se vyfukuje, vytlačuje vzduch
PROCESY V TECHNICE BUDOV cvičení 1, 2
 UNIVERZITA TOMÁŠE BATI VE ZLÍNĚ AKULTA APLIKOVANÉ INORMATIKY PROCESY V TECHNICE BUDOV cvičení, část Hana Charvátová, Dagmar Janáčová Zlín 03 Tento studijní materiál vznikl za finanční odory Evroského sociálního
UNIVERZITA TOMÁŠE BATI VE ZLÍNĚ AKULTA APLIKOVANÉ INORMATIKY PROCESY V TECHNICE BUDOV cvičení, část Hana Charvátová, Dagmar Janáčová Zlín 03 Tento studijní materiál vznikl za finanční odory Evroského sociálního
Stabilita prutu, desky a válce vzpěr (osová síla)
 Stabilita rutu, deky a válce vzěr (oová íla) Průběh ro ideálně římý rut (teoretický tav) F δ F KRIT Průběh ro reálně římý rut (reálný tav) 1 - menší očáteční zakřivení - větší očáteční zakřivení F Obr.1
Stabilita rutu, deky a válce vzěr (oová íla) Průběh ro ideálně římý rut (teoretický tav) F δ F KRIT Průběh ro reálně římý rut (reálný tav) 1 - menší očáteční zakřivení - větší očáteční zakřivení F Obr.1
EKONOMETRIE 4. přednáška Modely chování spotřebitele
 EKONOMETRIE 4. řednáška Modely chování sotřebitele Rozočtové omezení Sotřebitel ři svém rozhodování resektuje tzv. rozočtové omezení x + x y, kde x i množství i-té sotřební komodity, i cena i-té sotřební
EKONOMETRIE 4. řednáška Modely chování sotřebitele Rozočtové omezení Sotřebitel ři svém rozhodování resektuje tzv. rozočtové omezení x + x y, kde x i množství i-té sotřební komodity, i cena i-té sotřební
Pravdpodobnost výskytu náhodné veliiny na njakém intervalu urujeme na základ tchto vztah: f(x)
 NÁHODNÁ VELIINA Náhodná veliina je veliina, jejíž hodnota je jednoznan urena výsledkem náhodného pokusu (je-li tento výsledek dán reálným íslem). Jde o reálnou funkci definovanou na základním prostoru
NÁHODNÁ VELIINA Náhodná veliina je veliina, jejíž hodnota je jednoznan urena výsledkem náhodného pokusu (je-li tento výsledek dán reálným íslem). Jde o reálnou funkci definovanou na základním prostoru
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ APLIKOVANÁ FYZIKA MODUL 2 TERMODYNAMIKA
 YSOKÉ UČENÍ ECHNICKÉ BRNĚ FAKULA SAEBNÍ PAEL SCHAUER APLIKOANÁ FYZIKA MODUL ERMODYNAMIKA SUDIJNÍ OPORY PRO SUDIJNÍ PROGRAMY S KOMBINOANOU FORMOU SUDIA Recenzoval: Prof. RNDr. omáš Ficker, CSc. Pavel Schauer,
YSOKÉ UČENÍ ECHNICKÉ BRNĚ FAKULA SAEBNÍ PAEL SCHAUER APLIKOANÁ FYZIKA MODUL ERMODYNAMIKA SUDIJNÍ OPORY PRO SUDIJNÍ PROGRAMY S KOMBINOANOU FORMOU SUDIA Recenzoval: Prof. RNDr. omáš Ficker, CSc. Pavel Schauer,
Cvičení z termodynamiky a statistické fyziky
 Cvičení z termodynamiky a statistické fyziky 1 Matematické základy 1 Parciální derivace Necht F(x,y = xe x2 +y 2 Sočtěte F x, F y, 2 Úlný diferenciál I Bud 2 F x 2, 2 F x y, dω = A(x,ydx + B(x,ydy 2 F
Cvičení z termodynamiky a statistické fyziky 1 Matematické základy 1 Parciální derivace Necht F(x,y = xe x2 +y 2 Sočtěte F x, F y, 2 Úlný diferenciál I Bud 2 F x 2, 2 F x y, dω = A(x,ydx + B(x,ydy 2 F
Úvěr a úvěrové výpočty 1
 Modely analýzy a syntézy lánů MAF/KIV) Přednáška 8 Úvěr a úvěrové výočty 1 1 Rovnice úvěru V minulých řednáškách byla ro stav dluhu oužívána rovnice 1), kde ředokládáme, že N > : d = a b + = k > N. d./
Modely analýzy a syntézy lánů MAF/KIV) Přednáška 8 Úvěr a úvěrové výočty 1 1 Rovnice úvěru V minulých řednáškách byla ro stav dluhu oužívána rovnice 1), kde ředokládáme, že N > : d = a b + = k > N. d./
TROJFÁZOVÝ OBVOD SE SPOT EBI EM ZAPOJENÝM DO HV ZDY A DO TROJÚHELNÍKU
 TROJFÁZOVÝ OBVOD E POT EBI EM ZAPOJENÝM DO HV ZDY A DO TROJÚHELNÍKU Návod do m ení Ing. Vít zslav týskala, Ing. Václav Kolá Únor 2000 poslední úprava leden 2014 1 M ení v trojázových obvodech Cíl m ení:
TROJFÁZOVÝ OBVOD E POT EBI EM ZAPOJENÝM DO HV ZDY A DO TROJÚHELNÍKU Návod do m ení Ing. Vít zslav týskala, Ing. Václav Kolá Únor 2000 poslední úprava leden 2014 1 M ení v trojázových obvodech Cíl m ení:
Jak prochází světlo soustavou částečně propustných zrcadel?
 Jak rochází světlo soustavou částečně roustných zrcadel? Když světlo rochází oloroustným zrcadlem, olovina světla rojde a olovina se odrazí. Co se však stane, když takových zrcadel máme víc za sebou a
Jak rochází světlo soustavou částečně roustných zrcadel? Když světlo rochází oloroustným zrcadlem, olovina světla rojde a olovina se odrazí. Co se však stane, když takových zrcadel máme víc za sebou a
1. série. Různá čísla < 1 44.
 série Téma: Termínodeslání: Různá čísla ½ º Ò ½ ½º ÐÓ je řirozené q9+9 q 6+ 9 9 6 ¾º ÐÓ `5+ 6 998 není řirozené º ÐÓ Nechť c je řirozené číslo Rozhodněte, které z čísel c+ c a c c je větší a své tvrzení
série Téma: Termínodeslání: Různá čísla ½ º Ò ½ ½º ÐÓ je řirozené q9+9 q 6+ 9 9 6 ¾º ÐÓ `5+ 6 998 není řirozené º ÐÓ Nechť c je řirozené číslo Rozhodněte, které z čísel c+ c a c c je větší a své tvrzení
Základy elektrických pohonů, oteplování,ochlazování motorů
 Základy elektrických ohonů, otelování,ochlazování motorů Určeno ro studenty kombinované formy FS, ředmětu Elektrotechnika II an Dudek únor 2007 Elektrický ohon Definice (dle ČSN 34 5170): Elektrický ohon
Základy elektrických ohonů, otelování,ochlazování motorů Určeno ro studenty kombinované formy FS, ředmětu Elektrotechnika II an Dudek únor 2007 Elektrický ohon Definice (dle ČSN 34 5170): Elektrický ohon
2.6.6 Sytá pára. Předpoklady: 2604
 .6.6 Sytá ára Předolady: 604 Oaování: aaliny se vyařují za aždé teloty. Nejrychlejší částice uniají z aaliny a stává se z nich ára. Do isy nalijee vodu voda se ostuně vyařuje naonec zůstane isa rázdná,
.6.6 Sytá ára Předolady: 604 Oaování: aaliny se vyařují za aždé teloty. Nejrychlejší částice uniají z aaliny a stává se z nich ára. Do isy nalijee vodu voda se ostuně vyařuje naonec zůstane isa rázdná,
KATEDRA VOZIDEL A MOTOR. epl ování PSM #12/14. Karel Páv
 AEDRA VOZIDEL A MOOR elování M #/4 arel áv vody elování M / 7 Zvýšení hmotnotního nalnní vále ílem zvýšení tedního efektvního tlaku motoru (Downzng. Zvýšení elkové únnot motoru. elk m meh. z. Vntní tvorba
AEDRA VOZIDEL A MOOR elování M #/4 arel áv vody elování M / 7 Zvýšení hmotnotního nalnní vále ílem zvýšení tedního efektvního tlaku motoru (Downzng. Zvýšení elkové únnot motoru. elk m meh. z. Vntní tvorba
VLHKÝ VZDUCH STAVOVÉ VELIČINY
 VLHKÝ VZDUCH STAVOVÉ VELIČINY Vlhký vzduch - vlhký vzduch je směsí suchého vzduchu a vodní áry okuující solečný objem - homogenní směs nastává okud je voda ve směsi v lynném stavu - heterogenní směs ve
VLHKÝ VZDUCH STAVOVÉ VELIČINY Vlhký vzduch - vlhký vzduch je směsí suchého vzduchu a vodní áry okuující solečný objem - homogenní směs nastává okud je voda ve směsi v lynném stavu - heterogenní směs ve
Analytická metoda aneb Využití vektorů v geometrii
 KM/GVS Geometrické vidění světa (Design) nalytická metoda aneb Využití vektorů v geometrii Použité značky a symboly R, C, Z obor reálných, komleních, celých čísel geometrický vektor R n aritmetický vektor
KM/GVS Geometrické vidění světa (Design) nalytická metoda aneb Využití vektorů v geometrii Použité značky a symboly R, C, Z obor reálných, komleních, celých čísel geometrický vektor R n aritmetický vektor
Stavová rovnice. Ve stavu termodynamické rovnováhy termodynamicky homogenní soustavy jsou všechny vnitřní parametry Y i
 ermodynamický ostulát: Stavová rovnice e stavu termodynamické rovnováhy termodynamicky homogenní soustavy jsou všechny vnitřní arametry Y i určeny jako funkce všech vnějších arametrů X j a teloty Y i f
ermodynamický ostulát: Stavová rovnice e stavu termodynamické rovnováhy termodynamicky homogenní soustavy jsou všechny vnitřní arametry Y i určeny jako funkce všech vnějších arametrů X j a teloty Y i f
Pomoc v nouzi. (m B je hmotnost rozpouštědla v gramech)
 Pomo v nouz m / M n n n n n.. B B x m n g 000 mol kg M mb 0 m B (g mol ) (0 g) mb mb. n M n M m m B B B W B (m B je hmotnot rozouštědla v grameh).4 000 000 n 000 n n M V M V V M m ( ) 0 m m roztok mol
Pomo v nouz m / M n n n n n.. B B x m n g 000 mol kg M mb 0 m B (g mol ) (0 g) mb mb. n M n M m m B B B W B (m B je hmotnot rozouštědla v grameh).4 000 000 n 000 n n M V M V V M m ( ) 0 m m roztok mol
Termomechanika 8. přednáška Doc. Dr. RNDr. Miroslav Holeček
 Termomechanika 8. přednáška Doc. Dr. RNDr. Miroslav Holeček Upozornění: Tato prezentace slouží výhradně pro výukové účely Fakulty strojní Západočeské univerzity v Plzni. Byla sestavena autorem s využitím
Termomechanika 8. přednáška Doc. Dr. RNDr. Miroslav Holeček Upozornění: Tato prezentace slouží výhradně pro výukové účely Fakulty strojní Západočeské univerzity v Plzni. Byla sestavena autorem s využitím
Listopad Ing.Karel Páv,Ph.D.
 Základy -D modelování PSM Lstoad Ing.Karel Páv,Ph.D. Důvody ro modelování oběhu PSM / 7 [bar] 5 5 5 smulae měření Možnost redke oběhu ještě nevyrobeného motoru. Možnost sledování vlvu různýh arametrů,
Základy -D modelování PSM Lstoad Ing.Karel Páv,Ph.D. Důvody ro modelování oběhu PSM / 7 [bar] 5 5 5 smulae měření Možnost redke oběhu ještě nevyrobeného motoru. Možnost sledování vlvu různýh arametrů,
03 Návrh pojistného a zabezpečovacího zařízení
 03 Návrh ojistného a zabezečovacího zařízení Roman Vavřička ČVUT v raze, Fakulta strojní Ústav techniky rostředí 1/14 htt://ut.fs.cvut.cz Roman.Vavricka@fs.cvut.cz ojistné zařízení chrání zdroj tela roti
03 Návrh ojistného a zabezečovacího zařízení Roman Vavřička ČVUT v raze, Fakulta strojní Ústav techniky rostředí 1/14 htt://ut.fs.cvut.cz Roman.Vavricka@fs.cvut.cz ojistné zařízení chrání zdroj tela roti
M ENÍ PR TOKU VZDUCHU
 VUT V PRAZE, FAKULTA STROJNÍ Studijní obor Inteligentní budovy Exerimentální metody M ENÍ PR TOKU VZDUCHU SONDÁ Í RYCHLOSTNÍHO PROFILU PRANDTLOVOU SONDOU 2011 VUT V PRAZE Fakulta strojní Ústav techniky
VUT V PRAZE, FAKULTA STROJNÍ Studijní obor Inteligentní budovy Exerimentální metody M ENÍ PR TOKU VZDUCHU SONDÁ Í RYCHLOSTNÍHO PROFILU PRANDTLOVOU SONDOU 2011 VUT V PRAZE Fakulta strojní Ústav techniky
Dynamické programování
 ALG Dynamické rogramování Nejdelší rostoucí odoslounost Otimální ořadí násobení matic Nejdelší rostoucí odoslounost Z dané oslounosti vyberte co nejdelší rostoucí odoslounost. 5 4 9 5 8 6 7 Řešení: 4 5
ALG Dynamické rogramování Nejdelší rostoucí odoslounost Otimální ořadí násobení matic Nejdelší rostoucí odoslounost Z dané oslounosti vyberte co nejdelší rostoucí odoslounost. 5 4 9 5 8 6 7 Řešení: 4 5
1. Úkol. 2. Teorie. Fyzikální základy techniky
 Fyzikálí základy tehiky Protokol č.: Náze: Staoeí olytroikého exoetu a idikátoroého diagramu komresoru yraoáo de: 5..007 yraoali: Roma Stae, Odřej Soboda, Sabia Zoroá, Marti Smažil. Úkol Naším úkolem bylo
Fyzikálí základy tehiky Protokol č.: Náze: Staoeí olytroikého exoetu a idikátoroého diagramu komresoru yraoáo de: 5..007 yraoali: Roma Stae, Odřej Soboda, Sabia Zoroá, Marti Smažil. Úkol Naším úkolem bylo
TERMOMECHANIKA 12. Cykly tepelných motorů
 FSI U v Brně, Energetický útav Odbor termomechaniky a techniky rotředí rof. Ing. Milan Pavelek, Sc. ERMOMEHANIKA. ykly teelných motorů OSNOA. KAPIOLY Přehled cyklů teelných motorů ykly alovacích motorů
FSI U v Brně, Energetický útav Odbor termomechaniky a techniky rotředí rof. Ing. Milan Pavelek, Sc. ERMOMEHANIKA. ykly teelných motorů OSNOA. KAPIOLY Přehled cyklů teelných motorů ykly alovacích motorů
, kde J [mol.m -2.s -1 ] je difuzní tok, D [m 2.s -1 ] je celkový
![, kde J [mol.m -2.s -1 ] je difuzní tok, D [m 2.s -1 ] je celkový , kde J [mol.m -2.s -1 ] je difuzní tok, D [m 2.s -1 ] je celkový](/thumbs/62/46575607.jpg) FM / DIFUZE I. I. a II. FICKŮV ZÁKON Jméno: St. sk.: Datum: Autor vičení: Ing. Eva Novotná, Ph.D., 4enov@seznam.z Potřebné moudro : Cílem vičení je vytvořit reálný pohled na důležitost, mnohotvárnost a
FM / DIFUZE I. I. a II. FICKŮV ZÁKON Jméno: St. sk.: Datum: Autor vičení: Ing. Eva Novotná, Ph.D., 4enov@seznam.z Potřebné moudro : Cílem vičení je vytvořit reálný pohled na důležitost, mnohotvárnost a
PRŮTOK PLYNU OTVOREM
 PRŮTOK PLYNU OTVOREM P. Škrabánek, F. Dušek Univerzita Pardubice, Fakulta chemicko technologická Katedra řízení rocesů a výočetní techniky Abstrakt Článek se zabývá ověřením oužitelnosti Saint Vénantovavy
PRŮTOK PLYNU OTVOREM P. Škrabánek, F. Dušek Univerzita Pardubice, Fakulta chemicko technologická Katedra řízení rocesů a výočetní techniky Abstrakt Článek se zabývá ověřením oužitelnosti Saint Vénantovavy
IDEÁLNÍ PLYN II. Prof. RNDr. Emanuel Svoboda, CSc.
 IDEÁLNÍ PLYN II Prof. RNDr. Eanuel Svoboa, Sc. ZÁKLADNÍ RONIE PRO LAK IP F ýchoisko efinice tlaku vztahe S Náoba tvaru krychle, stejná rychlost olekul všei sěry (olekulární chaos, všechny sěry stejně ravěoobné)
IDEÁLNÍ PLYN II Prof. RNDr. Eanuel Svoboa, Sc. ZÁKLADNÍ RONIE PRO LAK IP F ýchoisko efinice tlaku vztahe S Náoba tvaru krychle, stejná rychlost olekul všei sěry (olekulární chaos, všechny sěry stejně ravěoobné)
Obr. 1: Řez masivním průřezem z RD zasaženým účinkům požáru
 Teorie: Dřevo a materiály na bázi dřeva jsou sloučeninami uhlíku, kyslíku, vodíku a dalších rvků řírodního ůvodu. Jedná se o hořlavé materiály, jejichž hořlavost lze do jisté míry omezit ovrchovou úravou,
Teorie: Dřevo a materiály na bázi dřeva jsou sloučeninami uhlíku, kyslíku, vodíku a dalších rvků řírodního ůvodu. Jedná se o hořlavé materiály, jejichž hořlavost lze do jisté míry omezit ovrchovou úravou,
Příklady k přednášce 1. Úvod. Michael Šebek Automatické řízení 2019
 Příklady k řednášce. Úvod Michael Šebek Atomatické řízení 09 08.0.09 Kyvadlo řízené momentem Pohybová rovnice (. Newtonův zákon ro rotaci) J ϕ = M ro moment setrvačnosti J = ml = M Flsinϕ c = M mgl sinϕ
Příklady k řednášce. Úvod Michael Šebek Atomatické řízení 09 08.0.09 Kyvadlo řízené momentem Pohybová rovnice (. Newtonův zákon ro rotaci) J ϕ = M ro moment setrvačnosti J = ml = M Flsinϕ c = M mgl sinϕ
Příklady k přednášce 1. Úvod
 Příklady k řednášce. Úvod Michael Šebek Atomatické řízení 08 9-6-8 Kyvadlo řízené momentem Atomatické řízení - Kybernetika a robotika Pohybová rovnice (. Newtonův zákon ro rotaci) J ϕ M ro moment setrvačnosti
Příklady k řednášce. Úvod Michael Šebek Atomatické řízení 08 9-6-8 Kyvadlo řízené momentem Atomatické řízení - Kybernetika a robotika Pohybová rovnice (. Newtonův zákon ro rotaci) J ϕ M ro moment setrvačnosti
Měření základních vlastností OZ
 Měření základních vlastností OZ. Zadání: A. Na operačním zesilovači typu MAA 74 a MAC 55 změřte: a) Vstupní zbytkové napětí U D0 b) Amplitudovou frekvenční charakteristiku napěťového přenosu OZ v invertujícím
Měření základních vlastností OZ. Zadání: A. Na operačním zesilovači typu MAA 74 a MAC 55 změřte: a) Vstupní zbytkové napětí U D0 b) Amplitudovou frekvenční charakteristiku napěťového přenosu OZ v invertujícím
Josef Keder, Lenka Janatová Český hydrometeorologický ústav
 ZHODNOENÍ MOŽNOSTI SNÍŽENÍ ČETNOSTI VÝSKYTU PŘEKRAČOVÁNÍ IMISNÍH LIMITŮ ESTOU REGULAE EMISÍ Josef Keder, Lenka Janatová Český hydrometeorologický ústav MOTIVAE Potřeba aplikace vhodných opatření k expozici
ZHODNOENÍ MOŽNOSTI SNÍŽENÍ ČETNOSTI VÝSKYTU PŘEKRAČOVÁNÍ IMISNÍH LIMITŮ ESTOU REGULAE EMISÍ Josef Keder, Lenka Janatová Český hydrometeorologický ústav MOTIVAE Potřeba aplikace vhodných opatření k expozici

