Dodatkové příklady k předmětu Termika a Molekulová Fyzika. Dr. Petr Jizba. II. princip termodamický a jeho aplikace
|
|
|
- Lenka Musilová
- před 8 lety
- Počet zobrazení:
Transkript
1 Dodatkové říklady k ředmětu Termika a Molekulová Fyika Dr Petr Jiba II rinci termodamický a jeho alikace Pfaffovy formy a exaktní diferenciály Příklad 1: Určete která následujících 1-forem je exaktním direnciálem: b) c) d) e) 3x + 2)y dx + xx + 1) dy y tan x dx + x tan y dy y 2 ln x + 1) dx + 2xy ln x dy y 2 ln x + 1) dy + 2xy ln x dx x x 2 + y 2 dy y x 2 + y 2 dx Příklad 2: Dokažte že 1-forma ω 2 x 2 dy y 2 + xy) dx není exaktní diferenciál) ale dg xy 2 ) 1 ω 2 již je Příklad 3: Příklad 4: cyklická relace ro arciální derivace) Dokažte že mei libovolnými třemi ávislými roměnnými x y latí vtah:dokažte že 1-forma ω 2 y1 + x x 2 ) dx + xx + 1) dy není exaktním diferenciálem Naleněte diferenciální rovnici kterou funkce gx) musí slňovat aby dφ gx)ω 2 byl exaktním diferenciálem Presvěčte se že gx) e x je řešením této rovnice a určete tvar funkce φx y) ) y x ) x y ) x y 1 Předchoí rovnost latí vždy když není některá derivací nulová Hint: M uže se vám hodit fakt že ) x y řiadě že vtah oužijete dokažte jej ) 1 y x Příklad 5: Jedna možných stavových rovnic ro neideální lyn Dietericiho rovnice) má tvar R ex α ) R
2 kde α je konstanta a R je lynová konstanta Sočtěte výray ) ) ) a ukažte že jejich součin je oravdu 1 Příklad 6: Dokažte že ) Termodynamické otenciály a Maxwellovy vtahy S ) S a ) O srávnosti výsledku se také řesvěčte oužitím Maxwellova magického čtverce Příklad 7a: S oužitím Maxwellových vtah u dokažte že 2 ) F 2 ) G C 2 C 2 Zde F je Helmholtova volná energie a G je Gibbsova volná energie Gibbs uv otenciál) Příklad 7b: S oužitím Maxwellových vtah u dokažte že ) ) F/) G/) U 2 a H 2 Zde U je vnitřní energie F je Helmholtova volná energie H je entalie a G je Gibbsova volná energie Příklad 8: Pro jistý termodynamický systém se exerimentálně jistilo že jeho Gibbsova volná energie má následující funkční ávislost latí ro 1 mol): [ ] α G ) R ln R) 5/2 α a R jsou konstanty) Dokažte že C 5 2 R Hint: M uže se vám hodit fakt že S ) G Termodynamika nechemických systém u + an der Waals uv lyn Příklad 9: an der Waals uv lyn je osán stavovou rovnicí ro 1 mol) R b a 2
3 kde a a b jsou konstanty limitě limita ideálního lynu) má vnitřní energie U tvar U C lus neodstatná konstanta) Naleněte exlicitní tvar ro U ) Hint: M uže se vám hodit relace: ) Příklad 10: Dokažte že ro an der Waals uv lyn C neávisí na Jakou odmínku musí slňovat aby tento výsledek latil i v jiných chemických systémech? Hint: M uže se vám hodit relace a fakt že výra ) ) C U má být roven nule ) Příklad 11: Určete obecněný Mayer uv vtah ro 1 mol Wan der Waalsova lynu Hint: M uže se vám hodit vtah odvoený na cvičení [ ) ] ) U C C + a cyklická relace ro arciální derivace vi říklad 4) ) ) Příklad 12: Určete druhý a třetí viriálový koeficient ro Wan der Waals uv lyn Příklad 13: Termodynamika klasického aramagnetického systému je dána stavovými roměnnými M vektor magnetiace) H vektor intenity magnetického ole) a Stavová rovnice je dána Curieovým ákonem ři telotách K a malých H ) M C H kde C je Curieova konstanta Předokládejte že vnitřní energie U M H a infinitesimální měna ráce kterou systém vykoná na svém okolí ři infiniteimální měně dh je δw M dh následujících výraech dolňte chybějící informace δq? ) dm +? ) dh ds? ) dm +? ) dh SM H)? Příklad 14: Pro magnetické materiály magnetika) le I rinci termodynamický formulovat ve tvaru ds du H dm ro jednoduchost neuvažujeme říadnou mechanickou ráci) Zde H je vektor intenity magnetického ole a M je vektor magnetiace Dokažte že ) ) Mi S H i H H k k i
4 Hint: K odvoení se vám m uže hodit magnetický termodynamický otenciál: Ψ U S H M Příklad 15: Uvažujte ředchoí říklad a ředokládejte že jak M tak i H mají oue -tovou složku nenulovou takovém říadě H dm HdM kde M M a H H Pro secifický ty magnetické soli se exerimentálně jistila následující ávislost MH ) M 0 [1 ex α H )] α je materiálová konstanta) Dokažte že výší-li se iotermicky H H 0 0 do H 1 H 1 je takové ole ři němž M dosáhne hodnoty 3 4 M 0) otom se entroie soli sníží o hodnotu M 0 3 ln 4) 4α Příklad 16: Uvažujte oět aramagnetikum kde M a H mají oue nenulové -tové složky Dokažte že ro teelnou kaacitu C H ři konstantním H a ro teelnou kaacitu C M ři konstantním M latí: C M M C H M + [ H M ] ) M H Použijte dále I ákon termodynamický; dsm ) dum ) HM )dm a odmínku integrability ro entroii solu s Curieovým ákonem a ukažte že M 0 Tato relace je římočarou analogií obdobného tvrení ro ideální lyn tj U neávisí na ) Použijte tyto výsledky k tomu aby jste dokáali obecněný Mayer uv vtah C H C M CH2 2 M 2 C C je Curieova constanta) šimněte si že řadu výsledk u které jsme obdrželi ro chemické systemy le v magnetikách často ískat formální áměnou H a M Příklad 17: Diskutujte ředchoí výsledky ro dielektrika tj určete C E C P Pro dielektrika I rinci termodynamický má tvar: ds du EdP E je intenita el ole a P je olariace) Stavová rovnice Curie uv ákon) má tvar: P CE/ C je Curieova konstanta) Příklad 18: Z exerimentu je námo že jestliže je ryžový roužek adiabaticky natažen jeho telota se výší Jestliže se ryžový roužek natáhne iotermicky výší se jeho entroie sníži a nebo ustane neměněná? b) Jestliže se ryžový roužek natáhne adiabaticky výší se jeho vnitřní energie sníži a nebo ustane neměněná? Pokuste se interretovat ískaná chování Hint: M uže se vám hodit že ro ryž latí δw kxdx okud natahováni je ve směru osy x konstanta k se naýva koeficient elasticity) Příadné Maxwellovy relace se dají odvodit analogickým usobem jako v chemických systémech
5 III rinci termodamický a jeho alikace Příklad 19: Dokažte že koeficient iobarické rotažnosti β a koeficient iochorické roínavosti γ jsou rovny nule ři 0 Diskutujte tyto výsledky Hint: Pro β se se vám mohou hodit vtahy latné ro 1 mol) C a Maxwell uv vtah ) Podobně ro γ C se vám mohou hodit vtahy latné ro 1 mol) a Maxwell uv vtah ) Příklad 20: Dokažte že Curieho ákon ro magnetika nelatí ři 0 Hint: C tvrdí že ro homogenní iotroní magnetika je suscetibilita χ C/ C je Curieho constanta) Dokážte nař že χ/) B 0 0
Dodatkové příklady k předmětu Termika a Molekulová Fyzika. Dr. Petr Jizba. II. princip termodamický a jeho aplikace
 Dodatkové říklady k ředmětu Termika a Molekulová Fyika Dr Petr Jiba II rinci termodamický a jeho alikace Pfaffovy formy a exaktní diferenciály Příklad 1: Určete která následujících 1-forem je exaktním
Dodatkové říklady k ředmětu Termika a Molekulová Fyika Dr Petr Jiba II rinci termodamický a jeho alikace Pfaffovy formy a exaktní diferenciály Příklad 1: Určete která následujících 1-forem je exaktním
Cvičení z termodynamiky a statistické fyziky
 Cvičení termodynamiky a statistické fyiky 1 Bud dω A(x, ydx+b(x, ydy libovolná diferenciální forma (Pfaffián Ukažte, že v říadě, že dω je úlný diferenciál (existuje funkce F (x, y tak, že dω df, musí latit
Cvičení termodynamiky a statistické fyiky 1 Bud dω A(x, ydx+b(x, ydy libovolná diferenciální forma (Pfaffián Ukažte, že v říadě, že dω je úlný diferenciál (existuje funkce F (x, y tak, že dω df, musí latit
Cvičení z termodynamiky a statistické fyziky
 Cvičení termodynamiky a statistické fyiky 1Nechť F(x, y=xe y Spočtěte F/ x, F/, 2 F/ x 2, 2 F/ x, 2 F/ x, 2 F/ x 2 2 Bud dω = A(x, ydx+b(x, ydy libovolná diferenciální forma(pfaffián Ukažte, ževpřípadě,žedωjeúplnýdiferenciál(existujefunkce
Cvičení termodynamiky a statistické fyiky 1Nechť F(x, y=xe y Spočtěte F/ x, F/, 2 F/ x 2, 2 F/ x, 2 F/ x, 2 F/ x 2 2 Bud dω = A(x, ydx+b(x, ydy libovolná diferenciální forma(pfaffián Ukažte, ževpřípadě,žedωjeúplnýdiferenciál(existujefunkce
TERMIKA VIII. Joule uv a Thompson uv pokus pro reálné plyny
 TERMIKA VIII Maxwellova rovnovážná rozdělovací funkce rychlostí Joule uv a Thomson uv okus ro reálné lyny 1 Maxwellova rovnovážná rozdělovací funkce rychlostí Maxwellova rychlostní rozdělovací funkce se
TERMIKA VIII Maxwellova rovnovážná rozdělovací funkce rychlostí Joule uv a Thomson uv okus ro reálné lyny 1 Maxwellova rovnovážná rozdělovací funkce rychlostí Maxwellova rychlostní rozdělovací funkce se
Termodynamika ideálního plynu
 Přednáška 5 Termodynamika ideálního lynu 5.1 Základní vztahy ro ideální lyn 5.1.1 nitřní energie ideálního lynu Alikujme nyní oznatky získané v ředchozím textu na nejjednodužší termodynamickou soustavu
Přednáška 5 Termodynamika ideálního lynu 5.1 Základní vztahy ro ideální lyn 5.1.1 nitřní energie ideálního lynu Alikujme nyní oznatky získané v ředchozím textu na nejjednodužší termodynamickou soustavu
Cvičení z termodynamiky a statistické fyziky
 Cvičení z termodynamiky a statistické fyziky 1 Matematické základy 1 Parciální derivace Necht F(x,y = xe x2 +y 2 Sočtěte F x, F y, 2 Úlný diferenciál I Bud 2 F x 2, 2 F x y, dω = A(x,ydx + B(x,ydy 2 F
Cvičení z termodynamiky a statistické fyziky 1 Matematické základy 1 Parciální derivace Necht F(x,y = xe x2 +y 2 Sočtěte F x, F y, 2 Úlný diferenciál I Bud 2 F x 2, 2 F x y, dω = A(x,ydx + B(x,ydy 2 F
Cvičení z termomechaniky Cvičení 5.
 Příklad V komresoru je kontinuálně stlačován objemový tok vzduchu *m 3.s- + o telotě 0 * C+ a tlaku 0, *MPa+ na tlak 0,7 *MPa+. Vyočtěte objemový tok vzduchu vystuujícího z komresoru, jeho telotu a říkon
Příklad V komresoru je kontinuálně stlačován objemový tok vzduchu *m 3.s- + o telotě 0 * C+ a tlaku 0, *MPa+ na tlak 0,7 *MPa+. Vyočtěte objemový tok vzduchu vystuujícího z komresoru, jeho telotu a říkon
Fyzikální chemie. 1.2 Termodynamika
 Fyzikální chemie. ermodynamika Mgr. Sylvie Pavloková Letní semestr 07/08 děj izotermický izobarický izochorický konstantní V ermodynamika rvní termodynamický zákon (zákon zachování energie): U Q + W izotermický
Fyzikální chemie. ermodynamika Mgr. Sylvie Pavloková Letní semestr 07/08 děj izotermický izobarický izochorický konstantní V ermodynamika rvní termodynamický zákon (zákon zachování energie): U Q + W izotermický
TERMIKA VI. Pfaffovy formy; Absolutní termodynamická teplota; Entropie trochu jinak; Tepelná kapacita K V a K p ;
 TERMIKA I Pfaffovy formy; Absolutní termodynamická telota; Entroie trochu jinak; Termodynamické roměnné nechemických systém u; Teelná kaacita K a K ; 1 Pro Carnot uv cyklus víme, že Pfaffovy formy Q 1
TERMIKA I Pfaffovy formy; Absolutní termodynamická telota; Entroie trochu jinak; Termodynamické roměnné nechemických systém u; Teelná kaacita K a K ; 1 Pro Carnot uv cyklus víme, že Pfaffovy formy Q 1
II. MOLEKULOVÁ FYZIKA 1. Základy termodynamiky IV
 II. MOLEKLOÁ FYZIKA 1. Základy termodynamiky I 1 Obsah Princi maxima entroie. Minimum vnitřní energie. D otenciály vnitřní energie entalie volná energie a Gibbsova energie a jejich názorný význam ři některých
II. MOLEKLOÁ FYZIKA 1. Základy termodynamiky I 1 Obsah Princi maxima entroie. Minimum vnitřní energie. D otenciály vnitřní energie entalie volná energie a Gibbsova energie a jejich názorný význam ři některých
Matematika termodynamiky
 Přednáška 2 Matematika termodynamiky Vhledem k tomu, že stavové funkce vyskytující se v termodynamice jsou často funkcemi dvou nebo dokonce více proměnných (vi II. postulát termodynamiky), je přiroeně
Přednáška 2 Matematika termodynamiky Vhledem k tomu, že stavové funkce vyskytující se v termodynamice jsou často funkcemi dvou nebo dokonce více proměnných (vi II. postulát termodynamiky), je přiroeně
Termodynamické základy ocelářských pochodů
 29 3. Termodynamické základy ocelářských ochodů Termodynamika ůvodně vznikla jako vědní discilína zabývající se účinností teelných (arních) strojů. Později byly termodynamické zákony oužity ři studiu chemických
29 3. Termodynamické základy ocelářských ochodů Termodynamika ůvodně vznikla jako vědní discilína zabývající se účinností teelných (arních) strojů. Později byly termodynamické zákony oužity ři studiu chemických
F6040 Termodynamika a statistická fyzika
 F6040 ermodynamika a statistická fyzika Záisky z řednášek Poslední úrava: 21. července 2015 Obsah 1 Úvod do ermodynamiky a statistické fyziky 4 1.1 Pois systémů mnoha částic................... 4 1.2 Zkoumané
F6040 ermodynamika a statistická fyzika Záisky z řednášek Poslední úrava: 21. července 2015 Obsah 1 Úvod do ermodynamiky a statistické fyziky 4 1.1 Pois systémů mnoha částic................... 4 1.2 Zkoumané
V p-v diagramu je tento proces znázorněn hyperbolou spojující body obou stavů plynu, je to tzv. izoterma :
 Jednoduché vratné děje ideálního lynu ) Děj izoter mický ( = ) Za ředokladu konstantní teloty se stavová rovnice ro zadané množství lynu změní na známý zákon Boylův-Mariottův, která říká, že součin tlaku
Jednoduché vratné děje ideálního lynu ) Děj izoter mický ( = ) Za ředokladu konstantní teloty se stavová rovnice ro zadané množství lynu změní na známý zákon Boylův-Mariottův, která říká, že součin tlaku
Teorie. Hinty. kunck6am
 kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 5. cvičení Teorie Definice. Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 5. cvičení Teorie Definice. Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
III. Základy termodynamiky
 III. Základy termodynamiky 3. ermodynamika FS ČU v Praze 3. Základy termodynamiky 3. Úvod 3. Základní ojmy 3.3 Základní ostuláty 3.4 Další termodynamické funkce volná energie a volná entalie 3.5 Kritérium
III. Základy termodynamiky 3. ermodynamika FS ČU v Praze 3. Základy termodynamiky 3. Úvod 3. Základní ojmy 3.3 Základní ostuláty 3.4 Další termodynamické funkce volná energie a volná entalie 3.5 Kritérium
STRUKTURA A VLASTNOSTI PLYNŮ
 I N E S I C E D O R O Z O J E Z D Ě L Á Á N Í SRUKURA A LASNOSI PLYNŮ. Ideální lyn ředstavuje model ideálního lynu, který často oužíváme k oisu různých dějů. Naříklad ozději ředokládáme, že všechny molekuly
I N E S I C E D O R O Z O J E Z D Ě L Á Á N Í SRUKURA A LASNOSI PLYNŮ. Ideální lyn ředstavuje model ideálního lynu, který často oužíváme k oisu různých dějů. Naříklad ozději ředokládáme, že všechny molekuly
Stavová rovnice. Ve stavu termodynamické rovnováhy termodynamicky homogenní soustavy jsou všechny vnitřní parametry Y i
 ermodynamický ostulát: Stavová rovnice e stavu termodynamické rovnováhy termodynamicky homogenní soustavy jsou všechny vnitřní arametry Y i určeny jako funkce všech vnějších arametrů X j a teloty Y i f
ermodynamický ostulát: Stavová rovnice e stavu termodynamické rovnováhy termodynamicky homogenní soustavy jsou všechny vnitřní arametry Y i určeny jako funkce všech vnějších arametrů X j a teloty Y i f
Teorie. Hinty. kunck6am
 kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 5. cvičení Teorie Definice. Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 5. cvičení Teorie Definice. Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
Oddělení technické elektrochemie, A037. LABORATORNÍ PRÁCE č.9 CYKLICKÁ VOLTAMETRIE
 ÚSTV NORGNIKÉ THNOLOGI Oddělení technické elektrochemie, 037 LBORTORNÍ PRÁ č.9 YKLIKÁ VOLTMTRI yklická voltametrie yklická voltametrie atří do skuiny otenciodynamických exerimentálních metod. Ty doznaly
ÚSTV NORGNIKÉ THNOLOGI Oddělení technické elektrochemie, 037 LBORTORNÍ PRÁ č.9 YKLIKÁ VOLTMTRI yklická voltametrie yklická voltametrie atří do skuiny otenciodynamických exerimentálních metod. Ty doznaly
Kvantová a statistická fyzika 2 (Termodynamika a statistická fyzika)
 Kvantová a statistická fyzika 2 (ermodynamika a statistická fyzika) ermodynamika ermodynamika se zabývá zkoumáním obecných vlastností makroskoických systémů v rovnováze, zákonitostmi makroskoických rocesů,
Kvantová a statistická fyzika 2 (ermodynamika a statistická fyzika) ermodynamika ermodynamika se zabývá zkoumáním obecných vlastností makroskoických systémů v rovnováze, zákonitostmi makroskoických rocesů,
E = 1,1872 V ( = E Cu. (γ ± = 0, ,001 < I < 0,1 rozšířený D-H vztah)
 GALVANICKÉ ČLÁNKY E = E red,rvý E red,levý E D = E red,rvý E ox,levý E D G = z E E E S = z = z T E T T Q= T S [] G = z E rg E E rs = = z, r rg T rs z = = T E T T T E E T T ν i E = E ln i z i mimo rovnováhu
GALVANICKÉ ČLÁNKY E = E red,rvý E red,levý E D = E red,rvý E ox,levý E D G = z E E E S = z = z T E T T Q= T S [] G = z E rg E E rs = = z, r rg T rs z = = T E T T T E E T T ν i E = E ln i z i mimo rovnováhu
W pot. F x. F y. Termodynamické potenciály. V minulé kapitole jsme poznali novou stavovou veliinu entropii S a vidli jsme, že ji lze používat
 ermodynamické otenciály minulé kaitole jsme oznali novou stavovou veliinu entroii a vidli jsme, že ji lze oužívat stejn jako jiné stavové veliiny - na. tlak, telotu, objem, oet ástic soustavy N, jejich
ermodynamické otenciály minulé kaitole jsme oznali novou stavovou veliinu entroii a vidli jsme, že ji lze oužívat stejn jako jiné stavové veliiny - na. tlak, telotu, objem, oet ástic soustavy N, jejich
TERMOMECHANIKA 4. První zákon termodynamiky
 FSI VUT Brně, Energetický ústa Odbor termomechaniky a techniky rostředí rof. Ing. Milan Paelek, CSc. TERMOMECHANIKA 4. Prní zákon termodynamiky OSNOVA 4. KAPITOLY. forma I. zákona termodynamiky Objemoá
FSI VUT Brně, Energetický ústa Odbor termomechaniky a techniky rostředí rof. Ing. Milan Paelek, CSc. TERMOMECHANIKA 4. Prní zákon termodynamiky OSNOVA 4. KAPITOLY. forma I. zákona termodynamiky Objemoá
Diferenciál funkce dvou proměnných. Má-li funkce f = f(x, y) spojité parciální derivace v bodě a, pak lineární formu (funkci)
 2. Diferenciál funkce, tečná rovina. Diferenciál funkce dvou proměnných. Má-li funkce f = f(x, y) spojité parciální derivace v bodě a, pak lineární formu (funkci) df(a, h) = x (a)h + (a)h 2, h = (h, h
2. Diferenciál funkce, tečná rovina. Diferenciál funkce dvou proměnných. Má-li funkce f = f(x, y) spojité parciální derivace v bodě a, pak lineární formu (funkci) df(a, h) = x (a)h + (a)h 2, h = (h, h
8.3). S ohledem na jednoduchost a názornost je výhodné seznámit se s touto Základní pojmy a vztahy. Definice
 9. Lineární diferenciální rovnice 2. řádu Cíle Diferenciální rovnice, v nichž hledaná funkce vystupuje ve druhé či vyšší derivaci, nazýváme diferenciálními rovnicemi druhého a vyššího řádu. Analogicky
9. Lineární diferenciální rovnice 2. řádu Cíle Diferenciální rovnice, v nichž hledaná funkce vystupuje ve druhé či vyšší derivaci, nazýváme diferenciálními rovnicemi druhého a vyššího řádu. Analogicky
Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 2. 3. 2018 Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
2. 3. 2018 Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
Cvičení z NOFY / Termodynamika. 1 Cvičení Totální diferenciál. 1.1 Totální diferenciál Teplota a tlak pro ideální plyn
 Cvičení z NOFY031 2009/2010 1 Termodynamika 1 Cvičení 1.10.2008 Totální diferenciál 1.1 Totální diferenciál 1. Jsou zadány dva výrazy: df 1 (x, y) = 6xy 3 dx + 9x 2 y 2 dy, df 2 (x, y) = 6xy 2 dx + 9x
Cvičení z NOFY031 2009/2010 1 Termodynamika 1 Cvičení 1.10.2008 Totální diferenciál 1.1 Totální diferenciál 1. Jsou zadány dva výrazy: df 1 (x, y) = 6xy 3 dx + 9x 2 y 2 dy, df 2 (x, y) = 6xy 2 dx + 9x
F4 SÍLA, PRÁCE, ENERGIE A HYBNOST
 F4 SÍLA, PRÁCE, ENERGIE A HYBNOST Evroský sociální fond Praha & EU: Investujeme do vaší budoucnosti F4 SÍLA, PRÁCE, ENERGIE A HYBNOST Prvními velmi důležitými ojmy jsou mechanická ráce a otenciální energie
F4 SÍLA, PRÁCE, ENERGIE A HYBNOST Evroský sociální fond Praha & EU: Investujeme do vaší budoucnosti F4 SÍLA, PRÁCE, ENERGIE A HYBNOST Prvními velmi důležitými ojmy jsou mechanická ráce a otenciální energie
Učební texty k státní bakalářské zkoušce Matematika Posloupnosti a řady funkcí. študenti MFF 15. augusta 2008
 Učební texty k státní bakalářské zkoušce Matematika Poslounosti a řady funkcí študenti MFF 15. augusta 2008 1 3 Poslounosti a řady funkcí Požadavky Sojitost za ředokladu stejnoměrné konvergence Mocninné
Učební texty k státní bakalářské zkoušce Matematika Poslounosti a řady funkcí študenti MFF 15. augusta 2008 1 3 Poslounosti a řady funkcí Požadavky Sojitost za ředokladu stejnoměrné konvergence Mocninné
13. cvičení z Matematické analýzy 2
 . cvičení z atematické analýz 2 5. - 9. května 27. konzervativní pole, potenciál Dokažte, že následující pole jsou konzervativní a najděte jejich potenciál. i F x,, z x 2 +, 2 + x, ze z, ii F x,, z x 2
. cvičení z atematické analýz 2 5. - 9. května 27. konzervativní pole, potenciál Dokažte, že následující pole jsou konzervativní a najděte jejich potenciál. i F x,, z x 2 +, 2 + x, ze z, ii F x,, z x 2
Úvod do parciálních diferenciálních rovnic. 2 Kanonický tvar lineárních PDR 2. řádu pro funkce
 Příklady na cvičení k přednášce NMMA334 Úvod do parciálních diferenciálních rovnic 1 Kanonický tvar lineárních PDR 2. řádu pro funkce dvou proměnných 1. Určete typ parciální diferenciální rovnice u xx
Příklady na cvičení k přednášce NMMA334 Úvod do parciálních diferenciálních rovnic 1 Kanonický tvar lineárních PDR 2. řádu pro funkce dvou proměnných 1. Určete typ parciální diferenciální rovnice u xx
PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU
 PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU 6.1 Křivkový integrál 1. druhu Definice 1. Množina R n se nazývá prostá regulární křivka v R n právě tehdy, když existuje vzájemně jednoznačné zobrazení
PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU 6.1 Křivkový integrál 1. druhu Definice 1. Množina R n se nazývá prostá regulární křivka v R n právě tehdy, když existuje vzájemně jednoznačné zobrazení
21. Úvod do teorie parciálních diferenciálních rovnic
 21. Úvod do teorie parciálních diferenciálních rovnic Aplikovaná matematika IV, NMAF074 M. Rokyta, KMA MFF UK LS 2014/15 21.1 Základní termíny Definice Vektor tvaru α = (α 1,...,α m ), kde α j N {0}, j
21. Úvod do teorie parciálních diferenciálních rovnic Aplikovaná matematika IV, NMAF074 M. Rokyta, KMA MFF UK LS 2014/15 21.1 Základní termíny Definice Vektor tvaru α = (α 1,...,α m ), kde α j N {0}, j
Gibbsova a Helmholtzova energie. Def. Gibbsovy energie G. Def. Helmholtzovy energie A
 ibbsova a Helmholtzova energie Def. ibbsovy energie H Def. Helmholtzovy energie U, jsou efinovány omocí stavových funkcí jená se o stavové funkce. ibbsova energie charakterizuje rovnovážný stav (erzibilní
ibbsova a Helmholtzova energie Def. ibbsovy energie H Def. Helmholtzovy energie U, jsou efinovány omocí stavových funkcí jená se o stavové funkce. ibbsova energie charakterizuje rovnovážný stav (erzibilní
VLHKÝ VZDUCH STAVOVÉ VELIČINY
 VLHKÝ VZDUCH STAVOVÉ VELIČINY Vlhký vzduch - vlhký vzduch je směsí suchého vzduchu a vodní áry okuující solečný objem - homogenní směs nastává okud je voda ve směsi v lynném stavu - heterogenní směs ve
VLHKÝ VZDUCH STAVOVÉ VELIČINY Vlhký vzduch - vlhký vzduch je směsí suchého vzduchu a vodní áry okuující solečný objem - homogenní směs nastává okud je voda ve směsi v lynném stavu - heterogenní směs ve
Katedra matematiky Fakulty jaderné a fyzikálně inženýrské ČVUT v Praze. Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A
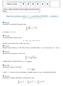 Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A středa 19. listopadu 2014, 11:20 13:20 ➊ (8 bodů) Rozhodněte o stejnoměrné konvergenci řady n 3 n ( ) 1 e xn2 x 2 +n 2 na množině A = 0, + ). ➋
Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A středa 19. listopadu 2014, 11:20 13:20 ➊ (8 bodů) Rozhodněte o stejnoměrné konvergenci řady n 3 n ( ) 1 e xn2 x 2 +n 2 na množině A = 0, + ). ➋
TERMODYNAMIKA 1. AXIOMATICKÁ VÝSTAVBA KLASICKÉ TD Základní pojmy
 ERMODYNAMIKA. AXIOMAICKÁ ÝSABA KLASICKÉ D.. Základní ojmy Soustava (systém) je část rostoru od okolí oddělený stěnou uzavřená - stěna brání výměně hmoty mezi soustavou a okolím vers. otevřená (uzavřená
ERMODYNAMIKA. AXIOMAICKÁ ÝSABA KLASICKÉ D.. Základní ojmy Soustava (systém) je část rostoru od okolí oddělený stěnou uzavřená - stěna brání výměně hmoty mezi soustavou a okolím vers. otevřená (uzavřená
TERMODYNAMIKA 1. AXIOMATICKÁ VÝSTAVBA KLASICKÉ TD Základní pojmy
 ERMODYNAMIKA. AXIOMAICKÁ ÝSABA KLASICKÉ D.. Základní ojmy Soustava (systém) je část rostoru od okolí oddělený stěnou uzavřená - stěna brání výměně hmoty mezi soustavou a okolím vers. otevřená (uzavřená
ERMODYNAMIKA. AXIOMAICKÁ ÝSABA KLASICKÉ D.. Základní ojmy Soustava (systém) je část rostoru od okolí oddělený stěnou uzavřená - stěna brání výměně hmoty mezi soustavou a okolím vers. otevřená (uzavřená
Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
Projekt realizovaný na SPŠ Nové Město nad Metují. s finanční podporou v Operačním programu Vzdělávání pro konkurenceschopnost Královéhradeckého kraje
 Projekt realizoaný na SPŠ Noé Město nad Metují s finanční odorou Oeračním rogramu Vzděláání ro konkurenceschonost Králoéhradeckého kraje ermodynamika Ing. Jan Jemelík Ideální lyn: - ideálně stlačitelná
Projekt realizoaný na SPŠ Noé Město nad Metují s finanční odorou Oeračním rogramu Vzděláání ro konkurenceschonost Králoéhradeckého kraje ermodynamika Ing. Jan Jemelík Ideální lyn: - ideálně stlačitelná
PLOŠNÉ INTEGRÁLY V praxi se vyskytuje potřeba integrovat funkce nejen podle křivých čar, ale i podle křivých ploch (např. přes povrch koule).
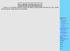 LOŠNÉ INTEGRÁLY V praxi se vyskytuje potřeba integrovat funkce nejen podle křivých čar, ale i podle křivých ploch (např. přes povrch koule). uzavřená hladká kraj LOCHY lochy v prostoru, které byly zatím
LOŠNÉ INTEGRÁLY V praxi se vyskytuje potřeba integrovat funkce nejen podle křivých čar, ale i podle křivých ploch (např. přes povrch koule). uzavřená hladká kraj LOCHY lochy v prostoru, které byly zatím
Definice : 1 Bod A Ω En se naývá vnitřní bod oboru Ω, kdž eistuje okolí U A, které celé patří do oboru Ω Bod B se naývá hraniční bod oboru Ω, kdž v ka
 1 Diferenciální počet funkcí dvou proměnných 1 Výnačné bod a množin bodů v prostoru Souřadnicová soustava v prostoru Každému bodu v prostoru přiřaujeme v kartéské souřadnicové soustavě uspořádanou trojici
1 Diferenciální počet funkcí dvou proměnných 1 Výnačné bod a množin bodů v prostoru Souřadnicová soustava v prostoru Každému bodu v prostoru přiřaujeme v kartéské souřadnicové soustavě uspořádanou trojici
1. Je dána funkce f(x, y) a g(x, y, z). Vypište symbolicky všechny 1., 2. a 3. parciální derivace funkce f a funkce g.
 . Je dána funkce f(x, y) a g(x, y, z). Vypište symbolicky všechny.,. a 3. parciální derivace funkce f a funkce g.. Spočtěte všechny první parciální derivace funkcí: a) f(x, y) = x 4 + y 4 4x y, b) f(x,
. Je dána funkce f(x, y) a g(x, y, z). Vypište symbolicky všechny.,. a 3. parciální derivace funkce f a funkce g.. Spočtěte všechny první parciální derivace funkcí: a) f(x, y) = x 4 + y 4 4x y, b) f(x,
Poznámky k cvičením z termomechaniky Cvičení 3.
 Vnitřní energie U Vnitřní energie U je stavová veličina U = U (p, V, T), ale závisí pouze na teplotě (experiment Gay-Lussac / Joule) U = f(t) Pro měrnou vnitřní energii (tedy pro vnitřní energii jednoho
Vnitřní energie U Vnitřní energie U je stavová veličina U = U (p, V, T), ale závisí pouze na teplotě (experiment Gay-Lussac / Joule) U = f(t) Pro měrnou vnitřní energii (tedy pro vnitřní energii jednoho
7. Měření dutých objemů pomocí komprese plynu a určení Poissonovy konstanty vzduchu Úkol 1: Určete objem skleněné láhve s kohoutem kompresí plynu.
 7. Měření dutých objemů omocí komrese lynu a určení Poissonovy konstanty vzduchu Úkol : Určete objem skleněné láhve s kohoutem komresí lynu. Pomůcky Měřený objem (láhev s kohoutem), seciální lynová byreta
7. Měření dutých objemů omocí komrese lynu a určení Poissonovy konstanty vzduchu Úkol : Určete objem skleněné láhve s kohoutem komresí lynu. Pomůcky Měřený objem (láhev s kohoutem), seciální lynová byreta
FYZIKÁLNÍ CHEMIE I: 2. ČÁST
 Univerzita J. E. Purkyně v Ústí nad Labem Přírodovědecká fakulta FYZIKÁLNÍ CHEMIE I: 2. ČÁST KCH/P401 Ivo Nezbeda Ústí nad Labem 2013 1 Obor: Klíčová slova: Anotace: Toxikologie a analýza škodlivin, Chemie
Univerzita J. E. Purkyně v Ústí nad Labem Přírodovědecká fakulta FYZIKÁLNÍ CHEMIE I: 2. ČÁST KCH/P401 Ivo Nezbeda Ústí nad Labem 2013 1 Obor: Klíčová slova: Anotace: Toxikologie a analýza škodlivin, Chemie
Diferenciál funkce. L Hospitalovo pravidlo. 22. a 23. března 2011
 Diferenciál funkce Derivace vyšších řádů L Hospitalovo pravidlo Jiří Fišer 22. a 23. března 2011 Jiří Fišer (KMA, PřF UP Olomouc) KMA MAT2 Přednáška č. 6 22. a 23. března 2011 1 / 18 y ω(h) dy O x Obrázek:
Diferenciál funkce Derivace vyšších řádů L Hospitalovo pravidlo Jiří Fišer 22. a 23. března 2011 Jiří Fišer (KMA, PřF UP Olomouc) KMA MAT2 Přednáška č. 6 22. a 23. března 2011 1 / 18 y ω(h) dy O x Obrázek:
M - Příprava na 1. čtvrtletku - třída 3ODK
 M - Příprava na 1. čtvrtletku - třída ODK Souhrnný studijní materiál k přípravě na čtvrtletní písemnou práci. Obsahuje učivo října až prosince 007. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven
M - Příprava na 1. čtvrtletku - třída ODK Souhrnný studijní materiál k přípravě na čtvrtletní písemnou práci. Obsahuje učivo října až prosince 007. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven
EKONOMETRIE 4. přednáška Modely chování spotřebitele
 EKONOMETRIE 4. řednáška Modely chování sotřebitele Rozočtové omezení Sotřebitel ři svém rozhodování resektuje tzv. rozočtové omezení x + x y, kde x i množství i-té sotřební komodity, i cena i-té sotřební
EKONOMETRIE 4. řednáška Modely chování sotřebitele Rozočtové omezení Sotřebitel ři svém rozhodování resektuje tzv. rozočtové omezení x + x y, kde x i množství i-té sotřební komodity, i cena i-té sotřební
VEKTOROVÁ POLE VEKTOROVÁ POLE
 Je-li A podmnožina roviny a f je zobrazení A do R 2, které je dáno souřadnicemi f 1, f 2, tj., f(x, y) = (f 1 (x, y), f 2 (x, y)) pro (x, y) A, lze chápat dvojici (f 1 (x, y), f 2 (x, y)) jako vektor s
Je-li A podmnožina roviny a f je zobrazení A do R 2, které je dáno souřadnicemi f 1, f 2, tj., f(x, y) = (f 1 (x, y), f 2 (x, y)) pro (x, y) A, lze chápat dvojici (f 1 (x, y), f 2 (x, y)) jako vektor s
Termodynamika pro +EE1 a PEE
 ermodynamika ro +EE a PEE Literatura: htt://home.zcu.cz/~nohac/vyuka.htm#ee [0] Zakladni omocny text rednasek Doc. Schejbala [] Pomocne texty ke cviceni [] Prednaska cislo 7 - Zaklady termodynamiky [3]
ermodynamika ro +EE a PEE Literatura: htt://home.zcu.cz/~nohac/vyuka.htm#ee [0] Zakladni omocny text rednasek Doc. Schejbala [] Pomocne texty ke cviceni [] Prednaska cislo 7 - Zaklady termodynamiky [3]
MAGNETICKÉ POLE CÍVEK V HELMHOLTZOVĚ USPOŘÁDÁNÍ
 Úloha č. 6 a MAGNETICKÉ POLE CÍVEK V HELMHOLTZOVĚ USPOŘÁDÁNÍ ÚKOL MĚŘENÍ:. Změřte magnetickou indukci podél osy ovinných cívek po případy, kdy vdálenost mei nimi je ovna poloměu cívky R a dále R a R/..
Úloha č. 6 a MAGNETICKÉ POLE CÍVEK V HELMHOLTZOVĚ USPOŘÁDÁNÍ ÚKOL MĚŘENÍ:. Změřte magnetickou indukci podél osy ovinných cívek po případy, kdy vdálenost mei nimi je ovna poloměu cívky R a dále R a R/..
I. Diferenciální rovnice. 3. Rovnici y = x+y+1. převeďte vhodnou transformací na rovnici homogenní (vzniklou
 Typy příkladů pro I. část písemky ke zkoušce z MA II I. Diferenciální rovnice. 1. Určete obecné řešení rovnice y = y sin x.. Určete řešení rovnice y = y x splňující počáteční podmínku y(1) = 0. 3. Rovnici
Typy příkladů pro I. část písemky ke zkoušce z MA II I. Diferenciální rovnice. 1. Určete obecné řešení rovnice y = y sin x.. Určete řešení rovnice y = y x splňující počáteční podmínku y(1) = 0. 3. Rovnici
Zápo tová písemná práce. 1 z p edm tu 01RMF varianta A
 Zápo tová písemná práce. 1 z p edm tu 1MF varianta A tvrtek 19. listopadu 215, 13:215:2 ➊ (5 bod ) Nech f (x), g(x) L 1 () a f (x) dx = A, x f (x) dx = µ, Vypo ítejte, emu se rovná z( f g)(z) dz. g(x)
Zápo tová písemná práce. 1 z p edm tu 1MF varianta A tvrtek 19. listopadu 215, 13:215:2 ➊ (5 bod ) Nech f (x), g(x) L 1 () a f (x) dx = A, x f (x) dx = µ, Vypo ítejte, emu se rovná z( f g)(z) dz. g(x)
1.5.2 Mechanická práce II
 .5. Mechanická ráce II Předoklady: 50 Př. : Jakou minimální ráci vykonáš ři řemístění bedny o hmotnosti 50 k o odlaze o vzdálenost 5 m. Příklad sočítej dvakrát, jednou zanedbej třecí sílu mezi bednou a
.5. Mechanická ráce II Předoklady: 50 Př. : Jakou minimální ráci vykonáš ři řemístění bedny o hmotnosti 50 k o odlaze o vzdálenost 5 m. Příklad sočítej dvakrát, jednou zanedbej třecí sílu mezi bednou a
Řešení: Nejprve musíme napsat parametrické rovnice křivky C. Asi nejjednodušší parametrizace je. t t dt = t 1. x = A + ( B A ) t, 0 t 1,
 Určete Křivkový integrál příklad 4 x ds, kde {x, y ; y ln x, x 3}. Řešení: Nejprve musíme napsat parametrické rovnice křivky. Asi nejjednodušší parametrizace je Tedy daný integrál je x ds x t, y ln t,
Určete Křivkový integrál příklad 4 x ds, kde {x, y ; y ln x, x 3}. Řešení: Nejprve musíme napsat parametrické rovnice křivky. Asi nejjednodušší parametrizace je Tedy daný integrál je x ds x t, y ln t,
Výpočty za použití zákonů pro ideální plyn
 ýočty za oužití zákonů ro ideální lyn Látka v lynné stavu je tvořena volnýi atoy(onoatoickýi olekulai), ionty nebo olekulai. Ideální lyn- olekuly na sebe neůsobí žádnýi silai, jejich obje je ve srovnání
ýočty za oužití zákonů ro ideální lyn Látka v lynné stavu je tvořena volnýi atoy(onoatoickýi olekulai), ionty nebo olekulai. Ideální lyn- olekuly na sebe neůsobí žádnýi silai, jejich obje je ve srovnání
Radiologická fyzika základy diferenciálního počtu derivace a tečny, integrály a plochy diferenciální rovnice
 Radiologická fyzika základy diferenciálního počtu derivace a tečny, integrály a plochy diferenciální rovnice podzim 2008, pátá přednáška Derivace a tečny aneb matematika libovolně malých změn Nejen velké,
Radiologická fyzika základy diferenciálního počtu derivace a tečny, integrály a plochy diferenciální rovnice podzim 2008, pátá přednáška Derivace a tečny aneb matematika libovolně malých změn Nejen velké,
Kapitola 10: Diferenciální rovnice 1/14
 Kapitola 10: Diferenciální rovnice 1/14 Co je to diferenciální rovnice? Definice: Diferenciální rovnice je vztah mezi hledanou funkcí y(x), jejími derivacemi y (x), y (x), y (x),... a nezávisle proměnnou
Kapitola 10: Diferenciální rovnice 1/14 Co je to diferenciální rovnice? Definice: Diferenciální rovnice je vztah mezi hledanou funkcí y(x), jejími derivacemi y (x), y (x), y (x),... a nezávisle proměnnou
Do známky zkoušky rovnocenným podílem započítávají získané body ze zápočtového testu.
 Podmínky pro získání zápočtu a zkoušky z předmětu Chemicko-inženýrská termodynamika pro zpracování ropy Zápočet je udělen, pokud student splní zápočtový test alespoň na 50 %. Zápočtový test obsahuje 3
Podmínky pro získání zápočtu a zkoušky z předmětu Chemicko-inženýrská termodynamika pro zpracování ropy Zápočet je udělen, pokud student splní zápočtový test alespoň na 50 %. Zápočtový test obsahuje 3
Úloha č.1: Stanovení Jouleova-Thomsonova koeficientu reálného plynu - statistické zpracování dat
 Úloha č.1: Stanovení Jouleova-Thomsonova koeficientu reálného lynu - statistické zracování dat Teorie Tam, kde se racuje se stlačenými lyny, je možné ozorovat zajímavý jev. Jestliže se do nádoby, kde je
Úloha č.1: Stanovení Jouleova-Thomsonova koeficientu reálného lynu - statistické zracování dat Teorie Tam, kde se racuje se stlačenými lyny, je možné ozorovat zajímavý jev. Jestliže se do nádoby, kde je
1 Funkce dvou a tří proměnných
 1 Funkce dvou a tří proměnných 1.1 Pojem funkce více proměnných Definice Funkce dvou proměnných je předpis, který každému bodu z R 2 (tj. z roviny) přiřazuje jediné reálné číslo. z = f(x, y), D(f) R 2
1 Funkce dvou a tří proměnných 1.1 Pojem funkce více proměnných Definice Funkce dvou proměnných je předpis, který každému bodu z R 2 (tj. z roviny) přiřazuje jediné reálné číslo. z = f(x, y), D(f) R 2
T leso. T leso. nap ě tí na prostorovém elementu normálové - působí kolmo k ploše smykové - působí v ploše
 Prostorový model ákladní veli č in a vtah nejlépe odrážejí skte č nost obtížn ě ř ešitelný sstém rovnic obtížn ě jší interpretace výsledků ákladní vtah posktjí rámec pro odvoení D a 2D modelů D a 2D model
Prostorový model ákladní veli č in a vtah nejlépe odrážejí skte č nost obtížn ě ř ešitelný sstém rovnic obtížn ě jší interpretace výsledků ákladní vtah posktjí rámec pro odvoení D a 2D modelů D a 2D model
y 10 20 Obrázek 1.26: Průměrová rovina válcové plochy
 36 KAPITOLA 1. KVADRIKY JAKO PLOCHY 2. STUPNĚ 2 1 2 1 1 y 1 2 Obráek 1.26: Průměrová rovina válcové plochy Věta: Je-li definována průměrová rovina sdružená s asymptotickým směrem, potom je s tímto směrem
36 KAPITOLA 1. KVADRIKY JAKO PLOCHY 2. STUPNĚ 2 1 2 1 1 y 1 2 Obráek 1.26: Průměrová rovina válcové plochy Věta: Je-li definována průměrová rovina sdružená s asymptotickým směrem, potom je s tímto směrem
HYDROPNEUMATICKÝ VAKOVÝ AKUMULÁTOR
 HYDROPNEUMATICKÝ AKOÝ AKUMULÁTOR OSP 050 ŠEOBECNÉ INFORMACE ýočet hydroneumatického akumulátoru ZÁKLADNÍ INFORMACE Při výočtu hydroneumatického akumulátoru se vychází ze stavové změny lynu v akumulátoru.
HYDROPNEUMATICKÝ AKOÝ AKUMULÁTOR OSP 050 ŠEOBECNÉ INFORMACE ýočet hydroneumatického akumulátoru ZÁKLADNÍ INFORMACE Při výočtu hydroneumatického akumulátoru se vychází ze stavové změny lynu v akumulátoru.
Fáze a fázové přechody
 Kvantová a statistická fyzika 2 (Termodynamika a statistická fyzika) Fáze a fázové přechody Pojem fáze je zobecněním pojmu skupenství, označuje homogenní část makroskopického tělesa. Jednotlivé fáze v
Kvantová a statistická fyzika 2 (Termodynamika a statistická fyzika) Fáze a fázové přechody Pojem fáze je zobecněním pojmu skupenství, označuje homogenní část makroskopického tělesa. Jednotlivé fáze v
Učební texty k státní bakalářské zkoušce Matematika Diferenciální rovnice. študenti MFF 15. augusta 2008
 Učební texty k státní bakalářské zkoušce Matematika Diferenciální rovnice študenti MFF 15. augusta 2008 1 7 Diferenciální rovnice Požadavky Soustavy lineárních diferenciálních rovnic prvního řádu lineární
Učební texty k státní bakalářské zkoušce Matematika Diferenciální rovnice študenti MFF 15. augusta 2008 1 7 Diferenciální rovnice Požadavky Soustavy lineárních diferenciálních rovnic prvního řádu lineární
Globální extrémy (na kompaktní množině)
 Globální extrémy (na kompaktní množině) Budeme hledat globální extrémy funkce f na uzavřené a ohraničené (tedy kompaktní) množině M. Funkce f může svého globálního extrému na M nabývat bud v nějaké bodě
Globální extrémy (na kompaktní množině) Budeme hledat globální extrémy funkce f na uzavřené a ohraničené (tedy kompaktní) množině M. Funkce f může svého globálního extrému na M nabývat bud v nějaké bodě
KLASICKÁ MECHANIKA. Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny.
 MECHANIKA 1 KLASICKÁ MECHANIKA Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny. Klasická mechanika rychlosti těles jsou mnohem menší než rychlost světla ve
MECHANIKA 1 KLASICKÁ MECHANIKA Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny. Klasická mechanika rychlosti těles jsou mnohem menší než rychlost světla ve
PRŮTOK PLYNU OTVOREM
 PRŮTOK PLYNU OTVOREM P. Škrabánek, F. Dušek Univerzita Pardubice, Fakulta chemicko technologická Katedra řízení rocesů a výočetní techniky Abstrakt Článek se zabývá ověřením oužitelnosti Saint Vénantovavy
PRŮTOK PLYNU OTVOREM P. Škrabánek, F. Dušek Univerzita Pardubice, Fakulta chemicko technologická Katedra řízení rocesů a výočetní techniky Abstrakt Článek se zabývá ověřením oužitelnosti Saint Vénantovavy
 !!! #!! # % & ()!+ %& #( ) +,,!,!!./0./01 2 34 % 00 (1!#! #! #23 + )!!,,5,!+ 4)!005!! 6 )! %,76!,8, )! 44 %!! #! #236!!1 1 5 6 5+!!1 ( 9 9!5 6 + /+ # % 7 8 % : 4; 2,/! = %
!!! #!! # % & ()!+ %& #( ) +,,!,!!./0./01 2 34 % 00 (1!#! #! #23 + )!!,,5,!+ 4)!005!! 6 )! %,76!,8, )! 44 %!! #! #236!!1 1 5 6 5+!!1 ( 9 9!5 6 + /+ # % 7 8 % : 4; 2,/! = %
1. série. Různá čísla < 1 44.
 série Téma: Termínodeslání: Různá čísla ½ º Ò ½ ½º ÐÓ je řirozené q9+9 q 6+ 9 9 6 ¾º ÐÓ `5+ 6 998 není řirozené º ÐÓ Nechť c je řirozené číslo Rozhodněte, které z čísel c+ c a c c je větší a své tvrzení
série Téma: Termínodeslání: Různá čísla ½ º Ò ½ ½º ÐÓ je řirozené q9+9 q 6+ 9 9 6 ¾º ÐÓ `5+ 6 998 není řirozené º ÐÓ Nechť c je řirozené číslo Rozhodněte, které z čísel c+ c a c c je větší a své tvrzení
Laplaceova transformace.
 Lalaceova transformace - studijní text ro cvičení v ředmětu Matematika -. Studijní materiál byl řiraven racovníky katedry E. Novákovou, M. Hyánkovou a L. Průchou za odory grantu IG ČVUT č. 300043 a v rámci
Lalaceova transformace - studijní text ro cvičení v ředmětu Matematika -. Studijní materiál byl řiraven racovníky katedry E. Novákovou, M. Hyánkovou a L. Průchou za odory grantu IG ČVUT č. 300043 a v rámci
14. cvičení z Matematické analýzy 2
 4. cvičení z atematické analýzy 2 8. - 2. ledna 28 4. (Greenova věta) Použijte Greenovu větu k nalezení práce síly F (x, y) (2xy 3, 4x 2 y 2 ) vykonané na částici podél křivky Γ, která je hranicí oblasti
4. cvičení z atematické analýzy 2 8. - 2. ledna 28 4. (Greenova věta) Použijte Greenovu větu k nalezení práce síly F (x, y) (2xy 3, 4x 2 y 2 ) vykonané na částici podél křivky Γ, která je hranicí oblasti
Nalezněte hladiny následujících funkcí. Pro které hodnoty C R jsou hladiny neprázdné
 . Definiční obor a hladiny funkce více proměnných Nalezněte a graficky znázorněte definiční obor D funkce f = f(x, y), kde a) f(x, y) = x y, b) f(x, y) = log(xy + ), c) f(x, y) = xy, d) f(x, y) = log(x
. Definiční obor a hladiny funkce více proměnných Nalezněte a graficky znázorněte definiční obor D funkce f = f(x, y), kde a) f(x, y) = x y, b) f(x, y) = log(xy + ), c) f(x, y) = xy, d) f(x, y) = log(x
Uzavřené a otevřené množiny
 Teorie: Uzavřené a otevřené množiny 2. cvičení DEFINICE Nechť M R n. Bod x M nazveme vnitřním bodem množiny M, pokud existuje r > 0 tak, že B(x, r) M. Množinu všech vnitřních bodů značíme Int M. Dále,
Teorie: Uzavřené a otevřené množiny 2. cvičení DEFINICE Nechť M R n. Bod x M nazveme vnitřním bodem množiny M, pokud existuje r > 0 tak, že B(x, r) M. Množinu všech vnitřních bodů značíme Int M. Dále,
Diferenciální počet funkcí více proměnných
 Vysoké učení technické v Brně Fakulta strojního inženýrství Diferenciální počet funkcí více proměnných Doc RNDr Miroslav Doupovec, CSc Neřešené příklady Matematika II OBSAH Obsah I Diferenciální počet
Vysoké učení technické v Brně Fakulta strojního inženýrství Diferenciální počet funkcí více proměnných Doc RNDr Miroslav Doupovec, CSc Neřešené příklady Matematika II OBSAH Obsah I Diferenciální počet
NMAF063 Matematika pro fyziky III Zápočtová písemná práce B Termín pro odevzdání 4. ledna 2019
 Jméno: Příklad 2 3 4 5 Celkem bodů Bodů 20 20 20 20 20 00 Získáno Zápočtová písemná práce určená k domácímu vypracování. Nutnou podmínkou pro získání zápočtu je zisk více jak 50 bodů. Pravidla jsou následující:.
Jméno: Příklad 2 3 4 5 Celkem bodů Bodů 20 20 20 20 20 00 Získáno Zápočtová písemná práce určená k domácímu vypracování. Nutnou podmínkou pro získání zápočtu je zisk více jak 50 bodů. Pravidla jsou následující:.
MFT - Matamatika a fyzika pro techniky
 MFT - Matamatika a fyzika pro techniky Pro každou přednášku by zde měl být seznam klíčových témat, odkaz na literaturu, zápočtový příklad k řešení a další příklady k procvičování převážně ze sbírky příkladů
MFT - Matamatika a fyzika pro techniky Pro každou přednášku by zde měl být seznam klíčových témat, odkaz na literaturu, zápočtový příklad k řešení a další příklady k procvičování převážně ze sbírky příkladů
4. Diferenciál a Taylorova věta
 4. Diferenciál a Taylorova věta Definice 4.1. Buď f : R n R, a Df. Řekneme, že f je diferencovatelná v bodě a, když h V n takový, že a + h Df platí f(a + h) f(a) gradf(a) h + h τ(h), kde lim τ(h) 0. Funkce
4. Diferenciál a Taylorova věta Definice 4.1. Buď f : R n R, a Df. Řekneme, že f je diferencovatelná v bodě a, když h V n takový, že a + h Df platí f(a + h) f(a) gradf(a) h + h τ(h), kde lim τ(h) 0. Funkce
22 Základní vlastnosti distribucí
 M. Rokyta, MFF UK: Aplikovaná matematika IV kap. 22: Základní vlastnosti distribucí 5 22 Základní vlastnosti distribucí 22.1 Temperované distribuce Definice. O funkci ϕ C (R m ) řekneme, že je rychle klesající
M. Rokyta, MFF UK: Aplikovaná matematika IV kap. 22: Základní vlastnosti distribucí 5 22 Základní vlastnosti distribucí 22.1 Temperované distribuce Definice. O funkci ϕ C (R m ) řekneme, že je rychle klesající
Transformujte diferenciální výraz x f x + y f do polárních souřadnic r a ϕ, které jsou definovány vztahy x = r cos ϕ a y = r sin ϕ.
 Ukázka 1 Necht má funkce z = f(x, y) spojité parciální derivace. Napište rovnici tečné roviny ke grafu této funkce v bodě A = [ x 0, y 0, z 0 ]. Transformujte diferenciální výraz x f x + y f y do polárních
Ukázka 1 Necht má funkce z = f(x, y) spojité parciální derivace. Napište rovnici tečné roviny ke grafu této funkce v bodě A = [ x 0, y 0, z 0 ]. Transformujte diferenciální výraz x f x + y f y do polárních
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ APLIKOVANÁ FYZIKA MODUL 2 TERMODYNAMIKA
 YSOKÉ UČENÍ ECHNICKÉ BRNĚ FAKULA SAEBNÍ PAEL SCHAUER APLIKOANÁ FYZIKA MODUL ERMODYNAMIKA SUDIJNÍ OPORY PRO SUDIJNÍ PROGRAMY S KOMBINOANOU FORMOU SUDIA Recenzoval: Prof. RNDr. omáš Ficker, CSc. Pavel Schauer,
YSOKÉ UČENÍ ECHNICKÉ BRNĚ FAKULA SAEBNÍ PAEL SCHAUER APLIKOANÁ FYZIKA MODUL ERMODYNAMIKA SUDIJNÍ OPORY PRO SUDIJNÍ PROGRAMY S KOMBINOANOU FORMOU SUDIA Recenzoval: Prof. RNDr. omáš Ficker, CSc. Pavel Schauer,
pouze u některých typů rovnic a v tomto textu se jím nebudeme až na
 Matematika II 7.1. Zavedení diferenciálních rovnic Definice 7.1.1. Rovnice tvaru F(y (n), y (n 1),, y, y, x) = 0 se nazývá diferenciální rovnice n-tého řádu pro funkci y = y(x). Speciálně je F(y, y, x)
Matematika II 7.1. Zavedení diferenciálních rovnic Definice 7.1.1. Rovnice tvaru F(y (n), y (n 1),, y, y, x) = 0 se nazývá diferenciální rovnice n-tého řádu pro funkci y = y(x). Speciálně je F(y, y, x)
Termomechanika 6. přednáška Doc. Dr. RNDr. Miroslav Holeček
 Termomechanika 6. přednáška Doc. Dr. RNDr. Miroslav Holeček Upozornění: Tato prezentace slouží výhradně pro výukové účely Fakulty strojní Západočeské univerzity v Plzni. Byla sestavena autorem s využitím
Termomechanika 6. přednáška Doc. Dr. RNDr. Miroslav Holeček Upozornění: Tato prezentace slouží výhradně pro výukové účely Fakulty strojní Západočeské univerzity v Plzni. Byla sestavena autorem s využitím
12.1 Úvod. Poznámka : Příklad 12.1: Funkce f(t) = e t2 nemá Laplaceův obraz. Příklad 12.2: a) L{1} = 1 p, p > 0 ; b) L{ eat } = 1, [ZMA15-P73]
![12.1 Úvod. Poznámka : Příklad 12.1: Funkce f(t) = e t2 nemá Laplaceův obraz. Příklad 12.2: a) L{1} = 1 p, p > 0 ; b) L{ eat } = 1, [ZMA15-P73] 12.1 Úvod. Poznámka : Příklad 12.1: Funkce f(t) = e t2 nemá Laplaceův obraz. Příklad 12.2: a) L{1} = 1 p, p > 0 ; b) L{ eat } = 1, [ZMA15-P73]](/thumbs/96/129935353.jpg) KAPITOLA 2: Lalaceova transformace [ZMA5-P73] 2. Úvod Lalaceovým obrazem funkce f(t) definované na, ) nazýváme funkci F () definovanou ředisem Definičním oborem funkce F F () = f(t) e t dt. je množina
KAPITOLA 2: Lalaceova transformace [ZMA5-P73] 2. Úvod Lalaceovým obrazem funkce f(t) definované na, ) nazýváme funkci F () definovanou ředisem Definičním oborem funkce F F () = f(t) e t dt. je množina
A[a 1 ; a 2 ; a 3 ] souřadnice bodu A v kartézské soustavě souřadnic O xyz
![A[a 1 ; a 2 ; a 3 ] souřadnice bodu A v kartézské soustavě souřadnic O xyz A[a 1 ; a 2 ; a 3 ] souřadnice bodu A v kartézské soustavě souřadnic O xyz](/thumbs/47/23721460.jpg) 1/15 ANALYTICKÁ GEOMETRIE Základní pojmy: Soustava souřadnic v rovině a prostoru Vzdálenost bodů, střed úsečky Vektory, operace s vektory, velikost vektoru, skalární součin Rovnice přímky Geometrie v rovině
1/15 ANALYTICKÁ GEOMETRIE Základní pojmy: Soustava souřadnic v rovině a prostoru Vzdálenost bodů, střed úsečky Vektory, operace s vektory, velikost vektoru, skalární součin Rovnice přímky Geometrie v rovině
Obrázek1:Nevratnáexpanzeplynupřesporéznípřepážkudooblastisnižšímtlakem p 2 < p 1
 Joule-Thomsonův jev Fyzikální raktikum z molekulové fyziky a termodynamiky Teoretický rozbor Entalie lynu Při Joule-Thomsonově jevu dochází k nevratné exanzi lynů do rostředí s nižším tlakem. Pro ilustraci
Joule-Thomsonův jev Fyzikální raktikum z molekulové fyziky a termodynamiky Teoretický rozbor Entalie lynu Při Joule-Thomsonově jevu dochází k nevratné exanzi lynů do rostředí s nižším tlakem. Pro ilustraci
KRUHOVÝ DĚJ S IDEÁLNÍM PLYNEM. Studijní text pro řešitele FO a ostatní zájemce o fyziku. Přemysl Šedivý. 1 Základní pojmy 2
 Obsah KRUHOÝ DĚJ S IDEÁLNÍM PLYNEM Studijní text ro řešitele FO a ostatní zájemce o fyziku Přemysl Šedivý Základní ojmy ztahy užívané ři oisu kruhových dějů s ideálním lynem Přehled základních dějů v ideálním
Obsah KRUHOÝ DĚJ S IDEÁLNÍM PLYNEM Studijní text ro řešitele FO a ostatní zájemce o fyziku Přemysl Šedivý Základní ojmy ztahy užívané ři oisu kruhových dějů s ideálním lynem Přehled základních dějů v ideálním
Funkce zadané implicitně
 Kapitola 8 Funkce zadané implicitně Začneme několika příklady. Prvním je známá rovnice pro jednotkovou kružnici x 2 + y 2 1 = 0. Tato rovnice popisuje křivku, kterou si však nelze představit jako graf
Kapitola 8 Funkce zadané implicitně Začneme několika příklady. Prvním je známá rovnice pro jednotkovou kružnici x 2 + y 2 1 = 0. Tato rovnice popisuje křivku, kterou si však nelze představit jako graf
Jméno... Cvičení den... hodina... Datum...rok... Počet listů... Varianta A
 æ æ Jméno... Cvičení den... hodina... Datum...rok... Počet listů.......... Varianta A 4 3 2 1 2 8 0 1 0 3 1. Vzhledem k reálnému parametru a diskutujte hodnost matice 2 1 0 1 2. 0 1 2 1 2 4 3 1 1 a 2.
æ æ Jméno... Cvičení den... hodina... Datum...rok... Počet listů.......... Varianta A 4 3 2 1 2 8 0 1 0 3 1. Vzhledem k reálnému parametru a diskutujte hodnost matice 2 1 0 1 2. 0 1 2 1 2 4 3 1 1 a 2.
Obyčejnými diferenciálními rovnicemi (ODR) budeme nazývat rovnice, ve kterých
 Obyčejné diferenciální rovnice Obyčejnými diferenciálními rovnicemi (ODR) budeme nazývat rovnice, ve kterých se vyskytují derivace neznámé funkce jedné reálné proměnné. Příklad. Bud dána funkce f : R R.
Obyčejné diferenciální rovnice Obyčejnými diferenciálními rovnicemi (ODR) budeme nazývat rovnice, ve kterých se vyskytují derivace neznámé funkce jedné reálné proměnné. Příklad. Bud dána funkce f : R R.
Matematika I A ukázkový test 1 pro 2014/2015
 Matematika I A ukázkový test 1 pro 2014/2015 1. Je dána soustava rovnic s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napište Frobeniovu větu (existence i počet řešení). b)
Matematika I A ukázkový test 1 pro 2014/2015 1. Je dána soustava rovnic s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napište Frobeniovu větu (existence i počet řešení). b)
1. Cvičení: Opakování derivace a integrály
 . Cvičení: Opakování derivace a integrál Derivace Příklad: Určete derivace následujících funkcí. f() e 5 ( 5 cos + sin ) f () 5e 5 ( 5 cos + sin ) + e 5 (5 sin + cos ) e 5 cos + 65e 5 sin. f() + ( + )
. Cvičení: Opakování derivace a integrál Derivace Příklad: Určete derivace následujících funkcí. f() e 5 ( 5 cos + sin ) f () 5e 5 ( 5 cos + sin ) + e 5 (5 sin + cos ) e 5 cos + 65e 5 sin. f() + ( + )
+ 2y y = nf ; x 0. závisí pouze na vzdálenosti bodu (x, y) od počátku, vyhovuje rovnici. y F x x F y = 0. x y. x x + y F. y = F
 Příkad 1 ( y ) Dokažte, že funkce F (x, y) = x n f x 2, kde f je spojitě diferencovatelná funkce, vyhovuje vztahu x F x + 2y F y = nf ; x 0 Ukažte, že každá funkce F (x, y), která má spojité parciální
Příkad 1 ( y ) Dokažte, že funkce F (x, y) = x n f x 2, kde f je spojitě diferencovatelná funkce, vyhovuje vztahu x F x + 2y F y = nf ; x 0 Ukažte, že každá funkce F (x, y), která má spojité parciální
Laplaceova transformace
 Lalaceova transformace EO2 Přednáška 3 Pavel Máša ÚVODEM Víme, že Fourierova transformace díky řísným odmínkám existence neexistuje ro řadu běžných signálů dokonce i funkce sin musela být zatlumena Jak
Lalaceova transformace EO2 Přednáška 3 Pavel Máša ÚVODEM Víme, že Fourierova transformace díky řísným odmínkám existence neexistuje ro řadu běžných signálů dokonce i funkce sin musela být zatlumena Jak
Základy elektrických pohonů, oteplování,ochlazování motorů
 Základy elektrických ohonů, otelování,ochlazování motorů Určeno ro studenty kombinované formy FS, ředmětu Elektrotechnika II an Dudek únor 2007 Elektrický ohon Definice (dle ČSN 34 5170): Elektrický ohon
Základy elektrických ohonů, otelování,ochlazování motorů Určeno ro studenty kombinované formy FS, ředmětu Elektrotechnika II an Dudek únor 2007 Elektrický ohon Definice (dle ČSN 34 5170): Elektrický ohon
Termodynamické potenciály
 Kapitola 1 Termodynamické potenciály 11 Vnitřní energie a U-formulace Fyzikání význam vnitřní energie: v průběhu adiabatického děje je vykonaná práce rovna úbytku vnitřní energie Platí pro vratné i pro
Kapitola 1 Termodynamické potenciály 11 Vnitřní energie a U-formulace Fyzikání význam vnitřní energie: v průběhu adiabatického děje je vykonaná práce rovna úbytku vnitřní energie Platí pro vratné i pro
