Vyjádření ke studentské anketě
|
|
|
- Jakub Vít Kašpar
- před 6 lety
- Počet zobrazení:
Transkript
1 Vyjádření ke studentské anketě Předměty: B3B01 KAT - Komplexní Analýza a transformace A8B01MCT - Matematika-komplexní proměnná a integrální transformace A3M01MKI - Matematika pro kybernetiku Vážené studentky a studenti, děkuji za vaši spolupráci během semestru a účast v anketě. Těší mě kladné komentáře, které převažují. Zamýšlím se nad kritickými poznámkami a náměty ke zlepšení. Především mě ale teší, že znalosti u zkoušky byly lepší než v prvním běhu předmětu v loňském roce. Řada studentů mi udělala radost jak zvládnutím písemné části, tak i porozuměním látce u části ústní. Mnoho studentů předmět nepodcenilo a pracovalo pravidelně již během semestru. Dialog, konzultace, a zájem studentů mě potěšily. Průchodnost předmětu se také výrazně zlepšila. K tomu se snažili přispět i vyučující. Nad rámec kontaktních hodin jsme se se studenty setkávali na dobrovolných konzultacích k přednášce (Komplexní pohovory), konzultacím ke cvičení (počítání příkladů navíc) i konzultacím ke zkoušce (byly propočítány veškeré teoretické i početní příklady z minulých písemek). Jsem rád, že mnozí studenti toto v anketě ocenili. Dále jsme změnili systém hodnocení tak, aby body ze semestru studentům u hodnocení zkoušky pouze pomáhaly a netvořily další nutný práh pro absolvování předmětu. I nadále budeme hledat cesty, jak studentům pomoci a přitom nesnižovat požadovanou úroveň znalostí. Rád bych stručně reagoval na některé komentáře studentů k hodnocení učitele i předmětů. Některé náměty se objevovaly i v loňské anketě, kde na ně bylo obsáhleji odpovězeno. Příkládám proto i vyjádření z loňského roku jako přílohu. Náročnost předmětu, hodinová dotace, kredity, apod. Řada studentů hodnotí předmět jako náročný a požadavky jako vysoké. K tomu se podrobněji vyjadřuji v reakci z loňského roku (viz níže). Předmět je koncovou matematickou analýzou, a proto je náročnější než Matematika I a II. Vzhledem k tomu, že obsahuje látku, která má mnoho aplikací, má i více typových úloh. Na druhé straně vše je založeno jen na několika principech a integrální transformace jsou do značné míry přeformulováním úloh z komplexní analýzy. Může se tedy 1
2 zdát, že dveří je mnoho. Klíčů k jejich otevírání je ale jen pár! Hodinová dotace předmětu a osnova je dána akreditací, tempo výkladu se tomu musí přizpůsobit. Možná by prospělo zvýšit dotaci na cvičení. Budeme nadále pořádat dobrovolná cvičení navíc a komplexní pohovory, i hledat cestu, jak více procvičit Fourierovu a Laplaceovu transformaci. Opět se objevuje snaha studentů srovnávat tento předmět s komplexní proměnnou na MFF UK. Tam se jde ovšem nesrovnatelně více jak do hloubky, tak i od šířky, což vím velice dobře jako absolvent tamní matematické analýzy. Některé výhrady byly vzneseny vůči počtu kreditů versus náročnosti. To neni v kompetenci vyučujících. Osobně bych bych se mírnému zvýšení kreditů nebránil. Na druhé straně je však třeba si uvědomit, že kredity nemohou úplně odrážet obtížnost. Pro mnoho studentů jsou matematiky obtížnější než ostatní předměty, ale dát jim za to více kreditů není reálné (například kvůli vyváženosti mezi profilovými a základními kurzy). Hodnocení v semestru a u zkoušky V některých komentářích se uvádí, že písemky v semestru jsou lehčí a jejich body se neodrazí v celkovém hodnocení. S prvním tvrzením souhlasím a nepovažuji to za problém. Tyto písemky slouží k podpoře průběžného studia, k získání zápočtu, jsou psány z menšího rozsahu učiva, neobsahují teorii, apod. K hodnocení ovšem přispěly. Přihlíželi jsme k nim u ústní části zkoušky, kde pomáhaly celkovou známku zlepšit (což mnoho studentů ocenilo i v této anketě). Ano, k postupu k ústní části je třeba, nezávisle na výsledcích ze semestru, napsat polovinu zkouškové písemky dobře. To považuji za správný a běžný požadavek. Polemizoval bych také s názorem, že u zkoušky by měly být k dispozici veškeré materiály, nebot je to na západní univerzitách běžné. Škoda, že studentka/student neřekli na jakých. Západní univerzity znám, sám na nich učím a podílím se na zkoušení (external examiner). Ze své osobní zkušenosti tak vím, že jsou tam velice striktní pravidla. Nejsou povoleny žádné studijní materiály, písemka se píše více méně jen jednou (ne 2-3 krát jako u nás), apod. Podle jednoho komentáře jem měl prohlásit, že vypíšu jen minimum termínů. Nic takého jsem neřekl a termínů bylo vypsáno dostatečně (předtermín plus každý týden termín pro 50 lidí - to je nadstandard ve srovnání s ostaními předměty). Různé Budu se snažit vylepšit stránku předmětu a zařadim kurz do Courseware. Zmiňované desetiminutové zpoždění na cvičení a pětiminutové na přednášce odmítám. Několikrát jsem ale na cvičení pozdě přišel a příště budu dochvilný. (Komplexními pohovory jsem ovšem případnou časovou ztrátu bohatě vyrovnal.) Kde je to možné, zpomalím výklad, a budu více psát na tabuli. Na druhé straně již téměř vše na tabuli píši a slidy jsou jen podpůrným materiálem. 2
3 Jsou však nezastupitelné v tom, že si studenti nemusí vše psát a že chrání studenty před mým špatným rukopisem. (Zde prosím studenty o toleranci, i já mam schovívavost k nečitelnosti mnohých písemek a snažím se je rozluštit.) Oceňuji posun názoru u některých studentů : "Stále si myslím, že matematik je tak trochu diagnóza, ale když má tak velké srdce jako prof. Hamhalter, tak na tom není nic špatného!" A děkuji také studentovi OES za krásnou básničku o předmětu, osvěžila mě! Těším se na další setkání a přeji hodně zdaru v dalším studiu. Jan Hamhalter, Březen 2019 Příloha vyjádření k anketě v roce 2018 Vážené studentky a studenti, děkuji za vaši účast v anketě, za kladná hodnocení, konstruktivní připomínky i kritické poznámky. Mé vyjádření k nim bude společné pro následující předměty, které byly vyučovány jednotně: B3B01 KAT - Komplexní Analýza a transformace A8B01MCT - Matematika-komplexní proměnná a integrální transformace A3M01MKI - Matematika pro kybernetiku Největší z těchto předmětů B3B01KAT byl vyučován v tomto semestru poprvé. Předmět se stejnou náplní komplexní analýzy a transformací jsem několik let učil v magisterské etapě. Jeho přesun (a redukci o stochastické procesy) do bakalářského studia považuji za správný. V minulém období byla výuka předmětu stabilně hodnocena studenty velmi dobře (známka přednášejícícho 1,3) a solidně byly hodnoceny i materiály (známka 1,4). Výuka ani materiály se nezměnily (materiály se dokonce rozrostly), a 3
4 přesto se hodnocení skokově zhoršilo (známka pro přednášející 1,7 pro materiály 2,26). Domnívám se, že hlavní příčinou není kvalita výuky nebo materiálů jako taková, ale malá úspěšnost studentů u zkoušky (cca 46 % průchodnost). Studenti dopadli hůře než dříve, což se do hodnocení ve studentské anketě často promítá. Nespokojenost respondentů s výsledkem zkoušky se projevila tónem, stylem i obsahem mnoha komentářů. Doufám, že po první zkušenosti se prospěch studentů zlepší. Vyučující se budou snažit předmět dále vylepšovat, nesnižovat jeho úrověň, a studenty vést k porozumění principům a systematické práci. Rád bych se ještě zevrubněji vyjádřil k některým okruhům připomínek. Obsah a náročnost předmětu, styl předášky, průběh zkoušení Komplexní proměnná a integrální transformace jsou tradičně základním matematickým předmětem na mnoha světových technických univerzitách. Na FEL ČVUT byla tato problematika přednášena od "nepaměti" ve druhém či třetím ročníku bakalářského studia. Pouze od roku 2010 do roku 2015 byla přesunuta do magisterské etapy programu KYR, a to s přidáním teorie stochastických procesů. Souhlasím se studenty, že předmět není lehký. Vyžaduje znalost předchozích matematických analýz, kombinuje je, obsahuje mnoho nových metod, pojmů a myšlenek. Vede k většímu počtu typových úloh, které se nedají naučit mechanicky bez hlubšího pochopení látky. Na druhé straně se nedomnívám, že je pro studenty nebetyčně složitý a nedá se systematickou prací během semestru a zkouškového období zvládnout. Řada studentů dostala hodnocení A (6 A z počtu 69 známek) a pochválila přínos předmětu. U ústní zkoušky jsem se přesvědčil, že jim nedělá problém všechny partie pochopit do hloubky. To vyvrací některé poznámky studentů, že nikdo předmět nepochopil a pro nikoho nebyl přínosem. Ve studentských komentářích se několikrát proti sobě stavěly dvě části předmětu: komplexní proměnná a integrální transformace. Integrálním transformacím se podle názoru některých věnovalo méně času a komplexní proměnná na rozdíl od nich nemá praktický význam. Nesouhlasím, myslím si totiž, že tato dvě témata nejdou od sebe oddělit. Vždyt například transformce Z je jenom jinak formulovaná úloha o Laurentově rozvoji a bez teorie singularit se nedají transformace pochopit a spočítat. Kdo dobře zvládne komplexní proměnou, neměl by mít s integrálními transformacemi problém. Cvičení měla poloviční dotaci než přednáška, proto na ní nebyla procvičena transformace Z. Nicméně na přednáškách byla tato transformace dostatečné probrána, včetně velkého množství příkladů a aplikací (viz slidy). Jak jsem již psal v Dopisu studentům na začátku semestru, těžištěm předmětu je přednáška. Slidy na ní byly promítány jako podklad - na tabuli jsem vše shrnul a vysvětlil, veškeré příklady a složitější úvahy jsem řešil s křídou v ruce. Myslím si, že pravidelná účast na přednášce je důležitým předpokladem úspěchu u zkoušky. Bohužel musím konstatovat, že od poloviny semestru nebyla účast na přednášce tak vysoká, jak by si to náročnost předmětu zasluhovala. Na cvičeních jsem nebyl spokojen se znalostmi některých studentů a upozorňoval na to. Výsledky dvou zápočtových testů dobře korelují s výsledky zkouškové písemky a měly být pro studenty varováním. Někteří studenti se pozastavují nad nízkým procentem úspěšných studentů před posledním termínem. To je pravda. Ale velký podíl na tom má i skutečnost, že přes nabízenou kapacitu chodilo v první polovině zkouškového období na zkoušky jen málo studentů. Ještě že jich více přišlo na poslední termín. 4
5 Studijní materiály Studijní materiály na tuto problematiku byly vytvářeny několik let kolektivem vyučujících. Ve srovnání s ostatními předměty se mi zdají být nadstandardní. Studentům jsou k dipozici (volně ke stažení) prezentace přednášek (350 stran) a Sbírka úloh v rozsahu (183 stran), která obsahuje jak řešené, tak i neřešené úlohy. Tato dvojice spolu se zápisky z přednášky tvoří základ, ze kterého vycházejí požadavky ke zkoušce. K dispozici jsou i zadání závěrečných písemek z minulých let. Navíc, pokud se student nespokojí s doporučenými zahraničními učebnicemi, má k dispozici skripta na komplexní proměnnou a nově i elektronická skripta na integrální trasformace. V jedné kritické poznámce se studentka/student diví, že skripta neměla za 10 let opravené vydání. To mě překvapuje, protože nové vydání vyšlo loni na podzim, a bylo studentům doporučeno. Chyby se opravovaly i v předchozích dotiscích. Jeden komentář kritizuje pozdní dodání skript na integrální transformace. To je mi líto, psaní tohoto textu jsem obětoval vánoční prázdniny, nebot jsem to dříve nestihl. Nicmémě, jedná se spíše o doplňkový materiál určený pro studenty s hlubší zájmem o problematiku. Obsahuje zejména složitější důkazy, které se nezkoušejí. V minulosti byla s materiály větší spokojenost (známka oscilovala kolem 1,3). Stejné materiály byly studentům také dány na sesterském předmětu KAN. Je zajímavé, že tam byly ale hodnoceny o dost lépe (známka 1,36) oproti studentům z KYR (známka 2,26). Možná se tedy do hodnocení materiálů promítla rozdílná průchodnost v obou předmětech. Zkoušková zadání a jejich návaznost na výuku V několika komentářích vyjadřují studenti názor, že příklady u zkoušky netestovaly porozumění látce a byly technicky a početně nadměrně náročné. S tímto názorem se vyhraněně neztožňuji. Naopak, snažili jsme se především zkoušet porozumění pojmům a metodám, a to jak u zkoušky písemné, tak i zkoušky ústní. Pokud student prokázal u ústní zkoušky že látce rozumí mohl si známku výrazně vylepšit. Každá písemka obsahovala teoretickou otázkou na pojem či větu, kde se nemuselo počítat téměř vůbec a stačila základní faktografická znalost a vhled do problematiky. Tyto úlohy však měly nejmenší úspěšnost, což není v souladu s tvrzením některých studentů, že látce porozuměli, ale byli zaskočeni zbytečně složitými výpočty a penalizací za numerické chyby. Myslím si, že to byl právě důraz na pochopení, který činil studentům největší potíže. Zadání nevedla ke složitým výpočtům či nepříjemným výrazům. Nerozumím v tomto smyslu poznámce jednoho studenta o rozkladu polynomu na ireducibilní činitele v rozsahu jednoho řádku A4. Pouze jednou se ve zkouškové písemce objevil polynom stupně tři (v tomto případě byl studentům napovězen jeden kořen), jinak se jednalo vesměs o kvadratické polynomy. Několik studentů tvrdí, že neuspěli, protože byli vlastně zkoušeni z předchozí analýzy. Konkrétně si jeden student ztěžuje, že musel zderivovat funkci arctg a tento "detail" si přece nemůže z Matematické analýzy 1 pamatovat. Tato funkce je důležitá a student by si ji pamatovat měl. Nicméně, hlavní námitkou proti této připomínce je skutečnost, že u všech elementárních komplexních funkcí byla jejich derivace odvozena na přednášce, a to včetně funkce arctg - viz slide strana 80. I když ovšem znalosti z předchozích matematik nejsou cíleně zkoušeny, je 5
6 třeba základní věci z nich znát (včetně střední a základní školy), nebot se na nich dále staví. V tomto jsou "koncové" matematiky těžší. Další námitky studentů se týkají skutečnosti, že na přednášce, cvičení a v materiálech jsou řešeny příklady lehčí než u zkoušky. S tím nemohu souhlasit. Zveřejňuji v závěrečném odstavci níže veškerá zadaní u zkoušek a připojuji u každého příkladu odkaz na přednášku či materiály, kde se podobná, ne-li stejná úloha řeší. Korektnost Chápu, že některé připomínky studentů mohou být po nezdaru u zkoušky expresivní. Přesto se mi v několika případech zdá, že překročily mez a poškodily anketu a její princip anonymity. Například: "Je to matematik, nejspíše za to nemůže. Je to něco mezi diagnózou a prokletím". K tomu dodávám, že za to mohu a "prokletí" je mi životní radostí. V dalším anketním lístku je předmět popsán jako reikarnace Dachau. To by podle mého soudu nemělo zaznít ani v nadsázce. Zadání písemek a jejich zdroje 1. [10 bodů] Je dána Laurentova řada 1 n= Zadání č.1 n 2 n zn + n=0 3 n 2 n n! zn. a) Určete součet f(z) této řady a její obor konvergence. b) Stanovte C zf(z) dz, kde C je kladně orientovaná kružninice z = 2. Zdroj: slajd str. 133, a) analogie sbírka i), Sbírka: , b) ii) 2. [10 bodů] Je dána funkce f(z) v oblasti G C. Uvažujme následující tvrzení (A) f(z) dz = 0 pro každou Jordanovu křivku C G. C (B) f(z) má primitivní funkci v G. (C) f(z) je holomorfní v G. a) Dokažte (B) (A). b) Dokažte či vyvrat te (C) (A). c) Formulujte Cauchyovu větu. Zdroj: slajdy 4.12 str. 97, 4.13 str. 99, 4.15 str. 101, str.103. a) Důsledek na slajdu 98, b) příklad na slajdu 86 a také poznámka na slajdu
7 3. [10 bodů] Je dána funkce f(t) = t t a) Stanovte Fourierovu transformaci funkce f(t) a spočtěte ˆf(0). b) Pro jakou funkci g(t) platí, že Fourierův obraz součinu g(t)f(t) je ˆf(p 2)? c) Určete Fourierův obraz funkce e t2 f(2t). Zdroj: a) Sbírka (i) pro a = 2, řešeno na cvičení; b),c) bezprostřední aplikace gramatiky a věty o konvoluci. 4. [10 bodů] Máme dánu diferenciální rovnici y (t) + y(t) = g(t) s počátečními podmínkami y(0) = y (0) = 0, kde { 1 pro t 4n, 4n + 1), n = 0, 1,... g(t) = 0 jinak a) Určetete Laplaceův obraz řešení rovnice. b) Necht P, Q jsou polynomy, pro jejichž stupeň platí st P < st Q, a necht T > 0. Zdůvodněte, že inverzní Laplaceův obraz k funkci a Laplaceova inverze k funkci P (p) Q(p) P (p) Q(p) (1 e pt ) si jsou na intervalu (0, T ) rovny. c) Stanovte analyticky řešení na intervalu (0, 4) a vyjádřete ho bez použití symboliky jednotkové funkce. Zdroje: Řešeno na přednášce na tabuli, Sbírka a mnohé další (3.3.14,...) b) řešeno na cvičení. 7
8 1. [10 bodů] Je dána funkce a) Stanovte Zadání č. 2 f(z) = z + i z i. A = {f(z) z < 2}. b) Určete, pro jaké K 0 zobrazí funkce f(z) přímku q : Re z = K na kružninici bez jednoho bodu. Pro tato K určete střed kružninice, na kterou se přímka q zobrazí. Zdroje: Řešeno na tabuli na přednášce, Sbírka a mnohé další (3.3.14,...) 2. [10 bodů] Vypočtěte (x 3) cos x x(x 2 + 1) dx. Zdroje: Obcházení pólů - řešeno na přednášce na tabuli, Sbírka 6.2.ě3 (jen místo sinus je zde kosinus a x 3 místo x 2). 3. [10 bodů] Funkce f(z) má pól řádu 3 v bodě z 0 = i. a) Určete typ singularity i pro funkci f(z) + b) Určete typ singularity i pro funkci z (z i) 4. f(z) + e 1 (z i). c) At (a n ) n= jsou koeficienty Laurentova rozvoje funkce f(z) v prstencovém okolí bodu z 0 = i. Jakou podmínku (nutnou a postačující) musí koeficienty splňovat, aby i byl pól řádu 3? Zdroje: Základní definice a slajd: věta 6.12, a) a b) typově ii) 4. [10 bodů] a) Odvod te Taylorolův rozvoj funkce v okolí bodu 0. g(z) = ln(1 + z) b) Určete inverzní Z-transformaci funkce (Návod: Využijte výsledek bodu a).) F (z) = ln z3 + 1 z 3. 8
9 c) Posloupnost (y n ) n=0 Z 0 má Z-obraz G(z) = F (z) kde funkce F je jako v b). Stanovte y 9. z (z 1) 2, Zdroje: a) Slajd str.167, b) Sbírka: (lehká modifikace) c) přímočaré využití věty o konvoluce a defininici konvoluce. 9
10 Zadání č [10 bodů] Máme funkce h(x, y) = 2x y, g(x, y) = e x sin y + h(x, y). a) Určete všechny celistvé funkce f(z) tak, že Re f(z) = h(x, y). b) Určete všechny celistvé funkce ω(z) tak, že Re ω(z) = g(x, y). c) Určete všechny celistvé funkce r(z) tak, že Im r(z) = g(x, y). Zdroj: přímo definice e z slide p.66 a zbude lineární funkce, řešeno na tabuli na přednášce, na cvičení a i ve sbírce např b) (je řešený). 2. [10 bodů] a) Formulujte větu o Laplaceově obrazu periodické funkce. b) Určete A > 0 tak, aby funkce F (p) = 1 p 1 p e Ap, T > 0, 1 e pt byla Laplaceovým obrazem periodické funkce s periodou T. Nakreslete graf vzoru funkce F. Zdroj: slajd str [10 bodů] Je dána funkce F (p) = 1 p e 2p. a) Aplikací metody reziduí vyjádřete Laplaceův vzor f(t) k funkci F (p) s použitím nekonečné řady b) Ukažte, že f(t) = t ω(t), kde ω(t) je periodická funkce s periodou 4. c) Stanovte analyticky funkci ω(t) na intervalu (0, 4) a nakreslete její graf. Návod: Užijte b). 10
11 Zdroj: Je přímo ze Sbírky pro a = 2. Zcela analogické slajdu: Příklad 9.25 str , zevrubně řešeno na přednášce. 4. [10 bodů] Jsou dány diferenční rovnice y n+3 y n+2 + 2y n = n 2 n, (1) y n+3 y n+2 + 2y n = 0. (2) a) Napište parametrické vyjádření Z-obrazu řešení rovnice (1) vyhovujícího podmínkám y 0 = y 1 = 0. b) Nalezněte řešení rovnice (2) splňující y 0 = y 1 = 0, y 2 = 1. Zdroj: typická úloha ze slajdů p a ze sbírky: a další. a) viz
12 Zadání č [10 bodů] Je dána funkce f(z) = 1 sin 1. z a) Stanovte izolované singularity funkce f(z) a určete jejich typ. b) Stanovte hlavní část Laurentova rozvoje funkce f(z) v bodě z 0 = 1 π. c) Spočtěte integrál C 1 z sin 1 dz, z kde C je kladně orientovaná kružnice z = 3π. Zdroje: Řešeno na cvičení, Sbírka: a) a b) je příkad ze sbírky c) je jednoduchá aplikace rezidua v nekonecnu. 2. [10 bodů] Vypočtěte 2π 0 dt a + b sin t, a > b > 0. (Při výpočtu se může hodit fakt, že pro kořeny z 1, z 2 polynomu z 2 + pz + q platí z 1 z 2 = q.) Zdroje: slide Příklad na str. 199 zaměněn jen sinus za kosinus. 3. [10 bodů] a) Formulujte větu o Fourierově obrazu derivace. b) Je dána funkce g(t) taková, že g(t), g (t) L 1 (R). Pomocí Fourierova obrazu G(p) funkce g(t) stanovte Fourierův obraz funkce f(t) = g (t) ( 1(t 1) 1(t 2) ). Zdroje: slajd: a) 8.17 Věta b) aplikace věty z a), obrazu konvoluce a výpočtu obrazu obdélníkového pulzu. 4. [10 bodů] Máme posloupnost (a n ) n=0 Z 0. Řešte diferenční rovnici y n+1 + n 3 k y n k = a n, y 0 = 0. k=0 Zdroje: slajdy: Sbírka: a další 12
13 Zadání č [10 bodů] a) Formulujte větu o integrálním vyjádření koeficientů mocninné řady. b) Funkce f(z) je holomorfní v kruhu Víme, že Ukažte, že K = {z C z < R}. f(z) M z K. f (n) (0) n!m R n. Zdroje: Slajdy: Věta 5.11 a základní odhad křivkového integrálu. 2. [10 bodů] Je dána funkce f(z) = 1 (1 z) 3. a) Rozviňte f(z) v Laurentovu řadu v oblasti {z C z > 1}. b) Určete res z 100 f(z). Zdroje: a) analogie příkladu ze slidu 165, b) analogie příkladu Sbírka [10 bodů] Je dána funkce F (p) = 1 (p + 1)(p 1)(1 e p ). Určete její vzor f(t) v Laplaceově transformaci, a to analyticky na intervalu (1, 2). Zdroje: Typický příklad řešený na tabuli na přednášce, Sbírka: (jen jiný interval) 4. [10 bodů] Je dána posloupnost (a n ) n=0 Z 0. Řešte diferenční rovnici y n+1 y n = n + a n, y 0 = 1. Zdroje: Standardní příklad na diferenční rovnice (slajdy, sbírka) viz.například Jan Hamhalter, březen
B3B01 KAT - Komplexní Analýza a transformace
 Vážené studentky a studenti, děkuji za vaši účast v anketě, za kladná hodnocení, konstruktivní připomínky i kritické poznámky. Mé vyjádření k nim bude společné pro následující předměty, které byly vyučovány
Vážené studentky a studenti, děkuji za vaši účast v anketě, za kladná hodnocení, konstruktivní připomínky i kritické poznámky. Mé vyjádření k nim bude společné pro následující předměty, které byly vyučovány
MKI Funkce f(z) má singularitu v bodě 0. a) Stanovte oblast, ve které konverguje hlavní část Laurentova rozvoje funkce f(z) v bodě 0.
 MKI -00 Funkce f(z) má singularitu v bodě 0. a) Stanovte oblast, ve které konverguje hlavní část Laurentova rozvoje funkce f(z) v bodě 0. V jakém rozmezí se může pohybovat poloměr konvergence regulární
MKI -00 Funkce f(z) má singularitu v bodě 0. a) Stanovte oblast, ve které konverguje hlavní část Laurentova rozvoje funkce f(z) v bodě 0. V jakém rozmezí se může pohybovat poloměr konvergence regulární
Komplexní analýza. Reziduová věta a její aplikace. Martin Bohata. Katedra matematiky FEL ČVUT v Praze
 Komplexní analýza Reziduová věta a její aplikace Martin Bohata Katedra matematiky FEL ČVUT v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Reziduová věta a její aplikace / Motivace Mějme
Komplexní analýza Reziduová věta a její aplikace Martin Bohata Katedra matematiky FEL ČVUT v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Reziduová věta a její aplikace / Motivace Mějme
Komplexní analýza. Laplaceova transformace. Martin Bohata. Katedra matematiky FEL ČVUT v Praze
 Komplexní analýza Laplaceova transformace Martin Bohata Katedra matematiky FEL ČVUT v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Laplaceova transformace 1 / 18 Definice Definice Laplaceovou
Komplexní analýza Laplaceova transformace Martin Bohata Katedra matematiky FEL ČVUT v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Laplaceova transformace 1 / 18 Definice Definice Laplaceovou
ŘADY KOMPLEXNÍCH FUNKCÍ
 ŘADY KOMPLEXNÍCH FUNKCÍ OBECNÉ VLASTNOSTI Řady komplexních čísel z n byly částečně probírány v kapitole o číselných řadách. Definice říká, že n=0 z n = z, jestliže z je limita částečných součtů řady z
ŘADY KOMPLEXNÍCH FUNKCÍ OBECNÉ VLASTNOSTI Řady komplexních čísel z n byly částečně probírány v kapitole o číselných řadách. Definice říká, že n=0 z n = z, jestliže z je limita částečných součtů řady z
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %% POJMY, JEJICHŽ ZNALOST SE OČEKÁVÁ %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %% POJMY, JEJICHŽ ZNALOST SE OČEKÁVÁ %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% množina komplexních čísel algebraický zápis komplexního
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %% POJMY, JEJICHŽ ZNALOST SE OČEKÁVÁ %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% množina komplexních čísel algebraický zápis komplexního
ZS: 2018/2019 NMAF063 F/3 Josef MÁLEK. Matematika pro fyziky III
 ZS: 2018/2019 NMAF063 F/3 Josef MÁLEK Matematika pro fyziky III OBECNÉ INFORMACE A SYLABUS Přednášející: Cvičící: Josef Málek Tomáš Los, Michal Pavelka, Michal Pavelka, Vít Průša Termíny přednášek: čtvrtek
ZS: 2018/2019 NMAF063 F/3 Josef MÁLEK Matematika pro fyziky III OBECNÉ INFORMACE A SYLABUS Přednášející: Cvičící: Josef Málek Tomáš Los, Michal Pavelka, Michal Pavelka, Vít Průša Termíny přednášek: čtvrtek
METODICKÝ NÁVOD MODULU
 Centrum celoživotního vzdělávání METODICKÝ NÁVOD MODULU Název Základy matematiky modulu: Zkratka: ZM Počet kreditů: 4 Semestr: Z/L Mentor: Petr Dolanský Tutor: Petr Dolanský I OBSAH BALÍČKU STUDIJNÍCH
Centrum celoživotního vzdělávání METODICKÝ NÁVOD MODULU Název Základy matematiky modulu: Zkratka: ZM Počet kreditů: 4 Semestr: Z/L Mentor: Petr Dolanský Tutor: Petr Dolanský I OBSAH BALÍČKU STUDIJNÍCH
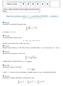
0 = 2e 1 (z 3 1)dz + 3z. z=0 z 3 4z 2 + 3z + rez. 4. Napište Fourierův rozvoj vzhledem k trigonometrickému systému periodickému
 2 1 1 0.8 0.6 0.4 0.2 0.2 0.4 0.6 0.8 1 x 1 2 Jméno a příjmení: ID.č. 9.5.2016 1. Řešte diferenciální rovnici: y + 2xy x 2 + 3 = sin x x 2 + 3. y = C cos x x 2 + 1 2. Vypočtěte z 2 e z dz, kde je křivka
2 1 1 0.8 0.6 0.4 0.2 0.2 0.4 0.6 0.8 1 x 1 2 Jméno a příjmení: ID.č. 9.5.2016 1. Řešte diferenciální rovnici: y + 2xy x 2 + 3 = sin x x 2 + 3. y = C cos x x 2 + 1 2. Vypočtěte z 2 e z dz, kde je křivka
FOURIEROVA TRANSFORMACE FOURIEROVA VĚTA
 FOURIEROVA TRANSFORMACE FOURIEROVA VĚTA V kapitole o Fourierových řadách byla dokázána Fourierova věta (připomeňte si, že f(x = (f(x + + f(x /2: VĚTA Necht f je po částech hladká na R a R f konverguje
FOURIEROVA TRANSFORMACE FOURIEROVA VĚTA V kapitole o Fourierových řadách byla dokázána Fourierova věta (připomeňte si, že f(x = (f(x + + f(x /2: VĚTA Necht f je po částech hladká na R a R f konverguje
Vybrané kapitoly z matematiky
 Vybrané kapitoly z matematiky VŠB-TU Ostrava 2017-2018 Vybrané kapitoly z matematiky 2017-2018 1 / 19 Základní informace předmět: 714-0513, 5 kreditů přednáší: Radek Kučera kontakt: radek.kucera@vsb.cz,
Vybrané kapitoly z matematiky VŠB-TU Ostrava 2017-2018 Vybrané kapitoly z matematiky 2017-2018 1 / 19 Základní informace předmět: 714-0513, 5 kreditů přednáší: Radek Kučera kontakt: radek.kucera@vsb.cz,
FOURIEROVA TRANSFORMACE
 FOURIEROVA TRANSFORMACE FOURIEROVA VĚTA V kapitole o Fourierových řadách byla dokázána (připomeňte si, že f(x) = (f(x + ) + f(x ))/2): VĚTA. Necht f je po částech hladká na R a R f konverguje. Potom f(x)
FOURIEROVA TRANSFORMACE FOURIEROVA VĚTA V kapitole o Fourierových řadách byla dokázána (připomeňte si, že f(x) = (f(x + ) + f(x ))/2): VĚTA. Necht f je po částech hladká na R a R f konverguje. Potom f(x)
Matematika. ochrana životního prostředí analytická chemie chemická technologie Forma vzdělávání:
 Studijní obor: Aplikovaná chemie Učební osnova předmětu Matematika Zaměření: ochrana životního prostředí analytická chemie chemická technologie Forma vzdělávání: denní Celkový počet vyučovacích hodin za
Studijní obor: Aplikovaná chemie Učební osnova předmětu Matematika Zaměření: ochrana životního prostředí analytická chemie chemická technologie Forma vzdělávání: denní Celkový počet vyučovacích hodin za
MATEMATIKA I - vybrané úlohy ze zkoušek v letech
 MATEMATIKA I - vybrané úlohy ze zkoušek v letech 008 0 doplněné o další úlohy. část DIFERENCIÁLNÍ POČET funkcí jedné proměnné Další část ( integrální počet) bude vydána na konci listopadu 9. 9. 0 Případné
MATEMATIKA I - vybrané úlohy ze zkoušek v letech 008 0 doplněné o další úlohy. část DIFERENCIÁLNÍ POČET funkcí jedné proměnné Další část ( integrální počet) bude vydána na konci listopadu 9. 9. 0 Případné
MATEMATIKA B 2. Integrální počet 1
 metodický list č. 1 Integrální počet 1 V tomto tématickém celku se posluchači seznámí s některými definicemi, větami a výpočetními metodami užívanými v části matematiky obecně známé jako integrální počet
metodický list č. 1 Integrální počet 1 V tomto tématickém celku se posluchači seznámí s některými definicemi, větami a výpočetními metodami užívanými v části matematiky obecně známé jako integrální počet
Matematika I A ukázkový test 1 pro 2014/2015
 Matematika I A ukázkový test 1 pro 2014/2015 1. Je dána soustava rovnic s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napište Frobeniovu větu (existence i počet řešení). b)
Matematika I A ukázkový test 1 pro 2014/2015 1. Je dána soustava rovnic s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napište Frobeniovu větu (existence i počet řešení). b)
Jméno a Příjmení. Třída. Škola
 Studentský dotazník Vážení studenti, cílem tohoto průzkumu je zjistit váš postoj k matematice a k výukovému nástroji Khan Academy. Vaše názory a odpovědi pomohou dalším studentům a učitelům při zapojování
Studentský dotazník Vážení studenti, cílem tohoto průzkumu je zjistit váš postoj k matematice a k výukovému nástroji Khan Academy. Vaše názory a odpovědi pomohou dalším studentům a učitelům při zapojování
Zimní semestr akademického roku 2014/ prosince 2014
 Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičení Zimní semestr akademického roku 24/25 2. prosince 24 Předmluva iii
Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičení Zimní semestr akademického roku 24/25 2. prosince 24 Předmluva iii
Separovatelné diferenciální rovnice
 Matematika 2, příklady na procvičení (Josef Tkadlec, 8. 6. 2009) Separovatelné diferenciální rovnice. Řešte diferenciální rovnici s počáteční podmínkou x = e x t, x() = 0. 2. Řešte diferenciální rovnici
Matematika 2, příklady na procvičení (Josef Tkadlec, 8. 6. 2009) Separovatelné diferenciální rovnice. Řešte diferenciální rovnici s počáteční podmínkou x = e x t, x() = 0. 2. Řešte diferenciální rovnici
Matematika I A ukázkový test 1 pro 2011/2012. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a
 Matematika I A ukázkový test 1 pro 2011/2012 1. Je dána soustava rovnic s parametrem a R x y + z = 1 a) Napište Frobeniovu větu. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a b) Vyšetřete počet řešení soustavy
Matematika I A ukázkový test 1 pro 2011/2012 1. Je dána soustava rovnic s parametrem a R x y + z = 1 a) Napište Frobeniovu větu. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a b) Vyšetřete počet řešení soustavy
Rovnice matematické fyziky cvičení pro akademický školní rok 2013-2014
 Harmonogram výuky předmětu Rovnice matematické fyziky cvičení pro akademický školní rok 2013-2014 Vedoucí cvičení: ing. Václav Klika, Ph.D. & MSc. Karolína Korvasová & & ing. Matěj Tušek, Ph.D. Katedra
Harmonogram výuky předmětu Rovnice matematické fyziky cvičení pro akademický školní rok 2013-2014 Vedoucí cvičení: ing. Václav Klika, Ph.D. & MSc. Karolína Korvasová & & ing. Matěj Tušek, Ph.D. Katedra
MATEMATIKA II - vybrané úlohy ze zkoušek ( 2015)
 MATEMATIKA II - vybrané úlohy ze zkoušek ( 2015 doplněné o další úlohy 13. 4. 2015 Nalezené nesrovnalosti ve výsledcích nebo připomínky k tomuto souboru sdělte laskavě F. Mrázovi ( e-mail: Frantisek.Mraz@fs.cvut.cz.
MATEMATIKA II - vybrané úlohy ze zkoušek ( 2015 doplněné o další úlohy 13. 4. 2015 Nalezené nesrovnalosti ve výsledcích nebo připomínky k tomuto souboru sdělte laskavě F. Mrázovi ( e-mail: Frantisek.Mraz@fs.cvut.cz.
B) výchovné a vzdělávací strategie jsou totožné se strategiemi vyučovacího předmětu Matematika.
 4.8.3. Cvičení z matematiky Předmět Cvičení z matematiky je vyučován v sextě a v septimě jako volitelný předmět. Vzdělávací obsah vyučovacího předmětu Cvičení z matematiky vychází ze vzdělávací oblasti
4.8.3. Cvičení z matematiky Předmět Cvičení z matematiky je vyučován v sextě a v septimě jako volitelný předmět. Vzdělávací obsah vyučovacího předmětu Cvičení z matematiky vychází ze vzdělávací oblasti
Tematický plán Obor: Informační technologie. Vyučující: Ing. Joanna Paździorová
 Tematický plán Vyučující: Ing. Joanna Paździorová 1. r o č n í k 5 h o d i n t ý d n ě, c e l k e m 1 7 0 h o d i n Téma- Tematický celek Z á ř í 1. Opakování a prohloubení učiva základní školy 18 1.1.
Tematický plán Vyučující: Ing. Joanna Paździorová 1. r o č n í k 5 h o d i n t ý d n ě, c e l k e m 1 7 0 h o d i n Téma- Tematický celek Z á ř í 1. Opakování a prohloubení učiva základní školy 18 1.1.
Otázky k ústní zkoušce, přehled témat A. Číselné řady
 Otázky k ústní zkoušce, přehled témat 2003-2004 A Číselné řady Vysvětlete pojmy částečný součet řady, součet řady, řadonverguje, řada je konvergentní Formulujte nutnou podmínku konvergence řady a odvoďte
Otázky k ústní zkoušce, přehled témat 2003-2004 A Číselné řady Vysvětlete pojmy částečný součet řady, součet řady, řadonverguje, řada je konvergentní Formulujte nutnou podmínku konvergence řady a odvoďte
Zimní semestr akademického roku 2014/ prosince 2014
 Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičení Zimní semestr akademického roku 2014/2015 2. prosince 2014 Předmluva
Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičení Zimní semestr akademického roku 2014/2015 2. prosince 2014 Předmluva
CZ 1.07/1.1.32/02.0006
 PO ŠKOLE DO ŠKOLY CZ 1.07/1.1.32/02.0006 Číslo projektu: CZ.1.07/1.1.32/02.0006 Název projektu: Po škole do školy Příjemce grantu: Gymnázium, Kladno Název výstupu: Prohlubující semináře Matematika (MI
PO ŠKOLE DO ŠKOLY CZ 1.07/1.1.32/02.0006 Číslo projektu: CZ.1.07/1.1.32/02.0006 Název projektu: Po škole do školy Příjemce grantu: Gymnázium, Kladno Název výstupu: Prohlubující semináře Matematika (MI
ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE. Matematika 0A1. Cvičení, zimní semestr. Samostatné výstupy. Jan Šafařík
 Vysoké učení technické v Brně Stavební fakulta ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE Matematika 0A1 Cvičení, zimní semestr Samostatné výstupy Jan Šafařík Brno c 2003 Obsah 1. Výstup č.1 2 2. Výstup
Vysoké učení technické v Brně Stavební fakulta ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE Matematika 0A1 Cvičení, zimní semestr Samostatné výstupy Jan Šafařík Brno c 2003 Obsah 1. Výstup č.1 2 2. Výstup
18 Fourierovy řady Úvod, základní pojmy
 M. Rokyta, MFF UK: Aplikovaná matematika III kap. 18: Fourierovy řady 7 18 Fourierovy řady 18.1 Úvod, základní pojmy Otázka J. Fouriera: Lze každou periodickou funkci napsat jako součet nějakých "elementárních"
M. Rokyta, MFF UK: Aplikovaná matematika III kap. 18: Fourierovy řady 7 18 Fourierovy řady 18.1 Úvod, základní pojmy Otázka J. Fouriera: Lze každou periodickou funkci napsat jako součet nějakých "elementárních"
SIGNÁLY A SOUSTAVY, SIGNÁLY A SYSTÉMY
 SIGNÁLY A SOUSTAVY, SIGNÁLY A SYSTÉMY TEMATICKÉ OKRUHY Signály se spojitým časem Základní signály se spojitým časem (základní spojité signály) Jednotkový skok σ (t), jednotkový impuls (Diracův impuls)
SIGNÁLY A SOUSTAVY, SIGNÁLY A SYSTÉMY TEMATICKÉ OKRUHY Signály se spojitým časem Základní signály se spojitým časem (základní spojité signály) Jednotkový skok σ (t), jednotkový impuls (Diracův impuls)
Katedra matematiky Fakulty jaderné a fyzikálně inženýrské ČVUT v Praze. Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A
 Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A středa 19. listopadu 2014, 11:20 13:20 ➊ (8 bodů) Rozhodněte o stejnoměrné konvergenci řady n 3 n ( ) 1 e xn2 x 2 +n 2 na množině A = 0, + ). ➋
Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A středa 19. listopadu 2014, 11:20 13:20 ➊ (8 bodů) Rozhodněte o stejnoměrné konvergenci řady n 3 n ( ) 1 e xn2 x 2 +n 2 na množině A = 0, + ). ➋
Diskrétní matematika. DiM /01, zimní semestr 2017/2018
 Diskrétní matematika Petr Kovář petr.kovar@vsb.cz Vysoká škola báňská Technická univerzita Ostrava DiM 470-2301/01, zimní semestr 2017/2018 O tomto souboru Tento soubor je zamýšlen především jako pomůcka
Diskrétní matematika Petr Kovář petr.kovar@vsb.cz Vysoká škola báňská Technická univerzita Ostrava DiM 470-2301/01, zimní semestr 2017/2018 O tomto souboru Tento soubor je zamýšlen především jako pomůcka
DEFINICE,VĚTYADŮKAZYKÚSTNÍZKOUŠCEZMAT.ANALÝZY Ib
 INFORMACE O PRŮBĚHU A POŽADAVKY KE ZKOUŠCE Z MAT. ANALÝZYIbVLS2010/11 Ke zkoušce mohou přistoupit studenti, kteří získali zápočet. Do indexu jej zapíši na zkoušce, pokud cvičící potvrdí, že na něj student
INFORMACE O PRŮBĚHU A POŽADAVKY KE ZKOUŠCE Z MAT. ANALÝZYIbVLS2010/11 Ke zkoušce mohou přistoupit studenti, kteří získali zápočet. Do indexu jej zapíši na zkoušce, pokud cvičící potvrdí, že na něj student
Zdrojem většiny příkladů je sbírka úloh 1. cvičení ( ) 2. cvičení ( )
 Příklady řešené na cvičení LA II - LS 1/13 Zdrojem většiny příkladů je sbírka úloh http://kam.mff.cuni.cz/~sbirka/ 1. cvičení (..13) 1. Rozhodněte, které z následujících operací jsou skalárním součinem
Příklady řešené na cvičení LA II - LS 1/13 Zdrojem většiny příkladů je sbírka úloh http://kam.mff.cuni.cz/~sbirka/ 1. cvičení (..13) 1. Rozhodněte, které z následujících operací jsou skalárním součinem
MATEMATIKA II - vybrané úlohy ze zkoušek (2015)
 MATEMATIKA II - vybrané úlohy ze zkoušek (2015) doplněné o další úlohy 24. 2. 2015 Nalezené nesrovnalosti ve výsledcích nebo připomínky k tomuto souboru sdělte laskavě F. Mrázovi (e-mail: Frantisek.Mraz@fs.cvut.cz
MATEMATIKA II - vybrané úlohy ze zkoušek (2015) doplněné o další úlohy 24. 2. 2015 Nalezené nesrovnalosti ve výsledcích nebo připomínky k tomuto souboru sdělte laskavě F. Mrázovi (e-mail: Frantisek.Mraz@fs.cvut.cz
ALGEBRA. Téma 5: Vektorové prostory
 SLEZSKÁ UNIVERZITA V OPAVĚ Matematický ústav v Opavě Na Rybníčku 1, 746 01 Opava, tel. (553) 684 611 DENNÍ STUDIUM Téma 5: Vektorové prostory Základní pojmy Vektorový prostor nad polem P, reálný (komplexní)
SLEZSKÁ UNIVERZITA V OPAVĚ Matematický ústav v Opavě Na Rybníčku 1, 746 01 Opava, tel. (553) 684 611 DENNÍ STUDIUM Téma 5: Vektorové prostory Základní pojmy Vektorový prostor nad polem P, reálný (komplexní)
Modernizace výuky na Fakultě stavební VUT v Brně v rámci bakalářských a magisterských studijních programů CZ.04.1.03/3.2.15.2/0292
 Modernizace výuky na Fakultě stavební VUT v Brně v rámci bakalářských a magisterských studijních programů CZ.04.1.03/3.2.15.2/0292 Název předmětu: Vyrovnávací kurz z matematiky Zabezpečující ústav: Ústav
Modernizace výuky na Fakultě stavební VUT v Brně v rámci bakalářských a magisterských studijních programů CZ.04.1.03/3.2.15.2/0292 Název předmětu: Vyrovnávací kurz z matematiky Zabezpečující ústav: Ústav
Maturitní témata z matematiky
 Maturitní témata z matematiky G y m n á z i u m J i h l a v a Výroky, množiny jednoduché výroky, pravdivostní hodnoty výroků, negace operace s výroky, složené výroky, tabulky pravdivostních hodnot důkazy
Maturitní témata z matematiky G y m n á z i u m J i h l a v a Výroky, množiny jednoduché výroky, pravdivostní hodnoty výroků, negace operace s výroky, složené výroky, tabulky pravdivostních hodnot důkazy
Státní závěrečná zkouška z oboru Matematika a její použití v přírodních vědách
 Státní závěrečná zkouška z oboru Matematika a její použití v přírodních vědách Ústní zkouška z oboru Náročnost zkoušky je podtržena její ústní formou a komisionálním charakterem. Předmětem bakalářské zkoušky
Státní závěrečná zkouška z oboru Matematika a její použití v přírodních vědách Ústní zkouška z oboru Náročnost zkoušky je podtržena její ústní formou a komisionálním charakterem. Předmětem bakalářské zkoušky
MATEMATICKÉ PRAKTIKUM
 MATEMATICKÉ PRAKTIKUM Sbírka řešených příkladů z matematiky pro studenty vysokých škol Miloš Kaňka Vědecký redaktor: prof. RNDr. Josef Matušů, DrSc. Miloš Kaňka Matematické praktikum Sbírka řešených příkladů
MATEMATICKÉ PRAKTIKUM Sbírka řešených příkladů z matematiky pro studenty vysokých škol Miloš Kaňka Vědecký redaktor: prof. RNDr. Josef Matušů, DrSc. Miloš Kaňka Matematické praktikum Sbírka řešených příkladů
MATURITNÍ TÉMATA Z MATEMATIKY
 MATURITNÍ TÉMATA Z MATEMATIKY 1. Základní poznatky z logiky a teorie množin Pojem konstanty a proměnné. Obor proměnné. Pojem výroku a jeho pravdivostní hodnota. Operace s výroky, složené výroky, logické
MATURITNÍ TÉMATA Z MATEMATIKY 1. Základní poznatky z logiky a teorie množin Pojem konstanty a proměnné. Obor proměnné. Pojem výroku a jeho pravdivostní hodnota. Operace s výroky, složené výroky, logické
Matematika I. dvouletý volitelný předmět
 Název předmětu: Zařazení v učebním plánu: Matematika I O7A, C3A, O8A, C4A dvouletý volitelný předmět Cíle předmětu Tento předmět je koncipován s cílem usnadnit absolventům gymnázia přechod na vysoké školy
Název předmětu: Zařazení v učebním plánu: Matematika I O7A, C3A, O8A, C4A dvouletý volitelný předmět Cíle předmětu Tento předmět je koncipován s cílem usnadnit absolventům gymnázia přechod na vysoké školy
Diskretizace. 29. dubna 2015
 MSP: Domácí příprava č. 3 Vnitřní a vnější popis diskrétních systémů Dopředná Z-transformace Zpětná Z-transformace Řešení diferenčních rovnic Stabilita diskrétních systémů Spojování systémů Diskretizace
MSP: Domácí příprava č. 3 Vnitřní a vnější popis diskrétních systémů Dopředná Z-transformace Zpětná Z-transformace Řešení diferenčních rovnic Stabilita diskrétních systémů Spojování systémů Diskretizace
2. Určte hromadné body, limitu superior a limitu inferior posloupností: 2, b n = n. n n n.
 Písemka matematika 3 s řešením 1. Vypočtěte lim n( 1 + n 2 n), n lim n (( 1 + 1 n e ) n ) n. 1/2, 1/ e 2. Určte hromadné body, limitu superior a limitu inferior posloupností: a n = sin nπ ( 2, b n = n
Písemka matematika 3 s řešením 1. Vypočtěte lim n( 1 + n 2 n), n lim n (( 1 + 1 n e ) n ) n. 1/2, 1/ e 2. Určte hromadné body, limitu superior a limitu inferior posloupností: a n = sin nπ ( 2, b n = n
7. Funkce jedné reálné proměnné, základní pojmy
 , základní pojmy POJEM FUNKCE JEDNÉ PROMĚNNÉ Reálná funkce f jedné reálné proměnné je funkce (zobrazení) f: X Y, kde X, Y R. Jde o zvláštní případ obecného pojmu funkce definovaného v přednášce. Poznámka:
, základní pojmy POJEM FUNKCE JEDNÉ PROMĚNNÉ Reálná funkce f jedné reálné proměnné je funkce (zobrazení) f: X Y, kde X, Y R. Jde o zvláštní případ obecného pojmu funkce definovaného v přednášce. Poznámka:
MATEMATIKA II - vybrané úlohy ze zkoušek v letech
 MATEMATIKA II - vybrané úlohy ze zkoušek v letech 2009 2012 doplněné o další úlohy 3. část KŘIVKOVÉ INTEGRÁLY, GREENOVA VĚTA, POTENIÁLNÍ POLE, PLOŠNÉ INTEGRÁLY, GAUSSOVA OSTROGRADSKÉHO VĚTA 7. 4. 2013
MATEMATIKA II - vybrané úlohy ze zkoušek v letech 2009 2012 doplněné o další úlohy 3. část KŘIVKOVÉ INTEGRÁLY, GREENOVA VĚTA, POTENIÁLNÍ POLE, PLOŠNÉ INTEGRÁLY, GAUSSOVA OSTROGRADSKÉHO VĚTA 7. 4. 2013
Gymnázium Jiřího Ortena, Kutná Hora
 Předmět: Náplň: Třída: Počet hodin: Pomůcky: Cvičení z matematiky algebra (CZMa) Systematizace a prohloubení učiva matematiky: Číselné obory, Algebraické výrazy, Rovnice, Funkce, Posloupnosti, Diferenciální
Předmět: Náplň: Třída: Počet hodin: Pomůcky: Cvičení z matematiky algebra (CZMa) Systematizace a prohloubení učiva matematiky: Číselné obory, Algebraické výrazy, Rovnice, Funkce, Posloupnosti, Diferenciální
Modelování systémů a procesů (11MSP) Bohumil Kovář, Jan Přikryl, Miroslav Vlček. 8. přednáška 11MSP pondělí 20. dubna 2015
 Modelování systémů a procesů (11MSP) Bohumil Kovář, Jan Přikryl, Miroslav Vlček Ústav aplikované matematiky ČVUT v Praze, Fakulta dopravní 8. přednáška 11MSP pondělí 20. dubna 2015 verze: 2015-04-14 12:31
Modelování systémů a procesů (11MSP) Bohumil Kovář, Jan Přikryl, Miroslav Vlček Ústav aplikované matematiky ČVUT v Praze, Fakulta dopravní 8. přednáška 11MSP pondělí 20. dubna 2015 verze: 2015-04-14 12:31
Gymnázium Jiřího Ortena, Kutná Hora
 Předmět: Cvičení z matematiky Náplň: Systematizace a prohloubení učiva matematiky Třída: 4. ročník Počet hodin: 2 Pomůcky: Učebna s dataprojektorem, PC, grafický program, tabulkový procesor Číselné obory
Předmět: Cvičení z matematiky Náplň: Systematizace a prohloubení učiva matematiky Třída: 4. ročník Počet hodin: 2 Pomůcky: Učebna s dataprojektorem, PC, grafický program, tabulkový procesor Číselné obory
Zimní semestr akademického roku 2014/ prosince 2014
 Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičení Zimní semestr akademického roku 2014/2015 7. prosince 2014 Předmluva
Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičení Zimní semestr akademického roku 2014/2015 7. prosince 2014 Předmluva
Komplexní analýza. Fourierovy řady. Martin Bohata. Katedra matematiky FEL ČVUT v Praze
 Komplexní analýza Fourierovy řady Martin Bohata Katedra matematiky FEL ČVU v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Fourierovy řady 1 / 20 Úvod Často se setkáváme s periodickými
Komplexní analýza Fourierovy řady Martin Bohata Katedra matematiky FEL ČVU v Praze bohata@math.feld.cvut.cz Martin Bohata Komplexní analýza Fourierovy řady 1 / 20 Úvod Často se setkáváme s periodickými
8.4. Shrnutí ke kapitolám 7 a 8
 8.4. Shrnutí ke kapitolám 7 a 8 Shrnutí lekce Úvodní 7. kapitola přinesla informace o druzích řešení diferenciálních rovnic prvního řádu a stručné teoretické poznatky o podmínkách existence a jednoznačnosti
8.4. Shrnutí ke kapitolám 7 a 8 Shrnutí lekce Úvodní 7. kapitola přinesla informace o druzích řešení diferenciálních rovnic prvního řádu a stručné teoretické poznatky o podmínkách existence a jednoznačnosti
Základy matematiky pro FEK
 Základy matematiky pro FEK 1. přednáška 22.9.2016 Blanka Šedivá KMA zimní semestr 2016/2017 Blanka Šedivá (KMA) Základy matematiky pro FEK zimní semestr 2016/2017 1 / 19 Organizační pokyny přednášející:
Základy matematiky pro FEK 1. přednáška 22.9.2016 Blanka Šedivá KMA zimní semestr 2016/2017 Blanka Šedivá (KMA) Základy matematiky pro FEK zimní semestr 2016/2017 1 / 19 Organizační pokyny přednášející:
Cvičení z Lineární algebry 1
 Cvičení z Lineární algebry Michael Krbek podzim 2003 2392003 Hodina Jsou dána komplexní čísla z = +2 i a w = 2 i Vyjádřete c algebraickém tvaru (z + w) 3,, (zw), z w 2 Řešte v komplexním oboru rovnice
Cvičení z Lineární algebry Michael Krbek podzim 2003 2392003 Hodina Jsou dána komplexní čísla z = +2 i a w = 2 i Vyjádřete c algebraickém tvaru (z + w) 3,, (zw), z w 2 Řešte v komplexním oboru rovnice
Požadavky k zápočtu a ke zkoušce z předmětu Matematická analýza 2 kód NMMA102, letní semestr 2012 2013. Luboš Pick
 Požadavky k zápočtu a ke zkoušce z předmětu Matematická analýza 2 kód NMMA102, letní semestr 2012 2013 Luboš Pick Obsah Popis předmětu 1 Zápočet 1 Zkouška 2 Celkové hodnocení zkoušky 4 Seznamy požadovaných
Požadavky k zápočtu a ke zkoušce z předmětu Matematická analýza 2 kód NMMA102, letní semestr 2012 2013 Luboš Pick Obsah Popis předmětu 1 Zápočet 1 Zkouška 2 Celkové hodnocení zkoušky 4 Seznamy požadovaných
Základy matematiky pracovní listy
 Dagmar Dlouhá, Michaela Tužilová Katedra matematiky a deskriptivní geometrie VŠB - Technická univerzita Ostrava Úvod Pracovní listy jsou určeny pro předmět Základy matematiky vyučovaný Katedrou matematiky
Dagmar Dlouhá, Michaela Tužilová Katedra matematiky a deskriptivní geometrie VŠB - Technická univerzita Ostrava Úvod Pracovní listy jsou určeny pro předmět Základy matematiky vyučovaný Katedrou matematiky
Teorie. Hinty. kunck6am
 kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 5. cvičení Teorie Definice. Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 5. cvičení Teorie Definice. Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
MATEMATIKA III. Olga Majlingová. Učební text pro prezenční studium. Předběžná verze
 Fakulta strojního inženýrství Univerzity J. E. Purkyně v Ústí nad Labem Pasteurova 7 Tel.: 475 285 511 400 96 Ústí nad Labem Fax: 475 285 566 Internet: www.ujep.cz E-mail: kontakt@ujep.cz MATEMATIKA III
Fakulta strojního inženýrství Univerzity J. E. Purkyně v Ústí nad Labem Pasteurova 7 Tel.: 475 285 511 400 96 Ústí nad Labem Fax: 475 285 566 Internet: www.ujep.cz E-mail: kontakt@ujep.cz MATEMATIKA III
Systematizace a prohloubení učiva matematiky. Učebna s dataprojektorem, PC, grafický program, tabulkový procesor. Gymnázium Jiřího Ortena, Kutná Hora
 Předmět: Náplň: Třída: Počet hodin: Pomůcky: Cvičení z matematiky Systematizace a prohloubení učiva matematiky 4. ročník 2 hodiny Učebna s dataprojektorem, PC, grafický program, tabulkový procesor Číselné
Předmět: Náplň: Třída: Počet hodin: Pomůcky: Cvičení z matematiky Systematizace a prohloubení učiva matematiky 4. ročník 2 hodiny Učebna s dataprojektorem, PC, grafický program, tabulkový procesor Číselné
Požadavky k písemné přijímací zkoušce z matematiky do navazujícího magisterského studia pro neučitelské obory
 Požadavky k písemné přijímací zkoušce z matematiky do navazujícího magisterského studia pro neučitelské obory Zkouška ověřuje znalost základních pojmů, porozumění teorii a schopnost aplikovat teorii při
Požadavky k písemné přijímací zkoušce z matematiky do navazujícího magisterského studia pro neučitelské obory Zkouška ověřuje znalost základních pojmů, porozumění teorii a schopnost aplikovat teorii při
16 Fourierovy řady Úvod, základní pojmy
 M. Rokyta, MFF UK: Aplikovaná matematika IV kap. 16: Fourierovy řady 1 16 Fourierovy řady 16.1 Úvod, základní pojmy Otázka J. Fouriera: Lze každou periodickou funkci napsat jako součet nějakých "elementárních"
M. Rokyta, MFF UK: Aplikovaná matematika IV kap. 16: Fourierovy řady 1 16 Fourierovy řady 16.1 Úvod, základní pojmy Otázka J. Fouriera: Lze každou periodickou funkci napsat jako součet nějakých "elementárních"
Bakalářská matematika I
 1. Funkce Diferenciální počet Mgr. Jaroslav Drobek, Ph. D. Katedra matematiky a deskriptivní geometrie Bakalářská matematika I Některé užitečné pojmy Kartézský součin podrobnosti Definice 1.1 Nechť A,
1. Funkce Diferenciální počet Mgr. Jaroslav Drobek, Ph. D. Katedra matematiky a deskriptivní geometrie Bakalářská matematika I Některé užitečné pojmy Kartézský součin podrobnosti Definice 1.1 Nechť A,
Seznámíte se s pojmem primitivní funkce a neurčitý integrál funkce jedné proměnné.
 INTEGRÁLNÍ POČET FUNKCÍ JEDNÉ PROMĚNNÉ NEURČITÝ INTEGRÁL NEURČITÝ INTEGRÁL Průvodce studiem V kapitole Diferenciální počet funkcí jedné proměnné jste se seznámili s derivováním funkcí Jestliže znáte derivace
INTEGRÁLNÍ POČET FUNKCÍ JEDNÉ PROMĚNNÉ NEURČITÝ INTEGRÁL NEURČITÝ INTEGRÁL Průvodce studiem V kapitole Diferenciální počet funkcí jedné proměnné jste se seznámili s derivováním funkcí Jestliže znáte derivace
Úlohy k přednášce NMAG 101 a 120: Lineární algebra a geometrie 1 a 2,
 Úlohy k přednášce NMAG a : Lineární algebra a geometrie a Verze ze dne. května Toto je seznam přímočarých příkladů k přednášce. Úlohy z tohoto seznamu je nezbytně nutné umět řešit. Podobné typy úloh se
Úlohy k přednášce NMAG a : Lineární algebra a geometrie a Verze ze dne. května Toto je seznam přímočarých příkladů k přednášce. Úlohy z tohoto seznamu je nezbytně nutné umět řešit. Podobné typy úloh se
Požadavky ke zkoušce. Ukázková písemka
 Požadavky ke zkoušce Zkouška z předmětu MATEMATIKA 1 má dvě části Písemná část: Písemná část se ještě dále rozděluje na praktickou část písemku a teoretickou část test. Písemka trvá 90 minut a je v ní
Požadavky ke zkoušce Zkouška z předmětu MATEMATIKA 1 má dvě části Písemná část: Písemná část se ještě dále rozděluje na praktickou část písemku a teoretickou část test. Písemka trvá 90 minut a je v ní
Matematická analýza I
 Matematická analýza I Cvičení 1 (4. 10. 2016) Definice absolutní hodnoty. Řešení nerovnic s absolutními hodnotami. Geometrická interpretace řešení nerovnice x + 1 < 3. Komplexní čísla a operace s nimi,
Matematická analýza I Cvičení 1 (4. 10. 2016) Definice absolutní hodnoty. Řešení nerovnic s absolutními hodnotami. Geometrická interpretace řešení nerovnice x + 1 < 3. Komplexní čísla a operace s nimi,
INOVACE MATEMATIKY PRO EKONOMY NA VŠE. Anketavroce2008
 INOVACE MATEMATIKY PRO EKONOMY NA VŠE Anketavroce2008 Dne 11.12.2008 se obrátil člen katedry matematiky doc. RNDr. Jiří Henzler, CSc. na všechny učitele Vysoké školy ekonomické v Praze s následující výzvou:
INOVACE MATEMATIKY PRO EKONOMY NA VŠE Anketavroce2008 Dne 11.12.2008 se obrátil člen katedry matematiky doc. RNDr. Jiří Henzler, CSc. na všechny učitele Vysoké školy ekonomické v Praze s následující výzvou:
MATEMATIKA B 2. Metodický list č. 1. Název tématického celku: Význam první a druhé derivace pro průběh funkce
 Metodický list č. 1 Význam první a druhé derivace pro průběh funkce Cíl: V tomto tématickém celku se studenti seznámí s některými základními pojmy a postupy užívanými při vyšetřování průběhu funkcí. Tématický
Metodický list č. 1 Význam první a druhé derivace pro průběh funkce Cíl: V tomto tématickém celku se studenti seznámí s některými základními pojmy a postupy užívanými při vyšetřování průběhu funkcí. Tématický
Úvod, základní pojmy, funkce
 Úvod, základní pojmy, funkce Michal Fusek Ústav matematiky FEKT VUT, fusekmi@feec.vutbr.cz 1. přednáška z ESMAT Michal Fusek (fusekmi@feec.vutbr.cz) 1 / 69 Obsah 1 Matematická logika 2 Množiny 3 Funkce,
Úvod, základní pojmy, funkce Michal Fusek Ústav matematiky FEKT VUT, fusekmi@feec.vutbr.cz 1. přednáška z ESMAT Michal Fusek (fusekmi@feec.vutbr.cz) 1 / 69 Obsah 1 Matematická logika 2 Množiny 3 Funkce,
Kapitola 1: Reálné funkce 1/20
 Kapitola 1: Reálné funkce 1/20 Funkce jedné proměnné 2/20 Definice: Necht M R. Jestliže každému x M je přiřazeno jistým předpisem f právě jedno y R, říkáme, že y je funkcí x. x... nezávisle proměnná (neboli
Kapitola 1: Reálné funkce 1/20 Funkce jedné proměnné 2/20 Definice: Necht M R. Jestliže každému x M je přiřazeno jistým předpisem f právě jedno y R, říkáme, že y je funkcí x. x... nezávisle proměnná (neboli
VZOROVÉ PŘÍKLADY Z MATEMATIKY A DOPORUČENÁ LITERATURA pro přípravu k přijímací zkoušce studijnímu oboru Nanotechnologie na VŠB TU Ostrava
 VZOROVÉ PŘÍKLADY Z MATEMATIKY A DOPORUČENÁ LITERATURA pro přípravu k přijímací zkoušce studijnímu oboru Nanotechnologie na VŠB TU Ostrava I Úprav algebraických výrazů zlomk, rozklad kvadratického trojčlenu,
VZOROVÉ PŘÍKLADY Z MATEMATIKY A DOPORUČENÁ LITERATURA pro přípravu k přijímací zkoušce studijnímu oboru Nanotechnologie na VŠB TU Ostrava I Úprav algebraických výrazů zlomk, rozklad kvadratického trojčlenu,
Přednášky z předmětu Aplikovaná matematika, rok 2012
 Přednášky z předmětu Aplikovaná matematika, rok 2012 Robert Mařík 23. ledna 2015 2 Obsah 1 Přednášky 2012 5 2 Písemky 2012 9 3 4 OBSAH Kapitola 1 Přednášky 2012 1. prednaska, 16.2.2012 -----------------------
Přednášky z předmětu Aplikovaná matematika, rok 2012 Robert Mařík 23. ledna 2015 2 Obsah 1 Přednášky 2012 5 2 Písemky 2012 9 3 4 OBSAH Kapitola 1 Přednášky 2012 1. prednaska, 16.2.2012 -----------------------
Jednou z nejdůležitějších funkcí, které se v matematice a jejích aplikacích používají je
 74 Příloha A Funkce Γ(z) Úvod Jednou z nejdůležitějších funkcí, které se v matematice a jejích aplikacích používají je nesporně funkce Γ(z). Její důležitost se vyrovná exponenciální funkci i funkcím goniometrickým.
74 Příloha A Funkce Γ(z) Úvod Jednou z nejdůležitějších funkcí, které se v matematice a jejích aplikacích používají je nesporně funkce Γ(z). Její důležitost se vyrovná exponenciální funkci i funkcím goniometrickým.
Mgr. Ladislav Zemánek Maturitní okruhy Matematika 2013-2014. 1. Obor reálných čísel
 Mgr. Ladislav Zemánek Maturitní okruhy Matematika 2013-2014 1. Obor reálných čísel - obor přirozených, celých, racionálních a reálných čísel - vlastnosti operací (sčítání, odčítání, násobení, dělení) -
Mgr. Ladislav Zemánek Maturitní okruhy Matematika 2013-2014 1. Obor reálných čísel - obor přirozených, celých, racionálních a reálných čísel - vlastnosti operací (sčítání, odčítání, násobení, dělení) -
Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
Poznámky k Fourierově transformaci
 Poznámky k Fourierově transformaci V těchto poznámkách jsou uvedeny základní vlastnosti jednorozměrné Fourierovy transformace a její aplikace na jednoduché modelové případy. Pro určitost jsou sdružené
Poznámky k Fourierově transformaci V těchto poznámkách jsou uvedeny základní vlastnosti jednorozměrné Fourierovy transformace a její aplikace na jednoduché modelové případy. Pro určitost jsou sdružené
sin(x) x lim. pomocí mocninné řady pro funkci sin(x) se středem x 0 = 0. Víme, že ( ) k=0 e x2 dx.
 Použití mocniných řad Nejprve si ukážeme dvě jednoduchá použití Taylorových řad. Příklad Spočtěte následující limitu: ( ) sin(x) lim. x x ( ) Najdeme lim sin(x) x x pomocí mocninné řady pro funkci sin(x)
Použití mocniných řad Nejprve si ukážeme dvě jednoduchá použití Taylorových řad. Příklad Spočtěte následující limitu: ( ) sin(x) lim. x x ( ) Najdeme lim sin(x) x x pomocí mocninné řady pro funkci sin(x)
SBÍRKA ÚLOH PRO PŘÍPRAVU NA PŘIJÍMACÍ ZKOUŠKY Z MATEMATIKY NA VŠ EKONOMICKÉHO SMĚRU
 SBÍRKA ÚLOH PRO PŘÍPRAVU NA PŘIJÍMACÍ ZKOUŠKY Z MATEMATIKY NA VŠ EKONOMICKÉHO SMĚRU Tento materiál vznikl v rámci realizace projektu: Globální vzdělávání pro udržitelný rozvoj v sítí spolupracujících škol,
SBÍRKA ÚLOH PRO PŘÍPRAVU NA PŘIJÍMACÍ ZKOUŠKY Z MATEMATIKY NA VŠ EKONOMICKÉHO SMĚRU Tento materiál vznikl v rámci realizace projektu: Globální vzdělávání pro udržitelný rozvoj v sítí spolupracujících škol,
Matematická analýza III.
 1. - limita, spojitost Miroslav Hušek, Lucie Loukotová UJEP 2010 Úvod Co bychom měli znát limity posloupností v R základní vlastnosti funkcí jedné proměnné (definiční obor, monotónnost, omezenost,... )
1. - limita, spojitost Miroslav Hušek, Lucie Loukotová UJEP 2010 Úvod Co bychom měli znát limity posloupností v R základní vlastnosti funkcí jedné proměnné (definiční obor, monotónnost, omezenost,... )
Renáta Bednárová, Petr Sládek. Pedagogická fakulta MU Brno, Univerzita obrany Brno
 Renáta Bednárová, Petr Sládek Pedagogická fakulta MU Brno, Univerzita obrany Brno Cíle Úvod Cíle projektu Charakteristika e-kurzu Několik poznámek k pedagogickému šetření Využití e-kurzu v praxi Možnosti
Renáta Bednárová, Petr Sládek Pedagogická fakulta MU Brno, Univerzita obrany Brno Cíle Úvod Cíle projektu Charakteristika e-kurzu Několik poznámek k pedagogickému šetření Využití e-kurzu v praxi Možnosti
Matematika 1 Jiˇr ı Fiˇser 19. z aˇr ı 2016 Jiˇr ı Fiˇser (KMA, PˇrF UP Olomouc) KMA MAT1 19. z aˇr ı / 19
 Matematika 1 Jiří Fišer 19. září 2016 Jiří Fišer (KMA, PřF UP Olomouc) KMA MAT1 19. září 2016 1 / 19 Zimní semestr KMA MAT1 1 Úprava algebraických výrazů. Číselné obory. 2 Kombinatorika, základy teorie
Matematika 1 Jiří Fišer 19. září 2016 Jiří Fišer (KMA, PřF UP Olomouc) KMA MAT1 19. září 2016 1 / 19 Zimní semestr KMA MAT1 1 Úprava algebraických výrazů. Číselné obory. 2 Kombinatorika, základy teorie
Cvičení z matematiky jednoletý volitelný předmět
 Název předmětu: Zařazení v učebním plánu: Cvičení z matematiky O8A, C4A, jednoletý volitelný předmět Cíle předmětu Obsah předmětu je zaměřen na přípravu studentů gymnázia na společnou část maturitní zkoušky
Název předmětu: Zařazení v učebním plánu: Cvičení z matematiky O8A, C4A, jednoletý volitelný předmět Cíle předmětu Obsah předmětu je zaměřen na přípravu studentů gymnázia na společnou část maturitní zkoušky
Gymnázium Česká a Olympijských nadějí, České Budějovice, Česká 64, 37021
 Maturitní témata MATEMATIKA 1. Funkce a jejich základní vlastnosti. Definice funkce, def. obor a obor hodnot funkce, funkce sudá, lichá, monotónnost funkce, funkce omezená, lokální a globální extrémy funkce,
Maturitní témata MATEMATIKA 1. Funkce a jejich základní vlastnosti. Definice funkce, def. obor a obor hodnot funkce, funkce sudá, lichá, monotónnost funkce, funkce omezená, lokální a globální extrémy funkce,
Kapitola 1: Reálné funkce 1/13
 Kapitola 1: Reálné funkce 1/13 Číselné množiny 2/13 N = {1, 2, 3, 4,... }... přirozená čísla N 0 = N {0} = {0, 1, 2, 3, 4,... } Z = {..., 2, 1, 0, 1, 2, 3, 4,... }... celá čísla Q = { p q p, q Z}... racionální
Kapitola 1: Reálné funkce 1/13 Číselné množiny 2/13 N = {1, 2, 3, 4,... }... přirozená čísla N 0 = N {0} = {0, 1, 2, 3, 4,... } Z = {..., 2, 1, 0, 1, 2, 3, 4,... }... celá čísla Q = { p q p, q Z}... racionální
Vzdělávací materiál. vytvořený v projektu OP VK. Název školy: Gymnázium, Zábřeh, náměstí Osvobození 20. Číslo projektu: CZ.1.07/1.5.00/34.
 Vzdělávací materiál vytvořený v projektu OP VK Název školy: Gymnázium, Zábřeh, náměstí Osvobození 20 Číslo projektu: Název projektu: Číslo a název klíčové aktivity: CZ.1.07/1.5.00/34.0211 Zlepšení podmínek
Vzdělávací materiál vytvořený v projektu OP VK Název školy: Gymnázium, Zábřeh, náměstí Osvobození 20 Číslo projektu: Název projektu: Číslo a název klíčové aktivity: CZ.1.07/1.5.00/34.0211 Zlepšení podmínek
Kapitola 7: Integrál. 1/17
 Kapitola 7: Integrál. 1/17 Neurčitý integrál - Motivační příklad 2/17 Příklad: Necht se bod pohybuje po přímce rychlostí a) v(t) = 3 [m/s] (rovnoměrný přímočarý pohyb), b) v(t) = 2t [m/s] (rovnoměrně zrychlený
Kapitola 7: Integrál. 1/17 Neurčitý integrál - Motivační příklad 2/17 Příklad: Necht se bod pohybuje po přímce rychlostí a) v(t) = 3 [m/s] (rovnoměrný přímočarý pohyb), b) v(t) = 2t [m/s] (rovnoměrně zrychlený
Organizace. Zápočet: test týden semestru (pátek) bodů souhrnný test (1 pokus) Zkouška: písemná část ( 50 bodů), ústní část
 Matematika I 1/15 2/15 Organizace Zápočet: test 6. + 11. týden semestru (pátek) 80 bodů 50 79 bodů souhrnný test (1 pokus) Zkouška: písemná část ( 50 bodů), ústní část www.vscht.cz/mat Výuka www.vscht.cz/mat/jana.nemcova
Matematika I 1/15 2/15 Organizace Zápočet: test 6. + 11. týden semestru (pátek) 80 bodů 50 79 bodů souhrnný test (1 pokus) Zkouška: písemná část ( 50 bodů), ústní část www.vscht.cz/mat Výuka www.vscht.cz/mat/jana.nemcova
19 Hilbertovy prostory
 M. Rokyta, MFF UK: Aplikovaná matematika III kap. 19: Hilbertovy prostory 34 19 Hilbertovy prostory 19.1 Úvod, základní pojmy Poznámka (připomenutí). Necht (X,(, )) je vektorový prostor se skalárním součinem
M. Rokyta, MFF UK: Aplikovaná matematika III kap. 19: Hilbertovy prostory 34 19 Hilbertovy prostory 19.1 Úvod, základní pojmy Poznámka (připomenutí). Necht (X,(, )) je vektorový prostor se skalárním součinem
Inverzní Laplaceova transformace
 Inverzní Laplaceova transformace Modelování systémů a procesů (MSP) Bohumil Kovář, Jan Přikryl, Miroslav Vlček Ústav aplikované matematiky ČVUT v Praze, Fakulta dopravní 6. přednáška MSP čtvrtek 30. března
Inverzní Laplaceova transformace Modelování systémů a procesů (MSP) Bohumil Kovář, Jan Přikryl, Miroslav Vlček Ústav aplikované matematiky ČVUT v Praze, Fakulta dopravní 6. přednáška MSP čtvrtek 30. března
maticeteorie 1. Matice A je typu 2 4, matice B je typu 4 3. Jakých rozměrů musí být matice X, aby se dala provést
 Úlohy k zamyšlení 1. Zdůvodněte, proč třetí řádek Hornerova schématu pro vyhodnocení polynomu p v bodě c obsahuje koeficienty polynomu r, pro který platí p(x) = (x c) r(x) + p(c). 2. Dokažte, že pokud
Úlohy k zamyšlení 1. Zdůvodněte, proč třetí řádek Hornerova schématu pro vyhodnocení polynomu p v bodě c obsahuje koeficienty polynomu r, pro který platí p(x) = (x c) r(x) + p(c). 2. Dokažte, že pokud
Teorie. Hinty. kunck6am
 kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 5. cvičení Teorie Definice. Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 5. cvičení Teorie Definice. Necht funkce f je definována na neprázdném otevřeném intervalu I. Řekneme, že funkce F je primitivní funkce k f na I, jestliže
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od podzimu 2016
 Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od podzimu 2016 Zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia
Zadání a řešení testu z matematiky a zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia od podzimu 2016 Zpráva o výsledcích přijímacího řízení do magisterského navazujícího studia
Text může být postupně upravován a doplňován. Datum poslední úpravy najdete u odkazu na stažení souboru. Veronika Sobotíková
 Tento text není samostatným studijním materiálem. Jde jen o prezentaci promítanou na přednáškách, kde k ní přidávám slovní komentář. Některé důležité části látky píšu pouze na tabuli a nejsou zde obsaženy.
Tento text není samostatným studijním materiálem. Jde jen o prezentaci promítanou na přednáškách, kde k ní přidávám slovní komentář. Některé důležité části látky píšu pouze na tabuli a nejsou zde obsaženy.
Anketa k využívání e learningu na FI pro studenty (jaro 2010)
 Anketa k využívání e learningu na FI pro studenty (jaro 2010) Odpovídá: žena 12 muž 98 Odpovídá: Jak dlouho studujete? 5% Jak dlouho studujete? 1. rok 1. rok 28 11% 15% 25% 2. rok žena 2. rok 27 3. rok
Anketa k využívání e learningu na FI pro studenty (jaro 2010) Odpovídá: žena 12 muž 98 Odpovídá: Jak dlouho studujete? 5% Jak dlouho studujete? 1. rok 1. rok 28 11% 15% 25% 2. rok žena 2. rok 27 3. rok
6. Bez použití funkcí min a max zapište formulí predikátového počtu tvrzení, že každá množina
 Instrukce: Příklady řešte výhradně elementárně, bez použití nástrojů z diferenciálního a integrálního počtu. Je-li součástí řešení úlohy podmnožina reálných čísel, vyjádřete ji jako disjunktní sjednocení
Instrukce: Příklady řešte výhradně elementárně, bez použití nástrojů z diferenciálního a integrálního počtu. Je-li součástí řešení úlohy podmnožina reálných čísel, vyjádřete ji jako disjunktní sjednocení
Matematická analýza pro informatiky I. Spojitost funkce
 Matematická analýza pro informatiky I. 6. přednáška Spojitost funkce Jan Tomeček tomecek@inf.upol.cz http://aix-slx.upol.cz/ tomecek/index Univerzita Palackého v Olomouci 18. března 2011 Jan Tomeček, tomecek@inf.upol.cz
Matematická analýza pro informatiky I. 6. přednáška Spojitost funkce Jan Tomeček tomecek@inf.upol.cz http://aix-slx.upol.cz/ tomecek/index Univerzita Palackého v Olomouci 18. března 2011 Jan Tomeček, tomecek@inf.upol.cz
ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE. Matematika I/1 BA06. Cvičení, zimní semestr
 Vysoké učení technické v Brně Stavební fakulta ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE Matematika I/1 BA06 Cvičení, zimní semestr DOMÁCÍ ÚLOHY Jan Šafařík Brno c 2014 1 (1) Určete rovnici kručnice o
Vysoké učení technické v Brně Stavební fakulta ÚSTAV MATEMATIKY A DESKRIPTIVNÍ GEOMETRIE Matematika I/1 BA06 Cvičení, zimní semestr DOMÁCÍ ÚLOHY Jan Šafařík Brno c 2014 1 (1) Určete rovnici kručnice o
Management rekreace a sportu. 10. Derivace
 Derivace Derivace Před mnoha lety se matematici snažily o obecné vyřešení úlohy, jak sestrojit tečnu k dané křivce a také yzici zápolili s problémem určení rychlosti nerovnoměrného pohybu K zásadnímu obratu
Derivace Derivace Před mnoha lety se matematici snažily o obecné vyřešení úlohy, jak sestrojit tečnu k dané křivce a také yzici zápolili s problémem určení rychlosti nerovnoměrného pohybu K zásadnímu obratu
Učební plán 4. letého studia předmětu matematiky. Učební plán 6. letého studia předmětu matematiky
 Učební plán 4. letého studia předmětu matematiky Ročník I II III IV Dotace 3 3+1 2+1 2+2 Povinnost povinný povinný povinný povinný Učební plán 6. letého studia předmětu matematiky Ročník 1 2 3 4 5 6 Dotace
Učební plán 4. letého studia předmětu matematiky Ročník I II III IV Dotace 3 3+1 2+1 2+2 Povinnost povinný povinný povinný povinný Učební plán 6. letého studia předmětu matematiky Ročník 1 2 3 4 5 6 Dotace
Význam a výpočet derivace funkce a její užití
 OPAKOVÁNÍ ZÁKLADŮ MATEMATIKY Metodický list č. 1 Význam a výpočet derivace funkce a její užití 1. dílčí téma: Výpočet derivace přímo z definice a pomocí základních vzorců. K tomuto tématu je třeba zopakovat
OPAKOVÁNÍ ZÁKLADŮ MATEMATIKY Metodický list č. 1 Význam a výpočet derivace funkce a její užití 1. dílčí téma: Výpočet derivace přímo z definice a pomocí základních vzorců. K tomuto tématu je třeba zopakovat
