Požadavky k zápočtu a ke zkoušce z předmětu Matematická analýza 2 kód NMMA102, letní semestr Luboš Pick

Transkript

1 Požadavky k zápočtu a ke zkoušce z předmětu Matematická analýza 2 kód NMMA102, letní semestr Luboš Pick

2

3 Obsah Popis předmětu 1 Zápočet 1 Zkouška 2 Celkové hodnocení zkoušky 4 Seznamy požadovaných vět, definic a klíčových pojmů 6 Vzorové příklady ze zápočtových písemkek 9 Vzorové zadání písemné části zkoušky 10 Vzor zadání zkušebních otázek pro ústní část zkoušky 10 iii

4

5 ZÁPOČET 1 Popis předmětu Jde o druhou část čtyřsemestrálního základního kursu matematické analýzy pro bakalářské obory Obecná matematika a MMIB. Věnuje se pokročilejším partiím diferenciálního počtu, základům počtu integrálního a základům teorie metrických prostorů. Kurs se skládá z přednášek a cvičení a je hodnocen zápočtem a zkouškou. Přednáška se koná pro větší množství (desítky až stovky) studentů najednou, přičemž přednášející u tabule vykládá především teoretické poznatky a ilustrativní příklady. Otázky v průběhu přednášky a diskuse po ní jsou vítány, jiná forma studentské aktivity (pobyt u tabule atd.) se nepředpokládá. Z látky přednášené na přednášce je potřeba složit zkoušku. Cvičení se koná pro menší množství (15-25) studentů najednou, typicky pro jeden kroužek. Na cvičeních se počítají příklady určené k procvičení dané tématiky. S aktivní účastí studentů (někdy i u tabule) se počítá. Náplň a formu cvičení určuje cvičící. Z početních technik prováděných na cvičeních je potřeba složit zápočet. Přechody mezi cvičeními jsou možné pouze ve zcela výjimečných a dobře odůvodněných případech. Přechody schvaluje přednášející. Všechny žádosti o změnu cvičení musí být podány přednášejícímu do Zápočet Zápočet bude udělen za 50% účast na cvičeních a dvě splněné zápočtové písemky. Studentům jiného než presenčního studia stačí k zápočtu dvě splněné zápočtové písemky. Během letního semestru budou uspořádány celkem čtyři zápočtové písemky: v úterý v 10:40 v posluchárně M1 (v rámci přednášky), v úterý v 10:40 v posluchárně M1 (v rámci přednášky), v pátek v 15:40 v posluchárně K1, v pátek v 15:40 v posluchárně K1. Každá zápočtová písemka bude obsahovat tři příklady z následujících oblastí matematické analýzy: opakování látky 1. semestru (výpočet limity posloupnosti, vyšetření konvergence číselné řady, výpočet limity funkce),

6 2 OBSAH Taylorův polynom, primitivní funkce, Newtonův integrál, limita nebo spojitost funkce více proměnných, totální diferenciál. Čas k vypracování každé zápočtové písemky je 30 minut. Běžné psací potřeby a veškeré písemné materiály jsou povoleny. Jakákoli technika (zejména kalkulačky, mobilní telefony apod.) je však zakázána. V každé zápočtové písemce bude za každý příklad udělen buď 1 bod (příklad splněn) nebo 0 bodů (příklad nesplněn). Písemka bude hodnocena jako splněná, pokud z ní student získá alespoň 2 body. Zkouška Písemná část. K písemné části zkoušky se mohou elektronicky prostřednictvím systému SIS přihlásit pouze studenti, kteří získali zápočet. Pro písemnou část zkoušky bude vypsáno právě pět termínů, a to v pondělí v 8:30 v posluchárně K1, v pondělí v 8:30 v posluchárně K1, v pondělí v 8:30 v posluchárně K1, v pondělí v 8:30 v posluchárně K1, ve středu v 8:30 v posluchárně K1. Mimo vypsané termíny nebude možné vykonat písemnou část zkoušky. Žádné další termíny nebudou vypsány. Studenti budou mít možnost se přihlašovat nebo odhlašovat do dne předcházejícího datu zkoušky včetně do 20:00 hodin. Pokud se student z vážného důvodu nemůže dostavit na písemnou část zkoušky, na kterou byl přihlášen a omluví se examinátorům elektronickou poštou, neztratí termín. V posluchárnách, v nichž se písemná část zkoušky bude konat, bude v době konání písemné části zkoušky vyvěšen zasedací pořádek. Prosíme studenty, aby se dostavili nejpozději v 8:15 a zaujali svá místa podle zasedacího pořádku. Před začátkem písemné části zkoušky bude provedena kontrola totožnosti studentů. Každý student se musí prokázat nějakým platným dokladem s fotografií (index, OP, ŘP, pas a podobně). Písemná část zkoušky bude obsahovat čtyři příklady z následujících partií matematické analýzy: Taylorův polynom nebo mocninná řada (10 bodů),

7 ZKOUŠKA 3 určení primitivní funkce k zadané funkci nebo výpočet určitého integrálu (15 bodů), vyšetření konvergence Newtonova integrálu (15 bodů), limita nebo spojitost funkce více proměnných, gradient nebo totální diferenciál (10 bodů). Jestliže student získá z písemné části zkoušky 28 nebo více bodů, postoupí k ústní části zkoušky. Jestliže získá 27 nebo méně bodů, bude zkouška hodnocena známkou neprospěl(a). Čas k vypracování písemné části je 120 minut. Běžné psací potřeby a veškeré písemné materiály jsou povoleny. Jakákoli technika (zejména kalkulačky, mobilní telefony apod.) je však zakázána. Bezprostředně po skončení písemné části (tedy přibližně v 10:35) bude na tabuli v posluchárně K1 předvedeno vzorové řešení. Účast na předvedení vzorového řešení je povolena (a doporučena) i studentům, kteří ten den písemnou zkoušku neskládali a teprve se připravují na některý z budoucích termínů. Odevzdané písemky budou opraveny během odpoledne v den konání písemné části zkoušky. Studentům, kteří úspěšně složí písemnou část zkoušky, bude přidělen čas ústní části zkoušky. Podrobný rozvrh ústní části zkoušky bude vyvěšen na webové stránce přednášejícího a bude pro všechny studenty závazný, je tedy nutné s tím počítat při plánování rozvrhu zkoušek. Studentům, jejichž písemná část zkoušky bude hodnocena známkou neprospěl(a), bude tato známka zapsána do SIS. Tito studenti se mohou dostavit následujícího dne k podrobnému vysvětlení jejich práce. Vysvětlování neúspěšných písemných prací bude probíhat v úterý od 8:00 do 9:50 v posluchárně K2, v úterý od 8:00 do 9:50 v posluchárně K2, v úterý od 8:00 do 9:50 v posluchárně K3, v úterý od 8:00 do 9:50 v posluchárně K2, ve čtvrtek od 8:00 do 9:50 v posluchárně K3, vždy od 8:00 do 9:50. Ústní část. Ústní část zkoušky se bude konat v úterý od 8:00 v posluchárně K4, v úterý od 8:00 v posluchárně K4, v úterý od 8:00 v posluchárně K2, v úterý od 8:00 v posluchárně K4, ve čtvrtek od 8:00 v posluchárně K2.

8 4 OBSAH Ústní část zkoušky bude obsahovat sedm otázek uspořádaných a přibližně hodnocených podle následujícího klíče: definice klíčového pojmu (0 bodů), formulace dvou vět a jedné definice (5+5+5 body), formulace a důkaz tří vět (celkem 35 bodů). K úspěšnému složení ústní části je třeba napsat správně definici klíčového pojmu a získat minimálně 30 bodů. Uvedené body jsou ovšem pouze orientační a slouží jako pomůcka pro zkoušejícího, nelze na jejich základě vznášet žádné námitky proti výsledku zkoušky. Po celou dobu ústní zkoušky platí, že student musí bezpečně ovládat veškeré klíčové pojmy, nejen ten, který si vylosuje. Prokáže-li se kdykoli během zkoušky, že student bezpečně neovládá kterýkoli z klíčových pojmů, bude zkouška hodnocena známkou neprospěl(a). Bude-li zkouška po ústní části hodnocena známkou neprospěl(a), je student povinen znovu složit obě části zkoušky (tedy i písemnou). Celkové hodnocení zkoušky K celkovému hodnocení známkou výborně je třeba, aby student ovládal všechny klíčové pojmy, dále aby s porozuměním ovládal definice a věty, znal důkazy všech vět a byl schopen aplikovat dosažené vědomosti na více či méně jednoduchých teoretických příkladech. Orientačně známka výborně odpovídá přibližně bodovému rozmezí K celkovému hodnocení známkou velmi dobře je třeba, aby student ovládal všechny klíčové pojmy, dále aby s porozuměním ovládal definice a věty, znal důkazy lehčích vět a byl schopen aplikovat dosažené vědomosti v jednoduchých teoretických příkladech. Může mít menší mezery v obtížnějších partiích. Orientačně známka velmi dobře odpovídá přibližně bodovému rozmezí K celkovému hodnocení známkou dobře je třeba, aby student ovládal všechny klíčové pojmy, dále aby s porozuměním ovládal definice a jednoduché věty a znal důkazy lehčích vět. Orientačně známka dobře odpovídá přibližně bodovému rozmezí

9 CELKOVÉ HODNOCENÍ ZKOUŠKY 5 Hodnocení známkou neprospěl(a) bude uplatněno, jestliže se během zkoušky prokáže, že student nezná některý z klíčových pojmů, neovládá věty nebo definice nebo není schopen dokázat ani nejjednodušší tvrzení. Orientačně hodnocení neprospěl(a) odpovídá přibližně bodovému rozmezí 0 57.

10 6 OBSAH Seznamy požadovaných vět, definic a klíčových pojmů Seznamy požadovaných vět, definic a klíčových pojmů se mohou v průběhu semestru mírně měnit v závislosti na přednášce. Jejich definitivní podoba bude včas oznámena na přednášce. Seznam klíčových pojmů. Taylorův polynom Taylorova řada, MacLaurinova řada mocninná řada, střed a poloměr konvergence primitivní funkce Riemannův integrál stejnoměrně spojitá funkce Newtonův integrál konvergentní a divergentní Newtonův integrál metrický prostor, metrika normovaný lineární prostor, norma otevřená a uzavřená množina, vnitřek a uzávěr množiny konvergence a limita posloupnosti v metrickém prostoru limita zobrazení vzhledem k množině derivace podle vektoru a parciální derivace, gradient, totální diferenciál, derivace zobrazení z R n do R m Jacobiho matice, jacobián prostor L.R n ; R m /, norma zobrazení Seznam požadovaných definic. polynom, stupeň polynomu, kořen polynomu symbol o racionální funkce dělení intervalu, zjemnění dělení horní a dolní součty, horní a dolní Riemannův integrál metriky v R n (eukleidovská, newyorská, maximová, diskrétní) metriky v C Œa; b (supremová, integrální), diskrétní metrika otevřená a uzavřená koule hromadný bod, derivace množiny, izolovaný bod vnitřní bod, vnitřek hraniční bod, hranice množiny vzdálenost bodu od množiny, průměr množiny zděděná metrika

11 SEZNAMY POŽADOVANÝCH VĚT, DEFINIC A KLÍČOVÝCH POJMŮ 7 Seznam požadovaných vět (není-li výslovně stanoveno jinak, jsou požadovány úplné důkazy). Taylorův polynom. o jednoznačnosti Taylorova polynomu obecný tvar zbytku Peanův tvar zbytku Lagrangeův tvar zbytku Cauchyův tvar zbytku aritmetika malého o (bez důkazu) skládání malého o (bez důkazu) Mocninné řady. o poloměru konvergence mocninné řady derivace mocninné řady Abelova věta Primitivní funkce. věta o jednoznačnosti primitivní funkce až na konstantu vztah spojitosti a existence primitivní funkce linearita primitivní funkce Darbouxova vlastnost derivace první věta o substituci druhá věta o substituci integrace per partes Určitý integrál. vlastnosti dělení aproximace Riemannova integrálu součty přes dělení s malou normou kritérium existence Riemannova integrálu vztah spojitosti a stejnoměrné spojitosti vztah spojitosti a riemannovské integrovatelnosti vztah monotonie a riemannovské integrovatelnosti vlastnosti Riemannova integrálu o derivaci funkce horní meze Riemannova integrálu charakterizace riemannovské integrovatelnosti vlastnosti Newtonova integrálu per partes pro Newtonův integrál věta o substituci pro Newtonův integrál Bolzanova Cauchyova podmínka pro funkce o newtonovské integrovatelnosti omezené spojité funkce na omezeném intervalu

12 8 OBSAH vztah Riemannova a Newtonova integrálu vztah spojitosti a existence Riemannova a Newtonova integrálu srovnávací kritérium pro konvergenci Newtonova integrálu limitní srovnávací kritérium pro konvergenci Newtonova integrálu Abelovo Dirichletovo kritérium konvergence Newtonova integrálu odhady Newtonova integrálu součinu dvou funkcí první věta o střední hodnotě druhá věta o střední hodnotě Metrické prostory. vlastnosti otevřených množin vztah otevřených a uzavřených množin vlastnosti uzavřených množin vlastnosti uzávěru vlastnosti konvergence v metrickém prostoru charakterizace spojitosti Heineova věta pro metrické prostory o spojitostísloženého zobrazení v bodě o limitě složeného zobrazení struktura otevřených množin na R Funkce více proměnných. vztah totálního diferencálu a parciálních derivací vztah existence totálního diferenciálu a spojitosti postačující podmínka pro existenci totálního diferenciálu geometrický význam gradientu o representaci derivace maticí vztah derivace a spojitosti vektorové funkce více proměnných postačující podmínka pro existenci derivace vektorové funkce více proměnných o derivaci složeného zobrazení řetízkové pravidlo

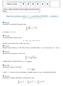
13 VZOROVÉ PŘÍKLADY ZE ZÁPOČTOVÝCH PÍSEMKEK 9 Vzorové příklady ze zápočtových písemkek Příklad 1. Nalezněte limitu posloupnosti fa n g, jestliže a n D 3.n C 1/3 C 2n.n 2 1/ 1 n 3 ; n 2 N: Příklad 2. Rozhodněte, zda číselná řada 1X 3n C 1 2n 2 nd1 konverguje, nebo diverguje a výsledek podrobně zdůvodněte. Příklad 3. Spočtě lim jxj arccotg.x/: x!1 Příklad 4. Napište Taylorův polynom funkce f.x/ D 1CxCx2 1 xcx 2 v bodě x D 0 až do řádu x 4 včetně. Spočtěte f.4/.0/. Příklad 5. Pomocí vhodně zvolené mocninné řady sečtěte číselnou řadu 1X. 1/ n 4 n.2n C 1/ : nd1 Příklad 6. Spočtěte primitivní funkci Z sin.log x/ dx x : Příklad 7. Spočtěte Newtonův integrál Z C dx q 1Cx x Příklad 8. Vyšetřete, zda konverguje Newtonův integrál Z p x log.1 C e x / dx: : Příklad 9. Spočtěte lim D Œx;y!Œ1;1 x C y x 2 xy C y 2 :

14 10 OBSAH Vzorové zadání písemné části zkoušky Příklad 1. S pomocí Taylorova polynomu vyšetřete konvergenci řady 1X tg sin 1 : (10 bodů) n 1 5 n 1 5 n 3 5 nd1 Příklad 2. Spočtěte Newtonův integrál Z 1 0 x 2 C x C 2.x 2 C 2/ 2 dx: (15 bodů).x C 1/ Příklad 3. Vyšetřete, pro které hodnoty parametru q 2 R konverguje Newtonův integrál Z 1 arccos x log q.1=x/ dx: (15 bodů) 0 Příklad 4. Nechť funkce f W R 2! R je definována předpisem ( e 1 x f.x; y/ D 2 Cy 2 ; Œx; y Œ0; 0 ; 0; Œx; y D Œ0; 0 : Vyšetřete, ve kterých bodech Œx; y 2 R 2 má funkce f totální diferenciál a spočtěte jej. (10 bodů) Vzor zadání zkušebních otázek pro ústní část zkoušky Otázka 1. Napište definici klíčového pojmu: Newtonův integrál. Otázka 2. Napište definici pojmu: metriky v C Œa; b (supremová, integrální), diskrétní metrika. Otázka 3. Napište znění věty: Darbouxova vlastnost derivace. Otázka 4. Napište znění věty: vztah totálního diferencálu a parciálních derivací. Otázka 5. Zformulujte a dokažte větu: vlastnosti uzávěru.

15 VZOR ZADÁNÍ ZKUŠEBNÍCH OTÁZEK PRO ÚSTNÍ ČÁST ZKOUŠKY 11 Otázka 6. Zformulujte a dokažte větu: vztah monotonie a riemannovské integrovatelnosti. Otázka 7. Zformulujte a dokažte větu: Peanův tvar zbytku.