Modelovánía experimentální zjišťovánímechanických vlastností nelineárních materiálů
|
|
|
- Silvie Vacková
- před 6 lety
- Počet zobrazení:
Transkript
1 Modelovánía experimentální zjišťovánímechanických vlastností nelineárních materiálů Biomechanika a lékařsképřístroje Projekt II LukášHorný Laboratoř biomechaniky člověka Ústavu mechaniky Fakulty strojní ČVUT v Praze
2 Teoretická část Svět nelineárnímechaniky solidů (T) Když se řekne lineární (T) Druhy a zdroje nelinearit (T3) Kdo to byl A.L. Cauchya kdo byl G. Green (T4) Kdo byl R.S. Rivlin
3 Kdyžse řekne lineární A co vlastněznamená, kdyžse řekne lineární? f(u)+ f(v)= f(u+ v) f(tu)= tf(u) Aditivita Homogenita Důsledky příméřešenírovnice f(x) = c jednoznačné řešení rovnice f(x) = c vektorový prostor řešení rovnice superpozice jednoznačná existence ortogonálního doplňku optimalizace
4 Kdyžse řekne lineární Uveďte příklad nějaké lineární závislosti v mechanice Ano, správně jsme tu dnes hlavně kvůli rovnici: σ= Eε Nějaké další návrhy? Co třeba pružina s hmotou? Učenec by řekl: lineární harmonický oscilátor
5 Kdyžse řekne lineární Jak se to más linearitou zjistíte, kdyžse zamyslíte nad některými operátory, které běžně používáme. Čili: kde se vzala derivace(funkce v bodě)? A co je to diferenciál?
6 Kdyžse řekne lineární Jak se to más energiív lineárním světě? Energie je kvadratická forma W= ½m(v v) W= ½Eε Promyslete si sami, pročpotenciálníenergie hmoty v tíhovém poli napíšeme W= mgh Aneb, kam zmizela druhá mocnina?
7 Kdyžse řekne nelineární Mechanická odezva pavoučího vlákna a pavučiny. (a) Tahová odezva vlákna (b) Model sítě ze spojitých vláken (c) Odezva defektní pavučiny (d) Rozdíl odezvy podle místa zatěžování (e) grafika k rozdílu odezvy (radiální vs spirální vlákno) SW Cranford et al. Nature 48, 7-78 (0) doi:0.038/nature0739
8 Druhy a zdroje nelinearit Nelinearita se v problému objevív nějakém okamžiku formulace modelu. Takže, co náš model úloha pružnosti obsahuje? Rovnice rovnováhy Geometrické rovnice Konstitutivní rovnice Okrajové a počáteční podmínky
9 Druhy a zdroje nelinearit Rovnice rovnováhy div(σ )+ b= D(ρv)/Dt Lineární člen Pole objemových sil může být nelineární Obsahuje nelinearitu skrze materiálovou derivaci Dv/Dt= v/ t + vgradv
10 Druhy a zdroje nelinearit Geometrické rovnice Vyjádření tenzoru deformace ε ij = ½( u i / x j + u j / x i ) Kompatibilita deformace ε ij / x k x l + ε kl / x i x j ε ik / x j x l ε jl / x i x k = 0 Týká se pouze úloh řešených přímo v deformacích. Předpokládaný tvar posuvů/deformace Např. konstantnost deformace v prostoru týká se pouze analytických úloh.
11 Geometrickánelinearita Velképosuvy Velkédeformace M o (x) Fw(x)= 0 Velképosuvy nemusínutněznamenat geometrickou nelinearitu Uvažujte deformaci jako poměr poloměrůna konci a na začátku nafukování Obrázek přejat z Interaktivní učebnice pružnosti a pevnosti, kolektiv autorůfsi VUT v Brně Pamplona DC, Gonçalves PB, Lopes SRX (006) Finite deformations of cylindrical membrane under internal pressure. Int J Mech Sci 48(6):
12 Velkédeformace ε ij = ½( u i / x j + u j / x i ) vs ε ij = ½( u i / x j + u j / x i + u k / x i u k / x j ) Smluvní napětí[kpa] Stretch λ= l/l Zdroj: Pryž LRG Treloar(944)
13 Velkédeformace Vycházíme z deformačního gradientu F dx= FdX F= Gradx F ik = x i / X K Musíme rozlišovat mezi počáteční (materiálovou) a průběžnou (prostorovou) konfigurací
14 Velkédeformace Odvozujeme několik měr deformace (a každá je energeticky konjugovaná s nějakou mírou napětí) C = F T F E = ½(F T F I) U F =RU lnu b = FF T e = ½(I F -T F - ) pravý Cauchy-Greenův tenzor deformace Green-Lagrangeův Pravý tenzor strečů Henckyho tenzor deformace levý Cauchy-Greenův Euler-Almansiho
15 Velkédeformace Příklad Homogenní deformace Uvažujme objekt tvaru krychle, který se deformuje do kvádru tak, že x = λ X x = λ X x 3 = λ 3 X 3 X 3 x 3 F ik = x i / X K F = x / X = λ F = x / X = λ F 33 = x 3 / X 3 = λ 3 F λ 0 0 = 0 λ λ 3 λ 3 E e E 3 e 3 F = F 3 = F 3 = F = F 3 = F 3 = 0 X x λ λ E e X x
16 Velkédeformace Příklad Homogenní deformace Tenzory deformace pak mají tvar: F λ 0 0 = 0 λ λ 3 λ 0 0 ε = 0 λ λ 3 C λ 0 0 = 0 λ λ 3 lnu lnλ 0 0 = 0 lnλ ln λ 3 E ( λ ) 0 0 = 0 ( λ ) ( λ 3 ) ( λ ) 0 0 e = 0 ( λ ) ( λ3 )
17 Velkédeformace Pozor! C λ 0 0 = 0 λ λ 3 λ λ 0 b = 0 0 λ 3 Maticová reprezentace totiž neukazuje bázové vektory C b λ 0 0 = 0 λ 0 = λ E E + λ E E + λ E E + 0 E E + E E + E E 0 0 λ 3 ( ) λ 0 0 = 0 λ 0 = λ e e + λ e e + λ e e + 0 e e + e e + e e 0 0 λ 3 ( ) Referenční báze {E,E,E 3 } Průběžná báze {e, e, e 3 }
18 Velkédeformace Pozor také na nesymetrické tenzory! Obecně totiž neplatí u v = v u Uvažujme prostý smyk podle obrázku X x k x = X + kx x = X x 3 = X 3 X x F k 0 = C k 0 = k + k Tenzory obsahující v názvu slovo deformace jsou symetrické. Proč?
19 Velkédeformace Míry deformace při jednoosém tahu True scale C = F T F F Míry deformace E = ½(F T F I) ε lnu e = ½(I F -T F - )
20 Materiálovánelinearita Napětí-deformace při tahovézkoušce pryže DorfmannA., Ogden R.W. (004) A constitutive model for the Mullins effect with permanent set in particle-reinforced rubber.intj Solid Struct 4 (7): Odezva podle množstvíplniva (% vs 60%) umožňující vulkanizaci
21 Materiálovánelinearita Měkké tkáně Napětí-deformace pro šlachu, nosorožčí a kočičí kůži Napětí-deformace pro prasečí cévy: aorta, vena cava, a. iliac, a. carotis Meyers M.A., Chen P.-Y., Lin A.Y.-M., Seki Y. (008) Biological materials: Structure and mechanical properties.progress Mater Sci 53():-06. SnowhillP.B., SilverF.H. (005) A mechanical model ofporcinevasculartissues-part II: Stress-strain and mechanical properties of juvenile porcine blood vessels. Cardiovasc Eng 5(4):57-69.
22 Materiálovánelinearita Jak efektivně popsat nelineární materiál? A. L. Cauchy vs. G. Green Konstitutivnírovnice tvoříme přímo (soustavou algebraických nebo diferenciálních) rovnic Obdobnějako zobecněný Hookeův zákon Předpokládáme existenci elastického potenciálu hyperelasticita Složky tenzoru napětídostaneme jako intenzitu elastického pole
23 Materiálovánelinearita Připomeňme si tíhový a elektrický potenciál Potenciál je měrná energie (v případě tíhy na jednotku hmotnosti). Představuje tedy práci, kterou by mohl vykonat jednotkový hmotný bod dík působení tíhového pole. V = U/m = mgh/m = gh Intenzita tíhového pole je pak dána: V/ h = g Potenciál elektrického pole náboje q je V = /(4πε)q /r když potenciální energie přenesená na částici s nábojem q ve vzdálenosti rje U = /(4πε)q q /r Intenzita elektrického pole je pak dána: E = - V/ r = /(4πε)q /r
24 Materiálovánelinearita Elastická potenciální energie U = ρw Hustota deformačníenergie (elastický potenciál) W = ½σ ij ε ij D formulace Hookeův zákon σ= Eε W= ½Eε W/ ε = Eε = σ
25 Materiálovánelinearita 3D zobecněný Hookeův zákon µ µ µ σ µ µ µ ε σ ε σ µ µ µ E ε 33 = σ 3 ( + µ )( µ ) µ ε σ ε 3 3 σ µ ε µ σ= Cε W = ½Cεε σ ij = W/ ε ij Ověřte si alespoň pro jednu složku
26 Materiálovánelinearita Elastický potenciál: Zajišťuje Implicitní splnění. zákona termodynamiky Zjednodušuje práci s nelineární materiálovou závislostí - mocninná, exponenciální, logaritmická Umožňuje snadnou implementaci anisotropie Ve forměvolnéenergie lze snadno rozšířit pro nevratnéděje (viskoelastický potenciál) Implementováno v MKP balících
27 Materiálovánelinearita Biomechanika V posledních padesáti letech se ukázal jako nejúspěšnější (u měkkých tkání kůže, cévy, srdce, vazy, ) model pro W navržený Y.C. Fungem(967) Elastomery W µ = α ( e αε ) Velice úspěšný model navržen R.W. Ogdenem(97) W n i= µ λ λ λ α ( α α α 3) 3 i i i i = + + i
28 Materiálovánelinearita Objektivita W R. S. Rivlin W = W(ε ij ) Invariance Wvůči transformaci souřadnic bude nejsnáze zajištěna formulací pomocí invariantů tenzoru deformace Důsledná aplikace invariantů Globální vs. Lokální v MKP Dnes existuje algebraická teorie konstitutivních rovnic (čili skalárních funkcí tenzorové proměnné)
29 Materiálovánelinearita Invarianty C Uvažujme homogenní deformaci x = λ X x = λ X x 3 = λ 3 X 3 C λ 0 0 = 0 λ λ 3 I C = λ + λ + λ 3 I C = λ λ + λ λ 3 + λ 3 λ I 3C = λ λ λ 3 = I b = I b = I 3 b
30 Materiálovánelinearita Neo-Hookeovský materiál Nejjednodušší model µ W = I ( ) 3 σ µ= 50 σ = µ λ λ µ= 0 µ= λ
31 Materiálovánelinearita Mooney-Rivlin µ υ W = I + I ( 3) ( 3) σ µ= ν = µ= ν = µ= ν = 0.5 µ= ν = 0. µ= ν = 0 µ= ν = -0.5 σ = µ λ + νλ λ λ µ= ν = 00 σ µ= ν = 0 µ= ν = 5 µ= ν = 0 λ
32 Materiálovánelinearita Gent µ J 3 m ln I W = Jm σ µ= J m = 0.4 µ= J m = 0.7 µ= J m = µ= J m = µ= J m = 0 σ = J µ Jmλ λ λ + 3 λ m λ
33 Materiálovánelinearita Poznámka Výše zmíněné modely W byly všechny: ISOTROPNÍ U všech jsme předpokládali nestlačitelný materiál J = detf= I 3C = I 3b = λ λ λ 3 =
34 Různémíry deformace dávajírůznémíry napětí Referenční konfigurace L A = BH AE x Průběžná konfigurace l a = bh ae x ae x f σ = a ( e e ) ( e e ) xx x x x x Průběžná konfigurace Skutečnénapětí σ = f/a P AE x ( e E ) = ( e E ) xx x X x X f A Smíšená konfigurace Smluvní napětí P = f/a S ( E ) σ ( ) P XX X X xx X X xx ( X X ) AE E = E x λ E = E λ E xx Referenční konfigurace DruhéPiola-KirchhoffovonapětíS= σ/λ x xx
35 Různémíry deformace dávajírůznémíry napětí Ještě jednou! Abychom získali druhépiola-kirchhoffovonapětís, transformuje skutečnénapětí σinverznítransformacík transformaci, která proběhla, když síla deformovala průřez do průběžné konfigurace; čili A a: a=λ x A DruhéPiola-Kirchhoffovonapětí tedy je S XX = (λ x ) - σ xx
36 Napětí Transformace mezi tenzory napětí Znovu připomeňme, že deformační gradient F převádí referenční vektor na zdeformovaný vektor x =FX S = F σf -T J σ = T J FSF P FS = S = F P P = JσF T σ = T J PF
37 Napětía elastický potenciál Míry napětí a deformace jsou konjugovány tak, že práce vnitřních sil (skalár) při deformaci je vždy stejná P = W F ( F) σ = ( ) F J W F F T σ = W J F C ( C) F T S W = = C ( C) W ( E) E
38 Nestlačitelný materiál Deformace elastomerůa měkkých tkáníjsou často modelovány jako isochorické děje dv J = = detf = I = I = λ λ λ = dv C b V takovém případěse na objemových složkách tenzoru deformace nekonána práce vnitřních sil. Takže odpovídajícísložky napětí nelze přímo určit z W. Zavádíme tudíž je jako neurčitý Lagrangeův multiplikátor p a určujeme z okrajových podmínek. W ( F) T ( C) p( J ) W = W + P = pf F W ( F) W T ( C) T σ = F pi = F F pi F C W ( C) S = pc C
39 Nelinearita okrajových podmínek Krom rovnic rovnováhy, kinematiky a materiálu, může nelinearita vniknou i v okrajových podmínkách. To je typické v kontaktních úlohách. Dead loading
40 Vybranépodpůrnézdroje Návrhy na úpravy nebo upozornění na chyby adresujte
Biomechanika srdečněcévnísoustavy a konstitutivnímodelování
 Biomechanika srdečněcévnísoustavy a konstitutivnímodelování Biomechanika a lékařsképřístroje Biomechanika I LukášHorný Laboratoř biomechaniky člověka Ústavu mechaniky Fakulty strojní ČVUT v Praze M Konstitutivní
Biomechanika srdečněcévnísoustavy a konstitutivnímodelování Biomechanika a lékařsképřístroje Biomechanika I LukášHorný Laboratoř biomechaniky člověka Ústavu mechaniky Fakulty strojní ČVUT v Praze M Konstitutivní
TENSOR NAPĚTÍ A DEFORMACE. Obrázek 1: Volba souřadnicového systému
 TENSOR NAPĚTÍ A DEFORMACE Obrázek 1: Volba souřadnicového systému Pole posunutí, deformace, napětí v materiálovém bodě {u} = { u v w } T (1) Obecně 9 složek pole napětí lze uspořádat do matice [3x3] -
TENSOR NAPĚTÍ A DEFORMACE Obrázek 1: Volba souřadnicového systému Pole posunutí, deformace, napětí v materiálovém bodě {u} = { u v w } T (1) Obecně 9 složek pole napětí lze uspořádat do matice [3x3] -
Modelovánía experimentální zjišťovánímechanických vlastností nelineárních materiálů
 Modelovánía experimentální zjišťovánímechanických vlastností nelineárních materiálů Biomechanika a lékařsképřístroje Projekt II LukášHorný Laboratoř biomechaniky člověka Ústavu mechaniky Fakulty strojní
Modelovánía experimentální zjišťovánímechanických vlastností nelineárních materiálů Biomechanika a lékařsképřístroje Projekt II LukášHorný Laboratoř biomechaniky člověka Ústavu mechaniky Fakulty strojní
Nelineární problémy a MKP
 Nelineární problémy a MKP Základní druhy nelinearit v mechanice tuhých těles: 1. materiálová (plasticita, viskoelasticita, viskoplasticita,...) 2. geometrická (velké posuvy a natočení, stabilita konstrukcí)
Nelineární problémy a MKP Základní druhy nelinearit v mechanice tuhých těles: 1. materiálová (plasticita, viskoelasticita, viskoplasticita,...) 2. geometrická (velké posuvy a natočení, stabilita konstrukcí)
Rozdíly mezi MKP a MHP, oblasti jejich využití.
 Rozdíly mezi, oblasti jejich využití. Obě metody jsou vhodné pro určitou oblast problémů. základě MKP vyžaduje rozdělení těles na vhodný počet prvků, jejichž analýza je poměrně snadná a pro většinu částí
Rozdíly mezi, oblasti jejich využití. Obě metody jsou vhodné pro určitou oblast problémů. základě MKP vyžaduje rozdělení těles na vhodný počet prvků, jejichž analýza je poměrně snadná a pro většinu částí
FAKULTA STAVEBNÍ NELINEÁRNÍ MECHANIKA. Telefon: WWW:
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ NELINEÁRNÍ MECHANIKA Bakalářské studium, 4. ročník Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ NELINEÁRNÍ MECHANIKA Bakalářské studium, 4. ročník Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz
Polární rozklad deformačního gradientu a tenzory přetvoření
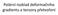 Polární rozklad deformačního gradientu a tenzory přetvoření https://en.wikipedia.org/wiki/finite_strain_theory Deformační gradient Musí tedy existovat jednoznačné zobrazení konfigurace : 1 t t x X, a inversní
Polární rozklad deformačního gradientu a tenzory přetvoření https://en.wikipedia.org/wiki/finite_strain_theory Deformační gradient Musí tedy existovat jednoznačné zobrazení konfigurace : 1 t t x X, a inversní
PRUŽNOST A PEVNOST II
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ PRUŽNOST A PEVNOST II Navazující magisterské studium, 1. ročník Alois Materna (přednášky) Jiří Brožovský (cvičení) Kancelář: LP C 303/1
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ PRUŽNOST A PEVNOST II Navazující magisterské studium, 1. ročník Alois Materna (přednášky) Jiří Brožovský (cvičení) Kancelář: LP C 303/1
Vlastnosti a zkoušení materiálů. Přednáška č.4 Úvod do pružnosti a pevnosti
 Vlastnosti a zkoušení materiálů Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze
Vlastnosti a zkoušení materiálů Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze
FAKULTA STAVEBNÍ. Telefon: WWW:
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ ZÁKLADY METODY KONEČNÝCH PRVKŮ Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast10.vsb.cz/brozovsky/
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ ZÁKLADY METODY KONEČNÝCH PRVKŮ Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast10.vsb.cz/brozovsky/
ÚVOD DO MODELOVÁNÍ V MECHANICE
 ÚVOD DO MODELOVÁNÍ V MECHANICE PRUŽNOST A PEVNOST Přednáška č. 5 Prof. Ing. Vladislav Laš. CSc. MECHANIKA PODDAJNÝCH TĚLES Úkolem PP z inženýrského hlediska je navrhnout součásti nebo konstrukce, které
ÚVOD DO MODELOVÁNÍ V MECHANICE PRUŽNOST A PEVNOST Přednáška č. 5 Prof. Ing. Vladislav Laš. CSc. MECHANIKA PODDAJNÝCH TĚLES Úkolem PP z inženýrského hlediska je navrhnout součásti nebo konstrukce, které
Nelineární úlohy při výpočtu konstrukcí s využitím MKP
 Nelineární úlohy při výpočtu konstrukcí s využitím MKP Obsah přednášky Lineární a nelineární úlohy Typy nelinearit (geometrická, materiálová, kontakt,..) Příklady nelineárních problémů Teorie kontaktu,
Nelineární úlohy při výpočtu konstrukcí s využitím MKP Obsah přednášky Lineární a nelineární úlohy Typy nelinearit (geometrická, materiálová, kontakt,..) Příklady nelineárních problémů Teorie kontaktu,
Nelineární analýza materiálů a konstrukcí (V-132YNAK) Přednáška 2 Princip metody konečných prvků
 Nelineární analýza materiálů a konstrukcí (V-132YNAK) Přednáška 2 Princip metody konečných prvků Petr Kabele petr.kabele@fsv.cvut.cz people.fsv.cvut.cz/~pkabele Petr Kabele, 2007-2014 Obsah Variační principy
Nelineární analýza materiálů a konstrukcí (V-132YNAK) Přednáška 2 Princip metody konečných prvků Petr Kabele petr.kabele@fsv.cvut.cz people.fsv.cvut.cz/~pkabele Petr Kabele, 2007-2014 Obsah Variační principy
Rovinná úloha v MKP. (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v. prostorové úlohy: u, v, w
 Rovinná úloha v MKP Hledané deformační veličiny viz klasická teorie pružnosti (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v desky: w, ϕ x, ϕ y prostorové úlohy: u,
Rovinná úloha v MKP Hledané deformační veličiny viz klasická teorie pružnosti (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v desky: w, ϕ x, ϕ y prostorové úlohy: u,
c B. Patzák 2012, verze 01
 Úvod do nelineárních problémů c B. Patzák (borek.patzak@fsv.cvut.cz), 2012, verze 01 Příklady nelineárního chování Problém vedení tepla, kde vlastnosti materiálu (koeficient vedení tepla) závisí na aktuální
Úvod do nelineárních problémů c B. Patzák (borek.patzak@fsv.cvut.cz), 2012, verze 01 Příklady nelineárního chování Problém vedení tepla, kde vlastnosti materiálu (koeficient vedení tepla) závisí na aktuální
Vícerozměrné úlohy pružnosti
 Přednáška 07 Rovinná napjatost nosné stěny Rovinná deformace Hlavní napětí Mohrova kružnice Metoda konečných prvků pro rovinnou napjatost Laméovy rovnice Příklady Copyright (c) 011 Vít Šmilauer Czech Technical
Přednáška 07 Rovinná napjatost nosné stěny Rovinná deformace Hlavní napětí Mohrova kružnice Metoda konečných prvků pro rovinnou napjatost Laméovy rovnice Příklady Copyright (c) 011 Vít Šmilauer Czech Technical
CAD/CAE. Fyzikální model. (fyzikální podstata problémů, počáteční a okrajové podmínky, materiálové modely)
 CAD/CAE ÚNOD: Jan Tippner, Václav Sebera, Miroslav Trcala, Eva Troppová. Fyzikální model (fyzikální podstata problémů, počáteční a okrajové podmínky, materiálové modely) Podpořeno projektem Průřezová inovace
CAD/CAE ÚNOD: Jan Tippner, Václav Sebera, Miroslav Trcala, Eva Troppová. Fyzikální model (fyzikální podstata problémů, počáteční a okrajové podmínky, materiálové modely) Podpořeno projektem Průřezová inovace
Úvod do nelineární pružnosti
 Úvod do nelineární pružnosti Lukáš Horný lukas.horny@fs.cvut.cz Ústav mechaniky, biomechaniky a mechatroniky, ČVUT FS Verze 05.05.09 Proč nelineární pružnost? Zdroje nelinearit Velké posuvy Velká natočení
Úvod do nelineární pružnosti Lukáš Horný lukas.horny@fs.cvut.cz Ústav mechaniky, biomechaniky a mechatroniky, ČVUT FS Verze 05.05.09 Proč nelineární pružnost? Zdroje nelinearit Velké posuvy Velká natočení
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6
 OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
Pružnost a pevnost. zimní semestr 2013/14
 Pružnost a pevnost zimní semestr 2013/14 Organizace předmětu Přednášející: Prof. Milan Jirásek, B322 Konzultace: pondělí 10:00-10:45 nebo dle dohody E-mail: Milan.Jirasek@fsv.cvut.cz Webové stránky předmětu:
Pružnost a pevnost zimní semestr 2013/14 Organizace předmětu Přednášející: Prof. Milan Jirásek, B322 Konzultace: pondělí 10:00-10:45 nebo dle dohody E-mail: Milan.Jirasek@fsv.cvut.cz Webové stránky předmětu:
Dnešní látka: Literatura: Kapitoly 3 a 4 ze skript Karel Rektorys: Matematika 43, ČVUT, Praha, Text přednášky na webové stránce přednášejícího.
 Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Pružnost a plasticita II CD03
 Pružnost a plasticita II CD3 uděk Brdečko VUT v Brně, Fakulta stavební, Ústav stavební mechanik tel: 5447368 email: brdecko.l @ fce.vutbr.cz http://www.fce.vutbr.cz/stm/brdecko.l/html/distcz.htm Obsah
Pružnost a plasticita II CD3 uděk Brdečko VUT v Brně, Fakulta stavební, Ústav stavební mechanik tel: 5447368 email: brdecko.l @ fce.vutbr.cz http://www.fce.vutbr.cz/stm/brdecko.l/html/distcz.htm Obsah
Obr. 0.1: Nosník se spojitým zatížením.
 Každý test obsahuje jeden příklad podobný níže uvedeným tpovým příkladům a několik otázek vbraných z níže uvedených testových otázek. Za příklad je možno získat maimálně bodů, celkový počet bodů z testu
Každý test obsahuje jeden příklad podobný níže uvedeným tpovým příkladům a několik otázek vbraných z níže uvedených testových otázek. Za příklad je možno získat maimálně bodů, celkový počet bodů z testu
Dynamika vázaných soustav těles
 Dynamika vázaných soustav těles Většina strojů a strojních zařízení, s nimiž se setkáváme v praxi, lze považovat za soustavy těles. Složitost dané soustavy závisí na druhu řešeného případu. Základem pro
Dynamika vázaných soustav těles Většina strojů a strojních zařízení, s nimiž se setkáváme v praxi, lze považovat za soustavy těles. Složitost dané soustavy závisí na druhu řešeného případu. Základem pro
Martin NESLÁDEK. 14. listopadu 2017
 Martin NESLÁDEK Faculty of mechanical engineering, CTU in Prague 14. listopadu 2017 1 / 22 Poznámky k úlohám řešeným MKP Na přesnost simulace pomocí MKP a prostorové rozlišení výsledků má vliv především:
Martin NESLÁDEK Faculty of mechanical engineering, CTU in Prague 14. listopadu 2017 1 / 22 Poznámky k úlohám řešeným MKP Na přesnost simulace pomocí MKP a prostorové rozlišení výsledků má vliv především:
KONSTITUČNÍ VZTAHY. 1. Tahová zkouška
 1. Tahová zkouška Tahová zkouška se provádí dle ČSN EN ISO 6892-1 (aktualizována v roce 2010) Je nejčastější mechanickou zkouškou kovových materiálů. Zkoušky se realizují na trhacích strojích, kde se zkušební
1. Tahová zkouška Tahová zkouška se provádí dle ČSN EN ISO 6892-1 (aktualizována v roce 2010) Je nejčastější mechanickou zkouškou kovových materiálů. Zkoušky se realizují na trhacích strojích, kde se zkušební
Co jsme udělali: Au = f, u D(A)
 Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Zde je uveden abecední seznam důležitých pojmů interaktivního učebního textu
 index 1 Rejstřík Zde je uveden abecední seznam důležitých pojmů interaktivního učebního textu Pružnost a pevnost. U každého termínu je uvedeno označení kapitoly a čísla obrazovek, na nichž lze pojem nalézt.
index 1 Rejstřík Zde je uveden abecední seznam důležitých pojmů interaktivního učebního textu Pružnost a pevnost. U každého termínu je uvedeno označení kapitoly a čísla obrazovek, na nichž lze pojem nalézt.
ÚVOD DO MODELOVÁNÍ V MECHANICE
 ÚVO O MOELOVÁNÍ V MECHNICE MECHNIK KOMPOZITNÍCH MTERIÁLŮ 2 Přednáška č. 7 Robert Zemčík 1 Zebry normální Zebry zdeformované 2 Zebry normální Zebry zdeformované 3 Zebry normální 4 Zebry zdeformované protažené?
ÚVO O MOELOVÁNÍ V MECHNICE MECHNIK KOMPOZITNÍCH MTERIÁLŮ 2 Přednáška č. 7 Robert Zemčík 1 Zebry normální Zebry zdeformované 2 Zebry normální Zebry zdeformované 3 Zebry normální 4 Zebry zdeformované protažené?
CAD/CAE. Fyzikální model. (fyzikální podstata problémů, počáteční a okrajové podmínky, materiálové modely)
 CAD/CAE ÚNOD: Jan Tippner, Václav Sebera, Miroslav Trcala, Eva Troppová. Fyzikální model (fyzikální podstata problémů, počáteční a okrajové podmínky, materiálové modely) Podpořeno projektem Průřezová inovace
CAD/CAE ÚNOD: Jan Tippner, Václav Sebera, Miroslav Trcala, Eva Troppová. Fyzikální model (fyzikální podstata problémů, počáteční a okrajové podmínky, materiálové modely) Podpořeno projektem Průřezová inovace
7. Základní formulace lineární PP
 p07 1 7. Základní formulace lineární PP Podle tvaru závislosti mezi vnějšími silami a deformačně napěťovými parametry tělesa dělíme pružnost a pevnost na lineární a nelineární. Lineární pružnost vyšetřuje
p07 1 7. Základní formulace lineární PP Podle tvaru závislosti mezi vnějšími silami a deformačně napěťovými parametry tělesa dělíme pružnost a pevnost na lineární a nelineární. Lineární pružnost vyšetřuje
Mechanika kontinua. Mechanika elastických těles Mechanika kapalin
 Mechanika kontinua Mechanika elastických těles Mechanika kapalin Mechanika kontinua Mechanika elastických těles Mechanika kapalin a plynů Kinematika tekutin Hydrostatika Hydrodynamika Kontinuum Pro vyšetřování
Mechanika kontinua Mechanika elastických těles Mechanika kapalin Mechanika kontinua Mechanika elastických těles Mechanika kapalin a plynů Kinematika tekutin Hydrostatika Hydrodynamika Kontinuum Pro vyšetřování
Kontraktantní/dilatantní
 Kontraktantní/dilatantní plasticita - úhel dilatance směr přírůstku plastické deformace Na základě experimentálního měření dospěl St. Venant k závěru, že směry hlavních napětí jsou totožné se směry přírůstku
Kontraktantní/dilatantní plasticita - úhel dilatance směr přírůstku plastické deformace Na základě experimentálního měření dospěl St. Venant k závěru, že směry hlavních napětí jsou totožné se směry přírůstku
Lineární stabilita a teorie II. řádu
 Lineární stabilita a teorie II. řádu Sestavení podmínek rovnováhy na deformované konstrukci Konstrukce s a bez počáteční imperfekce Výpočet s malými vs. s velkými deformacemi ANKC-C 1 Zatěžovacídráhy [Šejnoha,
Lineární stabilita a teorie II. řádu Sestavení podmínek rovnováhy na deformované konstrukci Konstrukce s a bez počáteční imperfekce Výpočet s malými vs. s velkými deformacemi ANKC-C 1 Zatěžovacídráhy [Šejnoha,
Inkrementální teorie plasticity - shrnutí
 Inkrementální teorie plasticity - shrnutí Aditivní zákon = e p. Hookeův zákon pro elastickou složku deformace =C: e. Podmínka plasticity f = f Y =0. Pravidlo zpevnění p e d =g, p,,d, d p,..., dy =h, p,y,
Inkrementální teorie plasticity - shrnutí Aditivní zákon = e p. Hookeův zákon pro elastickou složku deformace =C: e. Podmínka plasticity f = f Y =0. Pravidlo zpevnění p e d =g, p,,d, d p,..., dy =h, p,y,
Biomechanika a lékařské přístroje
 Biomechanika a lékařské přístroje Projekt II Lukáš Horný lukas.horny@fs.cvut.cz Ústav mechaniky, biomechaniky a mechatroniky, ČVUT FS 2018 Projekt II: O co nám půjde? Otázky odpovědi Konstrukce model konstrukce
Biomechanika a lékařské přístroje Projekt II Lukáš Horný lukas.horny@fs.cvut.cz Ústav mechaniky, biomechaniky a mechatroniky, ČVUT FS 2018 Projekt II: O co nám půjde? Otázky odpovědi Konstrukce model konstrukce
Pružnost a pevnost I
 Stránka 1 teoretické otázk 2007 Ing. Tomáš PROFANT, Ph.D. verze 1.1 OBSAH: 1. Tenzor napětí 2. Věta o sdruženosti smkových napětí 3. Saint Venantův princip 4. Tenzor deformace (přetvoření) 5. Geometrická
Stránka 1 teoretické otázk 2007 Ing. Tomáš PROFANT, Ph.D. verze 1.1 OBSAH: 1. Tenzor napětí 2. Věta o sdruženosti smkových napětí 3. Saint Venantův princip 4. Tenzor deformace (přetvoření) 5. Geometrická
2 Odvození pomocí rovnováhy sil
 Řetězovka Abstrakt: Ukážeme si, že řetěz pověšený mezi dvěma body v homogenním gravitačním poli se prohne ve tvaru grafu funkce hyperbolický kosinus. Odvození provedeme dvojím způsobem: pomocí rovnováhy
Řetězovka Abstrakt: Ukážeme si, že řetěz pověšený mezi dvěma body v homogenním gravitačním poli se prohne ve tvaru grafu funkce hyperbolický kosinus. Odvození provedeme dvojím způsobem: pomocí rovnováhy
8. Základy lomové mechaniky. Únava a lomová mechanika Pavel Hutař, Luboš Náhlík
 Únava a lomová mechanika Koncentrace napětí nesingulární koncentrátor napětí singulární koncentrátor napětí 1 σ = σ + a r 2 σ max = σ 1 + 2( / ) r 0 ; σ max Nekonečný pás s eliptickým otvorem [Pook 2000]
Únava a lomová mechanika Koncentrace napětí nesingulární koncentrátor napětí singulární koncentrátor napětí 1 σ = σ + a r 2 σ max = σ 1 + 2( / ) r 0 ; σ max Nekonečný pás s eliptickým otvorem [Pook 2000]
Numerické modelování v aplikované geologii
 Numerické modelování v aplikované geologii David Mašín Ústav hydrogeologie, inženýrské geologie a užité geofyziky Přírodovědecká fakulta Karlova Univerzita v Praze Přednášky pro obor Geotechnologie David
Numerické modelování v aplikované geologii David Mašín Ústav hydrogeologie, inženýrské geologie a užité geofyziky Přírodovědecká fakulta Karlova Univerzita v Praze Přednášky pro obor Geotechnologie David
Metoda konečných prvků Charakteristika metody (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika)
 Inovace studijního oboru Geotechnika Reg. č. CZ.1.07/2.2.00/28.0009 Metoda konečných prvků Charakteristika metody (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika) Doc. RNDr.
Inovace studijního oboru Geotechnika Reg. č. CZ.1.07/2.2.00/28.0009 Metoda konečných prvků Charakteristika metody (výuková prezentace pro 1. ročník navazujícího studijního oboru Geotechnika) Doc. RNDr.
Požadavky k písemné přijímací zkoušce z matematiky do navazujícího magisterského studia pro neučitelské obory
 Požadavky k písemné přijímací zkoušce z matematiky do navazujícího magisterského studia pro neučitelské obory Zkouška ověřuje znalost základních pojmů, porozumění teorii a schopnost aplikovat teorii při
Požadavky k písemné přijímací zkoušce z matematiky do navazujícího magisterského studia pro neučitelské obory Zkouška ověřuje znalost základních pojmů, porozumění teorii a schopnost aplikovat teorii při
Dynamika tekutin popisuje kinematiku (pohyb částice v času a prostoru) a silové působení v tekutině.
 Dynamika tekutin popisuje kinematiku (pohyb částice v času a prostoru) a silové působení v tekutině. Přehled proudění Vazkost - nevazké - vazké (newtonské, nenewtonské) Stlačitelnost - nestlačitelné (kapaliny
Dynamika tekutin popisuje kinematiku (pohyb částice v času a prostoru) a silové působení v tekutině. Přehled proudění Vazkost - nevazké - vazké (newtonské, nenewtonské) Stlačitelnost - nestlačitelné (kapaliny
Biomechanika II. Modely napjatosti a deformace cév, vliv zbytkových napětí a aktivní vlastnosti. Lukáš Horný
 Biomechanika II Modely napjatosti a deformace cév, vliv zbytkových napětí a aktivní vlastnosti ČVUT v Praze, fakulta strojní, ústav mechaniky, biomechaniky a mechatroniky Obor: Biomechanika a lékařské
Biomechanika II Modely napjatosti a deformace cév, vliv zbytkových napětí a aktivní vlastnosti ČVUT v Praze, fakulta strojní, ústav mechaniky, biomechaniky a mechatroniky Obor: Biomechanika a lékařské
Vibrace atomů v mřížce, tepelná kapacita pevných látek
 Vibrace atomů v mřížce, tepelná kapacita pevných látek Atomy vázané v mřížce nejsou v klidu. Míru jejich pohybu vyjadřuje podobně jako u plynů a kapalin teplota. - Elastické vlny v kontinuu neatomární
Vibrace atomů v mřížce, tepelná kapacita pevných látek Atomy vázané v mřížce nejsou v klidu. Míru jejich pohybu vyjadřuje podobně jako u plynů a kapalin teplota. - Elastické vlny v kontinuu neatomární
8 Elasticita kaučukových sítí
 8 Elasticita kaučukových sítí Elastomerní polymerní látky (např. kaučuky) tvoří ze / chemické příčné vazby a / fyzikální uzly. Vyznačují se schopností deformovat se již malou silou nejméně o 00 % své původní
8 Elasticita kaučukových sítí Elastomerní polymerní látky (např. kaučuky) tvoří ze / chemické příčné vazby a / fyzikální uzly. Vyznačují se schopností deformovat se již malou silou nejméně o 00 % své původní
vztažný systém obecné napětí předchozí OBSAH další
 p05 1 5. Deformace těles S deformací jako složkou mechanického pohybu jste se setkali už ve statice. Běžně je chápána jako změna rozměrů a tvaru tělesa. Lze ji popsat změnami vzdáleností různých dvou bodů
p05 1 5. Deformace těles S deformací jako složkou mechanického pohybu jste se setkali už ve statice. Běžně je chápána jako změna rozměrů a tvaru tělesa. Lze ji popsat změnami vzdáleností různých dvou bodů
Nauka o materiálu. Přednáška č.4 Úvod do pružnosti a pevnosti
 Nauka o materiálu Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze kluzu R e, odpovídající
Nauka o materiálu Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze kluzu R e, odpovídající
Vysoké učení technické v Brně, Fakulta strojního inženýrství MATEMATIKA 2
 Vysoké učení technické v Brně, Fakulta strojního inženýrství MATEMATIKA 2 Požadavky ke zkoušce pro skupinu C 1. ročník 2014/15 I. Diferenciální počet funkcí více proměnných 1. Funkce více proměnných (a)
Vysoké učení technické v Brně, Fakulta strojního inženýrství MATEMATIKA 2 Požadavky ke zkoušce pro skupinu C 1. ročník 2014/15 I. Diferenciální počet funkcí více proměnných 1. Funkce více proměnných (a)
Téma 1 Úvod do předmětu Pružnost a plasticita, napětí a přetvoření
 Pružnost a plasticita, 2.ročník kombinovaného studia Téma 1 Úvod do předmětu Pružnost a plasticita, napětí a přetvoření Základní pojmy, výchozí předpoklady Vztahy mezi vnitřními silami a napětími v průřezu
Pružnost a plasticita, 2.ročník kombinovaného studia Téma 1 Úvod do předmětu Pružnost a plasticita, napětí a přetvoření Základní pojmy, výchozí předpoklady Vztahy mezi vnitřními silami a napětími v průřezu
Numerické metody. Numerické modelování v aplikované geologii. David Mašín. Ústav hydrogeologie, inženýrské geologie a užité geofyziky
 Numerické modelování v aplikované geologii David Mašín Ústav hydrogeologie, inženýrské geologie a užité geofyziky Přírodovědecká fakulta Karlova Univerzita v Praze Přednášky pro obor Geotechnologie David
Numerické modelování v aplikované geologii David Mašín Ústav hydrogeologie, inženýrské geologie a užité geofyziky Přírodovědecká fakulta Karlova Univerzita v Praze Přednášky pro obor Geotechnologie David
Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra mechaniky. Diplomová práce
 Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra mechaniky Diplomová práce Identifikace materiálových parametrů pryžových segmentů tramvajových kol se zohledněním viskoelasticity Vypracoval:
Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra mechaniky Diplomová práce Identifikace materiálových parametrů pryžových segmentů tramvajových kol se zohledněním viskoelasticity Vypracoval:
Modelování a aproximace v biomechanice
 Modelování a aproximace v biomechanice Během většiny lidské aktivity působí v jednom okamžiku víc než jedna skupina svalů. Je-li úkolem analyzovat síly působící v kloubech a svalech během určité lidské
Modelování a aproximace v biomechanice Během většiny lidské aktivity působí v jednom okamžiku víc než jedna skupina svalů. Je-li úkolem analyzovat síly působící v kloubech a svalech během určité lidské
Cvičení 7 (Matematická teorie pružnosti)
 VŠB Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti (339) Pružnost a pevnost v energetice (Návo do cvičení) Cvičení 7 (Matematická teorie pružnosti) Autor: Jaroslav Rojíček Verze:
VŠB Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti (339) Pružnost a pevnost v energetice (Návo do cvičení) Cvičení 7 (Matematická teorie pružnosti) Autor: Jaroslav Rojíček Verze:
geologie a užité geofyziky Karlova Univerzita, Praha v geomechanice I
 1 Ústav hydrogeologie, inženýrské geologie a užité geofyziky Karlova Univerzita, Praha Přednášky pro předmět Matematické modelování v geomechanice I 1. část David Mašín 2 Obsah Úvod do matematického modelování
1 Ústav hydrogeologie, inženýrské geologie a užité geofyziky Karlova Univerzita, Praha Přednášky pro předmět Matematické modelování v geomechanice I 1. část David Mašín 2 Obsah Úvod do matematického modelování
Přednáška 08. Obecná trojosá napjatost
 Přednáška 8 Obecná trojosá napjatost Napětí statické rovnice Deformace geometrické rovnice Zobecněný Hookeův zákon Objemový modul pružnosti Oedometrický modul pružnosti Hlavní napětí, hlavní deformace
Přednáška 8 Obecná trojosá napjatost Napětí statické rovnice Deformace geometrické rovnice Zobecněný Hookeův zákon Objemový modul pružnosti Oedometrický modul pružnosti Hlavní napětí, hlavní deformace
ANALÝZA KONSTRUKCÍ. 5. přednáška
 ANALÝZA KONSTRUKCÍ 5. přednáška Nosné stěny rovinná napjatost Způsoby výpočtu napjatosti: Deformační metodou Primární neznámé: posuny u(,y), v(,y) Výchozí rovnice: statické Silovou metodou Primární neznámá:
ANALÝZA KONSTRUKCÍ 5. přednáška Nosné stěny rovinná napjatost Způsoby výpočtu napjatosti: Deformační metodou Primární neznámé: posuny u(,y), v(,y) Výchozí rovnice: statické Silovou metodou Primární neznámá:
Autor: Vladimír Švehla
 Bulletin of Applied Mechanics 1, 55 64 (2005) 55 Využití Castiglianovy věty při výpočtu deformací staticky určité případy zatížení tahem a tlakem Autor: Vladimír Švehla České vysoké učení technické, akulta
Bulletin of Applied Mechanics 1, 55 64 (2005) 55 Využití Castiglianovy věty při výpočtu deformací staticky určité případy zatížení tahem a tlakem Autor: Vladimír Švehla České vysoké učení technické, akulta
Napěťový vektor 3d. Díky Wikipedia za obrázek. n n n
 Míry napětí Napěťový vektor 3d n n2 2 n,. n n n Zatížené těleso rozdělíme myšleným řezem na dvě části. Na malou plošku v okolí materiálového bodu P působí napěťový vektor (n) (n, x, t), který je spojitou
Míry napětí Napěťový vektor 3d n n2 2 n,. n n n Zatížené těleso rozdělíme myšleným řezem na dvě části. Na malou plošku v okolí materiálového bodu P působí napěťový vektor (n) (n, x, t), který je spojitou
Matematická analýza pro informatiky I.
 Matematická analýza pro informatiky I. 10. přednáška Diferenciální počet funkcí více proměnných (II) Jan Tomeček jan.tomecek@upol.cz http://aix-slx.upol.cz/ tomecek/index Univerzita Palackého v Olomouci
Matematická analýza pro informatiky I. 10. přednáška Diferenciální počet funkcí více proměnných (II) Jan Tomeček jan.tomecek@upol.cz http://aix-slx.upol.cz/ tomecek/index Univerzita Palackého v Olomouci
Obsah PŘEDMLUVA 11 ÚVOD 13 1 Základní pojmy a zákony teorie elektromagnetického pole 23
 Obsah PŘEDMLUVA... 11 ÚVOD... 13 0.1. Jak teoreticky řešíme elektrotechnické projekty...13 0.2. Dvojí význam pojmu pole...16 0.3. Elektromagnetické pole a technické projekty...20 1. Základní pojmy a zákony
Obsah PŘEDMLUVA... 11 ÚVOD... 13 0.1. Jak teoreticky řešíme elektrotechnické projekty...13 0.2. Dvojí význam pojmu pole...16 0.3. Elektromagnetické pole a technické projekty...20 1. Základní pojmy a zákony
1 Ohyb desek - mindlinovské řešení
 1 OHYB DESEK - MINDLINOVSKÉ ŘEŠENÍ 1 1 Ohyb desek - mindlinovské řešení Kinematika přemístění Posun w se po tloušťce desky mění málo (vzhledem k hodnotě průhybu) w(x, y, z) = w(x, y) Normály ke střednicové
1 OHYB DESEK - MINDLINOVSKÉ ŘEŠENÍ 1 1 Ohyb desek - mindlinovské řešení Kinematika přemístění Posun w se po tloušťce desky mění málo (vzhledem k hodnotě průhybu) w(x, y, z) = w(x, y) Normály ke střednicové
Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 2. 3. 2018 Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
2. 3. 2018 Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
3.2 Základy pevnosti materiálu. Ing. Pavel Bělov
 3.2 Základy pevnosti materiálu Ing. Pavel Bělov 23.5.2018 Normálové napětí představuje vazbu, která brání částicím tělesa k sobě přiblížit nebo se od sebe oddálit je kolmé na rovinu řezu v případě že je
3.2 Základy pevnosti materiálu Ing. Pavel Bělov 23.5.2018 Normálové napětí představuje vazbu, která brání částicím tělesa k sobě přiblížit nebo se od sebe oddálit je kolmé na rovinu řezu v případě že je
MATEMATICKÝ MODEL CÉVNÍ STĚNY DVOUŠKÁLOVÁ METODA HOMOGENIZACE S UVAŽOVÁNÍM VELKÝCH DEFORMACÍ
 MATEMATICKÝ MODEL CÉVNÍ STĚNY DVOUŠKÁLOVÁ METODA HOMOGENIZACE S UVAŽOVÁNÍM VELKÝCH DEFORMACÍ Vladimír LUKEŠ, Eduard ROHAN 2 Abstract: Cévní stěna je modelována pomocí dvouškálové metody homogenizace, která
MATEMATICKÝ MODEL CÉVNÍ STĚNY DVOUŠKÁLOVÁ METODA HOMOGENIZACE S UVAŽOVÁNÍM VELKÝCH DEFORMACÍ Vladimír LUKEŠ, Eduard ROHAN 2 Abstract: Cévní stěna je modelována pomocí dvouškálové metody homogenizace, která
12. Únavové šíření trhliny. Únava a lomová mechanika Pavel Hutař, Luboš Náhlík
 Únava a lomová mechanika Proces únavového porušení Iniciace únavové trhliny v krystalu Cu (60 000 cyklů při 20 C) (převzato z [Suresh 2006]) Proces únavového porušení Jednotlivé stádia únavového poškození:
Únava a lomová mechanika Proces únavového porušení Iniciace únavové trhliny v krystalu Cu (60 000 cyklů při 20 C) (převzato z [Suresh 2006]) Proces únavového porušení Jednotlivé stádia únavového poškození:
Globální matice konstrukce
 Globální matice konstrukce Z matic tuhosti a hmotnosti jednotlivých prvků lze sestavit globální matici tuhosti a globální matici hmotnosti konstrukce, které se využijí v řešení základní rovnice MKP: [m]{
Globální matice konstrukce Z matic tuhosti a hmotnosti jednotlivých prvků lze sestavit globální matici tuhosti a globální matici hmotnosti konstrukce, které se využijí v řešení základní rovnice MKP: [m]{
2. Dynamika hmotného bodu
 . Dynamika hmotného bodu Syllabus:. Dynamika hmotného bodu. Newtonovy zákony. Síly působící při známém druhu pohybu. Pohybová rovnice hmotného bodu, vrhy, harmonický pohyb. Inerciální a neinerciální soustavy
. Dynamika hmotného bodu Syllabus:. Dynamika hmotného bodu. Newtonovy zákony. Síly působící při známém druhu pohybu. Pohybová rovnice hmotného bodu, vrhy, harmonický pohyb. Inerciální a neinerciální soustavy
Technologie a procesy sušení dřeva
 strana 1 Technologie a procesy sušení dřeva 5. Deformačně-napěťové pole ve dřevě během sušení Vytvořeno s podporou projektu Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v
strana 1 Technologie a procesy sušení dřeva 5. Deformačně-napěťové pole ve dřevě během sušení Vytvořeno s podporou projektu Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v
1. Úvod do pružnosti a pevnosti
 1. Úvod do pružnosti a pevnosti Mechanika je nejstarší vědní obor a její nedílnou součástí je nauka o pružnosti a pevnosti. Pružností nazýváme schopnost pevných těles získat po odstranění vnějších účinků
1. Úvod do pružnosti a pevnosti Mechanika je nejstarší vědní obor a její nedílnou součástí je nauka o pružnosti a pevnosti. Pružností nazýváme schopnost pevných těles získat po odstranění vnějších účinků
LDF MENDELU. Simona Fišnarová (MENDELU) LDR druhého řádu VMAT, IMT 1 / 22
 Lineární diferenciální rovnice druhého řádu Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF)
Lineární diferenciální rovnice druhého řádu Vyšší matematika, Inženýrská matematika LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF)
Dnešní látka Variačně formulované okrajové úlohy zúplnění prostoru funkcí. Lineární zobrazení.
 Předmět: MA4 Dnešní látka Variačně formulované okrajové úlohy zúplnění prostoru funkcí. Lineární zobrazení. Literatura: Kapitola 2 a)-c) a kapitola 4 a)-c) ze skript Karel Rektorys: Matematika 43, ČVUT,
Předmět: MA4 Dnešní látka Variačně formulované okrajové úlohy zúplnění prostoru funkcí. Lineární zobrazení. Literatura: Kapitola 2 a)-c) a kapitola 4 a)-c) ze skript Karel Rektorys: Matematika 43, ČVUT,
1 Vedení tepla stacionární úloha
 1 VEDENÍ TEPLA STACIONÁRNÍ ÚLOHA 1 1 Vedení tepla stacionární úloha Typický představitel transportních jevů Obdobným způsobem možno řešit například Fyzikální jev Neznámá Difuze koncentrace [3] Deformace
1 VEDENÍ TEPLA STACIONÁRNÍ ÚLOHA 1 1 Vedení tepla stacionární úloha Typický představitel transportních jevů Obdobným způsobem možno řešit například Fyzikální jev Neznámá Difuze koncentrace [3] Deformace
ÚVOD DO PROBLEMATIKY LOMOVÉ MECHANIKY KVAZIKŘEHKÝCH MATERIÁLŮ. Zbyněk Keršner Ústav stavební mechaniky FAST VUT v Brně
 ÚVOD DO PROBLEMATIKY LOMOVÉ MECHANIKY KVAZIKŘEHKÝCH MATERIÁLŮ Zbyněk Keršner Ústav stavební mechaniky FAST VUT v Brně 1 Motivace: trhliny v betonu mikrostruktura Vyhojování trhlin konstrukce Pražec po
ÚVOD DO PROBLEMATIKY LOMOVÉ MECHANIKY KVAZIKŘEHKÝCH MATERIÁLŮ Zbyněk Keršner Ústav stavební mechaniky FAST VUT v Brně 1 Motivace: trhliny v betonu mikrostruktura Vyhojování trhlin konstrukce Pražec po
10. Elasto-plastická lomová mechanika
 (J-integrál) Únava a lomová mechanika J-integrál je zobecněním hnací síly trhliny a umožňuje použití i v případech plastické deformace většího rozsahu: d J = A U da ( ) A práce vnějších sil působících
(J-integrál) Únava a lomová mechanika J-integrál je zobecněním hnací síly trhliny a umožňuje použití i v případech plastické deformace většího rozsahu: d J = A U da ( ) A práce vnějších sil působících
Katedra geotechniky a podzemního stavitelství
 Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Metoda okrajových prvků (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Metoda okrajových prvků (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
terminologie předchozí kapitoly: (ϕ, Ω) - plocha, S - geometrický obraz plochy
 2. Plošný integrál. Poznámka. Obecně: integrování přes k-rozměrné útvary (k-plochy) v R n. Omezíme se na případ k = 2, n = 3. Definice. Množina S R 3 se nazve plocha, pokud S = ϕ(), kde R 2 je otevřená
2. Plošný integrál. Poznámka. Obecně: integrování přes k-rozměrné útvary (k-plochy) v R n. Omezíme se na případ k = 2, n = 3. Definice. Množina S R 3 se nazve plocha, pokud S = ϕ(), kde R 2 je otevřená
Obecný Hookeův zákon a rovinná napjatost
 Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
1 Rozdělení mechaniky a její náplň
 1 Rozdělení mechaniky a její náplň Mechanika je nauka o rovnováze a pohybu hmotných útvarů pohybujících se rychlostí podstatně menší, než je rychlost světla (v c). Vlastnosti skutečných hmotných útvarů
1 Rozdělení mechaniky a její náplň Mechanika je nauka o rovnováze a pohybu hmotných útvarů pohybujících se rychlostí podstatně menší, než je rychlost světla (v c). Vlastnosti skutečných hmotných útvarů
Téma 1 Úvod do předmětu Pružnost a plasticita, napětí a přetvoření
 Pružnost a plasticita, 2.ročník kombinovaného studia Téma 1 Úvod do předmětu Pružnost a plasticita, napětí a přetvoření Základní pojmy, výchozí předpoklady Vztahy mezi vnitřními silami a napětími v průřezu
Pružnost a plasticita, 2.ročník kombinovaného studia Téma 1 Úvod do předmětu Pružnost a plasticita, napětí a přetvoření Základní pojmy, výchozí předpoklady Vztahy mezi vnitřními silami a napětími v průřezu
Bakalářská práce. České vysoké učení technické v Praze Fakulta strojní. Mechanické vlastnosti krčních tepen
 České vysoké učení technické v Praze Fakulta strojní Ústav mechaniky, biomechaniky a mechatroniky Bakalářská práce Mechanické vlastnosti krčních tepen 2016 Shchetinin Oleg Anotační list Jméno autora: Název
České vysoké učení technické v Praze Fakulta strojní Ústav mechaniky, biomechaniky a mechatroniky Bakalářská práce Mechanické vlastnosti krčních tepen 2016 Shchetinin Oleg Anotační list Jméno autora: Název
2. Určte hromadné body, limitu superior a limitu inferior posloupností: 2, b n = n. n n n.
 Písemka matematika 3 s řešením 1. Vypočtěte lim n( 1 + n 2 n), n lim n (( 1 + 1 n e ) n ) n. 1/2, 1/ e 2. Určte hromadné body, limitu superior a limitu inferior posloupností: a n = sin nπ ( 2, b n = n
Písemka matematika 3 s řešením 1. Vypočtěte lim n( 1 + n 2 n), n lim n (( 1 + 1 n e ) n ) n. 1/2, 1/ e 2. Určte hromadné body, limitu superior a limitu inferior posloupností: a n = sin nπ ( 2, b n = n
Počítačová dynamika tekutin (CFD) Základní rovnice. - laminární tok -
 Počítačová dynamika tekutin (CFD) Základní rovnice - laminární tok - Základní pojmy 2 Tekutina nemá vlastní tvar působením nepatrných tečných sil se částice tekutiny snadno uvedou do pohybu (výjimka některé
Počítačová dynamika tekutin (CFD) Základní rovnice - laminární tok - Základní pojmy 2 Tekutina nemá vlastní tvar působením nepatrných tečných sil se částice tekutiny snadno uvedou do pohybu (výjimka některé
Téma 12, modely podloží
 Téma 1, modely podloží Statika stavebních konstrukcí II., 3.ročník bakalářského studia Úvod Winklerův model podloží Pasternakův model podloží Pružný poloprostor Nosník na pružném Winklerově podloží, řešení
Téma 1, modely podloží Statika stavebních konstrukcí II., 3.ročník bakalářského studia Úvod Winklerův model podloží Pasternakův model podloží Pružný poloprostor Nosník na pružném Winklerově podloží, řešení
Analýza napjatosti PLASTICITA
 Analýza napjatosti PLASTICITA TENZOR NAPĚTÍ Teplota v daném bodě je skalár, je to tenzor nultého řádu, který nezávisí na změně souřadného systému Síla je vektor, je to tenzor prvního řádu, v trojrozměrném
Analýza napjatosti PLASTICITA TENZOR NAPĚTÍ Teplota v daném bodě je skalár, je to tenzor nultého řádu, který nezávisí na změně souřadného systému Síla je vektor, je to tenzor prvního řádu, v trojrozměrném
Přednáška č. 5: Jednorozměrné ustálené vedení tepla
 Přednáška č. 5: Jednorozměrné ustálené vedení tepla Motivace Diferenciální rovnice problému Gradient teploty Energetická bilance Fourierův zákon Diferenciální rovnice vedení tepla Slabé řešení Diskretizace
Přednáška č. 5: Jednorozměrné ustálené vedení tepla Motivace Diferenciální rovnice problému Gradient teploty Energetická bilance Fourierův zákon Diferenciální rovnice vedení tepla Slabé řešení Diskretizace
3.1. Newtonovy zákony jsou základní zákony klasické (Newtonovy) mechaniky
 3. ZÁKLADY DYNAMIKY Dynamika zkoumá příčinné souvislosti pohybu a je tedy zdůvodněním zákonů kinematiky. K pojmům používaným v kinematice zavádí pojem hmoty a síly. Statický výpočet Dynamický výpočet -
3. ZÁKLADY DYNAMIKY Dynamika zkoumá příčinné souvislosti pohybu a je tedy zdůvodněním zákonů kinematiky. K pojmům používaným v kinematice zavádí pojem hmoty a síly. Statický výpočet Dynamický výpočet -
Přednáška 08. Obecná trojosá napjatost. Napětí statické rovnice Deformace geometrické rovnice Zobecněný Hookeův zákon Příklad zemní tlak v klidu
 Přednáška 08 Obecná trojosá napjatost Napětí statické rovnice Deformace geometrické rovnice Zobecněný Hookeův ákon Příklad emní tlak v klidu Copyright (c) 2011 Vít Šmilauer Cech Technical University in
Přednáška 08 Obecná trojosá napjatost Napětí statické rovnice Deformace geometrické rovnice Zobecněný Hookeův ákon Příklad emní tlak v klidu Copyright (c) 2011 Vít Šmilauer Cech Technical University in
Interpolace, ortogonální polynomy, Gaussova kvadratura
 Interpolace, ortogonální polynomy, Gaussova kvadratura Petr Tichý 20. listopadu 2013 1 Úloha Lagrangeovy interpolace Dán omezený uzavřený interval [a, b] a v něm n + 1 různých bodů x 0, x 1,..., x n. Nechť
Interpolace, ortogonální polynomy, Gaussova kvadratura Petr Tichý 20. listopadu 2013 1 Úloha Lagrangeovy interpolace Dán omezený uzavřený interval [a, b] a v něm n + 1 různých bodů x 0, x 1,..., x n. Nechť
Fakt. Každou soustavu n lineárních ODR řádů n i lze eliminací převést ekvivalentně na jednu lineární ODR
 DEN: ODR teoreticky: soustavy rovnic Soustava lineárních ODR 1 řádu s konstantními koeficienty je soustava ve tvaru y 1 = a 11 y 1 + a 12 y 2 + + a 1n y n + b 1 (x) y 2 = a 21 y 1 + a 22 y 2 + + a 2n y
DEN: ODR teoreticky: soustavy rovnic Soustava lineárních ODR 1 řádu s konstantními koeficienty je soustava ve tvaru y 1 = a 11 y 1 + a 12 y 2 + + a 1n y n + b 1 (x) y 2 = a 21 y 1 + a 22 y 2 + + a 2n y
12. Prostý krut Definice
 p12 1 12. Prostý krut 12.1. Definice Prostý krut je označení pro namáhání přímého prizmatického prutu, jestliže jsou splněny prutové předpoklady, příčné průřezy se nedeformují, pouze se vzájemně natáčejí
p12 1 12. Prostý krut 12.1. Definice Prostý krut je označení pro namáhání přímého prizmatického prutu, jestliže jsou splněny prutové předpoklady, příčné průřezy se nedeformují, pouze se vzájemně natáčejí
11. přednáška 10. prosince Kapitola 3. Úvod do teorie diferenciálních rovnic. Obyčejná diferenciální rovnice řádu n (ODR řádu n) je vztah
 11. přednáška 10. prosince 2007 Kapitola 3. Úvod do teorie diferenciálních rovnic. Obyčejná diferenciální rovnice řádu n (ODR řádu n) je vztah F (x, y, y, y,..., y (n) ) = 0 mezi argumentem x funkce jedné
11. přednáška 10. prosince 2007 Kapitola 3. Úvod do teorie diferenciálních rovnic. Obyčejná diferenciální rovnice řádu n (ODR řádu n) je vztah F (x, y, y, y,..., y (n) ) = 0 mezi argumentem x funkce jedné
10 Funkce více proměnných
 M. Rokyta, MFF UK: Aplikovaná matematika II kap. 10: Funkce více proměnných 16 10 Funkce více proměnných 10.1 Základní pojmy Definice. Eukleidovskou vzdáleností bodů x = (x 1,...,x n ), y = (y 1,...,y
M. Rokyta, MFF UK: Aplikovaná matematika II kap. 10: Funkce více proměnných 16 10 Funkce více proměnných 10.1 Základní pojmy Definice. Eukleidovskou vzdáleností bodů x = (x 1,...,x n ), y = (y 1,...,y
Vícerozměrné úlohy pružnosti
 Přednáška 07 Víceroměrné úlohy Rovinná napjatost a deformace Hlavní napětí Mohrova kružnice Metoda konečných prvků pro úlohu rovinné napjatosti Příklady Copyright (c) 0 Vít Šmilauer Cech Technical University
Přednáška 07 Víceroměrné úlohy Rovinná napjatost a deformace Hlavní napětí Mohrova kružnice Metoda konečných prvků pro úlohu rovinné napjatosti Příklady Copyright (c) 0 Vít Šmilauer Cech Technical University
TENKOSTĚNNÉ A SPŘAŽENÉ KONSTRUKCE
 1 TENKOSTĚNNÉ A SPŘAŽENÉ KONSTRUKCE Michal Jandera Obsah přednášek 1. Stabilita stěn, nosníky třídy 4.. Tenkostěnné za studena tvarované profily: Výroba, chování průřezů, chování prutů. 3. Tenkostěnné
1 TENKOSTĚNNÉ A SPŘAŽENÉ KONSTRUKCE Michal Jandera Obsah přednášek 1. Stabilita stěn, nosníky třídy 4.. Tenkostěnné za studena tvarované profily: Výroba, chování průřezů, chování prutů. 3. Tenkostěnné
PRUŽNOST A PLASTICITA I
 Otázky k procvičování PRUŽNOST A PLASTICITA I 1. Kdy je materiál homogenní? 2. Kdy je materiál izotropní? 3. Za jakých podmínek můžeme použít princip superpozice účinků? 4. Vysvětlete princip superpozice
Otázky k procvičování PRUŽNOST A PLASTICITA I 1. Kdy je materiál homogenní? 2. Kdy je materiál izotropní? 3. Za jakých podmínek můžeme použít princip superpozice účinků? 4. Vysvětlete princip superpozice
Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
9. přednáška 26. listopadu f(a)h < 0 a pro h (0, δ) máme f(a 1 + h, a 2,..., a m ) f(a) > 1 2 x 1
 9 přednáška 6 listopadu 007 Věta 11 Nechť f C U, kde U R m je otevřená množina, a a U je bod Pokud fa 0, nemá f v a ani neostrý lokální extrém Pokud fa = 0 a H f a je pozitivně negativně definitní, potom
9 přednáška 6 listopadu 007 Věta 11 Nechť f C U, kde U R m je otevřená množina, a a U je bod Pokud fa 0, nemá f v a ani neostrý lokální extrém Pokud fa = 0 a H f a je pozitivně negativně definitní, potom
Téma 1 Úvod do předmětu Pružnost a plasticita, napětí a přetvoření
 Pružnost a plasticita, 2.ročník kombinovaného studia Téma 1 Úvod do předmětu Pružnost a plasticita, napětí a přetvoření Základní pojmy, výchozí předpoklady Vztahy mezi vnitřními silami a napětími v průřezu
Pružnost a plasticita, 2.ročník kombinovaného studia Téma 1 Úvod do předmětu Pružnost a plasticita, napětí a přetvoření Základní pojmy, výchozí předpoklady Vztahy mezi vnitřními silami a napětími v průřezu
Obsah PŘEDMLUVA...9 ÚVOD TEORETICKÁ MECHANIKA...15
 Obsah PŘEDMLUVA...9 ÚVOD...11 1. TEORETICKÁ MECHANIKA...15 1.1 INTEGRÁLNÍ PRINCIPY MECHANIKY... 16 1.1.1 Základní pojmy z mechaniky... 16 1.1.2 Integrální principy... 18 1.1.3 Hamiltonův princip nejmenší
Obsah PŘEDMLUVA...9 ÚVOD...11 1. TEORETICKÁ MECHANIKA...15 1.1 INTEGRÁLNÍ PRINCIPY MECHANIKY... 16 1.1.1 Základní pojmy z mechaniky... 16 1.1.2 Integrální principy... 18 1.1.3 Hamiltonův princip nejmenší
