Numerické modelování v aplikované geologii
|
|
|
- Václav Holub
- před 8 lety
- Počet zobrazení:
Transkript
1 Numerické modelování v aplikované geologii David Mašín Ústav hydrogeologie, inženýrské geologie a užité geofyziky Přírodovědecká fakulta Karlova Univerzita v Praze Přednášky pro obor Geotechnologie David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 1 / 49 Obsah Kontinuum 4 Napětí 5 Přetvoření David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 2 / 49
2 Způsoby řešení geomechanických úloh můžeme rozdělit na: Observační: Spolehnutí na pozorování, analogii a zkušenost Semianalytické: Kombinace observačních a matematických přístupů. Statistika, extrapolace, bez porozumění fyzikální podstaty jevů Analytické a numerické: Idealizace geologického prostředí matematickým modelem. Uzavřená (analytická) a numerická řešení. Přednáška se bude zabývat pouze posledním bodem. David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 3 / 49 V minulosti převládal zájem o analytické metody a fyzikální modelování (modelové zkoužky ve zmenšeném měřítku). o něm si řekneme později. Muir Wood (2004) Bakir et al. (1994) David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 4 / 49
3 Dnes, s rozvojem výpočetní techniky, začínají numerické metody nabývat výsadní postavení ve využití pro geotechnický design. Matematický model je nástroj pro pochopení problému, nikdy však ne přesným řešením. Pro jeho účelné využití je nutné znát jeho možnosti a omezení. Model vždy zjednodušuje velmi komplexní realitu. Je nutno dbát na to, aby byly vystihnuty nejdůležitější aspekty řešeného problému. David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 5 / 49 Postup při matematickém modelování 1 Zodpovězení otázky PROČ potřebuji matematický model. Co s jeho pomocí potřebuji vyřešit. 2 S tvorbou modelu je nutno začít co nejdříve. I předběžné výsledky mohou být využity pro plánování polních zkoušek a monitoringu. 3 Je nutno si rozmyslet kvalitativní očekávané výsledky. První model sestavený s pomocí kteréhokoliv programu nebude bezchybný! Chyby je možno odhalit jen pokud co nejjednodušší model postupně zesložit ujeme. 4 Vždy použijeme co nejjednodušší model, který stále vystihuje nejdůležitější aspekty řešeného problému. David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 6 / 49
4 Postup při matematickém modelování 5 V případě, že není možno sestavit model jenž vystihne základní charakteristiky řešeného problému (např. 2D výpočet pro případ s výraznými trojrozměrnými efekty), je možno provést sérii simulací pro získání výsledků v mezních případech. Z rozmezí získaných hodnot je možno odhadnout správné výsledky. David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 7 / 49 Oblasti aplikace počítačových modelů v geomechanice 1 Řešení komplexních geotechnických úloh, kde neexistuje uzavřené (analytické) řešení (interakce několika vlivů, komplikované geologické podmínky... ). feat.nl (2005) David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 8 / 49
5 Oblasti aplikace počítačových modelů v geomechanice 2 Pochopení i rozvoj tradičních metod (progresívní porušování, hledání kritické smykové plochy) Potts et al. (1997) David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 9 / 49 Oblasti aplikace počítačových modelů v geomechanice 3 Studie a zohlednění vlivu nelinearity (analytická řešení jsou pro lineárně pružný poloprostor, případně pro ideálně plastický materiál) Deane and Basset (1995) David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 10 / 49
6 Oblasti aplikace počítačových modelů v geomechanice 4 Vývoj jednoduchých empirických návrhových vztahů z numerických studií (např. deformace budovy nad výrubem tunelu) Francius et al. (2004) Mroueh and Shahour (2003) David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 11 / 49 Oblasti aplikace počítačových modelů v geomechanice 5 Interpretace údajů z monitoringu, využití pro plánování nejvhodnějších monitorovacích bodů. Rahim (2002) David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 12 / 49
7 Oblasti aplikace počítačových modelů v geomechanice 6 Interpretace laboratorních zkoušek (nerovnoměrné rozdělení napětí, lokalizace deformace) Vardoulakis (1977) Tejchman (2004) David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 13 / 49 Oblasti aplikace počítačových modelů v geomechanice 7 Řízení laboratorního programu (nestandardní dráhy napětí v okolí geotechnické konstrukce) Tang et al. (2000) David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 14 / 49
8 Maticový počet Vektor: Jednorozměrné pole skalárních veličin. Značíme v, v i. Jednotlivé komponenty (složky): v = v i = [v 1, v 2, v 3,..., v n ] V našem případě budeme většinou uvažovat kartrézskou soustavu souřadnic, t.j. n = 3. David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 15 / 49 Maticový počet Pokud má vektor fyzikální význam, pak je nezávislý na soustavě souřadnic. (Dojde ke změně jeho komponent, ale význam zůstane zachován). Např. vektor rychlosti: David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 16 / 49
9 Maticový počet Jeden vektor do druhého převádíme pomocí takzavené lineární transformace, kde lineárním operátorem je matice. t 1 t 2 t 3 = σ 11 σ 12 σ 13 σ 21 σ 22 σ 23 σ 31 σ 32 σ 33 n 1 n 2 n 3 nebo píšeme t i = σ ij n j Pokud má tato matice fyzikální význam (význam je nezávislý na soustavě souřadnic), nazýváme jí tenzorem. David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 17 / 49 Maticový počet Tenzor (druhého řádu): Lineární transformace jednoho vektoru do jiného vektoru (viz. dále). Značíme T, T ij, σ, σ ij. Stejně jako vektor můžeme tenzor vyjádřit pomocí komponent v určité soustavě souřadnic. Vektor je jednorozměrné pole skalárních veličin, tenzor druhého řádu můžeme vyjádřit pomocí matice: T = T 11 T 12 T 13 T 21 T 22 T 23 T 31 T 32 T 33 David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 18 / 49
10 Zápis operací s vektory a maticemi Budeme používat tzv, indexový zápis. Bude využíváno tzv. Einsteinovo indexování: Pokud se v součinu nebo v samostatně stojící proměnné vyskytnou dva stejné indexy, provede se součet proměnných probíhající přes tyto indexy. Součet neprobíhá pro tzv. volný index, který se vyskytuje i u proměnné na levé straně rovnice. David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 19 / 49 Zápis operací s vektory a maticemi Součet dvou matic: T ij = G ij + H ij T 11 T 12 T 13 T 21 T 22 T 23 T 31 T 32 T 33 = G 11 + H 11 G 12 + H 12 G 13 + H 13 G 21 + H 21 G 22 + H 22 G 23 + H 23 G 31 + H 31 G 32 + H 32 G 33 + H 33 David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 20 / 49
11 Zápis operací s vektory a maticemi Násobení matice skalární veličinou: C ij = at ij C 11 C 12 C 13 C 21 C 22 C 23 C 31 C 32 C 33 = at 11 at 12 at 13 at 21 at 22 at 23 at 31 at 32 at 33 David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 21 / 49 Zápis operací s vektory a maticemi Násobení matice vektorem: b i = T ij d j b 1 b 2 b 3 = T 11 d 1 + T 12 d 2 + T 13 d 3 T 21 d 1 + T 22 d 2 + T 23 d 3 T 31 d 1 + T 32 d 2 + T 33 d 3 Obdobně definujeme násobení dvou matic: T ik = σ ij ɛ jk David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 22 / 49
12 Zápis operací s vektory a maticemi Skalární součin dvou vektorů: c = t i v i c = t 1 v 1 + t 2 v 2 + t 3 v 3 David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 23 / 49 Zápis operací s vektory a maticemi Tenzorový součin: T ij = b i d j T 11 T 12 T 13 T 21 T 22 T 23 T 31 T 32 T 33 = b 1 d 1 b 1 d 2 b 1 d 3 b 2 d 1 b 2 d 2 b 2 d 3 b 3 d 1 b 3 d 2 b 3 d 3 David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 24 / 49
13 Maticové operátory Jednotková matice (tzv. Kroneckerovo delta) značíme 1 ij ij = Stopa Euklidovská norma Směr Deviátor tr σ = σ ij 1 ij σ = σ ij σ ij σ ij = σ ij σ dev (σ) = σ ij 1 ij tr(σ) 3 David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 25 / 49 Rotace soustavy souřadnic Při změně soustavy souřadnic se změní komponenty vektoru či tenzoru, přestože jejich fyzikální význam zůstane zachován. Pro případ vektoru jsou jeho nové komponenty v čárkovaných souřadnicích počítány pomocí v i = Q ij v j David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 26 / 49
14 Rotace soustavy souřadnic David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 27 / 49 Rotace soustavy souřadnic Transformační matici Q je pro 2D úlohu možno zapsat jako [ ] cos α sin α Q = sin α cos α Při pootočení souřadného systému pro tenzor se jeho nové komponenty vypočtou z T ij = Q ik T kl Q jl David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 28 / 49
15 Rotace soustavy souřadnic a vlastní čísla Pro matici T hledáme takový skalár λ a vektor n, aby platilo T ij n j = λn i n se označuje jako vlastní vektor a λ jako vlastní číslo. Rotaci souřadnic lze pro každou symetrickou matici (T ij = T ji ) rotovat tak, že prvky mimo hlavní diagonálu jsou rovné nule. Nenulové diagonální prvky jsou pak rovny vlastním číslům matice. David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 29 / 49 Invarianty tenzoru Invarianty jsou skalární veličiny vypočtené ze složek tenzoru, jejichž hodnota se nemění se změnou soustavy souřadnic. Rozlišujeme tři invarianty, jež značíme I 1, I 2 a I invariant I 1 = tr(t) 2. invariant I 2 = 1 2 (T ijt ij I 2 1 ) 3. invariant I 3 = det(t) David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 30 / 49
16 Invarianty tenzoru Pro diagonální tenzor T = T T T 33 se invarianty tedy vypočtou I 1 = T 11 + T 22 + T 33 I 2 = (T 11 T 22 + T 22 T 33 + T 33 T 11 ) I 3 = T 11 T 22 T 33 David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 31 / 49 Derivace Reprezentuje velikost změny funkce v nekonečně malém intervalu Matematická definice pro skalární funkci p (t) dp dt p = lim t 0 t David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 32 / 49
17 Derivace Derivaci definujeme i pro vektorové funkce. Derivace vektorové funkce p (t) má komponenty: dp dt = dp 1 dt dp 2 dt dp 3 dt David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 33 / 49 Gradient Gradient udává směr normály k průběhu funkce. Pro funkci dvou proměnných f (x1,x 2 ) zapisujeme grad f = f = f [ f =, f ] x i x 1 x 2 David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 34 / 49
18 Gradient Gradient funkce f (σ), kde σ je vektor, udává směr normály k ploše f (σ) : f (σ) σ = f σ 1 f σ 2 f σ 3 David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 35 / 49 Kontinuum Kontinuum Matematická definice kontinua: 1 Matematické funkce popisující kontinuum jsou spojité včetně svých derivací 2 Připouští se konečný počet ploch, kde podmínka 1. neplatí Kontinuum představuje spojité prostředí, kde jsou všechny veličiny definovány pro nekonečně malý bod. David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 36 / 49
19 Kontinuum Kontinuum Průběh měřené veličiny v závislosti na měřítku: David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 37 / 49 Napětí Napětí Pojem napětí zavedl Cauchy v roce Definoval jej jako sílu působící na danou plochu: σ = f ab David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 38 / 49
20 Napětí Napětí Popis napjatosti je v kontinuu složitější, definujeme normálové a smykové složky: Je zřejmé, že diagonální složky tenzoru napětí (T 11, T 22, T 33 ) jsou kolmé na infinitezimální krychli kontinua, nazýváme je proto napětí normálová (někdy značíme σ). Ostatní složky se nazývají napětí smyková (někdy značíme τ). David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 39 / 49 Napětí Napětí Pokud v bodě kontinua nepůsobí další síly či momenty (momenty mohou působit v tzv. polárním kontinuu) a bod je v rovnovážné poloze, tenzor napětí je symetrický, tzn. T ij = T ji Pro každý tenzor napětí lze pootočit soustavu souřadnic tak, aby smyková napětí (T ij pro i j) byla rovná nule. Nenulové diagonální členy se pak nazývají hlavní napětí. Hlavní napětí jsou vlastní čísla tenzoru napětí. David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 40 / 49
21 Napětí Znaménková konvence Napětí Komplikaci v orientaci v geotechnických výpočtech často přinášejí dvě různé znaménkové konvence. V mechanice kontinuua je zaběhnutá znaménková konvence jež označuje tahová napětí a přetvoření jako kladná, tlaková jako záporná. Tato konvence má za následek že výpočty geotechnických úloh jsou méně přehledné, nebot v geotechnice ve většině případů figurují tlaková napětí. Proto mechanika zemin většinou uvažuje tlaková napětí jako pozitivní. My budeme většinou uvažovat znaménkovou konvenci mechaniky kontinuua. David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 41 / 49 Napětí Invarianty napětí Napětí Pro popis stavu napjatosti často využíváme invarianty napětí, jejichž hodnota je nezávislá na souřadném systému. Střední napětí p je modifikovaným prvním invariantem napětí: p = I 1 3 = trt 3 "Deviátorové" napětí q je modifikovaný druhý invariant deviátoru napětí: 3 q = dev T 2 David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 42 / 49
22 Napětí Invarianty napětí Napětí Pro axisymetrický stav s diagonálním tenzorem napětí (např. pro běžnou triaxiální zkoušku): T a 0 0 T = 0 T r T r se vztahy pro výpočet invariantů redukují na p = T a + 2T r 3 q = T a T r Často se však pro triaxiální stav uvažuje q = T a T r Pro definici třetího používaného invariantu napětí si musíme vysvětlit pojem deviátorová rovina. David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 43 / 49 Napětí Invarianty napětí Napětí Deviátorová rovina je určena podmínkou trt = const. T 1 = T 2 = T 3 David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 44 / 49
23 Napětí Invarianty napětí Napětí V deviátorové rovině je konstantní první invariant napětí (střední napětí p). Je proto vhodná pro zobrazení stavu napjatosti s proměnným druhým a třetím invariantem napětí. Jako třetí invariant napětí se většinou uvažuje Lodeho úhel α cos 3α = J 3 2 ( 3 J 2 ) 3/2 David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 45 / 49 Přetvoření Přetvoření Přetvořením se označuje změna délky vztažená k původní délce. Následující výpočty jsou přesně platné pouze pro infinitezimální (nekonečně malá) přetvoření. Velká přetvoření jsou mimo náplň tohoto kurzu. Jednoosé přetvoření: ɛ 11 u 1 X 1 ɛ 22 u 2 X 2 David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 46 / 49
24 Přetvoření Přetvoření Pro čistý smyk jenž můžeme znázornit: definujeme úhlové přetvoření γ 12 jako γ 12 = 90 ψ = θ 12 + θ 21 tan θ 12 + tan θ 21 = u 1 X 2 + u 2 X 1 David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 47 / 49 Přetvoření Invarianty přetvoření Přetvoření Pro přetvoření využíváme následující invarianty: Objemové přetvoření ɛ v ɛ v = tr(ɛ) Smykové přetvoření ɛ s ɛ s = 2 3 dev(ɛ) David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 48 / 49
25 Přetvoření Invarianty přetvoření Přetvoření Pro axisymetrický stav s diagonálním tenzorem přetvoření (např. pro běžnou triaxiální zkoušku): ɛ a 0 0 ɛ = 0 ɛ r ɛ r se vztahy pro výpočet invariantů redukují na ɛ v = ɛ a + 2ɛ r ɛ s = 2 3 ɛ a ɛ r Pro triaxiální zkoušku se často uvažuje ɛ s = 2/3(ɛ a ɛ r ). Dále lze ukázat, že pro nedrénovanou triaxiální zkoušku platí ɛ s = ɛ a (a samozřejmě ɛ v = 0). David Mašín (Karlova Univerzita v Praze) Numerické modelování v aplikované geologii Geotechnologie 49 / 49
geologie a užité geofyziky Karlova Univerzita, Praha v geomechanice I
 1 Ústav hydrogeologie, inženýrské geologie a užité geofyziky Karlova Univerzita, Praha Přednášky pro předmět Matematické modelování v geomechanice I 1. část David Mašín 2 Obsah Úvod do matematického modelování
1 Ústav hydrogeologie, inženýrské geologie a užité geofyziky Karlova Univerzita, Praha Přednášky pro předmět Matematické modelování v geomechanice I 1. část David Mašín 2 Obsah Úvod do matematického modelování
Analýza napjatosti PLASTICITA
 Analýza napjatosti PLASTICITA TENZOR NAPĚTÍ Teplota v daném bodě je skalár, je to tenzor nultého řádu, který nezávisí na změně souřadného systému Síla je vektor, je to tenzor prvního řádu, v trojrozměrném
Analýza napjatosti PLASTICITA TENZOR NAPĚTÍ Teplota v daném bodě je skalár, je to tenzor nultého řádu, který nezávisí na změně souřadného systému Síla je vektor, je to tenzor prvního řádu, v trojrozměrném
geologie a užité geofyziky Karlova Univerzita, Praha Mechanika zemin a numerické modelování v geomechanice
 1 Ústav hydrogeologie, inženýrské geologie a užité geofyziky Karlova Univerzita, Praha Mechanika zemin a numerické modelování v geomechanice Přednáška pro studenty 2. ročníku geologie na PřFUK David Mašín
1 Ústav hydrogeologie, inženýrské geologie a užité geofyziky Karlova Univerzita, Praha Mechanika zemin a numerické modelování v geomechanice Přednáška pro studenty 2. ročníku geologie na PřFUK David Mašín
Numerické metody. Numerické modelování v aplikované geologii. David Mašín. Ústav hydrogeologie, inženýrské geologie a užité geofyziky
 Numerické modelování v aplikované geologii David Mašín Ústav hydrogeologie, inženýrské geologie a užité geofyziky Přírodovědecká fakulta Karlova Univerzita v Praze Přednášky pro obor Geotechnologie David
Numerické modelování v aplikované geologii David Mašín Ústav hydrogeologie, inženýrské geologie a užité geofyziky Přírodovědecká fakulta Karlova Univerzita v Praze Přednášky pro obor Geotechnologie David
TENSOR NAPĚTÍ A DEFORMACE. Obrázek 1: Volba souřadnicového systému
 TENSOR NAPĚTÍ A DEFORMACE Obrázek 1: Volba souřadnicového systému Pole posunutí, deformace, napětí v materiálovém bodě {u} = { u v w } T (1) Obecně 9 složek pole napětí lze uspořádat do matice [3x3] -
TENSOR NAPĚTÍ A DEFORMACE Obrázek 1: Volba souřadnicového systému Pole posunutí, deformace, napětí v materiálovém bodě {u} = { u v w } T (1) Obecně 9 složek pole napětí lze uspořádat do matice [3x3] -
Obecný Hookeův zákon a rovinná napjatost
 Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
Rozdíly mezi MKP a MHP, oblasti jejich využití.
 Rozdíly mezi, oblasti jejich využití. Obě metody jsou vhodné pro určitou oblast problémů. základě MKP vyžaduje rozdělení těles na vhodný počet prvků, jejichž analýza je poměrně snadná a pro většinu částí
Rozdíly mezi, oblasti jejich využití. Obě metody jsou vhodné pro určitou oblast problémů. základě MKP vyžaduje rozdělení těles na vhodný počet prvků, jejichž analýza je poměrně snadná a pro většinu částí
Základy matematiky pro FEK
 Základy matematiky pro FEK 2. přednáška Blanka Šedivá KMA zimní semestr 2016/2017 Blanka Šedivá (KMA) Základy matematiky pro FEK zimní semestr 2016/2017 1 / 20 Co nás dneska čeká... Závislé a nezávislé
Základy matematiky pro FEK 2. přednáška Blanka Šedivá KMA zimní semestr 2016/2017 Blanka Šedivá (KMA) Základy matematiky pro FEK zimní semestr 2016/2017 1 / 20 Co nás dneska čeká... Závislé a nezávislé
Maticí typu (m, n), kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru:
 3 Maticový počet 3.1 Zavedení pojmu matice Maticí typu (m, n, kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru: a 11 a 12... a 1k... a 1n a 21 a 22...
3 Maticový počet 3.1 Zavedení pojmu matice Maticí typu (m, n, kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru: a 11 a 12... a 1k... a 1n a 21 a 22...
16. Matematický popis napjatosti
 p16 1 16. Matematický popis napjatosti Napjatost v bodě tělesa jsme definovali jako množinu obecných napětí ve všech řezech, které lze daným bodem tělesa vést. Pro jednoznačný matematický popis napjatosti
p16 1 16. Matematický popis napjatosti Napjatost v bodě tělesa jsme definovali jako množinu obecných napětí ve všech řezech, které lze daným bodem tělesa vést. Pro jednoznačný matematický popis napjatosti
4. Napjatost v bodě tělesa
 p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
Kontraktantní/dilatantní
 Kontraktantní/dilatantní plasticita - úhel dilatance směr přírůstku plastické deformace Na základě experimentálního měření dospěl St. Venant k závěru, že směry hlavních napětí jsou totožné se směry přírůstku
Kontraktantní/dilatantní plasticita - úhel dilatance směr přírůstku plastické deformace Na základě experimentálního měření dospěl St. Venant k závěru, že směry hlavních napětí jsou totožné se směry přírůstku
7 Lineární elasticita
 7 Lineární elasticita Elasticita je schopnost materiálu pružně se deformovat. Deformace ideálně elastických látek je okamžitá (časově nezávislá) a dokonale vratná. Působí-li na infinitezimální objemový
7 Lineární elasticita Elasticita je schopnost materiálu pružně se deformovat. Deformace ideálně elastických látek je okamžitá (časově nezávislá) a dokonale vratná. Působí-li na infinitezimální objemový
Vektory a matice. Obsah. Aplikovaná matematika I. Carl Friedrich Gauss. Základní pojmy a operace
 Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
příkladů do cvičení. V textu se objeví i pár detailů, které jsem nestihl (na které jsem zapomněl) a(b u) = (ab) u, u + ( u) = 0 = ( u) + u.
 Několik řešených příkladů do Matematiky Vektory V tomto textu je spočteno několik ukázkových příkladů které vám snad pomohou při řešení příkladů do cvičení. V textu se objeví i pár detailů které jsem nestihl
Několik řešených příkladů do Matematiky Vektory V tomto textu je spočteno několik ukázkových příkladů které vám snad pomohou při řešení příkladů do cvičení. V textu se objeví i pár detailů které jsem nestihl
Rovinná úloha v MKP. (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v. prostorové úlohy: u, v, w
 Rovinná úloha v MKP Hledané deformační veličiny viz klasická teorie pružnosti (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v desky: w, ϕ x, ϕ y prostorové úlohy: u,
Rovinná úloha v MKP Hledané deformační veličiny viz klasická teorie pružnosti (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v desky: w, ϕ x, ϕ y prostorové úlohy: u,
Nelineární problémy a MKP
 Nelineární problémy a MKP Základní druhy nelinearit v mechanice tuhých těles: 1. materiálová (plasticita, viskoelasticita, viskoplasticita,...) 2. geometrická (velké posuvy a natočení, stabilita konstrukcí)
Nelineární problémy a MKP Základní druhy nelinearit v mechanice tuhých těles: 1. materiálová (plasticita, viskoelasticita, viskoplasticita,...) 2. geometrická (velké posuvy a natočení, stabilita konstrukcí)
Vlastní čísla a vlastní vektory
 5 Vlastní čísla a vlastní vektor Poznámka: Je-li A : V V lineární zobrazení z prostoru V do prostoru V někd se takové zobrazení nazývá lineárním operátorem, pak je přirozeným požadavkem najít takovou bázi
5 Vlastní čísla a vlastní vektor Poznámka: Je-li A : V V lineární zobrazení z prostoru V do prostoru V někd se takové zobrazení nazývá lineárním operátorem, pak je přirozeným požadavkem najít takovou bázi
Katedra geotechniky a podzemního stavitelství
 Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Metoda okrajových prvků (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
Katedra geotechniky a podzemního stavitelství Modelování v geotechnice Metoda okrajových prvků (prezentace pro výuku předmětu Modelování v geotechnice) doc. RNDr. Eva Hrubešová, Ph.D. Inovace studijního
Základy maticového počtu Matice, determinant, definitnost
 Základy maticového počtu Matice, determinant, definitnost Petr Liška Masarykova univerzita 18.9.2014 Matice a vektory Matice Matice typu m n je pravoúhlé (nebo obdélníkové) schéma, které má m řádků a n
Základy maticového počtu Matice, determinant, definitnost Petr Liška Masarykova univerzita 18.9.2014 Matice a vektory Matice Matice typu m n je pravoúhlé (nebo obdélníkové) schéma, které má m řádků a n
Cvičení 1. Napjatost v bodě tělesa Hlavní napětí Mezní podmínky ve víceosé napjatosti
 Cvičení 1 Napjatost v bodě tělesa Hlavní napětí Mezní podmínky ve víceosé napjatosti Napjatost v bodě tělesa Napjatost (napěťový stav) v bodě tělesa je množinou obecných napětí ve všech řezech, které lze
Cvičení 1 Napjatost v bodě tělesa Hlavní napětí Mezní podmínky ve víceosé napjatosti Napjatost v bodě tělesa Napjatost (napěťový stav) v bodě tělesa je množinou obecných napětí ve všech řezech, které lze
1 Projekce a projektory
 Cvičení 3 - zadání a řešení úloh Základy numerické matematiky - NMNM20 Verze z 5. října 208 Projekce a projektory Opakování ortogonální projekce Definice (Ortogonální projekce). Uvažujme V vektorový prostor
Cvičení 3 - zadání a řešení úloh Základy numerické matematiky - NMNM20 Verze z 5. října 208 Projekce a projektory Opakování ortogonální projekce Definice (Ortogonální projekce). Uvažujme V vektorový prostor
6. Vektorový počet Studijní text. 6. Vektorový počet
 6. Vektorový počet Budeme se pohybovat v prostoru R n, což je kartézská mocnina množiny reálných čísel R; R n = R R. Obvykle nám bude stačit omezení na případy n = 1, 2, 3; nicméně teorie je platná obecně.
6. Vektorový počet Budeme se pohybovat v prostoru R n, což je kartézská mocnina množiny reálných čísel R; R n = R R. Obvykle nám bude stačit omezení na případy n = 1, 2, 3; nicméně teorie je platná obecně.
8 Matice a determinanty
 M Rokyta, MFF UK: Aplikovaná matematika II kap 8: Matice a determinanty 1 8 Matice a determinanty 81 Matice - definice a základní vlastnosti Definice Reálnou resp komplexní maticí A typu m n nazveme obdélníkovou
M Rokyta, MFF UK: Aplikovaná matematika II kap 8: Matice a determinanty 1 8 Matice a determinanty 81 Matice - definice a základní vlastnosti Definice Reálnou resp komplexní maticí A typu m n nazveme obdélníkovou
Nauka o materiálu. Přednáška č.4 Úvod do pružnosti a pevnosti
 Nauka o materiálu Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze kluzu R e, odpovídající
Nauka o materiálu Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze kluzu R e, odpovídající
6. ANALYTICKÁ GEOMETRIE
 Vektorová algebra 6. ANALYTICKÁ GEOMETRIE Pravoúhlé souřadnice bodu v prostoru Poloha bodu v prostoru je vzhledem ke třem osám k sobě kolmým určena třemi souřadnicemi, které tvoří uspořádanou trojici reálných
Vektorová algebra 6. ANALYTICKÁ GEOMETRIE Pravoúhlé souřadnice bodu v prostoru Poloha bodu v prostoru je vzhledem ke třem osám k sobě kolmým určena třemi souřadnicemi, které tvoří uspořádanou trojici reálných
Vlastnosti a zkoušení materiálů. Přednáška č.4 Úvod do pružnosti a pevnosti
 Vlastnosti a zkoušení materiálů Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze
Vlastnosti a zkoušení materiálů Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze
Lineární zobrazení. 1. A(x y) = A(x) A(y) (vlastnost aditivity) 2. A(α x) = α A(x) (vlastnost homogenity)
 4 Lineární zobrazení Definice: Nechť V a W jsou vektorové prostory Zobrazení A : V W (zobrazení z V do W nazýváme lineárním zobrazením, pokud pro všechna x V, y V a α R platí 1 A(x y = A(x A(y (vlastnost
4 Lineární zobrazení Definice: Nechť V a W jsou vektorové prostory Zobrazení A : V W (zobrazení z V do W nazýváme lineárním zobrazením, pokud pro všechna x V, y V a α R platí 1 A(x y = A(x A(y (vlastnost
Změna koeficientů PDR při změně proměnných
 Změna koeficientů PR při změně proměnných Oldřich Vlach oto pojednání doplňuje přednášku M. Šofera na téma Nalezení složek tenzoru napjatosti pro případ rovinné úlohy s povrchem zatíženým kontaktním tlakem
Změna koeficientů PR při změně proměnných Oldřich Vlach oto pojednání doplňuje přednášku M. Šofera na téma Nalezení složek tenzoru napjatosti pro případ rovinné úlohy s povrchem zatíženým kontaktním tlakem
MATICE. a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij]
![MATICE. a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij] MATICE. a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij]](/thumbs/58/41721403.jpg) MATICE Matice typu m/n nad tělesem T je soubor m n prvků z tělesa T uspořádaných do m řádků a n sloupců: a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij] a m1 a m2 a mn Prvek a i,j je prvek matice A na místě
MATICE Matice typu m/n nad tělesem T je soubor m n prvků z tělesa T uspořádaných do m řádků a n sloupců: a 11 a 12 a 1n a 21 a 22 a 2n A = = [a ij] a m1 a m2 a mn Prvek a i,j je prvek matice A na místě
Hisab al-džebr val-muqabala ( Věda o redukci a vzájemném rušení ) Muhammada ibn Músá al-chvárizmího (790? - 850?, Chiva, Bagdád),
 1 LINEÁRNÍ ALGEBRA 1 Lineární algebra Slovo ALGEBRA pochází z arabského al-jabr, což znamená nahrazení. Toto slovo se objevilo v názvu knihy islámského matematika Hisab al-džebr val-muqabala ( Věda o redukci
1 LINEÁRNÍ ALGEBRA 1 Lineární algebra Slovo ALGEBRA pochází z arabského al-jabr, což znamená nahrazení. Toto slovo se objevilo v názvu knihy islámského matematika Hisab al-džebr val-muqabala ( Věda o redukci
AVDAT Vektory a matice
 AVDAT Vektory a matice Josef Tvrdík Katedra informatiky Přírodovědecká fakulta Ostravská univerzita Vektory x = x 1 x 2. x p y = y 1 y 2. y p Řádkový vektor dostaneme transpozicí sloupcového vektoru x
AVDAT Vektory a matice Josef Tvrdík Katedra informatiky Přírodovědecká fakulta Ostravská univerzita Vektory x = x 1 x 2. x p y = y 1 y 2. y p Řádkový vektor dostaneme transpozicí sloupcového vektoru x
1. Úvod do pružnosti a pevnosti
 1. Úvod do pružnosti a pevnosti Mechanika je nejstarší vědní obor a její nedílnou součástí je nauka o pružnosti a pevnosti. Pružností nazýváme schopnost pevných těles získat po odstranění vnějších účinků
1. Úvod do pružnosti a pevnosti Mechanika je nejstarší vědní obor a její nedílnou součástí je nauka o pružnosti a pevnosti. Pružností nazýváme schopnost pevných těles získat po odstranění vnějších účinků
Seriál II.II Vektory. Výfučtení: Vektory
 Výfučtení: Vektory Abychom zcela vyjádřili veličiny jako hmotnost, teplo či náboj, stačí nám k tomu jediné číslo (s příslušnou jednotkou). Říkáme jim skalární veličiny. Běžně se však setkáváme i s veličinami,
Výfučtení: Vektory Abychom zcela vyjádřili veličiny jako hmotnost, teplo či náboj, stačí nám k tomu jediné číslo (s příslušnou jednotkou). Říkáme jim skalární veličiny. Běžně se však setkáváme i s veličinami,
2D transformací. červen Odvození transformačního klíče vybraných 2D transformací Metody vyrovnání... 2
 Výpočet transformačních koeficinetů vybraných 2D transformací Jan Ježek červen 2008 Obsah Odvození transformačního klíče vybraných 2D transformací 2 Meto vyrovnání 2 2 Obecné vyjádření lineárních 2D transformací
Výpočet transformačních koeficinetů vybraných 2D transformací Jan Ježek červen 2008 Obsah Odvození transformačního klíče vybraných 2D transformací 2 Meto vyrovnání 2 2 Obecné vyjádření lineárních 2D transformací
Matematika B101MA1, B101MA2
 Matematika B101MA1, B101MA2 Zařazení předmětu: povinný předmět 1.ročníku bc studia 2 semestry Rozsah předmětu: prezenční studium 2 + 2 kombinované studium 16 + 0 / semestr Zakončení předmětu: ZS zápočet
Matematika B101MA1, B101MA2 Zařazení předmětu: povinný předmět 1.ročníku bc studia 2 semestry Rozsah předmětu: prezenční studium 2 + 2 kombinované studium 16 + 0 / semestr Zakončení předmětu: ZS zápočet
y = 2x2 + 10xy + 5. (a) = 7. y Úloha 2.: Určete rovnici tečné roviny a normály ke grafu funkce f = f(x, y) v bodě (a, f(a)). f(x, y) = x, a = (1, 1).
 III Diferenciál funkce a tečná rovina Úloha 1: Určete rovnici tečné roviny ke grafu funkce f = f(x, y) v bodě (a, f(a)) f(x, y) = 3x 3 x y + 5xy 6x + 5y + 10, a = (1, 1) Řešení Definičním oborem funkce
III Diferenciál funkce a tečná rovina Úloha 1: Určete rovnici tečné roviny ke grafu funkce f = f(x, y) v bodě (a, f(a)) f(x, y) = 3x 3 x y + 5xy 6x + 5y + 10, a = (1, 1) Řešení Definičním oborem funkce
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6
 OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
Matematika 1 MA1. 1 Analytická geometrie v prostoru - základní pojmy. 4 Vzdálenosti. 12. přednáška ( ) Matematika 1 1 / 32
 Matematika 1 12. přednáška MA1 1 Analytická geometrie v prostoru - základní pojmy 2 Skalární, vektorový a smíšený součin, projekce vektoru 3 Přímky a roviny 4 Vzdálenosti 5 Příčky mimoběžek 6 Zkouška;
Matematika 1 12. přednáška MA1 1 Analytická geometrie v prostoru - základní pojmy 2 Skalární, vektorový a smíšený součin, projekce vektoru 3 Přímky a roviny 4 Vzdálenosti 5 Příčky mimoběžek 6 Zkouška;
FAKULTA STAVEBNÍ NELINEÁRNÍ MECHANIKA. Telefon: WWW:
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ NELINEÁRNÍ MECHANIKA Bakalářské studium, 4. ročník Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ NELINEÁRNÍ MECHANIKA Bakalářské studium, 4. ročník Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz
Učební texty k státní bakalářské zkoušce Matematika Skalární součin. študenti MFF 15. augusta 2008
 Učební texty k státní bakalářské zkoušce Matematika Skalární součin študenti MFF 15. augusta 2008 1 10 Skalární součin Požadavky Vlastnosti v reálném i komplexním případě Norma Cauchy-Schwarzova nerovnost
Učební texty k státní bakalářské zkoušce Matematika Skalární součin študenti MFF 15. augusta 2008 1 10 Skalární součin Požadavky Vlastnosti v reálném i komplexním případě Norma Cauchy-Schwarzova nerovnost
10 Funkce více proměnných
 M. Rokyta, MFF UK: Aplikovaná matematika II kap. 10: Funkce více proměnných 16 10 Funkce více proměnných 10.1 Základní pojmy Definice. Eukleidovskou vzdáleností bodů x = (x 1,...,x n ), y = (y 1,...,y
M. Rokyta, MFF UK: Aplikovaná matematika II kap. 10: Funkce více proměnných 16 10 Funkce více proměnných 10.1 Základní pojmy Definice. Eukleidovskou vzdáleností bodů x = (x 1,...,x n ), y = (y 1,...,y
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Vektory Definice 011 Vektorem aritmetického prostorur n budeme rozumět uspořádanou n-tici reálných čísel x 1, x 2,, x n Definice 012 Definice sčítání
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Vektory Definice 011 Vektorem aritmetického prostorur n budeme rozumět uspořádanou n-tici reálných čísel x 1, x 2,, x n Definice 012 Definice sčítání
Polární rozklad deformačního gradientu a tenzory přetvoření
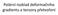 Polární rozklad deformačního gradientu a tenzory přetvoření https://en.wikipedia.org/wiki/finite_strain_theory Deformační gradient Musí tedy existovat jednoznačné zobrazení konfigurace : 1 t t x X, a inversní
Polární rozklad deformačního gradientu a tenzory přetvoření https://en.wikipedia.org/wiki/finite_strain_theory Deformační gradient Musí tedy existovat jednoznačné zobrazení konfigurace : 1 t t x X, a inversní
Vybrané kapitoly z matematiky
 Vybrané kapitoly z matematiky VŠB-TU Ostrava 2017-2018 Vybrané kapitoly z matematiky 2017-2018 1 / 19 Základní informace předmět: 714-0513, 5 kreditů přednáší: Radek Kučera kontakt: radek.kucera@vsb.cz,
Vybrané kapitoly z matematiky VŠB-TU Ostrava 2017-2018 Vybrané kapitoly z matematiky 2017-2018 1 / 19 Základní informace předmět: 714-0513, 5 kreditů přednáší: Radek Kučera kontakt: radek.kucera@vsb.cz,
Lineární algebra : Metrická geometrie
 Lineární algebra : Metrická geometrie (16. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 6. května 2014, 10:42 1 2 Úvod Zatím jsme se lineární geometrii věnovali v kapitole o lineárních
Lineární algebra : Metrická geometrie (16. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 6. května 2014, 10:42 1 2 Úvod Zatím jsme se lineární geometrii věnovali v kapitole o lineárních
Vlastní čísla a vlastní vektory
 Vlastní čísla a vlastní vektory 1 Motivace Uvažujme lineární prostor všech vázaných vektorů v rovině, které procházejí počátkem, a lineární zobrazení tohoto prostoru do sebe(lineární transformaci, endomorfismus)
Vlastní čísla a vlastní vektory 1 Motivace Uvažujme lineární prostor všech vázaných vektorů v rovině, které procházejí počátkem, a lineární zobrazení tohoto prostoru do sebe(lineární transformaci, endomorfismus)
Základy matematické teorie pružnosti Tenzor napětí a tenzor deformace Statické (Cauchyho) rovnice. Geometrické rovnice
 Přednáška 1 Základy matematické teorie pružnosti Tenzor napětí a tenzor deformace Statické (Cauchyho) rovnice Rozšířený Hookův zákon Geometrické rovnice Ondřej Jiroušek Ústav mechaniky a materiálů Fakulta
Přednáška 1 Základy matematické teorie pružnosti Tenzor napětí a tenzor deformace Statické (Cauchyho) rovnice Rozšířený Hookův zákon Geometrické rovnice Ondřej Jiroušek Ústav mechaniky a materiálů Fakulta
Napěťový vektor 3d. Díky Wikipedia za obrázek. n n n
 Míry napětí Napěťový vektor 3d n n2 2 n,. n n n Zatížené těleso rozdělíme myšleným řezem na dvě části. Na malou plošku v okolí materiálového bodu P působí napěťový vektor (n) (n, x, t), který je spojitou
Míry napětí Napěťový vektor 3d n n2 2 n,. n n n Zatížené těleso rozdělíme myšleným řezem na dvě části. Na malou plošku v okolí materiálového bodu P působí napěťový vektor (n) (n, x, t), který je spojitou
Matematická analýza III.
 2. Parciální derivace Miroslav Hušek, Lucie Loukotová UJEP 2010 Parciální derivace jsou zobecněním derivace funkce jedné proměnné. V této kapitole poznáme jejich základní vlastnosti a využití. Co bychom
2. Parciální derivace Miroslav Hušek, Lucie Loukotová UJEP 2010 Parciální derivace jsou zobecněním derivace funkce jedné proměnné. V této kapitole poznáme jejich základní vlastnosti a využití. Co bychom
Všechno, co jste kdy chtěli vědět o maticích, ale báli jste se zeptat
 Všechno, co jste kdy chtěli vědět o maticích, ale báli jste se zeptat Čtvercová matice n n, např. může reprezentovat: A = A A 2 A 3 A 2 A 22 A 23 A 3 A 32 A 33 matici koeficientů soustavy n lineárních
Všechno, co jste kdy chtěli vědět o maticích, ale báli jste se zeptat Čtvercová matice n n, např. může reprezentovat: A = A A 2 A 3 A 2 A 22 A 23 A 3 A 32 A 33 matici koeficientů soustavy n lineárních
0.1 Úvod do lineární algebry
 Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
Matematika KMI/PMATE 1 01 Úvod do lineární algebry 011 Lineární rovnice o 2 neznámých Definice 011 Lineární rovnice o dvou neznámých x, y je rovnice, která může být vyjádřena ve tvaru ax + by = c, kde
14. přednáška. Přímka
 14 přednáška Přímka Začneme vyjádřením přímky v prostoru Přímku v prostoru můžeme vyjádřit jen parametricky protože obecná rovnice přímky v prostoru neexistuje Přímka v prostoru je určena bodem A= [ a1
14 přednáška Přímka Začneme vyjádřením přímky v prostoru Přímku v prostoru můžeme vyjádřit jen parametricky protože obecná rovnice přímky v prostoru neexistuje Přímka v prostoru je určena bodem A= [ a1
ÚVOD DO MODELOVÁNÍ V MECHANICE
 ÚVOD DO MODELOVÁNÍ V MECHANICE PRUŽNOST A PEVNOST Přednáška č. 5 Prof. Ing. Vladislav Laš. CSc. MECHANIKA PODDAJNÝCH TĚLES Úkolem PP z inženýrského hlediska je navrhnout součásti nebo konstrukce, které
ÚVOD DO MODELOVÁNÍ V MECHANICE PRUŽNOST A PEVNOST Přednáška č. 5 Prof. Ing. Vladislav Laš. CSc. MECHANIKA PODDAJNÝCH TĚLES Úkolem PP z inženýrského hlediska je navrhnout součásti nebo konstrukce, které
Občas se používá značení f x (x 0, y 0 ), resp. f y (x 0, y 0 ). Parciální derivace f. rovnoběžného s osou y a z:
 PARCIÁLNÍ DERIVACE Jak derivovat reálné funkce více proměnných aby bylo možné tyto derivace použít podobně jako derivace funkcí jedné proměnné? Jestliže se okopíruje definice z jedné proměnné dostane se
PARCIÁLNÍ DERIVACE Jak derivovat reálné funkce více proměnných aby bylo možné tyto derivace použít podobně jako derivace funkcí jedné proměnné? Jestliže se okopíruje definice z jedné proměnné dostane se
2.6. VLASTNÍ ČÍSLA A VEKTORY MATIC
 .6. VLASTNÍ ČÍSLA A VEKTORY MATIC V této kapitole se dozvíte: jak jsou definována vlastní (charakteristická) čísla a vektory čtvercové matice; co je to charakteristická matice a charakteristický polynom
.6. VLASTNÍ ČÍSLA A VEKTORY MATIC V této kapitole se dozvíte: jak jsou definována vlastní (charakteristická) čísla a vektory čtvercové matice; co je to charakteristická matice a charakteristický polynom
Vlastní číslo, vektor
 [1] Vlastní číslo, vektor motivace: směr přímky, kterou lin. transformace nezmění invariantní podprostory charakteristický polynom báze, vzhledem ke které je matice transformace nejjednodušší podobnost
[1] Vlastní číslo, vektor motivace: směr přímky, kterou lin. transformace nezmění invariantní podprostory charakteristický polynom báze, vzhledem ke které je matice transformace nejjednodušší podobnost
Matematika (CŽV Kadaň) aneb Úvod do lineární algebry Matice a soustavy rovnic
 Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
Přednáška třetí (a pravděpodobně i čtvrtá) aneb Úvod do lineární algebry Matice a soustavy rovnic Lineární rovnice o 2 neznámých Lineární rovnice o 2 neznámých Lineární rovnice o dvou neznámých x, y je
Úvod do lineární algebry
 Úvod do lineární algebry 1 Aritmetické vektory Definice 11 Mějme n N a utvořme kartézský součin R n R R R Každou uspořádanou n tici x 1 x 2 x, x n budeme nazývat n rozměrným aritmetickým vektorem Prvky
Úvod do lineární algebry 1 Aritmetické vektory Definice 11 Mějme n N a utvořme kartézský součin R n R R R Každou uspořádanou n tici x 1 x 2 x, x n budeme nazývat n rozměrným aritmetickým vektorem Prvky
2 Vektorové normy. Základy numerické matematiky - NMNM201. Definice 1 (Norma). Norma je funkcionál splňující pro libovolné vektory x a y a pro
 Cvičení 1 Základy numerické matematiky - NMNM201 1 Základní pojmy opakování Definice 1 (Norma). Norma je funkcionál splňující pro libovolné vektory x a y a pro libovolný skalár α C následující podmínky:
Cvičení 1 Základy numerické matematiky - NMNM201 1 Základní pojmy opakování Definice 1 (Norma). Norma je funkcionál splňující pro libovolné vektory x a y a pro libovolný skalár α C následující podmínky:
Matice. Modifikace matic eliminační metodou. α A = α a 2,1, α a 2,2,..., α a 2,n α a m,1, α a m,2,..., α a m,n
 [1] Základní pojmy [2] Matice mezi sebou sčítáme a násobíme konstantou (lineární prostor) měníme je na jiné matice eliminační metodou násobíme je mezi sebou... Matice je tabulka čísel s konečným počtem
[1] Základní pojmy [2] Matice mezi sebou sčítáme a násobíme konstantou (lineární prostor) měníme je na jiné matice eliminační metodou násobíme je mezi sebou... Matice je tabulka čísel s konečným počtem
1.4. VEKTOROVÝ SOUČIN
 .4. VEKTOROVÝ SOUČIN V této kapitole se dozvíte: definici vektorového (také vnějšího) součinu, jeho vlastnosti a geometrický význam; co rozumíme pravotočivou ortonormální nebo ortogonální bází; definici
.4. VEKTOROVÝ SOUČIN V této kapitole se dozvíte: definici vektorového (také vnějšího) součinu, jeho vlastnosti a geometrický význam; co rozumíme pravotočivou ortonormální nebo ortogonální bází; definici
Slovo ALGEBRA pochází z arabského al-jabr, což znamená nahrazení. Toto slovo se objevilo v názvu knihy
 1 Lineární algebra Slovo ALGEBRA pochází z arabského al-jabr, což znamená nahrazení. Toto slovo se objevilo v názvu knihy islámského matematika Hisab al-džebr val-muqabala ( Věda o redukci a vzájemném
1 Lineární algebra Slovo ALGEBRA pochází z arabského al-jabr, což znamená nahrazení. Toto slovo se objevilo v názvu knihy islámského matematika Hisab al-džebr val-muqabala ( Věda o redukci a vzájemném
Přednáška 08. Obecná trojosá napjatost
 Přednáška 8 Obecná trojosá napjatost Napětí statické rovnice Deformace geometrické rovnice Zobecněný Hookeův zákon Objemový modul pružnosti Oedometrický modul pružnosti Hlavní napětí, hlavní deformace
Přednáška 8 Obecná trojosá napjatost Napětí statické rovnice Deformace geometrické rovnice Zobecněný Hookeův zákon Objemový modul pružnosti Oedometrický modul pružnosti Hlavní napětí, hlavní deformace
Eukleidovský prostor a KSS Eukleidovský prostor je bodový prostor, ve kterém je definována vzdálenost dvou bodů (metrika)
 Eukleidovský prostor a KSS Eukleidovský prostor je bodový prostor, ve kterém je definována vzdálenost dvou bodů (metrika) Kartézská soustava souřadnic je dána počátkem O a uspořádanou trojicí bodů E x,
Eukleidovský prostor a KSS Eukleidovský prostor je bodový prostor, ve kterém je definována vzdálenost dvou bodů (metrika) Kartézská soustava souřadnic je dána počátkem O a uspořádanou trojicí bodů E x,
Smyková pevnost zemin
 Smyková pevnost zemin 30. března 2017 Vymezení pojmů Smyková pevnost zemin - maximální vnitřní únosnost zeminy proti působícímu smykovému napětí Efektivní úhel vnitřního tření - část smykové pevnosti zeminy
Smyková pevnost zemin 30. března 2017 Vymezení pojmů Smyková pevnost zemin - maximální vnitřní únosnost zeminy proti působícímu smykovému napětí Efektivní úhel vnitřního tření - část smykové pevnosti zeminy
Poznámka. V některých literaturách se pro označení vektoru také používá symbolu u.
 Vektory, operace s vektory Ž3 Orientovaná úsečka Mějme dvojici bodů, (na přímce, v rovině nebo prostoru), které spojíme a vznikne tak úsečka. Pokud budeme rozlišovat, zda je spojíme od k nebo od k, říkáme,
Vektory, operace s vektory Ž3 Orientovaná úsečka Mějme dvojici bodů, (na přímce, v rovině nebo prostoru), které spojíme a vznikne tak úsečka. Pokud budeme rozlišovat, zda je spojíme od k nebo od k, říkáme,
1 Báze a dimenze vektorového prostoru 1
 1 Báze a dimenze vektorového prostoru 1 Báze a dimenze vektorového prostoru 1 2 Aritmetické vektorové prostory 7 3 Eukleidovské vektorové prostory 9 Levá vnější operace Definice 5.1 Necht A B. Levou vnější
1 Báze a dimenze vektorového prostoru 1 Báze a dimenze vektorového prostoru 1 2 Aritmetické vektorové prostory 7 3 Eukleidovské vektorové prostory 9 Levá vnější operace Definice 5.1 Necht A B. Levou vnější
VYBRANÉ PARTIE Z NUMERICKÉ MATEMATIKY
 VYBRANÉ PARTIE Z NUMERICKÉ MATEMATIKY Jan Krejčí 31. srpna 2006 jkrejci@physics.ujep.cz http://physics.ujep.cz/~jkrejci Obsah 1 Přímé metody řešení soustav lineárních rovnic 3 1.1 Gaussova eliminace...............................
VYBRANÉ PARTIE Z NUMERICKÉ MATEMATIKY Jan Krejčí 31. srpna 2006 jkrejci@physics.ujep.cz http://physics.ujep.cz/~jkrejci Obsah 1 Přímé metody řešení soustav lineárních rovnic 3 1.1 Gaussova eliminace...............................
VEKTORY. Obrázek 1: Jediný vektor. Souřadnice vektoru jsou jeho průměty do souřadných os x a y u dvojrozměrného vektoru, AB = B A
 VEKTORY Vektorem se rozumí množina všech orientovaných úseček, které mají stejnou velikost, směr a orientaci, což vidíme na obr. 1. Jedna konkrétní orientovaná úsečka se nazývá umístění vektoru na obr.
VEKTORY Vektorem se rozumí množina všech orientovaných úseček, které mají stejnou velikost, směr a orientaci, což vidíme na obr. 1. Jedna konkrétní orientovaná úsečka se nazývá umístění vektoru na obr.
Definice 28 (Ortogonální doplněk vektorového podprostoru). V k V n ; V k V. (Pech:AGLÚ/str D.5.1)
 14.3 Kolmost podprostorů 14.3.1 Ortogonální doplněk vektorového prostou Ve vektorovém prostoru dimenze 3 je ortogonálním doplňkem roviny (přesněji vektorového prostoru dimenze ) přímka na ní kolmá (vektorový
14.3 Kolmost podprostorů 14.3.1 Ortogonální doplněk vektorového prostou Ve vektorovém prostoru dimenze 3 je ortogonálním doplňkem roviny (přesněji vektorového prostoru dimenze ) přímka na ní kolmá (vektorový
2. Kinematika bodu a tělesa
 2. Kinematika bodu a tělesa Kinematika bodu popisuje těleso nebo také bod, který se pohybuje po nějaké trajektorii, křivce nebo jinak definované dráze v závislosti na poloze bodu na dráze, rychlosti a
2. Kinematika bodu a tělesa Kinematika bodu popisuje těleso nebo také bod, který se pohybuje po nějaké trajektorii, křivce nebo jinak definované dráze v závislosti na poloze bodu na dráze, rychlosti a
Kap. 3 Makromechanika kompozitních materiálů
 Kap. Makromechanika kompozitních materiálů Informační a vzdělávací centrum kompozitních technologií & Ústav mechaniky, biomechaniky a mechatroniky FS ČVU v Praze. listopadu 7 Základní pojmy a vztahy Notace
Kap. Makromechanika kompozitních materiálů Informační a vzdělávací centrum kompozitních technologií & Ústav mechaniky, biomechaniky a mechatroniky FS ČVU v Praze. listopadu 7 Základní pojmy a vztahy Notace
Globální matice konstrukce
 Globální matice konstrukce Z matic tuhosti a hmotnosti jednotlivých prvků lze sestavit globální matici tuhosti a globální matici hmotnosti konstrukce, které se využijí v řešení základní rovnice MKP: [m]{
Globální matice konstrukce Z matic tuhosti a hmotnosti jednotlivých prvků lze sestavit globální matici tuhosti a globální matici hmotnosti konstrukce, které se využijí v řešení základní rovnice MKP: [m]{
PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU
 PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU 6.1 Křivkový integrál 1. druhu Definice 1. Množina R n se nazývá prostá regulární křivka v R n právě tehdy, když existuje vzájemně jednoznačné zobrazení
PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU 6.1 Křivkový integrál 1. druhu Definice 1. Množina R n se nazývá prostá regulární křivka v R n právě tehdy, když existuje vzájemně jednoznačné zobrazení
Geometrické transformace pomocí matic
 Geometrické transformace pomocí matic Pavel Strachota FJFI ČVUT v Praze 2. dubna 2010 Obsah 1 Úvod 2 Geometrické transformace ve 2D 3 Geometrické transformace ve 3D Obsah 1 Úvod 2 Geometrické transformace
Geometrické transformace pomocí matic Pavel Strachota FJFI ČVUT v Praze 2. dubna 2010 Obsah 1 Úvod 2 Geometrické transformace ve 2D 3 Geometrické transformace ve 3D Obsah 1 Úvod 2 Geometrické transformace
Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague
 Tomáš Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague 1 / 63 1 2 3 4 5 6 7 8 9 10 11 2 / 63 Aritmetický vektor Definition 1 Aritmetický vektor x je uspořádaná
Tomáš Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague 1 / 63 1 2 3 4 5 6 7 8 9 10 11 2 / 63 Aritmetický vektor Definition 1 Aritmetický vektor x je uspořádaná
U Úvod do modelování a simulace systémů
 U Úvod do modelování a simulace systémů Vyšetřování rozsáhlých soustav mnohdy nelze provádět analytickým výpočtem.často je nutné zkoumat chování zařízení v mezních situacích, do kterých se skutečné zařízení
U Úvod do modelování a simulace systémů Vyšetřování rozsáhlých soustav mnohdy nelze provádět analytickým výpočtem.často je nutné zkoumat chování zařízení v mezních situacích, do kterých se skutečné zařízení
FAKULTA STAVEBNÍ. Telefon: WWW:
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ ZÁKLADY METODY KONEČNÝCH PRVKŮ Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast10.vsb.cz/brozovsky/
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ ZÁKLADY METODY KONEČNÝCH PRVKŮ Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast10.vsb.cz/brozovsky/
Dnešní látka Variačně formulované okrajové úlohy zúplnění prostoru funkcí. Lineární zobrazení.
 Předmět: MA4 Dnešní látka Variačně formulované okrajové úlohy zúplnění prostoru funkcí. Lineární zobrazení. Literatura: Kapitola 2 a)-c) a kapitola 4 a)-c) ze skript Karel Rektorys: Matematika 43, ČVUT,
Předmět: MA4 Dnešní látka Variačně formulované okrajové úlohy zúplnění prostoru funkcí. Lineární zobrazení. Literatura: Kapitola 2 a)-c) a kapitola 4 a)-c) ze skript Karel Rektorys: Matematika 43, ČVUT,
9 Kolmost vektorových podprostorů
 9 Kolmost vektorových podprostorů Od kolmosti dvou vektorů nyní přejdeme ke kolmosti dvou vektorových podprostorů. Budeme se zabývat otázkou, kdy jsou dva vektorové podprostory na sebe kolmé a jak to poznáme.
9 Kolmost vektorových podprostorů Od kolmosti dvou vektorů nyní přejdeme ke kolmosti dvou vektorových podprostorů. Budeme se zabývat otázkou, kdy jsou dva vektorové podprostory na sebe kolmé a jak to poznáme.
Lineární algebra : Skalární součin a ortogonalita
 Lineární algebra : Skalární součin a ortogonalita (15. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 30. dubna 2014, 09:00 1 2 15.1 Prehilhertovy prostory Definice 1. Buď V LP nad
Lineární algebra : Skalární součin a ortogonalita (15. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 30. dubna 2014, 09:00 1 2 15.1 Prehilhertovy prostory Definice 1. Buď V LP nad
10. Soustavy lineárních rovnic, determinanty, Cramerovo pravidlo
 0. Soustavy lineárních rovnic, determinanty, Cramerovo pravidlo (PEF PaA) Petr Gurka aktualizováno 9. prosince 202 Obsah Základní pojmy. Motivace.................................2 Aritmetický vektorový
0. Soustavy lineárních rovnic, determinanty, Cramerovo pravidlo (PEF PaA) Petr Gurka aktualizováno 9. prosince 202 Obsah Základní pojmy. Motivace.................................2 Aritmetický vektorový
Modelování systémů a procesů (11MSP) Bohumil Kovář, Jan Přikryl, Miroslav Vlček. 8. přednáška 11MSP pondělí 20. dubna 2015
 Modelování systémů a procesů (11MSP) Bohumil Kovář, Jan Přikryl, Miroslav Vlček Ústav aplikované matematiky ČVUT v Praze, Fakulta dopravní 8. přednáška 11MSP pondělí 20. dubna 2015 verze: 2015-04-14 12:31
Modelování systémů a procesů (11MSP) Bohumil Kovář, Jan Přikryl, Miroslav Vlček Ústav aplikované matematiky ČVUT v Praze, Fakulta dopravní 8. přednáška 11MSP pondělí 20. dubna 2015 verze: 2015-04-14 12:31
1 Linearní prostory nad komplexními čísly
 1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
Práce, energie a další mechanické veličiny
 Práce, energie a další mechanické veličiny Úvod V předchozích přednáškách jsme zavedli základní mechanické veličiny (rychlost, zrychlení, síla, ) Popis fyzikálních dějů usnadňuje zavedení dalších fyzikálních
Práce, energie a další mechanické veličiny Úvod V předchozích přednáškách jsme zavedli základní mechanické veličiny (rychlost, zrychlení, síla, ) Popis fyzikálních dějů usnadňuje zavedení dalších fyzikálních
Parametrické rovnice křivky
 Křivkový integrál Robert Mařík jaro 2014 Tento text je tištěnou verzí prezentací dostupných z http://user.mendelu.cz/marik/am. Křivkový integrál Jedná se o rozšíření Riemannova integrálu, kdy množinou
Křivkový integrál Robert Mařík jaro 2014 Tento text je tištěnou verzí prezentací dostupných z http://user.mendelu.cz/marik/am. Křivkový integrál Jedná se o rozšíření Riemannova integrálu, kdy množinou
Dodatek 2: Funkce dvou proměnných 1/9
 Dodatek 2: Funkce dvou proměnných 1/9 2/9 Funkce dvou proměnných Definice: Reálnou funkcí dvou reálných proměnných, definovanou na množině M R 2, rozumíme předpis f, který každé uspořádané dvojici reálných
Dodatek 2: Funkce dvou proměnných 1/9 2/9 Funkce dvou proměnných Definice: Reálnou funkcí dvou reálných proměnných, definovanou na množině M R 2, rozumíme předpis f, který každé uspořádané dvojici reálných
3.1. Newtonovy zákony jsou základní zákony klasické (Newtonovy) mechaniky
 3. ZÁKLADY DYNAMIKY Dynamika zkoumá příčinné souvislosti pohybu a je tedy zdůvodněním zákonů kinematiky. K pojmům používaným v kinematice zavádí pojem hmoty a síly. Statický výpočet Dynamický výpočet -
3. ZÁKLADY DYNAMIKY Dynamika zkoumá příčinné souvislosti pohybu a je tedy zdůvodněním zákonů kinematiky. K pojmům používaným v kinematice zavádí pojem hmoty a síly. Statický výpočet Dynamický výpočet -
1 Rozdělení mechaniky a její náplň
 1 Rozdělení mechaniky a její náplň Mechanika je nauka o rovnováze a pohybu hmotných útvarů pohybujících se rychlostí podstatně menší, než je rychlost světla (v c). Vlastnosti skutečných hmotných útvarů
1 Rozdělení mechaniky a její náplň Mechanika je nauka o rovnováze a pohybu hmotných útvarů pohybujících se rychlostí podstatně menší, než je rychlost světla (v c). Vlastnosti skutečných hmotných útvarů
Lineární algebra Operace s vektory a maticemi
 Lineární algebra Operace s vektory a maticemi Robert Mařík 26. září 2008 Obsah Operace s řádkovými vektory..................... 3 Operace se sloupcovými vektory................... 12 Matice..................................
Lineární algebra Operace s vektory a maticemi Robert Mařík 26. září 2008 Obsah Operace s řádkovými vektory..................... 3 Operace se sloupcovými vektory................... 12 Matice..................................
Derivace funkce. Přednáška MATEMATIKA č Jiří Neubauer
 Přednáška MATEMATIKA č. 9-11 Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Šotová, J., Doudová, L. Diferenciální počet funkcí jedné proměnné Motivační příklady
Přednáška MATEMATIKA č. 9-11 Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Šotová, J., Doudová, L. Diferenciální počet funkcí jedné proměnné Motivační příklady
Lineární algebra : Skalární součin a ortogonalita
 Lineární algebra : Skalární součin a ortogonalita (15. přednáška) František Štampach, Karel Klouda frantisek.stampach@fit.cvut.cz, karel.klouda@fit.cvut.cz Katedra aplikované matematiky Fakulta informačních
Lineární algebra : Skalární součin a ortogonalita (15. přednáška) František Štampach, Karel Klouda frantisek.stampach@fit.cvut.cz, karel.klouda@fit.cvut.cz Katedra aplikované matematiky Fakulta informačních
Diferenciál funkce dvou proměnných. Má-li funkce f = f(x, y) spojité parciální derivace v bodě a, pak lineární formu (funkci)
 2. Diferenciál funkce, tečná rovina. Diferenciál funkce dvou proměnných. Má-li funkce f = f(x, y) spojité parciální derivace v bodě a, pak lineární formu (funkci) df(a, h) = x (a)h + (a)h 2, h = (h, h
2. Diferenciál funkce, tečná rovina. Diferenciál funkce dvou proměnných. Má-li funkce f = f(x, y) spojité parciální derivace v bodě a, pak lineární formu (funkci) df(a, h) = x (a)h + (a)h 2, h = (h, h
Matematika 1 MA1. 2 Determinant. 3 Adjungovaná matice. 4 Cramerovo pravidlo. 11. přednáška ( ) Matematika 1 1 / 29
 Matematika 1 11. přednáška MA1 1 Opakování 2 Determinant 3 Adjungovaná matice 4 Cramerovo pravidlo 5 Vlastní čísla a vlastní vektory matic 6 Zkouška; konzultace; výběrová matematika;... 11. přednáška (15.12.2010
Matematika 1 11. přednáška MA1 1 Opakování 2 Determinant 3 Adjungovaná matice 4 Cramerovo pravidlo 5 Vlastní čísla a vlastní vektory matic 6 Zkouška; konzultace; výběrová matematika;... 11. přednáška (15.12.2010
MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA VEKTORY, MATICE
 MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA VEKTORY, MATICE Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipliny společného
MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA VEKTORY, MATICE Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipliny společného
MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA VEKTORY, MATICE
 MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA VEKTORY, MATICE Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipliny společného
MENDELOVA UNIVERZITA V BRNĚ LDF MT MATEMATIKA VEKTORY, MATICE Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipliny společného
1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004.
 Prostá regresní a korelační analýza 1 1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004. Problematika závislosti V podstatě lze rozlišovat mezi závislostí nepodstatnou, čili náhodnou
Prostá regresní a korelační analýza 1 1 Tyto materiály byly vytvořeny za pomoci grantu FRVŠ číslo 1145/2004. Problematika závislosti V podstatě lze rozlišovat mezi závislostí nepodstatnou, čili náhodnou
Matematika. Kamila Hasilová. Matematika 1/34
 Matematika Kamila Hasilová Matematika 1/34 Obsah 1 Úvod 2 GEM 3 Lineární algebra 4 Vektory Matematika 2/34 Úvod Zkouška písemná, termíny budou včas vypsány na Intranetu UO obsah: teoretická a praktická
Matematika Kamila Hasilová Matematika 1/34 Obsah 1 Úvod 2 GEM 3 Lineární algebra 4 Vektory Matematika 2/34 Úvod Zkouška písemná, termíny budou včas vypsány na Intranetu UO obsah: teoretická a praktická
Mechanika kontinua. Mechanika elastických těles Mechanika kapalin
 Mechanika kontinua Mechanika elastických těles Mechanika kapalin Mechanika kontinua Mechanika elastických těles Mechanika kapalin a plynů Kinematika tekutin Hydrostatika Hydrodynamika Kontinuum Pro vyšetřování
Mechanika kontinua Mechanika elastických těles Mechanika kapalin Mechanika kontinua Mechanika elastických těles Mechanika kapalin a plynů Kinematika tekutin Hydrostatika Hydrodynamika Kontinuum Pro vyšetřování
