XX. ročník BRKOS 2013/2014. Pomocný text
|
|
|
- Anna Matějková
- před 8 lety
- Počet zobrazení:
Transkript
1 XX. ročník BRKOS 203/204 Pomocný text Nekonečná série V šesté, nekonečné sérii se budeme zabývat tím, jak se různé matematické objekty chovají, když jejich standardní, konečné pojetí rozšíříme na nekonečno. Půjde zejména o posloupnosti a jejich ity, nekonečné součty a součiny. Na začátek si tedy definujeme posloupnost. Definice 6.. (Nekonečná) posloupnost reálných čísel je zobrazení, ve kterém každému přirozenému číslu přiřadíme jedno reálné číslo. Posloupnost značíme {a n }, kde a n je n-tý člen posloupnosti tedy reálné číslo, které přiřadíme přirozenému číslu n. Jednoduchým příkladem posloupnosti jsou třeba vzestupně seřazeny sudá přirozená čísla: 2, 4, 6, 8... Prvním členem je dvojka, tedy jedničce přiřadíme dvojku, dále dvojce čtyřku, trojce šestku a tak dále až do nekonečna. Obecně tak platí a n = 2n. V naší definici popisujeme posloupnosti reálných čísel. Můžeme samozřejmě podobně definovat posloupnosti přirozených, celých, nebo i komplexních čísel. Obecně posloupnost prvků množiny M je zobrazením z množiny přirozených čísel do množiny M. V této sérii však pracujeme zejména s reálnými čísly, proto nadále budeme hovořit o posloupnostech reálných čísel. Jak jsme již naznačili, konkrétní posloupnost můžeme popsat předpisem pro n-tý člen. Zápis a n = například vyjadřuje vzestupnou posloupnost druhých mocnin přirozených čísel:, 4, 9, 6... Existují i jiné způsoby, jak definovat konkrétní posloupnost. Jedním z nich je rekurentní (rekurzivní) vyjádření. Tehdy typicky nejprve řekneme, čemuž bude rovný první člen například a = 2 a dále vyjádříme člen a n+ pomocí člena a n, například: a n+ = 2a n. Dostáváme tak vlastně první člen a návod, jak z něj vypočítat druhý, z druhého třetí, atd. V tomto případě bude posloupnost vypadat následovně: 2, 4, 8, 6... Rekurentní vyjádření je v mnoha případech užitečné a často intuitivní, jeho nevýhodou však je, že abychom spočítali n-tý člen, musíme vypočítat všechny členy před ním. Typickou úlohou, se kterou se setkáváme, je najít pro posloupnost zadanou rekurentně její předpis pro n-tý člen. Nalezení samotného předpisu nemusí být vždy jednoduché a občas vyžaduje jisté zkušenosti. Typicky však pomůže spočítat si pár prvních členů a zkusit podle nich předpis uhodnout. Když už máme v rukou konkrétní předpis, jeho správnost ověříme tak, že ji dokážeme matematickou indukcí to už je většinou o něco lehčí problém. Postup si ukážeme na našem příkladu. Příklad 6.. Vyjádřete n-tý člen posloupnosti zadané rekurentně: a = 2, a n+ = 2a n. Řešení. Podíváme se na několik prvních členů: 2, 4, 8, 6. Snadno vidíme, že jde o mocniny dvojky, což je ostatně zřejmé z toho, že dvojku z prvního členu postupně násobíme dalšími dvojkami. Vzorec pro n-tý člen tedy zřejmě bude a n = 2 n. Jeho správnost ověříme BRKOS Team 204
2 XX. ročník BRKOS 203/204 indukcí. Pro první člen vzorec platí: a = 2 = 2, což je ve shodě s rekurentním zadáním. Předpokládejme nyní správnost vzorce pro n = k, tedy a k = 2 k. Z toho dokážeme platnost pro k + chceme tedy dokázat a k+ = 2 k+. Z rekurzivního předpisu máme a k+ = 2a k. Dosadíme podle indukčního předpokladu: a k+ = 2(2 k ) = 2 k+. Tím pádem jsme dokázali, že předpis a n = 2 n vyjadřuje tutéž posloupnost, jako rekurentní vztah ze zadání. Nyní představíme další důležitý pojem, a tím je ita posloupnosti. Definice 6.2. Posloupnost {a n } má vlastní itu L, značíme a n = L, když pro libovolné (malé) reálné ε > 0 existuje n 0 takové, že pro každé n n 0 platí a n L < ε. Co tedy znamená, že posloupnost má itu L? Znamená to, že ať vezmeme jakkoli malé číslo ε, bude existovat jisté hraniční n 0, tak že každý člen od a n0 až do nekonečna se bude od ity L lišit o méně, než je zvoleno ε. Limita tedy vyjadřuje, že členy posloupnosti se budou směrem do nekonečna přibližovat k číslu L a že se přiblíží libovolně blízko. Ukážeme si to na příkladu. Příklad 6.2. Určete itu posloupnosti a n = n. Řešení. Členy zadané posloupnosti budou vypadat následovně:, 2, 3, 4... Je zřejmé, že každý člen bude menší než ten před ním, vždy však bude větší od nuly. K nule se ve skutečnosti víme přiblížit libovolně blízko, itou posloupnosti tedy bude nula. Dokážeme to jednoduše pro libovolné ε (blízkost k nule) najdeme n 0 tak, že každý člen a n pro n n 0 bude od nuly rozdílný o méně, než ε. Mějme tedy libovolné ε > 0. Položíme n 0 = ε +. To znamená, že hodnotu ε nejprve zaokrouhlíme na celé číslo směrem dolů a pak k němu přičteme jedničku. Nyní dokážeme, že rozdíl člena a n0 a ity 0 bude menší než ε, čili a n0 0 = n 0 = < ε. Na dokazovanou nerovnost aplikujeme ekvivalentní úpravy: + ε ε + < ε ( < ε ε ε < ε ) + + Je zřejmé, že poslední nerovnost platí. Jelikož jsme použili ekvivalentní úpravy, platná je i dokazovaná nerovnost a tedy pro námi zvolené n 0 je a n0 dostatečně blízko nule. Zbývá nám dokázat, že to platí i pro každé další n n 0. Jak jsme však řekli, každý člen je menší než předchozí, zároveň však vždy větší od nuly. Tím pádem každé další a n bude k nule alespoň tak blízko jak a n0 a dokázali jsme tedy, že 0 je skutečně itou této posloupnosti. Ne každá posloupnost má itu. Například pro posloupnost a n = n žádnou vlastní itu nenajdeme. Vidíme, že tato posloupnost roste nad libovolnou mez, tedy její hodnota se vlastně blíží k nekonečnu. Zavedeme si proto pojem nevlastní ity. Definice 6.3. Posloupnost {a n } má nevlastní itu, resp., když pro libovolné reálné číslo h existuje n 0 takové, že pro každé n n 0 platí a n > h, resp. a n < h. BRKOS Team 204
3 XX. ročník BRKOS 203/204 Limita rovná nekonečnu tedy znamená, že ať zvolíme jakoukoliv horní mez (h), posloupnost ji časem překročí tak, že se pod ni už nevrátí (např. a n = n). Limita rovná zápornému nekonečnu naopak znamená, že posloupnost se dostane pod libovolnou dolní mez a nad ni se už nevrátí (např. a n = n). Platí, že každá posloupnost má nejvýše jednu itu. Pokud ji má a je jí reálné číslo (tedy jde o vlastní itu), říkáme že posloupnost konverguje, v opačném případě (ita neexistuje nebo je nevlastní) diverguje. Existují tedy i posloupnosti, které žádnou itu nemají například posloupnost a n = ( ) n, v níž se donekonečna střídají a. Při počítání it můžeme využít několik pravidel. Ať {a n } a {b n } jsou konvergentní posloupnosti a c je libovolné reálné číslo. Pak platí: (a n + b n ) = a n + (a n b n ) = a n (a nb n ) = a n c = c (ca n) = c a n Pokud je každý člen posloupnosti {b n } různý od nuly a i její ita je nenulová, platí: a n = a n Získané znalosti ukážeme na příkladu: Příklad 6.3. Určete itu posloupnosti a n = 3n2 2n+ 4. Řešení. 3 2n + = 4 3 2n n = + 4 = 3 2. n + n. n 4. n. n = = 3 Na základě uvedených znalostí o posloupnostech můžeme přejít k nekonečným řadám. Předpokládejme, že máme posloupnost {a k }. Nekonečná řada je vlastně součet všech jejích členů, tedy výraz ve tvaru a + a 2 + a zapisujeme také a k. Na první pohled se může zdát, že součet nekonečně mnoho čísel musí být také nekonečný, nemusí to tak však být vždy. Abychom mohli zkoumat nekonečné řady, zavedeme si nejdříve pojem částečného n součtu. Částečný součet posloupnosti, značíme a i nebo také s n, je součet jejích prvních n členů, tedy s n = a + a 2 + a a n. Je zřejmé, že takový součet umíme spočítat pro libovolné číslo n. Uvažme nyní posloupnost částečných součtů {s n }. Prvním členem této i= k= BRKOS Team 204
4 XX. ročník BRKOS 203/204 posloupnosti tedy bude vlastně první člen původní posloupnosti a, druhým bude součet jejích prvních dvou členů, třetím součet prvních tří členů atd. Čím dále tedy zajdeme v posloupnosti částečných součtů, tím více členů posloupnosti {a k } zahrneme do součtu s n. Naším cílem je najít součet všech členů bude nás tedy zajímat, jak se bude posloupnost částečných součtů vyvíjet směrem do nekonečna a právě tuto myšlenku vyjadřuje pojem ity. Součtem všech členů posloupnosti {a k }, pokud existuje, je ita posloupnosti její částečných součtů. Zapsáno formálně: k= a k = n i= a i = s n Pokud tedy máme vypočítat součet nekonečné řady, snažíme se nejprve najít předpis pro posloupnost částečných součtů. Jde o podobný úkol, jako hledání předpisu pro n-tý člen rekurentně zadané posloupnosti. Stačí si uvědomit, že posloupnost částečných součtů lze také zapsat rekurentně: s = a, s n+ = s n + a n+. Když vyjádříme posloupnost částečných součtů, stačí spočítat její itu. Pokud ta existuje a je to reálné číslo, jde o součet dané nekonečné řady. Ukážeme si postup na příkladu: Příklad 6.4. Určete součet nekonečné řady Řešení. Nejdříve si vypíšeme několik prvních členů posloupnosti: 2, 4, 8, 6... Následně si spočítáme několik prvních částečných součtů: 2, 3 4, 7 8, Nyní vidíme, že předpis pro částečný součet s n je s n = 2n 2. Jeho správnost ověříme indukcí. Platí s n = 2 = a. Předpokládáme platnost pro n = k, čili s k = 2k. Pro n = k + pak platí: s 2 k k+ = s k + a k+ = 2k + = 2(2k )+ = 2k+ 2+ = 2k+. Tím pádem jsme dokázali 2 k 2 k+ 2 k+ 2 k+ 2 k+ platnost našeho předpisu. Když se na něj nyní podíváme, už vidíme, že připočítáváním dalších členů se součet bude blížit jedničce, nikdy ji však nedosáhne. Tento odhad nyní potvrdíme spočítáním ity. k= s 2 n 2 n n = 2 n = 2 n. 2 k. 2 n 2 n = 2 n = 0 Vidíme tedy, že nekonečná řada čísel může mít konečný součet. Příklad který jsme uvedli je mimo jiné řešením známého filozofického paradoxu závodu Achillea a želvy. Podobně jako při posloupnostech také rozlišujeme konvergentní a divergentní řady, a to podle toho, jaká je posloupnost částečných součtů dané řady. Platí také, že posloupnost může mít konečný součet, jen pokud má itu rovnou nule (jde o nutnou, nikoliv však dostačující podmínku). Podobně jako nekonečné součty také můžeme zavést pojem nekonečného součinu značíme a k. Způsob jeho počítání je analogický nekonečným součtem konkrétní detaily k= proto už necháme na Vás. Doufáme, že Vás šestá série opět donutí nastartovat mozkové závity a přejeme hodně zdaru při jejím řešení! = BRKOS Team 204
5 XX. ročník BRKOS 203/204 Pomocný text Nekonečná série V šiestej, nekonečnej sérii sa budeme zaoberať tým, ako sa rôzne matematické objekty správajú, keď ich štandardné, konečné ponímanie rozšírime na nekonečno. Pôjde najmä o postupnusti a ich ity, nekonečné súčty a súčiny. Na začiatok si teda definujeme postupnosť. Definícia 6.. (Nekonečná) postupnosť reálnych čísel je zobrazenie, v ktorom každému prirodzenému číslu priradíme jedno reálne číslo. Postupnosť značíme {a n }, kde a n je n-tý člen postupnosti teda reálne číslo, ktoré priradíme prirodzenému číslu n. Jednoduchým príkladom postupnosti sú trebárs vzostupne zoradené párne prirodzené čísla: 2, 4, 6, 8... Prvým členom je dvojka, teda jedničke priradíme dvojku, ďalej dvojke štvorku, trojke šestu a tak ďalej až do nekonečna. Všeobecne tak platí a n = 2n. V našej definícii popisujeme postupnosti reálnych čísel. Môžeme samozrejme podobne definovať postupnosti prirodzených, celých, alebo aj komplexných čísel. Všeobecne postupnosť prvkov množiny M je zobrazením z množiny prirodzených čísel do množiny M. V tejto sérii však pracujeme najmä s reálnymi číslami, preto naďalej budeme hovoriť o postupnostiach reálnych čísel. Ako sme už naznačili, konkrétnu postupnosť môžeme popísať predpisom pre n-tý člen. Zápis a n = napríklad vyjadruje vzostupnú postupnosť druhých mocnín prirodzených čísel:, 4, 9, 6... Existujú aj iné spôsoby, ako definovať konkrétnu postupnosť. Jedným z nich je rekurentné (rekurzívne) vyjadrenie. Vtedy typicky najprv povieme, čomu bude rovný prvý člen napríklad a = 2 a ďalej vyjadríme člen a n+ pomocou člena a n, napríklad: a n+ = 2a n. Dostáme tak vlastne prvý člen a návod, ako z neho vypočítať druhý, z druhého tretí, atď. V tomto prípade bude postupnosť vyzerať nasledovne: 2, 4, 8, 6... Rekurentné vyjadrenie je v mnohých prípadoch užitočné a často intuitívne, jeho nevýhodou však je, že aby sme spočítali n-tý člen, musíme vypočítať všetky členy pred ním. Typickou úlohou, s ktorou sa stretávame, je nájsť pre postupnosť zadanú rekurentne jej predpis pre n-tý člen. Nájdenie samotného predpisu nemusí byť vždy jednoduché a občas vyžaduje isté skúsenosti. Typicky však pomôže spočítať si zopár prvých členov a skúsiť podľa nich predpis uhádnuť. Keď už máme v rukách konkrétny predpis, jeho správnosť overíme tak, že ju dokážeme matematickou indukciou to už je zväčša o niečo ľahší problém. Postup si ukážeme na našom príklade. Príklad 6.. Vyjadrite n-tý člen postupnosti zadanej rekurentne: a = 2, a n+ = 2a n. Riešenie. Pozrieme sa na niekoľko prvých členov: 2, 4, 8, 6. Ľahko vidíme, že ide o mocniny dvojky, čo je napokon zrejmé z toho, že dvojku z prvého člena postupne násobíme ďalšimi dvojkami. Vzorec pre n-tý člen teda zrejme bude a n = 2 n. Jeho správnosť overíme indukciou. Pre prvý člen vzorec platí: a = 2 = 2, čo je v zhode s rekurentným zadaním. Predpokladajme teraz správnosť vzorca pre n = k, teda a k = 2 k. Z toho dokážeme platnosť pre k + chceme teda dokázať a k+ = 2 k+. Z rekurzívneho predpisu máme a k+ = 2a k. Dosadíme podľa indukčného predpokladu: a k+ = 2(2 k ) = 2 k+. Tým pádom sme dokázali, že predpis a n = 2 n vyjadruje tú istú postupnosť, ako rekurentný vzťah zo zadania. BRKOS Team 204
6 XX. ročník BRKOS 203/204 Teraz predstavíme ďalší dôležitý pojem, a tým je ita postupnosti. Definícia 6.2. Postupnosť {a n } má vlastnú itu L, značíme a n = L, keď pre ľubovoľné (malé) reálne ε > 0 existuje n 0 také, že pre každé n n 0 platí a n L < ε. Čo teda znamená, že postupnosť má itu L? Znamená to, že nech zoberieme akokoľvek malé číslo ε, bude existovať isté hraničné n 0, tak že každý člen od a n0 až do nekonečna sa bude od ity L líšiť o menej, než je zvolené ε. Limita teda vyjadruje, že členy postupnosti sa budu smerom do nekonečna približovať k číslu L a že sa pribĺížia ľubovoľne blízko. Ukážeme si to na príklade. Príklad 6.2. Určite itu postupnosti a n = n. Riešenie. Členy zadanej postupnosti budú vyzerať nasledovne:, 2, 3, 4... Je zrejmé, že každý člen bude menší než ten pred ním, vždy však bude väčší od nuly. K nule sa v skutočnosti vieme priblížiť ľubovoľne blízko, itou postupnosti teda bude nula. Dokážeme to jednoducho pre ľubovoľné ε (blízkosť k nule) nájdeme n 0, tak že každý člen a n pre n n 0 bude od nuly rozdielny o menej, než ε. Majme teda ľubovoľné ε > 0. Položíme n 0 = ε +. To znamená, že hodnotu ε najprv zaokrúhe na celé číslo smerom dole a potom k nemu pričítame jedničku. Teraz dokážeme, že rozdiel člena a n0 a ity 0 bude menší než ε, čiže a n0 0 = n 0 = ε + < ε. Na dokazovanú nerovnosť aplikujeme ekvivalentné úpravy: ε + < ε ( < ε ε ε < ε ) + + Je zrejmé, že posledná nerovnosť platí. Nakoľko sme použili ekvivalentné úpravy, platná je aj dokazovaná nerovnosť a teda pre nami zvolené n 0 je a n0 dostatočne blízko nule. Zostáva nám dokázať, že to platí aj pre každé ďalšie n n 0. Ako sme však povedali, každý člen je menší než predchádzajúci, zároveň však vždy väčší od nuly. Tým pádom každé ďalšie a n bude k nule aspoň tak blízko ako a n0 a dokázali sme teda, že 0 je skutočne itou tejto postupnosti. Nie každá postupnosť má itu. Napríklad pre postupnosť a n = n žiadnu vlastnú itu nenájdeme. Vidíme, že táto postupnosť rastie nad ľubovoľnú hranicu, teda jej hodnota sa vlastne blíží k nekonečnu. Zavediemie si preto pojem nevlastnej ity. Definícia 6.3. Postupnosť {a n } má nevlastnú itu, resp., keď pre ľubovoľné reálne číslo h existuje n 0 také, že pre každé n n 0 platí a n > h, resp. a n < h. Limita rovná nekonečnu teda znamená, že nech zvolíme akúkoľvek hornú hranicu (h), postupnosť ju časom prekročí tak, že sa pod ňu už nevráti (napr. a n = n). Limita rovná zápornému nekonečnu naopak znamená, že postupnosť sa dostane pod ľubovoľnú dolnú hranicu a nad ňu sa už nevráti. Platí, že každá postupnosť má najviac jednu itu. Pokiaľ ju má a je ňou reálne číslo (teda ide o vlastnú itu), hovoríme že postupnosť konverguje, v opačnom prípade (ita neexistuje alebo je nevlastná) diverguje. Existujú BRKOS Team 204
7 XX. ročník BRKOS 203/204 teda aj postupnosti, ktoré žiadnu itu nemajú napríklad postupnosť a n = ( ) n, v ktorej sa donekonečna striedajú a. Pri počítaní ít môžeme využiť niekoľko pravidiel. Nech {a n } a {b n } sú konvergentné postupnosti a c je ľubovoľné reálne číslo. Potom platí: (a n + b n ) = a n + (a n b n ) = a n (a nb n ) = a n c = c (ca n) = c a n Pokiaľ je každý člen postupnosti {b n } rôzny od nuly a aj jej ita je nenulová, platí: a n = a n Získané znalosti ukážeme na príklade: Príklad 6.3. Určite itu postupnosti a n = 3n2 2n+ 4. Riešenie. 3 2n + = 4 3 2n n = + 4 = 3 2. n + n. n 4. n. n = = 3 Na základe uvedených znalostí o postupnostiach môžeme prejsť k nekonečným radom. Predpokladajme, že máme postupnosť {a k }. Nekonečný rad je vlastne súčet všetkých jej členov, teda výraz v tvare a + a 2 + a zapisujeme tiež a k. Na prvý pohľad sa môže zdať, že súčet nekonečne mnoho čísel musí byť tiež nekonečný, nemusí to tak však byť vždy. Aby sme mohli skúmať nekonečné rady, zavedieme si najskôr pojem čiastočného súčtu. n Čiastočný súčet postupnosti, značíme a i alebo tiež s n, je súčet jej prvých n členov, teda i= s n = a +a 2 +a a n. Je zrejmé, že takýto súčet vieme spočítať pre ľubovoľné číslo n. Uvážme teraz postupnosť čiastočných súčtov {s n }. Prvým členom tejto postupnosti teda bude vlastne prvý člen pôvodnej postupnosti a, druhým bude súčet jej prvých dvoch členov, tretím súčet prvých troch členov atď. Čím ďalej teda zájdeme v postupnosti čiastočných súčtov, tým viac členov postupnosti {a k } zahrnieme do súčtu s n. Naším ceľom je nájsť súčet všetkých členov bude nás teda zaujímať, ako sa bude postupnosť čiastočných súčtov vyvíjať smerom do nekonečna a k= BRKOS Team 204
8 XX. ročník BRKOS 203/204 práve túto myšlienku vyjadruje pojem ity. Súčtom všetkých členov postupnosti {a k }, ak existuje, je ita postupnosti jej čiastočných súčtov. Zapísané formálne: k= a k = n i= a i = s n Ak teda máme vypočítať súčet nekonečného radu, snažíme sa najprv nájsť predpis pre postupnosť čiastočných súčtov. Ide o podobnú úlohu, ako hľadanie predpisu pre n-tý člen rekurentne zadanej postupnosti. Stačí si uvedomiť, že postupnosť čiastočných súčtov možno tiež zapísať rekurentne: s = a, s n+ = s n + a n+. Keď vyjadríme postupnosť čiastočných súčtov, stačí spočítať jej itu. Pokiaľ tá existuje a je to reálne číslo, ide o súčet daného nekonečného radu. Ukážeme si postup na príklade: Príklad 6.4. Určite súčet nekonečného radu Riešenie. Najskôr si vypíšeme niekoľko prvých členov postupnosti: 2, 4, 8, 6... Následne si spočítame niekoľko prvých čiastkových súčtov: 2, 3 4, 7 8, Teraz vidíme, že predpis pre čiastkový súčet s n je s n = 2n 2. Jeho správnosť oveíme indukciou. Platí s n = 2 = a. Predpokladáme platnosť pre n = k, čiže s k = 2k. Pre n = k + potom platí: 2 k s k+ = s k + a k+ = 2k + = 2(2k )+ = 2k+ 2+ = 2k+. Tým pádom sme 2 k 2 k+ 2 k+ 2 k+ 2 k+ dokázali platnosť nášho predpisu. Keď sa naň teraz pozrieme, už vidíme, že pričítavaním ďalších členov sa súčet bude blížiť jedničke, nikdy ju však nedosiahne. Tento odhad teraz potvrdíme spočítaním ity. k= s 2 n 2 n n = 2 n = 2 n. 2 n 2 k. 2 n = 2 n = 0 Vidíme teda, že nekonečný rad čísel môže mať konečný súčet. Príklad ktorý sme uviedli je okrem iného riešením známeho filozofického paradoxu závodu Achillea a želvy. Podobne ako pri postupnostiach tiež rozlišujeme konvergentné a divergentné rady, a to podľa toho, aká je postupnosť čiastočných súčtov daného radu. Platí tiež, že postupnosť môže mať konečný súčet, len ak má itu rovnú nule (ide o nutnú, nie však dostačujúcu podmienku). Podobne ako nekonečné súčty tiež môžeme zaviesť pojem nekonečného súčinu značíme a k. Spôsob jeho počítania je analogický nekonečným súčtom konkrétne detaily k= preto už necháme na Vás. Dúfame, že Vás šiesta séria opäť donúti naštartovať mozgové závity a prajeme veľa zdaru pri jej riešení! = BRKOS Team 204
ČÍSELNÉ RADY. a n (1) n=1
 ČÍSELNÉ RADY Budeme sa zaoberať výrazmi, ktoré obsahujú nekonečne veľa sčítancov. Takéto výrazy budeme nazývať nekonečné rady. V nasledujúcom príklade je ilustrované, ako môže takýto výraz vzniknúť. Príklad.
ČÍSELNÉ RADY Budeme sa zaoberať výrazmi, ktoré obsahujú nekonečne veľa sčítancov. Takéto výrazy budeme nazývať nekonečné rady. V nasledujúcom príklade je ilustrované, ako môže takýto výraz vzniknúť. Príklad.
Zvyškové triedy podľa modulu
 Zvyškové triedy podľa modulu Tomáš Madaras 2011 Pre dané prirodzené číslo m 2 je relácia kongruencie podľa modulu m na množine Z reláciou ekvivalencie, teda jej prislúcha rozklad Z na systém navzájom disjunktných
Zvyškové triedy podľa modulu Tomáš Madaras 2011 Pre dané prirodzené číslo m 2 je relácia kongruencie podľa modulu m na množine Z reláciou ekvivalencie, teda jej prislúcha rozklad Z na systém navzájom disjunktných
Matematika Postupnosti
 Matematika 1-06 Postupnosti Definícia: Nekonečnou postupnosťou reálnych čísel nazývame zobrazenie f: N R množiny prirodzených čísel N do množiny reálnych čísel R. Označenie: a n n=1 = a 1, a 2,, a n, Matematika
Matematika 1-06 Postupnosti Definícia: Nekonečnou postupnosťou reálnych čísel nazývame zobrazenie f: N R množiny prirodzených čísel N do množiny reálnych čísel R. Označenie: a n n=1 = a 1, a 2,, a n, Matematika
Posloupnosti a jejich limity
 KMA/MAT Přednáška č. 7, Posloupnosti a jejich ity 5. listopadu 203 Motivační příklady Prozkoumejme, zatím laicky, následující posloupnosti: Posloupnost, 4, 9,..., n 2,... : Hodnoty rostou nade všechny
KMA/MAT Přednáška č. 7, Posloupnosti a jejich ity 5. listopadu 203 Motivační příklady Prozkoumejme, zatím laicky, následující posloupnosti: Posloupnost, 4, 9,..., n 2,... : Hodnoty rostou nade všechny
Limita a spojitost funkce. 3.1 Úvod. Definice: [MA1-18:P3.1]
![Limita a spojitost funkce. 3.1 Úvod. Definice: [MA1-18:P3.1] Limita a spojitost funkce. 3.1 Úvod. Definice: [MA1-18:P3.1]](/thumbs/94/120485064.jpg) KAPITOLA 3: Limita a spojitost funkce [MA-8:P3.] 3. Úvod Necht je funkce f definována alespoň na nějakém prstencovém okolí bodu 0 R. Číslo a R je itou funkce f v bodě 0, jestliže pro každé okolí Ua) bodu
KAPITOLA 3: Limita a spojitost funkce [MA-8:P3.] 3. Úvod Necht je funkce f definována alespoň na nějakém prstencovém okolí bodu 0 R. Číslo a R je itou funkce f v bodě 0, jestliže pro každé okolí Ua) bodu
Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H.
 FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
FUNKCIA, DEFINIČNÝ OBOR, OBOR HODNÔT Funkcia - priradenie (predpis), ktoré každému prvku z množiny D priraďuje práve jeden prvok množiny H. Množina D definičný obor Množina H obor hodnôt Funkciu môžeme
Kvadratické funkcie, rovnice, 1
 Kvadratické funkcie, rovnice, 1. ročník Kvadratická funkcia Kvadratickou funkciu sa nazýva každá funkcia na množine reálnych čísel R daná rovnicou y = ax + bx + c, kde a je reálne číslo rôzne od nuly,
Kvadratické funkcie, rovnice, 1. ročník Kvadratická funkcia Kvadratickou funkciu sa nazýva každá funkcia na množine reálnych čísel R daná rovnicou y = ax + bx + c, kde a je reálne číslo rôzne od nuly,
Funkcionální řady. January 13, 2016
 Funkcionální řady January 13, 216 f 1 + f 2 + f 3 +... + f n +... = f n posloupnost částečných součtů funkcionální řada konverguje na množine M konverguje posloupnost jeho částečných součtů na množine
Funkcionální řady January 13, 216 f 1 + f 2 + f 3 +... + f n +... = f n posloupnost částečných součtů funkcionální řada konverguje na množine M konverguje posloupnost jeho částečných součtů na množine
Lineárne nerovnice, lineárna optimalizácia
 Opatrenie:. Premena tradičnej škol na modernú Gmnázium Jozefa Gregora Tajovského Lineárne nerovnice, lineárna optimalizácia V tomto tete sa budeme zaoberat najskôr grafickým znázornením riešenia sústav
Opatrenie:. Premena tradičnej škol na modernú Gmnázium Jozefa Gregora Tajovského Lineárne nerovnice, lineárna optimalizácia V tomto tete sa budeme zaoberat najskôr grafickým znázornením riešenia sústav
Iracionálne rovnice = 14 = ±
 Iracionálne rovnice D. Rovnica je iracionálna, ak obsahuje neznámu pod odmocninou. P. Ak ide o odmocninu s párnym odmocniteľom, potom musíme stanoviť definičný obor pod odmocninou nesmie byť záporná hodnota
Iracionálne rovnice D. Rovnica je iracionálna, ak obsahuje neznámu pod odmocninou. P. Ak ide o odmocninu s párnym odmocniteľom, potom musíme stanoviť definičný obor pod odmocninou nesmie byť záporná hodnota
Limita funkcie. Čo rozumieme pod blížiť sa? y x. 2 lim 3
 Limita funkcie y 2 2 1 1 2 1 y 2 2 1 lim 3 1 1 Čo rozumieme pod blížiť sa? Porovnanie funkcií y 2 2 1 1 y 2 1 2 2 1 lim 3 1 1 1-1+ Limita funkcie lim f b a Ak ku každému číslu, eistuje také okolie bodu
Limita funkcie y 2 2 1 1 2 1 y 2 2 1 lim 3 1 1 Čo rozumieme pod blížiť sa? Porovnanie funkcií y 2 2 1 1 y 2 1 2 2 1 lim 3 1 1 1-1+ Limita funkcie lim f b a Ak ku každému číslu, eistuje také okolie bodu
0.1 Úvod do matematické analýzy
 Matematika I (KMI/PMATE) 1 0.1 Úvod do matematické analýzy 0.1.1 Limita a spojitost funkce Lineární funkce Lineární funkce je jedna z nejjednodušších a možná i nejpoužívanějších funkcí. f(x) = kx + q D(f)
Matematika I (KMI/PMATE) 1 0.1 Úvod do matematické analýzy 0.1.1 Limita a spojitost funkce Lineární funkce Lineární funkce je jedna z nejjednodušších a možná i nejpoužívanějších funkcí. f(x) = kx + q D(f)
8. Relácia usporiadania
 8. Relácia usporiadania V tejto časti sa budeme venovať ďalšiemu špeciálnemu typu binárnych relácií v množine M - reláciám Najskôr si uvedieme nasledujúce štyri definície. Relácia R definovaná v množine
8. Relácia usporiadania V tejto časti sa budeme venovať ďalšiemu špeciálnemu typu binárnych relácií v množine M - reláciám Najskôr si uvedieme nasledujúce štyri definície. Relácia R definovaná v množine
M úlohy (vyriešené) pre rok 2017
 M úlohy (vyriešené) pre rok 2017 Nájdite najmenšie prirodzené číslo, ktorého ciferný súčet je 2017 Ak má byť prirodzené číslo s daným ciferným súčtom čo najmenšie, musí mať čo najviac číslic 9 Pretože
M úlohy (vyriešené) pre rok 2017 Nájdite najmenšie prirodzené číslo, ktorého ciferný súčet je 2017 Ak má byť prirodzené číslo s daným ciferným súčtom čo najmenšie, musí mať čo najviac číslic 9 Pretože
Prevody z pointfree tvaru na pointwise tvar
 Prevody z pointfree tvaru na pointwise tvar Tomáš Szaniszlo 2010-03-24 (v.2) 1 Príklad (.(,)). (.). (,) Prevedenie z pointfree do pointwise tvaru výrazu (.(,)). (.). (,). (.(,)). (.). (,) Teraz je funkcia
Prevody z pointfree tvaru na pointwise tvar Tomáš Szaniszlo 2010-03-24 (v.2) 1 Príklad (.(,)). (.). (,) Prevedenie z pointfree do pointwise tvaru výrazu (.(,)). (.). (,). (.(,)). (.). (,) Teraz je funkcia
Přednáška 3: Limita a spojitost
 3 / 1 / 17, 1:38 Přednáška 3: Limita a spojitost Limita funkce Nejdříve je potřeba upřesnit pojmy, které přesněji popisují (topologickou) strukturu množiny reálných čísel, a to zejména pojem okolí 31 Definice
3 / 1 / 17, 1:38 Přednáška 3: Limita a spojitost Limita funkce Nejdříve je potřeba upřesnit pojmy, které přesněji popisují (topologickou) strukturu množiny reálných čísel, a to zejména pojem okolí 31 Definice
PŘEDNÁŠKA 2 POSLOUPNOSTI
 PŘEDNÁŠKA 2 POSLOUPNOSTI 2.1 Zobrazení 2 Definice 1. Uvažujme libovolné neprázdné množiny A, B. Zobrazení množiny A do množiny B je definováno jako množina F uspořádaných dvojic (x, y A B, kde ke každému
PŘEDNÁŠKA 2 POSLOUPNOSTI 2.1 Zobrazení 2 Definice 1. Uvažujme libovolné neprázdné množiny A, B. Zobrazení množiny A do množiny B je definováno jako množina F uspořádaných dvojic (x, y A B, kde ke každému
POSLOUPNOSTI A ŘADY INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ. Tento projekt je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky
 POSLOUPNOSTI A ŘADY Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu
POSLOUPNOSTI A ŘADY Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu
i j, existuje práve jeden algebraický polynóm n-tého stupˇna Priamym dosadením do (2) dostávame:
 0 Interpolácia 0 Úvod Hlavnou myšlienkou interpolácie je nájs t funkciu polynóm) P n x) ktorá sa bude zhodova t s funkciou fx) v n rôznych uzlových bodoch x i tj P n x) = fx i ) = f i = y i i = 0 n Niekedy
0 Interpolácia 0 Úvod Hlavnou myšlienkou interpolácie je nájs t funkciu polynóm) P n x) ktorá sa bude zhodova t s funkciou fx) v n rôznych uzlových bodoch x i tj P n x) = fx i ) = f i = y i i = 0 n Niekedy
Přednáška 6, 7. listopadu 2014
 Přednáška 6, 7. listopadu 204 Část 3: nekonečné řady Základní definice. Nekonečná řada, krátce řada, je posloupnost reálných čísel (a n ) R uvedená v zápisu a n = a + a 2 + a 3 +..., spolu s metodou přiřazující
Přednáška 6, 7. listopadu 204 Část 3: nekonečné řady Základní definice. Nekonečná řada, krátce řada, je posloupnost reálných čísel (a n ) R uvedená v zápisu a n = a + a 2 + a 3 +..., spolu s metodou přiřazující
Matematická analýza pro informatiky I. Limita posloupnosti (I)
 Matematická analýza pro informatiky I. 3. přednáška Limita posloupnosti (I) Jan Tomeček tomecek@inf.upol.cz http://aix-slx.upol.cz/ tomecek/index Univerzita Palackého v Olomouci 25. února 2011 tomecek@inf.upol.cz
Matematická analýza pro informatiky I. 3. přednáška Limita posloupnosti (I) Jan Tomeček tomecek@inf.upol.cz http://aix-slx.upol.cz/ tomecek/index Univerzita Palackého v Olomouci 25. února 2011 tomecek@inf.upol.cz
Limita a spojitost funkce a zobrazení jedné reálné proměnné
 Přednáška 4 Limita a spojitost funkce a zobrazení jedné reálné proměnné V několika následujících přednáškách budeme studovat zobrazení jedné reálné proměnné f : X Y, kde X R a Y R k. Protože pro každé
Přednáška 4 Limita a spojitost funkce a zobrazení jedné reálné proměnné V několika následujících přednáškách budeme studovat zobrazení jedné reálné proměnné f : X Y, kde X R a Y R k. Protože pro každé
3 Determinanty. 3.1 Determinaty druhého stupňa a sústavy lineárnych rovníc
 3 eterminanty 3. eterminaty druhého stupňa a sústavy lineárnych rovníc Začneme úlohou, v ktorej je potrebné riešiť sústavu dvoch rovníc o dvoch neznámych. a x + a 2 x 2 = c a 22 a 2 x + a 22 x 2 = c 2
3 eterminanty 3. eterminaty druhého stupňa a sústavy lineárnych rovníc Začneme úlohou, v ktorej je potrebné riešiť sústavu dvoch rovníc o dvoch neznámych. a x + a 2 x 2 = c a 22 a 2 x + a 22 x 2 = c 2
Nechť je číselná posloupnost. Pro všechna položme. Posloupnost nazýváme posloupnost částečných součtů řady.
 Číselné řady Definice (Posloupnost částečných součtů číselné řady). Nechť je číselná posloupnost. Pro všechna položme. Posloupnost nazýváme posloupnost částečných součtů řady. Definice (Součet číselné
Číselné řady Definice (Posloupnost částečných součtů číselné řady). Nechť je číselná posloupnost. Pro všechna položme. Posloupnost nazýváme posloupnost částečných součtů řady. Definice (Součet číselné
Spojitost a limita funkce
 Spojitost a ita funkce Okolí bodu Značení: a R ε > 0 označujeme O ε (a) = (a ε, a + ε) ε-ové okolí bodu a O + ε (a) = a, a + ε) pravé okolí, O ε (a) = (a ε, a levé okolí P ε (a) = O ε (a) \ {a} x a ε-ové
Spojitost a ita funkce Okolí bodu Značení: a R ε > 0 označujeme O ε (a) = (a ε, a + ε) ε-ové okolí bodu a O + ε (a) = a, a + ε) pravé okolí, O ε (a) = (a ε, a levé okolí P ε (a) = O ε (a) \ {a} x a ε-ové
POSLOUPNOSTI A ŘADY INVESTICE DO ROZVOJE VZDĚLÁVÁNÍ
 POSLOUPNOSTI A ŘADY Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu
POSLOUPNOSTI A ŘADY Gymnázium Jiřího Wolkera v Prostějově Výukové materiály z matematiky pro vyšší gymnázia Autoři projektu Student na prahu 21. století - využití ICT ve vyučování matematiky na gymnáziu
1 Linearní prostory nad komplexními čísly
 1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
1 Linearní prostory nad komplexními čísly V této přednášce budeme hledat kořeny polynomů, které se dále budou moci vyskytovat jako složky vektorů nebo matic Vzhledem k tomu, že kořeny polynomu (i reálného)
Rovnice přímky vypsané příklady. Parametrické vyjádření přímky
 Rovnice přímky vypsané příklady Zdroj: Vše kromě příkladu 3.4: http://kdm.karlin.mff.cuni.cz/diplomky/jan_koncel/rovina.php?kapitola=parametrickevyjadre ni Příklady 3.5 a 3.7-1 a 3: http://kdm.karlin.mff.cuni.cz/diplomky/jan_koncel/rovina.php?kapitola=obecnarovnice
Rovnice přímky vypsané příklady Zdroj: Vše kromě příkladu 3.4: http://kdm.karlin.mff.cuni.cz/diplomky/jan_koncel/rovina.php?kapitola=parametrickevyjadre ni Příklady 3.5 a 3.7-1 a 3: http://kdm.karlin.mff.cuni.cz/diplomky/jan_koncel/rovina.php?kapitola=obecnarovnice
p 2 q , tj. 2q 2 = p 2. Tedy p 2 je sudé číslo, což ale znamená, že
 KAPITOLA 1: Reálná čísla [MA1-18:P1.1] 1.1. Číselné množiny Přirozená čísla... N = {1,, 3,...} nula... 0, N 0 = {0, 1,, 3,...} = N {0} Celá čísla... Z = {0, 1, 1,,, 3,...} Racionální čísla... { p } Q =
KAPITOLA 1: Reálná čísla [MA1-18:P1.1] 1.1. Číselné množiny Přirozená čísla... N = {1,, 3,...} nula... 0, N 0 = {0, 1,, 3,...} = N {0} Celá čísla... Z = {0, 1, 1,,, 3,...} Racionální čísla... { p } Q =
Zavedení a vlastnosti reálných čísel
 Zavedení a vlastnosti reálných čísel jsou základním kamenem matematické analýzy. Konstrukce reálných čísel sice není náplní matematické analýzy, ale množina reálných čísel R je pro matematickou analýzu
Zavedení a vlastnosti reálných čísel jsou základním kamenem matematické analýzy. Konstrukce reálných čísel sice není náplní matematické analýzy, ale množina reálných čísel R je pro matematickou analýzu
Limita a spojitost funkce
 Přednáška 5 Limita a spojitost funkce V této přednášce se konečně dostaneme k diferenciálnímu počtu funkce jedné reálné proměnné. Diferenciální počet se v podstatě zabývá lokálním chováním funkce v daném
Přednáška 5 Limita a spojitost funkce V této přednášce se konečně dostaneme k diferenciálnímu počtu funkce jedné reálné proměnné. Diferenciální počet se v podstatě zabývá lokálním chováním funkce v daném
Zimní semestr akademického roku 2014/ prosince 2014
 Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičení Zimní semestr akademického roku 2014/2015 2. prosince 2014 Předmluva
Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičení Zimní semestr akademického roku 2014/2015 2. prosince 2014 Předmluva
7B. Výpočet limit L Hospitalovo pravidlo
 7B. Výpočet it L Hospitalovo pravidlo V prai často potřebujeme určit itu výrazů, které vzniknou operacemi nebo složením několika spojitých funkcí. Většinou pomohou pravidla typu ita součtu násobku, součinu,
7B. Výpočet it L Hospitalovo pravidlo V prai často potřebujeme určit itu výrazů, které vzniknou operacemi nebo složením několika spojitých funkcí. Většinou pomohou pravidla typu ita součtu násobku, součinu,
V této kapitole si zobecníme dříve probraný pojem limita posloupnosti pro libovolné funkce.
 Kapitola 7 Limita funkce V této kapitole budeme studovat pojem ita funkce, který lze zařadit mezi základní pojmy matematiky, speciálně pak matematické analýzy Využití ity funkce je široké Pomocí ity lze
Kapitola 7 Limita funkce V této kapitole budeme studovat pojem ita funkce, který lze zařadit mezi základní pojmy matematiky, speciálně pak matematické analýzy Využití ity funkce je široké Pomocí ity lze
1) Spočítejte limitu pomocí l Hospitalova pravidla, pokud selˇze, spočítejte ji klasicky:
 Příklady k desátému cvičení ) Spočítejte itu pomocí l Hospitalova pravidla pokud selˇze spočítejte ji klasicky:. 2. 3.. 5 + 3 2 8 π π sin 2 + ln(cos(3)) 3 2) Upravte na zlomek a pouˇzijte l Hospitalovo
Příklady k desátému cvičení ) Spočítejte itu pomocí l Hospitalova pravidla pokud selˇze spočítejte ji klasicky:. 2. 3.. 5 + 3 2 8 π π sin 2 + ln(cos(3)) 3 2) Upravte na zlomek a pouˇzijte l Hospitalovo
Nekonečné číselné řady. January 21, 2015
 Nekonečné číselné řady January 2, 205 IMA 205 Příklad 0 = 0 + 0 +... + 0 +... =? n= IMA 205 Příklad n= n 2 + n = 2 + 6 + 2 +... + n 2 +... =? + n s = 2 s 2 = 2 3... s 3 = 3 4 IMA 205 Příklad (pokr.) =
Nekonečné číselné řady January 2, 205 IMA 205 Příklad 0 = 0 + 0 +... + 0 +... =? n= IMA 205 Příklad n= n 2 + n = 2 + 6 + 2 +... + n 2 +... =? + n s = 2 s 2 = 2 3... s 3 = 3 4 IMA 205 Příklad (pokr.) =
Definice. Vektorový prostor V nad tělesem T je množina s operacemi + : V V V, tj. u, v V : u + v V : T V V, tj. ( u V )( a T ) : a u V které splňují
 Definice. Vektorový prostor V nad tělesem T je množina s operacemi + : V V V, tj. u, v V : u + v V : T V V, tj. ( u V )( a T ) : a u V které splňují 1. u + v = v + u, u, v V 2. (u + v) + w = u + (v + w),
Definice. Vektorový prostor V nad tělesem T je množina s operacemi + : V V V, tj. u, v V : u + v V : T V V, tj. ( u V )( a T ) : a u V které splňují 1. u + v = v + u, u, v V 2. (u + v) + w = u + (v + w),
verze 1.3 kde ρ(, ) je vzdálenost dvou bodů v R r. Redukovaným ε-ovým okolím nazveme ε-ové okolí bodu x 0 mimo tohoto bodu, tedy množinu
 Úvod Diferenciální počet více proměnných verze.3 Následující text popisuje základy diferenciálního počtu více proměnných. Měl by sloužit především studentům předmětu MATEMAT na Univerzitě Hradec Králové
Úvod Diferenciální počet více proměnných verze.3 Následující text popisuje základy diferenciálního počtu více proměnných. Měl by sloužit především studentům předmětu MATEMAT na Univerzitě Hradec Králové
Matematika (KMI/PMATE)
 Matematika (KMI/PMATE) Přednáška druhá aneb Úvod do matematické analýzy Limita a spojitost funkce Matematika (KMI/PMATE) 1 / 30 Osnova přednášky lineární funkce y = kx + q definice lineární funkce význam
Matematika (KMI/PMATE) Přednáška druhá aneb Úvod do matematické analýzy Limita a spojitost funkce Matematika (KMI/PMATE) 1 / 30 Osnova přednášky lineární funkce y = kx + q definice lineární funkce význam
Limita funkce. FIT ČVUT v Praze. (FIT) Limita funkce 3.týden 1 / 39
 Limita funkce FIT ČVUT v Praze 3.týden (FIT) Limita funkce 3.týden 1 / 39 Definice funkce. Zobrazení (f, D f ), jehož definiční obor D f i obor hodnot H f je podmnožinou množiny reálných čísel, se nazývá
Limita funkce FIT ČVUT v Praze 3.týden (FIT) Limita funkce 3.týden 1 / 39 Definice funkce. Zobrazení (f, D f ), jehož definiční obor D f i obor hodnot H f je podmnožinou množiny reálných čísel, se nazývá
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ
 ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
ANALYTICKÁ GEOMETRIE LINEÁRNÍCH ÚTVARŮ V ROVINĚ Parametrické vyjádření přímky v rovině Máme přímku p v rovině určenou body A, B. Sestrojíme vektor u = B A. Pro bod B tím pádem platí: B = A + u. Je zřejmé,
Maticí typu (m, n), kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru:
 3 Maticový počet 3.1 Zavedení pojmu matice Maticí typu (m, n, kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru: a 11 a 12... a 1k... a 1n a 21 a 22...
3 Maticový počet 3.1 Zavedení pojmu matice Maticí typu (m, n, kde m, n jsou přirozená čísla, se rozumí soubor mn veličin a jk zapsaných do m řádků a n sloupců tvaru: a 11 a 12... a 1k... a 1n a 21 a 22...
Pozičné číselné sústavy. Dejiny. Číselná sústava je spôsob, akým sú zapisované čísla pomocou znakov (nazývaných cifry).
 Duda, Džima, Mačák Pozičné číselné sústavy Číselná sústava je spôsob, akým sú zapisované čísla pomocou znakov (nazývaných cifry). Podľa spôsobu určenia hodnoty čísla z daného zápisu rozlišujeme dva hlavné
Duda, Džima, Mačák Pozičné číselné sústavy Číselná sústava je spôsob, akým sú zapisované čísla pomocou znakov (nazývaných cifry). Podľa spôsobu určenia hodnoty čísla z daného zápisu rozlišujeme dva hlavné
VECIT 2006 Tento materiál vznikol v rámci projektu, ktorý je spolufinancovaný Európskou úniou. 1/4
 Príklad 1 Naučte korytnačku príkaz čelenka. Porozmýšľajte nad využitím príkazu plnytrojuhol60: viem plnytrojuhol60 opakuj 3 [do 60 vp 120 Riešenie: definujeme ďalšie príkazy na kreslenie trojuholníka líšiace
Príklad 1 Naučte korytnačku príkaz čelenka. Porozmýšľajte nad využitím príkazu plnytrojuhol60: viem plnytrojuhol60 opakuj 3 [do 60 vp 120 Riešenie: definujeme ďalšie príkazy na kreslenie trojuholníka líšiace
Použitie grafického kalkulátora Casio ClassPad300 vo vyučovaní matematiky v tematickom celku POSTUPNOSTI
 Použitie grafického kalkulátora Casio ClassPad300 vo vyučovaní matematiky v tematickom celku POSTUPNOSTI Martina Bestrová Abstrakt: Ako hovorí už samotný názov, článok sa zaoberá použitím grafického kalkulátora
Použitie grafického kalkulátora Casio ClassPad300 vo vyučovaní matematiky v tematickom celku POSTUPNOSTI Martina Bestrová Abstrakt: Ako hovorí už samotný názov, článok sa zaoberá použitím grafického kalkulátora
Číselné posloupnosti
 Číselné posloupnosti Jiří Fišer KMA, PřF UP Olomouc ZS09 Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 1 / 43 Pojem posloupnosti Každé zobrazení N do R nazýváme číselná posloupnost. 1 a 1, 2 a 2, 3 a
Číselné posloupnosti Jiří Fišer KMA, PřF UP Olomouc ZS09 Jiří Fišer (KMA, PřF UP Olomouc) KMA MA2AA ZS09 1 / 43 Pojem posloupnosti Každé zobrazení N do R nazýváme číselná posloupnost. 1 a 1, 2 a 2, 3 a
1. Posloupnosti čísel
 1. Posloupnosti čísel 1.1. Posloupnosti a operace s nimi Definice 1.1 Posloupnost reálných čísel ( = reálná posloupnost ) je zobrazení, jehož definičním oborem je množina N a oborem hodnot je nějaká podmnožina
1. Posloupnosti čísel 1.1. Posloupnosti a operace s nimi Definice 1.1 Posloupnost reálných čísel ( = reálná posloupnost ) je zobrazení, jehož definičním oborem je množina N a oborem hodnot je nějaká podmnožina
Teorie informace a kódování (KMI/TIK) Reed-Mullerovy kódy
 Teorie informace a kódování (KMI/TIK) Reed-Mullerovy kódy Lukáš Havrlant Univerzita Palackého 10. ledna 2014 Primární zdroj Jiří Adámek: Foundations of Coding. Strany 137 160. Na webu ke stažení, heslo:
Teorie informace a kódování (KMI/TIK) Reed-Mullerovy kódy Lukáš Havrlant Univerzita Palackého 10. ledna 2014 Primární zdroj Jiří Adámek: Foundations of Coding. Strany 137 160. Na webu ke stažení, heslo:
Algoritmizace složitost rekurzivních algoritmů. Jiří Vyskočil, Marko Genyg-Berezovskyj 2010
 složitost rekurzivních algoritmů Jiří Vyskočil, Marko Genyg-Berezovskyj 2010 Vyjádřen ení složitosti rekurzivního algoritmu rekurentním m tvarem Příklad vyjádření složitosti rekurzivního algoritmu rekurencí:
složitost rekurzivních algoritmů Jiří Vyskočil, Marko Genyg-Berezovskyj 2010 Vyjádřen ení složitosti rekurzivního algoritmu rekurentním m tvarem Příklad vyjádření složitosti rekurzivního algoritmu rekurencí:
Množiny, relácie, zobrazenia
 Množiny, relácie, zobrazenia Množiny "Množina je súhrn predmetov, vecí, dobre rozlíšiteľných našou mysľou alebo intuíciou" "Množina je súbor rôznych objektov, ktoré sú charakterizované spoločnými vlastnosťami,
Množiny, relácie, zobrazenia Množiny "Množina je súhrn predmetov, vecí, dobre rozlíšiteľných našou mysľou alebo intuíciou" "Množina je súbor rôznych objektov, ktoré sú charakterizované spoločnými vlastnosťami,
Nejčastějšími funkcemi, s kterými se setkáváme v matematice i v jejích aplikacích, jsou
 4 Cíle Nejčastějšími funkcemi, s kterými se setkáváme v matematice i v jejích aplikacích, jsou funkce, jejichž ita v bodě 0 je rovna funkční hodnotě v tomto bodě Seznámíme se s vlastnostmi takových funkcí
4 Cíle Nejčastějšími funkcemi, s kterými se setkáváme v matematice i v jejích aplikacích, jsou funkce, jejichž ita v bodě 0 je rovna funkční hodnotě v tomto bodě Seznámíme se s vlastnostmi takových funkcí
Riešenie cvičení z 3. kapitoly
 Riešenie cvičení z 3. kapitoly Cvičenie 3.1. Prepíšte z prirodzeného jazyka do jazyka výrokovej logiky: (a) Jano pôjde na výlet a Fero pôjde na výlet; (1) vyjadrite túto vetu pomocou implikácie a negácie
Riešenie cvičení z 3. kapitoly Cvičenie 3.1. Prepíšte z prirodzeného jazyka do jazyka výrokovej logiky: (a) Jano pôjde na výlet a Fero pôjde na výlet; (1) vyjadrite túto vetu pomocou implikácie a negácie
Matematická analýza pro informatiky I. Limita funkce
 Matematická analýza pro informatiky I. 5. přednáška Limita funkce Jan Tomeček tomecek@inf.upol.cz http://aix-slx.upol.cz/ tomecek/index Univerzita Palackého v Olomouci 18. března 2011 Jan Tomeček, tomecek@inf.upol.cz
Matematická analýza pro informatiky I. 5. přednáška Limita funkce Jan Tomeček tomecek@inf.upol.cz http://aix-slx.upol.cz/ tomecek/index Univerzita Palackého v Olomouci 18. března 2011 Jan Tomeček, tomecek@inf.upol.cz
Limita a spojitost LDF MENDELU
 Limita a spojitost Základy vyšší matematiky LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Limita a spojitost Základy vyšší matematiky LDF MENDELU Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Matematika III. Miroslava Dubcová, Daniel Turzík, Drahoslava Janovská. Ústav matematiky
 Matematika III Řady Miroslava Dubcová, Daniel Turzík, Drahoslava Janovská Ústav matematiky Přednášky ZS 202-203 Obsah Číselné řady. Součet nekonečné řady. Kritéria konvergence 2 Funkční řady. Bodová konvergence.
Matematika III Řady Miroslava Dubcová, Daniel Turzík, Drahoslava Janovská Ústav matematiky Přednášky ZS 202-203 Obsah Číselné řady. Součet nekonečné řady. Kritéria konvergence 2 Funkční řady. Bodová konvergence.
Studentove t-testy. Metódy riešenia matematických úloh
 Studentove t-testy Metódy riešenia matematických úloh www.iam.fmph.uniba.sk/institute/stehlikova Jednovýberový t-test z prednášky Máme náhodný výber z normálneho rozdelenia s neznámymi parametrami Chceme
Studentove t-testy Metódy riešenia matematických úloh www.iam.fmph.uniba.sk/institute/stehlikova Jednovýberový t-test z prednášky Máme náhodný výber z normálneho rozdelenia s neznámymi parametrami Chceme
Příklad 1. Řešení 1a Máme vyšetřit lichost či sudost funkce ŘEŠENÉ PŘÍKLADY Z M1A ČÁST 3
 Příklad 1 Zjistěte, zda jsou dané funkce sudé nebo liché, případně ani sudé ani liché: a) =ln b) = c) = d) =4 +1 e) =sin cos f) =sin3+ cos+ Poznámka Všechny tyto úlohy řešíme tak, že argument funkce nahradíme
Příklad 1 Zjistěte, zda jsou dané funkce sudé nebo liché, případně ani sudé ani liché: a) =ln b) = c) = d) =4 +1 e) =sin cos f) =sin3+ cos+ Poznámka Všechny tyto úlohy řešíme tak, že argument funkce nahradíme
M - Kvadratické rovnice a kvadratické nerovnice
 M - Kvadratické rovnice a kvadratické nerovnice Určeno jako učební tet pro studenty dálkového studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase.
M - Kvadratické rovnice a kvadratické nerovnice Určeno jako učební tet pro studenty dálkového studia. VARIACE 1 Tento dokument byl kompletně vytvořen, sestaven a vytištěn v programu dosystem - EduBase.
IV. Základní pojmy matematické analýzy IV.1. Rozšíření množiny reálných čísel
 Matematická analýza IV. Základní pojmy matematické analýzy IV.1. Rozšíření množiny reálných čísel na množině R je definováno: velikost (absolutní hodnota), uspořádání, aritmetické operace; znázornění:
Matematická analýza IV. Základní pojmy matematické analýzy IV.1. Rozšíření množiny reálných čísel na množině R je definováno: velikost (absolutní hodnota), uspořádání, aritmetické operace; znázornění:
PODPROGRAMY. Vyčlenenie podprogramu a jeho pomenovanie robíme v deklarácii programu a aktiváciu vykonáme volaním podprogramu.
 PODPROGRAMY Podprogram je relatívne samostatný čiastočný algoritmus (čiže časť programu, ktorý má vlastnosti malého programu a hlavný program ho môže volať) Spravidla ide o postup, ktorý bude v programe
PODPROGRAMY Podprogram je relatívne samostatný čiastočný algoritmus (čiže časť programu, ktorý má vlastnosti malého programu a hlavný program ho môže volať) Spravidla ide o postup, ktorý bude v programe
3. přednáška 15. října 2007
 3. přednáška 15. října 2007 Kompaktnost a uzavřené a omezené množiny. Kompaktní množiny jsou vždy uzavřené a omezené, a v euklidovských prostorech to platí i naopak. Obecně to ale naopak neplatí. Tvrzení
3. přednáška 15. října 2007 Kompaktnost a uzavřené a omezené množiny. Kompaktní množiny jsou vždy uzavřené a omezené, a v euklidovských prostorech to platí i naopak. Obecně to ale naopak neplatí. Tvrzení
ANALYTICKÁ GEOMETRIE V ROVINĚ
 ANALYTICKÁ GEOMETRIE V ROVINĚ Analytická geometrie vyšetřuje geometrické objekty (body, přímky, kuželosečky apod.) analytickými metodami. Podle prostoru, ve kterém pracujeme, můžeme analytickou geometrii
ANALYTICKÁ GEOMETRIE V ROVINĚ Analytická geometrie vyšetřuje geometrické objekty (body, přímky, kuželosečky apod.) analytickými metodami. Podle prostoru, ve kterém pracujeme, můžeme analytickou geometrii
Řešení 1a Budeme provádět úpravu rozšířením směřující k odstranění odmocniny v čitateli. =lim = 0
 Příklad Vypočítejte ity funkcí: a) b) c) d) Poznámka Po dosazení do všech těchto úloh dostaneme nedefinovaný výraz. Proto je třeba provést úpravy vedoucí k vykrácení a následně k výsledku. Řešení a Budeme
Příklad Vypočítejte ity funkcí: a) b) c) d) Poznámka Po dosazení do všech těchto úloh dostaneme nedefinovaný výraz. Proto je třeba provést úpravy vedoucí k vykrácení a následně k výsledku. Řešení a Budeme
MOCNINY A ODMOCNINY Eva Zummerová
 MOCNINY A ODMOCNINY Eva Zummerová . Mocniny s prirodzeným exponentom Zápis a n (čítame a na n-tú ), kde a R, n N a platí : a n = a.a...a n činiteľov sa nazýva n-tá mocnina čísla a. Číslo a sa nazýva základ
MOCNINY A ODMOCNINY Eva Zummerová . Mocniny s prirodzeným exponentom Zápis a n (čítame a na n-tú ), kde a R, n N a platí : a n = a.a...a n činiteľov sa nazýva n-tá mocnina čísla a. Číslo a sa nazýva základ
Základy matematické analýzy
 Základy matematické analýzy Spojitost funkce Ing. Tomáš Kalvoda, Ph.D. 1, Ing. Daniel Vašata 2 1 tomas.kalvoda@fit.cvut.cz 2 daniel.vasata@fit.cvut.cz Katedra aplikované matematiky Fakulta informačních
Základy matematické analýzy Spojitost funkce Ing. Tomáš Kalvoda, Ph.D. 1, Ing. Daniel Vašata 2 1 tomas.kalvoda@fit.cvut.cz 2 daniel.vasata@fit.cvut.cz Katedra aplikované matematiky Fakulta informačních
Jednoduchá exponenciální rovnice
 Jednoduchá exponenciální rovnice Z běžné rovnice se exponenciální stává, pokud obsahuje proměnnou v exponentu. Obecně bychom mohli exponenciální rovnici zapsat takto: a f(x) = b g(x), kde a, b > 0. Typickým
Jednoduchá exponenciální rovnice Z běžné rovnice se exponenciální stává, pokud obsahuje proměnnou v exponentu. Obecně bychom mohli exponenciální rovnici zapsat takto: a f(x) = b g(x), kde a, b > 0. Typickým
HL Academy - Chata Lopata Emu (Brkos 2012) Řetězové zlomky / 27
 Řetězové zlomky HL Academy - Chata Lopata 2012 13.2. 18.2.2012 Emu (Brkos 2012) Řetězové zlomky 13.2. 18.2.2012 1 / 27 Obsah 1 Úvod 2 Základní pojmy 3 Konečné řetězové zlomky Sblížené zlomky Euklidův algoritmus
Řetězové zlomky HL Academy - Chata Lopata 2012 13.2. 18.2.2012 Emu (Brkos 2012) Řetězové zlomky 13.2. 18.2.2012 1 / 27 Obsah 1 Úvod 2 Základní pojmy 3 Konečné řetězové zlomky Sblížené zlomky Euklidův algoritmus
Že tuto definici znáte, ale stále přesně nevíte, jak funkci chápat? Ukážeme si konkrétní příklad. 1 2 3 4 5 Definiční obor (množina A)
 Funkce úvod Co je funkce Funkce je předpis, který číslu z množiny A přiřazuje právě jedno číslo z množiny B. Množina A je definiční obor funkce a množina B je obor hodnot funkce. Že tuto definici znáte,
Funkce úvod Co je funkce Funkce je předpis, který číslu z množiny A přiřazuje právě jedno číslo z množiny B. Množina A je definiční obor funkce a množina B je obor hodnot funkce. Že tuto definici znáte,
Posloupnosti a řady. a n+1 = a n + 4, a 1 = 5 a n+1 = a n + 5, a 1 = 5. a n+1 = a n+1 = n + 1 n a n, a 1 = 1 2
 Vlastnosti posloupností 90000680 (level ): Je dána posloupnost (an + b), ve které platí, že a = a a 4 = 8. Potom: Posloupnosti a řady 900006807 (level ): Které z čísel 5, 5, 8, 47 není členem posloupnosti
Vlastnosti posloupností 90000680 (level ): Je dána posloupnost (an + b), ve které platí, že a = a a 4 = 8. Potom: Posloupnosti a řady 900006807 (level ): Které z čísel 5, 5, 8, 47 není členem posloupnosti
Zpracoval: hypspave@fel.cvut.cz 7. Matematická indukce a rekurse. Řešení rekurentních (diferenčních) rovnic s konstantními koeficienty.
 Zpracoval: hypspave@fel.cvut.cz 7. Matematická indukce a rekurse. Řešení rekurentních (diferenčních) rovnic s konstantními koeficienty. (A7B01MCS) I. Matematická indukce a rekurse. Indukční principy patří
Zpracoval: hypspave@fel.cvut.cz 7. Matematická indukce a rekurse. Řešení rekurentních (diferenčních) rovnic s konstantními koeficienty. (A7B01MCS) I. Matematická indukce a rekurse. Indukční principy patří
Teoretická informatika Tomáš Foltýnek Teorie čísel Nekonečno
 Tomáš Foltýnek foltynek@pef.mendelu.cz Teorie čísel Nekonečno strana 2 Opakování z minulé přednášky Jak je definována podmnožina, průnik, sjednocení, rozdíl? Jak je definována uspořádaná dvojice a kartézský
Tomáš Foltýnek foltynek@pef.mendelu.cz Teorie čísel Nekonečno strana 2 Opakování z minulé přednášky Jak je definována podmnožina, průnik, sjednocení, rozdíl? Jak je definována uspořádaná dvojice a kartézský
7.1 Návrhové zobrazenie dotazu
 7.1 Návrhové zobrazenie dotazu Ovládanie návrhového zobrazenia, ktoré je jedným z možností zobrazenia dotazu, je nevyhnutné pri tvorbe zložitejších dotazov, pretože v ňom môžeme definovať akýkoľvek dotaz
7.1 Návrhové zobrazenie dotazu Ovládanie návrhového zobrazenia, ktoré je jedným z možností zobrazenia dotazu, je nevyhnutné pri tvorbe zložitejších dotazov, pretože v ňom môžeme definovať akýkoľvek dotaz
Diplomový projekt. Detská univerzita Žilinská univerzita v Žiline Matilda Drozdová
 Diplomový projekt Detská univerzita Žilinská univerzita v Žiline 1.7.2014 Matilda Drozdová Pojem projekt Projekt je určitá časovo dlhšia práca, ktorej výsledkom je vyriešenie nejakej úlohy Kto rieši projekt?
Diplomový projekt Detská univerzita Žilinská univerzita v Žiline 1.7.2014 Matilda Drozdová Pojem projekt Projekt je určitá časovo dlhšia práca, ktorej výsledkom je vyriešenie nejakej úlohy Kto rieši projekt?
11. téma: Zaokrúhľovanie, práca so zaokrúhlenými číslami
 11. téma: Zaokrúhľovanie, práca so zaokrúhlenými číslami I. Úlohy na úvod 1. a) Zaokrúhlite nadol, b) zaokrúhlite nahor, c) zaokrúhlite číslo 5,47 na desatiny, číslo 483,203 na jednotky, číslo 2 996 789
11. téma: Zaokrúhľovanie, práca so zaokrúhlenými číslami I. Úlohy na úvod 1. a) Zaokrúhlite nadol, b) zaokrúhlite nahor, c) zaokrúhlite číslo 5,47 na desatiny, číslo 483,203 na jednotky, číslo 2 996 789
NMAF 051, ZS Zkoušková písemná práce 16. ledna 2009
 Jednotlivé kroky při výpočtech stručně, ale co nejpřesněji odůvodněte. Pokud používáte nějaké tvrzení, nezapomeňte ověřit splnění předpokladů. Jméno a příjmení: Skupina: Příklad 3 5 Celkem bodů Bodů 8
Jednotlivé kroky při výpočtech stručně, ale co nejpřesněji odůvodněte. Pokud používáte nějaké tvrzení, nezapomeňte ověřit splnění předpokladů. Jméno a příjmení: Skupina: Příklad 3 5 Celkem bodů Bodů 8
Pojem limity funkce charakterizuje chování funkce v blízkém okolí libovolného bodu, tedy i těch bodů, ve kterých funkce není definovaná. platí. < ε.
 LIMITA FUNKCE Pojem ity unkce charakterizuje chování unkce v blízkém okolí libovolného bodu, tedy i těch bodů, ve kterých unkce není deinovaná Zápis ( ) L Přesněji to vyjadřuje deinice: znamená, že pro
LIMITA FUNKCE Pojem ity unkce charakterizuje chování unkce v blízkém okolí libovolného bodu, tedy i těch bodů, ve kterých unkce není deinovaná Zápis ( ) L Přesněji to vyjadřuje deinice: znamená, že pro
Multiplexor a demultiplexor
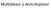 Multiplexor a demultiplexor Mux_DMux [2] Funkcia multiplexoru ako prepínača A D 1 D 0 Y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 3 x NAND Ak A = 0 výstup Y = D 0 a ak A = 1 výstup
Multiplexor a demultiplexor Mux_DMux [2] Funkcia multiplexoru ako prepínača A D 1 D 0 Y 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 3 x NAND Ak A = 0 výstup Y = D 0 a ak A = 1 výstup
Diferenciální rovnice 1
 Diferenciální rovnice 1 Základní pojmy Diferenciální rovnice n-tého řádu v implicitním tvaru je obecně rovnice ve tvaru,,,, = Řád diferenciální rovnice odpovídá nejvyššímu stupni derivace v rovnici použitému.
Diferenciální rovnice 1 Základní pojmy Diferenciální rovnice n-tého řádu v implicitním tvaru je obecně rovnice ve tvaru,,,, = Řád diferenciální rovnice odpovídá nejvyššímu stupni derivace v rovnici použitému.
Limita a spojitost funkce
 Limita a spojitost funkce Základ všší matematik Dana Říhová Mendelu Brno Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplin společného základu
Limita a spojitost funkce Základ všší matematik Dana Říhová Mendelu Brno Průřezová inovace studijních programů Lesnické a dřevařské fakult MENDELU v Brně (LDF) s ohledem na disciplin společného základu
Limita posloupnosti a funkce
 Limita posloupnosti a funkce Petr Hasil Přednáška z Matematické analýzy I c Petr Hasil (MUNI) Limita posloupnosti a funkce MA I (M1101) 1 / 90 Obsah 1 Posloupnosti reálných čísel Úvod Limita posloupnosti
Limita posloupnosti a funkce Petr Hasil Přednáška z Matematické analýzy I c Petr Hasil (MUNI) Limita posloupnosti a funkce MA I (M1101) 1 / 90 Obsah 1 Posloupnosti reálných čísel Úvod Limita posloupnosti
Přednáška 9, 28. listopadu 2014 Část 4: limita funkce v bodě a spojitost funkce
 Přednáška 9, 28. listopadu 2014 Část 4: limita funkce v bodě a spojitost funkce Zápisem f : M R rozumíme, že je dána funkce definovaná na neprázdné množině M R reálných čísel, což je množina dvojic f =
Přednáška 9, 28. listopadu 2014 Část 4: limita funkce v bodě a spojitost funkce Zápisem f : M R rozumíme, že je dána funkce definovaná na neprázdné množině M R reálných čísel, což je množina dvojic f =
Management rekreace a sportu. 10. Derivace
 Derivace Derivace Před mnoha lety se matematici snažily o obecné vyřešení úlohy, jak sestrojit tečnu k dané křivce a také yzici zápolili s problémem určení rychlosti nerovnoměrného pohybu K zásadnímu obratu
Derivace Derivace Před mnoha lety se matematici snažily o obecné vyřešení úlohy, jak sestrojit tečnu k dané křivce a také yzici zápolili s problémem určení rychlosti nerovnoměrného pohybu K zásadnímu obratu
Kombinatorická pravdepodobnosť (opakovanie)
 Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody kariet
Kombinatorická pravdepodobnosť (opakovanie) Metódy riešenia úloh z pravdepodobnosti a štatistiky Beáta Stehlíková, FMFI UK Bratislava www.iam.fmph.uniba.sk/institute/stehlikova Príklad 1: Zhody kariet
Pomocný text. Polynomy
 Pomocný text Polynomy Tato série bude o polynomech a to zejména o polynomech jedné proměnné (pokud nebude uvedeno explicitně, že jde o polynom více proměnných). Formálně je někdy polynom jedné proměnné
Pomocný text Polynomy Tato série bude o polynomech a to zejména o polynomech jedné proměnné (pokud nebude uvedeno explicitně, že jde o polynom více proměnných). Formálně je někdy polynom jedné proměnné
Ak stlačíme OK, prebehne výpočet a v bunke B1 je výsledok.
 Hľadanie riešenia: ak poznáme očakávaný výsledok jednoduchého vzorca, ale vstupná hodnota, ktorú potrebujeme k určeniu výsledku je neznáma. Aplikácia Excel hľadá varianty hodnoty v určitej bunke, kým vzorec,
Hľadanie riešenia: ak poznáme očakávaný výsledok jednoduchého vzorca, ale vstupná hodnota, ktorú potrebujeme k určeniu výsledku je neznáma. Aplikácia Excel hľadá varianty hodnoty v určitej bunke, kým vzorec,
Zápis predmetov do AiSu na aktuálny akademický rok
 Zápis predmetov do AiSu na aktuálny akademický rok UPOZORNENIE: Návod na zápis predmetov do AiSu je vypracovaný pre akademický rok 2015/2016. Študent si ale musí zvoliť vždy aktuálny akademický rok, do
Zápis predmetov do AiSu na aktuálny akademický rok UPOZORNENIE: Návod na zápis predmetov do AiSu je vypracovaný pre akademický rok 2015/2016. Študent si ale musí zvoliť vždy aktuálny akademický rok, do
3. LIMITA A SPOJITOST FUNKCE
 3. LIMITA A SPOJITOST FUNKCE Okolí reálného čísla a 3.1. Deinice Okolím reálného čísla a nazýváme otevřený interval a, a, kde je libovolné kladné číslo. Je to tedy množina reálných čísel x, která vyhovují
3. LIMITA A SPOJITOST FUNKCE Okolí reálného čísla a 3.1. Deinice Okolím reálného čísla a nazýváme otevřený interval a, a, kde je libovolné kladné číslo. Je to tedy množina reálných čísel x, která vyhovují
PLASTOVÉ KARTY ZÁKAZNÍKOV
 PLASTOVÉ KARTY ZÁKAZNÍKOV OBSAH 1 Plastové karty základné informácie... 1 2 Distribúcia plastových kariet zákazníkom... 1 2.1 Jednorázová hromadná distribúcia kariet... 1 2.2 Pravidelná distribúcia plastových
PLASTOVÉ KARTY ZÁKAZNÍKOV OBSAH 1 Plastové karty základné informácie... 1 2 Distribúcia plastových kariet zákazníkom... 1 2.1 Jednorázová hromadná distribúcia kariet... 1 2.2 Pravidelná distribúcia plastových
2 Fyzikální aplikace. Předpokládejme, že f (x 0 ) existuje. Je-li f (x 0 ) vlastní, pak rovnice tečny ke grafu funkce f v bodě [x 0, f(x 0 )] je
![2 Fyzikální aplikace. Předpokládejme, že f (x 0 ) existuje. Je-li f (x 0 ) vlastní, pak rovnice tečny ke grafu funkce f v bodě [x 0, f(x 0 )] je 2 Fyzikální aplikace. Předpokládejme, že f (x 0 ) existuje. Je-li f (x 0 ) vlastní, pak rovnice tečny ke grafu funkce f v bodě [x 0, f(x 0 )] je](/thumbs/102/152847701.jpg) Derivace funkce a jej geometrický význam Je dána funkce f) 3 6 + 9 + a naším úkolem je určit směrnici tečny v bodě [; f)] Pro libovolné lze směrnici sečny danou body [; f)] a [; f)] spočítat jako f) f)
Derivace funkce a jej geometrický význam Je dána funkce f) 3 6 + 9 + a naším úkolem je určit směrnici tečny v bodě [; f)] Pro libovolné lze směrnici sečny danou body [; f)] a [; f)] spočítat jako f) f)
Základy algoritmizácie a programovania
 Základy algoritmizácie a programovania Pojem algoritmu Algoritmus základný elementárny pojem informatiky, je prepis, návod, realizáciou ktorého získame zo zadaných vstupných údajov požadované výsledky.
Základy algoritmizácie a programovania Pojem algoritmu Algoritmus základný elementárny pojem informatiky, je prepis, návod, realizáciou ktorého získame zo zadaných vstupných údajov požadované výsledky.
1. podzimní série. KdyžseLenkatuhleozkouškovémnudila,přišlanato,žepokudproreálnáčísla a, b, cplatí nerovnosti
 1. podzimní série Téma: Triky Datumodeslání: ½½º Ò ¾¼½¼ ½º ÐÓ Ó Ýµ Miško vymyslel trik! Nejdříve požádá Tomáška, ať si vybere osmičku nebo devítku. Potom mu řekne, aby zvolené číslo vynásobil jakýmkoliv
1. podzimní série Téma: Triky Datumodeslání: ½½º Ò ¾¼½¼ ½º ÐÓ Ó Ýµ Miško vymyslel trik! Nejdříve požádá Tomáška, ať si vybere osmičku nebo devítku. Potom mu řekne, aby zvolené číslo vynásobil jakýmkoliv
4. Kombinatorika a matice
 4 Kombinatorika a matice 4 Princip inkluze a exkluze Předpokládejme, že chceme znát počet přirozených čísel menších než sto, která jsou dělitelná dvěma nebo třemi Označme N k množinu přirozených čísel
4 Kombinatorika a matice 4 Princip inkluze a exkluze Předpokládejme, že chceme znát počet přirozených čísel menších než sto, která jsou dělitelná dvěma nebo třemi Označme N k množinu přirozených čísel
Univerzita Karlova v Praze Pedagogická fakulta
 Univerzita Karlova v Praze Pedagogická fakulta SEMINÁRNÍ PRÁCE Z METOD ŘEŠENÍ 1 TEORIE ČÍSEL 000/001 Cifrik, M-ZT Příklad ze zadávacích listů 10 101 Dokažte, že číslo 101 +10 je dělitelné číslem 51 Důkaz:
Univerzita Karlova v Praze Pedagogická fakulta SEMINÁRNÍ PRÁCE Z METOD ŘEŠENÍ 1 TEORIE ČÍSEL 000/001 Cifrik, M-ZT Příklad ze zadávacích listů 10 101 Dokažte, že číslo 101 +10 je dělitelné číslem 51 Důkaz:
Kapitola Základní množinové pojmy Princip rovnosti. Dvě množiny S a T jsou si rovny (píšeme S = T ) prvek T je také prvkem S.
 1 Kapitola 1 Množiny 11 Základní množinové pojmy Pojem množiny nedefinujeme, pouze připomínáme, že množina je souhrn, nebo soubor navzájem rozlišitelných objektů, kterým říkáme prvky 111 Princip rovnosti
1 Kapitola 1 Množiny 11 Základní množinové pojmy Pojem množiny nedefinujeme, pouze připomínáme, že množina je souhrn, nebo soubor navzájem rozlišitelných objektů, kterým říkáme prvky 111 Princip rovnosti
Ďalší spôsob, akým je možné vygenerovať maticu je použitie zabudovaných funkcií na generovanie elementárnych matíc.
 MATICE MATLAB poskytuje obrovskú podporu práce s maticami. Táto hodina sa bude zaoberať základmi práce s maticami. Cieľom prvej časti hodiny je objasnenie základných princípov tvorby matíc, ich editáciu
MATICE MATLAB poskytuje obrovskú podporu práce s maticami. Táto hodina sa bude zaoberať základmi práce s maticami. Cieľom prvej časti hodiny je objasnenie základných princípov tvorby matíc, ich editáciu
9 Kolmost vektorových podprostorů
 9 Kolmost vektorových podprostorů Od kolmosti dvou vektorů nyní přejdeme ke kolmosti dvou vektorových podprostorů. Budeme se zabývat otázkou, kdy jsou dva vektorové podprostory na sebe kolmé a jak to poznáme.
9 Kolmost vektorových podprostorů Od kolmosti dvou vektorů nyní přejdeme ke kolmosti dvou vektorových podprostorů. Budeme se zabývat otázkou, kdy jsou dva vektorové podprostory na sebe kolmé a jak to poznáme.
MANUÁL K PROGRAMU MATEMATIKA 2.0 STIAHNUTIE A INŠTALÁCIA PROGRAMU:
 MANUÁL K PROGRAMU MATEMATIKA 2.0 Program na precvičovanie učiva z matematiky na nájdeme na stránke http://www.slunecnice.cz/sw/4321-matematika/. STIAHNUTIE A INŠTALÁCIA PROGRAMU: Po kliknutí na Stáhnout
MANUÁL K PROGRAMU MATEMATIKA 2.0 Program na precvičovanie učiva z matematiky na nájdeme na stránke http://www.slunecnice.cz/sw/4321-matematika/. STIAHNUTIE A INŠTALÁCIA PROGRAMU: Po kliknutí na Stáhnout
Pracovné prostredie MS EXCEL 2003.
 Pracovné prostredie MS EXCEL 2003. Tabuľkové kalkulátory sú veľmi praktické aplikácie pre realizáciu výpočtov, grafických prezentácií údajov, ako aj pe prácu s rôznymi údajmi ako s bázou dát. Tieto programy
Pracovné prostredie MS EXCEL 2003. Tabuľkové kalkulátory sú veľmi praktické aplikácie pre realizáciu výpočtov, grafických prezentácií údajov, ako aj pe prácu s rôznymi údajmi ako s bázou dát. Tieto programy
Metody výpočtu limit funkcí a posloupností
 Metody výpočtu limit funkcí a posloupností Martina Šimůnková, 6. listopadu 205 Učební tet k předmětu Matematická analýza pro studenty FP TUL Značení a terminologie R značí množinu reálných čísel, rozšířenou
Metody výpočtu limit funkcí a posloupností Martina Šimůnková, 6. listopadu 205 Učební tet k předmětu Matematická analýza pro studenty FP TUL Značení a terminologie R značí množinu reálných čísel, rozšířenou
Vektory a matice. Obsah. Aplikovaná matematika I. Carl Friedrich Gauss. Základní pojmy a operace
 Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
Vektory a matice Aplikovaná matematika I Dana Říhová Mendelu Brno Obsah 1 Vektory Základní pojmy a operace Lineární závislost a nezávislost vektorů 2 Matice Základní pojmy, druhy matic Operace s maticemi
