Předmět: SM02 PRŮBĚH VNITŘNÍCH SIL M(x), V(x), N(x) NA ROVINNÉM ŠIKMÉM PRUTU. prof. Ing. Michal POLÁK, CSc.
|
|
|
- Renáta Müllerová
- před 6 lety
- Počet zobrazení:
Transkript
1 Předmět: SM0 PRŮBĚH VNITŘNÍCH SIL M(), V(), N() NA ROVINNÉM ŠIKMÉM PRUTU pro. Ing. Michl POLÁK, CSc. Fkult stvení, ČVUT v Pre
2 PRŮBĚHY VNITŘNÍCH SIL M(), N(), V() NA ROVINNÉM ŠIKMÉM PRUTU:
3 ZATÍŽENÍ NA ŠIKMÝ PRUT: g () SVISLÉ SPOJITÉ ZATÍŽENÍ VZTAŽENÉ K ŠIKMÉ DÉLCE PRUTU NAPŘ. VLASTNÍ TÍHA KONSTRUKCE
4 ZATÍŽENÍ NA ŠIKMÝ PRUT: g () SVISLÉ SPOJITÉ ZATÍŽENÍ VZTAŽENÉ K VODOROVNÉ DÉLCE PRUTU NAPŘ. ZATÍŽENÍ SNĚHEM
5 ZATÍŽENÍ NA ŠIKMÝ PRUT: g () VODOROVNÉ SPOJITÉ ZATÍŽENÍ VZTAŽENÉ K ŠIKMÉ DÉLCE PRUTU
6 ZATÍŽENÍ NA ŠIKMÝ PRUT: g () VODOROVNÉ SPOJITÉ ZATÍŽENÍ VZTAŽENÉ K SVISLÉ DÉLCE PRUTU
7 ZATÍŽENÍ NA ŠIKMÝ PRUT: () SLOŽKA SPOJITÉHO ZATÍŽENÍ KOLMÁ KE STŘEDNICI PRUTU VZTAŽENÁ K ŠIKMÉ DÉLCE PRUTU () SLOŽKA SPOJITÉHO ZATÍŽENÍ ROVNOBĚŽNÁ SE STŘEDNICÍ PRUTU VZTAŽENÁ K ŠIKMÉ DÉLCE PRUTU
8 SOUŘADNÉ SYSTÉMY ŠIKMÉHO PRUTU: g, g GLOBÁLNÍ SOUŘADNÝ SYSTÉM, LOKÁLNÍ SOUŘADNÝ SYSTÉM PRUTU h g g
9 PŘEPOČET g ( g ) NA g () A g () NA g ( g ) : h dl g dl g dq g g ( g ) dq g = g ( g ). dl g g dq g dq g = g (). dl dl g dl dl g () dl g
10 PŘEPOČET g ( g ) NA g () A g () NA g ( g ) : dq g g ( g ) dl g dq g dq g = g ( g ). dl g dq g = g (). dl PRO PŘEPOČET PLATÍ: dq g = dq g g ( g ). dl g = g (). dl g ( g ). dl. cos = g (). dl dl g () g () = g ( g ). cos g ( g ) = g (). 1 cos dl g dl g dl dl g =dl cos α
11 ANALOGICKY VE VODOROVNÉM SMĚRU : dl g g () dl g ( g ) dl g dl g dl dl g = dl. sin g () = g ( g ). sin g ( g ) = g (). 1 sin
12 ŘEŠENÍ M(), N(), V() V LOKÁLNÍM SOUŘADNÉM SYSTÉMU: N hj M hj V hj h g () () g 1 g () g ( g ) 3 g () 4 g ( g ) g () = 1 g () + g ( g ). cos g () = 3 g () + 4 g ( g ). sin g () g () () = g (). cos + g (). sin () = - g (). sin + g (). cos T g g cos sin sin cos g g
13 ŘEŠENÍ M(), N(), V() V LOKÁLNÍM SOUŘADNÉM SYSTÉMU: g. sin g. cos N hj M hj h g V hj () () g () = 1 g () + g ( g ). cos g () = 3 g () + 4 g ( g ). sin g g g. sin g () g () g g. cos () = g (). cos + g (). sin () = - g (). sin + g (). cos T g g cos sin sin cos g g
14 PRO M(), N(), V() NA PRUTU (h,j) PLATÍ: N V d d M V d POSTUP INTEGRACE PRO RŮZNÉ TYPY SPOJITÉHO ZATÍŽENÍ SHODNÝ JAKO NA PRUTU VODOROVNÉM
15 PRO ROVNOMĚRNÉ SPOJITÉ ZATÍŽENÍ A : M hj N hj V Z hj g h F F X j L hj j L jk F = X. cos + Z. sin F = - X. sin + Z. cos N V M N V hj hj M V hj hj 1 N V M jh jh jh k N V hj hj M hj L V T L hj hj hj L X cos Z sin INTERVAL (h,j) ROVNICE N(), V(), M(): F F hj 1 N V L hj jk jk sin X cos Z N V jh jh F F
16 POLOHA A VELIKOST EXTRÉMU M(): dm d V V 0 V 0 EX hj EX EX V hj EX ( 0 ; L hj ) M EX M hj V hj EX 1 EX
17 N hj M hj h V hj F N L hj F j L jk k V M hj 1 8 L hj
18 PŘÍKLAD: VYKRESLETE PRŮBĚHY M(), N(), V() NA ZADANÉM NOSNÍKU: = 4 knm -1 1 =10 knm -1 1,154,308 F= kn,0 4,0 c VÝPOČET ŠIKMÝCH DÉLEK: cos sin 4 4,618,308 4,618 0,866 0,4998 L L L c 4,0,0 L cos,308 4,618 m 1,154,309 m,309 m 0,866
19 PŘÍKLAD: VYKRESLETE PRŮBĚHY M(), N(), V() NA ZADANÉM NOSNÍKU: = 4 knm -1 1 =10 knm -1 1,155,309 F= kn,0 4,0 c SLOUČENÍ ZATÍŽENÍ: 1 = 1 + cos α = ,866 = 13,465 knm -1
20 =13,465 knm -1 1,155,309 F= kn,0 4,0 c ROZKLAD ZATÍŽENÍ: F F = sin α = 13,465 0,4998 = 6,730 knm -1 = cos α = 13,465 0,866 = 11,663 knm -1 F = F sin α = 0,4998 = 1,000 kn F = F cos α = 0,866 = 1,73 kn
21 1,155,309 F =1,73 kn 30 o B B,0 4,0 c C = 6,730 knm -1 VÝPOČET REAKCÍ: S: B (L L ) F 0 c c : B L F (L L ) (L L ) 0 c c 1 ) S: C B F (L L 0 c c
22 1,155,309 F =1,73 kn 30 o B B,0 4,0 c C = 6,730 knm -1 VÝPOČET REAKCÍ: S: B (L Lc) F 0 B (L L c ) F 6,730(,309 4,618) 1 47,633 kn
23 1,155,309 F =1,73 kn 30 o B B,0 4,0 c C = 6,730 knm -1 VÝPOČET REAKCÍ: c : B L F (L L ) (L L ) 0 B c F (L L c ) L c 1 c 1 1,73(,309 4,618) 11,663(,309 4,618) 4,618 1 (L L c ) c 63,190 kn
24 1,155,309 F =1,73 kn 30 o B B,0 4,0 c C = 6,730 knm -1 VÝPOČET REAKCÍ: S: C B (L Lc) F 0 C B (L L c ) 63,190 11,663(,309 F 4,618) 1,73 19,33 kn
25 1,155,309 F =1,73 kn 30 o B B,0 4,0 c C = 6,730 knm -1 VÝPOČET M,N,V V BODECH NESPOJITOSTI : Průře, : N V F F M 0 knm 1,000 kn 1,73 kn
26 1,155,309 F =1,73 kn Průře, : N V M N 30 o B B,0 4,0 L 1 6,730,309 c C = 6,730 knm -1 V L 1,73 11,663,309 1 M V L 1 0 ( 1,73),309 11,663,309 35,090 knm VÝPOČET M,N,V V BODECH NESPOJITOSTI : 16,540 kn 8,66 kn M N V
27 =13,465 knm -1 1,155,309 F= kn 30 o,0 4,0 c VÝPOČET M,N,V V BODECH NESPOJITOSTI : M F L L 35,090 knm L,0 13,465,309,0
28 1,155,309 F =1,73 kn Průře,c : N V c c N V B B 30 o B B,0 4,0 16,540 47,633 ( 8,66) 63,160 c C = 6,73 knm -1 VÝPOČET M,N,V V BODECH NESPOJITOSTI : 31,093 kn 34,58 kn M N B V B
29 1,155,309 F =1,73 kn Průře c, : N V c c M N c 30 o B B,0 4,0 L c c C = 6,73 knm -1 ( 31,093) 6,730 4,618 VÝPOČET M,N,V V BODECH NESPOJITOSTI : 0,014 kn Vc Lc 34,58 11,663 4,618 19,33 kn 1 Mc Vc Lc Lc 1 ( 35,090) ( 34,58) 4,618 11,663 4,618 0,018 knm N c c M c V c
30 1,155,309 F =1,73 kn Průře c, : N c 0 kn V c C M c 0 knm 30 o B B,0 4,0 19,33 kn c C = 6,73 knm -1 N c 0,014 kn V c 19,33 kn M c 0,018 knm ROZDÍL ZAOKROUHLOVACÍ CHYBA KONTROLA KLADNÝ PRŮŘEZ (c,):
31 1,155,309 F =1,73 kn INTERVAL (,) N() N 30 o B B,0 4,0 1,000 6,730 V() V 1,73 11,663 1 M() M V 1,73 5,830 c C = 6,73 knm -1 URČENÍ PRŮBĚHU FUNKCÍ (), (), M(), N(), V(): M N V
32 1,155,309 F =1,73 kn INTERVAL (,c) N() N c 30 o B B,0 4,0 ( 31,093) 6,730 V() Vc 34,58 11,663 1 M() Mc Vc 35,090 34,58 5,83 c C = 6,73 knm -1 URČENÍ PRŮBĚHU FUNKCÍ (), (), M(), N(), V(): M c N c V c
33 1,155,309 F =1,73 kn V M V 0 EX EX EX c V c 30 o B B,0 4,0 EX 34,58 11,663 16,015 knm,960 m c C = 6,73 knm -1 EX ( 0 ; Lc ) ( 0 ; 4,618 ) 1 M(EX) Mc Vc EX EX 35,090 34,58,960 5,83,960 MAXIMUM M() NA INTERVALU (,c): M c N c V c
34 1,155,309 F =1,73 kn 30 o B B,0 4,0 c C = 6,73 knm -1 PRO VYKRESLENÍ PARABOL: c 1 L 11,663, L 11,663 4,618 c 7,773 knm 31,091 knm
35 N [kn] V [kn]
36 V [kn] M [knm]
37 PŘÍKLAD: VYKRESLETE PRŮBĚHY M(), N(), V() NA ZADANÉM NOSNÍKU: g ( g ) = g ( g ). cos g 3 g g g g g 3 cos g g
38 PŘÍKLAD: VYKRESLETE PRŮBĚHY M(), N(), V() NA ZADANÉM NOSNÍKU: g g g 3 cos g () = g (). sin () = g (). cos g 3 sin cos g g g 3 cos cos g g
39 PŘÍKLAD: VYKRESLETE PRŮBĚHY M(), N(), V() NA ZADANÉM NOSNÍKU: 3 sin cos g g g g cos g 3 cos 3 g sin cos cos sin cos 3 3 cos cos g g 3 cos 3 cos 4 cos cos
40 PŘÍKLAD: VYKRESLETE PRŮBĚHY M(), N(), V() NA ZADANÉM NOSNÍKU: N N M V d (3sin cos 3 ) 3 3 g C 1 (3sin cos 3 cos N 3 3 ) d sin cos sin cos sin cos 3 3 3
41 PŘÍKLAD: VYKRESLETE PRŮBĚHY M(), N(), V() NA ZADANÉM NOSNÍKU: M V N g 3 cos 3 cos 4 cos cos V M d (3cos V V 4 d ) cos (V 4 4 C (3cos 3 V 4 ) d cos cos ) d C M V 3 cos 4 4 4
1. výpočet reakcí R x, R az a R bz - dle kapitoly 3, q = q cosα (5.1) kolmých (P ). iz = P iz sinα (5.2) iz = P iz cosα (5.3) ix = P ix cosα (5.
 Kapitola 5 Vnitřní síly přímého šikmého nosníku Pojem šikmý nosník je používán dle publikace [1] pro nosník ležící v souřadnicové rovině xz, který je vůči vodorovné ose x pootočen o úhel α. Pro šikmou
Kapitola 5 Vnitřní síly přímého šikmého nosníku Pojem šikmý nosník je používán dle publikace [1] pro nosník ležící v souřadnicové rovině xz, který je vůči vodorovné ose x pootočen o úhel α. Pro šikmou
Stavební mechanika 2 (K132SM02)
 Stavení mechanika (K13SM0) ednáší: doc. Ing. Matj Lepš, Ph.D. Katedra mechaniky K13 místnost D034 e-mail: matej.leps@sv.cvut.cz konzultaní hodiny Pá 10:00-11:30 íklad: vykreslete prhy M(), N(), V() na
Stavení mechanika (K13SM0) ednáší: doc. Ing. Matj Lepš, Ph.D. Katedra mechaniky K13 místnost D034 e-mail: matej.leps@sv.cvut.cz konzultaní hodiny Pá 10:00-11:30 íklad: vykreslete prhy M(), N(), V() na
3. kapitola. Průběhy vnitřních sil na lomeném nosníku. Janek Faltýnek SI J (43) Teoretická část: Příkladová část: Stavební mechanika 2
 3. kapitola Stavební mechanika Janek Faltýnek SI J (43) Průběhy vnitřních sil na lomeném nosníku Teoretická část: Naším úkolem je v tomto příkladu vyšetřit průběh vnitřních sil na lomeném rovinném nosníku
3. kapitola Stavební mechanika Janek Faltýnek SI J (43) Průběhy vnitřních sil na lomeném nosníku Teoretická část: Naším úkolem je v tomto příkladu vyšetřit průběh vnitřních sil na lomeném rovinném nosníku
2.13 Rovinný obloukový nosník zatížený v rovině = staticky určitě podepřený rovinný obloukový prut
 .13 Rovinný obloukový nosník atížený v rovině = staticky určitě podepřený rovinný obloukový prut (střednice-rovinná křivka, atížení v rovině střednice) Geometrie obloukového prutu Poloha průřeu: s x =
.13 Rovinný obloukový nosník atížený v rovině = staticky určitě podepřený rovinný obloukový prut (střednice-rovinná křivka, atížení v rovině střednice) Geometrie obloukového prutu Poloha průřeu: s x =
Zjednodušená deformační metoda (2):
 Stavební mechanika 1SM Přednášky Zjednodušená deformační metoda () Prut s kloubově připojeným koncem (statická kondenzace). Řešení rovinných rámů s posuvnými patry/sloupy. Prut s kloubově připojeným koncem
Stavební mechanika 1SM Přednášky Zjednodušená deformační metoda () Prut s kloubově připojeným koncem (statická kondenzace). Řešení rovinných rámů s posuvnými patry/sloupy. Prut s kloubově připojeným koncem
A x A y. α = 30. B y. A x =... kn A y =... kn B y =... kn. Vykreslení N, V, M. q = 2kN/m M = 5kNm. F = 10 kn A c a b d ,5 2,5 L = 10
 Vzorový příklad k 1. kontrolnímu testu Prostý nosník Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A y y q = kn/m M = 5kNm F = 10 kn A c a b d 1 1 3,5,5 L = 10 α B B y x α = 30
Vzorový příklad k 1. kontrolnímu testu Prostý nosník Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A y y q = kn/m M = 5kNm F = 10 kn A c a b d 1 1 3,5,5 L = 10 α B B y x α = 30
Podmínky k získání zápočtu
 Podmínky k získání zápočtu 18 až 35 bodů 7 % aktivní účast, omluvená neúčast Odevzdání programů Testy: 8 nepovinných testů (-2 body nebo -3 body) 3 povinné testy s ohodnocením 5 bodů (povoleny 2 opravné
Podmínky k získání zápočtu 18 až 35 bodů 7 % aktivní účast, omluvená neúčast Odevzdání programů Testy: 8 nepovinných testů (-2 body nebo -3 body) 3 povinné testy s ohodnocením 5 bodů (povoleny 2 opravné
α = 210 A x =... kn A y =... kn A M =... knm
 Vzorový příklad k 1. kontrolnímu testu Konzola Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A M A y y q = kn/m M = - 5kNm A α B c a b d F = 10 kn 1 1 3,5,5 L = 10 x α = 10 A
Vzorový příklad k 1. kontrolnímu testu Konzola Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A M A y y q = kn/m M = - 5kNm A α B c a b d F = 10 kn 1 1 3,5,5 L = 10 x α = 10 A
* Modelování (zjednodušení a popis) tvaru konstrukce. pruty
 2. VNITŘNÍ SÍLY PRUTU 2.1 Úvod * Jak konstrukce přenáší atížení do vaeb/podpor? Jak jsou prvky konstrukce namáhány? * Modelování (jednodušení a popis) tvaru konstrukce. pruty 1 Prut: konstrukční prvek,
2. VNITŘNÍ SÍLY PRUTU 2.1 Úvod * Jak konstrukce přenáší atížení do vaeb/podpor? Jak jsou prvky konstrukce namáhány? * Modelování (jednodušení a popis) tvaru konstrukce. pruty 1 Prut: konstrukční prvek,
Zakřivený nosník. Rovinně zakřivený nosník v rovinné úloze geometrie, reakce, vnitřní síly. Stavební statika, 1.ročník bakalářského studia
 Stavební statika, 1.ročník bakalářského studia Zakřivený nosník Rovinně zakřivený nosník v rovinné úloze geometrie, reakce, vnitřní síly Katedra stavební mechaniky Fakulta stavební, VŠB - Technická univerzita
Stavební statika, 1.ročník bakalářského studia Zakřivený nosník Rovinně zakřivený nosník v rovinné úloze geometrie, reakce, vnitřní síly Katedra stavební mechaniky Fakulta stavební, VŠB - Technická univerzita
Kapitola 8. prutu: rovnice paraboly z = k x 2 [m], k = z a x 2 a. [m 1 ], (8.1) = z b x 2 b. rovnice sklonu střednice prutu (tečna ke střednici)
![Kapitola 8. prutu: rovnice paraboly z = k x 2 [m], k = z a x 2 a. [m 1 ], (8.1) = z b x 2 b. rovnice sklonu střednice prutu (tečna ke střednici) Kapitola 8. prutu: rovnice paraboly z = k x 2 [m], k = z a x 2 a. [m 1 ], (8.1) = z b x 2 b. rovnice sklonu střednice prutu (tečna ke střednici)](/thumbs/61/45546970.jpg) Kapitola 8 Vnitřní síly rovinně zakřiveného prutu V této kapitole bude na příkladech vysvětleno řešení vnitřních sil rovinně zakřivených nosníků, jejichž střednici tvoří oblouk ve tvaru kvadratické paraboly[1].
Kapitola 8 Vnitřní síly rovinně zakřiveného prutu V této kapitole bude na příkladech vysvětleno řešení vnitřních sil rovinně zakřivených nosníků, jejichž střednici tvoří oblouk ve tvaru kvadratické paraboly[1].
Stavební mechanika 2 (K132SM02)
 Stvení mecnik 2 (K132SM02) Přednáší: Jn Sýkor Ktedr mecniky K132 místnost D2016 e-mil: jn.sykor.1@fsv.cvut.cz konzultční odiny: Po 12-14 Kldné směry vnitřníc sil: Kldný průřez vnitřní síly jsou kldné ve
Stvení mecnik 2 (K132SM02) Přednáší: Jn Sýkor Ktedr mecniky K132 místnost D2016 e-mil: jn.sykor.1@fsv.cvut.cz konzultční odiny: Po 12-14 Kldné směry vnitřníc sil: Kldný průřez vnitřní síly jsou kldné ve
FAKULTA STAVEBNÍ. Stavební statika. Telefon: WWW:
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ Stavební statika Přednáška 2 pro kombinované studium Jiří Brožovský Kancelář: LP C 303/1 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ Stavební statika Přednáška 2 pro kombinované studium Jiří Brožovský Kancelář: LP C 303/1 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz
Stavební mechanika 2 (K132SM02) Přednáší: doc. Ing. Matěj Lepš, Ph.D. Katedra mechaniky K132 místnost D
 Stavební mechanika 2 (K132SM02) Přednáší: doc. Ing. Matěj Lepš, Ph.D. Katedra mechaniky K132 místnost D2034 e-mail: matej.leps@fsv.cvut.cz Organizace předtermínu a N & O zápočtových testů ze SM02 Předtermín
Stavební mechanika 2 (K132SM02) Přednáší: doc. Ing. Matěj Lepš, Ph.D. Katedra mechaniky K132 místnost D2034 e-mail: matej.leps@fsv.cvut.cz Organizace předtermínu a N & O zápočtových testů ze SM02 Předtermín
Prvky betonových konstrukcí BL01 6 přednáška. Dimenzování průřezů namáhaných posouvající silou prvky se smykovou výztuží, Podélný smyk,
 Prvky betonových konstrukcí BL01 6 přednáška Dimenzování průřezů namáhaných posouvající silou prvky se smykovou výztuží, Podélný smyk, Způsoby porušení prvků se smykovou výztuží Smyková výztuž přispívá
Prvky betonových konstrukcí BL01 6 přednáška Dimenzování průřezů namáhaných posouvající silou prvky se smykovou výztuží, Podélný smyk, Způsoby porušení prvků se smykovou výztuží Smyková výztuž přispívá
Šikmý nosník rovnoměrné spojité zatížení. L průmětu. zatížení kolmé ke střednici prutu (vítr)
 Šikmý nosník Šikmý nosník rovnoměrné spojité ztížení ztížení kolmé ke střednii prutu (vítr) q h - ztížení kolmé ke střednii prutu (vítr) - ztížení svislé zdáno n délku prutu (vlstní tíh) - ztížení svislé
Šikmý nosník Šikmý nosník rovnoměrné spojité ztížení ztížení kolmé ke střednii prutu (vítr) q h - ztížení kolmé ke střednii prutu (vítr) - ztížení svislé zdáno n délku prutu (vlstní tíh) - ztížení svislé
Stavební mechanika 2 (K132SM02)
 Stavební mechanika 2 (K132SM02) Přednáší: doc. Ing. Matěj Lepš, Ph.D. Katedra mechaniky K132 místnost D2034 e-mail: matej.leps@fsv.cvut.cz konzultační hodiny budou upřesněny později https://mech.fsv.cvut.cz/student/
Stavební mechanika 2 (K132SM02) Přednáší: doc. Ing. Matěj Lepš, Ph.D. Katedra mechaniky K132 místnost D2034 e-mail: matej.leps@fsv.cvut.cz konzultační hodiny budou upřesněny později https://mech.fsv.cvut.cz/student/
Betonové konstrukce (S) Přednáška 3
 Betonové konstrukce (S) Přednáška 3 Obsah Účinky předpětí na betonové prvky a konstrukce Silové působení kabelu na beton Ekvivalentní zatížení Staticky neurčité účinky předpětí Konkordantní kabel, Lineární
Betonové konstrukce (S) Přednáška 3 Obsah Účinky předpětí na betonové prvky a konstrukce Silové působení kabelu na beton Ekvivalentní zatížení Staticky neurčité účinky předpětí Konkordantní kabel, Lineární
FAKULTA STAVEBNÍ. Stavební statika. Telefon: WWW:
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ Stavební statika Vnitřní síly na nosnících Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW:
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ Stavební statika Vnitřní síly na nosnících Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW:
. 1 x. Najděte rovnice tečen k hyperbole 7x 2 2y 2 = 14, které jsou kolmé k přímce 2x+4y 3 = 0. 2x y 1 = 0 nebo 2x y + 1 = 0.
 Diferenciální počet příklad s výsledky ( Najděte definiční obor funkce f() = ln arcsin + ) D f = (, 0 Najděte rovnici tečny ke grafu funkce f() = 3 +, která je rovnoběžná s přímkou y = 4 4 y 4 = 0 nebo
Diferenciální počet příklad s výsledky ( Najděte definiční obor funkce f() = ln arcsin + ) D f = (, 0 Najděte rovnici tečny ke grafu funkce f() = 3 +, která je rovnoběžná s přímkou y = 4 4 y 4 = 0 nebo
7.1 Extrémy a monotonie
 KAPITOLA 7: Průběh funkce [ZMA13-P38] 7.1 Extrémy a monotonie Řekneme, že funkce f nabývá na množině M Df svého globálního maxima globálního minima A v bodě x 0, jestliže x 0 M, fx 0 = A a pro každé x
KAPITOLA 7: Průběh funkce [ZMA13-P38] 7.1 Extrémy a monotonie Řekneme, že funkce f nabývá na množině M Df svého globálního maxima globálního minima A v bodě x 0, jestliže x 0 M, fx 0 = A a pro každé x
ZDM PŘÍMÉ NOSNÍKY. Příklad č. 1. Miloš Hüttner SMR2 ZDM přímé nosníky cvičení 09. Zadání
 iloš Hüttner SR D přímé nosníky cvičení 09 adání D PŘÍÉ NOSNÍKY Příklad č. 1 Vykreslete průběhy vnitřních sil na konstrukci zobrazené na Obr. 1. Příklad převzat z katedrové wikipedie (originál ke stažení
iloš Hüttner SR D přímé nosníky cvičení 09 adání D PŘÍÉ NOSNÍKY Příklad č. 1 Vykreslete průběhy vnitřních sil na konstrukci zobrazené na Obr. 1. Příklad převzat z katedrové wikipedie (originál ke stažení
Výpočet vnitřních sil přímého nosníku III: šikmý nosník
 Stvení sttik,.ročník klářského studi Výpočet vnitřníh sil přímého nosníku III: šikmý nosník Výpočet vnitřníh sil šikmého nosníku - ztížení kolmé ke střednii prutu (vítr) - ztížení svislé zdáno n délku
Stvení sttik,.ročník klářského studi Výpočet vnitřníh sil přímého nosníku III: šikmý nosník Výpočet vnitřníh sil šikmého nosníku - ztížení kolmé ke střednii prutu (vítr) - ztížení svislé zdáno n délku
Výpočet vnitřních sil přímého nosníku III: šikmý nosník
 Stvení sttik,.ročník klářského studi Výpočet vnitřníh sil přímého nosníku III: šikmý nosník Výpočet vnitřníh sil šikmého nosníku - ztížení kolmé ke střednii prutu (vítr) - ztížení svislé zdáno n délku
Stvení sttik,.ročník klářského studi Výpočet vnitřníh sil přímého nosníku III: šikmý nosník Výpočet vnitřníh sil šikmého nosníku - ztížení kolmé ke střednii prutu (vítr) - ztížení svislé zdáno n délku
Kapitola 4. Tato kapitole se zabývá analýzou vnitřních sil na rovinných nosnících. Nejprve je provedena. Každý prut v rovině má 3 volnosti (kap.1).
 Kapitola 4 Vnitřní síly přímého vodorovného nosníku 4.1 Analýza vnitřních sil na rovinných nosnících Tato kapitole se zabývá analýzou vnitřních sil na rovinných nosnících. Nejprve je provedena rekapitulace
Kapitola 4 Vnitřní síly přímého vodorovného nosníku 4.1 Analýza vnitřních sil na rovinných nosnících Tato kapitole se zabývá analýzou vnitřních sil na rovinných nosnících. Nejprve je provedena rekapitulace
Stavební mechanika 3 132SM3 Přednášky. Deformační metoda: ZDM pro rámy s posuvnými styčníky, využití symetrie, výpočetní programy a kontrola výsledků.
 Stavební mechanika 12SM Přednášky Deformační metoda: ZDM pro rámy s posuvnými styčníky, využití symetrie, výpočetní programy a kontrola výsledků. Porovnání ODM a ZDM Příklad 1: (viz předchozí přednáška)
Stavební mechanika 12SM Přednášky Deformační metoda: ZDM pro rámy s posuvnými styčníky, využití symetrie, výpočetní programy a kontrola výsledků. Porovnání ODM a ZDM Příklad 1: (viz předchozí přednáška)
Předmět: SM01 Základní názvosloví stavebních konstrukcí, Zatížení stavebních konstrukcí Zatížení vlastní tíhou
 Předmět: SM01 Základní názvosloví stavebních konstrukcí, Zatížení stavebních konstrukcí Zatížení vlastní tíhou prof. Ing. Michal POLÁK, CSc. Fakulta stavební, ČVUT v Praze Základní názvosloví stavebních
Předmět: SM01 Základní názvosloví stavebních konstrukcí, Zatížení stavebních konstrukcí Zatížení vlastní tíhou prof. Ing. Michal POLÁK, CSc. Fakulta stavební, ČVUT v Praze Základní názvosloví stavebních
Stavební mechanika 1 (K132SM01)
 Stavební mechanika 1 (K132SM01) Přednáší: doc. Ing. Matěj Lepš, Ph.D. Katedra mechaniky K132 Termín opravného/náhradního zápočtového testu: 17.12.2014, 16:00-18:00, místnost B286. Na opravný/náhradní test
Stavební mechanika 1 (K132SM01) Přednáší: doc. Ing. Matěj Lepš, Ph.D. Katedra mechaniky K132 Termín opravného/náhradního zápočtového testu: 17.12.2014, 16:00-18:00, místnost B286. Na opravný/náhradní test
Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady. Část 1 - Test
 Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových charakteristik, oficiální přehled
Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových charakteristik, oficiální přehled
Spojitý nosník. Příklady
 Spojitý nosník Příklady Příklad, zadání A = konst. =, m I = konst. =,6 m 4 E = konst. = GPa q =kn / m F kn 3 = M = 5kNm F = 5kN 8 F3 = 8kN 4,5 . způsob řešení n p = (nepočítáme pootočení ve styčníku č.3)
Spojitý nosník Příklady Příklad, zadání A = konst. =, m I = konst. =,6 m 4 E = konst. = GPa q =kn / m F kn 3 = M = 5kNm F = 5kN 8 F3 = 8kN 4,5 . způsob řešení n p = (nepočítáme pootočení ve styčníku č.3)
Návrh a posudek osově namáhaného nosníku podle obou MS
 Návrh a posudek osově namáhaného nosníku podle obou MS 1) Statický rozbor 2) Dobře pochopit zadání definovat, v jakých hodnotách počítat (charakteristické x návrh.) 2) MSÚ nutný průřez dle MSÚ a) pevnost
Návrh a posudek osově namáhaného nosníku podle obou MS 1) Statický rozbor 2) Dobře pochopit zadání definovat, v jakých hodnotách počítat (charakteristické x návrh.) 2) MSÚ nutný průřez dle MSÚ a) pevnost
MATEMATIKA. Příklady pro 1. ročník bakalářského studia. II. část Diferenciální počet. II.1. Posloupnosti reálných čísel
 MATEMATIKA Příklady pro 1. ročník bakalářského studia II. část II.1. Posloupnosti reálných čísel Rozhodněte, zda posloupnost a n (n = 1, 2, 3,...) je omezená (omezená shora, omezená zdola) resp. monotónní
MATEMATIKA Příklady pro 1. ročník bakalářského studia II. část II.1. Posloupnosti reálných čísel Rozhodněte, zda posloupnost a n (n = 1, 2, 3,...) je omezená (omezená shora, omezená zdola) resp. monotónní
Pružnost a pevnost (132PRPE), paralelka J2/1 (ZS 2015/2016) Písemná část závěrečné zkoušky vzorové otázky a příklady.
 Pružnost a pevnost (132PRPE), paralelka J2/1 (ZS 2015/2016) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových
Pružnost a pevnost (132PRPE), paralelka J2/1 (ZS 2015/2016) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových
SMA2 Přednáška 09 Desky
 SMA Přednáška 09 Desk Měrné moment na deskách Diferenciální rovnice tenké izotropní desk Metod řešení diferenciální rovnice desk Přibližné řešení obdélníkových desek Příklad Copright (c) 01 Vít Šmilauer
SMA Přednáška 09 Desk Měrné moment na deskách Diferenciální rovnice tenké izotropní desk Metod řešení diferenciální rovnice desk Přibližné řešení obdélníkových desek Příklad Copright (c) 01 Vít Šmilauer
Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil
 Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil Souřadný systém, v rovině i prostoru Síla bodová: vektorová veličina (kluzný, vázaný vektor - využití),
Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil Souřadný systém, v rovině i prostoru Síla bodová: vektorová veličina (kluzný, vázaný vektor - využití),
Stavební mechanika 2 (K132SM02)
 Stavební mechanika (K13SM0) ednáší: doc. Ing. Matj Lepš, Ph.D. Katedra mechaniky K13 místnost D034 e-mail: matej.leps@fsv.cvut.cz konzultaní hodiny Pá 10:00-11:30 Matj Lepš 016 3.1 Prh vnitních sil po
Stavební mechanika (K13SM0) ednáší: doc. Ing. Matj Lepš, Ph.D. Katedra mechaniky K13 místnost D034 e-mail: matej.leps@fsv.cvut.cz konzultaní hodiny Pá 10:00-11:30 Matj Lepš 016 3.1 Prh vnitních sil po
Střední škola automobilní Ústí nad Orlicí
 Síla Základní pojmy Střední škola automobilní Ústí nad Orlicí vzájemné působení těles, které mění jejich pohybový stav nebo tvar zobrazuje se graficky jako úsečka se šipkou ve zvoleném měřítku m f je vektor,
Síla Základní pojmy Střední škola automobilní Ústí nad Orlicí vzájemné působení těles, které mění jejich pohybový stav nebo tvar zobrazuje se graficky jako úsečka se šipkou ve zvoleném měřítku m f je vektor,
2.8 Zobecnění vztahů mezi zatížením a vnitřními silami prutu (rovinný prut zatížený v rovině) df x =f x.ds df z =f z.ds. M+dM x. ds=r.dϕ.
 .8 Zobecnění vtahů mei atížením a vnitřními silami prutu (rovinný prut atížený v rovině) µ x N V M dm µ df df x =R. MdM x NdN VdV Náhradní břemena: df x = x. df =. dm µ =µ. Obecný rovinný prut: spojité
.8 Zobecnění vtahů mei atížením a vnitřními silami prutu (rovinný prut atížený v rovině) µ x N V M dm µ df df x =R. MdM x NdN VdV Náhradní břemena: df x = x. df =. dm µ =µ. Obecný rovinný prut: spojité
Pružnost a pevnost. 2. přednáška, 10. října 2016
 Pružnost a pevnost 2. přednáška, 10. října 2016 Prut namáhaný jednoduchým ohybem: rovnoměrně ohýbaný prut nerovnoměrně ohýbaný prut příklad výpočet napětí a ohybu vliv teplotních měn příklad nerovnoměrné
Pružnost a pevnost 2. přednáška, 10. října 2016 Prut namáhaný jednoduchým ohybem: rovnoměrně ohýbaný prut nerovnoměrně ohýbaný prut příklad výpočet napětí a ohybu vliv teplotních měn příklad nerovnoměrné
Statika 1. Reakce na rovinných staticky určitých konstrukcích. Miroslav Vokáč ČVUT v Praze, Fakulta architektury.
 reálných 3. přednáška Reakce na rovinných staticky určitých konstrukcích Miroslav Vokáč miroslav.vokac@cvut.cz ČVUT v Praze, Fakulta architektury 21. března 2016 Dřevěný trámový strop - Anežský klášter
reálných 3. přednáška Reakce na rovinných staticky určitých konstrukcích Miroslav Vokáč miroslav.vokac@cvut.cz ČVUT v Praze, Fakulta architektury 21. března 2016 Dřevěný trámový strop - Anežský klášter
1 ÚVOD 1. Odolání vlivům se prokazuje statickým resp. dynamickým výpočtem.
 1 ÚVOD 1 1 Úvod Stavební konstrukce musí být navržena (a provedena) tak, aby vyhovovala požadovanému účelu a odolala vlivům, které se mohou vyskytnout během její životnosti. Odolání vlivům se prokazuje
1 ÚVOD 1 1 Úvod Stavební konstrukce musí být navržena (a provedena) tak, aby vyhovovala požadovanému účelu a odolala vlivům, které se mohou vyskytnout během její životnosti. Odolání vlivům se prokazuje
Téma 7 Smyková napětí v ohýbaných nosnících
 Pružnost a plasticita,.ročník bakalářského studia Téma 7 Smková napětí v ohýbaných nosnících Základní vtah a předpoklad řešení Výpočet smkového napětí vbraných průřeů Dimenování nosníků namáhaných na smk
Pružnost a plasticita,.ročník bakalářského studia Téma 7 Smková napětí v ohýbaných nosnících Základní vtah a předpoklad řešení Výpočet smkového napětí vbraných průřeů Dimenování nosníků namáhaných na smk
Téma 5 Lomený a zakřivený nosník
 Stavební statika, 1.ročník bakalářského studia Téma 5 Lomený a zakřivený nosník Rovinně lomený nosník v rovinné úloze Rovinně lomený nosník v příčné úloze Prostorově lomený nosník Katedra stavební mechaniky
Stavební statika, 1.ročník bakalářského studia Téma 5 Lomený a zakřivený nosník Rovinně lomený nosník v rovinné úloze Rovinně lomený nosník v příčné úloze Prostorově lomený nosník Katedra stavební mechaniky
Kapitola 4: Průběh funkce 1/11
 Kapitola 4: Průběh funkce 1/11 Funkce monotonní 2/11 Věta: Necht je f spojitá a má derivaci na intervalu I. Potom platí (i) Je-li f (x) > 0 na I, je f rostoucí na I. (ii) Je-li f (x) 0 na I, je f neklesající
Kapitola 4: Průběh funkce 1/11 Funkce monotonní 2/11 Věta: Necht je f spojitá a má derivaci na intervalu I. Potom platí (i) Je-li f (x) > 0 na I, je f rostoucí na I. (ii) Je-li f (x) 0 na I, je f neklesající
Zakřivený nosník. Rovinně zakřivený nosník v rovinné úloze geometrie, reakce, vnitřní síly. Stavební statika, 1.ročník bakalářského studia
 Stavební statika, 1.ročník bakalářského stuia Zakřivený nosník Rovinně zakřivený nosník v rovinné úloze geometrie, reakce, vnitřní síly Katera stavební mechaniky Fakulta stavební, VŠB - Technická univerzita
Stavební statika, 1.ročník bakalářského stuia Zakřivený nosník Rovinně zakřivený nosník v rovinné úloze geometrie, reakce, vnitřní síly Katera stavební mechaniky Fakulta stavební, VŠB - Technická univerzita
Vnitřní síly v prutových konstrukcích
 Vnitřní síly v prutových konstrukcích Síla je vektorová fyikální veličina, která vyjadřuje míru působení těles nebo polí. Zavedení síly v klasické Newtonově mechanice (popis pohybu těles) dp dv F = = m
Vnitřní síly v prutových konstrukcích Síla je vektorová fyikální veličina, která vyjadřuje míru působení těles nebo polí. Zavedení síly v klasické Newtonově mechanice (popis pohybu těles) dp dv F = = m
Předmět: SM01 ZÁKLADNÍ NÁZVOSLOVÍ STAVEBNÍCH KONSTRUKCÍ, ZATÍŽENÍ STAVEBNÍCH KONSTRUKCÍ
 Předmět: SM01 ZÁKLADNÍ NÁZVOSLOVÍ STAVEBNÍCH KONSTRUKCÍ, ZATÍŽENÍ STAVEBNÍCH KONSTRUKCÍ prof. Ing. Michal POLÁK, CSc. Fakulta stavební, ČVUT v Praze ZÁKLADNÍ NÁZVOSLOVÍ STAVEBNÍCH KONSTRUKCÍ: KONSTRUKČNÍ
Předmět: SM01 ZÁKLADNÍ NÁZVOSLOVÍ STAVEBNÍCH KONSTRUKCÍ, ZATÍŽENÍ STAVEBNÍCH KONSTRUKCÍ prof. Ing. Michal POLÁK, CSc. Fakulta stavební, ČVUT v Praze ZÁKLADNÍ NÁZVOSLOVÍ STAVEBNÍCH KONSTRUKCÍ: KONSTRUKČNÍ
Stavební mechanika přednáška, 10. dubna 2017
 Stavební mechanika 3 7. přednáška, 10. dubna 2017 Stavební mechanika 3 7. přednáška, 10. dubna 2017 Obecná deformační metoda 8) poznámky k využití symetrie 9) využití výpočetních programů 10) kontrola
Stavební mechanika 3 7. přednáška, 10. dubna 2017 Stavební mechanika 3 7. přednáška, 10. dubna 2017 Obecná deformační metoda 8) poznámky k využití symetrie 9) využití výpočetních programů 10) kontrola
Téma 12, modely podloží
 Téma 1, modely podloží Statika stavebních konstrukcí II., 3.ročník bakalářského studia Úvod Winklerův model podloží Pasternakův model podloží Pružný poloprostor Nosník na pružném Winklerově podloží, řešení
Téma 1, modely podloží Statika stavebních konstrukcí II., 3.ročník bakalářského studia Úvod Winklerův model podloží Pasternakův model podloží Pružný poloprostor Nosník na pružném Winklerově podloží, řešení
Kapitola 4: Průběh funkce 1/11
 Kapitola 4: Průběh funkce 1/11 Funkce monotonní 2/11 Věta: Necht je f spojitá a má derivaci na intervalu I. Potom platí (i) Je-li f (x) > 0 na I, je f rostoucí na I. (ii) Je-li f (x) 0 na I, je f neklesající
Kapitola 4: Průběh funkce 1/11 Funkce monotonní 2/11 Věta: Necht je f spojitá a má derivaci na intervalu I. Potom platí (i) Je-li f (x) > 0 na I, je f rostoucí na I. (ii) Je-li f (x) 0 na I, je f neklesající
semestr: Letní 2014/2015 předmět: Stavební mechanika 2 (SM02)
 Požadavky pro písemné vypracování domácích cvičení cvičící: Vladimír Šána, B380 semestr: Letní 2014/2015 předmět: Stavební mechanika 2 (SM02) 1 Docházka na cvičení Docházka na cvičení je dobrovolná a nebude
Požadavky pro písemné vypracování domácích cvičení cvičící: Vladimír Šána, B380 semestr: Letní 2014/2015 předmět: Stavební mechanika 2 (SM02) 1 Docházka na cvičení Docházka na cvičení je dobrovolná a nebude
OHYB (Napjatost) M A M + qc a + b + c ) M A = 2M qc a + b + c )
 3.3 Řešené příklady Příklad 1: Pro nosník na obrázku vyšetřete a zakreslete reakce, T (x) a M(x). Dále určete M max a proveďte dimenzování pro zadaný průřez. Dáno: a = 0.5 m, b = 0.3 m, c = 0.4 m, d =
3.3 Řešené příklady Příklad 1: Pro nosník na obrázku vyšetřete a zakreslete reakce, T (x) a M(x). Dále určete M max a proveďte dimenzování pro zadaný průřez. Dáno: a = 0.5 m, b = 0.3 m, c = 0.4 m, d =
2. kapitola. Co jsou to vnitřní síly, jakými způsoby se dají určit, to vše jsme se naučili v první kapitole.
 2. kapitola Stavební mechanika 2 Janek Faltýnek SI J (43) Průběhy vnitřních sil Teoretická část: V tomto příkladu máme za úkol vyšetřit průběhy vnitřních sil na rovinné konstrukci zatížené libovolným spojitým
2. kapitola Stavební mechanika 2 Janek Faltýnek SI J (43) Průběhy vnitřních sil Teoretická část: V tomto příkladu máme za úkol vyšetřit průběhy vnitřních sil na rovinné konstrukci zatížené libovolným spojitým
Vzpěr jednoduchého rámu, diferenciální operátory. Lenka Dohnalová
 1 / 40 Vzpěr jednoduchého rámu, diferenciální operátory Lenka Dohnalová ČVUT, fakulta stavební, ZS 2015/2016 katedra stavební mechaniky a katedra matematiky, Odborné vedení: doc. Ing. Jan Zeman, Ph.D.,
1 / 40 Vzpěr jednoduchého rámu, diferenciální operátory Lenka Dohnalová ČVUT, fakulta stavební, ZS 2015/2016 katedra stavební mechaniky a katedra matematiky, Odborné vedení: doc. Ing. Jan Zeman, Ph.D.,
CVIČENÍ č. 10 VĚTA O ZMĚNĚ TOKU HYBNOSTI
 CVIČENÍ č. 10 VĚTA O ZMĚNĚ TOKU HYBNOSTI Stojící povrch, Pohybující se povrch Příklad č. 1: Vodorovný volný proud vody čtvercového průřezu o straně 25 cm dopadá kolmo na rovinnou desku. Určete velikost
CVIČENÍ č. 10 VĚTA O ZMĚNĚ TOKU HYBNOSTI Stojící povrch, Pohybující se povrch Příklad č. 1: Vodorovný volný proud vody čtvercového průřezu o straně 25 cm dopadá kolmo na rovinnou desku. Určete velikost
Definice derivace v bodě
 Definice derivace v bodě tgϕ = f ( ) f () f () : = tgϕ = lim f f () tgϕ = f f () Obecně: f f f ( ) ( ) : = lim f ( + h) f f : = lim h h Derivace zleva (zprava): f ( ) : = lim f f ( ) f ( ) : = lim + +
Definice derivace v bodě tgϕ = f ( ) f () f () : = tgϕ = lim f f () tgϕ = f f () Obecně: f f f ( ) ( ) : = lim f ( + h) f f : = lim h h Derivace zleva (zprava): f ( ) : = lim f f ( ) f ( ) : = lim + +
studentská kopie 3. Vaznice - tenkostěnná 3.1 Vnitřní (mezilehlá) vaznice
 3. Vaznice - tenkostěnná 3.1 Vnitřní (mezilehlá) vaznice Vaznice bude přenášet pouze zatížení působící kolmo k rovině střechy. Přenos zatížení působícího rovnoběžně se střešní rovinou bude popsán v poslední
3. Vaznice - tenkostěnná 3.1 Vnitřní (mezilehlá) vaznice Vaznice bude přenášet pouze zatížení působící kolmo k rovině střechy. Přenos zatížení působícího rovnoběžně se střešní rovinou bude popsán v poslední
STAVEBNÍ ÚPRAVY ZÁMEČNICKÉ DÍLNY V AREÁLU FIRMY ZLKL S.R.O. V LOŠTICÍCH P.Č. 586/1 V K.Ú. LOŠTICE
 Stavba : Objekt : STAVEBNÍ ÚPRAVY ZÁMEČNICKÉ DÍLNY V AREÁLU FIRMY ZLKL S.R.O. V LOŠTICÍCH P.Č. 586/1 V K.Ú. LOŠTICE - Dokumentace : Prováděcí projekt Část : Konstrukční část Oddíl : Ocelové konstrukce
Stavba : Objekt : STAVEBNÍ ÚPRAVY ZÁMEČNICKÉ DÍLNY V AREÁLU FIRMY ZLKL S.R.O. V LOŠTICÍCH P.Č. 586/1 V K.Ú. LOŠTICE - Dokumentace : Prováděcí projekt Část : Konstrukční část Oddíl : Ocelové konstrukce
Téma 8 Příčně zatížený rám a rošt
 Statika stavebních konstrukcí I.,.ročník bakalářského studia Téma 8 Příčně zatížený rám a rošt Základní vlastnosti příčně zatíženého rámu Jednoduchý příčně zatížený otevřený rám Základní vlastnosti roštu
Statika stavebních konstrukcí I.,.ročník bakalářského studia Téma 8 Příčně zatížený rám a rošt Základní vlastnosti příčně zatíženého rámu Jednoduchý příčně zatížený otevřený rám Základní vlastnosti roštu
ENÁ ŽELEZOBETONOVÁ DESKA S OTVOREM VE SLOUPOVÉM PRUHU
 P Ř Í K L A D Č. 4 LOKÁLNĚ PODEPŘENÁ ŽELEZOBETONOVÁ DESKA S OTVOREM VE SLOUPOVÉM PRUHU Projekt : FRVŠ 011 - Analýza metod výpočtu železobetonových lokálně podepřených desek Řešitelský kolektiv : Ing. Martin
P Ř Í K L A D Č. 4 LOKÁLNĚ PODEPŘENÁ ŽELEZOBETONOVÁ DESKA S OTVOREM VE SLOUPOVÉM PRUHU Projekt : FRVŠ 011 - Analýza metod výpočtu železobetonových lokálně podepřených desek Řešitelský kolektiv : Ing. Martin
IX. Vyšetřování průběhu funkce
 IX. Vyšetřování průběhu funkce Úvodní poznámky: Cíl: vyšetřit průběh dané funkce f. Zahrnuje: základní vlastnosti: D(f), spojitost, limity v krajních bodech, průsečíky s osami souřadnic, intervaly, kde
IX. Vyšetřování průběhu funkce Úvodní poznámky: Cíl: vyšetřit průběh dané funkce f. Zahrnuje: základní vlastnosti: D(f), spojitost, limity v krajních bodech, průsečíky s osami souřadnic, intervaly, kde
1/7. Úkol č. 9 - Pružnost a pevnost A, zimní semestr 2011/2012
 Úkol č. 9 - Pružnost a pevnost A, zimní semestr 2011/2012 Úkol řešte ve skupince 2-3 studentů. Den narození zvolte dle jednoho člena skupiny. Řešení odevzdejte svému cvičícímu. Na symetrické prosté krokevní
Úkol č. 9 - Pružnost a pevnost A, zimní semestr 2011/2012 Úkol řešte ve skupince 2-3 studentů. Den narození zvolte dle jednoho člena skupiny. Řešení odevzdejte svému cvičícímu. Na symetrické prosté krokevní
Zatížení stálá a užitná
 ZÁSADY OVĚŘOVÁNÍ EXISTUJÍCÍCH KONSTRUKCÍ Zatížení stálá a užitná prof. Ing. Milan Holický, DrSc. Kloknerův ústav, ČVUT v Praze 1. Zatížení stálá 2. Příklad stanovení stálého zatížení na základě zkoušek
ZÁSADY OVĚŘOVÁNÍ EXISTUJÍCÍCH KONSTRUKCÍ Zatížení stálá a užitná prof. Ing. Milan Holický, DrSc. Kloknerův ústav, ČVUT v Praze 1. Zatížení stálá 2. Příklad stanovení stálého zatížení na základě zkoušek
D STAVEBNĚ KONSTRUKČNÍ ŘEŠENÍ
 D.1.2 - STAVEBNĚ KONSTRUKČNÍ ŘEŠENÍ - TECHNICKÁ ZPRÁVA - STATICKÝ VÝPOČET Vypracoval: Ing. Andrej Smatana Autorizovaný inženýr pro statiku a dynamiku staveb ČKAIT: 1005325 Tel.: 608 363 318 web: www.statikastaveb.eu
D.1.2 - STAVEBNĚ KONSTRUKČNÍ ŘEŠENÍ - TECHNICKÁ ZPRÁVA - STATICKÝ VÝPOČET Vypracoval: Ing. Andrej Smatana Autorizovaný inženýr pro statiku a dynamiku staveb ČKAIT: 1005325 Tel.: 608 363 318 web: www.statikastaveb.eu
HUTNÍ PROJEKT OSTRAVA a.s. STATICKÝ VÝPOČET
 HUTNÍ PROJEKT OSTRAVA a.s. držitel certifikátu ISO 9001 a ISO 14001 STATICKÝ VÝPOČET Objednatel Stavba Objekt Část Stň : VÍTKOVICE ARÉNA, a.s. : STAVEBNÍ ÚPRAVY V HALE ČEZ ARÉNA : SO 003 STAVEBNÍ ÚPRAVY
HUTNÍ PROJEKT OSTRAVA a.s. držitel certifikátu ISO 9001 a ISO 14001 STATICKÝ VÝPOČET Objednatel Stavba Objekt Část Stň : VÍTKOVICE ARÉNA, a.s. : STAVEBNÍ ÚPRAVY V HALE ČEZ ARÉNA : SO 003 STAVEBNÍ ÚPRAVY
Požadavky pro písemné vypracování domácích cvičení
 Požadavky pro písemné vypracování domácích cvičení (cvičící: Vladimír Šána, B380) 1. Docházka na cvičení Docházka na cvičení je dobrovolná a nebude na ní brán zřetel při udělování zápočtů. Naopak budu
Požadavky pro písemné vypracování domácích cvičení (cvičící: Vladimír Šána, B380) 1. Docházka na cvičení Docházka na cvičení je dobrovolná a nebude na ní brán zřetel při udělování zápočtů. Naopak budu
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ 02 STATICKÝ VÝPOČET
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES 02 STATICKÝ VÝPOČET
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STAVEBNÍ ÚSTAV KOVOVÝCH A DŘEVĚNÝCH KONSTRUKCÍ FACULTY OF CIVIL ENGINEERING INSTITUTE OF METAL AND TIMBER STRUCTURES 02 STATICKÝ VÝPOČET
Osové namáhání osová síla N v prutu
 Osové nmáhání osová síl v prutu 3 typy úloh:. Pruty příhrdové konstrukce, táhl Dvě podmínky rovnováhy v kždém styčníku: F ix 0 F iz 0. Táhl podporující pevnou ztíženou desku R z M ib 0 P R R b P 6 6 P
Osové nmáhání osová síl v prutu 3 typy úloh:. Pruty příhrdové konstrukce, táhl Dvě podmínky rovnováhy v kždém styčníku: F ix 0 F iz 0. Táhl podporující pevnou ztíženou desku R z M ib 0 P R R b P 6 6 P
Funkce. RNDR. Yvetta Bartáková. Gymnázium, SOŠ a VOŠ Ledeč nad Sázavou
 Funkce RNDR. Yvetta Bartáková Gmnázium, SOŠ a VOŠ Ledeč nad Sázavou Derivace funkce VY INOVACE_05 0_M Gmnázium, SOŠ a VOŠ Ledeč nad Sázavou Definice Mějme funkci f definovanou v okolí bodu 0. Eistuje-li
Funkce RNDR. Yvetta Bartáková Gmnázium, SOŠ a VOŠ Ledeč nad Sázavou Derivace funkce VY INOVACE_05 0_M Gmnázium, SOŠ a VOŠ Ledeč nad Sázavou Definice Mějme funkci f definovanou v okolí bodu 0. Eistuje-li
Přímková a rovinná soustava sil
 Přímková a rovinná soustava sil 1) Souřadný systém - v prostoru - v rovině + y + 2) Síla P ( nebo F) - vektorová veličina - působiště velikost orientace Soustavy sil - přehled Soustavy sil můžeme rodělit
Přímková a rovinná soustava sil 1) Souřadný systém - v prostoru - v rovině + y + 2) Síla P ( nebo F) - vektorová veličina - působiště velikost orientace Soustavy sil - přehled Soustavy sil můžeme rodělit
Dvě varianty rovinného problému: rovinná napjatost. rovinná deformace
 Rovinný problém Řešíme plošné konstrukce zatížené a uložené v jejich střednicové rovině. Dvě varianty rovinného problému: rovinná napjatost rovinná deformace 17 Rovinná deformace 1 Obsahuje složky deformace
Rovinný problém Řešíme plošné konstrukce zatížené a uložené v jejich střednicové rovině. Dvě varianty rovinného problému: rovinná napjatost rovinná deformace 17 Rovinná deformace 1 Obsahuje složky deformace
PROHLÁŠENÍ O VLASTNOSTECH / VYHLÁSENI O PARAMETROCH DoP Nr. 500/1
 PROHLÁŠENÍ O VLASTNOSTECH / VYHLÁSENI O PARAMETROCH DoP Nr. 500/1 1. Jedinečný identifikační kód typu výrobku 3140.00 2. Typ: Překlad HELUZ 23,8/1000 Únosnost (včetně vlastní tíhy) / Únosnosť 13,15 kn
PROHLÁŠENÍ O VLASTNOSTECH / VYHLÁSENI O PARAMETROCH DoP Nr. 500/1 1. Jedinečný identifikační kód typu výrobku 3140.00 2. Typ: Překlad HELUZ 23,8/1000 Únosnost (včetně vlastní tíhy) / Únosnosť 13,15 kn
Pohybové možnosti volných hmotných objektů v rovině
 REAKCE ohyové možnosti volných hmotných ojektů v rovině Stupeň volnosti n v : možnost vykont jednu složku posunu v ose souřdného systému neo pootočení. m [00] +x volný hmotný od v rovině: n v =2 (posun
REAKCE ohyové možnosti volných hmotných ojektů v rovině Stupeň volnosti n v : možnost vykont jednu složku posunu v ose souřdného systému neo pootočení. m [00] +x volný hmotný od v rovině: n v =2 (posun
VŠB Technická univerzita Ostrava Fakulta stavební, Ludvíka Podéště 1875, Ostrava. Lenka Lausová, Vladimíra Michalcová STAVEBNÍ STATIKA
 VŠB Technická univerzita Ostrava Fakulta stavební, Ludvíka Podéště 1875, 708 33 Ostrava Anežka Jurčíková, Martin Krejsa, Lenka Lausová, Vladimíra Michalcová STAVEBNÍ STATIKA Vzdělávací pomůcka Ostrava
VŠB Technická univerzita Ostrava Fakulta stavební, Ludvíka Podéště 1875, 708 33 Ostrava Anežka Jurčíková, Martin Krejsa, Lenka Lausová, Vladimíra Michalcová STAVEBNÍ STATIKA Vzdělávací pomůcka Ostrava
Výpočet vnitřních sil přímého nosníku
 Stvení sttik, 1.ročník klářského studi ýpočet vnitřních sil přímého nosníku nitřní síly přímého vodorovného nosníku prostý nosník konzol nosník s převislým koncem Ktedr stvení mechniky Fkult stvení, ŠB
Stvení sttik, 1.ročník klářského studi ýpočet vnitřních sil přímého nosníku nitřní síly přímého vodorovného nosníku prostý nosník konzol nosník s převislým koncem Ktedr stvení mechniky Fkult stvení, ŠB
Veronika Drobná VB1STI02 Ing. Michalcová Vladimíra, Ph.D.
 Příklad 1: 3;4 3;4 = =4 9 2;1,78 = = 4 9 4=16 9 =1,78 =2 =2 2 4 9 =16 9 1 = 1+ =0,49 = 1+ =0,872 =0 =10 6+ 2,22=0 =3,7 6+ 2,22=0 =3,7 + =0 3,7+3,7=0 0=0 =60,64 =0 =0 + =0 =3,7 á čá 5+ 2,22=0 =3,7 5+ 2,22+
Příklad 1: 3;4 3;4 = =4 9 2;1,78 = = 4 9 4=16 9 =1,78 =2 =2 2 4 9 =16 9 1 = 1+ =0,49 = 1+ =0,872 =0 =10 6+ 2,22=0 =3,7 6+ 2,22=0 =3,7 + =0 3,7+3,7=0 0=0 =60,64 =0 =0 + =0 =3,7 á čá 5+ 2,22=0 =3,7 5+ 2,22+
Statika 1. Vnitřní síly na prutech. Miroslav Vokáč 11. dubna ČVUT v Praze, Fakulta architektury. Statika 1. M.
 Definování 4. přednáška prutech iroslav okáč miroslav.vokac@cvut.cz ČUT v Praze, Fakulta architektury 11. dubna 2016 prutech nitřní síly síly působící uvnitř tělesa (desky, prutu), které vznikají působením
Definování 4. přednáška prutech iroslav okáč miroslav.vokac@cvut.cz ČUT v Praze, Fakulta architektury 11. dubna 2016 prutech nitřní síly síly působící uvnitř tělesa (desky, prutu), které vznikají působením
Příklad 7 Průhyb nosníku - složitější případ
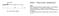 Příklad 7 Průhyb nosníku - složitější případ Zadání Nosník s proměnným průřezem je na obrázku. Průřezy a jsou obdélníkové, výška prvního průřezu je, násobkem výšky druhého průřezu. a) Pomocí metody integrace
Příklad 7 Průhyb nosníku - složitější případ Zadání Nosník s proměnným průřezem je na obrázku. Průřezy a jsou obdélníkové, výška prvního průřezu je, násobkem výšky druhého průřezu. a) Pomocí metody integrace
Rovinné přetvoření. Posunutí (translace) TEORIE K M2A+ULA
 Rovinné přetvoření Rovinné přetvoření, neboli, jak se také často nazývá, geometrická transformace je vlastně lineární zobrazení v prostoru s nějakou soustavou souřadnic. Jde v něm o přepočet souřadnic
Rovinné přetvoření Rovinné přetvoření, neboli, jak se také často nazývá, geometrická transformace je vlastně lineární zobrazení v prostoru s nějakou soustavou souřadnic. Jde v něm o přepočet souřadnic
NÁVRH OHYBOVÉ VÝZTUŽE ŽB TRÁMU
 NÁVRH OHYBOVÉ VÝZTUŽE ŽB TRÁU Navrhněte ohybovou výztuž do železobetonového nosníku uvedeného na obrázku. Kromě vlastní tíhy je nosník zatížen bodovou silou od obvodového pláště ostatním stálým rovnoměrným
NÁVRH OHYBOVÉ VÝZTUŽE ŽB TRÁU Navrhněte ohybovou výztuž do železobetonového nosníku uvedeného na obrázku. Kromě vlastní tíhy je nosník zatížen bodovou silou od obvodového pláště ostatním stálým rovnoměrným
RBZS 5. Schodiště Schodiště
 Schodiště podesta odpočívadlo hlavní podesta mezipodesta schodišťové rameno nástupní výstupní zrcadlo stupeň stupnice podstupnice jalový stupeň výška, šířka stupně Schodiště termíny přímočaré Typy schodišť
Schodiště podesta odpočívadlo hlavní podesta mezipodesta schodišťové rameno nástupní výstupní zrcadlo stupeň stupnice podstupnice jalový stupeň výška, šířka stupně Schodiště termíny přímočaré Typy schodišť
Atic, s.r.o. a Ing. arch. Libor Žák
 Atic, s.r.o. a Ing. arch. Libor Žák Riegrova, 62 00 Brno Sdružení tel. 2 286, 60 323 6 email: zak.apk@arch.cz Investor : Stavba : Objekt : Jihomoravský kraj Brno, Žerotínovo nám. 3/, PSČ 60 82 KOMPETENČNÍ
Atic, s.r.o. a Ing. arch. Libor Žák Riegrova, 62 00 Brno Sdružení tel. 2 286, 60 323 6 email: zak.apk@arch.cz Investor : Stavba : Objekt : Jihomoravský kraj Brno, Žerotínovo nám. 3/, PSČ 60 82 KOMPETENČNÍ
P Ř Í K L A D Č. 3 LOKÁLNĚ PODEPŘENÁ ŽELEZOBETONOVÁ DESKA S OTVOREM VE STŘEDNÍM PRUHU
 P Ř Í K L A D Č. 3 LOKÁLNĚ PODEPŘENÁ ŽELEZOBETONOVÁ DESKA S OTVOREM VE STŘEDNÍM PRUHU Projekt : FRVŠ 011 - Analýza metod výpočtu železobetonových lokálně podepřených desek Řešitelský kolektiv : Ing. Martin
P Ř Í K L A D Č. 3 LOKÁLNĚ PODEPŘENÁ ŽELEZOBETONOVÁ DESKA S OTVOREM VE STŘEDNÍM PRUHU Projekt : FRVŠ 011 - Analýza metod výpočtu železobetonových lokálně podepřených desek Řešitelský kolektiv : Ing. Martin
Projevy dotvarování na konstrukcích (na úrovni průřezových modelů)
 PŘEDNÁŠKY Projevy dotvarování na konstrukcích (na úrovni průřezových modelů) Volné dotvarování Vázané dotvarování Dotvarování a geometrická nelinearita Volné dotvarování Vývoj deformací není omezován staticky
PŘEDNÁŠKY Projevy dotvarování na konstrukcích (na úrovni průřezových modelů) Volné dotvarování Vázané dotvarování Dotvarování a geometrická nelinearita Volné dotvarování Vývoj deformací není omezován staticky
BO009 KOVOVÉ MOSTY 1 NÁVOD NA VÝPOČET VNITŘNÍCH SIL NA PODÉLNÝCH VÝZTUHÁCH ORTOTROPNÍ MOSTOVKY. AUTOR: Ing. MARTIN HORÁČEK, Ph.D.
 BO009 KOVOVÉ MOSTY 1 NÁVOD NA VÝPOČET VNITŘNÍCH SIL NA PODÉLNÝCH VÝZTUHÁCH ORTOTROPNÍ MOSTOVKY AUTOR: Ing. MARTIN HORÁČEK, Ph.D. Obsah Stanovení pérové konstanty poddajné podpory... - 3-1.1 Princip stanovení
BO009 KOVOVÉ MOSTY 1 NÁVOD NA VÝPOČET VNITŘNÍCH SIL NA PODÉLNÝCH VÝZTUHÁCH ORTOTROPNÍ MOSTOVKY AUTOR: Ing. MARTIN HORÁČEK, Ph.D. Obsah Stanovení pérové konstanty poddajné podpory... - 3-1.1 Princip stanovení
PASPORT MÍSTNÍCH KOMUNIKACÍ - Obec Deštné - ZIMNÍ ÚDRŽBA
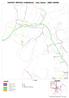 ÚK51 ÚK50 ÚK53 ÚK45 19c ÚK46 ÚK49 ÚK52 II/309 ÚK58 ÚK48 II/309 ÚK47 ÚK41 21c ÚK40 ÚK42 20c III/3093 ÚK43 ÚK44 ÚK38 13d II/310 13d ÚK30 ÚK39 ÚK37 ÚK36 ÚK35 ÚK34 ÚK21 10d 9c ÚK15 7c ÚK19 ÚK17 26c 27c 26c-M1
ÚK51 ÚK50 ÚK53 ÚK45 19c ÚK46 ÚK49 ÚK52 II/309 ÚK58 ÚK48 II/309 ÚK47 ÚK41 21c ÚK40 ÚK42 20c III/3093 ÚK43 ÚK44 ÚK38 13d II/310 13d ÚK30 ÚK39 ÚK37 ÚK36 ÚK35 ÚK34 ÚK21 10d 9c ÚK15 7c ÚK19 ÚK17 26c 27c 26c-M1
FYZIKA I. Složené pohyby (vrh šikmý)
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ FYZIKA I Složené pohb (vrh šikmý) Prof. RNDr. Vilém Mádr, CSc. Prof. In. Libor Hlaváč, Ph.D. Doc. In. Irena Hlaváčová, Ph.D. Mr. Art. Damar
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ FYZIKA I Složené pohb (vrh šikmý) Prof. RNDr. Vilém Mádr, CSc. Prof. In. Libor Hlaváč, Ph.D. Doc. In. Irena Hlaváčová, Ph.D. Mr. Art. Damar
Statický výpočet komínové výměny a stropního prostupu (vzorový příklad)
 KERAMICKÉ STROPY HELUZ MIAKO Tabulky statických únosností stropy HELUZ MIAKO Obsah tabulka č. 1 tabulka č. 2 tabulka č. 3 tabulka č. 4 tabulka č. 5 tabulka č. 6 tabulka č. 7 tabulka č. 8 tabulka č. 9 tabulka
KERAMICKÉ STROPY HELUZ MIAKO Tabulky statických únosností stropy HELUZ MIAKO Obsah tabulka č. 1 tabulka č. 2 tabulka č. 3 tabulka č. 4 tabulka č. 5 tabulka č. 6 tabulka č. 7 tabulka č. 8 tabulka č. 9 tabulka
Výpočet sedání kruhového základu sila
 Inženýrský manuál č. 22 Aktualizace 06/2016 Výpočet sedání kruhového základu sila Program: MKP Soubor: Demo_manual_22.gmk Cílem tohoto manuálu je popsat řešení sedání kruhového základu sila pomocí metody
Inženýrský manuál č. 22 Aktualizace 06/2016 Výpočet sedání kruhového základu sila Program: MKP Soubor: Demo_manual_22.gmk Cílem tohoto manuálu je popsat řešení sedání kruhového základu sila pomocí metody
PŘÍKLADY PŮSOBENÍ A VÝPOČTU ZATÍŽENÍ VLASTNÍ TÍHOU:
 PŘÍKLADY PŮSOBENÍ A VÝPOČTU ZATÍŽENÍ VLASTNÍ TÍHOU: Vykreslete zatížení zadaných prutů od vlastní tíhy, jsou-li rozměry průřezu b,h [m], objemová hmotnost ρ [kg.m -3 ] a tíhové zrychlení a g [m.s -2 ]
PŘÍKLADY PŮSOBENÍ A VÝPOČTU ZATÍŽENÍ VLASTNÍ TÍHOU: Vykreslete zatížení zadaných prutů od vlastní tíhy, jsou-li rozměry průřezu b,h [m], objemová hmotnost ρ [kg.m -3 ] a tíhové zrychlení a g [m.s -2 ]
trojkloubový nosník bez táhla a s
 Kapitola 10 Rovinné nosníkové soustavy: trojkloubový nosník bez táhla a s táhlem 10.1 Trojkloubový rám Trojkloubový rám se skládá ze dvou rovinně lomených nosníků v rovinné úloze s kloubovým spojením a
Kapitola 10 Rovinné nosníkové soustavy: trojkloubový nosník bez táhla a s táhlem 10.1 Trojkloubový rám Trojkloubový rám se skládá ze dvou rovinně lomených nosníků v rovinné úloze s kloubovým spojením a
Téma 6 Staticky neurčitý rovinný oblouk. kloubový příhradový nosník
 Stvení mechnik,.ročník klářského studi AST Tém 6 Stticky neurčitý rovinný olouk Stticky neurčitý rovinný klouový příhrdový nosník Zákldní vlstnosti stticky neurčitého rovinného olouku Dvoklouový olouk,
Stvení mechnik,.ročník klářského studi AST Tém 6 Stticky neurčitý rovinný olouk Stticky neurčitý rovinný klouový příhrdový nosník Zákldní vlstnosti stticky neurčitého rovinného olouku Dvoklouový olouk,
Normálová napětí v prutech namáhaných na ohyb
 Pružnost a plasticita, 2.ročník kombinovaného studia Normálová napětí v prutech namáhaných na ohb Základní vtah a předpoklad řešení Výpočet normálového napětí Dimenování nosníků namáhaných na ohb Složené
Pružnost a plasticita, 2.ročník kombinovaného studia Normálová napětí v prutech namáhaných na ohb Základní vtah a předpoklad řešení Výpočet normálového napětí Dimenování nosníků namáhaných na ohb Složené
Stavební mechanika 1 (K132SM01)
 Stavební mechanika 1 (K132SM01) Přednáší: doc. Ing. Matěj Lepš, Ph.D. Katedra mechaniky K132 Termín řádného zápočtového testu je středa 26.11 12:00 B286 Organizace testu: Studenti podle příjmení A-L 11:50-12:50
Stavební mechanika 1 (K132SM01) Přednáší: doc. Ing. Matěj Lepš, Ph.D. Katedra mechaniky K132 Termín řádného zápočtového testu je středa 26.11 12:00 B286 Organizace testu: Studenti podle příjmení A-L 11:50-12:50
Stěnové nosníky. Obr. 1 Stěnové nosníky - průběh σ x podle teorie lineární pružnosti.
 Stěnové nosníky Stěnový nosník je plošný rovinný prvek uložený na podporách tak, že prvek je namáhán v jeho rovině. Porovnáme-li chování nosníků o výškách h = 0,25 l a h = l, při uvažování lineárně pružného
Stěnové nosníky Stěnový nosník je plošný rovinný prvek uložený na podporách tak, že prvek je namáhán v jeho rovině. Porovnáme-li chování nosníků o výškách h = 0,25 l a h = l, při uvažování lineárně pružného
Ing. Jitka Řezníčková, CSc., Ing. Jan Šleichrt, Ing. Jan Vyčichl, Ph.D.
 Statika (18SAT) letní semestr 2016/2017 přednášky: Ing. Daniel Kytýř, Ph.D. cvičení: Ing. Tomáš Doktor, Ing. Petr Koudelka, Ing. Nela Krčmářová, Ing. Jitka Řezníčková, CSc., Ing. Jan Šleichrt, Ing. Jan
Statika (18SAT) letní semestr 2016/2017 přednášky: Ing. Daniel Kytýř, Ph.D. cvičení: Ing. Tomáš Doktor, Ing. Petr Koudelka, Ing. Nela Krčmářová, Ing. Jitka Řezníčková, CSc., Ing. Jan Šleichrt, Ing. Jan
Statika soustavy těles.
 Statika soustavy těles Základy mechaniky, 6 přednáška Obsah přednášky : uvolňování soustavy těles, sestavování rovnic rovnováhy a řešení reakcí, statická určitost, neurčitost a pohyblivost, prut a jeho
Statika soustavy těles Základy mechaniky, 6 přednáška Obsah přednášky : uvolňování soustavy těles, sestavování rovnic rovnováhy a řešení reakcí, statická určitost, neurčitost a pohyblivost, prut a jeho
BIOMECHANIKA KINEMATIKA
 BIOMECHANIKA KINEMATIKA MECHANIKA Mechanika je nejstarším oborem fyziky (z řeckého méchané stroj). Byla původně vědou, která se zabývala konstrukcí strojů a jejich činností. Mechanika studuje zákonitosti
BIOMECHANIKA KINEMATIKA MECHANIKA Mechanika je nejstarším oborem fyziky (z řeckého méchané stroj). Byla původně vědou, která se zabývala konstrukcí strojů a jejich činností. Mechanika studuje zákonitosti
VÝPOČET PŘETVOŘENÍ PŘÍHRADOVÝCH KONSTRUKCÍ SILOVOU METODOU řešený příklad pro BO004
 VÝPOČET PŘETVOŘENÍ PŘÍHRADOVÝCH KONSTRUKCÍ SILOVOU METODOU řešený příklad pro BO00 Slová metoda využívá prncp vrtuální práce. Zavádí se nový zatěžovací stav vrtuální zatížení. V tomto zatěžovacím stavu
VÝPOČET PŘETVOŘENÍ PŘÍHRADOVÝCH KONSTRUKCÍ SILOVOU METODOU řešený příklad pro BO00 Slová metoda využívá prncp vrtuální práce. Zavádí se nový zatěžovací stav vrtuální zatížení. V tomto zatěžovacím stavu
P Ř Í K L A D Č. 5 LOKÁLNĚ PODEPŘENÁ ŽELEZOBETONOVÁ DESKA S VÝRAZNĚ ROZDÍLNÝM ROZPĚTÍM NÁSLEDUJÍCÍCH POLÍ
 P Ř Í K L A D Č. 5 LOKÁLNĚ PODEPŘENÁ ŽELEZOBETONOVÁ DESKA S VÝRAZNĚ ROZDÍLNÝ ROZPĚTÍ NÁSLEDUJÍCÍCH POLÍ Projekt : FRVŠ 011 - Analýza metod výpočtu železobetonových lokálně podepřených desek Řešitelský
P Ř Í K L A D Č. 5 LOKÁLNĚ PODEPŘENÁ ŽELEZOBETONOVÁ DESKA S VÝRAZNĚ ROZDÍLNÝ ROZPĚTÍ NÁSLEDUJÍCÍCH POLÍ Projekt : FRVŠ 011 - Analýza metod výpočtu železobetonových lokálně podepřených desek Řešitelský
