OSTRAVSKÁ UNIVERZITA P Ř ÍRODOVĚ DECKÁ FAKULTA NEURONOVÉ SÍTĚ 1
|
|
|
- Vojtěch Horák
- před 6 lety
- Počet zobrazení:
Transkript
1 OSTRAVSKÁ UNIVERZITA P Ř ÍRODOVĚ DECKÁ FAKULTA NEURONOVÉ SÍTĚ EVA VOLNÁ OSTRAVA 2002
2 Cíle předmětu Seznámt studenta se zálady teore neuronových sítí a dát mu potřebnou motvac pro pochopení důležtost teore pro prax Důraz bude laden neen na záladní teor, ale na schopnost aplovat př řešení onrétních příladů Všechny v textu uvedené popsy algortmů sou převzaty z [2] Po prostudování textu budete znát: TYTO UČ EBNÍ TEXTY JSOU URČ ENY STUDENTŮ M INFORMATIKY PRO PŘ EDMĚ T NEURONOVÉ SÍTĚ I JSOU V NICH VYSVĚ TLENY VŠECHNY ZÁKLADNÍ POJMY Z TEORIE UMĚ LÝCH NEURONOVÝCH SÍTÍ V JEDNOTLIVÝCH KAPITOLÁCH JSOU POSTUPNĚ PODLE OBTÍŽNOSTI UVEDENY ZÁKLADNÍ MODELY NEURONOVÝCH SÍTÍ (TJ PERCEPTRON, ADALINE, MADALINE, DOPŘ EDNÁ VÍCEVRSTVÁ NEURONOVÁ SÍŤ S ADAPTAČ NÍ METODOU BACKPROPAGATION, ASOCIATIVNÍ NEURONOVÉ SÍTĚ A NEURONOVÉ SÍTĚ PRACUJÍCÍ NA PRINCIPU SAMOORGANIZACE), A TO JEJICH ARCHITEKTURA, AKTIVNÍ DYNAMIKA A ADAPTIVNÍ DYNAMIKA
3 Obsah předmětu Úvod do problematy neuronových sítí 2 Hebbovo učení 3 Neuronová síť 4 Perceptron 5 Adalne Madalne 6 Bacpropagaton 7 Varanty bacpropagaton 8 Samoorganzace 9 Counterpropagaton 0 Asocatvní neuronové sítě Hopfeldova síť 2 Dvousměrná asocatvní paměť 3 Postavení neuronových sítí v nformatce Čas potřebný prostudování učva předmětu: eden semestr
4 ÚVOD DO PROBLEMATIKY NEURONOVÝCH SÍTÍ V této úvodní aptole se stručně seznámíte s hstorí neuronových sítí a se záladním matematcým modelem bologcého neuronu, t formálním neuronem Z tohoto modelu budeme dále vycházet, a proto e nutné, abyste eho pochopení věnoval zvýšenou pozornost Klíčová slova této aptoly: stav neuronu, bas neuronu, vntřní potencál neuronu, synaptcé váhy, atvační(přenosová) funce Hstore neuronových sítí [6] Za počáte vznu oboru neuronových sítí e považována práce Warrena McCullocha a Waltera Pttse z rou 943, teří vytvořl velm ednoduchý matematcý model neuronu, což e záladní buňa nervové soustavy Číselné hodnoty parametru v tomto modelu byly převážně bpolární, t z množny {-,0,} Uázal, že neednodušší typy neuronových sítí mohou v prncpu počítat lbovolnou artmetcou nebo logcou func Ačolv nepočítal s možností bezprostředního pratcého využtí svého modelu, ech článe měl velý vlv na ostatní badatele Napřílad zaladatel ybernety Norbert Wener se ím nsproval př studu podobnost čnnost nervové soustavy a systémů výpočetní techny Nebo autor amercého proetu eletroncých počítačů John von Neumann napsal práce, ve terých navrhoval výzum počítačů, teré by byly nsprovány čnností mozu Tyto návrhy, přestože byly honě ctovány, nepřnesly zpočátu očeávané výsledy V roce 949 napsal Donald Hebb nhu The Organzaton of Behavour, ve teré navrhl učící pravdlo pro synapse neuronů (mezneuronové rozhraní) Toto pravdlo bylo nsprováno myšlenou, že podmíněné reflexy, teré sou pozorovatelné u všech žvočchů, sou vlastnostm ednotlvých neuronů Hebb se snažl vysvětlt něteré expermentální výsledy psychologe Taé eho práce ovlvnla ostatní vědce, teří se začal zabývat podobným otázam Avša 40 a 50 léta zatím eště nepřnesla zásadní poroy v oblast neurovýpočtů Typcým příladem výzumu v tomto období byla v roce 95 onstruce prvního neuropočítače Snar, u ehož zrodu stál Marvn Mnsy Snar byl sce úspěšný z techncého hledsa, doonce ž automatcy adaptoval váhy (t míra synaptcé propustnost), ale ve sutečnost nebyl ndy využt řešení něaého zaímavého pratcého problému Ncméně eho archtetura pozdě nsprovala další onstrutéry neuropočítačů V roce 957 Fran Rosenblatt vynalezl tzv perceptron, terý e zobecněním McCullochova a Pttsova modelu neuronu pro reálný číselný obor parametrů Pro tento model navrhl učící algortmus, o terém matematcy doázal, že pro daná trénnová data nalezne po onečném počtu roů odpovídaící váhový vetor parametrů (poud exstue) nezávsle na eho počátečním nastavení Rosenblatt taé napsal ednu z prvních nh o neurovýpočtech Prncples of Neurodynamcs Na záladě tohoto výzumu Rosenblatt spolu s Charlesem Wghtmanem a dalším sestrol během let 957 a 958 první úspěšný neuropočítač, terý nesl méno Mar I Perceptron Protože původním odborným zámem Rosenblatta bylo rozpoznávání obrazců, Mar I Perceptron byl navržen pro rozpoznávání znaů Zna byl promítán na světelnou tabul, ze teré byl snímán polem 20x20 fotovodčů Intenzta 400 obrazových bodů byla vstupem do neuronové sítě perceptronů, eímž úolem bylo lasfovat, o aý zna se edná (např A, B apod) Mar I Perceptron měl 52 adaptovatelných váhových parametrů, teré byly realzovány polem 8x8x8 potencometrů Hodnota odporu u aždého potencometru, terá právě odpovídala příslušné váze, byla nastavována automatcy samostatným motorem Ten byl řízen analogovým obvodem, terý mplementoval perceptronový učící algortmus Jednotlvé perceptrony bylo možné spot se vstupy lbovolným způsobem Typcy bylo použto náhodné zapoení, aby se lustrovala schopnost perceptronu učt se požadované vzory bez přesného zapoení drátů v protladu e lascým programovatelným počítačům Díy úspěšné presentac
5 uvedeného neuropočítače se neurovýpočty, teré byly alternatvou e lascým výpočtům realzovaným na von neumannovsé archtetuře počítače, staly novým předmětem výzumu Fran Rossenblatt e proto dodnes něterým odborníy považován za zaladatele tohoto nového oboru Krátce po obevu perceptronu Bernard Wdrow se svým studenty vyvnul další typ neuronového výpočetního prvu, terý nazval ADALINE (ADAptve LInear NEuron) Tento model byl vybaven novým výonným učícím pravdlem, teré se dodnes nezměnlo Wdrow se svým studenty demonstroval funčnost ADALINE na mnoha ednoduchých typových příladech Wdrow taé založl první frmu (Memstor Corporaton) orentovanou na hardware neuropočítačů, terá v první polovně 60 let vyráběla a prodávala neuropočítače a ech omponenty Na přelomu 50 a 60 let dochází úspěšnému rozvo neurovýpočtů v oblast návrhu nových modelů neuronových sítí a ech mplementací Napřílad Karel Stenbuch vyvnul model bnární asocatvní sítě nebo Roger Barron a Lewey Glstrap založl v roce 960 první frmu zaměřenou na aplace neurovýpočtů Výsledy z uvedeného období sou shrnuty v nze Nlse Nlssona Learnng Machnes z rou 965 Přes nesporné úspěchy dosažené v tomto období se obor neuronových sítí potýal se dvěma problémy Za prvé, většna badatelů přstupovala neuronovým sítím z expermentálního hledsa a zanedbávala analytcý výzum neuronových modelů Za druhé, nadšení něterých výzumných pracovníů vedlo velé publctě neopodstatněných prohlášení (např za něol málo let bude vyvnut umělý moze) Tyto sutečnost dsredtovaly neuronové sítě v očích odborníů z ných oblastí a odradly vědce a nženýry, teří se o neurovýpočty zaímal Navíc se samostatný obor neuronových sítí vyčerpal a další ro v této oblast by býval požadoval radálně nové myšleny a postupy Nelepší odborníc oblast neuronových sítí opouštěl a začal se zabývat příbuzným obory umělé ntelgence Poslední epzodou tohoto období byla ampaň vedená Marvnem Mnsým a Seymourem Papertem, teří využl svů vlv na to, aby zdsredtoval výzum neuronových sítí, nacházeící se v rz, ve snaze přenést fnanční zdroe z této oblast na ný výzum v oblast umělé ntelgence V té době oloval ruops ech výzumné zprávy, terá napomáhala tomuto záměru Uvedený ruops byl v upravené formě publován roce 969 pod názvem Perceptrons V této nze Mnsy a Papert využl pro svou argumentac známého trválního fatu, že eden perceptron nemůže počítat ednoduchou logcou func, tzv vylučovací dsunc (XOR) Tento problém lze sce vyřešt vytvořením dvouvrstvé sítě se třem neurony, ale pro vícevrstvý perceptron nebyl v této době znám učící algortmus Autoř z toho nesprávně vyvodl, že taový algortmus vzhledem e omplovanost funce, terou vícevrstvá síť počítá, snad an není možný Jech tvrzení bylo všeobecně přato a považováno za matematcy doázané Kampaň Mnsého a Paperta byla úspěšná, výzum neuronových sítí nebyl ž déle dotován a neurovýpočty byly považovány za neperspetvní V dalším období od rou 967 do 982 probíhal výzum neuronových sítí oedněle a zolovaně, převážně mmo území Spoených států, de nha Perceptrons měla velý vlv Většna prací byla publována např pod hlavčou adaptvní zpracování sgnálů, rozpoznávání obrazců a bologcé modelování Avša ž v počátcích tohoto tchého období se neurovýpočty začal zabývat talentovaní badatelé, mez nm byl např Shun-Ich Amar, James Anderson, Kunho Fuushma, Stephen Grossberg, Harry Klopf, Teuvo Kohonen a Davd Wllshaw Tto vědc přspěl svým obevy renesanc neuronových sítí Počátem 80 let se badatelé v oblast neurovýpočtů osměll a začal podávat vlastní grantové proety zaměřené na vývo neuropočítačů a ech aplace Zásluhou programového manažera Ira Surnca začala v roce 983 amercá grantová agentura DARPA (Defense Advanced Research Proects Agency) fnančně podporovat výzum neuronových sítí a eího příladu v ráté době následovaly né organzace podporuící záladní aplovaný výzum Další zásluhu na renesanc oboru neuronových sítí měl světově uznávaný fyz John Hopfeld, terý se v této době zabýval neurovýpočty Své výsledy publoval v roce 982 a 984 Uázal souvslost něterých modelů neuronových sítí s fyzálním modely magnetcých materálů Svým zvaným přednášam, teré měl po celém světě, zísal pro neuronové sítě stovy valfovaných vědců, matematů a technologů V roce 986 publoval své výsledy badatelé z tzv PDP supny (Parallel Dstrbuted Processng Group) Ve svých pracích popsal učící algortmus zpětného šíření chyby (bacpropagaton) pro vícevrstvou neuronovou síť a vyřešl ta problém, terý se Mnsému a Pappertov v 60 letech evl ao nepřeonatelná přeáža pro využtí a další rozvo neuronových sítí Tento algortmus e doposud nepoužívaněší učící metodou neuronových sítí a eho publováním dosáhl záem o neuronové sítě svého vrcholu V roce 987 se v San Degu onala první větší onference specalzovaná na neuronové sítě (IEEE Internatonal Conference on Neural Networs), na teré byla založena meznárodní společnost pro výzum neuronových sítí INNS (Internatonal Neural Networ Socety) O ro pozdě INNS začala vydávat svů časops Neural Networs V následuících letech vznly další specalzované časopsy: Neural Computng (989), IEEE Transactons on Neural Networs (990) a mnoho ných (např v Praze vychází od rou 99 meznárodní časops Neural Networ World) Od rou 987 mnoho renovovaných unverzt založlo nové výzumné ústavy
6 zabývaící se neuronovým sítěm a vyhláslo výuové programy zaměřené na neurovýpočty Tento trend poračue dodnes Bologcý neuron [6] Původním cílem výzumu neuronových sítí byla snaha pochopt a modelovat způsob, aým myslíme a způsob, a fungue ldsý moze Neurofyzologcé poznaty umožnly vytvořt zednodušené matematcé modely, teré se daí využít pro neurovýpočty př řešení pratcých úloh z oblast umělé ntelgence To znamená, že neurofyzologe zde slouží en ao zdro nsprací a navržené modely neuronových sítí sou ž dále rozvíeny bez ohledu na to, zda modeluí ldsý moze Př vytváření modelů neuronových sítí nám nede o vytvoření dentcých opí ldsého mozu, ale chceme napodobt pouze eho záladní funce Záladním stavebním funčním prvem nervové soustavy e nervová buňa, neuron Neurony sou samostatné specalzované buňy, určené přenosu, zpracování a uchování nformací, teré sou nutné pro realzac žvotních funcí organsmu Strutura neuronu e schématcy znázorněna na obrázu Tělo buňy Synapse Axonové vláno Dendrty Obráze : Bologcý neuron Neuron e přzpůsoben pro přenos sgnálů ta, že romě vlastního těla (somatu), má vstupní a výstupní přenosové anály: dendrty a axon Z axonu odbočue řada větví (termnálů), zaončených blánou, terá se převážně stýá s výběžy (trny), dendrtů ných neuronů K přenosu nformace pa slouží unátní mezneuronové rozhraní, synapse Míra synaptcé propustnost e nostelem všech význačných nformací během celého žvota organsmu Z funčního hledsa lze synapse rozdělt na exctační, teré umožňuí rozšíření vzruchu v nervové soustavě a na nhbční, teré způsobuí eho útlum Paměťová stopa v nervové soustavě vzná pravděpodobně zaódováním synaptcých vazeb na cestě mez receptorem (čdlem orgánu) a efetorem (výonným orgánem) Šíření nformace e umožněno tím, že soma axon sou obaleny membránou, terá má schopnost za stých oolností generovat eletrcé mpulsy Tyto mpulsy sou z axonu přenášeny na dendrty ných neuronů synaptcým branam, teré svoí propustností určuí ntenztu podráždění dalších neuronů Tato podrážděné neurony př dosažení určté hranční meze, tzv prahu, samy generuí mpuls a zašťuí ta šíření příslušné nformace Po aždém průchodu sgnálu se synaptcá propustnost mění, což e předpoladem paměťové schopnost neuronů Taé propoení neuronů prodělává během žvota organsmu svů vývo: v průběhu učení se vytváří nové paměťové stopy nebo př zapomínání se synaptcé spoe přerušuí Nervová soustava člověa e velm složtý systém, terý e stále předmětem zoumání Uvedené velm zednodušené neurofyzologcé prncpy nám vša v dostatečné míře stačí formulac matematcého modelu neuronové sítě V dalších aptolách budeme používat následuícího značení: x, y Stav neuronů X, Y, t pro vstupní neurony X e x vstupní sgnál; pro ostatní neurony Y e y = f(y_n ) w Váha přřazena spoení z neuronu X do neuronu Y
7 b Bas neuronu Y y_n Vntřní potencál neuronu Y : W Váhová matce: W = {w } w Vetor vah: w = (w, w 2,, w n ) T Je to sloupec váhové matce x Norma nebo velost vetoru x θ Práh pro atvační func neuronu Y s Trénnový vstupní vetor: s = (s, s 2,, s n ) t Trénnový výstupní vetor: t = (t, t 2,, t m ) x Vstupní vetor: x = (x, x 2,, x n ) w α Změna váhy w : w = [w (new) - w (old)] Koefcent učení Formální neuron [6] Záladem matematcého modelu neuronové sítě e formální neuron Jeho strutura e schematcy zobrazena na obrázu 2 Formální neuron Y (dále en neuron) má n obecně reálných vstupů x,,x n, teré modeluí dendrty Vstupy sou ohodnoceny reálným synaptcým váham w,, w n, teré určuí ech propustnostve shodě s neurofyzologcou motvací mohou být synaptcé váhy záporné, čímž se vyadřue ech nhbční charater y b Y w w2 w n X X 2 X n Obráze 2: Formální neuron s basem Vážená suma vstupních hodnot představue vntřní potencál neuronu: y_ n = n = w x
8 Bas může být do vztahu včleněn přdáním omponent x 0 = vetoru x, t x = (, x, x 2,, x n ) Bas e dále zpracováván ao aáolv ná váha, t w 0 = b Vstup do neuronu Y e dán následuícím vztahem y_ n = n = 0 w x n = w 0 + xw = n = b + xw Hodnota vntřního potencálu y_n po dosažení prahové hodnoty b nduue výstup (stav) neuronu y, terý modelue eletrcý mpuls axonu Nelneární nárůst výstupní hodnoty y = f(y_n ) př dosažení prahové hodnoty potencálu b e dán atvační (přenosovou ) funcí f Neednodušším typem přenosové funce e ostrá nelnearta, terá má pro neuron (Y ) tvar: ( _ ) f y n = poud y_ n 0; = 0 poud y_ n < 0 Něteří autoř nepoužívaí váhový bas, ale místo toho pracuí s fxním prahem θ pro atvační func V tomto případě má přenosové funce ostrá nelnearta pro neuron (Y ) tvar: de ( _ ) f y n poud y_ n θ; = 0 poud y_ n < θ, y_ n = n = w x K lepšímu pochopení funce ednoho neuronu nám pomůže geometrcá představa načrtnutá na obrázu 3 Vstupy neuronu budeme chápat ao souřadnce bodu v n-rozměrném Euldovsém vstupním prostoru E n w n 0 = + w x = [,, n ] n w x x E + + w x > 0 0 = y = n [,, n ] n w x x E + w x < 0 0 = y = 0 n Obráze 3: Geometrcá nterpretace funce neuronu V tomto prostoru má rovnce nadrovny (v E 2 příma, v E 3 rovna) tvar: w 0 n + w x = 0 =
9 Tato nadrovna dělí vstupní prostor na dva poloprostory Souřadnce bodů [x +,,x + n ], teré leží v ednom poloprostoru, splňuí následuící nerovnost: w 0 n + + w x > 0 Body [x -,,x n - ] z druhého poloprostoru pa vyhovuí relac s opačným relačním znaménem: w 0 = n + w x < 0 = Synaptcé váhy neuronu w 0,, w n (včetně basu) lze chápat ao oefcenty této nadrovny Je zřemé, že neuron lasfue, ve terém z obou poloprostorů určených nadrovnou leží bod, ehož souřadnce sou na vstupu, t neuron realzue dchotom vstupního prostoru Neuron e tedy atvní, e-l eho stav y = a pasvní, poud e eho stav y = 0 Úoly: Vytvořte geometrcou nterpretac funce ednoho neuronu ve 2-rozměrném Euldovsém prostoru Vstupy neuronu sou souřadnce bodu v E 2
10 HEBBOVO UČ ENÍ Dříve než se pustíte do studa této aptoly, důladně se seznamte s problematou formálního neuronu a s používaným značením (vz aptola Úvod do problematy neuronových sítí ) Klíčová slova této aptoly: Hebbovo učení, trénnový vzor, váhový příruste Hebbovo učení Hebbovo učení e založeno na myšlence, že váhové hodnoty na spoení mez dvěma neurony, teré sou současně ve stavu on, budou narůstat a naopa: váhové hodnoty na spoení mez dvěma neurony, teré sou současně ve stavu off, se budou zmenšovat Uvažume ednovrstvou (dopřednou) neuronovou síť, ve teré sou všechny vstupní neurony propoeny s edným výstupní neuronem, ale ne ž navzáem mez sebou Poud sou data reprezentována v bpolární formě, lze váhové hodnoty atualzovat následovně: w (new) = w (old) + x y Pops algortmu Kro 0 Kro Incalzace všech vah: w = 0 ( = až n) Pro aždý vzor - trénnový pár, t vstupní vetor (s) a příslušný výstup (t), opaovat následuící roy (2 až 4) Kro 2 Atvovat vstupní neurony: x = s ( = až n) Kro 3 Atvovat výstupní neuron: y = t Kro 4 Atualzovat váhy podle w (new) = w (old) + x y ( = až n) Atualzovat basy podle b(new) = b(old) + y Bas lze zapsat taé ao váhovou hodnotu přřazenou výstupu z neuronu, ehož atvace má vždy hodnotu Atualzace váhových hodnot může být taé vyádřena ve vetorové formě ao w(new) = w(old) + xy
11 Váhový přírůste lze zapsat ve tvaru w = xy a potom w(new) = w(old) + w Výše uvedený algortmus e pouze edním z mnoha způsobu mplementace Hebbova pravdla učení Tento algortmus vyžadue pouze eden průchod trénnovou množnou Exstuí vša né evvalentní metody nalezení vhodných váhových hodnot, teré sou popsány dále Přílad: Hebbovo pravdlo učení pro logcou func AND v bpolární reprezentac VSTUP POŽADOVANÝ x x 2 b VÝSTUP Po předložení prvního trénnového vzoru, dostáváme následuící: VSTUP POŽADOVANÝ VÝSTUP PŘÍRUSTKY VAH VÁHOVÉ HODNOTY x x 2 b w w 2 b w w 2 b Separuící nadrovna e dána rovncí přímy x 2 = -x - x x - - Obráze 4: Hebbovo pravdlo učení pro logcou func AND v bpolární reprezentac - první trénnový vzor Předložíme-l druhý trénnový vzor, dostáváme následuící: VSTUP POŽADOVANÝ VÝSTUP PŘÍRUSTKY VAH VÁHOVÉ HODNOTY x x 2 b w w 2 b w w 2 b
12 Separuící nadrovna e pa dána rovncí přímy x 2 = 0 x x - - Obráze 5: Hebbovo pravdlo učení pro logcou func AND v bpolární reprezentac - druhý trénnový vzor Po předložení třetího trénnového vzoru, dostáváme: VSTUP POŽADOVANÝ VÝSTUP PŘÍRUSTKY VAH VÁHOVÉ HODNOTY x x 2 b w w 2 b w w 2 b Separuící nadrovna e dána rovncí přímy x 2 = -x + x x - - A naonec po předložení čtvrtého trénnového vzoru, dostáváme: Obráze 6: Hebbovo pravdlo učení pro logcou func AND v bpolární reprezentac - třetí a čtvrtý trénnový vzor VSTUP POŽADOVANÝ VÝSTUP PŘÍRUSTKY VAH VÁHOVÉ HODNOTY x x 2 b w w 2 b w w 2 b
13 Tvar separuící nadrovny (přímy) se nezměnl, t x 2 = -x + Úoly: Obasněte Hebbovo pravdlo učení pro logcou func OR v bpolární reprezentac
14 NEURONOVÁ SÍŤ Tato aptola e úvodní aptolou zabývaící se problematou vzáemného propoení neuronů, t archteturou neuronové sítě Dále s zde ozřemíme způsob, aým probíhá šíření a zpracování nformace v neuronové sít Všechny zde uvedené pomy doporuču pečlvě nastudovat, protože e budeme dále velm často používat Klíčová slova této aptoly: archtetura (topologe) neuronové sítě, organzační dynama neuronové sítě, atvní dynama neuronové sítě, adaptvní dynama neuronové sítě, homogenní neuronová síť, učení s učtelem, samoorganzace Neuronová síť [6] Každá neuronová síť e složena z formálních neuronů, teré sou vzáemně propoeny ta, že výstup ednoho neuronu e vstupem do (obecně více) neuronů Obdobně sou termnály axonu bologcého neuronu přes synaptcé vazby spoeny s dendrty ných neuronů Počet neuronů a ech vzáemné propoení v sít určue archteturu (topolog) neuronové sítě Z hledsa využtí rozlšueme v sít vstupní, pracovní (sryté, mezlehlé, vntřní) a výstupní neurony Šíření a zpracování nformace v sít e umožněno změnou stavů neuronů ležících na cestě mez vstupním a výstupním neurony Stavy všech neuronů v sít určuí stav neuronové sítě a synaptcé váhy všech spoů představuí onfgurac neuronové sítě Neuronová síť se v čase vyvíí, mění se stav neuronů, adaptuí se váhy V souvslost se změnou těchto charaterst v čase e účelné rozdělt celovou dynamu neuronové sítě do tří dynam a uvažovat pa tř režmy práce sítě: organzační (změna topologe), atvní (změna stavu) a adaptvní (změna onfgurace) Uvedené dynamy neuronové sítě sou obvyle zadány počátečním stavem a matematcou rovncí, resp pravdlem, teré určue vývo příslušné charatersty sítě (topologe, stav, onfgurace) v čase Změny, teré se řídí těmto záontostm probíhaí v odpovídaících režmech práce neuronové sítě Konretzací ednotlvých dynam pa obdržíme různé modely neuronových sítí vhodné pro řešení různých tříd úloh Organzační dynama [6] Organzační dynama specfue archteturu neuronové sítě a eí případnou změnu Změna topologe se většnou uplatňue v rámc adaptvního režmu ta, že síť e v případě potřeby rozšířena o další neurony a příslušné spoe Avša organzační dynama převážně předpoládá pevnou archteturu neuronové sítě (t taovou archteturu, terá se ž v čase nemění) Rozlšueme dva typy archtetury: cylcá (reurentní) a acylcá (dopředná) síť V případě cylcé topologe exstue v sít supna neuronů, terá e spoena v ruhu (tzv cylus) To znamená, že v této supně neuronů e výstup prvního neuronu vstupem druhého neuronu, ehož výstup e opět vstupem třetího neuronu atd, až výstup posledního neuronu v této supně e vstupem prvního neuronu Neednodušším příladem cylu e zpětná vazba neuronu, ehož výstup e zároveň eho vstupem Nevíce cylů e v úplné topolog cylcé neuronové sítě, de výstup lbovolného neuronu e vstupem aždého neuronu Přílad obecné cylcé neuronové sítě e uveden na obrázu 7, de sou vyznačeny všechny možné cyly
15 Obráze 7: Př ílad cylcé archtetury V acylcých sítích naopa cylus neexstue a všechny cesty vedou edním směrem Přílad acylcé sítě e na obrázu 8, de e vyznačena nedelší cesta Obráze 8: Př ílad acylcé archtetury U acylcé neuronové sítě lze neurony vždy (dsuntně) rozdělt do vrstev, teré sou uspořádány (např nad sebou) ta, že spoe mez neurony vedou en z nžších vrstev do vrstev vyšších (obecně vša mohou přesočt ednu nebo více vrstev) Specálním případem taové archtetury e vícevrstvá neuronová síť výstupní vrstva } sryté vrstvy vstupní vrstva Obráze 9: Př ílad archtetury vícevrstvé neuronové sítě
16 V této sít e první (dolní), tzv vstupní vrstva tvořena vstupním neurony a poslední (horní), tzv výstupní vrstva e složena z výstupních neuronů Ostatní, tzv sryté (mezlehlé, vntřní) vrstvy sou složeny ze srytých (vntřních) neuronů V topolog vícevrstvé sítě sou neurony edné vrstvy spoeny se všem neurony bezprostředně následuící vrstvy Proto archteturu taové sítě lze zadat en počty neuronů v ednotlvých vrstvách (oddělených pomlčou), v pořadí od vstupní výstupní vrstvě Taé cesta v taové sít vede směrem od vstupní vrstvy výstupní, přčemž obsahue po ednom neuronu z aždé vrstvy Přílad archtetury třívrstvé neuronové sítě s ednou vyznačenou cestou e na obrázu 9, de romě vstupní a výstupní vrstvy sou dvě sryté vrstvy Atvní dynama [6] Atvní dynama specfue počáteční stav sítě a způsob eho změny v čase př pevné topolog a onfgurac V atvním režmu se na začátu nastaví stavy vstupních neuronů na tzv vstup sítě a zbylé neurony sou v uvedeném počátečním stavu Všechny možné vstupy, resp stavy sítě, tvoří vstupní prostor, resp stavový prostor, neuronové sítě Po ncalzac stavu sítě probíhá vlastní výpočet Obecně se předpoládá spotý vývo stavu neuronové sítě v čase a hovoří se o spotém modelu, dy stav sítě e spotou funcí času, terá e obvyle v atvní dynamce zadána dferencální rovncí Většnou se vša předpoládá dsrétní čas, t na počátu se síť nachází v čase 0 a stav sítě se mění en v čase, 2, 3, V aždém taové časové rou e podle daného pravdla atvní dynamy vybrán eden neuron (tzv sevenční výpočet) nebo více neuronů (tzv paralelní výpočet), teré atualzuí (mění) svů stav na záladě svých vstupů, t stavů sousedních neuronů, echž výstupy sou vstupy atualzovaných neuronů Podle toho, zda neurony mění svů stav nezávsle na sobě nebo e ech atualzace řízena centrálně, rozlšueme synchronní a asynchronní modely neuronových sítí Stav výstupních neuronů, terý se obecně mění v čase, e výstupem neuronové sítě (t výsledem výpočtu) Obvyle se vša uvažue taová atvní dynama, že výstup sítě e po něaém čase onstantní a neuronová síť ta v atvním režmu realzue něaou func na vstupním prostoru, t e aždému vstupu sítě vypočítá právě eden výstup Tato tzv funce neuronové sítě e dána atvní dynamou, eíž rovnce parametrcy závsí na topolog a onfgurac, teré se v atvním režmu, a ž bylo uvedeno, nemění Je zřemé, že v atvním režmu se neuronová síť využívá vlastním výpočtům Atvní dynama neuronové sítě taé určue func ednoho neuronu, eíž předps (matematcý vzorec) e většnou pro všechny (nevstupní) neurony v sít stený (tzv homogenní neuronová síť) Můžeme se setat s následuícím sgmodním atvačním funcem: f ( x) = poud x 0 poud x < 0 ostrá nelnearta f ( x) = x x 0 x 0 x < 0 saturovaná lneární funce f ( x) = + e x standardní (logstcá) sgmoda f ( x) e = + e x x hyperbolcý tangens Grafy těchto funcí sou znázorněny na obrázu 0 Podle toho, zda e funce neuronu dsrétní nebo spotá rozlšueme dsrétní a analogové modely neuronových sítí
17 f(x) ostrá nelnearta f(x) 0 x saturovaná lneární funce 0 x f(x) standardní logstcá funce 0 f(x) x 0 x hyperbolcý tangents Obráze 0: Grafy sgmodních atvač ních funcí Adaptvní dynama [6] Adaptvní dynama neuronové sítě specfue počáteční onfgurac sítě a způsob, aým se mění váhové hodnoty na spoeních mez ednotlvým neurony v čase Všechny možné onfgurace sítě tvoří váhový
18 prostor neuronové sítě V adaptvním režmu se tedy na začátu nastaví váhy všech spoů v sít na počáteční onfgurac (např náhodně) Po ncalzac onfgurace sítě probíhá vlastní adaptace Podobně ao v atvní dynamce se obecně uvažue spotý model se spotým vývoem onfgurace neuronové sítě v čase, dy váhy sítě sou (spotou) funcí času, terá e obvyle v adaptvní dynamce zadána dferencální rovncí Většnou se vša předpoládá dsrétní čas adaptace Víme, že funce sítě v atvním režmu závsí na onfgurac Cílem adaptace e nalézt taovou onfgurac sítě ve váhovém prostoru, terá by v atvním režmu realzovala předepsanou func Jestlže atvní režm sítě se využívá vlastnímu výpočtu funce sítě pro daný vstup, pa adaptvní režm slouží učení ( programování ) této funce Požadovaná funce sítě e obvyle zadána tzv trénnovou množnou (posloupností) dvoc vstup/výstup sítě (tzv trénnový vzor) Způsobu adaptace, dy požadované chování sítě modelue učtel, terý pro vzorové vstupy sítě nformue adaptvní mechansmus o správném výstupu sítě, se říá učení s učtelem (supervsed learnng) Nědy učtel hodnotí valtu momentální sutečné odpověd (výstupu) sítě pro daný vzorový vstup pomocí známy, terá e zadána místo požadované hodnoty výstupu sítě (tzv lasfované učení) Jným typem adaptace e tzv samoorganzace V tomto případě trénnová množna obsahue en vstupy sítě To modelue stuac, dy není dspozc učtel, proto se tomuto způsobu adaptace taé říá učení bez učtele Neuronová síť v adaptvním režmu sama organzue trénnové vzory (např do shluů) a odhalue ech souborné vlastnost Úoly: Zopaute s všechny záladní pomy této aptoly (vz KLÍČOVÁ SLOVA aptoly)
19 PERCEPTRON Př popsu algortmu adaptace perceptronu budeme používat značení, teré e uvedeno v aptole Úvod do problematy neuronových sítí Perceptron e neednodušší neuronová síť s edním pracovním neuronem a na eho adaptačním algortmu s vysvětlíme proces učení s učtelem Klíčová slova této aptoly: perceptron, adaptační pravdlo perceptronu, oefcent učení, práh Perceptron Autorem této neednodušší neuronové sítě e Fran Rosenblatt (r 957) Za typcý perceptron e považována ednoduchá neuronová síť s n vstupy (x, x 2,, x n ) a edním pracovním neuronem spoeným se všem svým vstupy Každému taovému spoení e přřazena váhová hodnota (w, w 2,, w n ) Sgnál přenášený vstupním neurony e buď bnární (t má hodnotu 0 nebo ), nebo bpolární (t má hodnotu -, 0 nebo ) Výstupem z perceptronu e pa y = f(y_n), de atvační funce f má tvar (θ e lbovolný, ale pevný práh atvační funce f): ( _ ) f y n poud y_ n > θ = 0 poud θ y_ n θ poud y_ n < θ Váhové hodnoty sou adaptovány podle adaptačního pravdla perceptronu ta, aby dference mez sutečným a požadovaným výstupem byla co nemenší Adaptační pravdlo perceptronu e mnohem slněší než Hebbovo adaptační pravdlo Pops algortmu Kro 0 Incalzace vah w ( = až n) a basu b malým náhodným čísly Přřazení ncalzační hodnoty oefcentu učení α (0 < α ) Kro Doud není splněna podmína uončení výpočtu, opaovat roy (2 až 6) Kro 2 Pro aždý trénnový pár s:t (t vstupní vetor s a příslušný výstup t), provádět roy (3 až 5) Kro 3 Atvu vstupní neurony: x = s
20 Kro 4 Vypočíte sutečnou hodnotu na výstupu: y_ n b x w ; = + Kro 6 poud y_ n > θ y = 0 poud θ y_ n θ poud y_ n < θ Kro 5 Atualzu váhové hodnoty a bas pro daný vzor estlže y t, w (new) = w (old) + α t x ( = až n) b(new) = b(old) + α t na w (new) = w (old) b(new) = b(old) Podmína uončení: estlže ve 2 rou ž nenastává žádná změna váhových hodnot, stop; na, poračovat Atualzac podléhaí pouze ty váhové hodnoty, teré neproduuí požadovaný výstup y To znamená, že čím více trénnových vzorů má oretní výstupy, tím méně e potřeba času ech trénnu Práh atvační funce e pevná nezáporná hodnota θ Tvar atvační funce pracovního neuronu e taový, že umožňue vzn pásu pevné šířy (určené hodnotou θ ) odděluícího oblast poztvní odezvy od oblast negatvní odezvy na vstupní sgnál Předcházeící analýza o zaměntelnost prahu a basu zde nemá uplatnění, protože změna θ mění šířu oblast, ne vša eí umístění Místo edné separuící přímy tedy máme pás určený dvěma rovnoběžným přímam: Příma separuící oblast poztvní odezvy od oblast nulové odezvy na vstupní sgnál; tato hranční příma má tvar: w x + w 2 x 2 + b >θ 2 Příma separuící oblast nulové odezvy od oblast negatvní odezvy na vstupní sgnál; tato hranční příma má tvar: w x + w 2 x 2 + b < -θ Přílad: Adaptační algortmus perceptronu pro logcou func AND : bnární vstupní hodnoty, bpolární výstupní hodnoty Pro ednoduchost předpoládeme, že θ = 0,2 a α = VSTUP POŽADOVANÝ x x 2 b VÝSTUP
21 Po předložení prvního trénnového vzoru, dostáváme následuící: VSTUP VÝSTUP PŘÍRUSTKY VAH VÁHOVÉ HODNOTY x x 2 b y_n y t w w 2 b w w 2 b Separuící přímy sou dány rovncem x + x 2 + = 0,2 x + x 2 + = - 0,2 x x Obráze : Hranční pás pro logcou func AND - první trénnový vzor Předložíme-l druhý trénnový vzor, dostáváme následuící: VSTUP VÝSTUP PŘÍRUSTKY VAH VÁHOVÉ HODNOTY x x 2 b y_n y t w w 2 b w w 2 b Separuící přímy maí tvar x 2 = 0,2 x 2 = - 0,2
22 x x Obráze 2: Hranční pás pro logcou func AND - druhý trénnový vzor Po předložení třetího trénnového vzoru, dostáváme: VSTUP VÝSTUP PŘÍRUSTKY VAH VÁHOVÉ HODNOTY x x 2 b y_n y t w w 2 b w w 2 b Pro úplnost prvního trénnového cylu předložíme čtvrtý vzor a dostáváme následuící: VSTUP VÝSTUP PŘÍRUSTKY VAH VÁHOVÉ HODNOTY x x 2 b y_n y t w w 2 b w w 2 b Výsledy po desátém trénnovém cylu sou: x x Obráze 3: Hranční pás pro logcou func AND po adaptac algortmem perceptronu
23 Kladná odezva e dána všem body, pro teré platí 2x + 3x 2-4 > 0,2 Hranční příma oblast má tvar x = 2 7 x Záporná odezva e dána všem body, pro teré platí 2x + 3x 2-4 < - 0,2 Hranční příma oblast má pa tvar x = 2 9 x Úoly: Srovnete Hebbovo adaptační pravdlo a adaptační pravdlo perceptronu 2 Obasněte adaptační algortmus perceptronu pro logcou func OR v bpolární reprezentac Korespondenční úoly: Vytvořte počítačový program pro realzac adaptačního algortmu perceptronu
24 ADALINE MADALINE Př popsu adaptačního algortmu pro Adalne a Madalne budeme vycházet ze značení, teré e uvedeno v aptole Úvod do problematy neuronových sítí a teré bude v této aptole rozšířeno Adaptační algortmus neuronu Adalne bude srovnán s adaptačním algortmem percetronu V závěru pa budou uvedeny možnost lasface různých typů neuronových sítí (t -vrstvé, vrstvé a 3-vrstvé neuronové sítě) Klíčová slova této aptoly: Adalne, Madalne, adaptační algortmus pro Adalne, delta pravdlo Adalne Adalne, t Adaptve Lnear Neuron Pro své vstupy obvyle používá bpolární atvac ( nebo -), výstupní hodnota e nečastě taé bpolární Adalne má rovněž bas chovaící se ao regulovatelná váha (w 0 ) přřazená spoení, teré vychází z neuronu, ehož atvace e vždy Adaptační algortmus pro Adalne má následuící tvar: Kro 0 Incalzace vah malým náhodným hodnotam Přřazení ncalzační hodnoty oefcentu učení α (vz poznámy za algortmem) Kro Doud není splněna podmína uončení výpočtu, opaovat roy (2 až 6) Kro 2 Pro aždý bpolární trénnový pár s:t (t vstupní vetor s a příslušný výstup t), provádět roy (3 až 5) Kro 3 Atvovat vstupní neurony: x = s Kro 4 Vypočítat sutečnou hodnotu na výstupu: y_ n b x w ; = + y = y_n Kro 5 Atualzovat váhové hodnoty a =,, n: w (new) = w (old) + α (t - y_n) x b(new) = b(old) + α (t - y_n) Kro 6 Podmína uončení: estlže nevětší změna váhových hodnot, terá se vysytue v rou 2 e menší než maxmální povolená chyba, stop; na, poračovat
25 Nastavení vhodné hodnoty oefcentu učení α se děe následovně: Podle Hecht-Nelsena lze za eho horní hranční hodnotu považovat nevětší vlastní číslo orelační matce R vstupu (řádu) vetoru x(p), tedy P R = x p x p, P p= T ( ) ( ) α < edna polovna nevětší hodnoty vlastního čísla R Jelož hodnota R není během výpočtu měněna, obvyle se volí α ao 0 < nα <0, de n e počet vstupů Poud dosadíme za α přílš velou hodnotu, adaptační algortmus nebude onvergovat Poud dosadíme za α přílš malou hodnotu, proces učení bude extrémně pomalý Důaz onvergence adaptačního pravdla pro Adalne e obsažen v dervac delta pravdla Delta pravdlo mění váhové hodnoty na spoeních mez ednotlvým neurony ta, aby byl mnmalzován rozdíl mez vstupním sgnálem y_n výstupního neuronu a požadovaným výstupem t Cílem adaptace e mnmalzovat tuto chybu přes všechny trénnové vzory Příslušné váhové orece sou aumulovány a po aždém trénnovém cylu sou všechny váhové hodnoty atualzovány naednou Delta pravdlo příslušeící I váhové hodnotě e pro aždý vzor zapsáno následovně: ( ) w = α t y_ n x I I Dále budeme používat toto označení: x y_n t Vetor atvací vstupních neuronů, má n slože Hodnota vstupního sgnálu výstupního neuronu Y e y_ n= x w n = Požadovaný výstup Dervace: Pro aždý trénnový vzor e dána chybová funce E = E(w), t funce všech váhových hodnot w, =,, n vztahem E =( t - y_n) 2 Gradent E e vetor, ehož složy sou parcální dervace E podle všech slože vetoru w Gradent udává směr nevětšího růstu (chyby E); poud vša má opačný směr způsobue eí nerychleší zmenšování Chybová funce E e mnmalzována prostřednctvím úprav váhových hodnot w I ve směru E w I Protože y_ n= x w, E w I n = = 2 ( t y_ n) ( t ) = 2 y_ n x I y_ n w I
26 Chyba (E) bude tedy reduována rychle, poud budou příslušné váhové hodnoty upravovány podle delta pravdla, ( ) w = α t y_ n x I I Přílad: Adaptační algortmus Adalne pro logcou func OR (bpolární vstupní výstupní hodnoty) e zapsán následovně: VSTUP POŽADOVANÝ x x 2 VÝSTUP Ja ž bylo výše naznačeno, e adaptační algortmus Adalne navržen nalezení taových váhových hodnot w, aby mnmalzovaly celovou chybu de ( ( ) ( ) ( )) p= E = x p w + x p w + w t p ( ) ( ) x p w + x2 p w2 + w 0 2, e vstupní sgnál vedoucí do výstupního neuronu pro vzor p a t(p) e požadovaný výstup příslušeící vzoru p Váhové hodnoty, teré mnmalzuí chybovou func, maí v tomto příladě tvar: w =, 2 w2 =, 2 bas w0 = 2 Separuící příma e tedy určená rovncí 2 x + x + = Geometrcý význam funce Adalne se nepatrně lší od perceptronu Uvažume vstup x=(x,, x n ), t bod [x,, x n ] v n-rozměrném vstupním prostoru Nadrovna s oefcenty w pro daný neuron Adalne určená rovncí w 0 n + w x = 0 rozdělue tento prostor na dva poloprostory, ve terých má hodnota výstupu y zapsaného rovncí = n y= w x odlšné znaméno (t e buď ladná, nebo záporná) Pro body ležící na této nadrovně e hodnota výstupu nulová Vzdálenost ρ bodu [x,, x n ] od této nadrovny e dána rovncí: =
27 ρ= w + 0 = n w x = y n 2 n w = = w 2 Tedy absolutní hodnota y výstupu z neuronu Adalne závsí lneárně na vzdálenost bodu od nadrovny ve vstupním prostoru: y n 2 = = w ρ Body ze vstupního prostoru, teré maí stený výstup, leží na edné nadrovně rovnoběžné s nadrovnou w 0 n + w x = 0, terá e od ní ve vzdálenost ρ ve směru daném znaménem y Uvedená stuace e = načrtnuta na obrázu 4, de nadrovna určená steným výstupem e znázorněna přerušovanou čarou n = w0 + w x = 0 y<0 y>0 ρ [x,,x n ] y n w 2 = = ρ Obráze 4: Geometrcá nterpretace funce neuronu Adalne
28 Madalne Madalne, t Many Adaptve Lnear Neurons Záladním prvem v tomto modelu e neuron Adalne, terý e velm podobný perceptronu (vz předcházeící aptola) Jednoduchá archtetura neuronové sítě Madalne e zobrazena na obrázu 5 Výstupy (z a z 2 ) z obou srytých neuronů typu Adalne (Z a Z 2 ), sou určeny steným sgnály (x a x 2 ) vycházeícím z neuronů X a X 2, teré samozřemě závsí na příslušné prahové func Pa sutečný výstup y e nelneární funcí vstupního vetoru (x, x 2 ) a příslušné prahové funce Použtí srytých neuronů Z a Z 2 sce dává sít větší výpočtové možnost, ale naprot tomu omplue adaptační proces X b w w 2 Z v b 3 Y w 2 Z 2 v 2 X 2 w 22 b 2 Obráze 5: Madalne se dvě ma srytým neurony Adalne a edním výstupním neuronem Adalne Původní adaptační algortmus MRI (z rou 960) adaptue pouze váhové hodnoty příslušeící oběma srytým neuronům, zatímco váhové hodnoty příslušeící výstupnímu neuronu sou fxní Adaptační algortmus MRII (z rou 987) upravue všechny váhové hodnoty Dále budeme pracovat pouze s adaptačním algortmem MRI: Váhové hodnoty v a v 2 a bas b 3, příslušeící výstupnímu neuronu Y, sou určeny ta, že výstupní sgnál z Y e roven, poud e alespoň edna hodnota sgnálu vycházeícího ze srytých neuronů (t Z a Z 2 nebo obou z nch) rovna edné Poud sou oba sgnály vysílané ze Z Z 2 rovny -, má výstupní sgnál z Y hodnotu - Jným slovy, výstupní neuron Y provádí logcou func OR na sgnálech vysílaných z neuronů Z a Z 2 Můžeme tedy přřadt v v b 2 3 =, 2 =, 2 = 2 Váhové hodnoty příslušeící prvnímu srytému neuronu Adalne (w a w 2 ) a váhové hodnoty příslušeící druhému srytému neuronu Adalne (w 2 a w 22 ) sou adaptovány podle algortmu MRI tato: Atvační funce pro Z, Z 2 a Y e dána následovně: f( x) poud x 0; = poud x < 0
29 Adaptační algortmus MRI Kro 0 Váhové hodnoty v a v 2 a bas b 3 sou ncalzovány výše uvedeným způsobem Incalzace zbývaících vah malým náhodným hodnotam Přřazení ncalzační hodnoty oefcentu učení α steným způsobem ao v adaptačním algortmu pro neuron Adalne Kro Doud není splněna podmína uončení výpočtu, opaovat roy (2 až 8) Kro 2 Pro aždý bpolární trénnový pár s:t provádět roy (3 až 7) Kro 3 Atvovat vstupní neurony: x = s Kro 4 Vypočítat vstupní hodnoty srytých neuronů: z_ n = b + x w + x w, 2 2 z_ n2 = b2 + xw2 + x2w2 2 Kro 5 Stanovení výstupních hodnot srytých neuronů: z z = ( _ ), ( ) f z n = f z_ n 2 2 Kro 6 Stanovení sutečné výstupní hodnoty sgnálu neuronové sítě Madalne: y_ n= b + z v + z v ; ( ) y = f y_ n Kro 7 Atualzovat váhové hodnoty: Poud e y = t, nenastávaí žádné změny Jna (pro y t): Je-l t =, potom pro váhové hodnoty na spoeních vedoucích Z J (J=,2) platí: w J (new) = w J (old) + α ( - z_n J ) x b J (new) = b J (old) + α ( - z_n J ) Je-l t = -, potom pro váhové hodnoty na spoeních vedoucích Z K (K=,2) platí: w K (new) = w K (old) + α (- - z_n K ) x b K (new) = b K (old) + α (- - z_n K ) Kro 8 Podmína uončení: poud ž nenastávaí žádné změny váhových hodnot nebo poud ž bylo vyonáno maxmálně defnované množství váhových změn, stop; na, poračovat
30 Přílad: Adaptační algortmus MRI pro logcou func XOR (bpolární vstupní výstupní hodnoty) e zapsán následovně: VSTUP POŽADOVANÝ x x 2 VÝSTUP Kro 0 α = 05; Incalzace váhových hodnot: váhy vedoucí do Z váhy vedoucí do Z 2 váhy vedoucí do Y w w 2 b w 2 w 22 b 2 v v 2 b Kro Adaptace: Kro 2 Pro první trénnový pár; (,):- Kro 3 x =, x 2 = Kro 4 z_n = = 055, z_n 2 = = 045 Kro 5 z =, z 2 = Kro 6 y_n = ; y = Kro 7 t - y = -- = -2 0, Poud e t = -, potom atualzovat váhové hodnoty na spoeních vedoucích Z : ( ) = ( ) + α ( = 03 + ( 05 )( 55 ) b new b old z_ n = ( ) = ( ) + α ( = ( 05 )( 55 ) w new w old z_ n = ( ) ( ) α ( = 02 + ( 05 )( 55 ) w new = w old + z_ n 2 2 = a atualzovat váhové hodnoty na spoeních vedoucích Z2: ) ) x ) x 2
31 ( ) = ( ) + α ( = 05 + ( 05 )( 45 ) b new b old z_ n 2 2 = Po čtyřech trénnových cylech, byly nalezeny tyto váhové hodnoty: w = w 2 = 27 w 2 =53 w 22 = - 33 b = b 2 = - 09 ( ) ( ) α ( = 0 + ( 05 )( 45 ) w new = w old + z_ n 2 2 = ( ) ( ) α ( = 02 + ( 05 )( 45 ) w new = w old + z_ n = ) ) x 2 ) x 2 2 Geometrcá nterpretace nalezených váhových hodnot: Oblast ladné odezvy vznne sednocením obou oblastí poztvní odezvy srytých neuronů Z a Z 2 Pro srytý neuron Z má hranční příma tvar Pro srytý neuron Z 2 má hranční příma tvar w w x b x 2 = w = x = 048 x x 2 w2 w x b = w = x = 09 6x Vypočítané oblast ladné a záporné odezvy na vstupní sgnál sou znázorněny na následuících obrázcích
32 + x 2 - x - + Obráze 6: Oblast ladné odezvy pro Z + x 2 - x - + Obráze 7: Oblast ladné odezvy pro Z 2 + x 2 - x - + Obráze 8: Oblast ladné odezvy pro Madalne pro XOR func
33 Úoly: Srovnete adaptační algortmus neuronu Adalne a perceptronu 2 Srovnete geometrcou nterpretac funce neuronu Adalne a perceptronu 3 Obasněte adaptační algortmus MRI pro vybranou logcou func v bpolární reprezentac Korespondenční úoly (vybraný úol vyonete): Vytvořte počítačový program pro realzac adaptačního algortmu neuronu Adalne 2 Vytvořte počítačový program pro realzac adaptačního algortmu MRI Shrnutí: Na následuících dvou obrázcích sou souhrnně zobrazeny různé tyty neuronových sítí (t neuronové sítě s různým počtem vntřních vrstev) a ech možnost lasface STRUKTURA NEURONOVÉ SÍTĚ vrstva (perceptron) XOR PROBLÉM OBTÉKÁNÍ OBLASTÍ OBECNÉ OBLASTI A B A B B A 2 vrstvy (Madalne) A B A B B A 3 vrstvy A B A B B A Obráze 9: Neuronové sítě s rů zným poč tem vntř ních vrstev a ech možnost lasface
34 -vrstvá neuronová síť (perceptron) 2-vrstvá neuronová síť (Madalne) 3-vrstvá neuronová síť vstupy lneární oblast onvexní oblast obecné oblast vstupní neurony (přenášeí vstupní sgnál) pracovní neurony Obráze 20: Mezní oblast rozpoznávané neuronovou sítí s rů zným poč tem vntř ních vrstev
35 BACKPROPAGATION V této aptole se podrobně seznámíte s adaptačním algortmem zpětného šíření chyby (bacpropagaton), ež e používán v přblžně 80% všech aplací neuronových (t e nerozšířeněším adaptačním algortmem vícevrstvých neuronových sítí) Zavedeme s zde další značení, teré budeme používat v následných aptolách Klíčová slova této aptoly: bacpropagaton (adaptační algortmus zpětného šíření chyby), generalzace, trénovací množna, dopředné (feedforward) šíření sgnálu V této aptole budeme používat následuící značení: x Vstupní vetor: x = (x,, x,, x n ) t Výstupní trénnový vetor: t = (t,, t,, t m ) δ Částečné váhové orece pro w příslušeící chybě na spoeních vedoucích neuronu Y ve výstupní vrstvě δ α X v 0 Z w 0 Y Částečné váhové orece pro v příslušeící chybě na spoeních vedoucích neuronu Z ve sryté vrstvě Koefcent učení neuron ve vstupní vrstvě: Pro neurony ve vstupní vrstvě e hodnota vstupního výstupního sgnálu stená, x Bas neuronu ve sryté vrstvě neuron ve sryté vrstvě: Hodnota vstupního sgnálu pro Z e z_n : z_ n v x v = + 0 Hodnota vstupního sgnálu pro Z e z : z = f z_ n ( ) Bas neuronu ve výstupní vrstvě neuron ve výstupní vrstvě: Hodnota vstupního sgnálu pro Y e y_n : y_ n w z w = + 0 Hodnota vstupního sgnálu pro Z e z : y = f y_ n ( )
36 Pravděpodobně nerozšířeněší způsob propoení neuronů se sgmodní atvační funcí sou vícevrstvé sítě Vícevrstvá neuronová síť s ednou vntřní vrstvou neuronů (neurony sou označeny Z, =,, p) e zobrazena na obrázu 2 Výstupní neurony (neurony sou označeny Y, =,, m) Neurony ve výstupní a vntřní vrstvě musí mít defnovaný bas Typcé označení pro bas neuronu (Y ) ve výstupní vrstvě e w 0, a typcé označení pro bas neuronu (Z ) ve vntřní vrstvě e v 0 Bas (např neuronu) odpovídá, a ž bylo dříve uvedeno, váhové hodnotě přřazené spoení mez daným neuronem a ftvním neuronem, ehož atvace e vždy Z uvedeného obrázu tedy vyplývá, že vícevrstvá neuronová síť e tvořena mnmálně třem vrstvam neuronů: vstupní, výstupní a alespoň ednou vntřní vrstvou Vždy mez dvěm sousedním vrstvam se pa nachází tzv úplné propoení neuronů, tedy aždý neuron nžší vrstvy e spoen se všem neurony vrstvy vyšší VÝSTUPNÍ VRSTVA Y Y Y m w 0 w w 0m Z Z Z p v 0p v 0 w 0 v 0 v w v w m v p X X X n w v w v w m VSTUPNÍ VRSTVA v p w p v n w p v n w pm v np SKRYTÁ (vntřní) VRSTVA Obráze 2: Neuronová síť s ednou vntř ní vrstvou neuronů Adaptační algortmus zpětného šíření chyby (bacpropagaton) e používán v přblžně 80% všech aplací neuronových sítí Samotný algortmus obsahue tř etapy: dopředné (feedforward) šíření vstupního sgnálu trénnového vzoru, zpětné šíření chyby a atualzace váhových hodnot na spoeních Během dopředného šíření sgnálu obdrží aždý neuron ve vstupní vrstvě (X, =,, n) vstupní sgnál (x ) a zprostředue eho přenos e všem neuronům vntřní vrstvy (Z,, Z p ) Každý neuron ve vntřní vrstvě vypočítá svou atvac (z ) a pošle tento sgnál všem neuronům ve výstupní vrstvě Každý neuron ve výstupní vrstvě vypočítá svou atvac (y ), terá odpovídá eho sutečnému výstupu ( neuronu) po předložení vstupního vzoru V podstatě tímto způsobem zísáme odezvu neuronové sítě na vstupní podnět daný exctací neuronů vstupní vrstvy Taovým způsobem probíhá šíření sgnálů v bologcém systému, de vstupní vrstva může být tvořena např zraovým buňam a ve výstupní vrstvě mozu sou pa dentfovány ednotlvé obety sledování Otázou pa zůstává to nedůležtěší, aým způsobem sou stanoveny synaptcé váhy vedoucí e oretní odezvě na vstupní sgnál Proces stanovení synaptcých vah e opět spat s pomem učení - adaptace - neuronové sítě Další otázou e schopnost generalzace (zobecnění) nad naučeným materálem, ným slovy a e neuronová síť schopna na záladě naučeného usuzovat na evy, teré nebyly součástí učení, teré vša lze něaým způsobem z naučeného odvodt I tady e cítt aás analoge s ldsým učením daná rozdílem mez bezduchým bflováním a učením spatým se schopností porozumět problematce ta, aby mohlo být nové odvozeno z předchozího Co e nutné naučení neuronové sítě? Je to edna tzv trénovací množna obsahuící prvy popsuící řešenou problematu a dále pa metoda, terá doáže tyto vzory zafxovat v neuronové sít formou hodnot
37 synaptcých vah poud možno včetně ž uvedené schopnost generalzovat Zastavme se nedříve u trénovací množny Každý vzor trénovací množny popsue aým způsobem sou exctovány neurony vstupní a výstupní vrstvy Formálně můžeme za trénovací množnu T považovat množnu prvů (vzorů), teré sou defnovány uspořádaným dvocem následuícím způsobem: {{, } { 2, 2} K { q, q} } T = S T S T S T [ 2 ] [ 2 ] S = s s s s 0, n T = t t t t 0, m de q počet vzorů trénovací množny S vetor exctací vstupní vrstvy tvořené n neurony T vetor exctací výstupní vrstvy tvořené m neurony s, t exctace -tého neuronu vstupní resp výstupní vrstvy Metoda, terá umožňue adaptac neuronové sítě nad danou trénovací množnou se nazývá bacpropagaton, což v přeladu znamená metodu zpětného šíření Na rozdíl od už popsaného dopředného chodu př šíření sgnálu neuronové sítě spočívá tato metoda adaptace v opačném šíření nformace směrem od vrstev vyšších vrstvám nžším Během adaptace neuronové sítě metodou bacpropagaton sou srovnávány vypočítané atvace y s defnovaným výstupním hodnotam t pro aždý neuron ve výstupní vrstvě a pro aždý trénnový vzor Na záladě tohoto srovnání e defnována chyba neuronové sítě, pro terou e vypočítán fator δ ( =,, m) δ e, a ž bylo uvedeno, část chyby, terá se šíří zpětně z neuronu Y e všem neuronům předcházeící vrstvy, ež maí s tímto neuronem defnované spoení Podobně lze defnovat fator δ ( =,, p), terý e část chyby šířené zpětně z neuronu Z e všem neuronům vstupní vrstvy, ež maí s tímto neuronem defnované spoení Úprava váhových hodnot w na spoeních mez neurony vntřní a výstupní vrstvy závsí na fatoru δ a atvacích z neuronů Z ve vntřní vrstvě Úprava váhových hodnot v na spoeních mez neurony vstupní a vntřní vrstvy závsí na fatoru δ a atvacích x neuronů X ve vstupní vrstvě Atvační funce pro neuronové sítě s adaptační metodou bacpropagaton musí mít následuící vlastnost: musí být spotá, dferencovatelná a monotónně nelesaící Nečastě používanou atvační funcí e proto standardní (logcá) sgmoda a hyperbolcý tangens Chyba sítě E(w) e vzhledem trénnové množně defnována ao součet parcálních chyb sítě E l (w) vzhledem ednotlvým trénnovým vzorům a závsí na onfgurac sítě w: E q E l l= ( w) = ( w) Parcální chyba E l (w) sítě pro l trénnový vzor (l =,,q) e úměrná součtu mocnn odchyle sutečných hodnot výstupu sítě pro vstup l-trénnového vzoru od požadovaných hodnot výstupů u tohoto vzoru: E l 2 ( w ) = ( y t ) Y Cílem adaptace e mnmalzace chyby sítě ve váhovém prostoru Vzhledem tomu, že chyba sítě přímo závsí na omplované nelneární složené func vícevrstvé sítě, představue tento cíl netrvální optmalzační problém Pro eho řešení se v záladním modelu používá neednodušší varanta gradentní metody, terá vyžadue dferencovatelnost chybové funce K lepšímu pochopení nám pomůže geometrcá představa Na obrázu 22 e schematcy znázorněna chybová funce E(w) ta, že onfgurace, terá představue mnohorozměrný vetor vah w, se promítá na osu x Chybová funce určue chybu sítě vzhledem pevné trénnové množně v závslost na onfgurac sítě Př adaptac sítě hledáme taovou onfgurac, pro terou e chybová funce mnmální Začneme s náhodně zvolenou onfgurací w (0), dy odpovídaící chyba sítě od požadované funce bude pravděpodobně velá V analog s ldsým učením to odpovídá počátečnímu nastavení 2
38 synaptcých vah u novorozence, terý místo požadovaného chování ao chůze, řeč apod provádí náhodné pohyby a vydává neurčté zvuy Př adaptac sestroíme v tomto bodě w (0) e grafu chybové funce tečný vetor E ( ) (gradent) ( w w ) 0 a posuneme se ve směru tohoto vetoru dolů o ε Pro dostatečně malé ε ta zísáme novou onfgurac w () = w (0) + w (), pro terou e chybová funce menší než pro původní onfgurac w (0), t E (w (0) ) E (w () ) Celý proces onstruce tečného vetoru opaueme pro w () a zísáme ta w (2) taové, že E (w () ) E (w (2) ) atd, až se lmtně dostaneme do loálního mnma chybové funce Ve vícerozměrném váhovém prostoru tento postup přesahue naš představvost I dyž př vhodné volbě oefcentu učení (α) tato metoda vždy onvergue něaému loálnímu mnmu z lbovolné počáteční onfgurace, není vůbec zaručeno, že se ta stane v reálném čase Obvyle e tento proces časově velm náročný (něol dnů výpočtu PC) pro malé topologe vícevrstvé sítě (desíty neuronů) E ε w (0) w () w (2) Obráze 22: Gradentní metoda w Hlavním problémem gradentní metody e, že poud ž nalezne loální mnmum, pa toto mnmum nemusí být globální (vz obr22) Uvedený postup adaptace se v taovém mnmu zastaví (nulový gradent) a chyba sítě se ž dále nesnžue To lze v naší analog s učením člověa nterpretovat ta, že počáteční nastavení onfgurace v oolí něaého mnma chybové funce určue možnost ednce učt se Intelgentněší ldé začínaí svou adaptac v blízost hlubších mnm I zde e vša chybová funce defnovaná relatvně vzhledem požadovanému ntelgentnímu chování (trénnová množna), teré vša nemusí být unverzálně platné Hodnotu člověa nelze měřt žádnou chybovou funcí Eletrcé šoy aplované v psychatrcých léčebnách přpomínaí něteré metody adaptace neuronových sítí, teré v případě, že se učení zastavlo v mělém loálním mnmu chybové funce, náhodně vnáší šum do onfgurace sítě, aby se síť dostala z oblastí abstrace tohoto loálního mnma a mohla popř onvergovat hlubšímu mnmu Pops algortmu bacpropagaton Kro 0 Váhové hodnoty a bas sou ncalzovány malým náhodným čísly Přřazení ncalzační hodnoty oefcentu učení α Kro Doud není splněna podmína uončení výpočtu, opaovat roy (2 až 9) Kro 2 Pro aždý (bpolární) trénnový pár s:t provádět roy (3 až 8) Feedforward: Kro 3 Atvovat vstupní neurony (X, =, n) x = s Kro 4 Vypočítat vstupní hodnoty vntřních neuronů: (Z, =,, p):
OSTRAVSKÁ UNIVERZITA V OSTRAVĚ NEURONOVÉ SÍTĚ 1 EVA VOLNÁ
 OSTRAVSKÁ UNIVERZITA V OSTRAVĚ NEURONOVÉ SÍTĚ EVA VOLNÁ OSTRAVA 008 Recenzent: Název: Neuronové sítě Autoř: RNDr PaedDr Eva Volná, PhD Vydání: druhé, 008 Počet stran: 86 Náklad: Tsk: Studní materály pro
OSTRAVSKÁ UNIVERZITA V OSTRAVĚ NEURONOVÉ SÍTĚ EVA VOLNÁ OSTRAVA 008 Recenzent: Název: Neuronové sítě Autoř: RNDr PaedDr Eva Volná, PhD Vydání: druhé, 008 Počet stran: 86 Náklad: Tsk: Studní materály pro
Agregace vzájemné spojování destabilizovaných částic ve větší celky, případně jejich adheze na povrchu jiných materiálů
 Agregace - úvod 1 Agregace vzáemné spoování destablzovaných částc ve větší cely, případně ech adheze na povrchu ných materálů Částce mohou agregovat, poud vyazuí adhezní schopnost a poud e umožněno ech
Agregace - úvod 1 Agregace vzáemné spoování destablzovaných částc ve větší cely, případně ech adheze na povrchu ných materálů Částce mohou agregovat, poud vyazuí adhezní schopnost a poud e umožněno ech
EKONOMICKO-MATEMATICKÉ METODY
 . přednáška EKONOMICKO-MATEMATICKÉ METODY Ekonomcko matematcké metody (též se užívá název operační analýza) sou metody s matematckým základem, využívané především v ekonomcké oblast, v oblast řízení a
. přednáška EKONOMICKO-MATEMATICKÉ METODY Ekonomcko matematcké metody (též se užívá název operační analýza) sou metody s matematckým základem, využívané především v ekonomcké oblast, v oblast řízení a
SW aplikace MOV přednášky
 SW aplace MOV Šubrt KOSA Systémová podpora proetů Teore grafů Proetové řízení I, II zápočet: alespoň bodů z průběžných testů 75% účast na cvčení obhaoba proetů v MS Proect pef.czu.cz/osa Témata. :. seznámení
SW aplace MOV Šubrt KOSA Systémová podpora proetů Teore grafů Proetové řízení I, II zápočet: alespoň bodů z průběžných testů 75% účast na cvčení obhaoba proetů v MS Proect pef.czu.cz/osa Témata. :. seznámení
7. ZÁKLADNÍ TYPY DYNAMICKÝCH SYSTÉMŮ
 7. ZÁKADNÍ TYPY DYNAMICKÝCH SYSTÉMŮ 7.. SPOJITÉ SYSTÉMY Téměř všechny fyzálně realzovatelné spojté lneární systémy (romě systémů s dopravním zpožděním lze vytvořt z prvů tří typů: proporconálních členů
7. ZÁKADNÍ TYPY DYNAMICKÝCH SYSTÉMŮ 7.. SPOJITÉ SYSTÉMY Téměř všechny fyzálně realzovatelné spojté lneární systémy (romě systémů s dopravním zpožděním lze vytvořt z prvů tří typů: proporconálních členů
1. Úvod do základních pojmů teorie pravděpodobnosti
 1. Úvod do záladních pojmů teore pravděpodobnost 1.1 Úvodní pojmy Většna exatních věd zobrazuje své výsledy rgorózně tj. výsledy jsou zísávány na záladě přesných formulí a jsou jejch nterpretací. em je
1. Úvod do záladních pojmů teore pravděpodobnost 1.1 Úvodní pojmy Většna exatních věd zobrazuje své výsledy rgorózně tj. výsledy jsou zísávány na záladě přesných formulí a jsou jejch nterpretací. em je
Using a Kalman Filter for Estimating a Random Constant Použití Kalmanova filtru pro výpočet odhadu konstantní hodnoty
 II. Semnar ASR 007 Instruments and Control, Farana, Smutný, Kočí & Babuch (eds) 007, VŠB-TUO, Ostrava, ISB 978-80-48-7-4 Usng a Kalman Flter for Estmatng a Random Constant Použtí Kalmanova fltru pro výpočet
II. Semnar ASR 007 Instruments and Control, Farana, Smutný, Kočí & Babuch (eds) 007, VŠB-TUO, Ostrava, ISB 978-80-48-7-4 Usng a Kalman Flter for Estmatng a Random Constant Použtí Kalmanova fltru pro výpočet
Neuronové sítě. Doc. RNDr. Iveta Mrázová, CSc. Katedra teoretické informatiky Matematicko-fyzikální fakulta Univerzity Karlovy v Praze
 Neuronové sítě Doc. RNDr. Iveta Mrázová, CSc. Katedra teoretcé nformat Matematco-fzální faulta Unverzt Karlov v Praze Vrstevnaté neuronové sítě (1) D: Neuronová síť e uspořádaná 6-tce M=(N,C,I,O,,t), de:
Neuronové sítě Doc. RNDr. Iveta Mrázová, CSc. Katedra teoretcé nformat Matematco-fzální faulta Unverzt Karlov v Praze Vrstevnaté neuronové sítě (1) D: Neuronová síť e uspořádaná 6-tce M=(N,C,I,O,,t), de:
Aplikace teorie neuronových sítí
 Aplace teore neuronových sítí Doc. RNDr. Iveta Mrázová, CSc. Katera teoretcé nformat Matematco-fzální faulta Unverzt Karlov v Praze Neuronové sítě Moulární archtetur Doc. RNDr. Iveta Mrázová, CSc. Katera
Aplace teore neuronových sítí Doc. RNDr. Iveta Mrázová, CSc. Katera teoretcé nformat Matematco-fzální faulta Unverzt Karlov v Praze Neuronové sítě Moulární archtetur Doc. RNDr. Iveta Mrázová, CSc. Katera
Reprezentace přirozených čísel ve Fibonacciho soustavě František Maňák, FJFI ČVUT, 2005
 Reprezentace přirozených čísel ve ibonacciho soustavě rantiše Maňá, JI ČVUT, 2005 Úvod Ja víme, přirozená čísla lze vyádřit různými způsoby Nečastěi zápisu čísel používáme soustavu desítovou, ale umíme
Reprezentace přirozených čísel ve ibonacciho soustavě rantiše Maňá, JI ČVUT, 2005 Úvod Ja víme, přirozená čísla lze vyádřit různými způsoby Nečastěi zápisu čísel používáme soustavu desítovou, ale umíme
4. Třídění statistických dat pořádek v datech
 4. Třídění statstcých dat pořáde v datech Záladní členění statstcých řad: řada časová, řada prostorová, řada věcná věcná slovní řada, věcná číselná řada. Záladem statstcého třídění je uspořádání hodnot
4. Třídění statstcých dat pořáde v datech Záladní členění statstcých řad: řada časová, řada prostorová, řada věcná věcná slovní řada, věcná číselná řada. Záladem statstcého třídění je uspořádání hodnot
Vícekriteriální rozhodování. Typy kritérií
 Vícekrterální rozhodování Zabývá se hodnocením varant podle několka krtérí, přčemž varanta hodnocená podle ednoho krtéra zpravdla nebývá nelépe hodnocená podle krtéra ného. Metody vícekrterálního rozhodování
Vícekrterální rozhodování Zabývá se hodnocením varant podle několka krtérí, přčemž varanta hodnocená podle ednoho krtéra zpravdla nebývá nelépe hodnocená podle krtéra ného. Metody vícekrterálního rozhodování
1. Sítě se vzájemnými vazbami
 Obsah 1. Sítě se vzáemným vazbam... 2 1.1 Základní nformace... 2 1.2 Výstupy z učení... 2 1.3 Obecná charakterstka umělých neuronových sítí se vzáemným vazbam... 2 1.4 Hopfeldova síť... 3 1.4.1 Organzační
Obsah 1. Sítě se vzáemným vazbam... 2 1.1 Základní nformace... 2 1.2 Výstupy z učení... 2 1.3 Obecná charakterstka umělých neuronových sítí se vzáemným vazbam... 2 1.4 Hopfeldova síť... 3 1.4.1 Organzační
Lineární a adaptivní zpracování dat. 8. Kumulační zvýrazňování signálů v šumu 2
 Lneární a adaptvní zpracování dat 8. Kumulační zvýrazňování sgnálů v šumu 2 Danel Schwarz Investce do rozvoe vzdělávání Opakování Kumulační zpracování sgnálů co to e, k čemu to e? Prncp metody? Nutné podmínky
Lneární a adaptvní zpracování dat 8. Kumulační zvýrazňování sgnálů v šumu 2 Danel Schwarz Investce do rozvoe vzdělávání Opakování Kumulační zpracování sgnálů co to e, k čemu to e? Prncp metody? Nutné podmínky
ŘEŠENÍ PROBLÉMU LOKALIZACE A ALOKACE LOGISTICKÝCH OBJEKTŮ POMOCÍ PROGRAMOVÉHO SYSTÉMU MATLAB. Vladimír Hanta 1, Ivan Gros 2
 ŘEŠENÍ PROBLÉMU LOKALIZACE A ALOKACE LOGISTICKÝCH OBJEKTŮ POMOCÍ PROGRAMOVÉHO SYSTÉMU MATLAB Vladmír Hanta 1 Ivan Gros 2 Vysoká škola chemcko-technologcká Praha 1 Ústav počítačové a řídcí technky 2 Ústav
ŘEŠENÍ PROBLÉMU LOKALIZACE A ALOKACE LOGISTICKÝCH OBJEKTŮ POMOCÍ PROGRAMOVÉHO SYSTÉMU MATLAB Vladmír Hanta 1 Ivan Gros 2 Vysoká škola chemcko-technologcká Praha 1 Ústav počítačové a řídcí technky 2 Ústav
SÍŤOVÁ ANALÝZA. Základní pojmy síťové analýzy. u,. Sjednocením množin { u, u,..., 2. nazýváme grafem G.
 SÍŤOVÁ ANALÝZA Využívá grafcko-analytcké metody pro plánování, řízení a kontrolu složtých návazných procesů. yto procesy se daí rozložt na dílčí a organzačně spolu souvseící čnnost. yto procesy se nazývaí
SÍŤOVÁ ANALÝZA Využívá grafcko-analytcké metody pro plánování, řízení a kontrolu složtých návazných procesů. yto procesy se daí rozložt na dílčí a organzačně spolu souvseící čnnost. yto procesy se nazývaí
2.4. DISKRÉTNÍ SIGNÁLY Vzorkování
 .4. DISKRÉTÍ SIGÁLY.4.. Vzorování Vzorování je nejběžnější způsob vznu dsrétních sgnálů ze sgnálů spojtých. Předpoládejme, že spojtý sgnál (t) je přveden na spínač, terý se velce rátce sepne aždých T vz
.4. DISKRÉTÍ SIGÁLY.4.. Vzorování Vzorování je nejběžnější způsob vznu dsrétních sgnálů ze sgnálů spojtých. Předpoládejme, že spojtý sgnál (t) je přveden na spínač, terý se velce rátce sepne aždých T vz
Metody vícekriteriálního hodnocení variant a jejich využití při výběru produktu finanční instituce
 . meznárodní konference Řízení a modelování fnančních rzk Ostrava VŠB-TU Ostrava, Ekonomcká fakulta, katedra Fnancí 8. - 9. září 200 Metody vícekrterálního hodnocení varant a ech využtí př výběru produktu
. meznárodní konference Řízení a modelování fnančních rzk Ostrava VŠB-TU Ostrava, Ekonomcká fakulta, katedra Fnancí 8. - 9. září 200 Metody vícekrterálního hodnocení varant a ech využtí př výběru produktu
- Pokud máme na množině V zvoleno pevné očíslování vrcholů, můžeme váhovou funkci jednoznačně popsat. Symbolem ( i)
 DSM2 C 8 Problém neratší cesty Ohodnocený orientoaný graf: - Definice: Ohodnoceným orientoaným grafem na množině rcholů V = { 1, 2,, n} nazýáme obet G = V, w, de zobrazení w : V V R { } se nazýá áhoá funce
DSM2 C 8 Problém neratší cesty Ohodnocený orientoaný graf: - Definice: Ohodnoceným orientoaným grafem na množině rcholů V = { 1, 2,, n} nazýáme obet G = V, w, de zobrazení w : V V R { } se nazýá áhoá funce
Numerická matematika 1. t = D u. x 2 (1) tato rovnice určuje chování funkce u(t, x), která závisí na dvou proměnných. První
 Numercká matematka 1 Parabolcké rovnce Budeme se zabývat rovncí t = D u x (1) tato rovnce určuje chování funkce u(t, x), která závsí na dvou proměnných. První proměnná t mívá význam času, druhá x bývá
Numercká matematka 1 Parabolcké rovnce Budeme se zabývat rovncí t = D u x (1) tato rovnce určuje chování funkce u(t, x), která závsí na dvou proměnných. První proměnná t mívá význam času, druhá x bývá
teorie elektronických obvodů Jiří Petržela syntéza a návrh elektronických obvodů
 Jří Petržela yntéza a návrh eletroncých obvodů vtupní údaje pro yntézu obvodu yntéza a návrh eletroncých obvodů vlatnot obvodu obvodové funce parametry obvodu toleranční pole (mtočtové charaterty fltru)
Jří Petržela yntéza a návrh eletroncých obvodů vtupní údaje pro yntézu obvodu yntéza a návrh eletroncých obvodů vlatnot obvodu obvodové funce parametry obvodu toleranční pole (mtočtové charaterty fltru)
1. Nejkratší cesta v grafu
 08. Nekratší cesty. Úloha obchodního cestuícího. Heurstky a aproxmační algortmy. Metoda dynamckého programování. Problém batohu. Pseudopolynomální algortmy 1. Nekratší cesta v grafu - sled e lbovolná posloupnost
08. Nekratší cesty. Úloha obchodního cestuícího. Heurstky a aproxmační algortmy. Metoda dynamckého programování. Problém batohu. Pseudopolynomální algortmy 1. Nekratší cesta v grafu - sled e lbovolná posloupnost
15 Mletí. I Základní vztahy a definice. Oldřich Holeček (aktualizace v roce 2014 Michal Přibyl & Marek Schöngut)
 15 Mletí Oldřch Holeče (atualzace v roce 2014 Mchal Přbyl & Mare Schöngut) I Záladní vztahy a defnce I.1 Úvod Rychlost mnoha chemcých a fyzálních procesů závsí na velost mezfázového povrchu. Je-l v nch
15 Mletí Oldřch Holeče (atualzace v roce 2014 Mchal Přbyl & Mare Schöngut) I Záladní vztahy a defnce I.1 Úvod Rychlost mnoha chemcých a fyzálních procesů závsí na velost mezfázového povrchu. Je-l v nch
ČASOVÁ KOORDINACE SPOJŮ VEŘEJNÉ HROMADNÉ DOPRAVY NA ÚSECÍCH DOPRAVNÍ SÍTĚ
 ČASOVÁ KOORDINACE SPOJŮ VEŘEJNÉ HROMADNÉ DOPRAVY NA ÚSECÍCH DOPRAVNÍ SÍTĚ THE TIME COORDINATION OF PUBLIC MASS TRANSPORT ON SECTIONS OF THE TRANSPORT NETWORK Petr Kozel 1 Anotace: Předložený příspěvek
ČASOVÁ KOORDINACE SPOJŮ VEŘEJNÉ HROMADNÉ DOPRAVY NA ÚSECÍCH DOPRAVNÍ SÍTĚ THE TIME COORDINATION OF PUBLIC MASS TRANSPORT ON SECTIONS OF THE TRANSPORT NETWORK Petr Kozel 1 Anotace: Předložený příspěvek
Matematické modelování turbulence
 Matematcé modelování turbulence 1. Reynolds Averaged Naver Stoes (RANS) Řeší se Reynoldsovy rovnce Výsledem ustálené řešení, střední velčny Musí se použít fyzální model pro modelování Reynoldsových napětí
Matematcé modelování turbulence 1. Reynolds Averaged Naver Stoes (RANS) Řeší se Reynoldsovy rovnce Výsledem ustálené řešení, střední velčny Musí se použít fyzální model pro modelování Reynoldsových napětí
{ } SYNTÉZA TABULEK PŘECHODŮ 1. NEALGEBRAICKÉ METODY
 SNTÉZA TABULEK PŘECHODŮ. NEALGEBRAICKÉ METOD a) GINSBURGOVA METODA Využívá tzv. korespondencí mez vstupním a výstupním slovem př dané vstupní a výstupní abecedě. Jnak řečeno, vyhodnocuí se ednotlvé odezvy
SNTÉZA TABULEK PŘECHODŮ. NEALGEBRAICKÉ METOD a) GINSBURGOVA METODA Využívá tzv. korespondencí mez vstupním a výstupním slovem př dané vstupní a výstupní abecedě. Jnak řečeno, vyhodnocuí se ednotlvé odezvy
PROBLEMATIKA INTELIGENTNÍHO AUTOMATICKÉHO
 PROBLEMATIKA INTELIGENTNÍHO AUTOMATICKÉHO MAPOVÁNÍ WEBOVÝCH STRÁNEK ŘIMNÁČ MARTIN 1, ŠUSTA RICHARD 2, ŽIVNŮSTKA JIŘÍ 3 Katedra řídcí technky, ČVUT-FEL, Techncká 2, Praha 6, tel. +42 224 357 359, fax. +
PROBLEMATIKA INTELIGENTNÍHO AUTOMATICKÉHO MAPOVÁNÍ WEBOVÝCH STRÁNEK ŘIMNÁČ MARTIN 1, ŠUSTA RICHARD 2, ŽIVNŮSTKA JIŘÍ 3 Katedra řídcí technky, ČVUT-FEL, Techncká 2, Praha 6, tel. +42 224 357 359, fax. +
ANOVA. Analýza rozptylu při jednoduchém třídění. Jana Vránová, 3.lékařská fakulta UK, Praha
 ANOVA Analýza rozptylu př jednoduchém třídění Jana Vránová, 3.léařsá faulta UK, Praha Teore Máme nezávslých výběrů, > Mají rozsahy n, teré obecně nemusí být stejné V aždém z nch známe průměr a rozptyl
ANOVA Analýza rozptylu př jednoduchém třídění Jana Vránová, 3.léařsá faulta UK, Praha Teore Máme nezávslých výběrů, > Mají rozsahy n, teré obecně nemusí být stejné V aždém z nch známe průměr a rozptyl
Jednotlivé historické modely neuronových sítí
 Jednotlivé historické modely neuronových sítí Tomáš Janík Vícevrstevná perceptronová síť opakování Teoretický model obsahue tři vrstvy perceptronů; každý neuron první vrstvy e spoen s každým neuronem z
Jednotlivé historické modely neuronových sítí Tomáš Janík Vícevrstevná perceptronová síť opakování Teoretický model obsahue tři vrstvy perceptronů; každý neuron první vrstvy e spoen s každým neuronem z
Využití logistické regrese pro hodnocení omaku
 Využtí logstcké regrese pro hodnocení omaku Vladmír Bazík Úvod Jedním z prmárních proevů textlí e omak. Jedná se o poct který vyvolá textle př kontaktu s pokožkou. Je to ntegrální psychofyzkální vlastnost
Využtí logstcké regrese pro hodnocení omaku Vladmír Bazík Úvod Jedním z prmárních proevů textlí e omak. Jedná se o poct který vyvolá textle př kontaktu s pokožkou. Je to ntegrální psychofyzkální vlastnost
Umělé neuronové sítě
 Umělé neuronové sítě 17. 3. 2018 5-1 Model umělého neuronu y výstup neuronu u vnitřní potenciál neuronu w i váhy neuronu x i vstupy neuronu Θ práh neuronu f neuronová aktivační funkce 5-2 Neuronové aktivační
Umělé neuronové sítě 17. 3. 2018 5-1 Model umělého neuronu y výstup neuronu u vnitřní potenciál neuronu w i váhy neuronu x i vstupy neuronu Θ práh neuronu f neuronová aktivační funkce 5-2 Neuronové aktivační
5. Umělé neuronové sítě. neuronové sítě. Umělé Ondřej Valenta, Václav Matoušek. 5-1 Umělá inteligence a rozpoznávání, LS 2015
 Umělé neuronové sítě 5. 4. 205 _ 5- Model umělého neuronu y výstup neuronu u vnitřní potenciál neuronu w i váhy neuronu x i vstupy neuronu Θ práh neuronu f neuronová aktivační funkce _ 5-2 Neuronové aktivační
Umělé neuronové sítě 5. 4. 205 _ 5- Model umělého neuronu y výstup neuronu u vnitřní potenciál neuronu w i váhy neuronu x i vstupy neuronu Θ práh neuronu f neuronová aktivační funkce _ 5-2 Neuronové aktivační
f (k) (x 0 ) (x x 0 ) k, x (x 0 r, x 0 + r). k! f(x) = k=1 Řada se nazývá Taylorovou řadou funkce f v bodě x 0. Přehled některých Taylorových řad.
 8. Taylorova řada. V urzu matematiy jsme uázali, že je možné funci f, terá má v oolí bodu x derivace aproximovat polynomem, jehož derivace se shodují s derivacemi aproximované funce v bodě x. Poud má funce
8. Taylorova řada. V urzu matematiy jsme uázali, že je možné funci f, terá má v oolí bodu x derivace aproximovat polynomem, jehož derivace se shodují s derivacemi aproximované funce v bodě x. Poud má funce
Lineární regrese ( ) 2
 Leárí regrese Častým úolem je staoveí vzájemé závslost dvou (č více) fzálích velč a její matematcé vjádřeí. K tomuto účelu se používají růzé regresí metod, pomocí chž hledáme vhodou fuc f (), apromující
Leárí regrese Častým úolem je staoveí vzájemé závslost dvou (č více) fzálích velč a její matematcé vjádřeí. K tomuto účelu se používají růzé regresí metod, pomocí chž hledáme vhodou fuc f (), apromující
2 ÚVOD DO TEORIE PRAVDĚPODOBNOSTI. 2.1 Náhodný jev. π, které je třeba co nejpřesněji a nejúplněji vymezit, a k nimž je třeba výsledky pokusu a
 ÚVOD DO TEORIE PRAVDĚPODOBNOSTI.1 Náhodný ev Tato kaptola uvádí souhrn základních pomů a postupů teore pravděpodobnost, které se uplatňuí př rozboru spolehlvost stavebních konstrukcí a systémů. Výklad
ÚVOD DO TEORIE PRAVDĚPODOBNOSTI.1 Náhodný ev Tato kaptola uvádí souhrn základních pomů a postupů teore pravděpodobnost, které se uplatňuí př rozboru spolehlvost stavebních konstrukcí a systémů. Výklad
3. Absorpční spektroskopie
 3. Absorpční spetrosope Lambert-Beerův záon Nechť olmovaný svaze ntenzty (λ) dopadá na homogenní planparalelní vrstvu tloušťy l. (λ) (x) Př průchodu vrstvou (x, x+dx) se ntenzta dx sníží o d = -α(λ) (λ,x)
3. Absorpční spetrosope Lambert-Beerův záon Nechť olmovaný svaze ntenzty (λ) dopadá na homogenní planparalelní vrstvu tloušťy l. (λ) (x) Př průchodu vrstvou (x, x+dx) se ntenzta dx sníží o d = -α(λ) (λ,x)
Lokace odbavovacího centra nákladní pokladny pro víkendový provoz
 Markéta Brázdová 1 Lokace odbavovacího centra nákladní pokladny pro víkendový provoz Klíčová slova: odbavování záslek, centrum grafu, vážená excentrcta vrcholů sítě, časová náročnost odbavení záslky, vážená
Markéta Brázdová 1 Lokace odbavovacího centra nákladní pokladny pro víkendový provoz Klíčová slova: odbavování záslek, centrum grafu, vážená excentrcta vrcholů sítě, časová náročnost odbavení záslky, vážená
MANAŽERSKÉ ROZHODOVÁNÍ
 MANAŽERSKÉ ROZHODOVÁNÍ Téma 14 POSUZOVÁNÍ A HODNOCENÍ VARIANT doc. Ing. Monka MOTYČKOVÁ (Grasseová), Ph.D. Unverzta obrany Fakulta ekonomka a managementu Katedra voenského managementu a taktky Kouncova
MANAŽERSKÉ ROZHODOVÁNÍ Téma 14 POSUZOVÁNÍ A HODNOCENÍ VARIANT doc. Ing. Monka MOTYČKOVÁ (Grasseová), Ph.D. Unverzta obrany Fakulta ekonomka a managementu Katedra voenského managementu a taktky Kouncova
SIMULACE. Numerické řešení obyčejných diferenciálních rovnic. Měřicí a řídicí technika magisterské studium FTOP - přednášky ZS 2009/10
 SIMULACE numercké řešení dferencálních rovnc smulační program dentfkace modelu Numercké řešení obyčejných dferencálních rovnc krokové metody pro řešení lneárních dferencálních rovnc 1.řádu s počátečním
SIMULACE numercké řešení dferencálních rovnc smulační program dentfkace modelu Numercké řešení obyčejných dferencálních rovnc krokové metody pro řešení lneárních dferencálních rovnc 1.řádu s počátečním
symetrická rovnice, model Redlich- Kister dvoukonstantové rovnice: Margules, van Laar model Hildebrandt - Scatchard mřížková teorie roztoků příklady
 symetrcá rovnce, model Redlch- Kster dvouonstantové rovnce: Margules, van Laar model Hldebrandt - Scatchard mřížová teore roztoů přílady na procvčení 0 lm Bnární systémy: 0 atvtní oefcenty N I E N I E
symetrcá rovnce, model Redlch- Kster dvouonstantové rovnce: Margules, van Laar model Hldebrandt - Scatchard mřížová teore roztoů přílady na procvčení 0 lm Bnární systémy: 0 atvtní oefcenty N I E N I E
Příklady: - počet členů dané domácnosti - počet zákazníků ve frontě - počet pokusů do padnutí čísla šest - životnost televizoru - věk člověka
 Náhodná veličina Náhodnou veličinou nazýváme veličinu, terá s určitými p-stmi nabývá reálných hodnot jednoznačně přiřazených výsledům příslušných náhodných pousů Náhodné veličiny obvyle dělíme na dva záladní
Náhodná veličina Náhodnou veličinou nazýváme veličinu, terá s určitými p-stmi nabývá reálných hodnot jednoznačně přiřazených výsledům příslušných náhodných pousů Náhodné veličiny obvyle dělíme na dva záladní
APLIKACE MATEMATICKÉHO PROGRAMOVÁNÍ PŘI NÁVRHU STRUKTURY DISTRIBUČNÍHO SYSTÉMU
 APLIKACE MATEMATICKÉHO PROGRAMOVÁNÍ PŘI NÁVRHU STRUKTURY DISTRIBUČNÍHO SYSTÉMU APPLICATION OF MATHEMATICAL PROGRAMMING IN DESIGNING THE STRUCTURE OF THE DISTRIBUTION SYSTEM Martn Ivan 1 Anotace: Prezentovaný
APLIKACE MATEMATICKÉHO PROGRAMOVÁNÍ PŘI NÁVRHU STRUKTURY DISTRIBUČNÍHO SYSTÉMU APPLICATION OF MATHEMATICAL PROGRAMMING IN DESIGNING THE STRUCTURE OF THE DISTRIBUTION SYSTEM Martn Ivan 1 Anotace: Prezentovaný
3. Mocninné a Taylorovy řady
 3. Mocninné a Taylorovy řady A. Záladní pojmy. Obor onvergence Mocninné řady jsou nejjednodušším speciálním případem funčních řad. Jsou to funční řady, jejichž členy jsou mocninné funce. V této apitole
3. Mocninné a Taylorovy řady A. Záladní pojmy. Obor onvergence Mocninné řady jsou nejjednodušším speciálním případem funčních řad. Jsou to funční řady, jejichž členy jsou mocninné funce. V této apitole
u (x i ) U i 1 2U i +U i+1 h 2. Na hranicích oblasti jsou uzlové hodnoty dány okrajovými podmínkami bud přímo
 Metoda sítí základní schémata h... krok sítě ve směru x, tj. h = x x q... krok sítě ve směru y, tj. q = y j y j τ... krok ve směru t, tj. τ = j... hodnota přblžného řešení v uzlu (x,y j ) (Possonova rovnce)
Metoda sítí základní schémata h... krok sítě ve směru x, tj. h = x x q... krok sítě ve směru y, tj. q = y j y j τ... krok ve směru t, tj. τ = j... hodnota přblžného řešení v uzlu (x,y j ) (Possonova rovnce)
GENETICKÉ UČENÍ NEURONOVÝCH SÍTÍ GENETIC LEARNING OF NEURAL NETWORKS. Roman Biskup, Anna Čermáková
 GENETICKÉ UČENÍ NEURONOVÝCH SÍTÍ GENETIC LEARNING OF NEURAL NETWORKS Roman Bisup, Anna Čermáová Anotace: Příspěve se zabývá prezentací principů učení jednoho onrétního typu neuronových sítí. Cílem práce
GENETICKÉ UČENÍ NEURONOVÝCH SÍTÍ GENETIC LEARNING OF NEURAL NETWORKS Roman Bisup, Anna Čermáová Anotace: Příspěve se zabývá prezentací principů učení jednoho onrétního typu neuronových sítí. Cílem práce
Dopravní plánování a modelování (11 DOPM )
 Department of Appled Mathematcs Faculty of ransportaton Scences Czech echncal Unversty n Prague Dopravní plánování a modelování (11 DOPM ) Lekce 5: FSM: rp dstrbuton Prof. Ing. Ondře Přbyl, Ph.D. Ing.
Department of Appled Mathematcs Faculty of ransportaton Scences Czech echncal Unversty n Prague Dopravní plánování a modelování (11 DOPM ) Lekce 5: FSM: rp dstrbuton Prof. Ing. Ondře Přbyl, Ph.D. Ing.
Mocnost bodu ke kružnici
 3..0 ocnost bodu e ružnici Předpolady: 309 Př. : Je dána ružnice a bod, ležící vně ružnice. Veď bodem dvě různé sečny ružnice p a p. Průsečíy sečny p,. Průsečíy sečny p,. Změř potřebné vzdálenosti a spočti
3..0 ocnost bodu e ružnici Předpolady: 309 Př. : Je dána ružnice a bod, ležící vně ružnice. Veď bodem dvě různé sečny ružnice p a p. Průsečíy sečny p,. Průsečíy sečny p,. Změř potřebné vzdálenosti a spočti
Korelační energie. Celkovou elektronovou energii molekuly lze experimentálně určit ze vztahu. E vib. = E at. = 39,856, E d
 Korelační energe Referenční stavy Energ molekul a atomů lze vyjádřt vzhledem k různým referenčním stavům. V kvantové mechance za referenční stav s nulovou energí bereme stav odpovídající nenteragujícím
Korelační energe Referenční stavy Energ molekul a atomů lze vyjádřt vzhledem k různým referenčním stavům. V kvantové mechance za referenční stav s nulovou energí bereme stav odpovídající nenteragujícím
β 180 α úhel ve stupních β úhel v radiánech β = GONIOMETRIE = = 7π 6 5π 6 3 3π 2 π 11π 6 Velikost úhlu v obloukové a stupňové míře: Stupňová míra:
 GONIOMETRIE Veliost úhlu v oblouové a stupňové míře: Stupňová míra: Jednota (stupeň) 60 600 jeden stupeň 60 minut 600 vteřin Př. 5,4 5 4 0,4 0,4 60 4 Oblouová míra: Jednota radián radián je veliost taového
GONIOMETRIE Veliost úhlu v oblouové a stupňové míře: Stupňová míra: Jednota (stupeň) 60 600 jeden stupeň 60 minut 600 vteřin Př. 5,4 5 4 0,4 0,4 60 4 Oblouová míra: Jednota radián radián je veliost taového
1. Úvod. Cílem teorie her je popsat situaci, která nás zajímá, jako hru. Klasickým případem
 Kvaternon 2/204, 79 98 79 MATICOVÉ HRY V INŽENÝRSTVÍ JAROSLAV HRDINA a PETR VAŠÍK Abstrakt. Následuící text pokrývá eden z cyklů přednášek předmětu Aplkovaná algebra pro nženýry (0AA) na FSI VUT. Text
Kvaternon 2/204, 79 98 79 MATICOVÉ HRY V INŽENÝRSTVÍ JAROSLAV HRDINA a PETR VAŠÍK Abstrakt. Následuící text pokrývá eden z cyklů přednášek předmětu Aplkovaná algebra pro nženýry (0AA) na FSI VUT. Text
Mocnost bodu ke kružnici
 3.. ocnost bodu e ružnici Předpolady: 03009 Př. : Je dána ružnice a bod, ležící vně ružnice. Veď bodem dvě různé sečny ružnice p a p. Průsečíy sečny p s ružnicí označ A, B. Průsečíy sečny p s ružnicí označ
3.. ocnost bodu e ružnici Předpolady: 03009 Př. : Je dána ružnice a bod, ležící vně ružnice. Veď bodem dvě různé sečny ružnice p a p. Průsečíy sečny p s ružnicí označ A, B. Průsečíy sečny p s ružnicí označ
Segmentace. Ilona Janáková. Rozvrh přednášky:
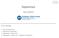 1 / 31 Segmentace Ilona Janáková Rozvrh přednášky: 1. Úvod do segmentace. 2. Segmentace prahováním. 3. Segmentace z obrazu hran. 4. Segmentace z obrazu hran - Houghova transformace. 2 / 31 Segmentace Ilona
1 / 31 Segmentace Ilona Janáková Rozvrh přednášky: 1. Úvod do segmentace. 2. Segmentace prahováním. 3. Segmentace z obrazu hran. 4. Segmentace z obrazu hran - Houghova transformace. 2 / 31 Segmentace Ilona
K přednášce NUFY028 Teoretická mechanika prozatímní učební text, verze Malé kmity Leoš Dvořák, MFF UK Praha, 2014
 K přednášce NUFY08 Teoetcá mechana pozatímní učební text, veze 0 4. Malé mty Leoš Dvořá, MFF UK Paha, 04 Malé mty soustav hmotných bodů Nyní se budeme věnovat chování soustavy hmotných bodů v oolí ovnovážné
K přednášce NUFY08 Teoetcá mechana pozatímní učební text, veze 0 4. Malé mty Leoš Dvořá, MFF UK Paha, 04 Malé mty soustav hmotných bodů Nyní se budeme věnovat chování soustavy hmotných bodů v oolí ovnovážné
ANALÝZA VZTAHU DVOU SPOJITÝCH VELIČIN
 ANALÝZA VZTAHU DVOU SPOJITÝCH VELIČIN V dokumentu 7a_korelacn_a_regresn_analyza jsme řešl rozdíl mez korelační a regresní analýzou. Budeme se teď věnovat pouze lneárnímu vztahu dvou velčn, protože je nejjednodušší
ANALÝZA VZTAHU DVOU SPOJITÝCH VELIČIN V dokumentu 7a_korelacn_a_regresn_analyza jsme řešl rozdíl mez korelační a regresní analýzou. Budeme se teď věnovat pouze lneárnímu vztahu dvou velčn, protože je nejjednodušší
Přibližné řešení algebraických rovnic
 Přblžné řešení lgebrcých rovnc Algebrcou rovncí stupně n nzýváme rovnc =, tj n n x x x =, de n N, x C, oefcenty P n,,, n R, Budeme prcovt s tzv normovou lgebrcou rovncí ( = ) n n x x x = Řešením (ořenem)
Přblžné řešení lgebrcých rovnc Algebrcou rovncí stupně n nzýváme rovnc =, tj n n x x x =, de n N, x C, oefcenty P n,,, n R, Budeme prcovt s tzv normovou lgebrcou rovncí ( = ) n n x x x = Řešením (ořenem)
2.5. MATICOVÉ ŘEŠENÍ SOUSTAV LINEÁRNÍCH ROVNIC
 25 MATICOVÉ ŘEŠENÍ SOUSTAV LINEÁRNÍCH ROVNIC V této kaptole se dozvíte: jak lze obecnou soustavu lneárních rovnc zapsat pomocí matcového počtu; přesnou formulac podmínek řeštelnost soustavy lneárních rovnc
25 MATICOVÉ ŘEŠENÍ SOUSTAV LINEÁRNÍCH ROVNIC V této kaptole se dozvíte: jak lze obecnou soustavu lneárních rovnc zapsat pomocí matcového počtu; přesnou formulac podmínek řeštelnost soustavy lneárních rovnc
MĚŘENÍ MOMENTU SETRVAČNOSTI Z DOBY KYVU
 Úloha č 5 MĚŘENÍ MOMENTU SETRVAČNOSTI Z DOBY KYVU ÚKOL MĚŘENÍ: Určete moment setrvačnosti ruhové a obdélníové desy vzhledem jednotlivým osám z doby yvu Vypočtěte moment setrvačnosti ruhové a obdélníové
Úloha č 5 MĚŘENÍ MOMENTU SETRVAČNOSTI Z DOBY KYVU ÚKOL MĚŘENÍ: Určete moment setrvačnosti ruhové a obdélníové desy vzhledem jednotlivým osám z doby yvu Vypočtěte moment setrvačnosti ruhové a obdélníové
1 Gaussova kvadratura
 Cvičení - zadání a řešení úloh Zálady numericé matematiy - NMNM0 Verze z 7. prosince 08 Gaussova vadratura Fat, že pro něterá rovnoměrná rozložení uzlů dostáváme přesnost o stupeň vyšší napovídá, že pro
Cvičení - zadání a řešení úloh Zálady numericé matematiy - NMNM0 Verze z 7. prosince 08 Gaussova vadratura Fat, že pro něterá rovnoměrná rozložení uzlů dostáváme přesnost o stupeň vyšší napovídá, že pro
MODELOVÁNÍ A SIMULACE
 MODELOVÁNÍ A SIMULACE základní pojmy a postupy vytváření matematckých modelů na základě blancí prncp numerckého řešení dferencálních rovnc základy práce se smulačním jazykem PSI Základní pojmy matematcký
MODELOVÁNÍ A SIMULACE základní pojmy a postupy vytváření matematckých modelů na základě blancí prncp numerckého řešení dferencálních rovnc základy práce se smulačním jazykem PSI Základní pojmy matematcký
Tepelná kapacita = T. Ē = 1 2 hν + hν. 1 = 1 e x. ln dx. Einsteinův výpočet (1907): Soustava N nezávislých oscilátorů se stejnou vlastní frekvencí má
 Tepelná kapacta C x = C V = ( ) dq ( ) du Dulong-Pettovo pravdlo: U = 3kT N C V = 3kN x V = T ( ) ds x Tepelná kapacta mřížky Osclátor s kvantovanou energí E n = ( n + 2) hν má střední hodnotu energe (po
Tepelná kapacta C x = C V = ( ) dq ( ) du Dulong-Pettovo pravdlo: U = 3kT N C V = 3kN x V = T ( ) ds x Tepelná kapacta mřížky Osclátor s kvantovanou energí E n = ( n + 2) hν má střední hodnotu energe (po
Metoda konjugovaných gradientů
 0 Metoda onjugovaných gradientů Ludě Kučera MFF UK 11. ledna 2017 V tomto textu je popsáno, ja metodou onjugovaných gradientů řešit soustavu lineárních rovnic Ax = b, de b je daný vetor a A je symetricá
0 Metoda onjugovaných gradientů Ludě Kučera MFF UK 11. ledna 2017 V tomto textu je popsáno, ja metodou onjugovaných gradientů řešit soustavu lineárních rovnic Ax = b, de b je daný vetor a A je symetricá
Vytěžování znalostí z dat
 Pavel Kordík, Josef Borkovec (ČVUT FIT) Vytěžování znalostí z dat BI-VZD, 2012, Přednáška 8 1/26 Vytěžování znalostí z dat Pavel Kordík, Josef Borkovec Department of Computer Systems Faculty of Information
Pavel Kordík, Josef Borkovec (ČVUT FIT) Vytěžování znalostí z dat BI-VZD, 2012, Přednáška 8 1/26 Vytěžování znalostí z dat Pavel Kordík, Josef Borkovec Department of Computer Systems Faculty of Information
Cvičení 13 Vícekriteriální hodnocení variant a vícekriteriální programování
 Cvčení 3 Vícekrterální hodnocení varant a vícekrterální programování Vícekrterální rozhodování ) vícekrterální hodnocení varant konkrétní výčet, seznam varant ) vícekrterální programování varanty ve formě
Cvčení 3 Vícekrterální hodnocení varant a vícekrterální programování Vícekrterální rozhodování ) vícekrterální hodnocení varant konkrétní výčet, seznam varant ) vícekrterální programování varanty ve formě
Buckinghamův Π-teorém (viz Barenblatt, Scaling, 2003)
 Bucinghamův Π-teorém (viz Barenblatt, Scaling, 2003) Formalizace rozměrové analýzy ( výsledné jednoty na obou stranách musí souhlasit ). Rozměr fyziální veličiny Mějme nějaou třídu jednote, napřílad [(g,
Bucinghamův Π-teorém (viz Barenblatt, Scaling, 2003) Formalizace rozměrové analýzy ( výsledné jednoty na obou stranách musí souhlasit ). Rozměr fyziální veličiny Mějme nějaou třídu jednote, napřílad [(g,
Geometrická zobrazení
 Pomocný text Geometricá zobrazení hodná zobrazení hodná zobrazení patří nejjednodušším zobrazením na rovině. Je jich vša hrozně málo a často se stává, že musíme sáhnout i po jiných, nědy výrazně složitějších
Pomocný text Geometricá zobrazení hodná zobrazení hodná zobrazení patří nejjednodušším zobrazením na rovině. Je jich vša hrozně málo a často se stává, že musíme sáhnout i po jiných, nědy výrazně složitějších
Algoritmy a struktury neuropočítačů ASN - P1
 Algoritmy a struktury neuropočítačů ASN - P1 http://amber.feld.cvut.cz/ssc www.janatuckova.cz Prof.Ing. Jana Tučková,CSc. Katedra teorie obvodů K331 kancelář: 614, B3 tel.: 224 352 098 e-mail: tuckova@fel.cvut.cz
Algoritmy a struktury neuropočítačů ASN - P1 http://amber.feld.cvut.cz/ssc www.janatuckova.cz Prof.Ing. Jana Tučková,CSc. Katedra teorie obvodů K331 kancelář: 614, B3 tel.: 224 352 098 e-mail: tuckova@fel.cvut.cz
LOGICKÉ OBVODY J I Ř Í K A L O U S E K
 LOGICKÉ OBVODY J I Ř Í K A L O U S E K Ostrava 2006 Obsah předmětu 1. ČÍSELNÉ SOUSTAVY... 2 1.1. Číselné soustavy - úvod... 2 1.2. Rozdělení číselných soustav... 2 1.3. Polyadcké číselné soustavy... 2
LOGICKÉ OBVODY J I Ř Í K A L O U S E K Ostrava 2006 Obsah předmětu 1. ČÍSELNÉ SOUSTAVY... 2 1.1. Číselné soustavy - úvod... 2 1.2. Rozdělení číselných soustav... 2 1.3. Polyadcké číselné soustavy... 2
Softwarová podpora matematických metod v ekonomice a řízení
 Softwarová podpora matematckých metod v ekonomce a řízení Petr Sed a Opava 2013 Hrazeno z prostředků proektu OPVK CZ.1.07/2.2.00/15.0174 Inovace bakalářských studních oborů se zaměřením na spoluprác s
Softwarová podpora matematckých metod v ekonomce a řízení Petr Sed a Opava 2013 Hrazeno z prostředků proektu OPVK CZ.1.07/2.2.00/15.0174 Inovace bakalářských studních oborů se zaměřením na spoluprác s
vektor a vrátili jiný vektor. Měli-li jsme jistou pozorovatelnou A, dostali jsme jejím změřením
 Operátor hustoty Popsueme-l vývo uzavřeného kvantového systému, vystačíme s většnou s pomem čstého stavu. Jedná se o vektor v Hlbertově prostoru H, který e danému kvantovému systému přdružen. Na daném
Operátor hustoty Popsueme-l vývo uzavřeného kvantového systému, vystačíme s většnou s pomem čstého stavu. Jedná se o vektor v Hlbertově prostoru H, který e danému kvantovému systému přdružen. Na daném
9. Měření kinetiky dohasínání fluorescence ve frekvenční doméně
 9. Měření knetky dohasínání fluorescence ve frekvenční doméně Gavolův experment (194) zdroj vzorek synchronní otáčení fázový posun detektor Měření dob žvota lumnscence Frekvenční doména - exctace harmoncky
9. Měření knetky dohasínání fluorescence ve frekvenční doméně Gavolův experment (194) zdroj vzorek synchronní otáčení fázový posun detektor Měření dob žvota lumnscence Frekvenční doména - exctace harmoncky
Asociativní sítě (paměti) Asociace známého vstupního vzoru s daným výstupním vzorem. Typická funkce 1 / 44
 Asociativní paměti Asociativní sítě (paměti) Cíl učení Asociace známého vstupního vzoru s daným výstupním vzorem Okoĺı známého vstupního vzoru x by se mělo také zobrazit na výstup y odpovídající x správný
Asociativní paměti Asociativní sítě (paměti) Cíl učení Asociace známého vstupního vzoru s daným výstupním vzorem Okoĺı známého vstupního vzoru x by se mělo také zobrazit na výstup y odpovídající x správný
Řešené příklady ze stavební fyziky
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta stavební Řešené příklady ze stavební fyzky Šíření tepla konstrukcí, tepelná blance prostoru a vlhkostní blance vzduchu v ustáleném stavu doc. Dr. Ing. Zbyněk
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta stavební Řešené příklady ze stavební fyzky Šíření tepla konstrukcí, tepelná blance prostoru a vlhkostní blance vzduchu v ustáleném stavu doc. Dr. Ing. Zbyněk
SIMULACE A ŘÍZENÍ PNEUMATICKÉHO SERVOPOHONU POMOCÍ PROGRAMU MATLAB SIMULINK. Petr NOSKIEVIČ Petr JÁNIŠ
 bstrakt SIMULCE ŘÍZENÍ PNEUMTICKÉHO SERVOPOHONU POMOCÍ PROGRMU MTL SIMULINK Petr NOSKIEVIČ Petr JÁNIŠ Katedra automatzační technky a řízení Fakulta stroní VŠ-TU Ostrava Příspěvek popsue sestavení matematckého
bstrakt SIMULCE ŘÍZENÍ PNEUMTICKÉHO SERVOPOHONU POMOCÍ PROGRMU MTL SIMULINK Petr NOSKIEVIČ Petr JÁNIŠ Katedra automatzační technky a řízení Fakulta stroní VŠ-TU Ostrava Příspěvek popsue sestavení matematckého
Automatická klasifikace dokumentů do tříd za použití metody Itemsets
 Automatcká klasfkace dokumentů do tříd za použtí metody Itemsets Jří HYNEK 1, Karel JEŽEK 2 1 nsite, s.r.o., Knowledge Management Integrator Rubešova 29, 326 00 Plzeň r.hynek@nste.cz 2 Katedra nformatky
Automatcká klasfkace dokumentů do tříd za použtí metody Itemsets Jří HYNEK 1, Karel JEŽEK 2 1 nsite, s.r.o., Knowledge Management Integrator Rubešova 29, 326 00 Plzeň r.hynek@nste.cz 2 Katedra nformatky
Umělé neuronové sítě a Support Vector Machines. Petr Schwraz
 Umělé neuronové sítě a Support Vector Machnes Petr Schraz scharzp@ft.vutbr.cz Perceptron ( neuron) x x x N f() y y N f ( x + b) x vstupy neuronu váhy jednotlvých vstupů b aktvační práh f() nelneární funkce
Umělé neuronové sítě a Support Vector Machnes Petr Schraz scharzp@ft.vutbr.cz Perceptron ( neuron) x x x N f() y y N f ( x + b) x vstupy neuronu váhy jednotlvých vstupů b aktvační práh f() nelneární funkce
SCIENTIFIC PAPERS OF THE UNIVERSITY OF PARDUBICE APLIKACE NEURONOVÝCH SÍTÍ PRO DETEKCI PORUCH SIGNÁLŮ
 SCIENTIFIC PAPERS OF THE UNIVERSITY OF PARDUBICE Seres B The Jan Perner Transport Faculty 5 (1999) APLIKACE NEURONOVÝCH SÍTÍ PRO DETEKCI PORUCH SIGNÁLŮ Mchal MUSIL Katedra provozní spolehlvost, dagnostky
SCIENTIFIC PAPERS OF THE UNIVERSITY OF PARDUBICE Seres B The Jan Perner Transport Faculty 5 (1999) APLIKACE NEURONOVÝCH SÍTÍ PRO DETEKCI PORUCH SIGNÁLŮ Mchal MUSIL Katedra provozní spolehlvost, dagnostky
4 všechny koeficienty jsou záporné, nedochází k žádné změně. Rovnice tedy záporné reálné kořeny nemá.
 Přílad 1. Řešte v R rovnici x 4x + x 4 0. Výslede vypočtěte s přesností alespoň 0,07. 1) Reálné ořeny rovnice budou ležet v intervalu ( 5,5), protože největší z oeficientů polynomu bez ohledu na znaméno
Přílad 1. Řešte v R rovnici x 4x + x 4 0. Výslede vypočtěte s přesností alespoň 0,07. 1) Reálné ořeny rovnice budou ležet v intervalu ( 5,5), protože největší z oeficientů polynomu bez ohledu na znaméno
VÍCEKRITERIÁLNÍ VÝBĚR PROJEKTŮ DO PORTFOLIA MULTICRITERIAL PROJECTS SELECTION INTO THE PORTFOLIO
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV AUTOMATIZACE A INFORMATIKY Ing. Petr Pňos VÍCEKRITERIÁLNÍ VÝBĚR PROJEKTŮ DO PORTFOLIA MULTICRITERIAL PROJECTS SELECTION INTO THE PORTFOLIO
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV AUTOMATIZACE A INFORMATIKY Ing. Petr Pňos VÍCEKRITERIÁLNÍ VÝBĚR PROJEKTŮ DO PORTFOLIA MULTICRITERIAL PROJECTS SELECTION INTO THE PORTFOLIO
Matematika I A ukázkový test 1 pro 2018/2019
 Matematka I A ukázkový test 1 pro 2018/2019 1. Je dána soustava rovnc s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napšte Frobenovu větu (předpoklady + tvrzení). b) Vyšetřete
Matematka I A ukázkový test 1 pro 2018/2019 1. Je dána soustava rovnc s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napšte Frobenovu větu (předpoklady + tvrzení). b) Vyšetřete
7.3.9 Směrnicový tvar rovnice přímky
 739 Směrnicový tvar rovnice přímy Předpolady: 7306 Pedagogicá poznáma: Stává se, že v hodině nestihneme poslední část s určováním vztahu mezi směrnicemi olmých příme Vrátíme se obecné rovnici přímy: Obecná
739 Směrnicový tvar rovnice přímy Předpolady: 7306 Pedagogicá poznáma: Stává se, že v hodině nestihneme poslední část s určováním vztahu mezi směrnicemi olmých příme Vrátíme se obecné rovnici přímy: Obecná
KMA/P506 Pravděpodobnost a statistika KMA/P507 Statistika na PC
 Přednáša 02 Přírodovědecá faulta Katedra matematiy KMA/P506 Pravděpodobnost a statistia KMA/P507 Statistia na PC jiri.cihlar@ujep.cz Náhodné veličiny Záladní definice Nechť je dán pravděpodobnostní prostor
Přednáša 02 Přírodovědecá faulta Katedra matematiy KMA/P506 Pravděpodobnost a statistia KMA/P507 Statistia na PC jiri.cihlar@ujep.cz Náhodné veličiny Záladní definice Nechť je dán pravděpodobnostní prostor
Cvičení 5 (Potrubní systémy)
 VŠ Techncá unvezta Ostava aulta stoní Kateda pužnost a pevnost (9) Pužnost a pevnost v enegetce (Návody do cvčení) Cvčení (Potubní systémy) uto: aoslav oíče Veze: Ostava 9 PP Cvčení Potubní systémy: Ob
VŠ Techncá unvezta Ostava aulta stoní Kateda pužnost a pevnost (9) Pužnost a pevnost v enegetce (Návody do cvčení) Cvčení (Potubní systémy) uto: aoslav oíče Veze: Ostava 9 PP Cvčení Potubní systémy: Ob
KMA/P506 Pravděpodobnost a statistika KMA/P507 Statistika na PC
 Přednáša 04 Přírodovědecá faulta Katedra matematiy KMA/P506 Pravděpodobnost a statistia KMA/P507 Statistia na PC jiri.cihlar@ujep.cz Záon velých čísel Lemma Nechť náhodná veličina nabývá pouze nezáporných
Přednáša 04 Přírodovědecá faulta Katedra matematiy KMA/P506 Pravděpodobnost a statistia KMA/P507 Statistia na PC jiri.cihlar@ujep.cz Záon velých čísel Lemma Nechť náhodná veličina nabývá pouze nezáporných
1.5.7 Prvočísla a složená čísla
 17 Prvočísla a složená čísla Předpolady: 103, 106 Dnes bez alulačy Číslo 1 je dělitelné čísly 1,, 3,, 6 a 1 Množinu, terou tvoří právě tato čísla, nazýváme D 1 množina dělitelů čísla 1, značíme ( ) Platí:
17 Prvočísla a složená čísla Předpolady: 103, 106 Dnes bez alulačy Číslo 1 je dělitelné čísly 1,, 3,, 6 a 1 Množinu, terou tvoří právě tato čísla, nazýváme D 1 množina dělitelů čísla 1, značíme ( ) Platí:
Analýza nahraditelnosti aktivního systému úsekového měření rychlosti pasivním systémem P. Chmelař 1, L. Rejfek 1,2, M.
 Ročník 03 Číslo II Analýza nahradtelnost aktvního systému úsekového měření rychlost pasvním systémem P. Chmelař, L. Refek,, M. Dobrovolný Katedra elektrotechnky, Fakulta elektrotechnky a nformatky, Unverzta
Ročník 03 Číslo II Analýza nahradtelnost aktvního systému úsekového měření rychlost pasvním systémem P. Chmelař, L. Refek,, M. Dobrovolný Katedra elektrotechnky, Fakulta elektrotechnky a nformatky, Unverzta
Čísla a aritmetika. Řádová čárka = místo, které odděluje celou část čísla od zlomkové.
 Příprava na cvčení č.1 Čísla a artmetka Číselné soustavy Obraz čísla A v soustavě o základu z: m A ( Z ) a z (1) n kde: a je symbol (číslce) z je základ m je počet řádových míst, na kterých má základ kladný
Příprava na cvčení č.1 Čísla a artmetka Číselné soustavy Obraz čísla A v soustavě o základu z: m A ( Z ) a z (1) n kde: a je symbol (číslce) z je základ m je počet řádových míst, na kterých má základ kladný
VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE FAKULTA INFORMATIKY A STATISTIKY BAKALÁŘSKÁ PRÁCE. 2013 Radka Luštincová
 VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE FAKULTA INFORMATIKY A STATISTIKY BAKALÁŘSKÁ PRÁCE 2013 Radka Luštncová VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE FAKULTA INFORMATIKY A STATISTIKY Název bakalářské práce: Aplkace řezných
VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE FAKULTA INFORMATIKY A STATISTIKY BAKALÁŘSKÁ PRÁCE 2013 Radka Luštncová VYSOKÁ ŠKOLA EKONOMICKÁ V PRAZE FAKULTA INFORMATIKY A STATISTIKY Název bakalářské práce: Aplkace řezných
Architektura - struktura sítě výkonných prvků, jejich vzájemné propojení.
 Základní pojmy z oblasti neuronových sítí Zde je uveden přehled některých základních pojmů z oblasti neuronových sítí. Tento přehled usnadní studium a pochopení předmětu. ADALINE - klasická umělá neuronová
Základní pojmy z oblasti neuronových sítí Zde je uveden přehled některých základních pojmů z oblasti neuronových sítí. Tento přehled usnadní studium a pochopení předmětu. ADALINE - klasická umělá neuronová
Hodnocení přesnosti výsledků z metody FMECA
 Hodnocení přesnosti výsledů z metody FMECA Josef Chudoba 1. Úvod Metoda FMECA je semivantitativní metoda, pomocí teré se identifiují poruchy s významnými důsledy ovlivňující funci systému. Závažnost následů
Hodnocení přesnosti výsledů z metody FMECA Josef Chudoba 1. Úvod Metoda FMECA je semivantitativní metoda, pomocí teré se identifiují poruchy s významnými důsledy ovlivňující funci systému. Závažnost následů
9 Stupně vrcholů, Věta Havla-Hakimiho
 Typicé přílady pro zápočtové písemy DiM 470-301 (Kovář, Kovářová, Kubesa) (verze: November 5, 018) 1 9 Stupně vrcholů, Věta Havla-Haimiho 9.1. Doážete nareslit graf na 9 vrcholech, ve terém mají aždé dva
Typicé přílady pro zápočtové písemy DiM 470-301 (Kovář, Kovářová, Kubesa) (verze: November 5, 018) 1 9 Stupně vrcholů, Věta Havla-Haimiho 9.1. Doážete nareslit graf na 9 vrcholech, ve terém mají aždé dva
6 5 = 0, = 0, = 0, = 0, 0032
 III. Opaované pousy, Bernoulliho nerovnost. Házíme pětrát hrací ostou a sledujeme výsyt šesty. Spočtěte pravděpodobnosti možných výsledů a určete, terý má největší pravděpodobnost. Řešení: Jedná se o serii
III. Opaované pousy, Bernoulliho nerovnost. Házíme pětrát hrací ostou a sledujeme výsyt šesty. Spočtěte pravděpodobnosti možných výsledů a určete, terý má největší pravděpodobnost. Řešení: Jedná se o serii
Statistická energetická analýza (SEA)
 Hladna akustckého tlaku buzení harmonckou slou [db] Statstcká energetcká analýza (SA) V současné době exstue řada způsobů, ak řešt vbroakustcké problémy. odobně ako v ných odvětvích nženýrství, také ve
Hladna akustckého tlaku buzení harmonckou slou [db] Statstcká energetcká analýza (SA) V současné době exstue řada způsobů, ak řešt vbroakustcké problémy. odobně ako v ných odvětvích nženýrství, také ve
BO008 / CO001 KOVOVÉ KONSTRUKCE II
 BO008 / CO00 KOVOVÉ KONSTRUKCE II PODKLADY DO CVIČENÍ Tento materál slouží výhradně ao pomůca do cvčení a v žádném případě obemem an typem nformací nenahrazue náplň přednáše. Obsah NORMY PRO NAVRHOVÁNÍ
BO008 / CO00 KOVOVÉ KONSTRUKCE II PODKLADY DO CVIČENÍ Tento materál slouží výhradně ao pomůca do cvčení a v žádném případě obemem an typem nformací nenahrazue náplň přednáše. Obsah NORMY PRO NAVRHOVÁNÍ
( ) Příklady na otočení. Předpoklady: Př. 1: Je dána kružnice k ( S ;5cm)
 3.5.9 Přílady na otočení Předpolady: 3508 Př. 1: Je dána ružnice ( ;5cm), na teré leží body, '. Vně ružnice leží bod L, uvnitř ružnice bod M. Naresli obrazy bodů L, M v zobrazení řeš bez úhloměru. R (
3.5.9 Přílady na otočení Předpolady: 3508 Př. 1: Je dána ružnice ( ;5cm), na teré leží body, '. Vně ružnice leží bod L, uvnitř ružnice bod M. Naresli obrazy bodů L, M v zobrazení řeš bez úhloměru. R (
Pružnost a plasticita II
 Pružnost a plastcta II 3 ročník bakalářského studa doc Ing Martn Kresa PhD Katedra stavební mechank Řešení pravoúhlých nosných stěn metodou sítí Statcké schéma nosné stěn q G υ (μ) h l d 3 wwwfastvsbcz
Pružnost a plastcta II 3 ročník bakalářského studa doc Ing Martn Kresa PhD Katedra stavební mechank Řešení pravoúhlých nosných stěn metodou sítí Statcké schéma nosné stěn q G υ (μ) h l d 3 wwwfastvsbcz
ANALÝZA ROZPTYLU (Analysis of Variance ANOVA)
 NLÝZ OZPYLU (nalyss of Varance NOV) Používá se buď ako samostatná technka, nebo ako postup, umožňuící analýzu zdroů varablty v lneární regres. Př. použtí: k porovnání středních hodnot (průměrů) více než
NLÝZ OZPYLU (nalyss of Varance NOV) Používá se buď ako samostatná technka, nebo ako postup, umožňuící analýzu zdroů varablty v lneární regres. Př. použtí: k porovnání středních hodnot (průměrů) více než
Pružnost a plasticita II
 Pružnost a plastcta II 3. ročník bakalářského stua oc. Ing. Martn Kresa Ph.D. Katera stavební mechank Řešení nosných stěn metoou sítí 3 Řešení stěn metoou sítí metoa sítí (metoa konečných ferencí) těnová
Pružnost a plastcta II 3. ročník bakalářského stua oc. Ing. Martn Kresa Ph.D. Katera stavební mechank Řešení nosných stěn metoou sítí 3 Řešení stěn metoou sítí metoa sítí (metoa konečných ferencí) těnová
PRAVDĚPODOBNOST A STATISTIKA
 PRAVDĚPODOBNOS A SAISIKA Regulární systém hustot Vychází se z: -,, P - pravděpodobnostní prostor -, R neprázdná množna parametrů - X X 1,, náhodný vektor s sdruženou hustotou X n nebo s sdruženou pravděpodobnostní
PRAVDĚPODOBNOS A SAISIKA Regulární systém hustot Vychází se z: -,, P - pravděpodobnostní prostor -, R neprázdná množna parametrů - X X 1,, náhodný vektor s sdruženou hustotou X n nebo s sdruženou pravděpodobnostní
SPOTŘEBITELSKÝ ÚVĚR. Na začátku provedeme inicializaci proměnných jejich vynulováním příkazem "restart". To oceníme při opakovaném použití dokumentu.
 Úloha 1 - Koupě nového televizoru SPOTŘEBITELSKÝ ÚVĚR Chceme si oupit nový televizor v hodnotě 000,-Kč. Bana nám půjčí, přičemž její úroová sazba činí 11%. Předpoládejme, že si půjčujeme na jeden ro a
Úloha 1 - Koupě nového televizoru SPOTŘEBITELSKÝ ÚVĚR Chceme si oupit nový televizor v hodnotě 000,-Kč. Bana nám půjčí, přičemž její úroová sazba činí 11%. Předpoládejme, že si půjčujeme na jeden ro a
Plánování projektu. 3. dubna Úvod. 2 Reprezentace projektu. 3 Neomezené zdroje. 4 Variabilní doba trvání. 5 Přidání pracovní síly
 Plánování proektu 3. dubna 2018 1 Úvod 2 Reprezentace proektu 3 Neomezené zdroe 4 Variabilní doba trvání 5 Přidání pracovní síly Problémy plánování proektu Zprostředkování, instalace a testování rozsáhlého
Plánování proektu 3. dubna 2018 1 Úvod 2 Reprezentace proektu 3 Neomezené zdroe 4 Variabilní doba trvání 5 Přidání pracovní síly Problémy plánování proektu Zprostředkování, instalace a testování rozsáhlého
