Základní list. Úplný základ - načítání knihoven, informace, restart. Základní informace. Jak dostat z Maplu další informace
|
|
|
- Nikola Kopecká
- před 6 lety
- Počet zobrazení:
Transkript
1 Základní list Úplný základ - načítání knihoven, informace, restart To, že čtete tento list znamená, že jste úspěšně zvládli spuštění Maplu a načtení listu do něj ;-). Pokud jste úplní začátečníci, chcete se něco dozvědět o Maplu a máte dost času můžete si pustit Starter tour (nalézá se jen v novějších verzích). Najdete jej v nabídce Help - Contents (pokud je samozřejmě ve Vaší verzi obsažena). Jinak doporučuji kurz RNDr Pavla Pyriha - odkaz na něj najdete na stránce, kde jste stáhli tento list. Základní informace Standartní funkce se zapisují v Maplu přirozeným způsobem - notací, používanou ve většině programech, kde se vyskytuje matematika. Stačí je psát tak, jak se například používají v programovacím jazyce Pascal. Proto uvedu pouze způsob zadávání exponenciely a logaritmu : > exp(x); > log(x)=ln(x); e x ln( x ) = ln( x ) A takhle vypadá absolutní hodnota a druhá odmocnina: > abs(-1); > sqrt(4); 1 2 Jak už by mělo být z předešlého zřejmé, každý příkaz je v Maplu nutné ukončit středníkem. Další možnost je ukončit ho dvojtečkou, což určuje, že Maple neprovede žádný výstup na obrazovku. > exp(x): Jak dostat z Maplu další informace Kromě systému nápovědy, který je mimochodem moc pěkný, existují v Maplu i další příkazy, které vám dají další informace o výpočtech a jejich průběhu. Nejzajímavějším takovým příkazem je infolevel. Nastavuje se pomocí přirozených čísel znamená nejméně informací, 5 nejvíce. Základní nastavení je 1. Infolevel se používá takto :
2 > infolevel[int]:=5; infolevel int := 5 Takto jsme právě zvýšili informace o průběhu výpočtů integrálu na 5. > Int(sin(x)/x, x=0..infinity)=int(sin(x)/x, x=0..infinity); int: Beginning integration with _EnvContinuous=_EnvContinuous, _EnvAll Solutions=_EnvAllSolutions, and _EnvCauchyPrincipalValue=_EnvCauchyPrinc ipalvalue. Definite Integration: Integrating expression on x=0..infinity Definite Integration: Using the integrators [Distribution, Piecewise, Series, O, Polynomial, Ln, LookUp, Cook, Ratpoly, Elliptic, EllipticTrig, MeijerGSpecial, Improper, Asymptotic, FTOC, MeijerG, Contour] Definite Integration: Trying method Distribution. Definite Integration: Finished method Distribution. Time elapsed: s. Definite Integration: Trying method Piecewise. Definite Integration: Finished method Piecewise. Time elapsed: s. Definite Integration: Trying method Series. Definite Integration: Finished method Series. Time elapsed: s. Definite Integration: Trying method O. Definite Integration: Finished method O. Time elapsed: s. Definite Integration: Trying method Polynomial. Definite Integration: Finished method Polynomial. Time elapsed: s. Definite Integration: Trying method Ln. Definite Integration: Finished method Ln. Time elapsed: s. Definite Integration: Trying method LookUp. IntegralTransform LookUp Integrator: Integral might be a fouriersin tr ansform with expr=1/x and s=1. LookUp Integrator: the specified integral found with the IntegralTrans form look up method. Definite Integration: Finished method LookUp. Time elapsed: s. Definite Integration: Method LookUp succeeded. Definite Integration: Finished sucessfully. Takhle tedy Maple počítá integrál 0 0 sin( x ) π dx = x 2 sin( x ) dx ;-). x Načítání knihoven Většina potřebných věcí se v Maplu ukrývá v různých knihovnách. Tyto knihovny se zpřístupní teprve po načtení. Toto řešení je dobré zejména vzhledem k obsáhlosti některých knihoven a způsobu jakým je to do nich uloženo. Pokud tedy počítáte s grupami nepotřebujete bředit paměť počítače knihovnou s numerickými funkcemi. Jednou z nejdůležitějších knihoven je knihovna Student obsahující základní funkce
3 potřebné k počítání příkladů z okruhu analýzy a kalkulu obecně. Tato knihovan (nebo alespoň většina, jejích funkcí - záleží na instalaci Maplu) se načítá automaticky po spuštění. Pro zábavu a obecné pobavení si ji načteme znova. > with(student); [ D, Diff, Doubleint, Int, Limit, Lineint, Product, Sum, Tripleint, changevar, completesquare, distance, equate, integrand, intercept, intparts, leftbox, leftsum, makeproc, middlebox, middlesum, midpoint, powsubs, rightbox, rightsum, showtangent, simpson, slope, summand, trapezoid] Podobnou práci na jiné brdo učiní i příkaz readlib. > readlib(student); table([ intercept = student/intercept, completesquare = student/cmpltsq, summand = student/summand, rightsum = student/rightsum, Int = student/int, leftbox = student/leftbox, rightbox = student/rightbox, powsubs = student/powsubs, Lineint = student/lineint, simpson = student/simpson, Sum = student/sum, equate = student/equate, slope = student/slope, middlebox = student/middlebox, makeproc = student/makeproc, changevar = student/changevar, showtangent = student/showtngt, trapezoid = student/trapezoid, Limit = student/limit, Product = student/product, Doubleint = student/doubleint, distance = student/distance, integrand = student/integrand, midpoint = student/midpoint, Tripleint = student/tripleint, D = D, leftsum = student/leftsum, middlesum = student/middlesum, Diff = student/diff, intparts = student/intparts ]) Můžeme také načítat jen jednotlivé příkazy, bez toho abychom načetli celou knihovnu. > with(student, rightsum); [ rightsum ] Restart Občas je výhodné vynulovat celou paměť, zbavit se zadefinovaných proměnných, funkcí i načtených knihoven. Pokud to chceme udělat stačí napsat: > restart; Další zajímavé operátory a funkce
4 Upravujeme výrazy Funkce simplify zjednodušuje výrazy. Provede krácení a vytýkání, umí i základní vzorce pro fce sin a cos. > (x^3-1)/(x-1)*(sin(x)^2-1)/cos(2*x)=simplify((x^3-1)/(x-1) *(sin(x)^2-1)/cos(2*x)); ( x 3 1 ) ( sin( x ) 2 1 ) = ( x 1 ) cos( 2 x ) cos( x ) 2 ( x 2 + x + 1 ) cos( 2 x ) Můžeme i určovat jaké úpravy se budou provádět viz. help na simplify. Podobné věci na trochu jiné brdo dělá funkce combine. > Limit(f(x),x=a)*Limit(g(x),x=a)=combine(Limit(f(x),x=a)*Li mit(g(x),x=a)); ( lim f( x )) ( lim g( x) ) = lim x a x a x a f( x ) g( x ) Opakem combine je expand: > (x+1)^4=expand((x+1)^4); ( x + 1 ) 4 = x x x x + 1 Vyčíslujeme Pro přibližné vyčíslení výrazu používáme funkci evalf. > Pi = evalf(pi); > Pi = evalf(pi, 20); π = π = Opět evalf je poměrně variabilní příkaz, více o jeho vatriantách viz. help na evalf. Na určení přesnosti můžeme použít, buď parametr v evalf, nebo globální parametr digits, který je standartně nastaven na 10. > Digits:=20; > e = evalf(exp(1)); Digits := 20 e =
5 Rozkládáme Zajímavou funkcí je factor. Pomůže nám faktorizovat polynomy. > x^4+7*x^3+17*x^2+17*x+6 = factor(x^4+7*x^3+17*x^2+17*x+6); x x x x + 6 = ( x + 3 ) ( x + 2 ) ( x + 1) 2 Rozklad se provádí pouze, lze-li rozložit celá čísla. Pokud to nejde, můžeme k tomu Maple donutit. > factor(x^3+3); > factor(x^3+3,3^(1/3)); / x ( x 2 x 3 ( 1 3 ) + 3 ( 2 3 ) ) ( x + 3 ( 1 3 ) ) Můžeme provádět i prvočíselný rozklad přírozených čísel. / / > ifactor(110160); ( 2) 4 ( 3 ) 4 ( 5 ) ( 17 ) Faktorizace na prvočísla není samozřejmě vždy ideální, ale lze ji provádět podle více metod viz help na ifactor. Více o práci s polynomy a faktorizaci viz list Algebra. Skládáme na více způsobů Nejdříve si ukážeme skládací operátor. Uplatníme ho později, např. při derivacích. > (sin@cos)(x); sin ( cos( x )) Můžeme použít, i dvojitý skládací operátor. Určuje kolikrát složíme funkci samu se sebou. > (sin@@(-1))(x); > (sin@@(3))(x); arcsin( x ) ( sin ( 3 ) )( x) Teď přijde na řadu jedna moc užitečná věc, která ušetří spoustu práce. Operátor $: > x := [i $ i=1..10];
6 x := [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ] Pomocí tohoto operátoru můžeme vytvářet skupiny čísel a z těch pak třeba počítat funkční hodnoty a pod. S tímto operátorem lze dělat i další fígle. Čísla například mohou být i necelá, skoky jsou opět po jedné: > z := {k $ k= 1/9..5}; z := {,,,, } Operátor $ je nadán i jistou mírou vlastní "chytrosti". > x := 5$4; x := 5, 5, 5, 5 Při vytváření jmen si vystačíme i jen s pouhou. (tečkou ;-)). > x := p.(5..10); x := p. ( ) Tak to je operátor, ale na podobné věci máme navíc i funkci, jmenuje se seq a je moc dobrá. Pomocí ní třeba konečně zjistíme jak, že je to s těmi siny ;-). > seq(sin(pi*i/4), i=0..8); ,, 1,, 0,, -1,, Pěkné. Ale pomocí jednoho příkazu navíc - nops, který vrací počet prvků v seznamu to ještě vylepšíme. > M := [seq(i/4, i=0..8)]; > [t,sin(t)]=[seq( [M[i],sin(M[i]*Pi)], i=1..nops(m))]; [ t, sin( t ) ] = M := 0, 1 1 3,,,,,,, [ 0, 0 ], 1 2 1,,,,,,,,, , [ 1, 0 ] 5, , , Můžeme dokonce přímo volat prvky v našem seznamu. > M_na_druhou := [seq( i^2,i=m)]; M_na_druhou := 0, 1 1 9,,,,,,, [ 2, 0 ]
7 Dostali jsme tedy možnost používat v Maple výhody cyklů a to bez toho abychom vůbec šáhli na nějaké programování. RootOf Nyní se podíváme na funkci RootOf. Tato funkce souvisí sice s Algebrou - vrací kořeny rovnic, ale sama se nám často objevuje na výstupu z mnoha dalších příkazů Maplu. Často se nám objeví něco jako: > RootOf(x^2+1=0); RootOf (( _Z. ( ) ) ) Nemusíme se hned lekat. Výsledky jsou prostě příslušné kořeny rovnice x = 0. Ty si můžeme vyčíslit třeba pomocí evalf nebo solve > evalf(rootof(x^2+1=0)); > solve(x^2+1=0); RootOf (( _Z. ( ) ) ) RootOf (( _Z. ( ) ) ) Bohužel aplikací evalf, některé kořeny ztrácíme. Tento problém naštěstí úplně vrací funkce allvalues: > allvalues(rootof(x^4+x^2+1)); RootOf ((_Z. ( ) ) 4 + ( _Z. ( ) ) ) Funkce signum a Heaviside Česky je to signum anglicky také, dělá to tohle: > sgn(-1) = signum(-1); > sgn( 1) = signum( 1); > sgn( 0) = signum( 0); > plot(signum(x), color=red,discont=true); sgn( -1) = -1 sgn( 1) = 1 sgn( 0) = 0
8 Podobně funguje funkce Heaviside: > Heaviside(-1); > Heaviside( 1); > Heaviside( 0); > plot(heaviside(x),x= ,color=red); 0 1 undefined Tedy platí (až na x = 0) Heaviside( x ) = signum( x) Přiřazujeme proměnným aneb assign V některých příkladech je potřeba proměnné přiřadit nějakou hodnotu. To se dělá (kromě :=) také funkcí assign: > assign(k=27);
9 > simplify(k^(1/3)); 3 Pokud se předchozího přiřazení chceme zbavit napíšeme: > k := 'k'; k := k Totéž můžeme (globálně a brutálně) provést i pomocí restart: > restart; Výroba nových funkcí ze starých Při většině problémů, které chceme v Maple spočítat, nepotřebujeme definovat vlastní funkce. Prostě rovnou napíšeme příslušnou funkcí například do integrálu apod.. Ovšem zvláště pokud kreslíme grafy a počítáme vícekrát funkční hodnoty, vyplatí se nám funkci nadefinovat. Používáme na to funkční operátor ->. > f:= x -> sin(x)*exp(x^2)+cos(x)*exp(-x^2); f := x sin( x ) e ( x2 ) + cos( x ) e ( x2 ) Pro získání funkční hodnoty nám pak stačí psát pouze : > f(pi); e ( π2 ) Pak můžeme snadno kreslit grafy : > plot(f(t), t=-pi..pi);
10 Proč je důležité používat funkcionální operátor? Podíváme se co by se stalo, kdybychom funkci špatně nadefinovali : > g:= sin(x)*x^3+3*x; g := sin( x ) x x Dostáváme dost mizerné výsledky : > g(pi); sin( x )( π ) x( π) x( π) A graf taky nic moc :( : > plot(g(x));
11 I když se nám podaří nakreslit graf následujícím způsobem. Doporučuji používat vždy funkční operátor > plot(g, x=0..pi);
12 Funkce můžeme definovat i po částech. Funguje to takhle: > piecewise(x>0,x^2,x<0, abs(x)); Teď si to nakreslíme: { x2 0 < x x x < 0 > f := x -> piecewise(x>0,x^2,x<0, abs(x)); > plot(f(x),x=-5..5); f := x piecewise ( 0 < x, x 2, x < 0, x )
13 Tímto způsobem můžeme samozřejmě popsat fci i na více než na dvou intervalech. Grafy Nejdříve si zadefinujeme nějakou pěknou funkci ;-) : > f := x -> x + 2*x^2*sin(1/x); f := x x + 2 x 2 sin 1 x Podíváme se na nějaký její jednoduchý graf. > plot(f(x), x=-1/2..1/2, y=-1/2..1/2, color=blue, numpoints=500,title=`tohle je graf ;-)`);
14 Tak takhle pěkně jsme to nakreslily, volba numpoints určuje v kolika bodech se funkční hodnoty kreslí. Bez ní by tento graf vypadal trochu nepěkně - nepřesně a hranatě ;-), ale uvětšiny ostatních grafů není potřeba. Označení y je standartní označení pro druhou osu, toto lze předefinovat pomocí volby axes - viz help na plot a na plot[options]. V případě, že funkce je nespojitá může nám nastat následující problém. > plot(1/(x-1), x=-4..6, y=-5..5);
15 Všimněte si nehezké čáry v bodě nespojitosti x = 1. Tu odstraníme přidáním podmínky discont=true > plot(1/(x-1), x=-4..6, y=-5..5, discont=true);
16 Nakreslit jeden graf nám často nestačí, a tak se teď budeme zabývat vytvářením více grafů najednou. S grafy manipuluje knihovna plots. > with(plots); [ animate, animate3d, animatecurve, arrow, changecoords, complexplot, complexplot3d, conformal, conformal3d, contourplot, contourplot3d, coordplot, coordplot3d, densityplot, display, dualaxisplot, fieldplot, fieldplot3d, gradplot, gradplot3d, graphplot3d, implicitplot, implicitplot3d, inequal, interactive, interactiveparams, intersectplot, listcontplot, listcontplot3d, listdensityplot, listplot, listplot3d, loglogplot, logplot, matrixplot, multiple, odeplot, pareto, plotcompare, pointplot, pointplot3d, polarplot, polygonplot, polygonplot3d, polyhedra_supported, polyhedraplot, rootlocus, semilogplot, setcolors, setoptions, setoptions3d, spacecurve, sparsematrixplot, surfdata, textplot, textplot3d, tubeplot ] Teď slíbených více grafů najednou. Zobrazujeme je pomocí funkce display. > plotf := plot(f(x), x=-1/2..1/2, y=-1/2..1/2, color=red, numpoints=500): > plot1 := plot(x+2*x^2, x=-1/2..1/2, y=-1/2..1/2,
17 linestyle=10,color=blue): > plot2 := plot(x-2*x^2, x=-1/2..1/2, y=-1/2..1/2, linestyle=10,color=blue): > display([plot1,plot2,plotf], title=`tohle jsou grafy ;-)`); Maple umí i jiné zajímavé "grafy". > plot1:= plot(sin(x),x=-pi/2..pi/2): > plot2:= plot(cos(x),x=-pi/2..pi/2,color=blue): > plot3:= textplot([[pi/4+0.2,sqrt(2)/2,`tady se protnou ;-)`],[-1,0.4,`A tady nic není`]],align={right}): > plot4:= pointplot([pi/4,sqrt(2)/2],symbol=circle): > display({plot1,plot2,plot3,plot4}, title=`hezké, ne?`);
18 Teď se podíváme na grafy implicitně zadané funkce. Takhle zobrazí Maple Descartesův list: > implicitplot(x^3+y^3-2*x*y=0, x=-2..2, y=-2..2,numpoints=5000, color=red);
19 Malá poznámka k volbě numpoints: tato volba není u většiny příkladů vůbec nutná. Obyčejně stačí základní nastavení (to je 50). Toto nastavení sice často nestačilo, ale Maple je nadán "přirozenou inteligencí" a sám volí hodnoty tak aby nakreslená křivka, co nejvíce odpovídala skutečné funkci. V některých příkladech bohužel jeho "chytrost" zklame. Descartův list je jedním z nich.. Můžeme zobrazit i paramatetrické funkce. Na to nám vystačí pouhá funkce plot. > plot([cos(t),sin(t), t=0..2*pi], title=`toto je kružnice. ;-)`);
20 Maple umí ještě i další triky s dvourozměrnými grafy. Než přejdeme ke grafům v trojrozměrném prostoru ukážeme si ještě jeden kousek pro fyziky: > fieldplot([cos(x),sin(y)],x=0..pi,y=0..2*pi, title=`vektorové pole ;-)`);
21 V trojrozměrném prostoru kreslíme grafy pomocí plot3d: > plot3d(1/5*x^2+sin(x*y), x=-pi..pi, y=-pi..pi, style=patch, axes=boxed, title=`takhle vypadá 3d graf ;-)`);
22 Grafy můžeme kreslit i v jiných souřadnicích než kartézských, například ve sférických. > plot3d({y*sin(x),x}, x=0..2*pi, y=-2*pi..2*pi, style=wireframe, coords=spherical, axes=frame, title=`průnik dvou 3d grafů ve sférických souřadnicích`);
23 > Poznámka : v nadpisu předchozího grafu můžeme vidět nemilé překvapení, které nám Maple připravuje s některými českými znaky :(. Nezbývá nám nic jiného než se těmto znakům vyhnout nebo počkat na novější verzi. Při kreslení dalších druhů grafů Vám dopomáhej Bůh a help na plots ;-). To jak se kreslí grafy k numerickým řešením diferenciálních rovnic najdete v listu Základy numerické matematiky. Použitá literatura Vojtěch Jarník : Úvod do počtu diferenciálního (Diferenciální počet I) Jiří Kopáček a kol.: Příklady z matematiky pro fyziky II.
2. přednáška (grafika a maplovský programovací jazyk)
 2. přednáška (grafika a maplovský programovací jazyk) Grafika v Maplu Mnoho možností nám poskytují balíky plots a plottools. restart; with(plots); [ animate, animate3d, animatecurve, arrow, changecoords,
2. přednáška (grafika a maplovský programovací jazyk) Grafika v Maplu Mnoho možností nám poskytují balíky plots a plottools. restart; with(plots); [ animate, animate3d, animatecurve, arrow, changecoords,
Co když chceme udělat funkci z něčeho, co jsme již pracně spočetli? > P4:=normal(eval(subs(n=4,1/2^n/n!*diff((x^2-1)^n,x$n))));
 restart; Procedury a funkce F:=(x)-sin(x)*exp(-x); F := x sin( x ) e ( x ) Co když chceme udělat funkci z něčeho, co jsme již pracně spočetli? P4:=normal(eval(subs(n=4,1/2^n/n!*diff((x^2-1)^n,x$n))));
restart; Procedury a funkce F:=(x)-sin(x)*exp(-x); F := x sin( x ) e ( x ) Co když chceme udělat funkci z něčeho, co jsme již pracně spočetli? P4:=normal(eval(subs(n=4,1/2^n/n!*diff((x^2-1)^n,x$n))));
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA INFORMAČNÍCH TECHNOLOGIÍ ÚSTAV POČÍTAČOVÝCH SYSTÉMŮ FACULTY OF INFORMATION TECHNOLOGY DEPARTMENT OF COMPUTER SYSTEMS SEMI-ANALYTICKÉ
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA INFORMAČNÍCH TECHNOLOGIÍ ÚSTAV POČÍTAČOVÝCH SYSTÉMŮ FACULTY OF INFORMATION TECHNOLOGY DEPARTMENT OF COMPUTER SYSTEMS SEMI-ANALYTICKÉ
MASARYKOVA UNIVERZITA. Funkce dvou proměnných: definiční obor, hledání extrémů, grafické znázornění
 MASARYKOVA UNIVERZITA PEDAGOGICKÁ FAKULTA Katedra matematiky Funkce dvou proměnných: definiční obor, hledání extrémů, grafické znázornění Bakalářská práce Brno 2016 Vedoucí práce: Mgr. Irena Budínová,
MASARYKOVA UNIVERZITA PEDAGOGICKÁ FAKULTA Katedra matematiky Funkce dvou proměnných: definiční obor, hledání extrémů, grafické znázornění Bakalářská práce Brno 2016 Vedoucí práce: Mgr. Irena Budínová,
Limity funkcí. Spočtěte následující limity: x, (Demidovič 411). x a) lim x 0. , b) lim x 1. , c) lim. 2 x 2 x 1
 Spočtěte následující limity: Limity funkcí Příklady řešené pomocí Maple V 1. a) lim x 0 x 2 1 2 x 2 x 1, b) lim x 1 x 2 1 2 x 2 x 1, c) lim x x 2 1 2 x 2 x 1, (Demidovič 411). Nejprve si zadefinujeme naší
Spočtěte následující limity: Limity funkcí Příklady řešené pomocí Maple V 1. a) lim x 0 x 2 1 2 x 2 x 1, b) lim x 1 x 2 1 2 x 2 x 1, c) lim x x 2 1 2 x 2 x 1, (Demidovič 411). Nejprve si zadefinujeme naší
Nula vyjde až po zjednodušení, které užívá pravidla pro práci s trigonometrickými funkcemi simplify(h1-h);
 Základní funkce a příkazy Maple jako kalkulátor. Červeně je zadání v jazyku systému MAPLE, černě jsou komentáře, modře pak výsledky. Příkaz necháme provést tak, že umístíme kursor (karetu, to co bliká
Základní funkce a příkazy Maple jako kalkulátor. Červeně je zadání v jazyku systému MAPLE, černě jsou komentáře, modře pak výsledky. Příkaz necháme provést tak, že umístíme kursor (karetu, to co bliká
Maple. Petr Kundrát. Ústav matematiky, FSI VUT v Brně. Maple a základní znalosti z oblasti obyčejných diferenciálních rovnic.
 Obyčejné diferenciální rovnice s počítačovou podporou - Maple Petr Kundrát Ústav matematiky, FSI VUT v Brně Tento soubor vznikl za účelem ilustrace použití prostředí Maple k řešení a vizualizaci řešení
Obyčejné diferenciální rovnice s počítačovou podporou - Maple Petr Kundrát Ústav matematiky, FSI VUT v Brně Tento soubor vznikl za účelem ilustrace použití prostředí Maple k řešení a vizualizaci řešení
Výpočet excentrického klikového mechanismu v systému MAPLE 11 Tomáš Svoboda Technická fakulta Česká Zemědělská Univerzita
 Výpočet excentrického klikového mechanismu v systému MAPLE 11 Tomáš Svoboda Technická fakulta Česká Zemědělská Univerzita ročník:2 studijní skupina:2 Page 1 Excentrický klikový mechanismus je zadán parametry
Výpočet excentrického klikového mechanismu v systému MAPLE 11 Tomáš Svoboda Technická fakulta Česká Zemědělská Univerzita ročník:2 studijní skupina:2 Page 1 Excentrický klikový mechanismus je zadán parametry
NMAF 051, ZS Zkoušková písemná práce 26. ledna x. x 1 + x dx. q 1. u = x = 1 u2. = 1 u. u 2 (1 + u 2 ) (1 u 2 du = 2.
 Jednotlivé kroky při výpočtech stručně, ale co nejpřesněji odůvodněte Pokud používáte nějaké tvrzení, nezapomeňte ověřit splnění předpokladů Jméno a příjmení: Skupina: Příklad 4 Celkem bodů Bodů 5 6 8
Jednotlivé kroky při výpočtech stručně, ale co nejpřesněji odůvodněte Pokud používáte nějaké tvrzení, nezapomeňte ověřit splnění předpokladů Jméno a příjmení: Skupina: Příklad 4 Celkem bodů Bodů 5 6 8
Internetová adresa osobní stránky:
 3 MAPLEOVSKÁ CVIČENÍ PRO DRUHÝ SEMESTR RNDr. Jiří Klaška, Dr. Internetová adresa osobní stránky: http://www.mat.fme.vutbr.cz/home/klaska E-mail: klaska@um.fme.vutbr.cz Úvod V rámci tří cvičení u počítače
3 MAPLEOVSKÁ CVIČENÍ PRO DRUHÝ SEMESTR RNDr. Jiří Klaška, Dr. Internetová adresa osobní stránky: http://www.mat.fme.vutbr.cz/home/klaska E-mail: klaska@um.fme.vutbr.cz Úvod V rámci tří cvičení u počítače
3.2 3DgrafyvMaple 106 KAPITOLA 3. UŽITÍ MAPLE PŘI ŘEŠENÍ KVADRIK
 106 KAPITOLA 3. UŽITÍ MAPLE PŘI ŘEŠENÍ KVADRIK > A2:=augment(submatrix(A,1..3,[1]),b,submatrix(A,1..3,[3])); Potom vypočítáme hodnotu x 2 : > x2:=det(a2)/det(a); Zadání matice. Matici M typu (2, 3) zadáme
106 KAPITOLA 3. UŽITÍ MAPLE PŘI ŘEŠENÍ KVADRIK > A2:=augment(submatrix(A,1..3,[1]),b,submatrix(A,1..3,[3])); Potom vypočítáme hodnotu x 2 : > x2:=det(a2)/det(a); Zadání matice. Matici M typu (2, 3) zadáme
Wolfram Alpha. v podobě html stránky, samotný výsledek je často doplněn o další informace (např. graf, jiné možné zobrazení výsledku a
 Wolfram Alpha jde o výpočetní prostředí z nejrůznějších oborů (matematika, fyzika, chemie, inženýrství... ) přístupné online: http://www.wolframalpha.com/ Jaké matematické výpočty Wolfram Alpha zvládá?
Wolfram Alpha jde o výpočetní prostředí z nejrůznějších oborů (matematika, fyzika, chemie, inženýrství... ) přístupné online: http://www.wolframalpha.com/ Jaké matematické výpočty Wolfram Alpha zvládá?
Diferenciální rovnice II
 Diferenciální rovnice II Cílem tohoto kurzu je ukázat si různé příklady použití počítačového algebraického systému Maple při řešení obyčejných diferenciálních rovnic. řádu a soustav obyčejných diferenciálních
Diferenciální rovnice II Cílem tohoto kurzu je ukázat si různé příklady použití počítačového algebraického systému Maple při řešení obyčejných diferenciálních rovnic. řádu a soustav obyčejných diferenciálních
> Limit((1-cos(x))/x^2, x=0)=limit((1-cos(x))/x^2, x=0); x 2 2. x 0. = undefined. x 0
 Matematická analýza Limity a nekonečné součiny V Maple není třeba rozlišovat mezi itou funkce a posloupnosti takže následující ita může být stejně tak dobře itou funkce i posloupnosti. Vše záleží na naší
Matematická analýza Limity a nekonečné součiny V Maple není třeba rozlišovat mezi itou funkce a posloupnosti takže následující ita může být stejně tak dobře itou funkce i posloupnosti. Vše záleží na naší
Základy numerické matematiky. Interpolace a aproximace funkcí
 Základy numerické matematiky Interpolace a aproximace funkcí Nejdříve se podíváme na interpolaci. Lagrangeovu interpolaci počítá Maple pomocí funkce interp. Jejími parametry jsou - soubor uzlů, funkčních
Základy numerické matematiky Interpolace a aproximace funkcí Nejdříve se podíváme na interpolaci. Lagrangeovu interpolaci počítá Maple pomocí funkce interp. Jejími parametry jsou - soubor uzlů, funkčních
Funkce a její vlastnosti
 funkce-vp.nb 1 Funkce a její vlastnosti Zadávání funkce a její obory Zadávání funkcí více proměnných je stejné jako u jedné proměnné In[1]:= f@x_, y_d := Sqrt@xyD In[2]:= f@3, 8D Out[2]= 2 6 In[3]:= f@2,
funkce-vp.nb 1 Funkce a její vlastnosti Zadávání funkce a její obory Zadávání funkcí více proměnných je stejné jako u jedné proměnné In[1]:= f@x_, y_d := Sqrt@xyD In[2]:= f@3, 8D Out[2]= 2 6 In[3]:= f@2,
1. Krivky. krivky zadane parametrickymi rovnicemi. Primka rovnobezna s osou y. Primka rovnobezna s osou x
 1. Krivky krivky zadane parametrickymi rovnicemi krivka K: x = f(t), y = g(t), t 2interval
1. Krivky krivky zadane parametrickymi rovnicemi krivka K: x = f(t), y = g(t), t 2interval
a 3 c 5 A 1 Programové prostředí
 Programové prostředí Program se skládá z několika různých typů řádků. 1. Řádek pro komentář = program jej neprovede. Vložíte jej stisknutím CTRL+T, přes menu Insert -> Text, kliknutím na. Řádek začíná
Programové prostředí Program se skládá z několika různých typů řádků. 1. Řádek pro komentář = program jej neprovede. Vložíte jej stisknutím CTRL+T, přes menu Insert -> Text, kliknutím na. Řádek začíná
Limita ve vlastním bodě
 Výpočty it Definice (a případné věty) jsou z knihy [] příklady z [] [] a []. Počítám u zkoušky dvacátou itu hlavu mám dávno už do čista vymytu papír se značkami skvěje z čela mi pot v proudech leje než
Výpočty it Definice (a případné věty) jsou z knihy [] příklady z [] [] a []. Počítám u zkoušky dvacátou itu hlavu mám dávno už do čista vymytu papír se značkami skvěje z čela mi pot v proudech leje než
Přednáška 3: Limita a spojitost
 3 / 1 / 17, 1:38 Přednáška 3: Limita a spojitost Limita funkce Nejdříve je potřeba upřesnit pojmy, které přesněji popisují (topologickou) strukturu množiny reálných čísel, a to zejména pojem okolí 31 Definice
3 / 1 / 17, 1:38 Přednáška 3: Limita a spojitost Limita funkce Nejdříve je potřeba upřesnit pojmy, které přesněji popisují (topologickou) strukturu množiny reálných čísel, a to zejména pojem okolí 31 Definice
FAKULTA STAVEBNÍ MATEMATIKA. Cvičení z matematiky s využitím systému MAPLE DOPLŇKOVÝ STUDIJNÍ MATERIÁL
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ JIŘÍ NOVOTNÝ MATEMATIKA Cvičení z matematiky s využitím systému MAPLE DOPLŇKOVÝ STUDIJNÍ MATERIÁL c Jiří Novotný, Brno 2015 Obsah Úvod 5 1 Funkce v MAPLE
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ JIŘÍ NOVOTNÝ MATEMATIKA Cvičení z matematiky s využitím systému MAPLE DOPLŇKOVÝ STUDIJNÍ MATERIÁL c Jiří Novotný, Brno 2015 Obsah Úvod 5 1 Funkce v MAPLE
Kapitola 9: Aplikace integrálů funkcí jedné proměnné
 Sbírka příkladů Matematika II pro strukturované studium Kapitola 9: Aplikace integrálů funkcí jedné proměnné Chcete-li ukončit prohlížení stiskněte klávesu Esc. Chcete-li pokračovat stiskněte klávesu Enter..
Sbírka příkladů Matematika II pro strukturované studium Kapitola 9: Aplikace integrálů funkcí jedné proměnné Chcete-li ukončit prohlížení stiskněte klávesu Esc. Chcete-li pokračovat stiskněte klávesu Enter..
1 LC - numerické řešení integrálu - rozšíření
 Pomůcka pro cvičení: 2. semestr Bc studia Numerické řešení integrálu-funkce daná tabelovanými hodnotami, funkce daná analyticky 1 LC - numerické řešení integrálu - rozšíření Pro numerický výpočet určitého
Pomůcka pro cvičení: 2. semestr Bc studia Numerické řešení integrálu-funkce daná tabelovanými hodnotami, funkce daná analyticky 1 LC - numerické řešení integrálu - rozšíření Pro numerický výpočet určitého
TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií
 TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií MATLB: přednáška 4 Numerické a analytické výpočty Zbyněk Koldovský Projekt ESF CZ.1.07/2.2.00/28.0050 Modernizace
TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií MATLB: přednáška 4 Numerické a analytické výpočty Zbyněk Koldovský Projekt ESF CZ.1.07/2.2.00/28.0050 Modernizace
Integrální počet funkcí jedné proměnné
 Integrální počet funkcí jedné proměnné Neurčité integrály Určité a nevlastní integrály Geometrické aplikace určitého integrálu. p.1/?? Neurčité integrály Příklad 7.1.1 Vhodnou metodou vypočítejte neurčitý
Integrální počet funkcí jedné proměnné Neurčité integrály Určité a nevlastní integrály Geometrické aplikace určitého integrálu. p.1/?? Neurčité integrály Příklad 7.1.1 Vhodnou metodou vypočítejte neurčitý
Úvod do programu MAXIMA
 Jedná se o rozpracovaný návod k programu wxmaxima pro naprosté začátečníky. Návod lze libovolně kopírovat a používat ke komerčním i osobním účelům. Momentálně chybí mnoho důležitých kapitol které budou
Jedná se o rozpracovaný návod k programu wxmaxima pro naprosté začátečníky. Návod lze libovolně kopírovat a používat ke komerčním i osobním účelům. Momentálně chybí mnoho důležitých kapitol které budou
Limita funkce. FIT ČVUT v Praze. (FIT) Limita funkce 3.týden 1 / 39
 Limita funkce FIT ČVUT v Praze 3.týden (FIT) Limita funkce 3.týden 1 / 39 Definice funkce. Zobrazení (f, D f ), jehož definiční obor D f i obor hodnot H f je podmnožinou množiny reálných čísel, se nazývá
Limita funkce FIT ČVUT v Praze 3.týden (FIT) Limita funkce 3.týden 1 / 39 Definice funkce. Zobrazení (f, D f ), jehož definiční obor D f i obor hodnot H f je podmnožinou množiny reálných čísel, se nazývá
Test M1-ZS12-2 M1-ZS12-2/1. Příklad 1 Najděte tečnu grafu funkce f x 2 x 6 3 x 2, která je kolmá na přímku p :2x y 3 0.
 Test M-ZS- M-ZS-/ Příklad Najděte tečnu grafu funkce f x x 6 3 x, která je kolmá na přímku p :x y 3 0. Zřejmě D f R. Přímka p má směrnici, tečna na ní kolmá má proto směrnici. Protože směrnice tečny ke
Test M-ZS- M-ZS-/ Příklad Najděte tečnu grafu funkce f x x 6 3 x, která je kolmá na přímku p :x y 3 0. Zřejmě D f R. Přímka p má směrnici, tečna na ní kolmá má proto směrnici. Protože směrnice tečny ke
Práce s kalkulátorem
 ..8 Práce s kalkulátorem Předpoklady: 007 Ke koupi kalkulátoru: Myslím, že každý student by si kalkulačku koupit měl. V současnosti sice existují dvě možné náhrady, které buď má (mobilní telefon) nebo
..8 Práce s kalkulátorem Předpoklady: 007 Ke koupi kalkulátoru: Myslím, že každý student by si kalkulačku koupit měl. V současnosti sice existují dvě možné náhrady, které buď má (mobilní telefon) nebo
Úvodní informace. 17. února 2018
 Úvodní informace Funkce více proměnných Přednáška první 17. února 2018 Obsah 1 Úvodní informace. 2 Funkce více proměnných Definiční obor Limita a spojitost Derivace, diferencovatelnost, diferenciál Úvodní
Úvodní informace Funkce více proměnných Přednáška první 17. února 2018 Obsah 1 Úvodní informace. 2 Funkce více proměnných Definiční obor Limita a spojitost Derivace, diferencovatelnost, diferenciál Úvodní
Matematická analýza pro informatiky I. Spojitost funkce
 Matematická analýza pro informatiky I. 6. přednáška Spojitost funkce Jan Tomeček tomecek@inf.upol.cz http://aix-slx.upol.cz/ tomecek/index Univerzita Palackého v Olomouci 18. března 2011 Jan Tomeček, tomecek@inf.upol.cz
Matematická analýza pro informatiky I. 6. přednáška Spojitost funkce Jan Tomeček tomecek@inf.upol.cz http://aix-slx.upol.cz/ tomecek/index Univerzita Palackého v Olomouci 18. března 2011 Jan Tomeček, tomecek@inf.upol.cz
Diferenciální rovnice I
 Diferenciální rovnice I V kurzu Diferenciální rovnice I se naučíme pomocí počítačového algebraického systému Maple hledat obecná a partikulární řešení obyčejných diferenciálních rovnic 1. řádu. Pro případ,
Diferenciální rovnice I V kurzu Diferenciální rovnice I se naučíme pomocí počítačového algebraického systému Maple hledat obecná a partikulární řešení obyčejných diferenciálních rovnic 1. řádu. Pro případ,
Nalezněte hladiny následujících funkcí. Pro které hodnoty C R jsou hladiny neprázdné
 . Definiční obor a hladiny funkce více proměnných Nalezněte a graficky znázorněte definiční obor D funkce f = f(x, y), kde a) f(x, y) = x y, b) f(x, y) = log(xy + ), c) f(x, y) = xy, d) f(x, y) = log(x
. Definiční obor a hladiny funkce více proměnných Nalezněte a graficky znázorněte definiční obor D funkce f = f(x, y), kde a) f(x, y) = x y, b) f(x, y) = log(xy + ), c) f(x, y) = xy, d) f(x, y) = log(x
Zimní semestr akademického roku 2014/ prosince 2014
 Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičení Zimní semestr akademického roku 2014/2015 7. prosince 2014 Předmluva
Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Obsah Cvičení Zimní semestr akademického roku 2014/2015 7. prosince 2014 Předmluva
Kapitola 7: Integrál. 1/17
 Kapitola 7: Integrál. 1/17 Neurčitý integrál - Motivační příklad 2/17 Příklad: Necht se bod pohybuje po přímce rychlostí a) v(t) = 3 [m/s] (rovnoměrný přímočarý pohyb), b) v(t) = 2t [m/s] (rovnoměrně zrychlený
Kapitola 7: Integrál. 1/17 Neurčitý integrál - Motivační příklad 2/17 Příklad: Necht se bod pohybuje po přímce rychlostí a) v(t) = 3 [m/s] (rovnoměrný přímočarý pohyb), b) v(t) = 2t [m/s] (rovnoměrně zrychlený
Grafy funkcí odvozených z funkcí sinus a cosinus I
 4..0 Grafy funkcí odvozených z funkcí sinus a cosinus I Předpoklady: 409 Pedagogická poznámka: Kvůli následující hodině je třeba dát pozor, příliš se nezaseknout na začátku hodiny a postupovat tak, aby
4..0 Grafy funkcí odvozených z funkcí sinus a cosinus I Předpoklady: 409 Pedagogická poznámka: Kvůli následující hodině je třeba dát pozor, příliš se nezaseknout na začátku hodiny a postupovat tak, aby
ˇ EDNA SˇKA 9 DALS ˇ I METODY INTEGRACE
 PŘEDNÁŠKA 9 DALŠÍ METODY INTEGRACE 1 9.1. Věta o substituci Věta 1 (O substituci) Necht je ϕ(x) prosté regulární zobrazení otevřené množiny X R n na množinu Y R n. Necht je M X, f(y) funkce definovaná
PŘEDNÁŠKA 9 DALŠÍ METODY INTEGRACE 1 9.1. Věta o substituci Věta 1 (O substituci) Necht je ϕ(x) prosté regulární zobrazení otevřené množiny X R n na množinu Y R n. Necht je M X, f(y) funkce definovaná
Ekonomická fakulta, Jihočeská univerzita v Českých Budějovicích. MATEMATICKÝ SOFTWARE MAPLE - MANUÁL Marek Šulista
 Ekonomická fakulta, Jihočeská univerzita v Českých Budějovicích MATEMATICKÝ SOFTWARE MAPLE - MANUÁL Marek Šulista Matematický software MAPLE slouží ke zpracování matematických problémů pomocí jednoduchého
Ekonomická fakulta, Jihočeská univerzita v Českých Budějovicích MATEMATICKÝ SOFTWARE MAPLE - MANUÁL Marek Šulista Matematický software MAPLE slouží ke zpracování matematických problémů pomocí jednoduchého
Úvod do programu MAPLE
 Úvod do programu MAPLE MAPLE V Release 9 (11) M. Jahoda Ústav chemického inženýrství VŠCHT Praha http://www.vscht.cz/uchi/maple http://www.maplesoft.com 2007 MAPLE pracovní plocha 2 MAPLE - nastavení fontů
Úvod do programu MAPLE MAPLE V Release 9 (11) M. Jahoda Ústav chemického inženýrství VŠCHT Praha http://www.vscht.cz/uchi/maple http://www.maplesoft.com 2007 MAPLE pracovní plocha 2 MAPLE - nastavení fontů
5.3. Implicitní funkce a její derivace
 Výklad Podívejme se na následující problém. Uvažujme množinu M bodů [x,y] R 2, které splňují rovnici F(x, y) = 0, M = {[x,y] D F F(x,y) = 0}, kde z = F(x,y) je nějaká funkce dvou proměnných. Je-li F(x,y)
Výklad Podívejme se na následující problém. Uvažujme množinu M bodů [x,y] R 2, které splňují rovnici F(x, y) = 0, M = {[x,y] D F F(x,y) = 0}, kde z = F(x,y) je nějaká funkce dvou proměnných. Je-li F(x,y)
Internetová adresa osobní stránky: http://www.mat.fme.vutbr.cz/home/klaska E-mail: klaska@um.fme.vutbr.cz
 3 MAPLEOVSKÁ CVIČENÍ PRO ZÁKLADNÍ KURZ MATEMATIKY RNDr. Jiří Klaška, Dr. Internetová adresa osobní stránky: http://www.mat.fme.vutbr.cz/home/klaska E-mail: klaska@um.fme.vutbr.cz Úvod Maple je program,
3 MAPLEOVSKÁ CVIČENÍ PRO ZÁKLADNÍ KURZ MATEMATIKY RNDr. Jiří Klaška, Dr. Internetová adresa osobní stránky: http://www.mat.fme.vutbr.cz/home/klaska E-mail: klaska@um.fme.vutbr.cz Úvod Maple je program,
- funkce, které integrujete aproximujte jejich Taylorovými řadami a ty následně zintegrujte. V obou případech vyzkoušejte Taylorovy řady
 Vzorové řešení domácího úkolu na 6. 1. 1. Integrály 1 1 x2 dx, ex2 dx spočítejte přibližně následují metodou - funkce, které integrujete aproximujte jejich Taylorovými řadami a ty následně zintegrujte.
Vzorové řešení domácího úkolu na 6. 1. 1. Integrály 1 1 x2 dx, ex2 dx spočítejte přibližně následují metodou - funkce, které integrujete aproximujte jejich Taylorovými řadami a ty následně zintegrujte.
1. sin(x + y) = sin(x) cos(y) + cos(x) sin(y) pro x, y R, cos(x + y) = cos(x) cos(y) sin(x) sin(y) pro x, y R;
 3. Elementární funkce. Věta C. Existují funkce sin(x) a cos(x) z R do R a číslo π (0, ) tak, že platí: 1. sin(x + y) = sin(x) cos(y) + cos(x) sin(y) pro x, y R, cos(x + y) = cos(x) cos(y) sin(x) sin(y)
3. Elementární funkce. Věta C. Existují funkce sin(x) a cos(x) z R do R a číslo π (0, ) tak, že platí: 1. sin(x + y) = sin(x) cos(y) + cos(x) sin(y) pro x, y R, cos(x + y) = cos(x) cos(y) sin(x) sin(y)
Laboratorní cvičení - Integrální počet v R
 Laboratorní cvičení - Integrální počet v R POZOR! Maple neuvádí ve výsledcích neurčitých integrálů integrační konstantu. Maple počítá integrály v oboru komplexních čísel. Neurčitý integrál Neurčitý integrál
Laboratorní cvičení - Integrální počet v R POZOR! Maple neuvádí ve výsledcích neurčitých integrálů integrační konstantu. Maple počítá integrály v oboru komplexních čísel. Neurčitý integrál Neurčitý integrál
Visualizace a animace. Jan Velechovský. Maple. plots Odkazy. Matlab. Animace Odkazy IDL. Odkazy. Gnuplot. 10. prosince Animace.
 10. prosince 2008 Proč vizualizace dat? Schopnost současně vnímat obrovské množství dat, tisíce čísel Obrázky jsou většinou to první co v textu upoutá Proč vizualizace dat? Schopnost současně vnímat obrovské
10. prosince 2008 Proč vizualizace dat? Schopnost současně vnímat obrovské množství dat, tisíce čísel Obrázky jsou většinou to první co v textu upoutá Proč vizualizace dat? Schopnost současně vnímat obrovské
Návod k programu Graph, verze 4.3
 Návod k programu Graph, verze 4.3 Obsah 1 Úvod 2 2 Popis pracovní lišty a nápovědy 2 2.1 Nastavení os...................................... 2 2.2 Nápověda....................................... 3 3 Jak
Návod k programu Graph, verze 4.3 Obsah 1 Úvod 2 2 Popis pracovní lišty a nápovědy 2 2.1 Nastavení os...................................... 2 2.2 Nápověda....................................... 3 3 Jak
Cvičení z matematické analýzy na FIT VUT s podporou Maple
 Cvičení z matematické analýzy na FIT VUT s podporou Maple Vlasta Krupková Vysoké Učení Technické Brno, Fakulta Elektrotechniky a komunikačních Technologií, Ústav matematiky, Technická 8,616 00 Brno e-mail:
Cvičení z matematické analýzy na FIT VUT s podporou Maple Vlasta Krupková Vysoké Učení Technické Brno, Fakulta Elektrotechniky a komunikačních Technologií, Ústav matematiky, Technická 8,616 00 Brno e-mail:
[obrázek γ nepotřebujeme, interval t, zřejmý, integrací polynomu a per partes vyjde: (e2 + e) + 2 ln 2. (e ln t = t) ] + y2
![[obrázek γ nepotřebujeme, interval t, zřejmý, integrací polynomu a per partes vyjde: (e2 + e) + 2 ln 2. (e ln t = t) ] + y2 [obrázek γ nepotřebujeme, interval t, zřejmý, integrací polynomu a per partes vyjde: (e2 + e) + 2 ln 2. (e ln t = t) ] + y2](/thumbs/102/153207878.jpg) 4.1 Křivkový integrál ve vektrovém poli přímým výpočtem 4.1 Spočítejte práci síly F = y i + z j + x k při pohybu hmotného bodu po orientované křivce, která je dána jako oblouk ABC na průnikové křivce ploch
4.1 Křivkový integrál ve vektrovém poli přímým výpočtem 4.1 Spočítejte práci síly F = y i + z j + x k při pohybu hmotného bodu po orientované křivce, která je dána jako oblouk ABC na průnikové křivce ploch
Lineární algebra s Matlabem cvičení 3
 Lineární algebra s Matlabem cvičení 3 Grafika v Matlabu Základní příkazy figure o vytvoří prázdné okno grafu hold on/hold off o zapne/vypne možnost kreslení více funkcí do jednoho grafu ezplot o slouží
Lineární algebra s Matlabem cvičení 3 Grafika v Matlabu Základní příkazy figure o vytvoří prázdné okno grafu hold on/hold off o zapne/vypne možnost kreslení více funkcí do jednoho grafu ezplot o slouží
Základy algoritmizace a programování
 Základy algoritmizace a programování Práce se symbolickými proměnnými Práce s grafikou Přednáška 11 7. prosince 2009 Symbolické proměnné Zjednodušení aritmetických výrazů simplify (s) Příklady: >>syms
Základy algoritmizace a programování Práce se symbolickými proměnnými Práce s grafikou Přednáška 11 7. prosince 2009 Symbolické proměnné Zjednodušení aritmetických výrazů simplify (s) Příklady: >>syms
Kapitola 7: Neurčitý integrál. 1/14
 Kapitola 7: Neurčitý integrál. 1/14 Neurčitý integrál 2/14 Definice: Necht f je funkce definovaná na intervalu I. Funkci F definovanou na intervalu I, pro kterou platí F (x) = f (x) x I nazýváme primitivní
Kapitola 7: Neurčitý integrál. 1/14 Neurčitý integrál 2/14 Definice: Necht f je funkce definovaná na intervalu I. Funkci F definovanou na intervalu I, pro kterou platí F (x) = f (x) x I nazýváme primitivní
4.3.1 Goniometrické rovnice
 .. Goniometrické rovnice Předpoklady: 6, 7 Názvosloví: Goniometrické rovnice: rovnice, ve kterých se neznámá objevuje uvnitř goniometrických funkcí. g x = a, kde Základní goniometrická rovnice: každá rovnice
.. Goniometrické rovnice Předpoklady: 6, 7 Názvosloví: Goniometrické rovnice: rovnice, ve kterých se neznámá objevuje uvnitř goniometrických funkcí. g x = a, kde Základní goniometrická rovnice: každá rovnice
Kvadratické nerovnice Předpoklady: Př. 1: Úvaha: Pedagogická poznámka:
 ..10 Kvadratické nerovnice Předpoklady: 01, 0, 0, 07 Př. 1: Vyřeš nerovnici 0. 0 - mohu rozložit na součin není to nic nového + 1 0 ( )( ) Hledám nulové body: 0 ( ) = = ( ) ( ; 1) ( 1; ) ( ; ) ( ) - -
..10 Kvadratické nerovnice Předpoklady: 01, 0, 0, 07 Př. 1: Vyřeš nerovnici 0. 0 - mohu rozložit na součin není to nic nového + 1 0 ( )( ) Hledám nulové body: 0 ( ) = = ( ) ( ; 1) ( 1; ) ( ; ) ( ) - -
7B. Výpočet limit L Hospitalovo pravidlo
 7B. Výpočet it L Hospitalovo pravidlo V prai často potřebujeme určit itu výrazů, které vzniknou operacemi nebo složením několika spojitých funkcí. Většinou pomohou pravidla typu ita součtu násobku, součinu,
7B. Výpočet it L Hospitalovo pravidlo V prai často potřebujeme určit itu výrazů, které vzniknou operacemi nebo složením několika spojitých funkcí. Většinou pomohou pravidla typu ita součtu násobku, součinu,
Spojitost a limita funkce, limita posloupnosti
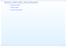 Spojitost a ita funkce, ita posloupnosti Spojitost funkce Limita funkcí Limita posloupností. p.1/14 Spojitost funkce Příklad 2.1.1 Vyšetřete spojitost funkce x sin 1 pro x 0, f(x) = x 1 pro x =0. Příklad
Spojitost a ita funkce, ita posloupnosti Spojitost funkce Limita funkcí Limita posloupností. p.1/14 Spojitost funkce Příklad 2.1.1 Vyšetřete spojitost funkce x sin 1 pro x 0, f(x) = x 1 pro x =0. Příklad
Geometrie v R n. z balíku student. Poznamenejme, že vlastně počítáme délku úsečky, která oba body spojuje. (b d)2 + (c a) 2
 Geometrie v R n Začněme nejjednodušší úlohou: Vypočtěme vzdálenost dvou bodů v rovině. Použijeme příkaz distance z balíku student. Poznamenejme, že vlastně počítáme délku úsečky, která oba body spojuje.
Geometrie v R n Začněme nejjednodušší úlohou: Vypočtěme vzdálenost dvou bodů v rovině. Použijeme příkaz distance z balíku student. Poznamenejme, že vlastně počítáme délku úsečky, která oba body spojuje.
Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague
 1 / 21 Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague 2 / 21 Řešíme následující úlohu: differencovatelnou funkci f : R R známe jen v konečném počtu bodů x 0,
1 / 21 Faculty of Nuclear Sciences and Physical Engineering Czech Technical University in Prague 2 / 21 Řešíme následující úlohu: differencovatelnou funkci f : R R známe jen v konečném počtu bodů x 0,
Systém je citlivý na velikost písmen CASE SENSITIVE rozeznává malá velká písmena, např. PROM=1; PROm=1; PRom=1; Prom=1; prom=1; - 5 různých proměnných
 Systém je citlivý na velikost písmen CASE SENSITIVE rozeznává malá velká písmena, např. PROM=1; PROm=1; PRom=1; Prom=1; prom=1; - 5 různých proměnných jakési nádoby na hodnoty jsou různých typů při běžné
Systém je citlivý na velikost písmen CASE SENSITIVE rozeznává malá velká písmena, např. PROM=1; PROm=1; PRom=1; Prom=1; prom=1; - 5 různých proměnných jakési nádoby na hodnoty jsou různých typů při běžné
ALGEBRA. 1. Pomocí Eukleidova algoritmu najděte největší společný dělitel čísel a a b. a) a = 204, b = 54, b) a = , b =
 ALGEBRA 1 Úkol na 13. 11. 2018 1. Pomocí Eukleidova algoritmu najděte největší společný dělitel čísel a a b. a) a = 204, b = 54, b) a = 353 623, b = 244 571. 2. Připomeňte si, že pro ε = cos 2π 3 + i sin
ALGEBRA 1 Úkol na 13. 11. 2018 1. Pomocí Eukleidova algoritmu najděte největší společný dělitel čísel a a b. a) a = 204, b = 54, b) a = 353 623, b = 244 571. 2. Připomeňte si, že pro ε = cos 2π 3 + i sin
Výukový materiál pro projekt Elektronická školička reg. č. CZ.1.07/1.3.05/ "Interaktivní DUMy"- interaktivity lze dosáhnout i v MS PowerPoint
 Výukový materiál pro projekt Elektronická školička reg. č. CZ.1.07/1.3.05/02.0041 "Interaktivní DUMy"- interaktivity lze dosáhnout i v MS PowerPoint Ing. Lenka Satková, 2012, str. 11 Materiál je publikován
Výukový materiál pro projekt Elektronická školička reg. č. CZ.1.07/1.3.05/02.0041 "Interaktivní DUMy"- interaktivity lze dosáhnout i v MS PowerPoint Ing. Lenka Satková, 2012, str. 11 Materiál je publikován
Wolfram Mathematica. Mgr. Jindřich Soukup 2. 7. 2012
 Wolfram Mathematica Mgr. Jindřich Soukup. 7. 0 Mathematica Tento soubor má sloužit jako první seznámení s programem Mathematica. Většina věcí je pouze přeložená z Help Tutorial.... V souboru je text a
Wolfram Mathematica Mgr. Jindřich Soukup. 7. 0 Mathematica Tento soubor má sloužit jako první seznámení s programem Mathematica. Většina věcí je pouze přeložená z Help Tutorial.... V souboru je text a
1) Spočítejte limitu pomocí l Hospitalova pravidla, pokud selˇze, spočítejte ji klasicky:
 Příklady k desátému cvičení ) Spočítejte itu pomocí l Hospitalova pravidla pokud selˇze spočítejte ji klasicky:. 2. 3.. 5 + 3 2 8 π π sin 2 + ln(cos(3)) 3 2) Upravte na zlomek a pouˇzijte l Hospitalovo
Příklady k desátému cvičení ) Spočítejte itu pomocí l Hospitalova pravidla pokud selˇze spočítejte ji klasicky:. 2. 3.. 5 + 3 2 8 π π sin 2 + ln(cos(3)) 3 2) Upravte na zlomek a pouˇzijte l Hospitalovo
1 Modelování systémů 2. řádu
 OBSAH Obsah 1 Modelování systémů 2. řádu 1 2 Řešení diferenciální rovnice 3 3 Ukázka řešení č. 1 9 4 Ukázka řešení č. 2 11 5 Ukázka řešení č. 3 12 6 Ukázka řešení č. 4 14 7 Ukázka řešení č. 5 16 8 Ukázka
OBSAH Obsah 1 Modelování systémů 2. řádu 1 2 Řešení diferenciální rovnice 3 3 Ukázka řešení č. 1 9 4 Ukázka řešení č. 2 11 5 Ukázka řešení č. 3 12 6 Ukázka řešení č. 4 14 7 Ukázka řešení č. 5 16 8 Ukázka
Je založen na pojmu derivace funkce a její užití. Z předchozího studia je třeba si zopakovat a orientovat se v pojmech: funkce, D(f), g 2 : y =
 0.1 Diferenciální počet Je částí infinitezimálního počtu, což je souhrnný název pro diferenciální a integrální počet. Je založen na pojmu derivace funkce a její užití. Z předchozího studia je třeba si
0.1 Diferenciální počet Je částí infinitezimálního počtu, což je souhrnný název pro diferenciální a integrální počet. Je založen na pojmu derivace funkce a její užití. Z předchozího studia je třeba si
10. přednáška (slovní úlohy vedoucí na extrémy - pokračování)
 10. přednáška (slovní úlohy vedoucí na extrémy - pokračování) Extremální úlohy Krabice Ze čtvercového kartónu o straně 60 cm odřízneme v rozích 4 menší čtverce. Ze zbytku poskládáme krabici bez víka (viz
10. přednáška (slovní úlohy vedoucí na extrémy - pokračování) Extremální úlohy Krabice Ze čtvercového kartónu o straně 60 cm odřízneme v rozích 4 menší čtverce. Ze zbytku poskládáme krabici bez víka (viz
Numerické metody a programování
 Projekt: Inovace výuky optiky se zaměřením na získání experimentálních dovedností Registrační číslo: CZ.1.07/2.2.00/28.0157 Numerické metody a programování Lekce 1 Tento projekt je spolufinancován Evropským
Projekt: Inovace výuky optiky se zaměřením na získání experimentálních dovedností Registrační číslo: CZ.1.07/2.2.00/28.0157 Numerické metody a programování Lekce 1 Tento projekt je spolufinancován Evropským
1 Základy práce s programem Maple
 1 ZÁKLADY PRÁCE S PROGRAMEM MAPLE 1 Základy práce s programem Maple Počítačový algebraický systém Maple TM je produktem kanadské společnosti Maplesoft, Waterloo Maple Inc. Jedná se o špičkový produkt v
1 ZÁKLADY PRÁCE S PROGRAMEM MAPLE 1 Základy práce s programem Maple Počítačový algebraický systém Maple TM je produktem kanadské společnosti Maplesoft, Waterloo Maple Inc. Jedná se o špičkový produkt v
PHP tutoriál (základy PHP snadno a rychle)
 PHP tutoriál (základy PHP snadno a rychle) Druhá, vylepšená offline verze. Připravil Štěpán Mátl, http://khamos.wz.cz Chceš se naučit základy PHP? V tom případě si prostuduj tento rychlý průvodce. Nejdříve
PHP tutoriál (základy PHP snadno a rychle) Druhá, vylepšená offline verze. Připravil Štěpán Mátl, http://khamos.wz.cz Chceš se naučit základy PHP? V tom případě si prostuduj tento rychlý průvodce. Nejdříve
Teorie. Hinty. kunck6am
 kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 2. cvičení Teorie Věta (Aritmetika derivací). Necht a R a necht f a g jsou funkce definované na nějakém okolí bodu a. Necht existují f (a) R a g (a) R.
kytaristka@gmail.com www.natur.cuni.cz/ kunck6am 2. cvičení Teorie Věta (Aritmetika derivací). Necht a R a necht f a g jsou funkce definované na nějakém okolí bodu a. Necht existují f (a) R a g (a) R.
Grafy relací s absolutními hodnotami
 ..5 Grafy relací s absolutními hodnotami Předpoklady: 0, 0, 03, 0, 05,, 3 Pedagogická poznámka: Tato hodina nepatří do klasických středoškolských osnov. Je reakcí na fakt, že relace s absolutními hodnotami
..5 Grafy relací s absolutními hodnotami Předpoklady: 0, 0, 03, 0, 05,, 3 Pedagogická poznámka: Tato hodina nepatří do klasických středoškolských osnov. Je reakcí na fakt, že relace s absolutními hodnotami
Zimní semestr akademického roku 2015/ ledna 2016
 Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Zimní semestr akademického roku 015/016 5. ledna 016 Obsah Cvičení Předmluva iii
Cvičení k předmětu BI-ZMA Tomáš Kalvoda Katedra aplikované matematiky FIT ČVUT Matěj Tušek Katedra matematiky FJFI ČVUT Zimní semestr akademického roku 015/016 5. ledna 016 Obsah Cvičení Předmluva iii
Numerické metody a programování. Lekce 1
 Numerické metody a programování Lekce 1 Numerické metody a programování Obsah přednášky 1. Mathematica: základy programování, symbolické výpočty, vizualizace dat. 2. Programování v prostředích Matlab/Octave.
Numerické metody a programování Lekce 1 Numerické metody a programování Obsah přednášky 1. Mathematica: základy programování, symbolické výpočty, vizualizace dat. 2. Programování v prostředích Matlab/Octave.
Primitivní funkce, určitý integrál, nevlastní
 Počítačový algebraický systém Maple jako pomůcka při studiu předmětu Matematika I a II. Primitivní funkce, určitý integrál, nevlastní integrály Program Maple může být velmi dobrým pomocníkem při hledání
Počítačový algebraický systém Maple jako pomůcka při studiu předmětu Matematika I a II. Primitivní funkce, určitý integrál, nevlastní integrály Program Maple může být velmi dobrým pomocníkem při hledání
8.4. Shrnutí ke kapitolám 7 a 8
 8.4. Shrnutí ke kapitolám 7 a 8 Shrnutí lekce Úvodní 7. kapitola přinesla informace o druzích řešení diferenciálních rovnic prvního řádu a stručné teoretické poznatky o podmínkách existence a jednoznačnosti
8.4. Shrnutí ke kapitolám 7 a 8 Shrnutí lekce Úvodní 7. kapitola přinesla informace o druzích řešení diferenciálních rovnic prvního řádu a stručné teoretické poznatky o podmínkách existence a jednoznačnosti
Programování v jazyku LOGO - úvod
 Programování v jazyku LOGO - úvod Programovací jazyk LOGO je určen pro výuku algoritmizace především pro děti školou povinné. Programovací jazyk pracuje v grafickém prostředí, přičemž jednou z jeho podstatných
Programování v jazyku LOGO - úvod Programovací jazyk LOGO je určen pro výuku algoritmizace především pro děti školou povinné. Programovací jazyk pracuje v grafickém prostředí, přičemž jednou z jeho podstatných
SLOŽENÉ ÚROKOVÁNÍ. částky naspořené po n letech při m úrokových obdobích za jeden rok platí formule
 Klasický termínovaný vklad SLŽENÉ ÚRKVÁNÍ PŘÍKLAD: Podnikatel uložil na klasický termínovaný vklad částku 300 000 Kč. Jaká bude výše kapitálu za 3 roky, jestliže úroková sazba činí 2% p.a. a je a) roční
Klasický termínovaný vklad SLŽENÉ ÚRKVÁNÍ PŘÍKLAD: Podnikatel uložil na klasický termínovaný vklad částku 300 000 Kč. Jaká bude výše kapitálu za 3 roky, jestliže úroková sazba činí 2% p.a. a je a) roční
4 Numerické derivování a integrace
 Břetislav Fajmon, UMAT FEKT, VUT Brno Téma je podrobně zpracováno ve skriptech [1], kapitola 7, strany 85-94. Jedná se o úlohu výpočtu (první či druhé) derivace či o výpočet určitého integrálu jinými metodami,
Břetislav Fajmon, UMAT FEKT, VUT Brno Téma je podrobně zpracováno ve skriptech [1], kapitola 7, strany 85-94. Jedná se o úlohu výpočtu (první či druhé) derivace či o výpočet určitého integrálu jinými metodami,
I. 7. Diferenciál funkce a Taylorova věta
 I. 7. Diferenciál funkce a Taylorova věta 343 I. 7. Diferenciál funkce a Taylorova věta Věta 26. Funkce f má v bodě x 0 diferenciál (je diferencovatelná v x 0 ) právě tehdy, když existuje vlastní derivace
I. 7. Diferenciál funkce a Taylorova věta 343 I. 7. Diferenciál funkce a Taylorova věta Věta 26. Funkce f má v bodě x 0 diferenciál (je diferencovatelná v x 0 ) právě tehdy, když existuje vlastní derivace
Kreslení elipsy Andrej Podzimek 22. prosince 2005
 Kreslení elipsy Andrej Podzimek 22. prosince 2005 Kreslení elipsy v obecné poloze O co půjde Ukázat přesný matematický model elipsy Odvodit vzorce pro výpočet souřadnic důležitých bodů Nalézt algoritmus
Kreslení elipsy Andrej Podzimek 22. prosince 2005 Kreslení elipsy v obecné poloze O co půjde Ukázat přesný matematický model elipsy Odvodit vzorce pro výpočet souřadnic důležitých bodů Nalézt algoritmus
Geometrie v R n. student. Poznamenejme, že vlastně počítáme délku úsečky, která oba body spojuje. (b d)2 + (c a) 2
 Geometrie v R n Začněme nejjednodušší úlohou: Vypočtěme vzdálenost dvou bodů v rovině. Použijeme příkaz distance z balíku student. Poznamenejme, že vlastně počítáme délku úsečky, která oba body spojuje.
Geometrie v R n Začněme nejjednodušší úlohou: Vypočtěme vzdálenost dvou bodů v rovině. Použijeme příkaz distance z balíku student. Poznamenejme, že vlastně počítáme délku úsečky, která oba body spojuje.
Integrace. Numerické metody 7. května FJFI ČVUT v Praze
 Integrace Numerické metody 7. května 2018 FJFI ČVUT v Praze 1 Úvod Úvod 1D Kvadraturní vzorce Gaussovy kvadratury Více dimenzí Programy 1 Úvod Úvod - Úloha Máme funkci f( x) a snažíme se najít určitý integrál
Integrace Numerické metody 7. května 2018 FJFI ČVUT v Praze 1 Úvod Úvod 1D Kvadraturní vzorce Gaussovy kvadratury Více dimenzí Programy 1 Úvod Úvod - Úloha Máme funkci f( x) a snažíme se najít určitý integrál
Bakalářská matematika I
 1. Funkce Diferenciální počet Mgr. Jaroslav Drobek, Ph. D. Katedra matematiky a deskriptivní geometrie Bakalářská matematika I Některé užitečné pojmy Kartézský součin podrobnosti Definice 1.1 Nechť A,
1. Funkce Diferenciální počet Mgr. Jaroslav Drobek, Ph. D. Katedra matematiky a deskriptivní geometrie Bakalářská matematika I Některé užitečné pojmy Kartézský součin podrobnosti Definice 1.1 Nechť A,
Kombinatorická minimalizace
 Kombinatorická minimalizace Cílem je nalézt globální minimum ve velké diskrétní množině, kde může být mnoho lokálních minim. Úloha obchodního cestujícího Cílem je najít nejkratší cestu, která spojuje všechny
Kombinatorická minimalizace Cílem je nalézt globální minimum ve velké diskrétní množině, kde může být mnoho lokálních minim. Úloha obchodního cestujícího Cílem je najít nejkratší cestu, která spojuje všechny
Vzorová písemka č. 1 (rok 2015/2016) - řešení
 Vzorová písemka č. rok /6 - řešení Pavla Pecherková. května 6 VARIANTA A. Náhodná veličina X je určena hustotou pravděpodobností: máme hustotu { pravděpodobnosti C x pro x ; na intervalu f x jinde jedná
Vzorová písemka č. rok /6 - řešení Pavla Pecherková. května 6 VARIANTA A. Náhodná veličina X je určena hustotou pravděpodobností: máme hustotu { pravděpodobnosti C x pro x ; na intervalu f x jinde jedná
7. Derivace složené funkce. Budeme uvažovat složenou funkci F = f(g), kde některá z jejich součástí
 202-m3b2/cvic/7slf.tex 7. Derivace složené funkce. Budeme uvažovat složenou funkci F = fg, kde některá z jejich součástí může být funkcí více proměnných. Předpokládáme, že uvažujeme funkce, které mají
202-m3b2/cvic/7slf.tex 7. Derivace složené funkce. Budeme uvažovat složenou funkci F = fg, kde některá z jejich součástí může být funkcí více proměnných. Předpokládáme, že uvažujeme funkce, které mají
MATEMATIKA III. Olga Majlingová. Učební text pro prezenční studium. Předběžná verze
 Fakulta strojního inženýrství Univerzity J. E. Purkyně v Ústí nad Labem Pasteurova 7 Tel.: 475 285 511 400 96 Ústí nad Labem Fax: 475 285 566 Internet: www.ujep.cz E-mail: kontakt@ujep.cz MATEMATIKA III
Fakulta strojního inženýrství Univerzity J. E. Purkyně v Ústí nad Labem Pasteurova 7 Tel.: 475 285 511 400 96 Ústí nad Labem Fax: 475 285 566 Internet: www.ujep.cz E-mail: kontakt@ujep.cz MATEMATIKA III
Primitivní funkce, určitý integrál, nevlastní integrály
 Primitivní funkce, určitý integrál, nevlastní integrály Program Maple může být velmi dobrým pomocníkem při hledání primitivních funkcí i při výpočtu určitých integrálů. Přesto se neobejdeme bez dobré znalosti
Primitivní funkce, určitý integrál, nevlastní integrály Program Maple může být velmi dobrým pomocníkem při hledání primitivních funkcí i při výpočtu určitých integrálů. Přesto se neobejdeme bez dobré znalosti
Derivace funkce Otázky
 funkce je jedním z hlavních nástrojů matematické analýzy. V příští části ukážeme, jak mnoho různorodých aplikací derivace má. Geometricky lze derivaci funkce v nějakém bodě chápat jako směrnici tečny grafu
funkce je jedním z hlavních nástrojů matematické analýzy. V příští části ukážeme, jak mnoho různorodých aplikací derivace má. Geometricky lze derivaci funkce v nějakém bodě chápat jako směrnici tečny grafu
Drsná matematika III 1. přednáška Funkce více proměnných: křivky, směrové derivace, diferenciál
 Drsná matematika III 1. přednáška Funkce více proměnných: křivky, směrové derivace, diferenciál Jan Slovák Masarykova univerzita Fakulta informatiky 16. 9. 2008 Obsah přednášky 1 Literatura 2 Funkce a
Drsná matematika III 1. přednáška Funkce více proměnných: křivky, směrové derivace, diferenciál Jan Slovák Masarykova univerzita Fakulta informatiky 16. 9. 2008 Obsah přednášky 1 Literatura 2 Funkce a
Soustavy nelineárních rovnic pomocí systému Maple. Newtonova metoda.
 Úvod Soustavy nelineárních rovnic pomocí systému Maple. Newtonova metoda. Mnoho technických problémů vede na řešení matematických úloh, které se následně převedou na úlohy řešení soustav nelineárních rovnic
Úvod Soustavy nelineárních rovnic pomocí systému Maple. Newtonova metoda. Mnoho technických problémů vede na řešení matematických úloh, které se následně převedou na úlohy řešení soustav nelineárních rovnic
Funkce a limita. Petr Hasil. Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF)
 Funkce a limita Petr Hasil Přednáška z matematiky Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Funkce a limita Petr Hasil Přednáška z matematiky Podpořeno projektem Průřezová inovace studijních programů Lesnické a dřevařské fakulty MENDELU v Brně (LDF) s ohledem na discipĺıny společného základu
Základy algoritmizace a programování
 Základy algoritmizace a programování Přednáška 1 Olga Majlingová Katedra matematiky, ČVUT v Praze 19. září 2011 Obsah Úvodní informace 1 Úvodní informace 2 3 4 Doporučená literatura web: http://marian.fsik.cvut.cz/zapg
Základy algoritmizace a programování Přednáška 1 Olga Majlingová Katedra matematiky, ČVUT v Praze 19. září 2011 Obsah Úvodní informace 1 Úvodní informace 2 3 4 Doporučená literatura web: http://marian.fsik.cvut.cz/zapg
Matematika I A ukázkový test 1 pro 2011/2012. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a
 Matematika I A ukázkový test 1 pro 2011/2012 1. Je dána soustava rovnic s parametrem a R x y + z = 1 a) Napište Frobeniovu větu. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a b) Vyšetřete počet řešení soustavy
Matematika I A ukázkový test 1 pro 2011/2012 1. Je dána soustava rovnic s parametrem a R x y + z = 1 a) Napište Frobeniovu větu. x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a b) Vyšetřete počet řešení soustavy
Matematická analýza ve Vesmíru. Jiří Bouchala
 Matematická analýza ve Vesmíru Jiří Bouchala Katedra aplikované matematiky jiri.bouchala@vsb.cz www.am.vsb.cz/bouchala - p. 1/19 typu: m x (sin x, cos x) R(x, ax +...)dx. Matematická analýza ve Vesmíru.
Matematická analýza ve Vesmíru Jiří Bouchala Katedra aplikované matematiky jiri.bouchala@vsb.cz www.am.vsb.cz/bouchala - p. 1/19 typu: m x (sin x, cos x) R(x, ax +...)dx. Matematická analýza ve Vesmíru.
MATEMATIKA II V PŘÍKLADECH
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ MATEMATIKA II V PŘÍKLADECH CVIČENÍ Č. Ing. Petra Schreiberová, Ph.D. Ostrava 0 Ing. Petra Schreiberová, Ph.D. Vysoká škola báňská Technická
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ MATEMATIKA II V PŘÍKLADECH CVIČENÍ Č. Ing. Petra Schreiberová, Ph.D. Ostrava 0 Ing. Petra Schreiberová, Ph.D. Vysoká škola báňská Technická
Ústav teoretické fyziky a astrofyziky Přírodovědecké fakulty Masarykovy Univerzity v Brně. 14. května 2007
 Rychlotest-řešení Ústav teoretické fyziky a astrofyziky Přírodovědecké fakulty Masarykovy Univerzity v Brně 14. května 2007 Příklad 1 Mějme funkci y = sin x rozhodněte zda směrnice tečny k dané křivce
Rychlotest-řešení Ústav teoretické fyziky a astrofyziky Přírodovědecké fakulty Masarykovy Univerzity v Brně 14. května 2007 Příklad 1 Mějme funkci y = sin x rozhodněte zda směrnice tečny k dané křivce
Derivace goniometrických. Jakub Michálek,
 Derivace goniometrických funkcí Jakub Michálek, Tomáš Kučera Shrnutí Odvodí se základní vztahy pro derivace funkcí sinus a cosinus za pomoci věty o třech limitách, odvodí se také dvě důležité limity. Vypočítá
Derivace goniometrických funkcí Jakub Michálek, Tomáš Kučera Shrnutí Odvodí se základní vztahy pro derivace funkcí sinus a cosinus za pomoci věty o třech limitách, odvodí se také dvě důležité limity. Vypočítá
Funkce Arcsin. Předpoklady: Některé dosud probírané funkce můžeme spojit do dvojic: 4 je číslo, jehož druhá mocnina se rovná 4.
 ..6 Funkce Arcsin Předpoklady: Některé dosud probírané funkce můžeme spojit do dvojic: Kvadratická funkce Druhá odmocnina y =, 0; ) y = je číslo, jehož druhá mocnina se rovná. - - - - - - y = y = Eponenciální
..6 Funkce Arcsin Předpoklady: Některé dosud probírané funkce můžeme spojit do dvojic: Kvadratická funkce Druhá odmocnina y =, 0; ) y = je číslo, jehož druhá mocnina se rovná. - - - - - - y = y = Eponenciální
Derivace funkce. Přednáška MATEMATIKA č Jiří Neubauer
 Přednáška MATEMATIKA č. 9-11 Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Šotová, J., Doudová, L. Diferenciální počet funkcí jedné proměnné Motivační příklady
Přednáška MATEMATIKA č. 9-11 Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Šotová, J., Doudová, L. Diferenciální počet funkcí jedné proměnné Motivační příklady
( ) ( ) Vzorce pro dvojnásobný úhel. π z hodnot goniometrických funkcí. Předpoklady: Začneme příkladem.
 Vzorce pro dvojnásobný úhel Předpoklady: 0 Začneme příkladem Př : Pomocí součtových vzorců odvoď vzorec pro sin x sin x sin x + x sin x cos x + cos x sin x sin x cos x Př : Pomocí součtových vzorců odvoď
Vzorce pro dvojnásobný úhel Předpoklady: 0 Začneme příkladem Př : Pomocí součtových vzorců odvoď vzorec pro sin x sin x sin x + x sin x cos x + cos x sin x sin x cos x Př : Pomocí součtových vzorců odvoď
