Zkou²ková písemná práce. 1/A z p edm tu 01RMF
|
|
|
- Bohumír Musil
- před 5 lety
- Počet zobrazení:
Transkript
1 Příjmení a jméno CELKEM Zkou²ková písemná práce. 1/A z p edm tu 01RMF 15/01/2016, 9:00 10:00 ➊ Je funkcionál denovaný p edpisem ze t ídy D (G), kde G = (1, + ). Vysv tlete! ( g; φ(x)) := R φ(x) x dx ➋ ƒemu se rovná L[ f (x) g(x)] a za jakým podmínek? Odvo te a výpo et podrobn ji komentujte. Neopome te diskutovat, zda f (x) g(x) má skute n Laplace v obraz! ➌ Vyslovte a dokaºte v tu o Parsevalov vzorci a Parsevalov rovnosti. ➍ Nech ˆL a ˆK jsou Volterrovy integrální operátory s jádry K (x, y) a L (x, y). Jakého tvaru je jádro M (x, y) integrálního operátoru ˆM := ˆL ˆK? Je ˆM také Volterr v? ➎ U kaºdé z níºe uvedených t íd uve te (ANO/NE), zda funkce h(x) = Θ(x)x 2 e 2x do dané t ídy pat í: D(R), S (R), P(R), L 1 (R). K postupu do dal²ího kola je t eba zodpov d t alespo 4 otázky správn. Mezi správn zodpov zenými úlohami MUSÍ být d kazová úloha. 3!
2 Jméno studenta (tiskacím písmem) ČÁST A BONUS CELKEM BODŮ Celkové hodnocení zkoušky (ve formátu A,B,C,D,E,F) : Podpis studenta: Zkou²ková písemná práce. 1/B z p edm tu 01RMF 15/01/2016, 10:30 11:30 ➊ (15 bod ) Vypo t te limitu ( sin 2 (µx) lim P 1 ) µ µx x δ(y). (1) Podrobn komentujte! Neopome te také komentovat, jak chápete sou in v levém argumentu tenzorového sou inu (1). Je denován korektn? ➋ (11 bod ) Dokaºte v tu: Nech f, g D a g je nitní. Pak existuje konvoluce f g a pro kaºdou testovací funkci φ( x) D platí ( f g, φ( x) ) = ( f ( x) g( y), η( y)φ( x + y) ), kde η( y) je libovolná testovací funkce, která... (dopl te!). ➌ (8 bod ) Nech ˆL je operátor s ist bodovým spektrem, jehoº spektrum leºí v R. Nech λ, µ σ( ˆL) a λ µ. Ozna me Q λ = {φ(x) H : ˆL(φ(x)) = λφ(x)}, Q µ = {ψ(x) H : ˆL(ψ(x))ψ = µψ(x)}. Dokaºte, ºe Q λ Q µ. Jsou v²echny p edpoklady této v ty nezbytné? Pro? Dále rozhodn te, zda jsou Q λ a Q µ vektorové prostory. Argumentujte. ➍ (6 bod ) Odvo te Fourier v obraz F[xye i(x+y) ].
3 Příjmení a jméno CELKEM Zkou²ková písemná práce. 2/A z p edm tu 01RMF 22/01/2016, 9:00 10:00 ➊ Leºí (ANO/NE) funkce Θ(x)e 3x, resp. distribuce Θ(x)e 3x v následující t íd? Va²i odpov zapi²te p ímo do tohoto zadání! D(R), S (R), P(R), D (R). ➋ Dokaºte, ºe zobrazení F : S S je spojité. ➌ Vyslovte a dokaºte (se v²emi náleºitostmi) základní v tu o e²ení diferenciální rovnice v D. ➍ Formulujte Cauchyovu úlohu pro dopravní rovnici a p eve te ji do e i zobecn ných funkcí. ➎ Jak je denována superstejnom rná konvergence v D(E r ) a jak konvergence v D (E r )? K postupu do dal²ího kola je t eba zodpov d t alespo 4 otázky správn. Mezi správn zodpov zenými úlohami MUSÍ být d kazové úlohy. 2 a 3!
4 Jméno studenta (tiskacím písmem) ČÁST A BONUS CELKEM BODŮ Celkové hodnocení zkoušky (ve formátu A,B,C,D,E,F) : Podpis studenta: Zkou²ková písemná práce. 2/B z p edm tu 01RMF 22/01/2016, 10:30 11:30 ➊ (9 bod ) e²te: φ(x) = 2 0 ( xe x 2 y 2 + xy 2 e x2 ) φ(y) dy 1 2 xe x2. Vysv tlete, pro p i e²ení této úlohy není moºné uºít ani metodu postupných aproximací ani metodu iterovaných jader. ➋ (10 bod ) Dokaºte komutativitu tenzorového sou inu. Postupujte formáln korektn a jednotlivé kroky d kazu komentujte. ➌ (14 bod ) Integrální transformace je denována p edpisem T [ f (x)] := R f (x)xe sx dx. Dokaºte, ºe Laplace v prostor P(R) m ºe být vhodným deni ním oborem takové transformace. V analogii ke znám j²ím integrálním transformacím se poté pokuste zformulovat co nejobecn j²í pravidlo pro T obraz konvoluce. P i hodnocení se ve zvý²ené mí e dbá na kreativitu e²ení a poctivost teoretických argumentací. ➍ (7 bod ) Jak souvisí hodnota funkcionálního diskriminantu D(x, y) s oblastmi excentricity parciální diferenciální rovnice druhého ádu? Dokaºte a své záv ry podrobn zd vod ujte.
5 Příjmení a jméno CELKEM Zkou²ková písemná práce. 3/A z p edm tu 01RMF 02/02/2016, 9:00 10:00 ➊ Vyslovte denici nosi e zobecn né funkce a podle ní rozhodn te, jak vypadá nosi zobecn né funkce 7 ( g, φ(x)) := x 3 φ(x) dx. 2 ➋ Vyslovte a dokaºte v tu o e²ení Fredholmovy integrální rovnice metodou postupných aproximací. Dokaºte také pomocné tvrzení o omezenosti Fredholmova integrálního operátoru. Kde se tohoto tvrzení v d kaze vyuºívá? ➌ Denujte Schwartz v prostor a rozhodn te, zda do n j funkce g(x) = x 2 e x2 pat í. ➍ Vyslovte a dokaºte v tu o ortogonalit vlastních funkcí. ➎ Vyslovte v tu o zjednodu²ení denice zobecn né konvoluce na D +(R). K postupu do dal²ího kola je t eba zodpov d t alespo 4 otázky správn. Mezi správn zodpov zenými úlohami MUSEJÍ být d kazové úlohy. 2 a 4!
6 Jméno studenta (tiskacím písmem) ČÁST A BONUS CELKEM BODŮ Celkové hodnocení zkoušky (ve formátu A,B,C,D,E,F) : Podpis studenta: Zkou²ková písemná práce. 3/B z p edm tu 01RMF 02/02/2016, 10:30 11:30 ➊ (9 bod ) Dokaºte, ºe e²ení Volterrovy integrální rovnice získané metodou postupných aproximací je jediné. Dokaºte také pot ebnou vlastnost týkající se mnoºin W 0 a W f. ➋ (7 bod ) Aplikací teorie integrálních transformací dokaºte rovnost x x1 x xn 2 xn f (x n ) dx n dx n 1... dx 3 dx 2 dx 1 = A x 0 (x s) n 1 f (s) ds. ƒemu musí rovna konstanta A? P i hodnocení se ve zvý²ené mí e dbá na kreativitu e²ení a poctivost teoretických argumentací. ➌ (12 bod ) Nech je dán operátor ˆL : H H s ist bodovým spektrem, jehoº v²echny vlastní ísla jsou prostá a jsou tvaru ( π ( π λ n = 8 cos 8i sin, (n N). 2n) 2n) Pokuste se co nejp esn ji ur it (a své tvrzení doloºit náleºitým výpo em) podobu mnoºiny { ˆL( f ) ˆL(g) U = f g } : f (x), g(x) H f (x) g(x). Jak se zm ní výsledek, bude-li mít kaºdé z vlastních ísel geometrickou násobnost rovnou t em? ➍ (12 bod ) Ve t íd zobecn ných funkcí vypo ítejte limitu ( x ) ( lim n n2 sin 2 P 1. n x)
7 Příjmení a jméno CELKEM Zkou²ková písemná práce. 4/A z p edm tu 01RMF 10/02/2016, 9:00 10:00 ➊ Dokaºte, ºe jsou-li f, g regulární distribuce s generátory f ( x), g( x) L 1 (E r ), pak f g existuje a je také regulární. Co je jejím generátorem? ➋ Vyslovte denice operátoru s ist bodovým spektrem a unfoldovaného spektra. ➌ Vyslovte a dokaºte v tu o zobecn né derivaci skokové funkce. ➍ Kde je chyba v následujícím tvrzení? A pro by to takto nemohlo fungovat? Nech f, g D +(R). Pak existuje konvoluce f g D +(R) a pro kaºdou testovací funkci φ(x) D(R) platí ( f g, φ(x) ) = ( f (x) g(y), η1 (x)η 2 (y)φ(x + y) ), kde η 1 (x), η 2 (y) D(R) jsou libovolné testovací funkce, které jsou na okolí intervalu 0, ) rovny jedné a existuje pro n K < 0 tak, ºe platí implikace x < K y < K η 1 (x) = η 2 (y) = 0. ➎ Odvo te obecný vztah mezi L[y (x)] a L[y(x)]. K postupu do dal²ího kola je t eba zodpov d t alespo 4 otázky správn. Mezi správn zodpov zenými úlohami MUSEJÍ být d kazové úlohy. 1 a 3!
8 Jméno studenta (tiskacím písmem) ČÁST A BONUS CELKEM BODŮ Celkové hodnocení zkoušky (ve formátu A,B,C,D,E,F) : Podpis studenta: Zkou²ková písemná práce. 4/B z p edm tu 01RMF 10/02/2016, 10:30 11:30 ➊ (7 bod ) Jaké jsou p edpoklady ve Fubiniov v t? A jak je jejich spln ní garantováno ve v t o zám n Fourierova vzoru a Fourierova obrazu v integrálu, tj. R f (x)g(x) dx = F(x)g(x) dx? Tvrzení dokaºte (2 body), ale podstatn více pozornosti v nujte podrobnému stanovení p edpoklad ve Fubiniov v t a zaru ení jejich R napln ní. ➋ (11 bod ) Nech je dán operátor ˆL s ist bodovým spektrem operující na Hilbertov prostoru H. Nech f (x) H je zvoleno pevn. Ozna me p íslu²nou operátorou bázi B = {φ 1 (x), φ 2 (x), φ 3 (x),...}. Pro zadané objekty je známo, ºe Vypo ítejte, emu se rovná podíl ˆL( f ) f. n N : ˆL f φ n = f φ 1 = π, 2 n n!, n N : f φ n+1 = f φ n. 3 x±i0. V t²í pozornost v nujte teo- ➌ (10 bod ) 1 Bez pouºití Sochockého vzorc a integrálních transformací vypo ítejte x retickým zd vodn ním. ➍ (12 bod ) Rozhodn te, denuje-li p edpis ( g; φ(x) ) := R ln x φ(x) dx zobecn nou funkci. Pokud ano, rozhodn te, je-li tato zobecn ná funkce regulární, a vypo t te její první derivaci.
9 Příjmení a jméno CELKEM Zkou²ková písemná práce. 5/A z p edm tu 01RMF 18/02/2016, 9:00 10:00 ➊ Vyslovte a dokaºte v tu o harmonickém e²ení dopravní rovnice. ➋ Denujte pojem meze integrálního jádra a pro Fredholmovo jádro dokaºte její kone nost. Dále ukaºte, ºe z existence meze plyne spojitost p íslu²ného operátoru v L 2 (G). Co je navíc nutno p edpokládat o G? ➌ Vyslovte a dokaºte Besselovu nerovnost. ➍ Denujte prostor testovacích funkcí. ➎ Denujte konvoluci v D a na jejím základ vypo ítejte f δ µ. Ve výpo tu ádn zd vodn te, pro na n kterém míst lze a na jiném nelze zam nit limitu a funkcionální závorky. Úlohu e²te pro f D, pro niº není garantováno, ºe je regulární. K postupu do dal²ího kola je t eba zodpov d t alespo 4 otázky správn. Mezi správn zodpov zenými úlohami MUSEJÍ být d kazové úlohy. 1 a 3!
10 Jméno studenta (tiskacím písmem) ČÁST A BONUS CELKEM BODŮ Celkové hodnocení zkoušky (ve formátu A,B,C,D,E,F) : Podpis studenta: Zkou²ková písemná práce. 5/B z p edm tu 01RMF 18/02/2016, 10:30 11:30 ➊ (10 bod ) Ukaºte, ºe znáte-li pro operátor s ist bodovým spektrem tzv. maticové elementy, tj. prvky tvaru ˆL(φ k ) φ n := β kn ur ené pro v²echny prvky operátorové báze, pak je pomocí nich (a také pomocí fourierovských koecient ) moºno vy íslit normu ˆL f pro libovolnou funkci f (x) H. Jakou podmínku byste kladli na maticové elementy, aby byla garantována hermiticita operátoru ˆL? Jaké vlastnosti má matice B = (β kn ) k,n? ➋ (8 bod ) Uºitím Laplaceovy transformace vypo t te ur itý integrál sin(x) x cos(x) 0 x 3 dx. ➌ (13 bod ) Rozhodn te, denuje-li p edpis ( h; φ(x) ) := 0 φ(x) x dx zobecn nou funkci. Pokud ano, rozhodn te, je-li tato zobecn ná funkce regulární, a maximáln zjednodu²te výraz x h. V odvození ukaºte místo, kde by argumentace selhala, kdyby v denici superstejnom rné konvergence nebylo garantováno stejnom rné omezení nosi e. ➍ (9 bod ) Zodpov zte a va²e tvrzení podpo te korektním výpo tem: Nech u(x, t) C 1 (R 2 ) \ C 2 (R 2 ). Nech w(x, t) je zobecn ná funkce generovaná klasickou funkcí Θ(t)u(x, t). ƒemu je v D (R 2 ) roven výraz w (x, t)? t Jak lze výsledek zjednodu²it za p edpokladu, ºe u(x, t) C (R 2 )?
11 Příjmení a jméno CELKEM Zkou²ková písemná práce. 6/A z p edm tu 01RMF 30/03/2016, 9:00 10:00 ➊ Nech ω(x) je Cimrmanova bu inka o jednotkovém polom ru, tj. ε = 1. U kaºdé z níºe uvedených t íd uve te (ANO/NE), zda funkce h(x) = ω(x)x 2 e 2x do dané t ídy pat í: D(R), S (R), P(R), L 1 (R). ➋ Z denice hermiticity operátoru odvo te podmínku pro jádro K ( x, y) : G G C integrálního operátoru ˆK denovaného na L 2 (G) posta ující pro to, aby ˆK byl hermiteovský. ➌ Vyslovte a dokaºte (se v²emi náleºitostmi) základní v tu o e²ení diferenciální rovnice v D (E r ). ➍ Denujte geometrickou násobnost vlastního ísla operátoru. ➎ Vyslovte a dokaºte v tu o harmonickém e²ení dopravní rovnice. K postupu do dal²ího kola je t eba zodpov d t alespo 4 otázky správn. Mezi správn zodpov zenými úlohami MUSEJÍ být d kazové úlohy. 3 a 5!
12 Jméno studenta (tiskacím písmem) ČÁST A BONUS CELKEM BODŮ Celkové hodnocení zkoušky (ve formátu A,B,C,D,E,F) : Podpis studenta: Zkou²ková písemná práce. 6/B z p edm tu 01RMF 30/03/2016, 10:30 11:30 ➊ (10 bod ) Pro parciální diferenciální operátor ˆL = t 2 a2 x 2 b, (a > 0 b > 0) x zformulujte p íslu²nou Cauchyovu úlohu, p eve te ji do prostoru zobecn ných funkcí a nalezn te fundamentální e²ení. Pro ú ely tohoto p íkladu si na základ vlastností Fourierova desatera odvo te Fourier v obraz funkce g(x) = e c(x d)2. ➋ (10 bod ) Rozhodn te, zda p edpis 0 3e 2x2 φ (x) dx (2) denujte zobecn nou funkci z D (R). Pokud ne, ukaºte na konkrétním p íklad, kde p edpis (2) selhává. Pokud ano, emu se taková distribuce rovná? Dále rozhodn te, zda p edpis (2) denujte zobecn nou funkci z S (R). ➌ (10 bod ) Dokaºte, ºe je-li g(x) P(R) hustotou pravd podobnosti, k níº existují v²echny necentrální momenty, pak lze sestavit Maclaurinovu adu jejího Laplaceova obrazu. Rozeberte také v²echny technikality na pozadí (analyti nost Laplaceova obrazu, obor konvergence, deni ní obor Laplaceova obrazu). Bude-li t eba, kla te na funkci g(x) dal²í omezení. ➍ (10 bod ) Ve t íd zobecn ných funkcí D (R 2 ) maximáln zjednodu²te výraz lim λ λ3 x 3 e λ2 x 2 P 1 x y2 d2 δ dy 2.
13 Příjmení a jméno CELKEM Zkou²ková písemná práce. 7/A z p edm tu 01RMF 04/05/2016, 9:00 10:00 ➊ Vyslovte a dokaºte (se v²emi náleºitostmi) základní v tu o e²ení diferenciální rovnice v D. ➋ Vyslovte a dokaºte v tu o e²ení Volterrovy integrální rovnice metodou postupných aproximací. Neopome te prokázat jednozna nost e²ení. ➌ Denujte regulární distribuci. ➍ Jak je zavedena konvergence v prostoru D (E r )? ➎ Jakého typu excentricity je diferenciální rovnice 4y 2 g x 2 + 4x 2 g x y (6x + 9y) 2 g y 2 = 0? K postupu do dal²ího kola je t eba zodpov d t alespo 4 otázky správn. Mezi správn zodpov zenými úlohami MUSEJÍ být d kazové úlohy. 1 a 2!
14 Jméno studenta (tiskacím písmem) ČÁST A BONUS CELKEM BODŮ Celkové hodnocení zkoušky (ve formátu A,B,C,D,E,F) : Podpis studenta: Zkou²ková písemná práce. 7/B z p edm tu 01RMF 04/05/2016, 10:30 11:30 ➊ (10 bod ) Dokaºte komutativitu tenzorového sou inu. Vyslovte téº zn ní lemmatu, bez kterého by nebylo moºno d kaz provést. ➋ (10 bod ) Dokaºte, ºe pokud je g(x) exponenciálního r stu, pak limita ln g(x) lim x + x vºdy existuje a její hodnota je rovna indexu r stu dané funkce. ➌ (10 bod ) Ve t íd zobecn ných funkcí D (R 2 ) maximáln zjednodu²te výraz Uºijte faktu, ºe R sin 2 (βx) dx = π β. x 2 lim c ex sin(cy) ( δ(x µ) sin(cy) P 1 cy y ). ➍ (10 bod ) Je dob e známo, ºe 1 lim e x2 2σ 2 D = δ. σ 0 + 2πσ Vy ale sestavte posloupnost regulárních distribucí, která konverguje k δ a své tvrzení dokaºte dv ma r znými postupy.
15 Příjmení a jméno CELKEM Zkou²ková písemná práce. 8/A z p edm tu 01RMF 31/05/2016, 13:00 14:00 ➊ Denujte omezenost a hermiteovskost operátoru. Jak jsou tyto pojmy provázány? ➋ Vyslovte a dokaºte v tu o Parsevalov vzorci a Parsevalov rovnosti. ➌ Vyslovte a dokaºte v tu o e²ení Fredholmovy integrální rovnice metodou postupných aproximací. Neopome te prokázat jednozna nost e²ení. ➍ Jak je zavedena superstejnom rná konvergence v prostoru testovacích funkcí? ➎ Nech ˆL a ˆK jsou Volterrovy integrální operátory s jádry K (x, y) a L (x, y). Jakého tvaru je jádro M (x, y) integrálního operátoru ˆM := ˆL ˆK? Je ˆM také Volterr v? K postupu do dal²ího kola je t eba zodpov d t alespo 4 otázky správn. Mezi správn zodpov zenými úlohami MUSEJÍ být d kazové úlohy. 2 a 3!
16 Jméno studenta (tiskacím písmem) ČÁST A BONUS CELKEM BODŮ Celkové hodnocení zkoušky (ve formátu A,B,C,D,E,F) : Podpis studenta: Zkou²ková písemná práce. 8/B z p edm tu 01RMF 31/05/2016, 14:30 15:30 ➊ (10 bod ) Prove te dekonvoluci 2Θ(x)x 2 g(x) = [3 4x + 2x 2 e 2x (3 + 2x)]Θ(x), g(x) =? ➋ (10 bod ) Pro kterou z funkcí xe x2, x 2 e x2 vrací kone ná ást P 1 x v bec P 1 x z p íslu²né t ídy? Podrobn komentujte! v t²í hodnotu? Kde má smysl tuto úlohu e²it? Je ➌ (10 bod ) Laplaceovou transformací e²te Cauchyovu úlohu pro integrodiferenciální rovnici x z + 3z 4 z(s) ds = 8Θ(x) & z(0 + ) = 2 & z (0 + ) = 9. 0 ➍ (10 bod ) Nech f ε (x, y) = Θ(x, y) xy x+y ε 4 e ε. Nech f ε je zobecn ná funkce, jejímº generátorem je funkce f ε (x, y). Vypo t te limitu lim ε 0+ f ε ve t íd D (R 2 ).
Zápo tová písemná práce. 1 z p edm tu 01RMF varianta A
 Zápo tová písemná práce. 1 z p edm tu 1MF varianta A tvrtek 19. listopadu 215, 13:215:2 ➊ (5 bod ) Nech f (x), g(x) L 1 () a f (x) dx = A, x f (x) dx = µ, Vypo ítejte, emu se rovná z( f g)(z) dz. g(x)
Zápo tová písemná práce. 1 z p edm tu 1MF varianta A tvrtek 19. listopadu 215, 13:215:2 ➊ (5 bod ) Nech f (x), g(x) L 1 () a f (x) dx = A, x f (x) dx = µ, Vypo ítejte, emu se rovná z( f g)(z) dz. g(x)
Záznam o ústní zkou²ce z p edm tu 01RMF (akademický ²kolní rok 2015/2016) P íjmení a jméno Datum Hodnocení Písemka Celkové hodnocení Podpis studenta
 báze v Hilbertov prostoru obory excentricity parciální diferenciální rovnice (a metoda jejich detekce pro PDR druhého ádu pro funkci dvou prom nných) fundamentální e²ení operátoru 1. ➋ Dokaºte: f( x),
báze v Hilbertov prostoru obory excentricity parciální diferenciální rovnice (a metoda jejich detekce pro PDR druhého ádu pro funkci dvou prom nných) fundamentální e²ení operátoru 1. ➋ Dokaºte: f( x),
Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A
 Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A st eda 19. listopadu 2015, 11:2013:20 ➊ (3 body) Pro diferenciální operátor ˆL je mnoºina W q denována p edpisem W q = { y(x) Dom( ˆL) : ˆL(y(x))
Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A st eda 19. listopadu 2015, 11:2013:20 ➊ (3 body) Pro diferenciální operátor ˆL je mnoºina W q denována p edpisem W q = { y(x) Dom( ˆL) : ˆL(y(x))
Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A
 Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A úterý 28. listopadu 2017, 9:2011:20 ➊ (8 bod ) Lze nebo nelze k rozhodnutí o stejnom rné konvergence ady ( 1) n+1 x ln(n) n 6 + n 2 x 4 na intervalu
Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A úterý 28. listopadu 2017, 9:2011:20 ➊ (8 bod ) Lze nebo nelze k rozhodnutí o stejnom rné konvergence ady ( 1) n+1 x ln(n) n 6 + n 2 x 4 na intervalu
Katedra matematiky Fakulty jaderné a fyzikálně inženýrské ČVUT v Praze Příjmení a jméno ➊ ➋ ➌ ➍ ➎ ➏ Bonus
 Zkoušková písemná práce č 1 z předmětu 1RMF čtvrtek 16 ledna 214, 9: 11: ➊ 11 bodů) Ve třídě zobecněných funkcí vypočítejte itu x ) n n2 sin 2 P 1 n x) ➋ 6 bodů) Aplikací Laplaceovy transformace vypočtěte
Zkoušková písemná práce č 1 z předmětu 1RMF čtvrtek 16 ledna 214, 9: 11: ➊ 11 bodů) Ve třídě zobecněných funkcí vypočítejte itu x ) n n2 sin 2 P 1 n x) ➋ 6 bodů) Aplikací Laplaceovy transformace vypočtěte
Zkou²ková písemná práce. 1 z p edm tu 01MAB4
 Zkou²ková písemná práce. 1 z p edm tu 1MAB4 29/5/218, 9: 11: ➊ (8 bod ) Pro parametry a > a b R vypo t te ur itý integrál e ax2 cos(bx2 ) 1 x Uºijte v tu o derivaci integrálu s parametrem. Spln ní p edpokladu
Zkou²ková písemná práce. 1 z p edm tu 1MAB4 29/5/218, 9: 11: ➊ (8 bod ) Pro parametry a > a b R vypo t te ur itý integrál e ax2 cos(bx2 ) 1 x Uºijte v tu o derivaci integrálu s parametrem. Spln ní p edpokladu
Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A
 Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A úterý 6. prosince 2016, 13:2015:20 ➊ (8 bod ) Vy²et ete stejnom rnou konvergenci ady na mnoºin R +. n=2 x n 1 1 4n 2 + x 2 ln 2 (n) ➋ (5 bod ) Detailn
Zápo tová písemná práce. 1 z p edm tu 01MAB3 varianta A úterý 6. prosince 2016, 13:2015:20 ➊ (8 bod ) Vy²et ete stejnom rnou konvergenci ady na mnoºin R +. n=2 x n 1 1 4n 2 + x 2 ln 2 (n) ➋ (5 bod ) Detailn
Zkou²ková písemná práce. 1 z p edm tu 01MAB4
 Zkou²ková písemná práce. 1 z p edm tu 01MAB4 25/05/2017, 9:00 11:00 ➊ (9 bod ) Nech je dvojrozm rná Lebesgueova míra generována vytvo ujícími funkcemi φ(x) = Θ(x)x 2 a ψ(y) = 7y. Vypo t te míru mnoºiny
Zkou²ková písemná práce. 1 z p edm tu 01MAB4 25/05/2017, 9:00 11:00 ➊ (9 bod ) Nech je dvojrozm rná Lebesgueova míra generována vytvo ujícími funkcemi φ(x) = Θ(x)x 2 a ψ(y) = 7y. Vypo t te míru mnoºiny
Zápo tová písemná práce. 1 z p edm tu 01MAB4 varianta A
 Zápo tová písemná práce. 1 z p edm tu 01MAB4 varianta A 18. dubna 2016, 11:2013:20 ➊ (1 bod) Nalezn te kritický bod soustavy generujících rovnic e x 6y 6z 2 + 12z = 13, 2e 2x 6y z 3 = 6. Uºijte faktu,
Zápo tová písemná práce. 1 z p edm tu 01MAB4 varianta A 18. dubna 2016, 11:2013:20 ➊ (1 bod) Nalezn te kritický bod soustavy generujících rovnic e x 6y 6z 2 + 12z = 13, 2e 2x 6y z 3 = 6. Uºijte faktu,
Zkou²ková písemná práce. 1 z p edm tu 01MAB4
 Katedra matematiky Fakulty jaderné a fyzikálně inženýrské ČVU v Praze Zkou²ková písemná práce. 1 z p edm tu 1MAB4 25/5/216, 9: 11: ➊ (11 bod ) Vypo ítejte abstraktní plo²nou míru mnoºiny M = (x, y) R 2
Katedra matematiky Fakulty jaderné a fyzikálně inženýrské ČVU v Praze Zkou²ková písemná práce. 1 z p edm tu 1MAB4 25/5/216, 9: 11: ➊ (11 bod ) Vypo ítejte abstraktní plo²nou míru mnoºiny M = (x, y) R 2
1. Spo t te limity (m ºete pouºívat l'hospitalovo pravidlo) x cotg x 1. c) lim. g) lim e x 1. cos(x) =
 I. L'HOSPITALOVO PRAVIDLO A TAYLOR V POLYNOM. Spo t te limity (m ºete pouºívat l'hospitalovo pravidlo) a) lim tg sin ( + ) / e e) lim a a i) lim a a, a > P ipome me si: 3 tg 4 2 tg b) lim 3 sin 4 2 sin
I. L'HOSPITALOVO PRAVIDLO A TAYLOR V POLYNOM. Spo t te limity (m ºete pouºívat l'hospitalovo pravidlo) a) lim tg sin ( + ) / e e) lim a a i) lim a a, a > P ipome me si: 3 tg 4 2 tg b) lim 3 sin 4 2 sin
nazvu obecnou PDR pro neznámou funkci
 Denice. Bu n N a Ω R d otev ená, d 2. Vztah tvaru F (x, u(x), Du(x),..., D (n 1) u(x), D (n) u(x)) = 0 x Ω (1) nazvu obecnou PDR pro neznámou funkci u : Ω R d R Zde je daná funkce. F : Ω R R d R dn 1 R
Denice. Bu n N a Ω R d otev ená, d 2. Vztah tvaru F (x, u(x), Du(x),..., D (n 1) u(x), D (n) u(x)) = 0 x Ω (1) nazvu obecnou PDR pro neznámou funkci u : Ω R d R Zde je daná funkce. F : Ω R R d R dn 1 R
I. VRSTEVNICE FUNKCE, OTEV ENÉ A UZAV ENÉ MNOšINY
 I. VRSTEVNICE FUNKCE, OTEV ENÉ A UZAV ENÉ MNOšINY 1. Ur ete a nakreslete deni ní obor a vrstevnice funkcí: a) f(, y) = + y b) f(, y) = y c) f(, y) = 2 + y 2 d) f(, y) = 2 y 2 e) f(, y) = y f) f(, y) =
I. VRSTEVNICE FUNKCE, OTEV ENÉ A UZAV ENÉ MNOšINY 1. Ur ete a nakreslete deni ní obor a vrstevnice funkcí: a) f(, y) = + y b) f(, y) = y c) f(, y) = 2 + y 2 d) f(, y) = 2 y 2 e) f(, y) = y f) f(, y) =
Text m ºe být postupn upravován a dopl ován. Datum poslední úpravy najdete u odkazu na staºení souboru. Veronika Sobotíková
 Tento text není samostatným studijním materiálem. Jde jen o prezentaci promítanou na p edná²kách, kde k ní p idávám slovní komentá. N které d leºité ásti látky pí²u pouze na tabuli a nejsou zde obsaºeny.
Tento text není samostatným studijním materiálem. Jde jen o prezentaci promítanou na p edná²kách, kde k ní p idávám slovní komentá. N které d leºité ásti látky pí²u pouze na tabuli a nejsou zde obsaºeny.
Skalární sou in. Úvod. Denice skalárního sou inu
 Skalární sou in Jedním ze zp sob, jak m ºeme dva vektory kombinovat, je skalární sou in. Výsledkem skalárního sou inu dvou vektor, jak jiº název napovídá, je skalár. V tomto letáku se nau íte, jak vypo
Skalární sou in Jedním ze zp sob, jak m ºeme dva vektory kombinovat, je skalární sou in. Výsledkem skalárního sou inu dvou vektor, jak jiº název napovídá, je skalár. V tomto letáku se nau íte, jak vypo
Integrování jako opak derivování
 Integrování jako opak derivování V tomto dokumentu budete seznámeni s derivováním b ºných funkcí a budete mít moºnost vyzkou²et mnoho zp sob derivace. Jedním z nich je proces derivování v opa ném po adí.
Integrování jako opak derivování V tomto dokumentu budete seznámeni s derivováním b ºných funkcí a budete mít moºnost vyzkou²et mnoho zp sob derivace. Jedním z nich je proces derivování v opa ném po adí.
Rovnice matematické fyziky cvičení pro akademický školní rok 2013-2014
 Harmonogram výuky předmětu Rovnice matematické fyziky cvičení pro akademický školní rok 2013-2014 Vedoucí cvičení: ing. Václav Klika, Ph.D. & MSc. Karolína Korvasová & & ing. Matěj Tušek, Ph.D. Katedra
Harmonogram výuky předmětu Rovnice matematické fyziky cvičení pro akademický školní rok 2013-2014 Vedoucí cvičení: ing. Václav Klika, Ph.D. & MSc. Karolína Korvasová & & ing. Matěj Tušek, Ph.D. Katedra
Vektor náhodných veli in - práce s více prom nnými
 Vektor náhodných veli in - práce s více prom nnými 12. kv tna 2015 N kdy k popisu n jaké situace pot ebujeme více neº jednu náhodnou veli inu. Nap. v k, hmotnost, vý²ku. Mezi t mito veli inami mohou být
Vektor náhodných veli in - práce s více prom nnými 12. kv tna 2015 N kdy k popisu n jaké situace pot ebujeme více neº jednu náhodnou veli inu. Nap. v k, hmotnost, vý²ku. Mezi t mito veli inami mohou být
Reálná ísla a posloupnosti Jan Malý
 Reálná ísla a posloupnosti Jan Malý Obsah 1. Reálná ísla 1 2. Posloupnosti 2 3. Hlub²í v ty o itách 4 1. Reálná ísla 1.1. Úmluva (T leso). Pod pojmem t leso budeme v tomto textu rozum t pouze komutativní
Reálná ísla a posloupnosti Jan Malý Obsah 1. Reálná ísla 1 2. Posloupnosti 2 3. Hlub²í v ty o itách 4 1. Reálná ísla 1.1. Úmluva (T leso). Pod pojmem t leso budeme v tomto textu rozum t pouze komutativní
P íklad 1 (Náhodná veli ina)
 P íklad 1 (Náhodná veli ina) Uvaºujeme experiment: házení mincí. Výsledkem pokusu je rub nebo líc, ºe padne hrana neuvaºujeme. Pokud hovo íme o náhodné veli in, musíme p epsat výsledky pokusu do mnoºiny
P íklad 1 (Náhodná veli ina) Uvaºujeme experiment: házení mincí. Výsledkem pokusu je rub nebo líc, ºe padne hrana neuvaºujeme. Pokud hovo íme o náhodné veli in, musíme p epsat výsledky pokusu do mnoºiny
5. Aplikace diferenciálního a integrálního po tu v jedné dimenzi ZS 2017/18 1 / 32
 5. Aplikace diferenciálního a integrálního po tu v jedné dimenzi Tomá² Sala MÚ UK, MFF UK ZS 2017/18 5. Aplikace diferenciálního a integrálního po tu v jedné dimenzi ZS 2017/18 1 / 32 5.1 Funkce spojité
5. Aplikace diferenciálního a integrálního po tu v jedné dimenzi Tomá² Sala MÚ UK, MFF UK ZS 2017/18 5. Aplikace diferenciálního a integrálního po tu v jedné dimenzi ZS 2017/18 1 / 32 5.1 Funkce spojité
Binární operace. Úvod. Pomocný text
 Pomocný text Binární operace Úvod Milí e²itelé, binární operace je pom rn abstraktní téma, a tak bude ob as pot eba odprostit se od konkrétních p íklad a podívat se na v c s ur itým nadhledem. Nicmén e²ení
Pomocný text Binární operace Úvod Milí e²itelé, binární operace je pom rn abstraktní téma, a tak bude ob as pot eba odprostit se od konkrétních p íklad a podívat se na v c s ur itým nadhledem. Nicmén e²ení
1. (18 bod ) Náhodná veli ina X je po et rub p i 400 nezávislých hodech mincí. a) Pomocí ƒeby²evovy nerovnosti odhadn te pravd podobnost
 (8 bod ) Náhodná veli ina X je po et rub p i nezávislých hodech mincí a) Pomocí ƒeby²evovy nerovnosti odhadn te pravd podobnost P ( X EX < ) (9 bod ) b) Formulujte centrální limitní v tu a pomocí ní vypo
(8 bod ) Náhodná veli ina X je po et rub p i nezávislých hodech mincí a) Pomocí ƒeby²evovy nerovnosti odhadn te pravd podobnost P ( X EX < ) (9 bod ) b) Formulujte centrální limitní v tu a pomocí ní vypo
Katedra matematiky Fakulty jaderné a fyzikálně inženýrské ČVUT v Praze. Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A
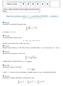 Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A středa 19. listopadu 2014, 11:20 13:20 ➊ (8 bodů) Rozhodněte o stejnoměrné konvergenci řady n 3 n ( ) 1 e xn2 x 2 +n 2 na množině A = 0, + ). ➋
Zápočtová písemná práce č. 1 z předmětu 01MAB3 varianta A středa 19. listopadu 2014, 11:20 13:20 ➊ (8 bodů) Rozhodněte o stejnoměrné konvergenci řady n 3 n ( ) 1 e xn2 x 2 +n 2 na množině A = 0, + ). ➋
1 Existence e²ení systému diferenciálních rovnic. 2 Jednozna nost e²ení pro systém diferenciálních rovnic
 1 Existence e²ení systému diferenciálních rovnic Denice. Funkci x : I R n, I otev ený interval, nazveme e²ením (DR), jestliºe 1. t I : (x(t), t) Ω 2. t I : x (t) vlastní 3. t I : x (t) = f(x(t), t) Lemma
1 Existence e²ení systému diferenciálních rovnic Denice. Funkci x : I R n, I otev ený interval, nazveme e²ením (DR), jestliºe 1. t I : (x(t), t) Ω 2. t I : x (t) vlastní 3. t I : x (t) = f(x(t), t) Lemma
Úvod do parciálních diferenciálních rovnic. 2 Kanonický tvar lineárních PDR 2. řádu pro funkce
 Příklady na cvičení k přednášce NMMA334 Úvod do parciálních diferenciálních rovnic 1 Kanonický tvar lineárních PDR 2. řádu pro funkce dvou proměnných 1. Určete typ parciální diferenciální rovnice u xx
Příklady na cvičení k přednášce NMMA334 Úvod do parciálních diferenciálních rovnic 1 Kanonický tvar lineárních PDR 2. řádu pro funkce dvou proměnných 1. Určete typ parciální diferenciální rovnice u xx
Text m ºe být postupn upravován a dopl ován. Datum poslední úpravy najdete u odkazu na staºení souboru. Veronika Sobotíková
 Tento text není smosttným studijním mteriálem. Jde jen o prezentci promítnou n p edná²kách, kde k ní p idávám slovní komentá. N které d leºité ásti látky pí²u pouze n tbuli nejsou zde obsºeny. Text m ºe
Tento text není smosttným studijním mteriálem. Jde jen o prezentci promítnou n p edná²kách, kde k ní p idávám slovní komentá. N které d leºité ásti látky pí²u pouze n tbuli nejsou zde obsºeny. Text m ºe
Transformace Aplikace Trojný integrál. Objem, hmotnost, moment
 Trojný integrál Dvojný a trojný integrál Objem, hmotnost, moment obecne ji I Nez zavedeme transformaci dvojne ho integra lu obecne, potr ebujeme ne kolik pojmu. Definice Necht je da no zobrazenı F : R2
Trojný integrál Dvojný a trojný integrál Objem, hmotnost, moment obecne ji I Nez zavedeme transformaci dvojne ho integra lu obecne, potr ebujeme ne kolik pojmu. Definice Necht je da no zobrazenı F : R2
QR, b = QS, c = QP. Dokaºte ºe vzdálenost bodu P od roviny spl uje. a (b c) d =
 . cvi ení -Opakování geometrie IR n, p íklady () Najd te velikost úhlu mezi hlavní diagonálou krychle a diagonálou jedné ze stran, která s ní má spole ný vrchol. (2) Dokaºte ºe x y = y x. (3) Dokaºte ºe
. cvi ení -Opakování geometrie IR n, p íklady () Najd te velikost úhlu mezi hlavní diagonálou krychle a diagonálou jedné ze stran, která s ní má spole ný vrchol. (2) Dokaºte ºe x y = y x. (3) Dokaºte ºe
2. Určte hromadné body, limitu superior a limitu inferior posloupností: 2, b n = n. n n n.
 Písemka matematika 3 s řešením 1. Vypočtěte lim n( 1 + n 2 n), n lim n (( 1 + 1 n e ) n ) n. 1/2, 1/ e 2. Určte hromadné body, limitu superior a limitu inferior posloupností: a n = sin nπ ( 2, b n = n
Písemka matematika 3 s řešením 1. Vypočtěte lim n( 1 + n 2 n), n lim n (( 1 + 1 n e ) n ) n. 1/2, 1/ e 2. Určte hromadné body, limitu superior a limitu inferior posloupností: a n = sin nπ ( 2, b n = n
Katedra matematiky Fakulty jaderné a fyzikálně inženýrské ČVUT v Praze Příjmení a jméno ➊ ➋ ➌ ➍ ➎ ➏ Bonus
 Zkoušková písemná práce č. 1 z předmětu 01MAB4 pondělí 25. května 2015, 9:00 11:00 Vypočítejte integrál y d(, y), kde Ω Objekt Ω načrtněte do obrázku! Ω = { (, y) R 2 :, y 0 4 + y 4 1 ( 4 + y 4 ) 3 16
Zkoušková písemná práce č. 1 z předmětu 01MAB4 pondělí 25. května 2015, 9:00 11:00 Vypočítejte integrál y d(, y), kde Ω Objekt Ω načrtněte do obrázku! Ω = { (, y) R 2 :, y 0 4 + y 4 1 ( 4 + y 4 ) 3 16
VYBRANÉ APLIKACE RIEMANNOVA INTEGRÁLU I. OBSAH A DÉLKA. (f(x) g(x)) dx.
 VYBRANÉ APLIKACE RIEMANNOVA INTEGRÁLU I. OBSAH A DÉLKA. Výpo et obsahu rovinných ploch a) Plocha ohrani ená k ivkami zadanými v kartézských sou adnicích. Obsah S rovinné plochy ohrani ené dv ma spojitými
VYBRANÉ APLIKACE RIEMANNOVA INTEGRÁLU I. OBSAH A DÉLKA. Výpo et obsahu rovinných ploch a) Plocha ohrani ená k ivkami zadanými v kartézských sou adnicích. Obsah S rovinné plochy ohrani ené dv ma spojitými
22 Základní vlastnosti distribucí
 M. Rokyta, MFF UK: Aplikovaná matematika IV kap. 22: Základní vlastnosti distribucí 5 22 Základní vlastnosti distribucí 22.1 Temperované distribuce Definice. O funkci ϕ C (R m ) řekneme, že je rychle klesající
M. Rokyta, MFF UK: Aplikovaná matematika IV kap. 22: Základní vlastnosti distribucí 5 22 Základní vlastnosti distribucí 22.1 Temperované distribuce Definice. O funkci ϕ C (R m ) řekneme, že je rychle klesající
Exponenciála matice a její užití. fundamentálních matic. Užití mocninných řad pro rovnice druhého řádu
 1 Tutoriál č. 3 Exponenciála matice a její užití řešení Cauchyovy úlohy pro lineární systémy užitím fundamentálních matic. Užití mocninných řad pro rovnice druhého řádu 0.1 Exponenciála matice a její užití
1 Tutoriál č. 3 Exponenciála matice a její užití řešení Cauchyovy úlohy pro lineární systémy užitím fundamentálních matic. Užití mocninných řad pro rovnice druhého řádu 0.1 Exponenciála matice a její užití
Záznam o ústní zkoušce z předmětu 01MAB4 (akademický školní rok 2017/2018) Příjmení a jméno studenta Finální hodnocení Datum ústní zkoušky
 hladká funkce na oblasti G E r 1. matematickým zápisem vystihněte geometrickou interpretaci abstraktního Lebesgueova integrálu Kam míří gradf( a)? Své tvrzení podpořte výpočtem. Jaký je rozdíl mezi symboly
hladká funkce na oblasti G E r 1. matematickým zápisem vystihněte geometrickou interpretaci abstraktního Lebesgueova integrálu Kam míří gradf( a)? Své tvrzení podpořte výpočtem. Jaký je rozdíl mezi symboly
Záludnosti velkých dimenzí
 Jan Vybíral KM/FJFI/ƒVUT 6. listopadu 2017 1/28 Warm-up Dva problémy na zah átí Geometrie R d Kolik bod je t eba rozmístit v jednotkové krychli [0, 1] d v dimenzi d, aby v kaºdém kvádru o objemu 1/10 leºel
Jan Vybíral KM/FJFI/ƒVUT 6. listopadu 2017 1/28 Warm-up Dva problémy na zah átí Geometrie R d Kolik bod je t eba rozmístit v jednotkové krychli [0, 1] d v dimenzi d, aby v kaºdém kvádru o objemu 1/10 leºel
Otázky k ústní zkoušce, přehled témat A. Číselné řady
 Otázky k ústní zkoušce, přehled témat 2003-2004 A Číselné řady Vysvětlete pojmy částečný součet řady, součet řady, řadonverguje, řada je konvergentní Formulujte nutnou podmínku konvergence řady a odvoďte
Otázky k ústní zkoušce, přehled témat 2003-2004 A Číselné řady Vysvětlete pojmy částečný součet řady, součet řady, řadonverguje, řada je konvergentní Formulujte nutnou podmínku konvergence řady a odvoďte
Limity funkcí v nevlastních bodech. Obsah
 Limity funkcí v nevlastních bodech V tomto letáku si vysv tlíme, co znamená, kdyº funkce mí í do nekone na, mínus nekone na nebo se blíºí ke konkrétnímu reálnému íslu, zatímco x jde do nekone na nebo mínus
Limity funkcí v nevlastních bodech V tomto letáku si vysv tlíme, co znamená, kdyº funkce mí í do nekone na, mínus nekone na nebo se blíºí ke konkrétnímu reálnému íslu, zatímco x jde do nekone na nebo mínus
I. Diferenciální rovnice. 3. Rovnici y = x+y+1. převeďte vhodnou transformací na rovnici homogenní (vzniklou
 Typy příkladů pro I. část písemky ke zkoušce z MA II I. Diferenciální rovnice. 1. Určete obecné řešení rovnice y = y sin x.. Určete řešení rovnice y = y x splňující počáteční podmínku y(1) = 0. 3. Rovnici
Typy příkladů pro I. část písemky ke zkoušce z MA II I. Diferenciální rovnice. 1. Určete obecné řešení rovnice y = y sin x.. Určete řešení rovnice y = y x splňující počáteční podmínku y(1) = 0. 3. Rovnici
INTEGRÁLY S PARAMETREM
 INTEGRÁLY S PARAMETREM b a V kapitole o integraci funkcí více proměnných byla potřeba funkce g(x) = f(x, y) dy proměnné x. Spojitost funkce g(x) = b a f(x, y) dy proměnné x znamená vlastně prohození limity
INTEGRÁLY S PARAMETREM b a V kapitole o integraci funkcí více proměnných byla potřeba funkce g(x) = f(x, y) dy proměnné x. Spojitost funkce g(x) = b a f(x, y) dy proměnné x znamená vlastně prohození limity
19 Hilbertovy prostory
 M. Rokyta, MFF UK: Aplikovaná matematika III kap. 19: Hilbertovy prostory 34 19 Hilbertovy prostory 19.1 Úvod, základní pojmy Poznámka (připomenutí). Necht (X,(, )) je vektorový prostor se skalárním součinem
M. Rokyta, MFF UK: Aplikovaná matematika III kap. 19: Hilbertovy prostory 34 19 Hilbertovy prostory 19.1 Úvod, základní pojmy Poznámka (připomenutí). Necht (X,(, )) je vektorový prostor se skalárním součinem
Pravd podobnost a statistika - cvi ení. Simona Domesová místnost: RA310 (budova CPIT) web:
 Pravd podobnost a statistika - cvi ení Simona Domesová simona.domesova@vsb.cz místnost: RA310 (budova CPIT) web: http://homel.vsb.cz/~dom0015 Cíle p edm tu vyhodnocování dat pomocí statistických metod
Pravd podobnost a statistika - cvi ení Simona Domesová simona.domesova@vsb.cz místnost: RA310 (budova CPIT) web: http://homel.vsb.cz/~dom0015 Cíle p edm tu vyhodnocování dat pomocí statistických metod
Diferenˇcní rovnice Diferenciální rovnice Matematika IV Matematika IV Program
 Program Diferenční rovnice Program Diferenční rovnice Diferenciální rovnice Program Frisch a Samuelson: Systém je dynamický, jestliže jeho chování v čase je určeno funkcionální rovnicí, jejíž neznámé závisí
Program Diferenční rovnice Program Diferenční rovnice Diferenciální rovnice Program Frisch a Samuelson: Systém je dynamický, jestliže jeho chování v čase je určeno funkcionální rovnicí, jejíž neznámé závisí
Dolní odhad síly pro ztrátu stability obecného prutu
 ƒeské vysoké u ení technické v Praze 9. února 216 Vedoucí seminární práce: doc. RNDr. Ivana Pultarová, Ph.D. prof. Ing. Milan Jirásek, DrSc. Osnova 1 2 Cíl práce Cíl práce Nalézt velikost síly, která zp
ƒeské vysoké u ení technické v Praze 9. února 216 Vedoucí seminární práce: doc. RNDr. Ivana Pultarová, Ph.D. prof. Ing. Milan Jirásek, DrSc. Osnova 1 2 Cíl práce Cíl práce Nalézt velikost síly, která zp
Úloha. 2 - Difrakce sv telného zá ení
 Úloha. - Difrakce sv telného zá ení Difrakci sv tla lze charakterizovat jako chování vlnových polí, které není moºné popsat pomocí zákon geometrické optiky. Lze ji p iblíºit jako ohyb nebo odchylku sv
Úloha. - Difrakce sv telného zá ení Difrakci sv tla lze charakterizovat jako chování vlnových polí, které není moºné popsat pomocí zákon geometrické optiky. Lze ji p iblíºit jako ohyb nebo odchylku sv
1.1 Existence a jednoznačnost řešení. Příklad 1.1: [M2-P1] diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu
![1.1 Existence a jednoznačnost řešení. Příklad 1.1: [M2-P1] diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu 1.1 Existence a jednoznačnost řešení. Příklad 1.1: [M2-P1] diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu](/thumbs/102/155926571.jpg) [M2-P1] KAPITOLA 1: Diferenciální rovnice 1. řádu diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu G(x, y, y, y,..., y (n) ) = 0 y (n) = F (x, y, y,..., y (n 1) ) Příklad 1.1:
[M2-P1] KAPITOLA 1: Diferenciální rovnice 1. řádu diferenciální rovnice (DR) řádu n: speciálně nás budou zajímat rovnice typu G(x, y, y, y,..., y (n) ) = 0 y (n) = F (x, y, y,..., y (n 1) ) Příklad 1.1:
NMAF063 Matematika pro fyziky III Zápočtová písemná práce B Termín pro odevzdání 4. ledna 2019
 Jméno: Příklad 2 3 4 5 Celkem bodů Bodů 20 20 20 20 20 00 Získáno Zápočtová písemná práce určená k domácímu vypracování. Nutnou podmínkou pro získání zápočtu je zisk více jak 50 bodů. Pravidla jsou následující:.
Jméno: Příklad 2 3 4 5 Celkem bodů Bodů 20 20 20 20 20 00 Získáno Zápočtová písemná práce určená k domácímu vypracování. Nutnou podmínkou pro získání zápočtu je zisk více jak 50 bodů. Pravidla jsou následující:.
Parciální diferenciální rovnice
 Parciální diferenciální rovnice Obsah kurzu Co bude obsahovat... úvod do PDR odvození některých PDR klasická teorie lineárních PDR 1. a 2. řádu řešení poč. a okraj. úloh vlastnosti řešení souvislost s
Parciální diferenciální rovnice Obsah kurzu Co bude obsahovat... úvod do PDR odvození některých PDR klasická teorie lineárních PDR 1. a 2. řádu řešení poč. a okraj. úloh vlastnosti řešení souvislost s
Nalezněte hladiny následujících funkcí. Pro které hodnoty C R jsou hladiny neprázdné
 . Definiční obor a hladiny funkce více proměnných Nalezněte a graficky znázorněte definiční obor D funkce f = f(x, y), kde a) f(x, y) = x y, b) f(x, y) = log(xy + ), c) f(x, y) = xy, d) f(x, y) = log(x
. Definiční obor a hladiny funkce více proměnných Nalezněte a graficky znázorněte definiční obor D funkce f = f(x, y), kde a) f(x, y) = x y, b) f(x, y) = log(xy + ), c) f(x, y) = xy, d) f(x, y) = log(x
Požadavky k písemné přijímací zkoušce z matematiky do navazujícího magisterského studia pro neučitelské obory
 Požadavky k písemné přijímací zkoušce z matematiky do navazujícího magisterského studia pro neučitelské obory Zkouška ověřuje znalost základních pojmů, porozumění teorii a schopnost aplikovat teorii při
Požadavky k písemné přijímací zkoušce z matematiky do navazujícího magisterského studia pro neučitelské obory Zkouška ověřuje znalost základních pojmů, porozumění teorii a schopnost aplikovat teorii při
Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 2. 3. 2018 Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
2. 3. 2018 Matematika II, úroveň A ukázkový test č. 1 (2018) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
MKI Funkce f(z) má singularitu v bodě 0. a) Stanovte oblast, ve které konverguje hlavní část Laurentova rozvoje funkce f(z) v bodě 0.
 MKI -00 Funkce f(z) má singularitu v bodě 0. a) Stanovte oblast, ve které konverguje hlavní část Laurentova rozvoje funkce f(z) v bodě 0. V jakém rozmezí se může pohybovat poloměr konvergence regulární
MKI -00 Funkce f(z) má singularitu v bodě 0. a) Stanovte oblast, ve které konverguje hlavní část Laurentova rozvoje funkce f(z) v bodě 0. V jakém rozmezí se může pohybovat poloměr konvergence regulární
Matematika II Limita a spojitost funkce, derivace
 Matematika II Limita a spojitost funkce, derivace RNDr. Renata Klufová, Ph. D. Jihoèeská univerzita v Èeských Budìjovicích EF Katedra aplikované matematiky a informatiky Prstencové a kruhové okolí bodu
Matematika II Limita a spojitost funkce, derivace RNDr. Renata Klufová, Ph. D. Jihoèeská univerzita v Èeských Budìjovicích EF Katedra aplikované matematiky a informatiky Prstencové a kruhové okolí bodu
Rovnice a nerovnice. Posloupnosti.
 .. Veronika Sobotíková katedra matematiky, FEL ƒvut v Praze, http://math.feld.cvut.cz/ 30. srpna 2018.. 1/75 (v reálném oboru) Rovnicí resp. nerovnicí v reálném oboru rozumíme zápis L(x) P(x), kde zna
.. Veronika Sobotíková katedra matematiky, FEL ƒvut v Praze, http://math.feld.cvut.cz/ 30. srpna 2018.. 1/75 (v reálném oboru) Rovnicí resp. nerovnicí v reálném oboru rozumíme zápis L(x) P(x), kde zna
Věta o sedlovém bodu a Fredholmova alternativa
 Věta o sedlovém bodu a Fredholmova alternativa Petr Tomiczek Fakulta Aplikovaných věd Západočeská univerzita Plzeň 2006 obsah 1 Rozklad Hilbertova prostoru Uzavřený lineární a samoadjungovaný operátor
Věta o sedlovém bodu a Fredholmova alternativa Petr Tomiczek Fakulta Aplikovaných věd Západočeská univerzita Plzeň 2006 obsah 1 Rozklad Hilbertova prostoru Uzavřený lineární a samoadjungovaný operátor
Co je to tensor... Vektorový prostor
 Vektorový prostor Co je to tensor... Tato ást je tu jen pro p ipomenutí, pokud nevíte co je to vektorový prostor, tak tení tohoto textu ukon ete na konci této v ty, neb zbytek textu by pro Vás nebyl ni
Vektorový prostor Co je to tensor... Tato ást je tu jen pro p ipomenutí, pokud nevíte co je to vektorový prostor, tak tení tohoto textu ukon ete na konci této v ty, neb zbytek textu by pro Vás nebyl ni
Matematická analýza KMA/MA2I 3. p edná²ka Primitivní funkce
 Matematická analýza KMA/MAI 3. p edná²ka Primitivní funkce Denice a základní vlastnosti P íklad Uvaºujme následující úlohu: Najd te funkci F : R R takovou, ºe F () R. Kdo zná vzorce pro výpo et derivací
Matematická analýza KMA/MAI 3. p edná²ka Primitivní funkce Denice a základní vlastnosti P íklad Uvaºujme následující úlohu: Najd te funkci F : R R takovou, ºe F () R. Kdo zná vzorce pro výpo et derivací
MATEMATIKA IV - PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE - ZÁPISKY Z. Obsah. 1. Parciální diferenciální rovnice obecně. 2. Kvaazilineární rovnice prvního řádu
 MATEMATIKA IV - PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE - ZÁPISKY Z PŘEDNÁŠEK JAN MALÝ Obsah 1. Parciální diferenciální rovnice obecně 1. Kvaazilineární rovnice prvního řádu 1 3. Lineární rovnice druhého řádu
MATEMATIKA IV - PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE - ZÁPISKY Z PŘEDNÁŠEK JAN MALÝ Obsah 1. Parciální diferenciální rovnice obecně 1. Kvaazilineární rovnice prvního řádu 1 3. Lineární rovnice druhého řádu
ZS: 2018/2019 NMAF063 F/3 Josef MÁLEK. Matematika pro fyziky III
 ZS: 2018/2019 NMAF063 F/3 Josef MÁLEK Matematika pro fyziky III OBECNÉ INFORMACE A SYLABUS Přednášející: Cvičící: Josef Málek Tomáš Los, Michal Pavelka, Michal Pavelka, Vít Průša Termíny přednášek: čtvrtek
ZS: 2018/2019 NMAF063 F/3 Josef MÁLEK Matematika pro fyziky III OBECNÉ INFORMACE A SYLABUS Přednášející: Cvičící: Josef Málek Tomáš Los, Michal Pavelka, Michal Pavelka, Vít Průša Termíny přednášek: čtvrtek
Město Mariánské Lázně
 Město Mariánské Lázně Městský úřad, odbor investic a dotací adresa: Městský úřad Mariánské Lázně, Ruská 155, 353 01 Mariánské Lázně telefon 354 922 111, fax 354 623 186, e-mail muml@marianskelazne.cz,
Město Mariánské Lázně Městský úřad, odbor investic a dotací adresa: Městský úřad Mariánské Lázně, Ruská 155, 353 01 Mariánské Lázně telefon 354 922 111, fax 354 623 186, e-mail muml@marianskelazne.cz,
Post ehy a materiály k výuce celku Funkce
 Post ehy a materiály k výuce celku Funkce 1) Grafy funkcí Je p edloºeno mnoºství výukových materiál v programu Graph - tvary graf základních i posunutých funkcí, jejich vzájemné polohy, Precizní zápis
Post ehy a materiály k výuce celku Funkce 1) Grafy funkcí Je p edloºeno mnoºství výukových materiál v programu Graph - tvary graf základních i posunutých funkcí, jejich vzájemné polohy, Precizní zápis
Písemná zkouška z Matematiky II pro FSV vzor
 Písemná zkouška z Matematik II pro FSV vzor. (0 bodů) Určete a nakreslete definiční obor funkce sin x f(x, ) = (Kalenda 00/) spočtěte její parciální derivace podle všech proměnných všude, kde existují,
Písemná zkouška z Matematik II pro FSV vzor. (0 bodů) Určete a nakreslete definiční obor funkce sin x f(x, ) = (Kalenda 00/) spočtěte její parciální derivace podle všech proměnných všude, kde existují,
Jméno: P íjmení: Datum: 17. ledna 2018 Nechci zápo et p i hodnocení niº²ím neº (nezávazné): vadí mi vystavení mého hodnocení na internetu.
 Jméno: P íjmení: Datum: 7. ledna 28 Nechci zápo et p i hodnocení niº²ím neº (nezávazné): vadí mi vystavení mého hodnocení na internetu. Rotující nádoba Otev ená válcová nádoba napln ná do poloviny vý²ky
Jméno: P íjmení: Datum: 7. ledna 28 Nechci zápo et p i hodnocení niº²ím neº (nezávazné): vadí mi vystavení mého hodnocení na internetu. Rotující nádoba Otev ená válcová nádoba napln ná do poloviny vý²ky
Seminá e. Ing. Michal Valenta PhD. Databázové systémy BI-DBS ZS 2010/11, sem. 1-13
 Seminá e Ing. Michal Valenta PhD. Katedra softwarového inºenýrství Fakulta informa ních technologií ƒeské vysoké u ení technické v Praze c Michal Valenta, 2010 Databázové systémy BI-DBS ZS 2010/11, sem.
Seminá e Ing. Michal Valenta PhD. Katedra softwarového inºenýrství Fakulta informa ních technologií ƒeské vysoké u ení technické v Praze c Michal Valenta, 2010 Databázové systémy BI-DBS ZS 2010/11, sem.
DERIVACE FUNKCE KOMPLEXNÍ PROMĚNNÉ
 DERIVACE FUNKCE KOMPLEXNÍ PROMĚNNÉ vlastnosti holomorfní DERIVACE U reálných funkcí více reálných proměnných nebylo možné definovat derivaci analogicky definici reálné jedné reálné proměnné (nešlo dělit...)
DERIVACE FUNKCE KOMPLEXNÍ PROMĚNNÉ vlastnosti holomorfní DERIVACE U reálných funkcí více reálných proměnných nebylo možné definovat derivaci analogicky definici reálné jedné reálné proměnné (nešlo dělit...)
Obsah. Pouºité zna ení 1
 Obsah Pouºité zna ení 1 1 Úvod 3 1.1 Opera ní výzkum a jeho disciplíny.......................... 3 1.2 Úlohy matematického programování......................... 3 1.3 Standardní maximaliza ní úloha lineárního
Obsah Pouºité zna ení 1 1 Úvod 3 1.1 Opera ní výzkum a jeho disciplíny.......................... 3 1.2 Úlohy matematického programování......................... 3 1.3 Standardní maximaliza ní úloha lineárního
Kapitola 8: Dvojný integrál 1/26
 Kapitola 8: vojný integrál 1/26 vojný integrál - osnova kapitoly 2/26 dvojný integrál přes obdélník definice výpočet (Fubiniova věta pro obdélník) dvojný integrál přes standardní množinu definice výpočet
Kapitola 8: vojný integrál 1/26 vojný integrál - osnova kapitoly 2/26 dvojný integrál přes obdélník definice výpočet (Fubiniova věta pro obdélník) dvojný integrál přes standardní množinu definice výpočet
Aplikace pravd podobnostních model v kurzovém sázení
 Aplikace pravd podobnostních model v kurzovém sázení 28.4.2016 Obsah 1 Kurzové sázení Tenis Kurz jako odhad pravd podobnosti Hodnocení kvality odhadu pravd podobnosti 2 Predikce pr b hu utkání Základní
Aplikace pravd podobnostních model v kurzovém sázení 28.4.2016 Obsah 1 Kurzové sázení Tenis Kurz jako odhad pravd podobnosti Hodnocení kvality odhadu pravd podobnosti 2 Predikce pr b hu utkání Základní
Ur itý integrál. Úvod. Denice ur itého integrálu
 V tomto lánku se budeme v novt ur itému integrálu, který dné funkci p i zuje íslo. My²lenk integrování pochází z geometrických poºdvk - zji² ování povrch, objem délek geometrických útvr. To znmená, ºe
V tomto lánku se budeme v novt ur itému integrálu, který dné funkci p i zuje íslo. My²lenk integrování pochází z geometrických poºdvk - zji² ování povrch, objem délek geometrických útvr. To znmená, ºe
Derivace funkce. Přednáška MATEMATIKA č Jiří Neubauer
 Přednáška MATEMATIKA č. 9-11 Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Šotová, J., Doudová, L. Diferenciální počet funkcí jedné proměnné Motivační příklady
Přednáška MATEMATIKA č. 9-11 Katedra ekonometrie FEM UO Brno kancelář 69a, tel. 973 442029 email:jiri.neubauer@unob.cz Šotová, J., Doudová, L. Diferenciální počet funkcí jedné proměnné Motivační příklady
e²ení systém lineárních rovnic pomocí s ítací, dosazovací a srovnávací metody
 e²ení systém lineárních rovnic pomocí s ítací, dosazovací a srovnávací metody V praxi se asto setkávame s p ípady, kdy je pot eba e²it více rovnic, takzvaný systém rovnic, obvykle s více jak jednou neznámou.
e²ení systém lineárních rovnic pomocí s ítací, dosazovací a srovnávací metody V praxi se asto setkávame s p ípady, kdy je pot eba e²it více rovnic, takzvaný systém rovnic, obvykle s více jak jednou neznámou.
Definice 1.1. Nechť je M množina. Funkci ρ : M M R nazveme metrikou, jestliže má následující vlastnosti:
 Přednáška 1. Definice 1.1. Nechť je množina. Funkci ρ : R nazveme metrikou, jestliže má následující vlastnosti: (1 pro každé x je ρ(x, x = 0; (2 pro každé x, y, x y, je ρ(x, y = ρ(y, x > 0; (3 pro každé
Přednáška 1. Definice 1.1. Nechť je množina. Funkci ρ : R nazveme metrikou, jestliže má následující vlastnosti: (1 pro každé x je ρ(x, x = 0; (2 pro každé x, y, x y, je ρ(x, y = ρ(y, x > 0; (3 pro každé
PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU
 PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU 6.1 Křivkový integrál 1. druhu Definice 1. Množina R n se nazývá prostá regulární křivka v R n právě tehdy, když existuje vzájemně jednoznačné zobrazení
PŘEDNÁŠKA 9 KŘIVKOVÝ A PLOŠNÝ INTEGRÁL 1. DRUHU 6.1 Křivkový integrál 1. druhu Definice 1. Množina R n se nazývá prostá regulární křivka v R n právě tehdy, když existuje vzájemně jednoznačné zobrazení
Primitivní funkce a Riemann uv integrál Lineární algebra Taylor uv polynom Extrémy funkcí více prom ˇenných Matematika III Matematika III Program
 Program Primitivní funkce a Riemannův integrál Program Primitivní funkce a Riemannův integrál Lineární algebra Program Primitivní funkce a Riemannův integrál Lineární algebra Taylorův polynom Program Primitivní
Program Primitivní funkce a Riemannův integrál Program Primitivní funkce a Riemannův integrál Lineární algebra Program Primitivní funkce a Riemannův integrál Lineární algebra Taylorův polynom Program Primitivní
24. Parciální diferenciální rovnice
 24. Parciální diferenciální rovnice Aplikovaná matematika IV, NMAF074 M. Rokyta, KMA MFF UK LS 2011/12 24.1 Rovnice vedení tepla Definice (Rovnice vedení tepla) Parciální diferenciální rovnici c(x)ρ(x)
24. Parciální diferenciální rovnice Aplikovaná matematika IV, NMAF074 M. Rokyta, KMA MFF UK LS 2011/12 24.1 Rovnice vedení tepla Definice (Rovnice vedení tepla) Parciální diferenciální rovnici c(x)ρ(x)
VYSOKÁ ŠKOLA POLYTECHNICKÁ JIHLAVA. Katedra matematiky. Matematika 2. pro technické obory. Petr Gurka, Stanislava Dvořáková
 VYSOKÁ ŠKOLA POLYTECHNICKÁ JIHLAVA Katedra matematiky Matematika 2 pro technické obory Petr Gurka, Stanislava Dvořáková 2019 Petr Gurka, Stanislava Dvořáková Matematika 2 pro technické obory 1. vydání
VYSOKÁ ŠKOLA POLYTECHNICKÁ JIHLAVA Katedra matematiky Matematika 2 pro technické obory Petr Gurka, Stanislava Dvořáková 2019 Petr Gurka, Stanislava Dvořáková Matematika 2 pro technické obory 1. vydání
Matematika I A ukázkový test 1 pro 2014/2015
 Matematika I A ukázkový test 1 pro 2014/2015 1. Je dána soustava rovnic s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napište Frobeniovu větu (existence i počet řešení). b)
Matematika I A ukázkový test 1 pro 2014/2015 1. Je dána soustava rovnic s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napište Frobeniovu větu (existence i počet řešení). b)
Kapitola 11: Lineární diferenciální rovnice 1/15
 Kapitola 11: Lineární diferenciální rovnice 1/15 Lineární diferenciální rovnice 2. řádu Definice: Lineární diferenciální rovnice 2-tého řádu je rovnice tvaru kde: y C 2 (I) je hledaná funkce a 0 (x)y +
Kapitola 11: Lineární diferenciální rovnice 1/15 Lineární diferenciální rovnice 2. řádu Definice: Lineární diferenciální rovnice 2-tého řádu je rovnice tvaru kde: y C 2 (I) je hledaná funkce a 0 (x)y +
3. Polynomy Verze 338.
 3. Polynomy Verze 338. V této kapitole se věnujeme vlastnostem polynomů. Definujeme základní pojmy, které se k nim váží, definujeme algebraické operace s polynomy. Diskutujeme dělitelnost polynomů, existenci
3. Polynomy Verze 338. V této kapitole se věnujeme vlastnostem polynomů. Definujeme základní pojmy, které se k nim váží, definujeme algebraické operace s polynomy. Diskutujeme dělitelnost polynomů, existenci
Práce s dokumentem. 1. Úvod do konstruování. 2. Statistické zpracování dat. 4. Analýza zatíºení a nap tí. Aktuální íslo revize: REV_40
 Aktuální íslo revize: REV_0 Práce s dokumentem Jednotlivé opravy (revize) jsou v dokumentu Errata ozna eny popiskem REV_a íslo revize ƒíslování revizí je provedeno chronologicky asov, tak jak p icházely
Aktuální íslo revize: REV_0 Práce s dokumentem Jednotlivé opravy (revize) jsou v dokumentu Errata ozna eny popiskem REV_a íslo revize ƒíslování revizí je provedeno chronologicky asov, tak jak p icházely
Transformujte diferenciální výraz x f x + y f do polárních souřadnic r a ϕ, které jsou definovány vztahy x = r cos ϕ a y = r sin ϕ.
 Ukázka 1 Necht má funkce z = f(x, y) spojité parciální derivace. Napište rovnici tečné roviny ke grafu této funkce v bodě A = [ x 0, y 0, z 0 ]. Transformujte diferenciální výraz x f x + y f y do polárních
Ukázka 1 Necht má funkce z = f(x, y) spojité parciální derivace. Napište rovnici tečné roviny ke grafu této funkce v bodě A = [ x 0, y 0, z 0 ]. Transformujte diferenciální výraz x f x + y f y do polárních
2. Ur íme sudost/lichost funkce a pr se íky s osami. 6. Na záv r na rtneme graf vy²et ované funkce. 8x. x 2 +4
 Pr b h funkce V této jednotce si ukáºeme jak postupovat p i vy²et ování pr b hu funkce. P edpokládáme znalost po ítání derivací a limit, které jsou dob e popsány v p edchozích letácích tohoto bloku. P
Pr b h funkce V této jednotce si ukáºeme jak postupovat p i vy²et ování pr b hu funkce. P edpokládáme znalost po ítání derivací a limit, které jsou dob e popsány v p edchozích letácích tohoto bloku. P
na za átku se denuje náhodná veli ina
 P íklad 1 Generujeme data z náhodné veli iny s normálním rozd lením se st ední hodnotou µ = 1 a rozptylem =. Rozptyl povaºujeme za známý, ale z dat chceme odhadnout st ední hodnotu. P íklad se e²í v následujícím
P íklad 1 Generujeme data z náhodné veli iny s normálním rozd lením se st ední hodnotou µ = 1 a rozptylem =. Rozptyl povaºujeme za známý, ale z dat chceme odhadnout st ední hodnotu. P íklad se e²í v následujícím
Matematika 4 FSV UK, LS Miroslav Zelený
 Matematika 4 FSV UK, LS 2017-18 Miroslav Zelený 13. Diferenční rovnice 14. Diferenciální rovnice se separovanými prom. 15. Lineární diferenciální rovnice prvního řádu 16. Lineární diferenciální rovnice
Matematika 4 FSV UK, LS 2017-18 Miroslav Zelený 13. Diferenční rovnice 14. Diferenciální rovnice se separovanými prom. 15. Lineární diferenciální rovnice prvního řádu 16. Lineární diferenciální rovnice
e²ení 5. série Binární kódy autor: Vlá a
 e²ení 5. série Binární kódy autor: Vlá a Úloha 4.1. Na zah átí si dáme snadn j²í p íklad. Ur it zná² hru Myslím si íslo a to má vlastnost, je to velice podobné. Tedy mám binární lineární kód délky 5, který
e²ení 5. série Binární kódy autor: Vlá a Úloha 4.1. Na zah átí si dáme snadn j²í p íklad. Ur it zná² hru Myslím si íslo a to má vlastnost, je to velice podobné. Tedy mám binární lineární kód délky 5, který
Tématické celky { kontrolní otázky.
 Tématické celky kontrolní otázky. Základy teorie pravdìpodobnosti..pravdìpodobnostní míra základní pojmy... Vysvìtlete pojem náhody, náhodného pokusu, náhodného jevu a jeho mno- ¾inovou interpretaci. Popi¹te
Tématické celky kontrolní otázky. Základy teorie pravdìpodobnosti..pravdìpodobnostní míra základní pojmy... Vysvìtlete pojem náhody, náhodného pokusu, náhodného jevu a jeho mno- ¾inovou interpretaci. Popi¹te
RNÉ MATERIÁLY. PSYCHODIAGNOSTIKA - VYHODNOCENÍ z , 13:19 hodin
 Strana 1 z 11 RNÉ MATERIÁLY PSYCHODIAGNOSTIKA - VYHODNOCENÍ z 14.11.2012, 13:19 hodin Kód probanda íjmení Jméno k Objednavatel el testování 3D60001025 íklad - Sériové íslo: Verze íslo: Vyhodnoceno: BFC6BC9F0D91
Strana 1 z 11 RNÉ MATERIÁLY PSYCHODIAGNOSTIKA - VYHODNOCENÍ z 14.11.2012, 13:19 hodin Kód probanda íjmení Jméno k Objednavatel el testování 3D60001025 íklad - Sériové íslo: Verze íslo: Vyhodnoceno: BFC6BC9F0D91
Zkouška ze Aplikované matematiky pro Arboristy (AMPA), LDF, minut. Součet Koeficient Body. 4. [10 bodů] Integrální počet. 5.
![Zkouška ze Aplikované matematiky pro Arboristy (AMPA), LDF, minut. Součet Koeficient Body. 4. [10 bodů] Integrální počet. 5. Zkouška ze Aplikované matematiky pro Arboristy (AMPA), LDF, minut. Součet Koeficient Body. 4. [10 bodů] Integrální počet. 5.](/thumbs/92/109752097.jpg) Zkouška ze Aplikované matematiky pro Arboristy (AMPA), LDF, 6.2.204 60 minut 2 3 4 5 6 Jméno:................................... Součet Koeficient Body. [2 bodů] V následující tabulce do každého z šesti
Zkouška ze Aplikované matematiky pro Arboristy (AMPA), LDF, 6.2.204 60 minut 2 3 4 5 6 Jméno:................................... Součet Koeficient Body. [2 bodů] V následující tabulce do každého z šesti
Pokyny k vyplnění Průběžné zprávy
 Pokyny k vyplnění Průběžné zprávy Verze: 2 Platná od: 15. 1. 2013 Doplnění nebo úpravy v pokynech jsou odlišeny červenou barvou písma. Termín pro podání elektronické verze průběžné zprávy obou částí je
Pokyny k vyplnění Průběžné zprávy Verze: 2 Platná od: 15. 1. 2013 Doplnění nebo úpravy v pokynech jsou odlišeny červenou barvou písma. Termín pro podání elektronické verze průběžné zprávy obou částí je
Kapitola 2: Spojitost a limita funkce 1/20
 Kapitola 2: Spojitost a limita funkce 1/20 Okolí bodu 2/20 Značení: a R, ε > 0 O ε (a) = (a ε, a + ε) ε-ové okolí bodu a O + ε (a) = a, a + ε) pravé okolí, O ε (a) = (a ε, a levé okolí P ε (a) = O ε (a)
Kapitola 2: Spojitost a limita funkce 1/20 Okolí bodu 2/20 Značení: a R, ε > 0 O ε (a) = (a ε, a + ε) ε-ové okolí bodu a O + ε (a) = a, a + ε) pravé okolí, O ε (a) = (a ε, a levé okolí P ε (a) = O ε (a)
se nazývá charakter grupy G. Dále budeme uvaºovat pouze kone né grupy G. Charaktery tvo í také grupu, s násobením denovaným
 Charaktery a Diskrétní Fourierova transforace Nejd leºit j²í kvantový algorite je Diskrétní Fourierova transforace (DFT) D vody jsou dva: DFT je pro kvantové po íta e exponenciáln rychlej²í neº pro po
Charaktery a Diskrétní Fourierova transforace Nejd leºit j²í kvantový algorite je Diskrétní Fourierova transforace (DFT) D vody jsou dva: DFT je pro kvantové po íta e exponenciáln rychlej²í neº pro po
+ 2y y = nf ; x 0. závisí pouze na vzdálenosti bodu (x, y) od počátku, vyhovuje rovnici. y F x x F y = 0. x y. x x + y F. y = F
 Příkad 1 ( y ) Dokažte, že funkce F (x, y) = x n f x 2, kde f je spojitě diferencovatelná funkce, vyhovuje vztahu x F x + 2y F y = nf ; x 0 Ukažte, že každá funkce F (x, y), která má spojité parciální
Příkad 1 ( y ) Dokažte, že funkce F (x, y) = x n f x 2, kde f je spojitě diferencovatelná funkce, vyhovuje vztahu x F x + 2y F y = nf ; x 0 Ukažte, že každá funkce F (x, y), která má spojité parciální
Lineární algebra : Metrická geometrie
 Lineární algebra : Metrická geometrie (16. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 6. května 2014, 10:42 1 2 Úvod Zatím jsme se lineární geometrii věnovali v kapitole o lineárních
Lineární algebra : Metrická geometrie (16. přednáška) František Štampach, Karel Klouda LS 2013/2014 vytvořeno: 6. května 2014, 10:42 1 2 Úvod Zatím jsme se lineární geometrii věnovali v kapitole o lineárních
DRN: Kořeny funkce numericky
 DRN: Kořeny funkce numericky Kořenem funkce f rozumíme libovolné číslo r splňující f(r) = 0. Fakt. Nechť f je funkce na intervalu a, b. Jestliže f(a) f(b) < 0 (tj. f(a) a f(b) mají opačná znaménka) a f
DRN: Kořeny funkce numericky Kořenem funkce f rozumíme libovolné číslo r splňující f(r) = 0. Fakt. Nechť f je funkce na intervalu a, b. Jestliže f(a) f(b) < 0 (tj. f(a) a f(b) mají opačná znaménka) a f
Home. Obsah. Strana 1 MATEMATIKA. Fullscreen PRO LETECKÉ. Tisk OBORY II. Konec
 Kurzy celoživotního vzdělávání Fakulta dopravní ČVUT MATEMATIKA Strana 1 PRO LETECKÉ OBORY II PŘEHLED LÁTKY 1 Metrické a normované prostory 2 Posloupnosti v metrických prostorech 3 Reálné funkce více reálných
Kurzy celoživotního vzdělávání Fakulta dopravní ČVUT MATEMATIKA Strana 1 PRO LETECKÉ OBORY II PŘEHLED LÁTKY 1 Metrické a normované prostory 2 Posloupnosti v metrických prostorech 3 Reálné funkce více reálných
TROJFÁZOVÝ OBVOD SE SPOT EBI EM ZAPOJENÝM DO HV ZDY A DO TROJÚHELNÍKU
 TROJFÁZOVÝ OBVOD E POT EBI EM ZAPOJENÝM DO HV ZDY A DO TROJÚHELNÍKU Návod do m ení Ing. Vít zslav týskala, Ing. Václav Kolá Únor 2000 poslední úprava leden 2014 1 M ení v trojázových obvodech Cíl m ení:
TROJFÁZOVÝ OBVOD E POT EBI EM ZAPOJENÝM DO HV ZDY A DO TROJÚHELNÍKU Návod do m ení Ing. Vít zslav týskala, Ing. Václav Kolá Únor 2000 poslední úprava leden 2014 1 M ení v trojázových obvodech Cíl m ení:
Projekty - Úvod do funkcionální analýzy
 Projekty - Úvod do funkcionální analýzy Projekt č. 1. Nechť a, b R, a < b. Dokažte, že prostor C( a, b ) = f : R R: f je spojitá na D(f) = a, b s metrikou je úplný. ρ(f, g) = max f(x) g(x) x a,b Projekt
Projekty - Úvod do funkcionální analýzy Projekt č. 1. Nechť a, b R, a < b. Dokažte, že prostor C( a, b ) = f : R R: f je spojitá na D(f) = a, b s metrikou je úplný. ρ(f, g) = max f(x) g(x) x a,b Projekt
Posloupnosti a řady. 28. listopadu 2015
 Posloupnosti a řady Přednáška 5 28. listopadu 205 Obsah Posloupnosti 2 Věty o limitách 3 Řady 4 Kritéria konvergence 5 Absolutní a relativní konvergence 6 Operace s řadami 7 Mocninné a Taylorovy řady Zdroj
Posloupnosti a řady Přednáška 5 28. listopadu 205 Obsah Posloupnosti 2 Věty o limitách 3 Řady 4 Kritéria konvergence 5 Absolutní a relativní konvergence 6 Operace s řadami 7 Mocninné a Taylorovy řady Zdroj
Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené
 28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
28. 2. 2017 Matematika II, úroveň A ukázkový test č. 1 (2017) 1. a) Napište postačující podmínku pro diferencovatelnost funkce n-proměnných v otevřené mn. M E n. Zapište a načrtněte množinu D, ve které
Dnešní látka: Literatura: Kapitoly 3 a 4 ze skript Karel Rektorys: Matematika 43, ČVUT, Praha, Text přednášky na webové stránce přednášejícího.
 Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
