NMAF063 Matematika pro fyziky III Zápočtová písemná práce B Termín pro odevzdání 4. ledna 2019

Transkript

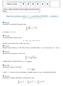
1 Jméno: Příklad Celkem bodů Bodů Získáno Zápočtová písemná práce určená k domácímu vypracování. Nutnou podmínkou pro získání zápočtu je zisk více jak 50 bodů. Pravidla jsou následující:. Příklady řešte samostatně bez cizí pomoci (spolužáci, starší kolegové a podobně. 2. Příklady lze řešit s použitím veškerých dosupných nástrojů (skripta, učebnice, software pro symbolické výpočty jako například Mathematica. 3. Pokud je příklad zadán ve stylu řešte diferenciální rovnici a pokud používáte software pro symbolické výpočty, není dovoleno použít funkce typu DSolve. Je naopak dovoleno použít bez dalšího komentáře výstup funkcí typu FourierTransform nebo Integrate. Je nutné explicitně uvést jednotlivé kroky řešení, dílčí výpočty lze svěřit software pro symbolické výpočty. 4. Pokud je příklad zadán ve stylu najděte Fourierovu transformaci funkce a pokud používáte software pro symbolické výpočty, není dovoleno použít funkce typu FourierTransform. Je naopak dovoleno použít bez dalšího komentáře výstup funkcí typu Apart, která provádí rozklad na parciální zlomky. 5. Numerická chyba v řešení znamená nulový bodový zisk za daný příklad. 6. Jednotlivé kroky při výpočtech stručně, ale přesně odůvodněte. Pokud používáte nějaké tvrzení, nezapomeňte ověřit splnění předpokladů. [20]. Zkoumejte posloupnost f n } + n definovanou jako 0 x < n, cn α f n (x n x < 0, cn α 0 x < n, 0 n x. Určete hodnotu parametrů α R + a c R tak, aby platilo f n δ, kde δ je derivace Dirac distribuce. Přesně specifikujte v jaké smyslu je konvergence definována. Chceme ukázat, že pro každou testovací funkci ϕ platí T fn, ϕ D (R,D(R T δ, ϕ D (R,D(R, kde konvergence je nyní standardní kovergence posloupnosti reálných čísel T fn, ϕ D (R,D(R, a kde distribuce T δ je definována jako T δ, ϕ D (R,D(R def T δ, ϕ D (R,D(R. Diracova distribuce T δ je zavedena standardním způsobem jako T δ, ϕ D (R,D(R def ϕ (0, kde ϕ značí klasickou derivaci testovací funkce ϕ. Musíme proto ukázat, že pro každou testovací funkci ϕ dostaneme T fn, ϕ D (R,D(R ϕ (0. (Ve smyslu posloupnosti čísel. Dualita T fn, ϕ D (R,D(R je reprezentována integrálem, nebot f n jsou lokálně integrovatelné funkce T fn, ϕ D (R,D(R f n (xϕ(x dx. (Využíváme standardního ztotožnění lokálně integrovatelných funkcí s příslušnými distribucemi. Po překladu definic do primitivních pojmů tedy chceme ukázat, že pro každou testovací funkci ϕ dostaneme f n (xϕ(x dx n + ϕ (0 Nyní již musíme pracně počítat. Označme si F n primitivní funkci k funkci f n aneb F n (x def ξ f n (ξ dξ

2 Podle věty o integraci per partes platí f n (xϕ(x dx u f n u F n + v ϕ v ϕ [F n(xϕ(x] + F n (xϕ (x dx F n (xϕ (x dx, kde jsme využili toho, že testovací funkce ϕ má kompaktní nosič, aneb je nenulová pouze uvnitř nějakého intervalu [A, B]. Nyní explicitně spočteme primitivní funkci F n, jest Jest 0 x (,, ( x + F n cn α, x [ n, 0], ( x + cn α x [ 0, n], 0, x ( n, +. ( F n (xϕ (x dx cn α x + χ n ( ( x,0 + + } χ n n (0, ϕ (x dx. Nyní provedeme substituci a ze zjevných důvodů zafixujeme α 2, ( cn α x + χ n ( x y n dx n dy ( x,0 + + n n y } χ (0, ϕ (x dx cn α n 2 Poslední integrál je ve vhodném tvaru pro itní přechod n +, f n (xϕ(x dx c y n + c } ( (y + χ(,0 + ( y + χ (0, ϕ y dy n α2 c y } ( (y + χ(,0 + ( y + χ (0, ϕ y dy n y (y + χ(,0 + ( y + χ (0, } ϕ ( y n dy. (y + χ(,0 + ( y + χ (0, } ϕ (0 dy cϕ (0 c ϕ (0. (Opět využíváme skutečnost, že testovací funkce je hladká funkce s kompaktním nosičem. Volbou α 2 a c tedy dostaneme požadovanou rovnost f n (xϕ(x dx n + ϕ (0. [20] 2. Pro f S (R řešte rovnici d3 f + k2 dx3 dx δ, kde δ je Dirac distribuce a k R + je konstanta. (Pozor, specifikace prostoru, ve kterém hledáte řešení, zde není pro jen okrasu, je to zásadní informace. Úlohu vyřešíme kupříkladu s použitím Fourierovy transformace. Použijeme Fourierovu transfroamci definovanou vztahem F[f](ξ def f(xe ix ξ dx, ( d 2 R d kde d je dimenze prostoru, na kterém pracujeme. S použitím tabulky Fourierových transformací zjistíme, že Fourierova transformace rovnice je iξ ( ξ 2 + k 2 F[f], kde jsme také využili známého vztahu pro Fourierovu transformaci Dirac distribuce. Zbývá najít inverzní Fourierovu transformaci [ f(x F ] iξ (ξ 2 + k 2 (x, což je snadné. (Připomínám, že je možné použít software pro symbolické výpočty. Výsledkem je f ekx χ (,0 + e kx χ (0,+ + sign x 2k 2,

3 což lze také zapsat jako f 2k 2 ( e k x sign x. Řešením homogenní rovnice (nulová pravá strana jsou funkce e kx, e kx a. Obecné řešení zdané rovnice získáme tak, že k řešení f ( 2k 2 e k x sign x. přičteme libovolné řešení homogenní rovnice, pokud je ovšem toto řešení v příslušném prostoru. Tuto podmínku splňuje pouze konstantní funkce, a proto je obecné řešení zadané rovnice dáno vztahem kde c je konstanta. [20] 3. Spočtěte Fourierovu transformaci funkce f 2k 2 ( e k x sign x + c, f(x sin (ωx, kde x R a ω R +, přesně specifikujte v jakém smyslu je v tomto případě Fourierova transformace definována. Abychom se bezpečně shodli na výsledku, tak připomínám, že užíváme následující definici Fourierovy transformace F[f](ξ def f(xe ix ξ dx, ( d 2 R d kde d je dimenze prostoru, na kterém pracujeme. Fourierovu transformaci budeme počítat jako Fourierovu transformaci ve smyslu distribucí. Jako vždy musíme vědět jak daná distribuce F[T ] působí na testovací funkce. Definice říká, že je nutné spočíst F[T ], ϕ S,S def T, F[ϕ] S,S. V našem případě musíme nejdříve interpretovat sin (ωx jakožto distribuci. Jest Tsin(ωx, ϕ S,S def Z definice Fourierovy transformace tedy musíme spočíst Tsin(ωy, F[ϕ] S,S y sin(ωy sin(ωxϕ(x dx. ( ϕ(xe ixy dx dy, kde jsme použili standardní definici Fourierovy transformace pro funkce. Sinus rozepíšeme jako komplexní exponenciálu, y ( + sin(ωy ϕ(xe ixy dx dy ( + e iωy y y ϕ(xe ixy dx dy e iωy ( Nyní stačí v získaném vzorci rozpoznat definici inverzní Fourierovy transformace, a využít skutečnosti, že Počítejme + ( + e iωy y F [F[f]] f. ϕ(xe ixy dx dy ( y e iωy F[ϕ](y dy y e iωy F[ϕ](y dy Obdobně naložíme s druhým integrálem a výsledkem je ( + sin(ωy ϕ(xe ixy dx y ( y e i( ωy F[ϕ](y dy ϕ(xe ixy dx dy. π F [F[ϕ](y] ( ω i 2 ϕ( ω. dy i π 2 ϕ( ω + i π 2 ϕ(ω,

4 přičemž poslední výraz lze zapsat jako π π i [ ϕ( ω + ϕ(ω] i 2 2 Celkem jsme tedy zjistili, že platí Tsin(ωx, F[ϕ] π i S,S 2 [ T δ(x+ω, ϕ + T S,S δ(x ω, ϕ ]. S,S ( Tδ(x ω T δ(x+ω, ϕ S,S, odkud plyne, že aneb π ( F[T sin(ωx ] i Tδ(ξ ω T δ(ξ+ω, 2 π F[sin(ωx] i [δ(ξ ω δ(ξ + ω]. 2 [20] 4. Spočtěte Fourierovu transformaci funkce f(x x 2, kde x R 3, přesně specifikujte v jakém smyslu je v tomto případě Fourierova transformace definována. Abychom se bezpečně shodli na výsledku, tak připomínám, že užíváme následující definici Fourierovy transformace F[f](ξ def f(xe ix ξ dx, ( d 2 R d kde d je dimenze prostoru, na kterém pracujeme. Naším úkolem je spočíst Fourierovu transformaci radiálně symetrické funkce. Můžeme použít vzorec, který jsme odvodili na cvičení F[f( x ](ξ 2 + f(r sin (r ξ r dr. ξ Po dosazení dostaneme F[f( x ](ξ R + 2 R ξ r0 sin (r ξ r dr r0 y r ξ ( dy ξ dr 2 ξ y + R y0 sin y y dy π ξ 2, kde jsme využili tabulkového integrálu R sin y dy π y + y0 y 2. [20] 5. Najděte Greenovu funkci pro úlohu dx 2 g, f x0 0, dx 0, xl kde g je daná funkce a L je kladná konstanta. (Aneb najděte funkci G(x, x takovou, že řešení úlohy lze zapsat jako f(x L x 0 G(x, x g(x dx. S použitím této Greenovy funkce pak řešte úlohu kde a, b jsou konstanty a h je daná funkce. dx 2 h, f x0 a, dx b, xl

5 Cílem je najít Green funkci, tedy funkci G(x, x, pro kterou by platilo Greenovu funkci najdeme jako řešení úlohy f(x L x 0 G(x, x g(x dx. d 2 G dx 2 δ(x x, G x0 0, dg dx 0, xl kde δ(x x je Dirac distribuce s nosičem v bodě x. Green funkci budeme hledat zvlášt na intervalech (0, x a (x, L, přičemž řešení na obou intervalech navážeme tak, aby skok ve funkční hodnotě druhé derivace vedl k Dirac distribuci. Pro x > x tedy řešíme úlohu a pro x < x řešíme úlohu d 2 G + dx 2 0, dg + dx 0, xl d 2 G dx 2 0, G x0 0. Řešení těchto úloh vede na aneb G(x, x G(x, x G + (x x > x, G (x x < x, D x > x, Ax x < x, kde A a D jsou konstanty závislé na x. Požadavek na spojitost funkce G(x, x při přechodu singularity v x je což v našem případě vede na rovnici Formální integrace rovnice d2 G dx 2 +ε x x G (x x x + G+ (x, Ax D δ(x x přes interval (x ε, x + ε vede na požadavek xx ε δ(x x dx +ε xx ε d 2 G dg+ dx dx2 dx kde ε je libovolné malé číslo, což znamená, že musí být splněna rovnost A. x +ε dg dx x ε, Green funkce je tedy dána vztahem a řešením původní úlohy je tedy funkce G(x, x x x < x, x x < x, f(x L x 0 L G(x, x g(x dx x g(x dx x g(x dx. x 0 x x

6 Je snadné přesvědčit se, že výsledek je skutečně řešením dané rovnice, podle věty o derivaci integrálu podle horní meze (základní věta diferenciálního a integrálního počtu dostaneme L L dx xg(x g(x dx + xg(x g(x dx, x x x x dx 2 g(x, a f je tudíž zjevně řešení původní diferenciální rovnice, a zároveň vidíme, že jsou splněny i okrajové podmínky. Chceme-li řešit úlohu s nenulovými okrajovými podmínkami, tedy úlohu dx 2 h, f x0 a, dx b, xl kde a, b jsou konstanty a h je daná funkce. Můžeme využít linearity příslušné rovnice a najít řešení jako součet funkcí f hmg a f bdr, kde f hmg řeší úlohu s nulovými okrajovými podmínkami, hmg dx 2 h, f hmg x0 0, hmg dx 0, xl a f bdr řeší úlohu s nulovou (speciální pravou stranou a nenulovými okrajovými podmínkami, tedy bdr dx 2 0, f bdr x0 a, bdr dx b. xl Zjevně a z předchozího výpočtu také víme, že f bdr (x a + bx L f hmg (x x g(x dx x g(x dx. x 0 x x Řešením úlohy s nenulovými okrajovými podmínkami je tudíž funkce L f(x f bdr (x + f hmg (x x g(x dx x g(x dx + bx + a. x 0 x x