5. Aproximace funkcí. Tento učební text byl podpořen z Operačního programu Praha- Adaptabilita. Hana Hladíková

Transkript

1 5 Aproximace funkcí Tento učební text byl podpořen z Operačního programu Praha- Adaptabilita Hana Hladíková

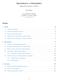
2 V praxi je často potřeba složitou funkci f nahradit funkcí jednodušší, která v nějakém vhodném smyslu napodobuje funkci f a která se snadno matematicky zpracovává a je vhodná pro využití na počítači V jiném případě funkční závislost, kterou se snažíme postihnout, nemusí být vždy známá Často vycházíme z hodnot, které jsme získali měřením Aproximovatfunkci f(x)znamenánahraditjifunkcí g(x),kterájekf(x)vjistémsmyslublízká Určímesystémjednoduchýchbázovýchfunkcí g 0 (x), g (x), g (x),, g n (x)funkci g(x)hledáme jakolineárníkombinacefunkcí g i,tjtj g(x)=c 0 g 0 (x)+c g (x)+c g (x)+ +c n g n (x)dle charakteru aproximační úlohy je nutné určit, podle jakých kritérií zvolit bázové funkce a koeficienty lineární kombinace Budeme zkoumat tři typy aproximace: a) aproximace na okolí bodu, b) interpolace, c) L aproximace Aproximace Taylorovým polynomem Nechťmáfunkce f(x)vintervalu x 0 h, x 0 + h spojitéderivacedo n+řádupotomprokaždé x x 0 h, x 0 + h platí, f(x)=t n (x)+r n+,kde T n (x)jetaylorůvpolynomn-téhostupně T n (x)=f(x 0 )+ f (x 0 )! (x x 0 )+ f (x 0 )! akde R n+ jetaylorůvzbytekvlagrangeovětvaru: (x x 0 ) + + f(n) (x 0 ) (x x 0 ) n n! R n+ = f(n+) (ξ) (n+)! (x x 0) n+, ξ x 0 h, x 0 + h Příklad:Aproximujmefunkci f(x)=cos(x)vbodě x 0 =0Taylorovýmpolynomem4stupně Projaké xsedopustímechybymenšínež0 3? Řešení: T 4 (x)=cos(0)+ cos (0)! =cos(0) sin(0)! sin(x) R 5 = (x 0)+ cos (0)! x cos(0)! (x 0) + cos(3) (0) 3! x + sin(0) 3! cos (5) (ξ) (x 0) 5 = (5)! (x 0) 3 + cos(4) (0) (x 0) 4 = 4! x 3 + cos(0) x 4 = x 4! 4 + x4 4 sin(ξ) x 5 x x 0,5 0 0 Obr5Taylorůvpolynom4stupněprofunkci f(x)=cos(x)vbodě x 0 =0

3 Interpolace Nechťjevn+bodech x 0, x, x,, x n D(f)dáno n+hodnot y 0 = f(x 0 ), y = f(x ),, y n = f(x n ) Prorůzné třídy funkcí Φ(x, a 0, a, a,, a n ) jednéproměnné x,kteréjsouurčenykoeficienty a 0, a, a,, a n hledámefunkci g(x)takovou, že g(x i, a 0, a, a,, a n )=y i Grafyfunkce f(x)ig(x)procházíbody[x i, y i ],pro,, n Tyto body se nazývají póly, proto se této metodě říká interpolace funkce- nahrazení grafu funkce mezi póly Volbou různých tříd funkcí obdržíme interpolaci polynomiální, splinovou, exponenciální Polynomiální interpolace Interpolační polynom Polynomnejvýšen-téhostupnějefunkcetvaru P n (x)=a 0 + a x+a x + +a n x n, x, a i R, n N Mějme n+bodů[x i, y i ]anechťplatí x i < x i+ Potomexistujeprávějedenpolynom P n (x)nejvýšen-téhostupně,prokterýplatí P n (x i )=y i, ntentopolynomnazývámeinterpolační polynom Vyjádříme-lipodmínky P n (x i )=y i,dostanemesoustavu n+rovnicon+neznámých,která lze zapsat maticově: x 0 (x 0 ) n (x 0 ) n a 0 y 0 x (x ) n (x ) n a y = x n (x n ) n (x n ) n Matice této soustavy má nenulový determinant(vandermontův determinant), proto má soustava právě jedno řešení Výše uvedená metoda(metoda neurčitých koeficientů) výpočtu interpolačního polynomu není příliš vhodná, protože tato matice soustavy je špatně podmíněná a s rostoucím počtem uzlů je značně náročná na počet operací Existuje několik vhodnějších metod výpočtu interpolačního polynomu, mezi nejznámější patří Newtonův a Lagrangeův interpolační polynom Odlišnost spočívá pouze v postupu a způsobu zápisu, jinak se jedná se o totožné polynomy (viz předchozí tvrzení o jednoznačnosti interpolačního polynomu) Příklad : Určete pomocí metody neurčitých koeficientů interpolační polynom pro funkci f(x) danou tabulkou: a n i 0 x i 0 3 y i a 0 = 3 3 a a 0 y n 3

4 a 0 =, a = 5 3, a = 3 P (x)=+ 5 3 x 3 x Lagrangeův tvar interpolačního polynomu Lagrangeůvinterpolačnípolynomn-téhostupně L n (x)hledámevetvaru L n (x)= n y i l i (x), l i (x)= (x x 0)(x x )(x x i )(x x i+ )(x x n ) (x i x 0 )(x i x )(x i x i )(x i x i+ )(x i x n ) Jezřejmé,žeplatí l j (x j )=al i (x j )=0pro i j,tedy L n (x)jeinterpolačnípolynomstupně ns uzly[x i, y i ] Lagrangeův interpolační polynom má spíše teoretický význam, pro praktické využití se příliš nehodípokudchcemepřidatjedenuzel,musímepřepočítatvšechnyfunkce l i (x) Příklad 3: Určete Lagrangeův interpolační polynom pro funkci f(x) danou tabulkou(viz předchozí příklad) Řešení: L (x)= y i l i (x)= (x x )(x x ) (x 0 x )(x 0 x ) + (x x 0)(x x ) (x x 0 )(x x ) +0 (x x 0)(x x ) (x x )(x x ) = (x )(x 3) 0)(x 3) 0)(x ) = +(x +0(x (0 )(0 3) ( 0)( 3) (3 0)(3 ) L (x)=+ 5 3 x 3 x Newtonův tvar interpolačního polynomu Nejdřívedefinujemepoměrnoudiferencik-téhořádufunkce f(x)probody[x i, f(x i )]takto: f[x i ]=y i, k=0, f[x i+, x i ]= yi+ yi x i+ x i, k=, f[x i+k, x i ]= f[x i+k,x i+] f[x i+k,x i] x i+k x i, < k n Newtonůvinterpolačnípolynomn-téhostupně N n (x)hledámevetvaru: N n (x)=f[x 0 ]+f[x, x 0 ](x x 0 )+f[x, x 0 ](x x 0 )(x x )+ +f[x n, x 0 ](x x 0 )(x x )(x x n ) Příklad 4: Určete Newtonův interpolační polynom pro funkci f(x) danou tabulkou(viz předchozí 3 příklad) i x i f(x i )=f[x i ] f[x i, x i ] f[x i, x i ] = = 3 0 = 3 N (x)=f[x 0 ]+f[x, x 0 ](x 0)+f[x, x 0 ](x 0)(x )= =+(x 0) 3 (x 0)(x )=+5 3 x 3 x 4

5 Chyba aproximace interpolačního polynomu Nechťmáfunkce f(x)vintervalu x 0, x n spojitéderivacedo n+hořádu, x i x 0, x n, x i < x j, i < ja P n (x)jeinterpolačnípolynompotomprokaždé x x 0, x n existuje ξ (x 0, x n )tak, že platí: f(x) P n (x)= f(n+) (ξ) (n+)! ω n(x),kde ω n (x)=(x x 0 )(x x )(x x n ) Pokudplatí,že f n+ (x) M, x x0, x n,potom Poznámka: f(x) P n (x) f (n+) (ξ) (n+)! ω n (x) M (n+)! ω n(x) ()Velikostchybyzávisína ω n (x)přizvětšenípočtuinterpolačníchuzlůnedocházíkzmenšení interpolační chyby Obr5 ω n (x) Naobrázku5jeznázorněnafunkce ω n (x) prorůzná nnaintervalu,5;,5 ase7 ekvidistantními uzly(vzdálenost mezi uzly je konstantní) () Pokud chceme aproximovat funkci mimo daný interval(extrapolace), není vhodné používat interpolační polynomy vyšších řádů (3) Se vzrůstajícím počtem uzlů roste oscilace interpolačního polynomu(obzvláště v okolí krajních bodů) Toto se projevuje velmi silně u ekvidistantního dělení Vhodnou volbou uzlů (např Čebyševovy polynomy) lze tuto oscilaci zmenšit (4) Funkce, které mají asymptotu není vhodné interpolovat pomocí polynomů, tento problém řeší výrazně lépe interpolace pomocí spline funkcí 5

6 Příklad 5: Rungeho problém Naintervalu 5;5 sekvidistantnímdělenímauzly: x i = 5+i,,,0kfunkci f(x)= +x (Rungehofunkce)nakreslímegrafinterpolačníhopolynomu P 0 (x) BudemezkoumatchybuinterpolacetétofunkceZgrafupolynomu P 0 (x)jezřejmé,žedocházík výrazné oscilaci v okolí krajních bodů Na Obrázku 53 je porovnán graf funkce f(x) a interpolačního polynomu P 0 (x)(oscilující) Obr53Rungehoproblém ω (x) (levýobr),rungehofunkceap 0 (x) MATLAB Interpolace polynomem V MATLABu v případě, že chceme zadaná(naměřená) data interpolovat polynomem n-tého stupně, můžeme to jednoduše provést pomocí funkce polyfit >> P=polyfit(X,Y,n), Xjevektor n+hodnotnezávisleproměnné, Y jevektor n+hodnotzávisleproměnné, nje stupeňpolynomuinterpolujícíbody[x i, y i ]apjevektorkoeficientůinterpolačníhopolynomu P(x), přičemž P(x)=p()x n + p()x n + +p(n)x+p(n+) Hodnoty polynomu P(x) ve všech prvcích vektoru X(např kvůli grafickému znázornění) lze zjistit funkcí polyval: >> YAP=polyval(P,X) P je vektor koeficientů aproximačního polynomu, X je vektor hodnot nezávisle proměnné a YAP je vektor hodnot aproximačního polynomu Interpolace pomocí spline funkcí V předchozím odstavci jsme zjistili, že interpolace pomocí polynomů i při poměrně vysokém počtu uzlů přináší problémy se značnou mírou oscilace Nyní rozdělíme vyšetřovaný interval na podintervaly a na jednotlivých podintervalech zkonstruujeme polynomy, vznikne tak po částech polynomiální funkce Vdalšímtextupředpokládáme,žemáme n+pólů[x i, y i ],pro,, n,prokteréplatí,že x i x 0, x n, x i < x j, i < joznačme h i = x i+ x i,,, n Spline funkce stupně m se nazývá taková funkce, která splňuje současně tyto podmínky: () po částech polynomiální funkce stupně m(je tvořená polynomy stupně m), ()výslednáfunkcejespojitádořádu m (derivaceaždo(m )-hořádujsouspojité)

7 Lineární spline funkce Lineární spline funkcejefunkce S (x),kterájespojitánaintervalu x 0, x n anakaždém intervalu x i, x i+,,, n, S (x)jepolynomprvníhostupněgrafemfunkce S (x)jelomená čára Prolineárníinterpolačnísplinefunkci S (x)platí S (x i )=y i,,, nplatítedy S (x)= y i+(x x i ) h i Kvadratická spline funkce + y i ( (x x ) i), x x i, x i+,,, n h i Kvadratickásplinefunkcejefunkce S (x),kterásplňujenásledujícívlastnosti: ) S (x)jekvadratickýmpolynomemnakaždémintervalu x i, x i+, (označímejej P i (x),platíproněj P i (x)=s (x), x x i, x i+ ) S (x)jespojitáamáspojitouprvníderivacipro x x 0, x n V praxi se více využívá kubická spline funkce, proto se jí budeme věnovat podrobněji Kubická spline funkce Kubickásplinefunkcejefunkce S 3 (x),kterásplňujenásledujícívlastnosti: ) S 3 (x)jekubickýmpolynomemnakaždémintervalu x i, x i+, (označímejej P i (x),platíproněj P i (x)=s 3 (x), x x i, x i+ ) S 3 (x)jespojitáamáspojitouprvníadruhouderivacipro x x 0, x n Musí tedy platit: () P i (x i )=y i,,, n(n+podmíneknarovnostfunkčníchhodnot), () P i (x i+ )=P i+ (x i+ ),,, n (n podmíneknaspojitostfunkce), (3) P i (x i+)=p i+ (x i+),,, n (n podmínekrovnostprvníchderivací), (4) P i (x i+)=p i+ (x i+),,, n (n podmínekrovnostdruhýchderivací) Na každém z n intervalů máme kubický polynom o neznámých 4 parametrech Celkem tedy hledáme4nneznámýchparametrůmáme3(n )+(n+)=4n podmínekabybylaspline funkce jednoznačně určena zbývá zvolit ještě dvě podmínky Podle volby těchto podmínek se rozlišují různé typy spline funkci, nejznámější jsou tyto dva typy: Kubickásplinefunkce,ukterésezvolízbývajícípodmínkytakto-S (x 0 )=S (x n )=0(tzv přirozené podmínky) se nazývá přirozená kubická spline funkce Kubickásplinefunkce,ukterésezvolízbývajícípodmínkytakto-S (x 0 )=f (x 0 ), S (x n )= f (x n )(tzvpodmínkytečen),kde f(x)jeinterpolovanáfunkce(platítedy f(x i )=y i )senazývá úplná kubická spline funkce Poznámka:Kubickásplinefunkce S 3 (x)jespojitá,máspojitouprvníadruhouderivacina x 0, x n S interpolovanou funkcí se shoduje v uzlových bodech, hodnoty derivací se u spline funkce a interpolované funkce mohou lišit Existence, jednoznačnost a chyba aproximace interpolační kubické přirozené spline funkce (resp úplné spline funkce) 7

8 Profunkci f(x),kterájedefinovanána x 0, x n,existujejedinápřirozenákubickásplinefunkce Profunkci f(x),kterájedefinovanána x 0, x n,existujejedináúplnákubickásplinefunkce Nechťmáfunkce f(x)vintervalu x 0, x n spojitéderivacedo4řádu,nechťjsou S 3p (x)přirozená splinefunkceas 3u (x)úplnásplinefunkcespóly[x i, f(x i )]adělením x i x 0, x n, x i < x j, i < j, nechť h i = x i+ x i,kde C= max{hi} min{h i},,, npakexistujekonstanta Ktak,žeplatí: -Propřirozenoukubickousplinefunkci S 3p f(x) S3p (x) C K (max {hi )}) -Proúplnoukubickousplinefunkci S 3u f (k) (x) S (k) 3 u (x) C K (max {h i }) 4 k, k=0,,3 Příklad : Rungeho problém Naintervalu 5;5 sekvidistantnímdělenímauzly: x i = 5+i, 0nakreslímegraf přirozenéinterpolačnísplinefunkce S 3p (x)kfunkci f(x)= +x (Rungehofunkce)Jezřejmé,že tato interpolace výrazně méně osciluje, než tomu bylo u interpolačních polynomů Na Obrázku 54 jeporovnángraffunkcef(x)(obrázekvlevo)as 3p (x)(vpravo),jevidět,žeseoptickytéměřneliší: Obr54Rungehofunkce(levýobrázek), S 3p (x)(pravýobrázek) B spline funkce Pro jednodušší manipulaci se spline funkcemi a určení bázových funkcí prostoru spline funkcí zavedemetzvb-splinymáme n+pólů[x i, y i ],pro,, n,prokteréplatí,že x i x 0, x n, 8

9 x i < x j, i < joznačme h i = x i+ x i,,, nprostorvšechsplinefunkcířádu kna tomtoděleníoznačíme Sp(x 0,, x n, k) Rekurentnídefinicebázovésplinefunkce B i,k (x): B i, (x)=, x x i, x i+ ), B i, (x)=0, x / x i, x i+ ),, n, B i,k (x)= x xi x i+k x i B i,k (x)+ x i+k x x i+k x i+ B i+,k (x) Vprostorusplinefunkcí S p (x 0,, x n, k)řádu klzevytvořitbázitvořenoub-spliny B k,, B n, kdyprokaždýspline s S p (x 0,, x n, k)platí,žejejlzenapsatjakolineárníkombinacitétobáze: s(x)= n i= k α i B i,k, x x 0, x n, α i R Základní vlastnosti B-splinů: ) B i,k (x) >0, x x i, x i+k ), ) B i,k (x)=0, x / x i, x i+k ), 3) s i=r+ k B i,k(x)=, x (x r, x s ), 0 r < s n Vdalšímtextu,prolepšínázornostpředpokládáme,žejsouuzlyekvidistantní x i+ x i = h,, n Vpřípaděneekvidistantníhoděleníjepostupobdobný,alezápissestávávýrazně obtížnějším Konstantní B spline funkce na rovnoměrném dělení B i, (x) =, x x i, x i+ ), B i, (x) =0, x (, x i ) x i+, ) B i+, (x)=, x x i+, x i+ ), B i+, (x)=0, x (, x i+ ) x i+, ) Lineární B spline funkce na rovnoměrném dělení B i, (x)= x xi x i+ x i B i, (x)+ xi+ x x i+ x i+ B i+, (x), x (, ) B i, (x)=0, x (, x i ) x i+, ) B i, (x)= x xi x i+ x i = x xi h, x x i, x i+ ), B i, (x)= xi+ x x i+ x i+ = xi+ x h, x x i+, x i+ ) Kvadratická B spline funkce na rovnoměrném dělení B i,3 (x)= x xi x i+ x i B i, (x)+ xi+3 x x i+3 x i+ B i+, (x), x (, ) B i,3 (x)=0, x (, x i ) x i+3, ) B i,3 (x)= (x xi)(x xi) h B i,3 (x)= (x xi)(xi+ x) h + xi+3 x h 0= (x xi) h, x x i, x i+ ), + (xi+3 x)(x xi+) h, x x i+, x i+ ), B i,3 (x)= x xi h 0+(xi+3 x) h = (xi+3 x) h, x x i+, x i+3 ), Kubická B spline funkce na rovnoměrném dělení B i,4 (x)= x xi x i+3 x i B i,3 (x)+ xi+4 x x i+4 x i+ B i+,3 (x), x (, ) 9

10 B i,4 (x)=0, x (, x i ) x i+4, ) B i,4 (x)= (x xi)3 h, x x 3 i, x i+ ), B i,4 (x)= x xi 3h B i,4 (x)= x xi 3h B i,4 (x)= x xi 3h ( ) (x xi)(x i+ x) h + (xi+3 x)(x xi+) h ( (x i+3 x) h + xi+4 x (x xi+)(x i+3 x) 3h h (0)+(xi+4 x) (x i+4 x) 3h h = (xi+4 x)3 h, x x 3 i+3, x i+4 ) + (xi+4 x)(x xi+) h 3, x x i+, x i+ ), ) + (xi+4 x)(x xi+) h, x x i+, x i+3 ), Obr 55 Znázornění 7 kubických bázových B splinů pro uzly 0,,,3,4na intervalu 0,4 Interpolace pomocí kubických B spline funkcí na rovnoměrném dělení Hledáme S S p (x 0,, x n,4)tak,aby S(x)= n i= 3 α i B i,4 (x) tak,že S(x j )=f j,,, n Jezřejmé,žemámeurčit n+3parametrůfunkčníchhodnotje n+,protozvolímeještědvě podmínky S (x 0 )=S (x n )=0(tzvpřirozenépodmínky)nasplinefunkciNyníjejiž Sjednoznačně určen Musíme vyřešit soustavu rovnic: S(x j )= n i= 3 α i B i (x j )=f j,,, n S (x 0 )=S (x n )=0 Pokudnynípostupnědosadíme x i dorekurentníhovzorceprobsplinefunkceavezmemevúvahu, že máme rovnoměrné dělení, dostaneme: B i 3,4 (x i )=, B i,4(x i )= 3, B i,4(x i )= Soustavu lze napsat v maticovém tvaru: B i,4 (x i )=0, B j,4 (x i )=0, x i (, x j ) x j+4, ) 0

11 α 3 α α α n α n = f 0 f f f n f n MATLAB interpolace funkce Prointerpolacifunkčníchhodnot yvzávislostina x(y= f(x))jekdispozicifunkce interp Prointerpolacifunkčníchhodnot zvzávislostina x, y(z= f(x, y))jekdispozicifunkce interp Základní syntaxe je >> YI = INTERP(X,Y,XI); kde Xjevektorbodůnaose x,vektor Yobsahujehodnotyvbodechvektoru X, XIjenovédělení intervalu vymezeném vektorem X(jiné než X) a Y I je vektor interpolovaných hodnot Hodnoty z vektorů X a Y sepoužijíjakopóly,jimižseproložípožadovanákřivkahodnotyvektoru Y I se následně počítají jako funkční hodnoty křivky v bodech vektoru XI Dělení intervalu XI může být jakkoliv jemné či hrubé a nemusí obsahovat původní body z vektoru X Přednastaveným typem interpolace je interpolace lineární Dalšími možnými typy interpolace jsou: o nearest - nejbližší soused(po částech konstantní funkce) o linear - lineární interpolace o spline - po částech kubická spline interpolace(spline) o pchip - po částech kubická interpolace zachovávající tvar(shape-preserving) o cubic - stejná metoda jako pchip o v5cubic - kubická interpolace z verze 5, která neumožňuje extrapolaci a používá spline pro neekvidistantní dělení X Tyto metody se zadávají pomocí syntaxe >> YI = INTERP(X,Y,XI, method ) Extrapolace dat se zadává pomocí stejné funkce jako interpolace, pouze se přidá parametr extrap: >> YI = INTERP(X,Y,XI, method, extrap ) Extrapolace je možná pouze pro metody cubic, pchip a spline, extrapolované části křivky pokračují podle předpisu poslední interpolované části křivky(mezi posledními dvěma póly) Pro interpolaci pomocí spline křivky volá funkce interp funkci s názvem spline Základní nastavení této funkce je takové, že vytváří přirozený spline(druhé derivace v koncových bodech křivky jsou rovny nule) Je zde však i možnost zadat velikosti krajních derivací, tedy tečný vektor křivky v krajníchbodechvtompřípaděsezadávektoryodvěhodnotydelšínežvektorxprvníaposlední hodnota je v tomto případě brána jako velikost první derivace v krajních bodech Funkce spline umožňuje interpolovat a extrapolovat při ekvidistantním i neekvidistantním dělení X V prostoru Matlab pro interpolaci ve dvou směrech používá INTERP Parametry pro různé typy interpolace zde jsou: o nearest - nejbližší soused(po částech konstantní plocha) o linear - bilineární interpolace o spline - spline interpolace o cubic - bikubická interpolace

12 Aproximace funkce V mnoha případech hodnoty funkce, kterou aproximujeme, získáme měřením a tyto hodnoty jsou zatíženy chybou Použití interpolace by v tomto případě napomáhalo k napodobení těchto chyb Interpolace také není vhodná, pokud je předpokládán jistý charakter aproximující funkce(třeba lineární či exponenciální závislost) a přitom žádná funkce v této třídě neprochází naměřenými hodnotami Provedeme proložení dat křivkou(curve fitting) Mějme x nezávisle proměnnou a f(x) je neznámá funkce proměnné x, kterou chceme aproximovat Provedli jsme m + měření(tedy získali jsme m+přibližnýchhodnot f i funkce f(x)prorůznéhodnoty x i,, m)obdrželijsme m+ uspořádanýchdvojic[x i, f i ] Podle očekávaného průběhu neznámé funkce f(x) zvolíme bázové funkce(polynomy, B-spliny, exponenciály)pokusímesejiaproximovatjakolineárníkombinaci nbázovýchfunkcí g 0 (x), g (x), g (x),, g n (x),tj f(x) R n (x)=a 0 g 0 (x)+a g (x)+a g (x)+ +a n g n (x), m < n, pokudby m=n,jednalobyseointerpolaci R n (x)senazýválineárníregresnífunkce Reziduum r i (x)jerozdílmezipozorovanouaaproximovanouhodnotouvuzlovýchbodech Označme g ij = g i (x j ), r i = r i (x), f i = f(x i ),potomlzereziduumnapsat: r i = f i n a j g ji,,, m Parametry a j určímetak,abyrezidua r i bylaminimálníjenutnésezamyslet,vjakémsmyslu budeme minimalizovat předchozí problém Nejobvyklejším přístupem je minimalizovat součet čverců reziduí(tzv metoda nejmenších čtverců) Metoda nejmenších čtverců V metodě nejmenších čtverců minimalizujeme součet čtverců reziduí, tj hledáme minimum funkce: m r = ri Obr 5 Metoda nejmenších čtverců

13 Hledáme minimum funkce S(a 0, a,, a n )= m m ri = f i Musíbýtsplněnapodmínkapro,, n 0= S(a 0, a,, n) a j = m f i n a j g ji n a j g ji g ji, Označíme-li m g r(x j )g s (x j )=(g r, g s ), m g r(x j )f j =(g r, f), r, s {0,,, n},lzetyto podmínky napsat jako: n a j (g j, g i )=(g i, f), i=,, m Dostanemesoustavu n+rovnicon+neznámých,kterálzezapsatmaticově: (g 0, g 0 ) (g 0, g ) (g 0, g n ) (g 0, g n ) (g, g 0 ) (g, g ) (g, g n ) (g, g n ) (g, g 0 ) (g, g ) (g, g n ) (g, g n ) (g n, g 0 ) (g n, g ) (g n, g n ) (g n, g n ) a 0 a a a n (g 0, f) (g, f) = (g, f) (g n, f) Tato soustava rovnic se nazývá normální soustava a její determinant se nazývá Grammův determinant Platí: )Grammůvdeterminantjenenulový,právěkdyžfunkce g 0 (x), g (x), g (x),, g n (x)jsou lineárněnezávislénamnožiněbodů x 0,, x n )Nechťjsoufunkce g 0 (x), g (x), g (x),, g n (x)namnožiněbodů x 0,, x m lineárněnezávislé,pakmánormálnísoustavajedinéřešení a 0, a,, a n Funkce n a j g ijenejlepšíaproximací(vesmyslunejmenšíchčtverců)funkce f(x)na množiněbodů x 0,, x m Poznámka:Pokudchcemejednotlivýmměřenímpřiřaditrůznouváhu(napříkladpokudjsouněkterá měření přesnější), potom se používá vážená metoda nejmenších čtverců a hledáme minimum funkce: m r w = ri w i Znamenáto,ževpůvodnímetoděnejmenšíchčtvercůmusímevynásobit f i ai-týřádekgrammovy maticečíslem w i Zbývá otázka volby vhodných bázových funkcí Je třeba je volit tak, aby bázové funkce funkce g 0 (x), g (x), g (x),, g n (x)bylylineárněnezávislénamnožiněbodů x 0,, x m Několikpříkladůvolbybázovýchfunkcí g j (x),,, n: () g j (x)=x j Vtomtopřípaděsoustavanormálníchrovnicbývášpatněpodmíněnásevzrůstajícím počtem bázových funkcí Proto je vhodné volit za bázové funkce ortogonální polynomy, u kterých má soustava normálních rovnic diagonální tvar(např polynomy Čebyševovy, Gramovy, Legendrovy, Leguerrovy), 3

14 () g 0 (x) =, g k = cos(kx), g k+ = sin(kx), k = 0,, n, x (c, c+π), c R (trigonometrické polynomy), (3) g j (x)=b j (x)(b-splinefunkce), (4) g j (x)=e jx (exponenciálnífunkce) Příklad 7: Napište normální soustavu rovnic pro proložení daných hodnot přímkou pomocí metody nejmenšíchčtverců(tedypro n=ag 0 (x)=, g (x)=x, S(a 0, a, x)=a 0 + a x) Řešení: Dostaneme soustavu rovnic o neznámých, kterou lze zapsat maticově: ( ) ( ) ( ) (g0, g 0 ) (g 0, g ) a0 (g0, f) = (g, g 0 ) (g, g ) (g, f) S(a 0, a )= 0= S(a 0, a ) a 0 = 0= S(a 0, a ) = a m (m+) x i m m x i x i a m (f i (a 0 + a x i )) m (f i (a 0 + a x i ))( ), m (f i (a 0 + a x i ))( x i ), ( a0 a m ) f(x i ) = m x i f(x i ) MATLAB Metoda nejmenších čtverců pro aproximaci polynomy V MATLABu v případě, že chceme zadaná(naměřená) data aproximovat polynomem n-tého stupně, můžeme to jednoduše provést pomocí funkce polyfit, která používá metodu nejmenších čtverců: >> P=polyfit(X,Y,n), X je vektor hodnot nezávisle proměnné, Y je vektor hodnot závisle proměnné, n je stupeň polynomu,jímžchcemeaproximovatbody[x i, y i ]apjevektorkoeficientůvýslednéhopolynomu P(x), přičemž P(x)=p()x n + p()x n + +p(n)x+p(n+) Hodnoty polynomu P(x) ve všech prvcích vektoru X(např kvůli grafickému znázornění) lze zjistit funkcí polyval: >> YAP=polyval(P,X) P je vektor koeficientů aproximačního polynomu, X je vektor hodnot nezávisle proměnné a YAP je vektor hodnot aproximačního polynomu Součet čtverců odchylek spočítáme jako součet prvků vektoru, který vznikl umocněním každého prvku vektoru rozdílů mezi YAPR a Y: >> S=sum((YAP-Y) ) 4