Matematická a experimentální analýza namáhání rotujícího prstence ovinovacího balicího stroje
|
|
|
- Pavel Svoboda
- před 9 lety
- Počet zobrazení:
Transkript
1 Matematická a experimentální analýza namáhání rotujícího prstence ovinovacího balicího stroje Bc. Josef Kamenický Vedoucí práce: Ing. Jiří Mrázek, Ph.D.; Ing. František Starý Abstrakt Tématem této práce je popis namáhání prstence rotujícího v ovinovacím balicím stroji Rotomatic Profi Double. Na prstenci jsou zavěšeny rámy cívek a elektrorozvaděče, které při vysokých otáčkách způsobují namáhání. V první části práce je řešen matematický popis namáhání. K výpočtům je použita jak analytická metoda, tak i metoda konečných prvků. V druhé části je popsáno experimentální zjišťování namáhání prstence. Na vybraných místech byly měřeny deformace pomocí tenzometrů. Klíčová slova Rotomatic Profi Double, porovnání analytické metody s MKP, tenzometrické měření 1. Úvod Ovinovací balicí stroj Rotomatic Profi Double slouží k balení zboží před expedicí z výrobního závodu. Umísťuje se buď přímo nad válečkové dopravníky, nebo se do něho paleta vkládá manipulačním zařízením. Zboží je srovnáno na dřevěné paletě (zpravidla Euro paleta) a paleta i se zbožím se důkladně ovine do tzv. stretch folie. Tím celý sloupec zboží na paletě získá kromě ochrany také vyšší stabilitu. Obr. 1. Konstrukce stroje Rotomatic Profi Double
2 Konstrukce stroje Rotomatic Profi Double je patrná z obr. 1. V rámu stroje je na řetězech zavěšen rám prstence. V něm rotuje prstenec s cívkami stretch folie. V horní části stroje se nachází přidržovač, který zajišťuje stabilitu zboží během balicího cyklu. Dále je na rámu prstence překrývací mechanismus, který folií překryje vrchní stranu sloupce zboží. Posledními částmi jsou mechanismy k zakončení folie, ty jsou umístěny taktéž na rámu prstence. Po zabalení palety se zbožím upraví konec stretch folie tak, aby nedošlo k samovolnému rozbalení, a zároveň konec folie drží do nového cyklu. 2. Popis prstence Sestava prstence je složena z několika základních celků. Na obr. 2 jsou tyto celky číselně označeny. Nosnou částí je zakroužený tenkostěnný uzavřený profil (1). K němu jsou přimontovány dva protilehlé rámy cívek (2) a dva protilehlé elektrické rozvaděče (3). Obr. 2. Konstrukce stroje Rotomatic Profi Double Cívky se stretch folií jsou umístěny ve dvou protilehlých rámech připevněných na rotujícím prstenci. Na něm se také nachází elektrické rozvaděče, taktéž proti sobě a vůči rámům cívek posunuty o 90. Prstenec rotuje v rámu prstence maximální rychlostí 60 otáček za minutu. Prstenec je v rámu veden pomocí kladek, které pojíždějí shora a z vnitřní strany zkrouženého L profilu. Rám prstence je umístěn v rámu stroje, ve kterém vykonává posuvný vertikální pohyb. Porovnáním odstředivých sil jednotlivých celků, působících při otáčkách 60 min -1, jsme získali přehled o vlivech jednotlivých celků na namáhání prstence. Největší vliv mají samozřejmě součásti s nejvyšší hmotností. Hmotnost každého rámu cívek, včetně samotných cívek folie, je 93,04 kg, rozvaděče 50,12 kg a vlastního prstence 68,2 kg. Menší vliv má také odstředivá síla působící na každý element profilu prstence. V následných výpočtech je tedy uvažováno se silami od rámů cívek, elektrických rozvaděčů a také s odstředivou silou vlastního prstence.
3 3. Výpočtové modely K analytickému výpočtu byl použit jeden výpočtový model a k výpočtu pomocí MKP byly použity dva typy modelů. Síly od rámů cívek jsou značeny FO, od elektrických rozvaděčů pak FR. Síly FR byly ve výpočtových modelech umístěny pod úhly 0 a p. Síly FO byly umístěny pod úhly p/2 a 3p/2. Výpočtem odstředivé síly rozvaděče a rámu cívky byly zjištěny tyto hodnoty: FR= 2 324,93 N a FO= 4 315,86 N. 3.1 Model pro analytický výpočet Pro analytický výpočet je zaveden tento model: rám v podstatě zakřivený prut, zatížený čtyřmi silami a spojitým zatížením. Schéma tohoto modelu je znázorněno na obr. 3. Síly působící na prut odpovídají odstředivým silám od dvou protilehlých rámů cívek a dvou protilehlých elektrických rozvaděčů. Spojité zatížení odpovídá vlastní odstředivé síle od rotace prstence. FO II. y qo I. NY +M FR a x MR NX FR/2 III. IV. FO Obr. 3. Model pro analytický výpočet 3.2 Model wire pro výpočet MKP Jedná se o drátový model, který svým zadáním a chováním odpovídá modelu pro analytický výpočet. Schéma tohoto modelu je uvedeno na obr. 4. Na drát působí čtyři síly umístěné po p/2 a odstředivá síla vznikající rotací prstence. Velikost těchto sil je shodná se silami v modelu analytického výpočtu. Síly jsou zadány manuálně dle hodnot vypočtených pro
4 danou úhlovou rychlost prstence. Velikost vlastní odstředivé síly prstence je zadána úhlovou rychlostí. Drát je spojen se středovým bodem pomocí Coupling Continuum distributing, a tento bod má definovány nulové posuvy ve všech třech směrech a také jsou definována nulová natočení v tomto bodě. Obr. 4. Drátový model pro výpočet MKP 3.3 Model solid - prstenec pro výpočet MKP Prstenec je zde vymodelován jako těleso. Síly jsou zadány stejným způsobem jako u předchozího modelu. Taktéž vlastní odstředivá síla prstence je zadána pomocí úhlové rychlosti prstence. Model je zobrazen na obr. 5. Uložení je řešeno stejným způsobem pomocí Coupling ke středovému bodu. Obr. 5. Model solid prstenec pro výpočet MKP
5 3.4 Model solid prstenec s kvádry pro výpočet MKP Tento výpočtový model, uvedený na obr. 6, vychází z reálného uspořádání největších hmot na prstenci. Základem je prstenec z předchozího modelu, k němu jsou připevněny čtyři kvádry o hmotnostech i těžištích odpovídajících příslušným zařízením zavěšeným na prstenci. Namáhání tohoto tělesa je zadáno pouze úhlovou rychlostí. Uložení je stejné jako u předchozího modelu. Obr. 6. Model solid prstenec s kvádry pro výpočet MKP 4. Výpočty Namáhání prstence bylo zjištěno jak analytickým výpočtem, tak výpočtem pomocí metody konečných prvků. Výsledky výpočtů jsou následně v 5. kapitole porovnány. 4.1 Analytický výpočet K tomuto výpočtu je použit výpočtový model prstence odpovídající zakřivenému prutu, zatíženému čtyřmi silami a spojitým zatížením, viz kapitola 3.1 a obr. 3. Výpočty jsou provedeny ve výpočetním programu MAPLE. Prstenec je v podstatě kruhový rám, je tedy třikrát staticky neurčitý. Z obr. 3 je vidět, že prut nahrazující rám je v jednom místě rozdělen. Jeden konec je vetknut a druhý zůstane volný. Protože se prut dělí v místě působiště síly FR, tato síla se rozdělí na dvě poloviny a na volném konci bude působit pouze jedna polovina této síly. Dále je pro výpočet nutné zavést deformační podmínky. Volný konec má vůči vetknutí nulové posunutí ve směru x a ve směru y, dále také nulový úhel natočení. Na volném konci jsou tedy zavedeny dvě vnitřní síly NX a NY, každá v příslušném směru, a jedna silová dvojice MR. Tyto síly a silová dvojice jsou tak veliké, aby zachovaly předepsané posuvy a úhel natočení (ty jsou nulové). Z obr. 3 je patrné rozdělení prutu na čtyři integrační pole. Na těchto polích vyjádřením vnitřních silových účinků získám průběh momentu. Rovnice na jednotlivých polích jsou:
6 ( ) ( ) ( ) (1) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) (2) (3) (4) V těchto rovnicích je qo spojité zatížení a jeho hodnota se spočte dle vztahu (5), ve kterém vystupuje hmotnost celého prstence m P a úhlová rychlost w. Namáhání je počítáno pro rotaci prstence při otáčkách 60 min -1, úhlová rychlost má tedy hodnotu w= 6,2831 rad*s -1. (5) Nejdříve je třeba vyjádřit deformační podmínky pro volný konec prutu. Pomocí Mohrova integrálu se vyjádří jednotlivé posuvy a úhel natočení. Výrazy pro výpočet uvedených deformací se musí rovnat nule. Pro posuv ve směru osy x platí výraz (6), ve směru osy y výraz (7) a pro úhel natočení výraz (8). { } (6) { ( ) ( ) ( ) ( ) } (7) { } (8) Rovnice (6) (8) tvoří soustavu tří rovnic o třech neznámých, a to NX, NY a MR. Dosazením známých hodnot získám řešení rovnice, viz výsledky (11) (13). Poloměr středové čáry profilu prstence je R= 1175 mm, modul pružnosti v tahu E= 2,1*10 5 Nmm -2. Kvadratický modul průřezu tenkostěnného obdélníkového profilu o šířce B= 50 mm, výšce H= 80 mm a tloušťce stěny t= 5 mm je J= mm 4. Velikosti odstředivých sil FR a FO jsou
7 Ohybové napětí [Nmm -2 ] vypočteny ze známých hmotností rámu cívky a elektrického rozvaděče. Hmotnost rozvaděče je 50,12 kg a hmotnost rámu cívky je 93,04 kg. Výpočet odstředivých sil je uveden ve vztazích (9) a (10). (9) (10) (11) (12) (13) Dosazením těchto výsledků do vztahů (1) (4) jsou získány rovnice (14) (17) popisující průběh ohybového momentu na daných polích. V těchto rovnicích je ohybový moment funkcí pouze úhlu a. (14) (15) (16) (17) Nyní se může vykreslit průběh ohybového napětí, viz obr. 7. Pro lepší porovnání maximální hodnoty a také pro následné porovnání s výpočty MKP je průběh napětí vykreslen v absolutní hodnotě. Průřezový modul v ohybu daného profilu prstence je Wo= mm 3. Průběh ohybového napětí na rotujícím prstenci Úhel a [ ] Obr. 7. Průběh ohybového napětí na prstenci analytické řešení
8 Při vykreslení závislosti velikosti ohybového napětí na otáčkách prstence jsou získány rovnice průběhu ohybového napětí jako funkce dvou proměnných, a to úhlu a a otáček prstence n. Tento průběh je zobrazen na obr. 8. Z obrázku je vidět, že nejkritičtějšími místy jsou ta pod úhly p/2 a 3p/2. To znamená místa upevnění rámů cívek, které jsou těžší nežli elektrické rozvaděče. Navíc napjatost v těchto místech roste mnohem rychleji než v ostatních místech. Maximální hodnota napětí je v místech pod úhly p/2 a 3p/2, a má hodnotu 60,75 Nmm -2. Lokální maxima mají hodnotu 21,54 Nmm -2. Obr. 8. Průběh ohybového momentu na prstenci v závislosti na jeho otáčkách 4.2 Výpočet MKP model wire Metodou konečných prvků je proveden výpočet drátového modelu z kapitoly 3.2. Velikost elementů je zvolena 10 mm. Na obr. 9 je vykreslen průběh napětí na prstenci. Špičky pod úhly p/2 a 3p/2 dosahují hodnoty 56 Nmm -2, maxima oblouků dosahují hodnoty 17 Nmm -2.
9 Ohybové napětí [Nmm -2 ] Ohybové napětí [Nmm -2 ] Průběh ohybového napětí na rotujícím prstenci Úhel a [ ] Obr. 9. Průběh ohybového napětí na prstenci model wire 4.3 Výpočet MKP model solid prstenec Výpočet je proveden na modelu z kapitoly 3.3, tedy plném tělese shodném s prstencem. K vysíťování je použito tetraedrů o velikosti 10 mm. Na obr. 10 je vykreslen průběh ohybového napětí na prstenci. Ve špičkách v místech pod úhly p/2 a 3p/2 je 50,9 Nmm -2, lokální maxima pak jsou 22,4 Nmm -2. Průběh ohybového napětí na rotujícím prstenci Úhel a [ ] Obr. 10. Průběh ohybového napětí na prstenci model solid prstenec
10 Ohybové napětí [Nmm -2 ] 4.4 Výpočet MKP model solid prstenec s kvádry K výpočtu je použit výpočtový model z kapitoly 3.4. Na prstenci jsou zavěšeny kvádry o odpovídajících hmotnostech. Síť tohoto tělesa se skládá z hexaedrů, jejichž velikost je 10 mm. Na obr. 11 je zobrazen průběh ohybového napětí, jehož maximální hodnota v místech pod úhly p/2 a 3p/2 je 36,13 Nmm -2. V místech pod úhly 0 a p má maximum hodnotu 16,39 Nmm Průběh ohybového napětí na rotujícím prstenci Úhel a [ ] Obr. 11. Průběh ohybového napětí na prstenci model solid prstenec s kvádry 5. Porovnání výsledků V předchozí kapitole byly pro každý výpočet napsány maximální hodnoty ohybového napětí. V tabulce 1 jsou tyto hodnoty porovnány, jsou zde také procentuálně vyjádřeny odchylky od analytického řešení. Tabulka 1. Porovnání výsledků jednotlivých výpočtů Analytický výpočet Vypočtené hodnoty Špička [Nmm -2 ] Lokální extrémy [Nmm -2 ] Špička [%] Odchylky Lokální extrémy [%] 60,75 21, Model wire ,8 21,1 Model solid prstenec Model solid prstenec s kvádry 50,9 22,4 16,2 4 36,13 16, ,9
11 Ohybové napětí [Nmm -2 ] Pro lepší srovnání výsledků jsou na obr. 12 vykresleny průběhy ohybového napětí z jednotlivých výpočtů do jednoho grafu. Průběh ohybového napětí je vykreslen pouze pro jednu polovinu prstence. V grafu jsou navíc vykresleny křivky udávající 80% respektive 60% hodnoty analytického řešení. Tím se nechá průběh napětí zhodnotit lépe, než jak je tomu při porovnávání hodnot pouze v několika bodech (viz tabulka 1). Průběh ohybového napětí na rotujícím prstenci Úhel a [ ] Analytické řešení 80% z analytického řešení 60% z analytického řešení MKP - wire - 4 síly + úhlová rychlost MKP - solid - 4 síly + úhlová rychlost - tetraedr MKP - solid - úhlová rychlost - hexaedr Obr. 12. Porovnání průběhu ohybového napětí na prstenci 6. Návrh ložiska Ke zvýšení tuhosti rotujícího členu by došlo při nahrazení prstence velko-průměrovým valivým ložiskem. Jako nejvhodnější ložisko bylo vybráno ložisko od výrobce Franke sestávající ze čtyř zkroužených drátů a valivých elementů. Ložisko je znázorněno na obr. 13. Výběr vhodného typu ložiska byl konzultován přímo s firmou Franke GmbH. Bylo vybráno ložisko s označením LEZ /16. Na obr. 14 je zobrazeno uložení valivého ložiska. Obr. 13. Ložisko od výrobce Franke (Zdroj:
12 Obr. 14. Uložení valivého ložiska 7. Tenzometrické měření Pomocí tenzometrického měření bylo zjišťováno namáhání nejen součástí tvořících rotující prstenec, ale součástí celého stroje Rotomatic Profi Double. Na základě analýzy provedené metodou konečných prvků byla vybrána místa, na kterých se měla měřit deformace pomocí tenzometrů. Na obr. 15 je například uveden rám cívky, na kterém byla označena 4 místa měření. Obr. 15. Rám cívky označení měřených míst
13 Vzhledem k velikosti měřeného stroje probíhalo měření přímo v areálu výrobce balicích strojů - firmy Pragometal, spol. s.r.o. Součástí tohoto projektu byla samozřejmě veškerá příprava měření. Z výsledků analýzy MKP byly vytvořeny podklady pro nalepení tenzometrů, byly připraveny části měřicího obvodu (kompenzační tenzometr, pájecí pole, kabely, konektory). Následně byly tenzometry nalepeny na zvolená místa měření. Po této přípravě následovalo vlastní měření, které probíhalo při několika zátěžných cyklech. Na obr. 16 je zobrazen rám cívky, na kterém jsou nalepeny tenzometry a pájecí pole. Obr. 16. Rám cívky tenzometrické měření 8. Závěr Tento článek popisuje namáhání rotujícího prstence zjištěné různými metodami analytických a MKP výpočtů a jejich porovnání. Pro výpočet metodou konečných prvků bylo použito více výpočtových modelů. Realitě nejvíce odpovídá model prstence se dvěma páry kvádrů o příslušných hmotnostech, které nahrazují rámy cívek a elektrické rozvaděče. V místě uchycení rámů cívek a rozvaděčů je ve skutečnosti zvýšená tuhost, což tento model, na rozdíl od drátového, splňuje. Zmíněný drátový model naopak odpovídá modelu analytickému, který má po celém obvodu konstantní tuhost, proto tento model tolik neodpovídá realitě. Té se více přibližuje výpočet na modelu s kvádry, neboť v místě rámů cívek a rozvaděčů bude vznikat vlivem odstředivé síly špička ohybového napětí. A záleží pak na tuhosti prstence v těchto místech, tedy na tuhosti elektrorozvaděčů a rámů cívek, jak výrazná a jak ostrá špička napětí zde bude vznikat. Z výpočtů bylo zjištěno, že prstenec je nejvíce namáhán v místech uložení rámů cívek a elektrických rozvaděčů. K porovnání výsledků výpočtů s výsledky tenzometrického měření bude třeba ještě zpracovat naměřená data. Poděkování Tato práce vznikla s podporou projektu MPO č. FR-TI3/281. Práce a celý výzkum byl podporován firmou Pragometal s.r.o.
14 Seznam symbolů E modul pružnosti v tahu (N. mm -2 ) FO odstředivá síla rámu cívky (N) FR odstředivá síla elektrického rozvaděče (N) J kvadratický modul průřezu (mm 4 ) MR vnitřní silová dvojice (N. mm) M ohybový moment (N. mm) NX vnitřní síla ve směru x (N) NY vnitřní síla ve směru y (N) R průměr prstence (mm) R průměr prstence (mm) da diferenciál úhlu (rad) m o hmotnost rámu cívky (kg) m p hmotnost profilu prstence (kg) m R hmotnost elektrického rozvaděče (kg) qo spojité zatížení (N. mm -1 ) u posuv ve směru osy x (mm) v posuv ve směru osy y (mm) a úhel (rad, ) f úhel natočení (rad) úhlová rychlost (rad. s -1 ) Seznam použité literatury DRASTÍK, František a kol. Strojnické tabulky pro konstrukci i dílnu. Ostrava: Montanex a.s., ISBN X. FRANKE GMBH. General Catalogue [online]. Aalen, Germany, 2011 [cit ]. Dostupné z: MICHALEC, Jiří a kol. Pružnost a pevnost I.. Praha: Vydavatelství ČVUT, Fakulta strojní. ISBN
MKP analýza konstrukčních řetězců ovinovacího balicího stroje FEM Analysis of Construction Parts of Wrapping Machine
 MKP analýza konstrukčních řetězců ovinovacího balicího stroje FEM Analysis of Construction Parts of Wrapping Machine Bc. Petr Kříbala Vedoucí práce: Ing. Jiří Mrázek, Ph.D., Ing. František Starý Abstrakt
MKP analýza konstrukčních řetězců ovinovacího balicího stroje FEM Analysis of Construction Parts of Wrapping Machine Bc. Petr Kříbala Vedoucí práce: Ing. Jiří Mrázek, Ph.D., Ing. František Starý Abstrakt
Systém nízkoúrovňových válečkových a řetězových dopravníků
 Systém nízkoúrovňových válečkových a řetězových dopravníků Bc. Vít Hanus Vedoucí práce: Ing. František Starý Abstrakt Tématem práce je návrh a konstrukce modulárního systému válečkových a řetězových dopravníků
Systém nízkoúrovňových válečkových a řetězových dopravníků Bc. Vít Hanus Vedoucí práce: Ing. František Starý Abstrakt Tématem práce je návrh a konstrukce modulárního systému válečkových a řetězových dopravníků
písemky (3 příklady) Výsledná známka je stanovena zkoušejícím na základě celkového počtu bodů ze semestru, ze vstupního testu a z písemky.
 POŽADAVKY KE ZKOUŠCE Z PP I Zkouška úrovně Alfa (pro zájemce o magisterské studium) Zkouška sestává ze vstupního testu (10 otázek, výběr správné odpovědi ze čtyř možností, rozsah dle sloupečku Požadavky)
POŽADAVKY KE ZKOUŠCE Z PP I Zkouška úrovně Alfa (pro zájemce o magisterské studium) Zkouška sestává ze vstupního testu (10 otázek, výběr správné odpovědi ze čtyř možností, rozsah dle sloupečku Požadavky)
Pružnost a pevnost. zimní semestr 2013/14
 Pružnost a pevnost zimní semestr 2013/14 Organizace předmětu Přednášející: Prof. Milan Jirásek, B322 Konzultace: pondělí 10:00-10:45 nebo dle dohody E-mail: Milan.Jirasek@fsv.cvut.cz Webové stránky předmětu:
Pružnost a pevnost zimní semestr 2013/14 Organizace předmětu Přednášející: Prof. Milan Jirásek, B322 Konzultace: pondělí 10:00-10:45 nebo dle dohody E-mail: Milan.Jirasek@fsv.cvut.cz Webové stránky předmětu:
Pružnost a pevnost I
 Stránka 1 teoretické otázk 2007 Ing. Tomáš PROFANT, Ph.D. verze 1.1 OBSAH: 1. Tenzor napětí 2. Věta o sdruženosti smkových napětí 3. Saint Venantův princip 4. Tenzor deformace (přetvoření) 5. Geometrická
Stránka 1 teoretické otázk 2007 Ing. Tomáš PROFANT, Ph.D. verze 1.1 OBSAH: 1. Tenzor napětí 2. Věta o sdruženosti smkových napětí 3. Saint Venantův princip 4. Tenzor deformace (přetvoření) 5. Geometrická
OTÁZKY VSTUPNÍHO TESTU PP I LS 2010/2011
 OTÁZKY VSTUPNÍHO TESTU PP I LS 010/011 Pomocí Thumovy definice, s využitím vrubové citlivosti q je definován vztah mezi součiniteli vrubu a tvaru jako: Součinitel tvaru α je podle obrázku definován jako:
OTÁZKY VSTUPNÍHO TESTU PP I LS 010/011 Pomocí Thumovy definice, s využitím vrubové citlivosti q je definován vztah mezi součiniteli vrubu a tvaru jako: Součinitel tvaru α je podle obrázku definován jako:
VŠB- Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti. Úvod do MKP Napěťová analýza tenzometrického snímače ve tvaru háku
 VŠB- Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti Úvod do MKP Napěťová analýza tenzometrického snímače ve tvaru háku Autor: Michal Šofer Verze 0 Ostrava 20 Zadání: Proveďte
VŠB- Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti Úvod do MKP Napěťová analýza tenzometrického snímače ve tvaru háku Autor: Michal Šofer Verze 0 Ostrava 20 Zadání: Proveďte
Téma 12, modely podloží
 Téma 1, modely podloží Statika stavebních konstrukcí II., 3.ročník bakalářského studia Úvod Winklerův model podloží Pasternakův model podloží Pružný poloprostor Nosník na pružném Winklerově podloží, řešení
Téma 1, modely podloží Statika stavebních konstrukcí II., 3.ročník bakalářského studia Úvod Winklerův model podloží Pasternakův model podloží Pružný poloprostor Nosník na pružném Winklerově podloží, řešení
Výpočet sedání kruhového základu sila
 Inženýrský manuál č. 22 Aktualizace 06/2016 Výpočet sedání kruhového základu sila Program: MKP Soubor: Demo_manual_22.gmk Cílem tohoto manuálu je popsat řešení sedání kruhového základu sila pomocí metody
Inženýrský manuál č. 22 Aktualizace 06/2016 Výpočet sedání kruhového základu sila Program: MKP Soubor: Demo_manual_22.gmk Cílem tohoto manuálu je popsat řešení sedání kruhového základu sila pomocí metody
Ing. Jan BRANDA PRUŽNOST A PEVNOST
 Ing. Jan BRANDA PRUŽNOST A PEVNOST Výukový text pro učební obor Technik plynových zařízení Vzdělávací oblast RVP Plynová zařízení a Tepelná technika (mechanika) Pardubice 013 Použitá literatura: Technická
Ing. Jan BRANDA PRUŽNOST A PEVNOST Výukový text pro učební obor Technik plynových zařízení Vzdělávací oblast RVP Plynová zařízení a Tepelná technika (mechanika) Pardubice 013 Použitá literatura: Technická
Teorie tkaní. Modely vazného bodu. M. Bílek
 Teorie tkaní Modely vazného bodu M. Bílek 2016 Základní strukturální jednotkou tkaniny je vazný bod, tj. oblast v okolí jednoho zakřížení osnovní a útkové nitě. Proces tkaní tedy spočívá v tvorbě vazných
Teorie tkaní Modely vazného bodu M. Bílek 2016 Základní strukturální jednotkou tkaniny je vazný bod, tj. oblast v okolí jednoho zakřížení osnovní a útkové nitě. Proces tkaní tedy spočívá v tvorbě vazných
OHYB (Napjatost) M A M + qc a + b + c ) M A = 2M qc a + b + c )
 3.3 Řešené příklady Příklad 1: Pro nosník na obrázku vyšetřete a zakreslete reakce, T (x) a M(x). Dále určete M max a proveďte dimenzování pro zadaný průřez. Dáno: a = 0.5 m, b = 0.3 m, c = 0.4 m, d =
3.3 Řešené příklady Příklad 1: Pro nosník na obrázku vyšetřete a zakreslete reakce, T (x) a M(x). Dále určete M max a proveďte dimenzování pro zadaný průřez. Dáno: a = 0.5 m, b = 0.3 m, c = 0.4 m, d =
Definujte poměrné protažení (schematicky nakreslete a uved te jednotky) Napište hlavní kroky postupu při posouzení prutu na vzpěrný tlak.
 00001 Definujte mechanické napětí a uved te jednotky. 00002 Definujte normálové napětí a uved te jednotky. 00003 Definujte tečné (tangenciální, smykové) napětí a uved te jednotky. 00004 Definujte absolutní
00001 Definujte mechanické napětí a uved te jednotky. 00002 Definujte normálové napětí a uved te jednotky. 00003 Definujte tečné (tangenciální, smykové) napětí a uved te jednotky. 00004 Definujte absolutní
Předpjatý beton Přednáška 4
 Předpjatý beton Přednáška 4 Obsah Účinky předpětí na betonové prvky a konstrukce Staticky neurčité účinky předpětí Konkordantní kabel Lineární transformace kabelu Návrh předpětí metodou vyrovnání zatížení
Předpjatý beton Přednáška 4 Obsah Účinky předpětí na betonové prvky a konstrukce Staticky neurčité účinky předpětí Konkordantní kabel Lineární transformace kabelu Návrh předpětí metodou vyrovnání zatížení
POŽADAVKY KE ZKOUŠCE Z PP I
 POŽADAVKY KE ZKOUŠCE Z PP I Zkouška úrovně Alfa (pro zájemce o magisterské studium) Zkouška sestává ze o vstupního testu (10 otázek, výběr správné odpovědi ze čtyř možností, rozsah dle sloupečku Požadavky)
POŽADAVKY KE ZKOUŠCE Z PP I Zkouška úrovně Alfa (pro zájemce o magisterské studium) Zkouška sestává ze o vstupního testu (10 otázek, výběr správné odpovědi ze čtyř možností, rozsah dle sloupečku Požadavky)
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6
 OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
Posouzení a optimalizace nosného rámu studentské formule
 Posouzení a optimalizace nosného rámu studentské formule Vypracoval: Martin Hloucal Vedoucí práce: Doc. Ing. Jan Zeman, Ph.D. 1 Co to je Formula Student/SAE Soutěž pro studenty technických vysokých škol,
Posouzení a optimalizace nosného rámu studentské formule Vypracoval: Martin Hloucal Vedoucí práce: Doc. Ing. Jan Zeman, Ph.D. 1 Co to je Formula Student/SAE Soutěž pro studenty technických vysokých škol,
Vybrané okruhy znalostí z předmětů stavební mechanika, pružnost a pevnost důležité i pro studium předmětů KP3C a KP5A - navrhování nosných konstrukcí
 Vybrané okruhy znalostí z předmětů stavební mechanika, pružnost a pevnost důležité i pro studium předmětů KP3C a KP5A - navrhování nosných konstrukcí Skládání a rozklad sil Skládání a rozklad sil v rovině
Vybrané okruhy znalostí z předmětů stavební mechanika, pružnost a pevnost důležité i pro studium předmětů KP3C a KP5A - navrhování nosných konstrukcí Skládání a rozklad sil Skládání a rozklad sil v rovině
Materiálové vlastnosti: Poissonův součinitel ν = 0,3. Nominální mez kluzu (ocel S350GD + Z275): Rozměry průřezu:
 Řešený příklad: Výpočet momentové únosnosti ohýbaného tenkostěnného C-profilu dle ČSN EN 1993-1-3. Ohybová únosnost je stanovena na základě efektivního průřezového modulu. Materiálové vlastnosti: Modul
Řešený příklad: Výpočet momentové únosnosti ohýbaného tenkostěnného C-profilu dle ČSN EN 1993-1-3. Ohybová únosnost je stanovena na základě efektivního průřezového modulu. Materiálové vlastnosti: Modul
Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady. Část 1 - Test
 Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových charakteristik, oficiální přehled
Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových charakteristik, oficiální přehled
Betonové konstrukce (S) Přednáška 3
 Betonové konstrukce (S) Přednáška 3 Obsah Účinky předpětí na betonové prvky a konstrukce Silové působení kabelu na beton Ekvivalentní zatížení Staticky neurčité účinky předpětí Konkordantní kabel, Lineární
Betonové konstrukce (S) Přednáška 3 Obsah Účinky předpětí na betonové prvky a konstrukce Silové působení kabelu na beton Ekvivalentní zatížení Staticky neurčité účinky předpětí Konkordantní kabel, Lineární
Sedmé cvičení bude vysvětlovat tuto problematiku:
 Sedmé cvičení bude vysvětlovat tuto problematiku: Velmi stručně o parciálních derivacích Castiglianova věta k čemu slouží Castiglianova věta jak ji použít Castiglianova věta staticky určité přímé nosníky
Sedmé cvičení bude vysvětlovat tuto problematiku: Velmi stručně o parciálních derivacích Castiglianova věta k čemu slouží Castiglianova věta jak ji použít Castiglianova věta staticky určité přímé nosníky
Mechanika s Inventorem
 CAD data Mechanika s Inventorem Optimalizace FEM výpočty 4. Prostředí aplikace Petr SCHILLING, autor přednášky Ing. Kateřina VLČKOVÁ, obsahová korekce Tomáš MATOVIČ, publikace 1 Obsah cvičení: Prostředí
CAD data Mechanika s Inventorem Optimalizace FEM výpočty 4. Prostředí aplikace Petr SCHILLING, autor přednášky Ing. Kateřina VLČKOVÁ, obsahová korekce Tomáš MATOVIČ, publikace 1 Obsah cvičení: Prostředí
Únosnost kompozitních konstrukcí
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta strojní Ústav letadlové techniky Únosnost kompozitních konstrukcí Optimalizační výpočet kompozitních táhel konstantního průřezu Technická zpráva Pořadové číslo:
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta strojní Ústav letadlové techniky Únosnost kompozitních konstrukcí Optimalizační výpočet kompozitních táhel konstantního průřezu Technická zpráva Pořadové číslo:
Pružnost a pevnost (132PRPE), paralelka J2/1 (ZS 2015/2016) Písemná část závěrečné zkoušky vzorové otázky a příklady.
 Pružnost a pevnost (132PRPE), paralelka J2/1 (ZS 2015/2016) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových
Pružnost a pevnost (132PRPE), paralelka J2/1 (ZS 2015/2016) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových
KONSTRUKČNÍ NÁVRH RÁMU LISU CKW 630 SVOČ FST Bc. Martin Konvalinka, Jiráskova 745, Nýrsko Česká republika
 KONSTRUKČNÍ NÁVRH RÁMU LISU CKW 630 SVOČ FST 2009 Bc. Martin Konvalinka, Jiráskova 745, 340 22 Nýrsko Česká republika ABSTRAKT Práce obsahuje pevnostní kontrolu rámu lisu CKW 630 provedenou analytickou
KONSTRUKČNÍ NÁVRH RÁMU LISU CKW 630 SVOČ FST 2009 Bc. Martin Konvalinka, Jiráskova 745, 340 22 Nýrsko Česká republika ABSTRAKT Práce obsahuje pevnostní kontrolu rámu lisu CKW 630 provedenou analytickou
Náhradní ohybová tuhost nosníku
 Náhradní ohybová tuhost nosníku Autoři: Doc. Ing. Jiří PODEŠVA, Ph.D., Katedra mechaniky, Fakulta strojní, VŠB - Technická univerzita Ostrava, e-mail: jiri.podesva@vsb.cz Anotace: Výpočty ocelových výztuží
Náhradní ohybová tuhost nosníku Autoři: Doc. Ing. Jiří PODEŠVA, Ph.D., Katedra mechaniky, Fakulta strojní, VŠB - Technická univerzita Ostrava, e-mail: jiri.podesva@vsb.cz Anotace: Výpočty ocelových výztuží
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STROJNÍ
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STROJNÍ Ústav mechaniky, biomechaniky a mechatroniky Odbor pružnosti a pevnosti Program pro analýzu napjatosti a deformaci hřídelů Studentská práce Jan Pecháček
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STROJNÍ Ústav mechaniky, biomechaniky a mechatroniky Odbor pružnosti a pevnosti Program pro analýzu napjatosti a deformaci hřídelů Studentská práce Jan Pecháček
Kapitola 8. prutu: rovnice paraboly z = k x 2 [m], k = z a x 2 a. [m 1 ], (8.1) = z b x 2 b. rovnice sklonu střednice prutu (tečna ke střednici)
![Kapitola 8. prutu: rovnice paraboly z = k x 2 [m], k = z a x 2 a. [m 1 ], (8.1) = z b x 2 b. rovnice sklonu střednice prutu (tečna ke střednici) Kapitola 8. prutu: rovnice paraboly z = k x 2 [m], k = z a x 2 a. [m 1 ], (8.1) = z b x 2 b. rovnice sklonu střednice prutu (tečna ke střednici)](/thumbs/61/45546970.jpg) Kapitola 8 Vnitřní síly rovinně zakřiveného prutu V této kapitole bude na příkladech vysvětleno řešení vnitřních sil rovinně zakřivených nosníků, jejichž střednici tvoří oblouk ve tvaru kvadratické paraboly[1].
Kapitola 8 Vnitřní síly rovinně zakřiveného prutu V této kapitole bude na příkladech vysvětleno řešení vnitřních sil rovinně zakřivených nosníků, jejichž střednici tvoří oblouk ve tvaru kvadratické paraboly[1].
Mechanika s Inventorem
 Mechanika s Inventorem 2. Základní pojmy CAD data FEM výpočty Petr SCHILLING, autor přednášky Ing. Kateřina VLČKOVÁ, obsahová korekce Optimalizace Tomáš MATOVIČ, publikace 1 Obsah přednášky: Lagrangeův
Mechanika s Inventorem 2. Základní pojmy CAD data FEM výpočty Petr SCHILLING, autor přednášky Ing. Kateřina VLČKOVÁ, obsahová korekce Optimalizace Tomáš MATOVIČ, publikace 1 Obsah přednášky: Lagrangeův
ρ 490 [lb/ft^3] σ D 133 [ksi] τ D 95 [ksi] Výpočet pružin Informace o projektu ? 1.0 Kapitola vstupních parametrů
![ρ 490 [lb/ft^3] σ D 133 [ksi] τ D 95 [ksi] Výpočet pružin Informace o projektu ? 1.0 Kapitola vstupních parametrů ρ 490 [lb/ft^3] σ D 133 [ksi] τ D 95 [ksi] Výpočet pružin Informace o projektu ? 1.0 Kapitola vstupních parametrů](/thumbs/50/26338473.jpg) N pružin i?..7 Vhodnost pro dynamické excelentní 6 [ F].. Dodávané průměry drátu,5 -,25 [in].3 - při pracovní teplotě E 2 [ksi].5 - při pracovní teplotě G 75 [ksi].7 Hustota ρ 4 [lb/ft^3]. Mez pevnosti
N pružin i?..7 Vhodnost pro dynamické excelentní 6 [ F].. Dodávané průměry drátu,5 -,25 [in].3 - při pracovní teplotě E 2 [ksi].5 - při pracovní teplotě G 75 [ksi].7 Hustota ρ 4 [lb/ft^3]. Mez pevnosti
NAMÁHÁNÍ NA KRUT NAMÁHÁNÍ NA KRUT
 Φd Předmět: Ročník: Vytvořil: Datum: MECHANIKA DRUHÝ ŠČERBOVÁ M. PAVELKA V. 8. KVĚTNA 2013 Název zpracovaného celku: NAMÁHÁNÍ NA KRUT NAMÁHÁNÍ NA KRUT KRUT KRUHOVÝCH PRŮŘEZŮ Součást je namáhána na krut
Φd Předmět: Ročník: Vytvořil: Datum: MECHANIKA DRUHÝ ŠČERBOVÁ M. PAVELKA V. 8. KVĚTNA 2013 Název zpracovaného celku: NAMÁHÁNÍ NA KRUT NAMÁHÁNÍ NA KRUT KRUT KRUHOVÝCH PRŮŘEZŮ Součást je namáhána na krut
Kˇriv e pruty Martin Fiˇser Martin Fiˇ ser Kˇ riv e pruty
 Obsah Dimenzování křivého tenkého prutu zde Deformace v daném místě prutu zde Castiglianova věta zde Dimenzování křivého tenkého prutu Mějme obecný křivý prut z homogeního izotropního materiálu. Obrázek:
Obsah Dimenzování křivého tenkého prutu zde Deformace v daném místě prutu zde Castiglianova věta zde Dimenzování křivého tenkého prutu Mějme obecný křivý prut z homogeního izotropního materiálu. Obrázek:
PROVOZ, DIAGNOSTIKA A ÚDRŽBA STROJŮ
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ PROVOZ, DIAGNOSTIKA A ÚDRŽBA STROJŮ ZÁKLADNÍ PORUCHY A JEJICH PROJEVY VE FREKVENČNÍCH SPEKTRECH doc. Ing. Helebrant František, CSc. Ing.
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ PROVOZ, DIAGNOSTIKA A ÚDRŽBA STROJŮ ZÁKLADNÍ PORUCHY A JEJICH PROJEVY VE FREKVENČNÍCH SPEKTRECH doc. Ing. Helebrant František, CSc. Ing.
1. Měření hodnoty Youngova modulu pružnosti ocelového drátu v tahu a kovové tyče v ohybu
 Měření modulu pružnosti Úkol : 1. Měření hodnoty Youngova modulu pružnosti ocelového drátu v tahu a kovové tyče v ohybu Pomůcky : - Měřící zařízení s indikátorovými hodinkami - Mikrometr - Svinovací metr
Měření modulu pružnosti Úkol : 1. Měření hodnoty Youngova modulu pružnosti ocelového drátu v tahu a kovové tyče v ohybu Pomůcky : - Měřící zařízení s indikátorovými hodinkami - Mikrometr - Svinovací metr
2.2 Mezní stav pružnosti Mezní stav deformační stability Mezní stav porušení Prvek tělesa a napětí v řezu... p03 3.
 obsah 1 Obsah Zde je uveden přehled jednotlivých kapitol a podkapitol interaktivního učebního textu Pružnost a pevnost. Na tomto CD jsou kapitoly uloženy v samostatných souborech, jejichž název je v rámečku
obsah 1 Obsah Zde je uveden přehled jednotlivých kapitol a podkapitol interaktivního učebního textu Pružnost a pevnost. Na tomto CD jsou kapitoly uloženy v samostatných souborech, jejichž název je v rámečku
( r ) 2. Měření mechanické hysterezní smyčky a modulu pružnosti ve smyku
 ěření mechanické hysterezní smyčky a modulu pružnosti ve smyku 1 ěření mechanické hysterezní smyčky a modulu pružnosti ve smyku Úkol č.1: Získejte mechanickou hysterezní křivku pro dráty různé tloušťky
ěření mechanické hysterezní smyčky a modulu pružnosti ve smyku 1 ěření mechanické hysterezní smyčky a modulu pružnosti ve smyku Úkol č.1: Získejte mechanickou hysterezní křivku pro dráty různé tloušťky
Zadání programu z předmětu Dynamika I pro posluchače kombinovaného studia v Ostravě a Uherském Brodu vyučuje Ing. Zdeněk Poruba, Ph.D.
 Zadání programu z předmětu Dynamika I pro posluchače kombinovaného studia v Ostravě a Uherském Brodu vyučuje Ing. Zdeněk Poruba, Ph.D. Ze zadaných třinácti příkladů vypracuje každý posluchač samostatně
Zadání programu z předmětu Dynamika I pro posluchače kombinovaného studia v Ostravě a Uherském Brodu vyučuje Ing. Zdeněk Poruba, Ph.D. Ze zadaných třinácti příkladů vypracuje každý posluchač samostatně
ZÁKLADNÍ PŘÍPADY NAMÁHÁNÍ
 7. cvičení ZÁKLADNÍ PŘÍPADY NAMÁHÁNÍ V této kapitole se probírají výpočty únosnosti průřezů (neboli posouzení prvků na prostou pevnost). K porušení materiálu v tlačených částech průřezu dochází: mezní
7. cvičení ZÁKLADNÍ PŘÍPADY NAMÁHÁNÍ V této kapitole se probírají výpočty únosnosti průřezů (neboli posouzení prvků na prostou pevnost). K porušení materiálu v tlačených částech průřezu dochází: mezní
Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil
 Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil Souřadný systém, v rovině i prostoru Síla bodová: vektorová veličina (kluzný, vázaný vektor - využití),
Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil Souřadný systém, v rovině i prostoru Síla bodová: vektorová veličina (kluzný, vázaný vektor - využití),
α = 210 A x =... kn A y =... kn A M =... knm
 Vzorový příklad k 1. kontrolnímu testu Konzola Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A M A y y q = kn/m M = - 5kNm A α B c a b d F = 10 kn 1 1 3,5,5 L = 10 x α = 10 A
Vzorový příklad k 1. kontrolnímu testu Konzola Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A M A y y q = kn/m M = - 5kNm A α B c a b d F = 10 kn 1 1 3,5,5 L = 10 x α = 10 A
1 Tuhé těleso a jeho pohyb
 1 Tuhé těleso a jeho pohyb Tuhé těleso (TT) působením vnějších sil se nemění jeho tvar ani objem nedochází k jeho deformaci neuvažuje se jeho částicová struktura, těleso považujeme za tzv. kontinuum spojité
1 Tuhé těleso a jeho pohyb Tuhé těleso (TT) působením vnějších sil se nemění jeho tvar ani objem nedochází k jeho deformaci neuvažuje se jeho částicová struktura, těleso považujeme za tzv. kontinuum spojité
MECHANIKA PODZEMNÍCH KONSTRUKCÍ Statické řešení výztuže podzemních děl
 STUDIJNÍ PODPORY PRO KOMBINOVANOU FORMU STUDIA NAVAZUJÍCÍHO MAGISTERSKÉHO PROGRAMU STAVEBNÍ INŽENÝRSTVÍ -GEOTECHNIKA A PODZEMNÍ STAVITELSTVÍ MECHANIKA PODZEMNÍCH KONSTRUKCÍ Statické řešení výztuže podzemních
STUDIJNÍ PODPORY PRO KOMBINOVANOU FORMU STUDIA NAVAZUJÍCÍHO MAGISTERSKÉHO PROGRAMU STAVEBNÍ INŽENÝRSTVÍ -GEOTECHNIKA A PODZEMNÍ STAVITELSTVÍ MECHANIKA PODZEMNÍCH KONSTRUKCÍ Statické řešení výztuže podzemních
Výpočtová dokumentace pro montážní přípravek oběžného kola Peltonovy turbíny
 Výpočtová dokumentace pro montážní přípravek oběžného kola Peltonovy turbíny Parametry Jako podklady pro výpočtovou dokumentaci byly zadavatelem dodány parametry: -hmotnost oběžného kola turbíny 2450 kg
Výpočtová dokumentace pro montážní přípravek oběžného kola Peltonovy turbíny Parametry Jako podklady pro výpočtovou dokumentaci byly zadavatelem dodány parametry: -hmotnost oběžného kola turbíny 2450 kg
Deformace nosníků při ohybu.
 Číslo projektu CZ.1.07/ 1.1.36/ 02.0066 Autor Pavel Florík Předmět Mechanika Téma Deformace nosníků při ohybu Metodický pokyn výkladový text s ukázkami Deformace nosníků při ohybu. Příklad č.2 Zalomený
Číslo projektu CZ.1.07/ 1.1.36/ 02.0066 Autor Pavel Florík Předmět Mechanika Téma Deformace nosníků při ohybu Metodický pokyn výkladový text s ukázkami Deformace nosníků při ohybu. Příklad č.2 Zalomený
Přijímací zkouška na navazující magisterské studium Studijní program Fyzika obor Učitelství fyziky matematiky pro střední školy
 Přijímací zkouška na navazující magisterské studium 013 Studijní program Fyzika obor Učitelství fyziky matematiky pro střední školy Studijní program Učitelství pro základní školy - obor Učitelství fyziky
Přijímací zkouška na navazující magisterské studium 013 Studijní program Fyzika obor Učitelství fyziky matematiky pro střední školy Studijní program Učitelství pro základní školy - obor Učitelství fyziky
Zapojení odporových tenzometrů
 Zapojení odporových tenzometrů Zadání 1) Seznamte se s konstrukcí a použitím lineárních fóliových tenzometrů. 2) Proveďte měření na fóliových tenzometrech zapojených do můstku. 3) Zjistěte rovnici regresní
Zapojení odporových tenzometrů Zadání 1) Seznamte se s konstrukcí a použitím lineárních fóliových tenzometrů. 2) Proveďte měření na fóliových tenzometrech zapojených do můstku. 3) Zjistěte rovnici regresní
trubku o délce l. Prut (nebo trubka) bude namáhán kroutícím momentem M K [Nm]. Obrázek 1: Prut namáhaný kroutícím momentem.
![trubku o délce l. Prut (nebo trubka) bude namáhán kroutícím momentem M K [Nm]. Obrázek 1: Prut namáhaný kroutícím momentem. trubku o délce l. Prut (nebo trubka) bude namáhán kroutícím momentem M K [Nm]. Obrázek 1: Prut namáhaný kroutícím momentem.](/thumbs/99/141481369.jpg) Namáhání krutem Uvažujme přímý prut neměnného kruhového průřezu (Obr.2), popřípadě trubku o délce l. Prut (nebo trubka) bude namáhán kroutícím momentem M K [Nm]. Obrázek : Prut namáhaný kroutícím momentem.
Namáhání krutem Uvažujme přímý prut neměnného kruhového průřezu (Obr.2), popřípadě trubku o délce l. Prut (nebo trubka) bude namáhán kroutícím momentem M K [Nm]. Obrázek : Prut namáhaný kroutícím momentem.
PŮDORYSNĚ ZAKŘIVENÁ KONSTRUKCE PODEPŘENÁ OBLOUKEM
 PŮDORYSNĚ ZAKŘIVENÁ KONSTRUKCE PODEPŘENÁ OBLOUKEM 1. Úvod Tvorba fyzikálních modelů, tj. modelů skutečných konstrukcí v určeném měřítku, navazuje na práci dalších řešitelských týmů z Fakulty stavební Vysokého
PŮDORYSNĚ ZAKŘIVENÁ KONSTRUKCE PODEPŘENÁ OBLOUKEM 1. Úvod Tvorba fyzikálních modelů, tj. modelů skutečných konstrukcí v určeném měřítku, navazuje na práci dalších řešitelských týmů z Fakulty stavební Vysokého
Střední průmyslová škola strojírenská a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191
 Název školy Název projektu Registrační číslo projektu Autor Název šablony Střední průmyslová škola strojírenská a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Modernizace výuky
Název školy Název projektu Registrační číslo projektu Autor Název šablony Střední průmyslová škola strojírenská a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Modernizace výuky
MKP v Inženýrských výpočtech
 Vysoké učení technické v Brně Fakulta strojního inženýrství ÚMTMB MKP v Inženýrských výpočtech Semestrální projekt (PMM II č. 25) Řešitel: Franta Vomáčka 2011/2012 1. Zadání Analyzujte a případně modifikujte
Vysoké učení technické v Brně Fakulta strojního inženýrství ÚMTMB MKP v Inženýrských výpočtech Semestrální projekt (PMM II č. 25) Řešitel: Franta Vomáčka 2011/2012 1. Zadání Analyzujte a případně modifikujte
4. Napjatost v bodě tělesa
 p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
Experimentální ověření možností stanovení příčné tuhosti flexi-coil pružin
 Jaromír Zelenka 1, Jakub Vágner 2, Aleš Hába 3, Experimentální ověření možností stanovení příčné tuhosti flexi-coil pružin Klíčová slova: vypružení, flexi-coil, příčná tuhost, MKP, šroubovitá pružina 1.
Jaromír Zelenka 1, Jakub Vágner 2, Aleš Hába 3, Experimentální ověření možností stanovení příčné tuhosti flexi-coil pružin Klíčová slova: vypružení, flexi-coil, příčná tuhost, MKP, šroubovitá pružina 1.
A x A y. α = 30. B y. A x =... kn A y =... kn B y =... kn. Vykreslení N, V, M. q = 2kN/m M = 5kNm. F = 10 kn A c a b d ,5 2,5 L = 10
 Vzorový příklad k 1. kontrolnímu testu Prostý nosník Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A y y q = kn/m M = 5kNm F = 10 kn A c a b d 1 1 3,5,5 L = 10 α B B y x α = 30
Vzorový příklad k 1. kontrolnímu testu Prostý nosník Zadání: Vypočtěte složky reakcí a vykreslete průběhy vnitřních sil. A x A y y q = kn/m M = 5kNm F = 10 kn A c a b d 1 1 3,5,5 L = 10 α B B y x α = 30
Materiály ke 12. přednášce z předmětu KME/MECHB
 Materiály ke 12. přednášce z předmětu KME/MECH Zpracoval: Ing. Jan Vimmr, Ph.D. Prutové soustavy Prutové soustavy představují speciální soustavy těles, které se uplatňují při navrhování velkorozměrových
Materiály ke 12. přednášce z předmětu KME/MECH Zpracoval: Ing. Jan Vimmr, Ph.D. Prutové soustavy Prutové soustavy představují speciální soustavy těles, které se uplatňují při navrhování velkorozměrových
PRUŽNOST A PLASTICITA I
 Otázky k procvičování PRUŽNOST A PLASTICITA I 1. Kdy je materiál homogenní? 2. Kdy je materiál izotropní? 3. Za jakých podmínek můžeme použít princip superpozice účinků? 4. Vysvětlete princip superpozice
Otázky k procvičování PRUŽNOST A PLASTICITA I 1. Kdy je materiál homogenní? 2. Kdy je materiál izotropní? 3. Za jakých podmínek můžeme použít princip superpozice účinků? 4. Vysvětlete princip superpozice
Martin NESLÁDEK. 14. listopadu 2017
 Martin NESLÁDEK Faculty of mechanical engineering, CTU in Prague 14. listopadu 2017 1 / 22 Poznámky k úlohám řešeným MKP Na přesnost simulace pomocí MKP a prostorové rozlišení výsledků má vliv především:
Martin NESLÁDEK Faculty of mechanical engineering, CTU in Prague 14. listopadu 2017 1 / 22 Poznámky k úlohám řešeným MKP Na přesnost simulace pomocí MKP a prostorové rozlišení výsledků má vliv především:
Střední průmyslová škola strojírenská a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191
 Název školy Název projektu Registrační číslo projektu Autor Název šablony Střední průmyslová škola strojírenská a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Modernizace výuky
Název školy Název projektu Registrační číslo projektu Autor Název šablony Střední průmyslová škola strojírenská a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Modernizace výuky
Příklad oboustranně vetknutý nosník
 Příklad oboustranně vetknutý nosník výpočet podle viskoelasticity: 4 L fˆ L w, t J t, t 384I 0 průhyb uprostřed co se změní v případě, fˆ že se zatížení M mění x t v čase? x Lx L H t t0 1 fl ˆ M fˆ 0,
Příklad oboustranně vetknutý nosník výpočet podle viskoelasticity: 4 L fˆ L w, t J t, t 384I 0 průhyb uprostřed co se změní v případě, fˆ že se zatížení M mění x t v čase? x Lx L H t t0 1 fl ˆ M fˆ 0,
VŠB- Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti. Úvod do MKP Napěťová analýza modelu s vrubem
 VŠB- Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti Úvod do MKP Autor: Michal Šofer Verze 0 Ostrava 2011 Zadání: Proveďte napěťovou analýzu součásti s kruhovým vrubem v místě
VŠB- Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti Úvod do MKP Autor: Michal Šofer Verze 0 Ostrava 2011 Zadání: Proveďte napěťovou analýzu součásti s kruhovým vrubem v místě
Experimentální hodnocení bezpečnosti mobilní fotbalové brány
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta strojní Ústav mechaniky, biomechaniky a mechatroniky Odbor mechaniky a mechatroniky Název zprávy Experimentální hodnocení bezpečnosti mobilní fotbalové brány
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta strojní Ústav mechaniky, biomechaniky a mechatroniky Odbor mechaniky a mechatroniky Název zprávy Experimentální hodnocení bezpečnosti mobilní fotbalové brány
Statika 1. Reakce na rovinných staticky určitých konstrukcích. Miroslav Vokáč ČVUT v Praze, Fakulta architektury.
 reálných 3. přednáška Reakce na rovinných staticky určitých konstrukcích Miroslav Vokáč miroslav.vokac@cvut.cz ČVUT v Praze, Fakulta architektury 21. března 2016 Dřevěný trámový strop - Anežský klášter
reálných 3. přednáška Reakce na rovinných staticky určitých konstrukcích Miroslav Vokáč miroslav.vokac@cvut.cz ČVUT v Praze, Fakulta architektury 21. března 2016 Dřevěný trámový strop - Anežský klášter
1. Změřte modul pružnosti v tahu E oceli z protažení drátu. 2. Změřte modul pružnosti v tahu E oceli a duralu nebo mosazi z průhybu trámku.
 1 Pracovní úkoly 1. Změřte modul pružnosti v tahu E oceli z protažení drátu. 2. Změřte modul pružnosti v tahu E oceli a duralu nebo mosazi z průhybu trámku. 3. Výsledky měření graficky znázorněte, modul
1 Pracovní úkoly 1. Změřte modul pružnosti v tahu E oceli z protažení drátu. 2. Změřte modul pružnosti v tahu E oceli a duralu nebo mosazi z průhybu trámku. 3. Výsledky měření graficky znázorněte, modul
ZÁKLADNÍ ÚLOHY TEORIE PLASTICITY Teoretické příklady
 Teorie plasticity VŠB TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ KATEDRA PRUŽNOSTI A PEVNOSTI ZÁKLADNÍ ÚLOHY TEORIE PLASTICITY Teoretické příklady 1. ŘEŠENÝ PŘÍKLAD NA TAH ŘEŠENÍ DLE DOVOLENÝCH NAMÁHÁNÍ
Teorie plasticity VŠB TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ KATEDRA PRUŽNOSTI A PEVNOSTI ZÁKLADNÍ ÚLOHY TEORIE PLASTICITY Teoretické příklady 1. ŘEŠENÝ PŘÍKLAD NA TAH ŘEŠENÍ DLE DOVOLENÝCH NAMÁHÁNÍ
ZDM PŘÍMÉ NOSNÍKY. Příklad č. 1. Miloš Hüttner SMR2 ZDM přímé nosníky cvičení 09. Zadání
 iloš Hüttner SR D přímé nosníky cvičení 09 adání D PŘÍÉ NOSNÍKY Příklad č. 1 Vykreslete průběhy vnitřních sil na konstrukci zobrazené na Obr. 1. Příklad převzat z katedrové wikipedie (originál ke stažení
iloš Hüttner SR D přímé nosníky cvičení 09 adání D PŘÍÉ NOSNÍKY Příklad č. 1 Vykreslete průběhy vnitřních sil na konstrukci zobrazené na Obr. 1. Příklad převzat z katedrové wikipedie (originál ke stažení
Globální matice konstrukce
 Globální matice konstrukce Z matic tuhosti a hmotnosti jednotlivých prvků lze sestavit globální matici tuhosti a globální matici hmotnosti konstrukce, které se využijí v řešení základní rovnice MKP: [m]{
Globální matice konstrukce Z matic tuhosti a hmotnosti jednotlivých prvků lze sestavit globální matici tuhosti a globální matici hmotnosti konstrukce, které se využijí v řešení základní rovnice MKP: [m]{
PRUŽNOST A PEVNOST 2 V PŘÍKLADECH
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ PRUŽNOST A PEVNOST 2 V PŘÍKLADECH doc. Ing. Karel Frydrýšek, Ph.D., ING-PAED IGIP Ing. Milan Sivera Ing. Richard Klučka Ing. Josef Sedlák
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ PRUŽNOST A PEVNOST 2 V PŘÍKLADECH doc. Ing. Karel Frydrýšek, Ph.D., ING-PAED IGIP Ing. Milan Sivera Ing. Richard Klučka Ing. Josef Sedlák
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ PRŮVODCE GB01-P03 MECHANIKA TUHÝCH TĚLES
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ Prof. RNDr. Zdeněk Chobola,CSc., Vlasta Juránková,CSc. FYZIKA PRŮVODCE GB01-P03 MECHANIKA TUHÝCH TĚLES STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ Prof. RNDr. Zdeněk Chobola,CSc., Vlasta Juránková,CSc. FYZIKA PRŮVODCE GB01-P03 MECHANIKA TUHÝCH TĚLES STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU
UPÍNACÍ DESKA KONÍKU SOUSTRUHU ŘADY SR SVOČ FST Bc. Milan Kušnír Západočeská univerzita v Plzni Univerzitní 8, Plzeň Česká republika
 UPÍNACÍ DESKA KONÍKU SOUSTRUHU ŘADY SR SVOČ FST 2009 Bc. Milan Kušnír Západočeská univerzita v Plzni Univerzitní 8, 306 14 Plzeň Česká republika ABSTRAKT Práce řeší uložení otočné vložky svršku koníka
UPÍNACÍ DESKA KONÍKU SOUSTRUHU ŘADY SR SVOČ FST 2009 Bc. Milan Kušnír Západočeská univerzita v Plzni Univerzitní 8, 306 14 Plzeň Česká republika ABSTRAKT Práce řeší uložení otočné vložky svršku koníka
Tuhost mechanických částí. Předepnuté a nepředepnuté spojení. Celková tuhosti kinematické vazby motor-šroub-suport.
 Tuhost mechanických částí. Předepnuté a nepředepnuté spojení. Celková tuhosti kinematické vazby motor-šroub-suport. R. Mendřický, M. Lachman Elektrické pohony a servomechanismy 31.10.2014 Obsah prezentace
Tuhost mechanických částí. Předepnuté a nepředepnuté spojení. Celková tuhosti kinematické vazby motor-šroub-suport. R. Mendřický, M. Lachman Elektrické pohony a servomechanismy 31.10.2014 Obsah prezentace
Stavební mechanika 3 132SM3 Přednášky. Deformační metoda: ZDM pro rámy s posuvnými styčníky, využití symetrie, výpočetní programy a kontrola výsledků.
 Stavební mechanika 12SM Přednášky Deformační metoda: ZDM pro rámy s posuvnými styčníky, využití symetrie, výpočetní programy a kontrola výsledků. Porovnání ODM a ZDM Příklad 1: (viz předchozí přednáška)
Stavební mechanika 12SM Přednášky Deformační metoda: ZDM pro rámy s posuvnými styčníky, využití symetrie, výpočetní programy a kontrola výsledků. Porovnání ODM a ZDM Příklad 1: (viz předchozí přednáška)
MODIFIKOVANÝ KLIKOVÝ MECHANISMUS
 MODIFIKOVANÝ KLIKOVÝ MECHANISMUS Michal HAJŽMAN Tento materiál je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky. Vyšetřování pohybu vybraných mechanismů v systému ADAMS
MODIFIKOVANÝ KLIKOVÝ MECHANISMUS Michal HAJŽMAN Tento materiál je spolufinancován Evropským sociálním fondem a státním rozpočtem České republiky. Vyšetřování pohybu vybraných mechanismů v systému ADAMS
Obr. 9.1 Kontakt pohyblivé části s povrchem. Tomuto meznímu stavu za klidu odpovídá maximální síla, která se nezývá adhezní síla,. , = (9.
 9. Tření a stabilita 9.1 Tření smykové v obecné kinematické dvojici Doposud jsme předpokládali dokonale hladké povrchy stýkajících se těles, kdy se silové působení přenášelo podle principu akce a reakce
9. Tření a stabilita 9.1 Tření smykové v obecné kinematické dvojici Doposud jsme předpokládali dokonale hladké povrchy stýkajících se těles, kdy se silové působení přenášelo podle principu akce a reakce
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/ HŘÍDELE A ČEPY
 Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 4.1.Hřídele a čepy HŘÍDELE A ČEPY Hřídele jsou základní strojní součástí válcovitého tvaru, která slouží k
Projekt: Inovace oboru Mechatronik pro Zlínský kraj Registrační číslo: CZ.1.07/1.1.08/03.0009 4.1.Hřídele a čepy HŘÍDELE A ČEPY Hřídele jsou základní strojní součástí válcovitého tvaru, která slouží k
Ing. Jan BRANDA PRUŽNOST A PEVNOST
 Ing. Jan BRANDA PRUŽNOST A PEVNOST Výukový text pro učební obor Technik plynových zařízení Vzdělávací oblast RVP Plynová zařízení a Tepelná technika (mechanika) Pardubice 2013 Aktualizováno: 2015 Použitá
Ing. Jan BRANDA PRUŽNOST A PEVNOST Výukový text pro učební obor Technik plynových zařízení Vzdělávací oblast RVP Plynová zařízení a Tepelná technika (mechanika) Pardubice 2013 Aktualizováno: 2015 Použitá
Namáhání ostění kolektoru
 Inženýrský manuál č. 23 Aktualizace 06/2016 Namáhání ostění kolektoru Program: MKP Soubor: Demo_manual_23.gmk Cílem tohoto manuálu je vypočítat namáhání ostění raženého kolektoru pomocí metody konečných
Inženýrský manuál č. 23 Aktualizace 06/2016 Namáhání ostění kolektoru Program: MKP Soubor: Demo_manual_23.gmk Cílem tohoto manuálu je vypočítat namáhání ostění raženého kolektoru pomocí metody konečných
Téma 3 Úvod ke staticky neurčitým prutovým konstrukcím
 Stavební mechanika, 2.ročník bakalářského studia AST Téma 3 Úvod ke staticky neurčitým prutovým konstrukcím Katedra stavební mechaniky Fakulta stavební, VŠB - Technická univerzita Ostrava Osnova přednášky
Stavební mechanika, 2.ročník bakalářského studia AST Téma 3 Úvod ke staticky neurčitým prutovým konstrukcím Katedra stavební mechaniky Fakulta stavební, VŠB - Technická univerzita Ostrava Osnova přednášky
Předmět: Ročník: Vytvořil: Datum: ŠČERBOVÁ M. PAVELKA V. NAMÁHÁNÍ NA OHYB
 Předmět: Ročník: Vytvořil: Datum: MECHNIK DRUHÝ ŠČERBOVÁ M. PVELK V. 14. ČERVENCE 2013 Název zpracovaného celku: NMÁHÁNÍ N OHYB D) VETKNUTÉ NOSNÍKY ZTÍŽENÉ SOUSTVOU ROVNOBĚŽNÝCH SIL ÚLOH 1 Určete maximální
Předmět: Ročník: Vytvořil: Datum: MECHNIK DRUHÝ ŠČERBOVÁ M. PVELK V. 14. ČERVENCE 2013 Název zpracovaného celku: NMÁHÁNÍ N OHYB D) VETKNUTÉ NOSNÍKY ZTÍŽENÉ SOUSTVOU ROVNOBĚŽNÝCH SIL ÚLOH 1 Určete maximální
VŠB Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti (339) Metoda konečných prvků MKP I (Návody do cvičení)
 VŠB Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti (339) Metoda konečných prvků MKP I (Návody do cvičení) Autoři: Martin Fusek, Radim Halama, Jaroslav Rojíček Verze: 0 Ostrava
VŠB Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti (339) Metoda konečných prvků MKP I (Návody do cvičení) Autoři: Martin Fusek, Radim Halama, Jaroslav Rojíček Verze: 0 Ostrava
Dvě varianty rovinného problému: rovinná napjatost. rovinná deformace
 Rovinný problém Řešíme plošné konstrukce zatížené a uložené v jejich střednicové rovině. Dvě varianty rovinného problému: rovinná napjatost rovinná deformace 17 Rovinná deformace 1 Obsahuje složky deformace
Rovinný problém Řešíme plošné konstrukce zatížené a uložené v jejich střednicové rovině. Dvě varianty rovinného problému: rovinná napjatost rovinná deformace 17 Rovinná deformace 1 Obsahuje složky deformace
III/2-1 Inovace a zkvalitnění výuky prostřednictvím ICT
 Název školy Název projektu Registrační číslo projektu Autor Střední průmyslová škola strojírenská a azyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Modernizace výuky CZ.1.07/1.5.00/34.1003
Název školy Název projektu Registrační číslo projektu Autor Střední průmyslová škola strojírenská a azyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Modernizace výuky CZ.1.07/1.5.00/34.1003
BEZSTYKOVÁ KOLEJ NA MOSTECH
 Ústav železničních konstrukcí a staveb 1 BEZSTYKOVÁ KOLEJ NA MOSTECH Otto Plášek Bezstyková kolej na mostech 2 Obsah Vysvětlení rozdílů mezi předpisem SŽDC S3 a ČSN EN 1991-2 Teoretický základ interakce
Ústav železničních konstrukcí a staveb 1 BEZSTYKOVÁ KOLEJ NA MOSTECH Otto Plášek Bezstyková kolej na mostech 2 Obsah Vysvětlení rozdílů mezi předpisem SŽDC S3 a ČSN EN 1991-2 Teoretický základ interakce
NÁVRH VÝZTUŽE ŽELEZOBETONOVÉHO VAZNÍKU S MALÝM OTVOREM
 NÁVRH VÝZTUŽE ŽELEZOBETONOVÉHO VAZNÍKU S MALÝM OTVOREM Předmět: Vypracoval: Modelování a vyztužování betonových konstrukcí ČVUT v Praze, Fakulta stavební Katedra betonových a zděných konstrukcí Thákurova
NÁVRH VÝZTUŽE ŽELEZOBETONOVÉHO VAZNÍKU S MALÝM OTVOREM Předmět: Vypracoval: Modelování a vyztužování betonových konstrukcí ČVUT v Praze, Fakulta stavební Katedra betonových a zděných konstrukcí Thákurova
METODIKA VÝPOČTU NÁHRADNÍ TUHOSTI NOSNÍKU.
 METODIKA VÝPOČTU NÁHRADNÍ TUHOSTI NOSNÍKU. THE METHODOLOGY OF THE BEAM STIFFNESS SUBSTITUTION CALCULATION. Jiří Podešva 1 Abstract The calculation of the horizontal mine opening steel support can be performed
METODIKA VÝPOČTU NÁHRADNÍ TUHOSTI NOSNÍKU. THE METHODOLOGY OF THE BEAM STIFFNESS SUBSTITUTION CALCULATION. Jiří Podešva 1 Abstract The calculation of the horizontal mine opening steel support can be performed
Vzpěr, mezní stav stability, pevnostní podmínky pro tlak, nepružný a pružný vzpěr Ing. Jaroslav Svoboda
 Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Inovace a zkvalitnění výuky prostřednictvím ICT Název: Téma: Autor: Číslo: Anotace: Mechanika, pružnost pevnost Vzpěr,
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Inovace a zkvalitnění výuky prostřednictvím ICT Název: Téma: Autor: Číslo: Anotace: Mechanika, pružnost pevnost Vzpěr,
Posouzení mikropilotového základu
 Inženýrský manuál č. 36 Aktualizace 06/2017 Posouzení mikropilotového základu Program: Soubor: Skupina pilot Demo_manual_36.gsp Cílem tohoto inženýrského manuálu je vysvětlit použití programu GEO5 SKUPINA
Inženýrský manuál č. 36 Aktualizace 06/2017 Posouzení mikropilotového základu Program: Soubor: Skupina pilot Demo_manual_36.gsp Cílem tohoto inženýrského manuálu je vysvětlit použití programu GEO5 SKUPINA
VŠB- Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti. Úvod do MKP Deformační analýza stojanu na kuželky
 VŠB- Technická univerzita Ostrava akulta strojní Katedra pružnosti a pevnosti Úvod do KP Autor: ichal Šofer Verze Ostrava Úvod do KP Zadání: Určete horizontální a vertikální posun volného konce stojanu
VŠB- Technická univerzita Ostrava akulta strojní Katedra pružnosti a pevnosti Úvod do KP Autor: ichal Šofer Verze Ostrava Úvod do KP Zadání: Určete horizontální a vertikální posun volného konce stojanu
NESTABILITY VYBRANÝCH SYSTÉMŮ. Úvod. Vzpěr prutu. Petr Frantík 1
 NESTABILITY VYBRANÝCH SYSTÉMŮ Petr Frantík 1 Úvod Úloha pokritického vzpěru přímého prutu je řešena dynamickou metodou. Prut se statickým zatížením je modelován jako nelineární disipativní dynamický systém.
NESTABILITY VYBRANÝCH SYSTÉMŮ Petr Frantík 1 Úvod Úloha pokritického vzpěru přímého prutu je řešena dynamickou metodou. Prut se statickým zatížením je modelován jako nelineární disipativní dynamický systém.
Hydromechanické procesy Hydrostatika
 Hydromechanické procesy Hydrostatika M. Jahoda Hydrostatika 2 Hydrostatika se zabývá chováním tekutin, které se vzhledem k ohraničujícímu prostoru nepohybují - objem tekutiny bude v klidu, pokud výslednice
Hydromechanické procesy Hydrostatika M. Jahoda Hydrostatika 2 Hydrostatika se zabývá chováním tekutin, které se vzhledem k ohraničujícímu prostoru nepohybují - objem tekutiny bude v klidu, pokud výslednice
Výpočet vnitřních sil na kruhovém ostění
 Výpočet vnitřních sil na kruhovém ostění Výpočet dle metody Zurabova-Bugajevové Metoda Zubarova-Bugajevové patří k metodám stanovení vnitřních sil na pružném ostění s předurčenou křivkou pasivního odporu.
Výpočet vnitřních sil na kruhovém ostění Výpočet dle metody Zurabova-Bugajevové Metoda Zubarova-Bugajevové patří k metodám stanovení vnitřních sil na pružném ostění s předurčenou křivkou pasivního odporu.
TÍHOVÉ ZRYCHLENÍ TEORETICKÝ ÚVOD. 9, m s.
 TÍHOVÉ ZRYCHLENÍ TEORETICKÝ ÚVOD Soustavu souřadnic spojenou se Zemí můžeme považovat prakticky za inerciální. Jen při několika jevech vznikají odchylky, které lze vysvětlit vlastním pohybem Země vzhledem
TÍHOVÉ ZRYCHLENÍ TEORETICKÝ ÚVOD Soustavu souřadnic spojenou se Zemí můžeme považovat prakticky za inerciální. Jen při několika jevech vznikají odchylky, které lze vysvětlit vlastním pohybem Země vzhledem
BIOMECHANIKA DYNAMIKA NEWTONOVY POHYBOVÉ ZÁKONY, VNITŘNÍ A VNĚJŠÍ SÍLY ČASOVÝ A DRÁHOVÝ ÚČINEK SÍLY
 BIOMECHANIKA DYNAMIKA NEWTONOVY POHYBOVÉ ZÁKONY, VNITŘNÍ A VNĚJŠÍ SÍLY ČASOVÝ A DRÁHOVÝ ÚČINEK SÍLY ROTAČNÍ POHYB TĚLESA, MOMENT SÍLY, MOMENT SETRVAČNOSTI DYNAMIKA Na rozdíl od kinematiky, která se zabývala
BIOMECHANIKA DYNAMIKA NEWTONOVY POHYBOVÉ ZÁKONY, VNITŘNÍ A VNĚJŠÍ SÍLY ČASOVÝ A DRÁHOVÝ ÚČINEK SÍLY ROTAČNÍ POHYB TĚLESA, MOMENT SÍLY, MOMENT SETRVAČNOSTI DYNAMIKA Na rozdíl od kinematiky, která se zabývala
Příklad 7 Průhyb nosníku - složitější případ
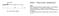 Příklad 7 Průhyb nosníku - složitější případ Zadání Nosník s proměnným průřezem je na obrázku. Průřezy a jsou obdélníkové, výška prvního průřezu je, násobkem výšky druhého průřezu. a) Pomocí metody integrace
Příklad 7 Průhyb nosníku - složitější případ Zadání Nosník s proměnným průřezem je na obrázku. Průřezy a jsou obdélníkové, výška prvního průřezu je, násobkem výšky druhého průřezu. a) Pomocí metody integrace
ANALÝZA NAPĚTÍ A DEFORMACÍ PRŮTOČNÉ ČOČKY KLAPKOVÉHO RYCHLOUZÁVĚRU DN5400 A POROVNÁNÍ HODNOCENÍ ÚNAVOVÉ ŽIVOTNOSTI DLE NOREM ČSN EN 13445-3 A ASME
 1. Úvod ANALÝZA NAPĚTÍ A DEFORMACÍ PRŮTOČNÉ ČOČKY KLAPKOVÉHO RYCHLOUZÁVĚRU DN5400 A POROVNÁNÍ HODNOCENÍ ÚNAVOVÉ ŽIVOTNOSTI DLE NOREM ČSN EN 13445-3 A ASME Michal Feilhauer, Miroslav Varner V článku se
1. Úvod ANALÝZA NAPĚTÍ A DEFORMACÍ PRŮTOČNÉ ČOČKY KLAPKOVÉHO RYCHLOUZÁVĚRU DN5400 A POROVNÁNÍ HODNOCENÍ ÚNAVOVÉ ŽIVOTNOSTI DLE NOREM ČSN EN 13445-3 A ASME Michal Feilhauer, Miroslav Varner V článku se
KMITÁNÍ PRUŽINY. Pomůcky: Postup: Jaroslav Reichl, LabQuest, sonda siloměr, těleso kmitající na pružině
 KMITÁNÍ PRUŽINY Pomůcky: LabQuest, sonda siloměr, těleso kmitající na pružině Postup: Těleso zavěsíme na pružinu a tu zavěsíme na pevně upevněný siloměr (viz obr. ). Sondu připojíme k LabQuestu a nastavíme
KMITÁNÍ PRUŽINY Pomůcky: LabQuest, sonda siloměr, těleso kmitající na pružině Postup: Těleso zavěsíme na pružinu a tu zavěsíme na pevně upevněný siloměr (viz obr. ). Sondu připojíme k LabQuestu a nastavíme
3.2 Základy pevnosti materiálu. Ing. Pavel Bělov
 3.2 Základy pevnosti materiálu Ing. Pavel Bělov 23.5.2018 Normálové napětí představuje vazbu, která brání částicím tělesa k sobě přiblížit nebo se od sebe oddálit je kolmé na rovinu řezu v případě že je
3.2 Základy pevnosti materiálu Ing. Pavel Bělov 23.5.2018 Normálové napětí představuje vazbu, která brání částicím tělesa k sobě přiblížit nebo se od sebe oddálit je kolmé na rovinu řezu v případě že je
Libor Kasl 1, Alois Materna 2
 SROVNÁNÍ VÝPOČETNÍCH MODELŮ DESKY VYZTUŽENÉ TRÁMEM Libor Kasl 1, Alois Materna 2 Abstrakt Příspěvek se zabývá modelováním desky vyztužené trámem. Jsou zde srovnány různé výpočetní modely model s prostorovými
SROVNÁNÍ VÝPOČETNÍCH MODELŮ DESKY VYZTUŽENÉ TRÁMEM Libor Kasl 1, Alois Materna 2 Abstrakt Příspěvek se zabývá modelováním desky vyztužené trámem. Jsou zde srovnány různé výpočetní modely model s prostorovými
VÝZKUM PROVOZNÍCH PARAMETRŮ DOPRAVNÍCH ZAŘÍZENÍ
 VÝZKUM PROVOZNÍCH PARAMETRŮ DOPRAVNÍCH ZAŘÍZENÍ Ing. Jiří Mrázek ČVUT v Praze, Fakulta strojní, Ústav výrobních strojů a mechanismů, Technická 4, 166 07 Praha 6, Jiri.Mrazek@fs.cvut.cz Neustálé zvyšování
VÝZKUM PROVOZNÍCH PARAMETRŮ DOPRAVNÍCH ZAŘÍZENÍ Ing. Jiří Mrázek ČVUT v Praze, Fakulta strojní, Ústav výrobních strojů a mechanismů, Technická 4, 166 07 Praha 6, Jiri.Mrazek@fs.cvut.cz Neustálé zvyšování
Stanovení kritických otáček vačkového hřídele Frotoru
 Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra mechaniky Stanovení ických otáček vačkového hřídele Frotoru Řešitel: oc. r. Ing. Jan upal Plzeň, březen 7 Úvod: Cílem předložené zprávy je
Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra mechaniky Stanovení ických otáček vačkového hřídele Frotoru Řešitel: oc. r. Ing. Jan upal Plzeň, březen 7 Úvod: Cílem předložené zprávy je
9. MĚŘENÍ SÍLY TENZOMETRICKÝM MŮSTKEM
 9. MĚŘENÍ SÍLY TENZOMETICKÝM MŮSTKEM Úvod: Tenzometry se používají např. pro: Měření deformací objektů. Měření síly, tlaku, krouticího momentu, momentu síly, mechanického napětí spojů. Měření zatížení
9. MĚŘENÍ SÍLY TENZOMETICKÝM MŮSTKEM Úvod: Tenzometry se používají např. pro: Měření deformací objektů. Měření síly, tlaku, krouticího momentu, momentu síly, mechanického napětí spojů. Měření zatížení
