RYCHLOST NEBO POHYB CHODCE DLE POŠKOZENÍ ZANECHANÝCH NA VOZIDLE
|
|
|
- Magdalena Vávrová
- před 6 lety
- Počet zobrazení:
Transkript
1 RYCHLOST NEBO POHYB CHODCE DLE POŠKOZENÍ ZANECHANÝCH NA VOZIDLE ABSTRAKT: PEDESTRIAN S SPEED OR MOVEMENT BASED ON IMPACT MARKS REMAINED ON THE VEHICLE Gbriel Pdurru 23 U nehod s chodci, které byly nlyzovány, byl veli důležitý pretre ve výpočtu ožnosti vyhnutí se nehodě rychlost chodce. Rychlost pohybu chodců se bere z grfů nebo tbulek, ve kterých se zznenává rychlost v souvislosti s věke, ntropoetrickýi údji, zvláštníi podínki pohybu td. V noh přípdech se všk popis pohybu chodce liší podle toho, zd jej popisují chodci svědkové, nebo řidič. Je zřejé, že ožnosti vyhnutí se nehodě jsou jiné, jedná-li se o norální chůzi, nebo o spěch či rychlý pohyb chodce. V toto článku nvrhujee způsob interpretce nlýzy podle stop znechných n vozidle, které uožňují vypočítt rychlost chůze chodce nebo stnovit druh pohybu chodce v okžiku, kdy došlo ke kolizi. KLÍČOVÁ SLOVA: nehod s chodci, pohyb chodce, rychlost chůze chodce, znechné stopy 1 ÚVOD Při nehodě ezi chodce vozidle hrje roli několik proěnných, tkže výsledke je složitý vzorec. V článku se budee zbývt různýi fktory, které při nehodě s chodci připdjí v úvhu, le zěříe se pouze n ty, které jsou přío propojeny s nvržený způsobe výpočtu. Dráh chodce vzdálenost projekce po kolizi s vozidle záleží hlvně n čtyřech fktorech. První fktore je typ vozidl jeho přední části. Evropští specilisté provedli výzku, n zákldě kterého rozčlenili přední část vozidl do čtyř typů: klínovou, trpezoidní (á tři podktegorie), pontonovou skříňovou [1]. Druhý fktore je konstituce chodce, hlvně hotnost výšk. Konstituce chodce závisí n věku deogrfické situci v ístě, kde došlo k nehodě.[2]. S figuríni [3] vyrobenýi n zákldě sttistik, tk by vyhovovly ntropoetrický údjů, byly provedeny experienty, jejichž výsledky byly ověřeny počítčovýi siulcei údji z nlýz skutečných nehod. Třetí důležitý fktore je ísto, kde ke kolizi, došlo poloh chodce ve vzthu k přední části vozidl. To je veli důležitý fktor, protože n ně závisí nožství energie, 23 Gbriel Pdurru, dipl. eng., M.Sc. - Ntionl Institute of Forensic Expertise, Buchrest Roni, district Lbortory of Isi 107
2 které ovlivní tělo chodce. Je znáo, že při kolizi s rohy přední části vozidl, dostává tělo chodce jen část energie, kterou by dostlo při kolizi s prostřední částí přední části vozidl. Čtvrtý důležitý pretre při provádění výzkuu nlýz nehod s chodci je rychlost chůze chodce. Rychlost chůze chodce je veli důležitá, protože podle ní lze stnovit, zd se řidič ohl kolizi vyhnout. Při rychlostech chodců vyšších než 10 k/h je jejich dráh znčně ovlivněn kolizí s vozidle. Dále popíšee způsob výpočtu rychlosti chůze chodců podle poškození zjištěného n vozidle po kolizi. 2 ZPŮSOB VÝPOČTU Výzku provedený Kllierise Schidte [4] ukázl, že ezi okžike kontktu boku oběti hlvy chodce s čelní skle vozidl uplyne dob si 120 s při rychlosti 28 k/h při kolizi, když je vozidle středně velké uto. Meissner kolektiv [5] provedli počítčovou studii dyniky kolize vozidlo-chodec poocí tetického odelu Mdyo figuríny Polr II. Studie byl proveden s běžný rodinný utoobile voze SUV při rychlosti 40 k/h. V přípdě utoobilu byl výsledná hodnot doby ezi kontkte boku hlvy 125 s v přípdě vozu SUV byl hodnot trvání si 100 s. Ve srovnání s testy prováděnýi n figurínách nsěrovných proti vystupující přední části vozidl, které je pro chodce éně trutické, vyšl v testech prováděných s neživýi těly (PMHS Post Morte Hun Subjects) dob ezi kontkte si 100 s. Jponští výzkuníci (Akiy kolektiv) [6] srovnávli skutečné výsledky s výsledky získnýi experientálně poocí figurín počítčové siulce poocí progru Mdyo verze 5.3. Závěre této studie je, že při rychlosti 40 k/h reprodukuje počítčová siulce přesně výsledky testů prováděných s neživýi těly i figuríni. Dob 120 s v přípdě nízkých rychlostí kolize do 30 k/h 100 s v přípdě vyšších rychlostí do 50 k/h bude použit v nše výzkuu. Pro dosžení přesných výsledků je sozřejě třeb provést experienty z použití: 1) stejného typu vozidl nebo co nejvíce podobného vozidl jko při nehodě 2) figuríny, která je shodná s ntropoetrickýi dty oběti. Po kolizi s chodce zůstávjí n vozidle znáky poškození deforce způsobené kontkte boku s kpotou kontkte hlvy oběti s čelní skle (obr.1). 108
3 Obr. 1. Kontkt boku s kpotou hlvy s čelní skle Vzdálenost ezi těito dvě stopi poškození bude oznčen jko s (obr. 2). Tto vzdálenost je ovlivněn fkte, že vlive setrvčnosti zchovává po krátkou dobu tělo oběti svůj původní pohyb. Obr. 2. Vzdálenost oznčená s ezi stopi poškození vzniklýi kontkte boku hlvy 109
4 Dob, která uplyne ezi kolizí rene hlvy, se dá vypočítt ze vzorce pro pohyb chodce, předpokládáe-li, že se jedná o lineární rovnoěrný pohyb: s t = (1) V p kde: V p = rychlost chodce </s>; s = vzdálenost <>. V toto čsové úseku zznená vozidlo ztrátu rychlosti ΔV vlive nárůstu hotnosti, kterou lze vyjádřit následující způsobe: ΔV = p Vi (2) kde: p = hotnost chodce <kg>; = hotnost vozidl <kg>; V i = rychlost vozidl v okžiku před kolizí. Ke ztrátě rychlosti ΔV dojde v době t, která je si s, jk bylo uvedeno výše. Této ztrátě rychlosti odpovídá d, které lze vypočítt poocí vzorce: d = ΔV t (3) Srovnání vzorce (1) vzorce (3) dostnee: s V p = ΔV d (4) Snížení rychlosti záleží n rychlosti kolize, hotnosti chodce době, která uplyne ezi kontkte s boke hlvou oběti. V přípdě rychlosti kolize ezi k/h, hotnosti chodce 75 kg hotnosti vozidl ezi kg je snížení rychlosti ezi 6,9-10 /s 2, což odpovídá snížení rychlosti n suché sfltové povrchu. Musíe zínit skutečnost, že hotnost vozidl předstvuje hotnost celého vozidl, i s náklde, psžéry řidiče. 110
5 Rychlost kolize lze vypočítt poocí vzdálenosti ujeté od okžiku, kdy došlo ke kolizi, ž do okžiku, kdy vozidlo zstvilo. (5). V i = 2 g f S </s> (5) Kobincí vzorce (2) (4) získáe: V p = s 1 d p V </s> (6) i V přípdě, kdy ke kolizi došlo při brzdění, lze vzorec (6) zkobinovný se vzorce (5) přepst následovně: kde: V p = s d p 1 </s> (7) 2 g f S f = koeficient dheze pneutik k povrchu silnice; S = vzdálenost ujetá vozidle po kolizi ž do zstvení; Pokud se v okžiku kolize zpolení rovná zpolení při brzdění, lze vzorec (6) přepst následovně: V p = s p g 2 f S </s> (8) nebo V p = 3,6 s p g 2 f S <k/h> (9) Poocí odhdu, který je dosttečně přesný, lze vzorec (9) přepst následovně: 1 V p = 7 s <k/h> S p 111
6 ExFoS - Expert Forensic Science 3 PŘÍPADOVÁ STUDIE Při nlýze nehody bylo poždováno uvedení toho, zd chodec běžel nebo kráčel norální rychlosti, to společně s rychlostí vozidl bylo podklde pro vyhodnocení toho, zd se nehodě dlo předejít. Poškození vozidl jko následek kolize s chodce je znázorněno n obrázcích 3 4. obr. 3. Poškození n čelní skle obr. 4. Poškození n přední světle 112
7 ExFoS - Expert Forensic Science Vzdálenost oznčená jko s ezi poškození vedle předního světl poškození n přední skle lze zěřit n nákresu vozidl ve skutečnosti (obr.5). Obr. 5 Vzdálenost oznčená s ezi znáki poškození n vozidle po kolizi Rychlost ut v okžiku kolize Vi, byl určen n zákldě brzdných stop (obr. 6) n 41 k/h. Silnice byl v tu dobu pokryt tenkou vrstvou sněhu (obr. 7). Obr.6 Nákres nehody v lé ěřítku Obr.7 Fotogrfie pořízená n ístě nehody 113
8 V utě byli přítoni řidič jeden spolucestující. Obětí byl žen ve věku 72 let o hotnosti si 70 kg. Vezee-li v úvhu skutečnost, že zpolení ut při brzdění bylo si 5,5 /s 2, odlišné od 7,2 /s 2, což je specifické zpolení při kolizi v toto přípdě, bude vzorec n výpočet rychlosti chodce následující (6): V p = s 1 d p V (6) i kde: = = 1110 kg; p = 70 kg; V i = 41 k/h = 19,72 /s; d = 7,1 /s 2 ; s = 0,39. Doszení získáe: V p = ,2 = 2,25 /s = 8,1 k/h 70 19,72 Podle nejnovějších výpočtů provedených polskýi specilisty [7] rychlost přecházení chodce tk ptří do ktegorie běhu. Osob, která zčl přecházet silnici, uvedl, že se pohybovli rychle, způsobe pohybu, pro který se v litertuře uvádí rychlost si 4,1 k/h. Výpočet toho, zd se dlo nehodě vyhnout, je proveden tk, že se vychází od íst, kde se ncházelo uto v okžiku, kdy zčl nebezpečná situce, použije se následující vzorec: S = V i S p V = 2, 9 p 4,1 41 = 29 = 41 2, 9 8,1 = 14,67 kde: S p = 2,9 vzdálenost, kterou ušel chodec od středu vozovky ž do íst kolize; Rychlost, při které by se nehodě dlo vyhnout brzdění, lze vypočítt poocí následujícího vzorce: 114
9 V ev = 3,6 d t 1 ExFoS - Expert Forensic Science îi 2 S d t 2 îi = 3, , = 50,09 k/h; 1 5,4 0,64 3, ,8 2 14,67 = = 32,35 k/h. 1 5,4 0,64 kde: t îi = 0,8 s trvání neúyslných zpoždění; Podle výše uvedených výpočtů je zřejé, že v přípdě, kdy by chodec přecházel vozovku vysokou rychlostí, ohl by se řidič vyhnout kolizi, pokud by zčl brzdit včs. Rychlost nutná k tou, by se nehodě dlo vyhnout, byl 50 k/h, což je rychlost vyšší než rychlost vozidl v okžiku kolize (která je stejná jko rychlost v okžiku před nehodou) 41 k/h. V přípdě, kdy by chodec přes vozovku běžel, by se řidič vozidl ohl nehodě vyhnout, pouze pokud by rychlost vozidl byl xiálně 32 k/h, což je rychlost nižší než skutečná rychlost vozidl 41 k/h. Rychlost pohybu vozidl 41 k/h byl nižší než xiální přijtelný liit pro tu část vozovky, kde k nehodě došlo. 4 SIMULACE NEHODY PŘÍPADU POMOCÍ V.CRASH 2.2 Siulční odely pro nehody vozidl s chodce lze úspěšně použít, pokud jsou správně určeny vstupní pretry. V toto přípdě jse použili progr V.Crsh 2.2, bycho zjistili, zd tetický odel určí správně íst, kde došlo k poškození. Zvolili jse utoobil VW Golf 3 chodce ženského pohlví, vysokého 1,6 o hotnosti 78 kg. V první přípdě, kdy rychlost chodce byl 4,1 k/h, byl vzdálenost s 20 c, ěřeno ezi první bode kontktu (levé přední světlo) (obr.8) bode poškození n přední skle (obr. 9). Poocí stejného odelu stejných pretrů kroě rychlosti chodce, která byl určen n 8,1 k/h zěnil pohyb chodce n běh, jse získli pro stejný bod prvního kontktu (obr.10) stejnou vzdálenost ezi body poškození jko při skutečné nehodě (obr.11). Tto siulce potvrzuje, že nvržený vzorec progr V.Crsh 2.2 lze se správně nstvenýi pretry úspěšně použít. 115
10 Obr.8 První bod kontktu Obr. 9 Vzdálenost s ezi body poškození 116
11 Obr.10 První bod kolize (rychlost chodce 8,1 k/h). Obr.11 Vzdálenost s ezi body poškození 117
12 5 ZÁVĚR ExFoS - Expert Forensic Science Cíle předložené studie je vzorec výpočtu, který by ěl být záklde pro výpočet rychlosti chodce, jenž byl obětí nehody s vozidle. Rychlost vypočítná n zákldě vzorce neá bsolutní hodnotu, le ůže pooci určit způsob chůze chodce. Jk je zřejé z prezentovné přípdové studie, je určení rychlosti chodce nebo způsobu pohybu chodce stnovení tohoto pretru zején důležité při zjišťování toho, zd bylo ožné se nehodě vyhnout. 6 LITERATURA [1]. Moser, A.; Hoschopf, H.; Steffn, H.; Ksnicky, G. - Vlidtion of PC-Crsh Pedestrin Model, SAE , Accident Reconstruction: Anlysis, Siultion nd Visuliztion (SP-1491); [2]. Sten, J.A.; Ko, S.; Guenther, D. A.; Heidinger, G. - A Deogrphic Anlysis nd Reconstruction of Selected Cses fro the Pedestrin Crsh Dt Study, SAE , Accident Reconstruction 2002 (SP-1666); [3]. Weyde, M.; Jger, S.; Knpe, M.; - Construction nd testing of pedestrin duy for relistic vehicle dge in experientl siultions of cr vs. pedestrin collisions - EVU ; [4]. Kllieris, D.; Schidt, G.; - New spects of pedestrin protection loding nd injury pttern in siulted pedestrin ccidents - SAE pper ; [5]. Meissner, M.; Rooj, L.; Bhll, J.; Longhtno, D.; Tkhshi, Y.; Dokko, Y.; Kikuchi, Y.; - A Multi-Body Coputtionl Study of the Kinetic nd Injury Response of Pedestrin with Vrible Stnce upon Ipct with Vehicle - SAE Vehicle Aggressivity nd Coptibility, structurl Crshworthiness, nd Pedestrin Sfety (SP-1878); [6]. Akiy, A.; Yoshid, S.; Mtsuhshi, T.; Shs, T.; Rngrjn, N.; Konosu, A.; Ishikw, H.; - Developent of Siultion Model nd Pedestrin Duy - SAE Advnces in Sfety technology 1999 (SP 1433); [7]. Zebl, J.; Ciepk, P.; Rez, A.; - Pedestrin speeds nd ccelertion - results of reserch on conteporry popultion - EVU ; Kontkt Gbriel Pdurru Str. Codrescu No. 11 A, D , Isi, Roni e-ils: contct@gpdurru.ro gbipdurru2004@yhoo.co tel:
Pístový efekt výtahů ve stavebních objektech
 Pístový efekt výthů ve stvebních objektech Ing. Jiří Pokorný, Ph.D. Hsičský záchrnný sbor Morvskoslezského krje úzení odbor Opv Těšínská 39, 746 01 Opv e-il: jiripokorny@ujil.cz Klíčová slov Pístový efekt,
Pístový efekt výthů ve stvebních objektech Ing. Jiří Pokorný, Ph.D. Hsičský záchrnný sbor Morvskoslezského krje úzení odbor Opv Těšínská 39, 746 01 Opv e-il: jiripokorny@ujil.cz Klíčová slov Pístový efekt,
( ) 1.5.2 Mechanická práce II. Předpoklady: 1501
 1.5. Mechnická práce II Předpokldy: 1501 Př. 1: Těleso o hmotnosti 10 kg bylo vytženo pomocí provzu do výšky m ; poprvé rovnoměrným přímočrým pohybem, podruhé pohybem rovnoměrně zrychleným se zrychlením
1.5. Mechnická práce II Předpokldy: 1501 Př. 1: Těleso o hmotnosti 10 kg bylo vytženo pomocí provzu do výšky m ; poprvé rovnoměrným přímočrým pohybem, podruhé pohybem rovnoměrně zrychleným se zrychlením
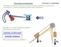
Základní principy fyziky semestrální projekt. Studium dynamiky kladky, závaží a vozíku
 Zákldní principy fyziky seestrální projekt Studiu dyniky kldky, závží vozíku Petr Luzr I/4 008/009 Zákldní principy fyziky Seestrální projekt Projekt zdl: Projekt vyprcovl: prof. In. rntišek Schuer, DrSc.
Zákldní principy fyziky seestrální projekt Studiu dyniky kldky, závží vozíku Petr Luzr I/4 008/009 Zákldní principy fyziky Seestrální projekt Projekt zdl: Projekt vyprcovl: prof. In. rntišek Schuer, DrSc.
(1) přičemž všechny veličiny uvažujeme absolutně. Její úpravou získáme vztah + =, (2) Přímé zvětšení Z je dáno vztahem Z = =, a a
 Úloh č. 3 Měření ohniskové vzdálenosti tenkých čoček 1) Pomůcky: optická lvice, předmět s průhledným milimetrovým měřítkem, milimetrové měřítko, stínítko, tenká spojk, tenká rozptylk, zdroj světl. ) Teorie:
Úloh č. 3 Měření ohniskové vzdálenosti tenkých čoček 1) Pomůcky: optická lvice, předmět s průhledným milimetrovým měřítkem, milimetrové měřítko, stínítko, tenká spojk, tenká rozptylk, zdroj světl. ) Teorie:
Obr. 1: Optická lavice s příslušenstvím při měření přímou metodou. 2. Určení ohniskové vzdálenosti spojky Besselovou metodou
 MĚŘENÍ PARAMETRŮ OPTICKÝCH SOUSTAV Zákldním prmetrem kždé zobrzovcí soustvy je především její ohnisková vzdálenost. Existuje několik metod k jejímu určení le téměř všechny jsou ztíženy určitou nepřesností
MĚŘENÍ PARAMETRŮ OPTICKÝCH SOUSTAV Zákldním prmetrem kždé zobrzovcí soustvy je především její ohnisková vzdálenost. Existuje několik metod k jejímu určení le téměř všechny jsou ztíženy určitou nepřesností
1.1.6 Měření pohybu. Předpoklady: Pomůcky: papírový šnek
 6 Měření pohybu Předpokldy: 0005 Poůcky: ppírový šnek Pedgogická poznák: Pokud nebudete provádět pokus se šneke (což nedoporučuji žáků se pokus líbí) ůžete stihnout látku této následující hodiny z jednu
6 Měření pohybu Předpokldy: 0005 Poůcky: ppírový šnek Pedgogická poznák: Pokud nebudete provádět pokus se šneke (což nedoporučuji žáků se pokus líbí) ůžete stihnout látku této následující hodiny z jednu
Laboratorní práce č. 6 Úloha č. 5. Měření odporu, indukčnosti a vzájemné indukčnosti můstkovými metodami:
 Truhlář Michl 3 005 Lbortorní práce č 6 Úloh č 5 p 99,8kP Měření odporu, indukčnosti vzájemné indukčnosti můstkovými metodmi: Úkol: Whetstoneovým mostem změřte hodnoty odporů dvou rezistorů, jejich sériového
Truhlář Michl 3 005 Lbortorní práce č 6 Úloh č 5 p 99,8kP Měření odporu, indukčnosti vzájemné indukčnosti můstkovými metodmi: Úkol: Whetstoneovým mostem změřte hodnoty odporů dvou rezistorů, jejich sériového
3. Kvadratické rovnice
 CZ..07/..08/0.0009. Kvdrtické rovnice se v tetice oznčuje lgebrická rovnice druhého stupně, tzn. rovnice o jedné neznáé, ve které neznáá vystupuje ve druhé ocnině (²). V zákldní tvru vypdá následovně:
CZ..07/..08/0.0009. Kvdrtické rovnice se v tetice oznčuje lgebrická rovnice druhého stupně, tzn. rovnice o jedné neznáé, ve které neznáá vystupuje ve druhé ocnině (²). V zákldní tvru vypdá následovně:
Pedagogická poznámka: Cílem hodiny je zopakování vztahu pro hustotu, ale zejména nácvik základní práce se vzorci a jejich interpretace.
 1.1.5 Hustota Předpoklady: 010104 Poůcky: voda, olej, váhy, dvojice kuliček, dvě stejné kádinky, dva oděrné válce. Pedagogická poznáka: Cíle hodiny je zopakování vztahu pro hustotu, ale zejéna nácvik základní
1.1.5 Hustota Předpoklady: 010104 Poůcky: voda, olej, váhy, dvojice kuliček, dvě stejné kádinky, dva oděrné válce. Pedagogická poznáka: Cíle hodiny je zopakování vztahu pro hustotu, ale zejéna nácvik základní
RYCHLOST CHODCŮ VÝSLEDKY VÝZKUMU V SOUČASNÉ POPULACI
 RYCHLOST CHODCŮ VÝSLEDKY VÝZKUMU V SOUČASNÉ POPULACI ABSTRAKT: Piotr Ciępka 3, Adam Reza 4, Jakub Zębala 5 Cílem článku je prezentovat výsledky výzkumu provedeného v Ústavu soudního inženýrství v Krakově,
RYCHLOST CHODCŮ VÝSLEDKY VÝZKUMU V SOUČASNÉ POPULACI ABSTRAKT: Piotr Ciępka 3, Adam Reza 4, Jakub Zębala 5 Cílem článku je prezentovat výsledky výzkumu provedeného v Ústavu soudního inženýrství v Krakově,
Potřeba tepla na vytápění budovy
 SPJ1 Podkldy pro cvičení Potřeb tepl n vytápění budovy In. Kil Stněk, 10/2010 kil.stnek@sv.cvut.cz 1 Sché výpočtu 1.1 Potřeb tepl n vytápění Potřebu tepl n vytápění budovy nd [kwh] vypočtee bilncování
SPJ1 Podkldy pro cvičení Potřeb tepl n vytápění budovy In. Kil Stněk, 10/2010 kil.stnek@sv.cvut.cz 1 Sché výpočtu 1.1 Potřeb tepl n vytápění Potřebu tepl n vytápění budovy nd [kwh] vypočtee bilncování
Posouzení stability svahu
 Verifikční nuál č. 3 Aktulizce 04/016 Posouzení stbility svhu Progr: Soubor: Stbilit svhu Deo_v_03.gst V toto verifikční nuálu je uveden ruční výpočet posouzení stbility svhu posouzení stbility svhu zbezpečeného
Verifikční nuál č. 3 Aktulizce 04/016 Posouzení stbility svhu Progr: Soubor: Stbilit svhu Deo_v_03.gst V toto verifikční nuálu je uveden ruční výpočet posouzení stbility svhu posouzení stbility svhu zbezpečeného
KATEDRA MATERIÁLOVÉHO INŽENÝRSTVÍ A CHEMIE. 123TVVM homogenizace (směšovací pravidla)
 KATEDRA MATERIÁLOVÉHO INŽENÝRSTVÍ A CHEMIE 23TVVM hoogenizce (sěšovcí prvidl) Hoogenizce Stvební teriály sou z hledisk zstoupení doinntních složek několikfázové systéy: Dvoufázové trice, vzduch (póry)
KATEDRA MATERIÁLOVÉHO INŽENÝRSTVÍ A CHEMIE 23TVVM hoogenizce (sěšovcí prvidl) Hoogenizce Stvební teriály sou z hledisk zstoupení doinntních složek několikfázové systéy: Dvoufázové trice, vzduch (póry)
25 Měrný náboj elektronu
 5 Měrný náboj elektronu ÚKOL Stnovte ěrný náboj elektronu e výsledek porovnejte s tbulkovou hodnotou. TEORIE Poěr náboje elektronu e hotnosti elektronu nzýváe ěrný náboj elektronu. Jednou z ožných etod
5 Měrný náboj elektronu ÚKOL Stnovte ěrný náboj elektronu e výsledek porovnejte s tbulkovou hodnotou. TEORIE Poěr náboje elektronu e hotnosti elektronu nzýváe ěrný náboj elektronu. Jednou z ožných etod
6. a 7. března Úloha 1.1. Vypočtěte obsah obrazce ohraničeného parabolou y = 1 x 2 a osou x.
 KMA/MAT Přednášk cvičení č. 4, Určitý integrál 6. 7. březn 17 1 Aplikce určitého integrálu 1.1 Počáteční úvhy o výpočtu obshu geometrických útvrů v rovině Úloh 1.1. Vypočtěte obsh obrzce ohrničeného prbolou
KMA/MAT Přednášk cvičení č. 4, Určitý integrál 6. 7. březn 17 1 Aplikce určitého integrálu 1.1 Počáteční úvhy o výpočtu obshu geometrických útvrů v rovině Úloh 1.1. Vypočtěte obsh obrzce ohrničeného prbolou
Ochrana před úrazem elektrickým proudem Společná hlediska pro instalaci a zařízení. 1. Definice
 ČSN EN 61 140 Ochrn před úrzem elektrickým proudem Společná hledisk pro instlci zřízení Tto mezinárodní norm pltí pro ochrnu osob zvířt před úrzem elektrickým proudem. Je určen pro poskytnutí zákldních
ČSN EN 61 140 Ochrn před úrzem elektrickým proudem Společná hledisk pro instlci zřízení Tto mezinárodní norm pltí pro ochrnu osob zvířt před úrzem elektrickým proudem. Je určen pro poskytnutí zákldních
Praktikum 1. Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. Úloha č...xvi... Název: Studium Brownova pohybu
 Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK Praktiku 1 Úloha č...xvi... Název: Studiu Brownova pohybu Pracoval: Jan Kotek stud.sk.: 17 dne: 7.3.2012 Odevzdal dne:... ožný počet
Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK Praktiku 1 Úloha č...xvi... Název: Studiu Brownova pohybu Pracoval: Jan Kotek stud.sk.: 17 dne: 7.3.2012 Odevzdal dne:... ožný počet
Křivkový integrál prvního druhu verze 1.0
 Křivkový integrál prvního druhu verze. Úvod Následující text popisuje výpočet křivkového integrálu prvního druhu. Měl by sloužit především studentům předmětu MATEMAT k příprvě n zkoušku. Mohou se v něm
Křivkový integrál prvního druhu verze. Úvod Následující text popisuje výpočet křivkového integrálu prvního druhu. Měl by sloužit především studentům předmětu MATEMAT k příprvě n zkoušku. Mohou se v něm
II. kolo kategorie Z5
 II. kolo ktegorie Z5 Z5 II 1 Z prvé kpsy klhot jsem přendl 4 pětikoruny do levé kpsy z levé kpsy jsem přendl 16 dvoukorun do prvé kpsy. Teď mám v levé kpse o 13 korun méně než v prvé. Ve které kpse jsem
II. kolo ktegorie Z5 Z5 II 1 Z prvé kpsy klhot jsem přendl 4 pětikoruny do levé kpsy z levé kpsy jsem přendl 16 dvoukorun do prvé kpsy. Teď mám v levé kpse o 13 korun méně než v prvé. Ve které kpse jsem
URČITÝ INTEGRÁL FUNKCE
 URČITÝ INTEGRÁL FUNKCE Formulce: Nším cílem je určit přibližnou hodnotu určitého integrálu I() = () d, kde předpokládáme, že unkce je n intervlu, b integrovtelná. Poznámk: Geometrický význm integrálu I()
URČITÝ INTEGRÁL FUNKCE Formulce: Nším cílem je určit přibližnou hodnotu určitého integrálu I() = () d, kde předpokládáme, že unkce je n intervlu, b integrovtelná. Poznámk: Geometrický význm integrálu I()
Teoretický souhrn k 2. až 4. cvičení
 SYSTÉMOVÁ ANALÝZA A MODELOVÁNÍ Teoretcký souhrn k 2. ž 4. cvčení ZS 2009 / 200 . Vyezení zákldních poů.. Systé e Systé e účelově defnovná nožn prvků vze ez n, která spolu se svý vstupy výstupy vykzue ko
SYSTÉMOVÁ ANALÝZA A MODELOVÁNÍ Teoretcký souhrn k 2. ž 4. cvčení ZS 2009 / 200 . Vyezení zákldních poů.. Systé e Systé e účelově defnovná nožn prvků vze ez n, která spolu se svý vstupy výstupy vykzue ko
Psychologická metodologie. NMgr. obor Psychologie
 Pržská vysoká škol psychosociálních studií, s.r.o. Temtické okruhy ke státní mgisterské zkoušce Psychologická metodologie NMgr. oor Psychologie 1 Vědecká teorie vědecká metod Vědecké vysvětlení, vědecký
Pržská vysoká škol psychosociálních studií, s.r.o. Temtické okruhy ke státní mgisterské zkoušce Psychologická metodologie NMgr. oor Psychologie 1 Vědecká teorie vědecká metod Vědecké vysvětlení, vědecký
Určení geometrických a fyzikálních parametrů čočky
 C Určení geoetrickýc a yzikálníc paraetrů čočky Úkoly :. Určete poloěry křivosti ploc čočky poocí séroetru. Zěřte tloušťku čočky poocí digitálnío posuvnéo ěřítka 3. Zěřte oniskovou vzdálenost spojné čočky
C Určení geoetrickýc a yzikálníc paraetrů čočky Úkoly :. Určete poloěry křivosti ploc čočky poocí séroetru. Zěřte tloušťku čočky poocí digitálnío posuvnéo ěřítka 3. Zěřte oniskovou vzdálenost spojné čočky
Popis fyzikálního chování látek
 Popis fyzikálního chování látek pro vysvětlení noha fyzikálních jevů již nevystačíe s pouhý echanický popise Terodynaika oblast fyziky, která kroě echaniky zkouá vlastnosti akroskopických systéů, zejéna
Popis fyzikálního chování látek pro vysvětlení noha fyzikálních jevů již nevystačíe s pouhý echanický popise Terodynaika oblast fyziky, která kroě echaniky zkouá vlastnosti akroskopických systéů, zejéna
1. Mechanika - úvod. [ X ] - měřící jednotka. { X } - označuje kvantitu (množství)
![1. Mechanika - úvod. [ X ] - měřící jednotka. { X } - označuje kvantitu (množství) 1. Mechanika - úvod. [ X ] - měřící jednotka. { X } - označuje kvantitu (množství)](/thumbs/24/3153976.jpg) . Mechanika - úvod. Základní pojy V echanice se zabýváe základníi vlastnosti a pohybe hotných těles. Chcee-li přeístit těleso (echanický pohyb), potřebujee k tou znát tyto tři veličiny: hota, prostor,
. Mechanika - úvod. Základní pojy V echanice se zabýváe základníi vlastnosti a pohybe hotných těles. Chcee-li přeístit těleso (echanický pohyb), potřebujee k tou znát tyto tři veličiny: hota, prostor,
1.1 Numerické integrování
 1.1 Numerické integrování 1.1.1 Úvodní úvhy Nším cílem bude přibližný numerický výpočet určitého integrálu I = f(x)dx. (1.1) Je-li znám k integrovné funkci f primitivní funkce F (F (x) = f(x)), můžeme
1.1 Numerické integrování 1.1.1 Úvodní úvhy Nším cílem bude přibližný numerický výpočet určitého integrálu I = f(x)dx. (1.1) Je-li znám k integrovné funkci f primitivní funkce F (F (x) = f(x)), můžeme
Ke schválení technické způsobilosti vozidla je nutné doložit: Musí být doložen PROTOKOL O TECHNICKÉ KONTROLE? ANO NE 10)
 ÚTAV INIČNÍ A MĚTKÉ DPRAVY.s., Prh 4,Chodovec, Türkov 1001,PČ 149 00 člen skupiny DEKRA www.usmd.cz,/ Přehled zákldních vrint pltných pro dovoz jednotlivých vozidel dle zákon č.56/2001b. ve znění zákon
ÚTAV INIČNÍ A MĚTKÉ DPRAVY.s., Prh 4,Chodovec, Türkov 1001,PČ 149 00 člen skupiny DEKRA www.usmd.cz,/ Přehled zákldních vrint pltných pro dovoz jednotlivých vozidel dle zákon č.56/2001b. ve znění zákon
VZDUCH V MÍSTNOSTI POMŮCKY NASTAVENÍ MĚŘICÍHO ZAŘÍZENÍ. Vzdělávací předmět: Fyzika. Tematický celek dle RVP: Látky a tělesa
 VZDUCH V MÍSTNOSTI Vzdělávací předět: Fyzika Teatický celek dle RVP: Látky a tělesa Teatická oblast: Měření fyzikálních veličin Cílová skupina: Žák 6. ročníku základní školy Cíle pokusu je určení rozěrů
VZDUCH V MÍSTNOSTI Vzdělávací předět: Fyzika Teatický celek dle RVP: Látky a tělesa Teatická oblast: Měření fyzikálních veličin Cílová skupina: Žák 6. ročníku základní školy Cíle pokusu je určení rozěrů
( ) ( ) Newtonův zákon II. Předpoklady:
 6 Newtonův zákon II Předpoklady: 0005 Př : Autoobil zrychlí z 0 k/h na 00 k/h za 8 s Urči velikost síly, která auto uvádí do pohybu, pokud autoobil váží,6 tuny Předpokládej rovnoěrně zrychlený pohybu auta
6 Newtonův zákon II Předpoklady: 0005 Př : Autoobil zrychlí z 0 k/h na 00 k/h za 8 s Urči velikost síly, která auto uvádí do pohybu, pokud autoobil váží,6 tuny Předpokládej rovnoěrně zrychlený pohybu auta
2.2.9 Grafické řešení rovnic a nerovnic
 ..9 Grfické řešení rovnic nerovnic Předpokldy: 0, 06 Př. : Řeš početně i grficky rovnici x + = x. Početně: Už umíme. x + = x x = x = K = { } Grficky: Kždá ze strn rovnice je výrzem pro lineární funkci
..9 Grfické řešení rovnic nerovnic Předpokldy: 0, 06 Př. : Řeš početně i grficky rovnici x + = x. Početně: Už umíme. x + = x x = x = K = { } Grficky: Kždá ze strn rovnice je výrzem pro lineární funkci
Úlohy školní klauzurní části I. kola kategorie C
 52. ročník mtemtické olympiády Úlohy školní kluzurní části I. kol ktegorie 1. Odtrhneme-li od libovolného lespoň dvojmístného přirozeného čísl číslici n místě jednotek, dostneme číslo o jednu číslici krtší.
52. ročník mtemtické olympiády Úlohy školní kluzurní části I. kol ktegorie 1. Odtrhneme-li od libovolného lespoň dvojmístného přirozeného čísl číslici n místě jednotek, dostneme číslo o jednu číslici krtší.
Souhrn základních výpočetních postupů v Excelu probíraných v AVT 04-05 listopad 2004. r r. . b = A
 Souhrn zákldních výpočetních postupů v Ecelu probírných v AVT 04-05 listopd 2004. Řešení soustv lineárních rovnic Soustv lineárních rovnic ve tvru r r A. = b tj. npř. pro 3 rovnice o 3 neznámých 2 3 Hodnoty
Souhrn zákldních výpočetních postupů v Ecelu probírných v AVT 04-05 listopd 2004. Řešení soustv lineárních rovnic Soustv lineárních rovnic ve tvru r r A. = b tj. npř. pro 3 rovnice o 3 neznámých 2 3 Hodnoty
1 Poznámka k termodynamice: Jednoatomový či dvouatomový plyn?
 Kvantová a statistická fyzika (erodynaika a statistická fyzika) 1 Poznáka k terodynaice: Jednoatoový či dvouatoový plyn? Jeden ol jednoatoového plynu o teplotě zaujíá obje V. Plyn však ůže projít cheickou
Kvantová a statistická fyzika (erodynaika a statistická fyzika) 1 Poznáka k terodynaice: Jednoatoový či dvouatoový plyn? Jeden ol jednoatoového plynu o teplotě zaujíá obje V. Plyn však ůže projít cheickou
r j Elektrostatické pole Elektrický proud v látkách
 Elektrostatiké pole Elektriký proud v látkáh Měděný vodiče o průřezu 6 protéká elektriký proud Vypočtěte střední ryhlost v pohybu volnýh elektronů ve vodiči jestliže předpokládáe že počet volnýh elektronů
Elektrostatiké pole Elektriký proud v látkáh Měděný vodiče o průřezu 6 protéká elektriký proud Vypočtěte střední ryhlost v pohybu volnýh elektronů ve vodiči jestliže předpokládáe že počet volnýh elektronů
Newtonův zákon I
 14 Newtonův zákon I Předpoklady: 104 Začnee opakování z inulé hodiny Pedaoická poznáka: Nejdříve nechá studenty vypracovat oba následující příklady, pak si zkontrolujee první příklad a studenti dostanou
14 Newtonův zákon I Předpoklady: 104 Začnee opakování z inulé hodiny Pedaoická poznáka: Nejdříve nechá studenty vypracovat oba následující příklady, pak si zkontrolujee první příklad a studenti dostanou
Náklady výroby elektrické energie
 Náklady výroby elektrické energie Marginální náklady (arginální ezní, přírůstkové) Marginální náklady jsou definovány jako přírůstek nákladů vyvolaných ezní přírůstke poptávky (produkce). MC = dtc dq TC
Náklady výroby elektrické energie Marginální náklady (arginální ezní, přírůstkové) Marginální náklady jsou definovány jako přírůstek nákladů vyvolaných ezní přírůstke poptávky (produkce). MC = dtc dq TC
. Potom (2) B pro danou periodickou funkci f ( ) x se nazývá Fourierova analýza.
 Učební text k přednášce UFY Fourierov nlýz, Fourierov trnsforce nhronické periodické vlny Fourierov nlýz Fourierův teoré: Funkce f ( x ) s prostorovou periodou ůže být rozvinut do řdy hronických funkcí
Učební text k přednášce UFY Fourierov nlýz, Fourierov trnsforce nhronické periodické vlny Fourierov nlýz Fourierův teoré: Funkce f ( x ) s prostorovou periodou ůže být rozvinut do řdy hronických funkcí
Laboratorní práce č.8 Úloha č. 7. Měření parametrů zobrazovacích soustav:
 Truhlář Michl 7.. 005 Lbortorní práce č.8 Úloh č. 7 Měření prmetrů zobrzovcích soustv: T = ϕ = p = 3, C 7% 99,5kP Úkol: - Změřte ohniskovou vzdálenost tenké spojky přímou Besselovou metodou. - Změřte ohniskovou
Truhlář Michl 7.. 005 Lbortorní práce č.8 Úloh č. 7 Měření prmetrů zobrzovcích soustv: T = ϕ = p = 3, C 7% 99,5kP Úkol: - Změřte ohniskovou vzdálenost tenké spojky přímou Besselovou metodou. - Změřte ohniskovou
( t) ( t) ( t) Nerovnice pro polorovinu. Předpoklady: 7306
 7.3.8 Nerovnice pro polorovinu Předpokldy: 736 Pedgogická poznámk: Příkld 1 není pro dlší průěh hodiny důležitý, má smysl pouze jko opkování zplnění čsu při zpisování do třídnice. Nemá smysl kvůli němu
7.3.8 Nerovnice pro polorovinu Předpokldy: 736 Pedgogická poznámk: Příkld 1 není pro dlší průěh hodiny důležitý, má smysl pouze jko opkování zplnění čsu při zpisování do třídnice. Nemá smysl kvůli němu
APLIKACE METODY RIPRAN V SOFTWAROVÉM INŽENÝRSTVÍ
 APLIKACE METODY RIPRAN V SOFTWAROVÉM INŽENÝRSTVÍ Brnislv Lcko VUT v Brně, Fkult strojního inženýrství, Ústv utomtizce informtiky, Technická 2, 616 69 Brno, lcko@ui.fme.vutbr.cz Abstrkt Příspěvek podává
APLIKACE METODY RIPRAN V SOFTWAROVÉM INŽENÝRSTVÍ Brnislv Lcko VUT v Brně, Fkult strojního inženýrství, Ústv utomtizce informtiky, Technická 2, 616 69 Brno, lcko@ui.fme.vutbr.cz Abstrkt Příspěvek podává
5.1.5 Základní vztahy mezi body, přímkami a rovinami
 5.1.5 Zákldní vzthy mezi body, přímkmi rovinmi Předpokldy: 510 Prostor má tři rozměry, skládá se z bodů přímk - jednorozměrná podmnožin prostoru (množin bodů), rovin - dvojrozměrná podmnožin prostoru (množin
5.1.5 Zákldní vzthy mezi body, přímkmi rovinmi Předpokldy: 510 Prostor má tři rozměry, skládá se z bodů přímk - jednorozměrná podmnožin prostoru (množin bodů), rovin - dvojrozměrná podmnožin prostoru (množin
1. Hmotnost a látkové množství
 . Hotnost a látkové nožství Hotnost stavební jednotky látky (například ato, olekly, vzorcové jednotky, eleentární částice atd.) označjee sybole a, na rozdíl od celkové hotnosti látky. Při požití základní
. Hotnost a látkové nožství Hotnost stavební jednotky látky (například ato, olekly, vzorcové jednotky, eleentární částice atd.) označjee sybole a, na rozdíl od celkové hotnosti látky. Při požití základní
5.1.5 Základní vztahy mezi body přímkami a rovinami
 5.1.5 Zákldní vzthy mezi body přímkmi rovinmi Předpokldy: 510 Prostor má tři rozměry, skládá se z bodů. Přímk - jednorozměrná podmnožin prostoru (množin bodů) Rovin - dvojrozměrná podmnožin prostoru (množin
5.1.5 Zákldní vzthy mezi body přímkmi rovinmi Předpokldy: 510 Prostor má tři rozměry, skládá se z bodů. Přímk - jednorozměrná podmnožin prostoru (množin bodů) Rovin - dvojrozměrná podmnožin prostoru (množin
2. Sestrojte graf závislosti prodloužení pružiny na působící síle y = i(f )
 1 Pracovní úkoly 1. Zěřte tuost k pěti pružin etodou statickou. 2. Sestrojte raf závislosti prodloužení pružiny na působící síle y = i(f ) 3. Zěřte tuost k pěti pružin etodou dynaickou. 4. Z doby kitu
1 Pracovní úkoly 1. Zěřte tuost k pěti pružin etodou statickou. 2. Sestrojte raf závislosti prodloužení pružiny na působící síle y = i(f ) 3. Zěřte tuost k pěti pružin etodou dynaickou. 4. Z doby kitu
Stanovení disociační konstanty acidobazického indikátoru. = a
 Stnovení disociční konstnty cidobzického indikátoru Teorie: Slbé kyseliny nebo báze disociují ve vodných roztocích jen omezeně; kvntittivní mírou je hodnot disociční konstnty. Disociční rekci příslušející
Stnovení disociční konstnty cidobzického indikátoru Teorie: Slbé kyseliny nebo báze disociují ve vodných roztocích jen omezeně; kvntittivní mírou je hodnot disociční konstnty. Disociční rekci příslušející
3.2.2 Rovnice postupného vlnění
 3.. Rovnice postupného vlnění Předpoklady: 310, 301 Chcee najít rovnici, která bude udávat výšku vlny v libovolné okažiku i libovolné bodě (v jedno okažiku je v různých ístech různá výška vlny). Veličiny
3.. Rovnice postupného vlnění Předpoklady: 310, 301 Chcee najít rovnici, která bude udávat výšku vlny v libovolné okažiku i libovolné bodě (v jedno okažiku je v různých ístech různá výška vlny). Veličiny
x + F F x F (x, f(x)).
 I. Funkce dvou více reálných proměnných 8. Implicitně dné funkce. Budeme se zbývt úlohou, kdy funkce není zdná přímo předpisem, který vyjdřuje závislost její hodnoty n hodnotách proměnných. Jeden z možných
I. Funkce dvou více reálných proměnných 8. Implicitně dné funkce. Budeme se zbývt úlohou, kdy funkce není zdná přímo předpisem, který vyjdřuje závislost její hodnoty n hodnotách proměnných. Jeden z možných
Zhoubný novotvar ledviny mimo pánvičku v ČR
 Aktuální informce Ústvu zdrvotnických informcí sttistiky České repuliky Prh 8.1.2004 1 Zhouný novotvr ledviny mimo pánvičku v ČR Počet hlášených onemocnění zhouným novotvrem ledviny mimo pánvičku (dg.
Aktuální informce Ústvu zdrvotnických informcí sttistiky České repuliky Prh 8.1.2004 1 Zhouný novotvr ledviny mimo pánvičku v ČR Počet hlášených onemocnění zhouným novotvrem ledviny mimo pánvičku (dg.
ALARM. Statistika dopravních nehod dětí
 ALARM Statistika dopravních nehod dětí leden 2006 Číslo projektu: 1F44/L/058/050 Zadavatel: Ministerstvo dopravy Styčný pracovník: Blanka Sunkovská Datum: leden 2006 Zodpovědný řešitel: Řešitel: Spoluřešitelé:
ALARM Statistika dopravních nehod dětí leden 2006 Číslo projektu: 1F44/L/058/050 Zadavatel: Ministerstvo dopravy Styčný pracovník: Blanka Sunkovská Datum: leden 2006 Zodpovědný řešitel: Řešitel: Spoluřešitelé:
Hyperbola, jejíž střed S je totožný s počátkem soustavy souřadnic a jejíž hlavní osa je totožná
 Hyperol Hyperol je množin odů, které mjí tu vlstnost, že solutní hodnot rozdílu jejich vzdáleností od dvou dných různých odů E, F je rovn kldné konstntě. Zkráceně: Hyperol = {X ; EX FX = }; kde symolem
Hyperol Hyperol je množin odů, které mjí tu vlstnost, že solutní hodnot rozdílu jejich vzdáleností od dvou dných různých odů E, F je rovn kldné konstntě. Zkráceně: Hyperol = {X ; EX FX = }; kde symolem
Úmrtnost v Česku a vybraných evropských krajinách
 Úmrtnost v Česku vybrných evropských krjinách Bohdn Lind Univerzit Prdubice, ústv mtemtiky Vývoj úmrtnosti v ČR v letech 197 1999 podle nejčstějších příčin V České republice zemřelo v roce 1999 19 768
Úmrtnost v Česku vybrných evropských krjinách Bohdn Lind Univerzit Prdubice, ústv mtemtiky Vývoj úmrtnosti v ČR v letech 197 1999 podle nejčstějších příčin V České republice zemřelo v roce 1999 19 768
(Text s významem pro EHP)
 9.9.2015 L 235/7 PROVÁDĚCÍ NAŘÍZENÍ KOMISE (EU) 2015/1502 ze dne 8. září 2015, kterým se stnoví minimální technické specifikce postupy pro úrovně záruky prostředků pro elektronickou identifikci podle čl.
9.9.2015 L 235/7 PROVÁDĚCÍ NAŘÍZENÍ KOMISE (EU) 2015/1502 ze dne 8. září 2015, kterým se stnoví minimální technické specifikce postupy pro úrovně záruky prostředků pro elektronickou identifikci podle čl.
Pluto již není planetou, z astronomie však nemizí
 uto již není plnetou, z stronomie všk nemizí Vldimír Štefl, Brno Cílem příspěvku je vysvětlit čtenářům - žákům i učitelům, proč bylo uto při svém objevu v roce 1930 oznčeno z plnetu nopk jké byly důvody,
uto již není plnetou, z stronomie všk nemizí Vldimír Štefl, Brno Cílem příspěvku je vysvětlit čtenářům - žákům i učitelům, proč bylo uto při svém objevu v roce 1930 oznčeno z plnetu nopk jké byly důvody,
3. PEVNOST V TLAKU BETONU NA VÝVRTECH
 3. PEVNOST V TLAKU BETONU NA VÝVRTECH Vývrty jsou válcové zkušební vzorky, získané z konstrukce poocí dobře chlazeného jádrového vrtáku. Vývrty jsou pečlivě vyšetřeny, upraveny buď zabroušení, anebo koncování
3. PEVNOST V TLAKU BETONU NA VÝVRTECH Vývrty jsou válcové zkušební vzorky, získané z konstrukce poocí dobře chlazeného jádrového vrtáku. Vývrty jsou pečlivě vyšetřeny, upraveny buď zabroušení, anebo koncování
Dodatečné informace č. 1 zadavatele k veřejné zakázce. Pronájem multifunkčních tiskových zařízení
 Dodtečné informce č. 1 zdvtele k veřejné zkázce Pronájem multifunkčních tiskových zřízení Zdvtel upřesňuje zdávcí dokumentci výše uvedené veřejné zkázky n služby, vyhlášené v souldu s podmínkmi 25 38 zákon
Dodtečné informce č. 1 zdvtele k veřejné zkázce Pronájem multifunkčních tiskových zřízení Zdvtel upřesňuje zdávcí dokumentci výše uvedené veřejné zkázky n služby, vyhlášené v souldu s podmínkmi 25 38 zákon
je nutná k tomu, aby byl odhad takto pořízený je potřebná k tomu, aby proměnné-instrumenty vysvětlující veličiny v rovnici je nahrazovaly co
 Obecná etod nstruentálních proěnných (G)IV (Generl Instruentl Vrbles ethod) v soustvě sultánních regresních rovnc utor etody: J.D. Srgn [958] Metod nstruentálních proěnných je jstý zobecnění dvoustupňové
Obecná etod nstruentálních proěnných (G)IV (Generl Instruentl Vrbles ethod) v soustvě sultánních regresních rovnc utor etody: J.D. Srgn [958] Metod nstruentálních proěnných je jstý zobecnění dvoustupňové
evod povahy kritérií v modelech vícekriteriální analýzy variant Anotace Klí ová slova Annotation Keywords Úvod
 Převod povhy krtérí v odelech vícekrterální nlýzy vrnt Mln Houšk, Ludl Döeová Ktedr operční systéové nlýzy PEF ČZU v Prze e-l: housk@pef.czu.cz, doeov@pef.czu.cz Anotce Př řešení úloh vícekrterální nlýzy
Převod povhy krtérí v odelech vícekrterální nlýzy vrnt Mln Houšk, Ludl Döeová Ktedr operční systéové nlýzy PEF ČZU v Prze e-l: housk@pef.czu.cz, doeov@pef.czu.cz Anotce Př řešení úloh vícekrterální nlýzy
SYLABUS PŘEDNÁŠKY 7 Z GEODÉZIE 1
 SYLABUS PŘEDNÁŠKY 7 Z GEODÉZIE 1 (Souřdnicové výpočty) 1 ročník bklářského studi studijní progrm G studijní obor G doc Ing Jromír Procházk CSc listopd 2015 1 Geodézie 1 přednášk č7 VÝPOČET SOUŘADNIC JEDNOHO
SYLABUS PŘEDNÁŠKY 7 Z GEODÉZIE 1 (Souřdnicové výpočty) 1 ročník bklářského studi studijní progrm G studijní obor G doc Ing Jromír Procházk CSc listopd 2015 1 Geodézie 1 přednášk č7 VÝPOČET SOUŘADNIC JEDNOHO
SEMINÁŘ I Teorie absolutních a komparativních výhod
 PODKLDY K SEMINÁŘŮM ŘEŠENÉ PŘÍKLDY SEMINÁŘ I eorie bsolutních komprtivních výhod Zákldní principy teorie komprtivních výhod eorie komprtivních výhod ve své klsické podobě odvozuje motivci k obchodu z rozdílných
PODKLDY K SEMINÁŘŮM ŘEŠENÉ PŘÍKLDY SEMINÁŘ I eorie bsolutních komprtivních výhod Zákldní principy teorie komprtivních výhod eorie komprtivních výhod ve své klsické podobě odvozuje motivci k obchodu z rozdílných
3. ROVNICE A NEROVNICE 85. 3.1. Lineární rovnice 85. 3.2. Kvadratické rovnice 86. 3.3. Rovnice s absolutní hodnotou 88. 3.4. Iracionální rovnice 90
 ROVNICE A NEROVNICE 8 Lineární rovnice 8 Kvdrtické rovnice 8 Rovnice s bsolutní hodnotou 88 Ircionální rovnice 90 Eponenciální rovnice 9 Logritmické rovnice 9 7 Goniometrické rovnice 98 8 Nerovnice 0 Úlohy
ROVNICE A NEROVNICE 8 Lineární rovnice 8 Kvdrtické rovnice 8 Rovnice s bsolutní hodnotou 88 Ircionální rovnice 90 Eponenciální rovnice 9 Logritmické rovnice 9 7 Goniometrické rovnice 98 8 Nerovnice 0 Úlohy
Obsah rovinného obrazce
 Osh rovinného orzce Nejjednodušší plikcí určitého integrálu je výpočet oshu rovinného orzce. Zčneme větou. Vět : Je-li funkce f spojitá nezáporná n n orázku níže roven f ( ) d. ;, je osh rovinného orzce
Osh rovinného orzce Nejjednodušší plikcí určitého integrálu je výpočet oshu rovinného orzce. Zčneme větou. Vět : Je-li funkce f spojitá nezáporná n n orázku níže roven f ( ) d. ;, je osh rovinného orzce
3. VÝVRTY: ODBĚR, POPIS A ZKOUŠENÍ V TLAKU
 3. VÝVRTY: ODBĚR, POPIS A ZKOUŠENÍ V TLAKU Vývrty jsou válcová zkušební tělesa, získaná z konstrukce poocí dobře chlazeného jádrového vrtáku. Vývrty získané jádrový vrtáke jsou pečlivě vyšetřeny, upraveny
3. VÝVRTY: ODBĚR, POPIS A ZKOUŠENÍ V TLAKU Vývrty jsou válcová zkušební tělesa, získaná z konstrukce poocí dobře chlazeného jádrového vrtáku. Vývrty získané jádrový vrtáke jsou pečlivě vyšetřeny, upraveny
SIMULACE PROCESU TUHNUTÍ A CHLADNUTÍ KRUHOVÉHO PREDLITKU SIMULATION OF SOLIDIFICATION PROCESS OF ROUND CC BLANK
 SIMULACE PROCESU TUHNUTÍ A CHLADNUTÍ KRUHOVÉHO PREDLITKU SIMULATION OF SOLIDIFICATION PROCESS OF ROUND CC BLANK Miroslav Príhoda Jirí Molínek René Pyszko VŠB Technická univerzita Ostrava, 17. listopadu
SIMULACE PROCESU TUHNUTÍ A CHLADNUTÍ KRUHOVÉHO PREDLITKU SIMULATION OF SOLIDIFICATION PROCESS OF ROUND CC BLANK Miroslav Príhoda Jirí Molínek René Pyszko VŠB Technická univerzita Ostrava, 17. listopadu
F9 SOUSTAVA HMOTNÝCH BODŮ
 F9 SOUSTAVA HMOTNÝCH BODŮ Evopský sociální fon Ph & EU: Investujee o vší buoucnosti F9 SOUSTAVA HMOTNÝCH BODŮ Nyní se nučíe popisovt soustvu hotných boů Přepokláeje, že áe N hotných boů 1,,, N N násleující
F9 SOUSTAVA HMOTNÝCH BODŮ Evopský sociální fon Ph & EU: Investujee o vší buoucnosti F9 SOUSTAVA HMOTNÝCH BODŮ Nyní se nučíe popisovt soustvu hotných boů Přepokláeje, že áe N hotných boů 1,,, N N násleující
Posluchači provedou odpovídající selekci a syntézu informací a uceleně je uvedou do teoretického základu vlastního měření.
 Úloh č. 9 je sestven n zákldě odkzu n dv prmeny. Kždý z nich přistupuje k stejnému úkolu částečně odlišnými způsoby. Níže jsou uvedeny ob zdroje v plném znění. V kždém z nich jsou pro posluchče cenné inormce
Úloh č. 9 je sestven n zákldě odkzu n dv prmeny. Kždý z nich přistupuje k stejnému úkolu částečně odlišnými způsoby. Níže jsou uvedeny ob zdroje v plném znění. V kždém z nich jsou pro posluchče cenné inormce
2. Je vozidlo NOVÉ 1)
 již PRVZVANÉ (lze využít i prohlídce před schválením způsobilosti nebo prohlídce před registrcí vozidl viz. MP 1/2006 MD ČR) DEKRA Automobil.s., Prh 4, Chodovec, Türkov 1001,PČ 149 00 člen skupiny DEKRA
již PRVZVANÉ (lze využít i prohlídce před schválením způsobilosti nebo prohlídce před registrcí vozidl viz. MP 1/2006 MD ČR) DEKRA Automobil.s., Prh 4, Chodovec, Türkov 1001,PČ 149 00 člen skupiny DEKRA
s N, r > s platí: Základní požadavek na krásu matematického pravidla: Musí být co nejobecnější s minimem a a = a = a. Nemohli bychom ho upravit tak,
 .6. Mocniny celý ocnitele I Předpokldy: 6, 6 Př. : Kteé ze dvou pvidel je teticky hezčí? ) Po kždé R, N pltí: +. ) Po kždé R,, N, > pltí:. Zákldní poždvek n káu tetického pvidl: Muí ýt co nejoecnější inie
.6. Mocniny celý ocnitele I Předpokldy: 6, 6 Př. : Kteé ze dvou pvidel je teticky hezčí? ) Po kždé R, N pltí: +. ) Po kždé R,, N, > pltí:. Zákldní poždvek n káu tetického pvidl: Muí ýt co nejoecnější inie
DOPRAVNÌ INŽENÝRSKÉ OPATØENÍ
 DOPRVNÍ ZNÈENÍ ve služách ezpeènosti silnièního provozu JNEV DOPRVNÌ INŽENÝRSKÉ OPTØENÍ OPRV OJÍZDNÝCH TRS PO REKONSTRUKCI ŽÏÁKOVSKÉHO MOSTU SILNICE I/9 MILEVSKO Vyprcovl: Lucie Kuklová Dtu: èervenec 7
DOPRVNÍ ZNÈENÍ ve služách ezpeènosti silnièního provozu JNEV DOPRVNÌ INŽENÝRSKÉ OPTØENÍ OPRV OJÍZDNÝCH TRS PO REKONSTRUKCI ŽÏÁKOVSKÉHO MOSTU SILNICE I/9 MILEVSKO Vyprcovl: Lucie Kuklová Dtu: èervenec 7
MINISTERSTVO PRO MÍSTNÍ ROZVOJ Národní orgán pro koordinaci POKYN PRO TVORBU A OBSAH ZPRÁVY O REALIZACI OPERAČNÍHO PROGRAMU PRO MONITOROVACÍ VÝBOR
 MINISTERSTVO PRO MÍSTNÍ ROZVOJ Národní orgán pro koordinci POKYN PRO TVORBU A OBSAH ZPRÁVY O REALIZACI OPERAČNÍHO PROGRAMU PRO MONITOROVACÍ VÝBOR ŘÍJEN 2014 MINISTERSTVO PRO MÍSTNÍ ROZVOJ Odbor řízení
MINISTERSTVO PRO MÍSTNÍ ROZVOJ Národní orgán pro koordinci POKYN PRO TVORBU A OBSAH ZPRÁVY O REALIZACI OPERAČNÍHO PROGRAMU PRO MONITOROVACÍ VÝBOR ŘÍJEN 2014 MINISTERSTVO PRO MÍSTNÍ ROZVOJ Odbor řízení
1.2.5 2. Newtonův zákon I
 15 Newtonův zákon I Předpoklady: 104 Z inulé hodiny víe, že neexistuje příý vztah (typu příé nebo nepříé úěrnosti) ezi rychlostí a silou hledáe jinou veličinu popisující pohyb, která je navázána na sílu
15 Newtonův zákon I Předpoklady: 104 Z inulé hodiny víe, že neexistuje příý vztah (typu příé nebo nepříé úěrnosti) ezi rychlostí a silou hledáe jinou veličinu popisující pohyb, která je navázána na sílu
VALIDACE METODY k 0 STANDARDIZACE V NEUTRONOVÉ AKTIVAČNÍ ANALÝZE PROGRAMEM KAYZERO FOR WINDOWS. MARIE KUBEŠOVÁ a,b,c a JAN KUČERA a,b. Úvod.
 Che. Listy 105, 261268 (2011) Lbortorní přístroje postupy VALIDACE METODY k 0 STANDARDIZACE V NEUTRONOVÉ AKTIVAČNÍ ANALÝZE PRORAMEM KAYZERO FOR WINDOWS MARIE KUBEŠOVÁ,b,c JAN KUČERA,b Ústv jderné fyziky
Che. Listy 105, 261268 (2011) Lbortorní přístroje postupy VALIDACE METODY k 0 STANDARDIZACE V NEUTRONOVÉ AKTIVAČNÍ ANALÝZE PRORAMEM KAYZERO FOR WINDOWS MARIE KUBEŠOVÁ,b,c JAN KUČERA,b Ústv jderné fyziky
Obsah přednášky : Dynamika mechanismů. dynamika mechanismů - metoda uvolňování, dynamika mechanismů - metoda redukce
 Obsh přednášky : Dynik echnisů dynik echnisů - etod uvolňování, dynik echnisů - etod edukce Dynik echnisů Dynik echnisů pojednává o vzthu ezi sili, působícíi n soustvu těles - echnisus, pohybe echnisu,
Obsh přednášky : Dynik echnisů dynik echnisů - etod uvolňování, dynik echnisů - etod edukce Dynik echnisů Dynik echnisů pojednává o vzthu ezi sili, působícíi n soustvu těles - echnisus, pohybe echnisu,
Praktikum I Mechanika a molekulová fyzika
 Oddělení fzikálních praktik při Kabinetu výuk obecné fzik MFF UK Praktiku I Mechanika a olekulová fzika Úloha č. II Název: Studiu haronických kitů echanického oscilátoru Pracoval: Matáš Řehák stud.sk.:
Oddělení fzikálních praktik při Kabinetu výuk obecné fzik MFF UK Praktiku I Mechanika a olekulová fzika Úloha č. II Název: Studiu haronických kitů echanického oscilátoru Pracoval: Matáš Řehák stud.sk.:
II. Faktory ovlivňující rozhodnutí o ukončení pracovní aktivity
 II. Fktory ovlivňující rozhodnutí o ukončení prcovní ktivity Hrnice pro odchod do strobního důchodu v ČR má rozhodující vliv n ukončení veškerých prcovních ktivit výrzně se projevuje i v pozdějším ukončení
II. Fktory ovlivňující rozhodnutí o ukončení prcovní ktivity Hrnice pro odchod do strobního důchodu v ČR má rozhodující vliv n ukončení veškerých prcovních ktivit výrzně se projevuje i v pozdějším ukončení
3.2.2 Rovnice postupného vlnění
 3.. Rovnice postupného vlnění Předpoklady: 310, 301 Chcee najít rovnici, která bude udávat výšku vlny v libovolné okažiku i libovolné bodě (v jedno okažiku je v různých ístech různá výška vlny). Veličiny
3.. Rovnice postupného vlnění Předpoklady: 310, 301 Chcee najít rovnici, která bude udávat výšku vlny v libovolné okažiku i libovolné bodě (v jedno okažiku je v různých ístech různá výška vlny). Veličiny
Elektrický proud v elektrolytech
 Elektrolytický vodič Elektrický proud v elektrolytech Vezěe nádobu s destilovanou vodou (ta nevede el. proud) a vlože do ní dvě elektrody, které připojíe do zdroje stejnosěrného napětí. Do vody nasypee
Elektrolytický vodič Elektrický proud v elektrolytech Vezěe nádobu s destilovanou vodou (ta nevede el. proud) a vlože do ní dvě elektrody, které připojíe do zdroje stejnosěrného napětí. Do vody nasypee
2.9.11 Logaritmus. Předpoklady: 2909
 .9. Logritmus Předpokld: 909 Pedgogická poznámk: Následující příkld vždují tk jeden půl vučovcí hodin. V přípdě potřeb všk stčí dojít k příkldu 6 zbtek jen ukázt, což se dá z jednu hodinu stihnout (nedoporučuji).
.9. Logritmus Předpokld: 909 Pedgogická poznámk: Následující příkld vždují tk jeden půl vučovcí hodin. V přípdě potřeb všk stčí dojít k příkldu 6 zbtek jen ukázt, což se dá z jednu hodinu stihnout (nedoporučuji).
Příklad 22 : Kapacita a rozložení intenzity elektrického pole v deskovém kondenzátoru s jednoduchým dielektrikem
 Příkld 22 : Kpcit rozložení intenzity elektrického pole v deskovém kondenzátoru s jednoduchým dielektrikem Předpokládné znlosti: Elektrické pole mezi dvěm nbitými rovinmi Příkld 2 Kpcit kondenzátoru je
Příkld 22 : Kpcit rozložení intenzity elektrického pole v deskovém kondenzátoru s jednoduchým dielektrikem Předpokládné znlosti: Elektrické pole mezi dvěm nbitými rovinmi Příkld 2 Kpcit kondenzátoru je
2.1.6 Relativní atomová a relativní molekulová hmotnost
 .1. Relativní atoová a elativní oleklová hotnost Předpoklady: Pedagogická poznáka: Tato a následjící dvě hodiny jso pokse a toch jiné podání pobleatiky. Standadní přístp znaená několik ne zcela půhledných
.1. Relativní atoová a elativní oleklová hotnost Předpoklady: Pedagogická poznáka: Tato a následjící dvě hodiny jso pokse a toch jiné podání pobleatiky. Standadní přístp znaená několik ne zcela půhledných
{ } ( ) ( ) 2.5.8 Vztahy mezi kořeny a koeficienty kvadratické rovnice. Předpoklady: 2301, 2508, 2507
 58 Vzth mezi kořen koefiient kvdrtiké rovnie Předpokld:, 58, 57 Pedgogiká poznámk: Náplň zřejmě přeshuje možnost jedné vučoví hodin, příkld 8 9 zůstvjí n vičení neo polovinu hodin při píseme + + - zákldní
58 Vzth mezi kořen koefiient kvdrtiké rovnie Předpokld:, 58, 57 Pedgogiká poznámk: Náplň zřejmě přeshuje možnost jedné vučoví hodin, příkld 8 9 zůstvjí n vičení neo polovinu hodin při píseme + + - zákldní
Ohýbaný nosník - napětí
 Pružnost pevnost BD0 Ohýbný nosník - npětí Teorie Prostý ohb, rovinný ohb Při prostém ohbu je průřez nmáhán ohbovým momentem otáčejícím kolem jedné z hlvních os setrvčnosti průřezu, obvkle os. oment se
Pružnost pevnost BD0 Ohýbný nosník - npětí Teorie Prostý ohb, rovinný ohb Při prostém ohbu je průřez nmáhán ohbovým momentem otáčejícím kolem jedné z hlvních os setrvčnosti průřezu, obvkle os. oment se
DOPRAVNÌ INŽENÝRSKÉ OPATØENÍ
 DOPRAVNÍ ZNAÈENÍ ve služách ezpeènosti silnièního provozu DOPRAVNÌ INŽENÝRSKÉ OPATØENÍ STAVBA PØELOŽKY SILNICE III/14539 (pøes ulici M. Horákov do ulice Strkonick) stvení èást 2 4. fáze Vyprcovl: Lucie
DOPRAVNÍ ZNAÈENÍ ve služách ezpeènosti silnièního provozu DOPRAVNÌ INŽENÝRSKÉ OPATØENÍ STAVBA PØELOŽKY SILNICE III/14539 (pøes ulici M. Horákov do ulice Strkonick) stvení èást 2 4. fáze Vyprcovl: Lucie
M A = M k1 + M k2 = 3M k1 = 2400 Nm. (2)
 5.3 Řešené příkldy Příkld 1: U prutu kruhového průřezu o průměrech d d b, který je ztížen kroutícími momenty M k1 M k2 (M k2 = 2M k1 ), viz obr. 1, vypočítejte rekční účinek v uložení prutu, vyšetřete
5.3 Řešené příkldy Příkld 1: U prutu kruhového průřezu o průměrech d d b, který je ztížen kroutícími momenty M k1 M k2 (M k2 = 2M k1 ), viz obr. 1, vypočítejte rekční účinek v uložení prutu, vyšetřete
( a) Okolí bodu
 0..5 Okolí bodu Předpokldy: 40 Pedgogická poznámk: Hodin zjevně překrčuje možnosti většiny studentů v 45 minutách. Myslím, že nemá cenu přethovt do dlší hodiny, příkldy s redukovnými okolími nejsou nutné,
0..5 Okolí bodu Předpokldy: 40 Pedgogická poznámk: Hodin zjevně překrčuje možnosti většiny studentů v 45 minutách. Myslím, že nemá cenu přethovt do dlší hodiny, příkldy s redukovnými okolími nejsou nutné,
2.1 - ( ) ( ) (020201) [ ] [ ]
![2.1 - ( ) ( ) (020201) [ ] [ ] 2.1 - ( ) ( ) (020201) [ ] [ ]](/thumbs/102/155984102.jpg) - FUNKCE A ROVNICE Následující zákldní znlosti je nezbytně nutné umět od okmžiku probrání ž do konce studi mtemtiky n gymnáziu. Vyždováno bude porozumění schopnost plikovt ne pouze mechnicky zopkovt. Některé
- FUNKCE A ROVNICE Následující zákldní znlosti je nezbytně nutné umět od okmžiku probrání ž do konce studi mtemtiky n gymnáziu. Vyždováno bude porozumění schopnost plikovt ne pouze mechnicky zopkovt. Některé
Výzkum dopravní bezpečnosti
 Výzkum dopravní bezpečnosti Ing: Karel Mulač Škoda Auto, TK/25 14.1.2011 Tento materiál vznikl jako součást projektu In-TECH 2, který je spolufinancován Evropským sociálním fondem a státním rozpočtem ČR.
Výzkum dopravní bezpečnosti Ing: Karel Mulač Škoda Auto, TK/25 14.1.2011 Tento materiál vznikl jako součást projektu In-TECH 2, který je spolufinancován Evropským sociálním fondem a státním rozpočtem ČR.
KEYWORDS: Truck-trailer combination, Brake systém, Technical status, Convential brake systém, Electronic brake systém, Disc brakes, Drum brakes
 ABSTRAKT: ExFoS - Expert Forensic Science BRZDĚNÍ JÍZDNÍCH SOUPRAV BRAKING OF TRUCK - TRAILERS Haring Andrej 14 Tématem příspěvku je brzdění jízdních souprav v kritických jízdních situacích a jejich vliv
ABSTRAKT: ExFoS - Expert Forensic Science BRZDĚNÍ JÍZDNÍCH SOUPRAV BRAKING OF TRUCK - TRAILERS Haring Andrej 14 Tématem příspěvku je brzdění jízdních souprav v kritických jízdních situacích a jejich vliv
Vlnová teorie. Ing. Bc. Michal Malík, Ing. Bc. Jiří Primas. TECHNICKÁ UNIVERZITA V LIBERCI Fakulta mechatroniky, informatiky a mezioborových studií
 Ing. Bc. Michl Mlík, Ing. Bc. Jiří Prims ECHNICKÁ UNIVERZIA V LIBERCI Fkult mechtroniky, informtiky mezioborových studií ento mteriál vznikl v rámci projektu ESF CZ.1.7/../7.47, který je spolufinncován
Ing. Bc. Michl Mlík, Ing. Bc. Jiří Prims ECHNICKÁ UNIVERZIA V LIBERCI Fkult mechtroniky, informtiky mezioborových studií ento mteriál vznikl v rámci projektu ESF CZ.1.7/../7.47, který je spolufinncován
VIRTUÁLNÍ SIMULACE S VYUŽITÍM BIOMECHANICKÝCH MODELŮ ČLOVĚKA JAKO PODPORA SOUDNÍHO ZNALECTVÍ
 Abstrakt VIRTUÁLNÍ SIMULACE S VYUŽITÍM BIOMECHANICKÝCH MODELŮ ČLOVĚKA JAKO PODPORA SOUDNÍHO ZNALECTVÍ Luděk Hynčík 1, Hana Kocková 2, Jan Kovanda 3, Petr Krejčí 4 Častou dopravní nehodou je střet chodce
Abstrakt VIRTUÁLNÍ SIMULACE S VYUŽITÍM BIOMECHANICKÝCH MODELŮ ČLOVĚKA JAKO PODPORA SOUDNÍHO ZNALECTVÍ Luděk Hynčík 1, Hana Kocková 2, Jan Kovanda 3, Petr Krejčí 4 Častou dopravní nehodou je střet chodce
4. cvičení z Matematiky 2
 4. cvičení z Mtemtiky 2 14.-18. březn 2016 4.1 Njděte ity (i (ii (iii (iv 2 +(y 1 2 +1 1 2 +(y 1 2 z 2 y 2 z yz 1 2 y 2 (,y (0,0 2 +y 2 2 y 2 (,y (0,0 2 +y 3 (i Pro funkci f(, y = 2 +(y 1 2 +1 1 2 +(y
4. cvičení z Mtemtiky 2 14.-18. březn 2016 4.1 Njděte ity (i (ii (iii (iv 2 +(y 1 2 +1 1 2 +(y 1 2 z 2 y 2 z yz 1 2 y 2 (,y (0,0 2 +y 2 2 y 2 (,y (0,0 2 +y 3 (i Pro funkci f(, y = 2 +(y 1 2 +1 1 2 +(y
Jelikož jsme chráněnou dílnou poskytujeme firmám náhradní plnění (viz. www.renoza.cz)! Ceník 2. Vážená paní/pane,
 1 2 Vážená paní/pane, v rukou držíte orientační ceník společnosti Renoza s.r.o. Vzhlede k tou, že u většiny našich výrobků není ožné uvést veškeré varianty, tvary a způsoby provedení, uvádíe zde jen nejběžnější
1 2 Vážená paní/pane, v rukou držíte orientační ceník společnosti Renoza s.r.o. Vzhlede k tou, že u většiny našich výrobků není ožné uvést veškeré varianty, tvary a způsoby provedení, uvádíe zde jen nejběžnější
metoda uvolňování metoda redukce G 1 G 2
 Dynik echnisů Dynik echnisů pojednává o vzthu ezi sili, působícíi n soustvu těles - echnisus, pohybe echnisu, těito sili způsobené. Seznáíe se se dvě zákldníi etodi řešení dyniky echnisů. etod uvolňování
Dynik echnisů Dynik echnisů pojednává o vzthu ezi sili, působícíi n soustvu těles - echnisus, pohybe echnisu, těito sili způsobené. Seznáíe se se dvě zákldníi etodi řešení dyniky echnisů. etod uvolňování
 ňď Ó Ó Š ť ř ř ř Č ř ť ř Ř Š Ě Č Č ř Č Ý Ě ť Ě ť ř ý ř Ř ť ň Ě Ý ř Ě ř ř ň ť Š Š Š ň ť Ó ť Á ť ř Ů Ú Ě Č ť ň Š ř Ď Č Š ň Ř Ě ň ý řň ř ř ř Č Š ť Š Š Š Ú Š Á Ý Ú Š Š Š Š Š ť Á ť ť Ě ť ť ť ř Ú Ú Ú Š Ů Š ý
ňď Ó Ó Š ť ř ř ř Č ř ť ř Ř Š Ě Č Č ř Č Ý Ě ť Ě ť ř ý ř Ř ť ň Ě Ý ř Ě ř ř ň ť Š Š Š ň ť Ó ť Á ť ř Ů Ú Ě Č ť ň Š ř Ď Č Š ň Ř Ě ň ý řň ř ř ř Č Š ť Š Š Š Ú Š Á Ý Ú Š Š Š Š Š ť Á ť ť Ě ť ť ť ř Ú Ú Ú Š Ů Š ý
1.2. MOCNINA A ODMOCNINA
 .. MOCNINA A ODMOCNINA V této kpitole se dozvíte: jk je defiová oci s přirozeý, celý, rcioálí oecý reálý epoete jké jsou její vlstosti; jk je defiová přirozeá odoci, jké jsou její vlstosti jk se dá vyjádřit
.. MOCNINA A ODMOCNINA V této kpitole se dozvíte: jk je defiová oci s přirozeý, celý, rcioálí oecý reálý epoete jké jsou její vlstosti; jk je defiová přirozeá odoci, jké jsou její vlstosti jk se dá vyjádřit
13. Soustava lineárních rovnic a matice
 @9. Soustv lineárních rovnic mtice Definice: Mtice je tbulk reálných čísel. U mtice rozlišujeme řádky (i=,..n), sloupce (j=,..m) říkáme, že mtice je typu (n x m). Oznčíme-li mtici písmenem A, její prvky
@9. Soustv lineárních rovnic mtice Definice: Mtice je tbulk reálných čísel. U mtice rozlišujeme řádky (i=,..n), sloupce (j=,..m) říkáme, že mtice je typu (n x m). Oznčíme-li mtici písmenem A, její prvky
Konzultace z předmětu MATEMATIKA pro první ročník dálkového studia
 - - Konzultce z předmětu MATEMATIKA pro první ročník dálkového studi ) Číselné obor ) Zákldní početní operce procentový počet ) Absolutní hodnot reálného čísl ) Intervl množinové operce ) Mocnin ) Odmocnin
- - Konzultce z předmětu MATEMATIKA pro první ročník dálkového studi ) Číselné obor ) Zákldní početní operce procentový počet ) Absolutní hodnot reálného čísl ) Intervl množinové operce ) Mocnin ) Odmocnin
ROZŠÍŘENÉ ASISTENČNÍ SYSTÉMY, POLO-AUTONOMNÍ/AUTONOMNÍ SYSTÉMY ŘÍZENÍ Z POHLEDU TECHNICKÝCH STANDARDŮ. Sdružení pro dopravní telematiku
 ROZŠÍŘENÉ ASISTENČNÍ SYSTÉMY, POLO-AUTONOMNÍ/AUTONOMNÍ SYSTÉMY ŘÍZENÍ Z POHLEDU TECHNICKÝCH STANDARDŮ Sdružení pro dopravní telematiku ORGANIZACE PRO TVORBU NOREM Normotvorné organizace z pohledu autonomních
ROZŠÍŘENÉ ASISTENČNÍ SYSTÉMY, POLO-AUTONOMNÍ/AUTONOMNÍ SYSTÉMY ŘÍZENÍ Z POHLEDU TECHNICKÝCH STANDARDŮ Sdružení pro dopravní telematiku ORGANIZACE PRO TVORBU NOREM Normotvorné organizace z pohledu autonomních
Obecně: K dané funkci f hledáme funkci ϕ z dané množiny funkcí M, pro kterou v daných bodech x 0 < x 1 <... < x n. (δ ij... Kroneckerovo delta) (4)
 KAPITOLA 13: Numerická integrce interpolce [MA1-18:P13.1] 13.1 Interpolce Obecně: K dné funkci f hledáme funkci ϕ z dné množiny funkcí M, pro kterou v dných bodech x 0 < x 1
KAPITOLA 13: Numerická integrce interpolce [MA1-18:P13.1] 13.1 Interpolce Obecně: K dné funkci f hledáme funkci ϕ z dné množiny funkcí M, pro kterou v dných bodech x 0 < x 1
2002 Katedra obecné elektrotechniky FEI VŠB-TU Ostrava Ing.Stanislav Kocman
 STEJNOSĚRNÉ STROJE 1. Princip činnosti stejnosměrného stroje 2. Rekce kotvy komutce stejnosměrných strojů 3. Rozdělení stejnosměrných strojů 4. Stejnosměrné generátory 5. Stejnosměrné motory 2002 Ktedr
STEJNOSĚRNÉ STROJE 1. Princip činnosti stejnosměrného stroje 2. Rekce kotvy komutce stejnosměrných strojů 3. Rozdělení stejnosměrných strojů 4. Stejnosměrné generátory 5. Stejnosměrné motory 2002 Ktedr
Chemie - cvičení 2 - příklady
 Cheie - cvičení 2 - příklady Stavové chování 2/1 Zásobník o objeu 50 obsahuje plynný propan C H 8 při teplotě 20 o C a přetlaku 0,5 MPa. Baroetrický tlak je 770 torr. Kolik kg propanu je v zásobníku? Jaká
Cheie - cvičení 2 - příklady Stavové chování 2/1 Zásobník o objeu 50 obsahuje plynný propan C H 8 při teplotě 20 o C a přetlaku 0,5 MPa. Baroetrický tlak je 770 torr. Kolik kg propanu je v zásobníku? Jaká
