Maxwellovo({Boltzmannovo) rozdìlení rychlostí

Transkript

1 Maxwellovo({Boltzmannovo) rozdìlení rychlostí Pravdìpodobnost, ¾e molekulu nalezneme 1/32 4. listopadu 2016 v krychlièce o velikosti dxdydz se souøadnicemi v intervalech [x, x + dx), [y, y + dy) a [z, z + dz) a zároveò s rychlostmi v intervalu [v x, v x + dv x ), [v y, v y + dv y ), [v z, v z + dv z ), je úmìrná Boltmannovu faktoru exp = exp ( E ) pot + E kin k B T ( ) ( Epot 1 exp 2 mv 2 x k B T k B T ) exp ( 1 2 mv 2 ) y k B T exp ( 1 2 mv 2 z k B T Pravdìpodobnost, ¾e molekulu nalezneme s rychlostmi v intervalech[v x, v x + dv x ), [v y, v y + dv y ), [v z, v z + dv z ) (bez ohledu na E pot ) je úmìrná exp ( 1 2 mv 2 ) x k B T exp ( 1 2 mv 2 ) y k B T exp ( 1 2 mv 2 z k B T ) )

2 [tchem/mbfunkce.sh] Maxwellovo{Boltzmannovo rozdìlení rychlostí jinak 2/32 Pøedpoklady: { π je izotropní { π lze slo¾it z nezávislých pøíspìvkù souøadnic, tj. { lim v π(v x, v y, v z ) = 0 π(v x, v y, v z ) = π(v x )π(v y )π(v z ) Jediná funkce, která tomu vyhovuje, je π(v x ) = const exp( const v 2 x) Ukázky funkcí: 1. x 2 + y 2 { je izotropní, ale není souèinem, má ¹patnou limitu 2. x 2 y 2 { je souèinem, není izotropní, má ¹patnou limitu 3 3. (1 + x 2 )(1 + y 2 { je souèinem, není izotropní ) 4. 3 exp( x 2 /2 y 2 /2) { vyhovuje Pøedpoklad: { rychlost je souètem mnoha malých náhodných þ¹»ouchancùÿ Centrální limitní vìta Gaussovo rozlo¾ení

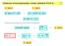
3 Experimentální ovìøení roz¹íøení spektrálních èar Dopplerovým jevem 3/32 molekulový paprsek: Stern, Zartman (1920): 1 = Pt drát pokrytý Ag a 2 = ¹tìrbina 3 = stínítko λ λ 0 λ = v x c Lammert (1929) páry Bi nebo Hg (?) credit: a podle jiných zdrojù cínová pícka

4 Pseudoexperimentální ovìøení a dùsledky [tchem/mbexp.sh] 4/32 Normalizované rozdìlení v jedné souøadnici: π(v x ) = 1 σ v 2π exp ( v 2 x 2σ 2 v ), σ 2 v = v 2 x = k BT m = RT M Rozdìlení rychlostí, tj. hustota pravdìpodobnosti, ¾e naleznu èástici s rychlostí v = v v intervalu [v, v + dv): π(v) = 4πv 2 π(v x )π(v y )π(v z ) = 2 π v 2 σ 3 v exp ( v 2 ) 2σ 2 v K N K 1000 K K 500 K 1000 K tchem/mbexp.sh: - přepni na NVE: e - záznam trajektorie: F - konec záznamu: F - konec: ESC ESC π(v x )/s.m -1 π(v)/s.m v x /m.s v/m.s -1

5 Dùsledky Støední rychlost v = 0 v π(v)dv = 8 π σ v = Støední kvadratická rychlost 8RT πm = 8kB T πm [cd maple; xmaple maxwell.mws] 5/32 v q = v 2 π(v)dv = 0 3RT M = 3kB T m Nejpravdìpodobnìj¹í rychlost dπ dv = 0 v max = 2RT M = 2kB T Souvislost: rychlost zvuku (κ = C p /C V ) m v zvuk = κrt M = κkb T m

6 Vsuvka: rychlost zvuku + 6/32 Mechanický model: m m m m Výchylka = y i, vzdálenost záva¾í = x. Síla pùsobící na hmotnost m v bodì i: F i = (y i+1 y i )K + (y i 1 y i )K = (y i+1 2y i + y i 1 )K x 2 2 y i x 2 K Newtonova pohyb.rov.: F i = m 2 y i t 2 vlnová rovnice x2 2 y i x 2 K = m 2 y i t 2 Kolik je tuhost pru¾iny K pro plyn? Odeèteme sílu v klidu ( m m = x) a pøi výchylce ( x + dy) na plochu A: (NB: p(x) je funkce výchylky) kde f i = A[p( x + dy) p( x)] = A p p V dy = A y V y dy =! Kdy pv κ = konst p V = κp V, Dále m = ρv = pm RT xa, dohromady: 2 yκrt x 2 M = 2 y t 2 v zvuk = V V = A( x+dy) y = A κrt M, y = y(x ± v zvukt) K = Aκp x

7 Pøíklady 7/32 Pøíklad Vypoètìte nejpravdìpodobnìj¹í rychlost molekuly N 2 za teploty 300 K. 422 m s 1 Pøíklad lidovky.cz ( ; foto ÈTK): ROSWELL { Raku¹an Felix Baumgartner vystoupal do stratosféry a vyskoèil ze svého heliového balonu ve vý¹ce 39 kilometrù.... Baumgartner jako první èlovìk na svìtì ve volném pádu pøekonal rychlost zvuku 1127,6 kilometru v hodinì. Jaká byla teplota ve vý¹ce, kde bylo rekordu dosa¾eno? Pøedpokládejte pro jednoduchost, ¾e vzduch se skládá z 20 % kyslíku a 80 % dusíku. Adiabatický pomìr vypoètìte z ekvipartièního principu. 30 C

8 Kinetická teorie plynù Pøedpoklady: 8/32 Mezi jednotlivými srá¾kami (vzájemnými i se stìnou nádoby) se molekuly pohybují pøímoèaøe a nepùsobí na sebe ¾ádnými odpudivými ani pøita¾livými silami. Plyn je natolik øídký, ¾e se molekuly srazí jen obèas. Proto jsou srá¾ky více ne¾ dvou èástic vzácné. Dal¹í zjednodu¹ení: modelové èástice budou tuhé a dokonale pru¾né (tuhé koule) { hrubá aproximace zvlá¹tì za ni¾¹ích teplot (vliv pøita¾livých interakcí) a pro nekulaté molekuly. Ji¾ umíte: stavovou rovnici ideálního plynu Lze poèítat: transportní vlastnosti (difuzivita, viskozita, tepelná vodivost), (alespoò èásteènì) rychlostní konstantu

9 Støední relativní rychlost molekul 9/32 v rel = v 1 v 2 π(v 1x )π(v 1y )π(v 1z )π(v 2x )π(v 2y )π(v 2z ) kde Výsledek π(v x ) = m 2πk B T exp v rel = 2 v dv 1x dv 1y dv 1z dv 2x dv 2y dv 2z ( mv 2 ) x 2k B T Nebo úvahou: 2 Gauss = Gauss s dvojnásobným rozptylem, tedy smìrodatnou odchylkou 2 tak velkou

10 Srá¾kový prùmìr a støední volná dráha molekuly 10/32 d = srá¾kový (kolizní) prùmìr (té¾ σ) úèinný prùøez = σ = πd 2 èíselná hustota = N = N/V = c/n A (té¾ ρ, ρ 1 ) ideální plyn: p = n V RT = crt = N V k BT = Nk B T Støední poèet srá¾ek jedné molekuly (z N v objemu V) za jednotku èasu Støední doba mezi srá¾kami r 1 = Nσv rel = 2Nσv v = 8 π k B T m τ 1 = 1 r 1 Støední volná dráha L (té¾ λ) = støední vzdálenost, kterou molekula urazí mezi dvìma srá¾kami L = v r 1 = v 2Nσv = 1 2Nσ = k BT 2σp = V 1 2σ

11 Støední volná dráha 11/32 Pøíklad. Jaká je støední volná dráha molekul ve vzduchu za bì¾ných podmínek (25 C, 1 bar)? L = 67 nm d η = kolizní prùmìr z viskozity d B = kolizní prùmìr z druhého viriálového koecientu (odchylky tlaku od ideálního plynu) d ρ = (M/ρN A ) 1/3 (odhad z hustoty kapaliny, pøi bodu varu nebo 20 C) plyn d η /pm d B /pm d ρ /pm plyn d η /pm d B /pm d ρ /pm He CH Ne N 2 O H CO Ar C 2 H O SO vzduch Cl CO C 6 H N CHCl ze suchého ledu, z kapaliny pøi 20 C: d ρ = 456 pm

12 Knudsenovo èíslo 12/32 Kn = L D L = støední volná dráha D = typická velikost (lineární rozmìr) otvoru/póru/pøedmìtu Knudsenùv (té¾ balistický) re¾im: Kn 1 molekuly se (témìø) navzájem nesrá¾ejí Normální (difuzní) re¾im: Kn 1 molekuly vykonávají Brownùv pohyb

13 Knudsenova efuze do vakua 13/32 Proudìní plynu malým otvorem, Kn 1 Pøibli¾nì: v v, J Nv p/ mk B T Pøesnìji (staèí uva¾ovat slo¾ku v x ): J = N = N 0 0 tok J je v èásticích v x π(v x )dv x /plochu/èas v x m 2πk B T exp ( v2 xm 2k B T kb T = N 2πm = Nv 4 = p 2πmkB T ) dv x credit: Wikipedia Graham: tì¾¹í molekuly unikají pomaleji Pou¾ití: tlak nasyc. par málo tìkavých látek molekulové paprsky; MBE (Molecular Beam Epitaxy) RHEED = Reection High Energy Electron Diraction

14 Knudsenova efuze do vakua a) ano (p s = Pa, d = m, σ = m 2, L = 1.1 m) b) s 1 (J = m 2 s 1 ) c) 40 s (pøibli¾nì pøedpokládáme výstupní úhel 1 rad, tedy atomy dopadají na plochu A = 100 cm 2, ta obsahuje N = A/d 2 = atomù, t = N/j [xcat ev/efuzearsen.ev] 14/32 Pøíklad. Pøi efuzi do vakua klesne tlak kyslíku v nádobì na polovinu za 10 minut. Za jak dlouho klesne tlak za jinak stejných podmínek, naplníme-li nádobu vodíkem? Jev probíhá izotermicky. 2.5 min Pøíklad. Knudsenova cela s arsenem je zahøáta na 220 C, prùmìr výstupního otvoru je D = 4 mm. a) Jsou splnìny pøedpoklady Knudsenovy efuze? b) Kolik atomù emituje cela za sekundu? c) Za jak dlouho se deponuje monomolekulární vrstva na terèíku ve vzdálenosti 10 cm? Kolizní prùmìr arsenu odhadnìte z hustoty. Data: ρ = 5.73 g cm 3, M = g mol 1. Konstanty Antoineovy rovnice (log 10 (p/pa) = A B/(T + C)) pro As jsou A = , B = , C = K.

15 Tok tepla ve ¹tìrbinì V Knudsenovì (balistickém) re¾imu platí 15/32 Kn = L z 1 molekuly se nesrá¾ejí tok tepla nezávisí na tlou¹»ce ¹tìrbiny (vzdálenosti mezi deskami) z Knudsenova stìna: èástice Pøedpoklad: deska = ideální Knudsenova stìnapo odrazu má náhodnou rychlost dle Maxwellova{ {Boltzmannova rozdìlení z J = Nv 4, J = Nv 4, J Q = 2JC V,1 T kde C V,1 = C V,m /N A = izochorická tepelná kapacita jedné molekuly Po dosazení (a s formálním znaménkem): J Q = 2JC V,1 T = 1 2 NvC V,1 T = NC V,1 2 π RT M T Pozn.: C V,obj = NC V,1 = cc V,m = objemová tepelná kapacita (c = látková koncentrace)

16 Tepelná vodivost plynu { objemová fáze 16/32 Pro Kn 1 si rozdìlíme ¹tìrbinu na vrstvy tlou¹»ky L a aplikujeme Knudsenùv výsledek (aproximace): z J = Nv 4, J = Nv 4, J Q 2JC V,1 T L z Gradient teploty: T = T z Mno¾ství tepla, které projde jednotkovou plochou J Q za jednotku èasu: J Q = λ T λ = J Q T/ z = 1 2 NvC V,1L = kb T C V,1 πm σ λ = tepelná vodivost. [J Q ] = J m 2 s 1 = W m 2, [λ] = W m 1 K 1 Pøesný výsledek (Chapman{Enskog) pro tuhé koule v limitì N 0: λ = 25π 64 NvC V,1L = πkb T m C V,1 σ

17 Tepelná vodivost plynu { objemová fáze Pøesný výsledek (Chapman{Enskog) pro tuhé koule v limitì N 0: λ = 25π 64 NvC V,1L = πkb T m C V,1 σ 17/32 1 A= m = 0.1 nm Pøíklad. (a) Vypoètìte tepelnou vodivost vzduchu (kolizní prùøezd = 3.7 A) pøi 25 C a srovnejte s experimentální hodnotou W m 1 K 1. Tepelnou kapacitu vypoètìte z ekvipartièního principu. (b) Opakujte výpoèet pouze s translaèní èástí tepelné kapacity. (a) W m 1 K 1, (b) W m 1 K 1 { experiment je mezi

18 Tepelná vodivost plynu { srovnání 18/32 Tlustá ¹tìrbina: J Q = λ T z NvC V,1 L T z Tenká ¹tìrbina: J Q NvC V,1 T = λ T L Dohromady: J Q λ T z + L J Q /J Q (0) 2 1 objemová fáze (tlustá ¹tìrbina) λ nezávisí na hustotì resp. tlaku (pro mìkké molekuly ponìkud závisí) λ 1/m 1/2 (tì¾¹í molekuly letí pomaleji) tok 1/m 1/2 λ 1/σ (proto¾e L 1/σ) λ C V,m (ale vibraèní a rotaèní èást ménì) T (exponent bývá vy¹¹í ne¾ 1/2 z dùvodu mìkkosti potenciálu a závislosti C V (T)) L 0 1 z Knudsenùv re¾im (úzká ¹tìrbina) tok tepla úmìrný hustotì tok nezávisí na σ, L λ C V,m (závisí na vlastnostech stìny) T

19 Tepelná vodivost plynu { zajímavosti lep¹í okna se plní Ar, Kr, SF 6 apod.: λ(ar)/λ(vzduch) = 0.67 (o nìco vìt¹í m a σ i ni¾¹í C V,m sni¾ují vodivost) λ(sf 6 )/λ(vzduch) = 0.5 vìt¹í m a σ sni¾ují vodivost, vìt¹í C V,m (èásteènì) zvy¹uje vodivost ale je to skleníkový plyn { dnes zakázán 19/32 Izolaèní schopnosti skelné vaty, pìnového PS ap. jsou dány pøedev¹ím plynem (vzduchem). Vzhledem k závislosti na T je koecient prostupu tepla za vy¹¹ích teplot vy¹¹í. Mikropórezní látky (SiO 2 aerogel) s dostateènì malými póry (ve srovnání se støední volnou dráhou) mohou mít tepelnou vodivost men¹í ne¾ vzduch. Dále se tato vodivost sní¾í pøidáním gratu (radiaèní èást tepelné vodivosti), lze dosáhnout ménì ne¾ polovinu tepelné vodivosti vzduchu.

20 Smyková viskozita smyková síla f = ηa dv x dy A = plocha dv x dy = gradient teèné rychlosti η = dynamická viskozita, [η] = Pa s Pou¾ijeme vzdálenost vrstev dy = L. Jedna molekula pøenese mezi vrstvami jedním smìrem ( ) hybnost y x dy A v 20/32 v +dv x x x mdv x = m dv x dy L Poèet molekul, které proteèou jednotkovou plochou jedním smìrem je podle Knudsenova výsledku 4 1Nv. (Nebo 1 6Nv pokud uva¾ujeme pohyb molekul jen v 1 ze 6 smìrù ±^x, ±^y, ±^z.) Obìma smìry ( ) se za jednotku èasu pøenese hybnost NvA mdv x dy L =! ηa dv x dy

21 Smyková viskozita II 21/32 kde ρ je hustota (hmotnost/objem) η = 1 2 NvmL = 1 2 ρvl Pøesnìj¹ím postupem (Enskog) pro tuhé koule: η = 5π 32 5π 5π ρvl = NvmL = N 8RT πm M 1 = 5 π N A 2Nσ 16 MRT N A σ T 1/2 Sutherland: T 3/2 /(T + C), C = 120 K (vzduch), C = 240 K (CO 2 ) nezávisí na tlaku Boyleùv experiment: tlumení kyvadla nezávisí na tlaku plynu Pøíklad. Viskozita vzduchu za normálních podmínek je Pa s. Vypoètìte a) (støední) prùmìr molekuly, b) støední volnou dráhu, c) maximální mo¾nou frekvenci ultrazvuku. a) σ = 3.7 A, b) L = 60 nm = 162 σ c) 7 GHz (v praxi 1{2 MHz, dosah centimetry)

22 Difuze [../simul/ar/miseni.sh] 22/32 Èástice v prostøedí stejných èástic (autodifuze, samodifuze, self-diusion). Za èas τ 1 = L/v urazí èástice vzdálenost L, pak zmìní smìr (pøedpokládejme, ¾e na zcela náhodný). r 2 = 6Dτ L 2 = 6Dτ 1 = 6DL/v D = 1 6 Lv = 1 3 Pøesnìj¹í teorie (Chapman{Enskog) pro tuhé koule: D = 3π 16 Lv (k B T) 3 πm 1 pσ L = 1 2Nσ v = 8 π k B T m klesá s rostoucí hustotou èi tlakem klesá s rostoucí hmotností èástic (separace izotopù v tì¾¹ím plynu) Pozn.: Difuze ve smìsi (rùzných molekul) je trochu slo¾itìj¹í

23 Jednotný popis kinematická viskozita plynu ν = η ρ = 5π 32 Lv 23/32 tepelná difuzivita (té¾ souèinitel teplotní vodivosti), pro teplo pak platí Fickovy zákony: λ α = = 25π C V,obj 64 Lv difuzivita (koecient autodifuze) D = 3π 16 Lv (konstanty pøesnì pro plyn z tuhých koulí za hustoty 0)

24 Knudsenova difuze (Knudsenùv tok) 24/32 Difuze plynu pórézním materiálem za podmínky, ¾e velikost pórù D (napø. prùmìr válcového póru) je men¹í ne¾ støední volná dráha L (èi srovnatelná). Pokud Kn 1: èástice se pohybuje pøímoèaøe mezi odrazy pøi odrazu se: { termalizuje (Maxwellovo{Boltzmannovo rozdìlení) = Knudsenova stìna { odrazí jako pru¾ná koule (vy¹¹í difuzivita) { nìco mezi Pou¾ití: vlastnosti pórézního materiálu

25 Knudsenova difuze ve válcovém póru 25/32 Pøibli¾nì: prùmìrný úhel 45, dráha r 2R 2, èas mezi odrazy τ r/v, D = r 2 /6τ = Rv Pøesnì: (výpoèet viz dále) D 1/ m (separace izotopù) D T 2π D = Rσ v 3 = π 6 Rv = π 8 6 R k B T π m

26 Knudsenova difuze ve válcovém póru II + 26/32 Pøesný výpoèet: Místo jednoho odrazu na Knudsenovì stìnì si pøedstavme dutinu, kde se èástice mnohokrát odrazí a pak vyletí. Pravdìpodobnost výletu ve smìru Ω = (θ, φ) je úmìrná prùmìtu plo¹ky do smìru kolmého k plo¹ce π(ω) cos θ dω, dω = dφ sin θdθ Válcový pór o polomìru R ve smìru ^y. Odraz ve smìru n = (sin θ cos φ, sin θ sin φ, cos θ) z bodu (0, 0, R) je dán parametrickou rovnicí pøímky l(a) = (0, 0, R) + a n a øe¹íme rovnici l(a) ^y = R. Ta má dvì øe¹ení, a = 0 (= výchozí bod (0, 0, R)), a = 2R cos θ cos 2 θ + sin 2 θ cos 2 φ

27 Knudsenova difuze ve válcovém póru II + 27/32 Dráha ve smìru osy póru (^y) je y = a sin θ sin φ za èas a/v, kde v má Maxwellovo{Boltzmannovo rozdìlení, Difuzivita je D = 1 2 π(v) = 1 (π/2) 1/2 σ 3 v y 2, kde = t exp 0 [ v2 2σ 2 v π(v)dv ] π/2 0, σ v = kb T m cos θ sin θdθ (pozn.: y 2 nezávisí na v, tak¾e výpoèet je jednoduchý). Integrály lze spoèítat snadno v Maple { viz dal¹í slajd 2π 0 dφ

28 Výpoèet integrálù [cd maple; xmaple knudsen.mws] + 28/32

29 Rychlostní konstanta ze srá¾kové teorie + 29/32 Poèet vzájemných srá¾ek v¹ech molekul v jednotce objemu za jednotku èasu r celk = r 1N 2 = 1 σn 2 v = 2σ p π k B T mk B T = 2σN2 A p2 1 π (RT) 3 M poèet vzájemných srá¾ek p 2, L 1/p

30 Rychlostní konstanta ze srá¾kové teorie + 30/32 2 A A 2 Pøedpoklad: molekuly zreagují v¾dy, jestli¾e k tomu mají pøi srá¾ce dost kinetické energie { alespoò aktivaèní energii E. Pravdìpodobnostní rozlo¾ení relativních rychlostí (jako T 2T): ( ) ( ) m 3/2 mv 2 π rel (v rel ) = 4π exp rel v 2 4πk B T 4k B T rel Molekula s v = v rel se bude srá¾et s ostatními s frekvencí (poèet srá¾ek za jednotku èasu) r 1 = v rel σ N Rychlost vzhledem k tì¾i¹ti páru je v rel /2 a energie je ) 2 = mv 2 rel E = 2 1 ( vrel 2 m 2 4 Naopak minimální rychlost v rel potøebná k reakci je v rel = 4E /m

31 Rychlostní konstanta ze srá¾kové teorie II + 31/32 Frekvence srá¾ek (tj. poèet srá¾ek vedoucích k reakci za jednotku èasu) Po substituci za E r reakce = N 2 v rel r reakce = 16π2 σ 2 N 2 2Vm 2 ( m 4πkT = 16π2 σ 2 N 2 2Vm 2 ( m 4πkT v rel σn 2 π rel (v rel )dv rel ) 3/2 E exp ) 3/2 exp ( E ( ) E E de k B T ) [ k B TE 0 ] +(k B T) 2 Pozn.: pro E = 0, tj. ka¾dá srá¾ka se poèítá, dostaneme r reakce = r celk Pøi jedné srá¾ce ubydou dvì molekuly. Reakèní rychlost vyjádøená jako úbytek koncentrace c = N/N A za jednotku èasu je tedy dc dτ = 2rN/N A = A(T) exp ( Ea,m RT k B T ) c 2 k(t) c 2 Realistiètìj¹í model uva¾uje jen radiální slo¾ku rychlosti pøi srá¾ce molekul tvaru koule, pak místo [k B TE ] vyjde [(k B T) 2 /2].

32 Rychlostní konstanta ze srá¾kové teorie III 32/32 Pøedexponenciální faktor dc dτ = k(t) c2 k(t) = A(T) exp ( Ea,m RT ) A(T) = E a,m πmkb T 4σ lépe: 2N Aσ kb T πm reakce je druhého øádu hlavní tepelná závislost je v exponenciálním faktoru zpøesnìní popisu srá¾ky modikuje pøedexponenciální faktor