Dopravní kinematika a grafy
|
|
|
- Tomáš Růžička
- před 10 lety
- Počet zobrazení:
Transkript
1 Dopraní kinemaika a grafy Sudijní ex pro řešiele F a oaní zájemce o fyziku Přemyl Šediý Io Volf bah 1 Základní pojmy dopraní kinemaiky 1.1 Poloha Rychlo Zrychlení Grafy dopraní kinemaice 7.1 Kinemaika a grafické znázornění ronoměrného pohybu Modeloání reálného pohybu pomocí ronoměrných pohybů Určení okamžié rychloi z grafu dráhy při neronoměrném pohybu Určení dráhy neronoměrného pohybu z grafu rychloi Kinemaika a grafické znázornění ronoměrně zrychleného a ronoměrnězpomalenéhopohybu Modeloání reálných pohybů pomocí ronoměrných a ronoměrněproměnnýchpohybů... 0 Výledky úloh 3 1
2 1 Základní pojmy dopraní kinemaiky 1.1 Poloha Pohyby dopraních proředků laků, ilničních ozidel po železničních raích a ilnicích popiujeme fyzikálně jako pohyby hmoných bodů ázaných na pené rajekorie. Poloha akoého hmoného bodu na rajekorii je doaečně určena jedinou ouřadnicí definoanou jako zdáleno od určiého zažného bodu. Abychom yačili kladnými ouřadnicemi, olíme zažný bod ždy na jednom konci železniční rai nebo ilnice. Souřadnicemi jou určeny aké polohy ýznač- ných objeků rozmíěných podél rajekorie. Například pro dálnici D1 Praha Brno Vyškojezažnýbodnajejímzačáku Praze na Kačeroě. Schéma éo dálnice, keré je příloze auomapy a jehožčájenaobr.1,náinformuje,že na ouřadnici 0,5 km je křižoaka Spořilo ýjezdem na Teplice, Ml. Bolela a Hr. Králoé, na črém kilomeru přijíždíme k prnímu benzinoému čerpadlu. něcodálebychomedoěděli,žeýjezd na Šoky a Věrný Jeníko má ouřadnici přeně 100 km ad. Pro orienaci řidičů jou odděloacím pruhu dálnice rozmíěnypokaždém0,5kmabulkyyznačením ouřadnice daného mía. Vzdáleno na ilnici amozřejmě neměříme zdušnoučarou.jeodélkarajekorie mezi zažným bodem a daným míem neboli dráha, kerou muí urazi ozidlo, aby e ze zažného bodu doalo do daného mía. br.1
3 1. Rychlo Řidič auomobilu leduje obykle průběh jízdy pomocí náramkoých hodinek a achomeru (rychloměru) umíěného na přírojoé dece před olanem (obr. ). Jeho ručka ukazuje eliko okamžié rychloi ozidla a na počíadle kilomerů čeme celkoou dráhu ujeou auomobilem od jeho uedení do proozu. Z fyzikálního hledika je okamžiá rychloauomobilu ekoroá eličina určená elikoí a měrem. Můžeme ji yjádři e aru =, kde jeelikookamžiérychloia jejednokoýměroýekor(obr.3). Připřímočarémpohybuležíekorya rajekorii(bod A),přikřiočarém pohybu leží ečně k rajekorii(bod B). Malý úek křié rajekorie můžeme ždy poažoa za čá kružnice určené ředem křioi S a poloměrem n křioi R. Jednokoý ekornměřující do ředu křioi e nazýá normáloý ekor A B S R , km/h br. br.3 Směr okamžié rychloi ozidla je ošem dán umíěním ilnice krajině, nemůžeme jej olini, a pokud nezabloudíme, ěšinou e o něj příliš nezajímáme. Za důležiou poažujeme jen eliko okamžié rychloi. Pro zjednodušení edy praxi obykle říkáme, že na achomeru čeme okamžiou rychlo ozidla. Nemůže-li dojí k nejanoi, yjadřujeme e někdy ako zkráceně i e fyzikálních úlohách. Konrolu achomeru můžeme jednoduše proé při jízdě álou rychloí, edy při ronoměrném pohybu. Jeliže údaj počíadla kilomerů zroe z hodnoy 1 čae 1 nahodnou čae,plaí = 1 1 =. 3
4 Příklad 1 Údaj počíadla kilomerů na achomeru e při jízdě álou rychloí zěšil o10kmza7minua0ekund.jakelkájerychloauomobilu? Řešení Při ýpoču můžeme použí hlaní jednoky SI, nebo počía jednokami kilomer, hodina a kilomer za hodinu: = = 10000m 440 =,7m 1. =3m 1, 10km ( ) =81,8km/h =8km/h.. h 3600 V éo a podobných úlohách dáme parně předno ýledku km/h. Nebude-li pohyb auomobilu přeně ronoměrný, zíkáme předcházejícím ýpočem pouze průměrnou rychlo p = 1 1 =. Noější achomery jou ybaeny i z. denním počíadlem kilomerů. To můžeme před jízdou ynuloa a měři jen dráhu dané jízdy. Použijeme-li pro měření jízdní doby opky, keré puíme okamžiku aru, můžeme průměrnou rychlo jízdy urči z jednoduššího zahu p =. Chceme-li urči okamžiou rychlo ozidla při neronoměrném pohybu, muíme změři dobu, za kerou projede ozidlo elmi malý přírůek dráhy. Výpoče zapiujeme e aru = ( ) pro 0 neboli = lim 0 =d d. Tako určují okamžiou rychlo cyklocompuery monoané na poroní kola(obr. 4), keré ukazují na dipleji podíl obodu kola a doby jednoho oběhu změřené pomocí magneického nímače. Tyo přiroje mají ošem ješě řadu dalších funkcí. Vedle okamžié rychloi mohou ukazoa i průměrnou rychlo od začáku jízdy, maximální rychlo, dobu jízdy, poče ujeých kilomerů od začáku jízdy nebo od doby uedení compuerudoproozu,frekencišlapáníaj. 4 br.4
5 1.3 Zrychlení Během jízdy ozidla e mění eliko jeho okamžié rychloi a zaáčkách i její měr.proberemeinejprepodleobr.5jízduzaáčkou.zadobu eozidlo přemíízbodu Adobodu Bajehorychloezměníz1na.Bude-lidoba elmi kráká, změní e eliko i měr rychloi jen neparně:.. 1 = =, α 5. V akoém případě můžeme z obr. 5a,b ododi n zahy: = 1= ( )= +, a = = α= 1 R = R, = Rn. A c) A α 1 an 1 B B α 1 S R a) b) d) =d br.5 kamžié zrychlení definoané zahem ( ) a= pro 0 nebolia= lim 0 d pak můžeme yjádři e aru: a= + = +. Rn=a+an Zrychlení při křiočarém pohybu můžeme edy rozloži na dě ložky: Tečnézrychlenía= a =a máeliko =. a a a an 5
6 Určuje čaoou změnu elikoi okamžié rychloi. Jeliže e rychlo zěšuje, jezlomek kladný a ečné zrychlení má měr ekoru okamžié rychloi (obr.5c).zmenšuje-lierychlo,jezlomek zápornýaečnézrychlenímá opačný měr než ekor okamžié rychloi(obr. 5d). Při ronoměrném pohybu je ečné zrychlení nuloé. Normáloénebolidořediézrychlenían= an =a Rnmáeliko n = R a míří ždy do ředu křioi daného úeku rajekorie. Určuje čaoou změnu měru okamžié rychloi. Při přímočarém pohybu je normáloé zrychlení nuloé a celkoé zrychlení chápeme i jako zrychlení ečné:a=a. V dopraní kinemaice, kde ná zajímá předeším eliko okamžié rychloi, e uplaní zrychlení ečné. Normáloé zrychlení je naopak důležié při řešení úloh z dynamiky jízdy zaáčce, kerými e omo exu nebudeme zabýa. 6
7 Grafy dopraní kinemaice K zíkání názorné předay o průběhu určiého pohybu použíáme grafy zobrazující záilo polohy nebo rychloi na čae. Polohu ozidla na ilnici můžeme urči dráhou, kerou ozidlo projelo, jeho zdálenoí od zažného bodu nebo polohoou ouřadnicí. U rychloi ozidla můžeme ledoa, jak e mění její eliko nebo polohoá ouřadnice. Ukážeme i o zjednodušeně na příkladu kuličky, kerou položíme na nakloněnou roinu do bodu A a udělíme ji počáeční rychlo0 zhůru podél nakloněnéroiny(obr.6).kuličkačae 1 doáhnenejyššíhobodu B,pake racízpěačae projedebodem Aměremdolů.Pohybpopíšemezhledem kezažnéouaě,jejížpočáekjebodě Aaoa xměřujezhůru podélnakloněnéroiny.jezřejmé,žečaoémineralu 0, 1 nenírozdíl mezidráhou,zdálenoí dodpočákuaouřadnicí x.nelišíeanieliko rychloi aouřadnice x.podoaženíbodu Bdráha dáleroe,alezdáleno d od počáku a ouřadnice x e zmenšují. Souřadnice rychloi změní znaménkoanadáleplaí x =.Poprůjezdubodem Aezměníznaménko ouřadnice x na záporné, ale zdáleno d po doažení nuly e opě zěšuje a nadáleplaí x= d. B x x d x 0 y A 1 d x 1 x br.6 Také při grafickém znázornění pohybu dopraního proředku nemuíme někerých případech rozlišoa dráhu, zdáleno od zažného bodu a polohoou ouřadnici, případně eliko rychloi a její ouřadnici. Jindy naopak muíme k rozdílům mezi nimi přihlíže. 7
8 .1 Kinemaika a grafické znázornění ronoměrného pohybu Naobr.7jougrafyrychoi ()adráhy () ronoměrného pohybu, při kerém e čaoém ineralu 1, zěšiladráhaz 1 na.plaí () = 1 = ( 1 )=. Přírůek dráhy je edy číelně roen obahu yšrafoaného obdélníka grafu rychloi. Dráha je lineární funkcí čau, graf dráhy ronoměrného pohybu je edy čáí přímky. Její ronici můžeme yjádři e aru: 1 1 α () 1 1 = 1 1 =, =( 1 ) br.7 Zolíme-li na odoroné a ilé oe ejná měříka, j. jednoce čau přiřadíme na odoroné oe ejně elký dílek jako jednoce dráhy na ilé oe, plaí pro odchylku α grafu dráhy od odoroné oy g α= { } { } = {}. Směrnice grafu g α je číelně rona elikoi rychloi ronoměrného pohybu.čímrmějšíjegrafdráhy,íměšíjerychlo.(toošemplaíipři jakékoli jiné olbě měříek na oách.) Vhodnou olbou počáečních podmínek pohybu můžeme dojí i k jiným ronicím grafu dráhy, uedeným na obr. 8. =+ 0 d 0 1 = =( 1) 1 P d 0 d1= 1( 1) d = d 0 ( ) br.8 br.9 8
9 Chceme-li jednom grafu zobrazi pohyby několika dopraních proředků, keré e po komunikaci pohybují oběma měry, použijeme mío grafu dráhy grafzdálenoiodzažnéhobodu d().jeliženapř.čae 1 yjedezmía Anějakéozidloálourychloí 1 měremkmíu Bležícímezdálenoi d 0 ačae yjededruhéozidlozmía Bálourychloí měremkmíu A, můžeme jejich pohyby popa ronicemi d 1 = 1 = 1 ( 1 )), 1 < < 1 + d 0 1, d = d 0 = d 0 ( )), < < + d 0, azobraziepolečnémgrafupodleobr.9.zprůečíku Poboučarpaknadno určímečaekáníobouozidelapolohumía,kdekekánídojde.keejnémuýledkudojdemeiřešenímronice d 1 = d. Příklad. Nákladníauomobilyjel7h00minzPrahydoBrnapodálniciD1apohyboaleálourychloí80km/h.Vzdálenoobouměje00km.V7h30min za ním yjel oobní auomobil jedoucí álou rychloí 110 km/h. Ve ejném okamžikuyjelnadálnicizbrnaměremnaprahujinýoobníauomobilaudržoal álou rychlo 100 km/h. Určee, kdy a kde e nákladní auomobil eká oběma oobními auomobily. Úlohu řeše nejpre graficky, poom počeně. Řešení Graf znázorňující, jak e mění zdálenoi šech ří ozidel od Prahy záiloi na čae, je na obr. 10. K jeho erojení byly použiy body zobrazující odjezdy jednoliých ozidel z jednoho měa a příjezdy do druhého měa. NákladníauomobilpojedezPrahydoBrna,5hapřijedeam9h30min. Prníoobníauomobilpojede(00/110)h. =1h49minadoBrnapřijede už9h19min. DruhýoobníauomobilpojedehapřijededoPrahy9h30min. Zpolohyprůečíků P 1 a P yčeme,ženákladníauomobilenejpreeká oobnímauomobilemjedoucímodbrnaao8h3 minezdálenoi 111kmodPrahy.obníauomobiljedoucíodPrahyjejpředjede8h50min e zdálenoi 147 km od Prahy. Pro počení řešení napíšeme nejpre ronice jednoliých pohybů: Nákladní auomobil: d 1 = 1 ( 1 ), 1 =80km/h, 1 =7,0h, 1. oobní auomobil: d = ( ), =110km/h, =7,5h, 9
10 . oobní auomobil: d 3 = d 0 3 ( 3 ), d 0 =00km, 3 =100km/h, 3 =7,5h, Při ýpoču použijeme jednoky km, h a km/h. Vzdálenoi, kde došlo k ekáníozidel,označíme d a d,přílušnéčay a.proauomobilyjedoucí ýmžměremřešímeronici d 1 = d : 1 ( 1 )= ( ) = =8,833h=8h50min, d = 1 ( 1 )=147km. Proauomobilyjedoucíopačnýmměremřešímeronici d 1 = d 3 : 1 ( 1 )=d 0 3 ( 3 ) = d =8,389h=8h3min, d = 1 ( 1 )=111km. Počení řešení úlohy není příliš ložié, ale nadno něm přehlédneme numerickou chybu. Čení z grafu je polehliější a dáá i doaečně přené ýledky, zejména když použijeme milimeroý papír. d km Brno 00 o P n P o 1 Praha br. 10 h 10
11 . Modeloání reálného pohybu pomocí ronoměrných pohybů V příkladu. jme řešili úlohu o pohybech po dálnici, kde za ideálních podmínek můžeme je álou rychloí. Někdy je možné i ložiější pohyby přibližně popa jako několik na ebe naazujících ronoměrných pohybů. Příklad 3 Cykliické záody mládeže budou probíha na rai dlouhé 9,5 km. čekáámenáledujícíprůběhjízdy:prníúekdélky6,0kmjeporoiněacyklié pojedou rychloí 30 km/h. Na druhém úeku délky,0 km je mírné oupání, cykliézmírnína0km/h.náledujeprudšíoupánídélce4,5km,kdee rychlo cykliů zmenší na 15 km/h, a odoroný úek délky 9,0 km, kerý projedou opě rychloí 30 km/h. Do cíle zbýá mírné kleání a cíloá roinka, kde předpokládáme rychlo 36,0 km/h. a) Určee celkoou dobu jízdy a průměrnou rychlo. b) Seroje grafy rychloi a dráhy. Poroneje celkoou dráhu a obah obrazce omezeného oou čau a grafem rychloi. Řešení a) Nejpre určíme doby průjezdu jednoliých úeků a celkoou dobu jízdy. 1 = 1 1 =0,0h=1min, = =0,10h=6min, 3 = 3 3 =0,30h=18min, 4 = 4 4 =0,30h=18min, 5 = 5 5 =0,0h=1min, Průměrná rychlo bude = =1,10h. p = =6,8km/h. b) Výledky ýpočů yužijeme k erojení grafů na obr. 11. brazec ohraničený oou čau a grafem rychloi e kládá z obdélníků, jejichž plošné obahy joučíelněronyoučinům 1 = 1 1, = až 5 = 5 5. Jednokoý plošný obah má yšrafoaný obdélníček leém dolním rohu obrazce, neboť 10km/h 0,1h=1km.Celkoýplošnýobahobrazceječíelněroencelkoé drázezáodníků, = Čaoýprůběhdráhyjezobrazen grafu (). 11
12 km/h , 0,4 0,6 0,8 1, h br. 11 km 5 0 ronoměrný pohyb průměrnou rychloí , 0,4 0,6 0,8 1,0 h V železniční praxi e ekááme grafickým jízdním řádem(grafikonem), kerý znázorňuje, jak e mění polohy šech laků na určié rai záiloi na čae.naobr.1idímečáakoéhografikonuproraťhalíčkůbrod Kolín Nymburk hl.n. Na horním a dolním okraji grafikonu je čaoá oa rozdělená po 10 minuách. U průečíku jednoliých grafů ynášecími čarami anic jou umíěny malé čílice, keré čaoý údaj upřeňují na minuy, případně půlminuy(podrženéčílice např.6čemejako6min30).napraéraně grafikonu je ilá oa, na keré čeme kilomeroé polohy anic, edy jejich ouřadnice. Podobně jako na dálnicích i podél železnic e nacházejí ouřadnicoé značky. Jou zhooeny jako paníky rozmíěné praidelně po 100 merech. Šikmé čáry grafikonu zobrazují záiloi poloh laků na čae. Pohyby laků obou měrech jou ošem idealizoány, jako by e kládaly ze amých ronoměrných pohybů. Grafikon edy popiuje reálné pohyby laků jen přibližně. 1
13 br. 1 13
14 Úloha 1 Z grafikonu na obr. 1 určee průměrné rychloi rychlíku č. 70 ANTNÍN DVŘÁKúecíchSělánadSázaou GolčůJeníkoaGolčůJeníko Kolín. Kilomeroé polohy anic jou 33,9 km, 67,1 km a 98,3 km. Příklad 4 Cykliické záody mládeže byly upořádány na okruhu délky 4 km, kerý mueli záodníci proje 5krá. Pael doáhl průměrné rychloi 40 km/h, Kája uraziljedenokruhza7min 30aJirkadoáhlcelkoéhočau4min 30. a) Určee pořadí záodníků cíli. b) Seroje graf záiloi polohy záodníků na čae a odhadněe, kdy a kde došlo k předjeí někerého pomalejšího z uedených ří záodníků záodníkem rychlejším. Řešení a)paelbylnejrychlejší,jedenokruhprojelza0,1h=6min.jirkabylnejpomalejší,jedenokruhprojelza8min 30.Pořadícíli:Pael,Kája,Jirka. b) Pro určení polohy záodníka na okruhu použijeme ouřadnici x 0, 4 km. Nakonciokruhueouřadnicezáodníkazměníze4kmna0kmaznoue začínázěšoa.zgrafunaobr.13idíme,žepaelpředjeljirkuojednokolo při ém črém okruhu. Ča a mío předjeí určíme ýpočem: 1 = m, kde 1 =11,11m 1, 3 =7,843m 1. = 4000m 1 3 =14. =0,4min, x= m. =1600m. V okamžiku, kdy Pael dojížděl do cíle, zbýalo Kájoi ješě jedno kolo. x km 4 3 Pael Kája Jirka br. 13 min 14
15 Úloha Auobuoá linka MHD pojuje mía A, B. Jejich zdáleno je 18 km a auobu ji překoná za 4 minu. Prní auobu yjíždí z koncoé anice A 6h0 min,dalšípraidelnýchineralech10 min.vkoncoéanici B čekají8 minaracejíepoejnéraezpě.zpáečníjízdarároněž4 minu. Kolik auobuů jedoucích proiměru poká ceující, kerý yjíždí ze anice A7h0min,akolikceující,kerýyjíždízeanice A8h0min? V jakých čaoých ineralech je budou pokáa? V auobuoé a nákladní dopraě e použíají achografy, keré zapiují na koouček papíru okamžiou rychlo ozidla a ujeou dráhu záiloi na čae.čáakoéhozáznamujenaobr.14.čára1jegrafokamžiérychloi. Čára popiuje činno řidiče(řízení, jiná práce, čekací doba, odpočinek). Zubaá čára 3 regiruje chod počíadla kilomerů během přechodu z jedné krajní polohy do druhé ujede ozidlo 5 km. Na rozdíl od železničního grafikonu, kerý je přibližný, pokyuje záznam z achografu přené informace o kuečném průběhu ledoané jízdy. br Vnašíukázceeauomobilpohyboalod16h5mindo18h0minpo dálniciaod18h30mindo19h0minpookreníilnicihuýmproozem. Prní čá jízdy e dá přibližně modeloa ronoměrným pohybem, při kerém 15
16 auomobilujelza88 mindráhu114km(odečenozčáry3)apohyboale rychloí 78 km/h. Druhá čá jízdy byla mnohem ložiější. Auomobil e několikrá muel zaaiaznourozje.za50 minujeljen40kmadoáhlprůměrnérychloi 48 km/h. Takoýo komplikoaný děj už nemůžeme ýižně modeloa ronoměrnými pohyby. Jednoliá rozjíždění a zaaení e šak dají doi přeně popa jako pohyby ronoměrně zrychlené a ronoměrně zpomalené..3 Určení okamžié rychloi z grafu dráhy při neronoměrném pohybu Včlánku.1jmeezabýaligrafemdráhy ronoměrného pohybu. Ten leží přímce, jejíž měrnice je, pokud zolíme na oe čauejnéměříkojakonaoedráhy,číelně rona elikoi konanní rychloi pohybu. Grafem dráhy neronoměrného pohybu je křika(obr. 15). Směrnice ečny grafu, kerá prochází bodem A o ouřadnicích [ 1, 1 ]abodem Boouřadnicích[, ], je číelně rona průměrné rychloi čaoémineralu 1, : g α= { 1 } { 1 } = { } { } = { p}. 1 A α 1 B B () B 1 br. 15 Chceme-liurčiokamžiourychločae 1,muímečaoýineral zmenšiknule.bod Bepřebody B, B přiblížíkbodu Aaečnagrafu přejdeečnubodě A.Velikookamžiérychloičae 1 jeedyčíelně ronaměrniciečnygrafubodě A: 1 ) ( 1 )=g α 1. Při pohybu dopraního proředku e okamžiá rychlo ždy mění pojiě (pokud ošem nedojde k nějaké haárii). Proo e pojiě mění i klon grafu dráhy. Graf má podobu hladké čáry bez orých zlomů. 1 Práěpopanýpoupeeyššímaemaicenazýáderioánífunkce ()bodě = 1 a zapiuje e zahem ( ( 1 )= lim 1 + ) ( 1 ). 0 α 16
17 .4 Určení dráhy neronoměrného pohybu z grafu rychloi Známe-li graf rychloi neronoměrného pohybu a chceme-li urči přírůek dráhyčaoémineralu 1,,můžemepoupoapodobnějakopříkladu 3 a nahradi neronoměrný pohyb řadou po obě jdoucích ronoměrných pohybů. Čaoý ineral rozdělíme na malé dílčí ineraly elikoi, e kerých e eliko okamžié rychloi změní jen neparně. Můžeme edy pohyby ěcho dílčích ineralech přibližně nahradi ronoměrnými pohyby rychlomi ronými kuečným okamžiým rychloem na počácích dílčích ineralů.grafemrychloiakozíkanéhonáhradníhopohybuje chodoá čára, kerá e liší od grafu kuečného pohybu ím méně, čím kraší ineraly zolíme(obr. 16). Elemenární přírůek dráhy náhradního pohybu = každém dílčím ineralu je číelně roen obahu jednoho obdélníkoého proužku( obr. 16 yznačeno šrafoaně). Celá dráha náhradního pohybu je číelně rona obahu yečkoané plochy. Při elmi jemném dělení ( 0) e náhradní pohyb prakicky neliší od kuečného pohybu a yečkoaná plocha přejde obrazec omezený grafem rychloi kuečného pohybu a oou čau(obr. 17). Vzahmezipočáečníhodnooudráhy 1,konečnouhodnooudráhy a obahem yečkoaného obrazce P je edy 1 = P, přičemž jednokoý obah má obdélník, jehož jednu ranu oří jednokoá úečka na oe čau a druhou ranu jednokoá úečka na oe rychloi. Jeliže čaynášímeekundácharychlom 1,odpoídájednokoémuobahu dráha1m.vynášíme-ličahodinácharychlokm h 1 jakopříkladu3, odpoídájednokoémuobahudráha1km. ) = () P () 1 1 br. 16 br. 17 Práěpopanýpoupeeyššímaemaicenazýáinegracefunkce ()ineralu 1, azíkanýýledekezapiujezahem 1 = d. 1 17
18 .5 Kinemaika a grafické znázornění ronoměrně zrychleného a ronoměrně zpomaleného pohybu Ronoměrně zrychlený je každý pohyb, při kerém e eliko okamžié rychloi záiloi na čae ronoměrně zěšuje. Tečné zrychlenía má konanní eliko a ejný měr jako okamžiá rychlo. Při ronoměrně zpomaleném pohybu e eliko okamžié rychloi záiloi na čae ronoměrně zmenšuje. Tečné zrychlenía má konanní eliko a opačný měr než okamžiá rychlo. Je-li pohyb přímočarý, nezniká normáloé zrychlení a celkoé zrychlenía e uplaňuje jako zrychlení ečné,a =a. V úlohách z dopraní kinemaiky čao použíáme označeníapro ečné zrychlení i případech, kdy e jedná o pohyb křiočarý, ale zajímáme e jen o eliko okamžié rychloi a její měr ná nezajímá. Téo nepřenoi e dopuíme i náledujících odacích. Ronoměrně zrychlené a ronoměrně zpomalené pohyby probíhají obykle jen na krákých úecích rajekorie. Proo je hodné při ýpočech použía pouze hlaní jednoky ouay SI. Budeme edy dráhu určoa merech, ča ekundách,rychlom 1 azrychlením. Průběh ronoměrně zrychleného pohybu nuloou počáeční rychloí znázorňují grafy na obr. 18. Ze zákona rychloi = a =a ododíme zákon dráhy. Dráha uražená od začáku pohybu je číelně rona obahu rojúhelníka omezenéhografemrychloi.položíme-li 0 =0(před arem ynulujeme počíadlo kilomerů), plaí = 1 a = =1 a = a. br
19 = 0+ a Průběh ronoměrně zrychleného pohybu nenuloou počáeční rychloí0 znázorňují grafy na obr. 19. Zákon rychloi má ar 0 ( 0+ ) = a+ 0. = 0+ 1 a 0 Dráhu uraženou čaoém ineralu 0, určíme jakoobahlichoběžníka.položíme-liopě 0 =0, plaí = ( 0+ ) = ( a) = a. br. 19 Průběh ronoměrně zpomaleného pohybu počáeční rychloí0 znázorňují grafy na obr. 0. Pohyb může probíha až do zaaení po dobu b,kerounazýámebrzdnádoba.zákonrychloi má ar = 0 a, dráhu uraženou čaoém ineralu 0,, kde < b, určíme opě jako obah lichoběžníka. Položíme-li 0 =0,plaí = ( 0+ ) = ( 0+ 0 a) = 0 1 a. 0 b ( 0+ ) = 0 a 0 b = 0 1 a obr. 0 Celkoádráha b ronoměrnězpomalenéhopohybuenazýábrzdnádráha. Vzahymezibrzdnoudobou b,počáečnírychloí 0,brzdnoudráhou b aelikoí ečného zrychlení a připomínají zákony ronoměrně zrychleného pohybu nuloou počáeční rychloí: b = 0 a, b= 0 b = 1 a b= 0 a Kdybychom oiž nafilmoali ronoměrně zpomalený pohyb nějakého ozidla až do zaaení a pak film puili pozpáku, doali bychom ronoměrně zrychlený pohyb nuloou počáeční rychloí, při kerém by couající ozidlo čae = b doáhlorychloi = 0. b 19
20 .6 Modeloání reálných pohybů pomocí ronoměrných a ronoměrně proměnných pohybů Příklad 4 Auomobil jedoucí rychloí 110 km/h začal brzdi a zaail e na dráze 100 m. Jakou rychloí e pohyboal e zdálenoi 10 m před míem zaaení? Řešení Budeme předpokláda, že celé brzdění proběhlo jako pohyb ronoměrně zpomalenýpočáečnírychloí 0 =110km/hacelkooubrzdnoudráhou b = 100m.Dopoledníhoúekubrzdnédráhyodélce 1 =10mjelauomobil počáečnírychloí 1.Zezahuproýpočebrzdnédráhyyjádřímeeliko zrychlení: b = 0 a, a= 0 = 1 =kon.. b 1 Úpraou doaneme: ( ) 1 = 1 1, 0 1 = 0 =10km h b 1 0,10=35km h 1. b Ke ejnému ýledku můžeme dojí z grafu rychloi na obr. 1. Celkoá brzdná dráha a polední úek brzdné dráhy jou číelně rony obahům yšrafoaného a ybareného rojúhelníka. Poměr obahů podobných rojúhelníků je roen druhé mocnině poměru podobnoi: ( ) 1 = k 1 =. b br. 1 Příklad 5 Určee, jakou dobu pořebuje oobní lak k překonání zdálenoi,4 km mezi ouedními anicemi, jeliže e rozjíždí e álým zrychlením o elikoi 0,70m,podoaženímaximálnírychloi90km/hepohybujeronoměrně anakonecbrzdíezrychlenímoelikoi0,55m aždozaaení.seroje graf rychloi a graf dráhy popaného pohybu. Řešení značení daných eličin: c =400m, m =90km h 1 =5m 1, a 1 =0,70m, a 3 =0,55m. Rozjezd a zaaení laku budeme nejpre yšeřoa jako amoané pohyby.vlakpořeboalkrozjezdudráhu 1,kerouprojelzadobu 1.Brzdění b 0
21 proběhlonadráze 3 zadobu 3.Plaí: 1 = m a 1. =36, 1 = m a 1. =450m, 3 = m a 3. =45, 3 = m a 3. =570m. Naronoměrnýpohybzbýádráha,keroulakprojedezadobu : = c 1 3. =1380m, = m =55 Celkoádobajízdyje c = =136. Graf rychloi na obr. má ar lichoběžníka. Z něj můžeme ododi jednodušší ýpoče celkoé doby jízdy. Plaí: c = m c m 1 m 3, c = c m = c m + m a 1 + m a 3. Grafdráhynaobr.ekládázúečkyadouúekůparaboly.Jednolié čái na ebe plynule naazují. Parabolu prním úeku popiuje funkce = 1 a 1.Parabolueřeímúekupopiujefunkce = c 1 a 3( c ). (Uaže, jak by ypadal pozpáku pušěný filmoý záznam pohybu.) Při krelení grafu byla použia abulka: / m m m () () br c 150 1
22 Úloha 3 Auomobilerozjíždělak,žepřizařazené jedničce doáhlběhemprních douekundrychloi7km/h,běhemdalšíchříekundpřizařazené dojce doáhlrychloi54km/h.pakřidičzařadil rojku aběhemdalšíchříekund doáhlrychloi7km/h,zařadil čyřku aběhempěiekunddoáhlrychloi90km/h,zařadil pěku apokračoaljízděálourychloí90km/h. Po deei ekundách ronoměrného pohybu i řidič šiml, že nemá dobře upeněný náklad, začal brzdi a během deíi ekund zaail, aby záadu odranil. Rozjezd poažuje za érii ronoměrně zrychlených pohybů a brzdění za ronoměrně zpomalený pohyb. Nakrelee graf rychloi a určee celkoou dráhu auomobilu. Úloha 4 Sprinerproběhldráhu100mza9,90.Předpokládejme,žeprních30me rozbíhal ronoměrně zrychleným pohybem, a pak běžel álou rychloí až do cíle. Určee rychlo druhé čái pohybu. Úloha 5 Nakřižoacezaaila načerenou děozidlaouedníchjízdníchpruzích. Pozměněěelnéignalizace nazelenou yrazilaoběozidlaak,žeprní ozidlodoáhlorychloi60km/h,kerájeomoúekupoolena,za8,3a druhéozidloza1,5. a) Rozjezd obou ozidel zakrelee do grafu (). Do éhož grafu aké zakrelee, jak e měnila záiloi na čae eliko relainí rychloi ozidel, j. eliko rychloi, kerou mělo jedno ozidlo e zažné ouaě pojené druhým ozidlem. b) Seroje graf, kerý znázorňuje, jak e během rozjezdu měnila zájemná zdáleno obou ozidel záiloi na čae. Pořebné zahy odoďe z grafu relainí rychloi.
23 Výledky úloh 1.69km/h,87km/h. Úlohu nejnáze yřešíme pomocí jednoduchého grafikonu. Z něj yčeme, že prní ceující poká 6 auobuů jedoucích proiměru a druhý jich poká 9. Budou-li e auobuy pohyboa álou rychloí, bude je pokáa praidelně každých 5 minu. x km m br. 3 h br. 4 = 1 1 +( 1+ ) + ( + 3 ) 3 + ( 3+ 4 ) =570m. 3
24 4. Z grafu rychloi ododíme: m c = 1 +, m br.5 m = 1+ c = 130m 9,9 = 1 =13,1m 1 =47,3km h 1. c 5.Danéeličiny: m =60km/h=16,7m 1, 1 =8,3, =1,5. a)grafrychloijenaobr.6.relainírychlo r ozidelenejpre ronoměrnězěšoalaačae 1 doáhlamaximálníhodnoy rm = m m 1 = m 1. Podoaženímaximaeronoměrnězmenšoalaačae klelananulu. b) Vzájemná zdáleno ozidel určiém čae je číelně rona obahu obrazce ohraničeného grafem relainí rychloi. Pro 0 < < 1 plaí: r = rm 1, d= r = m( 1 ) 1.. =3m. Včae = 1 doááme: d 1 = rm 1 = m( 1 ) 1 Včae = doáhnezdálenoozidelhodnoy d m = rm = m( 1 ). =35m adálejižneroe(obr.7). m 1 0 Pro 1 < < plaí: r = rm 1, d=d m r( ) m 10 1 = m( 1 ) m( ) = m( 1 ). d m 40 d m 30 d 1 0 rm r br. 6 br. 7 4
Rovnoměrný pohyb. velikost rychlosti stále stejná (konstantní) základní vztah: (pokud pohyb začíná z klidu) v m. s. t s
 Ronoměrný poyb eliko rycloi ále ejná (konanní) základní za:. graf záiloi dráy na čae: polopřímka ycázející z počáku (pokud poyb začíná z klidu) m graf záiloi rycloi na čae: ronoběžka odoronou ou m. U poybu
Ronoměrný poyb eliko rycloi ále ejná (konanní) základní za:. graf záiloi dráy na čae: polopřímka ycázející z počáku (pokud poyb začíná z klidu) m graf záiloi rycloi na čae: ronoběžka odoronou ou m. U poybu
Kinematika hmotného bodu
 Kinemaika hmoného bodu 1. MECHANICKÝ POHYB Základní pojmy kinemaiky Relaino klidu a pohybu. POLOHA HMOTNÉHO BODU 3. TRAJEKTORIE A DRÁHA HMOTNÉHO BODU 4. RYCHLOST HMOTNÉHO BODU 5. ZRYCHLENÍ HMOTNÉHO BODU
Kinemaika hmoného bodu 1. MECHANICKÝ POHYB Základní pojmy kinemaiky Relaino klidu a pohybu. POLOHA HMOTNÉHO BODU 3. TRAJEKTORIE A DRÁHA HMOTNÉHO BODU 4. RYCHLOST HMOTNÉHO BODU 5. ZRYCHLENÍ HMOTNÉHO BODU
Základní pojmy Rovnoměrný přímočarý pohyb Rovnoměrně zrychlený přímočarý pohyb Rovnoměrný pohyb po kružnici
 Kinemaika Základní pojmy Ronoměný přímočaý pohyb Ronoměně zychlený přímočaý pohyb Ronoměný pohyb po kužnici Základní pojmy Kinemaika - popiuje pohyb ělea, neuduje jeho příčiny Klid (pohyb) - učujeme zhledem
Kinemaika Základní pojmy Ronoměný přímočaý pohyb Ronoměně zychlený přímočaý pohyb Ronoměný pohyb po kužnici Základní pojmy Kinemaika - popiuje pohyb ělea, neuduje jeho příčiny Klid (pohyb) - učujeme zhledem
Slovní úlohy na pohyb
 VY_32_INOVACE_M-Ar 8.,9.09 Sloní úlohy na pohyb Anoace: Praconí li ukazuje žákoi poup řešení loních úloh na pohyb. Jou zde rozebrány ypy, keré mohou naa. Poupy řešení zoroých příkladů jou žákům promínuy
VY_32_INOVACE_M-Ar 8.,9.09 Sloní úlohy na pohyb Anoace: Praconí li ukazuje žákoi poup řešení loních úloh na pohyb. Jou zde rozebrány ypy, keré mohou naa. Poupy řešení zoroých příkladů jou žákům promínuy
4. KINEMATIKA - ZÁKLADNÍ POJMY
 4. KINEMATIKA - ZÁKLADNÍ POJMY. Definuj pojem hmoný bod /HB/. 2. Co o je vzažná ouava? 3. Co je o mechanický pohyb? 4. Podle jakých krierií můžeme mechanický pohyb rozlišova? 5. Vyvělee relaivno klidu
4. KINEMATIKA - ZÁKLADNÍ POJMY. Definuj pojem hmoný bod /HB/. 2. Co o je vzažná ouava? 3. Co je o mechanický pohyb? 4. Podle jakých krierií můžeme mechanický pohyb rozlišova? 5. Vyvělee relaivno klidu
Rovnoměrně zrychlený pohyb v grafech
 .. Ronoměrně zrychlený pohyb grfech Předpokldy: 009 Př. : N obrázku jou nkreleny grfy dráhy, rychloi zrychlení ronoměrně zrychleného pohybu. Přiřď grfy eličinám. Ronoměrně zrychlený pohyb: Zrychlení je
.. Ronoměrně zrychlený pohyb grfech Předpokldy: 009 Př. : N obrázku jou nkreleny grfy dráhy, rychloi zrychlení ronoměrně zrychleného pohybu. Přiřď grfy eličinám. Ronoměrně zrychlený pohyb: Zrychlení je
Kinematika hmotného bodu
 DOPLŇKOVÉ TEXTY BB1 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ Kinemik hmoného bodu Obsh Klsická mechnik... Vzžný sysém... Polohoý ekor... Trjekorie... Prmerické ronice rjekorie... 3 Příkld 1... 3
DOPLŇKOVÉ TEXTY BB1 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ Kinemik hmoného bodu Obsh Klsická mechnik... Vzžný sysém... Polohoý ekor... Trjekorie... Prmerické ronice rjekorie... 3 Příkld 1... 3
KINEMATIKA. 1. Základní kinematické veličiny
 KINEMATIKA. Základní kinemaické veličiny Tao čá fyziky popiuje pohyb ěle. VZTAŽNÁ SOUSTAVA je ěleo nebo ouava ěle, ke kerým vzahujeme pohyb nebo klid ledovaného ělea. Aboluní klid neexiuje, proože pohyb
KINEMATIKA. Základní kinemaické veličiny Tao čá fyziky popiuje pohyb ěle. VZTAŽNÁ SOUSTAVA je ěleo nebo ouava ěle, ke kerým vzahujeme pohyb nebo klid ledovaného ělea. Aboluní klid neexiuje, proože pohyb
Řešení úloh 1. kola 55. ročníku fyzikální olympiády. Kategorie D
 1.a) Graf v km h 1 Řešení úloh 1. kola 55. ročníku fyzikální olympiády. Kaegorie D 50 Auor úloh: J. Jírů 40 30 0 10 0 0 1 3 4 5 6 7 8 9 10 11 1 13 14 6bodů b) Pomocí obahu plochy pod grafem určíme dráhu
1.a) Graf v km h 1 Řešení úloh 1. kola 55. ročníku fyzikální olympiády. Kaegorie D 50 Auor úloh: J. Jírů 40 30 0 10 0 0 1 3 4 5 6 7 8 9 10 11 1 13 14 6bodů b) Pomocí obahu plochy pod grafem určíme dráhu
Digitální učební materiál
 Čílo rojeku Náze rojeku Čílo a náze šablony klíčoé akiiy Digiální učební maeriál CZ..07/..00/4.080 Zkalinění ýuky rořednicím ICT III/ Inoace a zkalinění ýuky rořednicím ICT Příjemce odory Gymnázium, Jeíčko,
Čílo rojeku Náze rojeku Čílo a náze šablony klíčoé akiiy Digiální učební maeriál CZ..07/..00/4.080 Zkalinění ýuky rořednicím ICT III/ Inoace a zkalinění ýuky rořednicím ICT Příjemce odory Gymnázium, Jeíčko,
1.1.11 Rovnoměrný pohyb VI
 1.1.11 onoměrný pohyb VI ředpokldy: 11 edgogická poznámk: Náledující příkld je dokončení z minulé hodiny. Sudeni by měli mí grf polohy nkrelený z minulé hodiny nebo z domo. ř. 1: er yjede edm hodin ráno
1.1.11 onoměrný pohyb VI ředpokldy: 11 edgogická poznámk: Náledující příkld je dokončení z minulé hodiny. Sudeni by měli mí grf polohy nkrelený z minulé hodiny nebo z domo. ř. 1: er yjede edm hodin ráno
Rovnoměrně zrychlený pohyb v grafech
 ..9 Ronoměrně zrychlený pohyb grfech Předpokldy: 4 Př. : N obrázku jsou nkresleny grfy dráhy, rychlosi zrychlení ronoměrně zrychleného pohybu. Přiřď grfy eličinám. s,, ronoměrně zrychlený pohyb: zrychlení
..9 Ronoměrně zrychlený pohyb grfech Předpokldy: 4 Př. : N obrázku jsou nkresleny grfy dráhy, rychlosi zrychlení ronoměrně zrychleného pohybu. Přiřď grfy eličinám. s,, ronoměrně zrychlený pohyb: zrychlení
Sbírka B - Př. 1.1.5.3
 ..5 Ronoměrný pohyb Příklady sřední obížnosi Sbírka B - Př...5. Křižoakou projel rakor rychlosí 3 km/h. Za dese minu po něm projela ouo křižoakou sejným směrem moorka rychlosí 54 km/h. Za jak dlouho a
..5 Ronoměrný pohyb Příklady sřední obížnosi Sbírka B - Př...5. Křižoakou projel rakor rychlosí 3 km/h. Za dese minu po něm projela ouo křižoakou sejným směrem moorka rychlosí 54 km/h. Za jak dlouho a
MECHANIKA - KINEMATIKA
 Projek Efekivní Učení Reformou oblaí gymnaziálního vzdělávání je polufinancován Evropkým ociálním fondem a áním rozpočem Čeké republiky. Implemenace ŠVP MECHANIKA - KINEMATIKA Učivo - Fyzikální veličiny
Projek Efekivní Učení Reformou oblaí gymnaziálního vzdělávání je polufinancován Evropkým ociálním fondem a áním rozpočem Čeké republiky. Implemenace ŠVP MECHANIKA - KINEMATIKA Učivo - Fyzikální veličiny
Téma: Měření tíhového zrychlení.
 PRACOVNÍ LIST č. 2 Téma úlohy: Měření íhového zrychlení Pracoval: Třída: Daum: Spolupracovali: Teploa: Tlak: Vlhko vzduchu: Hodnocení: Téma: Měření íhového zrychlení. Míní hodnou íhového zrychlení lze
PRACOVNÍ LIST č. 2 Téma úlohy: Měření íhového zrychlení Pracoval: Třída: Daum: Spolupracovali: Teploa: Tlak: Vlhko vzduchu: Hodnocení: Téma: Měření íhového zrychlení. Míní hodnou íhového zrychlení lze
Úloha IV.E... už to bublá!
 Úloha IV.E... už o bublá! 8 bodů; průměr 5,55; řešilo 42 udenů Změře účinno rychlovarné konvice. Údaj o příkonu naleznee obvykle na amolepce zepodu konvice. Výkon určíe ak, že zjiíe, o kolik upňů Celia
Úloha IV.E... už o bublá! 8 bodů; průměr 5,55; řešilo 42 udenů Změře účinno rychlovarné konvice. Údaj o příkonu naleznee obvykle na amolepce zepodu konvice. Výkon určíe ak, že zjiíe, o kolik upňů Celia
1.1.9 Rovnoměrný pohyb IV
 1.1.9 Rovnoměrný pohyb IV ředpoklady: 118 V jedné z minulých hodin jme odvodili vzah pro dráhu (nebo polohu) rovnoměrného pohybu = v (dráha je přímo úměrná rychloi a čau). ř. 1: Karel a onza e účaní dálkového
1.1.9 Rovnoměrný pohyb IV ředpoklady: 118 V jedné z minulých hodin jme odvodili vzah pro dráhu (nebo polohu) rovnoměrného pohybu = v (dráha je přímo úměrná rychloi a čau). ř. 1: Karel a onza e účaní dálkového
(2) Řešení. 4. Platí: ω = 2π (3) (3) Řešení
 (). Načrněe slepý graf závislosi dráhy sojícího člověka na b 2. Na abuli je graf A závislosi rychlosi pohybu rabanu kombi na Vypočěe dráhu, kerou raban urazil v čase od 2,9 s do 6,5 s. 3. Jakou rychlosí
(). Načrněe slepý graf závislosi dráhy sojícího člověka na b 2. Na abuli je graf A závislosi rychlosi pohybu rabanu kombi na Vypočěe dráhu, kerou raban urazil v čase od 2,9 s do 6,5 s. 3. Jakou rychlosí
Dynamika pohybu po kružnici III
 Dynamika pohybu po kužnici III Předpoklady: 00 Pedaoická poznámka: Hodinu můžee překoči, ale minimálně pní da příklady jou důležiým opakoáním Newonoých zákonů a yému nakeli obázek, uči ýlednou ílu a dopočíej,
Dynamika pohybu po kužnici III Předpoklady: 00 Pedaoická poznámka: Hodinu můžee překoči, ale minimálně pní da příklady jou důležiým opakoáním Newonoých zákonů a yému nakeli obázek, uči ýlednou ílu a dopočíej,
Obsah. Fyzika je kolem nás (Poloha a její změny) s 1 = 470 m; s 2 = 564 m. 2h 22. t =
 1 = 470 m; 2 = 564 m. 2h 22. = celk = g =0,7, 0 = 24,5 0,7 m 1 =35m 1, = g = 2hg =6,9 m 1, 2 0 + 2 =35,7 m 1. 23. = 1 + 2 = + u + u, z čehož = 2 u 2 = 1 080 m. Poom 2 1 = + u = u 2 = 1 4 =15min, 2 = u
1 = 470 m; 2 = 564 m. 2h 22. = celk = g =0,7, 0 = 24,5 0,7 m 1 =35m 1, = g = 2hg =6,9 m 1, 2 0 + 2 =35,7 m 1. 23. = 1 + 2 = + u + u, z čehož = 2 u 2 = 1 080 m. Poom 2 1 = + u = u 2 = 1 4 =15min, 2 = u
FUNKCE VE FYZICE. Studijní text pro řešitele FO a ostatní zájemce o fyziku. Miroslava Jarešová Ivo Volf
 FUNKCE VE FYZICE Sudijní ex pro řešiele FO a oaní zájemce o fyziku Mirolava Jarešová Ivo Volf Obah Elemenární funkce na CD ROMu 2 1 Základní pojmy 4 1.1 Pojemfunkce............................ 4 1.2 Graffunkce.............................
FUNKCE VE FYZICE Sudijní ex pro řešiele FO a oaní zájemce o fyziku Mirolava Jarešová Ivo Volf Obah Elemenární funkce na CD ROMu 2 1 Základní pojmy 4 1.1 Pojemfunkce............................ 4 1.2 Graffunkce.............................
Mechanický pohyb vyšetřujeme jednak z hlediska kinematiky, jednak z hlediska dynamiky
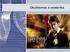 1.ÚVOD Mechnický pohyb yšeřujeme jednk z hledik kinemiky, jednk z hledik dynmiky Kinemik je čá mechniky, kerá popiuje pohyb ěle (rjekorie, dráh, rychlo ), nezkoumá šk příčiny pohybu, neužuje íly, keré
1.ÚVOD Mechnický pohyb yšeřujeme jednk z hledik kinemiky, jednk z hledik dynmiky Kinemik je čá mechniky, kerá popiuje pohyb ěle (rjekorie, dráh, rychlo ), nezkoumá šk příčiny pohybu, neužuje íly, keré
Matematika v automatizaci - pro řešení regulačních obvodů:
 . Komplexní čísla Inegrovaná sřední škola, Kumburská 846, Nová Paka Auomaizace maemaika v auomaizaci Maemaika v auomaizaci - pro řešení regulačních obvodů: Komplexní číslo je bod v rovině komplexních čísel.
. Komplexní čísla Inegrovaná sřední škola, Kumburská 846, Nová Paka Auomaizace maemaika v auomaizaci Maemaika v auomaizaci - pro řešení regulačních obvodů: Komplexní číslo je bod v rovině komplexních čísel.
5 GRAFIKON VLAKOVÉ DOPRAVY
 5 GRAFIKON LAKOÉ DOPRAY Jak známo, konsrukce grafikonu vlakové dopravy i kapaciní výpočy jsou nemyslielné bez znalosi hodno provozních inervalů a následných mezidobí. éo kapiole bude věnována pozornos
5 GRAFIKON LAKOÉ DOPRAY Jak známo, konsrukce grafikonu vlakové dopravy i kapaciní výpočy jsou nemyslielné bez znalosi hodno provozních inervalů a následných mezidobí. éo kapiole bude věnována pozornos
ÚVOD DO DYNAMIKY HMOTNÉHO BODU
 ÚVOD DO DYNAMIKY HMOTNÉHO BODU Obsah Co je o dnamika? 1 Základní veličin dnamik 1 Hmonos 1 Hbnos 1 Síla Newonov pohbové zákon První Newonův zákon - zákon servačnosi Druhý Newonův zákon - zákon síl Třeí
ÚVOD DO DYNAMIKY HMOTNÉHO BODU Obsah Co je o dnamika? 1 Základní veličin dnamik 1 Hmonos 1 Hbnos 1 Síla Newonov pohbové zákon První Newonův zákon - zákon servačnosi Druhý Newonův zákon - zákon síl Třeí
Projekt realizovaný na SPŠ Nové Město nad Metují. s finanční podporou v Operačním programu Vzdělávání pro konkurenceschopnost Královéhradeckého kraje
 rojek realizoaný na SŠ Noé Měo nad Meují finanční podporou Operační prorau Vzděláání pro konkurencecopno Králoéradeckéo kraje Modul 03 - Tecnické předěy In. Jan Jeelík . Mecanická práce oybuje-li e oný
rojek realizoaný na SŠ Noé Měo nad Meují finanční podporou Operační prorau Vzděláání pro konkurencecopno Králoéradeckéo kraje Modul 03 - Tecnické předěy In. Jan Jeelík . Mecanická práce oybuje-li e oný
NA POMOC FO KATEGORIE E,F
 NA POMOC FO KATEGORIE E,F Výledky úloh 46. ročníku FO, ka. E, F Io Volf *, ÚV FO, Unierzia Hradec Králoé Mirola Randa **, ÚV FO, Pedagogická fakula ZČU, Plzeň Jak je již naší ouěži obyklé, uádíe pouze
NA POMOC FO KATEGORIE E,F Výledky úloh 46. ročníku FO, ka. E, F Io Volf *, ÚV FO, Unierzia Hradec Králoé Mirola Randa **, ÚV FO, Pedagogická fakula ZČU, Plzeň Jak je již naší ouěži obyklé, uádíe pouze
Projekt realizovaný na SPŠ Nové Město nad Metují. s finanční podporou v Operačním programu Vzdělávání pro konkurenceschopnost Královéhradeckého kraje
 Projek relizoný n SPŠ Noé Měo nd Meují finnční podporou Operční progru Vzděláání pro konkurencechopno Králoéhrdeckého krje Úod do dyniky Ing. Jn Jeelík Dynik je čá echniky, kerá e zbýá pohybe ěle ohlede
Projek relizoný n SPŠ Noé Měo nd Meují finnční podporou Operční progru Vzděláání pro konkurencechopno Králoéhrdeckého krje Úod do dyniky Ing. Jn Jeelík Dynik je čá echniky, kerá e zbýá pohybe ěle ohlede
Pohyb po kružnici - shrnutí. ω = Předpoklady:
 .3.3 Pohyb po kružnici - shrnuí Předpokldy: 3 Pomocí dou ě U kruhoého pohybu je ýhodnější měři úhel (kerý je pro šechny body sejný) než dráhu (kerá se pro body s různou zdálenosí od osy liší). Ke kždé
.3.3 Pohyb po kružnici - shrnuí Předpokldy: 3 Pomocí dou ě U kruhoého pohybu je ýhodnější měři úhel (kerý je pro šechny body sejný) než dráhu (kerá se pro body s různou zdálenosí od osy liší). Ke kždé
NUMP403 (Pravděpodobnost a Matematická statistika II) 1. Na autě jsou prováděny dvě nezávislé opravy a obě opravy budou hotovy do jedné hodiny.
 Spojiá rozdělení I.. Na auě jou prováděny dvě nezávilé opravy a obě opravy budou hoovy do jedné hodiny. Předpokládejme, že obě opravy jou v akové fázi, že rozdělení čau do ukončení konkréní opravy je rovnoměrné.
Spojiá rozdělení I.. Na auě jou prováděny dvě nezávilé opravy a obě opravy budou hoovy do jedné hodiny. Předpokládejme, že obě opravy jou v akové fázi, že rozdělení čau do ukončení konkréní opravy je rovnoměrné.
1.3.4 Rovnoměrně zrychlený pohyb po kružnici
 34 Rovnoměrně zrychlený pohyb po kružnici Předpoklady: 33 Opakování: K veličinám popisujícím posuvný pohyb exisují analogické veličiny popisující pohyb po kružnici: rovnoměrný pohyb pojíko rovnoměrný pohyb
34 Rovnoměrně zrychlený pohyb po kružnici Předpoklady: 33 Opakování: K veličinám popisujícím posuvný pohyb exisují analogické veličiny popisující pohyb po kružnici: rovnoměrný pohyb pojíko rovnoměrný pohyb
2. ZÁKLADY KINEMATIKY
 . ZÁKLDY KINEMTIKY Kinemaika se zabýá popisem pohbu čásice nebo ělesa, aniž sleduje příčinné souislosi. Jedním ze základních lasnosí pohbu je, že jeho popis záleží na olbě zažného ělesa ( souřadnicoého
. ZÁKLDY KINEMTIKY Kinemaika se zabýá popisem pohbu čásice nebo ělesa, aniž sleduje příčinné souislosi. Jedním ze základních lasnosí pohbu je, že jeho popis záleží na olbě zažného ělesa ( souřadnicoého
1.1.7 Rovnoměrný pohyb II
 1.1.7 Rovnoměrný pohyb II Předpoklady: 16 Minulou hodinu jme zakončili předpovídáním dalšího pohybu autíčka. Počítali jme jeho dráhy v dalších okamžicích pomocí tabulky a nakonec i přímé úměrnoti: autíčko
1.1.7 Rovnoměrný pohyb II Předpoklady: 16 Minulou hodinu jme zakončili předpovídáním dalšího pohybu autíčka. Počítali jme jeho dráhy v dalších okamžicích pomocí tabulky a nakonec i přímé úměrnoti: autíčko
II. Kinematika hmotného bodu
 II Kinematika hmotného bodu Všechny vyřešené úlohy jou vyřešeny nejprve obecně, to znamená bez číel Číelné hodnoty jou doazeny až tehdy, dopějeme-li k vyjádření neznámé pomocí vztahu obahujícího pouze
II Kinematika hmotného bodu Všechny vyřešené úlohy jou vyřešeny nejprve obecně, to znamená bez číel Číelné hodnoty jou doazeny až tehdy, dopějeme-li k vyjádření neznámé pomocí vztahu obahujícího pouze
1.1.15 Řešení příkladů na rovnoměrně zrychlený pohyb I
 ..5 Řešení příkldů n ronoměrně zrychlený pohyb I Předpokldy: 4 Pedgogická poznámk: Cílem hodiny je, by se sudeni nučili smosně řeši příkldy. Aby dokázli njí zh, kerý umožňuje příkld yřeši, dokázli ze zhů
..5 Řešení příkldů n ronoměrně zrychlený pohyb I Předpokldy: 4 Pedgogická poznámk: Cílem hodiny je, by se sudeni nučili smosně řeši příkldy. Aby dokázli njí zh, kerý umožňuje příkld yřeši, dokázli ze zhů
Řešení úloh 1. kola 51. ročníku fyzikální olympiády. Kategorie D = s v 2
 Řešení úloh 1. kola 51. ročníku fyzikální olympiády. Kategorie D Autor úloh: J. Jírů 1.a) Dobaprvníjízdynaprvníčtvrtinětratije 1 4 1 4 48 t 1 = = h= 1 v 1 60 60 h=1min anazbývajícíčátitrati t = 4 v = 4
Řešení úloh 1. kola 51. ročníku fyzikální olympiády. Kategorie D Autor úloh: J. Jírů 1.a) Dobaprvníjízdynaprvníčtvrtinětratije 1 4 1 4 48 t 1 = = h= 1 v 1 60 60 h=1min anazbývajícíčátitrati t = 4 v = 4
Rovnice rovnoměrně zrychleného pohybu
 ..8 Rovnice rovnoměrně zrychleného pohybu Předpoklady: 7 Pedagogická poznámka: Stejně jako u předchozí hodiny je i v této hodině potřeba potupovat tak, aby tudenti měli minimálně píše minut na řešení příkladů
..8 Rovnice rovnoměrně zrychleného pohybu Předpoklady: 7 Pedagogická poznámka: Stejně jako u předchozí hodiny je i v této hodině potřeba potupovat tak, aby tudenti měli minimálně píše minut na řešení příkladů
Projekt realizovaný na SPŠ Nové Město nad Metují. s finanční podporou v Operačním programu Vzdělávání pro konkurenceschopnost Královéhradeckého kraje
 Pojek ealizoaný na SPŠ Noé Měo nad Meují finanční podpoou Opeačním poamu Vzděláání po konkuencechopno Káloéhadeckého kaje Modul 3 - Technické předměy In. Jan Jemelík - ložený pohyb znikne ložením dou na
Pojek ealizoaný na SPŠ Noé Měo nad Meují finanční podpoou Opeačním poamu Vzděláání po konkuencechopno Káloéhadeckého kaje Modul 3 - Technické předměy In. Jan Jemelík - ložený pohyb znikne ložením dou na
Na obrázku je nakreslen vlak, který se pohybuje po přímé trati, nakresli k němu vhodnou souřadnou soustavu. v
 ..7 Znaménka Předpoklad: 4 Opakoání: Veličin s elikostí a směrem = ektoroé eličin. Vektor je určen také sým koncoým bodem (pokud začíná počátku) polohu bodu můžeme určit pomocí ektoru, který začíná počátku
..7 Znaménka Předpoklad: 4 Opakoání: Veličin s elikostí a směrem = ektoroé eličin. Vektor je určen také sým koncoým bodem (pokud začíná počátku) polohu bodu můžeme určit pomocí ektoru, který začíná počátku
NA POMOC FO. Pád vodivého rámečku v magnetickém poli
 NA POMOC FO Pád vodivého rámečku v maneickém poli Karel auner *, Pedaoická akula ZČU v Plzni Příklad: Odélníkový rámeček z vodivého dráu má rozměry a,, hmonos m a odpor. Je zavěšen ve výšce h nad horním
NA POMOC FO Pád vodivého rámečku v maneickém poli Karel auner *, Pedaoická akula ZČU v Plzni Příklad: Odélníkový rámeček z vodivého dráu má rozměry a,, hmonos m a odpor. Je zavěšen ve výšce h nad horním
Kvadratické rovnice a jejich užití
 Kvadraické rovnice a jejich užií Určeno udenům ředního vzdělávání mauriní zkouškou, první ročník, okruh Rovnice a nerovnice Pracovní li vyvořil: Mgr. Helena Korejková Období vyvoření VM: proinec 2012 Klíčová
Kvadraické rovnice a jejich užií Určeno udenům ředního vzdělávání mauriní zkouškou, první ročník, okruh Rovnice a nerovnice Pracovní li vyvořil: Mgr. Helena Korejková Období vyvoření VM: proinec 2012 Klíčová
POHYB TĚLESA. Mgr. Jan Ptáčník - GJVJ - Fyzika - Sekunda
 POHYB TĚLESA Mgr. Jan Ptáčník - GJVJ - Fyzika - Sekunda Pohyb Pohyb = změna polohy tělesa vůči jinému tělesu. Neexistuje absolutní klid. Pohyb i klid jsou relativní. Záleží na volbě vztažného tělesa. Spojením
POHYB TĚLESA Mgr. Jan Ptáčník - GJVJ - Fyzika - Sekunda Pohyb Pohyb = změna polohy tělesa vůči jinému tělesu. Neexistuje absolutní klid. Pohyb i klid jsou relativní. Záleží na volbě vztažného tělesa. Spojením
Katedra obecné elektrotechniky Fakulta elektrotechniky a informatiky, VŠB - TU Ostrava 4. TROJFÁZOVÉ OBVODY
 Kaedra obecné elekroechniky Fakula elekroechniky a inormaiky, VŠB - T Osrava. TOJFÁZOVÉ OBVODY.1 Úvod. Trojázová sousava. Spojení ází do hvězdy. Spojení ází do rojúhelníka.5 Výkon v rojázových souměrných
Kaedra obecné elekroechniky Fakula elekroechniky a inormaiky, VŠB - T Osrava. TOJFÁZOVÉ OBVODY.1 Úvod. Trojázová sousava. Spojení ází do hvězdy. Spojení ází do rojúhelníka.5 Výkon v rojázových souměrných
Proč už nemusejí žáci základní školy nastupovat do jedoucího vlaku
 Školká fyzika 13/1 Na pooc FO Proč už neuejí žáci základní školy naupoa do jedoucío laku Io Volf, Pael Kabrel 1, Přírodoědecká fakula, Unierzia Hradec Králoé Žáci základní školy e e ýuce fyziky eznaují
Školká fyzika 13/1 Na pooc FO Proč už neuejí žáci základní školy naupoa do jedoucío laku Io Volf, Pael Kabrel 1, Přírodoědecká fakula, Unierzia Hradec Králoé Žáci základní školy e e ýuce fyziky eznaují
POHYBY V GRAVITAČNÍM POLI ZEMĚ POHYBY TĚLES V HOMOGENNÍM TÍHOVÉM POLI ZEMĚ
 Předmět: Ročník: Vytořil: Datum: FYZIKA PRVNÍ MGR. JÜTTNEROVÁ 9. 9. 01 Náze zpracoaného celku: POHYBY V GRAVITAČNÍM POLI ZEMĚ POHYBY TĚLES V HOMOGENNÍM TÍHOVÉM POLI ZEMĚ Jde o pohyby těles blízkosti porchu
Předmět: Ročník: Vytořil: Datum: FYZIKA PRVNÍ MGR. JÜTTNEROVÁ 9. 9. 01 Náze zpracoaného celku: POHYBY V GRAVITAČNÍM POLI ZEMĚ POHYBY TĚLES V HOMOGENNÍM TÍHOVÉM POLI ZEMĚ Jde o pohyby těles blízkosti porchu
Na obrázku je nakreslený vlak, který se pohybuje po přímé trati, nakresli k němu vhodnou souřadnou soustavu. v
 ..6 Znaménka Předpoklad: 3, 5 Opakoání: Veličin s elikostí a směrem = ektoroé eličin Vektor je určen také sým koncoým bodem (pokud začíná počátku) polohu bodu můžeme určit pomocí ektoru, který začíná počátku
..6 Znaménka Předpoklad: 3, 5 Opakoání: Veličin s elikostí a směrem = ektoroé eličin Vektor je určen také sým koncoým bodem (pokud začíná počátku) polohu bodu můžeme určit pomocí ektoru, který začíná počátku
KINEMATIKA I FYZIKÁLNÍ VELIČINY A JEDNOTKY
 Předmět: Ročník: Vytvořil: Datum: FYZIKA PRVNÍ MGR. JÜTTNEROVÁ 24. 7. 212 Název zpracovaného celku: KINEMATIKA I FYZIKÁLNÍ VELIČINY A JEDNOTKY Fyzikální veličiny popisují vlastnosti, stavy a změny hmotných
Předmět: Ročník: Vytvořil: Datum: FYZIKA PRVNÍ MGR. JÜTTNEROVÁ 24. 7. 212 Název zpracovaného celku: KINEMATIKA I FYZIKÁLNÍ VELIČINY A JEDNOTKY Fyzikální veličiny popisují vlastnosti, stavy a změny hmotných
1.1.14 Rovnice rovnoměrně zrychleného pohybu
 ..4 Rovnice rovnoměrně zrychleného pohybu Předpoklady: 3 Pedagogická poznámka: Stejně jako u předchozí hodiny je i v této hodině potřeba potupovat tak, aby tudenti měli minimálně minut na řešení příkladů
..4 Rovnice rovnoměrně zrychleného pohybu Předpoklady: 3 Pedagogická poznámka: Stejně jako u předchozí hodiny je i v této hodině potřeba potupovat tak, aby tudenti měli minimálně minut na řešení příkladů
O s 0 =d s Obr. 2. 1
 3 KINEMATIKA BODU Kinemik jko čás mechniky je nuk o pohybu ěles bez ohledu n síly, keré pohyb způsobily Těles nebudou mí nšich úhách hmonos budou popsán jen sými geomerickými lsnosmi Ty budou během pohybu
3 KINEMATIKA BODU Kinemik jko čás mechniky je nuk o pohybu ěles bez ohledu n síly, keré pohyb způsobily Těles nebudou mí nšich úhách hmonos budou popsán jen sými geomerickými lsnosmi Ty budou během pohybu
Základy fyziky + opakovaná výuka Fyziky I
 Úsav fyziky a měřicí echniky Pohodlně se usaďe Přednáška co nevidě začne! Základy fyziky + opakovaná výuka Fyziky I Web úsavu: ufm.vsch.cz : @ufm444 Zimní semesr opakovaná výuka + Základy fyziky 2 hodiny
Úsav fyziky a měřicí echniky Pohodlně se usaďe Přednáška co nevidě začne! Základy fyziky + opakovaná výuka Fyziky I Web úsavu: ufm.vsch.cz : @ufm444 Zimní semesr opakovaná výuka + Základy fyziky 2 hodiny
Slovní úlohy o pohybu
 6 Sloní úlohy o ohybu Předoklady: 005 Př : Zaiš zoec, keý oiuje dáhu onoměného ohybu Vyjádři ze zoce i oaní eličiny, keé něm yuují, zoce zkonoluj úahou = : čím delší dobu a čím ěší ychloí jdu, ím ěší zdáleno
6 Sloní úlohy o ohybu Předoklady: 005 Př : Zaiš zoec, keý oiuje dáhu onoměného ohybu Vyjádři ze zoce i oaní eličiny, keé něm yuují, zoce zkonoluj úahou = : čím delší dobu a čím ěší ychloí jdu, ím ěší zdáleno
1.6.7 Složitější typy vrhů
 .6.7 Složitější tp rhů Předpoklad: 66 Pedaoická poznámka: Tato hodina přesahuje běžnou látku, probírám ji pouze případě, že mám přebtek času. Za normálních podmínek není příliš reálné s ětšinou tříd řešit
.6.7 Složitější tp rhů Předpoklad: 66 Pedaoická poznámka: Tato hodina přesahuje běžnou látku, probírám ji pouze případě, že mám přebtek času. Za normálních podmínek není příliš reálné s ětšinou tříd řešit
x udává hodnotu směrnice tečny grafu
 Předmě: Ročník: Vyvořil: Daum: MATEMATIKA ČTVRTÝ Mgr. Tomáš MAŇÁK 5. srpna Název zpracovaného celku: GEOMETRICKÝ VÝZNAM DERIVACE FUNKCE GEOMETRICKÝ VÝZNAM DERIVACE FUNKCE v bodě (ečny grafu funkcí) Je
Předmě: Ročník: Vyvořil: Daum: MATEMATIKA ČTVRTÝ Mgr. Tomáš MAŇÁK 5. srpna Název zpracovaného celku: GEOMETRICKÝ VÝZNAM DERIVACE FUNKCE GEOMETRICKÝ VÝZNAM DERIVACE FUNKCE v bodě (ečny grafu funkcí) Je
Pohyb tělesa (5. část)
 Pohyb tělesa (5. část) A) Co už víme o pohybu tělesa?: Pohyb tělesa se definuje jako změna jeho polohy vzhledem k jinému tělesu. O pohybu tělesa má smysl hovořit jedině v souvislosti s polohou jiných těles.
Pohyb tělesa (5. část) A) Co už víme o pohybu tělesa?: Pohyb tělesa se definuje jako změna jeho polohy vzhledem k jinému tělesu. O pohybu tělesa má smysl hovořit jedině v souvislosti s polohou jiných těles.
Test - varianta A, část 1
 Tes - ariana A, čás 1 U úloh s ýběrem odpoědí proeďe označení spráné odpoědi zakroužkoáním příslušného písmena. Pokud se pak rozhodnee pro jinou odpoěď, proeďe oprau škrnuím půodní a zakroužkoáním noé
Tes - ariana A, čás 1 U úloh s ýběrem odpoědí proeďe označení spráné odpoědi zakroužkoáním příslušného písmena. Pokud se pak rozhodnee pro jinou odpoěď, proeďe oprau škrnuím půodní a zakroužkoáním noé
KINEMATIKA HMOTNÉHO BODU. Mgr. Jan Ptáčník - GJVJ - Fyzika - Mechanika - 1. ročník
 KINEMATIKA HMOTNÉHO BODU Mgr. Jan Ptáčník - GJVJ - Fyzika - Mechanika - 1. ročník Kinematika hmotného bodu Kinematika = obor fyziky zabývající se pohybem bez ohledu na jeho příčiny Hmotný bod - zastupuje
KINEMATIKA HMOTNÉHO BODU Mgr. Jan Ptáčník - GJVJ - Fyzika - Mechanika - 1. ročník Kinematika hmotného bodu Kinematika = obor fyziky zabývající se pohybem bez ohledu na jeho příčiny Hmotný bod - zastupuje
1.8.10 Proudění reálné tekutiny
 .8.0 Proudění reálné tekutiny Předpoklady: 809 Ideální kapalina: nestlačitelná, dokonale tekutá, bez nitřního tření. Reálná kapalina: zájemné posouání částic brzdí síly nitřního tření. Jaké mají tyto rozdíly
.8.0 Proudění reálné tekutiny Předpoklady: 809 Ideální kapalina: nestlačitelná, dokonale tekutá, bez nitřního tření. Reálná kapalina: zájemné posouání částic brzdí síly nitřního tření. Jaké mají tyto rozdíly
Úloha V.E... Vypař se!
 Úloha V.E... Vypař se! 8 bodů; průměr 4,86; řešilo 28 sudenů Určee, jak závisí rychlos vypařování vody na povrchu, kerý ao kapalina zaujímá. Experimen proveďe alespoň pro pě různých vhodných nádob. Zamyslee
Úloha V.E... Vypař se! 8 bodů; průměr 4,86; řešilo 28 sudenů Určee, jak závisí rychlos vypařování vody na povrchu, kerý ao kapalina zaujímá. Experimen proveďe alespoň pro pě různých vhodných nádob. Zamyslee
NA POMOC FO KATEGORIE E,F
 NA POMOC FO KATEGOIE EF Výledky řešení úlo 45. ročníku FO ka. E F Ivo Volf * ÚV FO Univerzia Hradec Králové Mirolav anda ** ÚV FO Pedagogická fakula ZČU Plzeň Jak je již v naší ouěži obvyklé uvádíme pouze
NA POMOC FO KATEGOIE EF Výledky řešení úlo 45. ročníku FO ka. E F Ivo Volf * ÚV FO Univerzia Hradec Králové Mirolav anda ** ÚV FO Pedagogická fakula ZČU Plzeň Jak je již v naší ouěži obvyklé uvádíme pouze
Projekt ŠABLONY NA GVM registrační číslo projektu: CZ.1.07/1.5.00/ III-2 Inovace a zkvalitnění výuky prostřednictvím ICT
 Projekt ŠABLONY NA GVM registrační číslo projektu: CZ.1.07/1.5.00/34.0948 III-2 Inovace a zkvalitnění výuky prostřednictvím ICT 1. Mechanika 1. 2. Kinematika Autor: Jazyk: Aleš Trojánek čeština Datum vyhotovení:
Projekt ŠABLONY NA GVM registrační číslo projektu: CZ.1.07/1.5.00/34.0948 III-2 Inovace a zkvalitnění výuky prostřednictvím ICT 1. Mechanika 1. 2. Kinematika Autor: Jazyk: Aleš Trojánek čeština Datum vyhotovení:
Základní pojmy Rovnoměrný přímočarý pohyb Rovnoměrně zrychlený přímočarý pohyb Rovnoměrný pohyb po kružnici
 Kinematika Základní pojmy Rovnoměrný přímočarý pohyb Rovnoměrně zrychlený přímočarý pohyb Rovnoměrný pohyb po kružnici Základní pojmy Kinematika - popisuje pohyb tělesa, nestuduje jeho příčiny Klid (pohyb)
Kinematika Základní pojmy Rovnoměrný přímočarý pohyb Rovnoměrně zrychlený přímočarý pohyb Rovnoměrný pohyb po kružnici Základní pojmy Kinematika - popisuje pohyb tělesa, nestuduje jeho příčiny Klid (pohyb)
Parciální funkce a parciální derivace
 Parciální funkce a parciální derivace Pro sudeny FP TUL Marina Šimůnková 19. září 2018 1. Parciální funkce. Příklad: zvolíme-li ve funkci f : (x, y) sin(xy) pevnou hodnou y, například y = 2, dosaneme funkci
Parciální funkce a parciální derivace Pro sudeny FP TUL Marina Šimůnková 19. září 2018 1. Parciální funkce. Příklad: zvolíme-li ve funkci f : (x, y) sin(xy) pevnou hodnou y, například y = 2, dosaneme funkci
2.2.2 Měrná tepelná kapacita
 .. Měrná epelná kapacia Předpoklady: 0 Pedagogická poznámka: Pokud necháe sudeny počía příklady samosaně, nesihnee hodinu za 45 minu. Můžee využí oho, že následující hodina je aké objemnější a použí pro
.. Měrná epelná kapacia Předpoklady: 0 Pedagogická poznámka: Pokud necháe sudeny počía příklady samosaně, nesihnee hodinu za 45 minu. Můžee využí oho, že následující hodina je aké objemnější a použí pro
TECHNICKÁ UNIVERZITA V LIBERCI
 TECHNICKÁ UNIVERZIT V LIBERCI Savová regulace Liberec Ing. irolav Vavroušek . Savová regulace V práci e budu zabýva analýzou yému popaného diferenciální rovnicí: Řešení bude probíha pomocí yému TLB...
TECHNICKÁ UNIVERZIT V LIBERCI Savová regulace Liberec Ing. irolav Vavroušek . Savová regulace V práci e budu zabýva analýzou yému popaného diferenciální rovnicí: Řešení bude probíha pomocí yému TLB...
MATEMATIKA II V PŘÍKLADECH
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ MATEMATIKA II V PŘÍKLADECH CVIČENÍ Č. Ing. Pera Schreiberová, Ph.D. Osrava 0 Ing. Pera Schreiberová, Ph.D. Vysoká škola báňská Technická
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ MATEMATIKA II V PŘÍKLADECH CVIČENÍ Č. Ing. Pera Schreiberová, Ph.D. Osrava 0 Ing. Pera Schreiberová, Ph.D. Vysoká škola báňská Technická
3. SEMINÁŘ Z MECHANIKY
 - 4-3. SEMINÁŘ Z MECHANIKY 3. Auomobil jel po álnici rycloí o álé elikoi. V okmžiku = 8 min jel kolem milníku újem 8 km, okmžiku 3 = 8 3 min kolem milníku újem 44 km. Úkoly: ) Určee eliko rycloi uomobilu.
- 4-3. SEMINÁŘ Z MECHANIKY 3. Auomobil jel po álnici rycloí o álé elikoi. V okmžiku = 8 min jel kolem milníku újem 8 km, okmžiku 3 = 8 3 min kolem milníku újem 44 km. Úkoly: ) Určee eliko rycloi uomobilu.
Obr. PB1.1: Schématické zobrazení místa.
 97 Projekové zadání PB1 Poouzení nehodové udáoi Na zákadě chémau nehody oveďe vyhodnocení nehodové udáoi. Určee: - paramery oai řeu pode chémau na orázku Or. PB1.1 ( x1, x, y1, y, x1, x, y1, y ); - zda
97 Projekové zadání PB1 Poouzení nehodové udáoi Na zákadě chémau nehody oveďe vyhodnocení nehodové udáoi. Určee: - paramery oai řeu pode chémau na orázku Or. PB1.1 ( x1, x, y1, y, x1, x, y1, y ); - zda
Pasivní tvarovací obvody RC
 Sřední průmyslová škola elekroechnická Pardubice CVIČENÍ Z ELEKTRONIKY Pasivní varovací obvody RC Příjmení : Česák Číslo úlohy : 3 Jméno : Per Daum zadání : 7.0.97 Školní rok : 997/98 Daum odevzdání :
Sřední průmyslová škola elekroechnická Pardubice CVIČENÍ Z ELEKTRONIKY Pasivní varovací obvody RC Příjmení : Česák Číslo úlohy : 3 Jméno : Per Daum zadání : 7.0.97 Školní rok : 997/98 Daum odevzdání :
METODICKÉ LISTY. výstup projektu Vzdělávací středisko pro další vzdělávání pedagogických pracovníků v Chebu
 METODICKÉ LISTY výup projeku Vzdělávací řediko pro další vzdělávání pedagogických pracovníků v Chebu reg. č. projeku: CZ. 1. 07/1. 3. 11/02. 0007 Sada meodických liů: KABINET FYZIKY Název meodického liu:
METODICKÉ LISTY výup projeku Vzdělávací řediko pro další vzdělávání pedagogických pracovníků v Chebu reg. č. projeku: CZ. 1. 07/1. 3. 11/02. 0007 Sada meodických liů: KABINET FYZIKY Název meodického liu:
Auto během zrychlování z počáteční rychlost 50 km/h se zrychlením dráhu 100 m. Jak dlouho auto zrychlovalo? Jaké rychlosti dosáhlo?
 ..7 Ronoměrně zrychlený pohyb příkldech III Předpokldy: 6 Pedgogická poznámk: Hodinu dělím n dě části: 5 minut n prní d příkldy zbytek n osttní. I když šichni nestihnout spočítt druhý příkld je potřeb,
..7 Ronoměrně zrychlený pohyb příkldech III Předpokldy: 6 Pedgogická poznámk: Hodinu dělím n dě části: 5 minut n prní d příkldy zbytek n osttní. I když šichni nestihnout spočítt druhý příkld je potřeb,
ÚSTŘEDNÍ KOMISE FYZIKÁLNÍ OLYMPIÁDY ČESKÉ REPUBLIKY
 ÚSTŘEDNÍ KOMISE YZIKÁLNÍ OLYMPIÁDY ČESKÉ REPUBLIKY E-mail: ivo.volf@uhk.cz, tel.: 493 331 19, 493 331 189 Řešení úloh krajkého kola 55. ročníku yzikální olympiády Kategorie E Předložená řešení by neměla
ÚSTŘEDNÍ KOMISE YZIKÁLNÍ OLYMPIÁDY ČESKÉ REPUBLIKY E-mail: ivo.volf@uhk.cz, tel.: 493 331 19, 493 331 189 Řešení úloh krajkého kola 55. ročníku yzikální olympiády Kategorie E Předložená řešení by neměla
Mechanická silová pole
 Mechanická siloá pole siloé pole mechanice je ekooé pole chaakeizoané z. inenziou siloého pole (inenziou síly): E m [ms ] inenzia je oožná se zychlením, keé siloé pole aném mísě uělí liboolnému ělesu Siloé
Mechanická siloá pole siloé pole mechanice je ekooé pole chaakeizoané z. inenziou siloého pole (inenziou síly): E m [ms ] inenzia je oožná se zychlením, keé siloé pole aném mísě uělí liboolnému ělesu Siloé
Obecná rovnice kvadratické funkce : y = ax 2 + bx + c Pokud není uvedeno jinak, tak definičním oborem řešených funkcí je množina reálných čísel.
 5. Funkce 9. ročník 5. Funkce ZOPAKUJTE SI : 8. ROČNÍK KAPITOLA. Funkce. 5.. Kvadratická funkce Obecná rovnice kvadratické funkce : y = ax + bx + c Pokud není uvedeno jinak, tak definičním oborem řešených
5. Funkce 9. ročník 5. Funkce ZOPAKUJTE SI : 8. ROČNÍK KAPITOLA. Funkce. 5.. Kvadratická funkce Obecná rovnice kvadratické funkce : y = ax + bx + c Pokud není uvedeno jinak, tak definičním oborem řešených
VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C)
 VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C) max. 3 body 1 Zjistěte, zda vektor u je lineární kombinací vektorů a, b, je-li u = ( 8; 4; 3), a = ( 1; 2; 3), b = (2; 0; 1). Pokud ano, zapište tuto lineární kombinaci.
VZOROVÝ TEST PRO 3. ROČNÍK (3. A, 5. C) max. 3 body 1 Zjistěte, zda vektor u je lineární kombinací vektorů a, b, je-li u = ( 8; 4; 3), a = ( 1; 2; 3), b = (2; 0; 1). Pokud ano, zapište tuto lineární kombinaci.
Určitý integrál
 030 Určiý inegrál Předpokld: 00309 V několik minulých hodinách jsme se učili inegro - hledli jsme primiiní funkce Kráké shrnuí: F x dokážeme posupem, kerý nzýáme derioání, njí zcel přesně Pro hezké funkce
030 Určiý inegrál Předpokld: 00309 V několik minulých hodinách jsme se učili inegro - hledli jsme primiiní funkce Kráké shrnuí: F x dokážeme posupem, kerý nzýáme derioání, njí zcel přesně Pro hezké funkce
Jméno autora: Mgr. Zdeněk Chalupský Datum vytvoření: 20. 8. 2012 Číslo DUM: VY_32_INOVACE_16_FY_A
 Jméno autora: Mgr. Zdeněk Chalupský Datum vytvoření: 20. 8. 2012 Číslo DUM: VY_32_INOVACE_16_FY_A Ročník: I. Fyzika Vzdělávací oblast: Přírodovědné vzdělávání Vzdělávací obor: Fyzika Tematický okruh: Mechanika
Jméno autora: Mgr. Zdeněk Chalupský Datum vytvoření: 20. 8. 2012 Číslo DUM: VY_32_INOVACE_16_FY_A Ročník: I. Fyzika Vzdělávací oblast: Přírodovědné vzdělávání Vzdělávací obor: Fyzika Tematický okruh: Mechanika
2.6.5 Výměny tepla při změnách skupenství
 2.6.5 Výměny epla při změnách skupensí Předpoklady: 2604 Opakoání: Teplo se spořeboáá na da druhy dějů: zyšoání eploy: Q = mc, změna skupensí: Q = mlx. Tepelné konsany ody: c( led ) = 2000 J kg K, l =
2.6.5 Výměny epla při změnách skupensí Předpoklady: 2604 Opakoání: Teplo se spořeboáá na da druhy dějů: zyšoání eploy: Q = mc, změna skupensí: Q = mlx. Tepelné konsany ody: c( led ) = 2000 J kg K, l =
2.2.8 Jiné pohyby, jiné rychlosti I
 2.2.8 Jiné poyby, jiné ryclosi I Předpoklady: 020207 Pomůcky: Vernier Go Moion, počíač, nafukovací míč, kyvadlo velké, závaží na pružině, nakloněná rovina s vozíkem Př. 1: Nejdelší přímou pravidelně provozovanou
2.2.8 Jiné poyby, jiné ryclosi I Předpoklady: 020207 Pomůcky: Vernier Go Moion, počíač, nafukovací míč, kyvadlo velké, závaží na pružině, nakloněná rovina s vozíkem Př. 1: Nejdelší přímou pravidelně provozovanou
1.1.18 Rovnoměrně zrychlený pohyb v příkladech IV
 8 Rovnoměně ychlený pohyb v příkladech IV Předpoklady: 7 Pedagogická ponámka: Česká škola v současné době budí ve sudenech předsavu, že poblémy se řeší ásadně najednou Sudeni ak mají obovské poblémy v
8 Rovnoměně ychlený pohyb v příkladech IV Předpoklady: 7 Pedagogická ponámka: Česká škola v současné době budí ve sudenech předsavu, že poblémy se řeší ásadně najednou Sudeni ak mají obovské poblémy v
3. V případě dvou na sebe kolmých posunutí o velikostech 3 cm a 4 cm obdržíme výsledné posunutí o velikosti a) 8 cm b) 7 cm c) 6 cm d) 5 cm *
 Fyzika 1 2009 Otázky za 2 body 1. Mezi tavové veličiny patří a) teplo b) teplota * c) práce d) univerzální plynová kontanta 2. Krychle má hranu o délce 2 mm. Jaký je její objem v krychlových metrech? a)
Fyzika 1 2009 Otázky za 2 body 1. Mezi tavové veličiny patří a) teplo b) teplota * c) práce d) univerzální plynová kontanta 2. Krychle má hranu o délce 2 mm. Jaký je její objem v krychlových metrech? a)
Zákony bilance. Bilance hmotnosti Bilance hybnosti Bilance momentu hybnosti Bilance mechanické energie
 Zákony bilance Bilance hmonosi Bilance hybnosi Bilance momenu hybnosi Bilance mechanické energie Koninuum ermodynamický sysém Pené ěleso = ěšinou uzařený sysém Konsanní hmonos - nezáisí na čase ochází
Zákony bilance Bilance hmonosi Bilance hybnosi Bilance momenu hybnosi Bilance mechanické energie Koninuum ermodynamický sysém Pené ěleso = ěšinou uzařený sysém Konsanní hmonos - nezáisí na čase ochází
vzdálenost těžiště (myslí se tím těžiště celého tělesa a ne jeho jednotlivých částí) od osy rotace
 Přehled příkladů 1) Valiý pohyb, zákon zachoání energie ) Těžiště tělesa nebo moment setračnosti ýpočet integrací - iz http://kf.upce.cz/dfjp/momenty_setracnosti.pdf Nejčastější chyby: záměna momentu setračnosti
Přehled příkladů 1) Valiý pohyb, zákon zachoání energie ) Těžiště tělesa nebo moment setračnosti ýpočet integrací - iz http://kf.upce.cz/dfjp/momenty_setracnosti.pdf Nejčastější chyby: záměna momentu setračnosti
2.2.4 Kalorimetrická rovnice
 ..4 Kalorieriká rovnie Předpoklady: 0 Poůky: dvě kádinky, vaříí voda, eploěr Vernier, Síháe eplou a udenou vodu při íhání i vody vyěňují eplo, uí dojí k rovnováze zíkáe vodu o jedné eploě. Pokud žádné
..4 Kalorieriká rovnie Předpoklady: 0 Poůky: dvě kádinky, vaříí voda, eploěr Vernier, Síháe eplou a udenou vodu při íhání i vody vyěňují eplo, uí dojí k rovnováze zíkáe vodu o jedné eploě. Pokud žádné
1.8.9 Bernoulliho rovnice
 89 Bernoulliho ronice Předpoklady: 00808 Pomůcky: da papíry, přicucáadlo, fixírka Konec minulé hodiny: Pokud se tekutina proudí trubicí s různými průměry, mění se rychlost jejího proudění mění se její
89 Bernoulliho ronice Předpoklady: 00808 Pomůcky: da papíry, přicucáadlo, fixírka Konec minulé hodiny: Pokud se tekutina proudí trubicí s různými průměry, mění se rychlost jejího proudění mění se její
BIOMECHANIKA. Studijní program, obor: Tělesná výchovy a sport Vyučující: PhDr. Martin Škopek, Ph.D.
 BIOMECHANIKA 4, Kinematika pohybu I. (zákl. pojmy - rovnoměrný přímočarý pohyb, okamžitá a průměrná rychlost, úlohy na pohyb těles, rovnoměrně zrychlený a zpomalený pohyb, volný pád) Studijní program,
BIOMECHANIKA 4, Kinematika pohybu I. (zákl. pojmy - rovnoměrný přímočarý pohyb, okamžitá a průměrná rychlost, úlohy na pohyb těles, rovnoměrně zrychlený a zpomalený pohyb, volný pád) Studijní program,
Práce a výkon při rekuperaci
 Karel Hlava 1, Ladislav Mlynařík 2 Práce a výkon při rekuperaci Klíčová slova: jednofázová sousava 25 kv, 5 Hz, rekuperační brzdění, rekuperační výkon, rekuperační energie Úvod Trakční napájecí sousava
Karel Hlava 1, Ladislav Mlynařík 2 Práce a výkon při rekuperaci Klíčová slova: jednofázová sousava 25 kv, 5 Hz, rekuperační brzdění, rekuperační výkon, rekuperační energie Úvod Trakční napájecí sousava
Řešení úloh 1. kola 60. ročníku fyzikální olympiády. Kategorie D Autor úloh: J. Jírů. = 30 s.
 Řešení úloh. kola 60. ročníku fyzikální olympiády. Kategorie D Autor úloh: J. Jírů.a) Doba jízdy na prvním úseku (v 5 m s ): t v a 30 s. Konečná rychlost jízdy druhého úseku je v v + a t 3 m s. Pro rovnoměrně
Řešení úloh. kola 60. ročníku fyzikální olympiády. Kategorie D Autor úloh: J. Jírů.a) Doba jízdy na prvním úseku (v 5 m s ): t v a 30 s. Konečná rychlost jízdy druhého úseku je v v + a t 3 m s. Pro rovnoměrně
2.1.4 Výpočet tepla a zákon zachování energie (kalorimetrická rovnice)
 ..4 Výpoče epla a zákon zachování energie (kalorimerická rovnice) Teplo je fyzikální veličina, předsavuje aké energii a je udíž možné (i nuné) jej měři. Proč je aké nuné jej měři? Např. je předměem obchodu
..4 Výpoče epla a zákon zachování energie (kalorimerická rovnice) Teplo je fyzikální veličina, předsavuje aké energii a je udíž možné (i nuné) jej měři. Proč je aké nuné jej měři? Např. je předměem obchodu
b) Maximální velikost zrychlení automobilu, nemají-li kola prokluzovat, je a = f g. Automobil se bude rozjíždět po dobu t = v 0 fg = mfgv 0
 Řešení úloh. kola 58. ročníku fyzikální olympiády. Kategorie A Autoři úloh: J. Thomas, 5, 6, 7), J. Jírů 2,, 4).a) Napíšeme si pohybové rovnice, ze kterých vyjádříme dobu jízdy a zrychlení automobilu A:
Řešení úloh. kola 58. ročníku fyzikální olympiády. Kategorie A Autoři úloh: J. Thomas, 5, 6, 7), J. Jírů 2,, 4).a) Napíšeme si pohybové rovnice, ze kterých vyjádříme dobu jízdy a zrychlení automobilu A:
ROVNOMĚRNĚ ZRYCHLENÉ A ZPOMALENÉ POHYBY. Studijní text pro soutěžící FO a ostatní zájemce o fyziku Ivo Volf, Přemysl Šedivý.
 ROVNOMĚRNĚ ZRYCHLENÉ A ZPOMALENÉ POHYBY Sudijní ex pro ouěžící FO a oaní zájece o fyziku Ivo Volf, Přeyl Šedivý Obah Úvod 1 Kineaika rovnoěrně zrychleného a rovnoěrně zpoaleného příočarého pohybu honého
ROVNOMĚRNĚ ZRYCHLENÉ A ZPOMALENÉ POHYBY Sudijní ex pro ouěžící FO a oaní zájece o fyziku Ivo Volf, Přeyl Šedivý Obah Úvod 1 Kineaika rovnoěrně zrychleného a rovnoěrně zpoaleného příočarého pohybu honého
ROVNOMĚRNĚ ZRYCHLENÝ POHYB, ZPOMALENÝ POHYB TEORIE. Zrychlení. Rychlost
 Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Vladislav Válek MGV_F_SS_1S1_D05_Z_MECH_Rovnomerne_zrychleny_pohyb_z pomaleny_pohyb_pl Člověk a příroda Fyzika
Škola: Autor: DUM: Vzdělávací obor: Tematický okruh: Téma: Masarykovo gymnázium Vsetín Mgr. Vladislav Válek MGV_F_SS_1S1_D05_Z_MECH_Rovnomerne_zrychleny_pohyb_z pomaleny_pohyb_pl Člověk a příroda Fyzika
Přípravný kurz z fyziky na DFJP UPa
 Přípravný kurz z fyziky na DFJP UPa 26. 28.8.2015 RNDr. Jan Zajíc, CSc. ÚAFM FChT UPa Pohyby rovnoměrné 1. Člun pluje v řece po proudu z bodu A do bodu B rychlostí 30 km.h 1. Při zpáteční cestě z bodu
Přípravný kurz z fyziky na DFJP UPa 26. 28.8.2015 RNDr. Jan Zajíc, CSc. ÚAFM FChT UPa Pohyby rovnoměrné 1. Člun pluje v řece po proudu z bodu A do bodu B rychlostí 30 km.h 1. Při zpáteční cestě z bodu
Jméno autora: Mgr. Zdeněk Chalupský Datum vytvoření: Číslo DUM: VY_32_INOVACE_18_FY_A
 Jméno autora: Mgr. Zdeněk Chalupský Datum vytvoření: 1. 10. 2012 Číslo DUM: VY_32_INOVACE_18_FY_A Ročník: I. Fyzika Vzdělávací oblast: Přírodovědné vzdělávání Vzdělávací obor: Fyzika Tematický okruh: Mechanika
Jméno autora: Mgr. Zdeněk Chalupský Datum vytvoření: 1. 10. 2012 Číslo DUM: VY_32_INOVACE_18_FY_A Ročník: I. Fyzika Vzdělávací oblast: Přírodovědné vzdělávání Vzdělávací obor: Fyzika Tematický okruh: Mechanika
Fyzikajekolemnás(Polohaajejízměny) Studijní text pro řešitele FO a ostatní zájemce o fyziku Ivo Volf Miroslava Jarešová.
 Fyzikajekolemnás(Polohaajejízměny) Sudijní ex pro řešiele F a osaní zájemce o fyziku Io Volf Miroslaa Jarešoá bsah Sloo úodem 3 1 Popis polohy ělesa 4 1.1 Jednorozměrnýprosor....................... 4 Příklad1
Fyzikajekolemnás(Polohaajejízměny) Sudijní ex pro řešiele F a osaní zájemce o fyziku Io Volf Miroslaa Jarešoá bsah Sloo úodem 3 1 Popis polohy ělesa 4 1.1 Jednorozměrnýprosor....................... 4 Příklad1
1.6.5 Vodorovný vrh. Předpoklady: Pomůcky: kulička, stůl, případně metr a barva (na měření vzdálenosti doapdu a výšky stolu).
 165 Vodoroný rh Předpoklad: 164 Pomůck: kulička, stůl, případně metr a bara (na měření zdálenosti doapdu a ýšk stolu) Pedaoická poznámka: Stejně jako předchozí i tato hodina stojí a padá s tím, jak dobře
165 Vodoroný rh Předpoklad: 164 Pomůck: kulička, stůl, případně metr a bara (na měření zdálenosti doapdu a ýšk stolu) Pedaoická poznámka: Stejně jako předchozí i tato hodina stojí a padá s tím, jak dobře
Vzorové příklady - 7. cvičení
 Voroé příklady - 7 cičení Voroý příklad 7 Nádobou na obráku protéká oda Nádoba je rodělena na tři ektory přepážkami otory Prní otor je čtercoý, o ploše S = cm, další da jou kruhoé, S = 5 cm, S = cm Otory
Voroé příklady - 7 cičení Voroý příklad 7 Nádobou na obráku protéká oda Nádoba je rodělena na tři ektory přepážkami otory Prní otor je čtercoý, o ploše S = cm, další da jou kruhoé, S = 5 cm, S = cm Otory
BIOMECHANIKA KINEMATIKA
 BIOMECHANIKA KINEMATIKA MECHANIKA Mechanika je nejstarším oborem fyziky (z řeckého méchané stroj). Byla původně vědou, která se zabývala konstrukcí strojů a jejich činností. Mechanika studuje zákonitosti
BIOMECHANIKA KINEMATIKA MECHANIKA Mechanika je nejstarším oborem fyziky (z řeckého méchané stroj). Byla původně vědou, která se zabývala konstrukcí strojů a jejich činností. Mechanika studuje zákonitosti
Diferenciální a integrální poet
 Diferenciální a inegrální poe princip a prae. úodní díl Úodem Tao publikace je urena m, keí alepo do njaké míry umí derioa a inegroa, ale myl cho innoí jim není zcela janý. Výklad je eden mén odborným
Diferenciální a inegrální poe princip a prae. úodní díl Úodem Tao publikace je urena m, keí alepo do njaké míry umí derioa a inegroa, ale myl cho innoí jim není zcela janý. Výklad je eden mén odborným
DERIVACE A MONOTÓNNOST FUNKCE DERIVACE A MONOTÓNNOST FUNKCE. y y
 Předmě: Ročník: Vvořil: Daum: MATEMATIKA ČTVRTÝ Mgr Tomáš MAŇÁK 5 srpna Název zpracovaného celku: DERIVACE A MONOTÓNNOST FUNKCE DERIVACE A MONOTÓNNOST FUNKCE je monoónní na celém svém deiničním oboru D
Předmě: Ročník: Vvořil: Daum: MATEMATIKA ČTVRTÝ Mgr Tomáš MAŇÁK 5 srpna Název zpracovaného celku: DERIVACE A MONOTÓNNOST FUNKCE DERIVACE A MONOTÓNNOST FUNKCE je monoónní na celém svém deiničním oboru D
Jednotky zrychlení odvodíme z výše uvedeného vztahu tak, že dosadíme za jednotlivé veličiny.
 1. Auto zrychlí rovnoměrně zrychleným pohybem z 0 km h -1 na 72 km h -1 za 10 sekund. 2. Auto zastaví z rychlosti 64,8 km h -1 rovnoměrně zrychleným (zpomaleným) pohybem za 9 sekund. V obou případech nakreslete
1. Auto zrychlí rovnoměrně zrychleným pohybem z 0 km h -1 na 72 km h -1 za 10 sekund. 2. Auto zastaví z rychlosti 64,8 km h -1 rovnoměrně zrychleným (zpomaleným) pohybem za 9 sekund. V obou případech nakreslete
