Josef Schmidt 1. 1
|
|
|
- Štěpán Horák
- před 5 lety
- Počet zobrazení:
Transkript
1 Řešené příkady ze skript ELMA v..95 Josef Schmidt 1 1 schmijos@fjfi.cvut.cz
2 Dostává se vám do rukou sbírka podrobně řešených příkadů ze skript Što: Eektřina a magnetismus. Každý z příkadů by mě víceméně tvořit samostatnou jednotku. Pro porozumění řešení daného příkadu často není nutné číst příkady předchozí nebo násedující (ae ne vždy...). Pokud je nějaký příkad výjimkou z tohoto pravida, je obvyke na přísušnou pasáž na jiném místě sbírky odkázáno. Řešený příkad se vždy sestává ze zadání, jeho řešení a případného dodatku. Dodatek není k (pochopení) řešení nutný, často příkad komentuje, rozšiřuje nebo se na výpočet dívá z jiného pohedu. Příkady jsou seřazeny do ogických ceků a často tedy nejsou v pořadí, v jakém jsou uvedeny ve skriptech. Nicméně, jejich číso je zachováno pro snadnější orientaci. Za obsahem náseduje seznam příkadů seřazený stejně jako ve skriptech, díky čemuž se dá ryche dohedat, kde daný příkad v této sbírce je. V aktuání verzi chybí některé nepodstatné dodatky, které se časem ( již brzy ) objeví. 1
3 Obsah Seznam příkadů 5 1 Zákady teorie reativity Diatace času a kontrakce déek Mion v atmosféře Protony proétající skrz gaaxii Hustota Dopperův jev Skádání rychostí Odvození vzorce pro skádání rychosti pomocí sožení Lorentzových transformací Kosmická od a raketa Kosmonaut na Měsíci Reativistická pohybová rovnice Hyperboický pohyb Reativistická energie a práce Urychovač Práce vynaožená na eektronu Rozpad mezonu Vazebná energie afa částice Sunce Eektrostatika.1 Přehed vzorců Couombův zákon Kuičky na nitích Nabité kapky Eektrostatická energie Tři náboje Nuová eektrostatická energie Nabitý čtyřstěn Rozpad jádra Gaussův zákon Náboj v krychi Eektrostatický potenciá a intenzita eektrického poe Nabitá tyč Nabité destičky Osa nabitého kruhového kotouče Půkuová supka
4 Skoro uzavřená kružnice Useknutý vrchík Potenciá mýdové bubiny.15 Eektrostatické poe Země.16 Dieektrická pevnost vzduchu Eektrický dipóový a kvadrupóový moment Bodové náboje Poarizovaná tyč Poarizovaná koue Sía eektrického dipóu Kvadrupóový moment bodových nábojů Kvadrupóový moment eipsoidu Kondenzátory ,.8 a.9 Deskový kondenzátor a.33 Vácový kondenzátor a Geiger-Müerův počítač Kuový kondenzátor Kapacita vedení Skádání kapacit Kondenzátor s poovičním dieektrikem Kondenzátor s proměnným dieektrikem Energie kondenzátoru Stacionární eektrické poe Přehed vzorců Skádání odporů Skádání odporů Skádání odporů Odpor vodičů Poměrné vodiče Napnutý drát Odporová kryche zoace v koaxiáním kabeu Svodový odpor kuového kondenzátoru Ohmův zákon Kryche z odporů Úbytky napětí v obvodu Poškozené teegrafní vedení Rozvětvený proud Vnitřní odpor baterie Vnitřní odpor baterie Votmetr a ampérmetr Joueovo tepo Dimenzování odporů Ztráty ve vedení Kirchhoffovy zákony Dvousmyčkový obvod Bbec zapojující baterie Definice proudu Rychost eektronů v drátu
5 Eektrony v urychovači Van der Graaffův proud Stacionární magnetické poe Reativita Letící kondenzátor Hustota proudu a 4.5 Transformace eektrického a magnetického poe Sía na vodič s proudem Obdéníková smyčka v magnetickém poi Biot-Savartův zákon Magnetické poe kruhové a poygonání smyčky Ohnutý drát Magnetické poe na ose čtvercové smyčky Trojúheník z drátu Kryche z drátu Tři dráty Ampérův zákon Trubka s proudem Vyvrtaná díra Soenoid Magnetický dipó Zemský magnetický dipó Lorentzova sía Komá poe Kruhový pohyb v magnetickém poi Pohyb v magnetickém poi po šroubovici Eektromagnetické poe Eektromagnetická indukce ndukce na koejích Pohybující se smyčka a 5.8 Rotující cívky Homopoární generátor Vastní a vzájemná indukčnost a 5.4 Vastní indukčnost vácové cívky Vastní indukčnost toroidání cívky Vzájemná indukčnost Vzájemná indukčnost LR a RC obvody a 5.1 RC obvod Energie kondenzátoru LR obvod Obvody se střídavým proudem Nabíjení baterie Spotřebič
6 Seznam příkadů 1 Zákady teorie reativity Mion v atmosféře Protony proétající skrz gaaxii Kosmická od a raketa Dopperův jev Hustota Kosmonaut na Měsíci Hyperboický pohyb Urychovač Práce vynaožená na eektronu Rozpad mezonu Vazebná energie afa částice Sunce Eektrostatika.1 Kuičky na nitích Nabité kapky Tři náboje Nuová eektrostatická energie Nabitý čtyřstěn Rozpad jádra Náboj v krychi Nabitá tyč Nabité destičky Osa nabitého kruhového kotouče Půkuová supka Potenciá mýdové bubiny Skoro uzavřená kružnice Useknutý vrchík Eektrostatické poe Země Dieektrická pevnost vzduchu Bodové náboje Poarizovaná tyč Poarizovaná koue Sía eektrického dipóu Kvadrupóový moment bodových nábojů Kvadrupóový moment eipsoidu Deskový kondenzátor Deskový kondenzátor
7 .9 Deskový kondenzátor Vácový kondenzátor Kuový kondenzátor Kapacita vedení Geiger-Müerův počítač Skádání kapacit Kondenzátor s poovičním dieektrikem Kondenzátor s proměnným dieektrikem Energie kondenzátoru Stacionární eektrické poe Poměrné vodiče Napnutý drát Odporová kryche Skádání odporů Skádání odporů Kryche z odporů Dvousmyčkový obvod zoace v koaxiáním kabeu Svodový odpor kuového kondenzátoru Poškozené teegrafní vedení Úbytky napětí v obvodu Vnitřní odpor baterie Rozvětvený proud Dimenzování odporů Ztráty ve vedení Votmetr a ampérmetr Bbec zapojující baterie Vnitřní odpor baterie Rychost eektronů v drátu Eektrony v urychovači Van der Graaffův proud Stacionární magnetické poe Letící kondenzátor Hustota proudu Obdéníková smyčka v magnetickém poi Transformace eektrického a magnetického poe Transformace eektrického a magnetického poe Komá poe Magnetické poe kruhové a poygonání smyčky Trojúheník z drátu Kryche z drátu Magnetické poe na ose čtvercové smyčky Ohnutý drát Vyvrtaná díra Trubka s proudem Tři dráty Soenoid
8 4.16 Zemský magnetický dipó Pohyb v magnetickém poi po šroubovici Kruhový pohyb v magnetickém poi Eektromagnetické poe Pohybující se smyčka ndukce na koejích Vastní indukčnost vácové cívky Vastní indukčnost vácové cívky Vastní indukčnost toroidání cívky Homopoární generátor Rotující cívka Rotující cívka Vzájemná indukčnost Vzájemná indukčnost RC obvod RC obvod Energie kondenzátoru LR obvod Nabíjení baterie Spotřebič
9 Kapitoa 1 Zákady teorie reativity 1.1 Diatace času a kontrakce déek Mion v atmosféře Mion v kosmickém záření by pozorován, jak v atmosféře urazi od svého vzniku do rozpadu vzdáenost d = 5km rychostí v =,99c. Jakou dobu existova v naší pozorovací soustavě, jakou dobu ve vastní kidové soustavě a jak siná vrstva atmosféry proša koem něho ve vastní soustavě? Řešení: Dobu života v naší pozorovací soustavě určíme jednoduše z kinematického vztahu t = d v = 5km,99c = 1, s = 16,8µs (1.1) (použii jsme přibižnou hodnotu rychosti světa c = m/s). Z našeho pohedu zároveň mionu ubíhá čas pomaeji vivem diatace času. Určeme tedy ze vztahu pro diataci vastní čas mionu: τ = t γ = t 1 v c = d v 1 v c =, s =,375µs. (1.) Z pohedu mionu koem něj atmosféra sviští rychostí v, tudíž bude kontrahovaná ve směru svého pohybu, dosazením do vztahu pro kontrakci déek získáme toušt ku atmosféry z pohedu mionu: d = d γ = d Stejného výsedku dosáhneme použitím kinematického vztahu 1 v = 75m. (1.3) c d = τ v = 75m, (1.4) kde jsme využii faktu, že koem mionu atmosféra etí rychostí v po dobu jeho vastního času života τ. Dodatek: V tomto příkadu je možné natrefit na reativistický paradox. Z pohedu mionu je to pozorovate na Zemi, kdo se pohybuje, tudíž diatace času postihuje jeho. Mion tedy na svých hodinkách během svého života naměří spočtený čas τ =,37µs a de něj pozorovatei na Zemi uběhne pouze τ = τ γ = τ 1 v =,335µs (místo t = 16,8µs). (1.5) c 8
10 Jak je to možné? Probém je zde s reativitou současnosti. Dvě udáosti, které se z jedné vztažné soustavy jeví, že nastay současně, tak v jiné vztažné soustavě vůbec současné být nemusí. V soustavě spojené s pozorovateem nazemi mámedvě současné udáosti: vznik mionua spuštění stopek pozorovateem na Zemi, stejně jsou zde současné udáosti: zánik mionu a zastavení stopek pozemského pozorovatee. V soustavě spojené s mionem tyto udáosti současné obecně nebudou! Z pohedu mionu tedy pozorovate na Zemi nejspíš zcea nepochopiteně spouští a zastavuje stopky úpně jindy, než v okamžiku, kdy mion vzniká a zaniká. Kvantifikujme nyní tyto úvahy. Napišme si prostorové a časové souřadnice jednotivých udáostí v soustavě spojené se Zemí a transformujme je pomocí Lorentzovy transformace do soustavy spojené s mionem. Vezměme jednu prostorovou souřadnici x jejíž počátek je v místě vzniku mionu a míří doů směrem k pozorovatei. Pak vznik mionu P V, začátek měření P M, zánik mionu P Z a konec měření P K mají prostoročasové souřadnice (x, t): P V = (,), P M = (d,), P Z = (d,t), P K = (d,t). (1.6) (pro jednoduchost uvažujeme, že mion se rozpadne přesně u nohou pozorovatee). O vznik mionu v O země x x zánik mionu Obrázek 1.1: Souřadnice x spojená s pozorovateem na Zemi, s počátkem v místě vzniku mionu. Souřadnice x spojená s pohybujícím se mionem, mion je umístěn v počátku. Souřadnicix zavedemetak,žebudemířit vesměrusouřadnicex,ajejípočátek budespojens pohybujícímsemionem. Zavedení souřadnicxax také viz obrázek 1.1. Mezi souřadnicemi (x,t) a (x,t ) v takto zavedených vztažných soustavách můžeme přejít násedujícími Lorentzovými transformacemi x = γ(x vt) = x vt, 1 v c t = γ (t v c x ) = t v c x 1 v c. (1.7) Po dosazení konkrétních hodnot souřadnic (x, t) pro jednotivé udáosti dostaneme souřadnice (x,t ) udáostí ve vztažné soustavě spojené s mionem (po řadě vznik mionu P V, začátek měření P M, zánik mionu P Z, konec měření P K ): P V = (,), P M (γd =, γ v ) ( c d, P Z =, t ) (, P K γ =, t ), (1.8) γ kde jsme pro získání fináních tvarů použii vztah d = vt. Vidíme tedy, že v soustavě spojené s mionem pozorovate na Zemi zača měření dávno před vznikem mionu v čase t M = γ v c d = 9
11 117µs (mion vznik v čase t V = s). Konec měření nasta (současně se zánikem mionu) v čase t Z = t K = t γ =,37µs. Cekově tedy pozorovate v soustavě spojené s mionem měři po dobu t m = t M t Z = t γ +γ v ( ) 1 c d = t γ +γv c = tγ = 119µs, (1.9) kde jsme opět použii vztah d = vt. Vastní čas měřícího pozorovatee pak je t m γ = t = 16,8µs, což je přesně hodnota, kterou jsme měi na začátku. Čas,335µs, který nás ved k ceé této úvaze, jednoduše představuje jen maou část vastního času stopujícího pozorovatee. O žádný paradox se tedy nejedná Protony proétající skrz gaaxii V kosmickém záření se vyskytují protony o energii E = 1 1 GeV. Za jak douho proetí naší Gaaxií v naší vztažné soustavě a ve své vastní? Řešení: Nejprve si spočteme rychosti proétajících protonů. Vztah mezi energií a rychostí získáme ze savného vztahu E = mc = m γc = E γ =, (1.1) 1 v c ( ) 1/ kde jsme zavedi označení faktoru γ = 1 v c a kidové energie E = m c. Vyjádřením rychosti dostaneme v = 1 E ( ) E c. (1.11) E Kidová energie protonu je přibižně E = 1GeV. Hodnota rychosti je pak v = 1 1 c (1,5 1 )c =, }{{} 5c. (1.1) x kde jsme použii aproximaci (Tayorův rozvoj do prvního řádu) 1+x 1 + x. Z hediska pozorovatee v gaaxii můžeme uvažovat v c. Jestiže uvažujeme déku naší Gaaxie = 1 sv.et, pak doba, za kterou protony skrze Gaaxii proetí z hediska pozorovatee v Gaaxii, je jednoduše t = v = 1et. (1.13) c Čas uběhý z hediska protonu získáme pomocí vztahu pro diataci času (zde musíme použít přesnou rychost v) τ = t γ = t 1 v c. (1.14) Ze vztahu (1.1) vidíme, že E E = 1 v, pro vastní čas protonu pak dostaneme c τ = t E E = 15 et 1 1 = 1 5 et = 315s. (1.15) Dodatek: Pokud se na situaci podíváme z pohedu protonů, Gaaxie koem nich sviští obrovskou rychostí v a je tedy extrémně zkrácená vivem kontrakce déek. Spočtěme tuto déku pomocí vztahu pro kontrakci déek (opět musíme použít přesnou rychost v): = γ = 1 v c = E E = 15 sv.et 1 1 = 1 5 sv.et = 315sv.s, (1.16) 1
12 což je méně než vzdáenost ze Země na Sunce. Tuto vzdáenost také můžeme dostat použitím kinematického vztahu = τv τc, (1.17) kde jsme využii faktu, že koem protonu Gaaxie etí rychostí přibižně c po dobu jeho vastního času průetu τ Hustota Těeso se vzhedem k dané vztažné soustavě pohybuje rychostí v =,8c. Určete poměr mezi jeho hustotou v této soustavě a hustotou kidovou. Řešení: Hustota v kidové soustavě ρ a hustota v pohybující se soustavě ρ jsou z definice dány vztahy ρ = m, ρ = m V V, (1.18) kde m a V jsou hmotnost a objem v kidové soustavě a m a V jsou hmotnost a objem v pohybující se soustavě. Objem se vivem Lorentzovy kontrakce déek transformuje jako V = V γ = V 1 v c. (1.19) Tento transformační vztah pyne z toho, že rozměr ve směru pohybu podéhá kontrakci, viz obrázek 1.. c c = c b V b = b V v a a = a γ Obrázek 1.: Objem a pohybující se objem. Při pohybu se zároveň zvětšuje hmotnost těesa, m = m γ. Dáme-i tyto vztahy dohromady, dostaneme výsedek: ρ = m V = m γ V = m γ = ρ γ. (1.) γ V Dopperův jev Fyzik hazardér, který přeje autem křižovatku na červenou a by zastaven poicistou, se háji tím, že v důsedku Dopperova jevu vidě místo červené zeenou. Fyzikáně vzděaný poicista ho však stejně pokutova, a to za nedovoenou rychost. Určete tuto rychost za předpokadu, že červené odpovídá spektrání čára λ = 7nm a zeené λ = 55nm. Řešení: Reativistický vztah mezi vysíanou frekvencí zdroje f a pozorovanou frekvencí f p, pokud se pozorovate přibižuje ke zdroji rychostí v (a tedy s faktorem β = v c ) je 1+β f p = 1 β f. (1.1) 11
13 Za frekvence dosadíme pomocí vnových déek, f = c λ : Nyní již jen vyjádříme faktor β: rychost fyzika hazardéra v autě tedy bya v = βc = 71km/s. c λ = 1+β c. (1.) 1 β λ β = λ λ λ =,37, (1.3) +λ Dodatek: Odvod me výše zmíněný vztah mezi frekvencemi f a f p. Uvažujme zdroj, který je v kidu, a k němu se přibižuje pozorovate rychostí v. Jaká bude perioda vnění T pro pozorovatee? Ten jede rychostí v vstříc vnopochám šířících se rychostí c. Perioda T udávající, za jak douho koem pozorovatee propuje jedna vnová déka, je pak dána rovnicí vt +ct = λ, (1.4) kde λ je vnová déka světa vysíaného zdrojem, viz také obrázek 1.3. Tedy T = λ v+c. λ P vt ct Obrázek 1.3: Pozorovate P jede rychostí v vstříc vnění sířící se proti němu rychostí c. Nesmíme ovšem zapomenout na to, že pohybujícímu pozorovatei jdou hodiny pomaeji. Perioda T, kterou jsme zatím určii, je dána časem v soustavě spojené se zdrojem vnění. Pohybujícímu se pozorovatei mezitím uběhne vastní čas τ daný vztahem pro diataci času: τ = T γ = T 1 v c = T 1 β. (1.5) Takže pozorovaná frekvence je f p = 1 τ, postupným dosazováním dostaneme výsedný vztah: f p = 1 τ = β T = 1 v +c = 1+β 1 β λ 1 β 1. Skádání rychostí c 1+β = λ 1 β f. (1.6) 1..1 Odvození vzorce pro skádání rychosti pomocí sožení Lorentzových transformací Naezněte zákon reativistického skádání rychostí v jednom směru sožením dvou Lorentzových transformací. Konkrétně naezněte tvar jedné Lorentzovy transformace, která bude ekvivaentní sožení dvou výše zmíněných transformací. 1
14 Řešení: Pro dvě soustavy (S) a (S ), které mají stejně orientované osy a soustava (S ) se vůči (S) pohybuje podé osy x (resp. x ) rychostí V, má Lorentzova transformace tvar 1 x = γ(x Vt), y = y, z = z, t = γ (t Vc ) x, γ = (1 V ) 1/. (1.7) Uvažujme tři vztažné soustavy (S), (S ) a (S ). Mezi soustavami (S) a (S ) přecházíme zadanou rychostí V, mezi (S ) a (S ) zadanou rychostí W a mezi (S) rovnou do (S ) přejdeme hedanou rychostí Y. Viz také obrázek 1.4. z (S) z (S ) z (S ) V W c Y x x x O O O y y y Obrázek 1.4: Tři vztažné soustavy (S), (S ) a (S ). Označme faktory gama indexem pode rychosti, kterou obsahují: γ = γ V = (1 V ) 1/ ) 1/, γ W = (1 W, γ Y = (1 Y ) 1/. (1.8) c Pak Lorentzovy transformace pro souřadnice x, x, x a t, t, t mezi soustavami (S) a (S ), (S ) a (S ), (S) a (S ) mají tvar ( x = γ V (x Vt), t = γ V t V ) c x, (1.9) ( x ( = γ W x Wt ), t = γ W t W ) c x, (1.3) ( x = γ Y (x Yt), t = γ Y t Y ) c x. (1.31) Nyní provedeme sožení Lorentzových transformací (1.3) a (1.9) a výsedek porovnáme s (1.31). Vezměme vztah pro transformaci x (1.3) a dosad me za x a t z (1.9) : ( ( x = γ W γ V (x Vt) Wγ V t V )) c x. (1.3) Výše uvedený výraz chceme upravit do tvaru x = γ Y (x Yt) (1.31) u proměnné t pak odečteme výraz pro soženou rychost Y. Upravujme tedy (1.3): (( x = γ W γ V 1 VW ) ) x (V +W)t = c [γ W γ V ( 1 VW c c )] ( x V +W 1 VW c t 1 Pro počátky soustav spývající v čase t = t =. Mohi bychom vzít i vztah pro transformaci t, ae postup by by v podstatě identický. ) c = γ Y (x Yt) (1.33) 13
15 Z posední rovnosti v předchozím výrazu dostáváme porovnáním hedaný vztah pro soženou rychost Y: Y = V +W 1 VW. (1.34) c Zároveň obdržíme vztah mezi gama koeficienty pro jednotivé rychosti, ( γ W γ V 1 VW ) c = γ Y ; (1.35) jeho patnost můžeme dokázat prostým rozepsáním všech gama faktorů (a dosazení konkrétní hodnoty rychosti Y) a násednou zdouhavou úpravou Kosmická od a raketa Z kosmické odi pohybující se vzhedem k Zemi rychostí v 1 =,8c bya ve směru jejího pohybu vypuštěna raketa rychostí v =,6c vzhedem k odi. Vastní déka rakety je = 1m. Jaká je déka této rakety z hediska pozorovatee v odi a z hediska pozorovatee na Zemi? Řešení: Vzorec pro reativistické skádání rychostí je násedující: v = v 1 +v 1+ v 1v c, (1.36) kde v je výsedná rychost, v 1 a v jsou původní rychosti se shodným kadným směrem. Po dosazení dostaneme konkrétní výsednou rychost v: v = (,8+,6)c =,946c. (1.37) 1+,6,8 Pro získání pozorovaných déek rakety musíme jen dosadit správné rychosti do vzorce pro kontrakci déek = γ = 1 v c, (1.38) kde je vastní (kidová) déka, déka po kontrakci a v přísušná rychost pohybu. Raketa z pohedu kosmonauta na kosmické odi má rychost v, z hediska pozorovatee na Zemi má právě soženou rychost v. Výsedné kontrahované déky tedy jsou: v = 1 1,6 = 8m, v = 1 1 (,946) = 3,4m. (1.39) Kosmonaut na Měsíci Kosmonaut na Měsíci pozoruje dvě kosmické odi bížící se k němu z opačných stran rychostmi v 1 =,8c a v =,9c. Jaká je rychost jedné z odí měřená z pauby druhé? Řešení: Jenom pro zajímavost si uvědomme, že kosmonaut pozoruje kosmické odi bížit se k sobě prostým součtem rychostí: v 1 +v = 1,7c. Jiná je situace pro pozorovatee na jednotivých kosmických odích, z jejich pohedu se k sobě kosmické odě bíží rychostí v = v 1 +v 1+ v 1v c = (,8+,9)c =,988c. (1.4) 1+,8,9 14
16 1.3 Reativistická pohybová rovnice Hyperboický pohyb Určete rychost a dráhu reativistické částice, na níž působí konstantní sía F. Porovnejte s rovnoměrně zrycheným pohybem v nereativistické fyzice a ukažte, že rychost částice nepřekročí rychost světa c. Řešení: Řešme reativistickou pohybovou rovnici, resp. její jednorozměrnou verzi Po dosazení γ = d dt (m γ v) = F, d dt (m γv) = F. (1.41) ( 1 v c ) 1/ a zintegrování pode času (sía F je konstantní) získáme m v = Ft+C 1, (1.4) 1 v c kde integrační konstantu C 1 určíme z počátečních podmínek. Uvažujeme-i nuovou rychost v čase nua, v() =, dostaneme C 1 =. Z předchozí rovnice vyjádříme rychost v(t): v(t) = Ftc m c +F t = Ft 1 m ) = 1+( Ft m c c 1+ ( m c Ft ). (1.43) Z posedního vyjádření zjevně v(t) < c pro ibovoný čas t, navíc patí im t + v(t) = c. Dráhu x(t) získáme integrací rychosti pode času: Ftc x(t) = v(t)dt = dt. (1.44) m c +F t Použitím substituce u = m c +F t, du = F tdt obdržíme výsedek x(t) = c du F u = F c u+c = c m F c +F t +C. (1.45) Pro počáteční podmínku x() = máme C = c F m c. Výsedek pak můžeme napsat ve tvaru: x(t) = m c ( ) Ft (1.46) F m c Na závěr ukážeme, jak se iší reativistický výsedek od nereativistického. Bude se nám hodit Tayorův poynom funkce (1+x) α, kde α R a x je bízké nue: (1+x) α = + k= ( ) α x k = 1+αx+ α(α 1) x +... (1.47) k Vezměme nyní funkce v(t) v prostředním vyjádření (1.43) a x(t) (1.46) a použijme Tayorův rozvoj na odmocniny v nich: ( 1+ ( ) ) Ft ±1/ = 1± 1 ( ) Ft + ±1 m c m c 15 ( ± 1 1) ( ) Ft , (1.48) m C
17 kde jsme uvažovai x = ( Ft m c) a tedy náš rozvoj patí jen pro časy t, kdy je x maé. Po dosazení těchto rozvojů do funkcí x(t) a v(t) (u poohy jsme použii rozvoj do druhého řádu, u rychosti jen do prvního řádu) dostaneme x(t) = 1 F t 1 m 8m , (1.49) ct4 F 3 F 3 v(t) = F t 1 m m (1.5) ct3 Vidíme tedy, že vzorce pro nereativistický pohyb jsou prvním přibížením pohybu reativistického. V tzv. nereativistické imitě c + dostaneme vzorce pro nereativistický pohyb. Dodatek: Proč se příkad jmenuje hyperboický pohyb? Protože trajektorií reativistického pohybu s působící konstantní siou je v prostoročasovém diagramu hyperboa. Pro snažší úpravy se nám bude hodit pozměnit počáteční podmínku počáteční poohy na x() = m c F = α. Pak integrační konstanta vyjde C = a výsedná závisost poohy na čase x(t) je x(t) = α 1+ c t α. (1.51) Úpravou získáme rovnici trajektorie v prostoročasovém diagramu s proměnnými (x, t) jako x c t = α, (1.5) což je rovnice hyperboy znázorněné na obrázku 1.5. Nereativistický pohyb x = 1 m t pak představuje pohyb paraboický. ct F α x Obrázek 1.5: Hyperboický pohyb zakresený v prostoročasovém diagramu. Dodatek: Ve skriptech je výsedek zapsán pomocí konstanty a = F m. Tato konstanta nepředstavuje zrychení částice. Pro reativistický pohyb je při působení konstantní síy zrychení nekonstantní. Skutečnou hodnotu zrychení získáme kasickým způsobem z kinematického vztahu: a(t) = dv(t) dt = d dt ( Ftc m c +F t ) = m Fc3 ( m c +F t ) 3/. (1.53) 16
18 1.4 Reativistická energie a práce Urychovač Urychovač dodává protonům energii E = 5 GeV. Jaké rychosti dosahují? (Kidová energie protonu je E =,938GeV.) Řešení: Vztah mezi energií a rychostí získáme ze savného vztahu E = mc = m γc = E γ =, (1.54) 1 v c ( ) 1/ kde jsme zavedi označení faktoru γ = 1 v c a kidové energie protonu E = m c. Vyjádřením rychosti získáme v = Práce vynaožená na eektronu E ( ) E c =,999998c. (1.55) E Jak vekou práci je třeba vynaožit na zvýšení rychosti eektronu z v 1 = 1,.1 8 m.s 1 na v =,4.1 8 m.s 1 pode nereativistické a reativistické mechaniky? (Kidová energie eektronu je,511mev.) Řešení: V nereativistické mechanice je práce rozdí kinetických energií objektu W = E K E K1 = 1 m v 1 m v1 = 1 ( v m c ) c v 1 c = 1 E ( β β1) =,4E =,13MeV, (1.56) kde jsme vztah zapsai pomocí reativistických veičin kidové energie E a faktoru β = v c ; v našem konkrétním případě máme β 1 = 5 a β = 4 5 (při použití přibižné hodnoty rychosti světa c = m/s). V reativistickém případě je práce rovna přímo rozdíu cekových energií těes: W = E E 1 = m c m 1 c = m c (γ γ 1 ) = E (γ γ 1 ) =.58E =.96MeV, (1.57) kde jsme ve výrazu použii faktor γ = (1 β ) 1/. Výsedné vztahy pro nereativistickou, resp. reativistickou, práci jsou W = 1 E ( β β 1), resp. W = E (γ γ 1 ). (1.58) Nereativistický vztah získáme z toho reativistického Tayorovým rozvojem faktoru γ do prvního řádu: γ = ( 1 β ) 1/ 1+ 1 β Rozpad mezonu Mezon π (s kidovou energií E π = 139,6MeV ) serozpadá z kidu namion µ (kidová energie E µ = 15,7MeV ) a antineutrino ν. Určete energii mionu a antineutrina a uvoněnou kinetickou energii. Řešení: Nejprve spočteme cekovou uvoněnou kinetickou energii. Ta je dána prostým rozdíem cekových kidových energií před a po rozpadu úbytek hmoty se muse přeměnit na kinetickou energii: E K = E π (E µ +E ν ) = E π E µ = 33,9MeV, (1.59) 17
19 kde jsme poožii kidovou energii antineutrina E ν rovnu nue. Současné experimenty sice ukazují, že hmotnost neutrin je nenuová, ae zároveň v řádu jednotek ev nebo méně (tedy asi o 8 řádů méně než jsou kidové hmotnosti mezonu π a mionu). Jak se kinetická energie rozděí mezi vzniké částice? K tomu musíme využít zákony zachování hybnosti a energie: Mezon π by na začátku v kidu a tedy p π = a E π = E π : Reativistický vztah mezi energií a hybností je p π = p µ +p ν, E π = E µ +E ν. (1.6) = p µ +p ν, E π = E µ +E ν. (1.61) E c = E c p p = 1 c (E E ). (1.6) Ze zákona zachování hybnosti pyne rovnost kvadrátů hybností, p µ = p ν, a po dosazení z výše uvedeného vztahu dostaneme (opět po poožení E ν ) 1 c (E µ E µ ) = 1 c (E ν E ν ) E µ E µ = E ν. (1.63) Dospěi jsme tedy k násedující soustavě dvou rovnic o neznámých E µ a E ν : E π = E µ +E ν, Eµ = E µ E ν. (1.64) Po rozožení pravé strany druhé rovnice na (E µ E ν )(E µ +E ν ) a dosazení z první se vyhneme řešení kvadratické rovnice a dostaneme sadu ineárních rovnic: E π = E µ +E ν, Sečtením a odečtením těchto rovnic dostaneme výsedky: ( ) ( E µ = 1 E π + E µ E π = 19,8MeV, E ν = 1 E µ E π = E µ E ν. (1.65) E π E µ E π ) = 9,8MeV. (1.66) Na závěr stojí za to ještě expicitně spočítat kinetickou energii rozpadých částic jednoduše odečtením kidových energií: E Kµ = E µ E µ = 4,1MeV, E K ν = E ν = 9,8MeV. (1.67) Vidíme, že nehmotné antineutrino odnáší většinu vzniké kinetické energie! Vazebná energie afa částice Určete vazebnou energii částice α v M ev, jsou-i kidové hmotnosti protonu, neutronu a částice α: m p = 1, kg, m n = 1, kg a m α = 6, kg. Řešení: Vazebná energie je dána rozdíem kidových energií produktu a jeho konstituentů: E V = m α c (m p +m n )c = 4, J = 8,8MeV, (1.68) kde jsme použii přibižnou hodnotu rychosti světa c = m/s. Záporné znaménko naznačuje, že při vzniku afa částice se tato energie uvoní. Přepočet mezi jouy a eektronvoty je dán násedující jednoduchou jednotkovou úvahou 1eV = (1e).V = 1e C C.V = 1e C J = 1, J. (1.69) 18
20 Sunce Energie sunečního záření, které dopadá za jednotku času na čtvereční metr na hranici zemské atmosféry, představujetakzvanousuneční konstantu K = 137W.m,střednívzdáenostZemě od Sunce je d = 1, m = 1AU. Zdrojem suneční energie je tzv. vodíkový cykus, při němž se vždy čtyři jádra vodíku (protony) o reativní atomové hmotnosti m rp = 1,8 mění na jádro héia (m rα = 4,39). Určete úbytek hmotnosti Sunceamnožství spáeného vodíkuzasekundu. Odhadněte dobu, během níž by se spáio množství vodíku odpovídající dnešní hmotnosti Sunce M =.1 3 kg. Řešení: Nejprve určíme cekový zářivý výkon Sunce P. Jestiže ve vzdáenosti d prochází jedním metrem čtverečním výkon K, pak cekový výkon získáme vynásobením pochou sféry o pooměru d: P = 4πd K = 3, W = 3, TW (1.7) Tato energie se bere z jaderných reakcí uvnitř Sunce, kde se maá část hmoty přeměňuje na energii (at už kinetickou poséze vyzářenou pomocí eektromagnetického záření anebo rovnou na gamma záření). Množství přeměňované hmoty určíme z rovnice E = mc, resp. její časové derivace: P = de dt = dm dt c dm dt = P c = 4πd K c = 4, kg/s = 4,169Mt/s, (1.71) kde jsme použii přibižnou hodnotu rychosti světa c = m/s. Toto je tedy cekový úbytek hmotnosti Sunce za jednotku času vivem přeměny hmoty na vyzářenou energii. Nyní určíme množství spáeného vodíku za jednotku času. Jedna reakce vodíkového cyku poskytne násedující množství energie: E 1 = mc = (4m p m α )c. (1.7) Cekový počet potřebných reakcí za jednu vteřinu pro výkon P pak je N = P E 1 = 4πd K (4m p m α )c. (1.73) Za jednu reakci se spáí 4m p vodíku, cekové množství spáeného vodíku pak je dm H dt = 4m p N = 4m p 4πd K (4m p m α )c = 4πd K (1 mα 4m p )c. (1.74) m V posedním vyjádření již vystupuje pouze poměr hmotností α m p a tedy hmotnosti můžeme dosadit v jakýchkoiv jednotkách, třeba pomocí reativních atomových hmotností: dm H dt = 4πd K (1 mrα 4m rp )c = 5, kg/s = 598,Mt/s. (1.75) PokudbySuncebyojenzvodíkuajadernéreakce bypoceou dobuprobíhaystejnourychostí, pak by se vodík propái za čas T = M dm H dt = 3, s = 16md. et. (1.76) Steární evouce je samozřejmě mnohem kompikovanější a současné modey předpovídají cekovou dobu spaování vodíku na přibižně 1 miiard et. 19
21 Kapitoa Eektrostatika.1 Přehed vzorců Couombův zákon Sía F C od bodového náboje Q působící na bodový náboj q je dána jako F C = qq r 4πε r 3, F C = 1 qq 4πε r, (.1) kde r je vektor spojující náboj Q s nábojem q (od Q ke q), r je jeho veikost a ε. = 8, F.m 1 je permitivita vakua. ~F C q ~r Obrázek.1: Couombův zákon (směr síy je zde zakresen pro souhasné náboje). Q Eektrostatická energie W soustavy bodových nábojů: W = α<β 1 4πε q α q β r αβ, (.) kde q α jsou jednotivé veikosti bodových nábojů a r αβ jsou vzdáenosti mezi jednotivými náboji. q 3 r 3 r 13 r 1 q q 1 Obrázek.: Eektrostatická energie soustavy tří bodových nábojů. Gaussův zákon vztahuje tok eektrického poe E uzavřenou pochou s cekovým nábojem Q obkopeným touto pochou: E ds = Q. (.3) ε S
22 Eement pochy je d S = nds, kde n je jednotkový normáový vektor k pošce veikosti ds, viz také obrázek.3. Normáa n je orientována tak, aby mířia ven z uzavřené pochy. ~n ~E ds S Q Obrázek.3: Uzavřená pocha S v Gaussově zákoně s bodovým nábojem Q a znázorněným eementem pochy d S = nds. Pokud vektor intenzity eektrického poe E je v daném místě k poše S tečný, pak do integráu nepřispívá, nebot E n a tedy E d S =. Pokud naopak vektor E je v daném místě komý k poše S, pak se skaární součin redukuje na E d S = EdS. V případě, že pracujeme s bodovými náboji a některý z nábojů eží přímo na poše, Gaussův zákon nepatí (neze vastně rozhodnout, zda náboj eží či neeží uvnitř pochy) 1! Část eektrických siočar pak totiž uniká ven z pochy a není započítána do cekového toku eektrického poe. Eektrostatický potenciá ϕ pro bodové náboje: ϕ = 1 q α, (.4) 4πε R α q α jsou náboje jednotivých částic. Pro spojité rozožení náboje; po řadě: dékové, pošné a objemové rozožení: ϕ = 1 τ 4πε R d, ϕ = 1 σ 4πε S R ds, ϕ = 1 ρ dv, (.5) 4πε V R kdeτ, σ aρjsoupořadě funkcedékové, pošné, objemové nábojové hustoty. Vzdáenost R (pro bodové náboje R α ) je vzdáenost mezi místem určování eektrostatického potenciáu ϕ o poohovém vektoru r a integračním eementem (d, ds, dv) o poohovém vektoru r, tzn. R = r r, viz obrázek.4. Pro bodové náboje má roi r poohový vektor částic r α, tzn. R α = r r α. α dv ρ(~r ) O ~r ~r ~R =~r ~r '(~r) =? Obrázek.4: Znázorněný vektor R = r r pro určování eektrostatického (skaárního) potenciáu ϕ. Vektor r je poohový vektor místa určování hodnoty ϕ( r), vektor r je poohový vektor eementu objemu dv. 1 Podobně je to v případě dékového a pošného rozožení náboje, pokud část křivky či část pochy s náboji eží na poše S v Gaussově zákoně. 1
23 Podrobně mají vzorce násedující tvary. Pro bodové náboje: a pro spojité rozožení nábojů: ϕ( r) = 1 τ( r ) 1 4πε r r d, ϕ( r) = 4πε ϕ( r) = 1 q α 4πε r r α, (.6) S α σ( r ) 1 r r ds, ϕ( r) = 4πε V ρ( r ) r r dv. (.7) ntenzita eektrického poe E (ve statickém případě): je definováno jako (Couombická) sía působící na jednotkový (testovací) náboj: E = F C q. (.8) Vektor intenzity eektrického poe E můžeme získat z eektrostatického potenciáu ϕ: ( E = gradϕ = ϕ ) x, ϕ y, ϕ. (.9) z Přímý výpočet pro bodové náboje: a pro spojité rozožení nábojů: E = 1 τ R 4πε R 3 d, E 1 = 4πε E = 1 Rα q α 4πε Rα 3, (.1) S α R σ R 3 ds, E 1 = 4πε V R ρ dv, (.11) R3 kde τ, σ a ρ jsou po řadě funkce dékové, pošné, objemové nábojové hustoty. Vektor R (pro bodové náboje R α ) je vzdáenost mezi místem určování intenzity eektrického poe E o poohovém vektoru r a integračním eementem (d, ds, dv) o poohovém vektoru r, tzn. R = r r, viz obrázek.5. Pro bodové náboje má roi r poohový vektor částic r α, tzn. R α = r r α. Vzdáenost R je veikost vektoru R, tzn. R = r r (pro bodové náboje máme R α = r r α ). dv ρ(~r ) ~R =~r ~r ~r ~E(~r) =? O ~r Obrázek.5: Znázorněný vektor R = r r pro určování intenzity eektrického poe E. Vektor r je poohový vektor místa určování hodnoty E( r), vektor r je poohový vektor eementu objemu dv. Podrobně mají vzorce násedující tvary. Pro bodové náboje: E( r) = 1 r r α q α 4πε r r α 3 (.1) α
24 a pro spojité rozožení nábojů: E( r) = 1 τ( r ) 4πε E( r) = 1 σ( r ) 4πε S E( r) = 1 ρ( r ) 4πε V r r r r 3 d, r r r r 3 ds, r r r r dv. (.13) 3 Mutipóový rozvoj eektrostatického potenciáu je dán vztahem ϕ( r) = 1 [ Q 4πε r + p r r i,j Q ] ijx i x j r , (.14) kde r je veikost poohového vektoru r, Q je cekový náboj, p je vektor dipóového momentu a (Q ij ) je tenzor kvadrupóového momentu. Tyto veičiny se určí de násedujících vzorců (vždy pro bodové náboje a spojité objemové rozožení náboje ): Cekový náboj: Dipóový moment: Q = q α, Q = α p = q α r α, p = α V V ρ( r) dv, (.15) ρ( r) r dv, (.16) Kvadrupóový moment: Q ij = ( q α 3xi x j δ ij r ) α, Q ij = α V ρ( r) ( 3x i x j δ ij r ) dv, (.17) kde q α jsou náboje jednotivých částic, r α = (x 1α,x α,x 3α ) = (x α,y α,z α ) jejich poohové vektory, pro zpřehednění zápisu používáme značení (x α,y α,z α ) = (x,y,z) α. Vektor r = (x 1,x,x 3 ) = (x,y,z) je poohový vektor eementu objemu dv, ρ( r) je funkce objemové nábojové hustoty. Eektrické napětí je definované jako práce vnějších si F při přemístění jednotkového náboje po dráze : U = 1 F d q, (.18) kded = td, d jeeement déky a tje jednotkový tečný vektor ke křivce. V eektrostatice je obvyke jedinou siou působící na náboj sía eektrická, F = qe, pak se tedy vzorec konkretizuje na U = E d. (.19) Kapacita kondenzátoru je definována jako náboj na kondenzátoru na jednotkové napětí: Jednotky: kapacita C [F] = [C.V 1 ], náboj Q [C], napětí U [V]. C = Q U. (.) Pro krátkost nejsou uvedenévzorce pro dékové a pošné rozožení náboje. Spočívají jen v záměně objemového integráu za dékový nebo pošný a v záměně funkce objemové nábojové hustoty za dékovou nebo pošnou. 3
25 Skádání kapacit: Vzorce pro sériové (vevo) a paraení (vpravo) zapojení kondenzátorů jsou 1 C = 1 C C, C = C 1 +C, (.1) viz obrázek.6. C 1 C C 1 C Obrázek.6: Skádání kapacit C 1 a C. Vevo je sériové zapojení a vpravo paraení.. Couombův zákon..1.1 Kuičky na nitích Dvě stejné maé kuičky o hmotnostech m = 1g visí na dvou nitích déky = 1m. Nabijeme-i je souhasným nábojem stejné veikosti q, rozestoupí se tak, že niti budou svírat pravý úhe. Určete veikost náboje q. ~F n Fn ~ ~F C FC ~ m m ~F g ~F g Obrázek.7: Kuičky na niti. Řešení: Aby byy kuičky v rovnováze, musí výsednice gravitační F g a Couombovy síy F C směřovat ve směru nití (pak mohou být vyrovnány napět ovou siou F n ). Veikost Couombovy síy mezi dvěma náboji je obecně dána vztahem F C = 1 4πε q 1 q r, (.) kde q 1, q jsou hodnoty jednotivých nábojů a r je vzdáenost mezi nimi. Pro nitě svírající pravý úhe a tedy pro odkon jednotivých nití o úhe 45 musí být veikosti gravitační a Couombovy síy stejné, F C = F g. Vzdáenost mezi kuičkami je z Pythagorovy věty r = a veikosti jednotivých si pak: F C = 1 q 4πε, F g = mg. (.3) Vyjádříme-i náboj q z rovnice rovnosti si, dostaneme F C = F g q = ± 8πε mg = 1, C, (.4) kde jsme pro numerický výsedek použii hodnotu permitivity vakua ε = 8, F.m 1 a gravitačního zrychení g = 9,81m.s. 4
26 ... Nabité kapky Na dvou stejných vodních kapkách je po jednom přebytečném eektronu, přičemž sía eektrického odpuzování je stejně veká jako sía gravitačního přitahování. Určete pooměr kapek. ~F C ~ Fg ~ Fg ~ FC d Obrázek.8: Kapky s přebytečným eektronem. Řešení: Kuičky jsou odpuzovány Couombovou siou F C a přitahovány gravitační siou F g, veikosti těchto si jsou obecně dány vztahy F C = 1 4πε q 1 q r, F gκ m 1m r, (.5) kde q 1, q jsou jednotivé náboje, m 1 a m hmotnosti těes, r je jejich vzdáenost. Tyto vzorce patí pro sféricky symetricky rozožený náboj a hmotu (Gaussova věta) r je vzdáenost jejich středů. Uvažujeme zde, že jediný přebytečný eektron na kapkách se nachází právě v jejich středu. Vzorce (.5) pak jsou konkrétně F C = 1 4πε e d, F g = κ m d, (.6) kde m jsou hmotnosti jednotivých kapek, e je veikost eementárního eektrického náboje a d je vzdáenost středů kapek. Hmotnost kapek vyjádříme pomocí jejich hustoty ρ a pooměru r: m = ρv = 4 3 πr3 ρ. (.7) Z rovnosti veikostí si F C = F g vyjádříme potřebný pooměr kapek: 9e r = 6 64π 3 ε κρ = 7, m = 76,3µm, (.8) kdejsmepronumerickývýsedekpoužiihodnotyeementárníhoeektrickéhonábojee = 1, C, permitivity vakua ε = 8, F.m 1, gravitační konstanty κ = 6, m 3.kg 1.s a hustoty vody ρ = 1kg.m 3..3 Eektrostatická energie Tři náboje Tři náboje e, e, e jsou umístěny v uvedeném pořadí ve stejných vzdáenostech a. Určete síy působící na každý náboj a eektrostatickou energii soustavy. e a e a e Obrázek.9: Tři náboje e, e, e ve vzdáenostech a od sebe. 5
27 Řešení: Couombova sía F C od bodového náboje Q působící na bodový náboj q je dána jako F C = qq r 4πε r3, (.9) kde r je vektor spojující náboj Q s nábojem q (od Q ke q) a r je jeho veikost. Tento zápis pak přirozeně vyjadřuje vastnost, že souhasné náboje se odpuzují a nesouhasné přitahují. Označme síu působící od i-tého náboje na j-tý jako F ij. Tyto síy jsou znázorněné na obrázku.1. Jejich veikosti jsou F 1 = F 1 = F 3 = F 31 = 1 e 4πε a, F 13 = F 31 = 1 e 4πε 4a. (.3) 1 3 e e e ~F 31 ~ F1 ~ F1 ~ F3 ~ F3 ~ F13 Obrázek.1: Jednotivé síy působící na náboje. Sía F ij představuje síu od i-tého náboje působící na j-tý náboj. Označíme-i F 1, F a F 3 cekové veikosti si působící po řadě zeva na jednotivé náboje dostaneme (de veikostí díčích si F ij (.3) a jejich směrů na obrázku.1): F 1 = F 3 = 1 ( e ) 4πε a e (a) = 1 3e 4πε 4a, F =. (.31) Směry těchto výsedných si jsou na obrázku.11. e e e ~F 1 ~ F3 Obrázek.11: Cekové síy působící na náboje. Sía F je nuová. Eektrostatická energie soustavy je dána obecným vztahem W = 1 q α q β, (.3) 4πε r αβ kdeq α jsounábojenajednotivýchčásticích ar αβ jsoujejichvzájemnévzdáenosti.zdekonkrétně W = 1 ( q1 q + q 1q 3 + q ) q 3 = 1 ( ) e 4πε r 1 r 13 r 3 4πε a + e a + e = 1 3e a 4πε a. (.33) α<β.3..4 Nuová eektrostatická energie Najděte takové uspořádání jednoho protonu a dvou eektronů na jedné přímce, aby eektrostatická energie soustavy bya nuová. Řešení: Na přímce jsou možné dvě neekvivaentní uspořádání jednoho protonu a dvou eektronů, viz obrázek.1. Vzdáenosti mezi náboji jsme označii obecně a a b. a b a b e p e e e p Obrázek.1: Dvě uspořádání jednoho protonu a dvou eektronů na přímce. 6
28 Eektrostatická energie pro soustavu tří nábojů je W = 1 4πε α<β q α q β r αβ = 1 4πε ( q1 q r 1 + q 1q 3 r 13 + q q 3 r 3 ), (.34) kde q α jsou náboje na jednotivých částicích a r αβ jsou jejich vzájemné vzdáenosti. Pro uspořádání eektron-proton-eektron máme výraz W = 1 ( ) e 4πε a + e a+b + e = e a +b +ab b 4πε ab(a+b). (.35) V čitatei máme součet samých kadných číse (vzdáenosti a a b musíme uvažovat kadné, jeikož jsme je použii jako hodnoty pro r 1, r 13 a r 3, které jsou vždy kadné), takže v uspořádání e-p-e nemůže být eektrostatická energie W nuová. Pro uspořádání eektron-eektron-proton dostáváme W = 1 4πε ( e Eektrostatická energie je rovna nue, W =, právě tehdy když b a ab = ) a + e a+b + e = e b a ab b 4πε ab(a+b). (.36) ( ) b b 1 = a a ( ) b a 1, = 1± 5. (.37) Poměr kadných vzdáeností musí být kadný, řešením tedy je poměr vzdáeností b a = 1+ 5, kdy je eektrostatická energie W uspořádání e-e-p nuová Nabitý čtyřstěn Najděte energii potřebnou k umístění čtyř eektronů do vrchoů čtyřstěnu o hraně a = 1 1 m, v jehož středu je proton. e e p e e Obrázek.13: Čtyřstěn s eektrony v jeho vrchoem a protonem v jeho středu. Řešení: Eektrostatická energie soustavy nábojů W je dána vztahem W = 1 4πε α<β q α q β r αβ, (.38) kde q α jsou náboje na jednotivých částicích a r αβ jsou jejich vzájemné vzdáenosti. Nebudeme zde vypisovat všech deset čenů této sumy pro 5 nábojů. Uvědomíme si, že díky symetrii čtyřstěnu máme jen dva různé druhy interakcí mezi náboji. Je to vzájemná interakce eektronů ve vrchoech čtyřstěnu všechny jsou stejně vzdáené na déku hrany čtyřstěnu a a 7
29 těchto hran je cekem šest. Druhou interakcí je proton ve středu čtyřstěnu působící na čtyři eektrony ve vzdáenosti r: W = 1 ) (6 e e +4. (.39) 4πε a r Vzdáenost středu čtyřstěnu od jeho vrchoů je 3 r = W = e 6 8 4πε a a, kde a je déka jeho hrany. Po dosazení: = 1, J, (.4) pronumerickývýsedekjsmepoužiihodnotyeementárníhoeektrickéhonábojee = 1, C a permitivity vakua ε = 8, F.m Rozpad jádra Atomová jádra těžkých prvků můžeme považovat za koue nabité s objemovou hustotou náboje ρ = C.m 3. Jak se změní eektrostatická energie při symetrickém rozpadu jádra uranu 9U na dvě stejná jádra paadia 46 Pd? Řešení: Eektrostatická energie objemově nabité koue o pooměru R s konstantní nábojovou hustotou ρ, resp. cekovým nábojem na koui Q, je W = 4πR5 ρ = 3 1 Q 15ε 54πε R. (.41) Náboj jádra uranu je Q U = 9e a náboj jádra paadia je Q Pd = 46e = 1 Q U. Jejich pooměry určíme ze vztahu pro cekový náboj Q objemově homogenně nabité koue: Q = ρv = ρ 4 3Q 3 πr3 R = 3 4πρ. (.4) Pooměry jader uranu a paadia tedy jsou 69e 69e R U = 3 πρ, R Pd = 3 πρ = R U 1 3. (.43) Změna eektrostatické energie W je W = W U W Pd = 3 ( 1 Q ) ( ) U Q Pd = 3 1 Q 1 U 1 54πε R U R Pd 54πε R 1 U 3 = 3 ( 1 πρ Q U ) 3 54πε 69e = 7, J, (.44) 4 kdejsmepronumerickývýsedekpoužiihodnotyeementárníhoeektrickéhonábojee = 1, C a permitivity vakua ε = 8, F.m 1. 3 Odvození záměrně vynecháváme... 8
30 .4 Gaussův zákon Náboj v krychi Bodový náboj je umístěn a) ve středu kryche, b) v jednom z rohů kryche. Určete tok intenzity eektrického poe každou ze stěn kryche. Q Q (a) Náboj uprostřed kryche. (b) Náboj v rohu kryche. Obrázek.14: Náboje v krychích. Řešení: Pro rešení této úohy použijeme Gaussův zákon. Ten říká, že tok intenzity eektrického poe Φ skrze uzavřenou pochu S je úměrný náboji Q v této poše uzavřenému: Φ = E ds = Q. (.45) ε S Pokud uvažujeme náboj uprostřed kryche, můžeme povrch kryche vzít jako uzavřenou pochu S v Gaussově zákoně. Cekový tok intenzity eektrického poe E krychí tedy je Φ = Q ε. Symetrie úohy říká, že každou ze stěn kryche musí téct stejný tok eektrického poe 4. Tento tok je zjevně roven Φ 1stěna = 1 6 Φ = Q 6ε. (.46) Pro náboj v rohu kryche je situace kompikovanější v tom, že Gaussův zákon nepatí v případě, že bodový náboj eží na zvoené poše S. Můžeme ae určit tok třemi stěnami kryche, v nichž náboj eží, přímo z definice toku intenzity eektrického poe: Φ = E ds. (.47) S Vektory eektrického poe E jsou radiání míří vždy přímo od nebo k náboji. To znamená, že vektory E jsou tečné ke stěnám, ve kterých náboj eží, viz obrázek.15. Q ~E ~E Obrázek.15: Vektory eektrické intenzity E pro náboj v rohu kryche jsou tečné ke stěnám, ve kterých náboj eží. 4 Kryche je symetrická při rotaci o násobky pravých úhů okoo os procházející středem kryche (a nábojem) komých na přísušné dvě stěny kryche. 9
Z toho se η využije na zajištění funkcí automobilu a na překonání odporu vzduchu. l 100 km. 2 body b) Hledáme minimum funkce θ = 1.
 Řešení úoh. koa 59. ročníku fyzikání oympiády. Kategorie A Autor úoh: J. Thomas.a) Na dráze vt bude zapotřebí objem paiva V θ θv t. Při jeho spáení se získá tepo Q mh ρv H ρθvh t. Z toho se η využije na
Řešení úoh. koa 59. ročníku fyzikání oympiády. Kategorie A Autor úoh: J. Thomas.a) Na dráze vt bude zapotřebí objem paiva V θ θv t. Při jeho spáení se získá tepo Q mh ρv H ρθvh t. Z toho se η využije na
Řešení úloh 1. kola 60. ročníku fyzikální olympiády. Kategorie B Autoři úloh: J. Thomas (1, 2, 3, 4, 5, 7), M. Jarešová (6)
 Řešení úoh 1. koa 60. ročníku fyzikání oympiády. Kategorie B Autoři úoh: J. Thomas (1, 2, 3, 4, 5, 7), M. Jarešová (6) h 1.a) Protože vzdáenost bodů K a O je cos α, je doba etu kuičky z bodu K do bodu
Řešení úoh 1. koa 60. ročníku fyzikání oympiády. Kategorie B Autoři úoh: J. Thomas (1, 2, 3, 4, 5, 7), M. Jarešová (6) h 1.a) Protože vzdáenost bodů K a O je cos α, je doba etu kuičky z bodu K do bodu
MAGNETICKÉ POLE. 1. Stacionární magnetické pole I I I I I N S N N
 MAGETCKÉ POLE 1. Stacionární magnetické poe V E S T C E D O R O Z V O J E V Z D Ě L Á V Á Í je část prostoru, kde se veičiny popisující magnetické poe nemění s časem. Vzniká v bízkosti stacionárních vodičů
MAGETCKÉ POLE 1. Stacionární magnetické poe V E S T C E D O R O Z V O J E V Z D Ě L Á V Á Í je část prostoru, kde se veičiny popisující magnetické poe nemění s časem. Vzniká v bízkosti stacionárních vodičů
7 Kvantová částice v centrálně symetrickém potenciálu.
 7 Kvantová částice v centráně symetrickém potenciáu. Představte si, že hodíte kámen do vody a chcete popsat vny, které vzniknou. Protože hadina je D, můžete vny popsat funkcí f x, y. Ae pokud jste chytří,
7 Kvantová částice v centráně symetrickém potenciáu. Představte si, že hodíte kámen do vody a chcete popsat vny, které vzniknou. Protože hadina je D, můžete vny popsat funkcí f x, y. Ae pokud jste chytří,
Jev elektromagnetické indukce
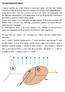 Jev eektromagnetické indukce V minuých kapitoách jsme si jistě uvědomii, že pojmy kid a pohyb, které byy vemi významné u mechanických dějů, při zkoumání eektrických a magnetických jevů nabyy přímo zásadní
Jev eektromagnetické indukce V minuých kapitoách jsme si jistě uvědomii, že pojmy kid a pohyb, které byy vemi významné u mechanických dějů, při zkoumání eektrických a magnetických jevů nabyy přímo zásadní
1.7 Magnetické pole stacionárního proudu
 1.7 Magnetické poe stacionárního proudu Pohybující se e. náboje (e. proud) vytvářejí magnetické poe. Naopak poe působí siou na pohybující se e. náboje. 1.7.1 E. proud, Ohmův zákon v diferenciáním tvaru
1.7 Magnetické poe stacionárního proudu Pohybující se e. náboje (e. proud) vytvářejí magnetické poe. Naopak poe působí siou na pohybující se e. náboje. 1.7.1 E. proud, Ohmův zákon v diferenciáním tvaru
Couloumbuv zákon stejne jako vetsina zakonu elektrostatiky jsou velmi podobna zakonum gravitacniho pole.
 1) Eektrostaticke poe, Cooumbuv zákon, Permitivita kazde dve teesa nabite eektrickym nabojem Q na sebe pusobi vzajemnou siou. Ta je vysise pomoci Couombovyho zákona: F = 1 4 Q Q 1 2 r r 2 0 kde první cast
1) Eektrostaticke poe, Cooumbuv zákon, Permitivita kazde dve teesa nabite eektrickym nabojem Q na sebe pusobi vzajemnou siou. Ta je vysise pomoci Couombovyho zákona: F = 1 4 Q Q 1 2 r r 2 0 kde první cast
Řešení úloh 1. kola 49. ročníku fyzikální olympiády. Kategorie D. Dosazením do rovnice(1) a úpravou dostaneme délku vlaku
 Řešení úoh koa 49 ročníku fyzikání oympiády Kategorie D Autořiúoh:JJírů(,3,4,5,6,),TDenkstein(), a) Všechny uvažované časy jsou měřené od začátku rovnoměrně zrychené pohybu vaku a spňují rovnice = at,
Řešení úoh koa 49 ročníku fyzikání oympiády Kategorie D Autořiúoh:JJírů(,3,4,5,6,),TDenkstein(), a) Všechny uvažované časy jsou měřené od začátku rovnoměrně zrychené pohybu vaku a spňují rovnice = at,
6.1.4 Kontrakce délek
 6..4 Kontrake déek Předpokady: 603 Existuje na Zemi jev, na kterém je diatae času opravdu vidět? Př. :Částie mion má poočas rozpadu (doba, za kterou se rozpadne přibižně poovina části) 2,2µs. Vysvěti,
6..4 Kontrake déek Předpokady: 603 Existuje na Zemi jev, na kterém je diatae času opravdu vidět? Př. :Částie mion má poočas rozpadu (doba, za kterou se rozpadne přibižně poovina části) 2,2µs. Vysvěti,
3.9. Energie magnetického pole
 3.9. nergie agnetického poe 1. Uět odvodit energii agnetického poe cívky tak, aby bya vyjádřena poocí paraetrů obvodu (I a L).. Znát vztah pro energii agnetického poe cívky jako funkci veičin charakterizujících
3.9. nergie agnetického poe 1. Uět odvodit energii agnetického poe cívky tak, aby bya vyjádřena poocí paraetrů obvodu (I a L).. Znát vztah pro energii agnetického poe cívky jako funkci veičin charakterizujících
2.1 Stáčivost v závislosti na koncentraci opticky aktivní látky
 1 Pracovní úkoy 1. Změřte závisost stočení poarizační roviny na koncentraci vodního roztoku gukozy v rozmezí 0 500 g/. Pro jednu zvoenou koncentraci proveďte 5 měření úhu stočení poarizační roviny. Jednu
1 Pracovní úkoy 1. Změřte závisost stočení poarizační roviny na koncentraci vodního roztoku gukozy v rozmezí 0 500 g/. Pro jednu zvoenou koncentraci proveďte 5 měření úhu stočení poarizační roviny. Jednu
1.5. DYNAMIKA OTÁČIVÉHO A SLOŽENÉHO POHYBU TĚLESA
 .5. OTÁČIVÉHO A SLOŽENÉHO POHYBU TĚLESA.5. ZÁKLADNÍ ROVNICE DYNAMIKY PRO ROTAČNÍ POHYB Fz F Z výsednce zrychujících s F m.a n m a t a n r z F Zrychující moment M F. r F. r z z z m.a t r6,5cm ρ r ω,ε r
.5. OTÁČIVÉHO A SLOŽENÉHO POHYBU TĚLESA.5. ZÁKLADNÍ ROVNICE DYNAMIKY PRO ROTAČNÍ POHYB Fz F Z výsednce zrychujících s F m.a n m a t a n r z F Zrychující moment M F. r F. r z z z m.a t r6,5cm ρ r ω,ε r
UNIVERZITA PARDUBICE FAKULTA CHEMICKO-TECHNOLOGICKÁ. katedra fyziky ZÁKLADY FYZIKY II. Pro obory DMML, TŘD a AID prezenčního studia DFJP
 UNIVERZITA PARDUBICE FAKULTA CHEMICKO-TECHNOLOGICKÁ katedra fyziky ZÁKLADY FYZIKY II Pro obory DMML, TŘD a AID prezenčního studia DFJP RNDr Jan Z a j í c, CSc, 005 4 MAGNETICKÉ JEVY 4 NESTACIONÁRNÍ ELEKTROMAGNETICKÉ
UNIVERZITA PARDUBICE FAKULTA CHEMICKO-TECHNOLOGICKÁ katedra fyziky ZÁKLADY FYZIKY II Pro obory DMML, TŘD a AID prezenčního studia DFJP RNDr Jan Z a j í c, CSc, 005 4 MAGNETICKÉ JEVY 4 NESTACIONÁRNÍ ELEKTROMAGNETICKÉ
F7 MOMENT SETRVAČNOSTI
 F7 MOMENT ETRVAČNOTI Evropský sociání fond Praha & EU: Investujeme do vaší budoucnosti F7 MOMENT ETRVAČNOTI V této části si spočteme některé jednoduché příkady na rotační pohyby a seznámíme se s někoika
F7 MOMENT ETRVAČNOTI Evropský sociání fond Praha & EU: Investujeme do vaší budoucnosti F7 MOMENT ETRVAČNOTI V této části si spočteme některé jednoduché příkady na rotační pohyby a seznámíme se s někoika
PRAKTIKUM II. Oddělení fyzikálních praktik při Kabinetu výuky obecné fyziky MFF UK. úlohač.19 Název: Měření s torzním magnetometrem
 Odděení fyzikáních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM II. úohač.19 Název: Měření s torzním magnetometrem Pracova: Lukáš Ledvina stud.skup.14 dne:16.10.2009 Odevzdadne: Možný počet
Odděení fyzikáních praktik při Kabinetu výuky obecné fyziky MFF UK PRAKTIKUM II. úohač.19 Název: Měření s torzním magnetometrem Pracova: Lukáš Ledvina stud.skup.14 dne:16.10.2009 Odevzdadne: Možný počet
Přehled veličin elektrických obvodů
 Přehled veličin elektrických obvodů Ing. Martin Černík, Ph.D Projekt ESF CZ.1.7/2.2./28.5 Modernizace didaktických metod a inovace. Elektrický náboj - základní vlastnost některých elementárních částic
Přehled veličin elektrických obvodů Ing. Martin Černík, Ph.D Projekt ESF CZ.1.7/2.2./28.5 Modernizace didaktických metod a inovace. Elektrický náboj - základní vlastnost některých elementárních částic
STRUKTURA A VLASTNOSTI KAPALIN
 I N V E S T I C E D O O Z V O J E V Z D Ě L Á V Á N Í STUKTUA A VLASTNOSTI KAPALIN. Povrchové napětí a) yzikání jev Povrch kapain se chová jako napjatá pružná membrána (důkaz vodoměrka, maé kapičky koue)
I N V E S T I C E D O O Z V O J E V Z D Ě L Á V Á N Í STUKTUA A VLASTNOSTI KAPALIN. Povrchové napětí a) yzikání jev Povrch kapain se chová jako napjatá pružná membrána (důkaz vodoměrka, maé kapičky koue)
Přijímací zkouška na navazující magisterské studium 2015
 Přijímací zkouška na navazující magisterské studium 205 Studijní program: Studijní obory: Fyzika FFUM Varianta A Řešení příkladů pečlivě odůvodněte. Příklad (25 bodů) Pro funkci f(x) := e x 2. Určete definiční
Přijímací zkouška na navazující magisterské studium 205 Studijní program: Studijní obory: Fyzika FFUM Varianta A Řešení příkladů pečlivě odůvodněte. Příklad (25 bodů) Pro funkci f(x) := e x 2. Určete definiční
6.1.4 Kontrakce délek
 6..4 Kontrake déek Předpokady: 603 Existuje na Zemi jev, na kterém je diatae času opravdu vidět? Př. :Částie mion má poočas rozpadu (doba, za kterou se rozpadne přibižně poovina části) 2,2μs. Vysvěti,
6..4 Kontrake déek Předpokady: 603 Existuje na Zemi jev, na kterém je diatae času opravdu vidět? Př. :Částie mion má poočas rozpadu (doba, za kterou se rozpadne přibižně poovina části) 2,2μs. Vysvěti,
Elastické deformace těles
 Eastické eformace těes 15 Na oceový rát ék L 15 m a průměru 1 mm zavěsíme závaží o hmotnosti m 110 kg přičemž Youngův mou pružnosti ocei v tahu E 16 GPa a mez pružnosti ocei σ P 0 Pa Určete reativní prooužení
Eastické eformace těes 15 Na oceový rát ék L 15 m a průměru 1 mm zavěsíme závaží o hmotnosti m 110 kg přičemž Youngův mou pružnosti ocei v tahu E 16 GPa a mez pružnosti ocei σ P 0 Pa Určete reativní prooužení
6. Rozptyl Leoš Dvořák, MFF UK Praha, Rozptyl
 K přednášce NUFY8 Teoretická mechanika 6. Rozpty Leoš Dvořák, MFF UK Praha, 14 Rozpty Z předchozí kapitoy umíme spočítat pohyb částice v poi centrání síy. Nyní toho využijeme pro případ ehké částice (napříkad
K přednášce NUFY8 Teoretická mechanika 6. Rozpty Leoš Dvořák, MFF UK Praha, 14 Rozpty Z předchozí kapitoy umíme spočítat pohyb částice v poi centrání síy. Nyní toho využijeme pro případ ehké částice (napříkad
7 Gaussova věta 7 GAUSSOVA VĚTA. Použitím Gaussovy věty odvod te velikost vektorů elektrické indukce a elektrické intenzity pro
 7 Gaussova věta Zadání Použitím Gaussovy věty odvod te velikost vektorů elektrické indukce a elektrické intenzity pro následující nabitá tělesa:. rovnoměrně nabitou kouli s objemovou hustotou nábojeρ,
7 Gaussova věta Zadání Použitím Gaussovy věty odvod te velikost vektorů elektrické indukce a elektrické intenzity pro následující nabitá tělesa:. rovnoměrně nabitou kouli s objemovou hustotou nábojeρ,
Skalární a vektorový popis silového pole
 Skalární a vektorový popis silového pole Elektrické pole Elektrický náboj Q [Q] = C Vlastnost materiálových objektů Interakce (vzájemné silové působení) Interakci (vzájemné silové působení) mezi dvěma
Skalární a vektorový popis silového pole Elektrické pole Elektrický náboj Q [Q] = C Vlastnost materiálových objektů Interakce (vzájemné silové působení) Interakci (vzájemné silové působení) mezi dvěma
Kmitavý pohyb trochu jinak
 Kmitavý pohyb trochu jinak JIŘÍ ESAŘ, PER BAROŠ Katedra fyziky, Pedaoická fakuta, JU České Budějovice Kmitavý pohyb patří mezi zákadní fyzikání děje. Většinou se tato část fyziky redukuje na matematický
Kmitavý pohyb trochu jinak JIŘÍ ESAŘ, PER BAROŠ Katedra fyziky, Pedaoická fakuta, JU České Budějovice Kmitavý pohyb patří mezi zákadní fyzikání děje. Většinou se tato část fyziky redukuje na matematický
Inovace předmětů studijních programů strojního inženýrství v oblasti teplotního namáhání
 Grantový projekt FRVŠ MŠMT č.97/7/f/a Inovace předmětů studijních programů strojního inženýrství v obasti tepotního namáhání Některé apikace a ukázky konkrétních řešení tepeného namáhání těes. Autorky:
Grantový projekt FRVŠ MŠMT č.97/7/f/a Inovace předmětů studijních programů strojního inženýrství v obasti tepotního namáhání Některé apikace a ukázky konkrétních řešení tepeného namáhání těes. Autorky:
1. Stanovení modulu pružnosti v tahu přímou metodou
 . Stanovení moduu pružnost v tahu přímou metodou.. Zadání úohy. Určte modu pružnost v tahu přímou metodou pro dva vzorky různých materáů a výsedky porovnejte s tabukovým hodnotam.. Z naměřených hodnot
. Stanovení moduu pružnost v tahu přímou metodou.. Zadání úohy. Určte modu pružnost v tahu přímou metodou pro dva vzorky různých materáů a výsedky porovnejte s tabukovým hodnotam.. Z naměřených hodnot
Modelování kmitavých soustav s jedním stupněm volnosti
 Modeování kmitavých soustav s jedním stupněm vonosti Zpracova Doc. RNDr. Zdeněk Haváč, CSc 1. Zákadní mode Zákadním modeem kmitavé soustavy s jedním stupněm vonosti je tzv. diskrétní podéně kmitající mode,
Modeování kmitavých soustav s jedním stupněm vonosti Zpracova Doc. RNDr. Zdeněk Haváč, CSc 1. Zákadní mode Zákadním modeem kmitavé soustavy s jedním stupněm vonosti je tzv. diskrétní podéně kmitající mode,
GAUSSŮV ZÁKON ELEKTROSTATIKY
 GAUSSŮV ZÁKON ELEKTROSTATIKY PLOCHA JAKO VEKTOR Matematický doplněk n n Elementární plocha ΔS ds Ploše přiřadíme vektor, který 1) je k této ploše kolmý 2) má velikost rovnou velikosti (obsahu) plochy Δ
GAUSSŮV ZÁKON ELEKTROSTATIKY PLOCHA JAKO VEKTOR Matematický doplněk n n Elementární plocha ΔS ds Ploše přiřadíme vektor, který 1) je k této ploše kolmý 2) má velikost rovnou velikosti (obsahu) plochy Δ
3.1. Newtonovy zákony jsou základní zákony klasické (Newtonovy) mechaniky
 3. ZÁKLADY DYNAMIKY Dynamika zkoumá příčinné souvislosti pohybu a je tedy zdůvodněním zákonů kinematiky. K pojmům používaným v kinematice zavádí pojem hmoty a síly. Statický výpočet Dynamický výpočet -
3. ZÁKLADY DYNAMIKY Dynamika zkoumá příčinné souvislosti pohybu a je tedy zdůvodněním zákonů kinematiky. K pojmům používaným v kinematice zavádí pojem hmoty a síly. Statický výpočet Dynamický výpočet -
Řešení úloh 1. kola 49. ročníku fyzikální olympiády. Kategorie A
 Řešení úoh 1 koa 49 ročníku fyzikání oympiády Kategorie A Autořiúoh:JJírů(1),PŠedivý(,,4,5,7),BVybíra(6) 1a) Při vobě směrů proudů pode obrázku sestavíme pode Kirchhoffových zákonů rovnice: R U e1 = R
Řešení úoh 1 koa 49 ročníku fyzikání oympiády Kategorie A Autořiúoh:JJírů(1),PŠedivý(,,4,5,7),BVybíra(6) 1a) Při vobě směrů proudů pode obrázku sestavíme pode Kirchhoffových zákonů rovnice: R U e1 = R
Univerzita Tomáše Bati ve Zlíně, Fakulta technologická Ústav fyziky a materiálového inženýrství
 Univerzita Tomáše Bati ve Zíně, Fakuta technoogická Ústav fyziky a materiáového inženýrství Jméno a příjmení Josef Novák Ročník / Skupina x Předmět Laboratorní cvičení z předmětu Datum měření xx. xx. xxxx
Univerzita Tomáše Bati ve Zíně, Fakuta technoogická Ústav fyziky a materiáového inženýrství Jméno a příjmení Josef Novák Ročník / Skupina x Předmět Laboratorní cvičení z předmětu Datum měření xx. xx. xxxx
ČÁST V F Y Z I K Á L N Í P O L E. 18. Gravitační pole 19. Elektrostatické pole 20. Elektrický proud 21. Magnetické pole 22. Elektromagnetické pole
 Kde se nacházíme? ČÁST V F Y Z I K Á L N Í P O L E 18. Gravitační pole 19. Elektrostatické pole 20. Elektrický proud 21. Magnetické pole 22. Elektromagnetické pole Mapování elektrického pole -jak? Detektorem.Intenzita
Kde se nacházíme? ČÁST V F Y Z I K Á L N Í P O L E 18. Gravitační pole 19. Elektrostatické pole 20. Elektrický proud 21. Magnetické pole 22. Elektromagnetické pole Mapování elektrického pole -jak? Detektorem.Intenzita
R2.213 Tíhová síla působící na tělesa je mnohem větší než gravitační síla vzájemného přitahování těles.
 2.4 Gravitační pole R2.211 m 1 = m 2 = 10 g = 0,01 kg, r = 10 cm = 0,1 m, = 6,67 10 11 N m 2 kg 2 ; F g =? R2.212 F g = 4 mn = 0,004 N, a) r 1 = 2r; F g1 =?, b) r 2 = r/2; F g2 =?, c) r 3 = r/3; F g3 =?
2.4 Gravitační pole R2.211 m 1 = m 2 = 10 g = 0,01 kg, r = 10 cm = 0,1 m, = 6,67 10 11 N m 2 kg 2 ; F g =? R2.212 F g = 4 mn = 0,004 N, a) r 1 = 2r; F g1 =?, b) r 2 = r/2; F g2 =?, c) r 3 = r/3; F g3 =?
Řešení úloh 1. kola 59. ročníku fyzikální olympiády. Kategorie D Autor úloh: J. Jírů
 Řešení úo. koa 59. ročníku fyzikání oympiáy. Kategorie D Autor úoh: J. Jírů Obr. 1 1.a) Označme v veikost rychosti pavce vzheem k voě a v 0 veikost rychosti toku řeky. Pak patí Číseně vychází α = 38. b)
Řešení úo. koa 59. ročníku fyzikání oympiáy. Kategorie D Autor úoh: J. Jírů Obr. 1 1.a) Označme v veikost rychosti pavce vzheem k voě a v 0 veikost rychosti toku řeky. Pak patí Číseně vychází α = 38. b)
Příklad 3 (25 bodů) Jakou rychlost musí mít difrakčním úhlu 120? -částice, abychom pozorovali difrakční maximum od rovin d hkl = 0,82 Å na
 Přijímací zkouška z fyziky 01 - Nav. Mgr. - varianta A Příklad 1 (5 bodů) Koule o poloměru R=10 cm leží na vodorovné rovině. Z jejího nejvyššího bodu vypustíme s nulovou počáteční rychlostí bod o hmotností
Přijímací zkouška z fyziky 01 - Nav. Mgr. - varianta A Příklad 1 (5 bodů) Koule o poloměru R=10 cm leží na vodorovné rovině. Z jejího nejvyššího bodu vypustíme s nulovou počáteční rychlostí bod o hmotností
KLASICKÁ MECHANIKA. Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny.
 MECHANIKA 1 KLASICKÁ MECHANIKA Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny. Klasická mechanika rychlosti těles jsou mnohem menší než rychlost světla ve
MECHANIKA 1 KLASICKÁ MECHANIKA Předmětem mechaniky matematický popis mechanického pohybu v prostoru a v čase a jeho příčiny. Klasická mechanika rychlosti těles jsou mnohem menší než rychlost světla ve
Okruhy, pojmy a průvodce přípravou na semestrální zkoušku v otázkách. Mechanika
 1 Fyzika 1, bakaláři AFY1 BFY1 KFY1 ZS 08/09 Okruhy, pojmy a průvodce přípravou na semestrální zkoušku v otázkách Mechanika Při studiu části mechanika se zaměřte na zvládnutí následujících pojmů: Kartézská
1 Fyzika 1, bakaláři AFY1 BFY1 KFY1 ZS 08/09 Okruhy, pojmy a průvodce přípravou na semestrální zkoušku v otázkách Mechanika Při studiu části mechanika se zaměřte na zvládnutí následujících pojmů: Kartézská
Fyzika 1 - rámcové příklady Kinematika a dynamika hmotného bodu, gravitační pole
 Fyzika 1 - rámcové příklady Kinematika a dynamika hmotného bodu, gravitační pole 1. Určete skalární a vektorový součin dvou obecných vektorů AA a BB a popište, jak závisí výsledky těchto součinů na úhlu
Fyzika 1 - rámcové příklady Kinematika a dynamika hmotného bodu, gravitační pole 1. Určete skalární a vektorový součin dvou obecných vektorů AA a BB a popište, jak závisí výsledky těchto součinů na úhlu
plochy oddělí. Dále určete vzdálenost d mezi místem jeho dopadu na
 Přijímací zkouška z fyziky 01 - Nav. Mgr. - varianta A Příklad 1 (5 bodů) Koule o poloměru R=10 cm leží na vodorovné rovině. Z jejího nejvyššího bodu vypustíme s nulovou počáteční rychlostí bod o hmotností
Přijímací zkouška z fyziky 01 - Nav. Mgr. - varianta A Příklad 1 (5 bodů) Koule o poloměru R=10 cm leží na vodorovné rovině. Z jejího nejvyššího bodu vypustíme s nulovou počáteční rychlostí bod o hmotností
Gyrační poloměr jako invariant relativistického pohybu. 2 Nerovnoměrný pohyb po kružnici v R 2
 Gyrační poloměr jako invariant relativistického pohybu nabité částice v konfiguraci rovnoběžného konstantního vnějšího elektromagnetického pole 1 Popis problému Uvažujme pohyb nabité částice v E 3 v takové
Gyrační poloměr jako invariant relativistického pohybu nabité částice v konfiguraci rovnoběžného konstantního vnějšího elektromagnetického pole 1 Popis problému Uvažujme pohyb nabité částice v E 3 v takové
Normálové napětí a přetvoření prutu namáhaného tahem (prostým tlakem) - staticky určité úlohy
 Pružnost a pasticita, 2.ročník bakaářského studia ormáové napětí a přetvoření prutu namáhaného tahem (prostým takem) - staticky určité úohy Zákadní vztahy a předpokady řešení apětí a přetvoření osově namáhaného
Pružnost a pasticita, 2.ročník bakaářského studia ormáové napětí a přetvoření prutu namáhaného tahem (prostým takem) - staticky určité úohy Zákadní vztahy a předpokady řešení apětí a přetvoření osově namáhaného
Diferenciální geometrie křivek
 Diferenciání geometrie křivek Poární souřadnice Kartézské souřadnice Poární souřadnice. y y M r M f x x rcosf y r sin f, r r x x y y f arctan x 1 Spiráy Archimedova spiráa r af r ae Logaritmická spiráa
Diferenciání geometrie křivek Poární souřadnice Kartézské souřadnice Poární souřadnice. y y M r M f x x rcosf y r sin f, r r x x y y f arctan x 1 Spiráy Archimedova spiráa r af r ae Logaritmická spiráa
Projekty - Vybrané kapitoly z matematické fyziky
 Projekty - Vybrané kapitoly z matematické fyziky Klára Švarcová klara.svarcova@tiscali.cz 1 Obsah 1 Průlet tělesa skrz Zemi 3 1.1 Zadání................................. 3 1. Řešení.................................
Projekty - Vybrané kapitoly z matematické fyziky Klára Švarcová klara.svarcova@tiscali.cz 1 Obsah 1 Průlet tělesa skrz Zemi 3 1.1 Zadání................................. 3 1. Řešení.................................
Matematika I (KX001) Užití derivace v geometrii, ve fyzice 3. října f (x 0 ) (x x 0) Je-li f (x 0 ) = 0, tečna: x = 3, normála: y = 0
 Rovnice tečny a normály Geometrický význam derivace funkce f(x) v bodě x 0 : f (x 0 ) = k t k t je směrnice tečny v bodě [x 0, y 0 = f(x 0 )] Tečna je přímka t : y = k t x + q, tj y = f (x 0 ) x + q; pokud
Rovnice tečny a normály Geometrický význam derivace funkce f(x) v bodě x 0 : f (x 0 ) = k t k t je směrnice tečny v bodě [x 0, y 0 = f(x 0 )] Tečna je přímka t : y = k t x + q, tj y = f (x 0 ) x + q; pokud
b) Maximální velikost zrychlení automobilu, nemají-li kola prokluzovat, je a = f g. Automobil se bude rozjíždět po dobu t = v 0 fg = mfgv 0
 Řešení úloh. kola 58. ročníku fyzikální olympiády. Kategorie A Autoři úloh: J. Thomas, 5, 6, 7), J. Jírů 2,, 4).a) Napíšeme si pohybové rovnice, ze kterých vyjádříme dobu jízdy a zrychlení automobilu A:
Řešení úloh. kola 58. ročníku fyzikální olympiády. Kategorie A Autoři úloh: J. Thomas, 5, 6, 7), J. Jírů 2,, 4).a) Napíšeme si pohybové rovnice, ze kterých vyjádříme dobu jízdy a zrychlení automobilu A:
OTÁZKY Z TEORIE ELEKTROMAGNETICKÉHO POLE Letní semestr 2003/2004 poslední úprava 25. června 2004
 OTÁZKY Z TEORIE ELEKTROMAGNETICKÉHO POLE Letní semestr 2003/2004 posední úprava 25. června 2004 1. ía současně působící na eektrický náboj v eektrickém a magnetickém poi (Lorentzova sía) [ ] F m = Q E
OTÁZKY Z TEORIE ELEKTROMAGNETICKÉHO POLE Letní semestr 2003/2004 posední úprava 25. června 2004 1. ía současně působící na eektrický náboj v eektrickém a magnetickém poi (Lorentzova sía) [ ] F m = Q E
Řešení úloh celostátního kola 49. ročníku fyzikální olympiády. Autořiúloh:P.Šedivý(1),L.Richterek(2),I.Volf(3)aB.Vybíral(4)
 Řešení úoh ceostátního ko 49. ročníku fyzikání oympiády. Autořiúoh:.Šedivý(1),L.Richterek(),I.Vof(3)B.Vybír(4) 1.) Oznčme t 1, t, t 3čsyzábesků, v 1, v, v 3přísušnérychostistředukoue, veikost zrychení
Řešení úoh ceostátního ko 49. ročníku fyzikání oympiády. Autořiúoh:.Šedivý(1),L.Richterek(),I.Vof(3)B.Vybír(4) 1.) Oznčme t 1, t, t 3čsyzábesků, v 1, v, v 3přísušnérychostistředukoue, veikost zrychení
Obvody s rozprostřenými parametry
 Obvody s rozprostřenými parametry EO2 Přednáška 12 Pave Máša - Vedení s rozprostřenými parametry ÚVODEM Každá kroucená dvojinka UTP patch kabeu je samostaným vedením s rozprostřenými parametry Impedance
Obvody s rozprostřenými parametry EO2 Přednáška 12 Pave Máša - Vedení s rozprostřenými parametry ÚVODEM Každá kroucená dvojinka UTP patch kabeu je samostaným vedením s rozprostřenými parametry Impedance
Obsah. 2 Moment síly Dvojice sil Rozklad sil 4. 6 Rovnováha 5. 7 Kinetická energie tuhého tělesa 6. 8 Jednoduché stroje 8
 Obsah 1 Tuhé těleso 1 2 Moment síly 2 3 Skládání sil 3 3.1 Skládání dvou různoběžných sil................. 3 3.2 Skládání dvou rovnoběžných, různě velkých sil......... 3 3.3 Dvojice sil.............................
Obsah 1 Tuhé těleso 1 2 Moment síly 2 3 Skládání sil 3 3.1 Skládání dvou různoběžných sil................. 3 3.2 Skládání dvou rovnoběžných, různě velkých sil......... 3 3.3 Dvojice sil.............................
Elektřina a magnetismus úlohy na porozumění
 Elektřina a magnetismus úlohy na porozumění 1) Prázdná nenabitá plechovka je umístěna na izolační podložce. V jednu chvíli je do místa A na vnějším povrchu plechovky přivedeno malé množství náboje. Budeme-li
Elektřina a magnetismus úlohy na porozumění 1) Prázdná nenabitá plechovka je umístěna na izolační podložce. V jednu chvíli je do místa A na vnějším povrchu plechovky přivedeno malé množství náboje. Budeme-li
Řešení úloh 1. kola 54. ročníku fyzikální olympiády. Kategorie C. s=v 0 t 1 2 at2. (1)
 Řešení úoh 1. koa 54. ročníku fyzikání oympiády. Kategorie C Autořiúoh:J.Jírů(1),J.Thomas(,3,5),M.Jarešová(4,7),P.Šedivý(6). 1.a) Během brzdění roste dráha s časem pode vzorce s=v 0 t 1 at. (1) Zevzorcepyne
Řešení úoh 1. koa 54. ročníku fyzikání oympiády. Kategorie C Autořiúoh:J.Jírů(1),J.Thomas(,3,5),M.Jarešová(4,7),P.Šedivý(6). 1.a) Během brzdění roste dráha s časem pode vzorce s=v 0 t 1 at. (1) Zevzorcepyne
Analýza napjatosti PLASTICITA
 Analýza napjatosti PLASTICITA TENZOR NAPĚTÍ Teplota v daném bodě je skalár, je to tenzor nultého řádu, který nezávisí na změně souřadného systému Síla je vektor, je to tenzor prvního řádu, v trojrozměrném
Analýza napjatosti PLASTICITA TENZOR NAPĚTÍ Teplota v daném bodě je skalár, je to tenzor nultého řádu, který nezávisí na změně souřadného systému Síla je vektor, je to tenzor prvního řádu, v trojrozměrném
Obvodové prvky a jejich
 Obvodové prvky a jejich parametry Ing. Martin Černík, Ph.D. Projekt ESF CZ.1.07/2.2.00/28.0050 Modernizace didaktických metod a inovace. Elektrický obvod Uspořádaný systém elektrických prvků a vodičů sloužící
Obvodové prvky a jejich parametry Ing. Martin Černík, Ph.D. Projekt ESF CZ.1.07/2.2.00/28.0050 Modernizace didaktických metod a inovace. Elektrický obvod Uspořádaný systém elektrických prvků a vodičů sloužící
7. Gravitační pole a pohyb těles v něm
 7. Gravitační pole a pohyb těles v něm Gravitační pole - existuje v okolí každého hmotného tělesa - představuje formu hmoty - zprostředkovává vzájemné silové působení mezi tělesy Newtonův gravitační zákon:
7. Gravitační pole a pohyb těles v něm Gravitační pole - existuje v okolí každého hmotného tělesa - představuje formu hmoty - zprostředkovává vzájemné silové působení mezi tělesy Newtonův gravitační zákon:
1. Náhodný vektor (X, Y ) má diskrétní rozdělení s pravděpodobnostní funkcí p, kde. p(x, y) = a(x + y + 1), x, y {0, 1, 2}.
 VIII. Náhodný vektor. Náhodný vektor (X, Y má diskrétní rozdělení s pravděpodobnostní funkcí p, kde p(x, y a(x + y +, x, y {,, }. a Určete číslo a a napište tabulku pravděpodobnostní funkce p. Řešení:
VIII. Náhodný vektor. Náhodný vektor (X, Y má diskrétní rozdělení s pravděpodobnostní funkcí p, kde p(x, y a(x + y +, x, y {,, }. a Určete číslo a a napište tabulku pravděpodobnostní funkce p. Řešení:
Derivace goniometrických funkcí
 Derivace goniometrických funkcí Shrnutí Jakub Michálek, Tomáš Kučera Odvodí se základní vztahy pro derivace funkcí sinus a cosinus za pomoci věty o třech itách, odvodí se také několik typických it pomocí
Derivace goniometrických funkcí Shrnutí Jakub Michálek, Tomáš Kučera Odvodí se základní vztahy pro derivace funkcí sinus a cosinus za pomoci věty o třech itách, odvodí se také několik typických it pomocí
Fyzikální korespondenční seminář UK MFF 10. II. 2
 10. ročník, úoha II. 2... magnetické kyvado (5 bodů; průměr?; řešio 60 studentů) V homogenním tíhovém poi (tíhové zrychení g = 9,81 m s 2 ) je na závěsu zanedbatené hmotnosti déky = 1,00 m umístěna maá
10. ročník, úoha II. 2... magnetické kyvado (5 bodů; průměr?; řešio 60 studentů) V homogenním tíhovém poi (tíhové zrychení g = 9,81 m s 2 ) je na závěsu zanedbatené hmotnosti déky = 1,00 m umístěna maá
Extrémy funkce dvou proměnných
 Extrémy funkce dvou proměnných 1. Stanovte rozměry pravoúhlé vodní nádrže o objemu 32 m 3 tak, aby dno a stěny měly nejmenší povrch. Označme rozměry pravoúhlé nádrže x, y, z (viz obr.). ak objem této nádrže
Extrémy funkce dvou proměnných 1. Stanovte rozměry pravoúhlé vodní nádrže o objemu 32 m 3 tak, aby dno a stěny měly nejmenší povrch. Označme rozměry pravoúhlé nádrže x, y, z (viz obr.). ak objem této nádrže
STACIONÁRNÍ MAGNETICKÉ POLE. Mgr. Jan Ptáčník - GJVJ - Fyzika - Elektřina a magnetismus - 3. ročník
 STACIONÁRNÍ MAGNETICKÉ POLE Mgr. Jan Ptáčník - GJVJ - Fyzika - Elektřina a magnetismus - 3. ročník Magnetické pole Vytváří se okolo trvalého magnetu. Magnetické pole vodiče Na základě experimentů bylo
STACIONÁRNÍ MAGNETICKÉ POLE Mgr. Jan Ptáčník - GJVJ - Fyzika - Elektřina a magnetismus - 3. ročník Magnetické pole Vytváří se okolo trvalého magnetu. Magnetické pole vodiče Na základě experimentů bylo
Linearní teplotní gradient
 Poznámky k semináři z předmětu Pružnost pevnost na K68 D ČVUT v Praze (pracovní verze). Tento materiá má pouze pracovní charakter a ude v průěhu semestru postupně dopňován. utor: Jan Vyčich E mai: vycich@fd.cvut.cz
Poznámky k semináři z předmětu Pružnost pevnost na K68 D ČVUT v Praze (pracovní verze). Tento materiá má pouze pracovní charakter a ude v průěhu semestru postupně dopňován. utor: Jan Vyčich E mai: vycich@fd.cvut.cz
Příklad 33 : Energie elektrického pole deskového kondenzátoru. Ověření vztahu mezi energií, kapacitou a veličinami pole.
 Přík 33 : Energie eektrického poe eskového konenzátoru. Ověření vzthu mezi energií, kpcitou veičinmi poe. Přepokáné znosti: Eektrické poe kpcit eskového konenzátoru Přík V eskovém konenzátoru je eektrické
Přík 33 : Energie eektrického poe eskového konenzátoru. Ověření vzthu mezi energií, kpcitou veičinmi poe. Přepokáné znosti: Eektrické poe kpcit eskového konenzátoru Přík V eskovém konenzátoru je eektrické
12 DYNAMIKA SOUSTAVY HMOTNÝCH BODŮ
 56 12 DYNAMIKA SOUSTAVY HMOTNÝCH BODŮ Těžiště I. impulsová věta - věta o pohybu těžiště II. impulsová věta Zákony zachování v izolované soustavě hmotných bodů Náhrada pohybu skutečných objektů pohybem
56 12 DYNAMIKA SOUSTAVY HMOTNÝCH BODŮ Těžiště I. impulsová věta - věta o pohybu těžiště II. impulsová věta Zákony zachování v izolované soustavě hmotných bodů Náhrada pohybu skutečných objektů pohybem
ELEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Posuvný proud a Poyntingův vektor
 ELEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Posuvný proud a Poyntingův vektor Peter Dourmashkin MIT 006, překlad: Jan Pacák (007) Obsah 10. POSUVNÝ PROUD A POYNTINGŮV VEKTOR 3 10.1 ÚKOLY 3 10. POSUVNÝ
ELEKTŘINA A MAGNETIZMUS Řešené úlohy a postupy: Posuvný proud a Poyntingův vektor Peter Dourmashkin MIT 006, překlad: Jan Pacák (007) Obsah 10. POSUVNÝ PROUD A POYNTINGŮV VEKTOR 3 10.1 ÚKOLY 3 10. POSUVNÝ
c) vysvětlení jednotlivých veličin ve vztahu pro okamžitou výchylku, jejich jednotky
 Harmonický kmitavý pohyb a) vysvětlení harmonického kmitavého pohybu b) zápis vztahu pro okamžitou výchylku c) vysvětlení jednotlivých veličin ve vztahu pro okamžitou výchylku, jejich jednotky d) perioda
Harmonický kmitavý pohyb a) vysvětlení harmonického kmitavého pohybu b) zápis vztahu pro okamžitou výchylku c) vysvětlení jednotlivých veličin ve vztahu pro okamžitou výchylku, jejich jednotky d) perioda
4. V jednom krychlovém metru (1 m 3 ) plynu je 2, molekul. Ve dvou krychlových milimetrech (2 mm 3 ) plynu je molekul
 Fyzika 20 Otázky za 2 body. Celsiova teplota t a termodynamická teplota T spolu souvisejí známým vztahem. Vyberte dvojici, která tento vztah vyjadřuje (zaokrouhleno na celá čísla) a) T = 253 K ; t = 20
Fyzika 20 Otázky za 2 body. Celsiova teplota t a termodynamická teplota T spolu souvisejí známým vztahem. Vyberte dvojici, která tento vztah vyjadřuje (zaokrouhleno na celá čísla) a) T = 253 K ; t = 20
Hlavní body. Teplotní závislosti fyzikálních veličin. Teplota, měření
 e r i k a Havní body epota, ěření epotní závisosti fyzikáních veičin Kinetická teorie pynů Maxweova rozděovací funkce epo, ěrné tepo, kaorietrie epota Je zákadní veičinou, kterou neze odvodit? Čověk ji
e r i k a Havní body epota, ěření epotní závisosti fyzikáních veičin Kinetická teorie pynů Maxweova rozděovací funkce epo, ěrné tepo, kaorietrie epota Je zákadní veičinou, kterou neze odvodit? Čověk ji
Theory Česky (Czech Republic)
 Q3-1 Velký hadronový urychlovač (10 bodů) Než se do toho pustíte, přečtěte si prosím obecné pokyny v oddělené obálce. V této úloze se budeme bavit o fyzice částicového urychlovače LHC (Large Hadron Collider
Q3-1 Velký hadronový urychlovač (10 bodů) Než se do toho pustíte, přečtěte si prosím obecné pokyny v oddělené obálce. V této úloze se budeme bavit o fyzice částicového urychlovače LHC (Large Hadron Collider
Téma 1: Elektrostatika I - Elektrický náboj Kapitola 22, str. 577 592
 Téma 1: Elektrostatika I - Elektrický náboj Kapitola 22, str. 577 592 Shrnutí: Náboj a síla = Coulombova síla: - Síla jíž na sebe náboje Q působí je stejná - Pozn.: hledám-li velikost, tak jen dosadím,
Téma 1: Elektrostatika I - Elektrický náboj Kapitola 22, str. 577 592 Shrnutí: Náboj a síla = Coulombova síla: - Síla jíž na sebe náboje Q působí je stejná - Pozn.: hledám-li velikost, tak jen dosadím,
FYZIKA I. Rovnoměrný, rovnoměrně zrychlený a nerovnoměrně zrychlený rotační pohyb
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ FYZIKA I Rovnoměrný, rovnoměrně zrychlený a nerovnoměrně zrychlený rotační pohyb Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D.
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ FYZIKA I Rovnoměrný, rovnoměrně zrychlený a nerovnoměrně zrychlený rotační pohyb Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D.
FYZIKA II. Petr Praus 7. Přednáška stacionární magnetické pole náboj v magnetickém poli
 FYZIKA II Petr Praus 7. Přednáška stacionární magnetické pole náboj v magnetickém poli Osnova přednášky Stacionární magnetické pole Lorentzova síla Hallův jev Pohyb a urychlování nabitých částic (cyklotron,
FYZIKA II Petr Praus 7. Přednáška stacionární magnetické pole náboj v magnetickém poli Osnova přednášky Stacionární magnetické pole Lorentzova síla Hallův jev Pohyb a urychlování nabitých částic (cyklotron,
FYZIKA I. Kyvadlový pohyb. Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D. Doc. Ing. Irena Hlaváčová, Ph.D. Mgr. Art.
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STRONÍ FYZIKA I Kyvadový pohyb Prof. RNDr. Viém Mádr, CSc. Prof. Ing. Libor Haváč, Ph.D. Doc. Ing. Irena Haváčová, Ph.D. Mgr. Art. Dagmar Mádrová
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STRONÍ FYZIKA I Kyvadový pohyb Prof. RNDr. Viém Mádr, CSc. Prof. Ing. Libor Haváč, Ph.D. Doc. Ing. Irena Haváčová, Ph.D. Mgr. Art. Dagmar Mádrová
Stacionární magnetické pole. Kolem trvalého magnetu existuje magnetické pole.
 Magnetické pole Stacionární magnetické pole Kolem trvalého magnetu existuje magnetické pole. Stacionární magnetické pole Pilinový obrazec magnetického pole tyčového magnetu Stacionární magnetické pole
Magnetické pole Stacionární magnetické pole Kolem trvalého magnetu existuje magnetické pole. Stacionární magnetické pole Pilinový obrazec magnetického pole tyčového magnetu Stacionární magnetické pole
1. Cvičení: Opakování derivace a integrály
 . Cvičení: Opakování derivace a integrál Derivace Příklad: Určete derivace následujících funkcí. f() e 5 ( 5 cos + sin ) f () 5e 5 ( 5 cos + sin ) + e 5 (5 sin + cos ) e 5 cos + 65e 5 sin. f() + ( + )
. Cvičení: Opakování derivace a integrál Derivace Příklad: Určete derivace následujících funkcí. f() e 5 ( 5 cos + sin ) f () 5e 5 ( 5 cos + sin ) + e 5 (5 sin + cos ) e 5 cos + 65e 5 sin. f() + ( + )
Vyřešením pohybových rovnic s těmito počátečními podmínkami dostáváme trajektorii. x = v 0 t cos α (1) y = h + v 0 t sin α 1 2 gt2 (2)
 Test a. Lučištník vystřelil z hradby vysoké 40 m šíp o hmotnosti 50 g rychlostí 60 m s pod úhlem 5 vzhůru vzhledem k vodorovnému směru. (a V jaké vzdálenosti od hradeb se šíp zabodl do země? (b Jaký úhel
Test a. Lučištník vystřelil z hradby vysoké 40 m šíp o hmotnosti 50 g rychlostí 60 m s pod úhlem 5 vzhůru vzhledem k vodorovnému směru. (a V jaké vzdálenosti od hradeb se šíp zabodl do země? (b Jaký úhel
Příklad 5.3. v 1. u 1 u 2. v 2
 Příklad 5.3 Zadání: Elektron o kinetické energii E se srazí s valenčním elektronem argonu a ionizuje jej. Při ionizaci se část energie nalétávajícího elektronu spotřebuje na uvolnění valenčního elektronu
Příklad 5.3 Zadání: Elektron o kinetické energii E se srazí s valenčním elektronem argonu a ionizuje jej. Při ionizaci se část energie nalétávajícího elektronu spotřebuje na uvolnění valenčního elektronu
Relativistická kinematika
 Relativistická kinematika 1 Formalismus čtyřhybnosti Pro řešení relativistických kinematických úloh lze často s výhodou použít formalismus čtyřhybnosti. Čtyřhybnost je čtyřvektor, který v sobě zahrnuje
Relativistická kinematika 1 Formalismus čtyřhybnosti Pro řešení relativistických kinematických úloh lze často s výhodou použít formalismus čtyřhybnosti. Čtyřhybnost je čtyřvektor, který v sobě zahrnuje
Necht na hmotný bod působí pouze pružinová síla F 1 = ky, k > 0. Podle druhého Newtonova zákona je pohyb bodu popsán diferenciální rovnicí
 Počáteční problémy pro ODR2 1 Lineární oscilátor. Počáteční problémy pro ODR2 Uvažujme hmotný bod o hmotnosti m, na který působí síly F 1, F 2, F 3. Síla F 1 je přitom úměrná výchylce y z rovnovážné polohy
Počáteční problémy pro ODR2 1 Lineární oscilátor. Počáteční problémy pro ODR2 Uvažujme hmotný bod o hmotnosti m, na který působí síly F 1, F 2, F 3. Síla F 1 je přitom úměrná výchylce y z rovnovážné polohy
Hlavní body - elektromagnetismus
 Elektromagnetismus Hlavní body - elektromagnetismus Lorenzova síla, hmotový spektrograf, Hallův jev Magnetická síla na proudovodič Mechanický moment na proudovou smyčku Faradayův zákon elektromagnetické
Elektromagnetismus Hlavní body - elektromagnetismus Lorenzova síla, hmotový spektrograf, Hallův jev Magnetická síla na proudovodič Mechanický moment na proudovou smyčku Faradayův zákon elektromagnetické
Příklady Kosmické záření
 Příklady Kosmické záření Kosmické částice 1. Jakou kinetickou energii získá proton při pádu z nekonečné výšky na Zem? Poloměr Zeměje R Z =637810 3 maklidováenergieprotonuje m p c 2 =938.3MeV. 2. Kosmickékvantum
Příklady Kosmické záření Kosmické částice 1. Jakou kinetickou energii získá proton při pádu z nekonečné výšky na Zem? Poloměr Zeměje R Z =637810 3 maklidováenergieprotonuje m p c 2 =938.3MeV. 2. Kosmickékvantum
Stav napjatosti materiálu.
 tav napjatosti materiáu. Zákad mechanik, 9. přednáška Obsah přednášk : jednoosý a dvojosý stav napjatosti, stav napjatosti ohýbaného nosníku, deformace ohýbaného nosníku, řešení statick neurčitých úoh
tav napjatosti materiáu. Zákad mechanik, 9. přednáška Obsah přednášk : jednoosý a dvojosý stav napjatosti, stav napjatosti ohýbaného nosníku, deformace ohýbaného nosníku, řešení statick neurčitých úoh
CVIČNÝ TEST 5. OBSAH I. Cvičný test 2. Mgr. Václav Zemek. II. Autorské řešení 6 III. Klíč 17 IV. Záznamový list 19
 CVIČNÝ TEST 5 Mgr. Václav Zemek OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 17 IV. Záznamový list 19 I. CVIČNÝ TEST 1 Zjednodušte výraz (2x 5) 2 (2x 5) (2x + 5) + 20x. 2 Určete nejmenší trojciferné
CVIČNÝ TEST 5 Mgr. Václav Zemek OBSAH I. Cvičný test 2 II. Autorské řešení 6 III. Klíč 17 IV. Záznamový list 19 I. CVIČNÝ TEST 1 Zjednodušte výraz (2x 5) 2 (2x 5) (2x + 5) + 20x. 2 Určete nejmenší trojciferné
Přijímací zkouška na navazující magisterské studium Studijní program Fyzika obor Učitelství fyziky matematiky pro střední školy
 Přijímací zkouška na navazující magisterské studium 013 Studijní program Fyzika obor Učitelství fyziky matematiky pro střední školy Studijní program Učitelství pro základní školy - obor Učitelství fyziky
Přijímací zkouška na navazující magisterské studium 013 Studijní program Fyzika obor Učitelství fyziky matematiky pro střední školy Studijní program Učitelství pro základní školy - obor Učitelství fyziky
Vzájemné silové působení
 magnet, magnetka magnet zmagnetované těleso. Původně vyrobeno z horniny magnetit, která má sama magnetické vlastnosti dnes ocelové zmagnetované magnety, ferity, neodymové magnety. dva magnetické póly (S-J,
magnet, magnetka magnet zmagnetované těleso. Původně vyrobeno z horniny magnetit, která má sama magnetické vlastnosti dnes ocelové zmagnetované magnety, ferity, neodymové magnety. dva magnetické póly (S-J,
Předmět: Ročník: Vytvořil: Datum: ŠČERBOVÁ M. PAVELKA V. NAMÁHÁNÍ NA OHYB A) NOSNÍKY NA DVOU PODPORÁCH ZATÍŽENÉ SOUSTAVOU ROVNOBĚŽNÝCH SIL
 Předmět: Ročník: Vytvoři: Datum: MECHANIKA DRUHÝ ŠČERBOVÁ M. PAVELKA V. 9. ČERVNA 2013 Název zpracovaného ceku: NAMÁHÁNÍ NA OHYB A) NOSNÍKY NA DVOU PODPORÁCH ZATÍŽENÉ SOUSTAVOU ROVNOBĚŽNÝCH SIL ÚLOHA 1
Předmět: Ročník: Vytvoři: Datum: MECHANIKA DRUHÝ ŠČERBOVÁ M. PAVELKA V. 9. ČERVNA 2013 Název zpracovaného ceku: NAMÁHÁNÍ NA OHYB A) NOSNÍKY NA DVOU PODPORÁCH ZATÍŽENÉ SOUSTAVOU ROVNOBĚŽNÝCH SIL ÚLOHA 1
Mezony π, mezony K, mezony η, η, bosony 1
 Mezony π, mezony K, mezony η, η, bosony 1 Mezony π, (piony) a) Nabité piony hmotnost, rozpady, doba života, spin, parita, nezachování parity v jejich rozpadech b) Neutrální piony hmotnost, rozpady, doba
Mezony π, mezony K, mezony η, η, bosony 1 Mezony π, (piony) a) Nabité piony hmotnost, rozpady, doba života, spin, parita, nezachování parity v jejich rozpadech b) Neutrální piony hmotnost, rozpady, doba
Dvojné a trojné integrály příklad 3. x 2 y dx dy,
 Spočtěte = { x, y) ; 4x + y 4 }. Dvojné a trojné integrály příklad 3 x y dx dy, Řešení: Protože obor integrace je symetrický vzhledem k ose x, tj. vzhledem k substituci [x; y] [x; y], a funkce fx, y) je
Spočtěte = { x, y) ; 4x + y 4 }. Dvojné a trojné integrály příklad 3 x y dx dy, Řešení: Protože obor integrace je symetrický vzhledem k ose x, tj. vzhledem k substituci [x; y] [x; y], a funkce fx, y) je
Téma 4 Výpočet přímého nosníku
 Stavební statika, 1.ročník bakaářského studia Téma 4 Výpočet přímého nosníku Výpočet nosníku v osové úoze Výpočet nosníku v příčné úoze ve svisé a vodorovné havní rovině Výpočet nosníku v krutové úoze
Stavební statika, 1.ročník bakaářského studia Téma 4 Výpočet přímého nosníku Výpočet nosníku v osové úoze Výpočet nosníku v příčné úoze ve svisé a vodorovné havní rovině Výpočet nosníku v krutové úoze
Příklady pro předmět Aplikovaná matematika (AMA) část 1
 Příklady pro předmět plikovaná matematika (M) část 1 1. Lokální extrémy funkcí dvou a tří proměnných Nalezněte lokální extrémy funkcí: (a) f 1 : f 1 (x, y) = x 3 3x + y 2 + 2y (b) f 2 : f 2 (x, y) = 1
Příklady pro předmět plikovaná matematika (M) část 1 1. Lokální extrémy funkcí dvou a tří proměnných Nalezněte lokální extrémy funkcí: (a) f 1 : f 1 (x, y) = x 3 3x + y 2 + 2y (b) f 2 : f 2 (x, y) = 1
ELT1 - Přednáška č. 6
 ELT1 - Přednáška č. 6 Elektrotechnická terminologie a odborné výrazy, měřicí jednotky a činitelé, které je ovlivňují. Rozdíl potenciálů, elektromotorická síla, napětí, el. napětí, proud, odpor, vodivost,
ELT1 - Přednáška č. 6 Elektrotechnická terminologie a odborné výrazy, měřicí jednotky a činitelé, které je ovlivňují. Rozdíl potenciálů, elektromotorická síla, napětí, el. napětí, proud, odpor, vodivost,
Parametrické rovnice křivky
 Křivkový integrál Robert Mařík jaro 2014 Tento text je tištěnou verzí prezentací dostupných z http://user.mendelu.cz/marik/am. Křivkový integrál Jedná se o rozšíření Riemannova integrálu, kdy množinou
Křivkový integrál Robert Mařík jaro 2014 Tento text je tištěnou verzí prezentací dostupných z http://user.mendelu.cz/marik/am. Křivkový integrál Jedná se o rozšíření Riemannova integrálu, kdy množinou
Kinetická teorie ideálního plynu
 Přednáška 10 Kinetická teorie ideálního plynu 10.1 Postuláty kinetické teorie Narozdíl od termodynamiky kinetická teorie odvozuje makroskopické vlastnosti látek (např. tlak, teplotu, vnitřní energii) na
Přednáška 10 Kinetická teorie ideálního plynu 10.1 Postuláty kinetické teorie Narozdíl od termodynamiky kinetická teorie odvozuje makroskopické vlastnosti látek (např. tlak, teplotu, vnitřní energii) na
Přednáška 12 Obecná deformační metoda, nelineární úlohy u prutových soustav
 Statika stavebních konstrukcí II., 3.ročník bakaářského studia Přednáška Obecná deformační metoda, neineární úohy u prutových soustav Fyzikáně neineární úoha Geometricky neineární úoha Konstrukčně neineární
Statika stavebních konstrukcí II., 3.ročník bakaářského studia Přednáška Obecná deformační metoda, neineární úohy u prutových soustav Fyzikáně neineární úoha Geometricky neineární úoha Konstrukčně neineární
3.1 Magnetické pole ve vakuu a v látkovén prostředí
 3. MAGNETSMUS 3.1 Magnetické pole ve vakuu a v látkovén prostředí 3.1.1 Určete magnetickou indukci a intenzitu magnetického pole ve vzdálenosti a = 5 cm od velmi dlouhého přímého vodiče, jestliže jím protéká
3. MAGNETSMUS 3.1 Magnetické pole ve vakuu a v látkovén prostředí 3.1.1 Určete magnetickou indukci a intenzitu magnetického pole ve vzdálenosti a = 5 cm od velmi dlouhého přímého vodiče, jestliže jím protéká
Základní pasivní a aktivní obvodové prvky
 OBSAH Strana 1 / 21 Přednáška č. 2: Základní pasivní a aktivní obvodové prvky Obsah 1 Klasifikace obvodových prvků 2 2 Rezistor o odporu R 4 3 Induktor o indukčnosti L 8 5 Nezávislý zdroj napětí u 16 6
OBSAH Strana 1 / 21 Přednáška č. 2: Základní pasivní a aktivní obvodové prvky Obsah 1 Klasifikace obvodových prvků 2 2 Rezistor o odporu R 4 3 Induktor o indukčnosti L 8 5 Nezávislý zdroj napětí u 16 6
Graf závislosti dráhy s na počtu kyvů n 2 pro h = 0,2 m. Graf závislosti dráhy s na počtu kyvů n 2 pro h = 0,3 m
 Řešení úloh 1. kola 59. ročníku fyzikální olympiády. Kategorie B Autoři úloh: J. Thomas (1,, 3, 4, 7), J. Jírů (5), P. Šedivý (6) 1.a) Je-li pohyb kuličky rovnoměrně zrychlený, bude pro uraženou dráhu
Řešení úloh 1. kola 59. ročníku fyzikální olympiády. Kategorie B Autoři úloh: J. Thomas (1,, 3, 4, 7), J. Jírů (5), P. Šedivý (6) 1.a) Je-li pohyb kuličky rovnoměrně zrychlený, bude pro uraženou dráhu
(1 + v ) (5 bodů) Pozor! Je nutné si uvědomit, že v a f mají opačný směr! Síla působí proti pohybu.
 Přijímací zkouška na navazující magisterské studium - 017 Studijní program Fyzika - všechny obory kromě Učitelství fyziky-matematiky pro střední školy, Varianta A Příklad 1 (5 bodů) Těleso s hmotností
Přijímací zkouška na navazující magisterské studium - 017 Studijní program Fyzika - všechny obory kromě Učitelství fyziky-matematiky pro střední školy, Varianta A Příklad 1 (5 bodů) Těleso s hmotností
Řešení úloh celostátního kola 59. ročníku fyzikální olympiády. Úlohy navrhl J. Thomas
 Řešení úlo celostátnío kola 59. ročníku fyzikální olympiády Úloy navrl J. Tomas 1.a) Rovnice rozpadu je 38 94Pu 4 He + 34 9U; Q E r [ m 38 94Pu ) m 4 He ) m 34 9U )] c 9,17 1 13 J 5,71 MeV. body b) K dosažení
Řešení úlo celostátnío kola 59. ročníku fyzikální olympiády Úloy navrl J. Tomas 1.a) Rovnice rozpadu je 38 94Pu 4 He + 34 9U; Q E r [ m 38 94Pu ) m 4 He ) m 34 9U )] c 9,17 1 13 J 5,71 MeV. body b) K dosažení
Základní otázky pro teoretickou část zkoušky.
 Základní otázky pro teoretickou část zkoušky. Platí shodně pro prezenční i kombinovanou formu studia. 1. Síla současně působící na elektrický náboj v elektrickém a magnetickém poli (Lorentzova síla) 2.
Základní otázky pro teoretickou část zkoušky. Platí shodně pro prezenční i kombinovanou formu studia. 1. Síla současně působící na elektrický náboj v elektrickém a magnetickém poli (Lorentzova síla) 2.
Fyzika II, FMMI. 1. Elektrostatické pole
 Fyzika II, FMMI 1. Elektrostatické pole 1.1 Jaká je velikost celkového náboje (kladného i záporného), který je obsažen v 5 kg železa? Předpokládejme, že by se tento náboj rovnoměrně rozmístil do dvou malých
Fyzika II, FMMI 1. Elektrostatické pole 1.1 Jaká je velikost celkového náboje (kladného i záporného), který je obsažen v 5 kg železa? Předpokládejme, že by se tento náboj rovnoměrně rozmístil do dvou malých
Řešení: Nejdříve musíme určit sílu, kterou působí kladka proti směru pohybu padajícího vědra a napíná tak lano. Moment síly otáčení kladky je:
 Přijímací zkouška na navazující magisterské studium - 16 Studijní program Fyzika - všechny obory kromě Učitelství fyziky-matematiky pro střední školy, Varianta A Příklad 1 (5 bodů) Jak dlouho bude padat
Přijímací zkouška na navazující magisterské studium - 16 Studijní program Fyzika - všechny obory kromě Učitelství fyziky-matematiky pro střední školy, Varianta A Příklad 1 (5 bodů) Jak dlouho bude padat
