Mechanika kontinua poddajných těles
|
|
|
- Milada Soukupová
- před 6 lety
- Počet zobrazení:
Transkript
1 I. ÚVOD Mechanka kontnua poddajných těles Mechanka kontnua je založena na objevných pracích Newtona, Eulera, Lagrangea a především Cauchyho. Aplkace počítačů umožnla řešt složté nelneární úlohy mechanky, které zace zpětně vyžadovaly hlubší teoretcké základy. Proto se v současné době pokračuje v ntenzvním bádání hledají se vztahy a závslost použtelné př formulac úloh s vysokým rychlostm zatěžování, vazby mez různým typy deformací a odpovídajcím růžně defnovaným napětím a pod. Mechanka kontnua je část mechanky, která se zabývá pohybem, deformací a napětí v těles a tekutnách. Pojem kontnuum je třeba chápat jako jeden z možných modelů hmoty a uvědomovat s přtom, že kontnuta spojtost prostředí je vlastně luze, která je v rozporu se skutečnou korpuskulární strukturou okolního světa. Předpokládá, že sledování prostředí je spojté. Má se zato, že všechny sledování vlastnost materálů obsaženého uvntř vytčeného nfntesmálního elementu jsou popsány spojtým funkcem prostorových souřadnc a navíc jsou stejné jako ty, které se dají expermentální zjstt u vzorků konečných velkos. Model kontnua, přjatý pro řešení určté třídy úloh, bude dávat správně výsledky pouze tehdy. Bude-l použt v rámc oboru své platnost. To však nelze matematcky dokázat. Jedným krterem je experment. Pokud výsledky expermentu nejsou v rozporu s tím, co model předpovídá, považuje se model za dobrý. Matematcký pops nelneárních dějů je složtý a pro úsporný a efektvní záps vyžaduje použtí tenzorového vyjádření vztahů. Proto jsou dále uvedeny stručné základy tenzorového a matcového počtu. II. NELINEÁRNÍ MECHANIKY KONTINUA. Skalár, vektor a tenzor [, ] Skaláry (tenzor nultého řádu) jsou jednoznačně určeny svým hodnotam a nezávsejí na souřadném systému. Příkladem skláru je teplota, hmotnost, hustota, apod. Vektory (tenzor prvního řádu) jsou určeny velkostí a směrem. Označují se polotučným stojatým písmeny, nebo kuznou ve složených závorkách ( v,v,v!, { v} ). Symbolem {v} označujeme sloupcový vektor. Operace s vektory Skalární součn je defnován vztahem n T T T T (.) = s = a b = ab = {}{} a b = {}{} a b = {}{} b a = {}{} b a Vektorový součn je defnován vztahem!!! j k c 0 a a!!! c= a b= a a a ; c a 0 a = ; c e a b = b b b c a a 0 jk j k (.)
2 Tenzory jsou velčny defnované transformačním vlastnostm. Kartézský tenzor.řádu je vektor se složkam a =α ja j ; a =α pa p (.)!!!!! kde α j = e.e j = cos( x,x j ),,j=,, jsou směrové kosny. e,e,e jsou jednotkové vektory souřadného systému x, x, x (obr.). x x x! P x e! O e! e! x x x Obr. Kartézský tenzor.řádu je určen se složkam a =α α a, a j p jq pq =α α a j p qj pq (.4) Symetrcký a antsymetrcký tenzor Operace s tenzory Násobení tenzorů j k kj T aj = aj T aj = aj [ ] [ ][ ] c = a b C=A B C = A B (.5) Skalární součn tenzorů vztahem s = A:B= tr n T ( ) j j j j = j= A B, kde operátor tr značí stopu. Tato operace je defnována n s= a b = a b (.6)
3 Invaranty tenzorů V mechance se př transformac souřadnc a určování hlavních hodnot tenzorů (jen dagonální prvky) setkáváme s koefcenty kubcké rovnce pro hlavní hodnoty tenzoru, které jsou nvarantam. Jsou tř I = a, I = aakk aka kj, (.7) I = aakkajj akakmam akaka jj, 6 + Invarant I lze vyjádřt jako determnant tenzoru a j, I = det a j Dervátor tenzoru je defnován d aj = aj akkδ j (.8) Druhý člen pravé strany představuje prvky tzv. kulového tenzoru. Hlavní hodnoty tenzorů Rovnce λ Iλ + I λ I = 0 (.9) určuje hlavní hodnoty tenzoru a j. Je-l a j symetrcký tenzor, jsou všechny tř nvaranty a hlavní hodnoty tenzoru reálná čísla. Prostřednctvím hlavních hodnot λ, λ, λ se nvaranty vyjádřují závslostm: I =λ +λ +λ, I =λλ +λλ +λλ, (.0) I =λλ λ,. Knematka přetvoření Knamatka studuje pohyb těles, anž se zábývá slam, které tento pohyb způsobují. Nejčastěj se použvá Lagrangeův pops pohybu [9]. To znamená závslost x = χ(x, t) (.) Na process deformace tělesa, popsaný funkc (.), se můžeme též dívat jako na transformační předps pro X x (Obr. ). Na obrázku je znázorněn pohyb tělesa z počáteční (referenční) konfgurace Ω 0 v čase t = 0 do okamžté konfgurace Ω v čase t. Tento pohyb bere v úvahu velká posunutí a velká přetvoření deformovaného tělesa. Význam jednotlvých velčn, kterým popsujeme deformac, je dobře patrný z obr. a z následujícího textu. Nejčastěj budeme označovat X materálové č lagrangeovské souřadnce. x prostorové č eulerovské souřadnce.
4 U, u posuvy t čas. Referenční konfgurace Okamžtá konfgurace X U(X,t) = u(x,t) χ x Ω 0 Ω tme t=0 X x tme t X, x e X, x O e e X, x Obr. Posuvy, deformační gradent Rozdl mez prostorovým a materálovým souřadncem defnuje posuv částce a nazývá se eulerovské formulace u(x, t) = x - X(x, t) (.) Lagrangeovská formulace je běžnější př popsu deformace poddajných těles U(X, t) = x(x, t) - X (.) Obě formulace př popsu jednoho a téhož deformačního procesu musejí dát stejné číselné výsledky, musejí tedy být vzájemně jednoznačně nvertovatelné. Podmínkou nvertovatelnost je nenulovost jacobánu transformace J = det F(X, t) (.4) kde x χ(x, t) F = = (.5) X X Skalární velčna J defnovaná vztahem (.4) se nazývá jacobán transformace. Tenzorová velčna, defnovaná vztahem (.5) je deformační gradent. Je defnovaná v konfgurac Ω, ale vztahuje se ke konfgurac Ω 0. Polární dekompozce (rozklad) 4
5 V každém bodu X Ω 0 a v čase t budeme mít následující polární dekompozce deformačního gradentu F = RU = VR, R T R = I, U = U T, V = V T (.6) kde R je ortogonální tenzor a U a V jsou poztvně defntní symetrcké tenzory dané vztahy U = F T F and V = F F T. Tenzor deformace Deformace tělesa, tj. změna jeho velkost a tvaru, se obvykle určuje stanovením posuvů jednotlvých částc a stanovením přetvoření v bezprostředním okolí částc. Míra deformace se nejlépe určuje posuvy vztaženým k celkovým rozměrům tělesa. Tyto míry jsou bez rozměrné a označují se přetvoření (stran), deformace nebo poměrné deformace. Míry přetvoření by neměly závset na zvolené soustavě souřadnc a na pohybu tělesa jako tuhého celku. Přpomeňme, že nfntesmální přetvoření, defnované vztahem (Cauchyův tenzor deformace) Tenzory deformace u ε = u + = u + u ( ) j j j j Xj X (.6) Tenzor deformace je vždy třosý. Může však v některých případech, kdy dochází k velkým deformacím (posuvům) v jedné rovně nebo ploše, být příčná změna rozměrů kontnua zanedbatelná. Greenova-Lagrangeova tenzoru deformace vyjádřeného v materálových souřadncích: G ε j = ( u j + u j + u k u kj ) (.7) Tenzor deformační gradent F zobrazuje vektor A v počáteční konfgurac na odpovídající vektor a v deformované konfgurac FA = a Deformac, která je výsledkem konečného pohybu, získáme ze změny délky tohoto vektoru a a A A = (FA) (FA) A A = A (F T F) A - A IA = A (C - I) A = A E A Z tohoto odvození vyplývají defnce pravého Cauchy-Greenova tenzoru deformace C a Green-Lagrangeova tenzoru deformace E. Uvádí se formálně jednodušší záps Greenova tenzoru deformace prostřednctvím materálového deformačního gradentů F ve tvaru E = (F T F - I) (.8) Formálně jednodušší záps Almansova tenzoru deformace prostřednctvím materálového deformačního gradentů F ve tvaru 5
6 A = (I - F -T F - ) (.9) Pravý Cauchyho-Greenyho deformační tenzor C C = F T F (.0) Levý Cauchyho-Greenyho deformační tenzor B B = F T F (.) Logartmcký tenzor přetvoření vztažený k materálním souřadncím je dán vztahem ε ol = lnu = lnc (.) Logartmcký tenzor přetvoření vztažený k prostorovým souřadncím je dán vztahem ε L = lnv = lnb (.) Deformační gradent a tenzory deformace mohou být rozloženy v součn sférské (dlatační) a zochorcké (dstorsní) část F = (J I) F (.4) C = F T F = J b = F F T = J E = (C - I) = J C, C = T F F (.5) b, b = F F T (.6) E + kde velčny s pruhem značí dstorsní část..4 Tenzory napětí ( J - ) I, E = ( C - I) (.7) Napětí je defnováno pomocí síl působících na elementární plošky. Síly rozdělujeme na vnější, působící na těleso z vnějšku, a na síly vntřní, udržující těleso kompaktní. Vnější síly mohou být objemové a povrchové. - Objemové síly působí jakoby na dálku na těleso nebo element. Jsou to síly gravtační, setrvačné, magnetcké a pod. Zpravdla se vztahují na jednotku objemu nebo hustoty (Nm -, Nkg - ). Ekvvalentní anglcký termín body forces. - Povrchové síly působí na krajovou část tělesa nebo elementu. Jsou to vlastně kontaktní síly. Tyto síly mají rozměr [N/m ]. Jejch anglcký název je surface forces nebo tracton forces. Povrchové síly jsou vlastně ty, které působí na vntřní povrch tělesa, obnažený v důsledku procesu uvolňování. Těmto slám se také říká vektory napětí jsou vztaženy na jednotku F plochy. Vektor napětí je obdobně jako výše defnován vztahem t = lm, kde F je S 0 S výslednce sl působících na plošku S. Vztah mez vektorem napětí a složkam tenzoru napětí je vyjádřen Cauchyho vztahem t = σ j n j nebo t = σ T n (.8) 6
7 Pro rovnnou napjatost můžeme Cauchyho vztah zobrazt. Po rozepsání dostaneme t =σ n+σ n t =σ n+σ n (.9) V matcovém tvaru je vztah (.8) vyjádřen t σ σ σ n t = σ σ σ. n (.0) t σ σ σ n Tenzor napětí σ j, tak jak zde bylo ukázáno, vyjádřuje okamžté síly vztažené ke geometr okamžté konfgurace. Označuje se Cauchyho skutečné napětí. V lneární mechance jsou deformace tělesa malé, a proto působící síly vztahují ke geometr počáteční konfgurace. To pak vede k pojmu nženýrského napětí. Použjeme-l horních levých ndexů pro rozlšení konfguračních vztahů, můžeme skutečný (Cauchyho) a nženýrský vektor napětí vyjádřt vztahy t t t Cauchy = t t = F t lm t t t eng = t 0 S 0 S t = F lm 0 0 S 0 S Těmto vektorům pak odpovídají tenzory skutečného a nženýrského napětí vztahy t = σ n t t t t t j j t t j j (.) t = σ n (.) Výhody použvání nženýrského napětí jsou nasnadě. Jejch výpočet je jednoduchý, vychází z geometre nezdeformované konfgurace a chyby tím vznkající jsou důsledku malých deformac zanedbatelné. Př řešení nelneárních úloh s velkým posuvy a s velkým deformacem nás však nženýrské napětí nechá na holčkách. Nebere v úvahu změnu geometre tělesa př jeho deformac. - První Polův-Krchhoffův tenzor napětí 0 t ρ t t T 0P= t 0F tσ ( P = J F σ σ = J PF ) (.) ρ - Druhý Polův-Krchhoffův tenzor napětí (symetrcký) ρ T S F F ( S= J F σf ρ 0 t t t t 0 = t 0 tσ0 T σ = J FSF ) (.4) Odvození obou zmíněných tenzorů je založeno na zákonu o zachování hmotnost a na matematcky konzstentních úvahách o přepočtu síly z jedné konfgurace do druhé (Fung 965, Okrouhlík 995,...). Tenzory jsou nezávslé na volbě souřadncového systému a nectlvé vůč pohybu tělesa jako tuhého celku. Nemají sce přímého fyzkálního významu, jsou však užtečným nástrojem př formulac přrůstkových metod vhodných pro řešení nelneárních úloh mechanky kontnua. Konjugované dvojce Míry deformace a míry napětí, jak je zřejmé z výše uvedeného, jsou rozdílné a proto je nutno zvolt vhodnou kombnac párů tenzoru deformace a tenzoru napětí. Je známo [], že pár : druhý Pola-Krchhoffa tenzor napětí a Greenův tenzor přetvoření jsou tzv. Energetcky konjugované. Energetcky konjugované pár je také Cauchyho tenzor napětí a nfntesmální 7
8 (nženýrský) tenzor přetvoření. O napětí a přetvoření říkáme, že jsou energetcky konjugované, jestlže jejch skalární součn davá mechankou prác. Mechanka práce povrchových a objemových sl v okamžté konfgurac je rovna (.5) W = σ jn juds + f judv S Použtím Gaussovy věty dostaneme W = V ( σju ) u σ j + fu dv = σ j + + f u dv (.6) x x x V j V j j Druhá část rovnce (.6) je levá část rovnce rovnováhy, a je tedy rovna nule. Využtím symetre tenzoru napětí může být mechancká práce výpočtena jako skalární součn Cauchyho tenzoru napětí a nfntesmálního přetvoření v okamžté konfgurac W = σ ju, jdv = σjε jdv = [ σ] :[ ε] dv (.7) V V V V referenční konfgurac se dá mechancká práce vyjádřt jako W = σε = (.8) V 0 j jdv SjEjd V 0 V Z hledska výkonové konjugovanost je známo [] pět dvojc. Uvedeme je v matcovém záps prostřednctvím Cauchyho tenzoru σ. První dvojc tvoří symetrcký druhý Pola-Krchhoffa tenzor napětí a Greenův tenzor přetvoření S= F F T J σ E = (F T F - I). Druhý dvojc tvoří Hllův symetrcký tenzor napětí a Almansův tenzor přetvoření T F J σf A = (I - F -T F - ). Třetí dvojc tvoří sdružený symetrcký tenzor napětí a Logartmcký tenzor přetvoření T R J σr ln ( = (F T F) / ) 4. Čtvrtou dvojc tvoří Boův symetrcký tenzor napětí a tenzor protažení ( T T F J σ R+R J σ F ) ( - I) 5. Pátou a poslední známou dvojc tvoří Černychův symetrcký tenzor napětí a nversní tenzor protažení ( F T J σ R+R T J σ F) (I - - ).5 Vztahy mez napětí a deformací Zobecněný Hookeův zákon můžeme vyjádřt v tenzorovém zápsu 8
9 σ j = Cjklε kl (, j, k, l =,, ) (.9) kde σ j a ε j jsou tenzory napětí a deformací druhého řádu a C jkl je tenzor čtvrtého řádu, jehož složky jsou konstanty tuhost materálu,, a jsou směry os souřadného systému. Všechny tyto tenzor jsou symetrcké, C jkl má nezavslých složek. Užjeme-l zkráceného zápsu, můžeme vztah mez napětím a deformacem zapsat v matcovému tvaru { σ} = [ C]{ ε} σ ε (.40) kde matce [ C ] je symetrcká matce 9x9. Můžeme nyní defnovat matc poddajnost a odpovídající vztah [ S ] = [ ] { ε} = [ S]{ σ} C (.50) ε σ (.5) Velčny všech jeho bodech shodné, budou hodnoty konstantní. Takové těleso nazýváme homogenním. C jkl jsou obecně funkcem místa (souřadnc). Jsou-l elastcké vlastnost tělesa ve C jkl společné všem bodům tělesa, budou tedy Jsou-l vlastnost prostředí v určtém bodě ve všech směrech stejné, říkáme o nch, že jsou v uvažovaném bodě zotropní. Je-l prostředí zotropní v každém bodě, mluvíme o zotropní prostředí. Jsou-l uvažované vlastnost v daném bodě prostředí v různých směrech různé, je prostředí v tomto bodě anzotropní a vztahuje-l se toto na celé prostředí, říkáme, že je celé prostředí anzotropní..6 Konsttutvní vztahy.6. Hyperelastcký materál Konsttutvní rovnce pro hyperelastcké materály vycházejí z postulátu exstence Helmholtzovy funkce volné energe Ψ, která je funkcí deformačního gradentu F. Napěťová odezva hyperelastckého materálu na deformac je odvozena z této skalární funkce deformační energe [9,] P = Ψ( F) F, (.5) T Ψ( F) T Ψ( F) σ= F = F J F J F, (.5) kde P je (nesymetrcký) první Pola-Krchhoffův tenzor napětí, σ je Cauchyho tenzor skutečných napětí a J je Jakobán deformačního gradentu. Alternatvní vztahy můžeme obdržet pro pravý Cauchy-Greenův tenzor deformace C, pro druhý (symetrcký) Pola- Krchhoffův tenzor napětí S a pro Green-Lagrangeův tenzor deformace E. Ψ( C) σ= F F C T J, (.54) ( ) P = Ψ C F C, (.55) 9
10 Ψ( C) Ψ( E) S = = C E, (.56) Funkce deformační energe musí být nvarantní př rotac tělesa jako tuhého celku. Pro zotropní hyperelastcký materál, jakým je kupř, pryž plněná sazem, lze vyjádřt Helmholtzův potencál v závslost na hlavních nvarantech jeho argumentů kupř. pravého Cauchy-Greenova tenzoru deformace C nebo jako funkcí prodloužení ( I ( ), I ( ), I ( )) Ψ=Ψ C C C, (.57) (,, ) Ψ=Ψ λ λ λ, (.58).6. Nestlačtelný hyperelastcký materál Celá řada polymerů př konečných deformacích téměr nemění svůj objem. Takové materály jsou považovány za nestlačtelné tj. deformace je zochorcká. Je to dealzace, která se v mechance kontnua často používá. Deformace je tedy stísněná a deformační podmínku lze vyjádřt jako J =. Obecnou konsttutvní rovnc pro nestlačtelný materál odvodíme z funkce deformační energe ve tvaru ( ) p( ) Ψ=Ψ F J (.59) kde p je neurčtý Lagrangeův násobtel, který lze považovat za hydrostatcký tlak. Jeho hodnotu lze určt z podmínek rovnováhy a z okrajových podmínek. Konsttutvní rovnce pak budou v obecném tvaru P = T Ψ( F) pf + F, (.60) Ψ( C) S = pc + C, (.6) Ψ( F) σ= pi+ F F T (.6).6. Stlačtelný hyperelastcký materál Pěnové elastomerské materály vykazují objemovou změnu př konečných deformací. Jednou podmínkou pro tyto materály je kladná hodnota objemové změny J. Protože se tyto materály chovají odlšně př objemové a smykové deformac, je třeba jejch deformac rozdělt na tzv. objemovou a zochorckou část. Deformační gradent F a pravý Cauchy- Greenův deformační tenzor C jsou podrobně jako v elastoplastctě rozloženy v součn složky odpovídají změně objemu (dlatační část) a složky zachovávající objem (dstorsní část) F = (J I) F (.6) C = F T F = (J I) C, C = T F F (.64) 0
11 Členy J I a (J I) jsou spojeny s deformací odpovídající změně objemu, zatímco členy F a C jsou modfkovaný deformační gradent a modfkovaný pravý Cauchy-Greenův tenzor deformace odpovídající dstors tvaru. Obdobně je rozložena funkce deformační energe Ψ ( ) =Ψ vol ( J) +Ψso ( ) kde vol ( J ) a so ( ) C C (.65) Ψ Ψ C jsou funkcí skalární hodnoty J a tenzory C, které popsují objemovou (dlatační) elastckou odezvu a zochorckou (dstorsní) elastckou odezvu materálu..6.4 Příčně zotropní materály Řada kompoztních materálů je složena z matce a vláknenné výztuže. Takový materál je anzotropní. Materál s výztuží pouze v jednom směru lze považovat za příčně zotropní s rovnou zotrope kolmou na směr vláken. Je-l tento materál schopen snášet konečné deformace, pak bude Helmholtzova volná energe funkcí dvou proměných pravého Cauchy- Greenova tenzoru deformace C a směrového vektoru vláken v nedeformované konfgurac a 0. Zavedeme-l tenzorový součn směrových vektorů A = a 0 a 0, pak deformační energ můžeme vyjádřt Ψ=Ψ( CA, ) (.66) Izotropní hyperelastcký materál může být reprezentován prvním třem nvaranty I, I a I pravého C č levého B Cauchy-Greenova tenzoru deformace, pro příčně zotropní materál je třeba přdat další dva nvaranty ( ) ( ) I Ca, = a.ca =λ, (.67) a I Ca, = a.ca, (.68) na kterých bude závset funkce deformační energe. Invarant I 4 je roven kvadrátu prodloužení ve směru vláken. Volná energe pro příčně zotropní materál, která je základem pro odvození konsttutvních rovnc, bude funkcí těchto pět nvarantů kde ( I ( ), I ( ), I ( ), I 4(, 0),I 5(, 0) ) Ψ=Ψ C C C C a C a (.69) Konsttutvní rovnce ve tvaru nvarantů 5 Ψ( ) ( ) Ia S = C, A Ψ = C, A C I C, (.70) I = I C, a= I = II-C C, a I = IC C I4 I5 = a0 a0, = a0 Ca 0 +a0c a0, C C Dosazením (.7) do (.70) dostaneme -, (.7) Ψ Ψ Ψ Ψ - Ψ Ψ S = + I I C+ I C + a0 a0 + a0 Ca 0 +a0c a 0, (.7) I I I I I4 I5
12 .6.5 Nestlačtelný příčně zotropní materál ) Předpokládejme, že matce příčně zotropního kompoztu je zotropní a nestlačtelná a že vlákna výztuže jsou schopna prodloužení. Z nestlačtelnost matrce vyplývá I = a ve vztahu pro volnou energ je nutné přdat člen s hydrostatckým tlakem Ψ=Ψ( I ( C), I ( C),I 4( C, a0), I 5( C, a0) )- ( ) p I, (.7) ) V případě zotropní a nestlačtelné matce a neprodlužtelných vláken máme I = a λ a = (I 4 = ) a do vztahu pro volnou energ přdáme neurčtý Lagrangeův násobtel q p I Ψ=Ψ( I ( C), I ( C), I 5( C, a0) )- ( )- ( 4 ).6.6 Kompoztní materál se dvěma skupnam výztužných vláken q I, (.74) Předpokládejme, že směrové vektory vláken v nedeformované konfgurac jsou a 0 a g 0. Analogcky můžeme defnovat dva tenzory A = a 0 a 0, G = g 0 g 0 (.75) A zavést funkc volné energe Ψ=Ψ( CA,G, ) (.76) K pět nvarantům v případu příčně zotropního materálu přídáme další tř ( ) ( ) ( ) ( ) I Cg, = g.cg =λ, g I Cg, = g.cg (.77) I Ca,, g = a.g a.cg Jsou-l skupny vláken navzájem kolmé, máme ortotropní materál. Za předpokladu, že matrce je zotropní a nestlačtelná a za předpokladu neprodlužtelnost vláken, můžeme Helmholtzovu funkcí volné energe zapsat ve tvaru p I q I Ψ=Ψ( I ( C), I ( C),I 5( C, a0),i 7( C, g0) )- ( )- ( 4 )- ( 6 ) r I, (.74) Jsou-l obě skupny vláken mechancky ekvvalentní pak, když nejsou nutně ortogonální, je materál v referenční konfgurac ortotropní..7 Funkce deformační energe V lteratuře lze najít celou řadu těchto funkcí pro stlačtelný nestlačtelný materál. Některé z nejčastěj užívaných (Neo-Hookean, Mooney-Rvln, Ogden, Blatz-Ko, ap.) jsou mplementovány do konečných prvků [9]..7. Funkce deformační energe pro zotropní materály a) Ogdenův model pro nestlačtelný materál (pryž, bomaterál ap.). Pryž je považována za nestlačtelnou (J = λ λ λ = ). Ogden zavádí deformační energ jako funkc hlavních prodloužení ve tvaru
13 N µ p αp αp αp Ψ = Ψ(λ, λ, λ ) = ( λ + λ + λ ) (.75) α p= p kde N je počet členů (větsnou N <=). Parametry µ p (smykové moduly) a bezrozměrné parametry α p je nutné určt expermentálně. Ogdenův model, který se v poslední době stal porpulární, má nekonstantní modul ve smyku a dává dobrou korelac v tahových zkouškách až do 700% deformace a je schopen zpevnění č změknutí př velkých deformacích. b) Mooney-Rvln, neo-hookeovský a Vargův model pro nestlačtelné materály. Tyto klascké modely pryžového materálu lze získat jako zvláštní případ Ogdenova modelu. Kupř. Mooney-Rvlnův model dostaneme položíme-l N =, α =, α = - Ψ = c ( λ + λ + λ - ) + c ( λ + λ + λ - ) = c (I ) + c (I ) (.76) kde ty konstanty c = µ / a c = µ / (µ = µ - µ ). Tento model dobře popsuje chován zotropní pryže př tahovém zatížení až do 00% deformace. Není adekvátní pro tlakové zatížení a není schopen posthnout zpevnění materálu př velkých deformacích. Pro N =, α = dostaváme neo-hookeovský model, který dává dobrou korelac s expermentálním daty do 40% deformace v tahu a do 90% deformace v čstém smyku Ψ = c ( λ + λ + λ - ) = c (I ) (.77) a Vargův model dostaneme pro N =, α = Ψ = c (λ + λ + λ ) (.78) c) Yeohův model U elastomerů vyztužených částcem sazí nebo křemíku se modul ve smyku výrazně mění s deformací nejprve se s rostoucí deformací snžuje a posléze opět stoupá př velkých deformacích. Ψ Expermenty ukazují, že je pro tyto materály blízké 0. Materálový model Yeohův I předpokládá deformační funkc, ve které chybí druhý nvarant Ψ = c (I ) + c (I ) + c (I ) (.79) Smykový modul obsahuje první a druhou mocnnu členu (I ) a aproxmuje expermentální závslost s dostatečnou přesností µ = c + c (I ) + c (I ) > 0 d) Blatz-Ko model pro pěnové elastomery Ve funkc deformační energe se kombnují teoretcké proměnné s expermentálním daty Ψ(I, I, I ) = f µ ( ) + ( β µ I β I I ) + ( f) + ( I ) β I β (.80)
14 ν kde β =, ν je Possonův poměr, µ je modul ve smyku a f [0,] je nterpolační ν parametr. e) Sant-Venant-Krchhoffův model Je to klascký nelneární model pro stlačtelné hyperelastcké materály. Je charakterzován funkcí deformační energe Ψ(E) = γ (tre) + µtre (.8) kde E je Green-Lagrangeův tenzor deformace, γ > 0 a µ > 0 jsou Lamého konstanty. Tento model je vhodný pro velké posuvy, ale nedoporučuje se pro velká stlačení..7. Funkce deformační energe pro anzotropní materály Funkce deformační energe (.66) a (.76) lze vyjádřt jako součet zotropní a anzotropní část Ψ = Ψ zo + Ψ anzo a) Příčně zotropní materál Bonet [5] použvá pro zotropní část deformační energe Sant-Venantův model (.8) pro malé deformace, pro nelneární deformace ho nahrazuje neo-hookeovským modelem (.77). Anzotropní část deformační energe je vyjádřena vztahem Ψ trn = [α + β(i ) + γ(i 4 )] (I 4 ) - α(i5 ) (.8) Je však nutné s uvědomt, že když je daný materál přčně zotropní v nedeformované konfgurac, nemusí to platt v deformované konfgurac. Vztah (.8) lze z tohoto důvodu upravt tak, že člen (I ), který je lneární funkcí C, nahradíme členem lnj. Ψ trn = [α + β lnj + γ(i 4 )] (I 4 ) - α(i5 ) (.8) b) Materál vyztužený dvěma skupnam vláken Holzapfel a kol. [6-8] používají k modelování zotropní část deformační energe neo- Hookeovský model (.77), který však může být nahrazen Ogdenovým (.75), nebo jným vhodným modelem. K modelování anzotropní část používají exponencální funkcí k k { [ ] } Ψ anzo = exp k ( I ) = 4,6 k >0 a k >0 jsou parametry materálů. III. VARIAČNÍ METODY MECHANIKY KONTINUA (.84) Složté problemy v mechance kontnua jsou těžké řešt přesně analytckou metodou. Proto se musíme uchýlt přblžné metody č numercké metody. Exstují v technce mnoho aplkace proměnných velčn hledat užtečný extrém. To je podstata varační metody. V nženýrských problémech a v problémech matematcké fyzky se velm často setkáváme s rovncem typu Ax = b (.) 4
15 kde b je prvek některého Hlbertova prostoru H a A je určtý operátor, nejčastější poztvní resp. poztvně defntní (defnční obor D A ) [0]. Řešením rovnce Ax = b pak rozumíme takový prvek x 0 D A, pro který platí Ax 0 = b (.) Je-l poztvní operátor A (poztvně defntní) úloha najít řešení x 0 rovnce Ax = b ekvvalentní úloze najít prvek x 0, mlmalzující kvadratcký funkconál Fx = (Ax, x) (b, x) (.) Pravě pro x = x 0 mnmální hodnoty na D A. Eulerova rovnce Funkce y(x), x (a, b). Řešt rovnc y(x) = 0, to znamená, že hledat mnmum funkconálu. Funkconál I(y) = b a F(x, y, y )dx Eulerova rovnce : Fy F " y' = 0, F y F F d F =, Fy' =, F" y' = y y' dx y '. Varační prncpy Tyto prncpy jsou vysvětleny ve vznkající Washzuově monograf [] spolu s celou řadou příkladů jejch užtí. Zde bude uveden jen jejch stručný přehled. Základem varačních prncpů je prncp vrtuálních prací, který lze formulovat následovně: Nechť mechancký systém s daným geometrckým vazbam je v rovnováze za působení soustavy sl. Pak součet všech vrtuálních prací δ W všech vnějších vntřních sl na lbovolných nekonečně malých vrtuálních posuvech vyhovujících daným geometrckým vazbám je roven nule: δ W = 0 (.5) Jestlže všechny vnější vntřní síly jsou konzervatvní, tj. mají potencál U, který je funkcí souřadnc, pak platí δ W = - δu (.6) a prncp vrtuálních prací vede k prncpu staconární hodnoty potencální energe U : Ze všech přípustných konfgurací soustavy je rovnovážných stav charakterzován staconární hodnotu potencální energe U: δu = 0. (.7) Tato formulace může být rozšířena na dynamcké problémy, kdy působí síly geometrcké vazby závsí na čase, použjeme-l d Alembertův prncp dynamcké rovnováhy a zahrneme-l vrtuální prác setrvačných sl: t t * δ Tdt + dwdt =0 (.8) t t 5
16 kde T je knetcká energe sytému, t a t je počáteční a konečný časový okamžk, ve kterých poloha systému odpovídá poloze př skutečném pohybu vrtuální posuvy jsou v těchto okamžcích rovny nule. Jestlže všechny vnější uvtřní síly mají potelcál U, pro který platí (.7), dostaváme Hamltonův prncp, který říká : Mez všem možných vrtuálním trajektorem systému je skutečná trajektore charakterzována staconární hodnotou funkconálu: t t ( ) T-U dt Zavedeme-l Lagrangeův knetcký potencál L = T U (.9) Pak Hamltonův prncp lze zapsat t t Ldt = 0 (.0) Varační metody mají šíroké použtí v pružností analyze za předpokladu malých deformací. Exstuje-l funkce energe napjatost a př varac posuvů zůstávají vnější síly nezměněné, pak prncp vrtuální práce vede k prncpu mnma deformační energe. Tento varační prncp spolu se zavedením Lagrangeových multplkatorů vede k celé řadě varačních prncpů včetně prncpu Hu-Washzuova, Hellnger-Ressnerova, prcpu mnma doplňkové energe a dalších. Defnujme funkc deformační energe A( ε j ) tak, že platí δa = σ j δε j, kde A= C jkl ε j ε kl (.) Dosadíme-l do (.) z Cauchyho vztahů pro deformace ε j = ( uj, + u, j ) (.) dostaneme funkc A(u ) a prncp vrtuální práce můžeme zapsat ve tvaru ( ) = 0 # δ Au dω XδudΩ pδud Γ (.) Ω Ω Γ p kde Ω je oblast, kterou zaujímá těleso, p # je vektor zatížení na část povrchu Γ p a X jsou hmotové síly. Defnujme funkc doplňkové deformační energe B ( ε j ) tak, že platí δb = ε δσ, kde B = S σσ (.4) j j jkl j kl potom prncp doplňkové vrtuální práce bude ve tvaru ( ) # j = 0 δ B σ dω uδ pd Γ (.5) Ω kde u # je vektor posuvu předepsaný na část povrchu Γ u a Γ u p = σ jn j. 6
17 Předpokládáme-l, že hmotové síly X, povrchová zatížení p # a posuvy u # jsou předpsány a př varacích se nemění, pak lze vyjádřt celkovou potencální energe a celku doplňkovou potencální energ jako: ( ) # Π= Au Xu dω pud Γ (.6) Ω a Π c = ( ) # Ω j Γ Γ p B σ dω u pd Γ (.7) u a prncp mnma celkové potencální energe a celkové doplňkové energe vyjádříme vztahy δπ = 0 a δπ c = 0 (.8) Platí-l lneárn vztah mez napětím a deformací, pak platí A = B, ve všech případech však platí A + B = σ j ε j. (.9) Hu-Washzův varační funkconál můžeme vyjádřt ve tvaru u u j H = A( ε ) + ( ) # # j Xu εj σj dω pud Γ u u pd Γ (.0) Ω xj x Γ p Γu kde εj, u, σj a p jsou vzájemně nezávslé velčny podrobené varacím, p # je vektor zatížení na část povrchu Γ p a u # je vektor posuvu předepsaný na část povrchu Γ u, A( ε j ) je energe napjatost a X jsou hmotové síly. Varací (.0) vzhledem k těmto osmnáct nezávslým velčnám dostáváme W u u σ j j δh = σ + + j δε j εj δσ j X δu dω Ω εj xj x xj + σ n p δudγ u u δ pdγ + σ n p δudγ = 0 ( # ) ( # ) ( ) j j j j Γ Γ Γ p u u (.) Staconární podmíky, které vyplývají z (.) jsou : Vztahy mez napětím a deformacem, Cauchyho vztahy, podmíky rovnováhy a okrajové podmínky na Γ u a Γ p. Fyzkální význam Lagrangeových multplkátorů p vyplývá z posledního výrazu v (.): jsou to povrchové síly na té část okraje, na které jsou předepsány posuvy. Funkconál Hellnger-Ressnerův lze odvodt z obecného funkconálu (.0). Velčny ε j jž nebudeme považovat za nezávslé a jejch varace δε j budou nulové, dále budeme předpokládat platnost Cauchyho vztahů (.) a lneární vztah mez napětí a deformací: ε j = S σ (.) jkl kl V takovém případě lze složky deformací zcela vyloučt z podntegrálního výrazu (.0) a získat funkconál: Π R = u u j σ + ( ) ( ) # # j Xu B σj dω pud Γ u u pd Γ Ω xj x Γ p Γu (.) kde u, σ a p jsou vzájemně nezávslé velčn podrobené varacím a funkce B plyne z (.4). j 7
18 Aplkujeme-l Hellnger-Ressnerův varační teorém spolu s Hamltonovým prncpem získáme funkconál: t t ( ) Φ= T-Π dt (.4) R a pohybové rovnce systému získáme z podmínky staconární hodnoty tohoto funkconálu: δφ = 0. (.5). Varační metody řešení okrajových úloh Uvažujeme soustavu m dferencálních rovnc y = f(x, y), x a, b (.6) s obecnou okrajovou podmínkou r(y(a), y(b)) = 0. (.7) Místo hledání řešení v určtých bodech, hledají varační metody řešení v jsté třídě funkcí, pokud je ϕ k (x) úplný systém funkcí, lze řešení napsat ( ) = ϕ ( ) y x a x (.8) k = k k a zbývá najít neznáme koefcenty a k. Samozřejmě se pak omezíme na konečný počet funkcí. Převedeme okrajové podmínky na homogenní a obyčejnou dferencální rovnc napíšeme ve tvaru A y(x) = f(x) (a) Lm y= 0 (b) Lm y= 0 kde A je dferencální operátor. Zvolíme bázové funkce ϕ k (x) takové, že splňují okrajové podmínky. V prostoru funkcí zavedeme skalární součn, často ( u,v) ( ) ( ) b = u x v x dx. Pozn. Většna metod je určena pro lneární operátory A, ale např. Galerknovu metodu lze užít pro nelneární operátory. Galerknova metoda Ay = f (Ay f, ϕ j ) = 0 j =,..., n Uvažujeme přblžné řešení ve tvaru n = ϕ y a n k k k = Po dosazení získáme systém rovnc pro koefcenty a k b b n Ayn f, ϕ j = Ayn f ϕ jdx = A a kϕk f, ϕ j dx = 0 a a k= ( ) ( ) Metoda konečných prvků (fnte element method) je varační metoda, která užívá specální bázové funkce, z nchž každá je nenulová jen v určtém krátkém ntervalu. Bázové funkce pro metodu konečných prvků mohou být například: a 8
19 ϕ = 0 pro x x ϕ= x x x x ϕ= x x x + x 0 pro x x x pro x x x + ϕ = pro x Uvedený tvar bázových funkcí lze použít, pokud dferencální rovnce obsahují maxmálně. dervac, jnak je třeba volt hladší bázové funkce (např. zvonové splny). + x 4. Metoda konečných prvků Metoda konečných prvků (FEM Fnte Element Method), se s výhodou používá pro řešení různých problémů v oblast mechanky poddajných těles. V metodě konečných prvků (MKP) vyplníme objem uvaženého tělesa mnoha náhradním částm jednoduchých geometrckých tvarů - ty nazýváme prvky a máme zato, že př vyplňování objemu nevznkly žadné umělé dutny a že prvky jsou pospojovány jen několka svým hrančním body. Konečným prvkem nazýváme zvolený element (objemu, plochy, délky) defnovaný uzly v rozích, popř. na hranách. Exstují mnohé způsoby jak vysvětlt a odvodt základní vztahy pro metodu konečných prvků. Jeden z nch, zde uvedený, je založen na prncpu vrtuálních prací. 4. Prncp vrtuálních prací Prncp vrtuálních prací hraje v mechance kontnua důležtou rol. Je též nazýván prncpem vrtuálnch posunutí. Duálním prncpem k prncpu vrtuálních posunutí je prncp vrtuálních sl []. Vrtuální práce je fktvní práce, kterou vykonají statcky přípustné síly a napětí př nfntesmálních knematky přístupných posunutí. Vrtuání práce δu, vykonaná vntřním slam, je rovna prác δw, vykonané vnějším slam δu = δw (4.) Vrtuání prác vnějších sl je dána vrtuání prác povrchových a objemových sl (4.) δw = δutds + δu fdv S V Vrtuání posuvy δu jsou myšlené, nkolv skutečné, nfntesmální posuvy udělené každé částc tělesa. Z výkonu vntřních sl podle (.5.76 []) se dá odvodt vrtuální práce sl ve tvaru δu = δεjσ jdv (4.) V Přpojíme-l vrtuální prác osamělých sl, se kterým se tak často pracuje v nženýrské prax dostaneme δ qq, (4.4) 9
20 můžeme celkovou blanc vrtuálních sl napsat ve tvaru, v něm se s ní často setkáváme v textech věnovaných metodě konečných prvků (Bathe, 996) u f dv + δ qq (4.5) δεjσ jdv = δutds + δ V S V Vyjádřeno slovy, vrtuální práce vntřních sl se rovná součtu vrtuální prácí sl obemových, povrchovývh a osamělých. Velčna δq, odpovdá předepsanému vrtuálnímu posunutí v místě působtě síly Q. 4. Soustavy nelnearních rovnc v MKP Se soustavam nelneárních rovnc se v metodě konečných prvků setkáváme často. 4.. Rovnce rovnováhy tělesa Statcká rovnce rovnováhy tělesa má po dskretzac tvar Ku = R (4.6) Kde K je matce tuhost, u vektor posunutí a R je vektor uzlových sl. Rovnc (4.6) lze přepsat do obecného tvaru g(u) = K(u)u R(u) = 0 (4.7) kde g(u) je gradent potencální energe, známy též jako rezduální vektor (out-of-balanceforce). 4.. Rovnce staconárního vedení tepla Rovnce staconárního vedení tepla vyjádřuje závslost mez přváděným výkonem Q a vektorem uzlových teplot T jako KT = Q (4.8) Tepelný tok Q na povrchu tělesa bývá nejčastěj popsán přestupem Q = α(t T 0 ), α = α(t) (9) kde T 0 je teplota okolí a α je součntel přestupu tepla. Protože α = α(t), bude matce tepelné vodvost K pravá strana Q funkcí teploty tělesa. Podobně jako (4.7) můžeme psát g(t) = K(T)T Q(T) = 0 (4.0) 4.. Konsttutvní vztahy Konsttutvní vztahy dávají do souvslost tenzor napětí σ s tenzorem deformace ε, např. Pro nelneárně pružný materál σ = Dε, kde D = D(ε), resp. D = D(σ) (4.) Můžeme považovat (4.) za soustavu nelneárních rovnc typu g(σ) = 0 nebo, což bude pro další účely výhodnější σ = f(σ), f(σ) = D(σ) ε, (4.) Základním algortmem řešsní soustav nelneárních rovnc na globální úrovní je Newtonova-Raphsonva (NR) metoda. 0
21 4. Newtonova-Raphsonova metoda Problém na globální úrovn můžeme formulovat následujícím způsobem: Hledáme řešení u, přčemž k dspozc máme jen aproxmac u n, tedy g(u n ) 0, g(u) = 0. (4.) Označme g n = g(u n ), u n+ = u n+ - u n (4.4) Defnujeme Jacoban (tangencální) matc g K j =, kde g = g (u j ),, j =,,...,N (4.5) u nebo stručně K n = g u j u n Dále defnujeme hessán (4.6) H jk = g u u j k, H n = g u u n (4.7) u n+ Rozvojem (4.) do Taylorovo řady v okolí bodu u n g(u) = g n + K n (u - u n ) + H n(u - u n ) + O(u - u n ) = 0 (4.8) Zanedbáním kvadratcké členy a členů vyšších řádů obdržíme výraz pro novou aproxmac K n (u n+ - u n ) = -g n (4.9) NR algortmus ) u 0 = 0 ) g n = g(u n ) = 0 ext ) sestavt K n = g/ u v bodě u n 4) K n u n+ = -g n 5) u n+ = u n + u n+ Nová aproxmac u n+ anuluje jen první dva členy řady (4.8). Zbytek, počítáme kvadratckým členem, představuje chybu aproxmace. Dá se tedy očekovat, že v následující terac, kdy bude elmnován rezduál H n(u - u n ) + O(u - u n ), vznkle chyba řádů O(u n+ - u n+ ) O(u n+ - u n ) 4 atd. Metoda bude zřejmě konvergovat kvadratcky.
22 LITERATURA [] Bohuslav Stříž, Mechanka textlí, část : Základy mechanky kontnua. Techncká unverzta v Lberc, 00. [] Bohuslav Stříž, Mechanka textlí, část : Aplkace mechanky kontnua. Techncká unverzta v Lberc, 00. [] Okrouhlík. M., Mechanka poddajných těles, numercká matematka a superpočítače. Ústav termomechanky, Praha 997. [4] Okrouhlík. M., Implementaton of Nonlnear Contunuum Mechancs n Fnte Element Codes. Insttute of Thermomechancs, Prague 995. [5] Bonet, J., Burton, A.J., A smple orthotropc, transversely sotropc hyperelastc consttutve equaton for large stran computatons, Comput. Methods Appl. Mech. Engrg. 6, 998, [6] Holzapfel, G.A., Gasser, T.C., Ogden, R.W., A new consttutve framework for arteral wall mechancs and a comparatve study of materal models, J. of Elastcty, Nov., 000. [7] Gerhard A. Holzapfel & Thomas C. Gasser, A vscoelastc model for fber-renforced compostes at fnte strans: Contnuum bass, computatonal aspects and applcatons, BIOMECH (gasser.pdf) [8] G. A. Holzapfel. Bomechancs of sort tssue. Graz, November 000. [9] Gerhard A. Holzapfel. Nonlnear sold mechancs, John Wley & Sons Ltd, Baffns Lane, Chchester West Sussex PO9 UD, England, 000. [0] Karel Rektorys a spolupracovníc. Přehled užté matematky. Praha 995. [] Washzu. K., Varatonal methods n elastcty and plastcty. th New York, USA, 98. [] Bohdana Marvalová, Určení efektvních mechanckých vlastností kompoztů vyztužených tkannou plátnové vazby.
MODELOVÁNÍ A SIMULACE
 MODELOVÁNÍ A SIMULACE základní pojmy a postupy vytváření matematckých modelů na základě blancí prncp numerckého řešení dferencálních rovnc základy práce se smulačním jazykem PSI Základní pojmy matematcký
MODELOVÁNÍ A SIMULACE základní pojmy a postupy vytváření matematckých modelů na základě blancí prncp numerckého řešení dferencálních rovnc základy práce se smulačním jazykem PSI Základní pojmy matematcký
Korelační energie. Celkovou elektronovou energii molekuly lze experimentálně určit ze vztahu. E vib. = E at. = 39,856, E d
 Korelační energe Referenční stavy Energ molekul a atomů lze vyjádřt vzhledem k různým referenčním stavům. V kvantové mechance za referenční stav s nulovou energí bereme stav odpovídající nenteragujícím
Korelační energe Referenční stavy Energ molekul a atomů lze vyjádřt vzhledem k různým referenčním stavům. V kvantové mechance za referenční stav s nulovou energí bereme stav odpovídající nenteragujícím
Numerická matematika 1. t = D u. x 2 (1) tato rovnice určuje chování funkce u(t, x), která závisí na dvou proměnných. První
 Numercká matematka 1 Parabolcké rovnce Budeme se zabývat rovncí t = D u x (1) tato rovnce určuje chování funkce u(t, x), která závsí na dvou proměnných. První proměnná t mívá význam času, druhá x bývá
Numercká matematka 1 Parabolcké rovnce Budeme se zabývat rovncí t = D u x (1) tato rovnce určuje chování funkce u(t, x), která závsí na dvou proměnných. První proměnná t mívá význam času, druhá x bývá
Energie elektrického pole
 Energe elektrckého pole Jž v úvodní kaptole jsme poznal, že nehybný (centrální elektrcký náboj vytváří v celém nekonečném prostoru slové elektrcké pole, které je konzervatvní, to znamená, že jakýkolv jný
Energe elektrckého pole Jž v úvodní kaptole jsme poznal, že nehybný (centrální elektrcký náboj vytváří v celém nekonečném prostoru slové elektrcké pole, které je konzervatvní, to znamená, že jakýkolv jný
Matematika I A ukázkový test 1 pro 2018/2019
 Matematka I A ukázkový test 1 pro 2018/2019 1. Je dána soustava rovnc s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napšte Frobenovu větu (předpoklady + tvrzení). b) Vyšetřete
Matematka I A ukázkový test 1 pro 2018/2019 1. Je dána soustava rovnc s parametrem a R x y + z = 1 x + y + 3z = 1 (2a 1)x + (a + 1)y + z = 1 a a) Napšte Frobenovu větu (předpoklady + tvrzení). b) Vyšetřete
Pružnost a plasticita II
 Pružnost a plastcta II 3 ročník bakalářského studa doc Ing Martn Kresa PhD Katedra stavební mechank Řešení pravoúhlých nosných stěn metodou sítí Statcké schéma nosné stěn q G υ (μ) h l d 3 wwwfastvsbcz
Pružnost a plastcta II 3 ročník bakalářského studa doc Ing Martn Kresa PhD Katedra stavební mechank Řešení pravoúhlých nosných stěn metodou sítí Statcké schéma nosné stěn q G υ (μ) h l d 3 wwwfastvsbcz
Sdílení tepla. Úvod - Přehled. Sdílení tepla mezi termodynamickou soustavou a okolím je podmíněno rozdílností teplot soustavy T.
 7.4.0 Úvod - Přehled Sdílení tepla Sdílení tepla mez termodynamckou soustavou a okolím je podmíněno rozdílností teplot soustavy T s a okolí T o. Teplo mez soustavou a okolím se sdílí třem základním způsoby:
7.4.0 Úvod - Přehled Sdílení tepla Sdílení tepla mez termodynamckou soustavou a okolím je podmíněno rozdílností teplot soustavy T s a okolí T o. Teplo mez soustavou a okolím se sdílí třem základním způsoby:
u (x i ) U i 1 2U i +U i+1 h 2. Na hranicích oblasti jsou uzlové hodnoty dány okrajovými podmínkami bud přímo
 Metoda sítí základní schémata h... krok sítě ve směru x, tj. h = x x q... krok sítě ve směru y, tj. q = y j y j τ... krok ve směru t, tj. τ = j... hodnota přblžného řešení v uzlu (x,y j ) (Possonova rovnce)
Metoda sítí základní schémata h... krok sítě ve směru x, tj. h = x x q... krok sítě ve směru y, tj. q = y j y j τ... krok ve směru t, tj. τ = j... hodnota přblžného řešení v uzlu (x,y j ) (Possonova rovnce)
ZÁPADOČESKÁ UNIVERZITA V PLZNI
 ZÁPADOČESKÁ UNIVERZITA V PLZNI FAKULTA STROJNÍ Semestrální práce z předmětu MM Stanovení deformace soustav ocelových prutů Václav Plánčka 6..006 OBSAH ZADÁNÍ... 3 TEORETICKÁ ČÁST... 4 PRAKTICKÁ ČÁST...
ZÁPADOČESKÁ UNIVERZITA V PLZNI FAKULTA STROJNÍ Semestrální práce z předmětu MM Stanovení deformace soustav ocelových prutů Václav Plánčka 6..006 OBSAH ZADÁNÍ... 3 TEORETICKÁ ČÁST... 4 PRAKTICKÁ ČÁST...
Numerická matematika A
 Numercká matematka A 5615 A1 Máme dánu soustava lneárních rovnc tvaru AX = B, kde 4 1 A = 1 4 1, B = 1 a Zapíšeme soustavu rovnc AX = B ve tvaru upravíme a následně (L + D + P X = B, DX = (L + P X + B,
Numercká matematka A 5615 A1 Máme dánu soustava lneárních rovnc tvaru AX = B, kde 4 1 A = 1 4 1, B = 1 a Zapíšeme soustavu rovnc AX = B ve tvaru upravíme a následně (L + D + P X = B, DX = (L + P X + B,
Osově namáhaný prut základní veličiny
 Pružnost a pevnost BD0 Osově namáhaný prut základní velčny ormálová síla půsoící v průřezu osově namáhaného prutu se získá ntegrací normálového napětí po ploše průřezu. da A Vzhledem k rovnoměrnému rozložení
Pružnost a pevnost BD0 Osově namáhaný prut základní velčny ormálová síla půsoící v průřezu osově namáhaného prutu se získá ntegrací normálového napětí po ploše průřezu. da A Vzhledem k rovnoměrnému rozložení
Mechanické vlastnosti materiálů.
 Mechancké vastnost materáů. Obsah přednášky : tahová zkouška, zákadní mechancké vastnost materáu, prodoužení př tahu nebo taku, potencání energe, řešení statcky neurčtých úoh Doba studa : as hodna Cí přednášky
Mechancké vastnost materáů. Obsah přednášky : tahová zkouška, zákadní mechancké vastnost materáu, prodoužení př tahu nebo taku, potencání energe, řešení statcky neurčtých úoh Doba studa : as hodna Cí přednášky
MĚRNÁ DEFORMAČNÍ ENERGIE OTEVŘENÉHO OCELOVÉHO
 MĚRNÁ DEFORMAČNÍ ENERGIE OTEVŘENÉHO OCELOVÉHO PROFILU NAMÁHANÉHO TLAKEM ZA OHYBU SPECIFIC STRAIN ENERGY OF THE OPEN CROSS-SECTION SUBJECTED TO COUPLED COMPRESSION AND BENDING I. Kološ 1 a P. Janas 2 Abstract
MĚRNÁ DEFORMAČNÍ ENERGIE OTEVŘENÉHO OCELOVÉHO PROFILU NAMÁHANÉHO TLAKEM ZA OHYBU SPECIFIC STRAIN ENERGY OF THE OPEN CROSS-SECTION SUBJECTED TO COUPLED COMPRESSION AND BENDING I. Kološ 1 a P. Janas 2 Abstract
TENSOR NAPĚTÍ A DEFORMACE. Obrázek 1: Volba souřadnicového systému
 TENSOR NAPĚTÍ A DEFORMACE Obrázek 1: Volba souřadnicového systému Pole posunutí, deformace, napětí v materiálovém bodě {u} = { u v w } T (1) Obecně 9 složek pole napětí lze uspořádat do matice [3x3] -
TENSOR NAPĚTÍ A DEFORMACE Obrázek 1: Volba souřadnicového systému Pole posunutí, deformace, napětí v materiálovém bodě {u} = { u v w } T (1) Obecně 9 složek pole napětí lze uspořádat do matice [3x3] -
Rozdíly mezi MKP a MHP, oblasti jejich využití.
 Rozdíly mezi, oblasti jejich využití. Obě metody jsou vhodné pro určitou oblast problémů. základě MKP vyžaduje rozdělení těles na vhodný počet prvků, jejichž analýza je poměrně snadná a pro většinu částí
Rozdíly mezi, oblasti jejich využití. Obě metody jsou vhodné pro určitou oblast problémů. základě MKP vyžaduje rozdělení těles na vhodný počet prvků, jejichž analýza je poměrně snadná a pro většinu částí
ALGORITMUS SILOVÉ METODY
 ALGORITMUS SILOVÉ METODY CONSISTENT DEFORMATION METHOD ALGORITHM Petr Frantík 1, Mchal Štafa, Tomáš Pal 3 Abstrakt Příspěvek se věnuje popsu algortmzace slové metody sloužící pro výpočet statcky neurčtých
ALGORITMUS SILOVÉ METODY CONSISTENT DEFORMATION METHOD ALGORITHM Petr Frantík 1, Mchal Štafa, Tomáš Pal 3 Abstrakt Příspěvek se věnuje popsu algortmzace slové metody sloužící pro výpočet statcky neurčtých
3 VYBRANÉ MODELY NÁHODNÝCH VELIČIN. 3.1 Náhodná veličina
 3 VBRANÉ MODEL NÁHODNÝCH VELIČIN 3. Náhodná velčna Tato kaptola uvádí stručný pops vybraných pravděpodobnostních modelů spojtých náhodných velčn s důrazem na jejch uplatnění př rozboru spolehlvost stavebních
3 VBRANÉ MODEL NÁHODNÝCH VELIČIN 3. Náhodná velčna Tato kaptola uvádí stručný pops vybraných pravděpodobnostních modelů spojtých náhodných velčn s důrazem na jejch uplatnění př rozboru spolehlvost stavebních
Statika soustavy těles v rovině
 Statka soustavy těles v rovně Zpracoval: Ing. Mroslav yrtus, Ph.. U mechancké soustavy s deálním knematckým dvojcem znázorněné na obrázku určete: počet stupňů volnost početně všechny reakce a moment M
Statka soustavy těles v rovně Zpracoval: Ing. Mroslav yrtus, Ph.. U mechancké soustavy s deálním knematckým dvojcem znázorněné na obrázku určete: počet stupňů volnost početně všechny reakce a moment M
Obecný Hookeův zákon a rovinná napjatost
 Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
Obecný Hookeův zákon a rovinná napjatost Základní rovnice popisující napěťově-deformační chování materiálu při jednoosém namáhání jsou Hookeův zákon a Poissonův zákon. σ = E ε odtud lze vyjádřit také poměrnou
Polární rozklad deformačního gradientu a tenzory přetvoření
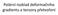 Polární rozklad deformačního gradientu a tenzory přetvoření https://en.wikipedia.org/wiki/finite_strain_theory Deformační gradient Musí tedy existovat jednoznačné zobrazení konfigurace : 1 t t x X, a inversní
Polární rozklad deformačního gradientu a tenzory přetvoření https://en.wikipedia.org/wiki/finite_strain_theory Deformační gradient Musí tedy existovat jednoznačné zobrazení konfigurace : 1 t t x X, a inversní
Analýza napjatosti PLASTICITA
 Analýza napjatosti PLASTICITA TENZOR NAPĚTÍ Teplota v daném bodě je skalár, je to tenzor nultého řádu, který nezávisí na změně souřadného systému Síla je vektor, je to tenzor prvního řádu, v trojrozměrném
Analýza napjatosti PLASTICITA TENZOR NAPĚTÍ Teplota v daném bodě je skalár, je to tenzor nultého řádu, který nezávisí na změně souřadného systému Síla je vektor, je to tenzor prvního řádu, v trojrozměrném
Biomechanika srdečněcévnísoustavy a konstitutivnímodelování
 Biomechanika srdečněcévnísoustavy a konstitutivnímodelování Biomechanika a lékařsképřístroje Biomechanika I LukášHorný Laboratoř biomechaniky člověka Ústavu mechaniky Fakulty strojní ČVUT v Praze M Konstitutivní
Biomechanika srdečněcévnísoustavy a konstitutivnímodelování Biomechanika a lékařsképřístroje Biomechanika I LukášHorný Laboratoř biomechaniky člověka Ústavu mechaniky Fakulty strojní ČVUT v Praze M Konstitutivní
VÝPOČTOVÉ MODELOVÁNÍ MECHANICKÝCH ZKOUŠEK KOMPOZITŮ PRYŽ-OCELOVÉ VLÁKNO
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ FACULTY OF MECHANICAL ENGINEERING ÚSTAV MECHANIKY TĚLES, MECHATRONIKY A BIOMECHANIKY INSTITUTE OF SOLID MECHANICS,
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ FACULTY OF MECHANICAL ENGINEERING ÚSTAV MECHANIKY TĚLES, MECHATRONIKY A BIOMECHANIKY INSTITUTE OF SOLID MECHANICS,
Kontraktantní/dilatantní
 Kontraktantní/dilatantní plasticita - úhel dilatance směr přírůstku plastické deformace Na základě experimentálního měření dospěl St. Venant k závěru, že směry hlavních napětí jsou totožné se směry přírůstku
Kontraktantní/dilatantní plasticita - úhel dilatance směr přírůstku plastické deformace Na základě experimentálního měření dospěl St. Venant k závěru, že směry hlavních napětí jsou totožné se směry přírůstku
Literatura: Kapitola 5 ze skript Karel Rektorys: Matematika 43, ČVUT, Praha, Text přednášky na webové stránce přednášejícího.
 Předmět: MA4 Dnešní látka: Metoda sítí pro 2D úlohy. Possonova rovnce. Vlnová rovnce. Rovnce vedení tepla. Lteratura: Kaptola 5 ze skrpt Karel Rektorys: Matematka 43, ČVUT, Praha, 2. Text přednášky na
Předmět: MA4 Dnešní látka: Metoda sítí pro 2D úlohy. Possonova rovnce. Vlnová rovnce. Rovnce vedení tepla. Lteratura: Kaptola 5 ze skrpt Karel Rektorys: Matematka 43, ČVUT, Praha, 2. Text přednášky na
Nelineární problémy a MKP
 Nelineární problémy a MKP Základní druhy nelinearit v mechanice tuhých těles: 1. materiálová (plasticita, viskoelasticita, viskoplasticita,...) 2. geometrická (velké posuvy a natočení, stabilita konstrukcí)
Nelineární problémy a MKP Základní druhy nelinearit v mechanice tuhých těles: 1. materiálová (plasticita, viskoelasticita, viskoplasticita,...) 2. geometrická (velké posuvy a natočení, stabilita konstrukcí)
SMR 1. Pavel Padevět
 SMR Pavel Padevět Oganzace předmětu Přednášející Pavel Padevět, K 3, D 09 e-mal: pavel.padevet@fsv.cvut.cz Infomace k předmětu: https://mech.fsv.cvut.cz/student SMR Heslo: odné číslo bez lomítka (případně
SMR Pavel Padevět Oganzace předmětu Přednášející Pavel Padevět, K 3, D 09 e-mal: pavel.padevet@fsv.cvut.cz Infomace k předmětu: https://mech.fsv.cvut.cz/student SMR Heslo: odné číslo bez lomítka (případně
FYZIKA I. Pohybová rovnice. Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D. Doc. Ing. Irena Hlaváčová, Ph.D. Mgr. Art.
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ FYZIKA I Pohybová rovnce Prof. RNDr. Vlém Mádr, CSc. Prof. Ing. Lbor Hlaváč, Ph.D. Doc. Ing. Irena Hlaváčová, Ph.D. Mgr. Art. Dagmar Mádrová
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ FYZIKA I Pohybová rovnce Prof. RNDr. Vlém Mádr, CSc. Prof. Ing. Lbor Hlaváč, Ph.D. Doc. Ing. Irena Hlaváčová, Ph.D. Mgr. Art. Dagmar Mádrová
Mechanika kontinua. Mechanika elastických těles Mechanika kapalin
 Mechanika kontinua Mechanika elastických těles Mechanika kapalin Mechanika kontinua Mechanika elastických těles Mechanika kapalin a plynů Kinematika tekutin Hydrostatika Hydrodynamika Kontinuum Pro vyšetřování
Mechanika kontinua Mechanika elastických těles Mechanika kapalin Mechanika kontinua Mechanika elastických těles Mechanika kapalin a plynů Kinematika tekutin Hydrostatika Hydrodynamika Kontinuum Pro vyšetřování
2. Definice pravděpodobnosti
 2. Defnce pravděpodobnost 2.1. Úvod: V přírodě se setkáváme a v přírodních vědách studujeme pomocí matematckých struktur a algortmů procesy dvojího druhu. Jednodušší jsou determnstcké procesy, které se
2. Defnce pravděpodobnost 2.1. Úvod: V přírodě se setkáváme a v přírodních vědách studujeme pomocí matematckých struktur a algortmů procesy dvojího druhu. Jednodušší jsou determnstcké procesy, které se
ANALÝZA VZTAHU DVOU SPOJITÝCH VELIČIN
 ANALÝZA VZTAHU DVOU SPOJITÝCH VELIČIN V dokumentu 7a_korelacn_a_regresn_analyza jsme řešl rozdíl mez korelační a regresní analýzou. Budeme se teď věnovat pouze lneárnímu vztahu dvou velčn, protože je nejjednodušší
ANALÝZA VZTAHU DVOU SPOJITÝCH VELIČIN V dokumentu 7a_korelacn_a_regresn_analyza jsme řešl rozdíl mez korelační a regresní analýzou. Budeme se teď věnovat pouze lneárnímu vztahu dvou velčn, protože je nejjednodušší
MOŽNOSTI MODELOVÁNÍ A ŘEŠENÍ STŘETU PŘI OBJASŇOVÁNÍ FINGOVANÝCH DOPRAVNÍCH NEHOD
 XV. konference absolventů studa technckého znalectví s meznárodní účastí MOŽNOSTI MODELOVÁNÍ A ŘEŠENÍ STŘETU PŘI OBJASŇOVÁNÍ FINGOVANÝCH DOPRAVNÍCH NEHOD Zdeněk Mrázek 1 1. Ř ešení stř etu u fngovaných
XV. konference absolventů studa technckého znalectví s meznárodní účastí MOŽNOSTI MODELOVÁNÍ A ŘEŠENÍ STŘETU PŘI OBJASŇOVÁNÍ FINGOVANÝCH DOPRAVNÍCH NEHOD Zdeněk Mrázek 1 1. Ř ešení stř etu u fngovaných
PRUŽNOST A PEVNOST II
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ PRUŽNOST A PEVNOST II Navazující magisterské studium, 1. ročník Alois Materna (přednášky) Jiří Brožovský (cvičení) Kancelář: LP C 303/1
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ PRUŽNOST A PEVNOST II Navazující magisterské studium, 1. ročník Alois Materna (přednášky) Jiří Brožovský (cvičení) Kancelář: LP C 303/1
Autor: Vladimír Švehla
 Bulletin of Applied Mechanics 1, 55 64 (2005) 55 Využití Castiglianovy věty při výpočtu deformací staticky určité případy zatížení tahem a tlakem Autor: Vladimír Švehla České vysoké učení technické, akulta
Bulletin of Applied Mechanics 1, 55 64 (2005) 55 Využití Castiglianovy věty při výpočtu deformací staticky určité případy zatížení tahem a tlakem Autor: Vladimír Švehla České vysoké učení technické, akulta
Maticová exponenciála a jiné maticové funkce
 Matcová exponencála a jné matcové funkce Motvace: Jž víte, že řešením rovnce y = ay, jsou funkce y(t = c e at, tj exponencály Pro tuto funkc platí, že y(0 = c, tj konstanta c je počáteční podmínka v bodě
Matcová exponencála a jné matcové funkce Motvace: Jž víte, že řešením rovnce y = ay, jsou funkce y(t = c e at, tj exponencály Pro tuto funkc platí, že y(0 = c, tj konstanta c je počáteční podmínka v bodě
KOMPLEXNÍ ČÍSLA. Algebraický tvar komplexního čísla
 KOMPLEXNÍ ČÍSLA Příklad Řešte na množně reálných čísel rovnc: x + = 0. x = Rovnce nemá v R řešení. Taková jednoduchá rovnce a nemá na množně reálných čísel žádné řešení! Co s tím? Zavedeme tzv. magnární
KOMPLEXNÍ ČÍSLA Příklad Řešte na množně reálných čísel rovnc: x + = 0. x = Rovnce nemá v R řešení. Taková jednoduchá rovnce a nemá na množně reálných čísel žádné řešení! Co s tím? Zavedeme tzv. magnární
2.5. MATICOVÉ ŘEŠENÍ SOUSTAV LINEÁRNÍCH ROVNIC
 25 MATICOVÉ ŘEŠENÍ SOUSTAV LINEÁRNÍCH ROVNIC V této kaptole se dozvíte: jak lze obecnou soustavu lneárních rovnc zapsat pomocí matcového počtu; přesnou formulac podmínek řeštelnost soustavy lneárních rovnc
25 MATICOVÉ ŘEŠENÍ SOUSTAV LINEÁRNÍCH ROVNIC V této kaptole se dozvíte: jak lze obecnou soustavu lneárních rovnc zapsat pomocí matcového počtu; přesnou formulac podmínek řeštelnost soustavy lneárních rovnc
Tepelná kapacita = T. Ē = 1 2 hν + hν. 1 = 1 e x. ln dx. Einsteinův výpočet (1907): Soustava N nezávislých oscilátorů se stejnou vlastní frekvencí má
 Tepelná kapacta C x = C V = ( ) dq ( ) du Dulong-Pettovo pravdlo: U = 3kT N C V = 3kN x V = T ( ) ds x Tepelná kapacta mřížky Osclátor s kvantovanou energí E n = ( n + 2) hν má střední hodnotu energe (po
Tepelná kapacta C x = C V = ( ) dq ( ) du Dulong-Pettovo pravdlo: U = 3kT N C V = 3kN x V = T ( ) ds x Tepelná kapacta mřížky Osclátor s kvantovanou energí E n = ( n + 2) hν má střední hodnotu energe (po
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6
 OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
OTÁZKY K PROCVIČOVÁNÍ PRUŽNOST A PLASTICITA II - DD6 POSUZOVÁNÍ KONSTRUKCÍ PODLE EUROKÓDŮ 1. Jaké mezní stavy rozlišujeme při posuzování konstrukcí podle EN? 2. Jaké problémy řeší mezní stav únosnosti
Vlastnosti a zkoušení materiálů. Přednáška č.4 Úvod do pružnosti a pevnosti
 Vlastnosti a zkoušení materiálů Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze
Vlastnosti a zkoušení materiálů Přednáška č.4 Úvod do pružnosti a pevnosti Teoretická a skutečná pevnost kovů Trvalá deformace polykrystalů začíná při vyšším napětí než u monokrystalů, tj. hodnota meze
Obr. 0.1: Nosník se spojitým zatížením.
 Každý test obsahuje jeden příklad podobný níže uvedeným tpovým příkladům a několik otázek vbraných z níže uvedených testových otázek. Za příklad je možno získat maimálně bodů, celkový počet bodů z testu
Každý test obsahuje jeden příklad podobný níže uvedeným tpovým příkladům a několik otázek vbraných z níže uvedených testových otázek. Za příklad je možno získat maimálně bodů, celkový počet bodů z testu
3 Základní modely reaktorů
 3 Základní modely reaktorů Rovnce popsující chování reakční směs v reaktoru (v čase a prostoru) vycházejí z blančních rovnc pro hmotu, energ a hybnost. Blanc lze formulovat pro extenzvní velčnu B v obecném
3 Základní modely reaktorů Rovnce popsující chování reakční směs v reaktoru (v čase a prostoru) vycházejí z blančních rovnc pro hmotu, energ a hybnost. Blanc lze formulovat pro extenzvní velčnu B v obecném
4. Napjatost v bodě tělesa
 p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
p04 1 4. Napjatost v bodě tělesa Předpokládejme, že bod C je nebezpečným bodem tělesa a pro zabránění vzniku mezních stavů je m.j. třeba zaručit, že napětí v tomto bodě nepřesáhne definované mezní hodnoty.
7 Lineární elasticita
 7 Lineární elasticita Elasticita je schopnost materiálu pružně se deformovat. Deformace ideálně elastických látek je okamžitá (časově nezávislá) a dokonale vratná. Působí-li na infinitezimální objemový
7 Lineární elasticita Elasticita je schopnost materiálu pružně se deformovat. Deformace ideálně elastických látek je okamžitá (časově nezávislá) a dokonale vratná. Působí-li na infinitezimální objemový
Odraz a lom rovinné monochromatické vlny na rovinném rozhraní dvou izotropních prostředí
 Odraz a lom rovnné monochromatcké vlny na rovnném rozhraní dvou zotropních prostředí Doplňující předpoklady: prostředí č.1, ze kterého vlna dopadá na rozhraní neabsorbuje (má r r reálný ndex lomu), obě
Odraz a lom rovnné monochromatcké vlny na rovnném rozhraní dvou zotropních prostředí Doplňující předpoklady: prostředí č.1, ze kterého vlna dopadá na rozhraní neabsorbuje (má r r reálný ndex lomu), obě
4/3.3. bodem v rovině (tvoří rovinný svazek sil), jsou vždy. rovnice z-ová. Pro rovnováhu takové soustavy
 STROJNICKÁ PŘÍRUČKA čá s t 4, d íl 3, k a p to la 3, str. 1 díl 3, Statka 4/3.3 ROVNOVÁHA TĚLESA Procházejí-l po uvolnění tělesa všechny síly jedním bodem v rovně (tvoří rovnný svazek sl), jsou vždy splněny
STROJNICKÁ PŘÍRUČKA čá s t 4, d íl 3, k a p to la 3, str. 1 díl 3, Statka 4/3.3 ROVNOVÁHA TĚLESA Procházejí-l po uvolnění tělesa všechny síly jedním bodem v rovně (tvoří rovnný svazek sl), jsou vždy splněny
Mechatronické systémy s elektronicky komutovanými motory
 Mechatroncké systémy s elektroncky komutovaným motory 1. EC motor Uvedený motor je zvláštním typem synchronního motoru nazývaný též bezkartáčovým stejnosměrným motorem (anglcky Brushless Drect Current
Mechatroncké systémy s elektroncky komutovaným motory 1. EC motor Uvedený motor je zvláštním typem synchronního motoru nazývaný též bezkartáčovým stejnosměrným motorem (anglcky Brushless Drect Current
Rovinná úloha v MKP. (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v. prostorové úlohy: u, v, w
 Rovinná úloha v MKP Hledané deformační veličiny viz klasická teorie pružnosti (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v desky: w, ϕ x, ϕ y prostorové úlohy: u,
Rovinná úloha v MKP Hledané deformační veličiny viz klasická teorie pružnosti (mohou být i jejich derivace!): rovinná napjatost a r. deformace (stěny,... ): u, v desky: w, ϕ x, ϕ y prostorové úlohy: u,
POTENCIÁL ELEKTRICKÉHO POLE ELEKTRICKÉ NAPĚTÍ
 POTENCIÁL ELEKTRICKÉHO POLE ELEKTRICKÉ NAPĚTÍ ELEKTRICKÝ POTENCIÁL Elektrcká potencální energe Newtonův zákon pro gravtační sílu mm F = G r 1 2 2 Coulombův zákon pro elektrostatckou sílu QQ F = k r 1 2
POTENCIÁL ELEKTRICKÉHO POLE ELEKTRICKÉ NAPĚTÍ ELEKTRICKÝ POTENCIÁL Elektrcká potencální energe Newtonův zákon pro gravtační sílu mm F = G r 1 2 2 Coulombův zákon pro elektrostatckou sílu QQ F = k r 1 2
Kinetika spalovacích reakcí
 Knetka spalovacích reakcí Základy knetky spalování - nauka o průběhu spalovacích reakcí a závslost rychlost reakcí na různých faktorech Hlavní faktory: - koncentrace reagujících látek - teplota - tlak
Knetka spalovacích reakcí Základy knetky spalování - nauka o průběhu spalovacích reakcí a závslost rychlost reakcí na různých faktorech Hlavní faktory: - koncentrace reagujících látek - teplota - tlak
Interpolace, ortogonální polynomy, Gaussova kvadratura
 Interpolace, ortogonální polynomy, Gaussova kvadratura Petr Tichý 20. listopadu 2013 1 Úloha Lagrangeovy interpolace Dán omezený uzavřený interval [a, b] a v něm n + 1 různých bodů x 0, x 1,..., x n. Nechť
Interpolace, ortogonální polynomy, Gaussova kvadratura Petr Tichý 20. listopadu 2013 1 Úloha Lagrangeovy interpolace Dán omezený uzavřený interval [a, b] a v něm n + 1 různých bodů x 0, x 1,..., x n. Nechť
Nelineární úlohy při výpočtu konstrukcí s využitím MKP
 Nelineární úlohy při výpočtu konstrukcí s využitím MKP Obsah přednášky Lineární a nelineární úlohy Typy nelinearit (geometrická, materiálová, kontakt,..) Příklady nelineárních problémů Teorie kontaktu,
Nelineární úlohy při výpočtu konstrukcí s využitím MKP Obsah přednášky Lineární a nelineární úlohy Typy nelinearit (geometrická, materiálová, kontakt,..) Příklady nelineárních problémů Teorie kontaktu,
KONSTITUČNÍ VZTAHY. 1. Tahová zkouška
 1. Tahová zkouška Tahová zkouška se provádí dle ČSN EN ISO 6892-1 (aktualizována v roce 2010) Je nejčastější mechanickou zkouškou kovových materiálů. Zkoušky se realizují na trhacích strojích, kde se zkušební
1. Tahová zkouška Tahová zkouška se provádí dle ČSN EN ISO 6892-1 (aktualizována v roce 2010) Je nejčastější mechanickou zkouškou kovových materiálů. Zkoušky se realizují na trhacích strojích, kde se zkušební
9. Měření kinetiky dohasínání fluorescence ve frekvenční doméně
 9. Měření knetky dohasínání fluorescence ve frekvenční doméně Gavolův experment (194) zdroj vzorek synchronní otáčení fázový posun detektor Měření dob žvota lumnscence Frekvenční doména - exctace harmoncky
9. Měření knetky dohasínání fluorescence ve frekvenční doméně Gavolův experment (194) zdroj vzorek synchronní otáčení fázový posun detektor Měření dob žvota lumnscence Frekvenční doména - exctace harmoncky
Ivana Linkeová SPECIÁLNÍ PŘÍPADY NURBS REPREZENTACE. 2 NURBS reprezentace křivek
 25. KONFERENCE O GEOMETRII A POČÍTAČOVÉ GRAFICE Ivana Lnkeová SPECIÁLNÍ PŘÍPADY NURBS REPREZENTACE Abstrakt Příspěvek prezentuje B-splne křvku a Coonsovu, Bézerovu a Fergusonovu kubku jako specální případy
25. KONFERENCE O GEOMETRII A POČÍTAČOVÉ GRAFICE Ivana Lnkeová SPECIÁLNÍ PŘÍPADY NURBS REPREZENTACE Abstrakt Příspěvek prezentuje B-splne křvku a Coonsovu, Bézerovu a Fergusonovu kubku jako specální případy
1. Spektrální rozklad samoadjungovaných operátorů 1.1. Motivace Vlastní čísla a vlastní vektory symetrické matice 1 1 A = 1 2.
 . Spektrální rozklad samoadjungovaných operátorů.. Motvace Vlastní čísla a vlastní vektory symetrcké matce A = A λe = λ λ = λ 3λ + = λ 3+ λ 3 Vlastní čísla jsou λ = 3+, λ = 3. Pro tato vlastní čísla nalezneme
. Spektrální rozklad samoadjungovaných operátorů.. Motvace Vlastní čísla a vlastní vektory symetrcké matce A = A λe = λ λ = λ 3λ + = λ 3+ λ 3 Vlastní čísla jsou λ = 3+, λ = 3. Pro tato vlastní čísla nalezneme
Numerická integrace konstitučních vztahů
 Numercká ntegrace konsttučních vztahů Po výočtu neznámých deformačních uzlových arametrů v každé terac NR metody je nutné stanovt naětí a deformace na rvcích. Nař. Jednoosý tah (vz obr. vravo) Pro nterval
Numercká ntegrace konsttučních vztahů Po výočtu neznámých deformačních uzlových arametrů v každé terac NR metody je nutné stanovt naětí a deformace na rvcích. Nař. Jednoosý tah (vz obr. vravo) Pro nterval
Relativistická kvantová mechanika
 Relatvstcká kvantová mechanka Mchal Lenc Poznámky k přednášce v jarním semestru Obrazy Postulát o kvantové kausaltě Evoluční operátor 3 Schrödngerův a Hesenbergův obraz 3 4 Interakční obraz4 Relatvta a
Relatvstcká kvantová mechanka Mchal Lenc Poznámky k přednášce v jarním semestru Obrazy Postulát o kvantové kausaltě Evoluční operátor 3 Schrödngerův a Hesenbergův obraz 3 4 Interakční obraz4 Relatvta a
1.1 Shrnutí základních poznatků
 1.1 Shrnutí základních poznatků Pojmem nádoba obvykle označujeme součásti strojů a zařízení, které jsou svým tvarem a charakterem namáhání shodné s dutými tělesy zatíženými vnitřním, popř. i vnějším tlakem.sohledemnatopovažujemezanádobyrůznápotrubíakotlovátělesa,alenapř.i
1.1 Shrnutí základních poznatků Pojmem nádoba obvykle označujeme součásti strojů a zařízení, které jsou svým tvarem a charakterem namáhání shodné s dutými tělesy zatíženými vnitřním, popř. i vnějším tlakem.sohledemnatopovažujemezanádobyrůznápotrubíakotlovátělesa,alenapř.i
LOGICKÉ OBVODY J I Ř Í K A L O U S E K
 LOGICKÉ OBVODY J I Ř Í K A L O U S E K Ostrava 2006 Obsah předmětu 1. ČÍSELNÉ SOUSTAVY... 2 1.1. Číselné soustavy - úvod... 2 1.2. Rozdělení číselných soustav... 2 1.3. Polyadcké číselné soustavy... 2
LOGICKÉ OBVODY J I Ř Í K A L O U S E K Ostrava 2006 Obsah předmětu 1. ČÍSELNÉ SOUSTAVY... 2 1.1. Číselné soustavy - úvod... 2 1.2. Rozdělení číselných soustav... 2 1.3. Polyadcké číselné soustavy... 2
vztažný systém obecné napětí předchozí OBSAH další
 p05 1 5. Deformace těles S deformací jako složkou mechanického pohybu jste se setkali už ve statice. Běžně je chápána jako změna rozměrů a tvaru tělesa. Lze ji popsat změnami vzdáleností různých dvou bodů
p05 1 5. Deformace těles S deformací jako složkou mechanického pohybu jste se setkali už ve statice. Běžně je chápána jako změna rozměrů a tvaru tělesa. Lze ji popsat změnami vzdáleností různých dvou bodů
Napěťový vektor 3d. Díky Wikipedia za obrázek. n n n
 Míry napětí Napěťový vektor 3d n n2 2 n,. n n n Zatížené těleso rozdělíme myšleným řezem na dvě části. Na malou plošku v okolí materiálového bodu P působí napěťový vektor (n) (n, x, t), který je spojitou
Míry napětí Napěťový vektor 3d n n2 2 n,. n n n Zatížené těleso rozdělíme myšleným řezem na dvě části. Na malou plošku v okolí materiálového bodu P působí napěťový vektor (n) (n, x, t), který je spojitou
Výslednice, rovnováha silové soustavy.
 Výslednce, ovnováha slové soustavy. Základy mechanky, 2. přednáška Obsah přednášky : výslednce a ovnováha slové soustavy, ovnce ovnováhy, postoová slová soustava Doba studa : as 1,5 hodny Cíl přednášky
Výslednce, ovnováha slové soustavy. Základy mechanky, 2. přednáška Obsah přednášky : výslednce a ovnováha slové soustavy, ovnce ovnováhy, postoová slová soustava Doba studa : as 1,5 hodny Cíl přednášky
ÚVOD DO MODELOVÁNÍ V MECHANICE
 ÚVOD DO MODELOVÁNÍ V MECHANICE PRUŽNOST A PEVNOST Přednáška č. 5 Prof. Ing. Vladislav Laš. CSc. MECHANIKA PODDAJNÝCH TĚLES Úkolem PP z inženýrského hlediska je navrhnout součásti nebo konstrukce, které
ÚVOD DO MODELOVÁNÍ V MECHANICE PRUŽNOST A PEVNOST Přednáška č. 5 Prof. Ing. Vladislav Laš. CSc. MECHANIKA PODDAJNÝCH TĚLES Úkolem PP z inženýrského hlediska je navrhnout součásti nebo konstrukce, které
KOMPLEXNÍ ČÍSLA. Algebraický tvar komplexního čísla
 KOMPLEXNÍ ČÍSLA Příklad 1 Řešte na množně reálných čísel rovnc: x + = 0. x = Rovnce nemá v R řešení. Taková jednoduchá rovnce a nemá na množně reálných čísel žádné řešení! Co s tím? Zavedeme tzv. magnární
KOMPLEXNÍ ČÍSLA Příklad 1 Řešte na množně reálných čísel rovnc: x + = 0. x = Rovnce nemá v R řešení. Taková jednoduchá rovnce a nemá na množně reálných čísel žádné řešení! Co s tím? Zavedeme tzv. magnární
Pružnost a plasticita II
 Pružnost a plastcta II 3. ročník bakalářského stua oc. Ing. Martn Krejsa, Ph.D. Katera stavební mechanky Moely položí Záklaové konstrukce Záklaové konstrukce zajšťují: přenesení tíhy vrchní stavby o položí
Pružnost a plastcta II 3. ročník bakalářského stua oc. Ing. Martn Krejsa, Ph.D. Katera stavební mechanky Moely položí Záklaové konstrukce Záklaové konstrukce zajšťují: přenesení tíhy vrchní stavby o položí
Téma 7, modely podloží
 Pružnost a plastcta II.,.ročník bakalářského stua, přenášky Janas, Téma 7, moely položí Úvo Wnklerův moel položí Pasternakův moel položí Pružný poloprostor Nosník na pružném Wnklerově položí, řešení ODM
Pružnost a plastcta II.,.ročník bakalářského stua, přenášky Janas, Téma 7, moely položí Úvo Wnklerův moel položí Pasternakův moel položí Pružný poloprostor Nosník na pružném Wnklerově položí, řešení ODM
Rovnováha soustavy hmotných bodů, princip virtuální práce
 K přednášce NUFY028 Teoretcká mechanka prozatímní učební text, verze 0. Prncp vrtuální práce Leoš Dvořák, MFF UK Praha, 204 Rovnováha soustav hmotných bodů, prncp vrtuální práce V této kaptole nepůjde
K přednášce NUFY028 Teoretcká mechanka prozatímní učební text, verze 0. Prncp vrtuální práce Leoš Dvořák, MFF UK Praha, 204 Rovnováha soustav hmotných bodů, prncp vrtuální práce V této kaptole nepůjde
Pružnost a plasticita II
 Pružnost a plastcta II 3. ročník bakalářského stua oc. Ing. Martn Kresa Ph.D. Katera stavební mechank Řešení nosných stěn metoou sítí 3 Řešení stěn metoou sítí metoa sítí (metoa konečných ferencí) těnová
Pružnost a plastcta II 3. ročník bakalářského stua oc. Ing. Martn Kresa Ph.D. Katera stavební mechank Řešení nosných stěn metoou sítí 3 Řešení stěn metoou sítí metoa sítí (metoa konečných ferencí) těnová
4EK211 Základy ekonometrie
 4EK211 Základy ekonometre Specální případy použtí MNČ Cvčení 8 Zuzana Dlouhá Specální případy použtí MNČ cvčení 1 7 = ekonometrcký model, který byl lneární v proměnných v parametrech MNČ můžeme použít,
4EK211 Základy ekonometre Specální případy použtí MNČ Cvčení 8 Zuzana Dlouhá Specální případy použtí MNČ cvčení 1 7 = ekonometrcký model, který byl lneární v proměnných v parametrech MNČ můžeme použít,
CHYBY MĚŘENÍ. uvádíme ve tvaru x = x ± δ.
 CHYBY MĚŘENÍ Úvod Představte s, že máte změřt délku válečku. Použjete posuvné měřítko a získáte určtou hodnotu. Pamětlv přísloví provedete ještě jedno měření. Ale ouha! Výsledek je jný. Co dělat? Měřt
CHYBY MĚŘENÍ Úvod Představte s, že máte změřt délku válečku. Použjete posuvné měřítko a získáte určtou hodnotu. Pamětlv přísloví provedete ještě jedno měření. Ale ouha! Výsledek je jný. Co dělat? Měřt
Iterační výpočty. Dokumentace k projektu pro předměty IZP a IUS. 22. listopadu projekt č. 2
 Dokumentace k projektu pro předměty IZP a IUS Iterační výpočty projekt č.. lstopadu 1 Autor: Mlan Setler, setl1@stud.ft.vutbr.cz Fakulta Informačních Technologí Vysoké Učení Techncké v Brně Obsah 1 Úvod...
Dokumentace k projektu pro předměty IZP a IUS Iterační výpočty projekt č.. lstopadu 1 Autor: Mlan Setler, setl1@stud.ft.vutbr.cz Fakulta Informačních Technologí Vysoké Učení Techncké v Brně Obsah 1 Úvod...
7. Základní formulace lineární PP
 p07 1 7. Základní formulace lineární PP Podle tvaru závislosti mezi vnějšími silami a deformačně napěťovými parametry tělesa dělíme pružnost a pevnost na lineární a nelineární. Lineární pružnost vyšetřuje
p07 1 7. Základní formulace lineární PP Podle tvaru závislosti mezi vnějšími silami a deformačně napěťovými parametry tělesa dělíme pružnost a pevnost na lineární a nelineární. Lineární pružnost vyšetřuje
Sylabus 18. Stabilita svahu
 Sylabus 18 Stablta svahu Stablta svahu Smykové plochy rovnná v hrubozrnných zemnách ev. u vrstevnatého ukloněného podloží válcová v jemnozrnných homogenních zemnách obecná nehomogenní podloží vč. stavebních
Sylabus 18 Stablta svahu Stablta svahu Smykové plochy rovnná v hrubozrnných zemnách ev. u vrstevnatého ukloněného podloží válcová v jemnozrnných homogenních zemnách obecná nehomogenní podloží vč. stavebních
České vysoké učení technické v Praze Fakulta biomedicínského inženýrství
 České vysoké učení techncké v Praze Fakulta bomedcínského nženýrství Úloha KA03/č. 4: Měření knematky a dynamky pohybu končetn pomocí akcelerometru Ing. Patrk Kutílek, Ph.D., Ing. Adam Žžka (kutlek@fbm.cvut.cz,
České vysoké učení techncké v Praze Fakulta bomedcínského nženýrství Úloha KA03/č. 4: Měření knematky a dynamky pohybu končetn pomocí akcelerometru Ing. Patrk Kutílek, Ph.D., Ing. Adam Žžka (kutlek@fbm.cvut.cz,
8a.Objektové metody viditelnosti. Robertsův algoritmus
 8a. OBJEKOVÉ MEODY VIDIELNOSI Cíl Po prostudování této kaptoly budete znát metody vdtelnost 3D objektů na základě prostorových vlastností těchto objektů tvořt algortmy pro určování vdtelnost hran a stěn
8a. OBJEKOVÉ MEODY VIDIELNOSI Cíl Po prostudování této kaptoly budete znát metody vdtelnost 3D objektů na základě prostorových vlastností těchto objektů tvořt algortmy pro určování vdtelnost hran a stěn
4EK211 Základy ekonometrie
 4EK211 Základy ekonometre Specální případy použtí MNČ Cvčení 9 Zuzana Dlouhá Specální případy použtí MNČ cvčení 1 8 = ekonometrcký model, který byl lneární v proměnných v parametrech MNČ můžeme použít,
4EK211 Základy ekonometre Specální případy použtí MNČ Cvčení 9 Zuzana Dlouhá Specální případy použtí MNČ cvčení 1 8 = ekonometrcký model, který byl lneární v proměnných v parametrech MNČ můžeme použít,
FAKULTA STAVEBNÍ. Telefon: WWW:
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ ZÁKLADY METODY KONEČNÝCH PRVKŮ Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast10.vsb.cz/brozovsky/
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STAVEBNÍ ZÁKLADY METODY KONEČNÝCH PRVKŮ Jiří Brožovský Kancelář: LP H 406/3 Telefon: 597 321 321 E-mail: jiri.brozovsky@vsb.cz WWW: http://fast10.vsb.cz/brozovsky/
Cvičení 7 (Matematická teorie pružnosti)
 VŠB Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti (339) Pružnost a pevnost v energetice (Návo do cvičení) Cvičení 7 (Matematická teorie pružnosti) Autor: Jaroslav Rojíček Verze:
VŠB Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti (339) Pružnost a pevnost v energetice (Návo do cvičení) Cvičení 7 (Matematická teorie pružnosti) Autor: Jaroslav Rojíček Verze:
VLIV VELIKOSTI OBCE NA TRŽNÍ CENY RODINNÝCH DOMŮ
 VLIV VELIKOSTI OBCE NA TRŽNÍ CENY RODINNÝCH DOMŮ Abstrakt Martn Cupal 1 Prncp tvorby tržní ceny nemovtost je sce založen na tržní nabídce a poptávce, avšak tento trh je značně nedokonalý. Nejvíce ovlvňuje
VLIV VELIKOSTI OBCE NA TRŽNÍ CENY RODINNÝCH DOMŮ Abstrakt Martn Cupal 1 Prncp tvorby tržní ceny nemovtost je sce založen na tržní nabídce a poptávce, avšak tento trh je značně nedokonalý. Nejvíce ovlvňuje
Jihočeská univerzita v Českých Budějovicích. Pedagogická fakulta Katedra fyziky. Bakalářská práce
 Jhočeská unverzta v Českých Budějovcích Pedagogcká fakulta Katedra fyzky Bakalářská práce České Budějovce 007 Tomáš Bürger Jhočeská unverzta v Českých Budějovcích Pedagogcká fakulta Katedra fyzky Generování
Jhočeská unverzta v Českých Budějovcích Pedagogcká fakulta Katedra fyzky Bakalářská práce České Budějovce 007 Tomáš Bürger Jhočeská unverzta v Českých Budějovcích Pedagogcká fakulta Katedra fyzky Generování
19 Eukleidovský bodový prostor
 19 Eukleidovský bodový prostor Eukleidovským bodovým prostorem rozumíme afinní bodový prostor, na jehož zaměření je definován skalární součin. Víme, že pomocí skalárního součinu jsou definovány pojmy norma
19 Eukleidovský bodový prostor Eukleidovským bodovým prostorem rozumíme afinní bodový prostor, na jehož zaměření je definován skalární součin. Víme, že pomocí skalárního součinu jsou definovány pojmy norma
1 Báze a dimenze vektorového prostoru 1
 1 Báze a dimenze vektorového prostoru 1 Báze a dimenze vektorového prostoru 1 2 Aritmetické vektorové prostory 7 3 Eukleidovské vektorové prostory 9 Levá vnější operace Definice 5.1 Necht A B. Levou vnější
1 Báze a dimenze vektorového prostoru 1 Báze a dimenze vektorového prostoru 1 2 Aritmetické vektorové prostory 7 3 Eukleidovské vektorové prostory 9 Levá vnější operace Definice 5.1 Necht A B. Levou vnější
7. ZÁKLADNÍ TYPY DYNAMICKÝCH SYSTÉMŮ
 7. ZÁKADNÍ TYPY DYNAMICKÝCH SYSTÉMŮ 7.. SPOJITÉ SYSTÉMY Téměř všechny fyzálně realzovatelné spojté lneární systémy (romě systémů s dopravním zpožděním lze vytvořt z prvů tří typů: proporconálních členů
7. ZÁKADNÍ TYPY DYNAMICKÝCH SYSTÉMŮ 7.. SPOJITÉ SYSTÉMY Téměř všechny fyzálně realzovatelné spojté lneární systémy (romě systémů s dopravním zpožděním lze vytvořt z prvů tří typů: proporconálních členů
Úloha 2: Měření modulu pružnosti v tahu a modulu pružnosti ve smyku
 Úloha 2: Měření modulu pružnost v tahu a modulu pružnost ve smyku FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 19.10.2009 Jméno: Frantšek Batysta Pracovní skupna: 11 Ročník a kroužek: 2. ročník,
Úloha 2: Měření modulu pružnost v tahu a modulu pružnost ve smyku FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Datum měření: 19.10.2009 Jméno: Frantšek Batysta Pracovní skupna: 11 Ročník a kroužek: 2. ročník,
Reologické modely technických materiálů při prostém tahu a tlaku
 . lekce Reologické modely technických materiálů při prostém tahu a tlaku Obsah. Základní pojmy Vnitřní síly napětí. Základní reologické modely technických materiálů 3.3 Elementární reologické modely creepu
. lekce Reologické modely technických materiálů při prostém tahu a tlaku Obsah. Základní pojmy Vnitřní síly napětí. Základní reologické modely technických materiálů 3.3 Elementární reologické modely creepu
Pružnost a pevnost I
 Stránka 1 teoretické otázk 2007 Ing. Tomáš PROFANT, Ph.D. verze 1.1 OBSAH: 1. Tenzor napětí 2. Věta o sdruženosti smkových napětí 3. Saint Venantův princip 4. Tenzor deformace (přetvoření) 5. Geometrická
Stránka 1 teoretické otázk 2007 Ing. Tomáš PROFANT, Ph.D. verze 1.1 OBSAH: 1. Tenzor napětí 2. Věta o sdruženosti smkových napětí 3. Saint Venantův princip 4. Tenzor deformace (přetvoření) 5. Geometrická
SIMULACE. Numerické řešení obyčejných diferenciálních rovnic. Měřicí a řídicí technika magisterské studium FTOP - přednášky ZS 2009/10
 SIMULACE numercké řešení dferencálních rovnc smulační program dentfkace modelu Numercké řešení obyčejných dferencálních rovnc krokové metody pro řešení lneárních dferencálních rovnc 1.řádu s počátečním
SIMULACE numercké řešení dferencálních rovnc smulační program dentfkace modelu Numercké řešení obyčejných dferencálních rovnc krokové metody pro řešení lneárních dferencálních rovnc 1.řádu s počátečním
Numerické metody optimalizace
 Numercké metody optmalzace Numercal optmzaton methods Bc. Mloš Jurek Dplomová práce 2007 Abstrakt Abstrakt česky Optmalzační metody představují vyhledávání etrémů reálných funkcí jedné nebo více reálných
Numercké metody optmalzace Numercal optmzaton methods Bc. Mloš Jurek Dplomová práce 2007 Abstrakt Abstrakt česky Optmalzační metody představují vyhledávání etrémů reálných funkcí jedné nebo více reálných
Martin NESLÁDEK. 14. listopadu 2017
 Martin NESLÁDEK Faculty of mechanical engineering, CTU in Prague 14. listopadu 2017 1 / 22 Poznámky k úlohám řešeným MKP Na přesnost simulace pomocí MKP a prostorové rozlišení výsledků má vliv především:
Martin NESLÁDEK Faculty of mechanical engineering, CTU in Prague 14. listopadu 2017 1 / 22 Poznámky k úlohám řešeným MKP Na přesnost simulace pomocí MKP a prostorové rozlišení výsledků má vliv především:
Dvě varianty rovinného problému: rovinná napjatost. rovinná deformace
 Rovinný problém Řešíme plošné konstrukce zatížené a uložené v jejich střednicové rovině. Dvě varianty rovinného problému: rovinná napjatost rovinná deformace 17 Rovinná deformace 1 Obsahuje složky deformace
Rovinný problém Řešíme plošné konstrukce zatížené a uložené v jejich střednicové rovině. Dvě varianty rovinného problému: rovinná napjatost rovinná deformace 17 Rovinná deformace 1 Obsahuje složky deformace
ANALÝZA A KLASIFIKACE DAT
 ANALÝZA A KLASIFIKACE DAT prof. Ing. Jří Holčík, CSc. INVESTICE Insttut DO bostatstky ROZVOJE VZDĚLÁVÁNÍ a analýz IV - pokračování KLASIFIKACE PODLE MINIMÁLNÍ VZDÁLENOSTI METRIKY PRO URČENÍ VZDÁLENOSTI
ANALÝZA A KLASIFIKACE DAT prof. Ing. Jří Holčík, CSc. INVESTICE Insttut DO bostatstky ROZVOJE VZDĚLÁVÁNÍ a analýz IV - pokračování KLASIFIKACE PODLE MINIMÁLNÍ VZDÁLENOSTI METRIKY PRO URČENÍ VZDÁLENOSTI
permutace, popisující nějaké symetrie, je i π permutace, popisující nějakou symetrii.
 DSM Cv Pólyova věta Budeme se zabývat objekty (na množně X - to jsou vrcholy těchto objektů) s různým prvky symetre (například to mohou být různé brože, tsky, ale také strukturní vzorce různých chemckých
DSM Cv Pólyova věta Budeme se zabývat objekty (na množně X - to jsou vrcholy těchto objektů) s různým prvky symetre (například to mohou být různé brože, tsky, ale také strukturní vzorce různých chemckých
Dynamika soustav hmotných bodů
 Dynamika soustav hmotných bodů Mechanický model, jehož pohyb je charakterizován pohybem dvou nebo více bodů, nazýváme soustavu hmotných bodů. Pro každý hmotný bod můžeme napsat pohybovou rovnici. Tedy
Dynamika soustav hmotných bodů Mechanický model, jehož pohyb je charakterizován pohybem dvou nebo více bodů, nazýváme soustavu hmotných bodů. Pro každý hmotný bod můžeme napsat pohybovou rovnici. Tedy
terminologie předchozí kapitoly: (ϕ, Ω) - plocha, S - geometrický obraz plochy
 2. Plošný integrál. Poznámka. Obecně: integrování přes k-rozměrné útvary (k-plochy) v R n. Omezíme se na případ k = 2, n = 3. Definice. Množina S R 3 se nazve plocha, pokud S = ϕ(), kde R 2 je otevřená
2. Plošný integrál. Poznámka. Obecně: integrování přes k-rozměrné útvary (k-plochy) v R n. Omezíme se na případ k = 2, n = 3. Definice. Množina S R 3 se nazve plocha, pokud S = ϕ(), kde R 2 je otevřená
21. Úvod do teorie parciálních diferenciálních rovnic
 21. Úvod do teorie parciálních diferenciálních rovnic Aplikovaná matematika IV, NMAF074 M. Rokyta, KMA MFF UK LS 2014/15 21.1 Základní termíny Definice Vektor tvaru α = (α 1,...,α m ), kde α j N {0}, j
21. Úvod do teorie parciálních diferenciálních rovnic Aplikovaná matematika IV, NMAF074 M. Rokyta, KMA MFF UK LS 2014/15 21.1 Základní termíny Definice Vektor tvaru α = (α 1,...,α m ), kde α j N {0}, j
Přednáška 08. Obecná trojosá napjatost
 Přednáška 8 Obecná trojosá napjatost Napětí statické rovnice Deformace geometrické rovnice Zobecněný Hookeův zákon Objemový modul pružnosti Oedometrický modul pružnosti Hlavní napětí, hlavní deformace
Přednáška 8 Obecná trojosá napjatost Napětí statické rovnice Deformace geometrické rovnice Zobecněný Hookeův zákon Objemový modul pružnosti Oedometrický modul pružnosti Hlavní napětí, hlavní deformace
Dnešní látka: Literatura: Kapitoly 3 a 4 ze skript Karel Rektorys: Matematika 43, ČVUT, Praha, Text přednášky na webové stránce přednášejícího.
 Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Předmět: MA4 Dnešní látka: Od okrajových úloh v 1D k o. ú. ve 2D Laplaceův diferenciální operátor Variačně formulované okrajové úlohy pro parciální diferenciální rovnice a metody jejich přibližného řešení
Nelineární analýza materiálů a konstrukcí (V-132YNAK) Přednáška 2 Princip metody konečných prvků
 Nelineární analýza materiálů a konstrukcí (V-132YNAK) Přednáška 2 Princip metody konečných prvků Petr Kabele petr.kabele@fsv.cvut.cz people.fsv.cvut.cz/~pkabele Petr Kabele, 2007-2014 Obsah Variační principy
Nelineární analýza materiálů a konstrukcí (V-132YNAK) Přednáška 2 Princip metody konečných prvků Petr Kabele petr.kabele@fsv.cvut.cz people.fsv.cvut.cz/~pkabele Petr Kabele, 2007-2014 Obsah Variační principy
Úvod do analytické mechaniky
 Úvod do analytické mechaniky Vektorová mechanika, která je někdy nazývána jako Newtonova, vychází bezprostředně z principů, které jsou vyjádřeny vztahy mezi vektorovými veličinami. V tomto případě např.
Úvod do analytické mechaniky Vektorová mechanika, která je někdy nazývána jako Newtonova, vychází bezprostředně z principů, které jsou vyjádřeny vztahy mezi vektorovými veličinami. V tomto případě např.
