9. SEMINÁŘ Z MECHANIKY
|
|
|
- Kamil Mareš
- před 5 lety
- Počet zobrazení:
Transkript
1 SENÁŘ Z ECHNKY 9 Sevční ( = 5 g ) se ozáčí z lidu Z jou dobu dosáne fevence 48 in, působí-li n něj oen síly N ěžišě? = ; ( ) 5 g 3 vzlede ose pocázející jeo () f = ; f = 48 in = 8 s ; = 3 N ; =? ω= π f =ε π f = ε= ε=, = π f 9 ěžý en je zdvián po nloněné ovině poocí dvou ln upevněnýc oníu onci nloněné oviny Honos ( ) ene je 4 g, výš ( ) nloněné oviny je její dél () l je ou silou je nuno ánou z ždé z ln? G l ; ; l ; g ; F =? Úlo je nlogicá použií volné ldy Podínou ovnováy ene ( í i jeo ovnoěné zvedání po nloněné ovině) je nulová výslednice sil působícíc n en F g sin g F + 4F = F 4F = F = = ; sin= F = 4 4 l 4l Ke sejnéu výsledu ůžee dojí i sovnání páce W vyonné dvě sili po dáze l s příůse poenciální enegie Ep ene při zvednuí jeo ěžišě o výšu Plí edy W = Ep Fl = g F g F = 4l 93 Plný oogenní íč onosi g poloěu c se poybuje yclosí 8 s Učee jeo (ožiou) ineicou enegii N jé dáze se zsví, je-li eno vlivéo odpou,5 c? = g ; = c ; v = 8 s ; ξ=,5 c E, s=? íč oná posuvný poyb yclosí v součsně se oáčí ole osy o pocázející ěžišě; poo E = E,pos + E,o = v + ω F
2 = = ω 5 ; v v E 5 = v + E 7 = v g 7 Fs v E s = ξ = v 7v s = ξg 94 Kulič o půěu 3 c vlící se po podlze se zsví z dobu s n dáze,4 Učee eno vlivéo odpou ezi uličou podlou d = 3 c ; = s ; s =,4 ; ξ=? = = = v ; s = = v v v v v s v = 7 = ; v =ω ; E = v + ω E = v 5 W = F s v W =ξ g s ; W = E E 7 4s = g 7 4s 4 ξ s = ξ= s 5 g 95 N osu činy ( ) jsou nvinuy dvě suny, eé jsou připevněny pevné vodoovné yči esliže činu pusíe, pdá záoveň se oáčí ylo pozoováno, že zyclení jejío pádu je Vypočěe ovou sílu v ždé suně á by usel bý o síl ve sunác, by oný sřed činy zůsávl sále ve sejné výši? g ; ; g ; =? N činu, poybující se oě očnío i posuvný poybe se zyclení, působí síl, složená z íové síly ecí ( g ) sun, eé jsou opčné ový silá ( = ; = ) Poo plí = g + = g = g = ( g ) Neá-li se čin poybov posuvný poybe (což je ovnocenné podínce = ), je nuno, by ová síl v ždé suně byl ovn polovině íy činy = = g 96 Svislý sloup o výšce se ácí ole svéo nejnižšío bodu Učee yclos dopdu jeo onío once o d ; g ; v =? oen sevčnosi vzlede ose pocázející ěžišě olo e sloupu: σ= ; d =ρd o
3 σ 3 σ = σ d = 3 = = σ = SENEOV vě po osu ácení sloupu (olou e sloupu) pocázející jeo once: 3 4 = + = + 3 = Úbye Ep poenciální enegie sloupu při polesu ěžišě o je oven jeo oční ineicé enegii E při dopdu n ze edy 3 Ep = E g = ω g = ω ω= 3 Nejvyšší bod sloupu se poybuje po užnici o poloěu, jeo obvodová yclos při dopdu je edy 3g v = ω= v = 3g 97 S řídelí o poloěu je pevně spojen plný oouč o poloěu onosi Hřídel i oouč jsou ze sejnéo eiálu, čási řídele vyčnívjící z oouče jí onos Přísoj je zvěšen n sivu dvě sejně dlouýi vlány připevněnýi řídeli Noáe-li vlán n řídel, oouč se zvedne Zčnou-li se vlán odoáv, oouč lesá Učee zyclení lesjícío O oouče ( )g + ; ; ; ; g =? g oen sevčnosi ěles vzlede ose je (sejně jo onos) diivní veličin je-li ěleso vořeno něoli (oogenníi) ělesy, je jeo oen sevčnosi vzlede libovolné příce oven souču oenů sevčnosi ěco ěles vzlede éo příce Osou o oáčení je pří olá ovině ppíu pocázející bode O SENEOV vě: ε= Koouč (, ):, =, válec ( ), :, = = +, = + ; = + = ( ) ( ) o ( ) ( + ) g ( + ) + ( + ) o ; = + g ε= o ε= ; = ε = ( + ) ( + ) + ( + ) g
4 N vodoovné sole leží cív nií ( ),, é bude posupné zyclení cívy, ánee-li z ni silou F? ý usí bý sě síly, á-li se cív poybov ve sěu npjé nii? o p ; ; ; F ; =? Po zyclení posuvnéo poybu (ěžišě) cívy dosáváe =ε = Disuse o sěu síly sěu zyclení Podle SENEOVY věy je oen sevčnosi cívy vzlede ose o = + oen síly vzlede ose o á velios = Fp = F( cos ) Z poybové ovnice oáčení cívy vyjádříe úlové zyclení ( cos ) ( s ) F co ε= ε= + + V nái zeslené přípdě obecně edy, dyž ; ccos =, se cív oáčí, že se její ěžišě posouvá zlev dopv (přibližně edy ve sěu síly cív je poslušná ni se při její poybu nvíjí) Po = ccos se cív neoáčí (oen síly vzlede ose o je nulový) je (přibližně) ve sěu síly vlečen C Po > ccos se cív při oáčení v opčné syslu, než v přípdě, posouvá zpv dolev cív je neposlušná ni se z ní při oáčení odvíjí 99 Sevční ( g F = ) je souose připevněn n řídeli ( =,5 ) onos i oen sevčnosi znedbáváe N řídeli je nvinuo lno, n něž visí závží ( = 4 g) S j velý zyclení se sevční ozáčí jou dáu - uzí závží z s? ( g = s ) Dynicé řešení Po zyclení poybu závží plí = g ; = s ; =,5 ; = 4 g ε, s =?, jeož
5 = g = ( g ) g Sevční je ozáčen silou, že poybová ovnice jeo očnío poybu ole pevné vodoovné osy pocázející ε= jeo ěžišě (olo ovině náesu) á v ( ) ε= Dosdíe-li do ooo výzu z z ε, dosnee g = ( g ) + = g = + g ε= +, ε=, s Dáu s závží z čs od zčáu jeo poybu z lidu učíe jo Enegeicé řešení s = s = g +, s = Souče ineicé enegie E,o očnío poybu sevčníu ineicé enegie E posuvnéo poybu závží je oven bsoluní odnoě úbyu Ep poenciální enegie závží; plí edy enegeicá bilnce Ep = E,o + E s = ω + g v Dosdíe-li do ooo výzu z ω výz v, dosnee v gs = + v Deivujee-li poslední ovnici podle čsu, obdžíe d s dv g = + v gv = + v d d s = + g v g = + ε= g + 9 N nloněné ovině ( ) se ncází oogenní ulič Po jé odnoy (sicéo) součiniele (y) N n g () řecí síly ezi uličou nloněnou ovinou nebude ulič při své poybu po nloněné ovině louz? Předpoládeje, že ulič (, ) při poybu po nloněné ovině nepoluzuje (jde o zv čisé vlení) Poybové ovnice posuvnéo poybu ěžišě uličy oce uličy (ole vodoovné osy pocázející ěžišě uličy olé e spádové příce nloněné oviny) p ůžee zps ve vu = g sin, y = = N g cos;
6 - 6 - ω= ; N = g cos je ece nloněné oviny n íu uličy; je oen sevčnosi uličy vzlede ose pocázející ěžišě; je velios zv dezní síly, zjišťující čisé válení uličy, což je sv, při něž je (ožiý) doyový bod uličy vůči nloněné ovině v lidu Z éo siuce je ožno složený poyb uličy převés n čisou oci ole osy pocázející bode P plí = v = ω, = ω z výše uvedenýc poybovýc ovnic dosáváe ω= + sin sin ω= g + = g gsin gsin = = + + ( +ϕ) g sin = ; ϕ= +ϕ g sin g sin ϕg sin ω= = ω= = +ϕ +ϕ á-li bý dezní silou řecí síl, usí po její velios pli Po uliču plí ϕg sin ϕ F = g cos = g +ϕ +ϕ 5 5 = ϕ= g 7 9 Přes pevnou ldu, jejíž onos je =,8 g, je veden doonle oebná ni znedbelné onosi N oncíc nii visí závží o onosec =, g =, g Učee zyclení sousvy při poybu závží následe íové síly síly npínjící ni =,8 g ; =, g ; =, g ;,, =? g g Uvžujee-li onos ldy, usíe opusi předsvu o sejně veliýc silác npínjícíc ni n obou snác ldy K ozáčení ldy o poloěu je oiž zpořebí nenulový výsledný oen = = ( ) co do veliosi ůznýc sil npínjícíc ni n obou snác ldy (v nše přípdě je > ) Poybová ovnice ldy je p = ε ( ) = ε Nedocází-li poluzování nii n obvodu ldy, je souvislos úlovéo zyclení ε ldy (posuvnéo) zyclení nii obou závží dán vze = ε Zpíšee duý poybový záon po obě závží závží =, g = ( g + )
7 závží = = g ; ( jsou ece nii n síly, eé je npínjí =, = ) Poybovou ovnici ldy ůžee po doszení z zps ve vu g ( ) ( ) = ε ( ) ( ) g g + = + + = ( ) g = + + g Poládáe-li ldu z oogenní oouč onosi poloěu, á její oen sevčnosi vzlede vodoovné ose pocázející ěžišě odnou ( ) = = g + + Dosdíe-li z zyclení do vyjádření sil, obdžíe po veliosi sil npínjící ni vzy = g, 4 + = g > Přes pevnou ldu uísěnou n oji solu je veden doonle oebná ni znedbelné onosi Honos ldy je =, g Závží onosi =,5 g upevněné n jedno onci nii leží n sole, n dué onci nii visí závží onosi =, g Součiniel řecí síly ezi pvní závží desou solu je =, Učee zyclení sousvy při poybu závží následe íové síly síly npínjící ni =,5 g ; =, g ; =, g ; =, ; = 9,8 s ; ( ) = = ε; ε= = g g = g,, =? g = + ; = g ( ) = = g g g g = ( ) = g, + + = ; 3, 43 s ( ) + + = g, =, 3 N ; + + ( ) + + = g, =,8 N + +
8 N pevné ldce onosi je upevněn nvinu doonle oebná ni znedbelné onosi N onci nii visí závží onosi Učee zyclení závží při jeo poybu následe íové síly sílu npínjící ni = ( + ) ; = ( ) g g + = ε; ( g ) = ε= = g = g 94 Do slenice vu očnío válce (,, ) = g, = g + + v ) nléváe plinu ( ) výšce ldiny ( bude í slenice s plinou nejvěší sbiliu ; ; ; ρ ; =? V souřdnicové syséu onéo sředu sousvy slenice + plin plí Položíe-li ρs = s P ( ) Sρ = =, dosnee = = Sρ + Sρ () ρ Při jé Nyní ledáe loální iniu éo funce v závislosi n poěnné (n výšce ldiny pliny v nádobě) Z podíny nulové pvní deivce dosnee posupně ( ) ( + ) d + = = d + = + Řešení éo vdicé ovnice dosnee (vyovující) řešení ve vu, ± + = = + = Dosdíe-li uo odnou poěnné do funce (), dosnee odnou jejío loálnío ini in ( ) = = + ( ) = = + +
9 in ( ) = + = = in = Sbili slenice s plinou je edy nejvěší (ěžišě sousvy je nejníže), je-li oný sřed sousvy slenice + plin v úovni ldiny pliny ve slenici Konéní odnou in = byco oli uči při znlosi odno (onsn)
4. SEMINÁŘ Z MECHANIKY
 - 9-4. SEMINÁŘ Z MECHNIKY 4. Čloěk drží jeden konec prkn, jeož druý konec leží n álci. Čloěk zčne posou prkno kupředu k, by se álec lil po odoroné roině bez prokluzoání by ni prkno po álci neklouzlo. Jkou
- 9-4. SEMINÁŘ Z MECHNIKY 4. Čloěk drží jeden konec prkn, jeož druý konec leží n álci. Čloěk zčne posou prkno kupředu k, by se álec lil po odoroné roině bez prokluzoání by ni prkno po álci neklouzlo. Jkou
11. cvičení z Matematiky 2
 11. cvičení z Mateatiky. - 6. května 16 11.1 Vypočtěte 1 x + y + z dv, kde : x + y + z 1. Věta o substituci á analogický tva a podínky pouze zanedbatelné nožiny nyní zahnují i plochy, oviny atd.: f dv
11. cvičení z Mateatiky. - 6. května 16 11.1 Vypočtěte 1 x + y + z dv, kde : x + y + z 1. Věta o substituci á analogický tva a podínky pouze zanedbatelné nožiny nyní zahnují i plochy, oviny atd.: f dv
Pohyb tělesa, základní typy pohybů, pohyb posuvný a rotační. Obsah přednášky : typy pohybů tělesa posuvný pohyb rotační pohyb geometrie hmot
 Pohyb tělesa, základní typy pohybů, pohyb posuvný a otační Obsah přednášky : typy pohybů tělesa posuvný pohyb otační pohyb geoetie hot Pohyb tělesa, základní typy pohybů, pohyb posuvný a otační posuvný
Pohyb tělesa, základní typy pohybů, pohyb posuvný a otační Obsah přednášky : typy pohybů tělesa posuvný pohyb otační pohyb geoetie hot Pohyb tělesa, základní typy pohybů, pohyb posuvný a otační posuvný
Řešení úloh krajského kola 58. ročníku fyzikální olympiády Kategorie B Autor úloh: J. Thomas
 Řešení úlo kajskéo kola 58 očníku fyzikální olympiády Kategoie B Auto úlo: J Tomas a) Doba letu střely od okamžiku výstřelu do zásau označíme t V okamžiku výstřelu se usa nacází ve vzdálenosti s měřené
Řešení úlo kajskéo kola 58 očníku fyzikální olympiády Kategoie B Auto úlo: J Tomas a) Doba letu střely od okamžiku výstřelu do zásau označíme t V okamžiku výstřelu se usa nacází ve vzdálenosti s měřené
Řešení testu 2b. Fyzika I (Mechanika a molekulová fyzika) NOFY ledna 2016
 Řešení testu b Fika I (Mecanika a molekulová fika NOFY. ledna 6 Příklad Zadání: Po kouli o poloměu se be pokluovaní valí malá koule o poloměu. Jaká bude úlová clost otáčení malé koule v okamžiku kd se
Řešení testu b Fika I (Mecanika a molekulová fika NOFY. ledna 6 Příklad Zadání: Po kouli o poloměu se be pokluovaní valí malá koule o poloměu. Jaká bude úlová clost otáčení malé koule v okamžiku kd se
( ) 1.7.8 Statika I. Předpoklady: 1707
 .7.8 Sik I Přeokly: 707 Peoická oznámk: Hoinu rozěluji n vě čási. V rvní čási (5 minu) očíáme rvní čyři říkly, ve ruhé (0 minu) zývjící ři. Př. : N koncích yče o hmonosi 0 k élce m jsou zvěšen závží o
.7.8 Sik I Přeokly: 707 Peoická oznámk: Hoinu rozěluji n vě čási. V rvní čási (5 minu) očíáme rvní čyři říkly, ve ruhé (0 minu) zývjící ři. Př. : N koncích yče o hmonosi 0 k élce m jsou zvěšen závží o
Kmitání, vlnění, akustika 1. Kmitavý pohyb
 Kiání, vnění, usi. Kivý pohb. Poje ivého pohbu Děj, eý se opuje v učié čsové inevu. Opuje-i se pvideně nějý pohbový sv nzýváe ho peiodicý pohb. Mění-i se pvideně s čse jiná fziání vsnos (epo, eeicé npěí,
Kiání, vnění, usi. Kivý pohb. Poje ivého pohbu Děj, eý se opuje v učié čsové inevu. Opuje-i se pvideně nějý pohbový sv nzýváe ho peiodicý pohb. Mění-i se pvideně s čse jiná fziání vsnos (epo, eeicé npěí,
Projekt realizovaný na SPŠ Nové Město nad Metují. s finanční podporou v Operačním programu Vzdělávání pro konkurenceschopnost Královéhradeckého kraje
 Projek realizovaný na SPŠ Nové Měso nad Meují s finanční podporou v Operační prograu Vzdělávání pro konkurenceschopnos Královéhradeckého kraje Modul 3 - Technické předěy ng. Jan Jeelík 4. Pohybová energie
Projek realizovaný na SPŠ Nové Měso nad Meují s finanční podporou v Operační prograu Vzdělávání pro konkurenceschopnos Královéhradeckého kraje Modul 3 - Technické předěy ng. Jan Jeelík 4. Pohybová energie
Příklad 70 Vypočet konstanty šíření (fázová konstanta, měrný útlum)
 Přílad 7 Vypočt onstanty šířní (fáová onstanta, ěný útlu) adání : Rovinná haonicá ltoagnticá vlna o itočtu : a) f 5 b) f 7 M c) f 9 G s šíří v postřdí s těito paaty:.[ S ], ε 8, µ. Vaianta a) Vaianta b)
Přílad 7 Vypočt onstanty šířní (fáová onstanta, ěný útlu) adání : Rovinná haonicá ltoagnticá vlna o itočtu : a) f 5 b) f 7 M c) f 9 G s šíří v postřdí s těito paaty:.[ S ], ε 8, µ. Vaianta a) Vaianta b)
Statika 1. Miroslav Vokáč ČVUT v Praze, Fakulta architektury. Statika 1. M. Vokáč. Plocha.
 Saika 1 Saika 1 2. přednáška ové veličin Saický momen Těžišě Momen servačnosi Hlavní ěžiš ové os a hlavní cenrální momen servačnosi Elipsa servačnosi Miroslav Vokáč miroslav.vokac@klok.cvu.cz Konrolní
Saika 1 Saika 1 2. přednáška ové veličin Saický momen Těžišě Momen servačnosi Hlavní ěžiš ové os a hlavní cenrální momen servačnosi Elipsa servačnosi Miroslav Vokáč miroslav.vokac@klok.cvu.cz Konrolní
Přijímací zkoušky do navazujícího magisterského studia Učitelství fyziky pro 2. stupeň ZŠ a Učitelství fyziky pro SŠ pro akademický rok 2011/2012
 řijíí ouš do ujíío iseséo sudi čielsí fi po. supeň Š čielsí fi po SŠ po deiý o 0/0 Koouč o poloěu 0 oosi se ůže oáče ole odooé os. N oouči je iuo eé láo. N oi lá isí áží o oosi. ou á oouč úloou los, uí-li
řijíí ouš do ujíío iseséo sudi čielsí fi po. supeň Š čielsí fi po SŠ po deiý o 0/0 Koouč o poloěu 0 oosi se ůže oáče ole odooé os. N oouči je iuo eé láo. N oi lá isí áží o oosi. ou á oouč úloou los, uí-li
metoda uvolňování metoda redukce G 1 G 2
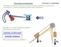 Dynik echnisů Dynik echnisů pojednává o vzthu ezi sili, působícíi n soustvu těles - echnisus, pohybe echnisu, těito sili způsobené. Seznáíe se se dvě zákldníi etodi řešení dyniky echnisů. etod uvolňování
Dynik echnisů Dynik echnisů pojednává o vzthu ezi sili, působícíi n soustvu těles - echnisus, pohybe echnisu, těito sili způsobené. Seznáíe se se dvě zákldníi etodi řešení dyniky echnisů. etod uvolňování
a polohovými vektory r k
 Mechania hmotných soustav Hmotná soustava (HS) je supina objetů, o teých je vhodné uvažovat jao o celu Pvy HS se pohybují účinem sil N a) vnitřních: Σ ( F + F + L+ F ) 0 i 1 i1 b) vnějších: síly od objetů,
Mechania hmotných soustav Hmotná soustava (HS) je supina objetů, o teých je vhodné uvažovat jao o celu Pvy HS se pohybují účinem sil N a) vnitřních: Σ ( F + F + L+ F ) 0 i 1 i1 b) vnějších: síly od objetů,
Dynamika tuhého tělesa. Petr Šidlof
 Dnaika tuhého tělesa Pet Šidlof Dnaika tuhého tělesa Pvní věta ipulsová F dp dt a t Zchlení těžiště Výslednice vnějších sil F A F B F C Celková hbnost soustav p p i Hotnost soustav i těžiště soustav se
Dnaika tuhého tělesa Pet Šidlof Dnaika tuhého tělesa Pvní věta ipulsová F dp dt a t Zchlení těžiště Výslednice vnějších sil F A F B F C Celková hbnost soustav p p i Hotnost soustav i těžiště soustav se
seznámit studenty se základními typy pohybu tělesa, s kinematikou a dynamikou posuvného a rotačního pohybu
 Dynaika, 5. přednáška Obsah přednášky : typy pohybů těesa posuvný pohyb otační pohyb geoetie hot Doba studia : asi,5 hodiny Cí přednášky : seznáit studenty se zákadníi typy pohybu těesa, s kineatikou a
Dynaika, 5. přednáška Obsah přednášky : typy pohybů těesa posuvný pohyb otační pohyb geoetie hot Doba studia : asi,5 hodiny Cí přednášky : seznáit studenty se zákadníi typy pohybu těesa, s kineatikou a
Posuvný a rotační pohyb tělesa.
 Posuvný a otační pohyb těesa. Zákady echaniky, 4. přednáška Obsah přednášky : typy pohybů těesa posuvný pohyb otační pohyb geoetie hot Doba studia : asi,5 hodiny Cí přednášky : seznáit studenty se zákadníi
Posuvný a otační pohyb těesa. Zákady echaniky, 4. přednáška Obsah přednášky : typy pohybů těesa posuvný pohyb otační pohyb geoetie hot Doba studia : asi,5 hodiny Cí přednášky : seznáit studenty se zákadníi
 ú ó ú ó ú ú ó š Í Ť ň ŠÍ Ů ň ú Ů ó š ú ú ň š ú š ť ť ú š š ú ť úť Ď š š ú ú ť ú É ú ó ú ť š É ú ó ú ú ó ú ť ť ó ú ó ť ú ň ú ó ú ú ó ó ó Ý ň ú ú ó ó óé ó ú ó ú ó ó Ó ň ó ó ó ú ú ó ó ó ó ó ó ó ó ú ó ó ú
ú ó ú ó ú ú ó š Í Ť ň ŠÍ Ů ň ú Ů ó š ú ú ň š ú š ť ť ú š š ú ť úť Ď š š ú ú ť ú É ú ó ú ť š É ú ó ú ú ó ú ť ť ó ú ó ť ú ň ú ó ú ú ó ó ó Ý ň ú ú ó ó óé ó ú ó ú ó ó Ó ň ó ó ó ú ú ó ó ó ó ó ó ó ó ú ó ó ú
FYZIKA I. Pohyb těles po podložce
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHICKÁ UIVERZITA OSTRAVA FAKULTA STROJÍ FYZIKA I Pohyb ěles po podložce Prof. RDr. Vilé Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D. Doc. Ing. Irena Hlaváčová, Ph.D. Mgr. Ar. Dagar Mádrová
VYSOKÁ ŠKOLA BÁŇSKÁ TECHICKÁ UIVERZITA OSTRAVA FAKULTA STROJÍ FYZIKA I Pohyb ěles po podložce Prof. RDr. Vilé Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D. Doc. Ing. Irena Hlaváčová, Ph.D. Mgr. Ar. Dagar Mádrová
Kinematika a dynamika soustavy těles
 Knemaka a dynamka sousay ěles Vyšeřoání poybu mecansmů Analycké yšeřoání poybu mecansmu le poés pomocí doé funkce j. au me souřadncem popsujícím polou nacío a nanýc členů. Posup je paný níže uedenéo příkladu.
Knemaka a dynamka sousay ěles Vyšeřoání poybu mecansmů Analycké yšeřoání poybu mecansmu le poés pomocí doé funkce j. au me souřadncem popsujícím polou nacío a nanýc členů. Posup je paný níže uedenéo příkladu.
Obsah přednášky : Dynamika mechanismů. dynamika mechanismů - metoda uvolňování, dynamika mechanismů - metoda redukce
 Obsh přednášky : Dynik echnisů dynik echnisů - etod uvolňování, dynik echnisů - etod edukce Dynik echnisů Dynik echnisů pojednává o vzthu ezi sili, působícíi n soustvu těles - echnisus, pohybe echnisu,
Obsh přednášky : Dynik echnisů dynik echnisů - etod uvolňování, dynik echnisů - etod edukce Dynik echnisů Dynik echnisů pojednává o vzthu ezi sili, působícíi n soustvu těles - echnisus, pohybe echnisu,
Gravitační pole. a nepřímo úměrná čtverci vzdáleností r. r r
 Newtonův avitační zákon: Gavitační pole ezi dvěa tělesy o hotnostech 1 a, kteé jsou od sebe vzdáleny o, působí stejně velké síly vzájené přitažlivosti, jejichž velikost je přío úěná součinu hotností 1
Newtonův avitační zákon: Gavitační pole ezi dvěa tělesy o hotnostech 1 a, kteé jsou od sebe vzdáleny o, působí stejně velké síly vzájené přitažlivosti, jejichž velikost je přío úěná součinu hotností 1
Napětí horninového masivu
 Npětí honinového msivu pimání npjtostí sekundání npjtostí účinky n stbilitu podzemního díl Dále můžeme uvžovt * bobtnání honiny * teplotní stv honiny J. Pušk MH 6. přednášk 1 Pimání npjtost gvitční (vyvolán
Npětí honinového msivu pimání npjtostí sekundání npjtostí účinky n stbilitu podzemního díl Dále můžeme uvžovt * bobtnání honiny * teplotní stv honiny J. Pušk MH 6. přednášk 1 Pimání npjtost gvitční (vyvolán
Pohyb tělesa. rovinný pohyb : Všechny body tělesa se pohybují v navzájem rovnoběžných rovinách. prostorový pohyb. posuvný pohyb. rotační.
 Pohyb těesa posuvný pohyb otační pohyb obecný ovinný pohyb posuvný pohyb ovinný pohyb : Všechny body těesa se pohybují v navzáje ovnoběžných ovinách. postoový pohyb sféický pohyb šoubový pohyb obecný postoový
Pohyb těesa posuvný pohyb otační pohyb obecný ovinný pohyb posuvný pohyb ovinný pohyb : Všechny body těesa se pohybují v navzáje ovnoběžných ovinách. postoový pohyb sféický pohyb šoubový pohyb obecný postoový
DOPLŇKOVÉ TEXTY BB01 PAVEL SCHAUER INTERNÍ MATERIÁL FAST VUT V BRNĚ TUHÉ TĚLESO
 DOPLŇKOÉ TXTY BB0 PAL SCHAUR INTRNÍ MATRIÁL FAST UT BRNĚ TUHÉ TĚLSO Tuhé těleso je těleso, o teé latí, že libovolná síla ůsobící na těleso nezůsobí jeho defoaci, ale ůže ít ouze ohybový účine. Libovolná
DOPLŇKOÉ TXTY BB0 PAL SCHAUR INTRNÍ MATRIÁL FAST UT BRNĚ TUHÉ TĚLSO Tuhé těleso je těleso, o teé latí, že libovolná síla ůsobící na těleso nezůsobí jeho defoaci, ale ůže ít ouze ohybový účine. Libovolná
Válcová momentová skořepina
 Válcová momenová skořepina Momenová skořepina je enkosěnné ěleso, jež nesplňuje předpoklady o membánové napjaosi. Válcová skořepina je vlášním případem skořepiny oačně symeické, musí edy splňova podmínky
Válcová momenová skořepina Momenová skořepina je enkosěnné ěleso, jež nesplňuje předpoklady o membánové napjaosi. Válcová skořepina je vlášním případem skořepiny oačně symeické, musí edy splňova podmínky
Tlumené kmity. Obr
 1.7.. Tluené kiy 1. Uě vysvěli podsau lueného kiavého pohybu.. Vysvěli význa luící síly. 3. Zná rovnici okažié výchylky lueného kiavého pohybu. 4. Uě popsa apliudu luených kiů. 5. Zná konsany charakerizující
1.7.. Tluené kiy 1. Uě vysvěli podsau lueného kiavého pohybu.. Vysvěli význa luící síly. 3. Zná rovnici okažié výchylky lueného kiavého pohybu. 4. Uě popsa apliudu luených kiů. 5. Zná konsany charakerizující
FYZIKA I. Rovnoměrný, rovnoměrně zrychlený a nerovnoměrně zrychlený rotační pohyb
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ FYZIKA I Rovnoměrný, rovnoměrně zrychlený a nerovnoměrně zrychlený rotační pohyb Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D.
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ FYZIKA I Rovnoměrný, rovnoměrně zrychlený a nerovnoměrně zrychlený rotační pohyb Prof. RNDr. Vilém Mádr, CSc. Prof. Ing. Libor Hlaváč, Ph.D.
Fakulta stavební ČVUT v Praze Katedra hydrauliky a hydrologie. Předmět HYA2 K141 FSv ČVUT. Hydrostatika
 aula savební ČVUT v Pae Kaeda hdauli a hdoloie Předmě HYA K4 Sv ČVUT Hdosaia Doc. In. Aleš Havlí, CSc., In. Tomáš Pice PhD. K4 HYA Hdosaia ŘEŠENÍ HYDROSTATICKÉ SÍLY VE SLOŽKÁCH Dvě navájem olmé vodoovné
aula savební ČVUT v Pae Kaeda hdauli a hdoloie Předmě HYA K4 Sv ČVUT Hdosaia Doc. In. Aleš Havlí, CSc., In. Tomáš Pice PhD. K4 HYA Hdosaia ŘEŠENÍ HYDROSTATICKÉ SÍLY VE SLOŽKÁCH Dvě navájem olmé vodoovné
třecí síla (tečná vazba podložky) F normálová reakce podložky výsledná reakce podložky Podmínky rovnováhy:
 SPŠ VOŠ KLADO SAIKA - PASIVÍ ODPORY PASIVÍ ODPORY Při vzájemném pohybu těles vznikjí v reálných vzbách psivní odpory, jejichž práce se mění v teplo. Psivní odpory předstvují ztráty, které snižují účinnost
SPŠ VOŠ KLADO SAIKA - PASIVÍ ODPORY PASIVÍ ODPORY Při vzájemném pohybu těles vznikjí v reálných vzbách psivní odpory, jejichž práce se mění v teplo. Psivní odpory předstvují ztráty, které snižují účinnost
Obecný rovinný pohyb. teorie současných pohybů, Coriolisovo zrychlení dynamika obecného rovinného pohybu,
 Obecný oinný pohyb ynik, 7. přednášk Obsh přednášky : teoie součsných pohybů, Coiolisoo zychlení dynik obecného oinného pohybu, ob studi : si 1,5 hodiny Cíl přednášky : seznáit studenty se zákldy teoie
Obecný oinný pohyb ynik, 7. přednášk Obsh přednášky : teoie součsných pohybů, Coiolisoo zychlení dynik obecného oinného pohybu, ob studi : si 1,5 hodiny Cíl přednášky : seznáit studenty se zákldy teoie
10 Transformace 3D. 10.1 Transformace a jejich realizace. Studijní cíl. Doba nutná k nastudování. Průvodce studiem
 Trnsformce 3D Sudijní cíl Teno blok je věnován rnsformcím 3D grfik. V eu budou popsán ákldní rnsformce v prosoru posunuí oočení kosení měn měřík používné při prcování 3D modelu. Jednolivé rnsformce budou
Trnsformce 3D Sudijní cíl Teno blok je věnován rnsformcím 3D grfik. V eu budou popsán ákldní rnsformce v prosoru posunuí oočení kosení měn měřík používné při prcování 3D modelu. Jednolivé rnsformce budou
Rotačně symetrické úlohy
 Roačně symeické úlohy Pužnos a pevnos Napěí a defomace zaíženého pužného ělesa Základní úloha pužnosi - Posup řešení úlohy ) podmínky ovnováhy ) vzahy mezi posuvy a převořeními 3) vyloučení posuvů ovnice
Roačně symeické úlohy Pužnos a pevnos Napěí a defomace zaíženého pužného ělesa Základní úloha pužnosi - Posup řešení úlohy ) podmínky ovnováhy ) vzahy mezi posuvy a převořeními 3) vyloučení posuvů ovnice
3. Kvadratické rovnice
 CZ..07/..08/0.0009. Kvdrtické rovnice se v tetice oznčuje lgebrická rovnice druhého stupně, tzn. rovnice o jedné neznáé, ve které neznáá vystupuje ve druhé ocnině (²). V zákldní tvru vypdá následovně:
CZ..07/..08/0.0009. Kvdrtické rovnice se v tetice oznčuje lgebrická rovnice druhého stupně, tzn. rovnice o jedné neznáé, ve které neznáá vystupuje ve druhé ocnině (²). V zákldní tvru vypdá následovně:
Dynamika tuhého tělesa
 Dnaika tuhého tělesa Pet Šidlof ECHNCKÁ UNVERZA V LBERC Fakulta echatonik, infoatik a eioboových studií ento ateiál vnikl v áci pojektu ESF CZ..7/../7.47 Reflexe požadavků půslu na výuku v oblasti autoatického
Dnaika tuhého tělesa Pet Šidlof ECHNCKÁ UNVERZA V LBERC Fakulta echatonik, infoatik a eioboových studií ento ateiál vnikl v áci pojektu ESF CZ..7/../7.47 Reflexe požadavků půslu na výuku v oblasti autoatického
Příklad 4 Ohýbaný nosník - napětí
 Příklad 4 Oýaný nosník - napěí Teorie Prosý o, rovinný o Při prosé ou je průře naáán oový oene oáčející kole jedné lavníc os servačnosi průřeu, ovkle os. oen se načí neo jeno. Běžněji je ožné se seka s
Příklad 4 Oýaný nosník - napěí Teorie Prosý o, rovinný o Při prosé ou je průře naáán oový oene oáčející kole jedné lavníc os servačnosi průřeu, ovkle os. oen se načí neo jeno. Běžněji je ožné se seka s
2. Sestrojte graf závislosti prodloužení pružiny na působící síle y = i(f )
 1 Pracovní úkoly 1. Zěřte tuost k pěti pružin etodou statickou. 2. Sestrojte raf závislosti prodloužení pružiny na působící síle y = i(f ) 3. Zěřte tuost k pěti pružin etodou dynaickou. 4. Z doby kitu
1 Pracovní úkoly 1. Zěřte tuost k pěti pružin etodou statickou. 2. Sestrojte raf závislosti prodloužení pružiny na působící síle y = i(f ) 3. Zěřte tuost k pěti pružin etodou dynaickou. 4. Z doby kitu
6. Optika. Konstrukce vlnoploch pro světlo:
 6. Opi 6. Záldní pojmy Těles, erá vysíljí svělo, jsou svěelné zdroje. Zářivá energie v nich vzniá přeměnou z energie elericé, chemicé, jderné. Zdrojem svěl mohou bý i osvělená ěles (vidíme je díy odrzu
6. Opi 6. Záldní pojmy Těles, erá vysíljí svělo, jsou svěelné zdroje. Zářivá energie v nich vzniá přeměnou z energie elericé, chemicé, jderné. Zdrojem svěl mohou bý i osvělená ěles (vidíme je díy odrzu
ý ý ů ů ý ů ř Š úř ř ř ů ř ý ř ů ň ý ř ň ó ř ý ů ř Ú ř ý Á ý ň ř ř ř ř ý ř ý ř Č ú
 ů Í Ě ď Ť Š ň Ž Č ř ý ť Í ř ý ý ř ř ď ř ř ď ů ř ý ý ů ů ý ů ř Š úř ř ř ů ř ý ř ů ň ý ř ň ó ř ý ů ř Ú ř ý Á ý ň ř ř ř ř ý ř ý ř Č ú Á ř ď ý ř ý Í ď ď ď Í ď ď Ú ř ď ř ď ř ý ď ó ý ú ů ř ď ř ď Ž ř ď ď Ž ř
ů Í Ě ď Ť Š ň Ž Č ř ý ť Í ř ý ý ř ř ď ř ř ď ů ř ý ý ů ů ý ů ř Š úř ř ř ů ř ý ř ů ň ý ř ň ó ř ý ů ř Ú ř ý Á ý ň ř ř ř ř ý ř ý ř Č ú Á ř ď ý ř ý Í ď ď ď Í ď ď Ú ř ď ř ď ř ý ď ó ý ú ů ř ď ř ď Ž ř ď ď Ž ř
Dynamika mechanismů. dynamika mechanismů - metoda uvolňování, dynamika mechanismů - metoda redukce. asi 1,5 hodiny
 Dynaika echanisů Dynaika I, 0. přednáška Obsah přednášky : dynaika echanisů - etoda uvolňování, dynaika echanisů - etoda edukce Doba studia : asi,5 hodiny Cíl přednášky : seznáit studenty se dvěa základníi
Dynaika echanisů Dynaika I, 0. přednáška Obsah přednášky : dynaika echanisů - etoda uvolňování, dynaika echanisů - etoda edukce Doba studia : asi,5 hodiny Cíl přednášky : seznáit studenty se dvěa základníi
1.5.4 Kinetická energie
 .5.4 Kineicá energie Předolady: 50 Energie je jeden z nejoužívanějších, ale aé nejhůře definovaelných ojmů ve sředošolsé fyzice. V běžném živoě: energie = něco, co ořebujeme vyonávání ráce. Vysyuje se
.5.4 Kineicá energie Předolady: 50 Energie je jeden z nejoužívanějších, ale aé nejhůře definovaelných ojmů ve sředošolsé fyzice. V běžném živoě: energie = něco, co ořebujeme vyonávání ráce. Vysyuje se
rovinná soustava sil (paprsky všech sil soustavy leží v jedné rovině) rovinný svazek sil rovinná soustava rovnoběžných sil
 3.3 Obecé soustav sl soustava sl seskupeí sl působících a těleso vláští případ: svaek sl (papsk všech sl soustav se potíaí v edo bodě) soustava ovoběžých sl (papsk všech sl soustav sou aváe ovoběžé) ová
3.3 Obecé soustav sl soustava sl seskupeí sl působících a těleso vláští případ: svaek sl (papsk všech sl soustav se potíaí v edo bodě) soustava ovoběžých sl (papsk všech sl soustav sou aváe ovoběžé) ová
PLASTICITA A CREEP PLASTICITA II
 Plasicia II /4 PLATICITA A CREEP PLATICITA II Zbyně Hubý zbyne.huby huby@fs.cvu.cz Plasicia II /4 Deviáoový ozlad enzou naěí, seální ozlad, invaiany, chaaeisicé ovnice Plasicia II /4 Tenzo naěí, enzo deviáou
Plasicia II /4 PLATICITA A CREEP PLATICITA II Zbyně Hubý zbyne.huby huby@fs.cvu.cz Plasicia II /4 Deviáoový ozlad enzou naěí, seální ozlad, invaiany, chaaeisicé ovnice Plasicia II /4 Tenzo naěí, enzo deviáou
Statika 2. Kombinace namáhání N + M y + M z. Miroslav Vokáč 19. října ČVUT v Praze, Fakulta architektury.
 2. přednáška N + M + M Jádro průřeu Šikmý ohb M + N M + N M + M + N Jádro průřeu Ecenrický lak a vloučeného ahu Konrolní oák Miroslav Vokáč miroslav.vokac@cvu.c ČVUT v Prae, Fakula archiekur 19. října
2. přednáška N + M + M Jádro průřeu Šikmý ohb M + N M + N M + M + N Jádro průřeu Ecenrický lak a vloučeného ahu Konrolní oák Miroslav Vokáč miroslav.vokac@cvu.c ČVUT v Prae, Fakula archiekur 19. října
é éž á ó ý ě č ě í ž é é š é í é š ě ě í é í ú úž ú é ž ě ž ď ý ý řě ě ě á š á š ř ý ďá ě ě ě ú Ž ý ť ě ž řěčí ě ž í šě š ž ř ř ěř ďá ó ř š Žá ě í ě ý
 Í Í Ý í í í ě ý á é í á ř č é á ý á ý ň ó š á č ě é ř ř čí é ú č ž é š á é á í á ř č Č á č ě š ě á í ď š á ř é í é ě á í čá ď Í ěč é é ěř é ě ší ě á í é žď á á š ř čí é š ě ž ýš á í é ě á ď ř ě í é á ú
Í Í Ý í í í ě ý á é í á ř č é á ý á ý ň ó š á č ě é ř ř čí é ú č ž é š á é á í á ř č Č á č ě š ě á í ď š á ř é í é ě á í čá ď Í ěč é é ěř é ě ší ě á í é žď á á š ř čí é š ě ž ýš á í é ě á ď ř ě í é á ú
PLASTICITA A CREEP PLASTICITA II
 Plasicia II /4 PLATICITA A CREEP PLATICITA II Zbyně Hubý zbyne.huby huby@fs.cvu.cz Plasicia II /4 Deviáoový ozlad enzou naěí, seální ozlad, invaiany, chaaeisicé ovnice Plasicia II /4 Tenzo naěí, enzo deviáou
Plasicia II /4 PLATICITA A CREEP PLATICITA II Zbyně Hubý zbyne.huby huby@fs.cvu.cz Plasicia II /4 Deviáoový ozlad enzou naěí, seální ozlad, invaiany, chaaeisicé ovnice Plasicia II /4 Tenzo naěí, enzo deviáou
ÚLOHA VÍCE TĚLES V NEBESKÉ MECHANICE
 ÚLOHA VÍCE TĚLES V NEBESKÉ ECHANICE SPECIFIKACE PROBLÉU Řeš úlohu ěles zaeá aléz pohyby ( foulova pohybové ovce a aléz ech řešeí) hoých bodů (esp ěles př zaedbáí duhoé oace) a eé působí pouze vzáeé gavačí
ÚLOHA VÍCE TĚLES V NEBESKÉ ECHANICE SPECIFIKACE PROBLÉU Řeš úlohu ěles zaeá aléz pohyby ( foulova pohybové ovce a aléz ech řešeí) hoých bodů (esp ěles př zaedbáí duhoé oace) a eé působí pouze vzáeé gavačí
ú é é č žé é é ě é é ž ř ž é ě ů Ř ň ž é é řď ú é Á ř é č ř ž ó ř ě ú ů é ě ě ř é č ž é ě ř ě Č ď ř ř č ž ě ě ů ě ř č ě é ž ů ř ó é ř č ř ě ě ř č é é
 Č é Č Í č č Á é č č ě ř ě ř é č č č ř ž ěř č č ř ě č č é ě é ě ž ů č Ý Ť é ř ě é ť ě ů ě é é ť ř ů ě ř ě ů č Š ě ó ó ž ť č ř ž ř ž ě č ž ř Š ž ě ó ž ě ž ě č Šř ú é é č žé é é ě é é ž ř ž é ě ů Ř ň ž é
Č é Č Í č č Á é č č ě ř ě ř é č č č ř ž ěř č č ř ě č č é ě é ě ž ů č Ý Ť é ř ě é ť ě ů ě é é ť ř ů ě ř ě ů č Š ě ó ó ž ť č ř ž ř ž ě č ž ř Š ž ě ó ž ě ž ě č Šř ú é é č žé é é ě é é ž ř ž é ě ů Ř ň ž é
č Ř Ě ů č ě ě ě ě č š ě Ž č úč úč ě č ú Š č ě š č Ž č Š ě š č ů úč Í Š ě ě Í Ú č č ě ú č č ě Á Ř Ř Ž Ý Ř Ř Í Ú Ž Ý č Ř Í Ř É ÍÚ Ř Ř Ř š ě č č Ř š ě š
 Ý Í Í Í Í č č ě Í č č č č č č č Š ě ě Š ě č č účí Í č č ě ě ě č ě Ř č úč ě č Ř Ě ů č ě ě ě ě č š ě Ž č úč úč ě č ú Š č ě š č Ž č Š ě š č ů úč Í Š ě ě Í Ú č č ě ú č č ě Á Ř Ř Ž Ý Ř Ř Í Ú Ž Ý č Ř Í Ř É ÍÚ
Ý Í Í Í Í č č ě Í č č č č č č č Š ě ě Š ě č č účí Í č č ě ě ě č ě Ř č úč ě č Ř Ě ů č ě ě ě ě č š ě Ž č úč úč ě č ú Š č ě š č Ž č Š ě š č ů úč Í Š ě ě Í Ú č č ě ú č č ě Á Ř Ř Ž Ý Ř Ř Í Ú Ž Ý č Ř Í Ř É ÍÚ
Veronika Drobná VB1STI02 Ing. Michalcová Vladimíra, Ph.D.
 Příklad 1: 3;4 3;4 = =4 9 2;1,78 = = 4 9 4=16 9 =1,78 =2 =2 2 4 9 =16 9 1 = 1+ =0,49 = 1+ =0,872 =0 =10 6+ 2,22=0 =3,7 6+ 2,22=0 =3,7 + =0 3,7+3,7=0 0=0 =60,64 =0 =0 + =0 =3,7 á čá 5+ 2,22=0 =3,7 5+ 2,22+
Příklad 1: 3;4 3;4 = =4 9 2;1,78 = = 4 9 4=16 9 =1,78 =2 =2 2 4 9 =16 9 1 = 1+ =0,49 = 1+ =0,872 =0 =10 6+ 2,22=0 =3,7 6+ 2,22=0 =3,7 + =0 3,7+3,7=0 0=0 =60,64 =0 =0 + =0 =3,7 á čá 5+ 2,22=0 =3,7 5+ 2,22+
Í Í ěč Š ěš ěš ř ř č ěš ř ř č Ů ě ř Ú ř ř ěž Úč ř č ěš ě č č Ž Ž ěš Ž Ž ř Ž ú Ž Ž Š ř č ř ř ěš Ž ří č ř ě ě č Ů ř č úč ř ěš ě Š č ř ě ě ěš ě Ž ř ř ěš
 ěš Š č ň ěš Š ň č ř č Ú č č č č Ú ě ě ě ř ě Ú č ž ř ř č ř č ď č Ž Ž ř č Ž čó ú š ú š Í Á Í ř ě Í Š ě Í ě Í š ě č ř ě Úč ě ř č Ú ř ř č č ěší ě č Ú Í ř ěž č Ž ř ě ěš Í Í ěč Š ěš ěš ř ř č ěš ř ř č Ů ě ř Ú
ěš Š č ň ěš Š ň č ř č Ú č č č č Ú ě ě ě ř ě Ú č ž ř ř č ř č ď č Ž Ž ř č Ž čó ú š ú š Í Á Í ř ě Í Š ě Í ě Í š ě č ř ě Úč ě ř č Ú ř ř č č ěší ě č Ú Í ř ěž č Ž ř ě ěš Í Í ěč Š ěš ěš ř ř č ěš ř ř č Ů ě ř Ú
MOMENT SETRVAČNOSTI. Obecná část Pomocí Newtonova pohybového zákona síly můžeme odvodit pohybovou rovnici pro rotační pohyb:
 MOMENT SETRVAČNOST Obecná část Pomocí Newtonova pohybového záona síly můžeme odvodit pohybovou rovnici pro rotační pohyb: dω M = = ε, (1) d t de M je moment vnější síly působící na těleso, ω úhlová rychlost,
MOMENT SETRVAČNOST Obecná část Pomocí Newtonova pohybového záona síly můžeme odvodit pohybovou rovnici pro rotační pohyb: dω M = = ε, (1) d t de M je moment vnější síly působící na těleso, ω úhlová rychlost,
Úč é ř é ž é é žň é č ž š é é é é ž ů úč ó ř ž é š ý ý š č ř č ř ů ř é č ý ý é ž é č č é ý é ť ž č ůž č č ř ů ý ř ř ůž é ů ý ý ů ž č ř ůž ý é ůž ř ř ž
 ď Á Ý š Á ý ý č ý š ř ů č č é č č č ú š é č Č ý ř ž ř é ž Č ř č ň š č č č č é Úč ž ř é é ř é č ř ý š ř ů ý ž č ř ř ř é ž é é Úč é ř é ž é é žň é č ž š é é é é ž ů úč ó ř ž é š ý ý š č ř č ř ů ř é č ý ý
ď Á Ý š Á ý ý č ý š ř ů č č é č č č ú š é č Č ý ř ž ř é ž Č ř č ň š č č č č é Úč ž ř é é ř é č ř ý š ř ů ý ž č ř ř ř é ž é é Úč é ř é ž é é žň é č ž š é é é é ž ů úč ó ř ž é š ý ý š č ř č ř ů ř é č ý ý
VÝPOČET PŘETVOŘENÍ STATICKY URIČTÝCH KONSTRUKCÍCH KOMPLEXNÍ PŘÍKLAD
 Miloš Hüne SMR neilové účink vičení 05 Zání VÝPOČET PŘETVOŘENÍ STATICKY URIČTÝCH KONSTRUKCÍCH KOMPLEXNÍ PŘÍKLAD Příkl č. Uvžje konki z O., vpočíeje vooovný pon v oě (znčený eploní ozžnoi vžje α 0 6 K -.
Miloš Hüne SMR neilové účink vičení 05 Zání VÝPOČET PŘETVOŘENÍ STATICKY URIČTÝCH KONSTRUKCÍCH KOMPLEXNÍ PŘÍKLAD Příkl č. Uvžje konki z O., vpočíeje vooovný pon v oě (znčený eploní ozžnoi vžje α 0 6 K -.
ž í
 ž š š č š š Č š č č š č ď é Š š ž é Š š ť é č š č šé č ť Š ť č š é š č š é é Š č é é ň é š š é é é č ň č é š é č é š é č š é č é é é č é ž Ť č š é š č Ý Š š Š ň š ť Š é é š č č č č č č ť é č é č č č
ž š š č š š Č š č č š č ď é Š š ž é Š š ť é č š č šé č ť Š ť č š é š č š é é Š č é é ň é š š é é é č ň č é š é č é š é č š é č é é é č é ž Ť č š é š č Ý Š š Š ň š ť Š é é š č č č č č č ť é č é č č č
Zada ní 2. Semina rní pra ce z pr edme tu Matematika pro informatiky (KI/MAI)
 Zaa ní. eina ní pa e z p ee u Maeaia po infoai (KI/MAI) Dau zaání. 5. 17 Poín paoání - einání páe se sláá z poaoé čási (ó Malabu) a eoé čási (poool o paoání). - Kažý suen oezáá pái sá za sebe. - uen si
Zaa ní. eina ní pa e z p ee u Maeaia po infoai (KI/MAI) Dau zaání. 5. 17 Poín paoání - einání páe se sláá z poaoé čási (ó Malabu) a eoé čási (poool o paoání). - Kažý suen oezáá pái sá za sebe. - uen si
Posouzení vyztužené stěny podle ČSN EN (Boulení stěn)
 9. Únosnos ve smu Posouzení vzužené sěn podle ČSN EN 99--5 (Boulení sěn) Používá se eorie roovanýc napěí. liv výzu je zarnu úměrně vššímu riicému napěí - po mírné úpravě soulasí s experimen. Únosnos ve
9. Únosnos ve smu Posouzení vzužené sěn podle ČSN EN 99--5 (Boulení sěn) Používá se eorie roovanýc napěí. liv výzu je zarnu úměrně vššímu riicému napěí - po mírné úpravě soulasí s experimen. Únosnos ve
MOMENT SETRVAČNOSTI. Obecná část Pomocí Newtonova pohybového zákona síly můžeme odvodit pohybovou rovnici pro rotační pohyb:
 MOMENT SETRVAČNOST Obecná část Pomocí Newtonova pohybového záona síly můžeme odvodit pohybovou rovnici pro rotační pohyb: dω M = = ε, (1) d t de M je moment vnější síly působící na těleso, ω úhlová rychlost,
MOMENT SETRVAČNOST Obecná část Pomocí Newtonova pohybového záona síly můžeme odvodit pohybovou rovnici pro rotační pohyb: dω M = = ε, (1) d t de M je moment vnější síly působící na těleso, ω úhlová rychlost,
FYZIKÁLNÍ PRAKTIKUM Ústav fyziky FEI VUT BRNO
 FYZIKÁLNÍ PRAKIKUM Úsav fyziky FEI VU BRNO Spolupracoval Příprava Šuranský Radek Opravy méno Ročník 1 Škovran an Předn. skup. B Měřeno dne 5.4. Učiel Sud. skupina 1 Kód 17 Odevzdáno dne 16.5. Hodnocení
FYZIKÁLNÍ PRAKIKUM Úsav fyziky FEI VU BRNO Spolupracoval Příprava Šuranský Radek Opravy méno Ročník 1 Škovran an Předn. skup. B Měřeno dne 5.4. Učiel Sud. skupina 1 Kód 17 Odevzdáno dne 16.5. Hodnocení
25 Měrný náboj elektronu
 5 Měrný náboj elektronu ÚKOL Stnovte ěrný náboj elektronu e výsledek porovnejte s tbulkovou hodnotou. TEORIE Poěr náboje elektronu e hotnosti elektronu nzýváe ěrný náboj elektronu. Jednou z ožných etod
5 Měrný náboj elektronu ÚKOL Stnovte ěrný náboj elektronu e výsledek porovnejte s tbulkovou hodnotou. TEORIE Poěr náboje elektronu e hotnosti elektronu nzýváe ěrný náboj elektronu. Jednou z ožných etod
Kmitání vynucené. kmitání při působení konstantní síly, harmonicky buzené kmitání amplitudová a fázová charakteristika.
 Kiání vynucené Osh přednášy : iání při půsoení onsnní síly, hronicy uzené iání pliudová fázová chrerisi Do sudi : si,5 hodiny Cíl přednášy : seznái sudeny se záoniosi vynuceného iání Kiání vynucené D =
Kiání vynucené Osh přednášy : iání při půsoení onsnní síly, hronicy uzené iání pliudová fázová chrerisi Do sudi : si,5 hodiny Cíl přednášy : seznái sudeny se záoniosi vynuceného iání Kiání vynucené D =
5.4.6 Objemy a povrchy rotačních těles I
 5.4.6 Objey a povchy otačních těle I Předpoklady: 050405 Pedagogická poznáka: Stejně jako u nohotěnů i u otačních těle e vzoce po objey a obahy e neodvozují, žáci ohou využívat tabulky a cíle hodin je,
5.4.6 Objey a povchy otačních těle I Předpoklady: 050405 Pedagogická poznáka: Stejně jako u nohotěnů i u otačních těle e vzoce po objey a obahy e neodvozují, žáci ohou využívat tabulky a cíle hodin je,
á í ý ť é ó Í č é ě é Í Í ú Ž Í é í á á ý á ý ě ť é ť á í č čť š é ť Ě í í č á á á á ě í ě ř ě Í š ů ě ř ů ú í ý Í ý é á í č á á ž é ř ř š š ý ý ú áš
 ý ť é ó Í č é ě é Í Í ú Ž Í é ý ý ě ť é ť č čť š é ť Ě č ě ě ě Í š ů ě ů ú ý Í ý é č ž é š š ý ý ú š ě Í č Í Í ú ě Á Í ť Í ě Í š š ň ú č š Ů Í č ď š éí é Č ě ů ý ó ěž š ě ť Í ž ě Č Í ý é Í ÁÉ ň ů Ů ě ú
ý ť é ó Í č é ě é Í Í ú Ž Í é ý ý ě ť é ť č čť š é ť Ě č ě ě ě Í š ů ě ů ú ý Í ý é č ž é š š ý ý ú š ě Í č Í Í ú ě Á Í ť Í ě Í š š ň ú č š Ů Í č ď š éí é Č ě ů ý ó ěž š ě ť Í ž ě Č Í ý é Í ÁÉ ň ů Ů ě ú
Jaroslav Reichl. Střední průmyslová škola sdělovací techniky Panská 3 Praha 1
 Střední půslová šola sdělovací techni Pansá Paha 1 Jaoslav Reichl, 017 učená studentů 4 očníu technicého lcea jao doplně e studiu apliované ateati Jaoslav Reichl Sbía úloh z apliované ateati, J Reichl,
Střední půslová šola sdělovací techni Pansá Paha 1 Jaoslav Reichl, 017 učená studentů 4 očníu technicého lcea jao doplně e studiu apliované ateati Jaoslav Reichl Sbía úloh z apliované ateati, J Reichl,
Hlavní body. Úvod do dynamiky. Dynamika translačních pohybů Dynamika rotačních pohybů
 Mechanka dynaka Hlavní body Úvod do dynaky. Dynaka tanslačních pohybů Dynaka otačních pohybů Úvod do dynaky Mechanka by byla neúplná, kdyby se nezabývala, důvody poč se tělesa dávají do pohybu, zychlují,
Mechanka dynaka Hlavní body Úvod do dynaky. Dynaka tanslačních pohybů Dynaka otačních pohybů Úvod do dynaky Mechanka by byla neúplná, kdyby se nezabývala, důvody poč se tělesa dávají do pohybu, zychlují,
=, kde P(x) a Q(x) jsou polynomy. Rozklad na parciální zlomky Parciální zlomky jsou speciální racionální lomené funkce. Rozlišujeme 2 typy:
 3 předáš INTEGRAE RAIONÁLNÍ LOMENÉ FUNKE Důležiou supiu fucí, eré můžeme (spoň eoreicy) iegrov v možiě elemeárích fucí, voří rcioálí lomeé fuce Kždou rcioálí lomeou fuci vru P( ) f ( ) =, de P() Q() jsou
3 předáš INTEGRAE RAIONÁLNÍ LOMENÉ FUNKE Důležiou supiu fucí, eré můžeme (spoň eoreicy) iegrov v možiě elemeárích fucí, voří rcioálí lomeé fuce Kždou rcioálí lomeou fuci vru P( ) f ( ) =, de P() Q() jsou
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ PRŮVODCE GB01-P03 MECHANIKA TUHÝCH TĚLES
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ Prof. RNDr. Zdeněk Chobola,CSc., Vlasta Juránková,CSc. FYZIKA PRŮVODCE GB01-P03 MECHANIKA TUHÝCH TĚLES STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ Prof. RNDr. Zdeněk Chobola,CSc., Vlasta Juránková,CSc. FYZIKA PRŮVODCE GB01-P03 MECHANIKA TUHÝCH TĚLES STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU
N. Určete velikosti sil, kterými trám působí na vzpěry.
 0. Tué těeo 0 N 0. béníoá tená e ozěy 0 c 90 c je otáčiá oe oy joucí její třee oé oině ey. N eu ůobí íy oe obázu. Učete eiot ě ýenéo oentu íy ě otáčení ey, teý tento oent íy zůobí. 0 N 0 c 0 N 90 c 0 N
0. Tué těeo 0 N 0. béníoá tená e ozěy 0 c 90 c je otáčiá oe oy joucí její třee oé oině ey. N eu ůobí íy oe obázu. Učete eiot ě ýenéo oentu íy ě otáčení ey, teý tento oent íy zůobí. 0 N 0 c 0 N 90 c 0 N
Mechanika tuhého tělesa
 Mechanika tuhého tělesa Tuhé těleso je ideální těleso, jehož tvar ani objem se působením libovolně velkých sil nemění Síla působící na tuhé těleso má pouze pohybové účinky Pohyby tuhého tělesa Posuvný
Mechanika tuhého tělesa Tuhé těleso je ideální těleso, jehož tvar ani objem se působením libovolně velkých sil nemění Síla působící na tuhé těleso má pouze pohybové účinky Pohyby tuhého tělesa Posuvný
MECHANICKÉ KMITÁNÍ NETLUMENÉ
 MECHANICKÉ KMITÁNÍ NETLUMENÉ Kitání je PERIODICKÝ pohyb hotného bodu (tělesa). Pohybuje se z jedné rajní polohy KP do druhé rajní polohy KP a zpět. Jaýoliv itající objet se nazývá OSCILÁTOR. A je aplituda
MECHANICKÉ KMITÁNÍ NETLUMENÉ Kitání je PERIODICKÝ pohyb hotného bodu (tělesa). Pohybuje se z jedné rajní polohy KP do druhé rajní polohy KP a zpět. Jaýoliv itající objet se nazývá OSCILÁTOR. A je aplituda
ó ž ž ě ě ě ě ě ů ě ď ž ů ě ě ů
 ž ě ž ě ě Č š Č š š ě ě š ž ó ž ž ě ě ě ě ě ů ě ď ž ů ě ě ů ž ž ěž ě ě ó ž ž ě ž ě ě ě ě ť ě š ě ň ů ě ň ě ž ž ž ť š ě ů ů š š Ň ěž ěž ěž ť ěž ó ůú ť ě ž ž ě ž ě ě ň ž ň ě ěž ě ě ů ě ě ů ě Á ě ě ů ě ě
ž ě ž ě ě Č š Č š š ě ě š ž ó ž ž ě ě ě ě ě ů ě ď ž ů ě ě ů ž ž ěž ě ě ó ž ž ě ž ě ě ě ě ť ě š ě ň ů ě ň ě ž ž ž ť š ě ů ů š š Ň ěž ěž ěž ť ěž ó ůú ť ě ž ž ě ž ě ě ň ž ň ě ěž ě ě ů ě ě ů ě Á ě ě ů ě ě
(2) Řešení. 4. Platí: ω = 2π (3) (3) Řešení
 (). Načrněe slepý graf závislosi dráhy sojícího člověka na b 2. Na abuli je graf A závislosi rychlosi pohybu rabanu kombi na Vypočěe dráhu, kerou raban urazil v čase od 2,9 s do 6,5 s. 3. Jakou rychlosí
(). Načrněe slepý graf závislosi dráhy sojícího člověka na b 2. Na abuli je graf A závislosi rychlosi pohybu rabanu kombi na Vypočěe dráhu, kerou raban urazil v čase od 2,9 s do 6,5 s. 3. Jakou rychlosí
á ž é á á á ž ý ě í š ě ší á ů ý ž ě ý č í ý ů ů í ě é ě ý ů ě í í á í š í ě í í í í é ě ě í í í ě í ý ě íč í é á ý í ý č í ž ž é Í ý á í č í í í í í
 á é á ě é í é í á Ž é á ěž ý č á íš č íí á í ý š ě ý ý ů íž í é é é ž é á ě ě ý á í ě š ě í ý ě á ů é í á č í í í é í ž é íč ý ž ý í í á í ý á á ý ý ží ý é č í í é í é ě í á č ě éč ě í í é Í Í í ě í ý
á é á ě é í é í á Ž é á ěž ý č á íš č íí á í ý š ě ý ý ů íž í é é é ž é á ě ě ý á í ě š ě í ý ě á ů é í á č í í í é í ž é íč ý ž ý í í á í ý á á ý ý ží ý é č í í é í é ě í á č ě éč ě í í é Í Í í ě í ý
V B r n ě, 2 4. b ř e z n a
 P E D A G O G I C K Á F A K U L T A M A S A R Y K O V Y U N I V E R Z I T Y V B R N Ě K a t e d r a o b č a n s k é v ý c h o v y V ý v o j č e s k o s l o v e n s k ý c h a č e s k ý c h p o l i t i c
P E D A G O G I C K Á F A K U L T A M A S A R Y K O V Y U N I V E R Z I T Y V B R N Ě K a t e d r a o b č a n s k é v ý c h o v y V ý v o j č e s k o s l o v e n s k ý c h a č e s k ý c h p o l i t i c
Dynamika hmotných bodů. 3. Hmotný bod o hmotnosti m = 10 kg se pohybuje po kružnici o poloměru r = 2 m,
 Dnik honých bodů 3 Honý bod o honosi kg se ohbuje o kužnici o oloěu 3 3 řičež jeho dáh áisí n čse odle hu s k kde k 5 /s Učee elikos ýsledné síl ůsobící n honý bod úhel α keý síá eko síl s ekoe chlosi
Dnik honých bodů 3 Honý bod o honosi kg se ohbuje o kužnici o oloěu 3 3 řičež jeho dáh áisí n čse odle hu s k kde k 5 /s Učee elikos ýsledné síl ůsobící n honý bod úhel α keý síá eko síl s ekoe chlosi
Č é
 Č Í Á Č é š Í ď ž š ř š ů ř é š š š é ž Í Í ť š š ú ó ř ř ž ý é é ůž é ž ň ž ý é ý ž ž š ůž ý ů ý ý š Š é Š Ž Ž é Č Ž Č Ž š Ž ž š ž é Č Ž ž é š Ž š š é š é é Ž ť é š Ž š š Í Í ř ř é ž ř é Ž Č Á é é ů ů
Č Í Á Č é š Í ď ž š ř š ů ř é š š š é ž Í Í ť š š ú ó ř ř ž ý é é ůž é ž ň ž ý é ý ž ž š ůž ý ů ý ý š Š é Š Ž Ž é Č Ž Č Ž š Ž ž š ž é Č Ž ž é š Ž š š é š é é Ž ť é š Ž š š Í Í ř ř é ž ř é Ž Č Á é é ů ů
VŠB- Technická univerzita Ostrava Fakulta strojní Katedra pružnosti a pevnosti. Úvod do MKP Napěťová analýza tenkostěnné tlakové nádoby
 VŠB- Technická univerzia Osrava Fakula srojní Kaedra pružnosi a pevnosi Úvod do MKP Auor: Michal Šofer Verze 0 Osrava 2011 Zadání: Proveďe napěťovou analýzu lakové nádoby v ísě D (v polovině válcové čási),
VŠB- Technická univerzia Osrava Fakula srojní Kaedra pružnosi a pevnosi Úvod do MKP Auor: Michal Šofer Verze 0 Osrava 2011 Zadání: Proveďe napěťovou analýzu lakové nádoby v ísě D (v polovině válcové čási),
r Co se stane se spektrem signá lu z obr.1.12, dojde-li k zvětšení jeho opakovací frekvence na 500Hz? Ř ešení: Viz obr.1.15
 r.5. Co se sane se spere signá lu z obr.., dojde-li zvěšení jeho opaovací frevence na 5Hz? Viz obr..5 u( )[ V] u( )[ V] 3 5 6 [ s] 3 5 6 [ s] s s U i, U [ V] U i,5 U [ V],,5,,,5,5 ϕ [ rad] π ϕ [ rad] π
r.5. Co se sane se spere signá lu z obr.., dojde-li zvěšení jeho opaovací frevence na 5Hz? Viz obr..5 u( )[ V] u( )[ V] 3 5 6 [ s] 3 5 6 [ s] s s U i, U [ V] U i,5 U [ V],,5,,,5,5 ϕ [ rad] π ϕ [ rad] π
Seznámíte se s principem integrace substituční metodou a se základními typy integrálů, které lze touto metodou vypočítat.
 4 Inegrace subsiucí 4 Inegrace subsiucí Průvodce sudiem Inegrály, keré nelze řeši pomocí základních vzorců, lze velmi časo řeši subsiuční meodou Vzorce pro derivace elemenárních funkcí a věy o derivaci
4 Inegrace subsiucí 4 Inegrace subsiucí Průvodce sudiem Inegrály, keré nelze řeši pomocí základních vzorců, lze velmi časo řeši subsiuční meodou Vzorce pro derivace elemenárních funkcí a věy o derivaci
Obsah dnešní přednášky : Obecný rovinný pohyb tělesa. Teorie současných pohybů, Coriolisovo zrychlení, dynamika obecného rovinného pohybu.
 Obsh dnešní řednášky : Obecný oinný ohyb těles. eoie součsných ohybů, Coiolisoo zychlení, dynik obecného oinného ohybu. Obecný oinný ohyb zákldní ozkld. osu osu = A otce = A otce A A A A efeenční bod sueosice
Obsh dnešní řednášky : Obecný oinný ohyb těles. eoie součsných ohybů, Coiolisoo zychlení, dynik obecného oinného ohybu. Obecný oinný ohyb zákldní ozkld. osu osu = A otce = A otce A A A A efeenční bod sueosice
1.7.2 Moment síly vzhledem k ose otáčení
 .7. oment síly vzhledem k ose otáčení Předpoklady 70 Pedagogická poznámka Situaci tochu komplikuje skutečnost, že žáci si ze základní školy pamatují součin a mají pocit, že se pouze opakuje notoicky známá
.7. oment síly vzhledem k ose otáčení Předpoklady 70 Pedagogická poznámka Situaci tochu komplikuje skutečnost, že žáci si ze základní školy pamatují součin a mají pocit, že se pouze opakuje notoicky známá
š í ý Í í ý č é á č í ů ý č ě ů á á í é č é á é š á č é ý í á ý ý í ž žá ý ý ř ě ý í ě é ž č é ó é í É é á č ý á ž Ž é ř í ší É ě é ě í á é č ý í ž ří
 š í ý Í í ý č á č í ů ý č ě ů á á í č á š á č ý í á ý ý í ž žá ý ý ř ě ý í ě ž č ó í É á č ý á ž Ž ř í ší É ě ě í á č ý í ž ří í ž ř Ě ř Í ď ář á č ý á í ř š š ě Ž í ý á á ý žá ý ý ž čí Ž í í í í č ř ě
š í ý Í í ý č á č í ů ý č ě ů á á í č á š á č ý í á ý ý í ž žá ý ý ř ě ý í ě ž č ó í É á č ý á ž Ž ř í ší É ě ě í á č ý í ž ří í ž ř Ě ř Í ď ář á č ý á í ř š š ě Ž í ý á á ý žá ý ý ž čí Ž í í í í č ř ě
Nakloněná rovina II
 1215 Nkloněná rovin II Předokldy: 1214 Pomůcky: siloměr 2,5 N, sd n měření řecí síly Pedoická oznámk: V éo následující hodině se nerobírá žádná nová lák Přeso jde o oměrně důležié hodiny, roože žáci se
1215 Nkloněná rovin II Předokldy: 1214 Pomůcky: siloměr 2,5 N, sd n měření řecí síly Pedoická oznámk: V éo následující hodině se nerobírá žádná nová lák Přeso jde o oměrně důležié hodiny, roože žáci se
Řešení soustav lineárních rovnic
 Řešeí sousv lieáríc rovic Sousv lieáríc rovic Sousvou m lieáríc rovic o ezámýc rozumíme sousvu : Kde ij i R M m m Čísl ij zýváme koeficiey sousvy čísl i soluí čley Uvedeou sousvu udeme zči Sm m M m Homogeí
Řešeí sousv lieáríc rovic Sousv lieáríc rovic Sousvou m lieáríc rovic o ezámýc rozumíme sousvu : Kde ij i R M m m Čísl ij zýváme koeficiey sousvy čísl i soluí čley Uvedeou sousvu udeme zči Sm m M m Homogeí
í é é á š ě í ý ž ď í é žřá čí ř é č í čí á ř á čí é á á á ž ď ř ú ě á í ý ž á ř š í ž ě á š ř ý ř á č í ř á ď ě á á í ě í á ďí é ď ř í č ř ž ř á é č
 ť ď ě ý Ž ý Ž ě ř šá ú é ě é žč ě á ó ž á ě č ď ě ž ří šě í á Ž é á ě č é é ě ě é ě ě ž žě ě řě ě ý á í ě ď ě á ž é á ě ý č ě áú ě á ýž ě ý ú í á ž č ř á ěž ěžš ž ó ě é á ř ě ř ě ž ě á ý í ý š ší á ě ší
ť ď ě ý Ž ý Ž ě ř šá ú é ě é žč ě á ó ž á ě č ď ě ž ří šě í á Ž é á ě č é é ě ě é ě ě ž žě ě řě ě ý á í ě ď ě á ž é á ě ý č ě áú ě á ýž ě ý ú í á ž č ř á ěž ěžš ž ó ě é á ř ě ř ě ž ě á ý í ý š ší á ě ší
Teorie současných pohybů, Coriolisovo zrychlení, dynamika obecného rovinného pohybu.
 Obsh dnešní řednášky : Alikoná echnik, 4. řednášk Obecný oinný ohyb těles. eoie součsných ohybů, Coiolisoo zychlení, dynik obecného oinného ohybu. Obecný oinný ohyb zákldní ozkld. Alikoná echnik, 4. řednášk
Obsh dnešní řednášky : Alikoná echnik, 4. řednášk Obecný oinný ohyb těles. eoie součsných ohybů, Coiolisoo zychlení, dynik obecného oinného ohybu. Obecný oinný ohyb zákldní ozkld. Alikoná echnik, 4. řednášk
č á ž á ž ý ý Ú ď ě é ř ářž ž ý ř ůž ř š á ů ž é á é ř ť á ě á ž É ř á é ř ť éž ě é é ě ů ě č é ě á é éř ý ě ě š ý š ř é ě š š á ě šá á é á ň é á ž á
 ďť č á ž á ž ý ý Ú ď ě é ř ářž ž ý ř ůž ř š á ů ž é á é ř ť á ě á ž É ř á é ř ť éž ě é é ě ů ě č é ě á é éř ý ě ě š ý š ř é ě š š á ě šá á é á ň é á ž á é ž š ý ř ášý ě ý ů é é á é ěž ř ý á š ů ž ě š š
ďť č á ž á ž ý ý Ú ď ě é ř ářž ž ý ř ůž ř š á ů ž é á é ř ť á ě á ž É ř á é ř ť éž ě é é ě ů ě č é ě á é éř ý ě ě š ý š ř é ě š š á ě šá á é á ň é á ž á é ž š ý ř ášý ě ý ů é é á é ěž ř ý á š ů ž ě š š
Měření napjatosti na povrchu tělesa Tenkostěnná trubka zatížená krutem a vnitřním přetlakem
 4. lekce Měření npjosi n povrcu ěles Tenkosěnná rubk zížená kruem vniřním přelkem Obs: 4.1 Úvod 4. Kru enkosěnné válcové rubk 4.3 Tenkosěnná lková válcová nádob 3 4.4 Dvouosá npjos Morov kružnice 4 4.5
4. lekce Měření npjosi n povrcu ěles Tenkosěnná rubk zížená kruem vniřním přelkem Obs: 4.1 Úvod 4. Kru enkosěnné válcové rubk 4.3 Tenkosěnná lková válcová nádob 3 4.4 Dvouosá npjos Morov kružnice 4 4.5
Hydrostatické váhy. HANA MALINOVÁ Katedra didaktiky fyziky, MFF UK. Princip hydrostatického vážení. Veletrh nápadů učitelů fyziky 14
 Velerh nápadů učielů fyziky 4 Hydrosaické váhy HANA MALINOVÁ Kaedra didakiky fyziky, MFF UK V příspěvku bude prezenována eoda hydrosaického vážení, kerá se používá na určování husoy různých aeriálů. Žáci
Velerh nápadů učielů fyziky 4 Hydrosaické váhy HANA MALINOVÁ Kaedra didakiky fyziky, MFF UK V příspěvku bude prezenována eoda hydrosaického vážení, kerá se používá na určování husoy různých aeriálů. Žáci
ě ě í ý ě á ý ů é á í ů á č š í ř í ó ě é á ž ý í ě ýč ář ř š ě ý ář ý á é á í š ě é í ř áž á á ě í ě á í í í á ý ří ě ý ě ší é á á í í ř ř á á í Í áž
 Á á í ý á í č é é á í í čí í ý á ů í é á í ř ů ý č é é ř í á é é ě ě í ý ě í é ý á í í í ý á í ž í č ý ý á ů ů řá é é á ý á ý ě í ý ě á ř á ř é š í ží í ě é ě é á á í á á ů ě ší ů á í í ů ě í é é ý š š
Á á í ý á í č é é á í í čí í ý á ů í é á í ř ů ý č é é ř í á é é ě ě í ý ě í é ý á í í í ý á í ž í č ý ý á ů ů řá é é á ý á ý ě í ý ě á ř á ř é š í ží í ě é ě é á á í á á ů ě ší ů á í í ů ě í é é ý š š
4. Střední radiační teplota; poměr osálání,
 Sálavé a průmyslové vyápění (60). Sřední radiační eploa; poměr osálání, operaivní a výsledná eploa.. 08 a.. 08 Ing. Jindřich Boháč TEPLOTY Sřední radiační eploa - r Sálavé vyápění = PŘEVÁŽNĚ sálavé vyápění
Sálavé a průmyslové vyápění (60). Sřední radiační eploa; poměr osálání, operaivní a výsledná eploa.. 08 a.. 08 Ing. Jindřich Boháč TEPLOTY Sřední radiační eploa - r Sálavé vyápění = PŘEVÁŽNĚ sálavé vyápění
NA POMOC FO KATEGORIE E,F
 NA POMOC FO KATEGOIE EF Výledky řešení úlo 45. ročníku FO ka. E F Ivo Volf * ÚV FO Univerzia Hradec Králové Mirolav anda ** ÚV FO Pedagogická fakula ZČU Plzeň Jak je již v naší ouěži obvyklé uvádíme pouze
NA POMOC FO KATEGOIE EF Výledky řešení úlo 45. ročníku FO ka. E F Ivo Volf * ÚV FO Univerzia Hradec Králové Mirolav anda ** ÚV FO Pedagogická fakula ZČU Plzeň Jak je již v naší ouěži obvyklé uvádíme pouze
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV AUTOMOBILNÍHO A DOPRAVNÍHO INŽENÝRSTVÍ FACULTY OF MECHANICAL ENGINEERING INSTITUTE OF AUTOMOTIVE ENGINEERING
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA STROJNÍHO INŽENÝRSTVÍ ÚSTAV AUTOMOBILNÍHO A DOPRAVNÍHO INŽENÝRSTVÍ FACULTY OF MECHANICAL ENGINEERING INSTITUTE OF AUTOMOTIVE ENGINEERING
3.2.2 Rovnice postupného vlnění
 3.. Rovnice postupného vlnění Předpoklady: 310, 301 Chcee najít rovnici, která bude udávat výšku vlny v libovolné okažiku i libovolné bodě (v jedno okažiku je v různých ístech různá výška vlny). Veličiny
3.. Rovnice postupného vlnění Předpoklady: 310, 301 Chcee najít rovnici, která bude udávat výšku vlny v libovolné okažiku i libovolné bodě (v jedno okažiku je v různých ístech různá výška vlny). Veličiny
Ž ÚČ ť ň ž Ž Č ň Ť Š ě ěž ó š ěňž Ú ňť ť ň Č š ě š ě Č ň š ě ů ť ů ň ě ěž Ž ě š ž ě ě ě ú Ó Ó š ž ž
 Ů ú ě ě š Ú ú ů ú Ž ú ž ě Ž ě ě ú ě ů ě ň ú ú ú ě ě ů ú š ň Ž ň ž Ž ú ž ň ěž Ž ň Ú š ě ě ž ě š ů š ň ž ň Ž ě Ž ÚČ ť ň ž Ž Č ň Ť Š ě ěž ó š ěňž Ú ňť ť ň Č š ě š ě Č ň š ě ů ť ů ň ě ěž Ž ě š ž ě ě ě ú Ó
Ů ú ě ě š Ú ú ů ú Ž ú ž ě Ž ě ě ú ě ů ě ň ú ú ú ě ě ů ú š ň Ž ň ž Ž ú ž ň ěž Ž ň Ú š ě ě ž ě š ů š ň ž ň Ž ě Ž ÚČ ť ň ž Ž Č ň Ť Š ě ěž ó š ěňž Ú ňť ť ň Č š ě š ě Č ň š ě ů ť ů ň ě ěž Ž ě š ž ě ě ě ú Ó
Í ž é é é é ž é š ů š š é ú é ůž Ú Ú š é é ž ž ž Í ž š Ú Ž é ď é ť é Í é š éů ů ť Š ů Í é Í Í š š ů ú é ž ž
 š é Ž é ť ť é ž ž é é ú ú ž é Č Ž é é Í Ž Ž é ž ů ť é ú ů š ú š š ď ů ž ž é ú ž š é ž é ú š š Š š Ž Ž é ů ž Í Í é šť é ž ť š Š š ů é š š ť ů ů š ž Í Č ť é ť ž ž Š Š ů ů ů é ť ů é ů Ž š é Í Í ž ž ť é Í
š é Ž é ť ť é ž ž é é ú ú ž é Č Ž é é Í Ž Ž é ž ů ť é ú ů š ú š š ď ů ž ž é ú ž š é ž é ú š š Š š Ž Ž é ů ž Í Í é šť é ž ť š Š š ů é š š ť ů ů š ž Í Č ť é ť ž ž Š Š ů ů ů é ť ů é ů Ž š é Í Í ž ž ť é Í
1.1.18 Rovnoměrně zrychlený pohyb v příkladech IV
 8 Rovnoměně ychlený pohyb v příkladech IV Předpoklady: 7 Pedagogická ponámka: Česká škola v současné době budí ve sudenech předsavu, že poblémy se řeší ásadně najednou Sudeni ak mají obovské poblémy v
8 Rovnoměně ychlený pohyb v příkladech IV Předpoklady: 7 Pedagogická ponámka: Česká škola v současné době budí ve sudenech předsavu, že poblémy se řeší ásadně najednou Sudeni ak mají obovské poblémy v
Matematika v automatizaci - pro řešení regulačních obvodů:
 . Komplexní čísla Inegrovaná sřední škola, Kumburská 846, Nová Paka Auomaizace maemaika v auomaizaci Maemaika v auomaizaci - pro řešení regulačních obvodů: Komplexní číslo je bod v rovině komplexních čísel.
. Komplexní čísla Inegrovaná sřední škola, Kumburská 846, Nová Paka Auomaizace maemaika v auomaizaci Maemaika v auomaizaci - pro řešení regulačních obvodů: Komplexní číslo je bod v rovině komplexních čísel.
Digitální učební materiál
 Číso projeu Název projeu Číso a název šabon íčové aivi Digiání učební aeriá CZ..7/.5./3.8 Zvainění výu prosřednicví ICT III/ Inovace a zvainění výu prosřednicví ICT Příjece podpor Gnáziu, Jevíčo, A. K.
Číso projeu Název projeu Číso a název šabon íčové aivi Digiání učební aeriá CZ..7/.5./3.8 Zvainění výu prosřednicví ICT III/ Inovace a zvainění výu prosřednicví ICT Příjece podpor Gnáziu, Jevíčo, A. K.
é é Ť í í íš ě é é á í Ěí é é á í Ť á Ž á Ť č é č í Ťá Í č é é ě ě í č š í é é ě ě ší Ť á ě á í š í é é á é ě Ť Í č é é í áš é Ť í á í á í í č é č í Ť
 Č č É á á é ě é č á í ž é Ťí ě á Ť ě é é í ž á Ž č ě č č č é í í ě í Ž é Ť é í é á ž ž á éč é á í á ž í ž Ťí í í č é á ď í á ž í í č í ě í č í ě š í ě í éž í Ť í šť á í á ě é í š Ť ž í í Ť ě ž í á ší é
Č č É á á é ě é č á í ž é Ťí ě á Ť ě é é í ž á Ž č ě č č č é í í ě í Ž é Ť é í é á ž ž á éč é á í á ž í ž Ťí í í č é á ď í á ž í í č í ě í č í ě š í ě í éž í Ť í šť á í á ě é í š Ť ž í í Ť ě ž í á ší é
é é ý ý Í Č ý é š ý é é é č ú č é š é é é é š Í é é é é é č é č č é ý č č č č Í č é č č č č š é é ú ý ý Č Í ň ů é é é č é č ý Č č é é č ý é é é ý ý š
 š é é č č Č č é é é č Č č é é č é ý ý Č é é š ú ú é Í é č č š ý Ýč ý č ú č č č č č č ú Í ý é é ó č ý š č ý ý č ý ý ů č ý Ť ý ů č ý č ý Í č ý é č ú Í ú ý š š é é é é ý ý Í Č ý é š ý é é é č ú č é š é é
š é é č č Č č é é é č Č č é é č é ý ý Č é é š ú ú é Í é č č š ý Ýč ý č ú č č č č č č ú Í ý é é ó č ý š č ý ý č ý ý ů č ý Ť ý ů č ý č ý Í č ý é č ú Í ú ý š š é é é é ý ý Í Č ý é š ý é é é č ú č é š é é
