4.1 Shrnutí základních poznatků
|
|
|
- Miroslava Staňková
- před 9 lety
- Počet zobrazení:
Transkript
1 4.1 Shrnutí základních poznatků V celé řadě konstrukcí se setkáváme s případy, kdy o nosnosti nerozhoduje pevnost materiálu, ale stabilitní stav rovnováhy. Tuto problematiku souhrnně nazýváme stabilita konstrukcí. Ztráta stability nejčastěji nastává při namáhání tlakem, ohybem a krutem, popř. při jejich kombinaci. S úlohami ztráty stability se setkáváme u tenkostěnných konstrukcí, u rovinných a zakřivených desek, u otevřených i uzavřených profilů nebo u tenkostěnných nosníků. Problém stability může nastat u nosného celku nebo jen u jeho částí. Potom hovoříme o lokální stabilitě. V rámci úloh stability je následující patrie zaměřena pouze na jeden ze základních případů, tzv. vzpěr. Dochází k němu při zatížení štíhlého prutu(vzpěry) tlakovou osovou silou.uvedemedvěteorie,znichžprvníjemožnépoužítvpružnéadruhouvnepružné oblasti zatěžování. Eulerova teorie vzpěru Je nazvána podle Leonharda Eulera, který se problematikou stability prutů v elastické oblasti zatěžování zabýval v 18. století. Dříve uveďme nejprve předpoklady platnosti této teorie: Materiál prutu je lineárně elastický(zatěžování probíhá v oblasti platnosti Hookeova zákona), homogenní a izotropní. Osaprutujepřímá,sílapůsobípřesněvoseprutubezvnějšíchivnitřníchexcentricit, případné klouby jsou bez tření. V souvislosti s těmito podmínkami se někdy hovoří o tzv. ideálním prutu. Při odvození teorie vzpěru přímých prutů však respektujeme i další předpoklady: Poměrnédeformace,kterémohouvznikat,jsoumalé,tj. ε 1. Respektujeme Saint-Venantův princip, při kterém se lokální charakter zatížení projevuje jen v jeho blízkém okolí. Vliv vlastní tíhy, popř. působení jiných primárních vnějších účinků, mimo osových sil, neuvažujeme. Prut je po částech prizmatický, tj. konstantního průřezu. V případě vzpěru, kdy zatěžující tlaková síla(obr. 1) působí v ose štíhlého prutu, nelze sestavit podmínky rovnováhy sil na nepřetvořeném tělese(prutu), jak je to obvyklé např. při odvození podmínek rovnováhy ohýbaných přímých prutů. V tomto případě vyvolá osová síla při průhybu prutu přídavný ohybový moment, který zpětně ovlivní napětí i 1
2 F l F x Obr.1:Prutdélky lzatíženýtlakovouosovousilou F. průhyb. Deformace již nejsou přímo úměrné velikosti osového zatížení a nemůžeme tak jejich vliv zanedbat. Hovoříme pak o teorii 2. řádu a při sestavování podmínek rovnováhy na elementárním hranolku přímého prutu(obr. 2) bereme v úvahu ještě další předpoklady. Respektujeme složku posuvu-průhybu v(x) jako rameno, na kterém vyvozují osové síly ohybový moment. Neuvažujeme vliv změny rozpětí a polohy příčného zatížení prutu. Normálová síla N(x), resp. posouvajicí síla T(x), působí rovnoběžně se souřadnicovou osou x,resp. y. Připouštíme platnost direfenciální rovnice průhybové čáry podle Euler-Bernoulliho nosníkové teorie. Z obr. 2 je potom zřejmé, jak sestavujeme diferenciální podmínky rovnováhy dle teorie 1.a2.řádunarovinnězatíženémelementuprutu.Vobecnémpřípadě,kdyuvažujemei vliv příčného zatížení q(x), kombinace vzpěru a ohybu, formulujeme dle teorie 1. řádu tzv. Schwedlerovu větu, pro kterou platí: dt(x) = q(x) a dm(x) = T(x), resp. Avšak, dle teorie 2. řádu nabývají tyto rovnice tvaru d 2 M(x) 2 = q(x). (1) dt(x) = q(x) a dm(x) = T(x) N(x) dv(x). (2) N M x T (a) q M+dM N+dN T+dT N M x T (b) q dv M+dM N+dN T+dT Obr. 2: Zatížení elementárního hranolku prutu dle teorie(a) 1. řádu,(b) 2. řádu. 2
3 Při namáhání prutu vzpěrem, viz obr. 1, neuvažujeme v diferenciálních rovnicích(2) vliv spojitého příčného zatížení a píšeme Zobr.1aobr.2jedálezřejmé(připoužitímetodyřezu),že q(x)=0. (3) N(x)= F pro F >0. (4) Pomocí vztahů(2) až(4) a pomocí direfenciální rovnice průhybové čáry d 2 v(x) = M(x) 2 EJ obdržíme po úpravě homogenní lineární diferenciální rovnici 4. řádu s konstantními koeficienty d 4 v(x) + F d 2 v(x) =0, (6) 4 EJ 2 kde E=konstjemodulpružnostivtahuaJ =konstjekvadratickýmomentprůřezu prutu(vztažený k hlavní centrální ose). Rovnice je často zavedením substitučních vztahů w(x)= v(x) l kde l je délka prutu, viz obr. 1, převedena do bezrozměrného tvaru d 4 w(ξ) 4 + η 2d2 w(ξ) 2 =0, (5) a ξ= x l, (7) kde η 2 = Fl2 EJ, (8) avtétopodobějeznámájakoeulerovarovnicevzpěruprutu. Předpokládejmeřešenírovnice(8)vetvaru w=e κξ.podosazenízad 2 w/ 2 ad 4 w/ 4 do(8)apodělenícelérovnicevýrazeme κξ dostanemepro κtzv.charakteristickourovnici κ 4 + η 2 κ 2 =0 skořeny κ 1,2 =0, κ 3 =iη, κ 4 = iη, (9) kdei= 1jeimaginárníjednotka.Protožekořen0jedvojnásovný,jefundamentální systém rovnice(8) dán funkcemi w 1 =e κ 1ξ =1, w 2 = ξe κ 2ξ = ξ, w 3 =e κ 3ξ =e iη ξ, w 4 =e κ 4ξ =e iη ξ, (10) nebo funkcemi v reálném tvaru w 1 =1, w 2 = ξ, w 3 =sinη ξ, w 4 =cos η ξ. (11) Obecným integrálem rovnice(8) je potom(píšeme jej v reálném tvaru) w(ξ)=c 1 + C 2 ξ+ C 3 sin η ξ+ C 4 cos η ξ, (12) přičemž C 1 až C 4 jsouintegračníkonstanty,kteréjenutnéurčitnazákladěokrajových podmínek konkrétní úlohy. 3
4 Známe-li obecné řešení(12) pro průhyb(vybočení) prutu, můžeme s jeho pomocí vyjádřit další veličiny, které budeme v dalším využívat. Pro úhel natočení přibližně platí: ϕ(x)= dv(x), ohybový moment dle rovnice(5) platí: M(x)= EJ d2 v(x) 2, resp. ϕ(ξ)=dw(ξ), (13) resp. M(ξ)= EJ l posouvajicísíludlerovnic(2)a(14)platí: [ T(x)= EJ d3 v(x) + F dv(x) ], resp. T(ξ)= 3 [ EJ d 2 w(ξ) 2, (14) d 3 w(ξ) + F dw(ξ) ]. (15) l 2 3 Čtyřiintegračníkonstanty C 1 až C 4 vypočtemezedvouokrajovýchpodmíneknakaždém konci prutu. Obdržíme tak soustavu čtyř homogenních lineárních algebraických rovnic, které lze formálně zapsat v maticovém tvaru Ac=0, (16) kdeaječtvercovámatice4.řádu,c=[c 1,C 2,C 3,C 4 ] T a0jenulovýsloupcovývektor dimenze 4. Podmínkou netriviálního řešení soustavy rovnic(16) je det(a)=0, (17) což vyjadřuje zároveň podmínku stability prutu. Na základě tohoto kritéria stability potom vypočteme velikost kritického zatížení a kritické síly. Sohledemnauloženíprutů,vizobr.3,sevpraxiobvyklesetkávámesečtyřmizákladními případy vzpěru v pružné oblasti řešení. F F F F l x (a) (b) (c) (d) Obr. 3: Základní případy uložení prutů. 4
5 I.případvzpěru,kdyjeprutnajednomkoncivetknutýanadruhémvolný obr.3a. Okrajové podmínky: v(0)=0, ϕ(0)=0, M(l)=0, T(l)=0. (18) Okrajové podmínky v bezrozměrném tvaru: w(0)=0, dw(0) =0, d 2 w(1) 2 =0, d 3 w(1) + η 2dw(1) 3 =0. (19) Kritérium stability: Kritickévzpěrnézatížení 1 : cos η=0 pro η 0. (20) η= π 2. (21) II.případvzpěru,kdyjeprutnajednomkoncipevněkloubověupevněnanadruhém kloubověupevněnaveden obr.3b. Okrajové podmínky: v(0)=0, M(0)=0, v(l)=0, M(l)=0. (22) Okrajové podmínky v bezrozměrném tvaru: w(0)=0, d 2 w(0) 2 =0, w(1)=0, d 2 w(1) 2 =0. (23) Kritérium stability: Kritické vzpěrné zatížení: sin η=0 pro η 0. (24) η= π. (25) III. případ vzpěru, kdy je prut na jednom konci vetknutý a na druhém kloubově upevněn aveden obr.3c. Okrajové podmínky: v(0)=0, ϕ(0)=0, v(l)=0, M(l)=0. (26) 1 Praktickývýznammajívevšechčtyřechpřípadechvzpěrupouzeuvedenékořeny.Vpřípaděostatních kořenů by musely mít pruty boční vedení. 5
6 Okrajové podmínky v bezrozměrném tvaru: w(0)=0, dw(0) =0, w(1)=0, d 2 w(1) 2 =0. (27) Kritérium stability: Kritické vzpěrné zatížení: tanη= η pro η 0. (28) η= π = 2π. (29) IV.případvzpěru,kdyjeprutnajednomkoncivetknutýanadruhémukončenposuvným vetknutím obr. 3d. Okrajové podmínky: v(0)=0, ϕ(0)=0, v(l)=0, ϕ(l)=0. (30) Okrajové podmínky v bezrozměrném tvaru: w(0)=0, dw(0) =0, w(1)=0, dw(1) =0. (31) Kritérium stability: 1 cos η= η sin η pro η 0. (32) 2 Kritické vzpěrné zatížení: η=2π. (33) Velikost kritické síly pro jednotlivé případy plyne z porovnání(8) s příslušnými velikostmi kritického vzpěrného zatížení. Z porovnání takto získaných vztahů je zřejmá jejich vzájemná vazba. Všechny případy můžeme vyjádřit jednotným vzorcem F kr = n π2 EJ min l 2, kde n= 1/4 pro I. případ vzpěru, 1 pro II. případ vzpěru, 2 pro III. případ vzpěru, 4 pro IV.případvzpěru, který je označován jako Eulerův vzorec vzpěru. Ze vzorce je patrné, že za kvadratický moment průřezu prutu je vždy nutné dosadit jeho minimální hodnotu. To plyne ze skutečnosti, že vybočení osově stlačovaného prutu nastane v rovině nejmenší ohybové tuhosti. Jestliže zavedeme tzv. poloměr setrvačnosti i a štíhlostní poměr λ pomocí vztahů (34) i 2 min= J min A a λ= l i min, (35) 6
7 σ kr σ k σ u Tetmayerova teorie Eulerova teorie 0 30 λ mez Obr. 4: Průběh kritického napětí dle Tetmayerovy a Eulerovy teorie vzpěru. λ můžeme vyjádřit velikost kritického napětí dle Eulera σ kr = F kr A = n π2 E λ 2, (36) kde Ajevelikostprůřezuprutu.Závislostí σ kr na λjehyperbola2.řádusasymptotami vsouřadnicovýchosách,jakjepatrnézobr.4. Jak již bylo dříve uvedeno, je použitelnost Eulerovy teorie vzpěru omezena platností Hookeova zákona, a je proto vázána podmínkou σ kr σ u, (37) tj.žekritickénapětínepřevýšímezúměrnostimateriálu,vizobr.4.napětí σ u odpovídá tzv.meznímuštíhlostnímupoměru λ mez,jehožhodnotuurčímevsouladusevzorcem(36) a podmínkou(37) jako ne λ mez = π. (38) σ u Vsouladusevztahem(37)pakmůžemevymezitpružnouoblastřešenívzpěrupodmínkou 2 Tetmayerova teorie vzpěru λ λ mez. (39) Řešení v nepružném oblasti vzpěru není dosud uspokojivě teoreticky nalezeno. Dimenzování se zde velmi často provádí na základě experimentů. Vznikají tak empirické vzorce, mezi které patří i Tetmayerův vztah. Pro houževnaté materiály je uváděn ve tvaru σ kr = σ T = a bλ, (40) 2 VpřípaděII.typuvzpěrusenavícnedoporučujezatěžovatprutnavzpěr,jestližeštíhlostnípoměr přesahuje hodnotu
8 zatímco pro křehké materiály je doplněn ještě o jeden člen σ kr = σ T = a bλ cλ 2. (41) Konstanty aab,popř. c,jsouzávislénapoužitémmateriáluamusíbýturčenyexperimentálně. Jestliže u houževnatého materiálu tyto konstanty neznáme, můžeme je přibližně určitzeznalosti σ u, λ mez amezekluzumateriálu σ k prohodnotu λ=0,resp. λ=30,viz obr. 4. Při malých štíhlostních poměrech λ 30 (42) přechází vzpěr v prostý tlak a není nutné jej uvažovat. Kritickousíluvnepružnéoblastidostanemezeznáméhonapětí σ T (vizvztah(40), popř.(41))jako F kr = F T = Aσ T. (43) Poznámka: Kritická síla je pouze teoretická hodnota a při praktickém výpočtu zatížení prutu je nutné brát v úvahu snížení nosnosti, která je zapříčeněna např. vlivem výrobní tolerance nebo nehomogenity materiálu. Tyto okolnosti zahrnujeme do výpočtu pomocí bezpečnosti k, což můžeme vyjádřit vztahem pro provozní sílu F, resp. napětí σ, F F kr k, resp. σ σ kr k. (44) Bezpečnost se obvykle uvažuje v elastickém i plastickém rozsahu vzpěru konstantní a pro běžnékonstrukceseudává k=
ŠROUBOVÉ SPOJE VÝKLAD
 ŠROUBOVÉ SPOJE VÝKLAD Šroubové spoje patří mezi rozebíratelné spoje s tvarovým stykem (lícovaný šroub), popřípadě silovým stykem (šroub prochází součástí volně, je zatížený pouze silou působící kolmo k
ŠROUBOVÉ SPOJE VÝKLAD Šroubové spoje patří mezi rozebíratelné spoje s tvarovým stykem (lícovaný šroub), popřípadě silovým stykem (šroub prochází součástí volně, je zatížený pouze silou působící kolmo k
Ztráta stability tenkých přímých prutů - vzpěr
 Ztráta stability tenkých přímých prutů - vzpěr Motivace štíhlé pruty namáhané tlakem mohou vybočit ze svého původně přímého tvaru a může dojít ke ztrátě stability a zhroucení konstrukce dříve, než je dosaženo
Ztráta stability tenkých přímých prutů - vzpěr Motivace štíhlé pruty namáhané tlakem mohou vybočit ze svého původně přímého tvaru a může dojít ke ztrátě stability a zhroucení konstrukce dříve, než je dosaženo
Únosnosti stanovené níže jsou uvedeny na samostatné stránce pro každý profil.
 Směrnice Obsah Tato část se zabývá polyesterovými a vinylesterovými konstrukčními profily vyztuženými skleněnými vlákny. Profily splňují požadavky na kvalitu dle ČSN EN 13706. GDP KORAL s.r.o. může dodávat
Směrnice Obsah Tato část se zabývá polyesterovými a vinylesterovými konstrukčními profily vyztuženými skleněnými vlákny. Profily splňují požadavky na kvalitu dle ČSN EN 13706. GDP KORAL s.r.o. může dodávat
Boulení stěn při normálovém, smykovém a lokálním zatížení (podle ČSN EN 1993-1-5). Posouzení průřezů 4. třídy. Boulení ve smyku, výztuhy stěn.
 3. Stabilita stěn. Boulení stěn při normálovém, smykovém a lokálním zatížení (podle ČSN EN 1993-1-5). Posouzení průřezů 4. třídy. Boulení ve smyku, výztuhy stěn. Boulení stěn Štíhlé tlačené stěny boulí.
3. Stabilita stěn. Boulení stěn při normálovém, smykovém a lokálním zatížení (podle ČSN EN 1993-1-5). Posouzení průřezů 4. třídy. Boulení ve smyku, výztuhy stěn. Boulení stěn Štíhlé tlačené stěny boulí.
4. přednáška OCELOVÉ KONSTRUKCE VŠB. Technická univerzita Ostrava Fakulta stavební Podéš 1875, éště. Miloš Rieger
 4. přednáška OCELOVÉ KOSTRUKCE VŠB Technická univerzita Ostrava Fakulta stavební Ludvíka Podéš éště 1875, 708 33 Ostrava - Poruba Miloš Rieger VZPĚRÁ ÚOSOST TLAČEÝCH PRUTŮ 1) Centrický tlak - Vzpěrná únosnost
4. přednáška OCELOVÉ KOSTRUKCE VŠB Technická univerzita Ostrava Fakulta stavební Ludvíka Podéš éště 1875, 708 33 Ostrava - Poruba Miloš Rieger VZPĚRÁ ÚOSOST TLAČEÝCH PRUTŮ 1) Centrický tlak - Vzpěrná únosnost
Vybrané okruhy znalostí z předmětů stavební mechanika, pružnost a pevnost důležité i pro studium předmětů KP3C a KP5A - navrhování nosných konstrukcí
 Vybrané okruhy znalostí z předmětů stavební mechanika, pružnost a pevnost důležité i pro studium předmětů KP3C a KP5A - navrhování nosných konstrukcí Skládání a rozklad sil Skládání a rozklad sil v rovině
Vybrané okruhy znalostí z předmětů stavební mechanika, pružnost a pevnost důležité i pro studium předmětů KP3C a KP5A - navrhování nosných konstrukcí Skládání a rozklad sil Skládání a rozklad sil v rovině
2.8 Zobecnění vztahů mezi zatížením a vnitřními silami prutu (rovinný prut zatížený v rovině) df x =f x.ds df z =f z.ds. M+dM x. ds=r.dϕ.
 .8 Zobecnění vtahů mei atížením a vnitřními silami prutu (rovinný prut atížený v rovině) µ x N V M dm µ df df x =R. MdM x NdN VdV Náhradní břemena: df x = x. df =. dm µ =µ. Obecný rovinný prut: spojité
.8 Zobecnění vtahů mei atížením a vnitřními silami prutu (rovinný prut atížený v rovině) µ x N V M dm µ df df x =R. MdM x NdN VdV Náhradní břemena: df x = x. df =. dm µ =µ. Obecný rovinný prut: spojité
3. Způsoby namáhání stavebních konstrukcí
 3. Způsoby namáhání stavebních konstrukcí Každému přetvoření stavební konstrukce odpovídá určitý druh namáhání, který poznáme podle výslednice vnitřních sil ve vyšetřovaném průřezu. Lze ji obecně nahradit
3. Způsoby namáhání stavebních konstrukcí Každému přetvoření stavební konstrukce odpovídá určitý druh namáhání, který poznáme podle výslednice vnitřních sil ve vyšetřovaném průřezu. Lze ji obecně nahradit
6 Mezní stavy únosnosti
 6 Mezní stavy únosnosti U dřevěných onstrucí musíme ověřit jejich mezní stavy, teré se vztahují e zřícení nebo jiným způsobům pošození onstruce, při nichž může být ohrožena bezpečnost lidí. 6. Navrhování
6 Mezní stavy únosnosti U dřevěných onstrucí musíme ověřit jejich mezní stavy, teré se vztahují e zřícení nebo jiným způsobům pošození onstruce, při nichž může být ohrožena bezpečnost lidí. 6. Navrhování
Modelování kmitavých soustav s jedním stupněm volnosti
 Modeování kmitavých soustav s jedním stupněm vonosti Zpracova Doc. RNDr. Zdeněk Haváč, CSc 1. Zákadní mode Zákadním modeem kmitavé soustavy s jedním stupněm vonosti je tzv. diskrétní podéně kmitající mode,
Modeování kmitavých soustav s jedním stupněm vonosti Zpracova Doc. RNDr. Zdeněk Haváč, CSc 1. Zákadní mode Zákadním modeem kmitavé soustavy s jedním stupněm vonosti je tzv. diskrétní podéně kmitající mode,
6 Mezní stavy únosnosti
 6 Mezní stavy únosnosti 6.1 Nosníky 6.1.1 Nosníky pozemních staveb Typické průřezy spřažených nosníků jsou na obr. 4. Betonová deska může být kompaktní nebo žebrová, případně může mít náběhy. Ocelový nosník
6 Mezní stavy únosnosti 6.1 Nosníky 6.1.1 Nosníky pozemních staveb Typické průřezy spřažených nosníků jsou na obr. 4. Betonová deska může být kompaktní nebo žebrová, případně může mít náběhy. Ocelový nosník
Inovace předmětů studijních programů strojního inženýrství v oblasti teplotního namáhání
 Grantový projekt FRVŠ MŠMT č.97/7/f/a Inovace předmětů studijních programů strojního inženýrství v obasti tepotního namáhání Některé apikace a ukázky konkrétních řešení tepeného namáhání těes. Autorky:
Grantový projekt FRVŠ MŠMT č.97/7/f/a Inovace předmětů studijních programů strojního inženýrství v obasti tepotního namáhání Některé apikace a ukázky konkrétních řešení tepeného namáhání těes. Autorky:
VY_32_INOVACE_C 08 09
 Název a adresa školy: Střední škola průmyslová a umělecká, Opava, příspěvková organizace, Praskova 399/8, Opava, 74601 Název operačního programu: OP Vzdělávání pro konkurenceschopnost, oblast podpory 1.5
Název a adresa školy: Střední škola průmyslová a umělecká, Opava, příspěvková organizace, Praskova 399/8, Opava, 74601 Název operačního programu: OP Vzdělávání pro konkurenceschopnost, oblast podpory 1.5
Euklidovský prostor Stručnější verze
 [1] Euklidovský prostor Stručnější verze definice Eulidovského prostoru kartézský souřadnicový systém vektorový součin v E 3 vlastnosti přímek a rovin v E 3 a) eprostor-v2, 16, b) P. Olšák, FEL ČVUT, c)
[1] Euklidovský prostor Stručnější verze definice Eulidovského prostoru kartézský souřadnicový systém vektorový součin v E 3 vlastnosti přímek a rovin v E 3 a) eprostor-v2, 16, b) P. Olšák, FEL ČVUT, c)
Fakulta strojního inženýrství VUT v Brně Ústav konstruování. KONSTRUOVÁNÍ STROJŮ převody. Přednáška 6
 Fakulta strojního inženýrství VUT v Brně Ústav konstruování KONSTRUOVÁNÍ STROJŮ převody Přednáška 6 Pevnostní výpočet čelních ozubených kol Don t force it! Use a bigger hammer. ANONYM Kontrolní výpočet
Fakulta strojního inženýrství VUT v Brně Ústav konstruování KONSTRUOVÁNÍ STROJŮ převody Přednáška 6 Pevnostní výpočet čelních ozubených kol Don t force it! Use a bigger hammer. ANONYM Kontrolní výpočet
2 MECHANICKÉ VLASTNOSTI SKLA
 2 MECHANICKÉ VLASTNOSTI SKLA Pevnost skla reprezentující jeho mechanické vlastnosti nejčastěji bývá hlavním parametrem jeho využití. Nevýhodou skel je jejich poměrně nízká pevnost v tahu a rázu (pevnost
2 MECHANICKÉ VLASTNOSTI SKLA Pevnost skla reprezentující jeho mechanické vlastnosti nejčastěji bývá hlavním parametrem jeho využití. Nevýhodou skel je jejich poměrně nízká pevnost v tahu a rázu (pevnost
NOSNÍK NA PRUŽNÉM PODLOŽÍ (WINKLEROVSKÉM)
 NOSNÍK NA PRUŽNÉ PODLOŽÍ (WINKLEROVSKÉ) Uvažujeme spojitý nosník na pružných podporách. Pružná podpora - odpor je úměrný zatlačení. Pružné podpory velmi blízko sebe - jejich účinek lze nahradit spojitou
NOSNÍK NA PRUŽNÉ PODLOŽÍ (WINKLEROVSKÉ) Uvažujeme spojitý nosník na pružných podporách. Pružná podpora - odpor je úměrný zatlačení. Pružné podpory velmi blízko sebe - jejich účinek lze nahradit spojitou
Pruty nam ahan e na vzpˇ er Martin Fiˇser Martin Fiˇ ser Pruty nam ahan e na vzpˇ er
 Obsah Úvod Eulerova teorie namáhání prutů na vzpěr První případ vzpěru zde Druhý případ vzpěru zde Třetí případ vzpěru zde Čtvrtý případ vzpěru zde Shrnutí vzorců potřebných pro výpočet Eulerovy teorie
Obsah Úvod Eulerova teorie namáhání prutů na vzpěr První případ vzpěru zde Druhý případ vzpěru zde Třetí případ vzpěru zde Čtvrtý případ vzpěru zde Shrnutí vzorců potřebných pro výpočet Eulerovy teorie
Projekty do předmětu MF
 Univerzita Palackého v Olomouci Přírodovědecká fakulta Katedra optiky ZÁVĚREČNÁ PRÁCE Projekty do předmětu MF Vypracoval: Miroslav Mlynář E-mail: mlynarm@centrum.cz Studijní program: B1701 Fyzika Studijní
Univerzita Palackého v Olomouci Přírodovědecká fakulta Katedra optiky ZÁVĚREČNÁ PRÁCE Projekty do předmětu MF Vypracoval: Miroslav Mlynář E-mail: mlynarm@centrum.cz Studijní program: B1701 Fyzika Studijní
N únosnost nýtů (při 2 střižných krčních nýtech zpravidla únosnost plynoucí z podmínky otlačení) Pak platí při rozteči (nýtové vzdálenosti) e
 Výpočet spojovacích prostředků a spojů (Prostý smyk) Průřez je namáhán na prostý smyk, působí-li na něj vnější síly, jejichž účinek lze ekvivalentně nahradit jedinou posouvající silou T v rovině průřezu
Výpočet spojovacích prostředků a spojů (Prostý smyk) Průřez je namáhán na prostý smyk, působí-li na něj vnější síly, jejichž účinek lze ekvivalentně nahradit jedinou posouvající silou T v rovině průřezu
Vzpěr, mezní stav stability, pevnostní podmínky pro tlak, nepružný a pružný vzpěr Ing. Jaroslav Svoboda
 Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Inovace a zkvalitnění výuky prostřednictvím ICT Název: Téma: Autor: Číslo: Anotace: Mechanika, pružnost pevnost Vzpěr,
Střední průmyslová škola a Vyšší odborná škola technická Brno, Sokolská 1 Šablona: Inovace a zkvalitnění výuky prostřednictvím ICT Název: Téma: Autor: Číslo: Anotace: Mechanika, pružnost pevnost Vzpěr,
9 Spřažené desky s profilovaným plechem v pozemních stavbách
 9 Spřažené desky s profilovaným plechem v pozemních stavbách 9.1 Všeobecně 9.1.1 Rozsah platnosti Tato kapitola normy se zabývá spřaženými stropními deskami vybetonovanými do profilovaných plechů, které
9 Spřažené desky s profilovaným plechem v pozemních stavbách 9.1 Všeobecně 9.1.1 Rozsah platnosti Tato kapitola normy se zabývá spřaženými stropními deskami vybetonovanými do profilovaných plechů, které
VZDĚLÁVACÍ KURZ SE ZAMĚŘENÍM NA PŘÍPRAVU NA PROFESNÍ KVALIFIKACI PROJEKTANT LEŠENÍ INFORMACE
 INFORMACE MÍSTO KONÁNÍ: HOTEL SLAVIA, VLADIVOSTOCKÁ 1460/10, PRAHA 10. Organizace kurzu Kurz je rozdělen do 8 seminářů pátek sobota vždy po 6-ti vyučovacích hodinách v kombinované formě studia prezenční
INFORMACE MÍSTO KONÁNÍ: HOTEL SLAVIA, VLADIVOSTOCKÁ 1460/10, PRAHA 10. Organizace kurzu Kurz je rozdělen do 8 seminářů pátek sobota vždy po 6-ti vyučovacích hodinách v kombinované formě studia prezenční
OVMT Mechanické zkoušky
 Mechanické zkoušky Mechanickými zkouškami zjišťujeme chování materiálu za působení vnějších sil, tzn., že zkoumáme jeho mechanické vlastnosti. Některé mechanické vlastnosti materiálu vyjadřují jeho odpor
Mechanické zkoušky Mechanickými zkouškami zjišťujeme chování materiálu za působení vnějších sil, tzn., že zkoumáme jeho mechanické vlastnosti. Některé mechanické vlastnosti materiálu vyjadřují jeho odpor
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ VÝZKUMNÁ ZPRÁVA STABILITA VYBRANÝCH KONFIGURACÍ KOLEJOVÉHO SVRŠKU
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ INFRAM a.s., Česká republika VÝZKUMNÁ ZPRÁVA STABILITA VYBRANÝCH KONFIGURACÍ KOLEJOVÉHO SVRŠKU Řešitel Objednatel Ing. Petr Frantík, Ph.D. Ústav stavební
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ INFRAM a.s., Česká republika VÝZKUMNÁ ZPRÁVA STABILITA VYBRANÝCH KONFIGURACÍ KOLEJOVÉHO SVRŠKU Řešitel Objednatel Ing. Petr Frantík, Ph.D. Ústav stavební
PLÁŠŤOVÉ PŮSOBENÍ TENKOSTĚNNÝCH KAZET
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ Doktorský studijní program: STAVEBNÍ INŽENÝRSTVÍ Studijní obor: POZEMNÍ STAVBY Ing. Jan RYBÍN THE STRESSED SKIN ACTION OF THIN-WALLED LINEAR TRAYS
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STAVEBNÍ Doktorský studijní program: STAVEBNÍ INŽENÝRSTVÍ Studijní obor: POZEMNÍ STAVBY Ing. Jan RYBÍN THE STRESSED SKIN ACTION OF THIN-WALLED LINEAR TRAYS
Technická mechanika - Statika
 Technická mechanika - Statika Elektronická učebnice Ing. Jaromír Petr Tento materiál byl vytvořen v rámci projektu CZ.1.07/1.1.07/03.0027 Tvorba elektronických učebnic O B S A H 1 Statika tuhých těles...
Technická mechanika - Statika Elektronická učebnice Ing. Jaromír Petr Tento materiál byl vytvořen v rámci projektu CZ.1.07/1.1.07/03.0027 Tvorba elektronických učebnic O B S A H 1 Statika tuhých těles...
Fakulta aplikovaných věd Katedra mechaniky
 Fakulta aplikovaných věd Katedra mechaniky Bakalářská práce Analýza stability vybraných druhů kompozitních nosníků Vypracoval: Petr Hanzlík Vedoucí práce: Ing. Tomáš Kroupa, Ph.D. Plzeň, 2014 Prohlášení
Fakulta aplikovaných věd Katedra mechaniky Bakalářská práce Analýza stability vybraných druhů kompozitních nosníků Vypracoval: Petr Hanzlík Vedoucí práce: Ing. Tomáš Kroupa, Ph.D. Plzeň, 2014 Prohlášení
Osové a deviační momenty setrvačnosti ploch (opakování ze 4. cvičení) Momenty setrvačnosti k otočeným osám Kroucení kruhových a mezikruhových průřezů
 Jedenácté cvičení bude vysvětlovat tuto problematiku: Osové a deviační momenty setrvačnosti ploch (opakování ze 4. cvičení) Momenty setrvačnosti k otočeným osám Kroucení kruhových a mezikruhových průřezů
Jedenácté cvičení bude vysvětlovat tuto problematiku: Osové a deviační momenty setrvačnosti ploch (opakování ze 4. cvičení) Momenty setrvačnosti k otočeným osám Kroucení kruhových a mezikruhových průřezů
7 Prostý beton. 7.1 Úvod. 7.2 Mezní stavy únosnosti. Prostý beton
 7 Prostý beton 7.1 Úvod Konstrukce ze slabě vyztuženého betonu mají výztuž, která nesplňuje podmínky minimálního vyztužení, požadované pro železobetonové konstrukce. Způsob porušení konstrukcí odpovídá
7 Prostý beton 7.1 Úvod Konstrukce ze slabě vyztuženého betonu mají výztuž, která nesplňuje podmínky minimálního vyztužení, požadované pro železobetonové konstrukce. Způsob porušení konstrukcí odpovídá
Vzájemně působící pomocný rám. Popis PGRT
 Popis Popis je konstrukce, v níž díky ukotvení mohou rámy, které ji tvoří, působit nikoli jako dva samostatné rámy, ale jako jeden rám podvozku. vykazuje mnohem větší odpor proti průhybu než pomocný rám
Popis Popis je konstrukce, v níž díky ukotvení mohou rámy, které ji tvoří, působit nikoli jako dva samostatné rámy, ale jako jeden rám podvozku. vykazuje mnohem větší odpor proti průhybu než pomocný rám
TÉMATICKÉ OKRUHY KE SZZ 2013/14 ING PLASTIKÁŘSKÁ TECHNOLOGIE
 TÉMATICKÉ OKRUHY KE SZZ 2013/14 PLASTIKÁŘSKÁ TECHNOLOGIE 1. Rovnice toku a třídění z reologického hlediska podle průběhu tokové křivky. 2. Aktivační energie viskózního toku Arteniova rovnice. 3. Kapilární
TÉMATICKÉ OKRUHY KE SZZ 2013/14 PLASTIKÁŘSKÁ TECHNOLOGIE 1. Rovnice toku a třídění z reologického hlediska podle průběhu tokové křivky. 2. Aktivační energie viskózního toku Arteniova rovnice. 3. Kapilární
PRVKY BETONOVÝCH KONSTRUKCÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ DOC. ING. LADISLAV ČÍRTEK, CSC PRVKY BETONOVÝCH KONSTRUKCÍ MODUL M05 NAVRHOVÁNÍ JEDNODUCHÝCH PRVKŮ STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ DOC. ING. LADISLAV ČÍRTEK, CSC PRVKY BETONOVÝCH KONSTRUKCÍ MODUL M05 NAVRHOVÁNÍ JEDNODUCHÝCH PRVKŮ STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU
6. T e s t o v á n í h y p o t é z
 6. T e s t o v á n í h y p o t é z Na základě hodnot z realizace náhodného výběru činíme rozhodnutí o platnosti hypotézy o hodnotách parametrů rozdělení nebo o jeho vlastnostech. Používáme k tomu vhodně
6. T e s t o v á n í h y p o t é z Na základě hodnot z realizace náhodného výběru činíme rozhodnutí o platnosti hypotézy o hodnotách parametrů rozdělení nebo o jeho vlastnostech. Používáme k tomu vhodně
Pružnost a pevnost. 2. přednáška, 10. října 2016
 Pružnost a pevnost 2. přednáška, 10. října 2016 Prut namáhaný jednoduchým ohybem: rovnoměrně ohýbaný prut nerovnoměrně ohýbaný prut příklad výpočet napětí a ohybu vliv teplotních měn příklad nerovnoměrné
Pružnost a pevnost 2. přednáška, 10. října 2016 Prut namáhaný jednoduchým ohybem: rovnoměrně ohýbaný prut nerovnoměrně ohýbaný prut příklad výpočet napětí a ohybu vliv teplotních měn příklad nerovnoměrné
Materiály charakteristiky potř ebné pro navrhování
 2 Materiály charakteristiky potřebné pro navrhování 2.1 Úvod Zdivo je vzhledem k velkému množství druhů a tvarů zdicích prvků (cihel, tvárnic) velmi různorodý stavební materiál s rozdílnými užitnými vlastnostmi,
2 Materiály charakteristiky potřebné pro navrhování 2.1 Úvod Zdivo je vzhledem k velkému množství druhů a tvarů zdicích prvků (cihel, tvárnic) velmi různorodý stavební materiál s rozdílnými užitnými vlastnostmi,
Stabilita tenkostěnných za studena tvarovaných Z vaznic v oblasti nadpodporových momentů. Stability of Cold-formed Z purlins in Support Region.
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta stavební Doktorský studijní program: STAVEBNÍ INŽENÝRSTVÍ Studijní obor: Konstrukce a dopravní stavby Stabilita tenkostěnných za studena tvarovaných Z vaznic
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta stavební Doktorský studijní program: STAVEBNÍ INŽENÝRSTVÍ Studijní obor: Konstrukce a dopravní stavby Stabilita tenkostěnných za studena tvarovaných Z vaznic
Určování výměr Srážka mapového listu Výpočet objemů Dělení pozemků
 Geodézie přednáška 9 Určování výměr Srážka mapového listu Výpočet objemů Dělení pozemků Ústav geoinformačních technologií Lesnická a dřevařská fakulta ugt.mendelu.cz tel.: 545134015 Určování výměr určování
Geodézie přednáška 9 Určování výměr Srážka mapového listu Výpočet objemů Dělení pozemků Ústav geoinformačních technologií Lesnická a dřevařská fakulta ugt.mendelu.cz tel.: 545134015 Určování výměr určování
POŽADAVKY KE ZKOUŠCE Z PP I
 POŽADAVKY KE ZKOUŠCE Z PP I Zkouška úrovně Alfa (pro zájemce o magisterské studium) Zkouška sestává ze o vstupního testu (10 otázek, výběr správné odpovědi ze čtyř možností, rozsah dle sloupečku Požadavky)
POŽADAVKY KE ZKOUŠCE Z PP I Zkouška úrovně Alfa (pro zájemce o magisterské studium) Zkouška sestává ze o vstupního testu (10 otázek, výběr správné odpovědi ze čtyř možností, rozsah dle sloupečku Požadavky)
Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady. Část 1 - Test
 Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových charakteristik, oficiální přehled
Pružnost a pevnost (132PRPE) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových charakteristik, oficiální přehled
Západočeská univerzita v Plzni. Fakulta aplikovaných věd Katedra matematiky. Geometrie pro FST 1. Pomocný učební text
 Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra matematiky Geometrie pro FST 1 Pomocný učební text František Ježek, Marta Míková, Světlana Tomiczková Plzeň 29. srpna 2005 verze 1.0 Předmluva
Západočeská univerzita v Plzni Fakulta aplikovaných věd Katedra matematiky Geometrie pro FST 1 Pomocný učební text František Ježek, Marta Míková, Světlana Tomiczková Plzeň 29. srpna 2005 verze 1.0 Předmluva
9. Úvod do teorie PDR
 9. Úvod do teorie PDR A. Základní poznatky o soustavách ODR1 Diferenciální rovnici nazveme parciální, jestliže neznámá funkce závisí na dvou či více proměnných (příslušná rovnice tedy obsahuje parciální
9. Úvod do teorie PDR A. Základní poznatky o soustavách ODR1 Diferenciální rovnici nazveme parciální, jestliže neznámá funkce závisí na dvou či více proměnných (příslušná rovnice tedy obsahuje parciální
III/2-1 Inovace a zkvalitnění výuky prostřednictvím ICT
 Název školy Název projektu Registrační číslo projektu Autor Střední průmyslová škola strojírenská a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Modernizace výuky CZ.1.07/1.5.00/34.1003
Název školy Název projektu Registrační číslo projektu Autor Střední průmyslová škola strojírenská a Jazyková škola s právem státní jazykové zkoušky, Kolín IV, Heverova 191 Modernizace výuky CZ.1.07/1.5.00/34.1003
strol. s.ucasl. Joseph E. Shigley The Iowa State University of Science and Technology Richard G. Budynas Institute of Technology
 Kon. ; ; nl strol. y; ; s.ucasl. Joseph E. Shigley University of Michigan Charles R. Mischke The Iowa State University of Science and Technology Richard G. Budynas Rochester Institute of Technology VYSOKE
Kon. ; ; nl strol. y; ; s.ucasl. Joseph E. Shigley University of Michigan Charles R. Mischke The Iowa State University of Science and Technology Richard G. Budynas Rochester Institute of Technology VYSOKE
MATURITNÍ OKRUHY STAVBA A PROVOZ STROJŮ TŘÍDA: 4SB ŠKOLNÍ ROK: 2015-2016 SPEZIALIZACE: TECHNICKÝ SOFTWARE
 1.A. VALIVÁ LOŽISKA a) dělení ložisek b) skladba ložisek c) definice základních pojmů d) výpočet ložisek d) volba ložisek 1.B. POHYBLIVÉ ČÁSTI PÍSTOVÉHO STROJE a) schéma pohyblivých částí klikového mechanismu
1.A. VALIVÁ LOŽISKA a) dělení ložisek b) skladba ložisek c) definice základních pojmů d) výpočet ložisek d) volba ložisek 1.B. POHYBLIVÉ ČÁSTI PÍSTOVÉHO STROJE a) schéma pohyblivých částí klikového mechanismu
Vedení tepla v MKP. Konstantní tepelné toky. Analogické úlohám statiky v mechanice kontinua
 Vedení tepla v MKP Stacionární úlohy (viz dále) Konstantní tepelné toky Analogické úlohám statiky v mechanice kontinua Nestacionární úlohy (analogické dynamice stavebních konstrukcí) 1 Základní rovnice
Vedení tepla v MKP Stacionární úlohy (viz dále) Konstantní tepelné toky Analogické úlohám statiky v mechanice kontinua Nestacionární úlohy (analogické dynamice stavebních konstrukcí) 1 Základní rovnice
Diplomová práce. Sbírka úloh z mechaniky kontinua PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO KATEDRA TEORETICKÉ FYZIKY. Vypracoval: Michal Kolář
 PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO KATEDRA TEORETICKÉ FYZIKY Diplomová práce Sbírka úloh z mechaniky kontinua Vypracoval: Michal Kolář studující V. ročníku obor M F studijní rok 00/003 Vedoucí
PŘÍRODOVĚDECKÁ FAKULTA UNIVERZITY PALACKÉHO KATEDRA TEORETICKÉ FYZIKY Diplomová práce Sbírka úloh z mechaniky kontinua Vypracoval: Michal Kolář studující V. ročníku obor M F studijní rok 00/003 Vedoucí
OTÁZKY VSTUPNÍHO TESTU PP I LS 2010/2011
 OTÁZKY VSTUPNÍHO TESTU PP I LS 010/011 Pomocí Thumovy definice, s využitím vrubové citlivosti q je definován vztah mezi součiniteli vrubu a tvaru jako: Součinitel tvaru α je podle obrázku definován jako:
OTÁZKY VSTUPNÍHO TESTU PP I LS 010/011 Pomocí Thumovy definice, s využitím vrubové citlivosti q je definován vztah mezi součiniteli vrubu a tvaru jako: Součinitel tvaru α je podle obrázku definován jako:
10.1 Úvod. 10.2 Návrhové hodnoty vlastností materiálu. 10 Dřevo a jeho chování při požáru. Petr Kuklík
 10 10.1 Úvod Obecná představa o chování dřeva při požáru bývá často zkreslená. Dřevo lze zapálit, může vyživovat oheň a dále ho šířit pomocí prchavých plynů, vznikajících při vysoké teplotě. Proces zuhelnatění
10 10.1 Úvod Obecná představa o chování dřeva při požáru bývá často zkreslená. Dřevo lze zapálit, může vyživovat oheň a dále ho šířit pomocí prchavých plynů, vznikajících při vysoké teplotě. Proces zuhelnatění
Příklad 7 Průhyb nosníku - složitější případ
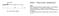 Příklad 7 Průhyb nosníku - složitější případ Zadání Nosník s proměnným průřezem je na obrázku. Průřezy a jsou obdélníkové, výška prvního průřezu je, násobkem výšky druhého průřezu. a) Pomocí metody integrace
Příklad 7 Průhyb nosníku - složitější případ Zadání Nosník s proměnným průřezem je na obrázku. Průřezy a jsou obdélníkové, výška prvního průřezu je, násobkem výšky druhého průřezu. a) Pomocí metody integrace
Sylabus k přednášce předmětu BK1 SCHODIŠTĚ Ing. Hana Hanzlová, CSc., Ing. Jitka Vašková, CSc.
 Schodiště jsou souborem stavebních prvků (schodišťová ramena, podesty, mezipodesty, podestové nosníky, schodnice a schodišťové stěny), které umožňují komunikační spojení různých výškových úrovní. V budovách
Schodiště jsou souborem stavebních prvků (schodišťová ramena, podesty, mezipodesty, podestové nosníky, schodnice a schodišťové stěny), které umožňují komunikační spojení různých výškových úrovní. V budovách
Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil
 Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil Souřadný systém, v rovině i prostoru Síla bodová: vektorová veličina (kluzný, vázaný vektor - využití),
Okruhy problémů k teoretické části zkoušky Téma 1: Základní pojmy Stavební statiky a soustavy sil Souřadný systém, v rovině i prostoru Síla bodová: vektorová veličina (kluzný, vázaný vektor - využití),
Fakulta strojního inženýrství VUT v Brně Ústav konstruování. KONSTRUOVÁNÍ STROJŮ strojní součásti. Přednáška 5
 Fakulta strojního inženýrství VUT v Brně Ústav konstruování KONSTRUOVÁNÍ STROJŮ strojní součásti Přednáška 5 Šrouby a šroubové spoje For want of a nail the shoe is lost; For want of a shoe the horse is
Fakulta strojního inženýrství VUT v Brně Ústav konstruování KONSTRUOVÁNÍ STROJŮ strojní součásti Přednáška 5 Šrouby a šroubové spoje For want of a nail the shoe is lost; For want of a shoe the horse is
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE. Úloha 2: Měření modulu pružnosti v tahu a ve smyku. Abstrakt
 FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Úoha : Měření moduu pružnosti v tahu a ve smyku Datum měření: 9. 10. 009 Jméno: Jiří Sabý Pracovní skupina: 1 Ročník a kroužek:. ročník, 1. kroužek, pátek 13:30 Spoupracovaa:
FYZIKÁLNÍ PRAKTIKUM FJFI ČVUT V PRAZE Úoha : Měření moduu pružnosti v tahu a ve smyku Datum měření: 9. 10. 009 Jméno: Jiří Sabý Pracovní skupina: 1 Ročník a kroužek:. ročník, 1. kroužek, pátek 13:30 Spoupracovaa:
Klopením rozumíme ztrátu stability při ohybu, při které dojde k vybočení prutu z roviny jeho prvotního ohybu (viz obr.). Obr.
 . cvičení Klopení nosníků Klopením rozumíme ztrátu stability při ohybu, při které dojde k vybočení prutu z roviny jeho prvotního ohybu (viz obr.). Obr. Ilustrace klopení Obr. Ohýbaný prut a tvar jeho ztráty
. cvičení Klopení nosníků Klopením rozumíme ztrátu stability při ohybu, při které dojde k vybočení prutu z roviny jeho prvotního ohybu (viz obr.). Obr. Ilustrace klopení Obr. Ohýbaný prut a tvar jeho ztráty
Úloha I.E... tři šedé vlasy dědy Aleše
 Úloha I.E... tři šedé vlasy dědy Aleše 8 bodů; průměr 4,28; řešilo 50 studentů Pokuste se určit některé napěťové charakteristiky v tahu u lidského vlasu. Z vašeho pokusu sestavte co nejpodrobnější graf
Úloha I.E... tři šedé vlasy dědy Aleše 8 bodů; průměr 4,28; řešilo 50 studentů Pokuste se určit některé napěťové charakteristiky v tahu u lidského vlasu. Z vašeho pokusu sestavte co nejpodrobnější graf
ŠROUBOVÝ A PROSTOROVÝ POHYB ROTAČNĚ SYMETRICKÉHO TĚLESA
 ŠROUBOVÝ A PROSTOROVÝ POHYB ROTAČNĚ SYMETRICKÉHO TĚLESA Zpracoval Doc. RNDr. Zdeněk Hlaváč, CSc Pojem šroubového pohybu Šroubový pohyb je definován jako pohyb, jejž lze ve vhodném referenčním bodě rozložit
ŠROUBOVÝ A PROSTOROVÝ POHYB ROTAČNĚ SYMETRICKÉHO TĚLESA Zpracoval Doc. RNDr. Zdeněk Hlaváč, CSc Pojem šroubového pohybu Šroubový pohyb je definován jako pohyb, jejž lze ve vhodném referenčním bodě rozložit
K přednášce NUFY028 Teoretická mechanika prozatímní učební text, verze 01 10. Spojitá prostředí: rovnice struny Leoš Dvořák, MFF UK Praha, 2014
 K přednášce NUFY8 Teoretická mechanika prozatímní učební text, verze 1 1 Spojitá prostředí: rovnice strun Leoš Dvořák, MFF UK Praha, 14 Spojitá prostředí: rovnice strun Dosud jsme se zabývali pohbem soustav
K přednášce NUFY8 Teoretická mechanika prozatímní učební text, verze 1 1 Spojitá prostředí: rovnice strun Leoš Dvořák, MFF UK Praha, 14 Spojitá prostředí: rovnice strun Dosud jsme se zabývali pohbem soustav
FAKULTA STAVEBNÍ VUT V BRNĚ PŘIJÍMACÍ ŘÍZENÍ DO MNSP STAVEBNÍ INŽENÝRSTVÍ PRO AKADEMICKÝ ROK 2008 2009
 FAKULTA STAVEBNÍ VUT V BRNĚ PŘIJÍMACÍ ŘÍZENÍ DO MNSP STAVEBNÍ INŽENÝRSTVÍ PRO AKADEMICKÝ ROK 2008 2009 OBOR: POZEMNÍ STAVBY (S) A. MATEMATIKA TEST. Hladina významnosti testu α při testování nulové hypotézy
FAKULTA STAVEBNÍ VUT V BRNĚ PŘIJÍMACÍ ŘÍZENÍ DO MNSP STAVEBNÍ INŽENÝRSTVÍ PRO AKADEMICKÝ ROK 2008 2009 OBOR: POZEMNÍ STAVBY (S) A. MATEMATIKA TEST. Hladina významnosti testu α při testování nulové hypotézy
4 Spojovací a kloubové hřídele
 4 Spojovací a kloubové hřídele Spojovací a kloubové hřídele jsou určeny ke stálému přenosu točivého momentu mezi jednotlivými částmi převodného ústrojí. 4.1 Spojovací hřídele Spojovací hřídele zajišťují
4 Spojovací a kloubové hřídele Spojovací a kloubové hřídele jsou určeny ke stálému přenosu točivého momentu mezi jednotlivými částmi převodného ústrojí. 4.1 Spojovací hřídele Spojovací hřídele zajišťují
Rotační skořepiny, tlakové nádoby, trubky. i Výpočet bez chyb. ii Informace o o projektu?
 Rotační skořepiny, tlakové nádoby, trubky i Výpočet bez chyb. ii Informace o o projektu? Kapitola vstupních parametrů 1. Výběr materiálu a nastavení jednotek 1.1 Jednotky výpočtu 1.2 Materiál SI Units
Rotační skořepiny, tlakové nádoby, trubky i Výpočet bez chyb. ii Informace o o projektu? Kapitola vstupních parametrů 1. Výběr materiálu a nastavení jednotek 1.1 Jednotky výpočtu 1.2 Materiál SI Units
Měřicí a řídicí technika Bakalářské studium 2007/2008. odezva. odhad chování procesu. formální matematický vztah s neznámými parametry
 MODELOVÁNÍ základní pojmy a postupy principy vytváření deterministických matematických modelů vybrané základní vztahy používané při vytváření matematických modelů ukázkové příklady Základní pojmy matematický
MODELOVÁNÍ základní pojmy a postupy principy vytváření deterministických matematických modelů vybrané základní vztahy používané při vytváření matematických modelů ukázkové příklady Základní pojmy matematický
PROFILY S VLNITOU STOJINOU POMŮCKA PRO PROJEKTANTY A ODBĚRATELE WT PROFILŮ
 Průběžná 74 100 00 Praha 10 tel: 02/67 31 42 37-8, 02/67 90 02 11 fax: 02/67 31 42 39, 02/67 31 53 67 e-mail:kovprof@ini.cz PROFILY S VLNITOU STOJINOU POMŮCKA PRO PROJEKTANTY A ODBĚRATELE WT PROFILŮ verze
Průběžná 74 100 00 Praha 10 tel: 02/67 31 42 37-8, 02/67 90 02 11 fax: 02/67 31 42 39, 02/67 31 53 67 e-mail:kovprof@ini.cz PROFILY S VLNITOU STOJINOU POMŮCKA PRO PROJEKTANTY A ODBĚRATELE WT PROFILŮ verze
SCIA.ESA PT. Posudky ocelových konstrukcí
 SCIA.ESA PT Posudky ocelových konstrukcí Posudky ocelových konstrukcí POSUDKY OCELOVÝCH KONSTRUKCÍ 1 Vítejte... 1 Děkujeme vám, že jste si zvolili systém ESA PT... 1 Úvod do posudků... 2 PARAMETRY A NASTAVENÍ
SCIA.ESA PT Posudky ocelových konstrukcí Posudky ocelových konstrukcí POSUDKY OCELOVÝCH KONSTRUKCÍ 1 Vítejte... 1 Děkujeme vám, že jste si zvolili systém ESA PT... 1 Úvod do posudků... 2 PARAMETRY A NASTAVENÍ
Platnost Bernoulli Navierovy hypotézy
 Přednáška 03 Diferenciální rovnice ohybu prutu Platnost Bernoulli Navierovy hypotézy Schwedlerovy věty Rovnováha na segmentech prutu Clebschova metoda integrace Příklady Copyright (c) 011 Vít Šmilauer
Přednáška 03 Diferenciální rovnice ohybu prutu Platnost Bernoulli Navierovy hypotézy Schwedlerovy věty Rovnováha na segmentech prutu Clebschova metoda integrace Příklady Copyright (c) 011 Vít Šmilauer
Česká republika - ŽENY
 2012 Česká republika - ŽENY věk qx px lx dx Lx Tx ex Dx Cx Nx Mx Sx Rx 0 0.002338 0.997662 100000 234 99804 8088058 80.88 100 000.00 229.43 4 164 194.04 22 355.11 130 483 842.84 1 731 180.86 1 0.000144
2012 Česká republika - ŽENY věk qx px lx dx Lx Tx ex Dx Cx Nx Mx Sx Rx 0 0.002338 0.997662 100000 234 99804 8088058 80.88 100 000.00 229.43 4 164 194.04 22 355.11 130 483 842.84 1 731 180.86 1 0.000144
2016 Česká republika ŽENY (aktuální k )
 2016 Česká republika ŽENY (aktuální k 27. 11. 2017) věk qx px lx dx Lx Tx ex Dx Cx Nx Mx Sx Rx 0 0.002462 0.997538 100 000.00 246.23 99787 8205207 82.05 100 000.00 243.07 5 066 877.57 34 975.90 176 922
2016 Česká republika ŽENY (aktuální k 27. 11. 2017) věk qx px lx dx Lx Tx ex Dx Cx Nx Mx Sx Rx 0 0.002462 0.997538 100 000.00 246.23 99787 8205207 82.05 100 000.00 243.07 5 066 877.57 34 975.90 176 922
ZÁKLADNÍ ÚLOHY TEORIE PLASTICITY Teoretické příklady
 Teorie plasticity VŠB TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ KATEDRA PRUŽNOSTI A PEVNOSTI ZÁKLADNÍ ÚLOHY TEORIE PLASTICITY Teoretické příklady 1. ŘEŠENÝ PŘÍKLAD NA TAH ŘEŠENÍ DLE DOVOLENÝCH NAMÁHÁNÍ
Teorie plasticity VŠB TECHNICKÁ UNIVERZITA OSTRAVA FAKULTA STROJNÍ KATEDRA PRUŽNOSTI A PEVNOSTI ZÁKLADNÍ ÚLOHY TEORIE PLASTICITY Teoretické příklady 1. ŘEŠENÝ PŘÍKLAD NA TAH ŘEŠENÍ DLE DOVOLENÝCH NAMÁHÁNÍ
Veronika Drobná VB1STI02 Ing. Michalcová Vladimíra, Ph.D.
 Příklad 1: 3;4 3;4 = =4 9 2;1,78 = = 4 9 4=16 9 =1,78 =2 =2 2 4 9 =16 9 1 = 1+ =0,49 = 1+ =0,872 =0 =10 6+ 2,22=0 =3,7 6+ 2,22=0 =3,7 + =0 3,7+3,7=0 0=0 =60,64 =0 =0 + =0 =3,7 á čá 5+ 2,22=0 =3,7 5+ 2,22+
Příklad 1: 3;4 3;4 = =4 9 2;1,78 = = 4 9 4=16 9 =1,78 =2 =2 2 4 9 =16 9 1 = 1+ =0,49 = 1+ =0,872 =0 =10 6+ 2,22=0 =3,7 6+ 2,22=0 =3,7 + =0 3,7+3,7=0 0=0 =60,64 =0 =0 + =0 =3,7 á čá 5+ 2,22=0 =3,7 5+ 2,22+
FAKULTA STAVEBNÍ MATEMATIKA II MODUL 2 STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ MATEMATIKA II MODUL KŘIVKOVÉ INTEGRÁLY STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Typeset by L A TEX ε c Josef Daněček, Oldřich Dlouhý,
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ FAKULTA STAVEBNÍ MATEMATIKA II MODUL KŘIVKOVÉ INTEGRÁLY STUDIJNÍ OPORY PRO STUDIJNÍ PROGRAMY S KOMBINOVANOU FORMOU STUDIA Typeset by L A TEX ε c Josef Daněček, Oldřich Dlouhý,
STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJNICKÁ A STŘEDNÍ ODBORNÁ ŠKOLA PROFESORA ŠVEJCARA, PLZEŇ, KLATOVSKÁ 109. Josef Gruber MECHANIKA I STATIKA
 STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJNICKÁ A STŘEDNÍ ODBORNÁ ŠKOLA PROFESORA ŠVEJCARA, PLZEŇ, KLATOVSKÁ 109 Josef Gruber MECHANIKA I STATIKA Vytvořeno v rámci Operačního programu Vzdělávání pro konkurenceschopnost
STŘEDNÍ PRŮMYSLOVÁ ŠKOLA STROJNICKÁ A STŘEDNÍ ODBORNÁ ŠKOLA PROFESORA ŠVEJCARA, PLZEŇ, KLATOVSKÁ 109 Josef Gruber MECHANIKA I STATIKA Vytvořeno v rámci Operačního programu Vzdělávání pro konkurenceschopnost
Statika 2. Vetknuté nosníky. Miroslav Vokáč 2. listopadu ČVUT v Praze, Fakulta architektury. Statika 2. M.
 3. přednáška Průhybová čára Mirosav Vokáč mirosav.vokac@kok.cvut.cz ČVUT v Praze, Fakuta architektury 2. istopadu 2016 Průhybová čára ohýbaného nosníku Znaménková konvence veičin M z x +q +w +ϕ + q...
3. přednáška Průhybová čára Mirosav Vokáč mirosav.vokac@kok.cvut.cz ČVUT v Praze, Fakuta architektury 2. istopadu 2016 Průhybová čára ohýbaného nosníku Znaménková konvence veičin M z x +q +w +ϕ + q...
Atic, s.r.o. a Ing. arch. Libor Žák
 Atic, s.r.o. a Ing. arch. Libor Žák Riegrova 44, 612 00 Brno Sdružení tel. 541 245 286, 605 323 416 email: zak.apk@arch.cz Investor : Stavba : Objekt : Jihomoravský kraj Brno, Žerotínovo nám. 3/5, PSČ
Atic, s.r.o. a Ing. arch. Libor Žák Riegrova 44, 612 00 Brno Sdružení tel. 541 245 286, 605 323 416 email: zak.apk@arch.cz Investor : Stavba : Objekt : Jihomoravský kraj Brno, Žerotínovo nám. 3/5, PSČ
+ ω y = 0 pohybová rovnice tlumených kmitů. r dr dt. B m. k m. Tlumené kmity
 Tlumené kmit V praxi téměř vžd brání pohbu nějaká brzdicí síla, jejíž původ je v třecích silách mezi reálnými těles. Matematický popis těchto sil bývá dosti komplikovaný. Velmi často se vsktuje tzv. viskózní
Tlumené kmit V praxi téměř vžd brání pohbu nějaká brzdicí síla, jejíž původ je v třecích silách mezi reálnými těles. Matematický popis těchto sil bývá dosti komplikovaný. Velmi často se vsktuje tzv. viskózní
ZÁKLADNÍ PŘÍPADY NAMÁHÁNÍ
 7. cvičení ZÁKLADNÍ PŘÍPADY NAMÁHÁNÍ V této kapitole se probírají výpočty únosnosti průřezů (neboli posouzení prvků na prostou pevnost). K porušení materiálu v tlačených částech průřezu dochází: mezní
7. cvičení ZÁKLADNÍ PŘÍPADY NAMÁHÁNÍ V této kapitole se probírají výpočty únosnosti průřezů (neboli posouzení prvků na prostou pevnost). K porušení materiálu v tlačených částech průřezu dochází: mezní
Pružnost a pevnost (132PRPE), paralelka J2/1 (ZS 2015/2016) Písemná část závěrečné zkoušky vzorové otázky a příklady.
 Pružnost a pevnost (132PRPE), paralelka J2/1 (ZS 2015/2016) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových
Pružnost a pevnost (132PRPE), paralelka J2/1 (ZS 2015/2016) Písemná část závěrečné zkoušky vzorové otázky a příklady Povolené pomůcky: psací a rýsovací potřeby, kalkulačka (nutná), tabulka průřezových
6. Střídavý proud. 6. 1. Sinusových průběh
 6. Střídavý proud - je takový proud, který mění v čase svoji velikost a smysl. Nejsnáze řešitelný střídavý proud matematicky i graficky je sinusový střídavý proud, který vyplývá z konstrukce sinusovky.
6. Střídavý proud - je takový proud, který mění v čase svoji velikost a smysl. Nejsnáze řešitelný střídavý proud matematicky i graficky je sinusový střídavý proud, který vyplývá z konstrukce sinusovky.
Zkoušky čtvercových sloupků ze za studena tvářené korozivzdorné oceli
 228 STAVEBNÍ OBZOR 8/2012 Zkoušky čtvercových sloupků ze za studena tvářené korozivzdorné oceli Ing. Michal JANDERA, Ph. D. prof. Ing. Josef MACHÁČEK, DrSc. ČVUT v Praze Fakulta stavební Článek popisuje
228 STAVEBNÍ OBZOR 8/2012 Zkoušky čtvercových sloupků ze za studena tvářené korozivzdorné oceli Ing. Michal JANDERA, Ph. D. prof. Ing. Josef MACHÁČEK, DrSc. ČVUT v Praze Fakulta stavební Článek popisuje
STATICKÝ VÝPOČET: PŘESTUPNÍ UZEL HULVÁKY 1.ETAPA: obj. SO 01 Sociální zařízení MHD obj. SO 02 Veřejné WC
 -1- STATICKÝ VÝPOČET: PROJEKTOVÁ DOKUMENTACE PRO REALIZACI PŘESTUPNÍ UZEL HULVÁKY 1.ETAPA: obj. SO 01 Sociální zařízení MHD obj. SO 0 Veřejné WC A) SVISLÉ ZATÍŽENÍ STŘECHY: SKLON: 9 o ; sin 0,156; cos
-1- STATICKÝ VÝPOČET: PROJEKTOVÁ DOKUMENTACE PRO REALIZACI PŘESTUPNÍ UZEL HULVÁKY 1.ETAPA: obj. SO 01 Sociální zařízení MHD obj. SO 0 Veřejné WC A) SVISLÉ ZATÍŽENÍ STŘECHY: SKLON: 9 o ; sin 0,156; cos
Lineární stabilita a teorie II. řádu
 Lineární stabilita a teorie II. řádu Sestavení podmínek rovnováhy na deformované konstrukci Konstrukce s a bez počáteční imperfekce Výpočet s malými vs. s velkými deformacemi ANKC-C 1 Zatěžovacídráhy [Šejnoha,
Lineární stabilita a teorie II. řádu Sestavení podmínek rovnováhy na deformované konstrukci Konstrukce s a bez počáteční imperfekce Výpočet s malými vs. s velkými deformacemi ANKC-C 1 Zatěžovacídráhy [Šejnoha,
PROBLÉMY STABILITY. 9. cvičení
 PROBLÉMY STABILITY 9. cvičení S pojmem ztráty stability tvaru prvku se posluchač zřejmě již setkal v teorii pružnosti při studiu prutů namáhaných osovým tlakem (viz obr.). Problematika je však obecnější
PROBLÉMY STABILITY 9. cvičení S pojmem ztráty stability tvaru prvku se posluchač zřejmě již setkal v teorii pružnosti při studiu prutů namáhaných osovým tlakem (viz obr.). Problematika je však obecnější
České vysoké učení technické v Praze Fakulta biomedicínského inženýrství
 České vysoké učení technické v Praze Fakulta biomedicínského inženýrství Úloha KA03/č. 8: Měření zatížení protéz dolních končetin tenzometrickou soupravou Metodický pokyn pro vyučující se vzorovým protokolem
České vysoké učení technické v Praze Fakulta biomedicínského inženýrství Úloha KA03/č. 8: Měření zatížení protéz dolních končetin tenzometrickou soupravou Metodický pokyn pro vyučující se vzorovým protokolem
VÝPOČET VLASTNÍCH FREKVENCÍ RÁMU
 VÝPOČET VLASTNÍCH FREKVENCÍ RÁMU MODELOVÁNÍ MECHANICKÝCH SOUSTAV Martin Bílek 0.3.05 Brdový list Náběh Horní činek Krajnice Nosný drát Nítěnka Dolní činek Závěs 5.5.05 Výpočet vlastních frekvencí pružně
VÝPOČET VLASTNÍCH FREKVENCÍ RÁMU MODELOVÁNÍ MECHANICKÝCH SOUSTAV Martin Bílek 0.3.05 Brdový list Náběh Horní činek Krajnice Nosný drát Nítěnka Dolní činek Závěs 5.5.05 Výpočet vlastních frekvencí pružně
STAVEBNÍ STATIKA. Ing. Petr Konečný, Ph.D. LPH 407/3. tel
 STAVEBNÍ STATIKA Ing. Petr Konečný, Ph.D. LPH 47/3 tel. 59 732 1394 petr.konecny@vsb.c http://fast1.vsb.c/konecny roklad síly v rovině síla pod úhlem γ - (k ose ) až -18 až +18 x A γ P P P x γ + x P x
STAVEBNÍ STATIKA Ing. Petr Konečný, Ph.D. LPH 47/3 tel. 59 732 1394 petr.konecny@vsb.c http://fast1.vsb.c/konecny roklad síly v rovině síla pod úhlem γ - (k ose ) až -18 až +18 x A γ P P P x γ + x P x
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE FAKULTA STROJNÍ ÚSTAV MECHANIKY, BIOMECHANIKY A MECHATRONIKY ZTRÁTA STABILITY PRUTŮ PROMĚNNÉHO PRŮŘEZU
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE AKULTA STROJNÍ ÚSTAV MECHANIKY, BIOMECHANIKY A MECHATRONIKY ZTRÁTA STABILITY PRUTŮ PROMĚNNÉHO PRŮŘEZU BAKALÁŘSKÁ PRÁCE Autor Matěj Mazur Vedoucí bakalářské práce Doc.
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE AKULTA STROJNÍ ÚSTAV MECHANIKY, BIOMECHANIKY A MECHATRONIKY ZTRÁTA STABILITY PRUTŮ PROMĚNNÉHO PRŮŘEZU BAKALÁŘSKÁ PRÁCE Autor Matěj Mazur Vedoucí bakalářské práce Doc.
4. Tenkostěnné za studena tvarované prvky. Návrh na únavu OK.
 4. Tenkostěnné za studena tvarované prvky. Návrh na únavu OK. Výroba, zvláštnosti návrhu, základní případy namáhání, spoje, navrhování z hlediska MSÚ a MSP. Návrh na únavu: zatížení, Wöhlerův přístup a
4. Tenkostěnné za studena tvarované prvky. Návrh na únavu OK. Výroba, zvláštnosti návrhu, základní případy namáhání, spoje, navrhování z hlediska MSÚ a MSP. Návrh na únavu: zatížení, Wöhlerův přístup a
MATEMATIKA IV - PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE - ZÁPISKY Z. Obsah. 1. Parciální diferenciální rovnice obecně. 2. Kvaazilineární rovnice prvního řádu
 MATEMATIKA IV - PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE - ZÁPISKY Z PŘEDNÁŠEK JAN MALÝ Obsah 1. Parciální diferenciální rovnice obecně 1. Kvaazilineární rovnice prvního řádu 1 3. Lineární rovnice druhého řádu
MATEMATIKA IV - PARCIÁLNÍ DIFERENCIÁLNÍ ROVNICE - ZÁPISKY Z PŘEDNÁŠEK JAN MALÝ Obsah 1. Parciální diferenciální rovnice obecně 1. Kvaazilineární rovnice prvního řádu 1 3. Lineární rovnice druhého řádu
Zakázka: D111029 Stavba: Sanace svahu Olešnice poškozeného přívalovými dešti v srpnu 2010 I. etapa Objekt: SO 201 Sanace svahu
 1 Technická zpráva ke statickému výpočtu... 2 1.1 Identifikační údaje... 2 1.1.1 Stavba... 2 1.1.2 Investor... 2 1.1.3 Projektant... 2 1.1.4 Ostatní... 2 1.2 Základní údaje o zdi... 3 1.3 Technický popis
1 Technická zpráva ke statickému výpočtu... 2 1.1 Identifikační údaje... 2 1.1.1 Stavba... 2 1.1.2 Investor... 2 1.1.3 Projektant... 2 1.1.4 Ostatní... 2 1.2 Základní údaje o zdi... 3 1.3 Technický popis
Předmět: Ročník: Vytvořil: Datum: ŠČERBOVÁ M. PAVELKA V. VZPĚR VZPĚR
 Předmět: Ročník: Vytvořil: Datum: MECHANIKA DRUHÝ ŠČERBOVÁ M. PAVELKA V. 8. ZÁŘÍ 2013 Název zpracovaného celku: VZPĚR VZPĚR U všech předcházejících druhů namáhání byla funkce součásti ohroţena překročením
Předmět: Ročník: Vytvořil: Datum: MECHANIKA DRUHÝ ŠČERBOVÁ M. PAVELKA V. 8. ZÁŘÍ 2013 Název zpracovaného celku: VZPĚR VZPĚR U všech předcházejících druhů namáhání byla funkce součásti ohroţena překročením
Elektronický učební text pro podporu výuky klasické mechaniky pro posluchače učitelství I. Mechanika hmotného bodu
 Elektronický učební text pro podporu výuky klasické mechaniky pro posluchače učitelství I Mechanika hmotného bodu Autor: Kateřina Kárová Text vznikl v rámci bakalářské práce roku 2006. Návod na práci s
Elektronický učební text pro podporu výuky klasické mechaniky pro posluchače učitelství I Mechanika hmotného bodu Autor: Kateřina Kárová Text vznikl v rámci bakalářské práce roku 2006. Návod na práci s
Podmínky k získání zápočtu
 Podmínky k získání zápočtu 18 až 35 bodů 7 % aktivní účast, omluvená neúčast Odevzdání programů Testy: 8 nepovinných testů (-2 body nebo -3 body) 3 povinné testy s ohodnocením 5 bodů (povoleny 2 opravné
Podmínky k získání zápočtu 18 až 35 bodů 7 % aktivní účast, omluvená neúčast Odevzdání programů Testy: 8 nepovinných testů (-2 body nebo -3 body) 3 povinné testy s ohodnocením 5 bodů (povoleny 2 opravné
1.1 Shrnutí základních poznatků
 1.1 Shrnutí základních poznatků Pojmem nádoba obvykle označujeme součásti strojů a zařízení, které jsou svým tvarem a charakterem namáhání shodné s dutými tělesy zatíženými vnitřním, popř. i vnějším tlakem.sohledemnatopovažujemezanádobyrůznápotrubíakotlovátělesa,alenapř.i
1.1 Shrnutí základních poznatků Pojmem nádoba obvykle označujeme součásti strojů a zařízení, které jsou svým tvarem a charakterem namáhání shodné s dutými tělesy zatíženými vnitřním, popř. i vnějším tlakem.sohledemnatopovažujemezanádobyrůznápotrubíakotlovátělesa,alenapř.i
Sedmé cvičení bude vysvětlovat tuto problematiku:
 Sedmé cvičení bude vysvětlovat tuto problematiku: Velmi stručně o parciálních derivacích Castiglianova věta k čemu slouží Castiglianova věta jak ji použít Castiglianova věta staticky určité přímé nosníky
Sedmé cvičení bude vysvětlovat tuto problematiku: Velmi stručně o parciálních derivacích Castiglianova věta k čemu slouží Castiglianova věta jak ji použít Castiglianova věta staticky určité přímé nosníky
χ je součinitel vzpěrnosti pro příslušný způsob vybočení.
 6.3 Vpěrná únosnost prutů 6.3. Tlačené prut stálého průřeu 6.3.. Vpěrná únosnost () Tlačený prut se má posuovat na vpěr podle podmínk: Ed 0, (6.46),Rd Ed je návrhová hodnota tlakové síl;,rd návrhová vpěrná
6.3 Vpěrná únosnost prutů 6.3. Tlačené prut stálého průřeu 6.3.. Vpěrná únosnost () Tlačený prut se má posuovat na vpěr podle podmínk: Ed 0, (6.46),Rd Ed je návrhová hodnota tlakové síl;,rd návrhová vpěrná
Definujte poměrné protažení (schematicky nakreslete a uved te jednotky) Napište hlavní kroky postupu při posouzení prutu na vzpěrný tlak.
 00001 Definujte mechanické napětí a uved te jednotky. 00002 Definujte normálové napětí a uved te jednotky. 00003 Definujte tečné (tangenciální, smykové) napětí a uved te jednotky. 00004 Definujte absolutní
00001 Definujte mechanické napětí a uved te jednotky. 00002 Definujte normálové napětí a uved te jednotky. 00003 Definujte tečné (tangenciální, smykové) napětí a uved te jednotky. 00004 Definujte absolutní
Kapka kapaliny na hladině kapaliny
 JEVY NA ROZHRANÍ TŘÍ PROSTŘEDÍ Kapka kapaliny na hladině kapaliny Na hladinu (viz obr. 11) kapaliny (1), nad níž je plynné prostředí (3), kápneme kapku jiné kapaliny (2). Vzniklé tři povrchové vrstvy (kapalina
JEVY NA ROZHRANÍ TŘÍ PROSTŘEDÍ Kapka kapaliny na hladině kapaliny Na hladinu (viz obr. 11) kapaliny (1), nad níž je plynné prostředí (3), kápneme kapku jiné kapaliny (2). Vzniklé tři povrchové vrstvy (kapalina
Autor: Vladimír Švehla
 Bulletin of Applied Mechanics 1, 55 64 (2005) 55 Využití Castiglianovy věty při výpočtu deformací staticky určité případy zatížení tahem a tlakem Autor: Vladimír Švehla České vysoké učení technické, akulta
Bulletin of Applied Mechanics 1, 55 64 (2005) 55 Využití Castiglianovy věty při výpočtu deformací staticky určité případy zatížení tahem a tlakem Autor: Vladimír Švehla České vysoké učení technické, akulta
Ohyb nastává, jestliže v řezu jakožto vnitřní účinek působí ohybový moment, tj. dvojice sil ležící v rovině kolmé k rovině řezu.
 Ohyb přímých prutů nosníků Ohyb nastává, jestliže v řeu jakožto vnitřní účinek působí ohybový moment, tj dvojice sil ležící v rovině kolmé k rovině řeu Ohybový moment určíme jako součet momentů od všech
Ohyb přímých prutů nosníků Ohyb nastává, jestliže v řeu jakožto vnitřní účinek působí ohybový moment, tj dvojice sil ležící v rovině kolmé k rovině řeu Ohybový moment určíme jako součet momentů od všech
215.1.18 REOLOGICKÉ VLASTNOSTI ROPNÝCH FRAKCÍ
 215.1.18 REOLOGICKÉ VLASTNOSTI ROPNÝCH FRAKCÍ ÚVOD Reologie se zabývá vlastnostmi látek za podmínek jejich deformace toku. Reologická měření si kladou za cíl stanovení materiálových parametrů látek při
215.1.18 REOLOGICKÉ VLASTNOSTI ROPNÝCH FRAKCÍ ÚVOD Reologie se zabývá vlastnostmi látek za podmínek jejich deformace toku. Reologická měření si kladou za cíl stanovení materiálových parametrů látek při
Analýza dynamiky pádu sportovní branky, vč. souvisejících aspektů týkajících se materiálu
 ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta elektrotechnická katedra řídicí techniky Technická 2, 166 27 Praha 6 13. listopadu 2009 Analýza dynamiky pádu sportovní branky, vč. souvisejících aspektů týkajících
ČESKÉ VYSOKÉ UČENÍ TECHNICKÉ V PRAZE Fakulta elektrotechnická katedra řídicí techniky Technická 2, 166 27 Praha 6 13. listopadu 2009 Analýza dynamiky pádu sportovní branky, vč. souvisejících aspektů týkajících
